TOP10 đề ôn tập cuối học kì 2 Toán 10 Cánh Diều (70% TN + 30% TL)

Tài liệu gồm 144 trang, tuyển tập 10 đề ôn tập kiểm tra cuối học kì 2 môn Toán 10 theo chương trình SGK Toán 10 Cánh Diều; các đề được biên soạn theo hình thức 70% trắc nghiệm kết hợp 30% tự luận, mời bạn đọc đón xem

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK2 Toán 10

Môn: Toán 10

Sách: Cánh diều

Thông tin:

144 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ 2 (CÁNH DIỀU)
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
TT
Nội dung kiến
thức
Đơn vị kiến thức
Mức độ nhận thức Tổng
% tổng
điểm
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
Số CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số CH
Thời
gian
(phút)
TN TL
1
V. Đại số tổ
hợp
1.Quy tắc cộng và quy tắc nhân 1 1 2
2. Hoán vị, chỉnh hợp
2
2
1*
1**
2
1
3. Tổ hợp 1 1 2
4. Nhị thức Newton
1
3
2
VI. Một số
yếu tố Thống
kê và xác suất
1.Số gần đúng và sai số
1
1
1
2. Các số đặc trưng đo xu thế trung tâm
của mẫu số liệu.
1
3. Các số đặc trưng đo mức độ phân tán
của mẫu số liệu
2 1
4. Xác suất cuả biến cố
3
3
1*
1**
5
1
1 1 2
3
X. PP tọa độ
trong mặt
phẳng
2. PT đường thẳng trong mp tọa độ 2 1
1*
1**
2
2
3. Vị trí tương đối và góc giữa 2 đường
thẳng. Khoảng cách từ 1 đểm đến đường
thẳng
2 1 2
4. PT đường tròn trong mp tọa độ
2
2
3
5. Ba đường Conic và ứng dụng
1
1
3
Tổng
20
15
2
2
35
4
Tỉ lệ (%)
40
30
20
10
100
Tỉ lệ chung (%)
70
30
100
Lưu ý:
- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
- Số điểm tính cho 1 câu trắc nghiệm là 0,20 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
Phần tự luận: (để được phong phú mình để nhiều lựa chọn) (3.0Đ)
- Hai câu vận dụng mỗi câu 1,0 điểm ta chọn ở 1* sao cho 1 câu Đại Số và 1 câu Hình học.
- Hai câu vận dụng cao mỗi câu 0,5 điểm ta chọn ở 1** sao cho 1 câu Đại Số và 1 câu Hình học.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 01
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Đo chiều dài của một cây thước, ta được kết quả
( )
45 0,3l cm= ±
thì sai số tương đối của phép
đo là:
A.
0,3
l
∆=
. B.
0,3
l
∆≤
. C.
3
10
l
δ
=
. D.
1
150
l
δ
≤
.
Câu 2: Điểm (thang điểm 10) của 11 học sinh cao điểm nhất trong một bài kiểm tra như sau:
10 9 10 8 9 10 9 7 8 9 10. Hãy tìm các tứ phân vị.
A.
1
7Q =
,
2
8
Q =
,
3
10Q =
B.
1
8
Q
=
,
2
10
Q =
,
3
10Q =
.
C.
1
8Q =
,
2
9Q =
,
3
10
Q =
. D.
1
8Q
=
,
2
9Q =
,
3
9Q =
.
Câu 3: Một cửa hàng giày thể thao đã thống kê cỡ giày của 20 khách hàng nữ được chọn ngẫu nhiên cho
kết quả như sau:
35 37 39 41 38 40 40 37 39 38 38 36 37 42 38 35 38 36 38 35
Tìm trung vị cho mẫu số liệu trên.
A.
36
. B.
37
. C.
38
. D.
39
.
Câu 4: Một mẫu số liệu thống kê có tứ phân vị lần lượt là
123
22, 27, 32QQ Q= = =
. Giá trị nào sau đây
là giá trị ngoại lệ của mẫu số liệu
A. 30. B. 9. C. 48. D. 46.
Câu 5: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai điểm
( )
3;1M −
và
( )
6; 4N −
. Tọa độ trọng
tâm
G
của tam giác
OMN
là
A.
( )
9; 5G −
. B.
( )
1;1G −
. C.
( )
1; 1G −
. D.
( )
3; 3G −
.
Câu 6: Cho đường
( )
( )
12
:
34
=−+
∈
= −
xt
dt
yt
. Véc tơ nào sau đây là véc tơ chỉ phương của
( )
d
?
A.
( )
1; 2=
a
. B.
( )
1; 3= −
a
. C.
( )
2; 4= −
a
. D.
( )
1; 2
= −
a
.
Câu 7: Trong mặt phẳng tọa độ
Oxy
, viết phương trình tham số của đường thẳng đi qua hai điểm
( )
3; 2M −
và
(
)
4;1N
.
A.
34
2
xt
yt
= +
=−+
. B.
43
12
xt
yt
= +
= −
. C.
13
32
xt
yt
= +
= −
. D.
3
23
xt
yt
= +
=−+
.
Câu 8: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10xy− + −=
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Câu 9: Khoảng cách từ điểm
1(1; )M −
đến đường thẳng
:3 4 0xy∆ ++=
là
A.
1
. B.
3 10
5
. C.
5
2
. D.
2 10
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Câu 10: Phương trình nào sau đây là phương trình đường tròn?
A.
22
6 10 30 0xy x y
. B.
22
3 2 30 0xy xy
.
C.
22
4 10 6 2 0xy xy 
. D.
22
2 4 8 1 0.x y xy 
.
Câu 11: Đường tròn
( )
C
có tâm
( )
2;3I −
và đi qua
( )
2; 3M −
có phương trình là:
A.
(
) ( )
22
2 3 52xy+ +− =
.
B.
( ) ( )
22
2 3 52xy+ +− =
.
C.
22
4 6 57 0xy xy++−−=
.
D.
22
4 6 39 0xy xy+++−=
.
Câu 12: Tọa độ các tiêu điểm của hypebol
( )
22
:1
94
xy
H −=
là
A.
( ) ( )
12
13;0 ; 13;0FF=−=
. B.
( ) ( )
12
0; 13 ; 0; 13FF=−=
.
C.
( ) ( )
12
0; 5 ; 0; 5FF=−=
. D.
( ) ( )
12
5;0 ; 5;0FF=−=
.
Câu 13: Một tổ có
6
học sinh nữ và
8
học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học
sinh của tổ đó đi trực nhật?
A.
28
. B.
48
. C.
14
. D.
8
.
Câu 14: Từ
4
số
1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số?
A.
12
. B.
6
. C.
64
. D.
24
.
Câu 15: Có bao nhiêu cách xếp
3
học sinh nam và
4
học sinh nữ theo hàng ngang?
A.
7!
. B.
144
. C.
2880
. D.
480
.
Câu 16: Từ
7
chữ số
1, 2, 3, 4, 5, 6, 7
có thể lập được bao nhiêu số tự nhiên có
4
chữ số đôi một khác
nhau?
A.
4
7
. B.
7
P
. C.
4
7
C
. D.
4
7
A
.
Câu 17: Cho tập hợp
{
}
1; 2;3; 4;5M =
. Số tập con gồm hai phần tử của tập hợp
M
là:
A. 11. B.
2
5
A
. C.
2
5
C
. D.
2
P
.
Câu 18: Khai triển
( )
5
2xy+
thành đa thức ta được kết quả sau
A.
5 4 32 23 4 5
10 40 80 80 32x xy xy xy xy y++ + ++
.
B.
5 4 32 23 4 5
10 40 40 10 2x xy xy xy xy y+++++
.
C.
5 4 32 23 4 5
10 40 80 40 32x xy xy xy xy y++ + ++
.
D.
5 4 32 23 4 5
10 20 20 10 2x xy xy xy xy y+++++
.
Câu 19: Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất xuất hiện mặt hai chấm là
A.
1
2
. B.
1
3
. C.
1
6
. D.
1
4
.
Câu 20: Một hộp chứa
10
quả cầu gồm
3
quả cầu màu xanh và
7
quả cầu màu đỏ, các quả cầu đôi một
khác nhau. Chọn ngẫu nhiên lần lượt hai quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn
ra cùng màu bằng
A.
7
30
. B.
8
15
. C.
7
15
. D.
5
11
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Câu 21: Từ một nhóm gồm
6
học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. Xác suất để
chọn được 2 học sinh nữ và 1 học sinh nam bằng
A.
3
10
. B.
1
5
. C.
1
6
. D.
1
2
.
Câu 22: Cho số gần đúng
23748023
α
=
với độ chính xác
101d =
. Hãy viết số quy tròn của số
A.
23749000
. B.
23748000
. C.
23746000
. D.
23747000
.
Câu 23: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?
A.
4,694
. B.
4,925
. C.
4,55
. D.
4,495
.
Câu 24: Trong mặt phẳng hệ tọa độ
,
Oxy
cho hai điểm
( ) ( )
2; 1 , 1; 7AB−
. Tọa độ điểm M thỏa mãn hệ
thức
30AM AB+=
 
là
A.
( )
1; 3M −
B.
( )
5; 5M
−
C.
( )
1; 1M −
D.
( )
3; 1M −
Câu 25: Đường thẳng
∆
đi qua điểm
( )
1; 2M
và song song với đường thẳng
:4 2 1 0dx y+ +=
có phương
trình tổng quát là
A.
4 2 30xy+ +=
. B.
2 40xy++=
. C.
2 30xy− +=
. D.
2 40xy+−=
.
Câu 26: Hai đường thẳng
12
: 5, : 9d mx y m d x my+=− + =
cắt nhau khi và chỉ khi
A.
1m ≠−
. B.
1m ≠
. C.
1
m
≠±
. D.
2m ≠
.
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( )
1; 2A
,
( )
5; 2B
,
( )
1; 3C
−
có phương trình
là.
A.
22
6 10x y xy+ + + −=
. B.
22
6 10x y xy+ − − −=
.
C.
22
6 10
x y xy+ − + −=
. D.
22
6 10
x y xy+ + − −=
.
Câu 28: Đường tròn
( )
C
đi qua
( )
1; 3A
,
( )
3;1B
và có tâm nằm trên đường thẳng
:2 7 0d xy−+=
có
phương trình là
A.
( ) ( )
22
7 7 102xy− +− =
. B.
( ) ( )
22
7 7 164xy+ ++ =
.
C.
( ) ( )
22
3 5 25xy− +− =
. D.
( ) ( )
22
3 5 25xy+ ++ =
.
Câu 29: Phương trình chính tắc của elip đi qua điểm
( )
0; 4−
A
và có một tiêu điểm
( )
2
3; 0F
là
A.
22
1
10 8
+=
xy
. B.
22
1
25 16
+=
xy
. C.
22
1
25 9
+=
xy
. D.
22
1
16 25
+=
xy
.
Câu 30: Cần xếp 3 nam, 3 nữ vào 1 hàng có 6 ghế. Hỏi có bao nhiêu cách xếp sao cho nam nữ ngồi xen
kẽ.
A.
36
. B.
720
. C.
78
. D.
72
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Câu 31: Có 4 cặp vợ chồng ngồi trên một dãy ghế dài. Có bao nhiêu cách sắp xếp sao cho vợ và chồng
của mỗi gia đình đều ngồi cạnh nhau.
A.
384
. B.
8!
. C.
4!.4!
. D.
48
.
Câu 32: Ở một Đoàn trường phổ thông có 5 thầy giáo, 4 cô giáo và 8 học sinh. Có bao nhiêu cách chọn
ra một đoàn công tác gồm 7 người trong đó có 1 trưởng đoàn là thầy giáo, 1 phó đoàn là cô giáo
và đoàn công tác phải có ít nhất 4 học sinh.
A.
6020
. B.
10920
. C.
9800
. D.
10290
.
Câu 33: Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số
1,2,3, 4,5,6
. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là một số chia hết cho
5
.
A.
1
6
. B.
1
12
. C.
1
2
. D.
1
4
.
Câu 34: Chọn ngẫu nhiên hai số khác nhau từ
25
số nguyên dương đầu tiên. Xác suất
để chọn được hai số có tổng là một số chẵn là
A.
13
25
. B.
12
25
. C.
1
2
. D.
313
625
.
Câu 35: Một nhóm gồm 12 học sinh trong đó có 7 học sinh nam và 5 học sinh nữ. Chọn ngẫu nhiên 3 học
sinh từ nhóm 12 học sinh đó đi lao động. Xác suất để trong ba học sinh được chọn có ít nhất một
học sinh nữ là:
A.
15
22
. B.
7
44
. C.
35
44
. D.
37
44
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có 8 người cùng vào thang máy ở tầng 1 của một tòa nhà cao 10 tầng và đi lên trên. Hỏi có bao
nhiêu cách sắp xếp để trong 8 người đó có đúng 2 người cùng ra ở 1 tầng và mỗi người còn lại
ra ở mỗi tầng khác nhau.
Câu 37: Trong mặt phẳng
,
Oxy
viết phương trình chính tắc của Elip
( )
E
có một tiêu điểm là
( )
1
2;0F −
và đi qua điểm
( )
2;3M
.
Câu 38: Gọi
S
là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập
{ }
1; 2;3; 4;5E =
. Chọn
ngẫu nhiên một số từ tập
S
. Xác xuất để số được chọn là một số chẵn bằng
Câu 39: Trong mặt phẳng
Oxy
cho parabol
( )
2
:8Py x=
. Đường thẳng
Δ
không trùng với trục
Ox
đi
qua tiêu điểm
F
của
( )
P
sao cho góc hợp bởi hai tia
Fx
và
Ft
là tia của
Δ
nằm phía trên trục
hoành một góc bằng
( )
0
90αα≠
. Biết
Δ
cắt
( )
P
tại hai điểm phân biệt
,MN
và tập hợp trung
điểm
I
của đoạn
MN
khi
α
thay đổi là một Parabol. Xác định phương trình của Parabol.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Đo chiều dài của một cây thước, ta được kết quả
( )
45 0,3l cm= ±
thì sai số tương đối của phép
đo là:
A.
0,3
l
∆=
. B.
0,3
l
∆≤
. C.
3
10
l
δ
=
. D.
1
150
l
δ
≤
.
Lời giải
Vì
0,3
l
∆≤
nên
0,3 1
45 150
l
l
l
δ
∆
=≤=
.
Câu 2: Điểm (thang điểm 10) của 11 học sinh cao điểm nhất trong một bài kiểm tra như sau:
10 9 10 8 9 10 9 7 8 9 10. Hãy tìm các tứ phân vị.
A.
1
7Q
=
,
2
8Q =
,
3
10
Q =
B.
1
8Q =
,
2
10Q
=
,
3
10Q =
.
C.
1
8Q =
,
2
9Q =
,
3
10Q
=
. D.
1
8
Q
=
,
2
9Q =
,
3
9Q =
.
Lời giải
Sắp xếp các giá trị theo thứ tự không giảm:
7 8 8 9 9 9 9 10 10 10 10
Trung vị của mẫu số liệu là:
2
9Q =
.
Tứ vị phân thứ nhất là
1
8Q
=
.
Tứ vị phân thứ ba là
3
10Q
=
.
Vậy
1
8Q =
,
2
9Q =
,
3
10Q =
là các tứ phân vị của mẫu số liệu trên.
Câu 3: Một cửa hàng giày thể thao đã thống kê cỡ giày của 20 khách hàng nữ được chọn ngẫu nhiên cho
kết quả như sau:
35 37 39 41 38 40 40 37 39 38 38 36 37 42 38 35 38 36 38 35
Tìm trung vị cho mẫu số liệu trên.
A.
36
. B.
37
. C.
38
. D.
39
.
Lời giải
Sắp xếp các giá trị theo thứ tự không giảm:
35 35 35 36 36 37 37 37 38 38 38 38 38 38 39 39 40 40 41 42
Vì
20n =
là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa:
38 38
2
Me
+
=
Câu 4: Một mẫu số liệu thống kê có tứ phân vị lần lượt là
123
22, 27, 32QQ Q= = =
. Giá trị nào sau đây
là giá trị ngoại lệ của mẫu số liệu
A. 30. B. 9. C. 48. D. 46.
Lời giải
Ta có
31
32 22 10
Q
QQ∆= − = − =
. Do đó
[ ]
13
1,5. ; 1,5. 7;47
QQ
QQ

− ∆ + ∆=

.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Do
[ ]
48 7;47
∉
nên là một giá trị ngoại lệ của mẫu số liệu.
Câu 5: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai điểm
( )
3;1M −
và
( )
6; 4N −
. Tọa độ trọng
tâm
G
của tam giác
OMN
là
A.
( )
9; 5G −
. B.
( )
1;1G −
. C.
( )
1; 1G −
. D.
( )
3; 3G −
.
Lời giải
Ta có:
( )
( )
360
1
33
1; 1
1 40
1
33
M NO
G
M NO
G
xxx
x
G
yyy
y
++
−+ +
= = =
⇒−
+− +
++
= = = −
.
Câu 6: Cho đường
( ) (
)
12
:
34
=−+
∈
= −
xt
dt
yt
. Véc tơ nào sau đây là véc tơ chỉ phương của
( )
d
?
A.
(
)
1; 2=
a
. B.
( )
1; 3= −
a
. C.
(
)
2; 4= −
a
. D.
( )
1; 2
= −
a
.
Lời giải
Dựa vào
( )
d
ta có VTCP:
( )
2; 4= −
a
Câu 7: Trong mặt phẳng tọa độ
Oxy
, viết phương trình tham số của đường thẳng đi qua hai điểm
( )
3; 2M −
và
( )
4;1N
.
A.
34
2
xt
yt
= +
=−+
. B.
43
12
xt
yt
= +
= −
. C.
13
32
xt
yt
= +
= −
. D.
3
23
xt
yt
= +
=−+
.
Lời giải
Gọi
d
là đường thẳng đi qua hai điểm
( )
3; 2M −
và
( )
4;1N
.
⇒
Đường thẳng
d
đi qua điểm
( )
3; 2M −
và nhận
( )
1; 3MN

làm vectơ chỉ phương.
Vậy phương trình tham số đường thẳng
d
:
( )
3
23
xt
t
yt
= +
∈
=−+
.
Câu 8: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10xy− + −=
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
+) Xét:
2 31
46 1
−
= ≠
−−
nên hai đường thẳng song.
Câu 9: Khoảng cách từ điểm
1(
1; )M −
đến đường thẳng
:3 4 0xy∆ ++=
là
A.
1
. B.
3 10
5
. C.
5
2
. D.
2 10
.
Lời giải
Khoảng cách từ điểm
1(1; )M −
đến đường thẳng
:3 4 0xy∆ ++=
là
( )
22
3.1 1 4
6 3 10
;.
5
10
31
dM
−+
∆= = =
+
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Câu 10: Phương trình nào sau đây là phương trình đường tròn?
A.
22
6 10 30 0xy x y
. B.
22
3 2 30 0xy xy
.
C.
22
4 10 6 2 0xy xy 
. D.
22
2 4 8 1 0.x y xy 
.
Lời giải
Phương trình đường tròn đã cho có dạng:
22
22 0x y ax by c+ − − +=
là phương trình đường
tròn
22
0.abc
⇔ + −>
Xét đáp án A, ta có
3, 5, 30
abc= = =
22
40abc⇒ + −=>
.
Câu 11: Đường tròn
( )
C
có tâm
( )
2;3I −
và đi qua
( )
2; 3M −
có phương trình là:
A.
( ) ( )
22
2 3 52xy+ +− =
.
B.
( ) ( )
22
2 3 52xy+ +− =
.
C.
22
4 6 57 0xy xy++−−=
.
D.
22
4 6 39 0xy xy+++−=
.
Lời giải
( )
2
2
4 6 52R IM= = +− =

.
Phương trình đường tròn tâm
( )
2;3I
−
,
52R =
là:
(
)
( )
22
2 3 52.
xy+ +− =
Câu 12: Tọa độ các tiêu điểm của hypebol
( )
22
:1
94
xy
H −=
là
A.
(
)
( )
12
13;0 ; 13;0FF
=−=
. B.
( )
( )
12
0; 13 ; 0; 13FF
=−=
.
C.
( )
( )
12
0; 5 ; 0; 5FF=−=
. D.
( )
( )
12
5;0 ; 5;0FF
=−=
.
Lời giải
Gọi
( ) ( )
12
;0 ; ;0F cFc=−=
là hai tiêu điểm của
( )
H
.
Từ phương trình
( )
22
:1
94
xy
H −=
, ta có:
2
9a =
và
2
4b =
suy ra
( )
2 22
13 13, 0c ab c c= + = ⇒= >
.
Vậy tọa độ các tiêu điểm của
(
)
H
là
( ) ( )
12
13;0 ; 13;0FF=−=
.
Câu 13: Một tổ có
6
học sinh nữ và
8
học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học
sinh của tổ đó đi trực nhật?
A.
28
. B.
48
. C.
14
. D.
8
.
Lời giải
Số cách chọn ngẫu nhiên một học sinh của tổ đi trực nhật là
6 8 14
+=
.
Câu 14: Từ
4
số
1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số?
A.
12
. B.
6
. C.
64
. D.
24
.
Lời giải
Gọi số cần lập là
,0abc a ≠
.
Chọn
a
có 4 cách chọn.
Chọn
b
có 4 cách chọn.
Chọn
c
có 4 cách chọn.
Theo qui tắc nhân, số các số lập được là :
3
4 64=
số.
Câu 15: Có bao nhiêu cách xếp
3
học sinh nam và
4
học sinh nữ theo hàng ngang?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
A.
7!
. B.
144
. C.
2880
. D.
480
.
Lời giải
Số cách xếp
3
học sinh nam và
4
học sinh nữ theo hàng ngang là
7!
.
Câu 16: Từ
7
chữ số
1, 2, 3, 4, 5, 6, 7
có thể lập được bao nhiêu số tự nhiên có
4
chữ số đôi một khác
nhau?
A.
4
7
. B.
7
P
. C.
4
7
C
. D.
4
7
A
.
Lời giải
Số các số tự nhiên có
4
chữ số đôi một khác nhau được lập từ
7
chữ số
1, 2, 3, 4, 5, 6, 7
là
4
7
A
Câu 17: Cho tập hợp
{
}
1; 2;3; 4;5
M =
. Số tập con gồm hai phần tử của tập hợp
M
là:
A. 11. B.
2
5
A
. C.
2
5
C
. D.
2
P
.
Lời giải
Mỗi tập con hai phần tử của tập hợp
M
là một tổ hợp chập 2 của 5 phần tử. Vậy số tập con hai
phần tử của tập hợp
M
là:
2
5
C
.
Câu 18: Khai triển
( )
5
2xy+
thành đa thức ta được kết quả sau
A.
5 4 32 23 4 5
10 40 80 80 32x xy xy xy xy y++ + ++
.
B.
5 4 32 23 4 5
10 40 40 10 2x xy xy xy xy y+++++
.
C.
5 4 32 23 4 5
10 40 80 40 32x xy xy xy xy y++ + ++
.
D.
5 4 32 23 4 5
10 20 20 10 2x xy xy xy xy y+++++
.
Lời giải
( ) ( ) ( ) ( ) ( ) ( )
5 1 2 3 45
05 14 23 32 4 5
55 5 5 5 5
2 2 2 2 22x y Cx Cx y Cx y Cx y Cx y C y+=+ + + + +
.
5 4 32 23 4 5
10 40 80 80 32x xy xy xy xy y=++ + ++
.
Câu 19: Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất xuất hiện mặt hai chấm là
A.
1
2
. B.
1
3
. C.
1
6
. D.
1
4
.
Lời giải
Gọi A là biến cố xuất hiện mặt hai chấm.
Ta có
( )
6n Ω=
,
( )
1nA=
.
Suy ra
( )
( )
(
)
1
6
nA
PA
n
= =
Ω
.
Câu 20: Một hộp chứa
10
quả cầu gồm
3
quả cầu màu xanh và
7
quả cầu màu đỏ, các quả cầu đôi một
khác nhau. Chọn ngẫu nhiên lần lượt hai quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn
ra cùng màu bằng
A.
7
30
. B.
8
15
. C.
7
15
. D.
5
11
.
Lời giải
Gọi biến cố
A
: “Hai quả cầu được chọn ra cùng màu”.
Số phần tử của không gian mẫu là:
( )
10.9 90n Ω= =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Chọn hai quả cầu cùng màu xảy ra
2
trường hợp: hoặc
2
quả cùng màu xanh hoặc
2
quả cùng
màu đỏ. Khi đó
( )
3.2 7.6 48nA=+=
.
Xác suất để hai quả cầu được chọn ra cùng màu là
( )
( )
( )
48 8
90 15
nA
PA
n
= = =
Ω
.
Câu 21: Từ một nhóm gồm
6
học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. Xác suất để
chọn được 2 học sinh nữ và 1 học sinh nam bằng
A.
3
10
. B.
1
5
. C.
1
6
. D.
1
2
.
Lời giải
Số phần tử của không gian mẫu là
( )
3
10
nCΩ=
.
Gọi A là biến cố: “Chọn được 2 học sinh nữ và 1 học sinh nam” thì
(
)
21
64
.nA CC
=
.
Xác suất chọn được 2 học sinh nữ và 1 học sinh nam là
( )
21
64
3
10
.
1
2
CC
PA
C
= =
.
Câu 22: Cho số gần đúng
23748023
α
=
với độ chính xác
101d =
. Hãy viết số quy tròn của số
A.
23749000
. B.
23748000
. C.
23746000
. D.
23747000
.
Lời giải
Độ chính xác
101d =
(hàng trăm) nên ta làm tròn số
23748023
α
=
đến hàng nghìn được kết
quả là
23748000
α
=
.
Câu 23: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?
A.
4,694
. B.
4,925
. C.
4,55
. D.
4,495
.
Lời giải
Số bạn học sinh trong lớp là
61538840n =+ +++=
(bạn)
Trong năm 2021, trung bình mỗi bạn trong lớp đọc số cuốn sách là:
6.3 15.4 3.5 8.6 8.7
4,925
40
x
+ +++
= =
Câu 24: Trong mặt phẳng hệ tọa độ
,Oxy
cho hai điểm
( ) ( )
2; 1 , 1; 7AB−
. Tọa độ điểm M thỏa mãn hệ
thức
30AM AB+=
 
là
A.
(
)
1; 3M −
B.
( )
5; 5M −
C.
( )
1; 1M −
D.
( )
3; 1M −
Lời giải
Gọi
( )
;M ab
Ta có
( )
2; 1=−−

AM a b
và
( )
3; 6= −

AB
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Lại có
( )
( )
3 2 30
3
30
1
3 1 60
− −=
=
+=⇔ ⇔

= −
−+=
 
a
a
AM AB
b
b
. Suy ra
( )
3; 1−M
.
Câu 25: Đường thẳng
∆
đi qua điểm
( )
1; 2
M
và song song với đường thẳng
:4 2 1 0dx y+ +=
có phương
trình tổng quát là
A.
4 2 30xy+ +=
. B.
2 40xy++=
. C.
2 30xy− +=
. D.
2 40xy+−=
.
Lời giải
Vì
// : 4 2 1 0dx y∆ + +=
: 4 2 0 , ( 1)x ym m⇒∆ + + = ≠
.
Mà
∆
đđi qua
(
)
1; 2
M
nên ta có
( )
4.1 2.2 0 8m m TM+ +=⇒=−
.
:4280 :2 40x y xy⇒∆ + − = ⇔∆ + − =
.
Câu 26: Hai đường thẳng
12
: 5, : 9d mx y m d x my
+=− + =
cắt nhau khi và chỉ khi
A.
1m ≠−
. B.
1m ≠
. C.
1
m
≠±
. D.
2m ≠
.
Lời giải
CÁCH 1
-Xét
0m =
thì
12
5 9d :y , d :x=−=
. Rõ ràng hai đường thẳng này cắt nhau nên
0m =
thỏa
mãn.
-Xét
0
m ≠
thì
1
:5d y mx m
=− +−
và
2
:9
x
dy
m
=−+
Hai đường thẳng
1
d
và
2
d
cắt nhaut
0
1
(2)
1
m
m
m
m
≠
⇔− ≠− ⇔
≠±
.
Từ và ta có
1m ≠±
.
CÁCH 2
1
d
và
2
d
theo thứ tự nhận các vectơ
12
1 1n ( m; ), n ( ;m )= =

làm vec tơ pháp tuyến.
1
d
và
2
d
cắt nhau
1
n⇔
và
2
n
không cùng phương
⇔
11 1m.m . m .≠ ⇔ ≠±
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( )
1; 2
A
,
( )
5; 2B
,
( )
1; 3C
−
có phương trình
là.
A.
22
6 10x y xy+ + + −=
. B.
22
6 10x y xy+ − − −=
.
C.
22
6 10x y xy+ − + −=
. D.
22
6 10x y xy+ + − −=
.
Lời giải
Gọi
( )
C
là phương trình đường tròn đi qua ba điểm
,,ABC
với tâm
( )
;I ab
( )
C⇒
có dạng:
22
22 0x y ax by c+ − − +=
. Vì đường tròn
( )
C
đi qua qua ba điểm
,,ABC
nên ta có hệ phương trình:
3
1424 0 24 5
1
25 4 10 4 0 10 4 29
2
1926 0 26 10
1
a
a bc a bc
a bc a bc b
a bc a bc
c
=
+− − += − − +=−


+− − +=⇔− − +=− ⇔ =−


+− + += − + +=−

= −
.
Vậy phương trình đường tròn cần tìm là
22
6 10x y xy+ − + −=
.
Câu 28: Đường tròn
( )
C
đi qua
( )
1; 3A
,
( )
3;1B
và có tâm nằm trên đường thẳng
:2 7 0d xy−+=
có
phương trình là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
A.
( ) ( )
22
7 7 102xy− +− =
. B.
( ) ( )
22
7 7 164xy+ ++ =
.
C.
( ) ( )
22
3 5 25xy− +− =
. D.
( ) ( )
22
3 5 25xy+ ++ =
.
Lời giải
Đường tròn
( )
C
có tâm
( )
;I ab
, bán kính
R
có phương trình là:
( ) ( ) ( )
22
2
*xa yb R− +− =
.
( )
;2 7I d Ia a∈⇒ +
.
( ) ( )
22
1 24AI a a= −+ +
2
5 14 17aa= ++
( ) ( )
22
3 26BI a a= −+ +
2
5 18 45aa= ++
Vì
( )
C
đi qua
( )
1; 3A
,
( )
3;1B
nên
AI BI=
⇔
22
AI BI=
⇔
22
5 14 17 5 18 45aa aa+ += + +
⇔
7a = −
Suy ra tâm
( )
7; 7I −−
, bán kính
22
164R AI= =
.
Vậy đường tròn
( )
C
có phương trình:
( ) ( )
22
7 7 164xy+ ++ =
.
Câu 29: Phương trình chính tắc của elip đi qua điểm
( )
0; 4−A
và có một tiêu điểm
( )
2
3; 0F
là
A.
22
1
10 8
+=
xy
. B.
22
1
25 16
+=
xy
. C.
22
1
25 9
+=
xy
. D.
22
1
16 25
+=
xy
.
Lời giải
Phương trình chính tắc của elip có dạng
( )
22
22
1 0+ = >>
xy
ab
ab
.
Ta có
2
2
2
2 22 2
16
1
16
39
25
=
=
= ⇒=


=+=
b
b
cc
abc a
.
Vậy elip có phương trình chính tắc là
22
1
25 16
+=
xy
.
Câu 30: Cần xếp 3 nam, 3 nữ vào 1 hàng có 6 ghế. Hỏi có bao nhiêu cách xếp sao cho nam nữ ngồi xen
kẽ.
A.
36
. B.
720
. C.
78
. D.
72
.
Lời giải
Có 6 cách chọn một người tuỳ ý ngồi vào chỗ thứ nhất. Tiếp đến, có 3 cách chọn một người khác
phái ngồi vào chỗ thứ 2. Lại có 2 cách chọn một người khác phái ngồi vào chỗ thứ 3, có 2 cách
chọn vào chỗ thứ 4, có 1 cách chọn vào chỗ thứ 5, có 1 cách chọn vào chỗ thứ 6.
Vậy có: cách.
Câu 31: Có 4 cặp vợ chồng ngồi trên một dãy ghế dài. Có bao nhiêu cách sắp xếp sao cho vợ và chồng
của mỗi gia đình đều ngồi cạnh nhau.
A.
384
. B.
8!
. C.
4!.4!
. D.
48
.
Lời giải
-Nhóm mỗi cặp vợ chồng lại với nhau có
2!.2!.2!.2!
cách
-Sắp xếp 4 cặp vợ chồng lên một dãy ghế dài có
4!
cách
-Theo quy tắc nhân, ta có
2!.2!.2!.2!.4! 384=
.
6.3.2.2.1.1 72=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Câu 32: Ở một Đoàn trường phổ thông có 5 thầy giáo, 4 cô giáo và 8 học sinh. Có bao nhiêu cách chọn
ra một đoàn công tác gồm 7 người trong đó có 1 trưởng đoàn là thầy giáo, 1 phó đoàn là cô giáo
và đoàn công tác phải có ít nhất 4 học sinh.
A.
6020
. B.
10920
. C.
9800
. D.
10290
.
Lời giải
Trường hợp 1: Đoàn có 1 thầy giáo, 1 cô giáo, và 5 học sinh có:
5
8
5.4. 1120C =
cách.
Trường hợp 2: Đoàn có 1 thầy giáo, 2 cô giáo, và 4 học sinh có:
24
48
5. . 4200AC =
cách.
Trường hợp 3: Đoàn có 2 thầy giáo, 1 cô giáo, và 4 học sinh có:
24
58
.4. 5600AC=
cách.
Vậy theo quy tắc cộng có:
1120 4200 5600 10920++=
cách.
Câu 33: Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số
1,2,3, 4,5,6
. Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là một số chia hết cho
5
.
A.
1
6
. B.
1
12
. C.
1
2
. D.
1
4
.
Lời giải
Số phần tử của không gian mẫu:
( )
3
6
120nAΩ= =
.
Gọi
A
là biến cố: "Số chọn được là một số chia hết cho
5
".
Số chia hết cho
5
được lập từ các chữ số trên có dạng
5ab
.
Chọn
2
số
,ab
từ các chữ số
1,2,3, 4,6
là một chỉnh hợp chập
2
của
5
phần tử.
Số cách chọn là
( )
2
5
20nA A= =
.
Vậy xác suất cần tìm là:
( )
( )
( )
20 1
120 6
nA
PA
n
= = =
Ω
.
Câu 34: Chọn ngẫu nhiên hai số khác nhau từ
25
số nguyên dương đầu tiên. Xác suất
để chọn được hai số có tổng là một số chẵn là
A.
13
25
. B.
12
25
. C.
1
2
. D.
313
625
.
Lời giải
Số cách chọn hai số khác nhau từ
25
số nguyên dương đầu tiên là
( )
2
25
C 300 300n= ⇒ Ω=
.
Gọi
A
là biến cố “Tổng hai số được chọn là một số chẵn’’.
Ta có hai trường hợp
Trường hợp 1: Chọn
2
số chẵn khác nhau từ tập
12
số chẵn có
2
12
C 66=
cách.
Trường hợp 2: Chọn
2
số lẻ khác nhau từ tập
13
số lẻ có
2
13
C 78=
cách.
Do đó
( ) 66 78 144
nA=+=
.
Vậy xác suất cần tìm là
144 12
P( )
300 25
A = =
.
Câu 35: Một nhóm gồm 12 học sinh trong đó có 7 học sinh nam và 5 học sinh nữ. Chọn ngẫu nhiên 3 học
sinh từ nhóm 12 học sinh đó đi lao động. Xác suất để trong ba học sinh được chọn có ít nhất một
học sinh nữ là:
A.
15
22
. B.
7
44
. C.
35
44
. D.
37
44
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Lời giải
Số cách chọn ba học sinh bất kì là
( )
3
12
220
nCΩ= =
Số cách chọn ba học sinh nam là
3
7
35C =
Số cách chọn ra ba học sinh mà có ít nhất một học sinh nữ là
33
12 7
185CC−=
Xác suất để chọn được ba học sinh có ít nhất một học sinh nữ là
185 37
220 44
P = =
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có 8 người cùng vào thang máy ở tầng 1 của một tòa nhà cao 10 tầng và đi lên trên. Hỏi có bao
nhiêu cách sắp xếp để trong 8 người đó có đúng 2 người cùng ra ở 1 tầng và mỗi người còn lại
ra ở mỗi tầng khác nhau.
Lời giải
Chọn 2 người trong 8 người có:
2
8
28C =
cách.
Chọn 1 tầng trong 9 tầng để cho 2 người đó cùng ra có:
9
cách.
Chọn 6 tầng trong 8 tầng còn lại cho 6 người còn lại có:
6
8
20160A =
cách.
Vậy theo quy tắc nhân có:
28.9.20160 5080320=
cách.
Câu 37: Trong mặt phẳng
,Oxy
viết phương trình chính tắc của Elip
(
)
E
có một tiêu điểm là
( )
1
2;0F
−
và đi qua điểm
( )
2;3M
.
Lời giải
Phương trình chính tắc của Elip có dạng:
( )
22
22
1, 0
xy
ab
ab
+ = >>
.
Vì Elip có một tiêu điểm là
( )
1
2;0F −
nên
2c =
22 2 2 2
44abc ab
⇒−==⇒=+
.
Mặt khác Elip đi qua điểm
( )
2;3M
nên
(
)
22
22 2 2
22
49 4 9 4936
11 1
4
4
bb
ab b b
bb
++
+=⇔ +=⇔ =
+
+
( )
( )
2
42
2
12
9 36 0
3
bn
bb
bl
=
⇔− −=⇔
= −
.
22
412416ab= += +=
.
Vậy phương trình chính tắc của elip
( )
E
cần tìm là:
22
1
16 12
xy
+=
.
Câu 38: Gọi
S
là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập
{ }
1; 2;3; 4;5E =
. Chọn
ngẫu nhiên một số từ tập
S
. Xác xuất để số được chọn là một số chẵn bằng
Lời giải
Gọi
A
là biến cố “số được chọn là một số chẵn”
Số các số tự nhiên có bốn chữ số khác nhau là
4
5
120
A =
Số phần tử của không gian mẫu
( )
1
120
120nCΩ= =
Số các số tự nhiên chẵn có bốn chữ số khác nhau
3
4
2 48A =
Số kết quả thuận lợi của biến cố
A
là
( )
1
48
48nA C= =
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Vậy xác xuất để số được chọn là một số chẵn là
( )
( )
( )
48 2
120 5
nA
PA
n
= = =
Ω
Câu 39: Trong mặt phẳng
Oxy
cho parabol
( )
2
:8Py x=
. Đường thẳng
Δ
không trùng với trục
Ox
đi
qua tiêu điểm
F
của
( )
P
sao cho góc hợp bởi hai tia
Fx
và
Ft
là tia của
Δ
nằm phía trên trục
hoành một góc bằng
( )
0
90αα≠
. Biết
Δ
cắt
( )
P
tại hai điểm phân biệt
,MN
và tập hợp trung
điểm
I
của đoạn
MN
khi
α
thay đổi là một Parabol. Xác định phương trình của Parabol.
Lời giải
Theo giả thiết ta có
( )
2; 0F
, đường thẳng
Δ
có hệ số góc
tank α
=
Suy ra
( )
Δ : 2 .tanyx α= −
. Xét hệ phương trình
( )
2
2 tan
8
yx α
yx
= −
=
Suy ra
2
tan . 8 16 tan 0αy y α−− =
2
Δ' 16 16tan 0α=+>
do đó phương trình luôn có hai nghiệm phân biệt, hệ phương trình có hai
nghiệm phân biệt điều này chứng tỏ rằng
Δ
cắt
( )
P
tại hai điểm phân biệt.
Gọi tọa độ hai giao điểm đó là
( ) ( )
;, ;
MM NN
Mx y Nx y
;
( )
;
II
Ix y
là trung điểm của
MN
Theo định lý Viét ta có:
84
0
tan 2 tan
MN
MN I
yy
yy y
αα
+
+ = >⇒ = =
.
Mặt khác từ ta có
( )
2
4
4 tan 2
2 tan
MN
MN MN I
xx
yy xx αx
α
+
+ = +− ⇒= = +
Suy ra
2
4. 2
4
I
I
y
x

= +


hay
2
48
II
yx= −
Vậy tập hợp điểm
I
là Parabol có phương trình:
2
48yx= −
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 02
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho tam giác
ABC
với
( )
3; 6A −
;
( )
9; 10B −
và
1
;0
3
G



là trọng tâm. Tọa độ
C
là:
A.
(
)
5; 4
C −
. B.
( )
5; 4C
. C.
( )
5; 4C −
. D.
( )
5; 4C −−
.
Câu 2: Chiều cao của một ngọn đồi là
347,13 0,2h mm= ±
. Độ chính xác
d
của phép đo trên là
A.
347,13dm
=
. B.
347,33m
. C.
0, 2dm=
. D.
346,93dm=
.
Câu 3: Tứ phân vị thứ nhất của mẫu số liệu: 27; 15; 18; 30; 19; 40; 100; 9; 46; 10; 200.
A. 18. B. 15. C. 40. D. 46.
Câu 4: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là:
A. 20. B. 22. C. 24. D. 26.
Câu 5: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
A. Bình phương của phương sai. B. Một nửa của phương sai.
C. Căn bậc hai của phương sai. D. Hiệu của số lớn nhất và số nhỏ nhất.
Câu 6: Trong hệ tọa độ
,Oxy
cho ba điểm
( )
2; 1A
,
( )
0; 3B −
,
( )
3; 1C
. Tìm tọa độ điểm
D
để
ABCD
là hình bình hành.
A.
(
)
5; 5
. B.
( )
5; 2−
. C.
(
)
5; 4−
. D.
( )
1; 4−−
.
Câu 7: Chỉ số IQ của một nhóm học sinh là:
60
78
80
64
70
76
80
74
86
90
Các tứ phân vị của mẫu số liệu là
A.
123
70; 77; 80QQ Q= = =
. B.
123
72; 78; 80QQQ
= = =
.
C.
123
70; 76; 80QQ Q= = =
. D.
123
70; 75; 80QQQ= = =
.
Câu 8: Nhiệt độ cao nhất của Hà Nội trong
7
ngày liên tiếp trong tháng tám được ghi lại là:
34; 34; 36; 35; 33; 31;30
(Độ C).
Độ lệch chuẩn của mẫu số liệu thuộc khoảng nào
A.
( )
1; 2
. B.
( )
3; 4
. C.
7
2;
2



. D.
3
0;
4



.
Câu 9: Cho đường thẳng
d
có phương trình
14
3
xt
yt
= −
=−+
. Một vectơ chỉ phương của
d
là
A.
( )
1; 4u = −
. B.
( )
4;1u =
. C.
( )
1; 3u = −
. D.
( )
4;1u = −
.
Câu 10: Trong mặt phẳng tọa độ
Oxy
, phương trình tham số của đường thẳng qua
( )
1; 2M −
,
( )
4;3N
là
A.
4
32
xt
yt
= +
= −
. B.
15
23
xt
yt
= +
=−−
. C.
33
45
xt
yt
= +
= +
. D.
13
25
xt
yt
= +
=−+
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
Câu 11: Xác định vị trí tương đối giữa hai đường thẳng
1
: 2 10∆ − +=
xy
và
2
: 3 6 10 0∆−+ − =
xy
.
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau.
Câu 12:
Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
3; 4M −
đến đường thẳng
:3 4 1 0xy∆ − −=
.
A.
8
5
. B.
24
5
. C.
12
5
. D.
24
5
−
.
Câu 13: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
A.
22
2 4 90xy xy+ + − +=
. B.
22
6 4 13 0xy xy+−+ +=
.
C.
22
228460
x y xy
+ − − −=
. D.
22
5 4 4 10x yxy+ + − +=
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
(
)
3;2A −
và
( )
1;4B
. Viết phương trình đường tròn
đường kính
AB
?
A.
22
6 502xy xy++ − +=
. B.
22
6 502xy xy−+ + +=
.
C.
22
6 502xy xy++ − −=
. D.
22
6 502xy xy−+ + −=
.
Câu 15: Tọa độ các tiêu điểm của hypebol
(
)
22
:1
16 9
xy
H −=
là
A.
(
) ( )
12
5; 0 ; 5;0FF=−=
. B.
( ) ( )
12
0; 5 ; 0;5FF=−=
.
C.
(
)
(
)
12
0; 7 ; 0; 7FF
=−=
. D.
( ) ( )
12
7;0 ; 7;0FF=−=
.
Câu 16: Có
3
cuốn sách Toán khác nhau và
4
cuốn sách Vật lí khác nhau. Hỏi có bao nhiêu cách chọn
một cuốn sách trong số các cuốn sách đó?
A.
12
. B.
7
. C.
3
. D.
4
.
Câu 17: Có bao nhiêu cách chọn một cặp đôi tham gia văn nghệ từ một nhóm gồm
7
bạn nam và
6
bạn
nữ?
A.
13
. B.
42
. C.
8
. D.
7
.
Câu 18: Từ các số
1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm
4
chữ số đôi một khác nhau.
A.
12
. B.
64
. C.
256
. D.
24
.
Câu 19: Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập
{ }
2, 3, 4, 5, 6A =
A.
4
5
C
. B.
4
6
C
. C.
4
5
A
. D.
4
6
A
.
Câu 20: Có bao nhiêu cách chọn ra
4
học sinh từ một tổ gồm 15 học sinh?
A.
32760
. B.
50625
. C.
60
. D.
1365
.
Câu 21: Có bao nhiêu số hạng trong khai triển nhị thức
( )
5
32x−
A.
4
. B.
5
. C.
6
. D.
2
.
Câu 22: Một lớp có
35
học sinh, trong đó có
5
học sinh tên Linh. Trong một lần kiểm tra bài cũ, thầy
giáo gọi ngẫu nhiên một học sinh trong lớp lên bảng. Xác suất để học sinh tên Linh lên bảng
bằng
A.
1
175
. B.
1
7
. C.
1
35
. D.
1
5
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
Câu 23: Cho tập hợp
{
}
1; 2; 4;5;8; 9A =
lấy ngẫu nhiên một số. Xác suất để lấy được một số chẵn là:
A.
1
.
3
. B.
1
.
2
.
C.
2
.
5
. D.
1
.
6
Câu 24: Để kiểm tra sản phẩm của một công ty sữa, người ta gửi đến bộ phận kiểm nghiệm
5
hộp sữa
cam,
4
hộp sữa nho và
3
hộp sữa dâu. Bộ phận kiểm nghiệm chọn ngẫu nhiên
3
hộp sữa để
phân tích mẫu. Xác suất để
3
hộp sữa được chọn đủ cả
3
loại là
A.
1
5
. B.
3
7
. C.
1
6
. D.
3
11
.
Câu 25: Viết phương trình tổng quát của đường thẳng đi qua
( )
3; 2−M
và song song với đường thẳng
:2 5 0
+−=
d xy
A.
2 70+ −=xy
. B.
2 40+−=xy
. C.
2 50
+ −=
xy
. D.
2 60+−=xy
.
Câu 26: Với giá trị nào của
m
thì hai đường thẳng
1
:2 4 0d xy m++− =
và
( )
2
: 3 2 10d m xy m+ + + −=
song song?
A.
1.m =
B.
1.m = −
C.
2.m =
D.
3.m =
Câu 27: Đường tròn
(
)
C
có tâm
( )
1;2I −
và cắt đường thẳng
:3 15 0d xy−− =
theo một dây cung có
độ dài bằng 6. Tìm phương trình đường tròn
( )
C
.
A.
(
) ( )
22
1 2 49xy
− ++ =
. B.
( )
( )
22
1 2 49
xy+ +− =
.
C.
(
) ( )
22
1 27
xy−++ =
. D.
(
) ( )
22
1 27xy
+ +− =
.
Câu 28: Trong mặt phẳng tọa độ
( )
Oxy
, cho đường tròn
( )
S
có tâm
I
nằm trên đường thẳng
yx= −
,
bán kính
3R =
và tiếp xúc với các trục tọa độ. Lập phương trình của
( )
S
, biết hoành độ tâm
I
là số dương.
A.
( ) ( )
22
3 39xy− +− =
. B.
( ) ( )
22
3 39xy− ++ =
.
C.
( ) ( )
22
3 39xy− −− =
. D.
( ) ( )
22
3 39xy+ ++ =
.
Câu 29: Phương trình chính tắc của parabol
( )
P
có tiêu điểm là
( )
5; 0F
là:
A.
2
20yx=
. B.
2
30yx=
. C.
2
15
yx=
. D.
2
10
yx=
.
Câu 30: Một bạn có
4
áo xanh,
3
áo trắng và
5
quần màu đen. Hỏi bạn đó có bao nhiêu cách chọn một
bộ quần áo để mặc?
A.
35
. B.
66
. C.
12
. D.
60
.
Câu 31: Số cách xếp 5 nam và 4 nữ thành một hàng ngang sao cho 4 nữ luôn đứng cạnh nhau là
A. 362880. B. 2880. C. 5760. D. 17280.
Câu 32: Một nhóm có
3
học sinh nam và
3
học sinh nữ. Nhóm muốn xếp theo hàng ngang để chụp ảnh
kỉ niệm. Có bao nhiêu cách xếp để không có bạn nam nào đứng kề nhau.
A.
6!
. B.
3!.3!
. C.
3
4
3!.A
. D.
3
4
3!.C
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 33: Từ hộp chứa 5 quả cầu trắng, 4 quả cầu xanh kích thước và khối lượng như nhau. Lấy ngẫu nhiên
3 quả cầu. Tính xác suất để 3 quả cầu lấy được có màu trắng?
A.
5
42
. B.
5
9
. C.
1
3
. D.
1
21
.
Câu 34: Một tổ học sinh có 7 nữ và 5 nam. Chọn ngẫu nhiên 3 học sinh. Xác suất để trong 3 học sinh
được chọn có đúng 1 học sinh nam bằng
A.
1
5
. B.
5
12
. C.
21
44
. D.
7
22
.
Câu 35: Một hộp đựng 12 cây viết được đánh số từ 1 đến 12. Chọn ngẫu nhiên 2 cây. Xác suất để chọn
được 2 cây có tích hai số là số chẵn
A.
6
11
. B.
17
22
. C.
5
22
. D.
5
11
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có
5
chữ số đôi một khác nhau và số đó chia hết cho
9
.
Câu 37: Trong mặt phẳng
,Oxy
cho Elip
( )
E
đi qua điểm
( )
2 3;2M
và
M
nhìn hai tiêu điểm của
( )
E
dưới một góc vuông. Viết phương trình chính tắc của
( )
E
đã cho.
Câu 38: Một cuộc họp có sự tham gia của
6
nhà Toán học trong đó có 4 nam và
2
nữ,
7
nhà Vật lý
trong đó có
3
nam và
4
nữ và
8
nhà Hóa học trong đó có
4
nam và
4
nữ. Người ta muốn lập
một ban thư kí gồm
4
nhà khoa học. Tính xác suất để ban thư kí được chọn phải có đủ cả
3
lĩnh
vực và có cả nam lẫn nữ.
Câu 39: Cho hypebol
( )
H
có hai tiêu điểm
12
;FF
nằm trên
Ox
và đối xứng qua gốc tọa độ
O
,
( )
H
đi
qua điểm
M
có hoành độ
5−
và
12
9 41
;
44
MF MF= =
. Viết phương trình chính tắc của hypebol
( )
H
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho tam giác
ABC
với
( )
3; 6A −
;
( )
9; 10B −
và
1
;0
3
G



là trọng tâm. Tọa độ
C
là:
A.
(
)
5; 4
C −
. B.
( )
5; 4C
. C.
( )
5; 4C −
. D.
(
)
5; 4
C
−−
.
Lời giải.
Chọn C
Ta có :
3
3
ABC G
ABC G
xxx x
yyy y
++=
++=
(
)
(
)
3
3
C G AB
C G AB
x x xx
y y yy
= −+
⇔
= −+
( )
5; 4C⇒−
.
Câu 2: Chiều cao của một ngọn đồi là
347,13 0,2h mm= ±
. Độ chính xác
d
của phép đo trên là
A.
347,13
dm=
. B.
347,33m
. C.
0, 2dm=
. D.
346,93
dm
=
.
Lời giải
Chọn C
Ta có
a
là số gần đúng của
a
với độ chính xác
d
qui ước viết gọn là
aad= ±
. Vậy độ chính xác
của phép đo là
0, 2
dm=
.
Câu 3: Tứ phân vị thứ nhất của mẫu số liệu: 27; 15; 18; 30; 19; 40; 100; 9; 46; 10; 200.
A. 18. B. 15. C. 40. D. 46.
Lời giải
Sắp xếp số liệu theo thứ tự không giảm: 9; 10; 15; 18; 19; 27; 30; 40; 46; 100; 200.
Tứ phân vị thứ nhì là trung vị của dãy số liệu là:
2
27Q =
.
Tứ phân vị thứ nhất là trung vị của dãy số liệu: 9; 10; 15; 18; 19.
Khi đó tứ phân vị thứ nhất là:
1
15Q =
.
Câu 4: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là:
A. 20. B. 22. C. 24. D. 26.
Lời giải
Số liệu trên đã sắp xếp theo thứ tự không giảm
Ta có
123
10; 19; 32QQQ= = =
Vậy khoảng tứ phân vị của mẫu số liệu trên là:
32 10 22
Q
∆= − =
.
Câu 5: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
A. Bình phương của phương sai. B. Một nửa của phương sai.
C. Căn bậc hai của phương sai. D. Hiệu của số lớn nhất và số nhỏ nhất.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
Chọn đáp án: C.
Câu 6: Trong hệ tọa độ
,Oxy
cho ba điểm
( )
2; 1A
,
( )
0; 3B −
,
( )
3; 1C
. Tìm tọa độ điểm
D
để
ABCD
là hình bình hành.
A.
( )
5; 5
. B.
(
)
5; 2
−
. C.
(
)
5; 4
−
. D.
( )
1; 4−−
.
Lời giải
Chọn A
Gọi
( )
;,Dxy
ABCD
là hình bình hành
( ) ( )
2; 1 3; 4AD BC x y⇔ = ⇔ − −=
 
23 5
14 5
xx
yy
−= =

⇔⇔

−= =

Vậy
( )
5; 5D
.
Câu 7: Chỉ số IQ của một nhóm học sinh là:
60
78
80
64
70
76
80
74
86
90
Các tứ phân vị của mẫu số liệu là
A.
123
70; 77; 80QQ Q= = =
. B.
123
72; 78; 80QQQ= = =
.
C.
123
70; 76; 80
QQQ= = =
. D.
123
70; 75; 80QQQ
= = =
.
Lời giải
Sắp xếp các giá trị này theo thứ tự không giảm
60
64
70
74
76
78
80
80
86
90
Vì
10n =
là số chẵn nên
2
Q
là số trung bình cộng của hai giá trị chính giữa:
(
)
2
76 78 : 2 77Q =+=
Ta tìm
1
Q
là trung vị của nửa số liệu bên trái
2
Q
60
64
70
74
76
và tìm được
1
70Q =
Ta tìm
3
Q
là trung vị của nửa số liệu bên phải
2
Q
78
80
80
86
90
và tìm được
3
80Q =
.
C
A
B
D
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
Câu 8: Nhiệt độ cao nhất của Hà Nội trong
7
ngày liên tiếp trong tháng tám được ghi lại là:
34; 34; 36; 35; 33; 31;30
(Độ C).
Độ lệch chuẩn của mẫu số liệu thuộc khoảng nào
A.
( )
1; 2
. B.
(
)
3; 4
. C.
7
2;
2



. D.
3
0;
4



.
Lời giải
Số trung bình cộng của mẫu số liệu là:
34 34 36 35 33 31 30
33,29
7
x
++++++
= ≈
Phương sai của mẫu số liệu là:
( )
7
2
2
1
3, 92
7
i
i
xx
s
=
−
= ≈
∑
Độ lệch chuẩn cần tính là:
3,92 1,98s ≈≈
.
Câu 9: Cho đường thẳng
d
có phương trình
14
3
xt
yt
= −
=−+
. Một vectơ chỉ phương của
d
là
A.
( )
1; 4u = −
. B.
( )
4;1u =
. C.
( )
1; 3u = −
. D.
( )
4;1u = −
.
Lời giải
Từ phương trình tham số của đường thẳng
d
là
14
3
xt
yt
= −
=−+
, suy ra
d
có một vectơ chỉ phương
là
( )
4;1u = −
.
Câu 10: Trong mặt phẳng tọa độ
Oxy
, phương trình tham số của đường thẳng qua
( )
1; 2M
−
,
( )
4;3N
là
A.
4
32
xt
yt
= +
= −
. B.
15
23
xt
yt
= +
=−−
. C.
33
45
xt
yt
= +
= +
. D.
13
25
xt
yt
= +
=−+
.
Lời giải
Đường thẳng có véctơ chỉ phương là
( )
3; 5MN =

và đi qua
( )
1; 2M
−
nên có phương trình tham
số là
13
25
xt
yt
= +
=−+
.
Câu 11: Xác định vị trí tương đối giữa hai đường thẳng
1
: 2 10∆ − +=xy
và
2
: 3 6 10 0∆−+ − =xy
.
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau.
Lời giải
Tọa độ giao điểm của
1
∆
và
2
∆
là nghiệm của hệ phương trình:
2 10
3 6 10 0
− +=
−+ −=
xy
xy
3 6 30
3 6 10 0
− +=
⇔
−+=
xy
xy
Hệ phương trình trên vô nghiệm nên hai đường thẳng
1
∆
và
2
∆
song song với nhau.
Câu 12:
Trong mặt phẳng
Oxy
, khoảng cách từ điểm
( )
3; 4M −
đến đường thẳng
:3 4 1 0xy∆ − −=
.
A.
8
5
. B.
24
5
. C.
12
5
. D.
24
5
−
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
Ta có:
(
)
( )
(
)
2
2
3.3 4. 4 1
24
,
5
34
dM
− −−
∆= =
+−
.
Câu 13: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
A.
22
2 4 90xy xy+ + − +=
. B.
22
6 4 13 0xy xy+−+ +=
.
C.
22
228460
x y xy+ − − −=
. D.
22
5 4 4 10x yxy+ + − +=
.
Lời giải
Một phương trình trở thành phương trình đường tròn khi
22
0abc+ −>
.
Phương trình
2 2 22
228460 4230x y xy xy xy+ −−−=⇔+−−−=
.
Có
2 2 22
2, 1, 3 21380a b c abc= = =−⇒ + −= + +=>
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
( )
3;2A
−
và
( )
1;4B
. Viết phương trình đường tròn
đường kính
AB
?
A.
22
6 502xy xy++ − +=
. B.
22
6 502xy xy−+ + +=
.
C.
22
6 502xy xy++ − −=
. D.
22
6 502xy xy−+ + −=
.
Lời giải
Ta có
( )
4; 2 20 2 5
AB AB= ⇒= =

.
Gọi
I
là trung điểm của
AB
, suy ra
( )
1; 3I −
.
Phương trình đường tròn tâm
I
, bán kính
5
2
AB
R = =
là
( )
( )
22
22
1 3 5 2 6 50x y xy xy+ + − =⇔ + + − +=
.
Câu 15: Tọa độ các tiêu điểm của hypebol
(
)
22
:1
16 9
xy
H −=
là
A.
( ) ( )
12
5; 0 ; 5;0FF=−=
. B.
( ) ( )
12
0; 5 ; 0;5FF=−=
.
C.
( )
( )
12
0; 7 ; 0; 7FF=−=
. D.
( ) ( )
12
7;0 ; 7;0FF=−=
.
Lời giải
Gọi
( ) ( )
12
;0 ; ;0F cFc=−=
là hai tiêu điểm của
( )
H
.
Từ phương trình
( )
22
:1
16 9
xy
H −=
, ta có:
2
16a =
và
2
9b
=
suy ra
( )
2 22
25 5, 0c ab c c= + = ⇒= >
.
Vậy tọa độ các tiêu điểm của
( )
H
là
( ) ( )
12
5; 0 ; 5;0FF=−=
.
Câu 16: Có
3
cuốn sách Toán khác nhau và
4
cuốn sách Vật lí khác nhau. Hỏi có bao nhiêu cách chọn
một cuốn sách trong số các cuốn sách đó?
A.
12
. B.
7
. C.
3
. D.
4
.
Lời giải
Chọn
1
cuốn sách trong
7
cuốn sách (
3
cuốn sách Toán và
4
cuốn sách Vật lý) có
7
cách
chọn.
Câu 17: Có bao nhiêu cách chọn một cặp đôi tham gia văn nghệ từ một nhóm gồm
7
bạn nam và
6
bạn
nữ?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
A.
13
. B.
42
. C.
8
. D.
7
.
Lời giải
Số cách chọn một bạn nam và một bạn nữ là:
7.6 42=
.
Câu 18: Từ các số
1,2,3,4
có thể lập được bao nhiêu số tự nhiên gồm
4
chữ số đôi một khác nhau.
A.
12
. B.
64
. C.
256
. D.
24
.
Lời giải
Mỗi số lập được là một hoán vị của
4
số, nên lập được:
4
4! 24
P
= =
số.
Câu 19: Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập
{ }
2, 3, 4, 5, 6
A =
A.
4
5
C
. B.
4
6
C
. C.
4
5
A
. D.
4
6
A
.
Lời giải
Số các số tự nhiên có 4 chữ số khác nhau được lập từ
A
là
4
5
A
.
Câu 20: Có bao nhiêu cách chọn ra
4
học sinh từ một tổ gồm 15 học sinh?
A.
32760
. B.
50625
. C.
60
. D.
1365
.
Lời giải
Số cách chọn ra
4
học sinh từ một tổ gồm 15 học sinh là
4
15
1365C =
.
Câu 21: Có bao nhiêu số hạng trong khai triển nhị thức
(
)
5
32
x−
A.
4
. B.
5
. C.
6
. D.
2
.
Lời giải
Ta có trong khai triển nhị thức
( )
n
ab+
thì có
1n +
số hạng.
Vì vậy trong khai triển
( )
5
32x
−
có
51 6 +=
số hạng.
Câu 22: Một lớp có
35
học sinh, trong đó có
5
học sinh tên Linh. Trong một lần kiểm tra bài cũ, thầy
giáo gọi ngẫu nhiên một học sinh trong lớp lên bảng. Xác suất để học sinh tên Linh lên bảng
bằng
A.
1
175
. B.
1
7
. C.
1
35
. D.
1
5
.
Lời giải
Số cách chọn một bạn học sinh trong lớp là
35
cách.
Số cách chọn một bạn tên Linh trong
5
bạn là
5
cách.
Vậy xác suất để học sinh tên Linh lên bảng là
51
35 7
=
.
Câu 23: Cho tập hợp
{ }
1; 2; 4;5;8; 9A =
lấy ngẫu nhiên một số. Xác suất để lấy được một số chẵn là:
A.
1
.
3
. B.
1
.
2
.
C.
2
.
5
. D.
1
.
6
Lời giải
Số phần tử không gian mẫu:
( )
6n Ω=
.
Biến cố số lấy được số chẵn là:
{
}
2; 4;8
A =
nên
( )
3nA=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
Suy ra
( )
( )
( )
31
62
nA
PA
n
= = =
Ω
.
Câu 24: Để kiểm tra sản phẩm của một công ty sữa, người ta gửi đến bộ phận kiểm nghiệm
5
hộp sữa
cam,
4
hộp sữa nho và
3
hộp sữa dâu. Bộ phận kiểm nghiệm chọn ngẫu nhiên
3
hộp sữa để
phân tích mẫu. Xác suất để
3
hộp sữa được chọn đủ cả
3
loại là
A.
1
5
. B.
3
7
. C.
1
6
. D.
3
11
.
Lời giải
Ta có:
3
12
( ) 220nCΩ= =
.
Gọi
A
là biến cố:”3 hộp sữa được chọn đủ cả 3 loại”.
111
543
60 3
() . . 60 ()
220 11
nA CCC PA= =⇒==
.
Câu 25: Viết phương trình tổng quát của đường thẳng đi qua
( )
3; 2−M
và song song với đường thẳng
:2 5 0
+−=
d xy
A.
2 70+ −=xy
. B.
2 40+−=xy
. C.
2 50
+ −=xy
. D.
2 60+−=xy
.
Lời giải
Vì đường thẳng song song với
:2 5 0+−=d xy
nên
(
)
2;1
= =

d
VTPT n n
Phương trình đường thẳng là:
( )
2 3 20 2 40− ++=⇔ +−=x y xy
Câu 26: Với giá trị nào của
m
thì hai đường thẳng
1
:2 4 0d xy m++− =
và
( )
2
: 3 2 10d m xy m+ + + −=
song song?
A.
1.m =
B.
1.m = −
C.
2.m =
D.
3.m =
Lời giải
Với
2
2
1
1
:2 0
4
:7 7 0
d xy
md
d xy
d
+=
= →
+
∩ =∅→
/
→
+=
loại
4.m
=
Với
4m
=
/
thì
( )
12
1
||
2
:2 4 0
31
: 3 2 10
1
21
1.
5
421
dd
d xy m
m
dm y
m
m
m
m
m
xm
++− =
= −
+
→ =
+ + − −=
−−
= ⇔ ⇔=−
/
/
= −
−
Câu 27: Đường tròn
( )
C
có tâm
( )
1;2I −
và cắt đường thẳng
:3 15 0d xy−− =
theo một dây cung có
độ dài bằng 6. Tìm phương trình đường tròn
( )
C
.
A.
( )
( )
22
1 2 49xy− ++ =
. B.
( ) ( )
22
1 2 49xy+ +− =
.
C.
( ) ( )
22
1 27xy−++ =
. D.
( ) ( )
22
1 27xy+ +− =
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
Gọi
H
là trung điểm dây
AB
3
2
AB
AH HB⇒===
và
IH AB⊥
.
Ta có
( )
;IH d I d=
( )
( )
2
2
3. 1 2 15
2 10
31
−−−
= =
+−
.
Xét
IAH
vuông tại
H
:
22 2
AI IH AH
= +
( )
2
2
2 10 3 49= +=
2
49R⇒=
.
Phương trình đường tròn
( )
C
:
( ) ( )
22
1 2 49xy+ +− =
.
Câu 28: Trong mặt phẳng tọa độ
( )
Oxy
, cho đường tròn
(
)
S
có tâm
I
nằm trên đường thẳng
yx= −
,
bán kính
3R =
và tiếp xúc với các trục tọa độ. Lập phương trình của
(
)
S
, biết hoành độ tâm
I
là số dương.
A.
( ) ( )
22
3 39xy− +− =
. B.
( ) ( )
22
3 39xy− ++ =
.
C.
( ) ( )
22
3 39xy− −− =
. D.
( ) ( )
22
3 39xy+ ++ =
.
Lời giải
Do tâm
I
nằm trên đường thẳng
( )
;y x Ia a=−⇒ −
, điều kiện
0a >
.
Đường tròn
( )
S
có bán kính
3R =
và tiếp xúc với các trục tọa độ nên:
( ) ( ) ( ) ( ) ( )
; ; 3 3 3 3 3; 3d I Ox d I Oy a a n a l I= =⇔ =⇔= ∨=− ⇒ −
.
Vậy phương trình
( ) ( ) ( )
22
:3 39Sx y− ++ =
.
Câu 29: Phương trình chính tắc của parabol
( )
P
có tiêu điểm là
( )
5; 0F
là:
A.
2
20yx=
. B.
2
30yx=
. C.
2
15
yx
=
. D.
2
10yx
=
.
Lời giải
Gọi phương trình chính tắc của parabol
( )
P
là:
( )
2
20y px p= >
.
Vì
( )
P
có tiêu điểm là
( )
5; 0F
nên
5
2
p
=
, tức là
10p =
. Vậy phương trình chính tắc của parabol
( )
P
là
2
20yx
=
.
Câu 30: Một bạn có
4
áo xanh,
3
áo trắng và
5
quần màu đen. Hỏi bạn đó có bao nhiêu cách chọn một
bộ quần áo để mặc?
A.
35
. B.
66
. C.
12
. D.
60
.
Lời giải
Có
7
cách chọn một cái áo để mặc và có
5
cách chọn một cái quần để mặc.
Theo quy tắc nhân thì có
7.5 35=
cách chọn một bộ quần áo để mặc.
H
I
B
A
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Câu 31: Số cách xếp 5 nam và 4 nữ thành một hàng ngang sao cho 4 nữ luôn đứng cạnh nhau là
A. 362880. B. 2880. C. 5760. D. 17280.
Lời giải
Ghép 4 nữ thành 1 nhóm có 4! Cách.
Hoán vị nhóm nữ trên với 5 nam có 6! Cách.
Vậy có
4!.6! 17280=
cách.
Câu 32: Một nhóm có
3
học sinh nam và
3
học sinh nữ. Nhóm muốn xếp theo hàng ngang để chụp ảnh
kỉ niệm. Có bao nhiêu cách xếp để không có bạn nam nào đứng kề nhau.
A.
6!
. B.
3!.3!
. C.
3
4
3!.A
. D.
3
4
3!.C
.
Lời giải
Xếp thứ tự
3
bạn nữ có
3!
cách.
Khi đó các bạn nam đứng ở các vị trí x.
Xếp thứ tự
3
bạn nam vào
4
vị trí x có
3
4
A
cách. Vậy có tất cả
3
4
3!.A
cách.
Câu 33: Từ hộp chứa 5 quả cầu trắng, 4 quả cầu xanh kích thước và khối lượng như nhau. Lấy ngẫu nhiên
3 quả cầu. Tính xác suất để 3 quả cầu lấy được có màu trắng?
A.
5
42
. B.
5
9
. C.
1
3
. D.
1
21
.
Lời giải
Số phần tử của không gian mẫu:
(
)
3
9
.Ω=
nC
Gọi A là biến cố “3 quả cầu lấy được có màu trắng”, ta có:
( )
3
5
.=nA C
Xác suất để trong 4 người được chọn đều là nam:
( )
3
5
3
9
5
42
= =
C
PA
C
.
Câu 34: Một tổ học sinh có 7 nữ và 5 nam. Chọn ngẫu nhiên 3 học sinh. Xác suất để trong 3 học sinh
được chọn có đúng 1 học sinh nam bằng
A.
1
5
. B.
5
12
. C.
21
44
. D.
7
22
.
Lời giải
Tổng số học sinh của tổ là
7512+=
.
Số cách chọn 3 học sinh trong số 12 học sinh là:
3
12
C
.
Số cách chọn 3 học sinh trong đó có đúng 1 học sinh nam là:
12
57
.CC
.
Xác suất để trong 3 học sinh được chọn có đúng 1 học sinh nam bằng
12
57
3
12
.
21
44
CC
C
=
.
Câu 35: Một hộp đựng 12 cây viết được đánh số từ 1 đến 12. Chọn ngẫu nhiên 2 cây. Xác suất để chọn
được 2 cây có tích hai số là số chẵn
A.
6
11
. B.
17
22
. C.
5
22
. D.
5
11
.
Lời giải
Ta có không gian mẫu
( )
2
12
nC
Ω=
.
Gọi A là biến cố “Chọn được hai cây có tích hai số là số chẵn”
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Trong 12 cây viết có 6 cây được đánh số chẵn, 6 cây được đánh số lẻ. Tích hai số là số chẵn
nếu ít nhất có 1 cây mang số chẵn
( )
2 11
6 66
51
n A C CC⇒=+=
(
)
( )
( )
17
22
nA
PA
n
⇒==
Ω
.
Vậy xác suất để chọn được hai cây có tích hai số là số chẵn là
17
22
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có
5
chữ số đôi một khác nhau và số đó chia hết cho
9
.
Lời giải
Gọi số có
5
chữ số đôi một khác nhau là
0
x abcde a

.
Các chữ số
,,, ,abcde
được lập từ
2
trong
4
cặp
1;8 , 2; 7 , 3; 6 , 4;5
và
1
trong
2
chữ số
0;9
.
Ta xét các trường hợp sau:
Trường hợp
1
: Trong
x
có chứa số
9
, không chứa số
0
: có
2
4
5. .4!C
số.
Trường hợp
2
: Trong
x
có chứa số
0
, không chứa số
9
: có
2
4
4. .4!C
số.
Do đó số các số cần tìm là
22
44
.4! 45. . .4! 1296CC 
.
Câu 37: Trong mặt phẳng
,Oxy
cho Elip
( )
E
đi qua điểm
( )
2 3;2M
và
M
nhìn hai tiêu điểm của
( )
E
dưới một góc vuông. Viết phương trình chính tắc của
( )
E
đã cho.
Lời giải
Ta có:
( )
( )
1
2
2 3; 2
2 3; 2
MF c
MF c
=−− −
=−−


với
( )
1
;0Fc−
và
( )
2
;0Fc
.
Từ giả thiết, ta suy ra
12
.0MF MF
=
 
⇔
( )( )
23 23 4 0cc−− − + =
⇔
2
16c =
.
Mà
(
)
(
)
2 3;2
ME∈
nên
22
12 4
1
ab
+=
⇔
22
12 4
1
16bb
+=
+
⇔
4
64b =
⇔
2
8b
=
2 22
24
abc⇒=+=
.
Vậy
22
32Sa b=+=
.
Câu 38: Một cuộc họp có sự tham gia của
6
nhà Toán học trong đó có 4 nam và
2
nữ,
7
nhà Vật lý
trong đó có
3
nam và
4
nữ và
8
nhà Hóa học trong đó có
4
nam và
4
nữ. Người ta muốn lập
một ban thư kí gồm
4
nhà khoa học. Tính xác suất để ban thư kí được chọn phải có đủ cả
3
lĩnh
vực và có cả nam lẫn nữ.
Lời giải
Ta có
4
21
( ) 5985nCΩ= =
+) Đặt
A
là biến cố chọn ra được
4
nhà khoa học có đầy đủ cả
3
lĩnh vực.
Khi đó:
Số cách chọn 2 nhà Toán học, 1 nhà Vật lý, 1 nhà Hóa học là:
211
6 78
. . 840
CCC=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Số cách chọn 1 nhà Toán học, 2 nhà Vật lý, 1 nhà Hóa học là:
121
678
. . 1008CCC
=
.
Số cách chọn 1 nhà Toán học, 1 nhà Vật lý, 2 nhà Hóa học là:
112
678
. . 1176
CCC
=
.
( )
840 1008 1176 3024nA⇒ =++=
+) Đặt
B
là biến cố chọn ra
4
nhà khoa học đủ cả
3
lĩnh vực mà trong đó
chỉ có nam hoặc chỉ có nữ.
Khi đó:
Số cách chọn chỉ có nam:
211 121 112
4 34 43 4 434
. . . . . . 192CCC CC C CCC
++=
.
Số cách chọn chỉ có nữ:
211 121 11 2
2 44 24 4 244
. . . . . . 112CCC CCC CCC++=
.
( )
192 112 304nB⇒ =+=
.
+) Vậy số cách chọn ra được
4
nhà khoa học có đày đủ cả
3
lĩnh vực, trong
đó có cả nam lẫ nữ là:
3024 304 2720−=
.
Hay
( ) 2720
nA=
Vậy
( )
( )
2720 544
()
5985 1197
nA
PA
n
= = =
Ω
Câu 39: Cho hypebol
( )
H
có hai tiêu điểm
12
;FF
nằm trên
Ox
và đối xứng qua gốc tọa độ
O
,
( )
H
đi
qua điểm
M
có hoành độ
5−
và
12
9 41
;
44
MF MF= =
. Viết phương trình chính tắc của hypebol
( )
H
.
Lời giải
Gọi phương trình chính tắc của đường hypebol
( )
H
có dạng:
22
22
1
xy
ab
−=
, trong đó
12
2
FF c=
mà
22
c ab
= +
.
Ta có
12
8 2a 4MF MF a− == ⇒=
.
Gọi
( ) (
) (
) ( )
( )
22
2 22 2
1 1 2 1 12 1
5; ; ;0 ; ;0 5 ; 5M yFcFc FMc yFMc y− − ⇒ =−+ =++
22 2
12
20 100 5 9FM FM c c b⇒ − =−=−⇒=⇒=
.
Vậy
( )
22
:1
16 9
xy
H −=
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 03
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho hai vectơ
a
và
b
khác
0
,
α
là góc tạo bởi 2 vectơ
a
và
b
khi
. ..ab a b= −


Chọn khẳng
định đúng.
A.
o
180
α
=
. B.
o
0
α
=
. C.
o
90
α
=
. D.
o
45
α
=
.
Câu 2: Đo chiều dài của một cây thước, ta được kết quả
45 0, 2 (cm)a = ±
. Khi đó sai số tuyệt đối của
phép đo được ước lượng là
A.
45
0, 2∆=
. B.
45
0, 2
∆≤
. C.
45
0, 2∆ ≤−
. D.
45
0, 2∆=−
.
Câu 3: Điểm thi tuyển sinh vào lớp
10
ba môn Toán, Văn, Tiếng Anh của một học sinh lần lượt là
8,0; 7,5; 8,2
. Điểm thi trung bình ba môn thi của học sinh đó là
A.
8,0
. B.
23,7
. C.
7,7
. D.
7,9
.
Câu 4: Mẫu số liệu sau cho biết cân nặng (đơn vị kg) của các học sinh Tổ 1 lớp 10A
45 46 42 50 38 42 44 42 40 60
Khoảng biến thiên của mẫu số liệu này là
A.
38
. B.
20
. C.
42
. D.
22
.
Câu 5: Cho mẫu số liệu
{ }
10,8,6, 2, 4
. Độ lệch chuẩn của mẫu gần bằng
A.
8
. B.
2,8
. C.
2, 4
. D.
6
.
Câu 6: Trong mặt phẳng
Oxy
, cho tam giác
ABC
biết
( ) ( ) ( )
1;1 , 2; 4 , 9; 3AB C−−
. Gọi
N
là điểm thuộc
cạnh
AC
sao cho
3=
AN CN
. Tính độ dài của vec tơ
BN

.
A.
4 29
. B.
29
. C.
2 29
. D.
3 29
.
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là
996 0,5mm
. Sai số tương đối
tối đa trong phép đo là bao nhiêu?
A.
0,05%
. B.
0,5%
. C.
0,04%.
D.
0,005%.
Câu 8: Tìm tứ phân vị của mẫu số liệu sau
12 3 6 15 27 33 31 18 29 54 1 8
A.
12 3
7, 17,5, 30QQ Q= = =
. B.
12 3
7, 16,5, 30QQ Q= = =
.
C.
12 3
7, 16,5, 30,5QQ Q= = =
. D.
12 3
7,5, 16,5, 30QQ Q= = =
.
Câu 9: Phương trình tổng quát của đường thẳng đi qua điểm
( )
2;1A −
và có vectơ pháp tuyến
( )
2;3n =
là
A.
2 3 50xy+ −=
. B.
3210xy− +=
. C.
2 3 10xy+ +=
. D.
3 2 80xy
− +=
.
Câu 10: Trong mặt phẳng tọa độ
Oxy
, phương trình tổng quát của đường thẳng đi qua hai điểm
( )
2;1A −
và
( )
2;4B
là
A.
3 4 10 0xy+ −=
. B.
34100xy−+=
. C.
4 3 50xy+ +=
. D.
4 3 50xy− +=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
Câu 11: Tính góc giữa hai đường thẳng
:3 7 0a xy−+=
và
: 3 10bx y− −=
A.
30°
. B.
90
°
. C.
60°
. D.
45°
.
Câu 12: Khoảng cách từ điểm
( )
3; 1
M
−
đến đường thẳng
2
:
12
xt
yt
=−+
∆
= +
nằm trong khoảng nào sau đây?
A.
(
)
1; 3
. B.
( )
3;5
. C.
(
)
7;9
. D.
( )
5;7
.
Câu 13: Trong mặt phẳng với hệ trục
Oxy
cho đường tròn
( )
( )
(
)
22
: 2 4 16− ++ =Cx y
. Đường tròn
( )
C
có toạ độ tâm
I
và bán kính
R
bằng
A.
( )
2; 4 ; 4−=
IR
. B.
( )
2; 4 ; 16−=IR
. C.
( )
2; 4 ; 4−=IR
. D.
( )
2; 4 ; 16−=
IR
.
Câu 14: Trong mặt phẳng với hệ toạ độ
Oxy
, phương trình đường tròn có tâm
( )
3;1I
và đi qua điểm
( )
2; 1−M
là
A.
( ) (
)
22
3 1 5.
+ ++ =xy
B.
( ) ( )
22
3 1 5.− +− =xy
C.
( ) ( )
22
3 1 5.− +− =
xy
D.
( ) ( )
22
3 1 5.+ ++ =xy
Câu 15: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A.
2
6yx= −
. B.
2
6yx=
. C.
2
6
xy= −
. D.
2
6xy=
.
Câu 16: Trường THPT A, khối
12
có
11
lớp, khối
11
có
10
lớp và khối
10
có
12
lớp. Thầy Tổ trưởng
tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn?
A.
3
. B.
33
. C.
11
. D.
10
.
Câu 17: Trong tủ quần áo của bạn Ngọc có
10
cái áo sơ mi đôi một khác nhau và
5
cái chân váy với hoa
văn khác nhau. Bạn Ngọc muốn chọn ra một bộ quần áo để đi dự tiệc sinh nhật. Hỏi bạn Ngọc
có bao nhiêu cách chọn?
A.
10
. B.
50
. C.
5
. D.
15
.
Câu 18: Có bao nhiêu cách xếp chỗ ngồi cho
4
bạn học sinh vào dãy có
4
ghế?
A.
4
cách. B.
8
cách. C.
12
cách. D.
24
cách.
Câu 19: Trong một lớp học có
20
học sinh nữ và
15
học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu
cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư?
A.
3
35
C
. B.
35!
. C.
35
3
A
. D.
3
35
A
.
Câu 20: Cho tập hợp
{ }
0;1; 2;3;4A =
. Số tập con gồm 2 phần tử của
A
là
A.
10
. B.
8
. C.
16
. D.
20
.
Câu 21: Trong khai triển nhị thức Niu-tơn của
( )
4
23x
−
có bao nhiêu số hạng?
A.
6
. B.
3
. C.
5
. D.
4
.
Câu 22: Có 2020 tấm thẻ được đánh số từ 1 đến 2020. Xét phép thử: lấy ngẫu nhiên 5 tấm thẻ trong số
2020 tấm thẻ đã cho. Tính số phấn tử của không gian mẫu.
A.
( )
5
2020
nCΩ=
. B.
( )
5
2020
nAΩ=
. C.
( )
1
2020
nCΩ=
. D.
( )
1
2020
nAΩ=
.
Câu 23: Một tổ học sinh gồm có 5 học sinh nữ và 7 học sinh nam, chọn ngẫu nhiên 2 học sinh. Tính xác
suất để 2 học sinh được chọn có cả học sinh nam và học sinh nữ?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
A.
1
3
. B.
1
6
. C.
35
66
. D.
3
55
Câu 24: Từ một hộp chứa
10
quả cầu màu đỏ và
5
quả cầu màu xanh, lấy ngẫu nhiên đồng thời
3
quả
cầu. Xác suất để lấy được
3
quả cầu màu xanh bằng
A.
24
91
. B.
12
91
. C.
2
91
. D.
1
12
.
Câu 25: Trong mặt phẳng
Oxy
, phương trình tổng quát của đường thẳng
∆
đi qua điểm
(
)
1; 2A −
và
song song đường thẳng
( )
d
có phương trình:
2 3 70xy− −=
là
A.
2 3 80xy− −=
. B.
2 3 80xy− +=
. C.
2 80xy− +=
. D. A.
Câu 26: Với giá trị nào của
m
thì hai đường thẳng
1
:3 4 10 0dxy++=
và
( )
2
2
: 2 1 10 0d m x my− + +=
trùng nhau?
A.
2m
±
. B.
1m
= ±
. C.
2m =
. D.
2m = −
.
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có phương trình
là.
A.
22
24 12 175 0xy x y++ − + =
. B.
22
24 12 175 0xy x y+− + + =
.
C.
22
24 12 175 0xy x y+− − + =
. D.
22
24 12 175 0xy x y++ + + =
.
Câu 28: Cho đường tròn
( )
22
: 2 4 40
Cx y x y+ − − −=
và điểm
( )
1; 5A
. Đường thẳng nào trong các
đường thẳng dưới đây là tiếp tuyến của đường tròn
( )
C
tại điểm
A
.
A.
50y −=
. B.
50y +=
. C.
50xy+−=
. D.
50xy−−=
.
Câu 29: Cho của hypebol
( )
22
:1
16 5
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
8
. B.
16
. C.
4
. D.
5
.
Câu 30: Tổ 1 của lớp 10A có 6 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một cặp
nam nữ từ tổ 1?
A.
11
. B.
30
. C.
6
. D.
5
.
Câu 31: Có 4 học sinh nam, 3 học sinh nữ và 2 thầy giáo xếp thành một hàng dọc tham gia một cuộc thi.
Hỏi có bao nhiêu cách xếp hàng sao cho nhóm 3 học sinh nữ luôn đứng cạnh nhau và nhóm hai
thầy giáo cũng đứng cạnh nhau?
A.
362880
. B.
14400
. C.
8640
. D.
288
.
Câu 32: Từ các chữ số
0,1, 2,3, 4,5,6,7
có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác
nhau và nhỏ hơn 2021?
A.
214
. B.
215
. C.
216
. D.
217
.
Câu 33: Gieo ngẫu nhiên
2
con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên
2
con xúc sắc bằng
1
”.
A.
2
9
. B.
1
9
. C.
5
18
. D.
5
6
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 34: Từ một đội văn nghệ có 5 nam và 8 nữ, cần lập một nhóm 4 người hát tốp ca một cách ngẫu
nhiên. Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng
A.
70
143
. B.
73
143
. C.
16
143
. D.
17
143
.
Câu 35: Từ một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng, người ta lấy ngẫu nhiên đồng thời 3 quả cầu.
Tính xác suất để trong 3 quả cầu được lấy có ít nhất 2 quả xanh.
A.
7
44
. B.
7
11
. C.
4
11
. D.
21
220
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho đa giác đều
(
)
H
có
48
đỉnh. Hỏi có bao nhiêu tam giác vuông có đỉnh là đỉnh của
( )
H
?
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
8;2M
. Viết phương trình đường thẳng
d
qua
M
và
d
cắt tia
Ox
,
Oy
lần lượt tại
( )
;0Aa
,
( )
0;Bb
sao cho tam giác
có diện tích nhỏ nhất.
Câu 38: Mật khẩu mở điện thoại của bác Bình là một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn
600.000. Bạn An được bác Bình cho biết thông tin ấy nhưng không cho biết mật khẩu chính xác
là số nào nên quyết định thử bấm ngẫu nhiên một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ
hơn 600.000. Tính xác suất để bạn An nhập một lần duy nhất mà đúng mật khẩu để mở được
điện thoại của bác Bình.
Câu 39: Hai thiết bị
A
và
B
dùng để ghi âm một vụ nổ đặt cách nhau
1
dặm, thiết bị
A
ghi được âm
thanh trước thiết bị
B
là 2 giây, biết vận tốc âm thanh là
1100 /
feet s
. Tìm các vị trí mà vụ nổ
có thể xảy ra.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho hai vectơ
a
và
b
khác
0
,
α
là góc tạo bởi 2 vectơ
a
và
b
khi
. ..
ab a b
= −


Chọn khẳng
định đúng.
A.
o
180
α
=
. B.
o
0
α
=
. C.
o
90
α
=
. D.
o
45
α
=
.
Lời giải
Ta có
(
)
. . .cos ,ab a b a b=

.
Mà theo giả thiết
..ab a b= −

, suy ra
(
)
( )
0
cos , 1 , 180
ab ab=−⇒ =
 
Câu 2: Đo chiều dài của một cây thước, ta được kết quả
45 0, 2 (cm)a = ±
. Khi đó sai số tuyệt đối của
phép đo được ước lượng là
A.
45
0, 2∆=
. B.
45
0, 2∆≤
. C.
45
0, 2∆ ≤−
. D.
45
0, 2∆=−
.
Lời giải
Ta có độ dài dài gần đúng của cây thước là
45a =
với độ chính xác
0, 2d =
Nên sai số tuyệt đối
45
0, 2d∆≤=
Câu 3: Điểm thi tuyển sinh vào lớp
10
ba môn Toán, Văn, Tiếng Anh của một học sinh lần lượt là
8,0; 7,5; 8,2
. Điểm thi trung bình ba môn thi của học sinh đó là
A.
8,0
. B.
23,7
. C.
7,7
. D.
7,9
.
Lời giải
Chọn D
Ta có điểm trung bình ba môn thi của học sinh là:
8,0 7 ,5 8,2
7,9
3
++
=
.
Câu 4: Mẫu số liệu sau cho biết cân nặng (đơn vị kg) của các học sinh Tổ 1 lớp 10A
45 46 42 50 38 42 44 42 40 60
Khoảng biến thiên của mẫu số liệu này là
A.
38
. B.
20
. C.
42
. D.
22
.
Lời giải
Khoảng biến thiên của mẫu số liệu là:
60 38 22R =−=
.
Câu 5: Cho mẫu số liệu
{ }
10,8,6, 2, 4
. Độ lệch chuẩn của mẫu gần bằng
A.
8
. B.
2,8
. C.
2, 4
. D.
6
.
Lời giải
Ta có
22222
10 8 6 2 4 (10 6) (8 6) (6 6) (2 6) (4 6)
6 8 2,8
55
xs
++++ −+−+−+−+−
= =⇒= = ≈
Độ lệch chuẩn là căn bậc hai của phương sai.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
Câu 6: Trong mặt phẳng
Oxy
, cho tam giác
ABC
biết
( ) ( ) ( )
1;1 , 2; 4 , 9; 3AB C−−
. Gọi
N
là điểm thuộc
cạnh
AC
sao cho
3=
AN CN
. Tính độ dài của vec tơ
BN

.
A.
4 29
. B.
29
. C.
2 29
. D.
3 29
.
Lời giải
Gọi
( )
;N ab
.
Ta có:
(
)
( )
(
)
3
7
3 3 7; 2
2
3
−=−
=
= ⇒= ⇔ ⇒ ⇒ −

= −
−=−
 
cN nA
CN N A
xx xx
a
AN CN AN NC N
b
yy yy
.
29⇒=

BN
.
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là
996 0,5
mm
. Sai số tương đối
tối đa trong phép đo là bao nhiêu?
A.
0,05%
. B.
0,5%
. C.
0,04%.
D.
0,005%.
Lời giải
Ta có độ dài gần đúng của cầu là
996a
với độ chính xác
d 0, 5
.
Vì sai số tuyệt đối
0, 5
a
d
nên sai số tương đối
0, 5
0, 05%
996
a
a
d
aa

.
Vậy sai số tương đối tối đa trong phép đo trên là
0, 05%
.
Câu 8: Tìm tứ phân vị của mẫu số liệu sau
12 3 6 15 27 33 31 18 29 54 1 8
A.
12 3
7, 17,5, 30QQ Q= = =
. B.
12 3
7, 16,5, 30QQ Q= = =
.
C.
12 3
7, 16,5, 30,5
QQ Q= = =
. D.
12 3
7,5, 16,5, 30
QQ Q= = =
.
Lời giải
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:
1 3 6 8 12 15 18 27 29 31 33 54
Trung vị của mẫu số liệu trên là
15 18
16,5
2
+
=
Trung vị của dãy
1 3 6 8 12 15
là
68
7
2
+
=
Trung vị của dãy
18 27 29 31 33 54
là
29 31
30
2
+
=
A
B
C
N
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
Vậy
12 3
7, 16,5, 30QQ Q= = =
.
Câu 9: Phương trình tổng quát của đường thẳng đi qua điểm
( )
2;1A −
và có vectơ pháp tuyến
( )
2;3n =
là
A.
2 3 50xy+ −=
. B.
3210xy− +=
. C.
2 3 10xy+ +=
. D.
3 2 80
xy− +=
.
Lời giải
Phương trình tổng quát của đường thẳng đi qua điểm
(
)
2;1A −
và có vectơ pháp tuyến
( )
2;3n =
có dạng là
( ) ( )
2 2 3 1 0 2 3 10x y xy+ + − = ⇔ + +=
.
Câu 10: Trong mặt phẳng tọa độ
Oxy
, phương trình tổng quát của đường thẳng đi qua hai điểm
( )
2;1A −
và
(
)
2;4B
là
A.
3 4 10 0xy+ −=
. B.
34100
xy−+=
. C.
4 3 50
xy
+ +=
. D.
4 3 50xy− +=
.
Lời giải
Đường thẳng
AB
nhận
( )
4;3AB =

làm vectơ chỉ phương, do đó một vectơ pháp tuyến của đường
thẳng
AB
là
( )
3; 4
n = −
.
Vậy phương trình tổng quát của đường thẳng
AB
là
( )
( )
3 24 10xy+ − −=
⇔
34100xy−+=
.
Câu 11: Tính góc giữa hai đường thẳng
:3 7 0a xy−+=
và
: 3 10bx y− −=
A.
30°
. B.
90°
. C.
60°
. D.
45°
.
Lời giải
Đường thẳng
a
có vectơ pháp tuyến là:
( )
1
3; 1n = −

;
Đường thẳng
b
có vectơ pháp tuyến là:
( )
2
1; 3
n
= −

.
Áp dụng công thức tính góc giữa hai đường thẳng có:
( )
( )
( )
12
12
1. 3 1 3
.
3
cos ,
2.2 2
.
nn
ab
nn
+− −
= = =


. Suy ra góc giữa hai đường thẳng bằng
30°
.
Câu 12: Khoảng cách từ điểm
( )
3; 1M −
đến đường thẳng
2
:
12
xt
yt
=−+
∆
= +
nằm trong khoảng nào sau đây?
A.
( )
1; 3
. B.
(
)
3;5
. C.
( )
7;9
. D.
(
)
5;7
.
Lời giải
Phươmg trình tổng quát đường thẳng
∆
là
2 50xy−+=
Khoảng cách từ điểm
M
đến đường thẳng
∆
là
( )
( )
2
2
2.3 1 5
12 5
5, 4
5
21
−− +
= ≈
+−
Câu 13: Trong mặt phẳng với hệ trục
Oxy
cho đường tròn
( ) ( ) ( )
22
: 2 4 16
− ++ =Cx y
. Đường tròn
( )
C
có toạ độ tâm
I
và bán kính
R
bằng
A.
( )
2; 4 ; 4−=IR
. B.
( )
2; 4 ; 16−=IR
. C.
( )
2; 4 ; 4−=IR
. D.
( )
2; 4 ; 16−=IR
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
Lời giải
Đường tròn
(
)
( )
(
)
22
: 2 4 16− ++ =
Cx y
. Do đó đường tròn
(
)
C
có toạ độ tâm
(
)
2; 4−I
và bán
kính
16 4= =R
.
Câu 14: Trong mặt phẳng với hệ toạ độ
O
xy
, phương trình đường tròn có tâm
(
)
3;1
I
và đi qua điểm
(
)
2; 1−M
là
A.
( )
( )
22
3 1 5.+ ++ =
xy
B.
( ) ( )
22
3 1 5.− +− =xy
C.
(
) ( )
22
3 1 5.− +− =xy
D.
( ) ( )
22
3 1 5.
+ ++ =xy
Lời giải
Vì đường tròn có tâm
(
)
3;1I
và đi qua điểm
( )
2; 1−M
nên bán kính của đường tròn là
( ) ( )
22
3 2 11 5= = − ++ =R MI
.
Vậy phương trình đường tròn cần tìm là
( ) ( )
22
3 15− +− =xy
.
Câu 15: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?
A.
2
6yx= −
. B.
2
6yx=
. C.
2
6xy= −
. D.
2
6xy=
.
Lời giải
Phương trình chính tắc của parabol có dạng
( )
2
20y px p= >
nên chỉ có trường hợp B là phương
trình chính tắc của đường parabol.
Câu 16: Trường THPT A, khối
12
có
11
lớp, khối
11
có
10
lớp và khối
10
có
12
lớp. Thầy Tổ trưởng
tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn?
A.
3
. B.
33
. C.
11
. D.
10
.
Lời giải
TH
1
: Chọn
1
lớp trong
11
lớp của khối
12
có
11
cách.
TH
2
: Chọn
1
lớp trong
10
lớp của khối
11
có
10
cách.
TH
3
: Chọn
1
lớp trong
12
lớp của khối
10
có
12
cách.
Theo quy tắc cộng ta được:
11 10 12 33++=
cách.
Câu 17: Trong tủ quần áo của bạn Ngọc có
10
cái áo sơ mi đôi một khác nhau và
5
cái chân váy với hoa
văn khác nhau. Bạn Ngọc muốn chọn ra một bộ quần áo để đi dự tiệc sinh nhật. Hỏi bạn Ngọc
có bao nhiêu cách chọn?
A.
10
. B.
50
. C.
5
. D.
15
.
Lời giải
Chọn
1
cái áo sơ mi trong
10
cái áo sơ mi có:
10
cách.
Chọn
1
cái chân váy trong
5
cái chân váy có:
5
cách.
Theo quy tắc nhân có:
10.5 50
=
cách.
Câu 18: Có bao nhiêu cách xếp chỗ ngồi cho
4
bạn học sinh vào dãy có
4
ghế?
A.
4
cách. B.
8
cách. C.
12
cách. D.
24
cách.
Lời giải
Xếp chỗ ngồi cho
4
học sinh vào dãy có
4
ghế có:
4! 24=
cách xếp.
Câu 19: Trong một lớp học có
20
học sinh nữ và
15
học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu
cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư?
A.
3
35
C
. B.
35!
. C.
35
3
A
. D.
3
35
A
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
Lời giải
Số cách chọn 3 học sinh làm lớp trưởng, lớp phó và bí thư là:
3
35
39270A =
.
Câu 20: Cho tập hợp
{ }
0;1; 2;3;4A
=
. Số tập con gồm 2 phần tử của
A
là
A.
10
. B.
8
. C.
16
. D.
20
.
Lời giải
Tập hợp
A
gồm có
5
phần tử.
Số tập con có
2
phần tử của tập
A
là:
2
5
10C
=
.
Câu 21: Trong khai triển nhị thức Niu-tơn của
( )
4
23x −
có bao nhiêu số hạng?
A.
6
. B.
3
. C.
5
. D.
4
.
Lời giải
Trong khai triển nhị thức Niu-tơn của
( )
4
23x −
có
415+=
số hạng.
Câu 22: Có 2020 tấm thẻ được đánh số từ 1 đến 2020. Xét phép thử: lấy ngẫu nhiên 5 tấm thẻ trong số
2020 tấm thẻ đã cho. Tính số phấn tử của không gian mẫu.
A.
(
)
5
2020
nCΩ=
. B.
(
)
5
2020
nAΩ=
. C.
(
)
1
2020
nCΩ=
. D.
( )
1
2020
nAΩ=
.
Lời giải
Số cách chọn ngẫu nhiên 5 tấm thẻ là:
5
100
C
.
Câu 23: Một tổ học sinh gồm có 5 học sinh nữ và 7 học sinh nam, chọn ngẫu nhiên 2 học sinh. Tính xác
suất để 2 học sinh được chọn có cả học sinh nam và học sinh nữ?
A.
1
3
. B.
1
6
. C.
35
66
. D.
3
55
Lời giải
Tổng số học sinh là:
5 7 12+=
Gọi
A
là biến cố trong hai học sinh được chọn, có cả học sinh nam và học sinh nữ. Ta có:
( )
2
12
nCΩ=
( )
11
57
.nA CC=
Vậy xác suất của biến cố
A
là:
( )
11
57
2
12
.
35
66
CC
PA
C
= =
.
Câu 24: Từ một hộp chứa
10
quả cầu màu đỏ và
5
quả cầu màu xanh, lấy ngẫu nhiên đồng thời
3
quả
cầu. Xác suất để lấy được
3
quả cầu màu xanh bằng
A.
24
91
. B.
12
91
. C.
2
91
. D.
1
12
.
Lời giải
Số phần tử của không gian mẫu là
( )
3
15
455nCΩ= =
.
Gọi biến cố
A
: “Lấy được
3
quả cầu màu xanh”.
Ta có
( )
3
5
10nA C= =
.
Xác suất để lấy được
3
quả cầu màu xanh bằng
( )
( )
( )
10 2
455 91
nA
pA
n
= = =
Ω
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
Câu 25: Trong mặt phẳng
Oxy
, phương trình tổng quát của đường thẳng
∆
đi qua điểm
( )
1; 2A −
và
song song đường thẳng
( )
d
có phương trình:
2 3 70
xy− −=
là
A.
2 3 80
xy− −=
. B.
2 3 80
xy
− +=
. C.
2 80xy− +=
. D. A.
Lời giải
Theo yêu cầu đề bài, đường thẳng
∆
đi qua điểm
( )
1; 2A −
và nhận vectơ
( )
2; 3n = −
làm
vectơ pháp tuyến.
Ta có phương trình tổng quát của đường thẳng
∆
là:
(
) (
)
2 1 3 2 0 2 3 80
x y xy− − + =⇔ − −=
.
Câu 26: Với giá trị nào của
m
thì hai đường thẳng
1
:3 4 10 0dxy++=
và
(
)
2
2
: 2 1 10 0d m x my− + +=
trùng nhau?
A.
2
m ±
. B.
1m = ±
. C.
2m =
. D.
2m = −
.
Lời giải
( )
12
2
2
2
1
2
: 2 1 10 0
2 1 10
3 4 10
:3 4 10 0
2 13
2.
4
dd
d m x my
mm
dxy
m
m
m
≡
− + +=
−
→ = =
++=
−=
⇔ ⇔=
=
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có phương trình
là.
A.
22
24 12 175 0xy x y++ − + =
. B.
22
24 12 175 0xy x y+− + + =
.
C.
22
24 12 175 0xy x y+− − + =
. D.
22
24 12 175 0xy x y++ + + =
.
Lời giải
Chọn C
Gọi phương trình đường tròn cần tìm có dạng:
( )
2 2 22
22 0 0x y ax by c a b c+ − − += + −>
.
Đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
nên ta có:
121 64 22 16 0 12
169 64 26 16 0 6
196 49 28 14 0 175
a bc a
a bc b
a bc c
+ − − += =


+ − − +=⇔ =


+ − − += =

Vậy phương trình đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7
ABC
là
22
24 12 175 0xy x y+− − + =
Câu 28: Cho đường tròn
( )
22
: 2 4 40Cx y x y+ − − −=
và điểm
( )
1; 5
A
. Đường thẳng nào trong các
đường thẳng dưới đây là tiếp tuyến của đường tròn
( )
C
tại điểm
A
.
A.
50y −=
. B.
50y +=
. C.
50xy+−=
. D.
50xy−−=
.
Lời giải
Đường tròn
( )
C
có tâm
( )
1; 2
I
( )
0;3
IA⇒=

.
Gọi
d
là tiếp tuyến của
( )
C
tại điểm
A
, khi đó
d
đi qua
A
và nhận vectơ
IA

là một VTPT.
Chọn một VTPT của
d
là
( )
0;1
d
n =

.
Vậy phương trình đường thẳng
d
là
50y −=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
Câu 29: Cho của hypebol
(
)
22
:1
16 5
xy
H
−=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
8
. B.
16
. C.
4
. D.
5
.
Lời giải
Gọi
1
F
và
2
F
là hai tiêu điểm của
( )
( )
22
22
: 1, 0, 0
xy
H ab
ab
−= > >
.
Điểm
( )
12
2M H MF MF a
∈⇔ − =
.
Từ phương trình
(
)
22
:1
16 5
xy
H
−=
suy ra
( )
2
16 4, 0a aa= ⇒= >
.
Vậy hiệu các khoảng cách từ mỗi điểm
M
nằm trên
( )
H
đến hai tiêu điểm có giá trị tuyệt đối
là
12
28
MF MF a
−==
.
Câu 30: Tổ 1 của lớp 10A có 6 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một cặp
nam nữ từ tổ 1?
A.
11
. B.
30
. C.
6
. D.
5
.
Lời giải
Số cách chọn ra một học sinh nam là: 6 cách chọn.
Số cách chọn ra một học sinh nữ là: 5 cách chọn.
Do đó theo quy tắc nhân thì chọn ra 1 cặp nam nữ sẽ có:
5.6 30=
cách chọn.
Câu 31: Có 4 học sinh nam, 3 học sinh nữ và 2 thầy giáo xếp thành một hàng dọc tham gia một cuộc thi.
Hỏi có bao nhiêu cách xếp hàng sao cho nhóm 3 học sinh nữ luôn đứng cạnh nhau và nhóm hai
thầy giáo cũng đứng cạnh nhau?
A.
362880
. B.
14400
. C.
8640
. D.
288
.
Lời giải
Xếp nhóm
A
gồm 3 học sinh nữ đứng cạnh nhau có:
3! 6=
cách.
Xếp nhóm
B
gồm 2 thầy giáo đứng cạnh nhau có:
2! 2=
cách.
Xếp nhóm
A
, nhóm
B
chung với 4 học sinh nam còn lại có:
6! 720=
cách.
Vậy theo quy tắc nhân có:
6.2.720 8640=
cách.
Câu 32: Từ các chữ số
0,1, 2,3, 4,5,6,7
có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác
nhau và nhỏ hơn 2021?
A.
214
. B.
215
. C.
216
. D.
217
.
Lời giải
Giả sử số tự nhiên thỏa mãn yêu cầu bài toán có dạng
abcd
.
TH1:
1a =
, ta chọn
,,bcd
bằng cách lấy 3 chữ số trong 7 chữ số còn lại nên có
3
7
210A =
số.
TH2:
2a =
, khi đó
0b =
và
1c =
và chọn
{ }
3; 4;5;6;7d ∈
nên
d
có
5
cách chọn, suy ra có 5
số thỏa mãn trường hợp này.
Vậy có
210 5 215+=
số thỏa mãn yêu cầu bài toán.
Câu 33: Gieo ngẫu nhiên
2
con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên
2
con xúc sắc bằng
1
”.
A.
2
9
. B.
1
9
. C.
5
18
. D.
5
6
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Số phần tử của không gian mẫu:
( )
6.6 36n Ω= =
.
Gọi
A
là biến cố thỏa mãn yêu cầu bài toán:
( ) ( ) (
) (
)
( )
( )
( ) ( ) ( ) ( )
{ }
1; 2 , 2; 1 , 3; 2 , 2; 3 , 3; 4 , 4; 3 , 4; 5 , 5; 4 , 5; 6 , 6; 5A =
nên
(
)
10
nA=
.
Vậy
( )
10 5
36 18
PA
= =
.
Câu 34: Từ một đội văn nghệ có 5 nam và 8 nữ, cần lập một nhóm 4 người hát tốp ca một cách ngẫu
nhiên. Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng
A.
70
143
. B.
73
143
. C.
16
143
. D.
17
143
.
Lời giải
Số cách chọn ra 4 người từ đội văn nghệ sao cho có ít nhất 3 nam là
31 4
58 5
.
CC C+
Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng
31 4
58 5
4
13
.
17
143
CC C
C
+
=
.
Câu 35: Từ một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng, người ta lấy ngẫu nhiên đồng thời 3 quả cầu.
Tính xác suất để trong 3 quả cầu được lấy có ít nhất 2 quả xanh.
A.
7
44
. B.
7
11
. C.
4
11
. D.
21
220
.
Lời giải
Số phần tử của không gian mẫu là
(
)
3
12
220nCΩ= =
.
Gọi
A
là biến cố: “3 quả cầu được lấy có ít nhất 2 quả xanh”.
Xét 2 trường hợp sau:
+ Trường hợp 1: Chọn 2 quả cầu xanh, 1 quả cầu vàng có
21
75
. 105CC=
cách.
+ Trường hợp 2: Chọn 3 quả cầu xanh có
3
7
35C
=
cách.
Suy ra
(
)
105 35 140
nA
= +=
.
Vậy xác suất cần tìm là
( )
(
)
( )
140 7
220 11
nA
pA
n
= = =
Ω
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho đa giác đều
(
)
H
có
48
đỉnh. Hỏi có bao nhiêu tam giác vuông có đỉnh là đỉnh của
( )
H
?
Lời giải
Đa giác đều
( )
H
có
48
đỉnh nên có
24
đường chéo đi qua tâm đường tròn ngoại tiếp đa giác
đều
( )
H
. Một tam giác vuông có đỉnh là đỉnh của
( )
H
thì phải có cạnh huyền là đường chéo
đi qua tâm đường tròn ngoại tiếp đa giác đều
( )
H
. Với một đường chéo như vậy của đa giác
đều
( )
H
sẽ tạo ra
46
tam giác vuông. Vậy số tam giác vuông có đỉnh là đỉnh của
( )
H
là
24.46 1104=
tam giác vuông.
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
8;2M
. Viết phương trình đường thẳng
d
qua
M
và
d
cắt tia
Ox
,
Oy
lần lượt tại
( )
;0Aa
,
( )
0;Bb
sao cho tam giác
có diện tích nhỏ nhất.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Ta có phương trình đường thẳng
d
có dạng:
1
xy
ab
+=
.
Do
d
đi qua
( )
8;2M
nên ta có
82
1
ab
+=
.
Mặt khác diện tích của tam giác vuông
ABO
là
1
.
2
ABO
S ab
∆
=
.
Áp dụng BĐT Cô si ta có:
8 2 8 2 16 4
1 2 . 12 12 8ab
a b a b ab
ab
= + ≥ ⇔≥ ⇔≥ ⇔ ≥
.
1
32
2
ab⇔≥
.
Ta có diện tích của tam giác vuông
ABO
nhỏ nhất bằng
32
khi
,ab
thỏa mãn hệ phương trình:
82
44
4 16
82 8 2
82 4 4
11
1
4
ab ab
ab a
ab
bb
ab bb
ab
= =
=

= =


⇔ ⇔ ⇔⇔

= =
+= +=


+=

.
Vậy
20ab+=
.
Câu 38: Mật khẩu mở điện thoại của bác Bình là một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn
600.000. Bạn An được bác Bình cho biết thông tin ấy nhưng không cho biết mật khẩu chính xác
là số nào nên quyết định thử bấm ngẫu nhiên một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ
hơn 600.000. Tính xác suất để bạn An nhập một lần duy nhất mà đúng mật khẩu để mở được
điện thoại của bác Bình.
Lời giải
Đặt
{ }
0,1, 2,3, 4,5,6,7,8,9
A
=
Gọi số tự nhiện lẻ có 6 chữa số là
x abcdef=
với
,,, ,,abcde f
thuộc
A
,
0a ≠
và
{ }
1,3,5,7,9
fB∈=
.
Vì
600.000x <
nên
{ }
1, 2,3, 4,5a ∈
.
Trường hợp 1:
{ }
1,3,5aa
∈⇒
có 3 cách chọn.
fa
≠
và
fB f
∈⇒
có 4 cách chọn.
Mỗi bộ
bcde
là một chỉnh hợp chập 4 của 8 phần tử còn lại thuộc tập
A ⇒
có
4
8
A
cách chọn.
Trường hợp này có
4
8
3.4. 20160A =
số.
Trường hợp 2:
{ }
2, 4aa∈⇒
có 2 cách chọn.
fB f∈⇒
có 5 cách chọn.
Mỗi bộ
bcde
là một chỉnh hợp chập 4 của 8 phần tử còn lại của tập
A ⇒
có
4
8
A
cách chọn.
Trường hợp này có
4
8
2.5. 16800A =
số.
Vậy có tất cả
20160 16800 36960+=
số tự nhiên lẻ có 6 chữ số.
Gọi C là biến cố bạn An nhập một lần theo gợi ý của bác Bình mà đúng mật khẩu mở điện
thoại.
Ta có
36960Ω=
;
1
C
Ω=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Vậy
1
36960
C
C
P
Ω
= =
Ω
.
Câu 39: Hai thiết bị
A
và
B
dùng để ghi âm một vụ nổ đặt cách nhau
1
dặm, thiết bị
A
ghi được âm
thanh trước thiết bị
B
là 2 giây, biết vận tốc âm thanh là
1100 /feet s
. Tìm các vị trí mà vụ nổ
có thể xảy ra.
Lời giải
Chọn hệ trục tọa độ
Oxy
mà
Ox
đi qua
A
và
B
,
Oy
là đường trung trực của
AB
.
Kí hiệu
1
d
là quãng đường âm thanh đi được từ vụ nổ đến thiết bị
A
,
2
d
là quãng đường âm
thanh đi được từ vụ nổ đến thiết bị
B
,
1
d
và
2
d
tính theo feet. Khi đó, do thiết bị
A
nhận âm
thanh nhanh hơn thiết bị
B
là
2
giây nên ta có phương trình:
21
2200 (1)
dd−=
Các điểm thỏa mãn
(1)
nằm trên một nhánh của Hypebol có phương trình:
22
22
1
xy
ab
−=
Ta có
5280
2640
2
c
= =
,
222
2200
1100, 5759600
2
a bca= = =−=
,
Vậy vụ nổ nằm trên một nhánh của Hypebol có phương trình:
22
1
1210000 5759600
xy
−=
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 04
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho
(
) ( )
5; 0 , 4;a bx=−=

. Tìm giá trị của
x
để hai vectơ
a
và
b
cùng
phương.
A.
4
. B.
1
−
. C.
0
. D.
5−
.
Câu 2: Cho hình chữ nhật có chiều dài bằng
10
3
, chiều rộng bằng 3. Để tính diện tích hình chữ nhật bạn
Giang lấy số gần đúng của
10
3
là 3,33. Hỏi sai số tuyệt đối của hình chữ nhật theo cách tính của
bạn Giang là bao nhiêu.
A.
0,1
. B.
0,01
. C.
1,11
. D.
0,11
.
Câu 3: Cho dãy số liệu
1; 2; 5; 7; 8; 9; 10
. Số trung vị của dãy trên bằng bao nhiêu?
A.
2
. B.
6
. C.
7
. D.
8
.
Câu 4: Một cửa hàng bán áo sơ mi thống kê số lượng áo bán ra trong tháng 6 như bảng sau.
Cỡ áo
37
38
39
40
41
42
Số lượng
35
42
50
38
32
48
Mốt của bảng số liệu trên bằng?
A.
42
. B.
39
. C.
50
. D.
41
.
Câu 5: Cho dãy số liệu
1; 3; 4; 6; 8; 9;11
. Phương sai của dãy trên bằng bao nhiêu?
A.
76
7
. B.
6
. C.
76
7
. D.
36
.
Câu 6: Cho hai vectơ
a
và
b
. Biết
2, 3ab
= =

và
(
)
0
, 30ab
=

. Tính
ab
+

.
A.
11
. B.
13
. C.
12
. D.
14
.
Câu 7: Biết rằng số trung vị trong mẫu số liệu sau ( đã sắp xếp theo thứ tự) bằng
14
. Tìm số nguyên
dương
x
.
2
1 3 4 13 1 18 19 21x −
A.
4x =
. B.
16x =
. C.
17x =
. D.
15x =
.
Câu 8: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị
kw
) hàng tháng của gia đình bạn An trong năm
2021 như sau:
163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là
10kw
.Gọi
;
QQ
′
∆∆
lần lượt
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây
là đúng
A.
QQ
′
∆=∆
. B.
10
QQ
′
∆=∆−
. C.
10
QQ
′
∆=∆−
D.
20
QQ
′
∆=∆−
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
Câu 9: Viết phương trình tổng quát của đường thẳng
∆
đi qua điểm
1; 3A
và có vectơ pháp tuyến
(3; 2)n = −
A.

3 2 30xy
. B.
3 2 30xy
. C.
3 2 70xy
. D.
3 2 70xy
.
Câu 10: Đường thẳng
d
đi qua
( ) ( )
0; 2 , 3; 0AB−
có phương trình theo đoạn chắn là
A.
1
23
xy
+=
−
. B.
1
32
xy
+=
−
. C.
0
23
xy
+=
−
. D.
0
32
xy
+=
−
.
Câu 11: Khoảng cách từ điểm
( )
1;1A
đến đường thẳng
5 12 6 0xy− −=
là
A.
13
. B.
13−
. C.
1−
. D.
1
.
Câu 12: Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:3 6 0d xy+−=
và đường thẳng
:
52
xt
yt
= −
∆
= −
. Góc giữa hai đường thẳng
d
và
∆
bằng
A.
30
°
. B.
135
°
. C.
45
°
. D.
90
°
.
Câu 13: Xác định tâm I và bán kính R của đường tròn
( ) ( ) ( )
22
:1 59Cx y− ++ =
.
A.
( 1; 5), 3IR
−=
. B.
9
( 1; 5),
2
IR−=
. C.
(1; 5), 3
IR−=
. D.
9
(1; 5),
2
IR
−=
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn tâm
(
)
2; 5I
−
và tiếp xúc với đường
thẳng
: 3 4 11 0
xy
∆− + + =
là
A.
( ) (
)
22
2 53
xy− ++ =
. B.
( ) ( )
22
2 59xy++−=
.
C.
(
) ( )
22
2 53xy
++−=
. D.
( ) ( )
22
2 59xy− ++ =
.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol?
A.
2
=
yx
. B.
2
6=yx
. C.
2
5= −
yx
. D.
2
2022
=yx
.
Câu 16: Trên kệ sách nhà bạn Lan có 7 quyển sách Toán khác nhau, 8 quyển sách Vật lý khác nhau và 9
quyển sách Lịch sử khác nhau. Hỏi bạn Lan có bao nhiêu cách chọn một quyển sách để đọc
A. 9. B. 8. C. 24. D. 7.
Câu 17: Một hộp đồ bảo hộ có 10 chiếc khẩu trang và 3 mặt nạ chống giọt bắn. Có bao nhiêu cách chọn
một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp đồ bảo hộ trên.
A.
10
. B.
30
. C.
13
. D.
3
.
Câu 18: Số hoán vị của tập
X
có 5 phần tử là
A.
5
. B.
24
. C.
120
. D.
60
.
Câu 19: Trong một hộp bánh có 10 chiếc bánh khác nhau. Có bao nhiêu cách lấy 3 chiếc bánh từ hộp đó
để phát cho các bạn An, Bình, Cường, mỗi bạn một chiếc?
A.
10
3
. B.
3
10
A
. C.
3
10
. D.
3
10
C
.
Câu 20: Lớp
11A
có
45
học sinh trong đó có
15
học sinh giỏi. Thầy giáo cần chọn một nhóm gồm
5
bạn học sinh của lớp
11A
đi dự trại hè. Hỏi thầy giáo đó có bao nhiêu cách chọn
1
nhóm sao cho
cả
5
bạn đều là học sinh giỏi.
A.
3003
. B.
360360
. C.
1221759
. D. Đáp án khác.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
Câu 21: Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của
( )
4
12x−
.
A.
1
. B.
1−
. C.
81
. D.
81
−
.
Câu 22: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xác suất để xuất hiện mặt có số chấm
chia hết cho 3 bằng
A.
1
2
. B.
1
3
. C.
1
6
. D.
2
3
.
Câu 23: Gieo ba con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên ba mặt lập thành
một cấp số cộng với cộng sai bằng 1 là bao nhiêu?
B.
1
6
. B.
1
36
. C.
1
9
. D.
1
27
.
Câu 24: Một tổ có
5
bạn nam và
7
bạn nữ, chọn một nhóm
3
bạn để tham gia biểu diễn văn nghệ. Xác
suất để chọn được
3
bạn nữ bằng
A.
21
220
. B.
1
22
. C.
7
44
. D.
5
44
.
Câu 25: Trong mặt phẳng
Oxy
cho điểm
( )
1;2M
và đường thẳng
: 4 20xy∆ + −=
. Viết phương trình
đường thẳng đi qua
M
và song song với
∆
.
A.
: 4 90dx y+ −=
. B.
: 4 90dx y+ +=
. C.
: 4 60dx y+ −=
. D.
: 4 60dx y
+ +=
.
Câu 26: Trong mặt phẳng với hệ tọa độ
Oxy
, hai đường thẳng có phương trình
( )
1
: 1 20
d mx m y m+− + =
và
2
:2 1 0d xy+ −=
song song khi và chỉ khi
A.
2.m =
B.
1.
m = −
C.
2.m = −
D.
1.
m =
Câu 27: Đường tròn
( )
C
đi qua
(
)
1; 3A
,
( )
3;1B
và có tâm nằm trên đường thẳng
:2 7 0d xy−+=
có
phương trình là
A.
( ) (
)
22
7 7 102xy
− +− =
. B.
( ) ( )
22
7 7 164xy+ ++ =
.
C.
( ) ( )
22
3 5 25xy− +− =
. D.
( ) ( )
22
3 5 25xy+ ++ =
.
Câu 28: Trong mặt phẳng tọa độ Oxy, cho đường tròn
( )
C
có phương trình
22
2 2 30xy xy+ − + −=
. Từ
điểm
( )
1;1A
kẻ được bao nhiêu tiếp tuyến đến đường tròn
( )
C
A. 1. B. 2. C. vô số. D. 0.
Câu 29: Phương trình chính tắc của elip có tổng các khoảng cách từ một điểm bất kỳ đến
hai tiêu điểm bằng
10
và có tiêu cự bằng
25
là
A.
22
1
10
25
+=
xy
. B.
22
1
25 20
+=
xy
. C.
22
1
25 5
+=
xy
. D.
22
1
100 20
+=
xy
.
Câu 30: Các thành phố
A
,
B
,
C
được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu
cách đi từ thành phố
A
đến thành phố
C
mà qua thành phố
B
chỉ một lần?
A.
6
. B.
12
. C.
8
. D.
4
.
A
B
C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 31: Một tổ có
7
người trong đó có An và Bình. Hỏi có bao nhiêu cách xếp
7
người vào bàn tròn có
7
ghế sao cho An và Bình ngồi cạnh nhau?
A.
720
. B.
240
. C.
5040
. D.
120
.
Câu 32: Có bao nhiêu cách xếp 5 bạn học sinh Tuấn, Tú, Tiến, Tân, Tiên vào 1 hàng ngang gồm 10 ghế
được đánh số từ 1 đến 10, sao cho Tuấn và Tiên luôn ngồi cạnh nhau?
A.
1890
. B.
252
. C.
3024
. D.
6048
.
Câu 33: Trên giá sách có
4
quyển sách Toán,
3
quyển sách Vật Lí và
2
quyển sách Hóa họ C. Lấy
ngẫu nhiên
3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán.
A.
1
3
. B.
37
42
. C.
5
6
. D.
19
21
Câu 34: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để
rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng
A.
1
3
. B.
2
3
. C.
5
18
. D.
13
18
.
Câu 35: Gieo một con súc xắc cân đối và đồng chất ba lần. Xác suất để ít nhất một lần xuất hiện mặt sáu
chấm là:
A.
125
216
. B.
91
216
. C.
25
216
. D.
81
216
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Từ một ban cán bộ Đoàn ở một trường học gồm có 20 học sinh, người ta muốn cử ra một nhóm
gồm 8 em đi tham gia hội trại với trường bạn. Biết rằng cần có một nhóm trưởng, hai bạn nhóm
phó, một bạn thủ quỹ và 4 bạn uỷ viên. Hỏi có bao nhiều cách chọn ra một nhóm học sinh như
vậy?
Câu 37: Viết phương trình chính tắc của hypebol
( )
H
có một tiêu điểm
( )
1
34;0F
−
và đi qua điểm
99
6;
25
A



.
Câu 38: Cho đa giác đều có 15 đỉnh, gọi
M
là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác
đã cho. Chọn ngẫu nhiên một tam giác thuộc tập
M
. Xác suất để chọn được một tam giác cân
nhưng không phải là tam giác đều bằng
Câu 39: Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có tiêu cự bằng
2 70 m
, độ
dài trục ảo bằng
2 42 m
. Biết chiều cao của tháp là
120m
và khoảng cách từ nóc tháp đến tâm
đối xứng của hypebol là
2
3
khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính
đáy của tháp.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho
( ) ( )
5; 0 , 4;a bx=−=

. Tìm giá trị của
x
để hai vectơ
a
và
b
cùng
phương.
A.
4
. B.
1
−
. C.
0
. D.
5−
.
Lời giải
( ) (
)
5; 0 , 4;a bx=−=

cùng phương
:. 0k a kb x⇔∃ = ⇒ =
Câu 2: Cho hình chữ nhật có chiều dài bằng
10
3
, chiều rộng bằng 3. Để tính diện tích hình chữ nhật bạn
Giang lấy số gần đúng của
10
3
là 3,33. Hỏi sai số tuyệt đối của hình chữ nhật theo cách tính của
bạn Giang là bao nhiêu.
A.
0,1
. B.
0,01
. C.
1,11
. D.
0,11
.
Lời giải
Diện tích hình chữ nhật đã cho
10
.3 10
3
S
= =
.
Diện tích hình chữ nhật khi bạn Giang tính
1
3,33.3 9,99S = =
.
Sai số tuyệt đối khi bạn Giang tính là
10 9,99 0,01−=
Câu 3: Cho dãy số liệu
1; 2; 5; 7; 8; 9; 10
. Số trung vị của dãy trên bằng bao nhiêu?
A.
2
. B.
6
. C.
7
. D.
8
.
Lời giải
Số trung vị của dãy trên là số đứng chính giữa xếp theo thứ tự không giảm. Vậy số trung vị của
dãy là
7
Câu 4: Một cửa hàng bán áo sơ mi thống kê số lượng áo bán ra trong tháng 6 như bảng sau.
Cỡ áo
37
38
39
40
41
42
Số lượng
35
42
50
38
32
48
Mốt của bảng số liệu trên bằng?
A.
42
. B.
39
. C.
50
. D.
41
.
Lời giải
Mốt của bảng trên là số lượng áo bán ra nhiều nhất của cỡ áo. vậy mốt bằng
39
Câu 5: Cho dãy số liệu
1; 3; 4; 6; 8; 9;11
. Phương sai của dãy trên bằng bao nhiêu?
A.
76
7
. B.
6
. C.
76
7
. D.
36
.
Lời giải
Số trung bình cộng của dãy số liệu trên là
13468911
6
7
x
++++++
= =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
Phương sai của dãy số liệu trên bằng
( ) ( )
(
) (
) ( ) ( ) ( )
222222 2
2
16 36 46 66 86 96 116
76
77
s
−+−+−+−+−+−+−
= =
Câu 6: Cho hai vectơ
a
và
b
. Biết
2, 3ab
= =

và
(
)
0
, 30ab
=

. Tính
ab+

.
A.
11
. B.
13
. C.
12
. D.
14
.
Lời giải
Ta có:
( )
( )
2
22
22
2 2 . .cos ,a b a b ab a b a b a b+ =++ = + +

( )
2
0
4 3 2.2. 3.cos30 13ab⇒ + =++ =

13ab
⇒+=

.
Câu 7: Biết rằng số trung vị trong mẫu số liệu sau ( đã sắp xếp theo thứ tự) bằng
14
. Tìm số nguyên
dương
x
.
2
1 3 4 13 1 18 19 21
x
−
A.
4x =
. B.
16x =
. C.
17x =
. D.
15x =
.
Lời giải
Số trung vị trong mẫu số liệu trên là
22
1 13 12
22
xx−+ +
=
Từ giả thiết suy ra
( )
( )
2
2
4
12
14 16
2
4
x tm
x
x
x loai
=
+
=⇔=⇔
= −
.
Vậy
4x =
.
Câu 8: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị
kw
) hàng tháng của gia đình bạn An trong năm
2021 như sau:
163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là
10kw
.Gọi
;
QQ
′
∆∆
lần lượt
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây
là đúng
A.
QQ
′
∆=∆
. B.
10
QQ
′
∆=∆−
. C.
10
QQ
′
∆=∆−
D.
20
QQ
′
∆=∆−
.
Lời giải
+) Sắp xếp mẫu số liệu năm 2021 theo thứ tự không giảm:
159 161 163 164 165 166 167 168 170 170 172 174
Mẫu số liệu gồm
12
giá trị nên số trung vị là
2
(166 167) : 2 166,5
Q =+=
Nửa số liệu bên trái là
159;161;163;164;165;166
gồm
6
giá trị
Khi đó
( )
1
163 164 : 2 163,5Q =+=
Nửa số liệu bên phải là
167;168;170;170;172;174
gồm
6
giá trị
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
Khi đó
3
170Q =
Khoảng tứ phân vị của mẫu số liệu bằng:
31
170 163,5 6,5
Q
QQ∆= − = − =
+) Sắp xếp mẫu số liệu năm 2022 theo thứ tự không giảm:
149 151 153 154 155 156 157 158 160 160 162 164
Mẫu số liệu gồm
12
giá trị nên số trung vị là
2
(156 157) : 2 156,5Q =+=
Nửa số liệu bên trái là
149;151;153;154;155;156
gồm
6
giá trị
Khi đó
1
(153 154) : 2 153,5Q =+=
Nửa số liệu bên phải là
157;158;160;160;162;164
gồm
6
giá trị
Khi đó
3
160
Q =
Khoảng tứ phân vị của mẫu số liệu bằng:
31
160 153,5 6,5
Q
QQ
′
∆= − = − =
Câu 9: Viết phương trình tổng quát của đường thẳng
∆
đi qua điểm
1; 3
A
và có vectơ pháp tuyến
(3; 2)
n = −
A.

3 2 30xy
. B.
3 2 30
xy
. C.
3 2 70xy
. D.
3 2 70xy
.
Lời giải
Phương trình đường thẳng cần tìm:
( )
(
)
3 1 2 3 0 3 2 90
x y xy− + − =⇔ + −=
.
Câu 10: Đường thẳng
d
đi qua
( ) ( )
0; 2 , 3; 0AB−
có phương trình theo đoạn chắn là
A.
1
23
xy
+=
−
. B.
1
32
xy
+=
−
. C.
0
23
xy
+=
−
. D.
0
32
xy
+=
−
.
Lời giải
Đường thẳng
d
đi qua
( ) (
)
0; 2 , 3; 0AB−
có phương trình theo đoạn chắn là:
1
32
xy
+=
−
Câu 11: Khoảng cách từ điểm
( )
1;1A
đến đường thẳng
5 12 6 0xy− −=
là
A.
13
. B.
13−
. C.
1−
. D.
1
.
Lời giải
Khoảng cách từ điểm
( )
1;1A
đến đường thẳng
:5 12 6 0xy∆ − −=
là
( )
( )
2
2
5.1 12.1 6
,1
5 12
dA
−−
∆= =
+−
.
Câu 12: Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:3 6 0d xy+−=
và đường thẳng
:
52
xt
yt
= −
∆
= −
. Góc giữa hai đường thẳng
d
và
∆
bằng
A.
30
°
. B.
135
°
. C.
45
°
. D.
90
°
.
Lời giải
+) Đường thẳng
d
có véc tơ pháp tuyến là:
( )
3;1
d
n =

.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
+) Đường thẳng
: : 2 5 0.
52
xt
xy
yt
= −
∆ ⇒∆ − + =
= −
Suy ra đường thẳng
∆
có véc tơ pháp
tuyến là:
( )
2; 1n
∆
= −

.
+) Gọi
α
là góc giữa hai đường thẳng
d
và
∆
. Ta có
( )
2
22 2
.
3.2 1.( 1)
2
cos 45 .
2
.
3 1. 2 1
d
d
nn
nn
αα
∆
°
∆
+−
= = = ⇒=
+ +−

 
Vậy góc giữa hai đường thẳng
d
và
∆
bằng
45
°
.
Câu 13: Xác định tâm I và bán kính R của đường tròn
( ) ( ) ( )
22
:1 59Cx y− ++ =
.
A.
( 1; 5), 3IR−=
. B.
9
( 1; 5),
2
IR−=
. C.
(1; 5), 3IR−=
. D.
9
(1; 5),
2
IR
−=
.
Lời giải
Đường tròn có tâm
(
)
1; 5 , 3IR−=
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn tâm
( )
2; 5I −
và tiếp xúc với đường
thẳng
: 3 4 11 0xy∆− + + =
là
A.
( )
(
)
22
2 53xy
− ++ =
. B.
( ) ( )
22
2 59xy++−=
.
C.
( ) (
)
22
2 53
xy++−=
. D.
( ) ( )
22
2 59xy− ++ =
.
Lời giải
Đường tròn tâm
I
tiếp xúc với đường thẳng
∆
có bán kính bằng khoảng cách từ điểm
I
đến
đường thẳng
∆
.
Suy ra,
(
)
( )
( )
2
2
3.2 4. 5 11
3 4 11
15
,3
55
34
II
xy
R dI
− + −+
−+ +
= ∆= = = =
−+
.
Vậy phương trình đường tròn tâm
( )
2; 5I −
, bán kính
3R
=
là:
( ) ( )
22
2 59xy− ++ =
.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol?
A.
2
=
yx
. B.
2
6=yx
. C.
2
5= −
yx
. D.
2
2022
=yx
.
Câu 16: Trên kệ sách nhà bạn Lan có 7 quyển sách Toán khác nhau, 8 quyển sách Vật lý khác nhau và 9
quyển sách Lịch sử khác nhau. Hỏi bạn Lan có bao nhiêu cách chọn một quyển sách để đọc
A. 9. B. 8. C. 24. D. 7.
Lời giải
Tổng số quyển sách:
7 8 9 24++=
quyển. Số cách chọn 1 quyển sách để đọc: 24 cách.
Câu 17: Một hộp đồ bảo hộ có 10 chiếc khẩu trang và 3 mặt nạ chống giọt bắn. Có bao nhiêu cách chọn
một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp đồ bảo hộ trên.
A.
10
. B.
30
. C.
13
. D.
3
.
Lời giải
Áp dụng quy tắc nhân, số cách chọn một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp
đồ bảo hộ trên là 10.3 = 30 cách.
Câu 18: Số hoán vị của tập
X
có 5 phần tử là
A.
5
. B.
24
. C.
120
. D.
60
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
Số hoán vị của tập
X
có 5 phần tử là
5! 120=
Câu 19: Trong một hộp bánh có 10 chiếc bánh khác nhau. Có bao nhiêu cách lấy 3 chiếc bánh từ hộp đó
để phát cho các bạn An, Bình, Cường, mỗi bạn một chiếc?
A.
10
3
. B.
3
10
A
. C.
3
10
. D.
3
10
C
.
Lời giải
Lấy 3 chiếc bánh từ 10 chiếc bánh, có
3
10
C
cách lấy.
Sau đó phát 3 chiếc bánh đã lấy cho 3 bạn, mỗi bạn một chiếc, có
3!
cách.
Vậy số cách cần tìm là:
33
10 10
.3!CA=
cách.
Câu 20: Lớp
11A
có
45
học sinh trong đó có
15
học sinh giỏi. Thầy giáo cần chọn một nhóm gồm
5
bạn học sinh của lớp
11A
đi dự trại hè. Hỏi thầy giáo đó có bao nhiêu cách chọn
1
nhóm sao cho
cả
5
bạn đều là học sinh giỏi.
A.
3003
. B.
360360
. C.
1221759
. D. Đáp án khác.
Lời giải
Số cách chọn
1
nhóm sao cho cả 5 bạn đều là học sinh giỏi bằng số cách chọn
5
học sinh trong
15
học sinh giỏi của lớp.
Vậy có
5
15
3003C
=
.
Câu 21: Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của
( )
4
12x−
.
A.
1
. B.
1−
. C.
81
. D.
81−
.
Lời giải
Tổng các hệ số trong khai triển nhị thức Niu-tơn của
( )
4
23x −
chính là giá trị của biểu thức
(
)
4
23x −
tại
1x =
.
Vậy
( )
4
1 2.1 1S =−=
.
Câu 22: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xác suất để xuất hiện mặt có số chấm
chia hết cho 3 bằng
A.
1
2
. B.
1
3
. C.
1
6
. D.
2
3
.
Lời giải
Không gian mẫu
{ }
1; 2;3; 4;5;6Ω=
( )
6n⇒ Ω=
.
Gọi
A
là biến cố “xuất hiện mặt có số chấm chia hết cho 3”, ta có
{ } (
)
3; 6 2A nA=⇒=
.
Vậy, xác suất để xuất hiện mặt có số chấm chia hết cho 3 là
( )
( )
( )
21
63
nA
PA
n
= = =
Ω
.
Câu 23: Gieo ba con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên ba mặt lập thành
một cấp số cộng với cộng sai bằng 1 là bao nhiêu?
B.
1
6
. B.
1
36
. C.
1
9
. D.
1
27
.
Lời giải
Số phần tử không gian mẫu là
3
6 216.=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
Các bộ ba số lập thành một cấp số cộng với công sai bằng 1 là
( ) ( ) ( ) ( )
1, 2,3 , 2,3, 4 , 3, 4,5 , 4,5,6 .
Các trường hợp trên với các hoán vị sẽ có
4.3! 24=
khả năng
thuận lợi cho biến cố.
Xác suất cần tìm là
24 1
.
216 9
=
Câu 24: Một tổ có
5
bạn nam và
7
bạn nữ, chọn một nhóm
3
bạn để tham gia biểu diễn văn nghệ. Xác
suất để chọn được
3
bạn nữ bằng
A.
21
220
. B.
1
22
. C.
7
44
. D.
5
44
.
Lời giải
Ta có số phân tử của không gian mẫu
( )
3
12
nCΩ=
.
Gọi
A
là biến cố chọn được
3
bạn nữ, ta có
( )
3
7
nA C=
.
Xác suất của biến cố
A
là
( )
( )
( )
3
7
3
12
7
44
nA
C
PA
nC
= = =
Ω
.
Câu 25: Trong mặt phẳng
Oxy
cho điểm
( )
1;2M
và đường thẳng
: 4 20xy∆ + −=
. Viết phương trình
đường thẳng đi qua
M
và song song với
∆
.
A.
: 4 90dx y+ −=
. B.
: 4 90dx y+ +=
. C.
: 4 60dx y+ −=
. D.
: 4 60dx y
+ +=
.
Lời giải
Ta có
d ⊥∆
, phương trình đường thẳng
d
có dạng:
:4 0dx y m+ +=
.
Mặt khác:
( )
1;2Md
∈
:
:1 4.2 0 9.
d mm+ +=⇔=−
Vậy phương trình đường thẳng
: 4 90dx y+ −=
.
Câu 26: Trong mặt phẳng với hệ tọa độ
Oxy
, hai đường thẳng có phương trình
( )
1
: 1 20d mx m y m+− + =
và
2
:2 1 0
d xy+ −=
song song khi và chỉ khi
A.
2.m =
B.
1.m = −
C.
2.m = −
D.
1.m =
Lời giải
(
)
12
1
||
2
2
1
12
2
0
.
: 12
1
2
21
:2 1 0
2
dd
dm
m
mx y m
mm
dx
m
m
y
m
+− + =
−
=
=
→ =
+−
/
−
−=
/
⇔⇔
=
=
−
Câu 27: Đường tròn
( )
C
đi qua
( )
1; 3A
,
( )
3;1B
và có tâm nằm trên đường thẳng
:2 7 0
d xy−+=
có
phương trình là
A.
( )
( )
22
7 7 102xy− +− =
. B.
( )
( )
22
7 7 164xy+ ++ =
.
C.
( ) ( )
22
3 5 25xy− +− =
. D.
( ) ( )
22
3 5 25xy+ ++ =
.
Lời giải
Đường tròn
( )
C
có tâm
( )
;
I ab
, bán kính
R
có phương trình là:
( ) ( ) ( )
22
2
*xa yb R− +− =
.
(
)
;2 7I d Ia a∈⇒ +
.
( ) ( )
22
1 24AI a a= −+ +
2
5 14 17aa= ++
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
( ) ( )
22
3 26
BI a a= −+ +
2
5 18 45
aa= ++
Vì
( )
C
đi qua
(
)
1; 3
A
,
( )
3;1B
nên
AI BI=
⇔
22
AI BI=
⇔
22
5 14 17 5 18 45aa aa
+ += + +
⇔
7
a = −
Suy ra tâm
( )
7; 7I −−
, bán kính
22
164R AI= =
.
Vậy đường tròn
( )
C
có phương trình:
( ) ( )
22
7 7 164xy+ ++ =
.
Câu 28: Trong mặt phẳng tọa độ Oxy, cho đường tròn
( )
C
có phương trình
22
2 2 30xy xy+ − + −=
. Từ
điểm
( )
1;1A
kẻ được bao nhiêu tiếp tuyến đến đường tròn
(
)
C
A. 1. B. 2. C. vô số. D. 0.
Lời giải
( )
C
có tâm
( )
1; 1I −
bán kính R=
22
1 (1) (3) 5+− −− =
Vì
2IA R= <
nên A nằm bên trong
( )
C
.Vì vậy không kẻ được tiếp tuyến nào tới đường tròn
( )
C
.
Câu 29: Phương trình chính tắc của elip có tổng các khoảng cách từ một điểm bất kỳ đến
hai tiêu điểm bằng
10
và có tiêu cự bằng
25
là
A.
22
1
10
25
+=
xy
. B.
22
1
25 20
+=
xy
. C.
22
1
25 5
+=
xy
. D.
22
1
100 20
+=
xy
.
Lời giải
Phương trình chính tắc của elip có dạng
( )
22
22
1 0+ = >>
xy
ab
ab
.
Ta có
2 22 2
2 10 5
2 25 5
20
= =


= ⇒=


=−=

aa
cc
b ac b
.
Vậy elip có phương trình chính tắc là
22
1
25 20
+=
xy
.
Câu 30: Các thành phố
A
,
B
,
C
được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu
cách đi từ thành phố
A
đến thành phố
C
mà qua thành phố
B
chỉ một lần?
A.
6
. B.
12
. C.
8
. D.
4
.
Lời giải
Ta có:
- Đi từ thành phố A đến thành phố B ta có 4 con đường để đi.
- Đi từ thành phố B đến thành phố C ta có 2 con đường để đi.
Vậy theo quy tắc nhân ta có
42 8×=
cách.
Câu 31: Một tổ có
7
người trong đó có An và Bình. Hỏi có bao nhiêu cách xếp
7
người vào bàn tròn có
7
ghế sao cho An và Bình ngồi cạnh nhau?
A.
720
. B.
240
. C.
5040
. D.
120
.
Lời giải
A
B
C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Ta buộc cặp hai bạn An và Bình và coi là một người thì có tất cả
6
người.
Suy ra có
5!
cách xếp
6
người này vào bàn tròn.
Nhưng hai bạn An và Bình có thể hoán vị để ngồi cạnh nhau.
Vậy có tất cả
5!.2! 240
=
cách xếp
7
người vào bàn tròn có
7
ghế sao cho An và Bình ngồi
cạnh nhau.
Câu 32: Có bao nhiêu cách xếp 5 bạn học sinh Tuấn, Tú, Tiến, Tân, Tiên vào 1 hàng ngang gồm 10 ghế
được đánh số từ 1 đến 10, sao cho Tuấn và Tiên luôn ngồi cạnh nhau?
A.
1890
. B.
252
. C.
3024
. D.
6048
.
Lời giải
Xem Tuấn và Tiên là khối
A
.
Xếp thứ tự khối
A
và 3 bạn Tú, Tiến, Tân vào các ghế trong hàng ngang có
4
9
A
cách.
Xếp vị trí cho Tuấn và Tiên trong khối
A
có
2!
cách xếp.
Vậy theo QTN, ta có
4
9
.2! 6048A =
cách.
Câu 33: Trên giá sách có
4
quyển sách Toán,
3
quyển sách Vật Lí và
2
quyển sách Hóa họ C. Lấy
ngẫu nhiên
3
quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán.
A.
1
3
. B.
37
42
. C.
5
6
. D.
19
21
Lời giải
Số phần tử của không gian mẫu
( )
3
9
84
nCΩ= =
.
Gọi
A
là biến cố sao cho ba quyển lấy ra có ít nhất một quyển sách Toán
A
⇒
là biến cố sao cho ba quyển lấy ra không có sách Toán
( )
3
5
10nA C⇒==
.
( )
PA⇒
( )
1 PA= −
10
1
84
= −
37
42
=
.
Câu 34: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để
rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng
A.
1
3
. B.
2
3
. C.
5
18
. D.
13
18
.
Lời giải
Có 2 trường hợp sau:
Trường hợp 1: 1 thẻ ghi số chẵn, 1 thẻ ghi số lẻ, suy ra có
11
45
20CC⋅=
cách rút.
Trường hợp 2: 2 thẻ ghi số chẵn, suy ra có
2
4
6C =
cách rút.
Suy ra xác suất bằng
2
9
20 6 13
18C
+
=
.
Câu 35: Gieo một con súc xắc cân đối và đồng chất ba lần. Xác suất để ít nhất một lần xuất hiện mặt sáu
chấm là:
A.
125
216
. B.
91
216
. C.
25
216
. D.
81
216
.
Lời giải
Ta có:
( ) 6.6.6 216n Ω= =
.
Gọi
A
là biến cố:”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó
A
là biến cố:”không có lần nào xuất hiện mặt sáu chấm”.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
( ) 5.5.5 125
nA
= =
. Vậy
125 91
() 1 () 1
216 216
PA PA
=− =−=
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Từ một ban cán bộ Đoàn ở một trường học gồm có 20 học sinh, người ta muốn cử ra một nhóm
gồm 8 em đi tham gia hội trại với trường bạn. Biết rằng cần có một nhóm trưởng, hai bạn nhóm
phó, một bạn thủ quỹ và 4 bạn uỷ viên. Hỏi có bao nhiều cách chọn ra một nhóm học sinh như
vậy?
Lời giải
Chọn ra hai em gồm nhóm trưởng và thủ quỹ có
2
20
A
cách.
Chọn ra hai em nhóm phó có
2
18
C
cách.
Chọn ra 4 uỷ viên từ 16 em còn lại có
4
16
C
cách.
Vậy có
224
20 18 16
. . 105814800
ACC
=
cách chọn ra nhóm học sinh đó.
Câu 37: Viết phương trình chính tắc của hypebol
( )
H
có một tiêu điểm
(
)
1
34;0
F −
và đi qua điểm
99
6;
25
A



.
Lời giải
Gọi pt chính tắc của hypebol
( )
H
:
( )
22
22
1 0, 0
xy
ab
ab
−= > >
.
( )
H
có một tiêu điểm
( )
1
34;0
F −
⇔
2 22 2 2
34 34 34c ab a b=⇔+=⇔=−
.
( )
1
Mặt khác do
( )
H
đi qua điểm
99
6;
25
A



nên
2
22
6 99
1
25
ab
−=
.
( )
2
Thay
( )
1
vào
( )
2
ta được:
( )
22
2
42
22
2
9 25
6 99
1 25 149 3366 0
374
34 25
25
ba
bb
bb
b loai
=⇒=
−=⇔+ −=⇔
−
−
=
.
Vậy
(
)
22
:1
25 9
xy
H −=
.
Câu 38: Cho đa giác đều có 15 đỉnh, gọi
M
là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác
đã cho. Chọn ngẫu nhiên một tam giác thuộc tập
M
. Xác suất để chọn được một tam giác cân
nhưng không phải là tam giác đều bằng
Lời giải
+ Số tam giác có ba đỉnh là ba đỉnh của đa giác đã cho là:
3
15
455=C
tam giá C.
Suy ra
( )
455Ω=n
.
+ Gọi
O
là tâm đường tròn ngoại tiếp đa giác đều.
Xét một đỉnh
A
bất kì của đa giác đều: có 7 cặp đỉnh của đa giác đối xứng với nhau qua
OA
,
hay có 7 tam giác cân tại đỉnh
A
.
Như vậy, với mỗi đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
+ Số tam giác đều có ba đỉnh là ba đỉnh của đa giác là
15
5
3
=
tam giá C.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều
thì đều cân tại ba đỉnh nên các tam giác đều được đếm ba lần.
+ Suy ra số tam giác cân nhưng không phải tam giác đều có ba đỉnh là ba đỉnh của đa giác đã
cho là:
7.15 3.5 90−=
.
Vậy, xác suất để chọn được một tam giác cân nhưng không phải là tam giác đều từ tập
M
bằng:
90 18
455 91
= =P
.
Câu 39: Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có tiêu cự bằng
2 70 m
, độ
dài trục ảo bằng
2 42 m
. Biết chiều cao của tháp là
120m
và khoảng cách từ nóc tháp đến tâm
đối xứng của hypebol là
2
3
khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính
đáy của tháp.
Lời giải
Phương trình chính tắc của hypebol có dạng
22
22
1
xy
ab
−=
, với
222
,a cb c a<=−
.
Ta có:
22
2 2 70 70
2 2 42 42
27
cc
bb
a cb
= ⇒=
= ⇒=
= −=
Vậy phương trình chính tắc của hypebol là:
22
1
28 42
xy
−=
.
Gọi khoảng cách từ tâm đối xứng đến đáy tháp là z.
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là
2
3
z
.
Ta có
2
120 72
3
zz z
+ = ⇒=
.
Thay
72y =
vào phương trình
22
1
28 42
xy
−=
ta tìm được
2 871x = ±
.
Thay
48y =
vào phương trình
22
1
28 42
xy
−=
ta tìm được
2 391x = ±
.
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là:
2 391m
;
2 871 .m
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 15
Sưu tầm và biên soạn
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 05
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho
( )
0;3A
;
( )
4;0B
;
( )
2; 5C −−
. Tính
.
AB BC
 
.
A.
16
. B.
9
. C.
10
−
. D.
9−
.
Câu 2: Hãy xác định sai số tuyệt đối của số
123456a =
biết sai số tương đối
0, 2%
a
δ
=
A. 246,912. B. 617280. C. 24691,2. D. 61728000
Câu 3: Cho các số liệu thống kê về sản lượng chè thu được trong
1
năm ( kg/sào) của
20
hộ gia đình
111
112
112
113
114
114
115
114
115
116
112
113
113
114
115
114
116
117
114
115
Tìm số mốt
A.
0
111M =
. B.
0
113
M =
. C.
0
114M =
. D.
0
117
M =
.
Câu 4: Số sản phẩm sản xuất mỗi ngày của một phân xưởng trong 9 ngày liên tiếp được ghi lại như sau:
27 26 21 28 25 30 26 23 26
Khoảng biến thiên của mẫu số liệu này là:
A. 8. B. 5. C. 6. D. 9.
Câu 5: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là:
A. 20. B. 22. C. 24. D. 26.
Câu 6: Cho ba điểm
( ) ( ) ( )
2; 4 , 6;0 , ;4A B Cm−
. Định
m
để
,,ABC
thẳng hàng?
A.
10m =
. B.
6m = −
. C.
2m =
. D.
10m
= −
.
Câu 7: Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75m với dụng cụ đo đảm bảo sai số tương
đối không vượt quá
1, 5‰
. Tính độ dài gần đúng của cầu.
A. 500,1m B. 499,9m C. 500 m D. 501 m
Câu 8: Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A1
Độ lệch chuẩn của mẫu số liệu trên là
A.
1, 5
. B.
1, 57
. C.
1, 58
. D.
1, 60
.
Câu 9: Trong mặt phẳng Oxy cho đường thẳng d:
24
1
xt
yt
= −
= +
. Vectơ nào dưới đây là một vectơ chỉ
phương của d?
A.
2
(2;1)u =
. B.
1
( 4;1)
u = −
. C.
3
(1; 3)u =

. D.
4
(2; 4)u
= −

.
Câu 10: Viết phương trình tổng quát của đường thẳng
d
qua
( )
1; 4M −−
và song song với đường thẳng
3 5 20xy+ −=
A.
: 4 20
dx y
−− − =
. B.
:3 5 23 0dx y++=
.
C.
:5 3 23 0dx y++=
. D.
: 3 5 23 0d xy−−+=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
Câu 11: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10
xy− + −=
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Câu 12: Khoảng cách từ điểm
(
)
2;0M
đến đường thẳng
13
24
xt
yt
= +
= +
là:
A.
2
. B.
2
5
. C.
10
5
. D.
5
2
.
Câu 13: Trong mặt phẳng với hệ trục tọa độ
Oxy
. Trong các phương trình sau, phương trình nào là
phương trình đường tròn?
A.
22
2 4 11 0+ − + −=xy xy
. B.
22
2 4 11 0−− + −=xy x y
.
C.
22
2 4 11 0
+− + +=xy xy
. D.
22
2 2 4 11 0+− + −=xy xy
.
Câu 14: Đường tròn
()C
tâm
(1; 4)I
và tiếp xúc với đườngthẳng
:4 3 4 0
xy∆ + +=
có phương trình là
A.
22
( 1) ( 4) 17xy−+− =
. B.
22
( 1) ( 4) 16xy−+− =
.
C.
22
( 1) ( 4) 25xy− +− =
. D.
22
( 1) ( 4) 16xy+ ++ =
Câu 15: Tọa độ các tiêu điểm của hypebol
( )
22
:1
94
xy
H −=
là
A.
( )
( )
12
13;0 ; 13;0
FF=−=
. B.
( )
( )
12
0; 13 ; 0; 13FF
=−=
.
C.
( )
( )
12
0; 5 ; 0; 5FF=−=
. D.
(
) ( )
12
5;0 ; 5;0FF
=−=
.
Câu 16: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một
học sinh trong lớp đi dự đại hội?
A.
20
. B.
35
. C.
15
. D.
300
.
Câu 17: Đi từ A đến B có 3 con đường,đi từ B đến C có 4 con đường.Hỏi đi từ A đến C có bao cách đi?
A. 7. B. 8. C. 10. D. 12.
Câu 18: Có
6
người đến nghe buổi hòa nhạc. Số cách sắp xếp
6
người này vào một hàng ngang
6
ghế
là
A.
6
. B.
2.6!
. C.
2
6
. D.
6!
.
Câu 19: Cho 6 chữ số
4, 5, 6, 7,8,9
. Hỏi có bao nhiêu số gồm 3 chữ số khác nhau được lập thành từ 6 chữ
số đó?
A.
180
. B.
120
. C.
256
. D.
216
.
Câu 20: Trong mặt phẳng cho tập hợp
S
gồm
10
điểm, trong đó không có
3
điểm nào thẳng hàng. Có
bao nhiêu tam giác có
3
đỉnh đều thuộc
S
?
A.
720.
B.
120.
C.
59049.
D.
3628800.
Câu 21: Mệnh đề nào dưới đây đúng?
A.
( )
4
04 13 22 2 3 3 4 4
44 4 4 4
3 .3 .3 .3 .3x CxCxCx CxC+= + + + +
.
B.
( )
4
432
3 12 54 108 324x xxx x+=+ + + +
.
A
B
C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
C.
( )
4
432
3 12 54 12 81
x xxxx+=+ + ++
.
D.
( )
4
4 32
3 108 54 108 81x xxxx+=+ + + +
.
Câu 22: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là:
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.
Câu 23: Từ một nhóm học sinh gồm có 5 nam và 6 nữ, chọn ngẫu nhiên ra 2 bạn. Tính xác suất để hai
bạn được chọn có cả nam và nữ.
A.
7
11
. B.
5
11
. C.
6
11
. D.
4
11
.
Câu 24: Một tổ có 4 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh lên bảng giải
bài tập. Xác suất để 3 học sinh được chọn có cả nam và nữ bằng
A.
1
6
. B.
5
6
. C.
3
5
. D.
2
5
.
Câu 25: Cho
( )
1;3M
và
( )
3;5N −
. Phương trình đường trung trực của đoạn thẳng
MN
là đường thẳng
nào dưới đây?
A.
2 70
xy+ −=
. B.
2 60
xy− +−=
. C.
2 70xy+ +=
. D.
2 60xy− ++=
.
Câu 26: Trong mặt phẳng tọa độ
( )
,Oxy
cho các điểm
( ) ( )
1; 2 , 2; 1−AB
. Đường thẳng
∆
đi qua điểm
A
, sao cho khoảng cách từ điểm
B
đến đường thẳng
∆
nhỏ nhất có phương trình là?
A.
3 50+−=xy
. B.
3 50
− +=xy
.
C.
3 10+ −=xy
. D.
3 10− −=xy
.
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( )
1; 2A
,
( )
5; 2B
,
( )
1; 3C −
có phương trình
là.
A.
22
6 10x y xy+ + + −=
. B.
22
6 10x y xy+ − − −=
.
C.
22
6 10x y xy+ − + −=
. D.
22
6 10x y xy+ + − −=
.
Câu 28: Cho đường thẳng
:3 4 19 0xy∆ − −=
và đường tròn
( ) ( ) ( )
22
: 1 1 25Cx y− +− =
. Biết đường
thẳng
∆
cắt
(
)
C
tại hai điểm phân biệt
A
và
B
, khi đó độ dài đọan thẳng
AB
là
A. 6. B. 3. C. 4. D. 8.
Câu 29: Cho của hypebol
( )
22
:1
16 9
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng
A.
8
. B.
6
. C.
4
. D.
5
.
Câu 30: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món, 1 loại quả tráng
miệng trong 5 loại quả tráng miệng và một loại nước uống trong 3 loại nước uống. Có bao nhiêu
cách chọn thực đơn?
A. 100. B. 15. C. 75. D. 25.
Câu 31: Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh
ngồi một ghế là
A.
6
10
C
. B.
6!
. C.
6
10
A
. D.
10
6
.
Câu 32: Mười hai đường thẳng có nhiều nhất bao nhiêu giao điểm?
A.
12
. B.
66
. C.
132
. D.
144
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 33: Thầy X có
15
cuốn sách gồm
4
cuốn sách toán,
5
cuốn sách lí và
6
cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên
8
cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ
3
môn.
A.
5
6
. B.
661
715
. C.
660
713
. D.
6
7
.
Câu 34: Một hộp chứa 11 viên bi được đánh số thứ tự từ 1 đến 11. Chọn ngẫu nhiên 3 viên bi rồi cộng
các số trên 3 viên bi đó với nhau. Xác suất để kết quả thu được là số chẵn bằng
A.
17
33
. B.
16
33
. C.
19
33
. D.
23
33
.
Câu 35: Một hộp chứa 5 bi xanh, 4 bi đỏ. Chọn ngẫu nhiên 2 bi từ hộp này. Xác suất để chọn được 2 bi
cùng màu là
A.
2
9
. B.
1
9
. C.
5
9
. D.
4
9
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu sô tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn và 3 chữ số lẻ?
Câu 37: Trong mặt phẳng
(Oxy)
cho điểm
(2; 4)M
và
13
:
2
xt
d
yt
= −
= +
.Viết phương trình đường thẳng song
song với đường thẳng
d
và cách điểm
M
một khoảng bằng
10
.
Câu 38: Cho tập hợp
{ }
0,1, 2,3, 4,5,6,7X =
. Gọi
S
là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một
khác nhau được lập từ tập hợp
X
. Chọn ngẫu nhiên một số từ
S
. Tính xác suất để chọn được
số chia hết cho 5.
Câu 39: Trong hệ trục tọa độ
Oxy
, cho Elip
( )
22
:1
25 16
xy
E +=
,
12
,FF
là hai tiêu điểm, hoành độ của
1
F
âm. Điểm
M
thuộc
( )
E
sao cho
12
2MF MF
=
. Hoành độ điểm
M
là
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho
(
)
0;3A
;
( )
4;0B
;
( )
2; 5C −−
. Tính
.AB BC
 
.
A.
16
. B.
9
. C.
10
−
. D.
9−
.
Lời giải
Ta có
( )
4; 3AB = −

;
(
)
6; 5
BC =−−

Vậy
.AB BC
 
(
) (
) (
)
4.6 3.5 9= − +− − =−
.
Câu 2: Hãy xác định sai số tuyệt đối của số
123456a =
biết sai số tương đối
0, 2%
a
δ
=
A. 246,912. B. 617280. C. 24691,2. D. 61728000
Giải
Ta có
246,912
a
a aa
a
a
δδ
∆
= ⇒∆ = =
.
Câu 3: Cho các số liệu thống kê về sản lượng chè thu được trong
1
năm ( kg/sào) của
20
hộ gia đình
111
112
112
113
114
114
115
114
115
116
112
113
113
114
115
114
116
117
114
115
Tìm số mốt
A.
0
111
M =
. B.
0
113M =
. C.
0
114M =
. D.
0
117M =
.
Lời giải
Nhìn vào bảng số liệu ta thấy giá trị
114
có tần số lớn nhất nên ta có
0
114M
=
.
Câu 4: Số sản phẩm sản xuất mỗi ngày của một phân xưởng trong 9 ngày liên tiếp được ghi lại như sau:
27 26 21 28 25 30 26 23 26
Khoảng biến thiên của mẫu số liệu này là:
A. 8. B. 5. C. 6. D. 9.
Lời giải
Số sản phẩm sản xuất thấp nhất và cao nhất lần lượt là 30 và 21. Vậy khoảng biến thiên của
mẫu số liệu này là 9.
Câu 5: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là:
A. 20. B. 22. C. 24. D. 26.
Lời giải
Số liệu trên đã sắp xếp theo thứ tự không giảm
Ta có
123
10; 19; 32QQQ= = =
Vậy khoảng tứ phân vị của mẫu số liệu trên là:
32 10 22
Q
∆= − =
.
Câu 6: Cho ba điểm
( ) (
) ( )
2; 4 , 6;0 , ;4A B Cm−
. Định
m
để
,,ABC
thẳng hàng?
A.
10m =
. B.
6m = −
. C.
2m =
. D.
10m = −
.
Lời giải
Chọn A
( ) ( )
4;4 ; 2;8 .AB AC m= = −
 
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
,,
ABC
thẳng hàng
,AB AC⇔
 
cùng phương
28
10
44
m
m
−
⇔ =⇔=
.
Câu 7: Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75m với dụng cụ đo đảm bảo sai số tương
đối không vượt quá
1, 5‰
. Tính độ dài gần đúng của cầu.
A. 500,1m B. 499,9m C. 500 m D. 501 m
Lời giải
Độ dài h của cây cầu là:
0,75
.1000 500
1, 5
d ≈=
(m)
Câu 8: Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A1
Độ lệch chuẩn của mẫu số liệu trên là
A.
1, 5
. B.
1, 57
. C.
1, 58
. D.
1, 60
.
Câu 9: Trong mặt phẳng Oxy cho đường thẳng d:
24
1
xt
yt
= −
= +
. Vectơ nào dưới đây là một vectơ chỉ
phương của d?
A.
2
(2;1)
u =
. B.
1
( 4;1)u = −
. C.
3
(1; 3)u =

. D.
4
(2; 4)u = −

.
Lời giải
Ta có
( 4;1)u = −
là một vectơ chỉ phương của d
Câu 10: Viết phương trình tổng quát của đường thẳng
d
qua
( )
1; 4M −−
và song song với đường thẳng
3 5 20xy+ −=
A.
: 4 20dx y−− − =
. B.
:3 5 23 0dx y++=
.
C.
:5 3 23 0dx y++=
. D.
: 3 5 23 0
d xy−−+=
.
Lời giải
Vì
d
song song với đường thẳng
3 5 20
xy
+ −=
nên phương trình của
d
có dạng
35 0x yc+ +=
( 2)c ≠−
.
Vì
d
đi qua điểm
( )
1; 4M −−
nên
3 20 0 23cc−− + = ⇒ =
.
Vậy phương trình tổng quát của
:3 5 23 0dx y++=
.
Câu 11: Xác định vị trí tương đối của
2
đường thẳng sau đây:
1
∆
:
2 3 10xy− +=
và
2
∆
:
4 6 10xy− + −=
.
A. Song song. B. Trùng nhau.
C. Vuông góc. D. Cắt nhau nhưng không vuông góc nhau.
Lời giải
+) Xét:
2 31
46 1
−
= ≠
−−
nên hai đường thẳng song.
Câu 12: Khoảng cách từ điểm
( )
2;0M
đến đường thẳng
13
24
xt
yt
= +
= +
là:
A.
2
. B.
2
5
. C.
10
5
. D.
5
2
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
Phương trình tổng quát
( )
4.2 3.0 2
:4 3 2 0 , 2
5
d x y d Md
−+
− +=⇒ = =
.
Câu 13: Trong mặt phẳng với hệ trục tọa độ
Oxy
. Trong các phương trình sau, phương trình nào là
phương trình đường tròn?
A.
22
2 4 11 0+ − + −=xy xy
. B.
22
2 4 11 0−− + −=xy x y
.
C.
22
2 4 11 0+−+ +=xy xy
. D.
22
2 2 4 11 0+− + −=xy xy
.
Lời giải
Phương trình
22
2 4 11 0+ − + −=
xy xy
là phương trình đường tròn.
Vì
22
1 4 11 16 0+ −=++ = >abc
trong đó
1; 2; 11.==−=−ab c
Câu 14: Đường tròn
()C
tâm
(1; 4)
I
và tiếp xúc với đườngthẳng
:4 3 4 0xy
∆ + +=
có phương trình là
A.
22
( 1) ( 4) 17
xy
− +− =
. B.
22
( 1) ( 4) 16xy−+− =
.
C.
22
( 1) ( 4) 25xy− +− =
. D.
22
( 1) ( 4) 16xy+ ++ =
Lời giải
( )
C
có bán kính
(
)
22
4.1 3.4 4
,4
34
R dI
++
= ∆= =
+
.
Do đó,
( )
C
có phương trình
22
( 1) ( 4) 16xy−+− =
.
Câu 15: Tọa độ các tiêu điểm của hypebol
( )
22
:1
94
xy
H −=
là
A.
( )
( )
12
13;0 ; 13;0FF=−=
. B.
( )
( )
12
0; 13 ; 0; 13FF
=−=
.
C.
( )
( )
12
0; 5 ; 0; 5FF=−=
. D.
( )
( )
12
5;0 ; 5;0FF=−=
.
Lời giải
Gọi
( ) ( )
12
;0 ; ;0F cFc=−=
là hai tiêu điểm của
( )
H
.
Từ phương trình
( )
22
:1
94
xy
H −=
, ta có:
2
9a =
và
2
4b
=
suy ra
( )
2 22
13 13, 0
c ab c c= + = ⇒= >
.
Vậy tọa độ các tiêu điểm của
( )
H
là
( )
(
)
12
13;0 ; 13;0FF
=−=
.
Câu 16: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một
học sinh trong lớp đi dự đại hội?
A.
20
. B.
35
. C.
15
. D.
300
.
Lời giải
Có 2 khả năng xẩy ra:
+) Học sinh được chọn là nam có 20 cách chọn.
+) Học sinh được chọn là nữ có 15 cách chọn.
Vậy theo quy tắc cộng có 20+15=35 cách chọn.
Câu 17: Đi từ A đến B có 3 con đường,đi từ B đến C có 4 con đường.Hỏi đi từ A đến C có bao cách đi?
A. 7. B. 8. C. 10. D. 12.
A
B
C
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
Lời giải
Theo quy tắc nhân ta có số cách đi từ A đến C là:
3.4 12=
. Vậy chọn đáp án D
Câu 18: Có
6
người đến nghe buổi hòa nhạc. Số cách sắp xếp
6
người này vào một hàng ngang
6
ghế
là
A.
6
. B.
2.6!
. C.
2
6
. D.
6!
.
Lời giải
Mỗi cách sắp xếp
6
người ngồi vào một hàng ngang
6
ghế là một hoán vị của
6
phần tử.
Vậy số cách sắp xếp là
6!
cách.
Câu 19: Cho 6 chữ số
4, 5, 6, 7,8,9
. Hỏi có bao nhiêu số gồm 3 chữ số khác nhau được lập thành từ 6 chữ
số đó?
A.
180
. B.
120
. C.
256
. D.
216
.
Lời giải
Gọi số cần tìm có dạng
abc
với
0,a abca≠ ≠≠≠
.
Chọn 3 chữ số khác nhau từ 6 chữ số đã cho và sắp xếp vào 3 vị trí
,,abc
có
3
6
120A =
cách.
Câu 20: Trong mặt phẳng cho tập hợp
S
gồm
10
điểm, trong đó không có
3
điểm nào thẳng hàng. Có
bao nhiêu tam giác có
3
đỉnh đều thuộc
S
?
A.
720.
B.
120.
C.
59049.
D.
3628800.
Lời giải
Số tam giác có
3
đỉnh đều thuộc
S
bằng số tổ hợp chập
3
của
10
phần từ và bằng
3
10
120C
=
Câu 21: Mệnh đề nào dưới đây đúng?
A.
( )
4
04 13 22 2 3 3 4 4
44 4 4 4
3 .3 .3 .3 .3x CxCxCx CxC
+= + + + +
.
B.
(
)
4
432
3 12 54 108 324
x xxx x+=+ + + +
.
C.
( )
4
432
3 12 54 12 81x xxxx
+=+ + ++
.
D.
( )
4
4 32
3 108 54 108 81x xxxx+=+ + + +
.
Lời giải
Ta có
( )
4
04 13 22 2 3 3 4 4
44 4 4 4
432
3 .3 .3 .3 .3
12 54 108 81
x CxCxCx CxC
xxx x
+= + + + +
=++++
Câu 22: Chọn ngẫu nhiên hai số khác nhau từ
15
số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là:
A.
1
7
. B.
8
15
. C.
4
15
. D.
1
14
.
Lời giải
Không gian mẫu
2
15
105C =
.
Để tổng hai số là một số lẻ ta chọn 1 số lẻ và 1 số chẵn nên ta có
8.7 56=
.
Xác suất cần tìm là
56 8
105 15
=
.
Câu 23: Từ một nhóm học sinh gồm có 5 nam và 6 nữ, chọn ngẫu nhiên ra 2 bạn. Tính xác suất để hai
bạn được chọn có cả nam và nữ.
A.
7
11
. B.
5
11
. C.
6
11
. D.
4
11
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
Lời giải
Số cách chọn 2 bạn trong tổng số 11 bạn:
2
11
()nCΩ=
Gọi A là biến cố: “Hai bạn được chọn có cả nam và nữ”. Ta có:
11
56
() .
nA CC
=
Từ đó, xác suất để hai bạn được chọn có cả nam và nữ là:
() 6
()
( ) 11
nA
PA
n
= =
Ω
.
Câu 24: Một tổ có 4 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh lên bảng giải
bài tập. Xác suất để 3 học sinh được chọn có cả nam và nữ bằng
A.
1
6
. B.
5
6
. C.
3
5
. D.
2
5
.
Lời giải
Ta có
(
)
3
9
84nCΩ= =
.
Gọi biến cố
:A
“3 học sinh được chọn có cả nam và nữ”
( )
12 21
45 4 5
. . 70nA CC CC⇒= + =
.
Vậy
( )
( )
( )
70 5
84 6
nA
pA
n
= = =
Ω
.
Câu 25: Cho
( )
1;3M
và
( )
3;5N −
. Phương trình đường trung trực của đoạn thẳng
MN
là đường thẳng
nào dưới đây?
A.
2 70xy
+ −=
. B.
2 60
xy− +−=
. C.
2 70xy+ +=
. D.
2 60xy− ++=
.
Lời giải
Ta có
(
)
4;2
MN = −

, đặt
(
)
2;1n = −
.
Gọi
I
là trung điểm của
MN
, ta có
( )
1;4
I −
.
Đường trung trực của đoạn thẳng
MN
là đường thẳng đi qua điểm
I
và nhận vectơ
n
làm
vectơ pháp tuyến, có phương trình:
( )
( )
2 11 4 0 2 60x y xy
− + + − = ⇔− + − =
.
Câu 26: Trong mặt phẳng tọa độ
( )
,Oxy
cho các điểm
( ) ( )
1; 2 , 2; 1−AB
. Đường thẳng
∆
đi qua điểm
A
, sao cho khoảng cách từ điểm
B
đến đường thẳng
∆
nhỏ nhất có phương trình là?
A.
3 50+−=xy
. B.
3 50− +=xy
.
C.
3 10+ −=
xy
. D.
3 10
− −=xy
.
Lời giải
Ta có
( )
1; 3= −

AB
.
Khoảng cách từ điểm
B
đến đường thẳng
∆
nhỏ nhất khi và chỉ khi
∆
đi qua
B
, suy ra véc-tơ

AB
là véc-tơ chỉ phương của
,∆
do đó đường thẳng
∆
có một véc-tơ pháp tuyến là
( )
3;1
∆

n
.
Vậy phương trình đường thẳng cần tìm là
( ) (
)
3 1 1 2 0 3 5 0.− + − =⇔ +−=x y xy
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( )
1; 2A
,
( )
5; 2B
,
( )
1; 3C −
có phương trình
là.
A.
22
6 10x y xy+ + + −=
. B.
22
6 10x y xy+ − − −=
.
C.
22
6 10x y xy+ − + −=
. D.
22
6 10x y xy+ + − −=
.
Lời giải
Gọi
( )
C
là phương trình đường tròn đi qua ba điểm
,,ABC
với tâm
( )
;I ab
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
( )
C⇒
có dạng:
22
22 0x y ax by c+ − − +=
. Vì đường tròn
( )
C
đi qua qua ba điểm
,,ABC
nên ta có hệ phương trình:
3
1424 0 24 5
1
25 4 10 4 0 10 4 29
2
1926 0 26 10
1
a
a bc a bc
a bc a bc b
a bc a bc
c
=
+− − += − − +=−


+− − +=⇔− − +=− ⇔ =−


+− + += − + +=−

= −
.
Vậy phương trình đường tròn cần tìm là
22
6 10x y xy+ − + −=
.
Câu 28: Cho đường thẳng
:3 4 19 0xy
∆ − −=
và đường tròn
( ) ( ) ( )
22
: 1 1 25Cx y− +− =
. Biết đường
thẳng
∆
cắt
(
)
C
tại hai điểm phân biệt
A
và
B
, khi đó độ dài đọan thẳng
AB
là
A. 6. B. 3. C. 4. D. 8.
Lời giải
Từ
(
)
3 19
:3 4 19 0 1
44
xy y x∆ − − =⇒= −
.
Thế
(
)
1
vào
( )
C
ta được
( )
2
2
3 23
1 25
44
xx

−+ − =


2
1
25 85 145
0.
29
16 8 16
5
x
xx
x
=
⇔ −+=⇔
=
+)
( )
1 4 1; 4 .
AA
xy A=⇒ =−⇒ −
+)
29 2 29 2
;.
5 5 55
BB
xyB

= ⇒ =−⇒ −


Độ dài đoạn thẳng
22
29 2
1 46
55
AB

= − +− + =


.
Câu 29: Cho của hypebol
( )
22
:1
16 9
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng
A.
8
. B.
6
. C.
4
. D.
5
.
Lời giải
Gọi
1
F
và
2
F
là hai tiêu điểm của
( ) ( )
22
22
: 1, 0, 0
xy
H ab
ab
−= > >
.
Điểm
( )
12
2M H MF MF a∈⇔ − =
.
Từ phương trình
( )
22
:1
16 9
xy
H −=
suy ra
( )
2
16 4, 0a aa= ⇒= >
.
Vậy hiệu các khoảng cách từ mỗi điểm
M
nằm trên
( )
H
đến hai tiêu điểm có giá trị tuyệt đối
là
12
28MF MF a−==
.
Câu 30: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món, 1 loại quả tráng
miệng trong 5 loại quả tráng miệng và một loại nước uống trong 3 loại nước uống. Có bao nhiêu
cách chọn thực đơn?
A. 100. B. 15. C. 75. D. 25.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
Lời giải
Chọn 1 món ăn trong 5 món: Có 5 cách chọn.
Chọn 1 loại quả tráng miệng trong 5 loại quả tráng miệng: Có 5 cách chọn.
Chọn 1 loại nước uống trong 3 loại nước uống: Có 3 cách chọn.
Theo quy tắc nhân, có 5.5.3 = 75 cách chọn thực đơn gồm 1 món ăn, 1 loại quả tráng miệng và
1 loại nước uống.
Câu 31: Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh
ngồi một ghế là
A.
6
10
C
. B.
6!
. C.
6
10
A
. D.
10
6
.
Lời giải
Mỗi cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh
ngồi một ghế là một chỉnh hợp chập 6 của 10.
Vậy số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học
sinh ngồi một ghế là
6
10
A
.
Câu 32: Mười hai đường thẳng có nhiều nhất bao nhiêu giao điểm?
A.
12
. B.
66
. C.
132
. D.
144
.
Lời giải
Để được nhiều giao điểm nhất thì mười hai đường thẳng này phải đôi một cắt nhau tại các điểm
phân biệt.
Như vậy có
2
12
66=C
.
Câu 33: Thầy X có
15
cuốn sách gồm
4
cuốn sách toán,
5
cuốn sách lí và
6
cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên
8
cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ
3
môn.
A.
5
6
. B.
661
715
. C.
660
713
. D.
6
7
.
Lời giải
Gọi A là biến cố “Số cuốn sách còn lại của thầy X có đủ 3 môn”, suy ra
A
là biến cố “Số cuốn
sách còn lại của thầy X không có đủ 3 môn”= “Thầy X đã lấy hết số sách của một môn học”.
Số phần tử của không gian mẫu là:
( )
n
Ω
8
15
C=
6435=
( )
44 53 62
4 11 5 10 6 9
...nA CC CC CC=++
486
=
( )
54
715
PA⇒=
( )
( )
1PA PA⇒=−
661
715
=
.
Câu 34: Một hộp chứa 11 viên bi được đánh số thứ tự từ 1 đến 11. Chọn ngẫu nhiên 3 viên bi rồi cộng
các số trên 3 viên bi đó với nhau. Xác suất để kết quả thu được là số chẵn bằng
A.
17
33
. B.
16
33
. C.
19
33
. D.
23
33
.
Lời giải
Không gian mẫu có số phần tử là:
3
11
()nCΩ=
.
Gọi A là biến cố: “Tổng các số trên 3 viên bi là số chẵn”
TH1: 3 viên bi được chọn đều được đánh số chẵn, có
3
5
C
cách chọn
TH2: 3 viên bi được chọn có 2 viên được đánh số lẻ và 1 viên được đánh số chẵn, có
21
65
.CC
Ta có:
3 21
5 65
) .(
nA C C C= +
Vậy xác suất cần tìm:
( )
( )
3 21
5 65
11
3
.
33
17
()
nA
C CC
PA
nC
= = =
Ω
+
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Câu 35: Một hộp chứa 5 bi xanh, 4 bi đỏ. Chọn ngẫu nhiên 2 bi từ hộp này. Xác suất để chọn được 2 bi
cùng màu là
A.
2
9
. B.
1
9
. C.
5
9
. D.
4
9
.
Lời giải
+ Số phần tử của không gian mẫu là:
( )
2
9
Ω=
nC
.
+ Gọi biến cố
A
: “ hai viên bi được chọn cùng màu”.
Ta có:
( )
22
54
= +nA C C
.
Vậy xác suất biến cố là
( )
(
)
( )
22
54
2
9
4
9
+
= = =
Ω
nA
CC
PA
nC
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu sô tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn và 3 chữ số lẻ?
Lời giải
Gọi
{ }
0;1; 2;3; 4;5;6;7;8;9A =
. Coi việc lập số có 6 chữ số như là sắp xếp các chữ số vào một
dãy 6 ô trống.
Có
3
5
C
cách lấy ra 3 chữ số lẻ và có
3
6
A
cách sắp xếp 3 chữ số này vào dãy 6 ô trống. Có
3
5
A
cách
sắp xếp 3 chữ số chẵn vào 3 ô trống còn lại. Như vậy có
333
565
. . 72000CAA=
dãy có 6 chữ số gồm
3 số chẵn, 3 số lẻ, kể cả trường hợp số 0 đứng đầu.
Xét trường hợp số 0 đứng đầu. Có
3
5
C
cách lấy ra 3 chữ số lẻ và có
3
5
A
cách sắp xếp 3 chữ số này
vào dãy 5 ô trống. Có
2
4
A
cách sắp xếp 2 chữ số chẵn vào 2 ô trống còn lại. Như vậy có
332
554
. . 7200CAA=
dãy có 6 chữ số có 0 đứng đầu, gồm 3 số chẵn, 3 số lẻ.
Từ đó có
72000 7200 64800−=
số thỏa mãn yêu cầu.
Câu 37: Trong mặt phẳng
(Oxy)
cho điểm
(2; 4)
M
và
13
:
2
xt
d
yt
= −
= +
.Viết phương trình đường thẳng song
song với đường thẳng
d
và cách điểm
M
một khoảng bằng
10
.
Lời giải
Xác định được véc tơ chỉ phương của đường thẳng
d
:
( 3;1)
d
u = −
Suy ra
: (1; 3)
d
VTTP n
=
Suy ra
: (1; 3)
d
VTTP n n
∆
= =

PT ĐT ∆ có dạng:
3 0, 7x yc c
+ + = ≠−
22
2 3.4
( , ) 10
13
c
dM
++
∆= =
+
4
14 10
24
c
c
c
= −
+= ⇔
= −
Vậy có 2 đường thẳng thỏa mãn :
3 40; 3 240xy xy+−= +−=
Câu 38: Cho tập hợp
{ }
0,1, 2,3, 4,5,6,7X =
. Gọi
S
là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một
khác nhau được lập từ tập hợp
X
. Chọn ngẫu nhiên một số từ
S
. Tính xác suất để chọn được
số chia hết cho 5.
Lời giải
Số các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ
X
là
( )
4
7
7. 5880nA
Ω= =
số.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Gọi A là biến cố chọn đượcsố chia hết cho
5
từ
S
.
Trường hợp 1: số có chữ số tận cùng bằng 5.
Khi đó, ta có
3
6
6.A
số thoả yêu cầu bài toán.
Trường hợp 2: số có chữ số tận cùng bằng 0.
Khi đó, ta có
4
7
A
số thoả yêu cầu bài toán.
Áp dụng quy tắc cộng ta có
(
)
34
67
6. 1560nA A A= +=
.
Suy ra xác suất của biến cố
A
là
( )
( )
( )
13
49
nA
PA
n
= =
Ω
.
Câu 39: Trong hệ trục tọa độ
Oxy
, cho Elip
(
)
22
:1
25 16
xy
E +=
,
12
,FF
là hai tiêu điểm, hoành độ của
1
F
âm. Điểm
M
thuộc
( )
E
sao cho
12
2MF MF=
. Hoành độ điểm
M
là:
Lời giải
Ta có
5a =
,
4b =
và
3c =
Với điểm
( ) ( )
00
;Mx y E∈
+)
(
)
12
21MF MF a+=
+)
( ) ( ) ( ) ( )
22 22
22
12 0 0 0
0 04MF MF x c y x c y cx

− = + +− − − +− =

mà
(
)
( )
22
1 2 212
1
MF MF MF MF MF MF−= − +
12 0
2
c
MF MF x
a
⇒−=
Từ và suy ra:
10
20
c
MF a x
a
c
MF a x
a
= +
= −
Nên theo yêu cầu bài toán ta có:
0 00
3 3 25
5 25
55 9
x xx

+ = − ⇒=


.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 06
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho hai véctơ
a
và
b
đều khác véctơ
0
. Khẳng định nào sau đây đúng?
A.
..ab a b=

. B.
( )
. . .cos ,ab a b a b
=

.
C.
( )
. . .cos ,ab ab a b=
 
. D.
( )
. . .sin ,
ab a b a b=

.
Câu 2: Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001.
A. 5,25. B. 5,24. C. 5,246. D. 5,2
Câu 3: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
160
178
150
164
168
176
156
172
Các tứ phân vị của mẫu số liệu là
A.
123
158; 164; 174
QQ Q= = =
. B.
123
158; 166; 174QQ Q= = =
.
C.
123
160; 168; 176QQQ= = =
. D.
123
150; 164; 178
QQQ= = =
.
Câu 4: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của Bình:
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu lần lượt là
A.
8R =
và
4
Q
∆=
. B.
10
R
=
và
3, 5
Q
∆=
.
C.
8
R =
và
3, 5
Q
∆=
. D.
10R =
và
4
Q
∆=
.
Câu 5: Chọn khẳng định đúng. Số liệu càng phân tán thì
A. Phương sai và độ lệch chuẩn càng lớn. B. Phương sai và độ lệch chuẩn càng nhỏ.
C. Phương sai và độ lệch chuẩn bằng nhau. D. Phương sai bằng số trung bình cộng.
Câu 6: Trong hệ tọa độ
Oxy
, cho
(
) ( ) (
)
2; 5 , 1; 1 , 3; 3A BC
. Tìm tọa độ đỉểm
E
sao cho
32AE AB AC
= −
  
A.
( )
3; 3−
. B.
( )
3; 3−
. C.
( )
3; 3−−
. D.
( )
2; 3−−
.
Câu 7: Bạn A đo chiều dài của một sân bóng ghi được
250 0,2m±
. Bạn B đo chiều cao của một cột cờ
được
15 0,1m±
. Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong
phép đo của bạn đó là bao nhiêu?
A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.
B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.
C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.
D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%.
Câu 8: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn
vị:
C
°
). Phương sai và độ lệch chuẩn của mẫu số liệu là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
A.
2
7,61; 2,76SS= ≈
B.
2
7; 2, 646= ≈SS
.
C.
2
7,7; 2,775= ≈SS
. D.
2
7,52; 2,742= ≈SS
.
Câu 9: Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5M −
và có vectơ chỉ phương
( )
1; 3u = −
là
A.
( )
2
53
xt
t
yt
= −
∈
=−+
. B.
( )
23
5
xt
t
yt
= +
∈
=−−
. C.
( )
12
35
xt
t
yt
=−+
∈
= −
. D.
( )
15
32
xt
t
yt
=
−−
∈
= +
.
Câu 10: Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
( )
3 ; 1A −
và
( )
1 ; 5B
A.
3 8 0xy−− =
B.
3 8 0xy+−=
C.
3 8 0xy−−− =
D.
3 8 0xy−+=
Câu 11: Tính góc giữa hai đường thẳng
1
: 2 10 0d xy−− =
và
2
: 3 9 0.dx y− +=
A.
o
30 .
B.
o
45 .
C.
o
60 .
D.
o
135 .
Câu 12: Cho 2 đường thẳng
( )
2
1
: 14 0d mx m y m− − +− =
và
( )
2
: 3 3 10d m xy m+ + − −=
. Tìm giá trị
của
m
để hai đường thẳng vuông góc với nhau.
A.
2
. B.
0
. C.
1
. D.
1−
.
Câu 13: Trong mặt phẳng với hệ tọa độ
,Oxy
phương trình nào sau đây là phương trình đường tròn?
A.
22
2 4 2 10x y xy+ − + −=
. B.
22
60xy+ +=
.
C.
22
4 2 10 0x y xy y+− −+=
. D.
22
4 6 12 0xy xy+− +−=
.
Câu 14: Đường tròn
( )
C
có tâm
( )
2;3I −
và đi qua
( )
2; 3M −
có phương trình là:
A.
( ) ( )
22
2 3 52xy+ +− =
.
B.
( ) ( )
22
2 3 52xy+ +− =
.
C.
22
4 6 57 0xy xy++−−=
.
D.
22
4 6 39 0xy xy+++−=
.
Câu 15: Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A.
2
2xy=
. B.
2
6yx=
. C.
2
4yx= −
. D.
2
8yx= −
.
Câu 16: Tổ 1 của lớp 10a1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1 bạn
học sinh của tổ 1 đi trực vệ sinh. Hỏi có bao nhiêu cách chọn.
A.
15
. B.
5
3
. C.
8
. D.
3
5
Câu 17: Bình có cái áo khác nhau, 4 chiếc quần khác nhau, 3 đôi giầy khác nhau và 2 chiếc mũ khác
nhau. Số cách chọn một bộ gồm quần, áo, giầy và mũ của Bình là
A. 120. B. 60. C. 5. D. 14.
Câu 18: Số cách sắp xếp
3
học sinh nam và
2
học sinh nữ vào một bàn dài có
5
ghế ngồi là
A.
3!.2!
. B.
5!
. C.
3!.2!.2!
. D.
5
.
Câu 19: Số chỉnh hợp chập
2
của
5
phần tử bằng
5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
A.
120
. B.
7
. C.
10
. D.
20
.
Câu 20: Một tổ có
6
học sinh nam và
9
học sinh nữ. Hỏi có bao nhiêu cách chọn
6
học sinh đi lao động,
trong đó có đúng
2
học sinh nam?
A.
24
69
.
CC
+
B.
24
69
..CC
C.
24
69
..AA
D.
24
96
..CC
Câu 21: Viết khai triển theo công thức nhị thức Niu-tơn
( )
5
2
xy−
.
A.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y−+ − + −
. B.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y−− − − +
.
C.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y++ + + +
. D.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y+− + − +
.
Câu 22: Từ một hộp chứa sáu quả cầu trắng và ba quả cầu đen, lấy ngẫu nhiên đồng thời ba quả. Tính xác
suất sao cho lấy được ba quả cùng màu
A.
1
. B.
1
4
. C.
3
. D.
4
.
Câu 23: Từ một hộp chứa
15
quả cầu gồm
10
quả màu đỏ và
5
quả màu xanh, lấy ngẫu nhiên đồng thời
hai quả. Xác suất để lấy được hai quả có màu khác nhau là
A.
10
21
. B.
2
21
. C.
1
7
. D.
3
7
.
Câu 24: Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết
cho 3 bằng
A.
3
20
. B.
1
20
. C.
1
3
. D.
3
10
.
Câu 25: Cho 2 điểm
( )
1;2 , (3;4).AB
Viết phương trình tổng quát đường trung trực của đoạn thẳng
AB
.
A.
5 0.
xy++=
B.
5 0.xy
−−=
C.
2 2 5 0.xy+ −=
D.
5 0.xy
+−=
Câu 26: Trong mặt phẳng
Oxy
, đường thẳng
∆
song song với đường thẳng
: 2 50dx y− +=
và cách
điểm
(1; 2)M −
một khoảng bằng
25
có phương trình là
A.
2 15 0xy− −=
. B.
2 15 0xy− −=
hoặc
2 50xy
− +=
.
C.
2 10 0xy−+=
. D.
2 10 0xy
−−=
hoặc
2 10 0
xy−+=
.
Câu 27: Trong hệ trục tọa độ
Oxy
, cho đường tròn
( )
C
đi qua hai điểm
( ) ( )
1; 2 , 3, 4AB
và tiếp xúc với
đường thẳng
:3 3 0
xy∆ +−=
, biết tâm của
( )
C
có tọa độ là những số nguyên. Phương trình
đường tròn
( )
C
là
A.
22
3 7 12 0.xy xy
B.
22
6 4 5 0.xy xy

C.
22
8 2 7 0.xy xy 
D.
22
2 8 20 0.
xy xy
Câu 28: Trong mặt phẳng tọa độ
Oxy
cho đường tròn
( )
C
có tâm
(
)
1; 1I −
bán kính
5R =
. Biết rằng
đường thẳng
( )
:3 4 8 0dxy− +=
cắt đường tròn
( )
C
tại hai điểm phân biệt
,AB
. Tính độ dài
đoạn thẳng
AB
.
A.
8AB
=
. B.
4AB =
. C.
3.AB =
. D.
6AB
=
.
Câu 29: Phương trình chính tắc của elip đi qua điểm
(
)
5; 0
và có tiêu cự bằng
25
là
A.
22
1
25 5
+=
xy
. B.
22
1
25 20
+=
xy
. C.
22
1
25 5
−=
xy
. D.
22
1
25 20
−=
xy
.
Câu 30: Có
9
cặp vợ chồng đi dự tiệc. Chọn một người đàn ông và một người phụ nữ trong bữa tiệc sao
cho hai người đó không là vợ chồng. Số cách chọn là
A.
81
. B.
64
. C.
9
. D.
72
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Câu 31: Lớp
8
12A
có
32
học sinh. Giáo viên chủ nhiệm muốn lập một ban cán sự của lớp gồm một lớp
trưởng, một bí thư, một lớp phó học tập và một lớp phó văn thể. Số cách lập nhóm ban cán sự là
A.
4
28
A
. B.
4!
. C.
4
32
A
. D.
4
32
C
.
Câu 32: Số đường chéo của đa giác đều có 20 cạnh là:
A. 170. B. 190. C. 360. D. 380.
Câu 33: Để kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để phân
tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là
A.
3
11
. B.
1
110
. C.
3
55
. D.
1
22
.
Câu 34: Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên đồng thời
3
quả. Xác suất để lấy được
3
quả màu đỏ bằng:
A.
5
.
12
B.
2
.
7
C.
7
44
D.
1
.
22
Câu 35: Một hộp phấn có 4 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên đồng thời 2 viên phấn
từ hộp trên. Tính xác suất để lấy được 2 viên phấn xanh.
A.
4
7
. B.
3
7
. C.
1
7
. D.
2
7
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có hai học sinh lớp
,A
ba học sinh lớp
B
và bốn học sinh lớp
C
xếp thành một hàng ngang sao
cho giữa hai học sinh lớp
A
không có học sinh nào lớp
.B
Hỏi có bao nhiêu cách xếp hàng như
vậy?
Câu 37: Trên mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có tọa độ các đỉnh là
( )
2;3A
,
( )
5;0B
và
( )
1;0C −
.Tìm tọa độ điểm
M
thuộc cạnh
BC
sao cho diện tích tam giác
MAB
bằng hai lần
diện tích tam giác
MAC
.
Câu 38: Một lớp có 35 đoàn viên trong đó có 15 nam và 20 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp
để tham dự hội trại 26 tháng 3. Tính xác suất để trong 3 đoàn viên được chọn có cả nam và nữ.
Câu 39: Cho parabol
2
( ): 4Py x=
và hai điểm
(0; 4), ( 6;4)AB−−
.
C
là điểm trên
()P
sao cho tam giác
ABC
có diện tích bé nhất. Tìm tọa độ điểm
C
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho hai véctơ
a
và
b
đều khác véctơ
0
. Khẳng định nào sau đây đúng?
A.
..ab a b=

. B.
( )
. . .cos ,ab a b a b=

.
C.
( )
. . .cos ,ab ab a b=
 
. D.
( )
. . .sin ,ab a b a b
=

.
Lời giải
Theo định nghĩa tích vô hướng của hai véctơ.
Câu 2: Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001.
A. 5,25. B. 5,24. C. 5,246. D. 5,2
Giải
Vì độ chính xác đến hàng phần nghìn nên ta quy tròn a đến hàng phần trăm, vậy số quy tròn của
a là 5,25.
Câu 3: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
160
178
150
164
168
176
156
172
Các tứ phân vị của mẫu số liệu là
A.
123
158; 164; 174QQ Q= = =
. B.
123
158; 166; 174QQ Q= = =
.
C.
123
160; 168; 176QQQ= = =
. D.
123
150; 164; 178QQQ= = =
.
Lời giải
Sắp xếp các giá trị này theo thứ tự không giảm
150
156
160
164
168
172
176
178
Vì
8
n =
là số chẵn nên
2
Q
là số trung bình cộng của hai giá trị chính giữa:
( )
2
164 168 : 2 166Q =+=
Ta tìm
1
Q
là trung vị của nửa số liệu bên trái
2
Q
150
156
160
164
và tìm được
( )
1
156 160 : 2 158Q =+=
Ta tìm
3
Q
là trung vị của nửa số liệu bên phải
2
Q
168
172
176
178
và tìm được
( )
3
172 176 : 2 174Q =+=
.
Câu 4: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của Bình:
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu lần lượt là
A.
8R =
và
4
Q
∆=
. B.
10R
=
và
3, 5
Q
∆=
.
C.
8R =
và
3, 5
Q
∆=
. D.
10R
=
và
4
Q
∆=
.
Lời giải
Sắp xếp mẫu số liệu theo thứ tự không giảm:
Khoảng biến thiên:
14 6 8R = −=
.
Mẫu số liệu có 16 giá trị nên ta có
2
9 10
9,5
2
Q
+
= =
;
1
88
8
2
Q
+
= =
và
3
11 12
11, 5
2
Q
+
= =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Vậy khoảng tứ phân vị là
31
11,5 8 3,5
Q
QQ∆= − = −=
.
Câu 5: Chọn khẳng định đúng. Số liệu càng phân tán thì
A. Phương sai và độ lệch chuẩn càng lớn. B. Phương sai và độ lệch chuẩn càng nhỏ.
C. Phương sai và độ lệch chuẩn bằng nhau. D. Phương sai bằng số trung bình cộng.
Lời giải
Dựa vào khái niệm.
Câu 6: Trong hệ tọa độ
Oxy
, cho
(
) ( ) ( )
2; 5 , 1; 1 , 3; 3A BC
. Tìm tọa độ đỉểm
E
sao cho
32AE AB AC= −
  
A.
( )
3; 3
−
. B.
( )
3; 3−
. C.
( )
3; 3−−
. D.
( )
2; 3−−
.
Lời giải
Chọn C
Gọi
( )
; Exy
.
Ta có
( )
32 2 2
AE AB AC AE AB AB AC BE CB= − ⇔−= − ⇔=
        
( ) ( )
14 3
1; 1 2 2; 2
14 3
xx
xy
yy
−=− =−

− −= − − ⇔ ⇔

−=− =−

Vậy
(
)
3; 3E
−−
.
Câu 7: Bạn A đo chiều dài của một sân bóng ghi được
250 0,2m±
. Bạn B đo chiều cao của một cột cờ
được
15 0,1m±
. Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong
phép đo của bạn đó là bao nhiêu?
A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.
B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.
C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.
D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%.
Giải
Phép đo của bạn A có sai số tương đối
1
0, 2
0,0008 0,08%
250
δ
≤= =
Phép đo của bạn B có sai số tương đối
2
0,1
0,0066 0,66%
15
δ
≤= =
Như vậy phép đo của bạn A có độ chính xác cao hơn.
Câu 8: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn
vị:
C
°
). Phương sai và độ lệch chuẩn của mẫu số liệu là
A.
2
7,61; 2,76SS= ≈
B.
2
7; 2, 646= ≈SS
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
C.
2
7,7; 2,775= ≈
SS
. D.
2
7,52; 2,742= ≈
SS
.
Lời giải
Dùng máy tính.
Câu 9: Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5M −
và có vectơ chỉ phương
( )
1; 3u = −
là
A.
( )
2
53
xt
t
yt
= −
∈
=−+
. B.
( )
23
5
xt
t
yt
= +
∈
=−−
.
C.
( )
12
35
xt
t
yt
=−+
∈
= −
. D.
( )
15
32
xt
t
yt
=−−
∈
= +
.
Lời giải
Phương trình tham số của đường thẳng đi qua điểm
( )
2; 5M −
và có vectơ chỉ phương
( )
1; 3u = −
có dạng là
( )
2
53
xt
t
yt
= −
∈
=−+
Câu 10: Viết phương trình tổng quát của đường thẳng đi qua 2 điểm
( )
3 ; 1A −
và
( )
1 ; 5B
A.
3 8 0xy−− =
B.
3 8 0
xy
+−=
C.
3 8 0xy−−− =
D.
3 8 0xy−+=
Lời giải
đường thẳng đi qua 2 điểm
( )
3 ; 1
A −
và
( )
1 ; 5B
có véc tơ chỉ phương là
( ) ( ) ( )
(
)
; 3 2;6 6; 2 2 3 1
3 3 10
8 0A yB
x
xn
y
=− ⇒= = ⇔ −−
⇒ − +=
=
+

Câu 11: Tính góc giữa hai đường thẳng
1
: 2 10 0
d xy−− =
và
2
: 3 9 0.dx y− +=
A.
o
30 .
B.
o
45 .
C.
o
60 .
D.
o
135 .
Lời giải
Ta có
(
)
( )
( )
( ) (
)
( ) ( )
12
;
22
2
1
2
1
22
2.1 1 . 3
1
2
0
2
: 2 10 0 2; 1
cos
: 3 9 1;
.1 3
3
1
dd
d
n
xy
dy
n
x
ϕ
ϕ
=
+
−− =→ = −
→
− +=→ =
−−
= =
+−
−
+−
45 .
ϕ
→=
Câu 12: Cho 2 đường thẳng
( )
2
1
: 14 0d mx m y m− − +− =
và
( )
2
: 3 3 10
d m xy m+ + − −=
. Tìm giá trị
của
m
để hai đường thẳng vuông góc với nhau.
A.
2
. B.
0
. C.
1
. D.
1−
.
Lời giải
Điều kiện:
( )
2
2
10mm+− + ≠
và
( )
2
3 10m + +≠
.
Véc tơ pháp tuyến của
1
d
là
(
)
1
;1n mm= −+

.
Véc tơ pháp tuyến của
2
d
là
( )
2
3;1nm= +

.
Hai đường thẳng vuông góc khi và chỉ khi
12
.0nn =

( ) ( )
3 10mm m⇔ + +− + =
( )
2
10 1mm⇔ + =⇔=−
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Câu 13: Trong mặt phẳng với hệ tọa độ
,Oxy
phương trình nào sau đây là phương trình đường tròn?
A.
22
2 4 2 10x y xy+ − + −=
. B.
22
60xy+ +=
.
C.
22
4 2 10 0x y xy y+− −+=
. D.
22
4 6 12 0xy xy+− +−=
.
Lời giải
Phương án A loại vì hệ số của
2
x
và
2
y
không bằng nhau.
Phương án B loại vì
22
60abc+ − =−<
.
Phương án C loại vì có số hạng chứa
xy
.
Phương án D nhận vì phương trình
( ) ( )
22
22
4 6 12 0 2 3 25xy xy x y+− + −=⇔− ++ =
là pt
đường tròn có tâm
( )
2; 3I −
, bán kính
5R =
.
Câu 14: Đường tròn
( )
C
có tâm
( )
2;3I −
và đi qua
( )
2; 3M −
có phương trình là:
A.
( ) ( )
22
2 3 52xy+ +− =
.
B.
( ) ( )
22
2 3 52xy+ +− =
.
C.
22
4 6 57 0xy xy++−−=
.
D.
22
4 6 39 0xy xy+++−=
.
Lời giải
( )
2
2
4 6 52R IM= = +− =

.
Phương trình đường tròn tâm
( )
2;3I −
,
52R =
là:
( ) ( )
22
2 3 52.xy+ +− =
Câu 15: Phương trình nào sau đây là phương trình chính tắc của đường parabol?
A.
2
2xy=
. B.
2
6yx=
. C.
2
4yx= −
. D.
2
8yx= −
.
Câu 16: Tổ 1 của lớp 10a1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1 bạn
học sinh của tổ 1 đi trực vệ sinh. Hỏi có bao nhiêu cách chọn.
A.
15
. B.
5
3
. C.
8
. D.
3
5
Lời giải
Th1: Chọn 1 học sinh nam có 3 cách chọn
Th2: Chọn 1 học sinh nữ có 5 cách chọn
Vậy có
35 8
cách chọn.
Câu 17: Bình có cái áo khác nhau, 4 chiếc quần khác nhau, 3 đôi giầy khác nhau và 2 chiếc mũ khác
nhau. Số cách chọn một bộ gồm quần, áo, giầy và mũ của Bình là
A. 120. B. 60. C. 5. D. 14.
Lời giải
Để chọn được bộ quần áo theo yêu cầu bài toán phải thực hiện liên tiếp các hành động:
+ Hành động 1: Chọn chiếc áo: Có 5 cách chọn.
+ Hành động 2: Chọn chiếc quần: Có 4 cách chọn.
+ Hành động 3: Chọn đôi giầy: Có 3 cách chọn.
+ Hành động 4: Chọn chiếc mũ: Có 2 cách chọn.
Vậy theo qui tắc nhân, có
5.4.3.2 120=
cách chọn.
Câu 18: Số cách sắp xếp
3
học sinh nam và
2
học sinh nữ vào một bàn dài có
5
ghế ngồi là
A.
3!.2!
. B.
5!
. C.
3!.2!.2!
. D.
5
.
Lời giải
Mỗi cách xếp
3
học sinh nam và
2
học sinh nữ vào một bàn dài có
5
ghế ngồi là 1 hoán vị của
5 phần tử. Vậy có
5!
cách sắp xếp.
Câu 19: Số chỉnh hợp chập
2
của
5
phần tử bằng
A.
120
. B.
7
. C.
10
. D.
20
.
5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Lời giải
Số chỉnh hợp chập
2
của
5
phần tử là
2
5
20
A
=
.
Câu 20: Một tổ có
6
học sinh nam và
9
học sinh nữ. Hỏi có bao nhiêu cách chọn
6
học sinh đi lao động,
trong đó có đúng
2
học sinh nam?
A.
24
69
.
CC
+
B.
24
69
..CC
C.
24
69
..AA
D.
24
96
..CC
Lời giải
Trong 6 học sinh phải có
2
học sinh nam và
4
học sinh nữ.
+ Chọn
2
học sinh nam có
2
6
C
cách.
+ Chọn
4
học sinh nữ có
4
9
C
cách.
Theo quy tắc nhân, ta có
24
69
.CC
cách chọn thỏa mãn yêu cầu.
Câu 21: Viết khai triển theo công thức nhị thức Niu-tơn
( )
5
2
xy−
.
A.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y−+ − + −
. B.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y−− − − +
.
C.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y++ + + +
. D.
10 8 62 43 24 5
5 10 10 5x xy xy xy xy y+− + − +
.
Lời giải
Ta có:
(
)
(
) (
)
( ) (
) (
) ( )
5
5
1 2 3 45
2 2 010182634425
55 5 5 5 5
x y x y Cx Cx y Cx y Cx y Cx y C y

− = +− = + −+ −+ −+ −+ −

Hay
( )
5
2 10 8 62 43 24 5
5 10 10 5
x y x xy xy xy xy y
−=− + − + −
.
Câu 22: Từ một hộp chứa sáu quả cầu trắng và ba quả cầu đen, lấy ngẫu nhiên đồng thời ba quả. Tính xác
suất sao cho lấy được ba quả cùng màu
A.
1
. B.
1
4
. C.
3
. D.
4
.
Lời giải
Gọi A là biến cố “lấy ba quả cầu cùng màu”.
Ta có
( )
3
9
84nCΩ= =
.
Lấy ba quả cầu cùng màu:
( )
33
63
21nA C C=+=
.
Xác suất lấy được ba quả cầu cùng màu là
() 1
()
() 4
nA
PA
n
= =
Ω
.
Câu 23: Từ một hộp chứa
15
quả cầu gồm
10
quả màu đỏ và
5
quả màu xanh, lấy ngẫu nhiên đồng thời
hai quả. Xác suất để lấy được hai quả có màu khác nhau là
A.
10
21
. B.
2
21
. C.
1
7
. D.
3
7
.
Lời giải
Không gian mẫu
Ω
: “lấy hai quả bất kì”
( )
2
15
nC⇒ Ω=
.
Biến cố
A
: “lấy hai quả có màu khác nhau”
( )
10.5 50nA⇒==
.
Vậy
(
)
( )
( )
10
21
nA
PA
n
= =
Ω
.
Câu 24: Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết
cho 3 bằng
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
A.
3
20
. B.
1
20
. C.
1
3
. D.
3
10
.
Lời giải
20n
3;6;9;12;15;18 6A nA 
63
20 10
nA
PA
n

Câu 25: Cho 2 điểm
( )
1;2 , (3;4).AB
Viết phương trình tổng quát đường trung trực của đoạn thẳng
AB
.
A.
5 0.
xy++=
B.
5 0.xy−−=
C.
2 2 5 0.
xy+ −=
D.
5 0.
xy+−=
Lời giải
+ Giả sử
∆
là đường trung trực của
AB
AB⇒∆⊥
tại trung điểm
M
của
AB
.
+ Tọa độ trung điểm
M
của
AB
là :
( )
2
2
2;3
3
2
AB
M
AB
M
xx
x
M
yy
y
+
= =
⇒
+
= =
.
+ Ta có
(
) ( ) ( )
2; 2 2 1;1 1;1AB n
∆
= = ⇒=
 
Suy ra phương trình tổng quát đường trung trực
∆
của đoạn thẳng
AB
là:
5 0.xy
+−=
Câu 26: Trong mặt phẳng
Oxy
, đường thẳng
∆
song song với đường thẳng
: 2 50dx y
− +=
và cách
điểm
(1; 2)M
−
một khoảng bằng
25
có phương trình là
A.
2 15 0xy− −=
. B.
2 15 0
xy− −=
hoặc
2 50xy− +=
.
C.
2 10 0xy−+=
. D.
2 10 0xy
−−=
hoặc
2 10 0xy
−+=
.
Lời giải
Vì
∆
song song với
: 2 50dx y
− +=
nên phương trình của
∆
có dạng:
( )
2 05x yc c− += ≠
Theo đề:
( )
14
;
5
c
dM
++
∆=
25=
⇔
5 10c+=
⇔
5 10
5 10
c
c
+=
+=−
⇔
( )
( )
5
15
cl
cn
=
= −
Vậy phương trình đường thẳng
∆
là:
2 15 0xy− −=
Câu 27: Trong hệ trục tọa độ
Oxy
, cho đường tròn
( )
C
đi qua hai điểm
( ) ( )
1; 2 , 3, 4AB
và tiếp xúc với
đường thẳng
:3 3 0xy∆ +−=
, biết tâm của
( )
C
có tọa độ là những số nguyên. Phương trình
đường tròn
( )
C
là
A.
22
3 7 12 0.xy xy
B.
22
6 4 5 0.xy xy

C.
22
8 2 7 0.xy xy

D.
22
2 8 20 0.
xy xy
Lời giải
Ta có :
(2; 2)AB =

; đoạn
AB
có trung điểm
( )
2;3M
⇒
Phương trình đường trung trực của đoạn
AB
là
: 50dx y+−=
.
Gọi
I
là tâm của
( )
C
Id⇒∈
( )
;5 , .Ia a a⇒ −∈
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Ta có:
( ) ( ) ( )
(
)
22
22
; 1 3 4 4;1 , 10.
10
a
R IA d I a a a I R
+
= = ∆= − + − = ⇔ = ⇒ =
Vậy phương trình đường tròn là:
( ) ( )
22
22
4 1 10 8 2 7 0.x y xy xy− + − = ⇔ + − − +=
Câu 28: Trong mặt phẳng tọa độ
Oxy
cho đường tròn
( )
C
có tâm
( )
1; 1
I −
bán kính
5R
=
. Biết rằng
đường thẳng
( )
:3 4 8 0dxy
− +=
cắt đường tròn
( )
C
tại hai điểm phân biệt
,AB
. Tính độ dài
đoạn thẳng
AB
.
A.
8AB =
. B.
4AB =
. C.
3.AB =
. D.
6AB =
.
Lời giải
Gọi
H
là trung điểm của đoạn thẳng
AB
. Ta có
IH AB⊥
và
(
)
(
)
(
)
2
2
3.1 4. 1 8
;3
34
IH d I AB
− −+
= = =
+−
.
Xét tam giác vuông
ta có:
2 2 2 22
5 3 16HA IA IH= − =−=
4 28HA AB HA⇒=⇒= =
Câu 29: Phương trình chính tắc của elip đi qua điểm
(
)
5; 0
và có tiêu cự bằng
25
là
A.
22
1
25 5
+=
xy
. B.
22
1
25 20
+=
xy
. C.
22
1
25 5
−=
xy
. D.
22
1
25 20
−=
xy
.
Lời giải
Phương trình chính tắc của elip có dạng
( )
22
22
1 0+ = >>
xy
ab
ab
.
Ta có
2
2
2
2 22 2
25
1
25
2 25 5
20
=
=
= ⇒=


=−=
a
a
cc
b ac b
.
Vậy elip có phương trình chính tắc là
22
1
25 20
+=
xy
.
Câu 30: Có
9
cặp vợ chồng đi dự tiệc. Chọn một người đàn ông và một người phụ nữ trong bữa tiệc sao
cho hai người đó không là vợ chồng. Số cách chọn là
A.
81
. B.
64
. C.
9
. D.
72
.
Lời giải
Chọn
1
người đàn ông trong
9
người đàn ông: có
9
cách.
Chọn
1
người phụ nữ trong
8
người phụ nữ không là vợ của người đàn ông đã chọn: có
8
cách
Theo quy tắc nhân: có
9.8 72=
cách chọn.
H
I
A
B
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Câu 31: Lớp
8
12A
có
32
học sinh. Giáo viên chủ nhiệm muốn lập một ban cán sự của lớp gồm một lớp
trưởng, một bí thư, một lớp phó học tập và một lớp phó văn thể. Số cách lập nhóm ban cán sự là
A.
4
28
A
. B.
4!
. C.
4
32
A
. D.
4
32
C
.
Lời giải
Mỗi cách chọn
4
học sinh từ
32
học sinh của lớp
8
12A
và phân
4
nhiệm vụ: Lớp trưởng, bí
thư, lớp phó học tập và lớp phó văn thể là một chỉnh hợp chập
4
của
32
phần tử.
Số cách chọn
4
học sinh từ
32
học sinh của lớp
8
12A
và phân
4
nhiệm vụ: Lớp trưởng, bí
thư, lớp phó học tập và lớp phó văn thể là số chỉnh hợp chập
4
của
32
phần tử.
Vậy số cách lập nhóm ban cán sự là
4
32
A
.
Câu 32: Số đường chéo của đa giác đều có 20 cạnh là:
A. 170. B. 190. C. 360. D. 380.
Lời giải
Đa giác đều có 20 cạnh nên có 20 đỉnh.
Từ 20 đỉnh của đa giác ta xác định được
2
20
C
đoạn thẳng.
Qua 2 đỉnh bất kì của đa giác ta luôn xác định được một đoạn thẳng có thể là đường chéo hoặc là
cạnh của đa giác đó.
Vậy số đường chéo của đa giác đều có 20 cạnh là
2
20
20 170C −=
.
Câu 33: Để kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để phân
tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là
A.
3
11
. B.
1
110
. C.
3
55
. D.
1
22
.
Lời giải
Tổng số hộp sữa được gửi đến để kiểm nghiệm là 12 hộp sữa.
Chọn ngẫu nhiên 3 hộp sữa từ 12 hộp sữa thì mỗi một cách chọn là một tổ hợp chập 3 của 12
phần tử. Các trường hợp đồng khả năng xảy ra.
Số phần tử của không gian mẫu là:
( )
3
12
220
nCΩ= =
.
Biến cố
A
: “3 hộp sữa được chọn có cả 3 loại”.
Như vậy sẽ chọn 1 hộp sữa cam, 1 hộp sữa dâu và 1 hộp sữa nho.
Số phần tử của biến cố
A
là:
( )
3.4.5 60nA= =
.
Xác suất của biến cố
A
là:
( )
( )
( )
60 3
220 11
nA
PA
n
= = =
Ω
.
Câu 34: Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên đồng thời
3
quả. Xác suất để lấy được
3
quả màu đỏ bằng:
A.
5
.
12
B.
2
.
7
C.
7
44
D.
1
.
22
Lời giải
Xác suất để lấy được
3
quả màu đỏ bằng:
( )
( )
( )
3
5
3
12
1
.
22
nA
C
PA
n
C
= = =
Ω
Câu 35: Một hộp phấn có 4 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên đồng thời 2 viên phấn
từ hộp trên. Tính xác suất để lấy được 2 viên phấn xanh.
A.
4
7
. B.
3
7
. C.
1
7
. D.
2
7
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Lời giải
Số phần tử của không gian mẫu là
( )
2
7
21nCΩ= =
.
Gọi
A
là biến cố: “ Chọn được 2 viên phấn xanh”.
Số phần tử của biến cố
A
là
(
)
2
3
3nA C= =
.
Vậy xác suất chọn được 2 viên phấn xanh từ hộp trên là
( )
( )
( )
31
21 7
nA
PA
n
= = =
Ω
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có hai học sinh lớp
,A
ba học sinh lớp
B
và bốn học sinh lớp
C
xếp thành một hàng ngang sao
cho giữa hai học sinh lớp
A
không có học sinh nào lớp
.B
Hỏi có bao nhiêu cách xếp hàng như
vậy?
Lời giải
Xếp
3
học sinh lớp
B
có
3!
cách xếp
1
B
2
B
3
B
4
Để giữa hai học sinh lớp
A
không có học sinh nào lớp
B
thì cả hai học sinh lớp
A
cùng được
xếp vào một vị trí trong 4 vị trí được đánh số ở trên nên có
2!.4
cách xếp
Xếp
4
học sinh lớp
C
vào cạnh các học sinh trên có
4
9
A
cách.
Theo QTN có
4
9
3!.2!.4. 145152A =
cách xếp thỏa đề.
Câu 37: Trên mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có tọa độ các đỉnh là
( )
2;3
A
,
( )
5;0B
và
( )
1;0C −
.Tìm tọa độ điểm
M
thuộc cạnh
BC
sao cho diện tích tam giác
MAB
bằng hai lần
diện tích tam giác
MAC
.
Lời giải
Ta có
( )
1
,.
2
ABM
S d A BM BM
∆
=
,
( )
1
,.
2
ACM
S d A CM CM
∆
=
.
Theo bài ra ta có diện tích tam giác
MAB
bằng hai lần diện tích tam giác
MAC
.
( ) ( )
11
,. 2. ,.
22
d A BM BM d A CM CM
⇒=
.
Mà
( ) ( )
( )
,,,dABM dACM dABC
= =
nên ta có
2.BM CM
=
.
Gọi
( )
;M xy
thuộc cạnh
BC
2
3
BM BC⇒=
 
.
Ta có
( )
5;BM x y= −

,
( )
6;0BC = −

( )
1
1; 0
0
x
M
y
=
⇒⇒
=
.
Câu 38: Một lớp có 35 đoàn viên trong đó có 15 nam và 20 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp
để tham dự hội trại 26 tháng 3. Tính xác suất để trong 3 đoàn viên được chọn có cả nam và nữ.
Lời giải
Ta có: Gọi A là biến cố “trong 3 đoàn viên được chọn có cả nam và nữ”
Số cách chọn 3 đoàn viên trong 35 đoàn viên để tham dự đại hội là:
3
35
C
Vậy
=
3
35
C
Trường hợp 1: trong 3 đoàn viên được chọn có 1 nam và 2 nữ có:
12
15 20
.CC
Trường hợp 2: trong 3 đoàn viên được chọn có 2 nam và 1 nữ có:
21
15 20
.CC
Vậy số cách chọn 3 đoàn viên có đủ cả nam và nữ là
12
15 20
.CC
+
21
15 20
.CC
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
( )
1 2 21
15 20 15 20
..nA CC CC= +
Xác suất để trong 3 đoàn viên được chọn có cả nam và nữ là:
( )
( )
( )
1 2 21
15 20 15 20
3
35
90
Ω 119
..
nA
CC C
P
C
nC
A =
+
= =
.
Câu 39: Cho parabol
2
( ): 4Py x
=
và hai điểm
(0; 4), ( 6;4)AB−−
.
C
là điểm trên
()
P
sao cho tam giác
ABC
có diện tích bé nhất. Tìm tọa độ điểm
C
.
Lời giải
( )
6;8AB = −

, suy ra vectơ pháp tuyến của đường thẳng
AB
là
(
)
4;3n
=
. Phương trình đường
thẳng
AB
là
4 3 12 0xy++=
.
Ta có
1
.
2
ABC
S CH AB=
. Do
AB
không đổi nên
ABC
S
nhỏ nhất
CH
⇔
nhỏ nhất.
Gọi
( )
();C xy P∈
, ta có:
( )
2
2
2
3 12
4 3 12
0
55
1 1 3 39
3 12
2
3
5 54
9
2
yy
xy
CH
yy y
++
++
= =


= ++ = + +



≥


Dấu
""=
xảy ra
3 39
0
2 2 16
yx
y +=⇔=−⇒=⇔
Do đó điểm
)
9
;
16
(
3
2
C P

−

∈

thì diện tích tam giác
ABC
nhỏ nhất.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 07
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho hình bình hành
ABCD
biết
( )
2;1A
,
( )
2; 1 ,B −
( )
2; 3C −−
. Tọa độ
giao điểm hai đường chéo của hình bình hành
ABCD
là
A.
( )
2;0
. B.
( )
2; 2
. C.
( )
0; 2
−
. D.
( )
0; 1
−
.
Câu 2: Quy tròn số
12,4567
đến hàng phần trăm ta được số.
A.
12,45
. B.
12,46
C.
12,457
D.
12,5
Câu 3: Tìm tứ phân vị của mẫu số liệu sau
3 4 6 7 8 9 10 12 13 16
A.
12 3
5, 8,5, 12QQ Q= = =
. B.
12 3
6, 8,5, 12QQ Q= = =
.
C.
12 3
6, 8,5, 12,5QQ Q
= = =
. D.
12 3
5, 8,5, 12, 5
QQ Q
= = =
.
Câu 4: Mẫu số liệu sau đây cho biết giá của một số loại giày trong cửa hàng
300 250300 360 350 650 450 500 300
Khoảng biến thiên của mẫu số liệu trên là
A.
400
. B.
300
. C.
650
. D.
250
.
Câu 5: Cho dãy số liệu thống kê:
1, 2,3, 4,5,6,7
. Phương sai của mẫu số liệu thống kê đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Câu 6: Biết rằng hai vec tơ
a
và
b
không cùng phương nhưng hai vec tơ
23ab+

và
(
)
1
ax b++

cùng
phương. Khi đó giá trị của
x
là
A.
1
2
. B.
3
2
−
. C.
1
2
−
. D.
3
2
.
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là
996 0,5mm
. Sai số tương đối
tối đa trong phép đo là bao nhiêu?
A.
0,05%
. B.
0,5%
. C.
0,04%.
D.
0,005%.
Câu 8: Để được cấp chứng chỉ môn Anh trình độ
2
A
của một trung tâm ngoại ngữ, học viên phải trải
qua
6
lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là
100
và phải đạt điểm trung bình
từ
70
điểm trở lên. Qua
5
lần thi Hoa đạt điểm trung bình là
64,5
điểm. Hỏi trong lần kiểm tra
cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ?
A.
97,5
. B.
92,5
. C.
95,5
. D.
97,8
.
Câu 9: Viết phương trình tổng quát của đường thẳng
∆
đi qua điểm
1; 3A
và có vectơ pháp tuyến
(3; 2)n =
A.
3 2 90xy 
. B.
3 2 60xy 
. C.
3 2 70xy 
. D.
3 2 80xy 
.
Câu 10: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường thẳng
d
cắt trục
Ox
,
Oy
lần lượt tại hai
điểm
( )
3;0A
và
( )
0; 2B −
. Đường thẳng
d
có phương trình là
A.
1
32
xy
−=−
. B.
1
23
xy
+=
−
. C.
1
32
xy
−=
. D.
0
32
xy
−=
.
Câu 11: Cho đường thẳng
1
: 2 3 15 0dxy++=
và
2
: 2 30dx y− −=
. Khẳng định nào sau đây đúng?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
A.
1
d
và
2
d
cắt nhau và không vuông góc với nhau.
B.
1
d
và
2
d
song song với nhau.
C.
1
d
và
2
d
trùng nhau.
D.
1
d
và
2
d
vuông góc với nhau.
Câu 12: Xác định
m
để
2
đường thẳng
: 2 30dx y 
và
: 30
d x my
vuông góc với nhau.
A.
2.m

B.
1
.
2
m

C.
2.m
D.
1
.
2
m
Câu 13: Tọa độ tâm
I
và bán kính
R
của đường tròn
( ) ( )
2
2
:1 8Cx y++=
là
A.
( )
1; 0 , 8.IR−=
B.
(
)
1;0 , 64.
IR
−=
C.
( )
1; 0 , 2 2 .IR−=
D.
( )
1; 0 , 2 2 .IR=
Câu 14: Cho đường tròn có phương trình
22
6 2 60
xy xy+ − + +=
và điểm
( )
1; 1A −
. Phương trình tiếp
tuyến của tại điểm
A
là
A.
1y =
. B.
1x =
. C.
2x =
. D.
2y =
.
Câu 15: Tọa độ các tiêu điểm của hypebol
( )
22
:1
16 9
xy
H −=
là
A.
( ) ( )
12
5; 0 ; 5; 0FF=−=
. B.
( ) ( )
12
0; 5 ; 0;5FF=−=
.
C.
( ) ( )
12
0; 7 ; 0; 7FF=−=
. D.
( ) ( )
12
7;0 ; 7;0FF=−=
.
Câu 16: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả ấy?
A.
48
. B.
24
. C.
14
. D.
18
.
Câu 17: Từ các chữ số 1;2;3;4;5, hỏi có thể lập được bao nhiêu số có hai chữ số khác nhau?
A.
25
. B.
20
. C.
10
. D.
9
.
Câu 18: Có bao nhiêu cách xếp 5 quyển sách gồm toán, lý, hóa, sinh, địa lên một kệ sách dài?
A.
120
. B.
60
. C.
48
. D.
24
.
Câu 19: Một câu lạc bộ có
20
thành viên. Số cách chọn một ban quản lí gồm
1
chủ tịch,
1
phó chủ tịch,
1
thư kí là
A.
13800
. B.
6900
. C.
7200
. D.
6840
.
Câu 20: Số cách chọn
5
học sinh trong một lớp có
25
học sinh nam và
16
học sinh nữ là
A.
55
25 16
CC+
. B.
5
25
C
. C.
5
41
A
. D.
5
41
C
.
Câu 21: Đa thức
(
)
5432
32 80 80 40 10 1Px x x x x x= − + − +−
là khai triển của nhị thức nào?
A.
( )
5
12x−
. B.
( )
5
12x+
. C.
( )
5
21x −
. D.
( )
5
1x −
.
Câu 22: Gieo một đồng xu cân đối và đồng chất liên tiếp bốn lần. Gọi
B
là biến cố “Kết quả bốn lần gieo
là như nhau”. Xác định biến cố
B
.
A.
{ }
;B SSSS NNNN=
B.
{ }
;B SNSN NSNS=
.C.
{ }
B NNNN=
. D.
{ }
B SSSS=
.
Câu 23: Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ đánh số từ
1
đến. Tính xác suất để tổng
của các số trên hai thẻ lấy ra là số chẵn.
A.
5
9
. B.
4
9
. C.
1
9
. D.
5
3
.
Câu 24: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc
bút. Tính xác suất để hai chiếc bút lấy được cùng màu?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
A.
28
5
. B.
8
15
. C.
1
7
. D.
7
15
.
Câu 25: Cho
( )
1;3M
và
(
)
3;5
N
−
. Phương trình đường trung trực của đoạn thẳng
MN
là đường thẳng
nào dưới đây?
A.
2 70xy+ −=
. B.
2 60xy− +−=
. C.
2 70xy+ +=
. D.
2 60xy
− ++=
.
Câu 26: Phương trình đường thẳng
d
qua
( )
1; 2M
và chắn trên hai trục toạ độ những đoạn bằng nhau là
A.
30
xy−−=
. B.
30
xy−+=
. C.
30xy+−=
. D.
30xy−+ − =
.
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có phương trình
là.
A.
22
24 12 175 0xy x y++ − + =
. B.
22
24 12 175 0xy x y+− + + =
.
C.
22
24 12 175 0xy x y+− − + =
. D.
22
24 12 175 0xy x y++ + + =
.
Câu 28: Cho Đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có bán kính
R
bằng
A.
2
. B.
1
. C.
5
. D.
2
.
Câu 29: Cho parabol có phương trình:
2
4 20yx=
. Phương trình đường chuẩn của parabol là:
A.
5
4
x =
. B.
4
5
x =
. C.
4
5
x = −
. D.
5
4
x = −
.
Câu 30: Một người có 7 đôi tất trong đó có 3 đôi tất trắng và 5 đôi giày trong đó có 2 đôi giày đen. Người
này không thích đi tất trắng cùng với giày đen. Hỏi người đó có bao nhiêu cách chọn tất và giày
thỏa mãn điều kiện trên?
A.
29
. B.
36.
C.
18.
D.
35.
Câu 31: Từ một lớp gồm 16 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh tham
gia đội Thanh niên xung kích, trong đó có 2 học sinh nam và 3 học sinh nữ.
A.
23
16 18
..CC
. B.
23
16 18
..AA
. C.
32
16 18
..CC
. D.
32
16 18
..AA
Câu 32: Cho
*
, ,1mn m∈>
. Giả sử
a
và
b
là hai đường thẳng song song. Trên đường thẳng
a
cho
m
điểm phân biệt màu đỏ, trên đường thẳng
b
cho
n
điểm phân biệt màu xanh. Số tam giác có 2
đỉnh màu đỏ và một đỉnh màu xanh thuộc tập hợp các điểm đã cho là
A.
12
.
mn
CC
. B.
21 1 2
..
mn mn
CC CC+
. C.
21
mn
CC+
. D.
21
.
mn
CC
.
Câu 33: Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống nhau,
một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp theo
hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là
A.
1
7
. B.
1
2 6!×
. C.
2
7!
. D.
1
7!
.
Câu 34: Một lớp có 20 nam sinh và 23 nữ sinh. Giáo viên chọn ngẫu nhiên 5 học sinh đi test Covid. Tính
xác suất
P
để 5 học sinh được chọn có cả nam và nữ.
A.
0,85P ≈
. B.
0,97P ≈
C.
0,96P ≈
. D.
0,95P ≈
.
Câu 35: Chọn ngẫu nhiên hai số khác nhau từ
30
số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng
A.
14
29
. B.
28
29
. C.
7
29
. D.
1
2
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 6 chữ số khác nhau trong đó 2 số kề nhau không cùng là số chẵn?
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:4 2 1 0dx y+ +=
và điểm
( )
1;1A
. Xác định
tọa độ hình chiếu vuông góc của
A
lên
d
.
Câu 38: Trong buổi sinh hoạt nhóm của lớp, tổ một có học sinh gồm học sinh nữ trong đó có Bí
thư và học sinh nam trong đó có Lớp trưởng. Chia tổ thành nhóm, mỗi nhóm gồm học
sinh và phải có ít nhất học sinh nữ. Xác suất để Bí thư và Lớp trưởng không ở cùng một nhóm
là
Câu 39: Cho hypebol
( )
22
:1
16 9
xy
H −=
. Tìm tọa độ điểm
M
thuộc
( )
H
sao cho
1
MF
vuông góc với
2
MF
.
---------- HẾT ----------
12
4
8
3
4
1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho hình bình hành
ABCD
biết
( )
2;1A
,
(
)
2; 1 ,
B
−
(
)
2; 3
C −−
. Tọa độ
giao điểm hai đường chéo của hình bình hành
ABCD
là
A.
( )
2;0
. B.
( )
2; 2
. C.
( )
0; 2−
. D.
(
)
0; 1
−
.
Lời giải
Giao điểm hai đường chéo là trung điểm của
AC
.
Vậy tọa độ giao điểm hai đường chéo là
(
)
0; 1I
−
.
Câu 2: Quy tròn số
12,4567
đến hàng phần trăm ta được số.
A.
12,45
. B.
12,46
C.
12,457
D.
12,5
Lời giải
Quy tròn số
12,4567
đến hàng trăm ta được số
12,46
.
Câu 3: Tìm tứ phân vị của mẫu số liệu sau
3 4 6 7 8 9 10 12 13 16
A.
12 3
5, 8,5, 12QQ Q= = =
. B.
12 3
6, 8,5, 12
QQ Q= = =
.
C.
12 3
6, 8,5, 12,5QQ Q= = =
. D.
12 3
5, 8,5, 12, 5QQ Q= = =
.
Lời giải
Trung vị của mẫu số liệu trên là
89
8,5
2
+
=
Trung vị của dãy
34678
là
6
Trung vị của dãy
9 10 12 13 16
là
12
Vậy
12 3
6, 8,5, 12QQ Q= = =
.
Câu 4: Mẫu số liệu sau đây cho biết giá của một số loại giày trong cửa hàng
300 250300 360 350 650 450 500 300
Khoảng biến thiên của mẫu số liệu trên là
A.
400
. B.
300
. C.
650
. D.
250
.
Lời giải
Khoảng biến thiên của mẫu số liệu là:
650 250 400R =−=
.
Câu 5: Cho dãy số liệu thống kê:
1, 2,3, 4,5,6,7
. Phương sai của mẫu số liệu thống kê đã cho là
A.
2
. B.
3
. C.
4
. D.
1
.
Lời giải
1234567
4
7
x
++++++
= =
Vậy phương sai của mẫu số liệu:
(
)
7
2
2
1
1
4
7
xi
i
s xx
=
= −=
∑
.
Câu 6: Biết rằng hai vec tơ
a
và
b
không cùng phương nhưng hai vec tơ
23ab+

và
( )
1ax b++

cùng
phương. Khi đó giá trị của
x
là
A.
1
2
. B.
3
2
−
. C.
1
2
−
. D.
3
2
.
Lời giải
Ta có
23ab+

và
(
)
1
ax b++

cùng phương nên có tỉ lệ:
11 1
23 2
x
x
+
= ⇒=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là
996 0,5mm
. Sai số tương đối
tối đa trong phép đo là bao nhiêu?
A.
0,05%
. B.
0,5%
. C.
0,04%.
D.
0,005%.
Lời giải
Ta có độ dài gần đúng của cầu là
996a
với độ chính xác
d 0, 5
.
Vì sai số tuyệt đối
0, 5
a
d
nên sai số tương đối
0, 5
0, 05%
996
a
a
d
aa

.
Vậy sai số tương đối tối đa trong phép đo trên là
0, 05%
.
Câu 8: Để được cấp chứng chỉ môn Anh trình độ
2
A
của một trung tâm ngoại ngữ, học viên phải trải
qua
6
lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là
100
và phải đạt điểm trung bình
từ
70
điểm trở lên. Qua
5
lần thi Hoa đạt điểm trung bình là
64,5
điểm. Hỏi trong lần kiểm tra
cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ?
A.
97,5
. B.
92,5
. C.
95,5
. D.
97,8
.
Lời giải
Gọi
x
là số điểm trong lần kiểm tra cuối mà Hoa cần đạt được để được cấp chứng chỉ
Ta có số điểm qua
5
lần thi của Hoa là
64,5.5 322,5=
.
Khi đó
322,5
70 70.6 322,5 97,5
6
x
x
+
≥ ⇔≥ − =
.
Vậy
12 3
7, 16,5, 30QQ Q= = =
.
Câu 9: Viết phương trình tổng quát của đường thẳng
∆
đi qua điểm
1; 3A
và có vectơ pháp tuyến
(3; 2)n =
A.
3 2 90xy 
. B.
3 2 60xy 
. C.
3 2 70xy 
. D.
3 2 80xy 
.
Lời giải
Phương trình đường thẳng cần tìm:
( ) (
)
3 1 2 3 0 3 2 90x y xy
− + − =⇔ + −=
.
Câu 10: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường thẳng
d
cắt trục
Ox
,
Oy
lần lượt tại hai
điểm
( )
3;0A
và
( )
0; 2B −
. Đường thẳng
d
có phương trình là
A.
1
32
xy
−=−
. B.
1
23
xy
+=
−
. C.
1
32
xy
−=
. D.
0
32
xy
−=
.
Lời giải
Phương trình đường thẳng đi qua hai điểm
( )
3;0
A
và
( )
0; 2B −
viết dưới dạng đoạn chắn là
:1 1
3 2 32
x y xy
d + =⇔−=
−
.
Câu 11: Cho đường thẳng
1
: 2 3 15 0dxy
++=
và
2
: 2 30dx y− −=
. Khẳng định nào sau đây đúng?
A.
1
d
và
2
d
cắt nhau và không vuông góc với nhau.
B.
1
d
và
2
d
song song với nhau.
C.
1
d
và
2
d
trùng nhau.
D.
1
d
và
2
d
vuông góc với nhau.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Đường thẳng
1
: 2 3 15 0dxy++=
có một vectơ pháp tuyến là
( )
1
2;3n =

và đường thẳng
2
: 2 30dx y− −=
có một vectơ pháp tuyến là
( )
2
1; 2n = −

.
Ta thấy
23
12
≠
−
và
12
. 2.1 3.( 2) 4 0nn = + − =−≠

.
Vậy
1
d
và
2
d
cắt nhau và không vuông góc với nhau.
Câu 12: Xác định
m
để
2
đường thẳng
: 2 30
dx y 
và
: 30
d x my
vuông góc với nhau.
A.
2.m 
B.
1
.
2
m 
C.
2.m
D.
1
.
2
m
Lời giải
: 2 30
dx y

có VTPT là
1; 2n
.
: 30
d x my
có VTPT là
1;nm

.
Để
d
vuông góc với
d
thì
1
. 0 12 0 .
2
nn m m
 

Câu 13: Tọa độ tâm
I
và bán kính
R
của đường tròn
( ) ( )
2
2
:1 8Cx y++=
là
A.
( )
1; 0 , 8.IR−=
B.
(
)
1;0 , 64.
IR
−=
C.
( )
1; 0 , 2 2 .IR−=
D.
( )
1; 0 , 2 2 .IR=
Lời giải
Từ phương trình đường tròn ta suy ra tọa độ tâm và bán kính là
(
)
1; 0 , 2 2 .
IR−=
Câu 14: Cho đường tròn có phương trình
22
6 2 60xy xy+ − + +=
và điểm
(
)
1; 1A −
. Phương trình tiếp
tuyến của tại điểm
A
là
A.
1y =
. B.
1x =
. C.
2x =
. D.
2y =
.
Lời giải
Ta có tâm đường tròn
( )
3; 1I −
, tiếp tuyến của tại điểm A nhận
( )
2;0AI =

làm vectơ pháp
tuyến nên có phương trình là
( ) ( )
2 10 10xy−+ +=
hay
1x =
.
Câu 15: Tọa độ các tiêu điểm của hypebol
( )
22
:1
16 9
xy
H −=
là
A.
( ) ( )
12
5; 0 ; 5; 0FF=−=
. B.
( ) ( )
12
0; 5 ; 0;5FF=−=
.
C.
( ) (
)
12
0; 7 ; 0; 7FF=−=
. D.
( ) ( )
12
7;0 ; 7;0FF=−=
.
Lời giải
Gọi
( ) ( )
12
;0 ; ;0F cFc=−=
là hai tiêu điểm của
( )
H
.
Từ phương trình
( )
22
:1
16 9
xy
H −=
, ta có:
2
16a =
và
2
9b =
suy ra
( )
2 22
25 5, 0c ab c c= + = ⇒= >
.
Vậy tọa độ các tiêu điểm của
( )
H
là
( ) ( )
12
5; 0 ; 5; 0FF
=−=
.
Câu 16: Có
8
quả ổi và
6
quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả ấy?
A.
48
. B.
24
. C.
14
. D.
18
.
Lời giải
Theo quy tắc cộng có
8 6 14+=
cách chọn ra một quả trong các quả đã cho.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Câu 17: Từ các chữ số 1;2;3;4;5, hỏi có thể lập được bao nhiêu số có hai chữ số khác nhau?
A.
25
. B.
20
. C.
10
. D.
9
.
Lời giải
Gọi số có hai chữ số khác nhau là
(
)
;0
ab a b a
≠≠
.
Ta có: Chọn
a
có 5 cách chọn.
Chọn
b
có 4 cách chọn.
Vậy theo quy tắc nhân ta có 4.5=20.
Câu 18: Có bao nhiêu cách xếp 5 quyển sách gồm toán, lý, hóa, sinh, địa lên một kệ sách dài?
A.
120
. B.
60
. C.
48
. D.
24
.
Lời giải
Số cách xếp là số các hoán vị của
5
phần tử là
5
5! 120P = =
cách.
Câu 19: Một câu lạc bộ có
20
thành viên. Số cách chọn một ban quản lí gồm
1
chủ tịch,
1
phó chủ tịch,
1
thư kí là
A.
13800
. B.
6900
. C.
7200
. D.
6840
.
Lời giải
Số cách chọn một ban quản lí gồm
1
chủ tịch,
1
phó chủ tịch,
1
thư kí là:
3
20
6840
A
=
Câu 20: Số cách chọn
5
học sinh trong một lớp có
25
học sinh nam và
16
học sinh nữ là
A.
55
25 16
CC+
. B.
5
25
C
. C.
5
41
A
. D.
5
41
C
.
Lời giải
Tổng số học sinh của lớp là
25 16 41+=
học sinh.
Mỗi cách chọn theo yêu cầu của đề là 1 tổ hợp chập 5 của 41 phần tử.
Nên có
5
41
C
cách chọn theo yêu cầu của đề.
Câu 21: Đa thức
(
)
5432
32 80 80 40 10 1Px x x x x x= − + − +−
là khai triển của nhị thức nào?
A.
( )
5
12x−
. B.
( )
5
12x+
. C.
( )
5
21x −
. D.
(
)
5
1x −
.
Lời giải
Vì hệ số của
5
x
là 32 và dấu trong khai triển đan xen nên chọn đáp án C.
Câu 22: Gieo một đồng xu cân đối và đồng chất liên tiếp bốn lần. Gọi
B
là biến cố “Kết quả bốn lần gieo
là như nhau”. Xác định biến cố
B
.
A.
{ }
;B SSSS NNNN=
B.
{ }
;B SNSN NSNS=
.C.
{ }
B NNNN=
. D.
{ }
B SSSS=
.
Lời giải
Kết quả của bốn lần gieo là như nhau nên ta có hai trường hợp là: cả bốn lần gieo đều là mặt sấp
xuất hiện và cả bốn lần gieo đều là mặt ngửa xuất hiện. Vậy
{ }
;B SSSS NNNN=
.
Câu 23: Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ đánh số từ
1
đến. Tính xác suất để tổng
của các số trên hai thẻ lấy ra là số chẵn.
A.
5
9
. B.
4
9
. C.
1
9
. D.
5
3
.
Lời giải
Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ có
( )
2
9
36nC
ω
= =
Gọi
A
là biến cố tổng của các số trên hai thẻ lấy ra là số chẵn
TH1. Lấy được hai thẻ ghi số lẻ có :
2
5
10C =
cách.
TH2. Lấy được hai thẻ ghi số chẵn có :
2
4
6C =
cách. Vậy
( )
16nA=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Xác suất để tổng của các số trên hai thẻ lấy ra là số chẵn là :
(
)
4
9
pA
=
.
Câu 24: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc
bút. Tính xác suất để hai chiếc bút lấy được cùng màu?
A.
28
5
. B.
8
15
. C.
1
7
. D.
7
15
.
Lời giải
Số phần tử của không gian mẫu là:
( )
2
15
105nC
Ω= =
Gọi
A
là biến cố “ lấy được hai chiếc bút cùng màu ”, tức là lấy được hai chiếc bút màu đen
hoặc hai chiếc bút màu xanh
22
78
( ) 49
nA C C⇒ =+=
Xác suất của biến cố
A
là:
( )
( ) 49 7
( ) 105 15
nA
PA
n
= = =
Ω
.
Câu 25: Cho
(
)
1;3M
và
(
)
3;5N
−
. Phương trình đường trung trực của đoạn thẳng
MN
là đường thẳng
nào dưới đây?
A.
2 70xy+ −=
. B.
2 60xy− +−=
. C.
2 70xy+ +=
. D.
2 60xy
− ++=
.
Lời giải
Ta có
( )
4;2MN
= −

, đặt
( )
2;1n = −
.
Gọi
I
là trung điểm của
MN
, ta có
( )
1;4I
−
.
Đường trung trực của đoạn thẳng
MN
là đường thẳng đi qua điểm
I
và nhận vectơ
n
làm
vectơ pháp tuyến, có phương trình:
( )
( )
2 11 4 0 2 60x y xy
− + + − = ⇔− + − =
.
Câu 26: Phương trình đường thẳng
d
qua
( )
1; 2
M
và chắn trên hai trục toạ độ những đoạn bằng nhau là
A.
30
xy−−=
. B.
30
xy
−+=
. C.
30xy+−=
. D.
30xy−+ − =
.
Lời giải
Vì đường thẳng
d
qua
( )
1; 2M
và chắn trên hai trục toạ độ những đoạn bằng nhau nên đường
thẳng cần tìm song song với đường thẳng
yx= −
hoặc
yx=
.
Vậy đường thẳng
d
có có dạng
y xa= +
hoặc
y xb=−+
.
Vì đường thẳng đi qua
( )
1; 2M
nên
1yx= +
hoặc
3yx=−+
.
Vậy
: 10dx y− +=
hoặc
: 30dx y−−=
.
Câu 27: Trong mặt phẳng
Oxy
, đường tròn đi qua ba điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có phương trình
là.
A.
22
24 12 175 0xy x y++ − + =
. B.
22
24 12 175 0xy x y+− + + =
.
C.
22
24 12 175 0xy x y+− − + =
. D.
22
24 12 175 0xy x y++ + + =
.
Lời giải
Chọn C
Gọi phương trình đường tròn cần tìm có dạng:
( )
2 2 22
22 0 0x y ax by c a b c+ − − += + −>
.
Đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
nên ta có:
121 64 22 16 0 12
169 64 26 16 0 6
196 49 28 14 0 175
a bc a
a bc b
a bc c
+ − − += =


+ − − +=⇔ =


+ − − += =

ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Vậy phương trình đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
là
22
24 12 175 0xy x y+− − + =
Câu 28: Cho Đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có bán kính
R
bằng
A.
2
. B.
1
. C.
5
. D.
2
.
Lời giải
Gọi phương trình đường tròn cần tìm có dạng:
( )
2 2 22
22 0 0x y ax by c a b c+ − − += + −>
.
Đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7
ABC
nên ta có:
121 64 22 16 0 12
169 64 26 16 0 6
196 49 28 14 0 175
a bc a
a bc b
a bc c
+ − − += =


+ − − +=⇔ =


+ − − += =

Ta có
22
5R abc= + −=
Vậy phương trình đường tròn đi qua 3 điểm
( ) ( ) ( )
11;8 , 13;8 , 14;7ABC
có bán kính là
5R =
.
Câu 29: Cho parabol có phương trình:
2
4 20yx=
. Phương trình đường chuẩn của parabol là:
A.
5
4
x
=
. B.
4
5
x =
. C.
4
5
x = −
. D.
5
4
x = −
.
Lời giải
Ta có:
( )
2
5
: 4 20 2 5
2
Py x p p= ⇒ =⇒=
.
Vậy
( )
P
có phương trình đường chuẩn là:
5
:
4
x∆=−
.
Câu 30: Một người có 7 đôi tất trong đó có 3 đôi tất trắng và 5 đôi giày trong đó có 2 đôi giày đen. Người
này không thích đi tất trắng cùng với giày đen. Hỏi người đó có bao nhiêu cách chọn tất và giày
thỏa mãn điều kiện trên?
A.
29
. B.
36.
C.
18.
D.
35.
Lời giải
Cách 1:
Trường hợp 1:
Chọn
1
đôi tất trắng có
3
cách.
Chọn
1
đôi giày không phải màu đen có
3
cách.
Do đó có
3.3 9
cách chọn 1 đôi tất trắng và 1 đôi giày không phải màu đen.
Trường hợp 2:
Chọn
1
đôi tất không phải màu trắng có
4
cách.
Chọn
1
đôi giày
bất kỳ có
5
cách.
Do đó có
4.5 20
cách chọn 1 đôi tất không phải màu trắng và 1 đôi giày bất kỳ.
Theo quy tắc cộng, ta có
9 20 29
cách chọn 1 đôi tất và 1 đôi giày thỏa mãn yêu cầu.
Cách 2:
Số cách chọn ra 1 đôi tất và 1 đôi giày bất kỳ là:
7.5 35
cách.
Số cách chọn ra 1 đôi tất trắng và 1 đôi giày đen là:
3.2 6
cách.
Vậy ta có
35 6 29
cách chọn 1 đôi tất và 1 đôi giày thỏa mãn yêu cầu.
Câu 31: Từ một lớp gồm 16 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh tham
gia đội Thanh niên xung kích, trong đó có 2 học sinh nam và 3 học sinh nữ.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
A.
23
16 18
..
CC
. B.
23
16 18
..
AA
. C.
32
16 18
..CC
. D.
32
16 18
..AA
Lời giải
Chọn 2 học sinh nam trong số 16 học sinh nam thì có
2
16
C
cách chọn.
Chọn 3 học sinh nữ trong số 18 học sinh nữ thì có
3
18
C
cách chọn.
Áp dụng quy tắc nhân, sẽ có
23
16 18
.CC
cách chọn 2 học sinh nam và 3 học sinh nữ.
Câu 32: Cho
*
, ,1mn m∈>
. Giả sử
a
và
b
là hai đường thẳng song song. Trên đường thẳng
a
cho
m
điểm phân biệt màu đỏ, trên đường thẳng
b
cho
n
điểm phân biệt màu xanh. Số tam giác có 2
đỉnh màu đỏ và một đỉnh màu xanh thuộc tập hợp các điểm đã cho là
A.
12
.
mn
CC
. B.
21 1 2
..
mn mn
CC CC+
. C.
21
mn
CC+
. D.
21
.
mn
CC
.
Lời giải
Chọn 2 đỉnh màu đỏ từ
m
điểm có
2
m
C
cách chọn.
Chọn 1 đỉnh màu xanh từ
n
điểm có
1
m
C
cách chọn.
Theo quy tắc nhân ta có số tam giác thỏa mãn là
21
.
mn
CC
.
Câu 33: Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống nhau,
một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp theo
hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là
A.
1
7
. B.
1
2 6!×
. C.
2
7!
. D.
1
7!
.
Lời giải
Hoán vị 7 chữ cái này ta được 1 dãy 7 chữ cái, tuy nhiên trong đó có 2 chữ T giống nhau nên khi
hoán vị 2 chữ T này cho nhau không tạo dãy mới.
Vì vậy sẽ có:
7!
2!
Ω=
dãy khác nhau.
Xác suất để tạo thành dãy THPTCLS là
12
7!
7!
2!
P = =
.
Câu 34: Một lớp có 20 nam sinh và 23 nữ sinh. Giáo viên chọn ngẫu nhiên 5 học sinh đi test Covid. Tính
xác suất
P
để 5 học sinh được chọn có cả nam và nữ.
A.
0,85P
≈
. B.
0,97P ≈
C.
0,96P ≈
. D.
0,95P ≈
.
Lời giải
Số phần tử của không gian mẫu là:
( )
5
43
nCΩ=
.
Gọi
A
là biến cố: “5 học sinh được chọn có cả nam và nữ”.
Ta có:
( )
( )
5 55
43 20 23
5
43
0,95
C CC
PA
C
−+
= ≈
.
Câu 35: Chọn ngẫu nhiên hai số khác nhau từ
30
số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng
A.
14
29
. B.
28
29
. C.
7
29
. D.
1
2
.
Lời giải
Chọn hai số khác nhau từ
30
số nguyên dương đầu tiên: có
2
30
C
cách chọn.
Suy ra
( )
2
30
nCΩ=
.
Gọi
A
là biến cố: “Chọn được hai số có tổng là một số chẵn”
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Ta xét hai trường hợp:
TH1: Hai số được chọn là hai số lẻ: có
2
15
C
cách chọn.
TH2: Hai số được chọn là hai số chẵn: có
2
15
C
cách chọn.
Suy ra
( )
22
15 15
nA C C= +
.
Vậy xác suất cần tìm là:
( )
( )
( )
22
15 15
2
30
14
29
nA
CC
PA
nC
+
= = =
Ω
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 6 chữ số khác nhau trong đó 2 số kề nhau không cùng là số chẵn?
Lời giải
Gọi số đó là .
Theo đề bài, ta có A có nhiều nhất 3 chữ số chẵn.
TH1: A có chữ số chẵn:
chẵn: số cách chọn A: .
lẻ: số cách chọn A: .
TH2: A có chữ số chẵn:
chẵn, suy ra lẻ. số cách chọn A: .
lẻ, có cách chọn vị trí không kề nhau của chữ số chẵn. số cách chọn A:
.
TH3: A có 3 chữ số chẵn:
chẵn, suy ra lẻ, có cách chọn vị trí không kề nhau của chữ số chẵn. số cách chọn
A: .
lẻ, có cách chọn vị trí không kề nhau của chữ số chẵn. số cách chọn A:
. Suy ra tổng số trường hợp: cách.
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:4 2 1 0dx y+ +=
và điểm
( )
1;1A
. Xác định
tọa độ hình chiếu vuông góc của
A
lên
d
.
Lời giải
Đường thẳng
d
có một VTPT
( )
4;2n =
suy ra
d
có một VTCP
( )
2;4u = −
.
Ta có
13
;2 , 1;2
22
H d H t t t AH t t

∈⇒ −− ∈⇒ = −−−



.
Hình chiếu vuông góc của
A
lên
d
là
H
nên
( ) ( )
32
. 0 1 . 2 2 .4 0 10 4 0
25
AH u t t t t
−

= ⇔ − − + − − = ⇔− − = ⇔ =



.
Vậy
23
;
5 10
H
−



.
Câu 38: Trong buổi sinh hoạt nhóm của lớp, tổ một có học sinh gồm học sinh nữ trong đó có Bí
thư và học sinh nam trong đó có Lớp trưởng. Chia tổ thành nhóm, mỗi nhóm gồm học
sinh và phải có ít nhất học sinh nữ. Xác suất để Bí thư và Lớp trưởng không ở cùng một nhóm
là
Lời giải
123456
A aaaaaa=
1
1
a
1
45
.CP
1
a
1 14
5 54 5
C .( . ).CC P
2
1
a
2
a
11 13
4 5 44 4
.C .( . ).C CC P
1
a
6
2
2
12 3
5 5 24
C .( .6. ).C PA
1
a
2
a
3
2
2
11 2 2
45 4 2 4
.C .( .3. ).C C PA
1
a
1
2
2
13 2
5 5 34
C .( .1. ).C PA
37800
12
4
8
3
4
1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Theo yêu cầu bài toán ta cần chia tổ một thành ba nhóm, trong đó một nhóm có, hai nhóm còn
lại có vai trò như nhau gồm. Suy ra số phần tử của không gian mẫu là:
Gọi là biến cố
Bí thư và Lớp trưởng cùng một nhóm . Ta có các trường hợp sau:
●Trường hợp thứ nhất: Bí thư và Lớp trưởng thuộc nhóm. Số cách xếp là:
.
●Trường hợp thứ hai: Bí thư và Lớp trưởng thuộc nhóm. Số cách xếp là
.
Suy ra .
Vậy xác suất để Bí thư và Lớp trưởng cùng một nhóm Suy ra xác
suất để Bí thư và Lớp trưởng không cùng một nhóm là
Câu 39: Cho hypebol
( )
22
:1
16 9
xy
H −=
. Tìm tọa độ điểm
M
thuộc
( )
H
sao cho
1
MF
vuông góc với
2
MF
.
Lời giải
Gọi
( ) ( ) ( )
22
; 1 ; 1
16 9
xy
M xy H∈ ⇒−=
Ta có
2
2 22
12
2
16
25 5 2 10
9
a
c a b c FF c
b
=
⇒ = + = ⇒=⇒ = =
=
.
Vì
12
MF MF⊥
nên tam giác
12
MF F
vuông tại
M
. Do đó
M
thuộc đường tròn
( )
C
có đường
kính
12
FF
.
( )
( )
( )
12
22
â 0; 0
: 25
t m
Bn 5á ní k h
2
C
O
F
R
y
F
Cx
= =
+
=
⇒
( ) ( )
22
25 ; 2MC xy∈ ⇒+=
Từ
( )
1
và
( )
2
, ta có
22
2
2
22
544
4 34
1
25
5
16 9
81
9
25
25
5
xy
x
x
y
xy
y
=
= ±
−=

⇔⇒


=
+=
= ±
Vậy
1234
4 34 9 4 34 9 4 34 9 4 34 9
;; ;; ; ; ;
55 55 5 5 5 5
MM M M
 
− − −−
 
  
 
.
---------- HẾT ----------
( )
( )
( ) ( )
13 13
26 13
22
48
...
. . 3360.
2!
CC CC
n CCΩ= =
A
''
''
( )
( ) ( )
13 13
26 13
11
37
...
1. . . 420
2!
CC CC
CC =
( ) ( ) ( )
2 13 22
7 35 2 2
1. . . . . 630C CC C C =
( ) 420 630 1050nA=+=
( ) 1050 5
() .
( ) 3360 16
nA
PA
n
= = =
Ω
5 11
() 1 .
16 16
PA=−=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 08
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho
( ) ( )
; và B ;
AA BB
Axy xy
. Tọa độ trung điểm
I
của đoạn thẳng
AB
là
A.
;
22
−−



A BA B
x xy y
I
. B.
;
22
++



A BA B
x xy y
I
.
C.
;
33
++



A BA B
x xy y
I
. D.
;
22
++



AABB
xyxy
I
.
Câu 2: Giá trị gần đúng của
28
chính xác đến hàng phần trăm là
A.
5,656
. B.
5, 65
. C.
5, 66
. D.
5,657
Câu 3: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau.
Số cuốn sách
3
4
5
6
7
Số bạn 6 15 3 8 8
Tìm mốt của mẫu số liệu trên
A.
7
. B.
5
. C.
6
. D.
4
.
Câu 4: Bảng sau cho biết thời gian chạy cự li 100m của các bạn trong lớp (đơn vị giây)
Thời gian 12 13 14 15 16
Số bạn 4 7 3 18 8
Hãy tính thời gian chạy trung bình cự li 100m của các bạn trong lớp.
A.
14,094
. B.
14,245
. C.
14,475
. D.
14,75
.
Câu 5: Số ôtô đi qua một cây cầu mỗi ngày trong một tuần đếm được như sau: 83; 74; 71; 79; 83; 69;
92. Phương sai và độ lệch chuẩn lần lượt là
A. 78,71 và 8,87. B. 52,99 và 7,28. C. 61,82 và 7,86. D. 55,63 và 7,46.
Câu 6: Cho
(0,1)a
=
,
( 1; 2)b
= −
,
( 3; 2)c =−−
. Tọa độ của
324u abc=+−

là
A.
(
)
10; 15
−
. B.
( )
15;10
. C.
( )
10;15
. D.
( )
10;15−
.
Câu 7: Kết quả đo chiều dài một cây cầu là
152,65am=
với độ chính xác
0,05m
. Viết số quy tròn của
số
a
và ước lượng sai số tương đối của số quy tròn đó.
A.
152,7
và
0,033%
a
δ
<
. B.
152,7
và
0,066%
a
δ
<
.
C.
152,7
và
0,013%
a
δ
<
. D.
152,7
và
0,065%
a
δ
=
Câu 8: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của mười hai thí
sinh theo thứ tự không giảm như sau:
56667777788x
Tìm
x
biết số trung bình của thời gian thi nghề của các thí sinh trên là
109
12
.
A.
35
. B.
33
. C.
34
. D.
36
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
Câu 9: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP
u
=(3;–4) là
A.
32
.
4
xt
yt


. B.
23
.
34
xt
yt


C.
23
.
14
xt
yt


. D.
12
.
43
xt
yt


.
Câu 10: Trong mặt phẳng tọa độ
Oxy
đường thẳng đi qua
( 1; 4)A
−
và song song trục
Ox
A.
10
x
−=
. B.
40y +=
. C.
10
x +=
. D.
40
y −=
.
Câu 11: Tính góc giữa hai đường thẳng
1
:2 5 2 0dxy+ −=
và
2
:3 7 3 0dxy− +=
.
A.
0
30
. B.
0
135
. C.
0
45
. D.
0
60
.
Câu 12: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
3
:
4
= −
= −
xt
d
yt
và
2
1
:
11 2
=
=−−
x
d
yt
Góc giữa hai
đường thẳng
1
d
và
2
d
bằng
A.
60
. B.
45
. C.
90
. D.
30
.
Câu 13: Phương trình đường tròn có tâm
( )
0; 2I
và bán kính
5=
R
là
A.
22
4 21 0+−+=xy y
. B.
22
4 21 0++−=xy y
.
C.
22
4 21 0+−−=xy y
. D.
22
4 21 0+−−=xy x
.
Câu 14: Trong hệ trục tọa độ
Oxy
, cho đường tròn
(
)
(
)
22
( ): 1 2 8
Cx y− ++ =
. Phương trình tiếp tuyến
d
của
()C
tai điểm
(3; 4)A
−
là
A.
: 10dx y
+ +=
. B.
: 2 11 0dx y
− −=
. C.
: 70dx y
−−=
. D.
: 70dx y
−+=
.
Câu 15: Phương trình nào sau đây là phương trình chính tắc của một elip?
A.
22
1
4 25
xy
−=
. B.
22
1
4 25
xy
+=−
. C.
22
1
52
xy
+=
. D.
22
0
4 25
xy
+=
.
Câu 16: Lớp 10A có 25 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một học sinh để
tham gia vào đội thanh niên tình nguyện của trường biết rằng tất cả các bạn trong lớp đều có khả
năng tham gia.
A.
40
. B.
25
. C.
15
. D.
10
.
Câu 17: Có bao nhiêu số tự nhiên có 2 chữ số mà cả hai chữ số đều là lẻ
A.
50
. B.
25
. C.
20
. D.
10
.
Câu 18: Số cách xếp
3
nam sinh và
4
nữ sinh vào một dãy ghê hàng ngang có
7
chỗ ngồi là
A.
4!.3
. B.
7!
. C.
4!.3!
. D.
4!
.
Câu 19: Một nhóm học sinh có
10
người. Cần chọn
3
học sinh trong nhóm để làm
3
công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việ C. Số cách chọn là
A.
3
10
. B.
30
. C.
3
10
C
. D.
3
10
A
.
Câu 20: Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con.
A. 1326. B. 104. C. 26. D. 2652
Câu 21: Trong khai triển nhị thức Niu-tơn của
( )
4
13x+
, số hạng thứ
2
theo số mũ tăng dần của
x
là
A.
108x
. B.
2
54x
. C.
1
. D.
12x
.
Câu 22: Xếp
7
học sinh
,,,,,,ABC DEFG
vào một chiếc bàn dài có đúng 7 ghế. Tính xác suất để học
sinh
D
không ngồi đầu bàn.
A.
4
7
. B.
7
3
. C.
3
7
. D.
5
7
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
Câu 23: Chọn ngẫu nhiên một số tự nhiên nhỏ hơn
15
. Tính xác suất để chọn được số chẵn
A.
8
15
. B.
1
2
. C.
7
15
. D.
4
7
.
Câu 24: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời
3
quả cầu.
Xác suất để lấy được
3
quả cầu màu xanh bằng
A.
24
455
. B.
4
165
. C.
4
455
. D.
24
165
.
Câu 25: Cho 2 điểm
( )
1;2 , (3;4).AB
Viết phương trình tổng quát đường trung trực của đoạn thẳng
AB
.
A.
5 0.xy
++=
B.
5 0.
xy−−=
C.
2 2 5 0.xy+ −=
D.
5 0.xy
+−=
Câu 26: Trong mặt phẳng
Oxy
, khoảng cách giữa hai đường thẳng song song
1
:3 4 3 0xyd − −=
và
2
:3 4 8 0xyd − −=
là
A. 4. B. 3. C. 1. D. 2.
Câu 27: Trong mặt phẳng tọa độ Oxy, cho đường tròn
22
( ) : 4 2 20 0
Cx y x y+−−−=
phương trình tiếp
tuyến của
( )
C
vuông góc với đường thẳng
:3 4 9 0xy∆ + +=
là
A.
4 3 30 0
xy
−+=
và
4 3 20 0xy−−=
. B.
4 3 20 0xy−+=
và
4 3 30 0
xy
−−=
.
C.
4 3 30 0
xy−−=
và
4 3 20 0
xy−−=
. B.
4 3 20 0xy−+=
và
4 3 30 0
xy−+=
.
Câu 28: Cho tam giác
ABC
có
( ) (
)
( )
1;1, 3;2, 5;5A BC
−−
. Toạ độ tâm đường tròn ngoại tiếp tam giác
ABC
là
A.
47 13
;
10 10

−


. B.
47 13
;
10 10



. C.
47 13
;
10 10

−−


. D.
47 13
;
10 10

−


.
Câu 29: Cho của hypebol
( )
22
:1
16 5
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
8
. B.
16
. C.
4
. D.
5
.
Câu 30: Có bao nhiêu số tự nhiên gồm bốn chữ số khác nhau và chia hết cho 5?.
A. 952. B. 1800. C. 1008. D. 1620.
Câu 31: Có
5
nhà toán học nam,
3
nhà toán học nữ và
4
nhà vật lý nam. Lập một đoàn công tác có
3
người cần có cả nam và nữ, trong đó có cả nhà toán học và nhà vật lý. Hỏi có bao nhiêu cách
lập?
A.
60
. B.
90
. C.
20
. D.
12
.
Câu 32: Cho tứ giác
ABCD
. Trên mỗi cạnh
,,,AB BC CD DA
lấy 7 điểm phân biệt và không có điểm nào
trùng với 4 đỉnh
,,,ABC D
. Hỏi từ
32
điểm đã cho lập được bao nhiêu tam giác?
A.
4960.
B.
4624.
C.
7140.
D.
6804.
Câu 33: Trong một lớp học gồm có
18
học sinh nam và
17
học sinh nữ. Giáo viên gọi ngẫu nhiên
4
học
sinh lên bảng giải bài tập. Xác suất để
4
học sinh được gọi có cả nam và nữ là:
A.
68
75
. B.
65
71
. C.
443
506
. D.
69
77
.
Câu 34: Chọn ngẫu nhiên hai số phân biệt từ
15
số nguyên dương đầu tiên. Xác suất để tích hai số được
chọn là một số chẵn bằng
A.
1
5
. B.
4
15
. C.
4
5
. D.
11
15
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 35: Từ một tổ gồm 10 nam và 8 nữ chọn ra một đoàn đại biểu gồm 6 người để tham dự hội nghị. Xác
suất để đoàn đại biểu được chọn có đúng 2 nữ bằng
A.
151
221
. B.
35
221
. C.
70
221
. D.
29
221
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp . Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác
nhau được lập thành từ các chữ số của tập
A
, đồng thời có đúng 2 chữ số lẻ và 2 chữ số lẻ đó
đứng cạnh nhau.
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
2;1M
và đường tròn
( ) ( ) ( )
22
:1 24Cx y− +− =
. Viết
phương trình đường thẳng
( )
d
qua điểm
M
và cắt
( )
C
tại hai điểm phân biệt
;AB
sao cho độ
dài
AB
ngắn nhất.
Câu 38: Xếp
5
quyển sách Toán và
5
quyển sách Văn khác nhau lên một kệ dài. Tính xác suất để
2
quyển sách cùng một môn nằm cạnh nhau.
Câu 39: Vệ tinh nhân tạo đầu tiên được Liên Xô phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là
một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là
22
2 22
22
1, 0, 0,
xy
abcab
ab
+=> > =−
. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là
583
dặm và xa nhất là
1342
dặm. Tìm tỷ số
c
a
, biết bán kính của Trái Đất xấp xỉ
4000
dặm.
---------- HẾT ----------
{ }
0; 1; 2; 3; 4; 5; 6
A =
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng
Oxy
, cho
( ) ( )
; và B ;
AA BB
Axy xy
. Tọa độ trung điểm
I
của đoạn thẳng
AB
là
A.
;
22
−−



A BA B
x xy y
I
. B.
;
22
++



A BA B
x xy y
I
.
C.
;
33
++



A BA B
x xy y
I
. D.
;
22
++



AABB
xyxy
I
.
Lời giải
Ta có:
I
là trung điểm của đoạn thẳng nên
2
2
AB
I
AB
I
xx
x
yy
y
+
=
+
=
.
Vậy
;
22
++



A BA B
x xy y
I
.
Câu 2: Giá trị gần đúng của
28
chính xác đến hàng phần trăm là
A.
5,656
. B.
5, 65
. C.
5, 66
. D.
5,657
Lời giải
Sử dụng máy tính cầm tay ta tính được
2 8 5,656854249...=
Vậy số quy tròn là
5, 66
.
Câu 3: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau.
Số cuốn sách 3 4 5 6 7
Số bạn 6 15 3 8 8
Tìm mốt của mẫu số liệu trên
A.
7
. B.
5
. C.
6
. D.
4
.
Lời giải
Mốt của mẫu số liệu trên là: 4
Câu 4: Bảng sau cho biết thời gian chạy cự li 100m của các bạn trong lớp (đơn vị giây)
Thời gian 12 13 14 15 16
Số bạn 4 7 3 18 8
Hãy tính thời gian chạy trung bình cự li 100m của các bạn trong lớp.
A.
14,094
. B.
14,245
. C.
14,475
. D.
14,75
.
Lời giải
Số bạn học sinh trong lớp là
4 7 3 18 8 40
n =+++ +=
(bạn)
Thời gian chạy trung bình cự li 100m của các bạn trong lớp là:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
4.12 7.13 3.14 18.15 8.16
14,475
40
x
+++ +
= =
Câu 5: Số ôtô đi qua một cây cầu mỗi ngày trong một tuần đếm được như sau: 83; 74; 71; 79; 83; 69;
92. Phương sai và độ lệch chuẩn lần lượt là
A. 78,71 và 8,87. B. 52,99 và 7,28. C. 61,82 và 7,86. D. 55,63 và 7,46.
Lời giải
Ta có:
( )
1
69 71 74 79 83.2 92 78,7
7
x = ++++ + ≈
.
Phương sai:
(
) ( ) ( ) (
)
( )
222 22
2
1
69 78,7 71 78,7 74 78,7 2. 83 78,7 92 78,7 55,63
7
S

=−+−+−+−+− ≈

.
Độ lệch chuẩn:
2
7,46SS= ≈
.
Câu 6: Cho
(0,1)a
=
,
( 1; 2)
b = −
,
( 3; 2)
c =−−
. Tọa độ của
324u abc=+−

là
A.
(
)
10; 15
−
. B.
( )
15;10
. C.
(
)
10;15
. D.
(
)
10;15
−
.
Lời giải
( )
3 2 4 10;15
=+−=

uabc
.
Câu 7: Kết quả đo chiều dài một cây cầu là
152,65
am=
với độ chính xác
0,05m
. Viết số quy tròn của
số
a
và ước lượng sai số tương đối của số quy tròn đó.
A.
152,7
và
0,033%
a
δ
<
. B.
152,7
và
0,066%
a
δ
<
.
C.
152,7
và
0,013%
a
δ
<
. D.
152,7
và
0,065%
a
δ
=
Lời giải
Vì độ chính xác đến hàng phần trăm nên ta quy tròn số
a
đến hàng phần chục là
152,7
. Ta có
152,6 152,7 0,1 152,7 0aa≤ ≤ ⇒− ≤ − ≤
hay
152,7 0,1
a
a∆= − ≤
. Vậy sai số tương đối là
0,1
0,066%
152,7
a
a
a
δ
∆
=≤<
.
Câu 8: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của mười hai thí
sinh theo thứ tự không giảm như sau:
56667777788x
Tìm
x
biết số trung bình của thời gian thi nghề của các thí sinh trên là
109
12
.
A.
35
. B.
33
. C.
34
. D.
36
.
Lời giải
Số trung bình là
5 3.6 4.7 2.8 109
35
12 12
++++
= = ⇔=
x
xx
.
Câu 9: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP
u
=(3;–4) là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
A.
32
.
4
xt
yt


. B.
23
.
34
xt
yt


C.
23
.
14
xt
yt


. D.
12
.
43
xt
yt


.
Lời giải
đường thẳng (d) đi qua M(–2;3) và có VTCP
3; 4 3; 4uu


có phương trình
23
.
34
xt
yt


Câu 10: Trong mặt phẳng tọa độ
Oxy
đường thẳng đi qua
( 1; 4)A −
và song song trục
Ox
A.
10x −=
. B.
40y
+=
. C.
10x +=
. D.
40y −=
.
Lời giải
Vì đường thẳng đi qua
( 1; 4)A −
và song song trục
Ox
nên có véc tơ pháp tuyến
( )
0;1j
nên có
phương trình
40y
−=
.
Câu 11: Tính góc giữa hai đường thẳng
1
:2 5 2 0
dxy
+ −=
và
2
:3 7 3 0dxy− +=
.
A.
0
30
. B.
0
135
. C.
0
45
. D.
0
60
.
Lời giải
Đường thẳng
1
:2 5 2 0dxy+ −=
có vectơ pháp tuyến
( )
1
2;5n
=
.
Đường thẳng
2
:3 7 3 0
dxy− +=
có vectơ pháp tuyến
( )
2
3; 7n = −
.
Góc giữa hai đường thẳng được tính bằng công thức
( )
( )
( )
12
12
12
12
2
222
.
2.3 5.( 7)
29 1
cos , cos ,
29 2 2
.
2 5. 3 7
nn
dd nn
nn
+−
= = = = =
+ +−



( )
0
12
; 45
dd⇒=
Vậy góc tạo bởi đường thẳng
1
d
và
2
d
bằng
0
45
.
Câu 12: Trong mặt phẳng
,Oxy
cho hai đường thẳng
1
3
:
4
= −
= −
xt
d
yt
và
2
1
:
11 2
=
=−−
x
d
yt
Góc giữa hai
đường thẳng
1
d
và
2
d
bằng
A.
60
. B.
45
. C.
90
. D.
30
.
Lời giải
Ta có đường thẳng
1
d
và
2
d
lần lượt có vecto chỉ phương là
( )
1
1; 1u =−−
,
( )
2
0; 2u = −
.
Gọi
ϕ
là góc giữa
1
d
và
2
d
.
12
12
. 1.0 2
2
cos 45
.2
22
uu
uu
ϕϕ
−+
= = = ⇒=


.
Câu 13: Phương trình đường tròn có tâm
( )
0; 2I
và bán kính
5=R
là
A.
22
4 21 0+−+=xy y
. B.
22
4 21 0++−=xy y
.
C.
22
4 21 0+−−=xy y
. D.
22
4 21 0+−−=xy x
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
Phương trình đường tròn có tâm
( )
0; 2I
và bán kính
5=R
là:
( )
2
2
2 25+− =xy
22
4 21 0⇔+−−=xy y
.
Câu 14: Trong hệ trục tọa độ
Oxy
, cho đường tròn
( ) ( )
22
( ): 1 2 8Cx y− ++ =
. Phương trình tiếp tuyến
d
của
()C
tai điểm
(3; 4)A −
là
A.
: 10dx y+ +=
. B.
: 2 11 0dx y− −=
. C.
: 70dx y−−=
. D.
: 70dx y−+=
.
Lời giải
Đường tròn
()C
có tâm
(1; 2)I −
.
Tiếp tuyến tại
A
có vectơ pháp tuyến là
(2; 2)n IA= = −

Phương trình tiếp tuyến của đường tròn tại
A
là:
2( 3) 2( 4) 0 7 0x y xy− − + =⇔−−=
.
Câu 15: Phương trình nào sau đây là phương trình chính tắc của một elip?
A.
22
1
4 25
xy
−=
. B.
22
1
4 25
xy
+=−
. C.
22
1
52
xy
+=
. D.
22
0
4 25
xy
+=
.
Lời giải
Phương trình chính tắc của một elip có dạng
22
22
1
xy
ab
+=
với
22
0ab>>
.
Câu 16: Lớp 10A có 25 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một học sinh để
tham gia vào đội thanh niên tình nguyện của trường biết rằng tất cả các bạn trong lớp đều có khả
năng tham gia.
A.
40
. B.
25
. C.
15
. D.
10
.
Lời giải
Số cách chọn được 1 học sinh nam: có 25.
Số cách chọn được 1 học sinh nữ: có 15.
Vậy để chọn một học sinh trong lớp 10A tham gia vào đội thanh niên tình nguyện của trường có:
25 15 40+=
.
Câu 17: Có bao nhiêu số tự nhiên có 2 chữ số mà cả hai chữ số đều là lẻ
A.
50
. B.
25
. C.
20
. D.
10
.
Lời giải
Gọi số tự nhiên có hai chữ số mà cả hai chữ số đều lẻ là .
Số cách chọn số là cách.
Số cách chọn số là cách.
Vậy có số thỏa mãn yêu cầu bài toán.
Câu 18: Số cách xếp
3
nam sinh và
4
nữ sinh vào một dãy ghê hàng ngang có
7
chỗ ngồi là
A.
4!.3
. B.
7!
. C.
4!.3!
. D.
4!
.
Lời giải
Xếp
3
nam sinh và
4
nữ sinh vào một dãy ghê hàng ngang có
7
chỗ ngồi có
7!
cách.
Câu 19: Một nhóm học sinh có
10
người. Cần chọn
3
học sinh trong nhóm để làm
3
công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việ C. Số cách chọn là
A.
3
10
. B.
30
. C.
3
10
C
. D.
3
10
A
.
Lời giải
Số cách chọn
3
em học sinh là số cách chọn
3
phần tử khác nhau trong
10
phần tử có phân biệt
có thứ tự nên số cách chọn thỏa yêu cầu là
3
10
A
.
Câu 20: Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con.
ab
a
5
b
5
5.5 25=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
A. 1326. B. 104. C. 26. D. 2652
Lời giải
Số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con:
2
52
C
1326=
.
Câu 21: Trong khai triển nhị thức Niu-tơn của
( )
4
13x+
, số hạng thứ
2
theo số mũ tăng dần của
x
là
A.
108x
. B.
2
54x
. C.
1
. D.
12x
.
Lời giải
Ta có
( )
( )
44
4
44
00
13 3 3
k
k kk k
kk
x Cx Cx
= =
+= =
∑∑
.
Do đó số hạng thứ
2
theo số mũ tăng dần của
x
ứng với
1k =
, tức là
11
4
3 12
Cx x=
.
Câu 22: Xếp
7
học sinh
,,,,,,ABC DEFG
vào một chiếc bàn dài có đúng 7 ghế. Tính xác suất để học
sinh
D
không ngồi đầu bàn.
A.
4
7
. B.
7
3
. C.
3
7
. D.
5
7
.
Lời giải
+ Xét phép thử: “Xếp
7
học sinh vào
7
ghế”, ta có
( )
7! 5040n Ω= =
.
+ Gọi
K
là biến cố: “Xếp
D
không ngồi đầu bàn”.
+ Ta tìm
( )
nK
:
Xếp
D
vào bàn sao cho
D
không ngồi đầu bàn, có 5 cách xếp.
Xếp 6 học sinh còn lại vào 6 ghế còn lại, có
6! 720=
cách xếp.
Vậy số cách xếp sao cho
D
không ngồi đầu bàn là
( )
5.720 3600nK = =
cách.
+ Xác suất cần tìm là
(
)
( )
( )
3600 5
5040 7
nK
pK
n
= = =
Ω
.
Câu 23: Chọn ngẫu nhiên một số tự nhiên nhỏ hơn
15
. Tính xác suất để chọn được số chẵn
A.
8
15
. B.
1
2
. C.
7
15
. D.
4
7
.
Lời giải
Ta có tập các số tự nhiên nhỏ hơn
15
là
{ }
0;1;2;3;...;14S =
nên có
7
số lẻ và
8
số chẵn.
Số phần tử không gian mẫu:
( )
15n
Ω=
.
Gọi A là biến cố: ‘‘Chọn được số chẵn’’ thì
( ) ( )
( )
( )
8
8.
15
nA
nA pA
n
=⇒==
Ω
Câu 24: Từ một hộp chứa
11
quả cầu màu đỏ và
4
quả cầu màu xanh, lấy ngẫu nhiên đồng thời
3
quả cầu.
Xác suất để lấy được
3
quả cầu màu xanh bằng
A.
24
455
. B.
4
165
. C.
4
455
. D.
24
165
.
Lời giải
Ta có
( )
3
15
nC
Ω=
.
Gọi
A
là biến cố “lấy được
3
quả cầu màu xanh” suy ra
( )
3
4
nA C=
Vậy xác suất để lấy ra được
3
quả cầu màu xanh là
( )
3
4
3
15
4
455
C
PA
C
= =
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
Câu 25: Cho 2 điểm
(
)
1;2 , (3;4).AB
Viết phương trình tổng quát đường trung trực của đoạn thẳng
AB
.
A.
5 0.
xy++=
B.
5 0.
xy−−=
C.
2 2 5 0.xy+ −=
D.
5 0.
xy+−=
Lời giải
+ Giả sử
∆
là đường trung trực của
AB
AB⇒∆⊥
tại trung điểm
M
của
AB
.
+ Tọa độ trung điểm
M
của
AB
là :
( )
2
2
2;3
3
2
AB
M
AB
M
xx
x
M
yy
y
+
= =
⇒
+
= =
.
+ Ta có
( ) ( ) ( )
2; 2 2 1;1 1;1AB n
∆
= = ⇒=
 
Suy ra phương trình tổng quát đường trung trực
∆
của đoạn thẳng
AB
là:
5 0.
xy+−=
Câu 26: Trong mặt phẳng
Oxy
, khoảng cách giữa hai đường thẳng song song
1
:3 4 3 0xyd − −=
và
2
:3 4 8 0xyd − −=
là
A. 4. B. 3. C. 1. D. 2.
Lời giải
Lấy
( )
2
0; 2A d− ∈
.
Do
12
dd
nên
( ) ( )
12 1
22
3.0 4
1
2
,
3
.( ) 3
,
( 4)
dddd dA =
−+
=
−
− − −−
=
Câu 27: Trong mặt phẳng tọa độ Oxy, cho đường tròn
22
( ) : 4 2 20 0Cx y x y+−−−=
phương trình tiếp
tuyến của
( )
C
vuông góc với đường thẳng
:3 4 9 0
xy∆ + +=
là
A.
4 3 30 0xy−+=
và
4 3 20 0
xy−−=
. B.
4 3 20 0
xy−+=
và
4 3 30 0xy−−=
.
C.
4 3 30 0xy−−=
và
4 3 20 0
xy−−=
. B.
4 3 20 0
xy−+=
và
4 3 30 0xy−+=
.
Lời giải
Đường tròn
( )
C
có tâm
( )
2;1I
và bán kính
22
2 1 20 5R = ++ =
.
Đường thẳng d vuông góc với
:3 4 9 0
xy∆ + +=
:4 3 0d x ym⇒ − +=
.
d
là tiếp tuyến của
( ) ( )
,C d Id R⇔=
( )
2
2
4.2 3.1
5.
43
m−+
⇔=
+−
5 25 30 : 4 3 30 0
5 25 20 : 4 3 20 0
m m dx y
m m dx y
−= = − + =

⇔ ⇔⇔

−=− =− − − =

.
Câu 28: Cho tam giác
ABC
có
( )
( )
( )
1;1, 3;2, 5;5A BC−−
. Toạ độ tâm đường tròn ngoại tiếp tam giác
ABC
là
A.
47 13
;
10 10

−


. B.
47 13
;
10 10



. C.
47 13
;
10 10

−−


. D.
47 13
;
10 10

−


.
Lời giải
Gọi
( )
;Ixy
là tâm đường tròn ngoại tiếp tam giác
ABC
.
Ta có:
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
22 2 2
22
22 2 2 2 2
47
1132
4 6 11
10
8 8 48 13
1155
10
x
xyx y
AI BI x y
xy
AI CI
xyx y
y
=
− ++ =− +−
= +=

⇔ ⇔⇔

−=
=
− ++ =− ++

= −
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
47 13
;
10 10
I

−


⇒
.
Câu 29: Cho của hypebol
(
)
22
:1
16 5
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
(
)
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
8
. B.
16
. C.
4
. D.
5
.
Lời giải
Gọi
1
F
và
2
F
là hai tiêu điểm của
(
) (
)
22
22
: 1, 0, 0
xy
H ab
ab
−= > >
.
Điểm
(
)
12
2M H MF MF a∈⇔ − =
.
Từ phương trình
( )
22
:1
16 5
xy
H −=
suy ra
( )
2
16 4, 0a aa= ⇒= >
.
Vậy hiệu các khoảng cách từ mỗi điểm
M
nằm trên
( )
H
đến hai tiêu điểm có giá trị tuyệt đối
là
12
28MF MF a
−==
.
Câu 30: Có bao nhiêu số tự nhiên gồm bốn chữ số khác nhau và chia hết cho 5?.
A. 952. B. 1800. C. 1008. D. 1620.
Lời giải
Gọi số tự nhiên cần tìm có dạng:
abcd
. Do chia hết cho 5 nên
{ }
0;5d ∈
Trường hợp 1: với
0d =
ta có:
Chọn d có 1 cách.
Chọn a có 9 cách
Chọn b có 8 cách
Chọn c có 7 cách
Vậy trường hợp 1 có:
9.8.7 504=
số
Trường hợp 2: với
5d =
ta có:
Chọn d có 1 cách.
Chọn a có 8 cách
Chọn b có 8 cách
Chọn c có 7 cách
Vậy trường hợp 1 có:
8.8.7 448=
số
Vậy có:
504 448 952+=
số thỏa yêu cầu bài toán.
Câu 31: Có
5
nhà toán học nam,
3
nhà toán học nữ và
4
nhà vật lý nam. Lập một đoàn công tác có
3
người cần có cả nam và nữ, trong đó có cả nhà toán học và nhà vật lý. Hỏi có bao nhiêu cách
lập?
A.
60
. B.
90
. C.
20
. D.
12
.
Lời giải
Để lập đội công tác ta chia làm các trường hợp sau:
+ Số cách chọn đội công tác gồm 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam có
5.3.4 60
=
cách
+ Số cách chọn đội công tác gồm 1 nhà toán học nữ, 2 nhà vật lý nam có
2
4
3. 18C =
cách
+ Số cách chọn đội công tác gồm 2 nhà toán học nữ, 1 nhà vật lý nam có
21
34
. 12CC=
cách
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Vậy số cách lập là
60 18 12 90++=
cách.
Câu 32: Cho tứ giác
ABCD
. Trên mỗi cạnh
,,,AB BC CD DA
lấy 7 điểm phân biệt và không có điểm nào
trùng với 4 đỉnh
,,,ABCD
. Hỏi từ
32
điểm đã cho lập được bao nhiêu tam giác?
A.
4960.
B.
4624.
C.
7140.
D.
6804.
Lời giải
Số tam giác lập được là số cách chọn
3
điểm trong
32
điểm đã cho sao cho không có
3
điểm
nào thẳng hàng.
Số cách chọn
3
điểm như trên là
33
32 9
4 4624CC−=
Số tam giác lập được thoả mãn đề bài là 4624.
Câu 33: Trong một lớp học gồm có
18
học sinh nam và
17
học sinh nữ. Giáo viên gọi ngẫu nhiên
4
học
sinh lên bảng giải bài tập. Xác suất để
4
học sinh được gọi có cả nam và nữ là:
A.
68
75
. B.
65
71
. C.
443
506
. D.
69
77
.
Lời giải
Ta có:
(
)
4
35
52360
nCΩ= =
.
Số cách gọi
4
học sinh lên bảng giải bài tập mà cả
4
bạn đều là nữ là:
4
17
C
Số cách gọi
4
học sinh lên bảng giải bài tập mà cả
4
bạn đều là nam là:
4
18
C
Gọi
A
là biến cố: “
4
học sinh được gọi có cả nam và nữ”.
Suy ra:
( )
( )
4 44
35 17 18
46920nA C C C=−+=
.
Vậy xác suất để
4
học sinh được gọi có cả nam và nữ là:
( )
( )
( )
46920 69
52360 77
nA
pA
n
= = =
Ω
.
Câu 34: Chọn ngẫu nhiên hai số phân biệt từ
15
số nguyên dương đầu tiên. Xác suất để tích hai số được
chọn là một số chẵn bằng
A.
1
5
. B.
4
15
. C.
4
5
. D.
11
15
.
Lời giải
Số phần tử của không gian mẫu:
( )
2
15
105nCΩ= =
.
Gọi A là biến cố: “Tích hai số được chọn là một số chẵn”.
Trường hợp 1: Chọn hai số đều là số chẵn. Số cách chọn :
2
7
21C
=
.
Trường hợp 2: Chọn một số chẵn và một số lẻ. Số cách chọn :
11
78
. 56CC=
.
Do đó:
( )
2 11
7 78
. 77CAnCC=+=
. Suy ra:
(
)
( )
( )
77 11
105 15
P A
n
An
= = =
Ω
.
Câu 35: Từ một tổ gồm 10 nam và 8 nữ chọn ra một đoàn đại biểu gồm 6 người để tham dự hội nghị. Xác
suất để đoàn đại biểu được chọn có đúng 2 nữ bằng
A.
151
221
. B.
35
221
. C.
70
221
. D.
29
221
.
Lời giải
Chọn ngẫu nhiên một đoàn đại biểu gồm 6 người từ tổ gồm 18 người.
Ta có
( )
6
18
nC
Ω
=
.
Gọi
A
là biến cố trong 6 đại biểu được chọn có đúng 2 người là nữ.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Chọn 2 đại biểu nữ từ 8 đại biểu nữ có
2
8
C
cách.
Chọn 4 đại biểu nam từ 10 đại biểu nam có
4
10
C
cách.
Từ đó có
( )
24
8 10
.nA CC=
.
Vậy
( )
( )
( )
24
8 10
6
18
.
70
221
nA
CC
PA
n
C
Ω
= = =
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp . Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác
nhau được lập thành từ các chữ số của tập
A
, đồng thời có đúng 2 chữ số lẻ và 2 chữ số lẻ đó
đứng cạnh nhau.
Lời giải
Vì chữ số lẻ đứng kề nhau nên ta gom số lẻ thành số , có bộ .
Gọi số cần chọn có dạng với .
` ● Trường hợp 1. , suy ra có cách chọn.
+) Có vị trí để xếp chữ số , ứng với mỗi cách xếp có cách xếp hai phần tử trong
.
+) Chọn thứ tự chữ số từ tập để xếp vào vị trí trống còn lại, có cách.
Do đó trường hợp này có số.
● Trường hợp 2. , suy ra có cách chọn.
+) Nếu xếp vào vị trí đầu tiên nên có 1 cách, ứng với cách xếp này có cách xếp hai phần
tử trong . Chọn chữ số từ tập chữ số còn lại để xếp vào vị trí trống còn lại, có
cách. Suy ra có tất cả số.
+) Nếu xếp vào vị trí thứ hoặc thứ thì có cách, ứng với cách xếp này có cách xếp
hai phần tử trong . Chọn chữ số từ tập chữ số còn lại để xếp vào vị trí trống còn lại,
có cách. Do đó số. Xét riêng trường hợp chữ số đứng đầu thì có
số. Suy ra có số.
Do đó trường hợp này có số.
Vậy có số thỏa mãn.
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho điểm
( )
2;1M
và đường tròn
( ) ( ) ( )
22
:1 24Cx y− +− =
. Viết
phương trình đường thẳng
( )
d
qua điểm
M
và cắt
( )
C
tại hai điểm phân biệt
;AB
sao cho độ
dài
AB
ngắn nhất.
Lời giải
{ }
0; 1; 2; 3; 4; 5; 6A =
2
2
M
2
3
3C =
M
abcd
{ }
0; 2; 4; 6d ∈
0d =
d
1
3
M
M
2!
M
2
{ }
2; 4; 6
2
2
3
A
2
3
1.3.2!. 36A =
{ }
2; 4; 6d ∈
d
3
M
2!
M
2
3
2
2
3
A
2
3
3.1.2!. 36A =
M
2
3
2
2!
M
2
3
2
2
3
A
2
3
3.2.2!. 72A =
0
1
2
3.2.2!. 24A =
72 24 48−=
36 48 84+=
( )
3. 36 84 360+=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Đường tròn
( )
C
có tâm
( )
1; 2I
, bán kính
2R =
.
22IM R= <=
nên điểm
M
nằm trong đường tròn.
Giả sử gọi
H
là trung điểm của
AB
.
Ta có
22 2
2 2. 2 4AB HB IB IH IH= = −=−
Vì
2
IH IM≤=
nên
22
24 24 22AB IH IM=−≥− =
do đó
AB
ngắn nhất khi
IH IM=
Lúc đó đường thẳng
d
qua
( )
2;1M
và nhận
( )
1; 1IM = −

làm vecto pháp tuyến
( ) ( ) ( ) ( )
:1 2 1 1 0 : 1 0 1; 1d x y d xy a c− − − = ⇔ −+ += ⇒ =− =
Câu 38: Xếp
5
quyển sách Toán và
5
quyển sách Văn khác nhau lên một kệ dài. Tính xác suất để
2
quyển sách cùng một môn nằm cạnh nhau.
Lời giải
+
( )
10!n Ω=
+ Đặt biến cố
A
: Có hai quyển sách cùng môn nằm cạnh nhau
Khi đó
A
: Các quyển sách cùng môn không nằm cạnh nhau
Có
( )
2.5!.5!
nA=
(
) ( )
(
)
10! 2.5!.5! 3600000
nA n nA= Ω− = − =
(
)
( )
( )
125
126
nA
PA
n
⇒==
Ω
.
Câu 39: Vệ tinh nhân tạo đầu tiên được Liên Xô phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là
một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là
22
2 22
22
1, 0, 0,
xy
abcab
ab
+=> > =−
. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là
583
dặm và xa nhất là
1342
dặm. Tìm tỷ số
c
a
, biết bán kính của Trái Đất xấp xỉ
4000
dặm.
Lời giải
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm
1
F
của elip.
Khi đó elip có phương trình là:
22
22
1, 0, 0
xy
ab
ab
+= > >
Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là
583
dặm và xa nhất là
1342
dặm,
mà bán kính của Trái Đất xấp xỉ 4000 dặm nên vệ tinh cách tâm Trái Đất gần nhất là
4583
dặm
và xa nhất là
5342
dặm.
Giả sử vệ tinh được biểu thị là điểm
(; )Mxy
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 15
Sưu tầm và biên soạn
Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là:
1
c
MF a x
a
= +
Và ta có
1
a c MF a c−≤ ≤+
Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là
ac
−
và
ac
+
4583 4962,5
5342 379,5
ac a
ac c
−= =

⇒⇒

+= =

Suy ra
0,076
c
a
≈
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 09
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong hệ tọa độ
,Oxy
cho
( )
( )
5;2 , 10;8AB
. Tìm tọa độ của vectơ
?AB

A.
( )
15;10AB =

. B.
(
)
2;4
AB
=

. C.
(
)
5;6
AB
=

. D.
( )
50;16AB =

.
Câu 2: Trong mặt phẳng tọa độ Oxy, gọi
( )
2;0E
−
,
( )
0; 2 3F
lần lượt là hình chiếu của điểm M lên
các trục tọa độ Ox, Oy. Độ dài của vectơ
OM

là
A.
22
. B.
4
. C.
2
. D.
3
.
Câu 3: Khi sử dụng máy tính bỏ túi với
10
chữ số thập phân ta được:
8 2,828427125=
. Giá trị gần
đúng của
8
chính xác đến hàng phần trăm là
A.
2,81
. B.
2,83
. C.
2,82
. D.
2,80
.
Câu 4: Hãy tìm trung vị cho mẫu số liệu điểm kiểm tra môn Toán của Lớp 11B:
3 5 6 7 1 10 3 4
A.
4,5
. B.
4
. C.
5
. D.
5,5
.
Câu 5: Người ta đã thống kê số gia cầm bị tiêu hủy trong vùng dịch của 6 xã A,B,.,F như sau (đơn vị:
nghìn con):
Xã
A
B
C
D
E
F
Số lượng gia cầm bị
tiêu hủy
12 25 27 15 45 5
Tìm trung vị cho mẫu số liệu về số gia cầm bị tiêu huỷ đã cho.
A.
20
. B.
21
. C.
21, 5
. D.
27
.
Câu 6: Nhiệt độ của thành phố Vinh ghi nhận trong
10
ngày qua lần lượt là:
24 21 30 34 28 35 33 36 25 27
Khoảng tứ phân vị của mẫu số liệu bằng:
A.
12
Q
∆=
. B.
11
Q
∆=
. C.
13
Q
∆=
D.
9
Q
∆=
.
Câu 7: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị
kw
) hàng tháng của gia đình bạn An trong năm
2021 như sau:
163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là
10kw
.Gọi
;
QQ
′
∆∆
lần lượt
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây
là đúng
A.
QQ
′
∆=∆
. B.
10
QQ
′
∆=∆−
. C.
10
QQ
′
∆=∆−
D.
20
QQ
′
∆=∆−
.
Câu 8: Các giá trị bất thường của mẫu số liệu
5
,
6
,
19
,
21
,
22
,
23
,
24
,
25
,
26
,
27
,
28
,
31
,
35
,
38
,
42
là
A.
5, 42
. B.
5, 6,38, 42
. C.
5, 6, 42
. D.
5,35,38, 42
.
Câu 9: Đường thẳng
∆
đi qua điểm
( )
1; 4M
và có vectơ pháp tuyến
( )
2;3=
n
có phương trình tổng
quát là
A.
2 3 14 0+−=xy
. B.
2 3 10 0++=xy
. C.
4 10 0−+ − =xy
. D.
4 10 0−+ + =xy
.
Câu 10: Viết phương trình đường thẳng đi qua điểm
( )
2;5M −
và cắt hai trục tọa độ tại hai điểm
A
và
B
sao cho
M
là trung điểm của
AB
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
A.
5 2 15 0xy+ +=
. B.
2 5 20 0xy−+=
. C.
5 2 20 0xy−+=
. D.
2 5 20 0yx
−+=
.
Câu 11: Tính góc giữa hai đường thẳng
: 3 2 0 ': 3 1 0 x y và x y∆ − + = ∆ + −=
?
A. 90
o
. B. 120
o
. C. 60
o
. D. 30
o
.
Câu 12: Tìm côsin góc giữa 2 đường thẳng
1
:4 3 1 0xy∆ − +=
và
2
66
:
18
xt
yt
= +
∆
= −
.
A.
7
25
. B.
1
. C.
24
25
. D.
6
25
.
Câu 13: Xác định tâm và bán kính của đường tròn
( ) ( ) (
)
22
: 1 2 9.Cx y
+ +− =
A. Tâm
( )
1; 2 ,I −
bán kính
3R =
. B. Tâm
( )
1; 2 ,
I −
bán kính
9R =
.
C. Tâm
( )
1; 2 ,I −
bán kính
3R =
. D. Tâm
( )
1; 2 ,I −
bán kính
9R =
.
Câu 14: Trong mặt phẳng với hệ toạ độ
Oxy
, phương trình đường tròn có tâm
( )
3;1I
và đi qua điểm
( )
2; 1
−M
là
A.
(
) (
)
22
3 1 5.+ ++ =xy
B.
( ) ( )
22
3 1 5.
− +− =xy
C.
( ) (
)
22
3 1 5.− +− =xy
D.
( ) ( )
22
3 1 5.+ ++ =xy
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol?
A.
2
3yx=
. B.
2
4yx=
. C.
2
5yx
=
. D.
2
4yx=
.
Câu 16: Trong kì thi vấn đáp môn toán lớp 11, Ban giám khảo đã chuẩn bị 25 câu đại số, 15 câu hình học
và 10 câu giải tích. Thí sinh được quyền chọn một câu để trả lời. Số khả năng chọn câu hỏi của
mỗi thí sinh là
A.
3750
. B.
50
. C.
375
. D.
150
.
Câu 17: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
1
cái
bút và
1
quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
90
. B.
70
. C.
80
. D.
60
.
Câu 18: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là
A.
9!
. B.
9
. C.
1
. D.
9
9
.
Câu 19: Năm 2021, cuộc thi Hoa hậu Hòa bình Quốc tế lần thứ 9 được tổ chức tại Thái Lan và có tổng
cộng 59 thí sinh tham gia. Hỏi có bao nhiêu các chọn ra 5 người bao gồm một Hoa hậu và bốn Á
hậu 1, 2, 3, 4?
A.
5
59
A
. B.
5
59
C
. C.
14
59 58
AA+
. D.
14
59 58
.CC
.
Câu 20: Trong mặt phẳng cho
15
điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác
trong có đỉnh là
3
trong số
15
đã cho là
A.
3
15
C
. B.
15!
. C.
3
15
. D.
3
15
A
.
Câu 21: Tìm hệ số của
22
xy
trong khai triển nhị thức Niu-tơn của
( )
4
2
xy+
.
A.
32
. B.
8
. C.
24
. D.
16
.
Câu 22: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác
suất để được 3 quả cầu khác màu là
A.
3
7
. B.
3
5
. C.
3
14
. D.
3
11
.
Câu 23: Có
30
chiếc thẻ được đánh số thứ tự từ
1
đến
30
. Chọn ngẫu nhiên
1
chiếc thẻ, tính xác suất để
chọn được thẻ ghi số chia hết cho
3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
A.
1
3
. B.
1
2
. C.
3
10
. D.
2
3
.
Câu 24: Từ một hộp chứa
10
quả bóng gồm 4 quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
1
6
. B.
1
30
. C.
3
5
. D.
2
5
.
Câu 25: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
2;0 , 0;3 , 3;1ABC−
. Đường thẳng
d
đi qua
B
và song song với
AC
có phương trình tổng quát là
A.
15 15 0
xy− +=
. B.
5 30xy+−=
. C.
5 15 0xy+−=
. D.
5 30xy++=
.
Câu 26: Trong mặt phẳng
Oxy
cho 3 điểm
( ) ( ) ( )
1;4 , 3; 1 , 6;2AB C−
không thẳng hàng. Tính khoảng
cách từ điểm
A
đến đường thẳng
BC
.
A.
(
)
32
;
2
d A BC
=
. B.
( )
2
;
2
d A BC
=
. C.
( )
2
;
7
d A BC =
. D.
( )
72
;
2
d A BC =
.
Câu 27: Đường tròn
( )
C
đi qua hai điểm
( )
1;1A
,
( )
5;3B
và có tâm
I
thuộc trục hoành có phương trình
là
A.
( )
2
2
4 10
xy
+ +=
. B.
( )
2
2
4 10xy− +=
. C.
( )
2
2
4 10xy− +=
. D.
( )
2
2
4 10xy
+ +=
.
Câu 28: Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
( )
22
: 22 0L x y ax by c
+ − − +=
ngoại tiếp tam
giác
ABC
, với
( ) ( ) ( )
1;0 , 0;–2 , 2;–1AB C
. Khi đó giá trị của biểu thức
abc++
bằng
A.
2
3
. B.
2
3
−
. C.
1
3
−
. D.
1
3
.
Câu 29: Phương trình chính tắc của
( )
E
có tiêu cự bằng
6
và đi qua điểm
( )
5; 0A
là:
A.
22
1
100 81
xy
+=
. B.
22
1
25 16
xy
+=
. C.
22
1
15 16
xy
+=
. D.
22
1
25 9
xy
+=
.
Câu 30: Trong hội nghị học sinh giỏi của trường, khi ra về các em bắt tay nhau. Biết rằng có
120
cái bắt
tay và giả sử không em nào bị bỏ sót cũng như bắt tay không lặp lại
2
lần. Số học sinh dự hội
nghị thuộc khoảng nào sau đây?
A.
( )
13;18
. B.
( )
21;26
. C.
( )
17;22
. D.
( )
9;14
.
Câu 31: Một lớp có
30
học sinh gồm
20
nam và
10
nữ. Hỏi có bao nhiêu cách chọn ra một nhóm
3
học
sinh sao cho nhóm đó có ít nhất một học sinh nữ?
A.
1140
. B.
2920
. C.
1900
. D.
900
.
Câu 32: Cho tập hợp
{ }
1;2;3;4;5;6;7A =
. Hỏi từ tập
A
có thể lập được bao nhiêu số tự nhiên có
6
chữ số khác nhau và phải có mặt các chữ số
1
,
2
,
3
sao cho chúng không đứng cạnh nhau?
A.
567
. B.
576
. C.
5040
. D.
840
.
Câu 33: Một nhóm gồm
12
học sinh trong đó có
6
học sinh khối 12,
4
học sinh khối
11
và
2
học sinh
khối 10. Chọn ngẫu nhiên
3
học sinh tham gia đội xung kích. Tính xác suất để
3
học sinh được
chọn không cùng một khối?
A.
1
5
. B.
6
55
. C.
12
55
. D.
49
55
.
Câu 34: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
A.
1
2
. B.
1
3
. C.
1
. D.
2
3
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 35: Một người chọn ngẫu nhiên
2
chiếc giày từ
5
đôi giày cỡ khác nhau. Tính xác suất để
2
chiếc
giày được chọn tạo thành một đôi.
A.
1
2
. B.
1
10
. C.
7
9
. D.
1
9
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp . Có bao nhiêu số tự nhiên chẵn có chữ số khác nhau
được lập thành từ các chữ số của tập đồng thời phải có mặt ba chữ số và chúng đứng
cạnh nhau?
Câu 37: Cho điểm
( )
1; 2M
và đường thẳng
:2 5 0d xy+−=
. Toạ độ của điểm đối xứng với điểm
M
qua
d
là
Câu 38: Một hộp đựng
10
viên bi có kích thước khác nhau, trong đó có
7
viên bi màu đỏ và
3
viên bi
màu xanh. Chọn ngẫu nhiên
2
viên bi từ hộp trên. Xác suất để
2
viên bi được chọn có ít nhất
một viên bi màu xanh bằng
Câu 39: Cho elip
( )
E
có độ dài trục lớn bằng
15
và đi qua điểm
M
sao cho
0
1
2
90F MF =
. Biết diện tích
tam giác
12
MF F
bằng 26. Phương trình chính tắc của elip
( )
E
là.
---------- HẾT ----------
{ }
0; 1; 2; 3; 4; 5; 6; 7A =
6
A
0; 1; 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong hệ tọa độ
,Oxy
cho
( )
( )
5;2 , 10;8AB
. Tìm tọa độ của vectơ
?AB

A.
(
)
15;10
AB
=

. B.
(
)
2;4
AB
=

. C.
(
)
5;6
AB
=

. D.
( )
50;16AB =

.
Lời giải
Chọn C
Áp dụng công thức
(
) ( )
; 5;6 .
B AB A
AB x x y y=− −=

Câu 2: Trong mặt phẳng tọa độ Oxy, gọi
( )
2;0E
−
,
( )
0; 2 3F
lần lượt là hình chiếu của điểm M lên
các trục tọa độ Ox, Oy. Độ dài của vectơ
OM

là
A.
22
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn B
Tọa độ của điểm
( )
2; 2 3M = −
Độ dài của vectơ
OM

là
( )
( )
2
2
2 2 3 16 4OM =−+ = =

Câu 3: Khi sử dụng máy tính bỏ túi với
10
chữ số thập phân ta được:
8 2,828427125=
. Giá trị gần
đúng của
8
chính xác đến hàng phần trăm là
A.
2,81
. B.
2,83
. C.
2,82
. D.
2,80
.
Lời giải
Chọn B
Giá trị gần đúng của
8 2,828427125=
chính xác đến hàng phần trăm là
2,83
.
Câu 4: Hãy tìm trung vị cho mẫu số liệu điểm kiểm tra môn Toán của Lớp 11B:
3 5 6 7 1 10 3 4
A.
4,5
. B.
4
. C.
5
. D.
5,5
.
Câu 5: Người ta đã thống kê số gia cầm bị tiêu hủy trong vùng dịch của 6 xã A,B,.,F như sau (đơn vị:
nghìn con):
Xã
A
B
C
D
E
F
Số lượng gia cầm bị
tiêu hủy
12 25 27 15 45 5
Tìm trung vị cho mẫu số liệu về số gia cầm bị tiêu huỷ đã cho.
A.
20
. B.
21
. C.
21, 5
. D.
27
.
Lời giải
Chọn A
Sắp xếp mẫu số liệu đã cho theo thứ tự không giảm ta được: 5 12 15 25 27 45
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
Mẫu số liệu đã cho có 6 giá trị nên trung vị của mẫu đó là
15 25
20
2
+
=
.
Câu 6: Nhiệt độ của thành phố Vinh ghi nhận trong
10
ngày qua lần lượt là:
24 21 30 34 28 35 33 36 25 27
Khoảng tứ phân vị của mẫu số liệu bằng:
A.
12
Q
∆=
. B.
11
Q
∆=
. C.
13
Q
∆=
D.
9
Q
∆=
.
Lời giải
Chọn D
Ta sắp xếp mẫu số liệu theo thứ tự không giảm:
21 24 25 27 28 30 33 34 35 36
Mẫu số liệu gồm 10 giá trị nên số trung vị là
2
(28 30) : 2 29Q =+=
Nửa số liệu bên trái là
21; 24; 25; 27;28
gồm
5
giá trị, số chính giữa là
25
Khi đó
1
25Q =
Nửa số liệu bên phải là
30;33; 34; 35; 36
gồm
5
giá trị, số chính giữa là
34
Khi đó
3
34Q =
Khoảng tứ phân vị của mẫu số liệu bằng:
31
34 25 9
Q
QQ
∆= − = − =
Câu 7: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị
kw
) hàng tháng của gia đình bạn An trong năm
2021 như sau:
163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là
10
kw
.Gọi
;
QQ
′
∆∆
lần lượt
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây
là đúng
A.
QQ
′
∆=∆
. B.
10
QQ
′
∆=∆−
. C.
10
QQ
′
∆=∆−
D.
20
QQ
′
∆=∆−
.
Lời giải
Chọn A
+) Sắp xếp mẫu số liệu năm 2021 theo thứ tự không giảm:
159 161 163 164 165 166 167 168 170 170 172 174
Mẫu số liệu gồm
12
giá trị nên số trung vị là
2
(166 167) : 2 166,5
Q =+=
Nửa số liệu bên trái là
159;161;163;164;165;166
gồm
6
giá trị
Khi đó
( )
1
163 164 : 2 163,5Q =+=
Nửa số liệu bên phải là
167;168;170;170;172;174
gồm
6
giá trị
Khi đó
3
170Q =
Khoảng tứ phân vị của mẫu số liệu bằng:
31
170 163,5 6,5
Q
QQ∆= − = − =
+) Sắp xếp mẫu số liệu năm 2022 theo thứ tự không giảm:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
149 151 153 154 155 156 157 158 160 160 162 164
Mẫu số liệu gồm
12
giá trị nên số trung vị là
2
(156 157) : 2 156,5Q =+=
Nửa số liệu bên trái là
149;151;153;154;155;156
gồm
6
giá trị
Khi đó
1
(153 154) : 2 153,5Q =+=
Nửa số liệu bên phải là
157;158;160;160;162;164
gồm
6
giá trị
Khi đó
3
160Q
=
Khoảng tứ phân vị của mẫu số liệu bằng:
31
160 153,5 6,5
Q
QQ
′
∆= − = − =
Câu 8: Các giá trị bất thường của mẫu số liệu
5
,
6
,
19
,
21
,
22
,
23
,
24
,
25
,
26
,
27
,
28
,
31
,
35
,
38
,
42
là
A.
5, 42
. B.
5, 6,38, 42
. C.
5, 6, 42
. D.
5,35,38, 42
.
Lời giải
Chọn A
Mẫu số liệu có các tứ phân vị
1
21Q =
,
2
25Q =
,
3
31
Q =
. Suy ra khoảng tứ phân vị
10Q∆=
.
Khi đó
1
3
6
2
QQ−∆=
,
1
3
41
2
QQ+∆=
nên các giá trị
5
,
42
là các giá trị bất thường của mẫu
số liệu trên
Câu 9: Đường thẳng
∆
đi qua điểm
( )
1; 4M
và có vectơ pháp tuyến
( )
2;3=
n
có phương trình tổng
quát là
A.
2 3 14 0
+−=
xy
. B.
2 3 10 0++=xy
. C.
4 10 0−+ − =
xy
. D.
4 10 0
−+ + =xy
.
Lời giải
Đường thẳng
∆
đi qua điểm
( )
1; 4M
và có vectơ pháp tuyến
( )
2;3=
n
có phương trình tổng
quát là
( ) ( )
2 1 3 4 0 2 3 14 0−+ − =⇔ + − =x y xy
.
Câu 10: Viết phương trình đường thẳng đi qua điểm
( )
2;5M −
và cắt hai trục tọa độ tại hai điểm
A
và
B
sao cho
M
là trung điểm của
AB
.
A.
5 2 15 0xy+ +=
. B.
2 5 20 0xy−+=
. C.
5 2 20 0xy−+=
. D.
2 5 20 0yx−+=
.
Lời giải
Gọi
( )
;0
A
A Ox A x∈⇒
và
( )
0;
B
B Oy B y∈⇒
.
Vì
M
là trung điểm của
AB
nên ta có:
24
2 10
AB M A
AB M B
xx x x
yy y y
+= =−

⇒

+= =

.
Suy ra phương trình đường thẳng
AB
là
1 5 2 20 0
4 10
xy
xy+=⇔−+=
−
.
Câu 11: Tính góc giữa hai đường thẳng
: 3 2 0 ': 3 1 0 x y và x y∆ − + = ∆ + −=
?
A. 90
o
. B. 120
o
. C. 60
o
. D. 30
o
.
Lời giải
∆
có vectơ pháp tuyến là
( )
1
1; 3n = −

.
'∆
có vectơ pháp tuyến là
( )
2
1; 3n =

.
Khi đó:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
(
)
( )
( )
( )
12
'
12
22
22
12
1.1 3 3
.
2
1
cos ; cos( ; )
2
4. 4
| |.
1 3 .1 3
nn
nn
nn
+−
−
∆∆ = = = = =
+− +




.
Vậy góc giữa hai đường thẳng
, '
∆∆
là
0
60
.
Câu 12: Tìm côsin góc giữa 2 đường thẳng
1
:4 3 1 0xy
∆ − +=
và
2
66
:
18
xt
yt
= +
∆
= −
.
A.
7
25
. B.
1
. C.
24
25
. D.
6
25
.
Lời giải
Ta có vec tơ pháp tuyến của hai đường thẳng là:
(
)
1
n 4; 3
∆
= −

.
( )
2
n 8; 6
∆
=

( )
( )
12
12
cos , cos n , n
∆∆
⇒ ∆∆ =
 
( )
2
2 22
4.8 3.6 7
25
4 3 .8 6
−
= =
+− +
.
Câu 13: Xác định tâm và bán kính của đường tròn
( )
(
) (
)
22
: 1 2 9.Cx y+ +− =
A. Tâm
( )
1; 2 ,I −
bán kính
3R =
. B. Tâm
(
)
1; 2 ,I −
bán kính
9R =
.
C. Tâm
( )
1; 2 ,I −
bán kính
3R =
. D. Tâm
(
)
1; 2 ,I −
bán kính
9R
=
.
Lời giải
Đường tròn
( ) ( )
( )
22
:1 29Cx y+ +− =
có tâm
( )
1; 2 ,
I
−
bán kính
3R =
.
Câu 14: Trong mặt phẳng với hệ toạ độ
Oxy
, phương trình đường tròn có tâm
( )
3;1
I
và đi qua điểm
(
)
2; 1−M
là
A.
( ) ( )
22
3 1 5.+ ++ =xy
B.
( ) ( )
22
3 1 5.− +− =xy
C.
( ) ( )
22
3 1 5.− +− =xy
D.
( ) ( )
22
3 1 5.+ ++ =xy
Lời giải
Vì đường tròn có tâm
( )
3;1I
và đi qua điểm
( )
2; 1−M
nên bán kính của đường tròn là
( ) ( )
22
3 2 11 5= = − ++ =R MI
.
Vậy phương trình đường tròn cần tìm là
( ) ( )
22
3 15− +− =
xy
.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol?
A.
2
3yx=
. B.
2
4yx
=
. C.
2
5yx=
. D.
2
4yx=
.
Câu 16: Trong kì thi vấn đáp môn toán lớp 11, Ban giám khảo đã chuẩn bị 25 câu đại số, 15 câu hình học
và 10 câu giải tích. Thí sinh được quyền chọn một câu để trả lời. Số khả năng chọn câu hỏi của
mỗi thí sinh là
A.
3750
. B.
50
. C.
375
. D.
150
.
Lời giải
Công việc chọn câu hỏi của thí sinh được hoàn thành bởi một trong các hành động: chọn 1 câu
hỏi đại số, chọn 1 câu hỏi hình học, chọn 1 câu hỏi giải tích.
Theo quy tắc cộng có
25 15 10 50++=
khả năng chọn câu hỏi cho mỗi thí sinh.
Câu 17: Có
10
cái bút khác nhau và
8
quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn
1
cái
bút và
1
quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?
A.
90
. B.
70
. C.
80
. D.
60
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
Lời giải
Số cách chọn
1
cái bút là
10
.
Số cách chọn
1
quyển sách là
8
.
Vậy theo quy tắc nhân, số cách chọn
1
cái bút và
1
quyển sách là:
10.8 80=
.
Câu 18: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là
A.
9!
. B.
9
. C.
1
. D.
9
9
.
Lời giải
Số cách xếp cần tìm là:
9
9!
P
=
.
Câu 19: Năm 2021, cuộc thi Hoa hậu Hòa bình Quốc tế lần thứ 9 được tổ chức tại Thái Lan và có tổng
cộng 59 thí sinh tham gia. Hỏi có bao nhiêu các chọn ra 5 người bao gồm một Hoa hậu và bốn Á
hậu 1, 2, 3, 4?
A.
5
59
A
. B.
5
59
C
. C.
14
59 58
AA+
. D.
14
59 58
.CC
.
Lời giải
Số cách chọn một Hoa hậu và bốn Á hậu 1, 2, 3, 4 sẽ tương ứng chọn 5 người trong 59 người
có phân biệt thứ tự. Suy ra số cách chọn là
5
59
A
.
Câu 20: Trong mặt phẳng cho
15
điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác
trong có đỉnh là
3
trong số
15
đã cho là
A.
3
15
C
. B.
15!
. C.
3
15
. D.
3
15
A
.
Lời giải
Ta chọn ba điểm bất kì trong
15
điểm đã cho thành lập được một tam giác, suy ra số tam giác
được tạo thành là
3
15
C
.
Câu 21: Tìm hệ số của
22
xy
trong khai triển nhị thức Niu-tơn của
( )
4
2xy+
.
A.
32
. B.
8
. C.
24
. D.
16
.
Lời giải
Ta có
( ) (
)
44
4
44
44
00
2 2 .2 .
k
k k k k kk
kk
x y Cx y C x y
−−
= =
+= =
∑∑
.
Số hạng chứa
22
xy
trong khai triển trên ứng với
42
2
2
k
k
k
−=
⇔=
=
.
Vậy hệ số của
22
xy
trong khai triển của
( )
4
2xy+
là
22
4
.2 24C =
.
Câu 22: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác
suất để được 3 quả cầu khác màu là
A.
3
7
. B.
3
5
. C.
3
14
. D.
3
11
.
Lời giải
Ta có
( )
3
12
220nCΩ= =
.
Gọi A là biến cố “chọn được 3 quả cầu khác màu”. Ta có
( )
5.4.3 60nA= =
.
Suy ra
( )
( )
( )
3
11
nA
PA
n
= =
Ω
.
Vậy chọn đáp án D.
Câu 23: Có
30
chiếc thẻ được đánh số thứ tự từ
1
đến
30
. Chọn ngẫu nhiên
1
chiếc thẻ, tính xác suất để
chọn được thẻ ghi số chia hết cho
3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
A.
1
3
. B.
1
2
. C.
3
10
. D.
2
3
.
Lời giải
Ta có
( )
1
30
nCΩ=
Gọi
A
là biến cố: “thẻ ghi số chia hết cho
3
’’
{ }
3,6,9,12,15,18, 21, 24,27,30A =
(
)
10
nA
⇒=
.
Xác suất của biến cố
A
là
( )
( )
( )
10 1
30 3
nA
PA
n
= = =
Ω
.
Câu 24: Từ một hộp chứa
10
quả bóng gồm 4 quả màu đỏ và
6
quả màu xanh, lấy ngẫu nhiên đồng thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
1
6
. B.
1
30
. C.
3
5
. D.
2
5
.
Lời giải
Lấy ngẫu nhiên đồng thời 3 quả cầu từ 10 quả bóng đã cho có
3
10
C
cách.
Lấy được
3
quả màu xanh từ
6
quả màu xanh đã cho có
3
6
C
cách.
Vậy xác suất để lấy được
3
quả màu xanh là
3
6
3
10
1
6
C
P
C
= =
.
Câu 25: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
( ) ( ) ( )
2;0 , 0;3 , 3;1ABC−
. Đường thẳng
d
đi qua
B
và song song với
AC
có phương trình tổng quát là
A.
15 15 0
xy− +=
. B.
5 30xy+−=
. C.
5 15 0xy+−=
. D.
5 30xy
++=
.
Lời giải
Ta có
( )
5;1AC = −

.
Vì đường thẳng
d
song song với
AC
nên
d
nhận
AC

là vectơ chỉ phương.
Suy ra vectơ pháp tuyến của
d
là
( )
1; 5n =
.
Phương trình đường thẳng
d
qua
( )
0;3B
có vectơ pháp tuyến
( )
1; 5n =
là
( ) ( )
1 0 5 3 0 5 15 0x y xy− + − =⇔+ − =
.
Câu 26: Trong mặt phẳng
Oxy
cho 3 điểm
( ) ( ) ( )
1;4 , 3; 1 , 6;2AB C−
không thẳng hàng. Tính khoảng
cách từ điểm
A
đến đường thẳng
BC
.
A.
(
)
32
;
2
d A BC =
. B.
( )
2
;
2
d A BC =
.
C.
(
)
2
;
7
d A BC
=
. D.
( )
72
;
2
d A BC =
.
Lời giải
Đường thẳng
BC
có một vtcp
( )
3;3u BC= =

⇒
một vtpt
( )
1; 1n −
.
Phương trình đường thẳng
BC
đi qua
( )
3; 1B −
; nhận véc tơ pháp tuyến
( )
1; 1n −
là:
( ) ( )
13110 40x y xy− − + =⇔−−=
Khoảng cách từ điểm
( )
1; 4A
đến đường thẳng
: 40BC x y−−=
:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
( )
(
)
2
2
144
72
;
2
11
d A BC
−−
= =
+−
.
Câu 27: Đường tròn
( )
C
đi qua hai điểm
( )
1;1A
,
( )
5;3B
và có tâm
I
thuộc trục hoành có phương trình
là
A.
( )
2
2
4 10xy+ +=
. B.
( )
2
2
4 10xy− +=
. C.
( )
2
2
4 10xy− +=
. D.
( )
2
2
4 10
xy
+ +=
.
Lời giải
Gọi
( )
;0I x Ox∈
;
22
IA IB
=
( ) ( )
22
22
1 15 3xx⇔−+=−+
22
2 1 1 10 25 9xx x x⇔ − ++= − + +
4x⇔=
. Vậy tâm đường tròn là
(
)
4;0I
và bán kính
( )
2
2
1 4 1 10R IA= = − +=
.
Phương trình đường tròn
( )
C
có dạng
( )
2
2
4 10
xy
− +=
.
Câu 28: Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
( )
22
: 22 0L x y ax by c+ − − +=
ngoại tiếp tam
giác
ABC
, với
( ) ( ) ( )
1;0 , 0;–2 , 2;–1AB C
. Khi đó giá trị của biểu thức
abc
++
bằng
A.
2
3
. B.
2
3
−
. C.
1
3
−
. D.
1
3
.
Lời giải
Vì các điểm
,,ABC
nằm trên đường tròn
( )
L
nên ta có hệ phương trình sau:
()
()
()
AL
BL
CL
∈
∈
∈
22
22
22
1 0 2. .1 2. .0 0
0 ( 2) 2. .0 2. .( 2) 0
2 ( 1) 2. .2 2. .( 1) 0
a bc
ab c
ab c
+ − − +=
⇔ +− − − − + =
+− − − − + =
21
44
42 5
ac
bc
a bc
− +=−
⇔ +=−
− + +=−
5
6
7
6
2
3
a
b
c
=
−
⇔=
=
.
Khi đó giá trị của biểu thức
1
3
abc++=
.
Câu 29: Phương trình chính tắc của
( )
E
có tiêu cự bằng
6
và đi qua điểm
( )
5; 0A
là:
A.
22
1
100 81
xy
+=
. B.
22
1
25 16
xy
+=
. C.
22
1
15 16
xy
+=
. D.
22
1
25 9
xy
+=
.
Lời giải
Chọn B
Do
( )
E
có tiêu cự bằng
6
nên
26
c =
3.
c⇒=
Do
( )
E
đi qua điểm
( )
5; 0A
nên
5a =
2 22
25 9 16b ac⇒ = − = −=
.
Phương trình chính tắc của
( )
E
là
( )
22
:1
25 16
xy
E +=
.
Câu 30: Trong hội nghị học sinh giỏi của trường, khi ra về các em bắt tay nhau. Biết rằng có
120
cái bắt
tay và giả sử không em nào bị bỏ sót cũng như bắt tay không lặp lại
2
lần. Số học sinh dự hội
nghị thuộc khoảng nào sau đây?
A.
( )
13;18
. B.
( )
21;26
. C.
( )
17;22
. D.
( )
9;14
.
Lời giải
Cách 1:
Gọi số học sinh dự hội nghị là
x
học sinh. Đk
0x >
.
Mỗi em sẽ bắt tay với
1x −
bạn còn lại.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Do bắt tay không lặp lại
2
lần nên số cái bắt tay là:
(
)
1
2
xx
−
.
Theo đề bài ta có phương trình:
( )
2
16 ( )
1
120 220 0
15 ( )
2
xn
xx
xx
xl
=
−
= ⇔ −− =⇔
= −
Vậy số học sinh dự hội nghị là 16.
Cách 2: Cứ 2 học sinh thì có 1 cái bắt tay. Vậy số cái bắt tay là số tổ hợp chập 2 của x.
Vậy ta có:
(
)
2
1
120 120
2
x
xx
C
−
=⇔=
. Giải ra ta cũng được
16
x =
.
Câu 31: Một lớp có
30
học sinh gồm
20
nam và
10
nữ. Hỏi có bao nhiêu cách chọn ra một nhóm
3
học
sinh sao cho nhóm đó có ít nhất một học sinh nữ?
A.
1140
. B.
2920
. C.
1900
. D.
900
.
Lời giải
Cách 1:
Để chọn ra 3 học sinh trong đó có ít nhất một học sinh nữ ta có các phương án sau:
Phương án 1: Chọn 1 học sinh nữ và 2 học sinh nam, có
12
10 20
.CC
cách thực hiện.
Phương án 2: Chọn 2 học sinh nữ và 1 học sinh nam, có
21
10 20
.CC
cách thực hiện.
Phương án 3: Chọn 3 học sinh nữ, có
3
10
C
cách thực hiện.
Theo quy tắc cộng, ta có:
1 2 21 3
10 20 10 20 10
. . 2920
CC CC C+ +=
cách chọn ra một nhóm 3 học sinh sao
cho nhóm đó có ít nhất một học sinh nữ.
Cách 2:
Có
3
30
C
cách chọn ra 3 học sinh từ 30 học sinh, trong đó có
3
20
C
cách chọn ra 3 học sinh, không
có học sinh nữ.
Suy ra có
33
30 20
2920CC−=
cách chọn ra một nhóm 3 học sinh sao cho nhóm đó có ít nhất một
học sinh nữ.
Câu 32: Cho tập hợp
{ }
1;2;3;4;5;6;7A =
. Hỏi từ tập
A
có thể lập được bao nhiêu số tự nhiên có
6
chữ số khác nhau và phải có mặt các chữ số
1
,
2
,
3
sao cho chúng không đứng cạnh nhau?
A.
567
. B.
576
. C.
5040
. D.
840
.
Lời giải
Lấy ra
3
chữ số khác
1
,
2
,
3
từ tập A có
3
4
C
cách.
Xếp
3
chữ số này có
3!
cách, coi 3 số trên là 3 vách ngăn sẽ tạo ra 4 vị trí xếp
3
chữ số
1
,
2
,
3
vào
3
trong
4
vị trí đó có
3
4
A
cách.
Vậy số các số lập được là:
33
44
.3!. 576CA=
.
Câu 33: Một nhóm gồm
12
học sinh trong đó có
6
học sinh khối 12,
4
học sinh khối
11
và
2
học sinh
khối 10. Chọn ngẫu nhiên
3
học sinh tham gia đội xung kích. Tính xác suất để
3
học sinh được
chọn không cùng một khối?
A.
1
5
. B.
6
55
. C.
12
55
. D.
49
55
.
Lời giải
Số phần tử của không gian mẫu
( )
3
12
220nCΩ= =
.
Gọi biến cố
A
: “ Ba học sinh được chọn không cùng một khối ”.
Khi đó, biến cố
A
: “ Ba học sinh được chọn cùng một khối ”.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Ta có
( )
33
64
24nA C C=+=
.
Xác suất của biến cố
A
là:
( )
24 6
220 55
PA= =
.
Vậy xác suất của biến cố
A
là:
( )
( )
6 49
11
55 55
PA PA=− =−=
.
Câu 34: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là
A.
1
2
. B.
1
3
. C.
1
. D.
2
3
.
Lời giải
Gieo một con súc sắc cân đối và đồng chất. Ta có không gian mẫu
{ }
1; 2;3; 4;5;6Ω=
.
Số phần tử của không gian mẫu là
( )
6n Ω=
.
Gọi
A
là biến cố mặt có số chấm chẵn xuất hiện. Ta có
{ }
2; 4;6A =
.
Suy ra số phần tử của biến cố
A
là
( )
3nA=
.
Vậy xác suất của biến cố là
( )
( )
( )
31
62
nA
pA
n
= = =
Ω
.
Câu 35: Một người chọn ngẫu nhiên
2
chiếc giày từ
5
đôi giày cỡ khác nhau. Tính xác suất để
2
chiếc
giày được chọn tạo thành một đôi.
A.
1
2
. B.
1
10
. C.
7
9
. D.
1
9
.
Lời giải
Chọn ngẫu nhiên
2
chiếc giày từ
5
đôi giày cỡ khác nhau có
2
10
C
cách.
Không gian mẫu là
2
10
CΩ=
.
Biến cố A : “Hai chiếc giày được chọn tạo thành một đôi”.
Vì chỉ có 5 đôi giày nên số phần tử của biến cố A là :
5A =
.
Vậy xác suất của biến cố A là :
2
10
51
9
A
P
C
= =
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp . Có bao nhiêu số tự nhiên chẵn có chữ số khác nhau
được lập thành từ các chữ số của tập đồng thời phải có mặt ba chữ số và chúng đứng
cạnh nhau?
Lời giải
Gọi số cần tìm có dạng .
Trường hợp 1: , suy ra có cách chọn.
Xếp các chữ số vào vị trí và có cách.
Chọn thứ tự từ tập có cách.
Do đó trường hợp này có số.
Trường hợp 2: . Tương tự như trường hợp 1 nên có số.
{ }
0; 1; 2; 3; 4; 5; 6; 7A =
6
A
0; 1; 2
123456
aaaaaa
6
0a =
6
a
1
1; 2
4
a
5
a
2
123
, , aaa
{ }
3; 4; 5; 6; 7
3
5
A
3
5
1.2. 120A =
6
2a =
120
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Trường hợp 3: , suy ra có cách chọn.
Xếp các chữ số đứng cạnh nhau có cách.
Chọn thứ tự hai chữ số từ tập để xếp vào hai vị trí còn lại có cách.
Do đó trường hợp này có số.
Vậy có số thỏa mãn.
Câu 37: Cho điểm
( )
1; 2M
và đường thẳng
:2 5 0d xy+−=
. Toạ độ của điểm đối xứng với điểm
M
qua
d
là
Lời giải
Phương trình đường thẳng
∆
qua
( )
1; 2M
và vuông góc với
d
là
: 2 30xy∆ − +=
.
Tìm tọa độ giao điểm
I
của
∆
và
d
là nghiệm của hệ phương trình
7
2 50
7 11
5
;
2 3 0 11
55
5
x
xy
I
xy
y
=
+−=

⇔⇒


− +=

=
.
( )
;
MM
Mx y
′′
′
đối xứng với điểm
M
qua
d
I⇒
là trung điểm
MM
′
.
79
2. 1
2
9 12
55
2
;
2 11
12
55
2. 2
55
2
MM
M
I
M IM
MM M IM
M
I
xx
x
x
x xx
M
y y y yy
y
y
′
′
′
′′
′
+
= −=
=
= −


′
⇒⇒ ⇔ ⇒


+=−


= −=
=
.
Câu 38: Một hộp đựng
10
viên bi có kích thước khác nhau, trong đó có
7
viên bi màu đỏ và
3
viên bi
màu xanh. Chọn ngẫu nhiên
2
viên bi từ hộp trên. Xác suất để
2
viên bi được chọn có ít nhất
một viên bi màu xanh bằng
Lời giải
* Không gian mẫu.
Chọn ngẫu nhiên
2
viên bi từ hộp có
10
viên bi ta có không gian mẫu là
( )
2
10
C 45n Ω= =
cách
chọn.
Gọi
A
là biến cố chọn được ít nhất một viên bi màu xanh.
* Số phần tử thuận lợi cho biến cố
.A
TH1: Chọn được 1 viên bi xanh, 1 viên bi đỏ có
11
37
CC⋅
cách chọn.
TH2: Chọn được 2 viên bi màu xanh có
2
3
C
cách chọn.
Do đó số phần tử thuận lợi cho biến cố
A
là
( )
11 2
37 3
C C C 24nA=⋅+=
cách chọn.
* Xác suất xảy ra của biến cố
A
Xác suất để
2
viên được chọn có ít nhất một viên bi màu xanh là
( )
( )
( )
24 8
.
45 15
nA
PA
n
= = =
Ω
Câu 39: Cho elip
( )
E
có độ dài trục lớn bằng
15
và đi qua điểm
M
sao cho
0
1
2
90F MF =
. Biết diện tích
tam giác
12
MF F
bằng 26. Phương trình chính tắc của elip
( )
E
là.
Lời giải
Ta có
12
26
MF F
S =
,
0
12
90F MF =
12
. 52MF MF⇒=
và
( )
2
22
12
2MF MF c+=
.
Độ dài trục lớn bằng 15
12
2 15MF MF a⇒+==
.
{ }
6
4; 6a ∈
6
a
2
0; 1; 2
3.3! 2! 16−=
{ } { }
6
3; 4; 5; 6; 7 \ a
2
4
A
2
4
2.16. 384A =
120 120 384 624++ =
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 15
Sưu tầm và biên soạn
Mà
( )
2
22
1 2 1 2 12
2.MF MF MF MF MF MF+ =++
.
( ) ( )
22
2
121
15 2 2.52
4
cc⇔ = + ⇒=
.
Mà
2
15 104
24
ab=⇒=
.
Vậy phương trình chính tắc của elip
( )
E
là
(
)
E
:
22
1
225 104
44
xy
+=
.
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 3 điểm
( 1;3), (3; 4), ( 5; 2)ABC− − −−
. Tìm tọa độ
trọng tâm G của tam giác ABC.
A.
( )
1; 1G −−
B.
1
;1
3
G

−


C.
11
;
33
G

−−


D.
( )
1; 1G
−
Câu 2: Trong hệ tọa độ
,
Oxy
cho ba điểm
(
) (
)
(
)
1;1 , 3;2 , 6;5 .AB C
Tìm tọa độ điểm
D
để tứ giác
ABCD
là hình bình hành.
A.
( )
4;3 .D
B.
(
)
3; 4 .D
C.
( )
4; 4 .D
D.
( )
8; 6 .D
Câu 3: Theo thống kê, dân số Việt Nam năm
2022
là
79715675
người. Giả sử sai số tuyệt đối của số
liệu thống kê này nhỏ hơn
10000
người. Hãy viết số quy tròn của số trên
A.
79710000
người. B.
79716000
người. C.
79720000
người. D.
79700000
người.
Câu 4: Hãy tìm số trung bình của mẫu số liệu khi cho bảng tần số dưới đây:
A. 8,29 B. 9,28 C. 8,73 D. 8,37.
Câu 5: Tìm mốt của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17; 17.
A. 17. B. 13 C. 14 D. 15.
Câu 6: Tìm tứ phân vị thứ ba của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17.
A. 16,5. B. 16 C. 15,5 D. 15.
Câu 7: Điểm thi HK1 của một học sinh lớp 10 như sau:
9
9
7
8
9
7
10
8
8
Khoảng biến thiên của mẫu số liệu là
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 8: Cho mẫu số liệu
10
;
8
;
6
;
2
;
4
. Độ lệch chuẩn của mẫu là
A.
8
. B.
2, 4
. C.
2,8
. D.
6
.
Câu 9: Cho đường thẳng
()d
có phương trình
1
32
xt
yt
= −
= +
. Khi đó, đương thẳng
()d
có 1 véc tơ pháp
tuyến là:
A.
( 1; 2)n = −
. B.
(1; 2)n =
. C.
(2;1)n =
. D.
(2; 1)n = −
.
Câu 10: Cho
ABC∆
có
( )
2; 1 ; (4;5); ( 3; 2)−−A BC
Viết phương trình tổng quát của đường cao
AH
.
A.
7 3 11 0xy+ −=
. B.
3 7 1 0
xy+ +=
.
C.
7 3 11 0xy+ +=
. D. −7x + 3y + 11 = 0
Câu 11: Khoảng cách từ điểm
5; 1M
đến đường thẳng
3 2 13 0xy 
là:
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 2
Sưu tầm và biên soạn
A.
2 13
. B.
28
13
. C.
26
. D.
13
2
.
Câu 12: Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng
( )
− −=: 2 10dx y
và
( )
′
+−=3 11 0dx y
.
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
135
.
Câu 13: Phương trình đường tròn có tâm
( )
2; 4I −
và bán kính
5R =
là:
A.
( ) ( )
22
2 45xy− ++ =
. B.
( ) ( )
22
2 5 25xy++−=
.
C.
( )
(
)
22
2 4 25xy+ +− =
. D.
( ) ( )
22
2 4 25xy− ++ =
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn
( )
1; 3I −
và tiếp xúc với trục tung có
phương trình là
A.
( ) (
)
22
1 31xy− ++ =
. B.
( )
( )
22
1 33
xy
−++ =
.
C.
( ) (
)
22
1 39xy− ++ =
. D.
( ) ( )
22
1 33xy− ++ =
.
Câu 15: Trong mặt phẳng
,Oxy
phương trình elip:
22
1
25 16
xy
+=
có một tiêu điểm là
A.
( )
0; 4
. B.
( )
0; 5
. C.
(
)
5;0
−
. D.
( )
3; 0
.
Câu 16: Có bao nhiêu cách chọn một học sinh từ một nhóm gồm
8
học sinh nam và
9
học sinh nữ?
A.
8
. B.
17
. C.
72
. D.
9
.
Câu 17: Một đội văn nghệ chuẩn bị được
2
vở kịch,
3
điệu múa và
6
bài hát. Tại hội diễn văn nghệ,
mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ trên có
bao nhiêu cách chọn chương trình biểu diễn, biết chất lượng các vở kịch, điệu múa, bài hát là
như nhau?
A.
11
. B.
18
. C.
25
. D.
36
.
Câu 18: Với năm chữ số
1, 2,3, 4,7
có thể lập được bao nhiêu số có
5
chữ số đôi một khác nhau và chia
hết cho
2
?
A.
120
. B.
24
. C.
48
. D.
1250
.
Câu 19: Một tổ có 15 học sinh. Hỏi có bao nhiêu cách chọn 2 học sinh từ tổ đó để giữ hai chức vụ tổ
trưởng và tổ phó?
A.
2
15
C
. B.
2
15
A
. C.
8
15
A
. D.
2
15
.
Câu 20: Lớp
11A
có
20
bạn nam và
22
bạn nữ. Có bao nhiêu cách chọn ra hai bạn tham gia hội thi
cắm hoa do nhà trường tổ chức
A.
42
. B.
861
. C.
1722
. D.
84
.
Câu 21: Tìm số hạng không chứa
x
trong khai triển nhị thức Niu-tơn của
4
3
1
x
x

+


.
A.
1
. B.
4
. C.
6
. D.
12
.
Câu 22: Gieo một con súc sắc cân đối đồng chất ba lần. Xác suất tích số chấm trong ba lần gieo bằng
6
là
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 3
Sưu tầm và biên soạn
A.
1
2
. B.
5
108
. C.
5
9
. D.
1
24
.
Câu 23: Có 10 tấm thẻ được đánh số từ 1 đến 10. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2 tấm
thẻ đều ghi số chẵn là
A.
2
9
. B.
1
4
. C.
7
9
. D.
1
2
.
Câu 24: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả màu đỏ. Chọn ngẫu nhiên đồng thời 2
quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng
A.
8
11
. B.
5
22
. C.
6
11
. D.
5
11
.
Câu 25: Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
( )
1; 0A
,
(
)
2; 1B
−
,
( )
1;1C
. Phương trình chính tắc
đường thẳng
( )
d
đi qua
A
và song song với
BC
là
A.
22
12
xy−+
=
−
. B.
12
12
xy−−
=
−
. C.
12
12
xy
−−
=
. D.
12
12
xy−−
=
−−
.
Câu 26: Đường Thẳng
: 3 0(, )ax by a b∆ + −= ∈
đi qua điểm
( )
1;1N
và cách điểm
( )
2;3M
một
khoảng bằng
5
. Khi đó
2ab−
bằng
A. 5. B. 2. C. 4. D. 0.
Câu 27: Lập phương trình đường tròn đi qua hai điểm
( ) ( )
3; 0 , 0; 2AB
và có tâm thuộc đường thẳng
:0dx y+=
.
A.
22
1 1 13
2 22
xy

− ++ =


. B.
22
1 1 13
2 22
xy

+ ++ =


.
C.
22
1 1 13
2 22
xy

− +− =


. D.
22
1 1 13
2 22
xy

+ +− =


.
Câu 28: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn
( )
1; 3I −
và tiếp xúc với trục tung có
phương trình là
A.
( ) ( )
22
1 31xy− ++ =
. B.
( ) ( )
22
1 33xy−++ =
.
C.
( ) ( )
22
1 39xy− ++ =
. D.
( ) ( )
22
1 33xy− ++ =
.
Câu 29: Cho của hypebol
( )
22
:1
94
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
(
)
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
6
. B.
3
. C.
4
. D.
5
.
Câu 30: Một hộp đựng 6 viên bi đen đánh số từ 1 đến 6 và 5 viên bi xanh đánh số từ 1 đến 5. Hỏi có bao
nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
A.
25
. B.
25
. C.
30
. D.
36
.
Câu 31: Một tổ có
6
học sinh nam và
9
học sinh nữ. Hỏi có bao nhiêu cách chọn
6
học sinh đi lao động,
trong đó có đúng
2
học sinh nam?
A.
24
69
+CC
Strong. B.
24
69
.CC
. C.
24
69
.AA
. D.
24
96
CC
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 4
Sưu tầm và biên soạn
Câu 32: Một nhóm công nhân gồm 8 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành
một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao
nhiêu cách lập tổ công tác.
A.
4060
. B.
12880
. C.
1286
. D.
8120
.
Câu 33: Cho hai hộp, hộp I chứa 4 viên bi đỏ và 3 viên bi xanh, hộp II chứa 5 viên bi đỏ và 2 viên bi
xanh. Lấy ngẫu nhiên từ mỗi hộp ra 2 viên bi. Tính xác suất để các viên bi lấy ra cùng màu.
A.
131
1001
. B.
9
143
. C.
131
441
. D.
1
7
.
Câu 34: Hai bạn lớp
A
và hai bạn lớp
B
được xếp vào 4 ghế hàng ngang. Xác xuất sao cho các bạn cùng
lớp không ngồi cạnh nhau bằng
A.
1
3
. B.
1
4
. C.
1
2
. D.
2
3
.
Câu 35: Bạn An có
7
cái kẹo vị hoa quả và
6
cái kẹo vị socola. An lấy ngẫu nhiên
5
cái kẹo cho vào
hộp để tặng cho em. Tính xác suất để
5
cái kẹo có cả vị hoa quả và vị socola.
A.
140
143
. B.
79
156
. C.
103
117
. D.
14
117
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa
hai chữ số 5 và 9 ?
Câu 37: Cho
( )
22
: 4 6 12 0Cx y x y+−+ −=
và đường thăng
( )
: 40d xy++=
. Viêt phương trình đường
thẳng
( )
∆
song song
( )
d
và cắt đường tròn
( )
C
theo một dây cung có độ dài bằng 8.
Câu 38: Tại môn bóng đá SEA Games 31 tổ chức tại Việt Nam có 10 đội bóng tham dự trong đó có 2 đội
tuyển Việt Nam và Thái Lan. Ban tổ chức chia ngẫu nhiên 10 đội tuyển thành 2 bảng: bảng A và
bảng B, mỗi bảng có 5 đội. Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một
bảng đấu là
Câu 39: Trên bờ biển có hai trạm thu phát tín hiệu
A
và
B
cách nhau
6km
, người ta xây một cảng biển
cho tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng
2 5 km
.
Một con tàu hàng M nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến
A
và
B
luôn là
2 6 km
. Khi neo đậu tại cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu?
---------- HẾT ----------
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 5
Sưu tầm và biên soạn
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 3 điểm
( 1;3), (3; 4), ( 5; 2)
ABC− − −−
. Tìm tọa độ
trọng tâm G của tam giác ABC.
A.
( )
1; 1G −−
B.
1
;1
3
G

−


C.
11
;
33
G

−−


D.
( )
1; 1
G −
Lời giải:
Chọn A
G là trọng tâm tam giác ABC nên ta có:
135
1
3
342
1
3
G
G
x
y
−+ −
= = −
−−
= = −
Câu 2: Trong hệ tọa độ
,Oxy
cho ba điểm
(
)
( )
( )
1;1 , 3;2 , 6;5 .
AB C
Tìm tọa độ điểm
D
để tứ giác
ABCD
là hình bình hành.
A.
( )
4;3 .D
B.
(
)
3; 4 .D
C.
( )
4; 4 .D
D.
(
)
8; 6 .D
Lời giải:
Chọn D
Gọi
(
)
;.Dxy
Ta có
( )
( )
2;1
.
6 ;5
AB
DC x y
=
=−−


Tứ giác
ABCD
là hình bình hành
AB DC⇔=
 
( )
26 4
4; 4 .
15 4
xx
D
yy
=−=

⇔ ⇔⇒

=−=

Câu 3: Theo thống kê, dân số Việt Nam năm
2022
là
79715675
người. Giả sử sai số tuyệt đối của số
liệu thống kê này nhỏ hơn
10000
người. Hãy viết số quy tròn của số trên
A.
79710000
người. B.
79716000
người. C.
79720000
người. D.
79700000
người.
Lời giải:
Chọn D
Độ chính xác đến hàng chục nghìn nên ta quy tròn số gần đúng đến hàng trăm nghìn.
Câu 4: Hãy tìm số trung bình của mẫu số liệu khi cho bảng tần số dưới đây:
A. 8,29 B. 9,28 C. 8,73 D. 8,37.
Lời giải:
Chọn A
Áp dụng công thức tính số trung bình của mẫu số liệu.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 6
Sưu tầm và biên soạn
Câu 5: Tìm mốt của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17; 17.
A. 17. B. 13 C. 14 D. 15.
Lời giải:
Chọn A
Mốt là 17 vì giá trị này xuất nhiều nhất là 3.
Câu 6: Tìm tứ phân vị thứ ba của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17.
A. 16,5. B. 16 C. 15,5 D. 15.
Lời giải:
Chọn A
Sắp xếp mẫu theo thứ tự không giảm: 11,13,14,14,15,15,16,17,17. Kích thước mẫu là 9. Trung
vịcủa mẫu là giá trị thứ 5 là 15. Khi đó tứ phân vị thứ ba là trung bình cộng của giá trị thứ 7 và
thứ 8 bằng 16,5.
Câu 7: Điểm thi HK1 của một học sinh lớp 10 như sau:
9
9
7
8
9
7
10
8
8
Khoảng biến thiên của mẫu số liệu là
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải:
Chọn C
Khoảng biến thiên là
10 7 3
R = −=
.
Câu 8: Cho mẫu số liệu
10
;
8
;
6
;
2
;
4
. Độ lệch chuẩn của mẫu là
A.
8
. B.
2, 4
. C.
2,8
. D.
6
.
Lời giải:
Chọn C
Giá trị trung bình của dãy số liệu là
108642
6
5
x
++++
= =
.
Độ lệch chuẩn của dãy số liệu là
2222
(10 6) (8 6) (4 6) (2 6)
2,8.
5
s
−+−+−+−
= ≈
Câu 9: Cho đường thẳng
()d
có phương trình
1
32
xt
yt
= −
= +
. Khi đó, đương thẳng
()d
có 1 véc tơ pháp
tuyến là:
A.
( 1; 2)n = −
. B.
(1; 2)n =
. C.
(2;1)n =
. D.
(2; 1)n = −
.
Lời giải
Đường thẳng d có véc tơ chỉ phương
( 1; 2)u = −
nên có 1 véc tơ pháp tuyến
(2;1)n
=
.
Câu 10: Cho
ABC∆
có
( )
2; 1 ; (4;5); ( 3; 2)−−A BC
Viết phương trình tổng quát của đường cao
AH
.
A.
7 3 11 0xy+ −=
. B.
3 7 1 0xy+ +=
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 7
Sưu tầm và biên soạn
C.
7 3 11 0
xy
+ +=
. D. −7x + 3y + 11 = 0
Lời giải
Đường cao
AH
có véc tơ pháp tuyến
( ) ( )
7; 3 7;3BC =−− =−

.
Nên phương trình đường cao
AH
là
( ) ( )
7 2 3 1 0 7 3 11 0x y xy−+ +=⇔ + − =
Câu 11: Khoảng cách từ điểm
5; 1M
đến đường thẳng
3 2 13 0xy 
là:
A.
2 13
. B.
28
13
. C.
26
. D.
13
2
.
Lời giải
Khoảng cách
22
3.5 2. 1 13
26
2 13
13
32
d


.
Câu 12: Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng
( )
− −=: 2 10dx y
và
( )
′
+−=3 11 0
dx y
.
A.
0
30
. B.
0
45
. C.
0
60
. D.
0
135
.
Lời giải
(
) ( )
'
1; 2 , 1; 3
dd
nn=−=
 
Gọi
α
là góc tạo bởi hai vectơ pháp tuyến của hai đường thẳng
( )
.
52
cos
2
5. 10
.
dd
dd
nn
nn
α
′
′
−
= = = −
 
 
0
135
α
⇒=
Suy ra góc giữa hai đường thẳng bằng
0
45
Câu 13: Phương trình đường tròn có tâm
(
)
2; 4I −
và bán kính
5R =
là:
A.
( ) ( )
22
2 45xy− ++ =
. B.
( ) ( )
22
2 5 25xy++−=
.
C.
( ) ( )
22
2 4 25xy
+ +− =
. D.
( ) ( )
22
2 4 25xy− ++ =
.
Lời giải
Phương trình đường tròn có tâm
( )
2; 4I −
và bán kính
5R =
là
( ) ( )
22
2 4 25xy
+ +− =
.
Câu 14: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn
( )
1; 3I −
và tiếp xúc với trục tung có
phương trình là
A.
( ) (
)
22
1 31xy
−++ =
. B.
( ) ( )
22
1 33xy−++ =
.
C.
( ) ( )
22
1 39xy− ++ =
. D.
(
) ( )
22
1 33xy− ++ =
.
Lời giải
Trục tung
:0Oy x =
⇒
đường tròn đã cho có bán kính
( )
,1R d I Oy= =
.
Vậy phương trình đường tròn cần tìm là
( ) ( )
22
1 31
xy− ++ =
.
Câu 15: Trong mặt phẳng
,Oxy
phương trình elip:
22
1
25 16
xy
+=
có một tiêu điểm là
A.
( )
0; 4
. B.
( )
0; 5
. C.
( )
5;0−
. D.
( )
3; 0
.
Lời giải
Theo giả thiết ta suy ra
22
25; 16ab= =
, khi đó
22
3c ab= −=
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 8
Sưu tầm và biên soạn
Ta có hai tiêu điểm
( )
1
3; 0
F −
và
(
)
2
3; 0F
.
Câu 16: Có bao nhiêu cách chọn một học sinh từ một nhóm gồm
8
học sinh nam và
9
học sinh nữ?
A.
8
. B.
17
. C.
72
. D.
9
.
Lời giải
Áp dụng quy tắc cộng ta có số cách chọn một học sinh từ một nhóm gồm
8
học sinh nam và
9
học sinh nữ là
8 9 17+=
.
Câu 17: Một đội văn nghệ chuẩn bị được
2
vở kịch,
3
điệu múa và
6
bài hát. Tại hội diễn văn nghệ,
mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ trên có
bao nhiêu cách chọn chương trình biểu diễn, biết chất lượng các vở kịch, điệu múa, bài hát là
như nhau?
A.
11
. B.
18
. C.
25
. D.
36
.
Lời giải
Số cách chọn chương trình biễu diễn văn nghệ của đội trên là:
2.3.6 36=
.
Câu 18: Với năm chữ số
1, 2,3, 4,7
có thể lập được bao nhiêu số có
5
chữ số đôi một khác nhau và chia
hết cho
2
?
A.
120
. B.
24
. C.
48
. D.
1250
.
Lời giải
Gọi số cần tìm là
n abcde=
, vì
n
chia hết cho
2
nên có
2
cách chọn
e
.
Bốn chữ số còn lại được chọn và sắp từ bốn trong năm chữ số trên nên có
4!
cách.
Vậy có tất cả
2 4! 48×=
số các số cần tìm.
Câu 19: Một tổ có 15 học sinh. Hỏi có bao nhiêu cách chọn 2 học sinh từ tổ đó để giữ hai chức vụ tổ
trưởng và tổ phó?
A.
2
15
C
. B.
2
15
A
. C.
8
15
A
. D.
2
15
.
Lời giải
Số cách chọn 2 học sinh trong 15 học sinh để làm hai chức vụ tổ trưởng và tổ phó là
2
15
A
.
Câu 20: Lớp
11A
có
20
bạn nam và
22
bạn nữ. Có bao nhiêu cách chọn ra hai bạn tham gia hội thi
cắm hoa do nhà trường tổ chức
A.
42
. B.
861
. C.
1722
. D.
84
.
Lời giải
Số cách chọn hai bạn trong lớp có
42
bạn học sinh là:
2
42
861C =
.
Câu 21: Tìm số hạng không chứa
x
trong khai triển nhị thức Niu-tơn của
4
3
1
x
x

+


.
A.
1
. B.
4
. C.
6
. D.
12
.
Lời giải
Ta có
( )
44
44
3 3 44
44
00
11
k
k
k kk
kk
x C x Cx
xx
−
−
= =

+= =


∑∑
.
Số hạng không chứa
x
trong khai triển trên ứng với
4 40 1kk
−=⇔=
.
Vậy số hạng không chứa
x
trong khai triển
4
3
1
x
x

+


là
1
4
4C =
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 9
Sưu tầm và biên soạn
Câu 22: Gieo một con súc sắc cân đối đồng chất ba lần. Xác suất tích số chấm trong ba lần gieo bằng
6
là
A.
1
2
. B.
5
108
. C.
5
9
. D.
1
24
.
Lời giải
Số phần tử của không gian mẫu là
( )
6.6.6 216n Ω= =
.
Gọi
A
là biến cố: “Tích số chấm trong ba lần gieo bằng 6”.
Các trường hợp thuận lợi cho biến cố
A
là
( ) ( ) (
) ( ) ( ) ( ) ( ) ( ) ( )
{
}
1;1;6 , 1;6;1 , 1;2;3 , 1;3;2 , 2;1;3 , 2;3;1 , 3;1;2 , 3;2;1 , 6;1;1
.
Suy ra
( )
9nA
=
.
Vậy xác suất cần tính là
( )
91
216 24
PA= =
.
Câu 23: Có 10 tấm thẻ được đánh số từ 1 đến 10. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2 tấm
thẻ đều ghi số chẵn là
A.
2
9
. B.
1
4
. C.
7
9
. D.
1
2
.
Lời giải
Phép thử T là: “ Chọn ngẫu nhiên hai thẻ từ tập hợp gồm 10 thẻ”.
Số phần tử của không gian mẫu:
(
)
2
10
45nCΩ= =
.
Trong 10 số nguyên dương từ 1 đến 10 gồm 5 số lẻ và 5 số chẵn. Để chọn được hai tấm thẻ đều
ghi số chẵn, ta cần chọn được 2 tấm thẻ từ 5 thẻ ghi số chẵn.
Gọi
A
là biến cố: “Chọn được hai tấm thẻ đều ghi số chẵn”, suy ra
( )
2
5
10nA C= =
.
Vậy xác suất của biến cố
A
là:
( )
( )
( )
10 2
45 9
nA
PA
n
= = =
Ω
.
Câu 24: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả màu đỏ. Chọn ngẫu nhiên đồng thời 2
quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng
A.
8
11
. B.
5
22
. C.
6
11
. D.
5
11
.
Lời giải
Số cách chọn ngẫu nhiên đồng thời 2 quả cầu từ hộp đó là
2
11
C 55=
.
Số cách chọn ngẫu nhiên đồng thời 2 quả cầu cùng màu từ hộp đó là
22
56
C C 25+=
.
Xác suất để 2 quả cầu chọn ra cùng màu bằng
25 5
55 11
=
.
Câu 25: Trong mặt phẳng tọa độ
Oxy
, cho ba điểm
( )
1; 0A
,
( )
2; 1B −
,
( )
1;1C
. Phương trình chính tắc
đường thẳng
( )
d
đi qua
A
và song song với
BC
là
A.
22
12
xy−+
=
−
. B.
12
12
xy−−
=
−
. C.
12
12
xy−−
=
. D.
12
12
xy−−
=
−−
.
Lời giải
( )
1; 2BC = −

. Đường thẳng
d
nhận vecto
BC

làm vecto chỉ phương.
Thay
( )
1; 0;1A
vào các đáp án ta có phương án
A
thỏa mãn.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 10
Sưu tầm và biên soạn
Câu 26: Đường Thẳng
: 3 0(, )ax by a b∆ + −= ∈
đi qua điểm
( )
1;1N
và cách điểm
( )
2;3M
một
khoảng bằng
5
. Khi đó
2ab−
bằng
A. 5. B. 2. C. 4. D. 0.
Lời giải
Đường Thẳng
: 30ax by∆ + −=
đi qua điểm
( )
1;1N
, ta có
30 3
ab b a
+−=⇒=−
.
Suy ra
: (3 ) 3 0ax a y∆ + − −=
,
Khi đó
2
22
2 (3 ).3 3
( ,) 5 5 2 1 0 1
(3 )
aa
dM a a a
aa
+− −
∆= ⇔ = ⇔ − += ⇒ =
+−
,
Với
12ab=⇒=
Vậy:
20ab−=
.
Câu 27: Lập phương trình đường tròn đi qua hai điểm
( ) ( )
3; 0 , 0; 2AB
và có tâm thuộc đường thẳng
:0dx y+=
.
A.
22
1 1 13
2 22
xy

− ++ =


. B.
22
1 1 13
2 22
xy

+ ++ =


.
C.
22
1 1 13
2 22
xy

− +− =


. D.
22
1 1 13
2 22
xy

+ +− =


.
Lời giải
( )
3; 0A
,
( )
0; 2B
,
:0dx y+=
.
Gọi
I
là tâm đường tròn vậy
( )
;Ix x−
vì
Id
∈
.
22
IA IB=
( )
( )
22
22
32x xx x⇔− +=++
6 94 4xx⇔− + = +
1
2
x⇔=
. Vậy
11
;
22
I

−


.
22
1 1 26
3
22 2
IA

=−+ =


là bán kính đường tròn.
Phương trình đường tròn cần lập là:
22
1 1 13
2 22
xy

− ++ =


.
Câu 28: Trong mặt phẳng tọa độ
Oxy
, phương trình đường tròn
( )
1; 3I −
và tiếp xúc với trục tung có
phương trình là
A.
( )
( )
22
1 31xy− ++ =
. B.
( ) ( )
22
1 33xy−++ =
.
C.
( ) ( )
22
1 39xy− ++ =
. D.
( ) ( )
22
1 33xy− ++ =
.
Lời giải
Trục tung
:0Oy x =
⇒
đường tròn đã cho có bán kính
( )
,1R d I Oy= =
.
Vậy phương trình đường tròn cần tìm là
(
) ( )
22
1 31xy− ++ =
.
Câu 29: Cho của hypebol
(
)
22
:1
94
xy
H −=
. Hiệu các khoảng cách từ mỗi điểm nằm trên
( )
H
đến hai
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
A.
6
. B.
3
. C.
4
. D.
5
.
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 11
Sưu tầm và biên soạn
Gọi
1
F
và
2
F
là hai tiêu điểm của
( ) ( )
22
22
: 1, 0, 0
xy
H ab
ab
−= > >
.
Điểm
(
)
12
2
M H MF MF a
∈⇔ − =
.
Từ phương trình
( )
22
:1
94
xy
H −=
suy ra
( )
2
9 3, 0
a aa
=⇒= >
.
Vậy hiệu các khoảng cách từ mỗi điểm
M
nằm trên
(
)
H
đến hai tiêu điểm có giá trị tuyệt đối là
12
26
MF MF a
−==
.
Câu 30: Một hộp đựng 6 viên bi đen đánh số từ 1 đến 6 và 5 viên bi xanh đánh số từ 1 đến 5. Hỏi có bao
nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số?
A.
25
. B.
25
. C.
30
. D.
36
.
Lời giải
Cách 1:
TH1.
Số cách chọn 1 viên bi đen được đánh số từ 1 đến 5: Có 5 cách chọn.
Số cách chọn 1 viên bi xanh được đánh số từ 1 đến 5: Có 4 cách chọn.
Theo quy tắc nhân có:
5.4 20=
cách.
TH2.
Số cách chọn 1 viên bi đen được đánh số 6: Có 1 cách chọn.
Số cách chọn 1 viên bi xanh được đánh số từ 1 đến 5: Có 5 cách chọn.
Theo quy tắc nhân có:
1.5 5
=
cách.
Vậy theo quy tắc cộng ta có
20 5 25+=
cách chọn.
Cách 2:
Chọn 1 bi xanh là 5 cách chọn.
Chọn 1 bi đen là 5 cách chọn
Vậy có
5.5 25=
cách chọn.
Câu 31: Một tổ có
6
học sinh nam và
9
học sinh nữ. Hỏi có bao nhiêu cách chọn
6
học sinh đi lao động,
trong đó có đúng
2
học sinh nam?
A.
24
69
+CC
Strong. B.
24
69
.CC
. C.
24
69
.AA
. D.
24
96
CC
.
Lời giải
Chọn
4
học sinh nữ có
4
9
C
cách, chọn
2
học sinh nam có
2
6
C
cách.
Có
24
69
.CC
cách chọn
6
học sinh đi lao động, trong đó có đúng
2
học sinh nam.
Câu 32: Một nhóm công nhân gồm 8 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành
một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao
nhiêu cách lập tổ công tác.
A.
4060
. B.
12880
. C.
1286
. D.
8120
.
Lời giải
Chọn 2 trong 8 nam làm tổ trưởng và tổ phó có
2
8
A
cách.
•
Chọn 3 tổ viên, trong đó có nữ
+) chọn 1 nữ và 2 nam có
2
6
5.C
cách.
+) chọn 2 nữ và 1 nam có
2
5
6.C
cách.
+) chọn 3 nữ có
3
5
C
cách.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 12
Sưu tầm và biên soạn
Vậy có
( )
+ +=
2 2 23
8 6 55
A 5.C 6.C C 8120
cách.
Câu 33: Cho hai hộp, hộp I chứa 4 viên bi đỏ và 3 viên bi xanh, hộp II chứa 5 viên bi đỏ và 2 viên bi
xanh. Lấy ngẫu nhiên từ mỗi hộp ra 2 viên bi. Tính xác suất để các viên bi lấy ra cùng màu.
A.
131
1001
. B.
9
143
. C.
131
441
. D.
1
7
.
Lời giải
Số phần tử không gian mẫu
22
77
. 441CCΩ= =
.
Gọi
A
là biến cố: “Các viên bi lấy ra cùng màu”.
Trường hợp 1: cùng màu đỏ:
22
45
. 60CC=
.
Trường hợp 2: cùng màu xanh:
22
32
.3CC=
.
60 3 63
A
Ω= +=
.
Vậy
( )
63 1
441 7
A
PA
Ω
= = =
Ω
.
Câu 34: Hai bạn lớp
A
và hai bạn lớp
B
được xếp vào 4 ghế hàng ngang. Xác xuất sao cho các bạn cùng
lớp không ngồi cạnh nhau bằng
A.
1
3
. B.
1
4
. C.
1
2
. D.
2
3
.
Lời giải
Mỗi cách xếp
4
học sinh vào
4
ghế hàng ngang là một hoán vị của
4
phần tử
Số phần tử của không gian mẫu là
4
4! 24
P
= =
Gọi
C
là biến cố “ Các bạn cùng lớp không ngồi cùng nhau”
Đánh số thứ tự cho 4 ghế là
1,2,3,4
. Hai bạn cùng lớp không ngồi cạnh nhau thì hai bạn cùng
lớp mỗi bạn phải ngồi ghế cùng mang số chẵn hoặc ghế cùng mang số lẻ. Khi đó
( )
2.2.2 8nC = =
Vậy
(
)
81
24 3
PC = =
.
Câu 35: Bạn An có
7
cái kẹo vị hoa quả và
6
cái kẹo vị socola. An lấy ngẫu nhiên
5
cái kẹo cho vào
hộp để tặng cho em. Tính xác suất để
5
cái kẹo có cả vị hoa quả và vị socola.
A.
140
143
. B.
79
156
. C.
103
117
. D.
14
117
.
Lời giải
Số phần tử không gian mẫu:
( )
5 14 23 32 41 5
7 76 76 76 76 6
....n C CC CC CC CC CΩ=+++++
1287=
.
Gọi
A
là biến cố: “ An lấy ngẫu nhiên
5
cái kẹo có cả vị hoa quả và vị socola”.
( )
14 23 32 41
76 76 76 76
. . . . 1260nA CC CC CC CC=+++=
.
Vậy
( )
( )
(
)
1260 140
1287 143
nA
PA
n
= = =
Ω
.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa
hai chữ số 5 và 9 ?
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 13
Sưu tầm và biên soạn
Lập số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa hai chữ
số 5 và 9.
Trường hợp 1 : 3 chữ số 1, 5, 9 đứng 3 vị trí đầu.
- Chữ số 1 đứng vị trí số 2 có : 1 cách chọn.
- Sắp xếp 2 chữ số 5, 9 bên cạnh chữ số 1 có :
2!
cách chọn.
- Chọn 4 số trong 7 chữ số còn lại xếp vào 3 vị trí còn lại có :
4
7
A
cách chọn.
Suy ra có :
4
7
2! 1680
A =
số.
Trường hợp 2 : 3 chữ số 1, 5, 9 không đứng ở vị trí đầu tiên
- Chọn ví trí cho chữ số 1 có : 4 cách chọn.
- Sắp xếp 2 chữ số 5, 9 bên cạnh chữ số 1 có :
2!
cách chọn.
- Chọn 1 chữ số cho vị trí đầu tiên có : 6 cách chọn.
- Chọn 3 chữ số xếp vào 3 vị trí còn lại có :
3
6
A
Suy ra có :
3
6
4.6.2! 5760
A
=
số.
Vậy có
7440
số.
Câu 37: Cho
(
)
22
: 4 6 12 0Cx y x y+−+ −=
và đường thăng
( )
: 40d xy++=
. Viêt phương trình đường
thẳng
( )
∆
song song
( )
d
và cắt đường tròn
( )
C
theo một dây cung có độ dài bằng 8.
Lời giải
( )
C
có tâm
( )
2; 3I −
và
5R =
.
Gọi
,AB
là giao điểm của
( )
∆
và đường tròn
( )
C
8AB⇒=
.
Kẻ
OH AB⊥
tại
H
H⇒
là trung điểm A B.
2 2 22
54 3OH OA AH= − = −=
( ) ( ) ( ) ( )
// : 0 4d xyc c∆ ⇒∆ + + = ≠
( )
( )
( )
( )
23
32 1
, 3 1 32
32 1
2
c
cn
d I OH c
cn
−+
= +
∆ = ⇔ =⇔ −= ⇔
=−+
Vây phương trình đường thẳng
(
)
∆
là
32 1 0xy+ + +=
hoặc
32 1 0xy+ − +=
.
Câu 38: Tại môn bóng đá SEA Games 31 tổ chức tại Việt Nam có 10 đội bóng tham dự trong đó có 2 đội
tuyển Việt Nam và Thái Lan. Ban tổ chức chia ngẫu nhiên 10 đội tuyển thành 2 bảng: bảng A và
bảng B, mỗi bảng có 5 đội. Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một
bảng đấu là
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 14
Sưu tầm và biên soạn
Số cách phân 10 đội tuyển thành 2 bảng A và B, mỗi bảng có 5 đội là
5
10
C
.
Số cách phân 10 đội tuyển thành 2 bảng A và B, mỗi bảng có 5 đội sao cho đội tuyển Việt Nam
và đội tuyển Thái Lan nằm cùng một bảng là:
*Trường hợp Việt Nam và Thái Lan cùng nằm ở bảng A: chọn thêm 3 đội từ 8 đội còn lại vào
bảng A có
3
8
C
cách.
*Trường hợp Việt Nam và Thái Lan cùng nằm ở bảng B: tương tự cũng có
3
8
C
cách.
Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một bảng đấu là
3
8
5
10
2
4
.
9
C
P
C
= =
Câu 39: Trên bờ biển có hai trạm thu phát tín hiệu
A
và
B
cách nhau
6km
, người ta xây một cảng biển
cho tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng
2 5 km
.
Một con tàu hàng M nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến
A
và
B
luôn là
2 6 km
. Khi neo đậu tại cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu?
Lời giải
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Page 15
Sưu tầm và biên soạn
Chọn hệ trục toạ độ
Oxy
như hình trên, trong đó
1km
ứng với 1 đơn vị.
Do
( ) ( )
26
3; 0 , 3; 0
MA MB
AB
−=
−
nên
M
thuộc hypebol
( )
22
:1
63
xy
H −=
.
Cảng biển xây theo hình elip có trục lớn là
6AB =
và tiêu cự là
25
( )
22
:1
94
xy
E⇒ +=
Khi con tàu
M
neo đậu thì chính là tại vị trí
I
:
Lúc này toạ độ của
I
thoả mãn hệ
22
2
22
2
126
1
6 3 17
12
1
17
94
xy
x
xy
y
−= =

⇔


=
+=
.
Khi đó khoảng cách từ con tàu
M
đến bờ biển là
12
17
km
.
---------- HẾT ----------
| 1/144
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

- - Lư TT C C T 3 2 1
ác ác u ỉ l
c c ý ệ T : kê
âu hỏi âu hỏi c ỉ X yế N Tổ h lệ t VI V ộ r . P và xác u . Đ i u n (% n phẳ on t . dung g P ố M hợ t g ( g m ại hứ ở ở t ) ng T ọa đ ột p s c c % s hố c ặt s ố t k ấp độ ấp độ ) u ng ố ộ ất ổ iến v nhận bi 5 4 t t 3 2 c 1 4. X c 3. c 2. 1.S 4. N 3. T 2. H 1.Q ận dụng v . . P hẳ hẳ . V . P á . ủa ủa B c ng ng. K T C C a T ị T phé ọa m m ố gầ á á á h ổ hợ oá uy t đư đư t đư c c c r độ c í s ẫ s ẫ ị s t ế ờ p t u s u s n vị t ờ hoả t v ng C ư ờ uấ ố đặ ố đặ n đúng và hứ ắ p c ng ơ ng o t ố l ố l c c , c à v à t t ng c ng đối á ủa c N ộ t n V uả i c i c Đ ận dụng c hông hi r hẳ vé ệ t ệ t hỉ ng và oni òn t u bi r u e ơ r w nh hợ n á ng t e ư . ư c c c c ng đo ng đo x t vị và rong h t và t t o . ế s on M quy t o n c a k M r ể ứ ừ ong i B s p ÔN: i g u 1 i ố ố ế A ao l ng dụng m óc ể m n l để u t u t ắ t T à c p t m ứ c gi h m p t hứ c nhâ T RẬN độ phâ hế ức à c ác ọa ữ OÁN đế ác c độ a ọa c t 2 đư t r n âu hỏ n đư độ ọa ung t c ĐỀ đ â n t , L u hỏi ờ ờ ộ â ng á i t ng m ỚP K n r I t ắc Ể ự l 10 ngh 20 C M 1 2 2 2 1 3 2 1 1 1 1 2 1 Số uậ H N hậ – T n. iệ 40 n biế T RA m ( k phú gi Th H hác an ờ ỜI t) i t CUỐI h quan 4 l 70 GI 15 C 1 2 1 1 1 3 1 1 1 2 1 Số T H A hô N KỲ 30 ng ựa c ( Mức L phú gi Th hiể ÀM 2 an ờ u ( t họn ) i độ CÁ B nhậ , t ÀI NH r 2 1* 1* 1* C Số ong đó c H V n t ậ : n dụng 2 hức 90 phút DI 0 (phú gi Th Ề an U ờ ó t duy ) i ) 30 nhất S 1** 1** 1** V ố 2 C ận dụng H 1 l 1 0 ựa c (phú gi Th c an ờ a họ t) i o n đúng. 35 TN 3 3 2 2 2 5 1 3 2 2 2 Số C H Tổ TL 4 2 1 1 n g (phú gi Th an ờ t) i % 100 100 điể tổ m n g - - Phầ đi - H H ể Số ai ai m n c đượ đi c t âu âu ự ể m l v v uậ c q t ậ ậ í n n n: nh uy dụ dụ ( đị c để ho n n nh t g c g m đư 1 ao m ợ r c ỗi on â c u c ph g m t ỗi âu r on ắc c 1,0 đi a t âu g ph nghi rận. 0,5 ể ú ệ m m m đi t ì l ể a c n à m h 0,2 t h để a c ọn 0 n h ở đ h i ọ 1* s i ể n ề m/ ở u l c 1** s ao c ự âu; a c s h h ố ao c o 1 ọn đi ) ể h c ( m o 1 c âu 3.0Đ c Đ ủa âu ại ) c S â Đ u ố v ại tự S à 1 c luận ố v à 1 c âu đư H ợ âu ì c n h quy H h ìn ọc đị h . nh h ọc tr . ong hướ ng dẫn chấm nhưng phải tươ ng ứng với tỉ lệ
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 01
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Đo chiều dài của một cây thước, ta được kết quả l = 45± 0,3(cm) thì sai số tương đối của phép đo là: A. ∆ = . B. ∆ ≤ . C. 3 δ = . D. 1 δ ≤ . l 0,3 l 0,3 l 10 l 150
Câu 2: Điểm (thang điểm 10) của 11 học sinh cao điểm nhất trong một bài kiểm tra như sau:
10 9 10 8 9 10 9 7 8 9 10. Hãy tìm các tứ phân vị.
A. Q = 7,Q = 8 ,Q = 10
B. Q = 8 ,Q =10 ,Q = 10 . 1 2 3 1 2 3
C. Q = 8 ,Q = 9,Q = 10 .
D. Q = 8 ,Q = 9,Q = 9 . 1 2 3 1 2 3
Câu 3: Một cửa hàng giày thể thao đã thống kê cỡ giày của 20 khách hàng nữ được chọn ngẫu nhiên cho kết quả như sau:
35 37 39 41 38 40 40 37 39 38 38 36 37 42 38 35 38 36 38 35
Tìm trung vị cho mẫu số liệu trên. A. 36. B. 37 . C. 38. D. 39.
Câu 4: Một mẫu số liệu thống kê có tứ phân vị lần lượt là Q = 22, Q = 27, Q = 32 1 2 3 . Giá trị nào sau đây
là giá trị ngoại lệ của mẫu số liệu A. 30. B. 9. C. 48. D. 46.
Câu 5: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai điểm M ( 3 − ; ) 1 và N (6; 4 − ) . Tọa độ trọng
tâm G của tam giácOMN là A. G(9; 5 − ) . B. G( 1; − ) 1 . C. G(1;− ) 1 . D. G(3; 3 − ). x = 1 − + 2t
Câu 6: Cho đường (d ): 
(t ∈) . Véc tơ nào sau đây là véc tơ chỉ phương của (d)?  y = 3 − 4t    
A. a = (1;2). B. a = ( 1; − 3). C. a = (2; 4 − ) . D. a = ( 1; − 2) .
Câu 7: Trong mặt phẳng tọa độ Oxy , viết phương trình tham số của đường thẳng đi qua hai điểm M (3; 2 − ) và N (4; ) 1 . x = 3 + 4tx = 4 + 3tx = 1+ 3tx = 3 + t A.  . B.  . C.  . D.  . y = 2 − + ty = 1− 2ty = 3 − 2ty = 2 − + 3t
Câu 8: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ ∆
1 : 2x − 3y +1 = 0 và 2 : 4
− x + 6y −1 = 0 . A. Song song. B. Trùng nhau. C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau.
Câu 9: Khoảng cách từ điểm M (1; 1
− ) đến đường thẳng ∆ : 3x + y + 4 = 0 là A. 1. B. 3 10 . C. 5 . D. 2 10 . 5 2 Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 10: Phương trình nào sau đây là phương trình đường tròn? A. 2 2
x y 6x10y 30  0 . B. 2 2
x y 3x2y 30  0 . 2 2
C. 4x y 10x6y2  0 . D. 2 2
x  2y 4x8y 1 0. .
Câu 11: Đường tròn (C) có tâm I ( 2;
− 3) và đi qua M (2; 3
− ) có phương trình là:
A. (x + )2 + ( y − )2 2 3 = 52 . 2 2
B. (x + 2) + ( y −3) = 52 . C. 2 2
x + y + 4x − 6y −57 = 0. D. 2 2
x + y + 4x + 6y −39 = 0. 2 2
Câu 12: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 9 4
A. F = − 13;0 ; F = 13;0 1 ( ) 2 ( ).
B. F = 0;− 13 ; F = 0; 13 . 1 ( ) 2 ( )
C. F = 0;− 5 ; F = 0; 5 .
D. F = − 5;0 ; F = 5;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
Câu 13: Một tổ có 6 học sinh nữ và 8 học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học
sinh của tổ đó đi trực nhật? A. 28 . B. 48 . C. 14. D. 8 .
Câu 14: Từ 4 số 1,2,3,4 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số? A. 12. B. 6 . C. 64 . D. 24 .
Câu 15: Có bao nhiêu cách xếp 3 học sinh nam và 4 học sinh nữ theo hàng ngang? A. 7!. B. 144. C. 2880 . D. 480 .
Câu 16: Từ 7 chữ số 1, 2, 3, 4, 5, 6, 7có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau? A. 4 7 . B. P7 . C. 4 C . D. 4 A . 7 7
Câu 17: Cho tập hợp M = {1;2;3;4; }
5 . Số tập con gồm hai phần tử của tập hợp M là: A. 11. B. 2 A . C. 2 C . D. P . 5 5 2
Câu 18: Khai triển (x + y)5 2
thành đa thức ta được kết quả sau A. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 80x y + 80xy + 32y . B. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 40x y +10xy + 2y . C. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 80x y + 40xy + 32y . D. 5 4 3 2 2 3 4 5
x +10x y + 20x y + 20x y +10xy + 2y .
Câu 19: Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất xuất hiện mặt hai chấm là A. 1 . B. 1 . C. 1 . D. 1 . 2 3 6 4
Câu 20: Một hộp chứa 10 quả cầu gồm 3 quả cầu màu xanh và 7 quả cầu màu đỏ, các quả cầu đôi một
khác nhau. Chọn ngẫu nhiên lần lượt hai quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn ra cùng màu bằng A. 7 . B. 8 . C. 7 . D. 5 . 30 15 15 11 Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 21: Từ một nhóm gồm 6 học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. Xác suất để
chọn được 2 học sinh nữ và 1 học sinh nam bằng A. 3 . B. 1 . C. 1 . D. 1 . 10 5 6 2
Câu 22: Cho số gần đúng α = 23748023 với độ chính xác d =101. Hãy viết số quy tròn của số A. 23749000 . B. 23748000 . C. 23746000 . D. 23747000 .
Câu 23: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách? A. 4,694 . B. 4,925. C. 4,55. D. 4,495 .
Câu 24: Trong mặt phẳng hệ tọa độ Oxy, cho hai điểm A(2; ) 1 , B( 1;
− 7) . Tọa độ điểm M thỏa mãn hệ
  
thức 3AM + AB = 0 là
A. M (1; − 3)
B. M (5; − 5) C. M (1; − ) 1 D. M (3; − ) 1
Câu 25: Đường thẳng ∆ đi qua điểm M (1;2) và song song với đường thẳng d : 4x + 2y +1= 0có phương
trình tổng quát là
A. 4x + 2y + 3 = 0 .
B. 2x + y + 4 = 0 .
C. x − 2y + 3 = 0.
D. 2x + y − 4 = 0 .
Câu 26: Hai đường thẳng d :mx + y = m −5,d :x + my = 9 cắt nhau khi và chỉ khi 1 2 A. m ≠ 1 − . B. m ≠ 1. C. m ≠ 1 ± . D. m ≠ 2 .
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(1;2) , B(5;2) , C (1; 3 − ) có phương trình là. A. 2 2
x + y + 6x + y −1 = 0 . B. 2 2
x + y − 6x − y −1 = 0 . C. 2 2
x + y − 6x + y −1 = 0 . D. 2 2
x + y + 6x − y −1 = 0 .
Câu 28: Đường tròn (C) đi qua A(1;3) , B(3; )
1 và có tâm nằm trên đường thẳng d : 2x − y + 7 = 0 có phương trình là
A. (x − )2 + ( y − )2 7 7 =102 .
B. (x + )2 + ( y + )2 7 7 =164 .
C. (x − )2 + ( y − )2 3 5 = 25 .
D. (x + )2 + ( y + )2 3 5 = 25 .
Câu 29: Phương trình chính tắc của elip đi qua điểm A(0; 4
− ) và có một tiêu điểm F 3;0 là 2 ( ) 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. + = 1. B. + = 1. C. + = 1. D. + = 1. 10 8 25 16 25 9 16 25
Câu 30: Cần xếp 3 nam, 3 nữ vào 1 hàng có 6 ghế. Hỏi có bao nhiêu cách xếp sao cho nam nữ ngồi xen kẽ. A. 36. B. 720 . C. 78. D. 72 . Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 31: Có 4 cặp vợ chồng ngồi trên một dãy ghế dài. Có bao nhiêu cách sắp xếp sao cho vợ và chồng
của mỗi gia đình đều ngồi cạnh nhau. A. 384. B. 8!. C. 4!.4!. D. 48 .
Câu 32: Ở một Đoàn trường phổ thông có 5 thầy giáo, 4 cô giáo và 8 học sinh. Có bao nhiêu cách chọn
ra một đoàn công tác gồm 7 người trong đó có 1 trưởng đoàn là thầy giáo, 1 phó đoàn là cô giáo
và đoàn công tác phải có ít nhất 4 học sinh. A. 6020 . B. 10920. C. 9800. D. 10290.
Câu 33: Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số
1,2,3,4,5,6 . Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là một số chia hết cho 5 . A. 1 . B. 1 . C. 1 . D. 1 . 6 12 2 4
Câu 34: Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất
để chọn được hai số có tổng là một số chẵn là A. 13 . B. 12 . C. 1 . D. 313 . 25 25 2 625
Câu 35: Một nhóm gồm 12 học sinh trong đó có 7 học sinh nam và 5 học sinh nữ. Chọn ngẫu nhiên 3 học
sinh từ nhóm 12 học sinh đó đi lao động. Xác suất để trong ba học sinh được chọn có ít nhất một học sinh nữ là: A. 15 . B. 7 . C. 35 . D. 37 . 22 44 44 44
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có 8 người cùng vào thang máy ở tầng 1 của một tòa nhà cao 10 tầng và đi lên trên. Hỏi có bao
nhiêu cách sắp xếp để trong 8 người đó có đúng 2 người cùng ra ở 1 tầng và mỗi người còn lại
ra ở mỗi tầng khác nhau.
Câu 37: Trong mặt phẳng Oxy, viết phương trình chính tắc của Elip (E) có một tiêu điểm là F 2; − 0 1 ( )
và đi qua điểm M (2;3).
Câu 38: Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập E = {1;2;3;4; } 5 . Chọn
ngẫu nhiên một số từ tập S . Xác xuất để số được chọn là một số chẵn bằng
Câu 39: Trong mặt phẳng Oxy cho parabol (P) 2
: y = 8x . Đường thẳng Δ không trùng với trục Ox đi
qua tiêu điểm F của (P) sao cho góc hợp bởi hai tia Fx và Ft là tia của Δ nằm phía trên trục
hoành một góc bằng α( 0
α ≠ 90 ). Biết Δ cắt (P) tại hai điểm phân biệt M , N và tập hợp trung
điểm I của đoạn MN khi α thay đổi là một Parabol. Xác định phương trình của Parabol.
---------- HẾT ---------- Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Đo chiều dài của một cây thước, ta được kết quả l = 45± 0,3(cm) thì sai số tương đối của phép đo là: A. ∆ = . B. ∆ ≤ . C. 3 δ = . D. 1 δ ≤ . l 0,3 l 0,3 l 10 l 150 Lời giải Vì ∆ ≤ nên l 0,3 1 δ ∆ = ≤ = . l 0,3 l l 45 150
Câu 2: Điểm (thang điểm 10) của 11 học sinh cao điểm nhất trong một bài kiểm tra như sau:
10 9 10 8 9 10 9 7 8 9 10. Hãy tìm các tứ phân vị.
A. Q = 7,Q = 8 ,Q = 10
B. Q = 8 ,Q =10 ,Q = 10 . 1 2 3 1 2 3
C. Q = 8 ,Q = 9,Q = 10 .
D. Q = 8 ,Q = 9,Q = 9 . 1 2 3 1 2 3 Lời giải
Sắp xếp các giá trị theo thứ tự không giảm: 7 8 8 9 9 9 9 10 10 10 10
Trung vị của mẫu số liệu là: Q = 9. 2
Tứ vị phân thứ nhất là Q = 8 . 1
Tứ vị phân thứ ba là Q = 10 . 3
Vậy Q = 8 ,Q = 9,Q = 10 là các tứ phân vị của mẫu số liệu trên. 1 2 3
Câu 3: Một cửa hàng giày thể thao đã thống kê cỡ giày của 20 khách hàng nữ được chọn ngẫu nhiên cho kết quả như sau:
35 37 39 41 38 40 40 37 39 38 38 36 37 42 38 35 38 36 38 35
Tìm trung vị cho mẫu số liệu trên. A. 36. B. 37 . C. 38. D. 39. Lời giải
Sắp xếp các giá trị theo thứ tự không giảm:
35 35 35 36 36 37 37 37 38 38 38 38 38 38 39 39 40 40 41 42
Vì n = 20 là số chẵn nên trung vị là trung bình cộng của hai giá trị chính giữa: 38 38 Me + = 2
Câu 4: Một mẫu số liệu thống kê có tứ phân vị lần lượt là Q = 22, Q = 27, Q = 32 1 2 3 . Giá trị nào sau đây
là giá trị ngoại lệ của mẫu số liệu A. 30. B. 9. C. 48. D. 46. Lời giải
Ta có ∆ = Q − Q = − =
. Do đó Q −1,5.∆ Q + ∆  =  . Q ; 1,5. Q 7;47 1 3  [ ] Q 32 22 10 3 1 Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Do 48∉[7;47] nên là một giá trị ngoại lệ của mẫu số liệu.
Câu 5: Trong mặt phẳng với hệ trục tọa độ Oxy , cho hai điểm M ( 3 − ; ) 1 và N (6; 4 − ) . Tọa độ trọng
tâm G của tam giácOMN là A. G(9; 5 − ) . B. G( 1; − ) 1 . C. G(1;− ) 1 . D. G(3; 3 − ). Lời giải x + x + x − + + M N O 3 6 0 x = = =  G 1 Ta có:  3 3  ⇒ G − . y + y +  y + − + M N O ( ) (1; )1 1 4 0 y = = = − G 1  3 3 x = 1 − + 2t
Câu 6: Cho đường (d ): 
(t ∈) . Véc tơ nào sau đây là véc tơ chỉ phương của (d)?  y = 3 − 4t    
A. a = (1;2). B. a = ( 1; − 3). C. a = (2; 4 − ) . D. a = ( 1; − 2) . Lời giải
Dựa vào (d ) ta có VTCP: a = (2; 4 − )
Câu 7: Trong mặt phẳng tọa độ Oxy , viết phương trình tham số của đường thẳng đi qua hai điểm M (3; 2 − ) và N (4; ) 1 . x = 3 + 4tx = 4 + 3tx = 1+ 3tx = 3 + t A.  . B.  . C.  . D.  . y = 2 − + ty = 1− 2ty = 3 − 2ty = 2 − + 3t Lời giải
Gọi d là đường thẳng đi qua hai điểm M (3; 2 − ) và N (4; ) 1 . 
⇒ Đường thẳng d đi qua điểm M (3; 2
− ) và nhận MN (1;3) làm vectơ chỉ phương. x = 3 + t
Vậy phương trình tham số đường thẳng d :  (t ∈). y = 2 − + 3t
Câu 8: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ ∆
1 : 2x − 3y +1 = 0 và 2 : 4
− x + 6y −1 = 0 . A. Song song. B. Trùng nhau. C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải 2 3 − 1 +) Xét: = ≠
nên hai đường thẳng song. 4 − 6 1 −
Câu 9: Khoảng cách từ điểm M (1; 1
− ) đến đường thẳng ∆ : 3x + y + 4 = 0 là A. 1. B. 3 10 . C. 5 . D. 2 10 . 5 2 Lời giải
Khoảng cách từ điểm M (1; 1
− ) đến đường thẳng ∆ : 3x + y + 4 = 0 là − +
d (M ∆) 3.1 1 4 6 3 10 ; = = = . 2 2 3 +1 10 5 Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 10: Phương trình nào sau đây là phương trình đường tròn? A. 2 2
x y 6x10y 30  0 . B. 2 2
x y 3x2y 30  0 . 2 2
C. 4x y 10x6y2  0 . D. 2 2
x  2y 4x8y 1 0. . Lời giải
Phương trình đường tròn đã cho có dạng: 2 2
x + y − 2ax − 2by + c = 0 là phương trình đường tròn 2 2
⇔ a + b − c > 0.
Xét đáp án A, ta có a = 3,b = 5,c = 30 2 2
⇒ a + b − c = 4 > 0 .
Câu 11: Đường tròn (C) có tâm I ( 2;
− 3) và đi qua M (2; 3
− ) có phương trình là:
A. (x + )2 + ( y − )2 2 3 = 52 . 2 2
B. (x + 2) + ( y −3) = 52 . C. 2 2
x + y + 4x − 6y −57 = 0. D. 2 2
x + y + 4x + 6y −39 = 0. Lời giải  2 R = IM = 4 + ( 6 − )2 = 52 .
Phương trình đường tròn tâm I ( 2;
− 3) , R = 52 là: ( x + )2 + ( y − )2 2 3 = 52. 2 2
Câu 12: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 9 4
A. F = − 13;0 ; F = 13;0 1 ( ) 2 ( ).
B. F = 0;− 13 ; F = 0; 13 . 1 ( ) 2 ( )
C. F = 0;− 5 ; F = 0; 5 .
D. F = − 5;0 ; F = 5;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( ) Lời giải Gọi F = − ;0 c ; F = ;0 c
là hai tiêu điểm của (H ) . 1 ( ) 2 ( ) 2 2
Từ phương trình ( ) : x y H − = 1, ta có: 2 a = 9 và 2 b = 4 suy ra 9 4 2 2 2
c = a + b =13 ⇒ c = 13,(c > 0) .
Vậy tọa độ các tiêu điểm của (H ) là F = − 13;0 ; F = 13;0 . 1 ( ) 2 ( )
Câu 13: Một tổ có 6 học sinh nữ và 8 học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học
sinh của tổ đó đi trực nhật? A. 28 . B. 48 . C. 14. D. 8 . Lời giải
Số cách chọn ngẫu nhiên một học sinh của tổ đi trực nhật là 6 + 8 =14 .
Câu 14: Từ 4 số 1,2,3,4 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số? A. 12. B. 6 . C. 64 . D. 24 . Lời giải
Gọi số cần lập là abc,a ≠ 0 .
Chọn a có 4 cách chọn.
Chọn b có 4 cách chọn.
Chọn c có 4 cách chọn.
Theo qui tắc nhân, số các số lập được là : 3 4 = 64 số.
Câu 15: Có bao nhiêu cách xếp 3 học sinh nam và 4 học sinh nữ theo hàng ngang? Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 7!. B. 144. C. 2880 . D. 480 . Lời giải
Số cách xếp 3 học sinh nam và 4 học sinh nữ theo hàng ngang là 7!.
Câu 16: Từ 7 chữ số 1, 2, 3, 4, 5, 6, 7có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau? A. 4 7 . B. P7 . C. 4 C . D. 4 A . 7 7 Lời giải
Số các số tự nhiên có 4 chữ số đôi một khác nhau được lập từ 7 chữ số 1, 2, 3, 4, 5, 6, 7là 4 A 7
Câu 17: Cho tập hợp M = {1;2;3;4; }
5 . Số tập con gồm hai phần tử của tập hợp M là: A. 11. B. 2 A . C. 2 C . D. P . 5 5 2 Lời giải
Mỗi tập con hai phần tử của tập hợp M là một tổ hợp chập 2 của 5 phần tử. Vậy số tập con hai
phần tử của tập hợp M là: 2 C . 5
Câu 18: Khai triển (x + y)5 2
thành đa thức ta được kết quả sau A. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 80x y + 80xy + 32y . B. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 40x y +10xy + 2y . C. 5 4 3 2 2 3 4 5
x +10x y + 40x y + 80x y + 40xy + 32y . D. 5 4 3 2 2 3 4 5
x +10x y + 20x y + 20x y +10xy + 2y . Lời giải
(x + 2y)5 = C x +C x (2y)1 +C x (2y)2 +C x (2y)3 +C x(2y)4 +C (2y)5 0 5 1 4 2 3 3 2 4 5 . 5 5 5 5 5 5 5 4 3 2 2 3 4 5
= x +10x y + 40x y + 80x y + 80xy + 32y .
Câu 19: Gieo một con súc sắc cân đối, đồng chất một lần. Xác suất xuất hiện mặt hai chấm là A. 1 . B. 1 . C. 1 . D. 1 . 2 3 6 4 Lời giải
Gọi A là biến cố xuất hiện mặt hai chấm.
Ta có n(Ω) = 6 , n( A) =1. n A Suy ra P( A) ( ) 1 = = . n(Ω) 6
Câu 20: Một hộp chứa 10 quả cầu gồm 3 quả cầu màu xanh và 7 quả cầu màu đỏ, các quả cầu đôi một
khác nhau. Chọn ngẫu nhiên lần lượt hai quả cầu từ hộp đó. Xác suất để hai quả cầu được chọn ra cùng màu bằng A. 7 . B. 8 . C. 7 . D. 5 . 30 15 15 11 Lời giải
Gọi biến cố A : “Hai quả cầu được chọn ra cùng màu”.
Số phần tử của không gian mẫu là: n(Ω) =10.9 = 90 . Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Chọn hai quả cầu cùng màu xảy ra 2 trường hợp: hoặc 2 quả cùng màu xanh hoặc 2 quả cùng
màu đỏ. Khi đó n( A) = 3.2 + 7.6 = 48 . n A 48 8
Xác suất để hai quả cầu được chọn ra cùng màu là P( A) ( ) = = = . n(Ω) 90 15
Câu 21: Từ một nhóm gồm 6 học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. Xác suất để
chọn được 2 học sinh nữ và 1 học sinh nam bằng A. 3 . B. 1 . C. 1 . D. 1 . 10 5 6 2 Lời giải
Số phần tử của không gian mẫu là n(Ω) 3 = C . 10
Gọi A là biến cố: “Chọn được 2 học sinh nữ và 1 học sinh nam” thì n( A) 2 1 = C .C . 6 4 2 1 C .
Xác suất chọn được 2 học sinh nữ và 1 học sinh nam là P( A) C 1 6 4 = = . 3 C 2 10
Câu 22: Cho số gần đúng α = 23748023 với độ chính xác d =101. Hãy viết số quy tròn của số A. 23749000 . B. 23748000 . C. 23746000 . D. 23747000 . Lời giải
Độ chính xác d =101(hàng trăm) nên ta làm tròn số α = 23748023 đến hàng nghìn được kết quả là α = 23748000 .
Câu 23: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như
bảng sau. Hỏi trong năm 2021, trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách? A. 4,694 . B. 4,925. C. 4,55. D. 4,495 . Lời giải
Số bạn học sinh trong lớp là n = 6 +15+ 3+ 8+ 8 = 40 (bạn)
Trong năm 2021, trung bình mỗi bạn trong lớp đọc số cuốn sách là: 6.3 15.4 3.5 8.6 8.7 x + + + + = = 4,925 40
Câu 24: Trong mặt phẳng hệ tọa độ Oxy, cho hai điểm A(2; ) 1 , B( 1;
− 7) . Tọa độ điểm M thỏa mãn hệ
  
thức 3AM + AB = 0 là
A. M (1; − 3)
B. M (5; − 5) C. M (1; − ) 1 D. M (3; − ) 1 Lời giải
Gọi M (a; b)  
Ta có AM = (a − 2; b − ) 1 và AB = ( 3 − ; 6) Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
   3
 (a − 2) − 3 = 0 a = 3
Lại có 3AM + AB = 0 ⇔  ⇔  . Suy ra M (3; − ) 1 . 3  (b − ) 1 + 6 = 0 b = 1 −
Câu 25: Đường thẳng ∆ đi qua điểm M (1;2) và song song với đường thẳng d : 4x + 2y +1= 0có phương
trình tổng quát là
A. 4x + 2y + 3 = 0 .
B. 2x + y + 4 = 0 .
C. x − 2y + 3 = 0.
D. 2x + y − 4 = 0 . Lời giải
Vì ∆ // d : 4x + 2y +1 = 0 ⇒ ∆ :4x + 2y + m = 0,(m ≠ 1).
Mà ∆ đđi qua M (1;2) nên ta có 4.1+ 2.2 + m = 0 ⇒ m = 8 − (TM ) .
⇒ ∆ :4x + 2y −8 = 0 ⇔ ∆ : 2x + y − 4 = 0 .
Câu 26: Hai đường thẳng d :mx + y = m −5,d :x + my = 9 cắt nhau khi và chỉ khi 1 2 A. m ≠ 1 − . B. m ≠ 1. C. m ≠ 1 ± . D. m ≠ 2 . Lời giải CÁCH 1 -Xét m = 0 thì 1 d : y = 5 − , d2
:x = 9. Rõ ràng hai đường thẳng này cắt nhau nên m = 0 thỏa mãn.
-Xét m ≠ 0 thì d : y = −mx + m − 5 và x = − + 1 d : y 9 2 m 1 m ≠ 0
Hai đường thẳng d và d cắt nhaut ⇔ − ≠ − ⇔ . 1 2 m  (2) mm ≠ 1 ± Từ và ta có m ≠ 1 ± . CÁCH 2   1
d và d2 theo thứ tự nhận các vectơ 1 n = ( m 1 ; ), 2
n = (1;m ) làm vec tơ pháp tuyến. 1
d và d2 cắt nhau ⇔ 1 n và 2
n không cùng phương ⇔ m.m ≠ 1 1 . ⇔ m ≠ 1 ± .
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(1;2) , B(5;2) , C (1; 3 − ) có phương trình là. A. 2 2
x + y + 6x + y −1 = 0 . B. 2 2
x + y − 6x − y −1 = 0 . C. 2 2
x + y − 6x + y −1 = 0 . D. 2 2
x + y + 6x − y −1 = 0 . Lời giải
Gọi (C) là phương trình đường tròn đi qua ba điểm ,
A B,C với tâm I ( ; a b) ⇒ (C) có dạng: 2 2
x + y − 2ax − 2by + c = 0 . Vì đường tròn (C) đi qua qua ba điểm , A B,C
nên ta có hệ phương trình: a = 3 1
 + 4 − 2a − 4b + c = 0  2
− a − 4b + c = 5 −     1
25 + 4 −10a − 4b + c = 0 ⇔  10
− a − 4b + c = 29 − ⇔ b  = − . 2 1  9 2a 6b c 0  2a 6b c 10  + − + + = − + + = −   c = 1 − 
Vậy phương trình đường tròn cần tìm là 2 2
x + y − 6x + y −1 = 0 .
Câu 28: Đường tròn (C) đi qua A(1;3) , B(3; )
1 và có tâm nằm trên đường thẳng d : 2x − y + 7 = 0 có phương trình là Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
A. (x − )2 + ( y − )2 7 7 =102 .
B. (x + )2 + ( y + )2 7 7 =164 .
C. (x − )2 + ( y − )2 3 5 = 25 .
D. (x + )2 + ( y + )2 3 5 = 25 . Lời giải
Đường tròn (C) có tâm I ( ;
a b) , bán kính R có phương trình là: (x − a)2 + ( y − b)2 2 = R (*) .
I ∈ d ⇒ I ( ;2 a a + 7) .
AI = (a − )2 + ( a + )2 1 2 4 2 = 5a +14a +17
BI = (a − )2 + ( a + )2 3 2 6 2 = 5a +18a + 45
Vì (C) đi qua A(1;3) , B(3; ) 1 nên AI = BI ⇔ 2 2 AI = BI ⇔ 2 2
5a +14a +17 = 5a +18a + 45 ⇔ a = 7 − Suy ra tâm I ( 7; − 7 − ) , bán kính 2 2 R = AI =164.
Vậy đường tròn (C) có phương trình: (x + )2 + ( y + )2 7 7 =164 .
Câu 29: Phương trình chính tắc của elip đi qua điểm A(0; 4
− ) và có một tiêu điểm F 3;0 là 2 ( ) 2 2 x y 2 2 x y 2 2 x y 2 2 x y A. + = 1. B. + = 1. C. + = 1. D. + = 1. 10 8 25 16 25 9 16 25 Lời giải 2 2 x y
Phương trình chính tắc của elip có dạng +
= 1 (a > b > 0) . 2 2 a b 16 =1 2  2 b = 16 b  Ta có 2 c = 3 ⇒ c = 9 .  2 2 2  2 a = b + c a = 25    2 2 x y
Vậy elip có phương trình chính tắc là + = 1. 25 16
Câu 30: Cần xếp 3 nam, 3 nữ vào 1 hàng có 6 ghế. Hỏi có bao nhiêu cách xếp sao cho nam nữ ngồi xen kẽ. A. 36. B. 720 . C. 78. D. 72 . Lời giải
Có 6 cách chọn một người tuỳ ý ngồi vào chỗ thứ nhất. Tiếp đến, có 3 cách chọn một người khác
phái ngồi vào chỗ thứ 2. Lại có 2 cách chọn một người khác phái ngồi vào chỗ thứ 3, có 2 cách
chọn vào chỗ thứ 4, có 1 cách chọn vào chỗ thứ 5, có 1 cách chọn vào chỗ thứ 6.
Vậy có: 6.3.2.2.1.1 = 72 cách.
Câu 31: Có 4 cặp vợ chồng ngồi trên một dãy ghế dài. Có bao nhiêu cách sắp xếp sao cho vợ và chồng
của mỗi gia đình đều ngồi cạnh nhau. A. 384. B. 8!. C. 4!.4!. D. 48 . Lời giải
-Nhóm mỗi cặp vợ chồng lại với nhau có 2!.2!.2!.2! cách
-Sắp xếp 4 cặp vợ chồng lên một dãy ghế dài có 4! cách
-Theo quy tắc nhân, ta có 2!.2!.2!.2!.4!= 384. Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 32: Ở một Đoàn trường phổ thông có 5 thầy giáo, 4 cô giáo và 8 học sinh. Có bao nhiêu cách chọn
ra một đoàn công tác gồm 7 người trong đó có 1 trưởng đoàn là thầy giáo, 1 phó đoàn là cô giáo
và đoàn công tác phải có ít nhất 4 học sinh. A. 6020 . B. 10920. C. 9800. D. 10290. Lời giải
Trường hợp 1: Đoàn có 1 thầy giáo, 1 cô giáo, và 5 học sinh có: 5 5.4.C =1120 cách. 8
Trường hợp 2: Đoàn có 1 thầy giáo, 2 cô giáo, và 4 học sinh có: 2 4
5.A .C = 4200 cách. 4 8
Trường hợp 3: Đoàn có 2 thầy giáo, 1 cô giáo, và 4 học sinh có: 2 4
A .4.C = 5600 cách. 5 8
Vậy theo quy tắc cộng có: 1120 + 4200 + 5600 =10920 cách.
Câu 33: Gọi S là tập hợp các số tự nhiên có ba chữ số đôi một khác nhau được lập thành từ các chữ số
1,2,3,4,5,6 . Chọn ngẫu nhiên một số từ S, tính xác suất để số được chọn là một số chia hết cho 5 . A. 1 . B. 1 . C. 1 . D. 1 . 6 12 2 4 Lời giải
Số phần tử của không gian mẫu: n(Ω) 3 = A =120 6 .
Gọi A là biến cố: "Số chọn được là một số chia hết cho 5 ".
Số chia hết cho 5 được lập từ các chữ số trên có dạng ab5.
Chọn 2 số a,b từ các chữ số 1,2,3,4,6 là một chỉnh hợp chập 2 của 5 phần tử.
Số cách chọn là n( A) 2 = A = 20 5 . n A
Vậy xác suất cần tìm là: P( A) ( ) 20 1 = = = . n(Ω) 120 6
Câu 34: Chọn ngẫu nhiên hai số khác nhau từ 25 số nguyên dương đầu tiên. Xác suất
để chọn được hai số có tổng là một số chẵn là A. 13 . B. 12 . C. 1 . D. 313 . 25 25 2 625 Lời giải
Số cách chọn hai số khác nhau từ 25 số nguyên dương đầu tiên là 2
C = 300 ⇒ n Ω = 300 . 25 ( )
Gọi A là biến cố “Tổng hai số được chọn là một số chẵn’’. Ta có hai trường hợp
Trường hợp 1: Chọn 2 số chẵn khác nhau từ tập 12 số chẵn có 2 C = 66 cách. 12
Trường hợp 2: Chọn 2 số lẻ khác nhau từ tập 13 số lẻ có 2 C = 78 cách. 13 Do đó n( ) A = 66 + 78 =144.
Vậy xác suất cần tìm là 144 12 P( ) A = = . 300 25
Câu 35: Một nhóm gồm 12 học sinh trong đó có 7 học sinh nam và 5 học sinh nữ. Chọn ngẫu nhiên 3 học
sinh từ nhóm 12 học sinh đó đi lao động. Xác suất để trong ba học sinh được chọn có ít nhất một học sinh nữ là: A. 15 . B. 7 . C. 35 . D. 37 . 22 44 44 44 Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số cách chọn ba học sinh bất kì là n(Ω) 3 = C = 220 12
Số cách chọn ba học sinh nam là 3 C = 35 7
Số cách chọn ra ba học sinh mà có ít nhất một học sinh nữ là 3 3 C − C =185 12 7 185 37
Xác suất để chọn được ba học sinh có ít nhất một học sinh nữ là P = = 220 44
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có 8 người cùng vào thang máy ở tầng 1 của một tòa nhà cao 10 tầng và đi lên trên. Hỏi có bao
nhiêu cách sắp xếp để trong 8 người đó có đúng 2 người cùng ra ở 1 tầng và mỗi người còn lại
ra ở mỗi tầng khác nhau. Lời giải
Chọn 2 người trong 8 người có: 2 C = 28 cách. 8
Chọn 1 tầng trong 9 tầng để cho 2 người đó cùng ra có: 9 cách.
Chọn 6 tầng trong 8 tầng còn lại cho 6 người còn lại có: 6 A = 20160 cách. 8
Vậy theo quy tắc nhân có: 28.9.20160 = 5080320 cách.
Câu 37: Trong mặt phẳng Oxy, viết phương trình chính tắc của Elip (E) có một tiêu điểm là F 2; − 0 1 ( )
và đi qua điểm M (2;3). Lời giải 2 2
Phương trình chính tắc của Elip có dạng: x y +
=1, a > b > 0 . 2 2 ( ) a b
Vì Elip có một tiêu điểm là F 2; − 0 nên c = 2 1 ( ) 2 2 2 2 2
⇒ a − b = c = 4 ⇒ a = b + 4 . 2 2
Mặt khác Elip đi qua điểm M (2;3) nên 4 9 4 9 4b + 9b + 36 + = 1 ⇔ + = 1 ⇔ = 1 2 2 2 2 2 a b b + 4 b b ( 2 b + 4) 2 b =12(n) 4 2
⇔ b − 9b − 36 = 0 ⇔  . 2 b = 3 −  (l) 2 2
a = b + 4 =12 + 4 =16 . 2 2
Vậy phương trình chính tắc của elip (E) cần tìm là: x y + =1. 16 12
Câu 38: Gọi S là tập các số tự nhiên có bốn chữ số khác nhau được lập từ tập E = {1;2;3;4; } 5 . Chọn
ngẫu nhiên một số từ tập S . Xác xuất để số được chọn là một số chẵn bằng Lời giải
Gọi A là biến cố “số được chọn là một số chẵn”
Số các số tự nhiên có bốn chữ số khác nhau là 4 A =120 5
Số phần tử của không gian mẫu n(Ω) 1 = C =120 120
Số các số tự nhiên chẵn có bốn chữ số khác nhau 3 2A = 48 4
Số kết quả thuận lợi của biến cố A là n( A) 1 = C = 48 48 Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 n A 48 2
Vậy xác xuất để số được chọn là một số chẵn là P( A) ( ) = = = n(Ω) 120 5
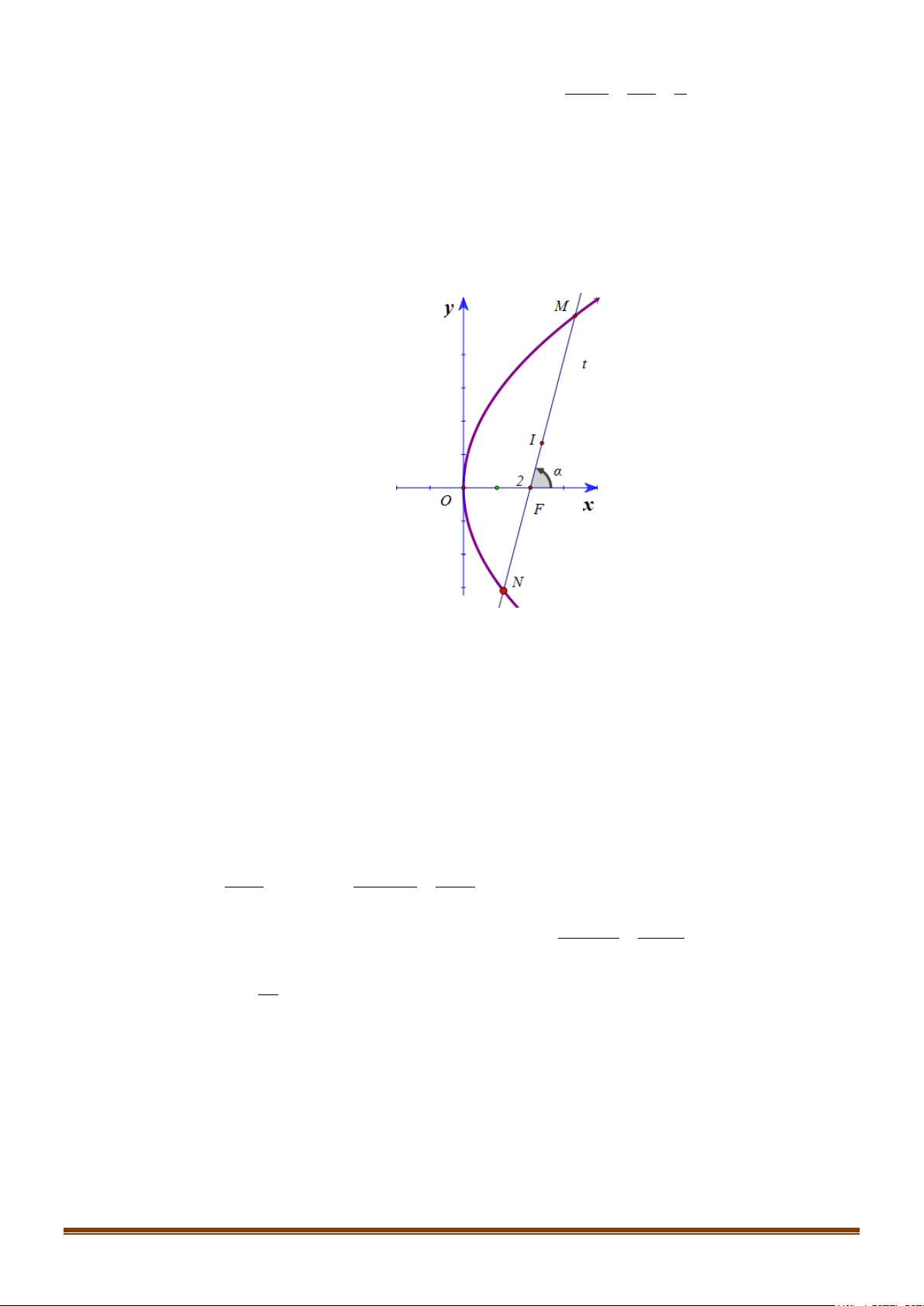
Câu 39: Trong mặt phẳng Oxy cho parabol (P) 2
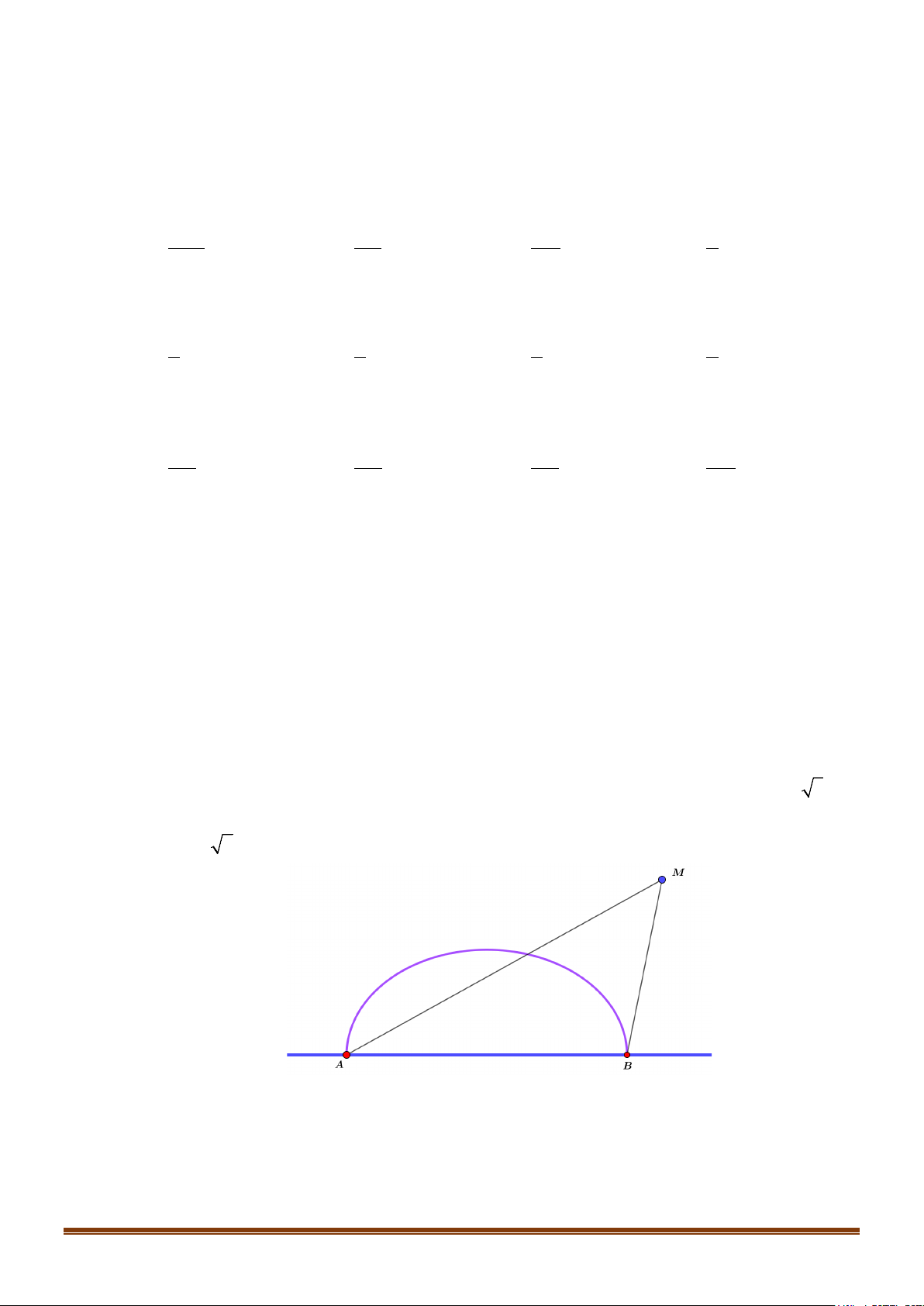
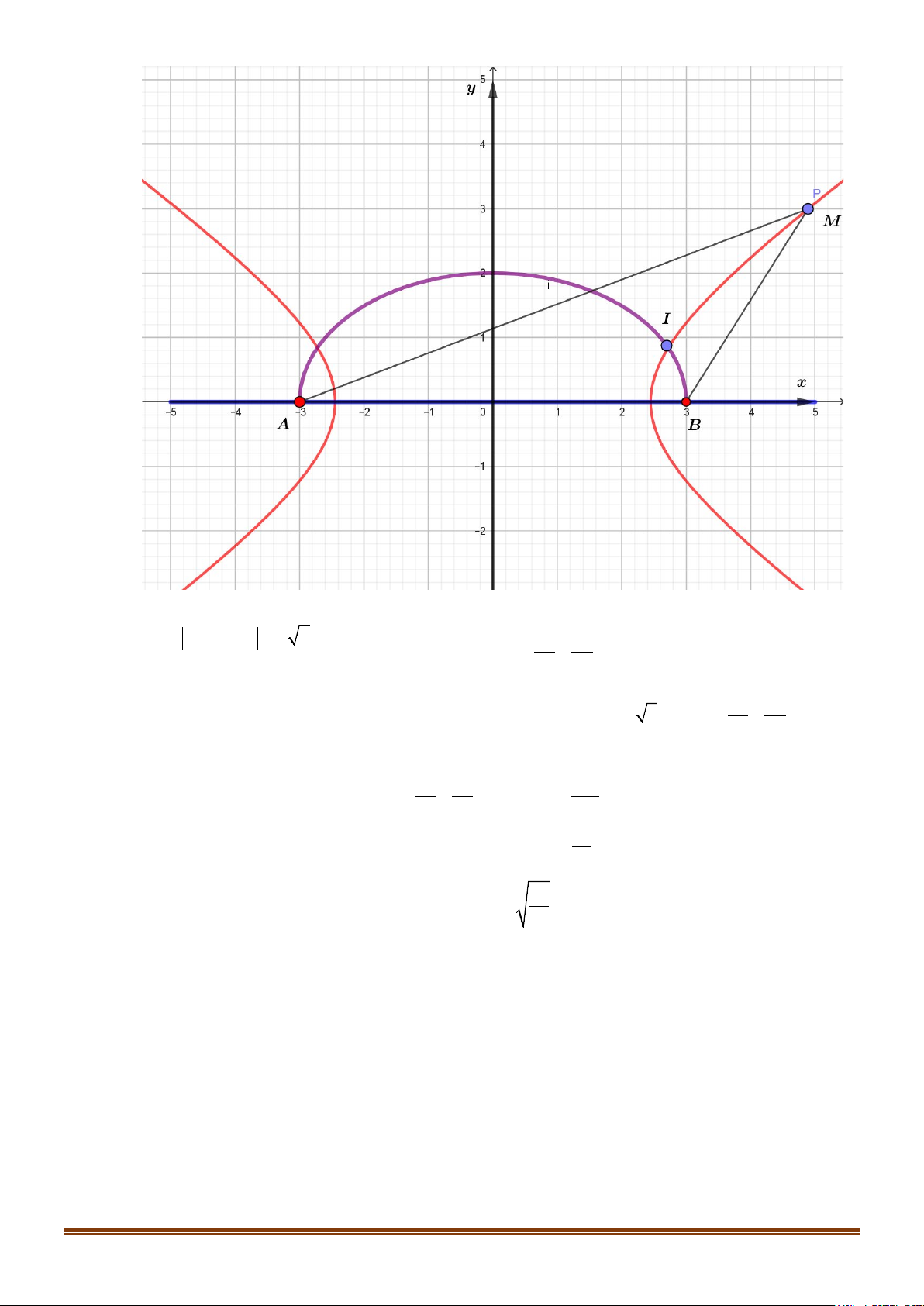
: y = 8x . Đường thẳng Δ không trùng với trục Ox đi
qua tiêu điểm F của (P) sao cho góc hợp bởi hai tia Fx và Ft là tia của Δ nằm phía trên trục
hoành một góc bằng α( 0
α ≠ 90 ). Biết Δ cắt (P) tại hai điểm phân biệt M , N và tập hợp trung
điểm I của đoạn MN khi α thay đổi là một Parabol. Xác định phương trình của Parabol. Lời giải
Theo giả thiết ta có F (2; 0) , đường thẳng Δ có hệ số góc k = tan α
y =(x − 2)tan α
Suy ra Δ : y =(x − 2).tan α . Xét hệ phương trình  2 y = 8x Suy ra 2 tan .
α y −8y −16 tan α = 0 2
Δ ' =16 +16 tan α > 0 do đó phương trình luôn có hai nghiệm phân biệt, hệ phương trình có hai
nghiệm phân biệt điều này chứng tỏ rằng Δ cắt (P) tại hai điểm phân biệt.
Gọi tọa độ hai giao điểm đó là M (x y
N x y ; I (x y là trung điểm của MN I ; I ) M ; M ) , ( N; N )
Theo định lý Viét ta có: 8 y + y M N 4 y + y = > ⇒ y = = . M N 0 tan I α 2 tan α Mặt khác từ ta có x + x
y + y = x + x − α ⇒ x = = + M N ( M N ) M N 4 4 tan I 2 2 2 tan α 2 Suy ra x 4. yI  = + hay 2 y = x − I 4 I 8 I   2  4 
Vậy tập hợp điểm I là Parabol có phương trình: 2 y = 4x −8 .
---------- HẾT ---------- Page 14
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 02
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho tam giác ABC với A( 3 − ;6) ; B(9; 1 − 0) và 1 G  ;0 
là trọng tâm. Tọa độC là: 3   
A. C (5;− 4) . B. C (5;4) . C. C ( 5; − 4). D. C ( 5; − − 4) .
Câu 2: Chiều cao của một ngọn đồi là h = 347,13m ± 0,2m . Độ chính xác d của phép đo trên là
A. d = 347,13m.
B. 347,33m .
C. d = 0,2m .
D. d = 346,93m .
Câu 3: Tứ phân vị thứ nhất của mẫu số liệu: 27; 15; 18; 30; 19; 40; 100; 9; 46; 10; 200. A. 18. B. 15. C. 40. D. 46.
Câu 4: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là: A. 20. B. 22. C. 24. D. 26.
Câu 5: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
A. Bình phương của phương sai.
B. Một nửa của phương sai.
C. Căn bậc hai của phương sai.
D. Hiệu của số lớn nhất và số nhỏ nhất.
Câu 6: Trong hệ tọa độ Oxy, cho ba điểm A(2; ) 1 , B(0; 3 − ) , C (3; )
1 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. (5; 5) . B. (5; 2 − ) . C. (5; 4 − ) . D. ( 1; − 4 − ) .
Câu 7: Chỉ số IQ của một nhóm học sinh là: 60 78 80 64 70 76 80 74 86 90
Các tứ phân vị của mẫu số liệu là
A. Q = 70;Q = 77;Q = 80 .
B. Q = 72;Q = 78;Q = 80 . 1 2 3 1 2 3
C. Q = 70;Q = 76;Q = 80 .
D. Q = 70;Q = 75;Q = 80 . 1 2 3 1 2 3
Câu 8: Nhiệt độ cao nhất của Hà Nội trong 7 ngày liên tiếp trong tháng tám được ghi lại là:
34; 34; 36; 35; 33; 31;30 (Độ C).
Độ lệch chuẩn của mẫu số liệu thuộc khoảng nào A. (1;2) . B. (3;4). C.  7 2;     . D. 3 0; . 2     4  x =1− 4t
Câu 9: Cho đường thẳng d có phương trình 
. Một vectơ chỉ phương của d là y = 3 − + t     A. u = (1; 4 − ) . B. u = (4; ) 1 . C. u = (1; 3 − ). D. u = ( 4; − ) 1 .
Câu 10: Trong mặt phẳng tọa độ Oxy , phương trình tham số của đường thẳng qua M (1; 2 − ) , N (4;3) là x = 4 + tx =1+ 5tx = 3 + 3tx =1+ 3t A.  . B.  . C.  . D.  . y = 3 − 2ty = 2 − − 3ty = 4 + 5ty = 2 − + 5t Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 11: Xác định vị trí tương đối giữa hai đường thẳng ∆ : x − 2y +1= 0 và ∆ : 3
− x + 6y −10 = 0 . 1 2
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau.
Câu 12: Trong mặt phẳng Oxy , khoảng cách từ điểm M (3;− 4) đến đường thẳng ∆ :3x − 4y −1 = 0 . A. 8 . B. 24 . C. 12 . D. 24 − . 5 5 5 5
Câu 13: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y + 2x − 4y + 9 = 0 . B. 2 2
x + y − 6x + 4y +13 = 0 . C. 2 2
2x + 2y −8x − 4y − 6 = 0 . D. 2 2
5x + 4y + x − 4y +1= 0.
Câu 14: Trong mặt phẳng tọa độ Oxy , cho hai điểm A( 3;
− 2) và B(1;4) . Viết phương trình đường tròn
đường kính AB ? A. 2 2
x + y + 2x − 6y + 5 = 0 . B. 2 2
x + y − 2x + 6y + 5 = 0 . C. 2 2
x + y + 2x − 6y − 5 = 0 . D. 2 2
x + y − 2x + 6y − 5 = 0 . 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 16 9 A. F = 5; − 0 ; F = 5;0 . B. F = 0; 5 − ; F = 0;5 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
C. F = 0;− 7 ; F = 0; 7 .
D. F = − 7;0 ; F = 7;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
Câu 16: Có 3 cuốn sách Toán khác nhau và 4 cuốn sách Vật lí khác nhau. Hỏi có bao nhiêu cách chọn
một cuốn sách trong số các cuốn sách đó? A. 12. B. 7 . C. 3. D. 4 .
Câu 17: Có bao nhiêu cách chọn một cặp đôi tham gia văn nghệ từ một nhóm gồm 7 bạn nam và 6 bạn nữ? A. 13. B. 42 . C. 8. D. 7 .
Câu 18: Từ các số 1,2,3,4 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau. A. 12. B. 64 . C. 256 . D. 24 .
Câu 19: Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập A = {2, 3, 4, 5, } 6 A. 4 C . B. 4 C . C. 4 A . D. 4 A . 5 6 5 6
Câu 20: Có bao nhiêu cách chọn ra 4 học sinh từ một tổ gồm 15 học sinh? A. 32760. B. 50625. C. 60 . D. 1365.
Câu 21: Có bao nhiêu số hạng trong khai triển nhị thức ( − )5 3 2x A. 4 . B. 5. C. 6 . D. 2 .
Câu 22: Một lớp có 35 học sinh, trong đó có 5 học sinh tên Linh. Trong một lần kiểm tra bài cũ, thầy
giáo gọi ngẫu nhiên một học sinh trong lớp lên bảng. Xác suất để học sinh tên Linh lên bảng bằng A. 1 . B. 1 . C. 1 . D. 1 . 175 7 35 5 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 23: Cho tập hợp A = {1;2;4;5;8; }
9 lấy ngẫu nhiên một số. Xác suất để lấy được một số chẵn là: A. 1.. B. 1 . C. 2.. D. 1 . 3 2 . 5 6
Câu 24: Để kiểm tra sản phẩm của một công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp sữa
cam, 4 hộp sữa nho và 3 hộp sữa dâu. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp sữa để
phân tích mẫu. Xác suất để 3 hộp sữa được chọn đủ cả 3 loại là A. 1 . B. 3 . C. 1 . D. 3 . 5 7 6 11
Câu 25: Viết phương trình tổng quát của đường thẳng đi qua M (3; 2
− ) và song song với đường thẳng
d : 2x + y − 5 = 0
A. x + 2y − 7 = 0 .
B. 2x + y − 4 = 0 .
C. x + 2y − 5 = 0.
D. 2x + y − 6 = 0 .
Câu 26: Với giá trị nào của m thì hai đường thẳng d : 2x + y + 4 − m = 0 và d : m + 3 x + y + 2m −1= 0 2 ( ) 1 song song? A. m =1. B. m = 1. − C. m = 2. D. m = 3.
Câu 27: Đường tròn (C) có tâm I ( 1;
− 2) và cắt đường thẳng d :3x − y −15 = 0 theo một dây cung có
độ dài bằng 6. Tìm phương trình đường tròn (C).
A. (x − )2 + ( y + )2 1 2 = 49 .
B. (x + )2 + ( y − )2 1 2 = 49 .
C. (x − )2 + ( y + )2 1 2 = 7 .
D. (x + )2 + ( y − )2 1 2 = 7 .
Câu 28: Trong mặt phẳng tọa độ (Oxy), cho đường tròn (S ) có tâm I nằm trên đường thẳng y = −x ,
bán kính R = 3 và tiếp xúc với các trục tọa độ. Lập phương trình của (S ) , biết hoành độ tâm I là số dương.
A. (x − )2 + ( y − )2 3 3 = 9.
B. (x − )2 + ( y + )2 3 3 = 9.
C. (x − )2 −( y − )2 3 3 = 9 .
D. (x + )2 + ( y + )2 3 3 = 9 .
Câu 29: Phương trình chính tắc của parabol (P) có tiêu điểm là F (5;0) là: A. 2 y = 20x . B. 2 y = 30x . C. 2 y =15x . D. 2 y =10x .
Câu 30: Một bạn có 4 áo xanh, 3 áo trắng và 5 quần màu đen. Hỏi bạn đó có bao nhiêu cách chọn một bộ quần áo để mặc? A. 35. B. 66 . C. 12. D. 60 .
Câu 31: Số cách xếp 5 nam và 4 nữ thành một hàng ngang sao cho 4 nữ luôn đứng cạnh nhau là A. 362880. B. 2880. C. 5760. D. 17280.
Câu 32: Một nhóm có 3 học sinh nam và 3 học sinh nữ. Nhóm muốn xếp theo hàng ngang để chụp ảnh
kỉ niệm. Có bao nhiêu cách xếp để không có bạn nam nào đứng kề nhau. A. 6!. B. 3!.3!. C. 3 3!.A . D. 3 3!.C . 4 4 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 33: Từ hộp chứa 5 quả cầu trắng, 4 quả cầu xanh kích thước và khối lượng như nhau. Lấy ngẫu nhiên
3 quả cầu. Tính xác suất để 3 quả cầu lấy được có màu trắng? A. 5 . B. 5 . C. 1 . D. 1 . 42 9 3 21
Câu 34: Một tổ học sinh có 7 nữ và 5 nam. Chọn ngẫu nhiên 3 học sinh. Xác suất để trong 3 học sinh
được chọn có đúng 1 học sinh nam bằng A. 1 . B. 5 . C. 21 . D. 7 . 5 12 44 22
Câu 35: Một hộp đựng 12 cây viết được đánh số từ 1 đến 12. Chọn ngẫu nhiên 2 cây. Xác suất để chọn
được 2 cây có tích hai số là số chẵn A. 6 . B. 17 . C. 5 . D. 5 . 11 22 22 11
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau và số đó chia hết cho 9.
Câu 37: Trong mặt phẳng Oxy, cho Elip (E) đi qua điểm M (2 3;2) và M nhìn hai tiêu điểm của (E)
dưới một góc vuông. Viết phương trình chính tắc của (E) đã cho.
Câu 38: Một cuộc họp có sự tham gia của 6 nhà Toán học trong đó có 4 nam và 2 nữ, 7 nhà Vật lý
trong đó có 3 nam và 4 nữ và 8 nhà Hóa học trong đó có 4 nam và 4 nữ. Người ta muốn lập
một ban thư kí gồm 4 nhà khoa học. Tính xác suất để ban thư kí được chọn phải có đủ cả 3 lĩnh
vực và có cả nam lẫn nữ.
Câu 39: Cho hypebol (H ) có hai tiêu điểm F; F 1
2 nằm trên Ox và đối xứng qua gốc tọa độ O , ( H ) đi qua điểm M 9 41 có hoành độ 5
− và MF = ; MF =
. Viết phương trình chính tắc của hypebol 1 2 4 4 (H ) .
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Cho tam giác ABC với A( 3 − ;6) ; B(9; 1 − 0) và 1 G  ;0 
là trọng tâm. Tọa độC là: 3   
A. C (5;− 4) . B. C (5;4) . C. C ( 5; − 4). D. C ( 5; − − 4) . Lời giải. Chọn C
x + x + x = x
 x = x − x + x C 3 G ( A B ) A B C 3 Ta có : G  ⇔ ⇒ C ( 5; − 4) . y  + y + y =  y
y = y − y + y
C 3 G ( A B ) A B C 3 G
Câu 2: Chiều cao của một ngọn đồi là h = 347,13m ± 0,2m . Độ chính xác d của phép đo trên là
A. d = 347,13m.
B. 347,33m .
C. d = 0,2m .
D. d = 346,93m . Lời giải Chọn C
Ta có a là số gần đúng của a với độ chính xác d qui ước viết gọn là a = a ± d . Vậy độ chính xác
của phép đo là d = 0,2m .
Câu 3: Tứ phân vị thứ nhất của mẫu số liệu: 27; 15; 18; 30; 19; 40; 100; 9; 46; 10; 200. A. 18. B. 15. C. 40. D. 46. Lời giải
Sắp xếp số liệu theo thứ tự không giảm: 9; 10; 15; 18; 19; 27; 30; 40; 46; 100; 200.
Tứ phân vị thứ nhì là trung vị của dãy số liệu là: Q = 27 . 2
Tứ phân vị thứ nhất là trung vị của dãy số liệu: 9; 10; 15; 18; 19.
Khi đó tứ phân vị thứ nhất là: Q =15 . 1
Câu 4: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là: A. 20. B. 22. C. 24. D. 26. Lời giải
Số liệu trên đã sắp xếp theo thứ tự không giảm
Ta có Q = 10;Q = 19;Q = 32 1 2 3
Vậy khoảng tứ phân vị của mẫu số liệu trên là: ∆ = − = . Q 32 10 22
Câu 5: Chọn khẳng định đúng trong bốn phương án sau đây. Độ lệch chuẩn là:
A. Bình phương của phương sai.
B. Một nửa của phương sai.
C. Căn bậc hai của phương sai.
D. Hiệu của số lớn nhất và số nhỏ nhất. Lời giải Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Chọn đáp án: C.
Câu 6: Trong hệ tọa độ Oxy, cho ba điểm A(2; ) 1 , B(0; 3 − ) , C (3; )
1 . Tìm tọa độ điểm D để ABCD là hình bình hành. A. (5; 5) . B. (5; 2 − ) . C. (5; 4 − ) . D. ( 1; − 4 − ) . Lời giải Chọn A A B D C   Gọi D( ;
x y), ABCD là hình bình hành ⇔ AD = BC ⇔ (x − 2; y − ) 1 = (3; 4) x − 2 = 3 x = 5 ⇔  ⇔ y 1 4  − = y = 5 Vậy D(5; 5) .
Câu 7: Chỉ số IQ của một nhóm học sinh là: 60 78 80 64 70 76 80 74 86 90
Các tứ phân vị của mẫu số liệu là
A. Q = 70;Q = 77;Q = 80 .
B. Q = 72;Q = 78;Q = 80 . 1 2 3 1 2 3
C. Q = 70;Q = 76;Q = 80 .
D. Q = 70;Q = 75;Q = 80 . 1 2 3 1 2 3 Lời giải
Sắp xếp các giá trị này theo thứ tự không giảm 60 64 70 74 76 78 80 80 86 90
Vì n =10 là số chẵn nên Q là số trung bình cộng của hai giá trị chính giữa: 2 Q = 76 + 78 : 2 = 77 2 ( )
Ta tìm Q là trung vị của nửa số liệu bên trái Q 1 2 60 64 70 74 76
và tìm được Q = 70 1
Ta tìm Q là trung vị của nửa số liệu bên phải Q 3 2 78 80 80 86 90
và tìm được Q = 80 . 3 Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 8: Nhiệt độ cao nhất của Hà Nội trong 7 ngày liên tiếp trong tháng tám được ghi lại là:
34; 34; 36; 35; 33; 31;30 (Độ C).
Độ lệch chuẩn của mẫu số liệu thuộc khoảng nào A. (1;2) . B. (3;4). C.  7 2;     . D. 3 0; . 2     4  Lời giải
Số trung bình cộng của mẫu số liệu là: 34 34 36 35 33 31 30 x + + + + + + = ≈ 33,29 7 7 ∑(x − x i )2
Phương sai của mẫu số liệu là: 2 i 1 s = = ≈ 3,92 7
Độ lệch chuẩn cần tính là: s ≈ 3,92 ≈1,98 . x =1− 4t
Câu 9: Cho đường thẳng d có phương trình 
. Một vectơ chỉ phương của d là y = 3 − + t     A. u = (1; 4 − ) . B. u = (4; ) 1 . C. u = (1; 3 − ). D. u = ( 4; − ) 1 . Lời giải x =1− 4t
Từ phương trình tham số của đường thẳng d là 
, suy ra d có một vectơ chỉ phương y = 3 − + t  là u = ( 4; − ) 1 .
Câu 10: Trong mặt phẳng tọa độ Oxy , phương trình tham số của đường thẳng qua M (1; 2 − ) , N (4;3) là x = 4 + tx =1+ 5tx = 3 + 3tx =1+ 3t A.  . B.  . C.  . D.  . y = 3 − 2ty = 2 − − 3ty = 4 + 5ty = 2 − + 5t Lời giải 
Đường thẳng có véctơ chỉ phương là MN = (3;5) và đi qua M (1; 2
− ) nên có phương trình tham x =1+ 3t số là  . y = 2 − + 5t
Câu 11: Xác định vị trí tương đối giữa hai đường thẳng ∆ : x − 2y +1= 0 và ∆ : 3
− x + 6y −10 = 0 . 1 2
A. Cắt nhau và không vuông góc với nhau. B. Trùng nhau.
C. Vuông góc với nhau. D. Song song với nhau. Lời giải
Tọa độ giao điểm của ∆ và ∆ là nghiệm của hệ phương trình: 1 2
x − 2y +1 = 0 3
x − 6y + 3 = 0  ⇔   3
− x + 6y −10 = 0 3
x − 6y +10 = 0
Hệ phương trình trên vô nghiệm nên hai đường thẳng ∆ và ∆ song song với nhau. 1 2
Câu 12: Trong mặt phẳng Oxy , khoảng cách từ điểm M (3;− 4) đến đường thẳng ∆ :3x − 4y −1 = 0 . A. 8 . B. 24 . C. 12 . D. 24 − . 5 5 5 5 Lời giải Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 3.3− 4. 4 − −1 24
Ta có: d (M ,∆) ( ) = = . 2 + (− )2 5 3 4
Câu 13: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y + 2x − 4y + 9 = 0 . B. 2 2
x + y − 6x + 4y +13 = 0 . C. 2 2
2x + 2y −8x − 4y − 6 = 0 . D. 2 2
5x + 4y + x − 4y +1= 0. Lời giải
Một phương trình trở thành phương trình đường tròn khi 2 2
a + b − c > 0 . Phương trình 2 2 2 2
2x + 2y −8x − 4y − 6 = 0 ⇔ x + y − 4x − 2y −3 = 0 . Có 2 2 2 2
a = 2,b =1,c = 3
− ⇒ a + b − c = 2 +1 + 3 = 8 > 0 .
Câu 14: Trong mặt phẳng tọa độ Oxy , cho hai điểm A( 3;
− 2) và B(1;4) . Viết phương trình đường tròn
đường kính AB ? A. 2 2
x + y + 2x − 6y + 5 = 0 . B. 2 2
x + y − 2x + 6y + 5 = 0 . C. 2 2
x + y + 2x − 6y − 5 = 0 . D. 2 2
x + y − 2x + 6y − 5 = 0 . Lời giải 
Ta có AB = (4;2) ⇒ AB = 20 = 2 5 .
Gọi I là trung điểm của AB , suy ra I ( 1; − 3).
Phương trình đường tròn tâm I , bán kính AB R = = 5 là 2
(x + )2 +( y − )2 2 2 1
3 = 5 ⇔ x + y + 2x − 6y + 5 = 0. 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ): x y H − = 1 là 16 9 A. F = 5; − 0 ; F = 5;0 . B. F = 0; 5 − ; F = 0;5 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
C. F = 0;− 7 ; F = 0; 7 .
D. F = − 7;0 ; F = 7;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( ) Lời giải Gọi F = − ;0 c ; F = ;0 c
là hai tiêu điểm của (H ) . 1 ( ) 2 ( ) 2 2
Từ phương trình ( ) : x y H − = 1, ta có: 2 a =16 và 2 b = 9 suy ra 16 9 2 2 2
c = a + b = 25 ⇒ c = 5,(c > 0) .
Vậy tọa độ các tiêu điểm của (H ) là F = 5; − 0 ; F = 5;0 . 1 ( ) 2 ( )
Câu 16: Có 3 cuốn sách Toán khác nhau và 4 cuốn sách Vật lí khác nhau. Hỏi có bao nhiêu cách chọn
một cuốn sách trong số các cuốn sách đó? A. 12. B. 7 . C. 3. D. 4 . Lời giải
Chọn 1 cuốn sách trong 7 cuốn sách (3 cuốn sách Toán và 4 cuốn sách Vật lý) có 7 cách chọn.
Câu 17: Có bao nhiêu cách chọn một cặp đôi tham gia văn nghệ từ một nhóm gồm 7 bạn nam và 6 bạn nữ? Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 13. B. 42 . C. 8. D. 7 . Lời giải
Số cách chọn một bạn nam và một bạn nữ là: 7.6 = 42 .
Câu 18: Từ các số 1,2,3,4 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau. A. 12. B. 64 . C. 256 . D. 24 . Lời giải
Mỗi số lập được là một hoán vị của 4 số, nên lập được: P = 4! = 24 4 số.
Câu 19: Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập A = {2, 3, 4, 5, } 6 A. 4 C . B. 4 C . C. 4 A . D. 4 A . 5 6 5 6 Lời giải
Số các số tự nhiên có 4 chữ số khác nhau được lập từ A là 4 A . 5
Câu 20: Có bao nhiêu cách chọn ra 4 học sinh từ một tổ gồm 15 học sinh? A. 32760. B. 50625. C. 60 . D. 1365. Lời giải
Số cách chọn ra 4 học sinh từ một tổ gồm 15 học sinh là 4 C =1365. 15
Câu 21: Có bao nhiêu số hạng trong khai triển nhị thức ( − )5 3 2x A. 4 . B. 5. C. 6 . D. 2 . Lời giải
Ta có trong khai triển nhị thức ( + )n
a b thì có n +1 số hạng.
Vì vậy trong khai triển ( − )5
3 2x có 5 +1 = 6 số hạng.
Câu 22: Một lớp có 35 học sinh, trong đó có 5 học sinh tên Linh. Trong một lần kiểm tra bài cũ, thầy
giáo gọi ngẫu nhiên một học sinh trong lớp lên bảng. Xác suất để học sinh tên Linh lên bảng bằng A. 1 . B. 1 . C. 1 . D. 1 . 175 7 35 5 Lời giải
Số cách chọn một bạn học sinh trong lớp là 35 cách.
Số cách chọn một bạn tên Linh trong 5 bạn là 5 cách.
Vậy xác suất để học sinh tên Linh lên bảng là 5 1 = . 35 7
Câu 23: Cho tập hợp A = {1;2;4;5;8; }
9 lấy ngẫu nhiên một số. Xác suất để lấy được một số chẵn là: A. 1.. B. 1 . C. 2.. D. 1 . 3 2 . 5 6 Lời giải
Số phần tử không gian mẫu: n(Ω) = 6 .
Biến cố số lấy được số chẵn là: A = {2;4; }
8 nên n( A) = 3. Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 n A Suy ra P( A) ( ) 3 1 = = = . n(Ω) 6 2
Câu 24: Để kiểm tra sản phẩm của một công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp sữa
cam, 4 hộp sữa nho và 3 hộp sữa dâu. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp sữa để
phân tích mẫu. Xác suất để 3 hộp sữa được chọn đủ cả 3 loại là A. 1 . B. 3 . C. 1 . D. 3 . 5 7 6 11 Lời giải Ta có: 3 n(Ω) = C = 220 12 .
Gọi A là biến cố:”3 hộp sữa được chọn đủ cả 3 loại”. 1 1 1 60 3 n( )
A = C .C .C = 60 ⇒ P( ) A = = . 5 4 3 220 11
Câu 25: Viết phương trình tổng quát của đường thẳng đi qua M (3; 2
− ) và song song với đường thẳng
d : 2x + y − 5 = 0
A. x + 2y − 7 = 0 .
B. 2x + y − 4 = 0 .
C. x + 2y − 5 = 0.
D. 2x + y − 6 = 0 . Lời giải  
Vì đường thẳng song song với d : 2x + y − 5 = 0 nên VTPT n = n = d (2; )1
Phương trình đường thẳng là: 2(x −3) + y + 2 = 0 ⇔ 2x + y − 4 = 0
Câu 26: Với giá trị nào của m thì hai đường thẳng d : 2x + y + 4 − m = 0 và d : m + 3 x + y + 2m −1= 0 2 ( ) 1 song song? A. m =1. B. m = 1. − C. m = 2. D. m = 3. Lời giải
d : 2x + y = 0 Với 1 m = 4  →  
→ d ∩ d =/ ∅ 
→ loại m = 4. 1 2
d : 7x + y + 7 =  0 2 Với m =/ 4 thì
d : 2x + y + 4 − m = 0 1 + − m − m = − d d m 2 1 1 || 3 1   → = =/ ⇔  ⇔ m = 1. −
d : m + 3 x + y − 2m −1 = 0  2 1 4 − mm /= 5 − 2 ( ) 1 2
Câu 27: Đường tròn (C) có tâm I ( 1;
− 2) và cắt đường thẳng d :3x − y −15 = 0 theo một dây cung có
độ dài bằng 6. Tìm phương trình đường tròn (C).
A. (x − )2 + ( y + )2 1 2 = 49 .
B. (x + )2 + ( y − )2 1 2 = 49 .
C. (x − )2 + ( y + )2 1 2 = 7 .
D. (x + )2 + ( y − )2 1 2 = 7 . Lời giải Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 I A H B
Gọi H là trung điểm dây AB AB ⇒ AH = HB =
= 3 và IH ⊥ AB . 2 3.(− ) 1 − 2 −15
Ta có IH = d (I ;d ) = = 2 10 . 2 3 + (− )2 1
Xét IAH vuông tại H : 2 2 2
AI = IH + AH = ( )2 2 2 10 + 3 = 49 2 ⇒ R = 49 .
Phương trình đường tròn (C): (x + )2 + ( y − )2 1 2 = 49 .
Câu 28: Trong mặt phẳng tọa độ (Oxy), cho đường tròn (S ) có tâm I nằm trên đường thẳng y = −x ,
bán kính R = 3 và tiếp xúc với các trục tọa độ. Lập phương trình của (S ) , biết hoành độ tâm I là số dương.
A. (x − )2 + ( y − )2 3 3 = 9.
B. (x − )2 + ( y + )2 3 3 = 9.
C. (x − )2 −( y − )2 3 3 = 9 .
D. (x + )2 + ( y + )2 3 3 = 9 . Lời giải
Do tâm I nằm trên đường thẳng y = −x ⇒ I ( ;
a − a) , điều kiện a > 0 .
Đường tròn (S ) có bán kính R = 3 và tiếp xúc với các trục tọa độ nên:
d (I;Ox) = d (I;Oy) = 3 ⇔ a = 3 ⇔ a = 3(n) ∨ a = 3
− (l) ⇒ I (3;−3) .
(S):(x −3)2 +( y +3)2 Vậy phương trình = 9.
Câu 29: Phương trình chính tắc của parabol (P) có tiêu điểm là F (5;0) là: A. 2 y = 20x . B. 2 y = 30x . C. 2 y =15x . D. 2 y =10x . Lời giải
Gọi phương trình chính tắc của parabol (P) là: 2
y = 2 px( p > 0).
Vì (P) có tiêu điểm là F (5;0) nên p = 5 , tức là p =10. Vậy phương trình chính tắc của parabol 2
(P) là 2y = 20x .
Câu 30: Một bạn có 4 áo xanh, 3 áo trắng và 5 quần màu đen. Hỏi bạn đó có bao nhiêu cách chọn một bộ quần áo để mặc? A. 35. B. 66 . C. 12. D. 60 . Lời giải
Có 7 cách chọn một cái áo để mặc và có 5 cách chọn một cái quần để mặc.
Theo quy tắc nhân thì có 7.5 = 35 cách chọn một bộ quần áo để mặc. Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 31: Số cách xếp 5 nam và 4 nữ thành một hàng ngang sao cho 4 nữ luôn đứng cạnh nhau là A. 362880. B. 2880. C. 5760. D. 17280. Lời giải
Ghép 4 nữ thành 1 nhóm có 4! Cách.
Hoán vị nhóm nữ trên với 5 nam có 6! Cách. Vậy có 4!.6!=17280 cách.
Câu 32: Một nhóm có 3 học sinh nam và 3 học sinh nữ. Nhóm muốn xếp theo hàng ngang để chụp ảnh
kỉ niệm. Có bao nhiêu cách xếp để không có bạn nam nào đứng kề nhau. A. 6!. B. 3!.3!. C. 3 3!.A . D. 3 3!.C . 4 4 Lời giải
Xếp thứ tự 3 bạn nữ có 3! cách.
Khi đó các bạn nam đứng ở các vị trí x.
Xếp thứ tự 3 bạn nam vào 4 vị trí x có 3
A cách. Vậy có tất cả 3 3!.A cách. 4 4
Câu 33: Từ hộp chứa 5 quả cầu trắng, 4 quả cầu xanh kích thước và khối lượng như nhau. Lấy ngẫu nhiên
3 quả cầu. Tính xác suất để 3 quả cầu lấy được có màu trắng? A. 5 . B. 5 . C. 1 . D. 1 . 42 9 3 21 Lời giải
Số phần tử của không gian mẫu: n(Ω) 3 = C . 9
Gọi A là biến cố “3 quả cầu lấy được có màu trắng”, ta có: n( A) 3 = C . 5 3 C
Xác suất để trong 4 người được chọn đều là nam: P( A) 5 5 = = . 3 C 42 9
Câu 34: Một tổ học sinh có 7 nữ và 5 nam. Chọn ngẫu nhiên 3 học sinh. Xác suất để trong 3 học sinh
được chọn có đúng 1 học sinh nam bằng A. 1 . B. 5 . C. 21 . D. 7 . 5 12 44 22 Lời giải
Tổng số học sinh của tổ là 7 + 5 =12 .
Số cách chọn 3 học sinh trong số 12 học sinh là: 3 C . 12
Số cách chọn 3 học sinh trong đó có đúng 1 học sinh nam là: 1 2 C .C . 5 7 1 2 C .C
Xác suất để trong 3 học sinh được chọn có đúng 1 học sinh nam bằng 21 5 7 = . 3 C 44 12
Câu 35: Một hộp đựng 12 cây viết được đánh số từ 1 đến 12. Chọn ngẫu nhiên 2 cây. Xác suất để chọn
được 2 cây có tích hai số là số chẵn A. 6 . B. 17 . C. 5 . D. 5 . 11 22 22 11 Lời giải
Ta có không gian mẫu n(Ω) 2 = C . 12
Gọi A là biến cố “Chọn được hai cây có tích hai số là số chẵn” Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Trong 12 cây viết có 6 cây được đánh số chẵn, 6 cây được đánh số lẻ. Tích hai số là số chẵn
nếu ít nhất có 1 cây mang số chẵn ⇒ n( A) 2 1 1 = C + C C = 51 6 6 6
⇒ P( A) n( A) 17 = = . n(Ω) 22
Vậy xác suất để chọn được hai cây có tích hai số là số chẵn là 17 . 22
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau và số đó chia hết cho 9. Lời giải
Gọi số có 5 chữ số đôi một khác nhau là x abcdea  0. Các chữ số a, ,
b c,d,e được lập từ 2 trong 4 cặp 1;  8 ,2;7,3;  6 ,4;  5 và 1 trong 2 chữ số 0;9.
Ta xét các trường hợp sau:
Trường hợp 1: Trong x có chứa số 9, không chứa số 0 : có 2 5.C .4! số. 4
Trường hợp 2 : Trong x có chứa số 0 , không chứa số 9: có 2 4.C .4! số. 4
Do đó số các số cần tìm là 2 2
5.C .4! 4.C .4!1296. 4 4
Câu 37: Trong mặt phẳng Oxy, cho Elip (E) đi qua điểm M (2 3;2) và M nhìn hai tiêu điểm của (E)
dưới một góc vuông. Viết phương trình chính tắc của (E) đã cho. Lời giải 
MF = −c − 2 3; 2 − 1  ( ) Ta có:  với F − ;0 c và F ;0 c . 2 ( ) 1 ( )
MF = c − 2 3; 2 − 2  ( )
 
Từ giả thiết, ta suy ra MF .MF = 0 ⇔ (−c − 2 3)(c − 2 3)+ = ⇔ 2c =16. 1 2 4 0 Mà 12 4
M (2 3;2)∈(E) nên + =1 2 2 a b ⇔ 12 4 + = 1 ⇔ 4 b = 64 ⇔ 2 b = 8 2 2 2
⇒ a = b + c = 24 . 2 2 b +16 b Vậy 2 2
S = a + b = 32 .
Câu 38: Một cuộc họp có sự tham gia của 6 nhà Toán học trong đó có 4 nam và 2 nữ, 7 nhà Vật lý
trong đó có 3 nam và 4 nữ và 8 nhà Hóa học trong đó có 4 nam và 4 nữ. Người ta muốn lập
một ban thư kí gồm 4 nhà khoa học. Tính xác suất để ban thư kí được chọn phải có đủ cả 3 lĩnh
vực và có cả nam lẫn nữ. Lời giải Ta có 4
n(Ω) = C = 5985 21
+) Đặt A là biến cố chọn ra được 4 nhà khoa học có đầy đủ cả 3 lĩnh vực. Khi đó:
Số cách chọn 2 nhà Toán học, 1 nhà Vật lý, 1 nhà Hóa học là: 2 1 1
C .C .C = 840 6 7 8 . Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Số cách chọn 1 nhà Toán học, 2 nhà Vật lý, 1 nhà Hóa học là: 1 2 1
C .C .C =1008 6 7 8 .
Số cách chọn 1 nhà Toán học, 1 nhà Vật lý, 2 nhà Hóa học là: 1 1 2
C .C .C =1176 6 7 8 .
⇒ n( A) = 840 +1008 +1176 = 3024
+) Đặt B là biến cố chọn ra 4 nhà khoa học đủ cả 3 lĩnh vực mà trong đó
chỉ có nam hoặc chỉ có nữ. Khi đó:
Số cách chọn chỉ có nam: 2 1 1 1 2 1 1 1 2
C .C .C + C .C .C + C .C .C =192 . 4 3 4 4 3 4 4 3 4
Số cách chọn chỉ có nữ: 2 1 1 1 2 1 1 1 2
C .C .C + C .C .C + C .C .C =112 . 2 4 4 2 4 4 2 4 4
⇒ n(B) =192 +112 = 304 .
+) Vậy số cách chọn ra được 4 nhà khoa học có đày đủ cả 3 lĩnh vực, trong
đó có cả nam lẫ nữ là: 3024 −304 = 2720. Hay n( ) A = 2720 Vậy n( A) 2720 544 P( ) A = = = n(Ω) 5985 1197
Câu 39: Cho hypebol (H ) có hai tiêu điểm F; F 1
2 nằm trên Ox và đối xứng qua gốc tọa độ O , ( H ) đi qua điểm M 9 41 có hoành độ 5
− và MF = ; MF =
. Viết phương trình chính tắc của hypebol 1 2 4 4 (H ) . Lời giải 2 2
Gọi phương trình chính tắc của đường hypebol (H ) x y có dạng: −
=1, trong đó F F = 2c 2 2 a b 1 2 mà 2 2
c = a + b .
Ta có MF − MF = 8 = 2a ⇒ a = 4 . 1 2 Gọi M ( 5
− ; y ); F (− ;0 c ); F ( ;0 c ) 2
⇒ F M = (c − 5)2 2 2
+ y ; F M = (c + 5)2 2 + y 1 1 2 1 1 2 1 2 2 2
⇒ F M − F M = 20 − c = 100 −
⇒ c = 5 ⇒ b = 9 . 1 2 2 2 Vậy ( ) : x y H − =1. 16 9
---------- HẾT ---------- Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 03
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).       
Câu 1: Cho hai vectơ a và b khác 0 , α là góc tạo bởi 2 vectơ a và b khi a.b = − a . b .Chọn khẳng định đúng. A. o α =180 . B. o α = 0 . C. o α = 90 . D. o α = 45 .
Câu 2: Đo chiều dài của một cây thước, ta được kết quả a = 45± 0,2(cm) . Khi đó sai số tuyệt đối của
phép đo được ước lượng là A. ∆ = 0,2 . B. ∆ ≤ 0,2 . C. ∆ ≤ 0, − 2 . D. ∆ = 0, − 2 . 45 45 45 45
Câu 3: Điểm thi tuyển sinh vào lớp 10 ba môn Toán, Văn, Tiếng Anh của một học sinh lần lượt là
8,0; 7,5; 8,2 . Điểm thi trung bình ba môn thi của học sinh đó là A. 8,0. B. 23,7 . C. 7,7 . D. 7,9 .
Câu 4: Mẫu số liệu sau cho biết cân nặng (đơn vị kg) của các học sinh Tổ 1 lớp 10A 45 46 42 50 38 42 44 42 40 60
Khoảng biến thiên của mẫu số liệu này là A. 38. B. 20 . C. 42 . D. 22 .
Câu 5: Cho mẫu số liệu {10,8,6,2, }
4 . Độ lệch chuẩn của mẫu gần bằng A. 8 . B. 2,8. C. 2,4 . D. 6 .
Câu 6: Trong mặt phẳng Oxy , cho tam giác ABC biết A(1; ) 1 , B(2; 4 − ),C (9; 3
− ). Gọi N là điểm thuộc 
cạnh AC sao cho AN = 3CN . Tính độ dài của vec tơ BN . A. 4 29 . B. 29 . C. 2 29 . D. 3 29 .
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là 996m  0,5m . Sai số tương đối
tối đa trong phép đo là bao nhiêu? A. 0,05% . B. 0,5% . C. 0,04%. D. 0,005%.
Câu 8: Tìm tứ phân vị của mẫu số liệu sau
12 3 6 15 27 33 31 18 29 54 1 8
A. Q = 7,Q =17,5,Q = 30 .
B. Q = 7,Q =16,5,Q = 30 . 1 2 3 1 2 3
C. Q = 7,Q =16,5,Q = 30,5 .
D. Q = 7,5,Q =16,5,Q = 30 . 1 2 3 1 2 3 
Câu 9: Phương trình tổng quát của đường thẳng đi qua điểm A( 2; − )
1 và có vectơ pháp tuyến n = (2;3) là
A. 2x + 3y − 5 = 0 .
B. 3x − 2y +1 = 0 .
C. 2x + 3y +1 = 0.
D. 3x − 2y +8 = 0 .
Câu 10: Trong mặt phẳng tọa độ Oxy , phương trình tổng quát của đường thẳng đi qua hai điểm A( 2 − ) ;1 và B(2;4) là
A. 3x + 4y −10 = 0 .
B. 3x − 4y +10 = 0 .
C. 4x + 3y + 5 = 0 .
D. 4x −3y + 5 = 0 . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 11: Tính góc giữa hai đường thẳng a : 3x − y + 7 = 0 và b : x − 3y −1= 0 A. 30° . B. 90° . C. 60°. D. 45°. x = 2 − + t
Câu 12: Khoảng cách từ điểm M (3;− )
1 đến đường thẳng ∆ : 
nằm trong khoảng nào sau đây? y =1+ 2t A. (1;3) . B. (3;5) . C. (7;9) . D. (5;7).
Câu 13: Trong mặt phẳng với hệ trục Oxy cho đường tròn (C) (x − )2 + ( y + )2 : 2
4 =16. Đường tròn (C)
có toạ độ tâm I và bán kính R bằng A. I (2; 4 − ); R = 4 . B. I (2; 4
− ); R =16. C. I ( 2; − 4); R = 4 . D. I ( 2; − 4); R =16.
Câu 14: Trong mặt phẳng với hệ toạ độ Oxy , phương trình đường tròn có tâm I (3; ) 1 và đi qua điểm M (2; ) 1 − là
A. (x + )2 + ( y + )2 3 1 = 5.
B. (x − )2 + ( y − )2 3 1 = 5.
C. (x − )2 + ( y − )2 3 1 = 5.
D. (x + )2 + ( y + )2 3 1 = 5.
Câu 15: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol? A. 2 y = 6 − x . B. 2 y = 6x . C. 2 x = 6 − y . D. 2 x = 6y .
Câu 16: Trường THPT A, khối 12 có 11 lớp, khối 11 có 10 lớp và khối 10 có 12 lớp. Thầy Tổ trưởng
tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn? A. 3. B. 33. C. 11. D. 10.
Câu 17: Trong tủ quần áo của bạn Ngọc có 10 cái áo sơ mi đôi một khác nhau và 5 cái chân váy với hoa
văn khác nhau. Bạn Ngọc muốn chọn ra một bộ quần áo để đi dự tiệc sinh nhật. Hỏi bạn Ngọc có bao nhiêu cách chọn? A. 10. B. 50. C. 5. D. 15.
Câu 18: Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế? A. 4 cách. B. 8 cách. C. 12 cách. D. 24 cách.
Câu 19: Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu
cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư? A. 3 C . B. 35!. C. 35 A . D. 3 A . 35 3 35
Câu 20: Cho tập hợp A = {0;1;2;3; }
4 . Số tập con gồm 2 phần tử của A là A. 10. B. 8 . C. 16. D. 20 .
Câu 21: Trong khai triển nhị thức Niu-tơn của ( x − )4 2 3 có bao nhiêu số hạng? A. 6 . B. 3. C. 5. D. 4 .
Câu 22: Có 2020 tấm thẻ được đánh số từ 1 đến 2020. Xét phép thử: lấy ngẫu nhiên 5 tấm thẻ trong số
2020 tấm thẻ đã cho. Tính số phấn tử của không gian mẫu. A. n(Ω) 5 = C . B. n(Ω) 5 = A . C. n(Ω) 1 = C . D. n(Ω) 1 = A . 2020 2020 2020 2020
Câu 23: Một tổ học sinh gồm có 5 học sinh nữ và 7 học sinh nam, chọn ngẫu nhiên 2 học sinh. Tính xác
suất để 2 học sinh được chọn có cả học sinh nam và học sinh nữ? Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 1 . B. 1 . C. 35 . D. 3 3 6 66 55
Câu 24: Từ một hộp chứa 10 quả cầu màu đỏ và 5 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả
cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng A. 24 . B. 12 . C. 2 . D. 1 . 91 91 91 12
Câu 25: Trong mặt phẳng Oxy , phương trình tổng quát của đường thẳng ∆ đi qua điểm A(1; − 2) và
song song đường thẳng (d ) có phương trình: 2x −3y − 7 = 0 là
A. 2x − 3y −8 = 0 .
B. 2x −3y +8 = 0 .
C. x − 2y + 8 = 0. D. A.
Câu 26: Với giá trị nào của m thì hai đường thẳng
d :3x + 4y +10 = 0 và d : 2m −1 x + m y +10 = 0 trùng nhau? 2 ( ) 2 1 A. m ± 2. B. m = 1 ± . C. m = 2 . D. m = 2 − .
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(11;8), B( 13;8), C ( 14;7) có phương trình là. A. 2 2
x + y + 24x −12y +175 = 0 . B. 2 2
x + y − 24x +12y +175 = 0 . C. 2 2
x + y − 24x −12y +175 = 0 . D. 2 2
x + y + 24x +12y +175 = 0 .
Câu 28: Cho đường tròn (C) 2 2
: x + y − 2x − 4y − 4 = 0 và điểm A(1;5) . Đường thẳng nào trong các
đường thẳng dưới đây là tiếp tuyến của đường tròn (C) tại điểm A .
A. y − 5 = 0.
B. y + 5 = 0 .
C. x + y −5 = 0.
D. x − y − 5 = 0 . 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 5
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 8 . B. 16. C. 4 . D. 5.
Câu 30: Tổ 1 của lớp 10A có 6 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một cặp nam nữ từ tổ 1? A. 11. B. 30. C. 6 . D. 5 .
Câu 31: Có 4 học sinh nam, 3 học sinh nữ và 2 thầy giáo xếp thành một hàng dọc tham gia một cuộc thi.
Hỏi có bao nhiêu cách xếp hàng sao cho nhóm 3 học sinh nữ luôn đứng cạnh nhau và nhóm hai
thầy giáo cũng đứng cạnh nhau? A. 362880. B. 14400. C. 8640 . D. 288 .
Câu 32: Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác
nhau và nhỏ hơn 2021? A. 214 . B. 215 . C. 216 . D. 217 .
Câu 33: Gieo ngẫu nhiên 2 con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên 2 con xúc sắc bằng 1”. A. 2 . B. 1 . C. 5 . D. 5 . 9 9 18 6 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 34: Từ một đội văn nghệ có 5 nam và 8 nữ, cần lập một nhóm 4 người hát tốp ca một cách ngẫu
nhiên. Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng 70 73 A. . B. . C. 16 . D. 17 . 143 143 143 143
Câu 35: Từ một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng, người ta lấy ngẫu nhiên đồng thời 3 quả cầu.
Tính xác suất để trong 3 quả cầu được lấy có ít nhất 2 quả xanh. A. 7 . B. 7 . C. 4 . D. 21 . 44 11 11 220
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho đa giác đều (H ) có 48 đỉnh. Hỏi có bao nhiêu tam giác vuông có đỉnh là đỉnh của (H ) ?
Câu 37: Trong mặt phẳng tọa độ Oxy , cho điểm M (8;2). Viết phương trình đường thẳng d qua M và
d cắt tia Ox , Oy lần lượt tại A(a;0), B(0;b) sao cho tam giác ABO có diện tích nhỏ nhất.
Câu 38: Mật khẩu mở điện thoại của bác Bình là một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn
600.000. Bạn An được bác Bình cho biết thông tin ấy nhưng không cho biết mật khẩu chính xác
là số nào nên quyết định thử bấm ngẫu nhiên một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ
hơn 600.000. Tính xác suất để bạn An nhập một lần duy nhất mà đúng mật khẩu để mở được
điện thoại của bác Bình.
Câu 39: Hai thiết bị A và B dùng để ghi âm một vụ nổ đặt cách nhau 1 dặm, thiết bị Aghi được âm
thanh trước thiết bị B là 2 giây, biết vận tốc âm thanh là 1100 feet / s . Tìm các vị trí mà vụ nổ có thể xảy ra.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).       
Câu 1: Cho hai vectơ a và b khác 0 , α là góc tạo bởi 2 vectơ a và b khi a.b = − a . b .Chọn khẳng định đúng. A. o α =180 . B. o α = 0 . C. o α = 90 . D. o α = 45 . Lời giải       Ta có .
a b = a . b .cos(a,b).         Mà theo giả thiết .
a b = − a . b , suy ra
(a b) = − ⇒(a b) 0 cos , 1 , =180
Câu 2: Đo chiều dài của một cây thước, ta được kết quả a = 45± 0,2(cm) . Khi đó sai số tuyệt đối của
phép đo được ước lượng là A. ∆ = 0,2 . B. ∆ ≤ 0,2 . C. ∆ ≤ 0, − 2 . D. ∆ = 0, − 2 . 45 45 45 45 Lời giải
Ta có độ dài dài gần đúng của cây thước là a = 45 với độ chính xác d = 0,2
Nên sai số tuyệt đối ∆ ≤ d = 0,2 45
Câu 3: Điểm thi tuyển sinh vào lớp 10 ba môn Toán, Văn, Tiếng Anh của một học sinh lần lượt là
8,0; 7,5; 8,2 . Điểm thi trung bình ba môn thi của học sinh đó là A. 8,0. B. 23,7 . C. 7,7 . D. 7,9 . Lời giải Chọn D
Ta có điểm trung bình ba môn thi của học sinh là: 8,0 + 7,5+ 8,2 = 7,9 . 3
Câu 4: Mẫu số liệu sau cho biết cân nặng (đơn vị kg) của các học sinh Tổ 1 lớp 10A 45 46 42 50 38 42 44 42 40 60
Khoảng biến thiên của mẫu số liệu này là A. 38. B. 20 . C. 42 . D. 22 . Lời giải
Khoảng biến thiên của mẫu số liệu là: R = 60 − 38 = 22 .
Câu 5: Cho mẫu số liệu {10,8,6,2, }
4 . Độ lệch chuẩn của mẫu gần bằng A. 8 . B. 2,8. C. 2,4 . D. 6 . Lời giải Ta có 2 2 2 2 2 10 +8+ 6 + 2 + 4
(10 − 6) + (8− 6) + (6 − 6) + (2 − 6) + (4 − 6) x = = 6 ⇒ s = = 8 ≈ 2,8 5 5
Độ lệch chuẩn là căn bậc hai của phương sai. Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 6: Trong mặt phẳng Oxy , cho tam giác ABC biết A(1; ) 1 , B(2; 4 − ),C (9; 3
− ). Gọi N là điểm thuộc 
cạnh AC sao cho AN = 3CN . Tính độ dài của vec tơ BN . A. 4 29 . B. 29 . C. 2 29 . D. 3 29 . Lời giải A N B C Gọi N ( ; a b) .   3  (x − x x x c N ) = − n Aa = 7
Ta có: AN = 3CN ⇒ AN = 3NC ⇔  ⇒  ⇒ N (7; 2 − ) . 3  ( y − y y y b C N ) = − N A  = 2 −  ⇒ BN = 29 .
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là 996m  0,5m . Sai số tương đối
tối đa trong phép đo là bao nhiêu? A. 0,05% . B. 0,5% . C. 0,04%. D. 0,005%. Lời giải
Ta có độ dài gần đúng của cầu là a  996 với độ chính xác d  0,5. Vì sai số tuyệt đối  d
  d  0,5 nên sai số tương đối 0,5 a     0, 05% . a a a a 996
Vậy sai số tương đối tối đa trong phép đo trên là 0,05%.
Câu 8: Tìm tứ phân vị của mẫu số liệu sau
12 3 6 15 27 33 31 18 29 54 1 8
A. Q = 7,Q =17,5,Q = 30 .
B. Q = 7,Q =16,5,Q = 30 . 1 2 3 1 2 3
C. Q = 7,Q =16,5,Q = 30,5 .
D. Q = 7,5,Q =16,5,Q = 30 . 1 2 3 1 2 3 Lời giải
Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:
1 3 6 8 12 15 18 27 29 31 33 54
Trung vị của mẫu số liệu trên là 15 +18 =16,5 2
Trung vị của dãy 1 3 6 8 12 15 là 6 + 8 = 7 2
Trung vị của dãy 18 27 29 31 33 54 là 29 + 31 = 30 2 Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Vậy Q = 7,Q =16,5,Q = 30 . 1 2 3 
Câu 9: Phương trình tổng quát của đường thẳng đi qua điểm A( 2; − )
1 và có vectơ pháp tuyến n = (2;3) là
A. 2x + 3y − 5 = 0 .
B. 3x − 2y +1 = 0 .
C. 2x + 3y +1 = 0.
D. 3x − 2y +8 = 0 . Lời giải
Phương trình tổng quát của đường thẳng đi qua điểm A( 2; − )
1 và có vectơ pháp tuyến n = (2;3)
có dạng là 2(x + 2) + 3( y − )
1 = 0 ⇔ 2x + 3y +1 = 0 .
Câu 10: Trong mặt phẳng tọa độ Oxy , phương trình tổng quát của đường thẳng đi qua hai điểm A( 2 − ) ;1 và B(2;4) là
A. 3x + 4y −10 = 0 .
B. 3x − 4y +10 = 0 .
C. 4x + 3y + 5 = 0 .
D. 4x −3y + 5 = 0 . Lời giải 
Đường thẳng AB nhận AB = (4;3) làm vectơ chỉ phương, do đó một vectơ pháp tuyến của đường 
thẳng AB là n = (3; 4 − ) .
Vậy phương trình tổng quát của đường thẳng AB là
3(x + 2) − 4( y − )
1 = 0 ⇔ 3x − 4y +10 = 0 .
Câu 11: Tính góc giữa hai đường thẳng a : 3x − y + 7 = 0 và b : x − 3y −1= 0 A. 30° . B. 90° . C. 60°. D. 45°. Lời giải 
Đường thẳng a có vectơ pháp tuyến là: n = 3;−1 1 ( ); 
Đường thẳng b có vectơ pháp tuyến là: n = 1;− 3 2 ( ).
Áp dụng công thức tính góc giữa hai đường thẳng có:   1. 3 n n + (− ) 1 (− 3 . ) cos(a,b) 3 1 2 =   = =
. Suy ra góc giữa hai đường thẳng bằng 30° . n . n 2.2 2 1 2 x = 2 − + t
Câu 12: Khoảng cách từ điểm M (3;− )
1 đến đường thẳng ∆ : 
nằm trong khoảng nào sau đây? y =1+ 2t A. (1;3) . B. (3;5) . C. (7;9) . D. (5;7). Lời giải
Phươmg trình tổng quát đường thẳng ∆ là 2x − y + 5 = 0 2.3− (− ) 1 + 5 12 5
Khoảng cách từ điểm M đến đường thẳng ∆ là = ≈ 5,4 2 + (− )2 5 2 1
Câu 13: Trong mặt phẳng với hệ trục Oxy cho đường tròn (C) (x − )2 + ( y + )2 : 2
4 =16. Đường tròn (C)
có toạ độ tâm I và bán kính R bằng A. I (2; 4 − ); R = 4 . B. I (2; 4
− ); R =16. C. I ( 2; − 4); R = 4 . D. I ( 2; − 4); R =16. Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Đường tròn (C) (x − )2 + ( y + )2 : 2
4 =16. Do đó đường tròn (C) có toạ độ tâm I (2; 4 − ) và bán kính R = 16 = 4 .
Câu 14: Trong mặt phẳng với hệ toạ độ Oxy , phương trình đường tròn có tâm I (3; ) 1 và đi qua điểm M (2; ) 1 − là
A. (x + )2 + ( y + )2 3 1 = 5.
B. (x − )2 + ( y − )2 3 1 = 5.
C. (x − )2 + ( y − )2 3
1 = 5. D. (x + )2 + ( y + )2 3 1 = 5. Lời giải
Vì đường tròn có tâm I (3; )
1 và đi qua điểm M (2; ) 1
− nên bán kính của đường tròn là
R = MI = ( − )2 + ( + )2 3 2 1 1 = 5 .
Vậy phương trình đường tròn cần tìm là (x − )2 + ( y − )2 3 1 = 5 .
Câu 15: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol? A. 2 y = 6 − x . B. 2 y = 6x . C. 2 x = 6 − y . D. 2 x = 6y . Lời giải
Phương trình chính tắc của parabol có dạng 2
y = 2 px( p > 0) nên chỉ có trường hợp B là phương
trình chính tắc của đường parabol.
Câu 16: Trường THPT A, khối 12 có 11 lớp, khối 11 có 10 lớp và khối 10 có 12 lớp. Thầy Tổ trưởng
tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn? A. 3. B. 33. C. 11. D. 10. Lời giải
TH 1: Chọn 1 lớp trong 11 lớp của khối 12 có 11 cách.
TH 2 : Chọn 1 lớp trong 10 lớp của khối 11 có 10 cách.
TH 3: Chọn 1 lớp trong 12 lớp của khối 10 có 12 cách.
Theo quy tắc cộng ta được: 11+10 +12 = 33 cách.
Câu 17: Trong tủ quần áo của bạn Ngọc có 10 cái áo sơ mi đôi một khác nhau và 5 cái chân váy với hoa
văn khác nhau. Bạn Ngọc muốn chọn ra một bộ quần áo để đi dự tiệc sinh nhật. Hỏi bạn Ngọc có bao nhiêu cách chọn? A. 10. B. 50. C. 5. D. 15. Lời giải
Chọn 1 cái áo sơ mi trong 10 cái áo sơ mi có: 10 cách.
Chọn 1 cái chân váy trong 5 cái chân váy có: 5 cách.
Theo quy tắc nhân có: 10.5 = 50 cách.
Câu 18: Có bao nhiêu cách xếp chỗ ngồi cho 4 bạn học sinh vào dãy có 4 ghế? A. 4 cách. B. 8 cách. C. 12 cách. D. 24 cách. Lời giải
Xếp chỗ ngồi cho 4 học sinh vào dãy có 4 ghế có: 4!= 24 cách xếp.
Câu 19: Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu
cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư? A. 3 C . B. 35!. C. 35 A . D. 3 A . 35 3 35 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số cách chọn 3 học sinh làm lớp trưởng, lớp phó và bí thư là: 3 A = 39270 . 35
Câu 20: Cho tập hợp A = {0;1;2;3; }
4 . Số tập con gồm 2 phần tử của A là A. 10. B. 8 . C. 16. D. 20 . Lời giải
Tập hợp A gồm có 5 phần tử.
Số tập con có 2 phần tử của tập A là: 2 C =10 . 5
Câu 21: Trong khai triển nhị thức Niu-tơn của ( x − )4 2 3 có bao nhiêu số hạng? A. 6 . B. 3. C. 5. D. 4 . Lời giải
Trong khai triển nhị thức Niu-tơn của ( x − )4 2 3 có 4 +1 = 5 số hạng.
Câu 22: Có 2020 tấm thẻ được đánh số từ 1 đến 2020. Xét phép thử: lấy ngẫu nhiên 5 tấm thẻ trong số
2020 tấm thẻ đã cho. Tính số phấn tử của không gian mẫu. A. n(Ω) 5 = C . B. n(Ω) 5 = A . C. n(Ω) 1 = C . D. n(Ω) 1 = A . 2020 2020 2020 2020 Lời giải
Số cách chọn ngẫu nhiên 5 tấm thẻ là: 5 C . 100
Câu 23: Một tổ học sinh gồm có 5 học sinh nữ và 7 học sinh nam, chọn ngẫu nhiên 2 học sinh. Tính xác
suất để 2 học sinh được chọn có cả học sinh nam và học sinh nữ? A. 1 . B. 1 . C. 35 . D. 3 3 6 66 55 Lời giải
Tổng số học sinh là: 5 + 7 =12
Gọi A là biến cố trong hai học sinh được chọn, có cả học sinh nam và học sinh nữ. Ta có: n(Ω) 2 = C 12 n( A) 1 1 = C .C 5 7 1 1 C .
Vậy xác suất của biến cố C 35
A là: P( A) 5 7 = = . 2 C 66 12
Câu 24: Từ một hộp chứa 10 quả cầu màu đỏ và 5 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3 quả
cầu. Xác suất để lấy được 3 quả cầu màu xanh bằng A. 24 . B. 12 . C. 2 . D. 1 . 91 91 91 12 Lời giải
Số phần tử của không gian mẫu là n(Ω) 3 = C = 455 . 15
Gọi biến cố A : “Lấy được 3 quả cầu màu xanh”. Ta có n( A) 3 = C =10. 5
Xác suất để lấy được 3 quả cầu màu xanh bằng
p( A) n( A) 10 2 = = = n(Ω) 455 91 Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 25: Trong mặt phẳng Oxy , phương trình tổng quát của đường thẳng ∆ đi qua điểm A(1; − 2) và
song song đường thẳng (d ) có phương trình: 2x −3y − 7 = 0 là
A. 2x −3y −8 = 0 .
B. 2x −3y +8 = 0 .
C. x − 2y + 8 = 0. D. A. Lời giải
Theo yêu cầu đề bài, đường thẳng ∆ đi qua điểm A(1; − 2) và nhận vectơ n = (2 ; −3) làm vectơ pháp tuyến.
Ta có phương trình tổng quát của đường thẳng ∆ là: 2(x − )
1 − 3( y + 2) = 0 ⇔ 2x − 3y −8 = 0 .
Câu 26: Với giá trị nào của m thì hai đường thẳng
d :3x + 4y +10 = 0 và d : 2m −1 x + m y +10 = 0 trùng nhau? 2 ( ) 2 1 A. m ± 2. B. m = 1 ± . C. m = 2 . D. m = 2 − . Lời giải
d :(2m − ) 2 2
1 x + m y +10 = 0 2 d ≡d 2m −1 m 10 1 2  → = =
d :3x + 4y +10 = 0 3 4 10 1 2m −1 = 3 ⇔  ⇔ m = 2. 2 m = 4
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(11;8), B( 13;8), C ( 14;7) có phương trình là. A. 2 2
x + y + 24x −12y +175 = 0 . B. 2 2
x + y − 24x +12y +175 = 0 . C. 2 2
x + y − 24x −12y +175 = 0 . D. 2 2
x + y + 24x +12y +175 = 0 . Lời giải Chọn C
Gọi phương trình đường tròn cần tìm có dạng: 2 2
x + y − ax − by + c = ( 2 2 2 2
0 a + b − c > 0) .
Đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) nên ta có: 121 
+ 64 − 22a −16b + c = 0 a =12 169   64 26a 16b c 0 b  + − − + = ⇔  = 6 196  49 28a 14b c 0  + − − + = c =   175
Vậy phương trình đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) là 2 2
x + y − 24x −12y +175 = 0
Câu 28: Cho đường tròn (C) 2 2
: x + y − 2x − 4y − 4 = 0 và điểm A(1;5) . Đường thẳng nào trong các
đường thẳng dưới đây là tiếp tuyến của đường tròn (C) tại điểm A .
A. y − 5 = 0.
B. y + 5 = 0 .
C. x + y −5 = 0.
D. x − y − 5 = 0 . Lời giải 
Đường tròn (C) có tâm I (1;2) ⇒ IA = (0;3) . 
Gọi d là tiếp tuyến của (C) tại điểm A , khi đó d đi qua A và nhận vectơ IA là một VTPT. 
Chọn một VTPT của d là n = . d (0; ) 1
Vậy phương trình đường thẳng d là y − 5 = 0. Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 5
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 8 . B. 16. C. 4 . D. 5. Lời giải 2 2
Gọi F và F là hai tiêu điểm của ( ) : x y H −
= 1, a > 0,b > 0 . 2 2 ( ) 1 2 a b
Điểm M ∈(H ) ⇔ MF − MF = 2a . 1 2 2 2
Từ phương trình ( ) : x y H − = 1 suy ra 2
a =16 ⇒ a = 4,(a > 0) . 16 5
Vậy hiệu các khoảng cách từ mỗi điểm M nằm trên (H ) đến hai tiêu điểm có giá trị tuyệt đối
là MF − MF = 2a = 8. 1 2
Câu 30: Tổ 1 của lớp 10A có 6 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một cặp nam nữ từ tổ 1? A. 11. B. 30. C. 6 . D. 5 . Lời giải
Số cách chọn ra một học sinh nam là: 6 cách chọn.
Số cách chọn ra một học sinh nữ là: 5 cách chọn.
Do đó theo quy tắc nhân thì chọn ra 1 cặp nam nữ sẽ có: 5.6 = 30 cách chọn.
Câu 31: Có 4 học sinh nam, 3 học sinh nữ và 2 thầy giáo xếp thành một hàng dọc tham gia một cuộc thi.
Hỏi có bao nhiêu cách xếp hàng sao cho nhóm 3 học sinh nữ luôn đứng cạnh nhau và nhóm hai
thầy giáo cũng đứng cạnh nhau? A. 362880. B. 14400. C. 8640 . D. 288 . Lời giải
Xếp nhóm A gồm 3 học sinh nữ đứng cạnh nhau có: 3!= 6 cách.
Xếp nhóm B gồm 2 thầy giáo đứng cạnh nhau có: 2!= 2 cách.
Xếp nhóm A , nhóm B chung với 4 học sinh nam còn lại có: 6!= 720 cách.
Vậy theo quy tắc nhân có: 6.2.720 = 8640 cách.
Câu 32: Từ các chữ số 0,1,2,3,4,5,6,7 có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác
nhau và nhỏ hơn 2021? A. 214 . B. 215 . C. 216 . D. 217 . Lời giải
Giả sử số tự nhiên thỏa mãn yêu cầu bài toán có dạng abcd .
TH1: a =1, ta chọn b, c, d bằng cách lấy 3 chữ số trong 7 chữ số còn lại nên có 3 A = 210 số. 7
TH2: a = 2 , khi đó b = 0 và c =1 và chọn d ∈{3;4;5;6; }
7 nên d có 5 cách chọn, suy ra có 5
số thỏa mãn trường hợp này.
Vậy có 210 + 5 = 215 số thỏa mãn yêu cầu bài toán.
Câu 33: Gieo ngẫu nhiên 2 con xúc sắc cân đối đồng chất. Tìm xác suất của biến cố: “ Hiệu số chấm
xuất hiện trên 2 con xúc sắc bằng 1”. A. 2 . B. 1 . C. 5 . D. 5 . 9 9 18 6 Lời giải Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Số phần tử của không gian mẫu: n(Ω) = 6.6 = 36.
Gọi A là biến cố thỏa mãn yêu cầu bài toán: A = ( { 1; 2), (2 )
; 1 , (3; 2), (2; 3), (3; 4), (4; 3), (4; 5), (5; 4), (5; 6), (6; 5)} nên n( A) =10. Vậy P( A) 10 5 = = . 36 18
Câu 34: Từ một đội văn nghệ có 5 nam và 8 nữ, cần lập một nhóm 4 người hát tốp ca một cách ngẫu
nhiên. Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng 70 73 A. . B. . C. 16 . D. 17 . 143 143 143 143 Lời giải
Số cách chọn ra 4 người từ đội văn nghệ sao cho có ít nhất 3 nam là 3 1 4
C .C + C 5 8 5 3 1 4
Xác suất để trong 4 người được chọn có ít nhất 3 nam bằng C .C + C 17 5 8 5 = . 4 C 143 13
Câu 35: Từ một hộp chứa 7 quả cầu xanh, 5 quả cầu vàng, người ta lấy ngẫu nhiên đồng thời 3 quả cầu.
Tính xác suất để trong 3 quả cầu được lấy có ít nhất 2 quả xanh. A. 7 . B. 7 . C. 4 . D. 21 . 44 11 11 220 Lời giải
Số phần tử của không gian mẫu là n(Ω) 3 = C = 220 . 12
Gọi A là biến cố: “3 quả cầu được lấy có ít nhất 2 quả xanh”. Xét 2 trường hợp sau:
+ Trường hợp 1: Chọn 2 quả cầu xanh, 1 quả cầu vàng có 2 1
C .C =105 cách. 7 5
+ Trường hợp 2: Chọn 3 quả cầu xanh có 3 C = 35 cách. 7
Suy ra n( A) =105 + 35 =140 . n A 140 7
Vậy xác suất cần tìm là p( A) ( ) = = = . n(Ω) 220 11
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho đa giác đều (H ) có 48 đỉnh. Hỏi có bao nhiêu tam giác vuông có đỉnh là đỉnh của (H ) ? Lời giải
Đa giác đều (H ) có 48 đỉnh nên có 24 đường chéo đi qua tâm đường tròn ngoại tiếp đa giác
đều (H ) . Một tam giác vuông có đỉnh là đỉnh của (H ) thì phải có cạnh huyền là đường chéo
đi qua tâm đường tròn ngoại tiếp đa giác đều (H ) . Với một đường chéo như vậy của đa giác
đều (H ) sẽ tạo ra 46 tam giác vuông. Vậy số tam giác vuông có đỉnh là đỉnh của (H ) là 24.46 =1104 tam giác vuông.
Câu 37: Trong mặt phẳng tọa độ Oxy , cho điểm M (8;2). Viết phương trình đường thẳng d qua M và
d cắt tia Ox , Oy lần lượt tại A(a;0), B(0;b) sao cho tam giác ABO có diện tích nhỏ nhất. Lời giải Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Ta có phương trình đường thẳng d có dạng: x y + = 1. a b
Do d đi qua M (8;2) nên ta có 8 2 + = 1. a b
Mặt khác diện tích của tam giác vuông ABO là 1 S = . ∆ a b ABO . 2
Áp dụng BĐT Cô si ta có: 8 2 8 2 16 4 1 = + ≥ 2 . ⇔ 1≥ 2 ⇔ 1≥ 2 ⇔ ab ≥ 8. a b a b ab ab 1 ⇔ ab ≥ 32. 2
Ta có diện tích của tam giác vuông ABO nhỏ nhất bằng 32 khi a,b thỏa mãn hệ phương trình: 8 2 = a = 4ba = 4b a b   a = 4ba =16  ⇔ 8 2 ⇔  8 2 ⇔  ⇔ . 8 2 + =   1 + =  1 b  4 b  =  = 4 + = 1 a b 4b b a b
Vậy a + b = 20 .
Câu 38: Mật khẩu mở điện thoại của bác Bình là một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ hơn
600.000. Bạn An được bác Bình cho biết thông tin ấy nhưng không cho biết mật khẩu chính xác
là số nào nên quyết định thử bấm ngẫu nhiên một số tự nhiên lẻ gồm 6 chữ số khác nhau và nhỏ
hơn 600.000. Tính xác suất để bạn An nhập một lần duy nhất mà đúng mật khẩu để mở được
điện thoại của bác Bình. Lời giải
Đặt A = {0,1,2,3,4,5,6,7,8, } 9
Gọi số tự nhiện lẻ có 6 chữa số là x = abcdef với a,b,c,d, ,
e f thuộc A , a ≠ 0 và
f ∈ B = {1,3,5,7 } ,9 .
Vì x < 600.000 nên a ∈{1,2,3,4, } 5 .  Trường hợp 1: a ∈{1,3 }
,5 ⇒ a có 3 cách chọn.
f ≠ a và f ∈ B ⇒ f có 4 cách chọn.
Mỗi bộ bcde là một chỉnh hợp chập 4 của 8 phần tử còn lại thuộc tập A ⇒ có 4 A cách chọn. 8 Trường hợp này có 4 3.4.A = 20160 số. 8  Trường hợp 2: a ∈{2, }
4 ⇒ a có 2 cách chọn.
f ∈ B ⇒ f có 5 cách chọn.
Mỗi bộ bcde là một chỉnh hợp chập 4 của 8 phần tử còn lại của tập A ⇒ có 4 A cách chọn. 8 Trường hợp này có 4 2.5.A =16800 số. 8
Vậy có tất cả 20160 +16800 = 36960 số tự nhiên lẻ có 6 chữ số.
Gọi C là biến cố bạn An nhập một lần theo gợi ý của bác Bình mà đúng mật khẩu mở điện thoại. Ta có Ω = 36960; Ω = . C 1 Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Ω Vậy C 1 P = = . C Ω 36960
Câu 39: Hai thiết bị A và B dùng để ghi âm một vụ nổ đặt cách nhau 1 dặm, thiết bị Aghi được âm
thanh trước thiết bị B là 2 giây, biết vận tốc âm thanh là 1100 feet / s . Tìm các vị trí mà vụ nổ có thể xảy ra. Lời giải
Chọn hệ trục tọa độ Oxy mà Ox đi qua A và B , Oy là đường trung trực của AB . Kí hiệu d d
1 là quãng đường âm thanh đi được từ vụ nổ đến thiết bị A , 2 là quãng đường âm
thanh đi được từ vụ nổ đến thiết bị B , d d
1 và 2 tính theo feet. Khi đó, do thiết bị A nhận âm
thanh nhanh hơn thiết bị B là 2 giây nên ta có phương trình: d − d = 2200 (1) 2 1
Các điểm thỏa mãn (1) nằm trên một nhánh của Hypebol có phương trình: 2 2 x y − = 1 2 2 a b Ta có 5280 c = = 2640 , 2200 2 2 2 a =
=1100, b = c − a = 5759600 2 2 , 2 2
Vậy vụ nổ nằm trên một nhánh của Hypebol có phương trình: x y − =1. 1210000 5759600
---------- HẾT ---------- Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 04
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).    
Câu 1: Trong mặt phẳng Oxy , cho a = ( 5;
− 0), b = (4; x). Tìm giá trị của x để hai vectơ a và b cùng phương. A. 4 . B. 1 − . C. 0 . D. 5 − .
Câu 2: Cho hình chữ nhật có chiều dài bằng 10 , chiều rộng bằng 3. Để tính diện tích hình chữ nhật bạn 3
Giang lấy số gần đúng của 10 là 3,33. Hỏi sai số tuyệt đối của hình chữ nhật theo cách tính của 3 bạn Giang là bao nhiêu. A. 0,1. B. 0,01. C. 1,11. D. 0,11.
Câu 3: Cho dãy số liệu 1; 2; 5; 7; 8; 9;10 . Số trung vị của dãy trên bằng bao nhiêu? A. 2 . B. 6 . C. 7 . D. 8 .
Câu 4: Một cửa hàng bán áo sơ mi thống kê số lượng áo bán ra trong tháng 6 như bảng sau. Cỡ áo 37 38 39 40 41 42 Số lượng 35 42 50 38 32 48
Mốt của bảng số liệu trên bằng? A. 42 . B. 39. C. 50. D. 41.
Câu 5: Cho dãy số liệu 1; 3; 4; 6; 8; 9;11. Phương sai của dãy trên bằng bao nhiêu? 76 A. . B. 6 . C. 76 . D. 36. 7 7        
Câu 6: Cho hai vectơ a và b . Biết a = 2, b = 3 và (a b) 0
, = 30 . Tính a + b . A. 11 . B. 13 . C. 12 . D. 14 .
Câu 7: Biết rằng số trung vị trong mẫu số liệu sau ( đã sắp xếp theo thứ tự) bằng 14. Tìm số nguyên dương x . 2
1 3 4 13 x −1 18 19 21 A. x = 4 . B. x =16 . C. x =17 . D. x =15.
Câu 8: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị kw) hàng tháng của gia đình bạn An trong năm
2021 như sau: 163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là 10kw .Gọi ∆ ∆′ lần lượt Q ; Q
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây là đúng A. ∆ = ∆′ . B. ∆′ = ∆ − . C. ∆ = ∆′ − D. ∆′ = ∆ − . Q Q 20 Q Q 10 Q Q 10 Q Q Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 9: Viết phương trình tổng quát của đường thẳng ∆ đi qua điểm A1; 
3 và có vectơ pháp tuyến n = (3; 2−)
A. 3x2y3  0 .
B. 3x2y  3  0 . C. 3x2y7  0 . D. 3x2y 7  0 .
Câu 10: Đường thẳng d đi qua A(0; 2
− ), B(3;0) có phương trình theo đoạn chắn là x y x y x y x y A. + =1. B. + =1. C. + = 0. D. + = 0 . 2 − 3 3 2 − 2 − 3 3 2 −
Câu 11: Khoảng cách từ điểm A(1; )
1 đến đường thẳng 5x −12y − 6 = 0 là A. 13. B. 13 − . C. 1 − . D. 1. x = − t
Câu 12: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x + y −6=0 và đường thẳng ∆: y= 5 − 2t
. Góc giữa hai đường thẳng d và ∆ bằng A. 30° . B. 135° . C. 45° . D. 90° .
Câu 13: Xác định tâm I và bán kính R của đường tròn (C) (x − )2 + ( y + )2 : 1 5 = 9 . A. I( 1; − 5), R = 3. B. 9 I( 1; − 5), R = . C. I(1; 5 − ), R = 3. D. 9 I(1; 5 − ), R = . 2 2
Câu 14: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn tâm I (2;−5) và tiếp xúc với đường
thẳng ∆ :− 3x + 4y +11 = 0 là
A. (x − )2 + ( y + )2 2 5 = 3.
B. (x + )2 + ( y − )2 2 5 = 9.
C. (x + )2 + ( y − )2 2 5 = 3.
D. (x − )2 + ( y + )2 2 5 = 9.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol? A. 2 y = x . B. 2 y = 6x . C. 2 y = 5 − x . D. 2 y = 2022x .
Câu 16: Trên kệ sách nhà bạn Lan có 7 quyển sách Toán khác nhau, 8 quyển sách Vật lý khác nhau và 9
quyển sách Lịch sử khác nhau. Hỏi bạn Lan có bao nhiêu cách chọn một quyển sách để đọc A. 9. B. 8. C. 24. D. 7.
Câu 17: Một hộp đồ bảo hộ có 10 chiếc khẩu trang và 3 mặt nạ chống giọt bắn. Có bao nhiêu cách chọn
một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp đồ bảo hộ trên. A. 10. B. 30. C. 13. D. 3.
Câu 18: Số hoán vị của tập X có 5 phần tử là A. 5. B. 24 . C. 120. D. 60 .
Câu 19: Trong một hộp bánh có 10 chiếc bánh khác nhau. Có bao nhiêu cách lấy 3 chiếc bánh từ hộp đó
để phát cho các bạn An, Bình, Cường, mỗi bạn một chiếc? A. 10 3 . B. 3 A . C. 3 10 . D. 3 C . 10 10
Câu 20: Lớp 11A có 45 học sinh trong đó có 15 học sinh giỏi. Thầy giáo cần chọn một nhóm gồm 5
bạn học sinh của lớp 11A đi dự trại hè. Hỏi thầy giáo đó có bao nhiêu cách chọn 1 nhóm sao cho
cả 5 bạn đều là học sinh giỏi. A. 3003. B. 360360. C. 1221759. D. Đáp án khác. Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 21: Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của ( − )4 1 2x . A. 1. B. 1 − . C. 81. D. 81 − .
Câu 22: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xác suất để xuất hiện mặt có số chấm chia hết cho 3 bằng A. 1 . B. 1 . C. 1 . D. 2 . 2 3 6 3
Câu 23: Gieo ba con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên ba mặt lập thành
một cấp số cộng với cộng sai bằng 1 là bao nhiêu? B. 1 . B. 1 . C. 1 . D. 1 . 6 36 9 27
Câu 24: Một tổ có 5 bạn nam và 7 bạn nữ, chọn một nhóm 3 bạn để tham gia biểu diễn văn nghệ. Xác
suất để chọn được 3 bạn nữ bằng A. 21 . B. 1 . C. 7 . D. 5 . 220 22 44 44
Câu 25: Trong mặt phẳng Oxy cho điểm M (1;2) và đường thẳng ∆ : x + 4y − 2 = 0 . Viết phương trình
đường thẳng đi qua M và song song với ∆ .
A. d : x + 4y −9 = 0 .
B. d : x + 4y + 9 = 0 . C. d : x + 4y − 6 = 0 . D. d : x + 4y + 6 = 0.
Câu 26: Trong mặt phẳng với hệ tọa độ Oxy , hai đường thẳng có phương trình
d : mx + m −1 y + 2m = 0 và d : 2x + y −1 = 0 song song khi và chỉ khi 1 ( ) 2 A. m = 2. B. m = 1. − C. m = 2. − D. m =1.
Câu 27: Đường tròn (C) đi qua A(1;3) , B(3; )
1 và có tâm nằm trên đường thẳng d : 2x − y + 7 = 0 có phương trình là
A. (x − )2 + ( y − )2 7 7 =102 .
B. (x + )2 + ( y + )2 7 7 =164 .
C. (x − )2 + ( y − )2 3 5 = 25 .
D. (x + )2 + ( y + )2 3 5 = 25 .
Câu 28: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C)có phương trình 2 2
x + y − 2x + 2y − 3 = 0 . Từ điểm A(1; )
1 kẻ được bao nhiêu tiếp tuyến đến đường tròn (C) A. 1. B. 2. C. vô số. D. 0.
Câu 29: Phương trình chính tắc của elip có tổng các khoảng cách từ một điểm bất kỳ đến
hai tiêu điểm bằng 10 và có tiêu cự bằng 2 5 là 2 2 2 2 2 2 2 2
A. x + y = 1.
B. x + y = 1.
C. x + y = 1.
D. x + y = 1. 10 2 5 25 20 25 5 100 20
Câu 30: Các thành phố A , B , C được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu
cách đi từ thành phố A đến thành phố C mà qua thành phố B chỉ một lần? A B C A. 6 . B. 12. C. 8. D. 4 . Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 31: Một tổ có 7 người trong đó có An và Bình. Hỏi có bao nhiêu cách xếp 7 người vào bàn tròn có
7 ghế sao cho An và Bình ngồi cạnh nhau? A. 720 . B. 240 . C. 5040. D. 120 .
Câu 32: Có bao nhiêu cách xếp 5 bạn học sinh Tuấn, Tú, Tiến, Tân, Tiên vào 1 hàng ngang gồm 10 ghế
được đánh số từ 1 đến 10, sao cho Tuấn và Tiên luôn ngồi cạnh nhau? A. 1890. B. 252 . C. 3024. D. 6048.
Câu 33: Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật Lí và 2 quyển sách Hóa họ C. Lấy
ngẫu nhiên 3 quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán. A. 1 . B. 37 . C. 5 . D. 19 3 42 6 21
Câu 34: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để
rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng A. 1 . B. 2 . C. 5 . D. 13 . 3 3 18 18
Câu 35: Gieo một con súc xắc cân đối và đồng chất ba lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là: A. 125 . B. 91 . C. 25 . D. 81 . 216 216 216 216
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Từ một ban cán bộ Đoàn ở một trường học gồm có 20 học sinh, người ta muốn cử ra một nhóm
gồm 8 em đi tham gia hội trại với trường bạn. Biết rằng cần có một nhóm trưởng, hai bạn nhóm
phó, một bạn thủ quỹ và 4 bạn uỷ viên. Hỏi có bao nhiều cách chọn ra một nhóm học sinh như vậy?
Câu 37: Viết phương trình chính tắc của hypebol (H ) có một tiêu điểm F − 34;0 và đi qua điểm 1 ( )  99  A6 ; . 25   
Câu 38: Cho đa giác đều có 15 đỉnh, gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác
đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M . Xác suất để chọn được một tam giác cân
nhưng không phải là tam giác đều bằng
Câu 39: Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có tiêu cự bằng 2 70 m , độ
dài trục ảo bằng 2 42 m . Biết chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm 2
đối xứng của hypebol là khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính 3 đáy của tháp.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).    
Câu 1: Trong mặt phẳng Oxy , cho a = ( 5;
− 0), b = (4; x). Tìm giá trị của x để hai vectơ a và b cùng phương. A. 4 . B. 1 − . C. 0 . D. 5 − . Lời giải     a = ( 5;
− 0), b = (4; x) cùng phương ⇔ k
∃ :a = k.b ⇒ x = 0
Câu 2: Cho hình chữ nhật có chiều dài bằng 10 , chiều rộng bằng 3. Để tính diện tích hình chữ nhật bạn 3
Giang lấy số gần đúng của 10 là 3,33. Hỏi sai số tuyệt đối của hình chữ nhật theo cách tính của 3 bạn Giang là bao nhiêu. A. 0,1. B. 0,01. C. 1,11. D. 0,11. Lời giải
Diện tích hình chữ nhật đã cho 10 S = .3 =10 . 3
Diện tích hình chữ nhật khi bạn Giang tính S = 3,33.3 = 9,99 1 .
Sai số tuyệt đối khi bạn Giang tính là 10 −9,99 = 0,01
Câu 3: Cho dãy số liệu 1; 2; 5; 7; 8; 9;10 . Số trung vị của dãy trên bằng bao nhiêu? A. 2 . B. 6 . C. 7 . D. 8 . Lời giải
Số trung vị của dãy trên là số đứng chính giữa xếp theo thứ tự không giảm. Vậy số trung vị của dãy là 7
Câu 4: Một cửa hàng bán áo sơ mi thống kê số lượng áo bán ra trong tháng 6 như bảng sau. Cỡ áo 37 38 39 40 41 42 Số lượng 35 42 50 38 32 48
Mốt của bảng số liệu trên bằng? A. 42 . B. 39. C. 50. D. 41. Lời giải
Mốt của bảng trên là số lượng áo bán ra nhiều nhất của cỡ áo. vậy mốt bằng 39
Câu 5: Cho dãy số liệu 1; 3; 4; 6; 8; 9;11. Phương sai của dãy trên bằng bao nhiêu? 76 A. . B. 6 . C. 76 . D. 36. 7 7 Lời giải
Số trung bình cộng của dãy số liệu trên là 1 3 4 6 8 9 11 x + + + + + + = = 6 . 7 Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Phương sai của dãy số liệu trên bằng
(1−6)2 +(3−6)2 +(4−6)2 +(6−6)2 +(8−6)2 +(9−6)2 +(11−6)2 2 76 s = = 7 7        
Câu 6: Cho hai vectơ a và b . Biết a = 2, b = 3 và (a b) 0
, = 30 . Tính a + b . A. 11 . B. 13 . C. 12 . D. 14 . Lời giải   2 2 2   2  2    
Ta có: ( a + b ) = a + b + 2ab = a + b + 2 a . b .cos(a,b)     ⇒ ( a + b )2 0
= 4 + 3 + 2.2. 3.cos30 =13 ⇒ a + b = 13 .
Câu 7: Biết rằng số trung vị trong mẫu số liệu sau ( đã sắp xếp theo thứ tự) bằng 14. Tìm số nguyên dương x . 2
1 3 4 13 x −1 18 19 21 A. x = 4 . B. x =16 . C. x =17 . D. x =15. Lời giải 2 2
Số trung vị trong mẫu số liệu trên là x −1+13 x +12 = 2 2 2 x +12 x = 4 (tm) Từ giả thiết suy ra 2 = 14 ⇔ x =16 ⇔  . 2 x = 4 −  (loai) Vậy x = 4 .
Câu 8: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị kw) hàng tháng của gia đình bạn An trong năm
2021 như sau: 163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là 10kw .Gọi ∆ ∆′ lần lượt Q ; Q
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây là đúng A. ∆ = ∆′ ∆′ = ∆ − ∆ = ∆′ − ∆′ = ∆ − Q Q . B. Q Q 10 . C. Q Q 10 D. Q Q 20 . Lời giải
+) Sắp xếp mẫu số liệu năm 2021 theo thứ tự không giảm: 159 161 163 164 165 166 167 168 170 170 172 174
Mẫu số liệu gồm 12 giá trị nên số trung vị là Q = (166 +167) : 2 =166,5 2
Nửa số liệu bên trái là 159;161;163;164;165;166gồm 6 giá trị
Khi đó Q = 163+164 : 2 =163,5 1 ( )
Nửa số liệu bên phải là 167;168;170;170;172;174 gồm 6 giá trị Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Khi đó Q =170 3
Khoảng tứ phân vị của mẫu số liệu bằng: ∆ = Q − Q = − = Q 170 163,5 6,5 3 1
+) Sắp xếp mẫu số liệu năm 2022 theo thứ tự không giảm: 149 151 153 154 155 156 157 158 160 160 162 164
Mẫu số liệu gồm 12 giá trị nên số trung vị là Q = (156 +157) : 2 =156,5 2
Nửa số liệu bên trái là 149;151;153;154;155;156gồm 6 giá trị
Khi đó Q = (153+154) : 2 =153,5 1
Nửa số liệu bên phải là 157;158;160;160;162;164 gồm 6 giá trị Khi đó Q =160 3
Khoảng tứ phân vị của mẫu số liệu bằng: ∆′ = Q − Q = − = Q 160 153,5 6,5 3 1
Câu 9: Viết phương trình tổng quát của đường thẳng ∆ đi qua điểm A1; 
3 và có vectơ pháp tuyến n = (3; 2−)
A. 3x2y3  0 .
B. 3x2y  3  0 . C. 3x2y7  0 . D. 3x2y 7  0 . Lời giải
Phương trình đường thẳng cần tìm: 3(x − )
1 + 2( y − 3) = 0 ⇔ 3x + 2y − 9 = 0 .
Câu 10: Đường thẳng d đi qua A(0; 2
− ), B(3;0) có phương trình theo đoạn chắn là x y x y x y x y A. + =1. B. + =1. C. + = 0. D. + = 0 . 2 − 3 3 2 − 2 − 3 3 2 − Lời giải x y
Đường thẳng d đi qua A(0; 2
− ), B(3;0) có phương trình theo đoạn chắn là: + =1 3 2 −
Câu 11: Khoảng cách từ điểm A(1; )
1 đến đường thẳng 5x −12y − 6 = 0 là A. 13. B. 13 − . C. 1 − . D. 1. Lời giải
Khoảng cách từ điểm A(1; )
1 đến đường thẳng ∆ :5x −12y − 6 = 0 là − −
d ( A ∆) 5.1 12.1 6 , = = 1. 2 5 + ( 12 − )2 x = − t
Câu 12: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 3x + y −6=0 và đường thẳng ∆: y= 5 − 2t
. Góc giữa hai đường thẳng d và ∆ bằng A. 30° . B. 135° . C. 45° . D. 90° . Lời giải 
+) Đường thẳng d có véc tơ pháp tuyến là: n = . d (3 ) ;1 Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 x = − t +) Đường thẳng ∆: 
⇒ ∆ : 2x − y +5=0. Suy ra đường thẳng ∆ có véc tơ pháp y = 5 − 2t  tuyến là: n = − . ∆ (2; ) 1
+) Gọi α là góc giữa hai đường thẳng d và ∆ . Ta có   n n d . + − ∆ 3.2 1.( 1) 2 cosα =   = = ⇒ α = 45 .° n n d . ∆ 3 +1 . 2 + (− )2 2 2 2 2 1
Vậy góc giữa hai đường thẳng d và ∆ bằng 45° .
Câu 13: Xác định tâm I và bán kính R của đường tròn (C) (x − )2 + ( y + )2 : 1 5 = 9 . A. I( 1; − 5), R = 3. B. 9 I( 1; − 5), R = . C. I(1; 5 − ), R = 3. D. 9 I(1; 5 − ), R = . 2 2 Lời giải
Đường tròn có tâm I (1; 5 − ), R = 3 .
Câu 14: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn tâm I (2;−5) và tiếp xúc với đường
thẳng ∆ :− 3x + 4y +11 = 0 là
A. (x − )2 + ( y + )2 2 5 = 3.
B. (x + )2 + ( y − )2 2 5 = 9.
C. (x + )2 + ( y − )2 2 5 = 3.
D. (x − )2 + ( y + )2 2 5 = 9. Lời giải
Đường tròn tâm I tiếp xúc với đường thẳng ∆ có bán kính bằng khoảng cách từ điểm I đến đường thẳng ∆ . 3 − x + y + − + − + I 4 I 11 3.2 4.( 5) 11 15
Suy ra, R = d (I ,∆) = = = = 3 . (− )2 2 5 5 3 + 4
Vậy phương trình đường tròn tâm I (2;−5) , bán kính R = 3 là: (x − )2 + ( y + )2 2 5 = 9.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol? A. 2 y = x . B. 2 y = 6x . C. 2 y = 5 − x . D. 2 y = 2022x .
Câu 16: Trên kệ sách nhà bạn Lan có 7 quyển sách Toán khác nhau, 8 quyển sách Vật lý khác nhau và 9
quyển sách Lịch sử khác nhau. Hỏi bạn Lan có bao nhiêu cách chọn một quyển sách để đọc A. 9. B. 8. C. 24. D. 7. Lời giải
Tổng số quyển sách: 7 + 8 + 9 = 24 quyển. Số cách chọn 1 quyển sách để đọc: 24 cách.
Câu 17: Một hộp đồ bảo hộ có 10 chiếc khẩu trang và 3 mặt nạ chống giọt bắn. Có bao nhiêu cách chọn
một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp đồ bảo hộ trên. A. 10. B. 30. C. 13. D. 3. Lời giải
Áp dụng quy tắc nhân, số cách chọn một chiếc khẩu trang và một mặt nạ chống giọt bắn từ hộp
đồ bảo hộ trên là 10.3 = 30 cách.
Câu 18: Số hoán vị của tập X có 5 phần tử là A. 5. B. 24 . C. 120. D. 60 . Lời giải Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Số hoán vị của tập X có 5 phần tử là 5!=120
Câu 19: Trong một hộp bánh có 10 chiếc bánh khác nhau. Có bao nhiêu cách lấy 3 chiếc bánh từ hộp đó
để phát cho các bạn An, Bình, Cường, mỗi bạn một chiếc? A. 10 3 . B. 3 A . C. 3 10 . D. 3 C . 10 10 Lời giải
Lấy 3 chiếc bánh từ 10 chiếc bánh, có 3 C cách lấy. 10
Sau đó phát 3 chiếc bánh đã lấy cho 3 bạn, mỗi bạn một chiếc, có 3! cách.
Vậy số cách cần tìm là: 3 3
C .3!= A cách. 10 10
Câu 20: Lớp 11A có 45 học sinh trong đó có 15 học sinh giỏi. Thầy giáo cần chọn một nhóm gồm 5
bạn học sinh của lớp 11A đi dự trại hè. Hỏi thầy giáo đó có bao nhiêu cách chọn 1 nhóm sao cho
cả 5 bạn đều là học sinh giỏi. A. 3003. B. 360360. C. 1221759. D. Đáp án khác. Lời giải
Số cách chọn 1 nhóm sao cho cả 5 bạn đều là học sinh giỏi bằng số cách chọn 5 học sinh trong
15 học sinh giỏi của lớp. Vậy có 5 C = 3003. 15
Câu 21: Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của ( − )4 1 2x . A. 1. B. 1 − . C. 81. D. 81 − . Lời giải
Tổng các hệ số trong khai triển nhị thức Niu-tơn của ( x − )4 2
3 chính là giá trị của biểu thức ( x − )4 2 3 tại x =1. Vậy S = ( − )4 1 2.1 =1.
Câu 22: Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất. Xác suất để xuất hiện mặt có số chấm chia hết cho 3 bằng A. 1 . B. 1 . C. 1 . D. 2 . 2 3 6 3 Lời giải
Không gian mẫu Ω = {1;2;3;4;5; } 6 ⇒ n(Ω) = 6 .
Gọi A là biến cố “xuất hiện mặt có số chấm chia hết cho 3”, ta có A = {3; }
6 ⇒ n( A) = 2 . n A 2 1
Vậy, xác suất để xuất hiện mặt có số chấm chia hết cho 3 là P( A) ( ) = = = . n(Ω) 6 3
Câu 23: Gieo ba con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên ba mặt lập thành
một cấp số cộng với cộng sai bằng 1 là bao nhiêu? B. 1 . B. 1 . C. 1 . D. 1 . 6 36 9 27 Lời giải
Số phần tử không gian mẫu là 3 6 = 216. Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Các bộ ba số lập thành một cấp số cộng với công sai bằng 1 là
(1,2,3),(2,3,4),(3,4,5),(4,5,6). Các trường hợp trên với các hoán vị sẽ có 4.3!= 24 khả năng
thuận lợi cho biến cố. Xác suất cần tìm là 24 1 = . 216 9
Câu 24: Một tổ có 5 bạn nam và 7 bạn nữ, chọn một nhóm 3 bạn để tham gia biểu diễn văn nghệ. Xác
suất để chọn được 3 bạn nữ bằng A. 21 . B. 1 . C. 7 . D. 5 . 220 22 44 44 Lời giải
Ta có số phân tử của không gian mẫu n(Ω) 3 = C . 12
Gọi A là biến cố chọn được 3 bạn nữ, ta có n( A) 3 = C . 7 3 n A
Xác suất của biến cố A là P( A) ( ) C 7 7 = = = . n(Ω) 3 C 44 12
Câu 25: Trong mặt phẳng Oxy cho điểm M (1;2) và đường thẳng ∆ : x + 4y − 2 = 0 . Viết phương trình
đường thẳng đi qua M và song song với ∆ .
A. d : x + 4y −9 = 0 .
B. d : x + 4y + 9 = 0 . C. d : x + 4y − 6 = 0 . D. d : x + 4y + 6 = 0. Lời giải
Ta có d ⊥ ∆ , phương trình đường thẳng d có dạng: d : x + 4y + m = 0.
Mặt khác: M ( 1;2 )∈d : d :1+ 4.2 + m = 0 ⇔ m = 9. −
Vậy phương trình đường thẳng d : x + 4y − 9 = 0 .
Câu 26: Trong mặt phẳng với hệ tọa độ Oxy , hai đường thẳng có phương trình
d : mx + m −1 y + 2m = 0 và d : 2x + y −1 = 0 song song khi và chỉ khi 1 ( ) 2 A. m = 2. B. m = 1. − C. m = 2. − D. m =1. Lời giải
d : mx + m −1 y + 2m = 0 1 ( ) d d m m −1 2m 1|| 2   → = =/
d : 2x + y −1 = 0 2 1 1 − 2  1 − =/ 2 ⇔  ⇔ m = 2. m = 2m − 2
Câu 27: Đường tròn (C) đi qua A(1;3) , B(3; )
1 và có tâm nằm trên đường thẳng d : 2x − y + 7 = 0 có phương trình là
A. (x − )2 + ( y − )2 7 7 =102 .
B. (x + )2 + ( y + )2 7 7 =164 .
C. (x − )2 + ( y − )2 3 5 = 25 .
D. (x + )2 + ( y + )2 3 5 = 25 . Lời giải
Đường tròn (C) có tâm I ( ;
a b) , bán kính R có phương trình là: (x − a)2 + ( y − b)2 2 = R (*) .
I ∈ d ⇒ I ( ;2 a a + 7) .
AI = (a − )2 + ( a + )2 1 2 4 2 = 5a +14a +17 Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
BI = (a − )2 + ( a + )2 3 2 6 2 = 5a +18a + 45
Vì (C) đi qua A(1;3) , B(3; ) 1 nên AI = BI ⇔ 2 2 AI = BI ⇔ 2 2
5a +14a +17 = 5a +18a + 45 ⇔ a = 7 − Suy ra tâm I ( 7; − 7 − ) , bán kính 2 2 R = AI =164.
Vậy đường tròn (C) có phương trình: (x + )2 + ( y + )2 7 7 =164 .
Câu 28: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C)có phương trình 2 2
x + y − 2x + 2y − 3 = 0 . Từ điểm A(1; )
1 kẻ được bao nhiêu tiếp tuyến đến đường tròn (C) A. 1. B. 2. C. vô số. D. 0. Lời giải
(C) có tâm I (1;− )1 bán kính R= 2 2 1 + ( 1 − ) − ( 3 − ) = 5
Vì IA = 2 < R nên A nằm bên trong (C).Vì vậy không kẻ được tiếp tuyến nào tới đường tròn (C).
Câu 29: Phương trình chính tắc của elip có tổng các khoảng cách từ một điểm bất kỳ đến
hai tiêu điểm bằng 10 và có tiêu cự bằng 2 5 là 2 2 2 2 2 2 2 2
A. x + y = 1.
B. x + y = 1.
C. x + y = 1.
D. x + y = 1. 10 2 5 25 20 25 5 100 20 Lời giải 2 2
Phương trình chính tắc của elip có dạng x + y = 1 (a > b > 0) . 2 2 a b 2a = 10 a = 5  
Ta có 2c = 2 5 ⇒ c = 5 .  2 2 2  2
b = a − c b = 20   2 2
Vậy elip có phương trình chính tắc là x + y = 1. 25 20
Câu 30: Các thành phố A , B , C được nối với nhau bởi các con đường như hình vẽ. Hỏi có bao nhiêu
cách đi từ thành phố A đến thành phố C mà qua thành phố B chỉ một lần? A B C A. 6 . B. 12. C. 8. D. 4 . Lời giải Ta có:
- Đi từ thành phố A đến thành phố B ta có 4 con đường để đi.
- Đi từ thành phố B đến thành phố C ta có 2 con đường để đi.
Vậy theo quy tắc nhân ta có 4× 2 = 8 cách.
Câu 31: Một tổ có 7 người trong đó có An và Bình. Hỏi có bao nhiêu cách xếp 7 người vào bàn tròn có
7 ghế sao cho An và Bình ngồi cạnh nhau? A. 720 . B. 240 . C. 5040. D. 120 . Lời giải Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Ta buộc cặp hai bạn An và Bình và coi là một người thì có tất cả 6 người.
Suy ra có 5! cách xếp 6 người này vào bàn tròn.
Nhưng hai bạn An và Bình có thể hoán vị để ngồi cạnh nhau.
Vậy có tất cả 5!.2!= 240 cách xếp 7 người vào bàn tròn có 7 ghế sao cho An và Bình ngồi cạnh nhau.
Câu 32: Có bao nhiêu cách xếp 5 bạn học sinh Tuấn, Tú, Tiến, Tân, Tiên vào 1 hàng ngang gồm 10 ghế
được đánh số từ 1 đến 10, sao cho Tuấn và Tiên luôn ngồi cạnh nhau? A. 1890. B. 252 . C. 3024. D. 6048. Lời giải
Xem Tuấn và Tiên là khối A .
Xếp thứ tự khối A và 3 bạn Tú, Tiến, Tân vào các ghế trong hàng ngang có 4 A cách. 9
Xếp vị trí cho Tuấn và Tiên trong khối A có 2! cách xếp. Vậy theo QTN, ta có 4 A .2!= 6048 cách. 9
Câu 33: Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật Lí và 2 quyển sách Hóa họ C. Lấy
ngẫu nhiên 3 quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán. A. 1 . B. 37 . C. 5 . D. 19 3 42 6 21 Lời giải
Số phần tử của không gian mẫu n(Ω) 3 = C = 84 . 9
Gọi A là biến cố sao cho ba quyển lấy ra có ít nhất một quyển sách Toán
⇒ A là biến cố sao cho ba quyển lấy ra không có sách Toán ⇒ n( A) 3 = C =10 . 5 10
⇒ P( A) =1− P( A) =1− 37 = . 84 42
Câu 34: Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để
rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng A. 1 . B. 2 . C. 5 . D. 13 . 3 3 18 18 Lời giải Có 2 trường hợp sau:
Trường hợp 1: 1 thẻ ghi số chẵn, 1 thẻ ghi số lẻ, suy ra có 1 1
C ⋅C = 20 cách rút. 4 5
Trường hợp 2: 2 thẻ ghi số chẵn, suy ra có 2 C = 6 cách rút. 4
Suy ra xác suất bằng 20 + 6 13 = . 2 C 18 9
Câu 35: Gieo một con súc xắc cân đối và đồng chất ba lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm là: A. 125 . B. 91 . C. 25 . D. 81 . 216 216 216 216 Lời giải
Ta có: n(Ω) = 6.6.6 = 216.
Gọi A là biến cố:”ít nhất một lần xuất hiện mặt sáu chấm”.
Khi đó A là biến cố:”không có lần nào xuất hiện mặt sáu chấm”. Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 n( ) A = 5.5.5 =125. Vậy 125 91 P( ) A =1− P( ) A =1− = . 216 216
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Từ một ban cán bộ Đoàn ở một trường học gồm có 20 học sinh, người ta muốn cử ra một nhóm
gồm 8 em đi tham gia hội trại với trường bạn. Biết rằng cần có một nhóm trưởng, hai bạn nhóm
phó, một bạn thủ quỹ và 4 bạn uỷ viên. Hỏi có bao nhiều cách chọn ra một nhóm học sinh như vậy? Lời giải
Chọn ra hai em gồm nhóm trưởng và thủ quỹ có 2 A cách. 20
Chọn ra hai em nhóm phó có 2 C cách. 18
Chọn ra 4 uỷ viên từ 16 em còn lại có 4 C cách. 16 Vậy có 2 2 4
A .C .C =105814800 cách chọn ra nhóm học sinh đó. 20 18 16
Câu 37: Viết phương trình chính tắc của hypebol (H ) có một tiêu điểm F − 34;0 và đi qua điểm 1 ( )  99  A6 ; . 25    Lời giải 2 2 x y
Gọi pt chính tắc của hypebol (H ) : −
= 1 a > 0,b > 0 . 2 2 ( ) a b
(H ) có một tiêu điểm F − 34;0 ⇔ 2 2 2 2 2
c = 34 ⇔ a + b = 34 ⇔ a = 34 − b . ( ) 1 1 ( )  99  2 6 99
Mặt khác do (H ) đi qua điểm A6 ; nên − = 1. (2) 25    2 2 a 25b Thay ( ) 1 vào (2) ta được: 2 2  2 b = 9 ⇒ a = 25 6 99 4 2 1 25b 149b 3366 0  − = ⇔ + − = ⇔ . 2 2 2 374 34 − b 25b b −  = (loai)  25 2 2 x y Vậy (H ) : − = 1. 25 9
Câu 38: Cho đa giác đều có 15 đỉnh, gọi M là tập tất cả các tam giác có ba đỉnh là ba đỉnh của đa giác
đã cho. Chọn ngẫu nhiên một tam giác thuộc tập M . Xác suất để chọn được một tam giác cân
nhưng không phải là tam giác đều bằng Lời giải
+ Số tam giác có ba đỉnh là ba đỉnh của đa giác đã cho là: 3
C = 455 tam giá C. 15 Suy ra n(Ω) = 455 .
+ Gọi O là tâm đường tròn ngoại tiếp đa giác đều.
Xét một đỉnh A bất kì của đa giác đều: có 7 cặp đỉnh của đa giác đối xứng với nhau qua OA,
hay có 7 tam giác cân tại đỉnh A .
Như vậy, với mỗi đỉnh của đa giác có 7 tam giác nhận nó làm đỉnh tam giác cân.
+ Số tam giác đều có ba đỉnh là ba đỉnh của đa giác là 15 = 5 tam giá C. 3 Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Tuy nhiên, trong các tam giác cân đã xác định ở trên có cả tam giác đều, do mọi tam giác đều
thì đều cân tại ba đỉnh nên các tam giác đều được đếm ba lần.
+ Suy ra số tam giác cân nhưng không phải tam giác đều có ba đỉnh là ba đỉnh của đa giác đã cho là: 7.15 − 3.5 = 90 .
Vậy, xác suất để chọn được một tam giác cân nhưng không phải là tam giác đều từ tập M bằng: 90 18 P = = . 455 91
Câu 39: Một tháp làm nguội của một nhà máy có mặt cắt là hình hyperbol có tiêu cự bằng 2 70 m , độ
dài trục ảo bằng 2 42 m . Biết chiều cao của tháp là 120m và khoảng cách từ nóc tháp đến tâm 2
đối xứng của hypebol là khoảng cách từ tâm đối xứng đến đáy. Tính bán kính nóc và bán kính 3 đáy của tháp. Lời giải 2 2
Phương trình chính tắc của hypebol có dạng x y − = 1, với 2 2 2
a < c,b = c − a . 2 2 a b Ta có:
2c = 2 70 ⇒ c = 70
2b = 2 42 ⇒ b = 42 2 2
a = c − b = 2 7 2 2
Vậy phương trình chính tắc của hypebol là: x y − =1. 28 42
Gọi khoảng cách từ tâm đối xứng đến đáy tháp là z. 2
Suy ra khoảng cách từ tâm đối xứng đến nóc tháp là z . 3 Ta có 2
z + z =120 ⇒ z = 72 3 . 2 2
Thay y = 72 vào phương trình x y −
=1 ta tìm được x = 2 ± 871 . 28 42 2 2
Thay y = 48 vào phương trình x y −
=1 ta tìm được x = 2 ± 391. 28 42
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là: 2 391m ; 2 871 . m Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
---------- HẾT ---------- Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 05
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).  
Câu 1: Cho A(0;3) ; B(4;0) ;C ( 2; − 5 − ) . Tính A . B BC . A. 16. B. 9. C. 10 − . D. 9 − .
Câu 2: Hãy xác định sai số tuyệt đối của số a =123456 biết sai số tương đốiδ = a 0,2% A. 246,912. B. 617280. C. 24691,2. D. 61728000
Câu 3: Cho các số liệu thống kê về sản lượng chè thu được trong 1 năm ( kg/sào) của 20 hộ gia đình 111 112 112 113 114 114 115 114 115 116 112 113 113 114 115 114 116 117 114 115 Tìm số mốt A. M =111. B. M =113. C. M =114 .
D. M =117 . 0 0 0 0
Câu 4: Số sản phẩm sản xuất mỗi ngày của một phân xưởng trong 9 ngày liên tiếp được ghi lại như sau: 27 26 21 28 25 30 26 23 26
Khoảng biến thiên của mẫu số liệu này là: A. 8. B. 5. C. 6. D. 9.
Câu 5: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là: A. 20. B. 22. C. 24. D. 26.
Câu 6: Cho ba điểm A(2 ; 4
− ), B(6 ; 0),C (m ; 4) . Định m để ,
A B,C thẳng hàng?
A. m =10 . B. m = 6 − .
C. m = 2 . D. m = 10 − .
Câu 7: Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75m với dụng cụ đo đảm bảo sai số tương
đối không vượt quá 1,5‰ . Tính độ dài gần đúng của cầu. A. 500,1m B. 499,9m C. 500 m D. 501 m
Câu 8: Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A1
Độ lệch chuẩn của mẫu số liệu trên là A. 1,5. B. 1,57 . C. 1,58. D. 1,60 . x = 2 − 4t
Câu 9: Trong mặt phẳng Oxy cho đường thẳng d: 
. Vectơ nào dưới đây là một vectơ chỉ y =1+ t phương của d?    
A. u2 = (2;1) . B. u1 = ( 4 − ;1) .
C. u = (1;3). D. u = (2; 4 − ). 3 4
Câu 10: Viết phương trình tổng quát của đường thẳng d qua M ( 1; − 4
− ) và song song với đường thẳng
3x + 5y − 2 = 0
A. d : −x − 4y − 2 = 0 . B. d :3x + 5y + 23 = 0 .
C. d :5x + 3y + 23 = 0 . D. d : 3
− x − 5y + 23 = 0 . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 11: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ ∆
1 : 2x − 3y +1 = 0 và 2 : 4
− x + 6y −1 = 0 . A. Song song. B. Trùng nhau. C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau.  x =1+ 3t
Câu 12: Khoảng cách từ điểm M (2;0) đến đường thẳng  là: y = 2 + 4t 2 A. 2 . B. . C. 10 . D. 5 . 5 5 2
Câu 13: Trong mặt phẳng với hệ trục tọa độ Oxy . Trong các phương trình sau, phương trình nào là
phương trình đường tròn? A. 2 2
x + y − 2x + 4y −11 = 0. B. 2 2
x − y − 2x + 4y −11 = 0 . C. 2 2
x + y − 2x + 4y +11 = 0 . D. 2 2
2x + y − 2x + 4y −11 = 0 .
Câu 14: Đường tròn (C) tâm I(1; 4) và tiếp xúc với đườngthẳng ∆ : 4x + 3y + 4 = 0 có phương trình là A. 2 2
(x −1) + (y − 4) =17 . B. 2 2
(x −1) + (y − 4) =16 . C. 2 2
(x −1) + (y − 4) = 25 . D. 2 2
(x +1) + (y + 4) =16 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 9 4
A. F = − 13;0 ; F = 13;0 1 ( ) 2 ( ).
B. F = 0;− 13 ; F = 0; 13 . 1 ( ) 2 ( )
C. F = 0;− 5 ; F = 0; 5 .
D. F = − 5;0 ; F = 5;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
Câu 16: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một
học sinh trong lớp đi dự đại hội? A. 20 . B. 35. C. 15. D. 300.
Câu 17: Đi từ A đến B có 3 con đường,đi từ B đến C có 4 con đường.Hỏi đi từ A đến C có bao cách đi? A C B A. 7. B. 8. C. 10. D. 12.
Câu 18: Có 6 người đến nghe buổi hòa nhạc. Số cách sắp xếp 6 người này vào một hàng ngang 6 ghế là A. 6 . B. 2.6!. C. 2 6 . D. 6!.
Câu 19: Cho 6 chữ số 4,5,6,7,8,9. Hỏi có bao nhiêu số gồm 3 chữ số khác nhau được lập thành từ 6 chữ số đó? A. 180. B. 120. C. 256 . D. 216 .
Câu 20: Trong mặt phẳng cho tập hợp S gồm 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Có
bao nhiêu tam giác có 3 đỉnh đều thuộc S ? A. 720. B. 120. C. 59049. D. 3628800.
Câu 21: Mệnh đề nào dưới đây đúng? A. (x + 3)4 0 4 1 3 2 2 2 3 3 4 4
= C x + C x .3+ C x .3 + C .3 x + C .3 4 4 4 4 4 . B. (x + )4 4 3 2
3 = x +12x + 54x +108x + 324 . Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 C. (x + )4 4 3 2
3 = x +12x + 54x +12x + 81. D. (x + )4 4 3 2
3 = x +108x + 54x +108x + 81.
Câu 22: Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là: 1 8 4 1 A. 7 . B. 15. C. 15. D. 14.
Câu 23: Từ một nhóm học sinh gồm có 5 nam và 6 nữ, chọn ngẫu nhiên ra 2 bạn. Tính xác suất để hai
bạn được chọn có cả nam và nữ. A. 7 . B. 5 . C. 6 . D. 4 . 11 11 11 11
Câu 24: Một tổ có 4 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh lên bảng giải
bài tập. Xác suất để 3 học sinh được chọn có cả nam và nữ bằng 1 A. . B. 5 . C. 3 . D. 2 . 6 6 5 5
Câu 25: Cho M (1;3) và N ( 3;
− 5) . Phương trình đường trung trực của đoạn thẳng MN là đường thẳng nào dưới đây?
A. x + 2y − 7 = 0 . B. 2
− x + y − 6 = 0.
C. x + 2y + 7 = 0 . D. 2
− x + y + 6 = 0 .
Câu 26: Trong mặt phẳng tọa độ (Oxy), cho các điểm A(1;2), B(2; ) 1
− . Đường thẳng ∆ đi qua điểm A
, sao cho khoảng cách từ điểm B đến đường thẳng ∆ nhỏ nhất có phương trình là?
A. 3x + y − 5 = 0 .
B. x − 3y + 5 = 0 .
C. 3x + y −1 = 0 .
D. x − 3y −1 = 0 .
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(1;2) , B(5;2), C (1; 3 − ) có phương trình là. A. 2 2
x + y + 6x + y −1 = 0 . B. 2 2
x + y − 6x − y −1 = 0 . C. 2 2
x + y − 6x + y −1 = 0 . D. 2 2
x + y + 6x − y −1 = 0 .
Câu 28: Cho đường thẳng ∆ :3x − 4y −19 = 0 và đường tròn (C) (x − )2 + ( y − )2 : 1 1 = 25 . Biết đường
thẳng ∆ cắt (C) tại hai điểm phân biệt A và B , khi đó độ dài đọan thẳng AB là A. 6. B. 3. C. 4. D. 8. 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 9
tiêu điểm có giá trị tuyệt đối bằng A. 8 . B. 6 . C. 4 . D. 5.
Câu 30: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món, 1 loại quả tráng
miệng trong 5 loại quả tráng miệng và một loại nước uống trong 3 loại nước uống. Có bao nhiêu cách chọn thực đơn? A. 100. B. 15. C. 75. D. 25.
Câu 31: Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh ngồi một ghế là A. 6 C . B. 6!. C. 6 A . D. 10 6 . 10 10
Câu 32: Mười hai đường thẳng có nhiều nhất bao nhiêu giao điểm? A. 12. B. 66 . C. 132. D. 144. Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 33: Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn. A. 5 . B. 661 . C. 660 . D. 6 . 6 715 713 7
Câu 34: Một hộp chứa 11 viên bi được đánh số thứ tự từ 1 đến 11. Chọn ngẫu nhiên 3 viên bi rồi cộng
các số trên 3 viên bi đó với nhau. Xác suất để kết quả thu được là số chẵn bằng A. 17 . B. 16 . C. 19 . D. 23 . 33 33 33 33
Câu 35: Một hộp chứa 5 bi xanh, 4 bi đỏ. Chọn ngẫu nhiên 2 bi từ hộp này. Xác suất để chọn được 2 bi cùng màu là A. 2 . B. 1 . C. 5 . D. 4 . 9 9 9 9
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu sô tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn và 3 chữ số lẻ? x =1− 3t
Câu 37: Trong mặt phẳng (Oxy) cho điểm M (2;4) và d : 
.Viết phương trình đường thẳng song y = 2 + t
song với đường thẳng d và cách điểm M một khoảng bằng 10 .
Câu 38: Cho tập hợp X = {0,1,2,3,4,5,6, }
7 . Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một
khác nhau được lập từ tập hợp X . Chọn ngẫu nhiên một số từ S . Tính xác suất để chọn được số chia hết cho 5. 2 2
Câu 39: Trong hệ trục tọa độ Oxy , cho Elip ( ): x y E +
=1, F , F là hai tiêu điểm, hoành độ của F 25 16 1 2 1
âm. Điểm M thuộc (E) sao cho MF = 2MF 1
2 . Hoành độ điểm M là
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).  
Câu 1: Cho A(0;3) ; B(4;0) ;C ( 2; − 5 − ) . Tính A . B BC . A. 16. B. 9. C. 10 − . D. 9 − . Lời giải  
Ta có AB = (4;−3) ; BC = ( 6; − − 5)   Vậy A . B BC = 4.( 6 − ) + ( 3 − ).( 5 − ) = 9 − .
Câu 2: Hãy xác định sai số tuyệt đối của số a =123456 biết sai số tương đốiδ = a 0,2% A. 246,912. B. 617280. C. 24691,2. D. 61728000 Giải ∆ Ta có a δ = ⇒ ∆ = δ a = . a a a 246,912 a
Câu 3: Cho các số liệu thống kê về sản lượng chè thu được trong 1 năm ( kg/sào) của 20 hộ gia đình 111 112 112 113 114 114 115 114 115 116 112 113 113 114 115 114 116 117 114 115 Tìm số mốt A. M =111. B. M =113. C. M =114 .
D. M =117 . 0 0 0 0 Lời giải
Nhìn vào bảng số liệu ta thấy giá trị 114 có tần số lớn nhất nên ta có M =114 . 0
Câu 4: Số sản phẩm sản xuất mỗi ngày của một phân xưởng trong 9 ngày liên tiếp được ghi lại như sau: 27 26 21 28 25 30 26 23 26
Khoảng biến thiên của mẫu số liệu này là: A. 8. B. 5. C. 6. D. 9. Lời giải
Số sản phẩm sản xuất thấp nhất và cao nhất lần lượt là 30 và 21. Vậy khoảng biến thiên của mẫu số liệu này là 9.
Câu 5: Số lượng ly trà sữa một quán nước bán được trong 20 ngày qua là:
4, 5, 6, 8, 9, 11, 13, 16, 16, 18, 20, 21, 25, 30, 31, 33, 36, 37, 40, 41.
Khoảng tứ phân vị của mẫu số liệu trên là: A. 20. B. 22. C. 24. D. 26. Lời giải
Số liệu trên đã sắp xếp theo thứ tự không giảm
Ta có Q = 10;Q = 19;Q = 32 1 2 3
Vậy khoảng tứ phân vị của mẫu số liệu trên là: ∆ = − = . Q 32 10 22
Câu 6: Cho ba điểm A(2 ; 4
− ), B(6 ; 0),C (m ; 4) . Định m để ,
A B,C thẳng hàng?
A. m =10 . B. m = 6 − .
C. m = 2 . D. m = 10 − . Lời giải Chọn A  
AB = (4 ; 4) ; AC = (m − 2 ; 8). Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10   m − ,
A B, C thẳng hàng ⇔ AB, AC cùng phương 2 8 ⇔ = ⇔ m =10 . 4 4
Câu 7: Kết quả đo chiều dài một cây cầu có độ chính xác là 0,75m với dụng cụ đo đảm bảo sai số tương
đối không vượt quá 1,5‰ . Tính độ dài gần đúng của cầu. A. 500,1m B. 499,9m C. 500 m D. 501 m Lời giải
Độ dài h của cây cầu là: 0,75 d ≈ .1000 = 500 (m) 1,5
Câu 8: Cho bảng số liệu thống kê điểm kiểm tra của lớp 10A1
Độ lệch chuẩn của mẫu số liệu trên là A. 1,5. B. 1,57 . C. 1,58. D. 1,60 . x = 2 − 4t
Câu 9: Trong mặt phẳng Oxy cho đường thẳng d: 
. Vectơ nào dưới đây là một vectơ chỉ y =1+ t phương của d?    
A. u2 = (2;1) . B. u1 = ( 4 − ;1) .
C. u = (1;3). D. u = (2; 4 − ). 3 4 Lời giải  Ta có u = ( 4
− ;1) là một vectơ chỉ phương của d
Câu 10: Viết phương trình tổng quát của đường thẳng d qua M ( 1; − 4
− ) và song song với đường thẳng
3x + 5y − 2 = 0
A. d : −x − 4y − 2 = 0 . B. d :3x + 5y + 23 = 0 .
C. d :5x + 3y + 23 = 0 . D. d : 3
− x − 5y + 23 = 0 . Lời giải
Vì d song song với đường thẳng 3x + 5y − 2 = 0 nên phương trình của d có dạng
3x + 5y + c = 0 (c ≠ 2) − .
Vì d đi qua điểm M ( 1; − 4 − ) nên 3
− − 20 + c = 0 ⇒ c = 23.
Vậy phương trình tổng quát của d :3x + 5y + 23 = 0 .
Câu 11: Xác định vị trí tương đối của 2 đường thẳng sau đây: ∆ ∆
1 : 2x − 3y +1 = 0 và 2 : 4
− x + 6y −1 = 0 . A. Song song. B. Trùng nhau. C. Vuông góc.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải 2 3 − 1 +) Xét: = ≠
nên hai đường thẳng song. 4 − 6 1 −  x =1+ 3t
Câu 12: Khoảng cách từ điểm M (2;0) đến đường thẳng  là: y = 2 + 4t 2 A. 2 . B. . C. 10 . D. 5 . 5 5 2 Lời giải Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 − +
Phương trình tổng quát d x − y + = ⇒ d (M d ) 4.2 3.0 2 : 4 3 2 0 , = = 2 . 5
Câu 13: Trong mặt phẳng với hệ trục tọa độ Oxy . Trong các phương trình sau, phương trình nào là
phương trình đường tròn? A. 2 2
x + y − 2x + 4y −11 = 0. B. 2 2
x − y − 2x + 4y −11 = 0 . C. 2 2
x + y − 2x + 4y +11 = 0 . D. 2 2
2x + y − 2x + 4y −11 = 0 . Lời giải Phương trình 2 2
x + y − 2x + 4y −11 = 0 là phương trình đường tròn. Vì 2 2
a + b − c =1+ 4 +11 =16 > 0 trong đó a =1;b = 2 − ;c = 11. −
Câu 14: Đường tròn (C) tâm I(1; 4) và tiếp xúc với đườngthẳng ∆ : 4x + 3y + 4 = 0 có phương trình là A. 2 2
(x −1) + (y − 4) =17 . B. 2 2
(x −1) + (y − 4) =16 . C. 2 2
(x −1) + (y − 4) = 25 . D. 2 2
(x +1) + (y + 4) =16 Lời giải ( 4.1+ 3.4 + 4
C)có bán kính R = d (I,∆) = = 4. 2 2 3 + 4
Do đó, (C) có phương trình 2 2
(x −1) + (y − 4) =16 . 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 9 4
A. F = − 13;0 ; F = 13;0 1 ( ) 2 ( ).
B. F = 0;− 13 ; F = 0; 13 . 1 ( ) 2 ( )
C. F = 0;− 5 ; F = 0; 5 .
D. F = − 5;0 ; F = 5;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( ) Lời giải Gọi F = − ;0 c ; F = ;0 c
là hai tiêu điểm của (H ) . 1 ( ) 2 ( ) 2 2
Từ phương trình ( ) : x y H − = 1, ta có: 2 a = 9 và 2 b = 4 suy ra 9 4 2 2 2
c = a + b =13 ⇒ c = 13,(c > 0) .
Vậy tọa độ các tiêu điểm của (H ) là F = − 13;0 ; F = 13;0 . 1 ( ) 2 ( )
Câu 16: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một
học sinh trong lớp đi dự đại hội? A. 20 . B. 35. C. 15. D. 300. Lời giải Có 2 khả năng xẩy ra:
+) Học sinh được chọn là nam có 20 cách chọn.
+) Học sinh được chọn là nữ có 15 cách chọn.
Vậy theo quy tắc cộng có 20+15=35 cách chọn.
Câu 17: Đi từ A đến B có 3 con đường,đi từ B đến C có 4 con đường.Hỏi đi từ A đến C có bao cách đi? A C B A. 7. B. 8. C. 10. D. 12. Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Theo quy tắc nhân ta có số cách đi từ A đến C là: 3.4 =12 . Vậy chọn đáp án D
Câu 18: Có 6 người đến nghe buổi hòa nhạc. Số cách sắp xếp 6 người này vào một hàng ngang 6 ghế là A. 6 . B. 2.6!. C. 2 6 . D. 6!. Lời giải
Mỗi cách sắp xếp 6 người ngồi vào một hàng ngang 6 ghế là một hoán vị của 6 phần tử.
Vậy số cách sắp xếp là 6! cách.
Câu 19: Cho 6 chữ số 4,5,6,7,8,9. Hỏi có bao nhiêu số gồm 3 chữ số khác nhau được lập thành từ 6 chữ số đó? A. 180. B. 120. C. 256 . D. 216 . Lời giải
Gọi số cần tìm có dạng abc với a ≠ 0,a ≠ b ≠ c ≠ a .
Chọn 3 chữ số khác nhau từ 6 chữ số đã cho và sắp xếp vào 3 vị trí a,b,c có 3 A =120 cách. 6
Câu 20: Trong mặt phẳng cho tập hợp S gồm 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Có
bao nhiêu tam giác có 3 đỉnh đều thuộc S ? A. 720. B. 120. C. 59049. D. 3628800. Lời giải
Số tam giác có 3 đỉnh đều thuộc S bằng số tổ hợp chập 3 của 10 phần từ và bằng 3 C =120 10
Câu 21: Mệnh đề nào dưới đây đúng? A. (x + 3)4 0 4 1 3 2 2 2 3 3 4 4
= C x + C x .3+ C x .3 + C .3 x + C .3 4 4 4 4 4 . B. (x + )4 4 3 2
3 = x +12x + 54x +108x + 324 . C. (x + )4 4 3 2
3 = x +12x + 54x +12x + 81. D. (x + )4 4 3 2
3 = x +108x + 54x +108x + 81. Lời giải Ta có (x +3)4 0 4 1 3 2 2 2 3 3 4 4
= C x + C x .3+ C x .3 + C .3 x + C .3 4 4 4 4 4 4 3 2
= x +12x + 54x +108x + 81
Câu 22: Chọn ngẫu nhiên hai số khác nhau từ 15 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số lẻ là: 1 8 4 1 A. 7 . B. 15. C. 15. D. 14. Lời giải Không gian mẫu 2 C =105. 15
Để tổng hai số là một số lẻ ta chọn 1 số lẻ và 1 số chẵn nên ta có 8.7 = 56 . 56 8 Xác suất cần tìm là = 105 15 .
Câu 23: Từ một nhóm học sinh gồm có 5 nam và 6 nữ, chọn ngẫu nhiên ra 2 bạn. Tính xác suất để hai
bạn được chọn có cả nam và nữ. A. 7 . B. 5 . C. 6 . D. 4 . 11 11 11 11 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số cách chọn 2 bạn trong tổng số 11 bạn: 2 n(Ω) = C11
Gọi A là biến cố: “Hai bạn được chọn có cả nam và nữ”. Ta có: 1 1 n( ) A = C .C 5 6 n( ) A 6
Từ đó, xác suất để hai bạn được chọn có cả nam và nữ là: P( ) A = = . n(Ω) 11
Câu 24: Một tổ có 4 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh lên bảng giải
bài tập. Xác suất để 3 học sinh được chọn có cả nam và nữ bằng 1 A. . B. 5 . C. 3 . D. 2 . 6 6 5 5 Lời giải Ta có n(Ω) 3 = C = 84 . 9
Gọi biến cố A: “3 học sinh được chọn có cả nam và nữ” ⇒ n( A) 1 2 2 1
= C .C + C .C = 70. 4 5 4 5 n A Vậy p( A) ( ) 70 5 = = = . n(Ω) 84 6
Câu 25: Cho M (1;3) và N ( 3;
− 5) . Phương trình đường trung trực của đoạn thẳng MN là đường thẳng nào dưới đây?
A. x + 2y − 7 = 0 . B. 2
− x + y − 6 = 0.
C. x + 2y + 7 = 0 . D. 2
− x + y + 6 = 0 . Lời giải  Ta có MN = ( 4;
− 2) , đặt n = ( 2 − ) ;1 .
Gọi I là trung điểm của MN , ta có I ( 1; − 4).
Đường trung trực của đoạn thẳng MN là đường thẳng đi qua điểm I và nhận vectơ n làm
vectơ pháp tuyến, có phương trình: 2 − (x + )
1 +1( y − 4) = 0 ⇔ 2
− x + y − 6 = 0 .
Câu 26: Trong mặt phẳng tọa độ (Oxy), cho các điểm A(1;2), B(2; ) 1
− . Đường thẳng ∆ đi qua điểm A
, sao cho khoảng cách từ điểm B đến đường thẳng ∆ nhỏ nhất có phương trình là?
A. 3x + y − 5 = 0 .
B. x − 3y + 5 = 0 .
C. 3x + y −1 = 0 .
D. x − 3y −1 = 0 . Lời giải  Ta có AB = (1; 3 − ) .
Khoảng cách từ điểm B đến đường thẳng ∆ nhỏ nhất khi và chỉ khi ∆ đi qua B , suy ra véc-tơ  
AB là véc-tơ chỉ phương của ∆, do đó đường thẳng ∆ có một véc-tơ pháp tuyến là n . ∆ (3; ) 1
Vậy phương trình đường thẳng cần tìm là 3(x − )
1 +1( y − 2) = 0 ⇔ 3x + y − 5 = 0.
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(1;2) , B(5;2), C (1; 3 − ) có phương trình là. A. 2 2
x + y + 6x + y −1 = 0 . B. 2 2
x + y − 6x − y −1 = 0 . C. 2 2
x + y − 6x + y −1 = 0 . D. 2 2
x + y + 6x − y −1 = 0 . Lời giải
Gọi (C) là phương trình đường tròn đi qua ba điểm ,
A B,C với tâm I ( ; a b) Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 ⇒ (C) có dạng: 2 2
x + y − 2ax − 2by + c = 0 . Vì đường tròn (C) đi qua qua ba điểm , A B,C
nên ta có hệ phương trình: a = 3 1
 + 4 − 2a − 4b + c = 0  2
− a − 4b + c = 5 −     1
25 + 4 −10a − 4b + c = 0 ⇔  10
− a − 4b + c = 29 − ⇔ b  = − . 2 1  9 2a 6b c 0  2a 6b c 10  + − + + = − + + = −   c = 1 − 
Vậy phương trình đường tròn cần tìm là 2 2
x + y − 6x + y −1 = 0 .
Câu 28: Cho đường thẳng ∆ :3x − 4y −19 = 0 và đường tròn (C) (x − )2 + ( y − )2 : 1 1 = 25 . Biết đường
thẳng ∆ cắt (C) tại hai điểm phân biệt A và B , khi đó độ dài đọan thẳng AB là A. 6. B. 3. C. 4. D. 8. Lời giải Từ 3 19
∆ :3x − 4y −19 = 0 ⇒ y = x − ( ) 1 . 4 4 Thế ( ) 1 vào (C) ta được 2 (x )2  3 23 1 x  − + − =   25  4 4  x =1 25 2 85 145 x x 0  ⇔ − + = ⇔ 29 . 16 8 16 x =  5
+) x = ⇒ y = − ⇒ A − A 1 A 4 (1; 4). +) 29 2 29 2 x y B  = ⇒ = − ⇒ − B B  ; . 5 5  5 5  2 2 Độ dài đoạn thẳng 29   2 AB  1 4 = − + − + =     6 .  5   5  2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 9
tiêu điểm có giá trị tuyệt đối bằng A. 8 . B. 6 . C. 4 . D. 5. Lời giải 2 2
Gọi F và F là hai tiêu điểm của ( ) : x y H −
= 1, a > 0,b > 0 . 2 2 ( ) 1 2 a b
Điểm M ∈(H ) ⇔ MF − MF = 2a . 1 2 2 2
Từ phương trình ( ) : x y H − = 1 suy ra 2
a =16 ⇒ a = 4,(a > 0) . 16 9
Vậy hiệu các khoảng cách từ mỗi điểm M nằm trên (H ) đến hai tiêu điểm có giá trị tuyệt đối
là MF − MF = 2a = 8. 1 2
Câu 30: Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món, 1 loại quả tráng
miệng trong 5 loại quả tráng miệng và một loại nước uống trong 3 loại nước uống. Có bao nhiêu cách chọn thực đơn? A. 100. B. 15. C. 75. D. 25. Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Chọn 1 món ăn trong 5 món: Có 5 cách chọn.
Chọn 1 loại quả tráng miệng trong 5 loại quả tráng miệng: Có 5 cách chọn.
Chọn 1 loại nước uống trong 3 loại nước uống: Có 3 cách chọn.
Theo quy tắc nhân, có 5.5.3 = 75 cách chọn thực đơn gồm 1 món ăn, 1 loại quả tráng miệng và 1 loại nước uống.
Câu 31: Số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh ngồi một ghế là A. 6 C . B. 6!. C. 6 A . D. 10 6 . 10 10 Lời giải
Mỗi cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh
ngồi một ghế là một chỉnh hợp chập 6 của 10.
Vậy số cách sắp xếp 6 học sinh ngồi vào 6 trong 10 ghế trên một hàng ngang sao cho mỗi học sinh ngồi một ghế là 6 A . 10
Câu 32: Mười hai đường thẳng có nhiều nhất bao nhiêu giao điểm? A. 12. B. 66 . C. 132. D. 144. Lời giải
Để được nhiều giao điểm nhất thì mười hai đường thẳng này phải đôi một cắt nhau tại các điểm phân biệt. Như vậy có 2 C = 66 . 12
Câu 33: Thầy X có 15 cuốn sách gồm 4 cuốn sách toán, 5 cuốn sách lí và 6 cuốn sách hóa. Các cuốn
sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học
sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn. A. 5 . B. 661 . C. 660 . D. 6 . 6 715 713 7 Lời giải
Gọi A là biến cố “Số cuốn sách còn lại của thầy X có đủ 3 môn”, suy ra A là biến cố “Số cuốn
sách còn lại của thầy X không có đủ 3 môn”= “Thầy X đã lấy hết số sách của một môn học”.
Số phần tử của không gian mẫu là: n(Ω) 8 = C = 6435 15 661 n( A) 4 4 5 3 6 2
= C .C + C .C + C .C = 486 ⇒ P( A) 54 =
⇒ P( A) =1− P( A) = . 4 11 5 10 6 9 715 715
Câu 34: Một hộp chứa 11 viên bi được đánh số thứ tự từ 1 đến 11. Chọn ngẫu nhiên 3 viên bi rồi cộng
các số trên 3 viên bi đó với nhau. Xác suất để kết quả thu được là số chẵn bằng A. 17 . B. 16 . C. 19 . D. 23 . 33 33 33 33 Lời giải
Không gian mẫu có số phần tử là: 3 n(Ω) = C . 11
Gọi A là biến cố: “Tổng các số trên 3 viên bi là số chẵn”
TH1: 3 viên bi được chọn đều được đánh số chẵn, có 3 C cách chọn 5
TH2: 3 viên bi được chọn có 2 viên được đánh số lẻ và 1 viên được đánh số chẵn, có 2 1 C .C 6 5 Ta có: 3 2 1 n( )
A = C + C .C 5 6 5 n( A) 3 2 1 + Vậy xác suất cần tìm: C C .C 17 5 6 5 P( ) A = = = . n(Ω) 3 C 33 11 Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 35: Một hộp chứa 5 bi xanh, 4 bi đỏ. Chọn ngẫu nhiên 2 bi từ hộp này. Xác suất để chọn được 2 bi cùng màu là A. 2 . B. 1 . C. 5 . D. 4 . 9 9 9 9 Lời giải
+ Số phần tử của không gian mẫu là: n(Ω) 2 = C . 9
+ Gọi biến cố A : “ hai viên bi được chọn cùng màu”.
Ta có: n( A) 2 2 = C + C . 5 4 2 2 n A C +
Vậy xác suất biến cố là P( A) ( ) C 4 5 4 = . n(Ω) = = 2 C 9 9
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu sô tự nhiên gồm 6 chữ số khác nhau trong đó có 3 chữ số chẵn và 3 chữ số lẻ? Lời giải
Gọi A = {0;1;2;3;4;5;6;7;8; }
9 . Coi việc lập số có 6 chữ số như là sắp xếp các chữ số vào một dãy 6 ô trống. Có 3
C cách lấy ra 3 chữ số lẻ và có 3
A cách sắp xếp 3 chữ số này vào dãy 6 ô trống. Có 3 A cách 5 6 5
sắp xếp 3 chữ số chẵn vào 3 ô trống còn lại. Như vậy có 3 3 3
C .A .A = 72000 dãy có 6 chữ số gồm 5 6 5
3 số chẵn, 3 số lẻ, kể cả trường hợp số 0 đứng đầu.
Xét trường hợp số 0 đứng đầu. Có 3
C cách lấy ra 3 chữ số lẻ và có 3
A cách sắp xếp 3 chữ số này 5 5 vào dãy 5 ô trống. Có 2
A cách sắp xếp 2 chữ số chẵn vào 2 ô trống còn lại. Như vậy có 4 3 3 2
C .A .A = 7200 dãy có 6 chữ số có 0 đứng đầu, gồm 3 số chẵn, 3 số lẻ. 5 5 4
Từ đó có 72000 − 7200 = 64800 số thỏa mãn yêu cầu. x =1− 3t
Câu 37: Trong mặt phẳng (Oxy) cho điểm M (2;4) và d : 
.Viết phương trình đường thẳng song y = 2 + t
song với đường thẳng d và cách điểm M một khoảng bằng 10 . Lời giải
Xác định được véc tơ chỉ phương của đường thẳng d : u = − d ( 3;1)
Suy ra VTTP : n = d (1;3)
Suy ra VTTP : n = n = d ∆ (1;3)
PT ĐT ∆ có dạng: x + 3y + c = 0,c ≠ 7 − 2 + 3.4 + c d(M ,∆) = = 10 2 2 1 + 3 c = 4 − 14 + c =10 ⇔  c = 24 −
Vậy có 2 đường thẳng thỏa mãn : x + 3y − 4 = 0; x + 3y − 24 = 0
Câu 38: Cho tập hợp X = {0,1,2,3,4,5,6, }
7 . Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một
khác nhau được lập từ tập hợp X . Chọn ngẫu nhiên một số từ S . Tính xác suất để chọn được số chia hết cho 5. Lời giải
Số các số tự nhiên có 5 chữ số đôi một khác nhau được lập từ X là n(Ω) 4 = 7.A = 5880 số. 7 Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Gọi A là biến cố chọn đượcsố chia hết cho 5 từ S .
Trường hợp 1: số có chữ số tận cùng bằng 5. Khi đó, ta có 3
6.A số thoả yêu cầu bài toán. 6
Trường hợp 2: số có chữ số tận cùng bằng 0. Khi đó, ta có 4
A số thoả yêu cầu bài toán. 7
Áp dụng quy tắc cộng ta có n( A) 3 4
= 6.A + A =1560. 6 7 n A
Suy ra xác suất của biến cố 13
A là P( A) ( ) = = . n(Ω) 49 2 2
Câu 39: Trong hệ trục tọa độ Oxy , cho Elip ( ): x y E +
=1, F , F là hai tiêu điểm, hoành độ của F 25 16 1 2 1
âm. Điểm M thuộc (E) sao cho MF = 2MF 1
2 . Hoành độ điểm M là: Lời giải
Ta có a = 5 , b = 4 và c = 3
Với điểm M (x ; y ∈ E 0 0 ) ( )
+) MF + MF = 2a 1 1 2 ( ) +) 2 2
MF − MF =  x + c + y − 0  −  x − c + y − 0  = 4cx 1 2 ( 0 )2 ( )2 ( 0 )2 ( )2 0     mà 2 2
MF − MF = MF − MF MF + MF 2c ⇒ MF − MF = x 1 2 ( 1 2 ) ( 1 2 ) 1 2 0 ac
MF = a + x  1 0 Từ và suy ra:  ac
MF = a − x 2 0  a
Nên theo yêu cầu bài toán ta có: 3  3  25
5 + x = 25− x ⇒  x = . 0 0 0 5  5  9
---------- HẾT ---------- Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 06
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).   
Câu 1: Cho hai véctơ a và b đều khác véctơ 0 . Khẳng định nào sau đây đúng?           A. .
a b = a . b . B. .
a b = a . b .cos(a,b).             C. . a b = .
a b .cos(a,b) . D. .ab = a . b .sin(a,b) .
Câu 2: Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001. A. 5,25. B. 5,24. C. 5,246. D. 5,2
Câu 3: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
160 178 150 164 168 176 156 172
Các tứ phân vị của mẫu số liệu là
A. Q =158;Q =164;Q =174 .
B. Q =158;Q =166;Q =174 . 1 2 3 1 2 3
C. Q =160;Q =168;Q =176 .
D. Q =150;Q =164;Q =178 . 1 2 3 1 2 3
Câu 4: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của Bình:
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu lần lượt là
A. R = 8 và ∆ = .
B. R =10 và ∆ = . Q 3,5 Q 4
C. R = 8 và ∆ =
. D. R =10 và ∆ = . Q 4 Q 3,5
Câu 5: Chọn khẳng định đúng. Số liệu càng phân tán thì
A. Phương sai và độ lệch chuẩn càng lớn.
B. Phương sai và độ lệch chuẩn càng nhỏ.
C. Phương sai và độ lệch chuẩn bằng nhau.
D. Phương sai bằng số trung bình cộng.
Câu 6: Trong hệ tọa độ Oxy , cho A(2; 5), B(1; )
1 , C (3; 3) . Tìm tọa độ đỉểm E sao cho   
AE = 3AB − 2AC A. (3; − 3) . B. ( 3 − ; 3) . C. ( 3 − ; − 3) . D. ( 2; − − 3).
Câu 7: Bạn A đo chiều dài của một sân bóng ghi được 250 ± 0,2m . Bạn B đo chiều cao của một cột cờ
được 15 ± 0,1m . Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong
phép đo của bạn đó là bao nhiêu?
A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.
B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.
C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.
D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%.
Câu 8: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn
vị: °C ). Phương sai và độ lệch chuẩn của mẫu số liệu là Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 2
S = 7,61;S ≈ 2,76 B. 2
S = 7;S ≈ 2,646 . C. 2
S = 7,7;S ≈ 2,775 . D. 2
S = 7,52;S ≈ 2,742 . 
Câu 9: Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u = ( 1; − 3) là x = 2 − tx = 2 + 3tx = 1 − + 2tx = 1 − −5t A.
(t ∈). B.
(t ∈) . C.
(t∈) . D.  (t∈). y = 5 − + 3ty = 5 − − ty = 3−5ty = 3+ 2t
Câu 10: Viết phương trình tổng quát của đường thẳng đi qua 2 điểm A(3 ;− ) 1 và B(1 ; 5)
A. 3x − y − 8 = 0
B. 3x + y −8 = 0 C. 3
− x − y − 8 = 0 D. 3x − y + 8 = 0
Câu 11: Tính góc giữa hai đường thẳng d : 2x − y −10 = 0 và d : x −3y + 9 = 0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 135 .
Câu 12: Cho 2 đường thẳng d :mx −(m − ) 2
1 y + 4 − m = 0 và d : m + 3 x + y − 3m −1 = 0. Tìm giá trị 2 ( ) 1
của m để hai đường thẳng vuông góc với nhau. A. 2 . B. 0 . C. 1. D. 1 − .
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, phương trình nào sau đây là phương trình đường tròn? A. 2 2
x + 2y − 4 x + 2y −1 = 0 . B. 2 2 x + y + 6 = 0 . C. 2 2
x + y − 4 xy − 2y +10 = 0 . D. 2 2
x + y − 4 x + 6y −12 = 0 .
Câu 14: Đường tròn (C) có tâm I ( 2;
− 3) và đi qua M (2; 3
− ) có phương trình là:
A. (x + )2 + ( y − )2 2 3 = 52 . 2 2
B. (x + 2) + ( y −3) = 52 . C. 2 2
x + y + 4x − 6y −57 = 0. D. 2 2
x + y + 4x + 6y −39 = 0.
Câu 15: Phương trình nào sau đây là phương trình chính tắc của đường parabol? A. 2 x = 2y . B. 2 y = 6x . C. 2 y = 4 − x . D. 2 y = 8 − x .
Câu 16: Tổ 1 của lớp 10a1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1 bạn
học sinh của tổ 1 đi trực vệ sinh. Hỏi có bao nhiêu cách chọn. A. 15 . B. 5 3 . C. 8 . D. 3 5
Câu 17: Bình có 5 cái áo khác nhau, 4 chiếc quần khác nhau, 3 đôi giầy khác nhau và 2 chiếc mũ khác
nhau. Số cách chọn một bộ gồm quần, áo, giầy và mũ của Bình là A. 120. B. 60. C. 5. D. 14.
Câu 18: Số cách sắp xếp 3 học sinh nam và 2 học sinh nữ vào một bàn dài có 5 ghế ngồi là A. 3!.2!. B. 5!. C. 3!.2!.2!. D. 5.
Câu 19: Số chỉnh hợp chập 2 của 5 phần tử bằng Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 120 . B. 7 . C. 10 . D. 20 .
Câu 20: Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động,
trong đó có đúng 2 học sinh nam? A. 2 4 C + C . B. 2 4 C .C . C. 2 4 A .A . D. 2 4 C .C . 6 9 6 9 6 9 9 6
Câu 21: Viết khai triển theo công thức nhị thức Niu-tơn ( − )5 2 x y . A. 10 8 6 2 4 3 2 4 5
x − 5x y +10x y −10x y + 5x y − y . B. 10 8 6 2 4 3 2 4 5
x − 5x y −10x y −10x y − 5x y + y . C. 10 8 6 2 4 3 2 4 5
x + 5x y +10x y +10x y + 5x y + y . D. 10 8 6 2 4 3 2 4 5
x + 5x y −10x y +10x y − 5x y + y .
Câu 22: Từ một hộp chứa sáu quả cầu trắng và ba quả cầu đen, lấy ngẫu nhiên đồng thời ba quả. Tính xác
suất sao cho lấy được ba quả cùng màu A. 1. B. 1 . C. 3. D. 4 . 4
Câu 23: Từ một hộp chứa 15 quả cầu gồm 10 quả màu đỏ và 5 quả màu xanh, lấy ngẫu nhiên đồng thời
hai quả. Xác suất để lấy được hai quả có màu khác nhau là 10 2 1 3 A. . B. . C. . D. . 21 21 7 7
Câu 24: Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng A. 3 . B. 1 . C. 1 . D. 3 . 20 20 3 10
Câu 25: Cho 2 điểm A(1;2), B(3;4). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB .
A. x + y + 5 = 0.
B. x − y −5 = 0.
C. 2x + 2y − 5 = 0.
D. x + y −5 = 0.
Câu 26: Trong mặt phẳng Oxy , đường thẳng ∆ song song với đường thẳng d : x − 2y + 5 = 0 và cách điểm M (1; 2
− ) một khoảng bằng 2 5 có phương trình là
A. x − 2y −15 = 0.
B. x − 2y −15 = 0 hoặc x − 2y + 5 = 0.
C. x − 2y +10 = 0 .
D. x − 2y −10 = 0 hoặc x − 2y +10 = 0 .
Câu 27: Trong hệ trục tọa độ Oxy , cho đường tròn (C) đi qua hai điểm A(1;2), B(3,4) và tiếp xúc với
đường thẳng ∆ :3x + y − 3 = 0 , biết tâm của (C) có tọa độ là những số nguyên. Phương trình
đường tròn (C) là A. 2 2
x y 3x7y 12  0. B. 2 2
x y 6x4y 5  0. C. 2 2
x y 8x2y 7  0. D. 2 2
x y 2x8y  20  0.
Câu 28: Trong mặt phẳng tọa độ Oxy cho đường tròn (C ) có tâm I (1;− )
1 bán kính R = 5 . Biết rằng
đường thẳng (d ) :3x − 4y +8 = 0 cắt đường tròn (C ) tại hai điểm phân biệt , A B . Tính độ dài đoạn thẳng AB . A. AB = 8 . B. AB = 4 . C. AB = 3. . D. AB = 6.
Câu 29: Phương trình chính tắc của elip đi qua điểm (5;0)và có tiêu cự bằng 2 5 là 2 2 2 2 2 2 2 2
A. x + y = 1.
B. x + y = 1.
C. x − y = 1.
D. x − y = 1. 25 5 25 20 25 5 25 20
Câu 30: Có 9 cặp vợ chồng đi dự tiệc. Chọn một người đàn ông và một người phụ nữ trong bữa tiệc sao
cho hai người đó không là vợ chồng. Số cách chọn là A. 81. B. 64 . C. 9. D. 72 . Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 31: Lớp 12A có 8
32 học sinh. Giáo viên chủ nhiệm muốn lập một ban cán sự của lớp gồm một lớp
trưởng, một bí thư, một lớp phó học tập và một lớp phó văn thể. Số cách lập nhóm ban cán sự là A. 4 A . B. A . D. 4 C . 28 4!. C. 432 32
Câu 32: Số đường chéo của đa giác đều có 20 cạnh là: A. 170. B. 190. C. 360. D. 380.
Câu 33: Để kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để phân
tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là A. 3 . B. 1 . C. 3 . D. 1 . 11 110 55 22
Câu 34: Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu đỏ bằng: A. 5 . B. 2 . C. 7 D. 1 . 12 7 44 22
Câu 35: Một hộp phấn có 4 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên đồng thời 2 viên phấn
từ hộp trên. Tính xác suất để lấy được 2 viên phấn xanh. A. 4 . B. 3 . C. 1 . D. 2 . 7 7 7 7
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có hai học sinh lớp ,
A ba học sinh lớp B và bốn học sinh lớp C xếp thành một hàng ngang sao
cho giữa hai học sinh lớp A không có học sinh nào lớp .
B Hỏi có bao nhiêu cách xếp hàng như vậy?
Câu 37: Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C ( 1;
− 0) .Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần
diện tích tam giác MAC .
Câu 38: Một lớp có 35 đoàn viên trong đó có 15 nam và 20 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp
để tham dự hội trại 26 tháng 3. Tính xác suất để trong 3 đoàn viên được chọn có cả nam và nữ. Câu 39: Cho parabol 2
(P) : y = 4x và hai điểm ( A 0; 4 − ), B( 6;
− 4) . C là điểm trên (P) sao cho tam giác
ABC có diện tích bé nhất. Tìm tọa độ điểm C .
---------- HẾT ---------- Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).   
Câu 1: Cho hai véctơ a và b đều khác véctơ 0 . Khẳng định nào sau đây đúng?           A. .
a b = a . b . B. .
a b = a . b .cos(a,b).             C. . a b = .
a b .cos(a,b) . D. .ab = a . b .sin(a,b) . Lời giải
Theo định nghĩa tích vô hướng của hai véctơ.
Câu 2: Tìm số gần đúng của a = 5,2463 với độ chính xác d = 0,001. A. 5,25. B. 5,24. C. 5,246. D. 5,2 Giải
Vì độ chính xác đến hàng phần nghìn nên ta quy tròn a đến hàng phần trăm, vậy số quy tròn của a là 5,25.
Câu 3: Bảng sau đây cho biết chiều cao của một nhóm học sinh:
160 178 150 164 168 176 156 172
Các tứ phân vị của mẫu số liệu là
A. Q =158;Q =164;Q =174 .
B. Q =158;Q =166;Q =174 . 1 2 3 1 2 3
C. Q =160;Q =168;Q =176 .
D. Q =150;Q =164;Q =178 . 1 2 3 1 2 3 Lời giải
Sắp xếp các giá trị này theo thứ tự không giảm
150 156 160 164 168 172 176 178
Vì n = 8 là số chẵn nên Q là số trung bình cộng của hai giá trị chính giữa: 2 Q = 164 +168 : 2 =166 2 ( )
Ta tìm Q là trung vị của nửa số liệu bên trái Q 1 2 150 156 160 164
và tìm được Q = 156 +160 : 2 =158 1 ( )
Ta tìm Q là trung vị của nửa số liệu bên phải Q 3 2 168 172 176 178
và tìm được Q = 172 +176 : 2 =174 . 3 ( )
Câu 4: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của Bình:
Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu lần lượt là
A. R = 8 và ∆ = .
B. R =10 và ∆ = . Q 3,5 Q 4
C. R = 8 và ∆ =
. D. R =10 và ∆ = . Q 4 Q 3,5 Lời giải
Sắp xếp mẫu số liệu theo thứ tự không giảm:
Khoảng biến thiên: R =14 − 6 = 8 .
Mẫu số liệu có 16 giá trị nên ta có 9 10 Q + = = 9,5 ; 8 8 Q + = = 8 và 11 12 Q + = = 11,5. 2 2 1 2 3 2 Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Vậy khoảng tứ phân vị là ∆ = Q − Q = − = . Q 11,5 8 3,5 3 1
Câu 5: Chọn khẳng định đúng. Số liệu càng phân tán thì
A. Phương sai và độ lệch chuẩn càng lớn.
B. Phương sai và độ lệch chuẩn càng nhỏ.
C. Phương sai và độ lệch chuẩn bằng nhau.
D. Phương sai bằng số trung bình cộng. Lời giải Dựa vào khái niệm.
Câu 6: Trong hệ tọa độ Oxy , cho A(2; 5), B(1; )
1 , C (3; 3) . Tìm tọa độ đỉểm E sao cho   
AE = 3AB − 2AC A. (3; − 3) . B. ( 3 − ; 3) . C. ( 3 − ; − 3) . D. ( 2; − − 3). Lời giải Chọn C Gọi E ( ; x y). Ta có         
AE = 3AB − 2AC ⇔ AE − AB = 2( AB − AC) ⇔ BE = 2CB (  − = −  = −
x − y − ) = (− − ) x 1 4 x 3 1; 1 2 2; 2 ⇔  ⇔ y 1 4  − = − y = 3 − Vậy E ( 3 − ; −3) .
Câu 7: Bạn A đo chiều dài của một sân bóng ghi được 250 ± 0,2m . Bạn B đo chiều cao của một cột cờ
được 15 ± 0,1m . Trong 2 bạn A và B, bạn nào có phép đo chính xác hơn và sai số tương đối trong
phép đo của bạn đó là bao nhiêu?
A. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,08%.
B. Bạn B đo chính xác hơn bạn A với sai số tương đối là 0,08%.
C. Hai bạn đo chính xác như nhau với sai số tương đối bằng nhai là 0,08%.
D. Bạn A đo chính xác hơn bạn B với sai số tương đối là 0,06%. Giải
Phép đo của bạn A có sai số tương đối 0,2 δ ≤ = 0,0008 = 0,08% 1 250
Phép đo của bạn B có sai số tương đối 0,1 δ ≤ = 0,0066 = 0,66% 2 15
Như vậy phép đo của bạn A có độ chính xác cao hơn.
Câu 8: Biểu đồ sau ghi lại nhiệt độ lúc 12 giờ trưa tại một trạm quan trắc trong 10 ngày liên tiếp (đơn
vị: °C ). Phương sai và độ lệch chuẩn của mẫu số liệu là A. 2
S = 7,61;S ≈ 2,76 B. 2
S = 7;S ≈ 2,646 . Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 C. 2
S = 7,7;S ≈ 2,775 . D. 2
S = 7,52;S ≈ 2,742 . Lời giải
Dùng máy tính.
Câu 9: Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u = ( 1; − 3) là x = 2 − tx = 2 + 3t A.
(t ∈). B.  (t ∈) . y = 5 − + 3ty = 5 − − tx = 1 − + 2tx = 1 − − 5t C.
(t ∈) . D.  (t ∈) . y = 3− 5ty = 3+ 2t Lời giải
Phương trình tham số của đường thẳng đi qua điểm M (2;−5) và có vectơ chỉ phương u = ( 1; − 3) x = 2 − t có dạng là  (t ∈) y = 5 − + 3t
Câu 10: Viết phương trình tổng quát của đường thẳng đi qua 2 điểm A(3 ;− ) 1 và B(1 ; 5)
A. 3x − y − 8 = 0
B. 3x + y −8 = 0 C. 3
− x − y − 8 = 0 D. 3x − y + 8 = 0 Lời giải
đường thẳng đi qua 2 điểm A(3 ;− )
1 và B(1 ; 5) có véc tơ chỉ phương là   AB = ( 2;
− 6) ⇒ n = (6;2) = 2( ; 3 )
1 ⇔ 3x − y − 8 = 0
⇒ 3(x − 3) + y +1 = 0
Câu 11: Tính góc giữa hai đường thẳng d : 2x − y −10 = 0 và d : x −3y + 9 = 0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 135 . Lời giải Ta có  
d : 2x − y −10 = 0 → n = 2; 1 − + − − 1 1 ( ) ϕ= 2.1 1 . 3 d ;d ( ) ( ) ( 1 1 2 )   →cosϕ = = 
d : x − 3y + 9 = 0 → n = 1; 3  − + − + − 2 2 2 ( ) 2 2 ( )2 2 1 . 1 ( 3)2 → ϕ = 45 .
Câu 12: Cho 2 đường thẳng d :mx −(m − ) 2
1 y + 4 − m = 0 và d : m + 3 x + y − 3m −1 = 0. Tìm giá trị 2 ( ) 1
của m để hai đường thẳng vuông góc với nhau. A. 2 . B. 0 . C. 1. D. 1 − . Lời giải Điều kiện: 2 m + (−m + )2 1 ≠ 0 và (m + )2 3 +1 ≠ 0 . 
Véc tơ pháp tuyến của d = − + 1 là n ; m m 1 . 1 ( ) 
Véc tơ pháp tuyến của d = + 2 là n m 3;1 . 2 ( )
Hai đường thẳng vuông góc khi và chỉ khi n .n = 0 ⇔ m(m + 3) + (−m + ) 1 = 0 1 2 ⇔ (m + )2 1 = 0 ⇔ m = 1 − Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 13: Trong mặt phẳng với hệ tọa độ Oxy, phương trình nào sau đây là phương trình đường tròn? A. 2 2
x + 2y − 4 x + 2y −1 = 0 . B. 2 2 x + y + 6 = 0 . C. 2 2
x + y − 4 xy − 2y +10 = 0 . D. 2 2
x + y − 4 x + 6y −12 = 0 . Lời giải
Phương án A loại vì hệ số của 2 x và 2
y không bằng nhau. Phương án B loại vì 2 2
a + b − c = 6 − < 0 .
Phương án C loại vì có số hạng chứa xy .
Phương án D nhận vì phương trình 2 2
x + y − 4 x + 6y −12 = 0 ⇔ (x − 2)2 + ( y + 3)2 = 25là pt
đường tròn có tâm I (2; 3
− ) , bán kính R = 5.
Câu 14: Đường tròn (C) có tâm I ( 2;
− 3) và đi qua M (2; 3
− ) có phương trình là:
A. (x + )2 + ( y − )2 2 3 = 52 . 2 2
B. (x + 2) + ( y −3) = 52 . C. 2 2
x + y + 4x − 6y −57 = 0. D. 2 2
x + y + 4x + 6y −39 = 0. Lời giải  2 R = IM = 4 + ( 6 − )2 = 52 .
Phương trình đường tròn tâm I ( 2;
− 3) , R = 52 là: ( x + )2 + ( y − )2 2 3 = 52.
Câu 15: Phương trình nào sau đây là phương trình chính tắc của đường parabol? A. 2 x = 2y . B. 2 y = 6x . C. 2 y = 4 − x . D. 2 y = 8 − x .
Câu 16: Tổ 1 của lớp 10a1 có 3 học sinh nam và 5 học sinh nữ. Giáo viên chủ nhiệm muốn chọn 1 bạn
học sinh của tổ 1 đi trực vệ sinh. Hỏi có bao nhiêu cách chọn. A. 15 . B. 5 3 . C. 8 . D. 3 5 Lời giải
Th1: Chọn 1 học sinh nam có 3 cách chọn
Th2: Chọn 1 học sinh nữ có 5 cách chọn
Vậy có 3  5  8 cách chọn.
Câu 17: Bình có 5 cái áo khác nhau, 4 chiếc quần khác nhau, 3 đôi giầy khác nhau và 2 chiếc mũ khác
nhau. Số cách chọn một bộ gồm quần, áo, giầy và mũ của Bình là A. 120. B. 60. C. 5. D. 14. Lời giải
Để chọn được bộ quần áo theo yêu cầu bài toán phải thực hiện liên tiếp các hành động:
+ Hành động 1: Chọn chiếc áo: Có 5 cách chọn.
+ Hành động 2: Chọn chiếc quần: Có 4 cách chọn.
+ Hành động 3: Chọn đôi giầy: Có 3 cách chọn.
+ Hành động 4: Chọn chiếc mũ: Có 2 cách chọn.
Vậy theo qui tắc nhân, có 5.4.3.2 =120 cách chọn.
Câu 18: Số cách sắp xếp 3 học sinh nam và 2 học sinh nữ vào một bàn dài có 5 ghế ngồi là A. 3!.2!. B. 5!. C. 3!.2!.2!. D. 5. Lời giải
Mỗi cách xếp 3 học sinh nam và 2 học sinh nữ vào một bàn dài có 5 ghế ngồi là 1 hoán vị của
5 phần tử. Vậy có 5! cách sắp xếp.
Câu 19: Số chỉnh hợp chập 2 của 5 phần tử bằng A. 120 . B. 7 . C. 10 . D. 20 . Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số chỉnh hợp chập 2 của 5 phần tử là 2 A = 20 . 5
Câu 20: Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động,
trong đó có đúng 2 học sinh nam? A. 2 4 C + C . B. 2 4 C .C . C. 2 4 A .A . D. 2 4 C .C . 6 9 6 9 6 9 9 6 Lời giải
Trong 6 học sinh phải có 2 học sinh nam và 4 học sinh nữ.
+ Chọn 2 học sinh nam có 2 C cách. 6
+ Chọn 4 học sinh nữ có 4 C cách. 9
Theo quy tắc nhân, ta có 2 4
C .C cách chọn thỏa mãn yêu cầu. 6 9
Câu 21: Viết khai triển theo công thức nhị thức Niu-tơn ( − )5 2 x y . A. 10 8 6 2 4 3 2 4 5
x − 5x y +10x y −10x y + 5x y − y . B. 10 8 6 2 4 3 2 4 5
x − 5x y −10x y −10x y − 5x y + y . C. 10 8 6 2 4 3 2 4 5
x + 5x y +10x y +10x y + 5x y + y . D. 10 8 6 2 4 3 2 4 5
x + 5x y −10x y +10x y − 5x y + y . Lời giải Ta có: ( 2x − y)5 2
= x + (−y) 5 0 10 1 8
 = C x + C x (−y)1 2 6 + C x (−y)2 3 4 + C x (−y)3 4 2 + C x (−y)4 5 + C −y   5 5 5 5 5 5 ( )5 Hay (x − y)5 2 10 8 6 2 4 3 2 4 5
= x − 5x y +10x y −10x y + 5x y − y .
Câu 22: Từ một hộp chứa sáu quả cầu trắng và ba quả cầu đen, lấy ngẫu nhiên đồng thời ba quả. Tính xác
suất sao cho lấy được ba quả cùng màu A. 1. B. 1 . C. 3. D. 4 . 4 Lời giải
Gọi A là biến cố “lấy ba quả cầu cùng màu”. Ta có n(Ω) 3 = C = 84 . 9
Lấy ba quả cầu cùng màu: n( A) 3 3 = C + C = 21 6 3 .
Xác suất lấy được ba quả cầu cùng màu là n( ) A 1 P( ) A = = . n(Ω) 4
Câu 23: Từ một hộp chứa 15 quả cầu gồm 10 quả màu đỏ và 5 quả màu xanh, lấy ngẫu nhiên đồng thời
hai quả. Xác suất để lấy được hai quả có màu khác nhau là 10 2 1 3 A. . B. . C. . D. . 21 21 7 7 Lời giải
Không gian mẫu Ω : “lấy hai quả bất kì” ⇒ n(Ω) 2 = C . 15
Biến cố A : “lấy hai quả có màu khác nhau” ⇒ n( A) =10.5 = 50 . n A Vậy P( A) ( ) 10 = = . n(Ω) 21
Câu 24: Chọn ngẫu nhiên một số trong 20 số nguyên dương đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 3 . B. 1 . C. 1 . D. 3 . 20 20 3 10 Lời giải
n 20
A  3;6;9;12;15;1
8 n  A 6
P  n  A 6 3 A
n20 10
Câu 25: Cho 2 điểm A(1;2), B(3;4). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB .
A. x + y + 5 = 0.
B. x − y −5 = 0.
C. 2x + 2y − 5 = 0.
D. x + y −5 = 0. Lời giải
+ Giả sử ∆ là đường trung trực của AB ⇒ ∆ ⊥ AB tại trung điểm M của AB .  x + x A B x = =  M 2 + Tọa độ trung điểm 
M của AB là : 2  ⇒ M (2;3) . y + yA B y = = M 3  2  
+ Ta có AB = (2;2) = 2(1; ) 1 ⇒ n = ∆ (1; )1
Suy ra phương trình tổng quát đường trung trực ∆ của đoạn thẳng AB là:
x + y − 5 = 0.
Câu 26: Trong mặt phẳng Oxy , đường thẳng ∆ song song với đường thẳng d : x − 2y + 5 = 0 và cách điểm M (1; 2
− ) một khoảng bằng 2 5 có phương trình là
A. x − 2y −15 = 0.
B. x − 2y −15 = 0 hoặc x − 2y + 5 = 0.
C. x − 2y +10 = 0 .
D. x − 2y −10 = 0 hoặc x − 2y +10 = 0 . Lời giải
Vì ∆ song song với d : x − 2y + 5 = 0 nên phương trình của ∆ có dạng: x − 2y + c = 0 (c ≠ 5) + + Theo đề: ( ∆) 1 4 c d M ; = = 2 5 5  5 + c =10 c = 5 (l) ⇔ 5 + c =10 ⇔  ⇔  5 + c = 10 − c = 15 −  (n)
Vậy phương trình đường thẳng ∆ là: x − 2y −15 = 0
Câu 27: Trong hệ trục tọa độ Oxy , cho đường tròn (C) đi qua hai điểm A(1;2), B(3,4) và tiếp xúc với
đường thẳng ∆ :3x + y − 3 = 0 , biết tâm của (C) có tọa độ là những số nguyên. Phương trình
đường tròn (C) là A. 2 2
x y 3x7y 12  0. B. 2 2
x y 6x4y 5  0. C. 2 2
x y 8x2y 7  0. D. 2 2
x y 2x8y  20  0. Lời giải 
Ta có : AB = (2;2) ; đoạn AB có trung điểm M (2;3)
⇒ Phương trình đường trung trực của đoạn AB là d :x + y − 5 = 0.
Gọi I là tâm của (C) ⇒ I ∈d ⇒ I ( ;
a 5 − a),a ∈ .  Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 +
Ta có: R = IA = d (I ∆) = (a − )2 + (a − )2 2a 2 ; 1 3 =
⇔ a = 4 ⇒ I (4; ) 1 , R = 10. 10
Vậy phương trình đường tròn là: (x − )2 + ( y − )2 2 2 4
1 =10 ⇔ x + y −8x − 2y + 7 = 0.
Câu 28: Trong mặt phẳng tọa độ Oxy cho đường tròn (C ) có tâm I (1;− )
1 bán kính R = 5 . Biết rằng
đường thẳng (d ) :3x − 4y +8 = 0 cắt đường tròn (C ) tại hai điểm phân biệt , A B . Tính độ dài đoạn thẳng AB . A. AB = 8 . B. AB = 4 . C. AB = 3. . D. AB = 6. Lời giải A H B I
Gọi H là trung điểm của đoạn thẳng AB . Ta có IH ⊥ AB và − − +
IH = d (I AB ) 3.1 4.( ) 1 8 ; = = 3 . 2 3 + ( 4 − )2
Xét tam giác vuông AHI ta có: 2 2 2 2 2
HA = IA − IH = 5 − 3 = 16 ⇒ HA = 4 ⇒ AB = 2HA = 8
Câu 29: Phương trình chính tắc của elip đi qua điểm (5;0)và có tiêu cự bằng 2 5 là 2 2 2 2 2 2 2 2
A. x + y = 1.
B. x + y = 1.
C. x − y = 1.
D. x − y = 1. 25 5 25 20 25 5 25 20 Lời giải 2 2
Phương trình chính tắc của elip có dạng x + y = 1 (a > b > 0) . 2 2 a b 25 =1  2 2 aa = 25   Ta có 2 2c = 2 5 ⇒ c = 5 .  2 2 2  2
b = a − c b = 20    2 2
Vậy elip có phương trình chính tắc là x + y = 1. 25 20
Câu 30: Có 9 cặp vợ chồng đi dự tiệc. Chọn một người đàn ông và một người phụ nữ trong bữa tiệc sao
cho hai người đó không là vợ chồng. Số cách chọn là A. 81. B. 64 . C. 9. D. 72 . Lời giải
Chọn 1 người đàn ông trong 9 người đàn ông: có 9 cách.
Chọn 1 người phụ nữ trong 8 người phụ nữ không là vợ của người đàn ông đã chọn: có 8 cách
Theo quy tắc nhân: có 9.8 = 72 cách chọn. Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 31: Lớp 12A có 8
32 học sinh. Giáo viên chủ nhiệm muốn lập một ban cán sự của lớp gồm một lớp
trưởng, một bí thư, một lớp phó học tập và một lớp phó văn thể. Số cách lập nhóm ban cán sự là A. 4 A . B. A . D. 4 C . 28 4!. C. 432 32 Lời giải
Mỗi cách chọn 4 học sinh từ 32 học sinh của lớp 12A8 và phân 4 nhiệm vụ: Lớp trưởng, bí
thư, lớp phó học tập và lớp phó văn thể là một chỉnh hợp chập 4 của 32 phần tử.
Số cách chọn 4 học sinh từ 32 học sinh của lớp 12A8 và phân 4 nhiệm vụ: Lớp trưởng, bí
thư, lớp phó học tập và lớp phó văn thể là số chỉnh hợp chập 4 của 32 phần tử.
Vậy số cách lập nhóm ban cán sự là 4 A . 32
Câu 32: Số đường chéo của đa giác đều có 20 cạnh là: A. 170. B. 190. C. 360. D. 380. Lời giải
Đa giác đều có 20 cạnh nên có 20 đỉnh.
Từ 20 đỉnh của đa giác ta xác định được 2 C đoạn thẳng. 20
Qua 2 đỉnh bất kì của đa giác ta luôn xác định được một đoạn thẳng có thể là đường chéo hoặc là cạnh của đa giác đó.
Vậy số đường chéo của đa giác đều có 20 cạnh là 2 C − 20=170 . 20
Câu 33: Để kiểm tra chất lượng sản phẩm từ công ty sữa, người ta gửi đến bộ phận kiểm nghiệm 5 hộp
sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ngẫu nhiên 3 hộp để phân
tích mẫu. Xác suất để 3 hộp sữa được chọn có cả 3 loại là A. 3 . B. 1 . C. 3 . D. 1 . 11 110 55 22 Lời giải
Tổng số hộp sữa được gửi đến để kiểm nghiệm là 12 hộp sữa.
Chọn ngẫu nhiên 3 hộp sữa từ 12 hộp sữa thì mỗi một cách chọn là một tổ hợp chập 3 của 12
phần tử. Các trường hợp đồng khả năng xảy ra.
Số phần tử của không gian mẫu là: n(Ω) 3 = C = 220 . 12
Biến cố A : “3 hộp sữa được chọn có cả 3 loại”.
Như vậy sẽ chọn 1 hộp sữa cam, 1 hộp sữa dâu và 1 hộp sữa nho.
Số phần tử của biến cố A là: n( A) = 3.4.5 = 60 . n A 60 3
Xác suất của biến cố A là: P( A) ( ) = = = . n(Ω) 220 11
Câu 34: Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu đỏ bằng: A. 5 . B. 2 . C. 7 D. 1 . 12 7 44 22 Lời giải 3 n A C
Xác suất để lấy được 3 quả màu đỏ bằng: P( A) ( ) 5 1 = = = n(Ω) . 3 C 22 12
Câu 35: Một hộp phấn có 4 viên phấn trắng và 3 viên phấn xanh. Lấy ngẫu nhiên đồng thời 2 viên phấn
từ hộp trên. Tính xác suất để lấy được 2 viên phấn xanh. A. 4 . B. 3 . C. 1 . D. 2 . 7 7 7 7 Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số phần tử của không gian mẫu là n(Ω) 2 = C = 21. 7
Gọi A là biến cố: “ Chọn được 2 viên phấn xanh”.
Số phần tử của biến cố A là n( A) 2 = C = 3. 3 n A 3 1
Vậy xác suất chọn được 2 viên phấn xanh từ hộp trên là P( A) ( ) = = = . n(Ω) 21 7
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có hai học sinh lớp ,
A ba học sinh lớp B và bốn học sinh lớp C xếp thành một hàng ngang sao
cho giữa hai học sinh lớp A không có học sinh nào lớp .
B Hỏi có bao nhiêu cách xếp hàng như vậy? Lời giải
Xếp 3 học sinh lớp B có 3! cách xếp 1 B 2 B 3 B 4
Để giữa hai học sinh lớp A không có học sinh nào lớp B thì cả hai học sinh lớp A cùng được
xếp vào một vị trí trong 4 vị trí được đánh số ở trên nên có 2!.4 cách xếp
Xếp 4 học sinh lớp C vào cạnh các học sinh trên có 4 A cách. 9 Theo QTN có 4
3!.2!.4.A =145152 cách xếp thỏa đề. 9
Câu 37: Trên mặt phẳng tọa độ Oxy , cho tam giác ABC có tọa độ các đỉnh là A(2;3), B(5;0) và C ( 1;
− 0) .Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần
diện tích tam giác MAC . Lời giải Ta có 1 S = , 1 S = . ∆ d A CM CM ACM ( , ). ∆ d A BM BM ABM ( , ). 2 2
Theo bài ra ta có diện tích tam giác MAB bằng hai lần diện tích tam giác MAC . 1 ⇒ d ( A BM ) 1 , .BM = 2. d ( , A CM ).CM . 2 2 Mà d ( , A BM ) = d ( , A CM ) = d ( ,
A BC) nên ta có BM = 2.CM .  
Gọi M (x; y) thuộc cạnh BC 2 ⇒ BM = BC . 3   x =1
Ta có BM = (x −5; y ) , BC = ( 6; − 0) ⇒  ⇒ M (1;0) . y = 0
Câu 38: Một lớp có 35 đoàn viên trong đó có 15 nam và 20 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp
để tham dự hội trại 26 tháng 3. Tính xác suất để trong 3 đoàn viên được chọn có cả nam và nữ. Lời giải
Ta có: Gọi A là biến cố “trong 3 đoàn viên được chọn có cả nam và nữ”
Số cách chọn 3 đoàn viên trong 35 đoàn viên để tham dự đại hội là: 3 C35 n(Ω) Vậy = 3 C35
Trường hợp 1: trong 3 đoàn viên được chọn có 1 nam và 2 nữ có: 1 2 C .C 15 20
Trường hợp 2: trong 3 đoàn viên được chọn có 2 nam và 1 nữ có: 2 1 C .C 15 20
Vậy số cách chọn 3 đoàn viên có đủ cả nam và nữ là 1 2 C .C C .C 15 20 + 2 1 15 20 Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 n( A) 1 2 2 1
= C .C + C .C 15 20 15 20
Xác suất để trong 3 đoàn viên được chọn có cả nam và nữ là: 1 2 2 1 +
P( A) n( A) C .C C .C 90 15 20 15 20 = = = . n(Ω) 3 C 119 35 Câu 39: Cho parabol 2
(P) : y = 4x và hai điểm ( A 0; 4 − ), B( 6;
− 4) . C là điểm trên (P) sao cho tam giác
ABC có diện tích bé nhất. Tìm tọa độ điểm C . Lời giải   AB = ( 6;
− 8) , suy ra vectơ pháp tuyến của đường thẳng AB là n = (4;3). Phương trình đường
thẳng AB là 4x + 3y +12 = 0. Ta có 1 S
= CH AB . Do AB không đổi nên S
nhỏ nhất ⇔ CH nhỏ nhất. ABC . 2 ABC Gọi C ( ;
x y)∈(P) , ta có: 2 4x + 3y +12 y + 3y +12 CH = = 5 5 1 = (   y + y + ) 2 2 1  3  39 3 12 39 =  y + +   ≥ 5 5  2  4   20  Dấu " = "xảy ra 3 3 9
⇔ y + = 0 ⇔ y = − ⇒ x = 2 2 16  9 3 Do đó điểm C ;  − 
∈(P) thì diện tích tam giác ABC nhỏ nhất. 16 2 
---------- HẾT ---------- Page 14
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 07
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng Oxy , cho hình bình hành ABCD biết A(2; ) 1 , B(2;− ) 1 , C ( 2; − 3 − ) . Tọa độ
giao điểm hai đường chéo của hình bình hành ABCD là A. (2;0) . B. (2;2) . C. (0; 2 − ) . D. (0; ) 1 − .
Câu 2: Quy tròn số 12,4567 đến hàng phần trăm ta được số. A. 12,45 . B. 12,46 C. 12,457 D. 12,5
Câu 3: Tìm tứ phân vị của mẫu số liệu sau 3 4 6 7 8 9 10 12 13 16
A. Q = 5,Q = 8,5,Q =12 .
B. Q = 6,Q = 8,5,Q =12 . 1 2 3 1 2 3
C. Q = 6,Q = 8,5,Q =12,5 .
D. Q = 5,Q = 8,5,Q =12,5 . 1 2 3 1 2 3
Câu 4: Mẫu số liệu sau đây cho biết giá của một số loại giày trong cửa hàng
300 250300 360 350 650 450 500 300
Khoảng biến thiên của mẫu số liệu trên là A. 400 . B. 300. C. 650 . D. 250 .
Câu 5: Cho dãy số liệu thống kê: 1,2,3,4,5,6,7 . Phương sai của mẫu số liệu thống kê đã cho là A. 2 . B. 3. C. 4 . D. 1.      
Câu 6: Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 2a + 3b và a + (x + ) 1 b cùng
phương. Khi đó giá trị của x là A. 1 . B. 3 − . C. 1 − . D. 3 . 2 2 2 2
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là 996m  0,5m . Sai số tương đối
tối đa trong phép đo là bao nhiêu? A. 0,05% . B. 0,5% . C. 0,04%. D. 0,005%.
Câu 8: Để được cấp chứng chỉ môn Anh trình độ A của một trung tâm ngoại ngữ, học viên phải trải 2
qua 6 lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là 100 và phải đạt điểm trung bình
từ 70 điểm trở lên. Qua 5 lần thi Hoa đạt điểm trung bình là 64,5 điểm. Hỏi trong lần kiểm tra
cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ? A. 97,5. B. 92,5 . C. 95,5. D. 97,8.
Câu 9: Viết phương trình tổng quát của đường thẳng ∆ đi qua điểm A1; 
3 và có vectơ pháp tuyến n =(3;2)
A. 3x  2y9  0 .
B. 3x  2y6  0 . C. 3x  2y7  0 . D. 3x  2y8  0 .
Câu 10: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d cắt trục Ox , Oy lần lượt tại hai
điểm A(3;0) và B(0; 2
− ). Đường thẳng d có phương trình là A. x y − = 1 − . B. x y + = 1. C. x y − = 1. D. x y − = 0 . 3 2 2 − 3 3 2 3 2
Câu 11: Cho đường thẳng d : 2x + 3y +15 = 0 và d : x − 2y −3 = 0. Khẳng định nào sau đây đúng? 1 2 Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. d
d cắt nhau và không vuông góc với nhau. 1 và 2 B. d
d song song với nhau. 1 và 2 C. d d trùng nhau. 1 và 2 D. d
d vuông góc với nhau. 1 và 2
Câu 12: Xác định m để 2 đường thẳng d : x2y 3 0 và d: xmy3 0 vuông góc với nhau.
A. m  2. B. 1 m   .
C. m  2. D. 1 m  . 2 2
Câu 13: Tọa độ tâm I và bán kính R của đường tròn (C) (x + )2 2 : 1 + y = 8 là A. I ( 1; − 0), R = 8. B. I ( 1
− ;0), R = 64. C. I ( 1;
− 0), R = 2 2. D. I (1;0), R = 2 2.
Câu 14: Cho đường tròn có phương trình 2 2
x + y − 6x + 2y + 6 = 0 và điểm A(1;− ) 1 . Phương trình tiếp
tuyến của tại điểm A là A. y =1. B. x =1.
C. x = 2 . D. y = 2 . 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 16 9 A. F = 5; − 0 ; F = 5;0 . B. F = 0; 5 − ; F = 0;5 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
C. F = 0;− 7 ; F = 0; 7 .
D. F = − 7;0 ; F = 7;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
Câu 16: Có 8 quả ổi và 6 quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả ấy? A. 48. B. 24 . C. 14 . D. 18 .
Câu 17: Từ các chữ số 1;2;3;4;5, hỏi có thể lập được bao nhiêu số có hai chữ số khác nhau? A. 25 . B. 20 . C. 10. D. 9 .
Câu 18: Có bao nhiêu cách xếp 5 quyển sách gồm toán, lý, hóa, sinh, địa lên một kệ sách dài? A. 120. B. 60 . C. 48 . D. 24 .
Câu 19: Một câu lạc bộ có 20 thành viên. Số cách chọn một ban quản lí gồm 1 chủ tịch, 1phó chủ tịch, 1 thư kí là A. 13800. B. 6900 . C. 7200 . D. 6840 .
Câu 20: Số cách chọn 5 học sinh trong một lớp có 25 học sinh nam và 16 học sinh nữ là A. 5 5 C + C C A C 25 16 . B. 525. C. 541. D. 541.
Câu 21: Đa thức P(x) 5 4 3 2
= 32x −80x + 80x − 40x +10x −1 là khai triển của nhị thức nào? A. ( − )5 1 2x . B. ( + )5 1 2x . C. ( x − )5 2 1 . D. (x − )5 1 .
Câu 22: Gieo một đồng xu cân đối và đồng chất liên tiếp bốn lần. Gọi B là biến cố “Kết quả bốn lần gieo
là như nhau”. Xác định biến cố B .
A. B = {SSSS; NNNN} B. B = {SNSN; NSNS}.C. B = {NNNN}.
D. B = {SSSS} .
Câu 23: Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ đánh số từ 1 đến. Tính xác suất để tổng
của các số trên hai thẻ lấy ra là số chẵn. 4 1 5 A. 5 . B. . C. . D. . 9 9 9 3
Câu 24: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc
bút. Tính xác suất để hai chiếc bút lấy được cùng màu? Page 2
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 28 . B. 8 . C. 1 . D. 7 . 5 15 7 15
Câu 25: Cho M (1;3) và N ( 3;
− 5) . Phương trình đường trung trực của đoạn thẳng MN là đường thẳng nào dưới đây?
A. x + 2y − 7 = 0 . B. 2
− x + y − 6 = 0.
C. x + 2y + 7 = 0 . D. 2
− x + y + 6 = 0 .
Câu 26: Phương trình đường thẳngd qua M (1;2) và chắn trên hai trục toạ độ những đoạn bằng nhau là
A. x − y − 3 = 0 .
B. x − y + 3 = 0 .
C. x + y − 3 = 0 .
D. −x + y − 3 = 0 .
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(11;8), B( 13;8), C ( 14;7) có phương trình là. A. 2 2
x + y + 24x −12y +175 = 0 . B. 2 2
x + y − 24x +12y +175 = 0 . C. 2 2
x + y − 24x −12y +175 = 0 . D. 2 2
x + y + 24x +12y +175 = 0 .
Câu 28: Cho Đường tròn đi qua 3 điểm A(11;8), B( 13;8), C (
14;7) có bán kính R bằng A. 2 . B. 1. C. 5 . D. 2 .
Câu 29: Cho parabol có phương trình: 2
4y = 20x . Phương trình đường chuẩn của parabol là: A. 5 x = . B. 4 x = . C. 4 x = − . D. 5 x = − . 4 5 5 4
Câu 30: Một người có 7 đôi tất trong đó có 3 đôi tất trắng và 5 đôi giày trong đó có 2 đôi giày đen. Người
này không thích đi tất trắng cùng với giày đen. Hỏi người đó có bao nhiêu cách chọn tất và giày
thỏa mãn điều kiện trên? A. 29 . B. 36. C. 18. D. 35.
Câu 31: Từ một lớp gồm 16 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh tham
gia đội Thanh niên xung kích, trong đó có 2 học sinh nam và 3 học sinh nữ. A. 2 3 C .C .. B. 2 3 A .A .. C. 3 2 C .C .. D. 3 2 A .A . 16 18 16 18 16 18 16 18 Câu 32: Cho * ,
m n∈ ,m >1. Giả sử a và b là hai đường thẳng song song. Trên đường thẳng a cho m
điểm phân biệt màu đỏ, trên đường thẳng b cho n điểm phân biệt màu xanh. Số tam giác có 2
đỉnh màu đỏ và một đỉnh màu xanh thuộc tập hợp các điểm đã cho là A. 1 2 C C . B. 2 1 1 2
C C + C C . C. 2 1 C + C . D. 2 1 C C . m. m. n m. m. n n m n n
Câu 33: Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống nhau,
một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp theo
hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là A. 1 . B. 1 . C. 2 . D. 1 . 7 2×6! 7! 7!
Câu 34: Một lớp có 20 nam sinh và 23 nữ sinh. Giáo viên chọn ngẫu nhiên 5 học sinh đi test Covid. Tính
xác suất P để 5 học sinh được chọn có cả nam và nữ.
A. P ≈ 0,85.
B. P ≈ 0,97
C. P ≈ 0,96 . D. P ≈ 0,95.
Câu 35: Chọn ngẫu nhiên hai số khác nhau từ 30 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng A. 14 . B. 28 . C. 7 . D. 1 . 29 29 29 2
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 6 chữ số khác nhau trong đó 2 số kề nhau không cùng là số chẵn? Page 3
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 37: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 4x + 2y +1 = 0 và điểm A(1; ) 1 . Xác định
tọa độ hình chiếu vuông góc của A lên d .
Câu 38: Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Bí
thư và 8 học sinh nam trong đó có Lớp trưởng. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học
sinh và phải có ít nhất 1 học sinh nữ. Xác suất để Bí thư và Lớp trưởng không ở cùng một nhóm là 2 2
Câu 39: Cho hypebol ( ): x y H −
=1. Tìm tọa độ điểm M thuộc (H ) sao cho MF vuông góc với 16 9 1 MF . 2
---------- HẾT ---------- Page 4
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng Oxy , cho hình bình hành ABCD biết A(2; ) 1 , B(2;− ) 1 , C ( 2; − 3 − ) . Tọa độ
giao điểm hai đường chéo của hình bình hành ABCD là A. (2;0) . B. (2;2) . C. (0; 2 − ) . D. (0; ) 1 − . Lời giải
Giao điểm hai đường chéo là trung điểm của AC .
Vậy tọa độ giao điểm hai đường chéo là I (0;− ) 1 .
Câu 2: Quy tròn số 12,4567 đến hàng phần trăm ta được số. A. 12,45 . B. 12,46 C. 12,457 D. 12,5 Lời giải
Quy tròn số 12,4567 đến hàng trăm ta được số 12,46 .
Câu 3: Tìm tứ phân vị của mẫu số liệu sau 3 4 6 7 8 9 10 12 13 16
A. Q = 5,Q = 8,5,Q =12 .
B. Q = 6,Q = 8,5,Q =12 . 1 2 3 1 2 3
C. Q = 6,Q = 8,5,Q =12,5 .
D. Q = 5,Q = 8,5,Q =12,5 . 1 2 3 1 2 3 Lời giải
Trung vị của mẫu số liệu trên là 8 + 9 = 8,5 2
Trung vị của dãy 3 4 6 7 8 là 6
Trung vị của dãy 9 10 12 13 16 là 12
Vậy Q = 6,Q = 8,5,Q =12 . 1 2 3
Câu 4: Mẫu số liệu sau đây cho biết giá của một số loại giày trong cửa hàng
300 250300 360 350 650 450 500 300
Khoảng biến thiên của mẫu số liệu trên là A. 400 . B. 300. C. 650 . D. 250 . Lời giải
Khoảng biến thiên của mẫu số liệu là: R = 650 − 250 = 400 .
Câu 5: Cho dãy số liệu thống kê: 1,2,3,4,5,6,7 . Phương sai của mẫu số liệu thống kê đã cho là A. 2 . B. 3. C. 4 . D. 1. Lời giải 1 2 3 4 5 6 7 x + + + + + + = = 4 7 7
Vậy phương sai của mẫu số liệu: 1
s = ∑ x − x = . x ( i )2 2 4 7 i 1=      
Câu 6: Biết rằng hai vec tơ a và b không cùng phương nhưng hai vec tơ 2a + 3b và a + (x + ) 1 b cùng
phương. Khi đó giá trị của x là A. 1 . B. 3 − . C. 1 − . D. 3 . 2 2 2 2 Lời giải    
Ta có 2a + 3b và x + a + (x + )
1 b cùng phương nên có tỉ lệ: 1 1 1 = ⇒ x = . 2 3 2 Page 5
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 7: Độ dài của cái cầu bến thủy hai (Nghệ An) người ta đo được là 996m  0,5m . Sai số tương đối
tối đa trong phép đo là bao nhiêu? A. 0,05% . B. 0,5% . C. 0,04%. D. 0,005%. Lời giải
Ta có độ dài gần đúng của cầu là a  996 với độ chính xác d  0,5. Vì sai số tuyệt đối  d
  d  0,5 nên sai số tương đối 0,5 a     0, 05% . a a a a 996
Vậy sai số tương đối tối đa trong phép đo trên là 0,05%.
Câu 8: Để được cấp chứng chỉ môn Anh trình độ A của một trung tâm ngoại ngữ, học viên phải trải 2
qua 6 lần kiểm tra trắc nghiệm, thang điểm mỗi lần kiểm tra là 100 và phải đạt điểm trung bình
từ 70 điểm trở lên. Qua 5 lần thi Hoa đạt điểm trung bình là 64,5 điểm. Hỏi trong lần kiểm tra
cuối cùng Hoa phải đạt ít nhất là bao nhiêu điểm để được cấp chứng chỉ? A. 97,5. B. 92,5 . C. 95,5. D. 97,8. Lời giải
Gọi x là số điểm trong lần kiểm tra cuối mà Hoa cần đạt được để được cấp chứng chỉ
Ta có số điểm qua 5 lần thi của Hoa là 64,5.5 = 322,5.
Khi đó x + 322,5 ≥ 70 ⇔ x ≥ 70.6 − 322,5 = 97,5. 6
Vậy Q = 7,Q =16,5,Q = 30 . 1 2 3
Câu 9: Viết phương trình tổng quát của đường thẳng ∆ đi qua điểm A1; 
3 và có vectơ pháp tuyến n =(3;2)
A. 3x  2y9  0 .
B. 3x  2y6  0 . C. 3x  2y7  0 . D. 3x  2y8  0 . Lời giải
Phương trình đường thẳng cần tìm: 3(x − )
1 + 2( y − 3) = 0 ⇔ 3x + 2y − 9 = 0 .
Câu 10: Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d cắt trục Ox , Oy lần lượt tại hai
điểm A(3;0) và B(0; 2
− ). Đường thẳng d có phương trình là A. x y − = 1 − . B. x y + = 1. C. x y − = 1. D. x y − = 0 . 3 2 2 − 3 3 2 3 2 Lời giải
Phương trình đường thẳng đi qua hai điểm A(3;0) và B(0; 2
− ) viết dưới dạng đoạn chắn là : x y 1 x y d + = ⇔ − = 1. 3 2 − 3 2
Câu 11: Cho đường thẳng d : 2x + 3y +15 = 0 và d : x − 2y −3 = 0. Khẳng định nào sau đây đúng? 1 2 A. d
d cắt nhau và không vuông góc với nhau. 1 và 2 B. d
d song song với nhau. 1 và 2 C. d d trùng nhau. 1 và 2 D. d
d vuông góc với nhau. 1 và 2 Lời giải Page 6
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 
Đường thẳng d : 2x + 3y +15 = 0 có một vectơ pháp tuyến là n = 2;3 và đường thẳng 1 ( ) 1 
d : x − 2y − 3 = 0 n = 1; 2 − . 2
có một vectơ pháp tuyến là 2 ( )   Ta thấy 2 3 ≠
và n .n = 2.1+ 3.( 2) − = 4 − ≠ 0 . 1 2 − 1 2 Vậy d
d cắt nhau và không vuông góc với nhau. 1 và 2
Câu 12: Xác định m để 2 đường thẳng d : x2y 3 0 và d: xmy3 0 vuông góc với nhau.
A. m  2. B. 1 m   .
C. m  2. D. 1 m  . 2 2 Lời giải
d : x  2y  3  0 có VTPT là n1;2. 
d : x my 3  0 có VTPT là n1;m.  
Để d vuông góc với d thì 1 .
n n  0  1 2m  0  m  . 2
Câu 13: Tọa độ tâm I và bán kính R của đường tròn (C) (x + )2 2 : 1 + y = 8 là A. I ( 1; − 0), R = 8. B. I ( 1 − ;0), R = 64. C. I ( 1;
− 0), R = 2 2. D. I (1;0), R = 2 2. Lời giải
Từ phương trình đường tròn ta suy ra tọa độ tâm và bán kính là I ( 1; − 0), R = 2 2.
Câu 14: Cho đường tròn có phương trình 2 2
x + y − 6x + 2y + 6 = 0 và điểm A(1;− ) 1 . Phương trình tiếp
tuyến của tại điểm A là A. y =1. B. x =1.
C. x = 2 . D. y = 2 . Lời giải 
Ta có tâm đường tròn I (3;− )
1 , tiếp tuyến của tại điểm A nhận AI = (2;0) làm vectơ pháp
tuyến nên có phương trình là 2(x − ) 1 + 0( y + ) 1 = 0 hay x =1. 2 2
Câu 15: Tọa độ các tiêu điểm của hypebol ( ) : x y H − = 1 là 16 9 A. F = 5; − 0 ; F = 5;0 . B. F = 0; 5 − ; F = 0;5 . 1 ( ) 2 ( ) 1 ( ) 2 ( )
C. F = 0;− 7 ; F = 0; 7 .
D. F = − 7;0 ; F = 7;0 . 1 ( ) 2 ( ) 1 ( ) 2 ( ) Lời giải Gọi F = − ;0 c ; F = ;0 c
là hai tiêu điểm của (H ) . 1 ( ) 2 ( ) 2 2
Từ phương trình ( ) : x y H − = 1, ta có: 2 a =16 và 2 b = 9 suy ra 16 9 2 2 2
c = a + b = 25 ⇒ c = 5,(c > 0) .
Vậy tọa độ các tiêu điểm của (H ) là F = 5; − 0 ; F = 5;0 . 1 ( ) 2 ( )
Câu 16: Có 8 quả ổi và 6 quả xoài. Có bao nhiêu cách chọn ra một quả trong các quả ấy? A. 48. B. 24 . C. 14 . D. 18 . Lời giải
Theo quy tắc cộng có 8 + 6 = 14 cách chọn ra một quả trong các quả đã cho. Page 7
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 17: Từ các chữ số 1;2;3;4;5, hỏi có thể lập được bao nhiêu số có hai chữ số khác nhau? A. 25 . B. 20 . C. 10. D. 9 . Lời giải
Gọi số có hai chữ số khác nhau là ab(a ≠ ; b a ≠ 0) .
Ta có: Chọn a có 5 cách chọn.
Chọn b có 4 cách chọn.
Vậy theo quy tắc nhân ta có 4.5=20.
Câu 18: Có bao nhiêu cách xếp 5 quyển sách gồm toán, lý, hóa, sinh, địa lên một kệ sách dài? A. 120. B. 60 . C. 48 . D. 24 . Lời giải
Số cách xếp là số các hoán vị của 5 phần tử là P = 5!=120 cách. 5
Câu 19: Một câu lạc bộ có 20 thành viên. Số cách chọn một ban quản lí gồm 1 chủ tịch, 1phó chủ tịch, 1 thư kí là A. 13800. B. 6900 . C. 7200 . D. 6840 . Lời giải
Số cách chọn một ban quản lí gồm 1 chủ tịch, 1phó chủ tịch, 1 thư kí là: 3 A = 6840 20
Câu 20: Số cách chọn 5 học sinh trong một lớp có 25 học sinh nam và 16 học sinh nữ là A. 5 5 C + C C A C 25 16 . B. 525. C. 541. D. 541. Lời giải
Tổng số học sinh của lớp là 25 +16 = 41 học sinh.
Mỗi cách chọn theo yêu cầu của đề là 1 tổ hợp chập 5 của 41 phần tử. Nên có 5
C41 cách chọn theo yêu cầu của đề.
Câu 21: Đa thức P(x) 5 4 3 2
= 32x −80x + 80x − 40x +10x −1 là khai triển của nhị thức nào? A. ( − )5 1 2x . B. ( + )5 1 2x . C. ( x − )5 2 1 . D. (x − )5 1 . Lời giải Vì hệ số của 5
x là 32 và dấu trong khai triển đan xen nên chọn đáp án C.
Câu 22: Gieo một đồng xu cân đối và đồng chất liên tiếp bốn lần. Gọi B là biến cố “Kết quả bốn lần gieo
là như nhau”. Xác định biến cố B .
A. B = {SSSS; NNNN} B. B = {SNSN; NSNS}.C. B = {NNNN}.
D. B = {SSSS} . Lời giải
Kết quả của bốn lần gieo là như nhau nên ta có hai trường hợp là: cả bốn lần gieo đều là mặt sấp
xuất hiện và cả bốn lần gieo đều là mặt ngửa xuất hiện. Vậy B = {SSSS; NNNN}.
Câu 23: Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ đánh số từ 1 đến. Tính xác suất để tổng
của các số trên hai thẻ lấy ra là số chẵn. 4 1 5 A. 5 . B. . C. . D. . 9 9 9 3 Lời giải
Lấy ngẫu nhiên hai tấm thẻ trong một hộp chứa 9 tấm thẻ có n(ω) 2 = C = 36 9
Gọi A là biến cố tổng của các số trên hai thẻ lấy ra là số chẵn
TH1. Lấy được hai thẻ ghi số lẻ có : 2 C =10 cách. 5
TH2. Lấy được hai thẻ ghi số chẵn có : 2
C = 6 cách. Vậy n( A) =16. 4 Page 8
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Xác suất để tổng của các số trên hai thẻ lấy ra là số chẵn là : p( A) 4 = . 9
Câu 24: Một hộp đựng 7 chiếc bút bi đen và 8 chiếc bút bi xanh. Lấy đồng thời và ngẫu nhiên hai chiếc
bút. Tính xác suất để hai chiếc bút lấy được cùng màu? A. 28 . B. 8 . C. 1 . D. 7 . 5 15 7 15 Lời giải
Số phần tử của không gian mẫu là: n(Ω) 2 = = 15 C 105
Gọi A là biến cố “ lấy được hai chiếc bút cùng màu ”, tức là lấy được hai chiếc bút màu đen
hoặc hai chiếc bút màu xanh 2 2 ⇒ n( ) A = + = 7 C 8 C 49 Xác suất của biến cố n A
A là: P ( A) ( ) 49 7 = = = . n(Ω) 105 15
Câu 25: Cho M (1;3) và N ( 3;
− 5) . Phương trình đường trung trực của đoạn thẳng MN là đường thẳng nào dưới đây?
A. x + 2y − 7 = 0 . B. 2
− x + y − 6 = 0.
C. x + 2y + 7 = 0 . D. 2
− x + y + 6 = 0 . Lời giải  Ta có MN = ( 4;
− 2) , đặt n = ( 2 − ) ;1 .
Gọi I là trung điểm của MN , ta có I ( 1; − 4).
Đường trung trực của đoạn thẳng MN là đường thẳng đi qua điểm I và nhận vectơ n làm
vectơ pháp tuyến, có phương trình: 2 − ( x + )
1 +1( y − 4) = 0 ⇔ 2
− x + y − 6 = 0 .
Câu 26: Phương trình đường thẳngd qua M (1;2) và chắn trên hai trục toạ độ những đoạn bằng nhau là
A. x − y − 3 = 0 .
B. x − y + 3 = 0 .
C. x + y − 3 = 0 .
D. −x + y − 3 = 0 . Lời giải
Vì đường thẳng d qua M (1;2) và chắn trên hai trục toạ độ những đoạn bằng nhau nên đường
thẳng cần tìm song song với đường thẳng y = −x hoặc y = x .
Vậy đường thẳng d có có dạng y = x + a hoặc y = −x + b .
Vì đường thẳng đi qua M (1;2) nên y = x +1 hoặc y = −x + 3 .
Vậy d : x − y +1 = 0 hoặc d : x − y − 3 = 0.
Câu 27: Trong mặt phẳng Oxy , đường tròn đi qua ba điểm A(11;8), B( 13;8), C ( 14;7) có phương trình là. A. 2 2
x + y + 24x −12y +175 = 0 . B. 2 2
x + y − 24x +12y +175 = 0 . C. 2 2
x + y − 24x −12y +175 = 0 . D. 2 2
x + y + 24x +12y +175 = 0 . Lời giải Chọn C
Gọi phương trình đường tròn cần tìm có dạng: 2 2
x + y − ax − by + c = ( 2 2 2 2
0 a + b − c > 0) .
Đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) nên ta có: 121 
+ 64 − 22a −16b + c = 0 a =12 169   64 26a 16b c 0 b  + − − + = ⇔  = 6 196  49 28a 14b c 0  + − − + = c =   175 Page 9
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Vậy phương trình đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) là 2 2
x + y − 24x −12y +175 = 0
Câu 28: Cho Đường tròn đi qua 3 điểm A(11;8), B( 13;8), C (
14;7) có bán kính R bằng A. 2 . B. 1. C. 5 . D. 2 . Lời giải
Gọi phương trình đường tròn cần tìm có dạng: 2 2
x + y − ax − by + c = ( 2 2 2 2
0 a + b − c > 0) .
Đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) nên ta có: 121 
+ 64 − 22a −16b + c = 0 a =12 169   64 26a 16b c 0 b  + − − + = ⇔  = 6 196  49 28a 14b c 0  + − − + = c =   175 Ta có 2 2
R = a + b − c = 5
Vậy phương trình đường tròn đi qua 3 điểm A(11;8), B( 13;8), C ( 14;7) có bán kính là R = 5 .
Câu 29: Cho parabol có phương trình: 2
4y = 20x . Phương trình đường chuẩn của parabol là: A. 5 x = . B. 4 x = . C. 4 x = − . D. 5 x = − . 4 5 5 4 Lời giải Ta có: (P) 2 5
: 4y = 20x ⇒ 2 p = 5 ⇒ p = . 2
Vậy (P) có phương trình đường chuẩn là: 5 ∆ : x = − . 4
Câu 30: Một người có 7 đôi tất trong đó có 3 đôi tất trắng và 5 đôi giày trong đó có 2 đôi giày đen. Người
này không thích đi tất trắng cùng với giày đen. Hỏi người đó có bao nhiêu cách chọn tất và giày
thỏa mãn điều kiện trên? A. 29 . B. 36. C. 18. D. 35. Lời giải Cách 1: Trường hợp 1:
Chọn 1 đôi tất trắng có 3 cách.
Chọn 1 đôi giày không phải màu đen có 3 cách.
Do đó có 3.3  9 cách chọn 1 đôi tất trắng và 1 đôi giày không phải màu đen. Trường hợp 2:
Chọn 1 đôi tất không phải màu trắng có 4cách.
Chọn 1 đôi giày bất kỳ có 5 cách.
Do đó có 4.5  20 cách chọn 1 đôi tất không phải màu trắng và 1 đôi giày bất kỳ.
Theo quy tắc cộng, ta có 9 20  29 cách chọn 1 đôi tất và 1 đôi giày thỏa mãn yêu cầu. Cách 2:
Số cách chọn ra 1 đôi tất và 1 đôi giày bất kỳ là: 7.5  35 cách.
Số cách chọn ra 1 đôi tất trắng và 1 đôi giày đen là: 3.2  6 cách.
Vậy ta có 356  29 cách chọn 1 đôi tất và 1 đôi giày thỏa mãn yêu cầu.
Câu 31: Từ một lớp gồm 16 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh tham
gia đội Thanh niên xung kích, trong đó có 2 học sinh nam và 3 học sinh nữ. Page 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 2 3 C .C .. B. 2 3 A .A .. C. 3 2 C .C .. D. 3 2 A .A . 16 18 16 18 16 18 16 18 Lời giải
Chọn 2 học sinh nam trong số 16 học sinh nam thì có 2 C cách chọn. 16
Chọn 3 học sinh nữ trong số 18 học sinh nữ thì có 3 C cách chọn. 18
Áp dụng quy tắc nhân, sẽ có 2 3
C .C cách chọn 2 học sinh nam và 3 học sinh nữ. 16 18 Câu 32: Cho * ,
m n∈ ,m >1. Giả sử a và b là hai đường thẳng song song. Trên đường thẳng a cho m
điểm phân biệt màu đỏ, trên đường thẳng b cho n điểm phân biệt màu xanh. Số tam giác có 2
đỉnh màu đỏ và một đỉnh màu xanh thuộc tập hợp các điểm đã cho là A. 1 2 C C . B. 2 1 1 2
C C + C C . C. 2 1 C + C . D. 2 1 C C . m. m. n m. m. n n m n n Lời giải
Chọn 2 đỉnh màu đỏ từ m điểm có 2 C cách chọn. m
Chọn 1 đỉnh màu xanh từ n điểm có 1 C cách chọn. m
Theo quy tắc nhân ta có số tam giác thỏa mãn là 2 1 C C . m. n
Câu 33: Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống nhau,
một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp theo
hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là A. 1 . B. 1 . C. 2 . D. 1 . 7 2×6! 7! 7! Lời giải
Hoán vị 7 chữ cái này ta được 1 dãy 7 chữ cái, tuy nhiên trong đó có 2 chữ T giống nhau nên khi
hoán vị 2 chữ T này cho nhau không tạo dãy mới. 7!
Vì vậy sẽ có: Ω = dãy khác nhau. 2! 1 2
Xác suất để tạo thành dãy THPTCLS là P = 7! = . 7! 2!
Câu 34: Một lớp có 20 nam sinh và 23 nữ sinh. Giáo viên chọn ngẫu nhiên 5 học sinh đi test Covid. Tính
xác suất P để 5 học sinh được chọn có cả nam và nữ.
A. P ≈ 0,85.
B. P ≈ 0,97
C. P ≈ 0,96 . D. P ≈ 0,95. Lời giải
Số phần tử của không gian mẫu là: n(Ω) 5 = C . 43
Gọi A là biến cố: “5 học sinh được chọn có cả nam và nữ”. 5 C − ( 5 5 C + C 43 20 23 ) Ta có: P( A) = ≈ 0,95 . 5 C43
Câu 35: Chọn ngẫu nhiên hai số khác nhau từ 30 số nguyên dương đầu tiên. Xác suất để chọn được hai
số có tổng là một số chẵn bằng A. 14 . B. 28 . C. 7 . D. 1 . 29 29 29 2 Lời giải
Chọn hai số khác nhau từ 30 số nguyên dương đầu tiên: có 2 C cách chọn. 30 Suy ra n(Ω) 2 = C . 30
Gọi A là biến cố: “Chọn được hai số có tổng là một số chẵn” Page 11
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Ta xét hai trường hợp:
TH1: Hai số được chọn là hai số lẻ: có 2 C cách chọn. 15
TH2: Hai số được chọn là hai số chẵn: có 2 C cách chọn. 15 Suy ra n( A) 2 2 = C + C . 15 15 2 2 n A C + C 14
Vậy xác suất cần tìm là: P( A) ( ) 15 15 = = = . n(Ω) 2 C 29 30
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 6 chữ số khác nhau trong đó 2 số kề nhau không cùng là số chẵn? Lời giải
Gọi số đó là A = a a a a a a 1 2 3 4 5 6 .
Theo đề bài, ta có A có nhiều nhất 3 chữ số chẵn.
TH1: A có 1 chữ số chẵn: a 1 C .P
1 chẵn: số cách chọn A: 4 5 . a 1 1 4
C .(C .C ).P 1 lẻ: số cách chọn A: 5 5 4 5 .
TH2: A có 2 chữ số chẵn: a a 1 1 1 3
C .C .(C .C ).P
1 chẵn, suy ra 2 lẻ. số cách chọn A: 4 5 4 4 4 . a 6 2 2 1 lẻ, có
cách chọn vị trí không kề nhau của chữ số chẵn. số cách chọn A: 1 2 3
C .(C .6.P ).A 5 5 2 4 .
TH3: A có 3 chữ số chẵn: a a 3 2 2
1 chẵn, suy ra 2 lẻ, có cách chọn
vị trí không kề nhau của chữ số chẵn. số cách chọn A: 1 1 2 2
C .C .(C .3.P ).A 4 5 4 2 4 . a 1 2 2 1 lẻ, có cách chọn
vị trí không kề nhau của chữ số chẵn. số cách chọn A: 1 3 2
C .(C .1.P ).A 37800 5 5 3
4 . Suy ra tổng số trường hợp: cách.
Câu 37: Trong mặt phẳng tọa độ Oxy , cho đường thẳng d : 4x + 2y +1 = 0 và điểm A(1; ) 1 . Xác định
tọa độ hình chiếu vuông góc của A lên d . Lời giải  
Đường thẳng d có một VTPT n = (4;2) suy ra d có một VTCP u = ( 2; − 4) .  Ta có  1   3 H d H t; 2t ,t
AH t 1; 2t  ∈ ⇒ − − ∈ ⇒ = − − −  . 2 2     
Hình chiếu vuông góc của A lên d là H nên  
AH u = ⇔ (t − ) (− )  3  2 . 0 1 . 2 + 2
− t − .4 = 0 ⇔ 10
− t − 4 = 0 ⇔ t − =  .  2  5 Vậy  2 3 H − ;   . 5 10   
Câu 38: Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Bí
thư và 8 học sinh nam trong đó có Lớp trưởng. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học
sinh và phải có ít nhất 1 học sinh nữ. Xác suất để Bí thư và Lớp trưởng không ở cùng một nhóm là Lời giải Page 12
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Theo yêu cầu bài toán ta cần chia tổ một thành ba nhóm, trong đó một nhóm có, hai nhóm còn
lại có vai trò như nhau gồm. Suy ra số phần tử của không gian mẫu là: 1 3 1 3 n(Ω) = (
C .C . C .C 2 2 C .C . = 3360. 4 8 ) ( 2 6 ) ( 1 3 ) 2!
Gọi A là biến cố ' Bí thư và Lớp trưởng cùng một nhóm ' . Ta có các trường hợp sau:
●Trường hợp thứ nhất: Bí thư và Lớp trưởng thuộc nhóm. Số cách xếp là: 1 3 1 3 (
C .C . C .C 1 1 1.C .C . = 420 3 7 ) ( 2 6 ) ( 1 3 ) . 2!
●Trường hợp thứ hai: Bí thư và Lớp trưởng thuộc nhóm. Số cách xếp là ( 2 1.C ).( 1 3 C .C ).( 2 2 C .C = 630 7 3 5 2 2 ) . Suy ra n( ) A = 420 + 630 =1050 .
Vậy xác suất để Bí thư và Lớp trưởng cùng một nhóm n( ) A 1050 5 P( ) A = = = . Suy ra xác n(Ω) 3360 16
suất để Bí thư và Lớp trưởng không cùng một nhóm là 5 11 P( ) A =1− = . 16 16 2 2
Câu 39: Cho hypebol ( ): x y H −
=1. Tìm tọa độ điểm M thuộc (H ) sao cho MF vuông góc với 16 9 1 MF . 2 Lời giải 2 2 Gọi ( ; )∈( ) x y M x y H ⇒ − =1 ; ( ) 1 16 9 2 a =16 Ta có 2 2 2 
⇒ c = a + b = 25 ⇒ c = 5 ⇒ F F = 2c =10. 1 2 2 b  = 9
Vì MF ⊥ MF nên tam giác MF F vuông tại M . Do đó M thuộc đường tròn (C) có đường 1 2 1 2 kính F F . 1 2 tâm O(0;0) (C) F F ⇒ (C) 2 2 : x + y = 25 1 2 B n á kính R = = 5  2 M ∈(C) 2 2
⇒ x + y = 25 ; (2) 2 2   2 544 4 34  x y  − =1 x =  x = ± Từ ( ) 1 và (2) , ta có  25  5 16 9 ⇔  ⇒ 81   2 2  2  9 x + y = 25 y = = ±  25 y  5         Vậy 4 34 9 4 34 9 4 34 9 4 34 9 M  ; ;M  − ; ;M  ;− ;M − ;− . 1 2 3 4 5 5 5 5 5 5 5 5                 
---------- HẾT ---------- Page 13
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 08
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng Oxy , cho A(x y
x y . Tọa độ trung điểm I của đoạn thẳng AB
A; A ) và B ( B ; B ) là
A. x − x y y
x + x y + y A B I ; − A B A B A B   . B. I  ; . 2 2      2 2 
C. x + x y y
x + y x + y A B I ; + A B A A B B   . D. I  ; . 3 3      2 2 
Câu 2: Giá trị gần đúng của 2 8 chính xác đến hàng phần trăm là A. 5,656. B. 5,65. C. 5,66. D. 5,657
Câu 3: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như bảng sau. Số cuốn sách 3 4 5 6 7 Số bạn 6 15 3 8 8
Tìm mốt của mẫu số liệu trên A. 7 . B. 5. C. 6 . D. 4 .
Câu 4: Bảng sau cho biết thời gian chạy cự li 100m của các bạn trong lớp (đơn vị giây) Thời gian 12 13 14 15 16 Số bạn 4 7 3 18 8
Hãy tính thời gian chạy trung bình cự li 100m của các bạn trong lớp. A. 14,094 . B. 14,245 . C. 14,475 . D. 14,75.
Câu 5: Số ôtô đi qua một cây cầu mỗi ngày trong một tuần đếm được như sau: 83; 74; 71; 79; 83; 69;
92. Phương sai và độ lệch chuẩn lần lượt là A. 78,71 và 8,87. B. 52,99 và 7,28. C. 61,82 và 7,86. D. 55,63 và 7,46.    
Câu 6: Cho a = (0,1) ,b = ( 1; − 2) , c = ( 3 − ; 2
− ) . Tọa độ củau = 3a + 2b − 4c là A. (10; 15 − ). B. (15;10). C. (10;15). D. ( 10 − ;15).
Câu 7: Kết quả đo chiều dài một cây cầu là a =152,65m với độ chính xác 0,05m. Viết số quy tròn của
số a và ước lượng sai số tương đối của số quy tròn đó.
A. 152,7 và δ < .
B. 152,7 và δ < . a 0,066% a 0,033%
C. 152,7 và δ < .
D. 152,7 và δ = a 0,065% a 0,013%
Câu 8: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của mười hai thí
sinh theo thứ tự không giảm như sau: 5 6 6 6 7 7 7 7 7 8 8 x
Tìm x biết số trung bình của thời gian thi nghề của các thí sinh trên là 109 . 12 A. 35. B. 33. C. 34 . D. 36 . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 9: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP u =(3;–4) là x   3  2t x   2  3t x   2  3t x   1 2t A.  . . B.  . C.  . . D.  . . y   4  t      y  3  4t  y  1  4t 
y  4  3t 
Câu 10: Trong mặt phẳng tọa độ Oxy đường thẳng đi qua ( A 1;
− 4) và song song trục Ox
A. x −1 = 0 .
B. y + 4 = 0 .
C. x +1 = 0 .
D. y − 4 = 0 .
Câu 11: Tính góc giữa hai đường thẳng d : 2x + 5y − 2 = 0 và d :3x − 7y + 3 = 0 . 1 2 A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . x = 3 − x = 1 Câu 12: t
Trong mặt phẳng Oxy, cho hai đường thẳng d : và d : Góc giữa hai 1   y = 4 − t 2 y = 11 − − 2t
đường thẳng d và d bằng 1 2 A. 60 . B. 45 . C. 90 . D. 30 .
Câu 13: Phương trình đường tròn có tâm I (0;2) và bán kính R = 5 là A. 2 2
x + y − 4y + 21= 0 . B. 2 2
x + y + 4y − 21= 0 . C. 2 2
x + y − 4y − 21= 0 . D. 2 2
x + y − 4x − 21= 0 .
Câu 14: Trong hệ trục tọa độ Oxy , cho đường tròn C (x − )2 + ( y + )2 ( ) : 1
2 = 8 . Phương trình tiếp tuyến
d của (C) tai điểm (3 A ;− 4) là
A. d : x + y +1 = 0 .
B. d : x − 2y −11 = 0 . C. d : x − y − 7 = 0 . D. d : x − y + 7 = 0 .
Câu 15: Phương trình nào sau đây là phương trình chính tắc của một elip? 2 2 2 2 2 2 2 2 A. x y − =1. B. x y + = 1 − . C. x y + =1. D. x y + = 0. 4 25 4 25 5 2 4 25
Câu 16: Lớp 10A có 25 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một học sinh để
tham gia vào đội thanh niên tình nguyện của trường biết rằng tất cả các bạn trong lớp đều có khả năng tham gia. A. 40 . B. 25 . C. 15. D. 10.
Câu 17: Có bao nhiêu số tự nhiên có 2 chữ số mà cả hai chữ số đều là lẻ A. 50. B. 25 . C. 20 . D. 10.
Câu 18: Số cách xếp 3 nam sinh và 4 nữ sinh vào một dãy ghê hàng ngang có 7 chỗ ngồi là A. 4!.3. B. 7!. C. 4!.3!. D. 4!.
Câu 19: Một nhóm học sinh có 10 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việ C. Số cách chọn là A. 3 10 . B. 30. C. 3 C . D. 3 A . 10 10
Câu 20: Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con. A. 1326. B. 104. C. 26. D. 2652
Câu 21: Trong khai triển nhị thức Niu-tơn của ( + )4
1 3x , số hạng thứ 2 theo số mũ tăng dần của x là A. 108x . B. 2 54x . C. 1. D. 12x .
Câu 22: Xếp 7 học sinh ,
A B,C, D, E, F,G vào một chiếc bàn dài có đúng 7 ghế. Tính xác suất để học
sinh D không ngồi đầu bàn. A. 4 . B. 7 . C. 3 . D. 5 . 7 3 7 7 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 23: Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 15. Tính xác suất để chọn được số chẵn A. 8 . B. 1 . C. 7 . D. 4 . 15 2 15 7
Câu 24: Từ một hộp chứa 11 quả cầu màu đỏ và 4quả cầu màu xanh, lấy ngẫu nhiên đồng thời3quả cầu.
Xác suất để lấy được3quả cầu màu xanh bằng 24 4 4 24 A. . B. . C. . D. . 455 165 455 165
Câu 25: Cho 2 điểm A(1;2), B(3;4). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB .
A. x + y + 5 = 0.
B. x − y − 5 = 0.
C. 2x + 2y − 5 = 0.
D. x + y − 5 = 0.
Câu 26: Trong mặt phẳng Oxy , khoảng cách giữa hai đường thẳng song song d :3x − 4y −3 = 0 và 1
d :3x − 4y −8 = 0 là 2 A. 4. B. 3. C. 1. D. 2.
Câu 27: Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C) : x + y − 4x − 2y − 20 = 0 phương trình tiếp
tuyến của (C) vuông góc với đường thẳng ∆ :3x + 4y + 9 = 0 là
A. 4x − 3y + 30 = 0 và 4x − 3y − 20 = 0.
B. 4x − 3y + 20 = 0 và 4x − 3y − 30 = 0 .
C. 4x − 3y − 30 = 0 và 4x − 3y − 20 = 0.
B. 4x − 3y + 20 = 0 và 4x − 3y + 30 = 0 .
Câu 28: Cho tam giác ABC có A(1;− )
1 , B(3;2), C (5; 5
− ) . Toạ độ tâm đường tròn ngoại tiếp tam giác ABC là A.  47 13 ;  −        . B. 47 13  ; . C. 47 13 −  ;− . D. 47 13 −  ; . 10 10        10 10   10 10   10 10  2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 5
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 8 . B. 16. C. 4 . D. 5.
Câu 30: Có bao nhiêu số tự nhiên gồm bốn chữ số khác nhau và chia hết cho 5?. A. 952. B. 1800. C. 1008. D. 1620.
Câu 31: Có 5nhà toán học nam, 3nhà toán học nữ và 4 nhà vật lý nam. Lập một đoàn công tác có 3
người cần có cả nam và nữ, trong đó có cả nhà toán học và nhà vật lý. Hỏi có bao nhiêu cách lập? A. 60 . B. 90. C. 20 . D. 12.
Câu 32: Cho tứ giác ABCD . Trên mỗi cạnh AB, BC,CD, DA lấy 7 điểm phân biệt và không có điểm nào trùng với 4 đỉnh ,
A B,C, D . Hỏi từ 32 điểm đã cho lập được bao nhiêu tam giác? A. 4960. B. 4624. C. 7140. D. 6804.
Câu 33: Trong một lớp học gồm có 18 học sinh nam và 17 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học
sinh lên bảng giải bài tập. Xác suất để 4 học sinh được gọi có cả nam và nữ là: A. 68 . B. 65 . C. 443 . D. 69 . 75 71 506 77
Câu 34: Chọn ngẫu nhiên hai số phân biệt từ 15 số nguyên dương đầu tiên. Xác suất để tích hai số được
chọn là một số chẵn bằng A. 1 . B. 4 . C. 4 . D. 11 . 5 15 5 15 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 35: Từ một tổ gồm 10 nam và 8 nữ chọn ra một đoàn đại biểu gồm 6 người để tham dự hội nghị. Xác
suất để đoàn đại biểu được chọn có đúng 2 nữ bằng A. 151 . B. 35 . C. 70 . D. 29 . 221 221 221 221
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp A = {0; 1; 2; 3; 4; 5; }
6 . Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác
nhau được lập thành từ các chữ số của tập A , đồng thời có đúng 2 chữ số lẻ và 2 chữ số lẻ đó đứng cạnh nhau.
Câu 37: Trong mặt phẳng tọa độ Oxy , cho điểm M (2; )
1 và đường tròn (C) (x − )2 + ( y − )2 : 1 2 = 4. Viết
phương trình đường thẳng (d ) qua điểm M và cắt (C) tại hai điểm phân biệt ; A B sao cho độ
dài AB ngắn nhất.
Câu 38: Xếp 5 quyển sách Toán và 5 quyển sách Văn khác nhau lên một kệ dài. Tính xác suất để 2
quyển sách cùng một môn nằm cạnh nhau.
Câu 39: Vệ tinh nhân tạo đầu tiên được Liên Xô phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là
một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là 2 2 x y 2 2 2 +
=1,a > 0,b > 0,c = a − b . Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 2 2 a b
583 dặm và xa nhất là 1342 dặm. Tìm tỷ số c , biết bán kính của Trái Đất xấp xỉ 4000 dặm. a
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng Oxy , cho A(x y
x y . Tọa độ trung điểm I của đoạn thẳng AB
A; A ) và B ( B ; B ) là
A. x − x y y
x + x y + y A B I ; − A B A B A B   . B. I  ; . 2 2      2 2 
C. x + x y y
x + y x + y A B I ; + A B A A B B   . D. I  ; . 3 3      2 2  Lời giải x + x A B x =  I
Ta có: I là trung điểm của đoạn thẳng nên  2  . y + yA B y = I  2
Vậy  x + x y y A B I ; + A B   . 2 2   
Câu 2: Giá trị gần đúng của 2 8 chính xác đến hàng phần trăm là A. 5,656. B. 5,65. C. 5,66. D. 5,657 Lời giải
Sử dụng máy tính cầm tay ta tính được 2 8 = 5,656854249...Vậy số quy tròn là 5,66.
Câu 3: Thống kê số cuốn sách mỗi bạn trong lớp đã đọc trong năm 2021, bạn Lan thu được kết quả như bảng sau. Số cuốn sách 3 4 5 6 7 Số bạn 6 15 3 8 8
Tìm mốt của mẫu số liệu trên A. 7 . B. 5. C. 6 . D. 4 . Lời giải
Mốt của mẫu số liệu trên là: 4
Câu 4: Bảng sau cho biết thời gian chạy cự li 100m của các bạn trong lớp (đơn vị giây) Thời gian 12 13 14 15 16 Số bạn 4 7 3 18 8
Hãy tính thời gian chạy trung bình cự li 100m của các bạn trong lớp. A. 14,094 . B. 14,245 . C. 14,475 . D. 14,75. Lời giải
Số bạn học sinh trong lớp là n = 4 + 7 + 3+18+ 8 = 40 (bạn)
Thời gian chạy trung bình cự li 100m của các bạn trong lớp là: Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 4.12 7.13 3.14 18.15 8.16 x + + + + = = 14,475 40
Câu 5: Số ôtô đi qua một cây cầu mỗi ngày trong một tuần đếm được như sau: 83; 74; 71; 79; 83; 69;
92. Phương sai và độ lệch chuẩn lần lượt là A. 78,71 và 8,87. B. 52,99 và 7,28. C. 61,82 và 7,86. D. 55,63 và 7,46. Lời giải Ta có: 1
x = (69 + 71+ 74 + 79 + 83.2 + 92) ≈ 78,7 . 7 Phương sai: 2 1
S = (69 − 78,7)2 + (71− 78,7)2 + (74 − 78,7)2 + 2.(83− 78,7)2 + (92 − 78,7)2  ≈ 55,63 7   . Độ lệch chuẩn: 2
S = S ≈ 7,46 .    
Câu 6: Cho a = (0,1) ,b = ( 1; − 2) , c = ( 3 − ; 2
− ) . Tọa độ củau = 3a + 2b − 4c là A. (10; 15 − ). B. (15;10). C. (10;15). D. ( 10 − ;15). Lời giải    
u = 3a + 2b − 4c = (10;15) .
Câu 7: Kết quả đo chiều dài một cây cầu là a =152,65m với độ chính xác 0,05m. Viết số quy tròn của
số a và ước lượng sai số tương đối của số quy tròn đó.
A. 152,7 và δ < .
B. 152,7 và δ < . a 0,066% a 0,033%
C. 152,7 và δ < .
D. 152,7 và δ = a 0,065% a 0,013% Lời giải
Vì độ chính xác đến hàng phần trăm nên ta quy tròn số a đến hàng phần chục là 152,7 . Ta có
152,6 ≤ a ≤152,7 ⇒ 0
− ,1≤ a −152,7 ≤ 0 hay ∆ = a − ≤
. Vậy sai số tương đối là a 152,7 0,1 a 0,1 δ ∆ = ≤ < . a 0,066% a 152,7
Câu 8: Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của mười hai thí
sinh theo thứ tự không giảm như sau: 5 6 6 6 7 7 7 7 7 8 8 x
Tìm x biết số trung bình của thời gian thi nghề của các thí sinh trên là 109 . 12 A. 35. B. 33. C. 34 . D. 36 . Lời giải Số trung bình là
5 + 3.6 + 4.7 + 2.8 + x 109 x = = ⇔ x = 35. 12 12 
Câu 9: Phương trình tham số của đường thẳng (d) đi qua M(–2;3) và có VTCP u =(3;–4) là Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 x   3  2t x   2  3t A.  . . B.  . y   4  t    y  3  4t  x   2  3t x   1 2t C.  . . D.  . . y   1  4t   
y  4  3t  Lời giải  
đường thẳng (d) đi qua M(–2;3) và có VTCP u  3;4  u  3;4 có phương trình x   2  3t  . y   3  4t 
Câu 10: Trong mặt phẳng tọa độ Oxy đường thẳng đi qua ( A 1;
− 4) và song song trục Ox
A. x −1 = 0 .
B. y + 4 = 0 .
C. x +1 = 0 .
D. y − 4 = 0 . Lời giải
Vì đường thẳng đi qua ( A 1;
− 4) và song song trục Ox nên có véc tơ pháp tuyến j (0; ) 1 nên có
phương trình y − 4 = 0 .
Câu 11: Tính góc giữa hai đường thẳng d : 2x + 5y − 2 = 0 và d :3x − 7y + 3 = 0 . 1 2 A. 0 30 . B. 0 135 . C. 0 45 . D. 0 60 . Lời giải
Đường thẳng d : 2x + 5y − 2 = 0 có vectơ pháp tuyến 1 n = (2;5) . 1 
Đường thẳng d :3x − 7y + 3 = 0 có vectơ pháp tuyến n2 = (3; 7 − ) . 2
Góc giữa hai đường thẳng được tính bằng công thức     n .n ( 2.3+ 5.( 7 − ) 29 1
cos d ,d = cos n ,n =   = = = 1 2 ) ( ) 1 2 1 2 2 2 2 2 n . n + + − 29 2 2 1 2 2 5 . 3 ( 7) ⇒ (d ;d ) 0 = 45 1 2
Vậy góc tạo bởi đường thẳng d và d bằng 0 45 . 1 2 x = 3 − x = 1 Câu 12: t
Trong mặt phẳng Oxy, cho hai đường thẳng d : và d : Góc giữa hai 1    y = 4 − t 2 y = 11 − − 2t
đường thẳng d và d bằng 1 2 A. 60 . B. 45 . C. 90 . D. 30 . Lời giải
Ta có đường thẳng d và d lần lượt có vecto chỉ phương là   u = 1;
− −1 , u = 0;− 2 . 2 ( ) 1 ( ) 1 2
Gọi ϕ là góc giữa d và d . 1 2   u .u 1 − .0 + 2 2 1 2 cosϕ = = = ⇒ ϕ = 45   . u . u 2 2 2 1 2
Câu 13: Phương trình đường tròn có tâm I (0;2) và bán kính R = 5 là A. 2 2
x + y − 4y + 21= 0 . B. 2 2
x + y + 4y − 21= 0 . C. 2 2
x + y − 4y − 21= 0 . D. 2 2
x + y − 4x − 21= 0 . Lời giải Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Phương trình đường tròn có tâm I (0;2) và bán kính R = 5 là: 2
x + ( y − 2)2 = 25 2 2
⇔ x + y − 4y − 21= 0.
Câu 14: Trong hệ trục tọa độ Oxy , cho đường tròn C (x − )2 + ( y + )2 ( ) : 1
2 = 8 . Phương trình tiếp tuyến
d của (C) tai điểm (3 A ;− 4) là
A. d : x + y +1 = 0 .
B. d : x − 2y −11 = 0 . C. d : x − y − 7 = 0 . D. d : x − y + 7 = 0 . Lời giải
Đường tròn (C) có tâm I(1; 2) − .  
Tiếp tuyến tại A có vectơ pháp tuyến là n = IA = (2;− 2)
Phương trình tiếp tuyến của đường tròn tại A là: 2(x − 3) − 2(y + 4) = 0 ⇔ x − y − 7 = 0 .
Câu 15: Phương trình nào sau đây là phương trình chính tắc của một elip? 2 2 2 2 2 2 2 2 A. x y − =1. B. x y + = 1 − . C. x y + =1. D. x y + = 0. 4 25 4 25 5 2 4 25 Lời giải 2 2
Phương trình chính tắc của một elip có dạng x y + =1 với 2 2
a > b > 0 . 2 2 a b
Câu 16: Lớp 10A có 25 học sinh nam và 15 học sinh nữ. Hỏi có bao nhiêu cách chọn ra một học sinh để
tham gia vào đội thanh niên tình nguyện của trường biết rằng tất cả các bạn trong lớp đều có khả năng tham gia. A. 40 . B. 25 . C. 15. D. 10. Lời giải
Số cách chọn được 1 học sinh nam: có 25.
Số cách chọn được 1 học sinh nữ: có 15.
Vậy để chọn một học sinh trong lớp 10A tham gia vào đội thanh niên tình nguyện của trường có: 25+15= 40 .
Câu 17: Có bao nhiêu số tự nhiên có 2 chữ số mà cả hai chữ số đều là lẻ A. 50. B. 25 . C. 20 . D. 10. Lời giải
Gọi số tự nhiên có hai chữ số mà cả hai chữ số đều lẻ là ab .
Số cách chọn số a là 5 cách.
Số cách chọn số b là 5 cách.
Vậy có 5.5 = 25 số thỏa mãn yêu cầu bài toán.
Câu 18: Số cách xếp 3 nam sinh và 4 nữ sinh vào một dãy ghê hàng ngang có 7 chỗ ngồi là A. 4!.3. B. 7!. C. 4!.3!. D. 4!. Lời giải
Xếp 3 nam sinh và 4 nữ sinh vào một dãy ghê hàng ngang có 7 chỗ ngồi có 7! cách.
Câu 19: Một nhóm học sinh có 10 người. Cần chọn 3 học sinh trong nhóm để làm 3 công việc là tưới
cây, lau bàn và nhặt rác, mỗi người làm một công việ C. Số cách chọn là A. 3 10 . B. 30. C. 3 C . D. 3 A . 10 10 Lời giải
Số cách chọn 3 em học sinh là số cách chọn 3 phần tử khác nhau trong 10 phần tử có phân biệt
có thứ tự nên số cách chọn thỏa yêu cầu là 3 A . 10
Câu 20: Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con. Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 1326. B. 104. C. 26. D. 2652 Lời giải
Số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con: 2 C =1326 . 52
Câu 21: Trong khai triển nhị thức Niu-tơn của ( + )4
1 3x , số hạng thứ 2 theo số mũ tăng dần của x là A. 108x . B. 2 54x . C. 1. D. 12x . Lời giải 4 4 Ta có (1+ 3x)4 k = ∑C 3 k k
x = ∑C 3k kx . 4 ( ) 4 k =0 k =0
Do đó số hạng thứ 2 theo số mũ tăng dần của x ứng với k =1, tức là 1 1
C 3 x =12x . 4
Câu 22: Xếp 7 học sinh ,
A B,C, D, E, F,G vào một chiếc bàn dài có đúng 7 ghế. Tính xác suất để học
sinh D không ngồi đầu bàn. A. 4 . B. 7 . C. 3 . D. 5 . 7 3 7 7 Lời giải
+ Xét phép thử: “Xếp 7 học sinh vào 7 ghế”, ta có n(Ω) = 7!= 5040 .
+ Gọi K là biến cố: “Xếp D không ngồi đầu bàn”.
+ Ta tìm n(K ):
Xếp D vào bàn sao cho D không ngồi đầu bàn, có 5 cách xếp.
Xếp 6 học sinh còn lại vào 6 ghế còn lại, có 6!= 720 cách xếp.
Vậy số cách xếp sao cho D không ngồi đầu bàn là n(K ) = 5.720 = 3600 cách. n K
+ Xác suất cần tìm là p(K ) ( ) 3600 5 = = = . n(Ω) 5040 7
Câu 23: Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 15. Tính xác suất để chọn được số chẵn A. 8 . B. 1 . C. 7 . D. 4 . 15 2 15 7 Lời giải
Ta có tập các số tự nhiên nhỏ hơn 15là S = {0;1;2;3;...; }
14 nên có 7 số lẻ và 8 số chẵn.
Số phần tử không gian mẫu: n(Ω) =15. n A
Gọi A là biến cố: ‘‘Chọn được số chẵn’’ thì n( A) = ⇒ p( A) ( ) 8 8 = = n(Ω) . 15
Câu 24: Từ một hộp chứa 11 quả cầu màu đỏ và 4quả cầu màu xanh, lấy ngẫu nhiên đồng thời3quả cầu.
Xác suất để lấy được3quả cầu màu xanh bằng 24 4 4 24 A. . B. . C. . D. . 455 165 455 165 Lời giải Ta có n(Ω) 3 = C . 15
Gọi Alà biến cố “lấy được3quả cầu màu xanh” suy ra n( A) 3 = C 4 3 C 4
Vậy xác suất để lấy ra được 3 quả cầu màu xanh là P( A) 4 = = 3 C 455 15 Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 25: Cho 2 điểm A(1;2), B(3;4). Viết phương trình tổng quát đường trung trực của đoạn thẳng AB .
A. x + y + 5 = 0.
B. x − y − 5 = 0.
C. 2x + 2y − 5 = 0.
D. x + y − 5 = 0. Lời giải
+ Giả sử ∆ là đường trung trực của AB ⇒ ∆ ⊥ AB tại trung điểm M của AB .  x + x A B x = =  M 2
+ Tọa độ trung điểm M của AB là :  2  ⇒ M (2;3) . y + yA B y = = M 3  2  
+ Ta có AB = (2;2) = 2(1; ) 1 ⇒ n = ∆ (1; )1
Suy ra phương trình tổng quát đường trung trực ∆ của đoạn thẳng AB là: x + y − 5 = 0.
Câu 26: Trong mặt phẳng Oxy , khoảng cách giữa hai đường thẳng song song d :3x − 4y −3 = 0 và 1
d :3x − 4y −8 = 0 là 2 A. 4. B. 3. C. 1. D. 2. Lời giải Lấy A(0; 2 − )∈d . 2 − − − − Do 3.0 4.( 2) 3
d d nên d (d ,d = d , A d = = 1 1 2 ) ( 1 ) 1 2 2 2 3 − + ( 4) −
Câu 27: Trong mặt phẳng tọa độ Oxy, cho đường tròn 2 2
(C) : x + y − 4x − 2y − 20 = 0 phương trình tiếp
tuyến của (C) vuông góc với đường thẳng ∆ :3x + 4y + 9 = 0 là
A. 4x − 3y + 30 = 0 và 4x − 3y − 20 = 0.
B. 4x − 3y + 20 = 0 và 4x − 3y − 30 = 0 .
C. 4x − 3y − 30 = 0 và 4x − 3y − 20 = 0.
B. 4x − 3y + 20 = 0 và 4x − 3y + 30 = 0 . Lời giải
Đường tròn (C) có tâm I (2; ) 1 và bán kính 2 2 R = 2 +1 + 20 = 5 .
Đường thẳng d vuông góc với ∆ :3x + 4y + 9 = 0 ⇒ d : 4x − 3y + m = 0 . 4.2 − 3.1+ m
d là tiếp tuyến của (C) ⇔ d (I,d ) = R ⇔ = 5. 2 4 + ( 3 − )2 m − 5 = 25 m = 30
d : 4x − 3y + 30 = 0 ⇔ ⇔ ⇔  . m 5 25  m 20  − = − = −
d : 4x − 3y − 20 = 0
Câu 28: Cho tam giác ABC có A(1;− )
1 , B(3;2), C (5; 5
− ) . Toạ độ tâm đường tròn ngoại tiếp tam giác ABC là A.  47 13 ;  −        . B. 47 13  ; . C. 47 13 −  ;− . D. 47 13 −  ; . 10 10        10 10   10 10   10 10  Lời giải
Gọi I ( ;x y) là tâm đường tròn ngoại tiếp tam giác ABC .  47 AI = BI ( −  )2 1 + ( + )2 1 = ( −3)2 + ( − 2)2 2 2 4x + 6y =11 x x y x y =   10  ⇔  ⇔  ⇔  2 2 AI = CI (
x − )2 + ( y + )2 = ( x − )2 + ( y + )2 8
x − 8y = 48 13 1 1 5 5   y = − Ta có:  10 . Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 47 13 ⇒ I  ;  −  10 10   . 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 16 5
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 8 . B. 16. C. 4 . D. 5. Lời giải 2 2
Gọi F và F là hai tiêu điểm của ( ) : x y H −
= 1, a > 0,b > 0 . 2 2 ( ) 1 2 a b
Điểm M ∈(H ) ⇔ MF − MF = 2a . 1 2 2 2
Từ phương trình ( ) : x y H − = 1 suy ra 2
a =16 ⇒ a = 4,(a > 0) . 16 5
Vậy hiệu các khoảng cách từ mỗi điểm M nằm trên (H ) đến hai tiêu điểm có giá trị tuyệt đối
là MF − MF = 2a = 8. 1 2
Câu 30: Có bao nhiêu số tự nhiên gồm bốn chữ số khác nhau và chia hết cho 5?. A. 952. B. 1800. C. 1008. D. 1620. Lời giải
Gọi số tự nhiên cần tìm có dạng: abcd . Do chia hết cho 5 nên d ∈{0; } 5
Trường hợp 1: với d = 0 ta có: Chọn d có 1 cách. Chọn a có 9 cách Chọn b có 8 cách Chọn c có 7 cách
Vậy trường hợp 1 có: 9.8.7 = 504 số
Trường hợp 2: với d = 5 ta có: Chọn d có 1 cách. Chọn a có 8 cách Chọn b có 8 cách Chọn c có 7 cách
Vậy trường hợp 1 có: 8.8.7 = 448 số
Vậy có: 504 + 448 = 952số thỏa yêu cầu bài toán.
Câu 31: Có 5nhà toán học nam, 3nhà toán học nữ và 4 nhà vật lý nam. Lập một đoàn công tác có 3
người cần có cả nam và nữ, trong đó có cả nhà toán học và nhà vật lý. Hỏi có bao nhiêu cách lập? A. 60 . B. 90. C. 20 . D. 12. Lời giải
Để lập đội công tác ta chia làm các trường hợp sau:
+ Số cách chọn đội công tác gồm 1 nhà toán học nam, 1 nhà toán học nữ, 1 nhà vật lý nam có 5.3.4 = 60 cách
+ Số cách chọn đội công tác gồm 1 nhà toán học nữ, 2 nhà vật lý nam có 2 3.C =18 cách 4
+ Số cách chọn đội công tác gồm 2 nhà toán học nữ, 1 nhà vật lý nam có 2 1 C .C =12 cách 3 4 Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Vậy số cách lập là 60 +18 +12 = 90 cách.
Câu 32: Cho tứ giác ABCD . Trên mỗi cạnh AB, BC,CD, DA lấy 7 điểm phân biệt và không có điểm nào trùng với 4 đỉnh ,
A B,C, D . Hỏi từ 32 điểm đã cho lập được bao nhiêu tam giác? A. 4960. B. 4624. C. 7140. D. 6804. Lời giải
Số tam giác lập được là số cách chọn 3 điểm trong 32 điểm đã cho sao cho không có 3 điểm nào thẳng hàng.
Số cách chọn 3 điểm như trên là 3 3 C − 4C = 4624 32 9
Số tam giác lập được thoả mãn đề bài là 4624.
Câu 33: Trong một lớp học gồm có 18 học sinh nam và 17 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học
sinh lên bảng giải bài tập. Xác suất để 4 học sinh được gọi có cả nam và nữ là: A. 68 . B. 65 . C. 443 . D. 69 . 75 71 506 77 Lời giải Ta có: n(Ω) 4 = C = 52360 . 35
Số cách gọi 4 học sinh lên bảng giải bài tập mà cả 4 bạn đều là nữ là: 4 C 17
Số cách gọi 4 học sinh lên bảng giải bài tập mà cả 4 bạn đều là nam là: 4 C 18
Gọi A là biến cố: “4 học sinh được gọi có cả nam và nữ”. Suy ra: n( A) 4 = C − ( 4 4 C + C = 46920 . 35 17 18 )
Vậy xác suất để 4 học sinh được gọi có cả nam và nữ là:
p( A) n( A) 46920 69 = = = . n(Ω) 52360 77
Câu 34: Chọn ngẫu nhiên hai số phân biệt từ 15 số nguyên dương đầu tiên. Xác suất để tích hai số được
chọn là một số chẵn bằng 1 4 4 11 A. 5 . B. 15 . C. 5 . D. 15 . Lời giải
Số phần tử của không gian mẫu: n(Ω) 2 = C =105 15 .
Gọi A là biến cố: “Tích hai số được chọn là một số chẵn”.
Trường hợp 1: Chọn hai số đều là số chẵn. Số cách chọn : 2 C = 21. 7
Trường hợp 2: Chọn một số chẵn và một số lẻ. Số cách chọn : 1 1 C .C = 56 . 7 8 n A Do đó: n( A) 2 1 1
= C + C .C = 77 77 11 7 7 8 . Suy ra: P( A) ( ) = = = . n(Ω) 105 15
Câu 35: Từ một tổ gồm 10 nam và 8 nữ chọn ra một đoàn đại biểu gồm 6 người để tham dự hội nghị. Xác
suất để đoàn đại biểu được chọn có đúng 2 nữ bằng A. 151 . B. 35 . C. 70 . D. 29 . 221 221 221 221 Lời giải
Chọn ngẫu nhiên một đoàn đại biểu gồm 6 người từ tổ gồm 18 người. Ta có n(Ω ) 6 = 18 C .
Gọi A là biến cố trong 6 đại biểu được chọn có đúng 2 người là nữ. Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Chọn 2 đại biểu nữ từ 8 đại biểu nữ có 28 C cách.
Chọn 4 đại biểu nam từ 10 đại biểu nam có 410 C cách.
Từ đó có n( A) 2 4 = 8 C . 10 C . 2 4 n A Vậy P( A) ( ) 8 C . 10 C 70 = = = . n(Ω ) 6 18 C 221
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp A = {0; 1; 2; 3; 4; 5; }
6 . Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác
nhau được lập thành từ các chữ số của tập A , đồng thời có đúng 2 chữ số lẻ và 2 chữ số lẻ đó đứng cạnh nhau. Lời giải
Vì 2 chữ số lẻ đứng kề nhau nên ta gom 2 số lẻ thành số M , có 2 C = 3 M 3 bộ .
Gọi số cần chọn có dạng abcd với d ∈{0; 2; 4; } 6 .
` ● Trường hợp 1. d = 0 , suy ra d có 1 cách chọn.
+) Có 3 vị trí để xếp chữ số M , ứng với mỗi cách xếp M có 2! cách xếp hai phần tử trong M .
+) Chọn thứ tự 2 chữ số từ tập {2; 4; }
6 để xếp vào 2 vị trí trống còn lại, có 2 A3 cách.
Do đó trường hợp này có 2 1.3.2!.A = 36 3 số.
● Trường hợp 2. d ∈{2; 4; }
6 , suy ra d có 3 cách chọn.
+) Nếu xếp M vào vị trí đầu tiên nên có 1 cách, ứng với cách xếp này có 2! cách xếp hai phần
tử trong M . Chọn 2 chữ số từ tập 3 chữ số còn lại để xếp vào 2 vị trí trống còn lại, có 2 A3 cách. Suy ra có tất cả 2 3.1.2!.A = 36 3 số.
+) Nếu xếp M vào vị trí thứ 2 hoặc thứ 3 thì có 2 cách, ứng với cách xếp này có 2! cách xếp
hai phần tử trong M . Chọn 2 chữ số từ tập 3 chữ số còn lại để xếp vào 2 vị trí trống còn lại, có 2 A 2 3.2.2!.A = 72 0 3 cách. Do đó 3
số. Xét riêng trường hợp chữ số đứng đầu thì có 1 3.2.2!.A = 24 72 − 24 = 48 2 số. Suy ra có số.
Do đó trường hợp này có 36 + 48 = 84 số.
Vậy có 3.(36 + 84) = 360 số thỏa mãn.
Câu 37: Trong mặt phẳng tọa độ Oxy , cho điểm M (2; )
1 và đường tròn (C) (x − )2 + ( y − )2 : 1 2 = 4. Viết
phương trình đường thẳng (d ) qua điểm M và cắt (C) tại hai điểm phân biệt ; A B sao cho độ
dài AB ngắn nhất. Lời giải Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Đường tròn (C) có tâm I (1;2) , bán kính R = 2 .
IM = 2 < R = 2 nên điểm M nằm trong đường tròn.
Giả sử gọi H là trung điểm của AB . Ta có 2 2 2
AB = 2HB = 2. IB − IH = 2 4 − IH
Vì IH ≤ IM = 2 nên 2 2
AB = 2 4 − IH ≥ 2 4 − IM = 2 2 do đó AB ngắn nhất khi IH = IM 
Lúc đó đường thẳng d qua M (2; )
1 và nhận IM = (1;− ) 1 làm vecto pháp tuyến
(d ):1(x − 2) −1( y − )
1 = 0 ⇔ (d ) : −x + y +1 = 0 ⇒ a = 1; − c =1
Câu 38: Xếp 5 quyển sách Toán và 5 quyển sách Văn khác nhau lên một kệ dài. Tính xác suất để 2
quyển sách cùng một môn nằm cạnh nhau. Lời giải + n(Ω) =10!
+ Đặt biến cố A : Có hai quyển sách cùng môn nằm cạnh nhau
Khi đó A : Các quyển sách cùng môn không nằm cạnh nhau
Có n( A) = 2.5!.5!
n( A) = n(Ω) − n( A) =10!− 2.5!.5!= 3600000
⇒ P( A) n( A) 125 = = . n(Ω) 126
Câu 39: Vệ tinh nhân tạo đầu tiên được Liên Xô phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là
một đường elip nhận tâm Trái Đất là một tiêu điểm có phương trình quỹ đạo là 2 2 x y 2 2 2 +
=1,a > 0,b > 0,c = a − b . Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 2 2 a b
583 dặm và xa nhất là 1342 dặm. Tìm tỷ số c , biết bán kính của Trái Đất xấp xỉ 4000 dặm. a Lời giải
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F của elip. 1 2 2
Khi đó elip có phương trình là: x y +
=1, a > 0,b > 0 2 2 a b
Theo đề bài, ta có: vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm,
mà bán kính của Trái Đất xấp xỉ 4000 dặm nên vệ tinh cách tâm Trái Đất gần nhất là 4583dặm và xa nhất là 5342 dặm.
Giả sử vệ tinh được biểu thị là điểm M ( ; x y) . Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 c
Khi đó khoảng cách từ vệ tinh đến tâm Trái Đất là: MF = a + x 1 a
Và ta có a − c ≤ MF ≤ a + c 1
Vậy khoảng cách nhỏ nhất và lớn nhất từ vệ tinh đến tâm Trái Đất lần lượt là a − c và a + c
a − c = 4583 a = 4962,5 ⇒  ⇒ a c 5342  + = c = 379,5 c Suy ra ≈ 0,076 a
---------- HẾT ---------- Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 09
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). 
Câu 1: Trong hệ tọa độ Oxy, cho A(5;2), B(
10;8) . Tìm tọa độ của vectơ AB?    
A. AB = (15;10) .
B. AB = (2;4) .
C. AB = (5;6) .
D. AB = (50;16) .
Câu 2: Trong mặt phẳng tọa độ Oxy, gọi E ( 2;
− 0) , F (0;2 3) lần lượt là hình chiếu của điểm M lên 
các trục tọa độ Ox, Oy. Độ dài của vectơ OM là A. 2 2 . B. 4 . C. 2 . D. 3 .
Câu 3: Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: 8 = 2,828427125 . Giá trị gần
đúng của 8 chính xác đến hàng phần trăm là A. 2,81. B. 2,83. C. 2,82. D. 2,80.
Câu 4: Hãy tìm trung vị cho mẫu số liệu điểm kiểm tra môn Toán của Lớp 11B: 3 5 6 7 1 10 3 4 A. 4,5. B. 4 . C. 5. D. 5,5 .
Câu 5: Người ta đã thống kê số gia cầm bị tiêu hủy trong vùng dịch của 6 xã A,B,.,F như sau (đơn vị: nghìn con): Xã A B C D E F Số lượng gia cầm bị tiêu hủy 12 25 27 15 45 5
Tìm trung vị cho mẫu số liệu về số gia cầm bị tiêu huỷ đã cho. A. 20 . B. 21. C. 21,5 . D. 27 .
Câu 6: Nhiệt độ của thành phố Vinh ghi nhận trong 10 ngày qua lần lượt là:
24 21 30 34 28 35 33 36 25 27
Khoảng tứ phân vị của mẫu số liệu bằng: A. ∆ = . B. ∆ = . C. ∆ = D. ∆ = . Q 11 Q 9 Q 13 Q 12
Câu 7: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị kw ) hàng tháng của gia đình bạn An trong năm
2021 như sau: 163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là 10kw .Gọi ∆ ∆′ lần lượt Q ; Q
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây là đúng A. ∆ = ∆′ . B. ∆′ = ∆ − . C. ∆ = ∆′ − D. ∆′ = ∆ − . Q Q 10 Q Q 20 Q Q 10 Q Q
Câu 8: Các giá trị bất thường của mẫu số liệu 5,6 ,19, 21, 22 , 23, 24 , 25 , 26 , 27 , 28 ,31, 35,38, 42 là A. 5,42. B. 5,6,38,42. C. 5,6,42 . D. 5,35,38,42 . 
Câu 9: Đường thẳng ∆ đi qua điểm M (1;4) và có vectơ pháp tuyến n = (2;3) có phương trình tổng quát là
A. 2x + 3y −14 = 0 .
B. 2x + 3y +10 = 0. C. −x + 4y −10 = 0 . D. −x + 4y +10 = 0 .
Câu 10: Viết phương trình đường thẳng đi qua điểm M ( 2;
− 5) và cắt hai trục tọa độ tại hai điểm A và
B sao cho M là trung điểm của AB . Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
A. 5x + 2y +15 = 0.
B. 2x − 5y + 20 = 0 . C. 5x − 2y + 20 = 0 . D. 2y − 5x + 20 = 0 .
Câu 11: Tính góc giữa hai đường thẳng ∆ : x − 3y + 2 = 0 và
∆ ': x + 3y −1 = 0 ? A. 90o. B. 120o. C. 60o. D. 30o. x = 6 + 6t
Câu 12: Tìm côsin góc giữa 2 đường thẳng ∆ : 4x −3y +1= 0 ∆ : 1 và 2  . y =1−8t A. 7 . B. 1. C. 24 . D. 6 . 25 25 25
Câu 13: Xác định tâm và bán kính của đường tròn (C) (x + )2 + ( y − )2 : 1 2 = 9. A. Tâm I ( 1;
− 2), bán kính R = 3. B. Tâm I ( 1;
− 2), bán kính R = 9. C. Tâm I (1; 2
− ), bán kính R = 3. D. Tâm I (1; 2
− ), bán kính R = 9.
Câu 14: Trong mặt phẳng với hệ toạ độ Oxy , phương trình đường tròn có tâm I (3; ) 1 và đi qua điểm M (2; ) 1 − là
A. (x + )2 + ( y + )2 3 1 = 5.
B. (x − )2 + ( y − )2 3 1 = 5.
C. (x − )2 + ( y − )2 3
1 = 5. D. (x + )2 + ( y + )2 3 1 = 5.
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol? A. 2 y = 3x . B. 2 y = 4x . C. 2 y = 5x . D. 2 y = 4x .
Câu 16: Trong kì thi vấn đáp môn toán lớp 11, Ban giám khảo đã chuẩn bị 25 câu đại số, 15 câu hình học
và 10 câu giải tích. Thí sinh được quyền chọn một câu để trả lời. Số khả năng chọn câu hỏi của mỗi thí sinh là A. 3750. B. 50. C. 375. D. 150.
Câu 17: Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái
bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn? A. 90. B. 70 . C. 80 . D. 60 .
Câu 18: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là A. 9!. B. 9. C. 1. D. 9 9 .
Câu 19: Năm 2021, cuộc thi Hoa hậu Hòa bình Quốc tế lần thứ 9 được tổ chức tại Thái Lan và có tổng
cộng 59 thí sinh tham gia. Hỏi có bao nhiêu các chọn ra 5 người bao gồm một Hoa hậu và bốn Á hậu 1, 2, 3, 4? A. 5 A . B. 5 C . C. 1 4 A + A . D. 1 4 C .C . 59 59 59 58 59 58
Câu 20: Trong mặt phẳng cho 15 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác
trong có đỉnh là 3 trong số 15 đã cho là A. 3 C . A . 15 B. 15!. C. 3 15 . D. 315
Câu 21: Tìm hệ số của 2 2
x y trong khai triển nhị thức Niu-tơn của (x + y)4 2 . A. 32. B. 8 . C. 24 . D. 16.
Câu 22: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác
suất để được 3 quả cầu khác màu là A. 3 . B. 3 . C. 3 . D. 3 . 7 5 14 11
Câu 23: Có 30 chiếc thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên 1 chiếc thẻ, tính xác suất để
chọn được thẻ ghi số chia hết cho 3 Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 1 . B. 1 . C. 3 . D. 2 . 3 2 10 3
Câu 24: Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng 1 3 2 A. 1 . B. . D. 6 30 . C. 5 5 .
Câu 25: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(2;0), B(0;3),C ( 3 − ; )
1 . Đường thẳng d
đi qua B và song song với AC có phương trình tổng quát là
A. x −15y +15 = 0 .
B. 5x + y − 3 = 0 .
C. x + 5y −15 = 0 .
D. 5x + y + 3 = 0 .
Câu 26: Trong mặt phẳng Oxy cho 3 điểm A( 1;4 ), B( 3;−1 ),C ( 6;2 ) không thẳng hàng. Tính khoảng
cách từ điểm A đến đường thẳng BC .
A. d ( A BC) 3 2 ; =
. B. d ( A BC) 2 ; =
. C. d ( A BC) 2 ; =
. D. d ( A BC) 7 2 ; = . 2 2 7 2
Câu 27: Đường tròn (C) đi qua hai điểm A(1; )
1 , B(5;3) và có tâm I thuộc trục hoành có phương trình là A. (x + )2 2
4 + y =10. B. (x − )2 2
4 + y =10 . C. (x − )2 2
4 + y = 10 . D. (x + )2 2 4 + y = 10 .
Câu 28: Trong mặt phẳng tọa độ Oxy , cho đường tròn (L) 2 2
: x + y − 2ax − 2by + c = 0 ngoại tiếp tam
giác ABC , với A(1;0), B(0; – 2),C (2; – )
1 . Khi đó giá trị của biểu thức a + b + c bằng A. 2 . B. 2 − . C. 1 − . D. 1 . 3 3 3 3
Câu 29: Phương trình chính tắc của (E) có tiêu cự bằng 6 và đi qua điểm A(5;0) là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 100 81 25 16 15 16 25 9
Câu 30: Trong hội nghị học sinh giỏi của trường, khi ra về các em bắt tay nhau. Biết rằng có 120 cái bắt
tay và giả sử không em nào bị bỏ sót cũng như bắt tay không lặp lại 2 lần. Số học sinh dự hội
nghị thuộc khoảng nào sau đây? A. (13;18) . B. (21;26). C. (17;22) . D. (9;14) .
Câu 31: Một lớp có 30 học sinh gồm 20 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học
sinh sao cho nhóm đó có ít nhất một học sinh nữ? A. 1140. B. 2920 . C. 1900. D. 900.
Câu 32: Cho tập hợp A = {1;2;3;4;5;6;7} . Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên có 6
chữ số khác nhau và phải có mặt các chữ số 1, 2 , 3 sao cho chúng không đứng cạnh nhau? A. 567. B. 576. C. 5040. D. 840 .
Câu 33: Một nhóm gồm 12 học sinh trong đó có 6 học sinh khối 12, 4 học sinh khối 11 và 2 học sinh
khối 10. Chọn ngẫu nhiên 3học sinh tham gia đội xung kích. Tính xác suất để 3học sinh được
chọn không cùng một khối? A. 1 . B. 6 . C. 12 . D. 49 . 5 55 55 55
Câu 34: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là A. 1 . B. 1 . C. 1. D. 2 . 2 3 3 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 35: Một người chọn ngẫu nhiên 2 chiếc giày từ 5 đôi giày cỡ khác nhau. Tính xác suất để 2 chiếc
giày được chọn tạo thành một đôi. A. 1 . B. 1 . C. 7 . D. 1 . 2 10 9 9
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; }
7 . Có bao nhiêu số tự nhiên chẵn có 6 chữ số khác nhau
được lập thành từ các chữ số của tập A đồng thời phải có mặt ba chữ số 0; 1; 2 và chúng đứng cạnh nhau?
Câu 37: Cho điểm M (1;2) và đường thẳng d : 2x + y −5 = 0 . Toạ độ của điểm đối xứng với điểm M qua d là
Câu 38: Một hộp đựng 10 viên bi có kích thước khác nhau, trong đó có 7 viên bi màu đỏ và 3 viên bi
màu xanh. Chọn ngẫu nhiên 2 viên bi từ hộp trên. Xác suất để 2 viên bi được chọn có ít nhất
một viên bi màu xanh bằng
Câu 39: Cho elip (E) có độ dài trục lớn bằng 15và đi qua điểm M sao cho  0
F MF = 90 . Biết diện tích 1 2 tam giác MF F
1 2 bằng 26. Phương trình chính tắc của elip ( E ) là.
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). 
Câu 1: Trong hệ tọa độ Oxy, cho A(5;2), B(
10;8) . Tìm tọa độ của vectơ AB?    
A. AB = (15;10) .
B. AB = (2;4) .
C. AB = (5;6) .
D. AB = (50;16) . Lời giải Chọn C 
Áp dụng công thức AB = (x − x y − y = B A ; B A ) (5;6).
Câu 2: Trong mặt phẳng tọa độ Oxy, gọi E ( 2;
− 0) , F (0;2 3) lần lượt là hình chiếu của điểm M lên 
các trục tọa độ Ox, Oy. Độ dài của vectơ OM là A. 2 2 . B. 4 . C. 2 . D. 3 . Lời giải Chọn B
Tọa độ của điểm M = ( 2; − 2 3)  
Độ dài của vectơ OM là OM = (− ) + ( )2 2 2 2 3 = 16 = 4
Câu 3: Khi sử dụng máy tính bỏ túi với 10 chữ số thập phân ta được: 8 = 2,828427125 . Giá trị gần
đúng của 8 chính xác đến hàng phần trăm là A. 2,81. B. 2,83. C. 2,82. D. 2,80. Lời giải Chọn B
Giá trị gần đúng của 8 = 2,828427125 chính xác đến hàng phần trăm là 2,83.
Câu 4: Hãy tìm trung vị cho mẫu số liệu điểm kiểm tra môn Toán của Lớp 11B: 3 5 6 7 1 10 3 4 A. 4,5. B. 4 . C. 5. D. 5,5 .
Câu 5: Người ta đã thống kê số gia cầm bị tiêu hủy trong vùng dịch của 6 xã A,B,.,F như sau (đơn vị: nghìn con): Xã A B C D E F Số lượng gia cầm bị tiêu hủy 12 25 27 15 45 5
Tìm trung vị cho mẫu số liệu về số gia cầm bị tiêu huỷ đã cho. A. 20 . B. 21. C. 21,5 . D. 27 . Lời giải Chọn A
Sắp xếp mẫu số liệu đã cho theo thứ tự không giảm ta được: 5 12 15 25 27 45 Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 +
Mẫu số liệu đã cho có 6 giá trị nên trung vị của mẫu đó là 15 25 = 20 . 2
Câu 6: Nhiệt độ của thành phố Vinh ghi nhận trong 10 ngày qua lần lượt là:
24 21 30 34 28 35 33 36 25 27
Khoảng tứ phân vị của mẫu số liệu bằng: A. ∆ = . B. ∆ = . C. ∆ = D. ∆ = . Q 11 Q 9 Q 13 Q 12 Lời giải Chọn D
Ta sắp xếp mẫu số liệu theo thứ tự không giảm: 21 24 25 27 28 30 33 34 35 36
Mẫu số liệu gồm 10 giá trị nên số trung vị là Q = (28 + 30) : 2 = 29 2
Nửa số liệu bên trái là 21; 24; 25; 27;28gồm 5 giá trị, số chính giữa là 25 Khi đó Q = 25 1
Nửa số liệu bên phải là 30;33; 34; 35; 36 gồm 5 giá trị, số chính giữa là 34 Khi đó Q = 34 3
Khoảng tứ phân vị của mẫu số liệu bằng: ∆ = Q − Q = − = Q 34 25 9 3 1
Câu 7: Mẫu số liệu cho biết lượng điện tiêu thụ ( đơn vị kw ) hàng tháng của gia đình bạn An trong năm
2021 như sau: 163 165 159 172 167 168 170 161 164 174 170 166
Trong năm 2022 nhà bạn An giảm mức tiệu thụ điện mỗi tháng là 10kw .Gọi ∆ ∆′ lần lượt Q ; Q
là khoảng tứ phân vị của mẫu số liệu tiêu thụ điện năm 2021 năm 2022. Đẳng thức nào sau đây là đúng A. ∆ = ∆′ . B. ∆′ = ∆ − . C. ∆ = ∆′ − D. ∆′ = ∆ − . Q Q 10 Q Q 20 Q Q 10 Q Q Lời giải Chọn A
+) Sắp xếp mẫu số liệu năm 2021 theo thứ tự không giảm: 159 161 163 164 165 166 167 168 170 170 172 174
Mẫu số liệu gồm 12 giá trị nên số trung vị là Q = (166 +167) : 2 =166,5 2
Nửa số liệu bên trái là 159;161;163;164;165;166gồm 6 giá trị
Khi đó Q = 163+164 : 2 =163,5 1 ( )
Nửa số liệu bên phải là 167;168;170;170;172;174 gồm 6 giá trị Khi đó Q =170 3
Khoảng tứ phân vị của mẫu số liệu bằng: ∆ = Q − Q = − = Q 170 163,5 6,5 3 1
+) Sắp xếp mẫu số liệu năm 2022 theo thứ tự không giảm: Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 149 151 153 154 155 156 157 158 160 160 162 164
Mẫu số liệu gồm 12 giá trị nên số trung vị là Q = (156 +157) : 2 =156,5 2
Nửa số liệu bên trái là 149;151;153;154;155;156gồm 6 giá trị
Khi đó Q = (153+154) : 2 =153,5 1
Nửa số liệu bên phải là 157;158;160;160;162;164 gồm 6 giá trị Khi đó Q =160 3
Khoảng tứ phân vị của mẫu số liệu bằng: ∆′ = Q − Q = − = Q 160 153,5 6,5 3 1
Câu 8: Các giá trị bất thường của mẫu số liệu 5,6 ,19, 21, 22 , 23, 24 , 25 , 26 , 27 , 28 ,31, 35,38, 42 là A. 5,42. B. 5,6,38,42. C. 5,6,42 . D. 5,35,38,42 . Lời giải Chọn A
Mẫu số liệu có các tứ phân vị Q = 21 Q = 25 Q = 31 Q ∆ = 1 , 2 , 3
. Suy ra khoảng tứ phân vị 10 . Khi đó 3 Q − Q ∆ = 6 , 3 Q + Q
∆ = 41 nên các giá trị 5, 1
42 là các giá trị bất thường của mẫu 2 1 2 số liệu trên 
Câu 9: Đường thẳng ∆ đi qua điểm M (1;4) và có vectơ pháp tuyến n = (2;3) có phương trình tổng quát là
A. 2x + 3y −14 = 0 .
B. 2x + 3y +10 = 0. C. −x + 4y −10 = 0 . D. −x + 4y +10 = 0 . Lời giải
Đường thẳng ∆ đi qua điểm M (1;4) và có vectơ pháp tuyến n = (2;3) có phương trình tổng quát là 2(x − )
1 + 3( y − 4) = 0 ⇔ 2x + 3y −14 = 0.
Câu 10: Viết phương trình đường thẳng đi qua điểm M ( 2;
− 5) và cắt hai trục tọa độ tại hai điểm A và
B sao cho M là trung điểm của AB .
A. 5x + 2y +15 = 0.
B. 2x − 5y + 20 = 0 . C. 5x − 2y + 20 = 0 . D. 2y − 5x + 20 = 0 . Lời giải
Gọi A∈Ox ⇒ A(xA;0) và B∈Oy ⇒ B(0; yB ) .
xA + xB = 2 M xxA = 4 −
Vì M là trung điểm của AB nên ta có:  ⇒ . y
A + yB = 2 yM yB =   10 x y
Suy ra phương trình đường thẳng AB là +
=1 ⇔ 5x − 2y + 20 = 0. 4 − 10
Câu 11: Tính góc giữa hai đường thẳng ∆ : x − 3y + 2 = 0 và
∆ ': x + 3y −1 = 0 ? A. 90o. B. 120o. C. 60o. D. 30o. Lời giải  
∆ có vectơ pháp tuyến là n = 1;− 3 . ∆ ' có vectơ pháp tuyến là n = 1; 3 . 2 ( ) 1 ( ) Khi đó: Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10     n .n 1.1+ − 3 3 1 2 ( ) ( 2 − ' ∆ ∆ ) 1 cos ;
= cos(n ;n ) =  = = = . 1 2   | n |. n 1 + (− 3)2. 1 +( 3)2 2 2 4. 4 2 1 2
Vậy góc giữa hai đường thẳng ∆, ∆ ' là 0 60 . x = 6 + 6t
Câu 12: Tìm côsin góc giữa 2 đường thẳng ∆ : 4x −3y +1= 0 ∆ : 1 và 2  . y =1−8t A. 7 . B. 1. C. 24 . D. 6 . 25 25 25 Lời giải  
Ta có vec tơ pháp tuyến của hai đường thẳng là: n = − . n = ∆ (8;6) ∆ (4; 3) 1 2   4.8 − 3.6 7 ⇒ cos(∆ ,∆ = cos n = = . ∆ , n 1 2 ) ( 1 ∆2 ) + (− )2 2 2 2 25 4 3 . 8 + 6
Câu 13: Xác định tâm và bán kính của đường tròn (C) (x + )2 + ( y − )2 : 1 2 = 9. A. Tâm I ( 1;
− 2), bán kính R = 3. B. Tâm I ( 1;
− 2), bán kính R = 9. C. Tâm I (1; 2
− ), bán kính R = 3. D. Tâm I (1; 2
− ), bán kính R = 9. Lời giải
Đường tròn (C) (x + )2 + ( y − )2 : 1 2 = 9 có tâm I ( 1;
− 2), bán kính R = 3.
Câu 14: Trong mặt phẳng với hệ toạ độ Oxy , phương trình đường tròn có tâm I (3; ) 1 và đi qua điểm M (2; ) 1 − là
A. (x + )2 + ( y + )2 3 1 = 5.
B. (x − )2 + ( y − )2 3 1 = 5.
C. (x − )2 + ( y − )2 3
1 = 5. D. (x + )2 + ( y + )2 3 1 = 5. Lời giải
Vì đường tròn có tâm I (3; )
1 và đi qua điểm M (2; ) 1
− nên bán kính của đường tròn là
R = MI = ( − )2 + ( + )2 3 2 1 1 = 5 .
Vậy phương trình đường tròn cần tìm là (x − )2 + ( y − )2 3 1 = 5 .
Câu 15: Phương trình nào sau đây không phải là phương trình chính tắc của parabol? A. 2 y = 3x . B. 2 y = 4x . C. 2 y = 5x . D. 2 y = 4x .
Câu 16: Trong kì thi vấn đáp môn toán lớp 11, Ban giám khảo đã chuẩn bị 25 câu đại số, 15 câu hình học
và 10 câu giải tích. Thí sinh được quyền chọn một câu để trả lời. Số khả năng chọn câu hỏi của mỗi thí sinh là A. 3750. B. 50. C. 375. D. 150. Lời giải
Công việc chọn câu hỏi của thí sinh được hoàn thành bởi một trong các hành động: chọn 1 câu
hỏi đại số, chọn 1 câu hỏi hình học, chọn 1 câu hỏi giải tích.
Theo quy tắc cộng có 25 +15 +10 = 50 khả năng chọn câu hỏi cho mỗi thí sinh.
Câu 17: Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái
bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn? A. 90. B. 70 . C. 80 . D. 60 . Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Lời giải
Số cách chọn 1 cái bút là10.
Số cách chọn 1 quyển sách là 8 .
Vậy theo quy tắc nhân, số cách chọn 1 cái bút và 1 quyển sách là: 10.8 = 80 .
Câu 18: Số cách sắp xếp 9 học sinh ngồi vào một dãy gồm 9 ghế là A. 9!. B. 9. C. 1. D. 9 9 . Lời giải
Số cách xếp cần tìm là: P = 9!. 9
Câu 19: Năm 2021, cuộc thi Hoa hậu Hòa bình Quốc tế lần thứ 9 được tổ chức tại Thái Lan và có tổng
cộng 59 thí sinh tham gia. Hỏi có bao nhiêu các chọn ra 5 người bao gồm một Hoa hậu và bốn Á hậu 1, 2, 3, 4? A. 5 A . B. 5 C . C. 1 4 A + A . D. 1 4 C .C . 59 59 59 58 59 58 Lời giải
Số cách chọn một Hoa hậu và bốn Á hậu 1, 2, 3, 4 sẽ tương ứng chọn 5 người trong 59 người
có phân biệt thứ tự. Suy ra số cách chọn là 5 A . 59
Câu 20: Trong mặt phẳng cho 15 điểm phân biệt trong đó không có ba điểm nào thẳng hàng. Số tam giác
trong có đỉnh là 3 trong số 15 đã cho là A. 3 C . A . 15 B. 15!. C. 3 15 . D. 315 Lời giải
Ta chọn ba điểm bất kì trong 15 điểm đã cho thành lập được một tam giác, suy ra số tam giác được tạo thành là 3 C . 15
Câu 21: Tìm hệ số của 2 2
x y trong khai triển nhị thức Niu-tơn của (x + y)4 2 . A. 32. B. 8 . C. 24 . D. 16. Lời giải 4 4 Ta có (x + 2y)4 k 4−k
= ∑C x (2y)k k k 4
= ∑C .2 . −k k x y . 4 4 k =0 k =0 4 − k = 2 Số hạng chứa 2 2
x y trong khai triển trên ứng với  ⇔ k = 2. k = 2 Vậy hệ số của 2 2
x y trong khai triển của (x + y)4 2 là 2 2 C .2 = 24 . 4
Câu 22: Một bình đựng 5 quả cầu xanh, 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác
suất để được 3 quả cầu khác màu là A. 3 . B. 3 . C. 3 . D. 3 . 7 5 14 11 Lời giải Ta có n(Ω) 3 = C = 220 . 12
Gọi A là biến cố “chọn được 3 quả cầu khác màu”. Ta có n( A) = 5.4.3 = 60 . n A Suy ra P( A) ( ) 3 = = . n(Ω) 11
Vậy chọn đáp án D.
Câu 23: Có 30 chiếc thẻ được đánh số thứ tự từ 1 đến 30. Chọn ngẫu nhiên 1 chiếc thẻ, tính xác suất để
chọn được thẻ ghi số chia hết cho 3 Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 1 . B. 1 . C. 3 . D. 2 . 3 2 10 3 Lời giải Ta có n(Ω) 1 = C 30
Gọi A là biến cố: “thẻ ghi số chia hết cho 3’’
A = {3,6,9,12,15,18,21,24,27, }
30 ⇒ n( A) = 10 . n A 10 1
Xác suất của biến cố A là P( A) ( ) = = = n(Ω) 30 3 .
Câu 24: Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu xanh bằng 1 3 2 A. 1 . B. . D. 6 30 . C. 5 5 . Lời giải
Lấy ngẫu nhiên đồng thời 3 quả cầu từ 10 quả bóng đã cho có 310 C cách.
Lấy được 3 quả màu xanh từ 6 quả màu xanh đã cho có 36 C cách. 3 C
Vậy xác suất để lấy được 3 quả màu xanh là 1 6 P = = . 3 C 6 10
Câu 25: Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(2;0), B(0;3),C ( 3 − ; )
1 . Đường thẳng d
đi qua B và song song với AC có phương trình tổng quát là
A. x −15y +15 = 0 .
B. 5x + y − 3 = 0 .
C. x + 5y −15 = 0 .
D. 5x + y + 3 = 0 . Lời giải  Ta có AC = ( 5; − ) 1 . 
Vì đường thẳng d song song với AC nên d nhận AC là vectơ chỉ phương.
Suy ra vectơ pháp tuyến của d là n = (1;5) .
Phương trình đường thẳng d qua B(0;3) có vectơ pháp tuyến n = (1;5) là
1(x − 0) + 5( y − 3) = 0 ⇔ x + 5y −15 = 0.
Câu 26: Trong mặt phẳng Oxy cho 3 điểm A( 1;4 ), B( 3;−1 ),C ( 6;2 ) không thẳng hàng. Tính khoảng
cách từ điểm A đến đường thẳng BC .
A. d ( A BC) 3 2 ; =
. B. d ( A BC) 2 ; = . 2 2
C. d ( A BC) 2 ; = .
D. d ( A BC) 7 2 ; = . 7 2Lời giải   Đường thẳng 
BC có một vtcp u = BC = (3;3) ⇒ một vtpt n (1;− ) 1 .
Phương trình đường thẳng 
BC đi qua B (3;− )
1 ; nhận véc tơ pháp tuyến n (1;− ) 1 là:
1(x −3) −1( y + )
1 = 0 ⇔ x − y − 4 = 0
Khoảng cách từ điểm A(1;4) đến đường thẳng BC : x − y − 4 = 0 : Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 − − d ( A BC) 1 4 4 7 2 ; = = . 2 + (− )2 2 1 1
Câu 27: Đường tròn (C) đi qua hai điểm A(1; )
1 , B(5;3) và có tâm I thuộc trục hoành có phương trình là A. (x + )2 2
4 + y =10. B. (x − )2 2
4 + y =10 . C. (x − )2 2
4 + y = 10 . D. (x + )2 2 4 + y = 10 . Lời giải Gọi I ( ;0 x )∈Ox ; 2 2
IA = IB ⇔ ( − x)2 2 + = ( − x)2 2 1 1 5 + 3 2 2
⇔ x − 2x +1+1 = x −10x + 25 + 9
⇔ x = 4. Vậy tâm đường tròn là I (4;0) và bán kính R = IA = ( − )2 2 1 4 +1 = 10 .
Phương trình đường tròn (C) có dạng (x − )2 2 4 + y =10 .
Câu 28: Trong mặt phẳng tọa độ Oxy , cho đường tròn (L) 2 2
: x + y − 2ax − 2by + c = 0 ngoại tiếp tam
giác ABC , với A(1;0), B(0; – 2),C (2; – )
1 . Khi đó giá trị của biểu thức a + b + c bằng A. 2 . B. 2 − . C. 1 − . D. 1 . 3 3 3 3 Lời giải
Vì các điểm A, B,C nằm trên đường tròn (L) nên ta có hệ phương trình sau:  5 a =  A∈(L) 2 2 1  + 0 − 2. .1 a − 2. .0 b + c = 0  2 − a + c = 1 − 6      7 − B ∈(L) 2 2 ⇔ 0 + ( 2) − − 2. .0 a − 2. .( b 2)
− + c = 0 ⇔ 4b + c = 4 − ⇔ b  = . 6 C  ∈     (L) 2 2 2 + ( 1 − ) − 2. .2 a − 2. .( b 1 − ) + c = 0  4
− a + 2b + c = 5 −   2 c =  3
Khi đó giá trị của biểu thức 1
a + b + c = . 3
Câu 29: Phương trình chính tắc của (E) có tiêu cự bằng 6 và đi qua điểm A(5;0) là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 100 81 25 16 15 16 25 9 Lời giải Chọn B
Do (E) có tiêu cự bằng 6 nên 2c = 6 ⇒ c = 3.
Do (E) đi qua điểm A(5;0) nên a = 5 2 2 2
⇒ b = a − c = 25 − 9 =16 . 2 2
Phương trình chính tắc của (E) là ( ) : x y E + = 1. 25 16
Câu 30: Trong hội nghị học sinh giỏi của trường, khi ra về các em bắt tay nhau. Biết rằng có 120 cái bắt
tay và giả sử không em nào bị bỏ sót cũng như bắt tay không lặp lại 2 lần. Số học sinh dự hội
nghị thuộc khoảng nào sau đây? A. (13;18) . B. (21;26). C. (17;22) . D. (9;14) . Lời giải Cách 1:
Gọi số học sinh dự hội nghị là x học sinh. Đk x > 0 .
Mỗi em sẽ bắt tay với x −1 bạn còn lại. Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 x(x − ) 1
Do bắt tay không lặp lại 2 lần nên số cái bắt tay là: . 2 x(x − ) 1 x =16 (n)
Theo đề bài ta có phương trình: 2
=120 ⇔ x − x − 220 = 0 ⇔ 2  x = 15 − (l)
Vậy số học sinh dự hội nghị là 16.
Cách 2: Cứ 2 học sinh thì có 1 cái bắt tay. Vậy số cái bắt tay là số tổ hợp chập 2 của x. x x −1 2 ( ) Vậy ta có: C = ⇔ =
. Giải ra ta cũng được x =16 . x 120 120 2
Câu 31: Một lớp có 30 học sinh gồm 20 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học
sinh sao cho nhóm đó có ít nhất một học sinh nữ? A. 1140. B. 2920 . C. 1900. D. 900. Lời giải Cách 1:
Để chọn ra 3 học sinh trong đó có ít nhất một học sinh nữ ta có các phương án sau:
Phương án 1: Chọn 1 học sinh nữ và 2 học sinh nam, có 1 2
C .C cách thực hiện. 10 20
Phương án 2: Chọn 2 học sinh nữ và 1 học sinh nam, có 2 1
C .C cách thực hiện. 10 20
Phương án 3: Chọn 3 học sinh nữ, có 3
C cách thực hiện. 10
Theo quy tắc cộng, ta có: 1 2 2 1 3
C .C + C .C + C = 2920 cách chọn ra một nhóm 3 học sinh sao 10 20 10 20 10
cho nhóm đó có ít nhất một học sinh nữ. Cách 2: Có 3
C cách chọn ra 3 học sinh từ 30 học sinh, trong đó có 3
C cách chọn ra 3 học sinh, không 30 20 có học sinh nữ. Suy ra có 3 3
C − C = 2920 cách chọn ra một nhóm 3 học sinh sao cho nhóm đó có ít nhất một 30 20 học sinh nữ.
Câu 32: Cho tập hợp A = {1;2;3;4;5;6;7} . Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên có 6
chữ số khác nhau và phải có mặt các chữ số 1, 2 , 3 sao cho chúng không đứng cạnh nhau? A. 567. B. 576. C. 5040. D. 840 . Lời giải
Lấy ra 3 chữ số khác 1, 2 ,3 từ tập A có 3 C4 cách.
Xếp 3 chữ số này có 3! cách, coi 3 số trên là 3 vách ngăn sẽ tạo ra 4 vị trí xếp 3 chữ số 1, 2 ,
3 vào 3 trong 4 vị trí đó có 3 A4 cách.
Vậy số các số lập được là: 3 3 C .3!.A = 576 4 4 .
Câu 33: Một nhóm gồm 12 học sinh trong đó có 6 học sinh khối 12, 4 học sinh khối 11 và 2 học sinh
khối 10. Chọn ngẫu nhiên 3học sinh tham gia đội xung kích. Tính xác suất để 3học sinh được
chọn không cùng một khối? A. 1 . B. 6 . C. 12 . D. 49 . 5 55 55 55 Lời giải
Số phần tử của không gian mẫu n(Ω) 3 = C = 220 . 12
Gọi biến cố A : “ Ba học sinh được chọn không cùng một khối ”.
Khi đó, biến cố A : “ Ba học sinh được chọn cùng một khối ”. Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Ta có n( A) 3 3 = C + C = 24. 6 4
Xác suất của biến cố A là: P( A) 24 6 = = . 220 55
Vậy xác suất của biến cố A là:
P( A) = − P( A) 6 49 1 = 1− = . 55 55
Câu 34: Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm chẵn xuất hiện là A. 1 . B. 1 . C. 1. D. 2 . 2 3 3 Lời giải
Gieo một con súc sắc cân đối và đồng chất. Ta có không gian mẫu Ω = {1;2;3;4;5; } 6 .
Số phần tử của không gian mẫu là n(Ω) = 6 .
Gọi A là biến cố mặt có số chấm chẵn xuất hiện. Ta có A ={2;4; } 6 .
Suy ra số phần tử của biến cố A là n(A) = 3. n A
Vậy xác suất của biến cố là p( A) ( ) 3 1 = = = . n(Ω) 6 2
Câu 35: Một người chọn ngẫu nhiên 2 chiếc giày từ 5 đôi giày cỡ khác nhau. Tính xác suất để 2 chiếc
giày được chọn tạo thành một đôi. A. 1 . B. 1 . C. 7 . D. 1 . 2 10 9 9 Lời giải
Chọn ngẫu nhiên 2 chiếc giày từ 5 đôi giày cỡ khác nhau có 2 C cách. 10 Không gian mẫu là 2 Ω = C . 10
Biến cố A : “Hai chiếc giày được chọn tạo thành một đôi”.
Vì chỉ có 5 đôi giày nên số phần tử của biến cố A là : A = 5 .
Vậy xác suất của biến cố A là : 5 1 P = = . A 2 C 9 10
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; }
7 . Có bao nhiêu số tự nhiên chẵn có 6 chữ số khác nhau
được lập thành từ các chữ số của tập A đồng thời phải có mặt ba chữ số 0; 1; 2 và chúng đứng cạnh nhau? Lời giải
Gọi số cần tìm có dạng a a a a a a 1 2 3 4 5 6 .
Trường hợp 1: a = 0 a 1 6 , suy ra 6 có cách chọn.
Xếp các chữ số 1; 2 vào vị trí a a 2 4 và 5 có cách. Chọn thứ tự a , a , a {3; 4; 5; 6 } ; 7 3 A 1 2 3 từ tập có 5 cách.
Do đó trường hợp này có 3 1.2.A =120 5 số.
Trường hợp 2: a = 2 120 6
. Tương tự như trường hợp 1 nên có số. Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Trường hợp 3: a ∈ 4; 6 6 { } , suy ra a 2 6 có cách chọn.
Xếp các chữ số 0; 1; 2 đứng cạnh nhau có 3.3!− 2!=16 cách.
Chọn thứ tự hai chữ số từ tập {3; 4; 5; 6 } ; 7 \{a 2
6} để xếp vào hai vị trí còn lại có A4 cách.
Do đó trường hợp này có 2 2.16.A = 384 4 số.
Vậy có 120 +120 + 384 = 624 số thỏa mãn.
Câu 37: Cho điểm M (1;2) và đường thẳng d : 2x + y −5 = 0 . Toạ độ của điểm đối xứng với điểm M qua d là Lời giải
Phương trình đường thẳng ∆ qua M (1;2) và vuông góc với d là ∆ : x − 2y + 3 = 0 .
Tìm tọa độ giao điểm I của ∆ và d là nghiệm của hệ phương trình  7 2 + − 5 = 0 x x y =  5  7 11   I  ;  ⇔ ⇒ . x 2y 3 0 11   5 5  − + = y  =  5 M ′(x đối xứng với điểm ⇒ là trung điểm ′ y M qua d I MM ′. M ; M ′ )  x + x M M ′  7 9 x = x = − =  I   = −  M′ 2. 1 2 x ′ x x M 2 I M  5 5  9 12 ⇒  ⇒  ⇔  ⇒ M  ;  ′ . y y  + = −  ′ y ′ y y M M M 2 I M 11 12   5 5 y = y  = − = I M ′ 2. 2  2  5 5
Câu 38: Một hộp đựng 10 viên bi có kích thước khác nhau, trong đó có 7 viên bi màu đỏ và 3 viên bi
màu xanh. Chọn ngẫu nhiên 2 viên bi từ hộp trên. Xác suất để 2 viên bi được chọn có ít nhất
một viên bi màu xanh bằng Lời giải * Không gian mẫu.
Chọn ngẫu nhiên 2 viên bi từ hộp có 10 viên bi ta có không gian mẫu là n(Ω) 2 = 10 C = 45 cách chọn.
Gọi A là biến cố chọn được ít nhất một viên bi màu xanh.
* Số phần tử thuận lợi cho biến cố . A
TH1: Chọn được 1 viên bi xanh, 1 viên bi đỏ có 1 1 C3 ⋅C7 cách chọn.
TH2: Chọn được 2 viên bi màu xanh có 2 C3 cách chọn.
Do đó số phần tử thuận lợi cho biến cố A là n( A) 1 1 2
= C3 ⋅C7 + C3 = 24 cách chọn.
* Xác suất xảy ra của biến cố A n A
Xác suất để 2 viên được chọn có ít nhất một viên bi màu xanh là P( A) ( ) 24 8 = = = n(Ω) . 45 15
Câu 39: Cho elip (E) có độ dài trục lớn bằng 15và đi qua điểm M sao cho  0
F MF = 90 . Biết diện tích 1 2 tam giác MF F
1 2 bằng 26. Phương trình chính tắc của elip ( E ) là. Lời giải Ta có S = ,  0
F MF = 90 ⇒ MF .MF = 52 và 2 2
MF + MF = 2c . 1 2 ( )2 MF F 26 1 2 1 2 1 2
Độ dài trục lớn bằng 15 ⇒ MF + MF = 2a =15 1 2 . Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Mà (MF + MF )2 2 2
= MF + MF + 2MF .MF . 1 2 1 2 1 2 ⇔ ( )2 = ( c)2 2 121 15 2 + 2.52 ⇒ c = . 4 Mà 15 2 104 a = ⇒ b = . 2 4
Vậy phương trình chính tắc của elip (E) là 2 2 ( x y E): + =1 225 104 . 4 4
---------- HẾT ---------- Page 15
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KỲ II
Môn: TOÁN 10 – CÁNH DIỀU – ĐỀ SỐ 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 3 điểm ( A 1 − ;3), B(3; 4 − ),C( 5 − ; 2 − ) . Tìm tọa độ
trọng tâm G của tam giác ABC. A. G( 1; − − ) 1 B. 1 G  ; 1 −   C. 1 1 G  −  ;− G 1; 1 − 3      3 3  D. ( )
Câu 2: Trong hệ tọa độ Oxy, cho ba điểm A(1; ) 1 , B( 3;2), C (
6;5). Tìm tọa độ điểm D để tứ giác
ABCD là hình bình hành.
A. D(4;3).
B. D(3;4).
C. D(4;4).
D. D(8;6).
Câu 3: Theo thống kê, dân số Việt Nam năm 2022 là 79715675 người. Giả sử sai số tuyệt đối của số
liệu thống kê này nhỏ hơn 10000 người. Hãy viết số quy tròn của số trên
A. 79710000 người. B. 79716000 người. C. 79720000 người. D. 79700000 người.
Câu 4: Hãy tìm số trung bình của mẫu số liệu khi cho bảng tần số dưới đây: A. 8,29 B. 9,28 C. 8,73 D. 8,37.
Câu 5: Tìm mốt của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17; 17. A. 17. B. 13 C. 14 D. 15.
Câu 6: Tìm tứ phân vị thứ ba của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17. A. 16,5. B. 16 C. 15,5 D. 15.
Câu 7: Điểm thi HK1 của một học sinh lớp 10 như sau: 9 9 7 8 9 7 10 8 8
Khoảng biến thiên của mẫu số liệu là A. 1. B. 2 . C. 3. D. 0 .
Câu 8: Cho mẫu số liệu 10; 8 ; 6 ; 2 ; 4 . Độ lệch chuẩn của mẫu là A. 8 . B. 2,4 . C. 2,8. D. 6 .  x =1− t
Câu 9: Cho đường thẳng (d) có phương trình 
. Khi đó, đương thẳng (d) có 1 véc tơ pháp y = 3+ 2t tuyến là:     A. n = ( 1; − 2) . B. n = (1;2) . C. n = (2;1) . D. n = (2; 1) − . Câu 10: Cho A
∆ BC có A(2;− ) 1 ; B(4;5); C( 3
− ;2) Viết phương trình tổng quát của đường cao AH .
A. 7x + 3y −11 = 0. B. 3x + 7y + 1 = 0 .
C. 7x + 3y +11 = 0 . D. −7x + 3y + 11 = 0
Câu 11: Khoảng cách từ điểm M 5; 
1 đến đường thẳng 3x  2y 13  0 là: Page 1
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 2 13 . B. 28 . C. 26 . D. 13 . 13 2
Câu 12: Trong mặt phẳng Oxy , tính góc giữa hai đường thẳng (d) : x − 2y −1= 0 và (d′) x + 3y −11= 0 . A. 0 30 . B. 0 45 . C. 0 60 . D. 0 135 .
Câu 13: Phương trình đường tròn có tâm I ( 2;
− 4) và bán kính R = 5 là:
A. (x − )2 + ( y + )2 2 4 = 5 .
B. (x + )2 + ( y − )2 2 5 = 25 .
C. (x + )2 + ( y − )2 2 4 = 25.
D. (x − )2 + ( y + )2 2 4 = 25.
Câu 14: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn I (1; 3
− ) và tiếp xúc với trục tung có phương trình là
A. (x − )2 + ( y + )2 1 3 =1.
B. (x − )2 + ( y + )2 1 3 = 3 .
C. (x − )2 + ( y + )2 1 3 = 9 .
D. (x − )2 + ( y + )2 1 3 = 3 . 2 2
Câu 15: Trong mặt phẳng x y
Oxy, phương trình elip: + =1 25 16
có một tiêu điểm là A. (0;4) . B. (0; 5). C. (− 5;0). D. (3;0).
Câu 16: Có bao nhiêu cách chọn một học sinh từ một nhóm gồm 8 học sinh nam và 9học sinh nữ? A. 8 . B. 17 . C. 72 . D. 9.
Câu 17: Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn văn nghệ,
mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ trên có
bao nhiêu cách chọn chương trình biểu diễn, biết chất lượng các vở kịch, điệu múa, bài hát là như nhau? A. 11. B. 18. C. 25 . D. 36.
Câu 18: Với năm chữ số 1,2,3,4,7 có thể lập được bao nhiêu số có 5 chữ số đôi một khác nhau và chia hết cho 2 ? A. 120. B. 24 . C. 48 . D. 1250.
Câu 19: Một tổ có 15 học sinh. Hỏi có bao nhiêu cách chọn 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó? A. 2 C . B. 2 A . C. 8 A . D. 2 15 . 15 15 15
Câu 20: Lớp 11A có 20 bạn nam và 22 bạn nữ. Có bao nhiêu cách chọn ra hai bạn tham gia hội thi
cắm hoa do nhà trường tổ chức A. 42 . B. 861. C. 1722. D. 84 . 4
Câu 21: Tìm số hạng không chứa x trong khai triển nhị thức Niu-tơn của  1 3 x  +  . x    A. 1. B. 4 . C. 6 . D. 12.
Câu 22: Gieo một con súc sắc cân đối đồng chất ba lần. Xác suất tích số chấm trong ba lần gieo bằng 6 là Page 2
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 A. 1 . B. 5 . C. 5 . D. 1 . 2 108 9 24
Câu 23: Có 10 tấm thẻ được đánh số từ 1 đến 10. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2 tấm
thẻ đều ghi số chẵn là A. 2 . B. 1 . C. 7 . D. 1 . 9 4 9 2
Câu 24: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả màu đỏ. Chọn ngẫu nhiên đồng thời 2
quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng A. 8 . B. 5 . C. 6 . D. 5 . 11 22 11 11
Câu 25: Trong mặt phẳng tọa độ Oxy , cho ba điểm A(1;0), B(2;− ) 1 ,C (1; )
1 . Phương trình chính tắc
đường thẳng (d ) đi qua A và song song với BC là
A. x − 2 y + 2 − − − − − − = .
B. x 1 y 2 = .
C. x 1 y 2 = .
D. x 1 y 2 = . 1 2 − 1 − 2 1 2 1 − 2 −
Câu 26: Đường Thẳng ∆ : ax + by −3 = 0 (a,b∈) đi qua điểm N (1; )
1 và cách điểm M (2;3) một
khoảng bằng 5 . Khi đó a − 2b bằng A. 5. B. 2. C. 4. D. 0.
Câu 27: Lập phương trình đường tròn đi qua hai điểm A(3;0), B(0;2) và có tâm thuộc đường thẳng
d : x + y = 0 . 2 2 2 2 A.  1   1  13 x − +  1   1  13   y + =  . B. x + +   y + = . 2 2       2  2   2  2 2 2 2 2 C.  1   1  13 x − +  1   1  13   y − =  . D. x + +   y − = . 2 2       2  2   2  2
Câu 28: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn I (1; 3
− ) và tiếp xúc với trục tung có phương trình là
A. (x − )2 + ( y + )2 1 3 =1.
B. (x − )2 + ( y + )2 1 3 = 3 .
C. (x − )2 + ( y + )2 1 3 = 9 .
D. (x − )2 + ( y + )2 1 3 = 3 . 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 9 4
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 6 . B. 3. C. 4 . D. 5.
Câu 30: Một hộp đựng 6 viên bi đen đánh số từ 1 đến 6 và 5 viên bi xanh đánh số từ 1 đến 5. Hỏi có bao
nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số? A. 25 . B. 25 . C. 30. D. 36.
Câu 31: Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động,
trong đó có đúng 2 học sinh nam? A. 2 4
C + C Strong. B. 2 4 C .C . C. 2 4 A .A . D. 2 4 C C . 6 9 6 9 6 9 9 6 Page 3
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 32: Một nhóm công nhân gồm 8 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành
một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao
nhiêu cách lập tổ công tác. A. 4060 . B. 12880. C. 1286. D. 8120 .
Câu 33: Cho hai hộp, hộp I chứa 4 viên bi đỏ và 3 viên bi xanh, hộp II chứa 5 viên bi đỏ và 2 viên bi
xanh. Lấy ngẫu nhiên từ mỗi hộp ra 2 viên bi. Tính xác suất để các viên bi lấy ra cùng màu. A. 131 . B. 9 . C. 131 . D. 1 . 1001 143 441 7
Câu 34: Hai bạn lớp A và hai bạn lớp B được xếp vào 4 ghế hàng ngang. Xác xuất sao cho các bạn cùng
lớp không ngồi cạnh nhau bằng A. 1 . B. 1 . C. 1 . D. 2 . 3 4 2 3
Câu 35: Bạn An có 7 cái kẹo vị hoa quả và 6 cái kẹo vị socola. An lấy ngẫu nhiên 5 cái kẹo cho vào
hộp để tặng cho em. Tính xác suất để 5 cái kẹo có cả vị hoa quả và vị socola. A. 140 . B. 79 . C. 103 . D. 14 . 143 156 117 117
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa hai chữ số 5 và 9 ?
Câu 37: Cho (C) 2 2
: x + y − 4x + 6y −12 = 0 và đường thăng (d ): x + y + 4 = 0. Viêt phương trình đường
thẳng (∆) song song (d ) và cắt đường tròn (C) theo một dây cung có độ dài bằng 8.
Câu 38: Tại môn bóng đá SEA Games 31 tổ chức tại Việt Nam có 10 đội bóng tham dự trong đó có 2 đội
tuyển Việt Nam và Thái Lan. Ban tổ chức chia ngẫu nhiên 10 đội tuyển thành 2 bảng: bảng A và
bảng B, mỗi bảng có 5 đội. Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một bảng đấu là
Câu 39: Trên bờ biển có hai trạm thu phát tín hiệu A và B cách nhau 6km , người ta xây một cảng biển
cho tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng 2 5 km .
Một con tàu hàng M nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến A và B
luôn là 2 6 km . Khi neo đậu tại cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu?
---------- HẾT ---------- Page 4
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1: Trong mặt phẳng với hệ trục tọa độ Oxy, cho 3 điểm ( A 1 − ;3), B(3; 4 − ),C( 5 − ; 2 − ) . Tìm tọa độ
trọng tâm G của tam giác ABC. A. G( 1; − − ) 1 B. 1 G  ; 1 −   C. 1 1 G  −  ;− G 1; 1 − 3      3 3  D. ( ) Lời giải: Chọn A
G là trọng tâm tam giác ABC nên ta có:  1 − + 3− 5 G x = = 1 −  3  3− 4 − 2  G y = = 1 −  3
Câu 2: Trong hệ tọa độ Oxy, cho ba điểm A(1; ) 1 , B( 3;2), C (
6;5). Tìm tọa độ điểm D để tứ giác
ABCD là hình bình hành.
A. D(4;3).
B. D(3;4).
C. D(4;4).
D. D(8;6). Lời giải: Chọn D  AB =  (2; )1 Gọi D( ;
x y). Ta có  . DC =  (6− ;x5− y)   2 = 6 − xx = 4
Tứ giác ABCD là hình bình hành ⇔ AB = DC ⇔  ⇔  ⇒ D(4;4). 1  = 5 − yy = 4
Câu 3: Theo thống kê, dân số Việt Nam năm 2022 là 79715675 người. Giả sử sai số tuyệt đối của số
liệu thống kê này nhỏ hơn 10000 người. Hãy viết số quy tròn của số trên
A. 79710000 người. B. 79716000 người. C. 79720000 người. D. 79700000 người. Lời giải: Chọn D
Độ chính xác đến hàng chục nghìn nên ta quy tròn số gần đúng đến hàng trăm nghìn.
Câu 4: Hãy tìm số trung bình của mẫu số liệu khi cho bảng tần số dưới đây: A. 8,29 B. 9,28 C. 8,73 D. 8,37. Lời giải: Chọn A
Áp dụng công thức tính số trung bình của mẫu số liệu. Page 5
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 5: Tìm mốt của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17; 17. A. 17. B. 13 C. 14 D. 15. Lời giải: Chọn A
Mốt là 17 vì giá trị này xuất nhiều nhất là 3.
Câu 6: Tìm tứ phân vị thứ ba của mẫu số liệu sau: 11; 17; 13; 14; 15; 14; 15; 16; 17. A. 16,5. B. 16 C. 15,5 D. 15. Lời giải: Chọn A
Sắp xếp mẫu theo thứ tự không giảm: 11,13,14,14,15,15,16,17,17. Kích thước mẫu là 9. Trung
vịcủa mẫu là giá trị thứ 5 là 15. Khi đó tứ phân vị thứ ba là trung bình cộng của giá trị thứ 7 và thứ 8 bằng 16,5.
Câu 7: Điểm thi HK1 của một học sinh lớp 10 như sau: 9 9 7 8 9 7 10 8 8
Khoảng biến thiên của mẫu số liệu là A. 1. B. 2 . C. 3. D. 0 . Lời giải: Chọn C
Khoảng biến thiên là R =10 − 7 = 3.
Câu 8: Cho mẫu số liệu 10; 8 ; 6 ; 2 ; 4 . Độ lệch chuẩn của mẫu là A. 8 . B. 2,4 . C. 2,8. D. 6 . Lời giải: Chọn C
Giá trị trung bình của dãy số liệu là 10 8 6 4 2 x + + + + = = 6 . 5
Độ lệch chuẩn của dãy số liệu là 2 2 2 2 (10 6) (8 6) (4 6) (2 6) s − + − + − + − = ≈ 2,8. 5  x =1− t
Câu 9: Cho đường thẳng (d) có phương trình 
. Khi đó, đương thẳng (d) có 1 véc tơ pháp y = 3+ 2t tuyến là:     A. n = ( 1; − 2) . B. n = (1;2) . C. n = (2;1) . D. n = (2; 1) − . Lời giải  
Đường thẳng d có véc tơ chỉ phương u = ( 1;
− 2) nên có 1 véc tơ pháp tuyến n = (2;1) . Câu 10: Cho A
∆ BC có A(2;− ) 1 ; B(4;5); C( 3
− ;2) Viết phương trình tổng quát của đường cao AH .
A. 7x + 3y −11 = 0. B. 3x + 7y + 1 = 0 . Page 6
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
C. 7x + 3y +11 = 0 . D. −7x + 3y + 11 = 0 Lời giải 
Đường cao AH có véc tơ pháp tuyến BC = ( 7; − 3 − ) = −(7;3) .
Nên phương trình đường cao AH là 7(x − 2) + 3( y + )
1 = 0 ⇔ 7x + 3y −11 = 0
Câu 11: Khoảng cách từ điểm M 5; 
1 đến đường thẳng 3x  2y 13  0 là: A. 2 13 . B. 28 . C. 26 . D. 13 . 13 2 Lời giải 3.5  2.   1 13 Khoảng cách 26 d    2 13 . 2 2 3  2 13
Câu 12: Trong mặt phẳng Oxy , tính góc giữa hai đường thẳng (d) : x − 2y −1= 0 và (d′) x + 3y −11= 0 . A. 0 30 . B. 0 45 . C. 0 60 . D. 0 135 . Lời giải   n = − n = d (1; 2), d 1;3 ' ( )
Gọi α là góc tạo bởi hai vectơ pháp tuyến của hai đường thẳng   (α ) n n − d . d′ 5 2 cos =   = = − 0 ⇒ α = 135 n n d . ′ 5. 10 2 d
Suy ra góc giữa hai đường thẳng bằng 0 45
Câu 13: Phương trình đường tròn có tâm I ( 2;
− 4) và bán kính R = 5 là:
A. (x − )2 + ( y + )2 2 4 = 5 .
B. (x + )2 + ( y − )2 2 5 = 25 .
C. (x + )2 + ( y − )2 2 4 = 25.
D. (x − )2 + ( y + )2 2 4 = 25. Lời giải
Phương trình đường tròn có tâm I ( 2;
− 4) và bán kính R = 5 là (x + )2 + ( y − )2 2 4 = 25.
Câu 14: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn I (1; 3
− ) và tiếp xúc với trục tung có phương trình là
A. (x − )2 + ( y + )2 1 3 =1.
B. (x − )2 + ( y + )2 1 3 = 3 .
C. (x − )2 + ( y + )2 1 3 = 9 .
D. (x − )2 + ( y + )2 1 3 = 3 . Lời giải
Trục tung Oy :x = 0 ⇒đường tròn đã cho có bán kính R = d (I,Oy) =1.
Vậy phương trình đường tròn cần tìm là ( x − )2 + ( y + )2 1 3 = 1. 2 2
Câu 15: Trong mặt phẳng x y
Oxy, phương trình elip: + =1 25 16
có một tiêu điểm là A. (0;4) . B. (0; 5). C. (− 5;0). D. (3;0). Lời giải Theo giả thiết ta suy ra 2 2 a = 25; 16 b = , khi đó 2 2
c = a − b = 3 Page 7
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Ta có hai tiêu điểm F 3 − ;0 và F 3;0 . 2 ( ) 1 ( )
Câu 16: Có bao nhiêu cách chọn một học sinh từ một nhóm gồm 8 học sinh nam và 9học sinh nữ? A. 8 . B. 17 . C. 72 . D. 9. Lời giải
Áp dụng quy tắc cộng ta có số cách chọn một học sinh từ một nhóm gồm 8 học sinh nam và 9 học sinh nữ là 8+9=17 .
Câu 17: Một đội văn nghệ chuẩn bị được 2 vở kịch, 3 điệu múa và 6 bài hát. Tại hội diễn văn nghệ,
mỗi đội chỉ được trình diễn một vở kịch, một điệu múa và một bài hát. Hỏi đội văn nghệ trên có
bao nhiêu cách chọn chương trình biểu diễn, biết chất lượng các vở kịch, điệu múa, bài hát là như nhau? A. 11. B. 18. C. 25 . D. 36. Lời giải
Số cách chọn chương trình biễu diễn văn nghệ của đội trên là: 2.3.6 = 36.
Câu 18: Với năm chữ số 1,2,3,4,7 có thể lập được bao nhiêu số có 5 chữ số đôi một khác nhau và chia hết cho 2 ? A. 120. B. 24 . C. 48 . D. 1250. Lời giải
Gọi số cần tìm là n = abcde , vì n chia hết cho 2 nên có 2 cách chọn e .
Bốn chữ số còn lại được chọn và sắp từ bốn trong năm chữ số trên nên có 4! cách.
Vậy có tất cả 2× 4!= 48 số các số cần tìm.
Câu 19: Một tổ có 15 học sinh. Hỏi có bao nhiêu cách chọn 2 học sinh từ tổ đó để giữ hai chức vụ tổ trưởng và tổ phó? A. 2 C . B. 2 A . C. 8 A . D. 2 15 . 15 15 15 Lời giải
Số cách chọn 2 học sinh trong 15 học sinh để làm hai chức vụ tổ trưởng và tổ phó là 2 A . 15
Câu 20: Lớp 11A có 20 bạn nam và 22 bạn nữ. Có bao nhiêu cách chọn ra hai bạn tham gia hội thi
cắm hoa do nhà trường tổ chức A. 42 . B. 861. C. 1722. D. 84 . Lời giải
Số cách chọn hai bạn trong lớp có 42 bạn học sinh là: 2 C = 861. 42 4
Câu 21: Tìm số hạng không chứa x trong khai triển nhị thức Niu-tơn của  1 3 x  +  . x    A. 1. B. 4 . C. 6 . D. 12. Lời giải 4 4 4 − 4 Ta có  1 3   1 k x ∑C  + = ( 3x)k k k 4k −4 =     ∑C x . 4 4  xk =0  x k =0
Số hạng không chứa x trong khai triển trên ứng với 4k − 4 = 0 ⇔ k =1. 4
Vậy số hạng không chứa x trong khai triển  1 3 x  +  là 1 C = 4 . x    4 Page 8
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 22: Gieo một con súc sắc cân đối đồng chất ba lần. Xác suất tích số chấm trong ba lần gieo bằng 6 là A. 1 . B. 5 . C. 5 . D. 1 . 2 108 9 24 Lời giải
Số phần tử của không gian mẫu là n(Ω) = 6.6.6 = 216 .
Gọi A là biến cố: “Tích số chấm trong ba lần gieo bằng 6”.
Các trường hợp thuận lợi cho biến cố A là (
{ 1;1;6),(1;6; )1,(1;2;3),(1;3;2),(2;1;3),(2;3; )1,(3;1;2),(3;2 ) ;1 ,(6;1 ) ;1 }.
Suy ra n( A) = 9.
Vậy xác suất cần tính là P( A) 9 1 = = . 216 24
Câu 23: Có 10 tấm thẻ được đánh số từ 1 đến 10. Chọn ngẫu nhiên 2 thẻ. Xác suất để chọn được 2 tấm
thẻ đều ghi số chẵn là A. 2 . B. 1 . C. 7 . D. 1 . 9 4 9 2 Lời giải
Phép thử T là: “ Chọn ngẫu nhiên hai thẻ từ tập hợp gồm 10 thẻ”.
Số phần tử của không gian mẫu: n(Ω) 2 = C = 45 . 10
Trong 10 số nguyên dương từ 1 đến 10 gồm 5 số lẻ và 5 số chẵn. Để chọn được hai tấm thẻ đều
ghi số chẵn, ta cần chọn được 2 tấm thẻ từ 5 thẻ ghi số chẵn.
Gọi A là biến cố: “Chọn được hai tấm thẻ đều ghi số chẵn”, suy ra n( A) 2 = C =10 . 5 n A
Vậy xác suất của biến cố 10 2
A là: P( A) ( ) = = = . n(Ω) 45 9
Câu 24: Một hộp chứa 11 quả cầu gồm 5 quả màu xanh và 6 quả màu đỏ. Chọn ngẫu nhiên đồng thời 2
quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng A. 8 . B. 5 . C. 6 . D. 5 . 11 22 11 11 Lời giải
Số cách chọn ngẫu nhiên đồng thời 2 quả cầu từ hộp đó là 2 C = 55. 11
Số cách chọn ngẫu nhiên đồng thời 2 quả cầu cùng màu từ hộp đó là 2 2 C + C = 25. 5 6
Xác suất để 2 quả cầu chọn ra cùng màu bằng 25 5 = . 55 11
Câu 25: Trong mặt phẳng tọa độ Oxy , cho ba điểm A(1;0), B(2;− ) 1 ,C (1; )
1 . Phương trình chính tắc
đường thẳng (d ) đi qua A và song song với BC là
A. x − 2 y + 2 − − − − − − = .
B. x 1 y 2 = .
C. x 1 y 2 = .
D. x 1 y 2 = . 1 2 − 1 − 2 1 2 1 − 2 − Lời giải   BC = ( 1;
− 2). Đường thẳng d nhận vecto BC làm vecto chỉ phương. Thay A(1;0; )
1 vào các đáp án ta có phương án A thỏa mãn. Page 9
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Câu 26: Đường Thẳng ∆ : ax + by −3 = 0 (a,b∈) đi qua điểm N (1; )
1 và cách điểm M (2;3) một
khoảng bằng 5 . Khi đó a − 2b bằng A. 5. B. 2. C. 4. D. 0. Lời giải
Đường Thẳng ∆ : ax + by − 3 = 0 đi qua điểm N (1; )
1 , ta có a + b − 3 = 0 ⇒ b = 3− a .
Suy ra ∆ : ax + (3− a)y − 3 = 0 ,
2a + (3− a).3− 3 Khi đó 2
d(M ,∆) = 5 ⇔
= 5 ⇔ a − 2a +1 = 0 ⇒ a =1, 2 2 a + (3− a)
Với a =1⇒ b = 2
Vậy: 2a −b = 0.
Câu 27: Lập phương trình đường tròn đi qua hai điểm A(3;0), B(0;2) và có tâm thuộc đường thẳng
d : x + y = 0 . 2 2 2 2 A.  1   1  13 x − +  1   1  13   y + =  . B. x + +   y + = . 2 2       2  2   2  2 2 2 2 2 C.  1   1  13 x − +  1   1  13   y − =  . D. x + +   y − = . 2 2       2  2   2  2 Lời giải
A(3;0) , B(0;2) , d : x + y = 0 .
Gọi I là tâm đường tròn vậy I ( ;
x −x) vì I ∈d . 2 2 1
IA = IB ⇔ ( − x)2 2 2 3
+ x = x + (2 + x)2 ⇔ 6
− x + 9 = 4x + 4 ⇔ x = . Vậy 1 1 I  ;  − . 2 2 2    2 2 1   1  26 IA  = 3− + = 
là bán kính đường tròn. 2   2      2 2 2
Phương trình đường tròn cần lập là:  1   1  13 x − +   y + =  . 2 2      2
Câu 28: Trong mặt phẳng tọa độ Oxy , phương trình đường tròn I (1; 3
− ) và tiếp xúc với trục tung có phương trình là
A. (x − )2 + ( y + )2 1 3 =1.
B. (x − )2 + ( y + )2 1 3 = 3 .
C. ( x − )2 + ( y + )2 1 3 = 9 .
D. (x − )2 + ( y + )2 1 3 = 3 . Lời giải
Trục tung Oy :x = 0 ⇒đường tròn đã cho có bán kính R = d (I,Oy) =1.
Vậy phương trình đường tròn cần tìm là ( x − )2 + ( y + )2 1 3 = 1. 2 2
Câu 29: Cho của hypebol ( ) : x y H −
= 1. Hiệu các khoảng cách từ mỗi điểm nằm trên (H ) đến hai 9 4
tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? A. 6 . B. 3. C. 4 . D. 5. Lời giải Page 10
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 2 2
Gọi F và F là hai tiêu điểm của ( ) : x y H −
= 1, a > 0,b > 0 . 2 2 ( ) 1 2 a b
Điểm M ∈(H ) ⇔ MF − MF = 2a . 1 2 2 2
Từ phương trình ( ) : x y H − = 1 suy ra 2
a = 9 ⇒ a = 3,(a > 0) . 9 4
Vậy hiệu các khoảng cách từ mỗi điểm M nằm trên (H ) đến hai tiêu điểm có giá trị tuyệt đối là
MF − MF = 2a = 6 . 1 2
Câu 30: Một hộp đựng 6 viên bi đen đánh số từ 1 đến 6 và 5 viên bi xanh đánh số từ 1 đến 5. Hỏi có bao
nhiêu cách chọn hai viên bi từ hộp đó sao cho chúng khác màu và khác số? A. 25 . B. 25 . C. 30. D. 36. Lời giải Cách 1: TH1.
Số cách chọn 1 viên bi đen được đánh số từ 1 đến 5: Có 5 cách chọn.
Số cách chọn 1 viên bi xanh được đánh số từ 1 đến 5: Có 4 cách chọn.
Theo quy tắc nhân có: 5.4 = 20 cách. TH2.
Số cách chọn 1 viên bi đen được đánh số 6: Có 1 cách chọn.
Số cách chọn 1 viên bi xanh được đánh số từ 1 đến 5: Có 5 cách chọn.
Theo quy tắc nhân có: 1.5 = 5 cách.
Vậy theo quy tắc cộng ta có 20 + 5 = 25 cách chọn. Cách 2:
Chọn 1 bi xanh là 5 cách chọn.
Chọn 1 bi đen là 5 cách chọn
Vậy có 5.5 = 25 cách chọn.
Câu 31: Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động,
trong đó có đúng 2 học sinh nam? A. 2 4
C + C Strong. B. 2 4 C .C . C. 2 4 A .A . D. 2 4 C C . 6 9 6 9 6 9 9 6 Lời giải Chọn 4 học sinh nữ có 4
C cách, chọn 2 học sinh nam có 2 C 9 6 cách. Có 2 4 C .C 6
9 cách chọn 6 học sinh đi lao động, trong đó có đúng 2 học sinh nam.
Câu 32: Một nhóm công nhân gồm 8 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành
một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao
nhiêu cách lập tổ công tác. A. 4060 . B. 12880. C. 1286. D. 8120 . Lời giải
Chọn 2 trong 8 nam làm tổ trưởng và tổ phó có 2 A8 cách.
• Chọn 3 tổ viên, trong đó có nữ
+) chọn 1 nữ và 2 nam có 2 5.C6 cách.
+) chọn 2 nữ và 1 nam có 2 6.C5 cách. +) chọn 3 nữ có 3 C5 cách. Page 11
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10 Vậy có 2 A ( 2 5.C + 2 6.C + 3 8 6 5 C5 ) = 8120 cách.
Câu 33: Cho hai hộp, hộp I chứa 4 viên bi đỏ và 3 viên bi xanh, hộp II chứa 5 viên bi đỏ và 2 viên bi
xanh. Lấy ngẫu nhiên từ mỗi hộp ra 2 viên bi. Tính xác suất để các viên bi lấy ra cùng màu. A. 131 . B. 9 . C. 131 . D. 1 . 1001 143 441 7 Lời giải
Số phần tử không gian mẫu 2 2 Ω = C .C = 441 7 7 .
Gọi A là biến cố: “Các viên bi lấy ra cùng màu”.
Trường hợp 1: cùng màu đỏ: 2 2 C .C = 60 . 4 5
Trường hợp 2: cùng màu xanh: 2 2 C .C = 3. 3 2 Ω = + = A 60 3 63. Ω Vậy P( A) A 63 1 = = = . Ω 441 7
Câu 34: Hai bạn lớp A và hai bạn lớp B được xếp vào 4 ghế hàng ngang. Xác xuất sao cho các bạn cùng
lớp không ngồi cạnh nhau bằng A. 1 . B. 1 . C. 1 . D. 2 . 3 4 2 3 Lời giải
Mỗi cách xếp 4 học sinh vào 4 ghế hàng ngang là một hoán vị của 4 phần tử
Số phần tử của không gian mẫu là P = 4!= 24 4
Gọi C là biến cố “ Các bạn cùng lớp không ngồi cùng nhau”
Đánh số thứ tự cho 4 ghế là 1,2,3,4 . Hai bạn cùng lớp không ngồi cạnh nhau thì hai bạn cùng
lớp mỗi bạn phải ngồi ghế cùng mang số chẵn hoặc ghế cùng mang số lẻ. Khi đó
n(C) = 2.2.2 = 8 Vậy P(C) 8 1 = = . 24 3
Câu 35: Bạn An có 7 cái kẹo vị hoa quả và 6 cái kẹo vị socola. An lấy ngẫu nhiên 5 cái kẹo cho vào
hộp để tặng cho em. Tính xác suất để 5 cái kẹo có cả vị hoa quả và vị socola. A. 140 . B. 79 . C. 103 . D. 14 . 143 156 117 117 Lời giải
Số phần tử không gian mẫu: n(Ω) 5 1 4 2 3 3 2 4 1 5
= C + C .C + C .C + C .C + C .C + C = 1287 . 7 7 6 7 6 7 6 7 6 6
Gọi A là biến cố: “ An lấy ngẫu nhiên 5 cái kẹo có cả vị hoa quả và vị socola”. n( A) 1 4 2 3 3 2 4 1
= C .C + C .C + C .C + C .C =1260 . 7 6 7 6 7 6 7 6 n A 1260 140 Vậy P( A) ( ) = = = . n(Ω) 1287 143
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36: Có bao nhiêu số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa hai chữ số 5 và 9 ? Lời giải Page 12
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Lập số tự nhiên có 7 chữ số khác nhau từng đôi một, trong đó chữ số 1 đứng liền giữa hai chữ số 5 và 9.
Trường hợp 1 : 3 chữ số 1, 5, 9 đứng 3 vị trí đầu.
- Chữ số 1 đứng vị trí số 2 có : 1 cách chọn.
- Sắp xếp 2 chữ số 5, 9 bên cạnh chữ số 1 có : 2! cách chọn.
- Chọn 4 số trong 7 chữ số còn lại xếp vào 3 vị trí còn lại có : 4 A cách chọn. 7 Suy ra có : 4 2!A =1680 số. 7
Trường hợp 2 : 3 chữ số 1, 5, 9 không đứng ở vị trí đầu tiên
- Chọn ví trí cho chữ số 1 có : 4 cách chọn.
- Sắp xếp 2 chữ số 5, 9 bên cạnh chữ số 1 có : 2! cách chọn.
- Chọn 1 chữ số cho vị trí đầu tiên có : 6 cách chọn.
- Chọn 3 chữ số xếp vào 3 vị trí còn lại có : 3 A 6 Suy ra có : 3 4.6.2!A = 5760 số. 6 Vậy có 7440 số.
Câu 37: Cho (C) 2 2
: x + y − 4x + 6y −12 = 0 và đường thăng (d ): x + y + 4 = 0. Viêt phương trình đường
thẳng (∆) song song (d ) và cắt đường tròn (C) theo một dây cung có độ dài bằng 8. Lời giải
(C) có tâm I (2;−3) và R = 5. Gọi ,
A B là giao điểm của (∆) và đường tròn (C) ⇒ AB = 8.
Kẻ OH ⊥ AB tại H ⇒ H là trung điểm A B. 2 2 2 2
OH = OA − AH = 5 − 4 = 3
(∆) / /(d) ⇒ (∆): x + y + c = 0(c ≠ 4) − +  d ( c I ,(∆)) 2 3 c = 3 2 +1(n) = OH ⇔
= 3 ⇔ c −1 = 3 2 ⇔ 2 c = 3 − 2 +1  (n)
Vây phương trình đường thẳng (∆) là x + y + 3 2 +1 = 0 hoặc x + y −3 2 +1 = 0 .
Câu 38: Tại môn bóng đá SEA Games 31 tổ chức tại Việt Nam có 10 đội bóng tham dự trong đó có 2 đội
tuyển Việt Nam và Thái Lan. Ban tổ chức chia ngẫu nhiên 10 đội tuyển thành 2 bảng: bảng A và
bảng B, mỗi bảng có 5 đội. Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một bảng đấu là Lời giải Page 13
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Số cách phân 10 đội tuyển thành 2 bảng A và B, mỗi bảng có 5 đội là 5 C . 10
Số cách phân 10 đội tuyển thành 2 bảng A và B, mỗi bảng có 5 đội sao cho đội tuyển Việt Nam
và đội tuyển Thái Lan nằm cùng một bảng là:
*Trường hợp Việt Nam và Thái Lan cùng nằm ở bảng A: chọn thêm 3 đội từ 8 đội còn lại vào bảng A có 3 C cách. 8
*Trường hợp Việt Nam và Thái Lan cùng nằm ở bảng B: tương tự cũng có 3 C cách. 8 3 2
Xác suất để đội tuyển Việt Nam và đội tuyển Thái Lan nằm cùng một bảng đấu là C 4 8 P = = . 5 C 9 10
Câu 39: Trên bờ biển có hai trạm thu phát tín hiệu A và B cách nhau 6km , người ta xây một cảng biển
cho tàu hàng neo đậu là một nửa hình elip nhận AB làm trục lớn và có tiêu cự bằng 2 5 km .
Một con tàu hàng M nhận tín hiệu đi vào cảng biển sao cho hiệu khoảng cách từ nó đến A và B
luôn là 2 6 km . Khi neo đậu tại cảng thì khoảng cách từ con tàu đến bờ biển là bao nhiêu? Lời giải Page 14
Sưu tầm và biên soạn
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ II – TOÁN 10
Chọn hệ trục toạ độ Oxy như hình trên, trong đó 1km ứng với 1 đơn vị.
 MA− MB = 2 6 2 2 Do x y
nên M thuộc hypebol (H ) : − = 1. A  ( 3 − ;0), B(3;0) 6 3 2 2
Cảng biển xây theo hình elip có trục lớn là AB = 6 và tiêu cự là 2 5 ⇒ ( ) : x y E + = 1 9 4
Khi con tàu M neo đậu thì chính là tại vị trí I : 2 2  x y  2 126 − =1 x =   Lúc này toạ độ của   I thoả mãn hệ 6 3 17  ⇔  . 2 2  x y  2 12 + =1 y =  9 4  17
Khi đó khoảng cách từ con tàu M đến bờ biển là 12 km . 17
---------- HẾT ---------- Page 15
Sưu tầm và biên soạn
Document Outline

  • 00. MA TRẬN-TOÁN 10-CK2_CÁNH DIỀU
  • 01. ĐỀ 1 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 02. ĐỀ 2 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 03. ĐỀ 3 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 04. ĐỀ 4 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 05. ĐỀ 5 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 06. ĐỀ 6 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 07. ĐỀ 7 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 08. ĐỀ 8 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 09. ĐỀ 9 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)
  • 10. ĐỀ 10 - CUỐI HỌC KÌ 2 - TOÁN 10 - CÁNH DIỀU (70TN-30TL) (Bản word kèm giải chi tiết)