
ĐẶNG VIỆT ĐÔNG
TUYỂN TẬP 20 ĐỀ ÔN TẬP
HỌC KỲ II
MÔN TOÁN LỚP 10
NĂM HỌC 2020 - 2021

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 01
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho dãy số liệu thống kê:
48
,
36
,
33
,
38
,
32
,
48
,
42
,
33
,
39
. Khi đó số trung vị là
A.
38
. B.
40
. C.
32
. D.
36
.
Câu 2. Phương trình nào sau đây không phải là phương trình của một đường tròn?
A.
2 2
3 2 1 0
x y x y
. B.
2 2
6
x y
.
C.
2 2
2 4 0
x y x y xy
. D.
2 2
2 2 4 5 0
x y x y
.
Câu 3. Điểm cuối của góc lượng giác
ở góc phần tư thứ mấy nếu
sin ,tan
trái dấu?
A. Thứ
II
hoặc
IV.
B. Thứ
II
hoặc
III.
C. Thứ
I
hoặc
IV.
D. Thứ
I.
Câu 4. Điều kiện xác định của bất phương trình
2
1
2018 2 2019
2
x x
x
là
A.
2
x . B.
2
x .
C.
2
x . D.
2
x và
2
x .
Câu 5. Cho tam giác
ABC
có
AB c
,
AC b
,
BC a
, bán kính đường tròn ngoại tiếp và nội tiếp của
tam giác lần lượt là
R
,
r
. Mệnh đề nào dưới đây đúng?
A.
sin
a
R
A
. B.
2.sin
a
r
A
. C.
sin
a
r
A
. D.
2.sin
a
R
A
.
Câu 6. Chọn công thức sai?
A. sin sin 2sin .cos
2 2
a b a b
a b . B. cos cos 2cos .sin
2 2
a b a b
a b .
C.
sin sin 2cos .sin
2 2
a b a b
a b
.
D. cos cos 2sin .sin
2 2
a b a b
a b .
Câu 7. Trong hệ tọa độ
Oxy
cho elip
E
có phương trình chính tắc
2 2
1
80 31
x y
. Một tiêu điểm của elip
E
có tọa độ là
A.
7;0
. B.
0;7
. C.
7;0
. D.
0; 7
.
Câu 8. Có bao nhiêu điểm
M
trên đường tròn định hướng gốc
A
thỏa mãn sđ
, ?
3 3
k
AM k
A.
3
. B.
12
. C.
6
. D.
4
.
Câu 9. Cho
và
là hai góc khác nhau và bù nhau. Mệnh đề nào sau đây sai?
A.
cos cos
. B.
cot cot
.
C.
sin sin
. D.
tan tan
.
Câu 10. Tam giác với hai cạnh
,
a b
là
10,12
và góc
30
C có diện tích bằng bao nhiêu?
A.
28
. B.
14 5
. C.
10 3
. D.
30
.
Câu 11. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
rad 1
. B.
rad 60
.
C.
rad 180
. D.
180
rad
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 12. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng
1
:
2 4
x t
y t
,
t . Một vectơ chỉ
phương của đường thẳng là
A.
1; 4
u . B.
1;2
u . C.
2; 1
u . D.
4;1
u .
Câu 13. Nhị thức 2 3 x nhận giá trị dương khi và chỉ khi
A.
2
3
x . B.
3
2
x . C.
2
3
x . D.
3
2
x .
Câu 14. Nếu 2 2 a c b c thì bất đẳng thức nào sau đây đúng?
A. 3 3 . a b B.
2 2
.a b C. 2 2 .a b D.
1 1
.
a b
Câu 15. Khẳng định nào sau đây đúng?
A.
sin cos cos sin sin a b a b a b . B.
sin sin cos cos sin a b a b a b .
C.
sin sin cos cos sin a b a b a b . D.
sin cos cos sin sin a b a b a b .
Câu 16. Cho đường tròn
2 2
: 8 6 9 0 C x y x y . Tìm mệnh đề sai trong các mệnh đề sau.
A. Đường tròn
C đi qua điểm
1;0 .M B. Đường tròn
C có bán kính 4.R
C. Đường tròn
C không đi qua điểm
0;0 .O D. Đường tròn
C có tâm
4; 3 . I
Câu 17. Cho 3sin 4cos M x x. Chọn khẳng định đúng.
A. 5 5. M B. 5.M C. 5 . M D. 5. M
Câu 18. Tập nghiệm của bất phương trình
2
6 9 0 x x là:
A.
3; . B. . C.
\ 3 . D.
\ 3 .
Câu 19. Trong tất cả các hình chữ nhật có cùng diện tích
2
48m , hình chữ nhật có chu vi nhỏ nhất là:
A. 20. B.
16 3
. C.
20 3
. D. 16.
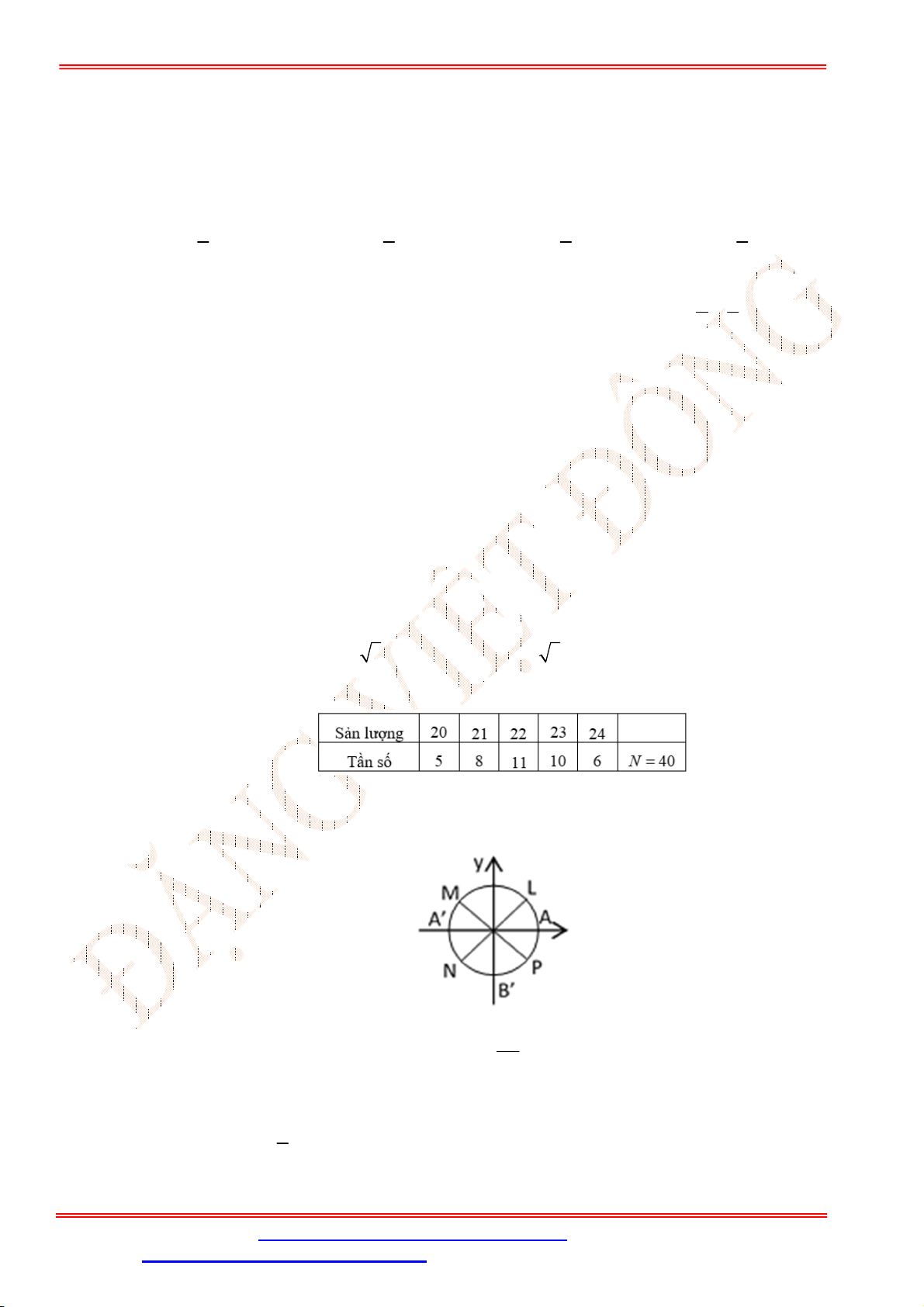
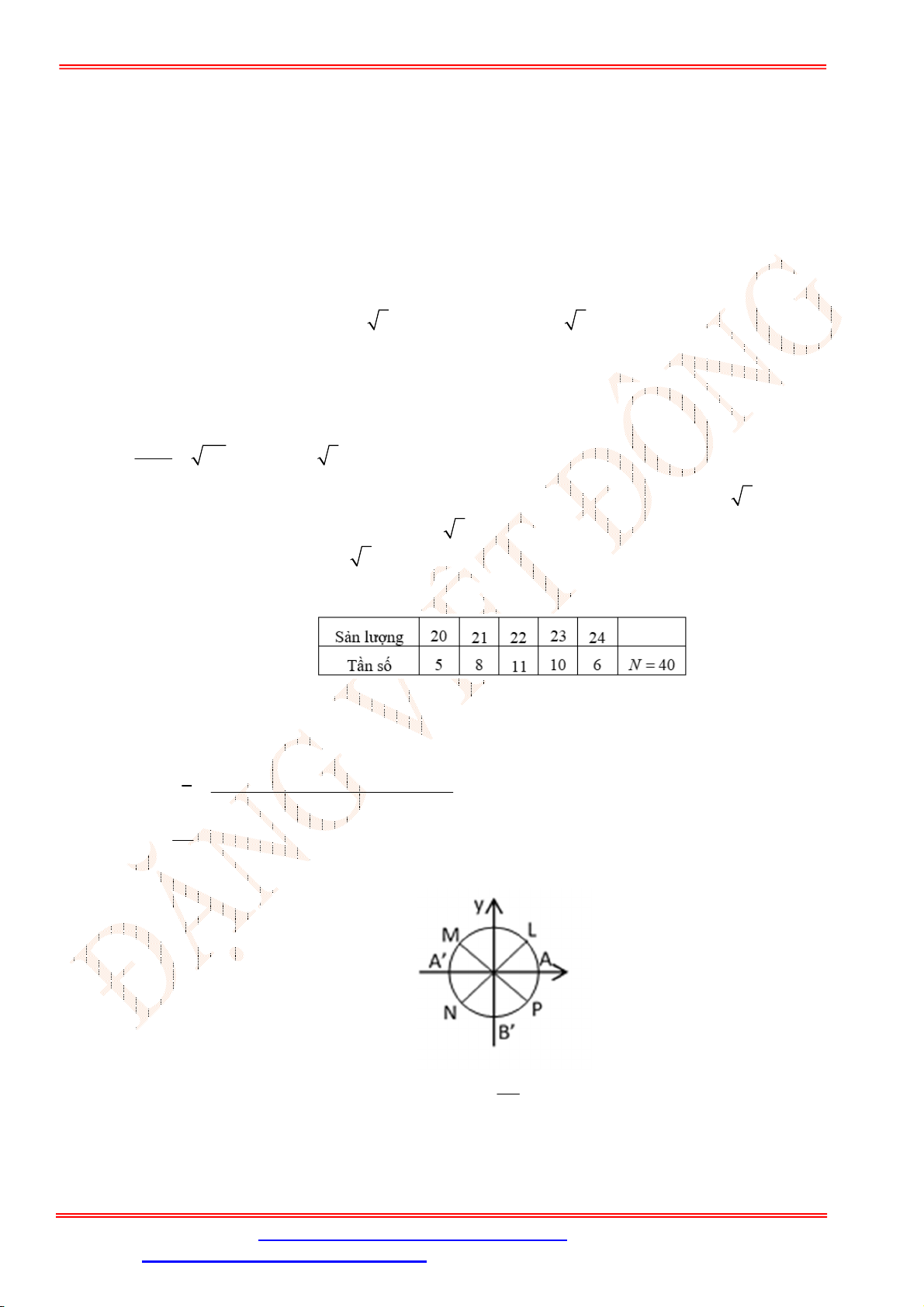
Câu 20. Sản lượng lúa (đơn vị ha) của 40 thửa ruộng có cùng diện tích được trình bày trong bảng số liệu
sau:
Tính phương sai của bảng số liệu.
A. 1,54. B. 1,53. C. 1,52. D. 1,55.
Câu 21. Cho , , ,L M N P lần lượt là điểm chính giữa các cung , ', ' ', 'AB BA A B B A.
Cung
có mút đầu trùng với A và số đo
3
4
k
hay
0 0
135 180
k .
Mút cuối của
ở đâu?
A. L hoặc P . B. M hoặc P . C. M hoặc N . D. L hoặc N .
Câu 22. Cho
5
sin cos
4
a a . Khi đó sin2a có giá trị bằng
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
5
2
. B.
2
. C.
3
32
. D.
9
16
.
Câu 23. Cho
7
cos
25
,
0 0
90 0
và các mệnh đề:
(I):
24
tan
7
(II):
24
sin
25
(III):
18
sin
25
(IV):
9
cot
24
Trong bốn mệnh đề trên có bao nhiêu mệnh đề sai?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 24. Cho hai điểm
2;3
A ,
4; 1
B . Phương trình đường trung trực
AB
.
A.
2 3 5 0
x y . B.
3 2 1 0
x y . C.
1 0
x y . D.
2 3 1 0
x y .
Câu 25. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
2 2
: 2 3 4
C x y . Gọi
1 2
,
là hai tiếp
tuyến của đường tròn
C
mà song song với đường thẳng
2 3
:
4 4
x t
d
y t
. Gọi
,
A B
lần lượt là giao
điểm của
1
với trục
,
Ox Oy
;
,
C D
lần lượt là giao điểm của
2
với trục
,
Ox Oy
. Diện tích của hình
thang
ABCD
tạo thành bằng
A.
50
.
3
B.
15.
C.
55
.
12
D.
11.
Câu 26. Cho
1
2
a và
1 1 2
a b ; đặt
tan
x a
và tan
y b
với
, 0;
2
x y
, thế thì
x y
bằng
A.
4
. B.
6
. C.
2
. D.
3
.
Câu 27. Tam giác
ABC
có trọng tâm
G
. Hai trung tuyến
6
BM
,
9
CN
và
0
120
BGC
. Tính độ dài
cạnh
AB
.
A.
2 13
AB . B.
13
AB . C.
2 11
AB
. D.
11
AB
.
Câu 28. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa tốt
nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp 2015
Khóa tốt nghiệp 2016
N
ữ
Nam
N
ữ
Nam
1 Giảng dạy 25 45 25 65
2
Ngân hàng
23
186
20
32
3
L
ậ
p
trình
25
120
12
58
4 Bảo hiểm 12 100 3 5
Trong số nữ sinh có việc làm ở Khóa tốt nghiệp 2015, tỷ lệ phần trăm của nữ trong lĩnh vực Giảng
dạy là bao nhiêu?
A.
11,2%
. B.
12,2%
. C.
15,0%
. D.
29,4%
.
Câu 29. Phương trình chính tắc của
E
có
5 4
c a
, độ dài trục nhỏ bằng
12
là
A.
2 2
1
25 36
x y
. B.
2 2
1
36 25
x y
. C.
2 2
1
64 36
x y
. D.
2 2
1
100 36
x y
.
Câu 30. Trong mặt phẳng
Oxy
, đường tròn
C
có tâm
1;3
I đi qua
3;1
M có phương trình là
A.
2 2
( 3) ( 1) 10
x y . B.
2 2
( 3) ( 1) 8
x y .
C.
2 2
( 1) ( 3) 8
x y . D.
2 2
( 1) ( 3) 10
x y .
Câu 31. Hãy chỉ ra đẳng thức sai.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
sin 4 sin6 sin 2
sin .sin 2 .sin3
4
.
B.
4cos .cos .cos cos2 cos2 cos2
a b b c c a a b b c c a
.
C.
sin10 sin6 sin 4
cos2 .sin5 .cos3
4
x x x
x x x .
D.
sin58 sin 42 sin72
sin 40 .cos10 .cos8
4
.
Câu 32. Cho đường thẳng đi qua hai điểm
3,0
A ,
0;4
B . Tìm tọa độ điểm
M
nằm trên
Oy
sao cho
diện tích tam giác
MAB
bằng
6
A.
0;8
. B.
1;0
. C.
0;0
và
0;8
. D.
0;1
.
Câu 33. Tìm số nguyên lớn nhất của
x
để
2 2
4 2 4
3
9 3
x x
f x
x
x x x
nhận giá trị âm.
A.
2
x . B.
1
x . C.
2
x . D.
1
x
.
Câu 34. Cho
2 2 3 2
1
f x x m m x m m
với
m
là tham số thực. Biết rằng có đúng 2 giá trị
1 2
,
m m
để
f x
không âm với mọi giá trị của
x
. Tính tổng
1 2
m m
.
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 35. Trong mặt phẳng tọa độ
Oxy
, cho các đường thẳng
1
:3 4 6 0
x y ,
2
:3 4 9 0
x y ,
3
:3 4 11 0
x y . Một đường thẳng
d
thay đổi cắt ba đường thẳng
1
,
2
,
3
lần lượt tại
A
,
B
,
C
. Giá trị nhỏ nhất của biểu thức
2
96
P AB
AC
bằng
A.
9
. B.
49
9
. C.
18
. D.
27
.
PHẦN II: TỰ LUẬN
Câu 36. Cho đường thẳng
1
:2 2 0
d x y ;
2
: 3 0
d x y và điểm
3;0
M . Viết phương trình đường
thẳng
đi qua điểm
M
, cắt
1
d
và
2
d
lần lượt tại
A
và
B
sao cho
M
là trung điểm của đoạn
AB
.
Câu 37.
Trong mặt phẳng
Oxy
, cho
2 2
: 2 1 5
C x y . Viết phương trình tiếp tuyến của
C
biết tiếp tuyến cắt
;
Ox Oy
lần lượt tại
;
A B
sao cho
2
OA OB
Câu 38. Tìm giá trị lớn nhất của
2 3 2 5
T x xy y x với
, 0
x y .
Câu 39.
Chứng minh rằng biểu thức sau đây không phụ thuộc vào x
6 6 2 2
sin os 3sin cos
A x c x x x
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 01
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
Câu 1. Cho dãy số liệu thống kê:
48
,
36
,
33
,
38
,
32
,
48
,
42
,
33
,
39
. Khi đó số trung vị là
A.
38
. B.
40
. C.
32
. D.
36
.
Lời giải
Chọn A
Dãy số liệu thống kê được xếp thành dãy không giảm là
32
,
33
,
33
,
36
,
38
,
39
,
42
,
48
,
48
.
Ta có số trung vị là
38
e
M .
Câu 2. Phương trình nào sau đây không phải là phương trình của một đường tròn?
A.
2 2
3 2 1 0
x y x y
. B.
2 2
6
x y
.
C.
2 2
2 4 0
x y x y xy
. D.
2 2
2 2 4 5 0
x y x y
.
Lời giải
Chọn C
Phương trình đường tròn có dạng tổng quát:
2 2
2 2 0
x y ax by c có tâm
;
I a b
, bán kính
2 2
R a b c
.
Điều kiện để phương trình này là phương trình đường tròn là
2 2
0
a b c .
Xét đáp án A.
2 2
3 9
; 1; 1; 0
2 4
a b c a b c nên là phương trình đường tròn.
Xét đáp án
B.
2 2
0; 0; 6; 6 0
a b c a b c nên là phương trình đường tròn.
Xét đáp án
D. Chia cả hai vế của phương trình cho
2
ta có:
2 2
5
2 0
2
x y x y .
2 2
5 41
1; ; 0; 0
4 16
a b c a b c nên là phương trình đường tròn.
Câu 3. Điểm cuối của góc lượng giác
ở góc phần tư thứ mấy nếu
sin ,tan
trái dấu?
A. Thứ
II
hoặc
IV.
B. Thứ
II
hoặc
III.
C. Thứ
I
hoặc
IV.
D. Thứ
I.
Lời giải
Chọn B
Câu 4. Điều kiện xác định của bất phương trình
2
1
2018 2 2019
2
x x
x
là
A.
2
x . B.
2
x .
C.
2
x . D.
2
x và
2
x .
Lời giải
Chọn D
Điều kiện xác định của bất phương trình là
2 0 2
2 0 2
x x
x x
Câu 5. Cho tam giác
ABC
có
AB c
,
AC b
,
BC a
, bán kính đường tròn ngoại tiếp và nội tiếp của
tam giác lần lượt là
R
,
r
. Mệnh đề nào dưới đây đúng?
A.
sin
a
R
A
. B.
2.sin
a
r
A
. C.
sin
a
r
A
. D.
2.sin
a
R
A
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D
Theo định lý sin ta có 2
sin 2.sin
a a
R R
A A
.
Câu 6. Chọn công thức sai?
A. sin sin 2sin .cos
2 2
a b a b
a b . B. cos cos 2cos .sin
2 2
a b a b
a b .
C.
sin sin 2cos .sin
2 2
a b a b
a b
.
D. cos cos 2sin .sin
2 2
a b a b
a b .
Lời giải
Chọn B
Theo công thức tổng thành tích:. cos cos 2cos .cos
2 2
a b a b
a b
Câu 7. Trong hệ tọa độ
Oxy
cho elip
E
có phương trình chính tắc
2 2
1
80 31
x y
. Một tiêu điểm của elip
E
có tọa độ là
A.
7;0
. B.
0;7
. C.
7;0
. D.
0; 7
.
Lời giải
Chọn C
Ta có:
2 2
8 1
:
0
1
3
x y
E
2
2
80
31
a
b
Mà
2 2 2
80 31 49 7
c a b c
Vậy
7;0
là tọa độ một tiêu điểm của
E
.
Câu 8. Có bao nhiêu điểm
M
trên đường tròn định hướng gốc
A
thỏa mãn sđ
, ?
3 3
k
AM k
A.
3
. B.
12
. C.
6
. D.
4
.
Lời giải
Chọn C
Số điểm cuối của cung
*
2
; ,
k
k n
n
là
n
điểm trên đường tròn lượng giác.
Câu 9. Cho
và
là hai góc khác nhau và bù nhau. Mệnh đề nào sau đây sai?
A.
cos cos
. B.
cot cot
.
C.
sin sin
. D.
tan tan
.
Lời giải
Chọn B
Mệnh đề A sai, sửa cho đúng là
cot cot
.
Câu 10. Tam giác với hai cạnh
,
a b
là
10,12
và góc
30
C có diện tích bằng bao nhiêu?
A.
28
. B.
14 5
. C.
10 3
. D.
30
.
Lời giải
Chọn D
Áp dụng công thức
1 1
sin .10.12.sin30 30
2 2
S ab C .
Câu 11. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
rad 1
. B.
rad 60
.
C.
rad 180
. D.
180
rad
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn C
Theo công thức đổi đơn vị đo góc, ta có:
180 .
rad
Câu 12. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường thẳng
1
:
2 4
x t
y t
,
t
. Một vectơ chỉ
phương của đường thẳng
là
A.
1; 4
u . B.
1;2
u . C.
2; 1
u . D.
4;1
u .
Lời giải
Chọn A
Câu 13. Nhị thức
2 3
x
nhận giá trị dương khi và chỉ khi
A.
2
3
x . B.
3
2
x . C.
2
3
x . D.
3
2
x .
Lời giải
Chọn B
Ta có
3
2 3 0
2
x x .
Câu 14. Nếu
2 2
a c b c
thì bất đẳng thức nào sau đây đúng?
A.
3 3 .
a b
B.
2 2
.
a b
C.
2 2 .
a b
D.
1 1
.
a b
Lời giải
Chọn C
Từ giả thiết, ta có
2 2 2 2 .
a c b c a b a b
Câu 15. Khẳng định nào sau đây đúng?
A.
sin cos cos sin sin
a b a b a b
. B.
sin sin cos cos sin
a b a b a b
.
C.
sin sin cos cos sin
a b a b a b
. D.
sin cos cos sin sin
a b a b a b
.
Lời giải
Chọn B
Câu 16. Cho đường tròn
2 2
: 8 6 9 0
C x y x y . Tìm mệnh đề sai trong các mệnh đề sau.
A. Đường tròn
C
đi qua điểm
1;0 .
M B. Đường tròn
C
có bán kính
4.
R
C. Đường tròn
C
không đi qua điểm
0;0 .
O D. Đường tròn
C
có tâm
4; 3 .
I
Lời giải
Chọn A
Đường tròn
2 2
: 8 6 9 0
C x y x y có tâm
4; 3
I và
2 2
4 3 9 4
R
Vậy đáp án A và B đúng.
Thay tọa độ điểm
0;0
O vào phương trình đường tròn
C
ta có
9 0
( vô lý).
Vậy đáp án C đúng.
Thay tọa độ điểm
1;0
M vào phương trình đường tròn
C
ta có
1 8 9 0
( vô lý).
Vậy đáp án D sai.
Câu 17. Cho
3sin 4cos
M x x
. Chọn khẳng định đúng.
A.
5 5.
M B.
5.
M C.
5 .
M
D.
5.
M
Lời giải
Chọn A
3 4
5 sin cos 5sin
5 5
M x x x
với
3 4
cos , sin
5 5
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có:
1 sin 1, 5 5sin 5,
x x x x .
Câu 18. Tập nghiệm của bất phương trình
2
6 9 0 x x là:
A.
3; . B. . C.
\ 3 . D.
\ 3 .
Lời giải
Chọn D
Ta có:
2
2
6 9 0 3 0 3 0 3 x x x x x .
Tập nghiệm của bất phương trình là
\ 3 .
Câu 19. Trong tất cả các hình chữ nhật có cùng diện tích
2
48m , hình chữ nhật có chu vi nhỏ nhất là:
A. 20. B.
16 3
. C.
20 3
. D. 16.
Lời giải
Chọn B
Gọi
a, b a 0, b 0 lần lượt là hai cạnh của hình chữ nhật. Ta có a.b 48 .
Áp dụng bất đẳng thức Cauchy cho hai số dương a, b:
a b
a.b a b 8 3
2
.
hình chữ nhật có chu vi nhỏ nhất khi
a b đạt giá trị nhỏ nhất a b 4 3 .
hình chữ nhật là hình vuông có cạnh 4 3 .
chu vi hình chữ nhật là
16 3
.
Câu 20. Sản lượng lúa (đơn vị ha) của 40 thửa ruộng có cùng diện tích được trình bày trong bảng số liệu
sau:
Tính phương sai của bảng số liệu.
A. 1,54. B. 1,53. C. 1,52. D. 1,55.
Lời giải
Chọn A
Ta có
5.20 8.21 11.22 10.23 6.24
22,1
40
x .
2 2 2 2 2
2
1
5 20 22,1 8 21 22,1 11 22 22,1 10 23 22,1 6 24 22,1 1,54
40
x
S .
Câu 21. Cho , , ,L M N P lần lượt là điểm chính giữa các cung , ', ' ', 'AB BA A B B A.
Cung
có mút đầu trùng với A và số đo
3
4
k
hay
0 0
135 180
k .
Mút cuối của
ở đâu?
A. L hoặc P . B. M hoặc P . C. M hoặc N . D. L hoặc N .
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D
Nhìn vào đường tròn lượng giác để đánh giá.
Câu 22. Cho
5
sin cos
4
a a . Khi đó
sin2
a
có giá trị bằng
A.
5
2
. B.
2
. C.
3
32
. D.
9
16
.
Lời giải
Chọn D
Ta có:
2
2 2
5 25 25
sin cos sin cos sin 2sin cos
4 16 16
25 9
sin 2 1
16 16
a a a a a a a cos a
a
.
Câu 23. Cho
7
cos
25
,
0 0
90 0
và các mệnh đề:
(I):
24
tan
7
(II):
24
sin
25
(III):
18
sin
25
(IV):
9
cot
24
Trong bốn mệnh đề trên có bao nhiêu mệnh đề sai?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B
Lập luận:
0 0
90 0 sin 0
mệnh đề (III), (I) sai.
Tính được:
2
2
7 24
sin 1 cos 1
25 25
(II) đúng.
cos 7
cot
sin 24
(IV) sai.
Vậy có ba mệnh đề sai.
Câu 24. Cho hai điểm
2;3
A ,
4; 1
B . Phương trình đường trung trực
AB
.
A.
2 3 5 0
x y . B.
3 2 1 0
x y . C.
1 0
x y . D.
2 3 1 0
x y .
Lời giải.
Chọn B
Trung điểm
AB
là
1;1
I ;
6; 4
AB là VTPT của đường trung trực của
AB
.
6 1 4 1 0
x y
3 2 1 0
x y .
Câu 25. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
2 2
: 2 3 4
C x y . Gọi
1 2
,
là hai tiếp
tuyến của đường tròn
C
mà song song với đường thẳng
2 3
:
4 4
x t
d
y t
. Gọi
,
A B
lần lượt là giao
điểm của
1
với trục
,
Ox Oy
;
,
C D
lần lượt là giao điểm của
2
với trục
,
Ox Oy
. Diện tích của hình
thang
ABCD
tạo thành bằng
A.
50
.
3
B.
15.
C.
55
.
12
D.
11.
Lời giải
Chọn A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Theo đề bài, ta có
C
có tâm
2;3
I và bán kính
4
R
.
Phương trình tiếp tuyến của
C
của đường tròn thỏa bài toán có dạng
4 3 0
x y c
Đồng thời thỏa
9
1
, 2
11
5
c
c
d I R
c
Do đó
1 2
:4 3 9 0; :4 3 11 0
x y x y
Suy ra
9 11 11
;0 , 0; 3 , ;0 , 0;
4 4 3
A B C D
15 55
;
4 12
AB CD và
2 4.
h R
Diện tích hình thang
ABCD
được tính bởi
1 1 15 55 50
.4.
2 2 4 12 3
S h AB CD
Câu 26. Cho
1
2
a và
1 1 2
a b ; đặt
tan
x a
và tan
y b
với
, 0;
2
x y
, thế thì
x y
bằng
A.
4
. B.
6
. C.
2
. D.
3
.
Lời giải:
Chọn A
1
1 1 2
3
1
1
2
2
a b
b
a
a
tan tan
tan
1 tan .tan
x y
x y
x y
1 1
2 3
1
1 1
1 .
2 3
4
x y .
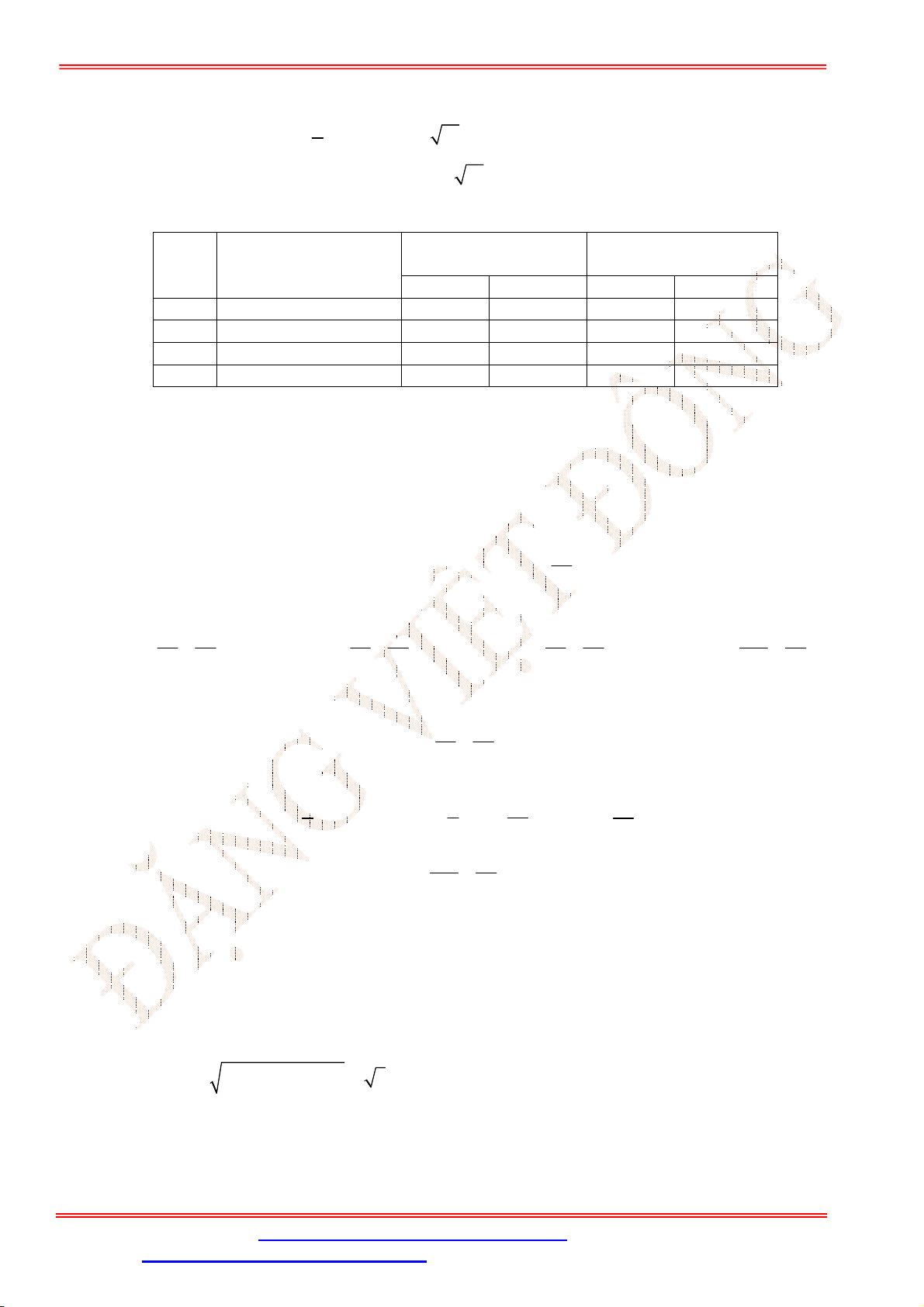
Câu 27. Tam giác
ABC
có trọng tâm
G
. Hai trung tuyến
6
BM ,
9
CN và
0
120
BGC . Tính độ dài
cạnh
AB
.
A.
2 13
AB . B.
13
AB . C.
2 11
AB
. D.
11
AB
.
Lời giải
Chọn A
Ta có:
BGC
và
BGN
là hai góc kề bù mà
0 0
120 120 .
BGC BGN
G
là trọng tâm của tam giác
ABC
2
4.
3
1
3.
3
BG BM
GN CN
Trong tam giác
BGN
ta có:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 2 2
2 . .cos
BN GN BG GN BG BGN
2
1
9 16 2.3.4. 13 13.
2
BN BN
N
là trung điểm của
2 2 13.
AB AB BN
Câu 28. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa tốt
nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp
2015
Khóa tốt nghiệp 2016
Nữ Nam Nữ Nam
1
Gi
ả
ng d
ạ
y
25
45
25
65
2
Ngân hàng
23
186
20
32
3 Lập trình 25 120 12 58
4
B
ả
o hi
ể
m
12
100
3
5
Trong số nữ sinh có việc làm ở Khóa tốt nghiệp 2015, tỷ lệ phần trăm của nữ trong lĩnh vực Giảng
dạy là bao nhiêu?
A.
11,2%
. B.
12,2%
. C.
15,0%
. D.
29,4%
.
Lời giải
Chọn D
Tổng số nữ sinh có việc làm ở Khóa tốt nghiệp 2015 là 85 người.
Nữ sinh có việc làm trong lĩnh vực Giảng dạy là 25 người.
Nên tỷ lệ phần trăm của nữ trong lĩnh vực Giảng dạy là
25
100% 29,4%
85
.
Câu 29. Phương trình chính tắc của
E
có
5 4
c a
, độ dài trục nhỏ bằng
12
là
A.
2 2
1
25 36
x y
. B.
2 2
1
36 25
x y
. C.
2 2
1
64 36
x y
. D.
2 2
1
100 36
x y
.
Lời giải
Chọn D
Phương trình chính tắc của
E
có dạng
2 2
2 2
1
x y
a b
với
2 2 2
b a c
.
Ta có độ dài trục nhỏ bằng 12 nên
2 12 6
b b .
Lại có:
4
5 4
5
c a c a
nên
2
2 2 2
4 9
5 25
b a a a
2 2 2
9
6 100
25
a a .
Vậy phương trình chính tắc của
E
là
2 2
1
100 36
x y
.
Câu 30. Trong mặt phẳng
Oxy
, đường tròn
C
có tâm
1;3
I đi qua
3;1
M có phương trình là
A.
2 2
( 3) ( 1) 10
x y . B.
2 2
( 3) ( 1) 8
x y .
C.
2 2
( 1) ( 3) 8
x y . D.
2 2
( 1) ( 3) 10
x y .
Lời giải
Chọn C
Ta có: bán kính đường tròn
C
có tâm
1;3
I đi qua
3;1
M là
2 2
3 1 1 3 8
R IM
.
Vậy phương trình đường tròn
C
có tâm
1;3
I đi qua
3;1
M là
2 2
( 1) ( 3) 8
x y .
Câu 31. Hãy chỉ ra đẳng thức sai.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
sin 4 sin6 sin 2
sin .sin 2 .sin3
4
.
B.
4cos .cos .cos cos2 cos2 cos2
a b b c c a a b b c c a
.
C.
sin10 sin6 sin 4
cos2 .sin5 .cos3
4
x x x
x x x .
D.
sin58 sin 42 sin72
sin 40 .cos10 .cos8
4
.
Lời giải
Chọn B
Kđ 1:
4cos cos cos 2 cos cos 2 .cos
2
2cos cos2 cos2
.
1 cos2 2cos cos2
.
Kđ 2:
sin8 sin2 cos2
1
cos2 sin5 cos3 sin10 sin6 sin 4
2 4
x x x
x x x x x x
.
Kđ 3:
sin50 sin30 cos8
sin58 sin42 sin8
sin 40 .cos10 .cos8
2 4
.
Kđ 4:
cos2 cos4 sin 2
sin 4 sin 6 sin 2
sin .sin .sin3
2 4
.
Câu 32. Cho đường thẳng đi qua hai điểm
3,0
A ,
0;4
B . Tìm tọa độ điểm
M
nằm trên
Oy
sao cho
diện tích tam giác
MAB
bằng
6
A.
0;8
. B.
1;0
. C.
0;0
và
0;8
. D.
0;1
.
Lời giải
Chọn C
Ta có
3;4
AB
5
AB .
Phương trình đường thẳng
AB
là
1
3 4
x y
4 3 12 0
x y .
Gọi
0;
M m Oy
2 2
3 12
,
3 4
m
d M AB
3 12
5
m
.
Diện tích tam giác
MAB
bằng
6
nên
3 12
1
.5 6
2 5
m
3 12 12
m
3 0
3 24
m
m
0 0;0
8 0;8
m M
m M
.
Câu 33. Tìm số nguyên lớn nhất của
x
để
2 2
4 2 4
3
9 3
x x
f x
x
x x x
nhận giá trị âm.
A.
2
x . B.
1
x . C.
2
x . D.
1
x
.
Lời giải
Chọn C
2 2 2
2 2
4 2 4 4 2 6 4 12
0 0 0
3 3 3
9 3
x x x x x x x x
f x
x x x x
x x x
.
2
3 20
0
3 3
x x
x x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
2
0
3 20 0
20
3
x
x x
x
.
0
3 3 0 3
3
x
x x x x
x
.
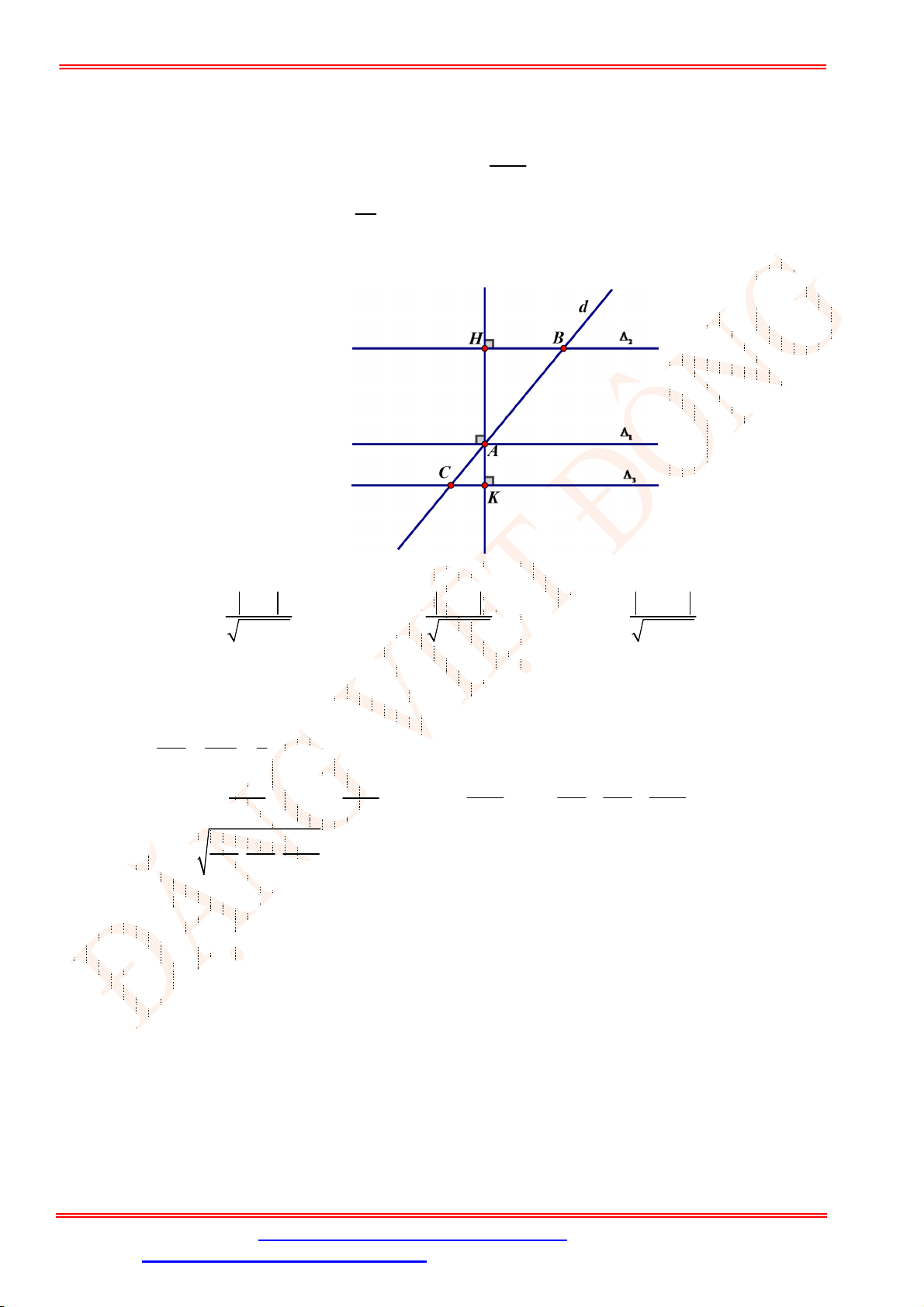
Bảng xét dấu:
Dựa vào bảng xét dấu, ta có
20
3
0 3 0
0 3
x
f x x
x
.
Vậy số nguyên lớn nhất để
0
f x là
2
x .
Câu 34. Cho
2 2 3 2
1
f x x m m x m m
với
m
là tham số thực. Biết rằng có đúng 2 giá trị
1 2
,
m m
để
f x
không âm với mọi giá trị của
x
. Tính tổng
1 2
m m
.
A.
1
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn A
Ta có:
2
2 3 2
1 0
0
1 4 0
a
f x x
m m m m
4 2 3 2 3 2
1 2 2 2 4 4 0
m m m m m m m
4 3 2
2 2 1 0
m m m m .
Trường hợp 1:
0 1 0
m (vô lý). Do đó
0
m không thỏa mãn bất phương trình.
Trường hợp 2:
0
m , chia cả 2 vế cho
2
m
ta được
2
2
2 1
2 1 0
m m
m m
2
2
1 1
2 1 0 1
m m
m m
.
Đặt
2 2
2
1 1
2
t m m t
m m
.
Khi đó
2
1 2 1 0 1
t t t
.
Với
2
1 5
1
2
1 1 1 0
1 5
2
m
t m m m
m
m
.
Vậy tổng
1 2
1
m m .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 35. Trong mặt phẳng tọa độ Oxy , cho các đường thẳng
1
:3 4 6 0 x y ,
2
:3 4 9 0 x y ,
3
:3 4 11 0
x y . Một đường thẳng d thay đổi cắt ba đường thẳng
1
,
2
,
3
lần lượt tại A ,
B , C . Giá trị nhỏ nhất của biểu thức
2
96
P AB
AC
bằng
A. 9. B.
49
9
. C. 18. D. 27 .
Lời giải
Chọn C
- Nhận thấy các đường thẳng
1
,
2
,
3
song song với nhau và
1 2
2 2
6 9
; 3
3 4
d ;
1 3
2 2
6 11
; 1
3 4
d ;
2 3
2 2
9 11
; 4
3 4
d
Suy ra:
1
nằm giữa
2
và
3
. Do đó nếu d cắt 3đường thẳng đó lần lượt tại A , B , C thì A nằm
giữa B và C .
- Qua A dựng đường thẳng vuông góc với
1
, cắt
2
và
3
lần lượt tại H và K
AB AH
AC AK
3
3
1
3. AB AC
2
96
P AB
AC
2
96
3. AC
AC
2
32
3.
AC
AC
2
32
3.
2 2
AC AC
AC
3
2
32
3.3. . .
2 2
Cauchy
AC AC
AC
18 . Dấu “=” xảy ra
4
12
AC
AB
.
Vậy
min
18P .
PHẦN II: TỰ LUẬN
Câu 36. Cho đường thẳng
1
:2 2 0 d x y ;
2
: 3 0 d x y và điểm
3;0M . Viết phương trình đường
thẳng đi qua điểm M , cắt
1
d
và
2
d
lần lượt tại A và B sao cho M là trung điểm của đoạn
AB .
Lời giải
1
; 2 2
A A A A
A x y d y x .
2
; 3
B B B B
B x y d y x .
Vì M là trung điểm của AB nên:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 6
11 16
2 2 2 3 0
3 3
A B M A B
A A
A B M A B
x x x x x
x y
y y y x x
.
Vậy
11 16
;
3 3
A
.
Đường thẳng là đường thẳng qua
A
và
M
. Từ đó suy ra
:8 24 0
x y .
Câu 37.
Trong mặt phẳng
Oxy
, cho
2 2
: 2 1 5
C x y . Viết phương trình tiếp tuyến của
C
biết tiếp tuyến cắt
;
Ox Oy
lần lượt tại
;
A B
sao cho
2
OA OB
Lời giải
C
có tâm
2;1
I , bán kính
5
R
Tiếp tuyến cắt
;
Ox Oy
lần lượt tại
;
A B
sao cho 2
OA OB
Tiếp tuyến có hệ số góc
1
2
OB
k
OA
.
Trường hợp 1: Với
1
2
k Phương trình tiếp tuyến có dạng
1
:
2
y x b
là tiếp tuyến của
;
C d I R
5
2
2
5
5
5
2
b
b
b
.
Suy ra phương trình tiếp tuyến cần tìm là
1 5
2 2
1 5
2 2
y x
y x
Trường hợp 2: Với
1
2
k Phương trình tiếp tuyến có dạng
1
:
2
d y x m
d
là tiếp tuyến của
;
C d I d R
9
4 2
2
5
1
5
2
b
m
b
.
Suy ra phương trình tiếp tuyến cần tìm là
1 9
2 2
1 1
2 2
y x
y x
Vậy có 4 tiếp tuyến thỏa mãn điều kiện.
Câu 38. Tìm giá trị lớn nhất của
2 3 2 5
T x xy y x với
, 0
x y .
Lời giải
Ta có:
2 3 2 5
T x xy y x
2 2 2
2
2 2 3 3 7
3 2 3 2 .
3 3 3 3 2 2 2
x x x x
T y y
2 2
0
2 3 7 7
3 ,
3 3 2 2 2
,
x
x
T y
x
y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dấu
" "
xảy ra khi và chỉ khi
2
2
9
3 0
3
4
1
2 3
0
4
3 2
x
y
x
x
y
.
Vậy
7
max
2
T khi và chỉ khi
9
4
1
4
x
y
.
Câu 39. Chứng minh rằng biểu thức sau đây không phụ thuộc vào x
6 6 2 2
sin os 3sin cos
A x c x x x
Lời giải
Ta có
6 6 2 2
sin os 3sin cos
A x c x x x
3
2 2 4 2 2 4 2 2
sin cos 3sin cos 3sin os 3sin cos
x x x x xc x x x
2 2 2 2
1 3sin cos sin cos 1 1 0 1
x x x x
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 02
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
PHẦN I: TRẮC NGHIỆM
Câu 1: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
0
m m x m
vô nghiệm?
A.
0
m
hay
1
m
. B.
0;1
m . C.
0
m
D.
;0 1;m
.
Câu 2: Tìm tập nghiệm của bất phương trình
2 7
1
4
x
x
?
A.
11;4
. B.
4;11
. C.
1;2;3
. D.
1;3
.
Câu 3: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có hai nghiệm
1
x
,
2
x
thỏa mãn
3 3
1 2
16
x x
.
A. Không tồn tại
m
. B.
2
m
. C.
1
m
. D.
1
m
hoặc
2
m
.
Câu 4: Cho tam giác
ABC
có
2
AB
cm,
1
AC
cm,
O
ˆ
60
A . Khi đó độ dài cạnh
BC
là:
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Câu 5: Cho ba điểm
1;4
A ,
3;2
B ,
5;4
C . Tọa độ tâm đường tròn ngoại tiếp tam giác
ABC
là:
A.
2;5
. B.
3
;2
2
. C.
9;10
. D.
3;4
.
Câu 6: Hình chiếu vuông góc của điểm
1;4
M xuống đường thẳng
: 2 2 0
x y
có tọa độ là:
A.
3;0
. B.
0;3
C.
2;2
D.
2; 2
Câu 7: Tính diện tích hình bình hành
ABCD
có
AB a
,
2
BC a
và góc
o
45
A
?
A.
2
2
a
. B.
2
2
a . C.
2
a
. D.
2
3
a .
Câu 8: Giá trị lớn nhất của biểu thức
4 7
sin cos
x x
là:
A.
2
. B.
1
. C.
1
2
. D.
1
.
Câu 9: Tập nghiệm của bất phương trình
2 2
2 4 3 3 2 1
x x x x
là
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;1
.
Câu 10: Tam giác
ABC
có
5
a
cm,
3
b
cm,
5
c
cm. Tính số đo góc
A
:
A.
O
45
. B.
O
30
. C.
O
90
. D.
o
72.54
.
Câu 11: Nếu cos sin 2 0
2
thì
bằng
A.
6
. B.
3
C.
4
D.
8
.
Câu 12: Biểu thức thu gọn của biểu thức
1
1 .tan
cos2
B x
x
là?
A.
tan2
x
B.
cot2
x
. C.
cos2
x
. D.
sin
x
.
Câu 13: Công thức nào sau đây là công thức Hê-rông:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
S pr
B.
S pr
C.
( )( )( )
S p p a p b p c
D.
( )( )( )
S p a p b p c
.
Câu 14: Điều kiện cần và đủ để tam giác
ABC
có góc
A
nhọn là?
A.
2 2 2
a b c
B.
2 2 2
a b c
C.
2 2 2
a b c
D.
2 2 2
a b c
.
Câu 15: Mệnh đề nào sau đây về tam giác
ABC
là SAI?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c
B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b
. D. Góc
A
tù khi và chỉ khi
2 2 2
b a c
.
Câu 16: Cho đường thẳng
có phương trình tổng quát:
2 3 1 0
x y
. Vecto nào sau đây là vecto chỉ
phương của đường thẳng
.
A.
(3;2)
. B.
(2;3)
. C.
( 3;2)
D.
(2; 3)
Câu 17: Tính
sin
, biết
5
cos
3
và
3
2
2
.
A.
1
3
B.
1
3
. C.
2
3
. D.
2
3
.
Câu 18: Cho
5
sin
3
a . Tính
cos2 sin
a a
A.
17 5
27
. B.
5
9
. C.
5
27
. D.
5
27
.
Câu 19: Tam giác
ABC
vuông tại
A
có
6
AB
cm,
10
BC
cm. Đường tròn nội tiếp tam giác đó có bán
kính
r
bằng
A.
1
cm. B.
2
cm. C.
2
cm. D.
3
cm.
Câu 20: Biến đổi thành tích biểu thức
sin7 sin5
sin7 sin5
ta được
A.
tan5 .tan
B.
cos2 .sin3
. C.
cot6 .tan
. D.
cos .sin
Câu 21: Trên mặt phẳng tọa độ
Oxy
cho hai vectơ
2 3
a i j
,
2
b i j
. Khi đó tọa độ vectơ
a b
là:
A.
2; 1
. B.
1;2
C.
1; 5
. D.
2; 3
.
Câu 22: Cho
cot 3
. Khi đó
3 3
3sin 2cos
12sin 4cos
có giá trị bằng
A.
1
4
. B.
5
4
. C.
3
4
D.
1
4
Câu 23: Cho sin cos
A
. Giá trị biểu thức
sin cos
bằng:
A.
2
1
2
A
B.
2
1
2
A
C.
1
2
A
D.
1
2
A
.
Câu 24: Trong mặt phẳng
Oxy
cho
2;3
A ,
4; 1
B
. Tọa độ của
OA OB
là
A.
2;4
B.
2; 4
. C.
3;1
D.
6; 2
Câu 25: Số đường thẳng đi qua điểm
5;6
M và tiếp xúc với đường tròn
2 2
: 1 2 1
C x y
là:
A. 0. B. 1. C. 2. D. 3.
Câu 26: Cho
0;3
A ,
4;2
B . Điểm
D
thỏa
2 2 0
OD DA DB
, tọa độ
D
là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
3;3
. B.
8;2
C.
8; 2
D.
5
2;
2
Câu 27: Trên mặt phẳng tọa độ
Oxy
, cho
ABC
vuông tại
A
có
1; 3
B
và
1;2
C . Tìm tọa độ điểm
H
là chân đường cao kẻ từ đỉnh
A
của
ABC
, biết
3
AB
,
4
AC
:
A.
24
1;
5
H
. B.
6
1;
5
H
C.
24
1;
5
H
. D.
6
1;
5
H
.
Câu 28: Cho
1
sin
3
a
với
2
a
. Tính
cos
a
.
A.
2 2
cos
3
a B.
2 2
cos
3
a C.
8
cos
9
a
D.
8
cos
9
a
.
Câu 29: Với mọi
x
, biểu thức
2 9
cos cos cos ... cos
5 5 5
x x x x
nhận giá trị bằng:
A.
10
. B.
10
. C.
0
. D.
1
.
Câu 30: Cho tam giác
ABC
có cạnh
BC a
, cạnh
CA b
. Tam giác
ABC
có diện tích lớn nhất khi góc
C
bằng
A.
o
60
B.
o
90
C.
o
150
. D.
o
120
Câu 31: Tìm tập nghiệm của bất phương trình
2 1 2
x x
.
A.
1
;3
3
. B.
1
;3
3
. C.
1
;3
3
. D.
1;3
Câu 32: Tam giác đều nội tiếp đường tròn bán kính
4
R
cm có diện tích là:
A.
13
cm
2
. B.
13 2
cm
2
. C.
12 3
cm
2
. D.
15
cm
2
.
Câu 33: Hệ bất phương trình
3 4 0
1
x x
x m
có nghiệm khi nào?
A.
5
m
B.
2
m
C.
5
m
D.
5
m
.
Câu 34: Phương trình nào dưới đây không là phương trình đường tròn?
A.
2 2
4 0
x y
. B.
2 2
2 0
x y x y
.
C.
2 2
0
x y x y
. D.
2 2
2 2 1 0
x y x y
.
Câu 35: Cho
3
tan
5
. Tính giá trị biểu thức
2 2
sin cos
sin cos
A
:
A.
15
16
B.
15
16
C.
5
6
D.
5
6
PHẦN II: TỰ LUẬN
Bài 1. Giải bất phương trình
2
2
3
1
4
x x
x
.
Bài 2. Cho tam giác
ABC
, biết
7, 8, 6
a b c
. Tính
S
và
a
h
.
Bài 3. Lập phương trình tiếp tuyến của đường tròn
2 2
: 6 2 0
C x y x y
, biết tiếp tuyến này vuông
góc với đường thẳng
:3 4 0
d x y
.
Bài 4. Tìm giá trị nhỏ nhất của hàm số
1 1
1
y
x x
với
0 1
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 02
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
PHẦN I: TRẮC NGHIỆM
1.C
2.
A
3.
D
4.
C
5.D
6.
C
7.
C
8.
D
9.D
10.
D
11.C 12.A 13.C 14.A 15.D 16.A 17.D 18.D 19.C 20.C
21.C
22.
A
23.A
24.
A
25.
C
26.
C
27.D
28.
B
29.C
30.
B
31.
A
32.D
33.
B
34.
B
35.A
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
PHẦN II: TỰ LUẬN
Câu hỏi Nội dung Điểm
Bài 1
(1,0 điểm)
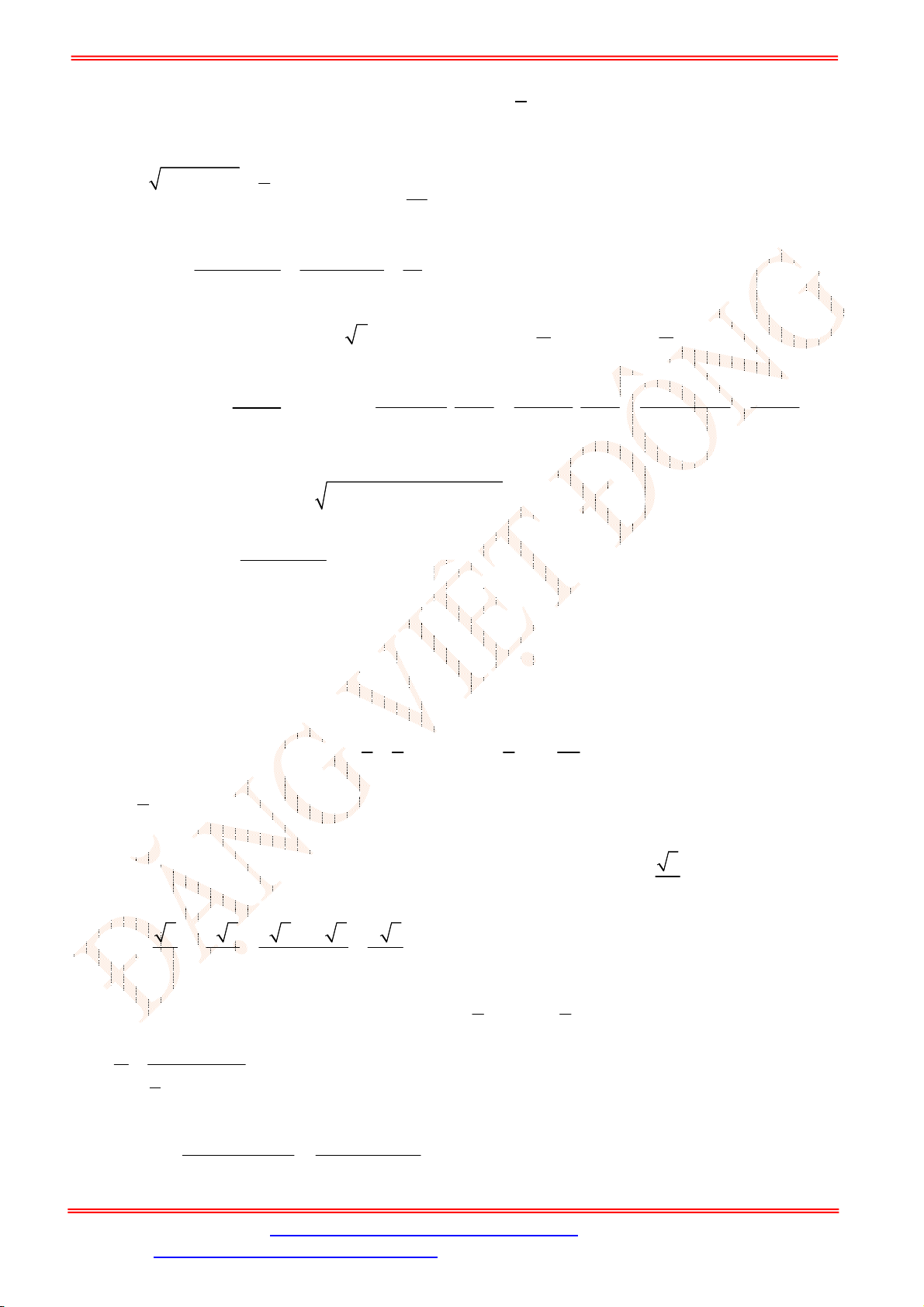
Bất phương trình
1
0
2 2
x
x x
Bảng xét dấu vế trái:
Đáp số 2 1, 2x x .
0,25
0,5
0,25
Bài 2
(1,0 điểm)
Áp dụng công thức Hê-rông với
21
2 2
a b c
p
Ta có
21 21 21 21 21 15
( )( )( ) 7 8 6
2 2 2 2 4
S p p a p b p c
Vì
1 21 15 1
7
2 4 2
a a
S ah h
nên suy ra
3 15
2
a
h .
0,25
0,25
0,25
0,25
Bài 3
(0,5 điểm)
Gọi tiếp tuyến cần tìm là
. Vì
vuông góc với d nên
: 3 0x y c
.
C có tâm
3; 1I và có bán kính 10R . Ta có tiếp xúc với
C
3 3
; 10 10
10
c
d I R c
.
Vậy tiếp tuyến cần tìm là : 3 10 0x y hay : 3 10 0x y .
0,25
0,25
Bài 4
(0,5 điểm)
Ta có
2
1 1 1 1 1
4
1 1 1
1
2
x x
y
x x x x x x
x x
Đẳng thức xảy ra khi
1
1
0;1
2
x x
x
x
.
Vậy giá trị nhỏ nhất của hàm số là 4 khi
1
2
x .
0,25
0,25

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
HƯỚNG DẪN CHI TIẾT 35 CÂU TRẮC NGHIỆM
Câu 1: Bất phương trình
2
0
m m x m
vô nghiệm khi và chỉ khi bất phương trình
2
0
m m x m
nghiệm đúng với mọi x
2
0
0.
0
m m
m
m
Chọn C.
Câu 2: Bất phương trình
2 7 11
1 0 11 4.
4 4
x x
x
x x
Vậy tập nghiệm là
11;4
. Chọn A.
Câu 3: Phương trình có nghiệm khi
0
2
2 0
m m
2
1
m
m
1
.
Theo định lý Vi-ét, ta có
1 2
1 2
2
2
x x m
x x m
. Theo đề bài,
3 3
1 2
16
x x
3
8 6 2 16
m m m
3 2
8 6 12 16 0
m m m
2
2 8 10 8 0
m m m
2 0
m
2
m
.
Kiểm tra điều kiện
1
, ta được
1
m
hoặc
2
m
. Chọn D.
Câu 4: Áp dụng định lý cô-sin, ta có
2 2 2 O
1
2. . .cos60 4 1 2.2.1. 3
2
BC AB AC AB AC
. Suy ra
3
BC cm. Chọn C.
Câu 5: Gọi phương trình đường tròn ngoại tiếp tam giác
ABC
là
2 2
: 2 2 0
C x y ax by d
. Do
C
đi qua các điểm
1;4
A ,
3;2
B và
5;4
C nên ta lập được hệ phương trình:
1 16 2 8 0 3
9 4 6 4 0 4
25 16 10 8 0 21
a b c a
a b c b
a b c c
.
Vậy tâm đường tròn cần tìm là
3;4
. Chọn D.
Câu 6: Đường thẳng qua
1;4
M và vuông góc với
: 2 2 0
x y
có phương trình
:2 6 0
x y
.
Hình chiếu vuông góc của
M
xuống
là giao điểm của
và
. Tọa độ giao điểm là nghiệm của hệ
phương trình
2 2 0 2
2 6 0 2
x y x
x y y
. Vậy tọa độ giao điểm cần tìm là
2;2
. Chọn C.
Câu 7: Góc
o o o
ˆ
180 45 135
B . Diện tích hình bình hành
ABCD
bằng
2
1
2. . . .sin
2
AB BC B a
. Chọn C.
Câu 8: Do
1 sin ,cos 1
x x
nên
4 7 2 2
sin cos sin cos 1
x x x x
. Vậy giá trị lớn nhất của biểu thức là
1
khi
2
x k
hay
2
x k
. Chọn D.
Câu 9: Đặt
2
3 2 0
t x x
2 2
2 3
x x t
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Bất phương trình cho trở thành:
2
2 3 5 0
t t
5
1
2
t
.
Suy ra
2
5
0 3 2
2
x x
2
2
0 3 2
25
3 2
4
x x
x x
3 1
x
x
3 1
x
. Chọn D.
Câu 10:
2 2 2 2 2 2
3 5 5 3
cos
2 2.3.5 10
b c a
A
bc
. Suy ra
o
72.54
A
. Chọn D.
Câu 11: Theo đề bài,
cos sin 2 sin2 1 2 2
2 4
k k
. Chọn C.
Câu 12: Ta có
1
1 .tan
cos2
B x
x
1 cos2 sin
.
cos2 cos
x x
x x
2
2cos sin
.
cos2 cos
x x
x x
2cos .sin
cos2
x x
x
sin2
cos2
x
x
tan2
x
.
Chọn A.
Câu 13: Công thức Hê-rông
S p p a p b p c
. Chọn C.
Câu 14: Ta có
2 2 2
cos
2
b c a
A
bc
. Góc
A
nhọn khi và chỉ khi
cos 0
A
hay
2 2 2
a b c
. Chọn A.
Câu 15: Phương án D là sai. Chọn D.
Câu 16: Một vectơ pháp tuyến của đường thẳng
:
2 3 1 0
x y
có tọa độ là
2;3
. Suy ra tọa độ
vectơ chỉ phương là
3;2
. Chọn A.
Câu 17: Ta có:
2 2
5 4
sin 1 cos 1
9 9
2
sin
3
. Do
3
2
2
nên
sin 0
. Vậy
2
sin
3
. Chọn D.
Câu 18: Ta có
2 3
cos2 sin 1 2sin sin sin 2sin
B a a a a a a
mà
5
sin
3
a
Suy ra
5 5 5 9 5 10 5 5
2
3 27 27 27
B
. Chọn D.
Câu 19: Tam giác
ABC
vuông tại A có diện tích
1 1
. .6.8 24
2 2
S AB AC
. Bán kính đường tròn nội tiếp
là
24
2
1
6 8 10
2
S
r
p
cm. Chọn C.
Câu 20: Ta có
sin7 sin5
sin7 sin5
2cos6 .sin
2sin6 .cos
cot6 .tan
. Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 21: Ta có
2 3 2; 3 ; 2 1;2
a i j a b i j b
suy ra
1; 5
a b
. Chọn C.
Câu 22: Ta có
2
2
3 3 3 3
1
3 2cot
3sin 2cos 3 2cot 1
sin
1 cot
12sin 4cos 12 4cot 12 4cot 4
. Chọn A.
Câu 23: Ta có
2
2
1 1
sin cos sin cos 1
2 2
A
. Chọn A.
Câu 24: Ta có
OA OB BA
và
2;4
BA
nên tọa độ của
OA OB
là
2;4
. Chọn A.
Câu 25: Đường tròn
C
có tâm
1;2
I và bán kính
1
R
. Ta có
2 2
5 1 6 2 4 2
IM R
, suy
ra điểm
M
nằm bên ngoài đường tròn. Do đó từ
M
kẻ được đúng hai tiếp tuyến đến
C
. Chọn C.
Câu 26: Gọi
;
D x y
. Theo đề
2 2 0
OD DA DB
2
OD AB
. Mà
4; 1
AB
2 8; 2
AB
8; 2
OD
. Vậy
8; 2
D
. Chọn C.
Câu 27: Ta có
2
.
AB BH BC
và
2
.
AC CH CB
. Do đó:
2
2
16
9
CH AC
BH AB
16
.
9
HC HB
.
Mà
,
HC HB
ngược hướng nên
16
9
HC HB
.
Khi đó, gọi
;
H x y
thì
1 ;2
HC x y
,
1 ; 3
HB x y
.
Suy ra:
16
1 1
9
16
2 3
9
x x
y y
1
6
5
x
y
6
1;
5
H
.
Câu 28: Ta có
2 2 2 2
8 2 2
sin cos 1 cos 1 sin cos
9 3
a a a a a . Vì
2
a
nên
2 2
cos
3
a
. Chọn B.
Câu 29: Ta có
5
cos cos
5
x x
;
6
cos cos
5 5
x x
;
2 7
cos cos
5 5
x x
;…
Vậy
2 9
cos cos cos ... cos 0
5 5 5
x x x x
. Chọn C.
Câu 30: Diện tích tam giác
ABC
được tính bằng công thức
1
sin
2
S ab C
. Do
o o
0 180
C
nên
0 sin 1
C
. Vậy diện tích lớn nhất khi
sin 1
C
hay
o
ˆ
90
C . Chọn B.
Câu 31: Bất phương trình
3
1
2 2 1 2 3
1 3
3
x
x x x x
x
. Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 32: Gọi cạnh của tam giác đều là
a
, ta có
o
2sin60
3
a a
R
, suy ra
3 4 3
a R . Diện tích
3
3
4 3
12 3
4 4.4
a
S
R
. Chọn C.
Câu 33: Hệ bất phương trình
3 4
1
x
x m
. Để hệ có nghiệm thì
1 3 2
m m
. Chọn B.
Câu 34: Xét phương án B:
2 2
2 0
x y x y
, có
1
2
a b
và
2
c
. Phương trình này không thỏa
điều kiện
2 2
0
a b c
nên không là phương trình đường tròn. Chọn B.
Câu 35: Vì
cos 0
, chia cả tử và mẫu của biểu thức cho
2
cos
, ta được
2
tan 15
tan 1 16
A
. Chọn A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 03
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho
ABC
có
4
a
,
5
c
,
150
B
. Tính diện tích tam giác
ABC
A.
10 3
S . B.
5
S . C.
5 3
S . D.
10
S .
Câu 2. Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của
x
?
A.
6 4
x x
. B.
2 2
6 4
x x
. C.
6 4
x x
. D. 6 4
x x
.
Câu 3. Bảng xét dấu sau là của biểu thức nào?
A.
2
f x x . B.
2 4
f x x
.
C.
16 8
f x x
. D.
2
f x x .
Câu 4. Tính giá trị của
89
cot .
6
A.
89 3
cot .
6 3
B.
89 3
cot .
6 3
C.
89
cot 3.
6
D.
89
cot 3.
6
Câu 5. Điều kiện xác định của bất phương trình
1
1
2
x
là:
A.
2
x . B.
2
x . C.
2
x . D.
2
x .
Câu 6. Góc lượng giác nào sau đây có cùng điểm cuối với góc
13
4
?
A.
3
4
. B.
3
4
. C.
4
. D.
3
2
.
Câu 7. Trong mặt phẳng tọa độ
Oxy
, cho elip
( )
E
có phương trình chính tắc
2 2
1
36 25
x y
. Độ dài trục
lớn của elip bằng
A.
36
. B.
12
. C.
25
. D.
10
.
Câu 8. Điểm cuối của
thuộc góc phần tư thứ ba
3
2
của đường tròn lượng giác. Khẳng
định nào sau đây là sai?
A.
0.
cot B.
0.
sin
C.
0.
cos D.
0.
tan
Câu 9. Phương trình nào sau đây không phải là phương trình đường tròn ?
A.
2 2
4 0
x y x y . B.
2 2
0
x y y .
C.
2 2
2 0
x y . D.
2 2
100 1 0
x y y .
Câu 10. Cho tam giác
ABC
vuông tại
A
góc
B
bằng
0
30
. Khẳng định nào sau đây là sai?
A.
1
cos
2
C . B.
3
sinC
2
. C.
1
sin
2
B . D.
1
cos
3
B .
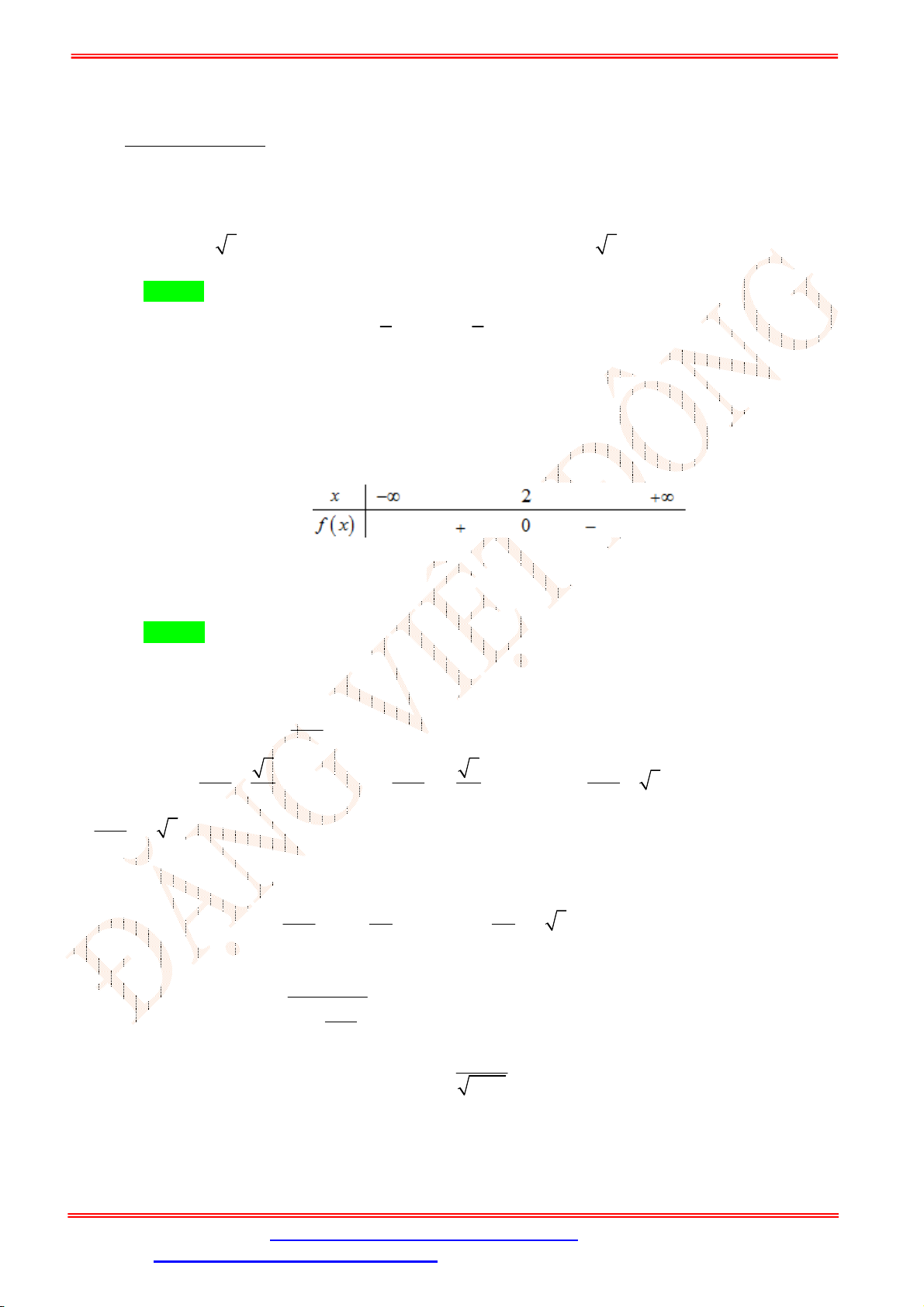
Câu 11. Cho đường thẳng
:3 2 10 0
d x y . Véc tơ nào sau đây là véctơ chỉ phương của
d
?
A.
3;2
u . B.
3; 2
u . C.
2; 3
u . D.
2; 3
u .
Câu 12. Kết quả điểm kiểm tra môn Toán trong một kì thi của
200
em học sinh được trình bày ở bảng
sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Số trung vị của bản phân bố tần số nói trên là:
A. 8. B.
7
. C.
6
. D. Đáp án khác
Câu 13. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
1
cos .cos3 cos4 cos2
2
x x x x
. B.
1
cos .cos cos2 cos2
2
x y x y
.
C.
1
cos .sin cos2 cos2
2
x y x y
. D.
sin sin sin
a b a b
.
Câu 14. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
( ): 4 2 1 0
C x y x y . Bán
kính đường tròn
C
là
A.
1
R
. B.
6
R . C.
6
R . D.
2
R
.
Câu 15. Số đo radian của góc
135
là
A.
6
. B.
3
4
. C.
2
3
. D.
2
.
Câu 16. Rút gọn biểu thức
sin2 .cos cos2 .sin
M x x x x
ta được kết quả
A.
sin
M x
. B.
cos3
M x
. C.
cos
M x
. D.
sin3
M x
.
Câu 17. Đường tròn
C
tâm
1;1
A và qua điểm
2; 1
B có phương trình là
A.
2 2
1 1 2
x y . B.
2 2
1 1 5
x y .
C.
2 2
1 1 5
x y . D.
2 2
1 1 1
x y .
Câu 18. Đường thẳng đi qua điểm và có vectơ chỉ phương có phương trình tổng
quát là:
A. B. C. D.
Câu 19. Tam giác
ABC
có
5, 7, 8
AB BC CA . Số đo góc
A
bằng:
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Câu 20. Lập phương trình chính tắc của Elip, biết hình chữ nhật cơ sở có chiều rộng bằng
10
và đường
chéo bằng
10 5
.
A.
2 2
1
225 400
x y
. B.
2 2
1
10 5
x y
. C.
2 2
1
400 100
x y
. D.
2 2
1
100 25
x y
.
Câu 21. Cho góc
thỏa mãn
3
cos
5
và
0
2
. Tính
5 3tan 6 4cot .
P a a
A.
6.
P B.
4.
P C.
6.
P D.
4.
P
Câu 22. Trên đường tròn lượng giác gốc
A
cho các cung có số đo:
I.
4
. II.
7
4
. III.
13
4
. IV.
71
4
.
Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ I và II. B. Chỉ I, II và IV.
C. Chỉ II, III và IV. D. Chỉ I, II và III.
Câu 23. Trong mặt phẳng tọa độ
Oxy
cho hai vectơ
; 1 , 2; 1
a x x b x x . Điều kiện của
x
để
. 3
a b
là
A.
0 1
x
. B.
2
x . C.
2 3
x . D.
2 1
x
.
Câu 24. Cho hai số thực
,
x y
không âm và thỏa mãn
2
2 12
x y . Giá trị lớn nhất của
P xy
là:
A.
4
. B.
8
. C.
13
. D.
13
4
.
d
0; 2
M
3;0
u
: 0.
d x
: 2 0.
d y
: 2 0.
d y
: 2 0.
d x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 25. Phương trình tiếp tuyến
d
của đường tròn
2 2
: 2 2 25
C x y tại điểm
2;1
M là
A.
:4 3 14 0.
d x y B.
:3 4 2 0.
d x y
C.
:4 3 11 0.
d x y D.
: 1 0.
d y
Câu 26. Cho mẫu số liệu thống kê:
2,4,6,8,10
. Phương sai của mẫu số liệu trên bằng bao nhiêu?
A.
8
. B.
10
. C.
40
. D.
6
.
Câu 27. Giá trị của biểu thức
2 2
tan cot
24 24
A bằng
A.
12 2 3
2 3
. B.
12 2 3
2 3
. C.
12 2 3
2 3
. D.
12 2 3
2 3
.
Câu 28. Cho
tan 2
x
và
o
0 90
x . Khi đó giá trị của
o
cos 30
x bằng:
A.
1
6
2
. B.
6 3
. C.
6
3
6
. D.
1 6
2 6
.
Câu 29. Tìm giá trị lớn nhất
M
và nhỏ nhất
m
của biểu thức
1 2 cos3 .
P x
A.
2, 2.
M m B.
0, 2.
M m
C.
3, 1.
M m D.
1, 1.
M m
Câu 30. Người ta điều tra ngẫu nhiên số cân nặng của 30 học sinh nữ một trường phổ thông, được ghi
trong bảng sau:
Số cân nặng (kg) 38 40 43 45 48 50
T
ần số
2
4
9
6
4
5
N = 30
T
ần suất (%)
6,67
13,33
30
20
13,33
16,67
Số cân nặng trung bình
x
, số trung vị
e
M
, mốt
0
M
của bảng thống kê trên là
A.
0
44; 44; 44.
e
x M M B.
0
44,5; 44; 43.
e
x M M
C.
0
45; 44; 43.
e
x M M D.
0
44; 44,5; 43.
e
x M M
Câu 31. Giải bất phương trình
3 2
2
1
x
x
x
được tập nghiệm là
A.
1
; 2;3
2
. B.
1
;1 2;
2
. C.
;1 2;
. D.
2;1 2;
.
Câu 32. Trong mặt phẳng tọa độ
Oxy
, cho điểm
2;2
M và hai đường thẳng
:2 3 1 0
x y
và
:2 3 0
d x y
. Một đường thẳng qua
M
cắt
và
d
lần lượt tại
A
và
B
sao cho
M
là
trung điểm của
AB
. Khi đó độ dài
AB
là
A.
2 2
AB
. B.
5
AB . C.
2
AB
. D.
4
AB
.
Câu 33. Cho góc
thỏa mãn
2
và
sin 2cos 1
. Tính
sin2
P
.
A.
24
.
25
P B.
2 6
.
5
P C.
24
.
25
P D.
2 6
.
5
P
Câu 34. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2
2 3 2
1
2 2
x mx m
,
x mx
nghiệm đúng với
mọi
x
.
A.
m 12 m 0
. B.
12 0
m . C.
4 m 0
. D.
4 m 4
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 35. Cho
ABC
nhọn, có
1;7
A ,
2;0
B ,
9;0
C đường cao
AH
. Xét các hình chữ nhật
MNPQ
với
M AB
;
N AC
; ,
P Q BC
. Điểm
;
M a b
thỏa mãn hình chữ nhật
MNPQ
có
diện tích lớn nhất, tính
P a b
.
A. 3. B. 5. C. 7. D. 1.
PHẦN II: TỰ LUẬN
Câu 36. Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
1;1 , 2;5
A B . Diện tích tam giác
ABC
bằng 6,
trọng tâm
G
của tam giác
ABC
nằm trên đường thẳng
: 3 0
x y . Tìm tọa độ điểm
C
của
tam giác
ABC
?
Câu 37. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 1 10
C x y . Lập phương trình tiếp
tuyến của đường tròn
C
biết tiếp tuyến tạo với
: 2 4 0
x y một góc bằng
45
.
Câu 38. Biết
, 0
x y ,
1.
x y Tìm giá trị nhỏ nhất của biểu thức
1 1
.
R x y
x y
Câu 39. Rút gọn các biểu thức sau:
0 0 0 0 0
os20 os40 os60 ... os160 os180
C c c c c c
.
------------- HẾT -------------
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 03
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho
ABC
có
4
a ,
5
c ,
150
B . Tính diện tích tam giác
ABC
A.
10 3
S . B.
5
S . C.
5 3
S . D.
10
S .
Lời giải
Chọn B
Diện tích tam giác
ABC
là
1
sin
2
S ac B
1
.4.5sin150
2
5
.
Câu 2. Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của
x
?
A.
6 4
x x
. B.
2 2
6 4
x x
. C.
6 4
x x
. D. 6 4
x x
.
Lời giải
Chọn D
Ta có:
6 4 6 4
x x (luôn đúng với mọi
x )
Câu 3. Bảng xét dấu sau là của biểu thức nào?
A.
2
f x x . B.
2 4
f x x
.
C.
16 8
f x x
. D.
2
f x x .
Lời giải
Chọn C
Ta thấy
16 8
f x x
có nghiệm
2
x đồng thời hệ số
8 0
a nên bảng xét dấu trên là
của biểu thức
16 8
f x x
.
Câu 4. Tính giá trị của
89
cot .
6
A.
89 3
cot .
6 3
B.
89 3
cot .
6 3
C.
89
cot 3.
6
D.
89
cot 3.
6
Lời giải
Chọn D
Cách 1. Ta có
89 5 5
cot cot 14 cot 3.
6 6 6
Cách 2. Hướng dẫn bấm máy tính.
Bấm lên màn hình
1
89
tan
6
và bấm dấu =. Màn hình hiện ra kết quả.
Câu 5. Điều kiện xác định của bất phương trình
1
1
2
x
là:
A.
2
x . B.
2
x . C.
2
x . D.
2
x .
Lời giải
Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Điều kiện xác định của bất phương trình
1
1
2
x
là:
2 0 2
x x .
Câu 6. Góc lượng giác nào sau đây có cùng điểm cuối với góc
13
4
?
A.
3
4
. B.
3
4
. C.
4
. D.
3
2
.
Lời giải
Chọn A
Ta có
13 3
4
4 4
nên góc lượng giác
3
4
có cùng điểm cuối với góc
13
4
.
Câu 7. Trong mặt phẳng tọa độ
Oxy
, cho elip
( )
E
có phương trình chính tắc
2 2
1
36 25
x y
. Độ dài trục
lớn của elip bằng
A.
36
. B.
12
. C.
25
. D.
10
.
Lời giải
Chọn B
Ta có
2
2
36 6 0
25 5
a a a
b b
Độ dài trục lớn của elip bằng
2 2.6 12
a .
Câu 8. Điểm cuối của
thuộc góc phần tư thứ ba
3
2
của đường tròn lượng giác. Khẳng
định nào sau đây là sai?
A.
0.
cot B.
0.
sin
C.
0.
cos D.
0.
tan
Lời giải
Chọn B
Điểm cuối của
thuộc góc phần tư thứ ba
0
0
0
0
sin
cos
tan
cot
Câu 9. Phương trình nào sau đây không phải là phương trình đường tròn ?
A.
2 2
4 0
x y x y . B.
2 2
0
x y y .
C.
2 2
2 0
x y . D.
2 2
100 1 0
x y y .
Lời giải.
Chọn A
Phương trình
2 2
4 0
x y x y không phải là phương trình đường tròn vì
2 2
7
0
2
a b c .
Câu 10. Cho tam giác
ABC
vuông tại
A
góc
B
bằng
0
30
. Khẳng định nào sau đây là sai?
A.
1
cos
2
C . B.
3
sinC
2
. C.
1
sin
2
B . D.
1
cos
3
B .
Lời giải
Chọn D
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ABC vuông tại A, góc B bằng
0
30 suy ra góc C bằng
0
60 .
0
3
sinC sin60
2
.
0
1
sin sin30
2
B .
0
3
cos cos30
2
B .
0
1
cos cos60
2
C .
Câu 11. Cho đường thẳng
:3 2 10 0 d x y . Véc tơ nào sau đây là véctơ chỉ phương của
d ?
A.
3;2
u . B.
3; 2
u . C.
2; 3
u . D.
2; 3
u .
Lời giải
Chọn C
Đường thẳng
d có một véctơ pháp tuyến là
3;2
n nên
d có một véctơ chỉ phương là
2; 3
u .
Câu 12. Kết quả điểm kiểm tra môn Toán trong một kì thi của 200 em học sinh được trình bày ở bảng
sau:
Số trung vị của bản phân bố tần số nói trên là:
A. 8. B. 7 . C. 6 . D. Đáp án khác
Lời giải
Chọn A
Số trung vị của bản phân bố tần số nói trên là: 8
Câu 13. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
1
cos .cos3 cos4 cos2
2
x x x x . B.
1
cos .cos cos2 cos2
2
x y x y .
C.
1
cos .sin cos2 cos2
2
x y x y . D.
sin sin sin a b a b .
Lời giải
Chọn A
1 1
cos .cos3 cos 3 cos 3 cos4 cos2
2 2
x x x x x x x x .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 14. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
( ): 4 2 1 0
C x y x y . Bán
kính đường tròn
C
là
A.
1
R
. B.
6
R . C.
6
R . D.
2
R
.
Lời giải
Chọn C
Có
2 2
2; 1, 1 6
a b c R a b c .
Câu 15. Số đo radian của góc
135
là
A.
6
. B.
3
4
. C.
2
3
. D.
2
.
Lời giải
Chọn B
Sử dụng máy tính bỏ túi ta tính được
3
135
4
.
Câu 16. Rút gọn biểu thức
sin2 .cos cos2 .sin
M x x x x
ta được kết quả
A.
sin
M x
. B.
cos3
M x
. C.
cos
M x
. D.
sin3
M x
.
Lời giải
Chọn A
Ta có
sin2 .cos cos2 .sin
M x x x x
sin(2 )
x x
sin
x
.
Câu 17. Đường tròn
C
tâm
1;1
A và qua điểm
2; 1
B có phương trình là
A.
2 2
1 1 2
x y . B.
2 2
1 1 5
x y .
C.
2 2
1 1 5
x y . D.
2 2
1 1 1
x y .
Lời giải
Chọn C
Ta có
1; 2
AB . Bán kính của đường tròn
C
là
5
AB .
Phương trình đường tròn tâm
1,1
A và bán kính
5
AB là:
2 2
1 1 5
x y .
Câu 18. Đường thẳng đi qua điểm và có vectơ chỉ phương có phương trình tổng
quát là:
A. B. C. D.
Lời giải
Chọn B
0
0; 2
: 2 0.
3;0 3 1; 0;1
d d
M
d
d
n
y
u
Câu 19. Tam giác
ABC
có
5, 7, 8
AB BC CA . Số đo góc
A
bằng:
A.
30 .
B.
45 .
C.
60 .
D.
90 .
Lời giải
Chọn C
Theo định lí hàm cosin, ta có
2 2 2 2 2 2
5 8 7 1
ˆ
cos
2 . 2.5.8 2
AB AC BC
A
AB AC
.
Do đó,
ˆ
60
A
.
Câu 20. Lập phương trình chính tắc của Elip, biết hình chữ nhật cơ sở có chiều rộng bằng
10
và đường
chéo bằng
10 5
.
A.
2 2
1
225 400
x y
. B.
2 2
1
10 5
x y
. C.
2 2
1
400 100
x y
. D.
2 2
1
100 25
x y
.
Lời giải
d
0; 2
M
3;0
u
: 0.
d x
: 2 0.
d y
: 2 0.
d y
: 2 0.
d x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D
Giả sử Elip có độ dài trục lớn là
2
a
, độ dài trục bé là
2
b
Hình chữ nhật có chiều rộng là
10
suy ta
2 10 5
b b
Đường chéo của hình chữ nhật cơ sở là
2 2 2
4 4 10 5 100
a b a
Vậy phương trình chính tắc của Elip là
2 2
1.
100 25
x y
Câu 21. Cho góc
thỏa mãn
3
cos
5
và
0
2
. Tính
5 3tan 6 4cot .
P a a
A.
6.
P B.
4.
P C.
6.
P D.
4.
P
Lời giải
Chọn D
Ta có
2
4 4
sin 1 cos tan
4
5 3
sin
3
5
0 cot
2 4
.
Thay
4
tan
3
3
cot
4
vào
P
, ta được
4
P
.
Câu 22. Trên đường tròn lượng giác gốc
A
cho các cung có số đo:
I.
4
. II.
7
4
. III.
13
4
. IV.
71
4
.
Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ I và II. B. Chỉ I, II và IV.
C. Chỉ II, III và IV. D. Chỉ I, II và III.
Lời giải
Chọn B
Có
7
2
4 4
và
71
18 9.2
4 4
nên
4
,
7
4
và
71
4
là các cung có điểm
cuối trùng nhau.
13
3
4 4
nên
13
4
là cung có điểm cuối không trùng với điểm cuối của các cung còn
lại.
Câu 23. Trong mặt phẳng tọa độ
Oxy
cho hai vectơ
; 1 , 2; 1
a x x b x x . Điều kiện của
x
để
. 3
a b
là
A.
0 1
x
. B.
2
x . C.
2 3
x . D.
2 1
x
.
Lời giải
Chọn D
Ta có:
2 2
. 3 2 2 1 3 2 0 2 1
a b x x x x x
.
Câu 24. Cho hai số thực
,
x y
không âm và thỏa mãn
2
2 12
x y . Giá trị lớn nhất của
P xy
là:
A.
4
. B.
8
. C.
13
. D.
13
4
.
Lời giải
Chọn B
Từ giả thiết, ta có
2
16 4 2 4 2 2 4 .2
x y x y x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Suy ra
8
xy . Dấu
'' ''
xảy ra khi
2; 4.
x y
Câu 25. Phương trình tiếp tuyến
d
của đường tròn
2 2
: 2 2 25
C x y tại điểm
2;1
M là
A.
:4 3 14 0.
d x y B.
:3 4 2 0.
d x y
C.
:4 3 11 0.
d x y D.
: 1 0.
d y
Lời giải
Chọn C
Đường tròn (C) có tâm
2; 2
I nên tiếp tuyến tại M có VTPT là
4;3 ,
n IM nên có
phương trình là:
4 2 3 1 0 4 3 11 0.
x y x y
Câu 26. Cho mẫu số liệu thống kê:
2,4,6,8,10
. Phương sai của mẫu số liệu trên bằng bao nhiêu?
A.
8
. B.
10
. C.
40
. D.
6
.
Lời giải
Chọn A
Số trung bình là :
x
2 4 6 8 10
5
6
.
Phương sai của mẫu số liệu trên là:
5
2
2
1
1
5
i
i
s x x
. Do đó
2
s
2 2 2 2 2
1
2 6 4 6 6 6 8 6 10 6
5
8
.
Câu 27. Giá trị của biểu thức
2 2
tan cot
24 24
A bằng
A.
12 2 3
2 3
. B.
12 2 3
2 3
. C.
12 2 3
2 3
. D.
12 2 3
2 3
.
Lời giải:
Chọn C
2 2
tan cot
24 24
A
2 2
1 1
1 1
cos sin
24 24
2 2
1
2
cos .sin
24 24
2
4
2
sin
12
8
2
1 cos
6
12 2 3
2 3
.
Câu 28. Cho
tan 2
x
và
o
0 90
x . Khi đó giá trị của
o
cos 30
x bằng:
A.
1
6
2
. B.
6 3
. C.
6
3
6
. D.
1 6
2 6
.
Lời giải
Chọn D
Ta có
tan 2
x
2
1
1 2 3
cos
x
1
cos
3
x .
Do
o
0 90
x nên
cos 0
x
1
cos
3
x .
Măt khác:
sin
tan
cos
x
x
x
2
sin tan .cos
3
x x x
.
Vậy
o
cos 30
C x
o o
cos cos30 sin sin30
x x
1 3 2 1
. .
2 2
3 3
3 6
6
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 29. Tìm giá trị lớn nhất
M
và nhỏ nhất
m
của biểu thức
1 2 cos3 .
P x
A.
2, 2.
M m B.
0, 2.
M m
C.
3, 1.
M m D.
1, 1.
M m
Lời giải
Chọn D
Ta có
1 cos3 1 0 cos3 1 0 2 cos3 2
x x x
1
1 1 2 cos3 1 1 1 .
1
M
x P
m
Câu 30. Người ta điều tra ngẫu nhiên số cân nặng của 30 học sinh nữ một trường phổ thông, được ghi
trong bảng sau:
S
ố cân nặng (kg)
38
40
43
45
48
50
Tần số 2 4 9 6 4 5 N = 30
Tần suất (%) 6,67 13,33 30 20 13,33 16,67
Số cân nặng trung bình
x
, số trung vị
e
M
, mốt
0
M
của bảng thống kê trên là
A.
0
44; 44; 44.
e
x M M B.
0
44,5; 44; 43.
e
x M M
C.
0
45; 44; 43.
e
x M M D.
0
44; 44,5; 43.
e
x M M
Lời giải.
ChọnD
Sử dụng MTCT theo các bước sau:
B1: mode 3 AC (chuyển sang chế độ thống kê)
B2: shift 1 1 1 (nhập bảng số liệu -kiểu cột dọc- theo bảng trên)
B3: shift 1 4 (gọi kết quả)
Ta được kết quả:
44,5.
x
Kết hợp với bảng trên thấy
0
43 45
44; 43.
2
e
M M
Vậy
0
44,5; 44; 43.
e
x M M
Chú ý: Cách sử dụng MTCT như trên có thể tìm được độ lệch chuẩn, phương sai. Tuy nhiên đối
với bài này (không yêu cầu tính độ lệch chuẩn/phương sai); nên học sinh có thể tính trung bình
bằng công thứch:
38.2 40.4 43.9 45.6 48.4 50.5
44,5.
30
x
Câu 31. Giải bất phương trình
3 2
2
1
x
x
x
được tập nghiệm là
A.
1
; 2;3
2
. B.
1
;1 2;
2
. C.
;1 2;
. D.
2;1 2;
.
Lời giải
Chọn B
Ta có
3 2
2
1
x
x
x
2
3 2 2 5 2
2 0 0
1 1
x x x
x
x x
.
Xét dấu vế trái

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dựa vào bảng xét dấu ta có tập nghiệm của bpt là
1
;1 2;
2
S
.
Câu 32. Trong mặt phẳng tọa độ Oxy , cho điểm
2;2M và hai đường thẳng :2 3 1 0x y và
:2 3 0d x y . Một đường thẳng qua M cắt và d lần lượt tại A và B sao cho M là
trung điểm của AB. Khi đó độ dài AB là
A.
2 2AB
. B.
5
AB . C. 2AB . D. 4AB .
Lời giải
Chọn A
2 1
:2 3 1 0 ;
3
a
A x y A a
:2 3 0 ;2 3B d x y B b b
Vì M là trung điểm của AB nên
4
2
4 1
3
2 1
2 2 6 20 3
2 3 4
3
A B M
A B M
a b
x x x
a b a
a
y y y a b b
b
1;1 ; 3;3 ; 2 2A B AB
.
Câu 33. Cho góc
thỏa mãn
2
và sin 2cos 1
. Tính sin2
P .
A.
24
.
25
P B.
2 6
.
5
P C.
24
.
25
P D.
2 6
.
5
P
Lời giải
Chọn C
Với
2
suy ra
sin 0
cos 0
.
Ta có
2
2
2 2
sin 2cos 1
1 2cos cos 1
sin cos 1
2
cos 0 loaïi
5cos 4cos 0
4
cos
5
.
Từ hệ thức
2 2
sin cos 1
, suy ra
3
sin
5
(do sin 0
).
Vậy
3 4 24
sin2 2sin .cos 2. .
5 5 25
P
.
Câu 34. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2
2 3 2
1
2 2
x mx m
,
x mx
nghiệm đúng với
mọi
x
.
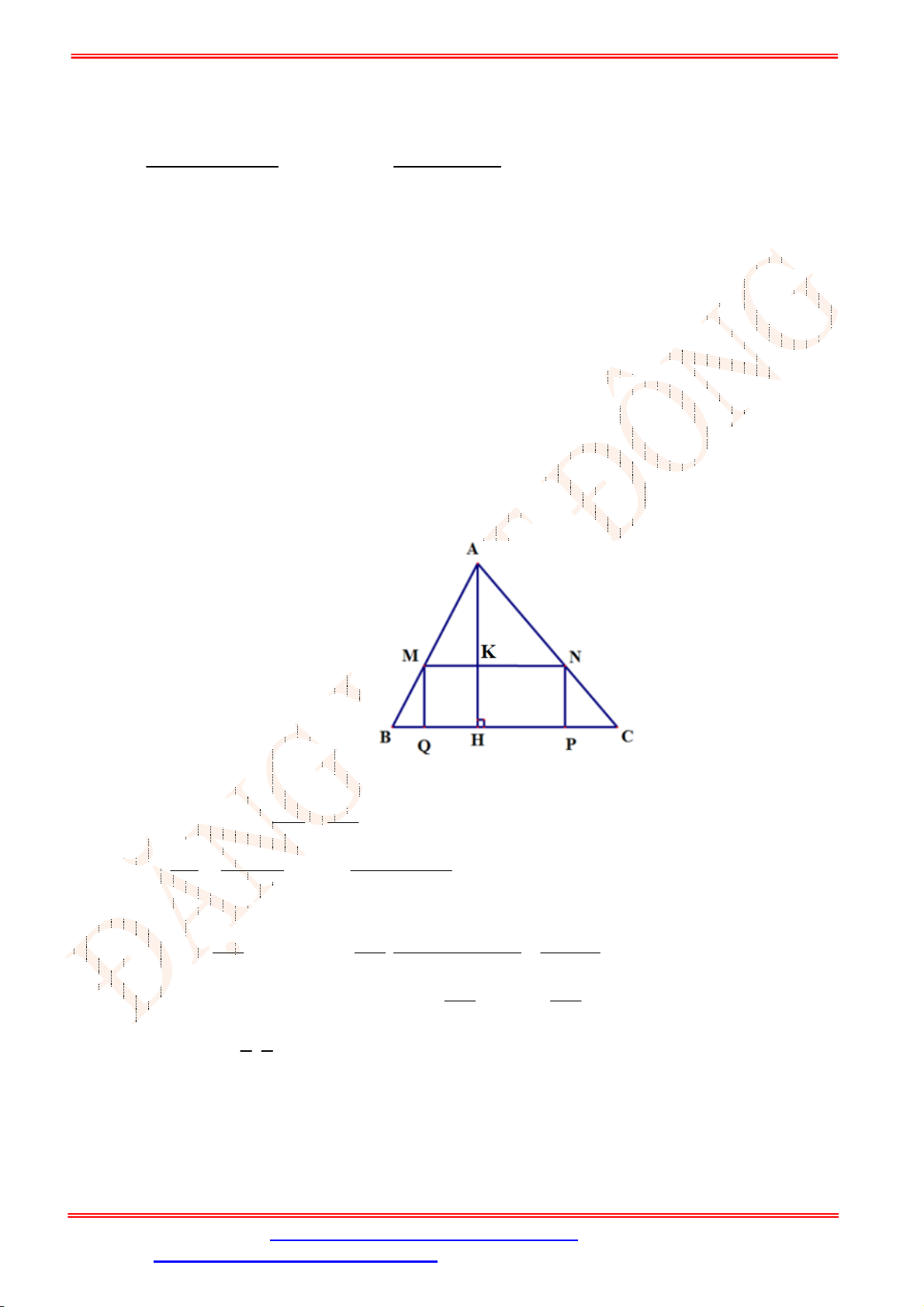
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
m 12 m 0
. B.
12 0
m . C.
4 m 0
. D.
4 m 4
.
Lời giải
Chọn C
2 2
2 2
2 3 2 3
1 0
2 2 2 2
x mx m x mx m
, x . , x .
x mx x mx
2
2
3 0
,
2 2 0
x mx m
x
x mx
2
2
12 0
16 0
m m
m
12 0
4 4
m
m
4 0
m .
Câu 35. Cho
ABC
nhọn, có
1;7
A ,
2;0
B ,
9;0
C đường cao
AH
. Xét các hình chữ nhật
MNPQ
với
M AB
;
N AC
; ,
P Q BC
. Điểm
;
M a b
thỏa mãn hình chữ nhật
MNPQ
có
diện tích lớn nhất, tính
P a b
.
A. 3. B. 5. C. 7. D. 1.
Lời giải
Chọn A
Tổng quát bài toán đặt
0
MQ x x AH
;
MN y AK AH x
Do
/ /
MN BC
MN AK
BC AH
( )
y AH x BC AH x
y
BC AH AH
Gọi
S
là diện tích hình chữ nhật
MNPQ
thì:
2
.
. .
2 4
x A
S
H x
BC
H
x
BC BC AH
x AH x
A
y
H A
Dấu
" "
xảy ra khi
2 2
AH AH
x AH x x MQ suy ra
M
là trung điểm của
AB
nên
tọa độ
1 7
;
2 2
M
. Vậy
3
P a b .
PHẦN II: TỰ LUẬN

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 36. Trong mặt phẳng
Oxy
, cho tam giác
ABC
có
1;1 , 2;5
A B . Diện tích tam giác
ABC
bằng 6,
trọng tâm
G
của tam giác
ABC
nằm trên đường thẳng
: 3 0
x y . Tìm tọa độ điểm
C
của
tam giác
ABC
?
Lời giải
Gọi
;
C x y
:
1;4 , 1; 1
AB AC x y .
Đường thẳng AB:
4 1 1 0 4 3 0
x y x y
4 3
,
17
x y
d C AB
4 3
1 1
. , 17. 6 4 3 12 1
2 2
17
ABC
x y
S AB d C AB x y
1 2
3 3
3
: 3 0 ; 3 2
1 5 3 15
3
3
x
a
a x
G x y G a a
y a y
a
Suy ra:
4 3 12 4 9
3 3 3 3
27 63 4
, ,
3 15 3 15
5 5 5
3 87 4
4 3 12 4 15
, ,
5 5 5
3 3 3 3
3 15 3 15
x y x y
a x a x
x y a
a y a y
x y x y
x y a
a x a x
a y a y
Vậy
27 63
;
5 5
C
hoặc
3 87
;
5 5
C
.
Câu 37. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 1 10
C x y . Lập phương trình tiếp
tuyến của đường tròn
C
biết tiếp tuyến tạo với
: 2 4 0
x y một góc bằng
45
.
Lời giải
Đường tròn
C
có tâm
1; 1
I và bán kính
10
R .
Giả sử tiếp tuyến là điểm
0 0
;
M x y
, khi đó phương trình tiếp tuyến có dạng
0 0 0 0 0 0
: 1 1 1 1 10 1 1 8 0 1
d x x y y x x y y x y .
Vì
2 2
0 0 0 0
; 1 1 10 2
M x y C x y .
Đường thẳng
d
tạo với
một góc bằng
0
45
khi và chỉ khi
0 0
0
2 2
0 0
2 1 1. 1
cos45
4 1. 1 1
x y
x y
0 0
0 0
0 0
6 2 3
2 1 5
4 2 4
y x
x y
y x
.
Giải hệ phương trình tạo bởi
2 , 3
ta được:
0
0 1
20
0
2
2
2;2
.
4; 2
4
2
x
y M
Mx
y

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Giải hệ phương trình tạo bởi
2 , 4
ta được:
0
0 3
40
0
0
4
0; 4
.
2;0
2
0
x
y M
Mx
y
Với
1
2;2
M , thay vào
1
ta được tiếp tuyến
1
: 3 8 0.
d x y
Với
2
4; 2
M , thay vào
1
ta được tiếp tuyến
2
: 3 14 0.
d x y
Với
3
0; 4
M , thay vào
1
ta được tiếp tuyến
3
: 3 12 0.
d x y
Với
4
2;0
M , thay vào
1
ta được tiếp tuyến
4
: 3 6 0.
d x y
Vậy có bốn tiếp tuyến
1 2 3 4
, , ,
d d d d
tới
C
thỏa mãn điều kiện đề bài.
Câu 38. Biết
, 0
x y ,
1.
x y Tìm giá trị nhỏ nhất của biểu thức
1 1
.
R x y
x y
Lời giải
Ta có
1 1
R x y
x y
1 1 3 1 1
4 4 4
x y
x y x y
Áp dụng bất đẳng thức
2
2 2
1 2
1 2
1 2 1 2
,
a a
a a
b b b b
dấu “=” xảy ra khi
1 2
1 2
a a
b b
.
Do đó
1 1 1
x y x y
1
1
1
3 1 1 3
.
4 4
x y
Ta có
1 1
R x y
x y
1 1 3 1 1
4 4 4
x y
x y x y
3 11
1 1 .
4 4
Dấu “=” xảy ra khi
1
.
2
x y
Vậy GTNN của
1 1
R x y
x y
là
11
4
.
Câu 39. Rút gọn các biểu thức sau:
0 0 0 0 0
os20 os40 os60 ... os160 os180
C c c c c c
.
Lời giải
Ta có:
0 0 0 0 0 0 0 0
os20 os160 os40 os140 os60 os120 os80 os100 1
C c c c c c c c c
=
0 0 0 0 0 0 0 0
os20 os20 os40 os40 os60 os60 os80 os80 1
c c c c c c c c
=
1
.
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 04
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
0
m m x m
vô nghiệm?
A.
0
m
hay
1
m
. B.
0;1
m
.
C.
0
m
D.
;0 1;m
.
Câu 2. Tìm tập nghiệm của bất phương trình
2 7
1
4
x
x
?
A.
11;4
. B.
4;11
. C.
1;2;3
. D.
1;3
.
Câu 3. Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có hai nghiệm
1
x
,
2
x
thỏa mãn
3 3
1 2
16
x x
.
A. Không tồn tại
m
. B.
2
m
. C.
1
m
. D.
1
m
hoặc
2
m
.
Câu 4. Cho tam giác
ABC
có
2
AB
cm,
1
AC
cm,
O
ˆ
60
A
. Khi đó độ dài cạnh
BC
là:
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Câu 5. Cho ba điểm
1;4
A ,
3;2
B ,
5;4
C . Tọa độ tâm đường tròn ngoại tiếp tam giác
ABC
là:
A.
2;5
. B.
3
;2
2
. C.
9;10
. D.
3;4
.
Câu 6. Hình chiếu vuông góc của điểm
1;4
M xuống đường thẳng
: 2 2 0
x y
có tọa độ là:
A.
3;0
. B.
0;3
. C.
2;2
. D.
2; 2
.
Câu 7. Tính diện tích hình bình hành
ABCD
có
AB a
,
2
BC a
và góc
o
45
A
?
A.
2
2
a
. B.
2
2
a
. C.
2
a
. D.
2
3
a
.
Câu 8. Giá trị lớn nhất của biểu thức
4 7
sin cos
x x
là:
A.
2
. B.
1
. C.
1
2
. D.
1
.
Câu 9. Tập nghiệm của bất phương trình
2 2
2 4 3 3 2 1
x x x x
là
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;1
.
Câu 10. Tam giác
ABC
có
5
a
cm,
3
b
cm,
5
c
cm. Tính số đo góc
A
:
A.
O
45
. B.
O
30
. C.
O
90
. D.
o
72.54
.
Câu 11. Nếu
cos sin 2 0
2
thì
bằng
A.
6
. B.
3
C.
4
D.
8
.
Câu 12. Biểu thức thu gọn của biểu thức
1
1 .tan
cos 2
B x
x
là?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
tan2
x
. B.
cot 2
x
. C.
cos2
x
. D.
sin
x
.
Câu 13. Công thức nào sau đây là công thức Hê-rông:
A.
S pr
. B.
S pr
.
C.
( )( )( )
S p p a p b p c
. D.
( )( )( )
S p a p b p c
.
Câu 14. Điều kiện cần và đủ để tam giác
ABC
có góc
A
nhọn là?
A.
2 2 2
a b c
. B.
2 2 2
a b c
. C.
2 2 2
a b c
. D.
2 2 2
a b c
.
Câu 15. Mệnh đề nào sau đây về tam giác
ABC
là SAI?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c
. B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b
. D. Góc
A
tù khi và chỉ khi
2 2 2
b a c
.
Câu 16. Cho đường thẳng
có phương trình tổng quát:
2 3 1 0
x y
. Vecto nào sau đây là vecto chỉ
phương của đường thẳng
.
A.
(3;2)
U
. B.
(2;3)
U
. C.
( 3;2)
U
D.
(2; 3)
U
Câu 17. Tính
sin
, biết
5
cos
3
và
3
2
2
.
A.
1
3
. B.
1
3
. C.
2
3
. D.
2
3
.
Câu 18. Cho
5
sin
3
a
. Tính
cos2 sin
a a
A.
17 5
27
. B.
5
9
. C.
5
27
. D.
5
27
.
Câu 19. Tam giác
ABC
vuông tại
A
có
6
AB
cm,
10
BC
cm. Đường tròn nội tiếp tam giác đó có bán
kính
r
bằng
A.
1
cm. B.
2
cm. C.
2
cm. D.
3
cm.
Câu 20. Biến đổi thành tích biểu thức
sin7 sin5
sin7 sin5
ta được
A.
tan5 .tan
B.
cos2 .sin3
. C.
cot6 .tan
. D.
cos .sin
.
Câu 21. Trên mặt phẳng tọa độ
Oxy
cho hai vectơ
2 3
a i j
,
2
b i j
. Khi đó tọa độ vectơ
a b
là:
A.
2; 1
. B.
1;2
. C.
1; 5
. D.
2; 3
.
Câu 22. Cho
cot 3
. Khi đó
3 3
3sin 2cos
12sin 4cos
có giá trị bằng
A.
1
4
. B.
5
4
. C.
3
4
. D.
1
4
.
Câu 23. Cho
sin cos
A
. Giá trị biểu thức
sin cos
bằng:
A.
2
1
2
A
. B.
2
1
2
A
. C.
1
2
A
. D.
1
2
A
.
Câu 24. Trong mặt phẳng
Oxy
cho
2;3
A ,
4; 1
B
. Tọa độ của
OA OB
là:
A.
2;4
B.
2; 4
. C.
3;1
. D.
6;2
.
Câu 25. Số đường thẳng đi qua điểm
5;6
M và tiếp xúc với đường tròn
2 2
: 1 2 1
C x y
là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A. 0. B. 1. C. 2. D. 3.
Câu 26. Cho
0;3
A ,
4;2
B . Điểm
D
thỏa
2 2 0
OD DA DB
, tọa độ
D
là:
A.
3;3
. B.
8;2
. C.
8; 2
. D.
5
2;
2
.
Câu 27. Trên mặt phẳng tọa độ
Oxy
, cho
ABC
vuông tại
A
có
1; 3
B
và
1;2
C . Tìm tọa độ điểm
H
là chân đường cao kẻ từ đỉnh
A
của
ABC
, biết
3
AB
,
4
AC
:
A.
24
1;
5
H
. B.
6
1;
5
H
C.
24
1;
5
H
. D.
6
1;
5
H
.
Câu 28. Cho
1
sin
3
a
với
2
a
. Tính
cos
a
.
A.
2 2
cos
3
a
. B.
2 2
cos
3
a
. C.
8
cos
9
a
. D.
8
cos
9
a
.
Câu 29. Với mọi
x
, biểu thức
2 9
cos cos cos ... cos
5 5 5
x x x x
nhận giá trị bằng:
A.
10
. B.
10
. C.
0
. D.
1
.
Câu 30. Cho tam giác
ABC
có cạnh
BC a
, cạnh
CA b
. Tam giác
ABC
có diện tích lớn nhất khi góc
C
bằng
A.
o
60
B.
o
90
C.
o
150
. D.
o
120
Câu 31. Tìm tập nghiệm của bất phương trình
2 1 2
x x
.
A.
1
;3
3
. B.
1
;3
3
. C.
1
;3
3
. D.
1;3
.
Câu 32. Tam giác đều nội tiếp đường tròn bán kính
4
R
cm có diện tích là:
A.
13
cm
2
. B.
13 2
cm
2
. C.
12 3
cm
2
. D.
15
cm
2
.
Câu 33. Hệ bất phương trình
3 4 0
1
x x
x m
có nghiệm khi nào?
A.
5
m
. B.
2
m
. C.
5
m
. D.
5
m
.
Câu 34. Phương trình nào dưới đây không là phương trình đường tròn?
A.
2 2
4 0
x y
. B.
2 2
2 0
x y x y
.
C.
2 2
0
x y x y
. D.
2 2
2 2 1 0
x y x y
.
Câu 35. Cho
3
tan
5
. Tính giá trị biểu thức
2 2
sin cos
sin cos
A
:
A.
15
16
B.
15
16
C.
5
6
D.
5
6
PHẦN II: TỰ LUẬN
Bài 1. Giải bất phương trình
2
2
3
1
4
x x
x
.
Bài 2. Cho tam giác
ABC
, biết
7, 8, 6
a b c
. Tính
S
và
a
h
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Bài 3. Lập phương trình tiếp tuyến của đường tròn
2 2
: 6 2 0
C x y x y
, biết tiếp tuyến này vuông
góc với đường thẳng
:3 4 0
d x y
.
Bài 4. Tìm giá trị nhỏ nhất của hàm số
1 1
1
y
x x
với
0 1
x
.
----------------------------------- HẾT-----------------------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 04
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
PHẦN I: TRẮC NGHIỆM
1.C 2.A 3.D 4.C 5.D 6.C 7.C 8.D 9.D 10.D
11.C
12.A
13.C
14.A
15.D
16.A
17.D
18.D
19.C
20.C
21.C 22.A 23.A 24.A 25.C 26.C 27.B 28.B 29.C 30.B
31.A
32
.C
33.B
34.B
35.A
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
HƯỚNG DẪN CHI TIẾT 35 CÂU TRẮC NGHIỆM
Câu 1. Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
0
m m x m
vô nghiệm?
A.
0
m
hay
1
m
. B.
0;1
m . C.
0
m
D.
;0 1;m
.
Lời giải
Chọn C
Bất phương trình
2
0
m m x m
vô nghiệm khi và chỉ khi bất phương trình
2
0
m m x m
nghiệm đúng với mọi x
2
0
0.
0
m m
m
m
Chọn C .
Câu 2. Tìm tập nghiệm của bất phương trình
2 7
1
4
x
x
?
A.
11;4
. B.
4;11
. C.
1;2;3
. D.
1;3
.
Lời giải
Chọn A
Bất phương trình
2 7 11
1 0 11 4.
4 4
x x
x
x x
Vậy tập nghiệm là
11;4
. Chọn A .
Câu 3. Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có hai nghiệm
1
x
,
2
x
thỏa mãn
3 3
1 2
16
x x
.
A. Không tồn tại
m
. B.
2
m
. C.
1
m
. D.
1
m
hoặc
2
m
.
Lời giải
Chọn D
Phương trình có nghiệm khi
0
2
2 0
m m
2
1
m
m
1
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Theo định lý Vi-ét, ta có
1 2
1 2
2
2
x x m
x x m
. Theo đề bài,
3 3
1 2
16
x x
3
8 6 2 16
m m m
3 2
8 6 12 16 0
m m m
2
2 8 10 8 0
m m m
2 0
m
2
m
.
Kiểm tra điều kiện
1
, ta được
1
m
hoặc
2
m
. Chọn D .
Câu 4. Cho tam giác
ABC
có
2
AB
cm,
1
AC
cm,
O
ˆ
60
A
. Khi đó độ dài cạnh
BC
là:
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Lời giải
Chọn C
Áp dụng định lý cô-sin, ta có
2 2 2 O
1
2. . .cos60 4 1 2.2.1. 3
2
BC AB AC AB AC
. Suy ra
3
BC
cm. Chọn C.
Câu 5. Cho ba điểm
1;4
A ,
3;2
B ,
5;4
C . Tọa độ tâm đường tròn ngoại tiếp tam giác
ABC
là:
A.
2;5
. B.
3
;2
2
. C.
9;10
. D.
3;4
.
Lời giải
Chọn D
Gọi phương trình đường tròn ngoại tiếp tam giác
ABC
là
2 2
: 2 2 0
C x y ax by d
. Do
C
đi qua các điểm
1;4
A ,
3;2
B và
5;4
C nên ta lập được hệ phương trình:
1 16 2 8 0 3
9 4 6 4 0 4
25 16 10 8 0 21
a b c a
a b c b
a b c c
.
Vậy tâm đường tròn cần tìm là
3;4
. Chọn D .
Câu 6. Hình chiếu vuông góc của điểm
1;4
M xuống đường thẳng
: 2 2 0
x y
có tọa độ là:
A.
3;0
. B.
0;3
. C.
2;2
. D.
2; 2
.
Lời giải
Chọn C
Đường thẳng qua
1;4
M và vuông góc với
: 2 2 0
x y
có phương trình
: 2 6 0
x y
. Hình chiếu vuông góc của
M
xuống
là giao điểm của
và
. Tọa độ giao điểm là nghiệm
của hệ phương trình
2 2 0 2
2 6 0 2
x y x
x y y
. Vậy tọa độ giao điểm cần tìm là
2;2
. Chọn C
.
Câu 7. Tính diện tích hình bình hành
ABCD
có
AB a
,
2
BC a
và góc
o
45
A
?
A.
2
2
a
. B.
2
2
a
. C.
2
a
. D.
2
3
a
.
Lời giải
Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Góc
o o o
ˆ
180 45 135
B
. Diện tích hình bình hành
ABCD
bằng
2
1
2. . . .sin
2
AB BC B a
. Chọn
C .
Câu 8. Giá trị lớn nhất của biểu thức
4 7
sin cos
x x
là:
A.
2
. B.
1
. C.
1
2
. D.
1
.
Lời giải
Chọn D
Do
1 sin ,cos 1
x x
nên
4 7 2 2
sin cos sin cos 1
x x x x
. Vậy giá trị lớn nhất của biểu thức
là
1
khi
2
x k
hay
2
x k
. Chọn D.
Câu 9. Tập nghiệm của bất phương trình
2 2
2 4 3 3 2 1
x x x x
là
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;1
.
Lời giải
Chọn D
Đặt
2
3 2 0
t x x
2 2
2 3
x x t
.
Bất phương trình cho trở thành:
2
2 3 5 0
t t
5
1
2
t
.
Suy ra
2
5
0 3 2
2
x x
2
2
0 3 2
25
3 2
4
x x
x x
3 1
x
x
3 1
x
. Chọn D .
Câu 10. Tam giác
ABC
có
5
a
cm,
3
b
cm,
5
c
cm. Tính số đo góc
A
:
A.
O
45
. B.
O
30
. C.
O
90
. D.
o
72.54
.
Lời giải
Chọn D
2 2 2 2 2 2
3 5 5 3
cos
2 2.3.5 10
b c a
A
bc
. Suy ra
o
72.54
A
. Chọn D.
Câu 11. Nếu
cos sin 2 0
2
thì
bằng
A.
6
. B.
3
C.
4
D.
8
.
Lời giải
Chọn C
Theo đề bài,
cos sin 2 sin2 1 2 2
2 4
k k
. Chọn C.
Câu 12. Biểu thức thu gọn của biểu thức
1
1 .tan
cos 2
B x
x
là?
A.
tan2
x
. B.
cot 2
x
. C.
cos2
x
. D.
sin
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A
Ta có
1
1 .tan
cos 2
B x
x
1 cos2 sin
.
cos2 cos
x x
x x
2
2cos sin
.
cos2 cos
x x
x x
2cos .sin
cos2
x x
x
sin2
cos2
x
x
tan2
x
. Chọn A .
Câu 13. Công thức nào sau đây là công thức Hê-rông:
A.
S pr
. B.
S pr
.
C.
( )( )( )
S p p a p b p c
. D.
( )( )( )
S p a p b p c
.
Lời giải
Chọn C
Công thức Hê-rông
S p p a p b p c
. Chọn C .
Câu 14. Điều kiện cần và đủ để tam giác
ABC
có góc
A
nhọn là?
A.
2 2 2
a b c
. B.
2 2 2
a b c
. C.
2 2 2
a b c
. D.
2 2 2
a b c
.
Lời giải
Chọn A
Ta có
2 2 2
cos
2
b c a
A
bc
. Góc
A
nhọn khi và chỉ khi
cos 0
A
hay
2 2 2
a b c
. Chọn A.
Câu 15. Mệnh đề nào sau đây về tam giác
ABC
là SAI?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c
. B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b
. D. Góc
A
tù khi và chỉ khi
2 2 2
b a c
.
Lời giải
Chọn D
Phương án D là sai. Chọn D.
Câu 16. Cho đường thẳng
có phương trình tổng quát:
2 3 1 0
x y
. Vecto nào sau đây là vecto chỉ
phương của đường thẳng
.
A.
(3;2)
U
. B.
(2;3)
U
. C.
( 3;2)
U
D.
(2; 3)
U
Lời giải
Chọn A
Một vectơ pháp tuyến của đường thẳng
:
2 3 1 0
x y
có tọa độ là
2;3
. Suy ra tọa độ
vectơ chỉ phương là
3;2
. Chọn A .
Câu 17. Tính
sin
, biết
5
cos
3
và
3
2
2
.
A.
1
3
B.
1
3
. C.
2
3
. D.
2
3
.
Lời giải
Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có:
2 2
5 4
sin 1 cos 1
9 9
2
sin
3
. Do
3
2
2
nên
sin 0
. Vậy
2
sin
3
. Chọn D.
Câu 18. Cho
5
sin
3
a
. Tính
cos2 sin
a a
A.
17 5
27
. B.
5
9
. C.
5
27
. D.
5
27
.
Lời giải
Chọn D
Ta có
2 3
cos 2 sin 1 2sin sin sin 2sin
B a a a a a a
mà
5
sin
3
a
Suy ra
5 5 5 9 5 10 5 5
2
3 27 27 27
B
. Chọn D .
Câu 19. Tam giác
ABC
vuông tại
A
có
6
AB
cm,
10
BC
cm. Đường tròn nội tiếp tam giác đó có bán
kính
r
bằng
A.
1
cm. B.
2
cm. C.
2
cm. D.
3
cm.
Lời giải
Chọn C
Tam giác
ABC
vuông tại A có diện tích
1 1
. .6.8 24
2 2
S AB AC
. Bán kính đường tròn nội
tiếp là
24
2
1
6 8 10
2
S
r
p
cm. Chọn C.
Câu 20. Biến đổi thành tích biểu thức
sin7 sin5
sin7 sin5
ta được
A.
tan5 .tan
B.
cos2 .sin3
. C.
cot6 .tan
. D.
cos .sin
.
Lời giải
Chọn C
Ta có
sin7 sin5
sin7 sin5
2cos6 .sin
2sin6 .cos
cot6 .tan
. Chọn C.
Câu 21. Trên mặt phẳng tọa độ
Oxy
cho hai vectơ
2 3
a i j
,
2
b i j
. Khi đó tọa độ vectơ
a b
là:
A.
2; 1
. B.
1;2
. C.
1; 5
. D.
2; 3
.
Lời giải
Chọn C
Ta có
2 3 2; 3 ; 2 1;2
a i j a b i j b
suy ra
1; 5
a b
. Chọn C.
Câu 22. Cho
cot 3
. Khi đó
3 3
3sin 2cos
12sin 4cos
có giá trị bằng

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
1
4
. B.
5
4
. C.
3
4
. D.
1
4
.
Lời giải
Chọn A
Ta có
2
2
3 3 3 3
1
3 2cot
3sin 2cos 3 2cot 1
sin
1 cot
12sin 4cos 12 4cot 12 4cot 4
. Chọn A .
Câu 23. Cho
sin cos
A
. Giá trị biểu thức
sin cos
bằng:
A.
2
1
2
A
. B.
2
1
2
A
. C.
1
2
A
. D.
1
2
A
.
Lời giải
Chọn A
Ta có
2
2
1 1
sin cos sin cos 1
2 2
A
. Chọn A.
Câu 24. Trong mặt phẳng
Oxy
cho
2;3
A ,
4; 1
B
. Tọa độ của
OA OB
là:
A.
2;4
B.
2; 4
. C.
3;1
. D.
6;2
.
Lời giải
Chọn A
Ta có
OA OB BA
và
2;4
BA
nên tọa độ của
OA OB
là
2;4
. Chọn A.
Câu 25. Số đường thẳng đi qua điểm
5;6
M và tiếp xúc với đường tròn
2 2
: 1 2 1
C x y
là:
A. 0. B. 1. C. 2. D. 3.
Lời giải
Chọn C
Đường tròn
C
có tâm
1;2
I và bán kính
1
R
. Ta có
2 2
5 1 6 2 4 2
IM R
,
suy ra điểm
M
nằm bên ngoài đường tròn. Do đó từ
M
kẻ được đúng hai tiếp tuyến đến
C
.
Chọn C .
Câu 26. Cho
0;3
A ,
4;2
B . Điểm
D
thỏa
2 2 0
OD DA DB
, tọa độ
D
là:
A.
3;3
. B.
8;2
. C.
8; 2
. D.
5
2;
2
.
Lời giải
Chọn C
Gọi
;
D x y
. Theo đề
2 2 0
OD DA DB
2
OD AB
. Mà
4; 1
AB
2 8; 2
AB
8; 2
OD
. Vậy
8; 2
D
. Chọn C.
Câu 27. Trên mặt phẳng tọa độ
Oxy
, cho
ABC
vuông tại
A
có
1; 3
B
và
1;2
C . Tìm tọa độ điểm
H
là chân đường cao kẻ từ đỉnh
A
của
ABC
, biết
3
AB
,
4
AC
:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
24
1;
5
H
. B.
6
1;
5
H
C.
24
1;
5
H
. D.
6
1;
5
H
.
Lời giải
Chọn B
Ta có
2
.
AB BH BC
và
2
.
AC CH CB
. Do đó:
2
2
16
9
CH AC
BH AB
16
.
9
HC HB
.
Mà
,
HC HB
ngược hướng nên
16
9
HC HB
.
Khi đó, gọi
;
H x y
thì
1 ;2
HC x y
,
1 ; 3
HB x y
.
Suy ra:
16
1 1
9
16
2 3
9
x x
y y
1
6
5
x
y
6
1;
5
H
.
Câu 28. Cho
1
sin
3
a
với
2
a
. Tính
cos
a
.
A.
2 2
cos
3
a
. B.
2 2
cos
3
a
. C.
8
cos
9
a
. D.
8
cos
9
a
.
Lời giải
Chọn B
Ta có
2 2 2 2
8 2 2
sin cos 1 cos 1 sin cos
9 3
a a a a a
. Vì
2
a
nên
2 2
cos
3
a
. Chọn B .
Câu 29. Với mọi
x
, biểu thức
2 9
cos cos cos ... cos
5 5 5
x x x x
nhận giá trị bằng:
A.
10
. B.
10
. C.
0
. D.
1
.
Lời giải
Chọn C
Ta có
5
cos cos
5
x x
;
6
cos cos
5 5
x x
;
2 7
cos cos
5 5
x x
;…
Vậy
2 9
cos cos cos ... cos 0
5 5 5
x x x x
. Chọn C .
Câu 30. Cho tam giác
ABC
có cạnh
BC a
, cạnh
CA b
. Tam giác
ABC
có diện tích lớn nhất khi góc
C
bằng
A.
o
60
B.
o
90
C.
o
150
. D.
o
120
Lời giải
Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Diện tích tam giác
ABC
được tính bằng công thức
1
sin
2
S ab C
. Do
o o
0 180
C
nên
0 sin 1
C
. Vậy diện tích lớn nhất khi
sin 1
C
hay
o
ˆ
90
C
. Chọn B .
Câu 31. Tìm tập nghiệm của bất phương trình
2 1 2
x x
.
A.
1
;3
3
. B.
1
;3
3
. C.
1
;3
3
. D.
1;3
.
Lời giải
Chọn A
Bất phương trình
2
2
2 0
1
2 2 1 1 3 3
2 2 1 2
3
3
2 1 2
x
x
x
x x x x
x x x
x
x x
.
Chọn A .
Câu 32. Tam giác đều nội tiếp đường tròn bán kính
4
R
cm có diện tích là:
A.
13
cm
2
. B.
13 2
cm
2
. C.
12 3
cm
2
. D.
15
cm
2
.
Lời giải
Chọn C
Gọi cạnh của tam giác đều là
a
, ta có
o
2sin 60
3
a a
R
, suy ra
3 4 3
a R
. Diện tích
3
3
4 3
12 3
4 4.4
a
S
R
. Chọn C .
Câu 33. Hệ bất phương trình
3 4 0
1
x x
x m
có nghiệm khi nào?
A.
5
m
. B.
2
m
. C.
5
m
. D.
5
m
.
Lời giải
Chọn B
Hệ bất phương trình
3 4
1
x
x m
. Để hệ có nghiệm thì
1 3 2
m m
. Chọn B.
Câu 34. Phương trình nào dưới đây không là phương trình đường tròn?
A.
2 2
4 0
x y
. B.
2 2
2 0
x y x y
.
C.
2 2
0
x y x y
. D.
2 2
2 2 1 0
x y x y
.
Lời giải
Chọn B
Xét phương án B:
2 2
2 0
x y x y
, có
1
2
a b
và
2
c
. Phương trình này không thỏa
điều kiện
2 2
0
a b c
nên không là phương trình đường tròn. Chọn B .
Câu 35. Cho
3
tan
5
. Tính giá trị biểu thức
2 2
sin cos
sin cos
A
:
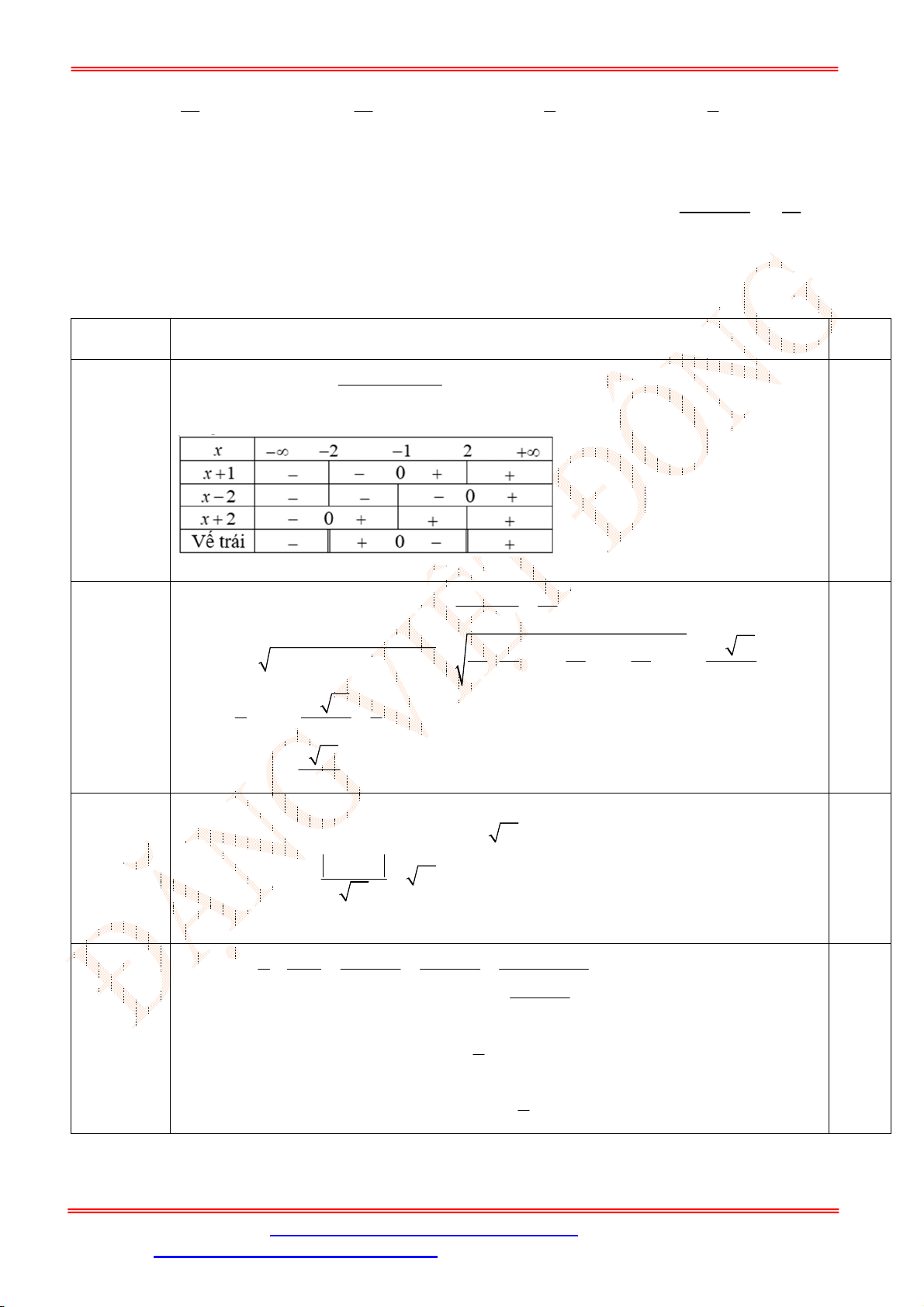
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
15
16
. B.
15
16
. C.
5
6
. D.
5
6
.
Lời giải
Chọn A
Vì cos 0
, chia cả tử và mẫu của biểu thức cho
2
cos
, ta được
2
tan 15
tan 1 16
A
. Chọn
A .
PHẦN II: TỰ LUẬN
Câu hỏi Nội dung Điểm
Bài 1
(1,0 điểm)
Bất phương trình
1
0
2 2
x
x x
Bảng xét dấu vế trái:
Đáp số
2 1, 2x x
.
0,25
0,5
0,25
Bài 2
(1,0 điểm)
Áp dụng công thức Hê-rông với
21
2 2
a b c
p
Ta có
21 21 21 21 21 15
( )( )( ) 7 8 6
2 2 2 2 4
S p p a p b p c
Vì
1 21 15 1
7
2 4 2
a a
S ah h
nên suy ra
3 15
2
a
h
.
0,25
0,25
0,25
0,25
Bài 3
(0,5 điểm)
Gọi tiếp tuyến cần tìm là
. Vì
vuông góc với d nên
:
3 0x y c
.
C có tâm
3; 1I và có bán kính
10R
. Ta có tiếp xúc với
C
3 3
; 10 10
10
c
d I R c
.
Vậy tiếp tuyến cần tìm là
: 3 10 0x y
hay
: 3 10 0x y
.
0,25
0,25
Bài 4
(0,5 điểm)
Ta có
2
1 1 1 1 1
4
1 1 1
1
2
x x
y
x x x x x x
x x
Đẳng thức xảy ra khi
1
1
0;1
2
x x
x
x
.
Vậy giá trị nhỏ nhất của hàm số là 4 khi
1
2
x
.
0,25
0,25

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 05
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh:
Tìm số trung vị của bảng số liệu trên.
A. 7. B. 8. C. 7.5. D. 7.3.
Câu 2. Với
là số thực bất kì. Khẳng định nào sau đây là sai?
A.
tan cot
2
. B.
cot cot
2
.
C.
cos sin
2
. D.
sin cos
2
.
Câu 3. Cho
2
. Kết quả đúng là
A.
sin 0;cos 0
. B.
sin 0;cos 0
.
C.
sin 0;cos 0
. D.
sin 0;cos 0
.
Câu 4. Trong mặt phẳng
Ox
y
, phương trình nào sau đây là phương trình của một đường tròn?
A.
2 2
4 2 8 3 0
x y xy x y
. B.
2 2
2 4 5 1 0
x y x y
.
C.
2 2
14 2 2018 0
x y x y
. D.
2 2
4 5 2 0
x y x y
.
Câu 5. Trong các công thức sau, công thức nào sai?
A. sin sin 2sin .cos
2 2
a b a b
a b . B. cos cos 2sin .sin
2 2
a b a b
a b .
C. sin sin 2cos .sin
2 2
a b a b
a b . D. cos cos 2sin .sin
2 2
a b a b
a b .
Câu 6. Đổi số đo của góc
2,5
sang đơn vị độ, phút, giây.
A.
0
2 5'0''
. B.
0
143 23'44''
. C.
0
2 30'00''
. D.
0
143 14'22''
.
Câu 7. Bất phương trình nào sau đây nhận
1
x
làm nghiệm?
A.
2
43 2 43 2 2
x x x x
. B.
1 1
0
3 1
x
x x
.
C.
3 4 2
x x x x
. D.
2
1 1
0
3 1
x
x x
.
Câu 8. Cho tam giác
ABC
, có
4cm, 12cm
AB AC và góc
120
BAC
. Tính diện tích tam giác
ABC
.
A.
12
. B.
24
. C.
12 3
. D.
24 3
.
Câu 9. Tọa độ tâm
I
và bán kính
R
của đường tròn
2 2
( ):( 1) ( 3) 16
C x y là:
A.
( 1;3), 4
I R B.
(1; 3), 4
I R C.
(1; 3), 16
I R D.
( 1;3), 16
I R
Câu 10. Elip
2 2
1
15 6
x y
có tiêu cự bằng
A.
9
. B.
4
. C.
6
. D.
8
.
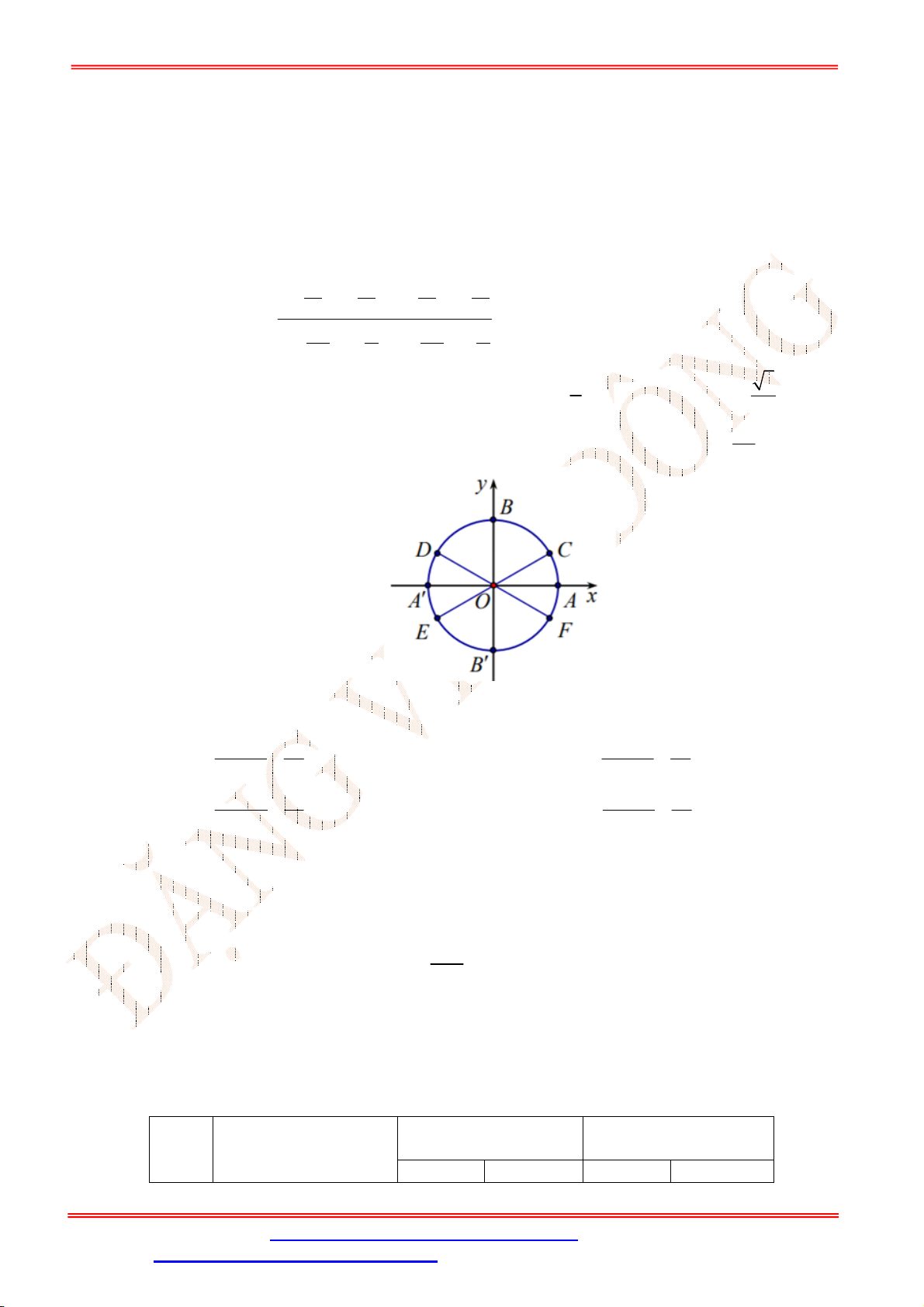
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 11. Trên mặt phẳng
Oxy
, cho đường thẳng
1 2
:
5 3
x t
d
y t
. Một vectơ chỉ phương của
d
là
A.
4
3; 2
u
. B.
1
1;5
u
.
C.
2
3;2
u
. D.
3
2; 3
u
.
Câu 12. Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
3
f x x
không âm?
A.
3; .
B.
; 3 .
C.
3; .
D.
; 3 .
Câu 13. Giá trị biểu thức
sin .cos sin .cos
15 10 10 15
2 2
cos .cos sin .sin
15 5 15 5
là
A.
1
. B.
1
. C.
3
2
. D.
3
2
.
Câu 14. Cho đường tròn lượng giác gốc
A
như hình vẽ. Điểm biểu diễn cung có số đo
5
2
là
A. điểm
B
. B. điểm
B
. C. điểm
E
. D. điểm
F
.
Câu 15. Cho tam giác
ABC
. Trung tuyến được tính theo công thức:
A. . B. .
C. . D. .
Câu 16. Cho
,
a b
là các số thực tùy ý. Mệnh đề nào sau đây đúng?
A. Nếu
a b
và
0
a
thì
2 2
a b
. B. Nếu
a b
và
0
b
thì
2 2
a b
.
C. Nếu
2 2
a b
thì
a b
. D. Nếu
a b
thì
2 2
a b
.
Câu 17. Chọn điểm
1;0
A làm điểm đầu của cung lượng giác trên đường tròn lượng giá Tìm điểm
cuối
M
của cung lượng giác có số đo
25
4
.
A.
M
là điểm chính giữa của cung phần tư thứ
IV
.
B.
M
là điểm chính giữa của cung phần tư thứ
II
.
C.
M
là điểm chính giữa của cung phần tư thứ
III
.
D.
M
là điểm chính giữa của cung phần tư thứ
I
.
Câu 18. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa
tốt nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp
2015
Khóa tốt nghiệp 2016
Nữ Nam Nữ Nam
a
m
2 2 2
2
2 4
a
b c a
m
2 2 2
2
2 4
a
b c a
m
2 2 2
2
2 4
a
a c b
m
2 2 2
2
4 2
a
b c a
m

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
1 Giảng dạy 25 45 25 65
2
Ngân hàng
23
186
20
32
3
L
ậ
p trình
25
120
12
58
4 Bảo hiểm 12 100 3 5
Tính cả hai khóa tốt nghiệp 2015 và 2016, lĩnh vực nào có tỷ lệ phần trăm nữ cao hơn các lĩnh
vực còn lại?
A. Lập trình. B. Bảo hiểm. C. Giảng dạy. D. Ngân hàng.
Câu 19. Tam giác
ABC
có
2, 3
AB AC
và
45
C
. Tính độ dài cạnh
BC
.
A.
6 2
.
2
BC B.
6.
BC
C.
5.
BC
D.
6 2
.
2
BC
Câu 20. Cho góc
thỏa mãn
5
cos
13
và
3
2
2
. Tính
tan2
P .
A.
120
.
119
P B.
119
.
120
P C.
120
.
119
P D.
119
.
120
P
Câu 21. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
8sin 3cos2
P x x
.
Tính
2
2 .
T M m
A.
130.
T B.
2.
T C.
112.
T D.
1.
T
Câu 22. Đường tròn
( )
C
có tâm
(2;3)
I và tiếp xúc với trục
Ox
có phương trình là:
A.
2 2
( 2) ( 3) 9
x y B.
2 2
( 2) ( 3) 4
x y
C.
2 2
( 2) ( 3) 3
x y
D.
2 2
( 2) ( 3) 9
x y
Câu 23. Viết phương trình tiếp tuyến của đường tròn
2 2
( ):( 2) ( 1) 25
C x y , biết tiếp tuyến song
song với đường thẳng
:4 3 14 0
d x y .
A.
4 3 14 0
x y hoặc
4 3 36 0
x y B.
4 3 14 0
x y
C.
4 3 36 0
x y D.
4 3 14 0
x y hoặc
4 3 36 0
x y
Câu 24. Cho dãy số liệu thống kê:
1,2,3,4,5,6,7
. Phương sai của mẫu số liệu thống kê đã cho là
A.
3
. B.
4
. C.
1
. D.
2
.
Câu 25. Cho elip
E
có độ dài trục lớn bằng
12
, độ dài trục bé bằng tiêu cự. Phương trình chính tắc
của
E
là:
A.
2 2
1
144 72
x y
. B.
2 2
1
36 18
x y
. C.
2 2
1
36 36
x y
. D.
2 2
1
144 144
x y
.
Câu 26. Nếu
tan 4tan
2 2
thì tan
2
bằng
A.
3sin
.
5 3cos
B.
3cos
.
5 3cos
C.
3cos
.
5 3cos
D.
3sin
.
5 3cos
Câu 27. Cho hai số thực
,
x y
thỏa mãn
2 3 7
x y . Giá trị lớn nhất của biểu thức
P x y xy
là:
A.
2
. B.
3
. C.
5
. D.
6
.
Câu 28. Bất phương trình
2
10 16 0
x x có tập nghiệm là
A.
8;
B.
2;8
C.
2;8
D.
;2

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 29. Cho góc
thỏa mãn
4
tan
3
và
2017 2019
2 2
. Tính
sin .
A.
4
sin
5
. B.
3
sin
5
. C.
4
sin
5
. D.
3
sin
5
.
Câu 30. Viết phương trình tham số của đường thẳng đi qua hai điểm
)
(3;
7
A và
.
(1;
7)
B
A.
7
x t
y t
. B.
7
x t
y
. C.
7
x t
y
. D.
3 7
1 7
x t
y t
.
Câu 31. Tìm tập xác định của hàm số
2
4 12 9
1
x x
y
x
A.
; 1
D . B.
3
; 1
2
D .
C.
3
; 1
2
D . D.
3
; 1 ;
2
D .
Câu 32. Cho biết
5
tan
7
x . Tính giá trị của biểu thức
5sin2 7cos2
P x x
.
A.
2.
P B.
9.
P C.
13.
P D.
7.
P
Câu 33. Điểm
;
A a b
thuộc đường thẳng
3
:
2
x t
d
y t
và cách đường thẳng
:2 3 0
x y một
khoảng bằng
2 5
và
0
a . Tính
.
P a b
.
A.
132
P . B.
72
P . C.
72
P . D.
132
P .
Câu 34. Trong mặt phẳng
Oxy
, cho
6;1
P
và
3; 2
Q
và đường thẳng
x 1 0
: 2
y
. Biết
;
M a b
thuộc
sao cho
MP MQ
ngắn nhất. Tính
2
T a b
A.
3
T
. B.
8
T
. C.
2
T
. D.
13
T
.
Câu 35. Tìm
m
để mọi
0;
x đều là nghiệm của bất phương trình
2 2 2
1 8 9 0
m x mx m
A.
3; 1
m . B.
3; 1
m . C.
3; 1
m . D.
m .
PHẦN II: TỰ LUẬN
Câu 36. Trong mặt phẳng với hệ tọa độ
Oxy
, lập phương trình đường thẳng d là đường thẳng song
song và cách đều hai đường thẳng
1 2
:3 6 0; : 6 2 1 0
x y x y .
Câu 37. Viết phương trình tiếp tuyến
của đường tròn
2 2
: 4 4 1 0
C x y x y biết đường thẳng
hợp với trục hoành một góc
0
45
.
Câu 38. Tìm giá trị nhỏ nhất của các biểu thức sau:
2 5
A x x .
Câu 39. Tính giá trị lượng giá của biểu thức lượng giác sau:
2
3 5
tan .tan .tan
8 8 8
P .
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 05
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh:
Tìm số trung vị của bảng số liệu trên.
A. 7. B. 8. C. 7.5. D. 7.3.
Lời giải
Chọn C
Sắp 20 điểm bài kiểm tra trong bảng số liệu đã cho theo thứ tự không giảm, ta có điểm 7 và
điểm 8 là hai điểm đứng giữa (đứng ở vị trí thứ 10 và 11) của dãy sắp thứ tự (n=20).
Vậy số trung vị của các con điểm đã cho trong bảng thống kê là:
7 8
7,5
2
e
M .
Câu 2. Với
là số thực bất kì. Khẳng định nào sau đây là sai?
A.
tan cot
2
. B.
cot cot
2
.
C.
cos sin
2
. D.
sin cos
2
.
Lời giải
Chọn B
cot tan
2
(cung phụ nhau).
Câu 3. Cho
2
. Kết quả đúng là
A.
sin 0;cos 0
. B.
sin 0;cos 0
.
C.
sin 0;cos 0
. D.
sin 0;cos 0
.
Lời giải
Chọn A
Vì
2
nên
sin 0;cos 0
.
Câu 4. Trong mặt phẳng
Ox
y
, phương trình nào sau đây là phương trình của một đường tròn?
A.
2 2
4 2 8 3 0
x y xy x y
. B.
2 2
2 4 5 1 0
x y x y
.
C.
2 2
14 2 2018 0
x y x y
. D.
2 2
4 5 2 0
x y x y
.
Lời giải
Chọn D
Phương án A: có tích
xy
nên không phải là phương trình đường tròn.
Phương án B: có hệ số bậc hai không bằng nhau nên không phải là phương trình đường tròn.
Phương án C: ta có
2 2
2 2
14 2 2018 0 7 1 1968 0
x y x y x y
không tồn
tại
,
x y
nên cũng không phải phương trình đường tròn.
Phương án D thỏa:
2 2
25 33
4 2 0
4 4
a b c
Câu 5. Trong các công thức sau, công thức nào sai?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A. sin sin 2sin .cos
2 2
a b a b
a b . B. cos cos 2sin .sin
2 2
a b a b
a b .
C. sin sin 2cos .sin
2 2
a b a b
a b . D. cos cos 2sin .sin
2 2
a b a b
a b .
Lời giải
Chọn B
Áp dụng công thức tổng thành tích: cos cos 2cos .cos
2 2
a b a b
a b .
Câu 6. Đổi số đo của góc
2,5
sang đơn vị độ, phút, giây.
A.
0
2 5'0''
. B.
0
143 23'44''
. C.
0
2 30'00''
. D.
0
143 14'22''
.
Lời giải
Chọn D
Cách 1:
Ta có:
0 0
0
180 180
1 2,5 2,5. 143 14'22''
rad
.
Cách 2: Sử dụng máy tính cầm tay fx-580VN X
Cách làm như câu 32.
Câu 7. Bất phương trình nào sau đây nhận
1
x
làm nghiệm?
A.
2
43 2 43 2 2
x x x x
. B.
1 1
0
3 1
x
x x
.
C.
3 4 2
x x x x
. D.
2
1 1
0
3 1
x
x x
.
Lời giải
Chọn C
+ Xét
3 4 2
x x x x
có TXĐ:
0;
D .
Thay
1
x
vào thấy thỏa mãn.
+ Xét
2
1 1
0
3 1
x
x x
có TXĐ:
\ 1; 3
D
.
+ Xét
2
43 2 43 2 2
x x x x
có TXĐ:
2;
D .
+ Xét
1 1
0
3 1
x
x x
có TXĐ:
\ 1;3
D
.
Thay
1
x
vào thấy không thỏa mãn .
Câu 8. Cho tam giác
ABC
, có
4cm, 12cm
AB AC và góc
120
BAC
. Tính diện tích tam giác
ABC
.
A.
12
. B.
24
. C.
12 3
. D.
24 3
.
Lời giải
Chọn C
1 1
. .sin .4.12.sin120 12 3
2 2
ABC
S AB AC BAC .
Câu 9. Tọa độ tâm
I
và bán kính
R
của đường tròn
2 2
( ):( 1) ( 3) 16
C x y là:
A.
( 1;3), 4
I R B.
(1; 3), 4
I R C.
(1; 3), 16
I R D.
( 1;3), 16
I R
Lời giải
Chọn B
Ta có
2 2
: 1 3 16 1; 3 , 16 4.
C x y I R

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 10. Elip
2 2
1
15 6
x y
có tiêu cự bằng
A.
9
. B.
4
. C.
6
. D.
8
.
Lời giải
Chọn C
Elip
2 2
1
15 6
x y
có
2
15
a ,
2
6
b suy ra
2 2 2
15 6 9
c a b
3
c .
Vậy tiêu cự của elip là
2 2.3 6
c .
Câu 11. Trên mặt phẳng
Oxy
, cho đường thẳng
1 2
:
5 3
x t
d
y t
. Một vectơ chỉ phương của
d
là
A.
4
3; 2
u
. B.
1
1;5
u
.
C.
2
3;2
u
. D.
3
2; 3
u
.
Lời giải
Chọn D
Ta có một vectơ chỉ phương của đường thẳng
d
là
3
2; 3
u
.
Câu 12. Với
x
thuộc tập hợp nào dưới đây thì nhị thức bậc nhất
3
f x x
không âm?
A.
3; .
B.
; 3 .
C.
3; .
D.
; 3 .
Lời giải
Chọn A
Nhị thức bậc nhất
3
f x x
không âm tức là
3 0 3.
f x x x
Vậy
3; .
x
Câu 13. Giá trị biểu thức
sin .cos sin .cos
15 10 10 15
2 2
cos .cos sin .sin
15 5 15 5
là
A.
1
. B.
1
. C.
3
2
. D.
3
2
.
Lời giải
Chọn A
sin sin
sin .cos sin .cos
15 10 6
15 10 10 15
1
2 2
2
cos .cos sin .sin
cos cos
15 5 15 5
15 5 3
.
Câu 14. Cho đường tròn lượng giác gốc
A
như hình vẽ. Điểm biểu diễn cung có số đo
5
2
là
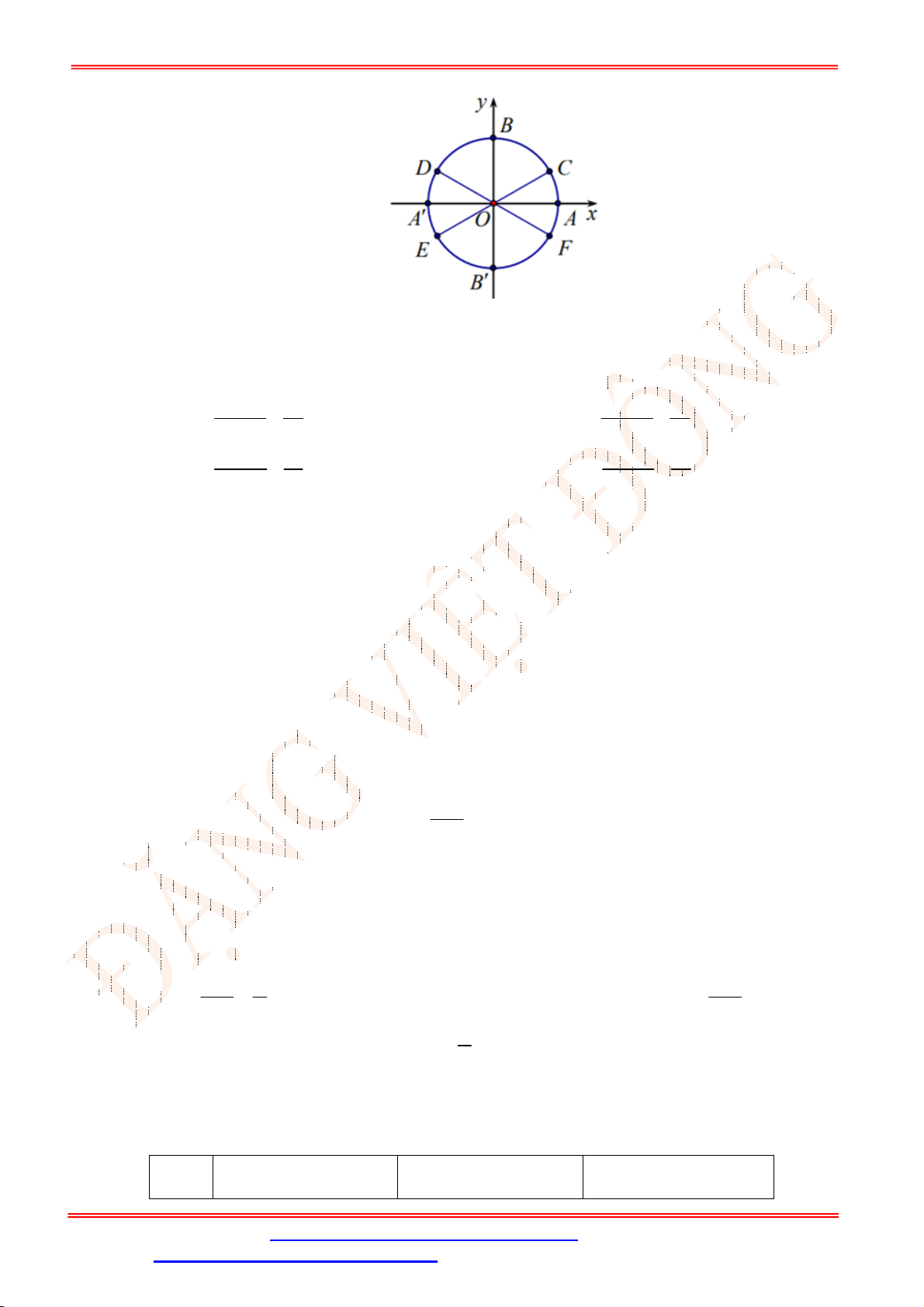
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A. điểm
B
. B. điểm
B
. C. điểm
E
. D. điểm
F
.
Lời giải
Chọn D
Câu 15. Cho tam giác
ABC
. Trung tuyến
a
m
được tính theo công thức:
A.
2 2 2
2
2 4
a
b c a
m
. B.
2 2 2
2
2 4
a
b c a
m
.
C.
2 2 2
2
2 4
a
a c b
m
. D.
2 2 2
2
4 2
a
b c a
m
.
Lời giải
Chọn B
Áp dụng công thức tính độ dài đường trung tuyến xuất phát từ đỉnh A nên chọn
Câu 16. Cho
,
a b
là các số thực tùy ý. Mệnh đề nào sau đây đúng?
A. Nếu
a b
và
0
a
thì
2 2
a b
. B. Nếu
a b
và
0
b
thì
2 2
a b
.
C. Nếu
2 2
a b
thì
a b
. D. Nếu
a b
thì
2 2
a b
.
Lời giải
Chọn A
Đáp án A,B,D sai vì thiếu điều kiện a, b là hai số không âm. Nếu a,b là hai số không âm thì
2 2
a b a b
.
Đáp án C đúng.
Câu 17. Chọn điểm
1;0
A làm điểm đầu của cung lượng giác trên đường tròn lượng giá Tìm điểm
cuối
M
của cung lượng giác có số đo
25
4
.
A.
M
là điểm chính giữa của cung phần tư thứ
IV
.
B.
M
là điểm chính giữa của cung phần tư thứ
II
.
C.
M
là điểm chính giữa của cung phần tư thứ
III
.
D.
M
là điểm chính giữa của cung phần tư thứ
I
.
Lời giải
Chọn D
Ta có:
25
3.2
4 4
nên điểm biểu diễn của cung lượng giác có số đo
25
4
trùng với điểm
biểu diễn của cung lượng giác có số đo
4
. Vì vậy,
M
là điểm chính giữa của cung phần tư
thứ
I
.
Câu 18. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa
tốt nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp
2015
Khóa tốt nghiệp 2016

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Nữ Nam Nữ Nam
1
Gi
ả
ng d
ạ
y
25
45
25
65
2
Ngân hàng
23
186
20
32
3 Lập trình 25 120 12 58
4
B
ả
o hi
ể
m
12
100
3
5
Tính cả hai khóa tốt nghiệp 2015 và 2016, lĩnh vực nào có tỷ lệ phần trăm nữ cao hơn các lĩnh
vực còn lại?
A. Lập trình. B. Bảo hiểm. C. Giảng dạy. D. Ngân hàng.
Lời giải
Chọn C
Tính cả hai khóa tốt nghiệp 2015 và 2016, ta có
Trong lĩnh vực Giảng dạy, tỉ lệ nữ là
50
100% 31,25%.
160
Trong lĩnh vực Ngân hàng, tỉ lệ nữ là
43
100% 16,48%.
261
Trong lĩnh vực Lập trình, tỉ lệ nữ là
37
100% 17,21%.
215
Trong lĩnh vực Bảo hiểm, tỉ lệ nữ là
15
100% 12,5%.
120
Kết luận: Trong lĩnh vực Giảng dạy có tỷ lệ phần trăm nữ cao hơn các lĩnh vực còn lại.
Câu 19. Tam giác
ABC
có
2, 3
AB AC
và
45
C
. Tính độ dài cạnh
BC
.
A.
6 2
.
2
BC B.
6.
BC
C.
5.
BC
D.
6 2
.
2
BC
Lời giải
Chọn D
Theo định lí hàm cosin, ta có
2 2
2 2 2 2
2. . .cos 2 3 2. 3. .cos 45
AB AC BC AC BC C BC BC
6 2
2
BC .
Câu 20. Cho góc
thỏa mãn
5
cos
13
và
3
2
2
. Tính
tan2
P .
A.
120
.
119
P B.
119
.
120
P C.
120
.
119
P D.
119
.
120
P
Lời giải
Chọn C
Ta có
2
sin2 2sin .cos
tan 2
cos2 2cos 1
P .
Mặt khác
2 2 2
12
sin cos 1 sin 1 cos sin
13
.
Do
3
2
2
nên
sin 0
12
sin
13
.
Khi đó
2
sin2 2sin .cos 120
tan2
cos2 2cos 1 119
P .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 21. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
8sin 3cos2
P x x
.
Tính
2
2 .
T M m
A.
130.
T B.
2.
T C.
112.
T D.
1.
T
Lời giải
Chọn D
Ta có
2 2 2 2
8sin 3cos2 8sin 3 1 2sin 2sin 3.
P x x x x x
Mà
2 2
1 sin 1 0 sin 1 3 2sin 3 5
x x x
2
5
3 5 2 1.
3
M
P T M m
m
Câu 22. Đường tròn
( )
C
có tâm
(2;3)
I và tiếp xúc với trục
Ox
có phương trình là:
A.
2 2
( 2) ( 3) 9
x y B.
2 2
( 2) ( 3) 4
x y
C.
2 2
( 2) ( 3) 3
x y
D.
2 2
( 2) ( 3) 9
x y
Lời giải
Chọn A
Ta có
2 2
2;3
: : 2 3 9.
; 3
I
C C x y
R d I Ox
Câu 23. Viết phương trình tiếp tuyến của đường tròn
2 2
( ):( 2) ( 1) 25
C x y , biết tiếp tuyến song
song với đường thẳng
:4 3 14 0
d x y .
A.
4 3 14 0
x y hoặc
4 3 36 0
x y B.
4 3 14 0
x y
C.
4 3 36 0
x y D.
4 3 14 0
x y hoặc
4 3 36 0
x y
Lời giải
Chọn C
Đường tròn (C) có tâm
2;1 , 5
I R và tiếp tuyến có dạng
:4 3 0 14 .
x y c c
Ta có
14
11
; 5 .
5
36
c l
c
R d I
c
Câu 24. Cho dãy số liệu thống kê:
1,2,3,4,5,6,7
. Phương sai của mẫu số liệu thống kê đã cho là
A.
3
. B.
4
. C.
1
. D.
2
.
Lời giải
Chọn B
1 2 3 4 5 6 7
4
7
x
Vậy phương sai của mẫu số liệu:
7
2
2
1
1
4
7
x i
i
s x x .
Câu 25. Cho elip
E
có độ dài trục lớn bằng
12
, độ dài trục bé bằng tiêu cự. Phương trình chính tắc
của
E
là:
A.
2 2
1
144 72
x y
. B.
2 2
1
36 18
x y
. C.
2 2
1
36 36
x y
. D.
2 2
1
144 144
x y
.
Hướng dẫn giải
Chọn B
E
có độ dài trục lớn bằng
12
nên
2 12 6
a a .
Độ dài trục bé bằng tiêu cự nên: 2 2
b c b c
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Mà:
2 2 2
b c a
nên
2 2 2 2
6 18
b b b .
Vậy phương trình
E
là:
2 2
1
36 18
x y
.
Câu 26. Nếu
tan 4tan
2 2
thì tan
2
bằng
A.
3sin
.
5 3cos
B.
3cos
.
5 3cos
C.
3cos
.
5 3cos
D.
3sin
.
5 3cos
Lời giải
Chọn A
Ta có:
2 2
tan tan 3tan 3sin .cos
3sin
2 2 2 2 2
tan .
2 5 3cos
1 tan .tan 1 4tan 1 3sin
2 2 2 2
Câu 27. Cho hai số thực
,
x y
thỏa mãn
2 3 7
x y . Giá trị lớn nhất của biểu thức
P x y xy
là:
A.
2
. B.
3
. C.
5
. D.
6
.
Lời giải
Chọn C
Ta có
2 2
2 2 3 3 7 5
6 1 1 2 2 3 3 36
4 4
x y
x y x y
.
Suy ra
5
x y xy .
Câu 28. Bất phương trình
2
10 16 0
x x có tập nghiệm là
A.
8;
B.
2;8
C.
2;8
D.
;2
Lời giải
Chọn B
Ta có
2
10 16 0 2 8 0 2 8
x x x x x .
Câu 29. Cho góc
thỏa mãn
4
tan
3
và
2017 2019
2 2
. Tính
sin .
A.
4
sin
5
. B.
3
sin
5
. C.
4
sin
5
. D.
3
sin
5
.
Lời giải
Chọn A
Ta có
2
2
2
2
1
4 1
1 tan
1
cos
3 cos
2017 2019
3
504.2 504.2
2 2
2 2
3
cos
5
. Mà
sin 4 sin 4
tan sin
3
cos 3 5
5
.
Câu 30. Viết phương trình tham số của đường thẳng đi qua hai điểm
)
(3;
7
A và
.
(1;
7)
B
A.
7
x t
y t
. B.
7
x t
y
. C.
7
x t
y
. D.
3 7
1 7
x t
y t
.
Lời giải
Chọn B
Ta thấy điểm
)
(3;
7
A không thuộc các đường thẳng có phương trình ở các phương án A, B,

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Hai điểm
)
(3;
7
A và
)
(1;
7
B đều thuộc đường thẳng có phương trình ở phương án
Câu 31. Tìm tập xác định của hàm số
2
4 12 9
1
x x
y
x
A.
; 1
D . B.
3
; 1
2
D .
C.
3
; 1
2
D . D.
3
; 1 ;
2
D .
Lời giải
Chọn B
Điều kiện
2
4 12 9
0
1
x x
x
. Ta xét các trường hợp sau
2
2
3
4 12 9 0
2 3 0
3
2
2
1 0
1
1
x
x x
x
x
x
x
x
.
2
2
4 12 9 0
2 3 0,
1
1 0
1
x x
x x
x
x
x
Vậy ta có điều kiện xác định của hàm số là
3
; 1
2
D .
Câu 32. Cho biết
5
tan
7
x . Tính giá trị của biểu thức
5sin2 7cos2
P x x
.
A.
2.
P B.
9.
P C.
13.
P D.
7.
P
Lời giải
Chọn D
2
2
2
10tan 14 10tan 14
5sin 2 7cos2 10sin .cos 14cos 7 7 7 7
1
1 tan
cos
x x
P x x x x x
x
x
.
Câu 33. Điểm
;
A a b
thuộc đường thẳng
3
:
2
x t
d
y t
và cách đường thẳng
:2 3 0
x y một
khoảng bằng
2 5
và
0
a . Tính
.
P a b
.
A.
132
P . B.
72
P . C.
72
P . D.
132
P .
Lời giải
Chọn A
Đường thẳng
và có vectơ pháp tuyến là
2; 1
n .
Điểm
A
thuộc đường thẳng
d
3 ;2
A t t
.
2
2 3 2 3
; 2 5
2 1
t t
d A
1 10
t
1 10
1 10
t
t
9
11
t
t
.
Với
9
t
12;11
A
. 12.11 132
ab .
Với
11
t
8; 2
A (loại).
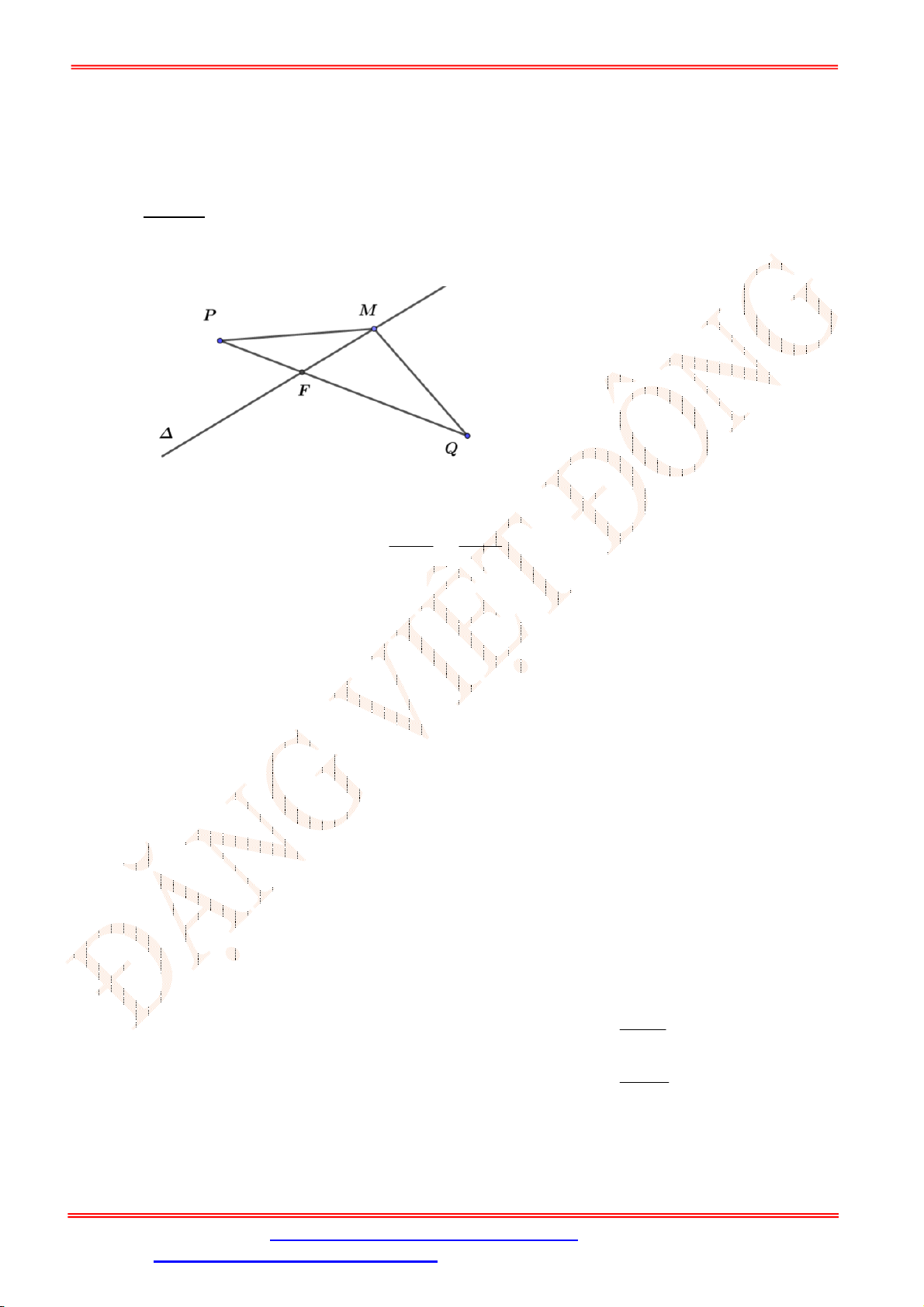
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 34. Trong mặt phẳng
Oxy
, cho
6;1
P
và
3; 2
Q
và đường thẳng
x 1 0
: 2
y
. Biết
;
M a b
thuộc
sao cho
MP MQ
ngắn nhất. Tính
2
T a b
A.
3
T
. B.
8
T
. C.
2
T
. D.
13
T
.
Lời giải
Chọn C
Đặt
10 0
, 2x 1
5 0
F P
F x y y P
F Q
và
Q
nằm về 2 phía với
.
Ta có:
MP MQ PQ
(không đổi) nên
min , ,
MP MQ PQ M P Q
thẳng hàng.
Điều này đồng nghĩa với
M F PQ
Phương trình đường thẳng
3 2
:
6 3 1 2
x y
PQ hay
: 3 3 0
PQ x y
Tọa độ
M
là nghiệm của hệ
2x 1 0 0
0; 1
3 3 0 1
y x
M
x y y
Vậy
2 2
T a b
.
Chọn C
Câu 35. Tìm
m
để mọi
0;
x đều là nghiệm của bất phương trình
2 2 2
1 8 9 0
m x mx m
A.
3; 1
m . B.
3; 1
m . C.
3; 1
m . D.
m .
Lời giải
Chọn A
- TH1:
2
1 0 1
m m
+ Với
1
m bất phương trình
8 8 0 1
x x loại
1
m .
+ Với
1
m bất phương trình
8 8 0 1
x x mọi
0;
x đều là nghiệm của bất
phương trình.
- TH1:
2
1 0 1
m m
Ta có
2
2
0 .
3
m m
Yêu cầu bài toán
2
2
1 2 1 2
2
2
2
1 0
8
1 0, 0,P . 0 0 3; 1
1
9
0
1
m
m
m S x x x x m
m
m
m
Vậy
3; 1
m .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
PHẦN II: TỰ LUẬN
Câu 36. Trong mặt phẳng với hệ tọa độ
Oxy
, lập phương trình đường thẳng d là đường thẳng song
song và cách đều hai đường thẳng
1 2
:3 6 0; : 6 2 1 0
x y x y .
Lời giải
Lấy điểm
1 2
1
2;0 ; 0;
2
M N ; Trung điểm của MN giả sử là:
1
1;
4
I
Vì đường thẳng
d
song song và cách đều hai đường thẳng
1 2
:3 6 0; : 6 2 1 0
x y x y .
:3 0
d x y c
I d
. Do đó:
13
4
c
Vậy phương trình đường thẳng
13
:3 0
4
d x y .
Câu 37. Viết phương trình tiếp tuyến
của đường tròn
2 2
: 4 4 1 0
C x y x y biết đường thẳng
hợp với trục hoành một góc
0
45
.
Lời giải
Giả sử phương trình đường thẳng
2 2
: 0, 0
ax by c a b
Đường thẳng
là tiếp tuyến với đường tròn (C) khi và chỉ khi
2
2 2
2 2
2 2
; 3 3 2 2 9 (*)
a b c
d I a b c a b
a b
Đường thẳng
hợp với trục hoành một góc
0
45
suy ra
0
2 2 2 2
cos ; cos45
b b
Ox a b
a b a b
hoặc
a b
TH1: Nếu
a b
thay vào (*) ta có
2 2
18 3 2
a c c a
, chọn
1 3 2
a b c
suy ra
: 3 2 0
x y
TH2: Nếu
a b
thay vào (*) ta có
2
2
3 2 4
18 4
3 2 4
c a
a a c
c a
Với
3 2 4
c a
, chọn
1, 1, 3 2 4 : 3 2 4 0
a b c x y
Với
3 2 4
c a
, chọn
1, 1, 3 2 4 : 3 2 4 0
a b c x y
Vậy có bốn đường thẳng thỏa mãn là
1,2 3
: 3 2 0, : 3 2 4 0
x y x y và
4
: 3 2 4 0
x y
Câu 38. Tìm giá trị nhỏ nhất của các biểu thức sau:
2 5
A x x .
Lời giải
Ta có
2 5 2 5 3
A x x x x
.
Dấu “
” xảy ra khi và chỉ khi
2 5 0 5 2
x x x .
Vậy giá trị nhỏ nhất của
A
là
3
, khi
5 2
x .
Câu 39. Tính giá trị lượng giá của biểu thức lượng giác sau:
2
3 5
tan .tan .tan
8 8 8
P .
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2
3 5
tan .tan .tan
8 8 8
P
Mà
3 5 3 5
, tan cot ,tan cot
8 8 2 8 8 2 8 8 8 8
Nên
tan .cot . tan cot 1
8 8 8 8
P .
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 06
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho tam giác
ABC
, chọn công thức đúng trong các phương án sau.
A.
2 2 2
2
2 4
a
a c b
m . B.
2 2 2
2
2 4
a
a b c
m .
C.
2 2 2
2
2 2
4
a
c b a
m . D.
2 2 2
2
2 4
a
b c a
m .
Câu 2. Trong các công thức sau, công thức nào đúng?
A.
sin – sin .cos cos .sin
a b a b a b
. B.
sin sin .cos cos.sin
a b a b b
.
C.
cos – cos .cos sin .sin
a b a b a b
. D.
cos cos .cos sin .sin
a b a b a b
.
Câu 3. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
9 4
x y
E . Tính tiêu cự của elip
E
.
A.
5
. B.
6
. C.
4
D.
2 5
.
Câu 4. Cho biểu thức
2 4.
f x x Tập hợp tất cả các giá trị của
x
để
0
f x là
A.
2; .
x B.
2; .
x C.
1
; .
2
x
D.
;2 .
x
Câu 5. Tìm mệnh đề sai trong các mệnh đề sau?
A.
, , a b a b a b
. B.
, 0
x a a x a a .
C.
, a b ac bc c
. D.
2 , 0, 0
a b ab a b .
Câu 6. Trong mặt phẳng
Ox
y
, cho đường tròn
2 2
: 2 3 9
C x y . Đường tròn
C
có tâm
và bán kính
A.
2; 3 ,R 3
I . B.
3;2 ,R 3
I .
C.
2;3 ,R 3
I . D.
2;3 ,R 9
I .
Câu 7. Tìm điều kiện xác định của bất phương trình
1
2
x
x
.
A.
2
x . B.
x . C.
2
x . D.
2
x .
Câu 8. Cho tam giác
ABC
có
0
7, 10, 120
a b C . Diện tích tam giác
ABC
có kết quả là
A.
31
ABC
S . B.
35 3
ABC
S . C.
35 3
2
ABC
S . D.
30
ABC
S .
Câu 9. Lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự
đó và các điểm
B
,
C
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240
. B. 120 360 ,
k k .
C. 240 360 ,
k k . D.
120
.
Câu 10. Cho
thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
A.
cot 0.
B.
sin 0.
C.
cos 0.
D.
tan 0.
Câu 11. Trong mặt phẳng với hệ tọa
Oxy
, cho đường thẳng
1
: ,
2 4
x t
t
y t
. Một véctơ chỉ
phương của đường thẳng
là.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
4;1
u . B.
1;2
u . C.
2;1
u . D.
1;4
u .
Câu 12. Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình của đường tròn?
A.
2 2
4 6 12 0
x y x y . B.
2 2
2 8 20 0
x y x y .
C.
2 2
4 10 6 2 0
x y x y . D.
2 2
2 4 8 1 0
x y x y .
Câu 13. Cho mẫu thống kê
28,16,13,18,12,28,13,19
. Trung vị của mẫu số liệu trên là bao nhiêu?
A.
18
. B.
20
. C.
14
. D.
17
.
Câu 14. Trong các công thức sau, công thức nào sai?
A. sin .cos
2 2
sin sin 2
b
b
a a b
a . B. cos .sin
2 2
sin – sin 2
a b
a b a b
.
C. cos .cos
2 2
cos cos 2
b
b
a a b
a . D. sin .sin
2 2
cos – cos 2
a b
a b a b
.
Câu 15. Cho góc lượng giác
. Tìm mệnh đề sai (giả thiết các vế đều có nghĩa).
A.
sin sin
. B.
tan tan
.
C.
sin sin
. D.
sin cos
2
.
Câu 16. Đổi sang radian góc có số đo
108
ta được
A.
3
2
. B.
3
5
. C.
4
. D.
10
.
Câu 17. Cho mẫu số liệu
10,8,6,2,4
. Độ lệch chuẩn của mẫu là
A.
2,8
. B.
2,4
. C.
6
. D.
8
.
Câu 18. Rút gọn biểu thức
1 sin cos2
sin2 cos
a a
A
a a
.
A.
tan .
B.
5
.
2
C.
2tan .
D.
1.
Câu 19. Viết phương trình tiếp tuyến của đường tròn
2 2
( ): 4 4 17 0
C x y x y , biết tiếp tuyến
song song với đường thẳng
:3 4 2018 0
d x y .
A.
3 4 23 0
x y hoặc
3 4 27 0
x y B.
3 4 23 0
x y hoặc
3 4 27 0
x y
C.
3 4 23 0
x y hoặc
3 4 27 0
x y D.
3 4 23 0
x y hoặc
3 4 27 0
x y
Câu 20. Nếu
sin 450 1 cos 540
thì
cos
có giá trị bằng
A.
1
2
. B.
1
2
. C.
1
. D.
1
.
Câu 21. Trên đường tròn lượng giác gốc
A
, cung lượng giác có các điểm biểu diễn tạo thành tam giác
đều là
A.
3
k
. B.
2
k
. C.
2
3
k
D.
k
.
Câu 22. Cho hàm số
4
1 .
1
y x x
x
Giá trị nhỏ nhất của
y
là
A.
3
. B.
5
. C.
2
. D.
4
.
Câu 23. Biểu thức
sin sin
3
P x x
có tất cả bao nhiêu giá trị nguyên?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 24. Đường trung trực của đoạn với và có phương trình là:
A. B.
C. D.
AB
1; 4
A
5;2
B
1 0.
x y
2 3 3 0.
x y
3 2 1 0.
x y
3 4 0.
x y
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 25. Phương trình chính tắc của
E
có tâm sai
4
5
e , độ dài trục nhỏ bằng
12
là
A.
2 2
1
36 25
x y
. B.
2 2
1
25 36
x y
. C.
2 2
1
64 36
x y
. D.
2 2
1
100 36
x y
.
Câu 26. Phương trình đường tròn
C
có tâm
1;3
I và đi qua gốc tọa độ là
A.
2 2
1 3 10
x y . B.
2 2
1 3 10.
x y
C.
2 2
10
x y . D.
2 2
100.
x y
Câu 27. Tập nghiệm
S
của bất phương trình
3 1 5 2
x x x x
là
A.
S . B.
5
;
2
S
. C.
5
;
2
S
. D.
S .
Câu 28. Cho tam giác
ABC
thỏa mãn
2 2 2
2 . 0
BC AC AB BC AC
số đo góc
C
là?
A.
45
. B.
30
. C.
150
. D.
60
.
Câu 29. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa
tốt nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp
2015
Khóa tốt nghiệp 2016
Nữ Nam Nữ Nam
1
Gi
ả
ng d
ạ
y
25
45
25
65
2 Ngân hàng 23 186 20 32
3
L
ậ
p trình
25
120
12
58
4 Bảo hiểm 12 100 3 5
Tính cả hai khóa tốt nghiệp
2015
và
2016
, số sinh viên làm trong lĩnh vực Ngân hàng nhiều
hơn số sinh viên làm trong lĩnh vực Giảng dạy là bao nhiêu phần trăm?
A.
67,2%
. B.
63,1%
. C.
62,0%
. D.
68,5%
.
Câu 30. Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?
1)
cos sin 2sin .
4
x x x
2)
cos sin 2cos .
4
x x x
3)
cos sin 2sin .
4
x x x
4)
cos sin 2sin .
4
x x x
A.
2.
B.
3.
C.
4.
D.
1.
Câu 31. Số các nghiệm nguyên thuộc tập
3;3
của bất phương trình
2
2
6
0
1 2
x x
x x x
là
A.
3
. B.
6
. C.
5
. D.
4
.
Câu 32. Cho
1;2 ; 3;2
A B và đường thẳng
:2 3 0
x y , điểm
C sao cho tam giác
ABC
cân ở
C
. Toạ độ của điểm
C
là:
A.
2;5
C . B.
2; 1
C . C.
1;1
C . D.
0;3
C .
Câu 33. Cho góc
thỏa mãn
cot 3 2
và
.
2
Tính
tan cot .
2 2
P
A.
19.
P B.
2 19.
P C.
2 19.
P D.
19.
P

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 34. Tất cả các giá trị của để bất phương trình thỏa mãn với mọi là
A. . B. . C. . D. .
Câu 35. Trong mặt phẳng tọa độ
Oxy
cho đường thẳng
d
tiếp xúc với đường tròn tâm
O
bán kính
1
,
cắt các trục
,
Ox Oy
lần lượt tại các điểm
A
và
B
. Giá trị nhỏ nhất của diện tích tam giác
OAB
có thể là
A.
1
2
. B.
1
. C.
2
. D.
4
.
PHẦN II: TỰ LUẬN
Câu 36. Cho đường thẳng
: 0
ax by c . Viết phương trình đường thẳng
đối xứng với đường
thẳng
a) qua trục hoành.
b) qua trục tung.
c) qua gốc tọa độ.
Câu 37. Lập phương trình tiếp tuyến chung của hai đường tròn sau:
2 2
1
: 4 5 0
C x y y và
2 2
2
: 6 8 16 0
C x y x y .
Câu 38. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
2
1
1
x
y
x x
.
Câu 39. Đơn giản các biểu thức
5
sin os tan tan
2 2 2
C x c x x x
------------- HẾT -------------
m
2
2 2 2
x m x mx
x
2
m
2
m
2 2
m
m

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 06
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Th
ờ
i gian làm bài
: 90 phút,
không tính th
ờ
i gian phát đ
ề
PHẦN I: TRẮC NGHIỆM
Câu 1. Cho tam giác
ABC
, chọn công thức đúng trong các phương án sau.
A.
2 2 2
2
2 4
a
a c b
m . B.
2 2 2
2
2 4
a
a b c
m .
C.
2 2 2
2
2 2
4
a
c b a
m . D.
2 2 2
2
2 4
a
b c a
m .
Lời giải
Chọn C
Câu 2. Trong các công thức sau, công thức nào đúng?
A.
sin – sin .cos cos .sin
a b a b a b
. B.
sin sin .cos cos.sin
a b a b b
.
C.
cos – cos .cos sin .sin
a b a b a b
. D.
cos cos .cos sin .sin
a b a b a b
.
Lời giải
Chọn C
Ta có
cos – cos .cos sin .sin
a b a b a b
.
Câu 3. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
9 4
x y
E . Tính tiêu cự của elip
E
.
A.
5
. B.
6
. C.
4
D.
2 5
.
Lời giải
Chọn D
Ta có
2
9
a ,
2
4
b
2 2 2
5
c a b
5
c .
Tiêu cự
2 2 5
c .
Câu 4. Cho biểu thức
2 4.
f x x Tập hợp tất cả các giá trị của
x
để
0
f x là
A.
2; .
x B.
2; .
x C.
1
; .
2
x
D.
;2 .
x
Chọn B
Ta có
0 2 4 0 2 2; .
f x x x x
Câu 5. Tìm mệnh đề sai trong các mệnh đề sau?
A.
, , a b a b a b
. B.
, 0
x a a x a a .
C.
, a b ac bc c
. D.
2 , 0, 0
a b ab a b .
Lời giải
Chọn C
, 0
a b ac bc c nên mệnh đề sai là
, a b ac bc c
.
Câu 6. Trong mặt phẳng
Ox
y
, cho đường tròn
2 2
: 2 3 9
C x y . Đường tròn
C
có tâm
và bán kính
A.
2; 3 ,R 3
I . B.
3;2 ,R 3
I .
C.
2;3 ,R 3
I . D.
2;3 ,R 9
I .
Lời giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn A
Từ phương trình đường tròn
C
, suy ra
C
có tâm
2; 3
I và bán kính
3
R .
Câu 7. Tìm điều kiện xác định của bất phương trình
1
2
x
x
.
A.
2
x . B.
x . C.
2
x . D.
2
x .
Lời giải
Chọn D
Điều kiện
2 0
x
2
x .
Câu 8. Cho tam giác
ABC
có
0
7, 10, 120
a b C . Diện tích tam giác
ABC
có kết quả là
A.
31
ABC
S . B.
35 3
ABC
S . C.
35 3
2
ABC
S . D.
30
ABC
S .
Lời giải
Chọn C
1 1 35 3
sin .7.10.sin120
2 2 2
ABC
S ab C .
Câu 9. Lục giác đều
ABCDEF
nội tiếp đường tròn lượng giác có gốc là
A
, các đỉnh lấy theo thứ tự
đó và các điểm
B
,
C
có tung độ dương. Khi đó góc lượng giác có tia đầu
OA
, tia cuối
OC
bằng
A.
240
. B. 120 360 ,
k k .
C. 240 360 ,
k k . D.
120
.
Lời giải
Chọn B
Theo bài ra ta có
0
120
AOC nên góc lượng giác có tia đầu
OA
, tia cuối
OC
có số đo bằng
0 0
120 360 ,
k k .
Câu 10. Cho
thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng?
A.
cot 0.
B.
sin 0.
C.
cos 0.
D.
tan 0.
Lời giải
Chọn C
thuộc góc phần tư thứ hai
sin 0
cos 0
tan 0
cot 0
Câu 11. Trong mặt phẳng với hệ tọa
Oxy
, cho đường thẳng
1
: ,
2 4
x t
t
y t
. Một véctơ chỉ
phương của đường thẳng
là.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
4;1
u . B.
1;2
u . C.
2;1
u . D.
1;4
u .
Lời giải
Chọn D
Một véctơ chỉ phương của đường thẳng
là
1;4
u .
Câu 12. Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình của đường tròn?
A.
2 2
4 6 12 0
x y x y . B.
2 2
2 8 20 0
x y x y .
C.
2 2
4 10 6 2 0
x y x y . D.
2 2
2 4 8 1 0
x y x y .
Lời giải
Chọn A
Vì hệ số của
2
x
khác hệ số của
2
y
nên A và D không phải là phương trình đường tròn.
B là phương trình đường tròn vì
2 2
4 9 12 25 0
a b c .
C không phải là phương trình đường tròn vì
2 2
1 16 20 3 0
a b c .
Câu 13. Cho mẫu thống kê
28,16,13,18,12,28,13,19
. Trung vị của mẫu số liệu trên là bao nhiêu?
A.
18
. B.
20
. C.
14
. D.
17
.
Lời giải
Chọn D
Mẫu thống kê trên có
8
số liệu được sắp xếp theo thứ tự không giảm là:
12,13,13,16,18,19,28,28
, nên trung vị của mẫu số liệu trên là
e
M
16 18
17
2
.
Câu 14. Trong các công thức sau, công thức nào sai?
A. sin .cos
2 2
sin sin 2
b
b
a a b
a . B. cos .sin
2 2
sin – sin 2
a b
a b a b
.
C. cos .cos
2 2
cos cos 2
b
b
a a b
a . D. sin .sin
2 2
cos – cos 2
a b
a b a b
.
Lời giải
Chọn D
Ta có sin .sin
2 2
cos – cos 2
a
a a
b
b b
.
Câu 15. Cho góc lượng giác
. Tìm mệnh đề sai (giả thiết các vế đều có nghĩa).
A.
sin sin
. B.
tan tan
.
C.
sin sin
. D.
sin cos
2
.
Lời giải
Chọn A
Ta có
sin sin
. nên D sai. Các phương án còn lại đều đúng theo tính chất.
Câu 16. Đổi sang radian góc có số đo
108
ta được
A.
3
2
. B.
3
5
. C.
4
. D.
10
.
Lời giải
Chọn B
Ta có 1
180
nên
108
108
180
3
5
.
Câu 17. Cho mẫu số liệu
10,8,6,2,4
. Độ lệch chuẩn của mẫu là
A.
2,8
. B.
2,4
. C.
6
. D.
8
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A
* Số trung bình:
2 4 6 8 10
6
5
x .
* Độ lệch chuẩn:
2 2 2 2 2
1
2 6 4 6 6 6 8 6 10 6 2,8
5
s .
Câu 18. Rút gọn biểu thức
1 sin cos2
sin2 cos
a a
A
a a
.
A.
tan .
B.
5
.
2
C. 2tan .
D. 1.
Lời giải
Chọn A
Ta có
2
sin 2sin 1
1 sin 2sin 1 sin
tan .
2sin .cos cos cos 2sin 1 cos
a a
a a a
A a
a a a a a a
Câu 19. Viết phương trình tiếp tuyến của đường tròn
2 2
( ): 4 4 17 0 C x y x y , biết tiếp tuyến
song song với đường thẳng :3 4 2018 0 d x y .
A. 3 4 23 0 x y hoặc 3 4 27 0 x y B. 3 4 23 0 x y hoặc 3 4 27 0 x y
C. 3 4 23 0 x y hoặc 3 4 27 0 x y D. 3 4 23 0 x y hoặc 3 4 27 0 x y
Lời giải
Chọn C
Đường tròn (C) có tâm
2; 2 , 5 I R và tiếp tuyến có dạng
:3 4 0 2018 .
x y c c
Ta có
23
2
; 5 .
27
5
c
c
R d I
c
Câu 20. Nếu
sin 450 1 cos 540
thì
cos
có giá trị bằng
A.
1
2
. B.
1
2
. C. 1. D. 1 .
Lời giải
Chọn A
sin 450 1 cos 540
sin 360 90 1 cos 360 180
sin 90 1 cos 180
1
cos 1 cos cos
2
.
Câu 21. Trên đường tròn lượng giác gốc
A , cung lượng giác có các điểm biểu diễn tạo thành tam giác
đều là
A.
3
k
. B.
2
k
. C.
2
3
k
D.
k .
Lời giải
Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Khi
0
k
, cung lượng giác có số đo là 0
rad
và có điểm biểu diễn là điểm
A
.
Khi
1
k
, cung lượng giác có số đo là
2
3
rad
và có điểm biểu diễn là điểm
M
.
Khi
2
k
, cung lượng giác có số đo là
4
3
rad
và có điểm biểu diễn là điểm
N
.
Tương tự với các giá trị k
ta được các điểm biểu diễn là
, ,
A M N
lập thành tam giác đều.
Câu 22. Cho hàm số
4
1 .
1
y x x
x
Giá trị nhỏ nhất của
y
là
A.
3
. B.
5
. C.
2
. D.
4
.
Lời giải
Chọn B
+) Áp dụng bất đẳng thức cô sy ta có
4 4
1 1 2. 1 . 1 5.
1 1
y x x
x x
+) Dấu
" "
xảy ra khi
1
4
1
1
3
x L
x
x
x
.
Câu 23. Biểu thức
sin sin
3
P x x
có tất cả bao nhiêu giá trị nguyên?
A.
1.
B.
2.
C.
3.
D.
4.
Lời giải
Chọn C
Áp dụng công thức sin sin 2cos sin
2 2
a b a b
a b , ta có
sin sin 2cos sin cos .
3 6 6 6
x x x x
Ta có
1 cos 1 1 1 1;0;1 .
6
P
x P P
Câu 24. Đường trung trực của đoạn với và có phương trình là:
A. B.
C. D.
Lời giải
Chọn B
Gọi I là trung điểm của AB và
d
là trung trực đoạn ATa có
1; 4 , 5;2 3; 1
:2 3 3 0.
4;6 2 2;3
d
A B I
d x
AB Bd
d
n A
y
Câu 25. Phương trình chính tắc của
E
có tâm sai
4
5
e , độ dài trục nhỏ bằng
12
là
A.
2 2
1
36 25
x y
. B.
2 2
1
25 36
x y
. C.
2 2
1
64 36
x y
. D.
2 2
1
100 36
x y
.
Lời giải
Chọn D
Ta có:
4
5
2 12
e
b
5 4
6
c a
b
2 2
25 16
6
c a
b
2 2 2
25 16
6
a b a
b
10
6
a
b
.
AB
1; 4
A
5;2
B
1 0.
x y
2 3 3 0.
x y
3 2 1 0.
x y
3 4 0.
x y

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy phương trình của
E
:
2 2
1
100 36
x y
.
Câu 26. Phương trình đường tròn
C
có tâm
1;3
I và đi qua gốc tọa độ là
A.
2 2
1 3 10
x y . B.
2 2
1 3 10.
x y
C.
2 2
10
x y . D.
2 2
100.
x y
Lời giải
Chọn A
Điểm
O
thuộc đường tròn
C
nên
10
R IO .
Đường tròn
C
có tâm
1;3
I và bán kính
10
R có phương trình
là
2 2
: 1 3 10
C x y .
Câu 27. Tập nghiệm
S
của bất phương trình
3 1 5 2
x x x x
là
A.
S . B.
5
;
2
S
. C.
5
;
2
S
. D.
S .
Lời giải
Chọn D
3 1 5 2
x x x x
2
3 0
x
(hiển nhiên).
Vậy
S .
Câu 28. Cho tam giác
ABC
thỏa mãn
2 2 2
2 . 0
BC AC AB BC AC
số đo góc
C
là?
A.
45
. B.
30
. C.
150
. D.
60
.
Lời giải
Chọn A
Đặt , ,
BC a AC b AB c
.
Khi đó
2 2 2
2 . 0
BC AC AB BC AC
2 2 2
2 . 0
a b c a b
2 2 2
2 . 2
cos 45
2 2 2
a b c a b
C C
ab ab
.
Câu 29. Số liệu thống kê tình hình việc làm của sinh viên nghành Toán sau khi tốt nghiệp của các khóa
tốt nghiệp 2015 và 2016 được trình bày trong bảng sau:
STT Lĩnh vực việc làm Khóa tốt nghiệp
2015
Khóa tốt nghiệp 2016
N
ữ
Nam
N
ữ
Nam
1 Giảng dạy 25 45 25 65
2
Ngân hàng
23
186
20
32
3 Lập trình 25 120 12 58
4
B
ả
o hi
ể
m
12
100
3
5
Tính cả hai khóa tốt nghiệp
2015
và
2016
, số sinh viên làm trong lĩnh vực Ngân hàng nhiều
hơn số sinh viên làm trong lĩnh vực Giảng dạy là bao nhiêu phần trăm?
A.
67,2%
. B.
63,1%
. C.
62,0%
. D.
68,5%
.
Lời giải
Chọn B
Tính cả hai khóa tốt nghiệp
2015
và
2016
, ở các lĩnh vực trong bảng số liệu,
Số sinh viên có việc làm trong lĩnh vực Ngân hàng là
261
( sinh viên ).
Số sinh viên có việc làm trong lĩnh vực Giảng dạy là
160
( sinh viên ).
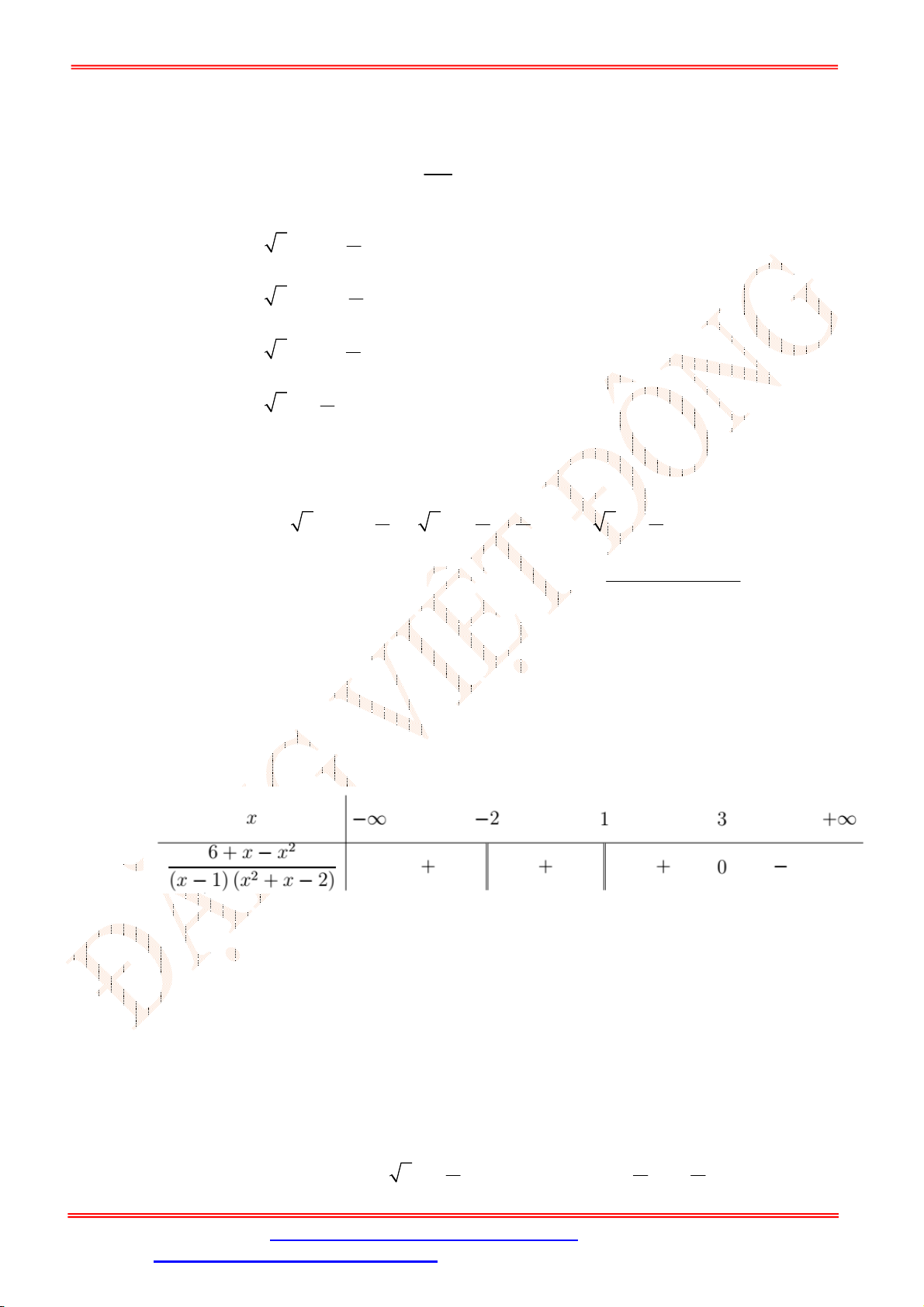
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Số sinh viên có việc làm trong lĩnh vực Ngân hàng hơn số sinh viên có việc làm trong lĩnh vực
Giảng dạy là
261 160 101
người.
Tỷ lệ phần trăm của sinh viên có việc làm trong lĩnh vực Ngân hàng nhiều hơn số sinh viên có
việc làm trong lĩnh vực Giảng dạy là
101
100% 63,1%
160
.
Câu 30. Có bao nhiêu đẳng thức dưới đây là đồng nhất thức?
1)
cos sin 2sin .
4
x x x
2)
cos sin 2cos .
4
x x x
3)
cos sin 2sin .
4
x x x
4)
cos sin 2sin .
4
x x x
A.
2.
B.
3.
C.
4.
D.
1.
Lời giải
Chọn A
Ta có cos sin 2cos 2cos 2sin
4 2 4 4
x x x x x
.
Câu 31. Số các nghiệm nguyên thuộc tập
3;3
của bất phương trình
2
2
6
0
1 2
x x
x x x
là
A.
3
. B.
6
. C.
5
. D.
4
.
Lời giải
Chọn D
2
1
1 2 0 1
2
x
x x x x
x
,
2
3
6 0
2
x
x x
x
.
Trục xét dấu:
Dựa trục xét dấu suy ra nghiệm nguyên thuộc tập
3;3
là
3; 1;0;2
S .
Câu 32. Cho
1;2 ; 3;2
A B và đường thẳng
:2 3 0
x y , điểm
C sao cho tam giác
ABC
cân ở
C
. Toạ độ của điểm
C
là:
A.
2;5
C . B.
2; 1
C . C.
1;1
C . D.
0;3
C .
Lời giải
Chọn B
Gọi tọa độ điểm
;2 3 1;2 1 , 3;2 1
C a a CA a a CB a a
Vì tam giác
ABC
cân ở
2 2 2 2
2 2
1 2 1 3 2 1
C CA CB a a a a
4 0 2 2; 1
2
a a C .
Câu 33. Cho góc
thỏa mãn
cot 3 2
và
.
2
Tính
tan cot .
2 2
P
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
19.
P B.
2 19.
P C.
2 19.
P D.
19.
P
Lời giải
Chọn B
Ta có
2 2
sin cos sin cos
2
2 2 2 2
tan cot .
2 2 sin
cos sin sin cos
2 2 2 2
P
Từ hệ thức
2
2
1 1
1 cot sin
sin
19
.
Do
sin 0
2
nên ta chọn
1
sin 2 19.
19
P
Câu 34. Tất cả các giá trị của
m
để bất phương trình
2
2 2 2
x m x mx
thỏa mãn với mọi
x
là
A.
2
m
. B.
2
m
. C.
2 2
m
. D.
m .
Lời giải
Chọn C
Ta có bpt
2
2 2 2
x m x mx
2
2
2 2 0
x m x m m
Đặt
0
t x m
. Bất phương trình đã cho có nghiệm với mọi
x
2 2
2 2 0, 0
t t m t
.
2 2 2 2
[0; )
2 2 , 0 min( 2 2)
t t m t m t t
2
2 2 2
m m
.
Câu 35. Trong mặt phẳng tọa độ
Oxy
cho đường thẳng
d
tiếp xúc với đường tròn tâm
O
bán kính
1
,
cắt các trục
,
Ox Oy
lần lượt tại các điểm
A
và
B
. Giá trị nhỏ nhất của diện tích tam giác
OAB
có thể là
A.
1
2
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn B
x
y
O
H
A
B
a
b
Gọi
;0
A a
0
a là giao điểm của đường thẳng
d
và trục
Ox
.
0;
B b
0
b là giao điểm của đường thẳng
d
và trục
Oy
.
Khi đó: ;
OA a OB b
1 1
.
2 2
OAB
S OAOB ab
1

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Xét tam giác vuông
OAB
có:
2 2 2 2
2 2 2 2 2
1 1 1 1 1
1 .
a b a b
OA OB OH a b
2 2 2 2
2 . 2
a b a b a b ab
Từ
1 1
OAB
S . Vậy
min
1
OAB
S .
PHẦN II: TỰ LUẬN
Câu 36. Cho đường thẳng
: 0
ax by c . Viết phương trình đường thẳng
đối xứng với đường
thẳng
a) qua trục hoành.
b) qua trục tung.
c) qua gốc tọa độ.
Lời giải
Xét điểm
;
M M
M x y
tùy ý thuộc .
a) Gọi
;
N N
N x y
là điểm đối xứng với M qua Ox.
Khi đó:
N M M N
N M M N
x x x x
y y y y
.
Do đó M
0
M M
ax by c
0
N N
ax by c
N
1
ax – by + c = 0.
Vậy phương trình đường thẳng đối xứng với qua Ox là ax – by + c = 0.
b) Gọi
;
P P
P x y
là điểm đối xứng với M qua Oy.
Khi đó ta có
P M M P
P M M P
x x x x
y y y y
. Do đó M
0
M M
ax by c
0
P P
ax by c
P
2
ax – by – c = 0.
Vậy phương trình đường thẳng đối xứng vơi qua Oy là ax – by – c = 0.
c) Gọi
;
Q Q
Q x y
là điểm đối xứng với M qua O.
Khi đó ta có
Q M M Q
Q M M Q
x x x x
y y y y
. Do đó M
0
M M
ax by c
0
Q Q
ax by c
Q
3
Câu 37. Lập phương trình tiếp tuyến chung của hai đường tròn sau:
2 2
1
: 4 5 0
C x y y và
2 2
2
: 6 8 16 0
C x y x y .
Lời giải
Đường tròn
1
C
có tâm
1
0;2
I bán kính
1
3
R
Đường tròn
2
C
có tâm
2
3; 4
I bán kính
2
3
R
Gọi tiếp tuyến chung của hai đường tròn có phương trình
: 0
ax by c với
2 2
0
a b
là tiếp tuyến chung của
1
C
và
2
C
1
2
( , ) 3
( , ) 3
d I
d I
2 2
2 2
2 3 *
3 4 3
b c a b
a b c a b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Suy ra
2
2 3 4
3 2
2
a b
b c a b c
a b
c
TH1: Nếu
2
a b
chọn
2, 1
a b
thay vào (*) ta được
2 3 5
c nên ta có 2 tiếp tuyến là
2 2 3 5 0
x y
TH2: Nếu
3 2
2
a b
c thay vào (*) ta được
2 2
2 2
b a a b
0
a hoặc
3 4 0
a b
+ Với 0
a c b
, chọn
1
b c
ta được
: 1 0
y
+ Với
3 4 0 3
a b c b
, chọn
4, 3, 9
a b c ta được
:4 3 9 0
x y
Vậy có 4 tiếp tuyến chung của hai đường tròn là:
2 2 3 5 0, 1 0,4 3 9 0
x y y x y .
Câu 38. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
2
1
1
x
y
x x
.
Lời giải
TXĐ:
D
Ta có:
2
1
1
1
x
y
x x
2
1
yx yx y x
2
1 1 0 2
yx y x y
TH1:
0
y
1 1
x .
Vậy
0
y thuộc miền giá trị của
f x
.
TH2:
0
y
Do
y
thuộc miền giá trị của
f x
Phương trình
2
có nghiệm
x
.
2
0
0
0
1
0
1
3 2 1 0
3
y
y
a
y
y y
.
2
1 0 0
y x x .
2
1
2 0 2
3
y x x
Vậy
1
min
3
y khi và chỉ khi
2
x .
max 1
y
khi và chỉ khi
0
x .
Câu 39. Đơn giản các biểu thức
5
sin os tan tan
2 2 2
C x c x x x
Lời giải
sin os tan tan cos cos 0
2 2 2
C x c x x x x x
------------- HẾT -------------

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 07
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
PHẦN TRẮC NGHIỆM
Câu 1: Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
0
m m x m
vô nghiệm?
A.
0
m
hay
1
m
. B.
0;1
m . C.
0
m
D.
;0 1;m
.
Câu 2: Tìm tập nghiệm của bất phương trình
2 7
1
4
x
x
?
A.
11;4
. B.
4;11
. C.
1;2;3
. D.
1;3
.
Câu 3: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có hai nghiệm
1
x
,
2
x
thỏa mãn
3 3
1 2
16
x x
.
A. Không tồn tại
m
. B.
2
m
. C.
1
m
. D.
1
m
hoặc
2
m
.
Câu 4: Cho tam giác
ABC
có
2
AB
cm,
1
AC
cm,
O
ˆ
60
A . Khi đó độ dài cạnh
BC
là:
A. 1 cm. B. 2 cm. C.
3
cm. D.
5
cm.
Câu 5: Cho ba điểm
1;4
A ,
3;2
B ,
5;4
C . Tọa độ tâm đường tròn ngoại tiếp tam giác
ABC
là:
A.
2;5
. B.
3
;2
2
. C.
9;10
. D.
3;4
.
Câu 6: Hình chiếu vuông góc của điểm
1;4
M xuống đường thẳng
: 2 2 0
x y
có tọa độ là:
A.
3;0
. B.
0;3
C.
2;2
D.
2; 2
Câu 7: Tính diện tích hình bình hành
ABCD
có
AB a
,
2
BC a
và góc
o
45
A
?
A.
2
2
a
. B.
2
2
a . C.
2
a
. D.
2
3
a .
Câu 8: Giá trị lớn nhất của biểu thức
4 7
sin cos
x x
là:
A.
2
. B.
1
. C.
1
2
. D.
1
.
Câu 9: Tập nghiệm của bất phương trình
2 2
2 4 3 3 2 1
x x x x
là
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;1
.
Câu 10: Tam giác
ABC
có
5
a
cm,
3
b
cm,
5
c
cm. Tính số đo góc
A
:
A.
O
45
. B.
O
30
. C.
O
90
. D.
o
72.54
.
Câu 11: Nếu cos sin 2 0
2
thì
bằng
A.
6
. B.
3
C.
4
D.
8
.
Câu 12: Biểu thức thu gọn của biểu thức
1
1 .tan
cos2
B x
x
là?
A.
tan2
x
B.
cot2
x
. C.
cos2
x
. D.
sin
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 13: Công thức nào sau đây là công thức Hê-rông:
A.
S pr
B.
S pr
C.
( )( )( )
S p p a p b p c
D.
( )( )( )
S p a p b p c
.
Câu 14: Điều kiện cần và đủ để tam giác
ABC
có góc
A
nhọn là?
A.
2 2 2
a b c
B.
2 2 2
a b c
C.
2 2 2
a b c
D.
2 2 2
a b c
.
Câu 15: Mệnh đề nào sau đây về tam giác
ABC
là SAI?
A. Góc
B
nhọn khi và chỉ khi
2 2 2
b a c
B. Góc
A
vuông khi và chỉ khi
2 2 2
a b c
.
C. Góc
C
tù khi và chỉ khi
2 2 2
c a b
. D. Góc
A
tù khi và chỉ khi
2 2 2
b a c
.
Câu 16: Cho đường thẳng
có phương trình tổng quát:
2 3 1 0
x y
. Vecto nào sau đây là vecto chỉ
phương của đường thẳng
.
A.
(3;2)
. B.
(2;3)
. C.
( 3;2)
D.
(2; 3)
Câu 17: Tính
sin
, biết
5
cos
3
và
3
2
2
.
A.
1
3
B.
1
3
. C.
2
3
. D.
2
3
.
Câu 18: Cho
5
sin
3
a . Tính
cos2 sin
a a
A.
17 5
27
. B.
5
9
. C.
5
27
. D.
5
27
.
Câu 19: Tam giác
ABC
vuông tại
A
có
6
AB
cm,
10
BC
cm. Đường tròn nội tiếp tam giác đó có bán
kính
r
bằng
A.
1
cm. B.
2
cm. C.
2
cm. D.
3
cm.
Câu 20: Biến đổi thành tích biểu thức
sin7 sin5
sin7 sin5
ta được
A.
tan5 .tan
B.
cos2 .sin3
. C.
cot6 .tan
. D.
cos .sin
Câu 21: Trên mặt phẳng tọa độ
Oxy
cho hai vectơ
2 3
a i j
,
2
b i j
. Khi đó tọa độ vectơ
a b
là:
A.
2; 1
. B.
1;2
C.
1; 5
. D.
2; 3
.
Câu 22: Cho
cot 3
. Khi đó
3 3
3sin 2cos
12sin 4cos
có giá trị bằng
A.
1
4
. B.
5
4
. C.
3
4
D.
1
4
Câu 23: Cho sin cos
A
. Giá trị biểu thức
sin cos
bằng:
A.
2
1
2
A
B.
2
1
2
A
C.
1
2
A
D.
1
2
A
.
Câu 24: Trong mặt phẳng
Oxy
cho
2;3
A ,
4; 1
B
. Tọa độ của
OA OB
là
A.
2;4
B.
2; 4
. C.
3;1
D.
6; 2
Câu 25: Số đường thẳng đi qua điểm
5;6
M và tiếp xúc với đường tròn
2 2
: 1 2 1
C x y
là:
A. 0. B. 1. C. 2. D. 3.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 26: Cho
0;3
A ,
4;2
B . Điểm
D
thỏa
2 2 0
OD DA DB
, tọa độ
D
là:
A.
3;3
. B.
8;2
C.
8; 2
D.
5
2;
2
Câu 27: Trên mặt phẳng tọa độ
Oxy
, cho
ABC
vuông tại
A
có
1; 3
B
và
1;2
C . Tìm tọa độ điểm
H
là chân đường cao kẻ từ đỉnh
A
của
ABC
, biết
3
AB
,
4
AC
:
A.
24
1;
5
H
. B.
6
1;
5
H
C.
24
1;
5
H
. D.
6
1;
5
H
.
Câu 28: Cho
1
sin
3
a
với
2
a
. Tính
cos
a
.
A.
2 2
cos
3
a B.
2 2
cos
3
a C.
8
cos
9
a
D.
8
cos
9
a
.
Câu 29: Với mọi
x
, biểu thức
2 9
cos cos cos ... cos
5 5 5
x x x x
nhận giá trị bằng:
A.
10
. B.
10
. C.
0
. D.
1
.
Câu 30: Cho tam giác
ABC
có cạnh
BC a
, cạnh
CA b
. Tam giác
ABC
có diện tích lớn nhất khi góc
C
bằng
A.
o
60
B.
o
90
C.
o
150
. D.
o
120
Câu 31: Tìm tập nghiệm của bất phương trình
2 1 2
x x
.
A.
1
;3
3
. B.
1
;3
3
. C.
1
;3
3
. D.
1;3
Câu 32: Tam giác đều nội tiếp đường tròn bán kính
4
R
cm có diện tích là:
A.
13
cm
2
. B.
13 2
cm
2
. C.
12 3
cm
2
. D.
15
cm
2
.
Câu 33: Hệ bất phương trình
3 4 0
1
x x
x m
có nghiệm khi nào?
A.
5
m
B.
2
m
C.
5
m
D.
5
m
.
Câu 34: Phương trình nào dưới đây không là phương trình đường tròn?
A.
2 2
4 0
x y
. B.
2 2
2 0
x y x y
.
C.
2 2
0
x y x y
. D.
2 2
2 2 1 0
x y x y
.
Câu 35: Cho
3
tan
5
. Tính giá trị biểu thức
2 2
sin cos
sin cos
A
:
A.
15
16
B.
15
16
C.
5
6
D.
5
6
PHẦN TỰ LUẬN
Bài 1. Giải bất phương trình
2
2
3
1
4
x x
x
.
Bài 2. Cho tam giác
ABC
, biết
7, 8, 6
a b c
. Tính
S
và
a
h
.
Bài 3. Lập phương trình tiếp tuyến của đường tròn
2 2
: 6 2 0
C x y x y
, biết tiếp tuyến này vuông
góc với đường thẳng
:3 4 0
d x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Bài 4. Tìm giá trị nhỏ nhất của hàm số
1 1
1
y
x x
với
0 1
x
.
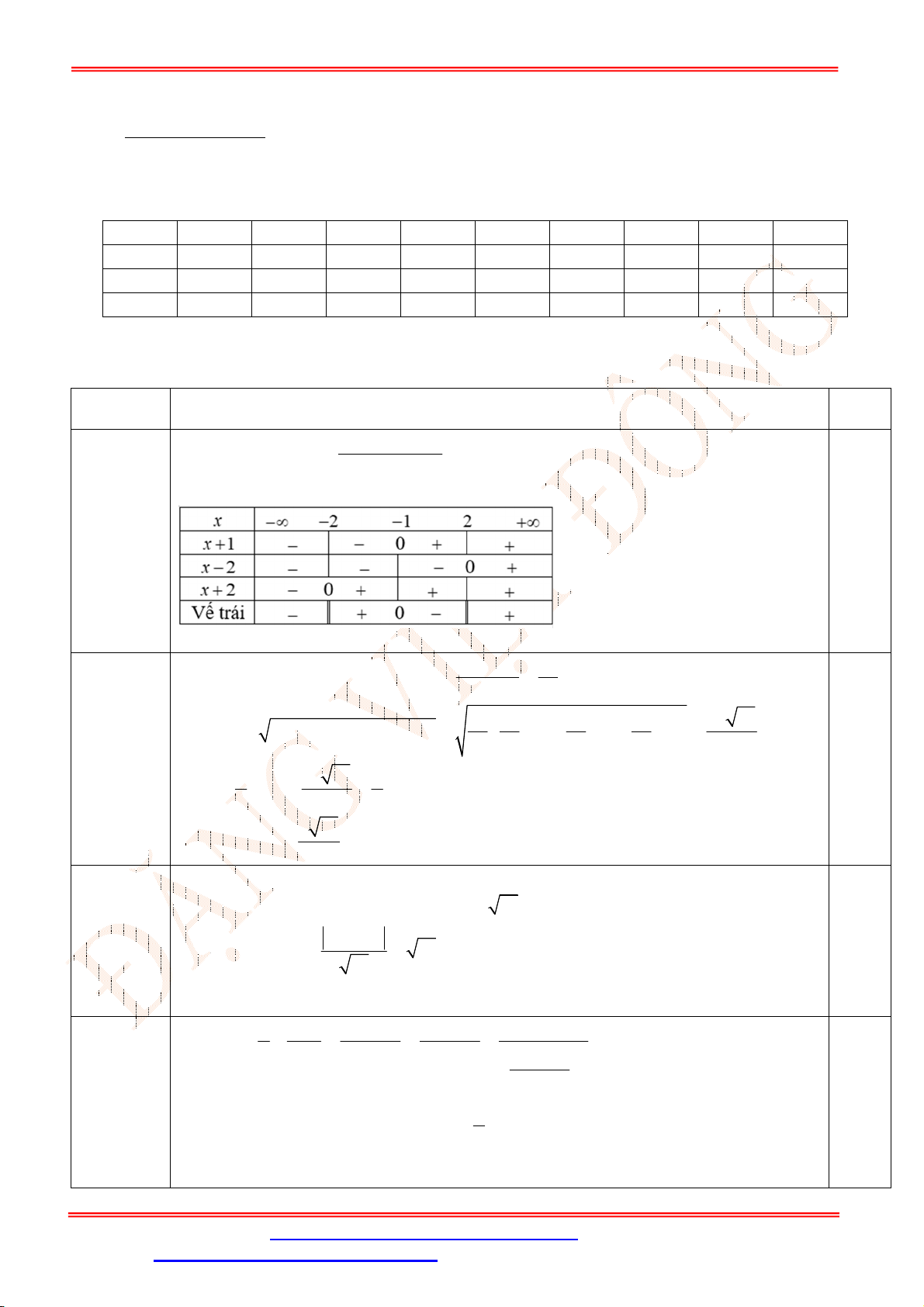
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 07
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. PHẦN TRẮC NGHIỆM
1.C 2.A 3.D 4.C 5.D 6.C 7.C 8.D 9.D 10.D
11.C 12.A 13.C 14.A 15.D 16.A 17.D 18.D 19.C 20.C
21.C 22.A 23.A 24.A 25.C 26.C 27.D 28.B 29.C 30.B
31.A 32.D 33.B 34.B 35.A
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
II. PHẦN TỰ LUẬN
Câu hỏi Nội dung Điểm
Bài 1
(1,0 điểm)
Bất phương trình
1
0
2 2
x
x x
Bảng xét dấu vế trái:
Đáp số 2 1, 2x x .
0,25
0,5
0,25
Bài 2
(1,0 điểm)
Áp dụng công thức Hê-rông với
21
2 2
a b c
p
Ta có
21 21 21 21 21 15
( )( )( ) 7 8 6
2 2 2 2 4
S p p a p b p c
Vì
1 21 15 1
7
2 4 2
a a
S ah h
nên suy ra
3 15
2
a
h .
0,25
0,25
0,25
0,25
Bài 3
(0,5 điểm)
Gọi tiếp tuyến cần tìm là
. Vì
vuông góc với d nên
: 3 0x y c
.
C có tâm
3; 1I và có bán kính 10R . Ta có tiếp xúc với
C
3 3
; 10 10
10
c
d I R c
.
Vậy tiếp tuyến cần tìm là : 3 10 0x y hay : 3 10 0x y .
0,25
0,25
Bài 4
(0,5 điểm)
Ta có
2
1 1 1 1 1
4
1 1 1
1
2
x x
y
x x x x x x
x x
Đẳng thức xảy ra khi
1
1
0;1
2
x x
x
x
.
0,25
0,25

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy giá trị nhỏ nhất của hàm số là
4
khi
1
2
x
.
HƯỚNG DẪN CHI TIẾT 35 CÂU TRẮC NGHIỆM
Câu 1: Bất phương trình
2
0
m m x m
vô nghiệm khi và chỉ khi bất phương trình
2
0
m m x m
nghiệm đúng với mọi x
2
0
0.
0
m m
m
m
Chọn C.
Câu 2: Bất phương trình
2 7 11
1 0 11 4.
4 4
x x
x
x x
Vậy tập nghiệm là
11;4
. Chọn A.
Câu 3: Phương trình có nghiệm khi
0
2
2 0
m m
2
1
m
m
1
.
Theo định lý Vi-ét, ta có
1 2
1 2
2
2
x x m
x x m
. Theo đề bài,
3 3
1 2
16
x x
3
8 6 2 16
m m m
3 2
8 6 12 16 0
m m m
2
2 8 10 8 0
m m m
2 0
m
2
m
.
Kiểm tra điều kiện
1
, ta được
1
m
hoặc
2
m
. Chọn D.
Câu 4: Áp dụng định lý cô-sin, ta có
2 2 2 O
1
2. . .cos60 4 1 2.2.1. 3
2
BC AB AC AB AC
. Suy ra
3
BC cm. Chọn C.
Câu 5: Gọi phương trình đường tròn ngoại tiếp tam giác
ABC
là
2 2
: 2 2 0
C x y ax by d
. Do
C
đi qua các điểm
1;4
A ,
3;2
B và
5;4
C nên ta lập được hệ phương trình:
1 16 2 8 0 3
9 4 6 4 0 4
25 16 10 8 0 21
a b c a
a b c b
a b c c
.
Vậy tâm đường tròn cần tìm là
3;4
. Chọn D.
Câu 6: Đường thẳng qua
1;4
M và vuông góc với
: 2 2 0
x y
có phương trình
:2 6 0
x y
.
Hình chiếu vuông góc của
M
xuống
là giao điểm của
và
. Tọa độ giao điểm là nghiệm của hệ
phương trình
2 2 0 2
2 6 0 2
x y x
x y y
. Vậy tọa độ giao điểm cần tìm là
2;2
. Chọn C.
Câu 7: Góc
o o o
ˆ
180 45 135
B . Diện tích hình bình hành
ABCD
bằng
2
1
2. . . .sin
2
AB BC B a
. Chọn
C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 8: Do
1 sin ,cos 1
x x
nên
4 7 2 2
sin cos sin cos 1
x x x x
. Vậy giá trị lớn nhất của biểu thức
là
1
khi
2
x k
hay
2
x k
. Chọn D.
Câu 9: Đặt
2
3 2 0
t x x
2 2
2 3
x x t
.
Bất phương trình cho trở thành:
2
2 3 5 0
t t
5
1
2
t
.
Suy ra
2
5
0 3 2
2
x x
2
2
0 3 2
25
3 2
4
x x
x x
3 1
x
x
3 1
x
. Chọn D.
Câu 10:
2 2 2 2 2 2
3 5 5 3
cos
2 2.3.5 10
b c a
A
bc
. Suy ra
o
72.54
A
. Chọn D.
Câu 11: Theo đề bài,
cos sin 2 sin2 1 2 2
2 4
k k
. Chọn C.
Câu 12: Ta có
1
1 .tan
cos2
B x
x
1 cos2 sin
.
cos2 cos
x x
x x
2
2cos sin
.
cos2 cos
x x
x x
2cos .sin
cos2
x x
x
sin2
cos2
x
x
tan2
x
. Chọn A.
Câu 13: Công thức Hê-rông
S p p a p b p c
. Chọn C.
Câu 14: Ta có
2 2 2
cos
2
b c a
A
bc
. Góc
A
nhọn khi và chỉ khi
cos 0
A
hay
2 2 2
a b c
. Chọn A.
Câu 15: Phương án D là sai. Chọn D.
Câu 16: Một vectơ pháp tuyến của đường thẳng
:
2 3 1 0
x y
có tọa độ là
2;3
. Suy ra tọa độ
vectơ chỉ phương là
3;2
. Chọn A.
Câu 17: Ta có:
2 2
5 4
sin 1 cos 1
9 9
2
sin
3
. Do
3
2
2
nên
sin 0
. Vậy
2
sin
3
. Chọn D.
Câu 18: Ta có
2 3
cos2 sin 1 2sin sin sin 2sin
B a a a a a a
mà
5
sin
3
a
Suy ra
5 5 5 9 5 10 5 5
2
3 27 27 27
B
. Chọn D.
Câu 19: Tam giác
ABC
vuông tại A có diện tích
1 1
. .6.8 24
2 2
S AB AC
. Bán kính đường tròn nội
tiếp là
24
2
1
6 8 10
2
S
r
p
cm. Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 20: Ta có
sin7 sin5
sin7 sin5
2cos6 .sin
2sin6 .cos
cot6 .tan
. Chọn C.
Câu 21: Ta có
2 3 2; 3 ; 2 1;2
a i j a b i j b
suy ra
1; 5
a b
. Chọn C.
Câu 22: Ta có
2
2
3 3 3 3
1
3 2cot
3sin 2cos 3 2cot 1
sin
1 cot
12sin 4cos 12 4cot 12 4cot 4
. Chọn A.
Câu 23: Ta có
2
2
1 1
sin cos sin cos 1
2 2
A
. Chọn A.
Câu 24: Ta có
OA OB BA
và
2;4
BA
nên tọa độ của
OA OB
là
2;4
. Chọn A.
Câu 25: Đường tròn
C
có tâm
1;2
I và bán kính
1
R
. Ta có
2 2
5 1 6 2 4 2
IM R
,
suy ra điểm
M
nằm bên ngoài đường tròn. Do đó từ
M
kẻ được đúng hai tiếp tuyến đến
C
. Chọn C.
Câu 26: Gọi
;
D x y
. Theo đề
2 2 0
OD DA DB
2
OD AB
. Mà
4; 1
AB
2 8; 2
AB
8; 2
OD
. Vậy
8; 2
D
. Chọn C.
Câu 27: Ta có
2
.
AB BH BC
và
2
.
AC CH CB
. Do đó:
2
2
16
9
CH AC
BH AB
16
.
9
HC HB
.
Mà
,
HC HB
ngược hướng nên
16
9
HC HB
.
Khi đó, gọi
;
H x y
thì
1 ;2
HC x y
,
1 ; 3
HB x y
.
Suy ra:
16
1 1
9
16
2 3
9
x x
y y
1
6
5
x
y
6
1;
5
H
.
Câu 28: Ta có
2 2 2 2
8 2 2
sin cos 1 cos 1 sin cos
9 3
a a a a a . Vì
2
a
nên
2 2
cos
3
a . Chọn B.
Câu 29: Ta có
5
cos cos
5
x x
;
6
cos cos
5 5
x x
;
2 7
cos cos
5 5
x x
;…
Vậy
2 9
cos cos cos ... cos 0
5 5 5
x x x x
. Chọn C.
Câu 30: Diện tích tam giác
ABC
được tính bằng công thức
1
sin
2
S ab C
. Do
o o
0 180
C
nên
0 sin 1
C
. Vậy diện tích lớn nhất khi
sin 1
C
hay
o
ˆ
90
C . Chọn B.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 31: Bất phương trình
3
1
2 2 1 2 3
1 3
3
x
x x x x
x
. Chọn A.
Câu 32: Gọi cạnh của tam giác đều là
a
, ta có
o
2sin60
3
a a
R
, suy ra
3 4 3
a R . Diện tích
3
3
4 3
12 3
4 4.4
a
S
R
. Chọn C.
Câu 33: Hệ bất phương trình
3 4
1
x
x m
. Để hệ có nghiệm thì
1 3 2
m m
. Chọn B.
Câu 34: Xét phương án B:
2 2
2 0
x y x y
, có
1
2
a b
và
2
c
. Phương trình này không thỏa
điều kiện
2 2
0
a b c
nên không là phương trình đường tròn. Chọn B.
Câu 35: Vì
cos 0
, chia cả tử và mẫu của biểu thức cho
2
cos
, ta được
2
tan 15
tan 1 16
A
. Chọn
A.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 08
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Tìm tất cả các giá trị của
x
để biểu thức
6 2
x
dương
A.
;3
x . B.
3;x
. C.
;6
x . D.
6;x
.
Câu 2. Cho
2
f x ax bx c
với
0
a
. Chọn mệnh đề đúng
A.
0
0,
0
a
f x x
. B.
0
0,
0
a
f x x
.
C.
0
0,
0
a
f x x
. D.
0
0,
0
a
f x x
.
Câu 3. Rút gọn biểu thức
2sin4
cos3 cos
x
x x
ta được biểu thức có dạng
sin 2
cos
a x
b x
. Giá trị của
2
a b
bằng
A.
2
. B.
5
. C.
5
. D.
3
.
Câu 4. Bất phương trình
2
5 2 0
x x x
có tập nghiệm là
A.
2;1 5;
. B.
; 2 1;5
. C.
; 2 1;5
. D.
2; 1 5;
.
Câu 5. Cho
1
cos
5
. Tính
2
sin
A.
2
24
sin
25
. B.
2
4
sin
5
. C.
2
25
sin
24
. D.
2
5
sin
4
.
Câu 6. Trong mặt phẳng
Oxy
, đường tròn
2 2
: 1 5 16
C x y
có tọa độ tâm
I
và bán kính
R
là:
A.
1;5 , 16
I R
. B.
1; 5 , 4
I R
. C.
1; 5 , 16
I R
. D.
1;5 , 4
I R
.
Câu 7. Hỏi
2
x
không là nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
A.
2
4 3 0
x x
. B.
2
4 3 0
x x
. C.
2 0
x
. D.
2 0
x
.
Câu 8. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
4 sin
K x
. Giá trị của
.
M m
bằng:
A.
. 15
M m
. B.
. 4
M m
. C.
. 15
M m
. D.
. 16
M m
.
Câu 9. Tập nghiệm của bất phương trình
1 2
x x
là:
A.
1
;
3
. B.
1
;2
3
. C.
1
;1
3
. D.
3;1
.
Câu 10. Phần không bị gạch (không thuộc đường thẳng d) trong hình sau đây là miền nghiệm của bất
phương trình nào?
A.
4 0
x y
. B.
2 4 0
x y
. C.
2 4 0
x y
. D.
4 0
x y
.
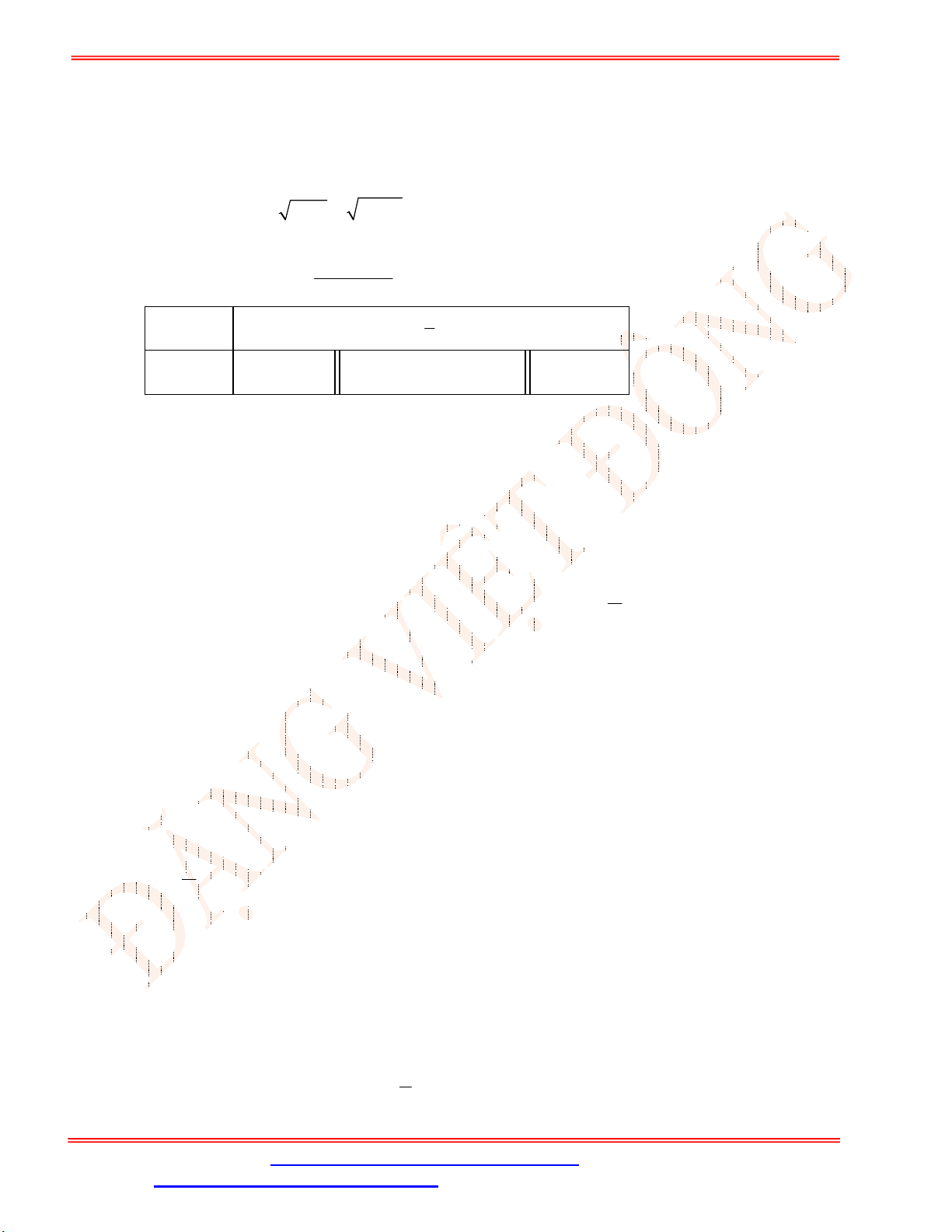
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 11. Cặp số nào sau đây là nghiệm của hệ bất phương trình
4 0
0
0
x y
x y
y
.
A.
5;3
. B.
1;1
. C.
4;4
. D.
2;1
.
Câu 12. Bất phương trình
2
7 5
x x
có cung tập nghiệm với bất phương trình
A.
2
12 0
x x
. B.
2
2 0
x x
. C.
2
2 0
x x
. D.
2
5 0
x x
.
Câu 13. Cho biểu thức
2
2 3 1
2
x x
f x
x x
có bảng xét dấu như sau:
x
f x
0
1
3
2
0
?
?
?
?
Xác định dấu trong các dấu hỏi theo thứ tự từ trái sang phải ?
A.
, , ,
. B.
, , ,
. C.
, , ,
. D.
, , ,
.
Câu 14. Bất phương trình
2
5 6 0
x x
có nghiệm là
A.
2
3
x
x
. B.
2 3
x
. C.
1
6
x
x
. D.
1 6
x
.
Câu 15. Tìm tất cả giá trị
m
để bất phương trình
2 2
2 1 3 0
x m x m
nghiệm đúng x
.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Câu 16. Cho
cos 0,7
. Tính giá trị của biểu thức
cos sin
2
P
bằng.
A.
0,7
P
. B.
0,49
P
. C.
0
P
. D.
0,14
P
.
Câu 17. Hệ bất phương trình
2
9 0
3 0
x
x
có nghiệm là
A.
3
x
. B.
3 3
x
. C.
3 3
x
. D.
3
x
.
Câu 18. Trong mặt phẳng
Oxy
tọa độ giao điểm của hai đường thẳng
: 2 3 0
x y
và
3
:
x t
d
y t
là
A.
0;3
. B.
2;1
. C.
2; 1
. D.
3;0
.
Câu 19. Cho
2
. Chọn khẳng định đúng:
A.
sin 0
. B.
tan 0
. C.
cos 0
. D.
cos 0
.
Câu 20. Cho hai số thực
a
và
b
. Chọn mệnh đề sai?
A.
2 2
a b a b
. B.
2 2
a b a b
.
C.
2 2
a b a b
. D.
2 2
a b a b
.
Câu 21. Chọn mệnh đề sai
A.
sin 2 2sin cos
x x x
. B.
2
cos 2 2cos 1
x x
.
C.
2 2
cos2 cos sin
x x x
. D.
2
cos2 2sin 1
x x
.
Câu 22. Giá trị nhỏ nhất của biểu thức
1
a
a
với
0
a
bằng
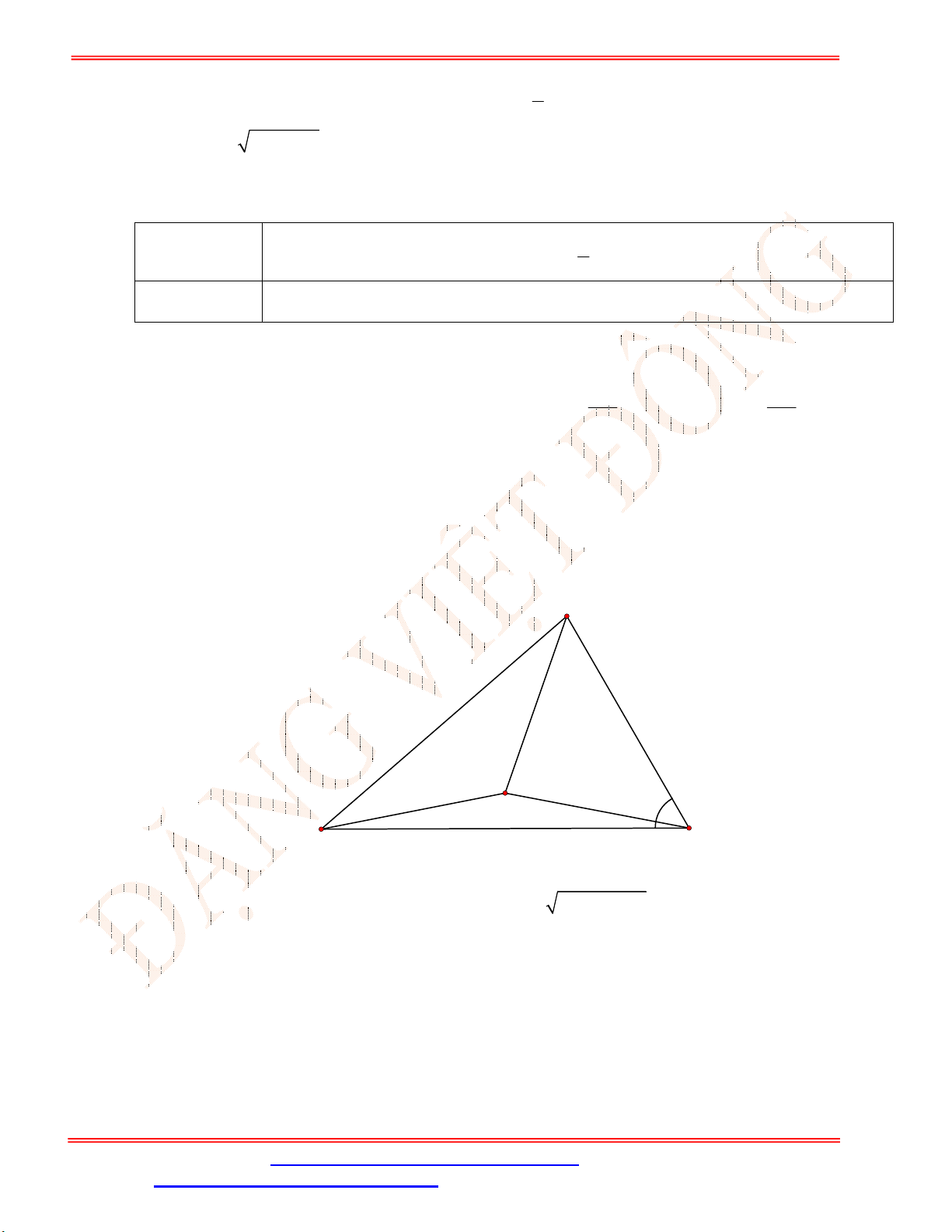
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
4
. B.
2
. C.
1
2
. D.
1
.
Câu 23. Hàm số
2
3
y x x
có tập xác định là
A.
;0
. B.
. C.
. D.
0;
.
Câu 24. Bảng xét dấu sau đây là của biểu thức
f x
nào?
x
3
2
f x
0
A.
2 3
f x x
. B.
3 2
f x x
. C.
3 2
f x x
. D.
2 3
f x x
.
Câu 25. Cho tam giác
ABC
vuông tại
A
có diện tích
S
. Chọn mệnh đề sai.
A.
2 2 2
BC AB AC
. B.
2 .
S AB AC
. C. sin
AC
B
BC
. D. cos
AC
B
BC
.
Câu 26. Khoảng cách từ nhà ông A đến nhà ông C bằng
50m,
AC
từ nhà ông B đến nhà ông C bằng
80m,
BC
góc tạo bởi đường thẳng
AB
và
BC
bằng
60
(như hình vẽ). Cả ba nhà muốn khoan
một cái giếng có đặt môtơ, vì muốn lực đẩy nước đến ba nhà như nhau nên họ quyết định đặt môtơ
ở vị trí
W
cách đều ba nhà
,
WA WB WC
rồi nối ống dẫn nước từ vị trí
W
về đến từng nhà,
chi phí lắp đặt
1m
ống dẫn nước là
25000
đồng. Chi phí mỗi nhà phải trả để lắp đặt đường ống
dẫn nước là (làm tròn đến hàng trăm)
60
Cái giêng W
Nhà ông A
Nhà ông B
Nhà ông C
A.
1120400
đồng B.
1050700
đồng C.
1020300
đồng D.
1010400
đồng
Câu 27. Số nghiệm nguyên của bất phương trình
2 2
2 2 3 6 4 0
x x x x
là
A.
3
B.
4
C.
2
D.
1
Câu 28. Trong mặt phẳng
Oxy
cho đường thẳng
: 2 3 0.
x y
Chọn mệnh đề sai
A. Một vectơ pháp tuyến của
là
1;2 .
n
B. Một vectơ chỉ phương của
là
2; 1 .
a
C. Một vectơ chỉ phương của
là
2;1 .
a
D. Một vectơ pháp tuyến của
là
1;2 .
n

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 29. Hệ bất phương trình
2 5 0
3 2 0
x
x
có tập nghiệm là
A.
5 3
;
2 2
B.
3
;
2
C.
5
;
2
D.
5 3
;
2 2
Câu 30. Cho
cos
2
.
cos 3
Tính
tan .tan .
B
A.
4
5
B.
1
5
C.
1
5
D.
2
5
Câu 31. Chọn mệnh đề đúng
A.
tan .cos 1
x x
. B.
2
2
1
1 tan
sin
x
x
. C.
2
2
1
1 cot
cos
x
x
. D.
2 2
cos 1 sin
x x
.
Câu 32. Trong mặt phẳng
Oxy
cho đường tròn
C
tâm
2; 3
I
, bán kính
10
R
và đường thẳng
: 3 0
d x y m
(với
m
là tham số). Tìm
m
để
d
tiếp xúc với
C
.
A.
1
25
m
m
. B.
3
17
m
m
. C.
2
18
m
m
. D.
1
21
m
m
.
Câu 33. Trong mặt phẳng
Oxy
cho
1;2
A và
5;0
B . Đường tròn
C
có đường kính
AB
có phương
trình là
A.
2 2
2 1 10
x y
. B.
2 2
2 1 10
x y
.
C.
2 2
2 1 40
x y
. D.
2 2
2 1 40
x y
.
Câu 34. Trong mặt phẳng
Oxy
, đường thẳng đi qua
2; 4
A
và nhận
4;3
u
là vec-tơ chỉ phương có
phương trình tham số là
A.
2 4
4 3
x t
y t
. B.
2 4
4 3
x y
. C.
4 2
3 4
x t
y t
. D.
2 4
4 3
x t
y t
.
Câu 35. Trong mặt phẳng
Oxy
cho hình chữ nhật
ABCD
có tâm
2; 4
I
, phương trình cạnh
: 2 5 0
CD x y
, phương trình cạnh
: 2 1 0
BC x y
. Diện tích
S
của hình chữ nhật
ABCD
bằng
A.
44
S
. B.
22
S
. C.
11
S
. D.
88
S
.
II - PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 1: (0,5 điểm) Giải bất phương trình:
2
5 6
0
2 3
x x
x
.
Câu 2: (0,5 điểm) Tính giá trị của biểu thức:
2
2cos 1
sin cos
x
A
x x
biết
3
cos sin
2
x x .
Câu 3: (2,0 điểm) Trong mặt phẳng với hệ tọa độ
Oxy
cho hai điểm
1; 3
A
,
2;1
B và đường thẳng
d
:
10 5
x t
y t
(
t
).
a) Viết phương trình tham số của đường thẳng
AB
?
b) Viết phương trình tổng quát của đường thẳng
đi qua
B
và vuông góc với đường thẳng
d
?
c) Viết phương trình đường tròn
C
tâm
A
tiếp xúc với trục hoành?
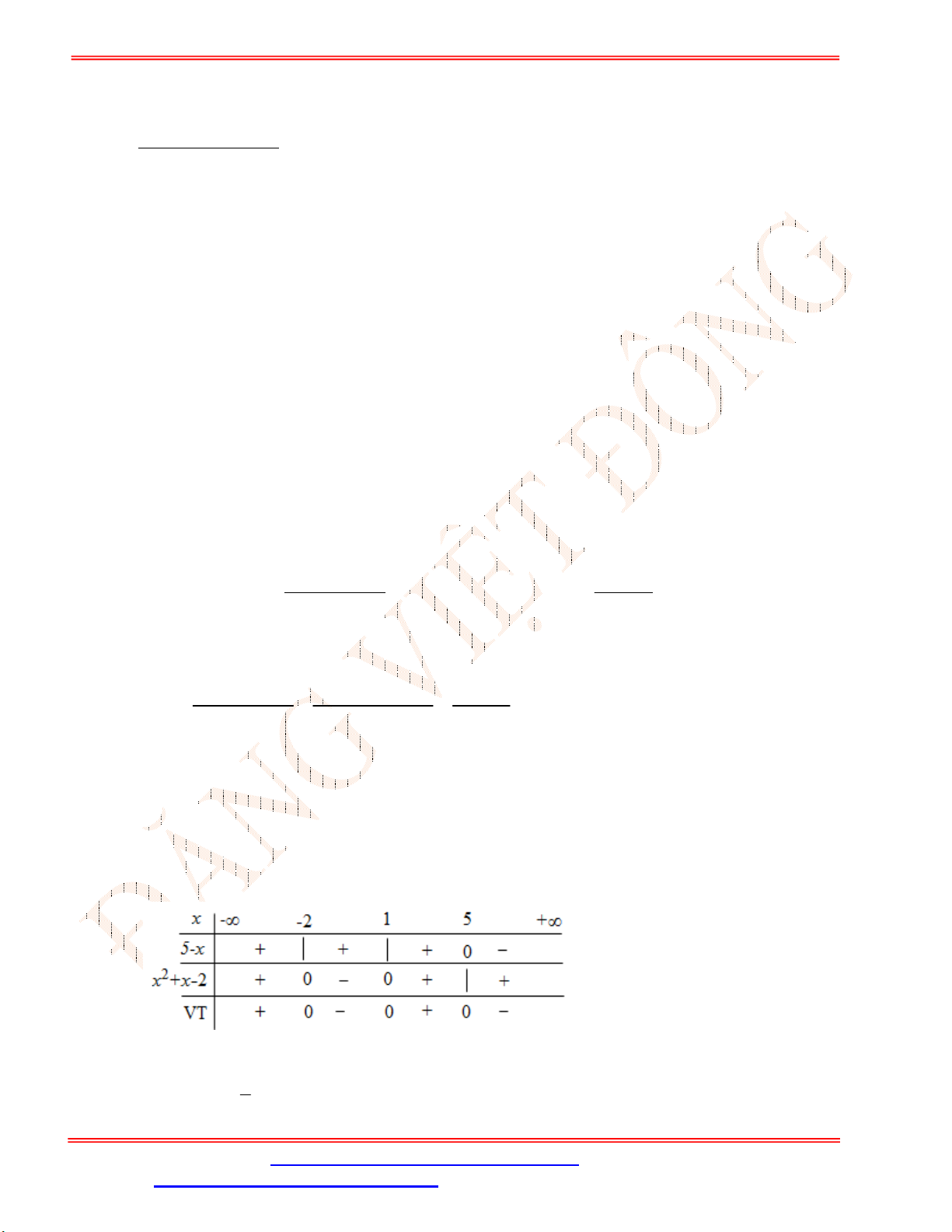
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 08
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I - PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1. Tìm tất cả các giá trị của
x
để biểu thức
6 2
x
dương
A.
;3
x . B.
3;x
. C.
;6
x . D.
6;x
.
Lời giải
Chọn A.
Ta có
6 2 0 2 6 3
x x x
.
Vậy
;3
x .
Câu 2. Cho
2
f x ax bx c
với
0
a
. Chọn mệnh đề đúng
A.
0
0,
0
a
f x x
. B.
0
0,
0
a
f x x
.
C.
0
0,
0
a
f x x
. D.
0
0,
0
a
f x x
.
Lời giải
Chọn C.
Câu 3. Rút gọn biểu thức
2sin4
cos3 cos
x
x x
ta được biểu thức có dạng
sin 2
cos
a x
b x
. Giá trị của
2
a b
bằng
A.
2
. B.
5
. C.
5
. D.
3
.
Lời giải
Chọn C.
Ta có
2sin4 2.2sin 2 cos2 2sin 2
cos3 cos 2cos2 cos cos
x x x x
x x x x x
(với điều kiện biểu thức có nghĩa).
Do đó
2
a
,
1
b
2
5
a b
.
Câu 4. Bất phương trình
2
5 2 0
x x x
có tập nghiệm là
A.
2;1 5;
. B.
; 2 1;5
. C.
; 2 1;5
. D.
2; 1 5;
.
Lời giải
Chọn C.
Lập bảng xét dấu vế trái
Từ bảng biến thiên suy ra tập nghiệm của bất phương trình là
; 2 1;5
.
Câu 5. Cho
1
cos
5
. Tính
2
sin

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2
24
sin
25
. B.
2
4
sin
5
. C.
2
25
sin
24
. D.
2
5
sin
4
.
Lời giải
Chọn A.
2
2 2
1 24
sin 1 cos 1
5 25
.
Câu 6. Trong mặt phẳng
Oxy
, đường tròn
2 2
: 1 5 16
C x y
có tọa độ tâm
I
và bán kính
R
là:
A.
1;5 , 16
I R
. B.
1; 5 , 4
I R
. C.
1; 5 , 16
I R
. D.
1;5 , 4
I R
.
Lời giải
Chọn B.
Ta có
1; 5 , 4
I R
.
Câu 7. Hỏi
2
x
không là nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
A.
2
4 3 0
x x
. B.
2
4 3 0
x x
. C.
2 0
x
. D.
2 0
x
.
Lời giải
Chọn D.
Thế
2
x
vào bất phương trình
2 0
x
không thỏa mãn.
Câu 8. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
4 sin
K x
. Giá trị của
.
M m
bằng:
A.
. 15
M m
. B.
. 4
M m
. C.
. 15
M m
. D.
. 16
M m
.
Lời giải
Chọn C.
Vì
1 sin 1
x
nên
3 4 sin 5
K x
Vậy
5
M
và
3
m
.
Câu 9. Tập nghiệm của bất phương trình
1 2
x x
là:
A.
1
;
3
. B.
1
;2
3
. C.
1
;1
3
. D.
3;1
.
Lời giải
Chọn C.
2 2
1 2 1 2
x x x x
2 2 2
2 1 4 3 2 1 0
x x x x x
1
1
3
x
.
Câu 10. Phần không bị gạch (không thuộc đường thẳng d) trong hình sau đây là miền nghiệm của bất
phương trình nào?
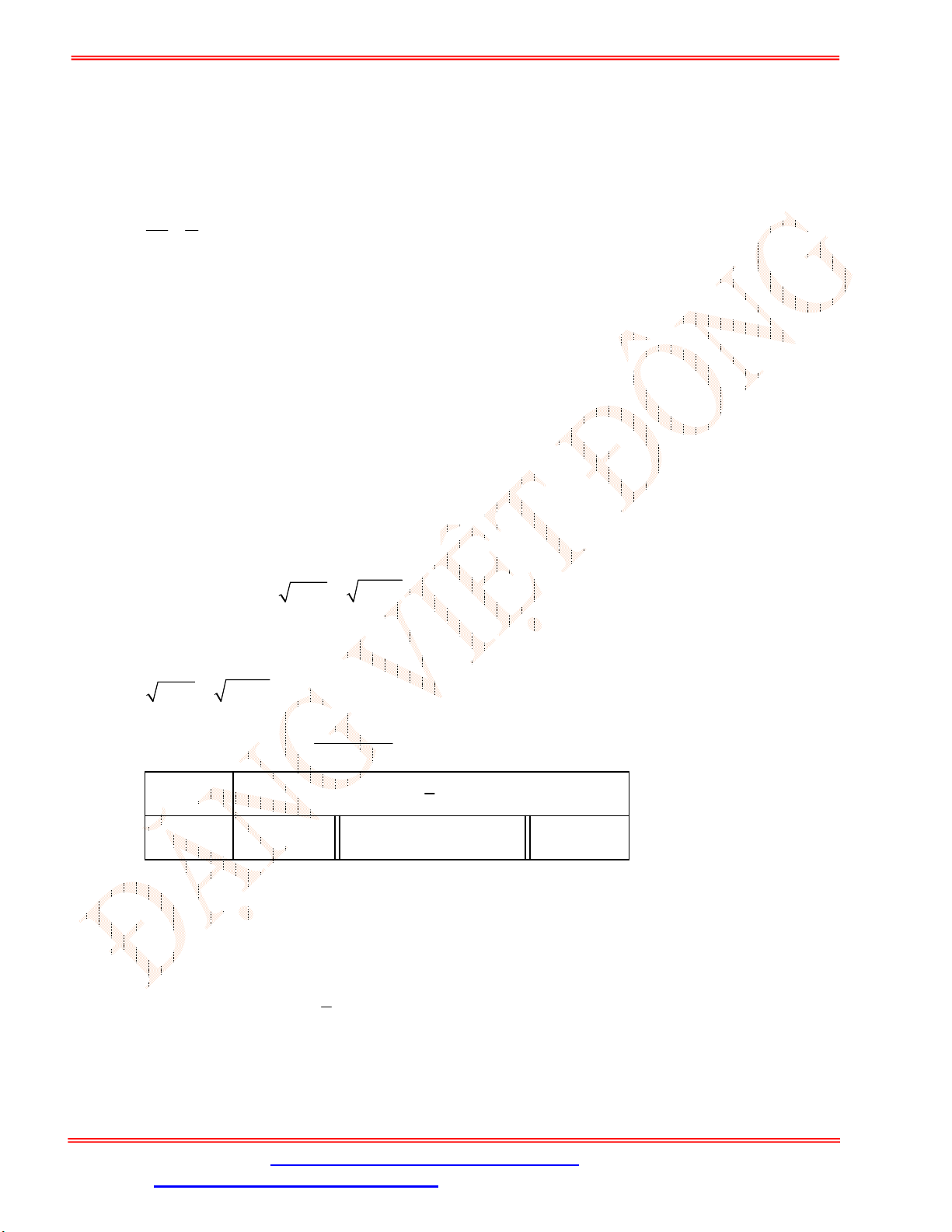
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
4 0
x y
. B.
2 4 0
x y
. C.
2 4 0
x y
. D.
4 0
x y
.
Lời giải
Chọn B.
Đường thẳng
d
đi qua hai điểm có tọa độ lần lượt là
4;0
và
0;2
nên phương trình
d
là:
1
4 2
x y
2 4 0
x y
.
Điểm
0;0
O
thuộc miền bị gạch
0 2.0 4 0
nên phần không bị gạch là miền nghiệm của bất
phương trình
2 4 0
x y
.
Câu 11. Cặp số nào sau đây là nghiệm của hệ bất phương trình
4 0
0
0
x y
x y
y
.
A.
5;3
. B.
1;1
. C.
4;4
. D.
2;1
.
Lời giải
Chọn D.
Cặp số
2;1
là nghiệm của hệ bất phương trình do
2 1 4 0
2 1 0
1 0
đúng.
Câu 12. Bất phương trình
2
7 5
x x
có cung tập nghiệm với bất phương trình
A.
2
12 0
x x
. B.
2
2 0
x x
. C.
2
2 0
x x
. D.
2
5 0
x x
.
Lời giải
Chọn C.
2 2 2
7 5 7 5 2 0
x x x x x x
.
Câu 13. Cho biểu thức
2
2 3 1
2
x x
f x
x x
có bảng xét dấu như sau:
x
f x
0
1
3
2
0
?
?
?
?
Xác định dấu trong các dấu hỏi theo thứ tự từ trái sang phải ?
A.
, , ,
. B.
, , ,
. C.
, , ,
. D.
, , ,
.
Lời giải
Chọn B.
Ta có:
2 0 0
x x
1
3 1 0
3
x x
2
0
2 0
2
x
x x
x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
0
x
là nghiệm bội chẵn,
1
2;
3
x x
là nghiệm bội lẻ
Bảng xét dấu :
x
f x
0
1
3
2
0
Câu 14. Bất phương trình
2
5 6 0
x x
có nghiệm là
A.
2
3
x
x
. B.
2 3
x
. C.
1
6
x
x
. D.
1 6
x
.
Lời giải
Chọn B.
Ta có:
2
2
5 6 0
3
x
x x
x
Bảng xét dấu :
x
f x
0
2
3
0
Dựa vào bảng xét dấu, ta có :
2
5 6 0
x x
2 3
x
.
Câu 15. Tìm tất cả giá trị
m
để bất phương trình
2 2
2 1 3 0
x m x m
nghiệm đúng x
.
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Lời giải
Chọn C.
Ta có :
2 2
2 1 3 0
x m x m
2
2
1 0
0
0
1 3 0
a
x
m m
2 4 0 2
m m
.
Câu 16. Cho
cos 0,7
. Tính giá trị của biểu thức
cos sin
2
P
bằng.
A.
0,7
P
. B.
0,49
P
. C.
0
P
. D.
0,14
P
.
Lời giải
Chọn B.
Ta có
cos sin
2
P
2
cos .cos (0,7)
0,49
.
Câu 17. Hệ bất phương trình
2
9 0
3 0
x
x
có nghiệm là
A.
3
x
. B.
3 3
x
. C.
3 3
x
. D.
3
x
.
Lời giải
Chọn C.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
2
3 3
9 0
3
3 0
x
x
x
x
3 3
x
.
Câu 18. Trong mặt phẳng
Oxy
tọa độ giao điểm của hai đường thẳng
: 2 3 0
x y
và
3
:
x t
d
y t
là
A.
0;3
. B.
2;1
. C.
2; 1
. D.
3;0
.
Lời giải
Chọn C.
Tọa độ giao điểm của
và
d
là nghiệm của hệ
2 3 0 6 2 3 0
3 3
x y t t
x t x t
y t y t
1
2
1
t
x
y
.
Câu 19. Cho
2
. Chọn khẳng định đúng:
A.
sin 0
. B.
tan 0
. C.
cos 0
. D.
cos 0
.
Lời giải
Chọn D.
Vì
2
nên
cos 0
.
Câu 20. Cho hai số thực
a
và
b
. Chọn mệnh đề sai?
A.
2 2
a b a b
. B.
2 2
a b a b
.
C.
2 2
a b a b
. D.
2 2
a b a b
.
Lời giải
Chọn A.
Ta có
2 2
a b a b
sai chẳng hạn:
2 1 2 2 2 1
(vô lý).
Câu 21. Chọn mệnh đề sai
A.
sin 2 2sin cos
x x x
. B.
2
cos 2 2cos 1
x x
.
C.
2 2
cos2 cos sin
x x x
. D.
2
cos2 2sin 1
x x
.
Lời giải
Chọn D.
2
cos2 1 2sin
x x
.
Câu 22. Giá trị nhỏ nhất của biểu thức
1
a
a
với
0
a
bằng
A.
4
. B.
2
. C.
1
2
. D.
1
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn B.
Áp dụng BĐT Cauchy – Schwarz cho hai số
a
và
1
a
:
1 1
2 .
a a
a a
1
2
a
a
.
Vậy giá trị nhỏ nhất của biểu thức
1
a
a
bằng
2
khi
1
a
.
Câu 23. Hàm số
2
3
y x x
có tập xác định là
A.
;0
. B.
. C.
. D.
0;
.
Lời giải
Chọn C.
Ta có
2
2
1 11
3 0
2 4
x x x
x
.
Vậy tập xác định của hàm số là
D
.
Câu 24. Bảng xét dấu sau đây là của biểu thức
f x
nào?
x
3
2
f x
0
A.
2 3
f x x
. B.
3 2
f x x
. C.
3 2
f x x
. D.
2 3
f x x
.
Lời giải
Chọn A.
Hàm số có dạng
f x ax b
có
0
a
và nhận
3
2
làm nghiệm nên
2 3
f x x
.
Câu 25. Cho tam giác
ABC
vuông tại
A
có diện tích
S
. Chọn mệnh đề sai.
A.
2 2 2
BC AB AC
. B.
2 .
S AB AC
. C. sin
AC
B
BC
. D. cos
AC
B
BC
.
Lời giải
Chọn D.
cos
AB
B
BC
.
Câu 26. Khoảng cách từ nhà ông A đến nhà ông C bằng
50m,
AC
từ nhà ông B đến nhà ông C bằng
80m,
BC
góc tạo bởi đường thẳng
AB
và
BC
bằng
60
(như hình vẽ). Cả ba nhà muốn khoan
một cái giếng có đặt môtơ, vì muốn lực đẩy nước đến ba nhà như nhau nên họ quyết định đặt môtơ
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ở vị trí
W
cách đều ba nhà
,
WA WB WC
rồi nối ống dẫn nước từ vị trí
W
về đến từng nhà,
chi phí lắp đặt
1m
ống dẫn nước là
25000
đồng. Chi phí mỗi nhà phải trả để lắp đặt đường ống
dẫn nước là (làm tròn đến hàng trăm)
60
Cái giêng W
Nhà ông A
Nhà ông B
Nhà ông C
A.
1120400
đồng B.
1050700
đồng C.
1020300
đồng D.
1010400
đồng
Lời giải
Chọn D
Do vị trí cái giếng cách đều ba nhà ông A, ông B, ông C nên vị trí cái giếng là tâm đường tròn
ngoại tiếp tam giác
ABC
Do đó đoạn đường về nhà ba ông bằng bán kính đường tròn ngoại tiếp
Ta có
2 2 2
2 . .cos60 4900 70.
AC BC BA BC BA AC
Khi đó
70
2sin60
3
AC
WA
Vậy số tiền mỗi nhà cần là:
70
25000. 1010400
3
đồng
Câu 27. Số nghiệm nguyên của bất phương trình
2 2
2 2 3 6 4 0
x x x x
là
A.
3
B.
4
C.
2
D.
1
Lời giải
Chọn A
Điều kiện:
2
3 6 4 0
x x
(luôn đúng)
Đặt
2
3 6 4, 0
t x x t
ta được bất phương trình
2
1 10
0 5 2 0 2
3 3
t t t t
Khi đó ta có
2 2
3 6 4 2 3 6 0 2 0
x x x x x
Các nghiệm nguyên là
2; 1;0
S
Câu 28. Trong mặt phẳng
Oxy
cho đường thẳng
: 2 3 0.
x y
Chọn mệnh đề sai
A. Một vectơ pháp tuyến của
là
1;2 .
n
B. Một vectơ chỉ phương của
là
2; 1 .
a
C. Một vectơ chỉ phương của
là
2;1 .
a
D. Một vectơ pháp tuyến của
là
1;2 .
n

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Câu 29. Hệ bất phương trình
2 5 0
3 2 0
x
x
có tập nghiệm là
A.
5 3
;
2 2
B.
3
;
2
C.
5
;
2
D.
5 3
;
2 2
Lời giải
Chọn B
Hệ bất phương trình
5
2 5 0
3
2
3 2 0 3
2
2
x
x
x
x
x
Vậy hệ bất phương trình có tập nghiệm là
3
;
2
Câu 30. Cho
cos
2
.
cos 3
Tính
tan .tan .
B
A.
4
5
B.
1
5
C.
1
5
D.
2
5
Lời giải
Chọn B
Ta có
cos
2 cos .cos sin .sin 2 1 tan .tan 2
cos 3 cos .cos sin .sin 3 1 tan .tan 3
1
3 3tan .tan 2 2tan .tan tan .tan
5
Câu 31. Chọn mệnh đề đúng
A.
tan .cos 1
x x
. B.
2
2
1
1 tan
sin
x
x
. C.
2
2
1
1 cot
cos
x
x
. D.
2 2
cos 1 sin
x x
.
Lời giải
Chọn D.
Ta có
2 2
cos sin 1
x x
2 2
cos 1 sin
x x
.
Câu 32. Trong mặt phẳng
Oxy
cho đường tròn
C
tâm
2; 3
I
, bán kính
10
R
và đường thẳng
: 3 0
d x y m
(với
m
là tham số). Tìm
m
để
d
tiếp xúc với
C
.
A.
1
25
m
m
. B.
3
17
m
m
. C.
2
18
m
m
. D.
1
21
m
m
.
Lời giải
Chọn D.
Điều kiện để
d
tiếp xúc với
C
là
,
d I d R
2 9
10
1 9
m
11 10
m
11 10
11 10
m
m
1
21
m
m
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 33. Trong mặt phẳng
Oxy
cho
1;2
A và
5;0
B . Đường tròn
C
có đường kính
AB
có phương
trình là
A.
2 2
2 1 10
x y
. B.
2 2
2 1 10
x y
.
C.
2 2
2 1 40
x y
. D.
2 2
2 1 40
x y
.
Lời giải
Chọn A.
Trung điểm
2;1
I của đoạn thẳng
AB
là tâm và
1
2
R AB
10
là bán kính của đường tròn
C
. Do đó phương trình đường tròn
C
là
2 2
2 1 10
x y
.
Câu 34. Trong mặt phẳng
Oxy
, đường thẳng đi qua
2; 4
A
và nhận
4;3
u
là vec-tơ chỉ phương có
phương trình tham số là
A.
2 4
4 3
x t
y t
. B.
2 4
4 3
x y
. C.
4 2
3 4
x t
y t
. D.
2 4
4 3
x t
y t
.
Lời giải
Chọn D.
Đường thẳng đi qua
2; 4
A
và nhận
4;3
u
làm vec-tơ chỉ phương nên PTTS là:
2 4
4 3
x t
y t
.
Câu 35. Trong mặt phẳng
Oxy
cho hình chữ nhật
ABCD
có tâm
2; 4
I
, phương trình cạnh
: 2 5 0
CD x y
, phương trình cạnh
: 2 1 0
BC x y
. Diện tích
S
của hình chữ nhật
ABCD
bằng
A.
44
S
. B.
22
S
. C.
11
S
. D.
88
S
.
Lời giải
Chọn A.
F
E
I
B
D
A
C
Gọi
E
và
F
lần lượt là trung điểm
CD
và
BC
2
AD IE
2 ;
d I CD
4 4 5
2.
4 1
2 5
.
2
CD IF
2 ,
d I BC
2 8 1
2.
1 4
22
5
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Suy ra
.
S AD CD
22
2 5.
5
44
.
II - PHẦN TỰ LUẬN (3 ĐIỂM)
Câu 1: (0,5 điểm) Giải bất phương trình:
2
5 6
0
2 3
x x
x
.
Câu 2: (0,5 điểm) Tính giá trị của biểu thức:
2
2cos 1
sin cos
x
A
x x
biết
3
cos sin
2
x x .
Câu 3: (2,0 điểm) Trong mặt phẳng với hệ tọa độ
Oxy
cho hai điểm
1; 3
A
,
2;1
B và đường thẳng
d
:
10 5
x t
y t
(
t
).
a) Viết phương trình tham số của đường thẳng
AB
?
b) Viết phương trình tổng quát của đường thẳng
đi qua
B
và vuông góc với đường thẳng
d
?
c) Viết phương trình đường tròn
C
tâm
A
tiếp xúc với trục hoành?
Lời giải
Câu 1: Đặt
2
5 6
2 3
x x
VT
x
Cho:
2
5 6 0 1
x x x
hoặc
6
5
x
.
2
2 3 0
3
x x
.
Bảng xét dấu:
x
1
2
3
6
5
VT
+
0
-
+
0
-
Vì
0
VT
nên
2 6
1; ;
3 5
x
.
Câu 2: Ta có:
2 2 2
sin cos cos sin
2cos 1 cos sin
cos sin
sin cos sin cos sin cos
x x x x
x x x
A x x
x x x x x x
.
Mà
3
cos sin
2
x x nên
3
2
A .
Câu 3:
a) Ta có:
1;4
AB VTCP
1;4
AB
u
.
Phương trình đường thẳng
AB
đi qua
1; 3
A
và
1;4
AB
VTCPu
:
AB
:
1
3 4
x t
y t
(
t
).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
b) Ta có:
d
:
10 5
x t
VTCP
y t
1;5
d
u
.
Vì
d
nên
VTCP
d
u
VTPT
1;5
n
.
Phương trình tổng quát đường thẳng
đi qua
2;1
B và
VTPT
1;5
n
:
:
1 2 5 1 0 5 7 0
x y x y
.
c) Ta có
Ox
:
0
y
.
Vì
C
tiếp xúc
Ox
nên bán kính của
C
là:
1.0 3.1
, 3
1
R d A Ox
.
Vậy phương trình đường tròn
C
có tâm
1; 3
A
và bán kính
3
R
:
C
:
2 2
1 3 9
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 09
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Trong mặt phẳng
Oxy
, cho hai đường thẳng
1 2
,
d d
lần lượt có phương trình tổng quát
7 13 1 0
x y
và
7 13 2 0
x y
. Xác định vị trí tương đối của hai đường thẳng
1 2
,
d d
A. Song song. B. Vuông góc. C. Cắt nhau. D. Trùng nhau.
Câu 2. Mệnh đề nào sau đây sai?
A.
0
1
360
rad
.
B.
0
1
180
rad
.
C. Trên đường tròn định hướng có vô số cung lượng giác có điểm đầu là
A
, điểm cuối là
B
.
D. Cung có số đó
rad
của đường tròn bán kính
R
có độ dài là
l R
.
Câu 3. Cho biểu thức
3
2sin sin 5 sin cos
2 2 2
A
với
,
5
k
k
thì
biểu thức
A
nhận bao nhiêu giá trị khác nhau.
A.
4
. B.
10
. C.
8
. D.
6
.
Câu 4. Cho bảng phân bố tần số: Tiền thưởng (triệu đồng) cho cán bộ công nhân viên của một công ty.
Tiền thưởng
2
3
4
5
6
Cộng
Tần số
5
15
10
6
7
43
Độ lệch chuẩn gần nhất với kết quả nào sau đây ?
A.
1,26
. B.
1,38
. C.
1,615
. D.
1,57
.
Câu 5. Trong mặt phẳng
Oxy
, cho đường thẳng
2 3
:
3 4
x t
d
y t
. Tìm tọa độ một vectơ chỉ phương của
d
.
A.
3; 4
. B.
4;3
. C.
4; 3
. D.
3;4
.
Câu 6. Cho
0
x
,
0
y
. Tìm giá trị lớn nhất của biểu thức
2 2
1 1
x y
P
x y
.
A.
1
2
M
. B.
1
4
M
. C.
1
M
. D.
2
M
.
Câu 7. Trên đường tròn lượng giác gốc
1;0
A cho cung lượng giác điểm đầu
A
và điểm cuối là
M
có
số đo
0
2
. Gọi
1
M
là điểm đối xứng của
M
qua gốc tọa độ
O
. Tìm số đo của cung
lượng giác có điểm đầu là
A
và điểm cuối là
1
M
.
A.
2
k
. B.
1 2
k
. C.
180
. D.
k
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 8. Trong mặt phẳng
Oxy
, cho elip
2 2
: 1
4 1
x y
E
và điểm
2;0
C . Có hai điểm
A
,
B
thuộc
E
thỏa mãn
A
,
B
đối xứng nhau qua trục hoành và tam giác
ABC
là tam giác đều. Tính độ dài đoạn
thẳng
AB
.
A.
3
. B.
2
. C.
8 3
5
. D.
8 3
7
.
Câu 9. Biết
3
;2
2
và
3
tan
7
. Tính giá trị biểu thức
cos sin
2 2
P
.
A.
1
4
P
. B.
1
4
P
. C.
1
2
P
. D.
1
2
P
.
Câu 10. Trong mặt phẳng
Oxy
, cho Elip
E
có một đỉnh trên trục lớn
3;0
A và một tiêu điểm là
2;0
F . Viết phương trình chính tắc của Elip
E
.
A.
2 2
1
9 4
x y
. B.
2 2
1
3 2
x y
. C.
2 2
1
5 9
x y
. D.
2 2
1
9 5
x y
.
Câu 11. Bất phương trình
f x a
với
0
a
tương đương với bất phương trình nào?
A.
f x a
. B.
f x a
hoặc
f x a
.
C.
a f x a
. D.
f x a
.
Câu 12. Tính tổng các nghiệm nguyên dương của bất phương trình
2
2
10
10
100
x
x
.
A.
40
. B.
0
. C.
45
. D.
9
.
Câu 13. Xác định mệnh đề đúng.
A.
3
sin3 3sin 4sin
a a a
. B.
3
sin3 4cos 3sin
a a a
.
C.
3
sin3 3sin 4cos
a a a
. D.
3
sin3 4sin 3sin
a a a
.
Câu 14. Trong mặt phẳng
Oxy
, tìm tọa độ tâm
I
và bán kính
R
của đường tròn có phương trình
2 2
1 2 4
x y
.
A. Tâm
1;2
I , bán kính
4
R
. B. Tâm
1;2
I , bán kính
2
R
.
C. Tâm
1; 2
I
, bán kính
4
R
. D. Tâm
1; 2
I
, bán kính
2
R
.
Câu 15. Cho biết
1
cos
3
a
,
1
cos
4
b
. Tính giá trị của biểu thức
cos cos
P a b a b
.
A.
119
144
P
. B.
263
144
P
. C.
11
14
P
. D.
119
144
P
.
Câu 16. Cho
7
4 .
2
Xác định mệnh đề đúng.
A.
2
1
tan 1
cos
B.
2
1
tan 1
sin
C.
2
1
tan 1
sin
D.
2
1
tan 1
cos
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2
2 3 0
mx mx
có tập nghiệm
bằng
.
A.
4
B.
2
C.
0
D.
3

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 18. Trong mặt phẳng
,
Oxy
cho đường tròn
2 2
: 4 4 6 0
C x y x y
và đường thẳng
: 2 3 0
d x my m
với
m
là tham số thực. Gọi
I
là tâm đường tròn
.
C
Tính tổng các giá trị
thực của tham số
m
tìm được để đường thẳng
d
cắt đường tròn
C
tại hai điểm phân biệt
,
A B
sao cho diện tích tam giác
ABI
lớn nhất.
A.
4
B.
0
C.
15
8
D.
8
15
Câu 19. Trong mặt phẳng
,
Oxy
cho elip
E
có phương trình chính tắc
2 2
1.
25 9
x y
Tính tỉ số giữa tiêu cự
và độ dài trục lớn elip
.
E
A.
5
3
B.
3
5
C.
4
5
D.
4
5
Câu 20. Trong mặt phẳng
,
Oxy
cho hình chữ nhật
ABCD
có điểm
6;2
I là giao điểm của hai đường
chéo
, .
AC BD
Điểm
1;5
M thuộc
AB
và trung điểm
E
của
CD
thuộc đường thẳng
: 5 0.
x y
Viết phương trình đường thẳng
.
AB
A.
4 19 0
4 0
x y
x y
B.
1 0
4 19 0
x
x y
C.
1 0
5 0
x
y
D.
5 0
4 19 0
y
x y
Câu 21. Trong mặt phẳng
Oxy
, tính bán kính đường tròn tiếp xúc với đường thảng
: 2 0
x y
tại
điểm
3;1
M và tâm nằm trên đường thẳng
: 2 2 0
d x y
.
A.
3
. B.
1
. C.
2
. D.
2
.
Câu 22. Cho
rad
là số đo của của một cung lượng giác tùy ý trên đường tròn lượng giác gốc
1;0
A có
điểm đầu là
A
và điểm cuối là
M
. Số đo của các cung lượng giác có cùng điểm đầu
A
và điểm
cuối
M
là :
A.
k
. B.
2
k
. C.
360
. D.
180
.
Câu 23. Trong mặt phẳng
Oxy
, tính khoảng cách từ
0;0
O đến đường thẳng
: 1
2 9
x y
d
.
A.
18
85
. B.
28
85
. C.
18
82
. D.
8
82
.
Câu 24. Cho biết
3 3
cos ,
5 2
.Tính giá trị biểu thức
5 11
cos tan
2 2
M
.
A.
3
16
M
. B.
31
20
M . C.
1
20
M . D.
4
5
M
.
Câu 25. Kết quả điều tra tuổi của 160 đoàn viên thanh niên được trình bày ở bảng phân bố tần số sau đây :
Tuổi 18 19 20 21 22 Cộng
Tần số 10 50 70 20 10 160
Phương sai của bảng phân bố tần số đã cho gần với kết quả nào sau đây ?
A.
0,902
. B.
1,42
. C.
1,435
. D.
2,104
.
Câu 26. Xác định mệnh đề đúng.
A.
1
cos cos sin sin
2
a b a b a b
. B.
cos cos 2cos cos
2 2
a b a b
a b
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
1
cos cos cos cos
2 2 2
a b a b
a b
. D.
cos cos 2sin sin
2 2
a b a b
a b
.
Câu 27. Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng có phương trình lần lượt là
2 5 0
x y
và
3 9 0.
x y
?
A.
45
. B.
30
. C.
60
. D.
90
.
Câu 28. Cho góc
thỏa mãn
3
2 2
và
1
sin
5
. Tính giá trị
sin 2
P
A.
2 6
25
P . B.
4 6
25
P . C.
2 6
25
P D.
4 6
25
P .
Câu 29. Trong mặt phẳng
Oxy
, đường tròn
;
C I R
có tâm
3;5
I và đi qua gốc tọa độ
O
có phương
trình là
A.
2 2
6 10 0
x y x y
. B.
2 2
6 10 2 0
x y x y
.
C.
2 2
6 10 0
x y x y
D.
2 2
6 10 0
x y x y
.
Câu 30. Cho
2
f x ax bx c
có
0
a
và có hai nghiệm phân biệt
1 2
,
x x
. Giả sử
1 2
x x
. Bảng xét dấu
nào sau đây là bảng xét dấu của
f x
A.
+-+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
.
B.
--
+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
C.
--
+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
D.
-
--
0
0
x
2
+∞
x
1
-∞
f(x)
x
.
Câu 31. Trên đường tròn lượng giác gốc
1;0
A cho cung lượng giác điểm đầu
A
và điểm cuối là
M
có
số đo là ,
2
k k
. Tìm số điểm
M
khác nhau.
A.
4
. B.
0
. C.
2
. D.
3
.
Câu 32. Trong mặt phẳng
Oxy
, cho đường thẳng
d
song song với đường thẳng
:3 2 6 0
x y
và
cắt
,
Ox Oy
tại
,
A B
sao cho
13
AB . Tính khoảng cách từ gốc tọa độ đến
d
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
7
13
. B.
6
13
. C.
3
13
. D.
5
13
.
Câu 33. Trong mặt phẳng
Oxy
, trong các phương trinh sau đây phương trình nào là phương trình chính tắc
của elip?
A.
2 2
1
9 16
x y
. B.
2 2
1
64 36
x y
. C.
2 2
1
16 9
x y
. D.
2 2
9 16 2
x y
.
Câu 34. Cho hàm số
cos4 4cos2 5
y x x m
. Tìm giá trị nguyên nhỏ nhất của tham số để giá trị nhỏ
nhất của hàm số đã cho lớn hơn
5
.
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 35. Xác định mệnh đề đúng.
A.
tan cot
. B.
tan cot
.
C.
tan tan
. D.
tan tan
.
II. TỰ LUẬN
Câu 1. Trong mặt phẳng
Oxy
, cho tam giác
ABC
với
2;3 , 1; 2 , 5;4
A B C . Viết phương trình
đường trung tuyến
AM
của tam giác
ABC
.
Câu 2. Trong mặt phẳng
Oxy
, viết phương trình đường tròn
C
có tâm
3;2
I và tiếp xúc với trục
hoành
Ox
.
Câu 3. Rút gọn biểu thức:
2
sin cos 1
1
cos sin
2 cos .cot
4
x x
P
x x
x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 09
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. TRẮC NGHIỆM
Câu 1. Trong mặt phẳng
Oxy
, cho hai đường thẳng
1 2
,
d d
lần lượt có phương trình tổng quát
7 13 1 0
x y
và
7 13 2 0
x y
. Xác định vị trí tương đối của hai đường thẳng
1 2
,
d d
A. Song song. B. Vuông góc. C. Cắt nhau. D. Trùng nhau.
Lời giải
Chọn A.
Vì
7 13 1
7 13 2
nên
1 2
/ /
d d
.
Câu 2. Mệnh đề nào sau đây sai?
A.
0
1
360
rad
.
B.
0
1
180
rad
.
C. Trên đường tròn định hướng có vô số cung lượng giác có điểm đầu là
A
, điểm cuối là
B
.
D. Cung có số đó
rad
của đường tròn bán kính
R
có độ dài là
l R
.
Lời giải
Chọn A.
0
1
180
rad
.
Câu 3. Cho biểu thức
3
2sin sin 5 sin cos
2 2 2
A
với
,
5
k
k
thì
biểu thức
A
nhận bao nhiêu giá trị khác nhau.
A.
4
. B.
10
. C.
8
. D.
6
.
Lời giải
Chọn D.
3
2sin sin 5 sin cos
2 2 2
A
2cos sin cos sin cos
Vậy
A
6
có giá trị khác nhau cos
5
k
với
0;9
k
.
Câu 4. Cho bảng phân bố tần số: Tiền thưởng (triệu đồng) cho cán bộ công nhân viên của một công ty.
Tiền thưởng
2
3
4
5
6
Cộng
Tần số
5
15
10
6
7
43
Độ lệch chuẩn gần nhất với kết quả nào sau đây ?
A.
1,26
. B.
1,38
. C.
1,615
. D.
1,57
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A.
Số tiền thưởng trung bình:
2.5 3.15 4.10 5.6 6.7
3,88
43
x
Phương sai của số liệu :
2 2 2 2 2
2
5 15 10 6 7
2 3,88 3 3,88 4 3,88 5 3,88 6 3,88 1,59
43 43 43 43 43
s
Độ lệch chuẩn:
2
1,26
s xấp xỉ .
Câu 5. Trong mặt phẳng
Oxy
, cho đường thẳng
2 3
:
3 4
x t
d
y t
. Tìm tọa độ một vectơ chỉ phương của
d
.
A.
3; 4
. B.
4;3
. C.
4; 3
. D.
3;4
.
Lời giải
Chọn D.
Câu 6. Cho
0
x
,
0
y
. Tìm giá trị lớn nhất của biểu thức
2 2
1 1
x y
P
x y
.
A.
1
2
M
. B.
1
4
M
. C.
1
M
. D.
2
M
.
Lời giải
Chọn B.
Ta có
2
1 0
x
2
1 4
x x
2
1
4
1
x
x
đẳng thức xảy ra khi
1
x
.
2
0
1
y
y
đẳng thức xảy ra khi và chỉ khi
0
y
.
2 2
1 1
x y
P
x y
1
4
đẳng thức xảy ra khi và chỉ khi
1
0
x
y
.
Vậy giá tri lớn nhất cần tìm là
1
4
.
Câu 7. Trên đường tròn lượng giác gốc
1;0
A cho cung lượng giác điểm đầu
A
và điểm cuối là
M
có
số đo
0
2
. Gọi
1
M
là điểm đối xứng của
M
qua gốc tọa độ
O
. Tìm số đo của cung
lượng giác có điểm đầu là
A
và điểm cuối là
1
M
.
A.
2
k
. B.
1 2
k
. C.
180
. D.
k
.
Lời giải
Chọn B.
Cung
1
MM
số đo của cung lượng giác có điểm đầu là
A
và điểm cuối là
1 2
k
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 8. Trong mặt phẳng
Oxy
, cho elip
2 2
: 1
4 1
x y
E
và điểm
2;0
C . Có hai điểm
A
,
B
thuộc
E
thỏa mãn
A
,
B
đối xứng nhau qua trục hoành và tam giác
ABC
là tam giác đều. Tính độ dài đoạn
thẳng
AB
.
A.
3
. B.
2
. C.
8 3
5
. D.
8 3
7
.
Lời giải
Chọn D.
C
B
A
Giả sử
;
A x y
,
;
B x y
với
2 2
x
,
1 1
y
,
0
y
.
Do tam giác
ABC
đều nên
AB AC
2
2 2
4 2
y x y
2
2
3 2
y x
.
Do
A E
2 2
1
4 1
x y
2
2
1
4
x
y
.
2
2
3 1 2
4
x
x
2
7 16 4 0
x x
2
2 0( )
2 48
7 49
x y loai
x y
.
2
8 3
4
7
AB y
.
Câu 9. Biết
3
;2
2
và
3
tan
7
. Tính giá trị biểu thức
cos sin
2 2
P
.
A.
1
4
P
. B.
1
4
P
. C.
1
2
P
. D.
1
2
P
.
Lời giải
Chọn C.
sin cos 2sin
2 2 2 4
P
.
Do
3
;2
2
5
;
2 4 4
2 sin 0
2 4
P
.
2
1 sin
P
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
3
tan
7
7
cot
3
.
2
2
1 9
sin
1 cot 16
Do
3
;2
2
sin 0
3
sin
4
.
2
1
4
P
1
2
P
.
Câu 10. Trong mặt phẳng
Oxy
, cho Elip
E
có một đỉnh trên trục lớn
3;0
A và một tiêu điểm là
2;0
F . Viết phương trình chính tắc của Elip
E
.
A.
2 2
1
9 4
x y
. B.
2 2
1
3 2
x y
. C.
2 2
1
5 9
x y
. D.
2 2
1
9 5
x y
.
Lời giải
Chọn D.
Một đỉnh trên trục lớn
3;0
A
3
a
.
Một tiêu điểm là
2;0
F
2
c
.
2 2 2
9 4 5
b a c
.
Vậy
2 2
: 1
9 5
x y
E
.
Câu 11. Bất phương trình
f x a
với
0
a
tương đương với bất phương trình nào?
A.
f x a
. B.
f x a
hoặc
f x a
.
C.
a f x a
. D.
f x a
.
Lời giải
Chọn C
Câu 12. Tính tổng các nghiệm nguyên dương của bất phương trình
2
2
10
10
100
x
x
.
A.
40
. B.
0
. C.
45
. D.
9
.
Lời giải
Chọn C
2
2
10
10
100
x
x
2
1000
0
100
x
2
100 0
x
10
x
10 10
x
.
Tổng các nghiệm nguyên dương của bất phương trình là
1 2 3 4 5 6 7 8 9 45
.
Câu 13. Xác định mệnh đề đúng.
A.
3
sin3 3sin 4sin
a a a
. B.
3
sin3 4cos 3sin
a a a
.
C.
3
sin3 3sin 4cos
a a a
. D.
3
sin3 4sin 3sin
a a a
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A
Câu 14. Trong mặt phẳng
Oxy
, tìm tọa độ tâm
I
và bán kính
R
của đường tròn có phương trình
2 2
1 2 4
x y
.
A. Tâm
1;2
I , bán kính
4
R
. B. Tâm
1;2
I , bán kính
2
R
.
C. Tâm
1; 2
I
, bán kính
4
R
. D. Tâm
1; 2
I
, bán kính
2
R
.
Lời giải
Chọn D
Đường tròn
2 2
1 2 4
x y
có tâm
1; 2
I
, bán kính
2
R
.
Câu 15. Cho biết
1
cos
3
a
,
1
cos
4
b
. Tính giá trị của biểu thức
cos cos
P a b a b
.
A.
119
144
P
. B.
263
144
P
. C.
11
14
P
. D.
119
144
P
.
Lời giải
Chọn A
Ta có
1
cos cos cos2 cos 2
2
P a b a b b a
2 2
1
2cos 2cos 2
2
a b
2 2
cos cos 1
a b
1 1 119
1
9 16 144
.
Câu 16. Cho
7
4 .
2
Xác định mệnh đề đúng.
A.
2
1
tan 1
cos
B.
2
1
tan 1
sin
C.
2
1
tan 1
sin
D.
2
1
tan 1
cos
Lời giải
Chọn D
Ta có
2 2
2 2
1 1
1 tan tan 1
cos cos
Do
7
4
2
nên
2
1
tan 0 tan 1.
cos
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
để bất phương trình
2
2 3 0
mx mx
có tập nghiệm
bằng
.
A.
4
B.
2
C.
0
D.
3
Lời giải
Chọn A
TH1: Với
0
m
ta có bất phương trình
3 0
(đúng x
) (TM)
TH2: Với
0
m
khi đó bất phương trình đúng
2
0
0 0
3 0
0 3 0
3 0
m
a m
x m
m
m m
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy các giá trị thỏa mãn là
3; 2; 1;0
m
Câu 18. Trong mặt phẳng
,
Oxy
cho đường tròn
2 2
: 4 4 6 0
C x y x y
và đường thẳng
: 2 3 0
d x my m
với
m
là tham số thực. Gọi
I
là tâm đường tròn
.
C
Tính tổng các giá trị
thực của tham số
m
tìm được để đường thẳng
d
cắt đường tròn
C
tại hai điểm phân biệt
,
A B
sao cho diện tích tam giác
ABI
lớn nhất.
A.
4
B.
0
C.
15
8
D.
8
15
Lời giải
Chọn B
H
B
A
I
Đường tròn
C
có tâm
2; 2
I
bán kính
2.
R
Đường thẳng
d
cắt đường tròn
C
tại hai điểm phân biệt
2
1 4
, 2
1
m
d I d R
m
2 2 2
4 30 4 30
16 8 1 2 2 14 8 1 0 .
14 14
m m m m m m
Khi đó
2 2
1 1
sin 1
2 2
IAB
S R AIB R
Do đó diện tích tam giác
IAB
lớn nhất
sin 1
AIB IA IB
Gọi
H
là trung điểm của
AB
ta có
HIA
vuông cân tại
H
do đó
1
IH
Hay
2 2
0
1 4 1 15 8 0
8
15
m
m m m m
m
Vậy
0.
m
Câu 19. Trong mặt phẳng
,
Oxy
cho elip
E
có phương trình chính tắc
2 2
1.
25 9
x y
Tính tỉ số giữa tiêu cự
và độ dài trục lớn elip
.
E
A.
5
3
B.
3
5
C.
4
5
D.
4
5
Lời giải
Chọn D
Ta có
2 2
25 5; 9 3
a a b b
Suy ra
25 9 4
c

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Suy ra
2 8 4
.
2 10 5
c
a
Câu 20. Trong mặt phẳng
,
Oxy
cho hình chữ nhật
ABCD
có điểm
6;2
I là giao điểm của hai đường
chéo
, .
AC BD
Điểm
1;5
M thuộc
AB
và trung điểm
E
của
CD
thuộc đường thẳng
: 5 0.
x y
Viết phương trình đường thẳng
.
AB
A.
4 19 0
4 0
x y
x y
B.
1 0
4 19 0
x
x y
C.
1 0
5 0
x
y
D.
5 0
4 19 0
y
x y
Lời giải
Chọn D
E
I(6;2)
C
A B
D
M(1;5)
Gọi
M
đối xứng với
M
qua
I
suy ra
11; 1
M
Gọi
;5E t t
ta có
6;3 , 11;6 t
IE t t M E t
Do
E
là trung điểm của
CD
nên
. 0 6 11 3 6 0
IE M E IE M E t t t t
2
7
2 26 84 0
6
t
t t
t
Suy ra
1 2
7; 2 , 6; 1
E E
Với
1
7; 2 1; 4
E IE
Đường thẳng
AB
có phương trình
1 4 5 0 4 19 0
x y x y
Với
2
6; 1 0; 3
E IE
Đường thẳng
AB
có phương trình
5 0.
y
Câu 21. Trong mặt phẳng
Oxy
, tính bán kính đường tròn tiếp xúc với đường thảng
: 2 0
x y
tại
điểm
3;1
M và tâm nằm trên đường thẳng
: 2 2 0
d x y
.
A.
3
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn D.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
+
IM
đi qua
3;1
M và vuông góc
: 2 0
x y
nên có phương trình
3 1 0
x y
4 0
x y
+ Tọa độ điểm
I
là nghiệm của hệ
2 2 0 2
2,2
4 0 2
x y x
I
x y y
+
2
2
2 2 2
, 2
1 1
R d I
.
Câu 22. Cho
rad
là số đo của của một cung lượng giác tùy ý trên đường tròn lượng giác gốc
1;0
A có
điểm đầu là
A
và điểm cuối là
M
. Số đo của các cung lượng giác có cùng điểm đầu
A
và điểm
cuối
M
là :
A.
k
. B.
2
k
. C.
360
. D.
180
.
Lời giải
Chọn B.
Câu 23. Trong mặt phẳng
Oxy
, tính khoảng cách từ
0;0
O đến đường thẳng
: 1
2 9
x y
d
.
A.
18
85
. B.
28
85
. C.
18
82
. D.
8
82
.
Lời giải
Chọn A.
+
: 1 9 2 18 0
2 9
x y
d x y
+
2 2
9.0 2.0 18
18
,
85
9 2
d O d
.
Câu 24. Cho biết
3 3
cos ,
5 2
.Tính giá trị biểu thức
5 11
cos tan
2 2
M
.
A.
3
16
M
. B.
31
20
M . C.
1
20
M . D.
4
5
M
.
Lời giải
Chọn B.
+ Có
5 11
cos tan cos 2 tan 5
2 2 2 2
M
cos tan sin cot
2 2
+ Vì
3
sin 0
2
I
d
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
+ Có
2
2
3 3 3 4
cos cos sin 1 cos 1
5 5 5 5
cos 3
cot
sin 4
. Vậy
4 3 31
5 4 20
M
.
Câu 25. Kết quả điều tra tuổi của 160 đoàn viên thanh niên được trình bày ở bảng phân bố tần số sau đây :
Tuổi 18 19 20 21 22 Cộng
Tần số 10 50 70 20 10 160
Phương sai của bảng phân bố tần số đã cho gần với kết quả nào sau đây ?
A.
0,902
. B.
1,42
. C.
1,435
. D.
2,104
.
Lời giải
Chọn A.
+ Ta có
18.10 19.50 20.70 21.20 22.10
19,8125
160
x
+ Phương sai
2 2 2 2 2
2
1
10. 18 50. 19 70. 20 20. 21 10. 22
160
s x x x x x
0,90234375
.
Câu 26. Xác định mệnh đề đúng.
A.
1
cos cos sin sin
2
a b a b a b
. B.
cos cos 2cos cos
2 2
a b a b
a b
.
C.
1
cos cos cos cos
2 2 2
a b a b
a b
. D.
cos cos 2sin sin
2 2
a b a b
a b
.
Lời giải
Chọn B.
Lý thuyết
Câu 27. Trong mặt phẳng
Oxy
, tính góc giữa hai đường thẳng có phương trình lần lượt là
2 5 0
x y
và
3 9 0.
x y
?
A.
45
. B.
30
. C.
60
. D.
90
.
Lời giải
Chọn A.
Gọi đường thẳng
:2 5 0
d x y
và
: 3 9 0.
x y
Ta có
2 2
2 2
2.1 1. 3
2
cos ,
2
2 1 . 1 3
d
.
, 45
d
.
Câu 28. Cho góc
thỏa mãn
3
2 2
và
1
sin
5
. Tính giá trị
sin 2
P
A.
2 6
25
P . B.
4 6
25
P . C.
2 6
25
P D.
4 6
25
P .
Lời giải
Chọn B.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
2
2 2
1 24
cos 1 sin 1
5 25
24
cos
5
(Vì
3
2 2
)
1 24 4 6
sin 2 2sin .cos 2. .
5 5 25
P
Câu 29. Trong mặt phẳng
Oxy
, đường tròn
;
C I R
có tâm
3;5
I và đi qua gốc tọa độ
O
có phương
trình là
A.
2 2
6 10 0
x y x y
. B.
2 2
6 10 2 0
x y x y
.
C.
2 2
6 10 0
x y x y
D.
2 2
6 10 0
x y x y
.
Lời giải
Chọn D.
Phương trình của đường tròn
C
có dạng
2 2 2 2
2 2 0 0
x y ax by c a b c
Vì đường tròn
;
C I R
có tâm
3;5
I nên ta có
2 2
2.3 2.5 0
x y x y c
Vì đường tròn
;
C I R
đi qua gốc tọa độ
O
nên ta có
0
c
Vậy đường tròn
;
C I R
có phương trình là
2 2
6 10 0
x y x y
Câu 30. Cho
2
f x ax bx c
có
0
a
và có hai nghiệm phân biệt
1 2
,
x x
. Giả sử
1 2
x x
. Bảng xét dấu
nào sau đây là bảng xét dấu của
f x
A.
+-+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
.
B.
--
+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
C.
--
+ 0
0
x
2
+∞
x
1
-∞
f(x)
x
D.
-
--
0
0
x
2
+∞
x
1
-∞
f(x)
x
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B.
Theo định lí dấu tam thức bậc hai thì
f x
cùng dấu với
a
trên
1 2
;
x x
, cùng dấu với
a
trên
1
;
x
và
2
;x
Câu 31. Trên đường tròn lượng giác gốc
1;0
A cho cung lượng giác điểm đầu
A
và điểm cuối là
M
có
số đo là ,
2
k k
. Tìm số điểm
M
khác nhau.
A.
4
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn A.
Có 4 điểm
M
khác nhau và cách nhau
2
là
1 2 3 4
1;0 , 0;1 , 1;0 , 0; 1
M M M M
.
Câu 32. Trong mặt phẳng
Oxy
, cho đường thẳng
d
song song với đường thẳng
:3 2 6 0
x y
và
cắt
,
Ox Oy
tại
,
A B
sao cho
13
AB . Tính khoảng cách từ gốc tọa độ đến
d
.
A.
7
13
. B.
6
13
. C.
3
13
. D.
5
13
.
Lời giải
Chọn B.
Vì
d
song song với đường thẳng
:3 2 6 0
x y
:3 2 0
d x y m
.
2
13
;0 , 0;
3 2 6
m m m
A B AB
2
13
13 6
6
m
m
.
:3 2 6 0
d x y
6
,
13
d O d
.
Câu 33. Trong mặt phẳng
Oxy
, trong các phương trinh sau đây phương trình nào là phương trình chính tắc
của elip?
A.
2 2
1
9 16
x y
. B.
2 2
1
64 36
x y
. C.
2 2
1
16 9
x y
. D.
2 2
9 16 2
x y
.
Lời giải
Chọn C.
Ta có
2 2
1
16 9
x y
là phương trình chính tắc của elip vì có
4 3
a b
.
Câu 34. Cho hàm số
cos4 4cos2 5
y x x m
. Tìm giá trị nguyên nhỏ nhất của tham số để giá trị nhỏ
nhất của hàm số đã cho lớn hơn
5
.
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn A.
Ta có
cos4 4cos2 5
y x x m
2
2cos 2 4cos2 4
x x m
2
2 cos2 1 2 2
x m m
min 2
y m
.
Theo đề
2 5 3
m m
4
m
.
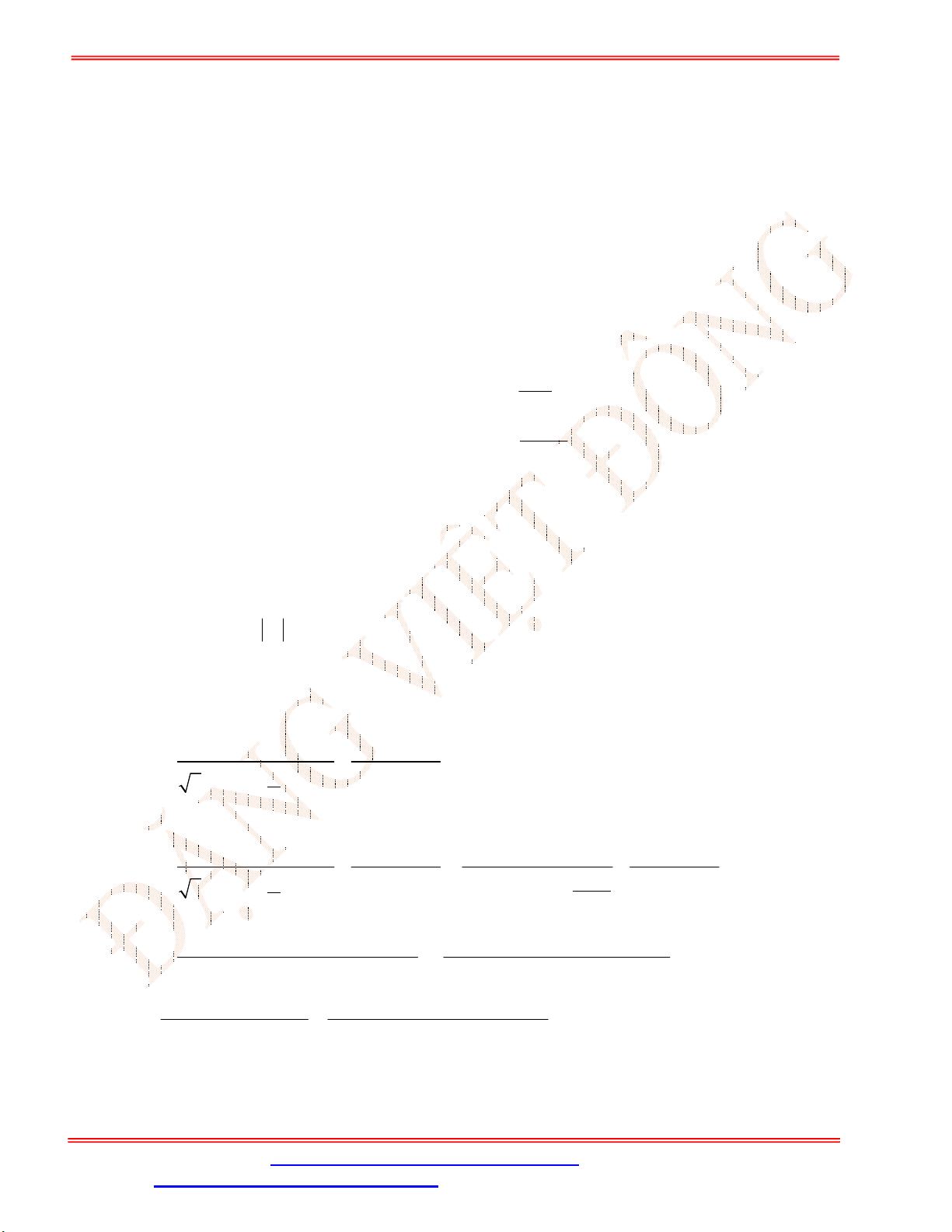
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 35. Xác định mệnh đề đúng.
A.
tan cot
. B.
tan cot
.
C.
tan tan
. D.
tan tan
.
Lời giải
Chọn C.
Ta có
tan tan
.
II. TỰ LUẬN
Câu 1. Trong mặt phẳng
Oxy
, cho tam giác
ABC
với
2;3 , 1; 2 , 5;4
A B C . Viết phương trình
đường trung tuyến
AM
của tam giác
ABC
.
Lời giải
Tọa độ trung điểm
M
của
BC
thỏa mãn :
1 5
2
2
2 4
1
2
M
M
x
y
2;1
M
0; 2
AM
1;0
AM
n
.
Vậy phương trình đường trung tuyến
AM
là:
2 0
x
.
Câu 2. Trong mặt phẳng
Oxy
, viết phương trình đường tròn
C
có tâm
3;2
I và tiếp xúc với trục
hoành
Ox
.
Lời giải
; 2
I
R d I Ox y
.
Vậy phương trình đường tròn cần tìm là:
2 2
3 2 4
x y
.
Câu 3. Rút gọn biểu thức:
2
sin cos 1
1
cos sin
2 cos .cot
4
x x
P
x x
x x
Lời giải
2
sin cos 1
1
cos sin
2 cos .cot
4
x x
P
x x
x x
2
sin cos 1
1
cos
cos sin
cos sin .
sin
x x
x
x x
x x
x
2
sin . sin cos 1 cos
cos sin .cos
x x x x
P
x x x
sin 1 2sin x 1 x
cos sin .cos
x xcos cos
x x x
2
x 1 2sin
cos sin cos sin
cos sin
cos sin .cos cos sin
cos x
x x x x
x x
x x x x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 10
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Cho hình vuông
ABCD
tâm
3;3
I , phương trình cạnh
: 1
AB y
. Gọi tọa độ điểm
;b
A a
và
;
B c d
. Khi đó
P a b c d
bằng
A.
6
. B.
9
. C.
8
. D.
5
.
Câu 2. Viết phương trình đường thẳng
đi qua điểm
2;5
G và có một VTPT là
2; 3
n
.
A.
2 3 19 0
x y
. B.
3 2 4 0
x y
.
C.
2 3 19 0
x y
. D.
3 2 4 0
x y
.
Câu 3. Giải bất phương trình
3 5 2
1
2 3
x x
x
A.
5
3
x
. B.
5
x
. C.
5
3
x
. D.
5
x
.
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai:
A.
4 4 2 2
sin cos 1 2sin cos
x x x x
. B.
2
sin cos 1 2sin cos
x x x x
.
C.
2
sin cos 1 2sin cos
x x x x
. D.
6 6 2 2
sin cos 1 sin cos
x x x x
.
Câu 5. Cho
4
sin
5
và 0
2
. tính
tan
.
A.
3
5
. B.
4
3
. C.
3
4
. D.
3
4
.
Câu 6. Biết
2
và
cot
,
cot
,
cot
theo thứ tự lập thành một cấp số cộng. Tích số
cot .cot
bằng
A.
2
. B.
3
. C.
2
. D.
3
.
Câu 7. Cho góc
x
thỏa mãn
0 0
0 90
x . Trong các mệnh đề sau, mệnh đề nào sai?
A.
cot 0
x
. B.
tan 0
x
. C.
sin 0
x
. D.
cos 0
x
.
Câu 8. Cho hai đường thẳng
1
: 2 4 0
d x y
;
2
:2 6 0
d x y
. Số đo góc giữa
1 2
;
d d
là
A.
0
60
. B.
0
45
. C.
0
30
. D.
0
90
.
Câu 9. Khẳng định nào sau đây đúng?
A.
0
cos cos 180
. B.
0
cot cot 180
.
C.
0
tan tan 180
. D.
0
sin sin 180
.
Câu 10. Tập nghiệm của bất phương trình
2
5 6 0
x x
là
A.
; 3 2;
. B.
; 3 2;
.
C.
; 2 3;
. D.
3; 2
.
Câu 11. Tính giá trị biểu thứ
2
tan tan sin
P
nếu cho
4
cos
5
,
3
2
.
A.
12
25
. B.
12
25
. C.
1
3
. D.
3
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 12. Cho
tan 3
x
. Tính
2 2
2 2
2sin 5sin cos cos
2sin sin cos cos
x x x x
A
x x x x
.
A.
2
11
A
. B.
4
A
. C.
22
4
A . D.
4
26
.
Câu 13. Nếu
tan cot 3
thì
2 2
tan cot
có giá trị bằng:
A.
11
. B.
9
. C.
12
. D.
10
.
Câu 14. Tìm tập nghiệm của bất phương trình
2
2
10
2
2 3
x x
x x
:
A.
; 4 1;1
. B.
3; 1 1;
. C.
4; 3 1;1
. D.
4; 1 3
.
Câu 15. Nếu
tan
và
tan
là hai nghiệm của phương trình
2
0
x px q
và
cot
và
cot
là hai
nghiệm của phương trình
2
0
x rx s
thì
s
r
bằng :
A.
1
pq
. B.
2
p
q
. C.
2
q
p
. D.
pq
.
Câu 16. Giải bất phương trình
3 2 0
x x
.
A.
2;3
. B.
2;3
. C.
;3
. D.
2;3
.
Câu 17. Giải hệ bất phương trình
3 6
5 3 2 15
x x
x x
.
A.
2 3
x
. B.
3 3
x
. C.
2 2
x
. D.
3 2
x
.
Câu 18. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 3 9
C x y
và điểm
2;1
A . Hai tiếp
tuyến kẻ từ
A
đến
C
tiếp xúc với
C
tại
,
M N
. Đường thẳng
MN
có phương trình
A.
4 2 0
x y
. B.
4 2 0
x y
. C.
4 2 0
x y
. D.
4 2 0
x y
.
Câu 19. Cho bất phương trình
2
3 10 2
x x x
. Khẳng định nào sau đây sai?
A. Bất phương trình có 7 nghiệm nguyên thuộc
0;20
.
B. Bất phương trình có một nghiêm thuộc
2;5
.
C. Bất phương trình có 7 nghiệm nguyên thuộc
5;10
.
D.
2
x
là nghiệm có giá trị nhò nhất của bất phương trình.
Câu 20. Trong mặt phẳng
Oxy
, cho các điểm
10;5
A ,
3;2
B ,
6; 5
C
. Phương trình đường tròn
ngoại tiếp tam giác
ABC
là
A.
2 2
4 4 16
x y
. B.
2
2
3 29
x y
.
C.
2
2
8 29
x y
. D.
2 2
4 4 29
x y
.
Câu 21. Vị trí tương đối của hai đường thẳng
1 2
2 3
: ; : 4 6 5 0
1 2
x t
d d x y
y t
là:
A. Cắt nhau B. Trùng nhau. C. Song song. D. Vuông góc
Câu 22. Giải bất phương trình
2 2 3
x x
A.
5
1
3
x x
. B.
3
2
x
. C.
5
3
x
. D.
3 5
2 3
x
.
Câu 23. Tìm giá trị của
m
để bất phương trình
2
2 2 2 0
m x m x m
vô nghiệm
A.
1 2
m
. B.
2
m
C.
1 2
m
. D.
2
m
.
Câu 24. Cho
2
2 3 3 1
y mx m x m
. Tìm
m
để
0
y
đúng với mọi giá trị
x
A.
9
2
m
. B.
1
m
. C.
1 0
m
. D.
9
1
2
m
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 25. Tìm tập nghiệm của bất phương trình:
2 2 1 13
x x x
A.
1
;9
2
. B.
9
2;
4
. C.
9
1;
2
. D.
3
;3
2
.
Câu 26. Tìm tập nghiệm của bất phương trình
2 2
1 4 4 4 0
x x x x
.
A.
2;1 4;
. B.
;1 2;
. C.
2;1 2;
. D.
; 2 1;2
.
Câu 27. Khẳng định nào sau đây sai? Với mọi
,
ta có:
A.
cos cos cos sin sin
. B.
tan tan tan
.
C.
cos cos cos sin sin
. D.
tan tan
tan
1 tan tan
.
Câu 28. Số nghiệm nguyên thuộc
20;20
của bất phương trình
2
8 2
x x
là
A.
32
. B.
34
. C.
36
. D.
30
.
Câu 29. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
2 2
: 4 8 16 0
C x y x y
. Tâm và
bán kính của
C
là
A.
2;4
I và
6
R
. B.
2; 4
I
và
6
R
. C.
2; 4
I
và
5
R
. D.
2;4
I và
5
R
.
Câu 30. Có bao nhiêu giá trị nguyên của
m
trong khoảng
3;3
để hệ bất phương trình
2
2 1 4
6 1 5 4
mx x m
x x
có nghiệm
A.
3
. B.
5
. C.
2
. D.
4
.
Câu 31. Tính khoảng cách giữa
5;1
M và
:3 4 1 0
x y
A.
3
. B.
10
. C.
2
. D.
5
.
Câu 32. Viết phương trình đường thẳng
đi qua hai điểm
2; 5
D
và
3; 1
E
A.
4 3 0
x y
. B.
4 18 0
x y
. C.
4 13 0
x y
. D.
3 1 0
x y
.
Câu 33. Viết phương trình đường thẳng
đi qua
2;5
H và vuông góc với đường thẳng
: x 3y 2 0
d
A.
3y 17 0
x
. B.
3y 13 0
x
. C.
3 y 11 0
x
. D.
3 y 1 0
x
.
Câu 34. Có bao nhiêu giá trị nguyên của
m
trong khoảng
5;5
để hệ bất phương trình
2
9 3
4 1 6
mx x m
x x
vô nghiệm.
A.
6
. B.
4
. C.
8
. D.
5
.
Câu 35. Cho bất phương trình
2
5 4 2 1 0
x x x
. Số nghiệm nguyên của bất phương trình là
A.
5
. B.
3
. C.
4
. D.
2
.
II. TỰ LUẬN
Câu 1. (1 điểm) Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 4 6 3 0
C x y x y
. Viết phương
trình tiếp tuyến của đường tròn biết tiếp tuyến vuông góc với đường thẳng
: 3 3 0
d x y
.
Câu 2. (1 điểm) Cho
sin 0
x
và
cos 1
x
. Chứng minh rằng :
sin 1 cos 2
1 cos sin sin
x x
x x x
.
Câu 3. (1 điểm) Giải bất phương trình
5 3 4 4 1
x x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 10
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. TRẮC NGHIỆM
Câu 1. Cho hình vuông
ABCD
tâm
3;3
I , phương trình cạnh
: 1
AB y
. Gọi tọa độ điểm
;b
A a
và
;
B c d
. Khi đó
P a b c d
bằng
A.
6
. B.
9
. C.
8
. D.
5
.
Lời giải
Chọn C.
I
A
B
C
D
Theo giả thiết ta có
1
b d
.
; ; 1 2
d I AB d I y
.
Vì
ABCD
là hình vuông nên
I
là trung điểm của hai đường chéo
AC
và
BD
và hai đường
chéo vuông góc nhau.
Tam giác
AIB
vuông cân tại
I
nên
2. ; 2 2
IA IB d I AB .
2
2 2
3 2 8
IA a
5
a
hoặc
1
a
.
Với
5 1
a b
.
Với
1 5
a b
.
Vậy
5 1 1 1 8
P
.
Câu 2. Viết phương trình đường thẳng
đi qua điểm
2;5
G và có một VTPT là
2; 3
n
.
A.
2 3 19 0
x y
. B.
3 2 4 0
x y
.
C.
2 3 19 0
x y
. D.
3 2 4 0
x y
.
Lời giải
Chọn A.
Phương trình đường thẳng
:
2 2 3 5 0
x y
Hay
2 3 19 0
x y
Câu 3. Giải bất phương trình
3 5 2
1
2 3
x x
x
A.
5
3
x
. B.
5
x
. C.
5
3
x
. D.
5
x
.
Lời giải
Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Bất phương trình tương đương :
3 2 5
1
2 3 3 2
x x
x
5
x
.
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai:
A.
4 4 2 2
sin cos 1 2sin cos
x x x x
. B.
2
sin cos 1 2sin cos
x x x x
.
C.
2
sin cos 1 2sin cos
x x x x
. D.
6 6 2 2
sin cos 1 sin cos
x x x x
.
Lời giải
Chọn D.
3 3 2 2
6 6 2 2 2 2 2 2
sin cos sin cos 1. sin sin .cos cos
x x x x x x x x
2 2 2 2 2 2
1 2sin cos sin cos 1 3sin cos
x x x x x x
.
Câu 5. Cho
4
sin
5
và 0
2
. tính
tan
.
A.
3
5
. B.
4
3
. C.
3
4
. D.
3
4
.
Lời giải
Chọn B.
Ta có
2 2 2 2
3
cos
16 9
5
sin cos 1 cos 1 cos
3
25 25
cos
5
.
Mà 0
2
nên
3
cos
5
.
Do đó
sin 4 5 4
tan . .
cos 5 3 3
Câu 6. Biết
2
và
cot
,
cot
,
cot
theo thứ tự lập thành một cấp số cộng. Tích số
cot .cot
bằng
A.
2
. B.
3
. C.
2
. D.
3
.
Lời giải
Chọn B.
Sai đề.
Chọn ;
2
thì
2
,
cot cot 2cot 0 ;cot .cot 0
.
Câu 7. Cho góc
x
thỏa mãn
0 0
0 90
x . Trong các mệnh đề sau, mệnh đề nào sai?
A.
cot 0
x
. B.
tan 0
x
. C.
sin 0
x
. D.
cos 0
x
.
Lời giải
Chọn D.
Câu 8. Cho hai đường thẳng
1
: 2 4 0
d x y
;
2
:2 6 0
d x y
. Số đo góc giữa
1 2
;
d d
là
A.
0
60
. B.
0
45
. C.
0
30
. D.
0
90
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D.
1 2 1 2
. 1.2 2. 1 0
n n d d
.
Câu 9. Khẳng định nào sau đây đúng?
A.
0
cos cos 180
. B.
0
cot cot 180
.
C.
0
tan tan 180
. D.
0
sin sin 180
.
Lời giải
Chọn D.
Câu 10. Tập nghiệm của bất phương trình
2
5 6 0
x x
là
A.
; 3 2;
. B.
; 3 2;
.
C.
; 2 3;
. D.
3; 2
.
Lời giải
Chọn A.
2
3
5 6 0
2
x
x x
x
.
Câu 11. Tính giá trị biểu thứ
2
tan tan sin
P
nếu cho
4
cos
5
,
3
2
.
A.
12
25
. B.
12
25
. C.
1
3
. D.
3
.
Lời giải
Chọn A.
Do
3
2
sin 0
.
2 2
sin 1 cos
16 9
1
25 25
.
3
sin
5
.
sin 3
tan
cos 4
.
2
3 3 9 12
tan tan sin .
4 4 25 25
P
.
Câu 12. Cho
tan 3
x
. Tính
2 2
2 2
2sin 5sin cos cos
2sin sin cos cos
x x x x
A
x x x x
.
A.
2
11
A
. B.
4
A
. C.
22
4
A . D.
4
26
.
Lời giải
Chọn A
Ta có
tan 3
x
cos 0
x
.
2 2
2 2
2sin 5sin cos cos
2sin sin cos cos
x x x x
A
x x x x
2
2
2tan 5tan 1
2tan tan 1
x x
x x
2
2
2.3 5.3 1 2
2.3 3 1 11
Câu 13. Nếu
tan cot 3
thì
2 2
tan cot
có giá trị bằng:
A.
11
. B.
9
. C.
12
. D.
10
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A.
2
2 2 2
tan cot tan cot 2tan .cot 3 2 11
.
Câu 14. Tìm tập nghiệm của bất phương trình
2
2
10
2
2 3
x x
x x
:
A.
; 4 1;1
. B.
3; 1 1;
. C.
4; 3 1;1
. D.
4; 1 3
.
Lời giải
Chọn C.
2
2
10
2
2 3
x x
x x
2
2
10
2 0
2 3
x x
x x
2
2
5 4
0
2 3
x x
x x
1 4
0
1 3
x x
x x
(*).
Bảng xét dấu
1 4
1 3
x x
f x
x x
f(x)
x
-
+ + - +
0
0
1-1
-3-4
(*)
4; 3 1;1
x
Câu 15. Nếu
tan
và
tan
là hai nghiệm của phương trình
2
0
x px q
và
cot
và
cot
là hai
nghiệm của phương trình
2
0
x rx s
thì
s
r
bằng :
A.
1
pq
. B.
2
p
q
. C.
2
q
p
. D.
pq
.
Lời giải
Chọn B.
tan
và
tan
là hai nghiệm của phương trình
2
0
x px q
tan tan
tan .tan
p
q
cot
và
cot
là hai nghiệm của phương trình
2
0
x rx s
cot cot
cot .cot
r
s
tan tan
tan .tan
1
tan .tan
r
s
1
p
r
q
s
q
2
s
p
r
q
.
Câu 16. Giải bất phương trình
3 2 0
x x
.
A.
2;3
. B.
2;3
. C.
;3
. D.
2;3
.
Lời giải
Chọn B.
Ta có:
2 0 2
3 2 0
3 0 3
x x
x x
x x
.
Câu 17. Giải hệ bất phương trình
3 6
5 3 2 15
x x
x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2 3
x
. B.
3 3
x
. C.
2 2
x
. D.
3 2
x
.
Lời giải
Chọn A.
Ta có:
3 6 3
2 3
5 3 2 15 2
x x x
x
x x x
.
Câu 18. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 1 3 9
C x y
và điểm
2;1
A . Hai tiếp
tuyến kẻ từ
A
đến
C
tiếp xúc với
C
tại
,
M N
. Đường thẳng
MN
có phương trình
A.
4 2 0
x y
. B.
4 2 0
x y
. C.
4 2 0
x y
. D.
4 2 0
x y
.
Lời giải
Chọn D.
2 2
: 1 3 9
C x y
có tâm
1; 3
I
và bán kính
3
R
.
Gọi
3
; 1
2
I
là trung điểm
IA
Đường tròn đường kính
IA
có phương trình
2 2
3 2 1 0
x y x y
Đường thẳng
MN
đi qua giao điểm của
C
và
IA
nên thoả hệ
2 2
2 2
3 2 1 0
4 2 0
2 6 1 0
x y x y
x y
x y x y
Câu 19. Cho bất phương trình
2
3 10 2
x x x
. Khẳng định nào sau đây sai?
A. Bất phương trình có 7 nghiệm nguyên thuộc
0;20
.
B. Bất phương trình có một nghiêm thuộc
2;5
.
C. Bất phương trình có 7 nghiệm nguyên thuộc
5;10
.
D.
2
x
là nghiệm có giá trị nhò nhất của bất phương trình.
Lời giải
Chọn B.
Ta có:
2
2
2
2
2 0
2 0
3 10 2
3 10 0
3 10 2
x
x
x x x
x x
x x x
.
2 2
2 4
2 5 4
x x
x x
x x x
Câu 20. Trong mặt phẳng
Oxy
, cho các điểm
10;5
A ,
3;2
B ,
6; 5
C
. Phương trình đường tròn
ngoại tiếp tam giác
ABC
là
A.
2 2
4 4 16
x y
. B.
2
2
3 29
x y
.
C.
2
2
8 29
x y
. D.
2 2
4 4 29
x y
.
Lời giải
Chọn C.
Phương trình đường tròn
C
có dạng:
2 2
2 2 0
x y ax by c
.
Do
, ,
A B C C
ta có hệ:
20 10 125 8
6 4 13 0
12 10 61 35
a b c a
a b c b
a b c c

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Do đó
C
có tâm
8;0
I và bán kính
29
R
Câu 21. Vị trí tương đối của hai đường thẳng
1 2
2 3
: ; : 4 6 5 0
1 2
x t
d d x y
y t
là:
A. Cắt nhau B. Trùng nhau. C. Song song. D. Vuông góc
Lời giải:
Chọn C
1 2 2
3;2 ; 4; 6 6;4
d d d
u n u
1 2
3 2
//
6 4
2.4 6. 1 5 0
d d
.
Câu 22. Giải bất phương trình
2 2 3
x x
A.
5
1
3
x x
. B.
3
2
x
. C.
5
3
x
. D.
3 5
2 3
x
.
Lời giải:
Chọn C
2 2 3
x x
2 3 2 2 3
x x x
2 3 2
2 2 3
x x
x x
5
3
1
x
x
5
3
x
.
Câu 23. Tìm giá trị của
m
để bất phương trình
2
2 2 2 0
m x m x m
vô nghiệm
A.
1 2
m
. B.
2
m
C.
1 2
m
. D.
2
m
.
Lời giải:
Chọn C
Xét
2 0 2
m m
2 0
vô lý
PTVN
Xét
2 0 2
m m
BPT vô nghiệm
2 0
0
m
2
2
2 2 0
m
m m m
2
2
2 6 4 0
m
m m
2
1 2
m
m
.
Câu 24. Cho
2
2 3 3 1
y mx m x m
. Tìm
m
để
0
y
đúng với mọi giá trị
x
A.
9
2
m
. B.
1
m
. C.
1 0
m
. D.
9
1
2
m
.
Lời giải:
Chọn B
Xét
0 1
m y
đúng
Xét
0
m
,
0
y
đúng với mọi giá trị
x
0
0
m
2
0
3 3 1 0
m
m m m
2 2
0
6 9 3 0
m
m m m m

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2
0
0
1
9
2 7 9 0
1
2
m
m
m
m m
m m
.
Câu 25. Tìm tập nghiệm của bất phương trình:
2 2 1 13
x x x
A.
1
;9
2
. B.
9
2;
4
. C.
9
1;
2
. D.
3
;3
2
.
Lời giải:
Chọn C
2 2 1 13
x x x
2
2 3 2 13
x x x
2
2 7 9 0
x x
9
1
2
x
.
Câu 26. Tìm tập nghiệm của bất phương trình
2 2
1 4 4 4 0
x x x x
.
A.
2;1 4;
. B.
;1 2;
. C.
2;1 2;
. D.
; 2 1;2
.
Lời giải
Chọn D
Cho
2
2
1 0 1
4 0 2
4 4 0 2
x x
x x
x x x
.
Bảng xét dấu
Vậy
; 2 1;2
S .
Câu 27. Khẳng định nào sau đây sai? Với mọi
,
ta có:
A.
cos cos cos sin sin
. B.
tan tan tan
.
C.
cos cos cos sin sin
. D.
tan tan
tan
1 tan tan
.
Lời giải
Chọn B
Ta có
tan tan
tan
1 tan tan
Câu 28. Số nghiệm nguyên thuộc
20;20
của bất phương trình
2
8 2
x x
là
A.
32
. B.
34
. C.
36
. D.
30
.
Lời giải
Chọn A
Ta có
2
8 2
x x
2
2 8 0
x x
Cho
2
4
2 8 0
2
x
x x
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Bảng xét dấu
Suy ra
; 2 4;x
.
Vì
; 2 4;
19; 18;...; 3;5;6;...;19
20;20
x
x S
x
Nên bất phương trình có
32
nghiệm nguyên thuộc
20;20
.
Câu 29. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
2 2
: 4 8 16 0
C x y x y
. Tâm và
bán kính của
C
là
A.
2;4
I và
6
R
. B.
2; 4
I
và
6
R
. C.
2; 4
I
và
5
R
. D.
2;4
I và
5
R
.
Lời giải
Chọn B
Ta có đường tròn
C
có tâm
2; 4
I
và bán kính
2
2
2 4 16 6
R
.
Câu 30. Có bao nhiêu giá trị nguyên của
m
trong khoảng
3;3
để hệ bất phương trình
2
2 1 4
6 1 5 4
mx x m
x x
có nghiệm
A.
3
. B.
5
. C.
2
. D.
4
.
Lời giải
Chọn D
Ta có
2
2 1 4 1
6 1 5 4 2
mx x m
x x
.
Giải
2
:
6 1 5 4 3
x x x
.
Giải
1
:
2
2 1 4
mx x m
2
2 1 4 1 3
m x m .
+ Nếu
1
2 1 0
2
m m
Khi đó
3 2 1
x m
.
Do đó hệ bất phương trình luôn có nghiệm suy ra các giá trị nguyên của
m
1
;3
2
thỏa mãn
là
1;2
m .
+ Nếu
1
2 1 0
2
m m
.
Khi đó
3 2 1
x m
.
Để hệ bất phương trình có nghiệm thì
2 1 3 2
m m
Suy ra các giá trị nguyên của
m
1
3;
2
thỏa mãn là
1;0
m .
Vậy có
4
giá trị nguyên của
m
thỏa mãn.
Câu 31. Tính khoảng cách giữa
5;1
M và
:3 4 1 0
x y
A.
3
. B.
10
. C.
2
. D.
5
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn C.
Ta có
2
2
3.5 4.1 1
, 2
3 4
d M
.
Câu 32. Viết phương trình đường thẳng
đi qua hai điểm
2; 5
D
và
3; 1
E
A.
4 3 0
x y
. B.
4 18 0
x y
. C.
4 13 0
x y
. D.
3 1 0
x y
.
Lời giải
Chọn C.
Đường thẳng
nhận
1;4
DE
làm véc tơ chỉ phương
véc tơ pháp tuyến
4; 1
n
: 4 2 5 0
x y
4 13 0
x y
.
Câu 33. Viết phương trình đường thẳng
đi qua
2;5
H và vuông góc với đường thẳng
: x 3y 2 0
d
A.
3y 17 0
x
. B.
3y 13 0
x
. C.
3 y 11 0
x
. D.
3 y 1 0
x
.
Lời giải
Chọn C.
Véc tơ chỉ phương của đường thẳng
d
là
3; 1
u
Vì
d
nên
nhận
3; 1
u
là véc tơ pháp tuyến.
2;5H
:3 2 5 0
x y
3 11 0
x y
.
Câu 34. Có bao nhiêu giá trị nguyên của
m
trong khoảng
5;5
để hệ bất phương trình
2
9 3
4 1 6
mx x m
x x
vô nghiệm.
A.
6
. B.
4
. C.
8
. D.
5
.
Lời giải
Chọn A.
Ta có
2
9 3
4 1 6
mx x m
x x
2
3 9 1
1
m x m
x
I
*Nếu
3
m
thì (1) vô nghiệm
I
vô nghiệm
3
m
(nhận)
2
* Nếu
5 3
m
thì
1 3
x m
I
vô nghiệm khi chỉ khi
3 1 2
m m
Kết hợp điều kiện
5 3
m
và m
ta được
2; 1;0;1;2
m
3
*Nếu
3 5
m
thì
1 3
x m
I
có nghiệm
3 5
m
(loại)
Từ
2
,
3
suy ra
2; 1;0;1;2;3
m .
Câu 35. Cho bất phương trình
2
5 4 2 1 0
x x x
. Số nghiệm nguyên của bất phương trình là
A.
5
. B.
3
. C.
4
. D.
2
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn B.
Điều kiện
1
x
Ta có
1
x
không phải là ngiệm của bất phương trình
2
5 4 2 1 0
x x x
1
x
Ta có
2
5 4 2 1 0
x x x
2
1 3 1 2 1 0
x x x
3
1 3 1 2 0
x x
Đặt
1, 0
t x t
ta được :
3
0
3 2 0
t
t t
2
0
1 2 0
t
t t t
2
0
2 0
t
t t
0 2
t
0 1 2 1 5
x x
x
2;3;4
x .
II. TỰ LUẬN
Câu 1. (1 điểm) Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 4 6 3 0
C x y x y
. Viết phương
trình tiếp tuyến của đường tròn biết tiếp tuyến vuông góc với đường thẳng
: 3 3 0
d x y
.
Lời giải
Đường tròn
C
có tâm
2;3
I và bán kính
4 9 3 10
R .
Gọi
là tiếp tuyến của đường tròn
C
: 3 3 0
d x y
có dạng :
3 0
x y m
.
Do
tiếp xúc
C
3
, 10
10
m
d I d R
3 10
m
13
7
m
m
.
Vậy
:3 13 0
:3 7 0
x y
x y
.
Câu 2. (1 điểm) Cho
sin 0
x
và
cos 1
x
. Chứng minh rằng :
sin 1 cos 2
1 cos sin sin
x x
x x x
.
Lời giải
sin 1 cos
1 cos sin
x x
VT
x x
2
2
sin 1 cos
1 cos sin
x x
x x
2 2cos 2
1 cos sin sin
x
VP
x x x
.
Câu 3. (1 điểm) Giải bất phương trình
5 3 4 4 1
x x x
Lời giải
Ta có:
5 3 4 4 1
x x x
2
1 0
5 3 4 0
1 0
5 3 4 16 1
x
x x
x
x x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 2
1
4
5
3
1
3 19 20 16 32 16
x
x x
x
x x x x
2
4
5 1
3
1
13 51 4 0
x x
x
x x
4
5 1
3
1
1
4
13
x x
x
x
5
4
4
3
x
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 11
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Đơn giản biểu thức
0 0
1 3
sin10 cos10
C
A.
0
8cos20
. B.
0
4sin20
. C.
0
4cos20
. D.
0
8sin 20
.
Câu 2. Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
1;2
A ,
3; 4
B
và đường thẳng
: 3 0
d x y
. Gọi
;
I a b
là tâm của đường tròn đi qua hai điểm
,
A B
và tiếp xúc với
d
. Tính hiệu
a b
?
A.
4
. B.
3
. C.
3
. D.
1
.
Câu 3. Tìm tất cả các giá trị của
m
để
2
2 1 4
f x mx m x m
luôn dương với
x
.
A.
0;m
. B.
1
; 1 ;
3
m
.
C.
1
1;
3
m
. D.
1
;
3
m
.
Câu 4. Một người đi bộ xuất phát từ vị trí
A
đến vị trí
B
. Sau khi người đó đi được
5
giờ
20
phút, một
người khác đi xe đạp cũng xuất phát từ
A
bắt đầu đuổi theo được
20
km
thì gặp người đi bộ. Tính
vận tốc của người đi bộ biết rằng vận tốc người đi xe đạp lớn hơn vận tốc người đi bộ là
12 /
km h
.
A.
5 /
km h
. B.
4 /
km h
. C.
3 /
km h
. D.
6 /
km h
.
Câu 5. Khi xét dấu biểu thức
2
2
3 10
1
x x
f x
x
ta có:
A.
0
f x
khi
1
x
. B.
0
f x
khi
5 1
x
hoặc
1 2
x
.
C.
0
f x
khi
1 1
x
. D.
0
f x
khi
5 2
x
.
Câu 6. Trong mặt phẳng
Oxy
, đường tròn tâm
2; 3
I
, và bán kính
4
R
có phương trình là:
A.
2 2
2 3 4
x y
. B.
2 2
2 3 16 0
x y
.
C.
2 2
2 3 16
x y
. D.
2 2
2 3 16
x y
.
Câu 7. Cho
2
cos
5
2
3
. Khi đó
sin
bằng:
A.
21
3
. B.
21
5
. C.
21
2
. D.
21
5
.
Câu 8. Một đường tròn có bán kính
15cm
. Tìm độ dài cung tròn có góc ở tâm bằng
30
.
A.
2
cm
5
. B.
5
cm
2
. C.
5
cm
3
. D.
cm
3
.
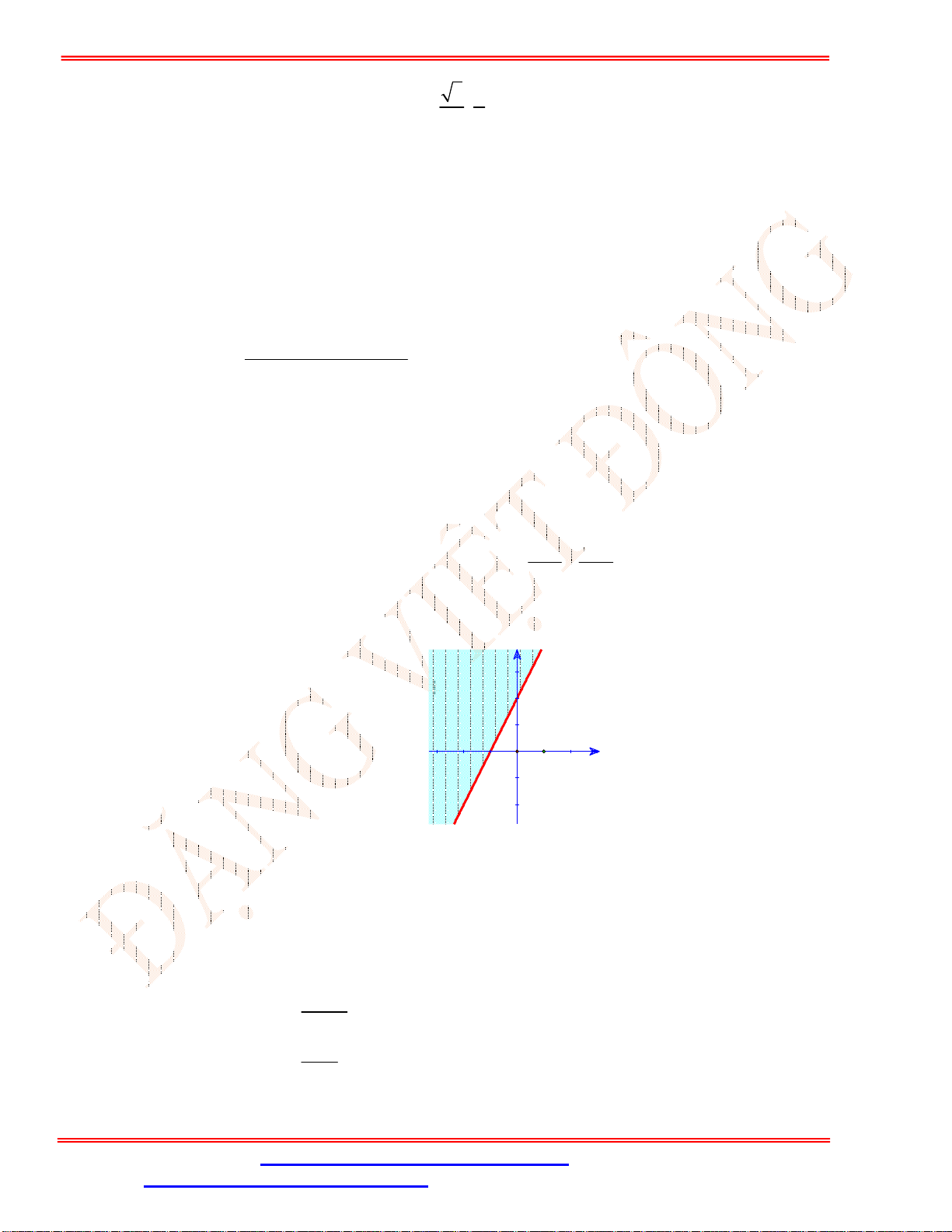
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 9. Trên đường tròn lượng giác, điểm
3 1
;
2 2
N
biểu diễn cung có số đo
. Tìm
, biết rằng
là
một trong bốn số đo cho dưới đây.
A.
210
. B.
210
. C.
30
. D.
30
.
Câu 10. Cho tam giác
ABC
. Hỏi mệnh đề nào sau đây sai?
A.
BC
là một vectơ chỉ phương của đường thẳng
BC
.
B. Trong mặt phẳng
Oxy
, các đường thẳng
AB
,
BC
,
CA
đều có hệ số góc.
C.
BC
là một vectơ pháp tuyến của đường cao
AH
.
D. Đường trung trực của
AB
nhận
AB
là vectơ pháp tuyến.
Câu 11. Biểu thức
sin sin3 sin5
cos cos3 cos5
x x x
A
x x x
.
A.
tan 3
x
. B.
cot
x
. C.
cot3
x
. D.
tan3
x
.
Câu 12. Cho biểu thức
1 2
f x x x
. Khẳng định nào sau đây đúng ?
A.
0
f x ,
1;
x . B.
0
f x ,
;2
x .
C.
0
f x ,
x
. D.
0
f x ,
1;2
x .
Câu 13. Cho
1
a
,
1
b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
1 1
a b
b a
.
A.
10
. B.
8
. C.
4
D.
6
.
Câu 14. Miền không tô đậm (không kể đường thẳng
d
) là miền nghiệm của bất phương trình nào ?
x
y
-1
2
O 1
A.
2 2
x y
. B.
2 2
x y
. C.
2 2 0
x y
D.
2 2 0
x y
.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
. Biết trung tuyến kẻ từ
A
và đường cao kẻ từ
B
lần lượt có phương trình
3 1 0
x y
và
1 0
x y
. Biết
1;2
M là trung điểm của
AB
. Giả sử
điểm
C
có tọa độ
;
C a b
. Tính tổng
a b
.
A.
3
. B.
3
. C.
4
D.
4
.
Câu 16. Hệ bất phương trình
4 3
6
2 5
1
2
3
x
x
x
x
có nghiệm là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
33
3
8
x . B.
5 33
2 8
x . C.
7 3
x
. D.
5
3
2
x .
Câu 17. Cho tam giác
ABC
có
0
60
B
,
0
45
C
,
5
AB
. Hỏi độ dài cạnh
AC
bằng bao nhiêu ?
A.
5 2
. B.
10
. C.
5 3
. D.
5 6
2
.
Câu 18. Tâm
I
và bán kính
R
của đường tròn
2 2
2 8 8 0
x y x y
là:
A.
1;4
I ,
5
R
. B.
1; 4
I
,
8
R
. C.
2;8
I ,
5
R
. D.
1; 4
I
,
5
R
.
Câu 19. Trong mặt phẳng
Oxy
, đường tròn có tâm
2; 1
I
, tiếp xúc với đường thẳng
:4 3 4 0
x y
có
phương trình là:
A.
2 2
2 1 3
x y
. B.
2 2
2 1 9
x y
.
C.
2 2
2 1 3
x y
. D.
2 2
2 1 9
x y
.
Câu 20. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 2 4 3 0
C x y x y
. Tiếp tuyến của
C
tại
2; 3
M
có phương trình là:
A.
5 0
x y
. B.
3 5 21 0
x y
. C.
2 1 0
x y
. D.
1 0
x y
.
Câu 21. Biết
2 2
25 9
sin ; os ;0
169 25 2 2
a c b a b
. Hãy tính
sin
a b
A.
56
65
. B.
33
65
. C.
33
65
. D.
56
65
.
Câu 22. Cho tam giác
ABC
có độ dài ba cạnh
, ,
a b c
và bán kính đường tròn ngoại tiếp là
R
. Biểu thức nào
sau đây dùng để tính
cos
C
A. cos
2
c
C
R
. B.
2 2 2
2
b c a
bc
. C.
2 2 2
2
a b c
ab
. D.
2 2 2
2
a c b
ac
.
Câu 23. Tập nghiệm của bất phương trình
3 2 2 7 0
x x
là:
A.
7 2
;
2 3
. B.
2 7
;
3 2
.
C.
7 3
;
2 2
. D.
7 3
; ;
2 2
.
Câu 24. Cho phương trình
2 2
0 1 0
ax by c a b
. Mệnh đề nào sau đây sai?
A. Điểm
0 0 0
;
M x y
thuộc đường thẳng
1
khi và chỉ khi
0 0
0
ax by c
.
B. Khi
0, 1
b là phương trình của đường thẳng song song hoặc trùng với trục
Oy
.
C.
1
là phương trình tổng quát của đường thẳng có vecto chỉ phương là
;
n a b
.
D. Khi
0, 1
a là phương trình của đường thẳng song song hoặc trùng với trục
Ox
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 25. Trên đường tròn lượng giác gốc
A
cho các cung có số đo.
I.
4
. II.
7
4
. III.
13
4
. IV.
5
9
.
Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ I,II và III. B. Chỉ I,II và IV. C. Chỉ II,III và IV. D. Chỉ I vàII.
Câu 26. Trên đường tròn định hướng gốc
A
có bao nhiêu điểm
M
thỏa mãn sđ
0
0
30 .45
AM k
, k
A.
6
. B.
8
. C.
4
. D.
10
.
Câu 27. Tập nghiệm
S
của hệ
2
2
7 6 0
8 15 0
x x
x x
là
A.
1;3
S . B. S
. C.
3;5
S . D.
1;3 5;6
S .
Câu 28. Trong các công thức lượng giác sau, công thức nào đúng với mọi ,
A.
tan tan
tan
1 tan .tan
. B.
tan tan tan
.
C.
cos cos cos sin sin
. D.
cos cos cos sin sin
.
Câu 29. Cho tam giác
ABC
thỏa mãn
2
2
tan sin
tan sin
B B
C C
. Khẳng định nào sau đây là đúng?
A. Tam giác
ABC
là tam giác tù. B. Tam giác
ABC
là tam giác đều.
C. Không tồn tại tam giác
ABC
. D. Tam giác
ABC
là tam giác vuông hoặc cân.
Câu 30. Tập nghiệm của bất phương trình
1
1
1
x
là
A.
;1
. B.
1;2
. C.
;1
. D.
1;2
.
Câu 31. Trong mặt phẳng
Oxy
, gọi
H
là trực tâm của tam giác
ABC
. Phương trình các cạnh và đường cao
của tam giác là
:7 4 0; :2 4 0; : 2 0
AB x y BH x y AH x y
. Phương trình đường cao
CH
của tam giác
ABC
là
A.
7 0
x y
. B.
7 2 0
x y
. C.
7 2 0
x y
. D.
7 2 0
x y
.
Câu 32. Tính các giá trị lượng giác của góc
60
.
A.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
B.
2 2
cos ;sin ;tan 1;cot 1
2 2
.
C.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
D.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
Câu 33. Cho đường thẳng
: 2 3 4 0
d x y
. Vectơ nào sau đây là vectơ pháp tuyến của
d
?
A.
4
2;3
n
. B.
2
4; 6
n
. C.
1
3;2
n
. D.
3
2; 3
n
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 34. Tập nghiệm của bất phương trình
2
4 3 0
x x
là
A.
3; 1
. B.
; 1 3;
.C.
; 3 1;
. D.
3; 1
.
Câu 35. Khi biểu diễn trên đường tròn lượng giác, cung lượng giác nào trong các cung lượng giác có số đo
dưới đây có cùng ngọn cung với cung lượng giác có số đo
4200
.
A.
8
. B.
120
. C.
120
. D.
130
.
Câu 36. Trong mặt phẳng
Oxy
, cho đường thẳng
:
d
2 1 0
x y
. Nếu đường thẳng
đi qua
1; 1
M
và song song với
d
thì
có phương trình:
A.
2 3 0
x y
. B.
2 1 0
x y
. C.
2 1 0
x y
. D.
2 3 0
x y
.
Câu 37. Cho
3
sin
4
. Khi đó
cos 2
bằng:
A.
7
4
. B.
7
4
. C.
1
8
. D.
1
8
.
Câu 38. Góc có số đo
3
16
được đổi sang số đo độ là:
A.
33 45
o
. B.
33 45
o
. C.
32 55
o
. D.
29 30
o
.
Câu 39. Trong các công thức lượng giác sau, công thức nào đúng với mọi ,
:
A.
sin 4
tan 2
cos2
. B.
1 tan
tan
1 tan 4
.
C.
sin sin .cos cos .sin
. D.
sin sin .cos cos .sin
.
Câu 40. Nhị thức
2 4
f x x
luôn âm trong khoảng nào sau đây:
A.
2;
. B.
0;
. C.
;2
. D.
;4
.
II. TỰ LUẬN ( 2 điểm).
Câu 1. (1 điểm).
Cho cung
thỏa mãn
1
sin
3
và 0
2
. Tính giá trị của biểu thức cos
3
.
Câu 2. (1 điểm).
Trong mặt phẳng tọa độ
Oxy
cho điểm
1; 4
A
và đường thẳng
d
:
2
4 5
x t
y t
,
t
. Viết
phương trình tổng quát của đường thẳng
qua
A
và song song với
d
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 11
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
I. TRẮC NGHIỆM
Câu 1. Đơn giản biểu thức
0 0
1 3
sin10 cos10
C
A.
0
8cos20
. B.
0
4sin20
. C.
0
4cos20
. D.
0
8sin 20
.
Lời giải
Chọn A.
0 0
1 3
sin10 cos10
C
0 0
0 0
cos10 3sin10
sin10 .cos10
0 0
0
2sin 30 10
1
sin 20
2
0 0
0
0
2sin20 cos20
4 8cos20
sin 20
.
Câu 2. Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
1;2
A ,
3; 4
B
và đường thẳng
: 3 0
d x y
. Gọi
;
I a b
là tâm của đường tròn đi qua hai điểm
,
A B
và tiếp xúc với
d
. Tính hiệu
a b
?
A.
4
. B.
3
. C.
3
. D.
1
.
Lời giải
Chọn D.
Ta thấy
1;2
A d
. Do đó
;
I a b
thuộc đường thẳng
đi qua
1;2
A và vuông góc với
d
.
Phương trình của đường thẳng
là:
1 0
x y
.
Do đó
; 1
I a b a b
.
Câu 3. Tìm tất cả các giá trị của
m
để
2
2 1 4
f x mx m x m
luôn dương với
x
.
A.
0;m
. B.
1
; 1 ;
3
m
.
C.
1
1;
3
m
. D.
1
;
3
m
.
Lời giải
Chọn D.
Để
2
2 1 4
f x mx m x m
luôn dương với
x
thì
2
2
0, 0 /
0
0
1
0
0
3
1 4 0
0
a b c k t m
m
a
m
a
m m
.
Câu 4. Một người đi bộ xuất phát từ vị trí
A
đến vị trí
B
. Sau khi người đó đi được
5
giờ
20
phút, một
người khác đi xe đạp cũng xuất phát từ
A
bắt đầu đuổi theo được
20
km
thì gặp người đi bộ. Tính
vận tốc của người đi bộ biết rằng vận tốc người đi xe đạp lớn hơn vận tốc người đi bộ là
12 /
km h
.
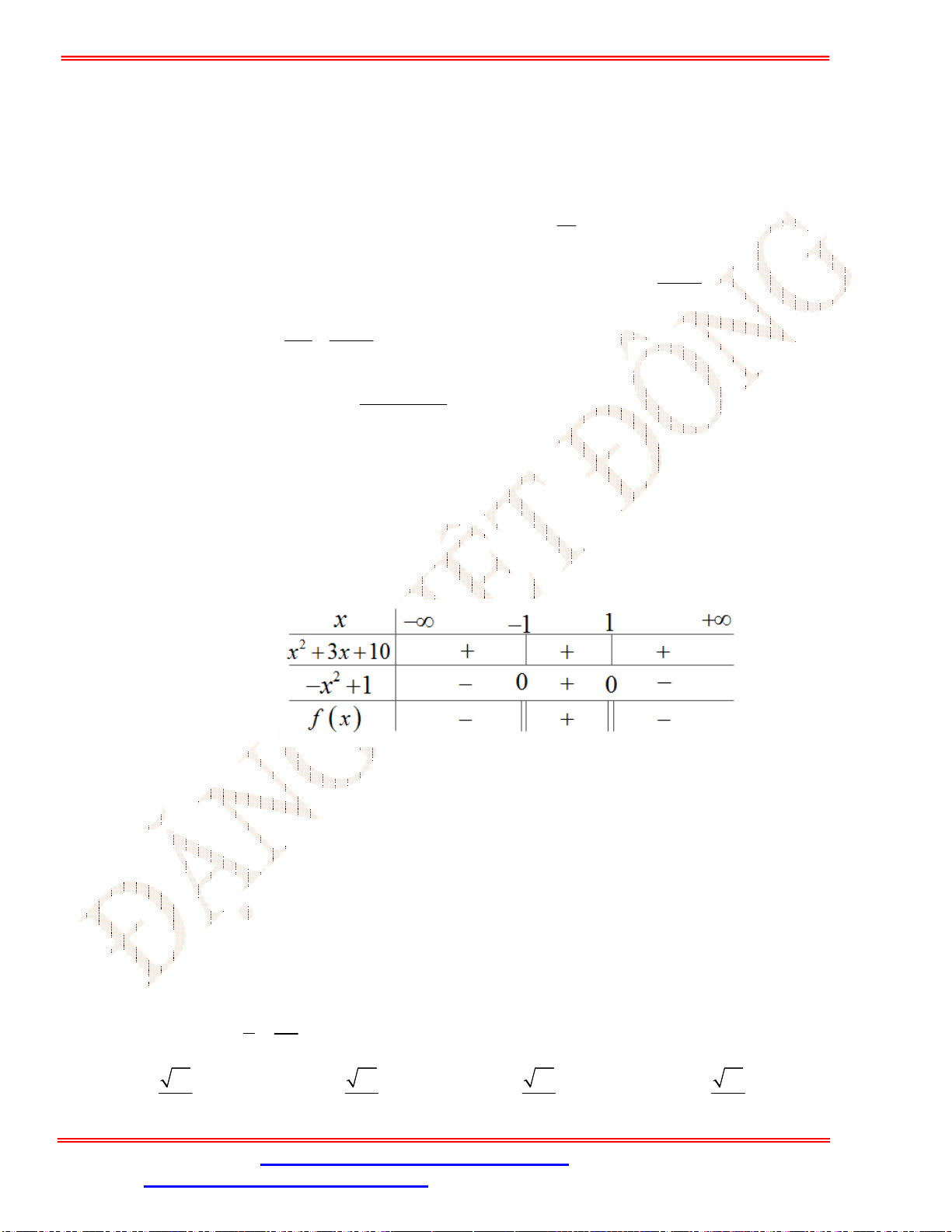
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
5 /
km h
. B.
4 /
km h
. C.
3 /
km h
. D.
6 /
km h
.
Lời giải
Chọn C.
Gọi vận tốc của người đi bộ là
/
v km h
. Khi đó vận tốc của người đi xe đạp là
12 /
v km h
.
Sau
5
giờ
20
phút người đi bộ đi được quãng đường là
16
3
v km
.
Lúc hai người gặp nhau thì người đi bộ đi thêm được quãng đường là
20
12
v
km
v
.
Ta có phương trình
16 20
20 3 /
3 12
v v
v km h
v
.
Câu 5. Khi xét dấu biểu thức
2
2
3 10
1
x x
f x
x
ta có:
A.
0
f x
khi
1
x
. B.
0
f x
khi
5 1
x
hoặc
1 2
x
.
C.
0
f x
khi
1 1
x
. D.
0
f x
khi
5 2
x
.
Lời giải
Chọn C.
Ta có bảng xét dấu của biểu thức
f x
như sau:
Vậy
0
f x
khi
1 1
x
.
Câu 6. Trong mặt phẳng
Oxy
, đường tròn tâm
2; 3
I
, và bán kính
4
R
có phương trình là:
A.
2 2
2 3 4
x y
. B.
2 2
2 3 16 0
x y
.
C.
2 2
2 3 16
x y
. D.
2 2
2 3 16
x y
.
Lời giải
Chọn D.
Đường tròn tâm
2; 3
I
, và bán kính
4
R
có phương trình là:
2 2
2 3 16
x y
.
Câu 7. Cho
2
cos
5
2
3
. Khi đó
sin
bằng:
A.
21
3
. B.
21
5
. C.
21
2
. D.
21
5
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn B.
Ta có
2 2
sin 1 cos
4 21
1
25 25
.
Vì
2
sin 0
3
. Do đó
21
sin
5
.
Câu 8. Một đường tròn có bán kính
15cm
. Tìm độ dài cung tròn có góc ở tâm bằng
30
.
A.
2
cm
5
. B.
5
cm
2
. C.
5
cm
3
. D.
cm
3
.
Lời giải
Chọn B.
Đường tròn (ứng với góc ở tâm là
360
) bán kính
R
có độ dài
2 .
R
. Do đó cung tròn có góc ở tâm
bằng
30
thì có độ dài cung tròn là:
30 .2 .
360
R
l
.15 5
6 6 2
R
.
Câu 9. Trên đường tròn lượng giác, điểm
3 1
;
2 2
N
biểu diễn cung có số đo
. Tìm
, biết rằng
là
một trong bốn số đo cho dưới đây.
A.
210
. B.
210
. C.
30
. D.
30
.
Lời giải
Chọn A.
x
y
-
3
2
N
1/2
O
Điểm
3 1
;
2 2
N
biểu diễn cung có số đo
suy ra
3
cos
2
và
1
sin
2
.
Vậy
210
.
Câu 10. Cho tam giác
ABC
. Hỏi mệnh đề nào sau đây sai?
A.
BC
là một vectơ chỉ phương của đường thẳng
BC
.
B. Trong mặt phẳng
Oxy
, các đường thẳng
AB
,
BC
,
CA
đều có hệ số góc.
C.
BC
là một vectơ pháp tuyến của đường cao
AH
.
D. Đường trung trực của
AB
nhận
AB
là vectơ pháp tuyến.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B.
-
BC
là một vectơ chỉ phương của đường thẳng
BC
nên A đúng.
- Vì
AH BC
nên
BC
là một vectơ pháp tuyến của đường cao
AH
suy ra C đúng.
- Đường trung trực của
AB
thì vuông góc với
AB
tại trung điểm của nó nên sẽ nhận
AB
làm vectơ
pháp tuyến, do đó D đúng.
- Lưu ý: Các đường thẳng vuông góc với trục
Ox
không có hệ số góc (hệ số góc không xác định), do
đó B sai vì trong các đường thẳng
AB
,
BC
,
CA
có thể có một đường vuông góc với trục
Ox
.
Câu 11. Biểu thức
sin sin3 sin5
cos cos3 cos5
x x x
A
x x x
.
A.
tan 3
x
. B.
cot
x
. C.
cot3
x
. D.
tan3
x
.
Lời giải
Chọn A.
sin5 sin sin3
sin sin3 sin5
cos cos3 cos5 cos5 cos cos3
x x x
x x x
A
x x x x x x
sin3 2cos2 1
2sin3 .cos2 sin3
tan3
2cos3 .cos2 cos3 cos3 2cos2 1
x x
x x x
x
x x x x x
Câu 12. Cho biểu thức
1 2
f x x x
. Khẳng định nào sau đây đúng ?
A.
0
f x ,
1;
x . B.
0
f x ,
;2
x .
C.
0
f x ,
x
. D.
0
f x ,
1;2
x .
Lời giải
Chọn D.
2
1 2 3 2
f x x x x x
Bảng xét dấu của
f x
x
f(x)
-∞
2
+∞1
0
0+
- -
Từ bảng xét dấu ta có
0
f x ,
1;2
x
Câu 13. Cho
1
a
,
1
b
. Tìm giá trị nhỏ nhất của biểu thức
2 2
1 1
a b
b a
.
A.
10
. B.
8
. C.
4
D.
6
.
Lời giải
Chọn B.
Đặt
1 0
x a
,
1 0
y b .
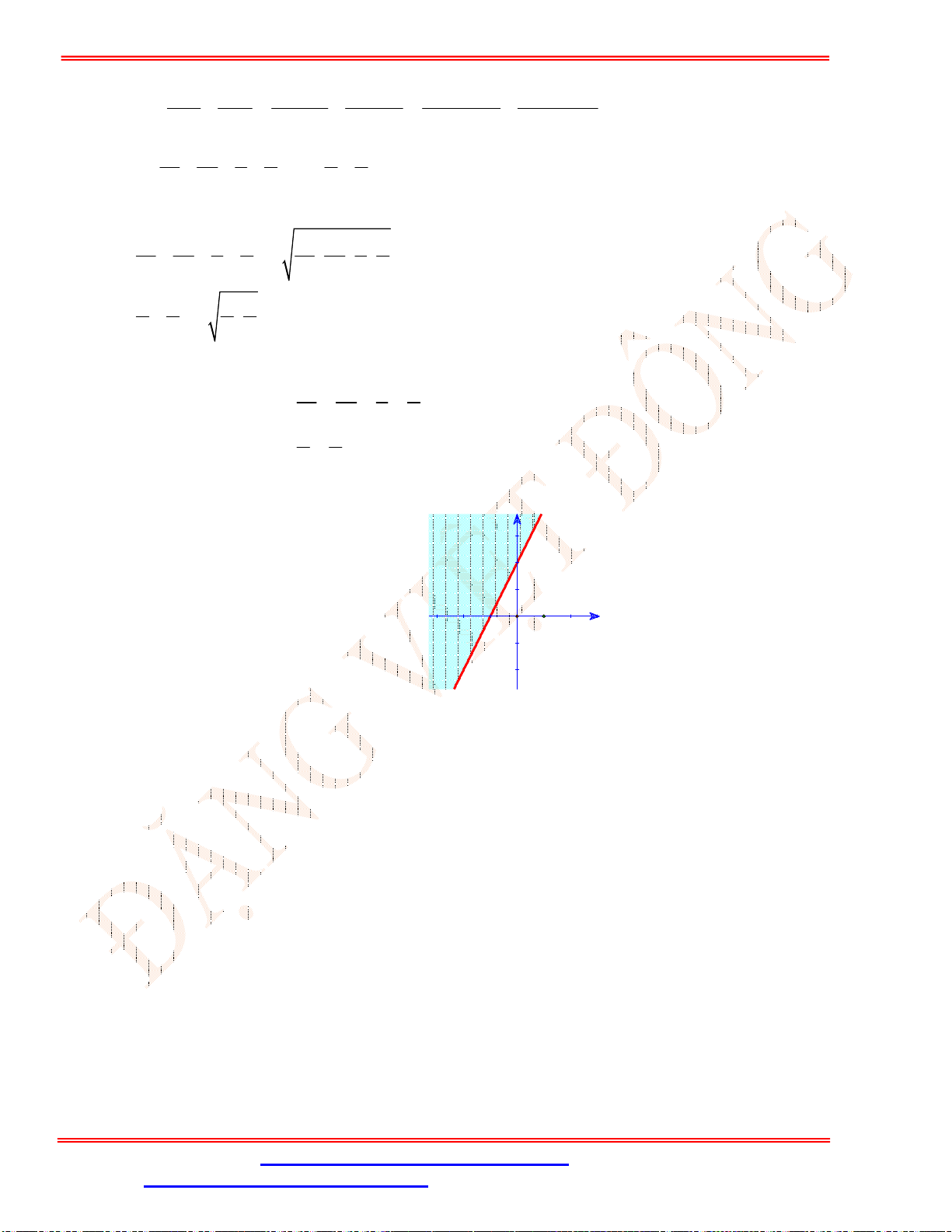
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 2
2 2 2 2
1 1
2 1 2 1
1 1
x y
a b x x y y
P
b a y x y x
2 2
1 1
2
x y x y
y x x y y x
.
Áp dụng bất đẳng thức Côsi ta có
2 2 2 2
4
1 1 1 1
4 4
x y x y
y x x y y x x y
.
2 2
x y x y
y x y x
.
Do đó
4 2.2 8
P
.
Dấu
" "
xảy ra
2 2
1 1
1 2
x y
y x x y
x y a b
x y
y x
.
Câu 14. Miền không tô đậm (không kể đường thẳng
d
) là miền nghiệm của bất phương trình nào ?
x
y
-1
2
O 1
A.
2 2
x y
. B.
2 2
x y
. C.
2 2 0
x y
D.
2 2 0
x y
.
Lời giải
Chọn D.
Đường thẳng
d
qua 2 điểm
1;0
và
0;2
nên
: 2 2 2 2 0
d y x x y
Ta có
2.0 0 2 0
nên miền không tô đậm (không kể đường thẳng
d
) là miền nghiệm của bất
phương trình
2 2 0
x y
.
Câu 15. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
. Biết trung tuyến kẻ từ
A
và đường cao kẻ từ
B
lần lượt có phương trình
3 1 0
x y
và
1 0
x y
. Biết
1;2
M là trung điểm của
AB
. Giả sử
điểm
C
có tọa độ
;
C a b
. Tính tổng
a b
.
A.
3
. B.
3
. C.
4
D.
4
.
Lời giải
Chọn B.
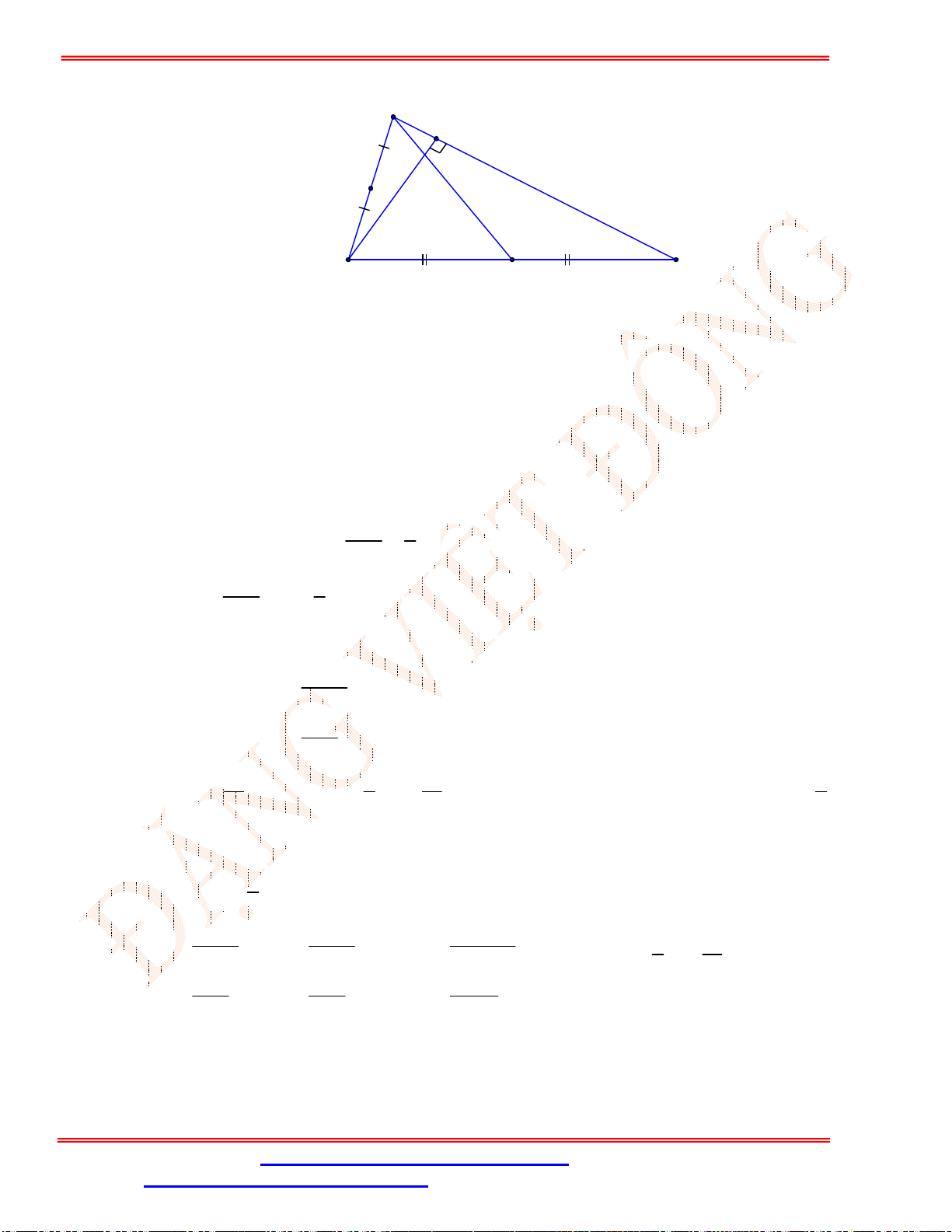
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
M
N
A
B
C
H
Ta có
1 3 ;t
A AM A t
M
là trung điểm
1 3 ;4
AB B t t
1 3 4 1 0 4 4 1
B BH t t t t
2;3
B ,
4;1
A .
Đường thẳng
AC
qua
A
và vuông góc với
BH
có phương trình
3 0
x y
; 3
C AC C c c
N
là trung điểm
2
;
2 2
c c
BC N
2
3. 1 0 2 3 2 0 2 4 2
2 2
c c
N AN c c c c
2; 5 2
C a ;
5
b
hay
3
a b
.
Câu 16. Hệ bất phương trình
4 3
6
2 5
1
2
3
x
x
x
x
có nghiệm là:
A.
33
3
8
x . B.
5 33
2 8
x . C.
7 3
x
. D.
5
3
2
x .
Lời giải
Chọn C
Điều kiện:
5
, 3
2
x x .
Ta có
4 3
6
2 5
1
2
3
x
x
x
x
4 3
6 0
2 5
1
2 0
3
x
x
x
x
8 33
0
2 5
7
0
3
x
x
x
x
5 33
; ;
2 8
7; 3
x
x
7; 3
x .
Câu 17. Cho tam giác
ABC
có
0
60
B
,
0
45
C
,
5
AB
. Hỏi độ dài cạnh
AC
bằng bao nhiêu ?
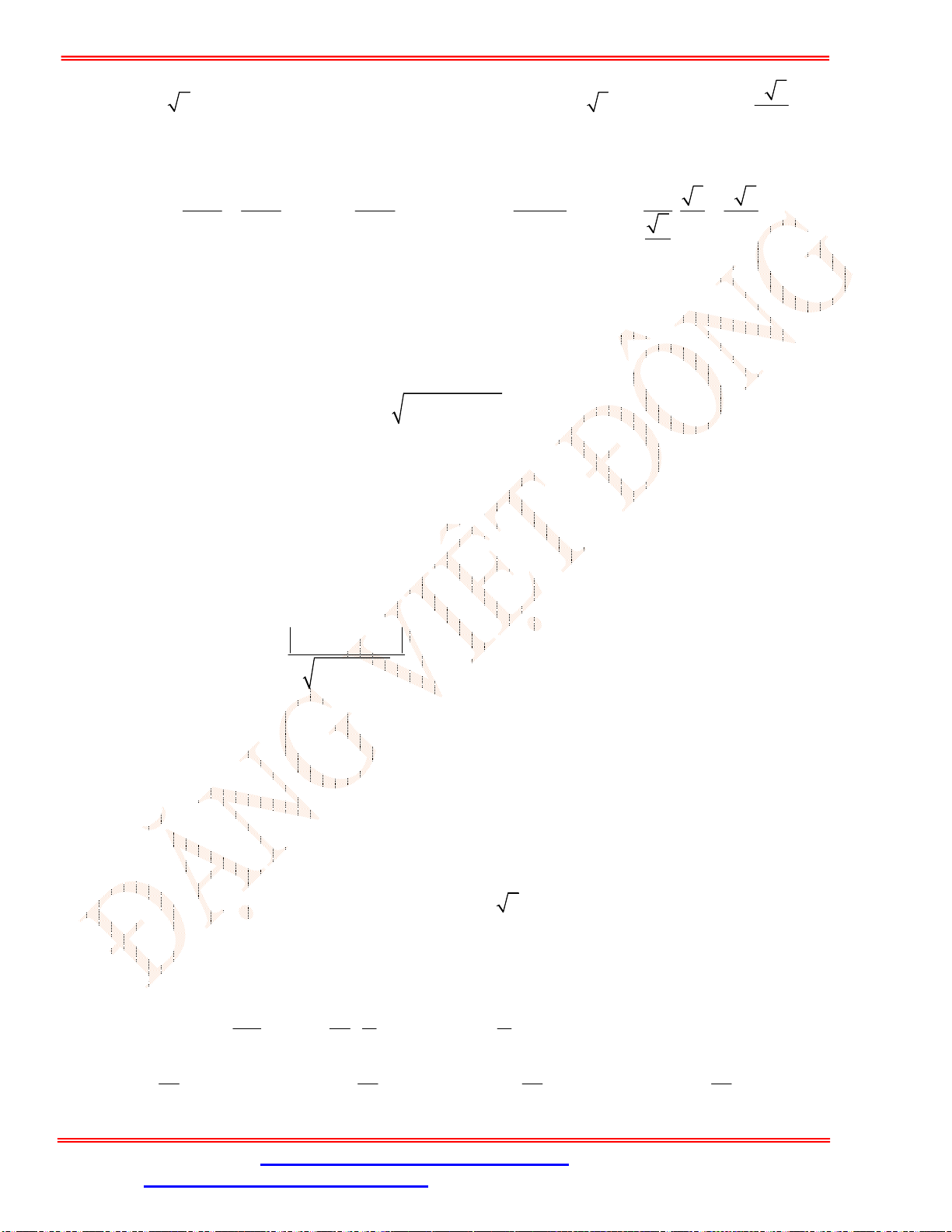
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
5 2
. B.
10
. C.
5 3
. D.
5 6
2
.
Lời giải
Chọn D
Ta có
sin sin
AC AB
B C
.sin
sin
AB
AC B
C
0
0
5 5 3 5 6
.sin60 .
sin 45 2 2
2
2
AC .
Câu 18. Tâm
I
và bán kính
R
của đường tròn
2 2
2 8 8 0
x y x y
là:
A.
1;4
I ,
5
R
. B.
1; 4
I
,
8
R
. C.
2;8
I ,
5
R
. D.
1; 4
I
,
5
R
.
Lời giải
Chọn A
Ta có tâm
1; 4
I
, bán kính
2
2
1 4 8 5
R
.
Câu 19. Trong mặt phẳng
Oxy
, đường tròn có tâm
2; 1
I
, tiếp xúc với đường thẳng
:4 3 4 0
x y
có
phương trình là:
A.
2 2
2 1 3
x y
. B.
2 2
2 1 9
x y
.
C.
2 2
2 1 3
x y
. D.
2 2
2 1 9
x y
.
Lời giải
Chọn B
Ta có
2
3
4.2 3 1 4
, 3
4 3
R d I
.
Nên phương trình đường tròn thỏa đề bài là
2 2
2 1 9
x y
.
Câu 20. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 2 4 3 0
C x y x y
. Tiếp tuyến của
C
tại
2; 3
M
có phương trình là:
A.
5 0
x y
. B.
3 5 21 0
x y
. C.
2 1 0
x y
. D.
1 0
x y
.
Lời giải
Chọn A
Đường tròn
C
có tâm
1; 2
I
, bán kính
2
R
.
Gọi
là tiếp tuyến của
C
tại
2; 3
M
.
: 2 2 1 3 3 2 0
x y
2 3 0
x y
5 0
x y
5 0
x y
.
Câu 21. Biết
2 2
25 9
sin ; os ;0
169 25 2 2
a c b a b
. Hãy tính
sin
a b
A.
56
65
. B.
33
65
. C.
33
65
. D.
56
65
.
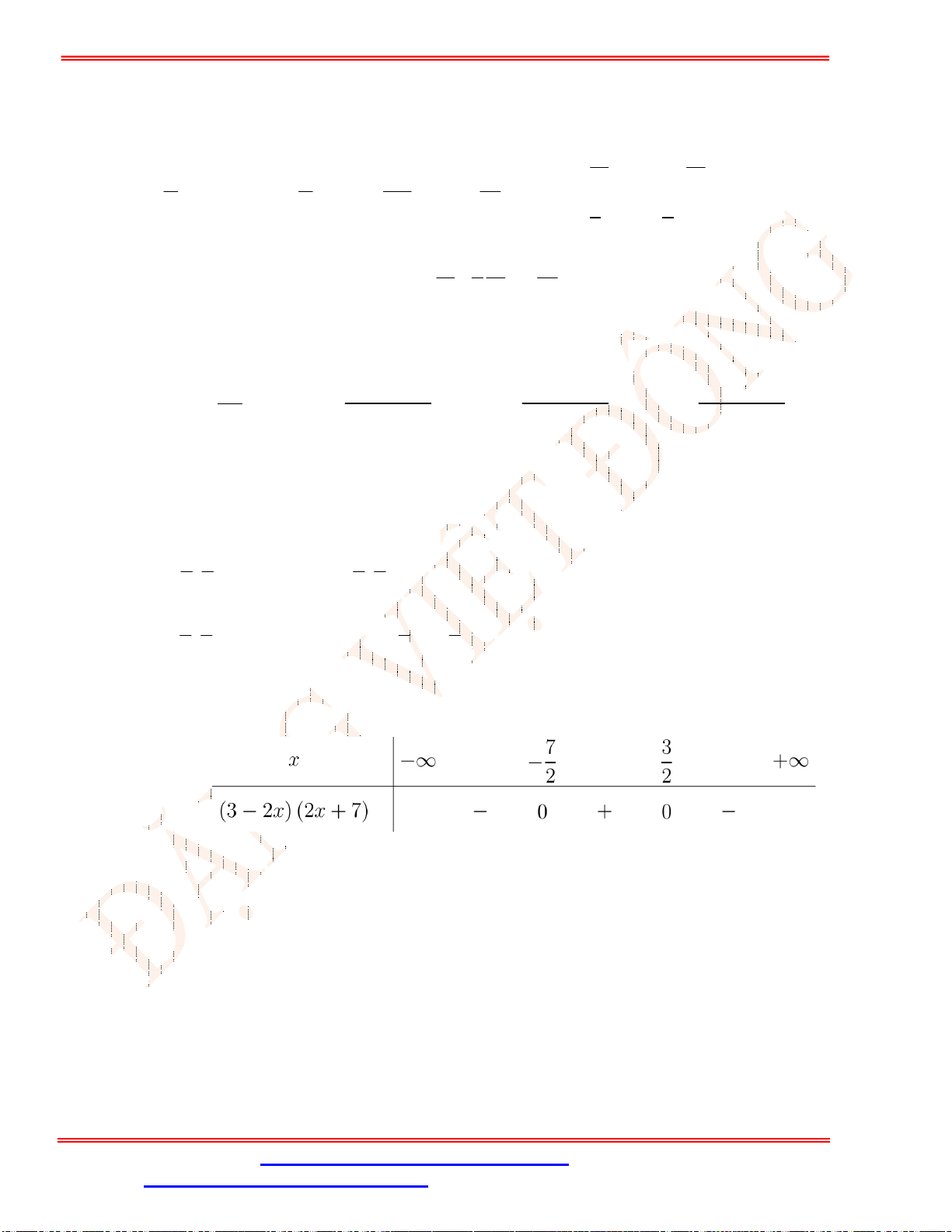
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn B.
Do
2 2
5 12
sin ;cos
25 9
13 13
;0 ;sin ; os
3 4
2 2 169 25
os ;sin
5 5
a a
a b a c b
c b b
.
Có
3 4 12 33
sin sin cos sin cos
13 5 13 65
a b a b b a
.
Câu 22. Cho tam giác
ABC
có độ dài ba cạnh
, ,
a b c
và bán kính đường tròn ngoại tiếp là
R
. Biểu thức nào
sau đây dùng để tính
cos
C
A. cos
2
c
C
R
. B.
2 2 2
2
b c a
bc
. C.
2 2 2
2
a b c
ab
. D.
2 2 2
2
a c b
ac
.
Lời giải
Chọn C.
Câu 23. Tập nghiệm của bất phương trình
3 2 2 7 0
x x
là:
A.
7 2
;
2 3
. B.
2 7
;
3 2
.
C.
7 3
;
2 2
. D.
7 3
; ;
2 2
.
Lời giải
Chọn C.
Câu 24. Cho phương trình
2 2
0 1 0
ax by c a b
. Mệnh đề nào sau đây sai?
A. Điểm
0 0 0
;
M x y
thuộc đường thẳng
1
khi và chỉ khi
0 0
0
ax by c
.
B. Khi
0, 1
b là phương trình của đường thẳng song song hoặc trùng với trục
Oy
.
C.
1
là phương trình tổng quát của đường thẳng có vecto chỉ phương là
;
n a b
.
D. Khi
0, 1
a là phương trình của đường thẳng song song hoặc trùng với trục
Ox
.
Lời giải
Chọn C.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
1
là phương trình tổng quát của đường thẳng có vecto pháp tuyến là
;
n a b
.
Câu 25. Trên đường tròn lượng giác gốc
A
cho các cung có số đo.
I.
4
. II.
7
4
. III.
13
4
. IV.
5
9
.
Hỏi các cung nào có điểm cuối trùng nhau?
A. Chỉ I,II và III. B. Chỉ I,II và IV. C. Chỉ II,III và IV. D. Chỉ I vàII.
Lời giải
Chọn D.
Câu 26. Trên đường tròn định hướng gốc
A
có bao nhiêu điểm
M
thỏa mãn sđ
0
0
30 .45
AM k
, k
A.
6
. B.
8
. C.
4
. D.
10
.
Lời giải
Chọn B.
Viết
0
0
0 0
.2.180
30 .45 30
8
k
k . Vậy chọn B.
Câu 27. Tập nghiệm
S
của hệ
2
2
7 6 0
8 15 0
x x
x x
là
A.
1;3
S . B. S
. C.
3;5
S . D.
1;3 5;6
S .
Lời giải
Chọn C.
2
7 6 0
x x
1 6
x
2
8 15 0
x x
3 5
x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy
3;5
S
Câu 28. Trong các công thức lượng giác sau, công thức nào đúng với mọi ,
A.
tan tan
tan
1 tan .tan
. B.
tan tan tan
.
C.
cos cos cos sin sin
. D.
cos cos cos sin sin
.
Lời giải
Chọn D.
Câu 29. Cho tam giác
ABC
thỏa mãn
2
2
tan sin
tan sin
B B
C C
. Khẳng định nào sau đây là đúng?
A. Tam giác
ABC
là tam giác tù. B. Tam giác
ABC
là tam giác đều.
C. Không tồn tại tam giác
ABC
. D. Tam giác
ABC
là tam giác vuông hoặc cân.
Lời giải
Chọn A.
2
2
tan sin
tan sin
B B
C C
cos sin
cos sin
C B
B C
sin .cos sin .cos
B B C C
sin 2 sin 2
B C
0
2 2
2 180 2
B C
B C
0
90
B C
B C
Vậy tam giác
ABC
là tam giác vuông hoặc cân.
Câu 30. Tập nghiệm của bất phương trình
1
1
1
x
là
A.
;1
. B.
1;2
. C.
;1
. D.
1;2
.
Lời giải
Chọn D.
1
1
1
x
2
0
1
x
x
1 2
x
.
Câu 31. Trong mặt phẳng
Oxy
, gọi
H
là trực tâm của tam giác
ABC
. Phương trình các cạnh và đường cao
của tam giác là
:7 4 0; :2 4 0; : 2 0
AB x y BH x y AH x y
. Phương trình đường cao
CH
của tam giác
ABC
là
A.
7 0
x y
. B.
7 2 0
x y
. C.
7 2 0
x y
. D.
7 2 0
x y
.
Lời giải
Chọn C
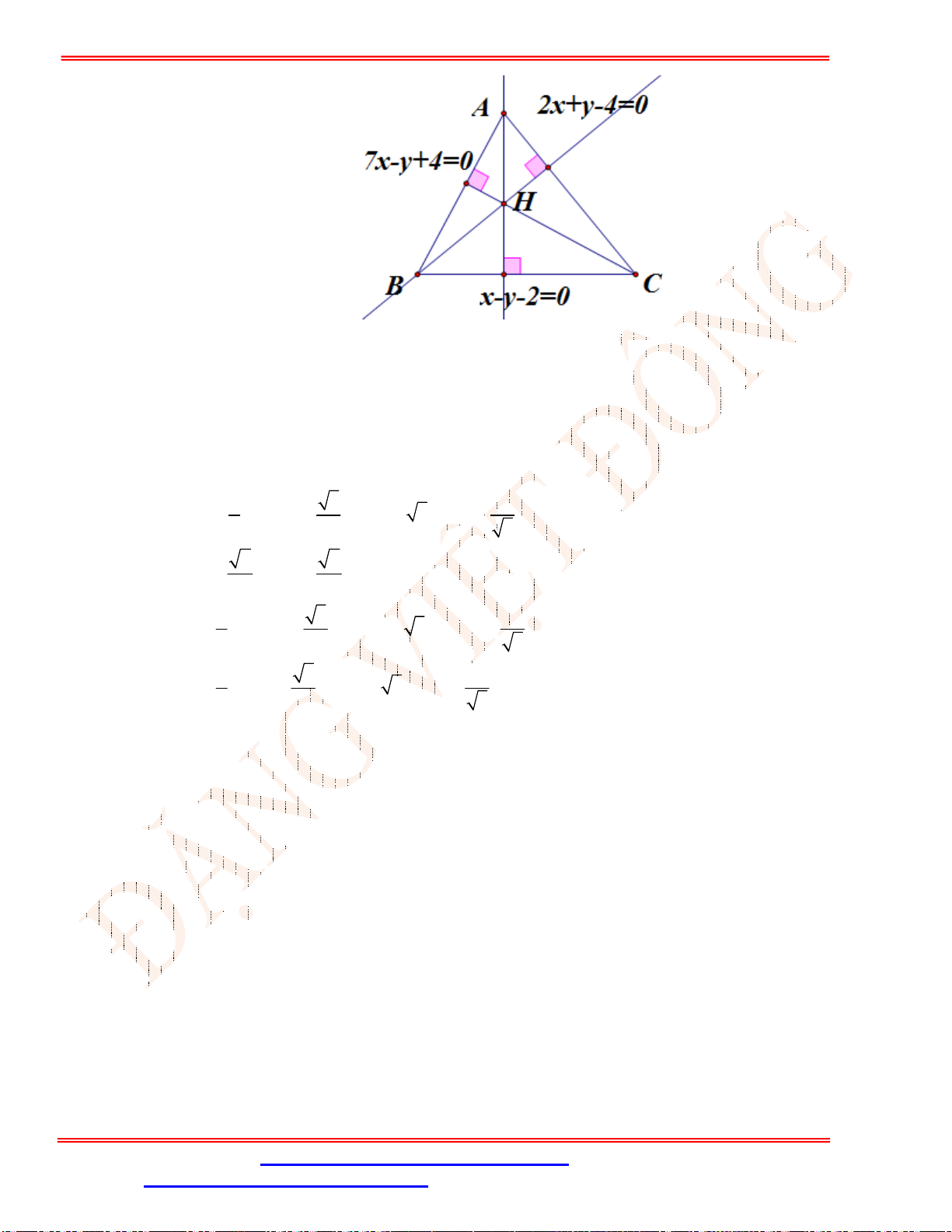
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có tọa độ trực tâm
H
là nghiệm của hệ phương trình
2 4 2
2;0
2 0
x y x
H
x y y
.
Đường cao
CH
nhận
1;7
AB
u
là vectơ pháp tuyến và đi qua
H
nên có phương trình
1. 2 7 0 7 2 0
x y x y
.
Câu 32. Tính các giá trị lượng giác của góc
60
.
A.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
B.
2 2
cos ;sin ;tan 1;cot 1
2 2
.
C.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
D.
1 3 1
cos ;sin ;tan 3;cot
2 2
3
.
Lời giải
Chọn C
Câu 33. Cho đường thẳng
: 2 3 4 0
d x y
. Vectơ nào sau đây là vectơ pháp tuyến của
d
?
A.
4
2;3
n
. B.
2
4; 6
n
. C.
1
3;2
n
. D.
3
2; 3
n
.
Lời giải
Chọn B
Ta có
2
4; 6 2. 2;3
n
.
Câu 34. Tập nghiệm của bất phương trình
2
4 3 0
x x
là
A.
3; 1
. B.
; 1 3;
.C.
; 3 1;
. D.
3; 1
.
Lời giải
Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
2
4 3 0
x x
1
3
x
x
. Vậy tập nghiệm là
; 3 1;S
.
Câu 35. Khi biểu diễn trên đường tròn lượng giác, cung lượng giác nào trong các cung lượng giác có số đo
dưới đây có cùng ngọn cung với cung lượng giác có số đo
4200
.
A.
8
. B.
120
. C.
120
. D.
130
.
Lời giải
Chọn B
Ta có
4200 120 12.360
, nên có cùng điểm ngọn với cung
120
.
Câu 36. Trong mặt phẳng
Oxy
, cho đường thẳng
:
d
2 1 0
x y
. Nếu đường thẳng
đi qua
1; 1
M
và song song với
d
thì
có phương trình:
A.
2 3 0
x y
. B.
2 1 0
x y
. C.
2 1 0
x y
. D.
2 3 0
x y
.
Lời giải
Chọn A.
Do
//
d
có dạng
2 0
x y m
1
m
Mà
1; 1M
3
m
(nhận)
Vậy
: 2 3 0
x y
.
Câu 37. Cho
3
sin
4
. Khi đó
cos 2
bằng:
A.
7
4
. B.
7
4
. C.
1
8
. D.
1
8
.
Lời giải
Chọn C.
Ta có:
cos2
2
1 2sin
2
3
1 2.
4
1
8
.
Câu 38. Góc có số đo
3
16
được đổi sang số đo độ là:
A.
33 45
o
. B.
33 45
o
. C.
32 55
o
. D.
29 30
o
.
Lời giải
Chọn A.
Ta có :
3
16
3
.180
16
o
33 45
o
.
Câu 39. Trong các công thức lượng giác sau, công thức nào đúng với mọi ,
:
A.
sin 4
tan 2
cos2
. B.
1 tan
tan
1 tan 4
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
sin sin .cos cos .sin
. D.
sin sin .cos cos .sin
.
Lời giải
Chọn D.
Câu 40. Nhị thức
2 4
f x x
luôn âm trong khoảng nào sau đây:
A.
2;
. B.
0;
. C.
;2
. D.
;4
.
Lời giải
Chọn C.
Ta có :
2 4 0
f x x
2
x
.
II. TỰ LUẬN ( 2 điểm).
Câu 1. (1 điểm).
Cho cung
thỏa mãn
1
sin
3
và 0
2
. Tính giá trị của biểu thức cos
3
.
Lời giải
Do 0
2
nên
cos 0
.
Ta có
1
sin
3
2
cos 1 sin
1
1
9
2 2
3
.
Do đó cos
3
cos cos sin sin
3 3
2 2 1 1 3
. .
3 2 3 2
2 2 3
6
.
Câu 2. (1 điểm).
Trong mặt phẳng tọa độ
Oxy
cho điểm
1; 4
A
và đường thẳng
d
:
2
4 5
x t
y t
,
t
. Viết
phương trình tổng quát của đường thẳng
qua
A
và song song với
d
.
Lời giải
Ta có
A d
. Đường thẳng
d
có véctơ chỉ phương
1;5
u nên ta chọn véc tơ pháp tuyến
5; 1
n
.
song song với
d
nên
có véc tơ pháp tuyến
5; 1
n
.
Vậy phưowng trình
có dạng:
5 9 0
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 12
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. [NB] Bất phương trình
5 6
5
1
x
x
có tập nghiệm
S
là
A.
1;S
. B.
S
.
C.
; 2 2;S
. D.
;2
S .
Câu 2. [TH] Cho biết
1
sin cos
2
x x
. Tính giá trị biểu thức
4 4
sin cos
M x x
.
A.
15
20
M . B.
23
32
M . C.
4
5
M
. D.
3
16
M
.
Câu 3. [TH] Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm có hoành độ dương thuộc đường thẳng
: 1 0
x y
sao cho
5
OM
. Khi đó hoành độ điểm
M
là
A.
5
x
. B.
4
x
. C.
3
x
. D.
2
x
.
Câu 4. [TH] Bất phương trình
2
1 5 4 0
x x x
có tập nghiệm
S
là
A.
4;S
. B.
;1 4;S
.
C.
4;S
. D.
1 4;S
.
Câu 5. [NB] Rút gọn biểu thức
2 2 2
sin cos tan
M x x x
bằng
A.
2
cot
x
. B.
2
1
sin
x
. C.
2
1
cos
x
. D.
2
2tan
x
.
Câu 6. [TH] Rút gọn biểu thức cos .cos
4 4
M
bằng
A.
1
cos2
2
M
. B.
1 2
cos
2 2
M
.
C.
cos
M
. D.
0
M
.
Câu 7. [VD] Trong mặt phẳng tọa độ
Oxy
, kẻ được bao nhiêu tiếp tuyến đến đường tròn
2 2
2 3 16
x y
biết tiếp tuyến song song với đường thẳng
3 4 2 0
x y
?
A. 2. B. 1. C. 0. D. Vô số.
Câu 8. [TH] Cho
5
cos
13
, 0
2
. Tính cos
3
.
A.
5 12 3
cos
3 26
. B.
5 12 3
cos
3 26
.
C.
12 5 3
cos
3 26
. D.
12 5 3
cos
3 26
.
Câu 9. [TH] Cho
2
2
f x x x m
. Tìm tất cả các giá trị của tham số
m
để
0
f x
,
x
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Câu 10. [VD]
S
là tập hợp tất các các giá trị nguyên dương của tham số
m
để phương trình
2 2 2
5 1 2 5 7 0
x m x m m
có hai nghiệm trái dấu. Hỏi tập hợp
S
có bao nhiêu phần
tử?
A. 4. B. Vô số. C. 0. D. 3.
Câu 11. [NB] Tập nghiệm của bất phương trình
2
7 6 0
x x
là
A.
;1 6;
. B.
6; 1
. C.
1;6
. D.
;1 6;
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 12. [TH] Cho cos2
m
. Hãy tính theo
m
giá trị của biểu thức
2 2
2sin 4cos
A
.
A. 3
A m
. B. 4
A m
. C. 3
A m
. D.
4 2
A m
.
Câu 13. [NB] Tập nghiệm của bất phương trình
3 6 0
x
là:
A.
; 2
. B.
; 3
. C.
2;
. D.
2;
.
Câu 14. [TH] Tập nghiệm
S
của hệ bất phương trình
2 0
2 1 2
x
x x
là
A.
;2
S . B.
3;S
. C.
3; 2
S
. D.
; 3
S
.
Câu 15. [NB] Điều kiện xác định của bất phương trình
3 0
x x
là:
A.
[0; )
. B.
9
{ }
1
;0
. C.
. D.
1
0;
9
.
Câu 16. [TH] Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2( 1) 4 8 0
x m x m
vô
nghiệm.
A.
[ 1;7]
m
. B.
( 1;7)
m
.
C.
( ; 1] [7; )
m
. D.
( 1; )
m
.
Câu 17. [NB] Viết phương trình đường thẳng đi qua
3;2
A và nhận
2; 4
n
làm véctơ pháp tuyến.
A.
3 2 4 0
x y
. B.
2 8 0
x y
. C.
2 7 0
x y
. D.
2 1 0
x y
.
Câu 18. [NB] Số
2
thuộc tập nghiệm của bất phương trình nào sau đây?
A.
2
2 2 0
x x
. B.
2 1 1
x x
.
C.
2
2 1 1
x x x
. D.
1
2 0
1
x
.
Câu 19. [NB] Cho
;
2
. Khẳng định nào dưới đây ĐÚNG ?
A.
cot 0
. B.
tan 0
. C.
cos 0
. D.
sin 0
.
Câu 20. [NB] Khẳng định nào sau đây SAI ?
A.
tan tan
x x
. B.
cos( ) cos
x x
.
C.
cot tan
2
x x
. D.
sin sin
x x
.
Câu 21. [TH] Cho tam giác
ABC
khẳng định nào sau đây ĐÚNG
A.
tan tan
A B C
. B.
cos cos
A B C
.
C.
sin sin
A B C
. D.
cot cot
A B C
.
Câu 22. [TH] Cho elip
2 2
: 1
25 16
x y
E
. Khẳng định nào sau đây ĐÚNG ?
A.
E
có tiêu cự bằng
3
.
B.
E
có hai tiêu điểm là
1 2
3;0 , 3;0
F F .
C.
E
có độ dài trục lớn bằng
5
.
D.
E
có độ dài trục bé bằng
4
.
Câu 23. [NB] Hàm số
2 6
f x x
có bảng xét dấu là
A. B.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C. D.
Câu 24. [TH] Cho
tan 3
. Tính
2sin 3cos
4sin 5cos
A
A.
9
7
B.
7
9
C.
9
7
D.
7
9
Câu 25. [VD] Trong mặt phẳng
Oxy
cho đường tròn
2 2
: 4 4 6 0
C x y x y
và đường thẳng
: 2 3 0
d x my m
với m là tham số thực. Gọi
I
là tâm đường tròn
C
. Tính tổng các giá
trị thực của tham số
m
tìm được để đường thẳng
d
cắt đường tròn
C
tại hai điểm phân biệt
,
M N
sao cho diện tích tam giác
IMN
lớn nhất?
A.
15
8
. B.
8
15
. C.
0
. D.
4
.
Câu 26. [NB] Trong mặt phẳng
Oxy
, cho đường thẳng
2 3
:
3 4
x t
d
y t
. Tìm tọa độ một vectơ chỉ phương
của
d
.
A.
3; 4
. B.
3;4
. C.
4; 3
D.
4;3
Câu 27. [TH] Tập nghiệm của bất phương trình
2
1
0
4 3
x
x x
A.
( 3; 1) [1; )
. B.
( ;1)
. C.
( 3;1)
. D.
( ; 3) ( 1;1]
.
Câu 28. [TH] Biết
5
tan
12
a thì tan
4
a
bằng:
A.
5
11
. B.
15
4
. C.
16
3
. D.
17
7
.
Câu 29. [TH] Tìm phương trình chính tắc của Elip có độ dài trục lớn bằng
4 10
và có một đỉnh là
(0;6)
B
.
A.
2 2
1
40 12
x y
. B.
2 2
1
160 32
x y
. C.
2 2
1
160 36
x y
D.
2 2
1
40 36
x y
.
Câu 30. [TH] Giải bất phương trình
3 2
2
1
x
x
x
được tập nghiệm là
A.
1
;1 2;
2
. B.
;1 2;
. C.
2;1 2;
. D.
1
; 2;3
2
.
Câu 31. [VD] Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
cân tại
A
, cạnh đáy
: 5 2 0
BC x y
, cạnh bên
:3 2 6 0
AB x y
, đường thẳng chứa cạnh
AC
đi qua điểm
6; 1
M
. Đỉnh
C
của tam giác có tọa độ là
;
a b
. Tính
2 3 ?
T a b
A.
5
T . B.
0
T . C.
15
T . D.
9
T .
Câu 32. [TH] Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
: 4 2 1 0
d x y
và điểm
1;1
A . Hình
chiếu vuông góc của
A
lên
d
là
;
H a b
. Khi đó
5 10
T a b
bằng
A.
4
T
. B.
1
T
. C.
5
T
. D.
1
T
.
Câu 33. [NB] Đường tròn
2 2
: 2 8 32 0
C x y x y
có tâm
I
và bán kính là
A.
2;8 , 10
I R
. B.
2; 8 , 10
I R . C.
1; 4 , 7
I R
. D.
1;4 , 5
I R
.
Câu 34. [TH] Cho
2; 1
A
,
4;5
B . Đường trung trực đoạn thẳng
AB
có phương trình là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
3 9 0
x y
. B.
3 2 18 0
x y
.
C.
3 7 0
x y
. D.
2 6 13 0
x y
.
Câu 35. [TH] Cho
2
sin
3
. Tính
cos2
?
A.
1
3
. B.
1
3
. C.
1
9
. D.
1
9
.
Câu 36. [TH] Góc giữa hai đường thẳng
1
: 2 15 0
d x y
và
2
:2 8 0
d x y
bằng :
A.
0
. B.
90
. C.
45
. D.
60
.
Câu 37. [TH] Có bao nhiêu giá trị của tham số
m
để hệ bất phương trình
3
3 3
x m
x m
có nghiệm duy
nhất.
A. 3. B. 2. C. 1. D. . Đáp án khác.
Câu 38. [VD] Rút gọn biểu thức
cos2 cos4 cos6
sin 2 sin 4 sin 6
P
.
A.
cot12
P
. B.
4cot
P
.
C.
cot 2 cot 4 cot 6
P
. D.
cot 4
P
.
Câu 39. [NB] Tập xác định
D
của hàm số
2
4 5
y x x
là
A.
; 5 1;D
. B.
5;1
D .
C.
; 5 1;D
. D.
5;1
D .
Câu 40. [TH] Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
1;1
A ,
3;3
B . Đường tròn đường kính
AB
có phương trình là
A.
2 2
1 2 5
x y
. B.
2 2
1 2 2 5
x y
.
C.
2 2
1 2 5
x y
. D.
2 2
1 2 20
x y
.
Câu 41. [TH] Cho đường tròn
2 2
: 1 2 25
C x y . Phương trình tiếp tuyến của
C
tại
5;1
M
là
A.
4 3 23 0
x y
. B.
4 3 17 0
x y
. C.
4 3 23 0
x y
. D.
4 3 23 0
x y
.
Câu 42. [NB] Đường tròn
C
có tâm
0;5
I và bán kính
4
R
có phương trình là
A.
2
2
5 16
x y . B.
2
2
5 2
x y . C.
2
2
5 4
x y . D.
2
2
5 16
x y .
Câu 43. [VD] Có bao nhiêu giá trị nguyên của tham số
10;10
m để bất phương trình
2
2 1 3 15 0
x m x m nghiệm đúng với mọi
1;2
x ?
A.
20
. B.
10
. C.
18
. D.
0
.
Câu 44. [TH] Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
sin sin
3 3
P
. Khi đó
M m
bằng
A. 1. B. 2. C. 0. C. 3.
Câu 45. [NB] Trên đường tròn lượng giác gốc
0;1
A , có bao nhiêu điểm cuối
M
biểu diễn cung
AM
thỏa mãn sđ
2
3
AM k
,
k
?
A.
2
. B.
4
. C.
6
. D.
1
.
Câu 46. [NB] Tập nghiệm của bất phương trình
2 6
0
5
x
x
là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
; 3 5;
. B.
3; 5
. C.
5;
. D.
; 3 5;
.
Câu 47. [TH] Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1;1
A ,
3;7
B ,
3; 2
C
. Gọi
M
là trung điểm của đoạn thẳng
AB
. Viết phương trình tham số của đường thẳng
CM
.
A.
1
4 3
x t
y t
. B.
1
4 3
x t
y t
. C.
4
1 3
x t
y t
. D.
4
1 3
x t
y t
.
Câu 48. [TH] Đường tròn đi qua ba điểm
0;4
A ,
3;4
B ,
3;0
C có bán kính bằng
A.
10
2
. B.
3
. C.
5
2
. D. 5.
Câu 49. [NB] Rút gọn biểu thức
sin2 .cos cos2 .sin
M x x x x
ta được kết quả
A.
sin3
M x
. B.
sin
M x
. C.
cos3
M x
. D.
cos
M x
.
Câu 50. [NB] Biết
3
cos 0
5 2
. Khi đó
tan
bằng
A.
4
3
. B.
1
2
. C.
3
4
. D.
2
3
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 12
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1A 2B 3C 4D 5C 6A 7B 8B 9A 10B 11D
12A
13A
14D
15A
16A
17D
18C
19C
20B 21C
22B 23C
24A
25B 26B 27D
28D
29D
30A
31D
32D
33C
34A
35C
36B 37C
38D
39B 40C
41A
42A
43C
44B 45D
46B 47B 48C
49B 50A
LỜI GIẢI CHI TIẾT
Câu 1. [NB] Bất phương trình
5 6
5
1
x
x
có tập nghiệm
S
là
A.
1;S
. B.
S
.
C.
; 2 2;S
. D.
;2
S .
Lời giải
Điều kiện:
1
x
.
Bất phương trình đã cho tương đương với
11
0 1 0 1
1
x x
x
.
Vậy
1;S
.
Câu 2. [TH] Cho biết
1
sin cos
2
x x
. Tính giá trị biểu thức
4 4
sin cos
M x x
.
A.
15
20
M . B.
23
32
M . C.
4
5
M
. D.
3
16
M
.
Lời giải
Ta có
1
sin cos
2
x x
2
2 2
1 1
sin cos sin cos 2sin cos
4 4
x x x x x x
.
Suy ra:
1 3
2sin .cos 1
4 4
x x
.
Ta lại có:
2 2
4 4 2 2 2 2 2 2
sin cos sin cos 2sin .cos 2sin .cos
M x x x x x x x x
2
2
2 2
2 2
1 1 1 3 23
= sin cos 2sin .cos 1 2sin .cos 1
2 2 2 4 32
x x x x x x
.
Câu 3. [TH] Trong mặt phẳng tọa độ
Oxy
, gọi
M
là điểm có hoành độ dương thuộc đường thẳng
: 1 0
x y
sao cho
5
OM
. Khi đó hoành độ điểm
M
là
A.
5
x
. B.
4
x
. C.
3
x
. D.
2
x
.
Lời giải
Do
M
thuộc đường thẳng
nên có tọa độ
; 1
M x x
. Khi đó theo đề bài ta có:
5
OM
2
2
1 5
x x
2
2 2 1 25
x x
2
12 0
x x
4
3
x
x
.
Do hoành độ điểm
M
dương nên
3
x
.
Câu 4. [TH] Bất phương trình
2
1 5 4 0
x x x
có tập nghiệm
S
là
A.
4;S
. B.
;1 4;S
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
4;S
. D.
1 4;S
.
Lời giải
Ta có:
2
1 5 4
f x x x x
.
Ta có
1
0
4
x
f x
x
.
Bảng xét dấu:
Vậy bất phương trình
2
1 5 4 0
x x x
có tập nghiệm
1 4;S
.
Câu 5. [NB] Rút gọn biểu thức
2 2 2
sin cos tan
M x x x
bằng
A.
2
cot
x
. B.
2
1
sin
x
. C.
2
1
cos
x
. D.
2
2tan
x
.
Lời giải
Ta có
2 2 2 2
2
1
sin cos tan 1 tan
cos
M x x x x
x
.
Câu 6. [TH] Rút gọn biểu thức cos .cos
4 4
M
bằng
A.
1
cos2
2
M
. B.
1 2
cos
2 2
M
.
C.
cos
M
. D.
0
M
.
Lời giải
Ta có:
1
cos .cos cos cos
4 4 2 4 4 4 4
M
1 1
cos2 cos cos2
2 2 2
.
Câu 7. [VD] Trong mặt phẳng tọa độ
Oxy
, kẻ được bao nhiêu tiếp tuyến đến đường tròn
2 2
2 3 16
x y
biết tiếp tuyến song song với đường thẳng
3 4 2 0
x y
?
A. 2. B. 1. C. 0. D. Vô số.
Lời giải
Đường tròn đã cho có tâm
2; 3
I
, bán kính
4
R
.
Theo giả thiết tiếp tuyến song song với đường thẳng
3 4 2 0
x y
nên tiếp tuyến có dạng
:3 4 0
x y m
,
2
m
.
Ta có
2
2
3.2 4. 3
, 4 18 20
3 4
m
d I R m
38 nhaän
2 loaïi
m
m
.
Suy ra
:3 4 38 0
x y
.
Vậy có 1 tiếp tuyến với đường tròn.
Câu 8. [TH] Cho
5
cos
13
, 0
2
. Tính cos
3
.
+
+
+|
0
x
2
5
x
+ 4
+
0
4
1 +∞
∞
f
(
x
)
x
1
x
0 0
0
+

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
5 12 3
cos
3 26
. B.
5 12 3
cos
3 26
.
C.
12 5 3
cos
3 26
. D.
12 5 3
cos
3 26
.
Lời giải
Vì 0
2
suy ra
sin 0
.
Ta có:
2
2 2 2
5 12
sin cos 1 sin 1 cos 1
13 13
(vì
sin 0
).
Vậy
5 1 12 3 5 12 3
cos cos cos sin sin . .
3 3 3 13 2 13 2 26
.
Câu 9. [TH] Cho
2
2
f x x x m
. Tìm tất cả các giá trị của tham số
m
để
0
f x
,
x
.
A.
1
m
. B.
1
m
. C.
1
m
. D.
1
m
.
Lời giải
Ta có
0,f x x
1 0 thoûa maõn
0
0 4 4 0 1
m m
.
Câu 10. [VD]
S
là tập hợp tất các các giá trị nguyên dương của tham số
m
để phương trình
2 2 2
5 1 2 5 7 0
x m x m m
có hai nghiệm trái dấu. Hỏi tập hợp
S
có bao nhiêu phần
tử?
A. 4. B. Vô số. C. 0. D. 3.
Lời giải
Phương trình đã có có hai nghiệm trái dấu khi và chỉ khi:
2 2
5 . 2 5 7 0 2 5 7 0
m m m m
7
1
m
m
.
Các giá trị nguyên dương thỏa mãn là các số nguyên dương lớn hơn 7. Vậy
S
có vô số phần tử.
Câu 11. [NB] Tập nghiệm của bất phương trình
2
7 6 0
x x
là
A.
;1 6;
. B.
6; 1
. C.
1;6
. D.
;1 6;
.
Lời giải
Đặt
2
7 6
f x x x
. Ta có bảng xét dấu của
f x
:
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là:
;1 6;
.
Câu 12. [TH] Cho cos2
m
. Hãy tính theo
m
giá trị của biểu thức
2 2
2sin 4cos
A
.
A. 3
A m
. B. 4
A m
. C. 3
A m
. D.
4 2
A m
.
Lời giải
Ta có
2
cos2 2cos 1
m
2
1
cos
2
m
;
2
cos 2 1 2sin
m
2
1
sin
2
m
.
2 2
1 1
2sin 4cos 2. 4. 3
2 2
m m
A m
.
Câu 13. [NB] Tập nghiệm của bất phương trình
3 6 0
x
là:
A.
; 2
. B.
; 3
. C.
2;
. D.
2;
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
3 6 0 2
x x
. Vậy tập nghiệm
; 2
S
.
Câu 14. [TH] Tập nghiệm
S
của hệ bất phương trình
2 0
2 1 2
x
x x
là
A.
;2
S . B.
3;S
. C.
3; 2
S
. D.
; 3
S
.
Lời giải
2 0 2
3
2 1 2 3
x x
x
x x x
. Vậy tập nghiệm
; 3
S
.
Câu 15. [NB] Điều kiện xác định của bất phương trình
3 0
x x
là
A.
[0; )
. B.
9
{ }
1
;0
. C.
. D.
1
0;
9
.
Lời giải
Điều kiện xác định của bất phương trình
3 0
x x
là:
0
x
Câu 16. [TH] Tìm tất cả các giá trị của tham số
m
để bất phương trình
2
2( 1) 4 8 0
x m x m
vô
nghiệm.
A.
[ 1;7]
m
. B.
( 1;7)
m
.
C.
( ; 1] [7; )
m
. D.
( 1; )
m
.
Lời giải
Ta có:
2
2
1 (4 8) 6 7
m m m m
.
Bất phương trình
2
2( 1) 4 8 0
x m x m
vô nghiệm khi và chỉ khi
2
2( 1) 4 8 0
x m x m
với mọi x
0 1 7
m
.
Câu 17. [NB] Viết phương trình đường thẳng đi qua
3;2
A và nhận
2; 4
n
làm véctơ pháp tuyến.
A.
3 2 4 0
x y
. B.
2 8 0
x y
. C.
2 7 0
x y
. D.
2 1 0
x y
.
Lời giải
Phương trình đường thẳng qua
3;2
A và nhận
2; 4
n
làm véctơ pháp tuyến là:
2 3 4 2 0 2 1 0
x y x y
.
Câu 18. [NB] Số
2
thuộc tập nghiệm của bất phương trình nào sau đây?
A.
2
2 2 0
x x
. B.
2 1 1
x x
.
C.
2
2 1 1
x x x
. D.
1
2 0
1
x
.
Lời giải
Thay
2
x
vào từng bất phương trình ta thấy đáp án C thỏa mãn.
Câu 19. [NB] Cho
;
2
. Khẳng định nào dưới đây ĐÚNG ?
A.
cot 0
. B.
tan 0
. C.
cos 0
. D.
sin 0
.
Lời giải
Với
sin 0
cos 0
;
tan 0
2
cot 0
.vậy đáp án đúng
cos 0
.
Câu 20. [NB] Khẳng định nào sau đây SAI ?
A.
tan tan
x x
. B.
cos( ) cos
x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
cot tan
2
x x
. D.
sin sin
x x
.
Lời giải
Áp dụng công thức cung đối :ta có
cos( ) cos
x x
suy ra B SAI.
Câu 21. [TH] Cho tam giác
ABC
khẳng định nào sau đây ĐÚNG
A.
tan tan
A B C
. B.
cos cos
A B C
.
C.
sin sin
A B C
. D.
cot cot
A B C
.
Lời giải
Trong tam giác
ABC
ta có: Tổng 3 góc
, ,
A B C
bằng
0
180
nên góc
A B
bù với góc
C
Do vậy
+)
tan tan
A B C
khẳng định A sai.
+)
cos cos
A B C
khẳng định B sai.
+)
cot cot
A B C
khẳng định D sai.
+)
sin sin
A B C
khẳng định C đúng.
Câu 22. [TH] Cho elip
2 2
: 1
25 16
x y
E
. Khẳng định nào sau đây ĐÚNG ?
A.
E
có tiêu cự bằng
3
.
B.
E
có hai tiêu điểm là
1 2
3;0 , 3;0
F F .
C.
E
có độ dài trục lớn bằng
5
.
D.
E
có độ dài trục bé bằng
4
.
Lời giải
Từ phương trình chính tắc
2 2
: 1
25 16
x y
E
.
Ta có:
+)
2
25 5
a a
nên trục lớn
2 10
a
. Do đó C sai.
+)
2
16 4
b b
trục bé
2 8
b
. Do đó D sai.
+) Vì
2 2 2
9
c a b
3
c
nên tiêu cự
2 6
c
. Do đó A sai.
+) Vì
3
c
nên hai tiêu điểm
1 2
3;0 , 3;0
F F . Vậy B đúng.
Câu 23. [NB] Hàm số
2 6
f x x
có bảng xét dấu là
A. B.
C. D.
Lời giải
Có
0
f x
3
x
Khi đó ta có bảng xét dấu
Câu 24. [TH] Cho
tan 3
. Tính
2sin 3cos
4sin 5cos
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
9
7
B.
7
9
C.
9
7
D.
7
9
Lời giải
Điều kiện:
2
x k
Ta có:
2sin 3cos
4sin 5cos
A
2sin 3cos
cos cos
4sin 5cos
cos cos
2tan 3
4tan 5
2.3 3
4.3 5
9
7
.
Câu 25. [VD] Trong mặt phẳng
Oxy
cho đường tròn
2 2
: 4 4 6 0
C x y x y
và đường thẳng
: 2 3 0
d x my m
với m là tham số thực. Gọi
I
là tâm đường tròn
C
. Tính tổng các giá
trị thực của tham số
m
tìm được để đường thẳng
d
cắt đường tròn
C
tại hai điểm phân biệt
,
M N
sao cho diện tích tam giác
IMN
lớn nhất?
A.
15
8
. B.
8
15
. C.
0
. D.
4
.
Lời giải
Đường tròn
2 2
: 4 4 6 0
C x y x y
có tâm
2 ; 2
I
và bán kính
4 4 6 2
r
.
Gọi
A
là hình chiếu của
I
lên
d
.
Ta có:
2 2
2 2 2 3 1 4
,
1 1
m m m
IA d I d
m m
. (Điều kiện:
2
IA ).
Ta có:
2 2
2
1 2
. . . 2 1
2 2
Cauchy
IMN
IA IA
S IA MN IA AM IA IA
.
Dấu
" "
xảy ra khi:
2 2 2
2
2 2 2
1 4
2 1 1 1 4 1
1
1 8 16 1 15 8 0
m
IA IA IA m m
m
m m m m m
Tổng các giá trị thực của tham số
m
:
8
15
S
.
Câu 26. [NB] Trong mặt phẳng
Oxy
, cho đường thẳng
2 3
:
3 4
x t
d
y t
. Tìm tọa độ một vectơ chỉ phương
của
d
.
A.
3; 4
. B.
3;4
. C.
4; 3
D.
4;3

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Một vectơ chỉ phương của
d
có tọa độ là
3;4
.
Câu 27. [TH] Tập nghiệm của bất phương trình
2
1
0
4 3
x
x x
A.
( 3; 1) [1; )
. B.
( ;1)
. C.
( 3;1)
. D.
( ; 3) ( 1;1]
.
Lời giải
Ta có
1 0 1
x x
,
2
1
4 3 0
3
x
x x
x
Bảng xét dấu
x
3
1
1
1
x
0
+
2
4 3
x x
0
0
+
+
2
1
4 3
x
x x
+
0
+
Dựa vào bảng xét dấu tập nghiệm của bất phương trình là
( ; 3) ( 1;1]
S
Câu 28. [TH] Biết
5
tan
12
a thì tan
4
a
bằng:
A.
5
11
. B.
15
4
. C.
16
3
. D.
17
7
.
Lời giải
5
tan tan 1
17
4 12
tan
5
4 7
1 tan .tan 1 .1
4 12
a
a
a
.
Câu 29. [TH] Tìm phương trình chính tắc của Elip có độ dài trục lớn bằng
4 10
và có một đỉnh là
(0;6)
B
.
A.
2 2
1
40 12
x y
. B.
2 2
1
160 32
x y
. C.
2 2
1
160 36
x y
D.
2 2
1
40 36
x y
.
Lời giải
Gọi phương trình chính tắc của
E
cần tìm là
2 2
2 2
1
x y
a b
.
Do
E
có độ dài trục lớn bằng
4 10
nên
4 10 2 10
2a a
.
Do
E
có một đỉnh là
(0;6)
B
nên
6
b
.
Vậy phương trình
E
là:
2 2
1
40 36
x y
.
Câu 30. [TH] Giải bất phương trình
3 2
2
1
x
x
x
được tập nghiệm là
A.
1
;1 2;
2
. B.
;1 2;
. C.
2;1 2;
. D.
1
; 2;3
2
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
3 2
2
1
x
x
x
2
3 2 2 5 2
2 0 0
1 1
x x x
x
x x
.
Xét dấu vế trái
Dựa vào bảng xét dấu ta có tập nghiệm của bpt là
1
;1 2;
2
S
.
Câu 31. [VD] Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác ABC cân tại A, cạnh đáy
: 5 2 0 BC x y
, cạnh bên
:3 2 6 0 AB x y
, đường thẳng chứa cạnh AC đi qua điểm
6; 1M . Đỉnh C của tam giác có tọa độ là
;a b . Tính 2 3 ? T a b
A.
5
T . B.
0
T . C.
15
T . D.
9
T .
Lời giải
Gọi d là đường thẳng đi qua M và song song với BC , khi đó d có vectơ pháp tuyến
1; 5n
Suy ra phương trình đường thẳng của
: 6 5 1 0 : 5 11 0 d x y d x y
Tọa độ giao điểm N của d và AB là nghiệm của hệ:
5 11 0 4
4; 3
3 2 6 0 3
x y x
N
x y y
Tam giác
ABC
cân tại A nên A nằm trên đường trung trực của
MN
.
Đường trung trực của MN đi qua trung điểm
1; 2I và nhận
10; 2
MN làm vectơ pháp
tuyến nên có phương trình:
10 1 2 2 0 5 3 0 x y x y
Khi đó tọa độ điểm A là nghiệm của hệ
3 2 6 0 0
0;3
5 3 0 3
x y x
A
x y y
Đường thẳng chứa cạnh AC đi qua điểm
0;3A và nhận
6; 4AM
làm vectơ chỉ phương
nên có phương trình là:
6
3 4
x t
AC
y t
có phương trình tổng quát là
2 3 9 0x y
.
Khi đó tọa độ điểm C là nghiệm của hệ
5 2 0 3
3;1 2.3 3.1 9
2 3 9 0 1
x y x
C T
x y y
.
Cách 2: Tác giả: Hà Nguyễn.
Gọi d là đường thẳng đi qua M và song song với
AB
, khi đó
d có vectơ pháp tuyến
3; 2n
.
Suy ra phương trình đường thẳng của
:3 6 2 1 0 :3 2 20 0d x y d x y
Tọa độ giao điểm
I
của d và
BC
là nghiệm của hệ:
3 2 20 0 8
8;2
5 2 0 2
x y x
I
x y y
.
I
B C
A
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Có
5 2;
C BC C c c
.
Do tam giác
ABC
cân tại
A
nên tam giác
MCI
cân tại
M
.
Suy ra
MC MI
2 2
5 8 1 13
c c
2
26 78 52 0
c c
1
2
c
c
.
+ Với
1 3;1
c C .
+ Với
2 8;2
c C (loại do
C I
).
Vậy
3;1
C
2.3 3.1 9
T
.
Câu 32. [TH] Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
: 4 2 1 0
d x y
và điểm
1;1
A . Hình
chiếu vuông góc của
A
lên
d
là
;
H a b
. Khi đó
5 10
T a b
bằng
A.
4
T
. B.
1
T
. C.
5
T
. D.
1
T
.
Lời giải
Đường thẳng
d
có một VTPT
4;2
n
suy ra
d
có một VTCP
2;4
u
.
Ta có
1 3
; 2 , 1; 2
2 2
H d H t t t AH t t
.
Hình chiếu vuông góc của
A
lên
d
là
H
nên
3 2
. 0 1 . 2 2 .4 0 10 4 0
2 5
AH u t t t t
.
Vậy
2 3 2 3
; ; 5 10 1
5 10 5 10
H a b T a b
.
Câu 33. [NB] Đường tròn
2 2
: 2 8 32 0
C x y x y
có tâm
I
và bán kính là
A.
2;8 , 10
I R
. B.
2; 8 , 10
I R . C.
1; 4 , 7
I R
. D.
1;4 , 5
I R
.
Lời giải
Đường tròn
C
có tâm
1; 4 , 1 16 32 7
I R
Câu 34. [TH] Cho
2; 1
A
,
4;5
B . Đường trung trực đoạn thẳng
AB
có phương trình là
A.
3 9 0
x y
. B.
3 2 18 0
x y
.
C.
3 7 0
x y
. D.
2 6 13 0
x y
.
Lời giải
Gọi
I
là trung điểm đoạn thẳng
AB
. Khi đó
3;2
I .
Đường trung trực của đoạn
AB
qua điểm
I
và nhận véctơ
2;6
AB
làm véctơ pháp tuyến
nên có phương trình là:
2 3 6 2 0
x y
2 6 18 0
x y
3 9 0
x y
.
Câu 35. [TH] Cho
2
sin
3
. Tính
cos2
?
A.
1
3
. B.
1
3
. C.
1
9
. D.
1
9
.
Lời giải
Ta có
2
2
2 1
cos2 1 2sin 1 2
3 9
.
Câu 36. [TH] Góc giữa hai đường thẳng
1
: 2 15 0
d x y
và
2
:2 8 0
d x y
bằng :
A.
0
. B.
90
. C.
45
. D.
60
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Ta có
1
d
có vectơ pháp tuyến
1
1; 2
n
,
2
d
có vectơ pháp tuyến
2
2;1
n
1 2 1 2 1 2
. 1.2 2 .1 0 , 90
n n d d d d
.
Câu 37. [TH] Có bao nhiêu giá trị của tham số
m
để hệ bất phương trình
3
3 3
x m
x m
có nghiệm duy
nhất.
A. 3. B. 2. C. 1. D. Đáp án khác.
Lời giải
Có
3 3
3 3 3 3
x m x m
x m x m
Hệ bất phương trình có nghiệm duy nhất khi và chỉ khi
3 3 3 3
m m m .
Vậy có một giá trị của
m
thỏa mãn yêu cầu bài toán.
Chọn đáp án C.
Câu 38. [VD] Rút gọn biểu thức
cos2 cos4 cos6
sin 2 sin 4 sin 6
P
.
A.
cot12
P
. B.
4cot
P
.
C.
cot 2 cot 4 cot 6
P
. D.
cot 4
P
.
Lời giải
Ta có:
cos6 cos2 cos4
cos2 cos4 cos6
sin 2 sin 4 sin6 sin6 sin 2 sin 4
P
2cos4 cos2 cos4
2sin4 cos2 sin 4
cos4 2cos2 1
sin 4 2cos2 1
cos4
cot 4
sin 4
.
Câu 39. [NB] Tập xác định
D
của hàm số
2
4 5
y x x
là
A.
; 5 1;D
. B.
5;1
D .
C.
; 5 1;D
. D.
5;1
D .
Lời giải
Điều kiện xác định:
2
4 5 0 5 1
x x x
.
Vậy tập xác định
5;1
D .
Câu 40. [TH] Trong mặt phẳng tọa độ
Oxy
, cho hai điểm
1;1
A ,
3;3
B . Đường tròn đường kính
AB
có phương trình là
A.
2 2
1 2 5
x y
. B.
2 2
1 2 2 5
x y
.
C.
2 2
1 2 5
x y
. D.
2 2
1 2 20
x y
.
Lời giải
Đặt
;
I I
I x y
là tâm của đường tròn đường kính
AB
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
1 3
1
2
1;2
1 3
2
2
I
I
x
I
y
.
Bán kính
2
2
2 1 5
R IA IA
.
Phương trình đường tròn đường kính
AB
là
2 2
1 2 5
x y
.
Câu 41. [TH] Cho đường tròn
2 2
: 1 2 25
C x y . Phương trình tiếp tuyến của
C
tại
5;1
M
là
A.
4 3 23 0
x y
. B.
4 3 17 0
x y
. C.
4 3 23 0
x y
. D.
4 3 23 0
x y
.
Lời giải
Đường tròn
2 2
: 1 2 25
C x y có tâm là
1; 2
I . Ta có
4;3
IM .
Tiếp tuyến của
C
tại
5;1
M đi qua
5;1
M và nhận
4;3
IM làm vectơ pháp tuyến nên
có phương trình tổng quát là
4 5 3 1 0 4 3 23 0
x y x y .
Câu 42. [NB] Đường tròn
C
có tâm
0;5
I và bán kính
4
R
có phương trình là
A.
2
2
5 16
x y . B.
2
2
5 2
x y . C.
2
2
5 4
x y . D.
2
2
5 16
x y .
Lời giải
Đường tròn
C
có tâm
0;5
I và bán kính
4
R
có phương trình là
2
2
5 16
x y .
Câu 43. [VD] Có bao nhiêu giá trị nguyên của tham số
10;10
m để bất phương trình
2
2 1 3 15 0
x m x m nghiệm đúng với mọi
1;2
x ?
A.
20
. B.
10
. C.
18
. D.
0
.
Lời giải
Ta có:
2
2 1 3 15
f x x m x m có hai nghiệm
1 2
5
; 3
2
m
x x
.
Vì
1 2
5 5
10
2 2
m
m x x
Khi đó bất phương trình
2
2 1 3 15 0
x m x m có tập nghiệm
5
;3
2
m
T
.
Bất phương trình nghiệm đúng với mọi
1;2
x
5 5
1;2 ;3 1 7
2 2
m m
m
.
Kết hợp điều kiện
10;10
m ta có
10 7
m
. Mà m
nên có
18
giá trị nguyên của
m
thỏa ycbt trong trường hợp này.
Vậy có
18
giá trị nguyên thỏa mãn yêu cầu bài toán.
Câu 44. [TH] Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
sin sin
3 3
P
. Khi đó
M m
bằng
A. 1. B. 2. C. 0. C. 3.
Lời giải
Ta có:
sin sin sin cos sin cos sin cos sin cos sin
3 3 3 3 3 3
P
.
Suy ra
1 1,P x
. Do đó
1
M
,
1
m
.
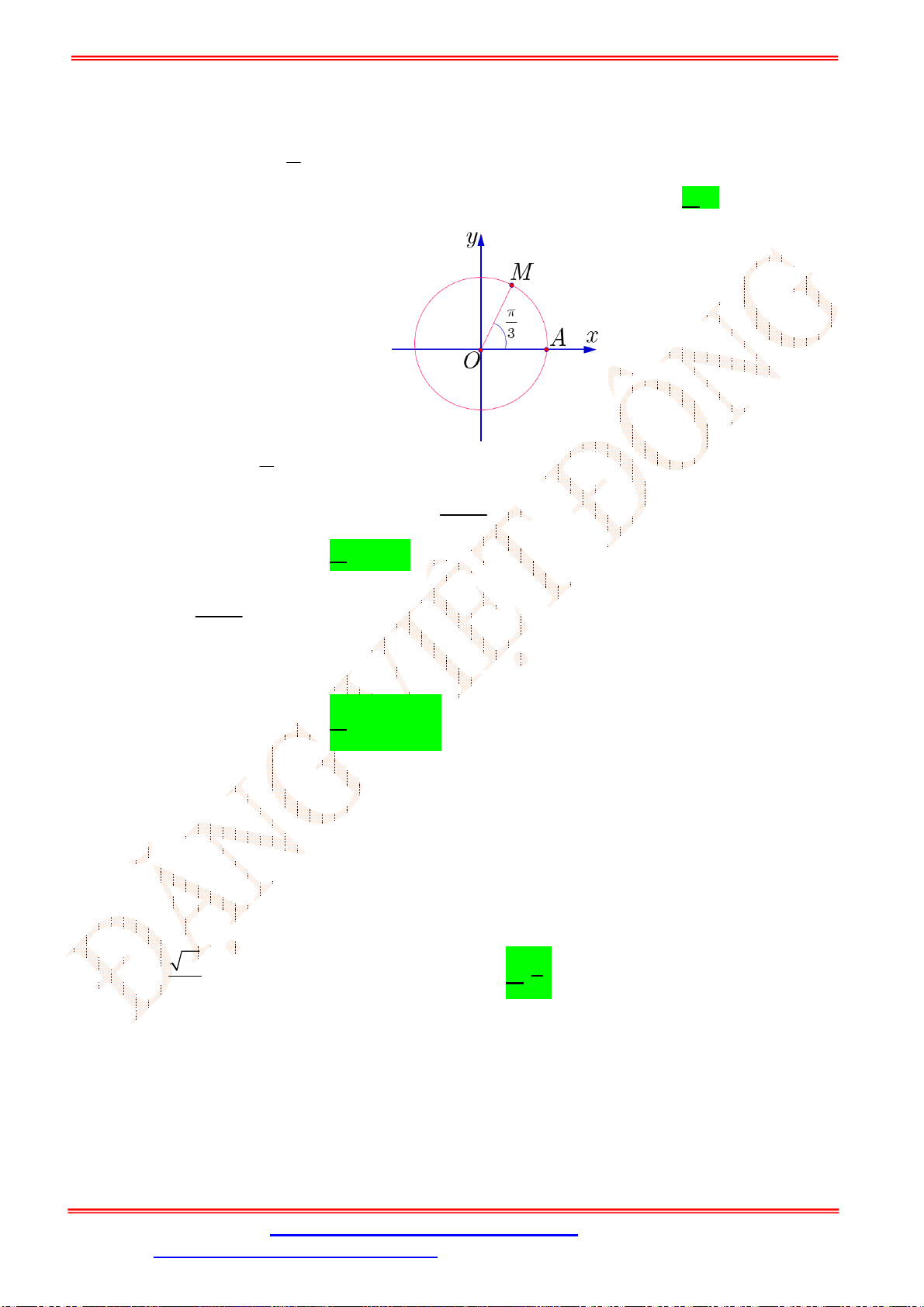
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy
2
M m
.
Câu 45. [NB] Trên đường tròn lượng giác gốc
0;1
A , có bao nhiêu điểm cuối
M
biểu diễn cung
AM
thỏa mãn sđ
2
3
AM k
,
k
?
A.
2
. B.
4
. C.
6
. D.
1
.
Lời giải
Ta có sđ
2
3
AM k
nên có 1 điểm
M
trên đường tròn.
Câu 46. [NB] Tập nghiệm của bất phương trình
2 6
0
5
x
x
là
A.
; 3 5;
. B.
3; 5
. C.
5;
. D.
; 3 5;
.
Lời giải
Ta có:
2 6
0 2 6 . 5 0 3 5
5
x
x x x
x
.
Câu 47. [TH] Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1;1
A ,
3;7
B ,
3; 2
C
. Gọi
M
là trung điểm của đoạn thẳng
AB
. Viết phương trình tham số của đường thẳng
CM
.
A.
1
4 3
x t
y t
. B.
1
4 3
x t
y t
. C.
4
1 3
x t
y t
. D.
4
1 3
x t
y t
.
Lời giải
Ta có
M
là trung điểm của đoạn thẳng
AB
nên
1;4
M . Suy ra
2;6
CM
.
Đường thẳng
CM
đi qua
1;4
M và nhận
1; 3
u
cùng phương với
CM
làm vectơ chỉ
phương nên có phương trình tham số là:
1
4 3
x t
y t
Câu 48. [TH] Đường tròn đi qua ba điểm
0;4
A ,
3;4
B ,
3;0
C có bán kính bằng
A.
10
2
. B.
3
. C.
5
2
. D. 5.
Lời giải
Giả sử phương trình đường tròn cần tìm có dạng
2 2
: 2 2 0
C x y ax by c
2 2
0
a b c
.
0;4 16 8 0 1
3;4 9 16 6 8 0 2
3;0 9 6 0 3
A C b c
B C a b c
C C a c

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Từ (1), (2), (3) ta có hệ phương trình
8 16
6 8 25
6 9
b c
a b c
a c
3
2
a
,
2
b
,
0
c
(nhận).
Vậy
2 2
5
2
R a b c
.
Câu 49. [NB] Rút gọn biểu thức
sin2 .cos cos2 .sin
M x x x x
ta được kết quả
A.
sin3
M x
. B.
sin
M x
. C.
cos3
M x
. D.
cos
M x
.
Lời giải
Chọn B
Ta có
sin2 .cos cos2 .sin
M x x x x
sin(2 )
x x
sin
x
.
Câu 50. [NB] Biết
3
cos 0
5 2
. Khi đó
tan
bằng
A.
4
3
. B.
1
2
. C.
3
4
. D.
2
3
.
Lời giải
Do 0
2
nên
sin 0
Khi đó:
2
4
sin 1 cos
5
.
Vậy:
sin 4
tan
cos 3
.
HẾT

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 13
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1: Viết phương trình đường tròn tâm
3; 2
I
và tiếp xúc với đường thẳng
2 1 0
x y
.
A.
2 2
9
3 2
5
x y
. B.
2 2
9
3 2
5
x y
.
C.
2 2
3
3 2
5
x y
. D.
2 2
81
3 2
5
x y
.
Câu 2: Xác định tâm
I
và tính bán kính
R
của đường tròn có phương trình
2 2
4 0
x y x
.
A.
2;0 , 2
I R
. B.
2;0 , 2
I R
. C.
2;0 , 2
I R . D.
2;0 , 2
I R .
Câu 3: Bộ số
;
x y
nào dưới đây KHÔNG phải là nghiệm của bất phương trình
2 5 1
x y
?
A.
0;2
. B.
2; 6
. C.
1; 3
. D.
2; 7
.
Câu 4: Điểm nào dưới đây KHÔNG thuộc đường thẳng
:3 1 0
d x y
?
A.
2; 5
. B.
1;0
. C.
0;1
. D.
1
;0
3
.
Câu 5:
Giải bất phương trình
1 2
0
2 1
x x
x
.
A.
1
1
2
2
x
x
. B.
1
1
2
2
x
x
. C.
1
1
2
2
x
x
. D.
1
1
2
2
x
x
.
Câu 6:
Chuyển phương trình đường thẳng sau về dạng tổng quát
1 2
2
x t
y t
.
A.
2 5 0
x y
. B.
2 3 0
x y
. C.
2 0
x y
. D.
2 4 0
x y
.
Câu 7: Cho hai đường thẳng
2 1 0
x y
và
2 2 0
x y
. Khi nói về vị trí tương đối của chúng,
khẳng định nào đúng?
A. Cắt nhau nhưng không vuông góc. B. Trùng nhau.
C. Song song. D. Vuông góc.
Câu 8:
Giải bất phương trình
2
1
2 1
x
x
.
A.
1
3
2
x
. B.
3
x
. C.
3
1
2
x
x
. D.
1
3
2
x
.
Câu 9: Công thức nào dưới đây là đúng về giá trị lượng giác của góc
? Giả sử các điều kiện xác
định được thỏa mãn.
A.
tan .cot 1
. B.
2 2
sin cos 2
. C.
cos tan .sin
. D.
2
2
1
tan 1.
sin
Câu 10: Hai góc lượng giác nào dưới đây được biểu diễn bởi cùng một điểm trên đường tròn lượng
giác?
A.
6
và
5
6
. B.
3
và
3
. C.
2
và
5
2
. D.
0
và
3
.
Câu 11: Viết phương trình tổng quát của đường thẳng đi qua
3;6
M
và có một vectơ pháp tuyến
2;1
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2 0
x y
. B.
3 6 0
x y
. C.
2 15 0
x y
. D.
2 12 0
x y
.
Câu 12: Công thức lượng giác nào dưới đây là sai? Giả sử các điều kiện xác định được thỏa mãn.
A.
2
2tan
tan 2
1 tan
a
a
a
. B.
sin sin cos sin cos .
a b a b b a
C.
sin 2 2sin cos .
a a a
D.
cos cos 2sin sin .
2 2
a b a b
a b
Câu 13: Tìm tất cả các giá trị của tham số
m
để bất phương trình 2
mx x m
có tập nghiệm là
.
A.
1
m
. B.
1
m
. C.
1
m
. D. m
.
Câu 14: Viết phương trình đoạn chắn của đường thẳng đi qua
5;0
M
và
0;3
N
.
A.
1
5 3
x y
. B.
0
5 3
x y
. C.
1
3 5
x y
. D.
0
3 5
x y
.
Câu 15: Giải hệ bất phương trình
2
2 5 4
4 5 0
x x
x x
.
A.
1 3
x
. B.
3
x
. C.
1
x
. D.
1 3
x
.
Câu 16: Góc lượng giác có số đo
60
thì có số đo bằng bao nhiêu theo rađian?
A.
3
. B.
2
3
. C.
5
6
. D.
3
4
.
Câu 17: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng
1 2
3
x t
y t
.
A.
( 2;1)
. B.
(1; 2)
. C.
(1;2)
. D.
( 4;2)
.
Câu 18: Viết phương trình đường thẳng đi qua điểm
(3;4)
M
và có hệ số góc
2
k
.
A.
2 10
y x
. B.
2 2
y x
. C.
2 2
y x
. D.
2 10
y x
.
Câu 19: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 ( 1) 1 0
x m x m
có hai nghiệm
dương phân biệt.
A.
9
1
m
m
. B.
9
m
. C. Không tồn tại
m
. D.
1 9
m
.
Câu 20: Tính khoảng cách từ điểm
(2;1)
M
đến đường thẳng
3 4 1 0
x y
.
A.
3
5
. B.
9
5
. C.
2
5
. D.
8
5
Câu 21: Tính giá trị biểu thức
sin .cos
6 6
2sin .cos
3 3
A
.
A.
3
2
. B.
1
2
. C.
1
3
. D.
1
.
Câu 22: Giải bất phương trình
2
4 0.
x
A.
2
2
x
x
. B.
2 2
x
. C.
2 2
x
. D.
2
2
x
x
.
Câu 23: Tính chất nào sau đây ĐÚNG với mọi góc lượng giác
bất kì và mọi số nguyên
k
thỏa mãn
các biểu thức xác định ?
A.
sin sin
k
. B.
cos 2 cos
k
.
C.
cos cos
k
. D.
1 tan 1
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 24: Viết phương trình tổng quát của đường thẳng đi qua
3;0
M
và song song với đường thẳng
2 100 0
x y
.
A.
2 6 0
x y
. B.
2 6 0
x y
. C.
2 6 0
x y
. D.
2 6 0
x y
.
Câu 25: Viết phương trình tiếp tuyến của đường tròn
2 2
1 5 5
x y
tại điểm
3; 4
M
thuộc
đường tròn.
A.
2 2 0
x y
. B.
2 5 0
x y
. C.
2 10 0
x y
. D.
2 11 0
x y
.
Câu 26: Viết phương trình đường tròn đường kính
AB
với
1; 2 , 3;0
A B .
A.
2 2
2 1 4
x y
. B.
2 2
2 1 16
x y
.
C.
2 2
2 1 8
x y
. D.
2 2
2 1 2
x y
.
Câu 27: Viết phương trình tổng quát của đường cao đỉnh
A
của tam giác
ABC
biết tọa độ các đỉnh
3;4 ,B 2;5 ,C 7;7
A .
A.
9 2 19 0
x y
. B.
9 2 35 0
x y
. C.
2 9 42 0
x y
. D.
2 9 30 0
x y
.
Câu 28: Giải bất phương trình
3 1 0
x
.
A.
1
3
x
. B.
1
3
x
. C.
1
3
x
. D.
1
3
x
.
Câu 29: Tìm điều kiện xác định của bất phương trình
1
1
3
x
x
.
A.
0 3
x
. B.
0
x
. C.
0 3
x
. D.
0 3
x
.
Câu 30: Giải bất phương trình
1 2 3 0
x x x
.
A. Vô nghiệm. B.
1 3
x
. C.
2 1
3
x
x
. D.
2
1 3
x
x
.
Câu 31: Viết phương trình tổng quát của đường thẳng đi qua
3; 1
M
và có một véc tơ chỉ phương
2; 1
.
A.
2 1 0
x y
. B.
2 7 0
x y
. C.
2 5 0
x y
. D.
2 5 0
x y
.
Câu 32: Cho
;
2
,
tan 3
. Tính
cos
.
A.
2
10
. B.
1
10
. C.
1
10
. D.
2
10
.
Câu 33: Giải bất phương trình
2
2 5 3 0
x x
.
A.
1
3
2
x
. B.
1
3
2
x
. C.
1
3
2
x
. D.
3
1
2
x
x
.
Câu 34: Tính độ dài cung tròn có số đo góc ở tâm bằng
6
của đường tròn lượng giác
A.
3
. B.
24
. C.
6
. D.
12
.
Câu 35: Cho phương trình
2
1 2 2 0
m x m x m
, với
m
là tham số. Tìm tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt.
A.
4
5
m
. B.
4
5
m
. C.
4
5
m
. D.
4
1
5
m
.
Câu 36: Cho phương trình
2
3 2 1 0
x m x m
, với
m
là tham số. Tìm tất cả các giá trị của
m
để
phương trình đã cho có nghiệm.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
8
9
m
. B.
8
9
m
. C. m
. D. không tồn tại
m
.
Câu 37: Cho
0;
2
,
1
sin
3
. Tính
tan
.
A.
2
4
. B.
1
3
. C.
2
2
. D.
1
3
.
Câu 38: Tính khoảng cách giữa hai điểm
3;4
M
và
1;0
N
.
A.
21
. B.
4 2
. C.
2 5
. D.
20
.
Câu 39: Tính cosin góc giữa hai đường thẳng
3x 10 0
y
và
2 4 5 0
x y
A.
2
5
. B.
2
10
. C.
2
20
. D.
2
2
.
Câu 40: Tìm tọa độ giao điểm của hai đường thẳng:
3x y 1 0
và
6x y 1 0
.
A.
1
;0
3
. B.
1
;0
3
. C.
0; 1
. D.
0;2
.
Câu 41: Viết phương trình đường tròn tâm I(2; 3), bán kính R = 2.
A.
2
2
x 2 (y 3) 4
. B.
2
2
x 2 (y 3) 4
.
C.
2
2
x 2 (y 3) 2
. D.
2
2
x 2 (y 3) 2
.
Câu 42: Cho góc lượng giác
0;
2
có
1
sin
3
. Tính
sin 2
.
A.
2 2
.
3
B.
4 2
.
9
C.
2 2
.
9
D.
2 2
.
9
Câu 43: Viết phương trình tổng quát của đường thẳng đi qua hai điểm
3;4
M
và
0;1
N
.
A.
7 0
x y
. B.
1 0
x y
. C.
1 0
x y
. D.
4 4 3 0
x y
.
Câu 44: Tìm tập nghiệm bất phương trình
2
4 3 0
x x
.
A.
; 3 1;
. B.
3; 1
. C.
; 3 1;
. D.
3; 1
.
Câu 45: Tìm tất cả các giá trị của tham số
m
để
2
1 1 0,f x mx m x m x
.
A.
0
1
3
m
m
. B.
0
m
. C.
1
m
. D.
1
1
3
m
m
.
Câu 46: Tìm tất cả giá trị của tham số
m
để hệ bất phương trình
2 1 3
x x
x m
có nghiệm.
A.
4.
m
B.
4.
m
C.
4.
m
D.
4.
m
Câu 47: Tìm tọa độ các giao điểm của đường tròn
2 2
: 1 3 4
C x y
và đường thẳng
: 4 0.
d x y
A.
1; 3 .
B. Không có giao điểm.C.
1; 3 ; 1; 5 .
D.
1; 5 .
Câu 48: Cho tứ giác
ABCD
có
1;7 , 1;1 , 5;1 , 7;5 .
A B C D
Tìm tọa độ giao điểm
I
của hai
đường chéo của tứ giác.
A.
4;2 .
I
B.
2;4 .
I
C.
2;3 .
I
D.
3;3 .
I
Câu 49: Trong tam giác
ABC
, hệ thức nào SAI?
A.
sin sin
A B C
. B.
cos
cos
A B C
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
cot
2 2
tan
A B C
. D.
sin cos
2 2
A B C
.
Câu 50: Giải bất phương trình
2
3 2
2 2
1
x x
x
x
.
A.
3
1
x
x
. B.
3 1
x
. C.
3 0
1
x
x
. D.
3
0 1
x
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 13
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.D 2.B 3.A 4.B 5.B 6.B 7.D 8.A 9.A 10.C
11.D 12.C 13.A 14.A 15.D 16.A 17.B 18.B 19.C 20.A
21.B 22.B 23.B 24.B 25.A 26.C 27.B 28.A 29.D 30.C
31.A 32.B 33.D 34.C 35.D 36.C 37.A 38.C 39.B 40.C
41.A 42.B 43.C 44.D 45.C 46b.B 47b.C 48b.D 49b.A 50b.C
46c.D 47c.C 48c.B 49c.D 50c.A
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN A: PHẦN CHUNG CHO TẤT CẢ CÁC HỌC SINH
Câu 1: Viết phương trình đường tròn tâm
3; 2
I và tiếp xúc với đường thẳng
2 1 0
x y .
A.
2 2
9
3 2
5
x y
. B.
2 2
9
3 2
5
x y .
C.
2 2
3
3 2
5
x y
. D.
2 2
81
3 2
5
x y .
Lời giải
Chọn D
Gọi đường thẳng có phương trình
2 1 0
x y là
.
Đường tròn tâm
I
tiếp xúc với
2
2
2.3 2 1
9
,
5
2 1
R d I R .
Vậy đường tròn cần tìm có phương trình:
2
2 2
9
3 2
5
x y hay
2 2
81
3 2
5
x y .
Câu 2: Xác định tâm
I
và tính bán kính
R
của đường tròn có phương trình
2 2
4 0
x y x .
A.
2;0 , 2
I R . B.
2;0 , 2
I R . C.
2;0 , 2
I R . D.
2;0 , 2
I R .
Lời giải
Chọn B
Đường tròn đã cho có tâm
2;0
I và có bán kính
2
2
2 0 0 2
R
.
Câu 3: Bộ số
;
x y
nào dưới đây KHÔNG phải là nghiệm của bất phương trình
2 5 1
x y
?
A.
0;2
. B.
2; 6
. C.
1; 3
. D.
2; 7
.
Lời giải
Chọn A
Với
0; 2
x y ,
2 5 2.0 5.2 10 1
x y (không là nghiệm của bất phương trình).
Với
2; 6
x y ,
2 5 2. 2 5. 6 26 1
x y (là nghiệm của bất phương trình).
Với
1; 3
x y ,
2 5 2.1 5. 3 17 1
x y (là nghiệm của bất phương trình).
Với
2; 7
x y ,
2 5 2. 2 5. 7 31 1
x y (là nghiệm của bất phương trình).
Câu 4: Điểm nào dưới đây KHÔNG thuộc đường thẳng
:3 1 0
d x y ?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2; 5
. B.
1;0
. C.
0;1
. D.
1
;0
3
.
Lời giải
Chọn B
Với
2; 5
x y ,
3 1 3.2 5 1 0
x y (thuộc đường thẳng
d
).
Với
1; 0
x y , 3 1 3.1 0 1
0
5
x y (không thuộc đường thẳng
d
).
Với
0; 1
x y
,
3 1 3.0 1 1 0
x y (thuộc đường thẳng
d
).
Với
1
; 0
3
x y ,
1
3 1 3. 0 1 0
3
x y (thuộc đường thẳng
d
).
Câu 5:
Giải bất phương trình
1 2
0
2 1
x x
x
.
A.
1
1
2
2
x
x
. B.
1
1
2
2
x
x
. C.
1
1
2
2
x
x
. D.
1
1
2
2
x
x
.
Lời giải
Chọn B
Vậy nghiệm của bất phương trình là
1
1
2
2
x
x
.
Câu 6:
Chuyển phương trình đường thẳng sau về dạng tổng quát
1 2
2
x t
y t
.
A.
2 5 0
x y . B.
2 3 0
x y . C.
2 0
x y . D.
2 4 0
x y .
Lời giải
Chọn B
Đường thẳng đã cho có điểm đi qua là
1;2
A
và VTCP
2;1
u
Suy ra VTPT của đường thẳng là
1; 2
n
Khi đó, PTTQ của đường thẳng:
1 1 2 2 0 2 3 0
x y x y .
Câu 7: Cho hai đường thẳng
2 1 0
x y
và
2 2 0
x y . Khi nói về vị trí tương đối của chúng,
khẳng định nào đúng?
A. Cắt nhau nhưng không vuông góc. B. Trùng nhau.
C. Song song. D. Vuông góc.
Lời giải
Chọn D
Đường thẳng
2 1 0
x y có VTPT
1
2; 1
n
Đường thẳng
2 2 0
x y có VTPT
2
1;2
n
Ta thấy:
1 2
. 2.1 1 .2 0
n n
nên hai đường thẳng đã cho vuông góc.
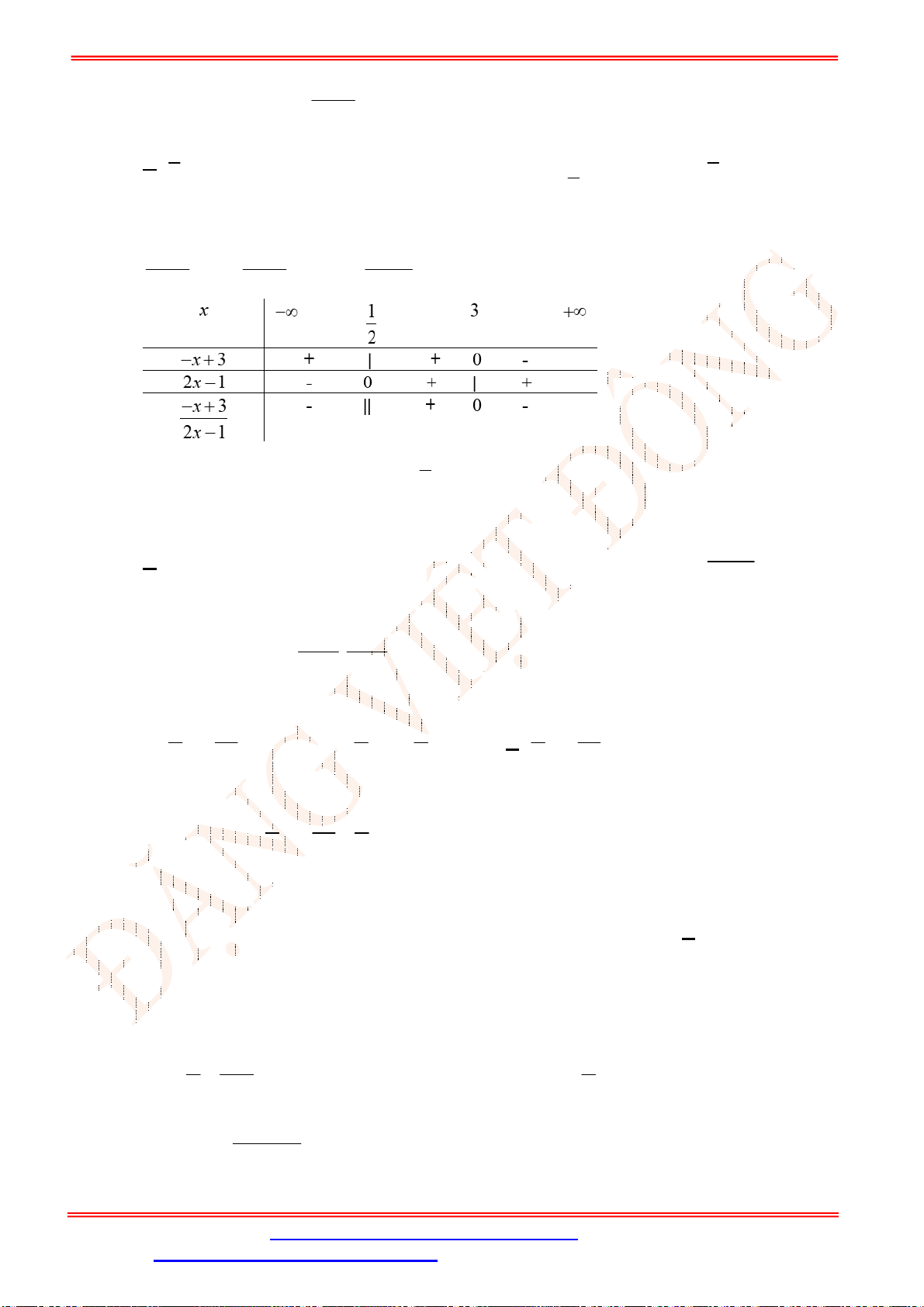
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 8:
Giải bất phương trình
2
1
2 1
x
x
.
A.
1
3
2
x . B.
3
x . C.
3
1
2
x
x
. D.
1
3
2
x .
Lời giải
Chọn A
2 2 3
1 1 0 0
2 1 2 1 2 1
x x x
x x x
Vậy nghiệm của bất phương trình là
1
3
2
x .
Câu 9: Công thức nào dưới đây là đúng về giá trị lượng giác của góc
? Giả sử các điều kiện xác
định được thỏa mãn.
A.
tan .cot 1
. B.
2 2
sin cos 2
. C.
cos tan .sin
. D.
2
2
1
tan 1.
sin
Lời giải
Chọn A
Ta có:
sin cos
tan .cot . 1
cos sin
.
Câu 10: Hai góc lượng giác nào dưới đây được biểu diễn bởi cùng một điểm trên đường tròn lượng
giác?
A.
6
và
5
6
. B.
3
và
3
. C.
2
và
5
2
. D.
0
và
3
.
Lời giải
Chọn C
Góc lượng giác
2
và
5
2
2 2
được biểu diễn bởi điểm
B
trên đường tròn lượng giác.
Câu 11: Viết phương trình tổng quát của đường thẳng đi qua
3;6
M và có một vectơ pháp tuyến
2;1
.
A.
2 0
x y . B.
3 6 0
x y . C.
2 15 0
x y . D.
2 12 0
x y .
Lời giải
Chọn D
Đường thẳng đi qua
3;6
M và có một vectơ pháp tuyến
2;1
có phương trình là
2. 3 1. 6 0 2 12 0
x y x y .
Do
5
3 3
nghiệm âm lớn nhất của phương trình là
3
.
Câu 12: Công thức lượng giác nào dưới đây là sai? Giả sử các điều kiện xác định được thỏa mãn.
A.
2
2tan
tan 2
1 tan
a
a
a
. B.
sin sin cos sin cos .
a b a b b a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
sin 2 2sin cos .
a a a
D.
cos cos 2sin sin .
2 2
a b a b
a b
Lời giải
Chọn C
Ta có
sin 2 2sin cos .
a a a
Câu 13: Tìm tất cả các giá trị của tham số
m
để bất phương trình 2
mx x m
có tập nghiệm là
.
A.
1
m . B.
1
m . C.
1
m . D.
m .
Lời giải
Chọn A
2
mx x m
1 2
m x m
Để bất phương trình có tập nghiệm là
thì
1 0 1
1
2 0 2
m m
m
m m
.
Câu 14: Viết phương trình đoạn chắn của đường thẳng đi qua
5;0
M và
0;3
N .
A.
1
5 3
x y
. B.
0
5 3
x y
. C.
1
3 5
x y
. D.
0
3 5
x y
.
Lời giải
Chọn A
Đường thẳng đi qua
5;0
M và
0;3
N có phương trình là
1
5 3
x y
.
Câu 15: Giải hệ bất phương trình
2
2 5 4
4 5 0
x x
x x
.
A.
1 3
x . B.
3
x . C.
1
x . D.
1 3
x .
Lời giải
Chọn D
2
2 5 4
3
1 3
1 5
4 5 0
x x
x
x
x
x x
.
Câu 16: Góc lượng giác có số đo
60
thì có số đo bằng bao nhiêu theo rađian?
A.
3
. B.
2
3
. C.
5
6
. D.
3
4
.
Lời giải
Chọn A
Góc lượng giác có số đo
60
thì có số đo bằng
3
rađian.
Câu 17: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng
1 2
3
x t
y t
.
A.
( 2;1)
. B.
(1; 2)
. C.
(1;2)
. D.
( 4;2)
.
Lời giải.
Chọn B
Vecto chỉ phương
(2;1)
u
vectơ pháp tuyến
(1; 2)
n
Câu 18: Viết phương trình đường thẳng đi qua điểm
(3;4)
M và có hệ số góc
2
k .
A.
2 10
y x . B.
2 2
y x . C.
2 2
y x . D.
2 10
y x .
Lời giải
Chọn B
2( 3) 4 2 2
y x x .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 19: Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 ( 1) 1 0
x m x m có hai nghiệm
dương phân biệt.
A.
9
1
m
m
. B.
9
m . C. Không tồn tại
m
. D.
1 9
m .
Lời giải
Chọn C
Để phương trình
2
2 ( 1) 1 0
x m x m có hai nghiệm dương phân biệt khi và chỉ khi
2
9
( 1) 8( 1) 0
0
1
( 1)
0 0
1
2
0
1
0
1
2
m
m m
m
m
S
m
P
m
m
Không tồn tại giá trị nào của
m
.
Câu 20: Tính khoảng cách từ điểm
(2;1)
M đến đường thẳng
3 4 1 0
x y .
A.
3
5
. B.
9
5
. C.
2
5
. D.
8
5
Lời giải
Chọn A
2 2
3.2 4.1 1
3
( , )
5
3 4
d M
.
Câu 21: Tính giá trị biểu thức
sin .cos
6 6
2sin .cos
3 3
A
.
A.
3
2
. B.
1
2
. C.
1
3
. D.
1
.
Lời giải
Chọn B
1 3
sin .cos
.
1
6 6
2 2
2
3 1
2sin .cos
2. .
3 3
2 2
A
.
Câu 22: Giải bất phương trình
2
4 0.
x
A.
2
2
x
x
. B.
2 2
x . C.
2 2
x . D.
2
2
x
x
.
Lời giải
Chọn B
2
4 0 2 2
x x
.
Câu 23: Tính chất nào sau đây ĐÚNG với mọi góc lượng giác
bất kì và mọi số nguyên
k
thỏa mãn
các biểu thức xác định ?
A.
sin sin
k
. B.
cos 2 cos
k
.
C.
cos cos
k
. D.
1 tan 1
.
Lời giải
Chọn B
cos 2 cos
k
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 24: Viết phương trình tổng quát của đường thẳng đi qua
3;0
M và song song với đường thẳng
2 100 0
x y .
A.
2 6 0
x y . B.
2 6 0
x y . C.
2 6 0
x y . D.
2 6 0
x y .
Lời giải
Chọn B
Đường thẳng đi qua điểm
3;0
M và song song với đường thẳng
2 100 0
x y có véctơ
pháp tuyến
2;1
n .
Phương trình đường thẳng là
2 3 1 0 0 2 6 0
x y x y .
Câu 25: Viết phương trình tiếp tuyến của đường tròn
2 2
1 5 5
x y tại điểm
3; 4
M thuộc
đường tròn.
A.
2 2 0
x y . B.
2 5 0
x y . C.
2 10 0
x y . D.
2 11 0
x y .
Lời giải
Chọn A
Ta có phương trình của đường tròn
2 2
1 5 5
x y nên tâm
1; 5
I .
Vì phương trình tiếp tuyến của đường tròn
2 2
1 5 5
x y tại điểm
3; 4
M nên
phương trình tiếp tuyến đi qua điểm
3; 4
M và nhận
2;1
IM là vectơ pháp tuyến.
Khi đó phương trình tiếp tuyến là:
2 3 1 4 0
x y
2 2 0
x y
2 2 0
x y .
Câu 26: Viết phương trình đường tròn đường kính
AB
với
1; 2 , 3;0
A B .
A.
2 2
2 1 4
x y . B.
2 2
2 1 16
x y .
C.
2 2
2 1 8
x y . D.
2 2
2 1 2
x y .
Lời giải
Chọn C
Vì đường tròn đường kính
AB
nên đường tròn có tâm
2; 1
I là trung điểm
AB
và bán kính
1
2 2
2
R AB .
Câu 27: Viết phương trình tổng quát của đường cao đỉnh
A
của tam giác
ABC
biết tọa độ các đỉnh
3;4 ,B 2;5 ,C 7;7
A .
A.
9 2 19 0
x y . B.
9 2 35 0
x y . C.
2 9 42 0
x y . D.
2 9 30 0
x y .
Lời giải
Chọn D
Do đường cao đỉnh
A
của tam giác
ABC
nên đi qua
3;4
A và nhận
9;2
BC làm vectơ pháp
tuyến. Khi đó phương trình đường cao đỉnh
A
có dạng:
9 3 2 4 0
x y
9 2 35 0
x y .
Câu 28: Giải bất phương trình
3 1 0
x .
A.
1
3
x . B.
1
3
x . C.
1
3
x . D.
1
3
x .
Lời giải
Chọn A
Ta có:
1
3 1 0
3
x x .
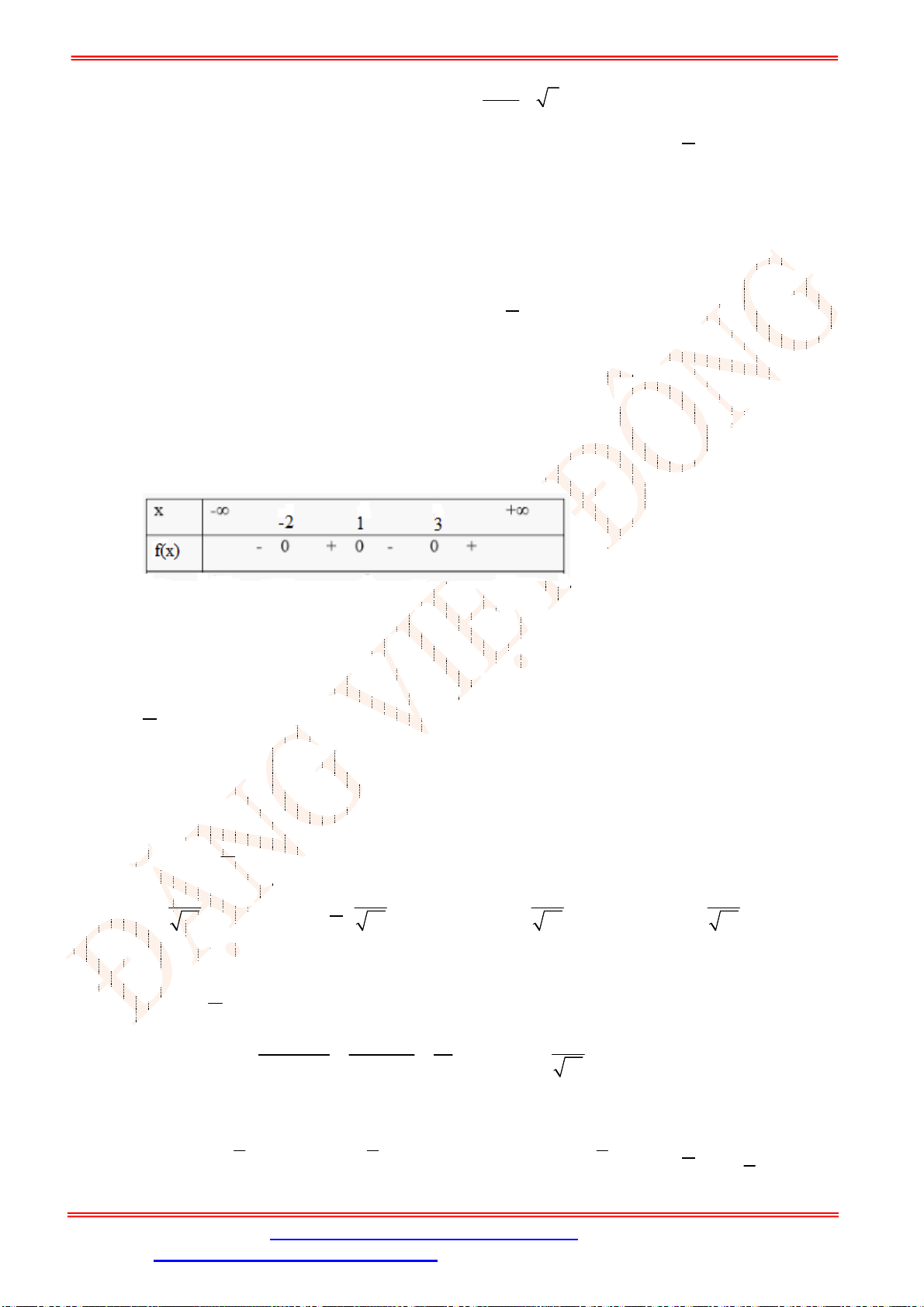
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 29: Tìm điều kiện xác định của bất phương trình
1
1
3
x
x
.
A.
0 3
x . B.
0
x . C.
0 3
x . D.
0 3
x .
Lời giải
Chọn D
Điều kiện xác định của bất phương trình
0
0 3
3
x
x
x
.
Câu 30: Giải bất phương trình
1 2 3 0
x x x .
A. Vô nghiệm. B.
1 3
x . C.
2 1
3
x
x
. D.
2
1 3
x
x
.
Lời giải
Chọn C
Đặt
1 2 3
f x x x x ,
1
0 2
3
x
f x x
x
Bảng xét dấu của
f x
:
Từ bảng xét dấu suy ra tập nghiệm của bpt
2 1
3
x
x
Câu 31: Viết phương trình tổng quát của đường thẳng đi qua
3; 1
M và có một véc tơ chỉ phương
2; 1
.
A.
2 1 0
x y . B.
2 7 0
x y . C.
2 5 0
x y . D.
2 5 0
x y .
Lời giải
Chọn A
Vectơ pháp tuyến của đường thẳng
1;2
n
Phương trình tổng quát của đường thẳng là
1 3 2 1 0 2 1 0
x y x y .
Câu 32: Cho
;
2
,
tan 3
. Tính
cos
.
A.
2
10
. B.
1
10
. C.
1
10
. D.
2
10
.
Lời giải
Chọn B
Vì
; cos 0
2
Ta có
2
2
2
1 1 1
cos
1 tan 10
1 3
1
cos
10
.
Câu 33: Giải bất phương trình
2
2 5 3 0
x x
.
A.
1
3
2
x . B.
1
3
2
x . C.
1
3
2
x . D.
3
1
2
x
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Ta có
2
2 5 3 0
x x
3
1
2
x
x
.
Câu 34: Tính độ dài cung tròn có số đo góc ở tâm bằng
6
của đường tròn lượng giác
A.
3
. B.
24
. C.
6
. D.
12
.
Lời giải
Chọn C
Ta có đường tròn lượng giác có bán kính
1
R
.
Do đó
6
l R
.
Câu 35: Cho phương trình
2
1 2 2 0
m x m x m , với
m
là tham số. Tìm tất cả các giá trị của
m
để phương trình đã cho có hai nghiệm phân biệt.
A.
4
5
m . B.
4
5
m . C.
4
5
m . D.
4
1
5
m .
Lời giải
Chọn D
Phương trình
2
1 2 2 0
m x m x m có hai nghiệm phân biệt
1 0
0
m
2
1
1
1
4
5 4 0
2 1 0
5
m
m
m
m
m
m m m
.
Vậy
4
1
5
m thì phương trình đã cho có hai nghiệm phân biệt.
Câu 36: Cho phương trình
2
3 2 1 0
x m x m , với
m
là tham số. Tìm tất cả các giá trị của
m
để
phương trình đã cho có nghiệm.
A.
8
9
m . B.
8
9
m . C.
m . D. không tồn tại
m
.
Lời giải
Chọn C
Phương trình
2
3 2 1 0
x m x m có nghiệm
0
2
2
3 2 4.1. 1 0 9 16 8 0
m m m m
2
8 8
3 0
3 9
m m .
Vậy
m phương trình luôn có nghiệm.
Câu 37: Cho
0;
2
,
1
sin
3
. Tính
tan
.
A.
2
4
. B.
1
3
. C.
2
2
. D.
1
3
.
Lời giải
Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Do
0; cos 0
2
. Do đó
2
2
1 2 2
cos 1 sin 1
3 3
.
Vậy
sin 1 2 2 2
tan :
cos 3 3 4
.
Câu 38: Tính khoảng cách giữa hai điểm
3;4
M và
1;0
N .
A.
21
. B.
4 2
. C.
2 5
. D.
20
.
Lời giải
Chọn C
Ta có
2 2
1 3 0 4 2 5
MN
.
Câu 39: Tính cosin góc giữa hai đường thẳng
3x 10 0
y và
2 4 5 0
x y
A.
2
5
. B.
2
10
. C.
2
20
. D.
2
2
.
Lời giải
Chọn B
Gọi
là góc giữa hai đường thẳng.
Hai vectơ pháp tuyến lần lượt là
1 2
3; 1 , 1;2
n n .
Vậy
2
2 2 2
3.1 1.2
1 2
cos
10
5 2
3 1 . 1 2
.
Câu 40: Tìm tọa độ giao điểm của hai đường thẳng:
3 1 0
x y và
6 1 0
x y .
A.
1
;0
3
. B.
1
;0
3
. C.
0; 1
. D.
0;2
.
Lời giải
Chọn C
Tọa độ giao điểm của hai đường thẳng đã cho là nghiệm hệ phương trình:
3 1 0 0
6 1 0 1
x y x
x y y
.
Vậy giao điểm cần tìm là (0; -1).
Câu 41: Viết phương trình đường tròn tâm I(2; 3), bán kính R = 2.
A.
2
2
2 ( 3) 4
x y . B.
2
2
2 ( 3) 4
x y .
C.
2
2
2 ( 3) 2
x y . D.
2
2
2 ( 3) 2
x y .
Lời giải
Chọn A.
Phương trình đường tròn có tâm I(2; 3), bán kính R = 2 là:
2 2
2 3 4
x y .
Câu 42: Cho góc lượng giác
0;
2
có
1
sin
3
. Tính
sin2
.
A.
2 2
.
3
B.
4 2
.
9
C.
2 2
.
9
D.
2 2
.
9
Lời giải
Chọn B
Vì
0;
2
nên
2
2
1 2 2
cos 0 cos 1 sin 1 .
3 3

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Từ đó,
1 2 2 4 2
sin 2 2sin .cos 2. . .
3 3 9
Câu 43: Viết phương trình tổng quát của đường thẳng đi qua hai điểm
3;4
M và
0;1
N .
A.
7 0
x y . B.
1 0
x y . C.
1 0
x y . D.
4 4 3 0
x y .
Lời giải
Chọn C
Ta có
3; 3
MN là 1 vectơ chỉ phương của đường thẳng suy ra 1 vectơ pháp tuyến của
đường thẳng là
1; 1
n .
Đường thẳng đi qua
0;1
N có 1 vectơ pháp tuyến của đường thẳng là
1; 1
n nên có
phương trình tổng quát là
1 0
x y .
Câu 44: Tìm tập nghiệm bất phương trình
2
4 3 0
x x
.
A.
; 3 1;
. B.
3; 1
. C.
; 3 1;
. D.
3; 1
.
Lời giải
Chọn D
Ta có
2
4 3 0 3 1
x x x
.
Vậy bất phương trình có tập nghiệm là
3; 1
S .
Câu 45: Tìm tất cả các giá trị của tham số
m
để
2
1 1 0,
f x mx m x m x .
A.
0
1
3
m
m
. B.
0
m . C.
1
m . D.
1
1
3
m
m
.
Lời giải
Chọn C
Trường hợp 1:
0 0
a m .
Suy ra
1 0 1 0 1
f x x f x x x (không thoả mãn).
Trường hợp 2:
0 0
a m
Suy ra
2
1 1 0,
f x mx m x m x
0
0
a
2
0
1 4 1 0
m
m m m
2
0
0
1
1
3 2 1 0
1
3
m
m
m
m
m m
m
.
Vậy với
1
m thì
0,
f x x .
Câu 46: Tìm tất cả giá trị của tham số
m
để hệ bất phương trình
2 1 3
x x
x m
có nghiệm.
A.
4.
m B.
4.
m C.
4.
m D.
4.
m
Lời giải
Chọn B
Bất phương trình đầu của hệ
2 1 3 4
x x x
1
;4
S
Bất phương trình hai của hệ
x m
2
;
S m
Hệ đã cho có nghiệm khi
1 2
4.
S S m
Vậy chọn B.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 47: Tìm tọa độ các giao điểm của đường tròn
2 2
: 1 3 4
C x y và đường thẳng
: 4 0.
d x y
A.
1; 3 .
B. Không có giao điểm. C.
1; 3 ; 1; 5 .
D.
1; 5 .
Lời giải
Chọn C
Tọa độ giao điểm là nghiệm hệ phương trình
2 2 2 2
1 3 4 1 3 4
4 0 4
x y x y
x y y x
2 2
1
1 1 4
4
4
x
x x
y x
y x
1
3
1
5
x
y
x
y
Vậy có hai giao điểm là
1; 3
và
1; 5 .
Câu 48: Cho tứ giác
ABCD
có
1;7 , 1;1 , 5;1 , 7;5 .
A B C D Tìm tọa độ giao điểm
I
của hai
đường chéo của tứ giác.
A.
4;2 .
I B.
2;4 .
I C.
2;3 .
I D.
3;3 .
I
Lời giải
Chọn D
Phương trình đường chéo
AC
:
1 7
6 6
x y
1 7 6 0
x y x y
Phương trình đường chéo
BD
:
1 1
1 2 2
8 4
x y
x y
2 3 0
x y
Tọa độ giao điểm
I
của hai đường chéo là nghiệm hệ phương trình
6 0 3
2 3 0 3
x y x
x y y
3;3
I
Vậy chọn D.
Câu 49: Trong tam giác
ABC
, hệ thức nào SAI?
A.
sin sin
A B C
. B.
cos cos
A B C
.
C.
tan cot
2 2
A B C
. D.
sin cos
2 2
A B C
.
Lời giải
Chọn A
Ta có
sin sin
A B C
.
Câu 50: Giải bất phương trình
2
3 2
2 2
1
x x
x
x
.
A.
3
1
x
x
. B.
3 1
x
. C.
3 0
1
x
x
. D.
3
0 1
x
x
.
Lời giải
Chọn C
Ta có
2
2
2
1
3 2 ( 1).(2 2)
3 2
2 2
1
1
3 2 ( 1).(2 2)
x
x x x x
x x
x
x
x
x x x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2
2
1
1
0
3 0
1
3
3 0
1
1
3 0
3 0
x
x
x
x x
x
x
x
x
x
x x
x
.
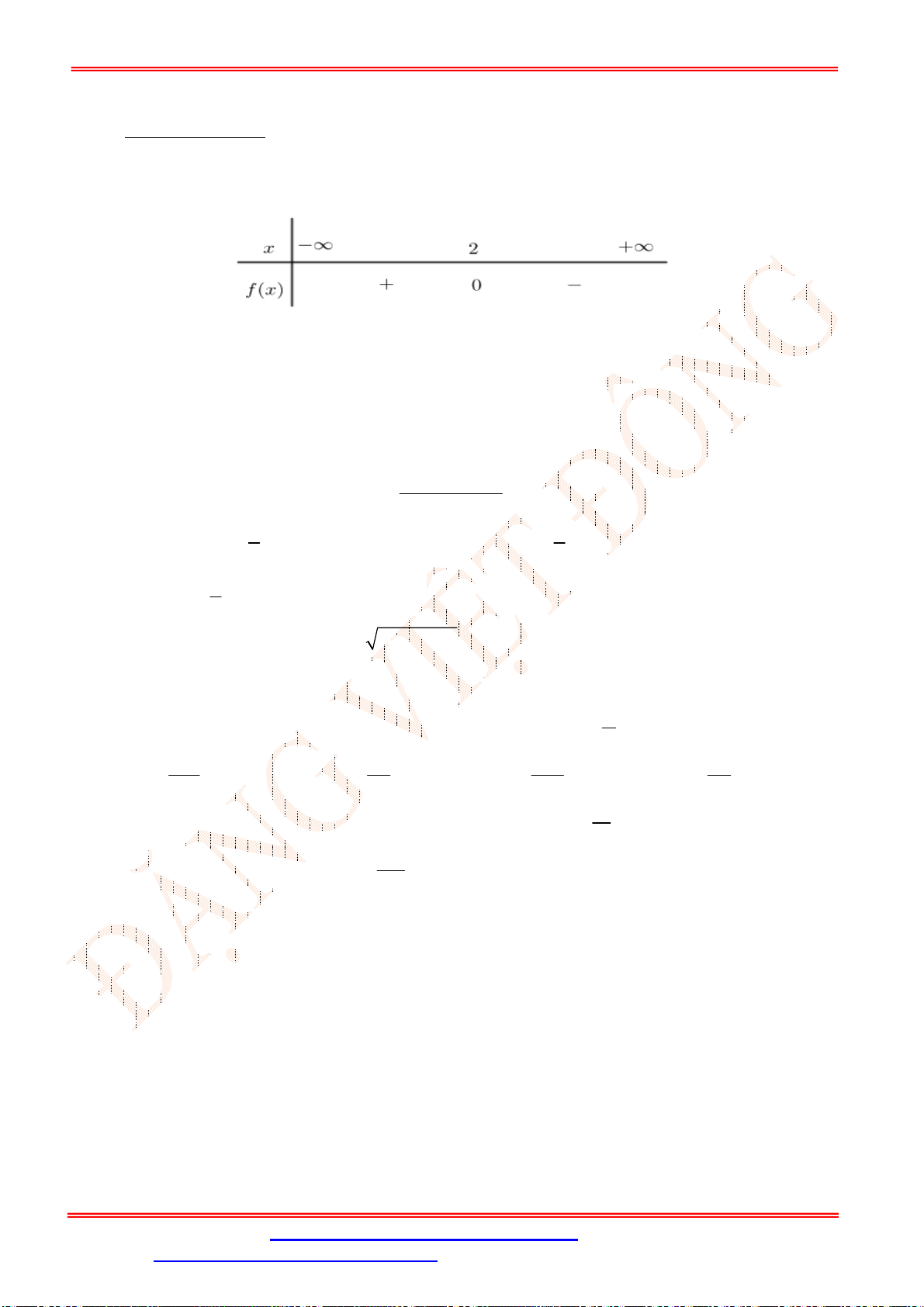
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 14
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Cho hàm số
y f x
có bảng xét dấu dưới đây.
Hỏi
y f x
là hàm số nào trong 4 đáp án sau?
A.
8 4
f x x
. B.
16 8
f x x
. C.
2
f x x
. D.
2 4
f x x
.
Câu 2. Cho tam thức bậc hai
2
0
f x ax bx c a
. Điều kiện cần và đủ để
0,f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Câu 3. Tập nghiệm của bất phương trình
2
( 1)(3 2 )
0
5 6
x x
x x
là
A.
3
( ;1) ;2 (3; )
2
. B.
3
1; (2;3)
2
.
C.
3
; (3; )
2
. D.
(1;2) (3; )
.
Câu 4. Tập xác định của hàm số
2
4 3
y x x
là
A.
. B.
( ;1) (3; )
. C.
( ;1] [3; )
. D.
[1;3]
.
Câu 5. Khi biểu diễn trên đường tròn lượng giác cung lượng giác nào trong các cung lượng giác có số
đo dưới đây có cùng điểm cuối với cung lượng giác có số đo
4
?
A.
10
3
. B.
5
4
. C.
25
4
. D.
7
4
.
Câu 6. Trên đường tròn bán kính
15
R
, độ dài của cung có số đo
15
là
A.
15
. B.
180
15.
. C.
15
. D.
.
Câu 7. Chọn khẳng định đúng?
A.
tan tan
.
B.
sin sin
.
C.
cot cot
. D.
cos cos
.
Câu 8. Khẳng định nào dưới đây sai?
A.
cos2 2cos 1
a a
. B.
2
2sin 1 cos2
a a
.
C.
sin sin cos sin cos
a b a b b a
. D.
sin2 2sin cos
a a a
.
Câu 9. Rút gọn biểu thức
cos 115 .cos –365 sin 115 .sin –365
M .
A.
cos 245
M
. B.
sin 480
M
.
C.
sin 245
M
. D.
cos 480
M
.
Câu 10. Công thức nào sau đây sai?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
1
sin sin cos cos
2
a b a b a b
. B.
–c c
1
s
2
o cos cos os
a b a b
a b
.
C.
cos cos cos
1
2
cosaa
b a b
b
.
D.
1
sin cos sin – sin
2
a b a b a b
.
Câu 11. Rút gọn biểu thức
4sin 2 .cos2
cos3 cos
x x
x x
(với điều kiện biểu thức có nghĩa), ta được biểu thức có dạng
sin 2
cos
a x
b x
với
, ,
a
a b
b
tối giản. Giá trị của
2
a b
bằng:
A.
2
. B.
5
. C.
5
. D.
3
.
Câu 12. Trong mặt phẳng
Oxy
, đường thẳng đi qua điểm
2; 4
A
và nhận
4;3
u
là vec-tơ chỉ
phương có phương trình tham số là:
A.
2 4
4 3
x t
y t
. B.
2 4
4 3
x y
. C.
4 2
3 4
x t
y t
. D.
2 4
4 3
x t
y t
.
Câu 13. Đường thẳng đi qua
1;2
A , nhận
(2; 4)
n
làm véctơ pháp tuyến có phương trình là:
A.
– 2 – 4 0
x y
. B.
4 0
x y
. C.
– 2 – 4 0
x y
. D.
– 2 3 0
x y
.
Câu 14. Cho đường thẳng
d
có phương trình tổng quát là
2019 2020 2021 0
x y
. Tìm khẳng định
sai trong các khẳng định sau:
A.
d
có véctơ pháp tuyến
(2019;2020)
n
.
B.
d
có véctơ chỉ phương
( 2020;2019)
u
.
C.
d
có hệ số góc
2019
2020
k .
D.
d
song song với đường thẳng
2019 2020 0
x y
.
Câu 15. Đường tròn có phương trình
2 2
10 24 0
x y y
thì bán kính bằng bao nhiêu?
A.
49
. B.
7
. C.
1
. D.
29
.
Câu 16. Trong mặt phẳng
Oxy
, phương trình nào sau đây là phương trình chính tắc của một elip?
A.
2 2
1
2 3
x y
. B.
2 2
1
9 8
x y
. C.
1
9 8
x y
. D.
2 2
1
9 1
x y
.
Câu 17. Tập nghiệm của bất phương trình
4
2
3
x
là
A.
; 3 1;
. B.
3; 1
. C.
1;
. D.
; 1
.
Câu 18. Các giá trị
m
làm cho biểu thức
2
4 5
f x x x m
luôn dương là:
A.
9
m . B.
9
m . C.
9
m . D.
m
.
Câu 19. Tìm
m
để bất phương trình
2
4 0
x mx m
vô nghiệm.
A.
0
m
. B.
0
m
. C.
1
0
4
m
. D.
1
4
0
m
m
.
Câu 20. Với
x
thuộc tập hợp nào dưới đây thì biểu thức
2
1
4 3
x
f x
x x
không dương?
A.
;1
S
. B.
3; 1 1;S
.
C.
; 3 1;1
S . D.
3;1
S .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 21. Góc có số đo
3
16
có số đo theo độ là
A.
o
33 45'
. B.
o
29 30'
. C.
o
32 55'
. D.
o
33 45'
.
Câu 22. Tập nghiệm của bất phương trình
2
2
2 3
4 2
x x
x x
là
A.
. B.
; 2 2;
.
C.
. D.
2;2
.
Câu 23. Cho
3
sin
5
và
2
. Tính
tan
.
A.
3
tan
4
. B.
3
tan
4
. C.
3
tan
4
. D.
4
tan
3
.
Câu 24. Biểu thức
3 4cos2 cos4
3 4cos2 cos4
có kết quả rút gọn bằng
A.
4
tan
. B.
4
tan
. C.
4
cot
. D.
4
cot
.
Câu 25. Rút gọn biểu thức
sin cos cos sin
A x y y x y y
.
A.
cos
A x
. B.
sin
A x
. C.
sin .cos2
A x y
. D.
cos .cos2
A x y
.
Câu 26. Rút gọn biểu thức
sin sin2 sin3
cos cos2 cos3
x x x
A
x x x
.
A.
tan6
A x
. B.
tan3
A x
.
C.
tan2
A x
. D.
tan tan2 tan3
A x x x
.
Câu 27. Cho
A
,
B
,
C
là các góc của tam giác
ABC
. Khẳng định nào sau đây Đúng?
A.
sin2 sin2 sin2 4cos cos cos
A B C A B C
.
B.
sin2 sin2 sin2 4cos cos cos
A B C A B C
.
C.
sin2 sin2 sin2 4sin sin sin
A B C A B C
.
D.
sin2 sin2 sin2 4sin sin sin
A B C A B C
.
Câu 28. Cho đường thẳng
2 2
:
3
x t
d t
y t
. Tìm điểm
M
trên đường thẳng
d
và cách điểm
0;1
A một khoảng bằng
5
.
A.
8 10
;
3 3
M
. B.
4;4
M hoặc
44 32
;
5 5
M
.
C.
4; 4
M
hoặc
24 2
;
5 5
M
. D.
4;4
M hoặc
24 2
;
5 5
M
.
Câu 29. Viết phương trình tổng quát của đường thẳng đi qua
2
điểm
2; 1
A
và
2;5
B .
A.
2 0
x . B.
2 7 9 0
x y . C.
2 0
x . D.
1 0
x y .
Câu 30. Cho tam giác
ABC
có
1;4
A
,
3;2
B
,
7;3
C
. Lập phương trình đường trung tuyến
AM
của tam giác
ABC
.
A.
8 3 4 0
x y
. B.
3 8 35 0
x y
.
C.
3 8 35 0
x y
. D.
8 3 20 0
x y
.
Câu 31. Trong mặt phẳng
Oxy
, đường tròn tâm
( 1;2)
I
và đi qua điểm
(2;1)
M
có phương trình là
A.
2 2
2 4 5 0
x y x y
. B.
2 2
2 4 3 0
x y x y
.
C.
2 2
2 4 5 0
x y x y
. D.
2 2
2 4 5 0.
x y x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 32. Trong mặt phẳng
Oxy
, cho elip
2 2
:3 4 48 0
E x y
và đường thẳng
: 2 4 0
d x y
.
Giao điểm của đường thẳng
d
và elip
E
có tọa độ là
A.
0; 4
và
2; 3
. B.
4;0
và
3;2
.
C.
0;4
và
2;3
. D.
4;0
và
2;3
.
Câu 33. Đường thẳng đi qua hai điểm
3;0
A và
0; 5
B
có phương trình là:
A.
1
3 5
x y
. B.
1
3 5
x y
. C.
1
5 3
x y
. D.
1
5 3
x y
.
Câu 34. Trong mặt phẳng tọa đô
Oxy
, biết đường thẳng
: 1
3 4
x y
cắt hai trục tọa độ tại hai điểm
phân biệt
A
và
B
. Tính diện tích
S
của tam giác
OAB
.
A.
6
S
. B.
12
S
. C.
4
S
. D.
3
S
.
Câu 35. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
tâm
I
bán kính
R
, đường thẳng
là tiếp
tuyến của đường tròn
C
tại điểm
M
. Chọn khẳng định đúng.
A.
,
d I R
. B.
,
d I R
. C.
,
d I R
. D.
,
d I R
.
Câu 36. Phương trình tiếp tuyến của đường tròn
C
:
2 2
1 5 4
x y tại điểm
3; 5
M
là.
A.
3 0
x . B.
3 0
x . C.
2 3 0
x y . D.
2 3 0
x y .
Câu 37. Đường tròn
C
có tâm
I
nằm trên đường thẳng
:2 4 0
d x y
và tiếp xúc với
:2 3 21 0
d x y
tại
3;5
H . Khi đó tâm
I
của
C
có tọa độ là:
A.
1; 2
I
. B.
1;2
I . C.
9 17
;
4 2
I
. D.
9 17
;
4 2
I
.
Câu 38. Trong mặt phẳng
Oxy
cho đường thẳng
1 2
: ,
3
x t
d t
y t
. Vectơ nào dưới đây là một
vectơ chỉ phương của
d
?
A.
1
1; 3
u
. B.
2
1;3
u
. C.
3
1; 2
u
. D.
4
2;1
u
.
Câu 39. Trong mặt phẳng
Oxy
, vectơ pháp tuyến của đường thẳng
:2 3 9 0
d x y
là:
A.
2; 3
n
. B.
2;3
n
. C.
2; 3
n
. D.
3; 2
n
.
Câu 40. Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:3 4 1 0
d x y
và điểm
1; 2
I
. Gọi
C
là đường tròn tâm
I
và cắt đường thẳng
d
tại hai điểm
,
A B
sao cho tam giác
IAB
có diện tích
bằng
4
. Phương trình đường tròn
C
là:
A.
2 2
1 2 8
x y
. B.
2 2
1 2 20
x y
.
C.
2 2
1 2 5
x y
. D.
2 2
1 2 16
x y
.
Câu 41. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
2 2 3
1
x mx m
y
x x
có tập xác định
là
?
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 42. Bất phương trình
2
2 2
2
3 1 3 9 5
0
4 5
x x x x
x x
có tập nghiệm là
A.
;1 2;
. B.
2;
.
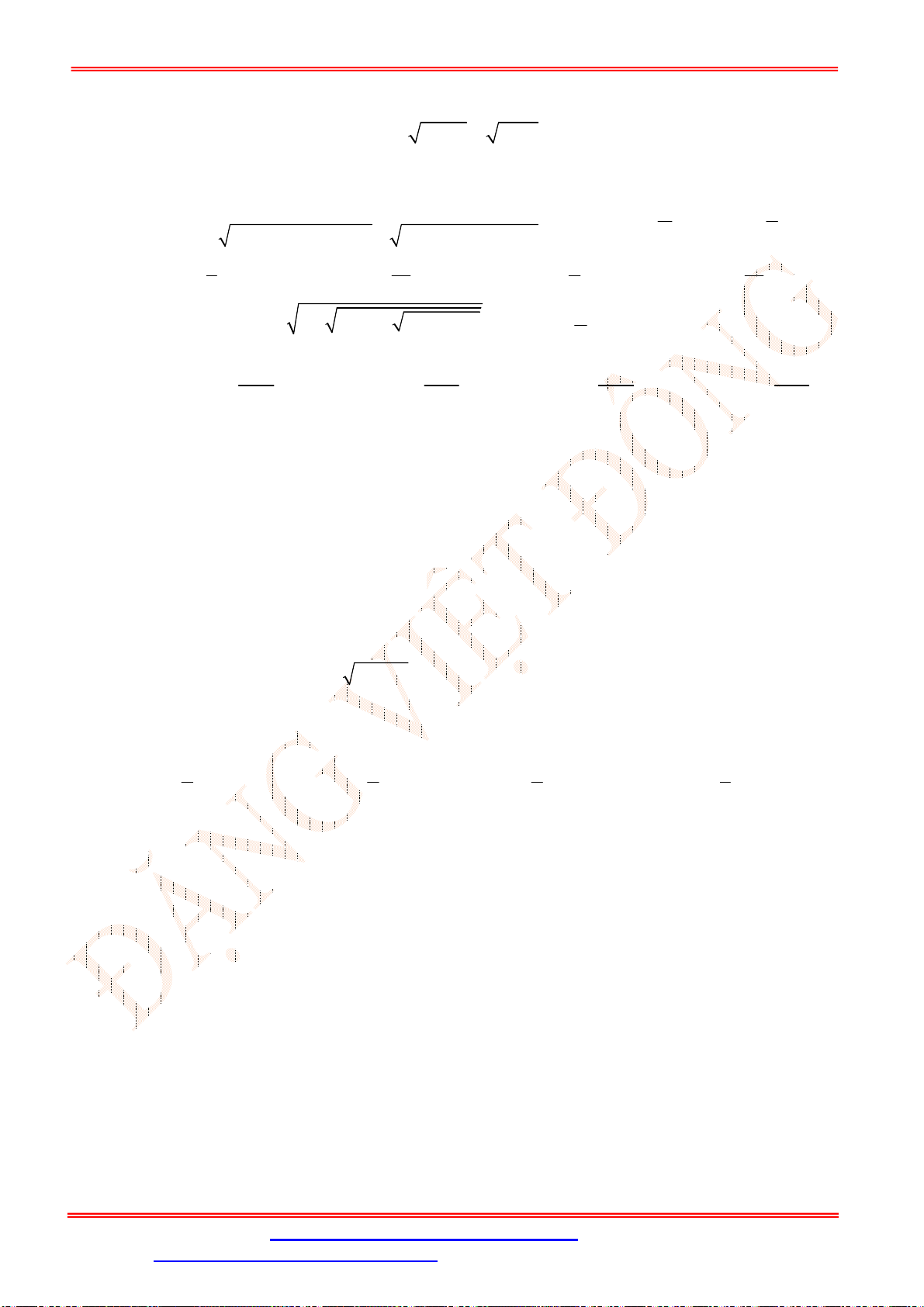
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
1;2
. D.
;1
.
Câu 43. Tập nghiệm của bất phương trình
2
3 1 6 3 14 8 0
x x x x
là nửa khoảng
;
a b
.
Tính tổng 3
S a b
.
A.
1
S
B.
2
S
C.
0
S
D.
4
S
Câu 44. Tính
2 2
cos 4cos 4 sin 4sin 4
M
biết
2
và
7
sin 2
9
.
A.
8
3
M
. B.
16
3
M
. C.
4
3
M
. D.
16
5
M
.
Câu 45. Cho biểu thức
2020
2 2 ... 2 2cos
Coù daáu caên baäc hai
P x
với
π
0
2
x . Hãy rút gọn biểu thức
P
.
A.
2020
2cos
2
x
P . B.
2021
2cos
2
x
P . C.
2020
2sin
2
x
P . D.
2021
2sin
2
x
P .
Câu 46. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hình chữ nhật
ABCD
có diện tích bằng 12, tâm
I
là
giao điểm của hai đường thẳng
1 2
: 3 0, : 6 0
d x y d x y
. Trung điểm cạnh
AD
là giao
điểm của
1
d
và
Ox
. Biết đỉnh
A
có tung độ dương, giả sử tọa độ
;
A a b
, khi đó giá trị
2
2
a b
là
A.
11
. B.
14
. C.
18
. D.
6
.
Câu 47. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
nội tiếp đường tròn tâm
1;2
I , bán kính
5
R
. Hai điểm
3;3
H ,
0; 1
K
lần lượt là chân đường cao kẻ từ
C
,
B
xuống cạnh
,
AB AC
. Tìm tọa độ điểm
A
, biết
A
có tung độ dương.
A.
5;5
A B.
3;5
A C.
4;6
A D.
2;6
A
Câu 48. Cho bất phương trình
2 2 2
2 2 5 9 1
x x x . Gọi
1 2 1 2
,
x x x x
là hai nghiệm nguyên
dương nhỏ nhất của bất phương trình
1
. Xác định giá trị của m để biểu thức
2
1 2 1 2
2 2 1
m x x m x x
đạt giá trị nhỏ nhất?
A.
5
2
. B.
5
4
. C.
5
2
. D.
5
8
.
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1; 2
A
, đường thẳng chứa tia phân giác
trong góc
C
có phương trình
: 3 0
d x y
, đường thẳng chứa cạnh
BC
đi qua điểm
4; 1
K
. Biết trọng tâm của tam giác
ABC
nằm trên đường thẳng có phương trình
: 2 2 0
x y
. Tìm tọa độ điểm
B
của tam giác đó?
A.
5; 2
B
. B.
5; 2
B
. C.
5; 2
B
. D.
5; 2
B
.
Câu 50. Trong mặt phẳng với hệ tọa độ
Oxy
. Cho đường tròn
C
:
2 2
1 2 9
x y
và điểm
2;3
M . Đường thẳng
qua
M
cắt đường tròn
C
tại hai điểm
,
A B
sao cho
2 2
18
MA MB
có phương trình là:
A.
2 1 0, 2 8 0
x y x y
. B.
2 1 0, 2 8 0
x y x y
.
C.
10 0, 5 0
x y x y
. D.
6 0, 3 0
x y x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
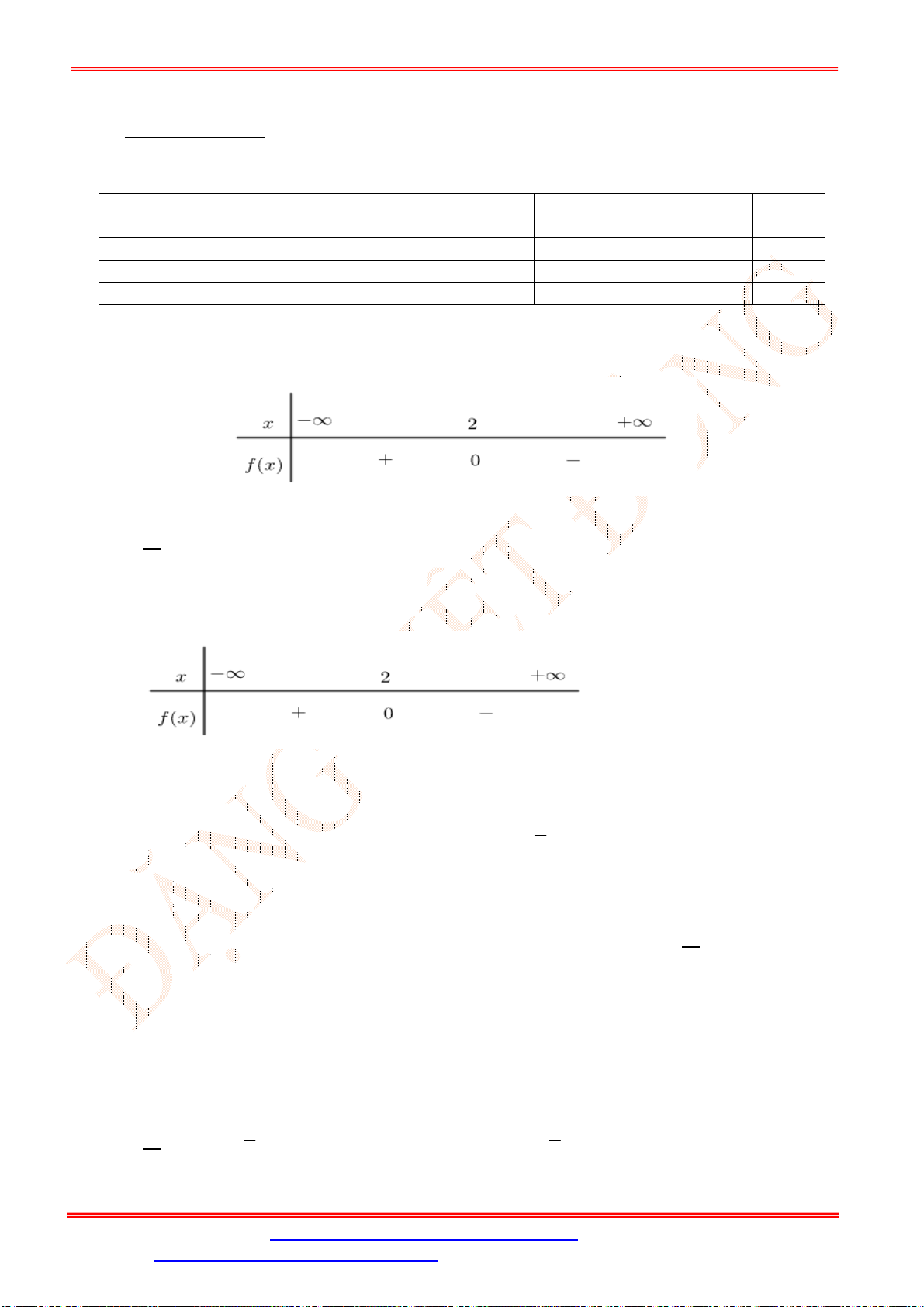
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 14
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.A 2.D 3.A 4.C 5.C 6.D 7.D 8.A 9.D 10.C
11.C 12.D 13.D 14.C 15.B 16.D 17.A 18.C 19.C 20.C
21.D 22.B 23.A 24.A 25.B 26.C 27.C 28.D 29.A 30.C
31.A 32.D 33.A 34.A 35.A 36.A 37.B 38.D 39.C 40.A
41.D 42.A 43.D 44.B 45.A 46.D 47.B 48.B 49.C 50.A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Cho hàm số
y f x
có bảng xét dấu dưới đây.
Hỏi
y f x
là hàm số nào trong 4 đáp án sau?
A.
8 4
f x x
. B.
16 8
f x x
. C.
2
f x x
. D.
2 4
f x x
.
Lời giải
Chọn A
Đáp án A
8 4
f x x
có
0
a
và
0 2
f x x
suy ra bảng xét dấu
Đáp án B
16 8
f x x
có
0
a
( Không thỏa mãn).
Đáp án C
2
f x x
có
0
a
và
0 2
f x x
( Không thỏa mãn).
Đáp án B
2 4
f x x
có
0
a
và
1
0
2
f x x
( Không thỏa mãn).
Câu 2. Cho tam thức bậc hai
2
0
f x ax bx c a
. Điều kiện cần và đủ để
0,f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Lời giải
Chọn D
Theo định lý dấu của tam thức bậc hai ta có
0
0,
0
a
f x x
.
Câu 3. Tập nghiệm của bất phương trình
2
( 1)(3 2 )
0
5 6
x x
x x
là
A.
3
( ;1) ;2 (3; )
2
. B.
3
1; (2;3)
2
.
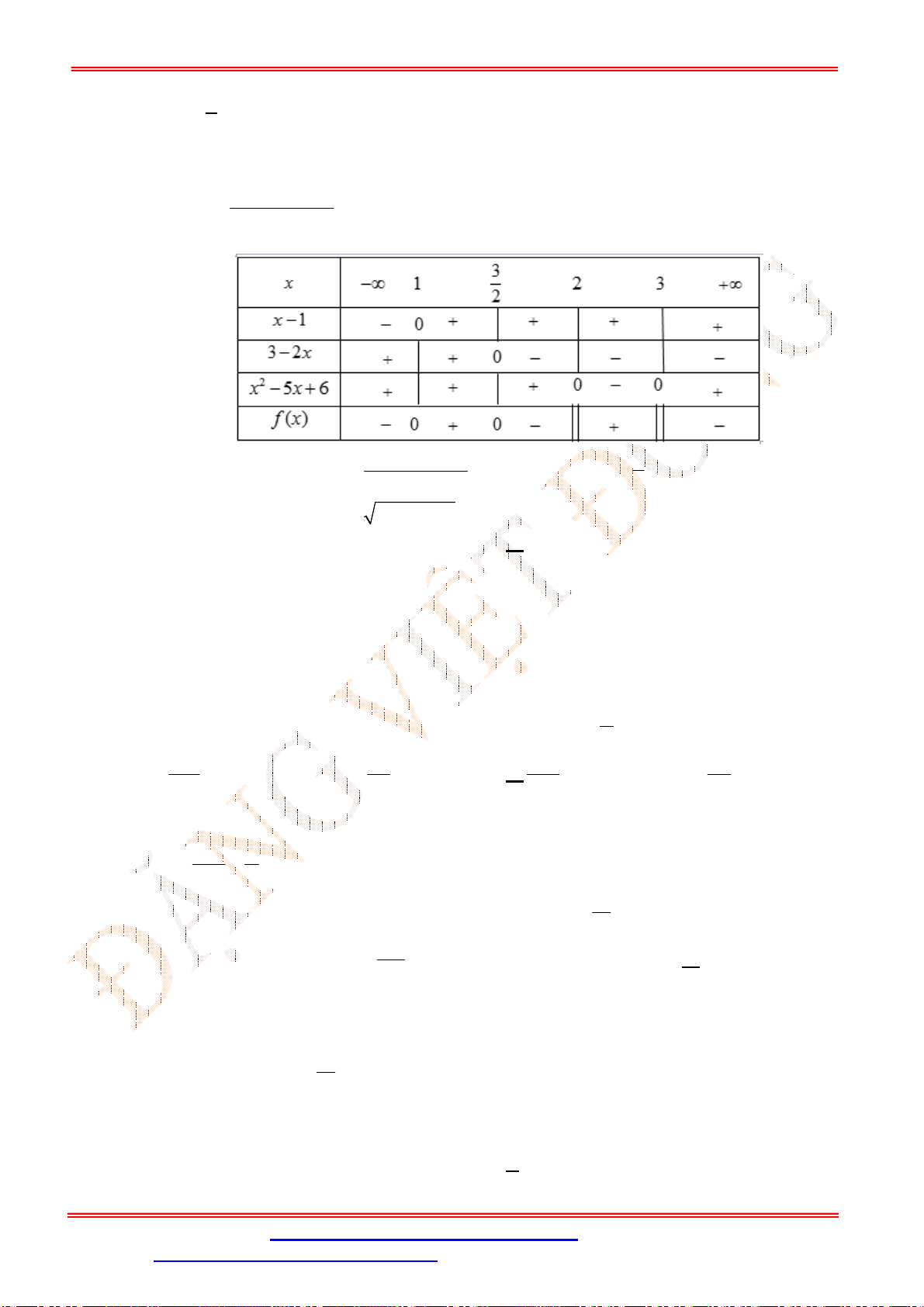
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
3
; (3; )
2
. D.
(1;2) (3; )
.
Lời giải
Chọn A
Đặt
2
( 1)(3 2 )
( )
5 6
x x
f x
x x
Ta có bảng xét dấu:
Từ bảng xét dấu ta có
2
( 1)(3 2 )
( ) 0
5 6
x x
f x
x x
3
( ;1) ;2 (3; )
2
x
.
Câu 4. Tập xác định của hàm số
2
4 3
y x x
là
A.
. B.
( ;1) (3; )
. C.
( ;1] [3; )
. D.
[1;3]
.
Lời giải
Chọn C
ĐK:
2
1
4 3 0 .
3
x
x x
x
Vậy TXĐ của hàm số là
D ( ;1] [3; )
Câu 5. Khi biểu diễn trên đường tròn lượng giác cung lượng giác nào trong các cung lượng giác có số
đo dưới đây có cùng điểm cuối với cung lượng giác có số đo
4
?
A.
10
3
. B.
5
4
. C.
25
4
. D.
7
4
.
Lời giải
Chọn C
Ta có
25
3.2
4 4
Câu 6. Trên đường tròn bán kính
15
R
, độ dài của cung có số đo
15
là
A.
15
. B.
180
15.
. C.
15
. D.
.
Lời giải.
Chọn D.
Độ dài cung là: 15.
15
l
.
Câu 7. Chọn khẳng định đúng?
A.
tan tan
.
B.
sin sin
.
C.
cot cot
. D.
cos cos
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
tan tan
sai vì
tan tan
.
sin sin
sai vì
sin sin
.
cot cot
sai vì
cot cot
.
Câu 8. Khẳng định nào dưới đây sai?
A.
cos2 2cos 1
a a
. B.
2
2sin 1 cos2
a a
.
C.
sin sin cos sin cos
a b a b b a
. D.
sin2 2sin cos
a a a
.
Lời giải
Chọn A
Ta có:
2
cos2 2cos 1
a a
nên A sai.
Và:
2
cos2 1 2sin 2sin 1 cos2
a a a a
nên B đúng.
Các đáp án C và D hiển nhiên đúng.
Câu 9. Rút gọn biểu thức
cos 115 .cos –365 sin 115 .sin –365
M .
A.
cos 245
M
. B.
sin 480
M
.
C.
sin 245
M
. D.
cos 480
M
.
Lời giải
Chọn D
Ta có công thức:
cos cos .cos sin .sin
a b a b a b
.
cos 115 .cos –365 sin 115 .sin –365
M
.
cos 115 365 cos 480
.
Câu 10. Công thức nào sau đây sai?
A.
1
sin sin cos cos
2
a b a b a b
. B.
–c c
1
s
2
o cos cos os
a b a b
a b
.
C.
cos cos cos
1
2
cosaa
b a b
b
.
D.
1
sin cos sin – sin
2
a b a b a b
.
Lời giải
Chọn C
Áp dụng công thức biến đổi tích thành tổng thì
cos cos cos cos .
1
2
a b a b
a b
Câu 11. Rút gọn biểu thức
4sin 2 .cos2
cos3 cos
x x
x x
(với điều kiện biểu thức có nghĩa), ta được biểu thức có dạng
sin 2
cos
a x
b x
với
, ,
a
a b
b
tối giản. Giá trị của
2
a b
bằng:
A.
2
. B.
5
. C.
5
. D.
3
.
Lời giải
Chọn C.
Ta có
4sin 2 cos2 4sin 2 cos 2 2sin 2
cos3 cos 2cos 2 cos cos
x x x x x
x x x x x
(với điều kiện biểu thức có nghĩa).
Do đó
2
a
,
1
b
2
5
a b
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 12. Trong mặt phẳng
Oxy
, đường thẳng đi qua điểm
2; 4
A
và nhận
4;3
u
là vec-tơ chỉ
phương có phương trình tham số là:
A.
2 4
4 3
x t
y t
. B.
2 4
4 3
x y
. C.
4 2
3 4
x t
y t
. D.
2 4
4 3
x t
y t
.
Lời giải
Chọn D.
Đường thẳng đi qua
2; 4
A
và nhận
4;3
u
làm vec-tơ chỉ phương nên PTTS là:
2 4
4 3
x t
y t
.
Câu 13. Đường thẳng đi qua
1;2
A , nhận
(2; 4)
n
làm véctơ pháp tuyến có phương trình là:
A.
– 2 – 4 0
x y
. B.
4 0
x y
. C.
– 2 – 4 0
x y
. D.
– 2 3 0
x y
.
Lời giải
Chọn D
PT đường thẳng cần tìm là :
2 1 4 2 0
x y
.
Vậy PT tổng quát đường thẳng cần tìm là:
2 3 0
x y
.
Câu 14. Cho đường thẳng
d
có phương trình tổng quát là
2019 2020 2021 0
x y
. Tìm khẳng định
sai trong các khẳng định sau :
A.
d
có véctơ pháp tuyến
(2019;2020)
n
.
B.
d
có véctơ chỉ phương
( 2020;2019)
u
.
C.
d
có hệ số góc
2019
2020
k .
D.
d
song song với đường thẳng
2019 2020 0
x y
.
Lời giải
Chọn C
Đường thẳng
d
có véctơ chỉ phương
( 2020;2019)
u
nên có hệ số góc
2
1
2019
2020
u
k
u
.
Câu 15. Đường tròn có phương trình
2 2
10 24 0
x y y
thì bán kính bằng bao nhiêu?
A.
49
. B.
7
. C.
1
. D.
29
.
Lời giải
Chọn B
Đường tròn
2 2
10 24 0
x y y
có tâm
0;5
I
, bán kính
2 2
0 5 24 7
R
.
Câu 16. Trong mặt phẳng
Oxy
, phương trình nào sau đây là phương trình chính tắc của một elip?
A.
2 2
1
2 3
x y
. B.
2 2
1
9 8
x y
. C.
1
9 8
x y
. D.
2 2
1
9 1
x y
.
Lời giải
Chọn D
Phương trình chính tắc của elip có dạng
2 2
2 2
1, 0
x y
a b
a b
nên chọn phương án
D
.
Câu 17. Tập nghiệm của bất phương trình
4
2
3
x
là
A.
; 3 1;
. B.
3; 1
. C.
1;
. D.
; 1
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn A
ĐK 3x .
Ta có
4 4 2 2
2 2 0 0 (1)
3 3 3
x
x x x
Bảng xét dấu :
Do đó
(1) ; 3 1;x
Vậy chọn đáp án A.
Câu 18. Các giá trị m làm cho biểu thức
2
4 5f x x x m luôn dương là:
A. 9m . B. 9m . C. 9m . D.
m
.
Lời giải
Chọn C
0 1 0
0, 9
0 4 ( 5) 0
a
f x x m
m
.
Vậy chọn đáp án C.
Câu 19. Tìm
m
để bất phương trình
2
4 0x mx m
vô nghiệm.
A. 0m . B. 0m . C.
1
0
4
m
. D.
1
4
0
m
m
.
Lời giải
Chọn C
Yêu cầu bài toán tương đương biểu thức
2
4f x x mx m
luôn nhận giá trị dương với mọi
x .
Ta có:
2
2
1 0
0
1
4 0, 0;
0 4
4 0
a
x mx m x m
m m
Câu 20. Với
x
thuộc tập hợp nào dưới đây thì biểu thức
2
1
4 3
x
f x
x x
không dương?
A.
;1S . B.
3; 1 1;S .
C.
; 3 1;1S . D.
3;1S .
Lời giải
Chọn C
2
1
4 3
x
f x
x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
1 0 1
x x
2
3
4 3 0
1
x
x x
x
Xét dấu
f x
:
Yêu cầu bài toán
0
f x
khi
; 3 1;1
x .
Câu 21. Góc có số đo
3
16
có số đo theo độ là
A.
o
33 45'
. B.
o
29 30'
. C.
o
32 55'
. D.
o
33 45'
.
Lời giải
Chọn D
Vì
o
180
1rad
nên
o o
o o
3 3 180 135
. 33,75 33 45'.
16 16 4
Câu 22. Tập nghiệm của bất phương trình
2
2
2 3
4 2
x x
x x
là
A.
. B.
; 2 2;
.
C.
. D.
2;2
.
Lời giải
Chọn B
Điều kiện:
2
x
.
2 2
2
2 3 2 3
0
4 2 2 2 2
x x x x
x x x x x
2
2 3 2
0
2 2
x x x
x x
2
2 8
0
2 2
x x
x x
Xét tam thức
2
2 8
f x x x
có
' 1 8 7 0
0
1 0
f x
a
với mọi x
.
Do đó
2
2
2 8
0 2 2 0
2.
2 2
x
x x
x x
x
x x
Vậy tập nghiệm của bất phương trình là
; 2 2;
.
Câu 23. Cho
3
sin
5
và
2
. Tính
tan
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
3
tan
4
. B.
3
tan
4
. C.
3
tan
4
. D.
4
tan
3
.
Lời giải
Chọn A
Ta có
2 2
cos 1 sin
4
cos
5
.
Vì
2
nên
4
cos
5
.
Tính được
3
tan
4
.
Câu 24. Biểu thức
3 4cos2 cos4
3 4cos2 cos4
có kết quả rút gọn bằng
A.
4
tan
. B.
4
tan
. C.
4
cot
. D.
4
cot
.
Lời giải
Chọn A
3 4cos2 cos4
3 4cos2 cos4
2
2 2
2
2 2
3 4 1 2sin 2 1 2sin 1
3 4 2cos 1 2 2cos 1 1
4
4
4
8sin
tan
8cos
.
Câu 25. Rút gọn biểu thức
sin cos cos sin
A x y y x y y
.
A.
cos
A x
. B.
sin
A x
. C.
sin .cos2
A x y
. D.
cos .cos2
A x y
.
Lời giải
Chọn B
Ta có
sin .cos cos .sin cos cos .cos sin .sin sin
A x y x y y x y x y y
2 2
sin .cos cos .sin .cos cos .cos .sin sin .sin
x y x y y x y y x y
2 2
sin . cos sin sin
x y y x
Vậy
sin
A x
.
Câu 26. Rút gọn biểu thức
sin sin2 sin3
cos cos2 cos3
x x x
A
x x x
.
A.
tan6
A x
. B.
tan3
A x
.
C.
tan2
A x
. D.
tan tan2 tan3
A x x x
.
Lời giải
Chọn C
Ta có
sin sin 2 sin3
cos cos2 cos3
x x x
A
x x x
2sin 2 .cos sin 2
2cos2 .cos cos2
x x x
x x x
sin 2
cos2
x
x
tan2
x
.
Vậy
tan2
A x
.
Câu 27. Cho
A
,
B
,
C
là các góc của tam giác
ABC
. Khẳng định nào sau đây Đúng?
A.
sin2 sin2 sin2 4cos cos cos
A B C A B C
.
B.
sin2 sin2 sin2 4cos cos cos
A B C A B C
.
C.
sin2 sin2 sin2 4sin sin sin
A B C A B C
.
D.
sin2 sin2 sin2 4sin sin sin
A B C A B C
.
Lời giải
Chọn C
Ta có
sin2 sin2 sin2
A B C
sin 2 sin2 sin2
A B C
2sin cos 2sin .cos
A B A B C C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2sin cos cos
C A B C
4sin .cos .cos
2 2
A B C A B C
C
4sin .cos .cos
2 2
C A B
4sin .sin .sin
C A B
.
Câu 28. Cho đường thẳng
2 2
:
3
x t
d t
y t
. Tìm điểm
M
trên đường thẳng
d
và cách điểm
0;1
A một khoảng bằng
5
.
A.
8 10
;
3 3
M
. B.
4;4
M hoặc
44 32
;
5 5
M
.
C.
4; 4
M
hoặc
24 2
;
5 5
M
. D.
4;4
M hoặc
24 2
;
5 5
M
.
Lời giải
Chọn D
M d
2 2 ;3
M t t
.
2 2 ;2
AM t t
.
5
AM
2 2
2 2 2 25
t t
2
5 12 17 0
t t
1
2
1 4;4
17 24 2
;
5 5 5
t M
t M
.
Vậy có hai điểm
M
thỏa mãn yêu cầu:
4;4
M hoặc
24 2
;
5 5
M
.
Câu 29. Viết phương trình tổng quát của đường thẳng đi qua
2
điểm
2; 1
A
và
2;5
B .
A.
2 0
x . B.
2 7 9 0
x y . C.
2 0
x . D.
1 0
x y .
Lời giải
Chọn A
0;6
AB
6 0;1
là 1 VTCP của đường thẳng
AB
.
Đường thẳng
AB
có 1 VTPT là
1;0
n
.
Đường thẳng
AB
đi qua điểm
2; 1
A
có phương trình tổng quát là
: 2 0
AB x
.
Câu 30. Cho tam giác
ABC
có
1;4
A
,
3;2
B
,
7;3
C
. Lập phương trình đường trung tuyến
AM
của tam giác
ABC
.
A.
8 3 4 0
x y
. B.
3 8 35 0
x y
.
C.
3 8 35 0
x y
. D.
8 3 20 0
x y
.
Lời giải
Chọn C
M
là trung điểm của đoạn thẳng
BC
nên
5
5;
2
M
.
3
4;
2
AM
là 1 VTCP của đường thẳng
AM
.
u
2
AM
8; 3
cũng là 1 VTCP của đường thẳng
AM
.
3;8
n
là 1 VTPT của
AM
.
Đường thẳng
AM
đi qua điểm
1;4
A có phương trình là
3( 1) 8( 4) 0
x y
3 8 35 0
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy
:3 8 35 0
AM x y
.
Câu 31. Trong mặt phẳng
Oxy
, đường tròn tâm
( 1;2)
I
và đi qua điểm
(2;1)
M
có phương trình là
A.
2 2
2 4 5 0
x y x y
. B.
2 2
2 4 3 0
x y x y
.
C.
2 2
2 4 5 0
x y x y
. D.
2 2
2 4 5 0.
x y x y
.
Lời giải
Chọn A
Đường tròn có tâm
1;2
I và đi qua
2;1
M thì có bán kính là
2
2
3 1 10
R IM .
Khi đó có phương trình là:
2 2
2 2
1 2 10 2 4 5 0
x y x y x y
.
Câu 32. Trong mặt phẳng
Oxy
, cho elip
2 2
:3 4 48 0
E x y
và đường thẳng
: 2 4 0
d x y
. Giao
điểm của đường thẳng
d
và elip
E
có tọa độ là
A.
0; 4
và
2; 3
. B.
4;0
và
3;2
.
C.
0;4
và
2;3
. D.
4;0
và
2;3
.
Lời giải
Chọn D
Tọa độ giao điểm của đường thẳng
d
và elip
E
là nghiệm của hệ phương trình
2 22
4
0
2 4 0 2 4
16 48 0
2
3 4 8 0
3
4
x
y
x y x y
y
x y y y
x
.
Câu 33. Đường thẳng đi qua hai điểm
3;0
A và
0; 5
B
có phương trình là:
A.
1
3 5
x y
. B.
1
3 5
x y
. C.
1
5 3
x y
. D.
1
5 3
x y
.
Lờigiải
Chọn A
Phương trình đường thẳng đi qua hai điểm
3;0
A và
0; 5
B
là
1
3 5
x y
1
3 5
x y
Câu 34. Trong mặt phẳng tọa đô
Oxy
, biết đường thẳng
: 1
3 4
x y
cắt hai trục tọa độ tại hai điểm
phân biệt
A
và
B
. Tính diện tích
S
của tam giác
OAB
.
A.
6
S
. B.
12
S
. C.
4
S
. D.
3
S
.
Lời giải
Chọn A
Ta có
cắt hai trục
,
Ox Oy
lần lượt tại
3;0 , 0;4
A B .
3 3
OA
,
4 4
OB
.
Diện tích của tam giác
OAB
là
1
. . 6
2
S OAOB
.
Câu 35. Trong mặt phẳng tọa độ
Oxy
cho đường tròn
C
tâm
I
bán kính
R
, đường thẳng
là tiếp
tuyến của đường tròn
C
tại điểm
M
. Chọn khẳng định đúng.
A.
,
d I R
. B.
,
d I R
. C.
,
d I R
. D.
,
d I R
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn A
Câu 36. Phương trình tiếp tuyến của đường tròn
C
:
2 2
1 5 4
x y tại điểm
3; 5
M
là.
A.
3 0
x . B.
3 0
x . C.
2 3 0
x y . D.
2 3 0
x y .
Lời giải
Chọn A
Đường tròn
C
có tâm
1; 5
I
, bán kính
2
R
Tiếp tuyến của
C
tại
3; 5
M
có véctơ pháp tuyến là
2;0
IM
.
Vậy phương trình tiếp tuyến của đường tròn
C
tại
3; 5
M
là
2 3 0 5 0 3 0.
x y x
Câu 37. Đường tròn
C
có tâm
I
nằm trên đường thẳng
:2 4 0
d x y
và tiếp xúc với
:2 3 21 0
d x y
tại
3;5
H . Khi đó tâm
I
của
C
có tọa độ là:
A.
1; 2
I
. B.
1;2
I . C.
9 17
;
4 2
I
. D.
9 17
;
4 2
I
.
Lời giải
Chọn B.
Gọi
1
d
là đường thẳng vuông góc với
d
tại
H
. Suy ra:
1
:3 2 1 0
d x y
.
Do
C
tiếp xúc với
d
tại
H
nên IH
d
, suy ra
1
I d
.
Mà
I d
nên
1
I d d
và tọa độ
1;2
I .
Câu 38. Trong mặt phẳng
Oxy
cho đường thẳng
1 2
: ,
3
x t
d t
y t
. Vectơ nào dưới đây là một
vectơ chỉ phương của
d
?
A.
1
1; 3
u
. B.
2
1;3
u
. C.
3
1; 2
u
. D.
4
2;1
u
.
Lời giải
Chọn D
Đường thẳng
0
0
: ,
x x at
d t
y y bt
có một vectơ chỉ phương là
;
u a b
.
Nên một vectơ chỉ phương của
1 2
:
3
x t
d
y t
là
4
2;1
u
.
Câu 39. Trong mặt phẳng
Oxy
, vectơ pháp tuyến của đường thẳng
:2 3 9 0
d x y
là:
A.
2; 3
n
. B.
2;3
n
. C.
2; 3
n
. D.
3; 2
n
.
Lời giải
Chọn C
Ta có vectơ pháp tuyến của đường thẳng
:2 3 9 0
d x y
là
2; 3
n
.
Câu 40. Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
:3 4 1 0
d x y
và điểm
1; 2
I
. Gọi
C
là đường tròn tâm
I
và cắt đường thẳng
d
tại hai điểm
,
A B
sao cho tam giác
IAB
có diện tích
bằng
4
. Phương trình đường tròn
C
là:
A.
2 2
1 2 8
x y
. B.
2 2
1 2 20
x y
.
C.
2 2
1 2 5
x y
. D.
2 2
1 2 16
x y
.
Lời giải
Chọn A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi
H
là hình chiếu của
I
trên
d
H
là trung điểm của
AB
và
2
2
3.1 4.( 2) 1
, 2
3 4
IH d I d
.
Ta có
1
. .
2
IAB
S IH AB
2 2.4
4
2
IAB
S
AB
IH
2
AH
.
Vì tam giác
IHA
vuông tại
A
nên
2 2 2 2 2
2 2 8
IA IH HA
8
R IA
Phương trình đường tròn
C
là:
2 2
1 2 8
x y
.
Câu 41. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2
2 2 3
1
x mx m
y
x x
có tập xác định
là
?
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn D
Điều kiện xác định của hàm số là
2
2
2 2 3
0
1
x mx m
x x
.
Vì
2
1 0,x x x
nên hàm số đã cho có tập xác định
khi và chỉ khi
2
2 2 3 0,x mx m x
0
0
a
2
2 3 0
1 0
m m
3 1
m
.
Mà
m
nên
3; 2; 1;0;1
m .
Vậy có
5
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 42. Bất phương trình
2
2 2
2
3 1 3 9 5
0
4 5
x x x x
x x
có tập nghiệm là
A.
;1 2;
. B.
2;
.
C.
1;2
. D.
;1
.
Lời giải
Chọn A
Ta có:
2
2
4 5 2 1 0
x x x
với mọi
x
.Do đó
2
2 2
2
2 2
2
3 1 3 9 5
0 3 1 3 9 5 0
4 5
x x x x
x x x x
x x
2
2 2
3 1 3 3 1 2 0
x x x x
.
Đặt
2
3 1
x x a
bất phương trình trên trở thành
2
1
3 2 0
2
a
a a
a
+ Với
2 2
2
1 3 1 1 3 2 0
1
x
a x x x x
x
d
B
A
I
H

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
+ Với
2 2
2 3 1 2 3 3 0
a x x x x
bất phương trình vô nghiệm.
Vậy tập nghiệm của bất phương trình là
;1 2;
.
Câu 43. Tập nghiệm của bất phương trình
2
3 1 6 3 14 8 0
x x x x
là nửa khoảng
;
a b
.
Tính tổng 3
S a b
.
A.
1
S
B.
2
S
C.
0
S
D.
4
S
Lời giải
Chọn D
Điều kiện:
1
6 *
3
x .
BPT:
2
3 1 6 3 14 8 0
x x x x
2
3 1 4 6 1 3 14 5 0
x x x x
3 15 5
5 3 1 0
3 1 4 6 1
x x
x x
x x
3 1
( 5)( 3 1) 0
3 1 4 6 1
x x
x x
Dễ thấy
3 1 1
3 1 0, ;6
3
3 1 4 6 1
x x
x x
.
Suy ra:
5 0 5
x x
. Kết hợp với điều kiện
*
ta được tập nghiệm của bất phương trình
đã cho là:
1 1
;5 ; 5 3 4
3 3
a b S a b
.
Câu 44. Tính
2 2
cos 4cos 4 sin 4sin 4
M
biết
2
và
7
sin 2
9
.
A.
8
3
M
. B.
16
3
M
. C.
4
3
M
. D.
16
5
M
.
Lờigiải
Chọn B
2 2
cos 4cos 4 sin 4sin 4 cos 2 sin 2 2 cos 2 sin
M
4 os sin
c
.
Mặt khác:
2
7 16
cos sin 1 sin 2 1
9 9
.
Do
2
nên
cos 0; sin 0
nên suy ra:
4
sin cos
3
.
Vậy
16
3
M
.
Câu 45. Cho biểu thức
2020
2 2 ... 2 2cos
Coù daáu caên baäc hai
P x
với
π
0
2
x . Hãy rút gọn biểu thức
P
.
A.
2020
2cos
2
x
P . B.
2021
2cos
2
x
P . C.
2020
2sin
2
x
P . D.
2021
2sin
2
x
P .
Lời giải
ChọnA
Ta có
2
2 2cos 2 1 cos 4cos 2cos
2 2
x x
x x
(Vì
π
0
2
x nên
cos 0
2
x
).
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2
2
2 2 2cos 2 2cos 4cos 2cos 2cos
2 4 4 2
x x x x
x
.
2
3
2 2 2 2cos 2 2cos 4cos 2cos 2cos
4 8 8 2
x x x x
x
.
…
Vậy
2019 2020
2019
2 2 2 ... 2 2cos 2 2cos 2cos
2 2
Coù daáu caên baäc hai
x x
P x
.
Câu 46. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hình chữ nhật
ABCD
có diện tích bằng 12, tâm
I
là
giao điểm của hai đường thẳng
1 2
: 3 0, : 6 0
d x y d x y
. Trung điểm cạnh
AD
là giao
điểm của
1
d
và
Ox
. Biết đỉnh
A
có tung độ dương, giả sử tọa độ
;
A a b
, khi đó giá trị
2
2
a b
là
A.
11
. B.
14
. C.
18
. D.
6
.
Lời giải
Chọn D
Vì
I
là giao điểm của hai đường thẳng
1 2
: 3 0, : 6 0
d x y d x y
nên
9 3
;
2 2
I
.
Gọi
M
là trung điểm cạnh
AD
. Do
M
là giao điểm của
1
d
và
Ox
nên
3;0
M .
Ta có:
2. 3 2
AB IM .
. 12 2 2
ABCD
S AB AD AD .
Vì 2 điểm
I
và
M
đều thuộc
1
d
nên đường thẳng
IM
chính là
1
d
.
AD
qua
M
và vuông góc với
1
d
AD
:
–3 0
x y
. Lại có
2
MA
Tọa độ
A
là nghiệm của hệ:
2
2
3 0
2
1
3 2
a b
a
b
a b
hoặc
4
1
a
b
Mà đỉnh
A
có tung độ dương nên
2;1
A . Khi đó
2
2 6
a b
.
Câu 47. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
nội tiếp đường tròn tâm
1;2
I , bán kính
5
R
. Hai điểm
3;3
H ,
0; 1
K
lần lượt là chân đường cao kẻ từ
C
,
B
xuống cạnh
,
AB AC
. Tìm tọa độ điểm
A
, biết
A
có tung độ dương.
A.
5;5
A B.
3;5
A C.
4;6
A D.
2;6
A
Lời giải
Chọn B
I
D
B
C
A
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Phương trình đường tròn
2 2
: 1 2 25C x y .
Kẻ Ax là tiếp tuyến của đường tròn tại A, suy ra Ax AI (như hình vẽ), ta có
xAC ABC
.
Từ giả thiết suy ra tứ giác HKCB là tứ giác nội tiếp, suy ra , suy ra
xAC AKH
, suy ra
||Ax HK AI HK .
Đường thẳng
AI
đi qua
1;2I và có VTPT
3;4KH
.
Phương trình
:3 1 4 2 0 3 4 11 0AI x y x y .
Khi đó tọa độ điểm
A
là nghiệm của hệ:
2 2
2
11 3
3 4 11 0
4
1 2 25
25 1 16.25
x
x y
y
x y
x
5
1
3
5
x
y
x
y
.
Do A có tung độ dương nên
3;5
A .
Câu 48. Cho bất phương trình
2 2 2
2 2 5 9 1x x x . Gọi
1 2 1 2
,x x x x là hai nghiệm nguyên
dương nhỏ nhất của bất phương trình
1 . Xác định giá trị của m để biểu thức
2
1 2 1 2
2 2 1m x x m x x đạt giá trị nhỏ nhất?
A.
5
2
. B.
5
4
. C.
5
2
. D.
5
8
.
Lời giải
Chọn B
Đặt
2
2 2
2
2 2 0
2
t
t x t x
.
Bất phương trình
1 trở thành
2 2
2 2
. 5. 9 2
2 2
t t
t
3 2
4 2
2 5 2 8 0 1 4 2 0 1
1
t
t t t t t t t
t
(vì 0t ).
Với 1t ta được
2
6
2
2 2 1
6
2
x
x
x
1 2
2, 3x x
2 2
1 2 1 2
2 2 1 2 5 3m x x m x x m m
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Tam thức bậc hai
2
2 5 3
m m
đạt giá trị nhỏ nhất tại
5
4
m
.
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
1; 2
A
, đường thẳng chứa tia phân giác
trong góc
C
có phương trình
: 3 0
d x y
, đường thẳng chứa cạnh
BC
đi qua điểm
4; 1
K
. Biết trọng tâm của tam giác
ABC
nằm trên đường thẳng có phương trình
: 2 2 0
x y
. Tìm tọa độ điểm
B
của tam giác đó?
A.
5; 2
B
. B.
5; 2
B
. C.
5; 2
B
. D.
5; 2
B
.
Lời giải
Chọn C
Gọi
H
là hình chiếu vuông góc của
A
trên
d
, tìm được
3; 0
H
.
Gọi
A
là điểm đối xứng của
A
qua
d
. Khi đó
5; 2
A
và nằm trên đường thẳng chứacạnh
BC
.
Đường thẳng
BC
đi qua
A
và
K
.
Phương trình đường thẳng chứa cạnh
BC
là :
3 1 0
x y
.
Tọa độ của điểm
C
là
3 0
2; 1
3 1 0
x y
C
x y
.
Gọi
3 1;
B t t
. Tọa độ trọng tâm
G
của tam giác
ABC
là
3 2 1
;
3 3
t t
G
.
Vì
G
nằm trên
nên
3 2 1
2. 2 0 2
3 3
t t
t
.
Vậy
5; 2
B
.
Câu 50. Trong mặt phẳng với hệ tọa độ
Oxy
. Cho đường tròn
C
:
2 2
1 2 9
x y
và điểm
2;3
M . Đường thẳng
qua
M
cắt đường tròn
C
tại hai điểm
,
A B
sao cho
2 2
18
MA MB
có phương trình là:
A.
2 1 0, 2 8 0
x y x y
. B.
2 1 0, 2 8 0
x y x y
.
C.
10 0, 5 0
x y x y
. D.
6 0, 3 0
x y x y
.
Lời giải
d
A'
H
A
B
C
K

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn A
Đường tròn
C
có tâm
1;2 , 3
I R
. Kiểm tra, ta thấy
M
nằm ngoài đường tròn
C
.
Ta có:
2 2 2
. 1
MA MB ME MI R
.
Theo đề bài ra ta có:
2 2
2
18
16 4
. 1
MA MB
MA MB AB
MA MB
.
Phương trình đường thẳng
2 2
: 2 3 0, 0
AB a x b y a b
hay
2 3 0
ax by a b
.
2
2
2 2
2
3
; 5 5
1
2
2
a b
a b
AB
d I AB R
a b
a b
.
+ Với
2
a b
, chọn
2; 1
a b
, ta được đường thẳng
2 1 0
x y
.
+ Với
1
2
a b
, chọn
1; 2
a b
, ta được đường thẳng
2 8 0
x y
.
Thay vào ta được phương trình đường thẳng cần tìm
2 1 0, 2 8 0
x y x y
.
F
E
A
I
M
B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 15
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1: (NB) Bất phương trình
2 1 1
2
x
x
có nghiệm là
A.
4
3
x
. B.
3
4
x
. C.
2
x
. D.
1
2
x
.
Câu 2: (NB) Tìm tập nghiệm của hệ bất phương trình
5 2 4
3 1 10
x
x
.
A.
1
;3
2
S
. B.
1
;3
2
S
. C.
1
;3
2
S
. D.
1
;3
2
S
.
Câu 3: (NB) Cho nhị thức bậc nhất
3 20
f x x
. Khẳng định nào sau đây đúng?
A.
0
f x
khi x
. B.
0
f x
khi
20
;
3
x
.
C.
0
f x
khi
5
2
x
. D.
0
f x
khi
20
;
3
x
.
Câu 4: (NB) Nhị thức
1
f x x
nhận giá trị dương khi nào?
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Câu 5: (NB) Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình:
3 4 12 0
2 0
x y
x y
A.
0;4
M
. B.
2;0
N
. C.
0;3
P
. D.
1;1
Q
.
Câu 6: (NB) Hệ bất phương trình
2 6 0
1 2
x
x x
có tập nghiệm là:
A.
3;S
. B.
;3
S
. C.
3
S
. D. Vô nghiệm.
Câu 7: (NB) Góc (cung) lượng giác
nào dưới đây mà hai giá trị
sin
và
cos
của nó trái dấu?
A.
300 .
B.
80
C.
95
D.
100 .
Câu 8: (NB) Trong các đẳng thức sau, đẳng thức nào đúng?
A.
sin 180 cos
o
a a
. B.
sin 180 sin
o
a a
.
C.
sin 180 sin
o
a a
. D.
sin 180 cos
o
a a
.
Câu 9: (NB) Điểm cuối của cung
trên đường tròn lượng giác thuộc góc phần tư thứ II.
Chọn khẳng định đúng?
A.
cot 0
. B.
sin 0
. C.
cos 0
. D.
tan 0
.
Câu 10: (NB) Cho
2
( ) ( 0)
f x ax bx c a
. Điều kiện cần và đủ để
( ) 0,
f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Câu 11: (NB) Cho
2
( ) ( 0)
f x ax bx c a
có hai nghiệm
1 2 1 2
,
x x x x
. Tam thức
( )
f x
nhận
giá trị dương khi và chỉ khi
x
thuộc tập hợp nào?
A.
1 2
;
x x
. B.
1 2
; ;x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
. D.
;
2
b
a
.
Câu 12: (NB) Đường thẳng
d
đi qua điểm
2;3
M
và có véctơ chỉ phương
4;1
u
có phương
trình tham số là
A.
2 4
:
3
x t
d t
y t
. B.
2 3
:
4
x t
d t
y t
.
C.
4 2
:
1 3
x t
d t
y t
. D.
2 4
:
3
x t
d t
y t
.
Câu 13: (NB) Trong mặt phẳng
Oxy
, cho đường thẳng
1
: ( )
2 2
x t
d t
y t
véctơ chỉ phương của
đường thẳng
d
là
A.
(1;2)
u
. B.
(2; 1)
u
C.
( 2;1)
u
. D.
( 1;2)
u
.
Câu 14: (NB) Nếu đơn vị của số liệu thống kê là
m
thì đơn vị của độ lệch chuẩn là
A.
2
m
. B.
3
m
. C.
m
. D. Không có đơn vị.
Câu 15: (NB) Điểm kiểm tra giữa kỳ 2 của một học sinh lớp 10 như sau:
2, 4, 6,8,10
.Phương sai của
mẫu số liệu trên là bao nhiêu?
A. 6 B. 8 C. 10 D. 40
Câu 16: (NB) Mệnh đề nào sau đây là sai?
A.
sin sin .cos sin cos
x y x y y x
.
B.
cos sin sin cos .cos
x y x y x y
.
C.
sin sin .cos sin cos
x y x y y x
.
D.
cos cos .cos sin sin
x y x y x y
.
Câu 17: (NB) Mệnh đề nào sau đây sai?
A.
tan tan .
B.
cot tan .
2
C.
sin cos .
2
D.
sin cos .
2
Câu 18: (NB) Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình đường tròn?
A.
2 2
2 1 0
x y x y
. B.
2 2
3 3 6 12 3 0
x y x y
.
C.
2 2
2 1 0
x y xy y
. D.
2 2
1 0
x y
.
Câu 19: (NB) Trong mặt phẳng toạ độ
Oxy
, cho hai điểm
( 2;3)
A
và
(6 ;5)
B
.
phương trình đường tròn
đường kính
AB
, có phương trình là
A.
2 2
( 2) ( 4) 17
x y
. B.
2 2
( 2) ( 4) 17
x y
.
C.
2 2
( 2) ( 4) 68
x y
. D.
2 2
( 2) ( 4) 68
x y
.
Câu 20: (NB) Phương trình chính tắc của elip có độ dài trục lớn bằng
10
, độ dài trục nhỏ bằng
8
là:
A.
2 2
x y
1
100 64
. B.
2 2
x y
1
25 16
. C.
2 2
x y
1
10 8
. D.
2 2
x y
1
5 4
.
Câu 21: (NB) Trong hệ tọa độ
Oxy
cho elip
E
có phương trình chính tắc
2 2
1
80 31
x y
. Một tiêu điểm
của elip
E
có tọa độ là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
0; 7
. B.
7;0
. C.
0;7
. D.
7;0
.
Câu 22: (TH) Tập nghiệm của bất phương trình
3 2
x x
là
A.
1
;
2
S
. B.
1
;
2
S
. C.
; 2
S
. D.
1 2
;
2 5
S
.
Câu 23: (TH) Tập nghiệm của hệ bất phương trình
5 3 1
4 2
3 5
x x
x
là
A.
3
;8
7
S
. B.
2;8
S
. C. S
. D.
2;8
S
.
Câu 24: (TH) Biểu thức
( ) 2 1
f x x
nhận giá trị dương trên khoảng nào trong các khoảng sau đây:
A.
2;3
. B.
1
;2
2
. C.
0;1
. D.
2;0
.
Câu 25: (TH) Tìm tất cả các giá trị thực của tham số
m
để hệ bất phương trình
2 1 3
0
x
x m
có nghiệm
duy nhất?
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Câu 26: (TH) Một chiếc đồng hồ có kim giờ
OG
chỉ số
9
và kim phút
OP
chỉ số
12
.
Số đo của góc lượng giác
( , )
OG OP
lúc đó là:
A.
2 , .
2
k k
B.
0
90 .360 , .
o
k k
C.
270 360 , .
o o
k k
D.
9
2 , .
10
k k
Câu 27: (TH) Cho
1
cos
2
x
. Khi đó giá trị của
2 2
3sin 4 cos
P x x
là
A.
3
4
. B.
13
4
. C.
3
4
. D.
13
4
.
Câu 28: (TH) Trong mặt phẳng
Oxy
, cho hai đường thẳng
1
2 1
:
1 3
x y
và
2
2
1 4
:
2
x m t
t
y mt
. Các giá trị của tham số
m
để
1
vuông góc với
2
là
A.
1
4
m
m
. B.
1
4
m
m
C.
1
4
m
m
. D.
1
4
m
m
.
Câu 29: (TH) Trong mặt phẳng
Oxy
, giả sử đường thẳng
d
có hệ số góc
k
và đi qua điểm
1;7 .
A
Để khoảng cách từ gốc toạ độ
O
đến
d
bằng
5
thì
k
bằng
A.
3
4
k
hoặc
4
3
k
. B.
3
4
k
hoặc
4
3
k
.
C.
3
4
k
hoặc
4
.
3
k
D.
3
4
k
hoặc
4
3
k
.
Câu 30: (TH) Trong hệ tọa độ
Oxy
, cho đường thẳng
: 2 3 0
x y
và điểm
3; 1
M
. Phương
trình đường thẳng
d
đi qua điểm
M
và vuông góc với đường thẳng
là:
A.
2 5 0
x y
. B.
2 7 0
x y
. C.
2 5 0
x y
. D.
2 1 0
x y
.
Câu 31: (TH) Tìm
m
để bất phương trình
2 2
1 1 1 0
m x m x
đúng với mọi
x
thuộc
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
1
1
m
m
. B.
1
5
3
m
m
. C.
1
1
m
m
. D.
1
5
3
m
m
.
Câu 32: (TH) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2 2 3
y x mx m
có tập
xác định là
.
A.
4
. B.
6
. C.
3
. D.
5
.
Câu 33: (TH) Rút gọn
cos cos sin sin
3 6 3 6
M a a
.
A.
cos
M a
. B.
sin
M a
. C.
1
sin
2
M a
. D.
cos2
M a
.
Câu 34: (TH) Tìm
m
để phương trình
2 2
2 2 5 0
x y x my
là phương trình đường tròn.
A.
2;2
m
. C.
; 2 2; .
m
B.
; 2 2; .
m
D.
2;2 .
m
Câu 35: (TH) Cho Elip
E
có phương trình chính tắc
2 2
1
16 9
x y
và hai tiêu điểm
1 2
,
F F
. Điểm
M
tùy ý thuộc
E
. Khi đó chu vi tam giác
1 2
MFF
bằng
A.
4 2 7
. B.
8 7
. C.
4 7
. D.
8 2 7
.
Câu 36: (VD) Cho hệ bất phương trình
1
1 2 4 0
x
m
x x
(
0
m
là tham số thực). Tìm tất cả các giá
trị của tham số
m
để hệ có đúng 3 nghiệm nguyên.
A.
0 3
m
. B.
\ 0;3
m
. C.
0
m
. D.
;3
m
.
Câu 37: (VD) Cho biểu thức
2
2.
1
x
f x
x
Tập hợp tất cả các giá trị của
x
thỏa mãn
0
f x
là
A.
; 1 .
B.
1; .
C.
4; 1 .
D.
; 4 1; .
Câu 38: (VD) Tìm tất cả các giá trị của y sao cho
2 2 2
2 2 2 4 3 0
x y z xy x z yz y
,
,x z
A.
3
y
. B.
0 3
y
. C.
0
y
. D.
0
y
hoặc
3
y
.
Câu 39: (VD) Gọi
S
là tập các giá trị của tham số
m
để bất phương trình
2
4 7 7 0
x mx m
có tập
nghiệm là
;
a b
sao cho
6
b a
. Khi đó tích các giá trị
m
là:
A.
1
2
. B.
1
2
. C.
3
2
. D.
3
2
.
Câu 40: (VD) Có bao nhiêu giá trị nguyên của
m
để biểu thức:
2
m 2 x 4 m 1 x m 1
luôn âm?
A. 1. B. 3. C. 2. D. 0.
Câu 41: (VD) Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho cung lượng giác
AM
có số đo
0
60
. Gọi
N
là điểm đối xứng với điểm
M
qua trục
O y
, số đo cung nhỏ
AN
là:
A.
120
o
. B.
0
240
.
C.
0
120
hoặc
0
240
. D.
0 0
120 .360 ,k k
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 42: (VD) Cho cung
x
thỏa mãn
1
sin cos
2
x x
. Khi đó
sin cos ,
a
P x x
b
trong đó
*
,
a b
và phân số
a
b
tối giản. Tính
a b
.
A.
13
. B.
19
. C.
11
. D.
5
.
Câu 43: (VD) Cho hai đường thẳng
1
: 3 3 0
d x y
và
2
3
: ( )
2
x t
d t
y t
và điểm
1;2
M
. Tìm
điểm
A
trên
1
d
và điểm
B
trên
2
d
sao cho
,
A B
đối xứng nhau qua
M
.
A.
3 4
; ;
5 5
A
7 16
;
5 5
B
. B.
3 4
; ;
5 5
A
7 16
;
5 5
B
.
C.
3 4
; ;
5 5
A
7 16
;
5 5
B
. D.
3 4
; ;
5 5
A
7 16
;
5 5
B
.
Câu 44: (VD) Giả sử
1 1
1 tan 1 tan tan
cos cos
n
x x m x
x x
cos 0; ,x m n
. Khi đó
n m
có giá trị bằng
A. 4 B. 3 C. 2 D. 1
Câu 45: (VD) Trong mặt phẳng
Oxy
cho hai điểm
4;0
A
,
0;3
B
. Phương trình đường tròn nội tiếp
tam giác
ABO
có dạng
2 2
1
x a y b
. Tính
2 3
S a b
.
A.
11
S
B.
2
S
C.
5
S
D.
8
S
Câu 46: (VD) Tìm phương trình chính tắc của elip nếu nó đi qua điểm
2 ; 3
A
và tỉ số của độ dài
trục lớn với tiêu cự bằng
2
3
.
A.
2 2
1
16 4
x y
. B.
2 2
1
4 3
x y
. C.
2 2
1
3 4
x y
. D.
2 2
1
4 16
x y
.
Câu 47: (VDC) Cho
(2 3)( 3 )
( )
x x m
f x
x m
. Có bao nhiêu giá trị nguyên của tham số
m
để
( ) 0, 1
f x x
?
A.
4
. B.
3
. C.
0
. D.
2
.
Câu 48: (VDC) Trong mặt phẳng
Oxy
, cho điểm
1;3 , 5;1
A B
. Phương trình đường thẳng
d
đi qua
A
sao cho khoảng cách từ
B
đến
d
là một số nguyên tố chẵn
A. Đường thẳng
3
x hoặc
4 3 13 0
x y
.
B. Đường thẳng
3
x hoặc
3 4 13 0
x y
.
C. Đường thẳng
3
y
hoặc
4 3 13 0
x y
.
D. Đường thẳng
3
y
hoặc
3 4 13 0
x y
.
Câu 1: (VDC) Cho
, 0;
2
x y
thỏa mãn
cos cos sin 1
x y x y x y
. Gọi
m
là giá trị
nhỏ nhất của biểu thức
4 4
sin sin
x y
P
y x
. Tìm khẳng định đúng trong các khẳng định sau
A.
1
0;
2
m
. B.
1 3
;
2
m
. C.
3
;1
m
. D.
1;
m
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 50: (VDC) Trong mặt phẳng với hệ tọa độ
Oxy
cho tam giác
ABC
có ba góc nhọn. Gọi
,
E F
lần
lượt là chân đường cao kẻ từ đỉnh
,
B C
. Đỉnh
3; 7
A
, trung điểm của
BC
là
2;3
M
và
đường tròn ngoại tiếp tam giác
AEF
có phương trình:
2 2
3 4 9
x y
. Khi đó, tích
hoành độ của điểm
B
và điểm
C
bằng
A.
4
. B.
4
. C.
61
. D.
61
.
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 15
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.A 2.D 3.D 4.D 5.C 6.A 7.D 8.C 9.B 10.A
11.B 12.D 13.D 14.C 15.B 16.D 17.C 18.B 19.A 20.B
21.D 22.A 23.A 24.D 25.B 26.A 27.D 28.D 29.D 30.D
31.B 32.D 33.B 34.B 35.D 36.B 37.C 38.B 39.B 40.D
41.A 42.C 43.A 44.B 45.C 46.A 47.D 48.C 49.B 50.C
HƯỚNG DẪN GIẢI
Câu 1: (NB) Bất phương trình
2 1 1
2
x
x
có nghiệm là
A.
4
3
x
. B.
3
4
x
. C.
2
x
. D.
1
2
x
.
Lời giải
Chọn A
Bất phương trình
2 1 1
2
x
x
2 1 1
2
x
x
3
2
2
x
4
3
x
Câu 2: (NB) Tìm tập nghiệm của hệ bất phương trình
5 2 4
3 1 10
x
x
.
A.
1
;3
2
S
. B.
1
;3
2
S
. C.
1
;3
2
S
. D.
1
;3
2
S
.
Lời giải
Chọn D
5 2 4
3 1 10
x
x
1
2
3
x
x
1
3
2
x
Vậy
1
;3
2
S
.
Câu 3: (NB) Cho nhị thức bậc nhất
3 20
f x x
. Khẳng định nào sau đây đúng?
A.
0
f x
khi x
. B.
0
f x
khi
20
;
3
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
0
f x
khi
5
2
x
. D.
0
f x
khi
20
;
3
x
.
Lời giải
Chọn D
20
3 20 0
3
x x
.
Câu 4: (NB) Nhị thức
1
f x x
nhận giá trị dương khi nào?
A.
1
x
. B.
1
x
. C.
1
x
. D.
1
x
.
Lời giải
Chọn D
Ta có
1 0
x
1
x
.
Câu 5: (NB) Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình
3 4 12 0
2 0
x y
x y
A.
0;4
M
. B.
2;0
N
. C.
0;3
P
. D.
1;1
Q
.
Lời giải
Chọn C
Điểm thuộc miền nghiệm của hệ bất phương trình là điểm có tọa độ thỏa mãn các bất phương
trình trong hệ bất phương trình đó.
Ta thay lần lượt tọa độ các điểm
, , ,
M N P Q
vào hệ bất phương trình đã cho thì chỉ có điểm
0;3
P
thỏa mãn. Thật vậy, ta xét điểm
P
, các điểm còn lại ta làm tương tự:
Ta thay
0; 3
x y
vào hệ bất phương trình đã cho ta được
3.0 4.3 12 0
0 3 2 0
(đúng).
Suy ra
0;3
P
thuộc miền nghiệm của hệ bất phương trình đã cho.
Câu 6: (NB) Hệ bất phương trình
2 6 0
1 2
x
x x
có tập nghiệm là
A.
3;S
. B.
;3
S
. C.
3
S
. D. Vô nghiệm.
Lời giải
Chọn A
2 6 0 3
3
1 2 1 2,
x x
x
x x x
.
Vậy tập nghiệm của hệ bất phương trình là
3;S
.
Câu 7: (NB) Góc (cung) lượng giác
nào dưới đây mà hai giá trị
sin
và
cos
của nó trái dấu?
A.
300 .
B.
80
C.
95
D.
100 .
Lời giải
Chọn D.
Vì góc phần tư thứ hai,
sin
mang dấu dương,
cos
mang dấu âm.
Câu 8: (NB) Trong các đẳng thức sau, đẳng thức nào đúng?
A.
sin 180 cos
o
a a
. B.
sin 180 sin
o
a a
.
C.
sin 180 sin
o
a a
. D.
sin 180 cos
o
a a
.
Lời giải
Chọn C
Sử dụng mối quan hệ của các cung có liên quan đặc biệt.
Câu 9: (NB) Điểm cuối của cung
trên đường tròn lượng giác thuộc góc phần tư thứ II.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn khẳng định đúng?
A.
cot 0
. B.
sin 0
. C.
cos 0
. D.
tan 0
.
Lời giải
Chọn B
Dựa vào bảng xác định dấu của các giá trị lượng giác ta có
sin 0
.
Câu 10: (NB) Cho
2
( ) ( 0)
f x ax bx c a
. Điều kiện cần và đủ để
( ) 0,
f x x
là
A.
0
0
a
. B.
0
0
a
. C.
0
0
a
. D.
0
0
a
.
Lời giải
Chọn A
( ) 0,
f x x
0
0
a
.
Câu 11: (NB) Cho
2
( ) ( 0)
f x ax bx c a
có hai nghiệm
1 2 1 2
,
x x x x
. Tam thức
( )
f x
nhận giá
trị dương khi và chỉ khi
x
thuộc tập hợp nào?
A.
1 2
;
x x
. B.
1 2
; ;x x
.
C.
. D.
;
2
b
a
.
Lời giải
Chọn B
Dựa theo định lí về dấu của tam thức bậc hai,
f x
cùng dấu với
a
với mọi
x
nằm ngoài
khoảng hai nghiệm.
Câu 12: (NB) Đường thẳng
d
đi qua điểm
2;3
M
và có véctơ chỉ phương
4;1
u
có phương trình
tham số là
A.
2 4
:
3
x t
d t
y t
. B.
2 3
:
4
x t
d t
y t
.
C.
4 2
:
1 3
x t
d t
y t
. D.
2 4
:
3
x t
d t
y t
.
Lời giải
Chọn D
Đường thẳng
d
đi qua điểm
2 ; 3
M
và có véctơ chỉ phương
4 ; 1
u
có phương trình tham số
là
2 4
:
3
x t
d t
y t
.
Câu 13: (NB) Trong mặt phẳng
Oxy
, cho đường thẳng
1
: ( )
2 2
x t
d t
y t
véctơ chỉ phương của
đường thẳng
d
là
A.
(1;2)
u
. B.
(2; 1)
u
C.
( 2;1)
u
. D.
( 1;2)
u
.
Lời giải
Chọn D
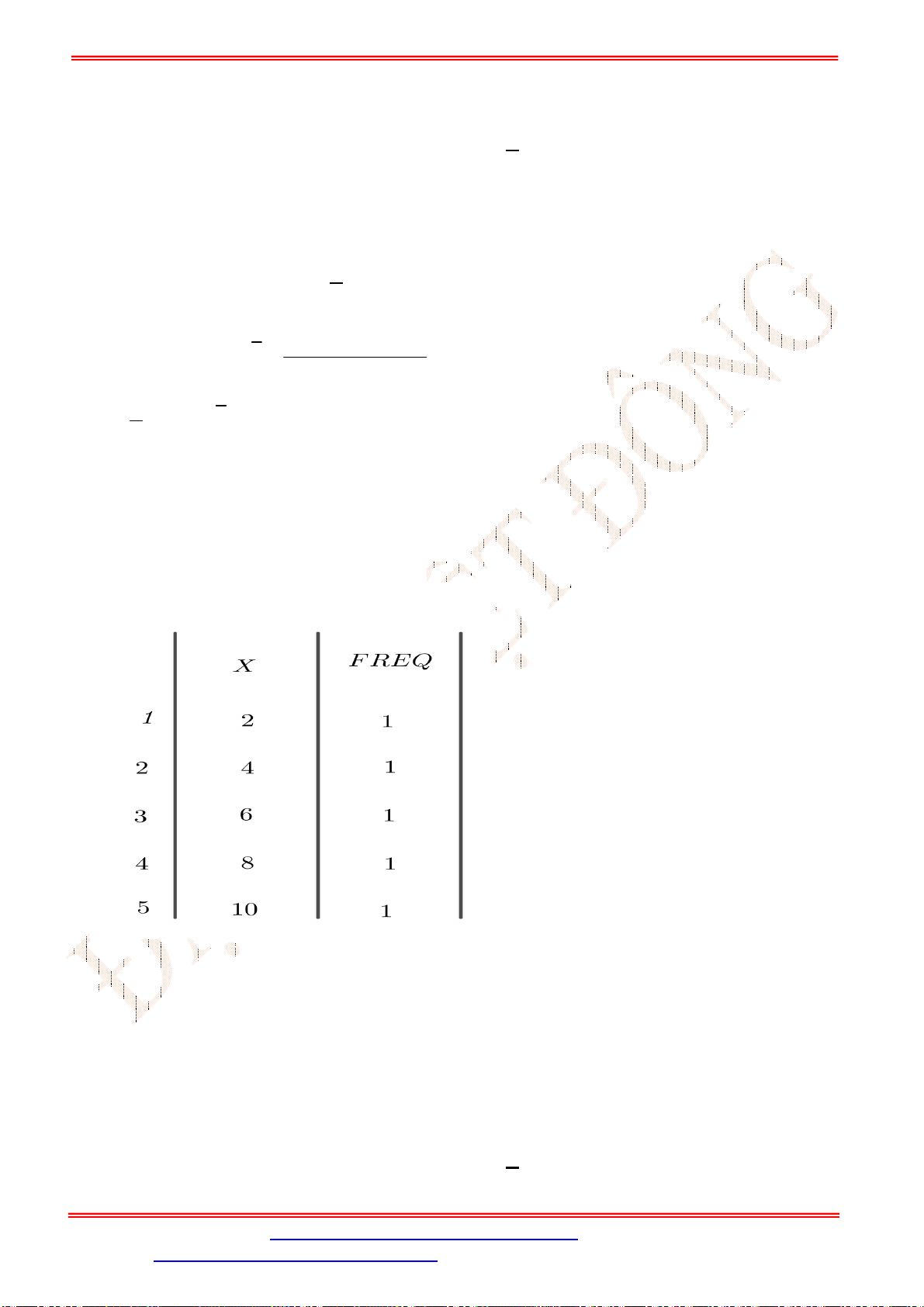
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Đường thẳng
d
có véctơ chỉ phương là
( 1; 2)
u
.
Câu 14: (NB) Nếu đơn vị của số liệu thống kê là
m
thì đơn vị của độ lệch chuẩn là
A.
2
m
. B.
3
m
. C.
m
. D. Không có đơn vị.
Lời giải
Chọn C
Độ lệch chuẩn của số liệu thống kê có đơn vị cùng với đơn vị của các số liệu trong mẫu thống kê.
Câu 15: (NB) Điểm kiểm tra giữa kỳ 2 của một học sinh lớp 10 như sau:
2, 4, 6,8,10
. Phương sai của
mẫu số liệu trên là bao nhiêu?
A. 6 B. 8 C. 10 D. 40
Lời giải
Chọn B
Cách 1: TỰ LUẬN:
2 4 6 8 10
6
5
x
.
2
5
2
1
1
8
5
i
i
s x x
.
Cách 2: CASIO:FX-570ES PLUS
Bước 1:Chuyển đổi máy tính về thống kê:
MODE 3 AC
.
Bước 2:Bật chức năng cột tần số:
SHIFT MODE
MŨI TÊN ĐI XUỐNG
4 1
START ON
.
Bước 3:Nhập dữ liệu:
1 1 1 1 AR
SHIFT Type V .
Lưu ý:Nhập dữ liệu xong ấn AC để thoát.
Bước 4:Tính giá trị độ lệch chuẩn:SHIFT
1 4 ar 3
V x
Kết quả:2.828427125
Bước 5:Tính phương sai:
2 2
Ans
x
Kết quả: 8
Đáp án:B
Câu 16: (NB) Mệnh đề nào sau đây là sai?
A.
sin sin .cos sin cos
x y x y y x
. B.
cos sin sin cos .cos
x y x y x y
.
C.
sin sin .cos sin cos
x y x y y x
. D.
cos cos .cos sin sin
x y x y x y
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D
Công thức đúng:
cos cos .cos sin sin
x y x y x y
.
Câu 17: (NB) Mệnh đề nào sau đây sai?
A.
tan tan .
B.
cot tan .
2
C.
sin cos .
2
D.
sin cos .
2
Lời giải
Chọn C
Công thức đúng là
sin cos
2
, đây là công thức cung hơn kém nhau
2
.
Câu 18: (NB)Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình đường tròn?
A.
2 2
2 1 0
x y x y
. B.
2 2
3 3 6 12 3 0
x y x y
.
C.
2 2
2 1 0
x y xy y
. D.
2 2
1 0
x y
.
Lời giải
Chọn B
Đáp án A sai vì có
2
y
.
Ta có:
2 2
3 3 6 12 3 0
x y x y
2 2
2 4 1 0
x y x y
Vì
2 2
1 2 1 6 0
nên phương trình trên là phương trình đường tròn
Do đó đáp án B đúng.
Đáp án C sai vì có
xy
.
Đáp án D sai vì có
2
1 0
R .
Câu 19: (NB) Trong mặt phẳng toạ độ
Oxy
, cho hai điểm
( 2;3)
A
và
(6 ;5)
B
.
phương trình đường tròn
đường kính
AB
, có phương trình là
A.
2 2
( 2) ( 4) 17
x y
. B.
2 2
( 2) ( 4) 17
x y
.
C.
2 2
( 2) ( 4) 68
x y
. D.
2 2
( 2) ( 4) 68
x y
.
Lời giải
Chọn A
Gọi
( ; )
I I
I x y
là tâm đường tròn cần tìm. Khi đó,
I
là trung điểm đoạn thẳng
AB
nên toạ độ điểm
I
là
2 6
2
2
3 5
4
2
I
I
x
y
.
Gọi bán kính đường tròn là
R
. Ta có
2
2 2 2 2
( 2 2) (3 4) 17
R IA
.
Do đó, phương trình đường tròn cần tìm là
2 2
( 2) ( 4) 17
x y
.
Câu 20: (NB) Phương trình chính tắc của elip có độ dài trục lớn bằng
10
, độ dài trục nhỏ bằng
8
là:
A.
2 2
x y
1
100 64
. B.
2 2
x y
1
25 16
. C.
2 2
x y
1
10 8
. D.
2 2
x y
1
5 4
.
Lời giải
Chọn B
Độ dài trục lớn bằng 10 suy ra
2 10 5.
a a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Độ dài trục nhỏ bằng 8 suy ra
2 8 4.
b b
Suy ra phương trình chính tắc của elip cần tìm là
2 2
x y
1
25 16
.
Câu 21: (NB) Trong hệ tọa độ
Oxy
cho elip
E
có phương trình chính tắc
2 2
1
80 31
x y
. Một tiêu điểm
của elip
E
có tọa độ là
A.
0; 7
. B.
7;0
. C.
0;7
. D.
7;0
.
Lời giải
Chọn D
Ta có:
2 2
80
: 1
31
x y
E
2
2
80
31
a
b
Mà
2 2 2
80 31 49 7
c a b c
Vậy
7;0
là tọa độ một tiêu điểm của
E
.
Câu 22: (TH) Tập nghiệm của bất phương trình
3 2
x x
là
A.
1
;
2
S
. B.
1
;
2
S
. C.
; 2
S
. D.
1 2
;
2 5
S
.
Lời giải
Chọn A
2 2
2
2 0
2
1
3 2
1
6 9 4 4
2
3 2
2
x
x
x
x x x
x x
x
x x
Vậy
1
;
2
S
.
Câu 23: (TH) Tập nghiệm của hệ bất phương trình
5 3 1
4 2
3 5
x x
x
là
A.
3
;8
7
S
. B.
2;8
S
. C. S
. D.
2;8
S
.
Lời giải
Chọn A
Ta có
5 3 1
3
5 6 2 7 3
3
4 2
8
7
5 3 5 2 8
7
3 5
2 8
x x
x x x
x
x
x x
x
x
.
Vậy tập nghiệm của hệ bất phương trình là
3
;8
7
S
.
Câu 24: (TH) Biểu thức
( ) 2 1
f x x
nhận giá trị dương trên khoảng nào trong các khoảng sau đây:
A.
2;3
. B.
1
;2
2
. C.
0;1
. D.
2;0
.
Lờigiải
Chọn D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Nhị thức bậc nhất
( ) 2 1
f x x
có hệ số
2 0
nên tất cả các giá trị của
x
làm cho biểu thức nhận
giá trị dương là:
1
;
2
x
, suy ra biểu thức nhận giá trị dương trên khoảng
2;0
.
Câu 25: (TH) Tìm tất cả các giá trị thực của tham số
m
để hệ bất phương trình
2 1 3
0
x
x m
có nghiệm
duy nhất?
A.
2
m
. B.
2
m
. C.
2
m
. D.
2
m
.
Lời giải
Chọn B
Bất phương trình
2 1 3 2
x x
nên có tập nghiệm là:
1
2;S
.
Bất phương trình 0
x m x m
nên có tập nghiệm là:
2
;
S m
.
Vậy hệ bất phương trình có nghiệm duy nhất khi và chỉ khi
2
m
.
Câu 26: (TH) Một chiếc đồng hồ có kim giờ
OG
chỉ số
9
và kim phút
OP
chỉ số
12
.
Số đo của góc lượng giác
( , )
OG OP
lúc đó là
A.
2 , .
2
k k
B.
0
90 .360 , .
o
k k
C.
270 360 , .
o o
k k
D.
9
2 , .
10
k k
Lời giải
Chọn A
Một chiếc đồng hồ có kim giờ
OG
chỉ số
9
và kim phút
OP
chỉ số
12
.
OG OP
Do đó số đo góc lượng giác
( , )
OG OP
là
1
. 2 2 , .
4
k k
Vậy chọn A.
Câu 27: (TH) Cho
1
cos
2
x
. Khi đó giá trị của
2 2
3sin 4 cos
P x x
là:
A.
3
4
. B.
13
4
. C.
3
4
. D.
13
4
.
Lời giải
Chọn D
Ta có:
2 2 2 2 2
1 13
3sin 4 cos 3(1 cos ) 4cos 3 cos 3
4 4
P x x x x x
.
Câu 28: (TH) Trong mặt phẳng
Oxy
, cho hai đường thẳng
1
2 1
:
1 3
x y
và
2
2
1 4
:
2
x m t
t
y mt
. Các giá trị của tham số
m
để
1
vuông góc với
2
là
A.
1
4
m
m
. B.
1
4
m
m
C.
1
4
m
m
. D.
1
4
m
m
.
Lời giải
Chọn D
1
có véctơ chỉ phương
1
1;3
u
;
2
có véctơ chỉ phương
2
2
4;
u m m
.
Ta thấy
2
0
u
vì
2
2 2
4 0,m m m
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Do đó
1 2 1 2
u u
1 2
. 0
u u
2
1 4 3 0
m m
2
3 4 0
m m
1
4
m
m
.
Câu 29: (TH) Trong mặt phẳng
Oxy
, giả sử đường thẳng
d
có hệ số góc
k
và đi qua điểm
1;7 .
A
Để khoảng cách từ gốc tọa độ
O
đến
d
bằng
5
thì
k
bằng
A.
3
4
k
hoặc
4
3
k
. B.
3
4
k
hoặc
4
3
k
.
C.
3
4
k
hoặc
4
.
3
k
D.
3
4
k
hoặc
4
3
k
.
Lời giải
Chọn D
Phương trình đường thẳng
d
là:
7 1 7 0
y k x kx y k
2
7
, 5 5
1
k
d O d
k
2 2
14 49 25 25
k k k
2
4
24 14 24 0
3
k k k
hoặc
3
4
k
.
Câu 30: (TH) Trong hệ tọa độ
Oxy
, cho đường thẳng
: 2 3 0
x y
và điểm
3; 1
M
. Phương trình
đường thẳng
d
đi qua điểm
M
và vuông góc với đường thẳng
là:
A.
2 5 0
x y
. B.
2 7 0
x y
. C.
2 5 0
x y
. D.
2 1 0
x y
.
Lời giải
Chọn D
Ta có: d
nên phương trình đường thẳng
d
có dạng
2 0
x y m
Mà
M d
nên
3 2( 1) 0 1
m m
Vậy phương trình đường thẳng
: 2 1 0
d x y
.
Câu 31: (TH) Tìm
m
để bất phương trình
2 2
1 1 1 0
m x m x
đúng với mọi
x
thuộc
A.
1
1
m
m
. B.
1
5
3
m
m
. C.
1
1
m
m
. D.
1
5
3
m
m
.
Lời giải
Chọn B
TH1:
2
1 0
1 0
1 0
m
m
1
m
.
TH2:
2
2
2
1 0
1 4 1 0
m
m m
1
5
3
m
m
Kết luận:
1
5
3
m
m
.
Câu 32: (TH) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
2
2 2 3
y x mx m
có tập xác
định là
?
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn D.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Hàm số
2
2 2 3
y x mx m
có tập xác định là
khi và chỉ khi
2
2 2 3 0
x mx m
với mọi
x
0
0
a
2
2 3 0
1 0
m m
3 1
m
. Do m
3; 2; 1;0;1
m
.
Vậy có
5
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 33: (TH) Rút gọn
cos cos sin sin
3 6 3 6
M a a
.
A.
cos
M a
. B.
sin
M a
. C.
1
sin
2
M a
. D.
cos2
M a
.
Lời giải
Chọn B
Ta có:
cos cos sin sin
3 6 3 6
M a a
cos cos sin
3 6 2
a a a
Câu 34: (TH) Tìm
m
để phương trình
2 2
2 2 5 0
x y x my
là phương trình đường tròn.
A.
2;2
m
. C.
; 2 2; .
m
B.
; 2 2; .
m
D.
2;2 .
m
Lời giải
Chọn B
Để phương trình trên là phương trình đường tròn thì
0
R
hay
2 2 2
1 5 4 0
R m m
; 2 2;m
.
Câu 35: (TH) Cho Elip
E
có phương trình chính tắc
2 2
1
16 9
x y
và hai tiêu điểm
1 2
,
F F
. Điểm
M
tùy
ý thuộc Elip
E
, khi đó chu vi tam giác
1 2
MFF
bằng
A.
4 2 7
. B.
8 7
. C.
4 7
. D.
8 2 7
.
Lời giải
Chọn D
Ta có
2 2
16; 9
a b
2 2 2
7 7
c a b c
.
Suy ra
1 2
2 2 7
FF c
Lại có
1 2
2 8
MF MF a
.
Vậy chu vi tam giác
1 2
MFF
bằng
1 2 1 2
8 2 7
MF MF FF
Câu 36: (VD) Cho hệ bất phương trình
1
1 2 4 0
x
m
x x
(
0
m
là tham số thực). Tìm tất cả các giá trị
của tham số
m
để hệ có đúng 3 nghiệm nguyên.
A.
0 3
m
. B.
\ 0;3
m
. C.
0
m
. D.
;3
m
.
Lời giải
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Hệ bất phương trình
1 (1)
1 2 4 0 (2)
x
m
x x
.
Giải bất phương trình (2):
1
1 2 4 0 4
2
x x x
Tập nghiệm
2
1
;4
2
S
. ( Tập nghiệm luôn có 3 số nguyên 1;2;3)
+) Trường hợp
0
m
ta có:
1
x
x m
m
nên tập nghiệm của phương trình (1) là
1
;
S m
Để hệ bất phương trình có đúng 3 nghiệm nguyên thì
3
m
.
+) Trường hợp
0
m
1
x
x m
m
nên tập nghiệm của phương trình (1) là
1
;S m
Khi đó, tập nghiệm của hệ bất phương trình
1 2 2
S S S S
Suy ra tập nghiệm của hệ bất phương trình
2
1
;4
2
S S
luôn có đúng ba nghiệm nguyên.
Vậy để hệ có đúng 3 nghiệm nguyên thì
;0 3;m
.
Câu 37: (VD) Cho biểu thức
2
2.
1
x
f x
x
Tập hợp tất cả các giá trị của
x
thỏa mãn
0
f x
là
A.
; 1 .
B.
1; .
C.
4; 1 .
D.
; 4 1; .
Lời giải
Chọn C
Ta có
2 4
2
1 1
x x
f x
x x
. Do đó ta có bảng xét dấu của
f x
như sau:
x
4 1
4
x
0
1
x
0
f x
0
Vậy tập hợp tất cả các giá trị của
x
thỏa mãn
0
f x
là
4; 1 .
x
Câu 38: (VD) Tìm tất cả các giá trị của y sao cho
2 2 2
2 2 2 4 3 0
x y z xy x z yz y
,
,x z
A.
3
y
. B.
0 3
y
. C.
0
y
. D.
0
y
hoặc
3
y
.
Lời giải
Chọn B
Ta có:
2 2 2
2 2 2 4 3 0
x y z xy x z yz y
,
x
2 2 2
2 2 4 3 0
x y z x y z yz y
,
x
2
2 2
2 4 3 0
y z y z yz y
2 2 2 2
2 2 4 3 0
y yz z y z yz y
2
2 3 0
z y z y
Mặt khác:
2
2 3 0,
z yz y z
2
3 0
y y
0 3
y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 39: (VD) Gọi
S
là tập các giá trị của tham số
m
để bất phương trình
2
4 7 7 0
x mx m
có tập
nghiệm là
;
a b
sao cho
6
b a
. Khi đó tích các giá trị
m
là:
A.
1
2
. B.
1
2
. C.
3
2
. D.
3
2
.
Lời giải
Chọn B
Ta có:
2
2 2
4 7 7 0 2 4 7 7
x mx m x m m m
2 2 2
2 4 7 7 2 4 7 7 2 4 7 7
x m m m m m m x m m m
Tập nghiệm của bất phương trình là:
2 2
2 4 7 7;2 4 7 7
m m m m m m
Theo đề ta có:
2
6 2 4 7 7 6
b a m m
2 2
4 7 7 3 4 7 2 0
m m m m
2
1
4
m
m
Vậy tích các giá trị
m
là:
1 1
2.
4 2
Câu 40: (VD) Có bao nhiêu giá trị nguyên của
m
để biểu thức:
2
m 2 x 4 m 1 x m 1
luôn âm?
A. 1. B. 3. C. 2. D. 0.
Lời giải
Chọn D
Xét biểu thức
2
2 4 1 1
f x m x m x m
.
TH1:
2
m
thì
3
4 3 0
4
f x x x . Suy ra
2
m
không thỏa mãn.
TH2:
2
m
thì
0,
f x x R
khi và chỉ khi:
2
2 2
2 0
2
0
4 8 4 2 0
' 0
2 1 2 1 0
m
m
a
m m m m
m m m
2
2
2
3 7 6 0
m
m
m
m
m m
.
Vậy không có giá trị nguyên nào của m để
f x
luôn âm.
Câu 41: (VD) Trên đường tròn với điểm gốc là
A
. Điểm
M
thuộc đường tròn sao cho cung lượng giác
AM
có số đo
0
60
. Gọi
N
là điểm đối xứng với điểm
M
qua trục
O y
, số đo cung nhỏ
AN
là:
A.
120
o
. B.
0
240
.
C.
0
120
hoặc
0
240
. D.
0 0
120 .360 ,k k
.
Lời giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn A.
Ta có
0
60AOM
,
0
60MON
Nên
0
120AON
.
Vậy số đo cung nhỏ AN bằng
0
120
.
Câu 42: (VD) Cho cung
x
thỏa mãn
1
sin cos
2
x x
. Khi đó
sin cos ,
a
P x x
b
trong đó
*
, a b
và phân số
a
b
tối giản. Tính a b .
A. 13. B. 19. C.
11
. D. 5.
Lời giải
Chọn C
Ta có:
1
cos sin
2
x x
2
2
1
cos sin
2
x x
2 2
1
cos sin 2sin .cos
4
x x x x
.
1
1 2sin .cos
4
x x
3
2sin .cos
4
x x
.
Ta có:
sin cos
P x x
2
2
sin cosP x x
2 2
sin cos 2sin .cosx x x x
1 2sin .cosx x
3
1
4
=
7
4
.
Do đó:
7
4
P
. Vậy 7 4 11a b .
Câu 43: (VD) Cho hai đường thẳng
1
: 3 3 0d x y
và
2
3
: ( )
2
x t
d t
y t
và điểm
1;2M
. Tìm
điểm
A
trên
1
d
và điểm
B
trên
2
d
sao cho
,A B
đối xứng nhau qua
M
.
A.
3 4
; ;
5 5
A
7 16
;
5 5
B
. B.
3 4
; ;
5 5
A
7 16
;
5 5
B
.
C.
3 4
; ;
5 5
A
7 16
;
5 5
B
. D.
3 4
; ;
5 5
A
7 16
;
5 5
B
Lời giải
Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
1
3 3 ;
A d A a a
2
3 ; 2
B d B t t
Ta có
,
A B
đối xứng nhau qua
M
nên
M
là trung điểm
AB
Do đó
4
3 3 3 2 3 4
5
2 4 2 4 8
5
a
a t a t
a t a t
t
Vậy
3 4
;
5 5
A
và
7 16
;
5 5
B
.
Câu 44: (VD) Giả sử
1 1
1 tan 1 tan tan
cos cos
n
x x m x
x x
cos 0; ,x m n
. Khi đó
n m
có giá trị bằng
A. 4 B. 3 C. 2 D. 1
Lời giải
Chọn B.
Ta có
2
2
1 1 1
1 tan 1 tan 1 tan
cos cos cos
x x x
x x x
2 2
1 tan 2 tan 1 tan 2tan
x x x x
1; 2; 3
n m m n
.
Câu 45: (VD) Trong mặt phẳng
Oxy
cho hai điểm
4;0
A
,
0;3
B
. Phương trình đường tròn nội tiếp tam
giác
ABO
có dạng
2 2
1
x a y b
. Tính
2 3
S a b
.
A.
11
S
B.
2
S
C.
5
S
D.
8
S
Lời giải
Chọn C
Tâm
;
I a b
thuộc đường phân giác góc phần tư thứ nhất nên
;
I a a
với
0
a
.
Đường tròn tiếp xúc với
,
OA Ox OB Oy
nên
a b r
.
Ta có
. 4.3
1
3 4 5
S OAOB
r
p OA OB AB
. Suy ra
1;1
I
.
Vậy
2 3 5
S a b
.
Câu 46: (VD) Tìm phương trình chính tắc của elip nếu nó đi qua điểm
2 ; 3
A
và tỉ số của độ dài trục
lớn với tiêu cự bằng
2
3
.
A.
2 2
1
16 4
x y
. B.
2 2
1
4 3
x y
. C.
2 2
1
3 4
x y
. D.
2 2
1
4 16
x y
.
Lời giải
Chọn A
Gọi phương trình elip cần tìm là:
2 2
2 2
1
x y
a b
với
0
a b
.
Theo đề bài ta có hệ phương trình:
2 2
4 3
1
2
3
a b
a
c
.
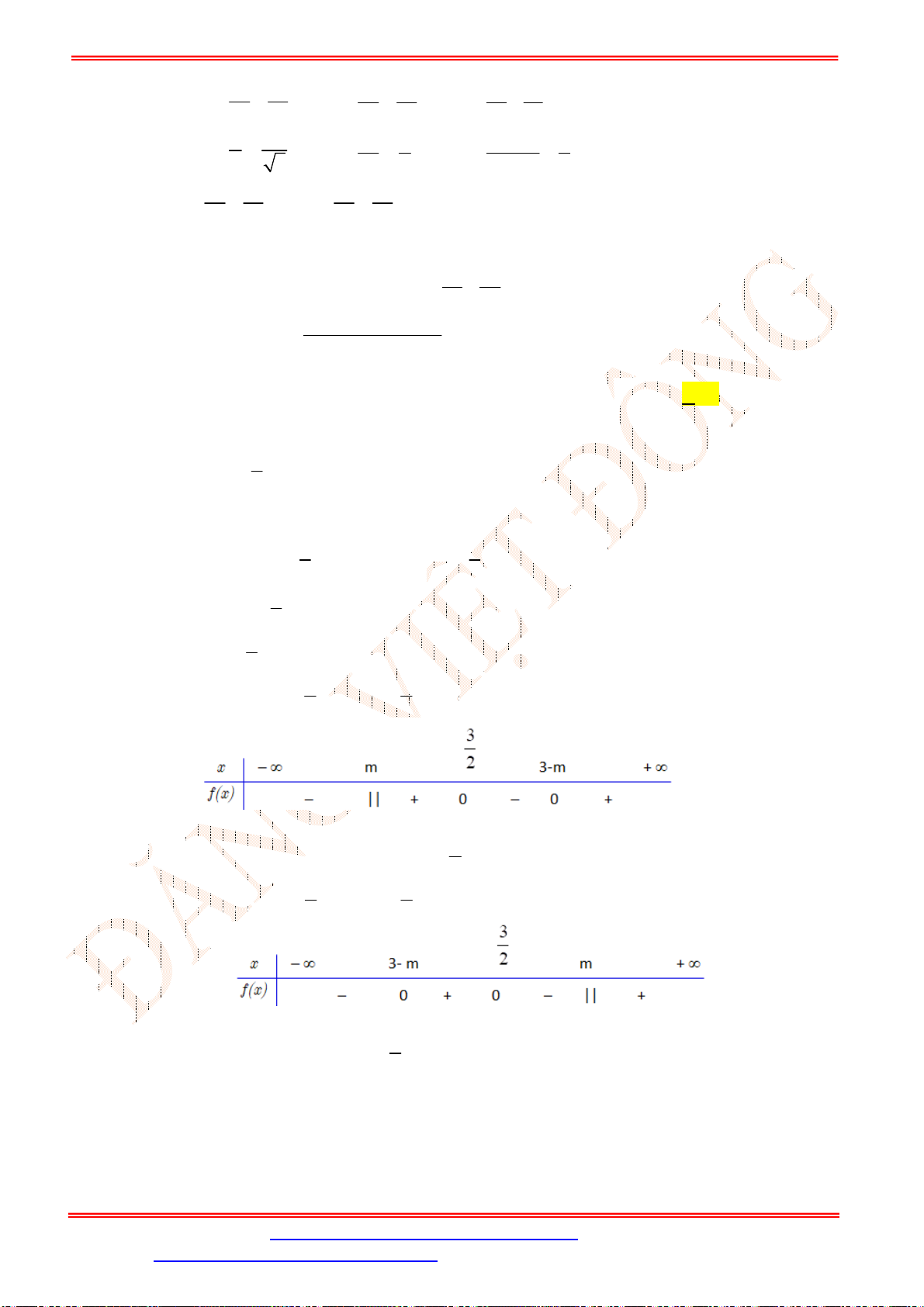
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có:
2 2
4 3
1
2
3
a b
a
c
2 2
2
2
4 3
1
4
3
a b
a
c
2 2
2
2 2
4 3
1
4
3
a b
a
a b
2 2
2 2
4 3
1
4
a b
a b
2 2
2 2
1 3
1
4
b b
a b
2
2
4
16
b
a
.
Vậy elip cần tìm có phương trình là:
2 2
1
16 4
x y
.
Câu 47: (VDC) Cho
(2 3)( 3 )
( )
x x m
f x
x m
. Có bao nhiêu giá trị nguyên của tham số
m
để
( ) 0, 1
f x x
?
A.
4
. B.
3
. C.
0
. D.
2
.
Lời giải
Chọn D
Xét
2 3 0
x
3
2
x
Xét
3 0
x m
3
x m
Xét
0
x m
x m
Nếu
3
3
2
m m m
thì
3
( ) 2 3,
2
f x x x
Suy ra
3
( ) 2 3,
2
f x x x
Do đó
3
( ) 0,
2
f x x
( thỏa mãn)
Nếu
3 3
3 3
2 2
m m m m
ta có bảng xét dấu
Do đó
( ) 0, 1 1
f x x m
Kết hợp điều kiện suy ra
3
1
2
m
Nếu
3 3
3 3
2 2
m m m m
ta có bảng xét dấu
Do đó
( ) 0, 1 3 1 2
f x x m m
Kết hợp điều kiện suy ra
3
2
2
m
Hợp các trường hợp ta được với
1;2
m
thì
( ) 0, 1
f x x
nên có 2 giá trị nguyên của
m
để
( ) 0, 1
f x x
.
Câu 48: (VDC) Trong mặt phẳng
Oxy
cho điểm
1;3 , 5;1
A B
. Phương trình đường thẳng
d
đi qua
A
sao cho khoảng cách từ
B
đến
d
là một số nguyên tố chẵn.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A. Đường thẳng
3
x hoặc
4 3 13 0
x y
.
B. Đường thẳng
3
x hoặc
3 4 13 0
x y
.
C. Đường thẳng
3
y
hoặc
4 3 13 0
x y
.
D. Đường thẳng
3
y
hoặc
3 4 13 0
x y
.
Lời giải
Chọn C
Đường thẳng
d
qua
1;3
A
và có véctơ pháp tuyến
;
n a b
có dạng:
2 2
( 1) ( 3) 0 ( 0)
a x b y a b
Khoảng cách từ
B
đến
d
là một số nguyên tố chẵn
2 2
(5 1) (1 3)
, 2 2
a b
d B d
a b
2 2 2 2
0
(4 2 ) 4( ) 12 16 0
4
3
a
a b a b a ab
a b
Với
0
a ta có đường thẳng
: ( 3) 0 3
d b y y
(vì
2 2
0
a b
).
Với
4
3
a b
ta có đường thẳng
4
: ( 1) ( 3) 0 4 3 13 0
3
d b x b y x y
(vì
2 2
0
a b
).
Câu 49: (VDC) Cho
, 0;
2
x y
thỏa mãn
cos cos sin 1
x y x y x y
. Gọi
m
là giá trị nhỏ
nhất của biểu thức
4 4
sin sin
x y
P
y x
. Tìm khẳng định đúng trong các khẳng định sau
A.
1
0;
2
m
. B.
1 3
;
2
m
. C.
3
;1
m
. D.
1;
m
.
Lời giải
Chọn B
cos cos sin 1
x y x y x y
cos2 cos2 2sin 2
x y x y
2 2
sin sin sin 1
x y x y
.
Do
, 0;
2
x y
nên
, , , 0;
2 2 2
x y x y
. Vậy ta xét các trường hợp:
*
2
x y
: Khi đó
0
2 2
0
2 2
x y
y x
sin sin cos 0
2
sin sin cos 0
2
x y y
y x x
2 2
1 sin sin sin cos cos sin sin 1
VT x y x y x y x y VP
: Không thỏa mãn
1
.
*
0
2
x y
: Khi đó
0
2 2
0
2 2
x y
y x
0 sin sin cos
2
0 sin sin cos
2
x y y
y x x
2 2
1 sin sin sin cos cos sin sin 1
VT x y x y x y x y VP
: Không thỏa mãn
1
.
*
2
x y
: Hiển nhiên thỏa mãn
1
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy
, 0;
, 0;
2
2
1
2
x y
x y
x y
.
Suy ra
2 2
2 2 2 2
4 4
sin sin sin cos
sin sin 2
x y x x
x y
P
y x x y x y
.
Mặt khác,
; ;
4 4
x y
thỏa mãn giả thiết bài cho và thỏa mãn
2
P
.
Vậy
2 1 3
;
2
m
.
Câu 50: (VDC) Trong mặt phẳng với hệ tọa độ
Oxy
cho tam giác
ABC
có ba góc nhọn. Gọi
,
E F
lần lượt
là chân đường cao kẻ từ đỉnh
,
B C
. Đỉnh
3; 7
A
, trung điểm của
BC
là
2;3
M
và đường
tròn ngoại tiếp tam giác
AEF
có phương trình:
2 2
3 4 9
x y
. Khi đó, tích hoành độ
của điểm
B
và điểm
C
bằng
A.
4
. B.
4
. C.
61
. D.
61
.
Lời giải
Chọn C
Gọi
H BE CF
, ta có tứ giác
AEHF
nội tiếp đường tròn
C
đường kính
AH
.
Theo giả thiết
2 2
: 3 4 9
C x y
Tâm
3; 4 3; 1
I H
0;6
AH
là vtpt của đường thẳng
BC
Đường thẳng
BC
nhận
1;0
u
làm vtcp
2
:
3
x t
BC
y
2;3
B t
2;3
M
là trung điểm của đoạn
BC
2;3
C t
Ta có
5;10 ; 5;4
AB t HC t
. 0
AB HC AB HC
5 5 40 0
t t
2
4 61
t
. 61
B C
x x
M(-2;3)
H
A(3;-7)
B
C
E
F
I

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 16
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Có bao nhiêu mệnh đề trong các câu dưới đây?
(1)
5
là số vô tỉ.
(2) Trăng hôm nay đẹp quá!
(3) Mấy giờ rồi?
(4) Nếu tôi đi bằng đầu thì bầu trời nằm dưới chân tôi.
(5) Bình phương của
3
là
6
.
A.
4
. B.
0
. C.
2
. D.
3
.
Câu 2. Mệnh đề nào sau đây là mệnh đề chứa biến?
A.
2A n n
là tập hợp các số tự nhiên chẵn.
B.
3
x .
C. Khủng long là loài bò sát.
D.
2
y x
là hàm số bậc nhất.
Câu 3. Cho tập hợp
2
1 , 6
A n n n
. Tập hợp nào sau đây là tập con của
A
?
A.
1;3;5;7
. B.
5;7;9;37
. C.
2;10;17;37
. D.
2;4;10;26
.
Câu 4. Cho hai tập hợp
1;2;4;7;9
X và
1;0;7;10
Y . Tập hợp
\
X Y
có bao nhiêu phần tử?
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số
2
3 1
2
x x
y
x
?
A.
1;3
M . B.
3;2
N . C.
0;1
P . D.
3;1
Q .
Câu 6. Tập xác định
D
của hàm số
3 1
y x
là
A.
0;D
. B.
0;D
. C.
1
;
3
D
. D.
1
;
3
D
.
Câu 7. Nghiệm của phương trình
2
5 6 0
x x
là
A.
2
3
x
x
. B.
2
3
x
x
. C.
2
3
x
x
. D.
2
3
x
x
.
Câu 8. Nghiệm của hệ phương trình
2 1
2 2
2 3
x y
y z
z x
là
A.
0
1
1
x
y
z
. B.
1
1
0
x
y
z
. C.
1
1
1
x
y
z
. D.
1
0
1
x
y
z
.
Câu 9. Với
x
thuộc tập hợp nào dưới đây thì đa thức
6 5 2 10 8
f x x x x x x
luôn
dương?
A.
. B.
. C.
;5
. D.
5;
.
Câu 10. Cho nhị thức bậc nhất
5 30
f x x
. Khẳng định nào sau đây đúng?
A.
0
f x
, x
. B.
0
f x
,
6;x
.
C.
0
f x
với
6
x
. D.
0
f x
,
;6
x .
Câu 11. Trong các tính chất sau, tính chất nào sai?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
a b
c d
a c b d
. B.
0
0
a b
c d
a b
d c
.
C.
0
0
a b
c d
ac bd
. D.
a b
c d
a c b d
.
Câu 12 . Đổi số đo
0
72
sang số đo radian.
A.
5
3
. B.
5
2
. C.
3
5
. D.
2
5
.
Câu 13. Cho đường tròn có bán kính
6 cm
. Tìm số đo (
rad
) của cung có độ dài là
3 cm
:
A.
0,5
. B.
3
. C.
2
. D.
1
.
Câu 14. Góc
18
có số đo bằng độ là:
A.
0
18
. B.
0
36
. C.
0
10
. D.
0
12
.
Câu 15. Véctơ là một đoạn thẳng:
A. Có hướng . B. Có hướng dương, hướng âm.
C. Có hai đầu mút. D. Thỏa cả ba tính chất trên.
Câu 16. Trong mặt phẳng
,
Oxy
cho hình bình hành
ABCD
. Gọi
G
là trọng tâm của tam giác
.
ACD
Biểu thị
AG
qua hai vectơ
AC
và
.
BC
A.
1 1
2 2
AG AC BC
. B.
1 1
3 3
AG AC BC
.
C.
1 2
3 3
AG AC BC
. D.
1 1
3 3
AG AC BC
.
Câu 17. Cho tam giác đều
ABC
nội tiếp đường tròn
( ; ).
O R
Tính
.
OBOC
theo
.
R
A.
2
1
.
2
OBOC R
. B.
2
.
OBOC R
.
C.
2
1
.
2
OBOC R
. D.
2
3
.
2
OBOC R
.
Câu 18. Cho tam giác
ABC
có trọng tâm
,
G
biết rằng
14,
BC
0
120 .
BGC
Bán kính đường tròn
ngoại tiếp tam giác
BGC
bằng
A.
14 3
3
. B.
3
14
. C.
14
. D.
1
14
.
Câu 19. Viết phương trình đường thẳng
d
đi qua
–2;3
M
và có VTCP
1;4
u
.
A.
2 3
1 4
x t
y t
. B.
2
3 4
x t
y t
. C.
2
3 4
x t
y t
. D.
1 2
4 3
x t
y t
.
Câu 20. Tìm tâm
I
và bán kính
R
của đường tròn
C
có phương trình là
2 2
4 2 1 0
x y x y
.
A. Tâm
2;1
I
, bán kính
6
R . B. Tâm
2;1
I
, bán kính
2
R
.
C. Tâm
2; 1
I
, bán kính
6
R . D. Tâm
2; 1
I
, bán kính
2
R
Câu 21. Mệnh đề phủ định của mệnh đề
2
, 2020 0
x x x
là
A.
2
, 2020 0
x x x
. B.
2
, 2020 0
x x x
.
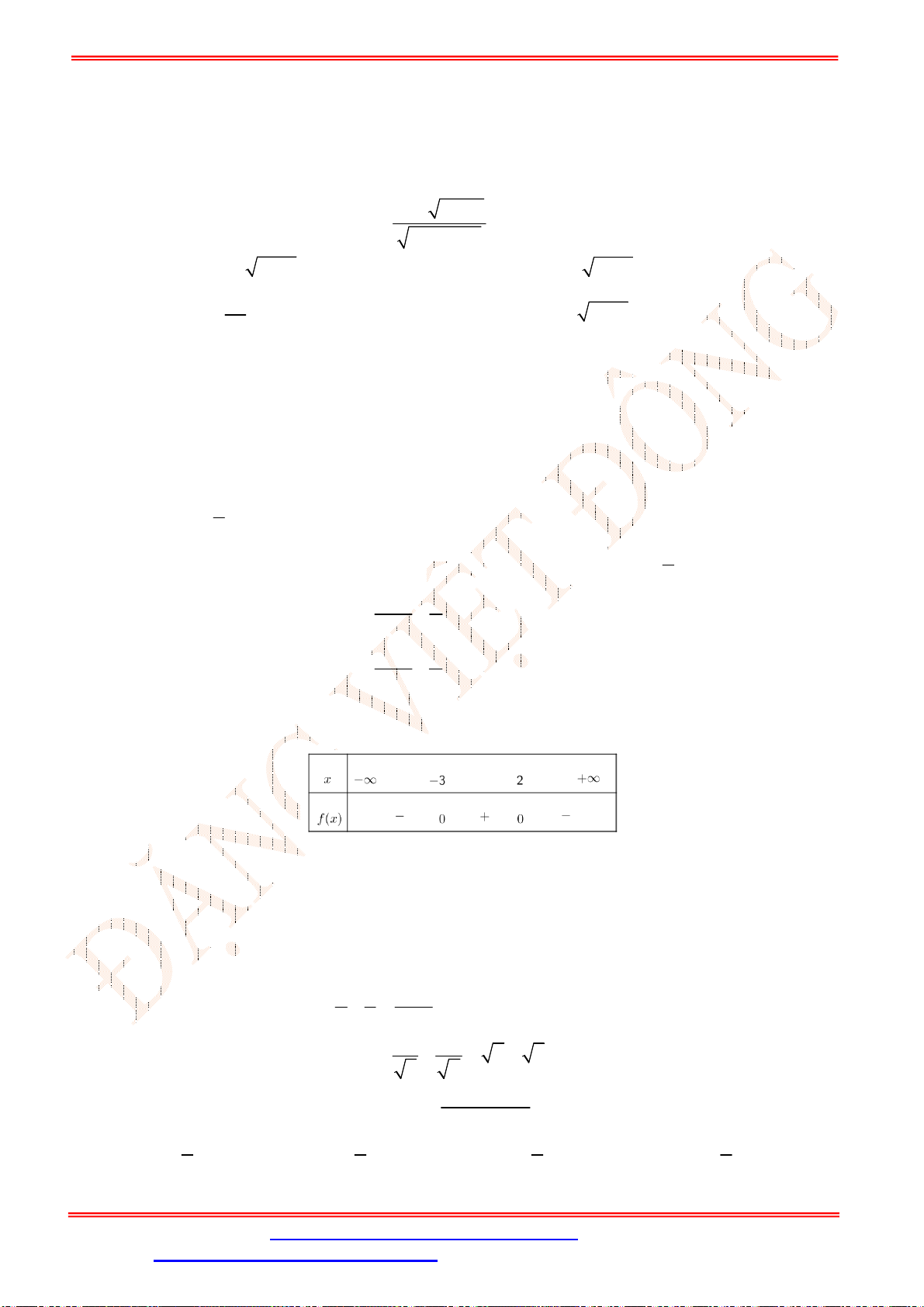
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
2
, 2020 0
x x x
. D.
2
, 2020 0
x x x
.
Câu 22. Cho các tập hợp
0;1;2;3;4
A
,
1;3;4;6;8
B
. Tập hợp
\ \
A B B A
bằng
A.
0;1;2;3;4;6;8
. B.
0;2;6;8
.
C.
1;2
. D.
.
Câu 23. Tìm tập xác định của hàm số
2
2
3 5
2020
x x
y
x
.
A. TXĐ:
2020
x . B. TXĐ:
2020;
.
C. TXĐ:
3
;
5
. D.TXĐ:
2020;
.
Câu 24. Biết đồ thị hàm số
2
, , , 0
y ax bx c a b c a
đi qua
(1;2)
A
và có đỉnh
(0;2020)
I
.
Tính
T a b c
A.
2020
T
. B.
4038
T
.
C.
4038
T
. D.
2020
T
.
Câu25. Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có
hai nghiệm
1
x
,
2
x
thỏa mãn
2 2
1 2
16
x x
.
A.
5
.
2
m
B.
2
m
.
C.
1
m
. D.
2
m
hoặc
5
2
m
.
Câu26. Nghiệm của hệ phương trình
4 1
5
2
5 2
3
2
x y
x y
là
A.
; 3;11
x y . B.
; 3;1
x y . C.
; 13;1
x y . D.
; 3;1
x y .
Câu 27. Hàm số nào sau đây có bảng xét dấu như hình bên dưới ?
A.
3
f x x
B.
2
3 2
f x x x
C.
2
6
f x x x
D.
2
6
f x x x
Câu 28 . Trong các mệnh đề sau, mệnh đề nào sai ?
A. Với mọi
,a b
ta có
2 2
0
a b ab
.
B. Nếu
a b
thì
3 3 2 2
a b ab a b
với mọi
,a b
.
C. Với mọi số thực
,
a b
:
1 1 4
a b a b
.
D. Với mọi số thực dương
,
a b
:
a b
a b
b a
.
Câu 29. Cho
tan 5
a
, giá trị của biểu thức
sin cos
cos sin
a a
A
a a
là
A.
2
3
. B.
2
3
. C.
3
2
. D.
3
2
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 30. Giá trị của biểu thức
3
2sin sin(5 ) sin cos
2 2 2
P x x x x
là
A.
3cos 2sin
x x
. B.
3cos
x
. C.
cos
x
. D.
cos
x
.
Câu 31. Cho các điểm
2;1 , 4;0 , 2;3
A B C . Tìm điểm
M
biết rằng
3 2
CM AC AB
A.
2; 5
M
. B.
5; 2
M
. C.
5;2
M . D.
2;5
M .
Câu 32. Trong mặt phẳng tọa độ
Oxy
cho bốn điểm
3; 2 , 7;1 , 0;1 , 8; 5
A B C D
. Khẳng định
nào sau đây là đúng?
A.
,
AB CD
đối nhau. B.
,
AB CD
cùng phương cùng hướng.
C.
, , ,
A B C D
thẳng hàng. D.
,
AB CD
cùng phương nhưng ngược hướng.
Câu 33. Cho tam giác
ABC
có độ dài các đường cao kẻ từ các đỉnh
, ,
A B C
lần lượt là
, ,
a b c
h h h
.
Nếu 2
a b c
h h h
thì
A.
2 1 1
sin sin sin
A B C
. B.
2sin sin sin
A B C
.
C.
2cos cos cos
A B C
. D.
2 1 1
cos cos cos
A B C
.
Câu 34. Trong mặt phẳng tọa độ
Oxy
cho điểm
1;2
M . Đường thẳng
đi qua
M
và cách gốc tọa
độ
O
một khoảng lớn nhất. Phương trình tham số của
là
A.
1
2 2
x t
y t
. B.
1
2 2
x t
y t
. C.
2 2
1
x t
y t
. D.
5 4
2
x t
y t
.
Câu 35. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
3; 2 , 3;1
A B và đường thẳng
d
có
phương trình:
2 3 0
x y
. Phương trình đường thẳng
song song với
d
và đi qua
trung điểm
M
của đoạn
AB
A.
2 1 0
x y
. B.
2 1 0
x y
. C.
2 1 0
x y
. D.
2 1 0
x y
.
Câu 36. Trong các mệnh đề sau, mệnh đề nào sai?
A.
n
,
2
11 2
n n
chia hết cho
11
. B.
n
,
2
1
n
chia hết cho
4
.
C. Tồn tại số nguyên tố chia hết cho
5
. D.
n
,
2
2 8 0
n
.
Câu 37. Cho hàm số
2
( ) ( 10) 1
y f x mx m x
. Có bao nhiêu giá trị nguyên của tham số m để hàm
số
( )
f x
nghịch biến trên khoảng
2 ;
?.
A.
3
. B. vô số. C.
1
. D.
2
.
Câu 38. Tìm số giá trị nguyên của tham số m để hàm số
2
2
2 3 5
( )
2 2020
x x
y f x
mx mx
có tập xác định
là
A.
2020
. B.
2019
. C.
2021
. D.
4040
.
Câu 39. Tìm tổng tất cả các giá trị nguyên của tham số
m
để phương trình (1) vô nghiệm
2
1 2 1 2 0 1
m x m x m .
A.
1
. B.
1
. C.
2
. D.
3
.
Câu 40. Cho hệ phương trình :
2 2
2 1
x y a
x y a
. Các giá trị thích hợp của tham số
a
để tổng bình
phương hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất
A.
1
.
2
a
B.
1.
a
C.
1.
a
. D.
1
.
2
a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 41. Gọi
S
là tập hợp các giá trị thực của tham số
a
để bất phương trình
2
2 2
9 8 0
2 1 2 0
x x
x a x a a
có nghiệm duy nhất. Tổng các phần tử của tập
S
bằng
A.
1
. B.
6
. C.
7
. D.
5
.
Câu 42. Cho
;
2 2
và
;
2
và
tan tan 1
. Gọi
S
là tập hợp các số đo của góc
thỏa
1 tan 1 tan 2
. Tổng các phần tử của tập
S
bằng
A.
5
4
. B.
4
. C.
4
. D.
3
2
.
Câu 43. Cho hình thoi
ABCD
tâm
O
có cạnh bằng
a
và
60
ABD
. Gọi
I
là điểm thỏa mãn
2 0
IC ID
. Tính tích vô hướng
.
AO BI
.
A.
2
.
4
a
AO BI
. B.
2
.
2
a
AO BI
. C.
2
.
2
a
AO BI
. D.
2
.
4
a
AO BI
.
Câu 44. Cho
1
cos2
4
a
. Tính
sin2 cos
a a
với 0
2
a
.
A.
3 10
16
. B.
3 10
8
. C.
5 6
8
. D.
5 6
16
.
Câu 45. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
x m
y
x m
trên đoạn
0;4
bằng
1
?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 46. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
2 4 4
m x x m
có nghiệm
âm?
A.
0
m
. B.
4
m
. C.
0 4
m . D.
0
m
và
4
m
.
Câu 47. Cho hệ phương trình
2
2 3 2
3 2 2 0
3 3 1 2 1 3 1
x y x y
x x x x y
. Gọi
0 0
;
x y
là một nghiệm
của hệ đã cho với
0
2
y
. Tính tổng
0 0
x y
.
A.
2 2
4
. B.
2 3
2
. C.
2 2
2
. D.
6 1
2
.
Câu 48. Cho hai số thực
,
x y
thỏa mãn
2 2
1.
x y xy
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của
.
S xy x y
Giá trị của
2
M m
bằng
A.
2 3
.
3
B.
2 3
.
9
C.
3
.
9
D.
3
.
3
Câu 49. Cho tam giác là tam giác đều có cạnh bằng
12
cm. Biết tập hợp các điểm thỏa mãn
3 4 3 4
MA MB MC MA MB MC
là một đường tròn. Xác định bán kính của đường tròn
đó?
A.
3 13
2
cm. B.
13
8
cm. C.
12 13
cm. D.
6 13
cm.
Câu 50: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
với
3; 4
A
, tâm đường tròn nội tiếp
ABC
M

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2;1
I , tâm đường tròn ngoại tiếp
1
;1
2
J
. Tính
,
d O BC
.
A.
2
. B.
2 5
. C.
10
. D.
5 2
.
………HẾT………..

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 16
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. Có bao nhiêu mệnh đề trong các câu dưới đây?
(1)
5
là số vô tỉ.
(2) Trăng hôm nay đẹp quá!
(3) Mấy giờ rồi?
(4) Nếu tôi đi bằng đầu thì bầu trời nằm dưới chân tôi.
(5) Bình phương của
3
là
6
.
A.
4
. B.
0
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta thấy câu (1), (4), (5) là các câu khẳng định nên là mệnh đề.
Câu (2) là câu cảm thán, (3) là câu nghi vấn nên không phải mệnh đề.
Câu 2. Mệnh đề nào sau đây là mệnh đề chứa biến?
A.
2A n n
là tập hợp các số tự nhiên chẵn.
B.
3
x .
C. Khủng long là loài bò sát.
D.
2
y x
là hàm số bậc nhất.
Lời giải
Chọn B
Mệnh đề chứa biến là mệnh đề có tính đúng sai phụ thuộc vào giá trị của biến.
Câu B đúng khi và chỉ khi
3
x và sai khi
3
x .
Câu 3. Cho tập hợp
2
1 , 6
A n n n
. Tập hợp nào sau đây là tập con của
A
?
A.
1;3;5;7
. B.
5;7;9;37
. C.
2;10;17;37
. D.
2;4;10;26
.
Lời giải
Chọn C
Lần lượt thay các giá trị
0,1,2,3,4,5,6
n , ta có
1;2;5;10;17;26;37
A . Vậy chỉ có đáp án
C thỏa mãn.
Câu 4. Cho hai tập hợp
1;2;4;7;9
X và
1;0;7;10
Y . Tập hợp
\
X Y
có bao nhiêu phần tử?
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn C
Ta có:
\ 1;2;4;9
X Y nên tập hợp
\
X Y
có
4
phần tử.
Câu 5. Điểm nào sau đây thuộc đồ thị hàm số
2
3 1
2
x x
y
x
?
A.
1;3
M . B.
3;2
N . C.
0;1
P . D.
3;1
Q .
Lời giải
Chọn D
Thay tọa độ của điểm
3;1
Q vào hàm số ta được mênh đề đúng, nên
3;1
Q là điểm thuộc đồ
thị hàm số.
Câu 6. Tập xác định
D
của hàm số
3 1
y x
là
A.
0;D
. B.
0;D
. C.
1
;
3
D
. D.
1
;
3
D
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn C
Điều kiện:
3 1 0
x
1
3
x
Vậy tập xác định
1
;
3
D
.
Câu 7. Nghiệm của phương trình
2
5 6 0
x x
là
A.
2
3
x
x
. B.
2
3
x
x
. C.
2
3
x
x
. D.
2
3
x
x
.
Lời giải
Chọn C
Vì
1 0
nên phương trình đã cho có hai nghiệm phân biệt là
2
x
,
3
x
.
Câu 8. Nghiệm của hệ phương trình
2 1
2 2
2 3
x y
y z
z x
là
A.
0
1
1
x
y
z
. B.
1
1
0
x
y
z
. C.
1
1
1
x
y
z
. D.
1
0
1
x
y
z
.
Lời giải
Chọn D
Từ phương trình
2 3
z x
suy ra
3 2 .
z x
Thay vào hai phương trình còn lại ta được hệ
phương trình, ta được
2 1
2 1 1
.
2 3 2 2
4 4 0
x y
x y x
y x
x y y
Từ đó ta được
3 2.1 1.
z
Vậy hệ phương trình có nghiệm
; ; 1;0;1
x y z
.
Câu 9. Với
x
thuộc tập hợp nào dưới đây thì đa thức
6 5 2 10 8
f x x x x x x
luôn
dương?
A.
. B.
. C.
;5
. D.
5;
.
Lời giải
Chọn A
6 5 2 10 8 0 0 5
x x x x x x
vô nghiệm.
Vậy
.
x
Câu 10. Cho nhị thức bậc nhất
5 30
f x x
. Khẳng định nào sau đây đúng?
A.
0
f x
, x
. B.
0
f x
,
6;x
.
C.
0
f x
với
6
x
. D.
0
f x
,
;6
x .
Lời giải
Chọn B
5 30 0 6
x x
.
Câu 11. Trong các tính chất sau, tính chất nào sai?
A.
a b
c d
a c b d
. B.
0
0
a b
c d
a b
d c
.
C.
0
0
a b
c d
ac bd
. D.
a b
c d
a c b d
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Câu 12 . Đổi số đo
0
72
sang số đo radian.
A.
5
3
. B.
5
2
. C.
3
5
. D.
2
5
.
Lời giải
Chọn D
Câu 13. Cho đường tròn có bán kính
6 cm
. Tìm số đo (
rad
) của cung có độ dài là
3 cm
:
A.
0,5
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn A
Theo công thức tính độ dài cung tròn ta có
.
180
a
l R R
nên
Ta có
3
0,5
6
l
R
.
Câu 14. Góc
18
có số đo bằng độ là:
A.
0
18
. B.
0
36
. C.
0
10
. D.
0
12
.
Lời giải
Chọn C
Ta có:
o o
o
180 180
1rad rad . 10
18 18
.
Câu 15. Véctơ là một đoạn thẳng:
A. Có hướng . B. Có hướng dương, hướng âm.
C. Có hai đầu mút. D. Thỏa cả ba tính chất trên.
Lời giải
Chọn A
Câu 16. Trong mặt phẳng
,
Oxy
cho hình bình hành
ABCD
. Gọi
G
là trọng tâm của tam giác
.
ACD
Biểu thị
AG
qua hai vectơ
AC
và
.
BC
A.
1 1
2 2
AG AC BC
. B.
1 1
3 3
AG AC BC
.
C.
1 2
3 3
AG AC BC
. D.
1 1
3 3
AG AC BC
.
Lời giải
Chọn D
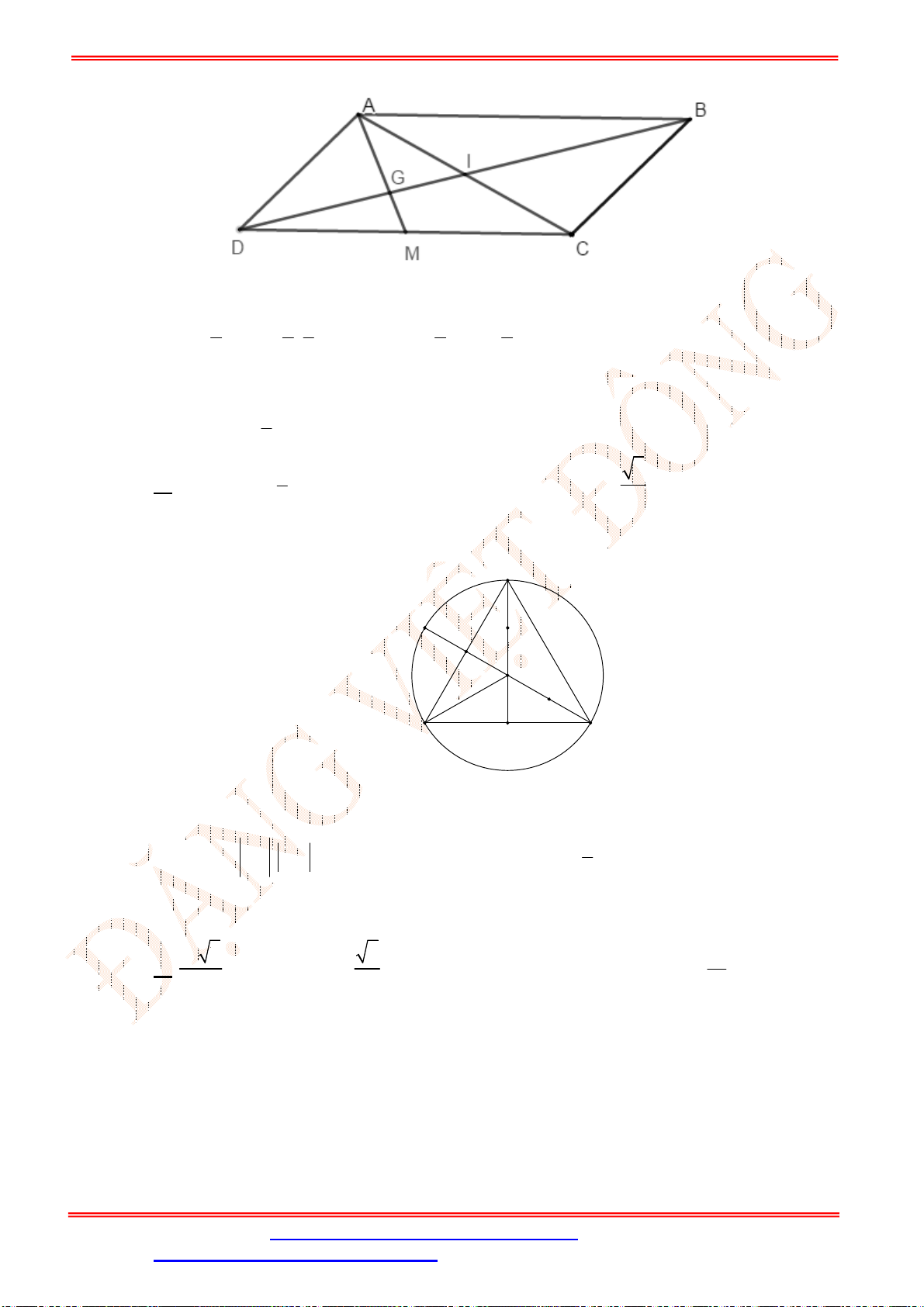
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi
M
là trung điểm của đoạn
CD
2 2 1 1 1
. .
3 3 2 3 3
AG AM AC AD AC BC
Câu 17. Cho tam giác đều
ABC
nội tiếp đường tròn
( ; ).
O R
Tính
.
OBOC
theo
.
R
A.
2
1
.
2
OBOC R
. B.
2
.
OBOC R
.
C.
2
1
.
2
OBOC R
. D.
2
3
.
2
OBOC R
.
Lời giải
Chọn C
Ta có
0
2 120 .
BOC BAC
Khi đó
0 2
1
. . .cos ; . .cos120 .
2
OBOC OB OC OB OC R R R
Câu 18. Cho tam giác
ABC
có trọng tâm
,
G
biết rằng
14,
BC
0
120 .
BGC
Bán kính đường tròn
ngoại tiếp tam giác
BGC
bằng
A.
14 3
3
. B.
3
14
. C.
14
. D.
1
14
.
Lời giải
Chọn A
M
H
C
A
B
O
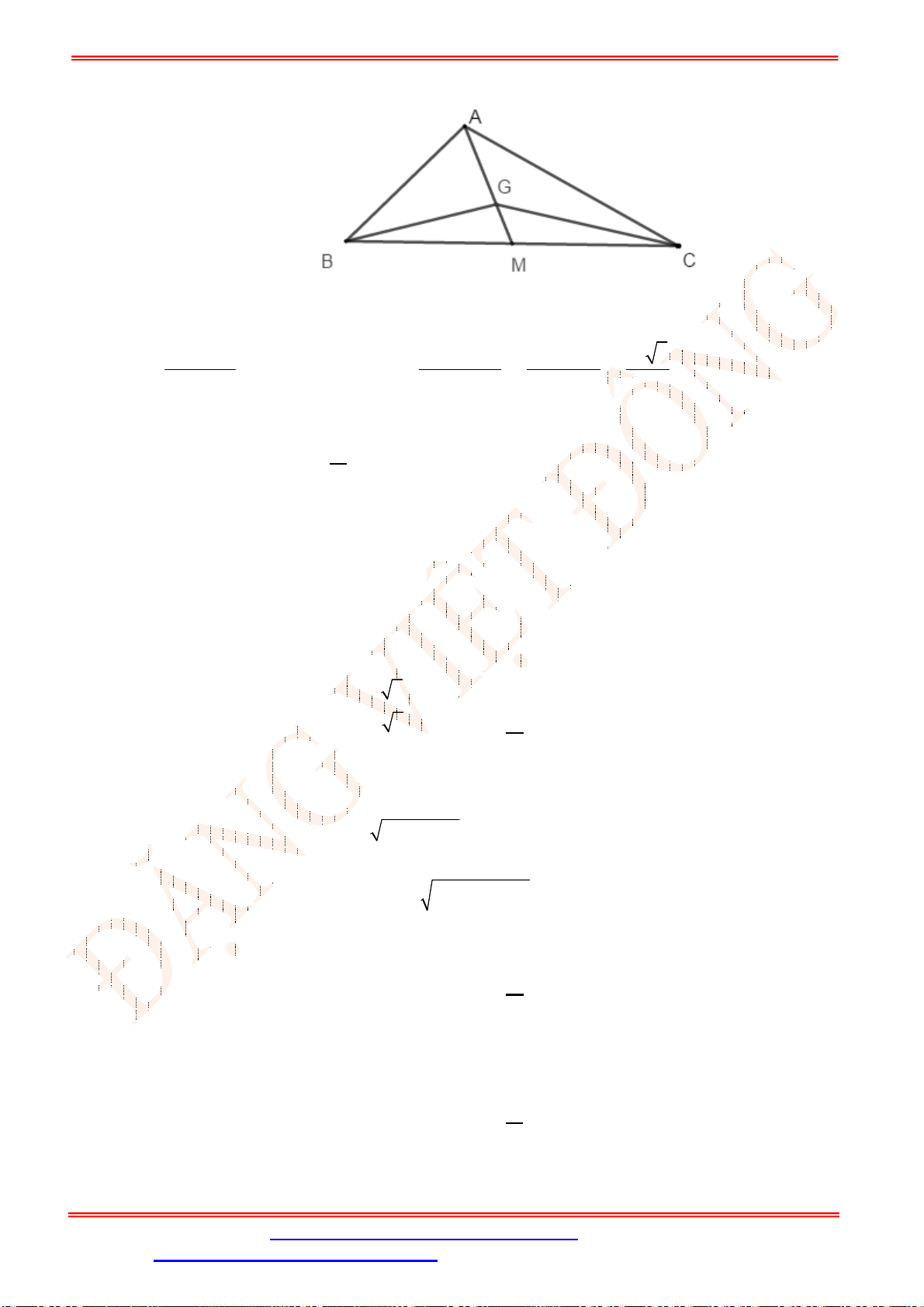
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Áp dụng định lý sin cho tam giác
BGC
ta có
( ) ( )
0
14 14 3
2 .
3
2sin120
sin 2sin
BGC BGC
BC BC
R R
BGC BGC
Câu 19. Viết phương trình đường thẳng
d
đi qua
–2;3
M
và có VTCP
1;4
u
.
A.
2 3
1 4
x t
y t
. B.
2
3 4
x t
y t
. C.
2
3 4
x t
y t
. D.
1 2
4 3
x t
y t
.
Lời giải
Chọn B
Đường thẳng
d
đi qua
–2;3
M
và có VTCP
1;4
u
có dạng
1
2
o
o
x x u t
y y u t
nên đường thẳng có phương trình:
2
3 4
x t
y t
Câu 20. Tìm tâm
I
và bán kính
R
của đường tròn
C
có phương trình là
2 2
4 2 1 0
x y x y
.
A. Tâm
2;1
I
, bán kính
6
R . B. Tâm
2;1
I
, bán kính
2
R
.
C. Tâm
2; 1
I
, bán kính
6
R . D. Tâm
2; 1
I
, bán kính
2
R
Lời giải
Chọn D
Phương trình đường tròn
C
có dạng là
2 2
2 2 0
x y ax by c
Tâm
;
I a b
và bán kính
2 2
R a b c
Suy ra
2; 1, 1
a b c
Như vậy tâm
2; 1
I
, bán kính
2
2
2 1 1 2
R
Câu 21. Mệnh đề phủ định của mệnh đề
2
, 2020 0
x x x
là
A.
2
, 2020 0
x x x
. B.
2
, 2020 0
x x x
.
C.
2
, 2020 0
x x x
. D.
2
, 2020 0
x x x
.
Lời giải
Chọn D
Mệnh đề phủ định của mệnh đề
2
, 2020 0
x x x
là
2
, 2020 0
x x x
.
Câu 22. Cho các tập hợp
0;1;2;3;4
A
,
1;3;4;6;8
B
. Tập hợp
\ \
A B B A
bằng
A.
0;1;2;3;4;6;8
. B.
0;2;6;8
.
C.
1;2
. D.
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B
Ta có :
\ 0;2
A B
\ 6;8
B A
Vậy
\ \ 0;2;6;8
A B B A
Câu 23. Tìm tập xác định của hàm số
2
2
3 5
2020
x x
y
x
.
A. TXĐ:
2020
x . B. TXĐ:
2020;
.
C. TXĐ:
3
;
5
. D.TXĐ:
2020;
.
Lời giải
Chọn D
Điều kiện xác định:
2
2
3 5 0
2020 0
2020 0
x
x
x
2
3 5 0
2020 0
x
x
5
3
2020
2020
x
x
x
2020
x
.
Vậy TXĐ:
2020;
.
Câu 24. Biết đồ thị hàm số
2
, , , 0
y ax bx c a b c a
đi qua
(1;2)
A
và có đỉnh
(0;2020)
I
.
Tính
T a b c
A.
2020
T
. B.
4038
T
.
C.
4038
T
. D.
2020
T
.
Lời giải
Chọn C
Do đồ thị hàm số
2
, , , 0
y ax bx c a b c a
đi qua
(1;2)
A
và có đỉnh
(0;2020)
I
.
Ta có :
2
2020
0
2
a b c
c
b
a
2018
2020
0
a
c
b
vậy
4038
T a b c
Câu25. Tìm tất cả các giá trị của tham số
m
để phương trình
2
2 2 0
x mx m
có
hai nghiệm
1
x
,
2
x
thỏa mãn
2 2
1 2
16
x x
.
A.
5
.
2
m
B.
2
m
.
C.
1
m
. D.
2
m
hoặc
5
2
m
.
Lời giải
Chọn D.
Phương trình có nghiệm khi
0
2
2 0
m m
1
.
Theo định lý Viet ta có
1 2
1 2
2
2
x x m
x x m
.
2 2
1 2
16
x x
2
4 2 2 16
m m
2
4 2 20 0
m m
2
5
2
m
m
.
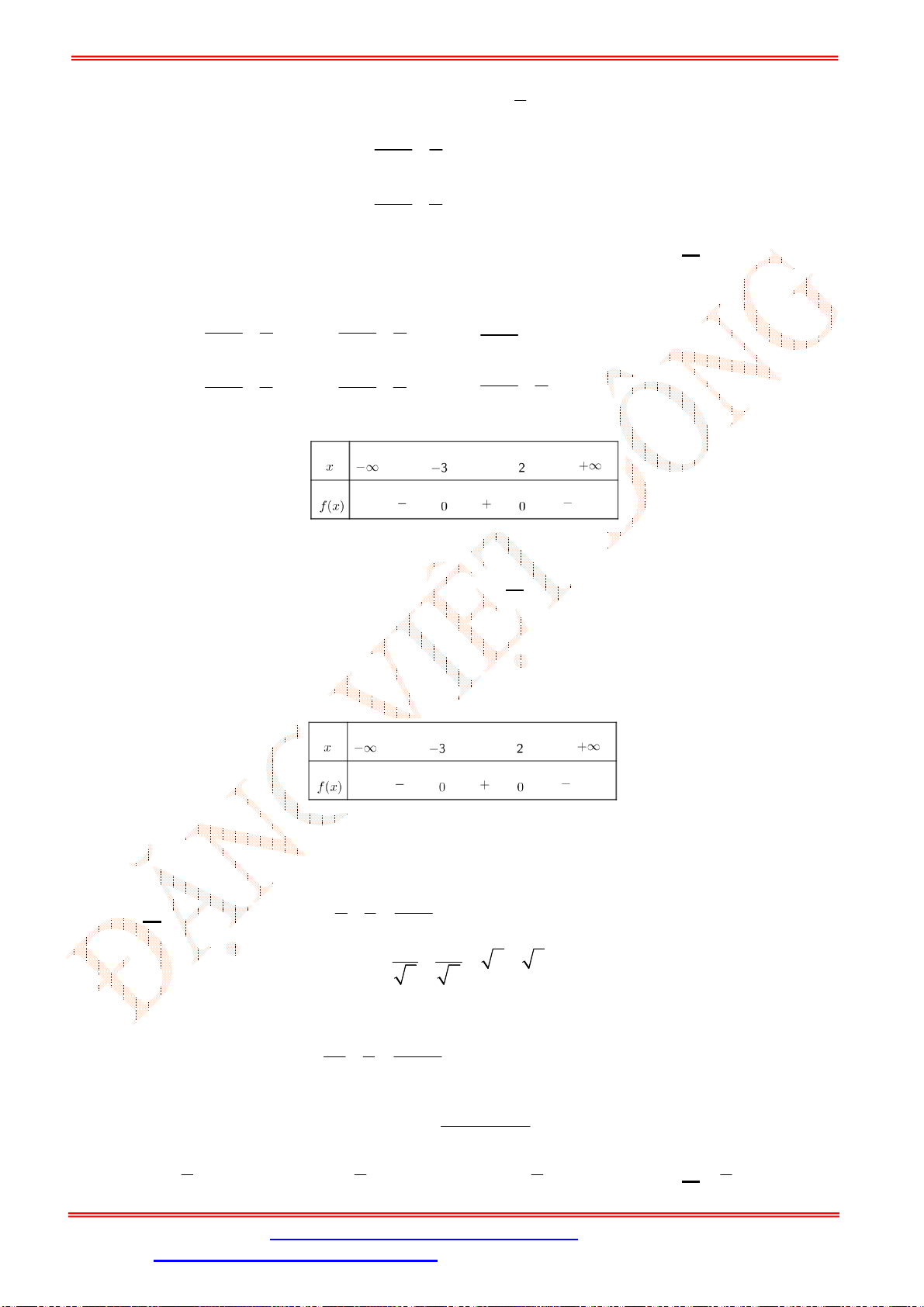
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Kiểm tra điều kiện
1
, ta được
2
m
hoặc
5
2
m
.
Câu26. Nghiệm của hệ phương trình
4 1
5
2
5 2
3
2
x y
x y
là
A.
; 3;11
x y . B.
; 3;1
x y . C.
; 13;1
x y . D.
; 3;1
x y .
Lời giải
Chọn D
Ta có:
4 1 8 2
13
5 10
13
3
2 2
2
5 2
5 2 5 2 1
3
3 3
2
2 2
x
x y x y
x
y
x y
x y x y
.
Câu 27 . Hàm số nào sau đây có bảng xét dấu như hình bên dưới ?
.
A.
3
f x x
B.
2
3 2
f x x x
C.
2
6
f x x x
D.
2
6
f x x x
Lời giải
Chọn D
Xét
2
2
6 0
3
x
x x
x
Khi đó ta có bảng xét dấu:
Câu 28 . Trong các mệnh đề sau, mệnh đề nào sai ?
A. Với mọi
,a b
ta có
2 2
0
a b ab
.
B. Nếu
a b
thì
3 3 2 2
a b ab a b
với mọi
,a b
.
C. Với mọi số thực
,
a b
:
1 1 4
a b a b
.
D. Với mọi số thực dương
,
a b
:
a b
a b
b a
.
Lời giải
Chọn C
Với
2, 4
a b
ta có:
1 1 4
2 4 2 4
(vô lý)
Vậy chọn đáp án C.
Câu 29. Cho
tan 5
a
, giá trị của biểu thức
sin cos
cos sin
a a
A
a a
là
A.
2
3
. B.
2
3
. C.
3
2
. D.
3
2
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Ta có
sin cos
sin cos tan 1 5 1 3
cos cos
cos sin
cos sin 1 tan 1 5 2
cos cos
a a
a a a
a a
A
a a
a a a
a a
Câu 30. Giá trị của biểu thức
3
2sin sin(5 ) sin cos
2 2 2
P x x x x
là
A.
3cos 2sin
x x
. B.
3cos
x
. C.
cos
x
. D.
cos
x
.
Lời giải
Chọn D
Ta có
3
2sin sin(5 ) sin cos
2 2 2
P x x x x
2cos sin sin sin
2
x x x x
2cos sin sin sin
2
x x x x
2cos cos cos
x x x
Câu 31. Cho các điểm
2;1 , 4;0 , 2;3
A B C . Tìm điểm
M
biết rằng
3 2
CM AC AB
A.
2; 5
M
. B.
5; 2
M
. C.
5;2
M . D.
2;5
M .
Lời giải
Chọn A
Gọi điểm
;
M x y
. Khi đó ta có:
2; 3
CM x y
,
4;2
AC
,
6; 1
AB
.
Theo giả thiết ta có:
3 2
CM AC AB
2 3.4 2.6
3 3.2 2. 1
x
y
2
5
x
y
.
Vậy
2; 5
M
.
Câu 32. Trong mặt phẳng tọa độ
Oxy
cho bốn điểm
3; 2 , 7;1 , 0;1 , 8; 5
A B C D
. Khẳng định
nào sau đây là đúng?
A.
,
AB CD
đối nhau. B.
,
AB CD
cùng phương cùng hướng.
C.
, , ,
A B C D
thẳng hàng. D.
,
AB CD
cùng phương nhưng ngược hướng.
Lời giải
Chọn D
Ta có:
4;3
AB
,
8; 6
CD
.
Nhận thấy:
2
CD AB
nên
,
AB CD
cùng phương nhưng ngược hướng.
Câu 33. Cho tam giác
ABC
có độ dài các đường cao kẻ từ các đỉnh
, ,
A B C
lần lượt là
, ,
a b c
h h h
.
Nếu 2
a b c
h h h
thì
A.
2 1 1
sin sin sin
A B C
. B.
2sin sin sin
A B C
.
C.
2cos cos cos
A B C
. D.
2 1 1
cos cos cos
A B C
.
Lời giải
Chọn A

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
1 1 1 2 2 2
. . . , ,
2 2 2
a b c a b c
S S S
S a h b h c h h h h
a b c
và
2 2 sin , 2 sin , 2 sin
sin sin sin
a b c
R a R A b R B c R C
A B C
Do đó
2 2 2 2 1 1
2 2
a b c
S S S
h h h
a b c a b c
2 1 1 2 1 1
2 sin 2 sin 2 sin sin sin sin
R A R B R C A B C
.
Câu 34. Trong mặt phẳng tọa độ
Oxy
cho điểm
1;2
M . Đường thẳng
đi qua
M
và cách gốc tọa
độ
O
một khoảng lớn nhất. Phương trình tham số của
là
A.
1
2 2
x t
y t
. B.
1
2 2
x t
y t
. C.
2 2
1
x t
y t
. D.
5 4
2
x t
y t
.
Lời giải
Chọn D
Gọi
H
là hình chiếu của
O
trên
. Khi đó OH
nên
,
d O OH OM
(không đổi).
Do đó
,
d O
lớn nhất bằng
OM
khi
H M
hay OM
.
Khi đó
có vectơ pháp tuyến là
1;2
OM
.
Phương trình tổng quát của
là:
1 1 2 2 0 2 5 0
x y x y
.
Từ đó suy ra
đi qua
5;0
N và có vectơ chỉ phương
4;2
u
.
Vậy phương trình tham số của
là
5 4
2
x t
y t
.
Câu 35. Trong mặt phẳng với hệ tọa độ
Oxy
, cho hai điểm
3; 2 , 3;1
A B và đường thẳng
d
có
phương trình:
2 3 0
x y
. Phương trình đường thẳng
song song với
d
và đi qua
trung điểm
M
của đoạn
AB
A.
2 1 0
x y
. B.
2 1 0
x y
. C.
2 1 0
x y
. D.
2 1 0
x y
.
Lời giải
Chọn D
Vì đường thẳng
song song với
d
nên phương trình đường thẳng
: 2 0
x y c
.
M
là trung điểm
1
0;
2
AB M
.
1
0 2. 0 1
2
M c c
.
Vậy phương trình đường thẳng
: 2 1 0
x y
.
Câu 36. Trong các mệnh đề sau, mệnh đề nào sai?
A.
n
,
2
11 2
n n
chia hết cho
11
. B.
n
,
2
1
n
chia hết cho
4
.
C. Tồn tại số nguyên tố chia hết cho
5
. D.
n
,
2
2 8 0
n
.
Lời giải
Chọn B
Đáp án A:
3
n
thì
2
11 2 44
n n
chia hết cho
11
: đáp án đúng.
Đáp án C: số
5
là số nguyên tố chia hết cho
5
: đáp án đúng.
Đáp án D:
2
2
2 8 0
2
n
n
n
: đáp án đúng.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Đáp án B sai vì
2
2 1
n k
n
n k
,với
k
nguyên dương.
Với
2 2
2 1 4 1
n k n k
không chia hết cho 4.
Với
2 2
2 1 1 4 4 2
n k n k k
không chia hết cho 4.
Câu 37. Cho hàm số
2
( ) ( 10) 1
y f x mx m x
. Có bao nhiêu giá trị nguyên của tham số m để hàm
số
( )
f x
nghịch biến trên khoảng
2 ;
?.
A.
3
. B. vô số. C.
1
. D.
2
.
Lời giải
Chọn A
+ m=0,
( ) 10x 1
f x
, hàm số này nghịch biến trên
nên m=0 thỏa
+m>0 không thỏa
+m<0, yêu cầu trở thành
( 10)
2 10 4 2
2
m
m m m
m
. Ta được
0 2
m
Vậy
0 2
m
nên có 3 giá trị nguyên của tham số m thỏa mãn.
Câu 38. Tìm số giá trị nguyên của tham số m để hàm số
2
2
2 3 5
( )
2 2020
x x
y f x
mx mx
có tập xác định
là
A.
2020
. B.
2019
. C.
2021
. D.
4040
.
Lời giải
Chọn A
Hàm số xác định khi
2
2 2
2 3 5 1
0 0
2 2020 2 2020
x x
mx mx mx mx
vì
2
2 3 5 0,
x x x R
Ta được:
2
2 2020 0,(1)
mx mx
Do đó hàm số có tập xác định là R khi (1) thỏa
x R
Ta xét hai trường hợp
+TH1:
0
m
thỏa
+TH2:
0
m
, yêu cầu là
2
0
0
2020 0
2020 0
2020 0
m
m
m
m
m m
Vậy
2019;0 ,m m
nên có 2020 giá trị nguyên của m thỏa
Câu 39. Tìm tổng tất cả các giá trị nguyên của tham số
m
để phương trình (1) vô nghiệm
2
1 2 1 2 0 1
m x m x m .
A.
1
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn B
Trường hợp 1:
1
m
.
Phương trình
1
trở thành:
3 0
(vô lý). Vậy
1
m
phương trình
1
vô nghiệm.
Trường hợp 2:
1
m
. Phương trình
1
là phương trình bậc hai.
Phương trình (1) vô nghiệm khi và chỉ khi
2
1 1 2 1 2 1 0
m m m m m
1
1
2
m . Vì
m
nên
0
m
.
Vậy tổng các giá trị của
m
là:
1 0 1
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 40. Cho hệ phương trình :
2 2
2 1
x y a
x y a
. Các giá trị thích hợp của tham số
a
để tổng bình
phương hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất
A.
1
.
2
a
B.
1.
a
C.
1.
a
. D.
1
.
2
a
Lời giải
Chọn D
Ta có :
2 2
2 1
x y a
x y a
4 2 4 2
2 1
x y a
x y a
5
5
3
5
a
x
a
y
2
2
2 2
2 2 2
5 9 10 110 25
2 5
1 1 9 9
2 2
5 25 25 5 5 2 10
2
a a a
a
a
y ax a
Đẳng thức xảy ra khi
1
2
a
.
Câu 41. Gọi
S
là tập hợp các giá trị thực của tham số
a
để bất phương trình
2
2 2
9 8 0
2 1 2 0
x x
x a x a a
có nghiệm duy nhất. Tổng các phần tử của tập
S
bằng
A.
1
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn C
Ta có
2
2 2
9 8 0
2 1 2 0
x x
x a x a a
1 8
2
x
a x a
.
Vậy hệ bất phương trình có nghiệm duy nhất
2 1 1
8 8
a a
a a
.
1;8
S nên tổng phần tử của tập
S
bằng
7
.
Câu 42. Cho
;
2 2
và
;
2
và
tan tan 1
. Gọi
S
là tập hợp các số đo của góc
thỏa
1 tan 1 tan 2
. Tổng các phần tử của tập
S
bằng
A.
5
4
. B.
4
. C.
4
. D.
3
2
.
Lời giải
Chọn D
Ta có
1 tan 1 tan 2
tan tan 1 tan tan
tan tan
1
1 tan tan
(vì
tan tan 1
)
tan 1
.
Mà
;
2 2
và
;
2
3
0
2
nên
4
hoặc
5
4
.
Suy ra
5
;
4 4
S
nên tổng các phần tử của tập
S
bằng
3
2
.
Câu 43. Cho hình thoi
ABCD
tâm
O
có cạnh bằng
a
và
60
ABD
. Gọi
I
là điểm thỏa mãn
2 0
IC ID
. Tính tích vô hướng
.
AO BI
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2
.
4
a
AO BI
. B.
2
.
2
a
AO BI
. C.
2
.
2
a
AO BI
. D.
2
.
4
a
AO BI
.
Lời giải
Chọn C
Ta có:
Do
ABCD
là hình thoi có cạnh bằng
a
và
60
ABD
nên
ABD
và
BCD
là các tam giác đều
cạnh
a
.
Ta có:
. . .
AO BI AO BD DI AO DI
2 2
. .
3 3
AO DC AO AB
2
2 3
. . .cos30
3 2 2
a a
a .
Câu 44. Cho
1
cos2
4
a
. Tính
sin2 cos
a a
với 0
2
a
.
A.
3 10
16
. B.
3 10
8
. C.
5 6
8
. D.
5 6
16
.
Lời giải
Chọn D
Do 0
2
a
nên
sin 0, cos 0
a a
.
Ta có:
1
cos2
4
a
2
2
1
2cos 1
4
1
1 2sin
4
a
a
2
2
5
cos
8
3
sin
8
a
a
10
cos
4
6
sin
4
a
a
.
Suy ra
2
sin2 cos 2sin cos
a a a a
6 5 5 6
2. .
4 8 16
.
Câu 45. Có bao nhiêu giá trị của tham số
m
để giá trị lớn nhất của hàm số
2
2
x m
y
x m
trên đoạn
0;4
bằng
1
?
A.
3
. B.
2
. C.
1
. D.
0
.
Lời giải
Chọn C
Điều kiện:
0;4
m
Ta có
2
2
2
0
m m
y
x m
0;4
x
.
Suy ra hàm số đồng biến trên
0;4
O
I
C
B
A
D

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
YCBT
4 1
0;4
y
m
2
2
1
4
0;4
m
m
m
2
6 0
0;4
m m
m
3
2
0;4
m
m
m
3
m
.
Câu 46. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
2 4 4
m x x m
có nghiệm
âm?
A.
0
m
. B.
4
m
. C.
0 4
m . D.
0
m
và
4
m
.
Lời giải
Chọn A
Ta có:
2
2 4 4 4 4 1
m x x m m m x m
Với
0: 1 0 4
m x
: Phương trình vô nghiệm
Với
4: 1 0 0
m x
: Phương trình nghiệm đúng với mọi x
Với
0
m
và
4
m
:
1
1 x
m
,
1
0 0
m
m
Do đó phương trình có nghiệm âm khi và chỉ khi
0
m
.
Câu 47. Cho hệ phương trình
2
2 3 2
3 2 2 0
3 3 1 2 1 3 1
x y x y
x x x x y
. Gọi
0 0
;
x y
là một nghiệm
của hệ đã cho với
0
2
y
. Tính tổng
0 0
x y
.
A.
2 2
4
. B.
2 3
2
. C.
2 2
2
. D.
6 1
2
.
Lời giải
Chọn B
Điều kiện
0
x
. Đặt
, 0
t x t
phương trình thứ nhất trở thành
2 2
3 2 2 3 2 2 0 2 1 2 0
t y t y t t yt y t t y t
2 1 0
t t y
2
1
t l
t y
Với
1
t y
ta được
1 1
x y x
y
Thay vào PT thứ 2 ta được
2 3 2
3 3 1 2 1 3
x x x x x
2
2
2
2 3 1
1 2 3 1 0
3 3 1
x x
x x x
x x x
2
2
2 3 1 0
1
1 0 *
3 3 1
x x
x
x x x
1
1
2
x tm
x tm
(PT
*
vô nghiệm vì
0
x
)
Với
1 2
x y
(loại). Với
1 2
1
2 2
x y
. Vậy
0 0
2 3
.
2
x y
Câu 48. Cho hai số thực
,
x y
thỏa mãn
2 2
1.
x y xy
Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá
trị nhỏ nhất của
.
S xy x y
Giá trị của
2
M m
bằng
2 3 2
3 3 1 2 2 1 0
x x x x x x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2 3
.
3
B.
2 3
.
9
C.
3
.
9
D.
3
.
3
Lời giải
Chọn A
Đặt ,xy t từ giả thiết
2 2
1 2 1.
x y xy xy xy xy t
Lại có
2
2 2
1
1 3 3 .
3
x y xy x y xy xy t
Vậy
1
;1 .
3
t
Xét
2
2 2 2 2 2 2 2 2 2 2
2 1 2 1S x y x y x y x y xy x y xy xy t t
Nếu
0 1,t
ta có
2
4. . . 1
2 2
t t
S t
Áp dụng BĐT
3
3
a b c
abc
với
, , 0,a b c
ta có
3
2
1
4
2 2
4. .
3 27
t t
t
S
Dấu bằng xảy ra khi và chỉ khi
2
1 0 .
2 3
t
t t
Nếu
1
0,
3
t
ta có
2
2
1
0
4
9
1 .
4
27
0 1
3
t
t t
t
Dấu bằng xảy ra khi và chỉ khi
1
.
3
t
Vậy
2
4
,
27
S
dấu bằng xảy ra khi và chỉ khi
1
3
t
hoặc
2
.
3
t
Do đó
2 3
2 3 2 3 2 3
9
2 .
9 9 3
2 3
9
M
S M m
m
Câu 49. Cho tam giác là tam giác đều có cạnh bằng 12cm. Biết tập hợp các điểm thỏa mãn
3 4 3 4MA MB MC MA MB MC
là một đường tròn. Xác định bán kính của đường tròn
đó?
A.
3 13
2
cm. B.
13
8
cm. C. 12 13 cm. D. 6 13 cm.
Lời giải
Chọn A
Gọi F là điểm sao cho 3CF CB
; dựng hình bình hành ACFD khi đó 3CD CA CB
.
ABC
M
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
E
CF
sao cho
DE CF
và gọi là điểm thỏa mãn
3 4 0 3 4 3 3 8 3 8
IA IB IC IA IB CI CI IA CI IB CI CA CB CI
. Khi đó
là điểm cố định.
Do tam giác
ABC
là tam giác đều nên có chiều cao bằng
12 3
6 3
2
DE cm.
Áp dụng định lí Pytago cho tam giác vuông
DEF
ta tính được
2 2
6
EF DF DE
Theo đề bài:
3 4 3 4
MA MB MC MA MB MC
8 3 4 3 3 4
MI IA IB IC MC CA MC CB MC
2
2 2 2
8 3 42 6 3 12 13
MI CA CB CE ED
12 13 3 13
8 2
IM
.
Vậy thuộc đường tròn tâm bán kính
3 13
2
cm.
Câu 50: Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
với
3; 4
A
, tâm đường tròn nội tiếp
2;1
I , tâm đường tròn ngoại tiếp
1
;1
2
J
. Tính
,
d O BC
.
A.
2
. B.
2 5
. C.
10
. D.
5 2
.
Lời giải
Chọn B
Gọi
( )
C
là đường tròn tâm
J
, bán kính
AJ
.
2
2
1 125
( ): 1 0; ( ) : 1
2 4
AI x y C x y
.
Gọi
9 7
( ) ;
2 2
D AI C D
.
Ta có:
BID BAI IBA CAD IBC DBC IBC IBD
DB DI
.
Mà
DC DB DC DB DI
.
Do đó
,
B C
là giao điểm của
( )
C
và
( ')
C
, với
( ')
C
là đường tròn tâm
D
bán kính
ID
.
Ta có:
2 2
9 7 25
( '):
2 2 2
C x y
.
I
I
M
I
D
I
J
A
B
C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Tọa độ
,
B C
thỏa hệ phương trình:
2
2
2 2
1 125
1
2 4
2 10 0
9 7 25
2 2 2
x y
x y
x y
.
Vậy
( ):2 10 0
BC x y
, 2 5
d O BC .
……………HẾT………….

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 17
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Một vectơ chỉ phương của đường thẳng
d
:
2 3
3
x t
y t
là
A.
2; 3
u
. B.
3; 1
u
. C.
3;1
u
. D.
3; 3
u
.
Câu 2. Trong các công thức sau, công thức nào sai ?
A.
1
cos cos cos – cos .
2
a b a b a b
B.
1
sin sin cos – – cos .
2
a b a b a b
C.
1
sin cos sin – s
2
.
in
a b a b a b
D.
1
sin cos sin cos .
2
a b a b a b
Câu 3. Cho nhị thức
2 3
f x x
, khẳng định nào sau đây là đúng?
A.
0,
f x
x . B.
0,
f x
3
;
2
x
.
C.
0,
f x
2
;
3
x
. D.
0,
f x
3
;
2
x
.
Câu 4. Giải bất phương trình
2 1 2 3
x x
thu được tập nghiệm có dạng
[ ; )
S a
. Số
a
bằng
A.
1
2
. B.
1
2
. C.
2
3
. D.
2
3
.
Câu 5. Đường thẳng đi qua
1;2
A
, nhận
1; 2
n
làm vectơ pháp tuyến có phương trình là
A.
2 4 0
x y
. B.
4 0
x y
. C.
2 5 0
x y
. D.
2 4 0
x y
.
Câu 6. Cho
1
sin
2
. Tính
cos2
E .
A.
1
2
. B.
3
2
. C.
3
2
. D.
1
2
.
Câu 7. Cho
sin 0
. Tính
cos
?
A.
cos 1
. B.
cos 0
. C.
cos 1
cos 1
. D.
cos 1
.
Câu 8. Cho 0
. Khẳng định nào sau đây đúng?
A.
sin 0.
B.
sin 0.
C.
cos 0.
D.
cos 0.
Câu 9. Trong hệ tọa độ
Oxy
, cho hai đường thẳng
1
:2 2 0
d x y
và
2
: 3 1 0
d x y
. Góc giữa
hai đường thẳng
1
d
,
2
d
có giá trị gần nhất với số đo nào dưới đây:
A.
98
. B.
99
. C.
82
. D.
80
.
Câu 10. Trong các phương trình dưới đây, đâu là phương trình đường tròn?
A.
2 2
2 2 5 0
x y x y
. B.
2 2
2 2 8 4 8 0
x y x y
.
C.
2 2
3 3 5 0
x y x y
. D.
2 2
2 2 8 4 8 0
x y x y
.
Câu 11. Phần gạch chéo ở hình vẽ dưới đây (tính cả các điểm nằm trên đường thẳng biên) biểu diễn
miền nghiệm của bất phương trình nào?
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
3 2 6
x y
. B.
3 2 6
x y
.
C.
2 3 6
x y
. D.
2 3 6
x y
.
Câu 12. Các tiêu điểm của elip
E
:
2 2
1
49 4
x y
là
A.
1 2
7;0 , 7;0
F F . B.
1 2
3 5;0 , 3 5;0
F F
.
C.
1 2
45;0 , 45;0
F F . D.
1 2
2;0 , 2;0
F F .
Câu 13. Cho tam thức bậc hai
2
6
f x x x
. Khẳng định nào sau đây đúng?
A.
0 2;3
f x x
. B.
0 ; 2 3;f x x
.
C.
0 ; 2
f x x
. D.
0 2;3
f x x
.
Câu 14. Cho
3
sin
5
α
và góc
α
thỏa mãn
90 180
α
. Khi đó:
A.
3
cot
4
α
. B.
4
cos
5
α
. C.
4
tan
3
α
. D.
4
cos
5
α
.
Câu 15. Số đo bằng đơn vị radian của góc
270
là :
A.
. B.
2
3
. C.
3
4
. D.
3
2
.
Câu 16. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 2 3 1
C x y
. Tọa độ tâm
I
là:
A.
2;3
I
. B.
2; 3
I
. C.
3
1;
2
I
. D.
3
1;
2
I
.
Câu 17. Cho điểm
0 0
;
M x y
và đường thẳng
:
0
ax by c
với
2 2
0
a b
. Khi đó khoảng cách
;
M
d
là ?
A.
0 0
;
2 2 2
M
ax by c
d
a b c
. B.
0 0
;
2 2 2
M
ax by c
d
a b c
.
C.
0 0
;
2 2
M
ax by c
d
a b
. D.
0 0
;
2 2
M
ax by c
d
a b
.
Câu 18. Cho hai đường thẳng
1
:
1 0
x y
và
2
:
1
x t
y t
. Khi đó hai đường thẳng này
A. vuông góc nhau. B. cắt nhau nhưng không vuông góc.
C. trùng nhau. D. song song với nhau.
Câu 19. Chọn điểm
1;0
A
làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm
O
2
3
y
x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
cuối
M
của cung lượng giác có số đo
4
.
A.
M
là điểm chính giữa của cung phần tư thứ
I
.
B.
M
là điểm chính giữa của cung phần tư thứ
II
.
C.
M
là điểm chính giữa của cung phần tư thứ
III
.
D.
M
là điểm chính giữa của cung phần tư thứ
IV
.
Câu 20. Tập nghiệm của bất phương trình
2
3 2 0
x x
là:
A.
;1 2;
. B.
2;
. C.
1;2
. D.
;1
.
Câu 21. Cho
ABC
có
(1;1)
A
,
(0; 2)
B
,
(4;2)
C
. Phương trình đường trung tuyến AM là
A.
2 3 0
x y
. B.
2 3 0
x y
. C.
2 0
x y
. D.
0
x y
.
Câu 22. Bất phương trình
2
1 2 1 3 0
m x m x m
với mọi
x khi
A.
1
m
. B.
2
m
. C.
1
m
. D.
2 7
m
.
Câu 23. Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình chính tắc của Elip có độ dài trục lớn gấp
đôi độ dài trục bé và có tiêu cự bằng
6
.
A.
2 2
1
12 9
x y
. B.
2 2
1
2 3 3
x y
. C.
2 2
1
12 6
x y
. D.
2 2
1
12 3
x y
.
Câu 24. Rút gọn biểu thức
sin sin cos
2 2
S x x x cos x
ta được
A.
0.
S
B.
sin .
S x
C.
2sin2 .
S x
D.
2 .
S sin x
Câu 25. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
3;1
A
và
2;5
B
. Hãy viết phương trình
đường tròn
C
nhận
AB
làm đường kính.
A.
2
2
1
3 41
2
x y
. B.
2 2
3 1 41
x y
.
C.
2
2
1 41
3
2 2
x y
. D.
2
2
1 41
3
2 4
x y
.
Câu 26. Trong mặt phẳng tọa độ
Oxy
cho điểm
5; 3
A
và đường thẳng
:3 4 20 0
d x y
. Viết
phương trình đường tròn
C
có tâm
A
và tiếp xúc với đường thẳng
d
.
A.
2 2
49
3 4
25
x y . B.
2 2
49
5 3
25
x y .
C.
2 2
7
5 3
5
x y
. D.
2 2
7
5 3
25
x y .
Câu 27. Viết phương trình tiếp tuyến của đường tròn
C
tại điểm
5; 2
M
biết đường tròn có phương
trình
2 2
2 1 10
x y
.
A.
3 13 0
x y
. B.
3 17 0
x y
. C.
3 17 0
x y
. D.
3 11 0
x y
.
Câu 28. Trong mặt phẳng
Oxy
, cho đường thẳng
: 1 0
x y
. Viết phương trình đường thẳng
d
đi
qua
1; 1
A và tạo với
một góc
0
45
.
A.
1 0
1 0
x
y
. B.
1 0
x y
. C.
1 0
x
. D.
1 0
y
.
Câu 29. Tập nghiệm của bất phương trình
3 4 2 4
2 2
x x
x x
là?
A.
2;8
. B.
; 2 8;
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
2;2 2;8
. D.
8;
.
Câu 30. Cho điểm
1;2
M
và đường thẳng
:
5 2
x t
t
y t
. Tọa độ của điểm
'
M
là điểm đối
xứng của điểm
M
qua đường thẳng
là:
A.
9 12
;
5 5
. B.
2 6
;
5 5
. C.
3
0;
5
. D.
3
; 5
5
.
Câu 31. Biết
5
sin
13
a
,
3
cos
5
b
,0
2 2
a b
. Hãy tính
sin
a b
.
A.
33
65
. B.
63
65
. C.
56
65
. D.
0
.
Câu 32. Cho phương trình
2
2 2 – 2 –1 0
x m x m
1
. Với giá trị nào của
m
thì phương trình
1
có
nghiệm:
A.
5
m
hoặc
1
m
. B.
5
m
hoặc
1
m
.
C.
5 1
m
. D.
1
m
hoặc
5
m
.
Câu 33. Tập nghiệm của bất phương trình
2
2 8 2 0
x x x
là
A.
2; .
B.
2; .
C.
4; .
D.
4; .
Câu 34. Số nghiệm nguyên thuộc khoảng
10;10
của bất phương trình
2
1 1
1 2
x x x
là
A.
10.
B.
8.
C.
9.
D.
11.
Câu 35. Cho đường thẳng
d
có phương trình
7
5 5
x t
t
y t
, phương trình tham số của đường
thẳng qua
2;3
M và song song với
d
là:
A.
2
3 5
x s
y s
. B.
5 2
1 3
x s
y s
. C.
5
x s
y s
. D.
3 5
2
x s
y s
.
Câu 36. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
đi qua hai điểm
1;0
A
,
1;2
B
và có
tâm
thuộc đường thẳng
:2 3 0
x y
. Tìm phương trình của đường tròn
C
.
A.
2 2
1 2 10
x y
. B.
2 2
2 1 10
x y
.
C.
2 2
2 1 10
x y
. D.
2 2
2 1 10
x y
.
Câu 37. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai đường thẳng
1
:
2
x t
d t
y t
;
: 3 4 2 0
x y
. Điểm
;
M a b d
thỏa
( , ) 2. ( , )
d M d M Ox
và
b 0
. Giá trị của biểu
thức
T a b
bằng
A.
13
11
. B.
11
3
. C.
40
11
. D.
33
11
.
Câu 38. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có hai đường cao là
BM
và
CN
. Giả
sử
BC
,
BM
,
CN
lần lượt có phương trình là
9 6 0
x y
,
3 8 0
x y
,
6 0
x y
.
Tọa độ đỉnh
A
là
A.
3; 1
A
. B.
6;0
A
. C.
0;2
A
. D.
2;4
A
.
Câu 39. Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
d
qua
(1;4)
M
và cắt hai tia
,
Ox Oy
lần lượt
tại
,
A B
sao cho diện tích tam giác
OAB
nhỏ nhất. Tính tổng các hoành độ và tung độ của
,
A B
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
0
. B.
16
. C.
10
. D.
5
.
Câu 40. Trong mặt phẳng tọa độ Oxy cho tam giác
ABC
có đường cao :2 3 12 0,AH x y đường
trung tuyến :2 3 0,AN x y với
N
thuộc đường thẳng
BC
gọi
1
;2
2
M
là trung điểm của
.AB
Biết điểm ( ; ).C a b Tính
2020P a b
A.
2019
B.
2020
C.
2021
D.
2022
Câu 41. Trong mặt phẳng với hệ tọa độ Oxy , cho đường tròn
C
có phương trình:
2 2
x y 4x 8y 5 0
. Phương trình đường thẳng vuông góc với đường thẳng
:d 3x 4y 12 0 và cắt đường tròn
C
theo một dây cung có độ dài bằng 8 là:
A. 4x 3y 19 0 và 4x 3y 11 0 . B. 4x 3y 5 0 và 4x 3y 35 0 .
C. 3x 4y 25 0 và 3x 4y 5 0 . D. 4x 3y 19 0 và 4x 3y 11 0 .
Câu 42. Có bao nhiêu giá trị nguyên của tham số
m
để hệ bất phương trình sau vô nghiệm:
2
2
7 12 0
3 0
x x
x m
A. Vô số B. 3 C.
5
D. 7
Câu 43. Trong không gian Oxy , cho đường tròn
2 2
: 2 6 1 0
C x y x y
. Viết phương trình tiếp
tuyến của đường tròn
C
, biết tiếp tuyến song song với đường thẳng :3 4 0.d x y
A. 3 4 0x y và 3 4 30 0x y . B.
3
2 0
2
x y và
3
2 15 0
2
x y .
C.
3 4 30 0
x y
. D.
3 4 30 0
x y
.
Câu 44. Trong mặt phẳng toạ độ Oxycho elip
2 2
: 1
25 9
x y
E
. Gọi
0 0
;M x y thuộc Elip thoả mãn
bán kính qua tiêu điểm này bằng 3 lần bán kính qua tiêu điểm kia. Khi đó giá trị
2 2
0 0
x y
bằng
A.
17
4
. B.
137
32
. C.
61
4
. D.
117
4
.
Câu 45. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh
C
của ngọn núi. Biết rằng độ cao
70mAB , phương nhìn AC tạo với phương nằm ngang góc
0
30
, phương nhìn BC tạo với
phương nằm ngang góc
0
15 30'
(tham khảo hình vẽ). Ngọn núi đó có độ cao so với mặt đất gần
nhất với giá trị nào sau đây?
A. 135m. B. 234m. C. 165m. D. 195m.
Câu 46. Cho đường tròn
2 2
:( 2) ( 1) 5
C x y
và điểm (3; 2)M . Gọi
1
M
,
2
M lần lượt là hai tiếp
điểm của hai tiếp tuyến kẻ từ M đến đường tròn
C ; Hãy viết phương trình của đường thẳng
1 2
M M
A.
1 2
( ): 3 4 0M M x y B.
1 2
( ): 3 4 0M M x y
C.
1 2
( ): 3 4 0M M x y D.
1 2
( ): 2 3 4 0M M x y

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 47. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
2
2
: 3 1
C x y
. Giả sử điểm
;
M x y
thuộc đường tròn
C
sao cho tổng khoảng cách từ
M
đến hai điểm
3;0
A ,
3;0
B là lớn
nhất. Khi đó giá trị
x y
là
A.
4
. B.
5
. C.
2
. D.
15
4
.
Câu 48. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
và đường thẳng
d
lần lượt có phương trình
2 2
2
1 2 3
x y
và
3 4 1 0
x y
. Viết phương trình đường thẳng
, biết
cắt
C
theo dây cung có độ dài lớn nhất và
tạo với
d
một góc
45
.
A.
4 3 2 0
x y
và
4 3 10 0
x y
.
B.
7 15 0
x y
và
7 5 0
x y
.
C.
3 2 4 3 0
x y
và
2 3 2 3 2 0
x y
.
D.
7 9 0
x y
và
7 13 0
x y
.
Câu 49. Cho phương trình đường tròn
2 2
: 9
C x y
tâm
I
và phương trình đường thẳng
: 1 2 1 0
m
d m x m y
với
m
là tham số nguyên. Biết đường thẳng
m
d
luôn cắt
đường tròn
C
tại hai điểm
,
A B
. Tính diện tích lớn nhất của tam giác
IAB
A.
5
. B.
6
. C.
7
. D.
8
.
Câu 50. Trong mặt phẳng
Oxy
, cho tam giác
ABC
có điểm
4;3
A
, đường phân giác trong
: 2 5 0
BI x y
, đường trung tuyến
: 4 13 10 0
BM x y
. Khi đó điểm
C
có hoành độ là:
A.
12
. B.
12
. C.
11
7
. D.
1
7
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 17
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.B 2.D 3.D 4.A 5.C 6.A 7.C 8.B 9.C 10.B
11.A 12.B 13.D 14.B 15.D 16.B 17.D 18.D 19.A 20.C
21.C 22.C 23.D 24.D 25.D 26.B 27.C 28.A 29.C 30.A
31.A 32.A 33.C 34.C 35.A 36.D 37.D 38.C 39.C 40.B
41.D 42.D 43.C 44.B 45.A 46.A 47.A 48.D 49.D 50.A
HƯỚNG DẪN GIẢI
Câu 1. Một vectơ chỉ phương của đường thẳng d :
2 3
3
x t
y t
là
A.
2; 3u
. B.
3; 1u
. C.
3;1u
. D.
3; 3u
.
Lời giải
Chọn B
Vectơ chỉ phương của đường thẳng d là
3; 1u
.
Câu 2. Trong các công thức sau, công thức nào sai ?
A.
1
cos cos cos – cos .
2
a b a b a b
B.
1
sin sin cos – – cos .
2
a b a b a b
C.
1
sin cos sin – s
2
.
in
a b a b a b
D.
1
sin cos sin cos .
2
a b a b a b
Lời giải
Chọn D
Công thức đúng là:
1
sin cos sin – s
2
.ina b a b a b
Câu 3. Cho nhị thức
2 3
f x x
, khẳng định nào sau đây là đúng?
A.
0,f x
x . B.
0,f x
3
;
2
x
.
C.
0,f x
2
;
3
x
. D.
0,f x
3
;
2
x
.
Lời giải
Chọn D
+)
3
0 .
2
f x x
+) Bảng xét dấu của
2 3f x x
.
+) Vậy
3
0 ; .
2
f x x
Câu 4. Giải bất phương trình
2 1 2 3
x x
thu được tập nghiệm có dạng
[ ; )S a
. Số a bằng
A.
1
2
. B.
1
2
. C.
2
3
. D.
2
3
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn A
+) Bảng xét dấu của
2 1
f x x
.
+) Xét hai trường hợp:
Với
1
2
x .
Khi đó:
1
2 1 2 3 1 2 2 3 4 2
2
x x x x x x
.
Kết hợp với
1
2
x , ta được:
1 1
;
2 2
x
.
Với
1
2
x
.
Khi đó:
2 1 2 3 2 1 2 3 1 3x x x x
(luôn đúng x )
Kết hợp với
1
2
x , ta được:
1
;
2
x
.
Vậy tập nghiệm của bất phương trình đã cho là
1
;
2
S
.
Câu 5. Đường thẳng đi qua
1;2A
, nhận
1; 2
n
làm vectơ pháp tuyến có phương trình là
A.
2 4 0x y
. B.
4 0x y
. C.
2 5 0x y
. D.
2 4 0x y
.
Lời giải
Chọn C
Phương trình đường thẳng cần tìm:
1. 1 2. 2 0 2 5 0 x y x y
.
Câu 6. Cho
1
sin
2
. Tính cos2
E .
A.
1
2
. B.
3
2
. C.
3
2
. D.
1
2
.
Lời giải
Chọn A
Ta có
2
2
1 1
cos2 1 2sin 1 2.
2 2
.
Câu 7. Cho sin 0 . Tính cos ?
A. cos 1 . B. cos 0 . C.
cos 1
cos 1
. D. cos 1 .
Lời giải
Chọn C
Ta có:
2 2 2
cos 1
sin cos 1 cos 1
cos 1
.
Câu 8. Cho 0 . Khẳng định nào sau đây đúng?
A. sin 0. B. sin 0. C. cos 0. D. cos 0.
Lời giải
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dựa vào bảng xét dấu của các giá trị lượng giác.
Ta có, với 0
sin 0.
Câu 9. Trong hệ tọa độ
Oxy
, cho hai đường thẳng
1
:2 2 0
d x y
và
2
: 3 1 0
d x y
. Góc giữa
hai đường thẳng
1
d
,
2
d
có giá trị gần nhất với số đo nào dưới đây:
A.
98
. B.
99
. C.
82
. D.
80
.
Lời giải
Chọn C
1
d
có vector pháp tuyến
1
2; 1
n
.
2
d
có vector pháp tuyến
2
1;3
n
.
Ta có:
1 2
1 2 1 2
2
2 2 2
1 2
2.1 1 .3
.
1
cos , cos ,
5 2
.
2 1 . 1 3
n n
d d n n
n n
.
1 2
, 81,86
d d
chọn C
Câu 10. Trong các phương trình dưới đây, đâu là phương trình đường tròn?
A.
2 2
2 2 5 0
x y x y
. B.
2 2
2 2 8 4 8 0
x y x y
.
C.
2 2
3 3 5 0
x y x y
. D.
2 2
2 2 8 4 8 0
x y x y
.
Lời giải
Chọn B
Phương án A, D: loại vì sai dạng phương trình đường tròn
Phương án C:
2 2 2 2
3 3
3 3 5 0 2. 2 5 0
2 2
x y x y x y x y
Ta có:
2 2
3 3 1
5 0
2 2 2
phương án C không phải phương trình đường tròn.
Phương án B:
2 2 2 2
2 2 8 4 8 0 2.2 2. 2 4 0
x y x y x y x y
Ta có:
2
2
2 2 4 8 0
phương án B là phương trình đường tròn.
Câu 11. Phần gạch chéo ở hình vẽ dưới đây (tính cả các điểm nằm trên đường thẳng biên) biểu diễn
miền nghiệm của bất phương trình nào?
A.
3 2 6
x y
. B.
3 2 6
x y
.
C.
2 3 6
x y
. D.
2 3 6
x y
.
Lời giải
Chọn A
Đường thẳng
đi qua hai điểm
2;0
A và
0;3
B có phương trình là
3 2 6
x y
nên phần
gạch chéo ở hình vẽ trên biểu diễn miền nghiệm của một trong hai bất phương trình
3 2 6
x y
O
2
3
y
x
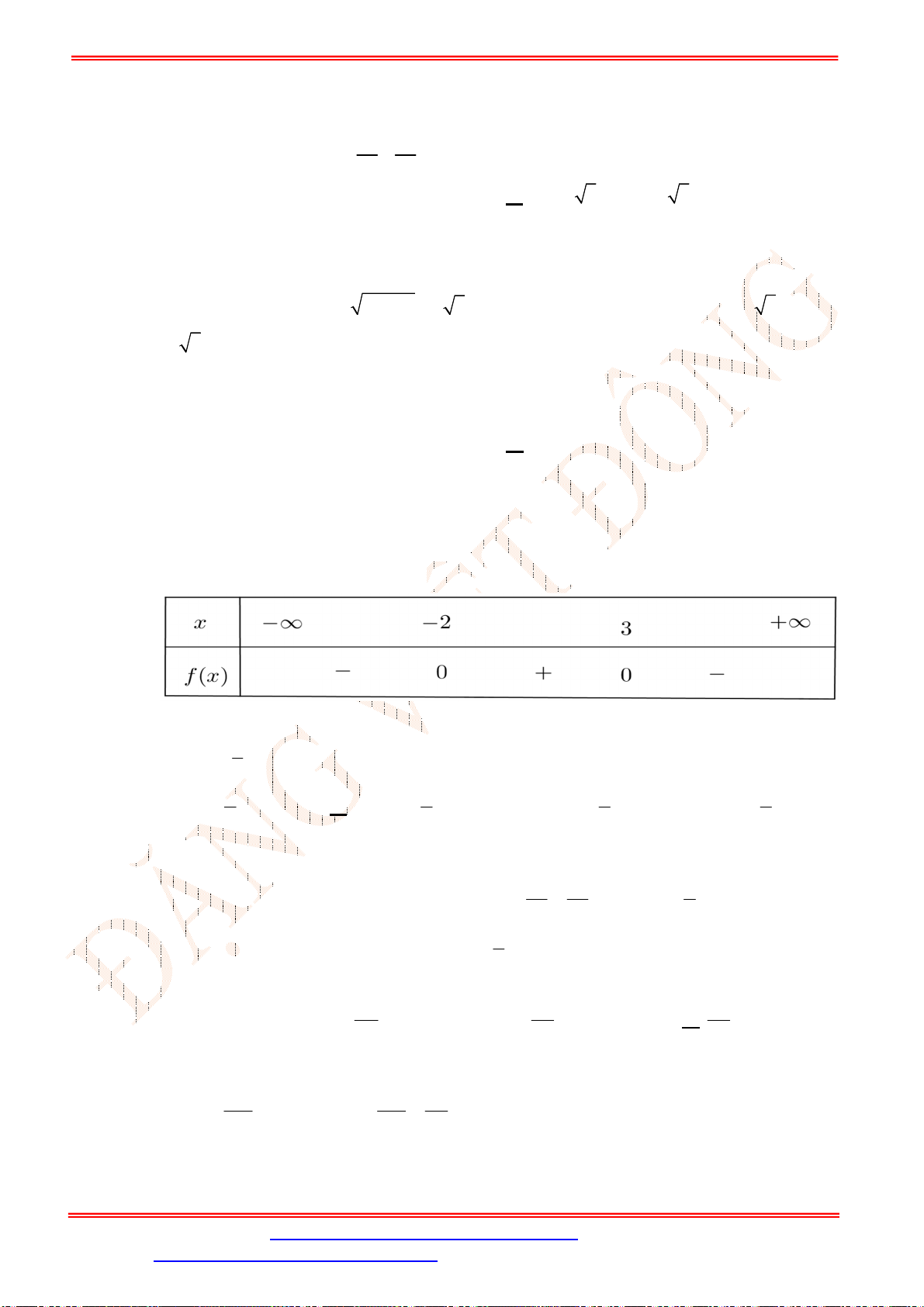
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
và 3 2 6x y . Dễ thấy điểm
0;0O thuộc miền nghiệm của bất phương trình 3 2 6x y
nên chọn A.
Câu 12. Các tiêu điểm của elip
E :
2 2
1
49 4
x y
là
A.
1 2
7;0 , 7;0F F . B.
1 2
3 5;0 , 3 5;0F F
.
C.
1 2
45;0 , 45;0F F . D.
1 2
2;0 , 2;0F F .
Lời giải
Chọn B
Ta có
7a
,
2b
nên
2 2
3 5c a b
. Do đó
E có hai tiêu điểm là
1
3 5;0F
và
2
3 5;0F
. Vậy chọn B.
Câu 13. Cho tam thức bậc hai
2
6
f x x x
. Khẳng định nào sau đây đúng?
A.
0 2;3f x x
. B.
0 ; 2 3;f x x
.
C.
0 ; 2f x x
. D.
0 2;3f x x
.
Lời giải
Chọn D
Ta có:
2
2
6 0
3
x
x x
x
.
Bảng xét dấu của
f x
:
Từ bảng xét dấu ta có:
0 2;3f x x
và
0 ; 2 3;f x x
Câu 14. Cho
3
sin
5
α
và góc α thỏa mãn 90 180α . Khi đó:
A.
3
cot
4
α
. B.
4
cos
5
α
. C.
4
tan
3
α
. D.
4
cos
5
α
.
Lời giải
Chọn B
Ta có:
2 2 2 2
9 16 4
sin cos 1 cos 1 sin 1 os
25 25 5
α α α α c α
.
Vì 90 180α nên cos 0α . Vậy:
4
cos
5
α
.
Câu 15. Số đo bằng đơn vị radian của góc
270
là :
A.
. B.
2
3
. C.
3
4
. D.
3
2
.
Lời giải
Chọn D
Ta có 1
180
3
270 270
180 2
.
Câu 16. Trong mặt phẳng
Oxy
, cho đường tròn
2 2
: 2 3 1C x y
. Tọa độ tâm I là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2;3
I
. B.
2; 3
I
. C.
3
1;
2
I
. D.
3
1;
2
I
.
Lời giải
Chọn B
Đường tròn
C
có tâm
;
I a b
và bán kính
R
có phương trình
2 2
2
:
C x a y b R
.
Vậy đường tròn
2 2
: 2 3 1
C x y
có tâm
2; 3
I
.
Câu 17. Cho điểm
0 0
;
M x y
và đường thẳng
:
0
ax by c
với
2 2
0
a b
. Khi đó khoảng cách
;
M
d
là ?
A.
0 0
;
2 2 2
M
ax by c
d
a b c
. B.
0 0
;
2 2 2
M
ax by c
d
a b c
.
C.
0 0
;
2 2
M
ax by c
d
a b
. D.
0 0
;
2 2
M
ax by c
d
a b
.
Lời giải
Chọn D
Công thức ở sách giáo khoa
Câu 18. Cho hai đường thẳng
1
:
1 0
x y
và
2
:
1
x t
y t
. Khi đó hai đường thẳng này
A. vuông góc nhau. B. cắt nhau nhưng không vuông góc.
C. trùng nhau. D. song song với nhau.
Lời giải
Chọn D
+ Từ
2
:
1
x t
y t
1 0
x y
+ Xét hệ phương trình :
1 0
1 0
x y
x y
, hệ vô nghiệm. Vậy
1 2
//
.
Câu 19. Chọn điểm
1;0
A
làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm
cuối
M
của cung lượng giác có số đo
4
.
A.
M
là điểm chính giữa của cung phần tư thứ
I
.
B.
M
là điểm chính giữa của cung phần tư thứ
II
.
C.
M
là điểm chính giữa của cung phần tư thứ
III
.
D.
M
là điểm chính giữa của cung phần tư thứ
IV
.
Lời giải
Chọn A
Theo giả thiết cung lượng giác đã cho có số đo bằng
4
, nên điểm
M
là điểm chính giữa của
cung phần tư thứ
I
.
Câu 20. Tập nghiệm của bất phương trình
2
3 2 0
x x
là:
A.
;1 2;
. B.
2;
. C.
1;2
. D.
;1
.
Lời giải
Chọn C
Ta có:
2
2
3 2 0
1
x
f x x x
x
.
Bảng xét dấu :

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dựa vào bảng xét dấu ta thấy
0 1 2.f x x
Câu 21. Cho ABC có
(1;1)A
,
(0; 2)B
,
(4;2)C
. Phương trình đường trung tuyến AM là
A.
2 3 0x y
. B.
2 3 0x y
. C.
2 0x y
. D.
0x y
.
Lời giải
Chọn C
M là trung điểm BC
(2;0)M
AM qua
(1;1)A
AM có 1 vtcp (1; 1)AM
AM có 1 vtpt (1;1)n
Phương trình tổng quát AM :
1.( 1) 1.( 1) 0 2 0x y x y
Câu 22. Bất phương trình
2
1 2 1 3 0 m x m x m
với mọi x khi
A. 1m . B. 2m . C. 1m . D. 2 7m .
Lời giải
Chọn C
2
1 2 1 3 0
m x m x m
1
Đặt
2
1 2 1 3f x m x m x m
TH1:
0 1 0 1
a m m
Khi đó,
1
trở thành:
4 0
( đúng x R )
1m thỏa yêu cầu bài toán.
TH2:
0 1
a m
2
1 1 3 4 4m m m m
Ta có:
0 1 0
0, 1
0 4 4 0
a m
f x x m
m
Vậy 1m thỏa yêu cầu bài toán.
Câu 23. Trong mặt phẳng với hệ tọa độ Oxy , viết phương trình chính tắc của Elip có độ dài trục lớn gấp
đôi độ dài trục bé và có tiêu cự bằng
6
.
A.
2 2
1
12 9
x y
. B.
2 2
1
2 3 3
x y
. C.
2 2
1
12 6
x y
. D.
2 2
1
12 3
x y
.
Lời giải
Chọn D
Elip cần tìm có dạng:
2 2
2 2
1
x y
a b
, ( 0)a b .
Ta có:
2 6 3c c
.
2 2 2
2 ;a b a b c
2 2
4 9b b
2
3b
2
3 9 12a .
Vậy phương trình elip cần tìm là:
2 2
1
12 3
x y
.
Câu 24. Rút gọn biểu thức
sin sin cos
2 2
S x x x cos x
ta được
A.
0.
S
B.
sin .
S x
C.
2sin2 .
S x
D.
2 .
S sin x
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
sin sin cos
2 2
.sin sin cos 2 sin 2 .
S x x x cos x
cosx x x x sinxcosx x
Câu 25. Trong mặt phẳng tọa độ
Oxy
cho hai điểm
3;1
A
và
2;5
B
. Hãy viết phương trình
đường tròn
C
nhận
AB
làm đường kính.
A.
2
2
1
3 41
2
x y
. B.
2 2
3 1 41
x y
.
C.
2
2
1 41
3
2 2
x y
. D.
2
2
1 41
3
2 4
x y
.
Lời giải
Chọn D
Gọi
I
là trung điểm đoạn
AB
1
;3
2
I
.
Đường tròn
C
nhận
AB
làm đường kính nên đường tròn
C
có tâm là điểm
1
;3
2
I
và có
bán kính
2
2 2 2
1 41
3 1 3
2 2
A I A I
R IA x x y y
. Phương trình đường
tròn
C
là
2
2
1 41
3
2 4
x y
.
Câu 26. Trong mặt phẳng tọa độ
Oxy
cho điểm
5; 3
A
và đường thẳng
:3 4 20 0
d x y
. Viết
phương trình đường tròn
C
có tâm
A
và tiếp xúc với đường thẳng
d
.
A.
2 2
49
3 4
25
x y . B.
2 2
49
5 3
25
x y .
C.
2 2
7
5 3
5
x y
. D.
2 2
7
5 3
25
x y .
Lời giải
Chọn B
Đường tròn
C
tâm
5; 3
A
và tiếp xúc với đường thẳng
d
nên khoảng cách từ tâm
A
đến
đường thẳng
d
chính bằng bán kính của đường tròn. Suy ra
2
2
3.5 4. 3 20
7
5
3 4
R
.
Phương trình đường tròn
C
là
2 2
49
5 3
25
x y .
Câu 27. Viết phương trình tiếp tuyến của đường tròn
C
tại điểm
5; 2
M
biết đường tròn có
phương trình
2 2
2 1 10
x y
.
A.
3 13 0
x y
. B.
3 17 0
x y
. C.
3 17 0
x y
. D.
3 11 0
x y
.
Lời giải
Chọn C
Đường tròn
C
có tâm
2; 1
I
suy ra
3; 1
IM
.
Phương trình tiếp tuyến của đường tròn
C
tại điểm
5; 2
M
là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
3 5 2 0
x y
3 17 0
x y
Câu 28. Trong mặt phẳng
Oxy
, cho đường thẳng
: 1 0
x y
. Viết phương trình đường thẳng
d
đi
qua
1; 1
A và tạo với
một góc
0
45
.
A.
1 0
1 0
x
y
. B.
1 0
x y
. C.
1 0
x
. D.
1 0
y
.
Lời giải
Chọn A
Phương trình đường thẳng
d
có dạng
1 1 0
A x B y
.
Theo giả thiết ta có
2 2 2 2
2
2
1 1
A B
A B
2 2
A B A B
0
AB
0
0
A
B
Với
0
A
chọn
1
B
. Vậy phương trình đường thẳng
d
là
1 0
y
Với
0
B
chọn
1
A
. Vậy phương trình đường thẳng
d
là
1 0
x
.
Câu 29. Tập nghiệm của bất phương trình
3 4 2 4
2 2
x x
x x
là?
A.
2;8
. B.
; 2 8;
.
C.
2;2 2;8
. D.
8;
.
Lời giải
Chọn C
Ta có:
2
3 4 2 4 3 4 2 4 10 16
0 0
2 2 2 2 2 2
x x x x x x
x x x x x x
Đặt
2
10 16
2 2
x x
f x
x x
.
Ta có:
2
2
10 16 0
8
x
x x
x
.
2 0 2
x x
2 0 2
x x
Ta có bảng xét dấu sau:
x
2
2
8
2
10 16
x x
+
|
+
0
0
+
2
x
|
0
+
|
+
2
x
0 +
|
+
|
+
f x
+
0 +
Vậy tập nghiệm của bất phương trình là:
2;2 2;8
S
.
Câu 30. Cho điểm
1;2
M
và đường thẳng
:
5 2
x t
t
y t
. Tọa độ của điểm
'
M
là điểm đối
xứng của điểm
M
qua đường thẳng
là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
9 12
;
5 5
. B.
2 6
;
5 5
. C.
3
0;
5
. D.
3
; 5
5
.
Lời giải
Chọn A
Gọi
H
là chân đường cao kẻ từ
M
đến đường thẳng
. Suy ra
;5 2
H h h
.
Ta có:
1; 2 , 1;3 2
u MH h h
.
Vì
7
. 0 1 2 3 2 0
5
MH MH u h h h
. Vậy
7 11
;
5 5
H
.
Gọi
'
M
là điểm đối xứng của
M
qua đường thẳng
. Suy ra
H
là trung điểm của đoạn
thẳng
'
MM
. Vậy tọa độ của điểm
'
M
là:
'
'
7 9
2 2. 1
5 5
11 12
2 2. 2
5 5
M H M
M H M
x x x
y y y
. Vậy
9 12
' ;
5 5
M
.
Câu 31. Biết
5
sin
13
a
,
3
cos
5
b
,0
2 2
a b
. Hãy tính
sin
a b
.
A.
33
65
. B.
63
65
. C.
56
65
. D.
0
.
Lời giải
Chọn A.
Ta có:
+)
2
cos 1 sin
a a
Do
cos 0
2
a a
2
5 12
cos 1
13 13
a
+)
2
sin 1 cos
b b
Do
0 sin 0
2
b b
2
3 4
sin 1
5 5
b
Vậy
5 3 12 4 33
sin sin .cos cos .sin . .
13 5 13 5 65
a b a b a b
.
Câu 32. Cho phương trình
2
2 2 – 2 –1 0
x m x m
1
. Với giá trị nào của
m
thì phương trình
1
có
nghiệm:
A.
5
m
hoặc
1
m
. B.
5
m
hoặc
1
m
.
C.
5 1
m
. D.
1
m
hoặc
5
m
.
Lời giải
Chọn A
Phương trình có nghiệm khi
2
'
0 2 2 1 0
m m
2
6 5 0
m m
1
5
m
m
.
Câu 33. Tập nghiệm của bất phương trình
2
2 8 2 0
x x x
là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2; .
B.
2; .
C.
4; .
D.
4; .
Lời giải
Chọn C
Điều kiện xác định
2
x
.
Ta có
2
2
2
2
2 8 2 0 4
2
2 8 0
4
x
x
x x x x
x
x x
x
.
Câu 34. Số nghiệm nguyên thuộc khoảng
10;10
của bất phương trình
2
1 1
1 2
x x x
là
A.
10.
B.
8.
C.
9.
D.
11.
Lời giải
Chọn C
Ta có
2
1 1
1 2
x x x
2 2
1 1 1
0 0
1 2 2
x
x x x x x
(1).
Bảng xét dấu
2
1
2
x
f x
x x
:
Từ bảng xét dấu, ta được tập nghiệm của bất phương trình là
2;1 1;S
.
Bất phương trình (1) có
9
nghiệm nguyên thuộc khoảng
10;10
là
1;2;3;4;5;6;7;8;9
.
Câu 35. Cho đường thẳng
d
có phương trình
7
5 5
x t
t
y t
, phương trình tham số của đường
thẳng qua
2;3
M và song song với
d
là:
A.
2
3 5
x s
y s
. B.
5 2
1 3
x s
y s
. C.
5
x s
y s
. D.
3 5
2
x s
y s
.
Lời giải
Chọn A
d
có một vtcp là
1;5
.
Đường thẳng cần tìm đi qua
–2;3
M và có vtcp là
1;5
nên có phương trình tham số
2
3 5
x s
s
y s
.
Câu 36. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
đi qua hai điểm
1;0
A
,
1;2
B
và có
tâm
thuộc đường thẳng
:2 3 0
x y
. Tìm phương trình của đường tròn
C
.
A.
2 2
1 2 10
x y
. B.
2 2
2 1 10
x y
.
C.
2 2
2 1 10
x y
. D.
2 2
2 1 10
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Cách 1:
Gọi
;3 2I x x
là tâm của đường tròn
C
. Vì
C
đi qua hai điểm
1;0
A
,
1;2
B
nên ta có
2 2 2 2
2 2
1 0 3 2 1 2 3 2
IA IB IA IB x x x x
2 2 2 2
1 3 2 1 1 2 4 8 2
x x x x x x
Suy ra
2; 1
I
. Do đó
C
có bán kính
2 2
1 2 0 1 10
R IA
.
Vậy
C
có phương trình
2 2
2 1 10
x y
.
Cách 2:
+ Gọi
I
là tâm của đường tròn
C
. Vì
C
đi qua hai điểm
1;0
A
,
1;2
B
nên ta có
IA IB
. Suy ra
I
thuộc đường trung trực
d
của đoạn thẳng
AB
.
d
đi qua trung điểm
0;1
M
của đoạn thẳng
AB
và nhận vectơ
2;2
AB
làm vectơ pháp
tuyến nên có phương trình
2 0 2 1 0 2 2 2 0 1 0
x y x y x y
.
+ Mà
I
nên tọa độ của
I
là nghiệm của hệ
1 0 2
2 3 0 1
x y x
x y y
.
Suy ra
2; 1
I
. Do đó
C
có bán kính
2 2
1 2 0 1 10
R IA
.
Vậy
C
có phương trình
2 2
2 1 10
x y
.
Câu 37. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hai đường thẳng
1
:
2
x t
d t
y t
;
: 3 4 2 0
x y
. Điểm
;
M a b d
thỏa
( , ) 2. ( , )
d M d M Ox
và
b 0
. Giá trị của biểu
thức
T a b
bằng
A.
13
11
. B.
11
3
. C.
40
11
. D.
33
11
.
Lời giải
Chọn D
Gọi
1 ;2 .
M t t d
Khi đó
3 1 4 2 2
( , ) 2. ( , ) 2. 2
5
t t
d M d M Ox t
11
9 20 10
9
9 20 10
9 20 10
29
11
t
t t
t t
t t
t
Với
11
,
9
t ta có
20
9
7
9
a
b
(loại)
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Với
29
,
11
t ta có
40
11
7
11
a
b
(nhận)
40 7 33
.
11 11 11
T a b
Câu 38. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
có hai đường cao là
BM
và
CN
. Giả
sử
BC
,
BM
,
CN
lần lượt có phương trình là
9 6 0
x y
,
3 8 0
x y
,
6 0
x y
.
Tọa độ đỉnh
A
là
A.
3; 1
A
. B.
6;0
A
. C.
0;2
A
. D.
2;4
A
.
Lời giải
Chọn C
Vì
B BC BM
nên tọa độ
B
thỏa hệ:
9 6 0 3
3; 1
3 8 0 1
x y x
B
x y y
.
Vì
C BC CN
nên tọa độ
C
thỏa hệ:
9 6 0 6
6;0
6 0 0
x y x
C
x y y
.
Ta có
AB CN
nên
AB
có vec tơ pháp tuyến
1;1
AB CN
n u
và qua
3; 1
B
nên
AB
có phương trình là
1 3 1 1 0 2 0
x y x y
.
Ta có:
AC BM
nên
AC
có vec tơ pháp tuyến
1;3
AC BM
n u
và qua
6;0
C
nên
AC
có
phương trình là
1 6 3 0 0 3 6 0
x y x y
.
Vì
A AB AC
nên tọa độ
A
thỏa hệ:
2 0 0
0;2
3 6 0 2
x y x
A
x y y
.
Câu 39. Trong mặt phẳng tọa độ
Oxy
, cho đường thẳng
d
qua
(1;4)
M
và cắt hai tia
,
Ox Oy
lần lượt
tại
,
A B
sao cho diện tích tam giác
OAB
nhỏ nhất. Tính tổng các hoành độ và tung độ của
,
A B
.
A.
0
. B.
16
. C.
10
. D.
5
.
Lời giải
Chọn C
Theo đề
( ;0), 0; (0; ); 0
A Ox A a a B Oy B b b
.
Ta có phương trình
: 1
x y
d
a b
. Mà
(1;4)
M d
nên
1 4
1
a b
.
Áp dụng bất đẳng thức Cauchy:
1 4 4
1 2 16
ab
a b ab
.
Diện tích tam giác
1 1 1
16 8
2 2 2
OAB
S OA OB a b
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dấu bằng xảy ra khi
1 4
2 (2;0)
1 4 8 (0;8)
1
a A
a b
b B
a b
.
Vậy tổng các hoành độ và tung độ của
,
A B
bằng 10.
Câu 40. Trong mặt phẳng tọa độ
Oxy
cho tam giác
ABC
có đường cao
:2 3 12 0,
AH x y
đường
trung tuyến
:2 3 0,
AN x y
với
N
thuộc đường thẳng
BC
gọi
1
;2
2
M
là trung điểm của
.
AB
Biết điểm
( ; ).
C a b
Tính
2020
P a b
A.
2019
B.
2020
C.
2021
D.
2022
Lời giải
Chọn B
Vì
A
là giao điểm của đường thẳng
AH
và đường thẳng
AN
nên tọa độ của
A
là nghiệm của
hệ:
2 3 12 0 2
( 3;2).
2 3 0 2
x y x
A
x y y
Vì
M
là trung điểm của
AB
nên
2 2
(2;2).
2 2
B M A B
B M A B
x x x x
B
y y y y
Phương trình đường thẳng
BC
đi qua
(2;2)
B
và vuông góc với đường cao
:2 3 12 0
AH x y
là:
3( 2) 2( 2) 0 :3 2 10 0.
x y BC x y
Do
N
là giao điểm của đường thẳng
:3 2 10 0
BC x y
và đường trung tuyến
:2 3 0,
AN x y
nên tọa độ
N
là nghiệm của hệ :
3 2 10 0 6
(6; 4).
2 3 0 4
x y x
N
x y y
Vì
N
là trung điểm của
BC
nên
2 10
(10; 10).
2 10
C N B
C N B
x x x
C
y y y
Câu 41. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
C
có phương trình:
2 2
x y 4x 8y 5 0
. Phương trình đường thẳng vuông góc với đường thẳng
:
d 3x 4y 12 0
và cắt đường tròn
C
theo một dây cung có độ dài bằng 8 là:
A.
4x 3y 19 0
và
4x 3y 11 0
. B.
4x 3y 5 0
và
4x 3y 35 0
.
C.
3x 4y 25 0
và
3x 4y 5 0
. D.
4x 3y 19 0
và
4x 3y 11 0
.
Lời giải
Chọn D
Đường tròn
:
2 2
C x y 4x 8y 5 0
có tâm
; ,
2
2
I 2 4 R 2 4 5 5
.
Gọi đường thẳng cần tìm là
.
Vì
d
nên phương trình
có dạng:
4x 3y m 0
.
Giả sử đường thẳng
cắt đường tròn
C
theo dây cung
AB
.
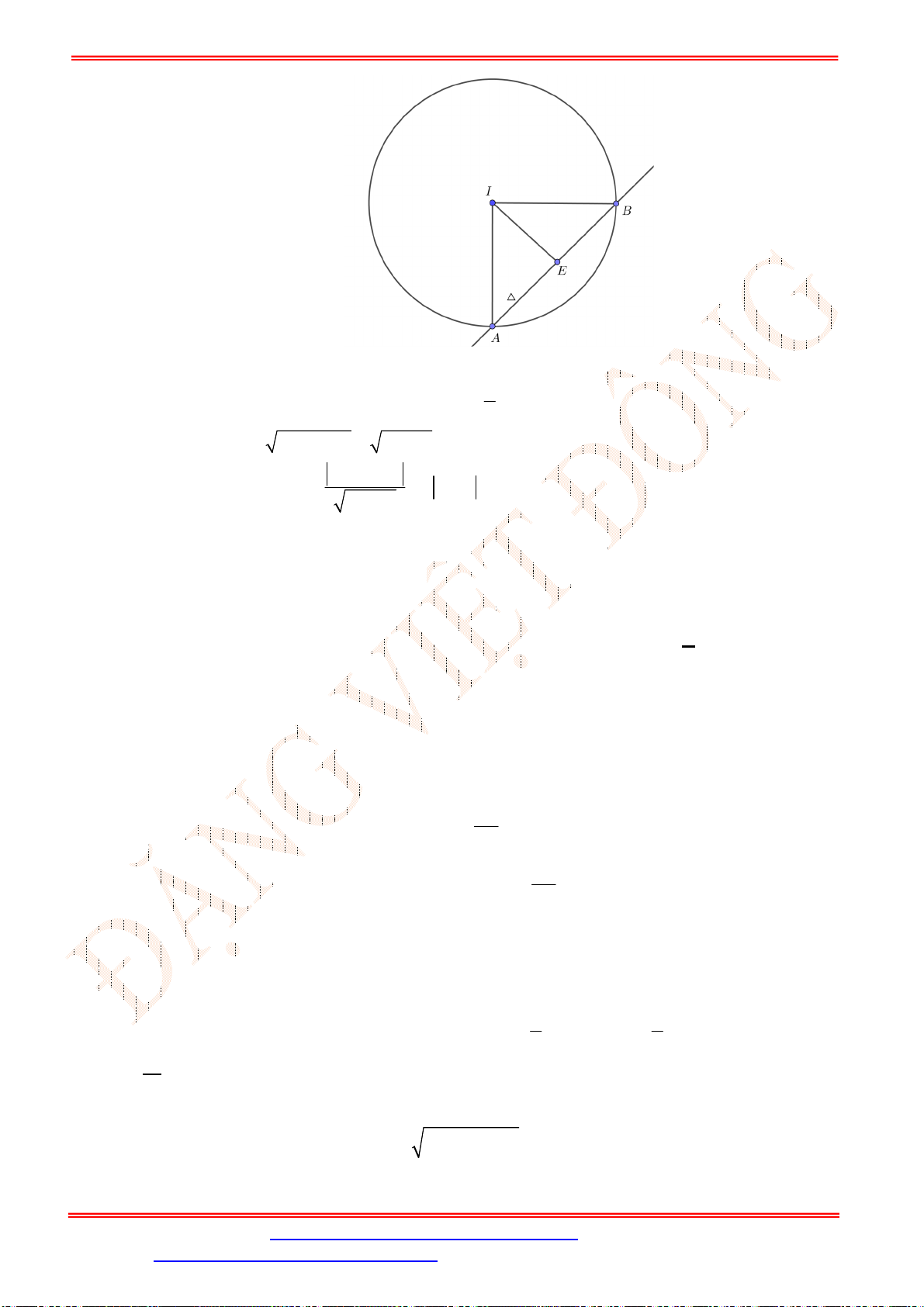
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi
E
là trung điểm đoạn
AB
suy ra
IE AB
1
AE AB 4
2
.
Xét :
2 2 2 2
IEA IE IA AE 5 4 3 .
Ta có
,
2 2
m 19
8 12 m
IE 3 d I m 4 15
m 11
4 3
.
Vậy phương trình đường thẳng cần tìm là 4x 3y 19 0 và 4x 3y 11 0 .
Câu 42. Có bao nhiêu giá trị nguyên của tham số
m
để hệ bất phương trình sau vô nghiệm:
2
2
7 12 0
3 0
x x
x m
A. Vô số B.
3
C.
5
D.
7
Lời giải
Chọn D
Ta có
2
2
7 12 0 1
3 0 2
x x
x m
Bất phương trình
1
có tập nghiệm
1
4; 3T
.
Bất phương trình
2
có tập nghiệm
2
1
;
3
m
T
.
Hệ bất phương trình vô nghiệm
2
2
1 2
3 9 3;3
3
m
T T m m
.
Vì m nên suy ra
0; 1; 2; 3m
. Vậy có
7
giá trị nguyên của
m
thỏa yêu cầu bài toán.
Câu 43. Trong không gian Oxy , cho đường tròn
2 2
: 2 6 1 0
C x y x y
. Viết phương trình tiếp
tuyến của đường tròn
C
, biết tiếp tuyến song song với đường thẳng :3 4 0.d x y
A. 3 4 0x y và 3 4 30 0x y . B.
3
2 0
2
x y
và
3
2 15 0
2
x y
.
C.3 4 30 0x y . D. 3 4 30 0x y .
Lời giải
Chọn C
C
có tâm
1; 3I
,
bán kính
2
2
1 3 1 3R .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vì tiếp tuyến
song song với đường thẳng :3 4d x y nên phương trình tiếp tuyến có dạng
3 4 0 0x y c c
.
Ta có:
2 2
0
3.1 4. 3
15 15
, 3 15 15 .
15 15
30
3 4
c l
c
c
d I R c
c
c n
Vậy phương trình tiếp tuyến :3 4 30 0.x y
Câu 44. Trong mặt phẳng toạ độ Oxycho elip
2 2
: 1
25 9
x y
E
. Gọi
0 0
;M x y thuộc Elip thoả mãn
bán kính qua tiêu điểm này bằng 3 lần bán kính qua tiêu điểm kia. Khi đó giá trị
2 2
0 0
x y
bằng
A.
17
4
. B.
137
32
. C.
61
4
. D.
117
4
.
Lời giải
Chọn B
Ta có:
2 2
: 1
25 9
x y
E
2
2
9
25 5
3
a a
b
b
Mặt khác
2 2 2
25 9 16 4 c a b c
Vì
0 0
; M x y E . Khi đó bán kính qua tiêu của M là
0 01 2
, . .
c c
MF a x MF a x
a a
Từ giả thiết suy ra:
1 2 1 2
2 1 2 1
3 3 0
3 3 0
MF MF MF MF
MF MF MF MF
2
1 2 2 1 1 2 1 2
2
0 0
2
2 2
0
2
2 2 4
2
0 0
2
3 . 3 0 16 . 3 0
16 . 3. 2 0
16 12
4 625
16 4 4 64
MF MF MF MF MF MF MF MF
c c
a x a x a
a a
c
a x a
a
c a a a
x x
a c
Mà
2
2
0
0
351
1 .9
25 64
x
M E y
Vậy
2 2
0 0
137
32
x y
Câu 45. Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh
C
của ngọn núi. Biết rằng độ cao
70mAB , phương nhìn AC tạo với phương nằm ngang góc
0
30
, phương nhìn BC tạo với
phương nằm ngang góc
0
15 30'
(tham khảo hình vẽ). Ngọn núi đó có độ cao so với mặt đất gần
nhất với giá trị nào sau đây?

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
135m
. B.
234m
. C.
165m
. D.
195m
.
Lời giải
Chọn A
Từ giả thiết, ta suy ra tam giác
ABC
có
0
60
CAB
,
0
105 30
ABC
và
70.
AB
Khi đó
0 0 0 0 0
180 180 180 165 30 14 30
A B C C A B
.
Theo định lí sin, ta có
sin sin
AC AB
B C
hay
0 0
70
sin105 30 sin14 30
AC
Do đó
0
0
70.sin105 30
269,4m
sin14 30
AC
.
Gọi
CH
là khoảng cách từ
C
đến mặt đất. Tam giác vuông
ACH
có cạnh
CH
đối diện với
góc
0
30
nên
269,4
134,7m
2 2
AC
CH .
Vậy ngọn núi cao khoảng
135
m
.
Câu 46. Cho đường tròn
2 2
:( 2) ( 1) 5
C x y
và điểm
(3; 2)
M
. Gọi
1
M
,
2
M
lần lượt là hai tiếp
điểm của hai tiếp tuyến kẻ từ
M
đến đường tròn
C
; Hãy viết phương trình của đường thẳng
1 2
M M
A.
1 2
( ): 3 4 0
M M x y
B.
1 2
( ): 3 4 0
M M x y
C.
1 2
( ): 3 4 0
M M x y
D.
1 2
( ): 2 3 4 0
M M x y
Lời giải
Chọn A
2 2
(2;1)
( ):( 2) ( 1) 5
5
Tâm I
C x y
R
Gọi
( ; )
n a b
là véc tơ pháp tuyến của tiếp tuyến cần tìm
2 2
( 0)
a b
Phương trình tiếp tuyến:
( ): ( 3) ( 2) 0 ( ): 3 2 0
a x b y ax by a b
( )
là tiếp tuyến của
C
2 2
2 2
2 3 2
( ; ) 5 3 5.
a b a b
d I R b a a b
a b
2 2 2 2 2 2
9 6 5( ) 2 3 2 0 ( 2 )(2 ) 0
2
2
b ab a a b a ab b a b a b
a b
b a
TH1:
2
a b
chọn
2; 1
a b
( ):2 8 0 2 8
x y y x
Tìm tọa độ tiếp điểm
1
M
của tiếp tuyến và đường tròn
2 2 2 2 2
1
( 2) ( 1) 5 ( 2) (2 9) 5 5 40 80 0
4 0 (4;0)
x y x x x x
x y M
TH2:
2
b a
chọn
1; 2
a b
( ): 2 1 0 2 1
x y x y
Tìm tọa độ tiếp điểm
2
M
của tiếp tuyến và đường tròn
2 2 2 2 2
2
( 2) ( 1) 5 ( 2 3) ( 1) 5 5 10 5 0
1 1 (1; 1)
x y y y y y
y x M
Phương trình của đường thẳng
1 2
M M

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
1 2
1 2 1 2
( 3; 1) (1; 3)
( ):1( 1) 3( 1) 0 ( ): 3 4 0
u M M n
M M x y M M x y
Vậy phương trình đường thẳng đi qua hai tiếp điểm là:
1 2
( ): 3 4 0
M M x y
Câu 47. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
2
2
: 3 1
C x y
. Giả sử điểm
;
M x y
thuộc đường tròn
C
sao cho tổng khoảng cách từ
M
đến hai điểm
3;0
A ,
3;0
B là lớn
nhất. Khi đó giá trị
x y
là
A.
4
. B.
5
. C.
2
. D.
15
4
.
Lời giải
Chọn A
Giả sử tọa độ của điểm
;
M x y
. Khi đó ta có:
2
2
3 1
x y
1
2
3 1 2 4
y y
2
.
Mặt khác:
2 2
2 2
3 3
MA MB x y x y
.
Áp dụng bất đẳng thức Cauchy-Schwarz ta có:
2
2 2 2 2
2 2 2 2 2 2
3 3 2 3 3 4 36
x y x y x y x y x y
.
Kết hợp với
1
,
2
ta có:
2
2 2
2 2
3 3 24 4 100
x y x y y
.
Vậy
10
MA MB
. Dấu
" "
xảy ra khi
0
4
x
y
.
Giá trị lớn nhất của
MA MB
bằng 10 khi
0;4
M .
Khi đó:
4
x y
.
Nhận xét
Bài này có thể giải dựa vào xét tương giao của Elip và đường tròn theo kiến thức lớp 10.
Câu 48. Trong mặt phẳng tọa độ
Oxy
, cho đường tròn
C
và đường thẳng
d
lần lượt có phương trình
2 2
2
1 2 3
x y
và
3 4 1 0
x y
. Viết phương trình đường thẳng
, biết
cắt
C
theo dây cung có độ dài lớn nhất và
tạo với
d
một góc
45
.
A.
4 3 2 0
x y
và
4 3 10 0
x y
.
B.
7 15 0
x y
và
7 5 0
x y
.
C.
3 2 4 3 0
x y
và
2 3 2 3 2 0
x y
.
D.
7 9 0
x y
và
7 13 0
x y
.
Lời giải
Chọn D
Đường tròn
C
có tâm
1;2
I , bán kính
3
R
.
Vì
cắt đường tròn
C
theo dây cung có độ dài lớn nhất nên
đi qua tâm
I
.
Gọi
;
n a b
là vecto pháp tuyến của
.
Suy ra
: 1 2 0
a x b y
: 2 0
ax by a b
.
d
có vecto pháp tuyến
3;4
d
n
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có:
cos , cos ,
d
d n n
.
.
d
d
n n
n n
2 2 2 2
3 4
cos45
3 4 .
a b
a b
2 2
3 4
1
2
5.
a b
a b
2 2
5 2 3 4
a b a b
2 2
7 48 7 0
a ab b
7
1
7
a b
a b
.
+) Với
7
a b
. Ta chọn
1
b
,
7
a
. Suy ra
:7 9 0
x y
.
+) Với
1
7
a b
. Ta chọn
7
b
,
1
a
. Suy ra
: 7 13 0
x y
.
Câu 49. Cho phương trình đường tròn
2 2
: 9
C x y
tâm
I
và phương trình đường thẳng
: 1 2 1 0
m
d m x m y
với
m
là tham số nguyên. Biết đường thẳng
m
d
luôn cắt
đường tròn
C
tại hai điểm
,
A B
. Tính diện tích lớn nhất của tam giác
IAB
A.
5
. B.
6
. C.
7
. D.
8
.
Lời giải
Chọn D
Từ giả thiết suy ra
0;0
I
Gọi
h
là khoảng cách từ
I
đến đường thẳng
m
d
thì ta có:
2 2
1
0 1
1 2
h h dom
m m
Mặt khác ta lại có:
2
2 2 4 2 2
9 9 7 1 1 8 0 1
IAB
S h h h h h h do h
Đẳng thức xảy ra khi và chỉ khi
1
h
, lúc này
1
m
hoặc
2
m
Vậy diện tích lớn nhất của tam giác
IAB
bằng
8
.
Câu 50. Trong mặt phẳng
Oxy
, cho tam giác
ABC
có điểm
4;3
A
, đường phân giác trong
: 2 5 0
BI x y
, đường trung tuyến
: 4 13 10 0
BM x y
. Khi đó điểm
C
có hoành độ là:
A.
12
. B.
12
. C.
11
7
. D.
1
7
.
Lời giải
Chọn A
E
D
M
A
B
C
d
I

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
+
B BI BM
, ta có hệ phương trình:
2 5 0 9
9; 2
4 13 10 0 2
x y x
B
x y y
+ Gọi
d
là đường thẳng qua
4;3
A
và vuông góc
: 2 5 0
BI x y
: 2 0
d BI d x y c
4;3 5 :2 5 0
A d c d x y
+ Gọi
E
là hình chiếu của
A
trên
BI
E d BI
, ta có hệ phương trình:
2 5 0 3
3;1
2 5 0 1
x y x
E
x y y
.
+ Gọi
D
là điểm đối xứng với
A
qua
BI
E
là trung điểm
AD
2 2
2; 1
2 1
D E A
D E A
x x x
D
y y y
+
D
là điểm đối xứng với
A
qua đường phân giác
BI
D BC
+
7;1
BD
+ Đường thẳng
BC
qua
9; 2
B
nhận
7;1
BD
làm vectơ chỉ phương có phương trình:
9 7
2
x t
t
y t
+
9 7 ; 2
C t t BC
+
M
là trung điểm
AC
13 7
13 7 1
2 2
;
1
2 2
2 2
A C
M
M M
M
x x
t
x
t t
M
y y t
y
+
13 7 1 13 7 1
; 4. 13. 10 0 3
2 2 2 2
t t t t
M BM t
Vậy:
9 7 12
C
x t
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 18
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1: Cho hình vuông
ABCD
cạnh bằng
a
. Gọi
E
là điểm đối xứng của
D
qua
C
. Tính
.
AE AB
.
A.
2
. 2
AE AB a
. B.
2
. 3
AE AB a
. C.
2
. 5
AE AB a
. D.
2
. 5
AE AB a
.
Câu 2: Trong mặt phẳng tọa độ
Oxy
, cho hai vectơ
1;2 , 2; 4 .
a b
Khi đó
cos ,
a b
bằng:
A.
3
5
. B.
3
5
. C. 1. D.
1
2
.
Câu 3: Hệ bất phương trình
2
1 0 1
0 2
x
x m
có nghiệm khi:
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 4: Cho
ABC
có
5
a
,
8
b
,
10
c
. Đẳng thức lượng giác nào sau đây là đúng:
A.
2sin 3sin sin
A B C
. B.
5
sin sin sin
8
C A B
.
C.
1
sin sin sin
3
A B C
. D.
sin 3sin
A B
.
Câu 5: Tập nghiệm của bất phương trình
3 2 0
x
là:
A.
3
;
2
. B.
3
;
2
. C.
3
;
2
. D.
3
;
2
.
Câu 6: Trong mặt phẳng tọa độ
,
Oxy
cho ba điểm
2;0
A ,
0;2
B và
0;7 .
C Tìm tọa độ
đỉnh thứ tư
D
của hình thang cân
.
ABCD
A.
7;0 .
D B.
7;0 , 2;9 .
D D C.
0;7 , 9;2 .
D D D.
9;2 .
D
Câu 7: Giá trị
m
thỏa mãn để giá trị lớn nhất của hàm số
2 1
f x x m
trên
1;3
bằng
5
thuộc khoảng nào:
A.
3; 2
. B.
3;4
. C.
0;1
. D.
1;2
.
Câu 8: Cho
a
là số thực bé hơn 2020. Giá trị lớn nhất của biểu thức
2 2
.cos 2020sin
P a x x
bằng
A.
2020
. B.
a
. C.
2020
a
. D.
2020
a
.
Câu 9: Tập nghiệm của bất phương trình
2
2 3 0
x x
là:
A.
3;1
. B.
1;3
. C.
1;3
. D.
3;1
.
Câu 10: Tập nghiệm của bất phương trình
3
8 2 4 1 14 8 1
x x x x x
có dạng
;
a b
c
, trong đó
,
a b
là các số nguyên tố. Tính giá trị biểu thức
T a b c
.
A.
2
. B.
6.
C.
5.
D.
8.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 11: Cho tan 3
. Tính giá trị của biểu thức
2
sin 2
cos2 3sin
P
.
A.
19
6
. B.
6
19
. C.
2
5
.
D.
5
2
.
Câu 12: Tìm tọa độ một véc tơ chỉ phương của đường thẳng có phương trình:
2
1 3
x t
t
y t
.
A.
1;3u
. B.
1;3u
. C.
3;1u
. D.
2;1u
.
Câu 13: Tìm giá trị lớn nhất của hàm số
3
1y x x với 0 1x .
A.
27
256
. B.
81
256
. C.
2
. D.
1
16
.
Câu 14: Trong mặt phẳng Oxy , cho đường thẳng
:5 2 8 0d x y . Véctơ pháp tuyến của
đường thẳng
d là
A.
2; 5n
. B.
5;2n
. C.
2;5n
. D.
5; 2n
.
Câu 15: Cho góc lượng giác
,Ou Ov có số đo
7
. Trong các số
29 22 6 41
; ; ;
7 7 7 7
,
những số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã
cho?
A.
29 41
;
7 7
. B.
29 22
;
7 7
. C.
22 41
;
7 7
. D.
6 41
;
7 7
.
Câu 16: Một người nông dân có 6 triệu đồng để làm một hàng rào chữ E dọc theo một
con sông (như hình vẽ) làm một khu đất có hai phần là hình chữ nhật để trồng rau.
Đối với mặt hàng rào song song bờ sông thì chi phí nguyên vật liệu là 60000 đồng
một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu
là 40000 đồng một mét. Tính diện tích lớn nhất của khu đất rào thu được.
A. 1245. B. 1250. C. 1255. D. 1260.
Câu 17: Trên đường tròn lượng giác, điểm biểu diễn của cung có số đo
11
3
có điểm cuối
thuộc góc phần tư nào?
A. Thứ nhất. B. Thứ hai. C. Thứ ba. D. Thứ tư.
Câu 18: Cho
3
cos
5
với 0
2
. Khi đó giá trị của biểu thức
sin 3cos
5sin 6
P
bằng
A.
2
5
P
. B.
1
5
P
. C.
1
5
P . D. 1P .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 19: Tìm tọa độ tâm của đường tròn
C
có phương trình
2 2
2 4 2020 0
x y x y
.
A.
1;2
I . B.
1; 2
I
. C.
1; 2
I
. D.
1;2
I .
Câu 20: Có bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để bất phương trình
3 2
2 0
x x m x m
nghiệm đúng với mọi
0
x
?
A.
7
. B.
8
. C.
9
. D.
10
.
Câu 21: Cho
3
sin
5
và
2 2
. Tính giá trị
cos
.
A.
4
5
. B.
16
25
. C.
4
5
. D.
4
5
.
Câu 22: Cho elip
2 2
:4 9 1
E x y
. Chọn khẳng định sai.
A. Độ dài trục nhỏ là
1
3
. B. Độ dài trục lớn là
1
.
C. Tiêu cự là
5
3
. D. Tiêu điểm là
1 2
5 5
;0 ; ;0
6 6
F F
.
Câu 23: Tìm tất cả các giá trị của tham số
m
để với mọi x
ta có
2
2
5
1 7
2 3 2
x x m
x x
.
A.
5
1
3
m
. B.
5
1
3
m
. C.
5
3
m
. D.
1
m
.
Câu 24: Phương trình đường tròn có tâm thuộc đường thẳng
: 2 0
x y
, tiếp xúc với
đường thẳng
:2 2 0
x y
đồng thời đường tròn đi qua điểm
1;3
M
là
A.
2 2
2 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
B.
2 2
2 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
C.
2 2
1 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
D.
2 2
2 1 5
x y
và
2 2
23 23 1885
4 8 16
x y
.
Câu 25: Cho hai đường thẳng
1
: 2 0
d x y
và
2
: 2 3 3 0
d x y
. Số đo của góc giữa hai
đường thẳng
1
d
và
2
d
gần với giá trị nào sau đây nhất?
A.
11 19
. B.
78 41
. C.
101 19
. D.
78 31
.
Câu 26: Cho tam giác
ABC
với
2;3 , 1; 1 , 10; 3
A B C
. Gọi
;
M a b
là điểm trên cạnh
BC
sao cho
DE
có độ dài nhỏ nhất với
,
D E
lần lượt là hình chiếu của
M
lên
,
AC AB
. Khi đó biểu thức
2 2
P a b
nhận giá trị bằng bao nhiêu?
A.
97
4
. B.
17
5
. C.
733
121
. D.
87
25
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 27: Cho hai đường thẳng
1
: 2 1 0
d x y
,
2
: 3 3 0.
d x y
Phương trình đường thẳng
d
đối xứng với
1
d
qua
2
d
là:
A.
2 2 0.
x y
. B.
2 2 0.
x y
. C.
2 2 0
x y
. D.
2 2 0
x y
.
Câu 28: Xác định tâm sai của elip (E):
2 2
1
25 9
x y
.
A.
5
4
. B.
4
5
. C.
5
3
. D.
3
5
.
Câu 29: Trong mặt phẳng
Oxy
, cho đường thẳng
:2 4 1 0
d x y
. Phương trình tham số
của đường thẳng
đi qua
6
(3;
)
A
và song song với đường thẳng
d
là
A.
3 2
6 4
x t
y t
. B.
4 3
2 6
x t
y t
. C.
3 4
6 2
x t
y t
. D.
3 2
6
x t
y t
.
Câu 30: Trong mặt phẳng tọa độ
,
Oxy
cho
ABC
có
2;1 , 2;3 ,C 0;2 .
A B Phương trình
tổng quát của đường thẳng chứa trung tuyến
CM
của
ABC
là:
A.
2 0
y
. B.
2 0
y
. C.
2 0
x y
. D.
2 0
x y
.
Câu 31: Đường tròn
(C)
có tâm
(1; 2)
I
và bán kính
2
R . Phương trình của đường tròn
(C)
là:
A.
2 2
2 4 3 0
x y x y
. B.
2 2
2 2 4 3 0
x y x y
.
C.
2 2
2 2 4 8 6 0
x y x y
. D.
2 2
2 4 2 0
x y x y
.
Câu 32: Tìm
a
để bất phương trình sau có nghiệm
3 2
3 1 1
x x a x x
A
3
a
. B.
3
a
. C.
2
a
. D.
3
a
.
Câu 33: Trong mặt phẳng tọa độ
O
xy
cho điểm
3 1
A ;
và đường thẳng
4 2
Δ
5 3
x t
:
y t
. Tìm
điểm
M
thuộc đường thẳng
Δ
sao cho
5 2
MA
?
A.
2 8
M ;
và
118 34
13 13
M ;
. B.
2 8
M ;
và
108 34
13 13
M ;
.
C.
2 8
M ;
và
118 34
13 13
M ;
. D.
2 8
M ;
và
118 34
13 13
M ;
.
Câu 34: Tìm số giá trị nguyên
m
để bất phương trình
2
1 2 7 0
x m x m
có tập
nghiệm
.
A.
5
. B.
7
. C.
11
. D.
15
.
Câu 35: Tìm tập hợp
S
tất cả các giá trị của tham số
m
để bất phương trình
8 7 3 8 2
m x mx m
có tập nghiệm là tập con của khoảng
1;
.
A.
5;S
. B.
3;S
. C.
5;S
. D.
3;S
.
Câu 36: Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức:
4 4 4 4
2 2 2 2
sin cos cos sin
sin cos cos sin
a x b y a x b y
H
c x d y c x d y
, với
, , , 0
a b c d
. Giá trị
,
M m
là:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A. ,
a c a b
M m
b d c d
. B. ,
a b a b
M m
c d c d
.
C. ,
a b a c
M m
c d b d
. D. ,
a c a c
M m
b d b d
.
Câu 37: Trong mặt phẳng với hệ tọa độ
Oxy
cho đường thẳng :
1
x t
y
và điểm
3; 2
P
.
Điểm
Q
,
PQ
khi đó tọa độ
Q
là:
A.
3;0
Q . B.
0;3
Q . C.
1;3
Q . D.
3;1
Q .
Câu 38: Tìm tập xác định của hàm số sau:
2
2
5 4
9 1
x x
y
x
.
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;4
.
Câu 39: Trên đoạn
2;2
, hàm số
2
1
mx
y
x
(với
0
m
) đạt giá trị nhỏ nhất tại
1
x
khi và
chỉ khi
A.
2
m
. B.
2
m
. C.
0
m
. D.
0
m
.
Câu 40: Trong hệ tọa độ
Oxy
, cho tam giác
ABC
vuông tại
A
và nội tiếp trong đường tròn
C
có phương trình:
2 2
6 2 5 0
x y x y
. Gọi
H
là hình chiếu vuông góc của
A
trên
BC
, đường tròn đường kính
AH
cắt
,
AB AC
lần lượt tại
,
M N
. Biết đường
thẳng chứa
,
M N
có phương trình
20 10 9 0
x y
. Khi đó hoành độ của điểm
A
là
A.
1
. B.
5
. C.
0
. D.
2
.
Câu 41: Mệnh đề nào sau đây sai?
A.
2 2
cos2 cos -sin
a a a
. B.
2 2
cos2 sin cos
a a a
C.
2
cos2 1 2sin
a a
. D.
2
cos2 2cos 1
a a
.
Câu 42: Cho
5
cos
13
a
0
2
a
. Giá trị
tan
a
là
A.
5
12
. B.
13
5
. C.
12
5
. D.
12
5
.
Câu 43: Có bao nhiêu giá trị nguyên của tham số
2020;2020
m để bất phương trình
2
1 1
4 2 2
2 2
x m x x m
luôn đúng với mọi
x
.
A.
2020
. B.
2018
. C.
4038
D.
4039
.
Câu 44: Hệ bất phương trình
2
1 2
2
3 3
3 4 0
x
x
x x
có tập nghiệm là
A.
5;
B.
; 4 1;
C.
4; 1
D.
5; 4 1;
Câu 45: Cho số thực
1
a
.Giá trị nhỏ nhất của biểu thức
4
1
P a
a
là
A.
4
. B.
6
. C.
3
. D.
5
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 46: Biểu thức
0 0 0 0 0
cos20 cos40 cos60 ... cos160 cos180
A có giá trị bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Câu 47: Cho
5 1;8
a m
và
2;
b m
, giá trị của tham số
m
để hai véctơ
a
và
b
vuông
góc với nhau là
A.
1
. B.
0
. C.
1
. D.
2
.
Câu 48: Cho
2
. Xác định dấu của các biểu thức sin
2
A.
sin 0
2
. B.
sin 0
2
. C.
sin 0
2
. D.
sin 0
2
.
Câu 49: Cho hình thang vuông
ABCD
có:
90
A B
, đáy bé
5
AD
, đáy lớn
15
BC
, và
12
AB
. Điểm
M
thuộc cạnh
AB
(không trùng
A
hoặc
B
) sao cho tổng
MD MC
nhỏ nhất. Khi đó tích độ dài .
AM BM
là
A.
18
. B.
20
. C.
27
. D.
36
.
Câu 50: Trong mặt phẳng tọa độ
Oxy
, cho
3
điểm
1;1
A ,
3;4
B ,
4; 1
C
. Gọi
I
là tâm
đường tròn ngoại tiếp tam giác
ABC
tọa độ tâm
I
là
A.
8 4
;
3 3
I
. B.
7 3
;
2 2
I
. C.
7 3
;
3 2
I
. D.
5 3
;
2 2
I
.
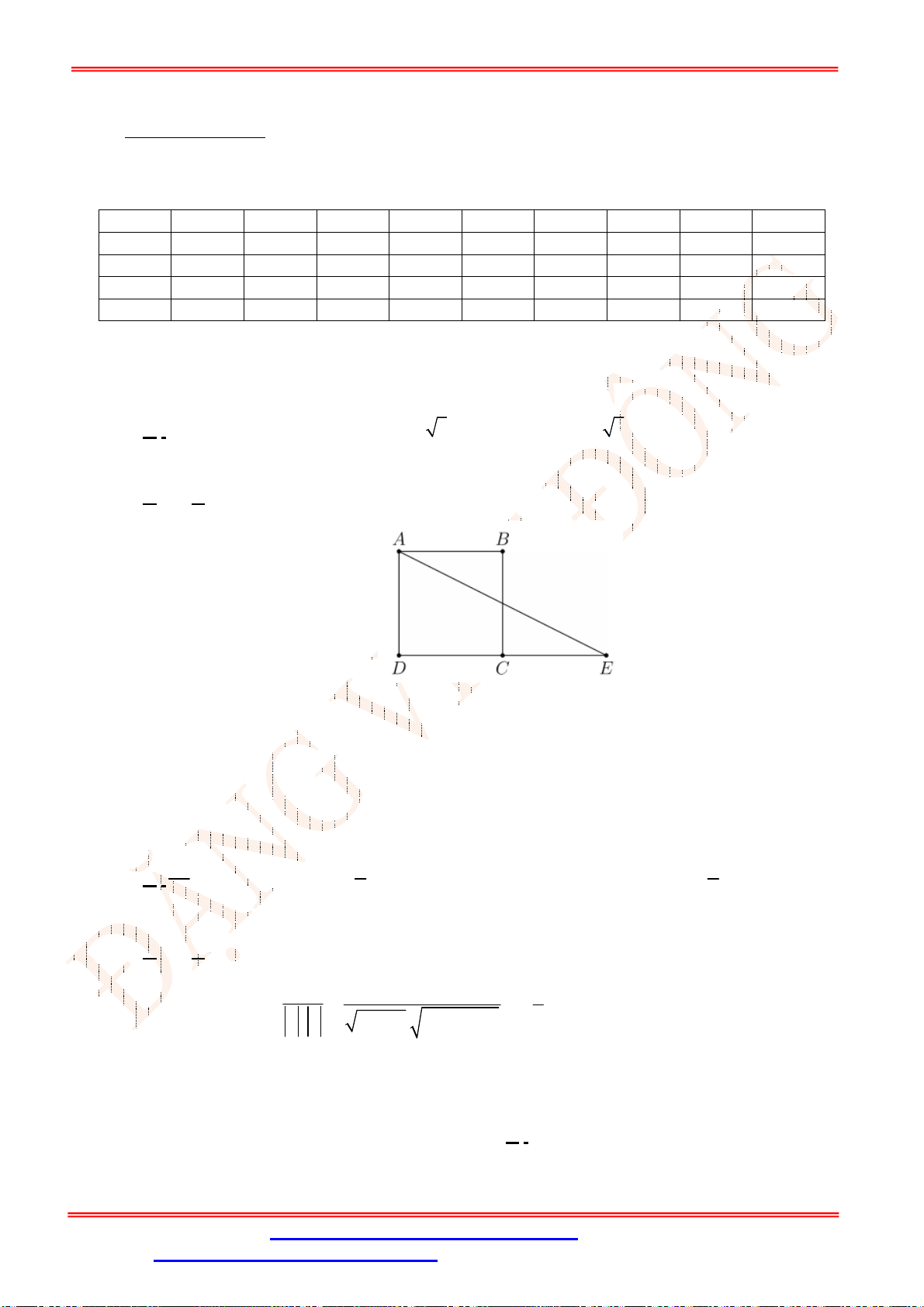
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 18
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.A 2.A 3.C 4.B 5.C 6.B 7.D 8.A 9.D 10.D
11.B 12.B 13.A 14.D 15.B 16.B 17.D 18.C 19.D 20.D
21.A 22.A 23.A 24.B 25.B 26.B 27.B 28.B 29.D 30.B
31.C 32.D 33.D 34.C 35.C 36.B 37.D 38.C 39.C 40.A
41.B 42.D 43.C 44.D 45.D 46.B 47.A 48.B 49.C 50.B
HƯỚNG DẪN GIẢI
Câu 1: Cho hình vuông
ABCD
cạnh bằng
a
. Gọi
E
là điểm đối xứng của
D
qua
C
. Tính
.
AE AB
.
A.
2
. 2
AE AB a
. B.
2
. 3
AE AB a
. C.
2
. 5
AE AB a
. D.
2
. 5
AE AB a
.
Lời giải
Chọn A
Vì
E
đối xứng với
D
qua
C
, suy ra
2 .
DE a
0 2
. . . . .cos , .2 .cos0 2
AE AB AD DE AB AD AB DE AB DE AB DE AB a a a
.
Câu 2: Trong mặt phẳng tọa độ
Oxy
, cho hai vectơ
1;2 , 2; 4 .
a b
Khi đó
cos ,
a b
bằng:
A.
3
5
. B.
3
5
. C. 1. D.
1
2
.
Lời giải
Chọn A
Ta có:
.
cos ,
.
a b
a b
a b
2
2 2 2
1.2 2. 4
3
.
5
1 2 . 2 4
Câu 3: Hệ bất phương trình
2
1 0 1
0 2
x
x m
có nghiệm khi:
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn C
Bất phương trình
1 1 1.
x
Suy ra
1
1;1
S .
Bất phương trình
2 .
x m
Suy ra
2
; .
S m
Hệ bất phương trình có nghiệm khi và chỉ khi
1 2
S S
1.
m
Câu 4: Cho
ABC
có
5
a
,
8
b
,
10
c
. Đẳng thức lượng giác nào sau đây là đúng:
A.
2sin 3sin sin
A B C
. B.
5
sin sin sin
8
C A B
.
C.
1
sin sin sin
3
A B C
. D.
sin 3sin
A B
.
Lời giải
Chọn B
Gọi
R
là bán kính đường tròn ngoại tiếp
ABC
. Theo định lí hàm sin trong tam giác ta có:
5 8 10
sin , sin , sin
2 2 2 2 2 2
a b c
A B C
R R R R R R
.
Lần lượt xét các phương án:
5 8 10 14 10
2sin 3sin sin 2. 3.
2 2 2 2 2
A B C
R R R R R
(vô lí). Phương án A sai.
5 10 5 5 8 5 5
sin sin sin .
8 2 2 8 2 2 2
C A B
R R R R R
. Đáp án B đúng.
1 5 8 1 10 13 10
sin sin sin .
3 2 2 3 2 2 6
A B C
R R R R R
(vô lí). Phương án C sai.
5 3.8
sin 3sin
2 2
A B
R R
( vô lí ). Phương án D sai.
Câu 5: Tập nghiệm của bất phương trình
3 2 0
x
là:
A.
3
;
2
. B.
3
;
2
. C.
3
;
2
. D.
3
;
2
.
Lời giải
Chọn C
Ta có:
3 2 0
x
2 3
x
3
2
x
.
Vậy tập nghiệm của bất phương trình đã cho là
3
;
2
S
.
Câu 6: Trong mặt phẳng tọa độ
,
Oxy
cho ba điểm
2;0
A ,
0;2
B và
0;7 .
C Tìm tọa độ
đỉnh thứ tư
D
của hình thang cân
.
ABCD

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
7;0 .
D B.
7;0 , 2;9 .
D D C.
0;7 , 9;2 .
D D D.
9;2 .
D
Lời giải
Chọn B
Gọi
;
D x y
. Có hai trường hợp sau xảy ra:
Trường hợp 1:
ABCD
là hình thang cân với hai đáy là
AB
và
CD
. Điều này xảy ra khi và
chỉ khi
( 0) (1)
(2)
CD k AB k
AC BD
.
Có
; 7
CD x y
và
2;2
AB
, do đó
2
(1) ; 7 2 ;2
2 7
x k
x y k k
y k
.
Khi đó
2 ;2 7
D k k
nên
2 2 2
2 2 2
(2) 2 7 2 2 5
AC BD k k
2
8 20 28 0
k k
1
7
2
k
k
.
Kết hợp với
0
k
ta được
7
2
k
, suy ra
7;0
D .
Trường hợp 2:
ABCD
là hình thang cân với hai đáy là
BC
và
AD
. Điều này xảy ra khi và
chỉ khi
( 0) (1)
(2)
AD kBC k
AC BD
.
Tương tự ta có
(1) 2;5
D k
và
9
(2)
5
k
. Do đó trường này ta được
2;9
D .
Vậy
7;0
D hoặc
2;9
D .
B
D
C
A
C
A
D
B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 7: Giá trị m thỏa mãn để giá trị lớn nhất của hàm số
2 1f x x m trên
1;3 bằng
5
thuộc khoảng nào:
A.
3; 2 . B.
3;4
. C.
0;1 . D.
1;2
.
Lời giải
Chọn D
Vì hàm số
2 1f x x m đồng biến trên
nên
1;3
max 3 2 2f x f m
.
Do đó
3
2 2 5
2
m m
.
Kết luận:
3
2
m
thỏa mãn.
Câu 8: Cho a là số thực bé hơn 2020. Giá trị lớn nhất của biểu thức
2 2
.cos 2020sinP a x x
bằng
A. 2020. B. a. C.
2020a
. D.
2020a
.
Lời giải
Chọn A
Ta có
2 2 2 2 2
2
.cos 2020sin 2020 cos 2020 cos sin
2020 cos 2020.
P a x x a x x x
a x
Do
2
2020 2020 0 2020 cos 0 2020.a a a x P
Như vậy giá trị lớn nhất của P là 2020, đạt được khi cos 0.x
Câu 9: Tập nghiệm của bất phương trình
2
2 3 0x x
là:
A.
3;1 . B.
1;3 . C.
1;3 . D.
3;1 .
Lời giải
Chọn D
2
1
2 3 0
3
x
x x
x
Bảng xét dấu:
Vậy
3;1S
Câu 10: Tập nghiệm của bất phương trình
3
8 2 4 1 14 8 1x x x x x
có dạng
;
a b
c
, trong đó ,a b là các số nguyên tố. Tính giá trị biểu thức T a b c .

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2
. B.
6.
C.
5.
D.
8.
Lời giải
Chọn D
Điều kiện
1
x
.
Bpt
3
8 2 4 1 1 8 1 16 1
x x x x x
3
3
8 2 4 1 4 1
x x x x
.
Đặt
2 , 4 1 2, 4
a x b x a b
. Bpt trở thành:
3 3
a a b b
2 2
1 0 0
a b a ab b a b
(do
2, 4
a b
nên
2 2
1 0
a ab b
).
Từ kết quả
2
2 4 0
2 4 1 2 4 1 1 0
2 4 1
x
a b x x x x x
x x
2
2
17 17
2
17 17
8
8
4 17 17 0
17 17
8
x
x
x
x
x x
x
.
Vậy
17, 17, 8 8
a b c T a b c
.
Câu 11: Cho
tan 3
. Tính giá trị của biểu thức
2
sin 2
cos 2 3sin
P
.
A.
19
6
. B.
6
19
. C.
2
5
.
D.
5
2
.
Lời giải
Chọn B
2 2 2 2
sin 2 2sin cos 2sin cos
cos 2 3sin 1 2sin 3sin 1 sin
P
.
Chia cả tử và mẫu của
P
cho
2
cos 0
và thay
2
2
sin 1
tan , 1 tan
cos cos
ta được
2
2tan 2.3 6
1 2tan 1 2.9 19
P
.
Phần trình bày trên có thể rút gọn như sau:
Vì
cos 0
nên
2 2 2 2 2 2 2
2sin cos 2sin cos 2tan 2.3 6
.
cos sin 3sin cos 2sin 1 2tan 1 3 19
P

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 12: Tìm tọa độ một véc tơ chỉ phương của đường thẳng
có phương trình:
2
1 3
x t
t
y t
.
A.
1;3
u
. B.
1;3
u
. C.
3;1
u
. D.
2;1
u
.
Lời giải
Chọn B
Câu 13: Tìm giá trị lớn nhất của hàm số
3
1
y x x
với
0 1
x
.
A.
27
256
. B.
81
256
. C.
2
. D.
1
16
.
Lời giải
Chọn A
Ta có:
3
1
1 .3 1 1 1
3
y x x x x x x
.
Do
0 1
x
nên
1 0
x
.
Áp dụng bất đẳng thức Côsi cho 4 số không âm
3 ,1 ,1
x x x
và
1
x
ta được:
4 4
1 3 (1 ) (1 ) (1 ) 1 3 27
. .
3 4 3 4 256
x x x x
y
.
Suy ra giá trị lớn nhất của hàm số bằng
27
256
đạt được khi
1
3 1
4
x x x
.
Câu 14: Trong mặt phẳng
Oxy
, cho đường thẳng
:5 2 8 0
d x y
. Véctơ pháp tuyến của
đường thẳng
d
là
A.
2; 5
n
. B.
5;2
n
. C.
2;5
n
. D.
5; 2
n
.
Lời giải
Chọn D
Từ phương trình tổng quát ta có véctơ pháp tuyến của đường thẳng
d
là
5; 2
n
.
Câu 15: Cho góc lượng giác
,
Ou Ov
có số đo
7
. Trong các số
29 22 6 41
; ; ;
7 7 7 7
,
những số nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã
cho?
A.
29 41
;
7 7
. B.
29 22
;
7 7
. C.
22 41
;
7 7
. D.
6 41
;
7 7
.
Lời giải
Chọn B
Hai góc có cùng tia đầu, tia cuối thì sai khác nhau một bội của
2
do đó
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vì
29
2 .2
7 7
,
22
3
7 7
,
6
7 7
và
41
3.2
7 7
nên các số
29 41
;
7 7
là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc đã
cho.
Câu 16: Một người nông dân có 6 triệu đồng để làm một hàng rào chữ
E
dọc theo một
con sông (như hình vẽ) làm một khu đất có hai phần là hình chữ nhật để trồng rau.
Đối với mặt hàng rào song song bờ sông thì chi phí nguyên vật liệu là
60000
đồng
một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu
là
40000
đồng một mét. Tính diện tích lớn nhất của khu đất rào thu được.
A.
1245
. B.
1250
. C.
1255
. D.
1260
.
Lời giải
Chọn B
Gia
sử đô
dai cu
a mô
t hang rao vuông goc bờ sông la
x m
va đô
dai cu
a hang rao song song với bờ sông la
, 0 .
y m x y
Khi đo, tô
ng sô tiên đê
mua hang rao la
3 .40000 .60000 6000000
x y
100 2
y x
.
Diê
n tich khu đât la
2
. 100 2 2 25 1250 1250.
S x y x x x
Vâ
y diê
n tich khu đât lớn nhât la
2
1250
m
khi
25
x m
va
50 .
y m
Câu 17: Trên đường tròn lượng giác, điểm biểu diễn của cung có số đo
11
3
có điểm cuối
thuộc góc phần tư nào?
A. Thứ nhất. B. Thứ hai. C. Thứ ba. D. Thứ tư.
Lời giải
Chọn D
Ta có
11
2.2
3 3
. Vậy điểm cuối của
2
cung
11
3
và
3
trùng nhau. Điểm cuối của
cung
3
thuộc cung phần tư thứ tư.
Câu 18: Cho
3
cos
5
với
0
2
. Khi đó giá trị của biểu thức
sin 3cos
5sin 6
P
bằng

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2
5
P
. B.
1
5
P
. C.
1
5
P
. D.
1
P
.
Lời giải
Chọn C
Ta có
2 2
9 16
sin 1 cos 1
25 25
.
Suy ra
4
sin
5
hoặc
4
sin
5
.
Vì
0
2
nên
sin 0
, do đó
4
sin
5
.
Vậy
4 6
sin 2cos 1
5 5
4
5sin 6 5
5. 6
5
P
.
Câu 19: Tìm tọa độ tâm của đường tròn
C
có phương trình
2 2
2 4 2020 0
x y x y
.
A.
1;2
I . B.
1; 2
I
. C.
1; 2
I
. D.
1;2
I .
Lời giải
Chọn D
Ta có
2 2
2 2
2 4 2020 0 1 2 2025
x y x y x y
.
Suy ra đường tròn
C
có tâm
1;2
I .
Câu 20: Có bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để bất phương trình
3 2
2 0
x x m x m
nghiệm đúng với mọi
0
x
?
A.
7
. B.
8
. C.
9
. D.
10
.
Lời giải
Chọn D
Ta có
3 2 3 2
2 0 2 1 0
x x m x m x x x m x
2 2
1 2 1 0 1 2 0
x x x m x x x x m
.
Với
0
x
thì
1 0
x
, khi đó
2
1 2 0
x x x m
với mọi
0
x
2
2 0
x x m
với
mọi
0
x
2
2
m x x
với mọi
0
x
.
Đặt
2
2
f x x x
. Lập bảng biến thiên hàm số
y f x
trên
0;

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Trên
0;
thì
max 1
f x
khi
1.
x
Suy ra:
3 2
2 0
x x m x m
đúng với mọi
0
x
khi
max
m f x
trên
0;
hay
1
m
.
Kết hợp với điều kiện
m
là số nguyên và
10;10
m
nên
1;2;3;4;5;6;7;8;9;10
m
.
Vậy có tất cả
10
giá trị của tham số
m
thỏa yêu cầu bài toán.
Câu 21: Cho
3
sin
5
và
2 2
. Tính giá trị
cos
.
A.
4
5
. B.
16
25
. C.
4
5
. D.
4
5
.
Lời giải
Chọn A
Ta có
2
2 2
3 16
cos 1 sin 1
5 25
.
Suy ra
4
cos
5
hoặc
4
cos
5
.
Vì
2 2
nên
cos 0
, vậy ta có
4
cos
5
.
Câu 22: Cho elip
2 2
:4 9 1
E x y
. Chọn khẳng định sai.
A. Độ dài trục nhỏ là
1
3
. B. Độ dài trục lớn là
1
.
C. Tiêu cự là
5
3
. D. Tiêu điểm là
1 2
5 5
;0 ; ;0
6 6
F F
.
Lời giải
Chọn A
2 2
2 2
:4 9 1 1.
1 1
4 9
x y
E x y
Khi đó:
2 2
1 1 5
; .
2 3 6
a b c a b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Do đó độ dài trục nhỏ là
2
2 .
3
b
Vậy khẳng định sai là: Độ dài trục nhỏ là
1
3
.
Câu 23: Tìm tất cả các giá trị của tham số
m
để với mọi x
ta có
2
2
5
1 7
2 3 2
x x m
x x
.
A.
5
1
3
m
. B.
5
1
3
m
. C.
5
3
m
. D.
1
m
.
Lời giải
Chọn A
Vì
2
2
3 7
2 3 2 2 0 , ,
4 8
x x x x
nên
2 2
2
2
2 2
1 2 3 2 5
5
1 7
2 3 2
5 7 2 3 2
x x x x m
x x m
x x
x x m x x
2
2
13 26 14 0 1
3 2 2 0 2
x x m
x x m
.
Tập nghiệm của bất phương trình
2
2
5
1 7
2 3 2
x x m
x x
là
khi và chỉ khi
1
và
2
cùng có
tập nghiệm là
.
Tập nghiệm của
1
là
khi và chỉ khi tam thức bậc hai
2
13 26 14
x x m
có biệt thức thu
gọn
13( 13 13 ) 0
m
1
m
(3).
Tập nghiệm của
2
là
khi và chỉ khi tam thức bậc hai
2
3 2 2
x x m
có biệt thức thu gọn
5 3 0
m
5
3
m
(4).
Kết hợp (3) và (4), ta có
5
1
3
m
.
Câu 24: Phương trình đường tròn có tâm thuộc đường thẳng
: 2 0
x y
, tiếp xúc với
đường thẳng
:2 2 0
x y
đồng thời đường tròn đi qua điểm
1;3
M
là
A.
2 2
2 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
B.
2 2
2 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
C.
2 2
1 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
D.
2 2
2 1 5
x y
và
2 2
23 23 1885
4 8 16
x y
.
Lời giải
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi tâm của đường tròn cần tìm là
2 ; : 2 0.
I t t x y
Theo giả thiết ta có:
2 2
2.2 2
; 2 1 3
5
t t
MI d I t t
2
3 2
5 10 10
5
t
t t
2
8 31 23 0
t t
1
23
8
t
t
.
Với
1
t
thì đường tròn cần tìm có tâm
2;1
I
, bán kính
5 ,
R IM và có phương trình là
2 2
2 1 5
x y
.
Với
23
8
t
thì đường tròn cần tìm có tâm
23 23
;
4 8
I
, bán kính
17 5
,
8
R IM và có phương
trình là
2 2
23 23 1445
4 8 64
x y
.
Vậy có hai đường tròn thỏa mãn yêu cầu của bài toán là
2 2
2 1 5
x y
và
2 2
23 23 1445
4 8 64
x y
.
Câu 25: Cho hai đường thẳng
1
: 2 0
d x y
và
2
: 2 3 3 0
d x y
. Số đo của góc giữa hai
đường thẳng
1
d
và
2
d
gần với giá trị nào sau đây nhất?
A.
11 19
. B.
78 41
. C.
101 19
. D.
78 31
.
Lời giải
Chọn B
Đường thẳng
1
: 2 0
d x y
có một vectơ pháp tuyến là
1
1; 1
n
.
Đường thẳng
2
: 2 3 3 0
d x y
có một vectơ pháp tuyến là
2
2;3
n
.
Gọi góc giữa
1
d
và
2
d
là
(0 90 )
.
Ta có
1 2
1 2
.
cos
.
n n
n n
2
2 2 2
2 3
1 1 . 2 3
26
26
78 41
.
Câu 26: Cho tam giác
ABC
với
2;3 , 1; 1 , 10; 3
A B C
. Gọi
;
M a b
là điểm trên cạnh
BC
sao cho
DE
có độ dài nhỏ nhất với
,
D E
lần lượt là hình chiếu của
M
lên
,
AC AB
. Khi đó biểu thức
2 2
P a b
nhận giá trị bằng bao nhiêu?
A.
97
4
. B.
17
5
. C.
733
121
. D.
87
25
.
Lời giải
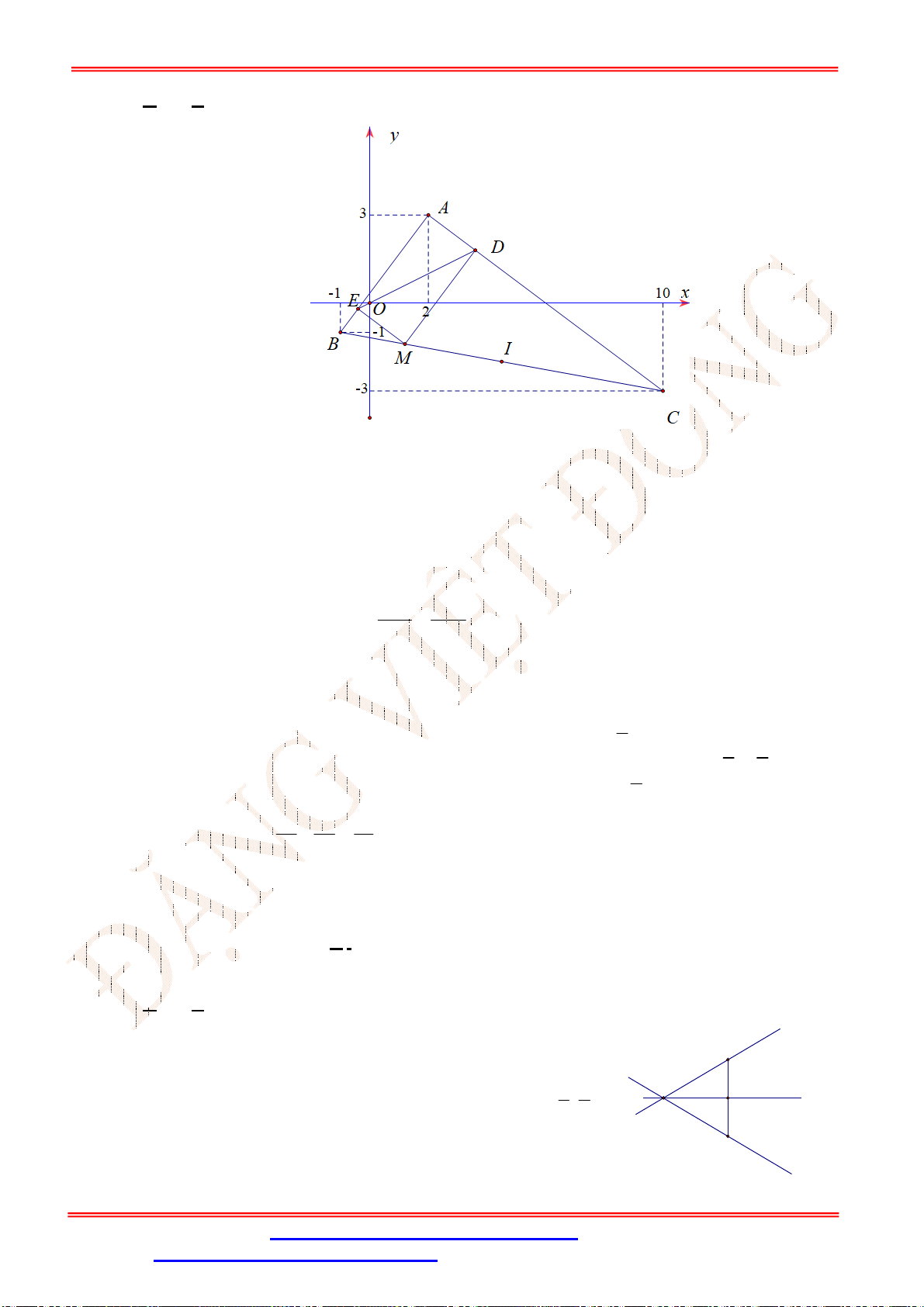
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B
Ta có
3; 4 , 8; 6
AB AC
. 3.8 4 6 0
AB AC
tam giác
ABC
vuông tại
A
.
Ta có
ADME
là hình chữ nhật nên
AM DE
.
Như thế
DE
nhỏ nhất
AM
nhỏ nhất
AM BC
M
là hình chiếu vuông góc của
A
lên
BC
.
Phương trình đường thẳng
BC
1 1
2 11 13 0
11 2
x y
x y
.
Đường thẳng qua
A
nhận
11; 2
BC
làm véctơ pháp tuyến có phương trình
11 2 2 3 0 11 2 16 0.
x y x y
Khi đó, tọa độ
M
là nghiệm của hệ
6
2 11 13 0
5
11 2 16 0 7
5
x
x y
x y
y
. Vậy
6 7
;
5 5
M
.
Từ đó suy ra
36 49 17
25 25 5
P .
Câu 27: Cho hai đường thẳng
1
: 2 1 0
d x y
,
2
: 3 3 0.
d x y
Phương trình đường thẳng
d
đối xứng với
1
d
qua
2
d
là:
A.
2 2 0.
x y
. B.
2 2 0.
x y
. C.
2 2 0
x y
. D.
2 2 0
x y
.
Lời giải
Chọn B
Gọi I là giao điểm của hai đường thẳng
1 2
,
d d
.
Tọa độ điểm
I
là nghiệm của hệ:
2 1 0
3 4
;
3 3 0
5 5
x y
I
x y
.
Lấy điểm
1
1 0
M ; d
. Đường thẳng
qua
M
và vuông góc
Δ
d
d
2
d
1
N
H
M
I

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
với
2
d
có phương trình:
3 3 0
x y .
Gọi
2
H d
, suy ra tọa độ điểm
H
là nghiệm của hệ:
3 3 0
3 6
3 3 0
5 5
x y
H ;
x y
Gọi
N d
.
d
đối xứng với
1
d
qua
2
d
, suy ra
H
là trung điểm
MN
.
1
2
1 12
5
12
5 5
2
5
N H M
N H M
x x x
N ;
y y y
.
3 4
qua ;
5 5
:
4 8
;
5 5
d
I
d
vtcp u IN
Phương trình d:
2 2 0.
x y
Câu 28: Xác định tâm sai của elip (E):
2 2
1
25 9
x y
.
A.
5
4
. B.
4
5
. C.
5
3
. D.
3
5
.
Lời giải
Chọn B
Ta có
2
25 5
a a
,
2
9 3
b b
2 2 2
16 4
c a b c
. Vậy tâm sai là
4
5
c
e
a
.
Câu 29: Trong mặt phẳng
Oxy
, cho đường thẳng
:2 4 1 0
d x y
. Phương trình tham số
của đường thẳng
đi qua
6
(3;
)
A
và song song với đường thẳng
d
là
A.
3 2
6 4
x t
y t
. B.
4 3
2 6
x t
y t
. C.
3 4
6 2
x t
y t
. D.
3 2
6
x t
y t
.
Lời giải
Chọn D
+) Đường thẳng
:2 4 1 0
d x y
2; 4
n
là véctơ pháp tuyến của đường thẳng
d
.
+)
/ /
d
2; 4
n
cũng là véctơ pháp tuyến của đường thẳng
.
2;1
u
là véctơ chỉ phương của đường thẳng
Mà đường thẳng
đi qua
6
(3;
)
A
nên phương trình tham số của đường thẳng
là
3 2
6
x t
y t
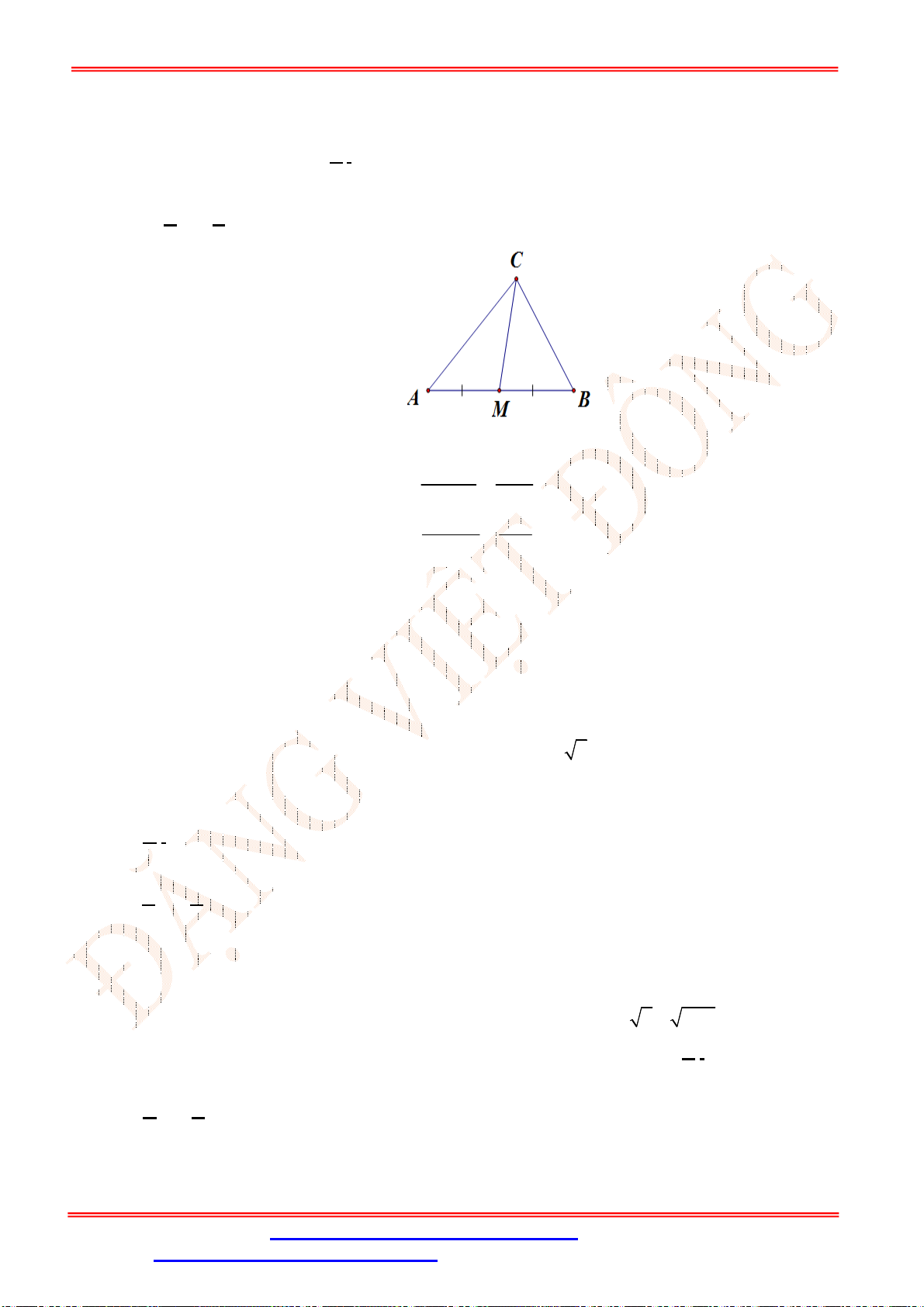
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 30: Trong mặt phẳng tọa độ
,
Oxy
cho
ABC
có
2;1 , 2;3 ,C 0;2 .
A B Phương trình
tổng quát của đường thẳng chứa trung tuyến
CM
của
ABC
là:
A.
2 0
y
. B.
2 0
y
. C.
2 0
x y
. D.
2 0
x y
.
Lời giải
Chọn B
Ta có
M
là trung điểm
2 2
2
2 2
2;2 .
1 3
2
2 2
A B
M
A B
M
x x
x
AB M
y y
y
Đường thẳng chứa trung tuyến
CM
nhận
2;0
CM làm
VTCP
Đường thẳng chứa trung
tuyến
CM
nhận
0;1
n
làm
VTPT
.
Đường thẳng chứa trung tuyến
CM
đi qua điểm
0;2
C và nhận véc tơ
0;1
n
làm VTPT có
phương trình:
0 0 1 2 0 2 0
x y y
.
Câu 31: Đường tròn
(C)
có tâm
(1; 2)
I
và bán kính
2
R . Phương trình của đường tròn
(C)
là:
A.
2 2
2 4 3 0
x y x y
. B.
2 2
2 2 4 3 0
x y x y
.
C.
2 2
2 2 4 8 6 0
x y x y
. D.
2 2
2 4 2 0
x y x y
.
Lời giải
Chọn C
Phương trình đường tròn
(C)
là
2 2 2 2
( 1) ( 2) 2 2 2 4 8 6 0
x y x y x y
.
Vậy chọn đáp án C
Câu 32: Tìm
a
để bất phương trình sau có nghiệm
3 2
3 1 1
x x a x x
A
3
a
. B.
3
a
. C.
2
a
. D.
3
a
.
Lời giải
Chọn D
Điều kiện:
1
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
BPT
3 2
1 3 1
x x x x a
1
.
Đặt
3 2
3 1 1
f x x x x x
.
1 2 1 2
, 1; ,
x x x x
, ta có
1 1 2 2
1 1
x x x x
,
3 2 3 2
1 1 2 2
1 3 3
x x x x
3 2 3 2
1 1 2 2
0 3 1 3 1
x x x x
Suy ra
3 2 3 2
1 1 1 1 2 2 2 2
3 1 1 3 1 1
x x x x x x x x
.
1 2
f x f x
,
1 2
, 1;x x
.
Suy ra
f x
đồng biến trên
1;
.
Mà
1 3
f
1
3
x ;
min f x
.
Suy ra:
1
có nghiệm
3
a .
Câu 33: Trong mặt phẳng tọa độ
O
xy
cho điểm
3 1
A ;
và đường thẳng
4 2
Δ
5 3
x t
:
y t
. Tìm
điểm
M
thuộc đường thẳng
Δ
sao cho
5 2
MA
?
A.
2 8
M ;
và
118 34
13 13
M ;
. B.
2 8
M ;
và
108 34
13 13
M ;
.
C.
2 8
M ;
và
118 34
13 13
M ;
. D.
2 8
M ;
và
118 34
13 13
M ;
.
Lời giải
Chọn D
Do
Δ 4 2 5 3
M M t; t
.
2 2
2 2
2
5 2 1 2 4 3 5 2
1 2 4 3 50
1
13 20 33 0
33
13
MA t t
t t
t
t t
t
+> Với
1 2 8
t M ;
+> Với
33 118 34
13 13 13
t M ;
Chọn D
truyphong.t0408@gmail.com

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 34: Tìm số giá trị nguyên
m
để bất phương trình
2
1 2 7 0
x m x m
có tập
nghiệm
.
A.
5
. B.
7
. C.
11
. D.
15
.
Lời giải
Chọn C
Đặt
2
1 2 7
f x x m x m
0,f x x
2
1 0
1 4 2 7 0
0
a
m m
2
6 27 0
m m
3 9
m
.
Do đó
2; 1;0;1;2;3;4;5;6;7;8
m . Vậy có
11
giá trị nguyên
m
.
Câu 35: Tìm tập hợp
S
tất cả các giá trị của tham số
m
để bất phương trình
8 7 3 8 2
m x mx m
có tập nghiệm là tập con của khoảng
1;
.
A.
5;S
. B.
3;S
. C.
5;S
. D.
3;S
.
Lời giải
Chọn C
Ta có
2 3
8 7 3 8 2 7 2 3
7
m
m x mx m x m x
.
Bất phương trình có tập nghiệm là
2 3
;
7
m
T
.
Để tập nghiệm là tập con của khoảng khoảng
1;
ta có
2 3
1 5
7
m
m
. Suy ra
5;m
.
Câu 36: Gọi
,
M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức:
4 4 4 4
2 2 2 2
sin cos cos sin
sin cos cos sin
a x b y a x b y
H
c x d y c x d y
, với
, , , 0
a b c d
. Giá trị
,
M m
là:
A. ,
a c a b
M m
b d c d
. B. ,
a b a b
M m
c d c d
.
C. ,
a b a c
M m
c d b d
. D. ,
a c a c
M m
b d b d
.
Lời giải
Chọn B
Ta có:
4 4 4 4
2 2 2 2 2 2 2 2
sin cos cos sin
sin cos cos sin sin cos cos sin
x x y y
H a b
c x d y c x d y c x d y c x d y

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có:
4 4 4 4
2 2 2 2 2 2
sin cos sin cos 1
sin cos cos sin sin cos
x x x x
c
c x d y c x d y c x c x
.
Dấu đẳng thức xảy ra khi
cos 0 cos 0
sin 0 cos 0
cos 0 sin 0
sin 0 sin 0
y x
x y
x x
y y
4 4 4 4
2 2 2 2 2 2
cos sin cos sin 1
sin cos cos sin cos sin
y y y y
d
c x d y c x d y d y d y
Dấu đẳng thức xảy ra khi
cos 0 cos 0
sin 0 cos 0
cos 0 sin 0
sin 0 sin 0
y x
x y
x x
y y
a b
H
c d
. Dấu đẳng thức xảy ra khi
cos 0
cos 0
sin 0
sin 0
x
y
x
y
.
Do đó, max
a b
H M
c d
Vì
2 2 2 2
sin cos sin cos
c d c x x d y y
Nên theo bất đẳng thức Bunhiakovski, ta có:
4 4
2 2 2 2
4 4
2 2 2 2
2 2 2 2
2
2 2
sin cos
sin cos cos sin
sin cos
sin cos cos sin
sin cos cos sin
sin cos 1
x x
c d
c x d y c x d y
x x
c x d y c x d y
c x d y c x d y
x x
.
Dấu đẳng thức xảy ra khi
2 2
2 2 2 2
sin cos
sin cos cos sin
x x
c x d y c x d y
2 2 2 2
cos cos sin sin cos .cos 0
x y x y x y x y

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Tương tự:
4 4
2 2 2 2
4 4
2 2 2 2
2 2 2 2
cos sin
sin cos cos sin
cos sin
sin cos cos sin 1
sin cos cos sin
y y
c d
c x d y c x d y
y y
c x d y c x d y
c x d y c x d y
Dấu đẳng thức xảy ra khi
2 2
2 2 2 2
cos sin
sin cos cos sin
y y
c x d y c x d y
4 4
cos cos cos cos cos cos 0 sin .sin 0
x y x y x y x y x y
Do đó:
a b a b
H
c d c d c d
. Dấu đẳng thức xảy ra khi
sin 0
cos 0
sin 0
cos 0
x y
x y
x y
x y
Vậy min
a b
H m
c d
.
Câu 37: Trong mặt phẳng với hệ tọa độ
Oxy
cho đường thẳng :
1
x t
y
và điểm
3; 2
P
. Điểm
Q
,
PQ
khi đó tọa độ
Q
là:
A.
3;0
Q . B.
0;3
Q . C.
1;3
Q . D.
3;1
Q .
Lời giải
Chọn D
+) Ta có vectơ chỉ phương của đường thẳng
là
1;0
u
.
+) Do
;1
Q Q t
. Do đó
3;3
PQ t
.
+) Vì
. 0 1. 3 0.3 0 3
PQ PQ u t t
.
Vậy
3;1
Q .
Câu 38: Tìm tập xác định của hàm số sau:
2
2
5 4
9 1
x x
y
x
.
A.
3;1
. B.
3;1
. C.
3;1
. D.
3;4
.
Lời giải:
Chọn C
Hàm số xác định khi
2
2
;1 4;
5 4 0
3;1
3;3
9 0
x
x x
x
x
x
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
.
Câu 39: Trên đoạn
2;2
, hàm số
2
1
mx
y
x
(với
0
m
) đạt giá trị nhỏ nhất tại
1
x
khi và
chỉ khi
A.
2
m
. B.
2
m
. C.
0
m
. D.
0
m
.
Lời giải
Chọn C
Vì
1
2
m
y nên bài toán trở thành tìm
0
m
để
2
1 2
mx m
x
,
2;2
x
.
Ta có
2
1 2
mx m
x
,
2;2
x
2
2 1 0
m x x
,
2;2
x
2
1 0
m x
,
2;2
x
0
m
.
Mà
0
m
nên
0
m
.
Câu 40: Trong hệ tọa độ
Oxy
, cho tam giác
ABC
vuông tại
A
và nội tiếp trong đường tròn
C
có phương trình:
2 2
6 2 5 0
x y x y
. Gọi
H
là hình chiếu vuông góc của
A
trên
BC
, đường tròn đường kính
AH
cắt
,
AB AC
lần lượt tại
,
M N
. Biết đường
thẳng chứa
,
M N
có phương trình
20 10 9 0
x y
. Khi đó hoành độ của điểm
A
là
A.
1
. B.
5
. C.
0
. D.
2
.
Lời giải
Chọn A
+) Do tam giác
ABC
vuông tại
A
và nội tiếp trong đường tròn
C
nên
C
là đường tròn
đường kính
BC
( tâm
3;1
I là trung điểm của
BC
)
+) Đường tròn đường kính
AH
cắt
,
AB AC
lần lượt tại
,
M N
nên ,
HM AB HN AC
+) Ta có
2 . .
. .
. .
. .
.
. 0
AI MN AB AC MA AN
AB MA AC AN
AB MH HA AC AH HN
AB HA AC AH
AC AB AH
BC AH
AI MN
(*)
+) Do đó
AI
có phương trình:
10 20 0
x y c
50
I AI c
:10 20 50 0 2 5 0
AI x y x y AI
N
M
H
I
B
C
A
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A AI C
nên tọa độ
A
thỏa mãn hệ:
2 2
5
0
2 5 0
6 2 5 0
1
2
x
y
x y
x y x y
x
y
5;0
1;2
A
A
+) Nếu
5;0
A khi đó
20 10 9 20 10 9 0
A A I I
x y x y
khi đó
,
A I
nằm cùng phía đối
với đường thẳng
MN
nên không thỏa mãn đề bài.
Vậy
1;2
A
Lưu ý: ngoài ra để chứng minh (*) ta có thể làm như sau:
Dựng tiếp tuyến
với đường tròn
I
tại
A
, khi đó
AI
. Nên để chứng minh
AI MN
ta đi chứng minh / /
MN
.
Thật vậy
Ta có:
1
1 1 1 1
1
90
90 / /
A C HAC
M N A M MN AI MN
HAC N
Câu 41: Mệnh đề nào sau đây sai?
A.
2 2
cos2 cos -sin
a a a
. B.
2 2
cos2 sin cos
a a a
C.
2
cos2 1 2sin
a a
. D.
2
cos2 2cos 1
a a
.
Lời giải
Chọn B
Câu 42: Cho
5
cos
13
a
0
2
a
. Giá trị
tan
a
là
A.
5
12
. B.
13
5
. C.
12
5
. D.
12
5
.
Lời giải
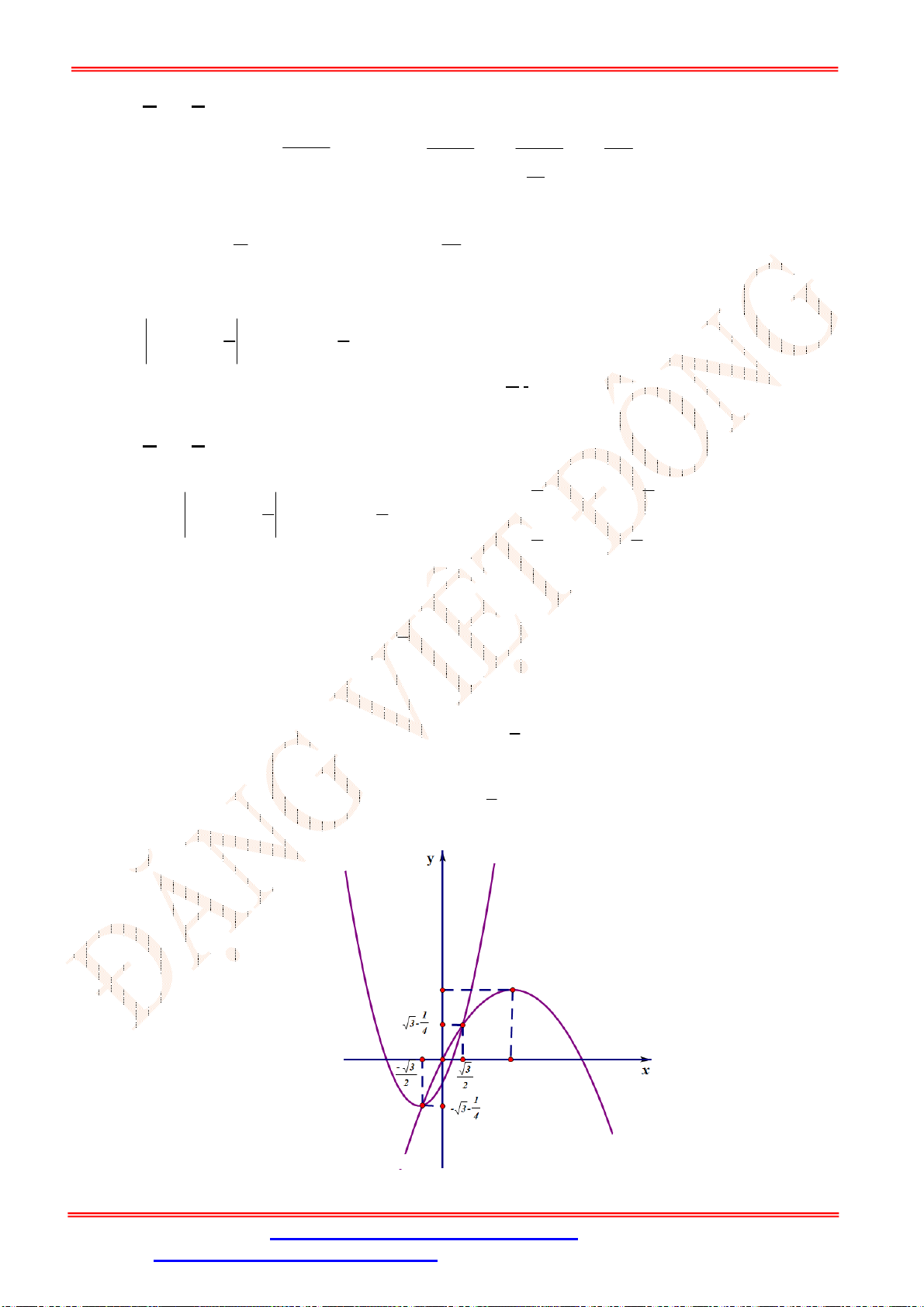
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D
Ta có:
2
2
1
1 tan
cos
a
a
2
2
2
1 1 144
tan 1 1
cos 25
5
13
a
a
Do: 0
2
a
nên
tan 0
a
12
tan
5
a .
Câu 43: Có bao nhiêu giá trị nguyên của tham số
2020;2020
m
để bất phương trình
2
1 1
4 2 2
2 2
x m x x m
luôn đúng với mọi
x
.
A.
2020
. B.
2018
. C.
4038
D.
4039
.
Lời giải
Chọn C
BPT
2
1 1
4 2 2
2 2
x m x x m
2
2
1 1
4 2 2
2 2
1 1
4 2 2
2 2
x m x x m
x m x x m
2
2
2 1 0
6 3 0
x x m
x x m
2
2
2 1
1
2
3
m x x
m x x
Ta cần tìm giá trị của tham số
m
sao cho
2
2
2 1
1
2
3
m x x
m x x
với mọi
x
.
Vẽ đồ thị các hàm số
2
2 1
y x x
và
2
1
2
3
y x x
trên cùng một hệ trục tọa độ.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Dựa vào đồ thị ta tìm được
1
3
4
m
hoặc
1
3
4
m
thỏa mãn ycbt.
Mặt khác:
2020;2020
m
,m
. Do đó
2020;...; 2;2;...;2020
m
.
Vậy có tất cả
4038
giá trị nguyên của tham số
m
thỏa mãn ycbt.
Câu 44: Hệ bất phương trình
2
1 2
2
3 3
3 4 0
x
x
x x
có tập nghiệm là
A.
5;
B.
; 4 1;
C.
4; 1
D.
5; 4 1;
Lời giải
Chọn D
2
2
5
1 2
3 1 2 6
2
4
3 3
3 4 0
3 4 0
1
x
x
x x
x
x
x x
x x
x
Vậy, hệ bất phương trình có tập nghiệm là:
5; 4 1;S
.
Câu 45: Cho số thực
1
a
.Giá trị nhỏ nhất của biểu thức
4
1
P a
a
là
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn D
Vì
1 1 0
a a
;
4
( 1) 1
1
P a
a
Áp dụng bất đẳng thức Côsi cho 2 số:
4 4
( 1) 2 ( 1). 4 4 1 5
1 1
a a P
a a
Dấu “=” xảy ra
2
3
4
1 ( 1) 4
1
1
a
a a
aa
3
a
( vì
1
a
)
Vậy giá trị nhỏ nhất của biểu thức
P
là
5
.
Câu 46: Biểu thức
0 0 0 0 0
cos20 cos40 cos60 ... cos160 cos180
A có giá trị bằng
A.
1
. B.
1
. C.
2
. D.
2
.
Lời giải
Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
0 0 0 0 0
0 0 0 0 0 0
cos20 cos40 cos60 ... cos160 cos180
cos20 cos160 cos40 cos140 ... cos80 cos100 cos1
80
0 0 ... 0 1
1
A
.
Câu 47: Cho
5 1;8
a m
và
2;
b m
, giá trị của tham số
m
để hai véctơ
a
và
b
vuông
góc với nhau là
A.
1
. B.
0
. C.
1
. D.
2
.
Lời giải
Chọn A
Dễ thấy hai véctơ
a
và
b
đều khác véc tơ không do đó
. 0 2. 5 1 8. 0 1
a b a b m m m
.
Câu 48: Cho
2
. Xác định dấu của các biểu thức sin
2
A.
sin 0
2
. B.
sin 0
2
. C.
sin 0
2
. D.
sin 0
2
.
Lời giải
Chọn B
Ta có
3
2 2 2
sin 0
2
Câu 49: Cho hình thang vuông
ABCD
có:
90
A B
, đáy bé
5
AD
, đáy lớn
15
BC
, và
12
AB
. Điểm
M
thuộc cạnh
AB
(không trùng
A
hoặc
B
) sao cho tổng
MD MC
nhỏ nhất. Khi đó tích độ dài .
AM BM
là
A.
18
. B.
20
. C.
27
. D.
36
.
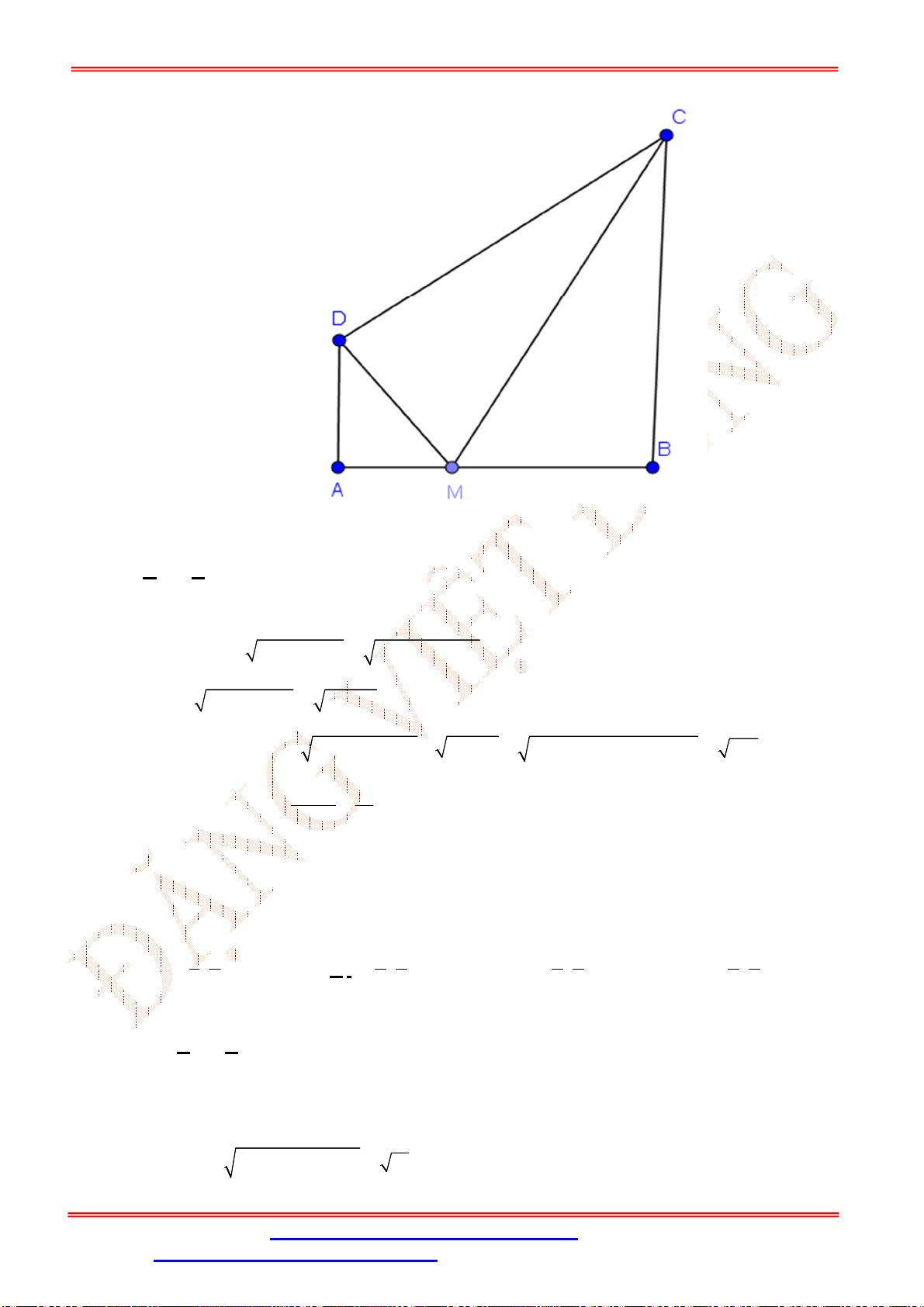
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn C
Đặt (0 12)AM x x khi đó: 12BM x
Ta có:
2 2 2 2
(12 ) 15MC MB BC x
2 2 2 2
5MD MA AD x
Khi đó:
2 2 2 2 2 2
(12 ) 15 5 (12 ) (15 5) 544MC MD x x x x
Dấu “=” xảy ra
12 15
3
5
x
x
x
Khi đó: 3; 9AM BM . Tích . 27AM BM . Chọn đáp án C
Câu 50: Trong mặt phẳng tọa độ Oxy , cho
3
điểm
1;1A
,
3;4B
,
4; 1C
. Gọi
I
là tâm
đường tròn ngoại tiếp tam giác
ABC
tọa độ tâm
I
là
A.
8 4
;
3 3
I
. B.
7 3
;
2 2
I
. C.
7 3
;
3 2
I
. D.
5 3
;
2 2
I
.
Lời giải
Chọn B
Cách 1.
Ta có:
2 2
3 1 4 1 13AB

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 2
4 1 1 1 13
AC
2 2
4 3 1 4 26
BC
2 2 2
AB AC BC
.
Vậy tam giác
ABC
vuông tại
A
. Từ đó suy ra, tâm
I
của đường tròn ngoại tiếp tam giác
ABC
là trung điểm của đoạn
BC
7 3
;
2 2
I
. Chọn B
Cách 2.
Ta có:
2;3
AB
;
3; 2
AC
. 2.3 2.3 0
AB AC
AB AC
tam giác
ABC
là
tam giác vuông tại
A
nên tâm
I
của đường tròn ngoại tiếp tam giác
ABC
là trung điểm của
cạnh
BC
7 3
;
2 2
I
. Chọn B

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 19
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Số 1x là nghiệm của bất phương trình nào sau đây?
A. 3 0x . B. 2 1 0x . C. 2 1 0x . D. 1 0x .
Câu 2. Tập nghiệm của hệ bất phương trình
2 1 3 2
3 0
x x
x
là:
A.
3;3 . B.
; 3 3; . C.
3; . D.
;3 .
Câu 3. Khẳng định nào sau đây sai?
A. Bất phương trình 0ax b có tập nghiệm là khi 0a và 0b
B. Nếu 0a thì bất phương trình 0ax b luôn có nghiệm.
C. Bất phương trình 0ax b vô nghiệm khi 0a và 0b .
D. Bất phương trình 0ax b vô nghiệm khi 0a .
Câu 4. Cho nhị thức bậc nhất ( ) 23 20f x x . Khẳng định nào sau đây đúng?
A ( ) 0f x với
20
;
23
x
. B. ( ) 0f x với
5
2
x .
C. ( ) 0f x với x . D. ( ) 0f x với
20
;
23
x
.
Câu 5. Cặp số
;x y nào sau đây không là nghiệm của bất phương trình 2 4x y ?
A.
1; 2 . B.
2; 1 . C.
9
;4
2
. D.
3
1;
5
.
Câu 6. Số giá trị nguyên của m để
1
2
x
y
là nghiệm của hệ bất phương trình
3
2 1 4
mx y
x m y
là:
A.
1
. B.
2
. C. 3. D. 5.
Câu 7. Có bao nhiêu số nguyên
x
thỏa
2
5 4 0x x
A. 1. B. 2 . C. 3. D. 4 .
Câu 8. Cho tam thức bậc hai
2
2 1 3x m x m với
m
là tham số. Điều kiện để tam thức đã cho
luôn dương với mọi giá trị của
m
là:
A.
2
2 1 4 3 0m m
. B.
2
2 1 4 3 0m m
.
C.
2
2 1 4 3 0m m
. D.
2
2 1 4 3 0m m
.
Câu 9. Điểm thi của lớp 10C của một trường Trung học Phổ Thông được trình bày ở bảng phân bố tần
số sau:

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Phương sai của bảng phân bố tần số đã cho là:
A.
0,94
B.
3,94.
C.
2,94.
D.
1,94.
Câu 10. Chọn câu đúng trong các câu trả lời sau đây: Phương sai bằng:
A. Một nửa của độ lệch chuẩn B. Căn bậc hai của độ lệch chuẩn.
C. Hai lần của độ lệch chuẩn. D. Bình phương của độ lệch chuẩn.
Câu 11. Cho đường tròn có bán kính
12 cm
. Tìm số đo (
rad
) của cung có độ dài là
6 cm
:
A. 0,5 . B. 3. C. 2. D. 1.
Câu 12. Góc
2
5
có số đo bằng độ là:
A.
18
. B.
36
. C.
72
. D.
12
.
Câu 13. Trong các giá trị sau,
sin
có thể nhận giá trị nào?
A.
2
. B.
4
3
. C.
0,7
. D.
5
2
.
Câu 14. Cho
5
cos
13
. Giá trị của
cos2
bằng
A.
119
169
. B.
219
169
. C.
219
169
. D.
119
169
.
Câu 15. Cho
1 1
cos , cos
3 4
a b
. Giá trị của biểu thức
cos( ).cos( )
P a b a b
bằng
A.
11
16
. B.
11
16
. C.
119
144
. D.
119
144
.
Câu 16. Trong hệ trục tọa độ
Oxy
, đường thẳng đi qua
1; 4
A
và nhận
2; 3
n
làm véc tơ pháp
tuyến có phương trình là:
A.
3 2 14 0
x y
. B.
3 2 14 0
x y
. C.
2 3 14 0
x y
. D.
2 3 14 0
x y
.
Câu 17. Trong hệ trục tọa độ
Oxy
, cho đường thẳng
d
:
5 4 2020 0
x y
. Véctơ nào sau đây là
véctơ pháp tuyến của
d
?
A.
1
4;2
n
. B.
2
4; 10
n
. C.
3
5;4
n
. D.
4
5; 4
n
.
Câu 18. Trong hệ trục tọa độ
Oxy
, cho đường tròn
C
có phương trình
2 2
4 2 4 0
x y x y
. Xác
định tọa độ tâm
I
và bán kính
R
của
C
.
A.
4;2
I ;
24
R . B.
2;1
I ;
3
R
.
C.
2; 1
I
;
3
R
. D.
4;2
I ;
4
R
.
Câu 19. Trong hệ trục tọa độ
Oxy
, phương trình đường tròn tâm
4;3
I bán kính
2
R
là
A.
2 2
4 3 4
x y
. B.
2 2
4 3 4
x y
.
C.
2 2
4 3 2
x y
. D.
2 2
4 3 2
x y
.
Câu 20. Trong mặt phẳng tọa độ
Oxy
, cho elip
E
có phương trình chính tắc
2 2
1
36 25
x y
. Độ dài trục
lớn của elip bằng
A.
10
. B.
36
. C.
12
. D.
25
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 21. Trong mặt phẳng tọa độ
Oxy
, phương trình nào dưới đây là phương trình chính tắc của elip ?
A.
2 2
1
9 4
x y
. B.
2 2
1
9 4
x y
. C.
2 2
1
4 9
x y
. D.
2 2
1
9 4
x y
.
Câu 22. Tổng tất cả các nghiệm nguyên dương của bất phương trình
2
2
1 20
x x x
là
A.28. B.21. C.
22
. D.
20
.
Câu 23. Số nghiệm nguyên của hệ bất phương trình
1
6 4 5
2
5 3
2 9
2
x x
x
x
là
A.
11
. B.
10
. C.12. D.
13
.
Câu 24. Biểu thức
(2 6)( 2020)
( )
( 3 9)
x x
f x
x x
nhận giá trị không âm khi nào?
A.
; 3 0;3 2020;x
. B.
; 3 0;3 2020;x
.
C
; 3 0;3 2020;x
. D.
; 3 0;3 2020;x
.
Câu 25 . Giải bất phương trình sau:
2020
1
2019
x
x
.
A.
1
; 2019 ;
2
x
. B.
1
; 2019 ;
2
x
.
C.
1
2019;
2
x
. D.
1
; 2019 ;
2
x
.
Câu 26 . Số giá trị nguyên của
x
để tam thức
2
2 7 9
f x x x
nhận giá trị âm là
A.
3
. B.
4
. C.
5
. D.
6
.
Câu 27. Tam thức
2
2 2 4
f x x m x m
âm với mọi
x
khi:
A.
14
2
m
m
. B.
14 2
m
. C.
2 14
m
. D.
14 2
m
.
Câu 28 . Đổi sang radian góc có số đó
108
ta được
A.
4
. B.
10
. C.
3
5
. D.
3
2
.
Câu 29. Đơn giản biểu thức
5
sin cos 13 3sin 5
2
D
.
A.
3sin 2cos
. B.
3sin
. C.
3sin
. D.
2cos 3sin
.
Câu 30. Tính
2
2
3tan tan
2 3tan
C
, biết
tan 2
2
A.
2
. B.
2
. C.
14
. D.
34
.
Câu 31. Cho
1;4
A và
3;6
B . Phương trình đường trung trực của đoạn thẳng
AB
là đường thẳng
nào dưới đây?
A.
7 0
x y
. B.
7 0
x y
. C.
2 2 7 0
x y
. D.
2 2 7 0
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 32. Cho đường thẳng
:3 4 2 0
x y
. Đường thẳng nào dưới đây song song và cách
một
khoảng cách bằng
1
?
A.
3 4 7 0
x y
. B.
3 4 3 0
x y
. C.
3 4 7 0
x y
. D.
3 4 1 0
x y
.
Câu 33. Cho hai đường thẳng
1
: 2 1 0
d x my m
và
2
2
:
5
x m t
d
y t
. Tìm các giá trị của tham số
m
để
1 2
,
d d
tạo với nhau một góc bằng
0
45
.
A.
3
m
. B.
3
1
3
m
m
. C.
3
1
3
m
m
. D. .
4 2 7
3
m
.
Câu 34. Phương trình đường tròn có tâm
1; 2
I
và tiếp xúc với đường thẳng
:3 4 1 0
x y
là
A.
2 2
36
1 2
25
x y . B.
2 2
36
1 2
25
x y .
C.
2 2
25
1 2
36
x y . D.
2 2
25
1 2
36
x y .
Câu 35. Trong mặt phẳng tọa độ
Oxy
, viết phương trình chính tắc của elip
E
có độ dài trục lớn bằng
10
và tiêu cự bằng
6
.
A.
2 2
: 1
25 9
x y
E
. B.
2 2
: 1
9 25
x y
E
. C.
2 2
: 1
25 16
x y
E
. D.
2 2
: 1
16 25
x y
E
.
Câu 36. Giá trị của
m
để hệ bất phương trình
2 4 0
2 0
x
mx m
vô nghiệm là
A.
2
0
3
m
. B.
2
3
m
. C.
3
m
. D.
2
0
3
m
.
Câu 37. Tìm tất cả các giá trị thực của tham số
m
để
1
f x m x m x
không âm với mọi
; 1 .
x m
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Câu 38. Giải bất phương trình sau:
2 2
1(*).
2
x
x
A.
0;S
B.
4
2;
3
S
C.
4
2; 0; .
3
S
D.
0; 2
S
Câu 39. Có bao nhiêu giá trị
m
nguyên để bất phương trình
2 2
3 2 1 2 3 2 0
x m x m m
nghiệm đúng với mọi
x
trên khoảng
2;
.
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 40. Trên đường tròn lượng giác có điểm gốc là
A
, cho tam giác
OMB
và tam giác
ONB
là các
tam giác đều. Cung
có mút đầu là
A
và mút cuối trùng với
,
B M
hoặc
N
. Số đo của cung
là

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
6 3
k
. B.
2
2 3
k
. C.
2 3
k
. D.
2
6 3
k
.
Câu 41. Nếu biết
4 4
sin cos 1
0; 0; 0
a b a b
a b a b
thì biểu thức
10 10
4 4
sin cos
M
a b
bằng:
A.
5 5
1 1
a b
. B.
4 4
1 1
a b
. C.
5
1
a b
. D.
4
1
a b
.
Câu 42. Cho
cos .sin sin
với
2
m
,
2
n
,
,
m n
. Khi đó:
A.
cos
cot 3cot
sin
. B.
cot 2cot
.
C.
cot 2cot
. D.
cos
cot 3cot
sin
.
Câu 43. Cho hai đường thẳng
1 2
: 2 2 0, : 2 3 0
d x y d x y
và điểm
(1;1)
M . Biết rằng có hai
đường thẳng
1 1 1 1 2 2 2 2
: 0, : 0
a x b y c a x b y c
đi qua M và cắt
1 2
,
d d
lần lượt tại
,
A B
sao cho
4
MA MB
. Tính
1 2
1 2
.
a a
T
b b
A.
1.
T
B.
1.
T
C.
340
.
341
T D.
340
.
341
T
Câu 44. Trong mặt phẳng tọa độ Oxy , cho đường thẳng
:2 6 0
x y
và điểm
2;2
A . Gọi
C
là
đường tròn đi qua A có tâm thuộc trục Oy, đồng thời tiếp xúc với
. Tính chu vi của đường
tròn
C
.
A.
5
. B.
2 5
. C.
5
. D.
10
.
Câu 45. Trong mặt phẳng tọa độ
Oxy
, đường thẳng
:3 4 12 0
d x y
cắt elip
2 2
: 1
16 9
x y
E
tại hai
điểm phân biệt
A
,
B
. Biết rằng điểm
0 0
;
C x y E
sao cho diện tích tam giác
ABC
bằng
6
, khi đó
0 0
.
x y
bằng
A.
5
. B.
1
. C.
6
. D.
3 2
.
Câu 46. Có bao nhiêu giá trị
m
nguyên,
2020;2020
m để đa thức
2 2
f x m x m x
không âm với mọi
; 2
x m
?
A. 2020. B. 2022. C. 2023. D. 2021.
Câu 47. Cho bất phương trình
2 2
2( 2) 2 0
x m x m
. Gọi tập
S
là tập các giá trị nguyên của
m
để
bất phương trình đã cho nghiệm đúng với mọi
0;2
x . Số phần tử của tập
S
là:
A. Vô số. B.
2
. C.
1
. D.
3
.
Câu 48. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
6 6
1
sin cos sin 4 .
2
A x x x
Giá trị của
8
m M
bằng
A. 10. B. 12. C. 13. D. 11.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
4;0
A , trung điểm của
BC
là
3;1
M . Gọi
,
E F
lần lượt là chân đường cao kẻ từ
B
và
C
của tam giác
ABC
. Biết đường
thẳng
EF
có phương trình
1 0
x
. Khoảng cách từ
A
đến đường thẳng
BC
là
A.
4 5
. B.
4 2
. C.
3 2
. D.
3 5
.
Câu 50. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
với
( 3; 4)
A
, tâm đường tròn nội tiếp
(2;1)
I
, tâm đường tròn ngoại tiếp
1
;1
2
J
. Tính
( , )
d O BC
.
A.
2
. B.
2 5
. C.
10
. D.
5 2
.
……………….HẾT……………

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 19
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1.B 2.A 3.D 4.D 5.D 6.C 7.D 8.C 9.D 10.D
11.A 12.C 13.C 14.D 15.D 16.D 17.D 18.C 19.B 20.C
21.A 22.A 23.C 24.D 25.A 26.C 27.D 28.C 29.B 30.A
31.B 32.C 33.C 34.A 35.C 36.A 37.B 38.C 39.D 40.B
41.D 42.B 43.D 44.B 45.C 46.C 47.D 48.A 49.D 50.B
HƯỚNG DẪN GIẢI
Câu 1. Số
1
x
là nghiệm của bất phương trình nào sau đây?
A.
3 0
x
. B.
2 1 0
x
. C.
2 1 0
x
. D.
1 0
x
.
Lời giải
Chọn B
Thay
1
x
vào các bất phương trình ta có phương án B đúng.
Câu 2. Tập nghiệm của hệ bất phương trình
2 1 3 2
3 0
x x
x
là:
A.
3;3
. B.
; 3 3;
. C.
3;
. D.
;3
.
Lời giải
Chọn A
Ta có
2 1 3 2
3 0
x x
x
3
3
x
x
3 3
x
.
Câu 3. Khẳng định nào sau đây sai?
A. Bất phương trình
0
ax b
có tập nghiệm là
khi
0
a
và
0
b
B. Nếu
0
a
thì bất phương trình
0
ax b
luôn có nghiệm.
C. Bất phương trình
0
ax b
vô nghiệm khi
0
a
và
0
b
.
D. Bất phương trình
0
ax b
vô nghiệm khi
0
a
.
Lời giải
Chọn D
Vì khi
0, 0
a b
thì bất phương trình
0
ax b
có vô số nghiệm .
Câu 4. Cho nhị thức bậc nhất
( ) 23 20
f x x
. Khẳng định nào sau đây đúng?
A
( ) 0
f x
với
20
;
23
x
. B.
( ) 0
f x
với
5
2
x
.
C.
( ) 0
f x
với x
. D.
( ) 0
f x
với
20
;
23
x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
Ta có:
20
( ) 0 23 20 0
23
f x x x .
Câu 5. Cặp số
;
x y
nào sau đây không là nghiệm của bất phương trình
2 4
x y
?
A.
1; 2
. B.
2; 1
. C.
9
;4
2
. D.
3
1;
5
.
Lời giải
Chọn D
+) Thay
1; 2
x y
vào bất phương trình, ta được:
2.1 2 4
(luôn đúng).
Cặp số
1; 2
là nghiệm của bất phương trình trên.
+) Thay
2; 1
x y
vào bất phương trình, ta được:
2.2 1 4
(luôn đúng).
Cặp số
2; 1
là nghiệm của bất phương trình trên.
+) Thay
9
; 4
2
x y
vào bất phương trình, ta được:
9
2. 4 4
2
(luôn đúng).
Cặp số
9
;4
2
là nghiệm của bất phương trình trên.
+) Thay
3
1;
5
x y
vào bất phương trình, ta được:
3
2.1 4
5
(Vô lí).
Cặp số
9
;4
2
không là nghiệm của bất phương trình trên.
Câu 6. Số giá trị nguyên của
m
để
1
2
x
y
là nghiệm của hệ bất phương trình
3
2 1 4
mx y
x m y
là:
A.
1
. B.
2
. C.
3
. D. 5.
Lời giải
Chọn C
Ta có
1
2
x
y
là nghiệm của hệ bất phương trình trên khi và chỉ khi
2 3
1
2 1
2 1 .2 4
2
m
m
m
m
m
.
Mà m
nên
2; 1;0
m
Câu 7. Có bao nhiêu số nguyên
x
thỏa
2
5 4 0
x x
A.
1
. B.
2
. C.
3
. D.
4
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn D
2
5 4 0 1 4x x x
, từ đó ta có
1;2;3;4x . Vậy có 4 số nguyên
x
thỏa.
Câu 8. Cho tam thức bậc hai
2
2 1 3x m x m với
m
là tham số. Điều kiện để tam thức đã cho
luôn dương với mọi giá trị của
m
là:
A.
2
2 1 4 3 0m m
. B.
2
2 1 4 3 0m m
.
C.
2
2 1 4 3 0m m
. D.
2
2 1 4 3 0m m
.
Lời giải
Chọn C
2
2
1 0
2 1 3 0, 2 1 4 3 0
0
x m x m x m m
.
Câu 9. Điểm thi của lớp 10C của một trường Trung học Phổ Thông được trình bày ở bảng phân bố tần
số sau:
Phương sai của bảng phân bố tần số đã cho là:
A. 0,94 B. 3,94. C. 2,94. D. 1,94.
Lời giải
Chọn D
Trong dãy số liệu về điểm thi của lớp 10C ta có:
1 1 2 2 6 6
1 1
... 7.5 5.6 10.7 12.8 4.9 2.10 7,175
40
x n x n x n x
n
Phương sai:
2 2 2
2
1 1 2 2 6 6
2 2 2
2 2 2
1
. . ... .
1
7. 5 7,175 5. 6 7,175 10. 7 7,175
40
12. 8 7,175 4. 9 7,175 2. 10 7,175
1,94
s n x x n x x n x x
n
Câu 10. Chọn câu đúng trong các câu trả lời sau đây: Phương sai bằng:
A. Một nửa của độ lệch chuẩn B. Căn bậc hai của độ lệch chuẩn.
C. Hai lần của độ lệch chuẩn. D. Bình phương của độ lệch chuẩn.
Lời giải
Chọn D
Ta có phương sai là:
2
x
s

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Độ lệch chuẩn:
2
x x
s s
Suy ra phương sai bằng bình phương của độ lệch chuẩn
Câu 11. Cho đường tròn có bán kính
12 cm
. Tìm số đo (
rad
) của cung có độ dài là
6 cm
:
A. 0,5 . B. 3. C. 2. D. 1.
Lời giải
Chọn A
Theo công thức tính độ dài cung tròn ta có
l R
nên suy ra
6
0,5
12
l
R
.
Câu 12. Góc
2
5
có số đo bằng độ là:
A.
18
. B.
36
. C.
72
. D.
12
.
Lời giải
Chọn C
Ta có:
o o
o
180 2 2 180
1rad rad . 72
5 5
.
Câu 13. Trong các giá trị sau,
sin
có thể nhận giá trị nào?
A.
2
. B.
4
3
. C.
0,7
. D.
5
2
.
Lời giải
Chọn C
Vì
1 sin 1
. Nên ta chọn C.
Câu 14. Cho
5
cos
13
. Giá trị của
cos2
bằng
A.
119
169
. B.
219
169
. C.
219
169
. D.
119
169
.
Lời giải
Chọn D
Ta có
2
2
5 119
cos2 2cos 1 2. 1
13 169
.
Câu 15. Cho
1 1
cos , cos
3 4
a b
. Giá trị của biểu thức
cos( ).cos( )
P a b a b
bằng
A.
11
16
. B.
11
16
. C.
119
144
. D.
119
144
.
Lời giải
Chọn D
Ta có
2
2 2
1 8
sin 1 os 1
3 9
a c a
và
2
2 2
1 15
sin 1 os 1
4 16
b c b
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
cos( ).cos( ) cos .cos sin .sin cos .cos sin .sin
P a b a b a b a b a b a b
2 2
2 2 2 2
1 1 8 15 119
cos .cos sin .sin . .
3 4 9 16 144
a b a b
Câu 16. Trong hệ trục tọa độ
Oxy
, đường thẳng đi qua
1; 4
A
và nhận
2; 3
n
làm véc tơ pháp
tuyến có phương trình là:
A.
3 2 14 0
x y
. B.
3 2 14 0
x y
. C.
2 3 14 0
x y
. D.
2 3 14 0
x y
.
Lời giải
Chọn D
Gọi
d
là đường thẳng đi qua
1; 4
A
và nhận
2; 3
n
làm VTPT
:2 1 3 4 0 2 3 14 0
d x y x y
.
Câu 17. Trong hệ trục tọa độ
Oxy
, cho đường thẳng
d
:
5 4 2020 0
x y
. Véctơ nào sau đây là
véctơ pháp tuyến của
d
?
A.
1
4;2
n
. B.
2
4; 10
n
. C.
3
5;4
n
. D.
4
5; 4
n
.
Lời giải
Chọn D
Ta có đường thẳng
d
có phương trình là
5 4 2020 0
x y
nên véctơ pháp tuyến của
d
là
5; 4
n
.
Câu 18. Trong hệ trục tọa độ
Oxy
, cho đường tròn
C
có phương trình
2 2
4 2 4 0
x y x y
. Xác
định tọa độ tâm
I
và bán kính
R
của
C
.
A.
4;2
I ;
24
R . B.
2;1
I ;
3
R
.
C.
2; 1
I
;
3
R
. D.
4;2
I ;
4
R
.
Lời giải
Chọn C
Đường tròn
C
có phương trình
2 2
2 2 0
x y ax by c
có tâm
;
I a b
và bán kính
2 2
R a b c
.
Ta có
2 4 2
a a
;
2 2 1
b b
;
4
c
. Khi đó
C
có tâm
2; 1
I
và bán kính
2
2
2 1 4 3
R
.
Câu 19. Trong hệ trục tọa độ
Oxy
, phương trình đường tròn tâm
4;3
I bán kính
2
R
là
A.
2 2
4 3 4
x y
. B.
2 2
4 3 4
x y
.
C.
2 2
4 3 2
x y
. D.
2 2
4 3 2
x y
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B
Đường tròn tâm
;
I a b
và bán kính
R
có phương trình
2 2
2
x a y b R
. Do đó, đường
tròn tâm
4;3
I và bán kính
2
R
có phương trình
2 2
2
4 3 2
x y
2 2
4 3 4
x y
.
Câu 20. Trong mặt phẳng tọa độ
Oxy
, cho elip
E
có phương trình chính tắc
2 2
1
36 25
x y
. Độ dài trục
lớn của elip bằng
A.
10
. B.
36
. C.
12
. D.
25
.
Lời giải
Chọn C
Xét
2 2
: 1
36 25
x y
E
.
Ta có:
2
2
36 6
5
25
a a
b
b
.
Suy ra độ dài trục lớn của
E
là
2 12
a
.
Câu 21. Trong mặt phẳng tọa độ
Oxy
, phương trình nào dưới đây là phương trình chính tắc của elip ?
A.
2 2
1
9 4
x y
. B.
2 2
1
9 4
x y
. C.
2 2
1
4 9
x y
. D.
2 2
1
9 4
x y
.
Lời giải
Chọn A
Phương trình chính tắc của elip có dạng:
2 2
2 2
1 0
x y
a b
a b
.
Phương án B, D: không đúng dạng phương trình elip
Phương án C không phải phương trình chính tắc elip vì
4 9
.
Câu 22. Tổng tất cả các nghiệm nguyên dương của bất phương trình
2
2
1 20
x x x
là
A.28. B.21. C.
22
. D.
20
.
Lời giải
Chọn A
Ta có
2
2
1 20 3 21 7
x x x x x
Tập nghiệm nguyên dương của bất phương trình là
1;2;3;4;5;6;7
S
Vậy tổng tất cả các nghiệm nguyên dương của bất phương trình đã cho là 28.
Câu 23. Số nghiệm nguyên của hệ bất phương trình
1
6 4 5
2
5 3
2 9
2
x x
x
x
là
A.
11
. B.
10
. C.12. D.
13
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn C
Ta có :
1
9
6 4 5
12 1 8 10 4 9
9
2
15
4
5 3 5 3 4 18 15
4
15
2 9
2
x x
x x x
x
x
x x x x
x
x
Mà x
nên
3;4;5;...;14
x .
Vậy số nghiệm nguyên của hệ bất phương trình đã cho là 12.
Câu 24. Biểu thức
(2 6)( 2020)
( )
( 3 9)
x x
f x
x x
nhận giá trị không âm khi nào?
A.
; 3 0;3 2020;x
. B.
; 3 0;3 2020;x
.
C
; 3 0;3 2020;x
. D.
; 3 0;3 2020;x
.
Lời giải
Chọn D
( ) 0
f x
(2 6)( 2020)
0
( 3 9)
x x
x x
(2 6)( 2020) 0
x x
3
2020
x
x
( )
f x
không xác định khi
( 3 9) 0
x x
0
3
x
x
Trục xét dấu của
( )
f x
:
Vậy
; 3 0;3 2020;x
.
Câu 25 . Giải bất phương trình sau:
2020
1
2019
x
x
.
A.
1
; 2019 ;
2
x
. B.
1
; 2019 ;
2
x
.
C.
1
2019;
2
x
. D.
1
; 2019 ;
2
x
.
Lời giải
Chọn A
Ta có
2020
1
2019
x
x
2020
1 0
2019
x
x
2 1
0
2019
x
x
Đặt
2 1
( )
2019
x
f x
x
.
( ) 0
f x
2 1
0
2019
x
x
1
2
x
.
( )
f x
không xác định khi
2019
x
.
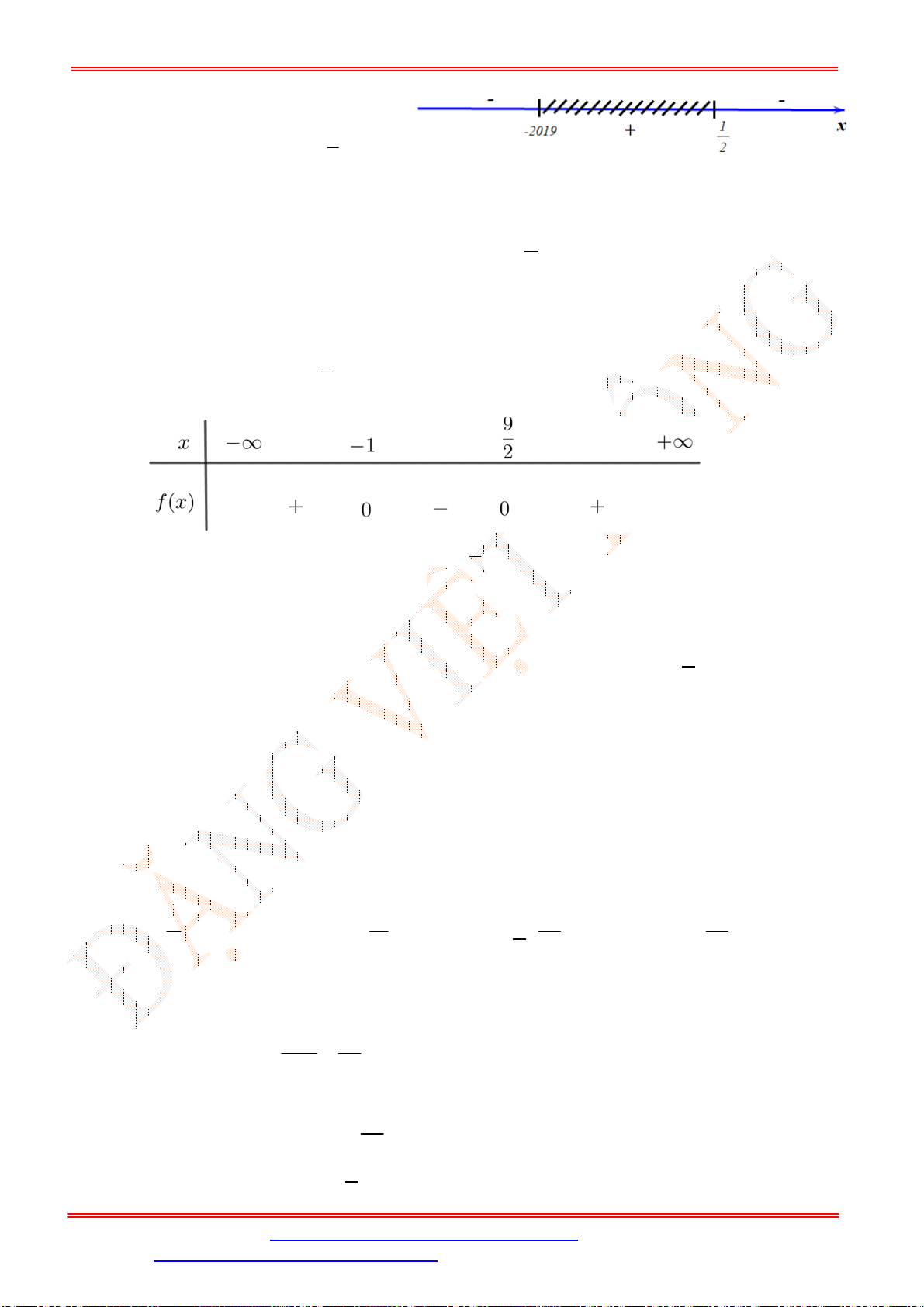
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Trục xét dấu của ( )f x :
Vậy
1
; 2019 ;
2
x
Câu 26 . Số giá trị nguyên của x để tam thức
2
2 7 9f x x x nhận giá trị âm là
A.
3
. B.
4
. C. 5. D. 6 .
Lời giải
Chọn C
Ta có
1
0
9
2
x
f x
x
BXD:
Dựa vào BXD ta thấy
9
0 1
2
f x x , do x nên
0;1;2;3;4x . Vậy có 5 giá trị
nguyên của x thảo mãn.
Câu 27. Tam thức
2
2 2 4f x x m x m âm với mọi x khi:
A.
14
2
m
m
. B. 14 2m . C. 2 14m . D. 14 2m .
Lời giải
Chọn D
Ta có
2
2
2 8 4 12 28m m m m
Khi đó
2
2
2 0
0, 12 28 0 14 2
12 28 0
f x x m m m
m m
.
Câu 28 . Đổi sang radian góc có số đó 108 ta được
A.
4
. B.
10
. C.
3
5
. D.
3
2
.
Lời giải
Chọn C
Ta có
108 108 .
180
3
5
.
Câu 29. Đơn giản biểu thức
5
sin cos 13 3sin 5
2
D
.
A. 3sin 2cos
. B. 3sin
. C. 3sin
. D. 2cos 3sin
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Lời giải
Chọn B
Ta có
5
sin cos 13 3sin 5
2
D
sin cos 3sin
2
cos cos 3sin
3sin
.
Câu 30. Tính
2
2
3tan tan
2 3tan
C
, biết
tan 2
2
A.
2
. B.
2
. C.
14
. D.
34
.
Lời giải
Chọn A
Ta có:
2
2tan
4
2
tan
3
1 tan
2
.
Suy ra:
2
2
4 4
3
3 3
2
4
2 3
3
C
.
Câu 31. Cho
1;4
A và
3;6
B . Phương trình đường trung trực của đoạn thẳng
AB
là đường thẳng
nào dưới đây?
A.
7 0
x y
. B.
7 0
x y
. C.
2 2 7 0
x y
. D.
2 2 7 0
x y
.
Lời giải
Chọn B
Ta có
2;2
AB
, đặt
1;1
n
.
Gọi
I
là trung điểm của
AB
, ta có
2;5
I .
Đường trung trực của đoạn thẳng
AB
là đường thẳng đi qua điểm
I
và nhận vectơ
n
làm
vectơ pháp tuyến, có phương trình:
1 2 1 5 0 7 0
x y x y
.
Câu 32. Cho đường thẳng
:3 4 2 0
x y
. Đường thẳng nào dưới đây song song và cách
một
khoảng cách bằng
1
?
A.
3 4 7 0
x y
. B.
3 4 3 0
x y
. C.
3 4 7 0
x y
. D.
3 4 1 0
x y
.
Lời giải
Chọn C
Gọi
là đường thẳng song song và cách
một khoảng cách bằng
1
.
Suy ra
:3 4 0 2
x y c c
.
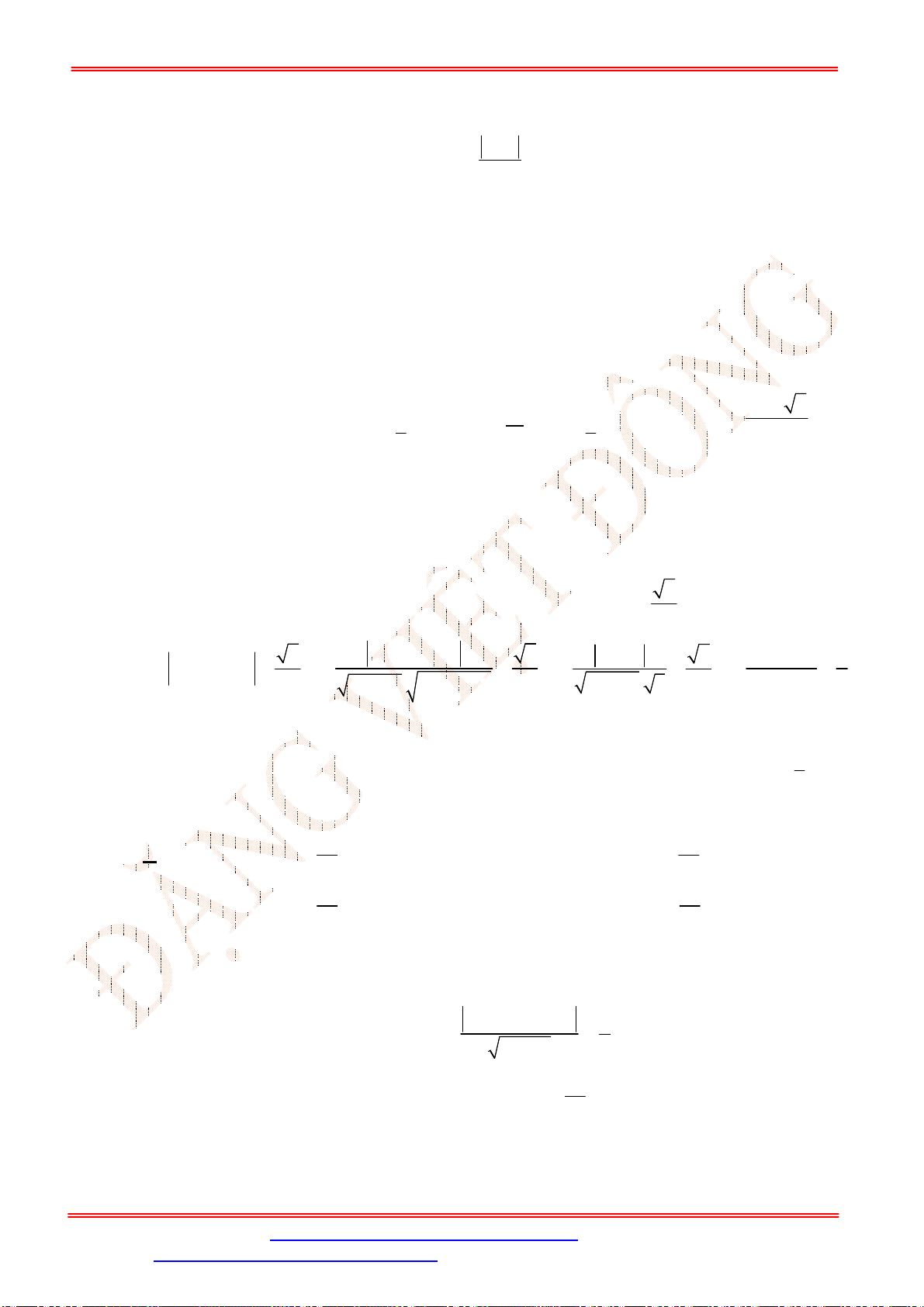
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn
2;2
A là điểm thuộc
.
Vì
nên
7
2
d , 1 d , ' 1 1
5
3
c tm
c
A
c tm
.
Với
7
c
,
có phương trình:
3 4 7 0
x y
.
Với
3
c
,
có phương trình:
3 4 3 0
x y
.
Câu 33. Cho hai đường thẳng
1
: 2 1 0
d x my m
và
2
2
:
5
x m t
d
y t
. Tìm các giá trị của tham số
m
để
1 2
,
d d
tạo với nhau một góc bằng
0
45
.
A.
3
m
. B.
3
1
3
m
m
. C.
3
1
3
m
m
. D. .
4 2 7
3
m
.
Lời giải
Chọn C
Vecto pháp tuyến của
1
d
,
2
d
lần lượt là
1
1;
n m
và
2
1; 2
n
.
Để
1 2
,
d d
tạo với nhau một góc bằng
0
45
thì
0
1 2
2
cos , cos45
2
d d
1 2
2
cos ,
2
n n
2
2 2 2
1.1 . 2
2
2
1 . 1 2
m
m
2 2
2 1
2
2
1 . 5
m
m
2
2
2 1
1
2
5 1
m
m
2
2
2 2 1 5 1
m m
2 2
8 8 2 5 5
m m m
2
3 8 3 0
m m
3
1
3
m
m
Câu 34. Phương trình đường tròn có tâm
1; 2
I
và tiếp xúc với đường thẳng
:3 4 1 0
x y
là
A.
2 2
36
1 2
25
x y . B.
2 2
36
1 2
25
x y .
C.
2 2
25
1 2
36
x y . D.
2 2
25
1 2
36
x y .
Lời giải
Chọn D
Bán kính của đường tròn là
R
,
d I
2 2
3.1 4. 2 1
3 4
6
5
Phương trình đường tròn cần tìm là:
2 2
36
1 2
25
x y .
Câu 35. Trong mặt phẳng tọa độ
Oxy
, viết phương trình chính tắc của elip
E
có độ dài trục lớn bằng
10
và tiêu cự bằng
6
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
A.
2 2
: 1
25 9
x y
E
. B.
2 2
: 1
9 25
x y
E
. C.
2 2
: 1
25 16
x y
E
. D.
2 2
: 1
16 25
x y
E
.
Lời giải
Chọn C
Độ dài trục lớn
2 10
a
5
a
Tiêu cự
2 6 3
c c
2
b
2 2
a c
2 2
5 3
16
Phương trình chính tắc của
2 2
2 2
: 1
x y
E
a b
2 2
1
25 16
x y
.
Câu 36. Giá trị của
m
để hệ bất phương trình
2 4 0
2 0
x
mx m
vô nghiệm là
A.
2
0
3
m
. B.
2
3
m
. C.
3
m
. D.
2
0
3
m
.
Lời giải
Chọn A
2 4 0 2
2 0 2
x x
mx m mx m
Nếu
0
m
BPT vô nghiệm (1)
Nếu
0
m
:
2
2
2
2
x
x
m
mx m
x
m
BPT vô nghiệm khi
2 3 2 3
2 0 0
2
m m
m
m m
. Kết hợp với điều kiện
0
m
ta
được
3
0
2
m
(2)
Nếu
0
m
:
2
2
2
2
x
x
m
mx m
x
m
BPT luôn có nghiệm với mọi
0
m
Vậy
2
0
3
m
thì BPT vô nghiệm.
Câu 37. Tìm tất cả các giá trị thực của tham số
m
để
1
f x m x m x
không âm với mọi
; 1 .
x m
A.
1.
m
B.
1.
m
C.
1.
m
D.
1.
m
Lời giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B
Xét bpt:
2
1 0 1 1
m x m x m x m
.
1
+ Xét
1m x
(không thỏa mãn).
+ Xét
1
m
thì
1 1
x m
không thỏa điều kiện nghiệm đã cho.
+ Xét
1
m
thì
1 1
x m
thỏa điều kiện nghiệm đã cho.
Vậy
1
m
.
Câu 38. Giải bất phương trình sau:
2 2
1(*).
2
x
x
A.
0;S
B.
4
2;
3
S
C.
4
2; 0; .
3
S
D.
0; 2
S
Lời giải
Chọn C
TH1:
2 2 0 1
x x
2 2 2 2 (2 2) ( 2)
(*) 1 1 0 0 0
2 2 2 2
x x x x x
x x x x
Ta có:
0
2 0 2
x
x x
BXD:
x
2
0
x
|
0
2
x
0
|
VT
0
Dựa vào BXD ta được:
2
0
x
x
So với điều kiện
1
x
suy ra
1
0;S
TH2:
2 2 0 1
x x

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
2 2
(*) 1
2
2 2
1 0
2
( 2x 2) (x 2)
0
2
3 4
0
2
x
x
x
x
x
x
x
Ta có:
4
3 4 0
3
x x
2 0 2
x x
BXD:
x
2
4
3
3 4
x
|
0
2
x
0
|
VT
||
|
Dựa vào bảng xét dấu ta được:
4
2
3
x
Kết hợp điều kiện suy ra
2
4
2;
3
S
Vậy
1 2
4
2; 0; .
3
S S S
Câu 39. Có bao nhiêu giá trị
m
nguyên để bất phương trình
2 2
3 2 1 2 3 2 0
x m x m m
nghiệm đúng với mọi
x
trên khoảng
2;
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn D
Đặt
2 2
3 2 1 2 3 2
f x x m x m m
. Ta có
f x
là tam thức bậc hai với
3 0
a
và
2
2 2
' 1 3 2 3 2 7 7 7 0
m m m m m
với mọi
m
.
Do đó phương trình
0
f x
có hai nghiệm phân biệt
1 2
,
x x
(giả sử
1 2
x x
).
Ta có
1 2 1 2
0, 2; 2 2 2 0
f x x x x x x
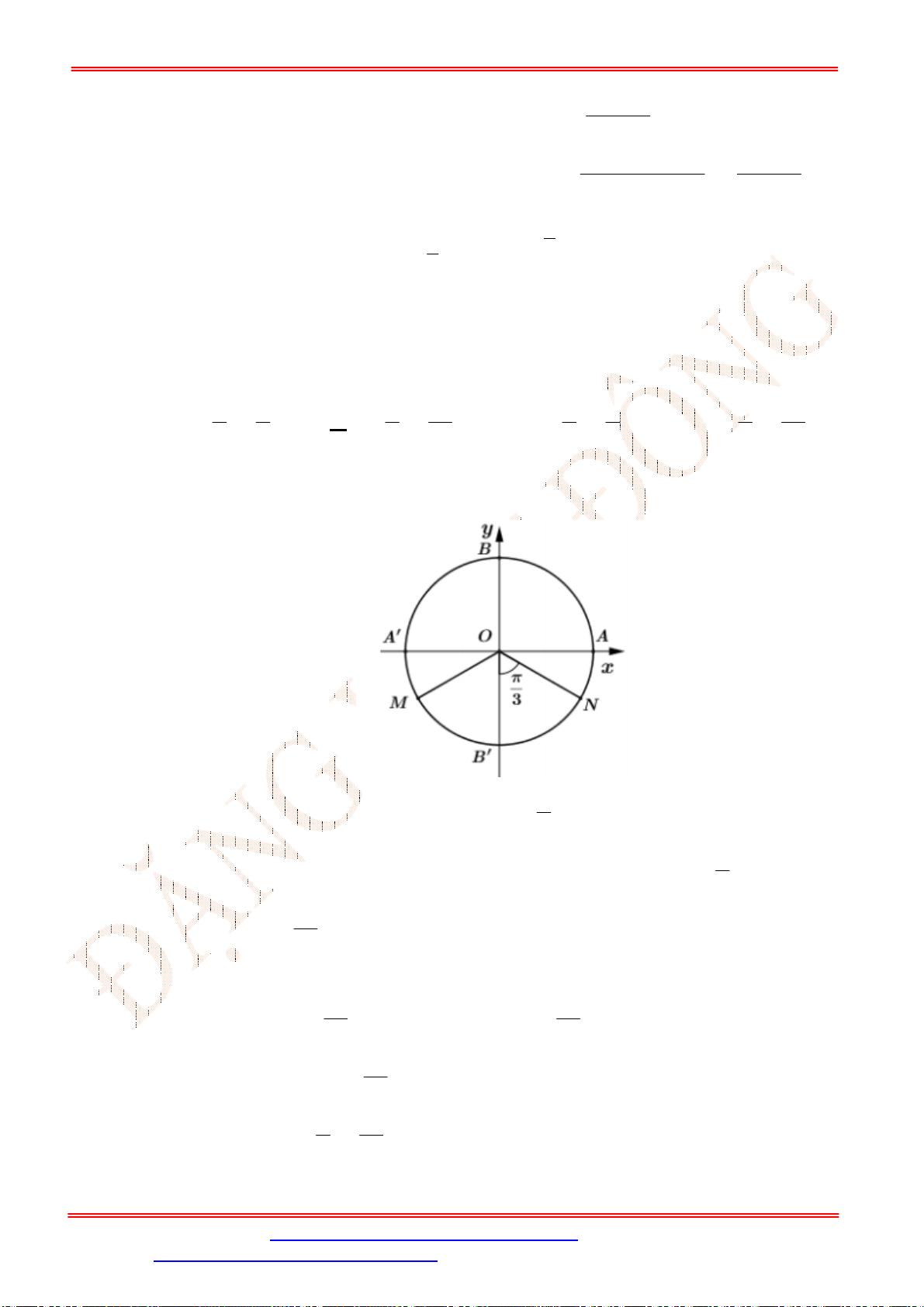
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
1 2
1 2
2
1 2 1 2
1 2
2 1
4
4
2 2 0
3
2 4 0
2 2 0
2 3 2
2 1
2. 4 0
3 3
m
x x
x x
x x x x
x x
m m
m
2
5
5
3
2
3
2 6 0
2
2
2
m
m
m
m m
m
.
Vì
m
nguyên nên
2, 1,0,1
m
.
Câu 40. Trên đường tròn lượng giác có điểm gốc là
A
, cho tam giác
OMB
và tam giác
ONB
là các
tam giác đều. Cung
có mút đầu là
A
và mút cuối trùng với
,
B M
hoặc
N
. Số đo của cung
là
A.
6 3
k
. B.
2
2 3
k
. C.
2 3
k
. D.
2
6 3
k
.
Lời giải
Chọn B
Cung
có mút đầu là
A
và mút cuối là
B
nên
,(1)
2
Tam giác
OMB
và tam giác
ONB
là các tam giác đều nên
3
MOB NOB
2
3
BA M MB N
.
Mặt khác cung
có mút đầu là
A
và mút cuối là
M
hoặc
N
nên
2 2
;
3 3
AM AB BM AB AN AM MN AM
Suy ra chu kỳ của cung
là
2
,(2)
3
Từ (1) và (2) ta có
2
,
2 3
k k
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 41. Nếu biết
4 4
sin cos 1
0; 0; 0
a b a b
a b a b
thì biểu thức
10 10
4 4
sin cos
M
a b
bằng:
A.
5 5
1 1
a b
. B.
4 4
1 1
a b
. C.
5
1
a b
. D.
4
1
a b
.
Lời giải
Chọn D
Đặt
2 2
sin ,(0 1) cos 1
u u u
Từ
4 4
sin cos 1
a b a b
ta suy ra
2 2 2 2
(1 ) 1 (1 ) 1
u u bu a u
a b a b ab a b
2
2 2
( ) 2 1
( ) 2 ( ) ( )
a b u au a
a b u a a b u a a b ab
ab a b
2 2 2 2
( ) 2 ( ) 0 [( ) ] 0
a
a b u a a b u a a b u a u
a b
.
Suy ra
2
2
sin
cos
a
a b
b
a b
(thỏa mãn
2 2
sin cos 1
).
Do đó
5 5
10 10
4 4 4 4 4
sin cos 1
( )
a b
a b a b
M
a b a b a b
.
Câu 42. Cho
cos .sin sin
với
2
m
,
2
n
,
,
m n
. Khi đó:
A.
cos
cot 3cot
sin
. B.
cot 2cot
.
C.
cot 2cot
. D.
cos
cot 3cot
sin
.
Lời giải
Chọn B
Ta có
cos .sin sin cos .sin sin
cos .sin sin .cos cos .sin
2cos .sin cos .sin
cos
2cos
sin sin
cot 2cot .
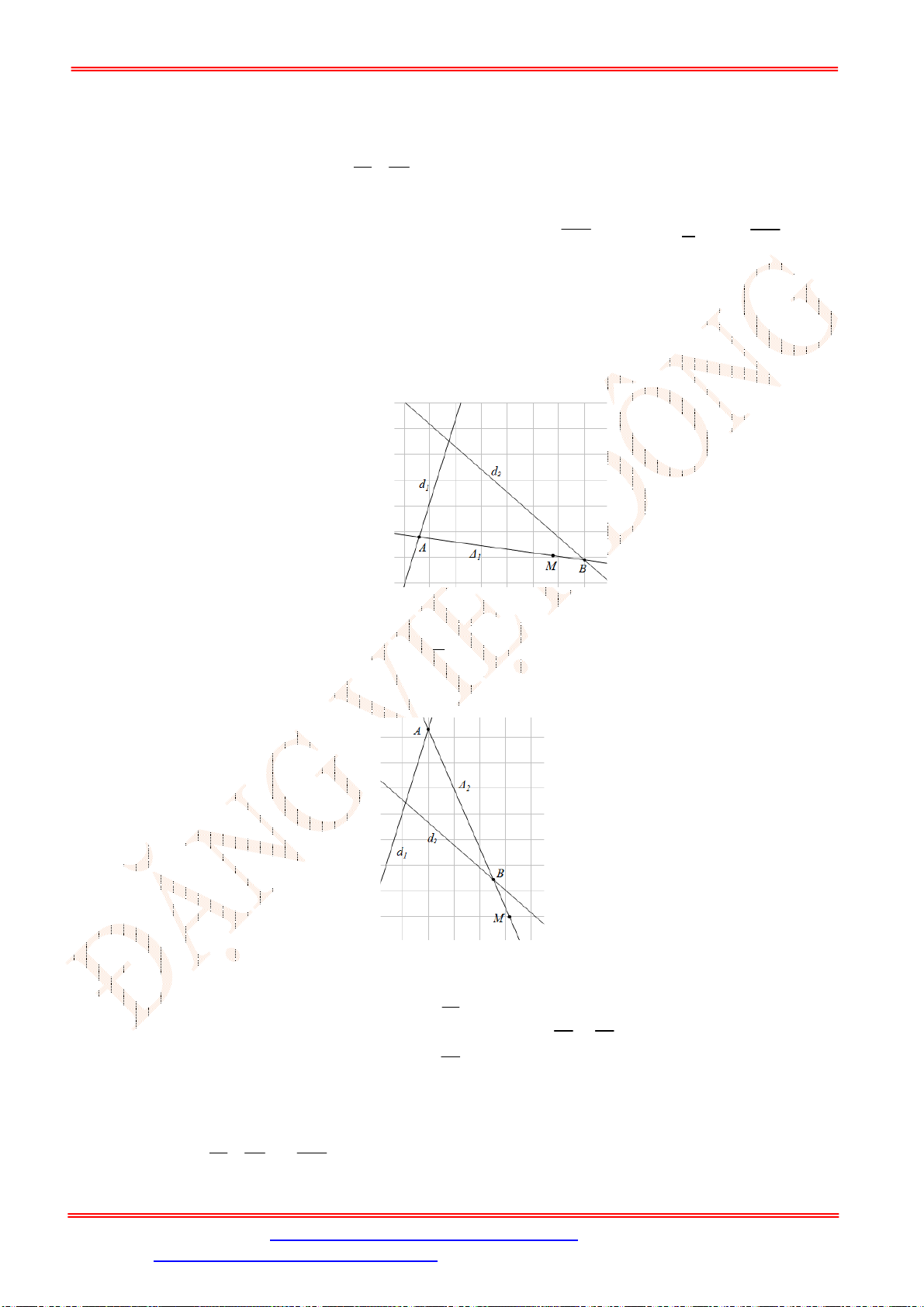
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 43. Cho hai đường thẳng
1 2
: 2 2 0, : 2 3 0
d x y d x y
và điểm
(1;1)
M . Biết rằng có hai
đường thẳng
1 1 1 1 2 2 2 2
: 0, : 0
a x b y c a x b y c
đi qua M và cắt
1 2
,
d d
lần lượt tại
,
A B
sao cho
4
MA MB
. Tính
1 2
1 2
.
a a
T
b b
A.
1.
T
B.
1.
T
C.
340
.
341
T D.
340
.
341
T
Lời giải
Chọn D
Gọi
1 2
2 2; ; ;2 3 2 3; 1 , 1;2 2
A a a d B b b d MA a a MB b b
TH 1:
4
MA MB
Khi đó ta có hệ
7
2 4 7
11;6
7
8 7
4
a
a b
MA
a b
b
. Từ đó
1
:6 11 5 0
x y
.
TH 2:
4
MA MB
Khi đó ta có hệ
11
2 4 1
31 14
3
; .
8 9
19
3 3
12
a
a b
MA
a b
b
Từ đó
2
:14 31 17 0
x y
.
Vậy
1 2
1 2
340
.
341
a a
T
b b

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 44. Trong mặt phẳng tọa độ Oxy , cho đường thẳng
:2 6 0
x y
và điểm
2;2
A . Gọi
C
là
đường tròn đi qua A có tâm thuộc trục Oy, đồng thời tiếp xúc với
. Tính chu vi của đường
tròn
C
.
A.
5
. B.
2 5
. C.
5
. D.
10
.
Lời giải
Chọn B
Gọi I là tâm của đường tròn
C
. Vì
0;
I Oy I a
.
Ta có
2
6
, 4 2
4 1
a
IA d I a
2 2
5 4 8 12 36
a a a a
2
4 8 4 0 1
a a a
0;1
I .
Suy ra
C
có bán kính là
5
R IA . Suy ra chu vi của đường tròn
C
là
2 2 5
R
.
Câu 45. Trong mặt phẳng tọa độ
Oxy
, đường thẳng
:3 4 12 0
d x y
cắt elip
2 2
: 1
16 9
x y
E
tại hai
điểm phân biệt
A
,
B
. Biết rằng điểm
0 0
;
C x y E
sao cho diện tích tam giác
ABC
bằng
6
, khi đó
0 0
.
x y
bằng
A.
5
. B.
1
. C.
6
. D.
3 2
.
Lời giải
Chọn C
Tọa độ giao điểm của
d
và
E
là nghiệm của hệ phương trình:
2 2
3 4 12 0
1
16 9
x y
x y
4
0
0
3
x
y
x
y
.
Vậy
4;0
A
và
0;3
B
5
AB
.
Điểm
0 0
;
C x y E
2 2
0 0
1
16 9
x y
1
.
0 0
0 0
3 4 12
1 1 1
. . ; .5. 3 4 12
2 2 5 2
ABC
x y
S AB d C AB x y
.
Mà
0 0
6 3 4 12 12
ABC
S x y
0 0
0 0
3 4 24 2
3 4 0 3
x y
x y
.
Từ
1
và
2
ta được
2
0 0
2 12 27 0
y y
(vô nghiệm).

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Từ
1
và
3
ta được
0 0
2
0
0 0
3
2 2
2
32 144
3
2 2
2
y x
y
y x
.
Khi đó
0 0
. 6
x y
.
Câu 46. Có bao nhiêu giá trị
m
nguyên,
2020;2020
m để đa thức
2 2
f x m x m x
không âm với mọi
; 2
x m
?
A. 2020. B. 2022. C. 2023. D. 2021.
Lời giải
Chọn C
Ta có:
2
2 2 2 4
f x m x m x m x m
Với
2
m
:
0. 0 0,f x x x
.
Với
2
m
:
2
0 2 4 0 2
f x m x m x m
Bảng xét dấu:
2
2 4 0, ; 2 2 0 2
m x m x m m m
.
Do đó
;2
m thỏa mãn:
0, ; 2
f x x m
.
Vậy có 2023 số
m
nguyên thỏa mãn yêu cầu bài toán.
Chọn đáp án C.
Câu 47. Cho bất phương trình
2 2
2( 2) 2 0
x m x m
. Gọi tập
S
là tập các giá trị nguyên của
m
để
bất phương trình đã cho nghiệm đúng với mọi
0;2
x . Số phần tử của tập
S
là:
A. Vô số. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn D
Đặt
2 2
2( 2) 2
f x x m x m
với hệ số
1 0
a
.
YCBT
. 0 0
. 2 0
a f
a f
2
2
2 0
4 6 0
m
m m
2 2
2 10 2 10
m
m
2 2 10
m
Vậy tập
S
thõa yêu cầu bài toán là
1;0;1
S .
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 48. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
6 6
1
sin cos sin 4 .
2
A x x x
Giá trị của
8
m M
bằng
A. 10. B. 12. C. 13. D. 11.
Lời giải
Chọn A
Ta có:
3
6 6 2 2 2 2 2 2
sin cos sin cos 3sin cos sin cos
x x x x x x x x
2
1 3. sin .cos
x x
2
sin 2
1 3.
2
x
2
3
1 sin 2
4
x
3 1 cos4
1 .
4 2
x
3
1 1 cos4
8
x
5 3cos4
.
8
x
Do đó
5 3 1 5 1
cos4 sin 4 3cos4 4sin4 .
8 8 2 8 8
A x x x x
Áp dụng BĐT Bunhiacopxki, ta có:
2
2 2 2 2
3cos4 4sin4 3 4 cos 4 sin 4 25.
x x x x
5 3cos4 4sin4 5.
x x
Do đó
5
0 .
4
A
Ta có:
0 3cos4 4sin 4 5 1
.
5
3cos4 4sin 4 5 2
4
A x x
A x x
Các phương trình
1
và
2
đều có nghiệm nên
giá trị lớn nhất của
A
là
5
4
và giá trị nhỏ nhất của
A
bằng
0.
Vậy
5
4
M
và
0
m
nên
5
8 0 8. 10.
4
m M
Câu 49. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
có
4;0
A , trung điểm của
BC
là
3;1
M . Gọi
,
E F
lần lượt là chân đường cao kẻ từ
B
và
C
của tam giác
ABC
. Biết đường
thẳng
EF
có phương trình
1 0
x
. Khoảng cách từ
A
đến đường thẳng
BC
là
A.
4 5
. B.
4 2
. C.
3 2
. D.
3 5
.
Lời giải
Chọn D
K
I
M
H
F
E
A
B
C
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi
I
là trung điểm của
EF
. Vì
1
2
ME MF BC
nên
MI EF
.
Phương trình
: 1
MI y
, suy ra
1;1
I .
Gọi
,
H K
lần lượt là hình chiếu của
A
trên
BC
và
EF
.
Ta có
10, 5 2
AI AM
và
2 2
4 1
, 3
1 0
AK d A EF
.
Vì tứ giác
BCEF
nội tiếp nên hai tam giác
ABC
và
AEF
đồng dạng nên ta có
,
5 2
5
,
10
d A BC
AH AM
d A EF AK AI
Suy ra
, 5 , 3 5
d A BC d A EF .
Câu 50. Trong mặt phẳng tọa độ
Oxy
, cho tam giác
ABC
với
( 3; 4)
A
, tâm đường tròn nội tiếp
(2;1)
I
, tâm đường tròn ngoại tiếp
1
;1
2
J
. Tính
( , )
d O BC
.
A.
2
. B.
2 5
. C.
10
. D.
5 2
.
Lời giải
Chọn B
Gọi
( )
C
là đường tròn tâm
J
, bán kính
AJ
2
2
1 125
( ): x y 1 0; ( ): 1
2 4
AI C x y
Gọi
( )
D AI C
. Khi đó tọa độ điểm
D
thỏa hệ phương trình:
2
2
3
4
x y 1 0
9
1 125
1
2
2 4
7
2
x
y
x
x y
y
D
I
J
A
B
C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Loại điểm
( 3; 4)
vì trùng
A
. Vậy
9 7
;
2 2
D
Ta có:
ˆ
BID BAI IBA CAD IBC DBC IBC IBD
DB DI
Mà
DC DB DC DB DI
.
Do đó
,
B C
là giao điểm của
( )
C
và
( ')
C
, với
( ')
C
là đường tròn tâm
D
bán kính
ID
.
Ta có:
2 2
9 7 25
( '):
2 2 2
C x y
Tọa độ
,
B C
thỏa hệ phương trình:
2
2
2 2
1 125
1
2 4
2 10 0
9 7 25
2 2 2
x y
x y
x y
Vậy
( ) : 2 10 0
BC x y
( , ) 2 5
d O BC
.
……………….HẾT……………

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 20
ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
Câu 1. Cho góc lượng giác
thỏa mãn
1
sin
3
, và
3
2
. Tính
sin 2
A.
7
9
. B.
4 2
9
. C.
4 2
9
. D.
2
3
.
Câu 2. Tìm
m
phương trình
2
3 2 3 0
m x mx m có hai nghiệm trái dấu.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Câu 3. Trong mặt phẳng với hệ tọa độ
Oxy
, phương trình tham số của đường thẳng đi qua
2;3
M
và song song với đường thẳng
7 5
1 5
x y
là
A.
5 2
1 3
x t
y t
. B.
5
x t
y t
. C.
2
3 5
x t
y t
D.
3 5
2
x t
y t
.
Câu 4. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
2 2
: 2 10 1 0
C x y x y
. Trong các
điểm
1;3 , 4; 1 , 2;1 , 3; 2
M N P Q
, điểm nào thuộc
C
?
A. Điểm
P
. B. Điểm
Q
. C. Điểm
N
. D. Điểm
M
.
Câu 5. Gọi
,
m M
lần lượt là nghiệm nguyên nhỏ nhất và lớn nhất của hệ bất phương trình
2
2
3
3 2
2 7 3
2 3 3 20
x x x
x x x x
. Tổng
m M
bằng
A.
3
. B.
2
. C.
6
. D.
7
.
Câu 6. Góc có số đo
120
đổi sang rađian là:
A.
3
2
. B.
2
3
. C.
4
. D.
10
.
Câu 7. Trong mặt phẳng với hệ trục tọa độ
Oxy
, tính góc giữa đường thẳng
3 1 0
x y
và trục
hoành.
A.
45
. B.
135
C.
60
. D.
120
.
Câu 8. Mệnh đề nào sau đây sai?
A.
2
cos2 1 2sin
a a
. B.
cos2 2sin cos
a a a
C.
2 2
cos2 cos sin
a a a
. D.
2
cos2 2cos 1
a a
.
Câu 9. Cho
1
cos
3
. Khi đó
cos 3
bằng
A.
1
3
. B.
1
3
. C.
2
3
. D.
2
3
.
Câu 10. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
9 4
x y
E
. Tính tiêu cự của elip
E
.
A.
6
. B.
4
C.
2 5
. D.
5
.
Câu 11. Số nghiệm nguyên của bất phương trình
2
2 3
x x là
A.
5
. B.
3
. C.
2
. D.
4
.
Câu 12. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho tam giác
ABC
có
2; 1
A
,
4;5
B ,
3;2
C .
Viết phương trình đường thẳng chứa đường cao của tam giác
ABC
đi qua đỉnh
C
.
A.
3 3 0
x y
. B.
3 11 0
x y
. C.
3 3 0
x y
. D.
1 0
x y
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 13. Phương trình
3 3
x x
có tập nghiệm là:
A.
;3
. B.
;3
. C.
3;
. D.
3
.
Câu 14. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường thẳng
( ): 2 3 1 0
x y . Một vec tơ chỉ
phương của đường thẳng
là :
A.
(3;2)
u . B.
(2; 3)
u . C.
(2;3)
u . D.
(3; 2)
u .
Câu 15. Cho tam giác
ABC
. Mệnh đề nào sau đây đúng?
A.
sin sin
2 2
A B C
. B.
cos cos
2 2
A B C
.
C.
sin( ) sin
A B C
. D.
cos( ) cos
A B C
.
Câu 16. Cho hàm số
, 0, ,
y ax b a a b
là tham số. Mệnh đề nào sau đây đúng?
A. Hàm số
y ax b
nhận giá trị dương trên
.
B. Hàm số
y ax b
nhận giá trị âm trên ;
b
a
.
C. Hàm số
y ax b
nhận giá trị âm trên
.
D. Hàm số
y ax b
nhận giá trị dương trên ;
b
a
.
Câu 17. Cho góc lượng giác
thỏa mãn
2
. Khẳng định nào sau đây đúng?
A.
cot 0
. B.
cos 0
. C.
tan 0
. D.
sin 0
.
Câu 18. Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình đường tròn?
A.
2 2
2 4 9 0
x y x y
. B.
2 2
2 2 4 8 19 0
x y x y
.
C.
2 2
2 6 15 0
x y x y
. D.
2 2
4 6 13 0
x y x y
.
Câu 19. Cho hàm số
2
f x ax bx c
với
0
a
. Biết rằng
0
a
,
2
4 0
b ac
. Mệnh đề nào
sau đây đúng?
A.
1 2
,
x x
:
0
f x
,
1 2
;
x x x
. B.
0
f x
, x
.
C.
1 2
,
x x
:
1 2
. 0
f x f x
. D.
0
f x
, x
.
Câu 20. Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
C
:
2 2
25
x y
. Phương trình tiếp
tuyến của đường tròn tại điểm
3;4
A là
A.
4 3 0
x y
. B.
4 3 24 0
x y
. C.
3 4 25 0
x y
. D.
3 4 25 0
x y
.
Câu 21. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
( ): 4 2 1 0
C x y x y
. Bán
kính đường tròn
C
là
A.
6
R . B.
2
R
. C.
1
R
. D.
6
R
.
Câu 22. Tập nghiệm của bất phương trình
2
2 1 0
x x
là
A.
1
;
4
. B.
. C.
1
\
4
. D.
.
Câu 23. Cho các góc lượng giác
,
a b
và
cos( )cos( ) sin( )sin( )
a b a b a b b
T a
. Mệnh đề sau
đây đúng?
A.
sin2
T b
. B.
cos2
T a
. C.
sin2
T a
. D.
cos2
T b
.
Câu 24. Biết rằng tập xác định của hàm số
2
1
2y x x
x
là
;D a
. Khẳng định nào sau
đây đúng?
A.
0
a
. B.
0
a
. C.
3 0
a
. D.
3
a
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 25. Cho các số
0, 0
a b
thỏa mãn
1
ab
. Mệnh đề nào sau đây đúng?
A.
1 2
a b
. B.
2
a b
. C.
0 1
a b
. D.
2
a b
.
Câu 26. Với mọi góc lượng giác
và số nguyên
k
, mệnh đề nào sau đây sai?
A.
sin 2 sin
k
. B.
cos cos
k
.
C.
tan tan
k
. D.
cot cot
k
.
Câu 27. Tập nghiệm của bất phương trình
2
1
x
là
A.
2;0
. B.
; 2
.
C.
; 2 0;
. D.
2;
.
Câu 28. Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình chính tắc của elip
E
biết rằng với mọi
điểm
M
thuộc
E
thì
1 2
10
MF MF
(
1 2
,
F F
là hai tiêu điểm của
E
)và tâm sai của
E
là
3
5
e
A.
2 2
1
100 36
x y
. B.
2 2
1
25 16
x y
. C.
2 2
1
100 64
x y
. D.
2 2
1
25 9
x y
.
Câu 29. Cho hai góc lượng giác , 0 ,
2
a b a b
thỏa mãn
1 3
tan ;tan
7 4
a b
. Tính
a b
.
A.
5
4
. B.
4
. C.
4
. D.
3
.
Câu 30. Tập nghiệm của bất phương trình
2 1 2
x x
là
A.
0;
. B.
1;
. C.
; 1
. D.
1;1
.
Câu 31. Có bao nhiêu giá trị nguyên thuộc
10;10
của
m
để bất phương trình
2
4 0
mx x m
vô
nghiệm?
A.
9
. B.
10
. C.
8
. D.
11
.
Câu 32. Biết rằng
1
cos 2 cos 2 sin cos 2 sin
2 3 2 12 12
x x x ax b
với mọi giá trị
của góc lượng giác
x
; trong đó
a
là số tự nhiên,
b
là số hữu tỉ thuộc
1
0;
2
. Mệnh đề nào sau
đây đúng?
A.
1
2
a b
. B.
3
2
a b
. C.
5
2
a b
. D.
2
a b
.
Câu 33. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
: 2 4 2 6 5 0
m
C x y mx m y m
(
m
là tham số). Tập hợp các điểm
m
I
là tâm của
đường tròn khi
m
thay đổi là
A. Parabol
2
: 2 1
P y x
. B. Đường thẳng
: 2 1
d y x
.
C. Parabol
2
: 2 1
P y x
. D. Đường thẳng
: 2 1
d y x
.
Câu 34. Cho
0 1
x
. Giá trị nhỏ nhất của biểu thức
4
1
1
x
f x
x x
bằng
A.
9
. B.
7
. C.
5
. D.
3
.
Câu 35. Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh
bằng
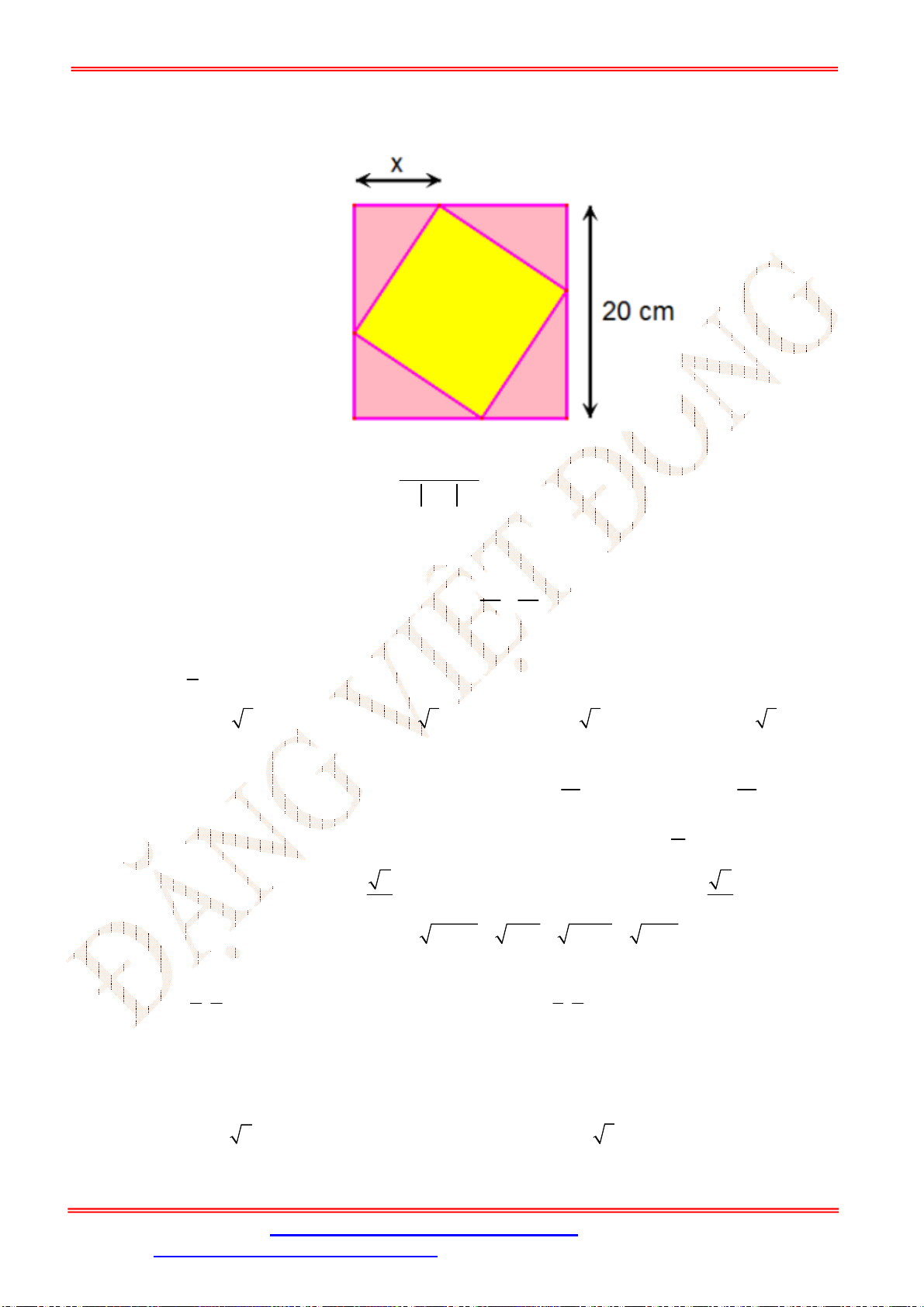
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
20
cm
, tạo thành bốn tam giác xung quanh như hình vẽ. Tìm tất cả các giá trị của
x
để diện
tích viên gạch không vượt quá
2
208
cm
.
A.
8 12
x
. B.
6 14
x
. C.
12 14
x
. D.
12 18
x
.
Câu 36. Tập nghiệm của bất phương trình
2
2 8
0
1
x x
x
là
A.
4; 1 1;2
. B.
4;2
.
C.
1;2
. D.
2; 1 1;2
.
Câu 37. Trong mặt phẳng tọa độ
Oxy
, cho Elip
2 2
: 1
25 9
x y
E
có hai tiêu điểm
1
F
,
2
F
. Biết điểm
M
có tung độ
M
y
dương thuộc Elip
E
sao cho bán kính đường tròn nội tiếp tam giác
1 2
MF F
bằng
4
3
. Mệnh đề nào sau đây là đúng?
A.
0; 3
M
y
. B.
2; 8
M
y
. C.
8;5
M
y
. D.
3;2
M
y
.
Câu 38. Tính tổng
2 2 2 2
sin 5 sin 10 sin 15 ... sin 85
S
.
A.
9
S
. B.
8
S
. C.
19
2
S . D.
17
2
S .
Câu 39. Cho góc lượng giác
thỏa mãn
sin cos 1
. Giá trị của sin
4
bằng
A.
1
. B.
2
2
. C.
1
. D.
2
2
.
Câu 40. Tập nghiệm của bất phương trình
2 4 1 2 1 4 3
x x x x x
là tập con của
tập hợp nào sau đây?
A.
2 1
;
3 2
. B.
1;0
. C.
1 2
;
3 3
. D.
0;1
.
Câu 41. Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường tròn
C
:
2 2
2
x a y b R
và đường thẳng
: 0
x y a b
. Biết đường thẳng
cắt đường tròn
C
tại 2 điểm
,
M N
phân biệt. Tính độ dài
MN
.
A.
2
MN R
. B.
2
MN R
. C.
3
MN R . D.
MN R
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 42. Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường thẳng
: 3 4 12 0
d x y
.
Phương trình đường thẳng
đi qua điểm
2; 1
M
và tạo với
d
một góc
0
45
có dạng
5 0
ax by
, trong đó
,
a b
cùng dấu. Khẳng định nào sau đây đúng?
A.
6
a b
. B.
8
a b
.
C.
8
a b
. D.
6
a b
.
Câu 43. Cho tam giác
ABC
có các góc thỏa mãn
sin sin cos cos
A B A B
. Tính số đo góc
C
của
tam giác
ABC
.
A.
0
90
. B.
0
120
. C.
0
60
. D.
0
45
.
Câu 44. Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
: 2 2 9
C x y
.
Phương trình các tiếp tuyến của đường tròn đi qua điểm
5; 1
A
là
A.
2 3 0
x y
hoặc
2 2 3 5 0
x y
. B.
4 0
x y
hoặc
6 0
x y
.
C.
3 4 1 0
x y
hoặc
4 3 13 0
x y
. D.
5
x
hoặc
1
y
.
Câu 45. Có bao nhiêu giá trị của
0
x
để hàm số
2
2 2 2
32 1 2 1
y x x x
đạt giá trị lớn nhất trên
1;1
tại
0
x x
?
A.
4
. B.
8
. C.
6
. D.
10
.
Câu 46. Tìm tập hợp các giá trị của
m
để bất phương tình
2
2 0
x x m
nghiệm đúng với mọi
0;3
x
A.
; 1
. B.
3;
. C.
1;
. D.
1;3
.
Câu 47. Có bao nhiêu giá trị của
m
để bất phương trình
2
1 0
m x m
vô nghiệm?
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 48. Cho góc lượng giác
a
thỏa mãn
2
sin 2 sin5 sin3
2
2cos 2 cos 1
a a a
a a
. Tính
sin
a
A.
1
4
. B.
1
. C.
1
. D.
1
4
.
Câu 49. Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hình chữ nhật có hai cạnh nằm trên hai đường
thẳng có phương trình lần lượt là
2 3 0; 2 5 0
x y x y
và tọa độ một đỉnh là
2;3
.
Diện tích hình chữ nhật đó là:
A.
12
5
(đvdt). B.
16
5
(đvdt). C.
9
5
(đvdt). D.
12
5
(đvdt).
Câu 50. Trong mặt phẳng với hệ trục tọa độ
Oxy
, viết phương trình đường tròn tâm
0;0
O cắt đường
thẳng
: 2 5 0
x y
tại hai điểm
;
M N
sao cho
4
MN
.
A.
2 2
9
x y
. B.
2 2
1
x y
. C.
2 2
21
x y
. D.
2 2
3
x y
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
ĐẶNG VIỆT ĐÔNG
ĐỀ SỐ 20
HDG ĐỀ KIỂM TRA HỌC KỲ II - NĂM HỌC 2020-2021
Môn: TOÁN, Lớp 10
Thời gian làm bài: 90 phút, không tính thời gian phát đề
BẢNG ĐÁP ÁN
1
B
2
B
3
C
4
C
5
A
6
B
7
C
8
B
9
A
10
C
11
D
12
C
13B
14
A
15
C
16
D
17
D
18
C
19
D
20
C
21
A
22
D
23B 24
A
25B
26B
27
C
28B
29B
30
D
31
A
32
D
33
D
34B 35
A
36
A
37
C
38
D
39
D
40
A
41B
42
C
43
A
44
D
45
A
46B
47
C
48B
49
D
50
A
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1: Cho góc lượng giác
thỏa mãn
1
sin
3
, và
3
2
. Tính
sin 2
A.
7
9
. B.
4 2
9
. C.
4 2
9
. D.
2
3
.
Lời giải
Chọn B
Ta có:
2
1 2 2
sin cos 1 sin
3 3
Theo giả thiết:
3 2 2
cos
2 3
1 2 2 4 2
sin 2 2sin .cos 2.
3 3 9
.
Câu 2: Tìm
m
phương trình
2
3 2 3 0
m x mx m có hai nghiệm trái dấu.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Lời giải
Chọn B
Điều kiện để phương trình
2
3 2 3 0
m x mx m có hai nghiệm trái dấu:
2
3 3 0
3 0 3
m m
m m
Câu 3: Trong mặt phẳng với hệ tọa độ
Oxy
, phương trình tham số của đường thẳng đi qua
2;3
M
và song song với đường thẳng
7 5
1 5
x y
là
A.
5 2
1 3
x t
y t
. B.
5
x t
y t
. C.
2
3 5
x t
y t
D.
3 5
2
x t
y t
.
Lời giải
Chọn C

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Do hai đường thẳng song song nên đường thẳng cần tìm nhận
1;5
u
là vectơ chỉ phương.
Do đó phương trình tham số là
2
3 5
x t
y t
.
Câu 4: Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
2 2
: 2 10 1 0
C x y x y
. Trong các
điểm
1;3 , 4; 1 , 2;1 , 3; 2
M N P Q
, điểm nào thuộc
C
?
A. Điểm
P
. B. Điểm
Q
. C. Điểm
N
. D. Điểm
M
.
Lời giải
Chọn C
Thay tọa độ các điểm vào phương trình của
C
thì chỉ có điểm
N
thỏa mãn phương trình
đường tròn. Vậy điểm
N C
.
Câu 5: Gọi
,
m M
lần lượt là nghiệm nguyên nhỏ nhất và lớn nhất của hệ bất phương trình
2
2
3
3 2
2 7 3
2 3 3 20
x x x
x x x x
. Tổng
m M
bằng
A.
3
. B.
2
. C.
6
. D.
7
.
Lời giải
Chọn A
Ta có hệ
2
2
2 2
3 3 2 3 2
3 2
2 7 3
4 4 7 3
6 12 8 3 3 20
2 3 3 20
x x x
x x x x
x x x x x x
x x x x
2
3
3
3 1
4 1
3 9 12 0
x
x
x
x
x x
. Do đó nghiệm nguyên nhỏ nhất là
3
x
và
nghiệm nguyên lớn nhất là
0
x
. Vậy
3
m M
.
Câu 6: Góc có số đo
120
đổi sang rađian là:
A.
3
2
. B.
2
3
. C.
4
. D.
10
.
Lời giải
Chọn B
Ta có:
2
120 .120
180 3
rad.
Câu 7: Trong mặt phẳng với hệ trục tọa độ
Oxy
, tính góc giữa đường thẳng
3 1 0
x y
và trục
hoành.
A.
45
. B.
135
C.
60
. D.
120
.
Lời giải
Chọn C
Đường thẳng
3 1 0
x y
có vectơ pháp tuyến là
3; 1
n
.
Trục
Ox
có vectơ pháp tuyến là
0;1
j
.
Gọi
là góc giữa đường thẳng
3 1 0
x y
và trục hoành.
Khi đó ta có
.
1
cos
2
.
n j
n j
60
.
Câu 8: Mệnh đề nào sau đây sai?
A.
2
cos2 1 2sin
a a
. B.
cos2 2sin cos
a a a

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
C.
2 2
cos2 cos sin
a a a
. D.
2
cos2 2cos 1
a a
.
Lời giải
Chọn B
Câu 9: Cho
1
cos
3
. Khi đó
cos 3
bằng
A.
1
3
. B.
1
3
. C.
2
3
. D.
2
3
.
Lời giải
Chọn A
cos 3
cos
1
3
.
Câu 10: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho elip
2 2
: 1
9 4
x y
E
. Tính tiêu cự của elip
E
.
A.
6
. B.
4
C.
2 5
. D.
5
.
Lời giải
Chọn C
Ta có
2
9
a
,
2
4
b
2 2 2
5
c a b
5
c .
Tiêu cự
2 2 5
c .
Câu 11: Số nghiệm nguyên của bất phương trình
2
2 3
x x là
A.
5
. B.
3
. C.
2
. D.
4
.
Lời giải
Chọn D
Điều kiện xác định của bất phương trình
0
2
x
x
.
2
2 3
x x
2
2 3
x x
2
2 3 0
x x
1 3
x
.
Kết hợp với điều kiện ở trên suy ra tập các nghiệm nguyên của bất phương trình là
1;0;2;3
T .
Câu 12: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho tam giác
ABC
có
2; 1
A
,
4;5
B ,
3;2
C .
Viết phương trình đường thẳng chứa đường cao của tam giác
ABC
đi qua đỉnh
C
.
A.
3 3 0
x y
. B.
3 11 0
x y
. C.
3 3 0
x y
. D.
1 0
x y
.
Lời giải
Chọn C
Đường cao đi qua đỉnh
3;2
C nhận vectơ
2;6
AB
làm véctơ pháp tuyến, sẽ có phương
trình là
2 3 6 2 0 3 3 0
x y x y
.
Câu 13: Phương trình
3 3
x x
có tập nghiệm là:
A.
;3
. B.
;3
. C.
3;
. D.
3
.
Lời giải
Chọn B
3 0 3
3 3 3
3 3 0
3 3
x x
x x x
x x x
x x x
Tập nghiệm của phương trình là:
;3
.
Cách 2

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Áp dụng định nghĩa
0
A A A
.
3 3 3 0 3
x x x x
. Tập nghiệm của phương trình là:
;3
.
Câu 14: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường thẳng
( ): 2 3 1 0
x y . Một vec tơ chỉ
phương của đường thẳng
là :
A.
(3;2)
u . B.
(2; 3)
u . C.
(2;3)
u . D.
(3; 2)
u .
Lời giải
Chọn A
( ): 2 3 1 0 2; 3
x y n là một véctơ pháp tuyến.
Suy ra một vectơ chỉ phương của
là :
3;2
u .
Câu 15: Cho tam giác
ABC
. Mệnh đề nào sau đây đúng?
A.
sin sin
2 2
A B C
. B.
cos cos
2 2
A B C
.
C.
sin( ) sin
A B C
. D.
cos( ) cos
A B C
.
Lời giải
Chọn C
sin sin sin
A B C A B C C
.
Câu 16: Cho hàm số
, 0, ,
y ax b a a b
là tham số. Mệnh đề nào sau đây đúng?
A. Hàm số
y ax b
nhận giá trị dương trên
.
B. Hàm số
y ax b
nhận giá trị âm trên ;
b
a
.
C. Hàm số
y ax b
nhận giá trị âm trên
.
D. Hàm số
y ax b
nhận giá trị dương trên ;
b
a
.
Lời giải
Chọn D.
Câu 17: Cho góc lượng giác
thỏa mãn
2
. Khẳng định nào sau đây đúng?
A.
cot 0
. B.
cos 0
. C.
tan 0
. D.
sin 0
.
Lời giải
Chọn D.
Câu 18: Trong mặt phẳng tọa độ
Oxy
, phương trình nào sau đây là phương trình đường tròn?
A.
2 2
2 4 9 0
x y x y
. B.
2 2
2 2 4 8 19 0
x y x y
.
C.
2 2
2 6 15 0
x y x y
. D.
2 2
4 6 13 0
x y x y
.
Lời giải
Chọn C.
Phương trình đường tròn có dạng
2 2
2 2 0
x y ax by c
với
2 2
0
a b c
.
Như vậy với
0
c
thì với mọi
a
,
b
phương trình trên luôn là phương trình đường tròn.
Phương trình :
2 2
2 6 15 0
x y x y
là phương trình đường tròn.
Câu 19: Cho hàm số
2
f x ax bx c
với
0
a
. Biết rằng
0
a
,
2
4 0
b ac
. Mệnh đề nào
sau đây đúng?
A.
1 2
,
x x
:
0
f x
,
1 2
;
x x x
. B.
0
f x
, x
.
C.
1 2
,
x x
:
1 2
. 0
f x f x
. D.
0
f x
, x
.
Lời giải
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn D.
Khi
2
4 0
b ac
thì
2
f x ax bx c
cùng dấu với
a
với mọi x
.
Vì
0
a
nên
0
f x
với x
.
Câu 20: Trong mặt phẳng với hệ tọa độ
Oxy
, cho đường tròn
C
:
2 2
25
x y
. Phương trình tiếp
tuyến của đường tròn tại điểm
3;4
A là
A.
4 3 0
x y
. B.
4 3 24 0
x y
. C.
3 4 25 0
x y
. D.
3 4 25 0
x y
.
Lời giải
Chọn C.
Đường tròn
C
có tâm
O
và có bán kính bằng
5
.
Tiếp tuyến của đường tròn tại
3;4
A và có vtpt là
3;4
OA
.
Phương trình của tiếp tuyến
3 3 4 4 0
x y
hay
3 4 25 0
x y
.
Câu 21: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
( ): 4 2 1 0
C x y x y
. Bán
kính đường tròn
C
là
A.
6
R . B.
2
R
. C.
1
R
. D.
6
R
.
Lời giải
Chọn A
Có
2 2
2; 1, 1 6
a b c R a b c .
Câu 22: Tập nghiệm của bất phương trình
2
2 1 0
x x
là
A.
1
;
4
. B.
. C.
1
\
4
. D.
.
Lời giải
Chọn D
Có
2
7 0
2 1 0,
2 0
x x x
a
.
Câu 23: Cho các góc lượng giác
,
a b
và
cos( )cos( ) sin( )sin( )
a b a b a b b
T a
. Mệnh đề sau
đây đúng?
A.
sin2
T b
. B.
cos2
T a
. C.
sin2
T a
. D.
cos2
T b
.
Lời giải
Chọn B
Ta có
cos( )cos( ) sin( )sin( ) cos cos2
a b a b a b a b a b aT
b a
.
Câu 24: Biết rằng tập xác định của hàm số
2
1
2y x x
x
là
;D a
. Khẳng định nào sau
đây đúng?
A.
0
a
. B.
0
a
. C.
3 0
a
. D.
3
a
.
Lời giải
Chọn A
Hàm số
2
1
2y x x
x
xác định khi
2
2 1
2 0
1
0
0
x x
x x
x
x
x
.
Vậy
1;D
0
a
.
Câu 25: Cho các số
0, 0
a b
thỏa mãn
1
ab
. Mệnh đề nào sau đây đúng?
A.
1 2
a b
. B.
2
a b
. C.
0 1
a b
. D.
2
a b
.
Lời giải

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Chọn B
Với hai số
0, 0
a b
, ta có:
2 2
a b ab
. Dấu
“ ”
xảy ra khi và chỉ khi
a b
.
Câu 26: Với mọi góc lượng giác
và số nguyên
k
, mệnh đề nào sau đây sai ?
A.
sin 2 sin
k
. B.
cos cos
k
.
C.
tan tan
k
. D.
cot cot
k
.
Lời giải
Chọn B
Vì
cos khi 2
cos
cos khi 2 1
k l
k
k l
, ,k l
.
Câu 27: Tập nghiệm của bất phương trình
2
1
x
là
A.
2;0
. B.
; 2
.
C.
; 2 0;
. D.
2;
.
Lời giải
Chọn C
Bất phương trình
0
2 2 2
1 1 0 0
2
x
x
xx x x
.
Vậy tập nghiệm của bất phương trình là:
; 2 0;S
Câu 28: Trong mặt phẳng với hệ tọa độ
Oxy
, viết phương trình chính tắc của elip
E
biết rằng với mọi
điểm
M
thuộc
E
thì
1 2
10
MF MF
(
1 2
,
F F
là hai tiêu điểm của
E
)và tâm sai của
E
là
3
5
e
A.
2 2
1
100 36
x y
. B.
2 2
1
25 16
x y
. C.
2 2
1
100 64
x y
. D.
2 2
1
25 9
x y
.
Lời giải
Chọn B
Gọi phương trình chính tắc của
E
có dạng
2 2
2 2
1, 0
x y
a b
a b
.
Vì
1 2
10
MF MF
2 10 5
a a
.
Tâm sai của
E
là
3
5
e
3
3
5
c
c
a
. Do đó
2 2 2 2
5 3 4
b a c
.
Vậy phương trình chính tắc của
E
là
2 2
1
25 16
x y
.
Câu 29: Cho hai góc lượng giác , 0 ,
2
a b a b
thỏa mãn
1 3
tan ;tan
7 4
a b
. Tính
a b
.
A.
5
4
. B.
4
. C.
4
. D.
3
.
Lời giải
Chọn B
Ta có
1 3
tan tan
7 4
tan 1
1 3
1 tan .tan
1 .
7 4
a b
a b
a b
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Mà 0 ,
2
a b
nên 0 a b
4
a b
.
Câu 30: Tập nghiệm của bất phương trình
2 1 2
x x
là
A.
0;
. B.
1;
. C.
; 1
. D.
1;1
.
Lời giải
Chọn D
Ta có
2 1 2
x x
2 2
2 0
3 3 1 1 1
2 2 1 2
1 1
x x
x
x x x
x x x
x x
.
Vậy tập nghiệm của bất phương trình là
1;1
S .
Câu 31: Có bao nhiêu giá trị nguyên thuộc
10;10
của
m
để bất phương trình
2
4 0
mx x m
vô
nghiệm?
A.
9
. B.
10
. C.
8
. D.
11
.
Lời giải
Chọn A.
Ta có
2
4 0
mx x m
vô nghiệm
2
4 0
mx x m
, x
.
I
Trường hợp :
0
m
, bất phương trình
I
thành
4 0 0
x x
0
m
không thỏa yêu
cầu bài toán.
Trường hợp :
0
m
,
2
4 0
mx x m
, x
2
0 0
2
0 4 0
m m
m
m
.
Mà
m
nguyên và
10;10
m nên
2;3;4;5;6;7;8;9;10
m .
Vậy có
9
giá trị của
m
thỏa yêu cầu bài toán.
Câu 32: Biết rằng
1
cos 2 cos 2 sin cos 2 sin
2 3 2 12 12
x x x ax b
với mọi giá trị
của góc lượng giác
x
; trong đó
a
là số tự nhiên,
b
là số hữu tỉ thuộc
1
0;
2
. Mệnh đề nào
sau đây đúng?
A.
1
2
a b
. B.
3
2
a b
. C.
5
2
a b
. D.
2
a b
.
Lời giải
Chọn D.
Ta có:
1
cos 2 cos 2 sin cos 2
2 3 2 12 12
x x x
1
cos 2 cos 2 sin cos 2
2 2 3 12 12
x x x
5
sin sin 2 sin cos 2
12 12 12 12
x x
sin 2 cos cos 2 sin sin 2
12 12 12 12
x x x
Suy ra
2, 0
a b
. Vậy
2
a b
.
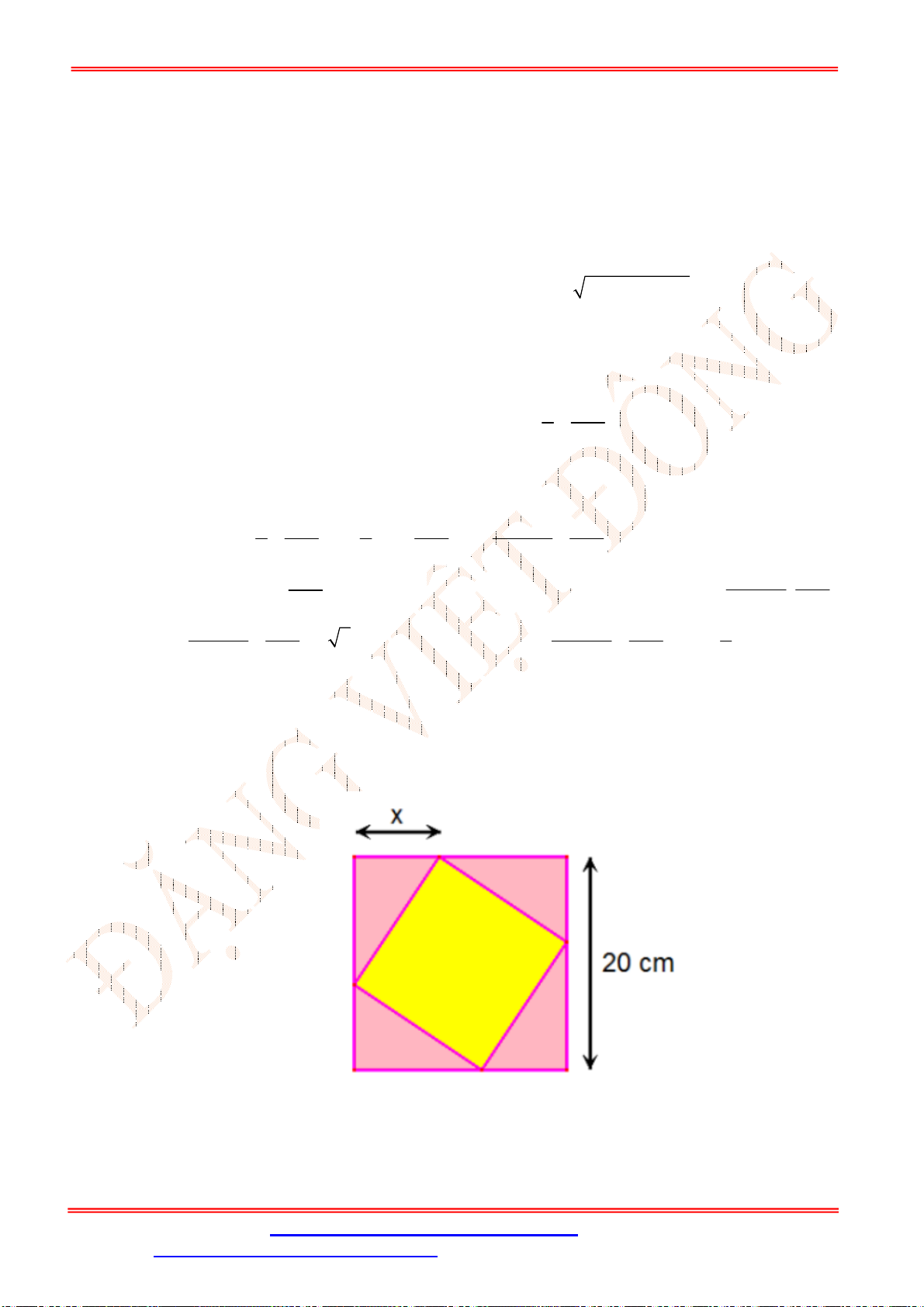
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 33: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
: 2 4 2 6 5 0
m
C x y mx m y m
(
m
là tham số). Tập hợp các điểm
m
I
là tâm của
đường tròn khi
m
thay đổi là
A. Parabol
2
: 2 1
P y x
. B. Đường thẳng
: 2 1
d y x
.
C. Parabol
2
: 2 1
P y x
. D. Đường thẳng
: 2 1
d y x
.
Lời giải
Chọn D.
Đường tròn
m
C
có tâm
; 2 1
I m m
và bán kính
2
5 10 6
R m m
.
Ta có:
2 1
2 1
I
I I
I
x m
y x
y m
. Suy ra tập hợp các điểm
m
I
là tâm của đường tròn khi
m
thay đổi là đường thẳng
: 2 1
d y x
.
Câu 34: Cho
0 1
x
. Giá trị nhỏ nhất của biểu thức
4
1
1
x
f x
x x
bằng
A.
9
. B.
7
. C.
5
. D.
3
.
Lời giải
Chọn B.
Ta có:
4 1
4 4
1 4 3 3
1 1 1
x
x x x
f x
x x x x x x
Vì
0 1
x
nên
0
1
x
x
. Áp dụng bất đẳng thức Cô si cho hai số
4 1
;
1
x
x
x x
ta
được:
4 1
2 4 4
1
x
x
x x
, đẳng thức xảy ra khi
4 1
2
1 3
x
x
x
x x
.
Khi đó
4 3 7
f x
. Vậy giá trị nhỏ nhất của biểu thức
f x
là
7
.
Câu 35: Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh
bằng
20
cm
, tạo thành bốn tam giác xung quanh như hình vẽ. Tìm tất cả các giá trị của
x
để diện
tích viên gạch không vượt quá
2
208
cm
.
A.
8 12
x
. B.
6 14
x
. C.
12 14
x
. D.
12 18
x
.
Lời giải
Chọn A.
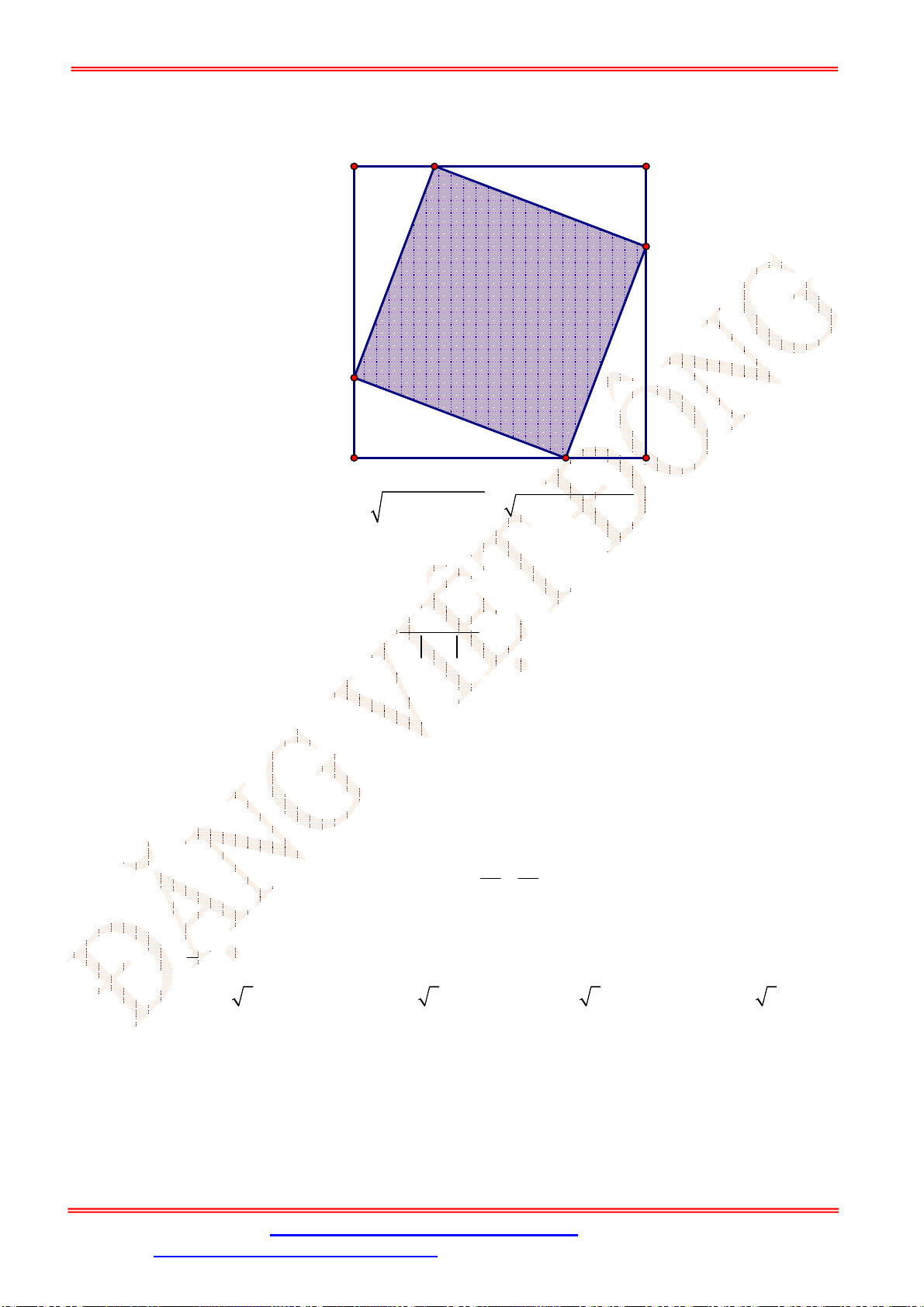
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Gọi
, , ,
E F G H
là bốn đỉnh của viên gạch hình vuông nội tiếp trong hình vuông
ABCD
có
cạnh
20
cm
như hình vẽ
20-
x
x
H
F
G
C
D
A
B
E
Ta có cạnh viên gạch là
2
2 2
20 2 40 400
EF x x x x
.
Diện tích của viên gạch là:
2 2
2 40 400
EF x x
.
Theo đề ta có diện tích viên gạch không vượt quá
2
208
cm
2 2
2 40 400 208
2 40 192 0 8 12
x x x x x
.
Câu 36: Tập nghiệm của bất phương trình
2
2 8
0
1
x x
x
là
A.
4; 1 1;2
. B.
4;2
.
C.
1;2
. D.
2; 1 1;2
.
Lời giải
Chọn A.
Điều kiện xác định
1
x
.
Bất phương trình
2
2 8 0 4 2 0 4 2
x x x x x
.
Vậy tập nghiệm của bất phương trình là
4; 1 1;2
.
Câu 37: Trong mặt phẳng tọa độ
Oxy
, cho Elip
2 2
: 1
25 9
x y
E
có hai tiêu điểm
1
F
,
2
F
. Biết điểm
M
có tung độ
M
y
dương thuộc Elip
E
sao cho bán kính đường tròn nội tiếp tam giác
1 2
MF F
bằng
4
3
. Mệnh đề nào sau đây là đúng?
A.
0; 3
M
y
. B.
2; 8
M
y
. C.
8;5
M
y
. D.
3;2
M
y
.
Lời giải
Chọn C.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
x
y
F
1
F
2
-4 -3
-2
-1
2
1
-2
-1 432
O
1
M
Ta có:
1 2 1 2
2 2 18
MF MF F F a c
.
Suy ra:
4
. 9. 12
3
MAB
S p r
. Suy ra
1 2
1
12 . 3
2
M M
y F F y
.
Câu 38: Tính tổng
2 2 2 2
sin 5 sin 10 sin 15 ... sin 85
S
.
A.
9
S
. B.
8
S
. C.
19
2
S . D.
17
2
S .
Lời giải
Chọn D.
2 2 2 2
sin 5 sin 10 sin 15 ... sin 85
S
2 2 2 2 2 2 2
sin 5 sin 85 sin 10 sin 80 ... sin 40 sin 50 sin 45
1 17
8
2 2
.
Câu 39: Cho góc lượng giác
thỏa mãn
sin cos 1
. Giá trị của sin
4
bằng
A.
1
. B.
2
2
. C.
1
. D.
2
2
.
Lời giải
Chọn D.
2 2
sin sin cos
4 2 2
.
Câu 40: Tập nghiệm của bất phương trình
2 4 1 2 1 4 3
x x x x x
là tập con của
tập hợp nào sau đây?
A.
2 1
;
3 2
. B.
1;0
. C.
1 2
;
3 3
. D.
0;1
.
Lời giải
Chọn A.
Điều kiện:
1
2
x
.
2 4 1 2 1 4 3
x x x x x
2 4 1 2 4 1 2 1 4 3 2 4 1
x x x x x x x x x
2 2
2 1 4 2 4 1 2 1 4 2 4 1
x x x x x x x x
2 1 4 2 4 1 9 6 0
x x x x x x x
.

ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Vậy tập nghiệm của bất phương trình là
1
;0
2
.
Câu 41: Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường tròn
C
:
2 2
2
x a y b R
và đường thẳng
: 0
x y a b
. Biết đường thẳng
cắt đường tròn
C
tại 2 điểm
,
M N
phân biệt. Tính độ dài
MN
.
A.
2
MN R
. B.
2
MN R
. C.
3
MN R . D.
MN R
.
Lời giải
Chọn B
Từ
C
:
2 2
2
x a y b R
ta có tâm
;
I a b
, bán kính
R
. Ta có
I
nên
MN
là
đường kính của đường tròn
C
2
MN R
.
Câu 42: Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường thẳng
: 3 4 12 0
d x y
.
Phương trình đường thẳng
đi qua điểm
2; 1
M
và tạo với
d
một góc
0
45
có dạng
5 0
ax by
, trong đó
,
a b
cùng dấu. Khẳng định nào sau đây đúng?
A.
6
a b
. B.
8
a b
.
C.
8
a b
. D.
6
a b
.
Lời giải
Chọn C
Từ
: 3 4 12 0
d x y
có vecto pháp tuyến
1
3; 4
n
,
: 5 0
ax by
có vecto pháp
tuyến
2
a;b
n
.
Khi đó
0 2 2
2 2
3 4
45 7 48 7 0
5
a b
cos a ab b
a b
7
b
a
hoặc
7
a b
( loại)
Mà
đi qua điểm
2; 1
M
nên ta có
2 5 0
a b
(*)
Với
7
b
a
kết hợp (*) suy ra
1, 7 8
a b a b
.
Câu 43: Cho tam giác
ABC
có các góc thỏa mãn
sin sin cos cos
A B A B
. Tính số đo góc
C
của
tam giác
ABC
.
A.
0
90
. B.
0
120
. C.
0
60
. D.
0
45
.
Lời giải
Chọn A
Từ
sin sin cos cos
A B A B
2sin 2
2 2 2 2
A B A B A B A B
cos cos cos
sin sin
2 2
A B C
A B C
.
Mà
0 0 0
180 2 180 90
A B C C C .
Câu 44: Trong mặt phẳng tọa độ với hệ trục tọa độ
Oxy
, cho đường tròn
2 2
: 2 2 9
C x y
.
Phương trình các tiếp tuyến của đường tròn đi qua điểm
5; 1
A
là
A.
2 3 0
x y
hoặc
2 2 3 5 0
x y
. B.
4 0
x y
hoặc
6 0
x y
.
C.
3 4 1 0
x y
hoặc
4 3 13 0
x y
. D.
5
x
hoặc
1
y
.
Lời giải
Chọn D
Từ
2 2
: 2 2 9
C x y
có tâm
2;2
I bán kính
3
R
.
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Từ điểm
5; 1
A
ta kiểm tra đường thẳng
: 5
d x
ta có
;
d I d R
5
x
là tiếp tuyến.
Câu 45: Có bao nhiêu giá trị của
0
x
để hàm số
2
2 2 2
32 1 2 1
y x x x
đạt giá trị lớn nhất trên
1;1
tại
0
x x
?
A.
4
. B.
8
. C.
6
. D.
10
.
Lời giải
Chọn A
Đặt
x cos
với
0;
, ta có
2
2 2 2
32 1 2 1
y cos cos cos
2 2 2 2 2
32 .sin . 2 8sin 2 . 2
y cos cos cos
2
2sin 4
y
0 2
y
Suy ra
max 2
y
khi
2
sin 4 1 4 0
cos
với
0;
3 5 7
; ; ;
8 8 8 8
Câu 46: Tìm tập hợp các giá trị của
m
để bất phương tình
2
2 0
x x m
nghiệm đúng với mọi
0;3
x
A.
; 1
. B.
3;
. C.
1;
. D.
1;3
.
Lời giải
Chọn B
2 2
2 0 2
x x m m x x
.
Đặt
2
0;3
2 , 0;3 max
f x x x m f x x m f x
.
Ta có bảng biến thiên của
f x
3
3
0
0x
y
1
+
∞
∞
-1
Vậy
3 3;m m
.
Câu 47: Có bao nhiêu giá trị của
m
để bất phương trình
2
1 0
m x m
vô nghiệm?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Chọn C
Bất phương rình vô nghiệm khi và chỉ khi
2
1
1 0
1
1
0
0
m
m
m
m
m
m
.
Câu 48: Cho góc lượng giác
a
thỏa mãn
2
sin 2 sin5 sin3
2
2cos 2 cos 1
a a a
a a
. Tính
sin
a
A.
1
4
. B.
1
. C.
1
. D.
1
4
.
Lời giải
Chọn B
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Ta có
2
sin 2 sin5 sin3
2
2cos 2 cos 1
a a a
a a
sin 2 2cos4 .sin
2
os4 cos
a a a
c a a
2sin cos os4
2
os4 cos
a a c a
c a a
sin 1
a
.
Câu 49: Trong mặt phẳng với hệ trục tọa độ
Oxy
, cho hình chữ nhật có hai cạnh nằm trên hai đường
thẳng có phương trình lần lượt là
2 3 0; 2 5 0
x y x y
và tọa độ một đỉnh là
2;3
.
Diện tích hình chữ nhật đó là:
A.
12
5
(đvdt). B.
16
5
(đvdt). C.
9
5
(đvdt). D.
12
5
(đvdt).
Lời giải
Chọn D
Vì hai phương trình đã cho là phương trình của hai đường thẳng cắt nhau nên giả sử
:2 3 0
AB x y
;
: 2 5 0
BC x y
Tọa độ đỉnh B là nghiệm của hpt
2 3 0
1 13
;
2 5 0
5 5
x y
B
x y
Ta thấy tọa độ đỉnh còn lại đều không thỏa hai phương trình đã cho nên đó chính là đỉnh
2;3 .
D
// ,
AD BC AD
đi qua
2;3 :
D AD
2 8 0
x y
Tọa độ đỉnh
A
là nghiệm của hpt
2 3 0
2 19
; .
2 8 0
5 5
x y
A
x y
2 2
1 2 13 19 3
,
5 5 5 5
5
AB
2 2
2 19 4
2 3
5 5
5
AD
3 4 12
. .
5
5 5
ABCD
S AB AD
. Vậy
12
5
ABCD
S
(đvdt).
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Ôn tập HKII Toán 10
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông
ID Tik Tok: dongpay
Câu 50: Trong mặt phẳng với hệ trục tọa độ
Oxy
, viết phương trình đường tròn tâm
0;0
O cắt đường
thẳng
: 2 5 0
x y
tại hai điểm
;
M N
sao cho
4
MN
.
A.
2 2
9
x y
. B.
2 2
1
x y
. C.
2 2
21
x y
. D.
2 2
3
x y
.
Lời giải
Chọn A
Gọi
R
là bán kính của đường tròn
C
thỏa đề bài.
không qua
0;0
O nên
MN
không phải là đường kính của
.
C
Gọi
H
là hình chiếu của
O
trên
thì
H
là trung điểm của
MN
1
2.
2
MH MN
2 2
5
; 5
1 2
OH d O
2 2
5 4 3.
R MO OH MH
Vậy
2 2
: 9.
C x y
---HẾT---
Bấm Tải xuống để xem toàn bộ.