







Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI HỌC SINH GIỎI CẤP THÀNH PHỐ
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2020 – 2021 MÔN VẬT LÝ 9
Đề chính thức THỜI GIAN 120 PHÚT (không kể thời gian giao đề)
Ngày 17 tháng 3 năm 2021
ĐỀ THI (gồm 2 trang, có 5 bài)
Câu 1. (4 điểm)
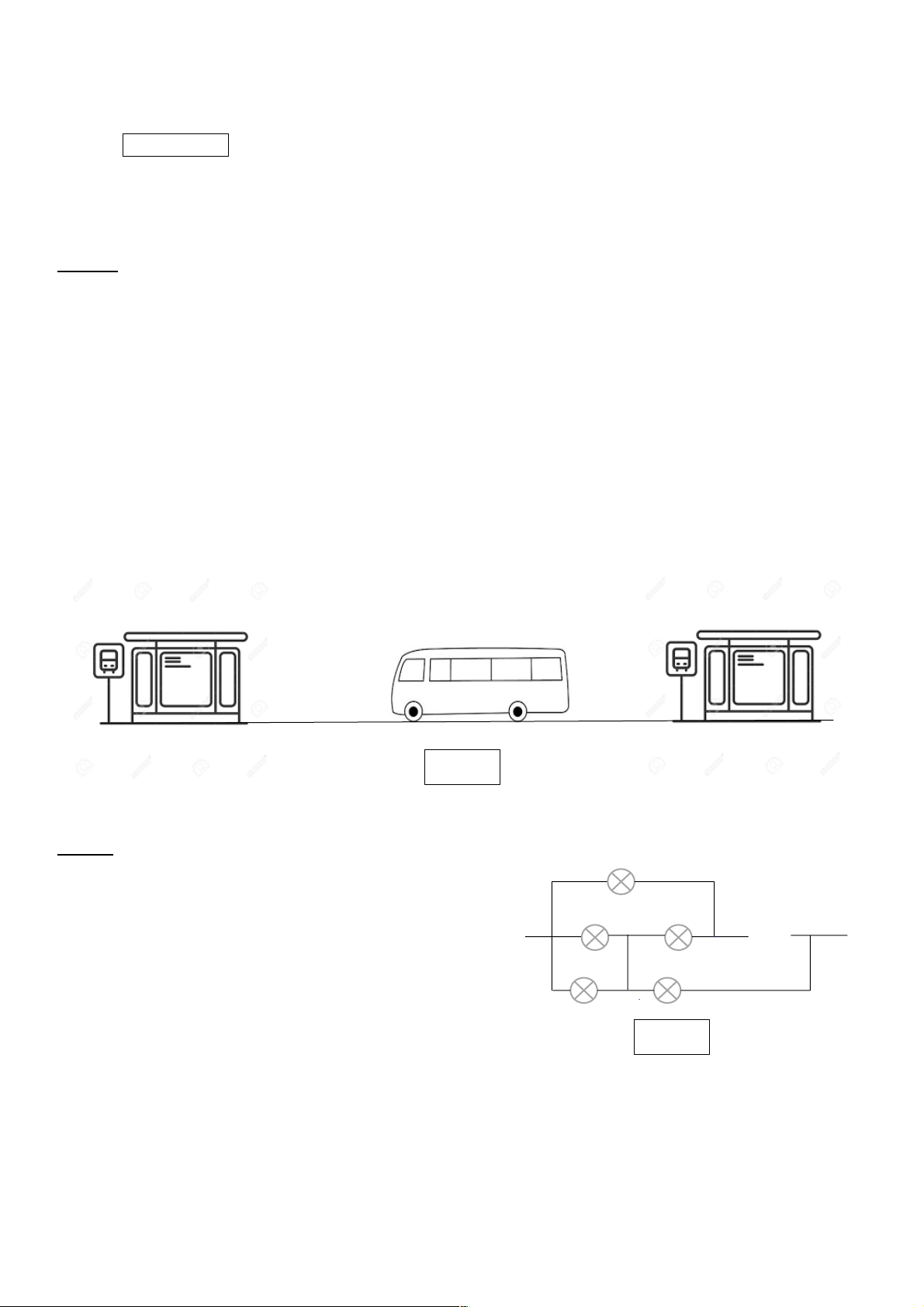
Một xe buýt di chuyển theo một lộ trình đã được định sẵn, theo quy định phải đi từ trạm A đến trạm
B trong khoảng thời gian t. Nếu đường vắng xe buýt đi từ trạm A đến trạm B với vận tốc 40 km/h thì
sẽ đến trạm B sớm hơn 20 phút so với thời gian quy định. Nếu là giờ tan tầm, tình trạng giao thông
ùn tắc, xe đi từ trạm A đến trạm B với vận tốc 15 km/h thì sẽ đến trạm B chậm hơn 20 phút so với thời gian quy định.
a. Tính chiều dài quãng đường AB giữa hai trạm và thời gian di chuyển theo quy định t.
b. Trong thực tế, do tình trạng giao thông trên tuyến đường, nên để di chuyển từ trạm A đến trạm B
theo đúng khoảng thời gian đã định sẵn t như câu a, xe buýt sẽ phải đi từ từ trạm A đến điểm C trên
quãng đường giữa hai trạm AB với vận tốc 40 km/h rồi đi từ C đến trạm B với vận tốc 15 km/h. Tính
quãng đường từ A đến C. Hình 1
Câu 2. (4 điểm)
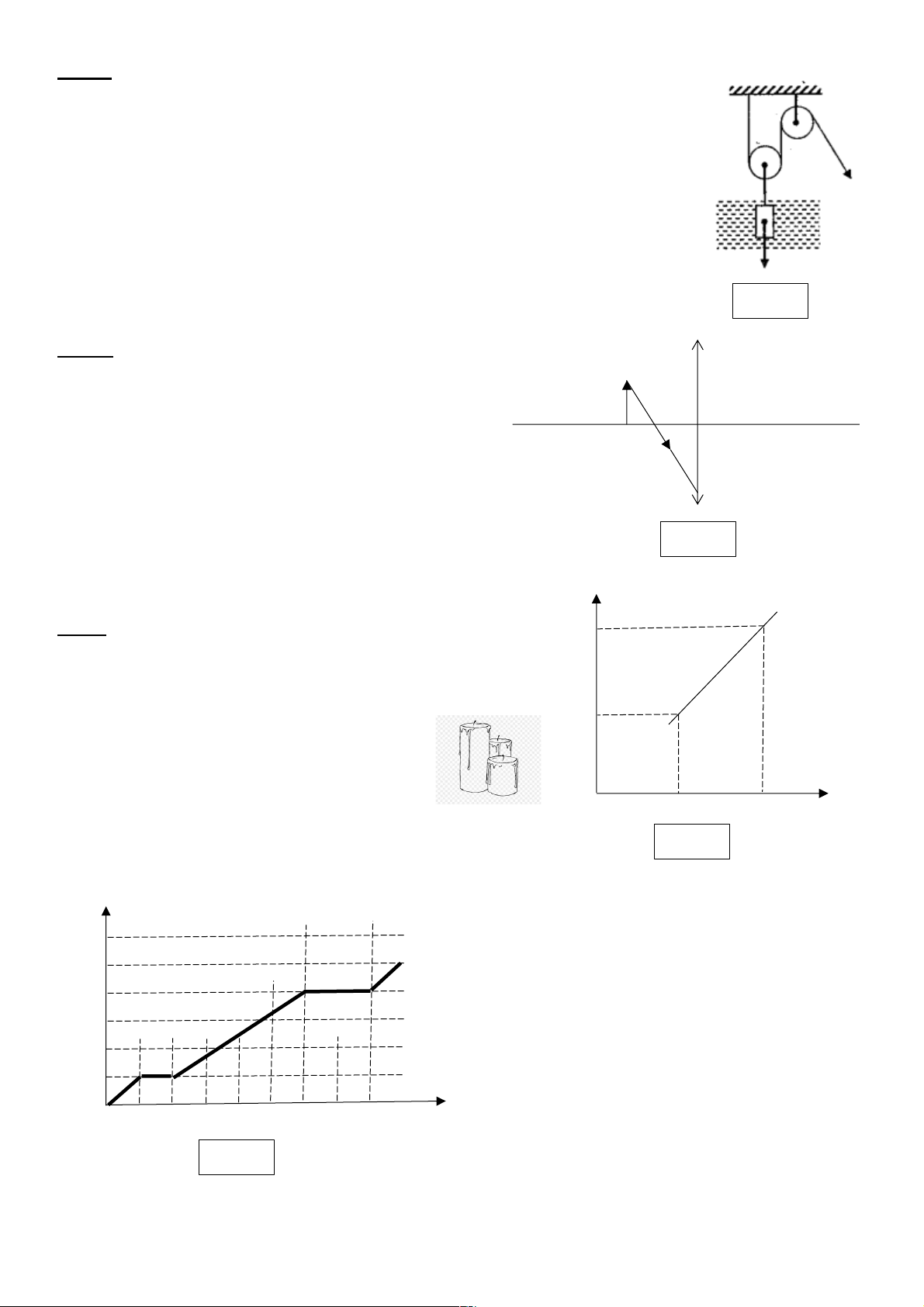
Một hệ thống chiếu sáng trang trí được lắp đặt với các
bóng đèn sợi đốt giống hệt nhau được lắp thành mạch
có dạng như hình vẽ 2. Xem các bóng đèn như những A M N B
điện trở thuần, điện áp đặt vào hai đầu A và B có giá -
trị không đổi là U. Mắc giữa M và N một vôn kế lý +
tưởng, giá trị đọc được trên vôn kế là 18 V. a. Tìm giá trị U.
b. Khi tháo vôn kế ra và thay bằng một ampe kế lý Hình 2
tưởng thì giá trị đọc được trên ampe kế là 1 A. Tính
giá trị điện trở của bóng đèn.
Bài 3. (4 điểm)
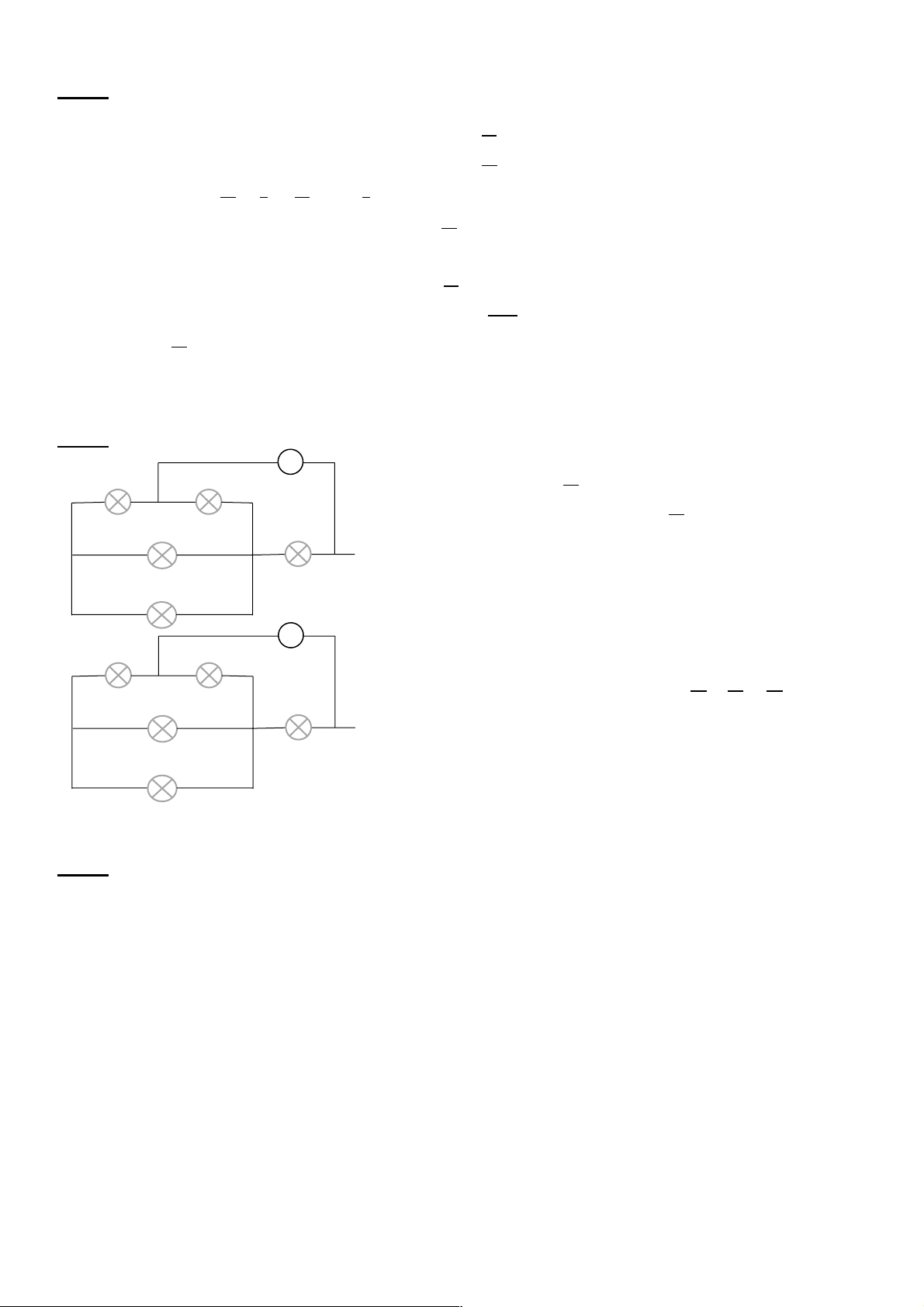
Một két sắt có khối lượng 500 kg, cao 50 cm chìm tới đáy một hồ sâu 10 m, để
trục vớt két sắt này lên, người ta sử dụng một hệ thống ròng rọc như hình vẽ 3.
Biết quá trình đưa vật từ đáy hồ lên, két sắt luôn chuyển động thẳng đều. Cho
trọng lượng riêng trung bình của két sắt là 90 000 N/m3 và của nước là 10 000
N/m3. Bỏ qua trọng lượng của các ròng rọc.
a. Tính lực kéo khi
- vật đã lên khỏi mặt nước.
- vật chìm hoàn toàn dưới nước.
b. Tính công của lực kéo vật khi vật chìm hoàn toàn trong nước. Hình 3
Câu 4. (4 điểm)
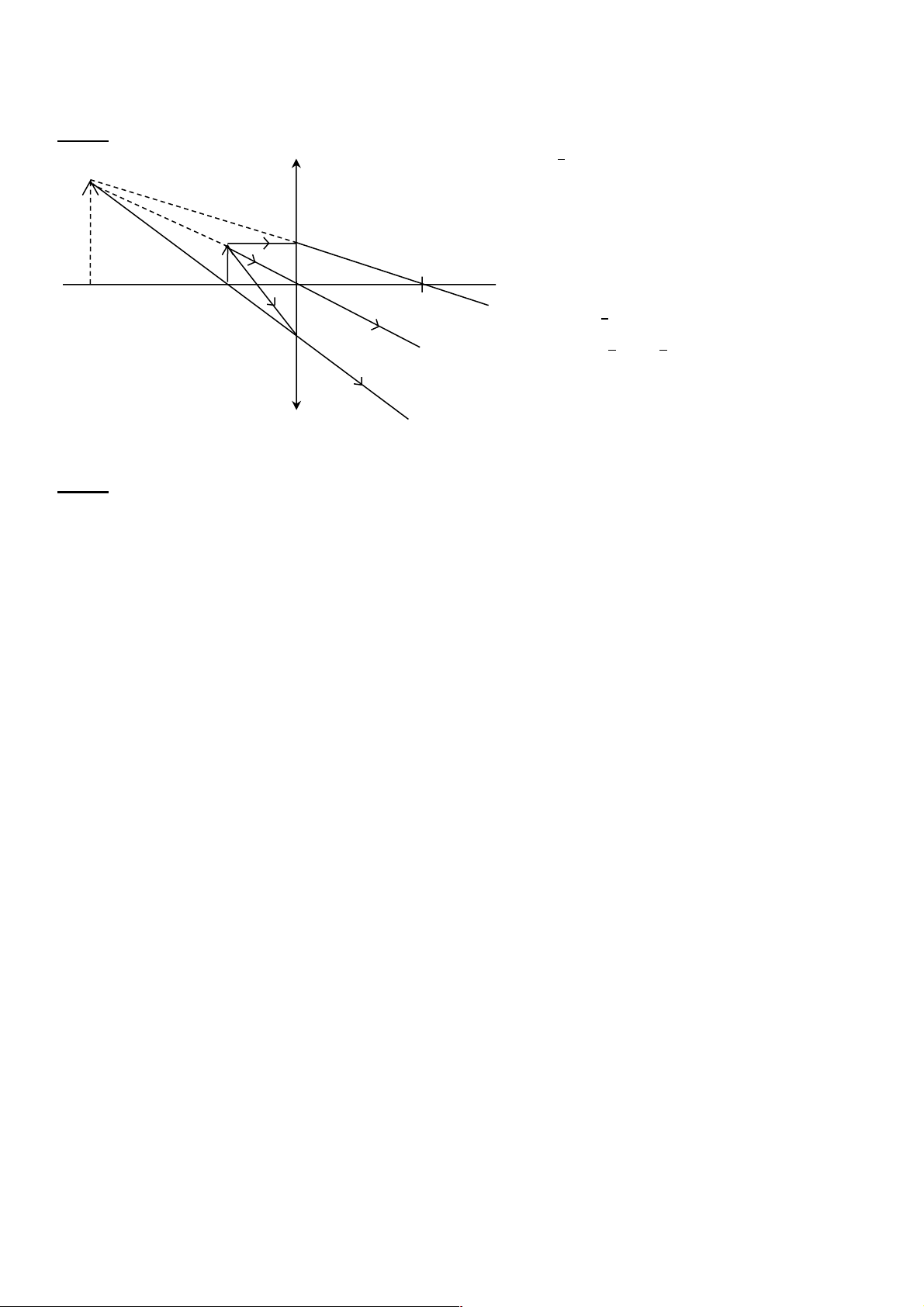
Vật sáng AB là một đoạn thẳng nhỏ hình mũi tên được B
đặt vuông góc với quang trục của một thấu kính hội tụ.
Điểm A nằm trên quang trục và cách quang tâm O một
khoảng được đo là OA = 10 mm. Một tia sáng đi từ B A O
đến gặp thấu kính tại điểm I (với OI = 2AB). Tia ló qua
thấu kính của tia sáng trên có đường kéo dài đi qua A. I
a. Vẽ ảnh của vật AB qua thấu kính.
b. Tìm tiêu cự của thấu kính này. Hình 4 V(cm3)
Bài 5. (4 điểm) 45
a. Xét đồ thị biểu diễn sự thay đổi thể tích của một khối khí
xác định khi thay đổi nhiệt độ như hình vẽ 5. Tính tỉ số khối
lượng riêng của của khối khí tại 50oC và 100oC.
b. Một nghệ nhân làm nến, sử dụng 50 g sáp 20
có nhiệt dung riêng là 0,6 kcal/kgoC, và nung
nóng cho đến khi sôi, tiến hành đo và vẽ đồ
thị biểu diễn giữa nhiệt độ của sáp theo thời T(oC)
gian, kết quả thu được như hình vẽ 6. 50 100
- Tìm nhiệt lượng cung cấp cho sáp trong một phút. Hình 5
- Tìm nhiệt độ sôi của sáp. T(oC) 250 200 150 100 50 t(phút) 1 2 3 4 5 6 7 8 Hình 6 ----- Hết -----
Hướng Dẫn Chấm (Tham khảo)
Câu 1. (4 điểm)
a. Gọi s là quãng đường AB
Thời gian xe chuyển động nếu xe đi với vận tốc v1, t! = " . #$
Thời gian xe chuyển động nếu xe đi với vận tốc v2, t% = " . !&
Theo bài ra ta có: t − " = ! và " − t = ! . (1 điểm) #$ ' !& '
Giải hệ trên: s = 16 km. Thời gian quy định là t = !! ≈ 0,73 h. (1 điểm) !&
b. Gọi s là quãng đường AC. 1
Thời gian xe chuyển động hết đoạn đường s1, t′! = "! . #$
Thời gian xe chuyển động hết đoạn đường s – s1, là t′% = "("! . !& Mà t′! + t′% = !!. (1 điểm) !&
Thay trên vào, giải phương trình trên được AC = 8 km. (1 điểm)
Câu 2. (4 điểm) V
a. Mạch khi này là như hình vẽ
Ta có R13 = 2R, và R1234 = !". #
Điện trở tương đương của mạch là 𝑅 R1 R $đ = &" (1 điểm) 3 # R5
I1 = I3 = I2/2, và I = I5 = U/(7R/5) = 5U/7R và U5 = 5U/7.
Nên U2 = 2U/7 và U3 = U/7, nên UMN = U3 + U5 = 6U/7 R2
Cuối cùng ta có U = 7UMN/6 = 21 V. (1 điểm) R4
b. Khi mắc ampe kế vào MN,
Ta chập đầu dây lại, ta có R1 // [(R2//R4) nt (R3//R5)] A
Ta có Rtđ = R/2, cường độ dòng chính là I = U/(R/2) = 2U/R.
Dòng qua ampe kế là: IA + I5 = I. (1 điểm) R1 R
Mà I5 = (U/2)/R = U/2R, và IA = I – I5, I 3 ' = !( − ( = *( = 1. ) !) !) R5 Nên R = 3U/2 = 31,5 Ω. (1 điểm) R2 R4
Câu 3. (4 điểm)
a. Trọng lượng của vật: P = 10m = 5 000 N.
Dùng ròng rọc động được lợi 2 lần về lực,
nên lực kéo khi vật đã lên khỏi mặt nước là F = P/2 = 2500 N.
Khi vật còn dưới nước thì thể tích chiếm chổ là V = P/dvật = 1/18 m3. (1 điểm)
Lực Archimède tác dụng lên vật FA = dn.V = 5000/9 = 555,55 N
Lực căng dây treo tác dụng lên vật: T = P – FA = 40000/9 = 4444,44 N
Lực kéo vật khi còn trong nước F = T/2 = 20000/9 = 2222,22 N (1 điểm)
b. Quãng đường vật di chuyển trong nước là s = h – Dh = 9,5 m. (1 điểm)
Do dùng ròng rọc động nên bị thiệt 2 lần về đường đi
nên công của lực kéo khi vật còn trong nước là
A = F.2s = 2222,22×2×9,5 = 2111109/50 = 42222,18 J. (1 điểm)
Câu 4. (4 điểm) AB = !OI B’ %
AB là đường trung bình của ∆ B’OI, AI = AB’ ∆ AOI = ∆ AA’B’ (1 điểm) A’B’ = OI = 2AB H B
A là trung điểm của OA’, OA’ = 20 mm ∆ FOH ~ ∆ FA’B’ (1 điểm)
OF/A’F = OH/A’B’ suy ra OF/(OF + OA’) = A’ A O F AB/A’B’ = ! (1 điểm) % I Suy ra OF = !OF + !OA’ % % Nên OF = OA’ = 20 mm. (1 điểm) Câu 5. (4 điểm)
a. Thể tích tại 50oC là 20 cm3. Thể tích tại 100oC là 45 cm3.
Khối lượng riêng = khối lượng/ thể tích. (1 điểm)
Tỉ số khối lượng riêng: = 45/20 = 9:4. Hoặc 4:9. (1 điểm)
b. Từ nhiệt dung riêng = 0,6 kcal/kgoC = 0,6 cal/goC.
Nhiệt lượng cần thiết cung cấp cho sáp trong mỗi phút là 0,6. 50. 50 = 1500 cal. (1 điểm)
Từ đồ thị ta thấy điểm sôi của sáp là 200 oC. (1 điểm)
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI HỌC SINH GIỎI CẤP THÀNH PHỐ
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2020 – 2021 MÔN VẬT LÝ 12
Đề chính thức THỜI GIAN 120 PHÚT (không kể thời gian giao đề)
Ngày 17 tháng 3 năm 2021
ĐỀ THI (gồm 2 trang, có 7 bài)
Bài 1. (3 điểm)
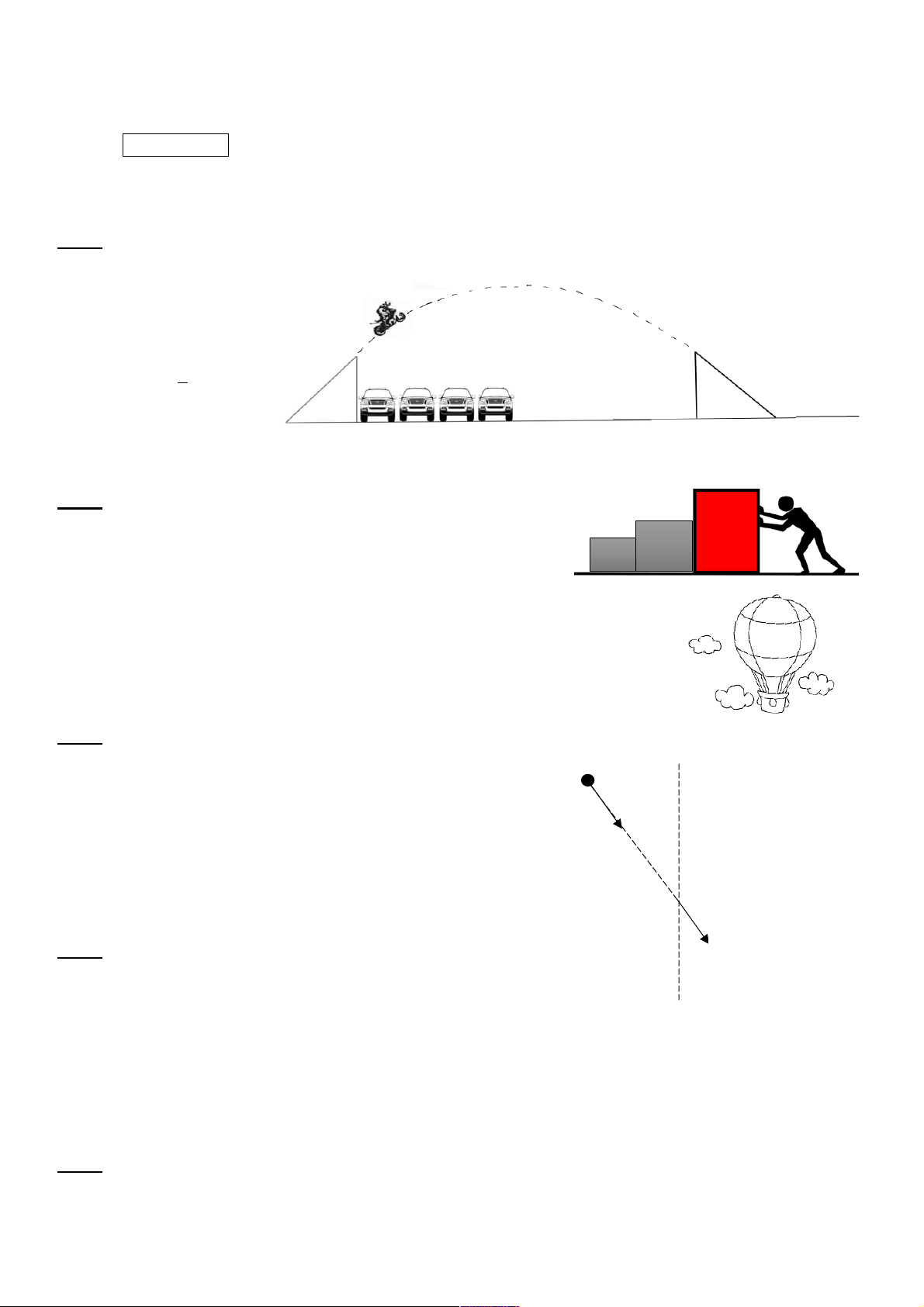
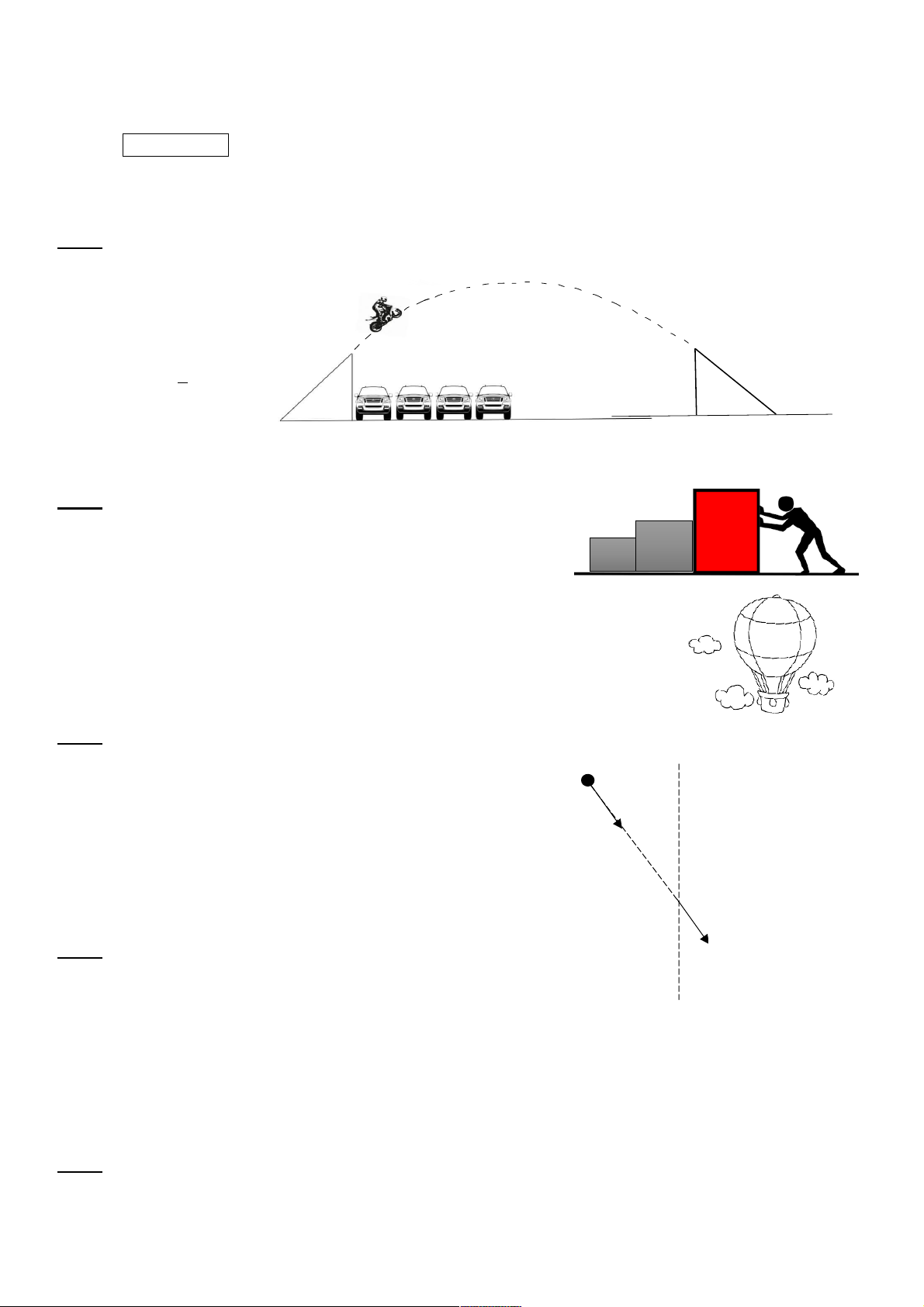
Một người lái xe mô tô mạo hiểm chuyển động qua một dốc nghiêng 45o, để bay qua một dãy các xe hơi được
xếp sát nhau, kỉ lục mà
người này hoàn thành là bay
qua 60 xe, biết chiều ngang
mỗi xe trung bình là 1,5 m.
Biết chiều dài của dốc nghiêng là 80√2 m và gia
tốc trọng trường là 10 m/s2.
Em hãy tìm vận tốc tối thiểu tại chân dốc nghiêng để người này có thể hoàn thành kỉ lục này.
Bài 2. (3 điểm)
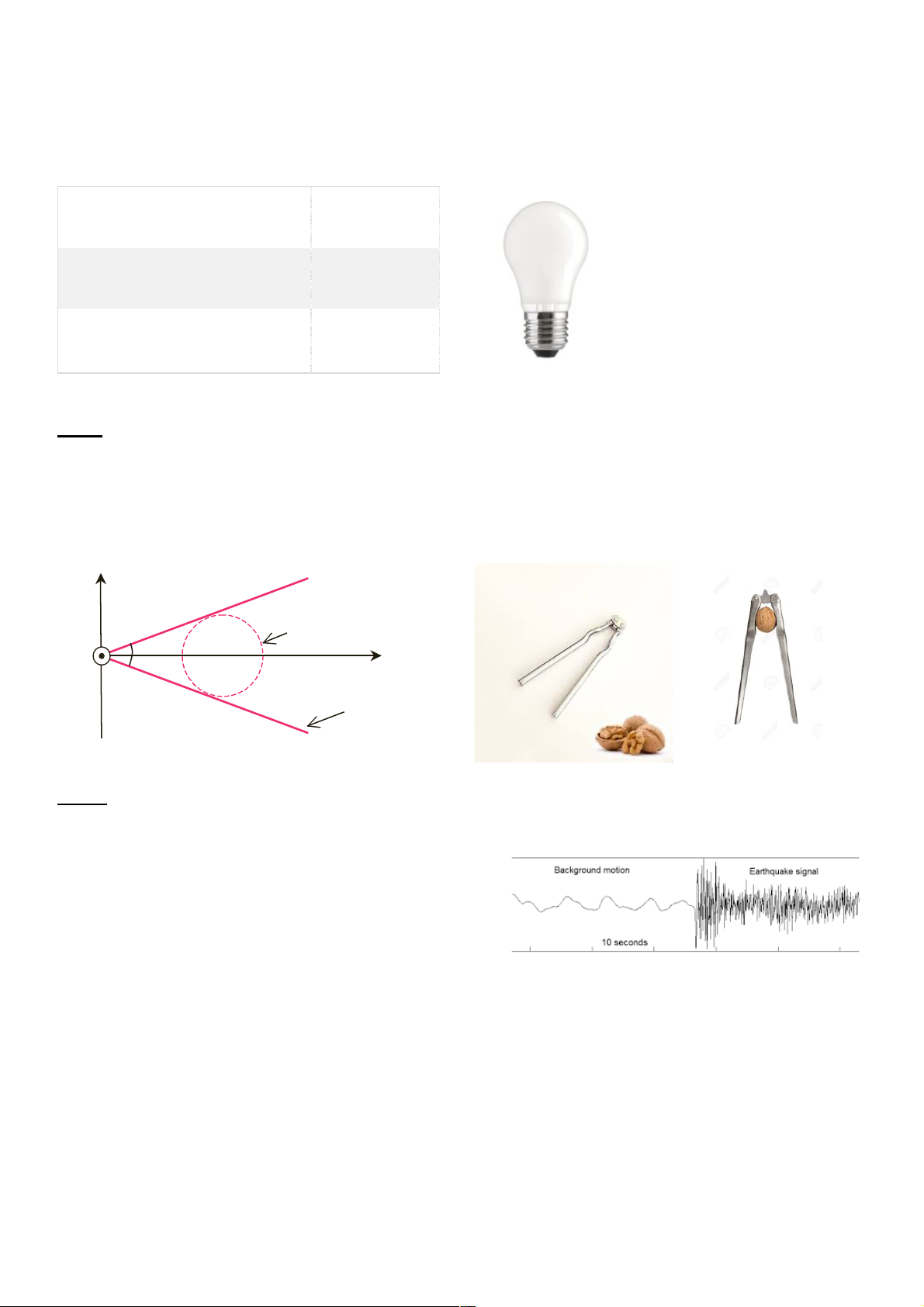
a. Một người làm việc sắp xếp các kiện hàng trong kho, cần chuẩn
bị các khối hàng để giao, ba kiện hàng A, B, C có các khối lượng
lần lượt là 40 kg, 20 kg và 10 kg đặt sát nhau trên mặt phẳng không
ma sát như hình vẽ. Nếu tác dụng một lực là 140 N vào vật 40 kg,
thì lực giữa mặt tiếp xúc giữa A và B là bao nhiêu?
b. Một khinh khí cầu có khối lượng m chuyển động đi xuống với một gia tốc a với
a < g. Hỏi cần phải bỏ đi một khối lượng bằng bao nhiêu để khinh khí cầu lại đi lên với gia tốc là a.
Bài 3. (3 điểm)
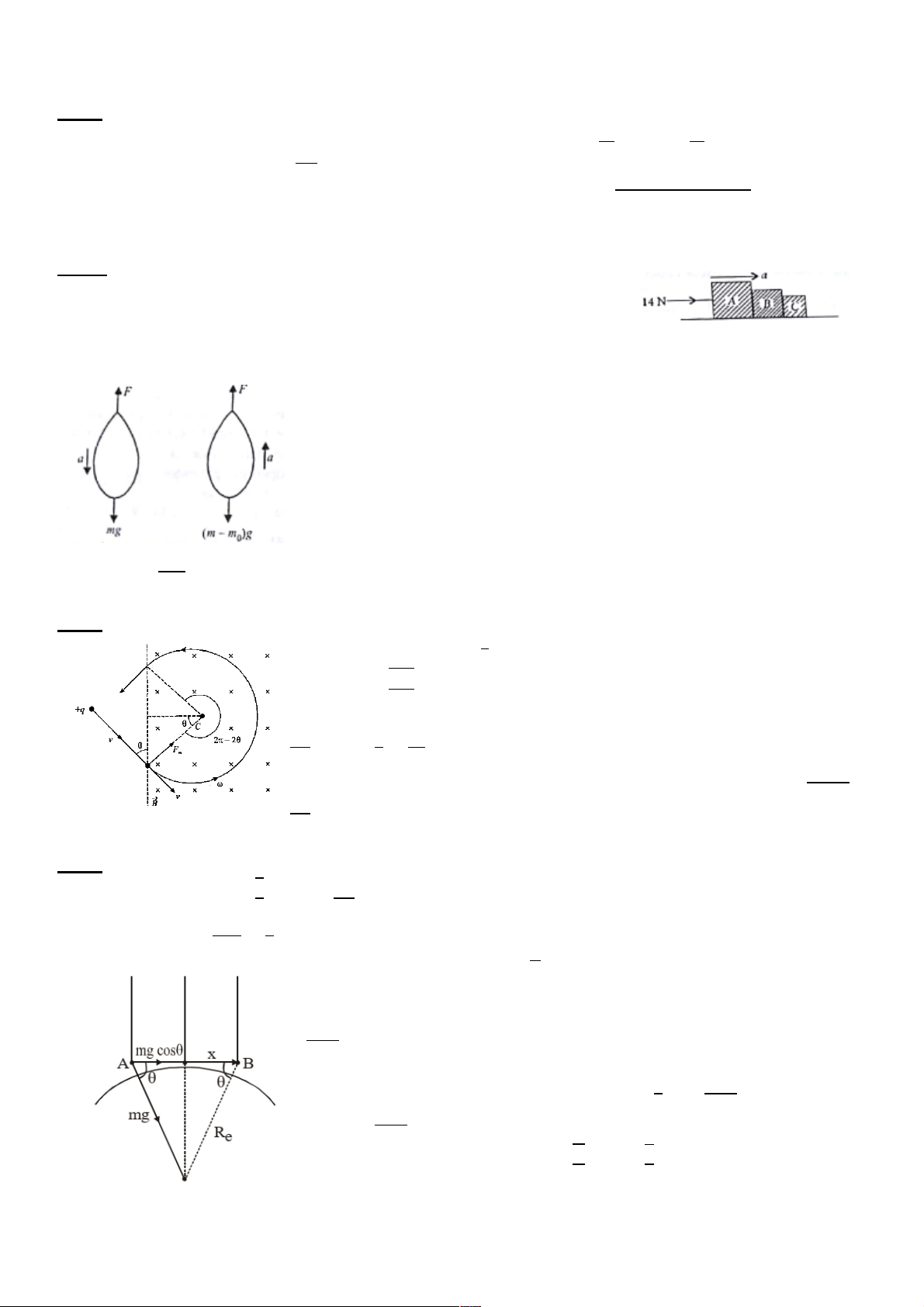
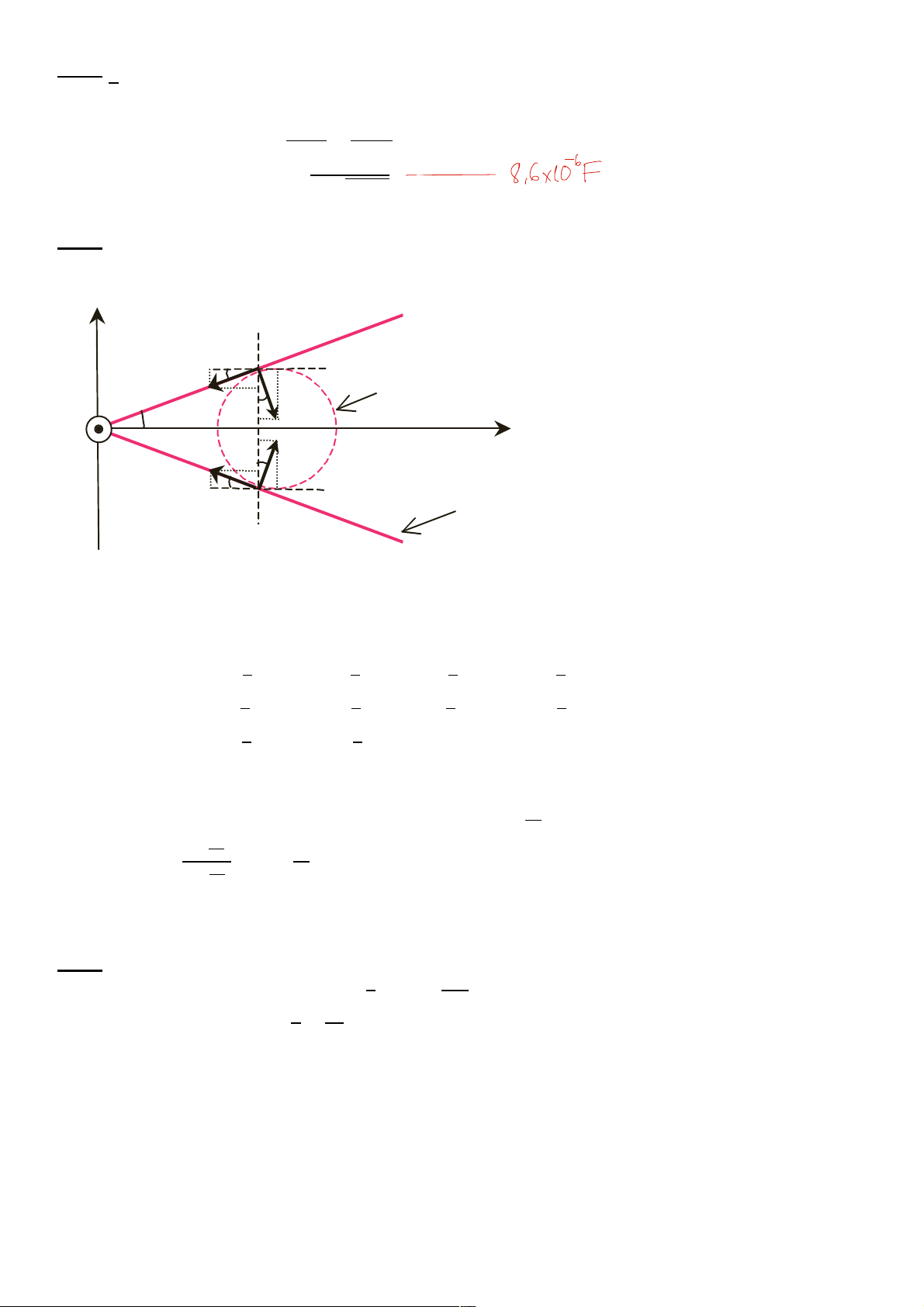
Một hạt mang điện có khối lượng m và điện tích q > 0 được tăng tốc
dưới một hiệu điện thế U. Đi vào một từ trường đều B như hình vẽ. +q 𝐵$⃗
Bỏ qua mọi tác dụng của trọng lực. X X X
a. Viết biểu thức vận tốc của hạt mang điện ngay trước khi đi vào từ X X trường đều. 𝑣⃗ X
b. Viết biểu thức thời gian mà hạt mang điện này ra khỏi vùng có từ 𝜃 X X X trường đều. X X X X
Bài 4. (3 điểm) X X
a. Một con lắc đơn có chu kì là 2 s trên mặt đất. Khi đem con lắc đơn X X X
này lên một hành tinh khác có khối lượng và đường kính gấp 2 lần
Trái đất, thì chu kì dao động bé của con lắc đơn này bằng bao nhiêu? X X X
b. Cho trái đất có bán kính là R và khối lượng là M, gia tốc trọng
trường sát mặt đất là g. Con lắc đơn có cấu tạo: vật nặng có khối X X X
lượng m, và chiều dài dây treo là vô cực, viết biểu thức chu kì dao
động bé của con lắc này trên Trái đất. Bỏ qua mọi sức cản.
Bài 5. (3 điểm)
a. Một bóng đèn điện được thiết kế cho một điện áp một chiều (DC) 12 V, nếu bóng đèn này được mắc vào
nguồn xoay chiều (AC) và cho ánh sáng bình thường, tìm điện áp cao nhất của nguồn xoay chiều này.
b. Một người đi du lịch nước ngoài mua một bóng đèn, trên vỏ hộp có ghi GE 31546 60A1 P VRS ES 110 Exercices 85
120 V BE, tra cứu trên mạng thì có được bảng số liệu như dưới đây. Khi quay về Việt Nam, người này muốn
sử dụng bóng đèn này cho nguồn điện tại nhà là 50 Hz và 220 V mà không hao tốn thêm điện năng, hỏi người Pour le cas a) :
này phải làm như thế nào để có thể sử dụng bóng đèn này đúng công suất tiêu thụ.
On négligera les frottements du palet dans l’air. Pour répondre à cette
question, on déterminera la distance maximale atteinte par le palet Elect lorsqu’on rica lance l le data
palet avec une vitesse initiale vo faisant un angle α
avec l’horizontale. Il faudra donc déterminer l’angle α permettant Dimming Capability
d’atteindre la distance maximale. Yes Pour le cas b) :
On prendra un coefficient de frottement entre la glace et le palet µ Nominal power [W] 60
C = 0,02. Puis on déterminera la distance maximale atteinte par le
palet lorsqu’il glisse sur la surface de la glace. v2 v2 RéponsesN : omi a) x n o o m al = lamp ------ vol ; tage b) xm [V = -]- - 120 2µCg g 2.3
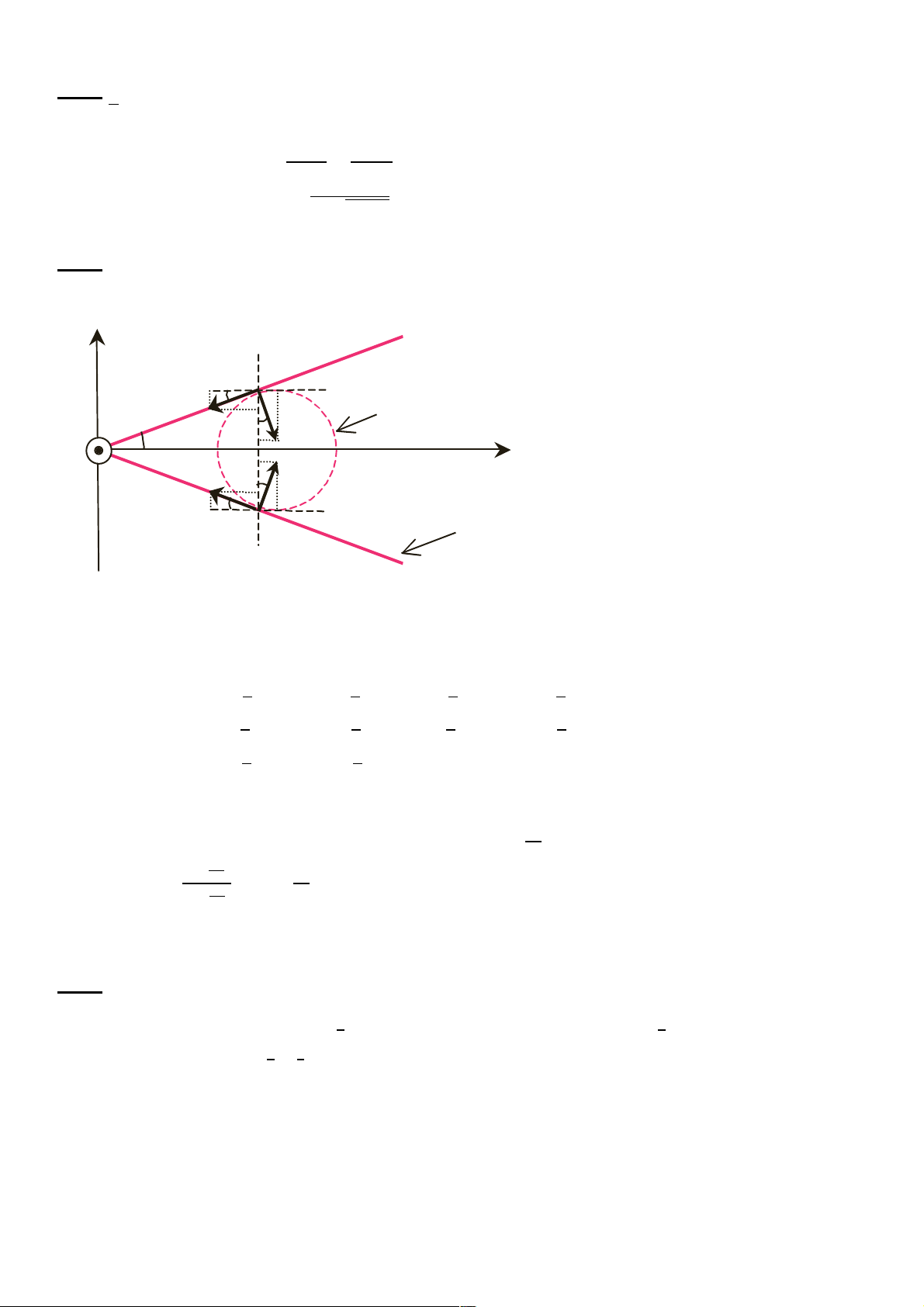
Mode d’emploi d’un casse-noix
Vous avez certainement remarqué que pour utiliser un casse-noix Bài 6. (schématisé (2 sur điể la m) fi
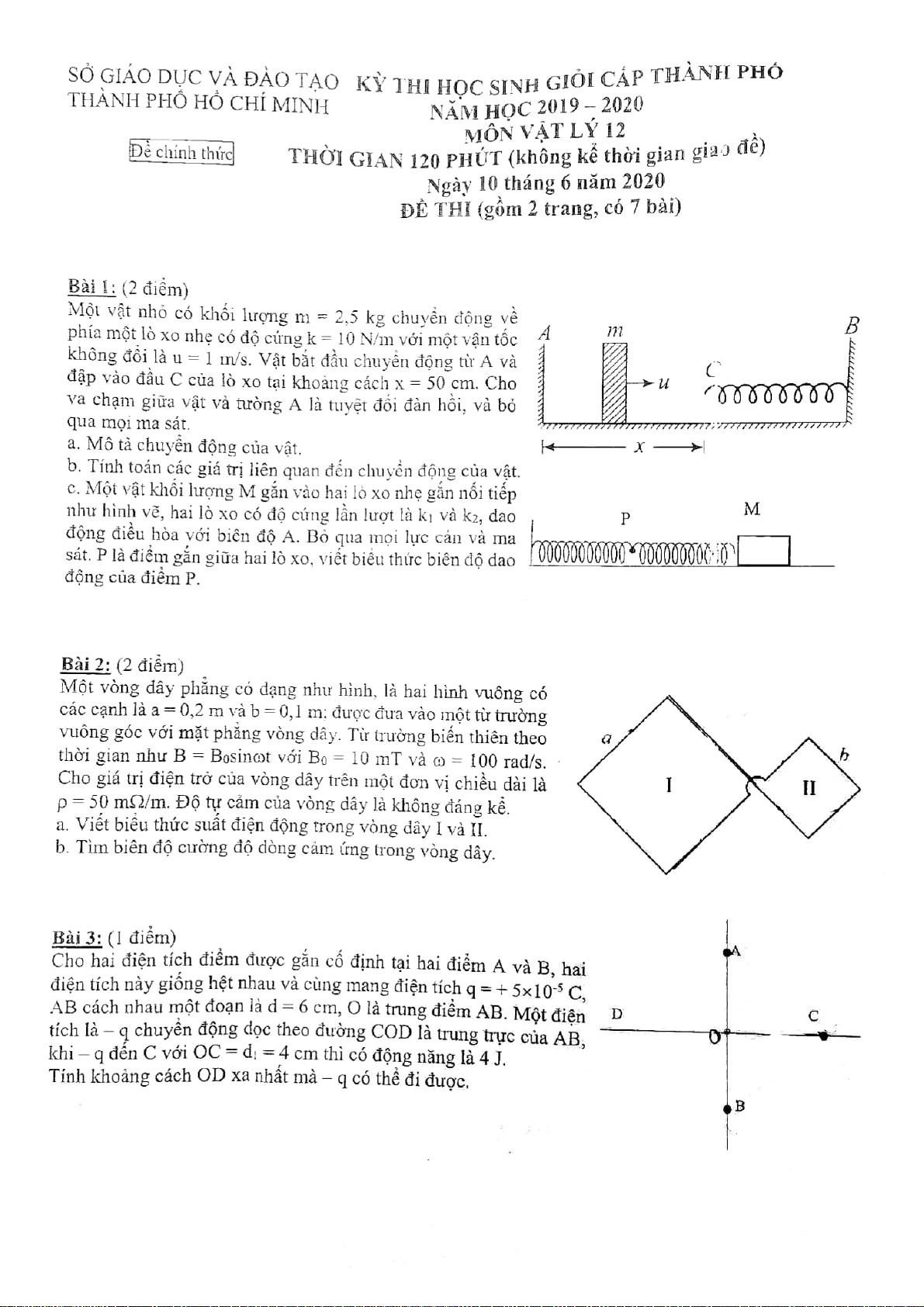
gure ci-dessous), il faut tout d’abord placer la noix Dụng entre cụ les dùng bras đ du ể làm vỡ vỏ casse-noix. hạt dẻ Ensuite cứ il ng f c aut ó cấu t serrer ạo là hai
(diminuercàng cứng như hình, để sử dụng, ta sẽ kẹp hạt dẻ gi l’angle ữ α a ) hai càng jusqu’à cứng, atteindre sau un đó k angle ẹp αc lại dư pour ới mộ lequel t góc la a noix tới một góc s’immobi-
tới hạn aC để cho hạt dẻ đứng yên. Tại góc tới lise. hạ En n ef giữ fet, aa vhai ant càng kẹp, d’atteindre khi cet hạt dẻ angle đã cố critique định, la ta noix xiết ch glisse ặt ha
entre i càng để làm bể vỏ hạt. Biết rằng hệ số ma sát
les bras du casse-noix. Une fois la noix immobilisée vous pouvez
giữa vỏ hạt và càng kẹp là µC = 0,3 và trọng lượng của hạt là không đáng kể so với các lực khác. Bỏ qua trọng
serrer les bras du casse-noix et casser la noix.
lượng của hạt, tìm aC. y Noix Hạt α z x Cas Kse ẹ -noix p Hạt
Sachant que pour le casse-noix de l’expérience, le coefficient de frot- Bài tement 7. entre (3 đi la ểm) noix
(qui a un diamètre de R = 3 cm) et un bras du
casse-noix est de µc = 0,3 et que le poids de la noix est négligeable dev
Động đất sinh ra sóng truyền
ant les autres forces, déterminez αtcrong .
lòng Trái đất, không giống như trong các môi trường chất lưu khác, trong lòng Réponse :
αđất có thể truyền cả sóng ngang (S) và sóng dọc (P). c = 33°
Tốc độ chuẩn của sóng S là khoảng 4,0 km/s, và sóng P là 2.4 Tarzan
8,0 km/s. Một địa chấn kế ghi nhận cả sóng P và sóng S từ
Tarzan qui a une masse m = 80 kg se saisit d’une liane attachée à un
tâm chấn của một trận động đất, ghi nhận cho thấy sóng P
point O et de longueur L = 4 m. Au départ la liane fait un angle θ
tới trước 4 phút so với sóng S. Giả sử sóng truyền trên m o par ột
đường thẳng, hỏi tâm chấn của trận động đất này cách địa
chấn kế một khoảng cách là bao nhiêu? www.biblio-scientifique.net -----Hết-----
Hướng dẫn chấm (tham khảo)
Bài 1. (3 điểm) " "
Do là vận tốc tối thiểu, xem như là ném nghiêng với tầm bay xa, là 𝑥 = !! sin 2𝜃 = !! (1 điểm) " "
Vận tốc bay đỉnh dốc là 𝑣# = -𝑥𝑔 = 30 m/s. với ℓ là chiều dài dốc. (1 điểm)
Vận tốc xuất phát điểm tại chân dốc xem như chạy chậm dần đều là 𝑣 = -𝑣$# + 2𝑔 sin 𝜃 × ℓ Thay số ta có v = 50 m/s. (1 điểm)
Bài 2. (3 điểm)
a. Gọi khối lượng chung của cả hệ là M = 70 kg. Gọi a là gia tốc của cả hệ.
Định luật 2 Newton: 140 = 70a suy ra a = 2 m/s2. Gọi F’ là lực tác dụng giữa các khối A và B.
ĐL 2 Newton một lần nữa là F – F’ = 40a suy ra 140 – F’= 40a suy ra F’ = 60 N. (1 điểm)
Study Physics Galaxy with www.puucho.com b.
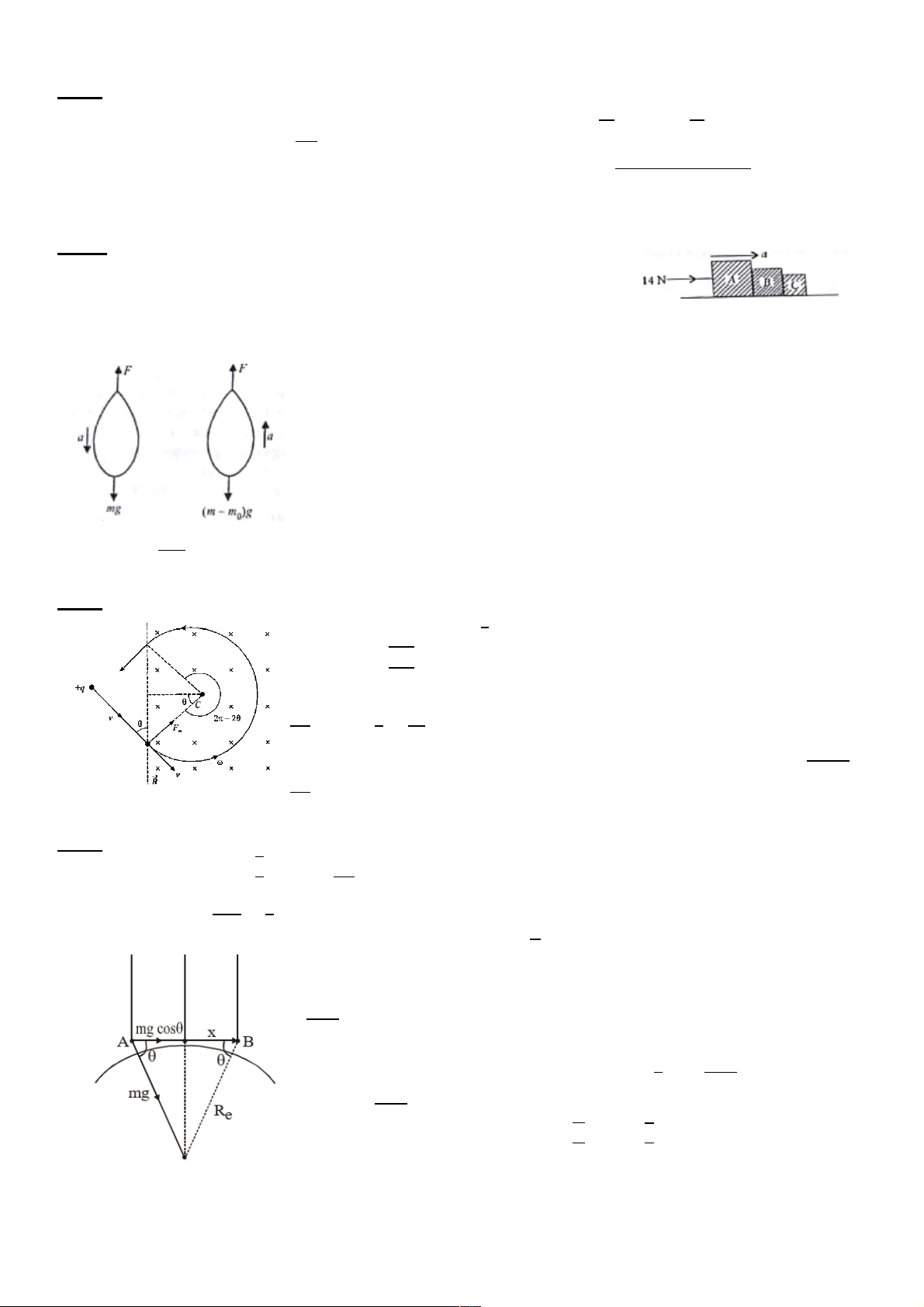
Khi khinh khí cầu đi xuống, F của không khí hướng lên, quả cầu đi xuống có gia tốc a. mg – F = ma
Gọi m0 là khối lượng được lấy ra khỏi khinh khí cầu sao cho khinh khí cầu
lại đi lên với gia tốc là a.
F – (m – m0)g = (m – m0)a (1 điểm)
Cộng hai phương trình vế theo vế m0g = 2ma – m0a. Suy ra m# = $%& (1 điểm) &'(
Bài 3. (3 điểm)
a. Ta có công thức 𝑞𝑈 = ) 𝑚𝑣$ $ suy ra 𝑣 = 8$*+ (1 điểm) ,
b. Khi vào trong từ trường đều hạt sẽ quay theo quỹ đạo tròn bán kính là 𝑅 = ,! → 𝜔 = ! = *- (1 điểm) *- . ,
Vậy thời gian mà hạt mang điện bay trong từ trường là 𝑡 = $/0$1 = 2 $, (𝜋 − 𝜃). (1 điểm) *-
Bài 4. (3 điểm)
a. Trên Trái đất: 𝑇 = 2𝜋8ℓ với 𝑔 = 45 " ."#
Trên hành tinh 𝑔6 = 4$5 = " ."$ $
Nên chu kì khi này là T’ = 2√2 s. (1 điểm)
b. Con lắc đơn sẽ dao động dọc theo đoạn AB.
Phương của trường hấp dẫn Trái đất là hướng tâm, và có độ lớn là 𝐹 = 45, = 𝑚𝑔 ."
Với M là khối lượng trái đất và R là bán kính trái đất.
Hình chiếu lên trục x là 𝐹7 = −𝐹. cos 𝜃 = −𝐹 7 = − 45, 𝑥 = −𝑘𝑥 . .% Với 𝑘 = 45, . (1 điểm) .%
Chu kì của con lắc đơn là 𝑇 = 2𝜋8, = 2𝜋8. (1 điểm) 8 " www.puucho.com
Bài 5. (3 điểm) a. 12 94 √2 = 17 V. (1 điểm)
Chapitre 2 • Lois de Newton et Forces
b. Mắc nối tiếp bóng đèn này với một tụ điện lý tưởng dòng qua mạch là I = P/U = 0,5 A là như nhau cho cả
mạch mắc nối tiếp. Ta có 𝐶 = ) = ; (1 điểm) $/9:& $/9+& For Ta ces có U2 = U2
appliquées au système : le poids P négligeable, les réactions C + U2B, Ta có 𝐶 = ; = 1,73.10-5 F. (1 điểm) $/9<+"0+" '
normales aux bras du casse-noix R n1 et R n2 et les forces de frotte-
Bài 6. (2 điểm)
ments entre les bras du casse-noix et la noix f 1 et f 2 .
Hệ hạt dẻ, hệ quy chiếu O,x, y, z.
Lực tác dụng vào hệ, như hình y f→1 → Noix R α/2 n1 z → x Rn2 f→2 Casse-noix
Bỏ qua trọng lựơng, định luật 2 Newton
Principe fondamental de la dynamique : 𝑅 $$$⃗ $$⃗ $$$⃗ $$⃗
=) + 𝑓) + 𝑅=$ + 𝑓$ = 𝑚𝑎⃗ Do đối xứng nên K𝑅 $$$⃗ $$$⃗ $$⃗ $$⃗
=)K = K𝑅=$K = 𝑅= và K𝑓)K = K𝑓$K = 𝑓 và f = µCRn. P + R + +
+ f = m a Hình c n1 f hiếu t 1 R rên Ox và n2 Oy l 2 à 𝑚𝑎
Pour des raisons de symétrie on peut écrire :
7 = 𝑚𝑥̈ = −𝑓) cos M>N + 𝑅 N − 𝑓 N + 𝑅 N $ =) sin M> $ $ cos M> $ =$ sin M> $ R 𝑚𝑎 = ? = 𝑚𝑦̈ = − = 𝑓) sin n1 R n2 R ; M>Nf− 𝑅 = N + 𝑓 1
f 2 = f et Nf+ 𝑅 = N, n $ =) cos M> $ $ sin M> $ = µ$ cos M> cRn (la noix $ S
glisse) uy ra: 𝑚𝑥̈ = −2𝑓 cos M>N + 2𝑅 N và 𝑚𝑦̈ = 0. (1 điểm) $ = sin M> $ Với f = µC.Rn.
La projection sur Ox et Oy donne :
Nên: 𝑚𝑥̈ = 2𝑅=[sin(𝛼/2) − 𝜇@ cos(𝛼/2)] và 𝑦̈ = 0 max Vỏ = hạt d mx˙˙ẻ đ = ứng yê – f1 n nê cos( n a
α/2) + R sin(α/2) – f cos(α/2) + R sin(α/2) x = 0, suy ra n1 → sin(𝛼@/2)
2 − 𝜇@ cos M>&N =n 0 2 . $ ABCD(&E may Nê=n ta c my˙˙ó: 𝜇 = – f " (
) + R cos(α/2) – f ( ) + R ( ) @ =1sin α/2 (
= tan M>&nN1 suy ra 𝛼 2sin α/2 n2cos α/2 FGAD &E $ @ = 2 tan0) 𝜇@ "
Thay số khi µC = 0,3 ta có aC = 33,4 o. (1 điểm)
mx˙˙ = – 2fcos(α/2) + 2R ( )
Ta thấy góc tới hạn không phụ thuộc vào kíc nsin α/2 h thước của hạt dẻ. C’est-à-dire : et avec f = µ cRn, my˙˙ = 0
Bài 7. (3 điểm)
Gọi x (km) là khoảng cách từ tâm chấn đến máy đo địa chấn. Thời gian để sóng S mx˙˙ đ = ến m 2Rná[y là sin t(α/2) – µ cos(α/2)] ) = H (s). Th
c ời gian để sóng P đến máy là t (s). (1 điểm) I $ = HJ
Và t) − t$ = 4 × 60 suy ra H − H y˙˙ = 4 × 0 60 suy ra x = 1920 km. (2 điểm) I J
On en déduit que pour que la noix soit immobile il faut ax = 0, c’est- à-dire :
mx˙˙ = 0 = 2Rn[sin(αc/2) – µccos(αc/2)] ⇒ (sin ( α
c/2) – µccos(αc/2) = 0) www.biblio-scientifique.net
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI HỌC SINH GIỎI CẤP THÀNH PHỐ
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2020 – 2021
MÔN VẬT LÝ 12 – CHUYÊN
Đề chính thức THỜI GIAN 120 PHÚT (không kể thời gian giao đề)
Ngày 17 tháng 3 năm 2021
ĐỀ THI (gồm 2 trang, có 7 bài)
Bài 1. (3 điểm)
Một người lái xe mô tô mạo hiểm chuyển động qua một dốc nghiêng 45o, để bay qua một dãy các xe hơi được
xếp sát nhau, kỉ lục mà
người này hoàn thành là bay
qua 60 xe, biết chiều ngang
mỗi xe trung bình là 1,5 m.
Biết chiều dài của dốc nghiêng là 80√2 m và gia
tốc trọng trường là 10 m/s2.
Em hãy tìm vận tốc tối thiểu tại chân dốc nghiêng để người này có thể hoàn thành kỉ lục này.
Bài 2. (3 điểm)
a. Một người làm việc sắp xếp các kiện hàng trong kho, cần chuẩn
bị các khối hàng để giao, ba kiện hàng A, B, C có các khối lượng
lần lượt là 40 kg, 20 kg và 10 kg đặt sát nhau trên mặt phẳng không
ma sát như hình vẽ. Nếu tác dụng một lực là 140 N vào vật 40 kg,
thì lực giữa mặt tiếp xúc giữa A và B là bao nhiêu?
b. Một khinh khí cầu có khối lượng m chuyển động đi xuống với một gia tốc a với
a < g. Hỏi cần phải bỏ đi một khối lượng bằng bao nhiêu để khinh khí cầu lại đi lên với gia tốc là a.
Bài 3. (3 điểm)
Một hạt mang điện có khối lượng m và điện tích q > 0 được tăng tốc
dưới một hiệu điện thế U. Đi vào một từ trường đều B như hình vẽ. +q 𝐵$⃗
Bỏ qua mọi tác dụng của trọng lực. X X X
a. Viết biểu thức vận tốc của hạt mang điện ngay trước khi đi vào từ X X trường đều. 𝑣⃗ X
b. Viết biểu thức thời gian mà hạt mang điện này ra khỏi vùng có từ 𝜃 X X X trường đều. X X X X
Bài 4. (3 điểm) X X
a. Một con lắc đơn có chu kì là 2 s trên mặt đất. Khi đem con lắc đơn X X X
này lên một hành tinh khác có khối lượng và đường kính gấp 2 lần
Trái đất, thì chu kì dao động bé của con lắc đơn này bằng bao nhiêu? X X X
b. Cho trái đất có bán kính là R và khối lượng là M, gia tốc trọng
trường sát mặt đất là g. Con lắc đơn có cấu tạo: vật nặng có khối X X X
lượng m, và chiều dài dây treo là vô cực, viết biểu thức chu kì dao
động bé của con lắc này trên Trái đất. Bỏ qua mọi sức cản.
Bài 5. (3 điểm)
a. Một bóng đèn điện được thiết kế cho một điện áp một chiều (DC) 12 V, nếu bóng đèn này được mắc vào
nguồn xoay chiều (AC) và cho ánh sáng bình thường, tìm điện áp cao nhất của nguồn xoay chiều này. Exercices 85
b. Một người đi du lịch nước ngoài mua một bóng đèn, trên vỏ hộp có ghi GE 31546 60A1 P VRS ES 110
120 V BE, tra cứu trên mạng thì có được bảng số liệu như dưới đây. Khi quay về Việt Nam, người này muốn Pour le cas a) :
sử dụng bóng đèn này cho nguồn điện tại nhà là 50 Hz và 220 V mà không hao tốn thêm điện năng, hỏi người
On négligera les frottements du palet dans l’air. Pour répondre à cette
này phải làm như thế nào để có thể sử dụng bóng đèn này đúng công suất tiêu thụ.
question, on déterminera la distance maximale atteinte par le palet
lorsqu’on lance le palet avec une vitesse initiale vo faisant un angle α avec Electrical d l’horizontale. at Il a f
audra donc déterminer l’angle α permettant
d’atteindre la distance maximale. Di Pour le cas mmi b) : ng Capability Yes
On prendra un coefficient de frottement entre la glace et le palet
µC = 0,02. Puis on déterminera la distance maximale atteinte par le Nominal power [W]
palet lorsqu’il glisse sur la surf 60 ace de la glace. v2 v2 Réponses : a) x o = ------ ; b) o m x = -- 2 m g Nominal lamp
µCg voltage [V] 120
2.3 Mode d’emploi d’un casse-noix
Vous avez certainement remarqué que pour utiliser un casse-noix
(schématisé sur la figure ci-dessous), il faut tout d’abord placer la noix Bài entre 6. (2 les điểm) bras
du casse-noix. Ensuite il faut serrer (diminuer D l’angle ụ α ng ) cụ dùng jusqu’à để làm atteindre v un ỡ vỏ angle h α ạ c t dẻ pour cứng c lequel ó la cấu t noix ạo là hai
s’immobi-càng cứng như hình, để sử dụng, ta sẽ kẹp hạt dẻ lise. gi En ữa ef ha fet, i acvàng ant cứng, sau d’atteindre đó cet kẹp lạ angle i dưới m critique ột la góc noix a tới m glisse ột góc entre
tới hạn aC để cho hạt dẻ đứng yên. Tại góc tới
les bras du casse-noix. Une fois la noix immobilisée vous pouvez
hạn giữa hai càng kẹp, khi hạt dẻ đã cố định, ta xiết chặt hai càng để làm bể vỏ hạt. Biết rằng hệ số ma sát
serrer les bras du casse-noix et casser la noix.
giữa vỏ hạt và càng kẹp là µC = 0,3 và trọng lượng của hạt là không đáng kể so với các lực khác. Tìm aC. y Noix Hạt α z x Cas Kse ẹ -noix p Hạt
Sachant que pour le casse-noix de l’expérience, le coefficient de frot- Bài tement 7. entre (3 đi la ểm) noix
(qui a un diamètre de R = 3 cm) et un bras du Đồ th casse-noix ị dư est ớ de i µđâ c y = biể 0,3 u et diễn que m le ột phầ poids n dòng de la xoa noix y c est hiều lý tưở
négligeable ng truyền đi giữa đám mây ở độ cao 1 km và mặt dev
đất, trong quá trình xảy hiện
ant les autres forces, déterminez αtcư.ợng sét. Giá trị I0 là 157 kA và T = 0,2 ms. Giả sử quá trình phóng điện diễn ra Réponse khi : α đi c ện t
= 33° rường trong không khí giữa đám mây và mặt đất có giá trị là E0 = 3´106 V/m.
a. Tính điện lượng tổng cộng được truyền trong quá trình phóng tia sét. 2.4 Tarzan
b. Tính cường độ dòng trung bình giữa đám mây và trái đất trong quá trình tia sét.
Tarzan qui a une masse m = 80 kg se saisit d’une liane attachée à un
c. Giả sử toàn bộ điện tích trên đám mây được phóng hết trong quá trình hình thành tia sét, tính điện dung của
point O et de longueur L = 4 m. Au départ la liane fait un angle θ
hệ đám mây đó và mặt đất. o par I www.biblio-scientifique.net 0 O T --Hết--
Hướng dẫn chấm (tham khảo)
Bài 1. (3 điểm) " "
Do là vận tốc tối thiểu, xem như là ném nghiêng với tầm bay xa, là 𝑥 = !! sin 2𝜃 = !! (1 điểm) " "
Vận tốc bay đỉnh dốc là 𝑣# = -𝑥𝑔 = 30 m/s. với ℓ là chiều dài dốc. (1 điểm)
Vận tốc xuất phát điểm tại chân dốc xem như chạy chậm dần đều là 𝑣 = -𝑣$# + 2𝑔 sin 𝜃 × ℓ Thay số ta có v = 50 m/s. (1 điểm)
Bài 2. (3 điểm)
a. Gọi khối lượng chung của cả hệ là M = 70 kg. Gọi a là gia tốc của cả hệ.
Định luật 2 Newton: 140 = 70a suy ra a = 2 m/s2. Gọi F’ là lực tác dụng giữa các khối A và B.
ĐL 2 Newton một lần nữa là F – F’ = 40a suy ra 140 – F’= 40a suy ra F’ = 60 N. (1 điểm)
Study Physics Galaxy with www.puucho.com b.
Khi khinh khí cầu đi xuống, F của không khí hướng lên, quả cầu đi xuống có gia tốc a mg – F = ma
Gọi m0 là khối lượng được lấy ra khỏi khinh khí cầu sao cho khinh khí cầu
lại đi lên với gia tốc là a.
F – (m – m0)g = (m – m0)a (1 điểm)
Cộng hai phương trình vế theo vế m0g = 2ma – m0a. Suy ra m# = $%& (1 điểm) &'(
Bài 3. (3 điểm)
a. Ta có công thức 𝑞𝑈 = ) 𝑚𝑣$ $ suy ra 𝑣 = 8$*+ (1 điểm) ,
b. Khi vào trong từ trường đều hạt sẽ quay theo quỹ đạo tròn bán kính là 𝑅 = ,! → 𝜔 = ! = *- (1 điểm) *- . ,
Vậy thời gian mà hạt mang điện bay trong từ trường là 𝑡 = $/0$1 = 2 $, (𝜋 − 𝜃). (1 điểm) *-
Bài 4. (3 điểm)
a. Trên Trái đất: 𝑇 = 2𝜋8ℓ với 𝑔 = 45 " ."#
Trên hành tinh 𝑔6 = 4$5 = " ."$ $
Nên chu kì khi này là T’ = 2√2 s. (1 điểm)
b. Con lắc đơn sẽ dao động dọc theo đoạn AB.
Phương của trường hấp dẫn Trái đất là hướng tâm, và có độ lớn là 𝐹 = 45, = 𝑚𝑔 ."
Với M là khối lượng trái đất và R là bán kính trái đất.
Hình chiếu lên trục x là 𝐹7 = −𝐹. cos 𝜃 = −𝐹 7 = − 45, 𝑥 = −𝑘𝑥 . .% Với 𝑘 = 45, . (1 điểm) .%
Chu kì của con lắc đơn là 𝑇 = 2𝜋8, = 2𝜋8. (1 điểm) 8 " www.puucho.com
Bài 5. (3 điểm) a. 12 94 √2 = 17 V. (1 điểm)
Chapitre 2 • Lois de Newton et Forces
b. Mắc nối tiếp bóng đèn này với một tụ điện lý tưởng dòng qua mạch là I = P/U = 0,5 A là như nhau cho cả
mạch mắc nối tiếp. Ta có 𝐶 = ) = ; (1 điểm) $/9:& $/9+& For Ta ces có U2 = U2
appliquées au système : le poids P négligeable, les réactions C + U2B, Ta có 𝐶 = ; = 1,73.10-5 F. (1 điểm) $/9<+"0+" '
normales aux bras du casse-noix R n1 et R n2 et les forces de frotte-
Bài 6. (2 điểm)
ments entre les bras du casse-noix et la noix f 1 et f 2 .
Hệ hạt dẻ, hệ quy chiếu O,x, y, z.
Lực tác dụng vào hệ, như hình y f→1 → Noix R α/2 n1 z → x Rn2 f→2 Casse-noix
Bỏ qua trọng lựơng, định luật 2 Newton
Principe fondamental de la dynamique : 𝑅 $$$⃗ $$⃗ $$$⃗ $$⃗
=) + 𝑓) + 𝑅=$ + 𝑓$ = 𝑚𝑎⃗ Do đối xứng nên K𝑅 $$$⃗ $$$⃗ $$⃗ $$⃗
=)K = K𝑅=$K = 𝑅= và K𝑓)K = K𝑓$K = 𝑓 và f = µCRn. P + R + +
+ f = m a Hình c n1 f hiếu t 1 R rên Ox và n2 Oy l 2 à 𝑚𝑎
Pour des raisons de symétrie on peut écrire :
7 = 𝑚𝑥̈ = −𝑓) cos M>N + 𝑅 N − 𝑓 N + 𝑅 N $ =) sin M> $ $ cos M> $ =$ sin M> $ R 𝑚𝑎 n1 = ? = 𝑚 R 𝑦̈ = − = 𝑓 n2 ) R sin ; M>Nf− 𝑅 = N + 𝑓 1
f 2 = f et Nf+ 𝑅 = N, n $ =) cos M> $ $ sin M> $ = µ$ cos M> cRn (la noix $ S
glisse) uy ra: 𝑚𝑥̈ = −2𝑓 cos M>N + 2𝑅 N và 𝑚𝑦̈ = 0. (1 điểm) $ = sin M> $ Với f = µC.Rn.
La projection sur Ox et Oy donne :
Nên: 𝑚𝑥̈ = 2𝑅=[sin(𝛼/2) − 𝜇@ cos(𝛼/2)] và 𝑦̈ = 0 max Vỏ = hạt d mx˙˙ẻ đ = ứng yê – f1 n nê cos( n a
α/2) + R sin(α/2) – f cos(α/2) + R sin(α/2) x = 0, suy ra n1 → sin(𝛼@/2)
2 − 𝜇@ cos M>&N =n 0 2 . $ ABCD(&E may Nê=n ta c my˙˙ó: 𝜇 = – f " (
) + R cos(α/2) – f ( ) + R ( ) @ =1sin α/2 (
= tan M>&nN1 suy ra 𝛼 2sin α/2 n2cos α/2 FGAD &E $ @ = 2 tan0) 𝜇@ "
Thay số khi µC = 0,3 ta có aC = 33,4 o. (1 điểm)
mx˙˙ = – 2fcos(α/2) + 2R ( )
Ta thấy góc tới hạn không phụ thuộc vào kíc nsin α/2 h thước của hạt dẻ. C’est-à-dire : et avec f = µ cRn, my˙˙ = 0
Bài 7. (3 điểm)
a. Điện lượng phóng ra là 𝑄 = ∫H 𝐼# sin M/ 𝑡N 𝑑𝑡 = $;!H = 20 C. (1 điểm) mx˙˙ = 2R # [ ( ) – Hµ ( / n sin α/2 ccos α/2)] b. Dòng điện t
rung bình là 𝐼 = I = $;! = 100 kA. (1 điểm) H / y˙˙ = 0
c. Điện trường tại thời điểm phóng sét E = 3´106 V/m.
Hiệu điện thế giữa đám mây và mặt đất U = E.d = 3´109 V.
On en déduit que pour que la noix soit immobile il faut a
Điện dung khi này là C = Q/U = 6,67´10-9 F. x = 0, c’est- (1 điểm) à-dire :
mx˙˙ = 0 = 2Rn[sin(αc/2) – µccos(αc/2)] ⇒ (sin ( α
c/2) – µccos(αc/2) = 0) www.biblio-scientifique.net



