Trắc nghiệm chương 1 giải tích 12 trích từ đề thi tốt nghiệp thpt 2020 có đáp án và lời giải
Trắc nghiệm chương 1 giải tích 12 trích từ đề thi tốt nghiệp THPT 2020 có đáp án và lời giải được soạn dưới dạng file word và PDF gồm 21 trang.Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mời các bạn cùng đón xem ở dưới.
Chủ đề: Tài liệu chung 297 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
Preview text:
BÀI TẬP TRẮC NGHIỆM CHƢƠNG 1 GIẢI TÍCH 12
TRÍCH TỪ ĐỀ THI TỐT NGHIỆP THPT 2020 ĐỢT 1 VÀ ĐỢT 2 2x 2
Câu 9.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Tiệm cận đứng của đồ thị hàm số y x là 1 A. x 2 .
B. x 1. C. x 1 . D. x 2 .
Câu 11. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)
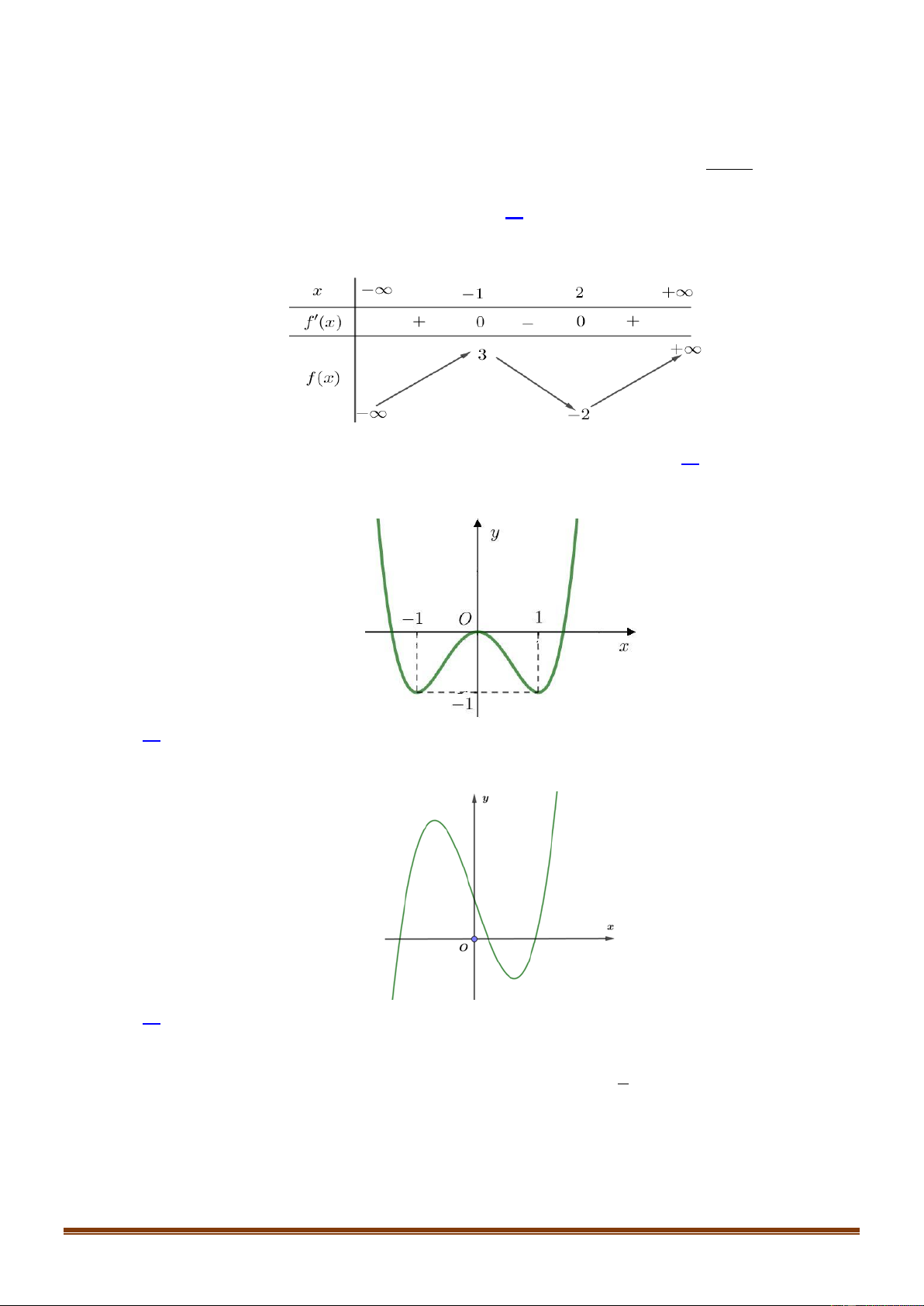
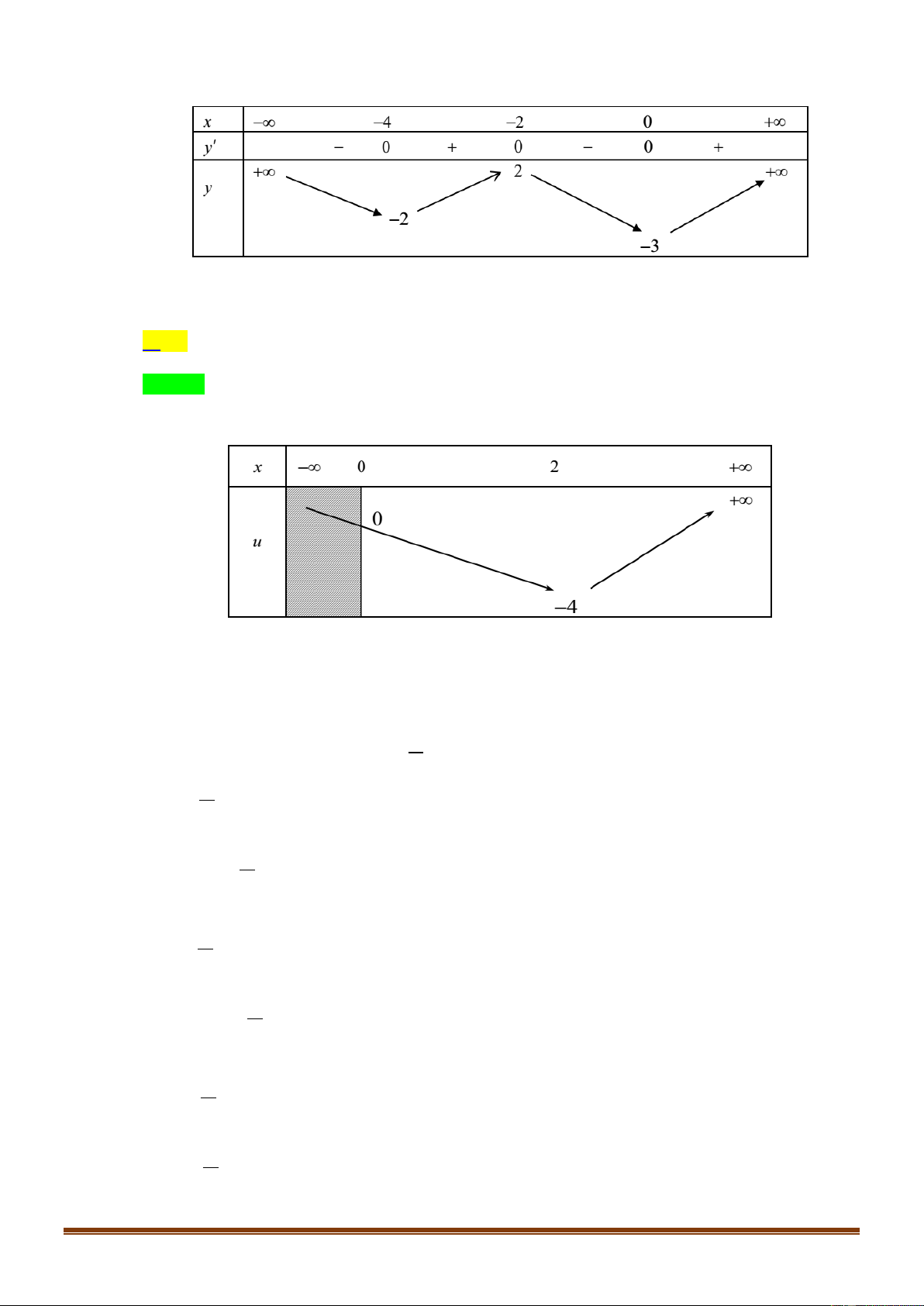
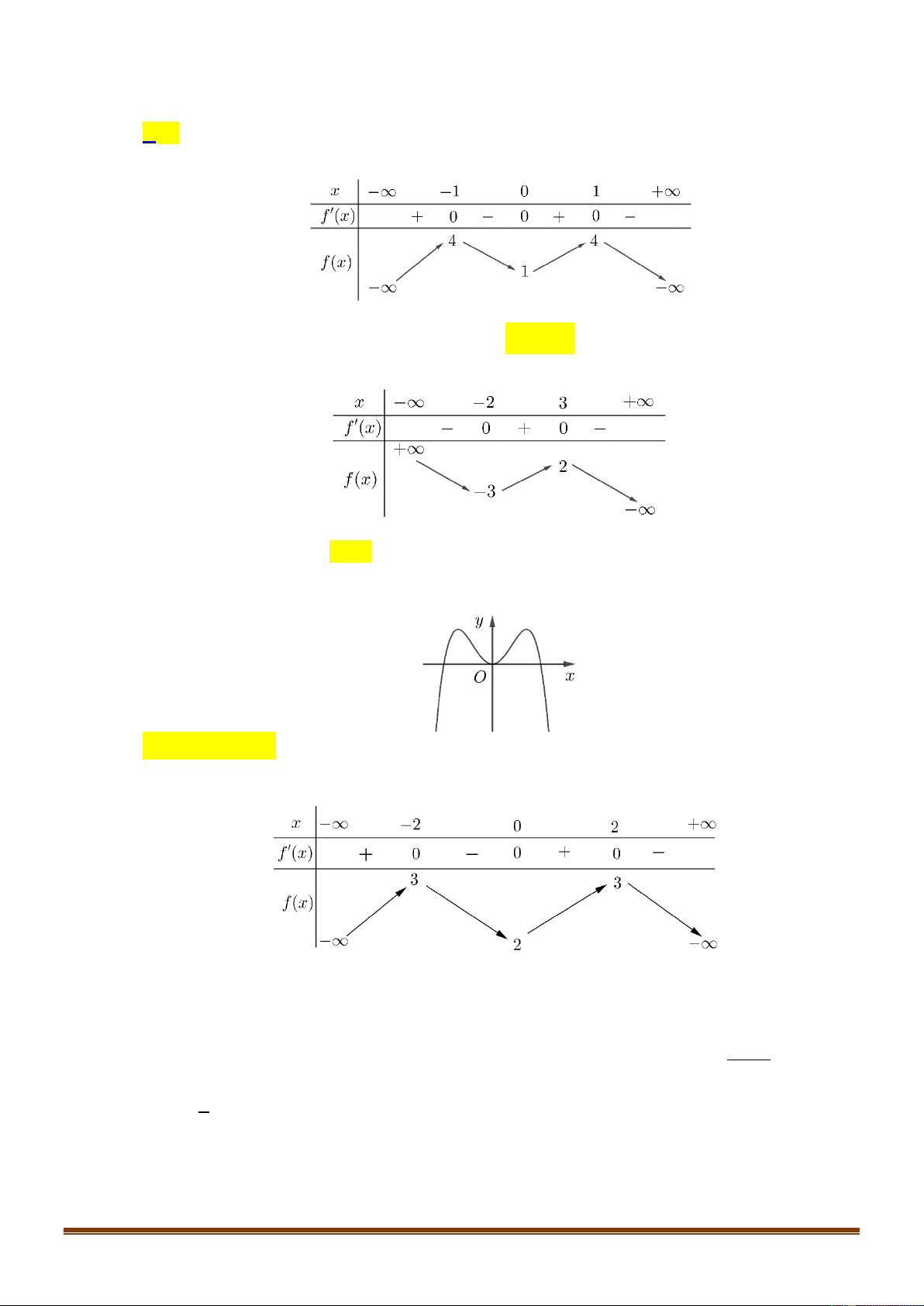
Cho hàm số f x có bảng biến thiên như sau :
Điểm cực đại của hàm số đã cho là A. x 3.
B. x 2. C. x 2. D. x 1.
Câu 19.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)
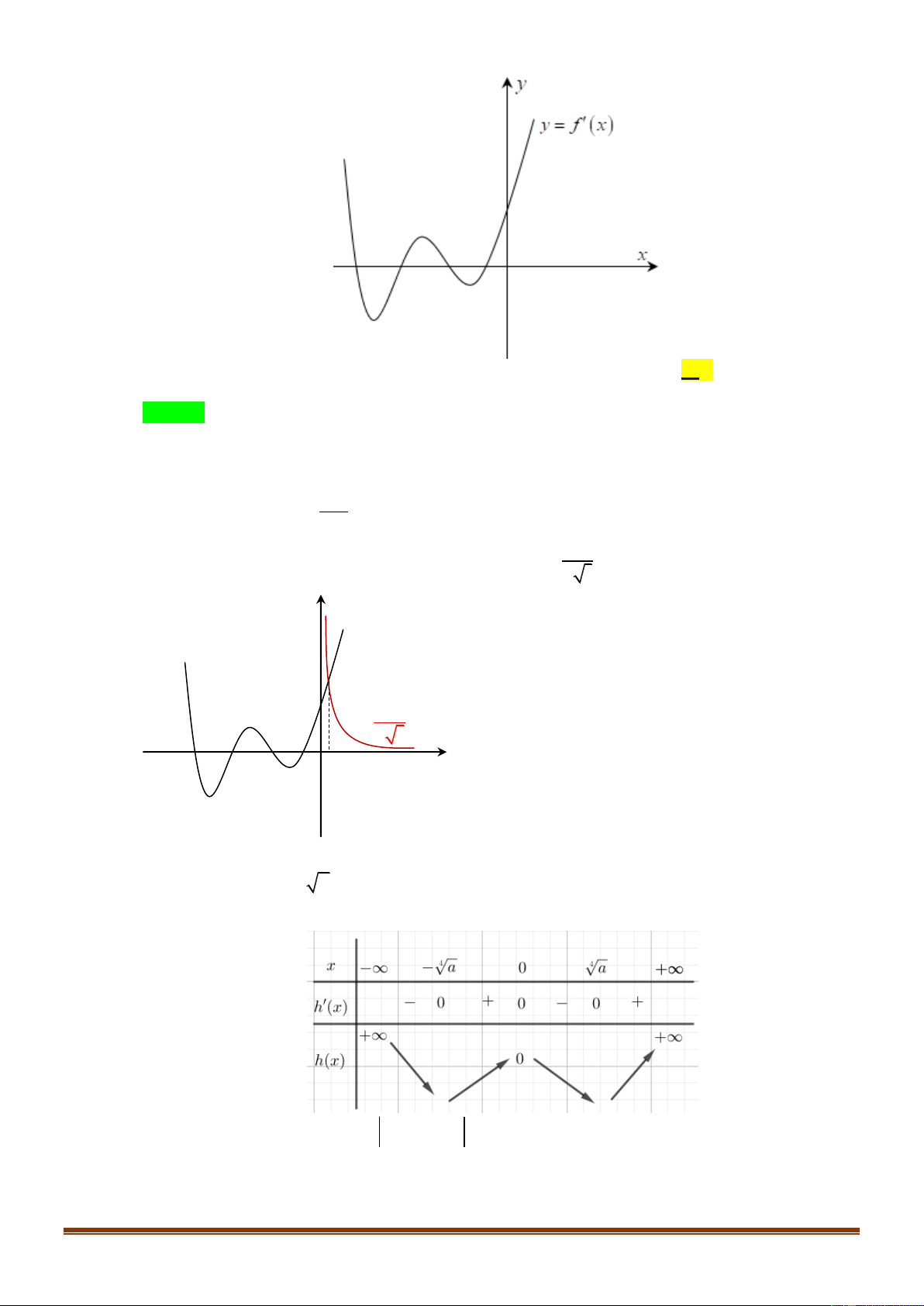
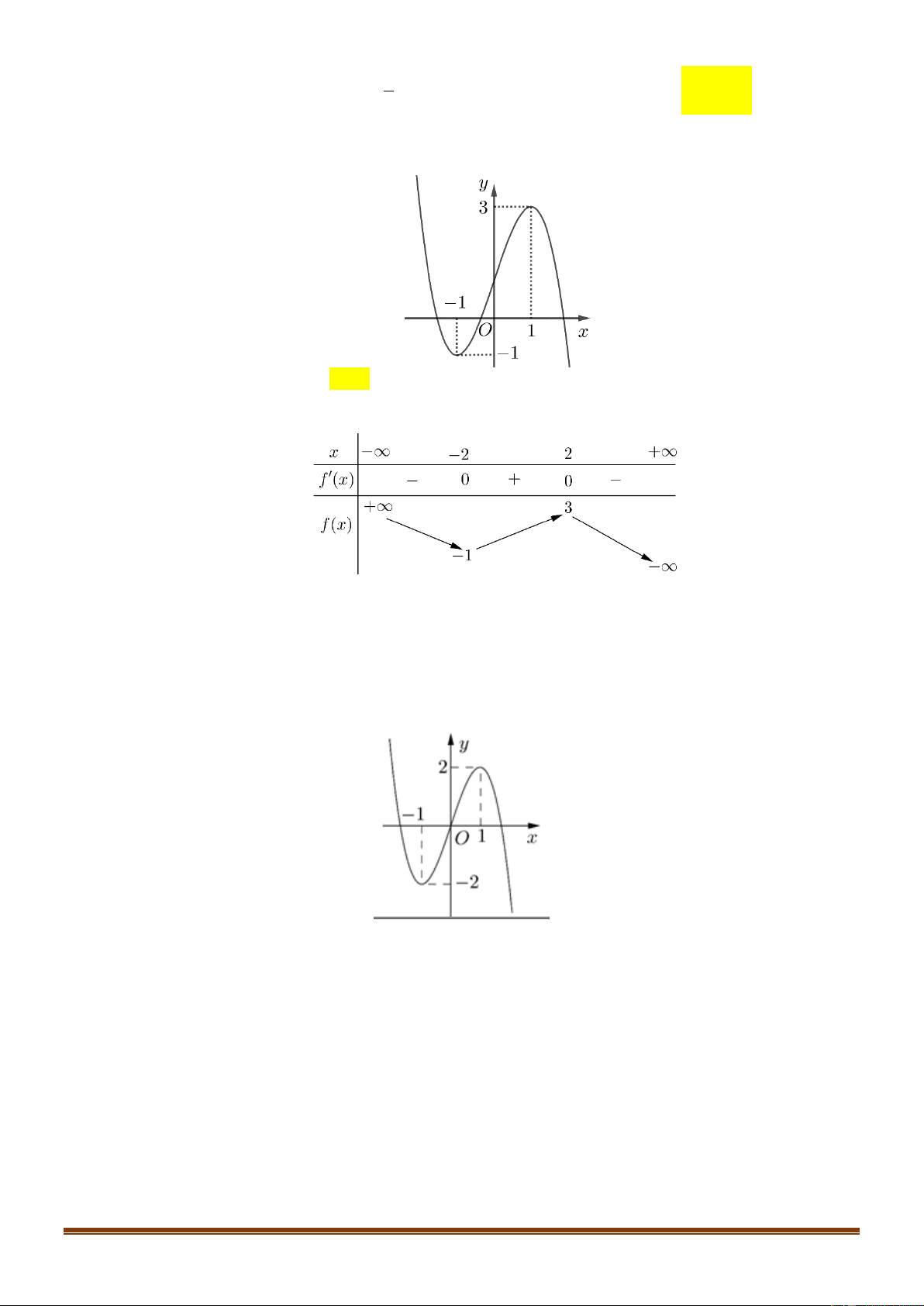
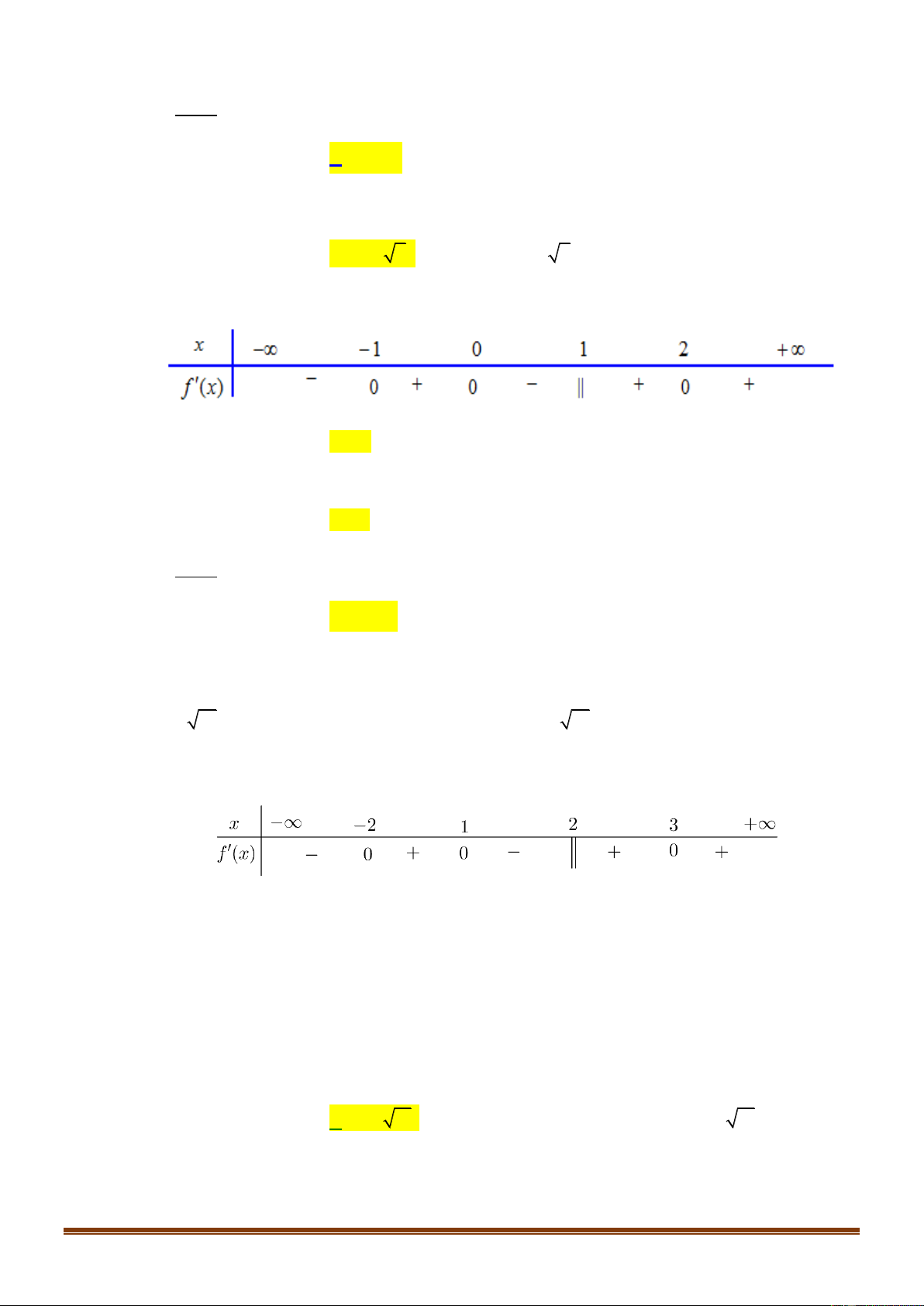
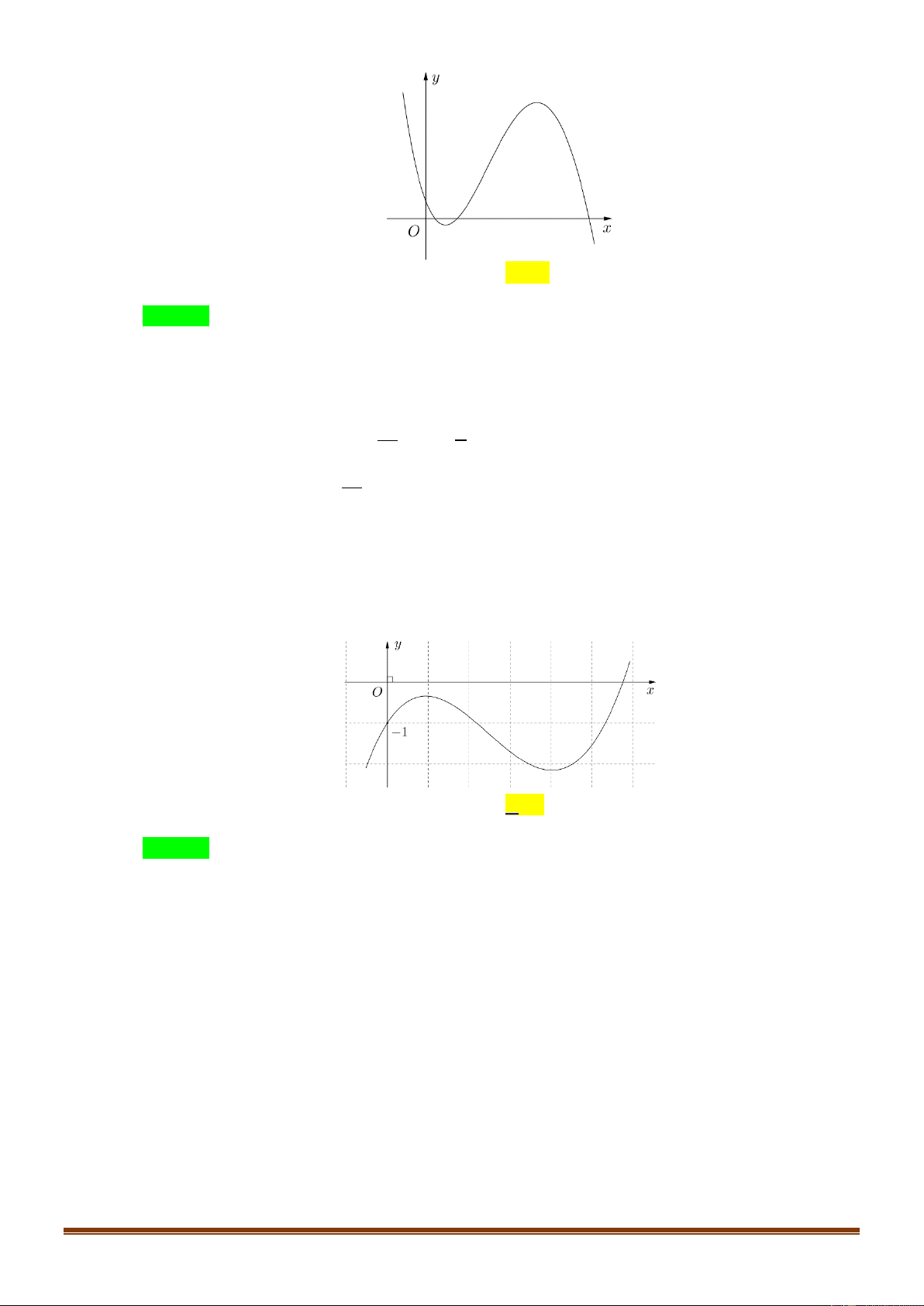
Cho hàm số y f x có đồ thị là đường cong hình
bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây ? A. 1 ;0 . B. ; 1 .
C. 0; . D. 0; 1 .
Câu 20. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Đồ thị của hàm số dưới đây có dạng như đường cong bên? A. 3
y x 3x 1. B. 4 2
y x 2x 1. C. 4 2
y x 2x 1. D. 3
y x 3x 1.
Câu 25.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)
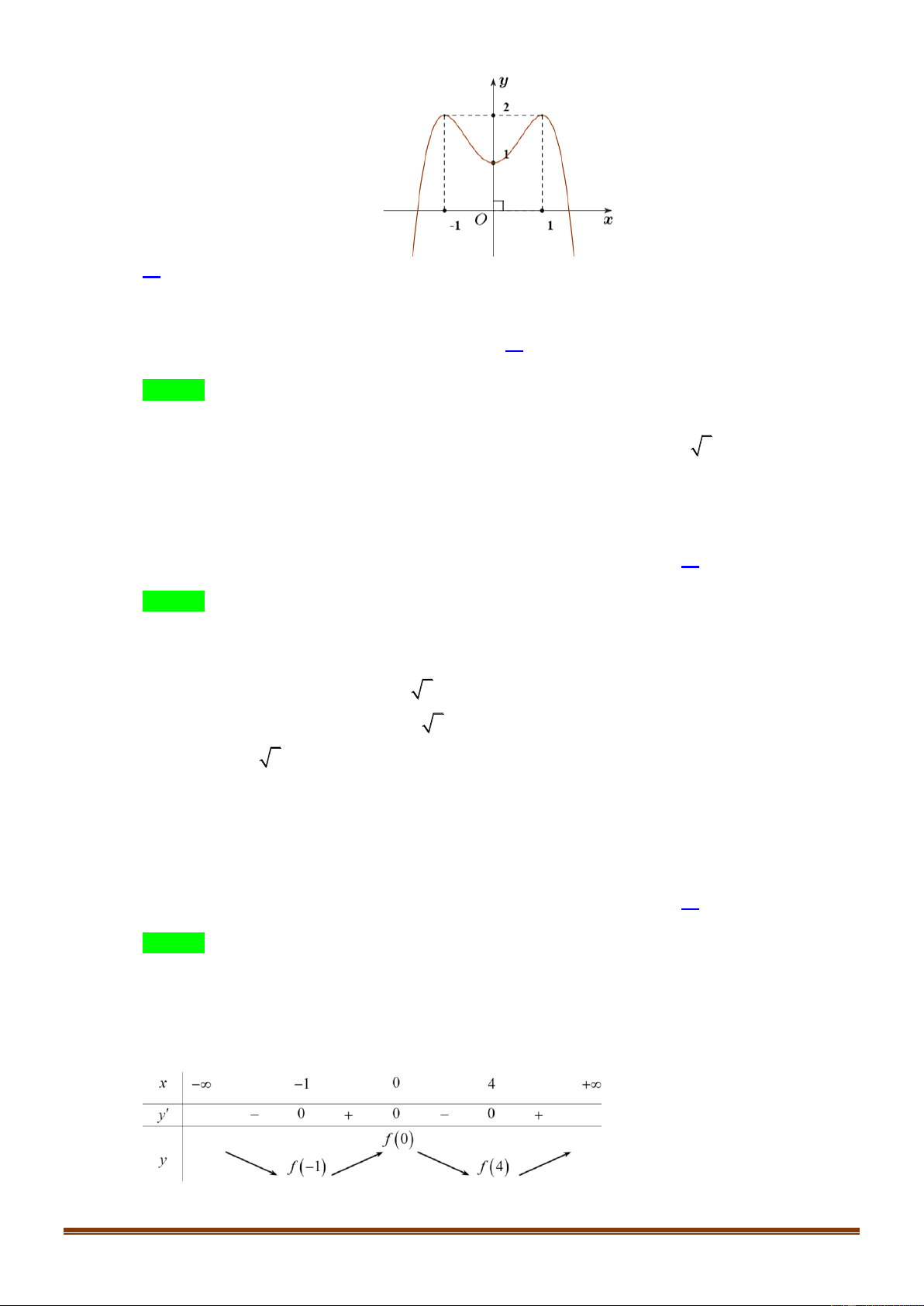
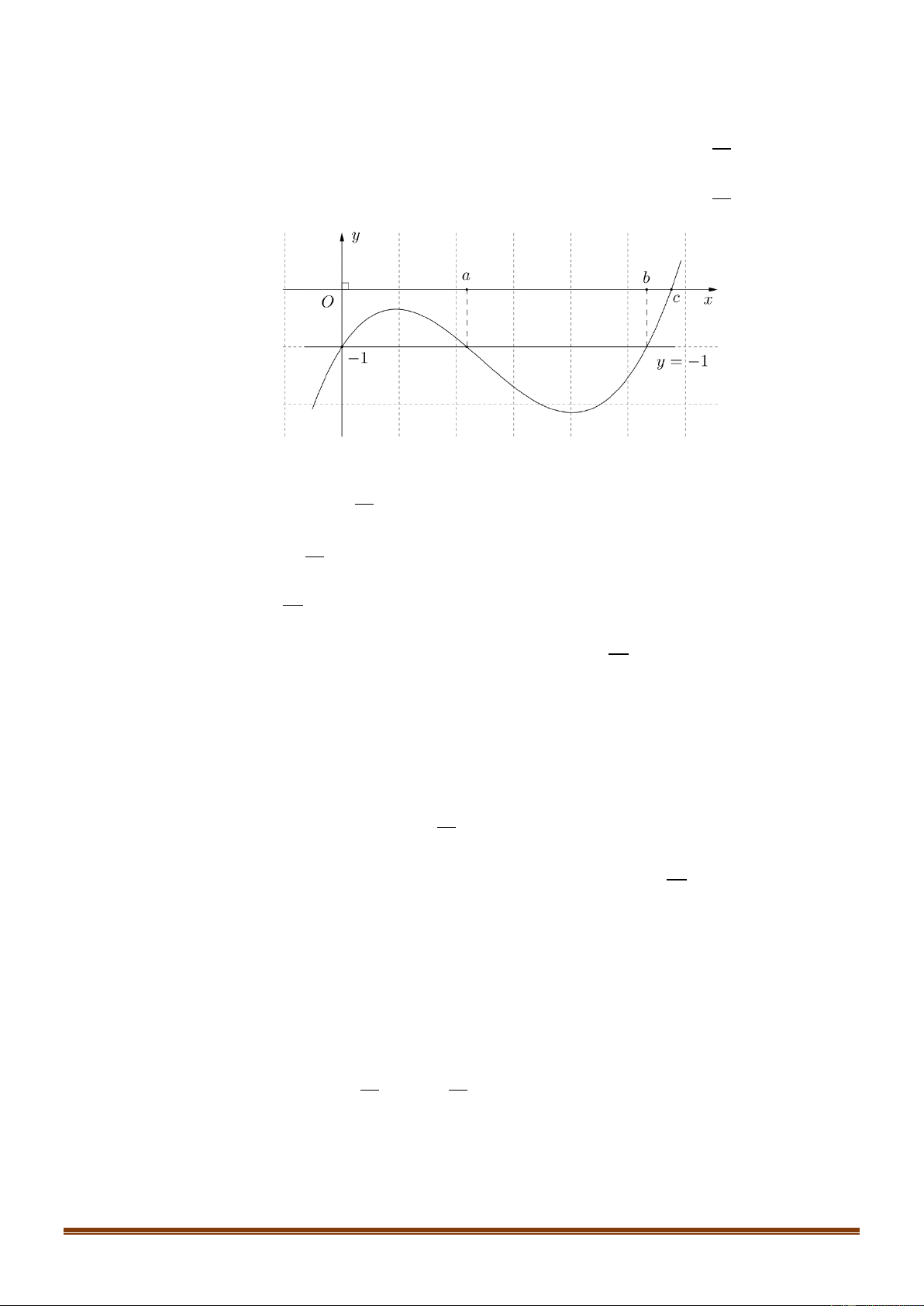
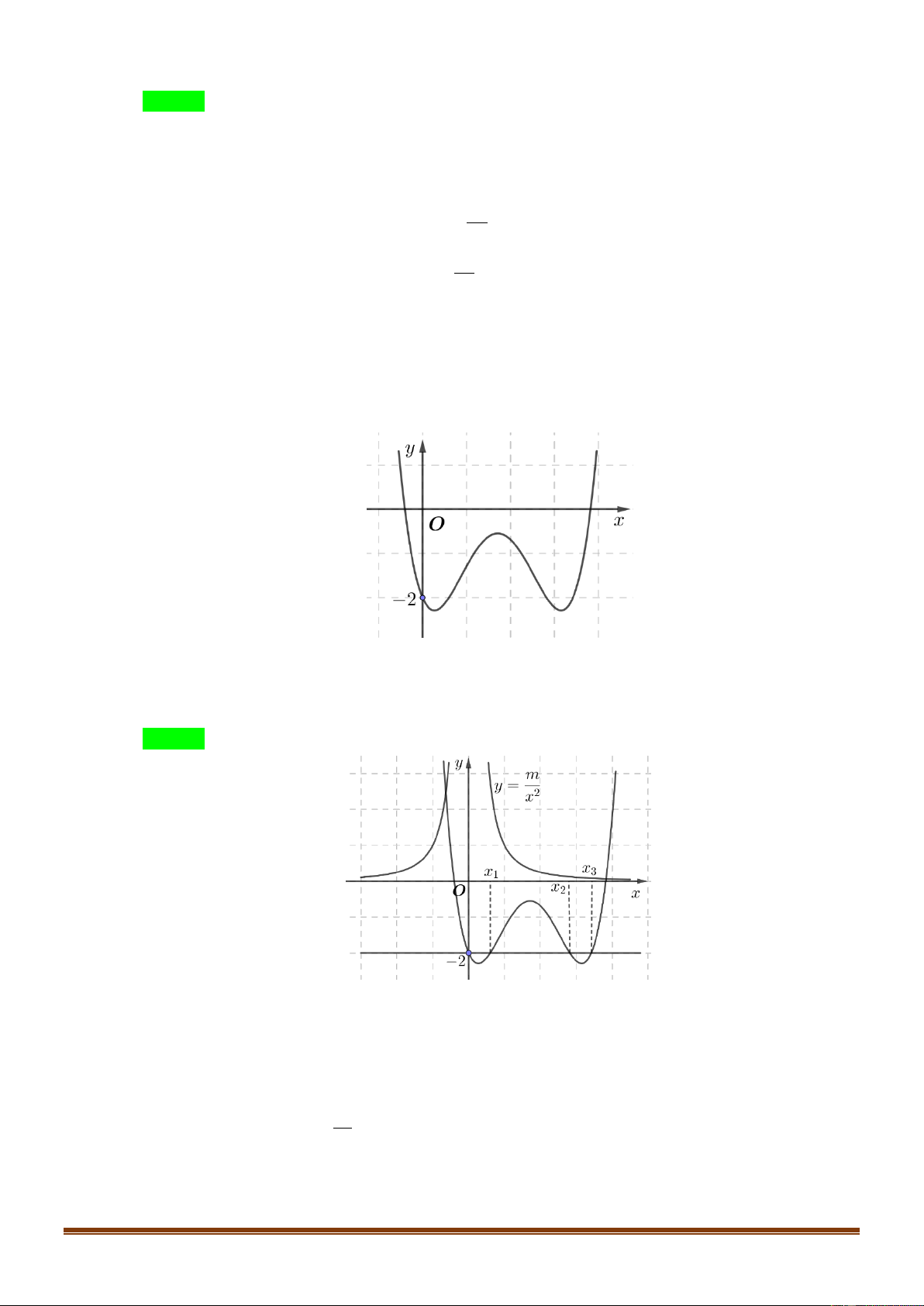
Cho hàm số bậc bốn y f x có đồ thị là đường
cong trong hình bên. Số nghiệm thực của phương trình f x 1 là 2 Trang1 A. 2 . B. 4 . C. 1. D. 3 .
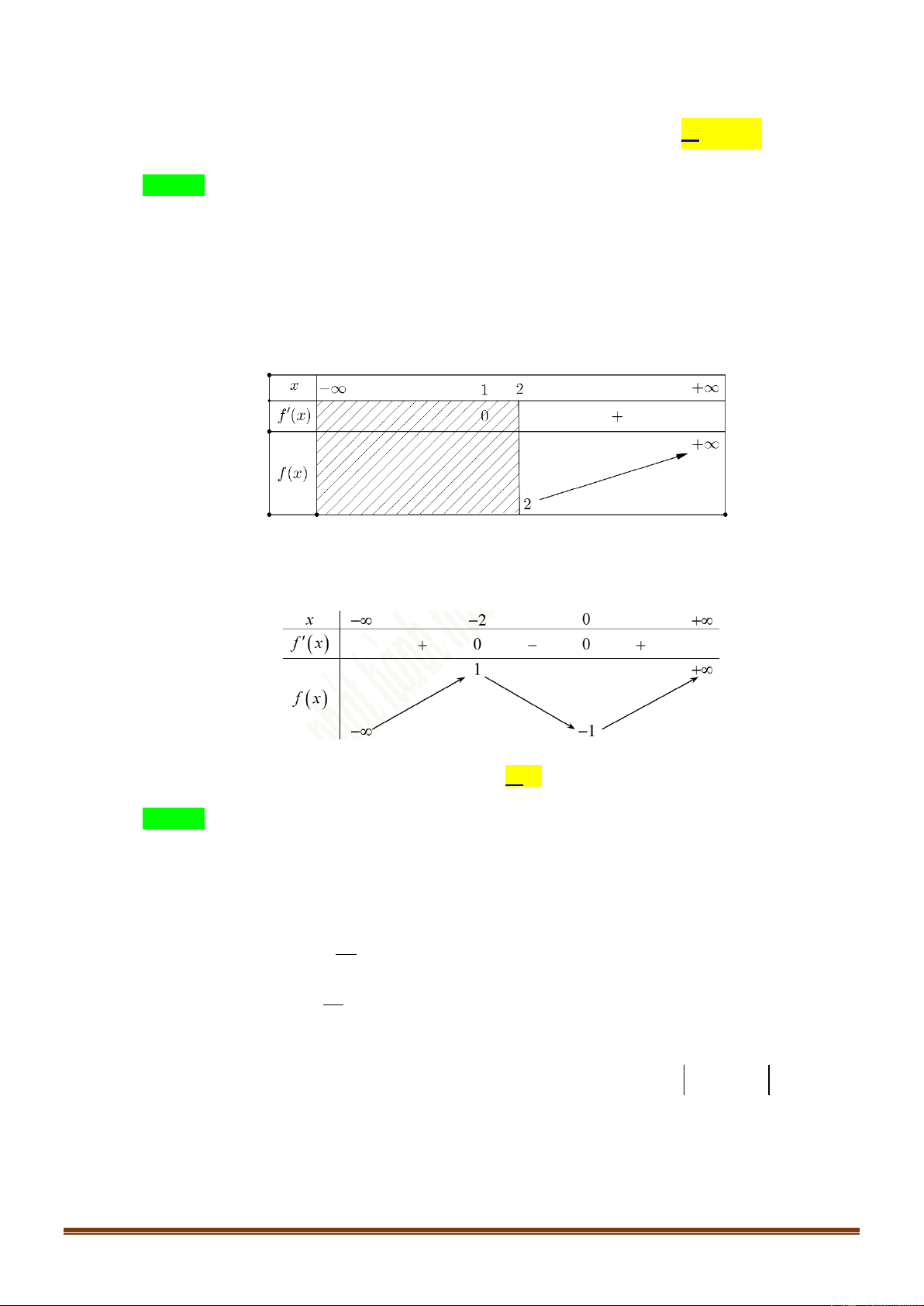
Câu 27.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Số giao điểm của đồ thị hàm số 3
y x 3x với trục hoành là A. 2 . B. 0 . C. 3 . D. 1. Lời giải Chọn C x 0
Phương trình hoành dộ giao điểm 3 2
x 3x 0 x(x 3) 0 . x 3 Vậy có 3 giao điểm.
Câu 32. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Giá trị nhỏ nhất của hàm số f x 4 2
x 10x 2 trên đoạn 0;9 bằng A. 2 . B. 11 . C. 26 . D. 27 . Lời giải Chọn D
Ta có f x 3 ' 4x 20x x 00;9
f ' x 0 3
4x 20x 0 x 5 0;9 x 5 0;9 f 0 2 ; f 5 2
7 ; f 9 5749.
Vậy min f x 2 7 . 0;9
Câu 33.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103) Cho hàm số f x có đạo hàm
f x x x x 3 1 4 , x
. Số điểm cực đại của hàm số đã cho là A. 2 . B. 3 . C. 4 . D.1. Chọn D x 0
f x 0 x x
1 x 43 0 x 1 . x 4
Lập bảng biến thiên của hàm số f x
Vậy hàm số đã cho có một điểm cực đại. Trang2
Câu 39. (Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Tập hợp tất cả các giá trị thực của tham số m để hàm số 3 2
y x 3x 2 m x đồng biến trên khoảng 2; là A. ; 1 . B. ; 2 . C. ; 1 . D. ; 2 . Lời giải Chọn D Ta có 2
y ' 3x 6x 2 m .
Để hàm số đồng biến trênkhoảng 2; khi và chỉ khi y ' 0, x 2; 2
3x 6x 2 m 0, x 2; 2
m 3x 6x 2, x 2; .
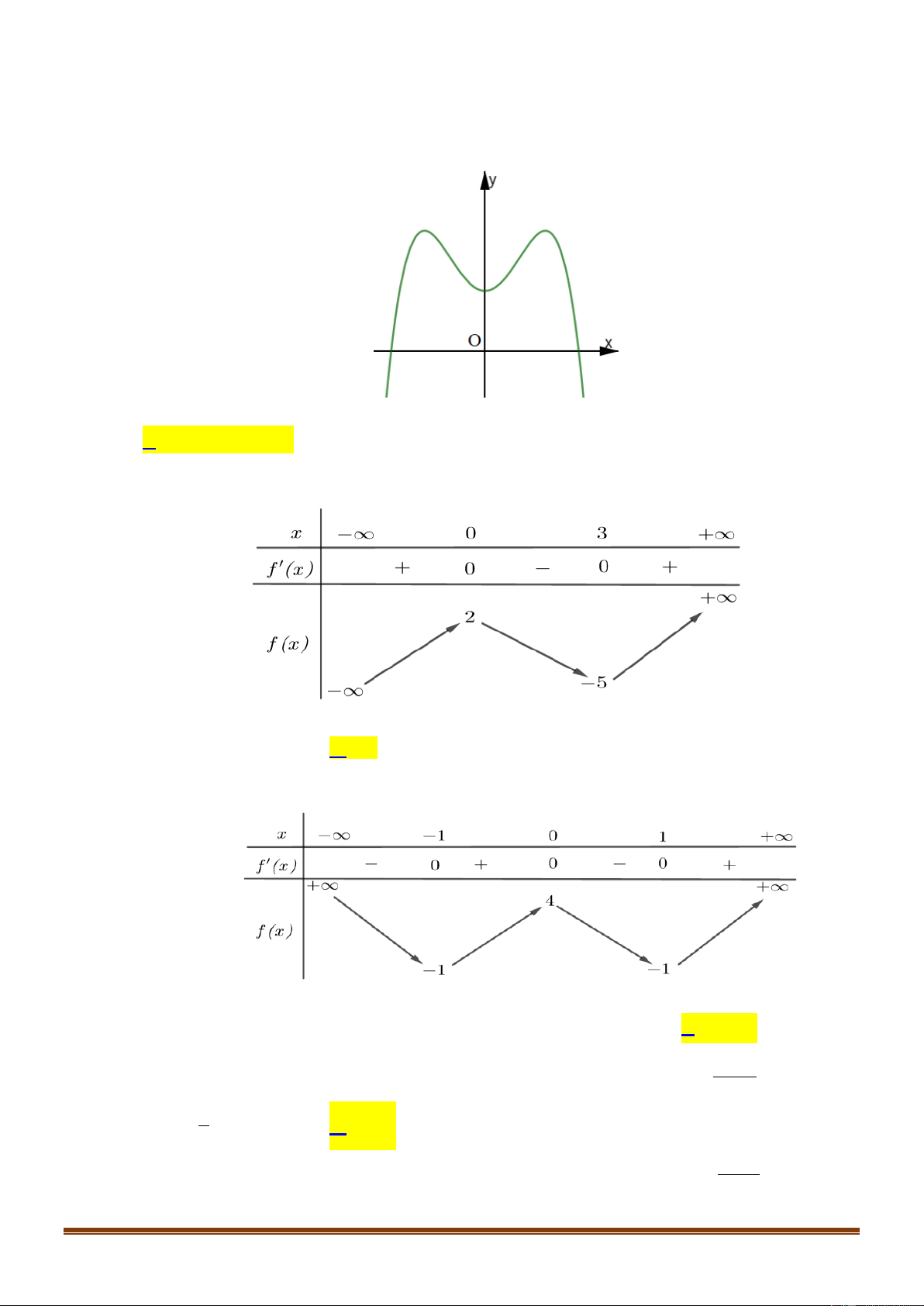
Xét hàm số f x 2
3x 6x 2, x 2;.
f ' x 6x 6 ; f ' x 0 6x 6 0 x 1. Bảng biến thiên:
Từ bảng biến thiên ta thấy m 2. Vậy m ; 2.
Câu 43.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Cho hàm số f x 3 2
ax bx cx d a, ,
b c, d có
bảng biến thiên như sau:
Có bao nhiêu số dương trong các số a, ,
b c, d ? A. 3. B. 4. C. 2. D.1. Lời giải Chọn C
lim f x a 0. x f 0 1 d 1 0. f x 2
3ax 2bx . c 2b 2 x x 2 b 3a 0 3a Ta có 1 2 . x x 0 c c 0 1 2 0 3a
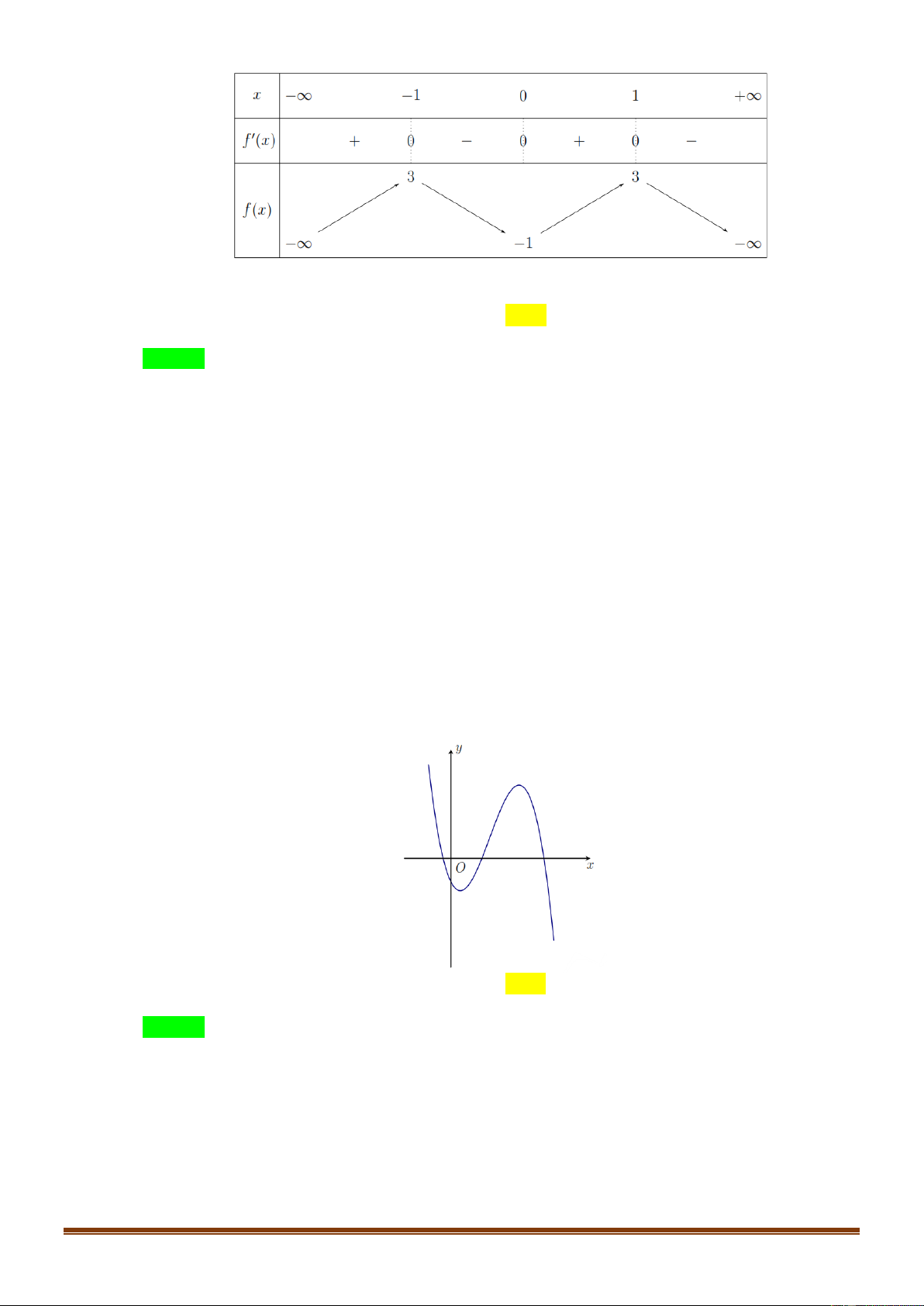
Câu 45.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Cho hàm số f x có f 0 0 . Biết y f x là hàm
số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số 4 2 g x f x x là Trang3 A. 4. B. 3. C. 6. D.5. Lời giải Chọn D
Xét hàm số 4 2 h x f x
x có hx 3 x f 4 4 x 2x . x 0
h x 0 f 1 4 x * 2 2x
Xét phương trình * : Đặt 4
t x thì * thành f t 1 với t 0 . 2 t y
y f t 1 y 2 t t a O
Dựa vào đồ thị, phương trình * có duy nhất một nghiệm a 0 . Khi đó, ta được 4 x a .
Bảng biến thiên của hàm số 4 2 h x f x x
Số cực trị của hàm số 4 2 g x f x
x bằng số cực trị của hàm 4 2 h x f x x và số
nghiệm đơn hoặc bội lẻ của phương trình h x 0 .
Dựa vào bảng biến thiên của hàm f x thì số cực trị của g x là 5. Trang4
Câu 49.(Đề tốt nghiệp 2020-Đợt 2 Mã đề 103)Cho hàm số f x có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 3
x 4x m có ít nhất ba
nghiệm thực phân biệt thuộc khoảng 0; ? A.15 . B.12 . C.14 . D.13 . Lời giải Chọn A Đặt 2
u x 4x (1) Ta có BBT sau: Ta thấy: + Với u 4
, phương trình (1) vô nghiệm. + Với u 4
, phương trình (1) có một nghiệm x 2 0 . + Với 4
u 0, phương trình (1) có hai nghiệm x 0 .
+ Vơi u 0 , phương trình (1) có một nghiệm x 0 Khi đó f m 2 3
x 4x m f u (2), ta thấy: 3
+ Nếu m 3 m 9 , phương trình (2) có một nghiệm u 0 nên phương trình đã cho có 3
một nghiệm x 0 . + Nếu m 3
2 9 m 6 , phương trình (2) có một nghiệm u 0 và một nghiệm 3 u 2
;0 nên phương trình đã cho có ba ngiệm x 0 . + Nếu m 2
m 6 , phương trình (2) có một nghiệm u 4
, một nghiệm u 2 ;0 và 3
một nghiệm u 0 nên phương trình đã cho có bốn nghiệm x 0 . + Nếu m 2
2 6 m 6 , phương trình (2) có một nghiệm u 4 , hai nghiệm 3 u 4
;0 và một nghiệm u 0 nên phương trình đã cho có năm nghiệm x 0 .
+ Nếu m 2 m 6 , phương trình (2) có một nghiệm u 4
, một nghiệm u 2 và một 3
nghiệm u 0 nên phương trình đã cho có ba nghiệm x 0 .
+ Nếu m 2 m 6 , phương trình (2) có một nghiệm u 4
và một nghiệm u 0 nên 3
phương trình đã cho có một nghiệm x 0 . Trang5 Vậy 9
m 6 có 15 giá trị m nguyên thỏa ycbt.
Câu 1: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y x 3x 1 . B. 3 2
y x 3x 1. C. 4 2
y x 2x 1. D. 4 2
y x 2x 1.
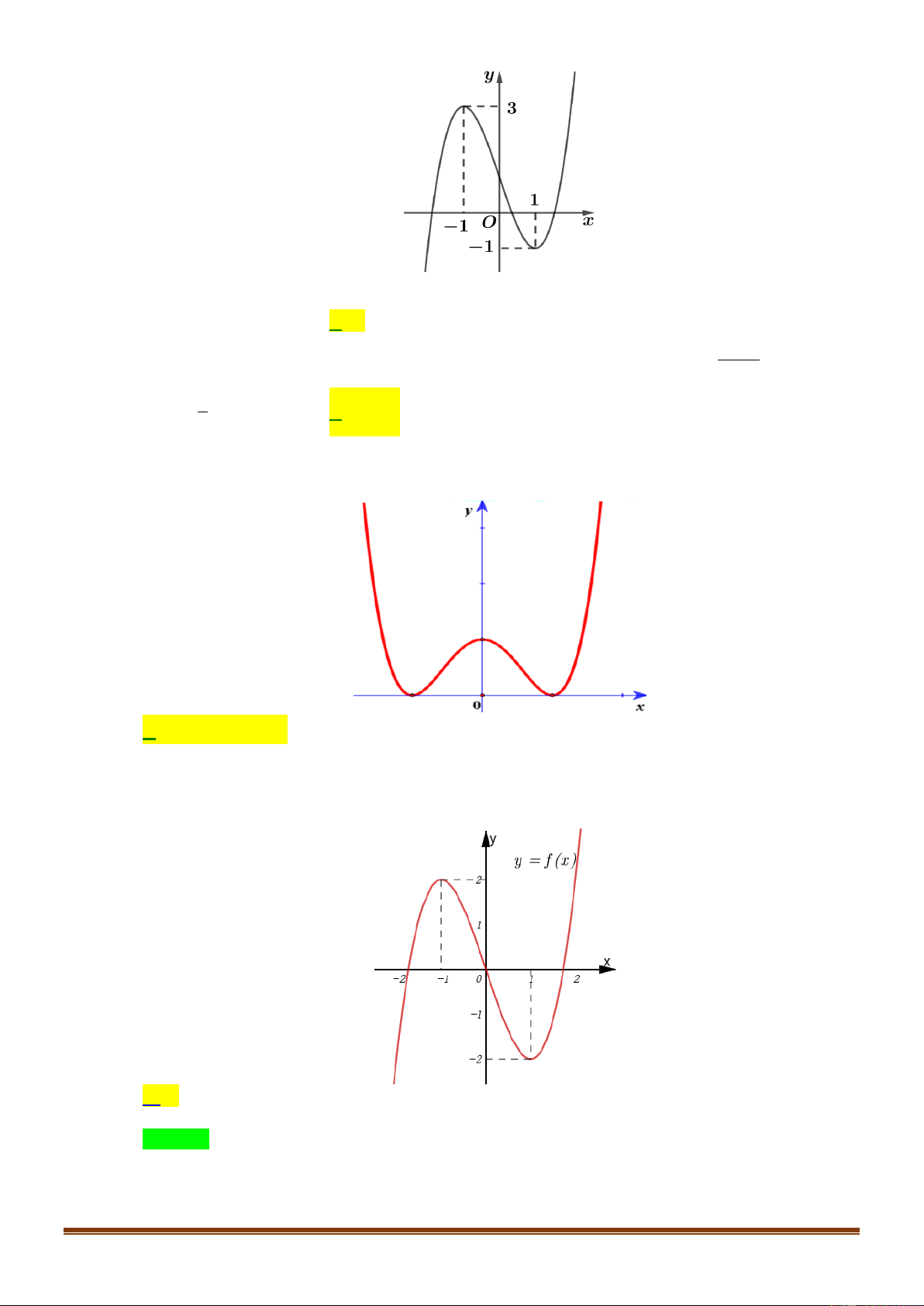
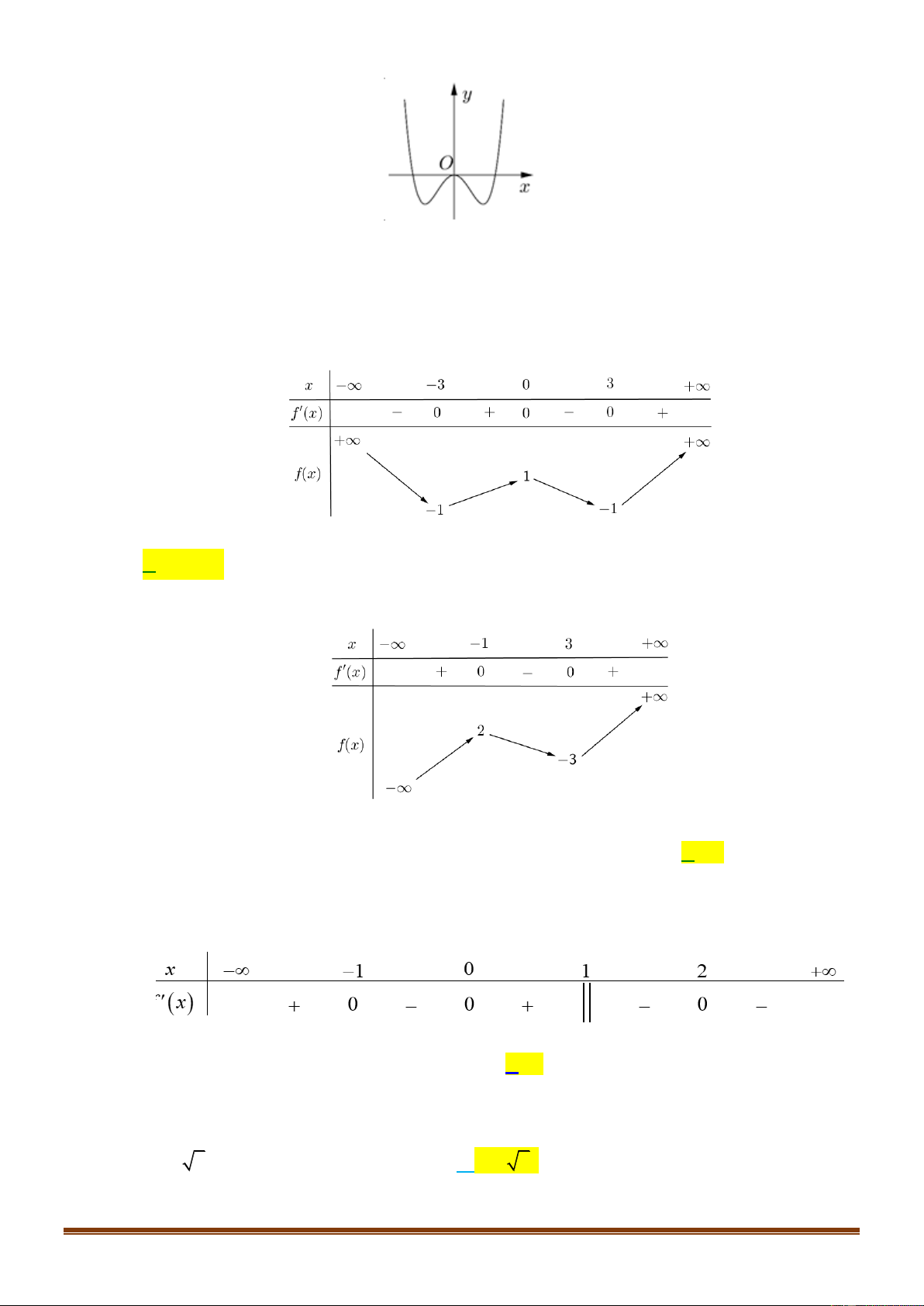
Câu 3: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 3 . B. 5 . C. 0 . D. 2 .
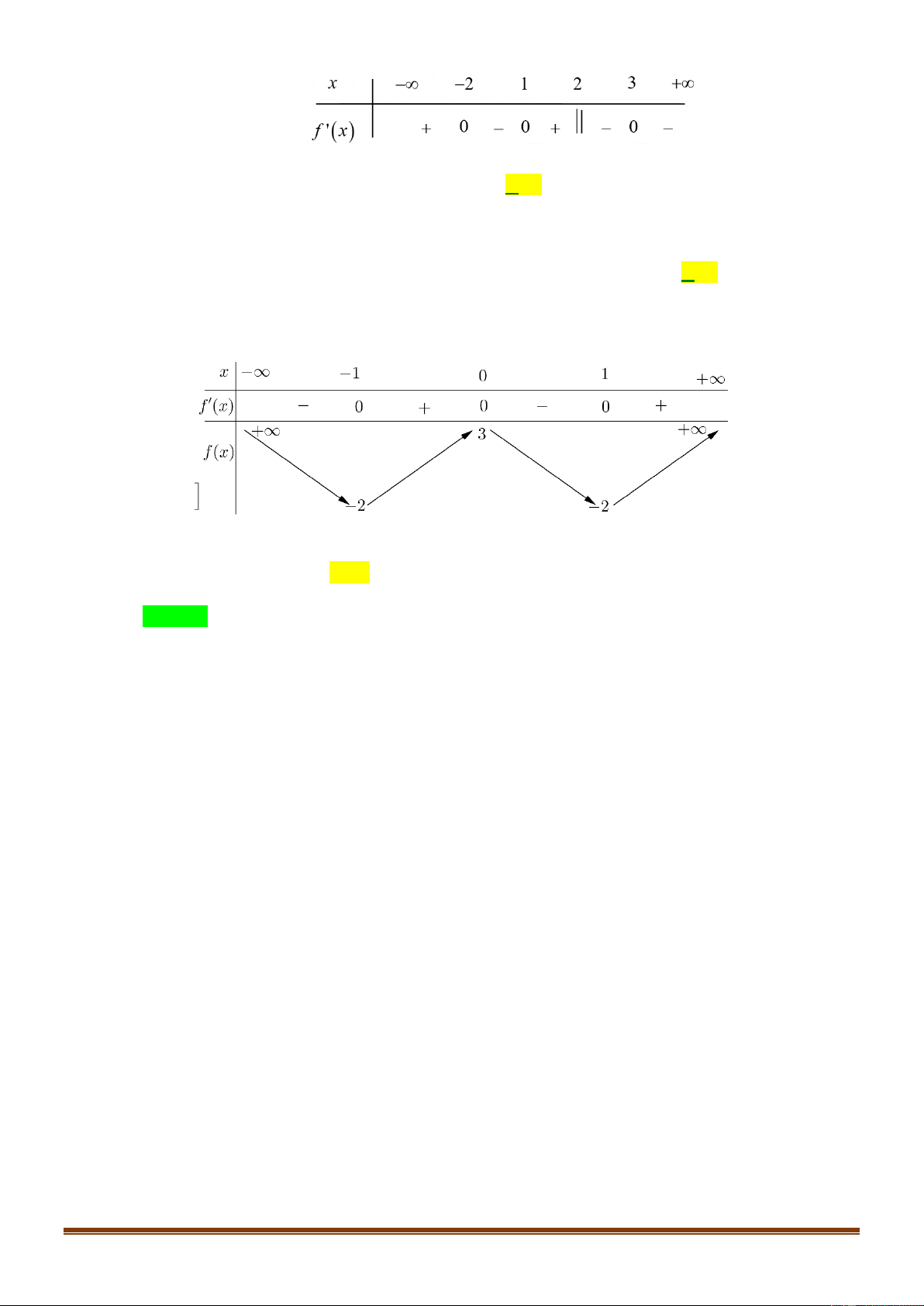
Câu 4: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. ; 1 . B. 0; 1 . C. 1 ;1 . D. 1 ;0 4x 1
Câu 11(Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Tiệm cận ngang của đồ thị hàm số y x là 1 1 A. y . B. y 4 . C. y 1. D. y 1. 4 5x 1
Câu 9: (Đề tốt nghiệp THPT 2020 mã đê 102)Tiệm cận ngang của đồ thị hàm số y là x 1 Trang6 A. y 1 1. B. y . C. y 1. D. y 5 . 5
Câu 11:(Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số bậc ba y f x có đồ thị là đường cong
trong hình bên. Số nghiệm thực của phương trình f x 1 là A. 0 . B. 3 . C. 1. D. 2 .
Câu 8: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 2 . B. 2 . C. 3 . D. 1.
Câu 15: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số bậc ba y f x có đồ thị là đường cong
trong hình bên. Số nghiệm thực của phương trình f x 1 là A. 1. B. 0 . C. 2 . D. 3 .
Câu 4: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình vẽ bên. Trang7
Số nghiệm thực của phương trình f x 2 là: A. 0 . B. 3 . C. 1. D. 2 . 3x 1
Câu 6: (Đề tốt nghiệp THPT 2020 mã đề 104)Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y . B. y 3 . C. y 1. D. y 1. 3
Câu 10:(Đề tốt nghiệp THPT 2020 mã đề 104)Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x 2x 1. B. 3 2
y x 3x 1. C. 3 2
y x 3x 1. D. 4 2
y x 2x 1.
Câu 16: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số bậc ba y f x có đồ thị là đường cong
trong hình bên. Số nghiệm thực của phương trình f x 1 là: A. 3 . B.1. C. 0 . D. 2 . Lời giải Chọn A.
Số nghiệm thực của phương trình f x 1
chính là số giao điểm của đồ thị hàm số
y f x và đường thẳng y 1. Trang8
Câu 26: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Số giao điểm của đồ thị hàm số 3 2
y x 3x và đồ thị hàm số 2
y 3x 3x là A. 3 . B.1. C. 2 . D. 0 .
Câu 17: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số f x có bảng biến thiên như sau.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 1; . B. 1 ;1 . C. 0; 1 . D. 1 ;0 .
Câu 18: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số f x có bảng biến thiên như sau.
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 2 . C. 2 . D. 3 .
Câu 20: (Đề tốt nghiệp THPT 2020 mã đê 102)Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x 2x . B. 3
y x 3x . C. 4 2
y x 2x . D. 3
y x 3x .
Câu 17: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số f (x) có bảng biến thiên như sau:
Hàm số đã chođồng biến trên khoảng nào dưới đây A. (2; 2) B. (0; 2) C. (2; 0) D. (2; ) . 2x 1
Câu 18: (Đề tốt nghiệp THPT 2020 mã đề 103)Tiệm cận ngang của đồ thị hàm số y x là: 1 1 A. y .
B. y 1.
C. y 1. D. y 2 . 2
Câu 19: (Đề tốt nghiệp THPT 2020 mã đề 103)Đồ thị của hàm số nào dưới đây có dạng như đường cong như hình bên Trang9 A. 4 2
y x 2x . B. 3 2
y x 3x . C. 4 2
y x 2x . D. 3 2
y x 3x .
Câu 16: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số f x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. 3 ;0. B. 3 ;3 . C. 0;3 . D. ; 3 .
Câu 17: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 3 . C. 1. D. 2 .
Câu 33: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số f x liên tục trên ¡ và có bảng xét dấu
của f x như sau:
Số điểm cực đại của hàm số đã cho là A. 4 . B.1. C. 2 . D. 3 .
Câu 36: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Giátrị nhỏ nhất của hàm số f x 3
x 24x trên đoạn 2;19 bằng A. 32 2 . B. 40 . C. 3 2 2 . D. 45 . Trang10
Câu 40: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Tập hợp tất cả các giá trị thực của tham số m để hàm số x 4 y
đồng biến trên khoảng ; 7 là x m A. 4;7 . B. 4;7 . C. 4;7 . D. 4; .
Câu 26: (Đề tốt nghiệp THPT 2020 mã đê 102)Giá trị nhỏ nhất của hàm số f x 3
x 21x trên đoạn 2;19 bằng A. 36 . B. 1 4 7 . C. 14 7 . D. 34 .
Câu 28: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm f x liên tục trên và có bảng xét dấu
f x như sau:
Số điểm cực tiểu của hàm số là A. 1. B. 2 . C. 3 . D. 4 .
Câu 33: (Đề tốt nghiệp THPT 2020 mã đê 102)Số giao điểm của đồ thị hàm số 3 2
y = x - x và đồ thị hàm số 2
y = - x + 5x là A. 2 . B. 3 . C. 1. D. 0 .
Câu 39: (Đề tốt nghiệp THPT 2020 mã đê 102)Tập hợp tất cả các giá trị thực của tham số m để hàm số x 5 y
đồng biến trên khoảng ; 8 là x m A. 5; . B. 5;8 . C. 5;8 . D. 5;8 .
Câu 35: (Đề tốt nghiệp THPT 2020 mã đề 103)Giá trị nhỏ nhất của hàm số 3
f (x) x 30x trên đoạn 2;19 bằng A. 20 10. B. 63. C. 20 10. D. 52.
Câu 36: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số f (x) liên tục trên và có bảng xét dấu
của f (x) như sau:
Số điểm cực tiểu của hàm số đã cho là A. 2. B. 4. C. 3. D. 1.
Câu 38: (Đề tốt nghiệp THPT 2020 mã đề 103)Số giao điểm của đồ thị hàm số 3 2
y x x và đồ thị hàm số 2
y x 5x A. 3. B. 0 . C. 1. D. 2.
Câu 29: (Đề tốt nghiệp THPT 2020 mã đề 104)Giá trị nhỏ nhất của hàm số f x 3
x 33x trên đoạn 2;19 bằng A. 72 . B. 2 2 11 . C. 58 . D. 22 11 .
Câu 34: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số f x liên tục trên R có bảng xét dấu f ' x Trang11
Số điểm cực đại của hàm số đã cho là: A. 3. B. 1. C. 2. D. 4.
Câu 37: (Đề tốt nghiệp THPT 2020 mã đề 104)Số giao điểm của đồ thị hàm số 2
y x 3x và đồ thị hàm số 3 2
y x x là A. 1. B. 0 . C. 2 . D. 3
Câu 44: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số bậc bốn f x có bảng biến thiên như sau:
Số điểm cực trị của hàm số g x x f x 2 4 1 là A. 11. B. 9 . C. 7 . D. 5 . Lời giải Chọn B.
Ta chọn hàm f x 4 2
5x 10x 3 . Đạo hàm
g x x f x 2 3 4
x f x f x 3 4 1 2 1
1 2x f x
1 2 f x
1 xf x 1 . x 0 3
2x f x 1 0
Ta có g x 0
f x . f
x xf x 1 0 2 1 1 0 2 f x
1 xf x 1 0 x 1 1,278 4 x 1 0, 606
+) f x
1 0 * 5 x 1 10 x 1 3 0 x 1 0 ,606 x 1 1 ,278
Phương trình có bốn nghiệm phân biệt khác 0 . t x 1
+) f x xf x 4 2 t
t t 3 2 1 1 0 2 5 10 3
1 20t 20t 0 t 1,199 t 0,731 4 3 2
30t 20t 40t 20t 6 0 t 0, 218 t 1,045
Phương trình có bốn nghiệm phân biệt khác 0 và khác các nghiệm của phương trình * .
Vậy số điểm cực trị của hàm số g x là 9 .
Câu 45: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số 3 2
y ax bx cx d , a , b ,
c d có đồ
thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ? Trang12 A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn C.
Ta có lim y a 0 . x
Gọi x , x là hoành độ hai điểm cực trị của hàm số suy ra x , x nghiệm phương trình 1 2 1 2 2
y 3ax 2bx c 0 nên theo định lý Viet: +) Tổng hai nghiệm 2b b x x
0 0 b 0. 1 2 3a a +) Tích hai nghiệm c x x 0 c 0 . 1 2 3a
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên d 0 .
Vậy có 2 số dương trong các số a , b , c , d .
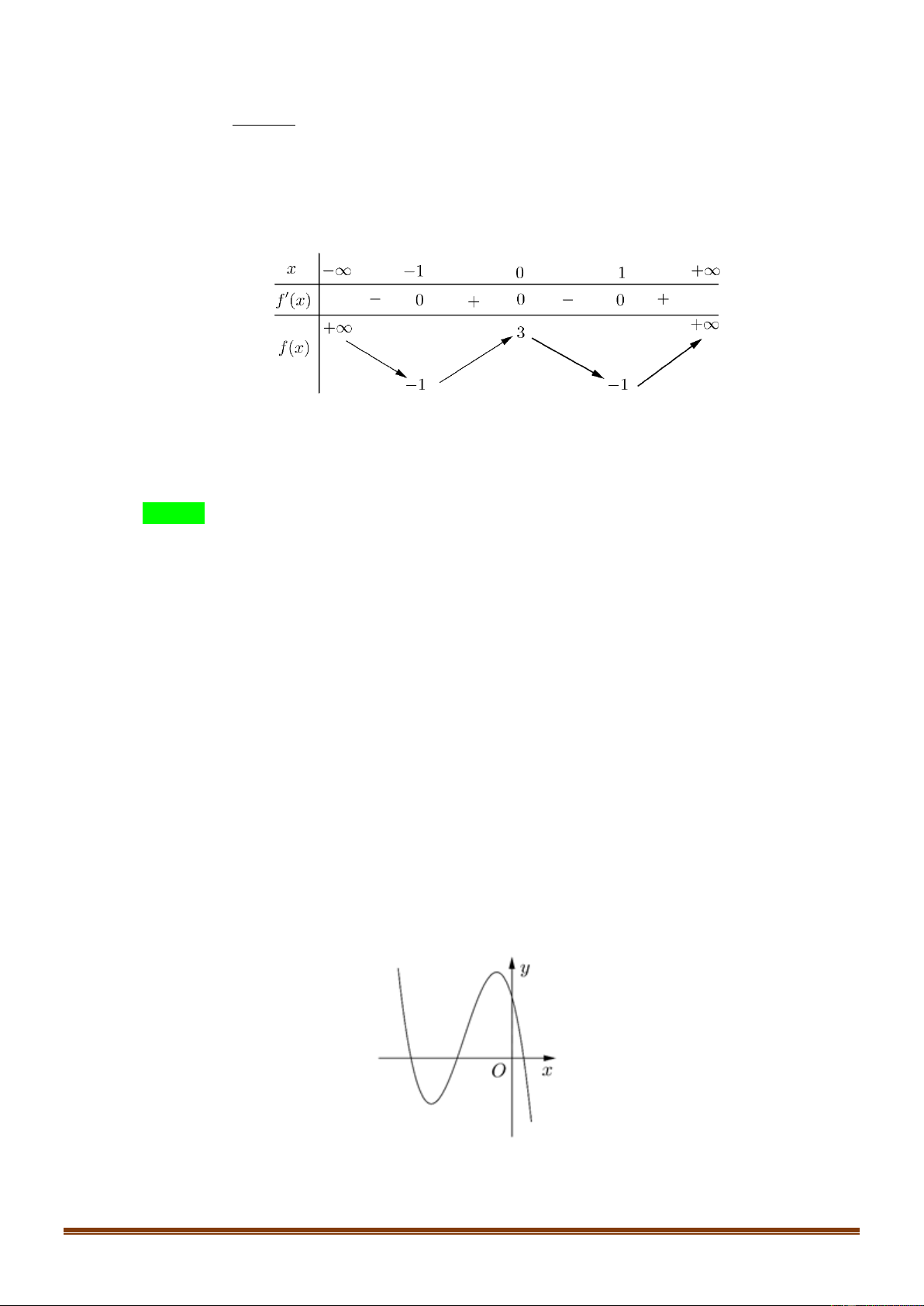
Câu 50: (Đề tốt nghiệp 2020-Đợt 1 Mã đề 101)Cho hàm số bậc ba y f (x) có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương trình f 3
x f (x) 1 0 là A. 8 . B. 5 . C. 6 . D. 4 . Lời giải Chọn C. Trang13 x 0 3 f (x) 0 x f (x) 0 3
( ) 1 0 3 ( ) 3 1 ( ) 0 a f x f x f x f x x f x a f (x) (do x 0) 3 x 3
x f (x) b 0 b f (x) (do x 0) 3 x
f (x) 0 có một nghiệm dương x c . k
Xét phương trình f (x)
với x 0, k 0 . 3 x k
Đặt g(x) f (x) . 3 x 3k g (
x) f '(x) . 4 x 3k
Với x c , nhìn hình ta ta thấy f (
x) 0 g (x) f (x) 0 4 x
g(x) 0 có tối đa một nghiệm. g(c) 0 Mặt khác
và g(x) liên tục trên ; c
lim g(x) x
g(x) 0 có duy nhất nghiệm trên ; c . k
Với 0 x c thì f (x) 0
g(x) 0 vô nghiệm. 3 x 3k
Với x 0 , nhìn hình ta ta thấy f (
x) 0 g (x) f (x) 0 4 x
g(x) 0 có tối đa một nghiệm.
lim g(x) 0 Mặt khác x 0
và g(x) liên tục trên ; 0 .
lim g(x) x
g(x) 0 có duy nhất nghiệm trên ; 0 .
Tóm lại g(x) 0 có đúng hai nghiệm trên \ 0 . a b
Suy ra hai phương trình f (x) , f (x)
có 4 nghiệm phân biệt khác 0 và khác c . 3 x 3 x
Vậy phương trình f 3
x f (x) 1 0 có đúng 6 nghiệm.
Câu 45: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số bậc bốn f x có bảng biến thiên như sau: Trang14
Số điểm cực trị của hàm số 4
g x x2 f x 1 là A. 7 . B. 8 . C. 5 . D. 9 . Lời giải Chọn C Ta có
g x x f x 4
x f x f x 3
x f x 3 2 2 . 1 4 1 1 2 . 1
f x
1 2xf x 1 x 0
Vậy g x 0 f x 1 0 1 f x
1 2xf x 1 0 2
Phương trình 1 có 4 nghiệm phân biệt
Phương trình 2 có f x 1 2
xf x
1 f x 2 x 1 f x
Từ bảng biến thiên suy ra hàm f x là bậc bốn trùng phương nên ta có
f x x4 x2 3 6
1 thay vào f x 2 x
1 f x vô nghiệm
Vậy hàm g x có 5 điểm cực trị.
Câu 46: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số y ax3 bx2 cx d a, ,
b c, d ¡ có đồ
thị là đường cong trong hình bên. Có bao nhiêu số dương trong các hệ số a,b, c, d ? A. 4 . B. 3 . C. 1 . D. 2 . Lời giải Chọn C
Ta có lim f x a 0 x
Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên ac 0 c 0
Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên ab 0 b 0
Đồ thị hàm số cắt trục tung ở dưới trục hoành d 0
Câu 50: (Đề tốt nghiệp THPT 2020 mã đê 102)Cho hàm số f x có đồ thị là đường cong như hình vẽ bên dưới. Trang15
Số nghiệm thực phân biệt của phương trình f 3
x f x 1 0 là A. 6 . B. 4 . C. 5 . D. 8 . Lời giải Chọn A 3
x f x a 6 ; 5 1
Dựa vào đồ thị, ta thấy f 3
x f x 1 0 f 3 x f x 3 1
x f x b 3 ; 2 2 3
x f x 0 3 x 0 x 0
+ Phương trình 3 tương đương . f x 0 x x , 6
x a 5 1 1 a b
+ Các hàm số g x
và h x
đồng biến trên các khoảng ;0
và 0; , và 3 x 3 x
nhận xét rằng x 0 không phải là nghiệm của phương trình 1 nên:
f x g x 1 . f
x h x
lim f x ;
lim f x 1 x x0 + Trên khoảng ;0
, ta có lim g x lim hx 0 nên các phương trình x x
lim g x lim h x x0 x0
f x g x và f x h x có nghiệm duy nhất.
lim f x ;
lim f x 1 x x0
+ Trên khoảng 0; , ta có lim g x lim hx 0 nên các phương trình x x
lim g x lim h x x0 x0
f x g x và f x h x có nghiệm duy nhất.
Do đó, phương trình f 3
x f x 1 0 có 6 nghiệm phân biệt.
Câu 41:] (Đề tốt nghiệp THPT 2020 mã đề 103)Tập hợp tất cả các giá trị thực của tham số m để hàm số x 2 y x
đồng biến trên khoảng ( ; 5) m A. (2;5] . B. [2;5) . C. (2; ) . D. (2;5) . Lời giải Chọn A Trang16
Tập xác định: D \ m . m 2 Ta có: y ' 2 (x m) y ' 0 x ( ; 5 ) m 2 0
Hàm số đồng biến trên khoảng ( ; 5 ) 2 m 5 . m( ; 5 ) m 5
Câu 44: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số bậc bốn f (x) có bảng biên thiên như sau:
Số điểm cực trị của hàm số 4 2
g(x) x [f (x 1)] là A. 7 . B. 5 . C. 9 . D. 11. Lời giải Chọn C Ta có : 4 2 2
f (x) 4x 8x 3 f (
x) 16x(x 1) Ta có 3 g (
x) 2x . f (x 1).[2 f (x 1) . x f ( x 1)] 3 x 0 (1) g (
x) 0 f (x 1) 0 (2)
2 f (x 1) .x f (x 1) 0 (3)
Phương trình (1) có x 0 (nghiệm bội ba).
Phương trình (2) có cùng số nghiệm với phương trình f (x) 0 nên (2) có 4 nghiệm đơn.
Phương trình (3) có cùng số nghiệm với phương trình : 4 2 2
2 f (x) (x 1). f (
x) 0 2(4x 8x 3) 16x(x 1)(x 1) 0 4 3 2
24x 16x 32x 16x 6 0 có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số g(x) 0 có tất cả 9 điểm cực trị.
Câu 46: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số 3 2
y ax bx cx d a, ,
b c, d có đồ
thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a,b, c, d ? A. 4 . B. 2 . C. 1 . D. 3 . Trang17 Lời giải Chọn C Ta có 2
y 3ax 2bx c . Dựa vào đồ thị ta thấy a 0 2 b 9ac 0 0 y 2b b 0
Hàm số có 2 cực trị âm nên S 0 0 3a c 0 P 0 c 0 3a
Đồ thị cắt trục Oy tại điểm 0;d nên d 0.
Vậy có đúng một số dương trong các số a,b, c, d
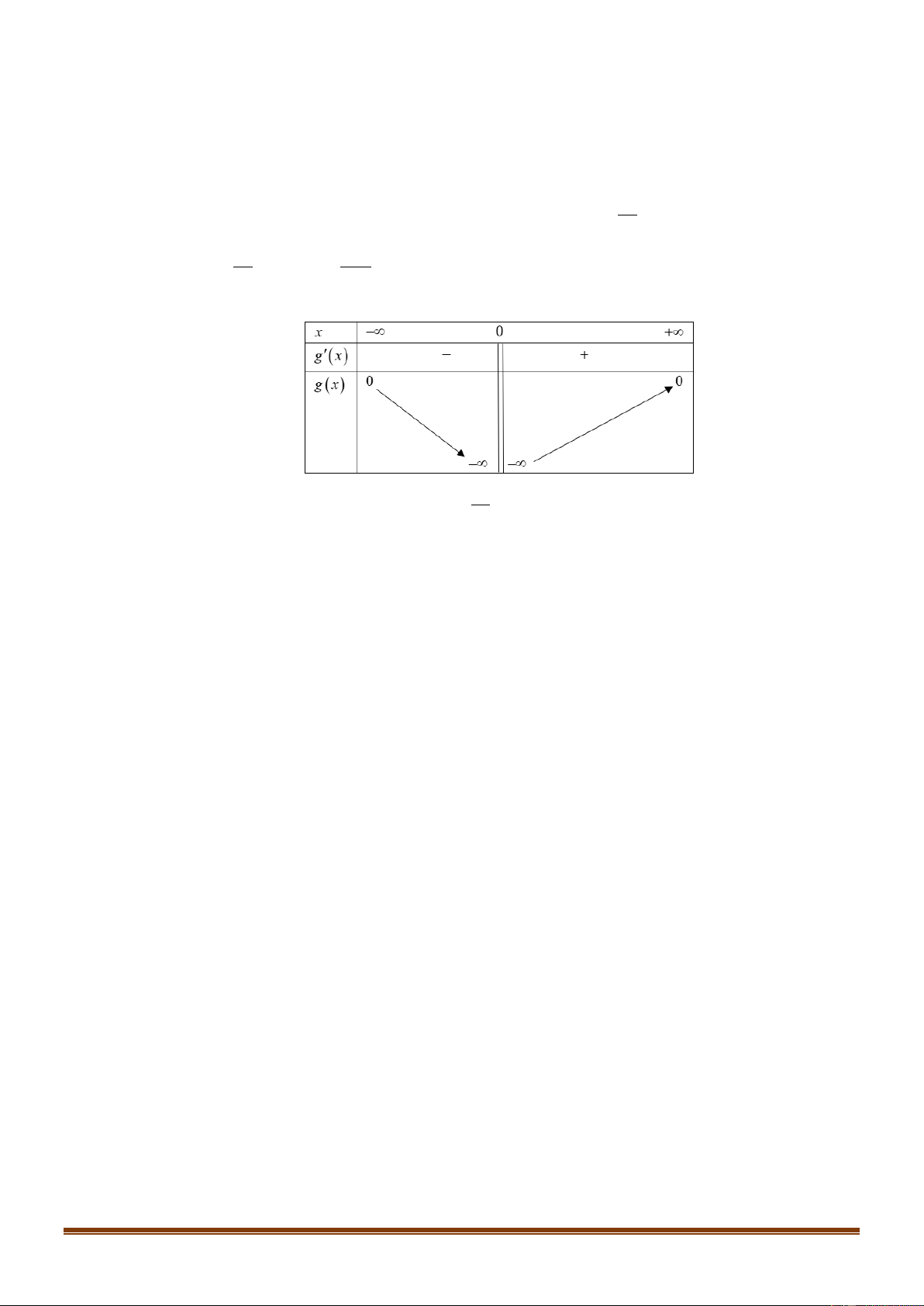
Câu 50: (Đề tốt nghiệp THPT 2020 mã đề 103)Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực phân biệt của phương trình f 2
x f (x) 2 0 là A. 8 . B. 12 . C. 6 . D. 9 . Lời giải Chọn D 2 x f (x) 0 x f x a f x f (x) 2 ( ) 1 2 2 0
với 0 a b c . 2
x f (x) b2 2
x f (x) c 3 m
Xét phương trình f (x) 1 m 0 . 2 x
Gọi , là hoành độ giao điểm của C : y f (x) và Ox ; 0 . Trang18 m m
(1) f (x)
0 . Đặt g(x) f (x) 2 x 2 x 2m Đạo hàm g (
x) f (x) . 3 x 2m
Trường hợp 1: x ; f ( x) 0;
0 g (x) 0 3 x m
Ta có lim g x , g( )
0 . Phương trình g x 0 có một nghiệm thuộc ; . 2 x
Trường hợp 2: x m f (x) 0 ,
0 suy ra g(x) 0 x (, ) . 2 x 2m
Trường hợp 3: x ; f ( x) 0;
0 g (x) 0 3 x m
Ta có lim g x , g( )
0 . Phương trình g x 0 có một nghiệm thuộc (;) . 2 x m
Vậy phương trình f x có hai nghiệm m 0. 2 x Ta có: 2
x f (x) 0 x 0 f (x) 0 : có ba nghiệm. Vậy phương trình 1 có 9 nghiệm.
Câu 42: (Đề tốt nghiệp THPT 2020 mã đề 104)Tập hợp tất cả các giá trị thực của tham số m để hàm số x 3 y ; 6 là x
đồng biến trên khoảng m A. 3;6 . B. 3;6 . C. 3; . D. 3;6 . Lời giải Chọn A
Hàm số xác định khi: x m 0 x m . x 3 m 3 y y x m x m2 y 0, x ; 6
Hàm số đồng biến trên khoảng ; 6 khi và chỉ khi: m ; 6 m 3 0 m 3 m 3 . m 3 m 6 6; m 6 m 6 Vậy: m3;6 .
Câu 46: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số bậc bốn f (x) có bảng biến thiên như sau Trang19
Số điểm cực trị của hàm số g x x f x 4 2 ( ) ( 1) A. 7 . B. 8 . C. 9 . D. 5 . Lời giải Chọn C
g x x f x 4 x f x 3 f x x f x 3 2 '( ) 2 ( 1) 4 ( 1) . '( 1) 2 (
1) . f (x 1) 2 .
x f '(x 1)
g '(x) 0 ta được + TH1: x 0 x a 2 x b( 2 ; 1 )
+ TH2: f (x 1) 0 x c ( 1 ;0) x d 0
+ TH3: f (x 1) 2 .
x f '(x 1) 0 .
Từ bảng biến thiên ta có hàm số thỏa mãn là 4 2 f (x) 5
x 10x 2
f (x 1) 2 .
x f '(x 1) 0 h x f (x 1) 2(x 1). f '(x 1) 2 f '(x 1) 0
Với t x 1 ta có: 4 2 3 3 h(t) 5
t 10t 2 2t( 2
0t 20t) 2( 2
0t 20t) 0 4 3 2 45
t 40t 50t 40t 2 0
Lập bảng biến thiên ta suy ra có 4 nghiệm t 4 nghiệm x Vậy có 9 cực trị.
Câu 50: (Đề tốt nghiệp THPT 2020 mã đề 104)Cho hàm số y f x có đồ thị là đường cong trong hình vẽ bên.
Số nghiê ̣m thực của phương trình f 2
x f x 2 là: A. 6. B. 12. C. 8. D. 9. Lời giải Chọn D 2
x f x 0 2
x f x a 0 Ta có: f 2
x f x 2 . 2 x f
x b 0 2 x f
x c 0 Trang20 x 0 Xét phương trình: 2
x f x 0
mà f x 0 có hai nghiệm 2
x . f x 0 có ba f x 0 nghiê ̣m. Xét phương trình: 2
x f x a 0 a Do 2
x 0 ; x 0 không là nghiê ̣m của phương trình f x 0 2 x a 2a
Xét g x g x 2 3 x x Bảng biến thiên: a
Từ bảng biến thiên với f x 0 f x có 2 nghiê ̣m. 2 x Tương tự: 2
x f x b và 2
x f x c ,
b c 0 mỗi phương trình cũng có hai nghiê ̣m.
Vâ ̣y số nghiê ̣m của phương trình f 2
x f x 2 là 9 nghiê ̣m. Trang21