Trắc nghiệm mũ-lôgarit trong các đề thi tốt nghiệp năm 2020-2019-2018 có lời giải
Trắc nghiệm mũ-lôgarit trong các đề thi tốt nghiệp năm 2020-2019-2018 có lời giải được soạn dưới dạng file PDF. Đề thi bao có 18 trang, bao gồm bộ câu hỏi trắc nghiệm. Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mờicác bạn cùng đón xem ở dưới.
Chủ đề: Tài liệu chung 297 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
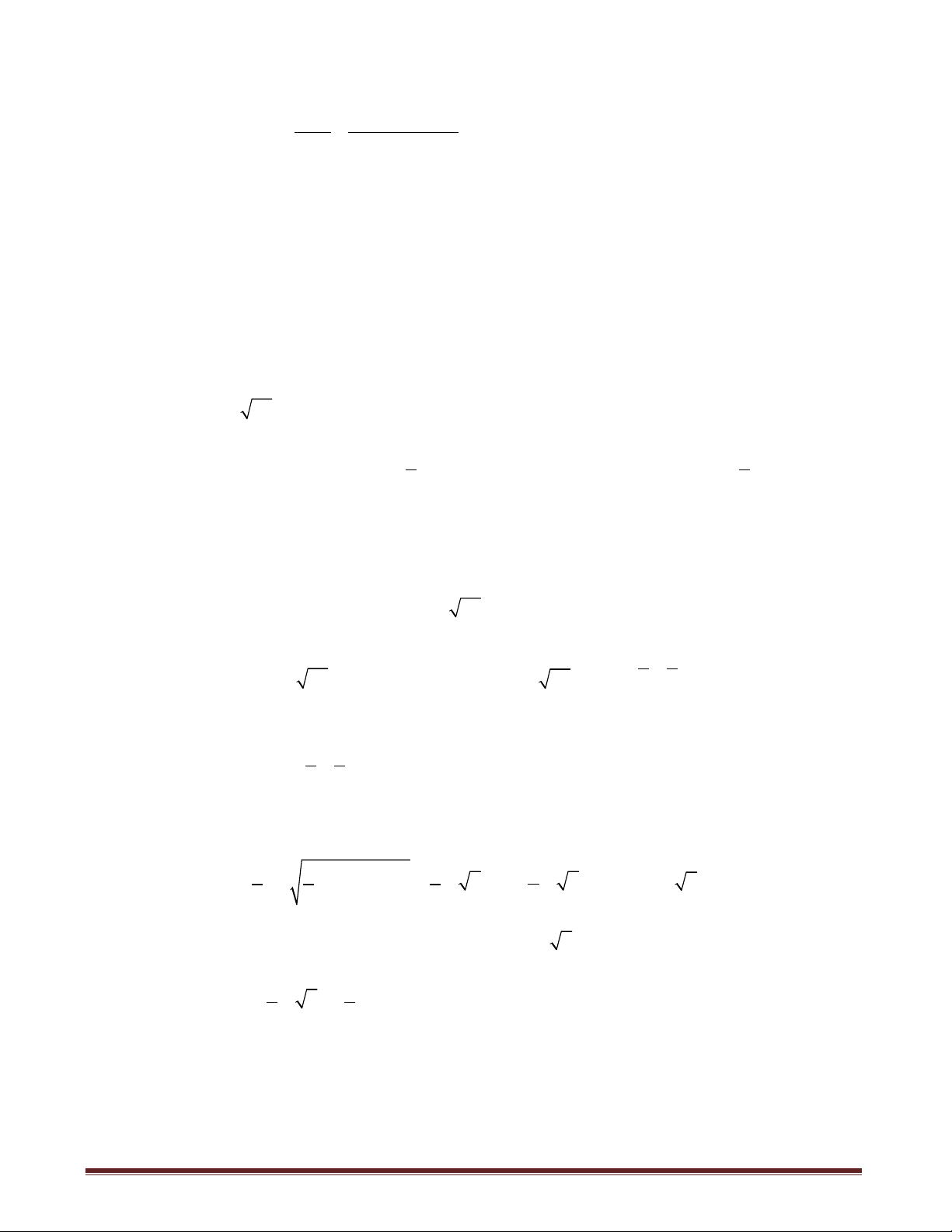
Preview text:
TRẮC NGHIỆM MŨ VÀ LÔGARIT TRONG CÁC ĐỀ THI TỐT NGHIỆP NĂM 2020-2019-2018
I. MỨC ĐỘ NHẬN BIẾT VÀ THÔNG HIỂU Câu 1. (TN LẦN 2-2020)
Với a là số thực dương tùy ý, log2 2a bằng A.1 log 2 a .
B. 1 log2 a .
C. 2 log2 a . D. 2 log2 a . Lời giải Chọn A log 2 2a
log2 2 log2 a 1 log2 a
Câu 2. (TN LẦN 2-2020)
Nghiê ̣m của phương trình log x 6 5 là 2
A. x 4 .
B. x 19 .
C. x 38. D. x 26 . Lời giải Chọn D
Điều kiện x 6 0 x 6
Ta có: log x 6 5 log x 6 log 2 x 6 32 x 326 x 26TM 2 5 2 2
Vâ ̣y nghiê ̣m của phương trình: x 26
Câu 3. (TN LẦN 2-2020)Với a, b là các số thực dương tùy ý thỏa mãn log a 2 log b 3, mệnh đề 3 9
nào dưới đây đúng?
A. a 27b .
B. a 9b . C. 4
a 27b . D. 2 a 27b . Lời giải Chọn A a a
Ta có: log a 2 log b 3 log a log b 3 log
3 27 a 27b . 3 9 3 3 3 b b
Câu 4. (TN LẦN 2-2020)
Tập nghiệm của bất phương trình log 2 36 x 3 là 3 A. ;
3 3; . B. ;3 . C. 3 ; 3 . D. 0; 3 . Lời giải Chọn C Ta có: log 2 36 x 2 2
3 36 x 27 9 x 0 3 x 3. 3
Câu 5. (TN LẦN 2-2020)
Với a là số thực dương tùy ý, log 3a bằng 3
A. 3 log a . B. 1 log a .
C. 3 log a . D. 1 log a . 3 3 3 3 Lời giải Chọn D
Ta có log 3a log 3 log a 1 log a . 3 3 3 3
Câu 6. (TN LẦN 2-2020)
Nghiệm của phương trình 2x 2 2 2x là A. x 2 . B. x 2 . C. x 4 .
D. x 4 . Lời giải Chọn B Trang1 2 x2 2
2x 2x 2 x x 2 .
Câu 7. (TN LẦN 2-2020)
Nghiệm của phương trình log x 7 5 là 2 A. x 18 . B. x 25 . C. x 39 . D. x 3. Lời giải Chọn B log x 7 5
5 x 7 2 x 25 . 2
Câu 8. (TN LẦN 2-2020)
Với a,b là các số thực dương tùy ý thỏa mãn log a 2log b 4 , mệnh 2 4
đề nào dưới đây đúng? A. 2 a 16b .
B. a 8b .
C. a 16b . D. 4 a 16b . Lời giải Chọn C Ta có
log a 2log b 4 2 4 1
log a 2log b 4 log a 2. log b 4 log a log b 4 2 2 2 2 2 2 2 2 a a 4 log
4 2 a 16b 2 b b
Câu 9. (TN LẦN 2-2020)
Tập nghiệm của bất phương trình log 2 31 x 3 là 3 A. ; 2 . B. 2 ;2. C. ; 2 2; . D. 0;2 . Lờigiải Chọn B log 2 31 x 2 2
3 31 x 27 x 4 0 x 2 ;2 . 3
Câu 10.(TN LẦN 1-2020)
Nghiệm của phương trình log x 2 3 là: 2
A. x 6 .
B. x 8.
C. x 11.
D. x 10 . Lời giải Chọn D
Điều kiện: x 2 0 x 2 . log
x 2 3 x 2 8 x 10 (thỏa). 2
Vậy phương trình có nghiệm x 10 .
Câu 11.(TN LẦN 1-2020)
Nghiệm của phương trình x 1 3 9 là
A. x 1.
B. x 2 . C. x 2 . D. x 1 . Lời giải Trang2 Chọn A Ta có: x 1 x 1 2 3
9 3 3 x 1 2 x 1.
Câu 12.(TN LẦN 1-2020)
Tập xác định của hàm số y log x là 3 A. (; 0) B. (0; )
C. (; ) D. [0; ) Lời giải Chọn B.
Điều kiện xác định: x 0 .
Câu 13.(TN LẦN 1-2020)
Với a,b là các số thực dương tùy ý và a 1, log b bằng 3 a 1 1
A. 3 log b
B. 3log b
C. log b D. log b a a 3 a 3 a Lời giải Chọn D 1 Ta có: log b log . b 3 3 a a
Câu 14.(TN LẦN 1-2020)
Tập nghiệm của bất phương trình 2 x 7 2 4 là A. (3; 3) . B. (0;3) . C. (;3) .
D. (3; ) . Lời giải Chọn A 2 2 Ta có : x - 7 2 < 4 x - 7 2 Û 2 < 2 2 Þ x - 7 < 2 2
Û x < 9 Þ x Î (- 3; ) 3 .
Câu 15.(TN LẦN 1-2020)
Cho a và b là hai số thực dương thỏa mãn log3(ab) 9
4a . Giá trị của 2 ab bằng A. 3 . B. 6. C. 2 D. 4 Lời giải Chọn D Ta có : log3(ab) 9
= 4a Û 2 log ab = log 4a Û log ( 2 2 a b = log 4a 2 2 Þ a b = 4a 3 ) 3 ( ) 3 ( ) 3 ( ) 2 Û ab = 4 .
Câu 16: (THAM KHẢO LẦN 2-2020)
Nghiệm của phương trình x 1 3 27 là A. x 4 . B. x 3 . C. x 2 . D. x 1 . Trang3 Lời giải Chọn A x 1 3 27 x 1 3
3 3 x 4 .
Câu 17: (THAM KHẢO LẦN 2-2020) Tập xác định của hàm số y log x là 2 A. [0; ) . B. ( ; ) . C. (0; ) . D. [2; ) . Lời giải Chọn C
Hàm số xác định khi x 0 . Vậy tập xác định D 0; .
Câu 18: (THAM KHẢO LẦN 2-2020)
Với a là số thực dương tùy ý, log 3 a bằng 2 3 1 A. log a . B. log a .
C. 3 log a . D. 3log a . 2 2 2 3 2 2 Lời giải Chọn D Ta có log 3 a 3log a . 2 2
Câu 19: (THAM KHẢO LẦN 2-2020) Tập nghiệm của bất phương trình log x 1 là A. 10; . B. 0; . C. 10; . D. ;10 . Lời giải Chọn C
log x 1 x 10 .
Vậy tập nghiệm của bất phương trình là 10; .
Câu 20: (THAM KHẢO LẦN 2-2020) Xét các số thực ; a b thỏa mãn log
3a.9b log 3 . Mệnh đề 3 9 nào là đúng?
A. a 2b 2 .
B. 4a 2b 1 . C. 4ab 1 .
D. 2a 4b 1 . Lời giải Chọn D a b a b 1 log 3 .9
log 3 log 3 log 9 3 9 3 3 2 1
a 2b 2a 4b 1. 2 Trang4
Câu 21: (THAM KHẢO LẦN 2-2020)
Tập nghiệm của bất phương trình 9x 2.3x 3 0 là A. 0; . B. 0; . C. 1; . D. 1; . Lời giải ChọnB t 1 Đặt 3x t
t 0 bất phương trình đã cho trở thành 2t 2t 3 0 t 3 loai
Với t 1 thì 3x 1 x 0 .
Câu22. (THAM KHẢO LẦN 1-2020) Nghiệm của phương trình log 2x 1 2 là 3 9 7
A. x 3.
B. x 5. C. x . D. x . 2 2 Lời giải Đáp án B log 2x 2
1 2 2x 1 3 x 5 3
Câu 23. (THAM KHẢO LẦN 1-2020) Xét tất cả các số dương a và b thỏa mãn log a log ab . 2 8
Mệnh đề nào dưới đây đúng? A. 2
a b . B. 3
a b .
C. a b . D. 2 a b . Lời giải Đáp án D 1 log a log ab log a log ab 2 8 2 2 3
3log a log ab 3
log a log ab 3 2
a ab a b . 2 2 2 2
Câu 24. (THAM KHẢO LẦN 1-2020) Tập nghiệm của bất phương trình 2 x 1 x x 9 5 5 là A. 2 ;4. B. 4 ;2. C. ;
24; . D. ;
42; . Lời giải Đáp án A 2 x 1 x x9 2 2 5 5
x 1 x x 9 x 2x 8 0 2 x 4 Trang5
Câu 25. (THAM KHẢO LẦN 1-2020) Cho x, y là các số thực dương thỏa mãn x
log x log y log
2x y . Giá trị của bằng 9 6 4 y 1 3 A. 2. B. .
C. log . D. log 2 . 2 2 2 3 2 Lời giải Đáp án B x 9t
Giả sử log x log y log (2x y) t . Suy ra: y 6t
2.9t 6t 4t 9 6 4
2x y 4t t 3 1 (loai) t 9 3 2 2. t 1 0 . 4 2 t 3 1 2 2 t x 9t 3 1 Ta có : . y 6t 2 2 Câu 26.(THPT QG-2019)
Với a là số thực dương tùy, 2 log a bằng 5 1 1 A. 2 log a .
B. 2 log a . C. log a log a 5 . D. 5 . 5 5 2 2 Lời giải Chọn A Ta có 2
log a 2log a . 5 5 Câu 27.(THPT QG-2019)
Nghiệm phương trình 2x 1 3 27 là A. x 5. B. x 1 . C. x 2 . D. x 4 . Lời giải Chọn C Ta có 2x 1 2 x 1 3 3 27 3
3 2x 1 3 x 2 . 2 Câu 28.(THPT QG-2019) Cho hàm số 3 2x x y có đạo hàm là 2 2 A. x 3 (2 3).2 . x x 2 ln 2 . B. x 3 2 x.ln 2 . C. 3 (2 3).2x x x 2 . D. 2 3 1 ( 3 ).2x x x x . Lời giải Chọn A Trang6 Câu 29.(THPT QG-2019) Cho và
là hai số thực dương thỏa mãn . Giá trị của a b 4 a b 16
4 log a log b bằng 2 2 A. 4 . B. 2 . C. 16 . D. 8 . Lời giải Chọn A Ta có 4 4
4log a log b log a log b log a b log 16 4 . 2 2 2 2 2 2 Câu 30(THPT QG-2019)
Nghiệm của phương trình log x 1 1 log 4x 1 3 3 là A. x 3. B. x 3 . C. x 4 . D. x 2 . Lời giải Chọn D
log x 1 1 log 4x 1 1 3 3 1 log 3
. x 1 log 4x 1 x x x 2 3 3 3 4 1 0 3 . Vậy
1 có một nghiệm x 2 .
Câu 31. (THPT QG-2018)Với a là số thực dương tùy ý, ln(5a)- ln(3a) bằng ln 5a 5 ln 5 A. .
B. ln 2a . C. ln . D. . ln 3a 3 ln 3 Lời giải Chọn C. 5a 5
Ta có ln (5a)- ln (3a)= ln = ln . 3a 3 x
Câu 32. (THPT QG-2018)Phương trình 2 1 2 32 có nghiệm là 5 3 A. x . B. x 2 . C. x . D. x 3. 2 2 Lời giải Chọn B. x Ta có 2 1 2
32 2x 1 5 x 2 .
II. MỨC ĐỘ VẬN DỤNG VÀ VẬN DỤNG CAO 2 2
Câu 1. (TN LẦN 2-2020)
Xét các số thực x, y thỏa mãn x y 1 2 2 2 2 2.4x x y x . Giá trị nhỏ 8x 4
nhất của biểu thức P
gần nhất với số nào dưới đây 2x y 1 Trang7 A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn C Nhận xét 2 2
x y 2x 2 0 ; x y 2 2 x y 1 2 2 2 Bất phương trình x y 1 2 2 2 2 2.4x x y x
x y x x 2 2 2 2 2 2 2 2
x y 2 x 1 2 2 2
x y 2x 2 . Đặt 2 2
t x y 2x 1
Bất phương trình 2t t 1 2t t 1 0 Đặt 2t f t
t 1. Ta thấy f 0 f 1 0 .
Ta có 2t f t ln 2 1 f t t 1
0 2 ln 2 1 t log 0,52 2 ln 2
Quan sats BBT ta thấy f t 0 0 t 1 2 2
0 x y 2x 1 1 x 2 2 1 y 1 1 8x 4 Xét P
2Px Py P 8x 4 2x y 1
P 4 8 2P x Py
P 4 2P 8 8 2P x 2P 8 Py
3P 12 8 2Px 1 Py
P 2 Px 2 Py
P2 P x 2 2 2 3 12 8 2 1 8 2 1 y Thế 1 vào ta có P 2 3 12 2 2 8 2P P 2
4P 40P 80 0
5 5 P 5 5 . 1 x 3 2 2 8 2P x 1 2 5 x 1 y x 1 y y 5 5 3 Dấu “=” xảy ra khi P y 5 2 2 5 5 x 2 2 1 y 1 y 1 y x 5 3 3 5 y 3
Vậy giá trị nhỏ nhất của P là 5 5 2,76 gần giá trị 3 nhất. Trang8
Câu 2. (TN LẦN 2-2020)
Có bao nhiêu cặp số nguyên dương ;
m n sao cho m n 10 và ứng với mỗi cặp ;
m n tồn tại đúng 3 số thực a 1 ;1 thỏa mãn m a n 2 2
ln a a 1 ? A. 7 . B. 8 . C. 10 . D. 9 . Lời giải Chọn D a m 2 m
Ta có 2a n ln 2
a a 1 ln 2
a a 1 . n
Xét hai hàm số f x 2 ln x
x 1 và 2 m g x x trên 1 ;1 . n 1 Ta có
f x 0 nên f x luôn đồng biến và 2 x 1
f x ln 1 2
x x 1 ln ln 2 x
x 1 f x nên f x là hàm 2
x x 1 số lẻ.
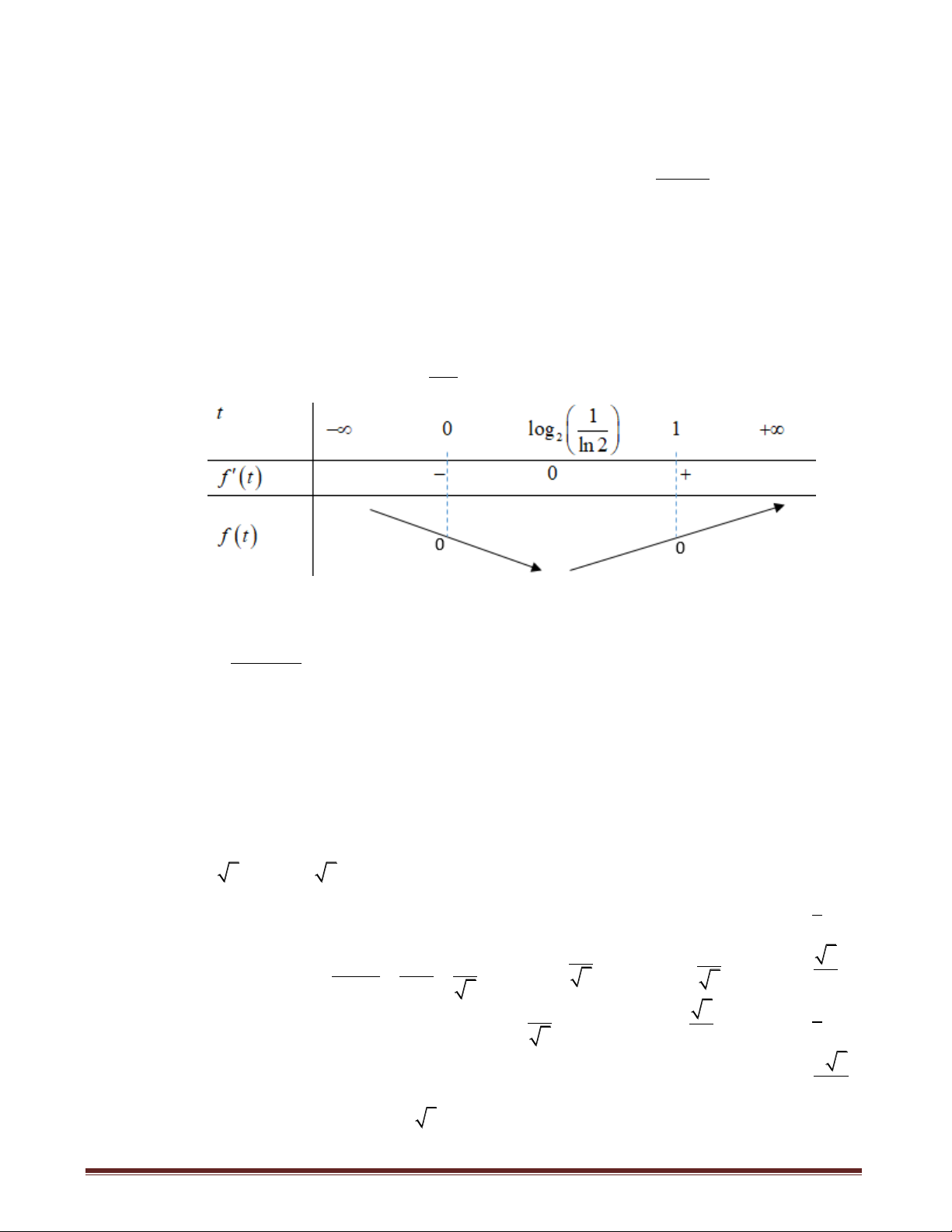
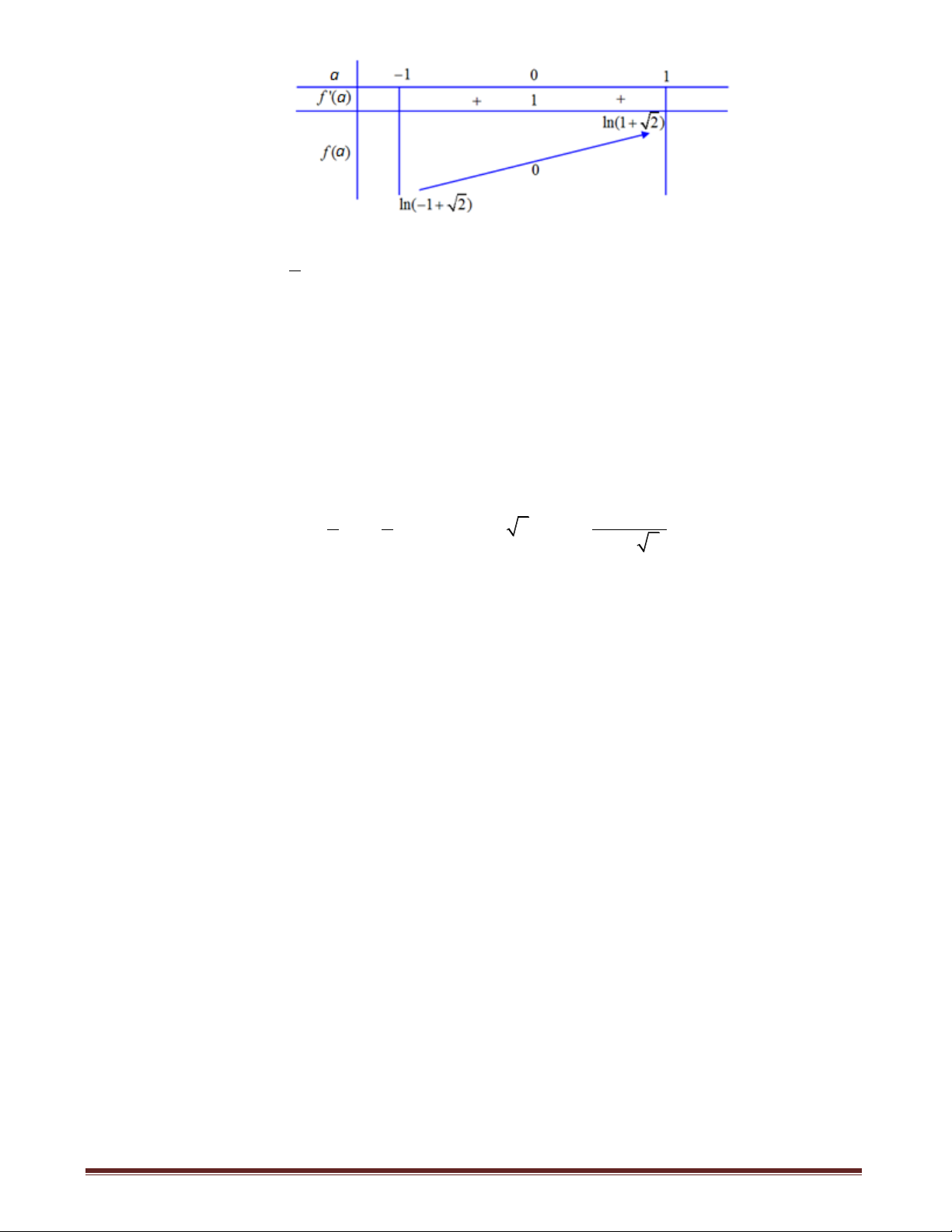
+ Nếu m chẵn thì g x là hàm số chẵn và có bảng biến thiên dạng
Suy ra phương trình có nhiều nhất 2 nghiệm, do đó m lẻ.
+ Nếu m lẻ thì hàm số g x là hàm số lẻ và luôn đồng biến.
Ta thấy phương trình luôn có nghiệm x 0 . Dựa vào tính chất đối xứng của đồ thị hàm số
lẻ, suy ra phương trình đã cho có đúng 3 nghiệm trên 1
;1 khi có 1 nghiệm trên 0; 1 , 2 2 hay f 1 g
1 ln 1 2 n . n
2,26 n 1; 2 ln 1 2
Đối chiếu điều kiện, với n 1 suy ra m 1;3;5;7;
9 , có 5 cặp số thỏa mãn
Với n 2 thì m 1;3;5;
7 có 4 cặp số thỏa mãn.
Vậy có 9 cặp số thỏa mãn bài toán. 2 2
Câu 3. (TN LẦN 2-2020)
Xét các số thực x và
y thỏa mãn x y 1 2 2 2 2 24x x y x . Giá trị 4 y
lớn nhất của biểu thức P 2x y gần nhất với số nào dưới đây? 1 A. 1 . B. 0 . C. 3 . D. 2 . Lời giải Chọn A 2 2 2 2 Ta có: x y 1 2 2 x x 2 x 1 y x y x 2 x x 2 2 2 2 4 2 2 1 y 1 . Đặt 2 2
t x 2x 1 y t 0 . Khi đó ta có 2t t 1, t 0 . Trang9 Đặt 2t f t t 1, t
0 , ta có: 2t f t
ln 2 1, cho f t 0 .
Ta nhận thấy phương trình f t 0 có một nghiệm nên phương trình f t 0 có tối đa hai nghiệm.
Mặt khác ta có f 0 f
1 0 . Suy ra phương trình f t 0 có hai nghiệm t 1 và t 0 .
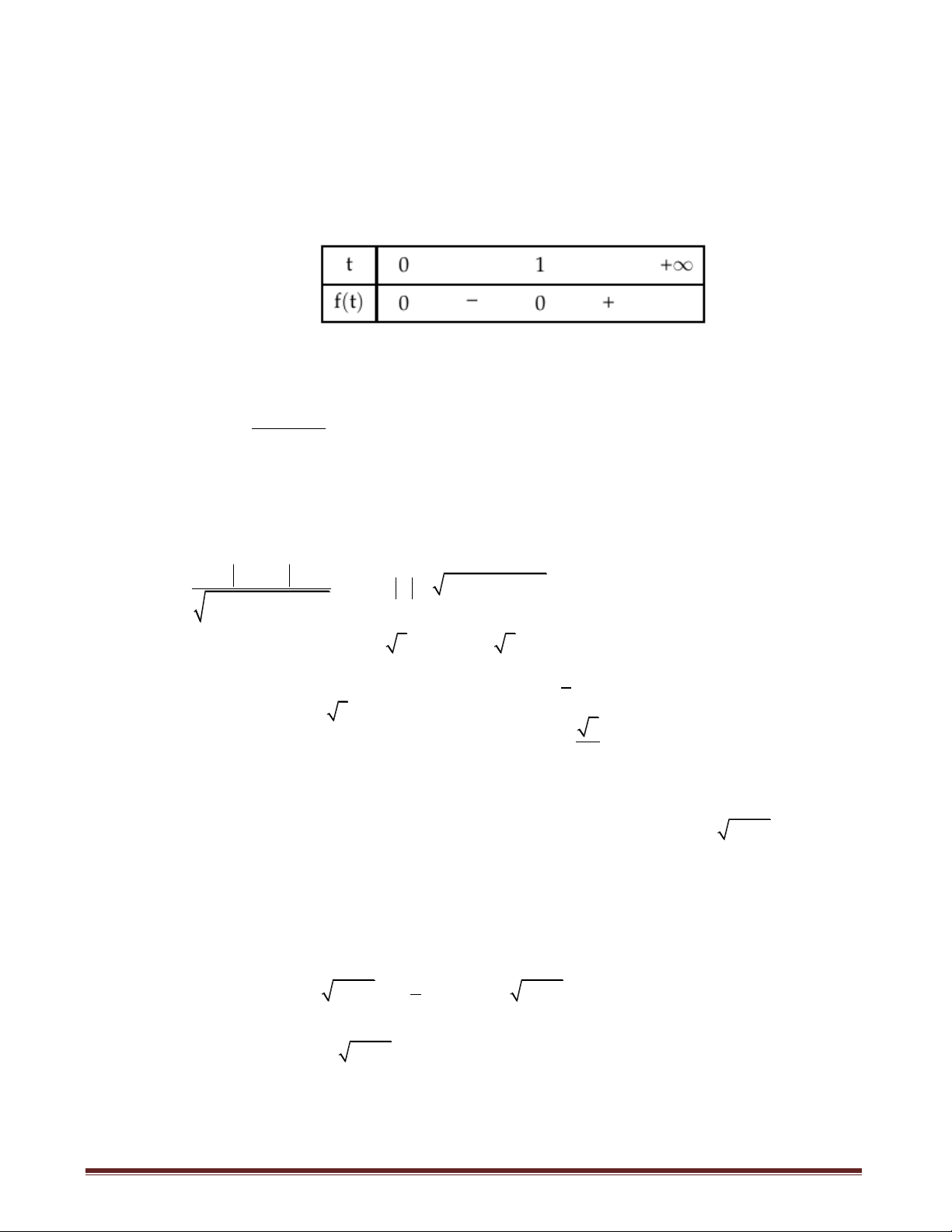
Khi đó ta có bảng xét dấu của hàm số f t như sau:
Khi đó f t 0 t 0
;1 . Suy ra x x y x 2 2 2 2 2 1 1 1 y 1 .
Khi đó tập hợp các điểm M ;
x y là một hình tròn S tâm I 1;0 , bán kính R 1. 4 y Ta có: P
2Px P 4 y P 0. 2x y 1
Khi đó ta cũng có tập hợp các điểm M ;
x y là một đường thẳng
: 2Px P 4 y P 0 .
Để và S có điểm chung, ta suy ra d I, 1. 2P P 2
1 3 P 5P 8P 16
2P2 P 42 2
4P 8P 16 0 1 5 P 1 5 . 1 x 3 Ta suy ra P 1
5 . Dấu " " xảy ra khi max 5 y 3
Câu 4. (TN LẦN 2-2020)
Có bao nhiêu cặp số nguyên dương ( ,
m n) sao cho m n 12 và ứng với mỗi cặp ( ,
m n) tồn tại đúng 3 số thực a (1,1) thỏa mãn m 2
2a n ln(a a 1) ? A.12 . B.10 . C.11. D. 9 . Lời giải Chọn D m 2 Ta có 2 m 2
2a n ln(a a 1)
a ln(a a 1) (*) n . Xét hàm 2
f (a) ln(a a 1) trên ( 1
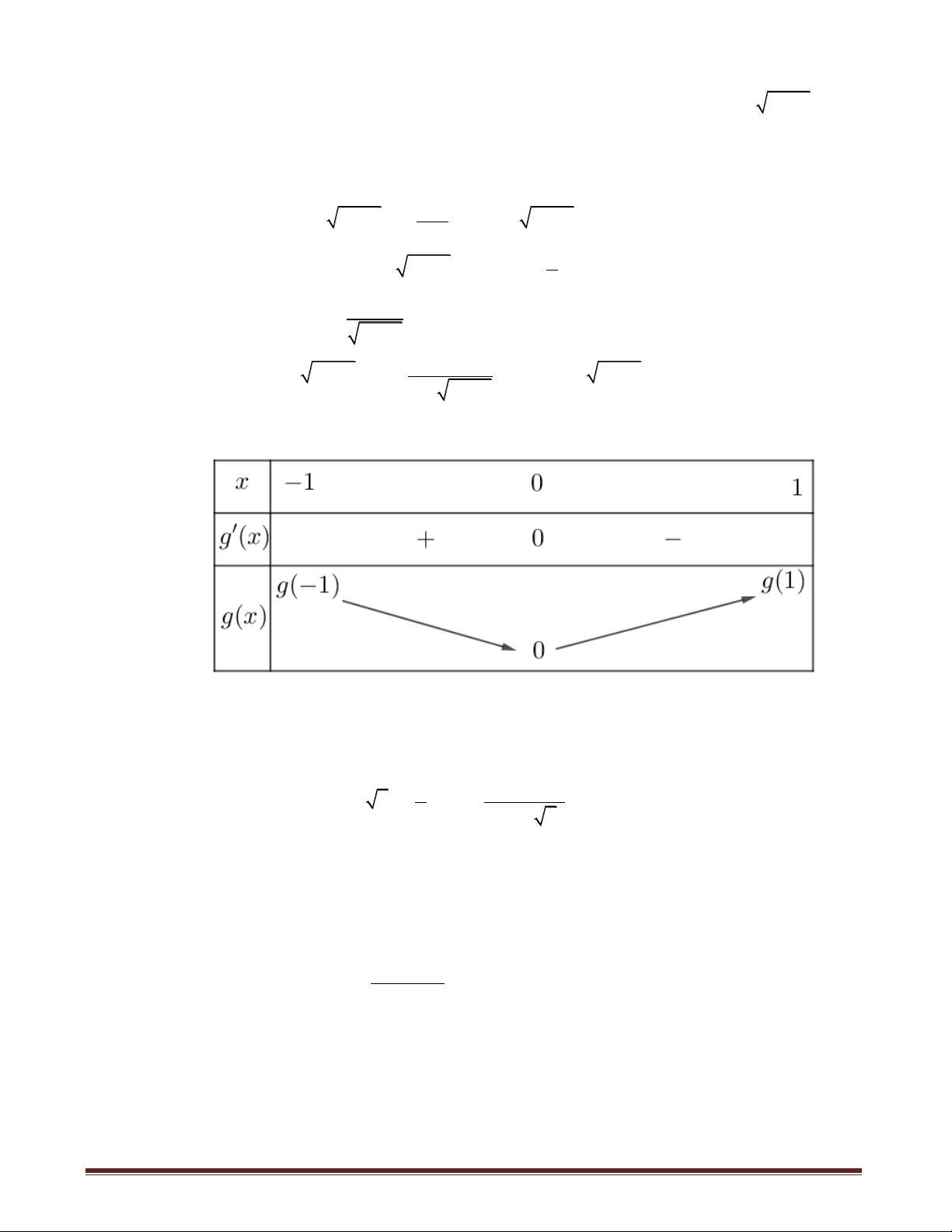
,1) (dễ thấy hàm f lẻ, đồng biến trên R ), có BBT: Trang10 2 Xét hàm ( ) . m g a a trên ( 1 ,1) . n
Với m chẵn, g(a) là hàm chẵn và g(a) 0, a
R , do đó (*) không thể có 3 nghiệm.
Với m lẻ, g(a) là hàm lẻ, đồng biến trên R và tiếp tuyến của đồ thị tại điểm a 0 là
đường thẳng y 0 .
Dễ thấy (*) có nghiệm a 0 (1;1) . Để (*) có đúng 3 nghiệm tức là còn có 2 nghiệm nữa
là a với 0 a 1. 0 0 2 m 2 2
Muốn vậy, thì g(1) .1
f (1) ln(1 2) n
2,26 n 1;n 2 n n ln(1 2) Cụ thể: + m 3;5;7; 9 thì n 1; 2 : Có 8 cặp ( , m n)
+ m 11 thì n 1 : Có 1 cặp ( , m n)
+ m 1: Đồ thị hàm số g(a) là đường thẳng ( g(a) a; g(a) 2a ) không thể cắt đồ thị hàm
số f (a) tại giao điểm a 0 được vì tiếp tuyến của hàm số f (a) tại điểm có hoành độ 0
a 0 là đường thẳng y a .
Vậy có cả thảy 9 cặp (m, n).
Câu 5.(TN LẦN 1-2020)
Có bao nhiêu số nguyên x sao cho ứng với mỗi x có không quá 127 số
nguyên y thỏa mãn log 2 x y log x y ? 3 2 A. 89 . B. 46 . C. 45 . D. 90 . Lời giải Chọn D Ta có log 2 x y log x y 1 3 2
Đặt t x y * (do x, y , x y 0 ) Trang11 (1) log 2
x x t log t g(t) log t log 2
x x t 0 2 3 2 2 3 1 1 Đạo hàm g ( t)
với mọi y . Do đó g t đồng biến trên 1; t ln 2 0 2
x x t ln 3
Vì mỗi x nguyên có không quá 127 giá trị t * nên ta có
g(128) 0 log 128 log 2
x x 128 0 2 3 2 7
x x 128 3 4 4,8 x 45,8
Như vậy có 90 giá trị thỏa yêu cầu bài toán
Câu 6:(THAM KHẢO LẦN 2-2020)
Xét các số thực dương a, ,
b x, y thỏa mãn a 1, b 1 và x y
a b ab . Giá trị nhỏ nhất của biểu thức P x 2 y thuộc tập hợp nào dưới đây? 5 5 A. 1; 2 . B. 2; . C. 3; 4 . D. ; 3 . 2 2 Lời giải Chọn D
Ta có a, b 1 và x, y 0 nên x ; y a b ; ab 1 1 1
x log b Do đó: x y
a b ab log x a log y b log ab . a a a 2 2 a
2y 1 log a b Khi đó, ta có: 3 1 P
log b log a . 2 2 a b
Lại do a, b 1 nên log , b log a 0 . a b 3 1 3 3 Suy ra P 2 log . b log a
2 , P 2 log b 2 . 2 2 a b 2 2 a
Lưu ý rằng, luôn tồn tại a, b 1 thỏa mãn log b 2 . a 3 5 Vậy min P 2 ; 3 . 2 2
Câu 7:(THAM KHẢO LẦN 2-2020)
Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa
mãn log x y log 2 2 x y ? 3 4 A. 3. B. 2. C. 1. D. Vô số Trang12 Lời giải Chọn B. x y 0 Điều kiện: . 2 2 x y 0 Điều kiện cần
x y 3t d
Đặt t log x y log 2 2 x y . 3 4 2 2
x y 4t C
Suy ra x, y tồn tại nếu đường thẳng d cắt đường tròn C tại ít nhất một điểm. 3t Hay
2t t log 2 0,8548. 3 2 2 x 1 log 2 3 2 0 x 3 Khi đó: 2 2 2 x y 4 3, 27 x 0 . x x 1 Điều kiện đủ: 4t t 1 0 y 3 1 t 0 Với x 1 . t t t
y 4t 1 4t 1 3t 2 2 1 f
t 9 2.3 2 4 0
Khi 0 0,8548 9t 4t t
f t 0 . Suy x 1 l . y 3t
Với x 0
4t 3t t 0 y 1t / m. 2 y 4t
y 3t 1 x 1
y t 0(t / m) . 2
y 4t 1
Câu 8. (THAM KHẢO LẦN 1-2020) Cho phương trình 2 log
2x m 2 log x m 2 0 (m là 2 2
tham số thực). Tập hợp tất cả các giá trị của m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1;2.
A. 1; 2 . B. 1; 2. C. 1;2 . D. 2; . Lời giải Đáp án C
Điều kiện: x 0 .
pt 1 log x2 m 2 log x m 2 0 2 2 Trang13 log x 1 2 2
log x mlog x m 1 0 2 2
log x m1 2
Ta có: x 1;2 log x 0;1 . 2
Vậy để phương trình đã cho có 2 nghiệm phân biệt thuộc đoạn 1; 2 khi và chỉ khi
0 m 11 1 m 2.
Câu 9.(THAM KHẢO LẦN 1-2020) Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 x 2000 và log 3 3 2 9y x x y ? 3 A. 2019. B. 6. C. 2020. D. 4. Lời giải Đáp án D + Ta có: log 3 3 2 9y 1log 1 2 9y x x y x x y 1 . 3 3
+ Đặt t log x 1 . Suy ra: 1 3t 3t x x 1. 3 Khi đó: t 2
1 3 2 3 y t y 2. Xét hàm số: 3h f h h
, ta có: 1 3 . h f h ln 3 0 h
nên hàm số f h đồng biến trên .
Do đó: 2 2 2 log 2
1 2 1 3 y 1 9y f t f y t y x y x x . 3
+ Do 0 x 2020 nên 1 1 2021 1 9y x
2021 0 y log 2021 3,46 . 9
Do y nên y 0;1; 2;
3 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 4 cặp số nguyên x; y thoả đề.
Câu 11.(THPT QG-2019) Cho phương trình 2 log x log
3x 1 log m m 9 3 ( là tham số thực). Có 3
tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có nghiệm A. 2 . B. 4 . C. 3 . D. Vô số. Lời giải Chọn A 1 Điều kiện: x 3
Phương trình tương đương với: 3x 1 3x 1
log x log 3x 1 log m log
log m m f x 3 3 3 3 3 x x Trang14 x 1 1
Xét f x 3 1 1 ; x
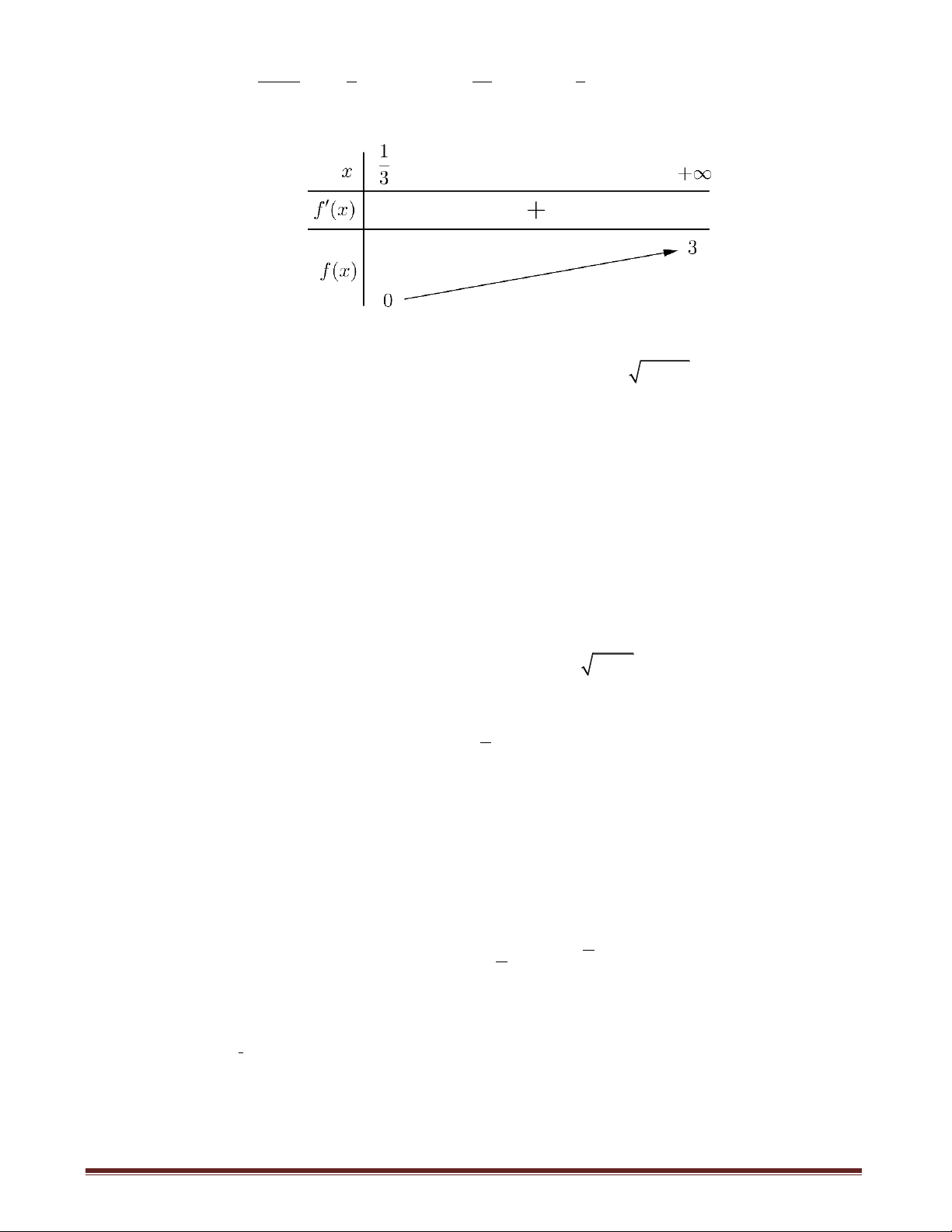
; ; f x 0; x ; x 3 2 x 3 Bảng biến thiên
Để phương trình có nghiệm thì m 0;3 , suy ra có 2 giá trị nguyên thỏa mãn Câu 12.(THPT QG-2019) Cho phương trình 2 4log log 5 7x x x m 0 m 2 2 ( là tham số
thực). Có tất cả bao nhiêu giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân biệt A. 49 . B. 47 . C. Vô số. D. 48 . Lời giải Chọn B x 0 Điều kiện: x log m 7
Với m 1, phương trình trở thành 2 4log log 5 7x x x 1 0 2 2 log x 1 2 2
4log x log x 5 0 2 2 5 log x 2 . 7x 1 0 4
x 0 (loai)
Phương trình này có hai nghiệm (thỏa)
Với m 2 , điều kiện phương trình là x log m 7 log x 1 x 2 2 2 5
4log x log x 5 0 2 2 5 Pt 4 log x x 2 2
7x m 0 4 x 7x m 7 m 5 4 Do x 2
2, 26 không là số nguyên, nên phương trình có đúng 2 nghiệm khi và chỉ khi Trang15 m 3 5 (nghiệm 4 x 2
không thỏa điều kiện và nghiệm x 2 thỏa điều kiện và khác 2 m 7 log m ) 7
Vậy m 3;4;5;...;4
8 . Suy ra có 46 giá trị của m .
Do đó có tất cả 47 giá trị của m
Câu 13. (THPT QG-2018) Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1 2 16 .4 m
5m 45 0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 13 . B. 3 . C. 6 . D. 4 . Lời giải Chọn B. Đặt 4x t
, t 0 . Phương trình đã cho trở thành 2 2
t 4mt 5m 45 0 * .
Với mỗi nghiệm t 0 của phương trình * sẽ tương ứng với duy nhất một nghiệm x của
phương trình ban đầu. Do đó, yêu cầu bài toán tương đương phương trình * có hai nghiệm
dương phân biệt. Khi đó 0 2 m 45 0 3 5 m 3 5
S 0 4m 0 m 0 3 m 3 5 . P 0 2 5m 45 0 m 3 m 3
Do m nên m 4;5; 6 .
Câu 14. (THPT QG-2018) Cho a 0 , b 0 thỏa mãn log a b a b
. Giá trị của a 2b bằng a b 2 2 9 1 log 3 2 1 2 3 2 1 6ab 1 7 5 A. 6 . B. 9 . C. . D. . 2 2 Lời giải Chọn C. Trang16 3
a 2b 1 1 log a b a b 2 2 9 1 0 3 2 1
Ta có a 0 , b 0 nên 2 2 9
a b 1 1 . log
3a 2b 1 0 6ab 1 6ab 1 1
Áp dụng BĐT Cô-si cho hai số dương ta được log a b a b a b a b a b 2 2 9
1 log ab 3 2 1 2 log a b 2 2 9 1 log 3 2 1 3 2 1 6 1 3 2 1 6ab 1 2 2 log a b log a b 2 2
9a b 1 6ab 1 ab 2 2 9 1 1 6 1 ab 2 2 9 1 6 1
a b2 3
0 3a b .
Vì dấu “ ” đã xảy ra nên log a b a b log b b b 2 2 1 log 3 1 3 1 2 a b 2 2 9 1 log 3 2 1 3 2 1 6ab 1 2b 1 2 1
2b 1 3b 1 2
2b 3b 3 0 b
(vì b 0 ). Suy ra a . 2 2 1
Vậy a 2b 7 3 . 2 2
Câu 15. (THPT QG-2018) Cho phương trình 5x m log
x m với m là tham số. Có bao nhiêu 5
giá trị nguyên của m 2
0;20 để phương trình đã cho có nghiệm? A. 20 . B. 19 . C. 9 . D. 21 . Lời giải Chọn B.
Điều kiện x m Ta có 5x log
5x log 5x m x m x x m x m x 5
x m log x m 5 5 log5 5 1 . Xét hàm số 5t f t t , 5t f t ln 5 1 0, t
, do đó từ 1 suy ra log 5x x x m m x . 5 1
Xét hàm số 5x g x x
, 1 5 .x g x
ln 5 , g x 0 x log
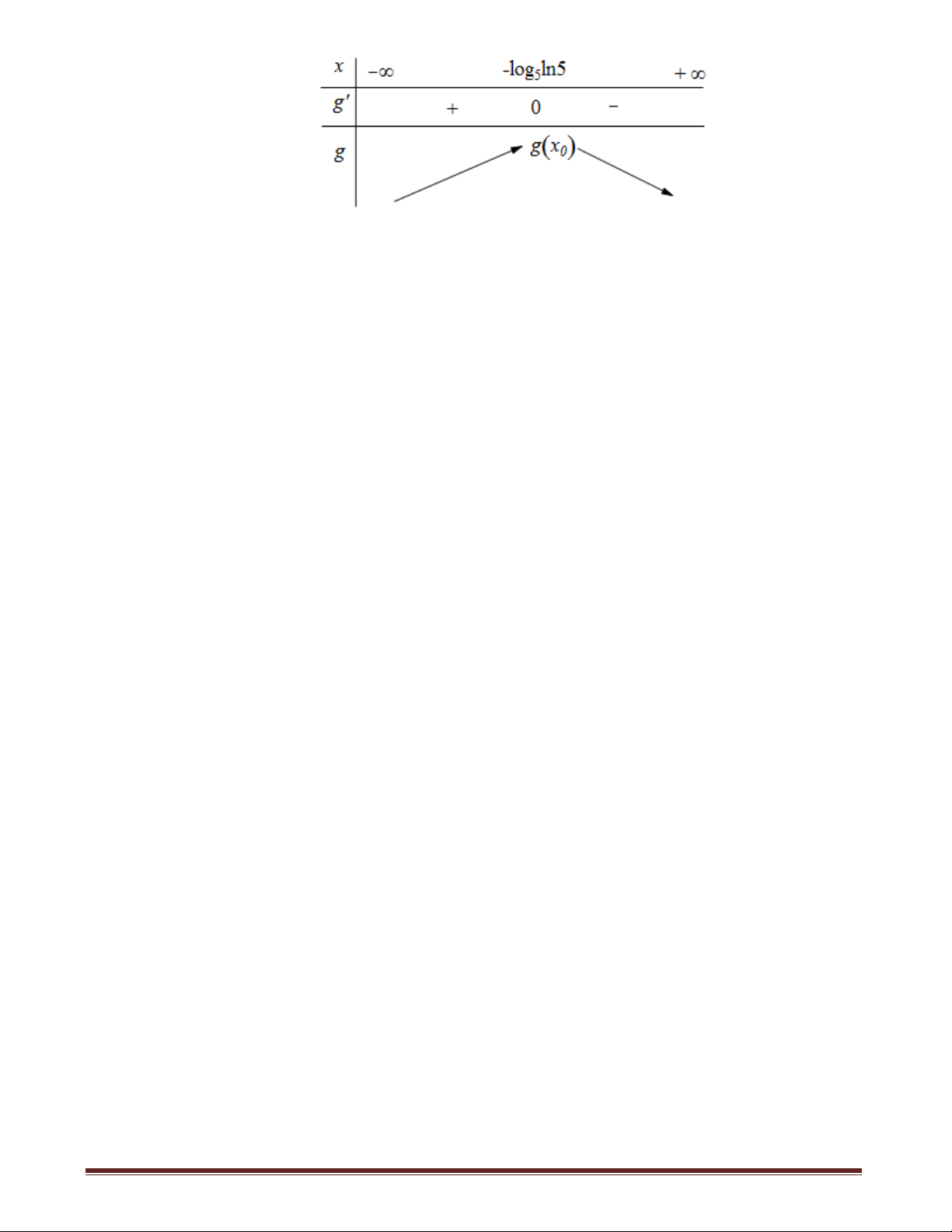
log ln 5 x . 5 5 0 ln 5 Bảng biến thiên Trang17
Do đó để phương trình có nghiệm thì m g x 0 ,92 . 0
Các giá trị nguyên của m 2 0;20 là 1 9; 1 8;...;
1 , có 19 giá trị m thỏa mãn. Trang18