Trắc Nghiệm Ôn Tập Giải Tích 12 Chương 1 Mức Độ 1 Và 2 Có Đáp Án

Trắc nghiệm ôn tập Giải Tích 12 Chương 1 Mức độ nhận biết 1 và 2 được biên soạn dưới dạng file PDF gồm 35 trang. Tài liệu ôn tập là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

60 30 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Trang1

CHƢƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ

I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ

KIẾN THỨC CẦN NHỚ:

1. Hàm số

 

y f x

đồng biến trên khoảng

     

; ' 0, ; .a b f x x a b   

Hàm số

 

y f x

đồng biến trên khoảng

 

;ab

thì nó đồng biến trên mọi khoảng con của khoảng

 

;ab

2.Hàm số

 

y f x

nghịch biến trên khoảng

     

; ' 0, ; .a b f x x a b   

Hàm số

 

y f x

nghịch biến trên khoảng

 

;ab

thì nó nghịch biến trên mọi khoảng con của

khoảng

 

;ab

DẠNG BÀI TẬP:

1. Dạng 1: Đọc bảng biến thiên:

Cách giải: Căn cứ vào bảng biến thiên, chỉ ra khoảng đồng biến, nghịch biến của hàm số.

Bài tập:

Câu 1:Cho hàm số có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới đây?

A. B.

C. D.

Câu 2: Cho hàm số

()y f x

có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

;1 

và nghịch biến

trên khoảng

 

1; 

B. Hàm số đồng biến trên khoảng

( ; ). 

C. Hàm số nghịch biến trên khoảng

 

;1 

và đồng biến

trên khoảng

 

1; 

D.Hàm số nghịch biến trên khoảng

 

1;1

∞

( )

 

2;2 .

 

0;2 .

 

2;0 .

 

2; .

-2

-1

∞

Trang2

Câu 3: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

1;0

 

1; 

 

0;1

 

;0

Câu 4: Cho hàm số

 

y f x

có bảng biến thiên như hình bên.

Mệnh đề nào sau đây đúng?

A.Hàm số nghịch biến trên khoảng

 

;1 

B.Hàm số nghịch biến trên khoảng

 

1; 

C.Hàm số đồng biến trên khoảng

 

1;1

D.Hàm số nghịch biến trên khoảng

 

1;1

Câu 5:Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số nghịch biến trong khoảng nào dưới đây?

 

1;1

. B.

 

0;1

 

4;

. D.

 

;2

Câu 6:Cho hàm số

 

y f x

có bảng biến thiên:

Hàm số đồng biến trên khoảng nào dưới đây?

 

;1 

. B.

 

;1 

và

 

1; 

 

1; 

. D.

 

1;1

Câu 6:Cho hàm sô

 

y f x

có bảng biến thiên như hnh v.

Mê



nh đê na



o sau đây la



sai?

A.Hàm số đã cho đồng biến trên khoảng

 

;1

B.Hàm số đã cho nghịch biến trên khoảng

 

0;3

C.Hàm số đã cho đồng biến trên khoảng

 

2;

D.Hàm số đã cho đồng biến trên khoảng

 

3; 

Câu 7:Cho hàm sô

 

y f x

có bảng biến thiên như hnh v.

Mệnh đề nào sau đây là đúng?

A.Hàm số đồng biến trên khoảng

 

3;4

B. Hàm số đồng biến trên khoảng

 

4;

∞

-6

∞

-2

∞

-1

∞

-1

∞

CĐ

-3

∞

Trang3

C.Hàm số nghịch biến trên khoảng

 

;4

.D.Hàm số nghịch biến trên khoảng

 

3;

Câu 8: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

 

0;

 

1;0

 

2;0

 

2; 

Câu 9:Cho hàm số

 

y f x

có bảng biến thiên như sau.

Khẳng định nào dưới đây đúng?

A.Hàm số đồng biến trên

 

1;1

B.Hàm số nghịch biến trên các khoảng

 

1;0

và

 

1; 

C. Hàm số đồng biến trên các khoảng

 

1;0

và

 

1; 

D.Hàm số đồng biến trên các khoảng

 

;1 

và

 

0;1

Câu 10: Cho hàm số

 

y f x

có bảng biến thiên như hnh v.

Hàm số

 

y f x

đồng biến trên khoảng nào sau đây?

 

0;3

 

1;3

 

1;2

 

0;

Câu 11: Cho hàm số có bảng biến thiên như sau:

Hàm số

 

y f x

đồng biến trên khoảng nào dưới đây?

 

;0

 

2;2

 

1;3

 

;2 

Câu 12: Cho hàm số

 

y f x

có bảng biến thiên như sau

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

 

5; 

 

3;0

 

2;4

 

5;2

Câu 13: Cho hàm số

 

y f x

có bảng xét dấu đạo hàm như

sau. Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng

 

;0 .

B. Hàm số nghịch biến trên khoảng

 

0;3 .

∞

-1

∞

Trang4

C. Hàm số đồng biến trên khoảng

 

2;0 .

D. Hàm số đồng biến trên khoảng

 

; 2 . 

Câu 14: Cho hàm số

 

có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới

đây?

 

;0

 

3; 

 

2;3

 

0;3

Câu 5: Hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào?

 

4; 

 

;0

 

;1





0;

Câu 16: Cho hàm số có bảng biến thiên như sau:

Hàm số đồng biến trên tập





;1

 

;0

 

;2 

 

1; 

Câu 17: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

 

2;1

 

1; 

 

;2 

 

1;0

Câu 18: Cho hàm số

 

có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới

đây?

 

2;2 .

 

0;2 .

 

2;0 .

 

2; .

Câu 19: Cho hàm số

 

y f x

có bảng biến thiên như sau:

Hàm số

 

nghịch biến trên khoảng nào dưới đây?

 

1;3

 

1;3

 

1;1

 

3;1

Trang5

Câu 20. Cho hàm số

()y f x

có bảng biến thiên như hnh v.

Mệnh đề nào sau đây đúng ?

A. Hàm số đã cho đồng biến trên khoảng

 

; 1 . 

B. Hàm số đã cho đồng biến trên khoảng

 

2; ,

C. Hàm số đã cho đồng biến trên khoảng

 

;2 .

D. Hàm số đã cho đồng biến trên

.

Câu 21. Cho hàm số

34y x x  

có bảng biến thiên sau, tìm

và

;2ab  

. B.

;4ab   

;1ab  

. D.

; 3.ab  

Câu 22.Cho hàm số

 

y f x

có bảng biến thiên như hnh v.

Khẳng định nào sau đây sai?

A. Hàm số nghịch biến trên khoảng

 

;1 

B. Hàm số nghịch biến trên khoảng

 

0;1

C. Hàm số đồng biến trên khoảng

 

2; 

D. Hàm số đồng biến trên khoảng

 

2; 

Câu 23: Cho hàm số

()y f x

có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (0,1) B.

( ;0)

(1; )

( 1;0)

2. Dạng 2: Đọc đồ thị hàm số

 

y f x

Cách giải: Hàm số

 

y f x

đồng biến trên khoảng

 

;ab

nếu đồ thị hàm số đi lên ( theo chiều từ trái sang

phải ) trên khoảng

 

;ab

Hàm số

 

y f x

nghịch biến trên khoảng

 

;ab

nếu đồ thị hàm số đi xuống ( theo chiều từ trái

sang phải ) trên khoảng

 

;ab

Bài tập:

Câu 1: Cho hàm số

 

y f x

có đồ thị là đường cong trong hình bên. Hàm số

đã cho nghịch biến trên khoảng nào dưới đây?

 

0;1

. B.

 

;0

 

0;

. D.

 

1;1

Trang6

Câu 2:Cho hàm số

 

y f x

có đồ thị là đường cong như hnh v. Hàm số đã cho đồng biến

trên khoảng nào dưới đây?

 

1;1

. B.

 

;0

 

0;1

. D.

 

0;

Câu 3: Cho hàm số

 

y f x

có đồ thị như hnh v. Hàm số đã cho đồng biến

trong khoảng nào?

 

1;0

 

2; 1

 

1;1

 

0;1

Câu 4: Cho hàm số bậc ba

 

y f x

có đồ thị như hnh bên. Hàm số đã

cho đồng biến trên khoảng nào, trong các khoảng dưới đây?

;









. B.

 

;1

 

0;1

. D.

 

1; 

Câu 5: Cho hàm số

 

y f x

xác định trên



và có đồ thị như hnh v .

Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới

đây?

 

;1

. B.

 

1;1

 

1; 

. D.

 

;1

Câu 6: Cho hàm số

 

y f x

có đồ thị như hnh v bên dưới

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

 

1;1

. B.

 

0;1

 

1; 

. D.

 

1;0

Câu 7: Cho hàm số y = f(x) có đồ thị như hnh v sau:

Khẳng định nào sau đây là đúng?

A.Hàm số đồng biến trên khoảng

 

; 

B.Hàm số nghịch biến trên

 

; 

C.Hàm số nghịch biến trên (; 0)

D.Hàm số đồng biến trên

󰇛

0; +

󰇜

Trang7

3. Dạng 3: Đọc đồ thị hàm số

 

'fx

Cách giải: Hàm số

 

y f x

đồng biến trên khoảng

 

;ab

nếu đồ thị hàm số

 

'fx

nằm phía trên trục

hoành

 

trên khoảng

 

;ab

Hàm số

 

y f x

nghịch biến trên khoảng

 

;ab

nếu đồ thị hàm số

 

'fx

nằm phía dƣới trục hoành

 

trên khoảng

 

;ab

Câu 1: Cho hàm số

 

xác định, liên tục trên



và có đồ thị của

hàm số

 

'fx

là đường cong như hnh v bên dưới. Hỏi khẳng định

nào đúng?

A. Hàm số

 

y f x

đồng biến trên khoảng

 

; 3 . 

B. Hàm số

 

y f x

nghịch biến trên khoảng

 

3; 2 .

C. Hàm số

 

y f x

đồng biến trên khoảng

 

2;0

D. Hàm số

 

y f x

nghịch biến trên khoảng

 

0;

4. Dạng 4: Tìm khoảng đơn điệu của hàm số

 

y f x

Cách giải :

Cách 1: Tự luận: Tính

 

''y f x

Lập bảng xét dấu của

 

''y f x

Căn cứ vào bảng xét dấu



kết luận.

Cách 2: Sử dụng máy tính cầm tay.

Câu 1: Hàm số

y x x x   

đồng biến trên:

 

;1 

và







 

;1 

và

 

2;









và

 

2;

;









Sử dụng máy tính:

qy1a2$Q)^4$+Q)qdpQ)+5$Q)rp2=

KQ:

50  

loại A, B

=p1a2= . KQ

  

Loại C. Chọn D

Câu 2: Hàm số







nghịch biến trên:



 

2;

 

;2

và

 

2;

 

;1 

và

 

1; 

Giải: Tập xác định của hàm số

 

\1D 



loại A, B, C. Chọn D

Trang8

Câu 3: Hàm số

  





đồng biến trên:

 

0;2

và

 

2;4

 

0;2

và

 

4;

 

;0

và

 

4;

 

;0

và

 

2;4

Sử dụng máy tính cầm tay ( Nhƣ câu 1)

Câu 4: Cho hàm số







. Phát biểu nào sau đây đúng?

A. Hàm số đồng biến trên khoảng

 

; 

B. Hàm số đồng biến trên mỗi khoảng

 

;1

và

 

1; 

C. Hàm số đồng biến trên khoảng

   

;1 1;  

D.Hàm số đồng biến trên khoảng

 

\1

Câu 5: Cho hàm số

3 3 2y x x x    

. Nhận định nào dưới đây là đúng ?

A. Hàm số nghịch biến trên

 

; 

B. Hàm số nghịch biến trên mỗi khoảng

 

;1

và

 

1; 

C. Hàm số nghịch biến trên khoảng

   

;1 1;  

D. Hàm số nghịch biến trên khoảng

 

\1

Câu 6: Cho hàm số







. Phát biểu nào sau đây đúng?

A. Hàm số nghịch biến trên các khoảng

 

0;2

và

 

2;3

B. Hàm số nghịch biến trên khoảng

 

1;3

C. Hàm số nghịch biến trên khoảng

   

1;2 2;3

D. Hàm số nghịch biến trên các khoảng

 

;1

và

 

3; 

Câu 7: Cho hàm số

3y x x

. Phát biểu nào sau đây sai?

A. Hàm số nghịch biến trên các khoảng

 

;0

và

 

2;3

B. Hàm số đồng biến trên khoảng

 

0;2

C. Hàm số nghịch biến trên khoảng

 

;2

và

 

2;3

D. Cả hai câu A và B đều kết luận đúng.

Câu 8: Cho hàm số

25y x x  

. Kết luận nào sau đây đúng?

A. Hàm số đồng biến với mọi x B. Hàm số nghịch biến với mọi x

C. Hàm số đồng biến trên khoảng

 

;1 

D. Hàm số đồng biến trên khoảng

 

1;0

và

 

1; 

Câu 9: Cho hàm số



. Kết luận nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng

 

;2

B. Hàm số đồng biến trên khoảng

 

2;

C. Hàm số đồng biến trên khoảng

 

2;2

D. Hàm số nghịch biến trên khoảng

 

2;2

Câu 10: Cho hàm số

y x x

. Hãy chọn khẳng định đúng?

A. Hàm số đồng biến trên khoảng

;



 





và nghịch biến trên khoảng

;









Trang9

B. Hàm số nghịch biến trên khoảng

;



 





và đồng biến trên khoảng

;









C. Hàm số đồng biến trên các khoảng

;



 





và

;









D.Hàm số nghịch biến trên các khoảng

;



 





và

;









Câu 11: Hàm số nào cho dưới đây đồng biến trên



2 2 2y x x x   

2 2 2y x x x    

2 16 31

y x x x    

2 3 9y x x  

Câu 12: Hàm số

2y x x  

nghịch biến trên khoảng















 

2;

 

1;2

Câu 13. Tìm tất cả các khoảng nghịch biến của hàm số

2 3.y x x  

( 1;0)

và

(1; ).

( ; 1) 

và

(0;1).

( 1;1).

( ; 1) 

và

(1; ).

Câu 14. Cho hàm số

2 3 1

y x x x    

Mệnh đề nào dƣới đây đúng?

A. Hàm số đồng biến trên khoảng

( ;1).

B. Hàm số nghịch biến trên khoảng

(1; ).

C. Hàm số nghịch biến trên khoảng

(1;3).

D. Hàm số đồng biến trên khoảng

(1;3).

Câu 15. Tìm các khoảng nghịch biến của hàm số







.\{2}R

( ;2)

và

(2; ).

( ;2).

Câu 16. Tìm các khoảng đồng biến hàm số

2 3 1.

y x x x   

( ;3).

(1; ).

(1;3).

( ;1)

và

(3; ).

Câu 17: Kết luận nào sau đây về tính đơn điệu của hàm số

2x 1







là đúng ?

A. Hàm số luôn luôn nghịch biến trên

 

R \ 1

B. Hàm số luôn luôn đồng biến trên

 

R \ 1

C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +)

D. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +).

Câu 18: Hàm số





nghịch biến trên khoảng nào

A. (-1; +∞). B. (-∞;0). C. [1; +∞). D. (1; +∞).

Câu 19: Hàm số

x 8x 7







đồng biến trên khoảng nào(chọn phƣơng án đúng nhất)

A. (-



;



)B. (

; +



) C. (-2;



) D. (-



;



) và ( ; +



)

Câu 20: Hàm số

y x 2x 1  

nghịch biến trên các khoảng nào sau đây?

A. (-



;0) B. (-



;

) C. (-



;1) D. (-



;



)

Trang10

Câu 21. Trong các hàm số sau, hàm số nào nghịch biến trên khoảng

( )

1;1-

. B.

31y x x= - +

. C.

. D.

Câu 22. Hàm số nào sau đây đồng biến trên

. B.

4 3 – 1y x x x= + +

– 2 – 1y x x=

. D.

y x x x= - + +

Câu 23. Hàm số nào sau đây đồng biến trên

yx=

. B.

. C.

3y x x=-

. D.

y x x x= - +

II. CỰC TRỊ CỦA HÀM SỐ

KIẾN THỨC CẦN NHỚ

1.Định nghĩa: Giả sử hàm số f xác định trên

 

KK 

và

xK

được gọi là điểm cực đại của hàm số f nếu tồn tại một khoảng

 

;a b K

chứa điểm

sao cho

       

, ; \ .f x f x x a b x  

Khi đó

 

được gọi là giá trị cực đại của hàm số f.

được gọi là điểm cực tiểu của hàm số f nếu tồn tại một khoảng

 

;a b K

chứa điểm

sao cho

       

, ; \ .f x f x x a b x  

Khi đó

 

được gọi là giá trị cực tiểu của hàm số f.

2.Điều kiện đủ để hàm số có cực trị:

Định lí 1: Giả sử hàm số fđạt cực trị tại điểm

. Khi đó, nếu f có đạo hàm tại điểm

thì

 

0.fx





Định lí 2:

a. Nếu

 



đổi dấu từ âm sang dương khi x đi qua điểm

(theo chiều tăng) th hàm số đạt cực tiểu tại điểm

b. Nếu

 



đổi dấu từ dương sang âm khi x đi qua điểm

(theo chiều tăng) th hàm số đạt cực đại tại điểm

Định lí 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng

 

;ab

chứa điểm

 

,0x f x





và f có đạo hàm cấp hai

khác 0 tại điểm

a) Nếu

 

0fx





thì hàm số f đạt cực đại tại điểm

b) Nếu

 

0fx





thì hàm số f đạt cực tiểu tại điểm

Nếu

 

0fx





th ta chưa thể kết luận được, cần lập bảng biến thiên hoặc bảng xét dấu đạo hàm.

Bảng tóm tắt các khái niệm

 

0 0 0

;M x f x

Điểm cực đại của

Giá trị cực đại(cực đại) của

Điểm cực đại của đồ thị hàm số

Điểm cực tiểu của

Giá trị cực tiểu(cực tiểu) của

Điểm cực tiểu của đồ thị hàm số

Điểm cực trị của

Cực trị của

Điểm cực trị của đồ thị hàm số

3.Quy tắc tìm cực trị của hàm số

3.1:Quy tắc 1: Lập bảng biến thiên hoặc bảng xét dấu

Trang11

Bước 1.Tìm

 



Bước 2. Tm các điểm

 

1,2,...

xi

tại đó đạo hàm bằng không hoặc hàm số liên tục nhưng không có đạo hàm.

Bước 3. Xét dấu

 



. Nếu

 



đổi dấu khi x qua điểm

thì hàm số đạt cực trị tại điểm

3.2:Quy tắc 2: Dùng định lý 3

Bước 1: Tìm

 



Bước 2: Tìm các nghiệm

 

1,2,...

xi

của phương trnh

 

0.fx





Bước 3: Tính

 



 Nếu

 





thì hàm số f đạt cực đại tại điểm

 Nếu

 





thì hàm số f đạt cực tiểu tại điểm

Nếu

 





thì ta lập bảng biến thiên để xác định điểm cực trị.

BÀI TẬP

1. Dạng 1: Đọc bảng biến thiên.

Câu 1. Cho hàm số có bảng biến thiên như sau:

Hàm số đã cho đạt cụrc đại tại

A. . B. C. . D.

Câu 2: Cho hàm số có bảng biến thiên như hnh v.

Tìm số điểm cực trị của hàm số.

A. 3. B. . C. 1. D. 2.

Câu 3: Hàm số liên tục trên và có bảng biến thiên

như hnh v.Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho có hai điểm cực trị.

B. Hàm số đã cho có đúng một điểm cực trị.

C. Hàm số đã cho không có giá trị cực tiểu.

D. Hàm số đã cho không có giá trị cực đại.

 

2x 

2.x 

1x 

1.x 

 

y f x

 

y f x

Điểm cực tiểu của đồ thị

hàm số

Điểm cực đại của đồ thị

hàm số

Giá trị cực tiểu

Giá trị cực đại

Điểm cực đại

Điểm cực tiểu

Điểm cực trị của hàm số

∞

( )

Trang12

Câu 4: Cho hàm số có bảng biến thiên như sau.

Giá trị cực đại của hàm số bằng

A. 1. B. 2. C. . D. 5.

Câu 5: Cho hàm số xác định, liên tục trên và có bảng biến thiên như hình v. Tìm giá trị cực đại

CĐ

và giá trị cực tiểu của hàm số đã cho

CĐ

y 

và . B.

CĐ

y 

và

CĐ

y 

và . D.

CĐ

y 

và

Câu 6: Cho hàm số có bảng biến thiên dưới đây.

Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số đạt cực đại tại

B. Hàm số đạt cực đại tại

C. Hàm số đạt cực đại tại

D. Hàm số đạt cực đại tại

Câu 7: Cho hàm số có bảng biến thiên như hnh v bên.

Mệnh đề nào dưới đây đúng?

A. Hàm số có điểm cực tiểu

B. Hàm số có điểm cực đại

C. Hàm số có điểm cực tiểu D. Hàm số có điểm cực tiểu

Câu 8: Cho hàm số có bảng biến thiên như hnh v.

Hỏi hàm số có bao nhiêu điểm cực trị?

A. Có một điểm. B. Có ba điểm.

C. Có hai điểm. D. Có bốn điểm.

Câu 9. Cho hàm số liên tục trên và có bảng biến

thiên như hnh v. Khẳng định nào sau đây là đúng?

A. Hàm số có giá trị cực tiểu bằng và bằng 1.

B. Hàm số đạt cực tiểu tại

C. Hàm số đạt cực đại tại

D. Hàm số có đúng hai điểm cực trị.

Câu 10.. Cho hàm số xác định, liên tục trên và có

bảng biến thiên như hnh v.Mệnh đề nào sau đây đúng?

A. Hàm số đạt cực đại tại và đạt cực tiểu tại

B. Hàm số có giá trị lớn nhất bằng và giá trị nhỏ nhất bằng

C. Hàm số có đúng một cực trị.

D. Hàm số có giá trị cực đại bằng 2.

Câu 11. Cho hàm số có bảng biến thiên như sau.

Hàm số đạt cực đại tại điểm nào trong các điểm sau đây?

A. . B. .

C. D.

Câu 12. Cho hàm số có bảng biến thiên như hnh

 

y f x

 

y f x

2y 

0.y 

0y 

2.y 

 

y f x

2.x 

2.x 

4.x 

3.x 

 

y f x

0.x 

5.x 

1.x 

1.x 

 

y f x

 

y f x

 

y f x

1

0.x 

 

y f x

2x 

1.x 

1.

 

y f x

2x 

3x 

2.x 

4.x 

 

y f x

Trang13

bên.

Chọn khẳng định sai.

A. Hàm số đạt cực đại tại

B. Hàm số có hai điểm cực trị.

C. Hàm số đạt cực tiểu tại

D. Hàm số có giá trị cực tiểu

Câu 13: Cho hàm số

 

y f x

xác định, liên tục trên



và có

bảng biến thiênnhư hnh v. Khẳng định nào sau đây là khẳng

định đúng?

A.Hàm số có đúng một cực trị.

B.Hàm số có giá trị cực tiểu bằng

C.Hàm số có giá trị lớn nhất bằng

và giá trị nhỏ nhất bằng

D.Hàm số đạt cực đại tại

0x 

và đạt cực tiểu tại

1x 

2. Dạng 2: Đọc đồ thị hàm số

Câu 1: Cho hàm số

a ( , , )y x bx cx d a b c    

có đồ thị như hnh v bên.

Số điểm cực trị của hàm số đã cho là

A. 2 B. 0 C. 3 D. 1

3. Dạng 3: Đọc bảng xét dấu hàm số

 

'fx

hoặc đồ thị hàm số

 

'fx

Chú ý: Qua

 

'fx

đổi dấu thì

là điểm cực trị của hàm số.

Câu 1: Cho hàm số

 

xác định và liên tục trên



,có đồ thị của hàm số

 

'fx

nhƣ hình vẽ. Hàm số

 

có bao nhiêu cực trị ?

A. 2. B. 3. C. 4. D. 5.

Câu2. Cho hàm số có bảng xét dấu của như sau:

Số điểm cực trị của hàm số đã cho là

A. 3. B. . C. 2. D. 1.

Câu 3. Cho hàm số xác định trên và

có bảng xét dấu của đạo hàm như sau:

Khi đó số điểm cực trị của hàm số là

A. 3. B. 2. C. 4. D. 1.

Câu 4. Cho hàm số có bảng xét dấu của

hàm đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là

A. 6. B. 4. C. 2. D. 3.

Câu 5. Cho hàm số liên tục trên và

0.x 

3.x 

3.y 

 



 

y f x

 

y f x

 

y f x

 

y f x

∞

-1

Trang14

có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho có bao nhiêu cực trị?

A. 3. B. 2. C. 1. D. 4.

Câu 6. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số

đã cho là

A. 3. B. 5. C. 2. D. 4.

Câu 7. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là

A. 2. B. 1. C. . D. 3.

Câu 8. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là

A. 3. B. 2. C. 5. D. 1.

Câu 9. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số là

A. 5. B. 2. C. 1. D. 3.

Câu 10.. Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho là

A. . B. 2. C. 3. D. 1.

Câu 11. Cho hàm số có . Số điểm cực trị của hàm số đã cho là

A. 2. B. 3. C. 4. D. 1.

Câu 12. Cho hàm số có đạo hàm , . Số điểm cực trị của hàm số đã cho là

A. . B. . C. . D. .

Câu 13. Cho hàm số liên tục trên

với bảng xét dấu đạo hàm như sau:

Số điểm cực trị của hàm số là.

A. . B.

C. . D. .

Câu 14. Cho hàm số . Hàm số có đồ thị như hnh v bên. Mệnh

đề nào dưới đây là đúng?

A.Hàm số đạt cực đại tại .

B.Hàm số có hai điểm cực trị.

C.Hàm số đạt cực tiểu tại .

D.Hàm số đạt cực tiểu tại .

Câu 15: Cho hàm số liên tục trên và có bảng xét dấu của như sau:

Số điểm cực đại của hàm số đã cho là

A. . B. . C. . D. .

Câu 16: Hàm số có đạo hàm trên khoảng . Cho đồ thị của

hàm số trên khoảng nhƣ sau:

Số điểm cực trị của hàm số trên K là:

 

        

2 3 4

1 2 3 4 ,f x x x x x



    

xR

 

       

2 3 4

1 2 3f x x x x x



  

 

    

12f x x x x  



 

y f x

    

1 2 ,f x x x x  



xR

 

y f x

     

12f x x x x  



 

    

12f x x x x  



 

   

'2f x x x

x

()y f x



()y f x

 

()y f x





 

0x 

 

1x 

 

1x 

 



( )

'fx

( )

'fx

( )



-

Trang15

A. 1 B. 2

C. 3 D. 4

4. Dạng 4:Tìm điểm cực trị của hàm số cụ thể

Thực hiện theo quy tắc tìm cực trị.

Sử dụng máy tính cầm tay.

Câu 1. Hàm số có

A. Ba điểm cực trị. B. Một điểm cực trị.

C. Không có điểm cực trị. D. Hai điểm cực trị.

Câu 2. Đồ thị hàm số nào sau đây có điểm cực trị.

A. . B. . C. . D. .

Câu 3. Số điểm cực trị của hàm số là.

A. . B. . C. . D. .

Câu 4. Cho ha



m sô . Tọa độ điểm cực đại của đồ thị hàm số là.

A. . B. . C. . D. .

Câu 5. Tm tọa độ điểm cực tiểu của đồ thị hàm số .

A. . B. . C. . D. .

Câu 6. Đồ thị hàm số có khoảng cách giữa hai điểm cực trị bằng.

A. . B. . C. . D. .

III. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ

KIẾN THỨC CẦN NHỚ

Cho hàm số

 

y f x

xác định trên tập D.

+) Số M được gọi là giá trị lớn nhất (GTLN) của hàm số

 

y f x

trên tập D nếu

 

f x M

với mọi

xD

và

tồn tại

xD

sao cho

 

f x M

Kí hiệu:

 

max

M f x

+) Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số

 

y f x

trên tập D nếu

 

f x m

với mọi

xD

và

tồn tại

xD

sao cho

 

f x m

Kí hiệu:

 

min

m f x

BÀI TẬP

Dạng 1: Tìm GTLN – GTNN của hàm số y = f(x) trên một khoảng

Bước 1. Tìm tập xác định (nếu đề chưa cho khoảng).

Bước 2. Tính

 



y f x

; tm các điểm mà đạo hàm bằng không hoặc không xác định.

Bước 3. Lập bảng biến thiên

Bước 4. Kết luận

Dạng 2: Tìm GTLN và GTNN của hàm số trên một đoạn

Bước 1. Tính

 



Bước 2. Tm các điểm

 

;

x a b

mà tại đó

 





hoặc

 



không xác định

 

1y x x

21y x x   

21y x x  

2 4 1y x x  

21y x x  

6 5 1y x x x   

y x x   

 

1; 2

 

1;2

 

1;2







32y x x  

 

1;4M

 

1;0M 

 

1;0M

 

1;4M 

32y x x  

Trang16

Bước 3. Tính

     

f a f x f b

Bước 4. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.

Khi đó

 

 

;

max

M f x

và

 

 

;

min

m f x

+) Hàm số

 

y f x

đồng biến trên đoạn [a; b] thì

   

max

min















f x f b

f x f a

+) Hàm số

 

y f x

nghịch biến trên đoạn [a; b] thì

   

max

min















f x f a

f x f b

Lƣu ý: Có thể dùng máy tính cầm tay để giải.

Bước 1. Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

 

y f x

trên miền (a; b) ta sử dụng máy tính Casio

với lệnh MODE 7

Bước 2. Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.

- Ta thiết lập miền giá trị của biến x Start a End b Step

ba

(có thể làm tròn để Step đẹp), hoặc chọn step 0,25

hay 0,5.

VÍ DỤ MẪU

Ví dụ 1. Cho hàm số

32   y x x

. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên [0; 3]. Giá

trị của

Mm

bằng

A. 8 B. 10 C. 6 D. 4

Hướng dẫn giải

Hàm số xác định và liên tục trên [0; 3]

Ta có

 

0 0; 3

0 3 6 0

2 0; 3







     









y x x

Khi đó

     

0 2, 2 6, 3 2  yyy

. Vậy

6; 2 8    M m M m

. Chọn A.

Sử dụng máy tính:

 

fx

pQ)qd+3Q)d+2=

Start0=

End 3=

Step 0.25=

Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.

Kết luận.

Ví dụ 2. Cho hàm số







. Giá trị của

 

2; 3

min max









bằng

A. 16 B.

Hướng dẫn giải

Ta có

 

0, 1





   



, do đó hàm số nghịch biến trên mỗi khoảng

   

; 1 ; 1;   

Hàm số nghịch

biến trên [2; 3].

Trang17

Do đó

 

 

 

 

2; 3

min 3 ; max 2 4

   y y y y

. Vậy

 

2; 3

5 89

min max 4



   





. Chọn D

Sử dụng máy tính:

 

fx

aQ)+2RQ)p1=

Start2=

End 3=

Step 0.25=

Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min.

Tính

 

2; 3

min max









. Kết luận.

Ví dụ 5. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số

4  y x x

Giá trị của biểu thức

P M m

bằng

 

2 2 1

 

2 2 1

21

21

Hướng dẫn giải

Tập xác định

 

2; 2D

.Ta có

 

1 , 2; 2





    



x x x

 

2 2; 2









    



   





y x x

   

2 2 2; 2 0; 2 2; 2 2      y y y y

Vậy

 

2 2, 2 2 2 2 2 2 1       M m P

. Chọn A

BÀI TẬP

Câu 1. Giá trị nhỏ nhất của hàm số trên đoạn bằng

A. 2. B.  . C.  . D. 

Câu 2. Gọi là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [1; 3]. Tính

A. 4. B. 9. C. 1. D. 5.

Câu 3. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [1; 3] bằng

A. . B. 20. C. 6. D.

Câu 4. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn bằng

A. 2. B. 3. C. 1. D. 4.

Câu 5. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số bằng

A. . B. 2. C. 1. D.

Câu 6. Giá trị nhỏ nhất của hàm số trên đoạn [1; 3] là

A. . B. . C. . D.

 

10 2f x x x  

 

1;2

 

1f x x

  

.Mm

 

f x x



31y x x   

 

0;2

2y x x  

22

2 2.

 

31f x x x  

 

[1;3]

min 3fx

 

[1;3]

min 6fx

 

[1;3]

min 37fx

 

[1;3]

min 5fx

Trang18

Câu 7. Gọi và là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập hợp

. Khi đó bằng

A. . B. . C. . D. −

Câu 8. Gọi lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn

. Khi đó tích bằng

A. . B. . C. . D.

Câu 9. Cho hàm số



. Giá trị nhỏ nhất của hàm số trên bằng

A. 2. B. . C. . D. 1.

Câu 10. Giá trị nhỏ nhất của hàm số là:

A. . B. 6. C. . D.

Câu 11. Giá trị lớn nhất của hàm số trên đoạn là

A. 11. B. 10.

C. . D. 15.

Câu 12. Giá trị lớn nhất của hàm số trên ] bằng

A. . B. . C. . D. 2.

Câu 13. Giá trị lớn nhất của hàm số trên đoạn [1; 3] bằng

A. . B. − . C. . D. 1.

Câu 14. Giá trị lớn nhất của hàm số trên đoạn bằng:

. B. 20.

. D.

Câu 15: Giá trị lớn nhất của hàm số trên đoạn bằng

A. . B. . C. . D. .

Câu 16: Giá trị nhỏ nhất của hàm số trên đoạn bằng

A. . B. . C. . D. .

Câu 17: Giá trị lớn nhất của hàm số trên đoạn bằng

A. . B. . C. . D. .

Câu 18: Giá trị lớn nhất của hàm số trên bằng

A. 4. B. 0. C. 20. D. –16.

Câu 19: Giá trị lớn nhất của hàm số trên đoạn bằng

A. . B. . C. . D. .

Câu 21: Giá trị nhỏ nhất của hàm số trên đoạn bằng











; 1 1;



   





T m M

22y x x x    









Mm

212

125

100

 

0;

18y x x  

32

6.

 

2 3 12 2f x x x x   

 

1;2



(0;3







2









155

( ) 3 2f x x x  

[ 3;3]

16

 

32f x x x  

 

3;3

16

 

3f x x x

 

3;3

18

2

 

32  f x x x

[ 3;3]

49y x x  

 

2;3

201

27x xy x+= -

[ ]

0;4

Trang19

A. . B. . C. . D. .

Câu 22: Giá trị nhỏ nhất của hàm số trên đoạn bằng

A. - 4. B. - 16. C. 0. D. 4.

Câu 23: Giá trị lớn nhất của hàm số trên đoạn bằng

A. . B. . C. . D. .

Câu 24: Tm giá trị nhỏ nhất m của hàm số trên đoạn

A. B. C. D.

Câu 25: Tm giá trị lớn nhất của hàm số trên đoạn

A. B. C. D.

IV. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ

KIẾN THỨC CẦN NHỚ

1. Định nghĩa

Đường thẳng

yy

được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số

 

y f x

nếu

 

lim





f x y

hoặc

lim





Đường thẳng

xx

được gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số

 

y f x

nếu ít nhất một trong các điều kiện sau được thỏa mãn:

   

lim ; lim





   

x x x x

f x f x

;

   

lim ; lim





   

x x x x

f x f x

DẠNG BÀI TẬP

Dạng 1. Xác định các đƣờng tiệm cận dựa vào định nghĩa

Ví dụ mẫu

Ví dụ 1: Cho hàm số

 

y f x

có

 

lim 3





và

 

lim 3





. Mệnh đề nào dưới đây đúng?

A.Đồ thị hàm số đã cho có hai tiệm cận ngang là

3y

và

3y

B.Đồ thị hàm số đã cho có hai tiệm cận ngang là

3x

và

3x

C.Đồ thị hàm số đã cho có đúng một tiệm cận ngang

D.Đồ thị hàm số đã cho không có tiệm cận ngang

Hướng dẫn giải

Vì

 

lim 3





nên

3y

là một đường tiệm cận ngang của đồ thị hàm số.

Vì

 

lim 3





nên

3y

là một đường tiệm cận ngang của đồ thị hàm số.

Chọn A

Dạng2. Xác định các đƣờng tiệm cận của đồ thị khi biết hàm số

Phƣơng pháp giải:Tiệm cận của đồ thị hàm số hữu tỷ

 



Điều kiện xác định

 

0gx

Tính các giới hạn

lim ; lim







nếu thỏa mãn định nghĩa của đường tiệm cận đứng và tiệm cận ngang thì kết

luận.

Chú ý:

259-

3y x x

 

4; 1

13y x x  

 

1; 2

7 11 2y x x x   

[0;2]

11m 

0m 

2m 

3m 

23y x x  

[0; 3]

9M 

83M 

1M 

6M 

Trang20

- Đối với hàm số phân thức hữu tỷ

 



với

   

1 1 0

... 0



     

n n n

f x a x a x a x a a

và

   

1 1 0

... 0



     

m m m

g x b x b x b x b b

Khi đó:

+ Nếu

nm

th đồ thị hàm số không có tiệm cận ngang.

+ Nếu

nm

th đồ thị hàm số có tiệm cận ngang là



+ Nếu

nm

th đồ thị hàm số có tiệm cận ngang là

0y

- Nếu đường thẳng

xx

là tiệm cận đứng của đồ thị hàm số thì

xx

là nghiệm của phương trnh

 

0gx

(ngƣợc lại nghiệm của

 

0gx

chƣa chắc đã là tiệm cận đứng của đồ thị).Hay nói cách khác

xx

là

các điểm gián đoạn của hàm số

- Điều kiện cần để đồ thị hàm số

 

y f x

có tiệm cận ngang là: Tập xác định của hàm số phải có khoảng vô

cực.

Tìm tiệm cận của đồ thị hàm số

, 0, 0



   



ax b

y c ad bc

cx d

Sử dụng máy tính cầm tay, với chức năng CALC

Câu 1. Tiệm cận ngang của đồ thị hàm số là

A. . B. . C. . D.

HD: Sử dụng máy tính

aQ)p2RQ)+1r99999999999999999=

KQ: 1



Chọn B.

Câu 2. Cho hàm số . Đường tiệm cận ngang của đồ thị hàm số trên là:

A. . B. . C. . D.

Câu 3. Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trnh?

A. . B. . C. . D.

Câu 4. Tm đường tiệm cận ngang của đồ thị hàm số

A. .B. . C. . D.

Câu 5. Đồ thị hàm số có tất cả bao nhiêu đường tiệm cận?

A. 2. B. . C. 1. D. 3.

Câu 6. Tm đường tiệm cận ngang của đồ thị hàm số

A. . B. . C. . D.

Câu 7. Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trnh nào dưới đây?

A. . B. . C. . D.







2y 

1y 

1x 

2.x 







4x 

2y 

4x 











5y 

0y 

1x 

1.y 







2y 

1x 

2x 

2.y 













1x 

2x 

2y 

2.y 





1x 

5y 

0x 

0.y 

Trang21

Câu 8. Đồ thị hàm số có các đường tiệm cận đứng, tiệm cận ngang lần lượt là

A. và . B. và C. và . D. và

aQ2)p3RQ)p1r9999999999999999=

KQ: 2



loại B, C.

=1 máy tính báo lỗi: Math ERROR



chọn A.

Câu 9. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số ?

A. . B. . C. . D.

Câu 10. Tiệm cận đứng của đồ thị hàm số là

A. . B. . C. . D.

Câu 11. Phương trnh các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số lần lượt là

A. và . B. và . C. và . D. và

Câu 12. Đồ thị hàm số có tiệm cận đứng là đường thẳng?

A. . B. . C. . D.

Câu 13. Hàm số nào có đồ thị nhận đuờng thẳng làm đường tiệm cận?

A. . B. . C. . D.

Câu 14. Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là

A. và . B. và . C. và . D. và

Dạng 3. Xác định các đƣờng tiệm cận của đồ thị hàm số dựa vào bảng biến thiên và đồ thị hàm số







1x 

2y 

2x 

1.y 

1x 

3y 

1x 

2.y 







2y 

y 

4y 

2.y 







2x 

2y 

3x 

3.y 







2x 

3y 

2y 

3x 

2x 

1y 

2x 

1.y 







3x 

2x 

2x 

3.x 

2x 









  













1x 

2y 

2x 

1y 

1x 

3y 

1x 

2.y 

Tcđ:

Tcn:

∞

( )

Trang22

Dựa vào bảng biến thiên của hàm số

 

y f x

xác định phƣơng trình các đƣờng tiệm cận đứng, tiệm cận

ngang, số các đƣờng tiệm cận của đồ thị hàm số

 

y f x

Chú ý: Nếu

ab

thì đồ thị hàm số có một đƣờng tiệm cận ngang.

Nếu

ab

thì đồ thị hàm số có hai đƣờng tiệm cận ngang.

Nếu











hoặc











thì đồ thị hàm số có một đƣờng tiệm cận ngang.

Nếu











thì đồ thị hàm số không có tiệm cận ngang.

Nếu cả hai bên

đều là số xác định ( không phải là



) thì đồ thị hàm số không có tiệm cận đứng.

Câu 1. Cho hàm số có bảng biến thiên như sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm

số đã cho là

A. B.

C. D.

Câu 2. Cho hàm số có bảng biến thiên. Đồ thị hàm

số có tiệm cận đứng là đường thẳng có phương trnh là

A. không tôn ta



i tiê



m câ



n đư



ng. B. .

C. . D. và .

Câu 3. Cho hàm số có bảng biến thiên sau. Hỏi

đồ thị hàm số đó có mấy tiệm cận.

A. . B. .

C. . D. .

Câu 4. Cho hàm số có bảng biến thiên như sau:

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho

là:

A. . B. .

C. . D. .

Câu 5. Cho hàm số có bảng biến thiên như sau:

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã

cho là

A. . B. .

C. . D.

 

y f x

()y f x

2x 

1x 

2x 

1x 

( )

y f x=

 

y f x

()y f x

f(x)

f'(x)

∞

Trang23

Câu 6. Cho hàm số có bảng biến thiên như sau.

Số đường tiệm cận ngang của đồ thị hàm số là

A. . B. .

C. . D. .

Câu 7. Cho hàm số xác định trên , liên tục trên

mỗi khoảng xác định và có bảng biến thiên như sau. Hỏi mệnh đề

nào dưới đây đúng?Số đường tiệm cận đư



ng của đồ thị hàm số là

A. . B. .

C. . D. .

Câu 8:Cho hàm số

 

y f x

có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là?

A.4. B.1.

C.2. D.3.

Câu 9:Cho hàm sô

 

y f x

có bảng biến thiên như hnh v.

Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là?

A.4. B.1.

C.2. D.3.

Câu 10:Cho hàm sô

 

y f x

có bảng biến thiên như hnh v.

Phương trnh đường tiệm cận ngang của đồ thị hàm số là:

1.x 

2.x 

1.y 

2.y 

Câu 11:Tổng số các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là

A. . B. 4. C.2. D.3.

Câu 12: Cho hàm số có bảng biến thiên như hnh v.

Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là

A. . B. .

C. . D. .

Câu 13:Đường thẳng là tiệm cận ngang của đồ thị hàm số nào

 

y f x

 

y f x

 

\1







 

y f x

2, 1xy

1, 2xy

1, 1xy

2, 2xy

2y 

∞

-1

∞

Trang24

sau đây?

A. . B. . C. . D. .

Câu 14:Số tiệm cận đứng của đồ thị hàm số

93x







là

A.3 B.2 C.0 D.1

Câu 15: Tiệm cận ngang của đồ thị hàm số







là

y 

. B.

4y 

. C.

1y 

. D.

1y 

Câu 16.Cho hàm số có bảng biến thiên sau:

Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:

A. 3. B. 1.

C. 2. D. 4.

V. NHẬN DẠNG ĐỒ THỊ HÀM SỐ

Bảng biến thiên và dạng đồ thị của hàm số bậc ba:

 

0.y ax bx cx d a    

Tập xác định:

D  

 

2 ' 2

' 3 2 0 ; 3

y ax bx c a b ac      

BẢNG BIẾN THIÊN

DẠNG ĐỒ THỊ

'0y 

có hai

nghiệm phân biệt

;xx

 

xx

Hệ số

0a 

'0y 

có hai

nghiệm phân biệt

;xx

 

xx

Hệ số

0a 





















()y f x

CĐ

∞

CĐ

∞

Trang25

'0y 

có nghiệm

kép

xx

Hệ số

0a 

'0y 

có nghiệm

kép

xx

Hệ số

0a 

'0y 

vô nghiệm

Hệ số

0a 

'0y 

vô nghiệm

Hệ số

0a 

Bảng biến thiên và dạng đồ thị của hàm số trùng phƣơng:

 

0.y ax bx c a   

Tập xác định:

D  

 

' 4 2 0 .y ax bx a  

BẢNG BIẾN THIÊN

DẠNG ĐỒ THỊ











∞

CĐ

∞

Trang26































Bảng biến thiên và dạng đồ thị của hàm số

 

0; 0 .

ax b

y c ad bc

cx d



   



Tập xác định:











Hàm số đồng biến trên

0.D ad bc  

Hàm số nghịch biến trên

0.D ad bc  

Đồ thị hàm số có tiệm cận ngang



tiệm cận đứng



BẢNG BIẾN THIÊN

DẠNG ĐỒ THỊ

0ad bc

∞

CĐ

∞

CĐ

∞

Trang27

0ad bc

Câu 1: Cho hàm số bậc ba:

 

0y ax bx cx d a    

có đồ thị nhƣ hình vẽ.Hãy

chọn mệnh đề đúng trong các mệnh đề sau.

0, 0, 0, 0.a b c d   

0, 0, 0, 0.a b c d   

0, 0, 0, 0.a b c d   

0, 0, 0, 0.a b c d   

Câu 2: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình

bên?

31y x x  

. B.

31y x x   

21y x x   

. D.

21y x x  

Câu3: Bảng biến thiên sau là của hàm số nào?

32y x x  

32y x x   

32y x x  

32y x x   

Câu 4: Đồ thị trong hnh v bên là của hàm số nào ?

34y x x  

34y x x   

34y x x  

34y x x   

Câu 5: Đồ thị sau đây là của hàm số nào ?

3 3 1y x x x   

31y x x   

31y x x  

31y x x   

∞

Trang28

Câu 6: Hnh v dưới đây là đồ thị của hàm số nào ?

32y x x   

43y x x   

32y x x  

43y x x  

Câu 7.Hàm số nào có đồ thị như hnh v .

)1(  xxy

)1(  xxy

)1(  xxy

)1(

 xxy

Câu 8. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

A. .

C. .

Câu 9.Đường cong trong hình v bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

Câu 10.

Đường cong trong hnh bên là đồ thị của hàm số nào dưới đây?

A. B.

C. D.

Câu 11.

Đường cong trong hình v bên là đồ thị của hàm số nào dưới đây?

A. . B.

C. . D.

3y x x

3.y x x  

2y x x

2.y x x  













1y x x  

3 1.y x x





















31y x x

3 1.y x x   

31y x x   

3 1.y x x

Trang29

Câu 12.

Đường cong trong hnh bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

Câu 13.

Đường cong trong hình v bên là đồ thị của hàm số nào dưới đây?

A. . B.

C. . D.

Câu 14.

Đường cong trong hình v bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

Câu 15:Đường cong trong hình v là đồ thị của hàm số nào dưới đây?

31y x x  

31y x x   

Câu 16. Đồ thị như hnh v là đồ thị của hàm số nào dưới đây?

A. . B.

C. D.

Câu 17

Đường cong trong hình v bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

32y x x   

2 1.y x x   

1y x x   

3 3.y x x   























21y x x  

2 1.y x x   

1y x x  

1.y x x   

34y x x  

3 4.y x x   

3 4.y x x  

3 4.y x x   

23y x x  

2 3.y x x  

23y x x   

Trang30

Câu 18.

Đường cong ở hnh bên là đồ thị của hàm số nào dưới đây. Hàm số đó là hàm số

nào?

A. .

C. .

Câu 20

Đường cong trong hnh bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

Câu 21.

Đường cong trong hnh bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

Câu 22

Đường cong trong hình v bên là đồ thị của hàm số

nào dưới đây?

A. . B.

C. . D.

Câu 23.

Đồ thị được cho ở hnh bên là đồ thị của hàm số nào dưới đây?

A. .

C. .

3 3.y x x  

32y x x  

3 2.y x x  

32y x x   

3 1.y x x  

3 2 1y x x  

2 3 1.y x x   

21y x x  

3 1.y x x   

1y x x  

4 1.y x x  

41y x x   

3 2 1.y x x x   



















31y x x   







31y x x  

2 1.y x x  

Trang31

VI. SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ

KIẾN THỨC CẦN NHỚ

Giả sử hàm số

 

y f x

có đồ thị là

 

;hàm số

 

y g x

có đồ thị là

 

Để tìm hoành độ giao

điểm của

 

và

 

,ta phải giải phƣơng trình

     

1f x g x

.Giả sử phƣơng trình

 

có

các nghiệm là

, ,...xx

Khi đó,các giao điểm của

 

và

 

là

 

1 1 1 2 2 2

; ; ; ;...M x f x M x f x

Vậy, số giao điểm của

 

và

 

là số nghiệm của phƣơng trình

     

1f x g x

BÀI TẬP

Câu 1.Cho hàm số có bảng biến thiên như sau:

Số nghiệm thực của phương trnh là:

A. 2.

B. 3.

C. 4.

D. 0.

Câu 2:Cho hàm số

 

y f x

có bảng biến thiên như sau:

Số nghiệm thực của phương trnh

 

2 3 0fx

là :

A. 4 B. 3

C. 2 D. 1

Câu 3: Cho hàm số

 

có bảng biến thiên như sau:

Số nghiệm thực của phương trnh

 

2 3 0fx

là :

. B.

. D.

()fx

3 ( ) 5 0fx

-2

∞

-2

∞

-2

∞

f(x)

f'(x)

Trang32

Câu 4:Cho hàm số

 

y f x

có bảng biến thiên như sau:

Số nghiệm thực của phương trnh

 

4fx

bằng:

A. 4. B. 3.

C. 2. D. 1.

Câu 5: Cho hàm số bậc ba có đồ thị là đường

cong trong hình bên. Số nghiệm thực của phương

trình là

A. . B. .

C. . D. .

Câu 6: Cho hàm số

 

y f x

có bảng biến thiên như sau

Số nghiệm thực của phương trnh

 

5 3 0fx

bằng :

A. 5. B. 4. C. 3. D. 2.

Câu 7:Cho hàm số

 

có bảng biến thiên như sau:

Số nghiệm thực của phương trnh

 

2 3 0fx

là :

A. 2. B. 1.

C. 4. D. 3.

Câu 8:Cho hàm số

a ( , , , )y x bx cx d a b c d    

. Đồ thị hàm số

()y f x

như hnh v bên.Số nghiệm thực của phương trnh

3 ( ) 4 0fx

là

A.3 B.0

C.1 D.2

 

y f x

 

1fx

-2

∞

-2

∞

-1

∞

f(x)

f'(x)

Trang33

Câu 9. Cho hàm số bậc bốn có đồ thị trong hình bên.

Số nghiệm của phương trnh là

A. 3. B. 2.

C. 1. D. 4.

Câu 10. Cho hàm số bậc bốn có đồ thị như hnh v.

Số nghiệm của phương trnh bằng

A. 1. B. 2.

C. 3. D. 4.

Câu 11. Cho hàm số liên tục trên và có bảng biến thiên

như sau. Số nghiệm của phương trnh là

A. 1. B. 2.

C. D. 3.

Câu 12. Cho hàm số có đồ thị như hnh v.

Số nghiệm của phương trnh là

A. 3. B. 1.

C. 2. D.

Câu 13. Cho hàm số có bảng biến thiên như hnh v

bên.Số nghiệm của phương trnh là

A. 1. B. 2.

C. 4. D. 3.

 

y f x

 

1fx

 

y f x

 

3 8 0fx

 

y f x

 

2 3 0fx

 

2 3 0fx

 

y f x

 

1fx

-1

∞

-1

∞

f(x)

f'(x)

Trang34

Câu 14. Cho hàm số có bảng biến thiên như sau:

Số nghiệm của phương trnh là:

A. 4. B.

C. 3. D. 2.

Câu 15.Cho hàm số có đồ thị như hnh v.

Tìm tất cả các giá trị thực của tham số để phương trnh có

bốn nghiệm thực phân biệt.

A. B.

C. D.

Câu 16. Cho hàm số có bảng biến thiên như

hình v:

Tìm tất cả các giá trị của để phương trnh có

3 nghiệm phân biệt.

A. . B. .

C. . D.

Câu 17. Cho hàm số có đồ thị như hnh v.

Số nghiệm của phương trnh là

A. 3. B. 1.

C. 2. D. 4.

Câu 18. Cho hàm số liên tục trên và có đồ thị như hnh bên.

Phương trnh có bao nhiêu nghiệm thực phân biệt?

A. 1. B. 2.

C. 3. D. 4.

Câu 19. Đồ thị ở hình bên là của hàm số .

Với giá trị nào của th phương trnh có ba nghiệm phân biệt?

A. . B. .

C. D.

 

y f x

 

2 5 0fx

21y x x   

21x x m   

1 2.m

1.m 

2.m

1 2.m

 

y f x

 

f x m

21m  

2 m

21m  

2 1.m  

 

y f x ax bx c   

 

2 3 0fx

 

y f x

 





23y x x  

20x x m  

3m 

4m 

0.m 

4.m 

Trang35

Câu 20.Cho hàm số xác định, liên tục trên và có

bảng biến thiên như hnh v.

Số nghiệm của phương trnh là

A. 2. B. .

C. 1. D. 3.

Câu 21. Cho hàm số có bảng biến thiên như hnh v.

Số nghiệm của phương trnh là

A. 1. B. 2.

C. 3. D.

Câu 22. Cho hàm số có đồ thị hàm số như hnh

v. Với giá trị nào của tham số phương trnh

có hai nghiệm phân biệt?

A. . B.

C. . D.

 

y f x

 

20fx

 

y f x

 

20fx

23y x x  

2 3 2 4x x m   











m











m 

Bấm Tải xuống để xem toàn bộ.

| 1/35

| | Tải xuống

Preview text:

CHƢƠNG I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
I. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
KIẾN THỨC CẦN NHỚ:
1. Hàm số y  f  x đồng biến trên khoảng  ;
a b  f ' x  0, x   ; a b.
Hàm số y  f  x đồng biến trên khoảng  ;
a bthì nó đồng biến trên mọi khoảng con của khoảng  ;ab.
2.Hàm số y  f  x nghịch biến trên khoảng  ;
a b  f ' x  0, x   ; a b.
Hàm số y  f  x nghịch biến trên khoảng  ;
a bthì nó nghịch biến trên mọi khoảng con của khoảng  ; a b. DẠNG BÀI TẬP:
1. Dạng 1: Đọc bảng biến thiên:
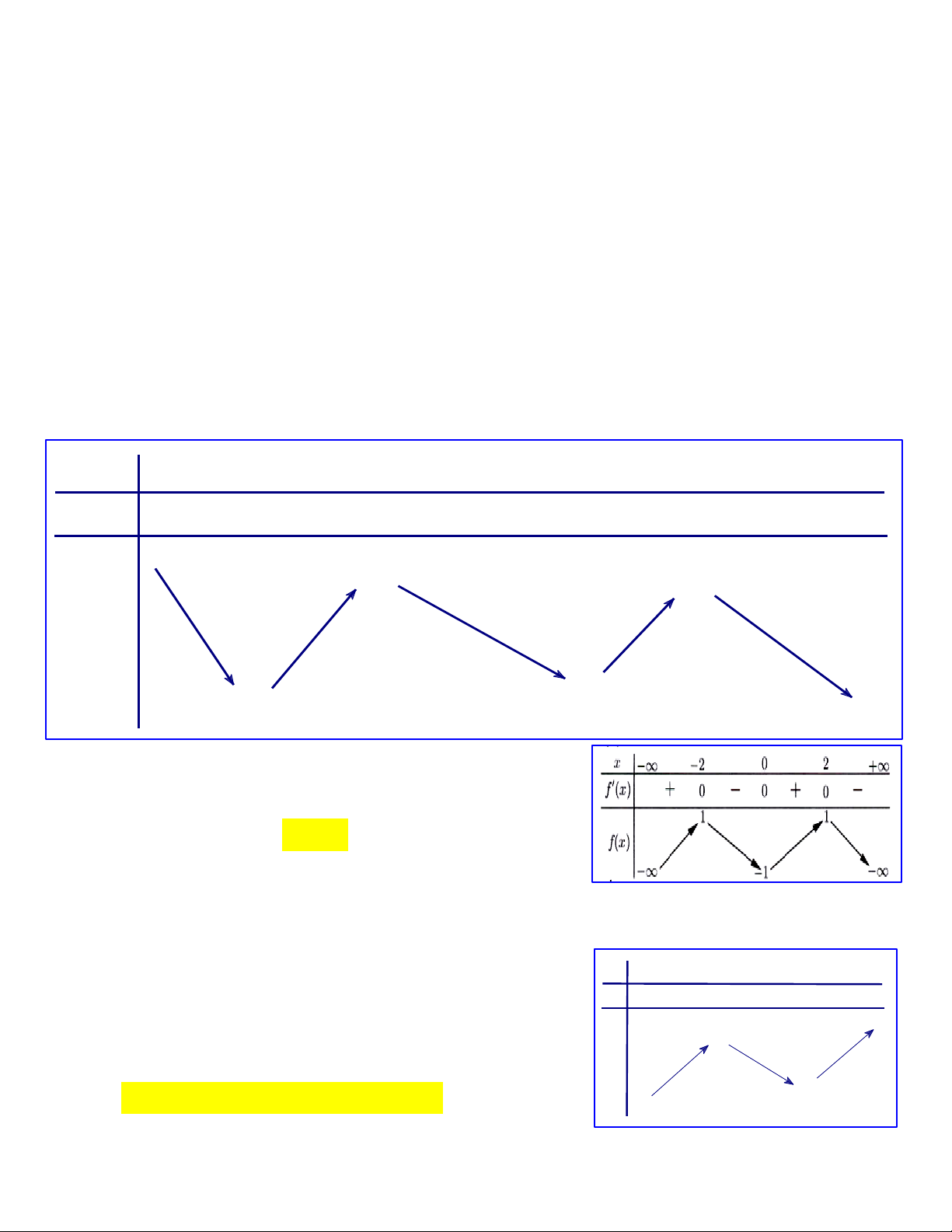
Cách giải: Căn cứ vào bảng biến thiên, chỉ ra khoảng đồng biến, nghịch biến của hàm số. x -∞ x1 x2 x3 x x 4 5 +∞ f'(x) - 0 + 0 - - 0 0 + 0 - +∞ f(x) y2 y5 y y4 1 -∞ Bài tập:
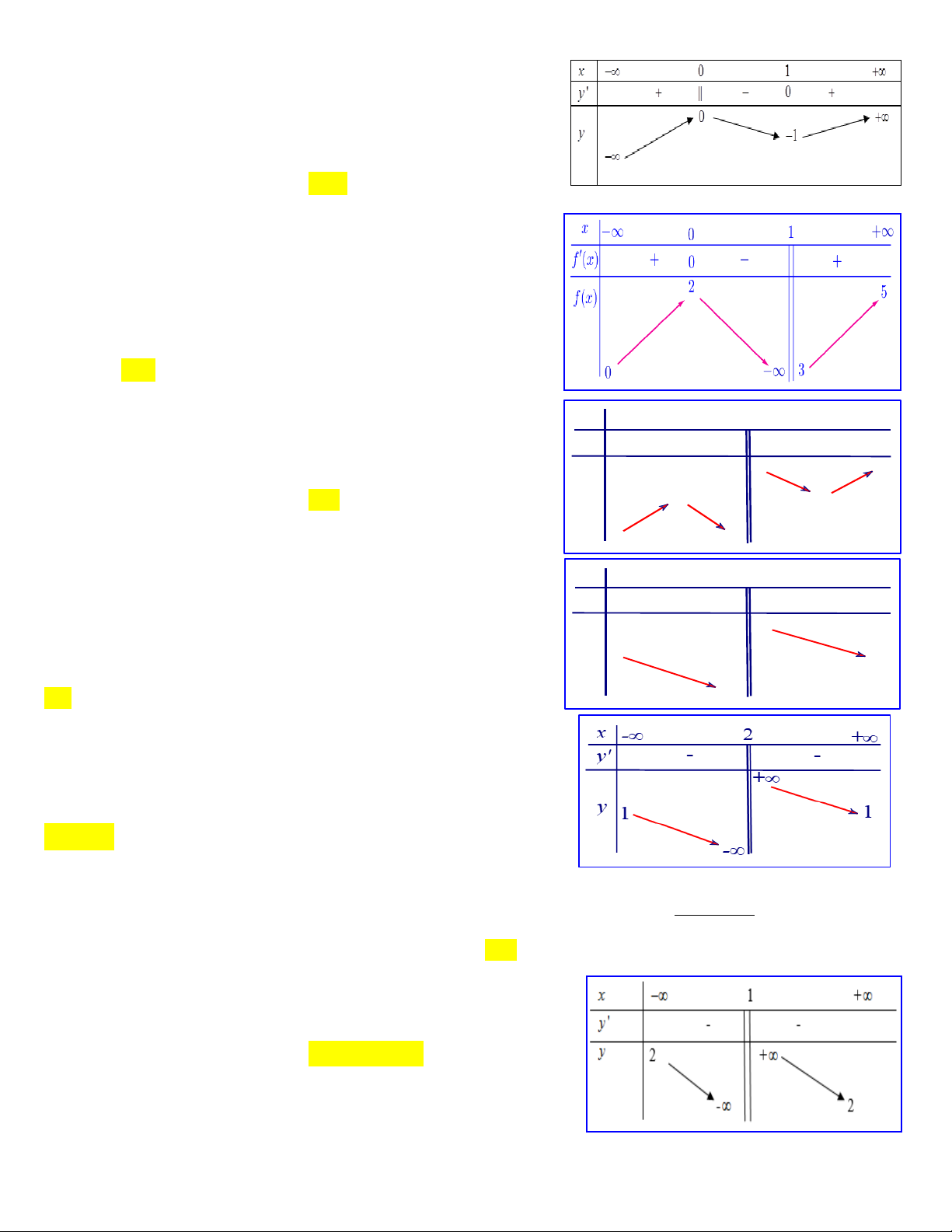
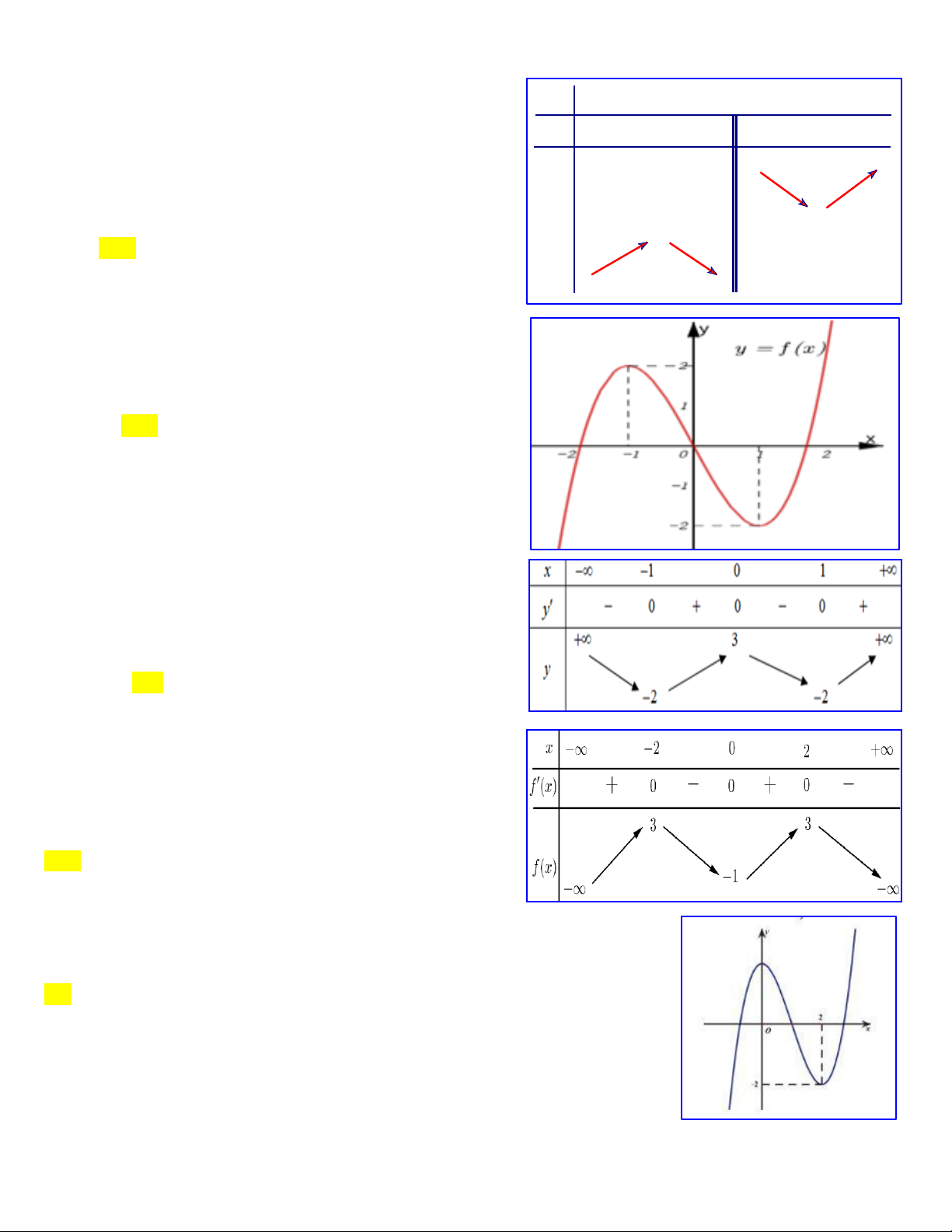
Câu 1:Cho hàm số f  x có bảng biến thiên như sau:
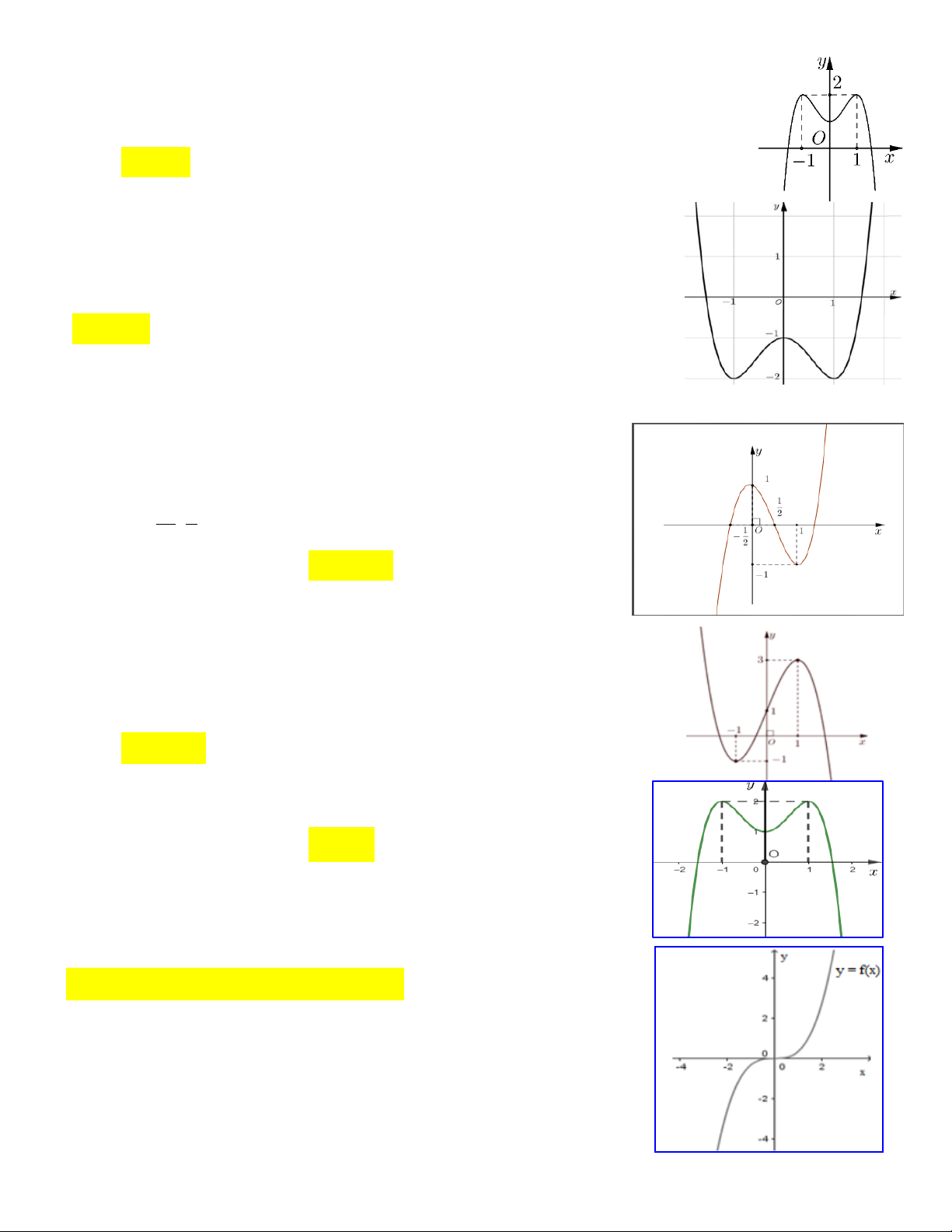
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới đây? A.  2  ;2. B. 0; 2. C.  2  ;0.
D. 2; . Câu 2:
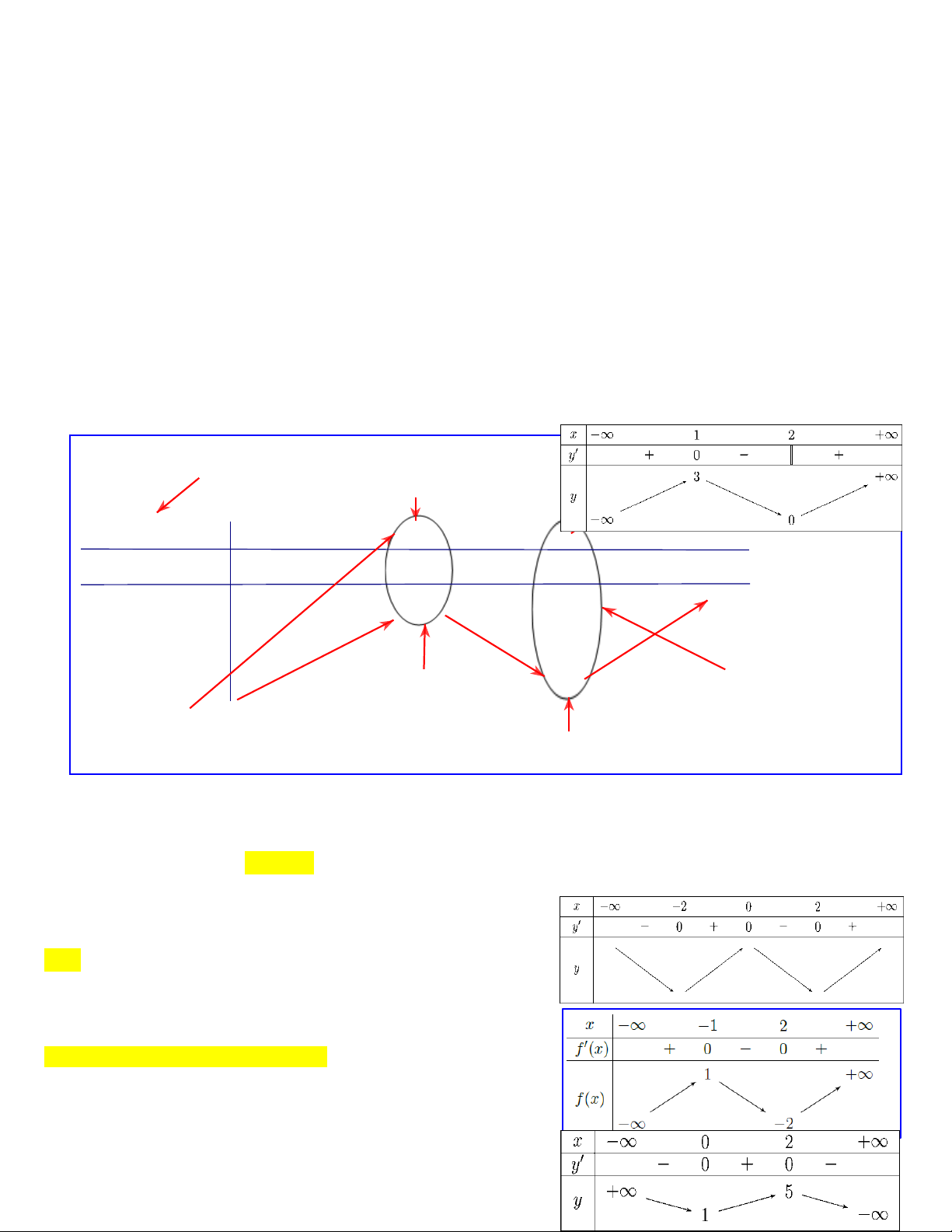
Cho hàm số y  f (x) có bảng biến thiên như sau:
Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;    1 và nghịch biến
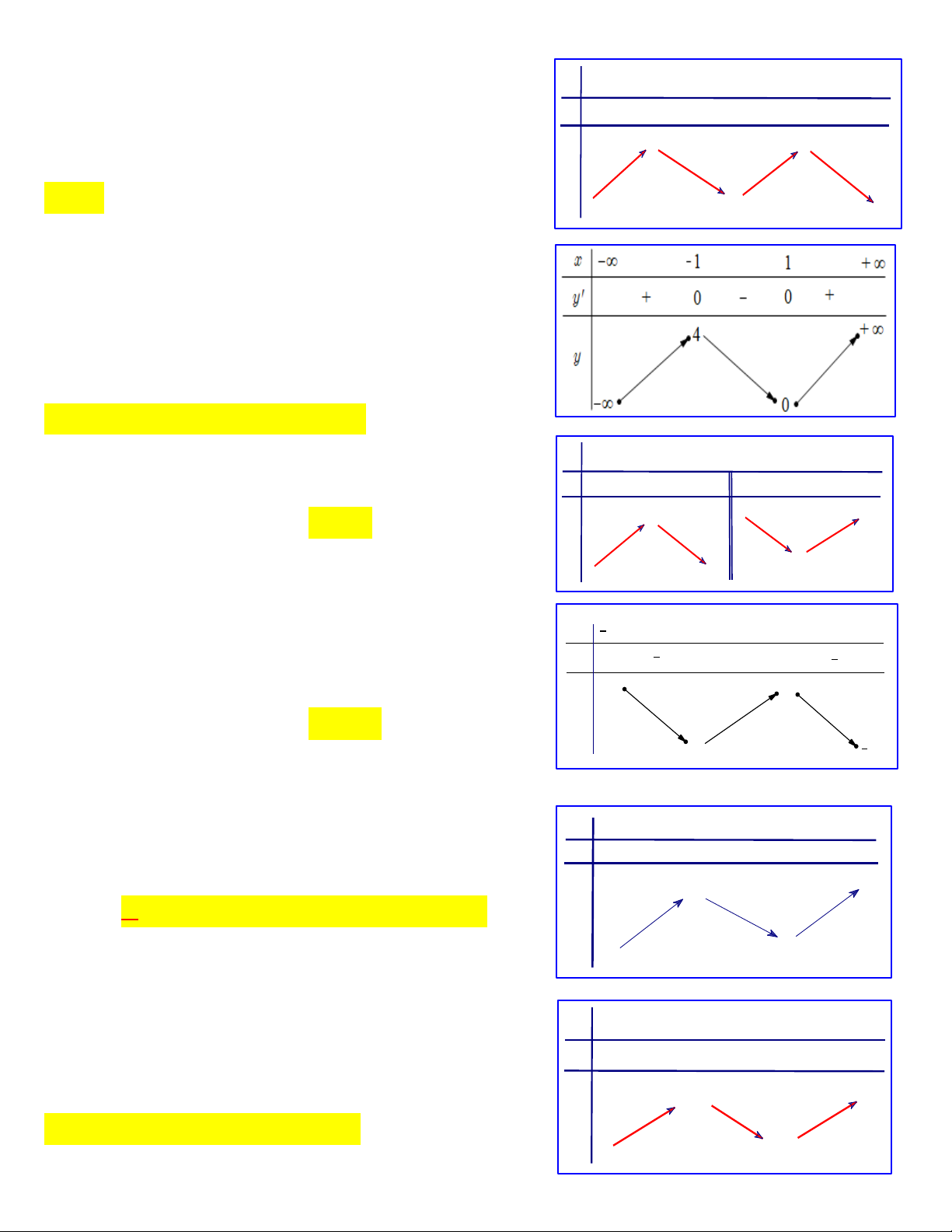
trên khoảng 1;  . x -∞ -1 1 +∞ y' + 0 - 0 +
B. Hàm số đồng biến trên khoảng (; ). +∞
C. Hàm số nghịch biến trên khoảng  ;    1 và đồng biến 2 y
trên khoảng 1;  -2
D.Hàm số nghịch biến trên khoảng  1   ;1 . -∞ Trang1
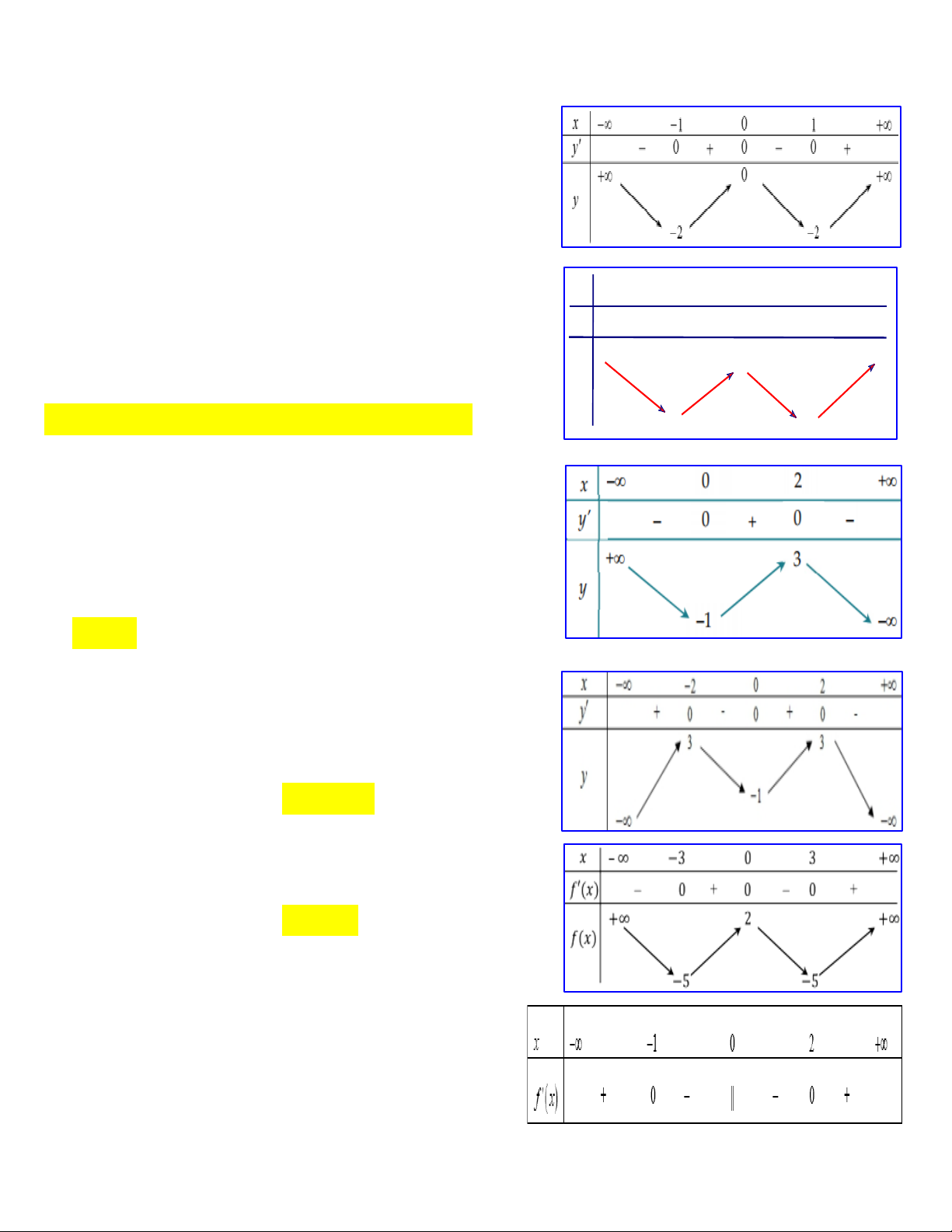
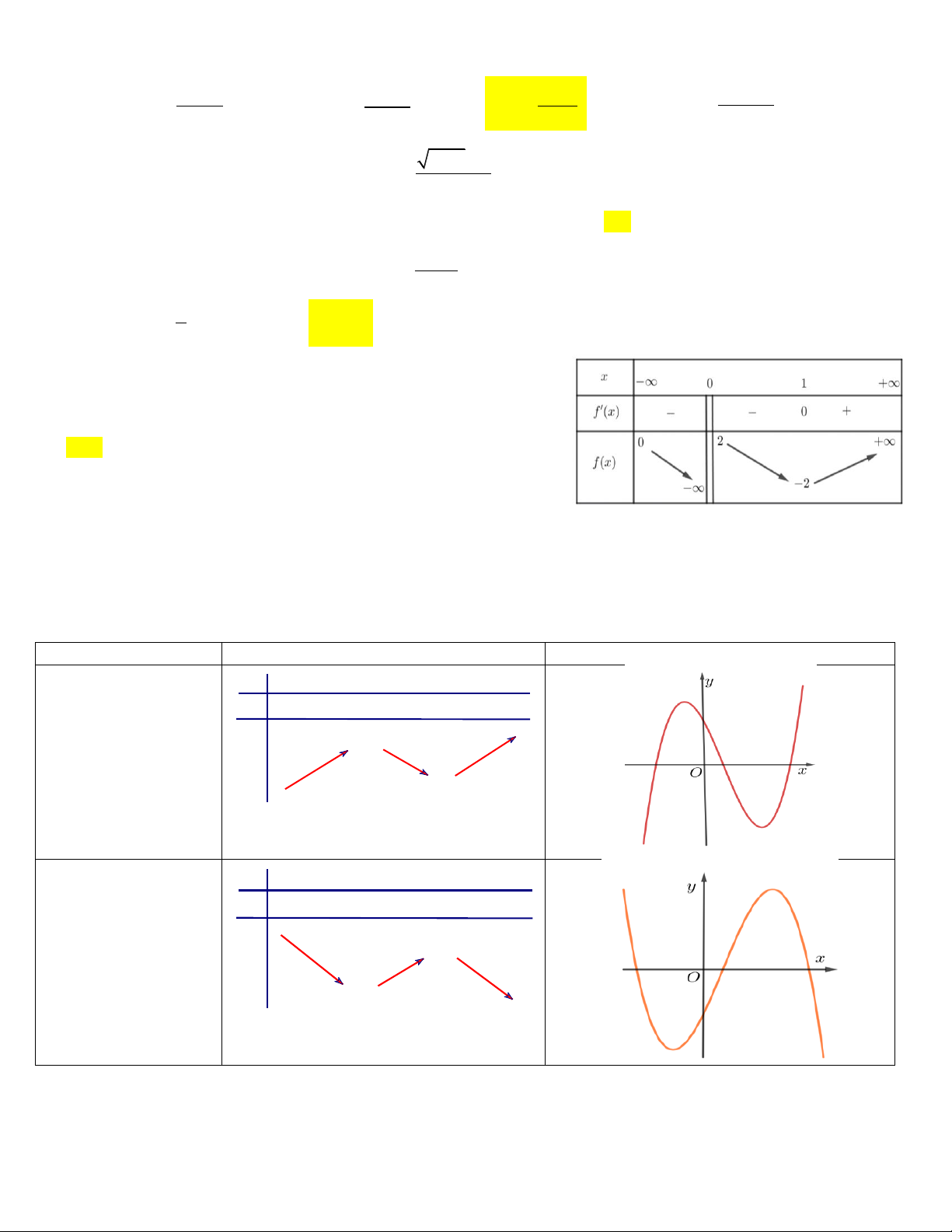
Câu 3: Cho hàm số y  f x có bảng biến thiên như sau: x -∞ -1 0 1 +∞
Hàm số y  f x đồng biến trên khoảng nào dưới đây? y' + 0 - 0 + 0 - A.  1  ;0 B. 1;  1 1 y C. 0;  1 D.  ;0   0 -∞ -∞
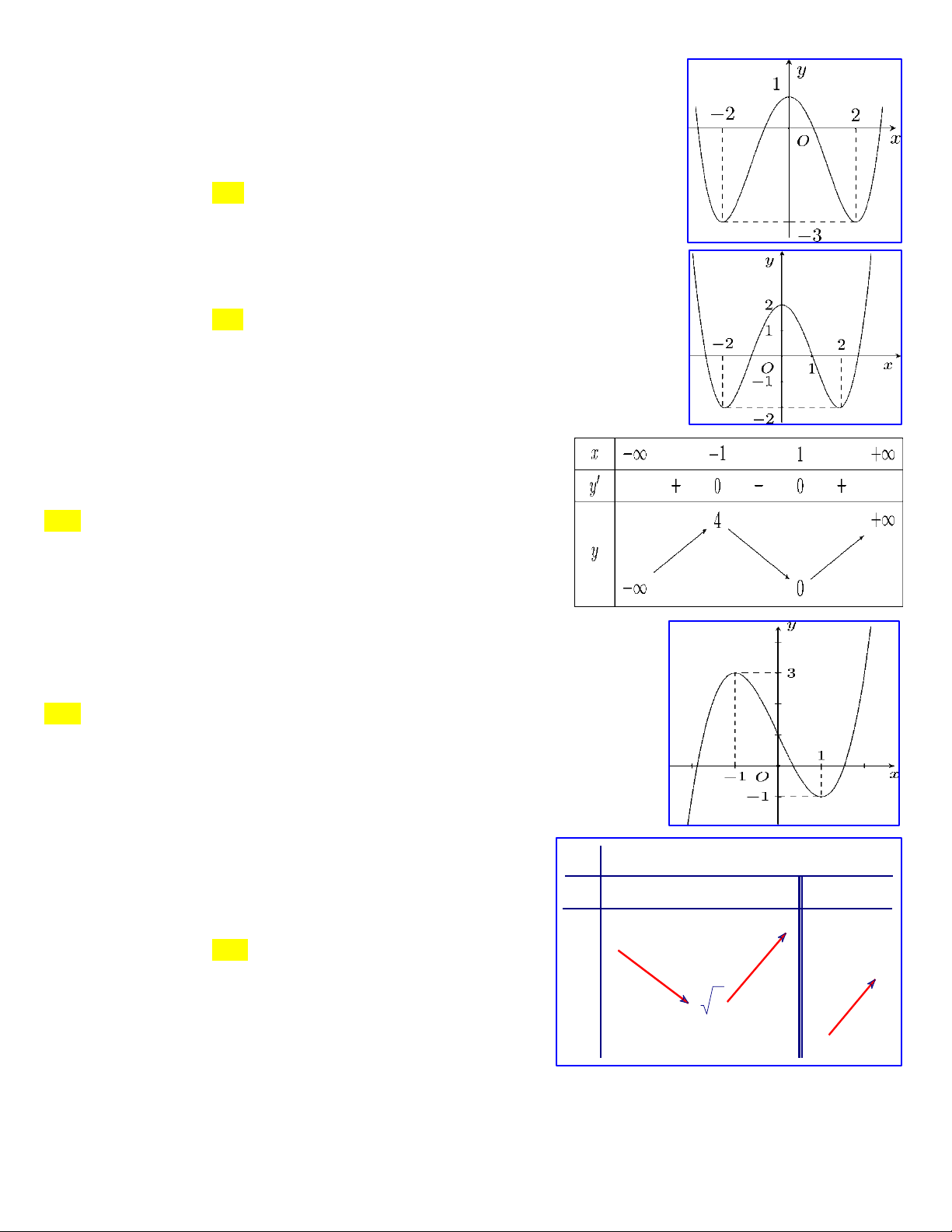
Câu 4: Cho hàm số y  f x có bảng biến thiên như hình bên.
Mệnh đề nào sau đây đúng?
A.Hàm số nghịch biến trên khoảng  ;    1 .
B.Hàm số nghịch biến trên khoảng 1;  .
C.Hàm số đồng biến trên khoảng  1   ;1 .
D.Hàm số nghịch biến trên khoảng  1   ;1 .
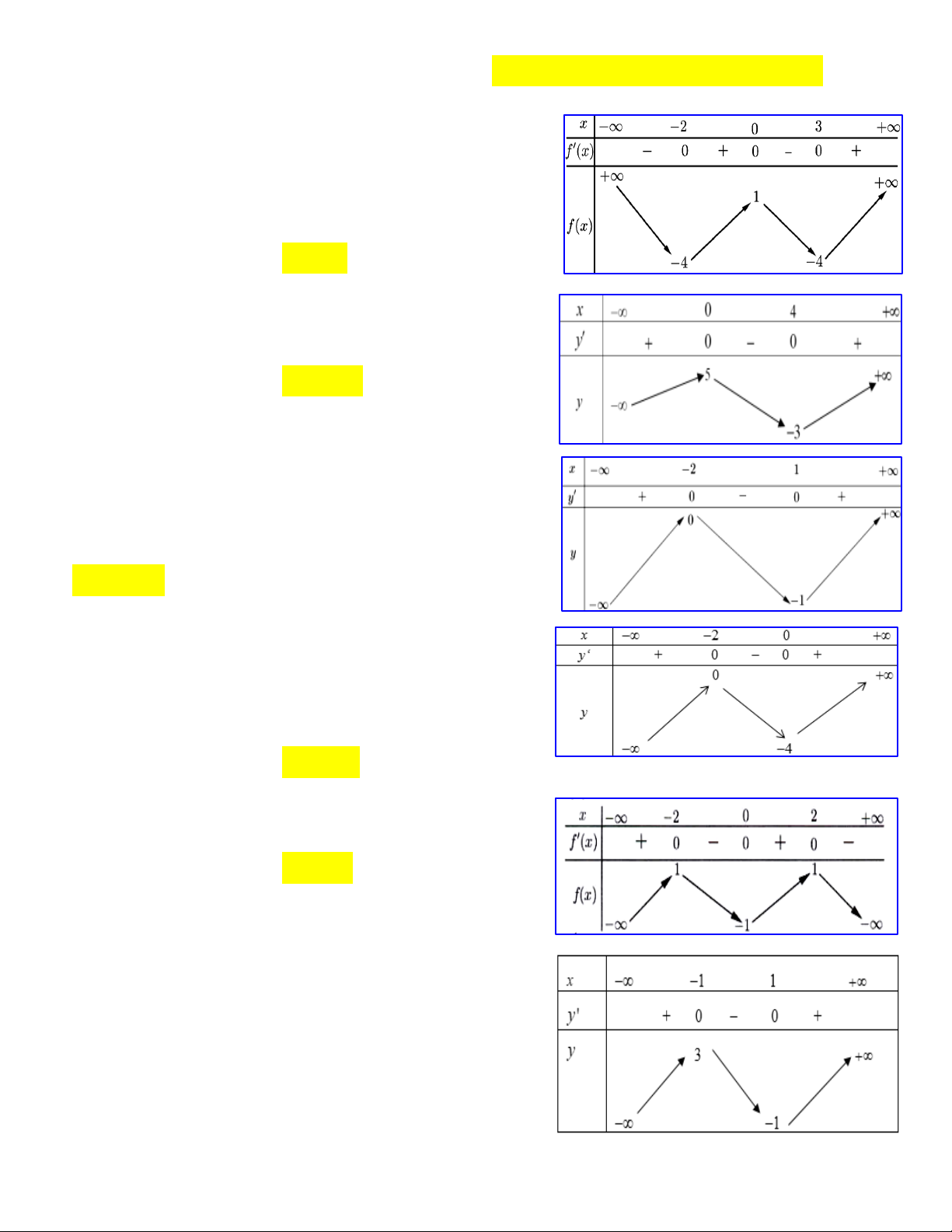
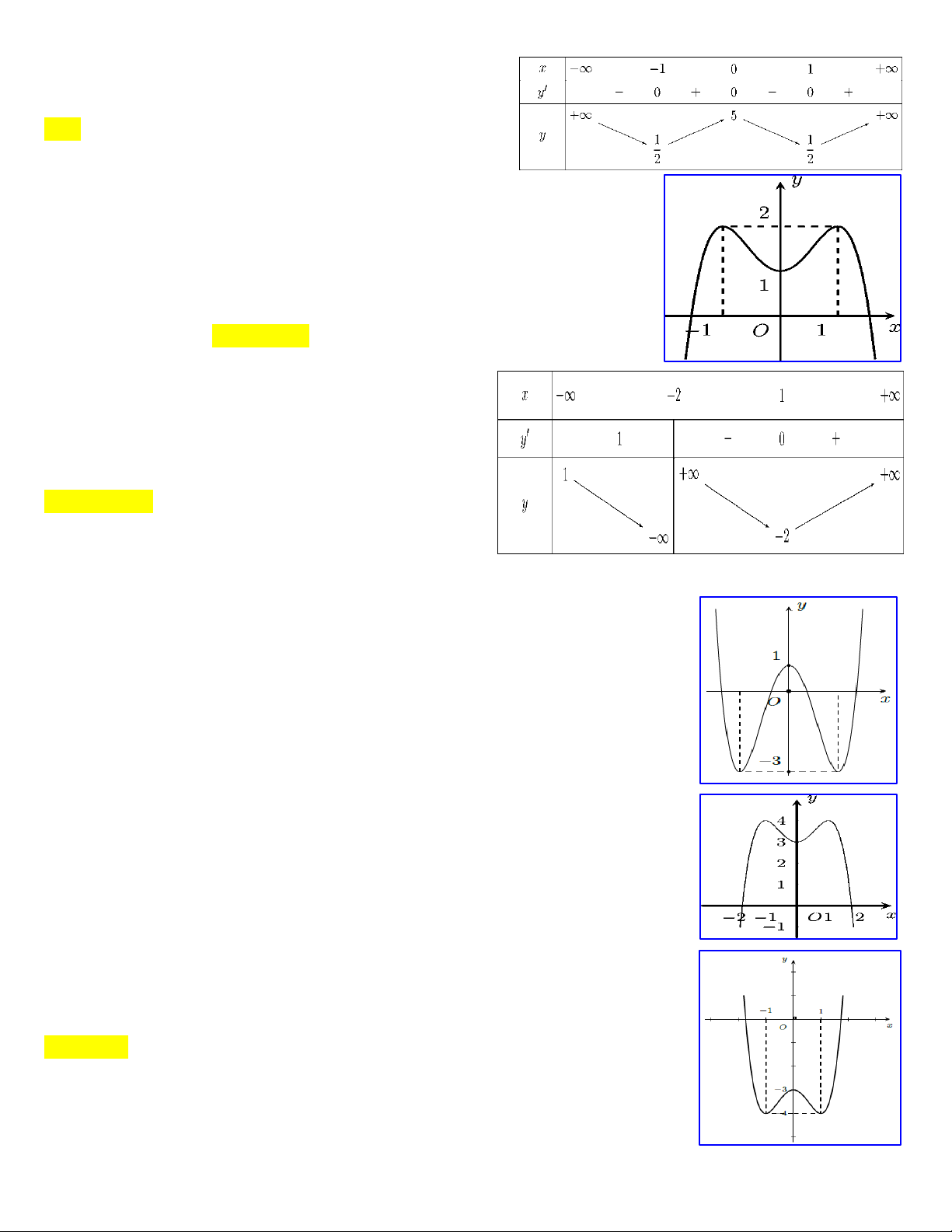
Câu 5:Cho hàm số y  f  x có bảng biến thiên như sau: x -∞ -1 0 1 +∞
Hàm số nghịch biến trong khoảng nào y' + 0 - - + dưới đây? 0 +∞ +∞ A.  1   ;1 . B. 0;  1 . 2 y C. 4;  . D.  ;  2 . 4 -∞ -∞
Câu 6:Cho hàm số y  f  x có bảng biến thiên: x ∞ 1 1 + ∞
Hàm số đồng biến trên khoảng nào dưới đây? y' 0 + 0 A.  ;    1 . B.  ;    1 và 1; . + ∞ -2 y C. 1;  . D.  1   ;1 . -6 ∞
Câu 6:Cho hàm số y  f  x có bảng biến thiên như hình vẽ. x -∞ 1 2 +∞
Mê ̣nh đề nào sau đây là sai? y' + 0 - 0 +
A.Hàm số đã cho đồng biến trên khoảng   ;1  . +∞ 3 y
B.Hàm số đã cho nghịch biến trên khoảng 0;3 .
C.Hàm số đã cho đồng biến trên khoảng 2;  . 0 -∞
D.Hàm số đã cho đồng biến trên khoảng 3;  .
Câu 7:Cho hàm số y  f  x có bảng biến thiên như hình vẽ. x -∞ -3 4 +∞
Mệnh đề nào sau đây là đúng? y' + - 0 0 +
A.Hàm số đồng biến trên khoảng  3  ;4. CĐ +∞ y
B. Hàm số đồng biến trên khoảng 4;  . CT -∞ Trang2
C.Hàm số nghịch biến trên khoảng  ;
 4 .D.Hàm số nghịch biến trên khoảng  3;   .
Câu 8: Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. 0;  B.  1  ;0 C.  2  ;0 D.  2;  
Câu 9:Cho hàm số y  f  x có bảng biến thiên như sau. x -∞ -1 0 1 +∞
Khẳng định nào dưới đây đúng? y' - 0 + 0 - 0 +
A.Hàm số đồng biến trên  1   ;1 . +∞ +∞ y 3
B.Hàm số nghịch biến trên các khoảng  1  ;0 và 1;
C. Hàm số đồng biến trên các khoảng  1
 ;0 và 1; . 0 0
D.Hàm số đồng biến trên các khoảng  ;    1 và 0;  1 .
Câu 10: Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Hàm số y  f x đồng biến trên khoảng nào sau đây? A. 0;3
B. 1;3 C. 1; 2
D. 0; 
Câu 11: Cho hàm số có bảng biến thiên như sau:
Hàm số y  f x đồng biến trên khoảng nào dưới đây? A.  ;0   B.  2  ;2
C. 1;3 D.  ;  2  
Câu 12: Cho hàm số y  f  x có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  5;   B.  3  ;0 C. 2; 4 D.  5  ;2
Câu 13: Cho hàm số y  f  x có bảng xét dấu đạo hàm như
sau. Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng  ;  0.
B. Hàm số nghịch biến trên khoảng 0;3. Trang3
C. Hàm số đồng biến trên khoảng  2  ;0.
D. Hàm số đồng biến trên khoảng  ;  2  .
Câu 14: Cho hàm số f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A.  ;0  
B. 3;  C.  2  ;3 D. 0;3
Câu 5: Hàm số y  f  x có bảng biến thiên như sau:
Hàm số đồng biến trên khoảng nào? A.  4;   B.  ;0   C.   ;1 
D. 0; 
Câu 16: Cho hàm số có bảng biến thiên như sau:
Hàm số đồng biến trên tập A.   ;1  B.  ;0   C.  ;  2   D.  1  ;
Câu 17: Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 2;  1
B. 1;  C.  ;  2   D.  1  ;0
Câu 18: Cho hàm số f  x có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào, trong các khoảng dưới đây? A.  2  ;2. B. 0; 2. C.  2  ;0.
D. 2; .
Câu 19: Cho hàm số y  f  x có bảng biến thiên như sau:
Hàm số f  x nghịch biến trên khoảng nào dưới đây? A. 1;3
B. 1;3 C.  1   ;1 D.  3   ;1 Trang4
Câu 20. Cho hàm số y  f (x) có bảng biến thiên như hình vẽ.
Mệnh đề nào sau đây đúng ?
A. Hàm số đã cho đồng biến trên khoảng  ;    1 .
B. Hàm số đã cho đồng biến trên khoảng 2; ,
C. Hàm số đã cho đồng biến trên khoảng  ;  2.
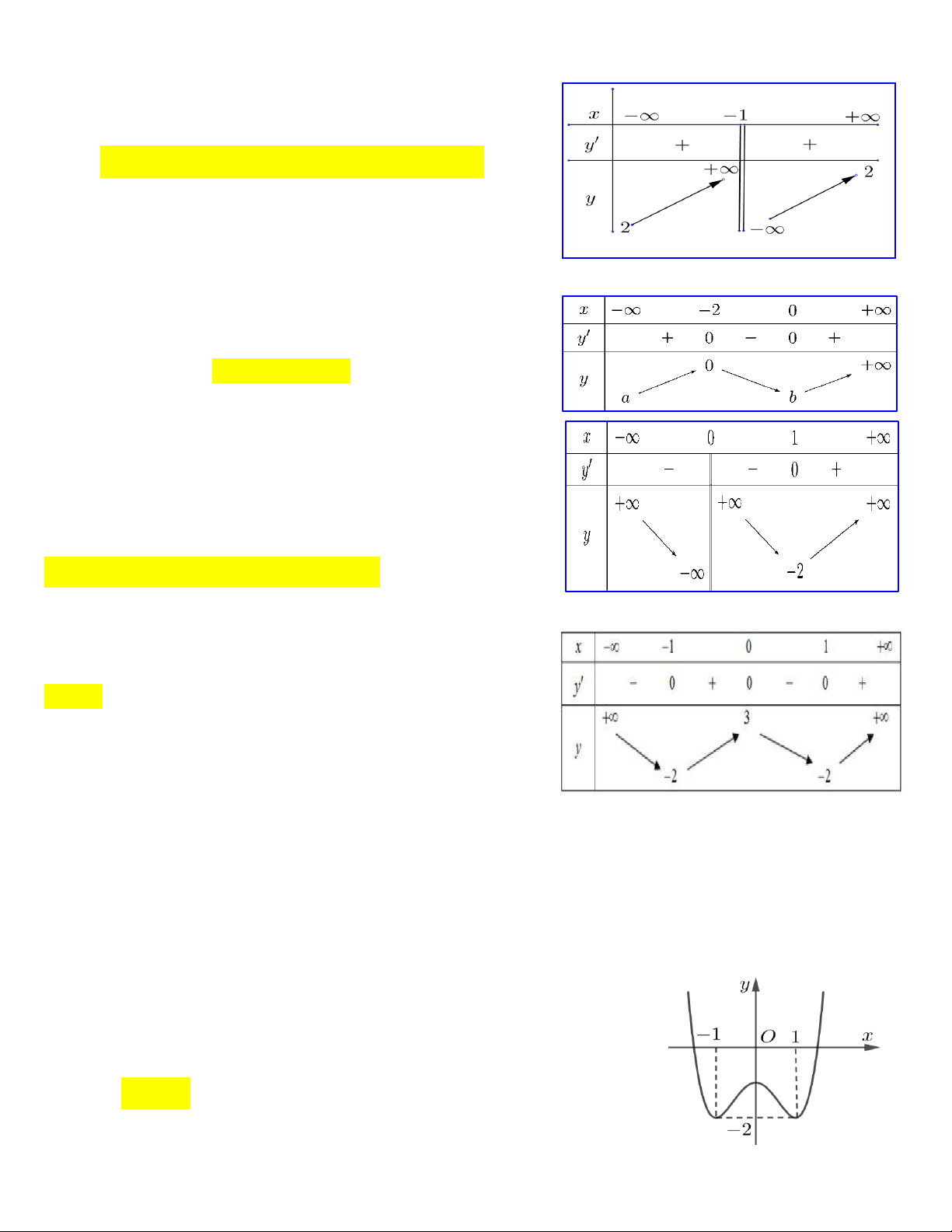
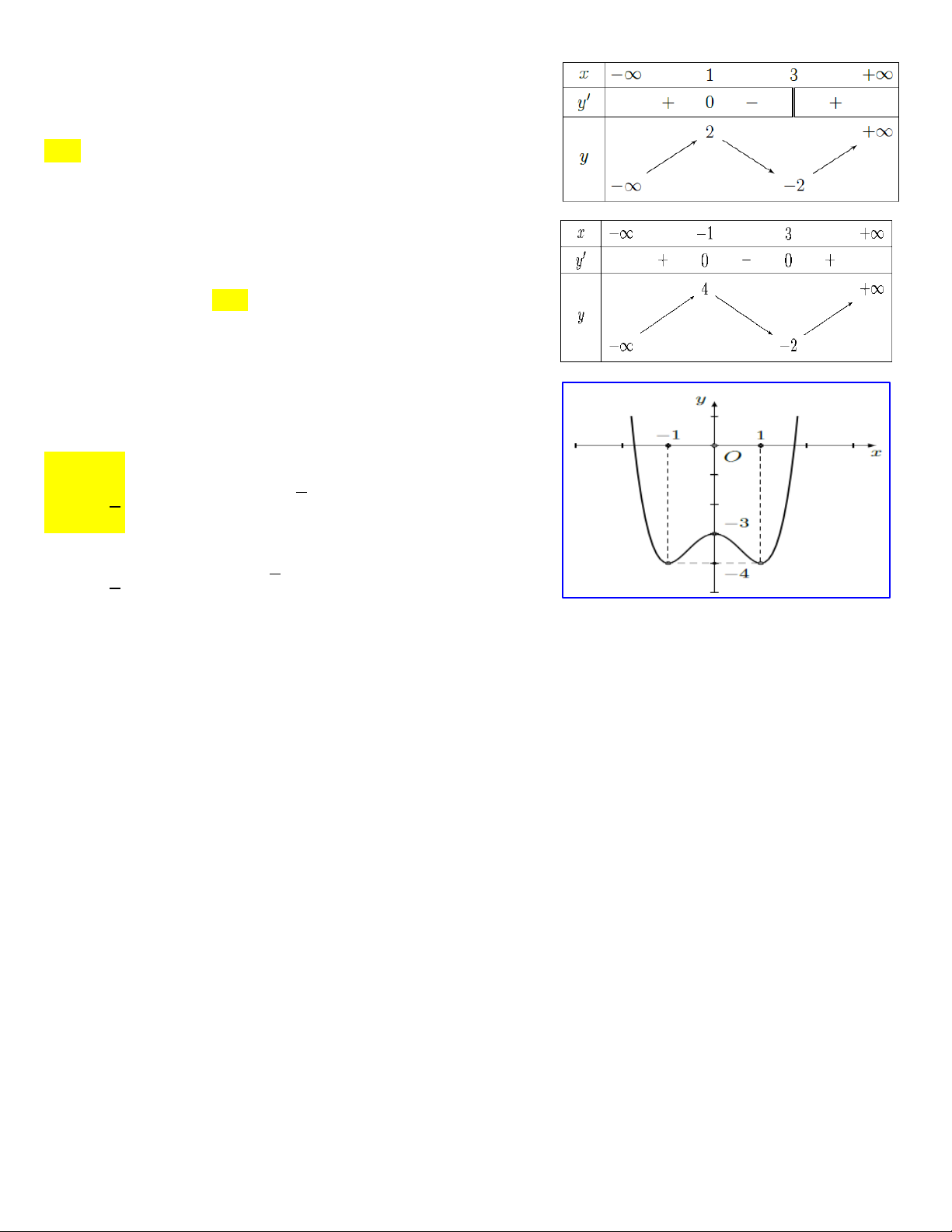
D. Hàm số đã cho đồng biến trên  . Câu 21. Cho hàm số 3 2
y  x  3x  4 có bảng biến thiên sau, tìm a và . b A. a   ;  b  2 . B. a  ;
 b  4 . C. a  ;
 b  1. D. a  ;  b  3.
Câu 22.Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên khoảng  ;    1 .
B. Hàm số nghịch biến trên khoảng 0;  1 .
C. Hàm số đồng biến trên khoảng 2;   .
D. Hàm số đồng biến trên khoảng  2;   .
Câu 23: Cho hàm số y  f (x) có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (0,1) B. (; 0) C. (1; ) D. (1; 0)
2. Dạng 2: Đọc đồ thị hàm số y  f  x:
Cách giải: Hàm số y  f  xđồng biến trên khoảng a;b nếu đồ thị hàm số đi lên ( theo chiều từ trái sang
phải ) trên khoảng a;b .
Hàm số y  f  xnghịch biến trên khoảng a;b nếu đồ thị hàm số đi xuống ( theo chiều từ trái
sang phải ) trên khoảng a;b . Bài tập: Câu 1:
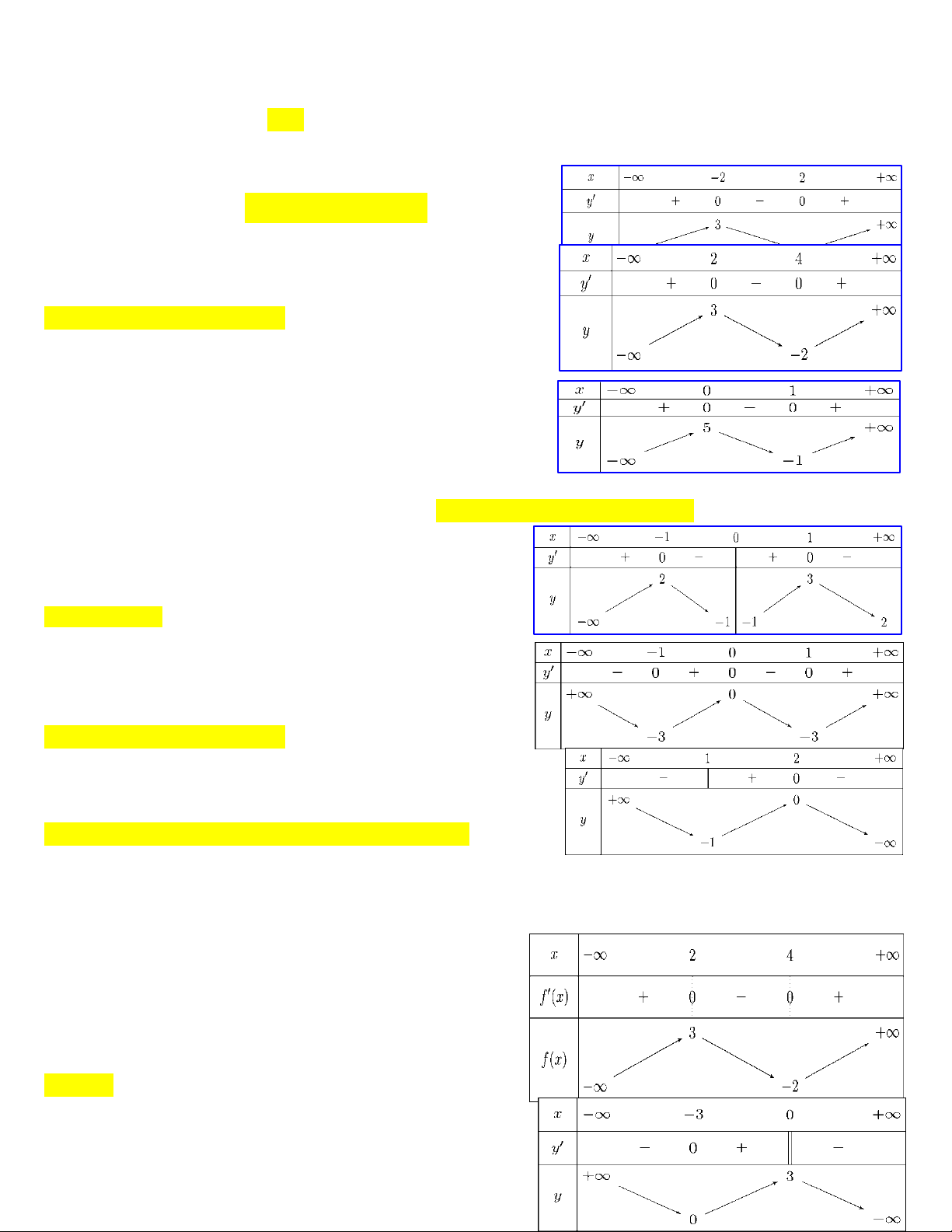
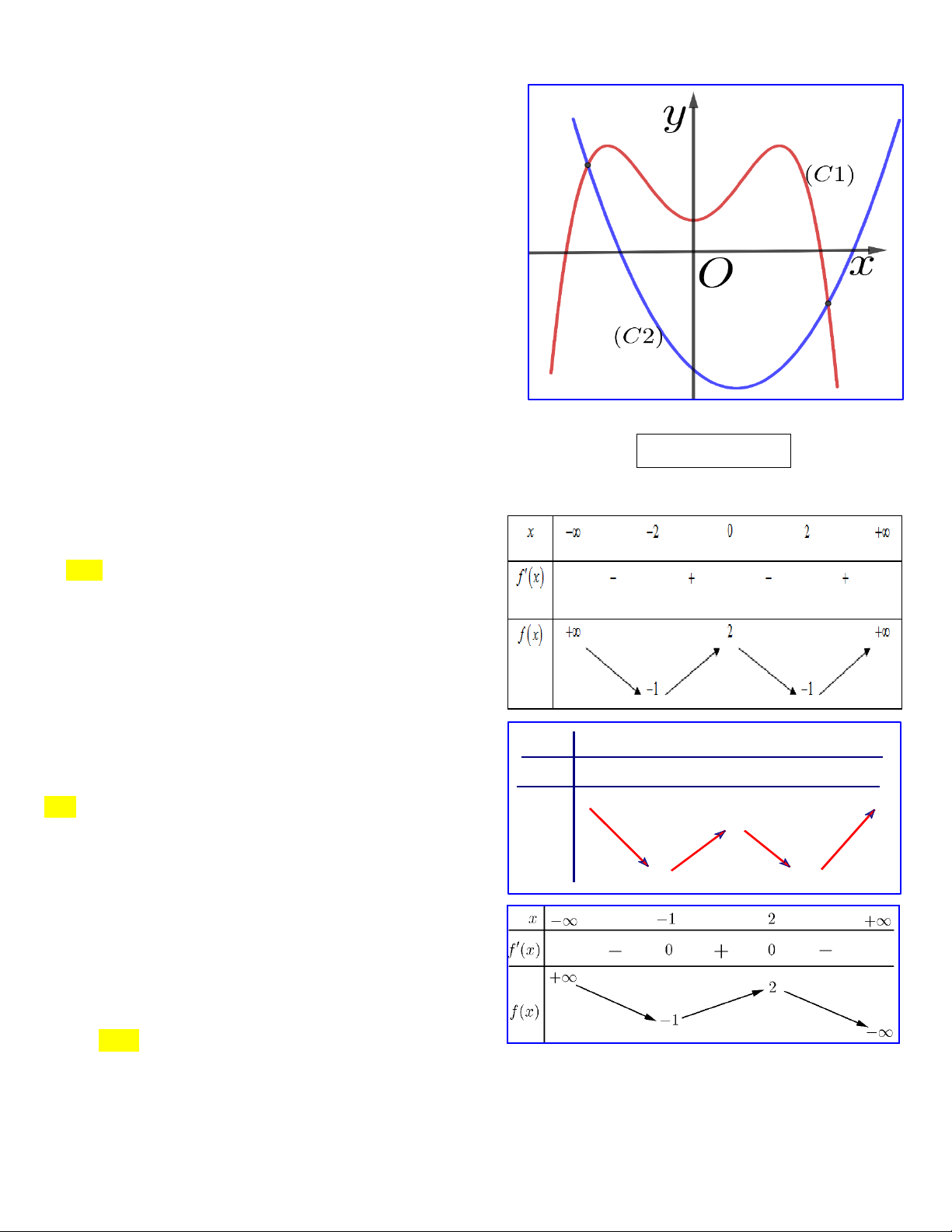
Cho hàm số y  f  x có đồ thị là đường cong trong hình bên. Hàm số
đã cho nghịch biến trên khoảng nào dưới đây? A. 0;  1 . B.  ;0  .
C. 0;  . D.  1   ;1 . Trang5
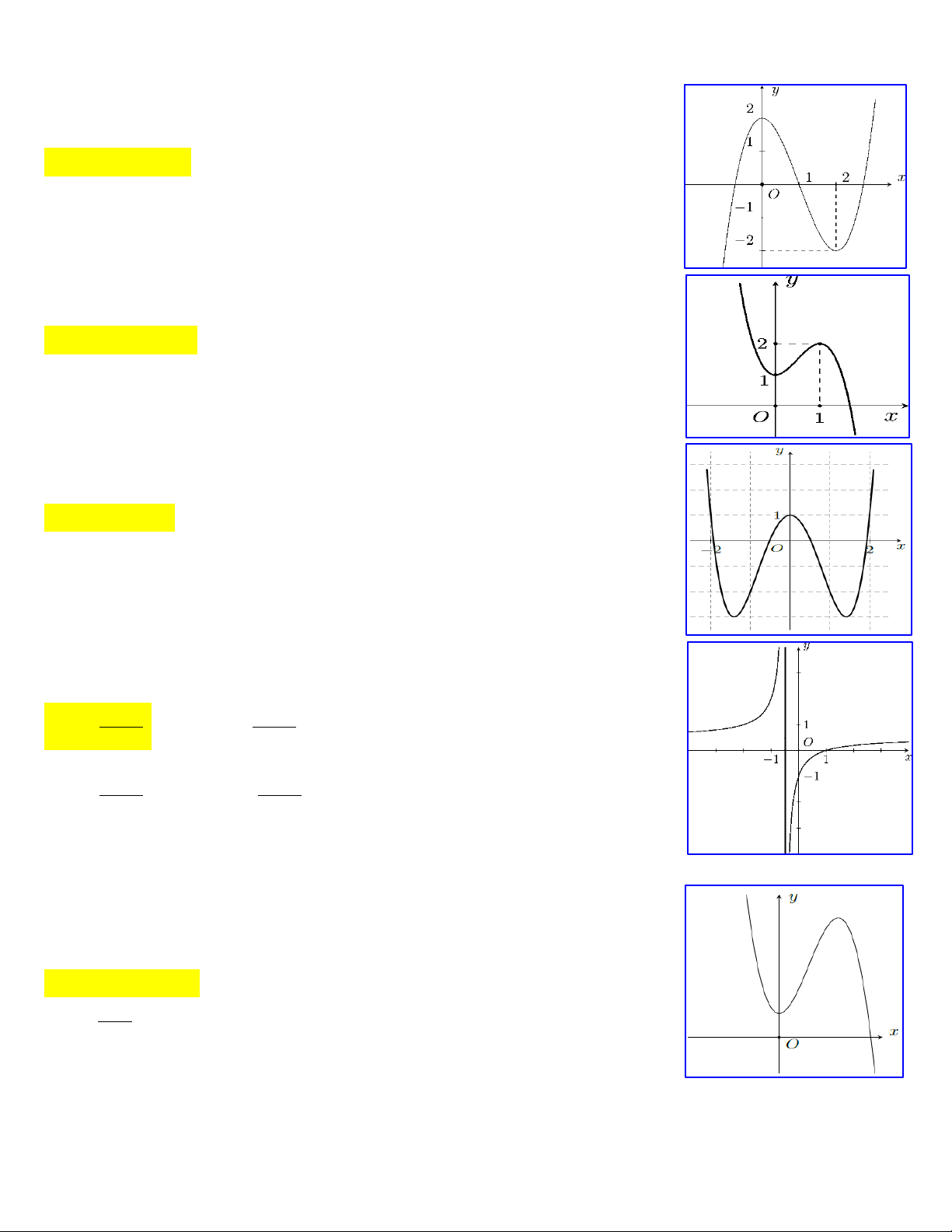
Câu 2:Cho hàm số y  f  x có đồ thị là đường cong như hình vẽ. Hàm số đã cho đồng biến
trên khoảng nào dưới đây? A.  1   ;1 . B.  ;  0. C. 0;  1 . D. 0;  .
Câu 3: Cho hàm số y  f  x có đồ thị như hình vẽ. Hàm số đã cho đồng biến trong khoảng nào? A.  1  ;0 B.  2  ;  1 C.  1   ;1 D. 0;  1 Câu 4:
Cho hàm số bậc ba y  f x có đồ thị như hình bên. Hàm số đã
cho đồng biến trên khoảng nào, trong các khoảng dưới đây?  1  1  A. ;  . B.   ;1  .  2 2  C. 0;  1 . D. 1;  . Câu 5:
Cho hàm số y  f  x xác định trên  và có đồ thị như hình vẽ .
Hàm số đã cho nghịch biến trên khoảng nào trong các khoảng dưới đây? A.   ;1  . B.  1   ;1 .
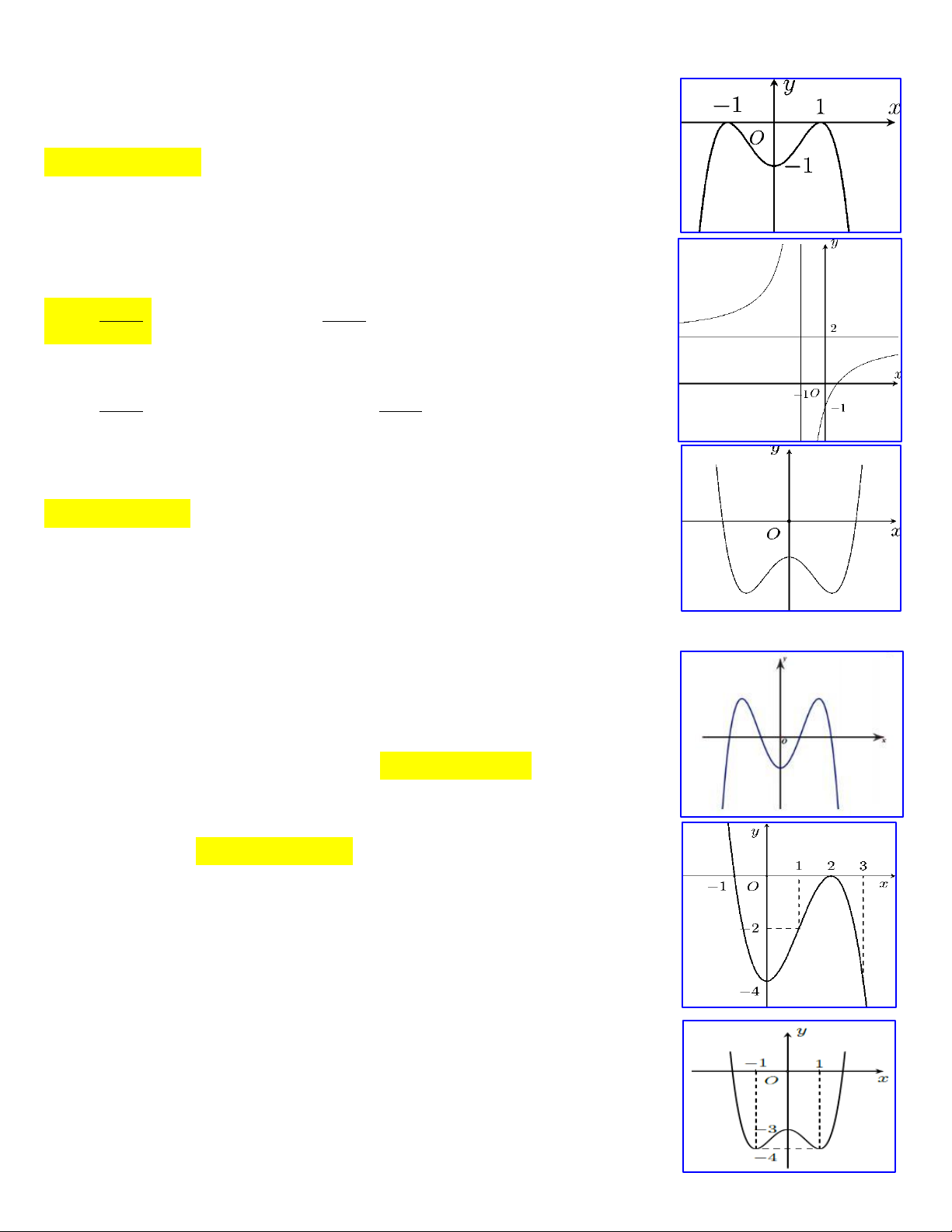
C. 1;  . D.   ;1  . Câu 6:
Cho hàm số y  f  x có đồ thị như hình vẽ bên dưới
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A.  1   ;1 . B. 0;  1 .
C. 1;  . D.  1  ;0 .
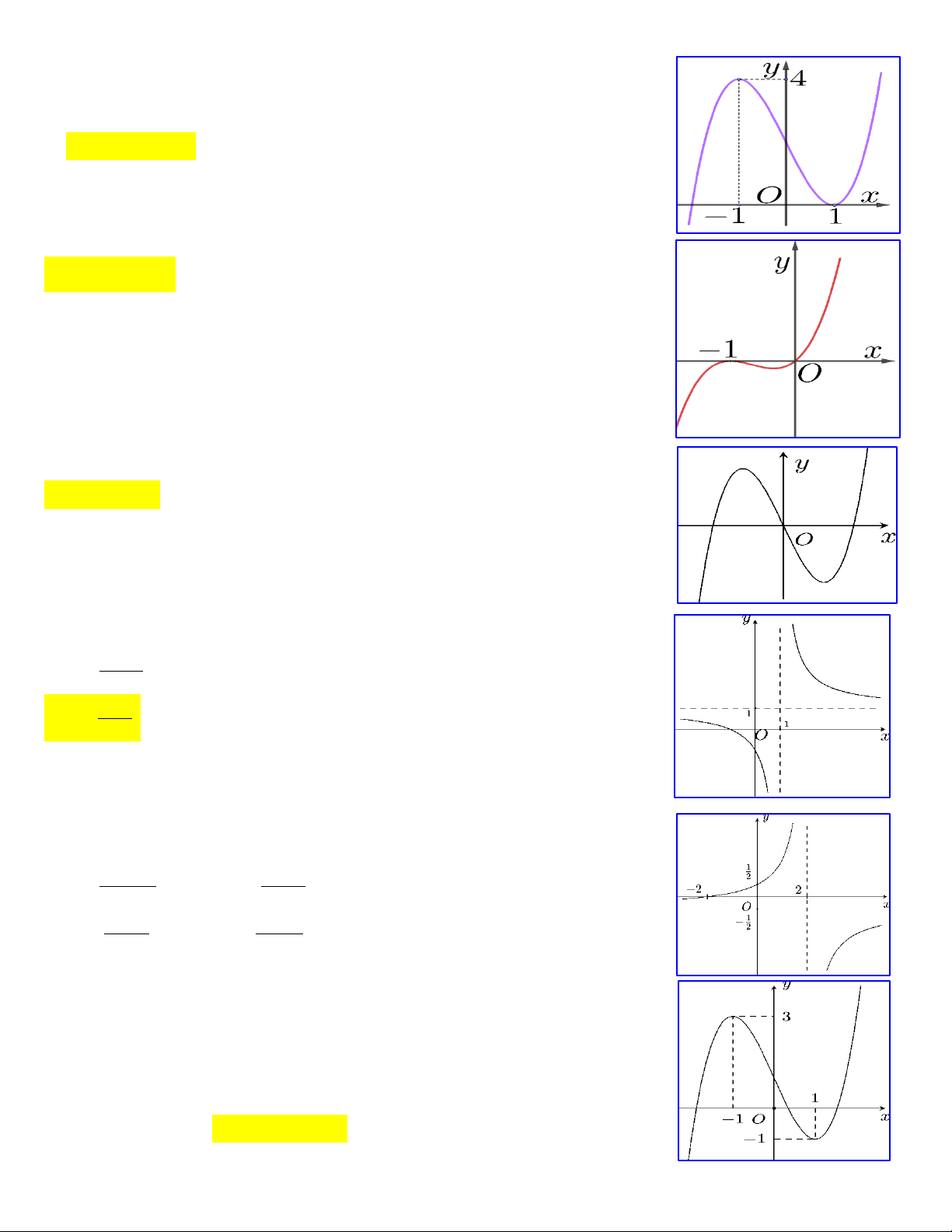
Câu 7: Cho hàm số y = f(x) có đồ thị như hình vẽ sau:
Khẳng định nào sau đây là đúng?
A.Hàm số đồng biến trên khoảng  ;  
B.Hàm số nghịch biến trên  ;  
C.Hàm số nghịch biến trên (−∞; 0)
D.Hàm số đồng biến trên 0; +∞ Trang6
3. Dạng 3: Đọc đồ thị hàm số f ' x :
Cách giải: Hàm số y  f  xđồng biến trên khoảng a;b nếu đồ thị hàm số f ' x nằm phía trên trục
hoành Ox trên khoảng a;b .
Hàm số y  f  xnghịch biến trên khoảng a;b nếu đồ thị hàm số f ' x nằm phía dƣới trục hoành
Oxtrên khoảng a;b.
Câu 1: Cho hàm số f  x xác định, liên tục trên  và có đồ thị của
hàm số f ' x là đường cong như hình vẽ bên dưới. Hỏi khẳng định nào đúng?
A. Hàm số y  f  x đồng biến trên khoảng  ;  3  .
B. Hàm số y  f  x nghịch biến trên khoảng  3  ; 2  .
C. Hàm số y  f  x đồng biến trên khoảng  2  ;0
D. Hàm số y  f  x nghịch biến trên khoảng 0;  .
4. Dạng 4: Tìm khoảng đơn điệu của hàm số y  f  x : Cách giải : Cách 1: Tự luận:
Tính y '  f ' x .
Lập bảng xét dấu của y '  f ' x
Căn cứ vào bảng xét dấu  kết luận.
Cách 2: Sử dụng máy tính cầm tay. 1 Câu 1: Hàm số 4 3 y 
x  x  x  5 đồng biến trên: 2  1  A.  ;    1 và ; 2   B.  ;    1 và 2;   2   1   1  C. 1  ; 
 và 2; D. ;     2   2  Sử dụng máy tính:
qy1a2$Q)^4$+Q)qdpQ)+5$Q)rp2=
KQ: 5  0  loại A, B 1 =p1a2= . KQ 
 0 Loại C. Chọn D 2  x Câu 2: Hàm số 2 y  nghịch biến trên: 1 x A.  B. 2;  C.  ;
 2 và 2; D.  ;    1 và  1  ;
Giải: Tập xác định của hàm số D   \  
1 loại A, B, C. Chọn D Trang7 2
x  2x  4
Câu 3: Hàm số y  đồng biến trên: x  2
A. 0; 2 và 2; 4
B. 0; 2 và 4;  C.  ;0   và 4; D.  ;0   và 2;4
Sử dụng máy tính cầm tay ( Nhƣ câu 1) x  Câu 4: Cho hàm số 1 y 
. Phát biểu nào sau đây đúng? 1 x
A. Hàm số đồng biến trên khoảng  ;  
B. Hàm số đồng biến trên mỗi khoảng   ;1  và 1;
C. Hàm số đồng biến trên khoảng   ;1  1;
D.Hàm số đồng biến trên khoảng  \   1 Câu 5: Cho hàm số 3 2
y  x  3x  3x  2 . Nhận định nào dưới đây là đúng ?
A. Hàm số nghịch biến trên  ;  
B. Hàm số nghịch biến trên mỗi khoảng   ;1  và 1;
C. Hàm số nghịch biến trên khoảng   ;1  1;
D. Hàm số nghịch biến trên khoảng  \   1 2 x  2x 1
Câu 6: Cho hàm số y 
. Phát biểu nào sau đây đúng? x  2
A. Hàm số nghịch biến trên các khoảng 0; 2 và 2;3
B. Hàm số nghịch biến trên khoảng 1;3
C. Hàm số nghịch biến trên khoảng 1; 2  2;3
D. Hàm số nghịch biến trên các khoảng   ;1  và 3; Câu 7: Cho hàm số 2 3
y  3x  x . Phát biểu nào sau đây sai?
A. Hàm số nghịch biến trên các khoảng  ;0   và 2;3
B. Hàm số đồng biến trên khoảng 0; 2
C. Hàm số nghịch biến trên khoảng  ;  2 và 2;3
D. Cả hai câu A và B đều kết luận đúng. Câu 8: Cho hàm số 4 2
y  x  2x  5 . Kết luận nào sau đây đúng?
A. Hàm số đồng biến với mọi x
B. Hàm số nghịch biến với mọi x
C. Hàm số đồng biến trên khoảng  ;    1
D. Hàm số đồng biến trên khoảng  1  ;0 và 1; Câu 9: Cho hàm số 4 y  x 
. Kết luận nào sau đây là đúng? x
A. Hàm số đồng biến trên khoảng  ;  2
B. Hàm số đồng biến trên khoảng 2; 
C. Hàm số đồng biến trên khoảng  2  ;2
D. Hàm số nghịch biến trên khoảng  2  ;2 Câu 10: Cho hàm số 4 2
y  x  x . Hãy chọn khẳng định đúng?  2   2 
A. Hàm số đồng biến trên khoảng   ;    
 và nghịch biến trên khoảng  ;     2   2   Trang8    
B. Hàm số nghịch biến trên khoảng 2   ;    
 và đồng biến trên khoảng 2  ;     2   2    2   2 
C. Hàm số đồng biến trên các khoảng   ;      và  ;     2   2      2 
D.Hàm số nghịch biến trên các khoảng 2   ;      và  ;     2   2  
Câu 11: Hàm số nào cho dưới đây đồng biến trên  ? A. 3 2
y  2x  2x  x  2 B. 3 2 y  2
 x  2x  x  2 2 3 2 C. 3 2 y  
x  2x 16x  31
D. y  2x  3x  9 3 Câu 12: Hàm số 2 y 
2  x  x nghịch biến trên khoảng  1   1  A. ; 2   B. 1  ;   C. 2;  D.  1  ;2  2   2 
Câu 13. Tìm tất cả các khoảng nghịch biến của hàm số 4 2
y  x  2x  3.
A. (1; 0) và (1; ). B. ( ;  1
 ) và (0;1). C. (1;1). D. ( ;  1
 ) và (1; ). 1 Câu 14. Cho hàm số 3 2 y  
x  2x  3x 1 Mệnh đề nào dƣới đây đúng? 3
A. Hàm số đồng biến trên khoảng ( ;
 1). B. Hàm số nghịch biến trên khoảng (1;).
C. Hàm số nghịch biến trên khoảng (1;3). D. Hàm số đồng biến trên khoảng (1;3). x 
Câu 15. Tìm các khoảng nghịch biến của hàm số 2 3 y  . x  2
A. R\{2}. B. ( ;
 2) và (2; ).
C. (2; ). D. ( ;  2). 1
Câu 16. Tìm các khoảng đồng biến hàm số 3 2 y 
x  2x  3x 1. 3 A. (;3).
B. (1; ). C. (1;3). D. ( ;
 1) và (3; ). 
Câu 17: Kết luận nào sau đây về tính đơn điệu của hàm số 2x 1 y  là đúng ? x 1
A. Hàm số luôn luôn nghịch biến trên R \   1 
B. Hàm số luôn luôn đồng biến trên R \   1 
C. Hàm số nghịch biến trên các khoảng (–; –1) và (–1; +)
D. Hàm số đồng biến trên các khoảng (–; –1) và (–1; +). x
Câu 18: Hàm số y 
nghịch biến trên khoảng nào 2 x  x A. (-1; +∞). B. (-∞;0). C. [1; +∞). D. (1; +∞). 2 x  8x  7
Câu 19: Hàm số y 
đồng biến trên khoảng nào(chọn phƣơng án đúng nhất) 2 x 1 1 1 1 A. (-  ; 
)B. ( 2 ; +  ) C. (-2; 
) D. (-  ; 
) và ( 2 ; +  ) 2 2 2 Câu 20: Hàm số 2
y  x  2x 1 nghịch biến trên các khoảng nào sau đây? 1 1 A. (-  ;0) B. (-  ; ) C. (-  ;1) D. (-  ;  ) 2 2 Trang9
Câu 21. Trong các hàm số sau, hàm số nào nghịch biến trên khoảng (- 1; ) 1 ? 1 1 1 A. y = . B. 3
y = x - 3x + 1 . C. y = . D. y = - . x 2 x x
Câu 22. Hàm số nào sau đây đồng biến trên ¡ ? x - 1 A. y = . B. 3 2
y = x + 4x + 3x – 1. x + 2 1 1 C. 4 2
y = x – 2x – 1. D. 3 2 y = x -
x + 3x + 1 . 3 2
Câu 23. Hàm số nào sau đây đồng biến trên ¡ ? 1 A. 2 y = x . B. y = . C. 3
y = x - 3x . D. 3 2
y = x - x + x . x
II. CỰC TRỊ CỦA HÀM SỐ
KIẾN THỨC CẦN NHỚ
1.Định nghĩa: Giả sử hàm số f xác định trên K K    và x  K 0 a)
x được gọi là điểm cực đại của hàm số f nếu tồn tại một khoảng  ;
a b  K chứa điểm x sao cho 0 0
f  x  f  x , x   ; a b \ x . 0     0
Khi đó f  x được gọi là giá trị cực đại của hàm số f. 0  b)
x được gọi là điểm cực tiểu của hàm số f nếu tồn tại một khoảng  ;
a b  K chứa điểm x sao cho 0 0
f  x  f  x , x   ; a b \ x . 0     0
Khi đó f  x được gọi là giá trị cực tiểu của hàm số f. 0 
2.Điều kiện đủ để hàm số có cực trị:
Định lí 1: Giả sử hàm số fđạt cực trị tại điểm x . Khi đó, nếu f có đạo hàm tại điểm x thì f x  0. 0  0 0 Định lí 2:
a. Nếu f  x đổi dấu từ âm sang dương khi x đi qua điểm x (theo chiều tăng) thì hàm số đạt cực tiểu tại điểm x . 0 0
b. Nếu f  x đổi dấu từ dương sang âm khi x đi qua điểm x (theo chiều tăng) thì hàm số đạt cực đại tại điểm x . 0 0
Định lí 3: Giả sử hàm số f có đạo hàm cấp một trên khoảng a;bchứa điểm x , f  x  0 và f có đạo hàm cấp hai 0  0
khác 0 tại điểm x . 0 a)
Nếu f  x  0 thì hàm số f đạt cực đại tại điểm x . 0  0 b)
Nếu f  x  0 thì hàm số f đạt cực tiểu tại điểm x . 0  0
Nếu f  x  0 thì ta chưa thể kết luận được, cần lập bảng biến thiên hoặc bảng xét dấu đạo hàm. 0 
Bảng tóm tắt các khái niệm x f  x M x ; f x 0  0  0 0  0
Điểm cực đại của f
Giá trị cực đại(cực đại) của f
Điểm cực đại của đồ thị hàm số f
Điểm cực tiểu của f
Giá trị cực tiểu(cực tiểu) của f
Điểm cực tiểu của đồ thị hàm số f
Điểm cực trị của f
Cực trị của f
Điểm cực trị của đồ thị hàm số f
3.Quy tắc tìm cực trị của hàm số
3.1:Quy tắc 1: Lập bảng biến thiên hoặc bảng xét dấu Trang10
Bước 1.Tìm f  x
Bước 2. Tìm các điểm x i 1,2,.. . tại đó đạo hàm bằng không hoặc hàm số liên tục nhưng không có đạo hàm. i
Bước 3. Xét dấu f  x . Nếu f  x đổi dấu khi x qua điểm x thì hàm số đạt cực trị tại điểm x . i i
3.2:Quy tắc 2: Dùng định lý 3
Bước 1: Tìm f  x
Bước 2: Tìm các nghiệm x i 1, 2,.. . của phương trình f  x  0. i
Bước 3: Tính f  x i 
 Nếu f x   0 thì hàm số f đạt cực đại tại điểm x . i i
 Nếu f x   0 thì hàm số f đạt cực tiểu tại điểm x . i i
Nếu f  x   0 thì ta lập bảng biến thiên để xác định điểm cực trị. i BÀI TẬP
1. Dạng 1: Đọc bảng biến thiên.
Điểm cực trị của hàm số Điểm cực đại
Điểm cực tiểu x -∞ x1 x2 + ∞ y' = f'(x) + 0 - 0 + y1 y = f(x)
Giá trị cực đại
Điểm cực tiểu của đồ thị y2 hàm số
Điểm cực đại của đồ thị hàm số
Giá trị cực tiểu
Câu 1. Cho hàm số f  x có bảng biến thiên như sau:
Hàm số đã cho đạt cụrc đại tại A. x  2
 . B. x  2.C. x 1. D. x  1. 
Câu 2: Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Tìm số điểm cực trị của hàm số.
A. 3. B. 0 . C. 1. D. 2.
Câu 3: Hàm số y  f  x liên tục trên R và có bảng biến thiên
như hình vẽ.Mệnh đề nào sau đây là đúng?
A. Hàm số đã cho có hai điểm cực trị.
B. Hàm số đã cho có đúng một điểm cực trị.
C. Hàm số đã cho không có giá trị cực tiểu.
D. Hàm số đã cho không có giá trị cực đại. Trang11
Câu 4: Cho hàm số y  f  x có bảng biến thiên như sau.
Giá trị cực đại của hàm số bằng
A. 1. B. 2. C. 0 . D. 5.
Câu 5: Cho hàm số y  f  x xác định, liên tục trên R và có bảng biến thiên như hình vẽ. Tìm giá trị cực đại
y và giá trị cực tiểu y của hàm số đã cho CĐ CT A. y  2
 và y  2 . B. y  0. CT y  3 và CĐ CĐ CT C. y
 2 và y  0. D. y  3 và y  2.  CĐ CT CĐ CT
Câu 6: Cho hàm số y  f  x có bảng biến thiên dưới đây.
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đạt cực đại tại x  2.
B. Hàm số đạt cực đại tại x  2. 
C. Hàm số đạt cực đại tại x  4.
D. Hàm số đạt cực đại tại x  3.
Câu 7: Cho hàm số y  f  x có bảng biến thiên như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A. Hàm số có điểm cực tiểu x  0.
B. Hàm số có điểm cực đại x  5.
C. Hàm số có điểm cực tiểu x  1. 
D. Hàm số có điểm cực tiểu x  1.
Câu 8: Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Hỏi hàm số y  f  x có bao nhiêu điểm cực trị?
A. Có một điểm.
B. Có ba điểm.
C. Có hai điểm. D. Có bốn điểm.
Câu 9. Cho hàm số y  f  x liên tục trên R và có bảng biến
thiên như hình vẽ. Khẳng định nào sau đây là đúng?
A. Hàm số có giá trị cực tiểu bằng 1và bằng 1.
B. Hàm số đạt cực tiểu tại x  0.
C. Hàm số đạt cực đại tại x  0.
D. Hàm số có đúng hai điểm cực trị.
Câu 10.. Cho hàm số y  f  x xác định, liên tục trên R và có
bảng biến thiên như hình vẽ.Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại x  2 và đạt cực tiểu tại x  1.
B. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1. 
C. Hàm số có đúng một cực trị.
D. Hàm số có giá trị cực đại bằng 2.
Câu 11. Cho hàm số y  f  x có bảng biến thiên như sau.
Hàm số đạt cực đại tại điểm nào trong các điểm sau đây? A. x  2  .
B. x  3. C. x  2.
D. x  4.
Câu 12. Cho hàm số y  f  x có bảng biến thiên như hình Trang12 bên. Chọn khẳng định sai.
A. Hàm số đạt cực đại tại x  0.
B. Hàm số có hai điểm cực trị.
C. Hàm số đạt cực tiểu tại x  3. 
D. Hàm số có giá trị cực tiểu y  3.
Câu 13: Cho hàm số y  f  x xác định, liên tục trên  và có x -∞ 0 1 +∞
bảng biến thiênnhư hình vẽ. Khẳng định nào sau đây là khẳng y' + - 0 + định đúng? +∞
A.Hàm số có đúng một cực trị. 0
B.Hàm số có giá trị cực tiểu bằng 1. y -1
C.Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1 -∞
D.Hàm số đạt cực đại tại x  0 và đạt cực tiểu tại x 1.
2. Dạng 2: Đọc đồ thị hàm số Câu 1: Cho hàm số 3
y  ax  bx  cx  d (a, ,
b c   ) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là A. 2 B. 0 C. 3 D. 1
3. Dạng 3: Đọc bảng xét dấu hàm số f ' x hoặc đồ thị hàm số f ' x
Chú ý: Qua x f ' x đổi dấu thì x là điểm cực trị của hàm số. 0 0
Câu 1: Cho hàm số f  x xác định và liên tục trên  ,có đồ thị của hàm số y
f ' x nhƣ hình vẽ. Hàm số f  x có bao nhiêu cực trị ? A. 2. B. 3. C. 4. D. 5. x O
Câu2. Cho hàm số f  x có bảng xét dấu của f  x như sau:
Số điểm cực trị của hàm số đã cho là
A. 3. B. 0 . C. 2. D. 1.
Câu 3. Cho hàm số y  f  x xác định trên R và
có bảng xét dấu của đạo hàm như sau:
Khi đó số điểm cực trị của hàm số y  f x là
A. 3. B. 2. C. 4. D. 1.
Câu 4. Cho hàm số y  f  x có bảng xét dấu của hàm đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A. 6. B. 4. C. 2. D. 3.
Câu 5. Cho hàm số y  f  x liên tục trên R và Trang13
có bảng xét dấu của đạo hàm như sau:
Hàm số đã cho có bao nhiêu cực trị?
A. 3. B. 2. C. 1. D. 4. 2 3 4
Câu 6. Cho hàm số f  x có đạo hàm f  x   x  
1  x  2  x  3  x  4 , x
 R . Số điểm cực trị của hàm số đã cho là A. 3. B. 5. C. 2. D. 4. 2 3 4
Câu 7. Cho hàm số f  x có đạo hàm f  x  x  x  
1  x  2  x  3 . Số điểm cực trị của hàm số đã cho là A. 2. B. 1. C. 0 . D. 3.
Câu 8. Cho hàm số f  x có đạo hàm f  x  x x   x  3 1
2 . Số điểm cực trị của hàm số đã cho là A. 3. B. 2. C. 5. D. 1.
Câu 9. Cho hàm số y  f  x có đạo hàm f  x  x x   x  2 1 2 , x
 R . Số điểm cực trị của hàm số là A. 5. B. 2. C. 1. D. 3. 2
Câu 10.. Cho hàm số y  f  x có đạo hàm f  x 3
 x x  
1  x  2 . Số điểm cực trị của hàm số đã cho là A. 0 . B. 2. C. 3. D. 1.
Câu 11. Cho hàm số f  x có f  x  x x   x  2 1
2 . Số điểm cực trị của hàm số đã cho là A. 2. B. 3. C. 4. D. 1.
Câu 12. Cho hàm số f  x có đạo hàm f  x  x  x  2 ' 2 , x
  . Số điểm cực trị của hàm số đã cho là A. 0 . B. 3 . C. 2 . D. 1 .
Câu 13. Cho hàm số y  f (x) liên tục trên 
với bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số y  f (x) là. A. 3 . B. 0 C.1. D. 2 .
Câu 14. Cho hàm số f  x . Hàm số y  f (
 x) có đồ thị như hình vẽ bên. Mệnh
đề nào dưới đây là đúng?
A.Hàm số f  x đạt cực đại tại x  0 .
B.Hàm số f  x có hai điểm cực trị.
C.Hàm số f  x đạt cực tiểu tại x  1  .
D.Hàm số f  x đạt cực tiểu tại x 1 .
Câu 15: Cho hàm số f  x liên tục trên ¡ và có bảng xét dấu của f  x như sau:
Số điểm cực đại của hàm số đã cho là A. 4 . B.1. C. 2 . D. 3 .
Câu 16: Hàm số f (x) có đạo hàm f '(x) trên khoảng K . Cho đồ thị của y
hàm số f '(x) trên khoảng K nhƣ sau:
Số điểm cực trị của hàm số f (x) trên K là: x - O Trang14 A. 1 B. 2 C. 3 D. 4
4. Dạng 4:Tìm điểm cực trị của hàm số cụ thể
Thực hiện theo quy tắc tìm cực trị.
Sử dụng máy tính cầm tay.
Câu 1. Hàm số y  x   x2 3 1 có
A. Ba điểm cực trị.
B. Một điểm cực trị.
C. Không có điểm cực trị.
D. Hai điểm cực trị.
Câu 2. Đồ thị hàm số nào sau đây có 3 điểm cực trị. A. 4 2
y  x  2x 1. B. 4 2
y  x  2x 1 . C. 4 2
y  2x  4x 1 . D. 4 2
y  x  2x 1 .
Câu 3. Số điểm cực trị của hàm số 3 2
y  x  6x  5x 1 là. A. 1. B. 4 . C. 2 . D. 3 . 3 x
Câu 4. Cho hàm số 2 2 y 
 2x  3x  . Tọa độ điểm cực đại của đồ thị hàm số là. 3 3   A. 1; 2   . B. 1; 2 . C.  1  2 ; 2 . D. 3; .    3 
Câu 5. Tìm tọa độ điểm cực tiểu M của đồ thị hàm số 3
y  x  3x  2 .
A. M 1; 4 . B. M  1  ;0 .
C. M 1;0 . D. M  1  ;4 .
Câu 6. Đồ thị hàm số 3 2
y  x  3x  2 có khoảng cách giữa hai điểm cực trị bằng. A. 5 . B. 20 . C. 2 . D. 2 5 .
III. GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ KIẾN THỨC CẦN NHỚ
Cho hàm số y  f  x xác định trên tập D.
+) Số M được gọi là giá trị lớn nhất (GTLN) của hàm số y  f  x trên tập D nếu f  x  M với mọi x  D và
tồn tại x  D sao cho f  x  M . 0  0
Kí hiệu: M  max f  x D
+) Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số y  f  x trên tập D nếu f  x  m với mọi x  D và
tồn tại x  D sao cho f  x  m 0  0
Kí hiệu: m  min f  x D BÀI TẬP
Dạng 1: Tìm GTLN – GTNN của hàm số y = f(x) trên một khoảng
Bước 1. Tìm tập xác định (nếu đề chưa cho khoảng).
Bước 2. Tính y  f  x ; tìm các điểm mà đạo hàm bằng không hoặc không xác định.
Bước 3. Lập bảng biến thiên
Bước 4. Kết luận
Dạng 2: Tìm GTLN và GTNN của hàm số trên một đoạn
Bước 1. Tính f  x
Bước 2. Tìm các điểm x  a b mà tại đó f  x
hoặc f  x không xác định i  i   0 i  ;  Trang15
Bước 3. Tính f a, f x , f b i  
Bước 4. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên.
Khi đó M  max f x và m  min f x a; b a; b max 
f  x  f b
+) Hàm số y  f  x đồng biến trên đoạn [a; b] thì  min 
f  x  f a max 
f  x  f a
+) Hàm số y  f  x nghịch biến trên đoạn [a; b] thì  min 
f  x  f b
Lƣu ý: Có thể dùng máy tính cầm tay để giải.
Bước 1. Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  f  x trên miền (a; b) ta sử dụng máy tính Casio với lệnh MODE 7
Bước 2. Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min. b  a
- Ta thiết lập miền giá trị của biến x Start a End b Step
(có thể làm tròn để Step đẹp), hoặc chọn step 0,25 19 hay 0,5. VÍ DỤ MẪU Ví dụ 1. Cho hàm số 3 2
y  x  3x  2 . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên [0; 3]. Giá
trị của M  m bằng A. 8 B. 10 C. 6 D. 4
Hướng dẫn giải
Hàm số xác định và liên tục trên [0; 3] x  0 0;  3 Ta có 2 y  0  3
 x  6x  0   x  2   0; 3
Khi đó y 0  2, y2  6, y3  2 . Vậy M  6; m  2  M  m  8 . Chọn A. Sử dụng máy tính:
w7 f  x  pQ)qd+3Q)d+2= Start0= End 3= Step 0.25=
Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min. Kết luận. x  2 2 2    
Ví dụ 2. Cho hàm số y 
. Giá trị của  min y    max y  bằng x  1  2; 3   2; 3  45 25 89 A. 16 B. C. D. 4 4 4
Hướng dẫn giải 3  Ta có y  
x  , do đó hàm số     
nghịch biến trên mỗi khoảng  ;  1 ; 1;  Hàm số nghịch x   0, 1 2 1 biến trên [2; 3]. Trang16 2 2 2       Do đó 5 89 y  y   5 min 3 
; max y  y 2  4 . Vậy 2
 min y   max y   4  . Chọn D    2;  3 2;  3 2  2; 3   2; 3   2  4 Sử dụng máy tính:
w7 f  x  aQ)+2RQ)p1= Start2= End 3= Step 0.25=
Quan sát bảng giá trị máy tính hiển thị, giá trị lớn nhất xuất hiện là max, giá trị nhỏ nhất xuất hiện là min. 2 2    
Tính  min y    max y  . Kết luận.  2; 3   2; 3 
Ví dụ 5. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số 2 y  x  4  x
Giá trị của biểu thức P  M  m bằng A. 2 2   1 B. 2 2   1 C. 2  1 D. 2 1
Hướng dẫn giải 2 x 4  x  x
Tập xác định D   2
 ; 2.Ta có y 1  , x   2  ; 2 2 2 4  x 4  x x  0  2 y  0 
4  x  x  
. y  2  2 2; y 2  0; y2  2; y 2    2  x  2     2  ; 2
Vậy M  2 2, m  2
  P  2 2  2  2  2 1. Chọn A BÀI TẬP
Câu 1. Giá trị nhỏ nhất của hàm số f  x 4 2
 x 10x  2 trên đoạn  1  ;2 bằng A. 2. B. ‐ 23. C. ‐ 22 . D. ‐ 7.
Câu 2. Gọi M , m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f  x 4
  x 1 trên đoạn [1; 3]. Tính M  . m x A. 4. B. 9. C. 1. D. 5.
Câu 3. Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số   4 f x  x  trên đoạn [1; 3] bằng x 65 52 A. . B. 20. C. 6. D. . 3 3
Câu 4. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3
y  x  3x 1 trên đoạn 0; 2 bằng A. 2. B. 3. C. 1. D. 4.
Câu 5. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y 
2  x  x bằng A. 2  2 . B. 2. C. 1. D. 2  2.
Câu 6. Giá trị nhỏ nhất của hàm số f  x 3
 x  3x 1 trên đoạn [1; 3] là
A. min f  x  3 . B. min f  x  6 . C. min f  x  37 . D. min f  x  5 [1;3] [1;3] [1;3] [1;3] Trang17 2 x 1
Câu 7. Gọi M và m là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên tập hợp x  2   D     3 ; 1  1;
. Khi đó T  m M bằng    2 1 3 3 A. . B. 0 . C. . D. − . 9 2 2
Câu 8. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y  x  2x  x  2 trên đoạn  1  1  ;
. Khi đó tích M m bằng    2  45 212 125 100 A. . B. . C. . D. . 4 27 36 9 1
Câu 9. Cho hàm số y  x 
. Giá trị nhỏ nhất của hàm số trên 0;  bằng x A. 2. B. 2 . C. 0 . D. 1.
Câu 10. Giá trị nhỏ nhất của hàm số 2
y  x  18  x là: A. 0 . B. 6. C. 3  2 . D. 6. 
Câu 11. Giá trị lớn nhất của hàm số f  x 3 2
 2x  3x 12x  2 trên đoạn  1  ;2 là A. 11. B. 10. C. 6 . D. 15. 1
Câu 12. Giá trị lớn nhất của hàm số y  x  trên (0;3 ] bằng x 28 8 A. . B. 0 . C. . D. 2. 9 3 3x 1
Câu 13. Giá trị lớn nhất của hàm số y  trên đoạn [1; 3] bằng x 1 5 A. 2  5 . B. − . C. . D. 1. 2 2 16  
Câu 14. Giá trị lớn nhất của hàm số 2 y  x  3 trên đoạn ; 4 bằng:   x  2  155 A. 24 . B. 20. C.12 . D. . 12
Câu 15: Giá trị lớn nhất của hàm số 3
f (x)  x  3x  2 trên đoạn [  3;3] bằng A. 16  . B. 20 . C. 0 . D. 4 .
Câu 16: Giá trị nhỏ nhất của hàm số f  x 3
 x 3x  2 trên đoạn  3  ;  3 bằng A. 20 . B. 4 . C. 0 . D. 16  .
Câu 17: Giá trị lớn nhất của hàm số f  x 3
 x  3x trên đoạn  3  ;  3 bằng A. 18 . B. 2 . C. 18  . D. 2  .
Câu 18: Giá trị lớn nhất của hàm số f  x 3
 x  3x  2 trên [  3;3] bằng A. 4. B. 0. C. 20. D. –16.
Câu 19: Giá trị lớn nhất của hàm số 4 2
y  x  4x  9 trên đoạn  2  ;  3 bằng A. 201. B. 2 . C. 9 . D. 54 .
Câu 21: Giá trị nhỏ nhất của hàm số 3 2
y = x + 2x - 7x trên đoạn [0; 4 ] bằng Trang18 A. - 259 . B. 68 . C. 0 . D. - 4 .
Câu 22: Giá trị nhỏ nhất của hàm số 3 2
y  x  3x trên đoạn  4  ;  1 bằng A. - 4. B. - 16. C. 0. D. 4.
Câu 23: Giá trị lớn nhất của hàm số 4 2
y  x  x 13 trên đoạn  1  ; 2 bằng 51 A. 25 . B. . C. 13 . D. 85 . 4
Câu 24: Tìm giá trị nhỏ nhất m của hàm số 3 2
y  x  7x  11x  2 trên đoạn [0; 2]
A. m  11
B. m  0 C. m  2 
D. m  3
Câu 25: Tìm giá trị lớn nhất M của hàm số 4 2
y  x  2x  3 trên đoạn [0; 3]
A. M  9
B. M  8 3
C. M  1
D. M  6
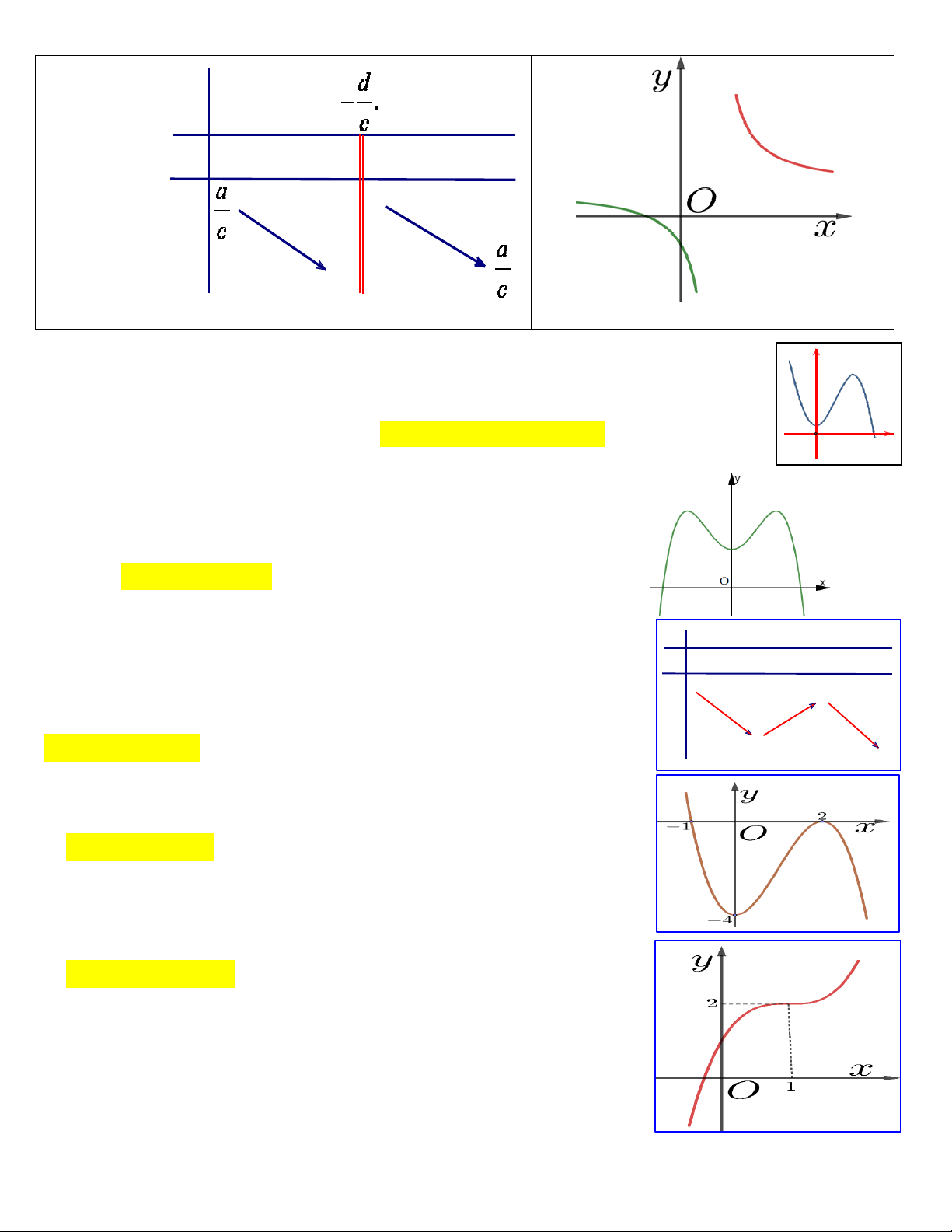
IV. ĐƢỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ KIẾN THỨC CẦN NHỚ 1. Định nghĩa
Đường thẳng y  y được gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số 0
y  f  x nếu lim f  x  y hoặc lim  y 0 0 x x
Đường thẳng x  x được gọi là đường tiệm cận đứng (gọi tắt là tiệm cận đứng) của đồ thị hàm số 0
y  f  x nếu ít nhất một trong các điều kiện sau được thỏa mãn:
lim f  x   ;
 lim f x  ; lim f x   ;
 lim f x   .     xx x xx x 0 0 x 0 0 x DẠNG BÀI TẬP
Dạng 1. Xác định các đƣờng tiệm cận dựa vào định nghĩa Ví dụ mẫu
Ví dụ 1: Cho hàm số y  f  x có lim f  x  3
 và lim f  x  3 . Mệnh đề nào dưới đây đúng? x x
A.Đồ thị hàm số đã cho có hai tiệm cận ngang là y  3 và y  3 
B.Đồ thị hàm số đã cho có hai tiệm cận ngang là x  3 và x  3 
C.Đồ thị hàm số đã cho có đúng một tiệm cận ngang
D.Đồ thị hàm số đã cho không có tiệm cận ngang
Hướng dẫn giải
Vì lim f  x  3  nên y  3
 là một đường tiệm cận ngang của đồ thị hàm số. x
Vì lim f  x  3 nên y  3 là một đường tiệm cận ngang của đồ thị hàm số. x Chọn A
Dạng2. Xác định các đƣờng tiệm cận của đồ thị khi biết hàm số  
Phƣơng pháp giải:Tiệm cận của đồ thị hàm số hữu tỷ  f x y g  x
Điều kiện xác định g  x  0 . Tính các giới hạn lim ;
y lim y nếu thỏa mãn định nghĩa của đường tiệm cận đứng và tiệm cận ngang thì kết  x x 0 x luận. Chú ý: Trang19  
- Đối với hàm số phân thức hữu tỷ  f x y với g  x f  x n n 1 
 a x  a x  ...  a x  a a  0 m m và g  x 1  b x  b x
 ...  b x  b b  0 m m 1  1 0  m  n n 1  1 0  n  Khi đó:
+ Nếu n  m thì đồ thị hàm số không có tiệm cận ngang. a
+ Nếu n  m thì đồ thị hàm số có tiệm cận ngang là y  n bm
+ Nếu n  m thì đồ thị hàm số có tiệm cận ngang là y  0
- Nếu đường thẳng x  x là tiệm cận đứng của đồ thị hàm số thì x  x là nghiệm của phương trình g  x  0 0 0
(ngƣợc lại nghiệm của g  x  0 chƣa chắc đã là tiệm cận đứng của đồ thị).Hay nói cách khác x  x là 0
các điểm gián đoạn của hàm số
- Điều kiện cần để đồ thị hàm số y  f  x có tiệm cận ngang là: Tập xác định của hàm số phải có khoảng vô cực. ax  b
Tìm tiệm cận của đồ thị hàm số y 
, c  0, ad  bc  0 : cx  d
Sử dụng máy tính cầm tay, với chức năng CALC x  2
Câu 1. Tiệm cận ngang của đồ thị hàm số y  là x 1
A. y  2 .
B. y  1 . C. x  1
 . D. x  2. HD: Sử dụng máy tính
aQ)p2RQ)+1r99999999999999999=
KQ: 1  Chọn B. 2x  3
Câu 2. Cho hàm số y 
. Đường tiệm cận ngang của đồ thị hàm số trên là: x  4  A. x  4
 . B. y  2 . C. x  3 4 . D. y  . 4 x  3
Câu 3. Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình? x 1
A. y  5 . B. y  0 . C. x 1 . D. y  1. 2  2x
Câu 4. Tìm đường tiệm cận ngang của đồ thị hàm số y  . x 1
A. y  2 .B. x  1  . C. x  2
 . D. y  2. 4x  4
Câu 5. Đồ thị hàm số y 
có tất cả bao nhiêu đường tiệm cận? 2 x  2x 1 A. 2. B. 0 . C. 1. D. 3. 2  2x
Câu 6. Tìm đường tiệm cận ngang của đồ thị hàm số y  . x 1 A. x  1
 . B. x  2
 . C. y  2 . D. y  2. 5
Câu 7. Tiệm cận ngang của đồ thị hàm số y 
là đường thẳng có phương trình nào dưới đây? x 1
A. x 1 .
B. y  5 .
C. x  0 . D. y  0. Trang20 2x  3
Câu 8. Đồ thị hàm số y 
có các đường tiệm cận đứng, tiệm cận ngang lần lượt là x 1
A. x 1 và y  2 .
B. x  2 và y  1. C. x 1 và y  3 . D. x  1  và y  2. aQ2)p3RQ)p1r9999999999999999=
KQ: 2  loại B, C.
=1 máy tính báo lỗi: Math ERROR  chọn A. 1 4x
Câu 9. Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số y  ? 2x 1 A. y  1 2 . B. y 
. C. y  4 . D. y  2. 2 3x  5
Câu 10. Tiệm cận đứng của đồ thị hàm số y  là x  2
A. x  2 . B. y  2 . C. x  3. D. y  3. 1 3x
Câu 11. Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y  lần lượt là x  2 A. x  2
 và y  3 . B. y  2 và x  3
 . C. x  2
 và y 1. D. x  2 và y  1. 7  2x
Câu 12. Đồ thị hàm số y 
có tiệm cận đứng là đường thẳng? x  2 A. x  3  .
B. x  2 . C. x  2  . D. x  3.
Câu 13. Hàm số nào có đồ thị nhận đuờng thẳng x  2 làm đường tiệm cận? 1 5x 1 1 A. y  . B. y 
. C. y  x  2  . D. y  . x 1 2  x x 1 x  2 2x  3
Câu 14. Đồ thị hàm số y 
có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x 1
A. x 1 và y  2 . B. x  2 và y  1 . C. x 1 và y  3 . D. x  1  và y  2.
Dạng 3. Xác định các đƣờng tiệm cận của đồ thị hàm số dựa vào bảng biến thiên và đồ thị hàm số Tcđ: x = x0 x - ∞ x0 +∞ y' = f'(x) ∞ y f(x) a = ∞ b Tcn: y = a Tcn: y = b Trang21
Dựa vào bảng biến thiên của hàm số y  f  x xác định phƣơng trình các đƣờng tiệm cận đứng, tiệm cận
ngang, số các đƣờng tiệm cận của đồ thị hàm số y  f  x
Chú ý: Nếu a  b thì đồ thị hàm số có một đƣờng tiệm cận ngang.
Nếu a  b thì đồ thị hàm số có hai đƣờng tiệm cận ngang. a   a   Nếu  hoặc 
thì đồ thị hàm số có một đƣờng tiệm cận ngang. b   b   a   Nếu 
thì đồ thị hàm số không có tiệm cận ngang. b  
Nếu cả hai bên x đều là số xác định ( không phải là  ) thì đồ thị hàm số không có tiệm cận đứng. 0
Câu 1. Cho hàm số y  f  x có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A. 4. B. 1. C. 3. D. 2.
Câu 2. Cho hàm số y  f (x) có bảng biến thiên. Đồ thị hàm
số có tiệm cận đứng là đường thẳng có phương trình là
A. không tồn ta ̣i tiê ̣m câ ̣n đứng. B. x  2  . C. x 1 . D. x  2  và x 1.
Câu 3. Cho hàm số y = f (x) có bảng biến thiên sau. Hỏi
đồ thị hàm số đó có mấy tiệm cận. A. 3 . B. 1. C. 4 . D. 2 .
Câu 4. Cho hàm số y  f  x có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là: A. 3 . B. 4 . C.1. D. 2 .
Câu 5. Cho hàm số y  f (x) có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã x ∞ cho là ∞ 2 + A. 4 . B. 2 . f'(x) C. 3 . D. 1 5 1 f(x) ∞ 5 Trang22
y  f  x Câu 6. Cho hàm số
có bảng biến thiên như sau.
Số đường tiệm cận ngang của đồ thị hàm số là A. 3 . B. 2 . C.1. D. 0 .
Câu 7. Cho hàm số y  f  x xác định trên  \   1 , liên tục trên
mỗi khoảng xác định và có bảng biến thiên như sau. Hỏi mệnh đề
nào dưới đây đúng?Số đường tiệm cận đứng của đồ thị hàm số là A. 3 . B. 2 . C.1. D. 0 . x -∞ -1 0 1 +∞
Câu 8:Cho hàm số y  f  x có bảng biến thiên như sau: y' + 0 - - 0 +
Tổng số đường tiệm cận đứng +∞ +∞
và ngang của đồ thị hàm số là? A.4. B.1. y 4 2 C.2. D.3. -∞ -∞ x -∞ 2 +∞
Câu 9:Cho hàm số y  f  x có bảng biến thiên như hình vẽ. y' - -
Tổng số đường tiệm cận đứng và ngang của đồ thị hàm số là? +∞ A.4. B.1. y 1 1 C.2. D.3. -∞
Câu 10:Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Phương trình đường tiệm cận ngang của đồ thị hàm số là: A. x  1. B. x  2. C. y  1. D. y  2. 2 x  3x  2
Câu 11:Tổng số các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y  là 3 2 x  2x A.1 . B. 4. C.2. D.3.
Câu 12: Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho lần lượt là
A. x  2, y  1 .
B. x  1, y  2 .
C. x  1, y  1.
D. x  2, y  2 .
Câu 13:Đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số nào Trang23 sau đây? x  2 2 1 x 1 2x 2x  3 A. y  . B. y  . C. y  . D. y  . 2x  4 1 2x 1 x x  2 x  9  3
Câu 14:Số tiệm cận đứng của đồ thị hàm số y  là 2 x  x A.3 B.2 C.0 D.1 4x 1
Câu 15: Tiệm cận ngang của đồ thị hàm số y  là x 1 1 A. y  . B. y  4 . C. y  1. D. y  1. 4
Câu 16.Cho hàm số y  f (x) có bảng biến thiên sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là: A. 3. B. 1. C. 2. D. 4.
V. NHẬN DẠNG ĐỒ THỊ HÀM SỐ 3 2
Bảng biến thiên và dạng đồ thị của hàm số bậc ba: y  ax  bx  cx  d a  0.
Tập xác định: D   2
y '  3ax  2bx  c a  0 ' 2
;   b  3ac y ' BẢNG BIẾN THIÊN DẠNG ĐỒ THỊ
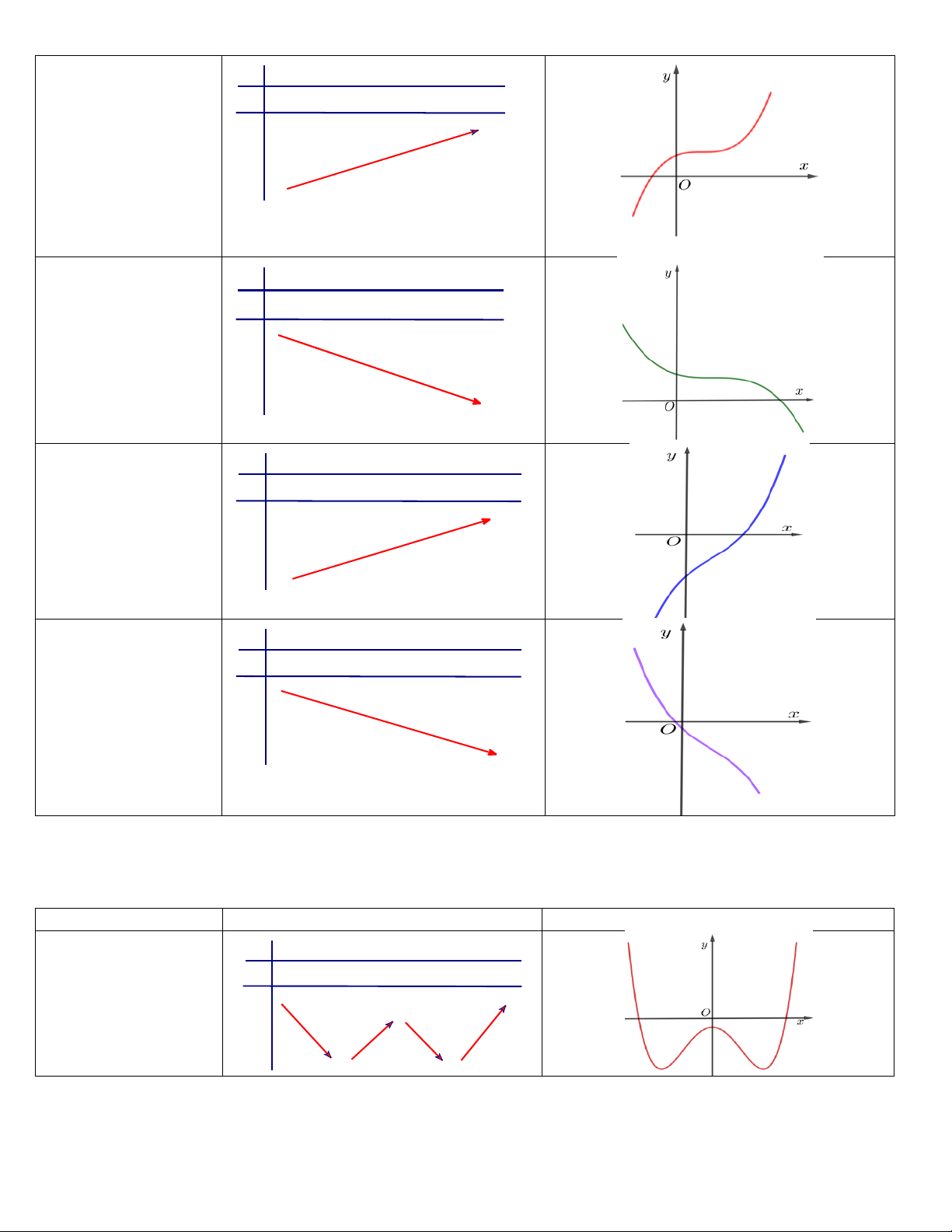
y '  0 có hai x -∞ x1 x2 +∞ nghiệm phân biệt y' + - 0 0 +
x ; x  x  x . +∞ 1 2  1 2 CĐ
Hệ số a  0 y CT -∞
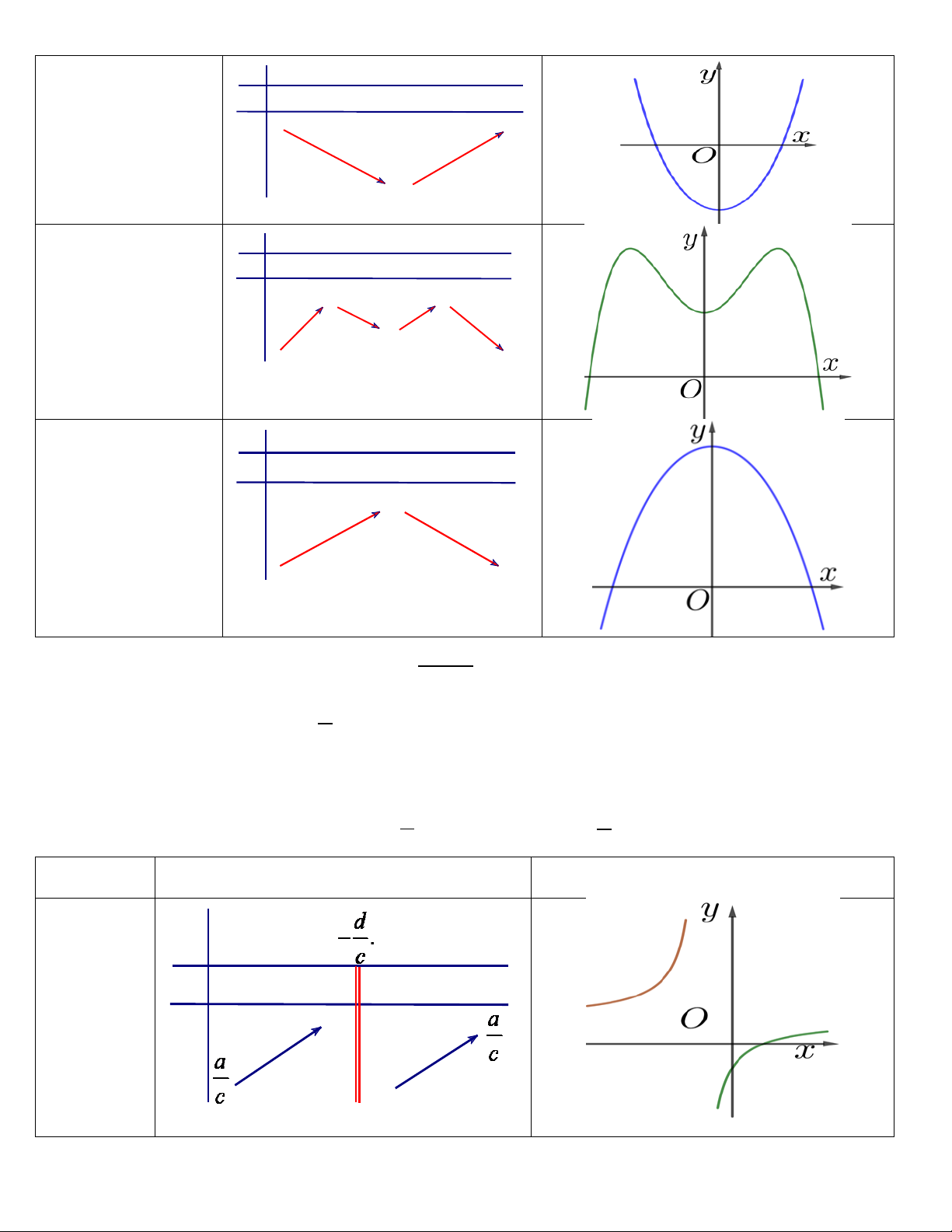
y '  0 có hai x -∞ x1 x2 +∞ nghiệm phân biệt y' - 0 + 0 -
x ; x  x  x . 1 2  1 2 +∞
Hệ số a  0 CĐ y CT -∞ Trang24
y '  0 có nghiệm x -∞ x1 +∞
kép x  x . y' 1 2 + 0 +
Hệ số a  0 +∞ y -∞
y '  0 có nghiệm x -∞ x1 +∞
kép x  x . 1 2 y' - - 0
Hệ số a  0 +∞ y -∞
y '  0 vô nghiệm x -∞ +∞
Hệ số a  0 y' + +∞ y -∞
y '  0 vô nghiệm x -∞ +∞
Hệ số a  0 y' - +∞ y -∞ 4 2
Bảng biến thiên và dạng đồ thị của hàm số trùng phƣơng: y  ax  bx  c a  0.
Tập xác định: D   3
y '  4ax  2bx a  0. BẢNG BIẾN THIÊN DẠNG ĐỒ THỊ x -∞ x1 x2 0 +∞ y' - 0 + 0 - 0 + a  0  +∞ +∞ b  0 CĐ y CT CT Trang25 x -∞ 0 +∞ y' - 0 + a  0 +∞ +∞  b  0 y CT x -∞ x1 0 x2 +∞ y' + 0 - 0 + 0 - a  0 CĐ CĐ  y b  0 CT -∞ -∞ x -∞ 0 +∞ y' + 0 - a  0 CĐ  y b  0 -∞ -∞ ax  b
Bảng biến thiên và dạng đồ thị của hàm số y 
c  0;ad bc  0. cx  d  d 
Tập xác định: D   \  .  c 
Hàm số đồng biến trên D  ad  bc  0.
Hàm số nghịch biến trên D  ad  bc  0. a d
Đồ thị hàm số có tiệm cận ngang y 
, tiệm cận đứng x   . c c BẢNG BIẾN THIÊN DẠNG ĐỒ THỊ
ad  bc  0 x -∞ +∞ y' + + +∞ y -∞ Trang26
ad  bc  0 x -∞ +∞ y' - - +∞ y -∞ 3 2
Câu 1: Cho hàm số bậc ba: y  ax  bx  cx  d a  0 có đồ thị nhƣ hình vẽ.Hãy y
chọn mệnh đề đúng trong các mệnh đề sau.
A. a  0,b  0,c  0, d  0.
B. a  0,b  0,c  0, d  0. x
C. a  0,b  0,c  0, d  0.
D. a  0,b  0,c  0, d  0. O Câu 2:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3 2
y  x  3x 1 . B. 3 2
y  x  3x 1. C. 4 2
y  x  2x 1. D. 4 2
y  x  2x 1.
Câu3: Bảng biến thiên sau là của hàm số nào? x -∞ 0 2 3 2    +∞ A. y x 3x 2 y' - 0 + 0 - 3 2     +∞ B. y x 3x 2 6 3 2    y C. y x 3x 2 2 D. 3 2
y  x  3x  2 -∞
Câu 4: Đồ thị trong hình vẽ bên là của hàm số nào ? A. 3
y  x  3x  4 B. 3 2
y  x  3x  4 C. 3
y  x  3x  4 D. 3 2
y  x  3x  4
Câu 5: Đồ thị sau đây là của hàm số nào ? A. 3 2
y  x  3x  3x 1 B. 3 2
y  x  3x 1 C. 3
y  x  3x 1 D. 3 2
y  x  3x 1 Trang27
Câu 6: Hình vẽ dưới đây là đồ thị của hàm số nào ? A. 3
y  x  3x  2 B. 3
y  x  4x  3 C. 3
y  x  3x  2 D. 3
y  x  4x  3
Câu 7.Hàm số nào có đồ thị như hình vẽ . 2
A. y  x(x  ) 1 2
B. y  x(x  ) 1 2
C. y  x(x  ) 1 2
D. y  x (x  ) 1
Câu 8. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y  x  3x . B. 3
y  x  3 . x C. 4 2
y  x  2x . D. 4 2
y  x  2x .
Câu 9.Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 2x 1 A. y  . x 1 x 1 B. y  . x 1 C. 4 2
y  x  x 1. D. 3
y  x  3x 1. Câu 10.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? x  2 x 1 A. y  B. y  . 2x  4 x  2 2x  3 x  3 C. y  D. y  . x  2 2x  4 Câu 11.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 3
y  x  3x 1. B. 3 2
y  x  3x 1. C. 3 2
y  x  3x 1. D. 3
y  x  3x 1. Trang28 Câu 12.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  3x  2 . B. 4 2
y  x  2x 1. C. 4 2
y  x  x 1. D. 4 2
y  x  3x  3. Câu 13.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? 2x 1 1  2x A. y  . B. y  . x 1 x  1 2x 1 2x 1 C. y  . D. y  . x 1 x 1 Câu 14.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  2x 1 . B. 4 2
y  x  2x 1. C. 3 2
y  x  x 1 . D. 3 2
y  x  x 1.
Câu 15:Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  3x 1 B. 3 2
y  x  3x 1 C. 3 2
y  x  3x 1 D. 4 2
y  x  3x 1
Câu 16. Đồ thị như hình vẽ là đồ thị của hàm số nào dưới đây? A. 3 2
y  x  3x  4 . B. 3 2
y  x  3x  4. C. 3 2
y  x  3x  4. D. 3 2
y  x  3x  4. Câu 17
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  2x  3 . B. 4 2
y  x  2x  3. C. 4 2
y  x  2x  3 . Trang29 D. 3 2
y  x  3x  3. Câu 18.
Đường cong ở hình bên là đồ thị của hàm số nào dưới đây. Hàm số đó là hàm số nào? A. 3 2
y  x  3x  2 . B. 3 2
y  x  3x  2. C. 3 2
y  x  3x  2 . D. 3 2
y  x  3x 1. Câu 20
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 2 3
y  3x  2x 1. B. 3 2 y  2
 x  3x 1. C. 3 2
y  x  2x 1 . D. 3 2
y  x  3x 1. Câu 21.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? A. 4 2
y  x  x 1. B. 4 2
y  x  4x 1. C. 4 2
y  x  4x 1 . D. 3 2
y  x  3x  2x 1. Câu 22
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? x 1 x  1 A. y  . B. y  . 2x 1 2x 1 2x 1 2x 1 C. y  . D. y  . x 1 x 1 Câu 23.
Đồ thị được cho ở hình bên là đồ thị của hàm số nào dưới đây? A. 3 2
y  x  3x 1. x 1 B. y  . x 1 C. 3 2
y  x  3x 1. D. 4
y  x  2x 1. Trang30
VI. SỰ TƢƠNG GIAO CỦA HAI ĐỒ THỊ KIẾN THỨC CẦN NHỚ
y  f  x
C ;hàm số 1  Giả sử hàm số có đồ thị là
y  g  x C . 2  có đồ thị là
Để tìm hoành độ giao điể
C C ,ta phải giải phƣơng trình 2  và 1  m của
f  x  g  x  
1 .Giả sử phƣơng trình   1 có
các nghiệm là x , x ,... 1 2
Khi đó,các giao điểm của C C M x ; f x ; M x ; f x ;... 1  1 1  2  2  2 2  1  và là  
Vậy, số giao điểm của C và C
là số nghiệm của phƣơng trình f  x  g  x   1 . 2  1  BÀI TẬP
Câu 1.Cho hàm số f (x) có bảng biến thiên như sau:
Số nghiệm thực của phương trình 3 f (x)  5  0 là: A. 2. B. 3. C. 4. D. 0.
Câu 2:Cho hàm số y  f  x có bảng biến thiên như sau: x -∞ -2 0 2 +∞
Số nghiệm thực của phương trình 2 f  x  3  0 là : f'(x) - + - 0 0 0 + +∞ A. 4 B. 3 +∞ 1 f(x) C. 2 D. 1 -2 -2
Câu 3: Cho hàm số f  x có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f  x  3  0 là : A. 1 . B. 2 . C. 3 . D. 0 . Trang31
Câu 4:Cho hàm số y  f  x có bảng biến thiên như sau: x -∞ -2 -1 0 +∞
Số nghiệm thực của phương trình f  x  4 bằng: f'(x) + 0 - - 0 + A. 4. B. 3. +∞ +∞ 2 f(x) -2 C. 2. D. 1. -∞ -∞ Câu 5:
Cho hàm số bậc ba y  f  x có đồ thị là đường
cong trong hình bên. Số nghiệm thực của phương
trình f  x  1  là A. 3 . B.1 . C. 0 . D. 2 .
Câu 6: Cho hàm số y  f  x có bảng biến thiên như sau
Số nghiệm thực của phương trình 5 f  x 3  0 bằng :
A. 5. B. 4. C. 3. D. 2.
Câu 7:Cho hàm số f  x có bảng biến thiên như sau:
Số nghiệm thực của phương trình 2 f  x  3  0 là : A. 2. B. 1. C. 4. D. 3. Câu 8:Cho hàm số 3
y  ax  bx  cx  d (a, ,
b c, d   ) . Đồ thị hàm số y  f (x)
như hình vẽ bên.Số nghiệm thực của phương trình 3 f (x)  4  0 là A.3 B.0 C.1 D.2 Trang32
Câu 9. Cho hàm số bậc bốn y  f  x có đồ thị trong hình bên.
Số nghiệm của phương trình f  x  1  là A. 3. B. 2. C. 1. D. 4.
Câu 10. Cho hàm số bậc bốn y  f  x có đồ thị như hình vẽ.
Số nghiệm của phương trình 3 f  x  8  0 bằng A. 1. B. 2. C. 3. D. 4.
Câu 11. Cho hàm số y  f  x liên tục trên R và có bảng biến thiên
như sau. Số nghiệm của phương trình 2 f  x  3  0 là A. 1. B. 2. C. 0. D. 3.
Câu 12. Cho hàm số f  x có đồ thị như hình vẽ.
Số nghiệm của phương trình 2 f  x  3  0 là A. 3. B. 1. C. 2. D. 0.
Câu 13. Cho hàm số y  f  x có bảng biến thiên như hình vẽ x -∞ -1 1 +∞
bên.Số nghiệm của phương trình f  x  1  là - f'(x) 0 + + +∞ A. 1. B. 2. 1 -1 f(x) - 2 C. 4. D. 3. -∞ Trang33
Câu 14. Cho hàm số y  f  x có bảng biến thiên như sau:
Số nghiệm của phương trình 2 f  x  5  0 là: A. 4. B. 0. C. 3. D. 2. Câu 15.Cho hàm số 4 2
y  x  2x 1 có đồ thị như hình vẽ.
Tìm tất cả các giá trị thực của tham số m để phương trình 4 2
x  2x 1  m có
bốn nghiệm thực phân biệt.
A. 1 m  2.
B. m  1.
C. m  2.
D. 1 m  2.
Câu 16. Cho hàm số y  f  x có bảng biến thiên như hình vẽ:
Tìm tất cả các giá trị của m để phương trình f  x  m có 3 nghiệm phân biệt. A. 2   m 1. B. 2   m. C. 2
  m 1. D. 2
  m 1. Câu 17. Cho hàm số    4 2 y
f x  ax  bx  c có đồ thị như hình vẽ.
Số nghiệm của phương trình 2 f  x  3  0 là A. 3. B. 1. C. 2. D. 4.
Câu 18. Cho hàm số y  f  x liên tục trên R và có đồ thị như hình bên.
Phương trình f  x   có bao nhiêu nghiệm thực phân biệt? A. 1. B. 2. C. 3. D. 4.
Câu 19. Đồ thị ở hình bên là của hàm số 4 2
y  x  2x  3 .
Với giá trị nào của m thì phương trình 4 2
x  2x  m  0 có ba nghiệm phân biệt? A. m  3  . B. m  4  .
C. m  0.
D. m  4. Trang34
Câu 20.Cho hàm số y  f  x xác định, liên tục trên R và có
bảng biến thiên như hình vẽ.
Số nghiệm của phương trình f  x  2  0 là A. 2. B. 0 . C. 1. D. 3.
Câu 21. Cho hàm số y  f  x có bảng biến thiên như hình vẽ.
Số nghiệm của phương trình f  x  2  0 là A. 1. B. 2. C. 3. D. 0. Câu 22. Cho hàm số 4 2
y  x  2x  3 có đồ thị hàm số như hình
vẽ. Với giá trị nào của tham số m phương trình 4 2
x  2x  3  2m  4 có hai nghiệm phân biệt? m  0  1 A. 1 . B. 0  m  . m  2  2 m  0  1 C. 1 . D. m  . m  2  2 Trang35

Trắc Nghiệm Ôn Tập Giải Tích 12 Chương 1 Mức Độ 1 Và 2 Có Đáp Án

Thông tin :

Tài liệu liên quan:

Hình nón là gì? Công thức tính diện tích xung quanh hình nón | Toán 12

Đề tham khảo kỳ thi tốt nghiệp THPT từ năm 2025 môn Toán

Đề thi thử TN THPT 2025 lần 1 môn Toán trường THPT Lương Tài 2 – Bắc Ninh

Lời giải chi tiết đề tham khảo kỳ thi tốt nghiệp THPT môn Toán từ năm 2025

Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bắc Giang