

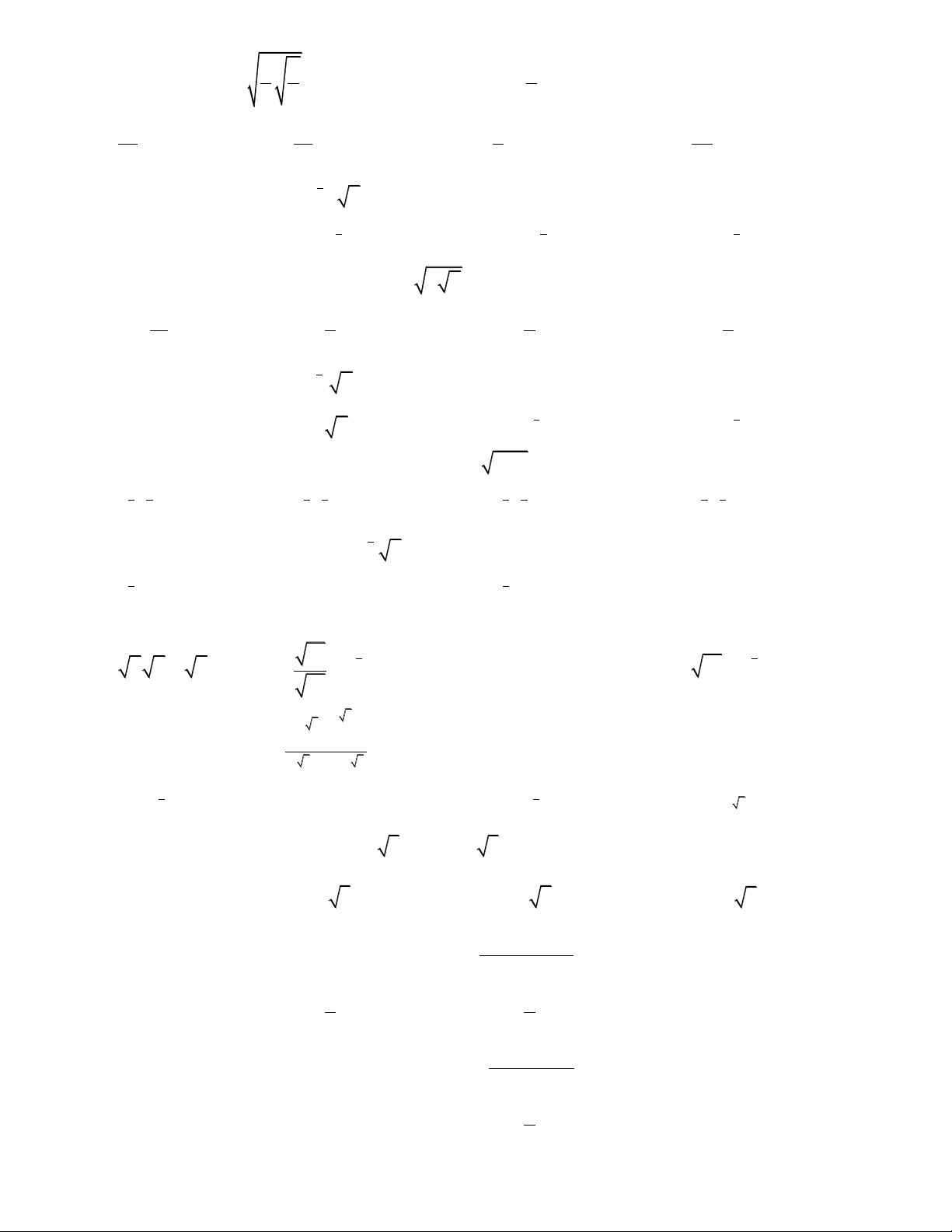


















Preview text:
CHƢƠNG II: LŨY THỪA – MŨ – LOGARIT
I. LŨY THỪA– HÀM SỐ LŨY THỪA
KIẾN THỨC CẦN NHỚ LŨY THỪA
1. Lũy thừa với số mũ nguyên
Cho n là một số nguyên dương.
• Với a tùy ý: n a . a . a ..a n thöø a soá • Với a 0: 0 a n 1 1; a
(a: cơ số, n: số mũ). n a Chú ý: 0
0 , 0n không có nghĩa.
Lũy thừa với số mũ nguyên có các tính chất tương tự như lũy thừa với số mũ nguyên dương.
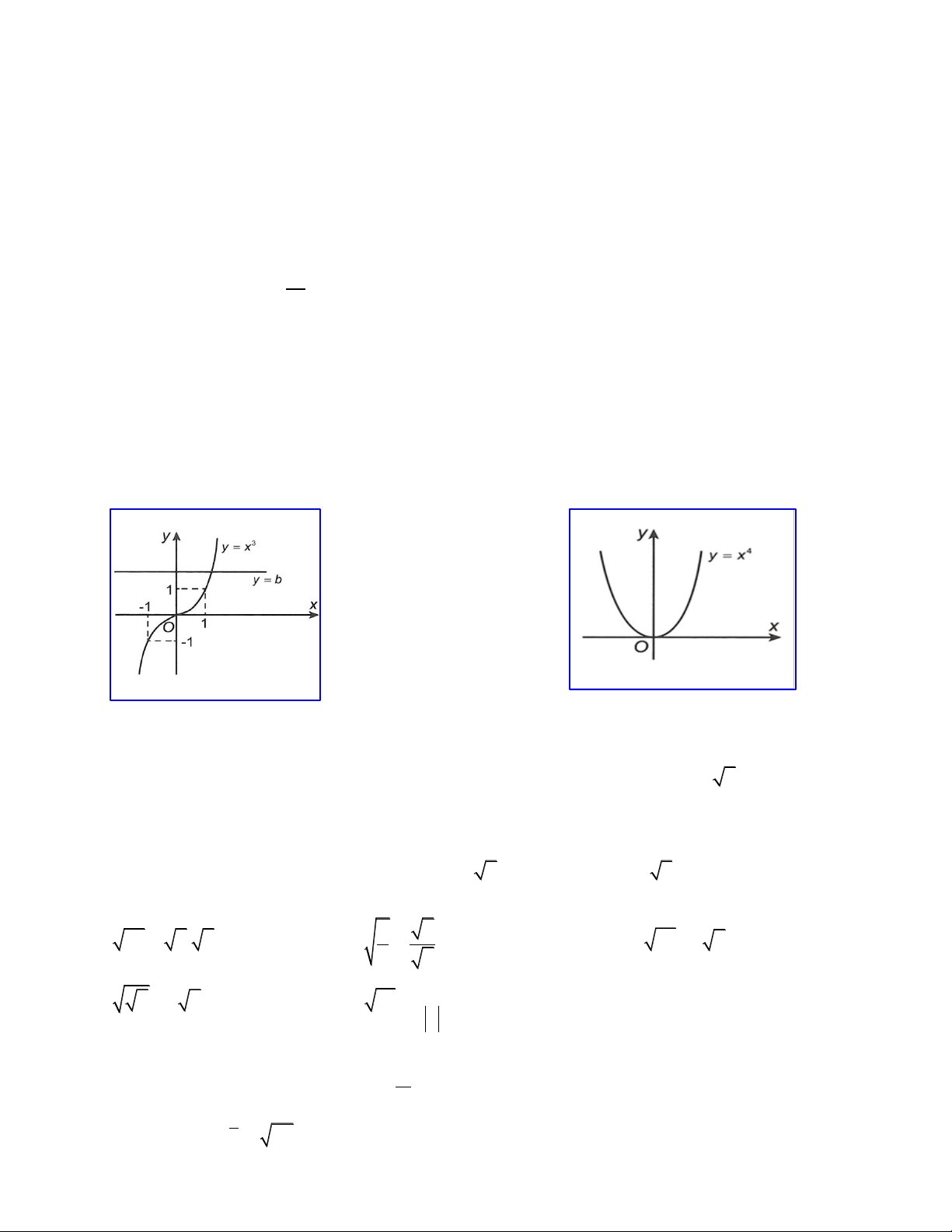
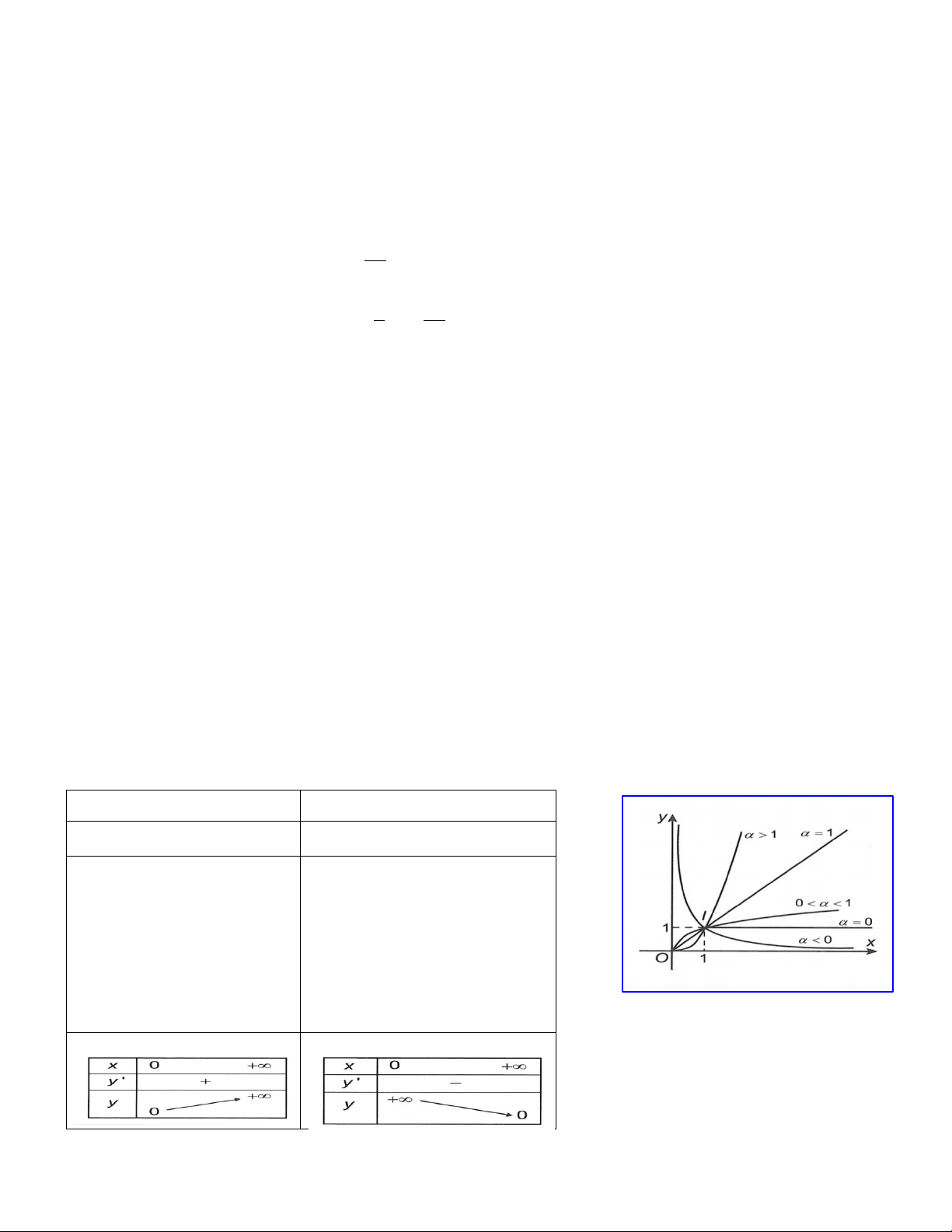
2. Phƣơng trình n x b*
• Với n lẻ: Phương trình (*) luôn có nghiệm duy nhất. • Với n chẵn:
+ Nếu b 0: Phương trình (*) có hai nghiệm trái dấu.
+ Nếu b 0: Phương trình (*) có một nghiệm x 0
+ Nếu b 0 : Phương trình (*) vô nghiệm. 3. Căn bậc n
Khái niệm: Cho b R , *
n N n 2 . Số a được gọi là căn bậc n của b nếu n a b .
• Với n lẻ và b R , phương trình n
x b có duy nhất một căn bậc n của b, ký hiệu là n b . • Với n chẵn:
b 0 : Không có căn bậc n của b.
b 0: Có một căn bậc n của 0 là 0.
b 0: Có hai căn trái dấu, ký hiệu giá trị dương là n b , còn giá trị âm là n b . Tính chất: Với , a b 0, * ,
m n N ; p Z ta có: n a a p • n n .n ab a ; b • n ,b 0;
• n p n a
a ,a 0; n b b a khi n leû • n m . n m a ; a • n n a a khi n chaü n.
4. Lũy thừa với số mũ hửu tỉ m
Cho số thực a dương và số hửu tỉ r , trong đó * m ,
Z n N . Lũy thừa của a với số mũ r được xác n m định như sau: r n m n
a a a .
5. Lũy thừa với số mũ vô tỉ Trang1
Cho a 0, là một số vô tỉ. Ta thừa nhận rằng luôn có một dãy số hữu tỉ r mà lim r và một n n n r
dãy số tương ứng n
a có giới hạn không phụ thuộc vào việc chọn dãy số r . n
Khi đó ta kí hiệu a lim rn
a là lũy thừa của a với số mũ . n
6. Lũy thừa với số mũ thực Tính chất
Với mọi a, b là các số thực dương; , là các số thực tùy ý, ta có: a
• a .a a ; • a ; • a . a ; a a a • . a b a .b ; • ; b b
So sánh hai lũy thừa
• So sánh cùng cơ số
- Nếu cơ số a 1 thì a a .
- Nếu cơ số 0 a 1thì a a .
• So sánh cùng số mũ
- Nếu số mũ 0thì a b 0 a b .
- Nếu số mũ 0 thì a b 0 a b . HÀM SỐ LŨY THỪA
1. Khái niệm hàm số lũy thừa Hàm số y x
,với R được gọi là hàm số lũy thừa.
Chú ý: Tập xác định của hàm số y x
tùy thuộc vào giá trị của .
Cụ thể: • nguyên dương: D R ;
• nguyên âm hoặc bằng 0: D \ R| 0 ;
• không nguyên: D 0;.
2. Đạo hàm của hàm số lũy thừa
Hàm số lũy thừa y x
, R có đạo hàm với mọi x 0 và: • x 1 x ; • u 1
u .u với u là biểu thức chứa x.
3. Khảo sát hàm số lũy thừa y x Đồ thị
y x , 0
y x , 0
a. Tập khảo sát: 0;
a. Tập khảo sát: 0; b. Sự biến thiên: b. Sự biến thiên: • 1 y x 0, > x 0 • 1 y x 0, > x 0
Hàm số luôn đồng biến.
Hàm số luôn nghịch biến.
• Giới hạn đặc biệt:
• Giới hạn đặc biệt:
lim x 0, lim x . lim x , lim x 0. x0 x x0 x • Tiệm cận: Không có. • Tiệm cận:
Trục Ox là tiệm cận ngang.
Trục Oy là tiệm cận đứng.
c. Bảng biến thiên:
c. Bảng biến thiên:
Nhận xét: Đồthị của hàm số lũy thừa luôn đi qua điểm I 1; 1 . Trang2 DẠNG BÀI TẬP Dạng 1: Lũy thừa
Bài toán 1. Viết lũy thừa với dạng số mũ hữu tỷ Phƣơng pháp giải
Tính chất của căn bậc n n a Khi n le û b 0 n a.n b Khi n leû n b • n a ab ; • n ;
n a .n b Khi n chaü n n b a Khi n chaü n b0 n b p a khi n leû
• n p n a
a ,a 0; • n m n.m a ;
a • n n a . a khi n chaü n
Công thức lũy thừa với số mũ thực m m m n a a a • m . m n m a a ; • m. n m n a a a ; • m n a ; • m. m a b . a b ; • . n a m b b Ví dụ mẫu:
Ví dụ 1: Cho x là số thực dương. Biểu thức 4 2 3 x
x được viết dưới dạng lũy thừa với số mũ hữu tỉ là 7 5 12 6 A. 12 x . B. 6 x . C. 7 x . D. 5 x . Hƣớng dẫn giải. 1 1 7 7 4 7 4 4 Ta có: 4 2 3 2 3 3 3 12 x x x x
x x x . Chọn A.
Sử dụng máy tính cầm tay:
Cho x một giá trị dƣơng bất kì, nhập vào máy tính, trừ lần lƣợt các đáp án cho đến khi nhận đƣợc kết
quả bằng 0 thì chọn.
Cho x 3 .
Thao tác trên máy tính: qs!o4$3dqs3$p3^7a12=
KQ: 0 Chọn A a b a
Ví dụ 2: Cho hai số thực dương a và b. Biểu thức 5 3
được viết dưới dạng lũy thừa với số mũ hữu tỉ b a b là 7 31 30 1 30 a 30 a 31 a 6 a A. . B. . C. . D. . b b b b Hƣớng dẫn giải 1 1 1 5 1 1 2 2 a b a
a a a a a 6 6 6 a a a a Ta có: 5 3 5 3 5 3 5 5 . Chọn D. b a b
b b b b b b b b b
Sử dụng máy tính cầm tay: Trang3
Cho a, b nhận a b giá trị dƣơng bất kì, nhập vào máy tính, trừ lần lƣợt các đáp án cho đến khi
nhận đƣợc kết quả bằng 0 thì chọn. a 3 a b a Cho . 5 3 b 5 b a b
Thao tác trên máy tính: qs!o5$3a5$qs5a3$s3a5$$$$ p(3a5$)^7a30=
KQ: 0, 0307 0 Loại A
!Eo31= KQ: 0, 3285 0 Loại B. Tƣơng tự, loại C chọn D.
Bài toán 2. Tính giá trị biểu thức Phƣơng pháp giải a
Công thức đặc biệt f x x
thì f x f 1 x 1. x a a
5 3x 3x
Ví dụ 1: Cho 9x 9x 23. Tính giá trị của biểu thức P ta được
1 3x 3x 3 1 5 A. 2. B. . C. . D. . 2 2 2 Hƣớng dẫn giải x x 2 3 3 5
Ta có: 9x 9x 23 3x 3x 25
3x 3x 5 loaïi
5 3x 3x 5 5 5
Từ đó, thế vào P Chọn D.
1 3x 3x . 1 5 2 BÀI TẬP
Câu 1: Khẳng định nào sau đây đúng? m A. n
a xác định với mọi a \ 0 ; n . B. n m n
a a ; a . m C. 0 a 1; a . D. n m n
a a ; a ; , m n . 2 2 2 3 a b
Câu 2: Rút gọn biểu thức
(với a 0,b 0và 2 3 a
b ) được kết quả a b 1 2 2 3 2 3 a b 2 2a A. 2. B. 2 2a . C. . D. . 2 3 a b 2 3 a b
Câu 3: Cho số thực dương a. Rút gọn 3 4 5
P a a a a ta được 25 37 53 43 A. 13 a . B. 13 a . C. 36 a . D. 60 a .
Câu 4: Viết biểu thức 3 2 P .
a a . a a 0 dưới dạng lũy thừa với số mũ hữu tỉ ta được 5 5 11 A. 3
P a . B. 6
P a . C. 6
P a . D. 2 P a . Trang4 m b a a
Câu 5: Viết biểu thức 5 3 , ,
a b 0 về dạng lũy thừa ta được m bằng a b b 2 4 2 2 A. . B. . C. . D. . 15 15 5 15 5
Câu 6: Rút gọn biếu thức 3 3
Q b : b với b 0 ta được 5 4 4 A. 2
Q b . B. 9
Q b . C. 3
Q b . D. 3 Q b .
Câu 7: Giả sử a là số thực dương, khác 1 và 3
a a được viết dưới dạng a .. Giá trị của là 11 5 2 1 A. . B. . C. . D. . 6 3 3 6 1
Câu 8: Rút gọn biểu thức 6 3
P x . x với x 0 ta được 1 2 A. 2
P x . B. P x. C. 8
P x . D. 9 P x .
Câu 9: Cho a, b là các số thực dương. Viết biểu thức 12 3 3
a b dưới dạng lũy thừa với số mũ hữu tỉ ta được 3 1 1 1 1 1 1 3 A. 4 2 a b . B. 4 9 a b . C. 4 4 a b . D. 4 4 a b . 2
Câu 10: Cho a là một số dương, viết 3 a
a dưới dạng lũy thừa với số mũ hữu tỉ ta được 7 1 A. 6 a . B. 3 a . C. 6 a . D. 2 a .
Câu 11: Cho a 0. Đẳng thức nào sau đây đúng? 3 5 a 7 A. 3 4
a a a. B. 6 a . C. a 4 2 6 a . D. 7 5 5 a a . 3 2 a a 3 1 3 1
Câu 12: Cho biểu thức P
, với a 0. Mệnh đề nào dưới đây đúng? 53 4 5 a .a 1 3 A. 2
P a . B. P . a C. 2
P a . D. 3 P a . 2017 2016
Câu 14: Giá trị của biểu thức P 7 4 3 74 3 bằng A. 1. B. 7 4 3. C. 7 4 3. D. 2016 7 4 3 .
10 2x 2x
Câu 16: Cho 4x 4x 14. Giá trị của biểu thức P là
3 2x 2x 1 6
A. P 2. B. P . C. P . D. P 7. 2 7
4 5x 5x
Câu 17: Cho 25x 25x 7. Giá trị của biểu thức P là
9 5x 5x 1
A. P 12. B. 1 P 12 . C. P . D. P 2. 9
Dạng 2: Hàm số lũy thừa Trang5
Bài toán 1. Tìm tập xác định của hàm số lũy thừa Phƣơng pháp giải
Ta tìm điều kiện xác định của hàm số y f x
, dựa vào số mũ của nó như sau:
• Nếu là số nguyên dương thì không có điều kiện xác định của f x.
• Nếu là số nguyên âm hoặc bằng 0 thì điều kiện xác định là f x 0.
• Nếu là số không nguyên thì điều kiện xác định là f x 0. Ví dụ mẫu
Ví dụ 1: Tập xác định của hàm số y x x 1 2 5 5 6 là A. \ 2; 3 . B. ; 2 3;. C. 2; 3 .
D. 3;.
Hƣớng dẫn giải: Số mũ 1
không phải là số nguyên. Do đó, điều kiện xác định của hàm số là: 5 2
x 5x 6 0 x2;
3 . Vậy tập xác định của hàm số đã cho là 2; 3 .Chọn C. si n 2018
Ví dụ 2: Tập xác định của hàm số y x là A. . B. 0;. C. \ 0 . D. 0; . Hƣớ si n 2018
ng dẫn giải: Ta có 0 y x
x nên tập xác định là \ 0 . Chọn C.
Ví dụ 3: Tập xác định của hàm số y x 2019 1 là A. . B. 0;. C. \ 0 . D. 0; .
Hƣớng dẫn giải: Vì số mũ 2019
là số nguyên âm nên điều kiện xác định của hàm số là
1 x 0, ngoài ra hàm số còn chứa căn thức bậc hai nên x 0. 1
x 0 luoân ñuùng x 0 Hàm số xác định
x 0. Vậy D 0; .Chọn D. x 0
Bài toán 2. Tính đạo hàm của hàm số lũy thừa Phƣơng pháp giải
Công thức tính đạo hàm • x 1
x x 0, ; • u 1
u .u với u là biểu thức chứa x. Ví dụ mẫu
Ví dụ 1: Tìm đạo hàm của hàm số y x 1 2 4 1 . 1 5
A. y 1 x 5 2 4 . B. y x1 x 5 2 4 . 4 2 5 1 C. y x1 x 5 2 4 . D. y x1 x 5 2 4 . 2 2 Hƣớng dẫn giải Trang6 1 5 5 1 1 1 1 Ta có: y 2 1 x 4 . 2 1 x 2 1 x 4 . 2
x x 2
1 x 4 . Chọn D. 4 4 2
Ví dụ 2: Tìm đạo hàm của hàm số y x4 2 3cos2 . A. y x3 24 2 3cos2 sin2 . x B. y x3 12 2 3cos2 sin2 . x C. y x3 24 2 3cos2 sin2 . x D. y x3 12 2 3cos2 sin2 . x Hƣớng dẫn giải 3 3
Ta có: y 42 3cos2x 2 3cos2x 42 3cos2x 6
sin2x x3 24 2 3cos2 sin2 . x Chọn A. BÀI TẬP
Câu 1:Tập xác định D của hàm số y x x 2 3 2 3 4 là
A. D \ 1 ; 4 . B. D ; 1 4; .
C. D . D. D ; 1 4;.
Câu 2: Trong các hàm số sau đây, hàm số nào có tập xác định D ? 1
A. y 2 x . B. y 2 . C. y 2 2 x .
D. y 2 x . 2 x
Câu 3: Tập xác định D của hàm số
x x 4 2 y 3 là A. 0; 3 .
B. D \ 0; 3 .
C. D .
D. D ; 0 3;.
Câu 4: Tập xác định của hàm số x x2019 2 2020 y 4 là A. ; 0 4; . B. ; 0 4;. C. 0; 4 . D. \ 0; 4 .
Câu 5: Tập xác định D của hàm số y x0 3 là
A. D ; 3 .
B. D ; 3.
C. D \ 3 . D. D . sin 2 x 3
Câu 6: Tập xác định D của hàm số y là x 2
A. D \ 2 ; 3 .
B. D , 2 3, .
C. D \ 3 . D. D ; 2 3;.
Câu 7: Tập xác định D của hàm số e
y x 2 x 1 là A. D 1 ; 1 .
B. D \ 1 ; 1 .
C. D 1;. D. D .
Câu 8. Tập xác định của hàm số y 2
x 3x 2 là A. R \ 1; 2 . B.
;1 2; . C. (1;2). D. ; 1 2; . LOGARIT KIẾN THỨC CẦN NHỚ Trang7 1. Khái niệm lôgarit
Cho hai số dương a, b với a 1 . Số thỏa mãn đẳng thức
a b được gọi là lôgarit cơ số a của b , và ký hiệu là log b . a 2. Tính chất log 0; log a 1 a a
Cho a,b 0, a 1. Ta có: log b a a ; b log a a
3. Quy tắc tính lôgarit
a. Lôgarit của một tích
Cho a, b , b 0 với a 1 , ta có: log (b b ) log b log b 1 2 a 1 2 a 1 a 2
Chú ý: Định lý trên có thể mở rộng cho tích của n số dương: log b ...b log b ... log b a 1 n a 1 a n trong đó ,
a b ,b ,...,b 0,a 1. 1 2 n
b. Lôgarit của một thƣơng b Cho ,
a b ,b 0 với a 1, ta có: 1 log
log b log b 1 2 a a 1 a 2 b2 Đặ 1 c biệt: log
log b a 0,b 0 . a a b
c. Lôgarit của một lũy thừa Cho hai số dương , a ,
b a 1. Với mọi , ta có: log b log b a a Đặ n 1 c biệt: log b log b a a n 4. Đổi cơ số log b Cho , a ,
b c 0; a 1;c 1, ta có: log c b a log a c 1 Đặ 1 c biệt: log b b log b log b a a 0. a 1; log a b
5. Lôgarit thập phân – lôgarit tự nhiên a. Lôgarit thập phân
Lôgarit thập phân là lôgarit cơ số 10. Với b 0, log b thường được viết là log b hoặc lgb . 10
b. Lôgarit tự nhiên
Lôgarit tự nhiên là lôgarit cơ số e . Với b 0, log b được viết là lnb. e DẠNG BÀI TẬP
Dạng 1. Tính giá trị của biểu thức không có điều kiện. Rút gọn biểu thức. Ví dụ 1: Cho , a b 0 và ,
a b 1, biểu thức 3 4 P log
b .log a bằng b a A. 6 B. 24 C. 12. D. 18. Hƣớng dẫn giải 3 1 Ta có : 3 4 3 4 P log
b .log a log b .log a .4.log . b 24.Chọn B. 1 b b a a 2 a 1 log b a 2 Trang8 Ví dụ 2:Cho ,
a b là các số thực dương thỏa mãn a 1, a b và log b 3. a b
Biến đổi biểu thức P log ta được b a a A. P 5 3 3. B. P 1
3.C. P 1 3. D. P 5 3 3. Hƣớng dẫn giải b 1 b a a 1 log log 1 3 1 a 3 1 Ta có: 2 2 P 1 3.Chọn C. 1 b log b 1 3 2 a log b 1 log 2 a a a
Phƣơng pháp giải trắc nghiệm: Chọn 3
a 2,b 2 . Bấm máy ta được P 1 3.Chọn C.
Dạng 2. Tính giá trị biểu thức theo một biểu thức đã cho Phƣơng pháp giải Để
tính log b theo m log ;
x n log y ta biến đổi b a .x .y . a a a
Từ đó suy ra log b log a .x .y m n . a a Ví dụ mẫu
Ví dụ 1. Cho log 27 .
a Khi đó giá trị của log 16 được tính theo a là 12 6 43 a 43 a 4a 2a A. . B. . C. . . 3 a 3 a 3 D. a 3 a Hƣớng dẫn giải log 27 3log 3 2a Ta có: 2 2 a log 27 log 3 . 12 2 log 12 2 log 3 3 a 2 2 43 4 4 4 a Khi đó log 16 4log 2 . Chọn A. 6 6 log 6 1 log 3 2a 3 a 2 2 1 3a
Sử dụng máy tính cầm tay:
i12$27qJz( Lưu log 27vào biến A) 12
Nhập log 16trừ lần lượt các đáp án cho đến khi được kết quả bằng 0 thì chọn. 6 i6$16$p(a4(3pJz)R3+Jz$)= KQ: 0 chọn A.
Ví dụ 2. Cho log 3 a; log 2 b Khi đó giá trị của log
30 được tính theo a là: 125 43 a 1 a a a A. . B. . C. . 3 b 31 b 3 D. . b 3 a Hƣớng dẫn giải lg30 1 lg3 1 a Ta có: log 30 .Chọn B. 125 lg125 31 lg2 31 b
Sử dụng máy tính tƣơng tự câu 1. g3)qJz; g2)qJx i125$30$p(a4(3pJz)R3pJx$)= KQ: 3
,0345... 0 loại A i125$30$p(a1+JzR3(1pJx)$)= KQ: 0 Chọn B. Trang9 BÀI TẬP
Câu 1: Với a là số thực dương tùy ý, 2 log a bằng 5 1 1
A. 2 log a B. 2+ log a C. log a D . + log a 5 5 2 5 2 5
Câu 2: Với a là số thực dương tùy ý, 2 log a bằng 7 1 1
A. 7 log a B. 2 log a C. log a D . + log a 2 7 2 7 2 2
Câu 3: Với a là số thực dương tùy ý, 2 log a bằng 7 1 1
A. 7 log a B.
+ log a C.
log a D . 2 log a 2 2 2 2 7 7
Câu 4: Với a là số thực dương tùy ý, 3 log a bằng 7 1
A. 7 log a B.
+ log a C. 3 log a D . 3+ log a 2 3 2 7 7
Câu 5: Với a là số thực dương tùy ý, 3 log a bằng 6 1
A. 6 log a B.
+ log a C. 3 log a D . 3+ log a 3 6 6 6
Câu 6: Với a là số thực dương tùy ý, 5 log a bằng 7 1
A. 5 log a B.
+ log a C. 7 log a D . 5+ log a 7 7 5 7 7
Câu 7: Với a là số thực dương tùy ý, 3 log a bằng 7 1 1
A. 7 log a B.
log a C. 3 log a D . + log a 2 3 7 7 3 7
Câu 8: Với a là số thực dương tùy ý, log a bằng 7 1 1
A. 7 log a B.
log a C. 3 log a D . log a 2 3 7 7 2 7
Câu 9: Với a là số thực dương tùy ý, 3 2 log a bằng 7 3 2
A. 3 log a B. log a C.
log a D . 3 log a 7 2 7 3 7 7
Câu 10: Với a là số thực dương và khác một, 3 2 log a bằng a 2 3 2 A. B. log a C.
log a D . 3 log a 3 2 a 3 2 3
Câu 11: Với a là số thực dương và khác một, 5 2 log a bằng a 2 3 5 2 A. 5 2 log a B. log a C. D . 3 a 2 a 2 5
Câu 12: Với a là số thực dương và khác một, log a bằng 2 a 3 A. 2 B.
log a C. 1 D . 3 log a 2 a 3 2
Câu 13: Khẳng định nào sau đây là khẳng định đúng khi a,b là các số thực dương khác một. A. logb a a b B. logb a a a C. loga b a a D. loga b a b
Câu 14: Cho 0 a 1 và x, y là hai số dương. Tìm mệnh đề đúng:
A. log (x y) log x log . y B. log ( .
x y) log x log y. a a a a a a C. log ( . x y) log . x log .
y D. log (x y) log . x log . y a a a a a a
Câu 15: Cho 0 a 1 và x, y là hai số dương. Tìm mệnh đề đúng: Trang10 x log x log x A. log a
B. log (x y) a a y log y a log y a a x C. log log x log . y
D. log (x y) log x log . y a a a y a a a
Câu 16: Cho a 0 và a 1. Khi đó biểu thức P log a có giá trị là: 3 a 1 1 A. 3. B. C. D. 3. 3 3 Câu 17: Biết log
a 2 với a 0 thì log a bằng: 6 6 A. 36.
B. 6. C. 1 D. 4 8log 7
Câu 18: Cho a 0 và a 1. Khi đó biểu thức 2 a P a có giá trị là: A. 2 7 . B. 4 7 . C. 6 7 . D. 8 7 .
Câu 19: Cho a 0 và a 1. Khi đó biểu thức log 4 a P a có giá trị là: 1 A. B. 2. C. 4. D.16. 2
Câu 20: Cho a 0 và a 1. Khi đó biểu thức 3 5
P log (a . a. a ) có giá trị là: a 1 37 A. B.10. C. 20. D. 15 10
Câu 21: Với a là số thực dương tùy ý, 3 log a bằng 6 1
A. 6 log a B.
+ log a C. 3 log a D . 3+ log a 3 6 6 6
Câu 22: Với a là số thực dương tùy ý, 5 log a bằng 7 1
A. 5 log a B.
+ log a C. 7 log a D . 5+ log a 7 7 5 7 7
Câu 23: Với a là số thực dương tùy ý, 3 log a bằng 7 1 1
A. 7 log a B.
log a C. 3 log a D . + log a 2 3 7 7 3 7
Câu 24: Với a là số thực dương tùy ý, log a bằng 7 1 1
A. 7 log a B.
log a C. 3 log a D . log a 2 3 7 7 2 7
Câu 25: Với a là số thực dương tùy ý, 3 2 log a bằng 7 3 2 A. 3 log a B. log a C.
log a D . 3 log a 7 2 7 3 7 7
Câu 26: Với a là số thực dương và khác một, 3 2 log a bằng a 2 3 2 A. B. log a C.
log a D . 3 log a 3 2 a 3 2 3
Câu 27: Với a là số thực dương và khác một, 5 2 log a bằng a 2 3 5 2 A. 5 2 log a B. log a C. D . 3 a 2 a 2 5
Câu 28: Với a là số thực dương và khác một, log a bằng 2 a 3 A. 2 B.
log a C. 1 D . 3 log a 2 a 3 2
Câu 29: Khẳng định nào sau đây là khẳng định đúng khi a,b là các số thực dương khác một. Trang11 A. logb a a b B. logb a a a C. loga b a a D. loga b a b
Câu 30: Cho 0 a 1 và x, y là hai số dương. Tìm mệnh đề đúng:
A. log (x y) log x log . y B. log ( .
x y) log x log y. a a a a a a C. log ( . x y) log . x log .
y D. log (x y) log . x log . y a a a a a a
Câu 31: Cho 0 a 1 và x, y là hai số dương. Tìm mệnh đề đúng: x log x log x A. log a
B. log (x y) a a y log y a log y a a x C. log log x log . y
D. log (x y) log x log . y a a a y a a a
Câu 32: Cho a 0 và a 1. Khi đó biểu thức P log a có giá trị là: 3 a 1 1 A. 3. B. C. D. 3. 3 3 Câu 33: Biết log
a 2 với a 0 thì log a bằng: 6 6 A. 36.
B. 6. C. 1 D. 4 8log 7
Câu 34: Cho a 0 và a 1. Khi đó biểu thức 2 a P a có giá trị là: A. 2 7 . B. 4 7 . C. 6 7 . D. 8 7 .
Câu 35: Cho a 0 và a 1. Khi đó biểu thức log 4 a P a có giá trị là: 1 A. B. 2. C. 4. D.16. 2
Câu 36: Cho a 0 và a 1. Khi đó biểu thức 3 5
P log (a . a. a ) có giá trị là: a 1 37 A. B.10. C. 20. D. 15 10 0 ,3 10 a
Câu 37: Với các số thực dương a , b bất kì, đặt M
. Mệnh đề nào dưới đây đúng? 3 5 b 1
A. log M 3log a log b .
B. log M 3log a 2 log b . 2 C. log M 3 log a 1 2 log b .
D. log M 3log a log b . 2 Câu 38: Cho log 5 ;
m log 5 n . Khi đó log 5 tính theo m và n là. 2 3 6 mn
A. m n . B. 2 2 m 1 n . C. . D. . m n m n
Câu 39: Với a, b là hai số thực dương và a 3 1, log a b bằng a a 3 3 3 2 4 2 A. log b . B. log b . C. log b . D. log b 2 2 a 2 a 3 9 a 3 a
Câu 40: Đặt log 6 ;
a log 7 b . Hãy biểu diễn log 7 theo a và b . 12 12 2 b b a a A. log 7 . B. log 7 . C. log 7 . D. log 7 . 2 1 2 a 1 2 a 1 2 b 1 b 2log a
Câu 41: Rút gọn biểu thức 3 2 P 3
log a .log 25 , với a là số thực dương khác 1 ta được: 5 a 2 2 2 2
A. P a 4 .
B. P a 4 .
C. P a 2 .
D. P a 2 .
Câu 42: Cho các số thức a , b , c thỏa mãn log b 9 log c 10 M log a c b a , a . Tính . Trang12 2 A. M 7 . B. M 3 . C. M 5 . D. M . 3 3 2 2
Câu 43: Cho a, b là các số thực dương khác 1 và thỏa mãn log b 3 . Tính giá trị của biểu thức a 3 b T log . b a a A. T 3 1 . B. T . C. T 4 . D. T 4 . 4
Câu 44: Cho a, b là các số thực dương, khác 1. Đặt log b . Tính theo giá trị của biểu thức: a 3
P log b log a 2 . a b 2 12 2 2 2 12 2 4 1 A. P . B. P . C. P . D. P . 2 2 2
Câu 45: Cho a log 5 . Tính log 1250 theo a . 2 4 1 4a 1 4a A. . B. .
C. 21 4a .
D. 21 4a . 2 2 4
Câu 46: Đặt log 2 a , khi đó log bằng 3 3 81 2 1 2
A. a 2 . B. 2 a 4 .
C. a 2 . D. 2a 4 . 2 4
Câu 47: Cho log 15 a . Tính A log 15 theo a. 3 25 a a a 2a A. A . B. A A A 2a 1 a . C. 1 21 . D. a a . 1
Câu 48: Đặt a log 3,b log 5, c log 7 . Biểu thức biểu diễn log 1050 theo a, b, c là. 2 2 2 60
1 a b 2c
1 a 2b c A. log 1050 . B. log 1050 . 60 1 2a b 60 2 a b
1 a 2b c
1 2a b c C. log 1050 . D. log 1050 . 60 1 2a b 60 2 a b
Câu 49: Đặt a = log 4, b = log 4. Hãy biểu diễn log 80 theo a và . b . 3 5 12 2 2a - 2ab 2 2a - 2ab A log 80 = .. B. log 80 = . 12 ab + b 12 ab a + 2ab a + 2ab C. log 80 = . D. log 80 = . 12 ab + b 12 ab
Câu 50:Với a là số thực dương tùy ý, log 2022 a bằng 4 1
A. 4044 log a .
B. 2022 log a .
C. 1011.log a . D. log a . 2 4 2 2 1011 HÀM SỐ MŨ KIẾN THỨC CẦN NHỚ 1. Hàm số mũ Định nghĩa: Hàm số x
y a a 0; a
1 được gọi là hàm số mũ cơ số a.
Tập xác định: Hàm số x
y a a 0; a
1 có tập xác định là . Đạo hàm: Hàm số x
y a a 0; a
1 có đạo hàm tại mọi x. x ' x a
a ln a ;Đặc biệt: x ' ex e . Trang13 u' ' u a
u a ln a ; u ' ' u e u e lim x a 0, lim x
a a 1 ; lim x a , lim x
a 0 0 a 1 . x x x x Sự biến thiên:
Khi a 1 hàm số luôn đồng biến.
Khi 0 a 1 hàm số luôn nghịch biến.
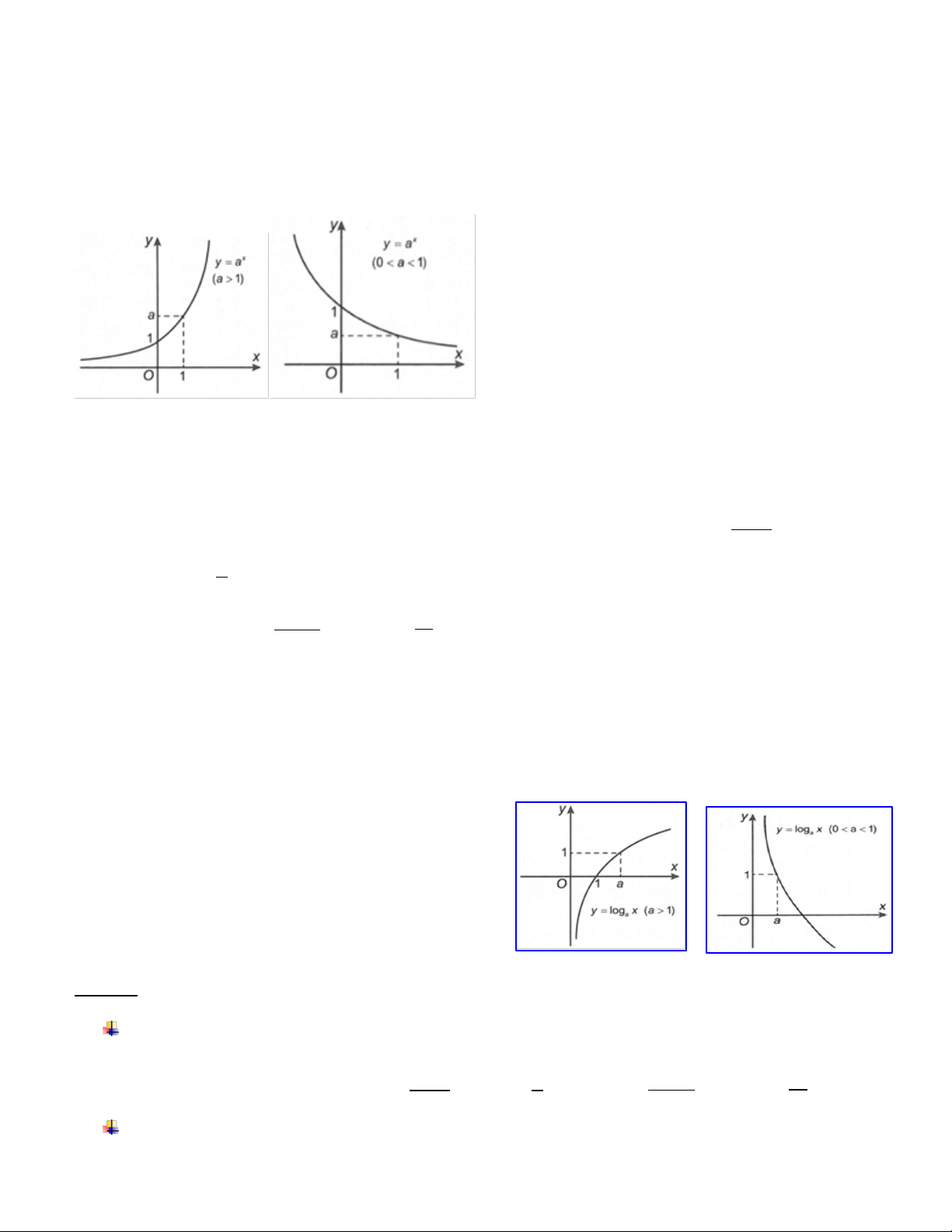
Đồ thị: Đồ thị hàm số có tiệm cận ngang là trục Ox và luôn đi qua các điểm 0;
1 , 1;a và nằm phía trên trục hoành. HÀM SỐ LOGARIT 2. Hàm số lôgarit
Định nghĩa: Hàm số y log x a 0; a
1 được gọi là hàm số lôgarit cơ số a. a
Tập xác định: Tập xác định: 0; .
Đạo hàm: Hàm số y log x a 0; a
1 có đạo hàm tại mọi x dương và x . a 1 log ' a x ln a
Đặc biệt: x 1 ln ' . x u u Hàm số hợp: u ; u ' ln ' a ' log ' u ln a u
Giới hạn đặc biệt: lim log x ,
lim log x a 1 ; a a x0 x lim log x ,
lim log x 0 a 1 . a a x0 x Sự biến thiên:
Khi a 1 hàm số luôn đồng biến.
Khi 0 a 1 hàm số luôn nghịch biến. Đồ thị
Đồ thị hàm số có tiệm cận đứng là trục Oy và luôn đi
qua các điểm 1;0, ; a
1 và nằm bên phải trục tung.
Nhận xét: Đồ thị của các hàm số x
y a và y log x a
a 0, a 1 đối xứng với nhau qua đường thẳng y x DẠNG BÀI TẬP
Dạng 1: Đạo hàm, sự biến thiên của hàm số
Bài toán 1: Tìm đạo hàm của các hàm số mũ – hàm số lôgarit Phƣơng pháp giải
Sử dụng công thức đạo hàm của hàm số mũ, lôgarit. 1 1 u u x ' x
ln ; u ' u' u a a a a a ln . a ; log x x ; u ; u ' ln ' a ' log ' a ' ; ln ' x ln a x u ln a u Ví dụ mẫu
Ví dụ 1: Khẳng định nào sau đây sai? Trang14 1
A. 3x ' 3x
ln3 B. x 1 ln '
C. log x ' D. 2x 2 ' x e e 3 x x ln 3 Hướng dẫn giải Ta có: 3x' 3 .x
ln 3 nên đáp án A đúng. x 1 ln '
nên đáp án B đúng. x 1 log x '
nên đáp án C đúng.
2x 2x 2 ' 2 '. 2. x e x e
e nên đáp án D sai. 3 xln3 Chọn D. Sử dụng máy tính.
Bài toán 2: Xét tính đồng biến, nghịch biến của hàm số mũ và hàm số lôgarit Phƣơng pháp giải Hàm số x
y a a 0; a
1 đồng biến khi a 1 và nghịch biến khi 0 a 1.
Hàm số y log x đồng biến khi a 1 và nghịch biến khi 0 a 1. a Ví dụ mẫu x
Ví dụ 1: Tìm a để hàm số y 2a 5 nghịch biến trên . 5 5 5 A. a 3 B. a 3
C. a 3 D. a 2 2 2
Hướng dẫn giải x 5
Hàm số y 2a 5 nghịch biến trên khi và chỉ khi 0 2a 5 1 a 3 . 2 Chọn A.
Ví dụ 2: Hàm số nào sau đây đồng biến trên ? x x 3
A. y log x B. y C. y
D. y log x 2 2 2 1 2 Hướng dẫn giải Ta có hàm số x
y a luôn đồng biến trên khi và chỉ khi a 1.
Ở phương án B, a
1 thỏa mãn khẳng định trên. 2
Ta loại phương án A và D vì hàm số y log x chỉ xác định trên 0; . a x 3 3
Ta loại phương án C, vì 0
1 nên hàm số y
nghịch biến trên 0; .Chọn B. 2 2
Ví dụ 3: Cho hàm số 2 3 x y x
e . Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng ;1 .
B. Hàm số nghịch biến trên khoảng 3 ; 1 .
C. Hàm số nghịch biến trên khoảng 1; .
D. Hàm số đồng biến trên khoảng 1;3 .
Hướng dẫn giải x 1 Ta có: x 2 x x y x e x e e 2 ' 2 . 3 .
. x 2x 3 . y' 0 . x 3 Bảng xét dấu: x -3 1 y’ + 0 - 0 + Chọn B. BÀI TẬP 2 Câu 1: Cho hàm số 3 2x x y có đạo hàm là Trang15 2 2 A. x 3 (2 3).2 . x x 2 ln 2 . B. x 3 2 x.ln 2 . C. 3 (2 3).2x x x 2 . D. 2 3 1 ( 3 ).2x x x x . 2 Câu 2: Hàm số 3 3x x y có đạo hàm là A. 2 3 2 3 .3x x x 2 . B. x 3 3 . x ln 3 . C. 2 2 3 1 3 .3x x x x . D. 2x 3 2 3 .3 . x x ln 3. 2 Câu 3: Hàm số 2x x y có đạo hàm là A. 2 2 1 2x x x x . B. 2 2 1 .2x x x 2 . C. 2x . x ln 2 . D. 2 2 1 .2x . x x ln 2 . 2 Câu 4: Hàm số 3x x y có đạo hàm là 2 x x A. 3 .ln 3 . B. 2 2 1 3x x x . C. 2 2 1 .3x x x x . D. 2 2 1 3x . x x ln 3 .
Câu 5: Tính đạo hàm của hàm số
2 2 2 x y x x e
A. ' 2 2 x y x e B. 2 ' 2 x y x e C. 2 ' x
y x e D. ' 2 x y xe 2
Câu 6: Đa ̣o hàm của hàm x x y e là: A. 2x x 2x 1 e B. x 2x 1 e C. 2 2x 1 x x e D. 2x 1 2x 1 e x
Câu 7: Đạo hàm của hàm số f x 1 là: 2 x x 1 1
A. f '(x) ln 2
B. f '(x) lg 2 2 2 x x 1 1
C. f '(x) ln 2
D. f '(x) lg 2 2 2
Câu 8: Đạo hàm của hàm số x y 2x 1 3 là: A. x
3 2 2x ln 3 ln 3 B. x
3 2 2x ln 3 ln 3 C. x x 1 2.3 2x 1 x.3 D. x 2.3 ln 3 x e
Câu 9: Đa ̣o hàm của hàm y là: x 1 x 2 xe x x xe x x 1 e e A. B. C. D. 2 2 x 2 1 x 1 x 1 x 1
Câu 10: Đa ̣o hàm của hàm 2 x y x 2x e là: A. 2 x x
2x 2 e B. 2 x x 2 e C. 2 x x x e D. 2 x x 2 e
Câu 11: Hàm số nào sau đây đồng biến trên ? x x x x 3 2 3 3 A. y B. y C. y D. y 3 2 2 3
Câu 12: Các giá trị thực của tham số a để hàm số 2 y log ,
x M a 4 nghịch biến trên tập xác định là M
A. 2 a 5
B. a 5
C. 5 a 2
; 2 a 5 D. a 2 x
Câu 13: Với giá trị nào của tham số a thì hàm số y 2
a 3a 3 đồng biến?
A. a 1
B. a 2
C. a 1;2
D. a ; 1 2; x
Câu 14: Hàm số y 2 3
a 10a 2 đồng biến trên ; khi Trang16 1 1 1 A. a ; B. a 3; C. a ; D. a ;3 3 3 3
Câu 15: Đạo hàm của hàm số y log 4x 1 là 3 1 4 ln 3 4 ln 3 A. y ' B. y ' C. y ' D. y ' 4x 1 ln 3 4x 1ln3 4x 1 4x 1
Câu 16: Tìm đạo hàm của hàm số y log ln 2x . 2 1 1 1 A. y ' B. y ' C. y ' D. y ' x ln 2 . x ln10 x ln 2 . x ln10 2x ln 2 . x ln10 x ln 2x
Câu 17: Cho hàm số f x 2
ln 4x x . Khẳng định nào sau đây đúng?
A. f '3 1 ,5
B. f '2 0
C. f '5 1 D. f ' 1 1
Câu 18: Tìm đạo hàm của hàm số y log 2 x x 1 . 5 2x 1 2x 1 1 A. y ' B. y '
C. y ' 2x 1 ln 5 D. y ' 2 x x 1 ln 5 2 x x 1
2x x 1ln5
Câu 19: Cho hàm số f x 4 ln x
1 . Đạo hàm f ' 1 bằng ln 2 1 A. B. 1 C. D. 2 2 2
Câu 20: Tìm đạo hàm của hàm số y 2 ln x x 1 1 2x 1 1 A. y ' B. y ' C. y ' D. y ' 2 2 x 1 2 x x 1 2 x x 1 2 x 1
Câu 21: Tìm đạo hàm của hàm số y 2
log x x . 1 2x 1 2x 1 2x 1 A. y B. y ' C. y ' D. y ' .log e 2 x xln10 2 x x
2x xloge 2 x x
Dạng 2: Tập xác định của hàm số chứa mũ – lôgarit
Bài toán 1. Tìm tập xác định của hàm số chứa mũ – lôgarit. Phƣơng pháp giải Hàm số x
y a a 0;a
1 có tập xác định là .
Hàm số y log xa 0;a
1 có tập xác định là 0; . a BÀI TẬP
Câu1. Tập xác định của hàm số y log x là 2
A. 0; . B. ;
. C. 0; . D. 2; . 3 x
Câu 2. Tập xác định của hàm số y log là 2 2x
A. D 3; . B. D 0; 3 . C. D ;
03; . D. D 0;3 .
Câu 3. Tập xác định của hàm số y x 2 log 2 là Trang17 A. R . B. R \
2 . C. 2; . D. 2; . 2
Câu 4. Tìm tập xác định D của hàm số x 2 e x y .
A. D R .B. D 0; 2.C. D R \0; 2 . D. D . 1
Câu 5. Tìm tập xác định D của hàm số y . x 5 e e
A. D (ln5; ). B. D [ln5; ) . C. D R \
5 . D. D 5; .
Câu 5. Tập xác định của hàm số y x 2 log 2 là A. R . B. R \
2 .C. 2; . D. 2; .
Câu 6. Tìm tập xác định của hàm số y log 2
x 3x 2 . 1 2 A.
;1 2; . B. (1;2). C. 2; . D. ;1 .
Câu 6. Tìm tập xác định của hàm số y log x 1 . 1 2 A. D ; 1 . B. D 1
; . C. D 1
; . D. D R \ 1 .
Câu 7. Tập xác định D của hàm số y log 2x 1 là 2022 1 1
A. D 0; . B. D R . C. D ; . D. D ; . 2 2
Câu 8. Tập xác định của hàm số y log x là 3
A. 0; . B. R \
0 . C. R . D. 0; . x 3
Câu 9. Tìm tập xác định D của hàm số y log . 2 x 2 A. D ;
3 2; . B. D 2; . C. D 3
;2 .D. D ; 3 2; .
Câu 10. Tìm tập xác định D của hàm số y log 3 x . 3
A. D 3; . B. D R \ 3 . C. D ;3 . D. D . R
Câu 11. Hàm số y log
2x 4x có tập xác định là 3 A. D R \ 0; 4 .
B. D 0; 4. C. D ;
04; . D. D 0;4 .
Câu 12. Tập xác định D của hàm số y x 23 2 là A. D R \ 2 . B. D 2;
. C. D 0; . D. D . R
Câu 13. Tập xác định D của hàm số f x ln 4 x là A. D ;
4 . B. D 4; . C. D R \ 4 . D. D ; 4.
Câu 14. Hàm số y log 3 2x có tập xác định là 3 3 3 3 A. ; . B. ; . C. ; . D. R. 2 2 2
Câu 15. Tập xác định của hàm số y log x 1 log x 3 là 2 2
A. D 1;3 . B. D
;1 .C. D 3; . D. D ; 1 3; . 10 x
Câu 16:Tập xác định D của hàm số y log3 là 2 x 3x 2
A. D 2;10
B. D 1;
C. D ; 10
D. D ; 1 2;10 Trang18
Câu 17. Tập xác định D của hàm số y x x 3 2 3 4 là A. D 1
;4. B. D 1
;4 .C. D R \ 1 ; 4 . D. D ; 1 4; .
Câu 18. Hàm số y log 2 4x x có tập xác định là 5
A. 0; . B. 0; 4 .C. R. D. 2;6 .
Câu 19: Tìm tập xác định D của hàm số y 3x x log x 4 2 2 1 . 2
A. D \ 0;1;
3 B. D 1;3 C. D 0;3 \ 1
D. D 1; 3 log100
Câu 20: Tìm tập xác định D của hàm số y x 2 log 2
x 2x 3 . 2
A. D 3;
B. D 2;3
C. D ; 1 3; D. D 1 ;3
Câu 21: Tìm tập xác định D của hàm số x y x 4 2 1 log 2 .
A. D 2;
B. D 0;
C. D 0; \ 2
D. D 0; \ 2 x 1
Câu 22: Tìm tập xác định D của hàm số y log . 2 x
A. D 1; B. D ;
0 1;
C. D 0;
1 D. D \ 0
Câu 23: Tìm tập xác định D của hàm số x y x 2 1 5 25 4
A. D ;3
B. D 4;
C. D
;3 D. D 3; \ 4 2
Câu 24: Tìm tập xác định D của hàm số 2 2022 x y
A. D 2; 2
B. D 2; 2 C. D 2; 2 D. D ; 2
PHƢƠNG TRÌNH MŨ – BẤT PHƢƠNG TRÌNH MŨ KIẾN THỨC CẦN NHỚ
1. Phƣơng trình mũ x a = b
+Nếu b 0 thì phương trình có nghiệm duy nhất x log b . a
+ Nếu b 0 thì phương trình vô nghiệm.
Đặc biệt: Phương trình x y
a a x y (biến đổi về cùng cơ số). f x gx
Dạng 1: Phương trình có dạng a a . f x g x
+ Nếu a 1 thì a a
nghiệm đúng với mọi x.
+ Nếu 0 a 1 thì f x g x. f x
Dạng 2: Phương trình có dạng a
b (với 0 a 1,b 0 ) f x a
b f x log b. a
2. Bất phƣơng trình mũ f x gx
Dạng 1: Bất phương trình có dạng a a . 1
+ Nếu a 1 thì
1 f x g x. Trang19
+ Nếu a 1 thì (1) nghiệm đúng x .
+ Nếu 0 a 1 thì
1 f x g x. f x
Dạng 2: Bất phương trình có dạng a
b (với b 0). (2)
+ Nếu a 1 thì 2 f x log . b a
+ Nếu 0 a 1 thì 2 f x log . b a f x
Dạng 3: Bất phương trình có dạng a . b 3
+ Nếu b 0 thì (3) nghiệm đúng x .
+ Nếu b 0, a 1 thì 3 f x log . b a
+ Nếu 0 a 1 thì 3 f x log . b a BÀI TẬP
Câu 1: Phương trình 9x 5.3x 6 0 có nghiệm là
A. x 1, x log 3. B. x 1 , x log 2.
C. x 1, x log 2. D. x 1 , x log 2. 2 3 3 3
Câu 2: Cho phương trình x x 1 4.4 9.2
8 0. Gọi x , x là hai nghiệm của phương trình trên. Khi đó, tích 1 2 x .x bằng 1 2 A. -1. B. 2. C. -2. D. 1.
Câu 3: Phương trình 3 x 9 x4 3
81có bao nhiêu nghiệm? A. 1. B. 2. C. 3. D. 4.
Câu 4: Phương trình x2 3
177147 có bao nhiêu nghiệm? A. 0. B. 1. C. 2. D. 3.
Câu 5: Phương trình 4x 10.2x
16 0 có bao nhiêu nghiệm? A. 1. B. 4. C. 3. D. 2.
Câu 6: Cho phương trình 2 x 4 x5 3
9.Tổng các lập phương các nghiệm thực của phương trình là A. 28. B. 27. C. 26. D. 25.
Câu 7: Cho phương trình 2 x 3x 8 2 x 1 3 9
, khi đó tập nghiệm của phương trình là 5 61 5 61
A. S 2; 5 . B. S ; . 2 2 5 61 5 61 C. S ; . D. S 2 ; 5 . 2 2
Câu 8: Nghiệm của phương trình: 2x1 3 27 là: A. x 5
B. x 1C. x 2 D. x 4
Câu 9: Nghiệm của phương trình: 2x1 3 27 là:
A. x 5 B. x 1C. x 2 D. x 4
Câu 10: Nghiệm của phương trình: 2x2 3 9 là:
A. x 5 B. x 1C. x 2 D. x 4
Câu 11: Nghiệm của phương trình: 2x1 3 3 là:
A. x 5 B. x 1C. x 2 D. x 4
Câu 12: Nghiệm của phương trình: 2x1 2 32 là:
A. x 3 B. x 1C. x 2 D. x 4
Câu 13: Nghiệm của phương trình: 2 x 3 2.2 1 là: Trang20 A. x 5 B. x 1 C. x 2 D. x 3
Câu 14: Nghiệm của phương trình: 2 x 3 4 2.2 2 là: A. x 5 B. x 1 C. x 2 D. x 3 2
Câu 15: Số nghiệm của phương trình là x 3x2 2 4 A. 2B. 1 C. 3 D. 0 2
Câu 16: Số nghiệm của phương trình là x 3x2 2 1 A. 2 B. 1 C. 3 D. 0 2
Câu 17: Số nghiệm của phương trình là x 3 2 x 1 A. 2 B. 1 C. 3 D. 0 2 x 3x
Câu 18: Số nghiệm của phương trình là 7 2 1 A. 2 B. 1 C. 3 D. 0 2 x 3x
Câu 19: Số nghiệm của phương trình là 7 5 78125 A. 2 B. 1 C. 3 D. 0
Câu 20: Tích các nghiệm của phương trình 2 2x 7x5 2 1 là 5 5 2 A. B. - C. D. 0 2 2 5
Câu 21: Tổng các nghiệm của phương trình là x2 x 1 4 2 A. - 2 B. 1 C. - 3 D. 0
Câu 22: Tổng các nghiệm của phương trình là x2 x 1 4 2 A. - 2 B. 5 C. - 3 D. 0
Câu 23: Tổng các nghiệm của phương trình là x2 x 1 3 9 A. - 2 B. 1 C. - 3 D. 0 x 2
Câu 24: Tổng các nghiệm của phương trình là x 1 16 2 A. - 2 B. 1 C. - 3 D. 0 2 x 5
Câu 25: Tích các nghiệm của phương trình là x 1 81 9 A. - 4 B. 1 C. - 3 D. 0 x 2
Câu 26: Tổng các nghiệm của phương trình là x 1 81 3 0 A. - 2 B. 1 C. - 3 D. 0 2 x 3x
Câu 27: Tích các nghiệm của phương trình là 4 5 25 A. 2 B. 1 C. - 3 D. 0
Câu 28. Nghiệm của phương trình x 1 3 27 là
A. x 4 .
B. x 3.
C. x 2 . D. x 1. x
Câu 29. Tìm nghiệm của phương trình 2 1 7 4 3 2 3. 1 3 1 A. x . B. x . C. x 1
. D. x . 4 4 4
Câu 30. Gọi x , x là nghiệm của phương trình 2 x 5 x 9 7
343. Tính x x . 1 2 1 2
A. x x 4 .
B. x x 6 . C. x x 5 . D. x x 3. 1 2 1 2 1 2 1 2
Câu 31. Phương trình x4 3 1 có nghiệm là A. x 4
. B. x 4 .
C. x 0 . D. x 5. 2
Câu 32. Có bao nhiêu giá trị x thoả mãn 5x 5x ? A. 0 . B. 3. C. 1. D. 2. Trang21
Câu 33. Tích tất cả các nghiệm của phương trình 2
3x x 9 bằng A. 2 . B. 1. C. 2. D. 3.
Câu 34. Tìm nghiệm của phương trình 9x 3x 6 0. A. x 2
. B. x 1 .
C. x 2 . D. x 3 2 3 x 1
Câu 35. Tập nghiệm của bất phương trình 2 x 1 3 là 3 1
A. S 1; . B. S ; 1; . 3 1 1
C. S ;1 . D. S ; . 3 3 2 x 5x x 1 1 1
Câu 36. Tập nghiệm của bất phương trình là 2 4 A. S ;
1 2;. B. S ;1 .
C. S \ 1; 2 .
D. S 2;.
Câu 38: Nghiệm của bất phương trình 2x 1 3 3 3 x là 3 2 2 2 A. x . B. x .
C. x . D. x . 2 3 3 3 x
Câu 39: Nghiệm của bất phương trình 2 x3 2 2 là
A. 1; . B. ; 0. C. ; 8 . D. 6; . 2 x 2 x 1 x5 2 5
Câu 40: Tập nghiệm của bất phương trình là 5 2 x 4 x 1 A. x 4.
B. x 1. C. . D. . x 1 x 4
PHƢƠNG TRÌNH – BẤT PHƢƠNG TRÌNH LOGARIT
KIẾN THỨC CƠ BẢN
PHƢƠNG TRÌNH LOGARIT 0 a 1
Dạng 1: log f x g x a loga f
x g x 0
Chú ý: Việc lựa chọn điều kiện f x 0 hoặc g x 0 tùy thuộc vào độ phức tạp của f x 0 và g x 0 0 a 1
Dạng 2: log f x b . a f x b a
BẤT PHƢƠNG TRÌNH LOGARIT a 1 0 f
x g x
Dạng 1: log f x g x a
loga 0a1 f
x g x 0 Trang22 a 1 a 1 0 f x b a f x b a
Dạng 2: log f x b
Dạng 3: log f x b a a 0 a 1 0 a 1 f x b a 0 f x b a BÀI TẬP
Câu 1. Nghiệm của phương trình log x 3 là 2
A. x 9 .
B. x 6 .
C. x 8. D. x 5.
Câu 2. Tìm tập nghiệm S của phương trình log 2
x 2x 3 log x 1 1 3 3 .
A. S 0;
5 .B. S
5 .C. S
0 .D. S 1; 5 .
Câu 3.Tìm tập nghiệm S của phương trình log 2x 1 log x 1 1 3 3 A. S
1 . B. S
4 .C. S
2 . D. S 3 .
Câu 4. Tìm tất cả các nghiệm của phương trình log x 5 4. 2
A. x 21.B. x 3. C. x 11. D. x 13.
Câu 5. Tìm nghiệm của phương trình log 3x 2 3. 3 29 11 25 A. x .B. x . C. x . D. x 87. 3 3 3
Câu 6. Giải phương trình log 2x 2 3. 2
A. x 3.
B. x 2 . C. x 5. D. x 4.
Câu 7: Phương trình x2 ln
7ln x 6 0 có bao nhiêu nghiệm? A. 1 B. 2 C. 3 D. 4
Câu 8. Cho phương trình log 5x 1 log x 1 5 5 1. Khi đặt log 5x t
1 , ta được phương trình nào 5 5 25 dưới đây? A. 2
t 1 0 . B. 2
t t 2 0 . C. 2
t 2 0 . D. 2
2t 2t 1 0.
Câu 9. Tập nghiệm của phương trình log
2x 3x 1 là: 0,25 3 2 2 3 2 2 A. {4}. B. ; .C. 1; 4 . D. 1 ; 4 . 2 2
Câu 10. Tập nghiệm của phương trình log 2
x 2x 4 2 là 2 A. 0; 2
. B. {2}. C. 0 . D. {0;2}.
Câu 11. Phương trình log
x 1 2 có nghiệm là 2 A. x 3
. B. x 1. C. x 3.D. x 8.
Câu 12. Tìm nghiệm của phương trình log x 2 2. 3
A. x 9 .
B. x 8.
C. x 11. D. x 10.
Câu 13. Gọi S là tập nghiệm của phương trình log x 1 log
x 3 1. Tìm S. 5 5 1 13 1 13 1 13 A. S 2 ; 4 . B. S ;
. C. S 4 . D. S . 2 2 2
Câu 14. Tìm tập nghiệm S của phương trình log x 4 4. 2 A. S 4 ;1
2 . B. S
4 . C. S 4;
8 . D. S 1 2 . Trang23
Câu 15: Phương trình log 2x 1 log
x 1 1 có nghiệm là 2 1 2 3 17 x 4 3 17 3 17 A. B. x C. x D. x 1 3 17 4 4 x 4
Câu 16: Tập nghiệm của phương trình log x 1 2 là 3 A. 3 B. 3 ; 4 C. 2 ; 3 D.4; 2 Trang24




