Trắc Nghiệm Ôn Tập Giải Tích 12 Chương 3 Mức 1 Và 2 Có Đáp Án

Trắc nghiệm ôn tập giải tích 12 chương 3 mục 1 và 2 được biên soạn dưới dạng file PDF gồm 42 trang.Tài liệu là kiến thức từ cơ bản đến nâng cao khác nhau và kèm sẵn đáp án để các em học sinh dễ dàng so sánh kết quả sao cho chuẩn xác nhất. Mời các em tham khảo thêm nhé!

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

41 trang 8 tháng trước

Tác giả:

Profile ha phan
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang1
NGUYÊN HÀM
1.1. Định nghĩa
Cho hàm số
fx
xác định trên
K
(
K
là khoảng, đoạn hay nửa khoảng). Hàm số
Fx
được gọi là
nguyên hàm của hàm số
fx
trên
K
nếu
F x f x'
với mọi
xK
.
Kí hiệu:

f x dx F x C
.
Định lí:
1) Nếu
Fx
là một nguyên hàm của
fx
trên
K
thì với mỗi hằng số
C
, hàm số
G x F x C
cũng là một nguyên hàm của
fx
trên
K
.
2) Nếu
Fx
là một nguyên hàm của hàm số
fx
trên
K
thì mọi nguyên hàm của
fx
trên
K
đều có dạng
, với
C
là một hằng số.
Do đó
F x C C,
là họ tất cả các nguyên hàm của
fx
trên
K
.
1.2. Tính chất của nguyên hàm
f x d x f x
và

f x dx f x C'
;
d f x f xdx dx
Nếu F(x) có đạo hàm thì:

d F x F x C( ) ( )

kf x dx k f x dx
với
k
là hằng số khác
0
.


f x g x dx f x dx g x dx
Công thức đổi biến số: Cho
y f u
và
Nếu

f x dx F x C( ) ( )
thì

f g x g x dx f u du( ) '( ) ( )
F u C()
1.3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số
fx
liên tục trên
K
đều có nguyên hàm trên
K
.
1.4. Bảng nguyên hàm các hàm số thƣờng gặp
1.
2.

dx x C
3.

x dx x C
1
1
1
1
16.
ax b
ax b c
a
1
1
dx , 1
1
4.
dx C
x
x
2
11
17.

x
xdx C
2
2
5.

dx x C
x
1
ln
18.
ax b c
ax b a
dx 1
ln
6.

xx
e dx e C
19.


ax b ax b
e d x e C
a
1
7.

x
x
a
a dx C
aln
20.

kx b
kx b
a
a dx C
ka
1
ln
8.

xdx x Ccos sin
21.
ax b dx ax b C
a
1
cos sin
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang2
9.
xdx x Csin cos
22.
ax b dx ax b C
a
1
sin cos
10.
x dx x Ctan . ln | cos |
23.
ax b ax b C
a
1
tan dx ln cos
11.

x dx x Ccot . ln | sin |
24.
ax b ax b C
a
1
cot dx ln sin
12.

dx x C
x
2
1
tan
cos
25.
dx ax b C
a
ax b
2
11
tan
cos
13.
dx x C
x
2
1
cot
sin
26.
dx ax b C
a
ax b
2
11
cot
sin
14.
x dx x C
2
1 tan tan
27.
ax b dx ax b C
a
2
1
1 tan tan
15.
x dx co x C
2
1 cot t
28.
ax b dx co ax b C
a
2
1
1 cot t
2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM
2.1. Phƣơng pháp đổi biến
2.1.1. Đổi biến dạng 1
Nếu :

f x dx F x C( ) ( )
và với
u t
là hàm số có đạo hàm thì :

f u du F t C( ) ( ( ))
2.1.1.1. Phƣơng pháp chung
Bước 1: Chọn
xt
, trong đó
t
là hàm số mà ta chọn thích hợp .
Bước 2: Lấy vi phân hai vế :
dx t dt'
Bước 3: Biến đổi :




f x dx f t t dt g t dt( ) '
Bước 4: Khi đó tính :

f x dx g t dt G t C( ) ( ) ( )
.
2.1.1.2. Các dấu hiệu đổi biến thƣờng gặp
Dấu hiệu
Cách chọn
ax
22
Đặt
x a sint
; với





t ;.
22
hoặc
x a cost
;
với


t 0; .
xa
22
Đặt
a
x
sint
.
; với





t ; \ 0
22
hoặc
a
x
cost
với





t 0; \ .
2
ax
22
Đặt
x a tant
; với





t ;.
22
hoặc
x a tcot
với
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang3
ax
ax
.
hoặc
ax
ax
.
Đặt
x acos t2
x a b x
Đặt
x a b a sin t
2
–()
ax
22
1
Đặt
x atant
; với





t ;.
22
2.1.2. Đổi biến dạng 2
Nếu hàm số f(x) liên tục thì đặt
xt
. Trong đó
t
cùng với đạo hàm của nó (
t'
là những
hàm số liên tục) thì ta được :



f x dx f t t dt g t dt G t C( ) ' ( ) ( )
.
2.1.2.1. Phƣơng pháp chung
Bước 1: Chọn t=
x
. Trong đó
x
là hàm số mà ta chọn thích hợp .
Bước 2: Tính vi phân hai vế :
dt t dt'
.
Bước 3: Biểu thị :




f x dx f t t dt g t d t( ) ' ( )
.
Bước 4: Khi đó :

I f x dx g t dt G t C( ) ( ) ( )
2.1.2.2. Các dấu hiệu đổi biến thƣờng gặp :
Dấu hiệu
Cách chọn
Hàm số có mẫu số
t
là mẫu số
Hàm số :
f x x;
tx
Hàm
a inx+b.cosx
fx
c inx+d.cosx+e
.s
.s




xx
t cos
2
tan ; 0
2
Hàm

fx
x a x b
1
Với :
xa0
và
xb0
.
Đặt :
t x a x b
Với
xa0
và
xb0
.
Đặt :
t x a x b
2.2. Phƣơng pháp nguyên hàm từng phần
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K:


u x v x dx u x v x v x u x dx( ). '( ) ( ). ( ) ( ). '( )
Hay


udv uv vdu
( với
du u x dx dv v x dx’ , ’
)
2.2.1. Phƣơng pháp chung
Bước 1: Ta biến đổi tích phân ban đầu về dạng :


I f x dx f x f x dx
12
( ) ( ). ( )
Bước 2: Đặt :


du f x dx
u f x
dv f x
v f x dx
1
1
2
2
' ( )
()
()
()
Bước 3: Khi đó :


u dv u v v du. . .
MỘT SỐ DẠNG NGUYÊN HÀM TỪNG PHẦN THƢỜNG GẶP
Ghi nhớ: Khi gặp
.sin
mx n
e ax b dx
hoặc
.
mx n
e cos ax b dx
luôn phải thực hiện phƣơng
pháp nguyên hàm từng phần hai lần liên tiếp.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang4
Dạng tích phân
Cách đặt
ax b
P x e dx
ax b
u P x
dv e dx
sin
..
mx n
P x dx
cos mx n
sin
.
u P x
mx n
dv dx
cos mx n
.ln
n
P x ax b dx
ln
.
n
u ax b
dv P x dx

sin
..
ax b
mx n
e dx
cos mx n
sin
.
ax b
ue
mx n
dv dx
cos mx n
Chọn u: Nhất lo,nhì đa, tam lƣợng, tứ mũ.
Bảng 1
Bảng 2
Quy tắc đƣờng chéo để tính tích phân từng phần
Áp dụng nhanh trong trƣờng hợp u là một đa thức bậc cao.
Ở cột u, lấy đạo hàm liên tiếp đến khi đƣợc kết quả bằng 0, hoặc đến khi lấy đạo hàm phức
tạp hơn, hoặc đến khi lặp lại thì dừng.
Ở cột v, tìm nguyên hàm tƣơng ứng của v.
VD: Trong bảng bên
Bảng 1:
12
. ' . '. ''.u v dx u v u v u v dx

Bảng 2:
1 2 3
. ' . '. ''. '''.u v dx u v u v u v u v
u"'
u"
-
( )
v
3
0
v
2
v
1
+
( )
+
( )
-
( )
v
u'
v'
u
Cột v (ng hàm)
Cột u ( đạo hàm)
+
( )
-
( )
+
( )
v
1
u''
v
u'
v'
u
( Nguyên hàm )
( Đạo hàm )
v
u
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang5
Ví dụ áp dụng: Tìm các nguyên hàm sau:
1.
2
2
x
x e dx
2.
21x cosxdx
3.
2
3 1 lnx xdx
Giải: Áp dụng quy tắc đƣờng chéo:
1:
2
2
x
x e dx
Căn cứ vào bảng ta đƣợc:
2
2
x
x e dx
22
11
2
24
xx
x e e C
2.
21x cosxdx
Căn cứ vào bảng ta đƣợc:
21x cosxdx
2 1 sin 2x x cosx C
3.
2
3 1 lnx xdx
Căn cứ vào bảng ta đƣợc:
2
3 1 lnx xdx
33
1
lnx x x x x dx
x
32
ln 1x x x x dx
3
3
ln
3
x
x x x x C
BÀI TẬP
2
+
x
e
2
x
v
u
+
-
+
e
2
x
1
4
0
e
2
x
1
2
1
-
cosx
1
-
2
x
sinx
v
u
+
-
+
0
cosx
2
x
x
3
1
x
1
-
x
2
3
lnx
-
v
u
+
-
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang6
Câu 1: Công thức tìm nguyên hàm nào sau đây chƣa đúng ?
A.
1
ln .dx x C
x

0x
B.
1
1.
1
x
x dx C
C.
0 1 .
ln
x
x
a
a dx C a
a
D.
2
1
tan .dx x C
cos x

Câu 2: Tìm nguyên hàm của hàm số
2
3
2 0 .f x x x
x
A.
22
3ln .f x dx x x C
B.
2
2
3
.f x dx x C
x
C.
2
3
.f x dx x C
x
D.
2
3
.f x dx x C
x
Câu 3: Hàm số
tan
x
F x e x C
là nguyên hàm của hàm số
fx
nào dưới đây?
A.
2
1
.
sin
x
f x e
x

B.
2
1
.
sin
x
f x e
x

C.
2
1
.
x
f x e
cos x

D.
cot .
x
f x e x
Câu 4. Họ nguyên hàm của hàm số
22
x
f x x
là
A.
2
2
ln2
x
xC
B.
2
2 .ln 2
x
xC
C.
2 2 .ln 2
x
C
D.
2
2
ln2
x
C
Câu 5: Biết
2 ln 3 1 .f x dx x x C
Tìm khẳng định đúng trong các khẳng định dưới đây:
A.
3 6 ln 9 1 .f x dx x x C
B.
3 3 ln 9 1 .f x dx x x C
C.
3 6 ln 3 1 .f x dx x x C
D.
3 2 ln 9 1 .f x dx x x C
Câu 6: Tìm nguyên hàm
Fx
của hàm số
x
f x e x
biết
02F
A.
2
1
2
x
x
F x e
. B.
2
1
2
x
x
F x e
. C.
2
1
2
x
x
F x e
. D.
2
1
2
x
x
F x e
.
Câu 7: Tính
F x xcosxdx
ta được kết quả
A.
sin .F x x x cosx C
B.
sin .F x x x cosx C
C.
sin .F x x x cosx C
D.
sin .F x x x cosx C
Câu 8. Họ nguyên hàm của hàm số
( ) 1
x
f x e

là
A.
x
e x C
. B.
x
e x C

. C.
x
e x C
. D.
x
e x C
.
Câu 9:
Fx
là một nguyên hàm của hàm số
2
23
0,
x
f x x
x

biết
1 1.F
Fx
là biểu
thức nào sau đây ?
A.
3
2 2.F x x
x
B.
3
2ln 2.F x x
x
C.
3
2 4.F x x
x
D.
3
2ln 4.F x x
x
Câu 10: Họ nguyên hàm của hàm số
()
x
f x e x
là
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang7
A.
2
.
x
e x C
B.
2
1
.
2
x
e x C
C.
2
11
.
12
x
e x C
x

D.
1.
x
eC
Câu 11. Họ nguyên hàm của hàm số
3
2
3
f x x 2
x
x
là:
A.
4
2
3ln 2 .ln 2
4
x
x
xC
B.
3
3
1
2
3
x
x
C
x
C.
4
32
4 ln 2
x
x
C
x
D.
4
3
2 .ln 2
4
x
x
C
x
Câu 12. Họ nguyên hàm của hàm số
( ) cos 1f x x
là:
A.
sinx C.x
B.
sinx C.x
C.
sinx C.
D.
sinx C.
Câu 13: Hàm số
32
( ) 5 4 7 10F x x x x C
là nguyên hàm của hàm số nào?
A.
2
( ) 5 4 7.f x x x
B.
4 3 2
5 4 7
( ) .
4 3 2
x x x
fx
C.
4 3 2
5 4 7
( ) 10 .
4 3 2
x x x
f x x
D.
2
( ) 15 8 7.f x x x
Câu 14. Họ nguyên hàm của hàm số
( ) 3
x
f x x
là
A.
2
3.
x
xC
B.
2
1
3.
2
x
xC
C.
2
31
.
ln3 2
x
xC
D.
3 1 .
x
C
Câu 15. Họ nguyên hàm của hàm số
( ) sin(2 1)f x x
là
A.
1
os(2 1) .
2
c x C
B.
1
os(2 1) .
2
c x C
C.
os(2 1) .c x C
D.
os(2 1) .c x C
Câu 16. Nguyên hàm của hàm số
1
J x dx
x




là
A.
2
( ) ln .F x x x C
B.
2
1
( ) ln .
2
F x x x C
C.
2
1
( ) ln( ) .
2
F x x x C
D.
2
( ) ln( ) .F x x x C
Câu 17: Họ nguyên hàm của hàm số
6
23
x
f x e x
là:
A.
62
1
43
6
x
e x x C
B.
62
43
x
e x x C
C.
62
3
x
e x x C
D.
62
1
3
6
x
e x x C
Câu 18: Nguyên hàm của hàm số
3
1
f x x
x

là:
A.
2
2
1
3f x dx x C
x
B.
4
ln
4
x
f x dx x C
C.
2
2
1
3f x dx x C
x
D.
4
ln
4
x
f x dx x C
Câu 19: Họ nguyên hàm của hàm số
1
23
fx
x
là:
A.
1
ln 2 3
2
xC
B.
1
ln 2 3
2
xC
C.
ln 2 3xC
D.
1
ln 2 3
ln 2
xC
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang8
Câu 20: Họ nguyên hàm của hàm số
2
1yx
là:
A.
3
x x C
B.
3
xC
C.
6xC
D.
3
3
x
xC
Câu 21: Họ nguyên hàm của hàm số
22x
f x e x
là:
A.
23
23
x
ex
F x C
B.
23x
F x e x C
C.
2
22
x
F x e x C
D.
3
2
3
x
x
F x e C
Câu 22: Nguyên hàm của hàm số
3
32f x x x
là hàm số nào trong các hàm số sau?
A.
2
33F x x x C
B.
4
2
32
3
x
F x x x C
C.
42
3
2
42
xx
F x x C
D.
42
2
42
xx
F x x C
Câu 23: Họ nguyên hàm của hàm số
2
f x x
x

là:
A.
2
2 ln
2
x
xC
B.
2
2
x
xC
C.
2
2
1 C
x

D.
2
2 ln
2
x
xC
Câu 24: Hàm số nào dưới đây là một nguyên hàm của hàm số
4
2f x x x
?
A.
42
2F x x x
B.
2
32F x x
C.
5
2
1
5
x
F x x
D.
42
42
xx
Fx
Câu 25: Họ nguyên hàm của hàm số
3x
f x e
là:
A.
31
31
x
e
f x dx C
x

B.
3
3
x
f x dx e C
C.
3
f x dx e C
D.
3
3
x
e
f x dx C
Câu 26: Họ nguyên hàm của hàm số
cosf x x x
là:
A.
2
sin
2
x
f x dx x C
B.
1 sinf x dx x C
C.
sin cosf x dx x x x C
D.
2
sin
2
x
f x dx x C
Câu 27: Hàm số
2
F x dx
có dạng:
A.
2
F x x C

B.
3
3
F x C

C.
22
2
x
F x C

D.
2F x x C

Câu 28: Cho hàm số
y F x
là một nguyên hàm của hàm số
2
yx
. Giá trị của
' 25F
bằng:
A. 125. B. 625. C. 5. D. 25.
Câu 29: Họ nguyên hàm của hàm số
31x
f x e
là:
A.
31
3
x
F x e C

B.
31
3 .ln 3
x
F x e C

C.
31
1
. ln 3
3
x
F x e C

D.
31
1
3
x
F x e C

ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang9
Câu 30. Cho
()Fx
là một nguyên hàm của hàm số
( ) 2
x
f x e x
thỏa mãn
3
(0)
2
F
. Tìm
()Fx
.
A.
2
3
()
2
x
F x e x
B.
2
1
( ) 2
2
x
F x e x
C.
2
5
()
2
x
F x e x
D.
2
1
()
2
x
F x e x
Câu 31. Hàm số
( )
3
x
F x e=
là một nguyên hàm của hàm số:
A.
( )
3
x
f x e=
. B.
( )
3
2
3.
x
f x x e=
. C.
( )
3
2
3
x
e
fx
x
=
. D.
( )
3
31
.
x
f x x e
-
=
.
Câu 32.Tìm nguyên hàm
()Fx
của hàm số thỏa mãn
2
2
F



.
A.
( ) cos sin 3F x x x
B.
( ) cos sin 3F x x x
C.
( ) cos sin 1F x x x
D.
( ) cos sin 1F x x x
Câu 33: Họ tất cả các nguyên hàm của hàm số
25f x x
là
A.
2
5.x x C
B.
2
2 5 .x x C
C.
2
2.xC
D.
2
.xC
Câu 34: Họ tất cả các nguyên hàm của hàm số là
A. . B. . C. . D. .
Câu 35:Họ tất cả các nguyên hàm của hàm số
23f x x
là
A.
2
2xC
. B.
2
3x x C
. C.
2
23x x C
. D.
2
xC
.
Câu 36: Họ tất cả các nguyên hàm của hàm số
24f x x
là
A.
2
24x x C
. B.
2
4x x C
. C.
2
xC
. D.
2
2xC
.
Câu 37: Nguyên hàm của hàm số
3
f x x x
là
A.
42
x x C
. B.
2
31xC
. C.
3
x x C
. D.
42
11
42
x x C
.
Câu 38: Nguyên hàm của hàm số
4
f x x x
là
A.
4
x x C
B.
3
41xC
. C.
52
x x C
. D.
52
11
52
x x C
.
Câu 39: Nguyên hàm của hàm số
42
y x x
là
A.
3
42x x C
. B.
53
11
53
x x C
. C.
42
x x C
D.
53
x x C
.
Câu 40: Nguyên hàm của hàm số
32
f x x x
là
A.
43
x x C
. B.
43
11
43
x x C
. C.
2
32x x C
. D.
32
x x C
.
Câu 41: Họ nguyên hàm của hàm số
1
54
fx
x
là
A.
1
ln 5 4
ln5
xC
B.
ln 5 4xC
C.
1
ln 5 4
5
xC
D.
1
ln 5 4
5
xC
Câu 42:Họ nguyên hàm của hàm số
2
x
f x x e
là
A.
2
x
eC
. B.
2 x
x e C
. C.
2
2
x
x e C
. D.
2 x
x e C
.
Câu 43. Hàm số
Fx
là một nguyên hàm của hàm số
fx
trên khoảng
K
nếu
A.
,F x f x x K
. B.
,.f x F x x K
( ) sin cosf x x x
26f x x
2
6x x C
2
2xC
2
26x x C
2
xC
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang10
C.
,F x f x x K
. D.
,.f x F x x K
Câu 44. Cho hàm số
2e
x
f x x
. Tìm một nguyên hàm
Fx
của hàm số
fx
thỏa mãn
0 2022.F
A.
e 2021.
x
Fx
B.
2
e 2021.
x
F x x
C.
2
e 2020.
x
F x x
D.
2
e 2021.
x
F x x
Câu 45. Họ nguyên hàm của hàm số
2
31f x x
là
A.
3
xC
. B.
3
3
x
xC
. C.
6xC
. D.
3
.x x C
Câu 46. Hàm số
cos 4 7f x x
có một nguyên hàm là
A.
sin 4 7xx
.B.
1
sin 4 7 3
4
x 
.C.
sin 4 7 1x 
. D. −
1
sin 4 7 3.
4
x 
Câu 47. Họ nguyên hàm của hàm số
2
cos f x x x
là
A.
2 sin x x C
. B.
3
1
sin
3
x x C
.C.
3
1
sin
3
x x C
. D.
3
sin .x x C
Câu 48. Họ nguyên hàm của hàm số
32
f x x x
là
A.
43
43
xx
C
.B.
43
xx
.C.
2
32xx
. D.
43
11
.
44
xx
Câu 49. Tìm họ nguyên hàm của hàm số
2
5
x
fx
?
A.
22
5 d 2.5
xx
x
ln5
C
. B.
2
2
5
5 d 2. .
ln 5
x
x
xC
C.
2
25
5d
2 ln 5
x
x
xC
. D.
1
2
25
5 d .
1
x
x
xC
x

Câu 50. Nguyên hàm của hàm số
3
41f x x x
là:
A.
42
x x x C
.B.
2
12 1xC
. C.
42
1
.
2
x x x C
D.
42
1
.
2
x x x C
Câu 51. Họ các nguyên hàm của hàm số
cos y x x
là
A.
2
1
sin
2
x x C
. B.
2
sin x x C
.C.
2
1
sin
2
x x C
.D.
2
sin .x x C
Câu 52. Nếu
3
de
3
x
x
f x x C
thì
fx
bằng
A.
2
3e
x
f x x
.B.
4
e
3
x
x
fx
.C.
2
e
x
f x x
. D.
4
e.
12
x
x
fx
Câu 53. Nguyên hàm của hàm số
2022
,f x x
xR
là hàm số nào trong các hàm số dưới đây?A.
2021
2022 ,F x x C
C R
. B.
2021
,F x x C
C R
.
C.
2023
,
2023
x
F x C
C R
. D.
2022
2021 ,F x x C
C R
.
Câu 54. Hàm số
2
e
x
Fx
là một nguyên hàm của hàm số nào dưới đây?
A.
2
2e
x
f x x
B.
2
2
e
x
f x x
C.
2
e
x
fx
D.
2
e
.
2
x
fx
x
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang11
Câu 55. Tìm tất cả các nguyên hàm của hàm số
3.
x
fx
A.
3
ln 3
x
C
. B.
3
ln 3
x
C

. C.
3
x
C

. D.
3
x
ln3
.C
Câu 56. Tìm tất cả các nguyên hàm của hàm số
sin 5 .f x x
A.
1
cos 5
5
xC
. B.
cos 5xC
. C.
-cos 5xC
. D. −
1
cos 5 .
5
xC
Câu 57. Họ nguyên hàm của hàm số
21f x x
là
A.
2
2F x x x
. B.
2Fx
. C.
F x C
. D.
2
.F x x x C
Câu 58. Họ nguyên hàm của hàm số
e
x
f x x
là
A.
2
e
x
xC
. B.
2
1
e
2
x
xC
. C.
2
11
e
12
x
xC
x

. D.
e 1 .
x
C
Câu 59.Tìm nguyên hàm
2
Fx
dx.
A.
2
F x x C

. B.
2 xC
. C.
3
3
F x C

. D.
22
.
2
x
F x C

Câu 60. Tìm tất cả nguyên hàm của hàm số
2
3.
2
x
f x x
A.
32
d
34
xx
f x x C
. B.
2
3
d.
2
x
f x x x C
C.
2
3
d
4
x
f x x x C
. D.
2
3
d
4
x
f x x x
.
Câu 61. Tìm họ nguyên hàm của hàm số
sin 3 1f x ax
(với
a
là tham số khác
0
).
A.
cos 3 1ax C
. B.
1
cos 3 1 .
3
ax C
a

C. −
1
cos 3 1
3
ax C
a

. D.
cos 3 1 .ax C
Câu 62: Họ các nguyên hàm của hàm số
sinf x x x
là:
A.
cos sinx x x C
B.
cos sinx x x C
C.
cos sinx x x C
D.
cos sinx x x C
Câu 63: Họ nguyên hàm của hàm số
4 1 lnf x x x
là:
A.
22
2 ln 3x x x
B.
22
2 lnx x x
C.
22
2 ln 3x x x C
D.
22
2 lnx x x C
Câu 64: Họ nguyên hàm của hàm số
2
3 1 lnf x x x
là:
A.
3
2
1 ln
3
x
x x x C
B.
3
3
ln
3
x
x x C
C.
3
2
1 ln
3
x
x x x x C
D.
3
3
ln
3
x
x x x C
Câu 65: Tất cả các nguyên hàm của hàm số
2
sin
x
fx
x
trên khoảng
0;
là:
A.
cot ln sinx x x C
B.
cot ln sinx x x C
C.
co t ln sinx x x C
D.
cot ln sinx x x C
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang12
Câu 66:Họ nguyên hàm của hàm số
cos
x
f x e x
là
A.
sin
x
e x C
. B.
1
sin
1
x
e
xC
x

. C.
sin
x
e x C
. D.
1
sin
1
x
e
xC
x

.
Câu 67:Tìm họ nguyên hàm
Fx
của hàm số
3
1f x x x
A.
43
42
xx
F x C
. B.
42
42
xx
F x x C
.
C.
3
4
2
x
F x x x C
. D.
3
3F x x C
.
Câu 68:Tìm tất cả nguyên hàm
Fx
của hàm số
1
f x x
x

.
A.
2
1
ln
2
F x x x C
. B.
2
1
ln
2
F x x x
.
C.
1 lnF x x C
D.
2
1
ln
2
F x x x C
.
Câu 69:Họ nguyên hàm của hàm số
21yx
là
A.
2
2
x
xC
. B.
21xC
. C.
2
x x C
. D.
2xC
.
Câu 70:Tính
sin3 dxx
A.
cos3xC
. B.
1
cos3
3
xC
. C.
1
cos3
3
xC
. D.
cos3xC
.
Câu 71:Họ nguyên hàm của hàm số
3
x
fx
là
A.
3 .ln3
x
C
. B.
3
ln3
x
C
. C.
1
3
1
x
C
x
. D.
1
3
x
C
.
Câu 72:Họ nguyên hàm của hàm số
sin2f x x
là:
A.
1
cos2
2
F x x C
. B.
cos2F x x C
.
C.
1
cos2
2
F x x C
. D.
cos2 F x x C
.
Câu 73:Họ nguyên hàm của hàm số
2
( ) 3 1f x x
là
A.
3
xC
B.
3
3
x
xC
C.
6xC
D.
3
x x C
Đề thi tốt nghiệp 2021
Mã đề 101
Câu 1: Cho hàm số
2
4f x x
. Khẳng định nào dưới đây đúng?
A.
d2f x x x C
. B.
2
d4f x x x x C
.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang13
C.
3
d4
3
x
f x x x C
. D.
3
d4f x x x x C
.
Câu 2: Cho hàm số
( ) 2
x
f x e
. Khẳng định nào dưới đây đúng?
A.
2
()d
x
f x x e C

. B.
( ) 2d
x
f x x e x C
.
C.
()d
x
f x x e C
. D.
( ) 2d
x
f x x e x C
.
Mã đề 102
Câu 1: Cho hàm số
2
3f x x
. Khẳng định nào dưới đây đúng?
A.
2
3f x dx x x C
. B.
3
3
3
x
f x dx x C
.
C.
3
3f x dx x x C
. D.
2f x dx x C
.
Câu 2: Cho hàm số
( ) 1.
x
f x e
Khẳng định nào dưới đây đúng?
A.
1
()
x
f x dx e C

. B.
()
x
f x dx e x C
.
C.
()
x
f x dx e x C
. D.
()
x
f x dx e C
.
Mã đề 103
Câu 1: Cho hàm số
2
1f x x
. Khẳng định nào dưới đây đúng?
A.
df x x x x C
. B.
3
d
3
x
f x x x C
.
C.
2
df x x x x C
. D.
d2f x x x C
.
Câu 2: Cho hàm số
( ) 3
x
f x e
. Khẳng định nào dưới đây đúng?
A.
( )d 3
x
f x x e x C
. B.
( )d
x
f x x e C
.
C.
3
( )d
x
f x x e C

. D.
( )d 3
x
f x x e x C
.
Mã đề 104
Câu 13: Cho hàm số
2
2f x x
. Khẳng định nào dưới đây đúng?
A.
d2f x x x C
. B.
3
d2
3
x
f x x x C
.
C.
2
d2f x x x x C
. D.
3
d2f x x x x C
.
Câu 23: Cho hàm số
( ) 4
x
f x e
. Khẳng định nào sau đây đúng?
A.
( ) 4
x
f x x e x C
d
. B.
()
x
f x x e C
d
.
C.
4
()
x
f x x e C

d
. D.
( ) 4
x
f x x e x C
d
.
Đề minh họa 2021
Câu 14: Cho hàm số
2
3 1.f x x
Trong các khẳng định sau, khẳng định nào đúng?
A.
3
3.f x dx x x C
B.
3
.f x dx x x C
C.
3
1
.
3
f x dx x x C
D.
3
.f x dx x C
Câu 15: Cho hàm số
cos2 .f x x
Trong các khẳng định sau, khẳng định nào đúng?
A.
1
sin 2 .
2
f x dx x C
B.
1
sin 2 .
2
f x dx x C
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang14
C.
2sin2 .f x dx x C
D.
2sin2 .f x dx x C
Đề thi tốt nghiệp 2020 ( Đợt 1 )
Mã đề 101
Câu 14:
2
x dx
bằng
A.
2xC
. B.
3
1
3
xC
. C.
3
xC
. D.
3
3xC
Mã đề 102
Câu 14: Họ nguyên hàm của hàm số
3
f x x
là
A.
4
4xC
. B.
2
3xC
. C.
4
xC
. D.
4
1
4
xC
.
Mã đề 103
Câu 1. bằng
A. B. C. D.
Mã đề 104
Câu 21:
5
x dx
bằng
A.
4
5xC
. B.
6
1
6
xC
. C.
6
xC
. D.
6
6xC
.
Đề thi tốt nghiệp 2020 ( Đợt 2 )
Câu 24.
2
3dxx
bằng
A.
3
3xC
. B.
6xC
. C.
3
1
3
xC
. D.
3
xC
.
Đề thi tham khảo lần 2 năm 2020
Câu 6. Hàm số
Fx
là một nguyên hàm của hàm số
fx
trên khoảng
K
nếu
A.
,
F x f x x K
B.
,
f x F x x K
C.
,
F x f x x K
D.
,
f x F x x K
Đề thi tham khảo lần 1 năm 2020
Câu 11: Họ tất cả các nguyên hàm của hàm số
cos 6f x x x
là
A.
2
sin 3x x C
. B.
2
sin 3x x C
. C.
2
sin 6x x C
. D.
sin xC
.
Đề thi THPT Quốc gia 2019
Mã đề 101
Câu 15. Họ tất cả các nguyên hàm của hàm số
25f x x
là
A.
2
5.x x C
. B.
2
2 5 .x x C
. C.
2
2.xC
. D.
2
.xC
.
Câu 31. Họ tất cả các nguyên hàm của hàm số
2
21
1
x
fx
x
trên khoảng
1; 
là
A.
2
2ln 1
1
xC
x
. B.
3
2ln 1
1
xC
x
.
C.
2
2ln 1
1
xC
x
. D.
3
2ln 1
1
xC
x
.
4
dx x
5
1
5
xC
3
4xC
5
xC
5
5xC
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang15
Mã đề 102
Câu 1. Họ tất cả các nguyên hàm của hàm số là
A. . B. . C. . D. .
Câu 34. Họ tất cả các nguyên hàm của hàm số trên khoảng là
A. . B. .
C. . D. .
Mã đề 103
Câu 12. Họ tất cả các nguyên hàm của hàm số
23f x x
là
A.
2
2xC
. B.
2
3x x C
. C.
2
23x x C
. D.
2
xC
.
Câu 34. Họ tất cả các nguyên hàm của hàm số
2
21
2
x
fx
x
trên khoảng
2; 
là:
A.
1
2ln 2
2
xC
x
. B.
1
2ln 2
2
xC
x
.
C.
3
2ln 2
2
xC
x
. D.
3
2ln 2
2
xC
x
.
Mã đề 104
Câu 8. Họ tất cả các nguyên hàm của hàm số
24f x x
là
A.
2
24x x C
. B.
2
4x x C
. C.
2
xC
. D.
2
2xC
.
Câu 35. Họ tất cả các nguyên hàm của hàm số
( )
( )
2
32
2
x
fx
x
-
=
-
trên khoảng
( )
2;+¥
là
A.
( )
4
3ln 2
2
xC
x
- + +
-
. B.
( )
2
3ln 2
2
xC
x
- + +
-
.
C.
( )
2
3ln 2
2
xC
x
- - +
-
. D.
( )
4
3ln 2
2
xC
x
- - +
-
.
Đề thi tham khảo kì thi THPT Quốc gia 2019
Câu 10: Họ nguyên hàm của hàm số
()
x
f x e x
là
A.
2
.
x
e x C
B.
2
1
.
2
x
e x C
C.
2
11
.
12
x
e x C
x

D.
1.
x
eC
Câu 33. Họ nguyên hàm của hàm số
4 1 lnf x x x
là
A.
22
2 ln 3x x x
B.
22
2 lnx x x
C.
22
2 ln 3x x x C
D.
22
2 lnx x x C
Đề thi THPT Quốc gia 2018
Mã đề 101
Câu 7: Nguyên hàm của hàm số
3
()f x x x
là
A.
42
x x C
B.
2
31xC
C.
3
x x C
D.
42
11
42
x x C
Mã đề 102
Câu 4. Nguyên hàm của hàm số
4
f x x x
là
26f x x
2
6x x C
2
2xC
2
26x x C
2
xC
2
31
()
( 1)
x
fx
x
(1; )
2
3ln( 1)
1
xC
x
1
3ln( 1)
1
xC
x
1
3ln( 1)
1
xC
x
2
3ln( 1)
1
xC
x
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang16
A.
4
x x C
B.
3
41xC
C.
52
x x C
D.
52
11
52
x x C
Mã đề 103
Câu 14. Nguyên hàm của hàm số
42
f x x x
là
A.
3
42x x C
B.
53
11
53
x x C
C.
42
x x C
D.
53
x x C
Đề thi tham khảo kì thi THPT Quốc gia 2018
Câu 9: Họ nguyên hàm của hàm số
2
f x 3x 1
là
A.
3
xC
B.
3
x
C
3
C.
6x C
D.
3
x x C
Đề thi THPT Quốc gia 2017
Mã đề 101
Câu 2: Tìm nguyên hàm của hàm số
( ) cos3f x x
A.
cos3 3sin3xdx x C
B.
sin3
cos3
3
x
xdx C
C.
sin3
cos3
3
x
xdx C

D.
cos3 sin3xdx x C
Câu 27:Cho hàm số
()fx
thỏa mãn
'( ) 3 5sinf x x
và
(0) 10f
. Mệnh đề nào dưới đây đúng ?
A.
( ) 3 5cos 5f x x x
B.
( ) 3 5cos 2f x x x
C.
( ) 3 5cos 2f x x x
D.
( ) 3 5cos 15f x x x
Câu 32:Cho
2
()F x x
là một nguyên hàm của hàm số
2
()
x
f x e
. Tìm nguyên hàm của hàm số
'2
()
x
f x e
A.
' 2 2
( ) 2
x
f x e dx x x C
B.
' 2 2
()
x
f x e dx x x C
C.
' 2 2
( ) 2 2
x
f x e dx x x C
D.
' 2 2
( ) 2 2
x
f x e dx x x C
Mã đề 102
Câu 2. Tìm nguyên hàm của hàm số
1
52
fx
x
A.
1
ln 5 2
5 2 5
dx
xC
x
. B.
1
ln(5 2)
5 2 2
dx
xC
x
.
C.
5ln 5 2
52
dx
xC
x
. D.
ln 5 2
52
dx
xC
x
.
Câu 40. Cho
( ) ( 1)
x
F x x e
là một nguyên hàm của hàm số
2
()
x
f x e
. Tìm nguyên hàm của hàm số
2
()
x
f x e
.
A.
2
( ) d (4 2 )
xx
f x e x x e C
B.
2
2
( ) d
2
xx
x
f x e x e C

C.
2
( ) d (2 )
xx
f x e x x e C
D.
2
( ) d ( 2)
xx
f x e x x e C
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3
Câu 10. Tìm nguyên hàm của hàm số
2
2
2
()f x x
x

.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang17
A.
3
2
()
3
x
f x dx C
x
. B.
3
1
()
3
x
f x dx C
x
.
C.
3
2
()
3
x
f x dx C
x
. D.
3
1
()
3
x
f x dx C
x
.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2
Câu 22. Tìm nguyên hàm của hàm số
( ) cos 2f x x
.
A.
1
( ) sin 2
2
f x dx x C
. B.
1
( ) sin 2
2
f x dx x C
.
C.
( ) 2sin2f x dx x C
. D.
( ) 2sin2f x dx x C
.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 23. Tìm nguyên hàm của hàm số
( ) 2 1f x x
.
A.
2
( ) (2 1) 2 1
3
f x dx x x C
. B.
1
( ) (2 1) 2 1
3
f x dx x x C
.
C.
1
( ) 2 1
3
f x dx x C
. D.
1
( ) 2 1
2
f x dx x C
.
TÍCH PHÂN
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA TÍCH PHÂN
1. Công thức tính tích phân
b
b
a
a
f x dx F x F b F a( ) ( ) ( ) ( )
.
* Nhận xét:Tích phân của hàm số
f
từ a đến b có thể kí hiệu bởi
b
a
f x dx()
hay
b
a
f t dt( ) .
Tích phân đó chỉ
phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
2. Tính chất của tích phân
Giả sử cho hai hàm số
( )
fx
và
( )
gx
liên tục trên
, , ,K a b c
là ba số bất kỳ thuộc
K
. Khi đó ta có :
1.
a
a
f x dx( ) 0
2.


ba
ab
f x dx f x dx( ) ( )
. 3.

b c b
a a c
f x dx f x dx f x dx( ) ( ) ( )
4.


b b b
a a a
f x g x dx f x dx g x dx( ) ( ) ( ) ( )
. 5.

bb
aa
kf x dx k f x dx( ) . ( )
.
6. Nếu f(x)
x a b0, ;


thì :


b
a
f x dx x a b( ) 0 ;
7. Nếu
bb
aa
x a b f x g x f x dx g x dx; : ( ) ( ) ( ) ( )



.
8. Nếu



x a b;
Nếu
M f x N()
thì
b
a
M b a f x dx N b a()
.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang18
PHƢƠNG PHÁP TÍNH TÍCH PHÂN
1. Phƣơng pháp đổi biến
1.1. Phƣơng pháp đổi biến số dạng 1
1.1.1. Định lí
Nếu 1) Hàm
x u t()
có đạo hàm liên tục trên



;
2) Hàm hợp
f u t( ( ))
được xác định trên



;
,
3)

u a u b( ) , ( )
Khi đó:


b
a
I f x dx f u t u t dt
'
( ) ( ( )) ( )
.
4.1.1.2. Phƣơng pháp chung
Bước 1: Đặt
x u t
Bước 2: Tính vi phân hai vế :
x u t dx u t dt( ) '( )
Đổi cận:


x b t
x a t
Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t
Vậy:




b
a
I f x dx f u t u t dt g t dt( ) ( ) '( ) ( )

G t G G( ) ( ) ( )
4.1.2. Phƣơng pháp đổi biến dạng 2
4.1.2.1. Định lí
Nếu hàm số
u u x()
đơn điệu và có đạo hàm liên tục trên đoạn


ab;
sao cho
f x dx g u x u x dx g u du( ) ( ) '( ) ( )
thì:


ub
b
a u a
I f x dx g u du
()
()
( ) ( )
.
4.1.2.2. Phƣơng pháp chung
Bước 1: Đặt
u u x du u x dx
'
( ) ( )
Bước 2: Đổi cận :


x b u u b
x a u u a
()
()
Bước 3: Chuyển tích phân đã cho sang tích phân theo
u
Vậy:


ub
bb
a a u a
I f x dx g u x u x dx g u d u
()
()
( ) ( ) . '( ) ( )
4.2. Phƣơng pháp tích phân từng phần
4.2.1. Định lí
Nếu
( )
ux
và
( )
vx
là các hàm số có đạo hàm liên tục trên


ab;
thì:


bb
aa
b
u x v x dx u x v x v x u x d x
a
''
( ) ( ) ( ) ( ) ( ) ( )
Hay
b
a
udv
b
uv
a
b
a
vdu
4.2.2. Phƣơng pháp chung
Bước 1: Viết
( )
f x dx
dưới dạng
udv uv dx
'
bằng cách chọn một phần thích hợp của
( )
fx
làm
( )
ux
và phần còn lại
dv v x dx'( )
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang19
Bước 2: Tính
du u d x'
và
v dv
v x dx'( )
Bước 3: Tính
b
a
vu x dx'( )
và
b
uv
a
BÀI TẬP
Câu 1. Nếu thì bằng
A. 16. B. 4. C. 2. D. 8.
Câu 2. Nếu thì bằng
A. 3. B. 4. C. 2. D.
Câu 3. Nếu và thì bằng bao nhiêu?
A. 3. B. 6. C. 12. D.
Câu 4. Nếu với thì giá trị của bằng
A. 9. B. 3. C. 6. D. 81.
Câu 5. Nếu với thì giá trị của bằng
A. 9. B. 3. C. 6. D. 81.
Câu 6. Nếu với thì giá trị của bằng
A. 9. B. 3. C. 6. D. 81.
Câu 7. Nếu thì bằng
A. . B. 2. C. 3. D. 4.
Câu 8. Cho hàm số liên tục trên đoạn . Nếu thì tích phân có giá
trị bằng
A. . B. 3. C. . D. −
Câu 9. Cho hàm số liên tục trên đoạn . Nếu thì tích phân có giá
trị bằng
A. . B. 3. C. . D. −
Câu 10. Cho các số thực . Nếu hàm số có đạo hàm là hàm liên tục trên thì
A. . B. .
C. . D. .
1
0
d4f x x
1
0
2 d 4f x x
2
1
d 3,f x x
5
2
d1f x x 
5
1
df x x
2.
5
2
d3f x x
7
5
d9f x x
7
2
df x x
6.
5
1
d
ln
21
x
c
x
cQ
c
5
1
d
ln
21
x
c
x
cQ
c
5
1
d
ln
21
x
c
x
cQ
c
2
1
d 3,f x x
5
2
d1f x x 
5
1
df x x
2
fx
0;3
3
0
d2f x x
3
0
[ 3 ]dx f x x
3
3
2
3
.
2
fx
0;3
3
0
d2f x x
3
0
[ 3 ( )]dxx f x
3
3
2
3
.
2
,a
()b a b
y f x
R
d
b
a
f x x f a f b
d
b
a
f x x f b f a

d
b
a
f x x f a f b

d
b
a
f x x f b f a
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang20
Câu 11 : Biết
1
0
2f x dx 
và
1
0
3,g x dx
khi đó
1
0
f x g x dx


bằng :
A. B. C. D.
Câu 12: Biết và khi đó bằng
A. . B. . C. . D. .
Câu 13: Biết
2
1
d2f x x
và
2
1
d6g x x
, khi đó
2
1
df x g x x


bằng
A.
4
.B.
8
.C.
8
. D.
4
.
Câu 14: Biết
11
00
( ) 2; ( ) 4f x dx g x dx

. Khi đó
1
0
( ) ( )f x g x dx
bằng
A. 6. B. -6. C.
2
. D.
2
.
Câu 15: Cho
2
1
1f x dx
và
4
1
3f t dt 
. Giá trị của
4
2
f u du
là:
A. -2 B.- 4 C. 4 D. 2
Câu 16: Cho
2
1
( ) 2f x dx
và
2
1
( ) 1g x dx

. Tính
2
1
2 ( ) 3 ( )I x f x g x dx
A.
5
2
I
B.
7
2
I
C.
17
2
I
D.
11
2
I
Câu 17 :Cho
10, 8, 7
d d c
a b a
f x dx f x dx f x dx
.
c
b
I f x dx
, ta được:
A.
5I 
B.
7I
C.
5I
D.
7I 
Câu 18: Biết
5
2
3f x dx
,
5
2
9g t dt
. Giá trị của
5
2
A f x g x dx

là:
A. 12B. 3 C. 6 D. 27
Câu 19: Biết
1 4 4
0 1 0
f(x)d 2, ( )d 3, g(x)d 4x f x x x
.Khẳng định nào sau đây SAI?
A.
4
0
( ) ( ) d 1f x g x x
.B.
44
00
f(x)d g(x)dxx

.C.
44
00
f(x)d g(x)dxx

.D.
4
0
f(x)d 5x
.
Câu 20: Biết
( ) 2
b
a
f x dx
và
( ) 3
b
c
f x dx
và a < b < c thì
()
c
a
f x dx
bằng bao nhiêu?
A. -1 B. 1 C. 5 D. -5
Câu 21. Xét , nếu đặt thì bằng
A. 2 eudu. B. 2 eudu. C. eudu. D. eudu.
Câu 22. Cho tích phânI . sinxdx. Nếu đặt thì kết quả nào sau đây đúng?
A. dt. B. dt. C. dt. D. dt.
5.
5.
1.
1.
1
0
3f x dx
1
0
4g x dx 
1
0
f x g x dx


7
7
1
1
2
2
x
0
edxx
2
ux
2
2
x
0
edxx
2
0
4
0
2
0
1
2
4
0
1
2
2
0
2 cos x

2 cos tx
2
3
It
3
2
It
2
3
2It
2
0
It
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang21
Câu 23. Cho tích phânI dx, giả sử đặt . Tìm mệnh đề đúng.
A. . B. dt. C. dt. D. dt.
Câu 24. Cho tích phânI dx. Nếu đặt thì
A. . B. dt. C. dt. D. dt.
Câu 25. Cho tích phânI dx. Đổi biến ta được kết quả nào sau đây?
A. dt. B. . C. . D. dt.
Câu 26. Cho tích phânI . Nếu đổi biến số thì
A. dt. B. dt. C. . D. dt.
Câu 27. Cho tích phânI dx. Với cách đặt ta được.
A. . B. dt. C. . D.
Câu 28. Cho tích phânI dx. Với cách đặt ta được.
A. . B. dt. C. . D.
Câu 29. Cho tích phân dx. Khi đặt thì tích phân đã cho trở thành
A. dt. B. dt. C. dt. D. dt.
Câu 30. Cho tích phân I dx. Viết dạng của khi đặt
A. dt. B. dt. C. dt. D. dt.
Câu 31. Cho . Khi đặt thì ta có
A. . B. . C. . D.
1
7
5
2
0
1
x
x
2
1tx
3
2
5
1
1
1
d
2
t
It
t
3
3
5
1
1t
I
t
3
2
4
1
1
1
2
t
t
3
4
4
1
1
3
2
t
t
3
0
11
x
x

1tx
2
2
1
2dI t t t
2
2
1
2I t t
2
2
1
22I t t
2
2
1
22I t t
e
1
1 ln x
x
1 ln tx
2
2
1
It
2
2
1
2dI t t
2
2
1
2dI t t
2
1
2It
1
2
0
d
4
x
x
2 sin ,xt
;
22
t





6
0
I
6
0
It
6
0
dt
I
t
3
0
I
1
3
0
1 x
3
1tx
1
3
0
3dI t t
1
2
0
3It
1
3
0
dI t t
1
0
3 d .I t t
1
3
0
1 x
3
1tx
1
3
0
3dI t t
1
2
0
3It
1
3
0
dI t t
1
0
3 d .I t t
4
2
0
9I x x
2
9tx
5
3
It
4
0
It
4
2
0
It
5
2
3
It
3
0
11
x
x

I
1.tx
2
2
1
22tt
2
2
1
22tt
2
2
1
2tt
2
2
1
2tt
e
d
e1
x
x
Ix
e1
x
t 
2
2dI t t
d
2
t
I
2dIt
2
d.I t t
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang22
Câu 32. Cho khi đặt ta có
A. dt. B. dt. C. dt. D. dt.
Câu 33. Với cách đổi biến thì tích phân trở thành
A. du. B. du. C. 2 du. D. du.
Câu 34. Với cách đổi biến thì tích phân trở thành
A. du. B. du. C. du. D. du.
Câu 35. Đổi biến thì tích phân trở thành
A. tdt. B. tdt. C. dt. D.
Câu 36: Giả sử
fx
là một hàm số liên tục trên khoảng
;

và
, , , ;a b c b c


. Mệnh đề nào
sau đây sai?
A.
.
b c b
a a c
f x dx f x dx f x dx
B.
.
b b c c
a a a
f x dx f x dx f x dx

C.
.
b b c b
a a b c
f x dx f x dx f x dx

D.
.
b c c
a a b
f x dx f x dx f x dx
Câu 37: Cho hàm số
3
yx
có một nguyên hàm là
Fx
. Khẳng định nào sau đây đúng?
A.
2 0 16.FF
B.
2 0 1.FF
C.
2 0 8.FF
D.
2 0 4.FF
Câu 38: Tích phân
0
cos
e
xdx
bằng
A.
sin .e
B.
cos .e
C.
sin .e
D.
cos .e
Câu 39: Tích phân
2
0
21I x dx
bằng
A.
5.I
B.
6.I
C.
2.I
D.
4.I
Câu 40: Cho
03
10
1; 3.f x dx f x dx


Tích phân
3
1
f x dx
bằng
A. 6. B. 4. C. 2. D. 0.
Câu 41:Cho
2
2
1f x dx
,
4
2
4.

f t dt
Giá trị của
4
2
I f y dy
là
A.
5.I
B.
3.I
C.
3.I 
D.
5.I 
1
2
0
1dI x x x

tx
1
2
0
1I t t
1
2
0
1I t t
1
2
0
1I t t
1
2
0
1I t t
1 3 ln ux
1
ln
d
1 3 ln
e
x
x
xx
2
2
1
2
1
3
u
2
2
1
2
1
9
u
2
2
1
1u
2
2
1
21
9
u
u
45ux
1
1
4 5dx x x
22
3
1
5
8
uu
22
1
1
5
8
uu
22
3
1
5
4
uu
2
3
1
5
8
uu
2 sin xt
1
2
0
d
4
x
x
6
0
3
0
6
0
6
0
d
.
t
t
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang23
Câu 42: Cho
50
c
a
f x dx
và
20.
c
b
f x dx
Giá trị
a
b
f x dx
bằng
A.
30.
B. 0. C. 70. D. 30.
Câu 43: Cho
1
0
2 12f x g x dx


và
1
0
5,g x dx
khi đó
1
0
f x dx
bằng
A.
2.
B. 12. C. 22. D. 2.
Câu 44: Cho
5
2
4f x dx
và
5
2
3,g x dx
khi đó
5
2
23f x g x dx


bằng
A. 1. B. 12. C. 7. D.
1.
Câu 45: Cho
2
0
3;f x dx 
4
2
6f x dx
và
4
0
8.g x dx
Khi đó
4
0
3f x g x dx


bằng
A. 14. B. 3. C. 17. D.
1.
Câu 46: Cho
2
1
25f x g x dx


và
2
1
2 3 4f x g x dx


. Khi đó
2
1
f x g x dx


bằng
A. 14. B. 3. C. 17. D.
1.
Câu 47: Cho hàm số
fx
liên tục trên
thỏa mãn
6
0
7f x dx
,
10
3
8f x dx
và
6
3
9.f x dx
Giá
trị của tích phân
10
0
I f x dx
bằng
A.
5.I
B.
6.I
C.
7.I
D.
8.I
Câu 48: Cho hàm số
fx
có đạo hàm trên đoạn
1;3
,
34f
và
3
1
7f x dx
. Khi đó
1f
bằng
A. 3. B. 11. C.
3.
D.
11.
Câu 49: Giá trị của
2
1
11
e
I dx
xx




là
A.
1
.I
e
B.
1
1.I
e

C.
1.I
D.
.Ie
Câu 50: Cho
,f x g x
là các hàm số có đạo hàm liên tục trên
0;1
và
1
0
.1g x f x dx
,
1
0
. 2.g x f x dx
Khi đó
1
0
.I f x g x dx


có giá trị là
A.
3.I
B.
1.I
C.
2.I
D.
1.I 
Câu 51: Cho hàm số
y f x
có đạo hàm là hàm liên tục trên
thỏa mãn
0 2, 1 6ff
. Khẳng
định nào sau đây là đúng?
A.
1
0
8.f x dx
B.
1
0
4.f x dx
C.
1
0
3.f x dx
D.
1
0
12.f x dx
Câu 52:Cho
2
1
4 2 1f x x dx


. Khi đó
2
1
f x dx
bằng
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang24
A. 1. B.
3.
C. 3. D.
1.
Câu 53: Cho hàm số
fx
liên tục trên
và
44
03
10, 4.f x dx f x dx

Tích phân
3
0
f x dx
bằng
A. 4. B. 7. C. 3. D. 6.
Câu 54: Với a, b là các tham số thực. Giá trị tích phân
2
0
3 2 1
b
x ax dx
bằng
A.
32
.b b a b
B.
32
.b b a b
C.
32
.b ba b
D.
2
3 2 1.b ab
Câu 55: Tích phân
1
0
3 1 3x x dx
bằng
A. 12. B. 9. C. 5. D. 6.
Câu 56:Biết
3
1
2
ln
x
dx a b c
x

, với
a, , , 9.b c c
Tổng
S a b c
là
A.
7.S
B.
5.S
C.
8.S
D.
6.S
Câu 57: Tích phân
1
0
1
1
I dx
x
có giá trị bằng
A.
ln2 1.
B.
ln2.
C.
ln2.
D.
1 ln2.
Câu 58: Cho hai tích phân
2
2
0
sinA xdx
và
2
2
0
cos .B xdx
Trong các khẳng định sau, khẳng định đúng
là
A.
2.AB
B.
.AB
C.
.AB
D.
1.AB
Câu 59: Cho hàm số
fx
liên tục trên
có
1
0
22f x dx
và
2
0
1 4.f x dx
Giá trị của
3
0
I f x dx
là
A.
5.I
B.
4.I
C.
6.I
D.
7.I
Câu 60:Cho
8
3
1 10f x dx
. Giá rị của
1
0
54J f x dx
là
A.
4.J
B.
10.J
C.
32.J
D.
2.J
Câu 61: Cho
9
0
27.f x dx
Giá trị của
0
3
3f x dx
là
A.
27.I
B.
3.I 
C.
9.I
D.
3.I
Câu 62: Giá trị của
2
2
0
sin .cosI x xdx
là
A.
0.I
B.
1.I
C.
1
.
3
I
D.
3
.
24
I
Câu 63: Cho hàm số
fx
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1
0
1 5, 12.f f x dx
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang25
Giá trị của
1
0
J xf x dx
là
A.
17.J 
B.
17.J
C.
7.J
D.
7.J 
Câu 64: Tích phân
2
1
3
x
I xe dx
nhận giá trị nào sau đây?
A.
3
1
36
.
e
I
e
B.
3
1
36
.
e
I
e
C.
3
36
.
e
I
e
D.
3
36
.
e
I
e
Câu 65: Giá trị của tích phân
1
0
21
x
I x e dx
là
A.
5 3.e
B.
1.e
C.
1.e
D.
5 1.e
Câu 66: Giá trị của
1
ln
e
I x xdx
là
A.
1
.
2
I
B.
2
1
2.
2
Ie
C.
2.I
D.
2
1
1.
4
Ie
Câu 67: Giá trị của tích phân
2
2
1
lnI x xdx
là
A.
87
ln2 .
39
B.
87
ln2 .
33
C.
24ln2 7.
D.
7
8ln 2 .
3
Câu 68: Giá trị của tích phân
5
4
1 ln 3I x x dx
là
A.
19
10ln 2 .
4
B.
19
10ln 2 .
4
C.
10ln2.
D.
19
10ln2.
4
Câu 69: Giá trị của tích phân
1
1 ln
e
x xdx
là
A.
2
5
.
4
e
B.
2
5
.
2
e
C.
2
5
.
2
e
D.
2
5
.
4
e
Câu70: Kết quả của
d
x
I xe x
là
A.
xx
I xe e C
. B.
xx
I e xe C
. C.
2
2
x
x
I e C
. D.
2
2
xx
x
I e e C
.
Câu71:Tính tích phân
1
0
d
32
x
I
x
A.
1
ln3
2
. B.
ln3
. C.
1
ln3
2
. D.
1
log3
2
.
Câu72:Cho hàm số
fx
có đạo hàm liên tục trên đoạn
;ab
và
2fa
,
4fb
. Tính
d
b
a
T f x x
.
A.
6T 
. B.
2T
. C.
6T
. D.
2T 
.
Câu73:Cho
2
0
d3f x x
. Tính
2
0
1df x x
?
A.
4
. B.
5
. C.
7
. D.
1
.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang26
Câu74:Tích phân
2
0
3
dx
x
bằng
A.
16
225
B.
5
log
3
C.
5
ln
3
D.
2
15
Đề thi tốt nghiệp THPT 2021
Mã đề 101
Câu 3: Nếu
4
1
d3f x x
và
4
1
d2g x x 
thì
4
1
df x g x x


bằng
A.
1
. B.
5
. C.
5
. D.
1
.
Câu 4: Nếu
3
0
d4f x x
thì
3
0
3df x x
bằng
A.
36
. B.
12
. C.
3
. D.
4
.
Câu 5: Nếu
2
0
d5f x x
thì
2
0
2 1 df x x


bằng
A. 8. B. 9. C. 10. D. 12.
Mã đề 102
Câu 3: Nếu
4
1
6f x dx
và
4
1
5g x dx 
thì
4
1
f x g x dx


bằng:
A.
1
. B.
11
. C.
1
. D.
11
.
Câu 4: Nếu
3
0
( )d 3f x x
thì
3
0
2 ( )df x x
bằng
A.
3
. B.
18
. C.
2
. D.
6
.
Câu 5: Nếu
2
0
( ) 3f x dx
thì
2
0
2 1 df x x


bằng
A.
6
. B.
4
. C.
8
. D.
5
.
Mã đề 103
Câu 3: Nếu
4
1
( )d 5f x x
và
4
1
( )d 4g x x 
thì
4
1
( ) ( ) df x g x x
bằng
A.
1
. B.
9
. C.
1
. D.
9
.
Câu 4: Nếu
3
0
d2f x x
thì
3
0
3df x x
bằng
A.
6
. B.
1
. C.
1
. D.
0
.
Câu 5: Nếu
2
0
d6f x x
thì
2
0
2 1 df x x


bằng
A.
12
. B.
10
. C.
11
. D.
14
Mã đề 104
Câu 3: Nếu
4
1
d4f x x
và
4
1
d3g x x 
thì
4
1
df x g x x


bằng
A.
1
. B.
7
. C.
1
. D.
7
.
Câu 10: Nếu
3
0
d3f x x
thì
3
0
4df x x
bằng
A.
3
. B.
12
. C.
36
. D.
4
.
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang27
Câu 32: Nếu
2
0
4f x dx
thì
2
0
2 1)f x dx


bằng
A.
8
. B.
10
. C.
7
. D.
6
.
Đề minh họa kì thi tốt nghiệp THPT năm 2021
Câu 16: Nếu
2
1
5f x dx
và
3
2
2f x dx 
thì
3
1
f x dx
bằng
A. 3. B. 7. C.
10.
D.
7.
Câu 17: Tích phân
2
3
1
x dx
bằng
A.
15
.
3
B.
17
.
4
C.
7
.
4
D.
15
.
4
Câu 33: Nếu
3
1
2 1 5f x dx


thì
3
1
f x dx
bằng
A. 3. B. 2. C.
3
.
4
D.
3
.
2
Đề thi tốt nghiệp THPT2020 ( Đợt 1 )
Mã đề 101
Câu 23: Biết
3
1
d3f x x
. Giá trị của
3
1
2df x x
bằng
A.
5
. B.
9
. C.
6
. D.
3
2
.
Câu 28: Biết
2
F x x
là một nguyên hàm của hàm số
fx
trên
. Giá trị của
2
1
2df x x


bằng
A.
5
. B.
3
. C.
13
3
. D.
7
3
.
Mã đề 102
Câu 1: Biết
5
1
d4f x x
. Giá trị của
5
1
3df x x
bằng
A.
7
. B.
4
3
. C.
64
. D.
12
.
Câu 34: Biết
3
F x x
là một nguyên hàm của hàm số
fx
trên
. Giá trị của
2
1
2 ( ) df x x
bằng
A.
23
4
. B.
7
. C.
9
. D.
15
4
.
Mã đề 103
Câu 2. Biết . Giá trị của bằng
A. . B. . C. . D. .
Câu 3. Biết là một nguyên hàm của hàm số trên . Giá trị của bằng
2
1
d2f x x
3
1
3df x x
5
6
2
3
8
3
()F x x
()fx
3
1
(1 ( ) d)x xf
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang28
A. 20. B. 22. C. 26. D. 28.
Mã đề 104
Câu 5: Biết
3
2
d 6.f x x
Giá trị của
3
2
2df x x
bằng
A.
36
. B.
3
. C.
12
. D.
8
.
Câu 38: Biết
2
F x x
là một nguyên hàm của hàm số
()fx
trên
. Giá trị của
3
1
1 ( )f x dx
bằng
A.
10
. B.
8
. C.
26
3
. D.
32
3
.
Đề thi tốt nghiệp THPT 2020 ( Đợt 2 )
Câu 8. Biết
2
1
d3f x x
và
2
1
d2g x x
. Khi đó
2
1
df x g x x


bằng?
A.
6
. B.
1
. C.
5
. D.
1
.
Câu 30. Biết
1
0
2 d 4f x x x


. Khi đó
1
0
df x x
bằng
A.
3
. B.
2
. C.
6
. D.
4
.
Đề thi tham khảo lần 2 năm 2020
Câu 18. Nếu
1
0
4
f x dx
thì
1
0
2
f x dx
bằng
A. 16 B. 4 C. 2 D. 8
Câu 33. Xét
2
2
0
x
xe dx
, nếu đặt
2
ux
thì
2
2
0
x
xe dx
bằng
A.
2
0
2
u
e du
B.
4
0
2
u
e du
C.
2
0
1
2
u
e du
D.
4
0
1
2
u
e du
Đề thi tham khảo lần 1 năm 2020
Câu 7: Nếu
2
1
2f x dx 
và
3
2
1f x dx
thì
3
1
f x dx
bằng
A.
3
. B.
1
. C. 1. D. 3.
Đề thi THPT Quốc gia 2019
Mã đề 101
Câu 11. Biết
1
0
2f x dx 
và
1
0
3,g x dx
khi đó
1
0
f x g x dx


bằng
A.
5.
. B.
5.
. C.
1.
. D.
1.
.
Câu 32. Cho hàm số
fx
. Biết
04f
và
2
2cos 1xxf
,
x
, khi đó
4
0
f x dx
bằng
A.
2
4
16
. B.
2
14
16

. C.
2
16 4
16


. D.
2
16 16
16


.
Mã đề 102
Câu 8. Biết và khi đó bằng
A. . B. . C. . D. .
1
0
3f x dx
1
0
4g x dx 
1
0
f x g x dx


7
7
1
1
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang29
Câu 33. Cho hàm số Biết và khi đó bằng
A. . B. . C. . D. .
Mã đề 103
Câu 4. Biết
2
1
d2f x x
và
2
1
d6g x x
, khi đó
2
1
df x g x x


bằng
A.
4
. B.
8
. C.
8
. D.
4
.
Câu 35. Cho hàm số
fx
. Biết
04f
và
2
2sin 1,f x x x
, khi đó
4
0
df x x
bằng
A.
2
15
16

. B.
2
16 16
16


. C.
2
16 4
16


. D.
2
4
16
.
Mã đề 104
Câu 15. Biết
11
00
( ) 2; ( ) 4f x dx g x dx

. Khi đó
1
0
( ) ( )f x g x dx
bằng
A. 6. B. -6. C.
2
. D.
2
.
Câu 32. Cho hàm số
()fx
. Biết
(0) 4f
và
2
'( ) 2sin 3,f x x x
, khi đó
4
0
()f x dx
bằng
A.
2
2
8
. B.
2
88
8


. C.
2
82
8


. D.
2
3 2 3
8


.
Đề thi tham khảo kì thi THPT Quốc gia 2019
Câu 6. Cho
1
0
( ) 2f x dx
và
1
0
g( ) 5x dx
, khi đó
1
0
( ) 2 ( )f x g x dx
bằng
A.
3.
B.
12.
C.
8.
D.
1.
Câu 38. Cho
1
2
0
ln2 ln3
2
xdx
a b c
x
với
,,abc
là các số hữu tỷ. Giá trị của
3abc
bằng
A. -2 B. -1 C. 2 D. 1
Đề thi THPT Quốc gia 2018
Mã đề 101
Câu 22:
2
31
1
x
e dx
bằng:
A.
52
1
()
3
ee
B.
52
1
3
ee
C.
52
ee
D.
52
1
()
3
ee
Câu 26: Cho
55
16
ln2 ln5 ln11,
9
dx
a b c
xx
với
,,abc
là các số hữu tỉ. Mệnh đề nào dưới đây đúng?
A.
a b c
B.
a b c
C.
3a b c
D.
3a b c
Mã đề 102
.fx
04f
2
'( ) 2cos 3, ,f x x x
4
0
( )df x x
2
2
8
2
88
8


2
82
8


2
68
8


ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang30
Câu 20.
1
31
0
x
e dx
bằng
A.
4
1
3
ee
B.
4
ee
C.
4
1
3
ee
D.
3
ee
Câu 27. Cho
21
5
ln3 ln5 ln7
4
dx
a b c
xx
, với a, b, c là các số hữu tỉ. Mệnh đề nào sau đây đúng?
A.
2a b c
B.
a b c
C.
a b c
D.
2a b c
Mã đề 103
Câu 19.
2
1
32
dx
x
bằng
A.
2ln2
B.
1
ln 2
3
C.
2
ln 2
3
D.
ln2
Câu 26. Cho
2
1
1 ln
e
x x dx ae be c
với a, b, c là các số hữu tỷ. Mệnh đề nào dưới đây đúng?
A.
a b c
B.
a b c
C.
a b c
D.
a b c
Đề thi tham khảo kì thi THPT Quốc gia 2018
Câu 19: Tích phân
2
0
dx
x3
bằng
A.
16
225
B.
5
log
3
C.
5
ln
3
D.
2
15
Câu 32: Biết
2
1
dx
a b c
x 1 x x x 1
với a, b, c là các số nguyên dương. Tính
P a b c.
A.
P 24
B.
P 12
C.
P 18
D.
P 46
Đề thi THPT Quốc gia 2017
Mã đề 101
Câu 25:Cho
6
0
( ) 12f x dx
. tính
2
0
(3 )I f x dx
A.
6I
B.
36I
C.
2I
D.
4I
Mã đề 102
Câu 12. Cho
()Fx
là nguyên hàm của hàm số
ln
()
x
fx
x
. Tính
( ) (1)F e F
A.
Ie
. B.
1
I
e
. C.
1
2
I
. D.
1I
.
Câu 21. Cho
2
1
( ) 2f x dx
và
2
1
( ) 1g x dx

. Tính
2
1
2 ( ) 3 ( )I x f x g x dx
A.
5
2
I
B.
7
2
I
C.
17
2
I
D.
11
2
I
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3
Câu 24. Tính tích phân
2
2
1
21I x x dx
bằng cách đặt
2
1ux
, mệnh đề nào dưới đây đúng ?
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang31
A.
3
0
2I udu
. B.
2
1
I udu
. C.
3
0
I udu
. D.
2
1
1
2
I udu
.
Câu 27. Cho
1
0
1
ln
12
x
dx e
ab
e

, với a, b là các số hữu tỉ. Tính
33
S a b
.
A.
2S
. B.
2S 
. C.
0S
. D.
1S
.
Câu 38. Cho hàm số
()fx
thỏa mãn
1
0
( 1) '( ) 10x f x dx
và
2 (1) (0) 2ff
. Tính
1
0
()I f x dx
.
A.
12I 
. B.
8I
. C.
12I
. D.
8I 
.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2 ( Đề thi thử nghiệm )
Câu 23. Cho hàm số
()fx
có đạo hàm trên đoạn
1;2 , (1) 1f
và
(2) 2f
. Tính
2
1
'( )I f x dx
.
A.
1I
. B.
1I 
. C.
3I
. D.
7
2
I
.
Câu 24. Biết
()Fx
là một nguyên hàm của hàm số
1
()
1
fx
x
và
(2) 1F
. Tính
(3)F
.
A.
(3) ln2 1F 
. B.
(3) ln2 1F 
. C.
1
(3)
2
F
. D.
7
(3)
4
F
.
Câu 25. Cho
4
0
( ) 16f x dx
. Tính
2
0
(2 )I f x dx
.
A.
32I
. B.
8I
. C.
16I
. D.
4I
.
Câu 26. Biết
4
2
3
ln2 ln3 ln5
dx
a b c
xx
, với a, b, c là các số nguyên. Tính
S a b c
.
A.
6S
. B.
2S
. C.
2S 
. D.
0S
.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 25. Tính tích phân
3
0
cos .sinI x xdx
.
A.
4
1
4
I

. B.
4
I

. C.
0I
. D.
1
4
I 
.
Câu 26. Tính tích phân
1
ln
e
I x xdx
.
A.
1
2
I
. B.
2
2
2
e
I
. C.
2
1
4
e
I
. D.
2
1
4
e
I
.
ỨNG DỤNG TÍCH PHÂN
1. Diện tích hình phẳng
1.1. Diện tích hình phẳng giới hạn bởi 1 đƣờng cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số liên tục trên đoạn , trục hoành và hai
y f x()


ab;
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang32
đường thẳng , được xác định:
1.2. Diện tích hình phẳng giới hạn bởi 2 đƣờng cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số , liên tục trên đoạn và hai
đường thẳng , được xác định:
- Nếu trên đoạn , hàm số không đổi dấu thì:
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi các đường , và hai đường thẳng ,
được xác định:
2. Thể tích vật thể và thể tích khối tròn xoay
2.1. Thể tích vật thể
Gọi là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm , . Giả
sử là hàm số liên tục trên đoạn .Khi đó thể tích vật thể B là
b
a
V S x dx
.
2.2. Thể tích khối tròn xoay
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường , trục
hoành và hai đường thẳng , quanh trục Oxlà
2
b
a
V f x dx


BÀI TẬP
Câu 1: Tính diện tích của những hình phẳng giới hạn bởi các đường
A.
9
2
B.
3
2
C.
5
4
D.
7
6
Câu 2: Tính diện tích của những hình phẳng giới hạn bởi các đường

2
( 6) ;yx

2
6y x x
A. 63 B. 72 C. 47 D. 35
Câu 3: Tính diện tích của những hình phẳng giới hạn bởi các đường
A.
9
2
B.
8
11
C.
7
9
D.
1
12
Câu 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
sin 1,yx
trục hoành và hai đường thẳng
0x
và
7
6
x
A.
37
1
26

B.
37
1
26

C.
37
1
23

D.
37
1
46

xa
xb
b
a
S f x dx()
y f x()
y g x()


ab;
xa
xb

b
a
S f x g x dx( ) ( )
[a b];
fx()

bb
aa
f x dx f x d x( ) ( )
x g y()
x h y()
yc
yd

d
c
S g y h y dy( ) ( )
B
Sx()
x
a x b()
Sx()
[a b];
y f x()
xa
xb
2
;2y x y x
32
;y x y x
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang33
Câu 5: Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số
2
cosyx
, trục hoành, trục tung và đường
thă
ng
x
.
A.
8
B.
6
C.
4
D.
2
Câu 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
yx
và
3
yx
.
A.
1
12
B.
1
9
C.
1
8
D.
1
15
Câu 7: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số
2
1yx
và
3yx
A.
6
2
B.
5
2
C.
11
2
D.
9
2
Câu 8: Các đường có phương trình
3
,1x y y
và
8x
A.
17
4
B.
17
2
C.
17
8
D.
27
4
Câu 9:Cho hình phẳng
D
giới hạn bởi đồ thị hai hàm số
y f x
,
y g x
liên tục trên đoạn
;ab
và
các đường thẳng
xa
,
xb
. Diện tích
S
của hình
D
được tính theo công thức nào dưới đây?
A.
πd
b
a
S f x g x x
. B.
d
b
a
S f x g x x
.
C.
2
d
b
a
S f x g x x


. D.
d
b
a
S f x g x x


.
Câu 10:Cho hàm số
fx
liên tục trên
, có đồ thị như hình vẽ. Gọi
S
là diện tích hình phẳng được giới hạn bởi đồ thị hàm số
fx
, trục
hoành và trục tung. Khẳng định nào sau đây đúng?
A.
0
dd
d
cd
S f x x f x x

. B.
0
dd
d
cd
S f x x f x x

.
C.
0
dd
d
cd
S f x x f x x

. D.
0
dd
d
cd
S f x x f x x

.
Câu 11:Cho hình phẳng
H
giới hạn bởi đồ thị hàm số
2
32y x x
, trục hoành và hai đường thẳng
1x
,
2x
. Quay
H
xung quanh trục hoành được khối tròn xoay có thể tích là
A.
2
2
1
3 2 dV x x x
. B.
2
2
2
1
3 2 dV x x x
.
C.
2
2
2
1
3 2 dV x x x
. D.
2
2
1
3 2 dV x x x
.
Câu 12:Cho hàm số
y f x
liên tục trên đoạn
;ab
. Gọi
D
là hình phẳng giới hạn bởi đồ thị hàm số
y f x
, trục hoành và hai đường thẳng
,x a x b a b
. Thể tích của khối tròn xoay tạo thành khi
quay
D
quanh trục hoành được tính theo công thức:
A.
2
b
a
V f x dx
B.
2
2
b
a
V f x dx
C.
22
b
a
V f x dx
D.
2
b
a
V f x dx
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang34
Câu 13: Gọi S là diện tích hình phẳng giới hạn bởi các đường
x
ye
,
0y
,
0x
,
2x
. Mệnh đề nào
dưới đây đúng?
A.
2
2
0
x
S e dx
. B.
2
0
x
S e dx
. C.
2
0
x
S e dx
. D.
2
2
0
x
S e dx
.
Câu 14: Diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
y x x
là
A.
37
12
. B.
9
4
I
. C.
81
12
. D. 13.
Câu 15. Diện tích của hình phẳng giới hạn bởi các đường và được tính
bởi công thức nào dưới đây?
A. . C. dx.
B. dx. D. dx.
Câu 16. Thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường , trục Ox và hai đường
thẳng khi quay quanh trục hoành được tính bởi công thức nào?
A. xdx. B. dx. C. xdx. D. dx.
Câu 17. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol và
đường thẳng xoay quanh trục Ox bằng
A. dx. B. dx. C. dx. D. dx.
Câu 18. Cho hàm số liên tục trên đoạn . Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng
A. dx. B. dx. C. dx. D. dx.
Câu 19. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số , trục hoành, hai đường thẳng
có công thức tính là
A. dx. B. dx. C. . D. dx.
Câu 20. Viết công thức tính thể tích của vật thể nằm giữa hai mặt phẳng và ln4, biết khi cắt
vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ ( ln4), ta được thiết diện
là một hình vuông có độ dài cạnh là
A. dx. dx. B. dx. D. dx.
Câu 21. Gọi là diện tích hình phẳng được tô đậm trong hình vẽ bên.
Công thức tính là
A. dx. B. dx.
S
2
2,yx
1,y 
0x
1x
1
2
0
2 1 dS x x

1
2
2
0
21Sx
1
2
0
21Sx
1
2
0
21Sx
yx
1; 4xx
4
1
V
4
1
||Vx
4
2
1
V
4
1
Vx
2
:P y x
:d y x
24
dx x x


11
24
00
dx x x


2
2
xX
1
2
0
xx
y f x
;ab
y f x
,xa
.xb
2
b
a
S f x
||
b
a
S f x
||
b
a
S f x
b
a
S f x
e
x
yx
2; 3xx
3
2
e
x
Sx
3
2
| e |
x
Sx
3
2
ed
x
S x x
3
2
e
x
Sx
V
0x
x
x
0 x
e.
x
x
ln 4
0
e
x
Vx
c.
ln 4
2
0
e
x
Vx
ln 4
0
e
x
Vx
ln 4
0
e
x
Vx
S
S
12
11
dS f x x f x


12
11
dS f x x f x


ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang35
C. dx. D. dx.
Câu 22. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol
và đường thẳng quay quanh trục Ox.
A. dx. B. dx. C. dx. D. dx.
Câu 23. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng
biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm.
A. . B. . C. 17 . D. 15
Câu 24.Đồ thị trong hình bên là của hàm số là diện tích hình phẳng
(phần tô đậm trong hình). Chọn khẳng định đúng.
A. dx. B. dx.
C. dx. D. dx.
Câu 25. Cho hàm số
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số và các đường thẳng
A. . B. . C. 10. D. 9.
Câu 26. Cho . Gọi là diện tích hình phẳng giới hạn bởi đồ thị hàm số và
trục hoành. Mệnh đề nào sau đây sai?
A. . B.
C. . D.
Câu 27. Tính thể tích V của vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường
quay quanh Ox.
A. . B. . C. . D.
Câu 28. Cho hình phẳng (H) giới hạn bởi Parabol và
đường cong có phương trình (hình vẽ).
Diện tích của hình phẳng (H) bằng
A. . B. C. . D.
2
1
S f x
2
1
S f x

2
:P y x
:2d y x
2
2
2
0
2xx
22
24
00
4dx x x


22
24
00
4dx x x


2
2
0
2xx
3
yx
1, 2xx
2
15
cm
4
2
17
cm
4
2
cm
2
cm .
,y f x
S
01
20
dS f x x f x


1
2
S f x
21
00
dS f x x f x


01
20
dS f x x f x


2
2
7 4 0 1
41
x khi x
fx
x khi x

fx
0,x
3,x
0.y
16
3
20
3
42
54f x x x
S
y f x
2
2
| | dS f x x
12
01
2 d 2 d .S f x x f x x

2
0
2 | |dS f x x
2
0
2 d .S f x x
2
1,yx
3
1yx
47
210
V
47
210
V
2
35
V
2
.
35
V
2
12
x
y
2
4
4
x
y 
2
12
x
43
3
А
43
.
6
А
43
6
2 4 3
.
3
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang36
Câu 29. Cho hàm số liên tục trên và có đồ thị (C) là đường cong như hình bên. Diện tích
hình phẳng giới hạn bởi đồ thị (C) , trục hoành và hai đường thẳng (phần tô đen) là
A. dx. B. dx. C. dx. D.
Câu 30. Cho hai hàm số và liên tục trên đoạn . Kí hiệu là hình phẳng giới
hạn bởi đồ thị hai hàm số và hai đường thẳng . Tính diện tích
của hình phẳng
A. dx. B. dx.
C. dx. D. dx.
Câu 31. Cho hàm số liên tục trên Gọi là diện tích hình
phẳng giới hạn bởi các đường và (như
hình vẽ bên).Mệnh đề nào sau đây đúng?
A. .
B. .
C. . D. .
Câu 32. Cho đồ thị hàm số trên như hình
vẽ.Biểu thức nào dưới đây có giá trị lớn nhất?
A. . B. .
C. . D. .
Câu 33. Gọi tam giác cong là hình phẳng giới hạn bởi đồ
thị các hàm số , , (tham khảo hình vẽ
bên). Diện tích của bằng
A. . B. .
C. . D. .
y f x
R
0,x
2x
2
0
fx
12
01
df x x f x

12
01
df x x f x

2
0
d.f x x
y f x
y g x
;ab
H
,y f x
y g x
,xa
()x b a b
S
.H
b
a
S f x g x
22
b
a
S f x g x

||
a
b
S f x g x
||
b
a
S f x g x
y f x
.¡
S
( )
, 0, 1y f x y x= = = -
5x =
15
11
( )d ( )dS f x x f x x
-
= - -
òò
15
11
( )d ( )dS f x x f x x
-
=+
òò
15
11
( )d ( )dS f x x f x x
-
=-
òò
15
11
( )d ( )dS f x x f x x
-
= - +
òò
()y f x=
0;8
éù
êú
ëû
1
0
()f x dx
ò
3
0
()f x dx
ò
5
0
()f x dx
ò
8
0
()f x dx
ò
( )
OAB
2
2yx=
3yx=-
0y =
( )
OAB
8
3
5
3
4
3
10
3
y
=
f(x)
y
x
O
5
1
-1
(
S
2
)
(
S
1
)
(
S
3
)
y
x
O
8
5
3
3
B
A
y
x
O
y=
3
-x
y=
2
x
2
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang37
Câu 34. Tính diện tích của hình phẳng (phần tô màu) trong hình
sau
A. . B. .
C. . D. .
Câu 35. Cho hàm số có đồ thị như hình dưới đây.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số và trục
là
A. .B. .
C. . D. .
Câu 36. Cho hàm số có đồ thị trên đoạn như hình vẽ
dưới đây. Tính tích phân .
A. B.
C. D.
Câu 37. Cho đồ thị hai hàm số và
như hình sau. Diện tích phần hình phẳng
được gạch sọc tính theo công thức nào dưới đây?
A. .
B. .
C. .
D. .
Câu 38. Diện tích phần hình phẳng gạch chéo trong hình vẽ
được tính theo công thức nào dưới đây?
A. .B. .
C. . D.
Đề thi tốt nghiệp 2020
S
8
3
S =
10
3
S =
11
3
S =
7
3
S =
y f x
y f x
Ox
S
20
01
ddf x x f x x

2
1
dS f x x
2
1
dS f x x

02
10
ddS f x x f x x


y f x
1;4
4
1
I f x dx
3.I
11
.
2
I
5.I
5
.
2
I
32
33y x x x
2
21y x x
12
3 2 3 2
11
2 2 d 2 2 dx x x x x x x x

2
32
1
2 2 dx x x x
12
3 2 3 2
11
2 2 d 2 2 dx x x x x x x x

2
32
1
2 2 dx x x x
2
2
1
2 2 4 dx x x

2
1
2 2 dxx

2
1
2 2 dxx
2
2
1
2 2 4 dx x x
4
2
O
x
y
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang38
Mã đề 101
Câu 29: Diện tích hình phẳng giới hạn bởi hai đường
2
4yx
và
24yx
bằng
A.
36
. B.
4
3
. C.
4
3
. D.
36
.
Mã đề 102
Câu 32: Diện tích hình phẳng giới hạn bởi hai đường
2
1yx
và
1yx
A.
6
. B.
13
6
. C.
13
6
. D.
1
6
.
Mã đề 103
Câu 4. Diện tích hình phẳng giới hạn bởi hai đường và bằng
A. . B. . C. . D. .
Mã đề 104
Câu 31: Diện tích hình phẳng giới hạn bởi hai đường
2
3yx
và
3yx
bằng
A.
125
6
. B.
1
6
. C.
125
6
. D.
6
.
Đề thi tốt nghiệp 2020 ( Đợt 2 )
Câu 29. Gọi
D
là hình phẳng giới hạn bởi các đường
2
, 0, 0
x
y e y x
và
1x
. Thể tích khối tròn
xoay tạo thành kho quay
D
quanh
Ox
bằng
A.
1
4
0
d
x
ex
. B.
1
2
0
d
x
ex
. C.
1
2
0
d
x
ex
. D.
1
4
0
d
x
ex
.
Đề thi tham khảo lần 2 năm 2020
Câu 34. Diện tích
S
của hình phẳng giới hạn bởi các đường
2
2 , 1, 0 y x y x
và
1x
được tính bởi
công thức nào dưới đây?
A.
1
2
0
21
S x dx
B.
1
2
0
1
21
2

S x dx
C.
1
2
2
0
21
S x dx
D.
1
2
0
21
S x dx
Đề thi tham khảo lần 1 năm 2020
Câu 29: Diện tích phần hình phẳng được gạch chép trong hình bên bằng
A.
2
2
1
2 2 4x x dx
. B.
2
2
1
2 2 4x x dx

.
C.
2
2
1
2 2 4x x dx
. D.
2
2
1
2 2 4x x dx

.
Đề thi THPT quốc gia 2019
Mã đề 101
Câu 29. Cho hàm số
fx
liên tục trên
R
. Gọi
S
là diện tích hình phẳng
giới hạn bởi các đường
, 0, 1y f x y x
và
4x
(như hình vẽ
bên). Mệnh đề nào dưới đây là đúng?
A.
14
11
S f x dx f x dx

. B.
14
11
S f x dx f x dx


.
C.
14
11
S f x dx f x dx


. D.
14
11
S f x dx f x dx

.
Mã đề 102
2
2yx
32yx
9
2
9
2
125
6
125
6
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang39
Câu 29. Cho hàm số liên tục trên . Gọi là diện tích hình phẳng giới hạn bởi các đường
, , và (như hình vẽ bên). Mệnh đề nào dưới đây đúng?
A. . B. .
C. . D. .
Mã đề 103
Câu 29. Cho hàm số
fx
liên tục trên
. Gọi
S
là diện tích hình
phẳng giới hạn bởi các đường
, 0, 1, 2y f x y x x
(như hình
vẽ bên). Mệnh đề nào dưới đây đúng?
A.
12
11
S f x dx f x dx

. B.
12
11
S f x dx f x dx

.
C.
12
11
S f x dx f x dx


. D.
12
11
S f x dx f x dx


.
Mã đề 104
Câu 24. Cho hàm số
fx
liên tục trên
R
. Gọi
S
là diện tích hình
phẳng giới hạn bởi các đường
, 0, 2y f x y x
và
3x
(như
hình vẽ bên). Mệnh đề nào dưới đây là đúng?
A.
13
21
S f x dx f x dx


. B.
13
21
S f x dx f x dx

.
C.
13
21
S f x dx f x dx


. D.
13
21
S f x dx f x dx

.
Đề thi tham khảo kì thi THPT Quốc gia 2019
Câu 24. Diện tích phần hình phẳng gạch chéo trong hình vẽ
bên được tính theo công thức nào dưới đây?
A.
2
2
1
2 2 4x x dx

B.
2
1
22x dx

C.
2
1
22x dx
D.
2
2
1
2 2 4x x dx
Đề thi THPT Quốc gia 2018
Mã đề 101
Câu 5: Gọi S là diện tích của hình phẳng giới hạn bởi các đường
, 0, 0, 2
x
y e y x x
. Mệnh đề nào
dưới đây đúng?
A.
2
2
0
x
S e dx
B.
2
0
x
S e dx
C.
2
0
x
S e dx
D.
2
2
0
x
S e dx
Mã đề 102
fx
S
y f x
0y
1x 
5x
15
11
S f x dx f x dx


15
11
S f x dx f x dx


15
11
S f x dx f x dx

15
11
S f x dx f x dx

ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang40
Câu 2. Gọi S là diện tích của hình phẳng giới hạn bởi các đường
2 , 0, 0, 2
x
y y x x
. Mệnh đề nào
dưới đây đúng?
A.
2
0
2
x
S dx
B.
2
2
0
2
x
S dx
C.
2
2
0
2
x
S dx
D.
2
0
2
x
S dx
Mã đề 103
Câu 4. Cho hình phẳng
H
giới hạn bởi các đường
2
3, 0, 0, 2y x y x x
. Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay
H
xung quanh trục Ox. Mệnh đề nào dưới đây đúng?
A.
2
2
2
0
3V x dx

B.
2
2
0
3V x dx

C.
2
2
2
0
3V x dx
D.
2
2
0
3V x dx
Đề thi tham khảo kì thi THPT quốc gia 2018
Câu 6: Cho hàm số
y f x
liên tục trên đoạn
a;b
. Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y f x
, trục hoành và hai đường thẳng
x a, x b a b
. Thể tích của khối tròn xoay tạo thành khi
quay D quanh trục hoành được tính theo công thức
A.
b
2
a
V f x dx
B.
b
2
a
V 2 f x dx
C.
b
22
a
V f x dx
D.
b
2
a
V f x dx
Câu 31: Cho (H) là hình phẳng giới hạn bởi parabol
2
y 3x ,
cung tròn có
phương trình
2
y 4 x
(với
0 x 2
) và trục hoành (phần tô đậm trong
hình vẽ). Diện tích của (H) bằng
A.
43
12

B.
43
12

C.
4 2 3 3
6
D.
5 3 2
3

Đề thi THPT Quốc gia 2017
Mã đề 101
Câu 14: Cho hình phẳng D giới hạn bởi đường cong
2 cosyx
, trục hoành và các đường
thẳng
0,
2
xx

. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
bao nhiêu ?
A.
1V

B.
( 1)V


C.
( 1)V


D.
1V

Mã đề 102
Câu 20. Cho hình phẳng D giới hạn bởi đường cong
2 sinyx
, trục hoành và các đường thẳng
0,xx

. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
A.
2( 1)V

B.
2 ( 1)V


C.
2
2V
D.
2V
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3
Câu 21. Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường
()y f x
, trục hoành và hai đường thẳng
1, 2xx
(như hình
vẽ bên). Đặt
02
10
( ) , ( )a f x dx b f x dx


, mệnh đề nào dưới đây
đúng ?
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Trang41
A.
S b a
. B.
S b a
.
C.
S b a
. D.
S b a
.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2
Câu 27. Cho hình thang cong (H) giới hạn bởi các đường
, 0, 0
x
y e y x
và
ln4x
. Đường thẳng
xk
(0 ln 4)k
chia (H) thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên.
Tìm k để
12
2SS
.
A.
2
ln 4
3
k
. B.
ln2k
.
C.
8
ln
3
k
. D.
ln3k
.
Câu 28. Ông An có một mảnh vườn hình elip có độ dài trục lớn
bằng 16m và độ dài trục bé bằng 10m. Ông muốn trồng hoa trên
một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng
(như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng /1 m
2
.
Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó ? (Số
tiền được làm tròn đến hàng nghìn.)
A. 7.862.000 đồng. B. 7.653.000 đồng.
C. 7.128.000 đồng. D. 7.826.000 đồng.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 22. Viết công thức tính thể tích V của khối tròn xoay được tạo thành khi quay hình thang cong, giới
hạn bởi đồ thị hàm số
()y f x
, trục Ox và hai đường thẳng
,x a x b
()ab
, xung quanh trục Ox.
A.
2
()
b
a
V f x dx
. B.
2
()
b
a
V f x dx
. C.
()
b
a
V f x dx
. D.
()
b
a
V f x dx
.
Câu 27. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
3
y x x
và đồ thị hàm số
2
y x x
.
A.
37
12
. B.
9
4
. C.
81
12
. D. 13.
Câu 28. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số
2( 1)
x
y x e
, trục tung và trục hoành. Tính
thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A.
42Ve
. B.
(4 2 )Ve

. C.
2
5Ve
. D.
2
( 5)Ve

.
| 1/41
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 NGUYÊN HÀM 1.1. Định nghĩa
Cho hàm số f x  xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F x  được gọi là
nguyên hàm của hàm số f x  trên K nếu F ' x   f x  với mọi x K . Kí hiệu:        f x dx F x C . Định lí:
1) Nếu F x  là một nguyên hàm của f x  trên K thì với mỗi hằng số C , hàm số
G x   F x  C cũng là một nguyên hàm của f x  trên K .
2) Nếu F x  là một nguyên hàm của hàm số f x  trên K thì mọi nguyên hàm của f x  trên K
đều có dạng F x  C , với C là một hằng số.
Do đó F x  C,C   là họ tất cả các nguyên hàm của f x  trên K .
1.2. Tính chất của nguyên hàm         f x dx f x  và '      
f x dx f x C ; d f xdx   f x  dx
 Nếu F(x) có đạo hàm thì:  ( )  ( )  d F x F x C
kf x dx  
k f x dx với k là hằng số khác 0 .  
f x   gx dx   f x dx   
gx dx
Công thức đổi biến số: Cho y f u và u g x . Nếu ( )  ( ) 
f x dx F x C thì f g x()g x '( d ) x  
f u( d)u F(u) C
1.3. Sự tồn tại của nguyên hàm
Định lí: Mọi hàm số f x  liên tục trên K đều có nguyên hàm trên K .
1.4. Bảng nguyên hàm các hàm số thƣờng gặp 1. 0   dx C 2.   dx x C  1  1    1     3.  1  x dx x C   1   1 16.    dx   ,    ax b ax b c 1 a   1 1 1 2 4.     dx C 17.    x xdx C x 2 x 2 1 dx 1 5.  ln   dx x C 18.  ln    ax b c x ax b a 6.    x x e dx e C  1  19.    ax b ax b e dx e C a x a kx b 1 a 7. x a dx    C 20. kx b a dx    C ln a k ln a 8. cos  sin   xdx x C 1 21. cos 
   sin      ax b dx ax b C a Trang1
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
9. sin xdx   co s x C  1 22. sin 
    cos     ax b dx ax b C a 10. t an .   ln | cos |   x dx x C 1 23. t an    dx   ln cos      ax b ax b C a 11. cot .  ln | sin |   x dx x C 1 24. cot    dx  ln sin      ax b ax b C a 1 1 1 12.  tan   dx x C 25.  tan    dx ax b C 2 cos x 2
cos ax b   a 1 1 1 13.   cot   dx x C 26.   cot    dx ax b C 2 sin x 2
sin ax b   a 14.   2 1 t an   tan   x dx x C 1 27. 1  2 t an     tan      ax b dx ax b C a 15.   2 1 cot    t   x dx co x C 1 28. 1  2 cot      t      ax b dx co ax b C a
2. CÁC PHƢƠNG PHÁP TÍNH NGUYÊN HÀM
2.1. Phƣơng pháp đổi biến
2.1.1. Đổi biến dạng 1 Nếu : ( )  ( ) 
f x dx F x C và với u   t  là hàm số có đạo hàm thì : ( )  ( (  ))   f u du F t C
2.1.1.1. Phƣơng pháp chung
Bước 1: Chọn x   t  , trong đó  t  là hàm số mà ta chọn thích hợp .
Bước 2: Lấy vi phân hai vế : dx   't dt
Bước 3: Biến đổi : f (x d ) x f
 t  't dt   
g t dt
Bước 4: Khi đó tính : f x ( d ) x g t ( d ) t G t ( )    C .
2.1.1.2. Các dấu hiệu đổi biến thƣờng gặp Dấu hiệu Cách chọn    
Đặt x a sint ; với t    ;
. hoặc x a cost ; a2  x 2  2 2 
với t  0;   . a     a Đặt x  .; với t    ;  \   0 hoặc x sint  2 2  cost x 2  a2  
với t  0;    \  .  2     
Đặt x a tant ; với t    ; . hoặc x a cot t  2 2  a2  x 2
với t  0; . Trang2
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 a x a x . hoặc .
Đặt x acos t 2 a x a x
x ab x
Đặt x a b ( a s ) in t 2 – 1    
Đặt x atant ; với t    ; . a2  x 2  2 2 
2.1.2. Đổi biến dạng 2
Nếu hàm số f(x) liên tục thì đặt x   t  . Trong đó  t  cùng với đạo hàm của nó ( ' t  là những
hàm số liên tục) thì ta được : f (x d ) x f    
t  't dt g t( d)t G t()     C .
2.1.2.1. Phƣơng pháp chung
Bước 1: Chọn t= x . Trong đó  x  là hàm số mà ta chọn thích hợp .
Bước 2: Tính vi phân hai vế : dt   't dt .
Bước 3: Biểu thị : f (x d ) x f
 t  't dt    g t ( d ) t .
Bước 4: Khi đó : I f x ( d ) x g t ( d ) t G t ( )    C
2.1.2.2. Các dấu hiệu đổi biến thƣờng gặp : Dấu hiệu Cách chọn Hàm số có mẫu số t là mẫu số
Hàm số : f x;  x  t   x  . s x x
Hàm    a inx+b.cosx f x t  t an ; cos  0
c. s inx+d.cosx+e 2  2  1
Với : x a  0 và x b  0 .
Hàm f x    
x a x b
Đặt : t x a x b
Với x a  0 và x b  0 . Đặt : t
x a  x b
2.2. Phƣơng pháp nguyên hàm từng phần
Nếu u(x) , v(x) là hai hàm số có đạo hàm liên tục trên K: u x ( ) v . '(x dx )
u(x) v . (x)  
v(x) u. '(x dx )
Hay udv uv  
vdu ( với du u’xdx, d v v’xdx )
2.2.1. Phƣơng pháp chung
Bước 1: Ta biến đổi tích phân ban đầu về dạng : I f x ( dx )  
f x().f (x dx ) 1 2
u f (x)
du f ' x ( dx )  1 
Bước 2: Đặt :    1 dv f x ( ) v   ( ) 2   f x dx 2
Bước 3: Khi đó : u dv .  u v .   vdu .
MỘT SỐ DẠNG NGUYÊN HÀM TỪNG PHẦN THƢỜNG GẶP   Ghi nhớ: Khi gặp mx n e .sin 
ax bdx hoặc mx n e .cos
ax bdx luôn phải thực hiện phƣơng
pháp nguyên hàm từng phần hai lần liên tiếp. Trang3
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 Dạng tích phân Cách đặt u
  Px
   axb P x e dx axb
dv e dx u   Px
sinmx n  P  x. 
sinmx n    .dx cos mx n dv          .dx cos mx n   lnn u  ax b   .lnn P x
ax bdx  dv P  x.dx axb u   e
sinmx n  axb e .   
sinmx n    .dx cos mx n dv         .dx cos mx n
Chọn u: Nhất lo,nhì đa, tam lƣợng, tứ mũ.
Cột u ( đạo hàm) Cột v (ng hàm) u v ( Đạo hàm ) u ( Nguyên hàm ) v' Bảng 1 (+) u v' Bảng 2 u' (+) (-) v u" v1 (+) u' v u"' (-) (-) v2 u'' (+) 0 v v 3 1
Quy tắc đƣờng chéo để tính tích phân từng phần
Áp dụng nhanh trong trƣờng hợp u là một đa thức bậc cao.
Ở cột u, lấy đạo hàm liên tiếp đến khi đƣợc kết quả bằng 0, hoặc đến khi lấy đạo hàm phức
tạp hơn, hoặc đến khi lặp lại thì dừng.
Ở cột v, tìm nguyên hàm tƣơng ứng của v. VD: Trong bảng bên Bảng 1:
u.v 'dx u.v u '.v u ' .v dx   1 2 Bảng 2:
u.v 'dx u.v u '.v u ' .v u ' '.v 1 2 3 Trang4
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Ví dụ áp dụng: Tìm các nguyên hàm sau: 1.     2 2 x x
e dx 2. 2x    1 cosx dx 3.  2 3x   1lnxdx
Giải: Áp dụng quy tắc đƣờng chéo: 1:     2 2 x x e dx
Căn cứ vào bảng ta đƣợc: u v x + 2 e2x  1 x 1    2 x 2 x x e dx  x  2 2 2 e
e C + 2 4 1 1 e2x - 2 + 1 0 e2x 4 2. 2x    1 cosx dx
Căn cứ vào bảng ta đƣợc: u v 2x - 1 cosx 2x   
1 cosx dx  2x  
1 sin x  2cosx C + sinx 2 - + 0 - cosx 3.  2 3x   1lnxdx
Căn cứ vào bảng ta đƣợc: u v  1 2 3 3 3x  
1lnxdx  x xln x   x xdx lnx x x2 3 - 1 +   3
x xx   2 ln x   1dx 1 -
x3 - x
 x x 3 x 3 ln x
x C x 3 BÀI TẬP Trang5
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 1: Công thức tìm nguyên hàm nào sau đây chƣa đúng ? 1  1   x A.
dx  ln x C. 
x  0 B. x dx   C      1 . x  1 x a 1 C. x a dx
C 0  a    1 . D.
dx  tan x  . C ln a 2 cos x 3
Câu 2: Tìm nguyên hàm của hàm số f x  2x x  0 . 2   x 3 A. f  x 2 2
dx x  3ln x C. B. f  x 2 dx x   C. 2 x 3 3 C. f  x 2 dx x
C. D. f  x 2 dx x   . C x x Câu 3: Hàm số   x
F x e  tan x C là nguyên hàm của hàm số f x nào dưới đây? x 1 x 1
A. f x  e
. B. f x  e  . 2 sin x 2 sin x x 1
C. f x  e  . D.   x
f x e  cot . x 2 cos x
Câu 4. Họ nguyên hàm của hàm số    2  2x f x x là 2x 2x A. 2 x   C B. 2  2x x .ln 2  C C. 2  2 . x ln 2  C D. 2   C ln 2 ln 2 Câu 5: Biết f
 xdx  2xln3x  1C. Tìm khẳng định đúng trong các khẳng định dưới đây: A. f
 3xdx  6xln9x  1C. B. f
 3xdx 3xln9x  1C. C. f
 3xdx  6xln3x  1C. D. f
 3xdx  2xln9x  1C. Câu 6:
Tìm nguyên hàm F x của hàm số   x
f x e x biết F 0  2 x x x x
A. F x 2 xe
1. B. F x 2 xe  1.
C. F x 2 xe
1. D. F x 2 xe  1. 2 2 2 2
Câu 7: Tính F x  xcosx dx  ta được kết quả
A. F x  x sin x cosx C.B. F x  x sin x cosx C.
C. F x  x sin x cosx C. D. F x  x sin x cosx C.
Câu 8. Họ nguyên hàm của hàm số ( ) x f x e  1là   A. x
e x C . B. x e
x C . C. x
e x C . D. x
e x C . 2x  3
Câu 9: F x là một nguyên hàm của hàm số f x 
x  0 , biết F  
1  1. F x là biểu 2   x thức nào sau đây ?
A. F x 3
 2x   2.
B. F x 3
 2ln x   2. x x
C. F x 3
 2x   4.
D. F x 3
 2ln x   4. x x
Câu 10: Họ nguyên hàm của hàm số ( ) x
f x e x là Trang6
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1 x 1 x 1 A. x 2
e x C. B. 2 e
x C. C. 2 e
x C. D. x
e 1  C. 2 x 1 2 3
Câu 11. Họ nguyên hàm của hàm số f x 3  x   2x là: 2 x 4 x 3 x 1 4 3 2x x 4 x 3 A. 2
 3ln x  2 .xln 2  C B. 
 2x C C.    C D.
  2 .xln 2  C 4 3 3 x 4 x ln 2 4 x
Câu 12. Họ nguyên hàm của hàm số f (x)  cos x 1 là:
A. sinx  x  C.
B. sinx  x  C. C. sinx  C. D. sinx  C. Câu 13: Hàm số 3 2
F (x)  5x  4x  7x 10  C là nguyên hàm của hàm số nào? 4 3 2 5x 4x 7x A. 2
f (x)  5x  4x  7.B. f (x)    . 4 3 2 4 3 2 5x 4x 7x
C. f (x)    10 . x D. 2
f (x)  15x  8x  7. 4 3 2
Câu 14. Họ nguyên hàm của hàm số ( )  3x f xx là 3x 1 x 1 A. x 2
3  x C. B. 2 3 
x C. C. 2
x C.D.3x 1 C. 2 ln 3 2
Câu 15. Họ nguyên hàm của hàm số f (x)  sin(2x 1) là 1 1 A.  os c
(2x 1)  C. B. o
c s(2x 1)  C. C.  os c
(2x 1)  C. D. os c
(2x 1)  C. 2 2  
Câu 16. Nguyên hàm của hàm số 1 J   x dx   là  x  1 A. 2
F(x)  ln x x C. B. 2
F (x)  ln x x C. 2 1 C. 2
F (x)  ln(x)  x C. D. 2
F (x)  ln(x)  x C. 2
Câu 17: Họ nguyên hàm của hàm số   6 x f x e   2x  3 là: 1 A. 6 x 2 e
 4x  3x C B. 6 x 2
e  4x  3x C 6 1 C. 6x 2 e
x  3x C D. 6 x 2
e x  3x C 6 1
Câu 18: Nguyên hàm của hàm số f x  3  x  là: x 1 x A. f  x 2 dx  3x   C B. f  x 4 dx   ln x C 2 x 4 1 x C. f  x 2 dx  3x   C D. f  x 4 dx   ln x C 2 x 4
Câu 19: Họ nguyên hàm của hàm số f x  1  là: 2x  3 1 1 1 A.
ln 2x  3  C B.
ln 2x  3  C
C. ln 2x  3  C D.
ln 2x  3  C 2 2 ln 2 Trang7
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 20: Họ nguyên hàm của hàm số 2
y x 1 là: 3 x A. 3
x x C B. 3 x C
C. 6x C D.x C 3
Câu 21: Họ nguyên hàm của hàm số f x 2 x 2
e x là: x e x
A. F x  2 3  
C B. F x 2 x 3
e x C 2 3 x C.   2  2 x F x e
 2x C
D. F x  3 2 xe   C 3
Câu 22: Nguyên hàm của hàm số f x 3
x  3x  2 là hàm số nào trong các hàm số sau? x
A. F x 2
 3x  3x C B. F x 4 2 
 3x  2x C 3 x x x x
C. F x  4 2 3  
 2x C
D. F x  4 2    2x C 4 2 4 2
Câu 23: Họ nguyên hàm của hàm số   2 f x x  là: x 2 x 2 x 2 2 x A.
 2 ln x C B.
x C C.1   C D.
 2 ln x C 2 2 2 x 2
Câu 24: Hàm số nào dưới đây là một nguyên hàm của hàm số f x 4  x  2x ? x x x
A. F x 4 2
x  2x
B. F x 2  3x  2
C. F x  5 2   x 1
D. F x  4 2   5 4 2
Câu 25: Họ nguyên hàm của hàm số   3x f x e là: x e A. f  x 3 1 dx   C B.    3  3 x f x dx e C 3x  1 x e C.    3
f x dx e C D. f  x 3 dx   C 3
Câu 26: Họ nguyên hàm của hàm số f x  x  cos x là: x A. f  x 2 dx
 sin x C B. f
 xdx 1sin x C 2 x C. f
 xdx xsinx cosx C D. f  x 2 dx
 sin x C 2 Câu 27: Hàm số   2 F x   dx  có dạng:   x A.   2
F x   x C
B. F x  3   C
C. F x 2 2   C
D. F x  2 x C 3 2
Câu 28: Cho hàm số y F x  là một nguyên hàm của hàm số 2
y x . Giá trị của F '25 bằng: A. 125. B. 625. C. 5. D. 25.
Câu 29: Họ nguyên hàm của hàm số f x 3x 1 e   là:   1 1 A.   3 1  3 x F x e
C B. Fx 3x 1  3e
. ln 3  C C. F x  3x 1 e  
. ln 3  C D. F x  3x 1 e    C 3 3 Trang8
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 3
Câu 30. Cho F (x) là một nguyên hàm của hàm số ( ) x
f x e  2x thỏa mãn F (0)  . Tìm F (x) . 2 x 1 x 3 A. 2
F (x)  e x B. 2
F (x)  2e x 2 2 x 1 x 5 C. 2
F (x)  e x D. 2
F (x)  e x 2 2 3 Câu 31. Hàm số ( ) x
F x = e là một nguyên hàm của hàm số: 3 x 3 3 e 3 A. ( ) x f x = e . B. ( ) 2 = 3 . x f x x e . C. f (x)= . D. ( ) 3 1 . x f x x e - = . 2 3x   
Câu 32.Tìm nguyên hàm F (x) của hàm số f (x)  sin x  cos x thỏa mãn F  2   .  2 
A. F (x)  cos x  sin x  3
B. F (x)   cos x  sin x  3
C. F (x)   cos x  sin x 1
D. F (x)   cos x  sin x  1
Câu 33: Họ tất cả các nguyên hàm của hàm số f x  2x  5 là A. 2
x  5x C. B. 2 2x  5x  . C C. 2 2x  . C D. 2 x  . C
Câu 34: Họ tất cả các nguyên hàm của hàm số f x  2x  6 là A. 2
x  6x C . B. 2
2x C . C. 2
2x  6x C . D. 2 x C .
Câu 35:Họ tất cả các nguyên hàm của hàm số f x  2x  3 là A. 2 2x C . B. 2
x  3x C . C. 2
2x  3x C . D. 2 x C .
Câu 36: Họ tất cả các nguyên hàm của hàm số f x  2x  4 là A. 2
2x  4x C . B. 2
x  4x C . C. 2 x C . D. 2 2x C .
Câu 37: Nguyên hàm của hàm số   3
f x x x là 1 1 A. 4 2
x x C . B. 2 3x 1 C . C. 3
x x C . D. 4 2 x x C . 4 2
Câu 38: Nguyên hàm của hàm số   4
f x x x là 1 1 A. 4
x x C B. 3 4x 1 C . C. 5 2
x x C . D. 5 2 x x C . 5 2
Câu 39: Nguyên hàm của hàm số 4 2
y x x là 1 1 A. 3
4x  2x C . B. 5 3 x x C . C. 4 2
x x C D. 5 3
x x C . 5 3
Câu 40: Nguyên hàm của hàm số   3 2
f x x x là 1 1 A. 4 3
x x C . B. 4 3 x x C . C. 2
3x  2x C . D. 3 2
x x C . 4 3
Câu 41: Họ nguyên hàm của hàm số f x 1  là 5x  4 1 1 1 A.
ln 5x  4  C
B. ln 5x  4  C
C. ln 5x  4  C
D. ln 5x  4  C ln 5 5 5
Câu 42:Họ nguyên hàm của hàm số    2 x f x x e là A. 2 x
e C . B. 2 x
x e C . C. 2 2 x
x e C . D. 2 x
x e C .
Câu 43. Hàm số F x là một nguyên hàm của hàm số f x trên khoảng K nếu
A. F x   f x, x   K .
B. f  x  F x, x   K. Trang9
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
C. F x  f x, x   K .
D. f  x  F x, x   K. Câu 44. Cho hàm số    2 ex f x x
. Tìm một nguyên hàm F x của hàm số f x thỏa mãn F 0  2022. A.   ex F x   2021. B.   2   ex F x x  2021. C.   2   ex F x x  2020. D.   2   ex F x x  2021.
Câu 45. Họ nguyên hàm của hàm số f x 2  3x 1 là 3 x A. 3
x C . B.
x C . C. 6x C . D. 3
x x C. 3
Câu 46. Hàm số f x  cos  4x  7 có một nguyên hàm là 1 1
A.  sin  4x  7  x .B. sin  4x  7  3 .C. sin  4x  7 1 . D. − si  n 4x  7  3. 4 4
Câu 47. Họ nguyên hàm của hàm số f x 2
x  cos x là 1 1
A. 2x  sin x C . B. 3
x  sin x C .C. 3
x  sin x C . D. 3
x  sin x C. 3 3
Câu 48. Họ nguyên hàm của hàm số   3 2
f x x x là 4 3 x x 1 1 A.   C .B. 4 3
x x .C. 2
3x  2x . D. 4 3 x x . 4 3 4 4
Câu 49. Tìm họ nguyên hàm của hàm số   25x f x  ? 2 x 5 x A. 2 x 2 5 d 2.5 x x   ln5 C . B. 2 5 dx  2.  C.  ln 5 x 1  x 25 x 25x C. 2 5 dx   C  . D. 2 5 dx   C.  2 ln 5 x 1
Câu 50. Nguyên hàm của hàm số f x 3
 4x x 1 là: 1 1 A. 4 2
x x x C .B. 2
12x 1  C . C. 4 2 x
x x C. D. 4 2 x
x x C. 2 2
Câu 51. Họ các nguyên hàm của hàm số y  cos x x là 1 1 A. 2 sin x
x C . B. 2
sin x x C .C. 2
 sin x x C .D. 2
 sin x x C. 2 2 x Câu 52. Nếu f  x 3 dx
 ex C thì f x bằng 3 x x A.   2  3  ex f x x
.B. f x 4 
 ex .C.   2   ex f x x
. D. f x 4   ex. 3 12
Câu 53. Nguyên hàm của hàm số f x 2022  x
,  x  R  là hàm số nào trong các hàm số dưới đây?A. F x 2021  2022x
C, C R .
B. F x 2021  x
C, C R . x
C. F x 2023 
C, C R .
D. F x 2022  2021x
C, C R . 2023 Câu 54. Hàm số   2 ex F x
là một nguyên hàm của hàm số nào dưới đây? 2 ex A.   2  2 ex f x x B.   2 2  ex f x x C.   2 ex f x
D. f x  . 2x Trang10
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 55. Tìm tất cả các nguyên hàm của hàm số   3 .x f x   3x 3x A. C . B.   C .
C. 3x C . D. 3 x ln3 . C  ln 3 ln 3
Câu 56. Tìm tất cả các nguyên hàm của hàm số f x  sin 5 . x 1 A.
cos 5x C .
B. cos 5x C .
C. -cos 5x C .
D. − 1 cos 5x C. 5 5
Câu 57. Họ nguyên hàm của hàm số f x  2x 1 là
A. F x 2
 2x x . B. F x  2 .
C. F x  C . D. F x 2
x x  . C
Câu 58. Họ nguyên hàm của hàm số    ex f xx là 1 x 1 x 1 A. 2
ex x C . B. 2 e 
x C . C. 2 e 
x C . D. ex 1 C. 2 x 1 2
Câu 59.Tìm nguyên hàm   2 F x    dx.   x A.   2
F x   x C .
B. 2 x C .
C. F x 3 
C . D. F x 2 2   C. 3 2 x
Câu 60. Tìm tất cả nguyên hàm của hàm số f x 2  3x  . 2 x x x A. f  x 3 2 dx    C . B. f  x 2 3 dx x   C. 3 4 2 x x C. f  x 2 3 dx x   C .
D. f x 2 3 dx x   . 4 4
Câu 61. Tìm họ nguyên hàm của hàm số f x  sin  3ax  
1 (với a là tham số khác 0 ). 1
A. cos  3ax   1  C . B. cos  3ax   1  C. 3a 1 C. − cos  3ax   1  C .
D.  cos  3ax   1  C. 3a
Câu 62: Họ các nguyên hàm của hàm số f x  x sin x là:
A. x cos x  sin x C
B. x cos x  sin x C
C. x cos x sin x C
D. x cos x  sin x C
Câu 63: Họ nguyên hàm của hàm số f x  4x 1 ln x là: A. 2 2
2x ln x  3x B. 2 2
2x ln x x C. 2 2
2x ln x  3x C D. 2 2
2x ln x x C
Câu 64: Họ nguyên hàm của hàm số f x   2 3x   1 ln x là: x 3 x
A. x x   3 2 1 ln x   C B. 3 x ln x   C 3 3 x 3 x
C. x x   3 2 1 ln x
x C D. 3 x ln x   x C 3 3 x
Câu 65: Tất cả các nguyên hàm của hàm số f x  
trên khoảng 0;  là: 2 sin x
A. x cot x  ln sin x   C
B. x cot x  ln sin x C
C. x cot x  ln sin x C
D. x cot x  ln sin x   C Trang11
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 66:Họ nguyên hàm của hàm số   x
f x e  cos x là x 1 e x 1 e A. x
e  sin x C . B.
 sin x C . C. x
e  sin x C . D.
 sin x C . x 1 x 1
Câu 67:Tìm họ nguyên hàm F x của hàm số f x 3
x x 1 x x x x
A. F x 4 3  
C . B. F x 4 2    x C . 4 2 4 2 x
C. F x 3 4  x   x C .
D. F x 3  3x C . 2
Câu 68:Tìm tất cả nguyên hàm F x của hàm số   1 f x x  . x 1 1
A. F x 2
x  ln x C .
B. F x 2
x  ln x . 2 2 1
C. F x  1 ln x C
D. F x 2
x  ln x C . 2
Câu 69:Họ nguyên hàm của hàm số y  2x 1 là 2 x A. x C .
B. 2x 1 C . C. 2
x x C .
D. 2x C . 2 Câu 70:Tính sin 3 d x x 1 1
A. cos3x C .
B.  cos 3x C .
C. cos 3x C .
D. cos3x C . 3 3
Câu 71:Họ nguyên hàm của hàm số   3x f x  là 3x x 1 3  A. 3 . x ln 3  C . B. C . C. C   . ln 3 x  . D. 1 3x C 1
Câu 72:Họ nguyên hàm của hàm số f x  sin 2x là:
A. F x 1
  cos 2x C .
B. F x  cos 2x C . 2
C. F x 1
 cos 2x C .
D. F x   cos 2x C . 2
Câu 73:Họ nguyên hàm của hàm số 2
f (x)  3x 1 là 3 x A. 3 x C B. x C
C. 6x C D. 3
x x C 3 Đề thi tốt nghiệp 2021 Mã đề 101 Câu 1:
Cho hàm số f x 2
x  4 . Khẳng định nào dưới đây đúng? A. f
 xdx  2x C . B. f  x 2
dx x  4x C . Trang12
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 x C. f  x 3 dx   4x C . D. f  x 3
dx x  4x C . 3 Câu 2: Cho hàm số ( ) x
f x e  2 . Khẳng định nào dưới đây đúng?  A. 2 ( )d x f x x eC  . B. ( )d x
f x x e  2x C  . C. ( )d x
f x x e C  . D. ( )d x
f x x e  2x C  . Mã đề 102 Câu 1:
Cho hàm số f x 2
x  3. Khẳng định nào dưới đây đúng? x A. f  x 2
dx x  3x C . B. f  x 3 dx
 3x C . 3 C. f  x 3
dx x  3x C . D. f
 xdx  2xC . Câu 2: Cho hàm số ( ) x
f x e 1. Khẳng định nào dưới đây đúng? A. 1 ( ) x f x dx e    C  . B. ( ) x
f x dx e x C  . C. ( ) x
f x dx e x C  . D. ( ) x
f x dx e C  . Mã đề 103 Câu 1:
Cho hàm số f x 2
x 1. Khẳng định nào dưới đây đúng? x A. f
 xdx x   x C . B. f  x 3 dx   x C . 3 C. f  x 2
dx x x C . D. f
 xdx  2xC . Câu 2: Cho hàm số ( ) x
f x e  3 . Khẳng định nào dưới đây đúng? A. ( )d x
f x x e  3x C  . B. ( )d x
f x x e C  . C. 3 ( )d x f x x e    C  . D. ( )d x
f x x e  3x C  . Mã đề 104
Câu 13: Cho hàm số f x 2
x  2 . Khẳng định nào dưới đây đúng? x A. f
 xdx  2xC . B. f  x 3 dx   2x C . 3 C. f  x 2
dx x  2x C . D. f  x 3
dx x  2x C .
Câu 23: Cho hàm số ( ) x
f x e  4 . Khẳng định nào sau đây đúng? A. ( ) x
f x x e  4x C  d . B. ( ) x
f x x e C  d . C. 4 ( ) x f x x eC  d . D. ( ) x
f x x e  4x C  d . Đề minh họa 2021
Câu 14: Cho hàm số f x 2
 3x 1. Trong các khẳng định sau, khẳng định nào đúng? A. f  x 3
dx  3x x  . C B. f  x 3
dx x x  . C 1 C. f  x 3 dx
x x C. D. f  x 3
dx x C. 3
Câu 15: Cho hàm số f x  cos 2 .
x Trong các khẳng định sau, khẳng định nào đúng? A. f  x 1 dx
sin 2x C. B. f  x 1
dx   sin 2x C. 2 2 Trang13
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 C. f
 xdx  2sin2x . C D. f
 xdx  2
 sin 2x C.
Đề thi tốt nghiệp 2020 ( Đợt 1 ) Mã đề 101 Câu 14: 2 x dx  bằng 1
A. 2x C . B. 3 x C . C. 3 x C . D. 3 3x C 3 Mã đề 102
Câu 14: Họ nguyên hàm của hàm số   3 f x x là 1 A. 4 4x C . B. 2 3x C . C. 4 x C . D. 4 x C . 4 Mã đề 103 Câu 1. 4 x dx bằng  1 A. 5 x C B. 3
4x C C. 5 x C D. 5 5x C 5 Mã đề 104 Câu 21: 5 x dx  bằng 1 A. 4 5x C . B. 6 x C . C. 6 x C . D. 6 6x C . 6
Đề thi tốt nghiệp 2020 ( Đợt 2 ) Câu 24. 2 3x dx  bằng 1 A. 3
3x C .
B. 6x C . C. 3
x C . D. 3
x C . 3
Đề thi tham khảo lần 2 năm 2020
Câu 6. Hàm số F x là một nguyên hàm của hàm số f x trên khoảng K nếu
A. F x   f x,x K
B. f  x  F x,x K
C. F x  f x,x K D. f  x  F x,x K
Đề thi tham khảo lần 1 năm 2020
Câu 11: Họ tất cả các nguyên hàm của hàm số f x  cos x  6x là A. 2
sin x  3x C . B. 2
sin x  3x C . C. 2
sin x  6x C .
D. sin x C .
Đề thi THPT Quốc gia 2019 Mã đề 101
Câu 15. Họ tất cả các nguyên hàm của hàm số f x  2x  5 là A. 2
x  5x C.. B. 2 2x  5x  . C . C. 2 2x  . C . D. 2 x  . C . 2x 1
Câu 31. Họ tất cả các nguyên hàm của hàm số f x     trên khoảng  1;  là x  2 1 A. x   2 2 ln 1   C . B. x   3 2 ln 1   C . x 1 x 1 C. x   2 2 ln 1   C x    C x . D.   3 2 ln 1 1 x . 1 Trang14
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 Mã đề 102
Câu 1. Họ tất cả các nguyên hàm của hàm số f x  2x  6 là A. 2
x  6x C . B. 2
2x C . C. 2
2x  6x C . D. 2
x C . 3x 1
Câu 34. Họ tất cả các nguyên hàm của hàm số f (x) 
trên khoảng (1; ) là 2 (x 1) 2 1
A. 3ln(x  1)   C .
B. 3ln(x  1)   C . x  1 x  1 1 2
C. 3ln(x  1)   C .
D. 3ln(x  1)   C . x  1 x  1 Mã đề 103
Câu 12. Họ tất cả các nguyên hàm của hàm số f x  2x  3 là A. 2
2x C . B. 2
x  3x C . C. 2
2x  3x C . D. 2
x C . 2x 1
Câu 34. Họ tất cả các nguyên hàm của hàm số f x   trên khoảng  2;   là: x  22 A. x   1 2 ln 2   C x    C x . B.   1 2 ln 2 2 x . 2 C. x   3 2 ln 2   C x    C x . D.   3 2 ln 2 2 x . 2 Mã đề 104
Câu 8. Họ tất cả các nguyên hàm của hàm số f x  2x  4 là A. 2
2x  4x C . B. 2
x  4x C . C. 2
x C . D. 2
2x C . 3x - 2
Câu 35. Họ tất cả các nguyên hàm của hàm số f (x)= trên khoảng (2;+ ¥ ) là (x - )2 2 4 2 A. 3ln (x - 2)+ + C . B. 3ln (x - 2)+ + C . x - 2 x - 2 2 4 C. 3ln (x - 2)- + C . D. 3ln (x - 2)- + C . x - 2 x - 2
Đề thi tham khảo kì thi THPT Quốc gia 2019
Câu 10: Họ nguyên hàm của hàm số ( ) x
f x e x là 1 x 1 x 1 A. x 2
e x C. B. 2 e
x C. C. 2 e
x C. D. x
e 1  C. 2 x 1 2
Câu 33. Họ nguyên hàm của hàm số f x  4x 1 ln x là A. 2 2
2x ln x  3x B. 2 2
2x ln x x C. 2 2
2x ln x  3x C D. 2 2
2x ln x x C
Đề thi THPT Quốc gia 2018 Mã đề 101
Câu 7: Nguyên hàm của hàm số 3
f (x)  x x là 1 1 A. 4 2
x x C B. 2 3x  1 C C. 3
x x C D. 4 2 x x C 4 2 Mã đề 102
Câu 4. Nguyên hàm của hàm số   4
f x x x là Trang15
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1 1 A. 4
x x C B. 3 4x 1  C C. 5 2
x x C D. 5 2 x x C 5 2 Mã đề 103
Câu 14. Nguyên hàm của hàm số   4 2
f x x x là 1 1 A. 3
4x  2x C B. 5 3 x x C C. 4 2
x x C D. 5 3
x x C 5 3
Đề thi tham khảo kì thi THPT Quốc gia 2018
Câu 9: Họ nguyên hàm của hàm số   2 f x  3x 1 là 3 x A. 3 x  C B.  C C. 6x  C D. 3 x  x  C 3
Đề thi THPT Quốc gia 2017 Mã đề 101
Câu 2: Tìm nguyên hàm của hàm số f (x)  cos 3x sin 3x
A. cos 3xdx  3sin 3x CB. cos 3xdx   C  3 sin 3x C. cos 3xdx   C
D. cos 3xdx  sin 3x C  3
Câu 27:Cho hàm số f (x) thỏa mãn f '(x)  3  5sin x và f (0)  10 . Mệnh đề nào dưới đây đúng ?
A. f (x)  3x  5cos x  5
B. f (x)  3x  5 cos x  2
C. f (x)  3x  5cos x  2
D. f (x)  3x  5 cos x 15 Câu 32:Cho 2
F (x)  x là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số ' 2 ( ) x f x e A. ' 2 x 2
f (x)e dx  x  2x CB. ' 2 2 ( ) x
f x e dx  x x CC. ' 2 x 2
f (x)e dx  2x  2x CD. ' 2x 2
f (x)e dx  2
x  2x CMã đề 102
Câu 2. Tìm nguyên hàm của hàm số f x 1  5x  2 dx 1 dx 1 A.
 ln 5x  2  C  . B.
  ln(5x  2)  C  . 5x  2 5 5x  2 2 dx dx C.
 5ln 5x  2  C  . D.
 ln 5x  2  C. 5x  2 5x  2 Câu 40. Cho ( )  ( 1) x F x x
e là một nguyên hàm của hàm số 2 ( ) x
f x e . Tìm nguyên hàm của hàm số 2 (  ) x f x e .  x x 2 A. 2 (
 ) xd  (4  2 ) x f x e x x e C B. 2 f (  x)e d x x e C 2 C. 2 (
 ) xd  (2  ) x f x e x x e C D. 2 (
 ) xd  (  2) x f x e x x e C
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3 2
Câu 10. Tìm nguyên hàm của hàm số 2
f (x)  x  . 2 x Trang16
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 3 x 2 3 x 1 A.
f (x)dx    C. B.
f (x)dx    C. 3 x 3 x 3 x 2 3 x 1 C.
f (x)dx    C. D.
f (x)dx    C. 3 x 3 x
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2
Câu 22. Tìm nguyên hàm của hàm số f (x)  cos 2x . 1 1 A.
f (x)dx  sin 2x C. B.
f (x)dx   sin 2x C. 2 2 C.
f (x)dx  2sin 2x C. D.
f (x)dx  2  sin 2x C.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 23. Tìm nguyên hàm của hàm số f (x)  2x 1. 2 1 A.
f (x)dx
(2x 1) 2x 1  C. B.
f (x)dx
(2x 1) 2x 1  C. 3 3 1 1 C.
f (x)dx   2x 1  C. D.
f (x)dx  2x 1  C. 3 2 TÍCH PHÂN
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT CỦA TÍCH PHÂN
1. Công thức tính tích phân b f (x d ) x b
F (x )  F b ( )   F a ( ) . a a b b
* Nhận xét:Tích phân của hàm số f từ a đến b có thể kí hiệu bởi  f (x d
) x hay  f t( d
) t. Tích phân đó chỉ a a
phụ thuộc vào f và các cận a, b mà không phụ thuộc vào cách ghi biến số.
2. Tính chất của tích phân
Giả sử cho hai hàm số f (x) và g (x) liên tục trên K , a, b, c là ba số bất kỳ thuộc K . Khi đó ta có : a b a b c b 1. f (x d ) x   0 2. f (x d ) x   
f x( d)x . 3. f(x dx )  f x ( dx )     f x( dx ) a a b a a c b b b b b
4. f (x )  g x ( )dx f x ( d ) x     
g x( d)x . 5. kf x ( dx )   k. f x ( dx ) . a a a a a b 6. Nếu f(x)  0, x   a  ;b 
 thì : f (x dx )  
0 x  a;b    a b b 7. Nếu x   a
 ;b : f (x)  g(x)  f (x dx )  g x ( dx )     . a a b
8. Nếu x  a;b 
 Nếu M f (x)  N thì M b a   f x ( dx )  N b   a  . a Trang17
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
PHƢƠNG PHÁP TÍNH TÍCH PHÂN
1. Phƣơng pháp đổi biến
1.1. Phƣơng pháp đổi biến số dạng 1 1.1.1. Định lí
Nếu 1) Hàm x u t
( ) có đạo hàm liên tục trên   ;    
2) Hàm hợp f (u t
( )) được xác định trên   ;     , 3) u
( )  a, u( )  b b
Khi đó: I f x dx    f u t u' ( ) ( ( )) t ( dt ) . a
4.1.1.2. Phƣơng pháp chung
Bước 1: Đặt x u t
Bước 2: Tính vi phân hai vế : x u t()  dx u ' t( d ) t x b t   Đổi cận:  x a t  
Bước 3: Chuyển tích phân đã cho sang tích phân theo biến t b    Vậy: I f x ( dx )
f u t()u ' t( dt )      g t( dt )  G t()
G() G   ( ) a  
4.1.2. Phƣơng pháp đổi biến dạng 2 4.1.2.1. Định lí
Nếu hàm số u u(x ) đơn điệu và có đạo hàm liên tục trên đoạn a;b   sao cho b u (b) f x ( d
) x g u x ( )u x '( d ) x g u ( d ) u thì: I f (x d ) x  
g u( d)u . a u (a )
4.1.2.2. Phƣơng pháp chung
Bước 1: Đặt u u x du u' ( ) (x d ) x x b u u b ( )
Bước 2: Đổi cận :  x a u u a ( )
Bước 3: Chuyển tích phân đã cho sang tích phân theo u b b u b ( ) Vậy: I f (x d
) x g u(x ) u . '(x d ) x     
g u( d)u a a u (a )
4.2. Phƣơng pháp tích phân từng phần 4.2.1. Định lí
Nếu u(x) và v(x) là các hàm số có đạo hàm liên tục trên a;b   thì: b b b b b b
u x v' x dx  u x v x    v x u' ( ) ( ) ( ) ( ) ( ) x ( d
) x Hay udv uv vdu a a a a a a
4.2.2. Phƣơng pháp chung
Bước 1: Viết f (x)dx dưới dạng udv uv d'x bằng cách chọn một phần thích hợp của f (x)
làm u(x) và phần còn lại dv v '(x d ) x Trang18
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Bước 2: Tính du u 'dx và v  dv  v x '( dx ) b b
Bước 3: Tính vu '(x d)x và uv a a BÀI TẬP 1 1 Câu 1. Nếu f
 xdx  4 thì 2 f
 xdx  4 bằng 0 0 A. 16. B. 4. C. 2. D. 8. 2 5 5 Câu 2. Nếu f
 xdx  3, f xdx  1  thì f
 xdx bằng 1 2 1 A. 3. B. 4. C. 2. D. 2.  5 7 7 Câu 3. Nếu f
 xdx  3 và f xdx  9 thì f xdx bằng bao nhiêu? 2 5 2 A. 3. B. 6. C. 12. D. 6.  5 dx Câu 4. Nếu  ln c với thì giá trị của bằng  c  Q c 2x 1 1 A. 9. B. 3. C. 6. D. 81. 5 dx Câu 5. Nếu  ln c với thì giá trị của bằng  c  Q c 2x 1 1 A. 9. B. 3. C. 6. D. 81. 5 dx Câu 6. Nếu  ln c với thì giá trị của bằng  c  Q c 2x 1 1 A. 9. B. 3. C. 6. D. 81. 2 5 5 Câu 7. Nếu f
 xdx  3, f xdx  1  thì f
 xdx bằng 1 2 1 A. 2  . B. 2. C. 3. D. 4. 3 3
Câu 8. Cho hàm số f x liên tục trên đoạn 0;  3 . Nếu f
 xdx  2 thì tích phân [x 3f
x]dx có giá 0 0 trị bằng 3 A. 3  3 . B. 3. C. . D. − . 2 2 3 3
Câu 9. Cho hàm số f x liên tục trên đoạn 0;  3 . Nếu f
 xdx  2 thì tích phân [x3f (x)]dx có giá  0 0 trị bằng 3 A. 3  3 . B. 3. C. . D. − . 2 2
Câu 10. Cho các số thực a, b(a b) . Nếu hàm số y f x có đạo hàm là hàm liên tục trên R thì b b A. f
 xdx f a f b . B. f
 xdx f b f a . a a b b C. f
 xdx f a f b . D. f
 xdx f b f a . a a Trang19
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1 1 1 Câu 11 : Biết
f xdx  2   và g
 xdx  3, khi đó  f
 x gxdx  bằng : 0 0 0 A. 5.  B. 5. C. 1.  D. 1. 1 1 1 Câu 12: Biết f
 xdx  3 và g
 xdx  4  khi đó  f
 x gxdx bằng  0 0 0 A. 7
 . B. 7 . C. 1. D. 1. 2 2 2 Câu 13: Biết f
 xdx  2 và g
 xdx  6, khi đó  f
 x gxdx  bằng 1 1 1 A. 4 .B. 8  .C. 8 . D. 4  . 1 1 1 Câu 14: Biết
f (x)dx  2; g(x)dx  4   
. Khi đó  f (x)  g(x)dx bằng 0 0 0 A. 6. B. -6. C. 2  . D. 2 . 2 4 4 Câu 15: Cho f
 xdx 1và f tdt  3   . Giá trị của
f udu  là: 1 1 2 A. -2 B.- 4 C. 4 D. 2 2 2 2 Câu 16: Cho
f (x)dx  2  và
g(x)dx  1  
. Tính I   x  2 f (x)  3g(x)dx 1  1  1  5 7 17 11 A. I B. I C. I D. I 2 2 2 2 d d c c Câu 17 :Cho f
 xdx 10, f
 xdx 8, f
 xdx  7 . I f
 xdx , ta được: a b a b A. I  5  B. I  7 C. I  5 D. I  7  5 5 5 Câu 18: Biết f
 xdx  3, g
 tdt  9. Giá trị của A   f
 x gxdx  là: 2 2 2
A. 12B. 3 C. 6 D. 27 1 4 4
Câu 19: Biết f(x)dx  2, f (x)dx  3, g(x)dx  4   
.Khẳng định nào sau đây SAI? 0 1 0 4 4 4 4 4 4
A.  f (x)  g(x)dx 1.B. f(x)dx  g(x)dx  
.C. f(x)dx  g(x)dx   .D. f(x)dx  5  . 0 0 0 0 0 0 b b c Câu 20: Biết
f (x)dx  2  và
f (x)dx  3 
và a < b < c thì f (x)dx  bằng bao nhiêu? a c a A. -1 B. 1 C. 5 D. -5 2 2 2 Câu 21. Xét x
xe dx , nếu đặt  2 thì x xe dx bằng  2 u x  0 0 2 4 2 1 4 1
A. 2 eudu. B. 2 eudu. C. eudu. D. eudu.     2 2 0 0 0 0  2
Câu 22. Cho tích phânI
2  cos x . sinxdx. Nếu đặt t  
x thì kết quả nào sau đây đúng?  2 cos 0  2 3 2 2 A. I t dt. B. I t dt. C. I  2
t dt. D. I t dt.     3 2 3 0 Trang20
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1 7 x
Câu 23. Cho tích phânI
dx, giả sử đặt t  1  x . Tìm mệnh đề đúng.  2   x 5 2 0 1 1 t  3 2 1 t  3 3 1 1 t  3 2 1 3 t  3 4 1 A. I
dt . B. I  dt. C. dt. D. dt.     5 2 t 5 t 4 2 t 4 2 t 1 1 1 1 3 x
Câu 24. Cho tích phânI
dx. Nếu đặt t x  thì  1 1 x 1 0 2 2 2 2
A. I   2t  2tdt . B. I   2
2t t  dt. C. I   2
2t  2t  dt. D. I   2
2t  2t  dt. 1 1 1 1 e 1 ln x
Câu 25. Cho tích phânI
dx. Đổi biến t  
x ta được kết quả nào sau đây?  1 ln x 1 2 2 2 2 A. 2
I t dt. B. 2
I  2 t dt . C. 2
I  2 t dt . D. I  2 t dt.     1 1 1 1 1 dx    
Câu 26. Cho tích phânI
. Nếu đổi biến số x t t   ; thì  2 sin ,   2   2 2  0 4 x     6 6 6 dt 3
A. I  dt. B. I t dt. C. I
. D. I  dt.     t 0 0 0 0 1
Câu 27. Cho tích phânI 3 
1 x dx. Với cách đặt t   x ta được.  3 1 0 1 1 1 1 A. 3
I  3 t dt . B. 2
I  3 t dt. C. 3
I t dt . D. I  3 tdt.     0 0 0 0 1
Câu 28. Cho tích phânI 3 
1 x dx. Với cách đặt t   x ta được.  3 1 0 1 1 1 1 A. 3
I  3 t dt . B. 2
I  3 t dt. C. 3
I t dt . D. I  3 tdt.     0 0 0 0 4
Câu 29. Cho tích phân 2
I x x  9 dx. Khi đặt t x
thì tích phân đã cho trở thành  2 9 0 5 4 4 5
A. I t dt. B. I t dt. C. 2
I t dt. D. 2
I t dt.     3 0 0 3 3 x
Câu 30. Cho tích phân I
dx. Viết dạng của khi đặt t x   I 1. 1 x 1 0 2 2 2 2 A.  2
2t  2t  dt. B.  2
2t  2t  dt. C.  2t  2t dt. D.  2
2t t  dt. 1 1 1 1 ex
Câu 31. Cho I  dx . Khi đặt x t   thì ta có  e 1 ex 1 t A. 2
I  2t dt . B. I  . C. I
t . D. I t t  d  2d  2d .  2 Trang21
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1  2
Câu 32. Cho I x x   
1 dx khi đặt t  x ta có 0 1 1 1 1 2 2 2 2
A. I   t t  
1 dt. B. I   tt  
1 dt. C. I tt  
1 dt. D. I tt   1 dt. 0 0 0 0 e ln x
Câu 33. Với cách đổi biến u  1 3 ln x thì tích phân dx trở thành  x 13 ln x 1 2 2 2 2 2 2 2 2 u 1 A.  2u  
1 du. B.  2u  
1 du. C. 2  2u   1 du. D. du.  3 9 9 u 1 1 1 1 1
Câu 34. Với cách đổi biến u
4x  5 thì tích phân x 4x  5dx trở thành 1 2 u  2 3 u  5 2 u  2 1 u  5 2 u  2 3 u  5 u  2 3 u  5 A. du. B. du. C. du. D. du.     8 8 4 8 1 1  1 1 1 dx
Câu 35. Đổi biến x  2 sin t thì tích phân trở thành  2  0 4 x     6 3 6 6 dt
A. tdt.
B. tdt. C. dt. D. .     t 0 0 0 0
Câu 36: Giả sử f x là một hàm số liên tục trên khoảng ;   và a, , b ,
c b c ;   . Mệnh đề nào sau đây sai? b c b b bc c A. f
 xdx f
 xdx f
 xd .x B. f
 xdx f
 xdxf
 xd .x a a c a a a b bc b b c c C. f
 xdx f
 xdx f
 xdx. D. f
 xdx f
 xdx f
 xd .x a a bc a a b Câu 37: Cho hàm số 3
y x có một nguyên hàm là F x . Khẳng định nào sau đây đúng?
A. F 2  F 0 16. B. F 2  F 0  1.
C. F 2  F 0  8.
D. F 2  F 0  4. e
Câu 38: Tích phân cos xdx  bằng 0 A. sin . e B.  cos . e C. sin . e D. cos . e 2
Câu 39: Tích phân I  2x   1dx bằng 0
A. I  5.
B. I  6.
C. I  2. D. I  4. 0 3 3 Câu 40: Cho f
 xdx 1; f
 xdx  3. Tích phân f
 xdx bằng 1  0 1  A. 6. B. 4. C. 2. D. 0. 2 4 4 Câu 41:Cho f
 xdx 1,    4.   f t dt Giá trị của I f
 ydy là 2  2  2
A. I  5.
B. I  3. C. I  3.  D. I  5.  Trang22
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 c c a Câu 42: Cho f
 xdx  50 và f
 xdx  20. Giá trị f xdx  bằng a b b A. 30.  B. 0. C. 70. D. 30. 1 1 1
Câu 43: Cho  f
 x2gxdx 12  và g
 xdx  5, khi đó f xdx  bằng 0 0 0 A. 2.  B. 12. C. 22. D. 2. 5 5 5 Câu 44: Cho f
 xdx  4 và g
 xdx  3, khi đó 2 f
 x3gxdx  bằng 2 2 2 A. 1. B. 12. C. 7. D. 1.  2 4 4 4 Câu 45: Cho
f xdx  3;   f
 xdx  6 và g
 xdx 8. Khi đó 3f
 x gxdx  bằng 0 2 0 0 A. 14. B. 3. C. 17. D. 1.  2 2 2
Câu 46: Cho  f
 x2gxdx 5  và 2 f
 x3gxdx  4   . Khi đó  f
 x gxdx  bằng 1 1 1 A. 14. B. 3. C. 17. D. 1.  6 10 6
Câu 47: Cho hàm số f x liên tục trên  thỏa mãn f
 xdx  7, f
 xdx 8 và f
 xdx  9. Giá 0 3 3 10
trị của tích phân I f
 xdx bằng 0
A. I  5.
B. I  6.
C. I  7. D. I  8. 3
Câu 48: Cho hàm số f x có đạo hàm trên đoạn 1; 
3 , f 3  4 và f
 xdx  7. Khi đó f  1 bằng 1 A. 3. B. 11. C. 3.  D. 11.  e  1 1 
Câu 49: Giá trị của I   dx   là 2  x x  1 1 1 A. I  . B. I  1.
C. I  1. D. I  . e e e 1
Câu 50: Cho f x, g x là các hàm số có đạo hàm liên tục trên 0  ;1 và g
 x.f xdx 1, 0 1 1  g
 x.f xdx  2. Khi đó I   f
 x.gx dx  có giá trị là 0 0
A. I  3.
B. I  1.
C. I  2. D. I  1. 
Câu 51: Cho hàm số y f x có đạo hàm là hàm liên tục trên  thỏa mãn f 0  2, f   1  6 . Khẳng
định nào sau đây là đúng? 1 1 1 1 A. f
 xdx 8. B. f
 xdx  4. C. f
 xdx  3. D. f
 xdx 12. 0 0 0 0 2 2
Câu 52:Cho 4 f
 x2xdx 1 
. Khi đó f xdx  bằng 1 1 Trang23
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 A. 1. B. 3.  C. 3. D. 1.  4 4 3
Câu 53: Cho hàm số f x liên tục trên  và f
 xdx 10, f
 xdx  4. Tích phân f xdx  bằng 0 3 0 A. 4. B. 7. C. 3. D. 6. b
Câu 54: Với a, b là các tham số thực. Giá trị tích phân  2 3x  2ax   1dx bằng 0 A. 3 2 b b a  . b B. 3 2 b b a  . b C. 3 2 b ba  . b D. 2
3b  2ab 1. 1
Câu 55: Tích phân 3x  
1  x  3 dx bằng 0 A. 12. B. 9. C. 5. D. 6. 3 x  2 Câu 56:Biết
dx a b ln c
, với a, b, c   , c  9. Tổng S a b c là x 1
A. S  7.
B. S  5.
C. S  8. D. S  6. 1 1
Câu 57: Tích phân I dx  có giá trị bằng x 1 0 A. ln 2 1. B. ln 2. C. ln 2. D.1 ln 2.   2 2
Câu 58: Cho hai tích phân 2 A  sin xdx  và 2 B  cos xd . x
Trong các khẳng định sau, khẳng định đúng 0 0 là A. A  2 . B B. A  . B C. A   . B
D. A B 1. 1 2 3
Câu 59: Cho hàm số f x liên tục trên  có 2 f
 xdx  2và f
 x 1dx  4.Giá trị của I f  xdx 0 0 0 là
A. I  5.
B. I  4.
C. I  6. D. I  7. 8 1 Câu 60:Cho f
 x 1dx 10. Giá rị của J f
 5x4dx là 3 0
A. J  4.
B. J 10.
C. J  32. D. J  2. 9 0 Câu 61: Cho f
 xdx  27. Giá trị của f   3  xdx là 0 3 
A. I  27. B. I  3. 
C. I  9. D. I  3.  2
Câu 62: Giá trị của 2 I  sin . x cos xdx  là 0 1 3 
A. I  0.
B. I  1. C. I  . D. I  . 3 24 1
Câu 63: Cho hàm số f x có đạo hàm liên tục trên đoạn 0 
;1 thỏa mãn f   1  5, f
 xdx 12. 0 Trang24
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1
Giá trị của J xf
 xdx là 0 A. J  17. 
B. J 17.
C. J  7. D. J  7.  2
Câu 64: Tích phân  3 x I xe dx
nhận giá trị nào sau đây? 1  3 3e  6 3 3e  6 3 3e  6 3 3e  6 A. I  . B. I  . C. I  . D. I  . 1 e 1 eee 1
Câu 65: Giá trị của tích phân  2   1 x I x e dx là 0
A. 5e 3.
B. e 1.
C. e 1. D. 5e 1. e
Câu 66: Giá trị của I x ln xdx  là 1 1 1 1 A. I  . B. I   2e 2.
C. I  2. D. I   2e  1. 2 2 4 2
Câu 67: Giá trị của tích phân 2
I x ln xdx  là 1 8 7 8 7 7 A. ln 2  . B. ln 2  .
C. 24ln 2  7. D. 8 ln 2  . 3 9 3 3 3 5
Câu 68: Giá trị của tích phân I  x  
1 ln  x  3 dx là 4 19 19 19 A.10 ln 2  . B.10 ln 2  . C.10ln 2. D. 10ln 2. 4 4 4 e
Câu 69: Giá trị của tích phân x   1ln xdx là 1 2 e  5 2 e  5 2 e  5 2 e  5 A. . B. . C. . D. . 4 2 2 4
Câu70: Kết quả của x
I xe dx  là 2 x 2 x A. x x
I xe e C . B. x x
I e xe C . C. x I e C . D. x x I
e e C . 2 2 1 dx
Câu71:Tính tích phân I   3  2x 0 1 1 1 A.  ln 3 . B. ln 3. C. ln 3 . D. log 3 . 2 2 2
Câu72:Cho hàm số f x có đạo hàm liên tục trên đoạn a ;b và f a  2
 , f b  4  . Tính b T f
 xdx . a A. T  6  . B. T  2 . C. T  6 . D. T  2  . 2 2 Câu73:Cho f
 xdx 3. Tính  f x  1dx ? 0 0 A. 4 . B. 5 . C. 7 . D. 1. Trang25
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 2 dx Câu74:Tích phân  bằng x  3 0 16 5 5 2 A. B. log C. ln D. 225 3 3 15
Đề thi tốt nghiệp THPT 2021 Mã đề 101 4 4 4 Câu 3: Nếu f
 xdx 3 và gxdx  2   thì  f
 x gx dx  bằng 1 1 1 A. 1. B. 5  . C. 5 . D. 1. 3 3 Câu 4: Nếu f
 xdx  4 thì 3f xdx  bằng 0 0 A. 36 . B. 12 . C. 3 . D. 4 . 2 2 Câu 5: Nếu f
 xdx  5 thì 2 f
 x1dx  bằng 0 0 A. 8. B. 9. C. 10. D. 12. Mã đề 102 4 4 4 Câu 3: Nếu f
 xdx  6 và gxdx  5   thì  f
 x gxdx  bằng: 1 1 1 A. 1. B. 11  . C. 1. D. 11. 3 3 Câu 4: Nếu
f (x)dx  3 
thì 2 f (x)dx  bằng 0 0 A. 3 . B. 18 . C. 2 . D. 6 . 2 2 Câu 5: Nếu
f (x)dx  3  thì 2 f
  x1 dx  bằng 0 0 A. 6 . B. 4 . C. 8 . D. 5 . Mã đề 103 4 4 4 Câu 3: Nếu
f (x)dx  5 
và g(x)dx  4  
thì  f (x)  g(x)dx bằng 1 1 1 A. 1. B. 9  . C. 1. D. 9 . 3 3 Câu 4: Nếu f
 xdx  2 thì 3f xdx  bằng 0 0 A. 6 . B. 1. C. 1. D. 0 . 2 2 Câu 5: Nếu f
 xdx  6 thì 2 f
 x1dx  bằng 0 0 A. 12 . B. 10 . C. 11. D. 14 Mã đề 104 4 4 4 Câu 3: Nếu f
 xdx  4 và gxdx  3   thì  f
 x gxdx  bằng 1 1 1 A. 1. B. 7  . C. 1. D. 7 . 3 3 Câu 10: Nếu f
 xdx  3 thì 4 f xdx  bằng 0 0 A. 3 . B. 12 . C. 36 . D. 4 . Trang26
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 2 2 Câu 32: Nếu f
 xdx  4 thì 2 f
 x1)dx  bằng 0 0 A. 8 . B. 10 . C. 7 . D. 6 .
Đề minh họa kì thi tốt nghiệp THPT năm 2021 2 3 3 Câu 16: Nếu f
 xdx 5 và f xdx  2   thì
f xdx  bằng 1 2 1 A. 3. B. 7. C. 10.  D. 7.  2 Câu 17: Tích phân 3 x dx  bằng 1 15 17 7 15 A. . B. . C. . D. . 3 4 4 4 3 3
Câu 33: Nếu 2 f
 x1 dx 5  thì
f xdx  bằng 1 1 3 3 A. 3. B. 2. C. . D. . 4 2
Đề thi tốt nghiệp THPT2020 ( Đợt 1 ) Mã đề 101 3 3 Câu 23: Biết f
 xdx 3. Giá trị của 2f xdx  bằng 1 1 3 A. 5 . B. 9 . C. 6 . D. . 2 2 Câu 28: Biết   2
F x x là một nguyên hàm của hàm số f x trên  . Giá trị của 2  f  xdx  bằng 1 13 7 A. 5 . B. 3 . C. . D. . 3 3 Mã đề 102 5 5 Câu 1: Biết f
 xdx  4. Giá trị của 3f xdx  bằng 1 1 4 A. 7 . B. . C. 64 . D. 12 . 3 2 Câu 34: Biết   3
F x x là một nguyên hàm của hàm số f x trên  . Giá trị của 2 f (x)dx bằng 1 23 15 A. . B. 7 . C. 9 . D. . 4 4 Mã đề 103 2 3 Câu 2. Biết f
 xdx  2. Giá trị của 3f
 xdx bằng 1 1 2 A. 5 . B. 6 . C. . D. 8 . 3 3 Câu 3. Biết 3
F (x)  x là một nguyên hàm của hàm số f (x) trên  . Giá trị của (1 f (x))dx bằng 1 Trang27
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 A. 20. B. 22. C. 26. D. 28. Mã đề 104 3 3 Câu 5: Biết f
 xdx  6. Giá trị của 2 f xdx  bằng 2 2 A. 36 . B. 3 . C. 12 . D. 8 . 3 Câu 38: Biết   2
F x x là một nguyên hàm của hàm số f (x) trên  . Giá trị của 1 f (x)dx bằng 1 26 32 A. 10 . B. 8 . C. . D. . 3 3
Đề thi tốt nghiệp THPT 2020 ( Đợt 2 ) 2 2 2 Câu 8. Biết f
 xdx 3 và g
 xdx  2. Khi đó  f
 x gxdx  bằng? 1 1 1 A. 6 . B. 1. C. 5 . D. 1. 1 1 Câu 30. Biết  f
  x 2xdx  4  . Khi đó
f x dx  bằng 0 0 A. 3 . B. 2 . C. 6 . D. 4 .
Đề thi tham khảo lần 2 năm 2020 1 1
Câu 18. Nếu  f xdx  4 thì 2
f xdx bằng 0 0 A. 16 B. 4 C. 2 D. 8 2 2 2 2
Câu 33. Xét  x xe dx , nếu đặt 2
u x thì  x xe dx bằng 0 0 2 4 2 1 4 1 A. 2 u e du B. 2 u e du C.uedu D.uedu 2 2 0 0 0 0
Đề thi tham khảo lần 1 năm 2020 2 3 3 Câu 7: Nếu
f xdx  2   và f
 xdx 1 thì f xdx  bằng 1 2 1 A. 3  . B. 1. C. 1. D. 3.
Đề thi THPT Quốc gia 2019 Mã đề 101 1 1 1 Câu 11. Biết
f xdx  2   và g
 xdx  3, khi đó  f
 x gxdx  bằng 0 0 0 A. 5.  . B. 5. . C. 1.  . D. 1. .  4
Câu 32. Cho hàm số f x . Biết f 0  4 và f  x 2
 2cos x 1, x   , khi đó f
 xdx bằng 0 2   4 2  14 2  16  4 2  16 16 A. . B. . C. . D. . 16 16 16 16 Mã đề 102 1 1 1 Câu 8. Biết f
 xdx  3 và g
 xdx  4  khi đó  f
 x gxdx bằng  0 0 0 A. 7  . B. 7 . C. 1. D. 1 . Trang28
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022  4
Câu 33. Cho hàm số f x. Biết f 0  4 và 2
f '(x)  2 cos x  3, x
   , khi đó f (x)dx bằng 0 2   2 2   8  8 2   8  2 2   6  8 A. . B. . C. . D. . 8 8 8 8 Mã đề 103 2 2 2 Câu 4. Biết f
 xdx  2 và g
 xdx  6 , khi đó  f
 x gxdx  bằng 1 1 1 A. 4 . B. 8  . C. 8 . D. 4  .  4
Câu 35. Cho hàm số f x . Biết f 0  4 và f  x 2
 2sin x 1, x   , khi đó f
 xdx bằng 0 2  15 2  16 16 2  16  4 2   4 A. . B. . C. . D. . 16 16 16 16 Mã đề 104 1 1 1 Câu 15. Biết
f (x)dx  2; g(x)dx  4   
. Khi đó  f (x)  g(x)dx bằng 0 0 0 A. 6. B. -6. C. 2  . D. 2 .  4
Câu 32. Cho hàm số f (x) . Biết f (0)  4 và 2
f '(x)  2sin x  3, x
  , khi đó f (x)dx  bằng 0 2   2 2   8 8 2   8  2 2 3  2  3 A. . B. . C. . D. . 8 8 8 8
Đề thi tham khảo kì thi THPT Quốc gia 2019 1 1 1 Câu 6. Cho
f (x)dx  2 
và g(x)dx  5 
, khi đó  f (x) 2g(x)dx bằng 0 0 0 A. 3.  B. 12. C. 8.  D. 1. 1 xdx Câu 38. Cho        a b c
với a, b, c là các số hữu tỷ. Giá trị của 3a b c bằng x  2 ln 2 ln 3 2 0 A. -2 B. -1 C. 2 D. 1
Đề thi THPT Quốc gia 2018 Mã đề 101 2  Câu 22: 3 x 1 e dx  bằng: 1 1 1 1 A. 5 2 (e e ) B. 5 2 e e C. 5 2 e e D. 5 2 (e e ) 3 3 3 55 dx Câu 26: Cho
a ln 2  bln 5  c ln11, 
với a, b, c là các số hữu tỉ. Mệnh đề nào dưới đây đúng? x x  9 16
A. a b c
B. a b c
C. a b  3c
D. a b  3  c Mã đề 102 Trang29
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 1 Câu 20. 3x 1 e dx  bằng 0 1 1 A.  4 e eB. 4 e e C.  4 e eD. 3 e e 3 3 21 dx Câu 27. Cho
a ln 3 bln 5  c ln 7 
, với a, b, c là các số hữu tỉ. Mệnh đề nào sau đây đúng? x x  4 5
A. a b  2  c
B. a b c
C. a b c
D. a b  2  c Mã đề 103 2 dx Câu 19.  bằng 3x  2 1 1 2 A. 2 ln 2 B. ln 2 C. ln 2 D. ln 2 3 3 e
Câu 26. Cho 1 xln x 2
dx ae be c với a, b, c là các số hữu tỷ. Mệnh đề nào dưới đây đúng? 1
A. a b c
B. a b c
C. a b c
D. a b c
Đề thi tham khảo kì thi THPT Quốc gia 2018 2 dx
Câu 19: Tích phân  bằng x  3 0 16 5 5 2 A. B. log C. ln D. 225 3 3 15 2 dx Câu 32: Biết  a  b  c 
với a, b, c là các số nguyên dương. Tính P  a  b  c. x 1 x  x x 1 1   A. P  24 B. P  12 C. P 18 D. P  46
Đề thi THPT Quốc gia 2017 Mã đề 101 6 2 Câu 25:Cho
f (x)dx  12  . tính I f (3x)dx 0 0 A. I  6 B. I  36 C. I  2 D. I  4 Mã đề 102 x
Câu 12. Cho F (x) là nguyên hàm của hàm số ln f (x) 
. Tính F (e)  F (1) x 1 1
A. I e . B. I  . C. I  . D. I  1 . e 2 2 2 2 Câu 21. Cho
f (x)dx  2  và
g(x)dx  1  
. Tính I   x  2 f (x)  3g(x)dx 1  1  1  5 7 17 11 A. I B. I C. I D. I 2 2 2 2
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3 2
Câu 24. Tính tích phân 2
I  2x x 1dx  bằng cách đặt 2
u x 1, mệnh đề nào dưới đây đúng ? 1 Trang30
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 3 2 3 2 1 A. I  2 udu  . B. I udu  . C. I udu  . D. I udu  . 2 0 1 0 1 1 dx 1 e Câu 27. Cho  a bln 
, với a, b là các số hữu tỉ. Tính 3 3
S a b . x e 1 2 0 A. S  2 . B. S  2  . C. S  0 . D. S  1. 1 1
Câu 38. Cho hàm số f (x) thỏa mãn (x 1) f '(x)dx  10 
và 2 f (1)  f (0)  2 . Tính I f (x)dx  . 0 0 A. I  12  . B. I  8 . C. I  12 . D. I  8  .
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2 ( Đề thi thử nghiệm ) 2
Câu 23. Cho hàm số f (x) có đạo hàm trên đoạn 1; 2, f (1)  1 và f (2)  2 . Tính I f '(x)dx  . 1 7 A. I  1. B. I  1  . C. I  3 . D. I  . 2 1
Câu 24. Biết F (x) là một nguyên hàm của hàm số f (x)  F  . Tính F(3) . x  và (2) 1 1 1 7
A. F (3)  ln 2 1 .
B. F (3)  ln 2 1 . C. F (3)  . D. F (3)  . 2 4 4 2 Câu 25. Cho
f (x)dx  16  . Tính I f (2x)dx  . 0 0
A. I  32 .
B. I  8 .
C. I  16 .
D. I  4 . 4 dx Câu 26. Biết
a ln 2  b ln 3 c ln 5 
, với a, b, c là các số nguyên. Tính S a b c . 2 x x 3
A. S  6 .
B. S  2 . C. S  2  .
D. S  0 .
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 25. Tính tích phân 3 I  cos . x sin xdx  . 0 1 1 A. 4 I    . B. 4 I    .
C. I  0 . D. I   . 4 4 e
Câu 26. Tính tích phân I x ln xdx  . 1 1 2 e  2 2 e 1 2 e 1 A. I . B. I . C. I . D. I . 2 2 4 4 ỨNG DỤNG TÍCH PHÂN
1. Diện tích hình phẳng
1.1. Diện tích hình phẳng giới hạn bởi 1 đƣờng cong và trục hoành
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x ) liên tục trên đoạn a;b , trục hoành và hai   Trang31
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 b
đường thẳng x a , x b được xác định: S f x ( ) dx a
1.2. Diện tích hình phẳng giới hạn bởi 2 đƣờng cong
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f (x ) , y g(x ) liên tục trên đoạn a;b và hai   b
đường thẳng x a , x b được xác định: S
f (x )  g(x ) dx a b b
- Nếu trên đoạn [a;b] , hàm số f (x ) không đổi dấu thì:
f (x ) dx f (x d ) x   a a
- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối
- Diện tích của hình phẳng giới hạn bởi các đường x g(y ) , x h(y ) và hai đường thẳng y c , d
y d được xác định: S g y ( )  h y ( ) dy c
2. Thể tích vật thể và thể tích khối tròn xoay
2.1. Thể tích vật thể
Gọi B là phần vật thể giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm a và b; S (x ) là
diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm x , a
(  x b) . Giả b
sử S (x ) là hàm số liên tục trên đoạn [a;b] .Khi đó thể tích vật thể B là V S  xdx. a
2.2. Thể tích khối tròn xoay
- Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y f (x ) , trục b
hoành và hai đường thẳng x a , x b quanh trục Oxlà V    f
 x 2 dxa BÀI TẬP
Câu 1: Tính diện tích của những hình phẳng giới hạn bởi các đường 2
y x ; y x  2 9 3 5 7 A. B. C. D. 2 2 4 6
Câu 2: Tính diện tích của những hình phẳng giới hạn bởi các đường y x  2 (
6) ; y x  2 6 x A. 63 B. 72 C. 47 D. 35
Câu 3: Tính diện tích của những hình phẳng giới hạn bởi các đường 3 2 y x ; y x 9 8 7 1 A. B. C. D. 2 11 9 12
Câu 4: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y  sin x 1, trục hoành và hai đường thẳng  x  0 và 7 x  6 3 7 3 7 3 7 3 7 A.  1 B.  1 C.  1 D.  1 2 6 2 6 2 3 4 6 Trang32
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 5: Tính diện tích hình phẳng giới hạn bởi : Đồ thị hàm số 2
y  cos x , trục hoành, trục tung và đường thẳng x  .     A. B. C. D. 8 6 4 2
Câu 6: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y x và 3 y x . 1 1 1 1 A. B. C. D. 12 9 8 15
Câu 7: Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số 2
y x 1 và y  3  x 6 5 11 9 A. B. C. D. 2 2 2 2
Câu 8: Các đường có phương trình 3
x y , y  1 và x  8 17 17 17 27 A. B. C. D. 4 2 8 4
Câu 9:Cho hình phẳng D giới hạn bởi đồ thị hai hàm số y f x , y g x liên tục trên đoạn  ; a b và
các đường thẳng x a , x b . Diện tích S của hình D được tính theo công thức nào dưới đây? b b A. S  π f
 x gx dx. B. S f
 x gx dx. a a b b
C. S   f
 x gx 2 dx  .
D. S   f
 x gxdx  . a a
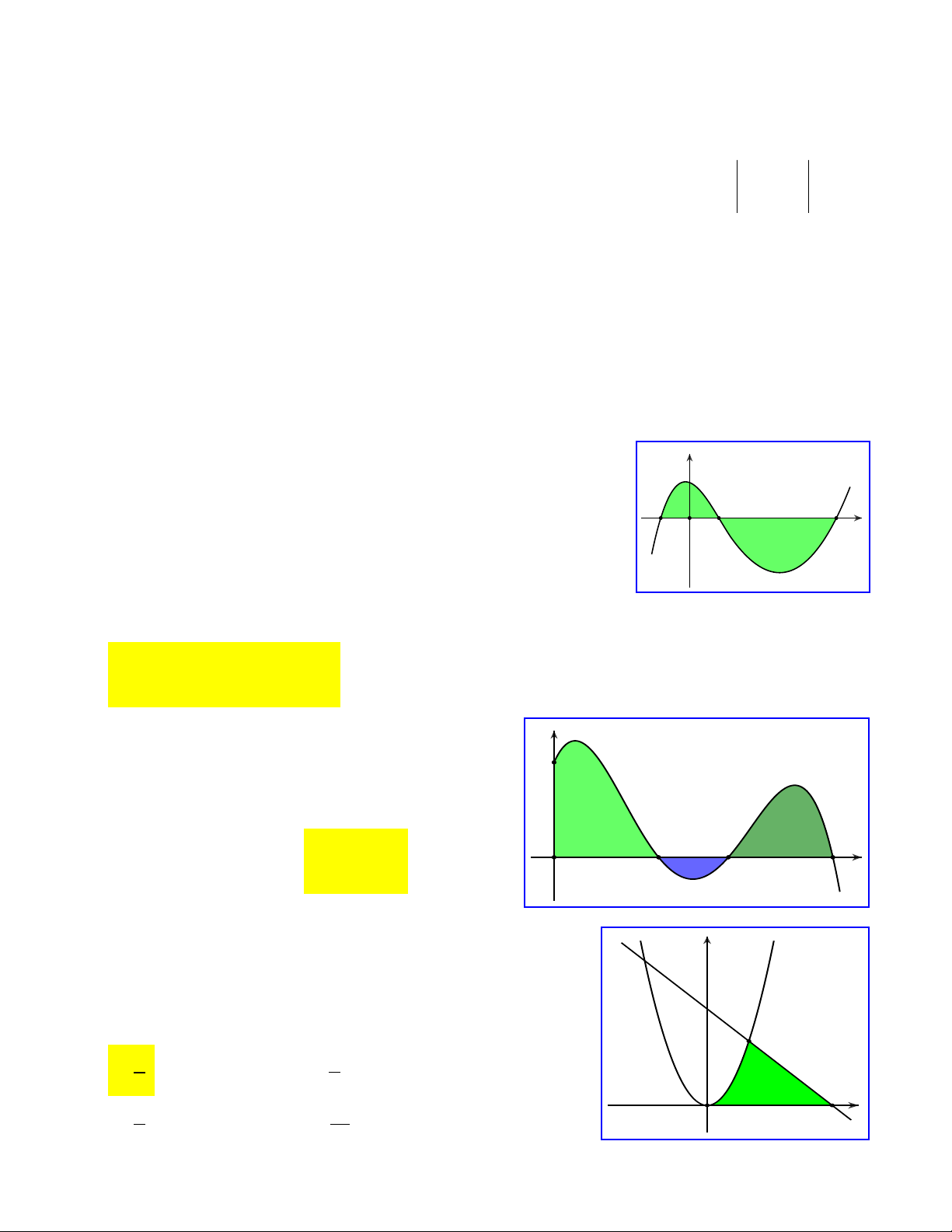
Câu 10:Cho hàm số f x liên tục trên  , có đồ thị như hình vẽ. Gọi S
là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f x , trục
hoành và trục tung. Khẳng định nào sau đây đúng? d 0 d 0 A. S f
 xdxf  xdx.
B. S   f
 xdxf  xdx . c d c d d 0 d 0
C. S   f
 xdxf
 xdx . D. S f
 xdxf  xdx. c d c d
Câu 11:Cho hình phẳng  H  giới hạn bởi đồ thị hàm số 2
y  x  3x  2 , trục hoành và hai đường thẳng
x 1, x  2 . Quay  H  xung quanh trục hoành được khối tròn xoay có thể tích là 2 2 2 A. 2 V
x  3x  2 dx  . B. 2 V
x  3x  2 dx  . 1 1 2 2 2
C. V    2
x  3x  2 dx . D. 2 V  
x  3x  2 dx  . 1 1
Câu 12:Cho hàm số y f x liên tục trên đoạn  ;
a b . Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y f x , trục hoành và hai đường thẳng x  ,
a x ba b . Thể tích của khối tròn xoay tạo thành khi
quay D quanh trục hoành được tính theo công thức: b b b b A. 2 V   f
 xdx B. 2 V  2 f
 xdx C. 2 2 V   f
 xdxD. 2 V   f
 xdx a a a a Trang33
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 13: Gọi S là diện tích hình phẳng giới hạn bởi các đường  x y
e , y  0 , x  0 , x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2 x S   e dx  . B. x S e dx  . C. x S   e dx  . D. 2 x S e dx  . 0 0 0 0
Câu 14: Diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x là 37 9 81 A. . B. I  . C. . D. 13. 12 4 12
Câu 15. Diện tích S của hình phẳng giới hạn bởi các đường 2
y  2x , y  1, x  0 và x 1 được tính
bởi công thức nào dưới đây? 1 1 2
A. S    2 2x   1dx . C. S   2 2x   1 dx. 0 0 1 1 B. S   2 2x   1 dx. D. S   2 2x   1 dx. 0 0
Câu 16. Thể tích của khối tròn xoay do hình phẳng giới hạn bởi các đường y
x , trục Ox và hai đường
thẳng x  1; x  4 khi quay quanh trục hoành được tính bởi công thức nào? 4 4 4 4
A. V   xdx. B. V  | x | dx. C. 2 V  
xdx. D. V   x dx.     1 1 1 1
Câu 17. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol  P 2 : y x và
đường thẳng d : y x xoay quanh trục Ox bằng 1 1 1 A. 2 4
x dx  x dx. B. 2 4
x dx  x dx. C.  
dx. D.   2
x x dx.      2 2 x X 0 0 0
Câu 18. Cho hàm số y f x liên tục trên đoạn  ;
a b . Viết công thức tính diện tích hình thang cong
giới hạn bởi đồ thị hàm số y f x , trục hoành và hai đường thẳng x a, x  . b b b b b A. 2 S f
 x dx. B. S  | f
 x| dx. C. S  | f
 x| dx. D. S f x dx. a a a a
Câu 19. Diện tích hình phẳng được giới hạn bởi đồ thị hàm số  ex y x
, trục hoành, hai đường thẳng
x  2; x  3 có công thức tính là 3 3 3 3 A.  ex S x dx. B.  | ex S x | dx. C.  ex S
x dx . D.   ex S x dx.     2  2  2  2 
Câu 20. Viết công thức tính thể tích V của vật thể nằm giữa hai mặt phẳng x  0 và x  ln4, biết khi cắt
vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x ( 0  x  ln4), ta được thiết diện
là một hình vuông có độ dài cạnh là ex x . ln 4 ln 4 ln 4 ln 4 2 A.  ex V x dx.   ex V x dx. B.   ex V x dx. D.  ex V x dx.  c.      0 0 0 0
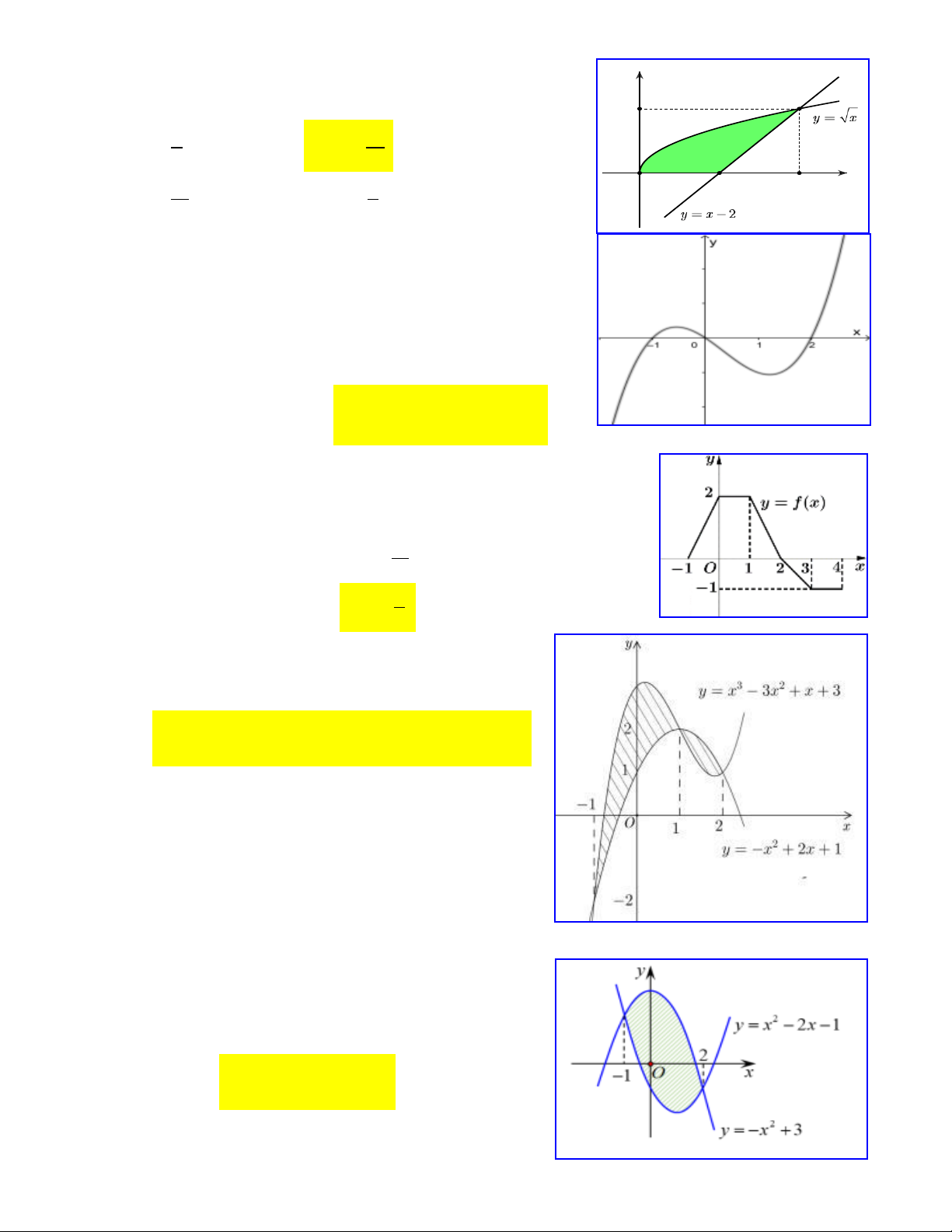
Câu 21. Gọi S là diện tích hình phẳng được tô đậm trong hình vẽ bên.
Công thức tính S là 1 2 1 2 A. S f
 xdxf xdx. B. S f
 xdxf x dx. 1  1 1  1 Trang34
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 2 2 C. S f
 x dx.
D. S   f  x dx. 1  1 
Câu 22. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol P 2
: y x và đường thẳng d : y  2x quay quanh trục Ox. 2 2 2 2 2 2 2 A.   2
x  2x dx. B. 2 4
 4x dx  x dx. C. 2 4
 4x dx  x dx. D. 2
 2x x dx.       0 0 0 0 0 0
Câu 23. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x , trục hoành và hai đường thẳng
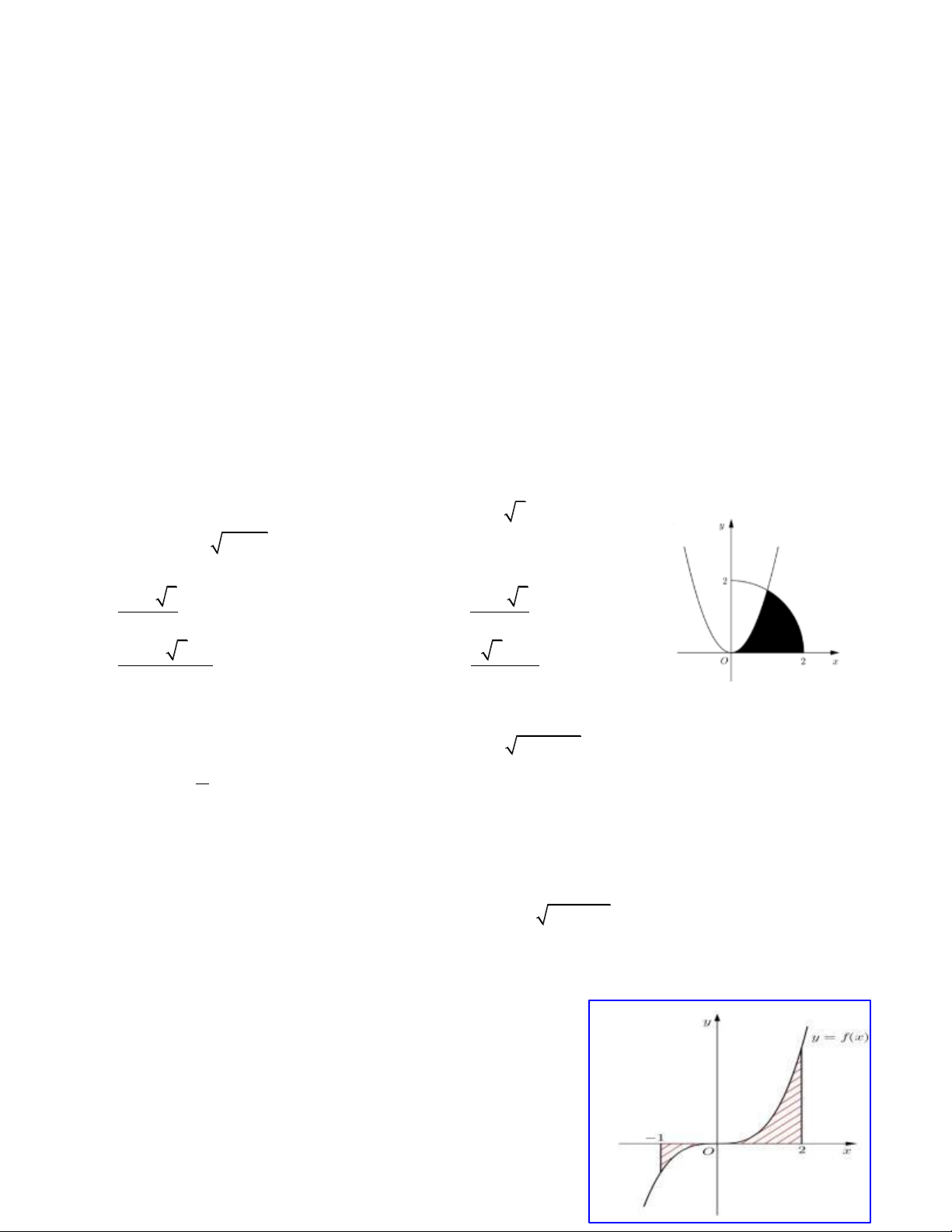
x  1, x  2 biết rằng mỗi đơn vị dài trên các trục tọa độ là 2 cm. 15 17 A. 2 cm . B. 2 cm . C. 17 2 cm . D. 15 2 cm . 4 4
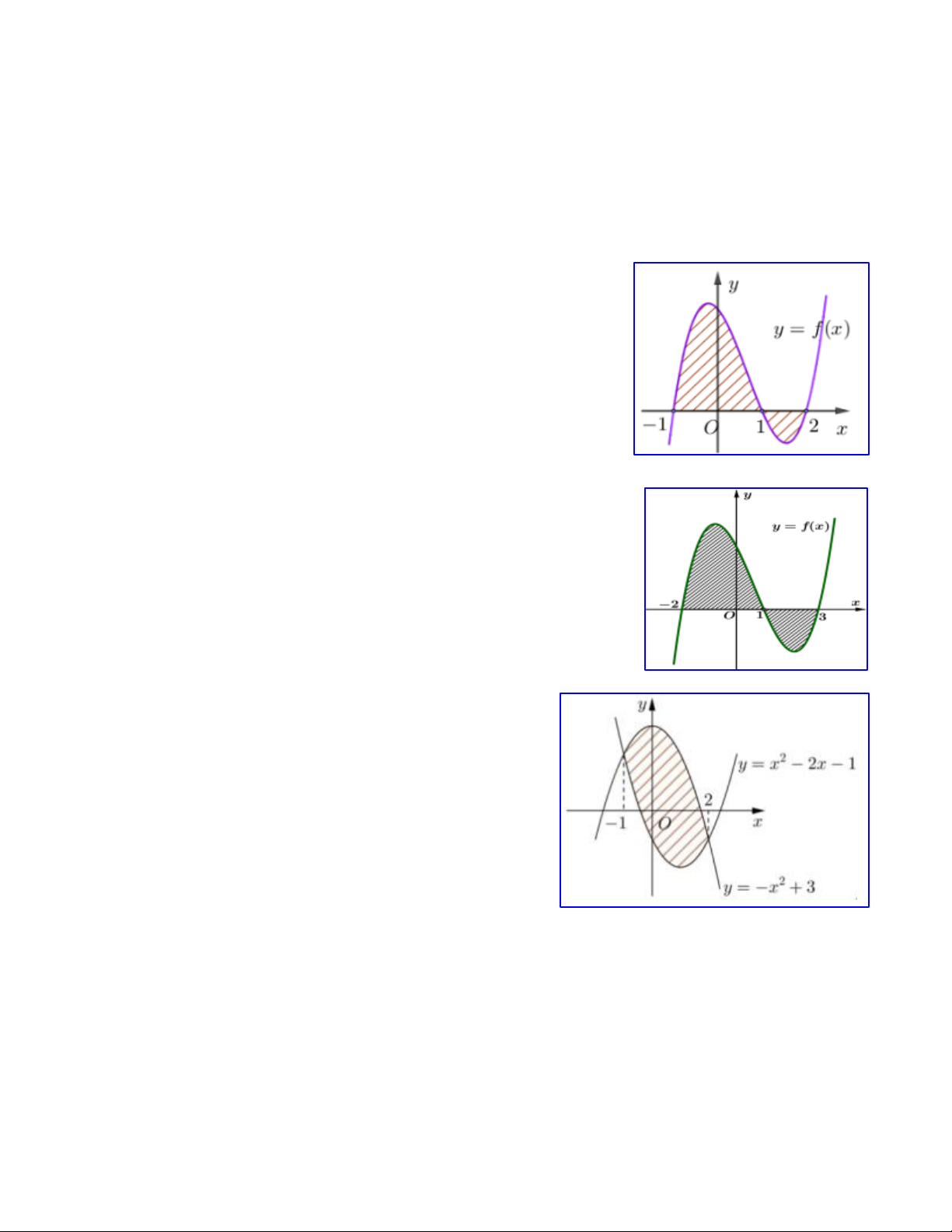
Câu 24.Đồ thị trong hình bên là của hàm số y f x, S là diện tích hình phẳng
(phần tô đậm trong hình). Chọn khẳng định đúng. 0 1 1 A. S f
 xdx f xdx. B. S f  xdx. 2  0 2  2  1 0 1 C. S f
 xdx f xdx. D. S f
 xdx f xdx. 0 0 2  0 2
7  4x khi0  x 1
Câu 25. Cho hàm số f x   2
4  x khi x 1
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số f x và các đường thẳng x  0, x  3, y  0. 16 20 A. . B. . C. 10. D. 9. 3 3
Câu 26. Cho f x 4 2
x  5x  4 . Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x và
trục hoành. Mệnh đề nào sau đây sai? 2 1 2 A. S  | f
 x|dx.
B. S  2 f  xdx 2  f
 xdx . 2  0 1 2 2
C. S  2 | f
 x|dx .
D. S  2 f  xdx . 0 0
Câu 27. Tính thể tích V của vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường 2 y x 1, 3
y x 1 quay quanh Ox. 47   A. V  47 . B. V  2 . C. V  2 . D. V  . 210 210 35 35 2 x
Câu 28. Cho hình phẳng (H) giới hạn bởi Parabol y  và 12 2
đường cong có phương trình x y  4  (hình vẽ). 4 2 x
Diện tích của hình phẳng (H) bằng 12 4А 3   4 3  А 4  24 3  3 A. . B. . C. . D. . 3 6 6 3 Trang35
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 29. Cho hàm số y f x liên tục trên R và có đồ thị (C) là đường cong như hình bên. Diện tích
hình phẳng giới hạn bởi đồ thị (C) , trục hoành và hai đường thẳng x  0, x  2 (phần tô đen) là 2 1 2 1 2 2
A. f x
  dx. B. f xdx f x dx. C. f xdx f x dx. D. f xdx . 0 0 1 0 1 0
Câu 30. Cho hai hàm số y f x và y g x liên tục trên đoạn  ;
a b . Kí hiệu H là hình phẳng giới
hạn bởi đồ thị hai hàm số y f x, y g x và hai đường thẳng x a, x b(a b) . Tính diện tích S của hình phẳng H. b b
A. S   f x  g x dx.
B. S    2 f x 2
g x dx. a a a b
C. S  | f
 x gx| dx.
D. S  | f
 x gx| dx. b a
Câu 31. Cho hàm số y f x liên tục trên ¡ . Gọi S là diện tích hình y
phẳng giới hạn bởi các đường y = f (x),y = 0,x = - 1 và x = 5 (như
hình vẽ bên).Mệnh đề nào sau đây đúng? y= f(x) 1 5 -1 O 1 5 x A. S = - f (x)dx -
f (x)dx . ò ò - 1 1 1 5 B. S = f (x)dx +
f (x)dx . ò ò - 1 1 1 5 1 5 C. S = f (x)dx -
f (x )dx . D. S = -
f (x )dx +
f (x )dx . ò ò ò ò - 1 1 - 1 1
Câu 32. Cho đồ thị hàm số y = f (x ) trên 0 é ;8 như ù hình êë úû y
vẽ.Biểu thức nào dưới đây có giá trị lớn nhất? 3 1 3 A.
f (x )dx . B.
f (x )dx . ò ò 0 0 (S ) 1 (S ) 3 5 8 C.
f (x )dx . D.
f (x )dx . ò ò O (S ) 3 5 8 x 2 0 0
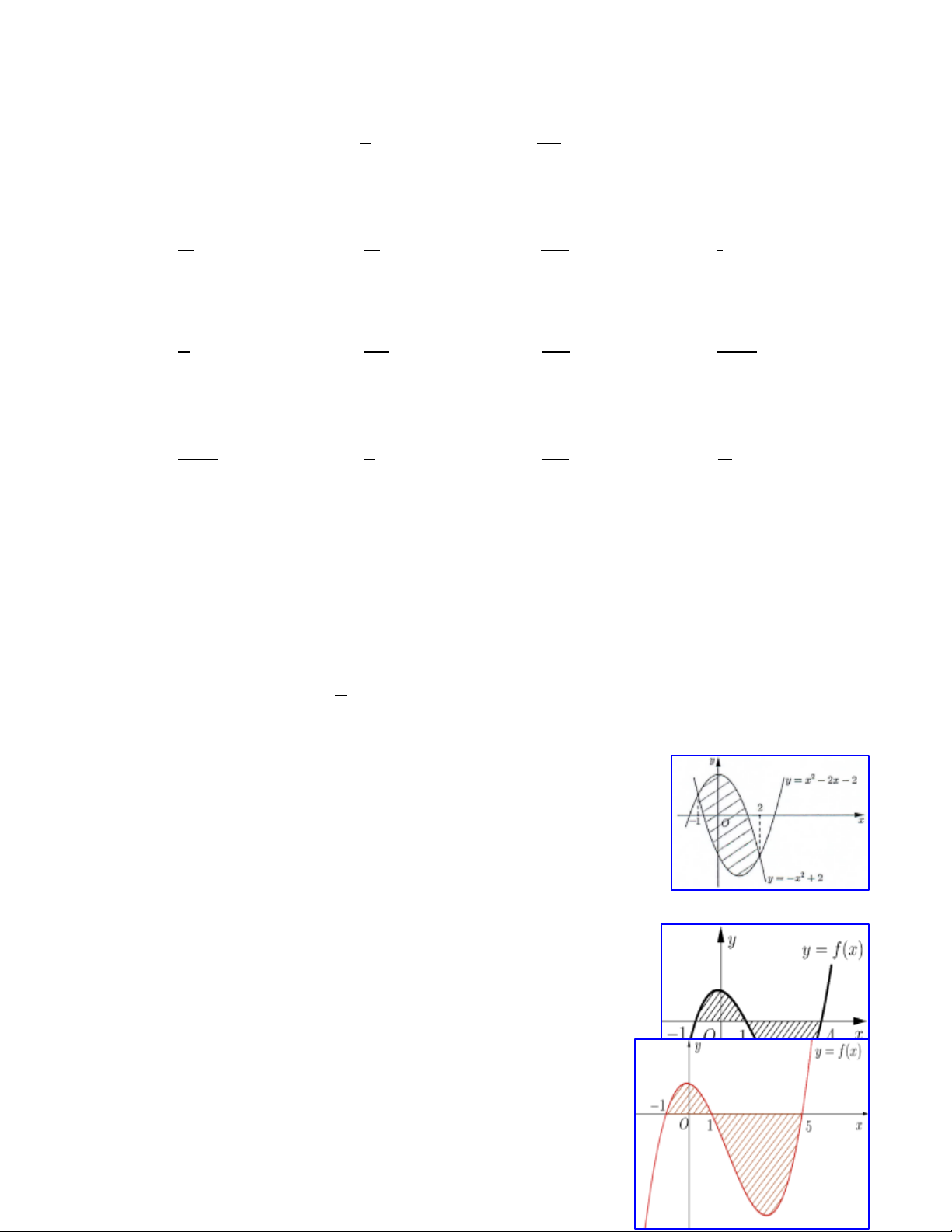
Câu 33. Gọi tam giác cong (OA B ) là hình phẳng giới hạn bởi đồ y thị các hàm số 2
y = 2x , y = 3 - x , y = 0 (tham khảo hình vẽ y= 2x2
bên). Diện tích của (OAB ) bằng A 8 5 A. . B. . 3 3 B x 4 10 O C. . D. . y= 3-x 3 3 Trang36
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 34. Tính diện tích S của hình phẳng (phần tô màu) trong hình y sau 8 10 A. S = . B. S = . 3 3 11 7 O 2 4 x C. S = . D. S = . 3 3
Câu 35. Cho hàm số y f x có đồ thị như hình dưới đây.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y f x và trục Ox là 2 0 2 A. S f
 xdxf
 xdx .B.S f
 xdx . 0 1 1  2 0 2 C. S   f
 xdx . D.S f
 xdxf
 xdx. 1  1 0
Câu 36. Cho hàm số y f x có đồ thị trên đoạn  1  ;4 như hình vẽ 4
dưới đây. Tính tích phân I f  xdx . 1  A. I  11 3. B. I  . 2 C. I  5 5. D. I  . 2
Câu 37. Cho đồ thị hai hàm số 3 2
y x  3x x  3 và 2
y  x  2x 1 như hình sau. Diện tích phần hình phẳng
được gạch sọc tính theo công thức nào dưới đây? 1 2 A.   3 2
x  2x x  2dx   3 2
x  2x x  2dx . 1  1 2 B.   3 2
x  2x x  2 dx . 1  1 2 C.   3 2
x  2x x  2dx   3 2
x  2x x  2dx . 1  1 2 D.   3 2
x  2x x  2dx . 1 
Câu 38. Diện tích phần hình phẳng gạch chéo trong hình vẽ
được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx .B.   2
x  2dx . 1  1  2 2
C.  2x  2dx . D.   2 2
x  2x  4dx 1  1  Đề thi tốt nghiệp 2020 Trang37
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022 Mã đề 101
Câu 29: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  4 và y  2x  4 bằng 4 4 A. 36 . B. . C. . D. 36 . 3 3 Mã đề 102 2
Câu 32: Diện tích hình phẳng giới hạn bởi hai đường y x 1 và y x 1  13 13 1 A. . B. . C. . D. . 6 6 6 6 Mã đề 103 Câu 4.
Diện tích hình phẳng giới hạn bởi hai đường 2
y x  2 và y  3x  2 bằng 9 9 125 125 A. . B. . C. . D. . 2 2 6 6 Mã đề 104
Câu 31: Diện tích hình phẳng giới hạn bởi hai đường 2
y x  3 và y x  3 bằng 125 1 125  A. . B. . C. . D. . 6 6 6 6
Đề thi tốt nghiệp 2020 ( Đợt 2 )
Câu 29. Gọi D là hình phẳng giới hạn bởi các đường 2 x
y e , y  0, x  0 và x 1. Thể tích khối tròn
xoay tạo thành kho quay D quanh Ox bằng 1 1 1 1 A. 4 xe dx  . B. 2 x e dx  . C. 2 xe dx  . D. 4 x e dx  . 0 0 0 0
Đề thi tham khảo lần 2 năm 2020
Câu 34. Diện tích S của hình phẳng giới hạn bởi các đường 2
y  2x , y  1
 , x  0 và x 1 được tính bởi
công thức nào dưới đây? 1 1 1 1 1 2
A. S    2 2x  
1dx B.S   2 2x  
1dx C.S   2 2x  
1 dx D.S   2 2x   1dx 2 0 0 0 0
Đề thi tham khảo lần 1 năm 2020
Câu 29: Diện tích phần hình phẳng được gạch chép trong hình bên bằng 2 2 A.   2 2
x  2x  4dx . B.   2
2x  2x  4dx . 1  1  2 2 C.   2 2
x  2x  4dx . D.   2
2x  2x  4dx . 1  1 
Đề thi THPT quốc gia 2019 Mã đề 101
Câu 29. Cho hàm số f x liên tục trên R . Gọi S là diện tích hình phẳng
giới hạn bởi các đường y f x, y  0, x  1
 và x  4 (như hình vẽ
bên). Mệnh đề nào dưới đây là đúng? 1 4 1 4
A. S   f
 xdxf
 xdx. B. S f
 xdxf
 xdx. 1  1 1  1 1 4 1 4 C. S f
 xdxf
 xdx. D. S   f
 xdxf
 xdx . 1  1 1  1 Mã đề 102 Trang38
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 29. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình phẳng giới hạn bởi các đường
y f x , y  0 , x  1
 và x  5 (như hình vẽ bên). Mệnh đề nào dưới đây đúng? 1 5 1 5 A. S f
 xdxf
 xdx. B. S f
 xdxf
 xdx. 1  1 1  1 1 5 1 5
C. S   f
 xdxf
 xdx . D. S   f
 xdxf
 xdx . 1  1 1  1 Mã đề 103
Câu 29. Cho hàm số f x liên tục trên  . Gọi S là diện tích hình
phẳng giới hạn bởi các đường y f x, y  0, x  1
 , x  2 (như hình
vẽ bên). Mệnh đề nào dưới đây đúng? 1 2 1 2 A. S   f
 xdxf
 xdx . B. S   f
 xdxf
 xdx. 1  1 1  1 1 2 1 2 C. S f
 xdxf
 xdx. D. S f
 xdxf
 xdx. 1  1 1  1 Mã đề 104
Câu 24. Cho hàm số f x liên tục trên R . Gọi S là diện tích hình
phẳng giới hạn bởi các đường y f x, y  0, x  2  và x  3 (như
hình vẽ bên). Mệnh đề nào dưới đây là đúng? 1 3 1 3 A. S f
 xdxf
 xdx . B. S   f
 xdxf
 xdx . 2  1 2  1 1 3 1 3 C. S f
 xdxf
 xdx . D. S   f
 xdxf
 xdx. 2  1 2  1
Đề thi tham khảo kì thi THPT Quốc gia 2019
Câu 24. Diện tích phần hình phẳng gạch chéo trong hình vẽ
bên được tính theo công thức nào dưới đây? 2 2 A.   2
2x  2x  4dx B.   2
x  2dx 1  1  2 2
C.  2x  2dx D.   2 2
x  2x  4dx 1  1 
Đề thi THPT Quốc gia 2018 Mã đề 101
Câu 5: Gọi S là diện tích của hình phẳng giới hạn bởi các đường x
y e , y  0, x  0, x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A. 2 x S   e dxB. x S e dxC. x S   e dxD. 2 x S e dx  0 0 0 0 Mã đề 102 Trang39
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
Câu 2. Gọi S là diện tích của hình phẳng giới hạn bởi các đường  2x y
, y  0, x  0, x  2 . Mệnh đề nào dưới đây đúng? 2 2 2 2 A.  2x S dxB. 2   2 x S dxC. 2  2 x S dxD.   2x S dx  0 0 0 0 Mã đề 103
Câu 4. Cho hình phẳng  H  giới hạn bởi các đường 2
y x  3, y  0, x  0, x  2 . Gọi V là thể tích của
khối tròn xoay được tạo thành khi quay  H  xung quanh trục Ox. Mệnh đề nào dưới đây đúng? 2 2 2 2 2 2
A.V    2
x  3 dx B.V    2 x  3 dx C.V   2 x  3 dx D.V   2 x  3dx 0 0 0 0
Đề thi tham khảo kì thi THPT quốc gia 2018
Câu 6: Cho hàm số y  f x liên tục trên đoạn a;b . Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số
y  f x , trục hoành và hai đường thẳng x  a, x  ba  b . Thể tích của khối tròn xoay tạo thành khi
quay D quanh trục hoành được tính theo công thức b b b b A. 2 V   f  xdx B. 2 V  2 f  xdx C. 2 2 V   f  xdx D. 2 V   f  xdx a a a a
Câu 31: Cho (H) là hình phẳng giới hạn bởi parabol 2 y  3x , cung tròn có phương trình 2 y 
4  x (với 0  x  2 ) và trục hoành (phần tô đậm trong
hình vẽ). Diện tích của (H) bằng 4  3 4  3 A. B. 12 12 4  2 3  3 5 3  2 C. D. 6 3
Đề thi THPT Quốc gia 2017 Mã đề 101
Câu 14: Cho hình phẳng D giới hạn bởi đường cong y  2  cos x , trục hoành và các đường 
thẳng x  0, x
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng 2 bao nhiêu ?
A.V   1
B. V  ( 1)
C.V  ( 1)
D. V   1 Mã đề 102
Câu 20. Cho hình phẳng D giới hạn bởi đường cong y
2  sin x , trục hoành và các đường thẳng
x  0, x   . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu ?
A.V  2(  1)
B.V  2 (  1) C. 2 V  2 D.V  2
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 3
Câu 21. Gọi S là diện tích hình phẳng (H) giới hạn bởi các đường
y f (x) , trục hoành và hai đường thẳng x  1, x  2 (như hình 0 2
vẽ bên). Đặt a
f (x)dx,b f (x)dx  
, mệnh đề nào dưới đây 1  0 đúng ? Trang40
ÔN TẬP GIẢI TÍCH 12 – CHƢƠNG III ÔN THI TỐT NGHIỆP THPT 2022
A. S b a .
B. S b a .
C. S b   a .
D. S b  a .
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 2
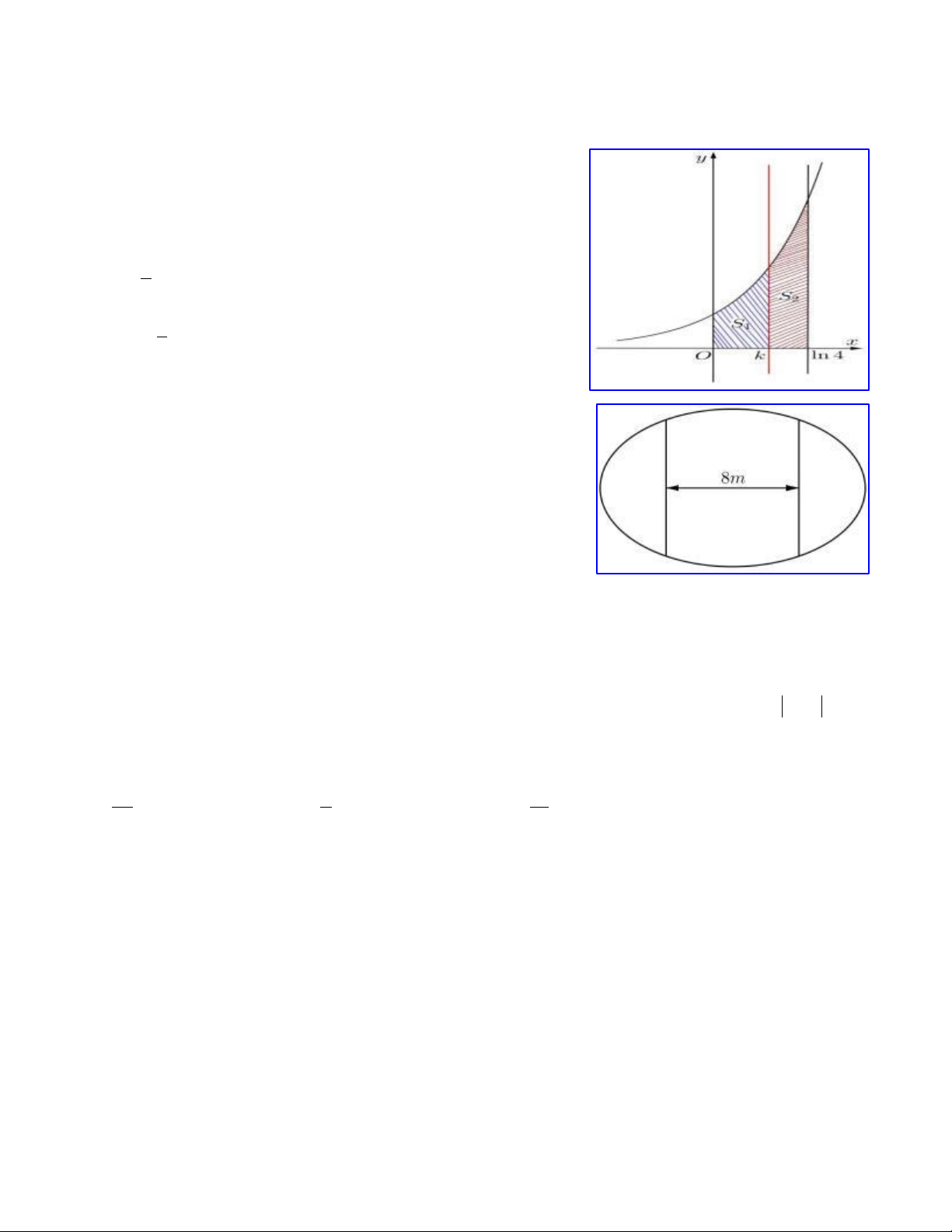
Câu 27. Cho hình thang cong (H) giới hạn bởi các đường x
y e , y  0, x  0 và x  ln 4 . Đường thẳng x k (0  k  ln 4)
chia (H) thành hai phần có diện tích là S và S như hình vẽ bên. 1 2
Tìm k để S  2S . 1 2 2 A. k  ln 4 .
B. k  ln 2 . 3 8
C. k  ln .
D. k  ln 3. 3
Câu 28. Ông An có một mảnh vườn hình elip có độ dài trục lớn
bằng 16m và độ dài trục bé bằng 10m. Ông muốn trồng hoa trên
một dải đất rộng 8m và nhận trục bé của elip làm trục đối xứng
(như hình vẽ). Biết kinh phí để trồng hoa là 100.000 đồng /1 m2.
Hỏi ông An cần bao nhiêu tiền để trồng hoa trên dải đất đó ? (Số
tiền được làm tròn đến hàng nghìn.) A. 7.862.000 đồng. B. 7.653.000 đồng. C. 7.128.000 đồng. D. 7.826.000 đồng.
Đề thi minh họa kì thi THPT Quốc gia 2017 – lần 1
Câu 22. Viết công thức tính thể tích V của khối tròn xoay được tạo thành khi quay hình thang cong, giới
hạn bởi đồ thị hàm số y f (x) , trục Ox và hai đường thẳng x a, x b (a b) , xung quanh trục Ox. b b b b A. 2 V   f (x)dx  . B. 2 V f (x)dx  . C. V   f (x)dx  . D. V f (x) dx  . a a a a
Câu 27. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 3
y x x và đồ thị hàm số 2
y x x . 37 9 81 A. . B. . C. . D. 13. 12 4 12
Câu 28. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số  2( 1) x y x
e , trục tung và trục hoành. Tính
thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox.
A. V  4  2e .
B. V  (4  2e) . C. 2 V e  5 . D. 2
V  (e  5) . Trang41