




Preview text:
lOMoAR cPSD| 45476132
HÀM SỐ MŨ VÀ LOGA – ĐỀ SỐ 1 .
Câu 1: Tập xác ịnh D của hàm số y log3 log x2 là A. D . B. D 0;1 . C. D 0; . D. D 1; .
Câu 2: Tập xác ịnh D của hàm số y x2 3x 2 2 là A. D \ 1;2 . B. D ; 1 2; . C. D ;1 2; . D. D \ 1;2 .
Câu 3: Tập nghiệm của bất phương trình log x 2 0 là 4 A. B. C. D. ; 1 . 2; 1 . 1; . 2; . Câu 4: Hàm số y x2 2x 2 ex có ạo hàm là D. A. 2x 2 ex . B. x e2 x . C. 2xex . 2x a4 a
2. Giá trị của loga b2 bằng: Câu 2 ex. 5: Biết log b b b A. 2. B. . C. 4 . D. . Câu 6: Gọi x ,x1 x
2 là hai nghiệm của phương trình 9x
4.3x 3 0. Tính tổng S x1 2 . A. S 1. B. S 4. C. S 9. D. S 10.
Câu 7: Biết log x2 6log a4 4log2 b log c
với a,b,c là các số thực dương bất kì. Tìm kết luận úng. 1 2 A. x a 3 3 2 . B. x a3 b2 c. C. x a c32 . D. x ac2 . b c b b
Câu 8: Tổng tất cả các nghiệm của phương trình 32x 2.3x 2 27 0 bằng A. 18. B. 27. C. 9. D. 3.
Câu 9: Cho hàm số y log x 2
2 . Tìm khẳng ịnh sai.
A. Hàm số ồng biến trên 0; .
B. Hàm số nghịch biến trên ;0 .
C. Hàm số có một iểm cực tiểu.
D. Đồ thị hàm số có ường tiệm cận. Câu 10: Cho 40
a log 52, b log 92 . Biểu diễn của theo a và b là: P log2 lOMoAR cPSD| 45476132 A. 1 3a P 3 a 2b. B. P 3 a b . C. P . D. P 3 a b . 2 2b
Câu 11: Tìm nghiệm của phương trình 2x 1 2x 1 2x 28. A. x 2. B. x 3. C. x . D. x 16.
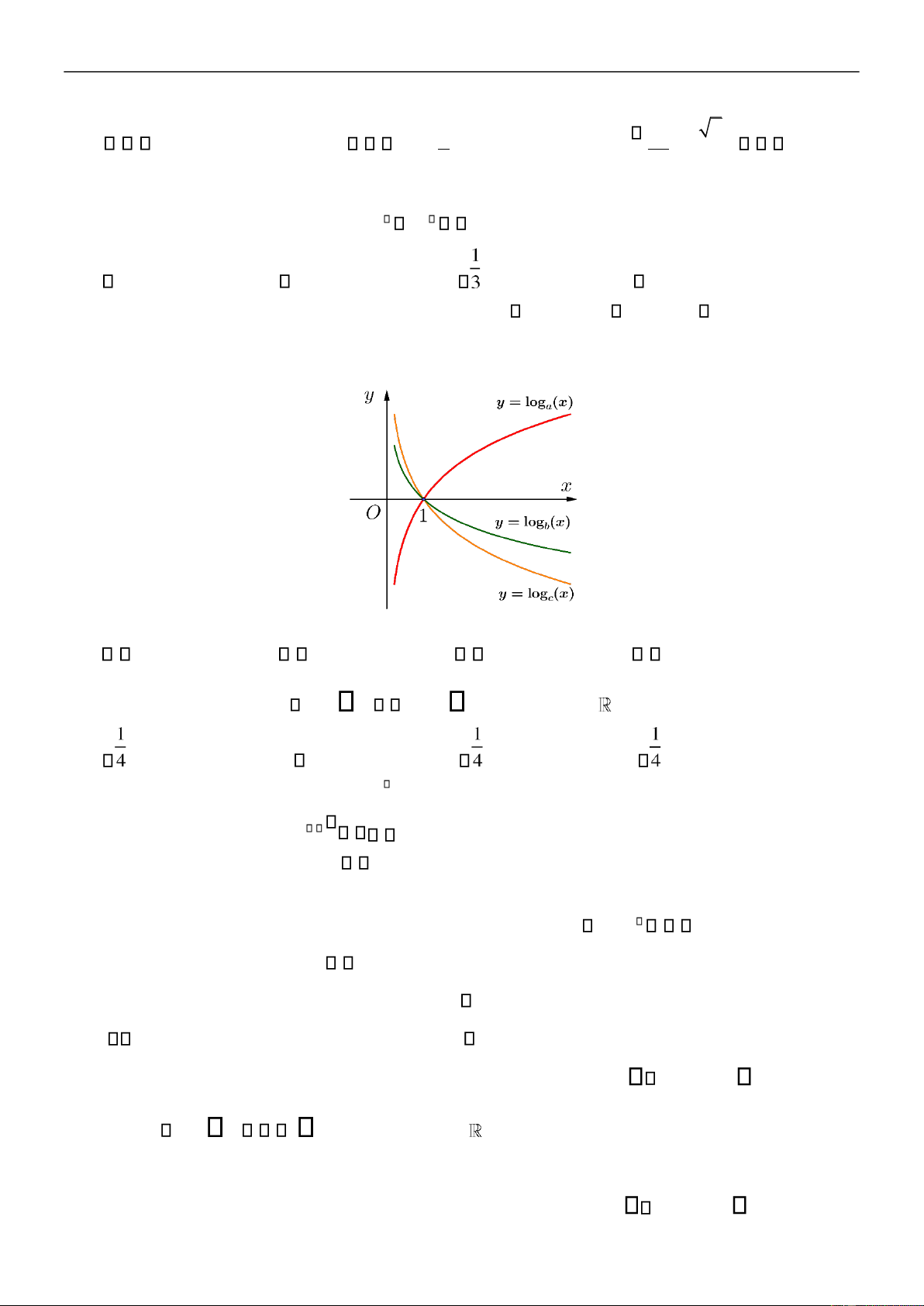
Câu 12: Cho ba số a , b , c dương và khác 1. Các hàm số y log xa , y log x , y log x có ồ thị b c như hình vẽ sau
Khẳng ịnh nào dưới ây úng? A. a c b. B. a b c. C. c b a . D. b c a .
Câu 13: [Mức ộ 3] Hàm số y log2 4x 2x m có tập xác ịnh là khi A. m . B. m 0 . C. m . D. m . 2x 10
Câu 14: Bất phương trình 2x 3x 4 2
1 có bao nhiêu nghiệm nguyên dương? 2 A. 6 . B. 4 . C. 3. D. 2 .
Câu 15: [Mức ộ 3] Tìm giá trị thực của tham số m ể phương trình 4x m.2x 1 m 2 0 có hai nghiệm
thực x1, x2 thỏa mãn x1 x2 2.
A. Không có giá trị nào của m. B. m 2. C. m 2. D. m 3.
Câu 16: [2D1-1.3-3] Có bao nhiêu gia trị nguyên của tham số m trong oạn 2019;2019 ể hàm số
y ln x 2 2 mx 1 ồng biến trên ? A. 2019. B. 2020. C. 4038. D. 1009. Câu 17: [Mức
ộ 3] Có bao nhiêu số nguyên m trên oạn 2020;2020 ể hàm số lOMoAR cPSD| 45476132 y log5
x22mx m 1 xác ịnh với mọi x 1;2 ? A. 4040. B. 2021. C. 2019. D. 2020.
Câu 18: Có bao nhiêu giá trị nguyên của tham số m ể tập nghiệm c ủa bất phương trình
ln x 2 2xm 2ln 2x 1 0 chứa úng hai số nguyên? A. 10 B. 3 C. 4 D. 9
Câu 19: Cho f x 2020x 2020 x . Gọi m0 là số lớn nhất trong số nguyên m thỏa f m 1 f m 2020
0 . Giá trị của m0 là 2020 A. m 0 2018. B. m0 2019. C. m0 2020. D. m0 2021.
Câu 20: [2D2-4.8-3] Bạn B vay một số tiền tại ngân hàng Agribank và trả góp số tiền ó trong vòng 3
tháng với mức lãi suất là 1% /tháng. Bạn B bắt ầu hoàn nợ, tháng thứ nhất bạn B trả ngân hàng
số tiền là 10 triệu ồng, tháng thứ 2 bạn B trả ngân hàng 20 triệu ồng và tháng cuối bạn B trả
ngân hàng 30 triệu ồng thì hết nợ. Vậy số tiền bạn B ã vay của ngân hàng là bao nhiêu. Chọn
kết quả gần úng nhất? A. 58 triệu ồng. B. 59 triệu ồng. C. 56 triệu ồng. D. 57 triệu ồng.
Câu 21: [2D2-4.0-3] Cho f x aln x
x2 1 bsinx 6 với a,b . Biết rằng f log loge 2.
Tính giá trị của f log ln10 . A. 10. B. 2 . C. 4 . D. 8.
Câu 22: [2D2-4.4-3] Cho hai số thực a 1,b 1. Gọi x ,x1 2 là hai nghiệm của phương trình a .bx x 12 1. x .x1 2 2
Trong trường hợp biểu thức S 1
x2 4x1 4x2 ạt giá trị nhỏ nhất, mệnh ề nào sau ây x úng? A. a b .
B. a.b 4. C. a.b 2. D. a b .
Câu 23: Cho số thực a,b 1 thỏa mãn iều kiện log2018 a log2019 b 20202. Tìm giá trị lớn nhất B.
log2019 2018 log2018 2019 . lOMoAR cPSD| 45476132
c ủ a bi ể u th ứ c P log a log
b ? C. D. 2020 log2019 2018 2020 log2018 2019 . 2019 2018 A. 2020 log . 2019 2018 log2018 2019
Câu 24: Số giá trị nguyên nhỏ hơn
2020 của tham số m ể phương 2020 .
trình log6 2020x m log4 log 2019 2018 log2018 2019 1010x có nghiệm là: A. 2020. B. 2021. C. 2019. D. 2022.
Câu 25: Có bao nhiêu cặp số nguyên (a;b) thỏa mãn 1 ab
100 ể phương trình abx bax có nghiệm nhỏ hơn 1? A. 4751. B. 4656. C. 2 . D. 4750.
Câu 26: Cho hàm s ố y f x liên t ụ c trên và có b ả ng xét d ấu ạo hàm như sau Bất phương trình f x ex2m úng với mọi x 1;1 khi và chỉ khi A. m f 0 1. B. m f 1 e. C. m f 0 1. D. m f 1 e.
Câu 27: [Mức ộ 3] Cho phương trình: log2 m x 4 log1 mx x2
0. Gọi S là tập hợp tất cả các 2
giá trị nguyên của tham số m ể phương trình ã cho có hai nghiệm phân biệt thỏa iều kiện x 1.
Tìm số phần tử của S . A. 2 . B. 0 . C. vô số. D. 1.
Câu 28: [2D2-6.6-4] Có bao nhiêu giá trị nguyên âm của tham số m sao cho phương trình 3x2 3x m 1 2 log2 x 2 5x m 2 có nghiệm? 2x x 1 A. Vô số. B. 4. C. 6. D. 5.
Câu 29: Tổng tất cả các giá trị của tham số m ể phương trình 3x 2x 1 2x m2 logx 2x 32 2 x m 2
có úng ba nghiệm phân biệt là A. 3. B. 2. C. 3. D. 2 .
Câu 30: [Mức ộ 4] Cho x,y,z là các số thực không âm thoả mãn2x 2y 2z
10. Giá trị lớn nhất của lOMoAR cPSD| 45476132 biểu thức P x y
3z gần nhất với số nào sau ây? A. 8 . B. 10 . C. 9 . D. 7 .
Câu 31: [Mức ộ 3] Cho hai số thực a,b lớn hơn 1 thỏa mãn a b
2020. Gọi m,n là hai nghiệm của phương trình log xa log xb 2log xa
2 0. Giá trị nhỏ nhất của biểu thức m.n 4a bằng A. 8076. B. 2028. C. 1011. D. 3622.
Câu 32: [2D1-1.2-4] Cho hàm số y f x có ạo hàm liên tục trên và có ồ thị hàm số y f x như
hình vẽ bên. Có bao nhiêu giá trị nguyên dương của tham số m ể hàm số y f x 1 20ln 2 xx
nghịch biến trên khoảng 1;1 ? m 2 A. 3. B. 6 . C. 4 . D. 5.
Câu 33: Cho các số thực a , b thỏa mãn a b 1 và 1 1 2020 . Giá trị của biểu thức log ab log ba P 1 1 bằng log bab log a ab A. 2014 . B. 2016 . C. 2018 . D. 2020 .
Câu 34: Cho cấp số cộng an , cấp số nhân bn thoả mãn a2 a1 0 , b 1 và hàm số 2 b1 f x x3 3x sao cho f a 2 2 f a 1 và f log b 2 2 2 f log b 2 1 . Tìm số
nguyên dương n nhỏ nhất sao cho bn 2019an A. 17. B. 14. C. 15. D. 16.
Câu 35: Xét các số thực dương a,b,c lớn hơn 1 ( với a b ) thỏa mãn 4 log ca log cb 25logab c. Giá
trị nhỏ nhất của biểu thức log ab log ca log bc bằng A. 5. B. 8. C. . D. 3. lOMoAR cPSD| 45476132




