Preview text:
Design, Analysis and Implementation of Algorithms
Pham Quang Dung and Do Phan Thuan
Computer Science Department, SoICT,
Hanoi University of Science and Technology. September 4, 2017 1 / 5 General answer
I Algorithms: A well-defined computational procedure that takes a set
of values as input and produces a set of values as output I Objectives of the course
F Skills: Design, analysis and implementation of algorithms Introduction Questions you may have I What are algorithms? I Why do we learn this course? 2 / 5 I Objectives of the course
F Skills: Design, analysis and implementation of algorithms Introduction Questions you may have I What are algorithms? I Why do we learn this course? General answer
I Algorithms: A well-defined computational procedure that takes a set
of values as input and produces a set of values as output 2 / 5 Introduction Questions you may have I What are algorithms? I Why do we learn this course? General answer
I Algorithms: A well-defined computational procedure that takes a set
of values as input and produces a set of values as output I Objectives of the course
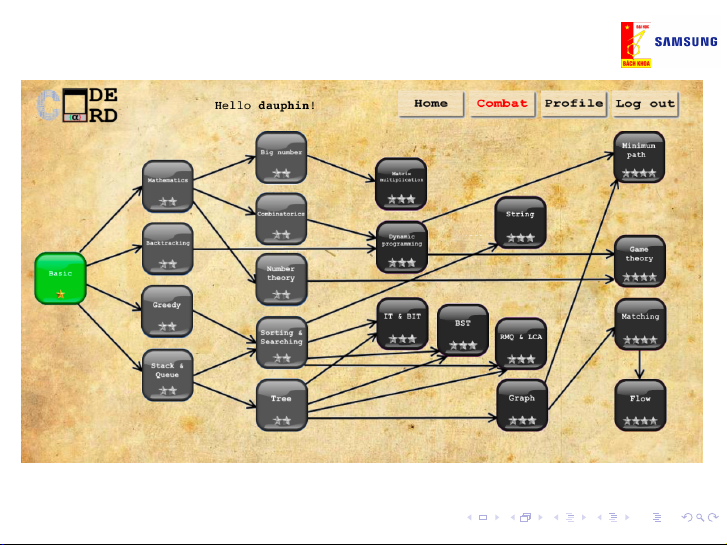
F Skills: Design, analysis and implementation of algorithms 2 / 5 Plan Basic
I Chapter 1: Introduction to algorithms and data structures (weeks 1-2)
I Chapter 2: Recursion, Backtracking, and Branch-and-Bound (weeks 3-5)
I Chapter 3: Greedy algorithms (weeks 6)
I Chapter 4: Divide-and-Conquer (week 7)
I Chapter 5: Dynamic Programming (weeks 8-9)
I Chapter 6: Graph algorithms and applications (weeks 10-11) Advances
I Chapter 7: Advanced data structures and applications (weeks 12-13)
I Chapter 8: Algorithms on Strings and applications (week 14-15) 3 / 5 4 / 5 References 1
T.H. Cormen, C.E. Leiserson, R.L. Rivest, C. Stein. Introduction to
Algorithms. Second Edition, MIT Press, 2001 2
Robert Lafore. Data structures and Algorithms in Java (2nd Edition) Sams Publishing, 2002 5 / 5
Introduction to Data Structures and Algorithms
Pham Quang Dung and Do Phan Thuan
Computer Science Department, SoICT,
Hanoi University of Science and Technology. January 19, 2018 1 / 1 First example
Find the largest weight subsequence of a given sequence of numbers
Given a sequence s = ha1, . . . , ani
a subsequence is s(i , j ) = hai , . . . , aj i, 1 ≤ i ≤ j ≤ n weight w (s(i , j )) = j X ak k=i
Problem: find the subsequence having largest weight
http://www.spoj.com/problems/MAXSUMSU/ Example
sequence: -2, 11, -4, 13, -5, 2
The largest weight subsequence is 11, -4, 13 having weight 20 2 / 1 How many subsequences?
Number of couple (i , j ) where 1 ≤ i ≤ j ≤ n n+n 2 This give a direct algorithm 3 / 1 Direct algorithm — O(n3)
Scan all possible subsequences n +n = n2+n 2 2
Compute and keep the largest weight subsequence 1
p u b l i c l o n g a l g o 1 ( int [] a ){ 2 int n = a . l e n g t h ; 3 l o n g max = a [ 0 ] ; 4
for ( int i = 0; i < n ; i + + ) { 5
for ( int j = i ; j < n ; j + + ) { 6 int s = 0; 7
for ( int k = i ; k <= j ; k ++) 8 s = s + a [ k ]; 9 max = max < s ? s : max ; 10 } 11 } 12 r e t u r n max ; 13 } 4 / 1 Direct algorithm Faster algorithm — O(n2) Observation: Pj a[k] = a[j ] + Pj−1 a[k] k=i k=i 1
p u b l i c l o n g a l g o 2 ( int [] a ){ 2 int n = a . l e n g t h ; 3 l o n g max = a [ 0 ] ; 4
for ( int i = 0; i < n ; i + + ) { 5 int s = 0; 6
for ( int j = i ; j < n ; j + + ) { 7 s = s + a [ j ]; 8 max = max < s ? s : max ; 9 } 10 } 11 r e t u r n max ; 12 } 5 / 1 Divide And Conquer
Divide the sequence into 2 subsequences at the middle s = s1 :: s2 The largest subsequence might I be in s1 or I be in s2 or
I start at some position of s1 and end at some position of s2 Java code: 1
p r i v a t e l o n g m a x S e q ( int i , int j ){ 2
if ( i == j ) r e t u r n a [ i ]; 3 int m = ( i + j ) / 2 ; 4
l o n g ml = m a x S e q ( i , m ); 5
l o n g mr = m a x S e q ( m +1 , j ); 6
l o n g m a x L = m a x L e f t ( i , m ); 7
l o n g m a x R = m a x R i g h t ( m +1 , j ); 8
l o n g m a x L R = m a x L + m a x R ; 9
l o n g max = ml > mr ? ml : mr ; 10
max = max > m a x L R ? max : m a x L R ; 11 r e t u r n max ; 12 } 13
p u b l i c l o n g a l g o 3 ( int [] a ){ 14 int n = a . l e n g t h ; 15
r e t u r n m a x S e q (0 , n - 1 ) ; 16 } 6 / 1
Divide and Conquer — O(n log n) 1
p r i v a t e l o n g m a x L e f t ( int i , int j ){ 2 l o n g m a x L = a [ j ]; 3 int s = 0; 4
for ( int k = j ; k >= i ; k - -){ 5 s += a [ k ]; 6
m a x L = m a x L > s ? m a x L : s ; 7 } 8 r e t u r n m a x L ; 9 } 10
p r i v a t e l o n g m a x R i g h t ( int i , int j ){ 11 l o n g m a x R = a [ i ]; 12 int s = 0; 13
for ( int k = i ; k <= j ; k + + ) { 14 s += a [ k ]; 15
m a x R = m a x R > s ? m a x R : s ; 16 } 17 r e t u r n m a x R ; 18 } 7 / 1 Dynamic programming General principle
Division: divide the initial problem into smaller similar problems (subproblems)
Storing solutions to subproblems: store the solution to subproblems into memory
Aggregation: establish the solution to the initial problem by
aggregating solutions to subproblems stored in the memory 8 / 1 Dynamic programming Largest subsequence Division:
I Let si be the weight of the largest subsequence of a1, . . . , ai ending at ai Aggregation: I s1 = a1
I si = max{si−1 + ai , ai }, ∀i = 2, . . . , n
I Solution to the original problem is max{s1, . . . , sn}
Number of basic operations is n (best algorithm) 9 / 1 Dynamic programming — O(n) 1
p u b l i c l o n g a l g o 4 ( int [] a ){ 2 int n = a . l e n g t h ; 3 l o n g max = a [ 0 ] ; 4 int [] s = new int [ n ]; 5 s [0] = a [ 0 ] ; 6 max = s [ 0 ] ; 7
for ( int i = 1; i < n ; i + + ) { 8
if ( s [ i -1] > 0) s [ i ] = s [ i -1] + a [ i ]; 9 e l s e s [ i ] = a [ i ]; 10
max = max > s [ i ] ? max : s [ i ]; 11 } 12 r e t u r n max ; 13 } 10 / 1 Analyzing algorithms
Resources (memory, bandwithd, CPU, etc.) required by the algorithms
Most concern is the computational time
Input size: number of items in the input
Running time: measured in term of the number of primitive operations performed 11 / 1 Analyzing algorithms algo1: T (n) = n3 + n2 + n 6 2 3 algo2: T (n) = n2 + n 2 2 algo3:
I Count the number of addition (”+”) operation T (n) ( 0 if n = 1 T (n) = T ( n ) + T ( n ) + cn if n > 1 2 2
I By induction: T (n) = n c logn algo4: T (n) = c n 12 / 1 Analyzing algorithms
Worst-case running time: the longest running time for any input of size n
Best-case running time: the shortest running time for any input of size n
Average-case running time: probabilistic analysis (make assumption of
a distribution of the input) yields expected running time 13 / 1