Ứng dụng ma trận trong xử lí ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng | Tiểu luận Toán kỹ thuật

BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC VĂN LANG -----F&E-----
KHOA KỸ THUẬT CƠ ĐIỆN VÀ MÁY TÍNH
TIỂU LUẬN THI KẾT THÚC HỌC PHẦN: TOÁN KỸ THUẬT
ỨNG DỤNG MA TRẬN TRONG XỬ LÝ ẢNH,
THỊ GIÁC MÁY TÍNH, NHẬN DẠNG VÀ PHÂN LOẠI ĐỐI TƯỢNG STTH: ĐINH LÊ ĐOAN NGỌ C MSSV: 2374601080016 STTH: HUỲNH NHẬT THẮNG MSSV: 2374601080027 STTH: NGUYỄN ĐĂNG KHO A MSSV: 2374601080011 STTH: NGUYỄN NGỌC LAN PHƯƠN G MSSV: 2374601080019
GIẢNG VIÊN HỖ TRỢ: TS – TRƯƠNG QUỐC TRÍ
TP HỒ CHÍ MINH, Ngày 06, tháng 12, năm 2023
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT MỤC L C Ụ
I. TÓM TẮT VỀ MA TRẬN ................................................................................................................... 3 II. GIỚI TH Ệ
I U ĐỀ TÀI NGHIÊN CỨU ............................................................................................. 3
1. MỤC ĐÍCH ............................................................................................................................................. 3
2. NỘI DUNG THỰC HIỆN .......................................................................................................................... 3
3. PHƯƠNG PHÁP - LÝ THUYẾT ................................................................................................................ 4 III. ỨNG Ụ
D NG TOÁN HỌC VÀO ĐỀ TÀI ........................................................................................ 4
1. MA TRẬN ............................................................................................................................................... 4
2. CÁC PHÉP TOÁN TRONG MA TRẬN ....................................................................................................... 5
A. CỘNG HAI MA TRẬN ............................................................................................................................. 5 B. NHÂN VÔ H Ớ
Ư NG VỚI MỘT SỐ ............................................................................................................. 5 C. MA T Ậ R N CHU Ể Y N Ị
V ........................................................................................................................... 6
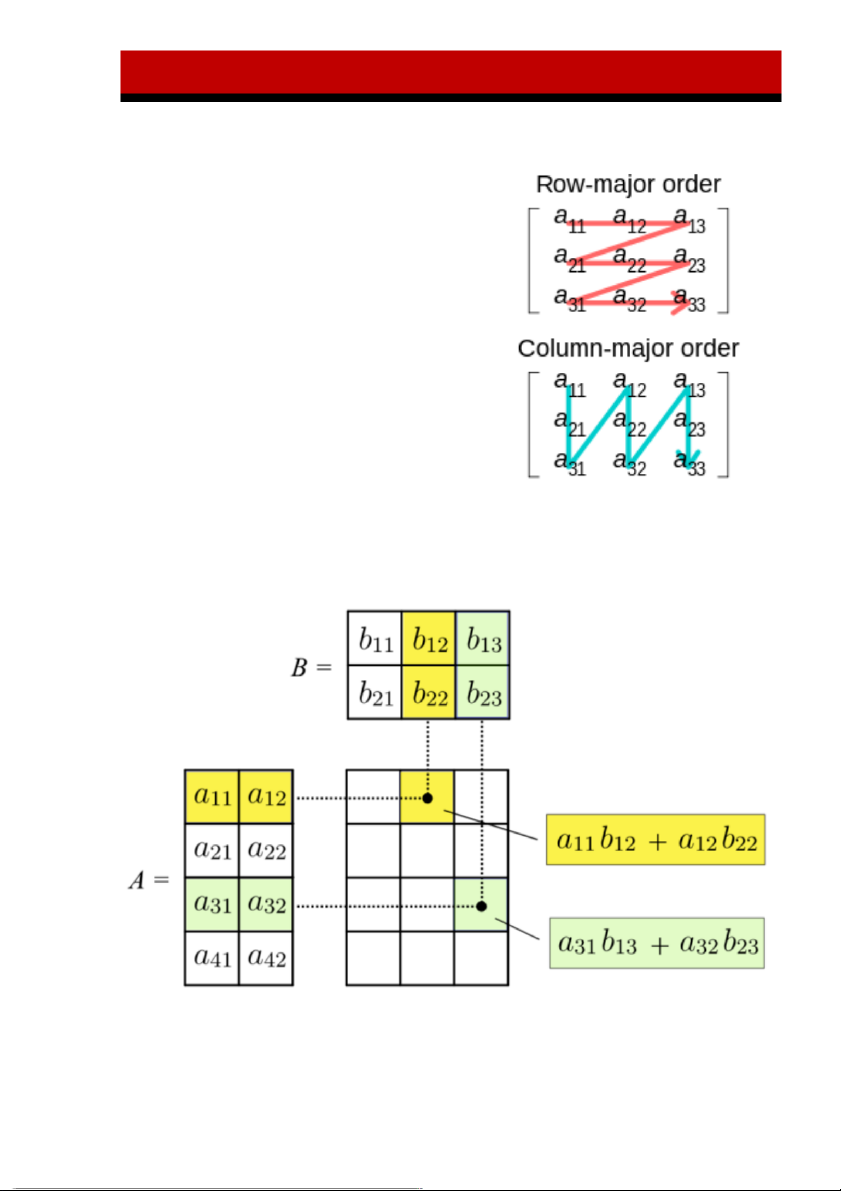
D. PHÉP NHÂN HAI MA TRẬN .................................................................................................................... 6
3. ẢNH ...................................................................................................................................................... .7
A. CẤU TẠO ............................................................................................................................................... 7 B. MA T Ậ R N Ả
NH ....................................................................................................................................... 8 C. MA T Ậ
R N RBG ..................................................................................................................................... 9
D. TENSOR ............................................................................................................................................... 10
4. TIỀN XỬ LÍ ẢNH ................................................................................................................................... 12 B. PHÓNG Ạ Đ I Ả
NH (SCALE) ................................................................................................................... 12 C. DỊCH CHU Ể Y N Ả
NH (TRANSLATION) ................................................................................................. 13
D. XOAY ẢNH (ROTATION) ...................................................................................................................... 14 E. BIẾN Ổ
Đ I AFFINE ................................................................................................................................. 15 5. LỌC Ả
NH .............................................................................................................................................. 17 A. NGUYÊN Ắ
T C CHUNG .......................................................................................................................... 17
IV. KẾT QUẢ ....................................................................................................................................... .18
MỘT SỐ BỘ LỌC LÀM MỊN ẢNH ................................................................................................................ .18
A. LỌC TRUNG BÌNH ................................................................................................................................... 18
B. LỌC GAUSS ............................................................................................................................................. 20
C. LỌC TRUNG VỊ ........................................................................................................................................ 22
D. BỘ LỌC BILATERAL (BỘ LỌC HAI CHIỀU) ............................................................................................ 23
V. THẢO LUẬN ........................................................................................................................................ 24
ĐÁNH GIÁ HIỆU SUẤT ................................................................................................................................. 24
VI. KẾT LUẬN ......................................................................................................................................... 24
CUỐI LỜI .................................................................................................................................................. 25 Trang 2 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT I. TÓM TẮT VỀ MA TRẬN
Ma trận là một công cụ toán học mạnh mẽ, được sử dụng rộng rãi trong xử lý ảnh,
thị giác máy tính, nhận dạng và phân loại đối tượng. Ma trận có thể biểu diễn các dữ
liệu ảnh, thực hiện các phép biến đổi hình học, áp dụng các bộ lọc và thuật toán,
cũng như trích xuất các đặc trưng và thông tin từ ảnh. Ma trận cũng là cơ sở của các
mô hình học máy và học sâu, giúp máy tính có khả năng nhận thức và hiểu ảnh một
cách chính xác và hiệu quả.
II. GIỚI THIỆU ĐỀ TÀI NGHIÊN CỨU 1. Mục đích
Mục đích của đề tài này là để nghiên cứu và trình bày về vai trò và ứng dụng của ma
trận trong xử lý ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng. Đề tài này
nhằm giúp người đọc hiểu được các khái niệm cơ bản của ma trận, các phương pháp
và lý thuyết liên quan, cũng như các ví dụ minh họa về cách sử dụng ma trận để giải
quyết các bài toán thực tế trong lĩnh vực xử lý ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng. 2. Nội dung thực hiện
- Giới thiệu về ma trận, các loại ma trận, các phép toán trên ma trận, và các tính chất của trận.
- Giới thiệu về xử lý ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng, và
các khái niệm cơ bản liên quan.
- Giải thích chi tiết ứng dụng của ma trận trong xử lý ảnh, thị giác máy tính, nhận
dạng và phân loại đối tượng, bao gồm:
§ Biểu diễn ảnh bằng ma trận và các định dạng ảnh phổ biến
§ Thực hiện các phép biến đổi hình học trên ảnh bằng ma trận, như chia tỷ
lệ, xoay, dịch chuyển, phép chiếu, và phép biến đổi affine
§ Áp dụng các bộ lọc và thuật toán trên ảnh bằng ma trận, như bộ lọc trung
bình, bộ lọc Gaussian, bộ lọc Sobel, bộ lọc Laplace, bộ lọc Canny, và thuật toán phân đoạn ảnh.
§ Trích xuất các đặc trưng và thông tin từ ảnh bằng ma trận, như histogram,
gradient, SIFT, SURF, HOG, và PCA
§ Sử dụng các mô hình học máy và học sâu dựa trên ma trận để nhận dạng
và phân loại đối tượng, như k-NN, SVM, mạng nơ-ron nhân tạo, mạng nơ-
ron tích chập, và mạng nơ-ron hồi quy
- Trình bày các kết quả thực nghiệm và đánh giá hiệu quả của các ứng dụng ma
trận trong xử lý ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng, bằng
cách sử dụng các hình ảnh và bảng biểu minh họa. Trang 3 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
3. Phương pháp - Lý thuyế t
- Phương pháp nghiên cứu tài liệu: tìm kiếm, đọc, và tổng hợp các tài liệu liên quan
đến ma trận, xử lý ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng, từ
các nguồn uy tín và chính xác như sách, báo khoa học, web chuyên ngành,…
- Phương pháp thực nghiệm: lập trình và chạy các ứng dựng ma trận trong xử lý
ảnh, thị giác máy tính, nhận dạng và phân loại đối tượng, bằng các sử dụng ngôn
ngữ lập trình Python và các thư viện hỗ trợ khác như NumPy,scikit-learn,
TensorFlow. Sử dụng các bộ dữ liệu ảnh phổ biến và đa dạng như MNIST,
CIFAR-10, ImageNet,…để kiểm tra và đánh giá hiệu quả của các ứng dụng về ma trận.
- Phương pháp phân tích và đánh giá: phân tích và đánh giá các kết quả thực
nghiệm của các ứng dụng ma trận trong xử lý ảnh, thị giác máy tính, nhận dạng
và phân loại đối tượng, bằng cách sử dụng các tiêu chí và chỉ số đo lường, như
độ chính xác, độ nhạy, độ đặc trưng, và thời gian xử lý.
III. ỨNG DỤNG TOÁN HỌC VÀO ĐỀ TÀI 1. Ma trận Định nghĩa:
Ma trận là một cấu trúc dữ liệu hai chiều được sắp xếp thành các hàng và cột, với
mỗi phần tử được xác định bằng chỉ số hàng và cột tương ứng. … … . . . . A = . . . . . . . . … Trang 4 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT Trong đó ma trận A gồm: § m: hàng § n: cột
2. Các phép toán trong ma trận
Cộng hai ma trận có cùng kích thước (cùng số hàng và cột)
Phép nhân vô hướng một số với ma trận là quá trình nhân mỗi phần tử của ma trận với một số hạng. Trang 5 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Ma trận chuyển vị là một ma trận mới
được tạo ra bằng cách đổi chỗ hàng
thành cột và ngược lại của ma trận ban
đầu. Cho một ma trận A và ma trận chuyển vị là
Nhân hai ma trận với điều kiện số cột của ma trận đầu tiên phải bằng số hàng của ma trận thứ hai. Trang 6 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT 3. Ảnh Trong tạo Ảnh kỹ thuật số,
Địa chỉ của một điểm ảnh tương ứng một hay một (tiếng
với tọa độ vật lý ITS. Pixel LCD được Anh: hay , viết tắt
sản xuất trong một mạng lưới hai
) là một điểm vật lý trong
chiều, và được sử dụng dấu chấm hoặc
một hình ảnh raster, hoặc một khối
đại diện hình vuông thông thường,
màu rất nhỏ và là đơn vị cơ bản nhất để
nhưng điểm ảnh CRT tương ứng với cơ
tạo nên một bức ảnh kỹ thuật số.
chế thời gian của chúng và tỷ lệ quét.
Một pixel không có kích thước cố định.
Mỗi điểm ảnh là một mẫu của một hình ảnh ban đầu, nhiều điểm ảnh hơn thường
cung cấp đại diện chính xác hơn của bản gốc. Cường độ của mỗi điểm ảnh có thể
thay đổi. Hình ảnh trong hệ thống màu sắc, màu sắc thường là ba hoặc bốn đại diện
trong lường độ thành phần như màu đỏ, xanh lá cây, và màu xanh, hoặc màu lục lam,
đỏ tươi, màu vàng, và màu đen. Hầu hết các chương trình ứng dụng đồ họa đều diễn
tả độ phân giải của hình ảnh bằng pixel dimensions - kích thước pixel, với số đo chiều ngang đi trước. Trang 7 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Bức ảnh trên kích thước 800 pixel 600 pixel,
có thể biểu diễn dưới dạng một ma trận kích thước 600 800 (vì
định nghĩa ma trận là số hàng nhân số cột). W1,1 W1,2 … W1,800 W2,1 W2,2 … W2,800 … … … … W600,1 W600,2 … W600,800
Trong đó mỗi phần tử wij là một pixel.
Như vậy có thể hiểu là mỗi pixel thì biểu diễn một màu và bức ảnh trên là sự kết hợp
rất nhiều pixel. Hiểu đơn giản thì in bức ảnh ra, kẻ ô vuông như chơi cờ ca rô với
800 đường thẳng ở chiều dài, 600 đường ở chiều rộng, thì mỗi ô vuông là một pixel,
biểu diễn một chấm màu. Trang 8 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT viết tắt của red (đỏ), green (xanh lục), blue (xanh
lam), là ba màu chính của ánh sáng khi
tách ra từ lăng kính. Khi trộn ba màu trên
theo tỉ lệ nhất định có thể tạo thành các màu khác màu.
Với mỗi bộ 3 số r, g, b nguyên trong
khoảng [0, 255] sẽ cho ra một màu khác
nhau. Do có 256 cách chọn r, 256 cách
chọn màu g, 256 cách chọn b.
Tổng số màu có thể tạo ra bằng hệ màu RGB là: 256 256 256 = 16777216 màu.
Để biểu diễn 1 màu ta cần 3 thông số (R, G, B) nên gọi wij = (rij, gij, bij) để biểu
diễn dưới dạng ma trận thì sẽ như sau:
Để tiện lưu trữ và xử lý không thể lưu trong 1 ma trận như thế kia mà sẽ tách mỗi
giá trị trong mỗi pixel ra một ma trận riêng.
Tách ma trận trên thành 3 ma trận cùng kích thước: mỗi ma trận lưu giá trị từng màu khác nhau red, green, blue Trang 9 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT Tổng quát: =>
Mỗi ma trận được tách ra được gọi là 1 channel nên ảnh màu được gọi là 3 channel:
channel red, channel green, channel blue.
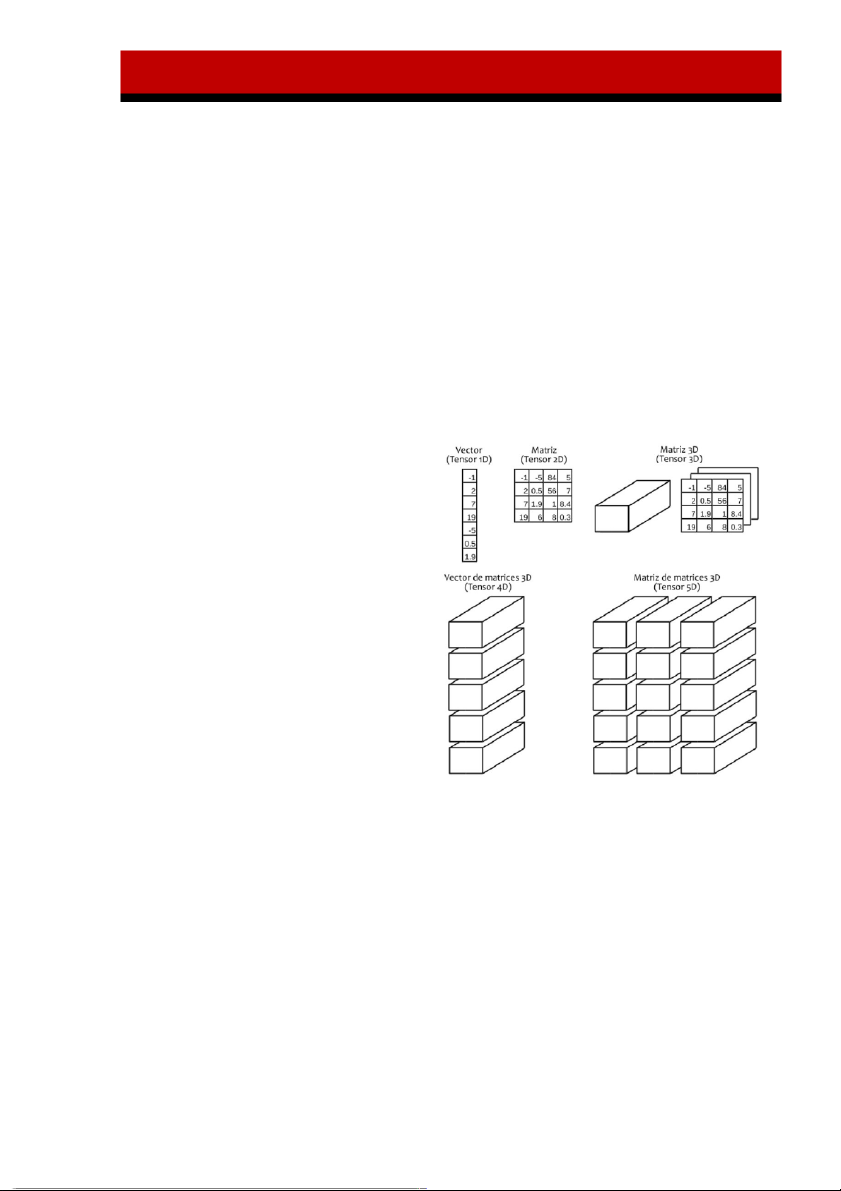
- Khi dữ liệu biểu diễn dạng 1
chiều, người ta gọi là vector,
mặc định khi viết vector sẽ viết dưới dạng cột.
- Khi dữ liệu dạng 2 chiều, người
ta gọi là ma trận, kích thước là số hàng số cột.
- Khi dữ liệu nhiều hơn 2 nhiều
thì sẽ được gọi là tensor, ví dụ
như dữ liệu có 3 chiều.
Để ý thì thấy là ma trận là sự kết hợp
của các vector cùng kích thước. Xếp
n vector kích thước m cạnh nhau thì sẽ được ma trận m n.
Thì tensor 3 chiều cũng là sự kết hợp của các ma trận cùng kích thước, xếp k ma
trận kích thước m n lên nhau sẽ được tensor kích thước m n k.
Do đó biểu diễn ảnh màu trên máy tính ở phần trên sẽ được biểu diễn dưới dạng
tensor 3 chiều kích thước 600 800 3 do có 3 ma trận (channel) màu red, green,
blue kích thước 600 800 chồng lên nhau. Trang 10 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Ví dụ biểu diễn ảnh màu kích thước 28 28, biểu diễn dưới dạng tensor 28 28 3
Tương tự ảnh màu, ảnh xám cũng có
kích thước 800 pixel 600 pixel, có
thể biểu diễn dưới dạng một ma
trận kích thước 600 800 (vì định
nghĩa ma trận là số hàng nhân số cột).
Tuy nhiên mỗi pixel trong ảnh xám
chỉ cần biểu diễn bằng một giá trị
nguyên trong khoảng từ [0,255] thay
vì (r, g, b) như trong ảnh màu. Do đó
khi biểu diễn ảnh xám trong máy tính
chỉ cần một ma trận là đủ. Trang 11 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Giá trị 0 là màu đen, 255 là màu trắng và giá trị pixel càng gần 0 thì càng tối và càng gần 255 thì càng sáng. 0 215 … 250 12 156 … 1 … … … … 244 255 … 12 4. Tiền xử lí ả nh
Đây là tập hợp các phép biến đổi hình ảnh từ một hình dạng này sang một hình
dạng khác thông qua việc làm thay đổi phương, chiều, góc, cạnh mà không làm
thay đổi nội dung chính của bức ảnh. Về mặt lý thuyết toán học một phép biến đổi
được định nghĩa như sao: Định nghĩa:
Mỗi một phép biến đổi hình học sẽ được xác định bởi một ma trận dịch
chuyển (translation matrix) M. Khi đó bất kì 1 điểm có tọa độ (x,y) trên ảnh
gốc thông qua phép biến đổi T sẽ có tọa độ trong không gian mới sau dịch
chuyển là T(x,y) theo công thức:
Scale ảnh là việc chúng ta thay đổi kích
Theo định nghĩa về phép biến đổi hình
thước dài, rộng của ảnh mà không làm
học thì một biến đổi phóng đại các
thay đổi tính chất song song của các
chiều (x, y) theo hệ số (a_{1}, a_{2})
đoạn thẳng trên ảnh gốc so với các trục
sẽ có ma trận dịch chuyển M là ma trận tọa độ X và Y.
đường chéo. Tức là ma trận vuông có
đường chéo chính là [a1,a2] và các
phần tử còn lại bằng 0. Trang 12 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Khi đó phép dịch chuyển sẽ là:
Ví dụ: Ta có 1 bức ảnh 800 x 600 pixels. Sau khi Scale gấp đôi kích thước của nó sẽ là 1600 x 1200 pixels
Ảnh sau khi scale sẽ chỉ thay đổi kích thước, không làm thay đổi nội dung ảnh.
Dịch chuyển ảnh thường được thực hiện trong trường hợp bạn muốn dịch chuyển
ảnh đến các vị trí khác nhau. Ví dụ tới các góc trái, phải, ở giữa, bên trên, bên dưới.
Phép dịch chuyển sẽ giữ nguyên tính chất song song của các đoạn thẳng sau dịch
chuyển đối với các trục X hoặc Y nếu trước dịch chuyển chúng cũng song song với
một trong hai trục này. Để dịch chuyển hình ảnh chúng ta phải xác định được (tx,
ty) là các giá trị di chuyển ảnh theo trục x và y.
Ma trận dịch chuyển M sẽ có dạng như bên dưới:
Giả sử mọi điểm ảnh đều nằm trên không
gian 2 chiều. Khi đó ta coi chiều thứ 3 là
một hằng số, chẳng hạn z=1. Khi đó phép
biến đổi (x,y) bất kì theo ma trận dịch chuyển M sẽ là: Trang 13 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Như vậy mỗi điểm tọa độ (x, y) đã được dịch chuyển tới một tọa độ mới là: (x + tx, y + ty)
Xoay ảnh được hiểu là ta quay một bức ảnh theo một góc xác định quanh một điểm
nào đó. Phép xoay sẽ không đảm bảo tính chất song song với các trục X hoặc Y như
phép dịch chuyển nhưng nó sẽ bảo toàn độ lớn góc. Nếu 3 điểm bất kì tại ảnh gốc
tạo thành một tam giác thì khi biến đổi qua phép xoay ảnh, chúng sẽ tạo thành một
tam giác đồng dạng với tam giác ban đầu.
Phép xoay của một hình ảnh tương
ứng với một góc (***) đạt được bằng
một ma trận dịch chuyển M như sau: Trang 14 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Trong biến đổi affine, toàn bộ các đường thẳng song song trong bức ảnh gốc giữ
nguyên tính chất song song ở ảnh đầu ra. Để tìm ma trận chuyển vị, chúng ta cần
xác định ra 3 điểm từ ảnh đầu vào và tọa độ tương ứng của chúng trong hình ảnh đầu ra. Trang 15 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
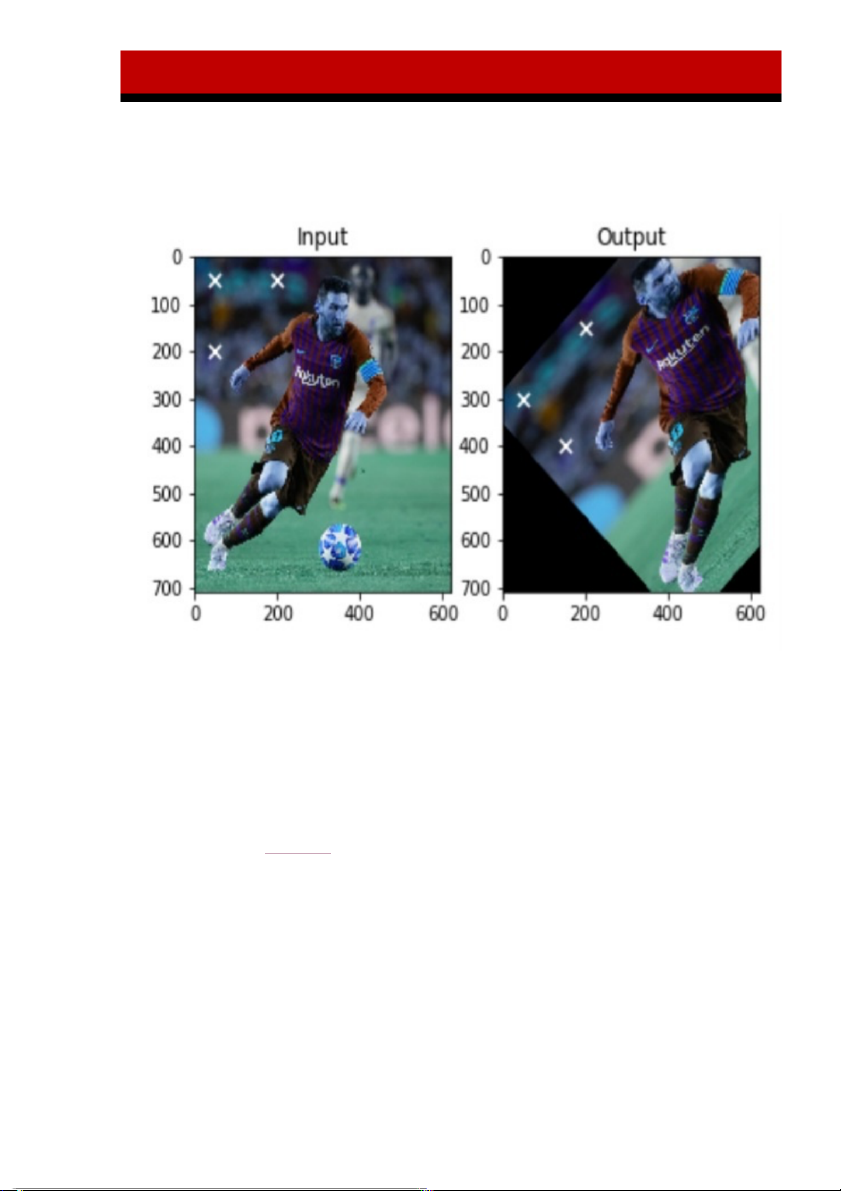
Kiểm tra ví dụ bên dưới, chúng ta cùng nhìn vào các điểm được lựa chọn (được đánh dấu x, màu trắng).
Như vậy sử dụng phép biến đổi Affine có thể giúp ta tạo thành nhiều biến thể, tư thế
khác nhau cho cùng một vật thể. Thường được áp dụng trong Data Augumentation
để làm giàu dữ liệu trong trường hợp số lượng ảnh không nhiều. Chẳng hạn với ảnh
mặt người đang chụp nghiêng ta có thể xoay theo các chiều sao cho từ mặt nghiêng
trở thành mặt chính diện hoặc như trong hình trên, hình ảnh messi đang chạy dáng
nghiêng đã được chuyển sang chạy dáng thẳng đứng và nghiêng với các độ lớn góc khác nhau.
Tham khảo thêm: Tại đây! Trang 16 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT 5. Lọc ả nh
- Nguyên tắc chung của các phương pháp lọc là cho ma trận ảnh nhân với một
ma trận lọc (Kernel). Ma trận lọc lọc (Kernel) còn có thể được gọi là cửa số
chập (trong phép nhân chập), cửa sổ lọc, mặt nạ,… Trong bài viết này tôi sử
dụng thuật ngữ ma trận lọc (Kernel).
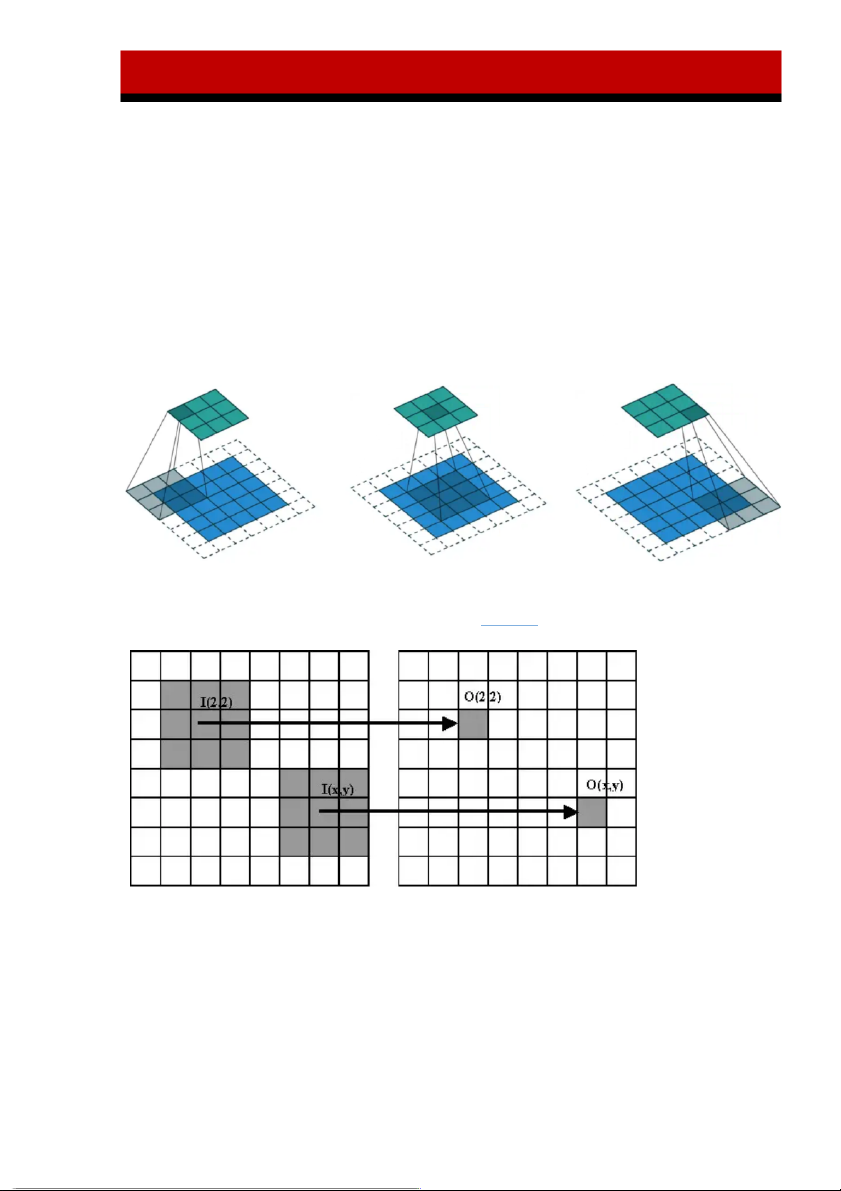
- Việc nhân ảnh với ma trận lọc giống như việc trượt ma trận lọc theo hàng trên
ảnh và nhân với từng vùng của ảnh, cộng các kết quả lại tạo thành kết quả của điểm ảnh trung tâm. Ma trận đầu vào I được nhân với ma trận lọc (phần xám ở hình trái) để tạo thành ma trận đầu ra O. Có 2 phép lọc ảnh là:
§ Tương quan (correlation): ma trận lọc sẽ đượt trượt đi và nhân với từng vùng của ảnh.
§ Tích chập (convolution): ma trận lọc sẽ được xoay 180 độ (theo cả chiều
ngang và dọc) trước khi thực hiện nhân. Trang 17 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
Với mỗi phép lọc ta có những ma trận lọc (Kernel) khác nhau, Với mỗi phép lọc ta
có những ma trận lọc (Kernel) khác nhau.
Khi nhân các phần tử tương ứng với nhau (giữa pixel, các điểm lân cận – các thành
phần trong kernel), đối với các phần tử ở cạnh thì sẽ có một số pixel bị khuyết, lúc
này, có nhiều cách giải quyết như bỏ qua, chèn thêm một (một số) hàng, cột mang
giá trị 0 hoặc bằng giá trị gần nhất, hoặc tạo một đối xứng gương ở cạnh ảnh.
Tổng T các phẩn tử trong ma trận M thường là 1.
§ T > 1: Ảnh sau khi thực hiện xong phép lọc số ảnh (I ) có độ sáng lớn hơn
so với ảnh ban đầu (I ).
§ T < 1: Ảnh sau khi thực hiện xong phép lọc số ảnh (I ) có độ sáng nhỏ hơn
so với ảnh ban đầu (I ).
Một số bộ lọc làm mịn ản h
Được xây dựng dựa trên ý tưởng tính giá trị một điểm ảnh bằng trung bình cộng các điểm ảnh xung quanh nó.
Ma trận lọc của lọc trung bình có dạng:
Cách lọc này thường được áp dụng cho
làm trơn ảnh vẫn muốn giữ lại biên không bị mờ. Trang 18 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
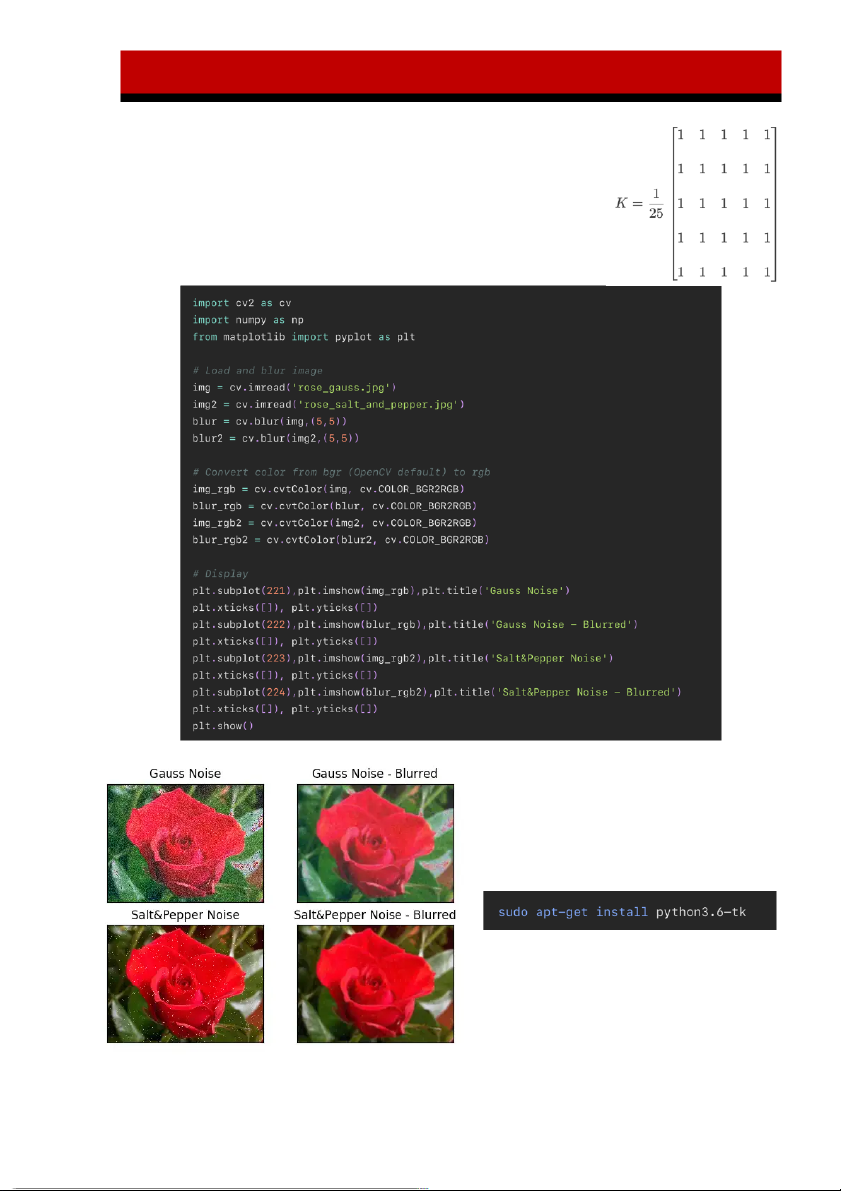
Code với Python - OpenCV: Đoạn code sau sẽ thực hiện lọc
ảnh với ma trận lọc trung bình 5 x 5.
Sau đây là kết quả khi chạy code:
cần cài gói matplotlib (dùng
pip) và tkinter để sử dụng với Python.
Với Python 3.6, việc cài đặt tkinter có thể sử dụng: Trang 19 / 25
BÁO CÁO ĐỒ ÁN CUỐI KỲ TOÁN KỸ THUẬT
§ Thực hiện bằng cách nhân chập ảnh đầu vào với một ma trận lọc Gauss sau
đó cộng chúng lại để tạo thành ảnh đầu ra.
§ Ý tưởng chung là giá trị mỗi điểm ảnh sẽ phụ thuộc nhiều vào các điểm ảnh
ở gần hơn là các điểm ảnh ở xa. Trọng số của sự phụ thuộc được lấy theo hàm
Gauss (cũng được sử dụng trong quy luật phân phối chuẩn)
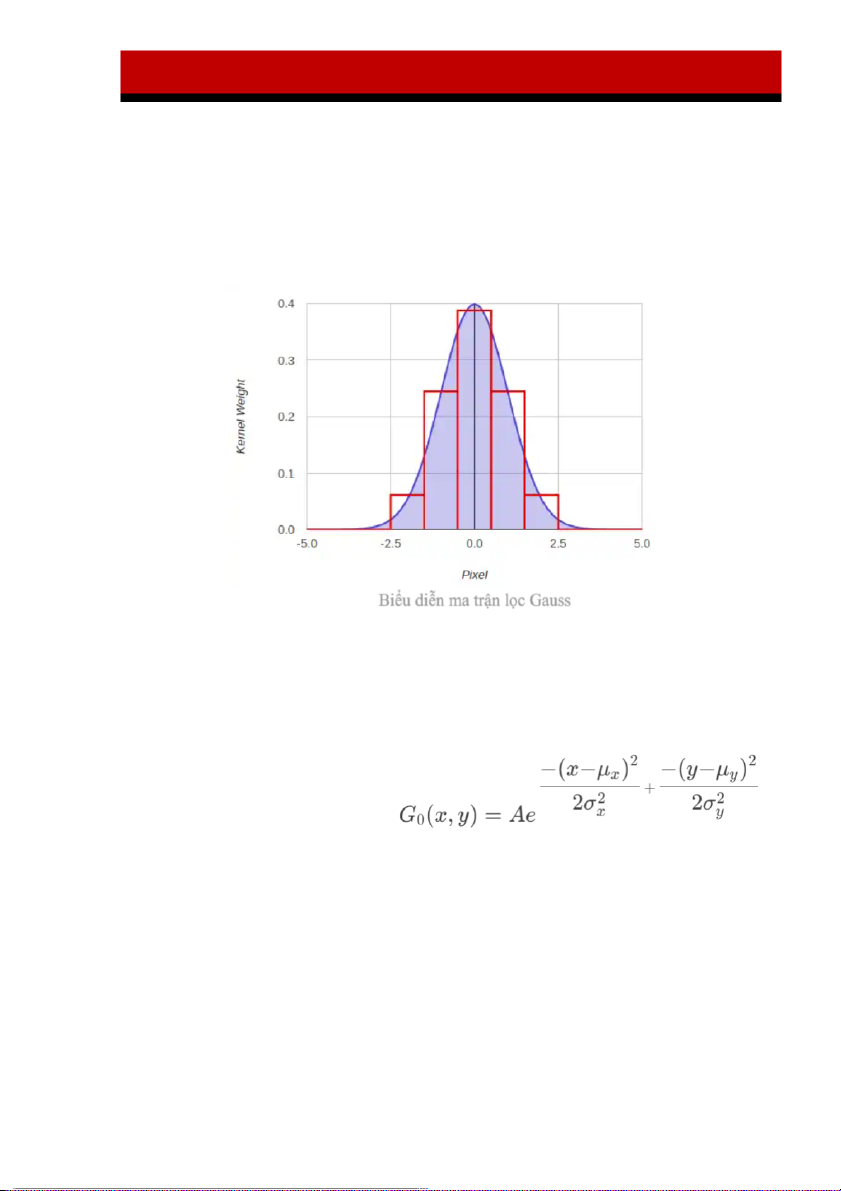
Giả sử ảnh là một chiều. Điểm ảnh ở trung tâm sẽ có trọng số lớn nhất. Các điểm
ảnh ở càng xa trung tâm sẽ có trọng số giảm dần khi khoảng cách từ chúng tới điểm
trung tâm tăng lên. Như vậy điểm càng gần trung tâm sẽ càng đóng góp nhiều hơn
vào giá trị điểm trung tâm.
Trên thực tế, việc lọc ảnh
dựa trên hàm Gauss 2 chiều
(ngang và dọc). Phân phối
chuẩn 2 chiều có thể biểu diễn dưới dạng:
§ Trong đó là trung bình (đỉnh), là phương sai của các biến số x và y.
§ Tham số quyết định tác động của bộ lọc Gauss lên ảnh. Độ lớn của ma trận
lọc (kernel) cần được lựa chọn cho đủ rộng.
Code thực tế lọc Gauss với Python - OpenCV: Trong OpenCV chúng ta sử dụng hàm
sau để lọc Gauss: cv.GaussianBlur(). Trang 20 / 25