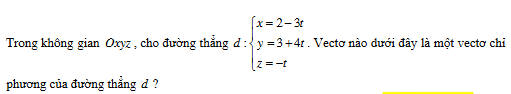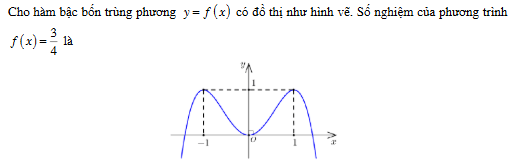Quiz: TOP 41 câu hỏi trắc nghiệm Đề ôn thi tốt nghiệp THPT 2025 toán phát triển minh họa giải chi tiết ( có đáp án ) | Đề thi THPT Quốc Gia
Câu hỏi trắc nghiệm
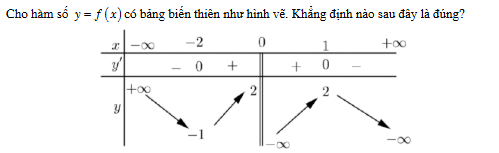
Cho hàm số y = f (x) có bảng biến thiên như hình vẽ, Khẳng định đúng là Hàm số đạt cực tiểu tại x = -2
Trong không gian Oxyz, phương trình mặt cầu tâm I (1;-2;3) bán kính R = 2 là
Trong không gian Oxyz, cho vecto OA = j - 2k. Tọa độ điểm A là (0;1;-2)
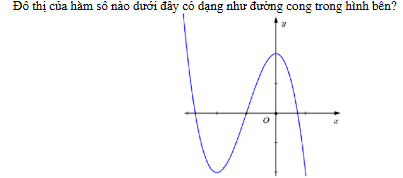
đồ thị của hàm số có dạng cong như hình bên là
Cho cấp số cộng có , . Số hạng bằng 11
Nếu và thì bằng 2
Với là các số thực dương khác 1. Khẳng định đúng là
Diện tích xung quanh của hình trụ tròn xoay có độ dài đường sinh và bán kính đáy được tính bằng công thức
Công thức đúng là
tập xác định D của hàm số y = là D = (-2;2)
Trong không gian , cho mặt phẳng . Vectơ là một vectơ pháp tuyến của (6;−4;3)
Mệnh đề sai là
Cho một khối chóp có thể tích bằng . Khi giảm diện tích đa giác đáy xuống lần thì thể tích khối chóp lúc đó bằng
Nghiệm của phương trình là .
Tập nghiệm của phương trình là .
Hàm số đã cho đồng biến trên khoảng (0;1)
Vecto là 1 vecto chỉ phương của đường thẳng d là .
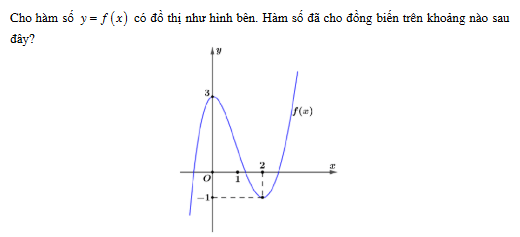
Hàm số đã cho đồng biến trên khoảng
Thể tích của khối lăng trụ có chiều cao bằng và diện tích đáy bằng được tính theo công thức V = Bh
Với là các số dương tuỳ ý, bằng 3lna - lnb
Diện tích toàn phần của hình nón có bán kính đáy và độ dài đường sinh bằng
Hàm số nào đồng biến trên từng khoảng xác định của nó là y =
số phức nghịch đảo của số phức z = 3 + 4i là
Số nghiệm của phương trình là 4
Có cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn xếp kề nhau
Trong không gian , cho điểm và mặt phẳng . Đường thẳng đi qua và vuông góc với có phương trình là
Cho số phức , . phần ảo của số phức
Cho số phức () thỏa mãn và . giá trị của biểu thức . là -8
Cho hàm số có đạo hàm . Hàm số đồng biến trên khoảng (1;2)
Cho hình lăng trụ đều có cạnh đáy bằng 1, cạnh bên bằng 2. Gọi C1 là trung điểm của . cosin của góc giữa hai đường thẳng và
Giá trị lớn nhất của hàm số bằng
Cho . Giá trị của tham số thuộc khoảng
Một con súc sắc cân đối đồng chất được gieo 5 lần. Xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba là
biết z= a + bi là số phức thỏa mãn (3-2i)z - 2iz = 15 - 8i. Tổng a + b là = 9
Cho bằng 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm 0, cạnh a. Cạnh bên SA vuông góc với đáy, góc SBD = 60 độ. Tính theo a khoảng cách giữa hai đường thẳng AB và SO là
Cho F(x) là một nguyên hàm của hàm số f(x) = . Hàm số F (x2 + x) có 5 điểm cực trị
Trong không gian với hệ tọa độ , cho đường thẳng và , . Phương trình mặt cầu đi qua có tâm thuộc đường thẳng là (x+1)2 + (y+1)2 + (z-2)2 = 17
Cho là các số thực lớn hơn 1 thoả mãn x2 - 6y2 . Tính
Câu. Có 6 giá trị nguyên dương của tham số để hàm số đồng biến trên khoảng
Xét () sao cho đồ thị hàm số có 4 điểm cực trị với hoành độ nguyên là . Gọi là hàm số bậc ba đi qua các điểm . Khi diện tích hình phẳng giới hạn bởi đồ thị hai hàm số và hai đường thẳng có diện tích bằng thì , với nguyên dương và phân số tối giản. .