Quiz: Top 20 câu hỏi trắc nghiệm môn Thống kê ứng dụng (có đáp án) | Đại học Kinh Tế - Luật, Đại học Quốc gia Thành phố Hồ Chí Minh
Q2:
Cho bảng kết quả thống kê mô tả từ Stata như sau:
Biến nào có phương sai cao nhất?
Q3:
Cho bảng dữ liệu về chiều cao của 50 SV UEL ngẫu nhiên được chọn như sau:
| Chiều cao (cm) | 140-145 | 145-150 | 150-155 | 155-160 | 160-165 |
| Số lượng | 5 | 10 | 22 | 7 | 6 |
Số yếu vị (mode) của bộ dữ liệu trên là bao nhiêu cm?
Giải thích
Chính xác! Chưa đúngModX = 150 + 5 x (((22-10):((22-10)+(22-7)))= 152,(2)
Bài toán sau dành cho câu 4, 5: Với X (Thu nhập) có kết quả từ phần mềm Stata như sau
Q10:
Một cửa hàng được gọi là có DOANH THU CAO (dt_cao) nếu doanh thu lớn hơn 290 triệu đồng/ngày. Bài toán ước lượng nên được sử dụng trong trường hợp này nếu muốn tìm hiểu về tỷ lệ các cửa hàng có doanh thu cao với độ tin cậy 95% là:
Q11:
Muốn đánh giá trọng lượng trung bình của trẻ sơ sinh, người ta tiến hành điều tra ngẫu nhiên 100 trẻ sơ sinh và thu được kết quả như sau:
Với độ tin cậy 95%, hãy ước lượng phương sai trọng lượng (kg2) của trẻ sơ sinh.
Q15:
Với ý kiến cho rằng thu nhập bình quân tại tỉnh A là 10 triệu đồng/tháng, kết quả kiểm định trên phần mềm Stata như sau
Hãy cho biết p-value là bao nhiêu ?
Q16:
Có ý kiến cho rằng mức chi tiêu trung bình của một người dân tỉnh A ít nhất là 7 triệu đồng/tháng. Kết quả kiểm định trên phần mềm Stata như sau
Tìm đáp án SAI
Q17:
Người ta muốn kiểm tra nhận định tỷ lệ ô tô nước ngoài chiếm 40% nên đã thử trên một mẫu thì được kết quả như sau:
Nhận định nào dưới đây là SAI?
Q19:
Có ý kiến cho rằng có sự khác biệt về thu nhập trung bình của người dân tại 2 tỉnh X và Y. Kết quả kiểm định trên phần mềm Stata như sau
Ta có các phát biểu sau
i. Giá trị kiểm định là -1.7150
ii. pvalue là 0.0863
iii. Chấp nhận H0 với mức ý nghĩa 5%
Đếm số phát biểu SAI
A. 0 B. 1 C. 2 D. 3
Q20:
Có ý kiến cho rằng tỷ lệ sinh viên ra trường có việc làm tại trường X cao hơn trường Y. Kết quả kiểm định trên phần mềm Stata như sau
Ta có các phát biểu sau
i. Giá trị kiểm định là 1.9819
ii. p-value là 0.0475 (X>Y nên là diff >0, p-value 0,0237)
iii. Chấp nhận H0 với mức ý nghĩa 1% (Vì p-value = 0,0237 > 1% nên k có cơ sở bác bỏ Ho)
Đếm số phát biểu SAI
Câu hỏi trắc nghiệm
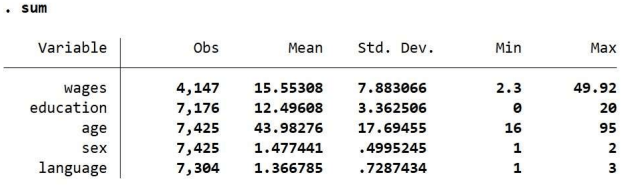
Dữ liệu của câu Q1 thuộc vào thang đo: Định danh (nominal)
Cột Std. Dev. -> age có gía trị lớn nhất
Cho bảng dữ liệu về chiều cao của 50 SV UEL ngẫu nhiên được chọn như sau:
| Chiều cao (cm) | 140-145 | 145-150 | 150-155 | 155-160 | 160-165 |
| Số lượng | 5 | 10 | 22 | 7 | 6 |
Số yếu vị (mode) của bộ dữ liệu trên là bao nhiêu cm?
ModX = 150 + 5 x (((22-10):((22-10)+(22-7)))= 152,(2)
Bài toán sau dành cho câu 4, 5: Với X (Thu nhập) có kết quả từ phần mềm Stata như sau
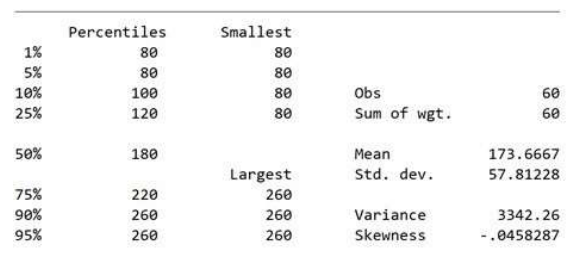
Trung vị (Med) là giá trị đứng ở vị trí giữa trong một dãy số đã được sắp xếp có thứ tự, theo hình
Med là 180 ứng với 50%, và Mean là 173, 6667. Vì Mean < Med -> lệch trái.
CV= S/ (X) = 57,81228 : 173, 6667 = 33,29%
Cho bảng dữ liệu về chiều dài của 50 con cá như sau:
| Chiều dài (mm) | Số lượng |
| 300-350 | 10 |
| 350-400 | 20 |
| 400-450 | 15 |
| 450-500 | 5 |
| Tổng | 50 |
Tính Med (trung vị) (đơn vị mm) của bộ dữ liệu này?
Bảng có 50 con cá, nên khoảng 25 26 sẽ là Med -> trong khoảng từ 350 -400.
Med = 350 + 50 x ((50/2-10)/20) = 387,5
P(420<X<480)= P(-2<Z<2) -> bấm máy tính Distribution – Normal CD với cận dưới -2, cận trên 2,
muy = 0 và xích ma = 1 ra 0,95445. Vậy số sp thỏa là 9544,5. -> A
Bài toán sau dành cho câu 8, 9: Thu nhập (USD/tuần) của các hộ gia đình được tóm tắt trong bảng sau
| Variable | Obs | Mean | Std. dev. | Min | Max |
| thu_nhap | 40 | 143.5 | 40.5 | 80 | 200 |
Áp dụng công thức ước lượng 1 mẫu, trường hợp ước lượng trung bình muy, có phương sai tổng
thể xích ma, có kqua là 143,5 +/- 40,5:(căn bậc hai 40)x1,96 -> D
Sai số : epsilon = 1,96 x 40,5 / (căn bậc 2 của n) = 10 -> n = 63,01 -> lấy ít nhất 64.
Đề hỏi THÊM -> 64 – 40= 24.
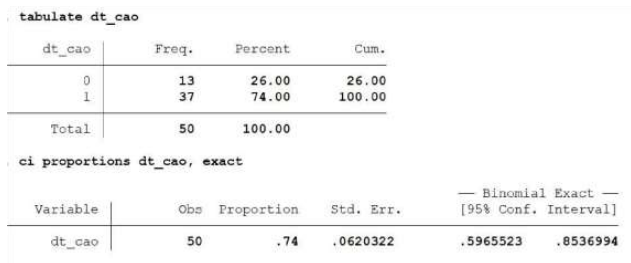
Bảng ở trên thể hiện khảo sát 50 cửa hàng, trong đó 13 cửa hàng có giá trị 0 là k có doanh thu cao và ngược lại với 1. Bảng này đánh lừa, k có liên quan tới câu hỏi.
Bảng thứ 2, cho thấy tỉ lệ cửa hàng có dthu cao, tin cậy 95% ở góc phải. -> A
Tìm S bấm máy tính, nhớ set cái Frequency trước khi vào MODE – 3 – 1 (1-VAR), đối với máy tính 570 (còn 580 tự mò tại k có máy đó) sẽ ra S=0,4983.
Áp dụng công thức ước lượng sẽ đụng tới bảng phụ lục 6 – chi bình phương, làm đúng là khi tra và dùng 2 số 129,6 và 74,22.
Kết quả: 99 x (0,4983)^2 / 129,6 ; 99 x (0,4983)^2 / 74,22
Áp dụng ước lượng 2 mẫu, trường hợp chưa biết phương sai tổng thể nhưng n1 và n2 đều >30.
Sai số epsilon = 1,96 x (căn bậc hai (150^2 /40 + 120^2 /50)) = 57,16…. (ĐTC 95% nên z = 1,96)
KTC cho muy1- muy2 = 1000 – 920 +/- 57,16 = (22.8405; 137.1595)
Sử dụng ước lượng sự khác biệt tỷ lệ 2 tổng thể (p1-p2) f 1 = 52/69 ; f 2 = 120/131; f ngang = (52+120)/(69+131) = 0,86.
Sai số epsilon = căn bậc hai ( f ngang x (1 - f ngang) x (1/n1 + 1/n2)) x z = căn bậc hai ( 0,86 x 0,14 x (1/69 + 1/131) x 1,96 = 0,10116…
Kqua (52/69 – 120/131 – 0,10116; 52/69 – 120/131 + 0,10116).
Update: Có 2 công thức tính trường hợp ‘ước lượng sự khác biệt tỷ lệ 2 tổng thể (p1-p2)’
Nếu mà áp dụng công thức trong giáo trình thống kê thì đáp án sẽ là B.
H (alpha) : muy khác 170.
Theo công thức, bác bỏ Ho nếu t-test < - z hay t-test > z.
Z = 1,96 (vì mức ý nghĩa 5%, tra z của 0.025 ở bảng), trung bình mẫu X ngang = 165,8 ; phương sai mẫu = 8,24697… (bấm máy)
t-test = (165,8 – 170)/(8,24697/ căn 9) = -1,52. Do t-test thuộc (-1,96;1,96) nên là k có căn cứ bác bỏ Ho.
P-value là 0.0375
Theo đề thì Ho là mean >= 7, Ha là mean < 7.
A. Đúng do góc bên phải, z = 6,3246.
B. p-value ở Ha: mean < 7 là 1,0000 lớn hơn mức ý nghĩa alpha 5% -> k bác bỏ đc Ho.
C. Vì B đúng nên C sai.
D. Theo hình.
Về câu B, Ho là p>= 0,4; Ha là p<0,4. Kiểm định p-value theo hình là 0,0357 < 10%. Bác bỏ Ho.
Kết quả kiểm định phương sai trên một mẫu từ phần mềm Stata như sau
| Obs Mean Std. err. Std. dev. [98% conf. interval] | |
| x | 10 . 47.43416 150 . . |
sd = sd(x) c = chi2 = 7.0069
H0: sd = 170 Degrees of freedom = 9
Ha: sd < 170 Ha: sd != 170 Ha: sd > 170
Pr(C < c) = 0.3636 2*Pr(C < c) = 0.7272 Pr(C > c) = 0.6364
Tìm đáp án ĐÚNG
A. 9 -> 7,0069 – S
B. 0,3636 -> 0,7272
C. Đ
D. Obs = 10.
iii. Ho là diff = 0, Ha là diff khác 0. Do p-value là 0,0863 > mức ý nghĩa 0,05 nên không có cơ sở bác bỏ Ho.
Số phát biểu SAI là: 1