Quiz: Top 70 câu trắc nghiệm Chương 2 kĩ thuật lập trình giao tiếp (có đáp án) | Đại học Kinh tế Kỹ thuật Công nghiệp

Dấu ; ở cuối mỗi hàng lệnh cho hiển thị kết quả của hàng lệnh đó. Dấu ; đều dùng để ngăn cách các lệnh.

Phép toán hình thức trong MATLAB được sử dụng Sau khai báo báo biến bằng từ khóa sym hoặc syms

Lệnh solve dùng để: Giải và tìm nghiệm của phương trình đại số

Lệnh diff(S) dùng để tính: Đạo hàm biểu thức symbolic S với biến của đạo hàm tự do

Lệnh diff(S,sym(‘v’)) dùng để tính: Đạo hàm biểu thức symbolic S với biến lấy đạo hàm là biến symbolic v

Lệnh diff(S,n) dùng để tính: Đạo hàm cấp n biểu thức S, n là số nguyên dương

Lệnh syms có nhiệm vụ: Tạo đối tượng (bao gồm cả biến) symbolic

Lệnh sym có nhiệm vụ: Tạo một số, một biến và một đối tượng symbolic

Lệnh int(S) dùng để tính: Tích phân không xác định của biểu thức symbolic S với biến tự do mặc định. Muốn biết biến mặc định ta dùng lệnh fìndsym.

Lệnh int(S,v) dùng để tính: Tích phân không xác định của biểu thức symbolic S với biến tích phân v

Lệnh int(S,a,b) dùng để tính: Tích phân không xác định của biểu thức symbolic S với biến tự do và cận lấy tích phân từ [a,b].

Lệnh int(S,v,a,b) dùng để tính: Tích phân không xác định của biểu thức symbolic S với biến tích phân v và cận lấy tích phân từ [a,b]

Lệnh limit(F) dùng để: Tìm giới hạn của biểu thức F khi a = 0

Lệnh limit(F,x,a) dùng để: Tìm giới hạn của biểu thức F khi x -> a

Lệnh limit(F,a) dùng để: Tìm giới hạn của biểu thức F với biến độc lập

Lệnh limit(F,x,a,‘right’) dùng để: Tìm giới hạn bên trái của biểu thức F

Lệnh laplace(F) dùng để: Lệnh laplace(F) dùng để biến đổi Laplace của hàm F với biến mặc nhiên độc lập t. Nó cho ta một hàm của s.

Lệnh limit(F,x,a,‘left’) dùng để: Tìm giới hạn bên trái của biểu thức F

Lệnh L = laplace(F,t) dùng để: Lệnh L = laplace(F,t) dùng để L là một hàm của t thay thế biến mặc nhiên s.

Lệnh L = laplace(F,w,z) dùng để: Lệnh L = laplace(F,w,z) dùng để L là hàm của z và F là hàm của w, nó thay thế các biến symbolic mặc nhiên s và t tương ứng.

Biến đổi Laplace ngược của hàm symbolic L với biến mặc nhiên độc lập s.
Nó cho ta một hàm của t. Dùng câu lệnh  F = ilaplace(L)

Biến đổi Laplace ngược của hàm symbolic L của F là hàm của y thay thế biến mặc nhiên t. Dùng câu lệnh  F = ilaplace(L,y)

Biến đổi Laplace ngược của hàm symbolic L của F là hàm của x và L là hàm của y, nó thay thế các biến symbolic mặc nhiên t và s. Dùng câu lệnh F = ilaplace(L,y,x)

Tổng của biểu thức symbolic theo biến symbolic k, k được xác định bằng lện findsym từ 0→k -1. Dùng câu lệnh symsum(S)

Tổng của biểu thức symbolic S theo biến symbolic v, v được xác định từ 0 -> k- 1. Dùng câu lệnh symsum(S,v)

Tích phân không xác định của biểu thức symbolic S với biến tích phân v và cận lấy tích phân từ [a,b]. Dùng câu lệnh int(S,v,a,b)

Tích phân không xác định của biểu thức symbolic S với biến tự do và cận lấy tích phân từ [a,b]. Dùng câu lệnh int(S,a,b)

Tích phân không xác định của biểu thức symbolic S với biến tích phân v. Dùng câu lệnh int(S,v)

Đạo hàm biểu thức symbolic S với biến của đạo hàm tự do. Dùng câu lệnh diff(S)

Đạo hàm biểu thức symbolic S với biến lấy đạo hàm là biến symbolic v. Dùng câu lệnh diff(S,‘v’) hay diff(S,sym(‘v’))

Đạo hàm cấp n biểu thức S, n là số nguyên dương. Dùng câu lệnh diff(S,n)

Tổng của biểu thức symbolic S theo symbolic v, v được xác định từ v = a đến v = b. Dùng câu lệnh symsum(S,a,b)

Giải hệ phương trình vi phân thường. Dùng câu lệnh y = dsolve('phương trình')

Giải hệ phương trình đại số phi tuyến. Dùng câu lệnh [biến 1, biến 2, …] = solve('phương trình 1', 'phương trình 2'…)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x y
>> diff(x^3+2*x+5*y, x)
Khi chạy chương trình, kết quả là: 3*x^2 + 2

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x y
>> diff(x^3+2*x+5*y, y)
lOMoAR cPSD|40190299
Khi chạy chương trình, kết quả là: 5

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> diff(x^4+5*x+6, x ,2)
Khi chạy chương trình, kết quả là: 12*x^2

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x y
>> diff(x^5+ 4*x^4+y^2+8*y, x )
Khi chạy chương trình, kết quả là: 5*x^4 + 16*x^3

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x y
>> diff(x^5+ 4*x^4+y^2+8*y, y )
Khi chạy chương trình, kết quả là: 2*y + 8

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> diff(4*x^6+ 2*x^5, x , 2 )
Khi chạy chương trình, kết quả là: 120*x^4 + 40*x^3

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms s t
>> f=sin(s*t);
>> diff(f,t)
Khi chạy chương trình, kết quả là: s*cos(s*t)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms s t
>> f=sin(s*t);
>> diff(f,s)
Khi chạy chương trình, kết quả là: t*cos(s*t)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms s t
>> f=sin(s*t);
>> diff(f,t,2)
Khi chạy chương trình, kết quả là: s^2*sin(s*t) + s^2*cos(s*t)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms s t
>> f=sin(s*t);
>> diff(f,s,2)
Khi chạy chương trình, kết quả là: -t^2*sin(s*t)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> f=sin(5*x);
>> diff(f)
Khi chạy chương trình, kết quả là: 5*cos(5*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> f=sin(5*x);
>> diff(f, 2)
Khi chạy chương trình, kết quả là: -25*sin(5*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> f=cos(5*x);
>> diff(f)
Khi chạy chương trình, kết quả là:  -5*sin(5*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> f=cos(5*x);
>> diff(f,2)
Khi chạy chương trình, kết quả là:  -25*cos(5*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> H=exp(x);
>> int(H)
Khi chạy chương trình, kết quả là: exp(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> H=exp(2*x);
>> int(H)
Khi chạy chương trình, kết quả là: exp(2*x)/2

Giải phương trình bậc 2 sau: b² +8c+2b=0 dùng câu lệnh solve('b^2+8*c+2*b=0')

Giải phương trình bậc 2 sau: b² +8c+2b=0 theo ẩn b dùng câu lệnh solve('b^2+8*c+2*b=0','b')

Giải phương trình bậc 2 sau: b² +8c+2b=0 theo ẩn c dùng câu lệnh solve('b^2+8*c+2*b=0','c')

Giải hệ phương trình sau: 4 y + 2 x - 1 = 0  dùng câu lệnh [x y] = solve('3*x+y+1', '4*y+2*x-1')

Trong cửa sổ Command Window của MATLAB thực hiện lệnh sau:
>> diff(sin(xy^2),x,2)
Khi chạy chương trình, kết quả là: Lỗi

Giải nhiều hệ phương trình, dùng câu lệnh solve('f(x)', 'g(x)', 'h(x)',…)

Giải theo biến được chỉ định là a, dùng câu lệnh solve(f,a)

Giải phương trình, dùng câu lệnh solve

Giải hệ phương trình sau: 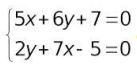 dùng câu lệnh [x y] = solve('5*x+6*y+7', '2*y+7*x-5')

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> H=2*exp(2*x);
>> int(H)
Khi chạy chương trình, kết quả là: exp(2*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> g=exp(x)*cos(x);
>> diff(g)
Khi chạy chương trình, kết quả là: exp(x)*cos(x) - exp(x)*sin(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> g=exp(x)*sin(x);
>> diff(g)
Khi chạy chương trình, kết quả là: exp(x)*cos(x) + exp(x)*sin(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> diff(x^5+4*x^4+5*y+8, x , 2)
Khi chạy chương trình, kết quả là: 20*x^3 + 48*x^2

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> g=cos(2*x);
>> diff(g)
Khi chạy chương trình, kết quả là:  -2*sin(2*x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> g=cos(x)+sin(x);
>> diff(g)
Khi chạy chương trình, kết quả là:  cos(x) - sin(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> H=cos(x);
>> int(H)
Khi chạy chương trình, kết quả là: sin(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x
>> H=sin(x);
>> int(H)
Khi chạy chương trình, kết quả là: -cos(x)

Trong cửa sổ Command Window của MATLAB thực hiện các lệnh sau:
>> syms x y
>> diff(x^3+2*x+5*y, x,3)
Khi chạy chương trình, kết quả là: 6

Giải hệ phương trình sau: 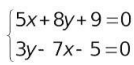dùng câu lệnh [x y] = solve('5*x+8*y+9', '3*y-7*x-5')

Giải hệ phương trình sau: 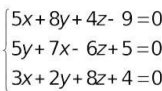dùng câu lệnh [x y z] = solve('5*x+8*y+4*z-9', '5*y+7*x-6*z+5', '3*x+2*y+8*z+4')