102 trang 88 lượt tải

05 đề ôn thi tốt nghiệp THPT năm 2025 môn Toán bám sát đề minh họa có đáp án

175

05 đề ôn thi tốt nghiệp THPT năm 2025 môn Toán bám sát đề minh họa có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 102 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem

Chủ đề: Đề thi THPTQG môn Toán năm 2025 340 tài liệu

Môn: Toán 2.2 K tài liệu

Tác giả:

Kim Ngân Lê

1 tháng trước

Danh sách Quiz

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 1

ĐỀ ÔN THI TỐT NGHIỆP THPT BÁM SÁT ĐỀ MINH HOẠ NĂM 2025

MÔN TOÁN

Thời gian 90 phút

ĐỀ SỐ 1

PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Họ nguyên hàm của hàm số





4 cos2

f x x

 

là

4 sin2

ln4 2

 

. B.

sin2

4 ln4

 

sin2

4 ln4

 

. D.

4 sin 2

ln4 2

 

Câu 2. Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số





y f x



, trục hoành, đường thẳng

x a x b

 

(như hình vẽ bên). Hỏi cách tính

nào dưới đây đúng?

 

S f x dx





. B.

   

c b

a c

S f x dx f x dx

 

 

   

c b

a c

S f x dx f x dx

  

 

. D.

   

c b

a c

S f x dx f x dx

 

 

Câu 3. Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi phân xưởng

cho như

Tuổi thọ (năm)

[1,5;2)

[2;2,5)

[2,5;3)

[3;3,5)

[3,5;4)

Số linh kiện của phân xưởng

4 9 13 8 6

Tính phương sai của mẫu số liệu ghép nhóm trên

0,145

. B.

0,245

. C.

0,445

. D.

0,355

Câu 4. Trong không gian

Oxyz

, cho ba điểm









2; 2;3 ; 1;3;4

A B

và





3; 1;5

C 

. Đường thẳng đi

qua

và song song với

có phương trình là:

2 4 1

2 2 3

x y z

  

 



2 2 3

2 4 1

x y z

  

 



2 2 3

4 2 9

x y z

  

 

2 2 3

2 4 1

x y z

  

 



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 2

Câu 5. Trong không gian

Oxyz

, cho mặt phẳng

( ):3 2 1 0

P x y z

   

. Véc tơ nào dưới đây là một

véc tơ pháp tuyến của

( )

( 3;1;2)

n  



. B.

n =(3;-1;2).

n =(3:1;2) .

n =(3;1;-2) .

Câu 6. Cho hàm số

(c 0, 0)

ax b

y ad bc

cx d



   



có đồ thị như hình vẽ.

Đồ thị hàm số đã cho có đường tiệm cận đứng bằng:



. B.

 

. C.



. D.

 

Câu 7. Tập nghiệm của bất phương trình

2 5



là





;log 5

 . B.





log 2;



. C.





;log 2

 . D.





log 5;



Câu 8. Nghiệm của phương trình





log 5 3



là



. B.



. C.



. D.



Câu 9. Cho hình chóp

S ABCD

có





SA ABCD

 và đáy

ABCD

là hình vuông. Từ

kẻ

AM SB



Khẳng định nào sau đây đúng?





AM SBD

 . B.





AM SBC

 . C.





SB MAC

 . D.





AM SAD

 .

Câu 10. Cho cấp số cộng





với



và công sai



. Giá trị của

bằng

. B.

. C.

. D.

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 3

Câu 11. Cho hình hộp

. ' ' ' '

ABCD A B C D

Chọn đẳng thức vectơ đúng:

' '

AC AB AB AD

  

   

. B.

' '

DB DA DD DC

  

   

AC AC AB AD

  

   

. D.

DB DA DD DC

  

   

Câu 12. Cho hàm số





f x

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

A. 3. B. -5. C. 0. D. 2.

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 1. Cho hàm số

2 1

( ) 2

f x e x



 

a) Hàm số đã cho có tập xác định





0;D

 

b) Đạo hàm của hàm số đã cho là

2 1

( ) 2 2

f x e





 

c) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn





0;2

lần lượt là



và

d) Tập nghiệm của bất phương trình

( ) 0

f x





là

;

 







 

Câu 2. Sau khi xuất phát, xe đạp di chuyển với tốc độ





2,01 0,025

v t t t

  , với

0 10

 

. Trong đó





v t

tính theo





m/s

, thời gian

tính theo

với



là thời điểm xe đạp xuất phát.

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang

a) Quãng đường xe đạp di chuyển được tính theo công thức là









2,01 0,05 0 10

s t t t   

b) Quãng đường xe đạp di chuyển được trong 3 giây là





8,82

c) Quãng đường xe đạp di chuyển được trong giây thứ 9 xấp xỉ





15,28

(kết quả làm tròn đến phần

trăm của mét).

d) Trong khoảng thời gian không quá 10s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe đạp là





2,51 /

m s

Câu 3. Một căn bệnh có 2% dân số mắc phải. Một phương pháp chẩn đoán được phát triển có tỷ lệ

chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số

trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 97%. Lấy một người đi

kiểm tra.

a) Xác suất để người đó mắc bệnh khi chưa kiểm tra là

0,02

b) Xác suất kết quả dương tính nếu người đó mắc bệnh là

0,99

c) Xác suất kết quả dương tính nếu người đó không mắc bệnh là

0,02

d) Biết rằng đã có kết quả chuẩn đoán là dương tính, xác suất để người đó thực sự bị bệnh là

0,35.

Câu 4. Một khu vực đã được thiết lập một hệ trục tọa độ

Oxyz

(đơn vị trên mỗi trục là mét). Một

flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu có phương trình

       

2 2 2

: 30 20 10 900

S x y z      . Bạn Trúc Linh đang sử dụng sử dụng máy tính tại điểm

nằm trên đường tròn





là giao của mặt cầu





và mặt đất. Biết mặt đất bằng phẳng và có phương

trình





: 0

P z



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 5

a) Mặt cầu





có toạ độ tâm và bán kính là





30; 20; 10

I    ,





R m

 .

b) Flycam cách mặt đất

mét.

c) Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn





là

14,14

mét (kết quả làm tròn đến hai chữ

số hàng thập phân của mét).

d) Đường tròn





có toạ độ tâm là





30;20;0

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này

với số vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1

áo, loại ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng ước tính nhu cầu của

khách không quá 100 cái cho cả 2 loại. Cửa hàng kinh doanh thu lãi lớn nhất được bao nhiêu triệu đồng?

Câu 2. Trường Lê Hồng Phong – Tây Hòa muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt

đất đến đỉnh là

2,25

mét, chiều rộng tiếp giáp với mặt đất là

mét. Giá thuê công nhân làm mỗi mét

vuông là

1,5

triệu đồng. Vậy số tiền nhà trường phải trả bao nhiêu triệu đồng ?

Câu 3. Mỗi chuyến xe buýt của hãng xe Phương Trang có sức chứa tối đa là

hành khách. Nếu một

chuyến xe buýt chở

hành khách thì giá tiền cho mỗi hành khách là

20 3

 



 

 

(nghìn đồng). Hỏi mỗi

chuyến xe buýt chở bao nhiêu hành khách thì hãng xe Phương Trang thu được số tiền nhiều nhất?

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang

Câu 4. Cho hộp

gồm

bi trắng và 5 bi đỏ, hộp

gồm

bi trắng và 4 bi đỏ. Bỏ ngẫu nhiên hai bi từ

hộp

sang hộp

. Sau đó lấy ngẫu nhiên từ hộp

một bi. Giả sử lấy được viên bi trắng. Tính xác suất

để lấy được bi trắng từ hộp

(kết quả làm tròn đến hàng phần trăm).

Câu 5. Cho hình lăng trụ đều

ABC A B C

  

có tất cả các cạnh có độ dài bằng 2 (tham khảo hình vẽ).

Tính khoảng cách giữa hai đường thẳng



và

A B



(làm tròn kết quả đến chữ số thập phân thứ nhất).

Câu 6. Giả sử Trái Đất có dạng hình cầu bán kính bằng

.10

m. Bạn Minh Hiền đang đứng trên mặt

đất. Có 3 vệ tinh báo về máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách Minh Hiền

3.10

vệ tinh thứ hai đang cách Minh Hiền

4.10

m và vệ tinh thứ ba đang cách Minh Hiền

5.10

m. Biết rằng

trong hệ trục toạ độ Oxyz (1 đơn vị =

m) cho trước với O là tâm Trái Đất, tại thời điểm vệ tinh thông

báo về máy chủ thì toạ độ của các vệ tinh lần lượt là









1 2

4;4;6 , 8;4;3

M M và





4;9;3

M . Biết tọa độ

vị trí của bạn Minh Hiền là





; ;

M x y z

. Tính giá trị biểu thức

2 3 4

T x y z

  

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 8

LỜI GIẢI CHI TIẾT

PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Họ nguyên hàm của hàm số





4 cos2

f x x

 

là

4 sin2

ln4 2

 

. B.

sin2

4 ln4

 

sin2

4 ln4

 

. D.

4 sin 2

ln4 2

 

Lời giải

Chọn D.

Ta có

 

4 sin2

4 cos2

ln4 2

x dx C

   



Câu 2. Gọi

là diện tích hình phẳng giới hạn bởi đồ thị hàm số





y f x



, trục hoành, đường thẳng

x a x b

 

(như hình vẽ bên). Hỏi cách tính

nào dưới đây đúng?

 

S f x dx





. B.

   

c b

a c

S f x dx f x dx

 

 

   

c b

a c

S f x dx f x dx

  

 

. D.

   

c b

a c

S f x dx f x dx

 

 

Lời giải

Chọn B.

   

c b

a c

S f x dx f x dx

 

 

Câu 3. Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi phân xưởng

cho như

Tuổi thọ (năm)

[1,5;2)

[2;2,5)

[2,5;3)

[3;3,5)

[3,5;4)

Số linh kiện của phân xưởng

4 9 13 8 6

Tính phương sai của mẫu số liệu ghép nhóm trên

0,145

. B.

0,245

. C.

0,445

. D.

0,355

Lời giải

Chọn D.

Ta có bảng số liệu với giá trị đại diện:

Tuổi thọ (năm)

[1,5;2)

[2;2,5)

[2,5;3)

[3;3,5)

[3,5;4)

Giá trị đại diện

1,75

2,25

2,75

3,25

3,75

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 9

Số linh kiện của phân xưởng

4 9 13 8 6

Tổng số linh kiện:

4 9 13 8 6 40

     

Giá trị trung bình

1,75.4 2,25.9 2,75.13 3,25.8 3,75.6 223

4 9 13 8 6 80

   

 

   

Phương sai:

 

2 2 2 2 2 2

1 223 2271

1,75 .4 2,25 .9 2,75 .13 3,25 .8 3,75 .6 0,355

40 80 6400

 

       

 

 

Câu 4. Trong không gian

Oxyz

, cho ba điểm









2; 2;3 ; 1;3;4

A B

và





3; 1;5

C 

. Đường thẳng đi

qua

và song song với

có phương trình là:

2 4 1

2 2 3

x y z

  

 



2 2 3

2 4 1

x y z

  

 



2 2 3

4 2 9

x y z

  

 

2 2 3

2 4 1

x y z

  

 



Lời giải

Chọn D.

Véctơ chỉ phương của đường thẳng cần tìm:





2; 4;1

BC  



Phương trình cần tìm là:

2 2 3

2 4 1

x y z

  

 



Câu 5. Trong không gian

Oxyz

, cho mặt phẳng

( ) :3 2 1 0

P x y z

   

. Véc tơ nào dưới đây là một

véc tơ pháp tuyến của

( )

( 3;1;2)

n  



. B.

n =(3;-1;2).

n =(3:1;2) .

n =(3;1;-2) .

Lời giải

Chọn B.

Véc tơ pháp tuyến của

( )

là:

(3; 1;2)

n  



Câu 6. Cho hàm số

(c 0, 0)

ax b

y ad bc

cx d



   



có đồ thị như hình vẽ.

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 10

Đồ thị hàm số đã cho có đường tiệm cận đứng bằng:



. B.

 

. C.



. D.

 

Lời giải

Chọn A.

Từ đồ thị hàm số ta thấy: hàm số đã cho có một tiệm cận đứng



Câu 7. Tập nghiệm của bất phương trình

2 5



là





;log 5

 . B.





log 2;



. C.





;log 2

 . D.





log 5;



Lời giải

Chọn D.

Ta có:

2 5 log 5

x  

. Tập nghiệm của bất phương trình là





log 5;S

 

Câu 8. Nghiệm của phương trình





log 5 3



là



. B.



. C.



. D.



Lời giải

Chọn A.

Ta có:





log 5 3



5 2 5 8

x x

   

 

Câu 9. Cho hình chóp

S ABCD

có





SA ABCD

 và đáy

ABCD

là hình vuông. Từ

kẻ

AM SB



Khẳng định nào sau đây đúng?





AM SBD

 . B.





AM SBC

 . C.





SB MAC

 . D.





AM SAD

 .

Lời giải

Chọn B.









SA ABCD SA BC   .

ABCD

là hình vuông nên





BC AB .

Từ

















1 , 2 3

BC SAB BC AM    .

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 11

Theo giả thiết, ta có





AM SB .

Từ













3 , 4

AM SBC

  .

Câu 10. Cho cấp số cộng





với



và công sai



. Giá trị của

bằng

. B.

. C.

. D.

Lời giải

Chọn A.

Ta có

2 1

7 4 11

u u d

    

Câu 11. Cho hình hộp

. ' ' ' '

ABCD A B C D

Chọn đẳng thức vectơ đúng:

' '

AC AB AB AD

  

   

. B.

' '

DB DA DD DC

  

   

AC AC AB AD

  

   

. D.

DB DA DD DC

  

   

Lời giải

Chọn B.

Theo quy tắc hình hộp ta có

' '

DB DA DD DC

  

   

Câu 12. Cho hàm số





f x

có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

A. 3. B. -5. C. 0. D. 2.

Lời giải

Chọn B.

Dựa vào bảng biến thiên ta có giá trị cực tiểu của hàm số bằng



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 12

PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn

đúng hoặc sai.

Câu 1. Cho hàm số

2 1

( ) 2

f x e x



 

a) Hàm số đã cho có tập xác định





0;D

 

b) Đạo hàm của hàm số đã cho là

2 1

( ) 2 2

f x e





 

c) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn





0;2

lần lượt là



và

d) Tập nghiệm của bất phương trình

( ) 0

f x





là

;

 







 

Lời giải

a) b) c) d)

SAI ĐÚNG ĐÚNG SAI

a) Hàm số đã cho có tập xác định





  

2 1 2 1

( ) 2 ( ) 2 2

x x

f x e x f x e

 



    

d) Hàm số đã cho xác định và liên tục trên





0;2

2 1 2 1

( ) 2 ( ) 2 2

x x

f x e x f x e

 



    

ta có:

2 1 2 1

( ) 0 2 2 0 1

x x

f x e e x

 



       

 

(0)

2 4

f e



 



 

 

 

Do đó:

[0;2]

max ( ) (2) 4

min ( ) 0

f x f e

f x f



  

 

 

 

 

Vậy giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn





0;2

lần lượt là



và

d) Ta có

2 1

( ) 0

2 2 0

2 1 0

f x







  

 

  

 

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 13

Vậy tập nghiệm của bất phương trình

( ) 0

f x





là

;

 







 

Câu 2. Sau khi xuất phát, xe đạp di chuyển với tốc độ





2,01 0,025

v t t t

  , với

0 10

 

. Trong đó





v t

tính theo





m/s

, thời gian

tính theo

với



là thời điểm xe đạp xuất phát.

a) Quãng đường xe đạp di chuyển được tính theo công thức là









2,01 0,05 0 10

s t t t   

b) Quãng đường xe đạp di chuyển được trong 3 giây là





8,82

c) Quãng đường xe đạp di chuyển được trong giây thứ 9 xấp xỉ





15,28

(kết quả làm tròn đến phần

trăm của mét).

d) Trong khoảng thời gian không quá 10s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe đạp là





2,51 /

m s

Lời giải

a) b) c) d)

SAI ĐÚNG ĐÚNG SAI

a) Quãng đường xe đạp di chuyển được phải là nguyên hàm của





v t

Khi đó









2,01 0,05 0 10

v t t t



   

là công thức tính gia tốc của vật.

b) Quãng đường xe đạp di chuyển được trong 3s là:

 

2 3

2,01 0,025

2,01 0,025 8,82

2 3

t t

t t dt m

 

   

 

 



c) Quãng đường xe đạp di chuyển được trong giây thứ 9

   

 

2 3

2,01 0,025

9 8 2,01 0,025 15,28

2 3

t t

s s t t dt m

 

     

 

 



d) Ta có:













 

0;10

2,01 0,025 0 10 max 17,6 /

v t t t t v t m s

     

khi





t s



Gia tốc xe đạp khi đó là













10 10 2,01 0,05.10 1,51 /

a v m s



   

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 14

Câu 3. Một căn bệnh có 2% dân số mắc phải. Một phương pháp chẩn đoán được phát triển có tỷ lệ

chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số

trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 97%. Lấy một người đi

kiểm tra.

a) Xác suất để người đó mắc bệnh khi chưa kiểm tra là

0,02

b) Xác suất kết quả dương tính nếu người đó mắc bệnh là

0,99

c) Xác suất kết quả dương tính nếu người đó không mắc bệnh là

0,02

d) Biết rằng đã có kết quả chuẩn đoán là dương tính, xác suất để người đó thực sự bị bệnh là

0,35.

Lời giải

a) b) c) d)

ĐÚNG ĐÚNG SAI SAI

a) Gọi

là biến cố “người đó mắc bệnh”

Xác suất để người đó mắc bệnh khi chưa kiểm tra:





2% 0,02

P A  

b) Gọi

là biến cố “kết quả kiểm tra người đó là dương tính”

Xác suất kết quả dương tính nếu người đó mắc bệnh là:





| 99% 0,99

P B A  

c) Xác xuất kết quả âm tính nếu người đó không mắc bệnh là:





| 97% 0,97

P B A  

Xác suất kết quả dương tính nếu người đó không mắc bệnh là:









| 1 | 1 0,97 0,03

P B A P B A    

d) Do đó xác suất để người đó không mắc bệnh khi chưa kiểm tra:





1 0,02 0,98

P A   

Xác suất để người đó thực sự bị bệnh là:

 









   

. |

0,02.0,99 33

| 0,402.

0,02.0,99 0,98.0,03 82

. | . |

P A P B A

P A B

P A P B A P A P B A

   



Câu 4. Một khu vực đã được thiết lập một hệ trục tọa độ

Oxyz

(đơn vị trên mỗi trục là mét). Một

flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu có phương trình

       

2 2 2

: 30 20 10 900

S x y z      . Bạn Trúc Linh đang sử dụng sử dụng máy tính tại điểm

nằm trên đường tròn





là giao của mặt cầu





và mặt đất. Biết mặt đất bằng phẳng và có phương

trình





: 0

P z



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 15

a) Mặt cầu





có toạ độ tâm và bán kính là





30; 20; 10

I    ,





R m

 .

b) Flycam cách mặt đất

mét.

c) Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn





là

14,14

mét (kết quả làm tròn đến hai chữ

số hàng thập phân của mét).

d) Đường tròn





có toạ độ tâm là





30;20;0

Lời giải

a) b) c) d)

ĐÚNG SAI SAI ĐÚNG

a) Mặt cầu





có tâm





30;20;10

I và có bán kính





R m



b) Khoảng cách Flycam đến mặt đất chính là khoảng cách từ tâm

đến





: 0

P z



Do đó:













, 10

d I P m



c) Gọi

là tâm của đường tròn





. Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn





chính

là

Ta có:

 

2 2 2 2

, 900 100 10 2 14,14

MJ R IJ R d I P m

 

       

 

d) Gọi

là hình chiếu vuông góc của

trên





Ta có:









30;20;0

J P J 

Vậy đường tròn





có toạ độ tâm là





30;20;0

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 16

PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.

Câu 1. Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này

với số vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1

áo, loại ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng ước tính nhu cầu của

khách không quá 100 cái cho cả 2 loại. Cửa hàng kinh doanh thu lãi lớn nhất được bao nhiêu triệu đồng?

Lời giải

Đáp án:

13,8

Gọi

x y

(cái) lần lượt là số áo dài tay và ngắn tay mà cửa hàng nên mua để kinh doanh có lãi nhất.

Điều kiện: 0, 0, ,x y x y

  



Theo yêu cầu bài toán, ta có hệ bất phương trình

100

8 6 720

x y













 



 



Ta cần tìm

x y

để biểu thức

150.000 120.000

F x y

 

đạt GTLN trên miền nghiệm của hệ trên

Biểu diễn miền nghiệm của hệ bất phương trình trên

Miền nghiệm là tứ giác

OABC

Các điểm có tọa độ như sau:

(0;0)

(0;100)

(60;40)

(90;0)

Tại

(0;0)



Tại

(0;100)

12.000.000



Tại

(60;40)

13.800.000



Tại

(90;0)

13.500.000



Vậy cửa hàng nên nhập 60 áo dài tay và 40 áo ngắn tay để kinh doanh thì có lãi nhất và lãi thu được là

13.800.000 đồng hay

13,8

triệu đồng

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang

Câu 2. Trường Lê Hồng Phong – Tây Hòa muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt

đất đến đỉnh là

2,25

mét, chiều rộng tiếp giáp với mặt đất là

mét. Giá thuê công nhân làm mỗi mét

vuông là

1,5

triệu đồng. Vậy số tiền nhà trường phải trả bao nhiêu triệu đồng ?

Lời giải

Đáp án:

6,75

Gọi phương trình parabol





P y ax bx c

  

. Do tính đối xứng của parabol nên ta có thể chọn hệ trục

tọa độ

Oxy

sao cho





có đỉnh

I Oy



(như hình vẽ).

 

 

 

 



 

 

 

 

 



Ta có hệ phương trình:

 

9 3

4 2

9 3

4 2

c I P

a b c A P

a b c B P



 



   





   











  











Vậy

 

P y x

  

Dựa vào đồ thị, diện tích cửa parabol là:

S x x



 

  

 

 



2 d

x x

 

  

 

 



3 4

 



 

 

 



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 18

Số tiền phải trả là:

1,5 6,75

 đồng.

Câu 3. Mỗi chuyến xe buýt của hãng xe Phương Trang có sức chứa tối đa là

hành khách. Nếu một

chuyến xe buýt chở

hành khách thì giá tiền cho mỗi hành khách là

20 3

 



 

 

(nghìn đồng). Hỏi mỗi

chuyến xe buýt chở bao nhiêu hành khách thì hãng xe Phương Trang thu được số tiền nhiều nhất?

Lời giải

Đáp án:

Số tiền thu được là :

 

20 3 20 9

40 1600 20

x x

f x x x x

 

    

 

 

(nghìn đồng)

Xét hàm số:

 

20 9

1600 20

f x x x

 

  

 

 

với

0 50

 

 

3 3

' 20 9

1600 10

f x x

 

  

 

 





 

' 0

3 3

9 0

1600 10

120

f x

x N

x L



   













Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy: GTLN của





f x

là

3200

khi



Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 19

Vậy một chuyến xe buýt thu được số tiền nhiều nhất là

3200

nghìn đồng khi có

hành khách.

Câu 4. Cho hộp

gồm

bi trắng và 5 bi đỏ, hộp

gồm

bi trắng và 4 bi đỏ. Bỏ ngẫu nhiên hai bi từ

hộp

sang hộp

. Sau đó lấy ngẫu nhiên từ hộp

một bi. Giả sử lấy được viên bi trắng. Tính xác suất

để lấy được bi trắng từ hộp

(kết quả làm tròn đến hàng phần trăm).

Lời giải

Đáp án:

0,14

Gọi

: “Bi lấy ra từ hộp II là bi của hộp

”

: “Bi lấy ra từ hộp

là bi của hộp

”

: “Lấy được bi trắng”

Ta có:

 

P K

 

;

 

P K

 

;

 

P A K

 

;

 

P A K

 

Áp dụng công thức xác suất toàn phần, ta có xác suất để lấy được bi trắng là:

         

1 1 2 2

1 1 5 3 7

. | . | . . 0,58

6 2 6 5 12

P A P K P A K P K P A K      .

Áp dụng công thức Bayes, xác suất để lấy được bi trắng của hộp

là:

 

   

 

1 1

. |

6 2

| 0,14

P K P A K

P K A

P A

   

Câu 5. Cho hình lăng trụ đều

ABC A B C

  

có tất cả các cạnh có độ dài bằng 2 (tham khảo hình vẽ).

Tính khoảng cách giữa hai đường thẳng



và

A B



(làm tròn kết quả đến chữ số thập phân thứ nhất).

Trả lời: ………………..

Lời giải

Đáp án:

0,9

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093

https://www.facebook.com/truongngocvy8/

Trang 20

Gọi

là điểm đối xứng của

qua

ta có tứ giác

ADA C

 

là hình bình hành do đó

A D AC

 

, suy ra

khoảng cách

( , ) ( ,( )) ( ,( ))

d AC BA d AC A BD d A A BD

    

 

Theo giả thiết

ABC A B C

  

là lăng trụ đều nên

( )

AA ABC





hay

( )

AA ABCD





suy ra

(1)

A A BD





Ta có

ABD



có

AB AD



nên là tam giác cân tại

, gọi

là trung điểm

ta có

(2)

AI BD



Xét tam giác

BCD



có

A I

lần lượt là trung điểm của

DC DB

nên

AI BC

 

Trong mặt phẳng

( ' )

A AI

dựng

; (3)

AH A I H A I

 

 

Từ (1) và (2) suy ra

( ' ) (4)

BD A AI BD AH

  

Từ (3) và (4) suy ra

( ' )

AH A BD



do đó khoảng cách ( ,( ))

d A SBD AH



Trong tam giác

A AI

vuông tại

ta có

2 2

. ' 2

0,9

( ')

AI AA

  



Câu 6. Giả sử Trái Đất có dạng hình cầu bán kính bằng

.10

m. Bạn Minh Hiền đang đứng trên mặt

đất. Có 3 vệ tinh báo về máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách Minh Hiền

3.10

vệ tinh thứ hai đang cách Minh Hiền

4.10

m và vệ tinh thứ ba đang cách Minh Hiền

5.10

m. Biết rằng

trong hệ trục toạ độ Oxyz (1 đơn vị =

m) cho trước với O là tâm Trái Đất, tại thời điểm vệ tinh thông

báo về máy chủ thì toạ độ của các vệ tinh lần lượt là









1 2

4;4;6 , 8;4;3

M M và





4;9;3

M . Biết tọa độ

vị trí của bạn Minh Hiền là





; ;

M x y z

. Tính giá trị biểu thức

2 3 4

T x y z

  

Bấm Tải xuống để xem toàn bộ.

Preview text:

Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
ĐỀ ÔN THI TỐT NGHIỆP THPT BÁM SÁT ĐỀ MINH HOẠ NĂM 2025 MÔN TOÁN
Thời gian 90 phút ĐỀ SỐ 1
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Họ nguyên hàm của hàm số    4x f x  cos 2x là 4x sin 2x sin 2x A.   C . B. 4x ln 4   C . ln 4 2 2 sin 2x 4x sin 2x C x . 4 ln 4   C . D.   C . 2 ln 4 2
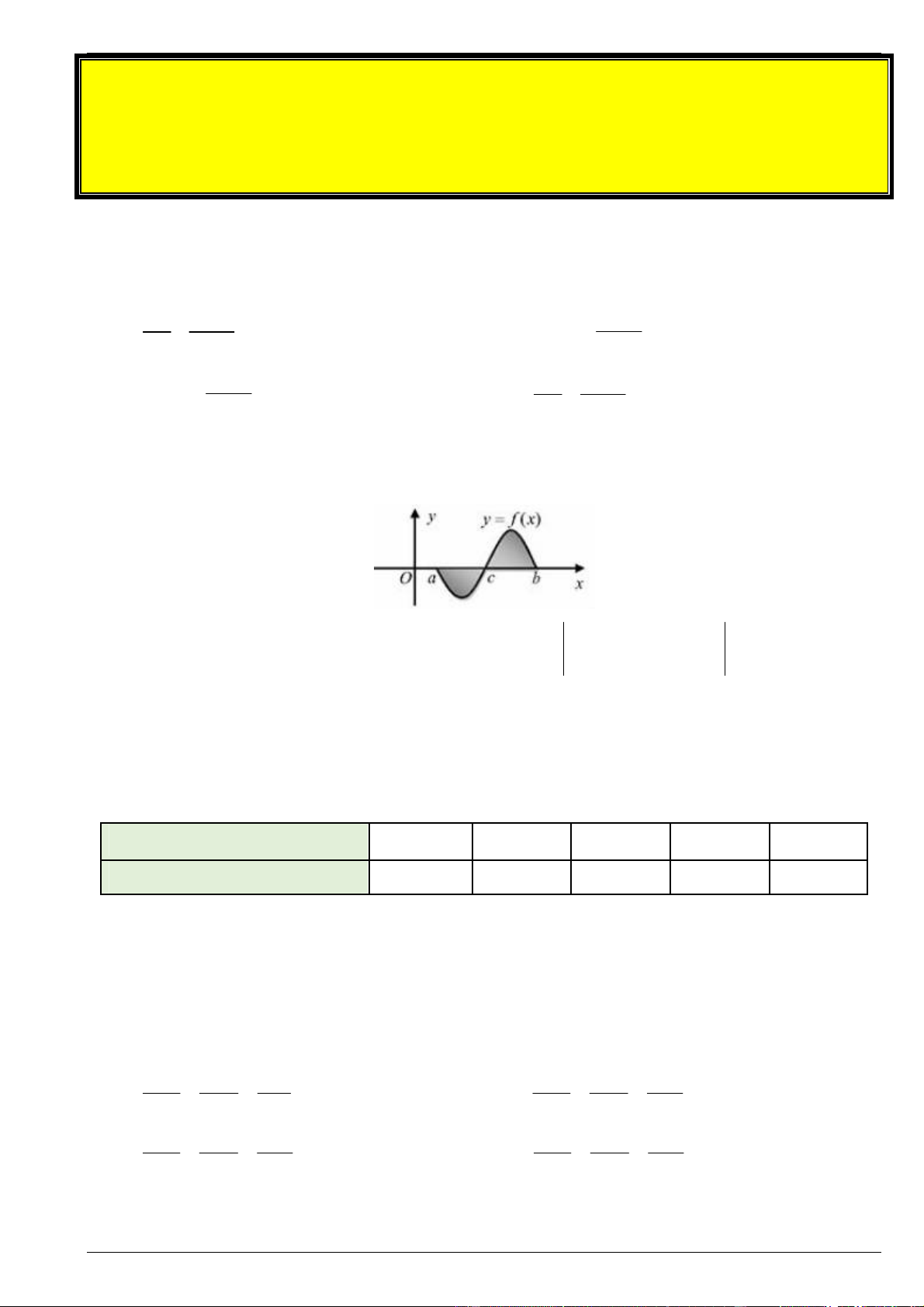
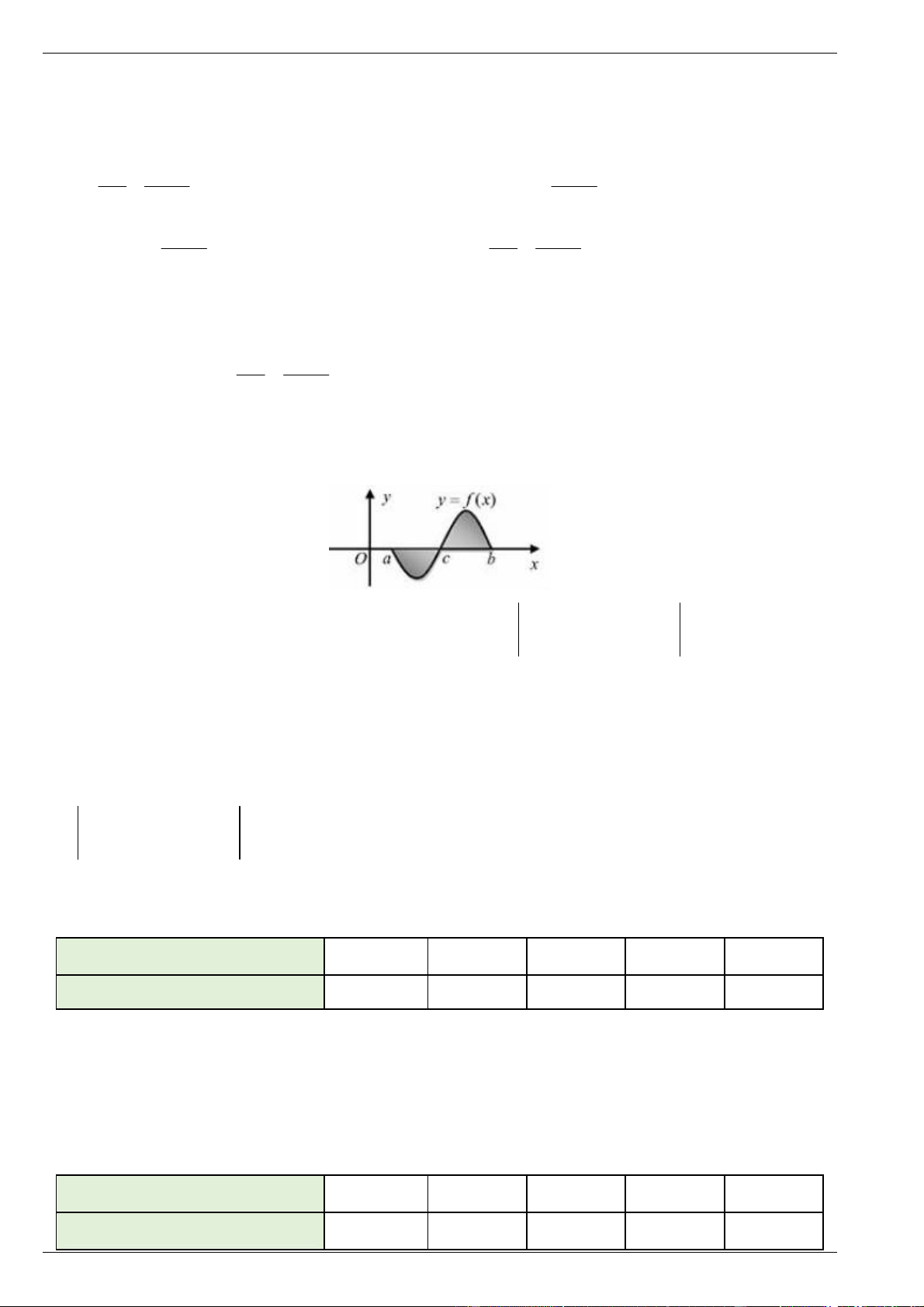
Câu 2. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành, đường thẳng x  ,
a x  b (như hình vẽ bên). Hỏi cách tính S nào dưới đây đúng? b c b A. S 
f  x dx  . B. S 
f  x dx  f  x dx   . a a c c b c b
C. S   f  x dx  f  x dx   . D. S 
f  x dx  f  x dx   . a c a c
Câu 3. Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi phân xưởng A cho như sau: Tuổi thọ (năm) [1,5; 2) [2; 2,5) [2,5;3) [3;3,5) [3,5; 4)
Số linh kiện của phân xưởng A 4 9 13 8 6
Tính phương sai của mẫu số liệu ghép nhóm trên A. 0,145 . B. 0, 245 . C. 0, 445 . D. 0,355 .
Câu 4. Trong không gian Oxyz , cho ba điểm A2; 2;3; B 1;3; 4 và C 3; 1;5 . Đường thẳng đi
qua A và song song với BC có phương trình là: x  2 y  4 z 1 x  2 y  2 z  3 A.   . B.   . 2 2 3 2 4  1 x  2 y  2 z  3 x  2 y  2 z  3 C.   . D.   . 4 2 9 2 4  1
https://www.facebook.com/truongngocvy8/ T r an g 1
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Câu 5. Trong không gian Oxyz , cho mặt phẳng (P) : 3x  y  2z 1  0 . Véc tơ nào dưới đây là một
véc tơ pháp tuyến của (P)  A. n  ( 3  ;1; 2) . B. n =(3; -1; 2). C. n =(3 :1; 2) . D. n =(3;1; -2) . 1 2 3 4 ax  b
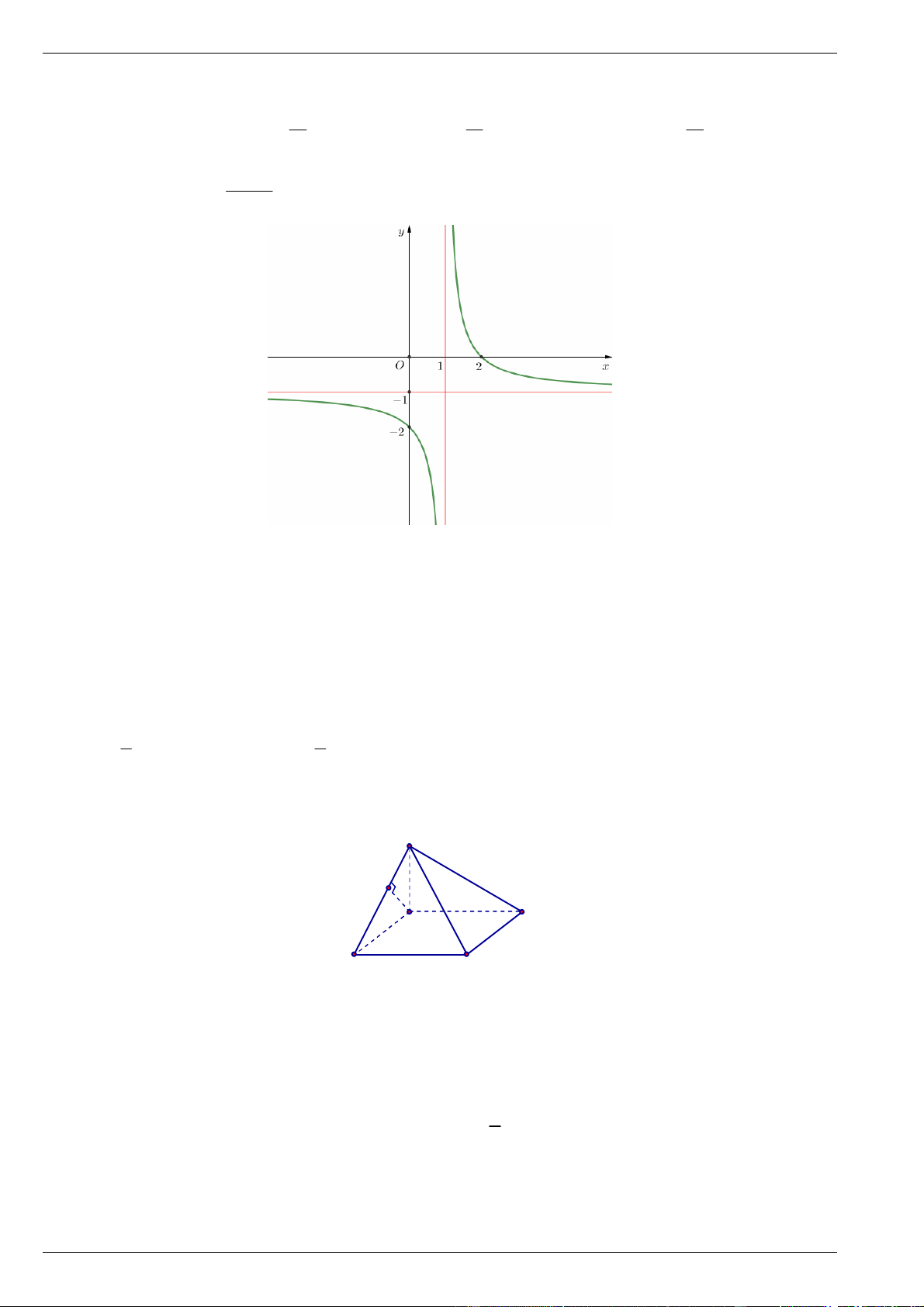
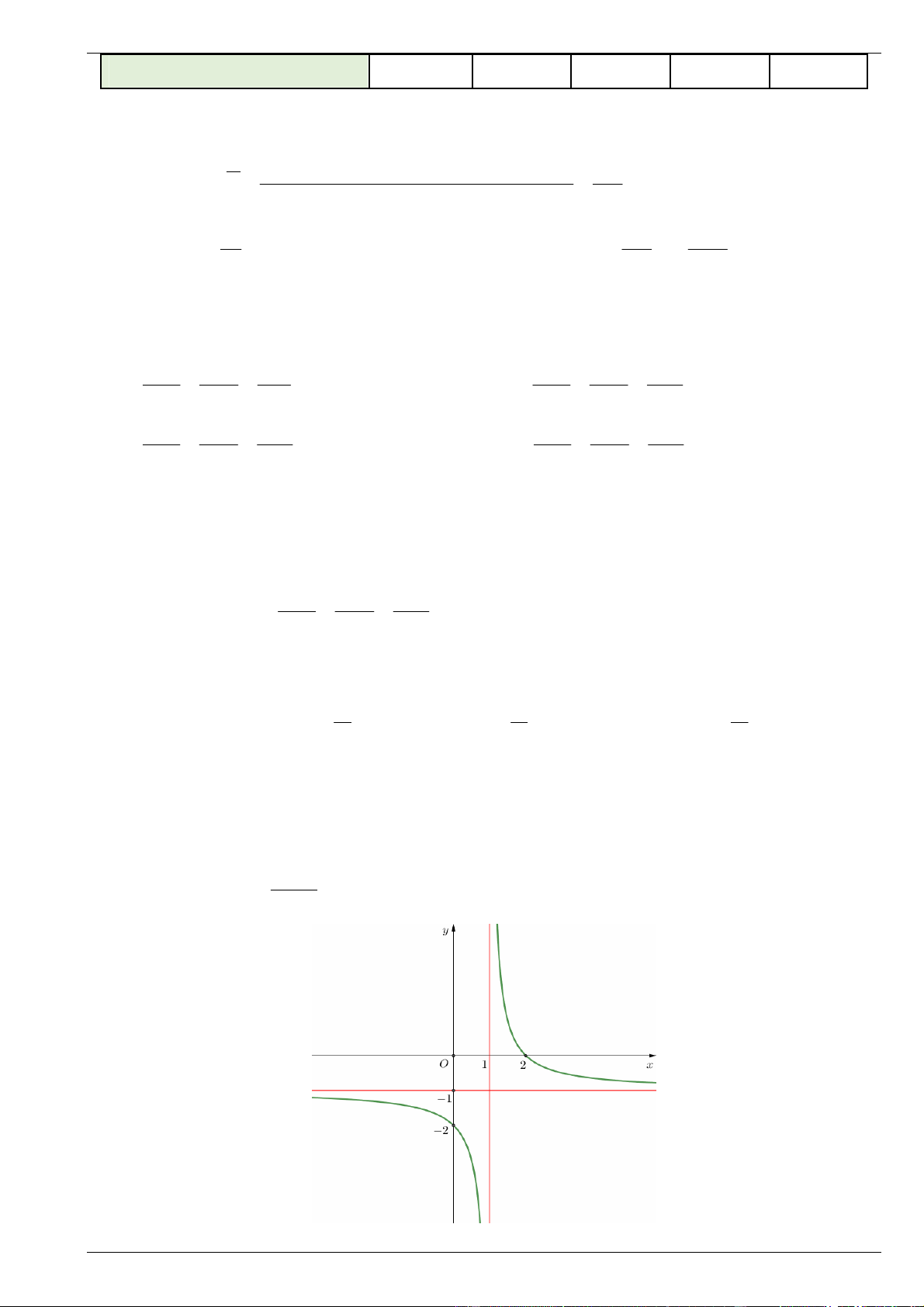
Câu 6. Cho hàm số y 
(c  0, ad  bc  0) có đồ thị như hình vẽ. cx  d
Đồ thị hàm số đã cho có đường tiệm cận đứng bằng: A. x  1 . B. x  1  . C. x  0 . D. y  1  .
Câu 7. Tập nghiệm của bất phương trình 2x  5 là
A. ; log 5 .
B. log 2;  .
C. ; log 2 .
D. log 5;  . 2  5  5  2 
Câu 8. Nghiệm của phương trình log 5x  3 là 2   8 9 A. x  . B. x  . C. x  8 . D. x  9 . 5 5
Câu 9. Cho hình chóp S.ABCD có SA   ABCD và đáy ABCD là hình vuông. Từ A kẻ AM  SB . S M D A B C
Khẳng định nào sau đây đúng?
A. AM   SBD .
B. AM   SBC  .
C. SB   MAC  .
D. AM   SAD .
Câu 10. Cho cấp số cộng u với u  7 và công sai d  4 . Giá trị của u bằng n  1 2 7 A. 11. B. 3 . C. . D. 28 . 4
https://www.facebook.com/truongngocvy8/ T r an g 2
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
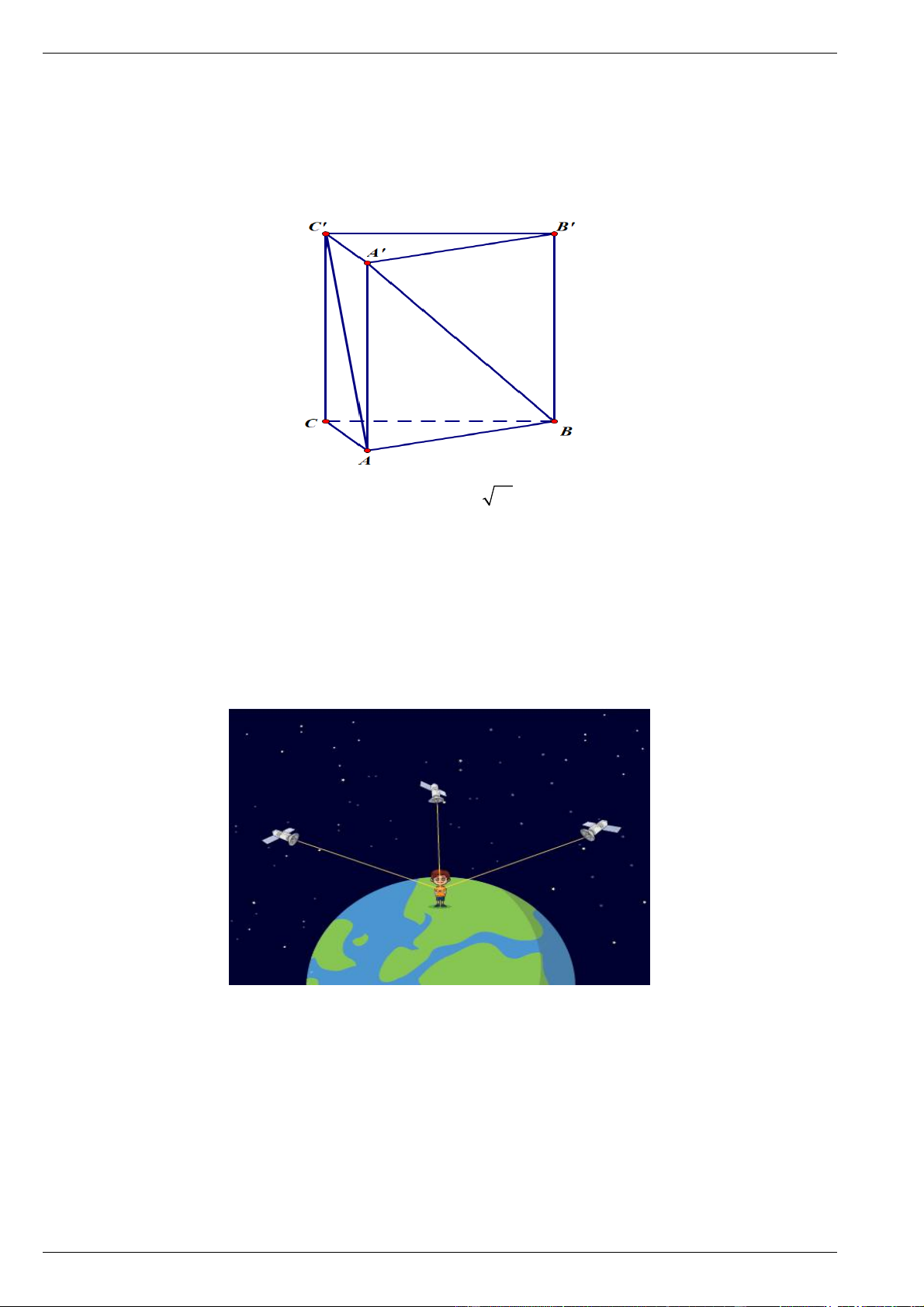
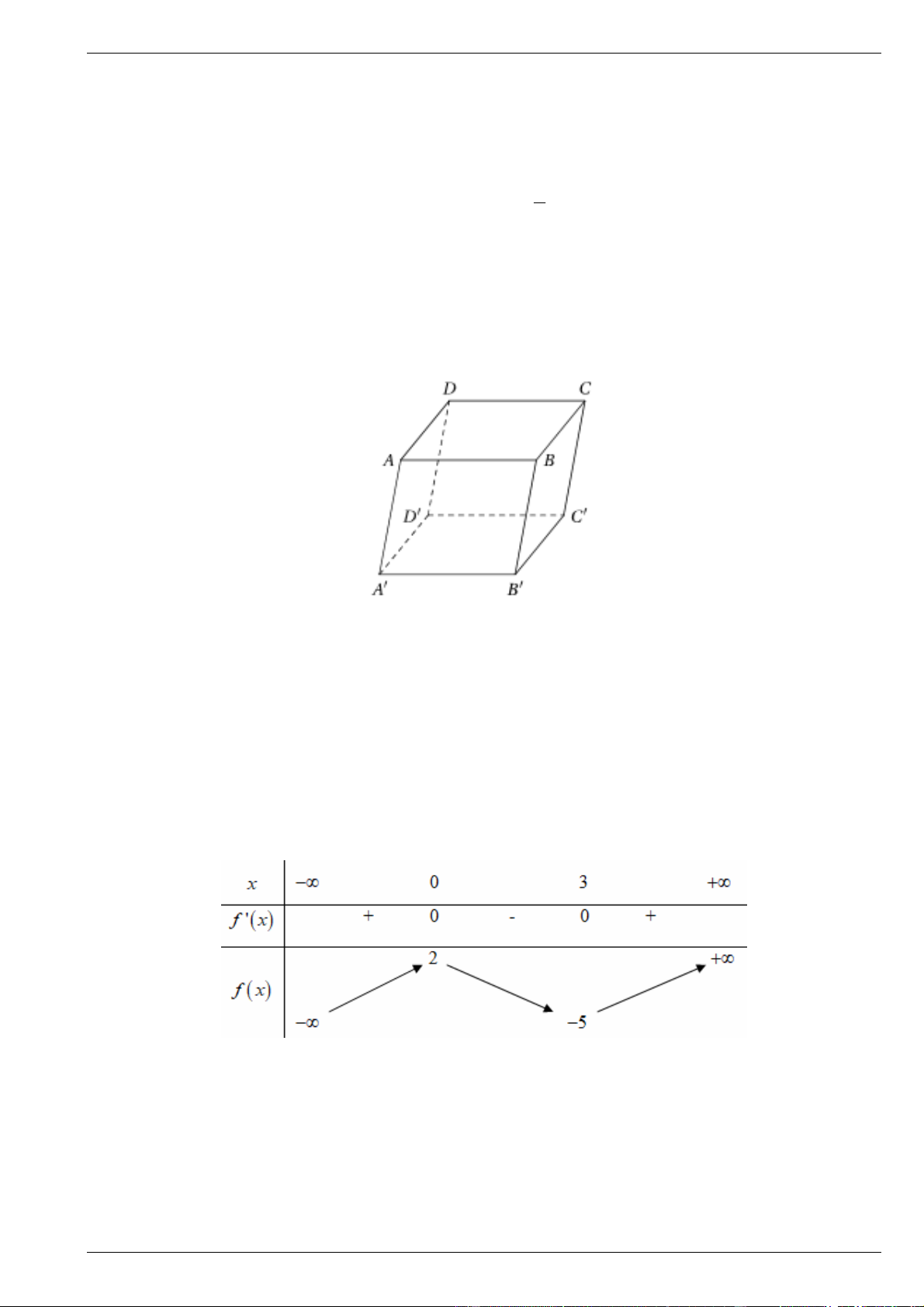
Câu 11. Cho hình hộp ABC .
D A ' B 'C ' D ' .
Chọn đẳng thức vectơ đúng:
    
  
A. AC '  AB  AB '  AD .
B. DB '  DA  DD '  DC . 
   
  
C. AC '  AC  AB  AD .
D. DB  DA  DD '  DC .
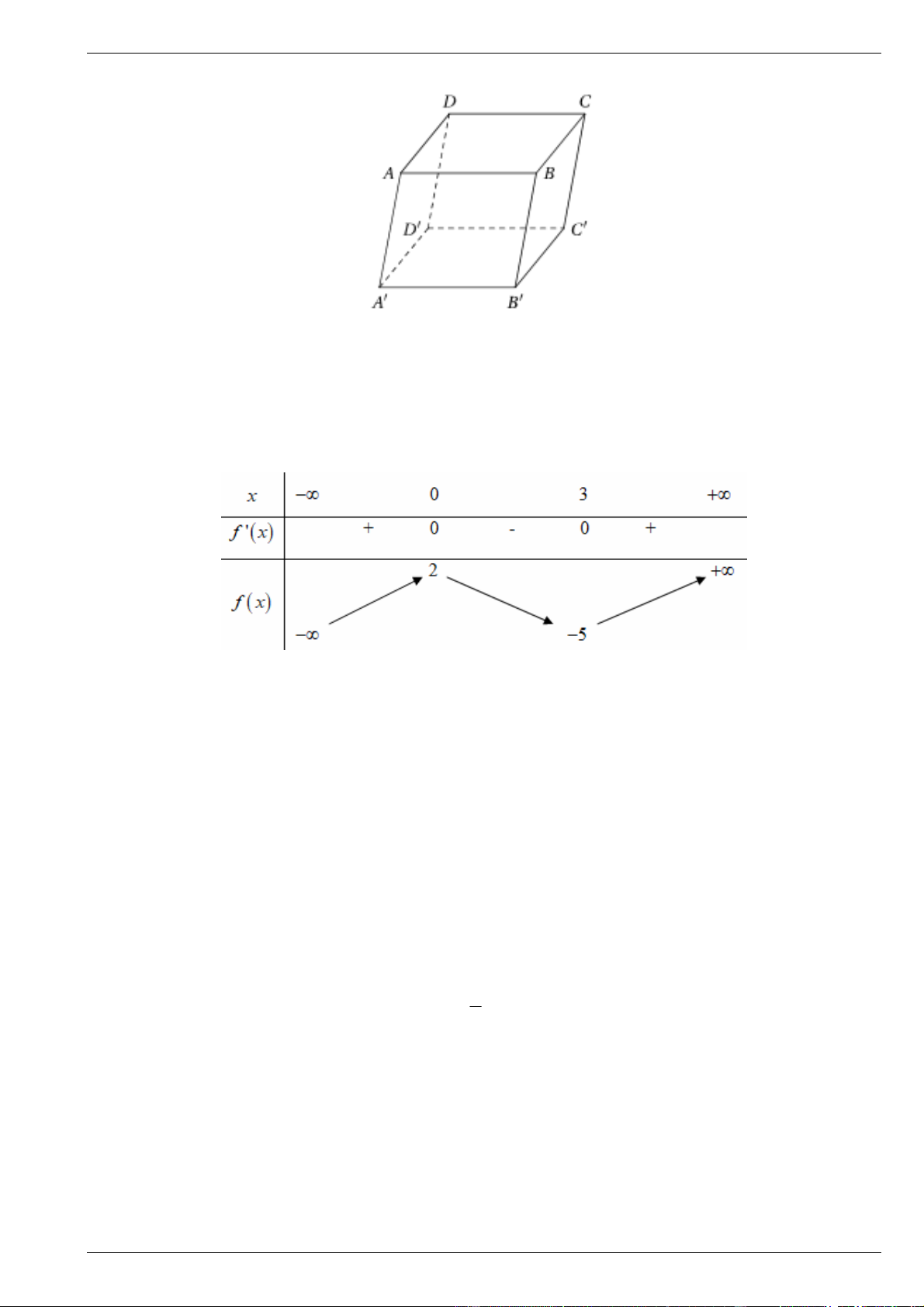
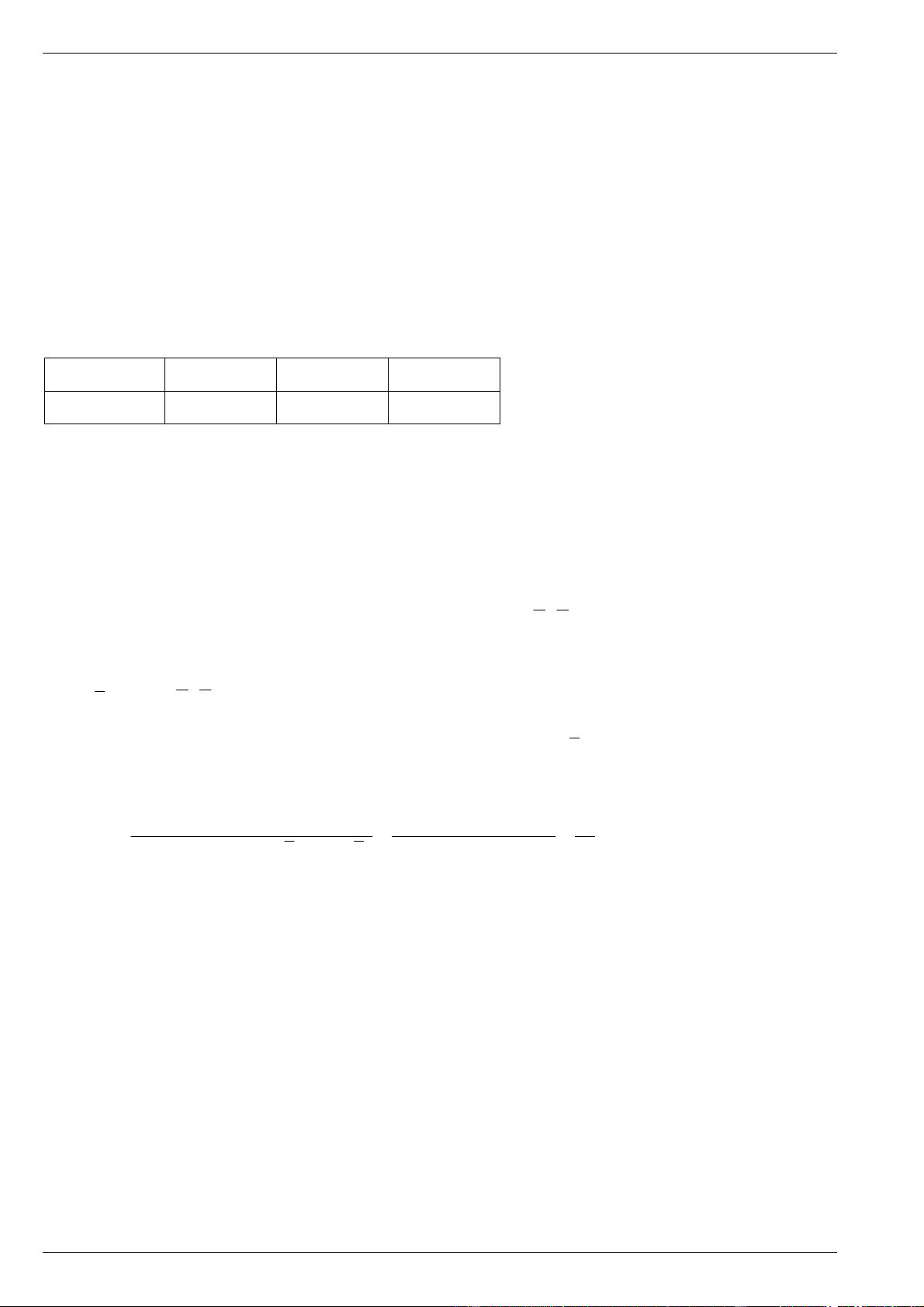
Câu 12. Cho hàm số f  x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 3. B. -5. C. 0. D. 2.
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2 x 1 f (x) e    2x
a) Hàm số đã cho có tập xác định D  0;   .
b) Đạo hàm của hàm số đã cho là 2 x 1 f (x) 2e     2 .
c) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn 0;2 lần lượt là 3 e  4 và 0 .  1 
d) Tập nghiệm của bất phương trình f (  x)  0 là ;    .  2 
Câu 2. Sau khi xuất phát, xe đạp di chuyển với tốc độ v t  2
 2, 01t  0, 025t , với 0  t  10 . Trong đó
v t  tính theo m/s , thời gian t tính theo s với t  0 là thời điểm xe đạp xuất phát.
https://www.facebook.com/truongngocvy8/ T r an g 3
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
a) Quãng đường xe đạp di chuyển được tính theo công thức là s t   2,01  0,05t 0  t  10
b) Quãng đường xe đạp di chuyển được trong 3 giây là 8,82 m .
c) Quãng đường xe đạp di chuyển được trong giây thứ 9 xấp xỉ 15, 28m (kết quả làm tròn đến phần trăm của mét).
d) Trong khoảng thời gian không quá 10s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe đạp là  2
2,51 m / s  .
Câu 3. Một căn bệnh có 2% dân số mắc phải. Một phương pháp chẩn đoán được phát triển có tỷ lệ
chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số
trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 97%. Lấy một người đi kiểm tra.
a) Xác suất để người đó mắc bệnh khi chưa kiểm tra là 0,02 .
b) Xác suất kết quả dương tính nếu người đó mắc bệnh là 0,99 .
c) Xác suất kết quả dương tính nếu người đó không mắc bệnh là 0, 02 .
d) Biết rằng đã có kết quả chuẩn đoán là dương tính, xác suất để người đó thực sự bị bệnh là 0,35.
Câu 4. Một khu vực đã được thiết lập một hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là mét). Một
flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu có phương trình
S   x  2   y  2   z  2 : 30 20 10
 900 . Bạn Trúc Linh đang sử dụng sử dụng máy tính tại điểm M
nằm trên đường tròn C  là giao của mặt cầu  S  và mặt đất. Biết mặt đất bằng phẳng và có phương
trình  P : z  0 .
https://www.facebook.com/truongngocvy8/ T r an g 4
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
a) Mặt cầu  S  có toạ độ tâm và bán kính là I  3  0; 20; 1
 0 , R  30m .
b) Flycam cách mặt đất 10 mét.
c) Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn C  là14,14 mét (kết quả làm tròn đến hai chữ
số hàng thập phân của mét).
d) Đường tròn C  có toạ độ tâm là 30;20;0 .
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này
với số vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1
áo, loại ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng ước tính nhu cầu của
khách không quá 100 cái cho cả 2 loại. Cửa hàng kinh doanh thu lãi lớn nhất được bao nhiêu triệu đồng?
Câu 2. Trường Lê Hồng Phong – Tây Hòa muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt
đất đến đỉnh là 2, 25 mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê công nhân làm mỗi mét
vuông là 1, 5 triệu đồng. Vậy số tiền nhà trường phải trả bao nhiêu triệu đồng ? Câu 3.
Mỗi chuyến xe buýt của hãng xe Phương Trang có sức chứa tối đa là 50 hành khách. Nếu một 2  x 
chuyến xe buýt chở x hành khách thì giá tiền cho mỗi hành khách là 20 3  
 (nghìn đồng). Hỏi mỗi  40 
chuyến xe buýt chở bao nhiêu hành khách thì hãng xe Phương Trang thu được số tiền nhiều nhất?
https://www.facebook.com/truongngocvy8/ T r an g 5
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Câu 4. Cho hộp I gồm 5 bi trắng và 5 bi đỏ, hộp II gồm 6 bi trắng và 4 bi đỏ. Bỏ ngẫu nhiên hai bi từ
hộp I sang hộp II . Sau đó lấy ngẫu nhiên từ hộp II một bi. Giả sử lấy được viên bi trắng. Tính xác suất
để lấy được bi trắng từ hộp I (kết quả làm tròn đến hàng phần trăm).
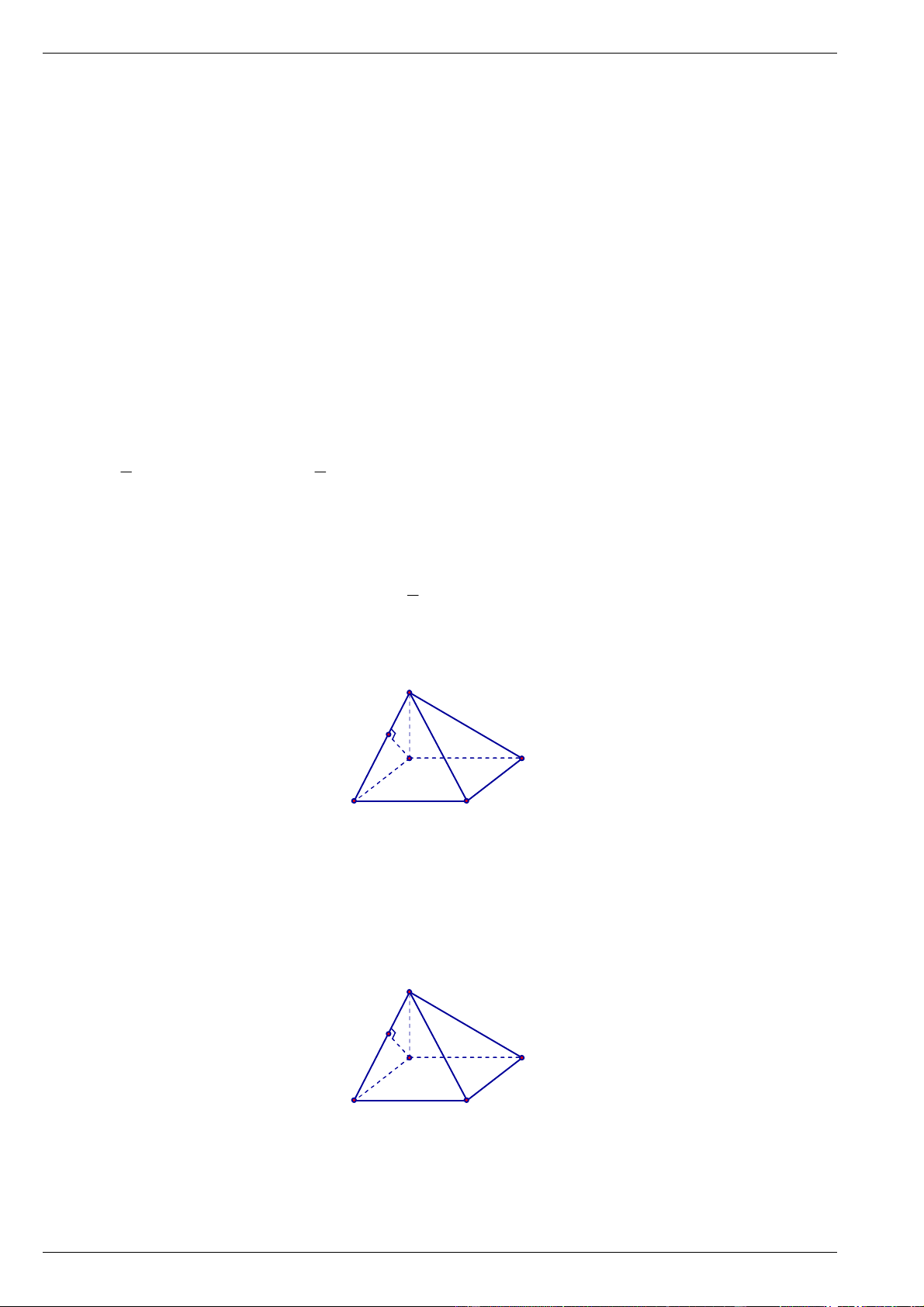
Câu 5. Cho hình lăng trụ đều ABC.AB C
  có tất cả các cạnh có độ dài bằng 2 (tham khảo hình vẽ).
Tính khoảng cách giữa hai đường thẳng AC và A B
 (làm tròn kết quả đến chữ số thập phân thứ nhất).
Câu 6. Giả sử Trái Đất có dạng hình cầu bán kính bằng 6
41.10 m. Bạn Minh Hiền đang đứng trên mặt
đất. Có 3 vệ tinh báo về máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách Minh Hiền 6 3.10 m,
vệ tinh thứ hai đang cách Minh Hiền 6
4.10 m và vệ tinh thứ ba đang cách Minh Hiền 6 5.10 m. Biết rằng
trong hệ trục toạ độ Oxyz (1 đơn vị = 6
10 m) cho trước với O là tâm Trái Đất, tại thời điểm vệ tinh thông
báo về máy chủ thì toạ độ của các vệ tinh lần lượt là M 4; 4; 6 , M 8; 4;3 và M 4;9;3 . Biết tọa độ 3   1   2  
vị trí của bạn Minh Hiền là M  ;
x y; z  . Tính giá trị biểu thức T  2x  3y  4z .
https://www.facebook.com/truongngocvy8/ T r an g 6
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
https://www.facebook.com/truongngocvy8/ T r an g 7
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
LỜI GIẢI CHI TIẾT
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Họ nguyên hàm của hàm số    4x f x  cos 2x là 4x sin 2x sin 2x A.   C . B. 4x ln 4   C . ln 4 2 2 sin 2x 4x sin 2x C x . 4 ln 4   C . D.   C . 2 ln 4 2 Lời giải Chọn D. x x Ta có  x  x 4 sin 2 4 cos 2 dx    C . ln 4 2
Câu 2. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y  f  x , trục hoành, đường thẳng x  ,
a x  b (như hình vẽ bên). Hỏi cách tính S nào dưới đây đúng? b c b A. S 
f  x dx  . B. S 
f  x dx  f  x dx   . a a c c b c b
C. S   f  x dx  f  x dx   . D. S 
f  x dx  f  x dx   . a c a c Lời giải Chọn B. c b S 
f  x dx  f  x dx   a c
Câu 3. Tuổi thọ của một số linh kiện điện tử (đơn vị: năm) được sản xuất bởi phân xưởng A cho như sau: Tuổi thọ (năm) [1,5; 2) [2; 2,5) [2,5;3) [3;3,5) [3,5; 4)
Số linh kiện của phân xưởng A 4 9 13 8 6
Tính phương sai của mẫu số liệu ghép nhóm trên A. 0,145 . B. 0, 245 . C. 0, 445 . D. 0,355 . Lời giải Chọn D.
Ta có bảng số liệu với giá trị đại diện: Tuổi thọ (năm) [1,5; 2) [2; 2,5) [2,5;3) [3;3,5) [3,5; 4) Giá trị đại diện 1, 75 2, 25 2, 75 3, 25 3, 75
https://www.facebook.com/truongngocvy8/ T r an g 8
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Số linh kiện của phân xưởng A 4 9 13 8 6
Tổng số linh kiện: n  4  9 13  8  6  40 1
1, 75.4  2, 25.9  2, 75.13  3, 25.8  3, 75.6 223
Giá trị trung bình x   1 4  9 13  8  6 80 2 1  223  2271 Phương sai: 2 s   2 2 2 2 2
1, 75 .4  2, 25 .9  2, 75 .13  3, 25 .8  3, 75 .6    0, 355 1    40  80  6400
Câu 4. Trong không gian Oxyz , cho ba điểm A2; 2;3; B 1;3; 4 và C 3; 1;5 . Đường thẳng đi
qua A và song song với BC có phương trình là: x  2 y  4 z 1 x  2 y  2 z  3 A.   . B.   . 2 2 3 2 4  1 x  2 y  2 z  3 x  2 y  2 z  3 C.   . D.   . 4 2 9 2 4  1 Lời giải Chọn D. 
Véctơ chỉ phương của đường thẳng cần tìm: BC  2; 4   ;1 . x  2 y  2 z  3
Phương trình cần tìm là:   . 2 4 1
Câu 5. Trong không gian Oxyz , cho mặt phẳng (P) : 3x  y  2z 1  0 . Véc tơ nào dưới đây là một
véc tơ pháp tuyến của (P)  A. n  ( 3  ;1; 2) . B. n =(3; -1; 2). C. n =(3 :1; 2) . D. n =(3;1; -2) . 1 2 3 4 Lời giải Chọn B. 
Véc tơ pháp tuyến của (P) là: n  (3; 1  ; 2) . 2 ax  b
Câu 6. Cho hàm số y 
(c  0, ad  bc  0) có đồ thị như hình vẽ. cx  d
https://www.facebook.com/truongngocvy8/ T r an g 9
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Đồ thị hàm số đã cho có đường tiệm cận đứng bằng: A. x  1 . B. x  1  . C. x  0 . D. y  1  . Lời giải Chọn A.
Từ đồ thị hàm số ta thấy: hàm số đã cho có một tiệm cận đứng x  1
Câu 7. Tập nghiệm của bất phương trình 2x  5 là
A. ; log 5 .
B. log 2;  .
C. ; log 2 .
D. log 5;  . 2  5  5  2  Lời giải Chọn D.
Ta có: 2x  5  x  log 5 . Tập nghiệm của bất phương trình là S  log 5; . 2  2
Câu 8. Nghiệm của phương trình log 5x  3 là 2   8 9 A. x  . B. x  . C. x  8 . D. x  9 . 5 5 Lời giải Chọn A. 8 Ta có: log 5x  3 3
 5x  2  5x  8  x  . 2   5
Câu 9. Cho hình chóp S.ABCD có SA   ABCD và đáy ABCD là hình vuông. Từ A kẻ AM  SB . S M D A B C
Khẳng định nào sau đây đúng?
A. AM   SBD .
B. AM   SBC  .
C. SB   MAC  .
D. AM   SAD . Lời giải Chọn B. S M D A B C
Do SA   ABCD  SA  BC   1 .
Do ABCD là hình vuông nên BC  AB 2 . Từ  
1 , 2  BC  SAB  BC  AM 3 .
https://www.facebook.com/truongngocvy8/ T r an g 10
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Theo giả thiết, ta có AM  SB 4 .
Từ 3, 4  AM  SBC  .
Câu 10. Cho cấp số cộng u với u  7 và công sai d  4 . Giá trị của u bằng n  1 2 7 A. 11. B. 3 . C. . D. 28 . 4 Lời giải Chọn A.
Ta có u  u  d  7  4  11 . 2 1
Câu 11. Cho hình hộp ABC .
D A ' B 'C ' D ' .
Chọn đẳng thức vectơ đúng:
    
  
A. AC '  AB  AB '  AD .
B. DB '  DA  DD '  DC . 
   
  
C. AC '  AC  AB  AD .
D. DB  DA  DD '  DC . Lời giải Chọn B. 
  
Theo quy tắc hình hộp ta có DB '  DA  DD '  DC
Câu 12. Cho hàm số f  x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 3. B. -5. C. 0. D. 2. Lời giải Chọn B.
Dựa vào bảng biến thiên ta có giá trị cực tiểu của hàm số bằng 5  .
https://www.facebook.com/truongngocvy8/ T r an g 11
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Câu 1. Cho hàm số 2 x 1 f (x) e    2x
a) Hàm số đã cho có tập xác định D  0;   .
b) Đạo hàm của hàm số đã cho là 2 x 1 f (x) 2e     2 .
c) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn 0;2 lần lượt là 3 e  4 và 0 .  1 
d) Tập nghiệm của bất phương trình f (  x)  0 là ;    .  2  Lời giải a) b) c) d) SAI ĐÚNG ĐÚNG SAI
a) Hàm số đã cho có tập xác định D  ;  b) 2 x 1  2 x 1
f (x)  e
 2x  f (x)  2e    2
d) Hàm số đã cho xác định và liên tục trên 0;2. 2 x 1  2 x 1
f (x)  e
 2x  f (x)  2e    2 x x 1 ta có: 2 1 2 1 f (
 x)  0  2e  2  0  e  1  x  2 1 f (0)  e  1  f  0    2  f 2 3  e  4 Do đó: 3
max f (x)  f (2)  e  4 x [  0;2]  1 
min f (x)  f  0   x [  0;2]  2 
Vậy giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên đoạn 0;2 lần lượt là 3 e  4 và 0 . d) Ta có f (  x)  0 2 x 1  2e   2  0 2 x 1  e   1  2x 1  0 1  x  2
https://www.facebook.com/truongngocvy8/ T r an g 12
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093  1 
Vậy tập nghiệm của bất phương trình f (  x)  0 là ;    .  2 
Câu 2. Sau khi xuất phát, xe đạp di chuyển với tốc độ v t  2
 2, 01t  0, 025t , với 0  t  10 . Trong đó
v t  tính theo m/s , thời gian t tính theo s với t  0 là thời điểm xe đạp xuất phát.
a) Quãng đường xe đạp di chuyển được tính theo công thức là s t   2,01  0,05t 0  t  10
b) Quãng đường xe đạp di chuyển được trong 3 giây là 8,82 m .
c) Quãng đường xe đạp di chuyển được trong giây thứ 9 xấp xỉ 15, 28m (kết quả làm tròn đến phần trăm của mét).
d) Trong khoảng thời gian không quá 10s đầu, khi vận tốc đạt giá trị lớn nhất thì gia tốc của xe đạp là  2
2,51 m / s  . Lời giải a) b) c) d) SAI ĐÚNG ĐÚNG SAI
a) Quãng đường xe đạp di chuyển được phải là nguyên hàm của vt 
Khi đó vt   2,01  0,05t 0  t  10 là công thức tính gia tốc của vật.
b) Quãng đường xe đạp di chuyển được trong 3s là: 3 3 2 3   2, 01t 0, 025t  2
2, 01t  0, 025t  dt    8,82   m . 2 3 0   0
c) Quãng đường xe đạp di chuyển được trong giây thứ 9 9 9 2 3  2, 01t 0, 025t 
s 9  s 8   2
2, 01t  0, 025t  dt    15, 28   m 2 3 8   8
d) Ta có: v t  2
 2, 01t  0, 025t 0  t  10  max v t   17,6m / s khi t  10s 0;10
Gia tốc xe đạp khi đó là a    v      2 10 10
2, 01 0, 05.10 1,51 m / s 
https://www.facebook.com/truongngocvy8/ T r an g 13
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Câu 3. Một căn bệnh có 2% dân số mắc phải. Một phương pháp chẩn đoán được phát triển có tỷ lệ
chính xác là 99%. Với những người bị bệnh, phương pháp này sẽ đưa ra kết quả dương tính 99% số
trường hợp. Với người không mắc bệnh, phương pháp này cũng chuẩn đoán đúng 97%. Lấy một người đi kiểm tra.
a) Xác suất để người đó mắc bệnh khi chưa kiểm tra là 0,02 .
b) Xác suất kết quả dương tính nếu người đó mắc bệnh là 0,99 .
c) Xác suất kết quả dương tính nếu người đó không mắc bệnh là 0, 02 .
d) Biết rằng đã có kết quả chuẩn đoán là dương tính, xác suất để người đó thực sự bị bệnh là 0,35. Lời giải a) b) c) d) ĐÚNG ĐÚNG SAI SAI
a) Gọi A là biến cố “người đó mắc bệnh”
Xác suất để người đó mắc bệnh khi chưa kiểm tra: P  A  2%  0,02
b) Gọi B là biến cố “kết quả kiểm tra người đó là dương tính”
Xác suất kết quả dương tính nếu người đó mắc bệnh là: P  B | A  99%  0,99
c) Xác xuất kết quả âm tính nếu người đó không mắc bệnh là: P B | A  97%  0,97 .
Xác suất kết quả dương tính nếu người đó không mắc bệnh là:
P B | A  1  PB | A  1 0,97  0,03
d) Do đó xác suất để người đó không mắc bệnh khi chưa kiểm tra: P  A  1 0,02  0,98
Xác suất để người đó thực sự bị bệnh là:
P  A.P B | A 0, 02.0,99 33
P  A | B     0, 402.
P  A.P  B | A  P A.PB | A 0, 02.0,99  0,98.0, 03 82
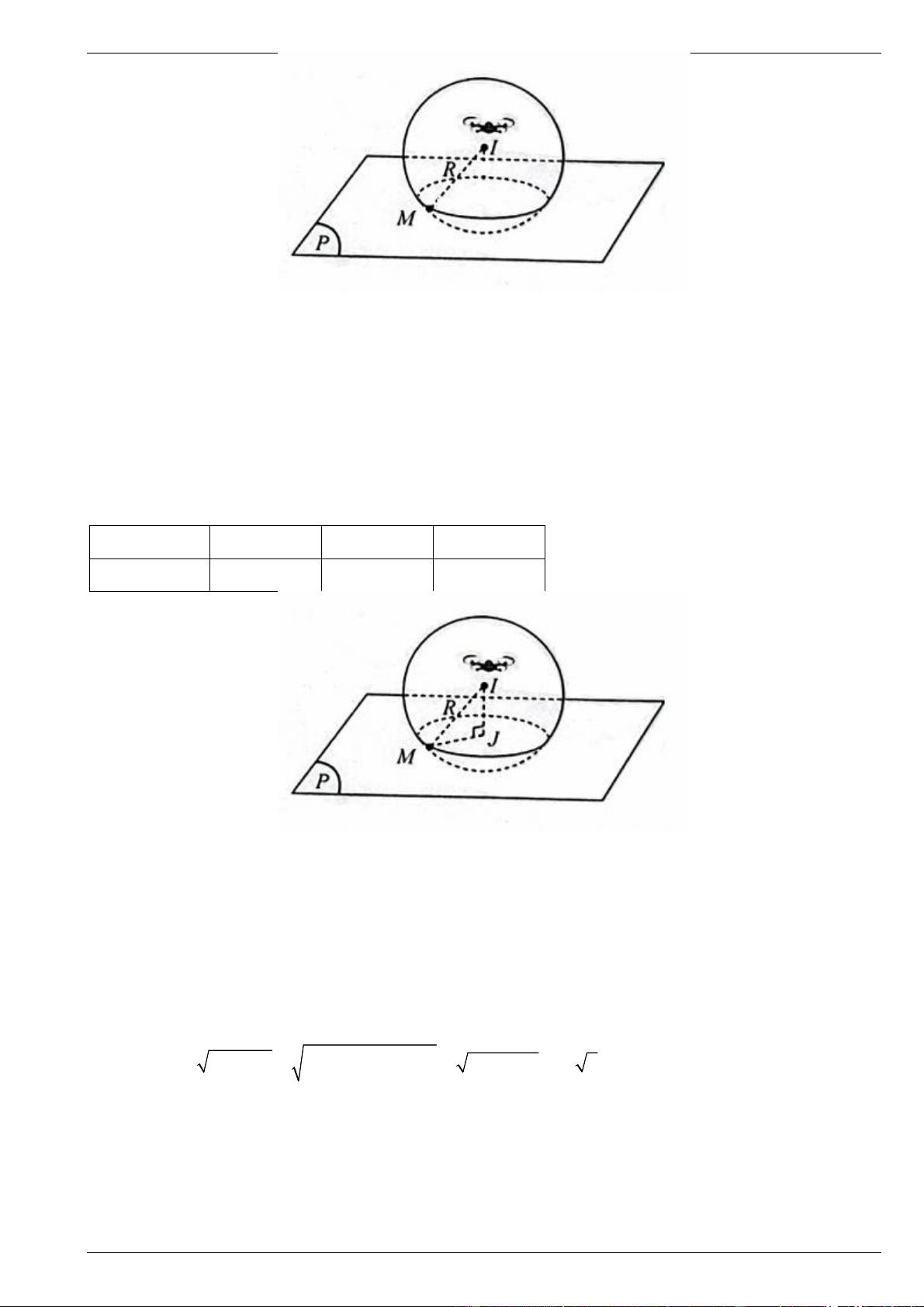
Câu 4. Một khu vực đã được thiết lập một hệ trục tọa độ Oxyz (đơn vị trên mỗi trục là mét). Một
flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu có phương trình
S   x  2   y  2   z  2 : 30 20 10
 900 . Bạn Trúc Linh đang sử dụng sử dụng máy tính tại điểm M
nằm trên đường tròn C  là giao của mặt cầu  S  và mặt đất. Biết mặt đất bằng phẳng và có phương
trình  P : z  0 .
https://www.facebook.com/truongngocvy8/ T r an g 14
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
a) Mặt cầu  S  có toạ độ tâm và bán kính là I  3  0; 20; 1
 0 , R  30m .
b) Flycam cách mặt đất 10 mét.
c) Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn C  là14,14 mét (kết quả làm tròn đến hai chữ
số hàng thập phân của mét).
d) Đường tròn C  có toạ độ tâm là 30;20;0 . Lời giải a) b) c) d) ĐÚNG SAI SAI ĐÚNG
a) Mặt cầu  S  có tâm I 30; 20;10 và có bán kính R  30m
b) Khoảng cách Flycam đến mặt đất chính là khoảng cách từ tâm I đến  P : z  0
Do đó: d  I, P  10m
c) Gọi J là tâm của đường tròn C  . Khoảng cách từ bạn Trúc Linh đến tâm của đường tròn C  chính là MJ 2 Ta có: 2 2 2 2 MJ  R  IJ 
R  d I,P  900 100  10 2  14,14m  
d) Gọi J là hình chiếu vuông góc của I trên  P .
Ta có: J   P  J 30; 20;0
Vậy đường tròn C  có toạ độ tâm là J 30; 20;0
https://www.facebook.com/truongngocvy8/ T r an g 15
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
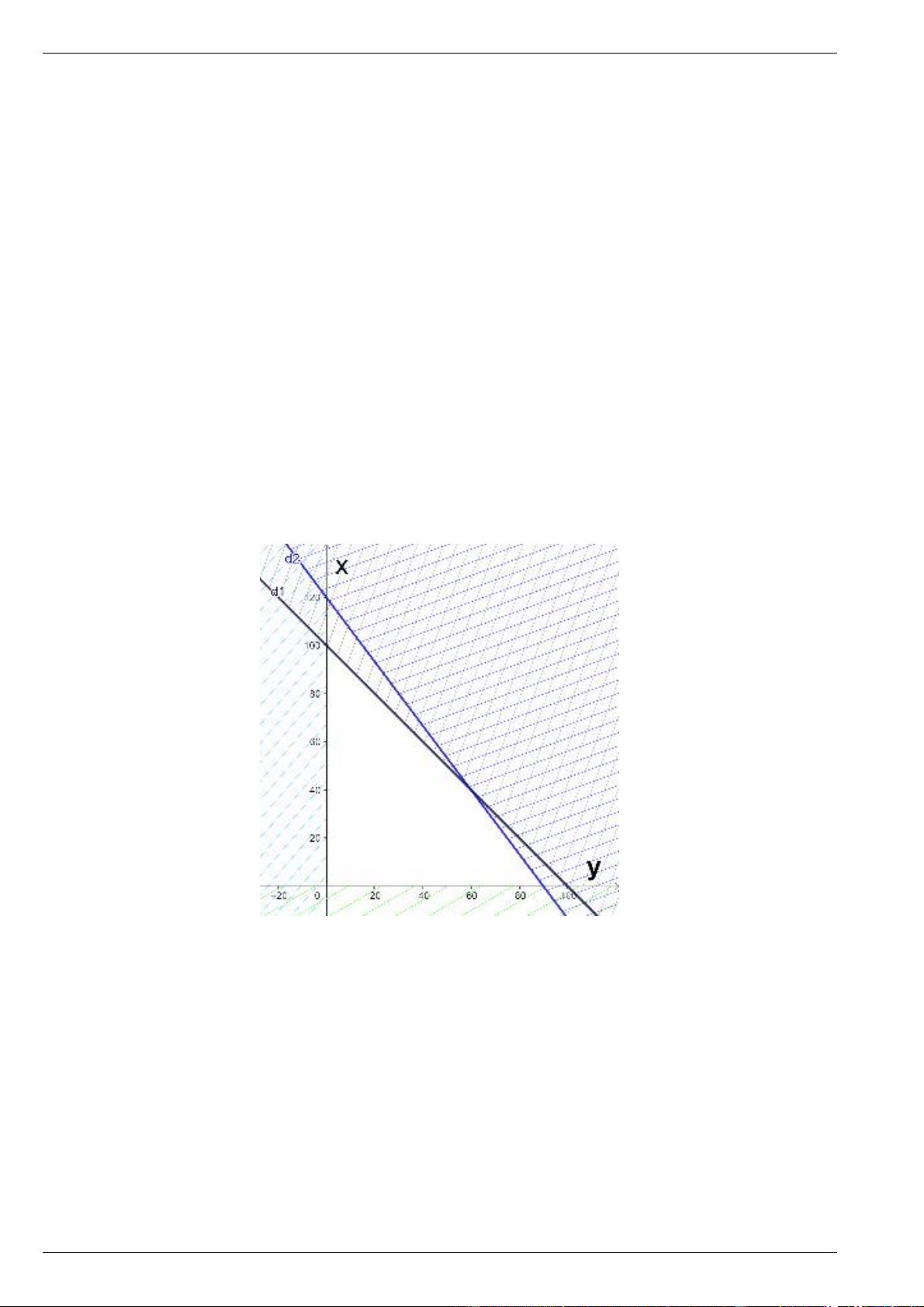
Câu 1. Cửa hàng thời trang Việt Tiến muốn kinh doanh thêm 2 loại áo thun mẫu mới trong dịp tết này
với số vốn đầu tư không quá 72 triệu đồng. Loại dài tay giá mua vào 800.000 đồng và lãi 150.000 đồng 1
áo, loại ngắn tay giá mua vào 600.000 đồng và lãi 120.000 đồng 1 áo. Cửa hàng ước tính nhu cầu của
khách không quá 100 cái cho cả 2 loại. Cửa hàng kinh doanh thu lãi lớn nhất được bao nhiêu triệu đồng? Lời giải
Đáp án: 13,8
Gọi x, y (cái) lần lượt là số áo dài tay và ngắn tay mà cửa hàng nên mua để kinh doanh có lãi nhất.
Điều kiện: x  0, y  0, , x y   x  0   y  0
Theo yêu cầu bài toán, ta có hệ bất phương trình  x  y  100  8
 x  6 y  720 
Ta cần tìm x, y để biểu thức F  150.000x 120.000 y đạt GTLN trên miền nghiệm của hệ trên
Biểu diễn miền nghiệm của hệ bất phương trình trên
Miền nghiệm là tứ giác OABC
Các điểm có tọa độ như sau: ( O 0;0) , (
A 0;100) , B(60;40) , C(90;0) Tại (
O 0;0) : F  0 Tại (
A 0;100) : F  12.000.000
Tại B(60; 40) : F  13.800.000
Tại C(90;0) : F  13.500.000
Vậy cửa hàng nên nhập 60 áo dài tay và 40 áo ngắn tay để kinh doanh thì có lãi nhất và lãi thu được là
13.800.000 đồng hay 13,8 triệu đồng
https://www.facebook.com/truongngocvy8/ T r an g 16
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
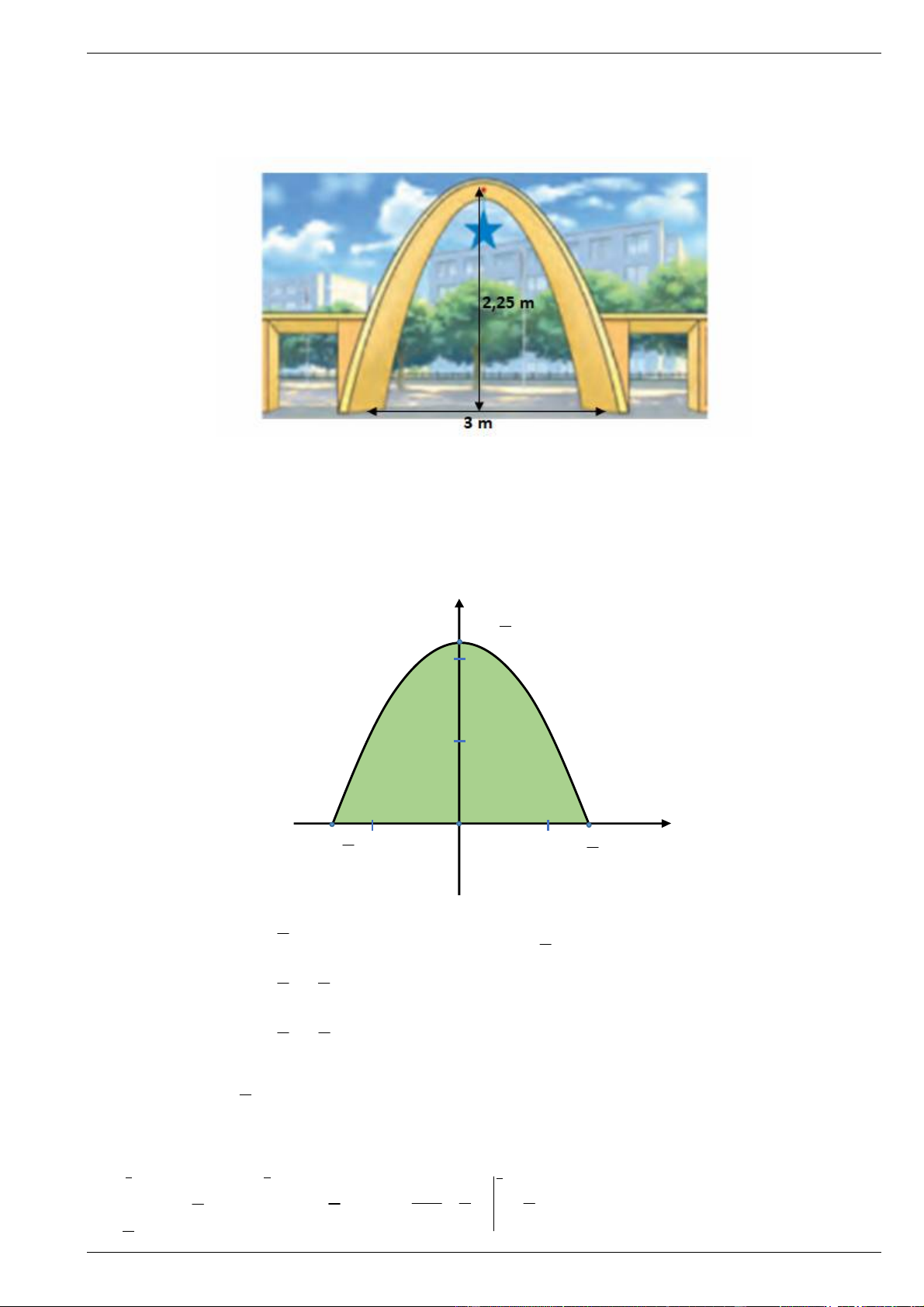
Câu 2. Trường Lê Hồng Phong – Tây Hòa muốn làm một cái cửa nhà hình parabol có chiều cao từ mặt
đất đến đỉnh là 2, 25 mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê công nhân làm mỗi mét
vuông là 1, 5 triệu đồng. Vậy số tiền nhà trường phải trả bao nhiêu triệu đồng ? Lời giải
Đáp án: 6, 75
Gọi phương trình parabol  P  2
: y  ax  bx  c . Do tính đối xứng của parabol nên ta có thể chọn hệ trục
tọa độ Oxy sao cho  P  có đỉnh I Oy (như hình vẽ). y  9  I 0;    4  2 1 1 1  3  O  3  x A  ; 0   B ; 0    2   2 
9  c,I P   9 4 c    4 9 3 
Ta có hệ phương trình:  a  b  c  0 AP  a  1  . 4 2  b   0 9 3  a  b  c  0 
BP   4 2 9 Vậy  P 2 : y  x  . 4
Dựa vào đồ thị, diện tích cửa parabol là: 3 3 9 2  9 2  9 3 4  x 9  9 2   S  x  dx  2 2    2 x  dx    2  x    m .  4  4 3 4 2 3   0   0 2
https://www.facebook.com/truongngocvy8/ T r an g 17
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093 9 Số tiền phải trả là: 1 . , 5  6, 75 đồng. 2 Câu 3.
Mỗi chuyến xe buýt của hãng xe Phương Trang có sức chứa tối đa là 50 hành khách. Nếu một 2  x 
chuyến xe buýt chở x hành khách thì giá tiền cho mỗi hành khách là 20 3  
 (nghìn đồng). Hỏi mỗi  40 
chuyến xe buýt chở bao nhiêu hành khách thì hãng xe Phương Trang thu được số tiền nhiều nhất? Lời giải Đáp án: 40 2 3  x   x 3 
Số tiền thu được là : f  x 2  20x 3   20  x  9x     (nghìn đồng)  40  1600 20   3  x 3 
Xét hàm số: f  x 2  20  x  9x 
 với 0  x  50 1600 20   2  3x 3 
f ' x  20  x  9   1600 10  
f ' x  0 2 3x 3   x  9  0 1600 10
 x  40  N 
 x 120L  Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy: GTLN của f  x là 3200 khi x  40
https://www.facebook.com/truongngocvy8/ T r an g 18
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Vậy một chuyến xe buýt thu được số tiền nhiều nhất là 3200 nghìn đồng khi có 40 hành khách.
Câu 4. Cho hộp I gồm 5 bi trắng và 5 bi đỏ, hộp II gồm 6 bi trắng và 4 bi đỏ. Bỏ ngẫu nhiên hai bi từ
hộp I sang hộp II . Sau đó lấy ngẫu nhiên từ hộp II một bi. Giả sử lấy được viên bi trắng. Tính xác suất
để lấy được bi trắng từ hộp I (kết quả làm tròn đến hàng phần trăm). Lời giải
Đáp án: 0,14
Gọi K : “Bi lấy ra từ hộp II là bi của hộp I ” 1
K : “Bi lấy ra từ hộp II là bi của hộp II ” 2
A : “Lấy được bi trắng” 1 C 1 1 C 5 1 C 1 1 C 3
Ta có: P  K  2   ; P  K  
; P  A | K  
; P  A | K   . 2  6 1  5 2  10 1 1 C 6 1 C 6 1 C 2 1 C 5 12 12 10 10
Áp dụng công thức xác suất toàn phần, ta có xác suất để lấy được bi trắng là: 1 1 5 3 7
P  A  P  K .P A | K  P K .P A | K  .  .   0,58 . 1   1   2   2  6 2 6 5 12
Áp dụng công thức Bayes, xác suất để lấy được bi trắng của hộp I là: 1 1 P  .
K .P A | K 1 1   1  P  6 2 K | A     0,14 . 1  P  A 7 7 12
Câu 5. Cho hình lăng trụ đều ABC.AB C
  có tất cả các cạnh có độ dài bằng 2 (tham khảo hình vẽ).
Tính khoảng cách giữa hai đường thẳng AC và A B
 (làm tròn kết quả đến chữ số thập phân thứ nhất).
Trả lời: ……………….. Lời giải Đáp án: 0,9
https://www.facebook.com/truongngocvy8/ T r an g 19
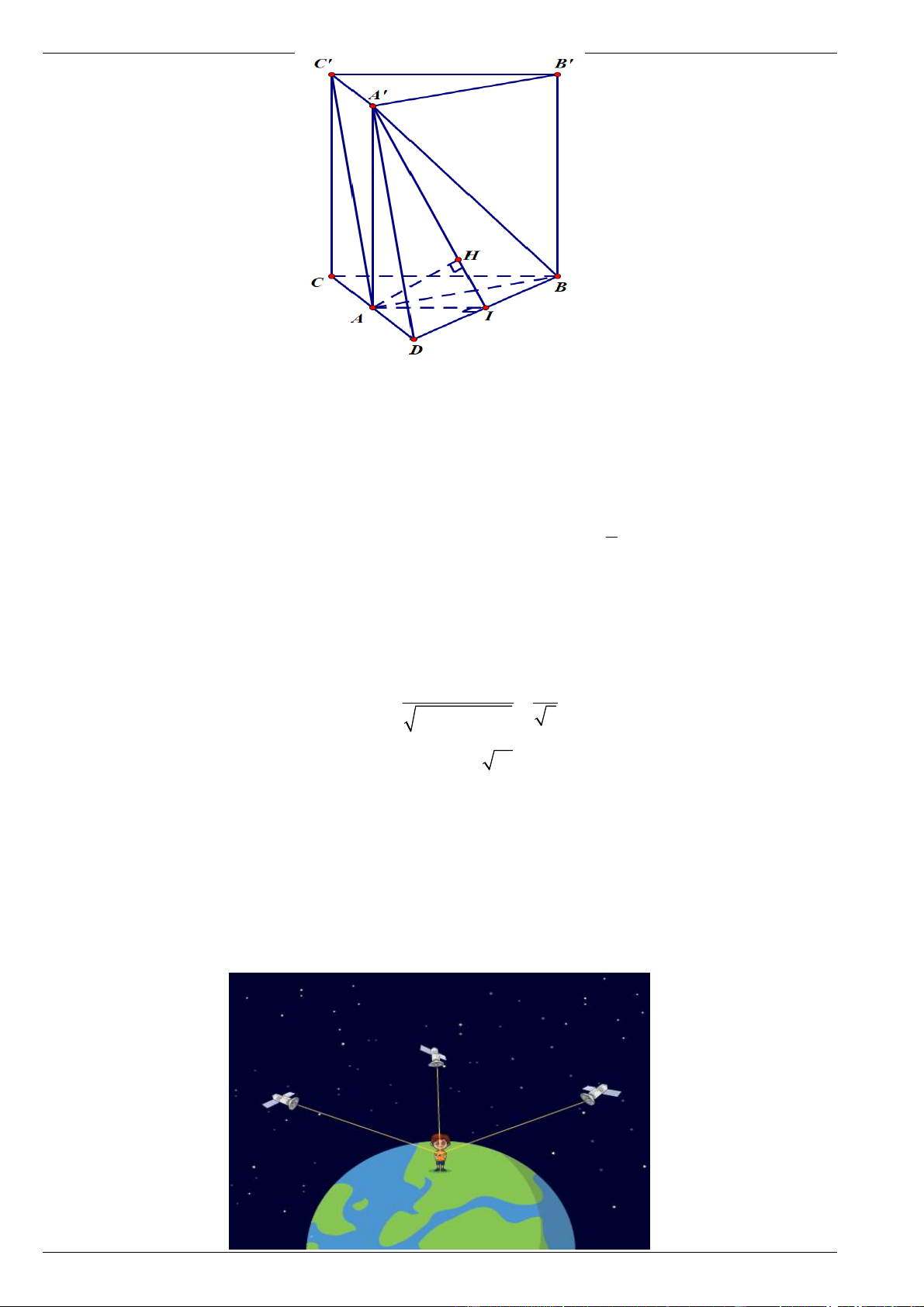
Đề ôn thi tốt nghiệp PTTH môn toán Năm 2025 có lời giải chi tiết Trương Ngọc Vỹ 0978 333 093
Gọi D là điểm đối xứng của C qua A ta có tứ giác ADA C
  là hình bình hành do đó AD//AC , suy ra
khoảng cách d ( AC ,  BA )
  d( AC , ( ABD))  d ( ,
A ( ABD)) .
Theo giả thiết ABC.AB C
  là lăng trụ đều nên AA  ( ABC) hay AA  ( ABCD) suy ra AA  BD (1) . Ta có A
 BD có AB  AD nên là tam giác cân tại A , gọi I là trung điểm BD ta có AI  BD (2) . 1
Xét tam giác BCD có ,
A I lần lượt là trung điểm của DC, DB nên AI  BC  1. 2
Trong mặt phẳng ( A' AI ) dựng AH  AI; H  AI (3) .
Từ (1) và (2) suy ra BD  ( A' AI )  BD  AH (4) .
Từ (3) và (4) suy ra AH  (A ' BD) do đó khoảng cách d ( ,
A (SBD))  AH . AI.AA ' 2
Trong tam giác A ' AI vuông tại A ta có AH    0,9 . 2 2 AI  (AA ') 5
Câu 6. Giả sử Trái Đất có dạng hình cầu bán kính bằng 6
41.10 m. Bạn Minh Hiền đang đứng trên mặt
đất. Có 3 vệ tinh báo về máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách Minh Hiền 6 3.10 m,
vệ tinh thứ hai đang cách Minh Hiền 6
4.10 m và vệ tinh thứ ba đang cách Minh Hiền 6 5.10 m. Biết rằng
trong hệ trục toạ độ Oxyz (1 đơn vị = 6
10 m) cho trước với O là tâm Trái Đất, tại thời điểm vệ tinh thông
báo về máy chủ thì toạ độ của các vệ tinh lần lượt là M 4; 4; 6 , M 8; 4;3 và M 4;9;3 . Biết tọa độ 3   1   2  
vị trí của bạn Minh Hiền là M  ;
x y; z  . Tính giá trị biểu thức T  2x  3y  4z .
https://www.facebook.com/truongngocvy8/ T r an g 20

05 đề ôn thi tốt nghiệp THPT năm 2025 môn Toán bám sát đề minh họa có đáp án

Tài liệu liên quan:

Đề cuối kỳ 2 Toán 12 năm 2024 – 2025 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối kỳ 2 Toán 11 năm 2024 – 2025 trường THPT Lê Hồng Phong – Đắk Lắk

Đề cuối kỳ 2 Toán 10 năm 2024 – 2025 trường THPT Lê Hồng Phong – Đắk Lắk

Đề thi thử tốt nghiệp THPT 2025 môn Toán Sở GD&ĐT Lào Cai

Đề thi thử tốt nghiệp THPT 2025 môn Toán Sở GD&ĐT Quảng Ninh