1 Ham so

1 HÀM SỐ 1 CHƯƠNG 1. HÀM SỐ 1
HÀM SỐ VÀ ĐỒ THỊ 1.1 HÀM SỐ
MỘT SỐ KHÁI NIỆM CƠ BẢN
• Nếu với mỗi giá trị x thuộc D, ta xác định được một và chỉ một giá trị tương ứng
f (x) thuộc tập hợp E thì ta có một hàm số.
• Ta gọi x là biến số và f (x) là hàm số của x.
• Tập hợp D được gọi là tập xác định của hàm số.
• Tập hợp E gồm tất cả các giá trị f (x) (tương ứng với x thuộc D) gọi là tập giá trị của hàm số.
• f là hàm số trên miền D, đồ thị của hàm số là tập hợp {(x; f (x) | x ∈ D)}. VÍ DỤ 1.1.
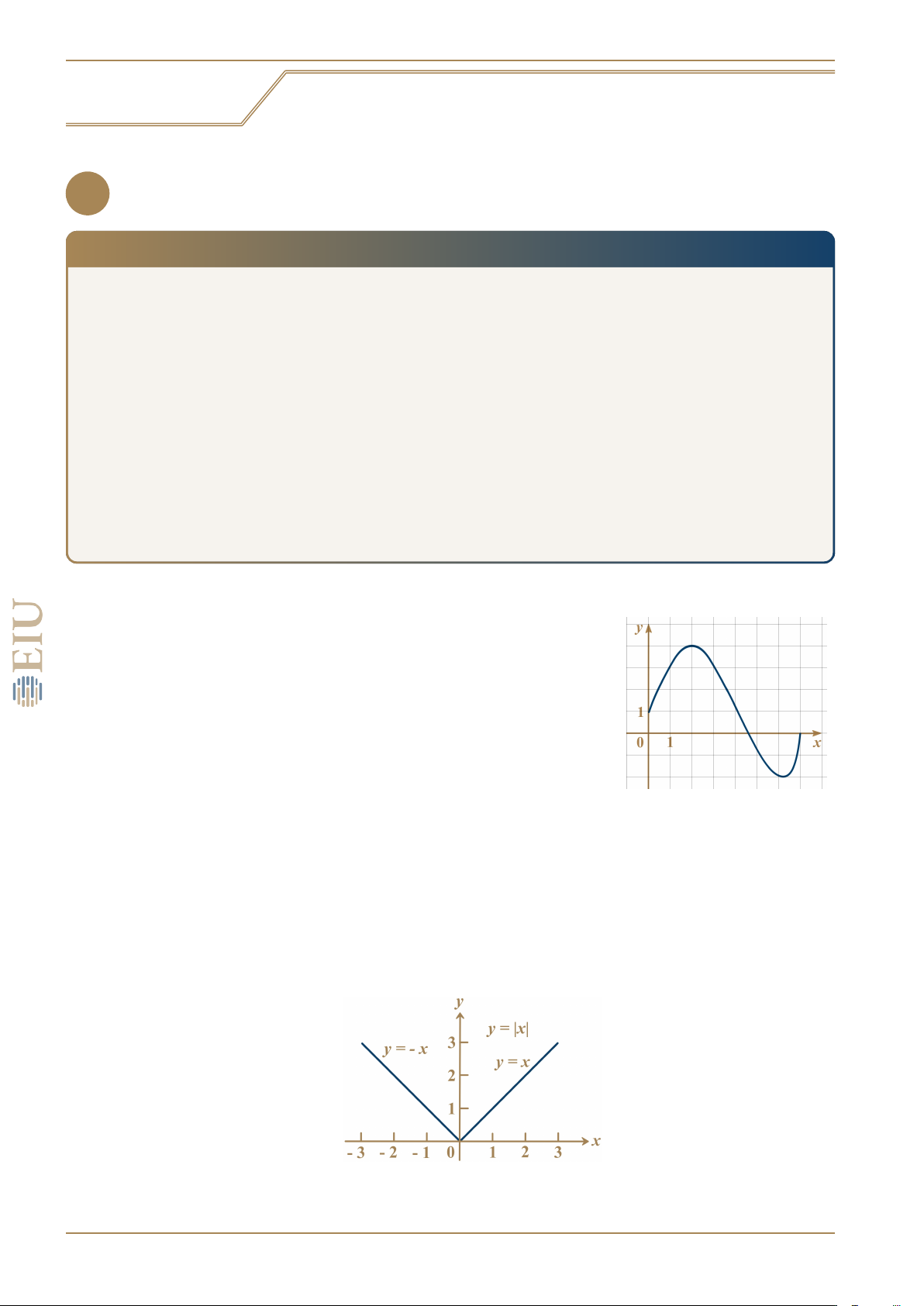
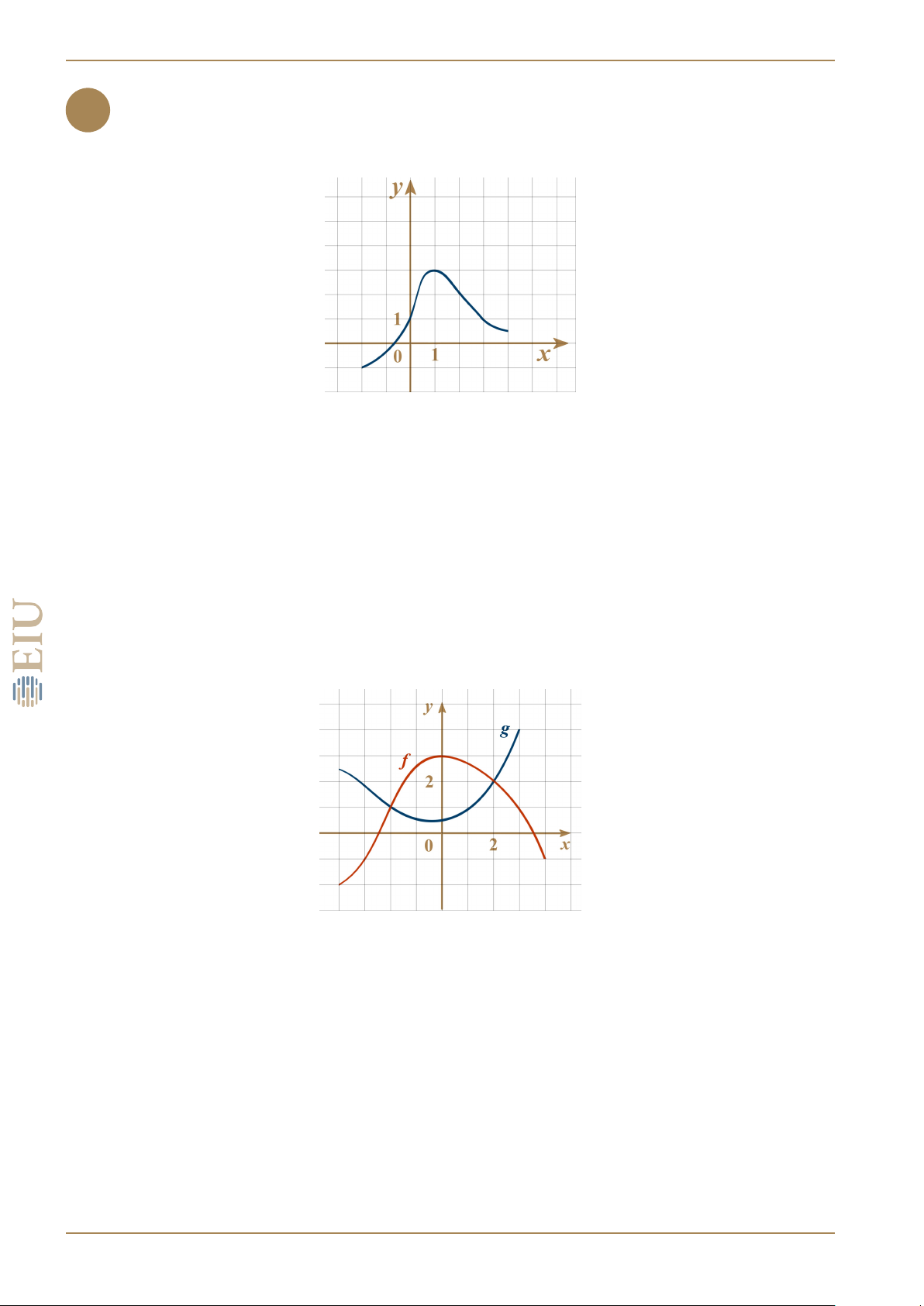
Cho hàm số f (x) có đồ thị như hình vẽ bên.
a) Tính f (1) và f (7).
b) Xác định tập xác định và tập giá trị của hàm số f . CHÚ Ý
Một hàm số có thể được cho bởi nhiều công thức. Chẳng hạn  x, x ≥ 0  
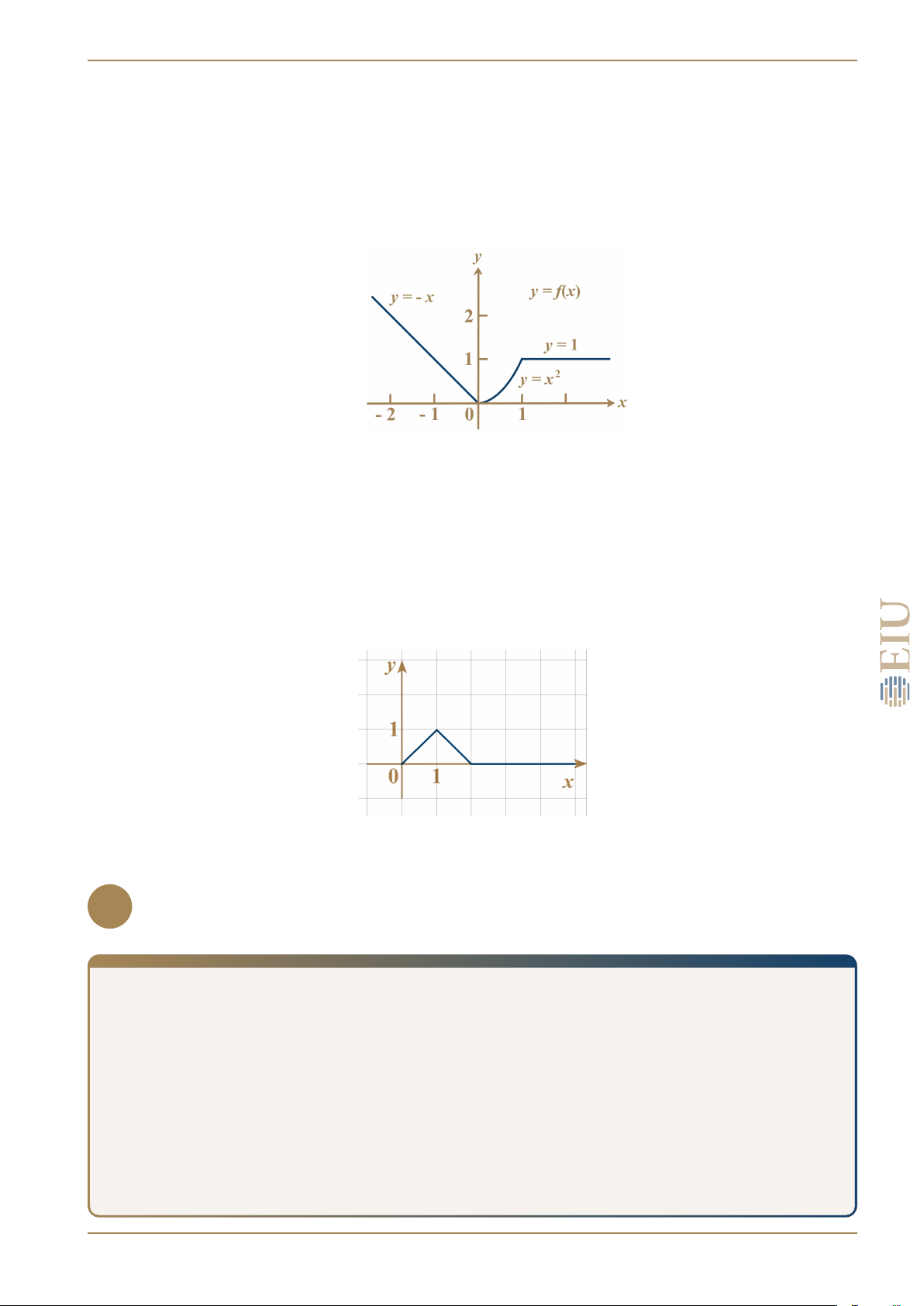
a) Xét hàm số f (x) = |x| = 
có đồ thị như hình vẽ.     − x, x < 0
Khi đó, với x ≥ 0 thì f (x) = x, với x < 0 thì f (x) = −x. LÊ NGUYỄN VIẾT TƯỜNG 2 1. HÀM SỐ VÀ ĐỒ THỊ   − x, x < 0      
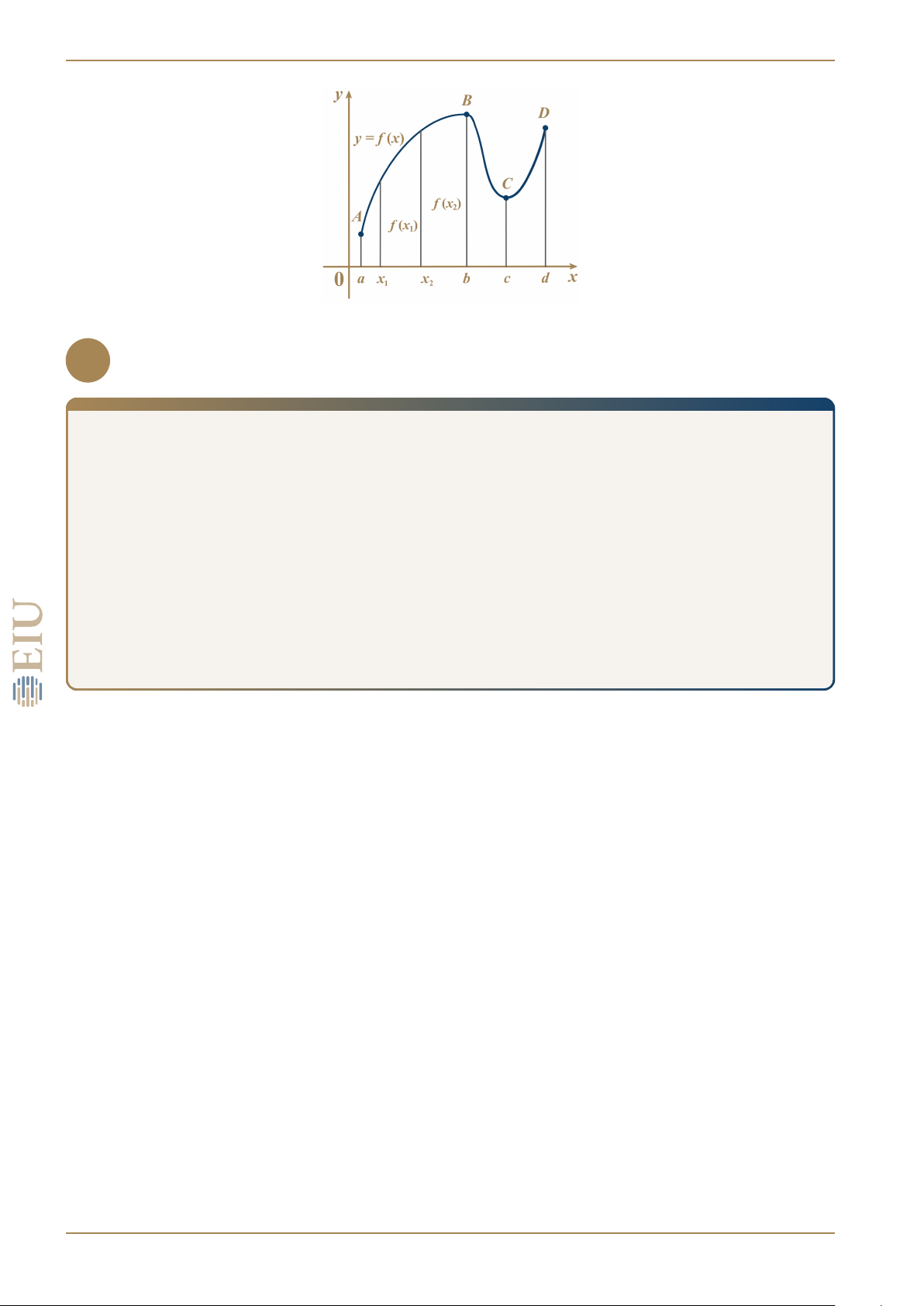
b) Xét hàm số f (x) = x2,
0 ≤ x ≤ 1 có đồ thị như hình vẽ.        1, x > 1
Khi đó, với x < 0 thì y = −x, với 0 ≤ x ≤ 1 thì y = x2 và với x > 1 thì y = 1.
VÍ DỤ 1.2. Xác định hàm số f (x) có đồ thị như hình vẽ sau:
1.2 HÀM SỐ ĐỒNG BIẾN. HÀM SỐ NGHỊCH BIẾN
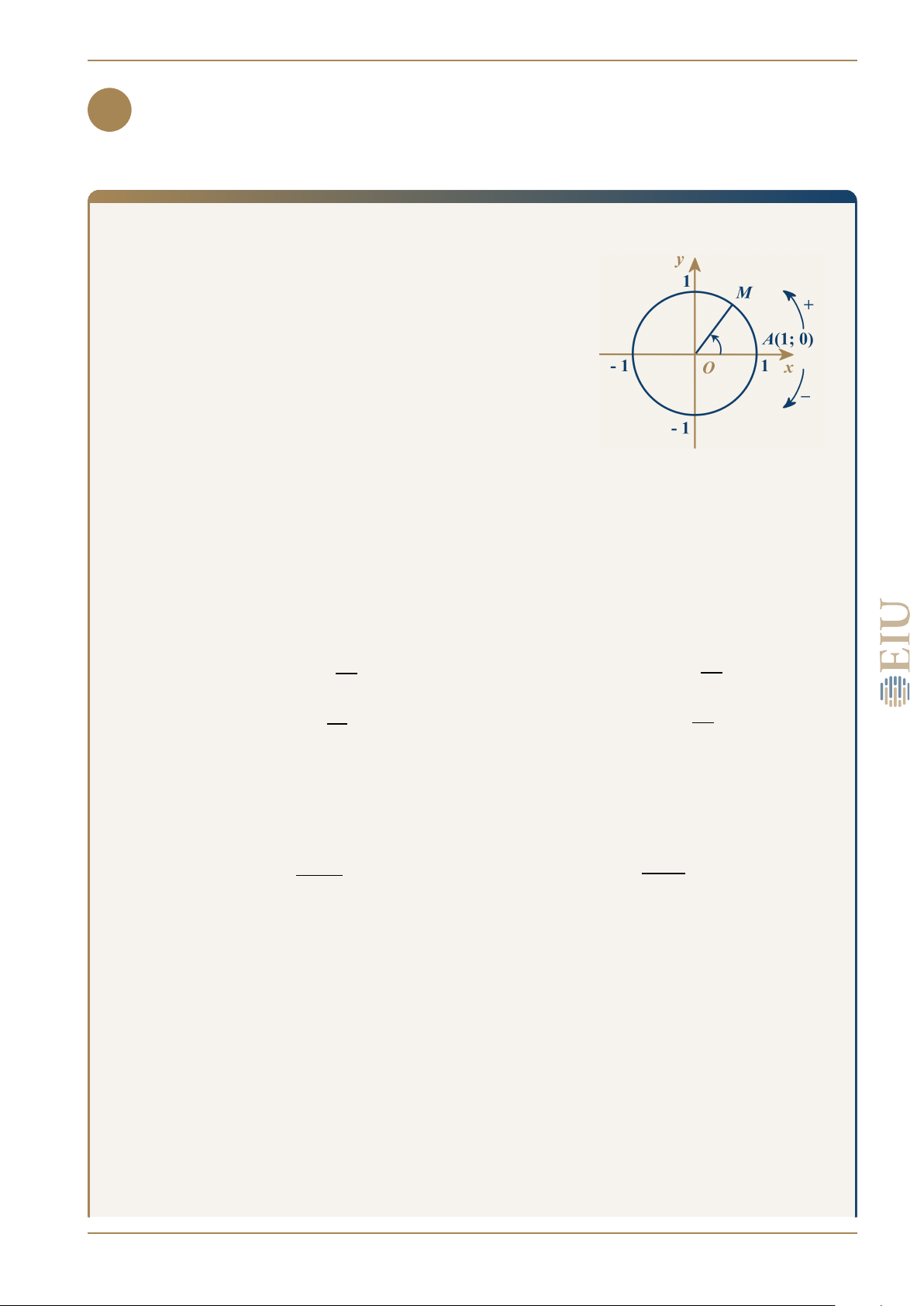
Với hàm số f (x) xác định trên khoảng (a; b), ta nói
• Hàm số đồng biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x1 < x2 ⇒ f (x1) < f (x2)
• Hàm số nghịch biến trên khoảng (a; b) nếu
∀x1, x2 ∈ (a; b), x2 < x2 ⇒ f (x1) > f (x2) 3 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ
1.3 HÀM SỐ CHẴN. HÀM SỐ LẺ. HÀM TUẦN HOÀN
Hàm số f (x) với tập xác định D được gọi là
• Hàm số chẵn nếu với mọi x ∈ D ta có −x ∈ D và f (−x) = f (x).
• Hàm số lẻ nếu với mọi x ∈ D ta có −x ∈ D và f (−x) = −f (x).
• Hàm số tuần hoàn nếu tồn tại một số T , 0 sao cho với mọi x ∈ D ta có x ± T ∈ D
và f (x + T ) = f (x).
Số dương T nhỏ nhất thoả mãn các điều kiện trên (nếu có) được gọi là chu kì của
hàm số tuần hoàn f (x). CHÚ Ý
• Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
• Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
VÍ DỤ 1.3. Xét tính chẵn, lẻ của các hàm số sau
a) f (x) = x2 + 1
b) g(x) = x3 + x
c) h(x) = sin 2x LÊ NGUYỄN VIẾT TƯỜNG 4 1. HÀM SỐ VÀ ĐỒ THỊ
1.4 MỘT SỐ HÀM CƠ BẢN HÀM LƯỢNG GIÁC
1. Đường tròn lượng giác
Trong mặt phẳng toạ độ Oxy, cho đường tròn tâm O
bán kính bằng 1. Trên đường tròn này, chọn điểm
A(1; 0) làm gốc, chiều dương là chiều ngược chiều
kim đồng hồ. Đường tròn cùng với gốc và chiều như
trên được gọi là đường tròn lượng giác.
Trên đường tròn lượng giác, điểm biểu diễn của góc
α là điểm M mà số đo của góc lượng giác (OA, OM ) bằng α.
2. Giá trị lượng giác của góc lượng giác
Trên đường tròn lượng giác, gọi M (xM ; yM ) là điểm biểu diễn của góc lượng giác có số đo α. Khi đó
• sine: sin α = y • M
cosine: cos α = xM
• tangent: tan α = yM
• cotangent: cot α = xM xM yM
• secant: sec α = 1
• cosecant: csc α = 1 xM yM
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
• sin2 α + cos2 α = 1
• tan α · cot α = 1 • 1 + tan2 α = 1 = sec2 α
• 1 + cot2 α = 1 = csc2 α cos2 α sin2 α
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
(a) Hai góc đối nhau (cos đối)
• sin(−α) = − sin α
• tan(−α) = − tan α
• cos(−α) = cos α
• cot(−α) = − cot α
(b) Hai góc bù nhau (bù sin)
• sin(π − α) = sin α
• tan(π − α) = − tan α
• cos(π − α) = − cos α
• cot(π − α) = − cot α 5 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ
(c) Hai góc phụ nhau (phụ chéo) • π π sin − α = cos α • tan − α = cot α 2 2 • π π cos − α = sin α • cot − α = tan α 2 2
5. Các công thức lượng giác
(a) Công thức cộng
• sin(α + ) = sin α cos + sin cos α
• sin(α − ) = sin α cos − sin cos α
• cos(α + ) = cos α cos − sin α sin
• cos(α − ) = cos α cos + sin α sin
• tan(α + ) = tan α + tan
• tan(α − ) = tan α − tan 1 − tan α tan 1 + tan α tan
(b) Công thức góc nhân đôi
• sin 2α = 2 sin α cos α
• cos 2α = cos2 α − sin2 α = 2 cos2 α − 1 = 1 − 2 sin2 α
• tan 2α = 2 tan α 1 − tan2 α
(c) Công thức biến đổi tổng thành tích • α + α − α + α −
sin α + sin = 2 sin cos
• sin α − sin = 2 cos sin 2 2 2 2 • α + α − α + α −
cos α +cos = 2 cos cos
• cos α−cos = −2 sin sin 2 2 2 2
(d) Công thức biến đối tích thành tổng
• cos α cos = 1 [cos(α + ) + cos(α − )] 2
• sin α cos = 1 [sin(α + ) + sin(α − )] 2 • 1
sin α sin = − [cos(α + ) − cos(α − )] 2
6. Định lý Cosine trong tam giác
Với mọi tam giác ABC, nếu đặt BC = a, CA = b, AB = c thì ta luôn có a2
= b2 + c2 − 2bc cos A b2
= c2 + a2 − 2ca cos B c2
= a2 + b2 − 2ab cos C Hệ quả
cos A = b2 + c2 − a2 ;
cos B = c2 + a2 − b2 ;
cos C = a2 + b2 − c2 2bc 2ca 2ab LÊ NGUYỄN VIẾT TƯỜNG 6 1. HÀM SỐ VÀ ĐỒ THỊ
HÀM MŨ - HÀM LOGARITHM
1. Phép tính luỹ thừa
Cho a, b là những số thực dương; γ, là những số thực bất kì. Khi đó
• aγ · a = aγ+
• (ab)γ = aγbγ
• (aγ) = aγ γ • aγ = a aγ− • = aγ a b bγ
2. Khái niệm logarithm
Cho hai số thực dương a, b với a , 1. Số thực γ thoả mãn đẳng thức aγ = b được
gọi là logarithm cơ số a của b và kí hiệu là log b. a
γ = log b ⇔ aγ = b. a CHÚ Ý
• Từ định nghĩa, ta có log 1 = 0; log a = 1; log ab = b;
aloga b = b. a a a
• log10b được viết là log b hoặc lg b. log b e
được viết là ln b.
3. Tính chất logarithm
Với 0 ≤ a , 1, M > 0, N > 0, ta có
• log (MN) = log M + log N
• log (Mγ) = γ log M (γ ∈ a a a a a R) • M log
= log M − log N • log log M a a M = 1 a N a a
4. Công thức đổi cơ số N
Cho các số dương a, b, N, a , 1, b , 1, ta có log N = logb . a log a b
Đặc biệt, ta có log N = 1 (N a , 1). log a N 7 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ 1.5 BÀI TẬP BÀI 1.
Cho hàm số f (x) có đồ thị như hình vẽ. a) Tính f (1).
b) Tìm x để f (x) = 1.
c) Tìm tập xác định và tập giá trị của f (x).
d) Hàm số đồng biến trên khoảng nào? BÀI 2.
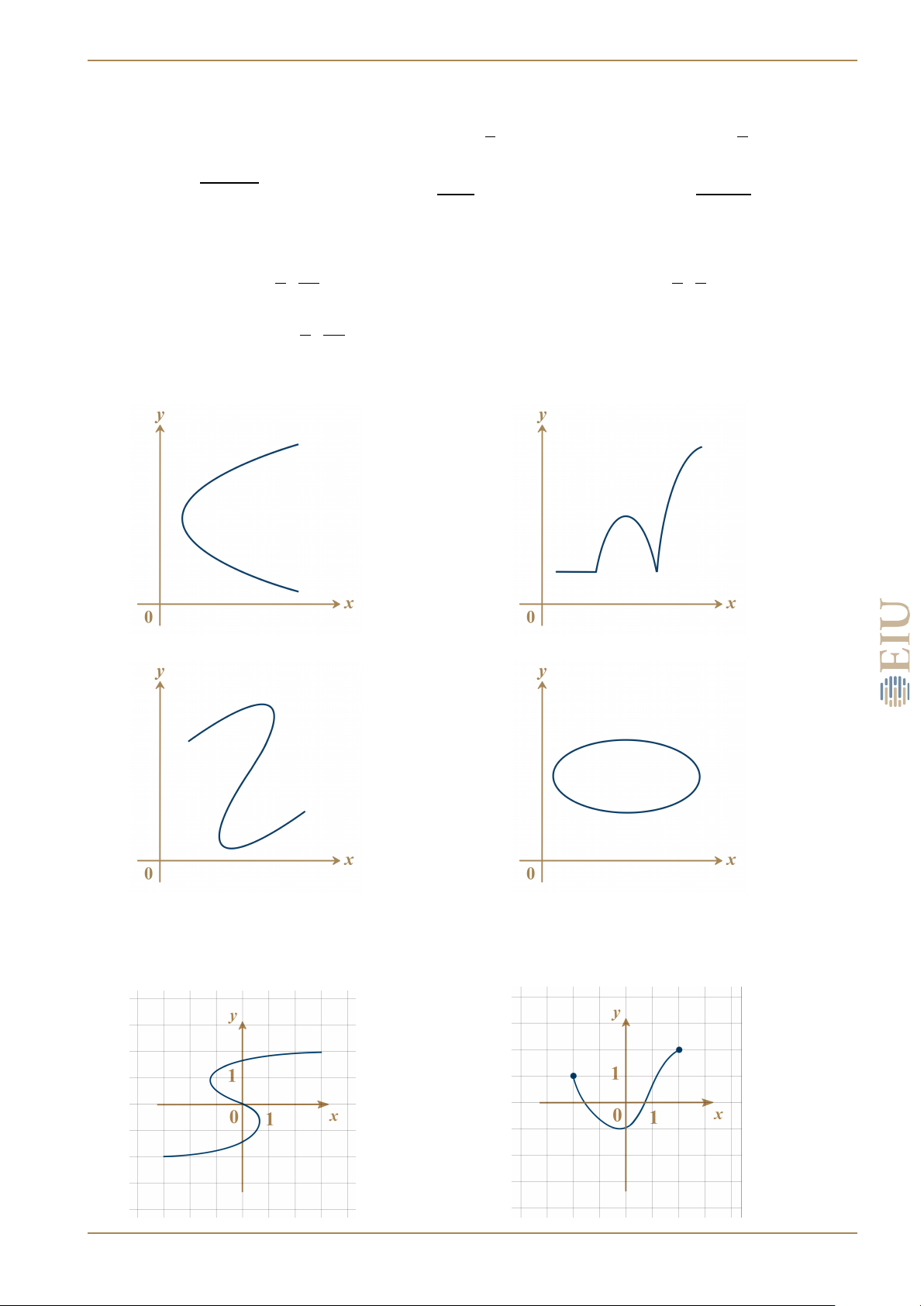
Cho các hàm số f (x) và g(x) có đồ thị như hình vẽ.
a) Tính f (−4) và g(3).
b) Tìm x để f (x) = g(x).
c) Hàm số f (x) đồng biến trên khoảng nào?
d) Tìm tập xác định và tập giá trị của f .
e) Tìm tập xác định và tập giá trị của g. LÊ NGUYỄN VIẾT TƯỜNG 8 1. HÀM SỐ VÀ ĐỒ THỊ
BÀI 3. Tìm tập xác định và tập giá trị của các hàm số sau: √ √
f (x) = 1 + x2 a) b) f (x) = 1 − x c) F (x) = sin x √ d) g(x) = x2 − 3x e) f (t) = 4 f) G(t) = 2 3 − t t2 − 16
BÀI 4. Tìm tập giá trị của các hàm số sau, biết π 7π π π
a) y = sin x, với x ∈ ; .
b) y = cos x, với x ∈ − ; . 4 6 6 3 π 3π
c) y = cos 2x, với x ∈ − ; . 2 2
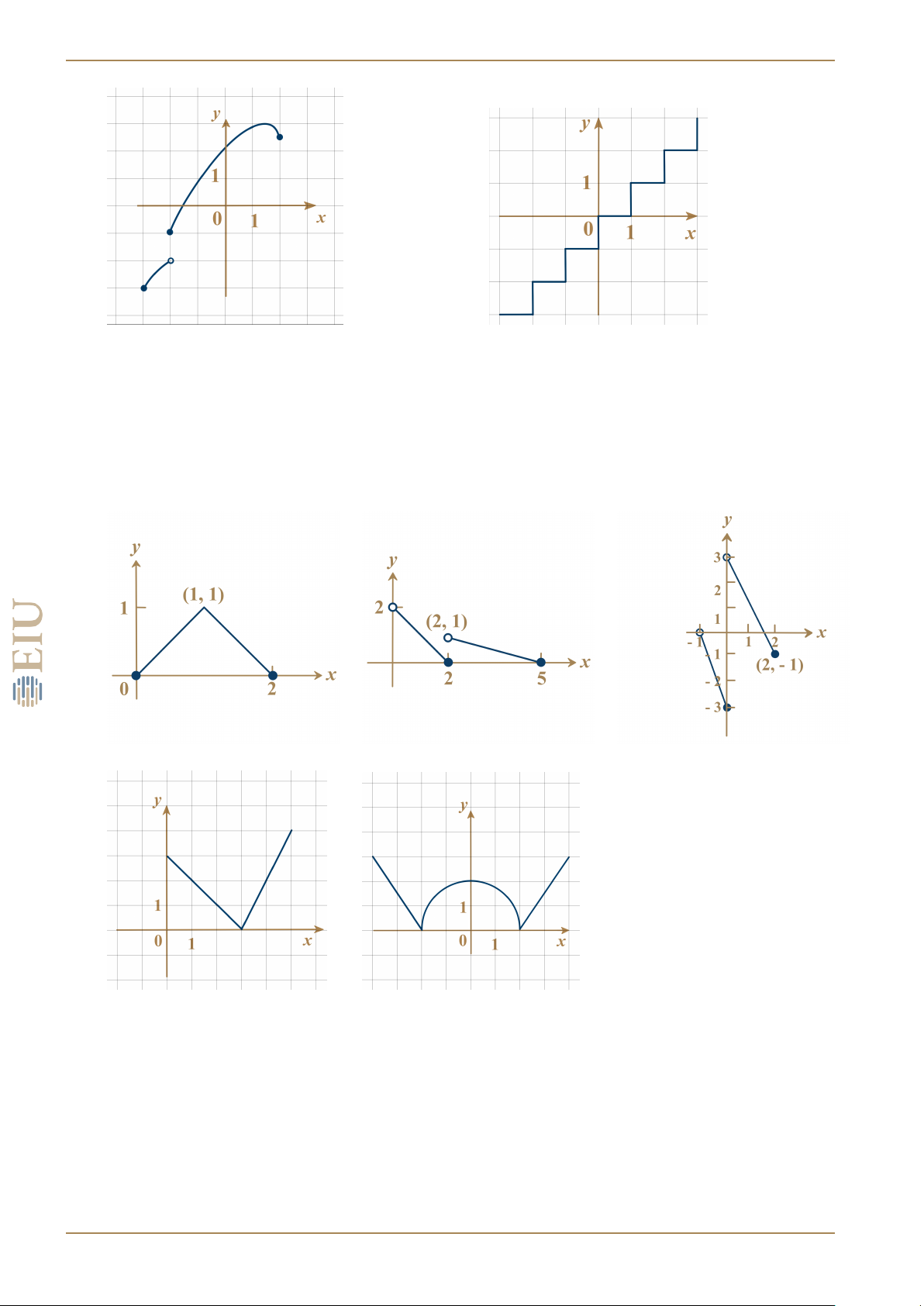
BÀI 5. Cho các đường cong sau, đường cong nào là đồ thị của một hàm số? a) b) c) d)
BÀI 6. Cho các đường cong sau, đường cong nào là đồ thị của một hàm số? Nếu là hàm số,
hãy tìm tập xác định và tập giá trị của nó. a) b) 9 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ c) d)
BÀI 7. Vẽ đồ thị của các hàm số sau:    x, 0 ≤ x ≤ 1 1 − x, 0 ≤ x ≤ 1 4 − x 2, x ≤ 1       a) f (x) =  b) g(x) =  c) F (x) =           2 − x, 1 < x ≤ 2 2 − x, 1 < x ≤ 2 x 2 + 2x, x > 1
BÀI 8. Xác định hàm số khi biết đồ thị của nó. a) b) c) d) e) LÊ NGUYỄN VIẾT TƯỜNG 10 1. HÀM SỐ VÀ ĐỒ THỊ
BÀI 9. Xác định tính chẵn, lẻ của các hàm số được cho bởi đồ thị sau: a) b) 11 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ 2 HÀM HỢP
2.1 KHÁI NIỆM HÀM HỢP
Cho hai hàm số f (x) và g(x), hàm số f ◦ g được xác định như sau
(f ◦ g)(x) = f (g(x))
được gọi là hàm hợp của f và g.
VÍ DỤ 2.1. Cho hàm số f (x) = x2 và g(x) = x − 3. Xác định f ◦ g và g ◦ f . √ √
VÍ DỤ 2.2. Cho hàm số f (x) =
x và g(x) =
2 − x. Hãy xác định: a) f ◦ g; b) g ◦ f ; c) f ◦ f ; d) g ◦ g.
VÍ DỤ 2.3. Tìm f ◦ g ◦ h, biết f (x) = x
, g(x) = x10, và h(x) = x + 3. x + 1
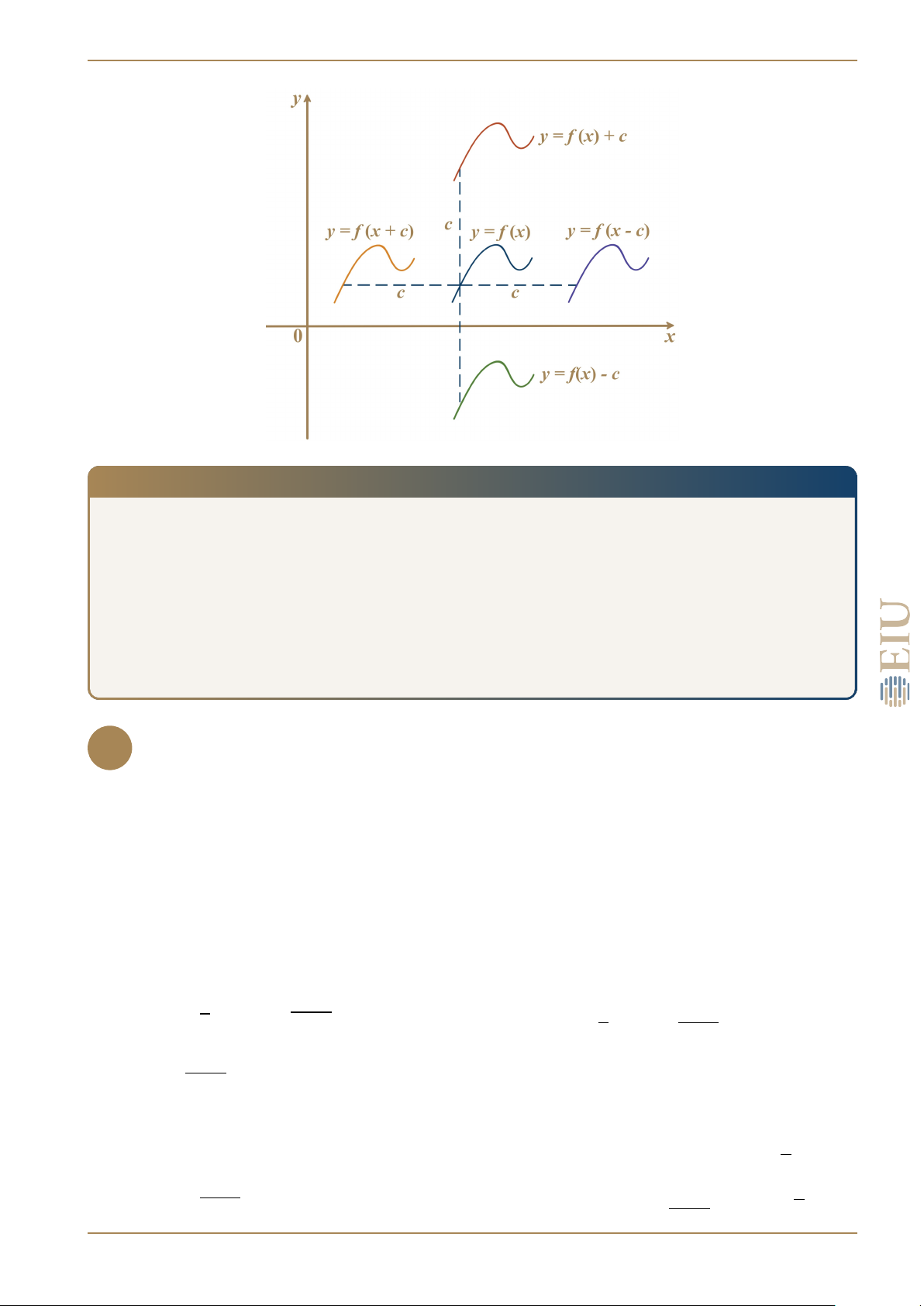
2.2 MỘT SỐ PHÉP BIẾN ĐỔI ĐỒ THỊ TỊNH TIẾN
Cho hàm số y = f (x) và số c > 0.
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = f (x) + c, ta tịnh tiến đồ thị hàm
số y = f (x) lên phía trên (theo phương Oy) c đơn vị.
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = f (x) − c, ta tịnh tiến đồ thị hàm
số y = f (x) xuống phía dưới (theo phương Oy) c đơn vị.
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = f (x + c), ta tịnh tiến đồ thị hàm
số y = f (x) sang trái (theo phương Ox) c đơn vị.
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = f (x − c), ta tịnh tiến đồ thị hàm
số y = f (x) sang phải (theo phương Ox) c đơn vị. LÊ NGUYỄN VIẾT TƯỜNG 12 2. HÀM HỢP ĐỐI XỨNG
Cho hàm số y = f (x).
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = f (−x), ta lấy đối xứng đồ thị
hàm số y = f (x) qua trục Oy.
• Từ đồ thị hàm số y = f (x) suy ra đồ thị hàm số y = −f (x), ta lấy đối xứng đồ thị
hàm số y = f (x) qua trục Ox. 2.3 BÀI TẬP
BÀI 10. Cho hàm số f (x) = x + 5 và g(x) = x2 − 3, hãy xác định: a) f (g(0)); b) g(f (0));
c) (f ◦ g)(x);
d) (g ◦ f )(x); e) f (f (−5)); f) g(g(2));
g) (f ◦ f )(x);
h) (g ◦ g)(x).
BÀI 11. Hãy xác định các hàm f ◦ g, g ◦ f, f ◦ f, g ◦ g, biết
a) f (x) = x2 − 1, g(x) = 2x + 1;
b) f (x) = 1 − 3x, g(x) = cos x; √ √ c) f (x) =
x, g(x) = 3 1 − x;
d) f (x) = x + 1 , g(x) = x + 1 ; x x + 2 e) f (x) = x
, g(x) = sin 2x. 1 + x
BÀI 12. Hãy xác định f ◦ g ◦ h, biết √
a) f (x) = 3x − 2, g(x) = sin x, h(x) = x2;
b) f (x) = |x − 4|, g(x) = 2x, h(x) = x; √ √ c) f (x) =
x − 3, g(x) = x2, h(x) = x3 + 2;
d) f (x) = tan x, g(x) = x
, h(x) = 3 x. x − 1 13 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ
BÀI 13. Cho bảng giá trị sau: x 1 2 3 4 5 6 f (x) 3 1 4 2 2 5 g(x) 6 3 2 1 2 3 Hãy xác định a) f (g(1)); b) g(f (1)); c) f (f (1)); d) g(g(1));
e) (g ◦ f )(3); f) (f ◦ g)(6). BÀI 14.
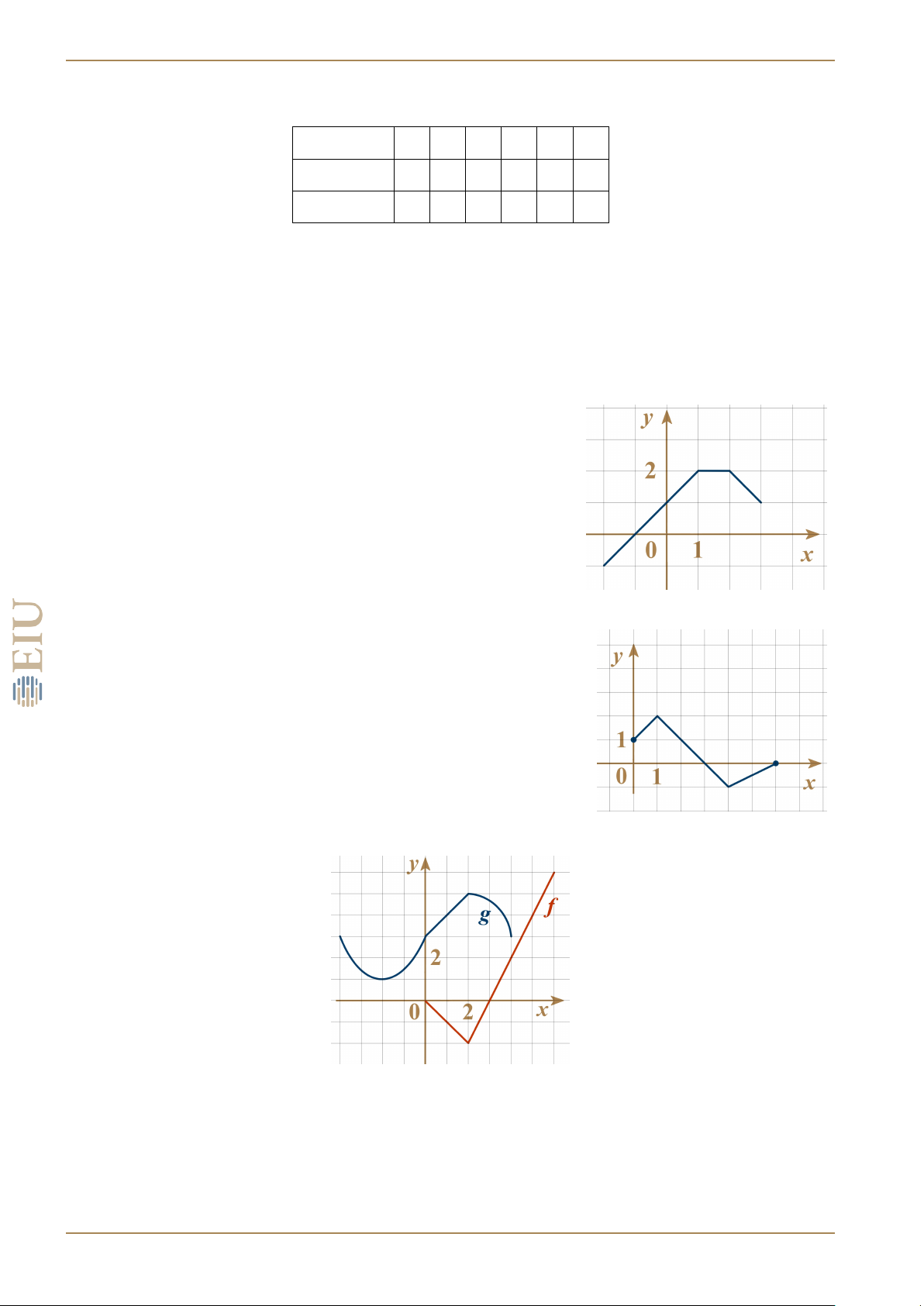
Cho hàm số f (x) có đồ thị như hình vẽ. Hãy vẽ đồ thị của các hàm sau:
a) y = f (x) − 2;
b) y = f (x − 2). BÀI 15.
Cho hàm số f (x) có đồ thị như hình vẽ. Hãy vẽ đồ thị của các hàm sau:
a) y = f (−x);
b) y = −f (x);
c) y = −f (−x).
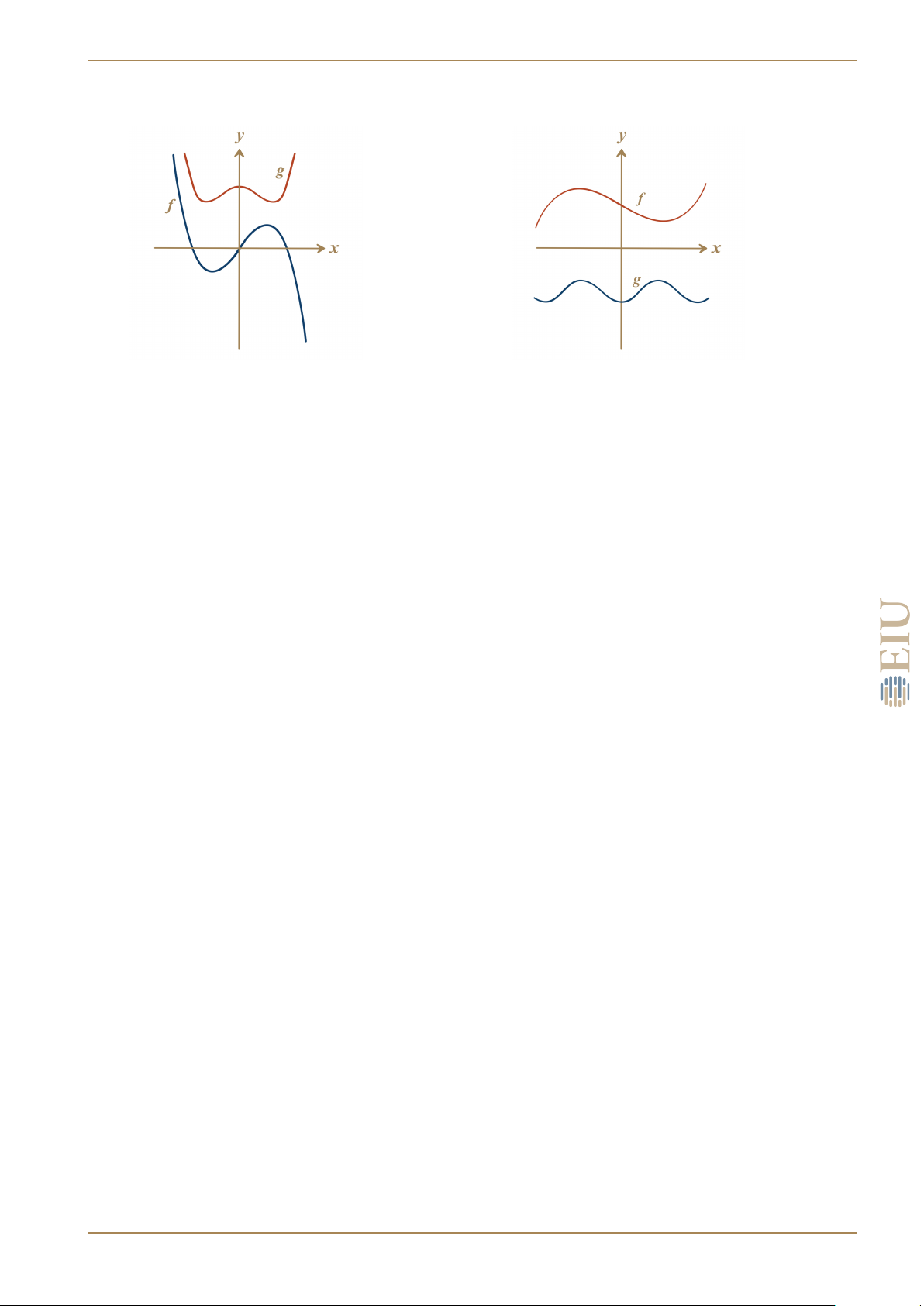
BÀI 16. Cho đồ thị của các hàm số f (x) và g(x) như hình vẽ Hãy xác định a) f (g(2)); b) g(f (0)); c) (f ◦ g)(0);
d) (g ◦ f )(6);
e) (g ◦ g)(−2);
f) (f ◦ f )(4). LÊ NGUYỄN VIẾT TƯỜNG 14 3. HÀM NGƯỢC 3 HÀM NGƯỢC 3.1 ĐỊNH NGHĨA
• Một hàm số f (x) được gọi là đơn ánh trên miền xác định D nếu f (x1) , f (x2) với mọi
x1 , x2 trên D. VÍ DỤ 3.1.
a) Hàm số y = x3 là đơn ánh.
Thật vậy, với mọi x 3 3 1 , x2 ta có x1 , x2 .
b) Hàm số y = x2 không là đơn ánh.
Thật vậy, ta có 1 , −1 nhưng 12 = (−1)2.
• Cho hàm số f là đơn ánh trên tập xác định D và có tập giá trị T.
Hàm ngược của nó (kí hiệu là f −1) được định nghĩa như sau
f −1(b) = a nếu f (a) = b.
Tập xác định của hàm f −1 là T và tập giá trị của f −1 là D. CHÚ Ý
a) f (x) có hàm ngược là f −1(x) khi và chỉ khi f f −1(x) = x và f −1 (f (x)) = x.
b) f −1(x) khác với (f (x))−1.
VÍ DỤ 3.2. Cho hàm số f (x) có f (1) = 5, f (3) = 7, và f (8) = −10. Hãy xác định f −1(7),
f −1(5), và f −1(−10).
3.2 TÌM HÀM NGƯỢC CỦA MỘT HÀM SỐ
CÁC BƯỚC TÌM HÀM NGƯỢC
• Bước 1: Đổi vị trí x và y, viết lại phương trình sau cho x = f (y).
• Bước 2: Giải phương trình vừa chuyển đổi để tìm y theo x.
• Bước 3: Khi có được y, biểu diễn nó dưới dạng y = f −1(x) và kết luận.
VÍ DỤ 3.3. Tìm hàm ngược của các hàm số sau: a) y = x3 + 2; b) y = 1 x + 1;
c) y = x2, với x ≥ 0. 2 15 LÊ NGUYỄN VIẾT TƯỜNG CHƯƠNG 1. HÀM SỐ 3.3 BÀI TẬP
BÀI 17. Trong các hàm số sau, hàm nào là đơn ánh?
a) f (x) = x2 − 2x;
b) f (x) = 10 − 3x; c) g(x) = 1 ;
d) g(x) = cos x. x
BÀI 18. Trong các hình vẽ sau, đâu là đồ thị của đơn ánh? a) b) c) d) e)
BÀI 19. Giả sử f là một đơn ánh có f (6) = 17, f −1(3) = 2. Tính f −1(17) và f (2).
BÀI 20. Giả sử f và g là các đơn ánh.
a) Cho f (x) = x5 + x3 + x. Tìm f −1(3) và f f −1(2).
b) Cho g(x) = 3 + x + ex. Tìm g−1(4). BÀI 21.
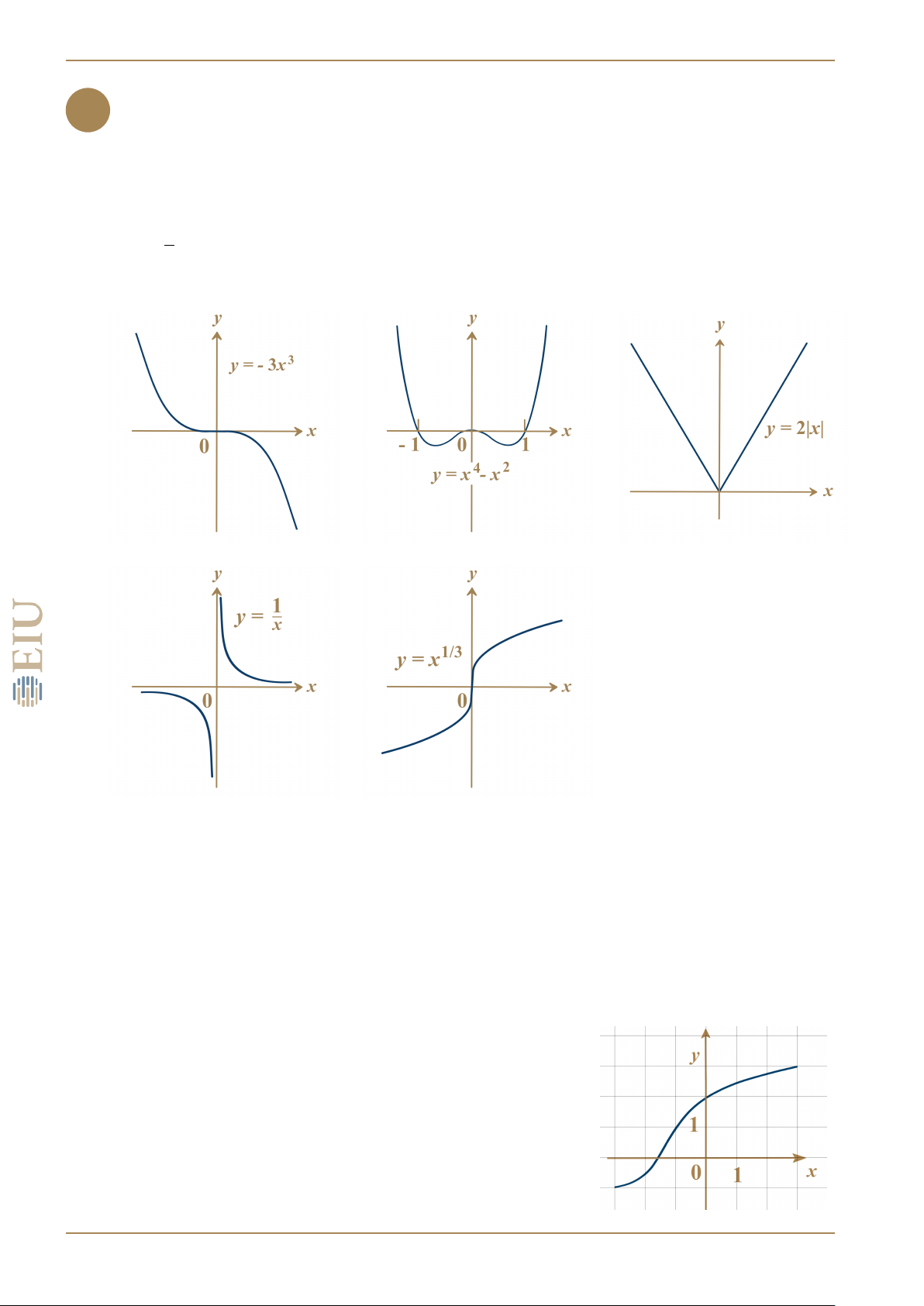
Cho hàm số y = f (x) có đồ thị như hình vẽ bên
a) Vì sao f (x) là đơn ánh?
b) Tìm tập xác định và tập giá trị của hàm f −1(x). c) Tính f −1(2). LÊ NGUYỄN VIẾT TƯỜNG 16 3. HÀM NGƯỢC
BÀI 22. Tìm hàm ngược của các hàm số sau: √ a) f (x) = 1 + 2 + 3x;
b) f (x) = 4x − 1 ;
c) f (x) = e2x−1; 2x + 3 1
d) y = x2 − x, với x ≥ ;
e) y = ln(x + 2); f) y = ex . 2 1 + 2ex 17 LÊ NGUYỄN VIẾT TƯỜNG