Tài liệu tổng hợp Vận dụng cao THPTQG

Biên soạn: Đội Ngũ Giáo Viên Trung Tâm Bồi Dưỡng Văn Hóa Trí Anh
CS1: Thái Hà: 0902.920.389
CS2: Hoàng Quốc Việt: 094.868.8992
CS3: Nguyễn Chí Thanh – Thành Công: 081.999.8992
Luyện thi các môn Toán – Lý – Hóa – Sinh – Anh
THPT QUỐC GIA – ĐGNL ĐHQGHN (HSA) – ĐGTD BKHN (TSA)
VDC THPTQG TAE PHẦN 5 (T PRO)
Câu 1: Cho hình chóp .
S ABCD có đáy ABCD là hình thoi cạnh 1 ;
ABC = 60 và SB =1. Hình chiếu vuông góc của điểm S lên mặt
phảng (ABC) trùng với trọng tâm tam giác ABC . Gọi  =  , B SC,D  .
Giá trị của cos là (làm tròn tới hàng phần mười)?
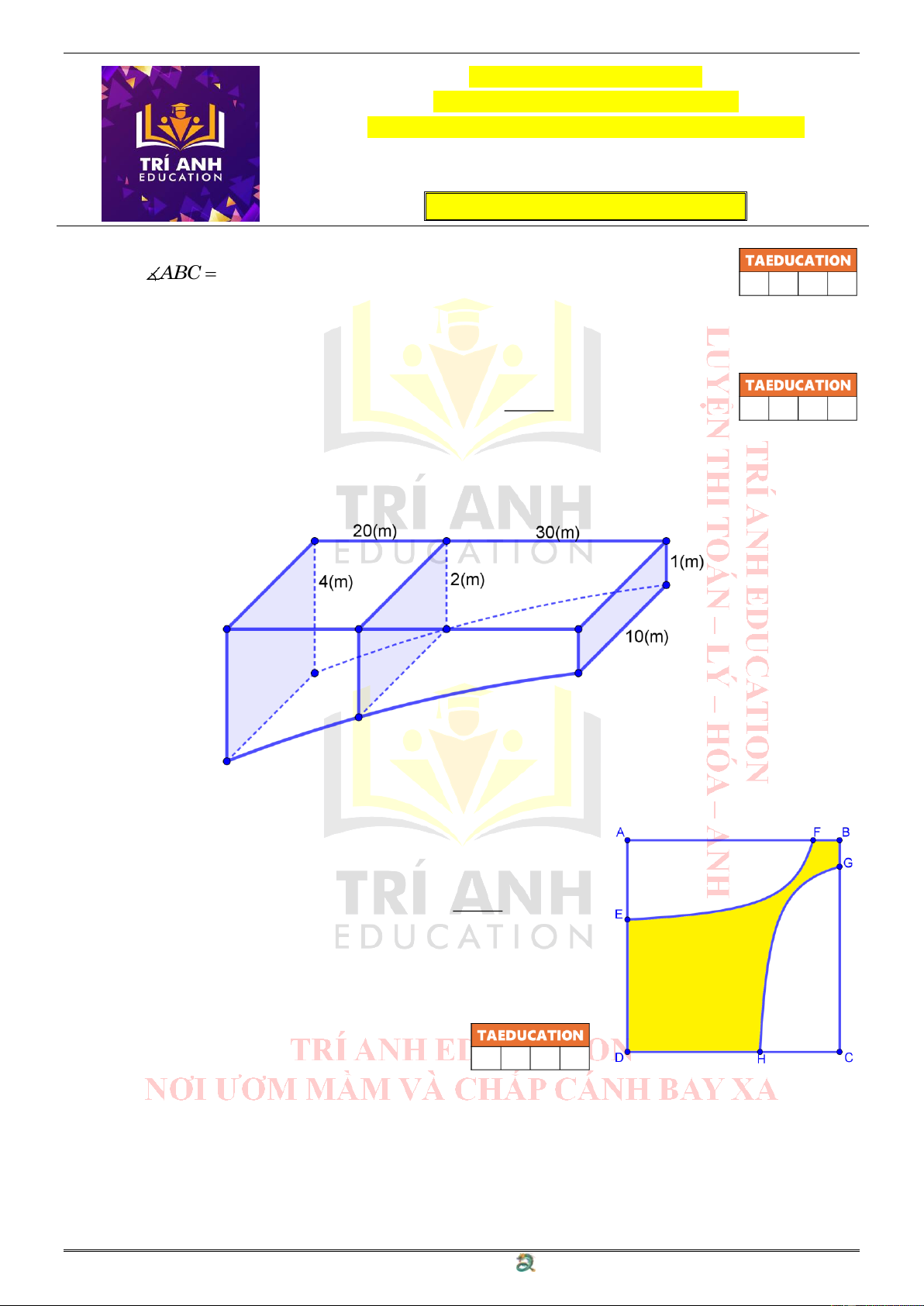
Câu 2: Một hồ bơi được thiết kế như hình vẽ dưới đây. Biết rằng các đường cong ax + b
phía dưới đều là các đường cong có dạng y =
và các mặt cắt đều là cx + d
hình chữ nhật có cùng chiều dài là 10(m). Thể tích lượng nước tối đa mà hồ bơi chứa được là bao nhiêu ( 3
m ) (làm tròn tới hàng phần mười)?
Câu 3: Một viên gạch có dạng hình vuông với kích thước mỗi
cạnh là 8(dm) được cho như hình vẽ bên trong đó độ
dài các cạnh FB =1(dm),AE = 3(dm) và đường cong ax + b
phía trên là đường cong có dạng y = đồng thời cx + d
tiệm cận với đường thẳng BC kéo dài. Biết rằng đường
cong phía dưới đối xứng với đường cong phía trên qua
đường thẳng BD . Tính diện tích phần hoa văn được tô
màu của viên gạch theo đơn vị ( 2 dm )
(làm tròn tới hàng phần mười)?
TRÍ tuệ được khai thông ANH dũng chép hóa rồng Trang 1/3
Biên soạn: Đội Ngũ Giáo Viên Trung Tâm Bồi Dưỡng Văn Hóa Trí Anh
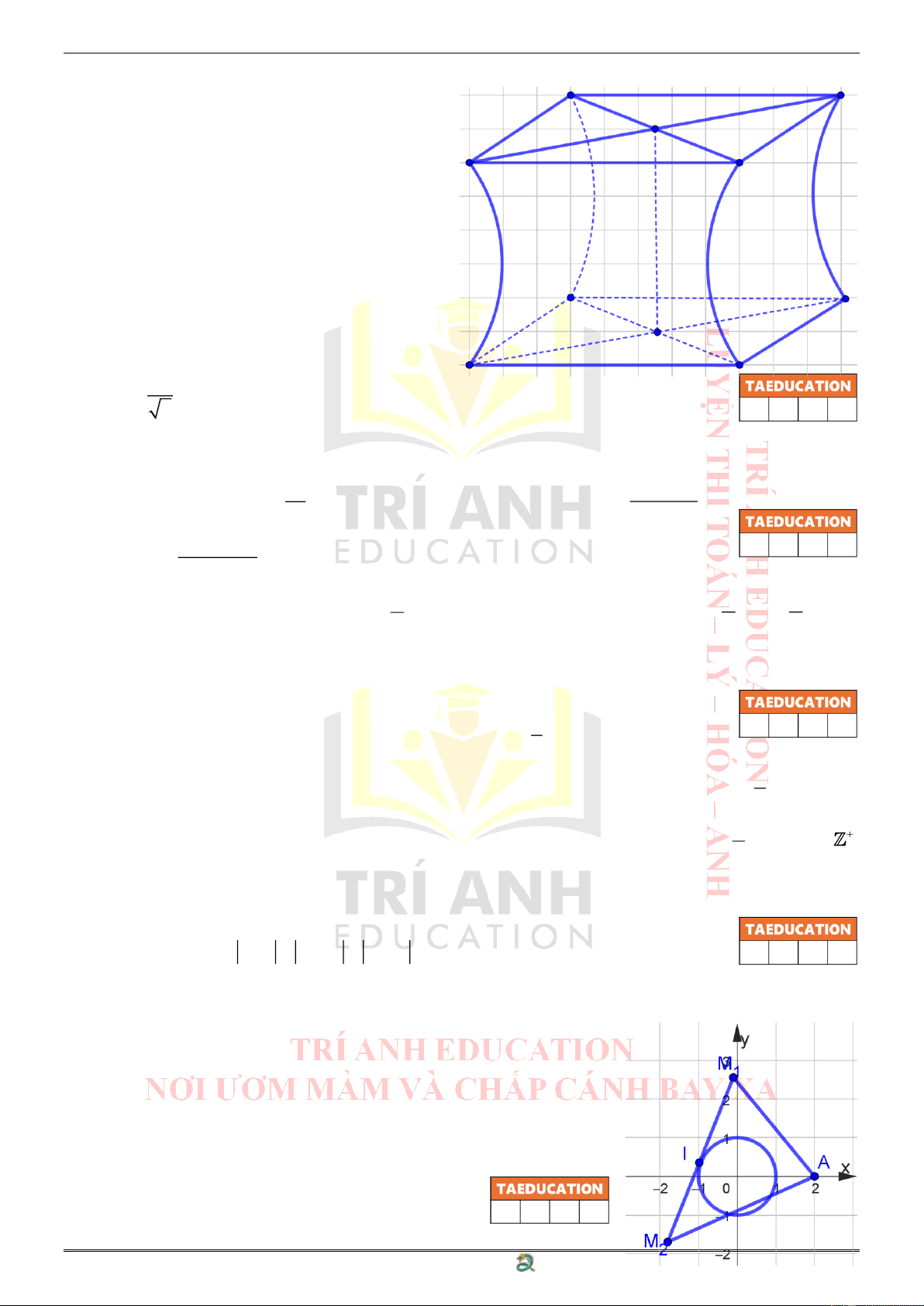
Câu 4: Người ta cần thiết kế một chiếc bàn
cách điệu bao gồm hai đáy là hai hình
vuông có cạnh đều bằng 1(m) và cách
nhau một khoảng cũng bằng 1(m)
sao cho đoạn nối tâm của hai hình
vuông vuông góc với hai mặt phẳng
đáy. Biết rằng trên mỗi mặt phẳng
chứa đường chéo của hình vuông, hai
đường cong ở hai bên là hai đường
Hyperbol và đoạn ngắn nhất nối giữa
hai điểm trên hai đường cong đó là
1 (m). Tính thể tích của chiếc bàn 2 đã cho theo đơn vị ( 3
m ) (làm tròn tới hàng phần mười)? 2 x f (x)
Câu 5: Biết rằng F (x) =
là một nguyên hàm của mỗi hàm số y = và 2 sin x + 2 xg(x) y =
với mọi x  0 . Diện tích hình phẳng giới hạn bởi các cos x + 2x       
đường y = f (x),y = g (x),x = và x =  bằng bao nhiêu biết rằng f = g (làm 2  2   2     
tròn tới hàng phần trăm)? Câu 6: Cho hàm số 3 2
y = x + ax + bx + c có đồ thị cắt trục hoành tại ba điểm 1
phân biệt. Biết rằng hàm số g (x) = f (x) f (x) − f  (x) 2  + 5 2  có 3 điểm 9
cực trị với hoành độ lần lượt là x  x  x đồng thời g (x = 3,g x = ,g x = 3. 1 ) ( 2) ( 3) 1 2 3 2 a
Diện tích hình phẳng giới hạn bởi đồ thị y = f (x) g(x) và trục hoành là với , a b +  b
và là phân số tối giản. Khi đó a + b = ?
Câu 7: Biết rằng tập hợp các điểm M (x; ;
y z) trong không gian Oxyz thỏa mãn
điều kiện: x −t + y − 2t + z − 3t 1 trong đó t  0  ;2   là một vật thể
(H). Thể tích của vật thể (H) khi đó là bao nhiêu (làm tròn tới hàng phần mười)
Câu 8: Cho điểm A (2;0) và đường tròn ( ) ;1 O . Giả sử có hai điểm
M ,M thỏa mãn điều kiện M M = 4 và đoạn thẳng 1 2 1 2
M M tiếp xúc với ( ) ;1 O
tại điểm I là trung điểm của 1 2
M M . Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu 1 2
thức P = AM + AM là bao nhiêu (làm tròn tới hàng 1 2 phần trăm)?
TRÍ tuệ được khai thông ANH dũng chép hóa rồng Trang 2/3
Biên soạn: Đội Ngũ Giáo Viên Trung Tâm Bồi Dưỡng Văn Hóa Trí Anh
Câu 9: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh a . Biết rằng khoảng a 10
cách giữa hai đường thẳng SB và AD là đồng thời 5
(SAB) ⊥ (SCD), (SAD) ⊥ (SBC) . Khi góc  = S  , A , B C 
 đạt giá trị lớn nhất thì giá trị
của cos là (làm tròn tới hàng phần trăm)?
Câu 10: Người ta thả hai quả bóng thăm dò không gian A,B
bay quanh Trái Đất theo quỹ đạo hình cầu với bán kính
không đổi R = 6400 (tâm Trái Đất là gốc tọa độ trong
hệ trục tọa độ Oxyz , mỗi đơn vị trên hệ tọa độ ứng với
1(km)) sao cho hai trái bóng luôn cách nhau một
khoảng không đổi AB = 3200 có nhiệm vụ truyền tín
hiệu đến một trạm vệ tinh được đặt ở vị trí điểm
M (0;8000;0) . Để tối ưu việc thu nhận tín hiệu, người
ta muốn chọn vị trí các vệ tinh sao cho hiệu bình phương khoảng cách 2 2
MA − MB giữa trạm tới hai
bóng A,B đạt giá trị lớn nhất. Giá trị lớn nhất khi đó là bao nhiêu (làm
tròn tới hàng phần mười theo đơn vị triệu (km))?
TRÍ tuệ được khai thông ANH dũng chép hóa rồng Trang 3/3