8-Noi dung on tap Co so Vat lý 2 - SPKHTN K46

NỘI DUNG ÔN TẬP – SƯ PHẠM KHOA HỌC TỰ NHIÊN

Phần Lý thuyết

Câu 1. Khái niệm điện trường. Vecto cường độ điện trường do một điện tích điểm gây ra.

Khái niệm điện trường. Điện trường là một dạng vật chất tồn tại xung quanh các điện tích và tác dụng lực điện lên các điện tích khác đặt trong nó.

Vecto cường độ điện trường do một điện tích điểm gây ra. Vectơ cường độ điện trường E do một điện tích điểm q gây ra tại một điểm được xác định bởi công thức: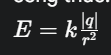

• k=9×10⁹ Nm²/C² (hằng số Coulomb trong chân không hoặc không khí).
• q là độ lớn điện tích điểm gây ra điện trường.
• r là khoảng cách từ điện tích điểm đến điểm khảo sát.

 Phương: Nằm trên đường thẳng nối điện tích điểm q với điểm khảo sát.

 Chiều:

• Hướng ra xa điện tích q nếu q>0.
• Hướng về phía điện tích q nếu q<0.

Câu 2. Nguyên lý chồng chất điện trường. Vecto cường độ điện trường do một vật tích điện gây ra.

Nguyên lý chồng chất điện trường phát biểu rằng, vectơ cường độ điện trường tổng hợp tại một điểm do nhiều điện tích gây ra bằng tổng các vectơ cường độ điện trường do từng điện tích riêng lẻ gây ra tại điểm đó. E=E1​​+E2​+...+En​​

Vecto cường độ điện trường do một vật tích điện gây ra. Vectơ cường độ điện trường do một vật tích điện gây ra tại một điểm được xác định bằng cách chia vật thành các phần tử điện tích nhỏ, tính cường độ điện trường do mỗi phần tử gây ra, sau đó tổng hợp (tích phân) các vectơ đó.

Câu 3. Điện thông và ý nghĩa điện thông. Nội dung định lý Ostrogradski – Gauss.

Điện thông là một đại lượng đặc trưng cho số đường sức điện trường xuyên qua một diện tích nhất định. Nó được tính bằng tích phân của tích vô hướng giữa vectơ cường độ điện trường và vectơ pháp tuyến của diện tích trên bề mặt đang xét. Ý nghĩa của điện thông: Cho biết mức độ "tập trung" của điện trường qua một bề mặt.

Nội dung định lý Ostrogradski - Gauss. Định lý Ostrogradski - Gauss (hay định lý Gauss cho điện trường) phát biểu rằng điện thông qua một mặt kín bất kỳ tỷ lệ với tổng đại số các điện tích nằm bên trong mặt kín đó. Công thức: 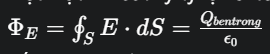trong đó Qbentrong​ là tổng điện tích bên trong mặt kín và ϵ0​ là hằng số điện môi của chân không.

Câu 4. Khái niệm điện thế, hiệu điện thế. Công thức xác định điện thế gây bởi một điện tích điểm và hệ điện tích điểm.

Điện thế tại một điểm trong điện trường là đại lượng đặc trưng cho khả năng sinh công của điện trường khi có một điện tích đặt tại điểm đó. Nó được định nghĩa là công của lực điện trường dịch chuyển một đơn vị điện tích dương từ điểm đó ra vô cùng (nếu chọn gốc điện thế ở vô cùng). Hiệu điện thế giữa hai điểm là công của lực điện trường để dịch chuyển một đơn vị điện tích dương giữa hai điểm đó, không phụ thuộc vào dạng đường đi. Nó cũng chính là sự chênh lệch điện thế giữa hai điểm.

Công thức xác định điện thế gây bởi một điện tích điểm và hệ điện tích điểm. Điện thế V do một điện tích điểm q gây ra tại một điểm cách nó một khoảng r là: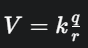

Điện thế do một hệ điện tích điểm gây ra tại một điểm bằng tổng đại số điện thế do từng điện tích điểm gây ra tại điểm đó: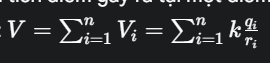

Câu 5. Thiết lập biểu thức vectơ cảm ứng từ B gây ra bởi một dòng điện thẳng nói chung. Xét các trường hợp riêng: dòng điện thẳng dài vô hạn, nửa đường thẳng, điểm đang xét thuộc đường thẳng chứa dòng điện.

Thiết lập biểu thức vectơ cảm ứng từ B gây ra bởi một dòng điện thẳng nói chung. Biểu thức vectơ cảm ứng từ B gây ra bởi một dòng điện thẳng nói chung được xác định bằng định luật Biot-Savart. 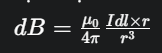trong đó dB là cảm ứng từ do phần tử dòng điện Idl gây ra, r là vectơ từ phần tử dòng điện đến điểm đang xét.

Dòng điện thẳng dài vô hạn: (chia 2πr)

Nửa đường thẳng: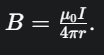

Điểm đang xét thuộc đường thẳng chứa dòng điện: B=0(vectơdlvà rcùng phương, dẫn đến dl×r=0)

Câu 6. Thiết lập biểu thức vectơ cảm ứng từ B gây ra bởi một dòng điện tròn. Xét các trường hợp riêng: tại điểm O nằm ở tâm dòng điện tròn, cung tròn chắn góc ở tâm 2.

Biểu thức vectơ cảm ứng từ B gây ra bởi một dòng điện tròn tại một điểm trên trục của vòng dây được tính bằng cách tích phân các đóng góp từ mỗi phần tử dòng điện theo định luật Biot-Savart: 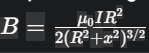trong đó R là bán kính vòng dây, x là khoảng cách từ tâm vòng dây đến điểm đang xét trên trục.

Tại điểm O nằm ở tâm dòng điện tròn: x=0, công thức trở thành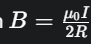

Cung tròn chắn góc ở tâm 2α: Cảm ứng từ tại tâm do một cung tròn gây ra là B=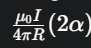

Câu 7. Định nghĩa đường cảm ứng từ. Nêu tính chất của đường cảm ứng từ. Vẽ phổ các đường sức của từ trường gây bởi một vài dòng điện (dòng điện thẳng, tròn, cuộn dây) và của vài loại nam châm (nam châm thẳng, nam châm chữ U.

Đường cảm ứng từ (hay đường sức từ) là những đường cong mà tiếp tuyến tại mỗi điểm trên đó cho biết chiều của vectơ cảm ứng từ tại điểm đó.

Tính chất của đường cảm ứng từ:

• Là những đường cong kín hoặc vô hạn ở hai đầu.
• Không cắt nhau.
• Nơi nào đường sức từ dày thì từ trường mạnh, nơi nào thưa thì từ trường yếu.
• Chiều của đường sức từ được xác định bằng quy tắc nắm tay phải (đối với dòng điện) hoặc từ cực Bắc ra cực Nam (đối với nam châm).

Vẽ phổ các đường sức của từ trường gây bởi một vài dòng điện (dòng điện thẳng, tròn, cuộn dây) và của vài loại nam châm (nam châm thẳng, nam châm chữ U). (Do giới hạn của văn bản, không thể vẽ hình trực tiếp. Tuy nhiên, mô tả các đường sức từ như sau):

• Dòng điện thẳng: Các đường sức từ là các đường tròn đồng tâm nằm trong mặt phẳng vuông góc với dây dẫn, tâm là điểm dây dẫn xuyên qua mặt phẳng đó.
• Dòng điện tròn: Các đường sức từ là các đường cong kín, xuyên qua lòng vòng dây và bao quanh vòng dây. Các đường sức từ sẽ dày đặc ở gần dây và thưa dần khi ra xa. Trên trục của vòng dây, các đường sức từ là các đường thẳng.
• Cuộn dây (ống dây solenoid): Bên trong ống dây, các đường sức từ là các đường thẳng song song, đều đặn, chỉ ra một từ trường đều. Bên ngoài ống dây, các đường sức từ loe ra và khép kín.
• Nam châm thẳng: Các đường sức từ đi ra từ cực Bắc và đi vào cực Nam, tạo thành các đường cong kín bên ngoài nam châm và đi từ cực Nam sang cực Bắc bên trong nam châm.
• Nam châm chữ U: Các đường sức từ đi ra từ cực Bắc và đi vào cực Nam, tạo thành một từ trường gần như đều giữa hai nhánh của chữ U.

Câu 8. Nêu định nghĩa và ý nghĩa của từ thông. Từ đó rút ra định lý O-G đối với từ trường.

ừ thông là một đại lượng đặc trưng cho số đường sức từ xuyên qua một diện tích nhất định. Nó được tính bằng tích phân của tích vô hướng giữa vectơ cảm ứng từ và vectơ pháp tuyến của diện tích trên bề mặt đang xét. Ý nghĩa của từ thông: Cho biết mức độ "tập trung" của từ trường qua một bề mặt.

Định lý Ostrogradski - Gauss đối với từ trường (Định lý Gauss về từ trường): Phát biểu rằng từ thông qua một mặt kín bất kỳ luôn bằng 0. Điều này thể hiện rằng không có "từ tích đơn" (monopole từ), tức là đường sức từ luôn là những đường cong kín.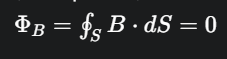

Câu 9. Phát biểu định lý Ampere (định lý về dòng toàn phần). Ứng dụng định lý Ampere tính cường độ từ trường H (và tính B) tại một điểm bên trong cuộn dây hình xuyến.

Định lý Ampere (định lý về dòng toàn phần): Tích phân đường của vectơ cường độ từ trường H(hoặc cảm ứng từ B) dọc theo một đường cong kín bất kỳ bằng tổng đại số các dòng điện xuyên qua mặt phẳng giới hạn bởi đường cong đó (nhân với μ0​ nếu tính cho B).

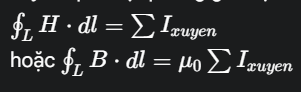
Ứng dụng định lý Ampere tính cường độ từ trường H (và tính B) tại một điểm bên trong cuộn dây hình xuyến. Đối với một cuộn dây hình xuyến có N vòng dây và bán kính trung bình R, dòng điện I chạy qua, cường độ từ trường H bên trong cuộn dây xuyến tại một điểm cách tâm R là: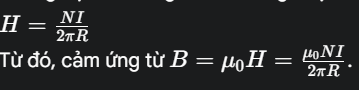

Câu 10. Tìm lực tác dụng giữa hai dòng điện thẳng song song dài vô hạn cùng chiều và ngược chiều nhau.

Cùng chiều: Hai dòng điện thẳng song song dài vô hạn cùng chiều sẽ hút nhau. Lực tác dụng lên mỗi đơn vị dài của dây dẫn được tính bằng: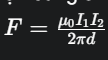

Ngược chiều: Hai dòng điện thẳng song song dài vô hạn ngược chiều sẽ đẩy nhau. Lực tác dụng lên mỗi đơn vị dài của dây dẫn cũng được tính bằng công thức trên.

Câu 11. Xác định vectơ từ trường do một điện tích chuyển động gây ra.

Vectơ từ trường B do một điện tích q chuyển động với vận tốc v gây ra tại một điểm cách điện tích một khoảng r được xác định bằng công thức: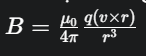

Câu 12. Xác định lực từ tác dụng lên hạt điện q chuyển động trong từ trường (lực Lorentz). Quỹ

đạo chuyển động của hạt như thế nào trong từ trường đều. Xét các trường hợp: B  v ,

B, v   .

B / /v và

Lực từ tác dụng lên hạt điện q chuyển động với vận tốc v trong từ trường B là lực Lorentz:F=q(vxB)

Độ lớn của lực: F=∣q∣vBsinα, trong đó α là góc giữa v và B.

Quỹ đạo chuyển động của hạt trong từ trường đều:

• Trường hợp B⊥v: Lực Lorentz luôn vuông góc với vận tốc, đóng vai trò là lực hướng tâm, làm cho hạt chuyển động tròn đều trong mặt phẳng vuông góc với B. Bán kính quỹ đạo được xác định bởi
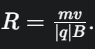
• Trường hợp B//v: Lực Lorentz bằng 0 (sinα=0), hạt chuyển động thẳng đều theo hướng ban đầu.
• Trường hợp (B,v)=α (góc bất kỳ): Hạt chuyển động theo quỹ đạo xoắn ốc (helix). Chuyển động này có thể phân tích thành hai thành phần: một chuyển động tròn trong mặt phẳng vuông góc với B và một chuyển động thẳng đều dọc theo hướng của B

Câu 13. Trình bày hiện tượng cảm ứng điện từ và hiện tượng tự cảm.

Hiện tượng cảm ứng điện từ: Là hiện tượng xuất hiện suất điện động cảm ứng (và dòng điện cảm ứng nếu mạch kín) trong một mạch kín khi từ thông qua mạch đó biến thiên theo thời gian.

Hiện tượng tự cảm: Là một trường hợp đặc biệt của hiện tượng cảm ứng điện từ, xảy ra trong một mạch điện có dòng điện biến đổi theo thời gian. Sự biến thiên của dòng điện trong mạch tạo ra sự biến thiên của từ thông riêng do chính dòng điện đó gây ra, dẫn đến xuất hiện một suất điện động tự cảm chống lại sự thay đổi của dòng điện đó.

Câu 14. Phát biểu định luật Lenzt (xác định chiều dòng điện cảm ứng) và định luật Faraday về suất điện động cảm ứng.

Định luật Lenzt: Chiều của dòng điện cảm ứng được sinh ra có tác dụng chống lại nguyên nhân sinh ra nó. (Tức là, từ trường do dòng điện cảm ứng sinh ra sẽ chống lại sự biến thiên của từ thông ban đầu).

Định luật Faraday về suất điện động cảm ứng: Suất điện động cảm ứng trong một mạch kín tỉ lệ với tốc độ biến thiên từ thông qua mạch đó.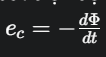

Câu 15. Dòng điện Foucault là gì? Nêu một số ứng dụng có lợi của dòng Foucault.

Dòng điện Foucault (dòng điện xoáy): Là dòng điện cảm ứng được tạo ra trong một khối vật dẫn khi vật dẫn đó chuyển động trong từ trường không đổi hoặc khi vật dẫn nằm trong từ trường biến thiên. Các dòng điện này tạo thành các vòng xoáy trong lòng vật dẫn.

Một số ứng dụng có lợi của dòng Foucault:

• Phanh điện từ: Dùng trong tàu hỏa, xe điện để tạo lực hãm mà không cần ma sát cơ học.
• Lò cảm ứng: Nung nóng kim loại bằng dòng Foucault.
• Thiết bị dò kim loại: Phát hiện kim loại ẩn dưới lòng đất.
• Đồng hồ đo điện: Đĩa nhôm quay do tác dụng của dòng Foucault.

Câu 16. Định nghĩa về dòng điện xoay chiều. Nguyên tắc tạo ra dòng điện xoay chiều.

Dòng điện xoay chiều: Là dòng điện có chiều và cường độ biến thiên tuần hoàn theo thời gian, thường là biến thiên điều hòa theo hàm sin hoặc cosin.

Nguyên tắc tạo ra dòng điện xoay chiều: Dựa trên hiện tượng cảm ứng điện từ. Khi một cuộn dây (hoặc khung dây) quay trong từ trường đều, hoặc một nam châm quay quanh một cuộn dây, từ thông qua cuộn dây biến thiên tuần hoàn, tạo ra một suất điện động cảm ứng xoay chiều và do đó là dòng điện xoay chiều trong mạch kín.

Câu 17. Quy tắc bàn tay phải xác định chiều dòng điện cảm ứng.

Quy tắc bàn tay phải (xác định chiều dòng điện cảm ứng): Đặt bàn tay phải sao cho các đường sức từ xuyên vào lòng bàn tay, ngón cái choãi ra 90 độ chỉ chiều chuyển động của dây dẫn, khi đó các ngón tay khép lại chỉ chiều của dòng điện cảm ứng trong dây dẫn.

Câu 18. Quy tắc bàn tay trái xác định lực từ tác dụng lên dây dẫn mang dòng điện, xác định lực lorenzt tác dụng lên hạt mang điện chuyển động trong từ trường. Quy tắc nắm tay phải (hoặc quy tắc vặn đinh ốc) xác định chiều vecto cảm ứng từ do dòng điện thẳng (hoặc tròn) gây ra.

Quy tắc bàn tay trái (xác định lực từ tác dụng lên dây dẫn mang dòng điện): Đặt bàn tay trái sao cho các đường sức từ xuyên vào lòng bàn tay, các ngón tay duỗi thẳng theo chiều dòng điện, khi đó ngón cái choãi ra 90⁰ chỉ chiều của lực từ tác dụng lên dây dẫn.

Quy tắc bàn tay trái (xác định lực Lorentz tác dụng lên hạt mang điện chuyển động trong từ trường): Đặt bàn tay trái sao cho các đường sức từ xuyên vào lòng bàn tay, các ngón tay duỗi thẳng theo chiều vận tốc của hạt mang điện dương (nếu là hạt mang điện âm thì chiều ngược lại), khi đó ngón cái choãi ra 90⁰ chỉ chiều của lực Lorentz tác dụng lên hạt.

Quy tắc nắm tay phải (hoặc quy tắc vặn đinh ốc) xác định chiều vecto cảm ứng từ do dòng điện thẳng (hoặc tròn) gây ra. Quy tắc nắm tay phải (hoặc quy tắc vặn đinh ốc):

• Đối với dòng điện thẳng: Đặt bàn tay phải nắm lấy dây dẫn sao cho ngón cái chỉ chiều dòng điện, khi đó các ngón tay khép lại chỉ chiều của vectơ cảm ứng từ (chiều đường sức từ) xung quanh dây dẫn.
• Đối với dòng điện tròn (hoặc cuộn dây): Nắm bàn tay phải sao cho các ngón tay khép lại chỉ chiều dòng điện trong vòng dây (hoặc các vòng dây của cuộn dây), khi đó ngón cái choãi ra chỉ chiều của vectơ cảm ứng từ xuyên qua tâm vòng dây (hoặc trục của cuộn dây).

Phần Bài tập

Bài tập định tính

BTĐT 1. Tại sao khi sơn những đồ vật nhỏ bằng phương pháp xì, muốn có lợi về kinh tế và trạnh được độc hại cho người công nhân, giữa ống phun và đồ vật người ta tạo ra một hiệu điện thế cao?

BTĐT 2. Màn chắn tĩnh điện là gì và hoạt động dựa trên hiện tượng Vật lý nào? Nêu một vài ứng dụng trong thực tế.

BTĐT 3. Tại sao đầu mút cột chống sét là mũi nhọn mà không phải là quả cầu? Cột chống sét hoạt động như thế nào? Cột chống sét có thể gây nguy hiểm cho toà nhà khi nào?

BTĐT 4. Một học sinh đã mắc lầm một vôn kế thay cho một ampe kế để đo cường độ dòng điện qua một bóng đèn. Khi đó độ nóng sáng của dây tóc bóng đèn sẽ như thế nào? Giải thích?

BTĐT 5. Một học sinh đã mắc lầm một ampe kế thay cho một vôn kế để đo hiệu điện thế trên một bóng đèn đang nóng sáng. Cường độ dòng điện trong mạch sẽ như thế nào? Giải thích?

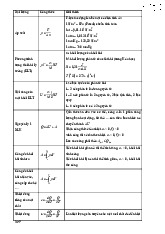
BTĐT 6. Muốn kiểm tra xem đường dây có bị đứt không người ta mắc vào mạch điện một vôn kế.

• • 1. Vôn kế sẽ chỉ như thế nào nếu được dây không bị đứt và hiệu điện thế đặt vào đường dây là 127 V.
    2. Có thể dùng ampe kế và bằng cách mắc đó để kiểm tra đường dây được không?

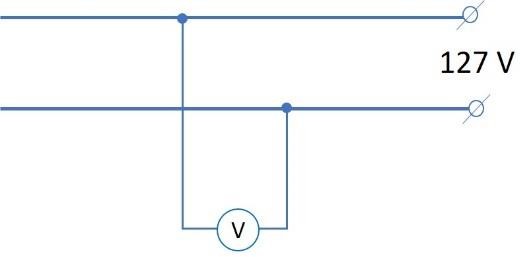
BTĐT 7. Số chỉ của vôn kế nào lớn hơn? Tại sao?

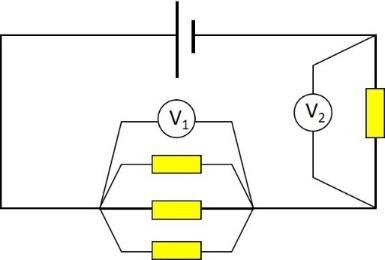
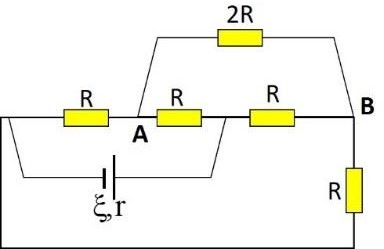
BTĐT 8. Xác định cường độ dòng điện chạy qua điện trở 2R.

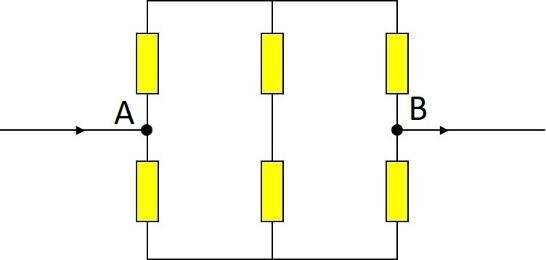
BTĐT 9. Xác định điện trở của phần mạch AB gồm 6 điện trở R như nhau.

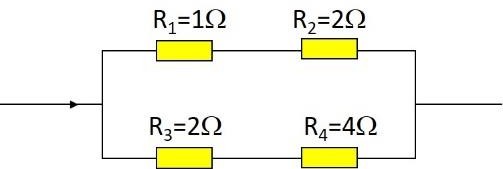
BTĐT 10. Trong các điện trở trên hình vẽ bên, điện trở nào toả nhiệt nhiều nhất.

BTĐT 11. Phải mắc các cuộn dây của hai thiết bị điện đun nóng nhúng trong cốc nước như thế nào để nước nhanh sôi.

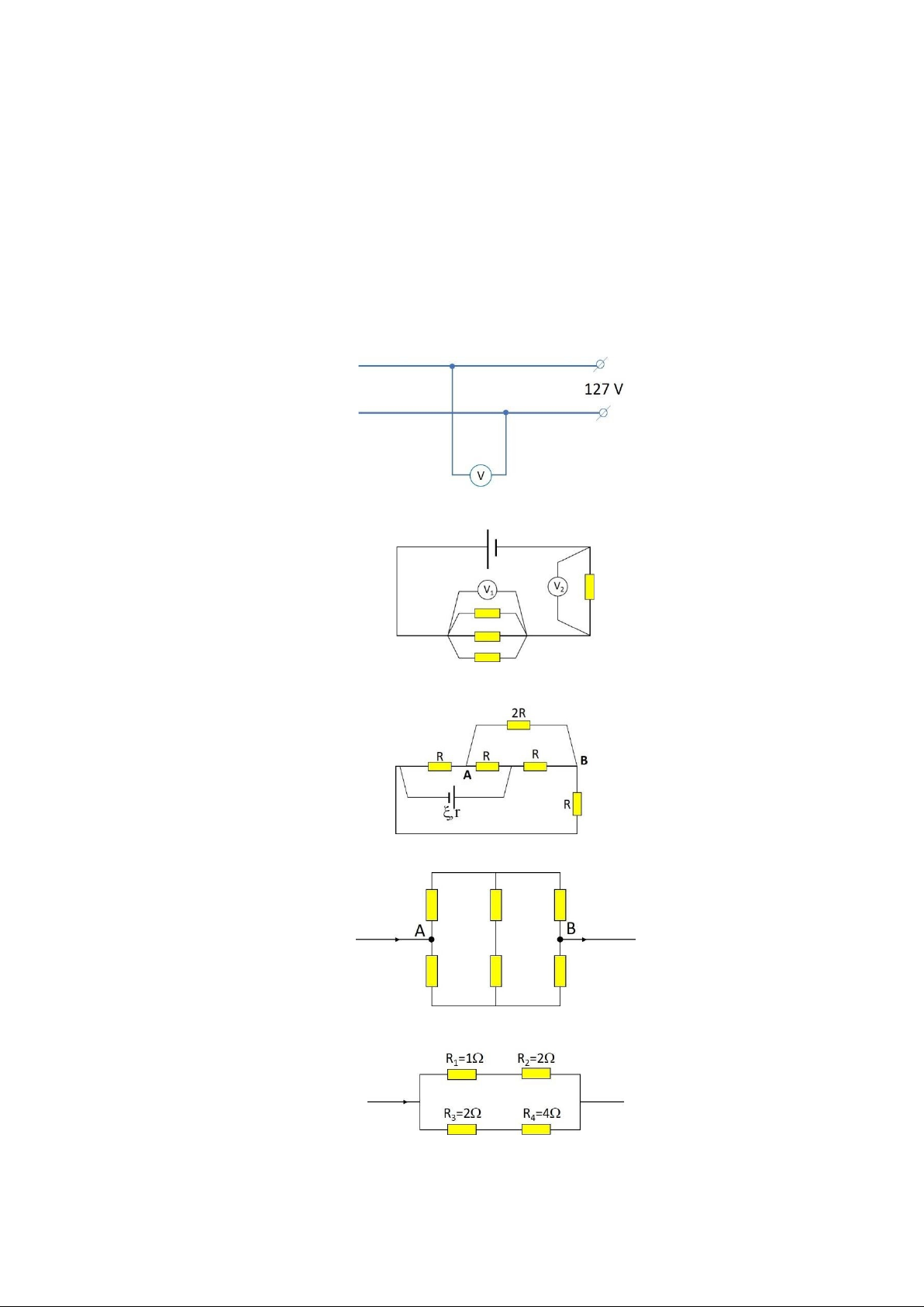
BTĐT 12. So sánh chỉ số của ampe kế trong các mạch điện vẽ ở hình bên dưới. Các mạch đó được lắp với các dụng cụ tương ứng như nhau.

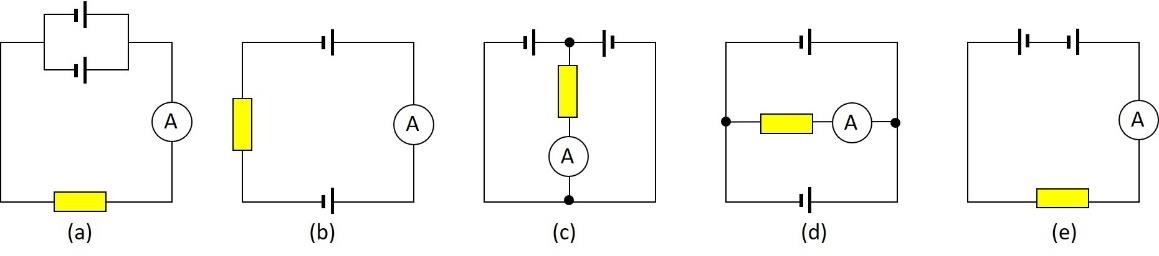
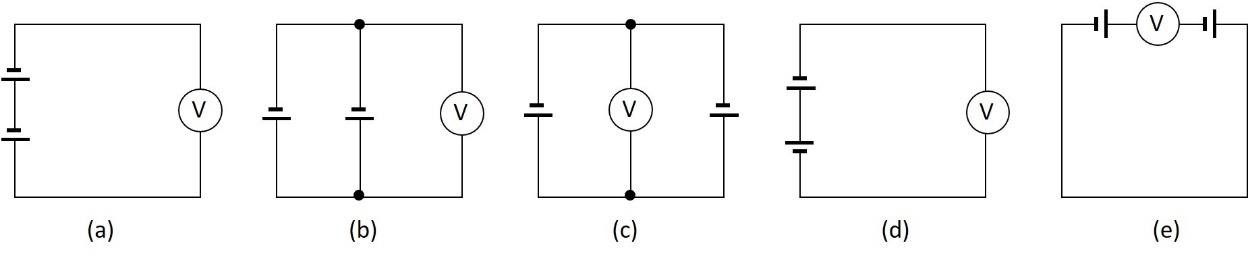
BTĐT 13. Hai pin giống nhau được ghép thành bộ như hình vẽ. Ở mỗi sơ đồ, vôn kế chỉ hiệu điện thế bao nhiêu nếu suất điện động mỗi pin là 1,5 V? Cho rằng điện trở trong các pin bằng không và điện trở của vôn kế rất lớn.

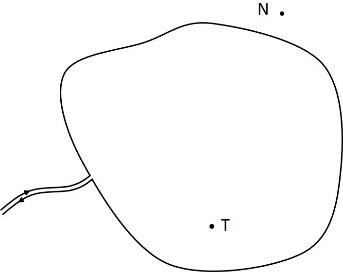
BTĐT 14. Cho một vòng kín phẳng dạng bất kỳ có dòng điện chạy qua. Xác định chiều của vecto cảm ứng từ tại điểm T nằm trong vòng và điểm N nằm ngoài vòng kín đó.

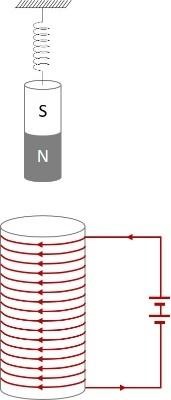
BTĐT 15. Treo một nam châm ở phía trên cuộn dây solenoid như hình vẽ. Cho cuộn dây có dòng điện một chiều đi qua cuộn dây thì sẽ có hiện tượng gì xảy ra với nam châm?

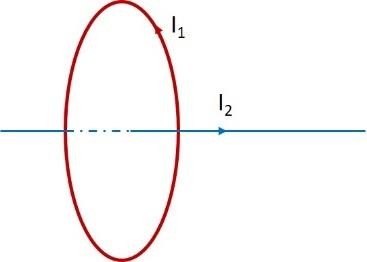
BTĐT 16. Dòng điện thẳng I2 đi qua trục của dòng điện tròn I1 (như hình vẽ). Lực tương tác giữa các dòng điện này như thế nào?

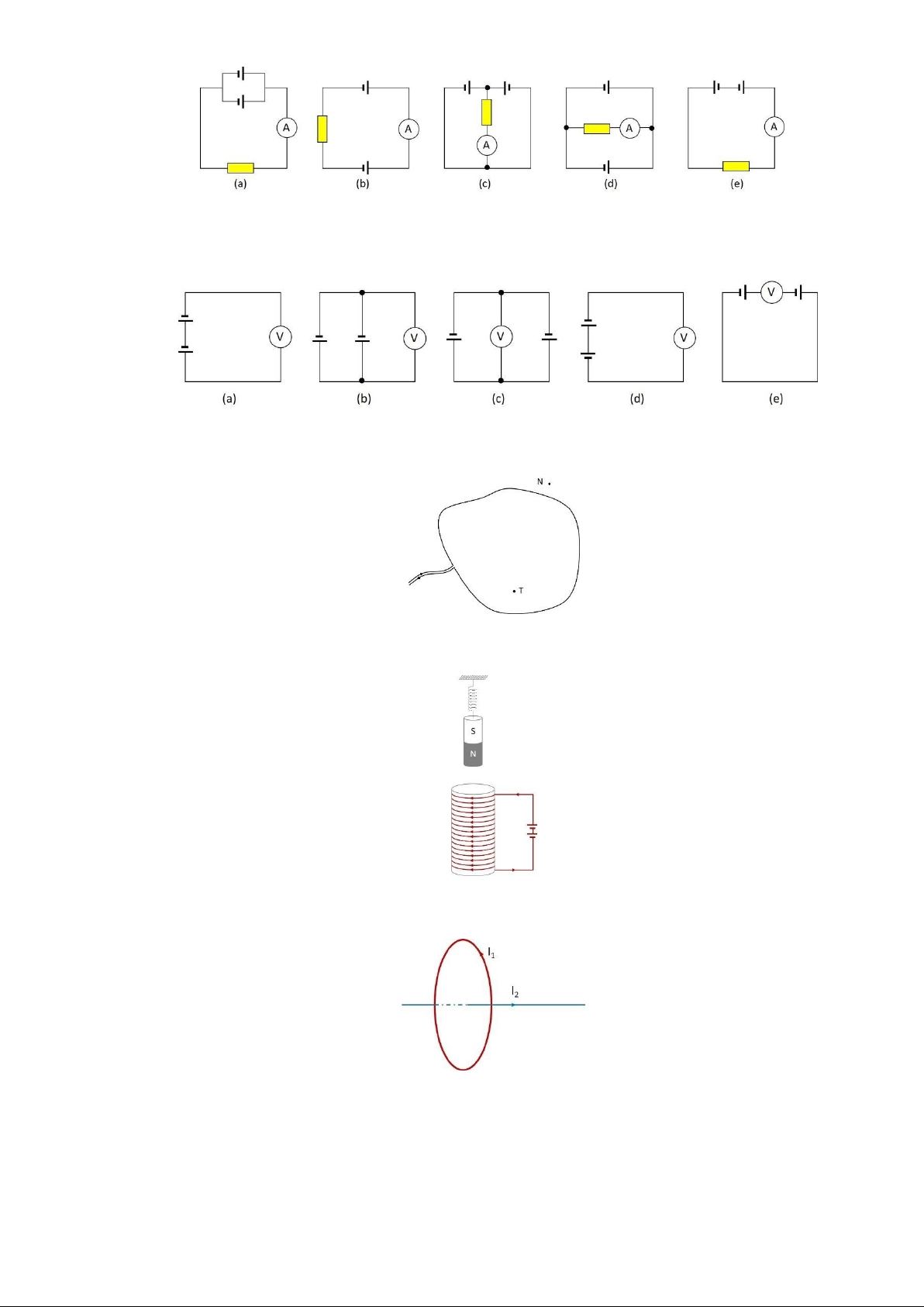
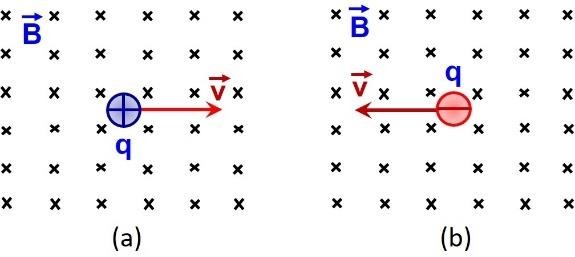
BTĐT 17. Một chùm hạt tích điện bay với vận tốc nào đó trong từ trường đều và vuông góc với vecto cảm ứng từ (hình vẽ bên chỉ vẽ một hạt để dễ hình dung). Trong từ trường này, các hạt đó sẽ chuyển động theo quỹ đạo như thế nào? Xác định công của lực từ tác dụng lên các hạt tích điện này?

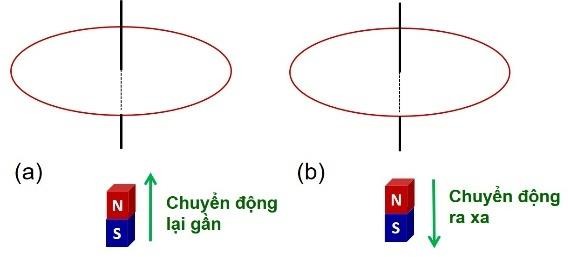
BTĐT 18. Nam châm di chuyển so với vòng dây kim loại với vận tốc nào đó. Xác định chiều dòng điện cảm ứng trong vòng day kim loại.

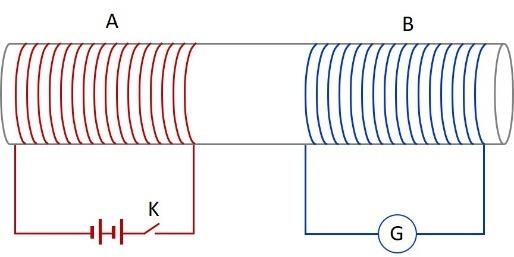
BTĐT 19. Dòng điện cảm ứng trong cuộn dây B sẽ như thế nào nếu trong cuộn A: (a) chuyển trạng thái khoá K từ ngắt sang đóng và (b) chuyển trạng thái khoá K từ đóng sang ngắt.

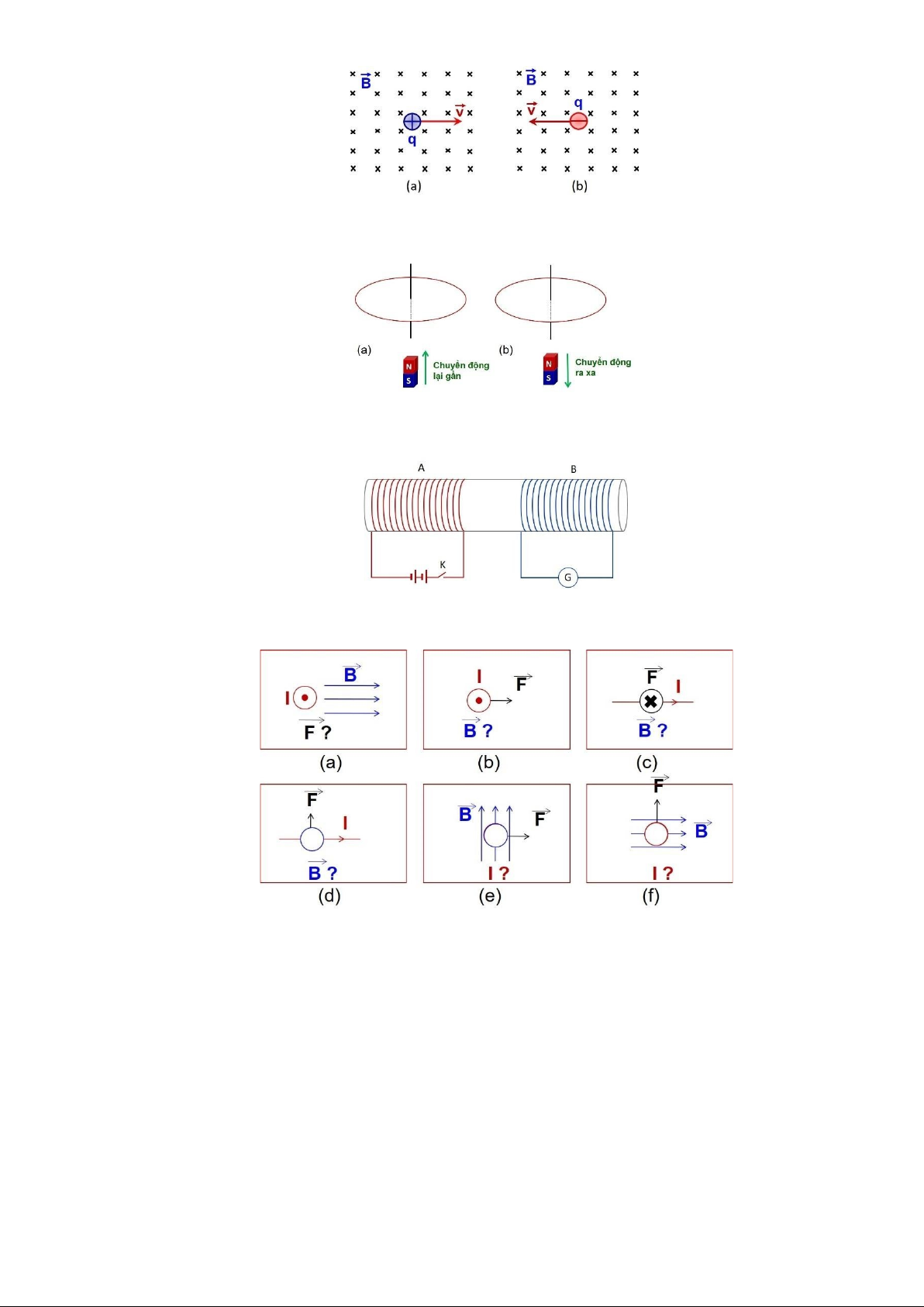
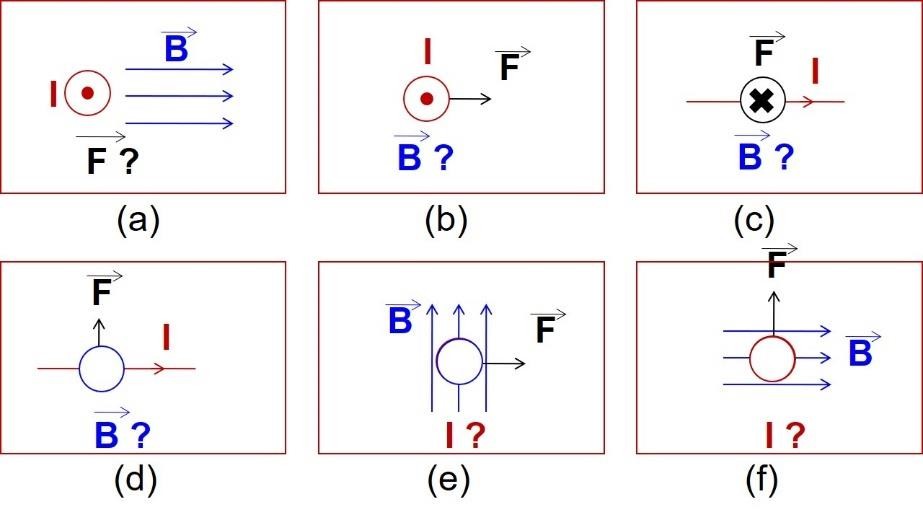
BTĐT 20. Xác định phương, chiều của một trong ba thành phần (dòng điện, lực từ tác dụng lên dây dẫn và vectơ cảm ứng từ) còn thiếu trong các hình vẽ sau:

Bài tập tự luận

Bài 1. Hai điện tích điểm cùng dấu q1 = q2 = q, đặt tại A và B cách nhau một khoảng 2a. Xét điểm M trên trung trực của hai điểm AB, cách đường thẳng AB một khoảng x. Xác định vectơ cường độ điện trường tại điểm M. Tìm x để EM đạt cực đại.

Bài 2. Xác định vectơ cường độ điện trường do vòng dây dẫn tròn bán kính R, tích điện đều với mật độ điện dài l gây ra tại điểm M trên trục vòng dây, cách tâm vòng dây một khoảng x. Xác định x để EM = 0; EM cực đại.

Bài 3. Xác định vectơ cường độ điện trường do đĩa tròn bán kính R, tích điện đều với mật độ điện mặt  gây ra tại điểm M trên trục đĩa, cách tâm đĩa một khoảng x.

Bài 4. Xác định cường độ điện trường tại điểm bên trong và bên ngoài khối cầu bán kính R, tích điện đều với mật độ điện khối . Cho biết hệ số điện môi ở trong và ngoài khối cầu đều bằng .

Bài 5. Xác định cường độ điện trường do mặt phẳng rộng vô hạn, tích điện đều với mật độ điện mặt  gây ra tại điểm cách mặt phẳng () một khoảng h. Cho biết hệ số điện môi là .

Bài 6. Một dây dẫn thẳng, dài vô hạn, tích điện đều với mật độ điện dài . Xác định cường độ điện trường tại điểm M cách dây dẫn môt đoạn r.

Bài 7. Vòng dây tròn, bán kính a, tích điện đều với điện tích tổng cộng Q. Tính điện thế tại tâm O của vòng dây và tại điểm M trên trục vòng dây, cách O một đoạn x. Suy ra hiệu điện thế UOM. Áp dụng số: a = 5cm; x = 12cm; Q = -2,6.10^{– 9} C. Xét 2 trường hợp: a) Gốc điện thế ở vô cùng;

1. Gốc điện thế tại O.

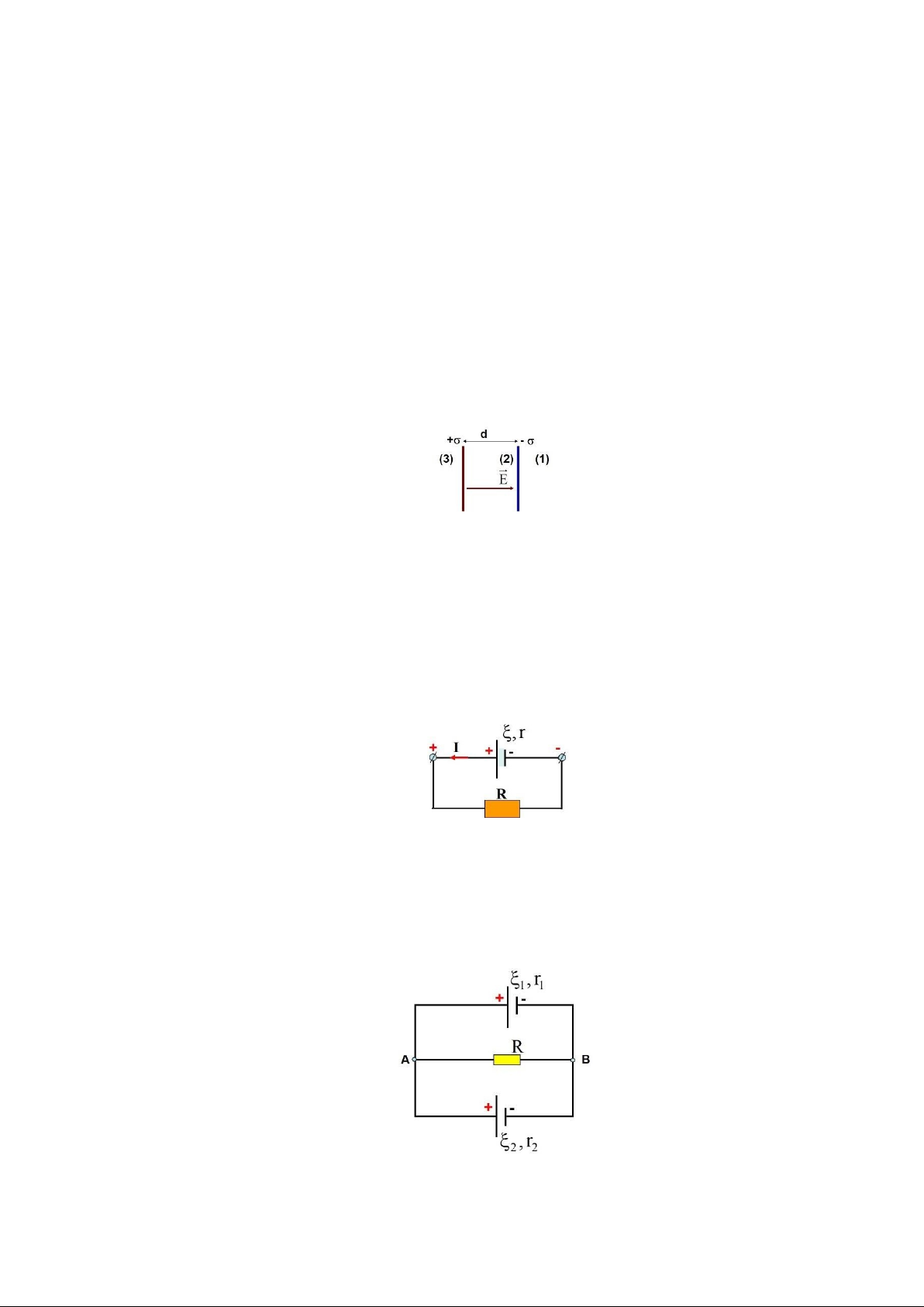
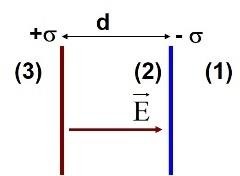
Bài 8. Hai mặt phẳng rộng vô hạn, tích điện đều với mật độ điện mặt ±, đặt cách nhau một khoảng d trong không khí.

• 1. Xác định sự phân bố cường độ điện trường và điện thế do 2 mặt phẳng này gây ra tại 3 vùng không gian tạo bởi 2 mặt phẳng này. Chọn gốc điện thế tại mặt phẳng tích điện âm.
  2. Cấu trúc linh kiện như trên là tụ điện phẳng. Xác định hiệu điện thế giữa 2 bản tụ và điện dung của tụ điện.

Bài 9. Hai mặt cầu bán kính R1, R2 (R1< R2), tích điện đều với điện tích +q và -q, đặt trong không khí. Xác định sự phân bố cường độ điện trường và điện thế do 2 mặt cầu này gây ra tại 3 vùng không gian tạo bởi 2 mặt cầu này. Chọn gốc điện thế tại mặt cầu tích điện âm.

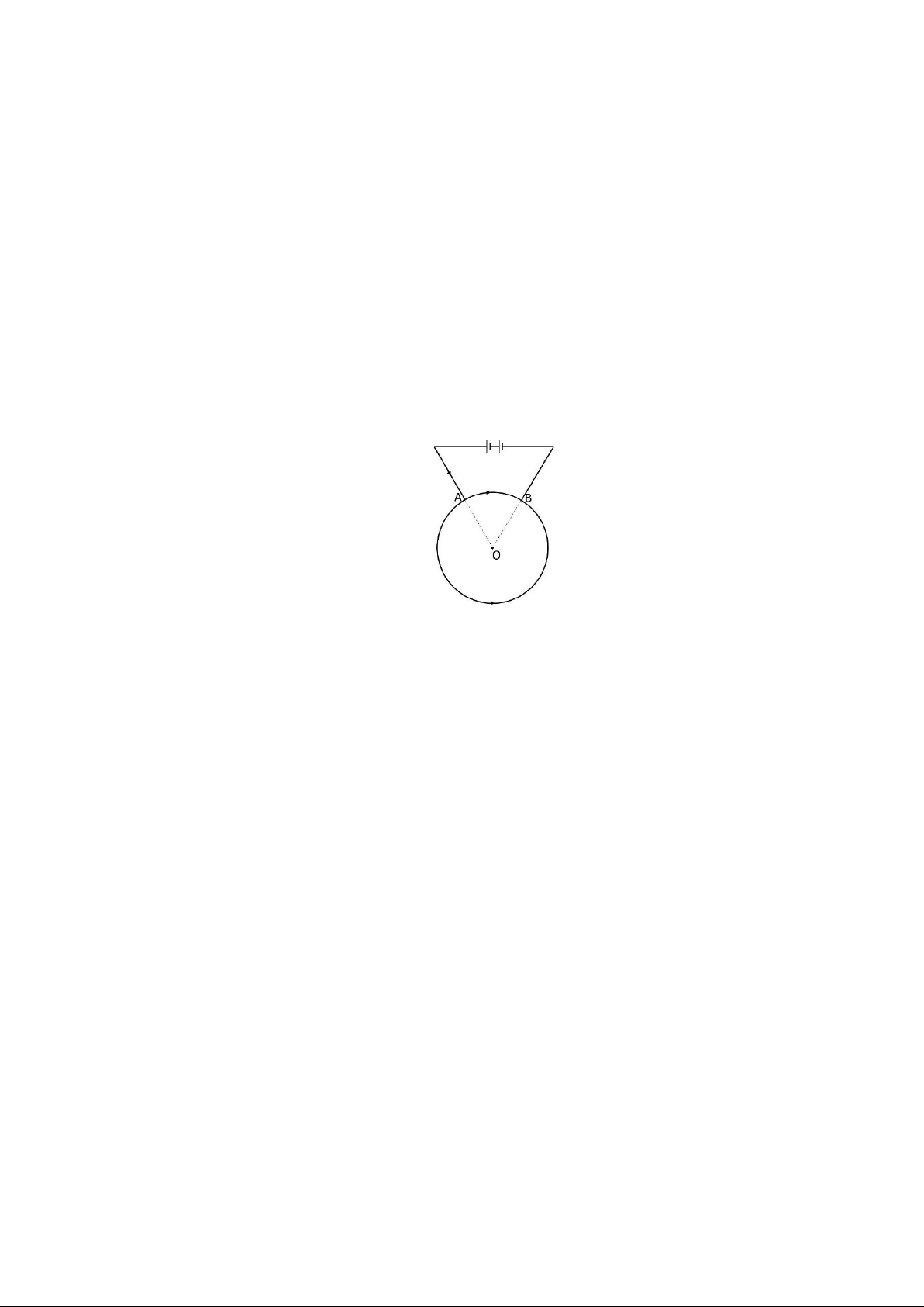
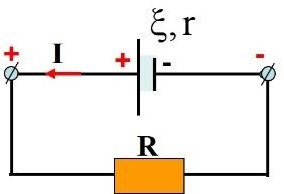
Bài 10. Cho mạch điện như hình vẽ. Cho biết:  = 6V; r = 2; R = 4 .

1. Tính cường độ dòng điện, công suất tiêu thụ của R, công suất và hiệu suất của nguồn điện.
2. Thay R’ (có giá trị khác R) thấy công suất của mạch ngoài vẫn không đổi. Tính R’.
3. Phải thay R =? để nguồn phát ra công suất lớn nhất? Tính giá trị Pmax.

Bài 11. Cho mạch điện có sơ đồ như hình vẽ. Cho biết 1 = 4V, 2 = 3V, r1 = r2 = 0,2, R = 0,4. Hãy tính:

1. Cường độ dòng điện qua các đoạn mạch.
2. Hiệu điện thế UAB và công suất tiêu thụ của R.

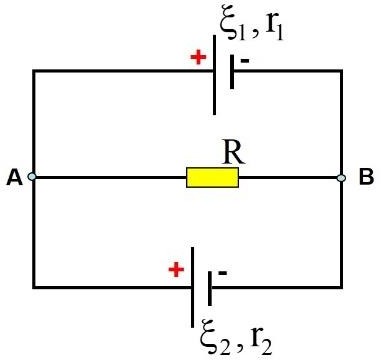
ĐS: I1 = 6A, I2 = 1A, I = 7A, UAB = 2,8V, PR = 19,6

Bài 12. Một acquy ôtô với suất điện động 12V và điện trở nội 0,040 được nạp với dòng 50A. Anh/Chị hãy xác định:

1. Hiệu điện thế giữa các điện cực của nó?
2. Công suất toả nhiệt trong acquy?
3. Công suất điện chuyển thành hoá năng?
4. Trả lời cho câu (a) và (b) như thế nào khi acquy được sử dụng để cấp 50A cho động cơ khởi động?

Bài 13. Một pin mặt trời cho một hiệu điện thế 0,10V khi một điện trở 500 được nối vào nó và cho hiệu điện thế 0,15V khi thay bằng điện trở 1000. Anh/Chị hãy xác định:

1. Điện trở nội và suất điện động của pin mặt trời?
2. Hiệu suất của pin khi chuyển năng lượng ánh sáng thành năng lượng nhiệt toả ra trên điện trở ngoài R = 1000. Biết rằng: diện tích của pin bằng 5,0cm² và nó nhận năng lượng sáng một đơn vị diện tích là bằng 2,0mW/cm².

Bài 14. Nối hai điểm A và B của một vòng dây dẫn hình tròn với hai cực của một nguồn điện một chiều. Phương của các dây nối đi qua tâm của vòng dây (hình vẽ). Bỏ qua ảnh hưởng của các đoạn dây nối. Xác định cường độ từ trường tại tâm của vòng dây.

Bài 15. Hai dây dẫn thẳng dài vô hạn song song đặt cách nhau 5cm. Dòng diện không đổi chạy trong các dây cùng chiều nhau và có cùng cường độ I1 = I2 =10A. Tìm vectơ cường độ từ trường gây bởi hai dòng điện tại một điểm cách đều mỗi dây dẫn 3cm.

Bài 16. Cho một dòng điện I chạy qua một dây dẫn đặc hình trụ, bán kính tiết diện thẳng của hình trụ bằng R. Anh/Chị hãy:

• 1. Xác định véctơ cường độ từ trường tại một điểm cách trục dây dẫn một đoạn r (với r > R và r < R).
  2. Vẽ đồ thị biểu diễn sự phụ thuộc của cường độ từ trường vào r.

Bài 17. Cho một vật dẫn hình trụ rỗng, bán kính ngoài và trong lần lượt là a và b có dòng điện không đổi I phân bố đều đi qua.

1. Xác định biểu thức cảm ứng từ B theo r, với b < r < a.
2. Xác định cảm ứng từ B khi r = a, r = b và khi b = 0

Bài 18. Cho một electron bay với vận tốc v = 4. 10⁷ m/s theo phương vuông góc với các đường cảm ứng từ của một từ trường đều có độ lớn cảm ứng từ B = 10^-3 T. Anh/Chị hãy:

1. Biểu diễn lực từ tác dụng lên electron và quỹ đạo chuyển động của electron.
2. Xác định bán kính quỹ đạo, chu kỳ quay và gia tốc chuyển động của electron.

Bài 19. Một hạt  có động năng 500 eV bay theo hướng vuông góc với đường sức từ của một từ trường đều có cảm ứng từ B = 0,1 T. Anh/Chị hãy xác định:

1. Lực tác dụng lên hạt ;
2. Bán kính quỹ đạo và chu kỳ quay của hạt trên quỹ đạo.

Chú thích: hạt  có cấu trúc 2 proton, 2 neutron và có khối lượng 4u (u = 1,66 10^-27 kg)