


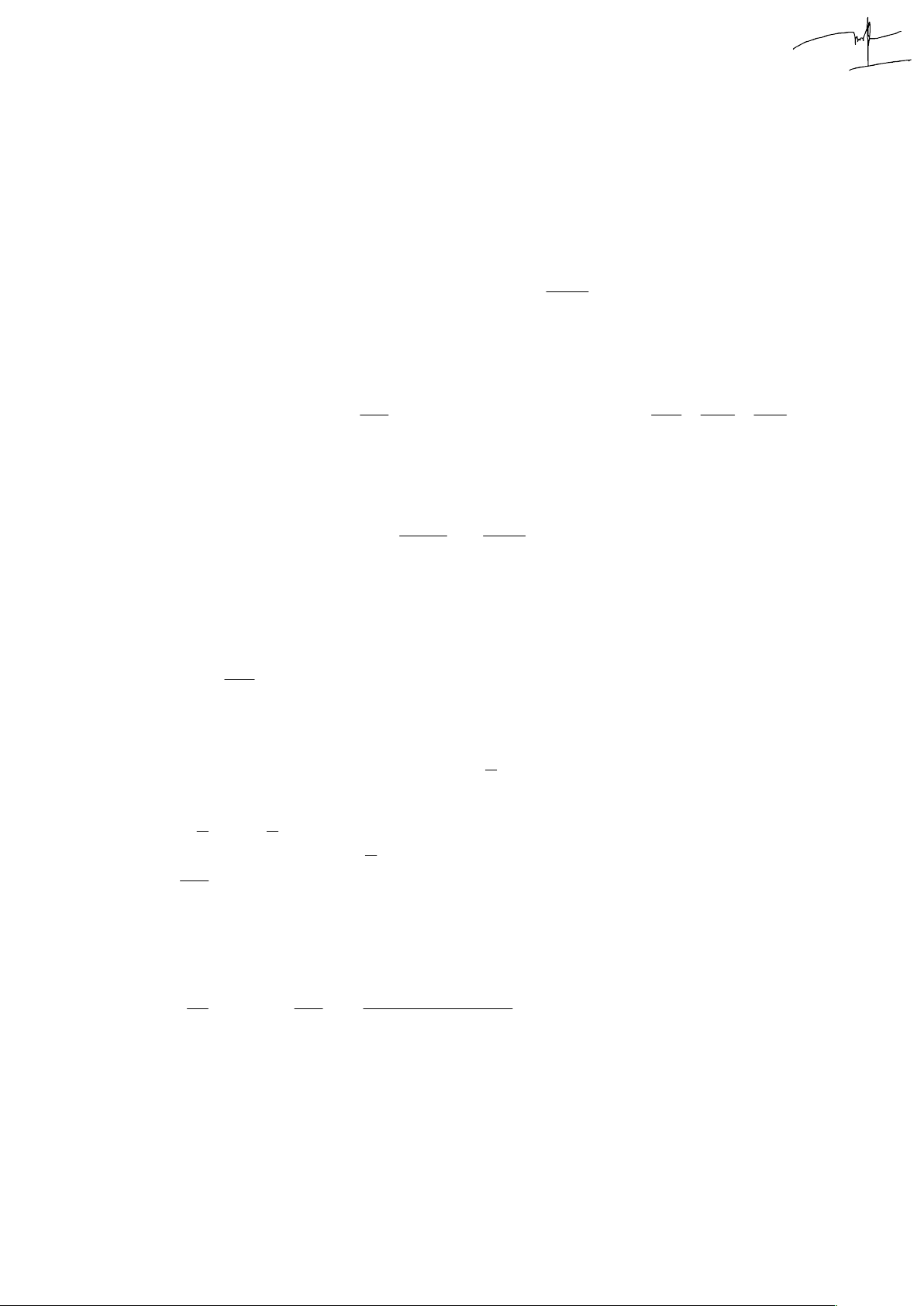




Preview text:
Đại lượng Công thức Giải thích
F: lực tác dụng lên bề mặt có diện tích S
1 N/m2 = 1Pa (Pascal) chuẩn tính toán F 1at = 9,81.104 N/m2 Áp suất p S 1 atm = 1,013.105 N/m2 1 mmHg = 133,23 N/m2 1 atm = 760 mmHg
m: khối lượng của khối khí Phương trình
M: khối lượng phân tử của chất khí (trong Hóa học) trạng thái khí lý m pV RT J M R 8,31 tưởng (KLT) mol.K T 0K t 0 273 C
i: số bậc tự do của phân tử khí
i = 3 nếu phân tử là đơn nguyên tử Nội năng của m i U RT
i = 5 nếu phân tử là 2 nguyên tử, 3 bậc tịnh tiến, 2 bậc một khối KLT M 2 quay
i = 6 nếu phân tử có 3 nguyên tử
Q là thức ăn đưa vào cơ thể, công A là 1 phần năng
lượng bạn hoạt động, hít thở … còn thừa bao nhiêu nó Nguyên lý 1 chuyển thành U Q U A ĐLH
Nhận công thì sẽ tỏa nhiệt. A < 0, Q < 0
Sinh công thì sẽ cần thu nhiệt. A > 0, Q > 0
Lúc nào cũng phải thỏa A Q sinh thu
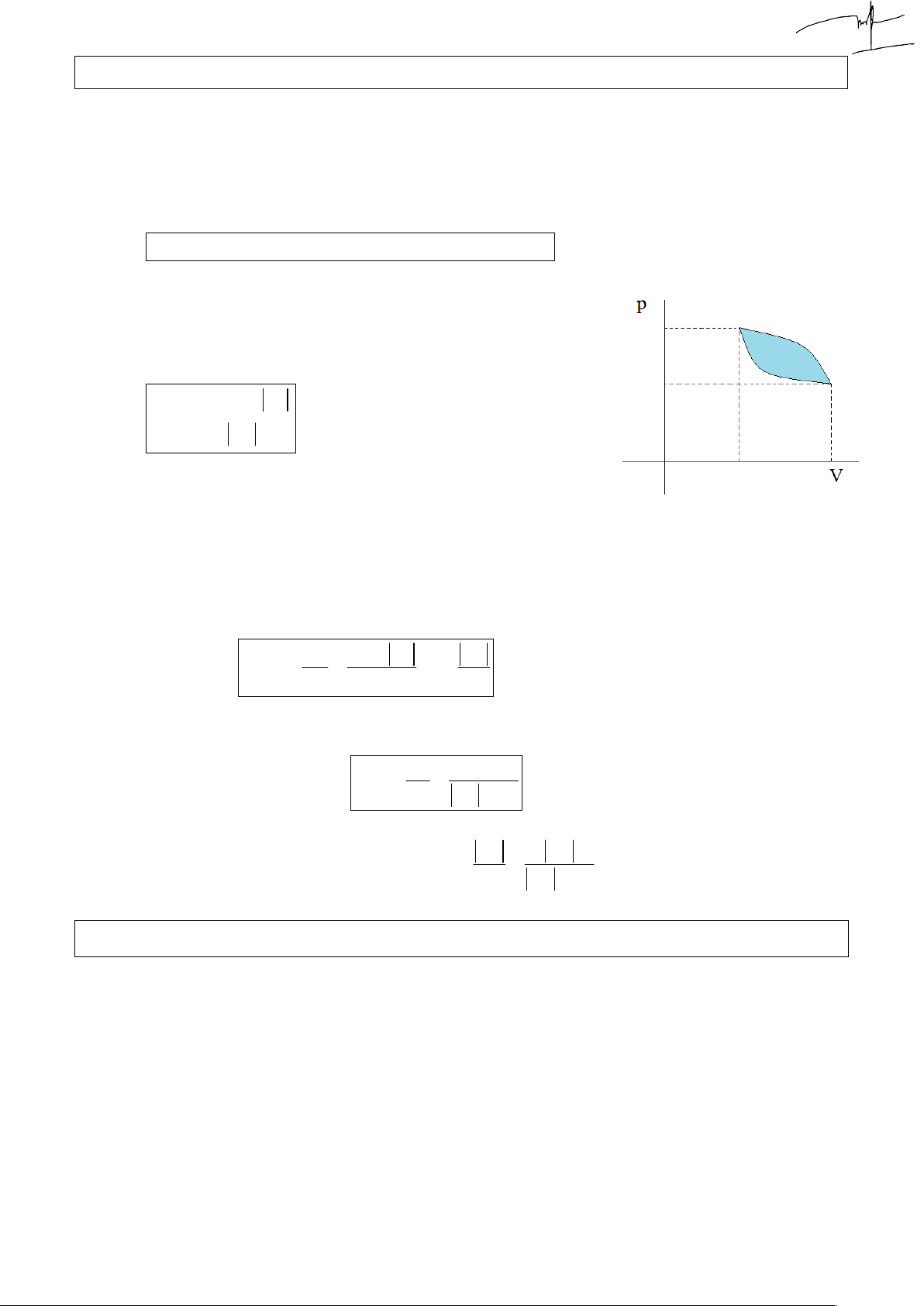
Nếu khối khí giãn nở thì thể tích tăng, A > 0, khối khí V Công do khối 2 A pdV sinh công. khí sinh ra 1 V
Nếu khối khí bị nén thì thể tích giảm, A < 0, khối khí thu công. Công do khối khí nhận vào, 2 V A pdV công cấp cho hệ 1 V … Nhiệt dung riêng của một dQ Q c mdT mT chất Nhiệt dung dQ Q C
Là nhiệt lượng cần truyền cho một mol chất đó để nhiệt ndT nT NTP riêng của phân C Mc
độ của nó tăng lên 1 độ tử m n (số mol) M
Các quá trình biến đổi: Đẳng tích Đẳng áp Đẳng nhiệt Đoạn nhiệt Đa biến 1 TV const pV const 1 1 TV const Tp const 1 pV const Tp const Phương p
là chỉ số đa biến. const V const pV const Hệ số Poisson - chỉ trình T T số đoạn nhiệt: 0 :đẳng áp C 1 : đẳng nhiệt p 2 1 1 C i v k : đoạn nhiệt
: đẳng tích Nhiệt dung i i C R C R C C C p 1 C 0 riêng V 2 2 T 1 V phân tử Công A m V m R m R T T 1 2 2 RT.ln T T 1 2 của khối M 1 M V M 1 0 pV V 1 2 1 1 1 khí sinh m p pV p V pV p V 1 1 2 2 1 1 2 2 1 RT.ln 1 1 ra M p2 U Q U Nhiệt Q m C T m C T v A 0 m C T M p M M Biến thiên nội m i R T m i R T 0 m i R T m i R T năng M 2 M 2 M 2 M 2 U Độ biến m V2 Rln thiên m T m T M V m 2 C 2 C 1 C ln T p ln v ln 0 2 Entropy M T M T M T 1 1 m p1 Rln 1 s M p2 NTP
So sánh độ dốc của đường đẳng nhiệt và đoạn nhiệt: Đẳng nhiệt : 0 dp p pV const pdV Vdp dV V
Đoạn nhiệt: là quá trình chất môi giới tiến hành hoàn toàn không
trao đổi nhiệt với môi trường bên ngoài: 1 0 dp p pV const p V dV V dp dV V
Vậy tan của góc nghiêng đường đoạn nhiệt lớn hơn đường đẳng nhiệt lần. 1. Đồ thị Entropy
Thấy đồ thị là đường thẳng vuông góc với trục s thì biết ngay là đoạn nhiệt, vì đoạn nhiệt s không đổi: Đẳng tích : m m V s C T C
p (màu đỏ là biến) thì hàm s có đồ thị theo T, p là đường v ln v ln M M nR cong có hình dạng sau: Tương tự, đẳng áp: m m p s C T C V
thì đồ thị cũng như vậy p ln p ln M M nR
Đẳng nhiệt s ~ lnV ~ ln p NTP 2. Chu trình khép kín
QH : nhiệt lượng truyền ra ngoài từ trong hệ / truyền từ bên ngoài vào trong hệ.
QL : nhiệt lượng bên trong hệ thoát ra ngoài / nhận từ bên ngoài vào trong hệ. Công của chu trình:
Cách 1: Act diện tích hình cong kín (p,V) = tích phân đường.
Nếu chu trình thuận chiều kim đồng hồ : A > 0
Nếu chu trình nghịch chiều kim đồng hồ: A < 0 A Q Q Cách 2: ctthuan H L A Q Q ctnghich H L
QH là tổng nhiệt lượng của những đoạn biến đổi có nhiệt lượng Q > 0,
tính theo bảng công thức số 2.
QL là tổng nhiệt lượng của những đoạn biến đổi có nhiệt lượng Q < 0
Hiệu suất nhiệt: trong chu trình thuận chiều, để đánh giá mức độ hoàn thiện của chu trình, người ta A Q Q Q dùng đại lượng này: ct H L HNhiet 1 H 0 H 1 Q Q Q H L L
Hệ số làm lạnh: đối với chu trình ngược chiều, để đánh giá mức độ hoàn thiện của chu trình máy Q Q
lạnh, người ta dùng đại lượng này: L L Lanh , có thể lớn hơn 1. A Q Q ct H L Q Q
Hệ số bơm nhiệt: trong chu trình bơm nhiệt H H , Nhiet Lanh 1 Nhiet A Q Q ct H L
3. Chu trình Carnot (nở – nở – nén – nén, đẳng trước đoạn sau)
Chu trình Carnot thuận nghịch cùng chiều: là chu trình bao gồm 2 quá trình đẳng nhiệt và đoạn
nhiệt xen kẽ nhau, có chiều cùng chiều kim đồng hồ.
Quá trình 1: Giãn nở đẳng nhiệt, chất môi giới hoàn toàn tiếp xúc với nguồn nóng, nên chất
môi giới nhận nhiệt QH > 0 từ nguồn nóng (TH = const), sinh công.
Quá trình 2: Giãn nở đoạn nhiệt, chất môi giới đi từ nguồn nóng TH đến nguồn lạnh có nhiệt độ TL, sinh công. NTP
Quá trình 3: Nén đẳng nhiệt, chất môi giới tiếp xúc hoàn toàn với nguồn lạnh (TL = const)
đồng thời nhả nhiệt lượng QL < 0 cho nguồn lạnh, nhận công.
Quá trình 4: Nén đoạn nhiệt, chất môi giới đi từ nguồn lạnh để trở về nguồn nóng ứng với
trạng thái ban đầu, nhận công. A Q Hiệu suất nhiệt: T ct H 1 L 1 L Nhiet Q Q T H H H o H
càng lớn khi độ chênh lệch nhiệt độ giữa 2 nguồn càng cao. Nhiet o H
chỉ phụ thuộc vào nhiệt độ 2 nguồn, không phụ thuộc vào tính chất của chất Nhiet môi giới. o H khi T hoặc T L 0 Nhiet 1
H (điều này không thể xảy ra). o H
khi T T hay nói cách khác khi chỉ có một nguồn nhiệt duy nhất. Nhiet 0 L H
Chu trình Carnot thuận nghịch ngược chiều: Nhận QL > 0, nhả ra QH < 0, nhưng Q Q H L Q Q T L L L 1
Hệ số làm lạnh: Lanh A Q Q T T T ct H L H L H 1 TL
Mọi tính chất của hệ số làm lạnh tương tự chu trình cùng chiều.
Hệ số bơm nhiệt (hiệu suất) : QH TH 1 Nhiet Q Q T T T H L H L 1 L TH
Nhiệt lượng truyền cho bên ngoài : Q Q A H L ct
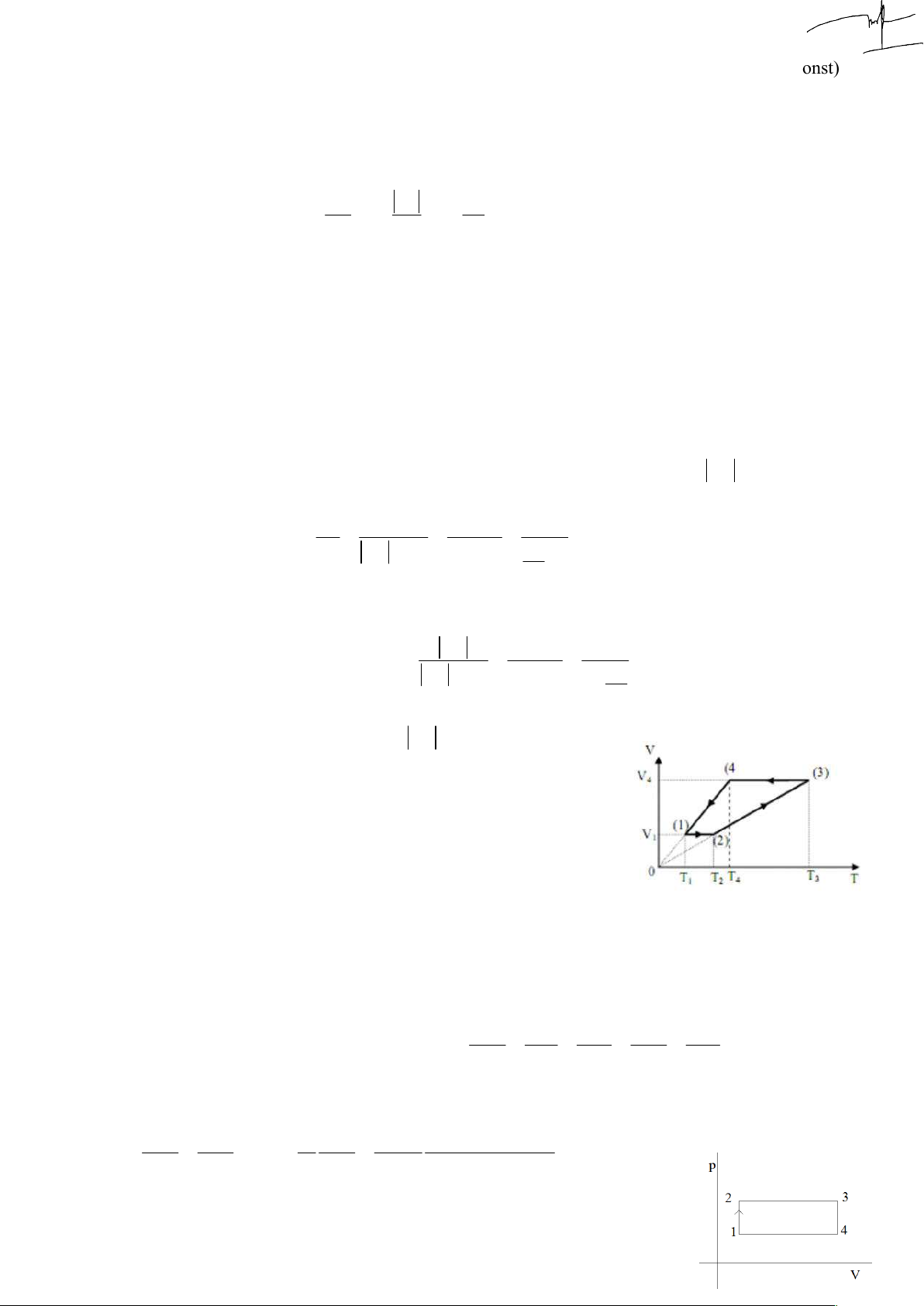
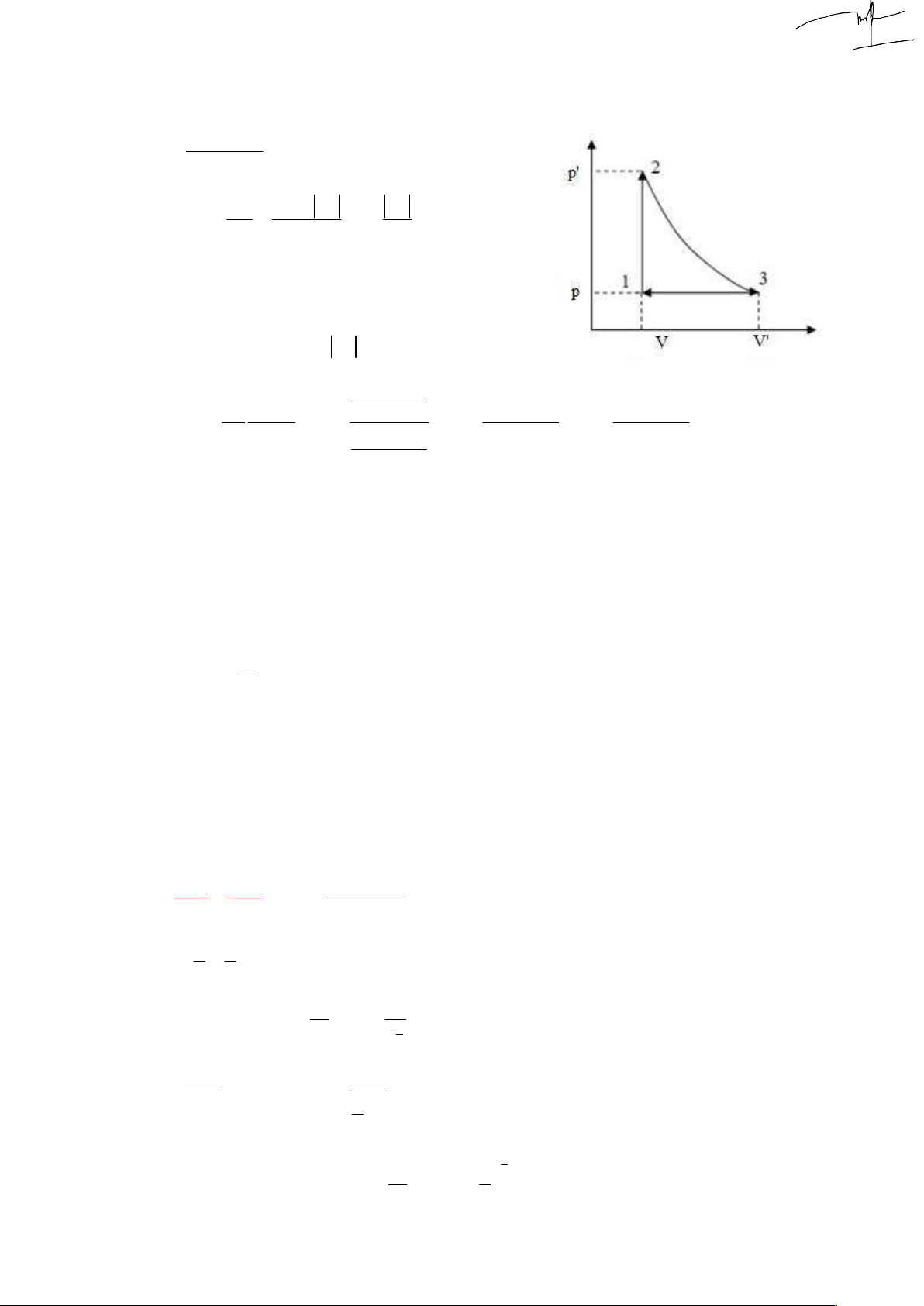
1. Một lượng khí lí tưởng đơn nguyên tử thực hiện chu trình
biến đổi như đồ thị hình sau. Biết 0 t 27 C; V 5lit; 1 1 0
t 127 C; V 6lit , ở điều kiện chuẩn, khối khí có thể tích 3 3
V 8,19lit . Sau mỗi chu trình biến đổi, khí sinh ra bao nhiêu 0 công. Đ/s: 20,26J 3 p 100.10 Pa Điều kiện chuẩn : 0 0 T 273 K 0
Chuỗi quá trình (màu đỏ là đã có số liệu): p V pV p V p V pV 0 0 1 1 2 1 2 3 1 3 nR T T T T T 0 1 2 3 4
2 3 đẳng áp: 3 3 p V p V T p V 400 100.10 .8,19.10 0 0 2 3 3 0 0 3 p 200.10 Pa 2 3 T T V T 6.10 273 0 3 3 0 NTP
4 1 đẳng áp, A p V V p V V p ? 41 1 3 1 1 3 1 1 3 3 p V p V p V T 100.10 .8,19.10 300 0 0 1 1 0 0 1 3 p 180.10 Pa 1 3 T T T V 273 5.10 0 1 0 1
Công của chu trình kín là tích phân đường (diện tích) của hình cong kín (p,V): A S p p V V J ct 200 180 3 .10 .6 5 3 .10 20 1234 2 1 3 1
Trong quá trình biến đổi từ (2) đến (3), khí sinh hay nhận bao nhiêu công ? Đ/s: sinh 456J
A p V V p V V 3 200.10 6 5 3 10 200J 23 2 3 2 2 3 1 Tính nhiệt độ T4: pV p V V 6 1 1 1 3 3 0
T T .300 360 K 360 273 C 87 C 1 0 0 4 T T V 5 1 4 1
2. Một bong bong nhỏ chứa 5mol Heli đơn nguyên tử được nhúng hoàn toàn vào trong nước.
Nước tăng thêm 200C thì khí Heli cũng tăng theo khi áp suất không đổi. Kết quả là bong
bong dãn ra. Nhiệt lượng Q cung cấp cho Heli là bao nhiêu trong quá trình dãn và nhiệt độ tăng. Đ/s: 2077J Đẳng áp: i 3 C R Q nC T J p 5.20,775.20 2077,5 p 1 1 .8,31 20,775 2 2
Độ biến thiên nội năng của Heli là bao nhiêu trong quá trình nhiệt độ tăng ? Đ/s: 1246J Đẳng áp: i 3 U n R T 5. .8,31.20 1246J 2 2
Công do khối khí Heli sinh ra để chống lại nước trong quá trình dãn và nhiệt độ tăng ? A Q U
2277,51246 1031,5J
3. Một động cơ làm việc theo chu trình Carnot với 2 Kmol khí lý tưởng 2 nguyên tử. Nhiệt độ
nguồn nóng là 4000C và nhiệt độ của nguồn lạnh là 200C. Mỗi chu trình hoạt động mất 1s.
Áp suất ở cuối quá trình giãn nở đẳng nhiệt bằng áp suất ở đầu quá trình nén đoạn nhiệt.
Công suất của động cơ. Đ/s: 18,4.103 kW Ta có p V p V p V p V 1 1 2 2 3 3 4 4 nR T T T T H H L L
Hệ số đoạn nhiệt trong chu trình : 2 7 1 i 5 Ta có : A T ct L 293 H Nhiet 1 1 0,565 Q T H H 673 Mà V p V p p 2 1 Q A nRT nRT hoặc 1 1 H H ln L ln 12 cần tìm tỉ số 2 V p V p p 1 2 1 2 4 7 5 1 1 1 7
Ta thấy từ (4) về (1) là đoạn nhiệt, p T L 293 1 1 T p T p 5 H L 18,366 1 4 p T H 673 4 NTP 3 A H Q J ct nhiet H 6 .
0,565.2.10 .8,31.673.ln 18,366 18,393.10
Theo đề, công này là trong 1s, nên công suất 6 P 18,393.10 W
4. Có 2 bình đựng cùng một chất khí, được nối với nhau bằng một ống có khóa. Áp suất ở
bình I là 2.105 Pa, ở bình II là 106 Pa. Mở khóa nhẹ nhàng để hai bình thông nhau sao cho
nhiệt độ không đổi. Khi đã cân bằng, áp suất ở cả 2 bình là 4.105 Pa. Tính dung tích của
bình II, biết dung tích bình I là 15 lít. Đ/s : 5 lít. 5
Thấy nhiệt độ không đổi mà nghĩ liền 2.10 pV p V V 15 3 lit là sai. Vì p 1 1 2 2 2 6 10 1, V1 và p2,
V2 là thông số của hai khối khí riêng, có số mol khí khác nhau chứ không phải là thông số của 2
quá trình của một khối khí.
Ở đây, ta dùng công thức : PV RT
, do R và T là như nhau nên ta có : PV PV PV 1 1 2 2 3 3 n n n n 1 2 3
Với V V V ; n n n , áp dụng tính chất các phân số bằng nhau : 3 1 2 3 1 2
PV PV PV V 5 P P 2.10 1 V V V 5 lit 1 1 2 2 1 2 2 1 5 1 P P 6.10 2
5. Một động cơ nhiệt lý tưởng chạy theo chu trình Carnot, có nguồn nóng ở nhiệt độ 1270C và
nguồn lạnh ở nhiệt độ 270C. Hiệu suất của máy là ? Đ/s : 25% 300 H Nhiet 1 0,25 25% 400
6. Một khối khí Heli có áp suất, thể tích, nội năng lần lượt là p, V, U. Biểu thức liên hệ giữa
chúng là ? Biết Heli đơn nguyên tử. Đ/s : 2 pV U 3 i 3 U n RT n RT 2 2 3 U PV PV 2 n RT
7. Một khối khí Nitơ có thể tích 8,3 lít, áp suất 15 at, nhiệt độ 270C. Khối lượng của khối khí đó là ? Đ/s : 0,137kg 3 4 m PV 8,3.10 .15.9,81.10 PV RT m M .28 137g M RT 300.8,31
8. Công thức nào giữa A p V hay A nR T
dùng để tính công thực hiện trong quá trình
biến đổi đẳng áp của n mol khí từ trạng thái (1) đến trạng thái (2) ? Đ/s : A nR T
Biến đổi đẳng áp nên V và T đổi, cùng tăng hoặc cùng giảm (do tỉ lệ thuận với nhau).
Giả sử V tăng, tức là khối khí sinh công (thu nhiệt bên ngoài vào) thì công dương, chọn công thức 2. NTP
Giả sử V giảm, tức là khối khí nhận công bên ngoài vào để sinh nhiệt, tức công âm, vẫn chọn công thức 2.
9. Tính độ biến thiên Entropy của 6,5g khí Hidro do nung nóng từ nhiệt độ 270C đến 1270C
trong điều kiện đẳng áp. Đ/s : 27J/K i 5 7 C R R R p 1 1 2 2 2 Độ biến thiên Entropy : m T 6,5 7 400 2 s C J K p ln . .8,31.ln 27,19 / M T 2 2 300 1
10. Có 10kg khí đựng trong bình kín ở áp suất 107 Pa. Người ta lấy một lượng khí cho tới khi
áp suất còn 2,5.106 Pa. Tính lượng khí đã lấy ra. Coi nhiệt độ không đổi. Đ/s: 7,5kg
Ta lưu ý bài toán này là khí đựng trong bình kín, nên thể tích cũng không đổi. 6 m VM m m p 2,5.10 1 2 2 V p RT m m .10 2,5 kg 2 1 7 M TR p p p 10 1 2 1
Vậy lượng khí đã lấy ra : m m m 7,5kg 1 2
11. Một vật có khối lượng 0,1kg đứng yên trên một mặt bàn nằm ngang không ma sát. Một vật
khác có cùng khối lượng, chuyển động với vận tốc 10m/s đến va chạm với vận tốc ban đầu.
Sau va chạm 2 vật dính vào nhau và tiếp tục chuyển động. Cả hai vật đều có cùng nhiệt độ
ban đầu là 3000K và nhiệt dung riêng 1,05.103J/kg.K. Giả sử năng lượng nhiệt tạo thành do
sự va chạm chia đều cho cả hai vật. Độ tăng nhiệt độ T
của hệ 2 vật sau va chạm là ? Đ/s: 1,2.10-2 (0K)
Nhiệt lượng sinh ra là do 1 phần động năng trước va chạm chuyển thành. Tức là động năng
không bảo toàn, nhưng động lượng vẫn bảo toàn. v0 . m v 2 . m v v 5 m / s 0 1 1 2
Nhiệt lượng được tạo thành: 1 2 1 2 1 2 1 2 Q W W mv mv J d d 2 .0,1.10 .2.0,1.5 2,5 0 1 0 1 2 2 2 2
Nhiệt lượng này làm tăng nhiệt độ: Q 2 Q mc T T 0 1,19.10 K mc
12. Có hai bình chứa hai chất khí khác nhau, được nối với nhau bằng một ống có khóa. Áp suất
và thể tích ở bình I là 1 at và 2 lít, ở bình II là 3 at và 3 lít. Mở khóa nhẹ nhàng để 2 bình
thông nhau, nhiệt độ không đổi. Tính áp suất trong 2 bình khi đã cân bằng. Đ/s: 2,2at pV p V p V V p V p V 1 1 2 2 1 2 RT
pV p V pV V 1 1 2 2 p 2,2at 1 1 2 2 1 2 n n n n V V 1 2 1 2 1 2
13. Trong một bình có thể tích 0,25m3 chứa hỗn hợp khí carbonic và hơi nước. Nhiệt độ của
khí là 3270C. Số phân tử khí carbonic và hơi nước lần lượt là 6,62.1021 và 0,9.1021. Tính áp
suất của 1kmol khí hỗn hợp. Đ/s theo E-learning: 249N/m2 NTP 21 6,62.10 n mol CO 0,011 2 23 6,022.10 21 0,9.10 n mol H O 0,0015 2 23 6,022.10 V n 11 3 CO CO 0,011 2 2 V m C 2O 50 V n H O H O 0,0015 2 2 3 3 V V V m CO H O 0,25 H2O 2 2 100 RT 8,21.327 273 p n 0,011. 246 V 11 2 N / m 1 1 50
Chênh lệch là do sai số lúc tính số mol. Đề bài hoặc là thừa 1kmol, hoặc là đáp án sai. Hoặc là mình giải sai.
14. Độ biến thiên Entropy trên đoạn giữa hai quá trình đoạn nhiệt trong chu trình Carnot
bằng 1kcal/độ. Hiệu số nhiệt độ giữa hai đường đẳng nhiệt là 1000C. Nhiệt lượng đã chuyển
hóa thành công trong chu trình này là ? Đ/s: 4,18.105 J. Ta có: m V m p 2 1 s Rln R ln 12 M V M p 1 2 m V m p 4 4 s Rln R ln 34 M V M p 3 3
Mà theo đề, độ biến thiên Entropy giữa 2 quá trình đoạn nhiệt, chính là nói đến độ biến thiên
Entropy của 2 quá trình đẳng nhiệt, và đề không phân biệt của giai đoạn đẳng nhiệt nào hết nên ta
gia cát dự là s s s 1 kcal / do 4184 J / do . Tính ra đáp án thì xem như là dự 12 34 đoán đúng. Ta có: m V2 Q RT s T H H .ln 12 H M V 1 A Q Q s T T J H L . H L 5 4184.100 4,184.10 m V4 Q RT s T L L .ln 34 L M V 3
15. Cho 0,05mol Chlorine (khí lý tưởng 2 nguyên tử) hoạt động
theo chu trình như hình. Với các thông số trạng thái 5 5 3 3
p p 10 Pa; p 5.10 Pa; V V 10 m . Độ tăng 1 3 2 1 2
nội năng ở quá trình 1-2 và công thực hiện bởi khí ở quá
trình 2-3 là ? Đ/s : 1000J và 805J i i 5 3 5 U n R T V p .10 .4.10 1000J 12 12 1 12 2 2 2 NTP 2 7 1 i 5
Tính A cho quá trình đẳng nhiệt 2-3 : m p2 A RT .ln
0,05.8,31.1203.ln5 804J 2 M p3 5 3 Với T p V 5.10 .10 2 2 0
2 tính dễ dàng từ phương trình : T 1203 K 2 nR 0,05.8,31
Bonus : Giả sử 2-3 là đoạn nhiệt, ta có các cách tính như sau :
Ta có hai công thức để tính A cho đoạn nhiệt : m R A T T và 1 A p V p V 2 2 3 3 2 3 M 1 1 1
Từ phương trình đoạn nhiệt Tp const suy ra T3. 1 1 1 2 p 2 7 0 T p T p T .T 5 .1203 760 K 2 2 3 3 3 2 p 3 R A n 8,31 T T 0,05. . 1203 760 460J 2 3 1 7 1 5
Nếu tính theo p, V thì từ phương trình đoạn nhiệt pV const , ta suy ra V3 : 7 p2 5 3 3 p V p V V .V 5.10 3,16.10 m 3 3 2 2 3 2 3 p3 1 A 5 3 5 3 10 .3,16.10 5.10 .10 460J 7 / 5 1
Tính theo công thức thứ 3 : A U nRT 0,05.8,31.760 1203 460J
16. Một khối khí lý tưởng biến đổi theo chu trình ABCD
trong đó AB và CD là hai quá trình đẳng áp, còn BC và
DA là hai quá trình đoạn nhiệt. Biết các nhiệt độ TA, TB,
TC, TD và số mol x. Hiệu suất của chu trình ABCD là? Đ/s: H 1 T T C D Nhiet T T B A A Q Q Q Ta có: ct H L HNhiet 1 L Q Q Q H H H
Với: Q nC T T Q Q AB p B A 0 H AB
Q nC T T Q nC T T CD p D C 0 L p C D H 1 T T C D T T B A NTP
17. Một động cơ nhiệt có tác nhân là 1 mol khí lý tưởng hoạt động theo chu trình như bên (quá
trình 2–3 : đoạn nhiệt, 3–1 : đẳng áp). Hiệu suất động cơ theo p, p’, V, V’, là ? pV V Đ/s: 1 V p p A Q Q Q Ta có: ct H L HNhiet 1 L Q Q Q H H H Với:
Q nC T T Q Q v 0 12 2 1 H 12
Q nC T T Q nC T T p 0 31 1 3 L p 3 1 pVV C p T T p V V p V V 3 1 nR H 1 1 1 1 C T T V p p V p p V p p v 2 1 nR
18. Cho hệ lúc đầu có số mol x = 1mol, thể tích V1 = 22,4 lít, nhiệt độ 270C. Lúc sau, V 2V . 2 1 Hằng số tự do i = 5.
Công của hệ trong trường hợp đẳng nhiệt là ? Đ/s: A = – 1727,6J
Do đẳng nhiệt nên để tăng thể tích ta chỉ có dùng công để nâng piston lên, thì tức là hệ nhận công
chứ khối khí không tự sinh công được. V2 A nRT.ln
1.8,31.300.ln 2 1728J V1
Công và nhiệt độ ở giai đoạn sau của hệ trong trường hợp đoạn nhiệt ? Đ/s: A = – 1516J và T = 2270K
Đoạn nhiệt thì nhiệt lượng không trao đổi với bên ngoài, nghĩa là không cung cấp nhiệt lượng
cho hệ được. Vậy để thể tích tăng trong đoạn nhiệt thì tác động công từ bên ngoài như trường hợp đẳng nhiệt. p V p V 1.8,31.300 1 1 2 2 n p 111294Pa 1 3 RT T R 22,4.10 1 2 2 7 1 i 5 V 1 1 pV p V p p .111294 42173Pa 1 1 2 2 2 1 7 V 2 5 2 1 A pV p V 1 J 1 7 3 3 111294.22,4.10 42173.22,4.10 .2 1509 1 1 2 2 1 5 7 1 1 Nhiệt độ T 5 1 1 V 1 1 0 2: T V TV T T .300 227,3 K 2 2 1 1 2 1 V 2 2 NTP 3 Hoặc tính theo n và p p V 42173.22,4.10 .2 2 2 0
2 đã tìm ra trước đó: T 227,3 K 2 nR 1.8,31
19. Một kilomol oxy được hơ nóng đẳng tích, nhiệt độ tuyệt đối của nó tăng lên 1,5 lần. Độ biến
thiên của Entropy của quá trình này là ? Đ/s: 8400J/K Ta có i 5 C R v .8,31 20,775 2 2 m T2 3 s C J K V ln 10 .20,775.ln1,5 8423 / M T1
20. Một mol khí Oxy coi là khí lý tưởng giãn đẳng nhiệt ở 370C từ 12 lít đến 19 lít. Tính công
của khí sinh ra trong quá trình đó. Đ/s: 1184J m V 19 2 A RT.ln 1.8,31.310.ln 1183 ,8J M V 12 1
21. Có 1g Oxy ở áp suất 3at sau khi hơ nóng đẳng áp nó chiếm thể tích 1 lít. Coi khí Oxy là lý
tưởng, tìm nhiệt độ sau khi hơ nóng. Đ/s: 1133K m 1 n mol M 32 4 3 p V p V p V 3.9,81.10 .10 1 1 2 2 2 2 0 n T 1133,28 K 2 T R T R nR 1 1 2 .8,31 32
22. Entropy của 4 mol khí lý tưởng gia tăng 23J/K do giãn nở đẳng nhiệt. Khi đó thể tích của
khối khí tăng lên bao nhiêu lần ? Đ/s: 2 lần. s 23 V V 2 2 nR 4.8,31 s nRln e e 1,99758 lần. V V 1 1
23. Một tủ lạnh gia đình có hiệu suất 4,7 lấy nhiệt từ buồng lạnh trong mỗi chu trình 250J. Cần
bao nhiêu công trong một chu trình để tủ lạnh hoạt động. Đ/s: 53J QH 250 A J Nhiet ct 53 Act 4,7
24. Một chậu bằng đồng có khối lượng 150g chứa 220g nước ở 200C. Một thanh đồng có khối
lượng 300g ở nhiệt độ cao rơi vào chậu nước, làm cho nước sôi và biến 5g nước thành hơi.
Nhiệt độ cuối của hệ là 1000C. Nhiệt độ ban đầu của thanh đồng và độ biến thiên Entropy
của hệ là bao nhiêu ? Biết nhiệt dung riêng của đồng là 390J/kg.K, nhiệt dung riêng của
nước là 4200J/kg.K, nhiệt hóa hơi của nước là 2,3.106J/kg. Đ/s: 11460K và 136J/K.
Chú ý : Hệ trung hòa khi thanh đồng, thau đồng, nước cùng 1000C.
Giai đoạn 1 – Nước tăng nhiệt độ từ 200C đến 1000C: 3 Q mc T 220.10 .4200.80 73920J 1
Giai đoạn 2 – Nhiệt lượng để nước hóa hơi, nhiệt tỏa ra nhưng vẫn do thanh đồng cung cấp: NTP 3 6 Q .
m L 5.10 .2,3.10 11500J 2
Nhiệt lượng làm cho chậu đồng 150g tăng lên đến 1000C: 3
Q mcT 150.10 .390.80 4680J 3
Vậy tổng nhiệt lượng của quá trình này:
Q 73900 11500 4680 90080J
Đây là nhiệt lượng do thanh đồng nóng truyền lại Q 90080 0 T 770 K 3 mc 300.10 .390
Nhiệt độ ban đầu của thanh đồng nóng: 0 T 373 770 1143 K Độ biến thiên Entropy :
Do không phải chu trình khí nên ta dùng công thức tổng quát: dQ ds T Đối với nước:
Giai đoạn 1 (thu nhiệt vào): Q mcT dQ mcdT (do T đổi nên lấy dT): 1 373 1 s mc dT mc lnT 220.10
.4200 ln 373 ln 293 223 J / K 293 373 3 1 293 T
Giai đoạn 2 (thu nhiệt vào): Q mL dQ Ldm (do m đổi nên lấy dm, T = 373 không đổi): 2
Ở đây bắt đầu có 2 hướng: 6 L 0,005 L 0,005 2,3.10 s dm m .0,005 31 J / K 2 0 0 T T 373 Đối với đồng:
Độ biến thiên Entropy của thanh đồng nóng (tỏa nhiệt ra): cũng đổi T nên lấy theo dT: 373 dT s mc mc lnT 300.10 .390. ln 373 ln1143 131 J / K 1143 373 3 3 1143 T
Độ biến thiên Entropy của thau đồng (thu nhiệt vào): 373 dT s mc mc lnT 150.10
.390. ln 373 ln 293 14 J / K 293 373 3 4 293 T 4 s s J K i 223 31 131 14 137 / i0 NTP



