9 Vật lý 9Chương 7Từ trường

Phần: Từ trường Chu Tiến Dũng
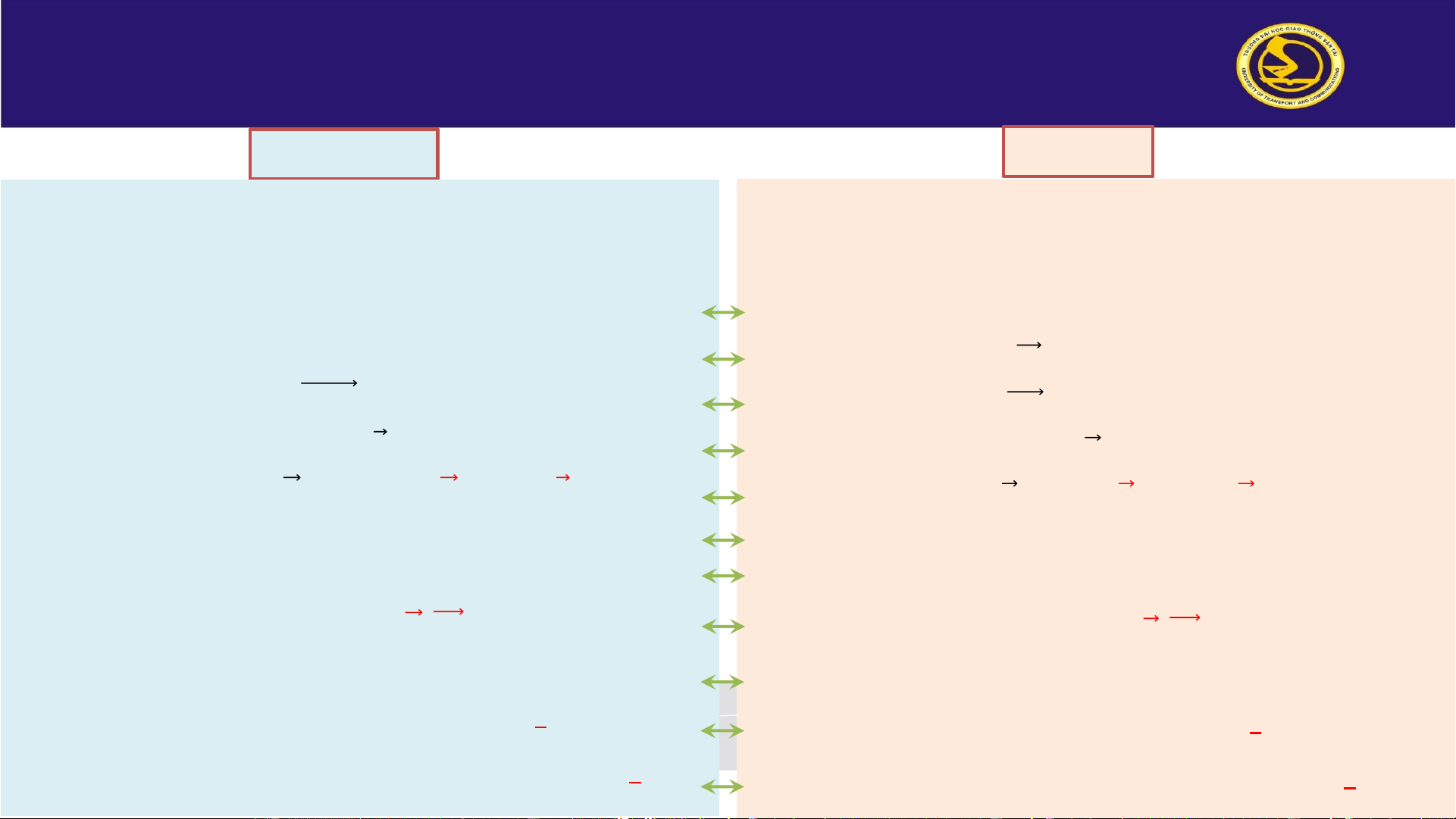
Bộ môn Vật lý – Khoa Khoa học Cơ bản – Trường Đại học Giao thông Vận tải Các khái niệm cơ bản Điện trường Từ trường
• Điện trường là « dạng vật chất đặc biệt » (khoảng không
✓ Từ trường là « dạng vật chất đặc biệt » (khoảng không
gian) tồn tại xung quanh mỗi vật mang điện (hay điện tích
gian) tồn tại xung quanh các dòng điện hoặc nam châm điểm)
• Vật dẫn mang điện tích: Q [C]
✓ Dây dẫn mang điện: 𝐼. Ԧ𝑙
• Điện tích điểm: q [C]
✓ Phần tử dòng điện: 𝐼. 𝑑𝑙 [A.m]
• Định luật Coulomb => 𝐹đ𝑖ệ𝑛 [N]
✓ Định luật Ampe => 𝐹𝑡ừ [N]
• Vectơ cường độ điện trường: 𝐸 [V/m]
✓ Vectơ cường độ từ trường: 𝐻 [A/m]
• Vectơ cảm ứng điện: 𝐷 [C/m2] với 𝐷 = 𝜀. 𝜀0. 𝐸
✓ Vectơ cảm ứng từ : 𝐵 [T] với 𝐵 = µ. 𝜇0. 𝐻 •
𝜀 – hằng số điện môi của môi trường
✓ µ - hằng số từ môi của môi trường
• 𝜀0 = 8,846. 10−12 (C2/N.m2) – hằng số điện môi
✓ 𝜇0 = 4𝜋. 10−7 (H/m) - hằng số từ môi
• Điện thông: Φ𝑒 = ׬ 𝑑Φ𝑒 = ׬ 𝐷. 𝑑𝑆 (𝑆)
✓ Từ thông: Φ𝑚 = ׬ 𝑑Φ𝑚 = ׬ 𝐵. 𝑑𝑆 (𝑆)
• Công của lực điện: A [J]
✓ Công của lực từ: A [J]
• Năng lượng điện trường 1 : W [J] với 𝑊 . 𝐸. 𝐷. 𝑉 1 E 𝐸 =
✓ Năng lượng từ trường 2 : W [J] với 𝑊 . 𝐵. 𝐻. 𝑉 H 𝐻 = 2
• Mật độ năng lượng điện trường 1 : w [J/m3] với 𝑤 . 𝐸. 𝐷 1 E 𝐸 =
✓ Mật độ năng lượng từ trường: w [J/m3] với 𝑤 . 𝐵. 𝐻 Chu Tiến Dũng 2 H 𝐻 = 2 Các khái niệm cơ bản
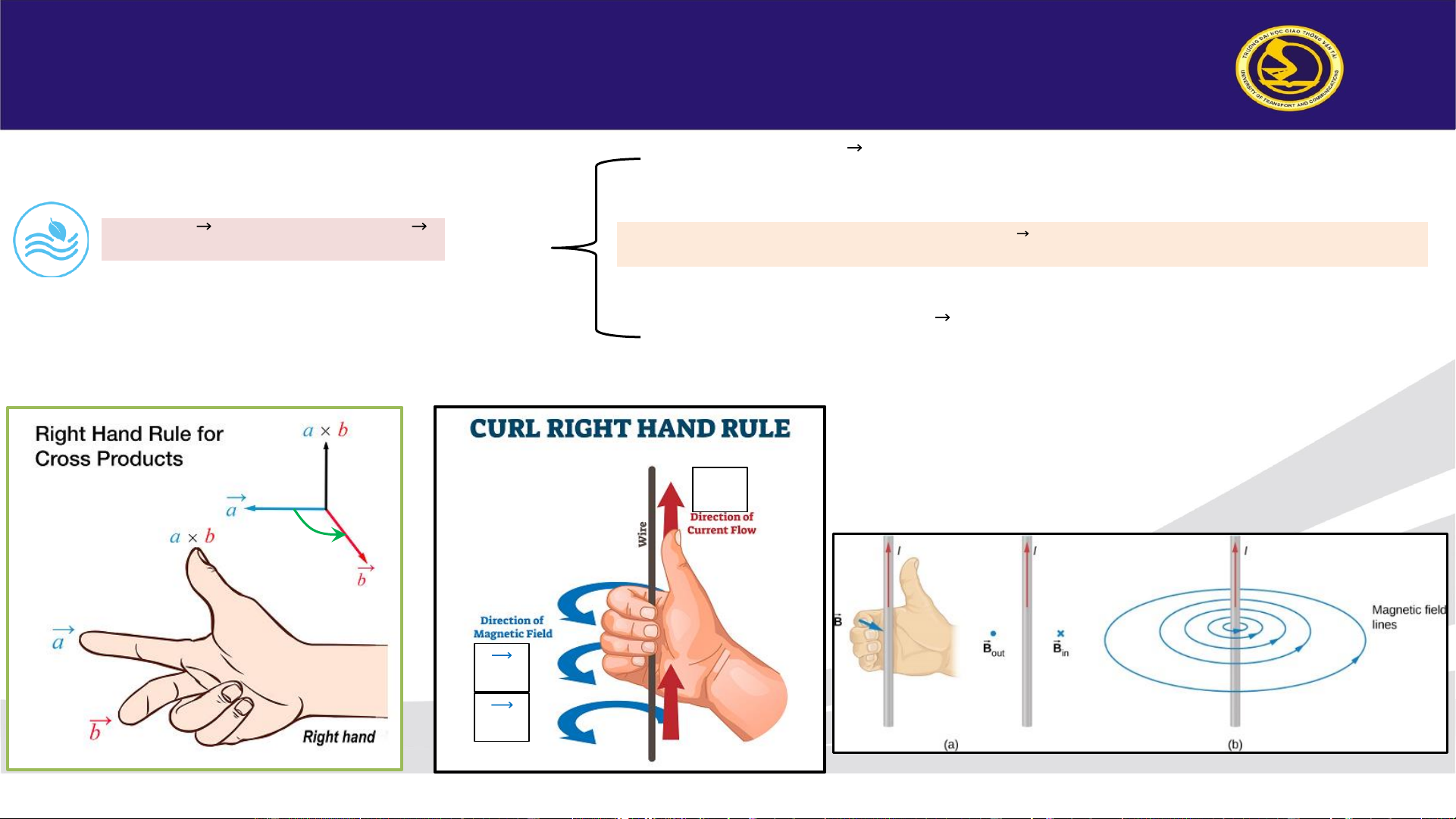
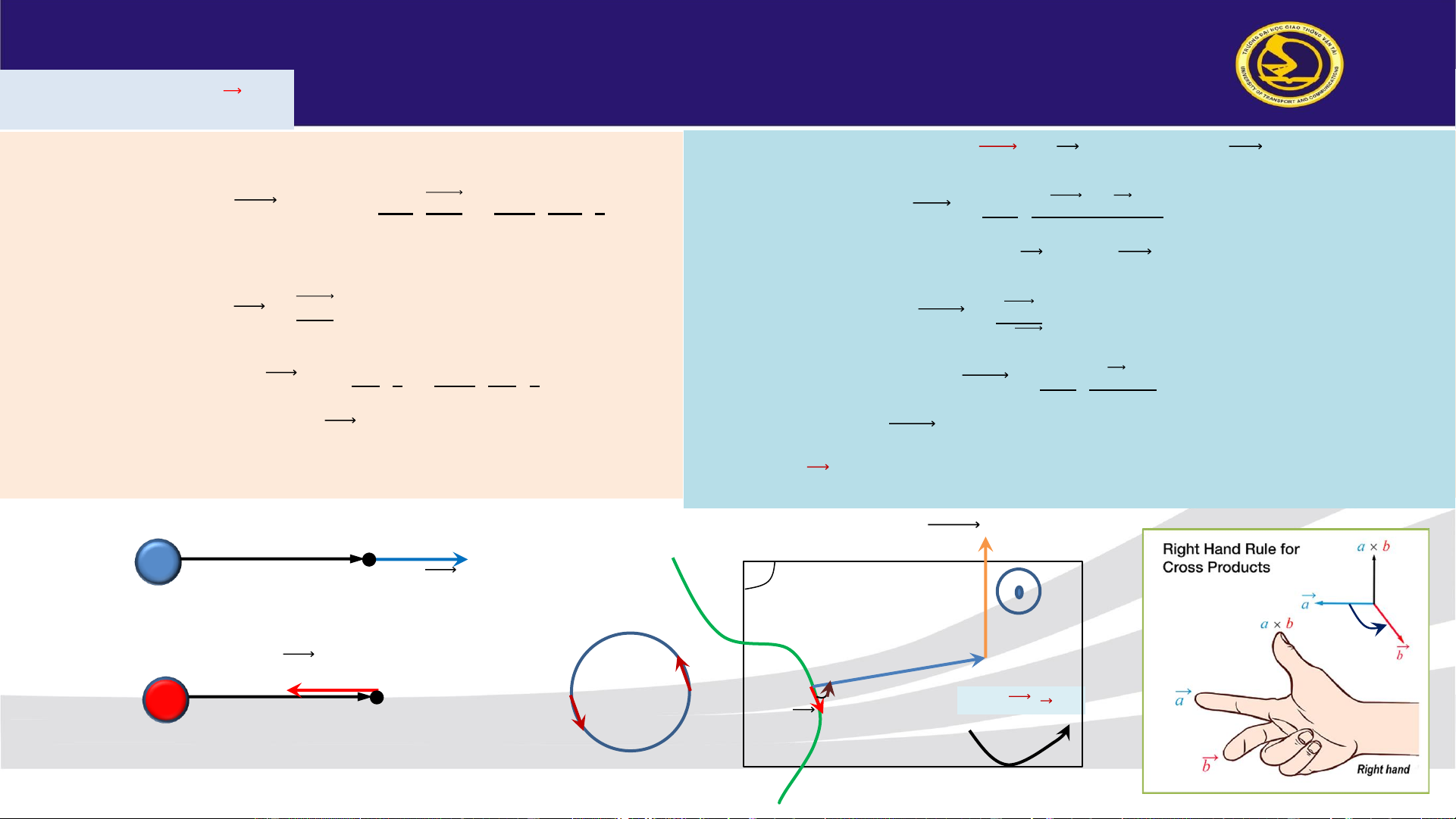
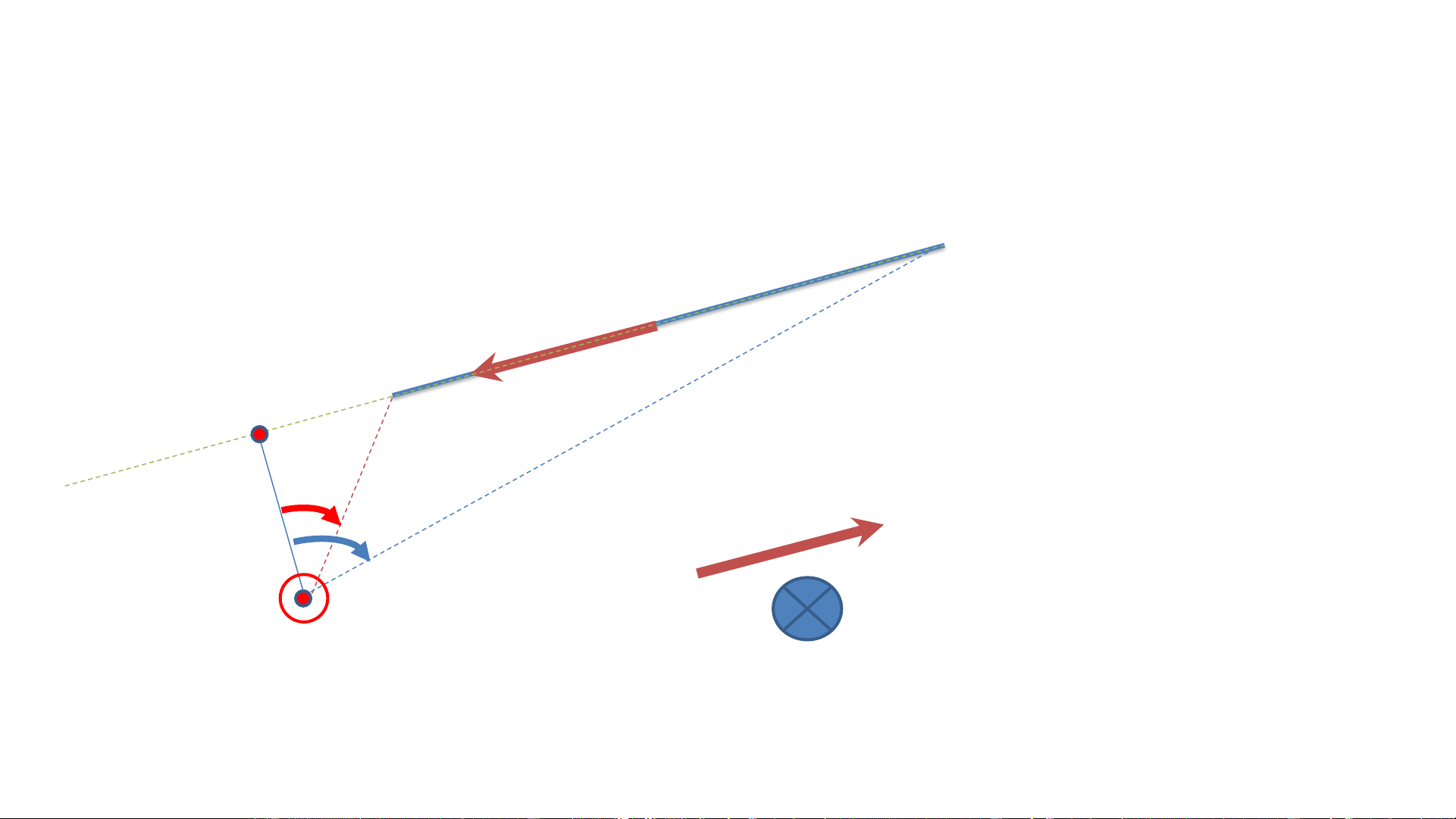
Phương: Ԧ𝑐⏊( Ԧ𝑎, 𝑏) Ԧ 𝑐 = Ԧ
𝑎ʌ𝑏 = 𝑎. 𝑏. 𝑠𝑖𝑛𝛼( Ԧ 𝑎, 𝑏) với Ԧ 𝑐
Chiều: thuận theo chiều quay từ Ԧ𝑎 sang 𝑏 (quy tắc vặn đinh ốc hay bàn tay phải)
Độ lớn: c = a.b.sin𝛼( Ԧ𝑎, 𝑏) I 𝛼 𝑩 𝑯 Chu Tiến Dũng
§1. Tương tác từ của dòng điện – Định luật Ampe
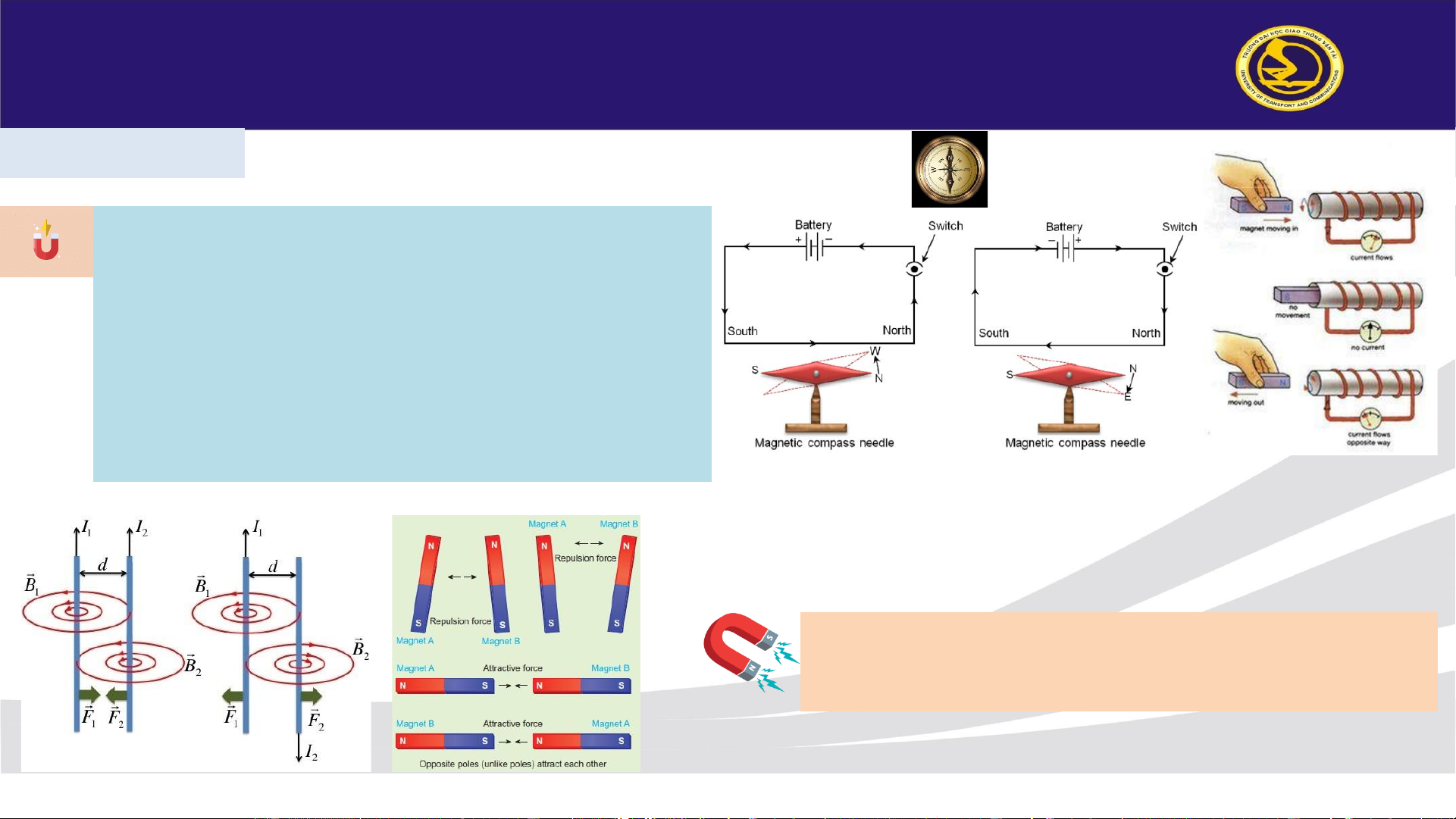
1. Tương tác từ là gì?
- Khi cho dòng điện đi qua dây dẫn (mạch điên) nằm gần
một kim nam châm, nó sẽ làm kim nam châm quay đi.
- Ngược lại, nam châm khi được đưa lại gần một cuộn dây
có điện chạy qua, nó có thể hút hoặc đẩy cuộn dây đó, hoặc
hơn nữa nam châm dịch chuyển trong ống dây có thể sinh ra dòng điện
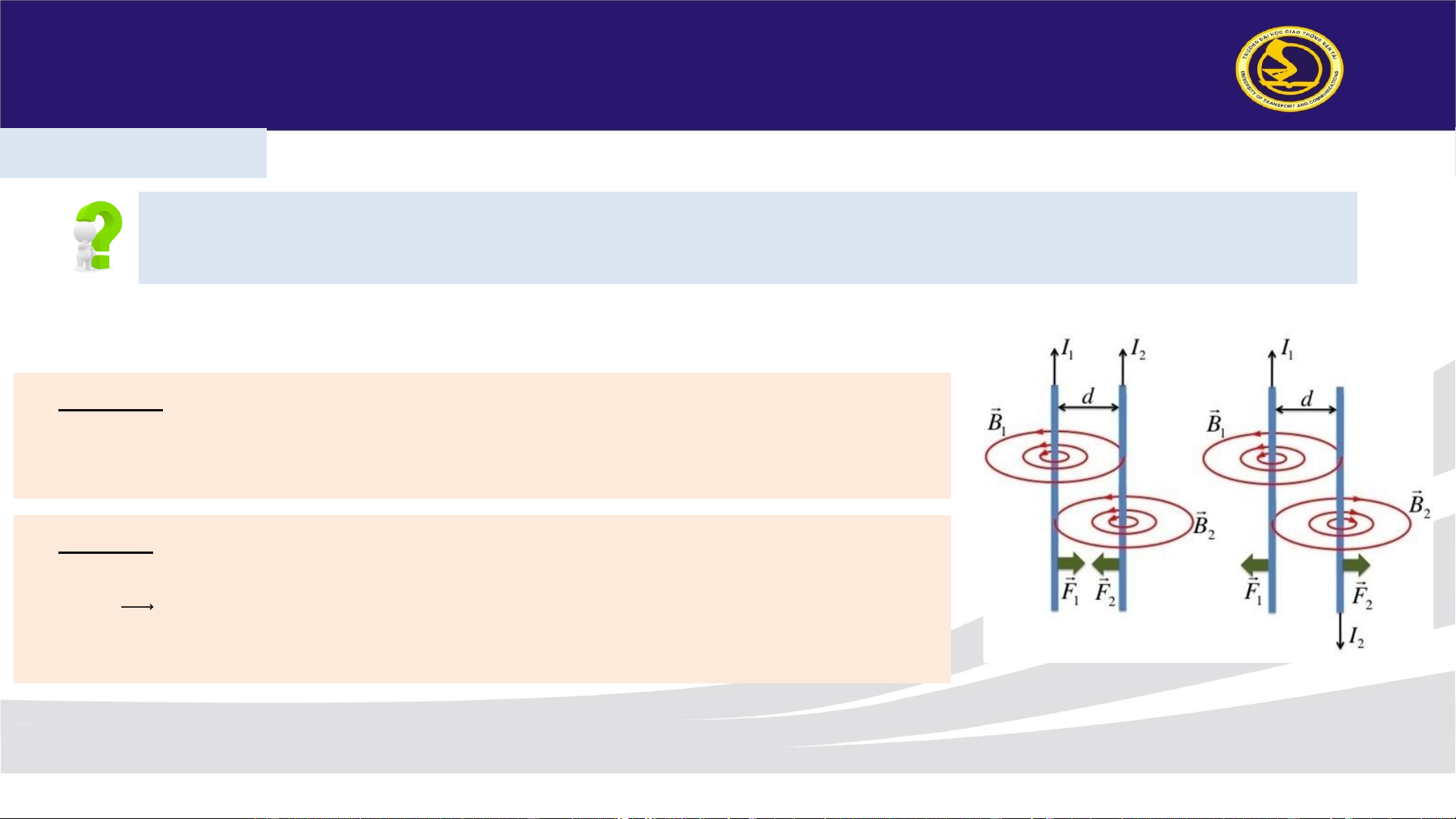
- Tương tự như hai thanh nam châm, hai dòng điện cũng có thể hút hoặc đẩy nhau Chu Tiến Dũng
§1. Tương tác từ của dòng điện – Định luật Ampe 2. Định luật Ampe
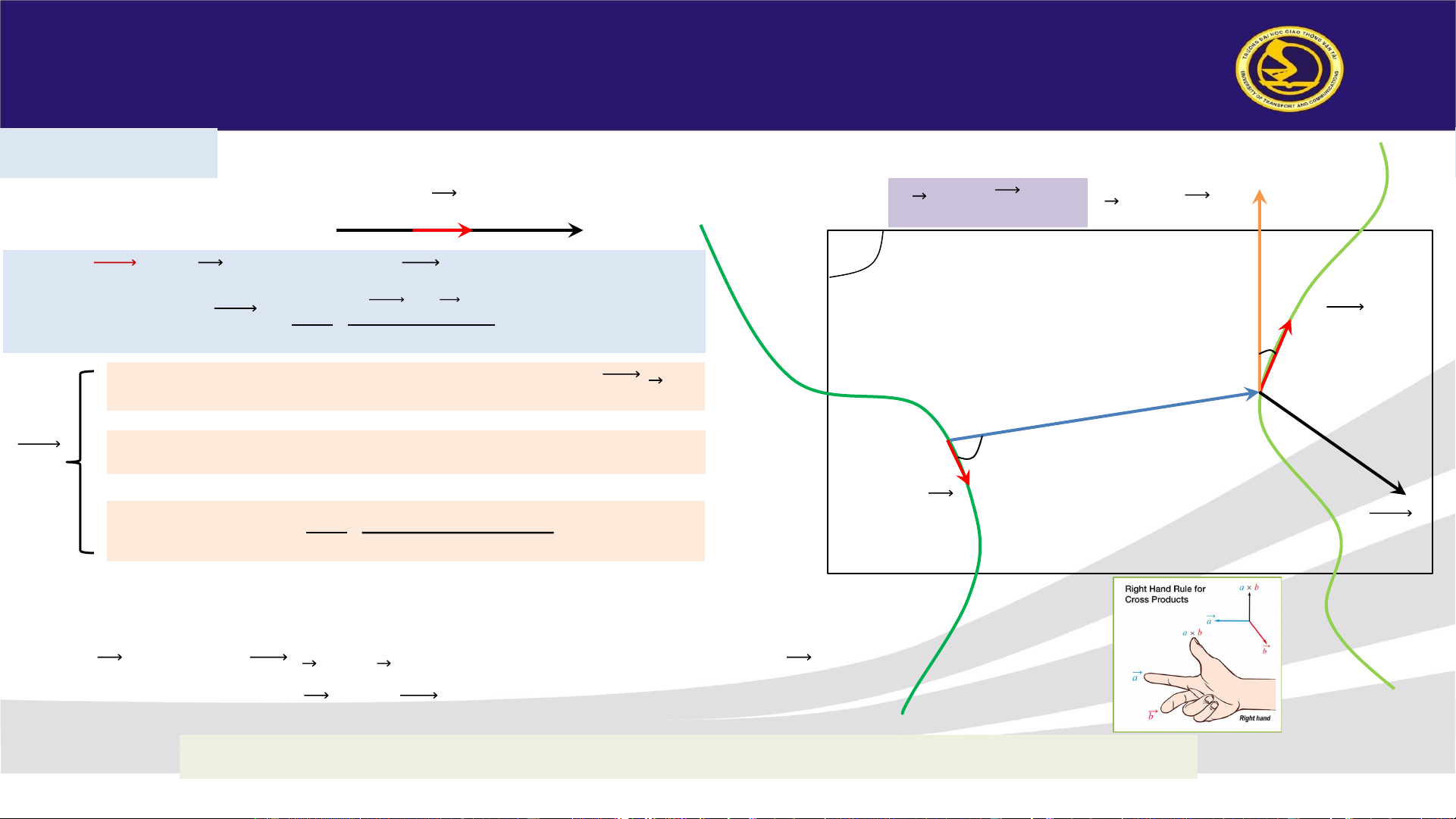
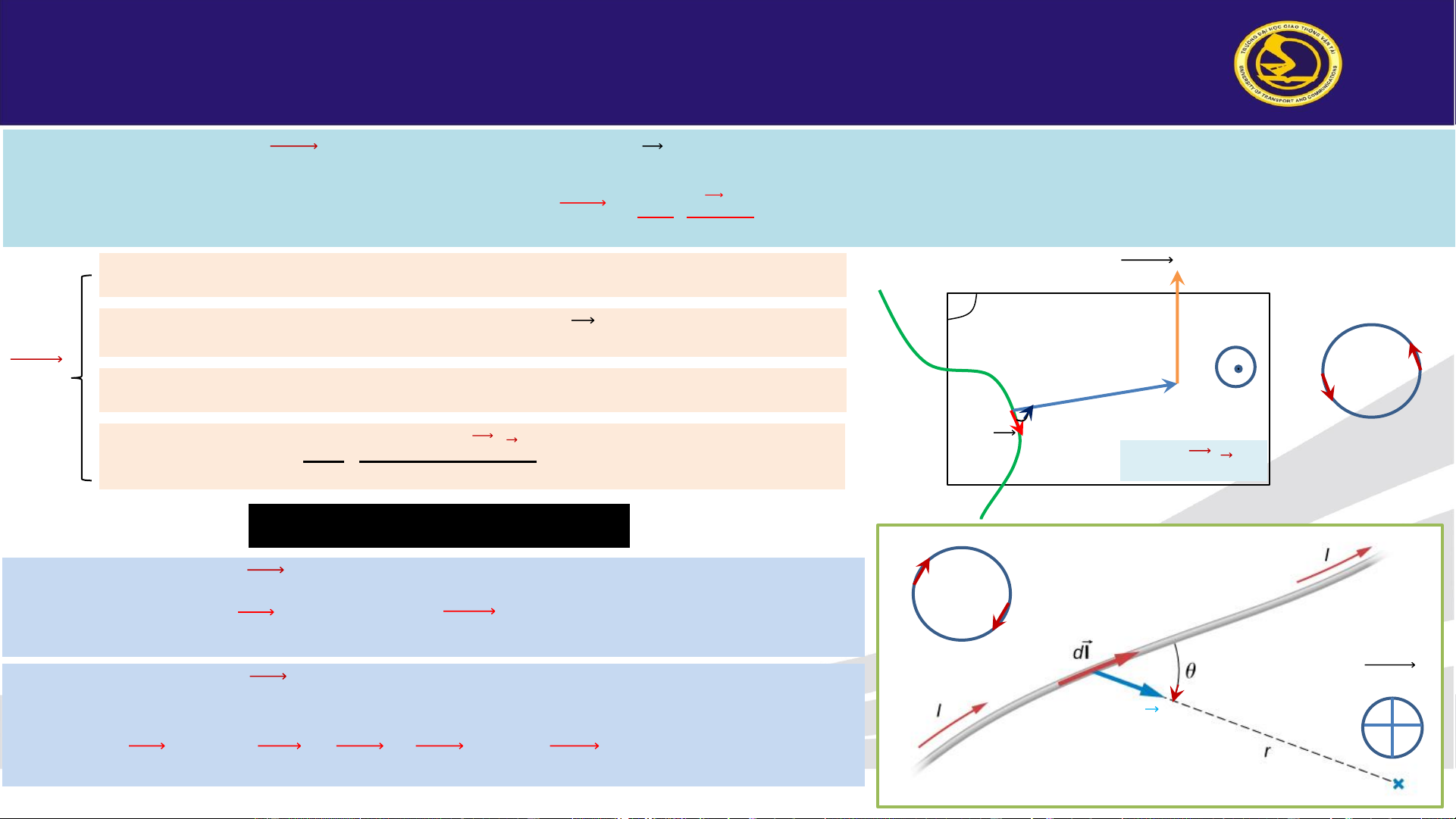
❖ Giới hạn: là định luật x/đ lực tương tác giữa hai phần tử dòng điện 𝑑𝑙 I
𝑛 ≡ (𝐼. 𝑑𝑙˄ Ԧ𝑟)
𝑛 ⊥ (𝐼. 𝑑𝑙, Ԧ𝑟) S
Từ lực 𝑑𝐹0 do 𝐼. 𝑑𝑙 tác dụng lên 𝐼0. 𝑑𝑙0: 𝜇.𝜇 𝐼 𝑑𝐹 0
0.𝑑𝑙0 ˄ (𝐼.𝑑𝑙˄ Ԧ 𝑟) 0 = . (7-1) 𝜃 𝐼 4𝜋 𝑟3 0 0. 𝑑𝑙0 Phương M
: vuông góc với mặt phẳng chứa (𝐼0. 𝑑𝑙0,𝑛) Ԧ𝑟 O 𝑑𝐹
Chiều: theo quy tắc bàn tay phải hay tam diện thuận 0 𝜃 𝐼. 𝑑𝑙 Độ lớn 𝜇.𝜇
𝐼.𝑑𝑙.𝑠𝑖𝑛𝜃.𝐼 : 𝑑𝐹 0 0.𝑑𝑙0.𝑠𝑖𝑛𝜃0 𝑑𝐹 0 = . (7-2) 0 4𝜋 𝑟2
▪ µ - độ từ thẩm của môi trường
▪ µ = 4𝜋. 10−7 (H/m) – hằng số từ 0
▪ θ (𝐼. 𝑑𝑙, Ԧ𝑟) ; θ (𝐼 0
0. 𝑑𝑙0, 𝑛) với 𝑛 - vectơ pháp tuyến của mp chứa (𝐼. 𝑑𝑙, Ԧ 𝑟) ≡ (S)
▪ r – khoảng cách giữa 𝐼. 𝑑𝑙 và 𝐼0. 𝑑𝑙0
➢ Chú ý: định luật Ampe thực chất là định luật tương tác từ giữa các dòng điện hữu hạn Chu Tiến Dũng
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường
1. Khái niệm từ trường -
Lực tương tác giữa 2 dòng điện được truyền từ dòng này sang dòng kia như thế nào? -
Khi chỉ có một dòng điện, tính chất của không gian xung quanh dòng điện ấy có bị biến đổi hay không?
➢ Khái niệm:
- Từ trường là « dạng vật chất đặc biệt » (khoảng không gian) tồn tại xung quanh mỗi dây dẫn
mang điện (hay dòng điện)
➢ Đặc điểm: -
Bất kỳ một dòng điện nào khác nằm trong khoảng không gian đó thì đều chịu tác dụng của
lực từ 𝐹𝑡ừ do từ trường đó đặt lên. -
Vận tốc truyền tương tác là hữu hạn và bằng vận tốc ánh sáng trong chân không. Chu Tiến Dũng
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường
2. Vectơ cảm ứng từ 𝑩 [T]
➢ Theo đ/luật Coulomb, lực điện của q lên q (đặt tại điểm M): ➢ 0
Theo đ/luật Ampe, từ lực 𝑑𝐹0do 𝐼𝑑𝑙 tác dụng lên 𝐼0𝑑𝑙0 (đặt tại điểm M): 𝑞.𝑞 𝑟 1 𝑞.𝑞 Ԧ 𝑟 𝐹 0 𝑞𝑞0 0
𝜇.𝜇0 𝐼0.𝑑𝑙0 ˄ (𝐼.𝑑𝑙˄ Ԧ𝑟) 𝑞𝑞 = Ԧ 𝐹 = 𝑘. . = . . (*) 𝑑𝐹 . 0 (*) 𝜀𝑟2 𝑟 4𝜋𝜀 0 = 0 𝜀𝑟2 𝑟 4𝜋 𝑟3
với Ԧ𝑟: bán kính vectơ hướng từ q đến q (điểm M) 0
với Ԧ𝑟: bán kính vectơ hướng từ 𝐼. 𝑑𝑙 đến 𝐼0. 𝑑𝑙0 (điểm M) 𝐹𝑞𝑞 Mà 𝐸 0 𝑑𝐹0 𝑀 = (**) Mà 𝑑𝐵 (**) 𝑞 𝑀 = 0 𝐼0.𝑑𝑙0  từ 𝑞 Ԧ 𝑟 1 𝑞 Ԧ 𝑟 (*) và (**) ta được: 𝐸
𝜇.𝜇0 (𝐼.𝑑𝑙˄ Ԧ𝑟) 𝑀 = 𝑘. . = . .
 từ (*) và (**) ta được: 𝑑𝐵 . (7-3) 𝜀𝑟2 𝑟 4𝜋𝜀 𝑀 = 0 𝜀𝑟2 𝑟 4𝜋 𝑟3
(vectơ cường độ điện trường 𝐸𝑀 tại điểm M bất kỳ trong điện (vectơ cảm ứng từ 𝑑𝐵𝑀 tại điểm M bất kỳ trong từ trường của 1 phần tử
trường của 1 điện tích điểm q)
dòng điện 𝐼𝑑𝑙) 𝐌 𝑑𝐵𝑀 + Ԧ𝑟 𝐸 S 𝑀 (𝑞 > 0) 𝐸 M 𝑀 𝐌 O - 𝜃 Ԧ𝑟 Ԧ𝑟 𝜃
θ (𝑰. 𝒅𝒍, 𝒓) 𝐼. 𝑑𝑙 (𝑞 < 0) Chu Tiến Dũng
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường
➢ Vectơ cảm ứng từ 𝐝𝐁𝐌 do 1 phần tử dòng điện Idl gây ra tại điểm M, cách phần tử một khoảng r là một vectơ có: 𝜇.𝜇 (𝐼.𝑑𝑙˄ Ԧ 𝑟) 𝑑𝐵 0 𝑀 = . (7-3) 4𝜋 𝑟3 - Gốc tại điểm M 𝑑𝐵𝑀 S
- Phương vuông góc với mặt phẳng chứa Idl và điểm M (tức (S) 𝑑𝐵𝑀 𝜃
- Chiều theo quy tắc vặn nút chai, bàn tay phải hay tam diện thuận M O Ԧ𝑟 𝜃 𝜇.𝜇
𝐼.𝑑𝑙.sin θ (𝑰.𝒅𝒍, 𝒓) 𝐼. 𝑑𝑙 - Độ lớn: 𝑑𝐵 0 𝑀 = .
θ (𝑰. 𝒅𝒍, 𝒓) 4𝜋 𝑟2
Nguyên lý chồng chất từ trường
❖ Vectơ cảm ứng từ 𝐁𝐌 do một dòng điện gây ra tại điểm M: 𝜃 𝐵𝑀 = ׬ 𝑑𝐵
𝑐ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛 𝑀 ❖ 𝒅𝑩 Vectơ cảm ứng từ 𝐁 𝑴
𝐌 của nhiều dòng điện bằng tổng các vec tơ cảm ứng O
từ do từng dòng điện sinh ra 𝒓 𝐵 𝑛
𝑀 = σ𝑖=1 𝐵𝑖𝑀 = 𝐵1𝑀 + 𝐵2𝑀 + ⋯ + 𝐵𝑛𝑀 M Chu Tiến Dũng
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường
3. Vectơ cường độ từ trường 𝑯 [A/m] 𝐻1 𝐻1
➢ Biểu thức:
𝑩 = µ. 𝝁𝟎. 𝑯 𝐻2 𝑩 ↑↑ 𝑯 𝐻2
𝐁 = µ. 𝛍𝟎. 𝐇 𝑑𝐵𝑀 S 𝑑𝐻𝑀 𝑑𝐻𝑀 M O Ԧ𝑟 𝑑𝐵𝑀 𝜃 θ O
(𝑰. 𝒅𝒍, 𝒓) 𝐼. 𝑑𝑙 𝒓 M Chu Tiến Dũng
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường 4. Ứng dụng
❖ Xác định vectơ cảm ứng từ 𝑩𝑴[T] tại một điểm M bất kỳ trong từ trường của một đoạn dòng điện thẳng (dây hữu hạn), và
của một dòng điện thẳng dài vô hạn 𝜇. 𝜇 (𝐼. 𝑑𝑙˄ Ԧ𝑟) 𝑑𝐵 0 𝑀 = . 𝐵𝑀 = න 𝑑𝐵𝑀 𝐼𝑑𝑙2 4𝜋 𝑟3 𝜽𝟐
𝑐ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛 𝜶𝟐 𝜶𝟏 B
➢ Dây AB dài hữu hạn l 𝑟 ▪ Phương 2
: 𝐵𝑀 ⊥ (𝐼. 𝑑𝑙, Ԧ𝑟) 𝜽
▪ Chiều: được x/đ theo quy tắc nắm bàn tay phải 𝐵𝑀 ▪ Độ lớn 𝜇.𝜇 : 𝐵 0.𝐼 𝑀 =
. (𝑐𝑜𝑠𝜽𝟏 − 𝑐𝑜𝑠𝜽𝟐) 𝐵 4𝜋.𝑅 𝜇.𝜇 𝜶 𝑀 0.𝐼 𝟐 hoặc: 𝐵𝑀 = . (𝑠𝑖𝑛𝜶 4𝜋.𝑅
𝟐 − 𝑠𝑖𝑛𝜶𝟏);𝜶𝟏(𝑅, 𝑟1) < 0 và 𝜶𝟐(𝑅, 𝑟2) > 0) l M trong đó 𝑅 𝜶𝟏
𝜽𝟏(𝐼𝑑𝑙1, 𝑟1), 𝜽𝟐(𝐼𝑑𝑙2, 𝑟2) và 𝜶𝟏(𝑅, 𝑟1), 𝜶𝟐(𝑅, 𝑟2) I.𝑑𝑙
• 𝑟1: vec tơ khoảng cách hướng từ 𝐼𝑑𝑙1 đến điểm M
• 𝑟2: vec tơ khoảng cách hướng từ 𝐼𝑑𝑙2 đến điểm M 𝜽𝟏
• R: khoảng cách ngắn nhất từ đoạn dây AB đến điểm M 𝑟1 𝐼𝑑𝑙1
➢ Dây AB dài vô hạn A 𝜃 𝜇. 𝜇0. 𝐼 1 → 00 𝑐𝑜𝑠𝜃1 → 1 𝛼1 → −900 𝑠𝑖𝑛𝛼1 → −1 𝜃 or 𝐵𝑀 = 2𝜋. 𝑅 2 → 1800 𝑐𝑜𝑠𝜃2 → −1 𝛼2 → +900 𝑠𝑖𝑛𝛼2 → +1
§2. Vectơ cảm ứng từ và vectơ cường độ từ trường ❖ 𝑨
Xác định vectơ cường độ từ trường 𝑯𝑴[ ] tại một điểm M bất kỳ trong từ trường của một đoạn dòng điện thẳng (dây hữu hạn), và của một 𝒎
dòng điện thẳng dài vô hạn 1 (𝐼. 𝑑𝑙˄ Ԧ𝑟) 𝐼𝑑𝑙 𝑑𝐻 . 2 𝑀 = 𝑑𝐻𝑀 𝜽𝟐 4𝜋 𝑟3 𝐻𝑀 = න
𝑐ả 𝑑ò𝑛𝑔 đ𝑖ệ𝑛 B
➢ Dây AB dài hữu hạn l 𝑟 ▪ Phương 2
: 𝐻𝑀 ⊥ (𝐼. 𝑑𝑙, Ԧ𝑟)
▪ Chiều: được x/đ theo quy tắc nắm bàn tay phải 𝐻𝑀 ▪ Độ lớn 𝐼 : 𝐻𝑀 =
. (𝑐𝑜𝑠𝜽𝟏 − 𝑐𝑜𝑠𝜽𝟐) 𝐻 4𝜋.𝑅 𝐼 𝜶 𝑀 𝟐 hoặc: 𝐻𝑀 = . (𝑠𝑖𝑛𝜶 4𝜋.𝑅
𝟐 − 𝑠𝑖𝑛𝜶𝟏); 𝜶𝟏(𝑅, 𝑟1) < 0 và 𝜶𝟐(𝑅, 𝑟2) > 0) l M trong đó 𝑅 𝜶𝟏
𝜽𝟏(𝐼𝑑𝑙1, 𝑟1), 𝜽𝟐(𝐼𝑑𝑙2, 𝑟2) và 𝜶𝟏(𝑅, 𝑟1), 𝜶𝟐(𝑅, 𝑟2) I.𝑑𝑙
• 𝑟1: vec tơ khoảng cách hướng từ 𝐼𝑑𝑙1 đến điểm M
• 𝑟2: vec tơ khoảng cách hướng từ 𝐼𝑑𝑙2 đến điểm M 𝜽𝟏
• R: khoảng cách ngắn nhất từ đoạn dây AB đến điểm M 𝑟1 𝐼𝑑𝑙1
➢ Dây AB dài vô hạn A 𝜃 𝐼 1 → 00 𝑐𝑜𝑠𝜃1 → 1 𝛼1 → −900 𝑠𝑖𝑛𝛼1 → −1 𝜃 or 𝐻𝑀 = 2𝜋. 𝑅 2 → 1800 𝑐𝑜𝑠𝜃2 → −1 𝛼2 → +900 𝑠𝑖𝑛𝛼2 → +1 B i A K M 𝑨
Tính vectơ cảm ứng từ 𝑩𝑴[T] và vectơ cường độ từ trường 𝑯𝑴[ ] tại một điểm M bất kỳ, nằm trong từ trường của nhiều đoạn dòng điện thẳng 𝒎
(nhiều dây hữu hạn), hay của nhiều dòng điện thẳng dài vô hạn và dây nửa vô hạn ➢ Cách làm: ❖ Chú ý:
1. Áp dụng nguyên lý chồng chất từ trường: -
Áp dụng các bước tương tự đối với 𝑯𝑴 (giống như 𝑩𝑴) 𝐵 𝑛 -
Công thức độ lớn (trong bước 4):
𝑀 = σ𝑖=1 𝐵𝑖𝑀 = 𝐵1𝑀 + 𝐵2𝑀 + ⋯ + 𝐵𝑛𝑀 (1)
▪ cho dòng thẳng hữu hạn
2. Phân tích chiều của các vectơ 𝑩 𝜇.𝜇0.𝐼 𝜇.𝜇0.𝐼
𝒊𝑴 thành phần (trên hình 𝐵𝑖𝑀 = . (𝑐𝑜𝑠𝜽 . (𝑠𝑖𝑛𝜶 4𝜋.𝑅
𝟏 − 𝑐𝑜𝑠𝜽𝟐) ; 𝐵𝑖𝑀 = 4𝜋.𝑅 𝟐 − 𝑠𝑖𝑛𝜶𝟏)
vẽ) => chiều của 𝐵 𝐼 𝐼 𝑀 or 𝐻𝑖𝑀 = . (𝑐𝑜𝑠𝜽 . (𝑠𝑖𝑛𝜶 4𝜋.𝑅
𝟏 − 𝑐𝑜𝑠𝜽𝟐) ; 𝐻𝑖𝑀 = 4𝜋.𝑅 𝟐 − 𝑠𝑖𝑛𝜶𝟏) 3. Nhận xét:
▪ cho dòng thẳng vô hạn • chiều của 𝜇.𝜇 𝐼 các 𝐵 0.𝐼
𝑖𝑀 => chuyển pt vectơ (1) thành pt đại số 𝐵𝑀 = or 𝐻 2𝜋.𝑅 𝑀 = 2𝜋.𝑅
• Nhận xét đặc điểm hình dạng của hình mà đầu bài cho ▪ cho dòng thẳng nửa vô hạn
=> pt đại số (2) (mối liên hệ giữa B và B ) M iM 𝜃1 → 00 𝑐𝑜𝑠𝜃1 → 1 𝜇.𝜇 𝐵 0.𝐼 𝑖𝑀 = . (1 − 𝑐𝑜𝑠𝜽𝟐)
4. Áp dụng công thức độ lớn: 𝜃2 𝑐𝑜𝑠𝜃2 4𝜋.𝑅 ▪ 𝜇.𝜇 𝐵 0.𝐼𝑖 𝜃1 𝑐𝑜𝑠𝜃1 𝜇.𝜇0.𝐼 𝑖𝑀 = . (𝑐𝑜𝑠𝜽 𝐻 . (𝑐𝑜𝑠𝜽 4𝜋.𝑅 𝟏 − 𝑐𝑜𝑠𝜽𝟐) 𝑖𝑀 𝜃 𝑖𝑀 = 𝟏 − 1) 2 → 00 𝑐𝑜𝑠𝜃2 → 1 4𝜋.𝑅 hoặc 𝜇.𝜇 : 𝐵 0.𝐼𝑖 𝑖𝑀 = . (𝑠𝑖𝑛𝜶 4𝜋.𝑅 𝟐 − 𝑠𝑖𝑛𝜶𝟏) 𝛼 𝑠𝑖𝑛𝛼 𝜇. 𝜇 𝑖𝑀 1 → −900 1 → −1 𝐵 0. 𝐼 . (𝑠𝑖𝑛𝜶 (lưu ý: 𝜶 𝛼 𝑠𝑖𝑛𝛼 𝑖𝑀 = 𝟐 − (−1))
𝟏(𝑅, 𝑟1) < 0 và 𝜶𝟐(𝑅, 𝑟2) > 0) 2(dương) 2 4𝜋. 𝑅
5. Kết luận: Phương, chiều và độ lớn của B 𝛼 𝑠𝑖𝑛𝛼 𝜇. 𝜇 M 1 (góc âm) 1
0. 𝐼 . (1 − 𝑠𝑖𝑛𝜶 Chu Tiến Dũng 𝛼 𝟏) 2 → +900 𝑠𝑖𝑛𝛼2 → +1 𝐵𝑖𝑀 = 4𝜋.𝑅
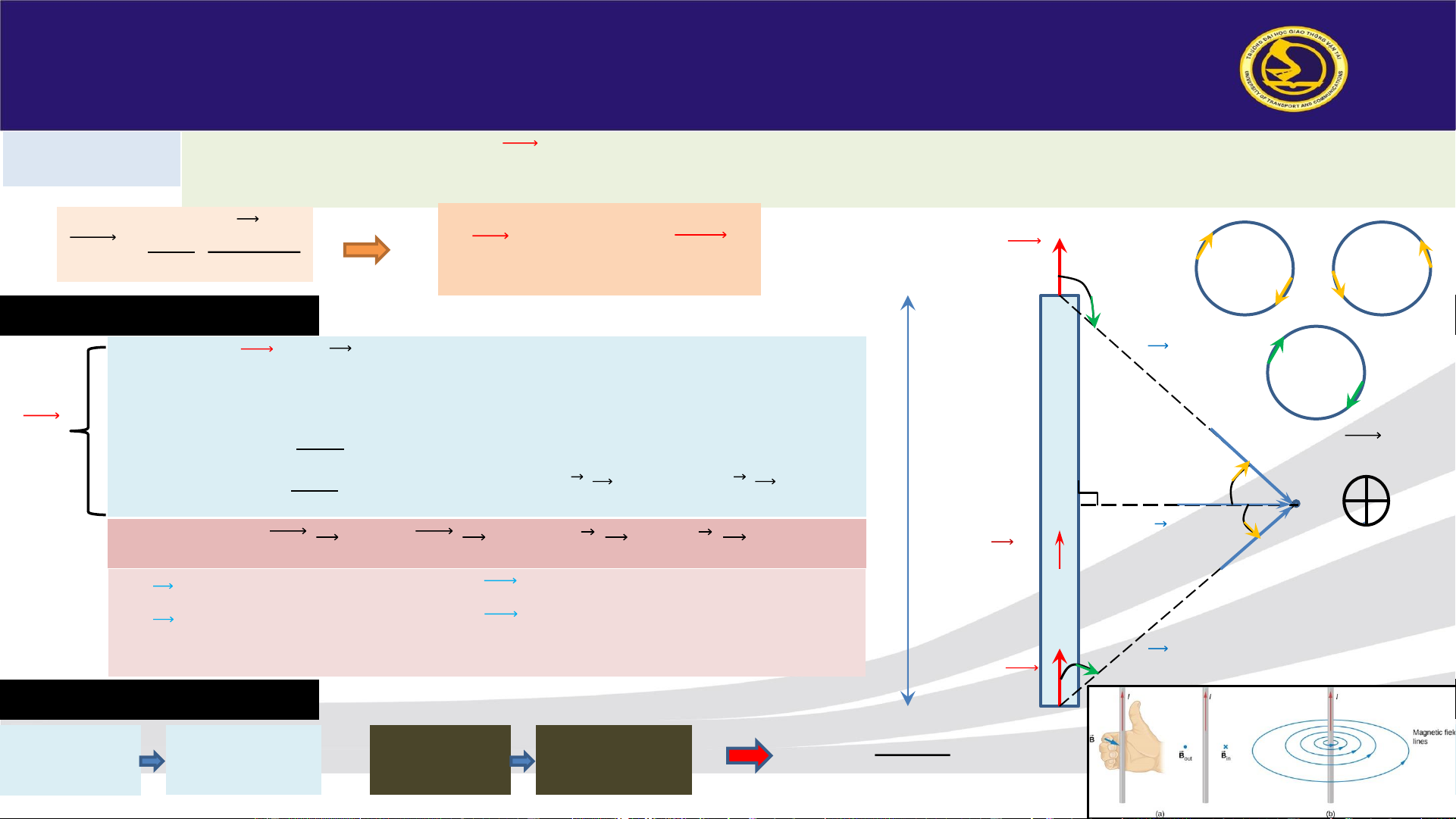
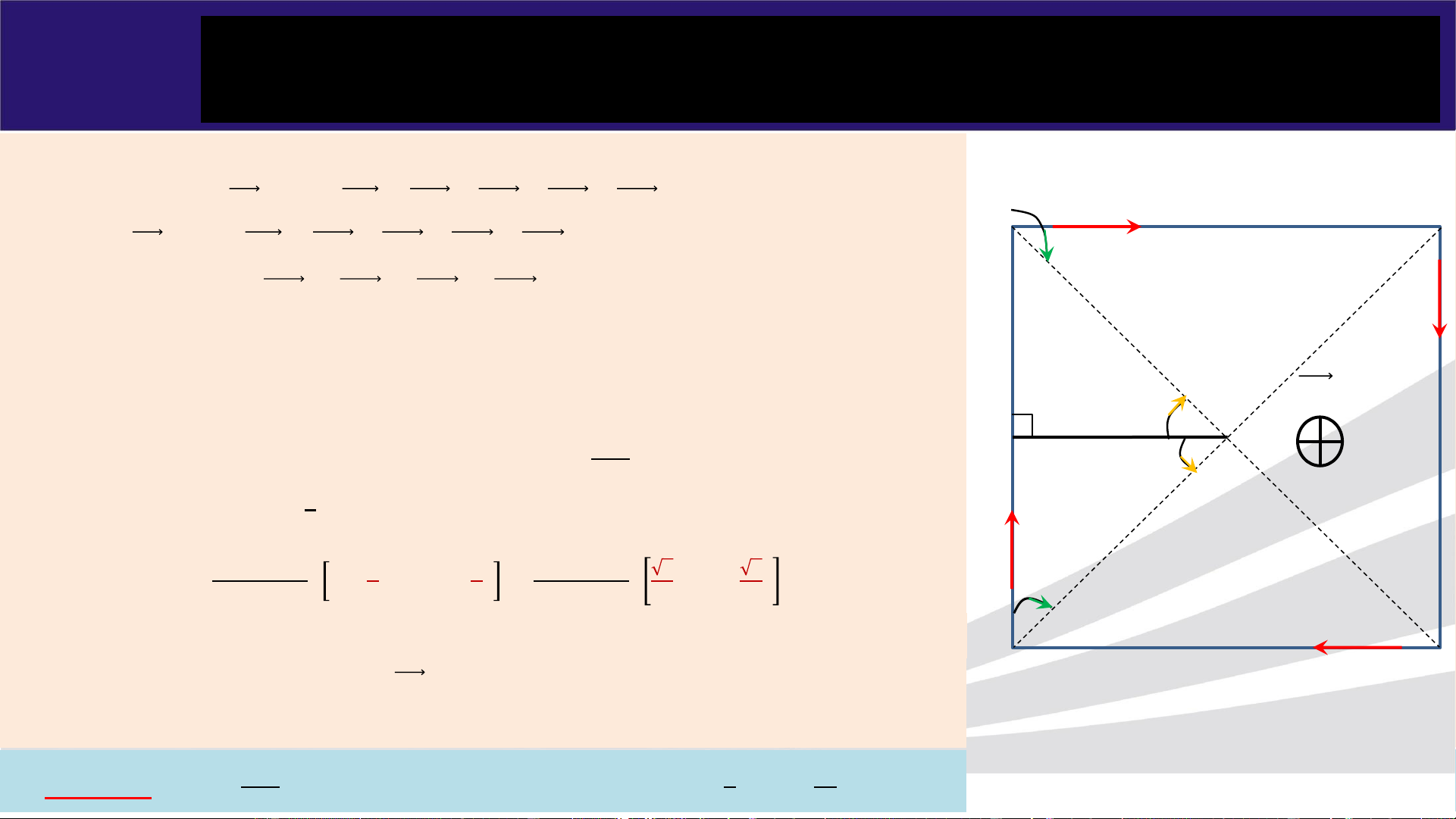
Luyện tập Một dây dẫn được uốn thành hình vuông ABCD có cạnh a = 10 (cm). Dòng điện chạy qua dây có
cường độ I = 1(A). Lấy 𝜇 = 1. Xác định vectơ cường độ từ trường tại tâm O hình vuông?
Áp dụng nguyên lý chồng chất từ trường: 𝐻 𝑛 𝜽
𝑂 = σ𝑖=1 𝐻𝑖𝑂 = 𝐻1𝑂 + 𝐻2𝑂 + 𝐻3𝑂 + 𝐻4𝑂 𝟐 C B Hay 𝐻 𝑛
𝑂 = σ𝑖=1 𝐻𝑖𝑂 = 𝐻𝐴𝐵 + 𝐻𝐵𝐶 + 𝐻𝐶𝐷 + 𝐻𝐷𝐴 (1) -
Theo hình vẽ, ta thấy 𝐻𝐴𝐵 ↑↑ 𝐻𝐵𝐶 ↑↑ 𝐻𝐶𝐷 ↑↑ 𝐻𝐷𝐴, có chiều hướng từ ngoài vào trong nên:
(1) => 𝐻𝑂 = 𝐻𝐴𝐵 + 𝐻𝐵𝐶 + 𝐻𝐶𝐷 + 𝐻𝐷𝐴 -
Mặt khác, do tứ giác là hình vuông, nên: 𝐻𝐴𝐵 = 𝐻𝐵𝐶 = 𝐻𝐶𝐷 = 𝐻𝐷𝐴 𝐻 Vậy: 𝐻 𝜶 𝑂 𝑂 = 4. 𝐻𝐴𝐵 (2) 𝟐 𝐼 -
Áp dụng công thức độ lớn cho dòng hữu hạn: 𝐻𝐴𝐵 =
. (𝑠𝑖𝑛𝜶𝟐 − 𝑠𝑖𝑛𝜶𝟏) R 𝜶 4𝜋.𝑅 𝟏 O 𝑎
với: 𝜶𝟐 > 0 và 𝜶𝟏< 0 và 𝑅 = = 5. 10−2(𝑚) 2 I 1 𝝅 𝝅 1 𝟐 𝟐 - Thay số: 𝐻 . 𝑠𝑖𝑛 − sin(− ) = . − (− ) =………(A/m) 𝜽 𝐴𝐵 = 𝟏 4𝜋.(5.10−2) 𝟒 𝟒 4𝜋.(5.10−2) 𝟐 𝟐 (3) -
Lấy đáp số (3) thay lại vào (2): 𝐻𝑂 = 4. 𝐻𝐴𝐵 =…(A/m) 𝐵𝑂 = 𝜇. 𝜇0. 𝐻𝑂 A a D
❖ Kết luận: vectơ cường độ từ trường 𝐻𝑂 tại tâm hình vuông có phương vuông góc với mp giấy
(mp chứa khung dây), có chiều hướng từ ngoài vào trong và có độ lớn 𝐻𝑂 =…(A/m) ▪ 𝑰 𝝅 𝟑𝝅
Cách khác: 𝑯𝑨𝑩 = . (𝒄𝒐𝒔𝜽 ; 𝜽 𝟒𝝅.𝑹 𝟏 − 𝒄𝒐𝒔𝜽𝟐) với 𝜽𝟏 = 𝟒 𝟐 = 𝟒 §3. Từ thông Điện 𝑁.𝑚2 thông Φ𝒆[ ] 𝐶 Từ thông Φ𝒎[Wb] 𝒏 𝒅𝑺 𝒅𝑺 𝑑𝑆 𝑫 𝑩 dS
𝑛 ≡ 𝑑𝑆: vectơ pháp tuyến của vi phân diện tích dS
𝑛 ≡ 𝑑𝑆: vectơ pháp tuyến của vi phân diện tích dS
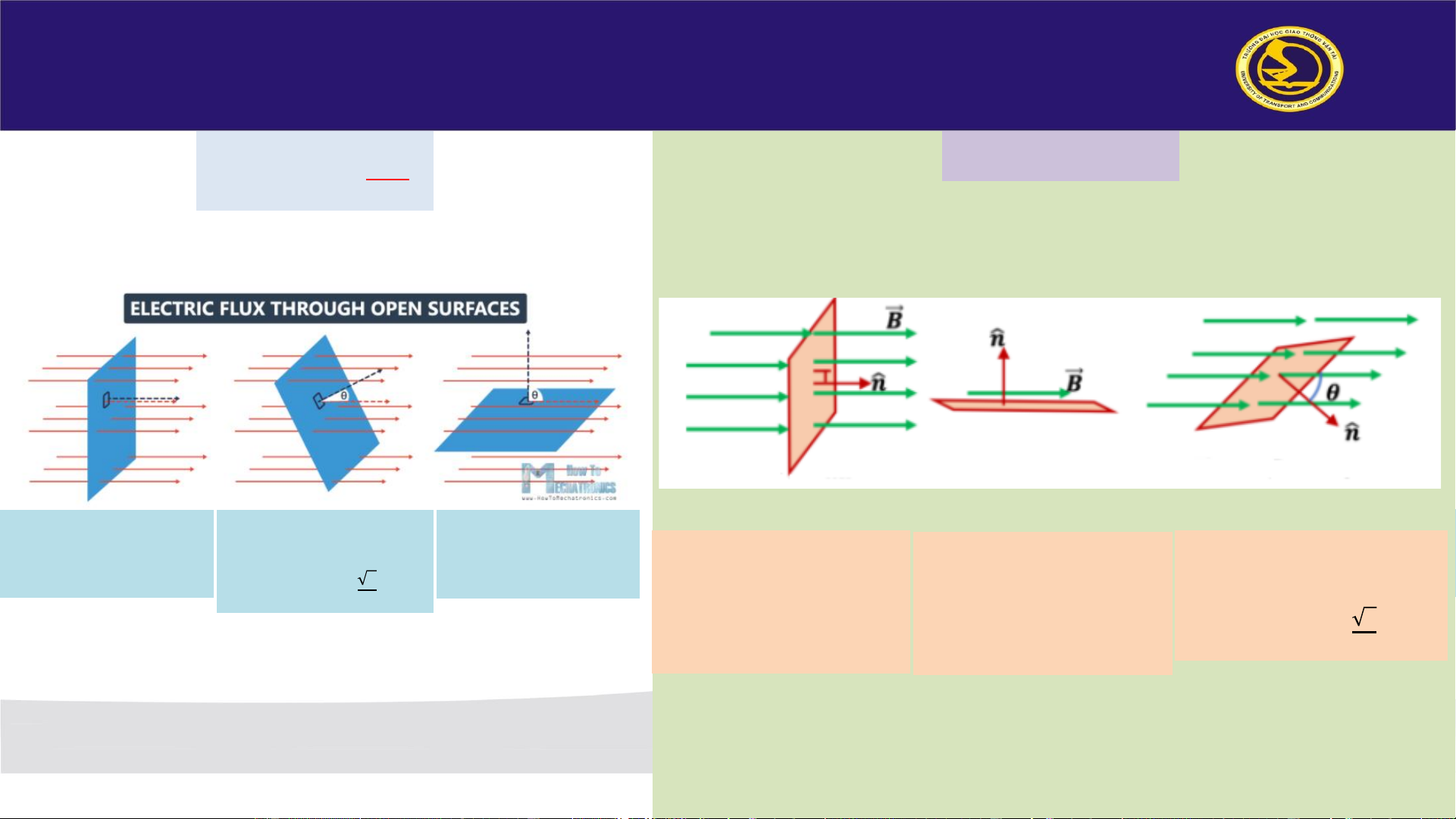
Điện thông gửi qua diện tích dS bất kỳ:
Từ thông gửi qua diện tích dS bất kỳ: 𝑑Φ 𝑑Φ
𝑒 = 𝐷. 𝑑𝑆 = 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑚 = 𝐵. 𝑑𝑆 = 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃
Điện thông gửi qua toàn bộ diện tích mặt (S):
Từ thông gửi qua toàn bộ diện tích mặt (S): Φ Φ
𝐵. 𝑑𝑆 = න 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑒 = න 𝐷. 𝑑𝑆 = න 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝜃 𝑚 = න (𝑆) (𝑆) (𝑆) (𝑆)
➢ Điện thông Φ𝒆 gửi qua 1 diện tích (S) bất kỳ được xác
➢ Từ thông Φ𝒎 gửi qua 1 diện tích (S) bất kỳ được xác định bằng tổng
định bằng tổng đại số các đường sức điện trường gửi
đại số các đường sức từ trường gửi qua diện tích (S) đó Chu Tiến quaDũ dng iện tích (S) đó §3. Từ thông Từ thông Φ Điện 𝑁.𝑚2 𝒎[Wb] thông Φ𝒆[ ] 𝐶
𝑑Φ𝑒 = 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑑Φ𝑒 = 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑑Φ𝑒 = 𝐷. 𝑑𝑆. 𝑐𝑜𝑠𝜃
= 𝐷. 𝑑𝑆. 𝑐𝑜𝑠00
= 𝐷. 𝑑𝑆. 𝑐𝑜𝑠300
= 𝐷. 𝑑𝑆. 𝑐𝑜𝑠900
𝑑Φ𝑚 = 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑑Φ𝑚 = 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃
𝑑Φ𝑚 = 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃 = 𝐷. 𝑑𝑆 3 = 𝐷. 𝑑𝑆. = 0
= 𝐵. 𝑑𝑆. 𝑐𝑜𝑠00
= 𝐵. 𝑑𝑆. 𝑐𝑜𝑠900
= 𝐵. 𝑑𝑆. 𝑐𝑜𝑠300 2 = 𝐵. 𝑑𝑆 = 0 3 = 𝐵. 𝑑𝑆. Max flux Zero flux 2 Chu Tiến Dũng §3. Từ thông
❖ Từ thông 𝜱𝒎[𝐖𝐛]
➢ Khái niệm: Từ thông Φ𝒎 gửi qua 1 diện tích (S) bất kỳ được
xác định bằng tổng đại số các đường sức từ trường gửi qua diện tích (S) đó
➢ Biểu thức: -
Từ thông gửi qua diện tích (dS): 𝑑Φ𝑚 = 𝐵. 𝑑𝑆 = 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃
Khi đó, từ thông gửi qua cả diện tích (S):
Φ𝑚 = ׬ 𝐵. 𝑑𝑆 = ׬ 𝐵. 𝑑𝑆. 𝑐𝑜𝑠𝜃 (𝑆) (𝑆)
➢ Trường hợp (S) nằm trong từ trường đều (𝐵 = 𝑐𝑜𝑛𝑠𝑡) và
với: B - vectơ cảm ứng từ (đều) tại một điểm bất kỳ trên diên tích (S) [T]
vuông góc với các đường cảm ứng từ (𝜃 = 00), thì :
S – diện tích mặt phẳng (S) [m2]
Φ𝑚 = ׬ 𝐵. 𝑑𝑆 = ׬ 𝐵. 𝑑𝑆 = 𝐵. 𝑆
- Đơn vị đo: [𝐖𝐛] (𝑆) (𝑆) Chu Tiến Dũng
§4: Định lý về dòng điện toàn phần
• Lưu số của vectơ cường độ từ trường • Định lý suất từ động: Lưu số của vectơ cường độ từ trường dọc theo một đường
dọc theo đường cong kín (C) là đại
cong kín (C) bất kỳ (một vòng) bằng tổng đại số cường độ của các dòng điện I
lượng về giá trị bằng tích phân của
xuyên qua diện tích giới hạn bởi đường cong (C).
𝐻. 𝑑𝑙 dọc theo toàn bộ đường cong đó: 𝑛
ර 𝐻. 𝑑𝑙 = ෍ 𝐼𝑖 (𝐶)
ර 𝐻. 𝑑𝑙 = ර 𝐻. 𝑑𝑙. cos(𝐻, 𝑑𝑙) 𝑖=1 (𝐶) (𝐶) Lưu ý:
- I sẽ mang dấu dương (I > 0) nếu dòng điện thứ i nhận chiều dịch chuyển trên đường cong (C) I i
làm chiều quay thuận xung quanh nó.
- I sẽ mang dấu âm (I < 0) nếu dòng điện thứ i nhận chiều dịch chuyển trên đường cong (C) i 𝐻
làm chiều quay nghịch xung quanh nó. O 𝑑𝜑 𝐼 𝐼 (C) 𝑑𝑙 1 2 (𝑪) 𝐼3 𝐼 Chu Tiến Dũng 4
§4: Định lý về dòng điện toàn phần 𝑛
ර 𝐻. 𝑑𝑙 = ෍ 𝐼𝑖 (𝐶) 𝑖=1
• Định lý suất từ động: Lưu số của vectơ
cường độ từ trường dọc theo một đường cong
kín (C) bất kỳ (một vòng) bằng tổng đại số
cường độ của các dòng điện I xuyên qua diện
tích giới hạn bởi đường cong (C). Chu Tiến Dũng
§4: Định lý về dòng điện toàn phần
• Cuộn dây điện hình xuyến: gồm N vòng dây quấn, trong đó dòng I chạy qua, với:
➢ b = R – bán kính trong của hình xuyến 1
➢ c = R – bán kính ngoài của hình xuyến 2 ➢ (C )
r – bán kính của đường cong kín (C ) (đi qua 1 điểm bất kỳ trong lòng cuộn dây hình 1 1 xuyến) => R < r < R 1 2
• Áp dụng định lý suất từ động: ׯ 𝐻. 𝑑𝑙 = σ𝑛 𝐼 (𝐶 𝑖=1 𝑖 = N.I (1) 1) - Ta có: ׯ 𝐻. 𝑑𝑙 = ׯ 𝐻. 𝑑𝑙 = 𝐻. ׯ 𝑑𝑙 = 𝐻. 2𝜋𝑟 (2) (𝐶1) (𝐶1) (𝐶1) -
Từ (1) và (2) suy ra: 𝐻. 2𝜋𝑟 = N.I (C ) 2 • Vậy: • 𝑁.𝐼 𝐻 = 2𝜋.𝑟
❖ Kết luận: Từ trường chỉ tồn tại trong lòng ống dây hình xuyến, có cường 𝑵.𝑰
Mà 𝐵 = 𝜇. 𝜇𝑜. 𝐻, nên 𝑩 = 𝝁. 𝝁𝒐.
độ giảm dần từ trong ra ngoài 𝟐𝝅.𝒓 Chu Tiến Dũng