Áp dụng casio trong Phương pháp tính để kiểm tra | Đại học Bách Khoa Hà Nội

1 Mục lục
Mục lục ...................................................................................................................................................... 1
1. Cách thiết lập số chữ số thập phân sau dấu phảy ..................................................................................... 2
2. Cách thiết lập đơn vị đo cho hàm lượng giác ............................................................................................ 2
3. Bài toán khoảng cách ly nghiệm ................................................................................................................ 2
4. Phương pháp lặp giải gần đúng phương trình f ( )
x 0. .................................................................... 3
Phương pháp chia đôi: .............................................................................................................................. 3
Phương pháp lặp đơn ............................................................................................................................... 5
Phương pháp dây cung ............................................................................................................................. 6
Phương pháp tiếp tuyến ........................................................................................................................... 7
5. Phương pháp lặp giải hệ phương trình AX  B...................................................................................... 8
Tính chuẩn của Vector: .............................................................................................................................. 8
6. Sơ đồ Hoocne tính giá trị đa thức .................................................. Ошибка! Закладка не определена.
7. Bình phương tối thiểu ............................................................................................................................. 14
8. Tính gần đúng tích phân .......................................................................................................................... 15
9. Giải gần đúng phương trình vi phân ....................................................................................................... 16
Công thức Euler hiện ............................................................................................................................... 16
Công thức Euler cải tiến .......................................................................................................................... 16
Công thức RK3, RK4 ................................................................................................................................. 16
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 2
1. Cách thiết lập số chữ số thập phân sau dấu phảy
Muốn hiển thị trên màn hình số thập phân đến 7 chữ số sau dấu phảy ta bấm như sau: qw317
Nhìn xem đáp án để bao nhiêu chữ số sau dấu phảy ta sẽ thiết lập bấy nhiêu chữ số.
2. Cách thiết lập đơn vị đo cho hàm lượng giác Đơn vị đo là độ: qw21 Đơn vị đo là radian: qw22
3. Bài toán khoảng cách ly nghiệm
Ví dụ: Cho phương trình 3 x 8
 x50. Khoảng nào sau đây là khoảng cách ly
nghiệm của phương trình đã cho? A. 1,5;  1 B.  1  ; 0  ,5 C. 1;1,  5 D.  0  ,5; 0 E. 1; 2
Nhận xét: Hàm số đã cho liên tục nên giá trị sẽ thay đổi liên tục từ dấu âm qua dấu
dương (trong các khoảng phân ly không có điểm gián đoạn).
Sử dụng Tabble của CASIO: Phím nhập Ý nghĩa qwRR11 Chỉ hiện 1 hàm f ( ) x khi nhập bảng w8
Chuyển sang chế độ bảng biểu [qdp8[p5= Nhập hàm số đã cho z1.5=2=0.2==
Nhập cận dưới (-1.5), cận trên
(2) và bước nhảy (0.2) cho bảng
Chú ý: Cận dưới là giá trị nhỏ nhất trong các
cận dưới của khoảng đã cho, cận trên là giá
trị lớn nhất trong các cận trên đã cho. Nếu
khoảng quá lớn ta chia nhỏ để kiểm tra hoặc
chọn bước lớn hơn để không vượt quá bộ nhớ.
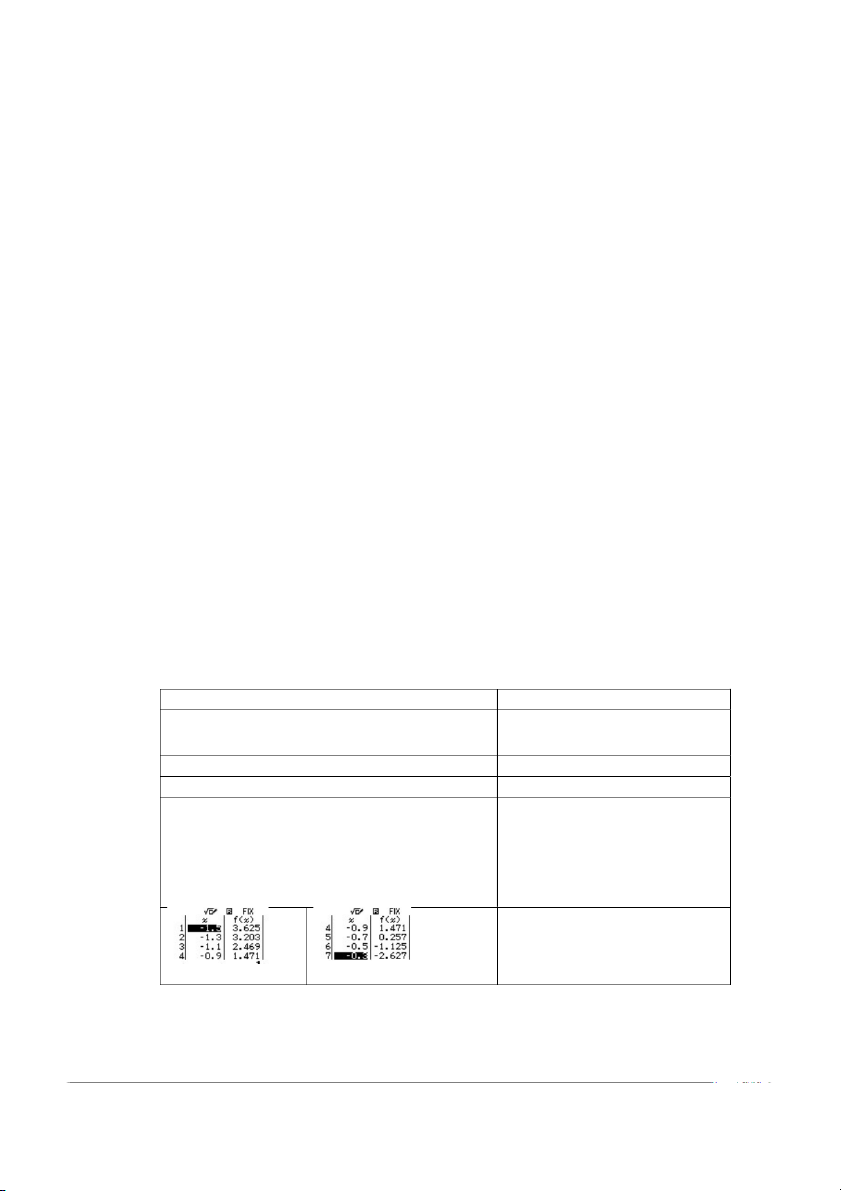
Từ bảng giá trị nhận thấy: * f ( )
x dương trên 1,5;  1 * f ( ) x đổi dấu trên  1  ; 0  ,5
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 3 * f ( ) x âm trên trên 1;1,  5 * f ( ) x âm trên 0,5; 0 * f ( ) x âm trên 1; 2 Chọn B
Chú ý: Có thể kiểm tra lại đáp án sử dụng
điề u kiện đủ của k.c.l Sử dụng CALC của CASIO: Phím nhập Ý nghĩa [qdp8[p5 Nhập hàm số đã cho rz1.5== 29 f ( 1.5)   8 rz1== f ( 1  ) 2
Nhận thấy giá trị tại 2 đầu mút ( 1  .5; 1
 ) đều dương nên loại đáp án này. Các đáp
án còn lại làm tương tự để tìm ra đoạn nào có giá trị tại 2 đầu mút trái dấu. Kiểm
tra bằng TABLE để đảm bảo không có 2 nghiệm nằm trong khoảng này (có thể có đáp án nhiễu).
4. Phương pháp lặp giải gần đúng phương trình f ( ) x 0. Phương pháp chia đôi: Ví dụ: Cho phương trình 3 x 8
 x50với một khoảng phân ly nghiệm là 1;0,  5 .
Nghiệm gần đúng của phương trình đã cho tìm được bằng PPCĐ sau 3 lần lặp gần
với kết quả nào nhất? A. -0.65562347 B. -0.68750000 C. -0.65323755 D. -0.66112031
Sử dụng SOLVE của CASIO ( sử dụng được cho mọi phương trình nhưng dễ bị
chọn nhầm do đáp án nhiễu) Phím bấm Ý nghĩa [qdp8[p5 Nhập hàm số
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 4 qrz1==
Tìm nghiệm của phương trình gần giá trị khởi đầu x  1.
Nếu chọn D là bị sai, chỉ sử dụng khi các đáp án rất xa nhau.
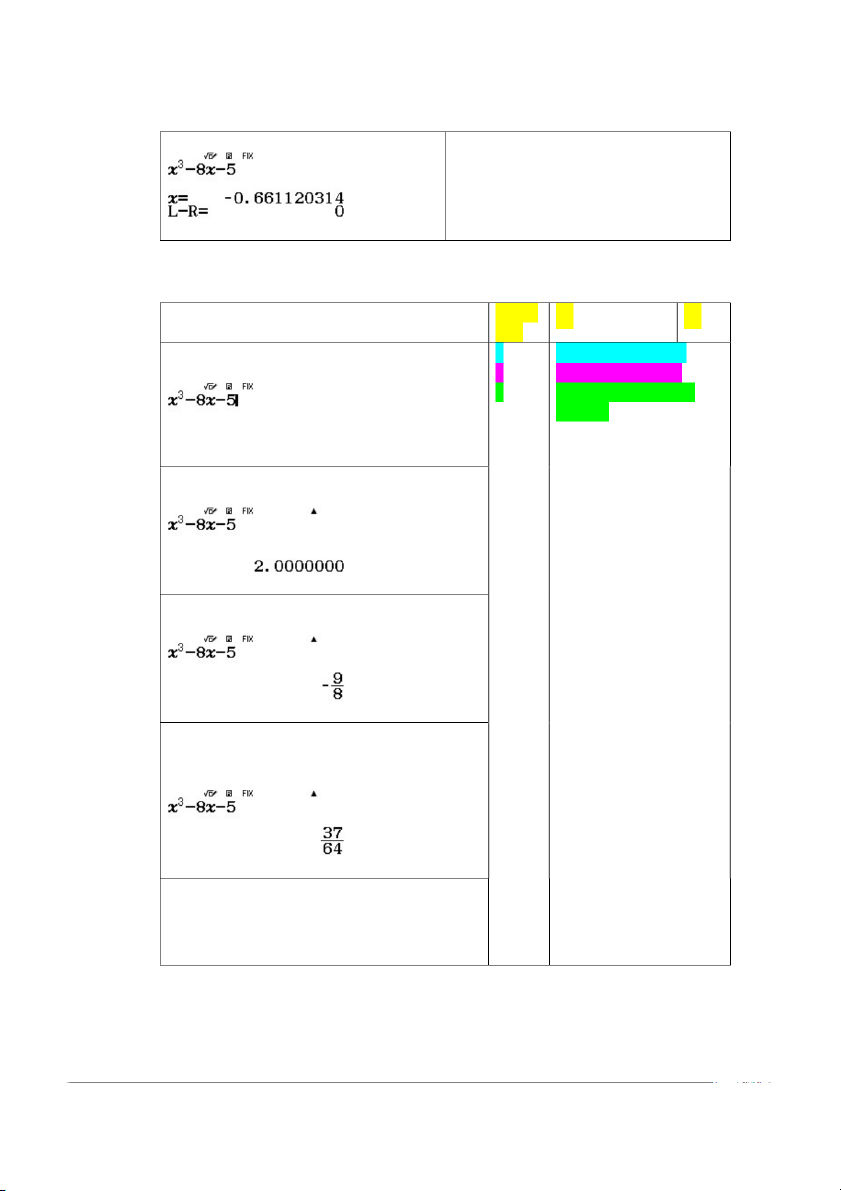
Sử dụng CALC của CASIO (dùng với số lần chia bất kỳ): Phím bấm #(chia a b n n đôi) Nhập hàm số: 1 -1 (+) -0.5 (-) [qdp8[p5 2 -0.75 (+) -0.5 (-) 3 -0.75 (+) -0.625(-) -0.6875
Thay x  1 vào hàm số: rz1==
Thay x  0.5 vào hàm số: rz0.5== Thay x ( 1   0  .5)/ 2 vào hàm số: r(z1+z0.5)P2 ==
ấn = để xem lại trung điểm Thay x ( 0  .75 0  .5) / 2 vào hàm số: (z0.75+z0.5) P2= =
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 5
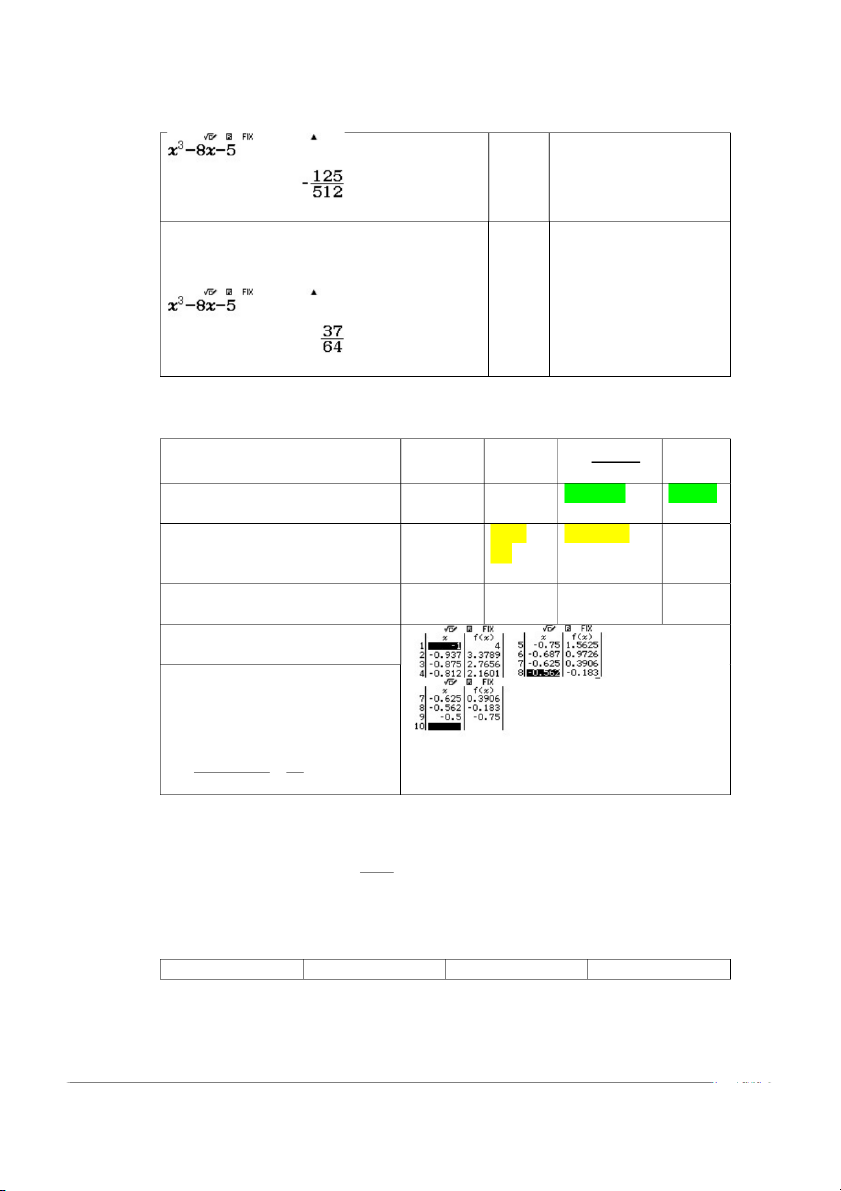
ấn = để xem lại trung điểm Thay x ( 0  .75 0  .625) / 2 vào hàm số: r(z1+z0.5)P2 ==
ấn = để xem lại trung điểm
Sử dụng Tabble của CASIO (dùng khi số lần chia ít hơn 4): Phím bấm #(chia a a  b b n n n đôi) c  n 2 Chọn chế độ bảng: 1 -1 (+) -0.75 (+) -0.5 (-) w8 Nhập hàm số: 2 -0.75 -0.625 (-) -0.5 (-) [qdp8[p5= (+) Nhập cận dưới: 3 -0.75 -0.6875 (+) -0.625 z1= (+) (-) Nhập cận trên: z0.5= Nhập bước: 0.0625
Ghi chú: lặp 3 lần nên ta chia đôi đoạn ( 1  ; 0  .5), tức là 0.5 (1) 1 h    0.0625 3 2 16 Phương pháp lặp đơn 3 x 5
Ví dụ: Cho phương trình x 
có khoảng phân ly nghiệm thực nghiệm thực là 8
( 1; 0 .5). Biết phương pháp lặp đơn hội tụ cho phương trình đã cho. Nghiệm gần
đúng sau 10 lần lặp với x  1  0
gần với giá trị nào dưới đây? A. 0
 .661120314 B.  0.661120323 C. 0.681320387 D. 0.361425314
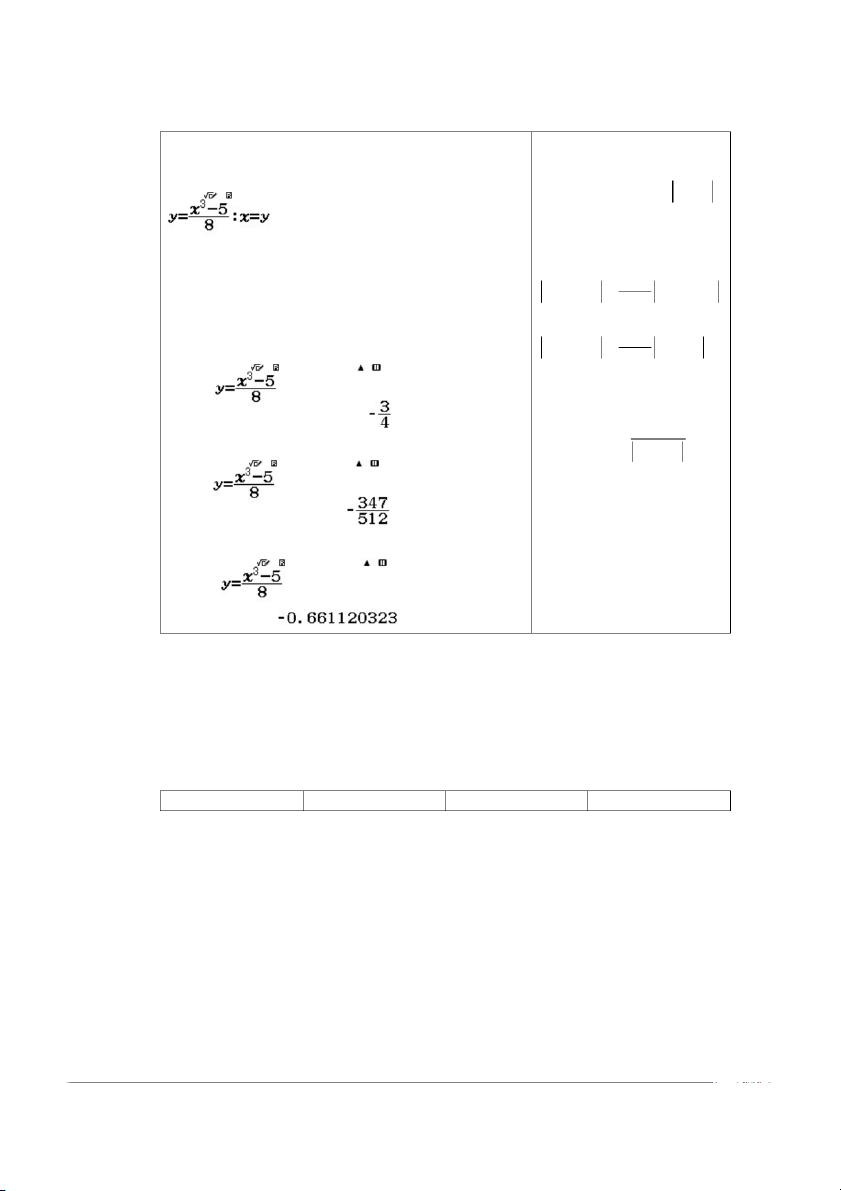
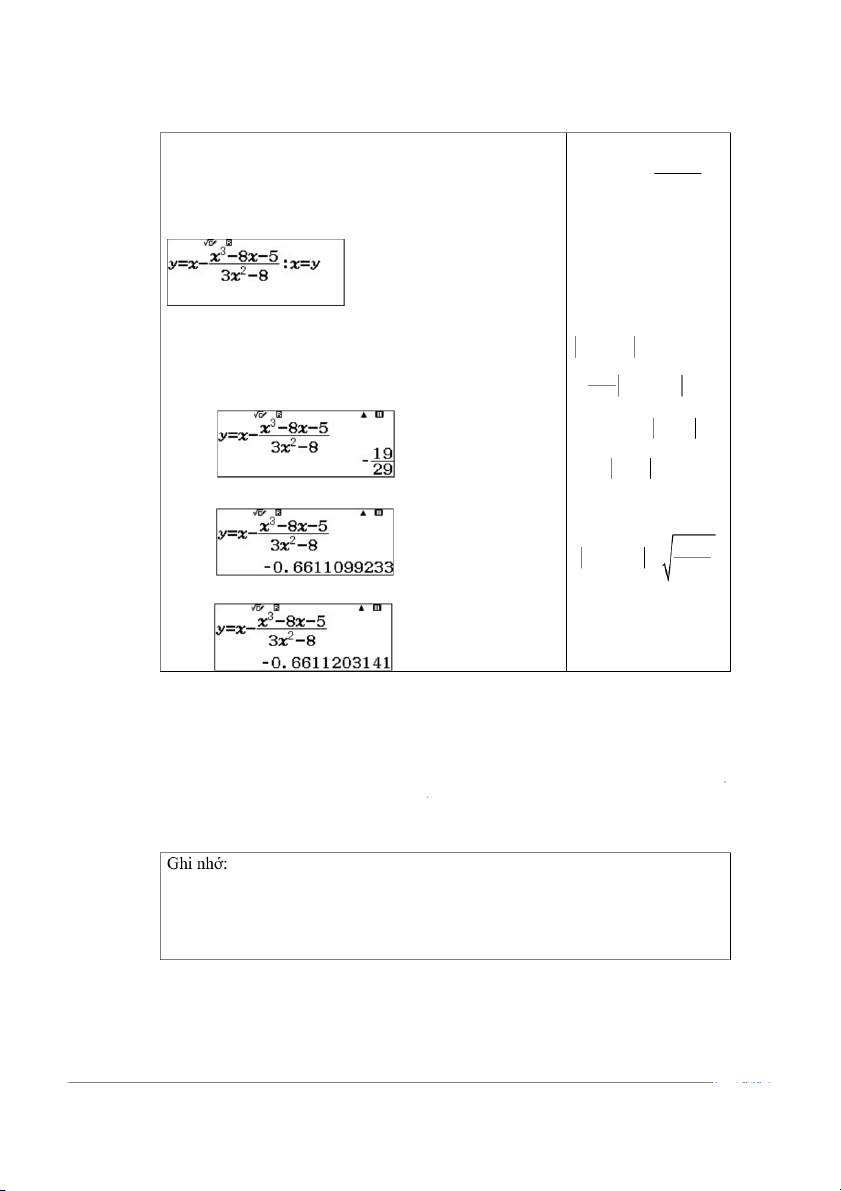
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 6 Nhập biểu thức lặp: Công thức lặp: Q)Qra[qdp5 x 1 (  x ) n  n R8$QyQ(QrQ)
Hệ số co: q  max(  '( ) x ) x [  a,b]
Điều kiện hội tụ: q 1. Đánh giá sai số: q
Nhập xấp xỉ ban đầu x  1  x    x  x 0 n1 n1 1 n  q rz1 Lặp = n q x     x  x n 1 1 0 1 q x1:
Số lần lặp cần thiết đề đạt sai số  cho trước:   (1 q)  n  log  . q     1 x x0  x : 2 … x : 10 Phương pháp dây cung
Ví dụ: Cho phương trình 3
x  8x  5  0 có khoảng phân ly nghiệm thực nghiệm
thực là (1; 0.5). Biết phương pháp dây cung hội tụ cho phương trình đã cho.
Nghiệm gần đúng sau 10 lần lặp với dây cung ở lần lặp đầu tiên là AB với ( A 1  ;2) và ( B 0  .5, 1
 .125) gần với giá trị nào dưới đây? A. 0  .6611203146 B. 0.6611203141 C. 0.6813203878 D. 0  .3614253148
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 7 Xác định d  0  .5; x  1  . f  Công thức lặp: 0 Tính ( 0.5): [qdp8[p5rz0.5== (d  x ) n x n 1  x  n  ( f (d )  f ( nx Điều kiện hội tụ: +) f '( ) x ; f '( ) x giữ Nhập biểu thức lặp: nguyên dấu trên [ a; b]. Q)Qr[pa(z0.5p[ +) chọn x ; d 0 sao cho )([qdp8[p5)Rza f (d) f '( ) x 0; f (x ) f( 9R8$p[qd+8[+5$Q 0 y[QrQ) Đánh giá sai số:   xn1 M1  1 m nx1 nx 1 m M  f '( ) x  m 0 1 1 x  [a;b]
Nhập xấp xỉ ban đầu x  1  0 rz1
Điều kiện dừng để đạt sai số  cho trước: Lặp = m 1 x n1  x  . n x M1  1 m 1: x : 2 … x : 10 Phương pháp tiếp tuyến
Ví dụ: Cho phương trình 3
x  8 x  5  0 có khoảng phân ly nghiệm thực nghiệm
thực là (1; 0.5). Biết phương pháp tiếp tuyến hội tụ cho phương trình đã cho.
Nghiệm gần đúng sau 4 lần lặp với phương pháp tiếp tuyến gần với giá trị nào dưới đây? A. 0  .6611203146 B. 0.6611203141 C. 0.6813203878 D. 0  .3614253148
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 8 Xác định x  0  .5. Công thức lặp: 0 Nhập biểu thức lặp: f ( x ) n n x 1  n x   Q)Qr[pa[qdp8[p f '( x ) n 5R3[dp8$Qy[QrQ Điều kiện hội tụ: +) ) f '( ) x ; f '( ) x giữ nguyên dấu trên [a ;b ]. +) chọn x sao 0 cho f ( x ) f (  ) x  0. 0 Đánh giá sai số:
Nhập xấp xỉ ban đầu x  0  .5 0  rz0.5 n x 1  Lặp = M2 2  x  x n 1 ;  n 2 1 m x 1: M2  max f '(x) ; [ , a ] b min f ('x)   1 m ; 0 [a,b ]
Điều kiện dừng để đạt x : sai số  cho trước: 2 2 1 m x x  . n 1   n M 2 … x : 5
5. Phương pháp lặp giải hệ phương trình AX B. Tính chuẩn của Vector: -40 3 4 4    4 30 4 2 A     1 2 -37 4     4 3 4 48 
 Để chuyển các phần tử của ma trận A thành trị tuyệt đối ta sử dụng phím ABS (q()  T
Để lấy riêng cột 1 của ma trận A ta tính AB với vector B[1,0,0,0] .(di
chuyển số 1 giúp ta lấy được các cột 2, 3, 4).
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 9
 Để lấy riêng dòng 1 của ma trận A ta tính BA với vector B  [1,0,0,0]. [1,0,0,0]T B
.(di chuyển số 1 giúp ta lấy được các dòng 2, 3, 4).
 Để cộng tổng các phần tử của vector cột 40, 4,1,1 T A   ta tính BA với 1   B(1,1,1,1).
 Để cộng tổng trị tuyệt đối các phần tử của vector cột 40, 4,1,1 T A   ta 1   tính BA với B (  1  ,1,1,1).
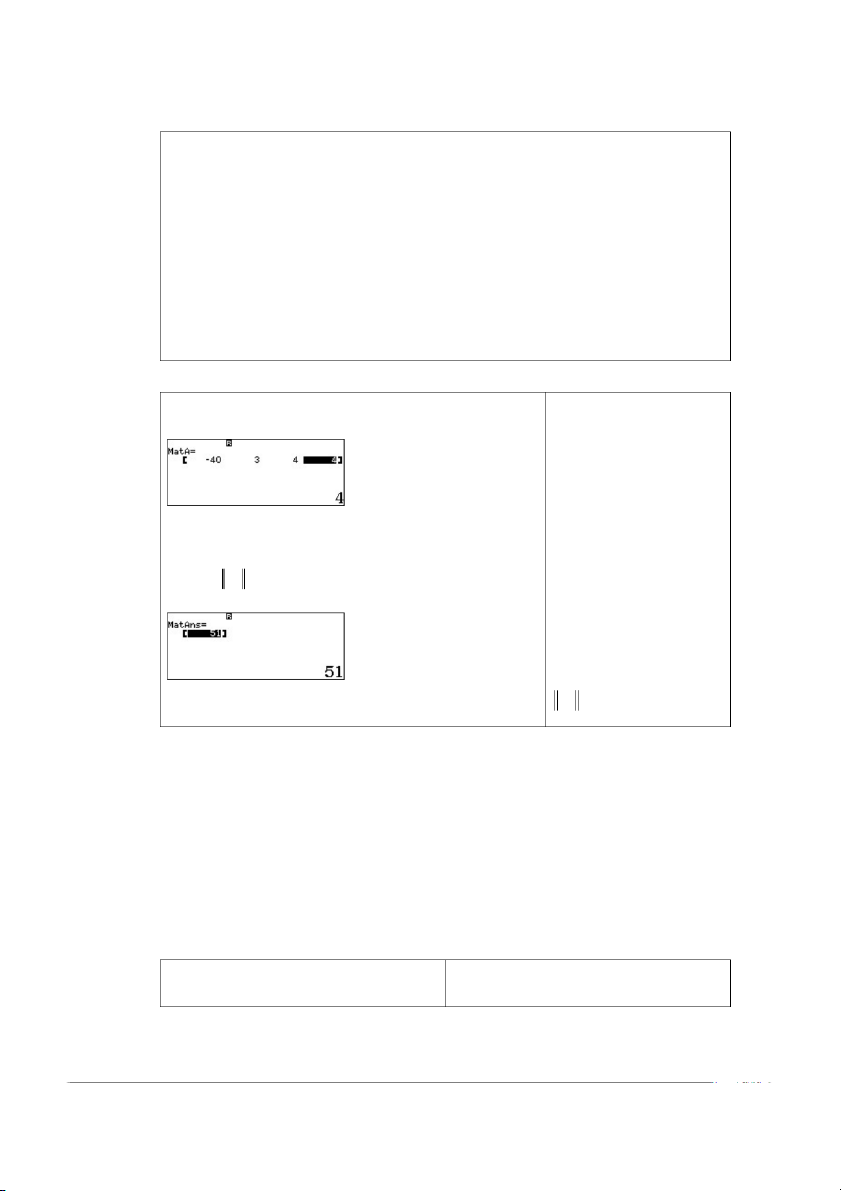
 Để cộng tổng các phần tử của vector dòng A  4  0,3,4,4 ta tính AB với 1   1 (1,1,1,1)T B  . Ví dụ: Nhập vector A : A  -40 3 4 4 1   1 w4114z40=3=4=4= Tạo vector B : T1241 z 1=1=1=1= T
B  1,1,1,1 (-1 xuất Ta tính A
hiện ở vị trí phần tử của 1  T3OT4= A mang dấu âm). 1
Ghi chú: Nếu A là vector cột ta dùng chuyển vị đưa 1 A 51 1  về vector hàng. Phương pháp lặp đơn:
Cho hệ phương trình X  BX  d trong đó
-0.08095 -0.07549 -0.02414   0.1109
B -0.09443 0.03703 0.03192       ; d  -0.0864  
 0.04384 -0.07115 0.03129      0.0077  
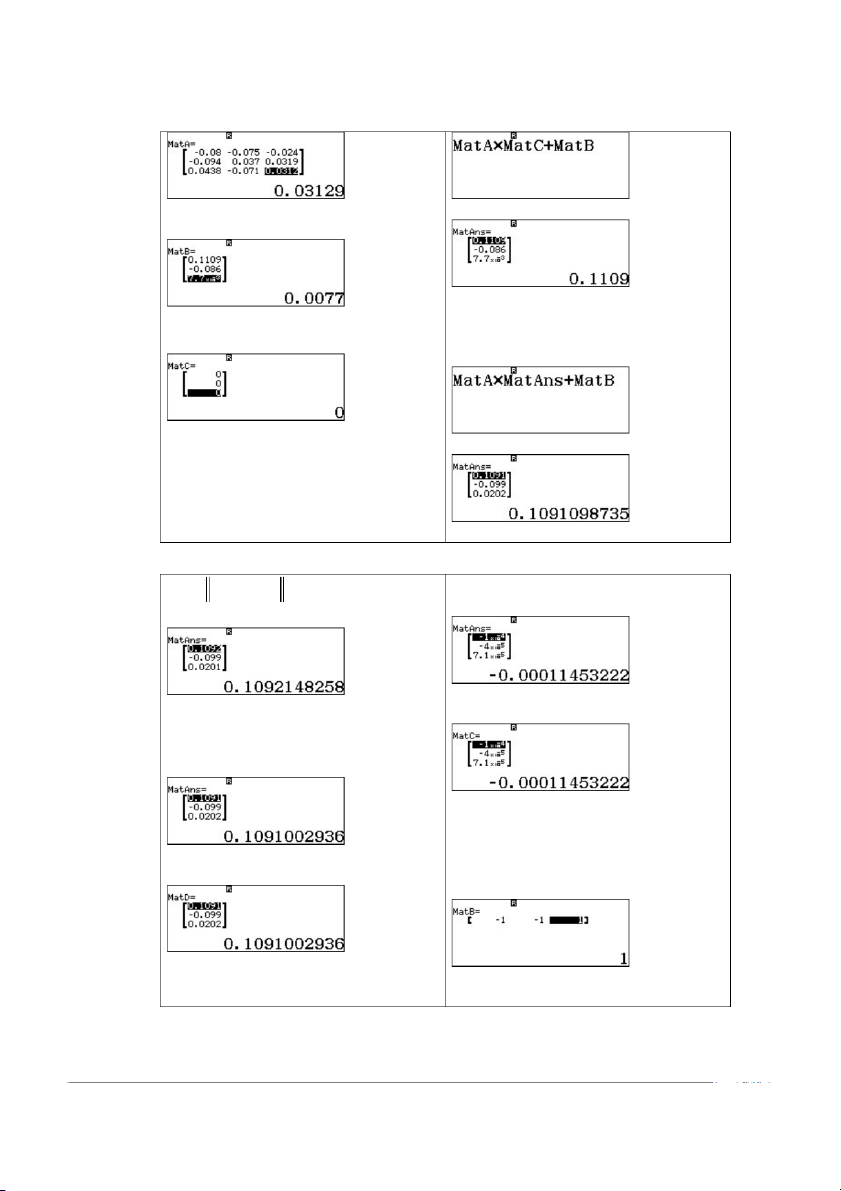
Sử dụng phương pháp lặp đơn giải hệ trên với 4 lần lặp với xấp xỉ ban đầu 0 (0,0,0)T X  . 1. Nhập ma trận B :
3. Nhập công thức lặp X  BX d n 1  n : w4133 T3OT5+T4
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 10 2. Nhập ma trận d : = T1231 Nhập vector 0
4. Sửa công thức thay MatC bằng X : T1331 MatAns: C!!!oTR1 5. Lặp {=C!=C!} Đánh giá sai số Tính n1 n X  X Tính hiệu 4 3 X  X :  CT6pT5=
Ở bước lặp thứ 3 ta lưu vector 3 X Lưu vào ma trận MatC Lưu vào ma trận MatC Ju Ju Tính tiếp vector 4 X C!=
Tính chuẩn hàng của vector 4 3 X  X
Tạo vector hàng MatB  [1,1,1] (chỗ 4 3 Lưu vào ma trận MatD
nào của vector X  X có dấu – thì để -1) Jj T1213z1 =z1=1= Nhân MatBxMatC
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 11 Ta tìm được 4 3 X  X  0.00023388637 1
Phương pháp lặp Gauss-Seidel
Cho hệ phương trình X   X   trong đó -0.08 -0.07 -0.02   0.11       -0.09 0.03 0.03  ;   -0.08    0.04 -0.07 0.03      0.01  
Sử dụng phương pháp lặp Gauss-Seidel giải hệ trên với 4 lần lặp với xấp xỉ ban đầu 0 (1,2,3)T X  .
Công thức lặp Gauss-Seidel
Nhập phương trình thứ 1
Hệ đã cho có thể viết lại dưới dạng QzQrz.08Qz lặp
+z.07Qx+z.0 ((A  x ;B  x ;C  x ) ) 1 2 3 2Qu+.11Qy A  -.08A + -.07B+-.02C+.11:
Nhập phương trình thứ 2 B=-.09A+.03B+.03C+-.08:
QxQrz.09Qz C=.04A+-.07B+.03C+.01 +.03Qx+.03Q u+z.08Qy
Nhập phương trình thứ 3 QuQr.04Qz+ z.07Qx+.03Q u+.01 Nhập dữ liệu R 1==
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 12 Ta nhận được 1 (0.03, 0.0827,0.016989)T X   Lặp {=} Lặp {=}
…………………………………………… Ta nhận được  0.1074024638    5 X  0.09177878719    0.02136149067   
6. Sơ đồ Hoocne tính giá trị đa thức Cho đa thức n n 1
P(x)  a x  a x      ... a x a n n 1 1 0
Ta biến đổi P(x)  (...(((a x  a      x a  x a  x a x a n n ) n ) n ) .... ) 1 2 3 1 0
Quá trình bấm máy CASIO theo sơ đồ Hoocne tính lần lượt các ngoặc từ trong ra ngoài.
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 13 Ví dụ: Cho đa thức 8 7 6 5 4 3 2
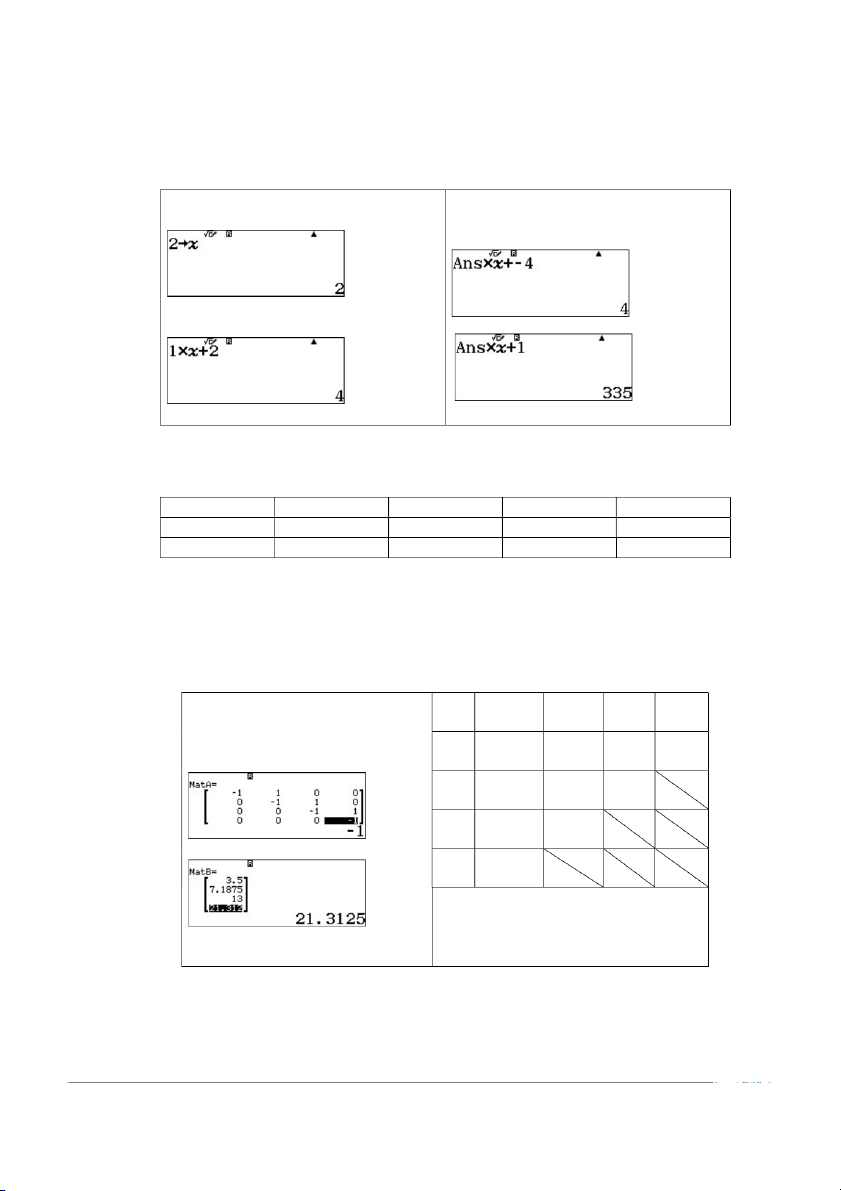
P(x)  x  2 x  4 x  x  x 12x  9 x  x 1. Tính P(2) sử dụng sơ đồ Hoocne Lưu 2 vào biến x
Tính ngoặc thứ 2,3,4… (từ trong ra 2J[ ngoài) Lặp {O[+z4=}
Tính ngoặc thứ 1 (từ trong ra ngoài) 1O[+2= ….
Vậy ta tìm được P(x)  335
8. Tính sai phân mốc cách đều
Ví dụ: Cho bảng giá trị Stt 0 1 2 3 x 1 1.5 2 2.5 y 3.5 7.1875 13 21.3125
Tính sai phân cấp 3 tại mốc x 1. 0 Công thức   y  y 0 y 1 0 k k    yr yr k 
Chuyển sang chế độ ma trận x y SP1 SP2 SP3 w4 Nhập vào ma trận 1 3.5 3.6875 2.125 0.375 w4144 1.5 7.1875 5.8125 2.5 2 13 8.3125 Nhập vào vector 2.5 21.3125
Nhận xét: Cột liền sau ít hơn cột liền trước 1 phần tử. Nhân MatAxMatB
Đối với bảng lớn hơn ta cần sử dụng cách bên nhiều lần
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 14
Nhân với ma trận MatA thức chất lấy
phần tử liền sau trừ đi phần tử liền trước của vector Nhân MatAxMatAns C!oTR1= Nhân MatAxMatAns C!=
7. Bình phương tối thiểu
Ví dụ: Cho bảng giá trị Stt 0 1 2 3 x 1 1.5 2 2.5 y 3.5 7.1875 13 21.3125
Tìm hàm thức nghiệm dạng 2
y  a bx cx sinh ra từ bảng giá trị trên. Ta sử dụng Statistics
Nhập bảng giá trị trên vào (có thể tính w6 toán với bảng dài) Chọn 3 Chọn T3
Ngoài ra có thể tính các tổng CT3
Ghi chú: Còn nhiều chức năng nữa ở MODE này,
các bạn tìm hiểu thêm về các dạng hàm thực nghiệm
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 15 T1 Have fun!
8. Tính gần đúng tích phân 2
Ví dụ:Tính gần đúng tích phân 2 x e dx 
sử dụng công thức hình thang? Simpson? 1 với bước h  0.1. Công thức hình thang Công thức Simpson Giải
Nhập vào máy tính CASIO biểu thức Lặp CRr1.1==m hàm số:
(Phần màu đỏ tùy chỉnh mốc) qh[d …….. Dùng r1==P2=m Dùng r2==P2=m Nhân M với h=0.1 QmO0.1=
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 16
Ghi chu: Với các hàm số có đạo hàm lớn trên khoảng tính tích phân thì sử dụng
y sẽ cho sai số lớn dẫn đến chọn nhầm đáp án nhiễu.
Hoàn toàn tương tư khi ta tính với công thức Simpson, chú ý nhân đúng hệ số
(tránh nhầm lẫn bằng cách viết các mốc chia ra giấy và đánh số, mốc lẻ nhân với 4
và mốc chắc nhân với 2, trừ 2 mốc đầu và cuối)
9. Giải gần đúng phương trình vi phân Công thức Euler hiện
Công thức Euler cải tiến Công thức RK3 Công thức RK4
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 17
Quy ước: A  y;x  x  Nhập vào máy tính CASIO
Nhập giá trị khởi đầu cho A và x QzQr Qz+ r1=0== 0.1O([ Qza2$)Qy Tính được y 1 1 Lặp {=} [Qr[+0.1 Tính được y  1.005 2 ……
Bấm CASIO cho công thức RK4
Quy ước: A  k ; B  k ;C  k ; D  k 1 2 3 4  Nhập vào máy tính CASIO Nhập x 0.1O[Q)P2 r .05= Nhập y 1+.5Qx= Lưu k  C 3 =Ju Nhập dữ liệu r0=1== Lưu k  A 1 Jz Nhập x r . 1= Nhập y 1+Qu= Lưu k  D Nhập x 4 r[+0.5O0.1= =Jj
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO 18 Nhập y Q)+0.5Qz= Lưu k  B 2 =Jx 1 Tính y  y  k  2k  2k k ) 1 0  1 2 3 4  6 C1+a1R6$ (Qz+2Qx +2Qu+Qj )=
SỬ DỤNG CASIO 580 VNX TRONG PHƯƠNG PHÁP TÍNH TAM DO