Chương VIII: quan hệ vuông góc trong không gian - Bài 1: hai đường thẳng vuông góc môn Toán 11

CHƯƠNG VIII: QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN
BÀI 1: HAI ĐƯỜNG THẲNG VUÔNG GÓC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
I. GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN
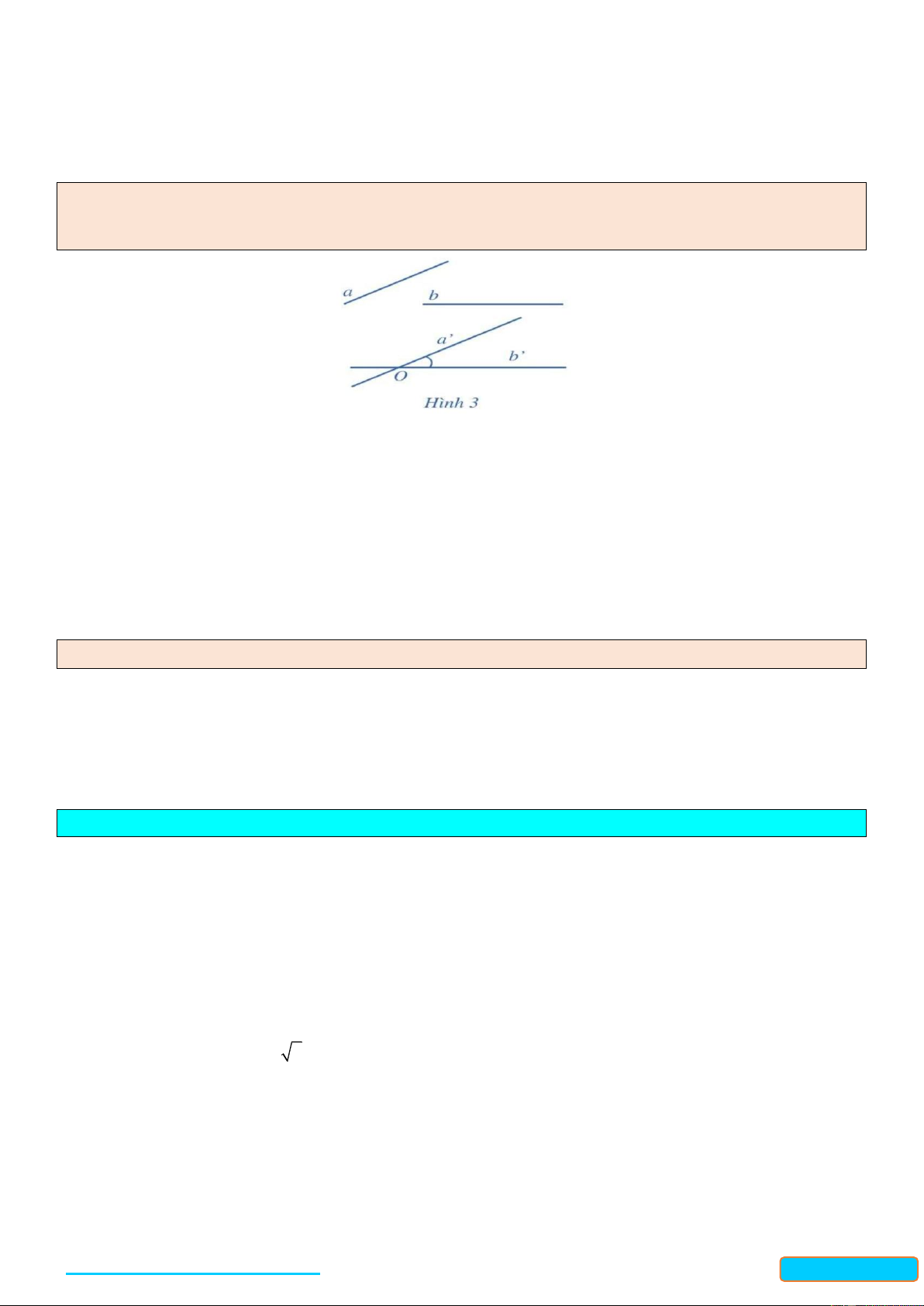
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a và b cùng đi qua điểm
O và lần lượt song song ( hoặc trùng) với a và b . Kí hiệu a,b hoặc a,b . Nhận xét: 
Góc giữa hai đường thẳng ,
a b không phụ thuộc vào vị trí điểm O (Hình 3). Thông thường, khi ta
tìm góc giữa hai đường thẳng ,
a b , ta chọn O thuộc a hoặc chọn O thuộc b . 
Góc giữa hai đường thẳng ,
a b bằng góc giữa hai đường thẳng ,
b a tức là a,b   , b a  . 
Góc giữa hai đường thẳng không vượt quá 90 . 
Nếu a//b thì a,c    ,
b c  với mọi đường thẳng c trong không gian.
II. HAI ĐƯỜNG THẲNG VUÔNG GÓC TRONG KHÔNG GIAN
Hai đường thẳng được gọi là vuông góc với nhau khi giữa chúng bằng 90 .
Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu a  b .
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Tính góc giữa hai đường thẳng 1. Phương pháp
 Lấy điểm O tùy ý ( ta có thể lấy điểm O thuộc một trong hai đường thẳng), qua đó vẽ các đường
thẳng lần lượt song song (hoặc trùng) với hai đường thẳng đã cho.
 Tính một góc trong các góc được tạo bởi giữa hai đường thẳng cắt nhau tại O.
 Nếu góc đó nhọn thì đó là góc cần tìm, nếu góc đó tù thì góc cần tính là góc bù với góc đã tính.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Cho biết
AB  CD  2a và MN  a 3 . Xác định góc tạo bởi hai đường thẳng AB và CD
Ví dụ 2. Cho hình lập phương ABC . D A B  C  D
  cạnh a . Gọi M, N, P lần lượt là trung điểm các cạnh A ,
B BC, C D
 . Xác định góc giữa hai đường thẳng MN và AP .
Ví dụ 3. Cho hình chóp S.ABC có tất cả các cạnh đều bằng a . Gọi I, J lần lượt là trung điểm của S ,
A BC . Tính số đo của góc hợp bởi IJ và SB . 1
Dạng 2. Chứng minh hai đường thẳng vuông góc trong không gian 1. Phương pháp
Cách 1: Dùng định nghĩa:     0 a b a, b  90 b/ /c
Cách 2: Dùng định lí:   a  b a  c
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Cho hình chóp .
S ABC có AB  AC , SAC  SAB . Chứng minh SA vuông góc với BC .
Ví dụ 2. Cho hình hộp ABC .
D MNPQ có sáu mặt đều là các hình vuông. Gọi E , F lần lượt là trung điểm
của AB và BC .
a) Chứng minh: EF  BD , EF  AM .
b) Tính góc giữa EF và AQ .
Ví dụ 3: Cho hình chop S.ABC co SA = SB = SC và ASB = BSC = CSA.
Chứng minh rang 𝑆𝐴 ⊥ 𝐵𝐶, 𝑆𝐵 ⊥ 𝐴𝐶 𝑣à 𝑆𝐶 𝐿 ⊥ 𝐴𝐵.
G. ĐỀ KIỂM TRA KẾT THÚC BÀI (LẤY ĐIỂM)
PHẦN 1 : TRẮC NGHIỆM 4 PHƯƠNG ÁN Câu 1:
Cho hình lập phương ABC . D A B  C  D
  . Góc giữa hai đường thẳng BA và CD bằng A. 60 . B. 90 . C. 45 . D. 30 . Câu 2:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng nhau. Gọi I và J lần lượt là trung điểm của SC
và BC . Số đo của góc  IJ ,CD bằng: A. 90 . B. 45 . C. 60 . D. 30 . Câu 3:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a . Gọi I và J lần lượt là trung điểm của SC và
BC . Góc giữa hai đường thẳng IJ và SC bằng A. 60 . B. 45 . C. 90 . D. 30 . Câu 4:
Cho hình lập phương ABC . D A B  C  D
 . Góc giữa hai đường thẳng A B
 và CD bằng A. 0 30 . B. 0 90 . C. 0 45 . D. 0 60 . Câu 5:
Cho hình lập phương ABC . D A B  C  D
  . Góc giữa hai đường thẳng A D  và B C   bằng     A. 90 . B. 60 . C. 30 . D. 45 . Câu 6:
Cho hình chóp tứ giác S.ABCD có tất cả các cạnh đều bằng a . Số đo góc giữa hai đường thẳng SA và CD bằng A. 30 . B. 90 . C. 60 . D. 45 . Câu 7: Cho lăng trụ ABCA B  C
  có tất cả các cạnh bằng nhau (tham khảo hình vẽ) 2
Góc giữa hai đường thẳng AB và C A   bằng A. 30 . B. 60 . C. 45 . D. 90 . Câu 8:
Cho hình lập phương ABC . D A B  C  D
  . Tính góc giữa hai đường thẳng CD và AC.' A. 45 . B. 60 . C. 90 . D. 30 . Câu 9:
Cho hình lập phương ABC . D A B  C  D
  có cạnh bằng a . Tính góc tạo bởi đường thẳng A B  và đường thẳng B C  . A. 60 . B. 45 . C. 30 . D. 90 .
Câu 10: Cho hình lập phương ABC . D A B  C  D
  . Góc giữa hai đường thẳng BA và CD bằng A. 90 . B. 45 . C. 30 . D. 60 .
Câu 11: Cho tứ diện ABCD với đáy BCD là tam giác vuông cân tại C . Các điểm M , N, ,
P Q lần lượt là trung điểm của A ,
B AC , BC,CD . Góc giữa MN và PQ bằng A. 0 45 . B. 0 60 . C. 0 30 . D. 0 0 .
Câu 12: Trong không gian cho hai tam giác đều ABC và ABC
¢ có chung cạnh AB và nằm trong hai mặt phẳng
khác nhau. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, C , B BC ¢ và C A ¢ . Tứ giác MNPQ là hình gì? A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang.
PHẦN 2 : TRẮC NGHIỆM ĐÚNG SAI Câu 1:
Cho hình chóp S.ABC có độ dài các cạnh SA  SB  SC  AB  AC  a và BC  a 2 . M, N lần lượt
là trung điểm của BC, AC. Các mệnh đề sau đúng hay sai?
a) Tam giác ABC vuông tại B .
b) MN vuông góc với AC .
c) Góc giữa hai đường thẳng MN và SB bằng 0 60 .
d) Góc giữa hai đường thẳng AB và SC bằng 0 60 . Câu 2:
Cho tứ diện đều ABCD. Gọi M , N, P lần lượt là trung điểm của cạnh BC , AD và AC ,  là góc giữa
hai đường thẳng AB và DM. Các mệnh đề sau đúng hay sai?
a) Tứ diện ABCD có tất cả các cạnh bằng nhau.
b) Góc giữa hai đường thẳng MP và BD 0 bằng 90 .
c) MN vuông góc với AD . 3 d) cos  . 4
PHẦN 3: TRẢ LỜI NGẮN   Câu 1:
Cho tứ diện ABCD có AB
CD 2. Gọi M , N lần lượt là trung điểm của AD và BC . Tính độ
dài đoạn thẳng MN biết góc giữa hai đường thẳng AB và MN bằng 30 (làm tròn kết quả đến hàng phần trăm). Câu 2:
Cho tứ diện ABCD có A ,
B AC, AD đôi một vuông góc với nhau, biết AB  AC  AD 1. Góc của
hai đường thẳng AB và CD bằng bao nhiêu độ? Câu 3:
Cho tứ diện ABCD có AC  1; BD  3. Gọi M, N lần lượt là trung điểm của AD và BC . Biết AC
vuông góc với BD . Tính độ dài MN . Kết quả làm tròn đến hàng phần chục. 3 Câu 4: Cho hình chóp .
S ABCD có đáy là hình vuông cạnh 2a , S
 AB đều và SC  2a 2 . Gọi H , K lần
lượt là trung điểm của AB, CD . Góc giữa đường thẳng AK và SH bằng bao nhiêu độ? PHẦN 4. TỰ LUẬN Câu 1:
Cho hình chóp S.ABCD có cạnh SA = x , tất cả các cạnh còn lại đều bằng a . Tính số đo của góc giữa hai
đường thẳng SA và SC. Câu 2:
Cho tứ diện ABCD có AC = ,
a BD = 3a . Gọi M, N lần lượt là trung điểm của AD và BC . Biết AC
vuông góc với BD . Tính MN . Câu 3:
Cho hình lăng trụ đều AB . C A B  C
  có cạnh đáy bằng 1, cạnh bên bằng 2 . Gọi C là trung điểm của 1
CC . Tính côsin của góc giữa hai đường thẳng BC và A B   . 1 Câu 4:
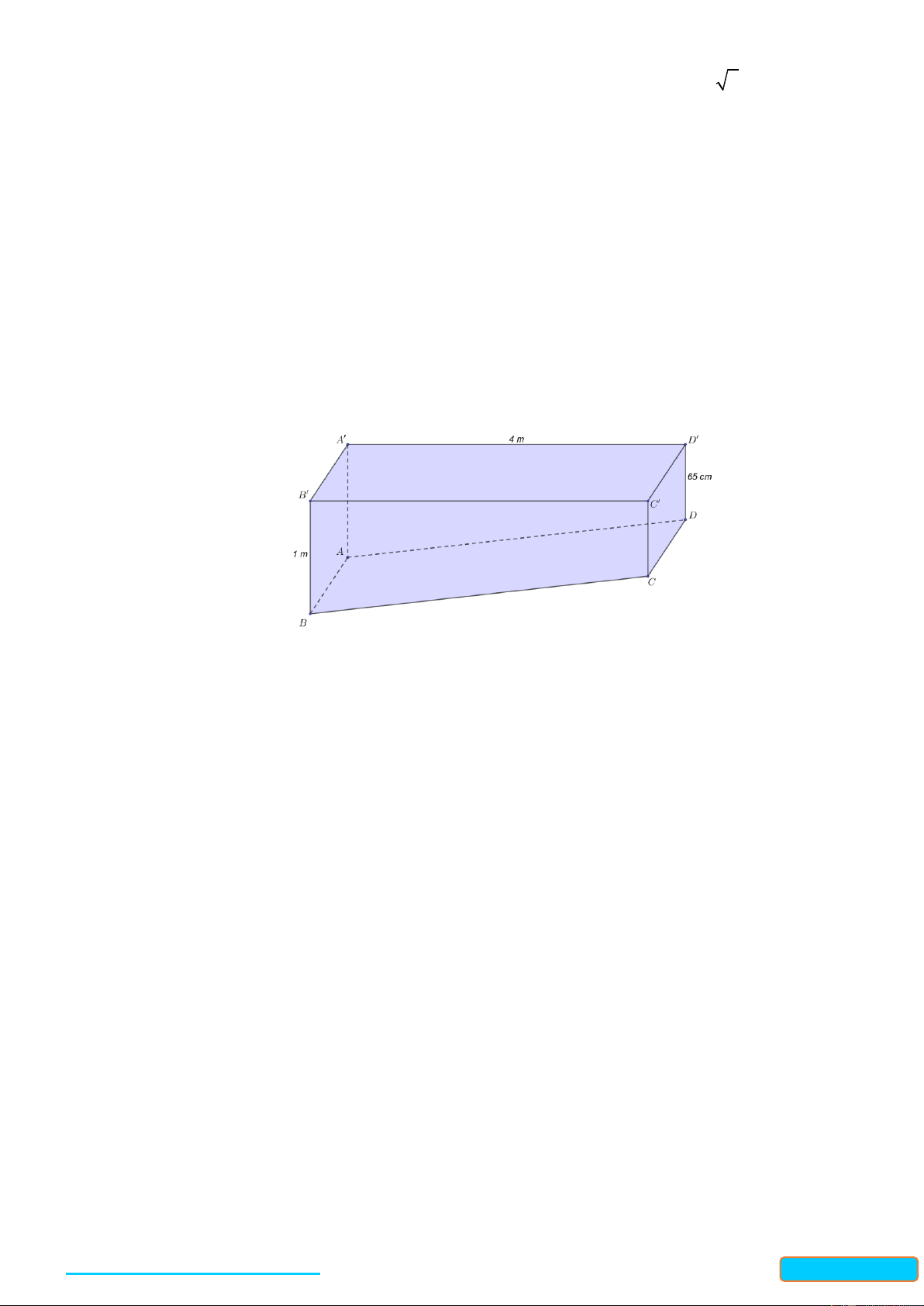
Bác Minh có một khối gỗ có kích thước như hình vẽ. Biết ABCD , A B  C  D  , A B  B  A , CDD C   là
các hình chữ nhật, A D  D  A , B C  C
 B là các hình thang vuông. Bác Minh muốn làm đẹp khối gỗ đó
bằng cách cắt khối gỗ theo mặt phẳng P đi qua C và song song với mặt phẳng  A B  C  D  .
Khi đó, bác Minh cần đặt mép BC của khối gỗ tạo với lưỡi cắt của máy cắt một góc bao nhiêu độ? HẾT 4