Bai 11 Đường đi ngắn nhất - Cây khung ngắn nhất môn Điện toán đám mây | Đại học Phenika

Nội dung
 Đường đi ngắn nhất  Thuật toán Dijkstra  Cây khung  Khái niệm
 Thuật toán tìm cây khung  Cây khung ngắn nhất  Thuật toán Kruskal Đường đi ngắn nhất
 Đường đi mà tổng trọng số của các cạnh trên đường đi nhỏ nhất
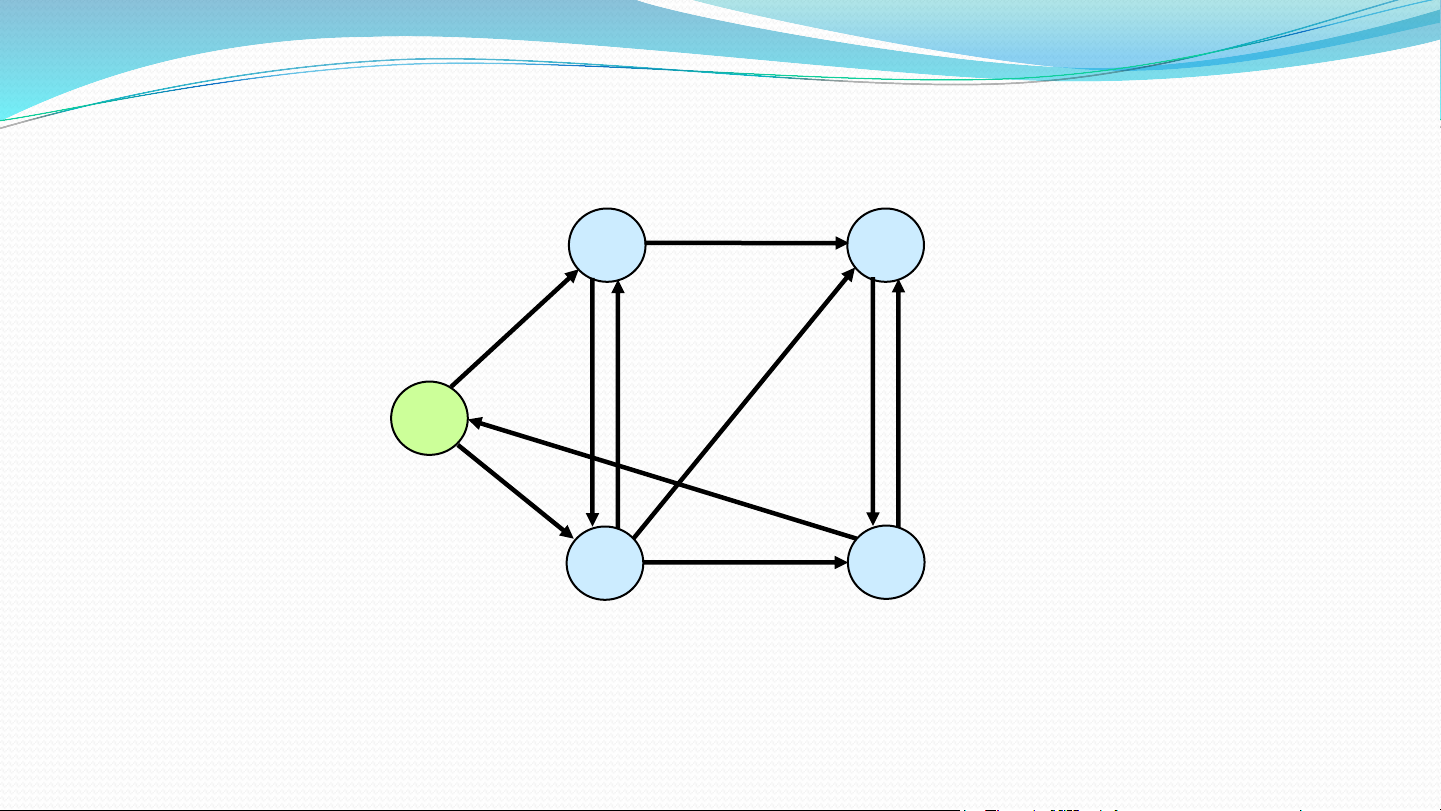
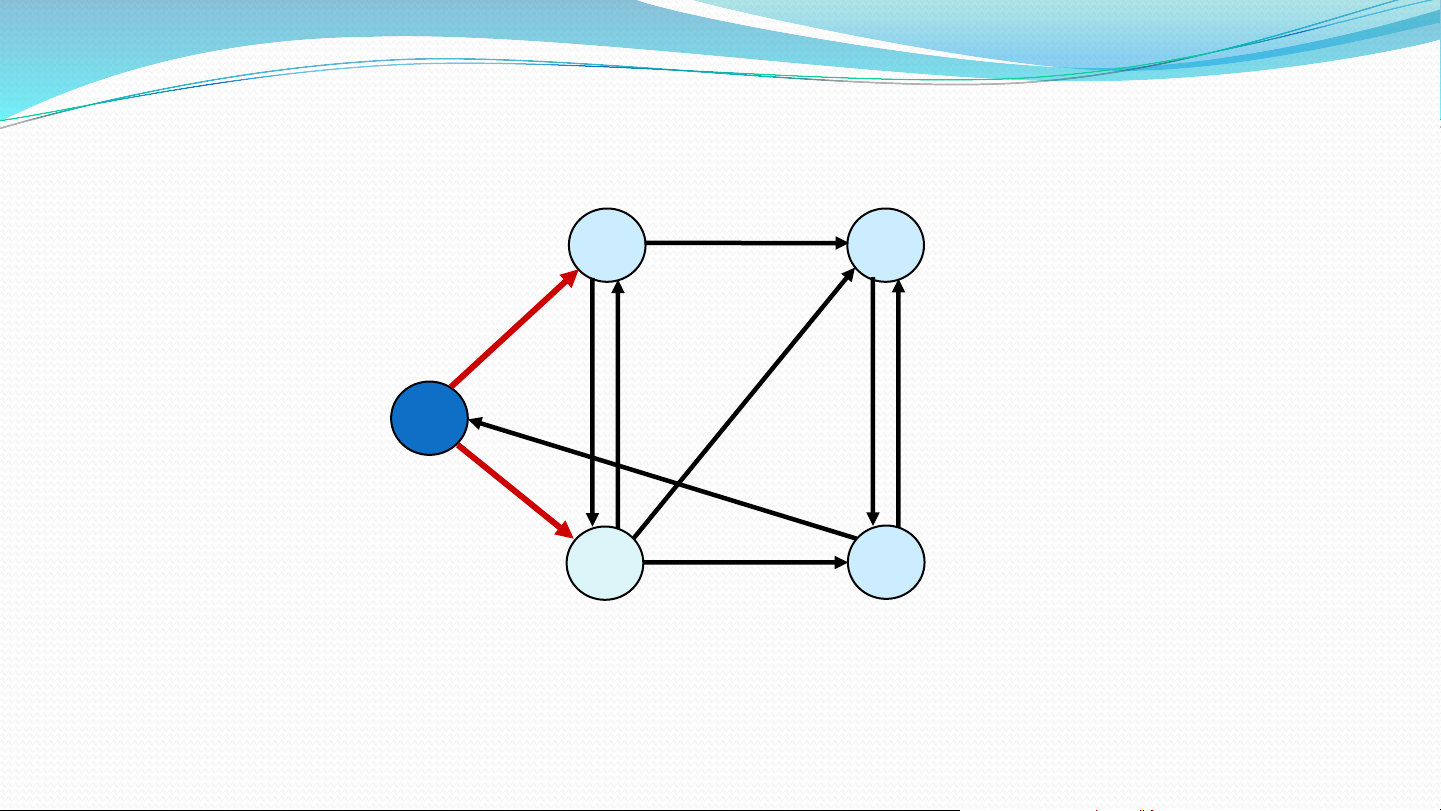
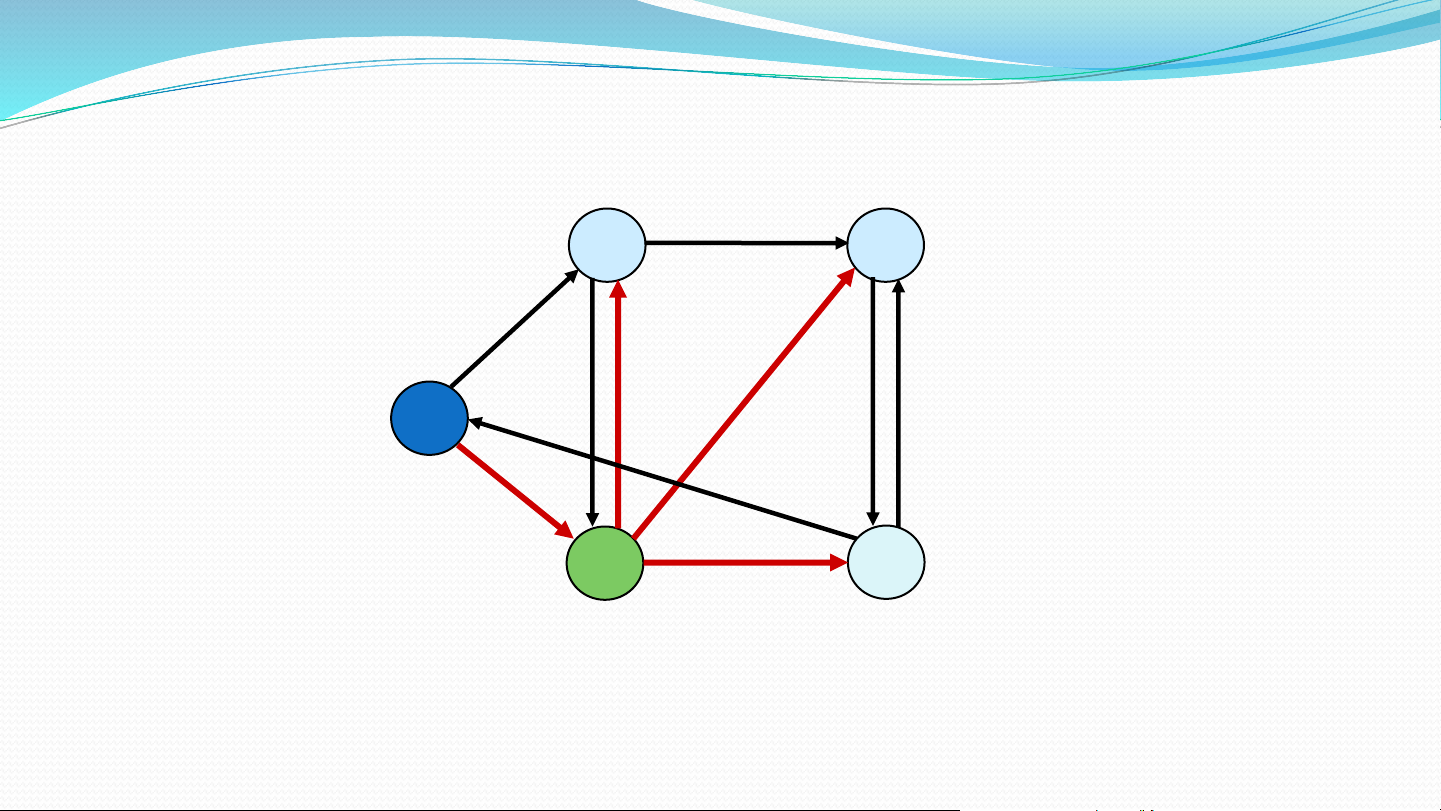
 Thuật toán Dijkstra
 Đồ̀ thị có trọng số không âm  Đỉnh xuất phát s
 Mảng dist[] lưu tổng trọng số ddnn từ s đến các đỉnh
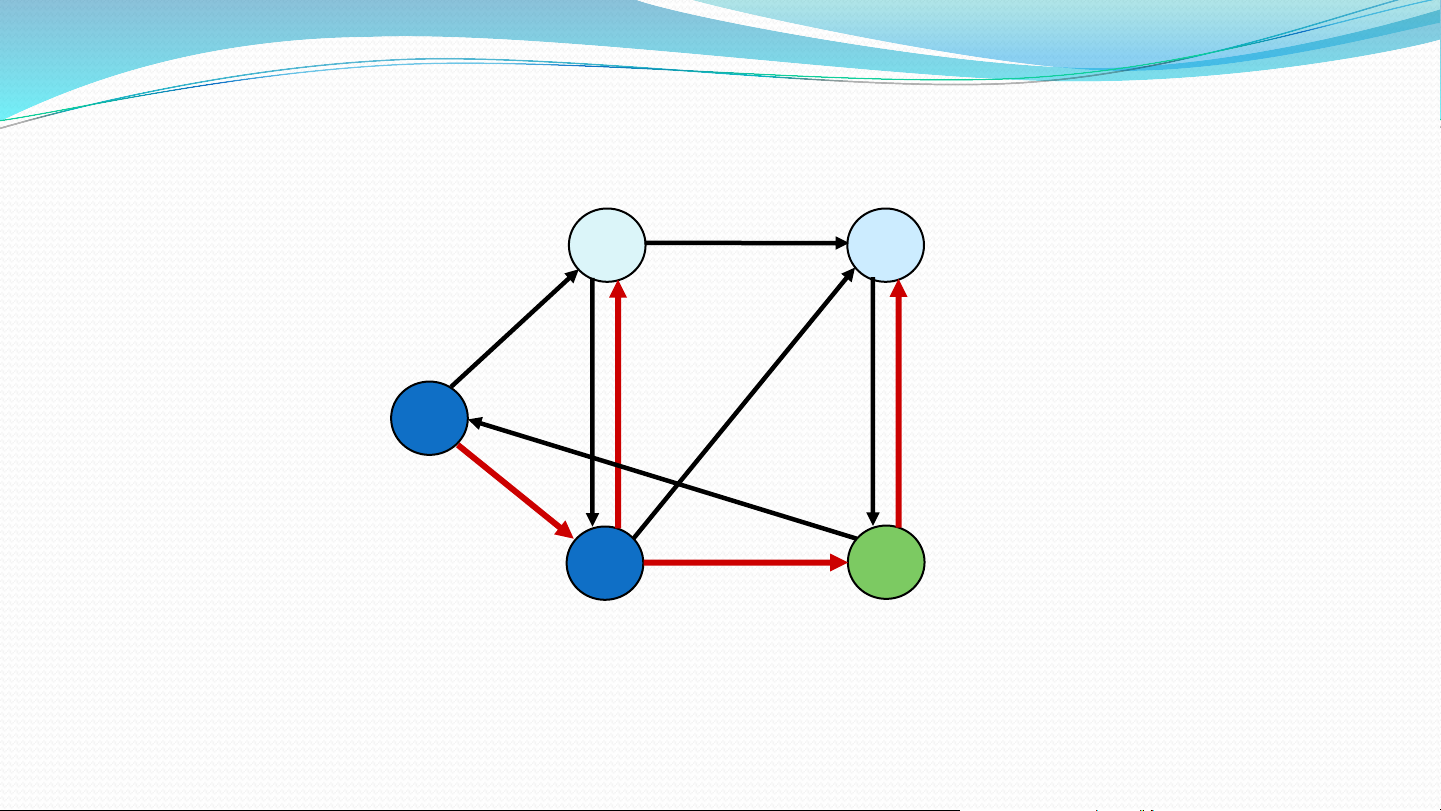
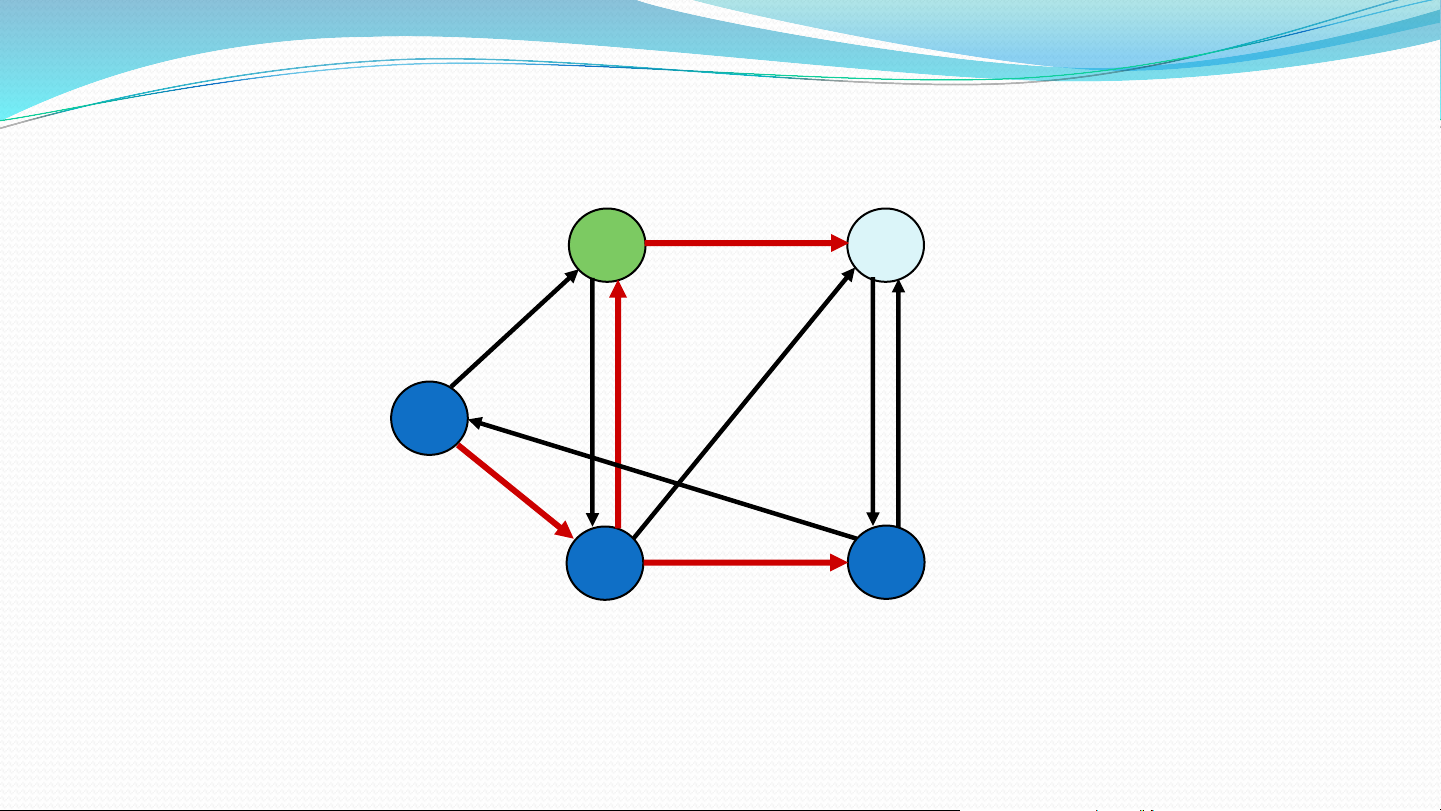
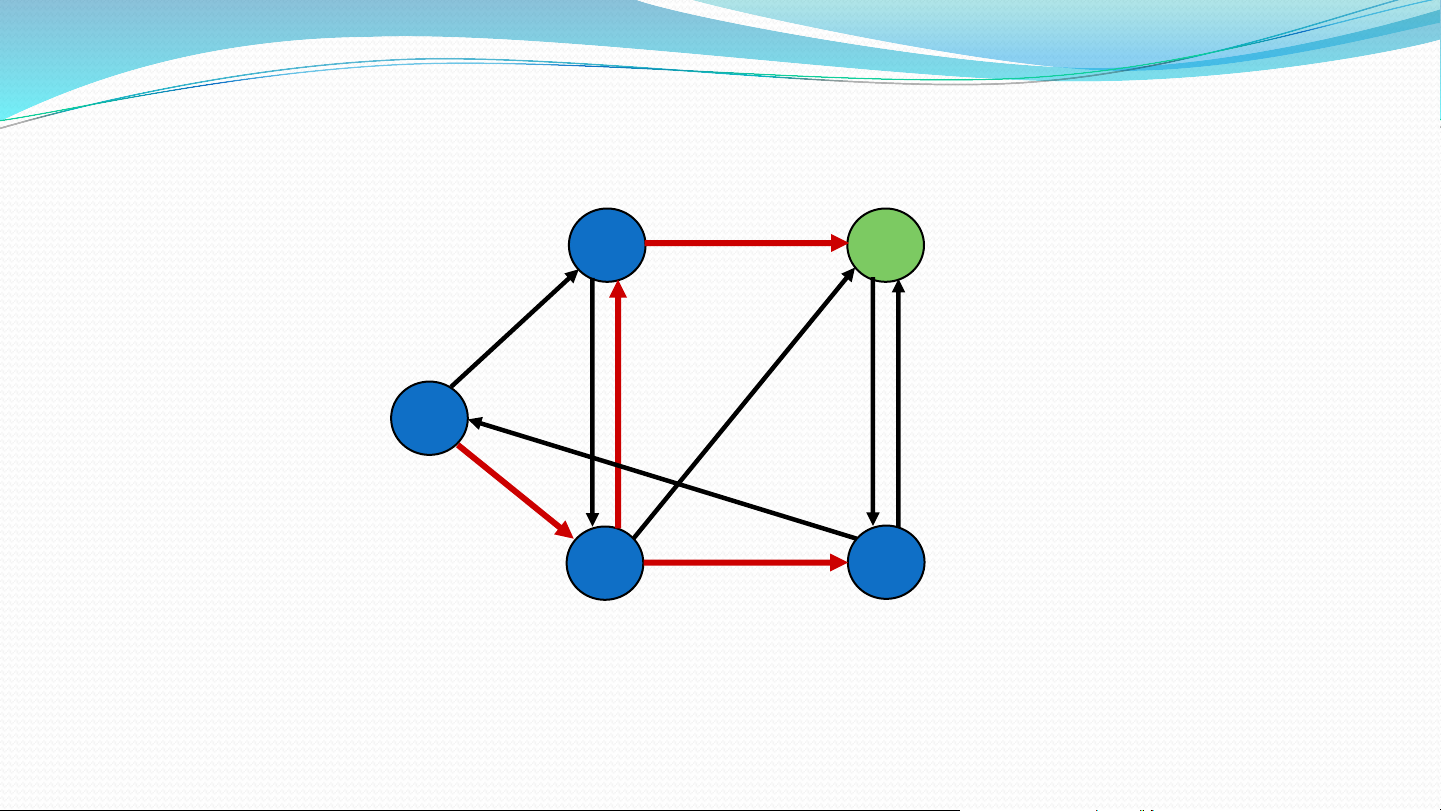
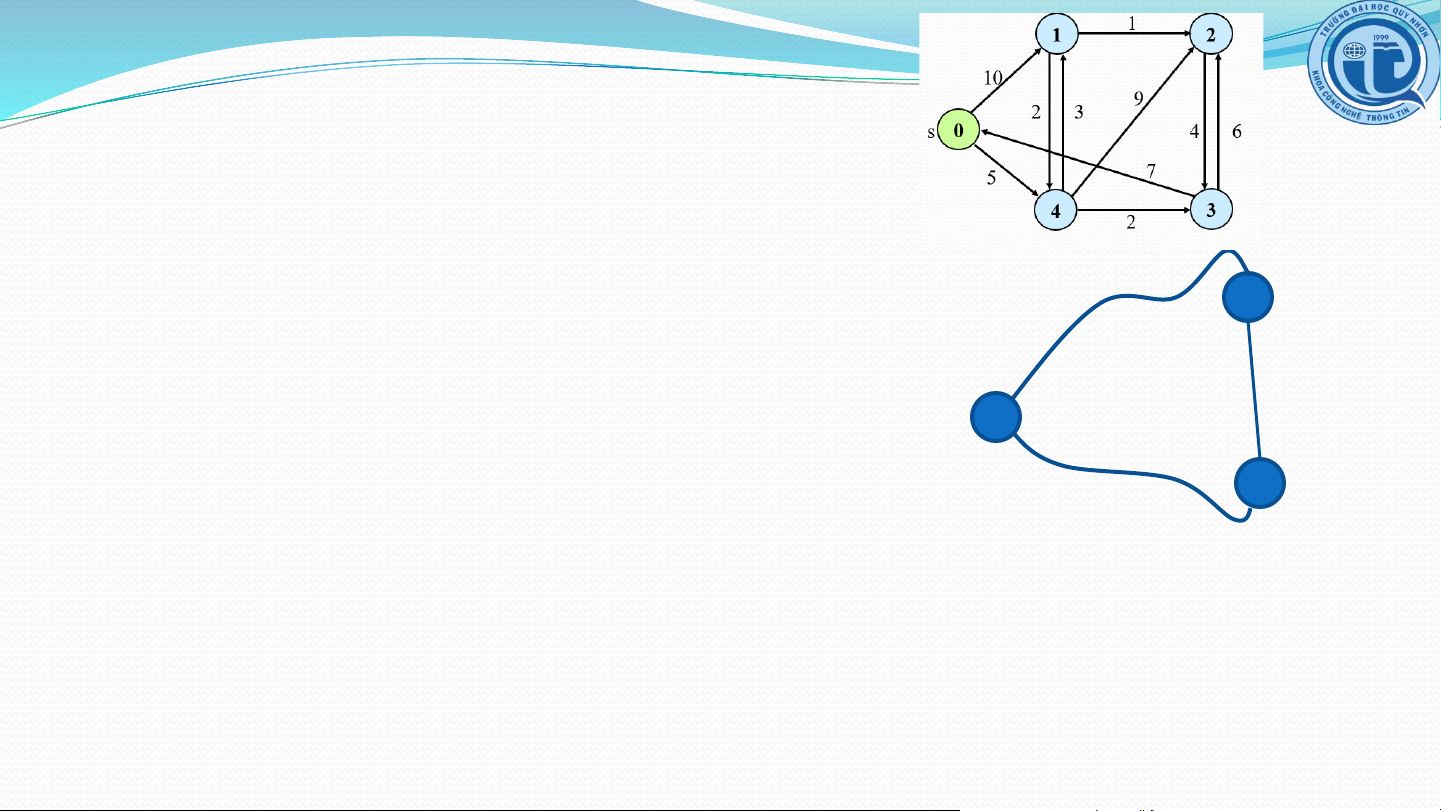
 Mảng parent[] lưu vết ddnn từ s đến các đỉnh Minh họa 1 1 2 10 Tìm đường đi 9 2 3 ngắn nhất từ 0 s 0 4 6 đến các đỉnh 5 7 4 3 2 Khởi tạo 10, 0 , -1 1 1 2 10 9 2 3 S = { 0 } s 0 4 6 5 7 4 3 2 5, 0 , -1 Chọn đỉnh, 8, 4 14, 4 10, 0 , -1 1 1 2 hiệu chỉnh 10 9 2 3 S = { 0, 4 } s 0 4 6 5 7 4 3 2 5, 5 0 , -1 , 0 7, 4 8, 4 13 14, 3 4 1 1 2 10 9 2 3 S = { 0, 4, 3 } s 0 4 6 5 7 4 3 2 5, 0 7, 4 , 8, 4 13 9 , 3 1 1 1 2 10 9 2 3 S = { 0, 4, 3, 1 } s 0 4 6 5 7 4 3 2 5, 0 7, 4 8, 4 9, 1 1 1 2 10 9 2 3
S = { 0, 4, 3, 1, 2 } s 0 4 6 5 7 4 3 2 5, 0 7, 4 Thuật toán Dijkstra  Khởi tạo: dist[u0]  Với mỗi đỉnh u: u0 
dist[u]= c[s, u], parent[u]=s, nếu có cạnh từ s đến u 
dist[u] = , parent[u] = -1, nếu ngược lại c[u0, v]  S = {s} s
 Tìm u0  S có dist[u0] = min{ d[v], vS } v dist[v]
 Kết nạp u0 vào tập S.
 Với mỗi đỉnh v  S, v kề với u0, nếu dist[v] > dist[u0] + c[u0,v]:
 dist[v] = dist[u0] + c[u0,v]  parent[v] = u0
 Lặp lại bước 2 cho đến khi S = V. Cài đặt #define MAX 100
void dijkstra(int c[MAX][MAX], int n, int s, int dist[], int parent[]) { bool S[MAX] = {false}; // Khởi tạo
for (int u = 0; u < n; u++) { if (c[s][u] < INF) { dist[u] = c[s][u]; parent[u] = s; } else { dist[u] = INF; parent[u] = -1; } } Cài đặt dist[s] = 0; S[s] = true; parent[s] = -1; // Lặp cho tới khi S = V
for (int i = 1; i < n; i++) { int u0 = -1; int minDist = INF;
// Tìm u0 không thuộc S có dist nhỏ nhất
for (int v = 0; v < n; v++) {
if (!S[v] && dist[v] < minDist) { minDist = dist[v]; u0 = v; } } Cài đặt if (u0 == -1) break; S[u0] = true; // Cập nhật dist
for (int v = 0; v < n; v++) {
if (!S[v] && c[u0][v] < INF) {
if (dist[v] > dist[u0] + c[u0][v]) {
dist[v] = dist[u0] + c[u0][v]; parent[v] = u0; } } } } } Cây khung
 Cho đồ thị G = là 1 đồ thị vô hướng, liên thông. Một cây
khung của đồ thị G là một đồ thị H có tập đỉnh là V và tập cạnh là
tập con của E thỏa điều kiện:
 H là một đồ thị liên thông (giữa mọi cặp đỉnh bất kỳ trong đồ thị đều tồn tại ít nhất một đường đi)  H không có chu trình
(Chu trình: 1 đường đi bắt đầu và kết thúc tại 1 đỉnh, trong đó tất cả các cạnh và đỉnh còn lại đều khác nhau) Nhận xét
 Một đồ thị có thể có nhiều cây khung.
 Số cạnh của cây khung bằng số đỉnh trừ 1.
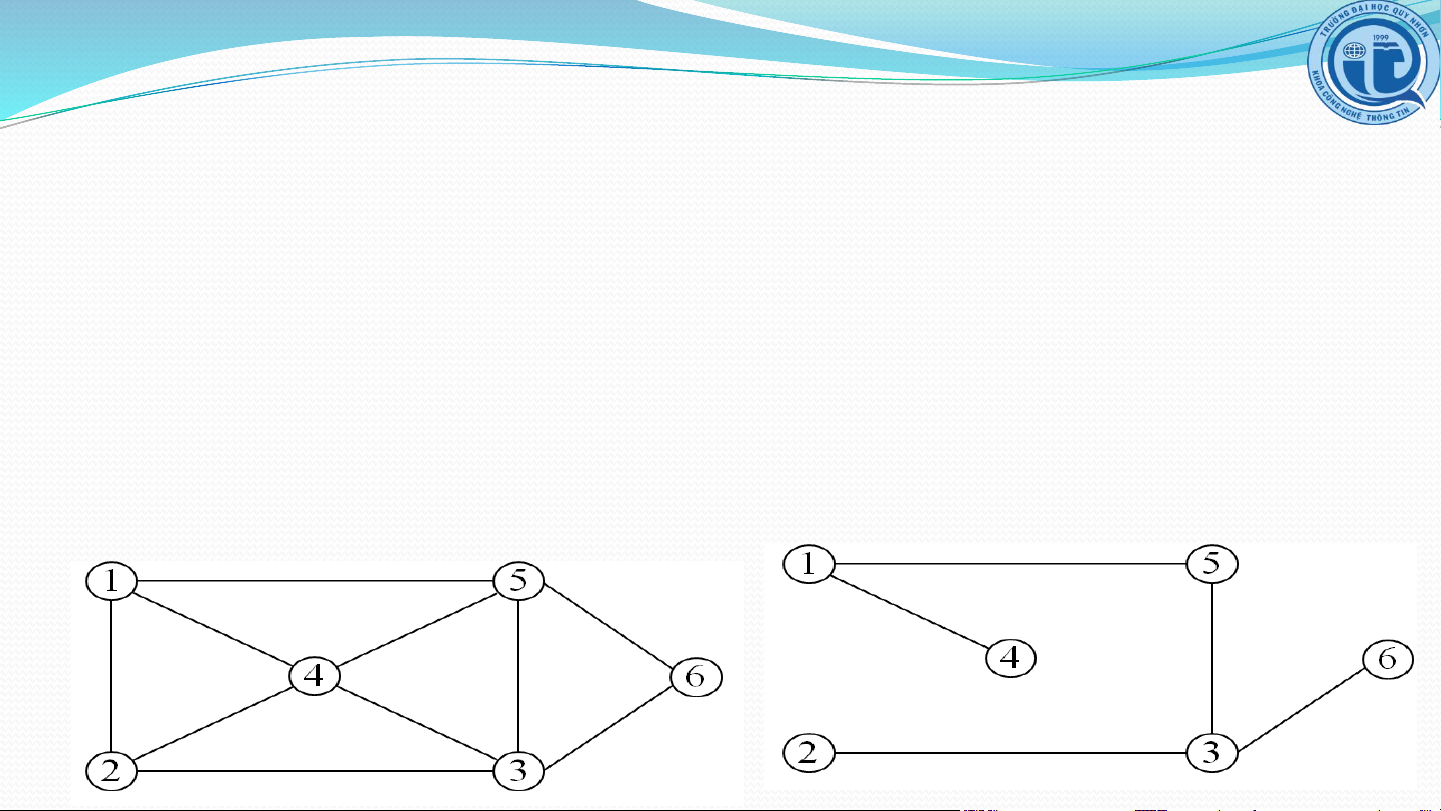
Thuật toán tìm cây khung
 Input: Đồ thị G
 Output: cây khung H của đồ̀ thị G  Action:
 Tạo một cây khung H có tập đỉnh trùng với tập đỉnh
của G và tập cạnh rỗng.
 Duyệt đồ thị G xuất phát từ đỉnh bất kỳ:
 Mỗi khi từ đỉnh v thăm đỉnh kề w thì đưa cạnh (v, w) vào cây khung. Cài đặt
AdjMatrixGraph spanningTree(AdjMatrixGraph g){
bool visted[MAXVERTICES] = {false}; AdjMatrixGraph h; h.numVertices = g.numVertices;
DFSSpanningTree(g, 0, h, visited); return h; }
void DFSSpanningTree(AdjMatrixGraph g, int v, AdjMatrixGraph &h, bool visited[]){ vistied[v] = true;
for(int w = 0; w < g.numVertices; w++)
if(g.adjMatrix[v][w]==1 && !visited[w]) { h.adjMatrix[v][w] = 1; h.adjMatrix[w][v] = 1;
DFSSpanningTree(g, w, h, visited); } } Cây khung ngắn nhất
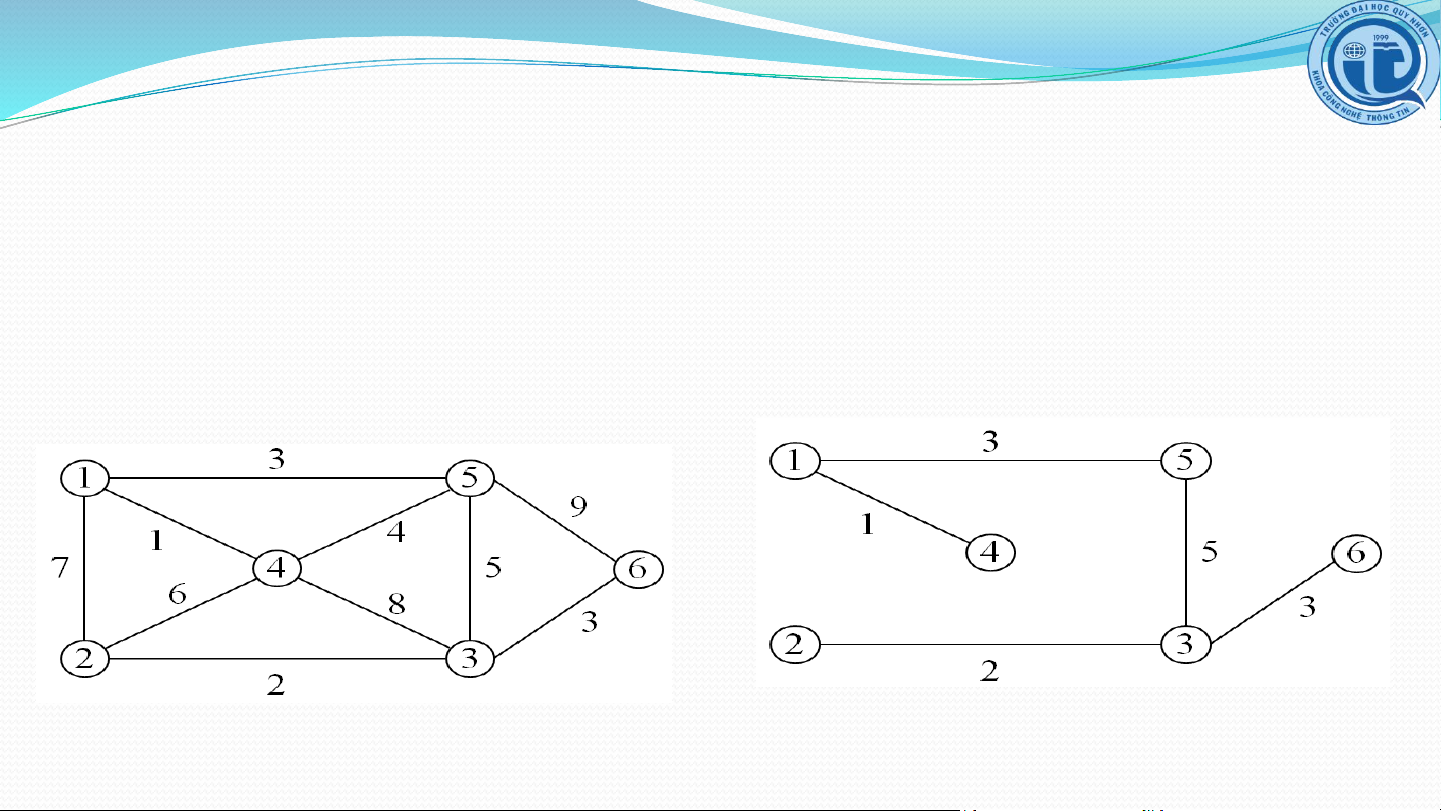
 H là cây khung ngắn nhất của đồ thị G nếu tổng các
trọng số của cây khung H là nhỏ nhất trong các cây khung của G. Thuật toán Kruskal
 Sắp xếp các cạnh của đồ thị theo thứ tự tăng của trọng số  Xuất phát T=  Lặp
 Chọn cạnh (u,v)E, có trọng số nhỏ nhất  E:=E \ {(u, v)}
 Nếu T{(u,v)} không chứa chu trình thì T:=T{(u,v)}  Đến khi |T|=|V|-1 Cài đặt
 Đồ thị biểu diễn danh sách cạnh
 Dùng mảng component[] để lưu thành phần liên thông của các đỉnh