32 trang 14 lượt tải

Bài 17 hàm số liên tục | Toán 11 kết nối tri thức

28

Bài 17 hàm số liên tục | Toán 11 kết nối tri thức. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!

Chủ đề: Chương 5: Giới hạn. Hàm số liên tục (KNTT) 82 tài liệu

Môn: Toán 11 3.7 K tài liệu

Sách: Kết nối tri thức

Tác giả:

Profile

Định Lương

3 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/32
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN C. BÀI TẬP TRẮC NGHIỆM (PHÂN MỨC ĐỘ)
1. Câu hỏi dành cho đối tượng học sinh trung bình – khá
Câu 1. Cho hàm số
y f x
liên tục trên
;a b
. Điều kiện cần và đủ để hàm số liên tục trên
;a b
là
A.
lim
x a
f x f a
và
lim
x b
f x f b
. B.
lim
x a
f x f a
và
lim
x b
f x f b
.
C.
lim
x a
f x f a
và
lim
x b
f x f b
. D.
lim
x a
f x f a
và
lim
x b
f x f b
.
Lời giải
Theo định nghĩa hàm số liên tục trên đoạn
;a b
. Chọn:
lim
x a
f x f a
và
lim
x b
f x f b
.
Câu 2. Cho hàm số
f x
xác định trên
;a b
. Tìm mệnh đề đúng.
A. Nếu hàm số
f x
liên tục trên
;a b
và
0f a f b
thì phương trình
0f x
không có
nghiệm trong khoảng
;a b
.
B. Nếu
0f a f b
thì phương trình
0f x
có ít nhất một nghiệm trong khoảng
;a b
.
C. Nếu hàm số
f x
liên tục, tăng trên
;a b
và
0f a f b
thì phương trình
0f x
không có nghiệm trong khoảng
;a b
.
D. Nếu phương trình
0f x
có nghiệm trong khoảng
;a b
thì hàm số
f x
phải liên tục trên
;a b
.
Lời giải
Vì
0f a f b
nên
f a
và
f b
cùng dương hoặc cùng âm. Mà
f x
liên tục, tăng trên
;a b
nên đồ thị hàm
f x
nằm trên hoặc nằm dưới trục hoành trên
;a b
hay phương trình
0f x
không có nghiệm trong khoảng
;a b
.
Câu 3. Cho hàm số
( )y f x
liên tục trên đoạn
;a b
. Mệnh đề nào dưới đây đúng?
A. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0f x
không có nghiệm nằm trong
;a b
.
B. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0f x
có ít nhất một nghiệm nằm trong
;a b
.
C. Nếu
( ). ( ) 0f a f b
thì phương trình
( ) 0f x
có ít nhất một nghiệm nằm trong
;a b
.
D. Nếu phương trình
( ) 0f x
có ít nhất một nghiệm nằm trong
;a b
thì
( ). ( ) 0f a f b
.
Lời giải
Chọn B
Vì theo định lý 3 trang 139/sgk.
Câu 4. Cho đồ thị của hàm số
y f x
như hình vẽ sau:
BÀI 17. HÀM SỐ LIÊN TỤC
• CHƯƠNG 5. GIỚI HẠN
• |FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
-4 -3 -2 -1 1 2 3 4 5
-2
-1
1
2
3
4
5
6
7
x
y
Chọn mệnh đề đúng.
A. Hàm số
y f x
có đạo hàm tại điểm
0x
nhưng không liên tục tại điểm
0x
.
B. Hàm số
y f x
liên tục tại điểm
0x
nhưng không có đạo hàm tại điểm
0x
.
C. Hàm số
y f x
liên tục và có đạo hàm tại điểm
0x
.
D. Hàm số
y f x
không liên tục và không có đạo hàm tại điểm
0x
.
Lời giải
Chọn B
Đồ thị là một đường liền nét, nhưng bị “gãy” tại điểm
0x
nên nó liên tục tại điểm
0x
nhưng
không có đạo hàm tại điểm
0x
.
Câu 5. Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại
1x
?
A. . B. .
C. . D. .
Lời giải
Chọn D
Vì
1 1
lim lim
x x
y y
nên hàm số không liên tục tại
1x
.
Câu 6. Cho các mệnh đề:
1. Nếu hàm số
y f x
liên tục trên
;a b
và
. 0f a f b
thì tồn tại
0
;x a b
sao cho
0
0f x
.
2. Nếu hàm số
y f x
liên tục trên
;a b
và
. 0f a f b
thì phương trình
0f x
có
nghiệm.
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
3. Nếu hàm số
y f x
liên tục, đơn điệu trên
;a b
và
. 0
f a f b
thì phương trình
0
f x
có nghiệm duy nhất.
A. Có đúng hai mệnh đề sai. B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai. D. Có đúng một mệnh đề sai.
Lời giải
Chọn D
Khẳng định thứ nhất sai vì thiếu tính liên tục trên đoạn
;a b
.
Câu 7. Cho hàm số
3
1
,khi 1
1
1 , khi 1
x
x
y
x
x
. Hãy chọn kết luận đúng
A.
y
liên tục phải tại
. B.
y
liên tục tại
.
C.
y
liên tục trái tại
1x
. D.
y
liên tục trên
.
Lời giải
Chọn A
Ta có:
1 1
y
.
Ta có:
1
lim 1
x
y
;
2
3
2
1 1 1 1
1 1
1
lim lim lim lim 1 4
1 1
x x x x
x x x
x
y x x
x x
Nhận thấy:
1
lim 1
x
y y
. Suy ra
y
liên tục phải tại
.
Câu 8. Cho hàm số
2
7 12
khi 3
3
1 khi 3
x x
x
y
x
x
. Mệnh đề nào sau đây đúng?
A. Hàm số liên tục nhưng không có đạo hàm tại
0
3
x
.
B. Hàm số gián đoạn và không có đạo hàm tại
0
3
x
.
C. Hàm số có đạo hàm nhưng không liên tục tại
0
3
x
.
D. Hàm số liên tục và có đạo hàm tại
0
3
x
.
Lời giải
Chọn D
2
3 3
7 12
lim lim 4 1 3
3
x x
x x
x y
x
nên hàm số liên tục tại
0
3
x
.
2 2 2
3 3 3
7 12 3 7.3 12 7 12
lim lim lim 4 1 ' 3 1
3 3
x x x
x x x x
x y
x x
.
Câu 9. Cho hàm số
2
khi 2
2 2
4 khi 2
x
x
f x
x
x
. Chọn mệnh đề đúng?
A. Hàm số liên tục tại
2
x
. B. Hàm số gián đoạn tại
2
x
.
C.
4 2
f
. D.
2
lim 2
x
f x
.
Lời giải
Chọn A
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Tập xác định:
D
2
lim
x
f x
2
2
lim
2 2
x
x
x
2
2 2 2
lim
2
x
x x
x
2
lim 2 2
x
x
4
2 4
f
2
lim 2
x
f x f
Vậy hàm số liên tục tại
2
x
.
Câu 10. Cho hàm số
3
2 1x
f x
x x
. Kết luận nào sau đây đúng?
A. Hàm số liên tục tại
1
x
. B. Hàm số liên tục tại
0
x
.
C. Hàm số liên tục tại
1x
. D. Hàm số liên tục tại
1
2
x
.
Lời giải
Chọn D
Tại
1
2
x
, ta có:
3
1 1
2 2
2 1 1
lim lim 0
1 2
x x
x
f x f
x
. Vậy hàm số liên tục tại
2
x
.
Câu 11. Hàm số nào sau đây liên tục tại
1
x
:
A.
2
1
1
x x
f x
x
. B.
2
2
2
1
x x
f x
x
. C.
2
1
x
x
x
f
x
. D.
1
1x
x
x
f
.
Lời giải
A)
2
1
1
x x
f x
x
1
lim
x
f x

suy ra
f x
không liên tục tại
1
x
.
B)
2
2
2
1
x x
f x
x
1 1
2
lim lim
1
x x
x
x
x
f

suy ra
f x
không liên tục tại
1
x
.
C)
2
1
x
x
x
f
x
2
1 1
1
lim lim 3 1
x x
x
f
x
f
x
x
suy ra
f x
liên tục tại
1
x
.
D)
1
1x
x
x
f
1 1
1
lim lim
1
x x
x
x
x
f
suy ra
f x
không liên tục tại
1
x
.
Câu 12. Hàm số nào dưới đây gián đoạn tại điểm
0
1
x
.
A.
2
1 2
y x x
. B.
2 1
1
x
y
x
. C.
1
x
y
x
. D.
2
1
1
x
y
x
.
Lời giải
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Ta có
2 1
1
x
y
x
không xác định tại
0
1
x
nên gián đoạn tại
0
1
x
.
Câu 13. Hàm số nào sau đây gián đoạn tại
2
x
?
A.
3 4
2
x
y
x
. B.
siny x
. C.
4 2
2 1
y x x
D.
tany x
.
Lời giải
Chọn A
Ta có:
3 4
2
x
y
x
có tập xác định:
\ 2
D
, do đó gián đoạn tại
2
x
.
Câu 14. Hàm số
1
x
y
x
gián đoạn tại điểm
0
x
bằng?
A.
0
2018
x
. B.
0
1
x
. C.
0
0
x
D.
0
1
x
.
Lời giải
Chọn D
Vì hàm số
1
x
y
x
có TXĐ:
\ 1
D
nên hàm số gián đoạn tại điểm
0
1
x
.
Câu 15. Cho hàm số
2
3
1
x
y
x
. Mệnh đề nào sau đây đúng?
A. Hàm số không liên tục tại các điểm
1
x
. B. Hàm số liên tục tại mọi
x
.
C. Hàm số liên tục tại các điểm
1
x
. D. Hàm số liên tục tại các điểm
1x
.
Lời giải
Chọn A
Hàm số
2
3
1
x
y
x
có tập xác định
\ 1
. Do đó hàm số không liên tục tại các điểm
1
x
.
Câu 16. Trong các hàm số sau, hàm số nào liên tục trên
?
A.
3
y x x
. B.
coty x
. C.
2 1
1
x
y
x
. D.
2
1
y x
.
Lời giải
Chọn A
Vì
3
y x x
là đa thức nên nó liên tục trên
.
Câu 17. Cho bốn hàm số
3
1
2 3 1 f x x x
,
2
3 1
2
x
f x
x
,
3
cos 3 f x x
và
4 3
log
f x x
. Hỏi có
bao nhiêu hàm số liên tục trên tập
?
A.
1
. B.
3
. C.
4
. D.
2
.
Lời giải
* Ta có hai hàm số
2
3 1
2
x
f x
x
và
4 3
log
f x x
có tập xác định không phải là tập
nên không
thỏa yêu cầu.
* Cả hai hàm số
3
1
2 3 1 f x x x
và
3
cos 3 f x x
đều có tập xác định là
đồng thời liên tục
trên
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 18. Trong các hàm số sau, hàm số nào liên tục trên
?
A.
tan 5f x x
. B.
2
3
5
x
f x
x
. C.
6
f x x
. D.
2
5
4
x
f x
x
.
Lời giải
Chọn D
Hàm số
2
5
4
x
f x
x
là hàm phân thức hữu tỉ và có TXĐ là
D
do đó hàm số
2
5
4
x
f x
x
liên tục trên
.
2. Câu hỏi dành cho đối tượng học sinh khá-giỏi
Câu 19. Cho hàm số
2
1 cos
khi 0
1 khi 0
x
x
f x
x
x
.
Khẳng định nào đúng trong các khẳng định sau?
A.
f x
có đạo hàm tại
0
x
. B.
2 0
f
.
C.
f x
liên tục tại
0
x
. D.
f x
gián đoạn tại
0
x
.
Lời giải
Hàm số xác định trên
Ta có
0 1
f
và
2
2
2
0 0 0
2sin
1 cos 1
2
lim lim lim
2
4.
2
x x x
x
x
f x
x
x
Vì
0
0 lim
x
f f x
nên
f x
gián đoạn tại
0
x
. Do đó
f x
không có đạo hàm tại
0
x
.
0
x
2
1 cos
0
x
f x
x
nên
2 0.
f
VậyA, B,C sai.
Câu 20. Cho hàm số
2
3
cos , 0
,0 1
1
, 1
x x x
x
f x x
x
x x
. Khẳng định nào sau đây đúng?
A. Hàm số
f x
liên tục tại mọi điểm
x
thuộc
.
B. Hàm số
f x
bị gián đoạn tại điểm
0
x
.
C. Hàm số
f x
bị gián đoạn tại điểm
1x
.
D. Hàm số
f x
bị gián đoạn tại điểm
0
x
và
1x
.
Lời giải
*
f x
liên tục tại
0
x
và
1x
.
* Tại
0
x
0 0
lim lim cos 0
x x
f x x x
,
2
0 0
lim lim 0
1
x x
x
f x
x
,
0 0
f
.
Suy ra
0 0
lim lim 0
x x
f x f x f
. Hàm số liên tục tại
0
x
.
* Tại
1x
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
2
1 1
1
lim lim
1 2
x x
x
f x
x
,
3
1 1
lim lim 1
x x
f x x
.
Suy ra
1 1
lim lim
x x
f x f x
. Hàm số gián đoạn tại
1x
.
Câu 21. Tìm m để hàm số
2
4
2
( )
2
2
x
khi x
f x
x
m khi x
liên tục tại
2
x
A.
4
m
. B.
2
m
. C.
4
m
. D.
0
m
.
Lời giải
Chọn A
Hàm số liên tục tại
2
x
khi và chỉ khi
2
2 2
4
lim lim 4
2
x x
x
m m m
x

Câu 22. Cho hàm số
3
1
khi 1
( )
1
2 1 khi 1
x
x
y f x
x
m x
. Giá trị của tham số
m
để hàm số liên tục tại điểm
0
1
x
là:
A.
1
2
m
. B.
2
m
. C.
1
m
. D.
0
m
.
Lời giải
Chọn C
Ta có
(1) 2 1
f m
3
2
1 1 1
1
lim lim lim( 1) 3
1
x x x
x
y x x
x
Để hàm số liên tục tại điểm
0
1
x
thì
1
(1) lim 2 1 3 1
x
f y m m
.
Câu 23. Để hàm số
2
3 2 khi 1
4 khi 1
x x x
y
x a x
liên tục tại điểm
1
x
thì giá trị của
a
là
A.
4
. B. 4. C. 1. D.
1
.
Lời giải
Chọn B
Hàm số liên tục tại
1
x
khi và chỉ khi
1 1
lim lim 1
x x
y y y


2
1 1
lim 4 lim 3 2 1
x x
x a x x y
4 0 4
a a
.
Câu 24. Tìm giá trị thực của tham số
m
để hàm số
3 2
2 2
1
1
3 1
x x x
khi x
f x
x
x m khi x
liên tục tại
1x
.
A.
0
m
. B.
6
m
. C.
4
m
. D.
2
m
.
Lời giải
Chọn A
Ta có:
1 3
f m
.
2
3 2
2
1 1 1 1
1 2
2 2
lim lim lim lim 2 3
1 1
x x x x
x x
x x x
f x x
x x
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Để hàm số
f x
liên tục tại
1x
thì
1
lim 1 3 3 0
x
f x f m m
.
Câu 25. Cho hàm số
2016
2
1
2018 1 2018
1
x x
khi x
f x
x x
k khi x
. Tìm
k
để hàm số
f x
liên tục tại
1x
.
A.
2 2019
k . B.
2017. 2018
2
k
. C.
1
k
. D.
20016
2019
2017
k
.
Lời giải
Chọn A
Ta có:
2016
2016
1 1
1 1 2018 1 2018
2
lim lim
2017 2017
2018 1 2018
x x
x x x x
x x
x
x x
2015 2014
1
1 ... 1 1 2018 1 2018
lim
2017 1
x
x x x x x x
x
2 2019
Để hàm số liên tục tại
1x
1
lim 1
x
f x f
2 2019
k .
Câu 26. Cho hàm số
1
1
1
1
x
khi x
f x
x
a khi x
. Tìm
a
để hàm số liên tục tại
0
1
x
.
A.
0
a
. B.
1
2
a
. C.
1
2
a
. D.
1
a
.
Lời giải
Chọn C
Ta có
1
lim
x
f x
1
1
lim
1
x
x
x
1
1
lim
1 1
x
x
x x
1
1
lim
1
x
x
1
2
.
Để hàm số liên tục tại
0
1
x
khi
1
lim 1
x
f x f
1
2
a
.
Câu 27. Biết hàm số
3 1
1
x b khi x
f x
x a khi x
liên tục tại
1x
. Mệnh đề nào dưới đây đúng?
A.
2a b
. B.
2a b
. C.
2a b
. D.
2a b
.
Lời giải
Chọn A
1
lim 1 3
x
f x f b
;
1
lim 1
x
f x a
. Để liên tục tại x=-1 ta có
3 1 2b a a b
Câu 28. Cho hàm số
3
khi x 3
1 2
khi x=3
x
f x
x
m
. Hàm số đã cho liên tục tại
3
x
khi
?
m
A.
1
. B.
1
. C.
4
. D.
4
.
Lời giải
Chọn D
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
3
f m
3 3
3
lim lim
1 2
x x
x
f x
x
3
3 1 2
lim
3
x
x x
x
3
lim 1 2 4
x
x
Để hàm số liên tục tại
3
x
thì
3
lim 3
x
f x f
Suy ra,
4
m
.
Câu 29. Biết hàm số
2
5 khi 1
2 3 khi 1
ax bx x
f x
ax b x
liên tục tại
1x
Tính giá trị của biểu thức
4P a b
.
A.
4P
. B.
5
P
. C.
5
P
. D.
4P
.
Lời giải
Chọn B
Ta có:
2
1 1
lim lim 5 5 1
x x
f x ax bx a b f
.
1 1
lim lim 2 3 2 3
x x
f x ax b a b
.
Do hàm số liên tục tại
1x
nên
5 2 3 4 5
a b a b a b
.
Câu 30. Tìm
m
để hàm số
2
1
( )
1
1 1
x x
khi x
f x
x
m khi x
liên tục tại
1x
A.
0
m
. B.
1
m
. C.
1
m
D.
2
m
.
Lời giải
Chọn D
TXĐ:
D R
Ta có
2
1 1 1
lim ( ) lim lim 1
1
x x x
x x
f x x
x
Và
(1) 1
f m
.
Hàm số liên tục tại
1x
1 1 2
m m
Câu 31. Có bao nhiêu số tự nhiên
m
để hàm số
2
2
3 2
1
1
1 1
x x
khi x
f x
x
m m khi x
liên tục tại điểm
1x
?
A. 0. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
2
1
3 2
lim
1
x
x x
x
1
1 2
lim
1
x
x x
x
1
lim 2 1
x
x
.
Để hàm số
f x
liên tục tại điểm
1x
cần:
1
lim 1
x
f x f
2
1 1
m m
2
0 (TM)
0
1 (L)
m
m m
m
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 32. Tìm
a
để hàm số
2 2
khi 2
2
2 khi 2
x
x
f x
x
x a x
liên tục tại
2
x
?
A.
15
4
. B.
15
4
. C.
1
4
. D.
1
.
Lời giải
Chọn B
Ta có
2 4
f a
.
Ta tính được
2 2 2
2 4 1 1
lim lim lim
4
2 2
2 2 2
x x x
x
f x
x
x x
.
Hàm số đã cho liên tục tại
2
x
khi và chỉ khi
2
1 15
2 lim 4
4 4
x
f f x a a
.
Vậy hàm số liên tục tại
2
x
khi
15
4
a
.
Câu 33. Cho hàm số
2
2
3 2
2
2 2
4 6 2
x x
khi x
f x
x
m x m khi x
,
m
là tham số. Có bao nhiêu giá trị của
m
để hàm
số đã cho liên tục tại
2
x
?
A.
3
. B.
0
. C.
2
. D.
1
Lời giải
Chọn D
Ta có
2
2 2 2 2
2 1 2 2
3 2
lim ( ) lim lim lim 1 2 2 4
2
2 2
x x x x
x x x
x x
f x x x
x
x
2 2
2 2
lim ( ) lim 4 6 2 4 6
x x
f x m x m m m
2
(2) 2 4 6
f m m
Để hàm số liên tục tại
2
x
thì
2 2
2 2
lim ( ) lim ( ) (2) 2 4 6 4 2 4 2 0 1
x x
f x f x f m m m m m
Vậy có một giá trị của
m
thỏa mãn hàm số đã cho liên tục tại
2
x
.
Câu 34. Cho hàm số
2
2
3 2 1 2
, 1
1
4 1
x x
x
f x
x
m x
. Hàm số
f x
liên tục tại
0
1
x
khi
A.
3
m
. B.
3
m
. C.
7
m
. D.
7
m
.
Lời giải
Chọn A
Tập xác định
D
,
0
1x
.
Ta có
1 4
f m
.
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
2
1 1
3 2 1 2
lim lim
1 1
x x
x x
f x
x x
1
2
1 3 5
lim
1 1 3 2 1 2
x
x x
x x x x
1
2
3 5
lim 1
1 3 2 1 2
x
x
x x x
Hàm số
f x
liên tục tại
0
1
x
khi và chỉ khi
1
lim 1 4 1 3
x
x f m m
.
Câu 35. Tìm giá trị của tham số
m
để hàm số
2
2
3 2
khi 1
1
2 khi 1
x x
x
f x
x
mx x
liên tục tại
1
x
.
A.
3
2
m
. B.
5
2
m
. C.
3
2
m
. D.
5
2
m
.
Lời giải
Chọn D
- Ta có:
+
1 2
f m
.
+
1
lim 2
x
f x m
.
+
2
2
1 1
3 2
lim lim
1
x x
x x
f x
x
1 1
1 2
2 1
lim lim
1 1 1 2
x x
x x
x
x x x
.
- Hàm số liên tục tại
1
x
1 1
1 lim lim
x x
f f x f x
1 5
2
2 2
m m
.
Câu 36. Cho hàm số
2
2
4 2
khi 0
( )
5
2 khi 0
4
x
x
x
f x
a x
. Tìm giá trị thực của tham số
a
để hàm số
( )f x
liên tục tại
0
x
.
A.
3
4
a
. B.
4
3
a
. C.
4
3
a
. D.
3
4
a
.
Lời giải
.
Chọn D
Tập xác định:
D
.
2 2
2
2
0 0 0
2 2
4 2 4 2
4 2
lim ( ) lim lim
4 2
x x x
x x
x
f x
x
x x
2
2 2 2
0 0
4 4 1 1
lim lim
4
( 4 2) 4 2
x x
x
x x x
.
5
(0) 2
4
f a
.
Hàm số
( )f x
liên tục tại
0
0 lim ( ) (0)
x
x f x f
5 1
2
4 4
a
3
4
a
.
Vậy
3
4
a
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 37. Cho hàm số
2
2 3 khi 1
3 1 khi 1
x x x
f x
x m x
. Tìm
m
để hàm số liên tục tại
0
1
x
.
A.
1
m
. B.
3
m
. C.
0
m
. D.
2
m
.
Lời giải
Chọn C
TXĐ
D
Ta có
1 2
f m
.
1
lim
x
f x
2
1
lim 2 3
x
x x
2
.
Hàm số liên tục tại
0
1
x
1
lim 1
x
f x f
2 2
m
0
m
.
Câu 38. Cho hàm số
2
3 2
2
( )
2
2
x x
x
f x
x
a x
khi
khi
. Hàm số liên tục tại
2
x
khi
a
bằng
A.
1
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn A
Hàm số liên tục tại
2
x
2
lim ( ) (2)
x
f x f
.
Ta có
2
2 2 2
3 2
(2) ,lim ( ) lim lim( 1) 1
2
x x x
x x
f a f x x
x
. Do đó
1
a
Câu 39. Cho hàm số
3
3
1 2
2 3
x
khi x
f x
x
mx khi x
. Hàm số liên tục tại điểm
x
khi
m
bằng:
A.
2
. B.
4
. C.
4
. D.
2
.
Lời giải
Chọn A
Tập xác định
D
.
Ta có
3 3 2
f m
và
3
lim
x
f x
3
3
lim
1 2
x
x
x
3
lim 1 2
x
x
4
.
Hàm số đã cho liên tục tại điểm
x
3
lim 3
x
f x f
3 2 4
m
2
m
.
Câu 40. Tìm
m
để hàm số
2
16
4
4
1 4
x
khi x
f x
x
mx khi x
liên tục tại điểm
4
x
.
A.
7
4
m
. B.
8
m
. C.
7
4
m
. D.
8
m
.
Lời giải
Chọn A
Ta có
4
lim 4
x
f x f
4 1
m
;
2
4 4
16
lim lim
4
x x
x
f x
x
4
lim 4
x
x
8
.
Hàm số liên tục tại điểm
4
x
4 4
lim lim 4
x x
f x f x f
4 1 8
m
7
4
m
.
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Câu 41. Tìm tất cả các giá trị của tham số
m
để hàm số liên tục tại
2
x
.
A.
3
m
. B.
2m
. C.
2
m
. D. Không tồn tại
m
.
Lời giải
Chọn A
Ta có
2
2 2 2 2
2
2
lim lim lim lim 2
2 2
x x x x
x x
x x
f x x
x x
.
2 2
lim lim 4 2 4
x x
f x mx m
Hàm số liên tục tại
2
x
khi
2 2
lim lim 2 4 2 3
x x
f x f x m m
.
Câu 42. Cho hàm số
3
1
.
1
1
x m
khi x
f x
x
n khi x
Để hàm số liên tục tại
0
1x
thì giá trị của biểu
thức
m n
tương ứng bằng:
A.
3
.
4
B.
1.
C.
1
.
2
D.
9
.
4
Lời giải
Chọn D
Ta có:
1 .f n
2
1 1
3
lim lim .
1 3
x x
x m
f x
x x m
Hàm số liên tục tại
1x
2
1 1
3
lim 1 lim (1).
1 3
x x
x m
f x f n
x x m
1
lim
x
f x
tồn tại khi
1
là nghiệm của phương trình:
2
2
1 3 0 .
2
m
m
m
+ Khi
2m
thì
1 1
1 1 1
1 lim lim .
4
3 2
1 3 2
x x
x
n n n
x
x x
+ Khi
2m
thì
1
1
1 lim
3 2
x
n
x
suy ra không tồn tại
.n
Vậy
1 9
2 .
4 4
m n
Câu 43. Cho hàm số
3 2
6 11 6
khi 3
3
khi 3
x x x
x
f x
x
m x
. Tìm giá trị của
m
để hàm số liên tục tại
x
?
A.
1
m
. B.
2
m
. C.
3
m
. D.
0
m
.
Lời giải
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Chọn B
Ta có:
3
f m
.
3 2
3 3
6 11 6
lim lim
3
x x
x x x
f x
x
2
3
lim 3 2 2
x
x x
.
Câu 44. Giới hạn
2
0
cos3 cos7
lim
x
x x
x
. Tìm giá trị của
m
để hàm số liên tục tại
x
?
A.
40
. B.
0
. C.
4
. D.
20
.
Lời giải
Chọn B
Ta có:
2
0
cos3 cos7
lim
x
x x
x
2
0
2sin 5 sin 2
lim
x
x x
x
2.5.2 20
.
Câu 45. Tìm
m
để hàm số
2
2
2
1
( )
1
2 khi 1
x x
khi x
f x
x
mx m x
liên tục tại
1.
x
A.
3
1;
2
m
. B.
1
m
. C.
3
2
m
. D.
3
1; .
2
m
.
Lời giải
Chọn A
Tập xác định
D R
.
*
2
( 1) 2f m m
*
2 2
1 1
lim ( ) lim ( 2 ) 2
x x
f x mx m m m
.
*
2
1 1
2
lim ( ) lim
1
x x
x x
f x
x

1 1
( 1)( 2)
lim lim ( 2) 3.
1
x x
x x
x
x
 
Hàm số liên tục tại
1
x
khi và chỉ khi
1 1
lim ( ) lim ( ) ( 1)
x x
f x f x f
 
2 2
2 3 2 3 0
m m m m
1
.
3
2
m
m
Vậy các giá trị của m là
3
1; .
2
m
Câu 46. Tìm các giá trị của tham số
m
để hàm số
2
2
3 2
2
2
1 2
x x
khi x
f x
x x
mx m khi x
liên tục tại điểm
2
x
.
A.
1
6
m
. B.
1
6
m
. C.
1
2
m
. D.
1
2
m
.
Lời giải
Chọn B
Ta có:
2
2
2 2 2
2 1
3 2 1 1
lim lim lim
2 2 2
x x x
x x
x x x
x x x x x
.
2 3 1
f m
.
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Để hàm số liên tục tại điểm
2
x
1
3 1
2
m
1
6
m
.
Câu 47. Cho hàm số
2
2
4 2
khi 0
5
2 khi 0
4
x
x
x
f x
a x
. Tìm các giá trị thực của tham số
a
để hàm
số
f x
liên tục tại
0
x
.
A.
3
4
a
. B.
4
3
a
. C.
4
3
a
. D.
3
4
a
.
Lời giải
Chọn D
+ Ta có
5
0 2
4
f a
.
+
2 2
2
2
0 0 0 0
2 2
4 2 1 1
lim lim lim lim .
4
4 2
4 2
x x x x
x x
f x
x
x
x x
Hàm số
f x
liên tục tại
0
x
khi
0
5 1 3
lim 0 2
4 4 4
x
f x f a a
.
Câu 48. Cho hàm số
2
3
1 2 1
khi
4 3 1 2
, , ,
1
khi
2 2
ax bx
x
x x
f x a b c
c
x
. Biết hàm số liên tục tại
1
2
x
.
Tính
S abc
.
A.
36
S
. B.
18
S
. C.
36
S
. D.
18
S
.
Lời giải
Chọn A
Ta có
2
2
2
2 2
2
3
2 2
2 2
1 2
4 3
1 2
4 3 1
2 1 1 1 2 2 1 1 1 2
ax bx
a b x bx
ax bx
x x
x x ax bx x x ax bx
.
Để hàm số liên tục tại
2
2 2
3
4 3 2 1
1
3
2
1 2 0
3
4 2
m
a b x bx m x
x b
a b
a
.
Khi đó
2 2
3
2
1 1
2
2 2
1 2 12 12 3
lim lim
4 3 1
2 1 1 3 1 3 2
x x
ax bx x x
x x
x x x x
1
2
2
3 3
lim 2 4
3
2
1 3 1 3 2
2
x
c
c
x x x
.
Vậy
3 3 4 36
S abc
.
Câu 49. Tìm
a
để hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
a x
liên tục tại điểm
0
1
x
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
1
a
. B.
0
a
. C.
2
a
. D.
1
a
.
Lời giải
Chọn C
Tập xác định
D R
.
1
f a
.
2
1 1 1
1
lim lim lim 1 2
1
x x x
x
f x x
x
.
f x
liên tục tại
0
1
x
khi và chỉ khi
1
lim 1 2
x
f x f a
.
Câu 50. Tìm giá trị thực của tham số m để hàm số
2
2
khi 2
( )
2
khi =2
x x
x
f x
x
m x
liên tục tại x=2.
A.
3.
m
B.
1.
m
C.
2.
m
D.
0.
m
Lời giải
Chọn A
Ta có:
2
2 2 2
2 ( 2)( 1)
lim lim lim( 1) 3.
2 2
x x x
x x x x
x
x x
Hàm số liên tục tại x=2
2
lim ( ) (2) 3.
x
f x f m
Câu 51. Để hàm số
2
2 3 1
1
2 1
1
x x
khi x
x
f x
m khi x
liên tục tại
1x
thì giá trị
m
bằng
A.
0,5
. B.
1,5
. C.
1
. D.
2
.
Lời giải
Chọn A
1
f m
.
2
1 1 1 1
1 2 1
2 3 1 2 1 1
lim lim lim lim
2 1 2 1 2 2
x x x x
x x
x x x
f x
x x
.
Để hàm số
f x
liên tục tại
1x
thì
1
1
lim 1
2
x
f x f m
.
Câu 52. Cho hàm số
2
2
khi 1
1
3 khi 1
x x
x
f x
x
m x
. Tìm tất cả các giá trị thực của tham số m để hàm số
gián đoạn tại
1.
x
A.
2.
m
B.
1.
m
C.
2.
m
D.
3.
m
Lời giải
Tập xác định của hàm số là
.
Hàm số gián đoạn tại
1x
khi
2
1 1
2
lim 1 lim 3
1
x x
x x
f x f m
x
1 1
1 2
lim 3 lim 2 3 3 3 1.
1
x x
x x
m x m m m
x
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Câu 53. Tìm tất cả các giá trị của
m
để hàm số
1 1
khi 0
1
khi 0
1
x x
x
x
f x
x
m x
x
liên tục tại
0
x
.
A.
1
m
. B.
2
m
. C.
1
m
. D.
0
m
.
Lời giải
Ta có
0 0
1
lim lim 1
1
x x
x
f x m m
x
.
0 0
1 1
lim lim
x x
x x
f x
x
0 0
2 2
lim lim 1
1 1 1 1
x x
x
x x x x x
.
0 1
f m
Để hàm liên tục tại
0
x
thì
0 0
lim lim 0
x x
f x f x f
1 1 2
m m
.
Câu 54. Cho hàm số
1
khi 0
1
khi 0
2
ax
e
x
x
f x
x
. Tìm giá trị của
a
để hàm số liên tục tại
0
0
x
.
A.
1
a
. B.
1
2
a
. C.
1
a
. D.
1
2
a
.
Lời giải
Tập xác định:
D
.
0 0 0
1 1
lim lim lim .
ax ax
x x x
e e
f x a a
x ax
.
1
0
2
f
; hàm số liên tục tại
0
0
x
khi và chỉ khi:
0
1
lim 0
2
x
f x f a
.
Câu 55. Cho hàm số
2
2
( 2) 2
khi 1
( )
3 2
8 khi 1
ax a x
x
f x
x
a x
. Có tất cả bao nhiêu giá trị của
a
để hàm số
liên tục tại
1x
?
A.
1
. B.
0
. C.
3
. D.
2
.
Lời giải
Tập xác định:
3;D
.
1
lim
x
f x
2
1
2 2
lim
3 2
x
ax a x
x
.
1
1 2 3 2
lim
1
x
x ax x
x
.
1
lim 2 3 2
x
ax x
4 2
a
.
2
1 8
f a
.
Hàm số đã cho liên tục tại
1x
khi
1
lim 1
x
f x f
2
4 2 8
a a
0
4
a
a
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy có
2
giá trị của
a
để hàm số đã cho liên tục tại
1x
.
Câu 56. Giá trị của tham số
a
để hàm số
2 2
khi 2
2
2 khi 2
x
x
y f x
x
a x x
liên tục tại
2
x
.
A.
1
4
. B.
1
. C.
15
4
. D.
4
.
Lời giải
Ta có:
2 2 2 2
2 2 2 1 1
lim lim lim lim
2 4
2 2
2 2 2
x x x x
x x
f x
x
x
x x
.
Hàm số liên tục tại
2
x
2
lim 2
x
f x f
1
4
4
a
15
4
a
.
Câu 57. Hàm số
2
1 1
1
x khi x
f x
x m khi x
liên tục tại điểm
0
1
x
khi
m
nhận giá trị
A.
2
m
. B.
2
m
. C.
1
m
. D.
1
m
.
Lời giải
Ta có
2
1 1
lim lim 1 2
x x
f x x
;
1 1
lim lim 1
x x
f x x m m
. Để hàm số liên tục tại
0
1
x
thì
1 1
lim lim 2 1 1
x x
f x f x m m
.
Câu 58. Cho hàm số
2 1 5
khi 4
4
2 khi 4
x x
x
f x
x
a x
. Tìm tất cả các giá trị thực của tham số
a
để hàm số liên tục tại
0
4
x
.
A.
5
2
a
. B.
11
6
a
. C.
a
. D.
2
a
.
Lời giải
4 4 4 4
2 1 5 4 1 1
lim lim lim lim
4 6
2 1 5
4 2 1 5
x x x x
x x x
f x
x
x x
x x x
4 2
f a
.
Hàm số liên tục tại
0
4
x
khi:
4
lim 4
x
f x f
1
2
6
a
11
6
a
.
Câu 59. Tìm tham số thực
m
để hàm số
y f x
2
12
khi 4
4
1 khi 4
x x
x
x
mx x
liên tục tại điểm
0
4
x
.
A.
4
m
. B.
3
m
. C.
2
m
. D.
5
m
.
Lời giải
Tập xác định:
D
.
Ta có:
Điện thoại: 0946798489 TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
+
2
4 4
12
lim lim
4
x x
x x
f x
x

4
3 4
lim
4
x
x x
x
4
lim 3
x
x
7
.
+
4 4 1
f m
.
Hàm số
f x
liên tục tại điểm
0
4
x
khi và chỉ khi
4
lim 4
x
f x f
4 1 7
m
2
m
.
Câu 60. Tìm giá trị của tham số
m
để hàm số
3 1 2
khi 1
1
khi 1
x
x
f x
x
m x
liên tục tại điểm
0
1
x
.
A.
3
m
. B.
1
m
. C.
3
4
m
. D.
1
2
m
.
Lời giải
Ta có
1
3 1 2
lim
1
x
x
x
2
1
3 1 2
lim
1 3 1 2
x
x
x x
1
3 3
lim
4
3 1 2
x
x
.
Với
1
f m
ta suy ra hàm số liện tục tại
1
x
khi
3
4
m
.
Câu 61. Cho hàm số
2
3 2
khi 1
1
1
khi 1
4
x
x
x
f x
m m x
. Tìm tất cả các giá trị của tham số thực
m
để
hàm số
f x
liên tục tại
1x
.
A.
0;1
m
. B.
0; 1
m
. C.
1
m
. D.
0
m
.
Lời giải
Ta có
1 1 1
3 2 1 1
lim lim lim
1 4
3 2
x x x
x
f x
x
x
;
2
1
1
1 lim
4
x
f f x m m
.
Để hàm số
f x
liên tục tại
1x
thì
2
1 1
4 4
m m
1
0
m
m
.
Câu 62. Tìm
a
để hàm số liên tục trên
:
3 2
2 khi 1
2 2
khi 1.
1
x a x
f x
x x x
x
x
A.
2
a
. B.
1
a
. C.
2
a
. D.
1
a
.
Lời giải
Khi
1x
thì
2
f x x a
là hàm đa thức nên liên tục trên khoảng
;1
.
Khi
1x
thì
3 2
2 2
1
x x x
f x
x
là hàm phân thức hữu tỉ xác định trên khoảng
1;
nên
liên tục trên khoảng
1;
.
Xét tính liên tục của hàm số tại điểm
1x
, ta có:
+
1 2
f a
.
+
1 1
lim lim 2 2
x x
f x x a a
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+
2
3 2
2
1 1 1 1
1 2
2 2
lim lim lim lim 2 3
1 1
x x x x
x x
x x x
f x x
x x
.
Hàm số
f x
liên tục trên
hàm số
f x
liên tục tại
1x
1 1
lim lim 1
x x
f x f x f
2 1 3
a
1
a
.
Câu 63. Tìm tất cả các giá trị thực của
m
để hàm số
2
2
2
2
2
2
x x
khi x
f x
x
m khi x
liên tục tại
2
x
.
A.
3
m . B.
1
m
. C.
3
m
. D.
1
m
.
Lời giải
Hàm số
f x
liên tục tại
2
lim 2
x
f x f
2
2
2
2
lim
2
x
x x
m
x
2
3
m
3
m
.
Câu 64. Tìm
m
để hàm số
2
4 3
1
( )
1
2 1
x x
khi x
f x
x
mx khi x
liên tục tại điểm
1
x
.
A.
2
m
. B.
0
m
. C.
4
m
. D.
4
m
.
Lời giải
Ta có:
1
lim
x
f x
2
1
4 3
lim
1
x
x x
x
1
1 3
lim
1
x
x x
x
1
lim 3
x
x
2
.
1
lim
x
f x
1
lim 2
x
mx
2
m
.
1 2
f m
.
Để hàm số đã cho liên tục tại điểm
1
x
thì
1 1
lim lim 1
x x
f x f x f
2 2
m
0
m
.
Câu 65. Cho hàm số
3
8
2
2
2 1 2
x
khi x
f x
x
m khi x
. Tìm
m
để hàm số liên tục tại điểm
0
2
x
.
A.
3
2
m
. B.
13
2
m
. C.
11
2
m
. D.
1
2
m
.
Lời giải
2 2 1
f m
.
2
3
2
2 2 2 2
2 2 4
8
lim lim lim lim 2 4 12
2 2
x x x x
x x x
x
f x x x
x x
.
Hàm số liên tục tại
0
2
x
2
11
2 lim 2 1 12
2
x
f f x m m
.
Câu 66. Cho hàm số
2
2 2
2 8
khi 2
( )
2
5 khi 2
x x
x
f x
x
m x mx x
m
. Biết hàm số
f x
liên tục tại
0
2
x
.
Số giá trị nguyên của
m
thỏa mãn yêu cầu bài toán là
A.
3
. B.
2
. C.
1
. D.
0
.

Tài liệu khác của Toán 11

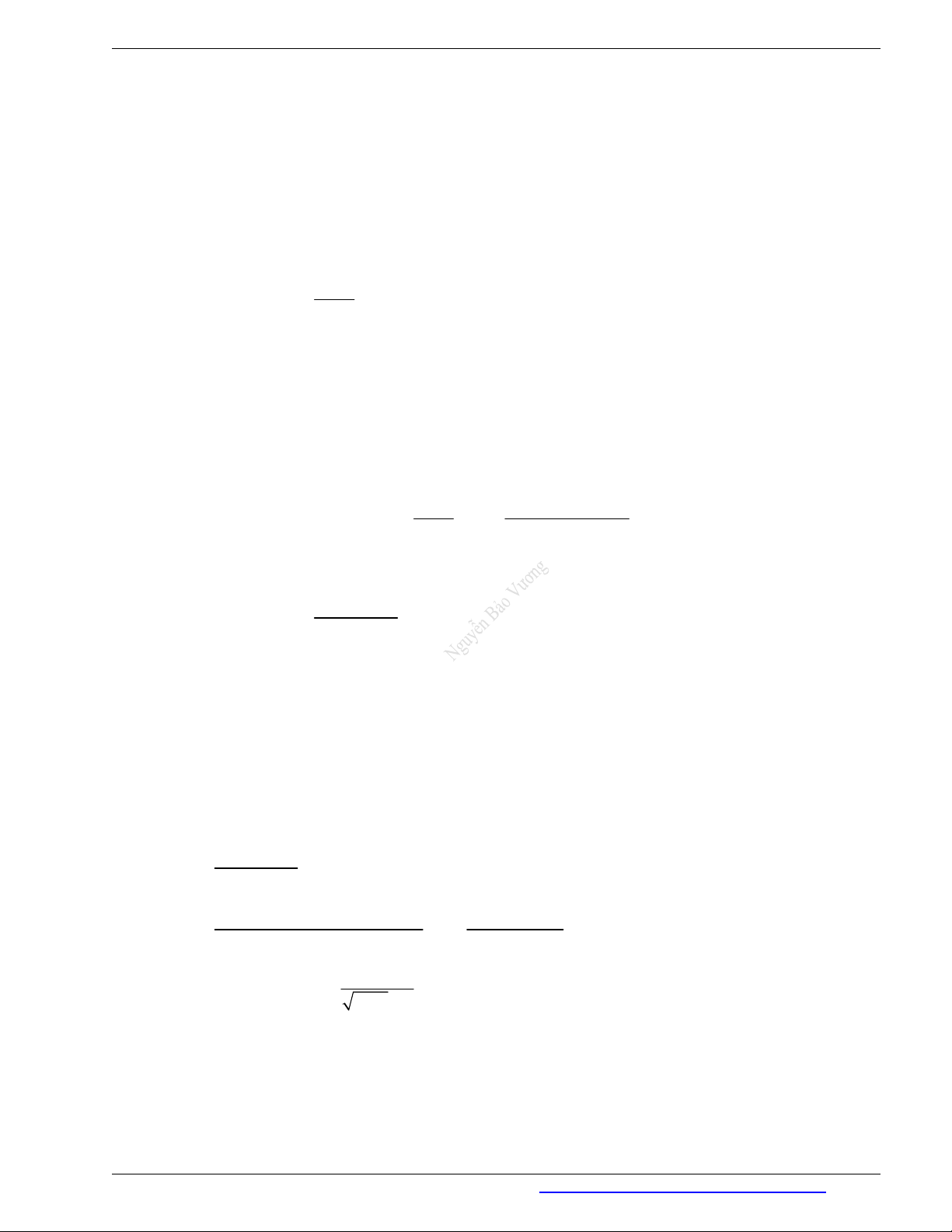
Preview text:

TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Điện thoại: 0946798489 BÀI 17. HÀM SỐ LIÊN TỤC
• CHƯƠNG 5. GIỚI HẠN
• |FanPage: Nguyễn Bảo Vương
PHẦN C. BÀI TẬP TRẮC NGHIỆM (PHÂN MỨC ĐỘ)
1. Câu hỏi dành cho đối tượng học sinh trung bình – khá Câu 1.
Cho hàm số y f x liên tục trên a;b . Điều kiện cần và đủ để hàm số liên tục trên a;b là
A. lim f x  f a và lim f x  f b .
B. lim f x  f a và lim f x  f b . x a  x b  x a  x b 
C. lim f x  f a và lim f x  f b .
D. lim f x  f a và lim f x  f b . x a  x b  x a  x b  Lời giải
Theo định nghĩa hàm số liên tục trên đoạn a;b . Chọn: lim f x  f a và lim f x  f b . x a  x b  Câu 2.
Cho hàm số f x xác định trên a;b . Tìm mệnh đề đúng.
A. Nếu hàm số f x liên tục trên a;b và f af b  0 thì phương trình f x  0 không có
nghiệm trong khoảng a;b .
B. Nếu f af b  0 thì phương trình f x  0 có ít nhất một nghiệm trong khoảng  ; a b .
C. Nếu hàm số f x liên tục, tăng trên a;b và f af b  0 thì phương trình f x  0
không có nghiệm trong khoảng  ; a b .
D. Nếu phương trình f x  0 có nghiệm trong khoảng  ;
a b thì hàm số f x phải liên tục trên a;b . Lời giải
Vì f af b  0 nên f a và f b cùng dương hoặc cùng âm. Mà f x liên tục, tăng trên
a;b nên đồ thị hàm f x nằm trên hoặc nằm dưới trục hoành trên a;b hay phương trình
f x  0 không có nghiệm trong khoảng a;b . Câu 3.
Cho hàm số y f (x) liên tục trên đoạn  ;
a b . Mệnh đề nào dưới đây đúng?
A. Nếu f (a). f (b)  0 thì phương trình f (x)  0 không có nghiệm nằm trong  ; a b .
B. Nếu f (a). f (b)  0 thì phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ; a b .
C. Nếu f (a). f (b)  0 thì phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ; a b .
D. Nếu phương trình f (x)  0 có ít nhất một nghiệm nằm trong  ;
a b thì f (a). f (b)  0 . Lời giải Chọn B
Vì theo định lý 3 trang 139/sgk. Câu 4.
Cho đồ thị của hàm số y f x như hình vẽ sau:
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ y 7 6 5 4 3 2 1 x -4 -3 -2 -1 1 2 3 4 5 -1 -2
Chọn mệnh đề đúng.
A. Hàm số y f x có đạo hàm tại điểm x  0 nhưng không liên tục tại điểm x  0 .
B. Hàm số y f x liên tục tại điểm x  0 nhưng không có đạo hàm tại điểm x  0 .
C. Hàm số y f x liên tục và có đạo hàm tại điểm x  0 .
D. Hàm số y f x không liên tục và không có đạo hàm tại điểm x  0 . Lời giải Chọn B
Đồ thị là một đường liền nét, nhưng bị “gãy” tại điểm x  0 nên nó liên tục tại điểm x  0 nhưng
không có đạo hàm tại điểm x  0 . Câu 5.
Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x  1 ? A. . B. . C. . D. . Lời giải Chọn D
Vì lim y  lim y nên hàm số không liên tục tại x  1 . x 1 x 1   Câu 6. Cho các mệnh đề:
1. Nếu hàm số y f x liên tục trên a;b và f a. f b  0 thì tồn tại x a;b sao cho 0   f x  0 . 0 
2. Nếu hàm số y f x liên tục trên a;b và f a. f b  0 thì phương trình f x  0 có nghiệm.
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
3. Nếu hàm số y f x liên tục, đơn điệu trên a;b và f a. f b  0 thì phương trình
f x  0 có nghiệm duy nhất.
A. Có đúng hai mệnh đề sai.
B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai.
D. Có đúng một mệnh đề sai. Lời giải Chọn D
Khẳng định thứ nhất sai vì thiếu tính liên tục trên đoạn a;b . 3 1   x  , khi x  1 Câu 7.
Cho hàm số y   1 x
. Hãy chọn kết luận đúng 1  , khi x  1 
A. y liên tục phải tại x  1 .
B. y liên tục tại x  1 .
C. y liên tục trái tại x  1 .
D. y liên tục trên  . Lời giải Chọn A Ta có: y   1  1 . 1 x   2 3 1 1  x x x
Ta có: lim y  1; lim y  lim  lim  lim         2 1 x x  4 x 1  x 1  x 1  1 x x 1  1 x x 1 
Nhận thấy: lim y y  
1 . Suy ra y liên tục phải tại x  1 . x 1  2
x  7x 12  khi x  3 Câu 8. Cho hàm số y   x  3
. Mệnh đề nào sau đây đúng? 1 khi x  3 
A. Hàm số liên tục nhưng không có đạo hàm tại x  3. 0
B. Hàm số gián đoạn và không có đạo hàm tại x  3. 0
C. Hàm số có đạo hàm nhưng không liên tục tại x  3. 0
D. Hàm số liên tục và có đạo hàm tại x  3. 0 Lời giải Chọn D 2 x  7x 12 lim
 lim  x  4  1
  y 3 nên hàm số liên tục tại x  3. 0 x3 x3 x  3  2
x  7x 12   2 3  7.3 12  2
x  7x 12 lim  lim
 lim  x  4  1
  y '3  1. x3 x3 x3 x  3 x  3  x  2 khi x  2  Câu 9.
Cho hàm số f x   x  2  2 . Chọn mệnh đề đúng? 4 khi x  2 
A. Hàm số liên tục tại x  2 .
B. Hàm số gián đoạn tại x  2 .
C. f 4  2 .
D. lim f x  2 . x2 Lời giải Chọn A
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
Tập xác định: D   x  2
x  2 x  2  2
lim f x  lim  lim
 lim  x  2  2  4 x2 x2 x  2  2 x2 x  2 x2 f 2  4
 lim f x  f 2 x2
Vậy hàm số liên tục tại x  2 . 2x 1
Câu 10. Cho hàm số f x 
. Kết luận nào sau đây đúng? 3 x x
A. Hàm số liên tục tại x  1 .
B. Hàm số liên tục tại x  0 . 1
C. Hàm số liên tục tại x  1 .
D. Hàm số liên tục tại x  . 2 Lời giải Chọn D 1 2x 1  1  Tại x
, ta có: lim f x  lim
 0  f   . Vậy hàm số liên tục tại x  2 . 2 3 1 1 xxx 1  2  2 2
Câu 11. Hàm số nào sau đây liên tục tại x 1 : 2 x x 1 2 x x  2 2 x x 1 x
A. f x 
. B. f x 
. C. f x 
. D. f x 1  . x 1  2 x 1  x x 1 Lời giải 2 x x 1
A) f x  x 1 
lim f x   suy ra f x không liên tục tại x 1.  x 1  2 x x  2
B) f x  2 x 1   f xx 2 lim  lim
  suy ra f x không liên tục tại x 1.   x 1  x 1  x 1 2 x x 1
C) f x  x 2  x f xx 1 lim  lim  3  f  
1 suy ra f x liên tục tại x 1. x 1  x 1  x x
D) f x 1  x 1  f xx 1 lim  lim
  suy ra f x không liên tục tại x 1.   x 1  x 1  x 1
Câu 12. Hàm số nào dưới đây gián đoạn tại điểm x  1. 0 2x 1 x x 1
A. y   x   2
1 x  2 . B. y  . C. y  . D. y  . x 1 x 1 2 x 1 Lời giải
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 2x 1 Ta có y
không xác định tại x  1 nên gián đoạn tại x  1. x 1 0 0
Câu 13. Hàm số nào sau đây gián đoạn tại x  2 ? 3x  4 A. y  .
B. y  sin x . C. 4 2
y x  2x 1
D. y  tan x . x  2 Lời giải Chọn A 3x  4 Ta có: y
có tập xác định: D   \  
2 , do đó gián đoạn tại x  2 . x  2 x
Câu 14. Hàm số y
gián đoạn tại điểm x bằng? x 1 0 A. x  2018 . B. x  1. C. x  0 D. x  1  . 0 0 0 0 Lời giải Chọn D x Vì hàm số y
có TXĐ: D   \  
1 nên hàm số gián đoạn tại điểm x  1  . x 1 0 x  3
Câu 15. Cho hàm số y
. Mệnh đề nào sau đây đúng? 2 x 1
A. Hàm số không liên tục tại các điểm x  1 .
B. Hàm số liên tục tại mọi x   .
C. Hàm số liên tục tại các điểm x  1 .
D. Hàm số liên tục tại các điểm x  1 . Lời giải Chọn A x  3 Hàm số y
có tập xác định  \  
1 . Do đó hàm số không liên tục tại các điểm x  1 . 2 x 1
Câu 16. Trong các hàm số sau, hàm số nào liên tục trên  ? 2x 1 A. 3
y x x .
B. y  cot x . C. y  . D. 2 y x 1 . x 1 Lời giải Chọn A Vì 3
y x x là đa thức nên nó liên tục trên  . 3x 1
Câu 17. Cho bốn hàm số f x 3
 2x  3x 1, f x  , f
x  cos x  3 và f
x  log x . Hỏi có 4   3   2   1 x  2 3
bao nhiêu hàm số liên tục trên tập  ? A. 1. B. 3 . C. 4 . D. 2 . Lời giải 3x 1
* Ta có hai hàm số f x  và f
x  log x có tập xác định không phải là tập  nên không 4   2   x  2 3 thỏa yêu cầu.
* Cả hai hàm số f x 3
 2x  3x 1 và f
x  cos x  3 đều có tập xác định là  đồng thời liên tục 3   1 trên  .
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
Câu 18. Trong các hàm số sau, hàm số nào liên tục trên  ? 2 x  3 x  5
A. f x  tan x  5 .
B. f x  .
C. f x  x  6 .
D. f x  . 5  x 2 x  4 Lời giải Chọn D x  5
Hàm số f x 
là hàm phân thức hữu tỉ và có TXĐ là D   do đó hàm số 2 x  4 x  5 f x  liên tục trên  . 2 x  4
2. Câu hỏi dành cho đối tượng học sinh khá-giỏi 1   cos x  khi x  0
Câu 19. Cho hàm số f x 2   x . 1  khi x  0 
Khẳng định nào đúng trong các khẳng định sau?
A. f x có đạo hàm tại x  0 .
B. f  2   0 .
C. f x liên tục tại x  0 .
D. f x gián đoạn tại x  0 . Lời giải
Hàm số xác định trên x 2 2sin 1 cos x 1
Ta có f 0  1 và f x 2 lim  lim  lim  2 2 x0 x0 x0 xx 2  4.   2 
Vì f 0  lim f x nên f x gián đoạn tại x  0 . Do đó f x không có đạo hàm tại x  0 . x0 1 cos x x
  0 f x 
 0 nên f  2   0.VậyA, B,C sai. 2 x
x cos x, x  0  2  x
Câu 20. Cho hàm số f x  , 0  x  1 
. Khẳng định nào sau đây đúng? 1 x  3 x , x  1 
A. Hàm số f x liên tục tại mọi điểm x thuộc  .
B. Hàm số f x bị gián đoạn tại điểm x  0 .
C. Hàm số f x bị gián đoạn tại điểm x  1 .
D. Hàm số f x bị gián đoạn tại điểm x  0 và x  1 . Lời giải
* f x liên tục tại x  0 và x  1. * Tại x  0 2 x
lim f x  lim x cos x  0 , lim f x  lim
 0 , f 0  0 . x 0 x 0   x 0 x 0   1 x
Suy ra lim f x  lim f x  f 0 . Hàm số liên tục tại x  0 . x 0 x 0   * Tại x  1
Trang 6 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 2 x 1
lim f x  lim  , lim f x 3  lim x  1. x 1 x 1   1 x 2 x 1 x 1  
Suy ra lim f x  lim f x . Hàm số gián đoạn tại x  1 . x 1 x 1   2  x  4  khi x  2 
Câu 21. Tìm m để hàm số f (x)   x  2
liên tục tại x  2  m khi x  2  A. m  4 . B. m  2 . C. m  4 . D. m  0 . Lời giải Chọn A 2  x  4 
Hàm số liên tục tại x  2 khi và chỉ khi lim
 lim m m m  4    x 2  x 2 x  2    3  x 1  khi x  1
Câu 22. Cho hàm số y f (x)   x 1
. Giá trị của tham số m để hàm số liên tục tại điểm
2m 1 khi x  1  x  1 là: 0 1 A. m   . B. m  2 . C. m  1. D. m  0 . 2 Lời giải Chọn C
Ta có f (1)  2m 1 3 x 1 2 lim y  lim
 lim(x x 1)  3 x 1  x 1  x 1 x 1 
Để hàm số liên tục tại điểm x  1thì f (1)  lim y  2m  1  3  m  1. 0 x 1  2
x  3x  2 khi x  1 
Câu 23. Để hàm số y  
liên tục tại điểm x  1
 thì giá trị của a là 4x a khi x  1   A. 4  . B. 4. C. 1. D. 1. Lời giải Chọn B
Hàm số liên tục tại x  1
 khi và chỉ khi lim y  lim y  y   1 x 1 x 1  
 lim 4x a  lim    
a  4  0  a  4 .    2 x
3x 2 y   1 x 1  x 1  3 2
x x  2x  2  khi x  1
Câu 24. Tìm giá trị thực của tham số m để hàm số f x   x 1
liên tục tại x 1. 3  x m khi x  1  A. m  0. B. m  6. C. m  4 . D. m  2 . Lời giải Chọn A Ta có: f   1  m  3.
x x x   x   1  2 3 2 x  2 2 2 
lim f x  lim  lim  lim  2 x  2  3. x 1  x 1  x 1  x 1 x 1 x 1 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
Để hàm số f x liên tục tại x 1 thì lim f x   f 1  3  m  3  m  0 . x 1 2016  xx  2  khi x  1
Câu 25. Cho hàm số f x   2018x 1  x  2018
. Tìm k để hàm số f x liên tục tại k khi x  1  x  1 . 2017. 2018 20016
A. k  2 2019 . B. k  . C. k  1 . D. k  2019 . 2 2017 Lời giải Chọn A xx   2016 2016 x 1 x  
1  2018x 1  x  2018 2  Ta có: lim  lim x 1  x 1
2018x 1  x  2018  2017x  2017  x   1  2015 2014 xx
 ...  x 1 
1  2018x 1  x  2018  lim  2 2019 x 1  2017  x   1
Để hàm số liên tục tại x  1  lim f x  f   1  k  2 2019 . x 1   x 1  khi x  1
Câu 26. Cho hàm số f x   x 1
. Tìm a để hàm số liên tục tại x  1. 0 a khi x  1  1 1 A. a  0 . B. a   . C. a  . D. a  1 . 2 2 Lời giải Chọn C x 1 x 1 1 1
Ta có lim f x  lim  lim  lim  . x 1  x 1  x 1 x 1   x   1  x   1 x 1  x 1 2 1
Để hàm số liên tục tại x  1 khi lim f x  f   1  a  . 0 x 1  2
 x b khi x   
Câu 27. Biết hàm số f x  3 1  
liên tục tại x  1
. Mệnh đề nào dưới đây đúng? x
  a khi x  1 
A. a b  2 . B. a  2  b .
C. a  2  b .
D. a b  2 . Lời giải Chọn A
lim f x  f  
1  b  3 ; lim f x  a  1. Để liên tục tại x=-1 ta có b  3  a  1  a b  2 x 1  x 1   3  x khi x  3 
Câu 28. Cho hàm số f x   x 1  2
. Hàm số đã cho liên tục tại x  3 khi m  ? m khi x=3  A. 1  . B. 1. C. 4 . D. 4 . Lời giải Chọn D
Trang 8 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG f 3  m 3  x
3  x x 1  2 lim f  x  lim  lim
 lim  x 1  2  4 x3 x3 x  1  2 x3 x  3 x3
Để hàm số liên tục tại x  3 thì lim f  x  f 3 x3 Suy ra, m  4  . 2
ax bx  5 khi x  1
Câu 29. Biết hàm số f x  
liên tục tại x  1 Tính giá trị của biểu thức 2ax  3b khi x  1 
P a  4b . A. P  4 . B. P  5 . C. P  5 . D. P  4 . Lời giải Chọn B
Ta có: lim f x  lim       .    2 ax bx 5 a b 5 f   1 x 1  x 1 
lim f x  lim 2ax  3b  2a  3b . x 1 x 1  
Do hàm số liên tục tại x  1 nên a b  5  2a  3b a  4b  5 . 2  x xkhi x  1
Câu 30. Tìm m để hàm số f (x)   x 1
liên tục tại x  1
m 1 khi x  1  A. m  0 . B. m  1. C. m  1 D. m  2 . Lời giải Chọn D TXĐ: D R 2 x x
Ta có lim f (x)  lim  lim x  1 x 1  x 1  x 1 x 1 
Và f (1)  m 1.
Hàm số liên tục tại x  1  m 1  1  m  2 2
x  3x  2  khi x  1
Câu 31. Có bao nhiêu số tự nhiên m để hàm số f x   x 1
liên tục tại điểm x  1?  2 m m 1 khi x  1  A. 0. B. 3 . C. 2 . D. 1. Lời giải Chọn D 2 x  3x  2  x   1  x  2 lim  lim
 lim x  2  1  . x 1  x 1 x 1  x 1 x 1 
Để hàm số f x liên tục tại điểm x  1 cần: lim f x  f   1 x 1  2
m m  1  1 m  0 (TM) 2
m m  0   . m  1  (L) 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/x  2  2  khi x  2
Câu 32. Tìm a để hàm số f x   x  2
liên tục tại x  2 ? 2x a khi x  2  15 15 1 A. . B.  . C. . D. 1 . 4 4 4 Lời giải Chọn B
Ta có f 2  4  a . x  2  4 1 1
Ta tính được lim f x  lim  lim  . x2
x2  x  2 x  2  2 x2 x  2  2 4 1 15
Hàm số đã cho liên tục tại x  2 khi và chỉ khi f 2  lim f x  4  a   a   . x2 4 4 15
Vậy hàm số liên tục tại x  2 khi a   . 4 2
x 3x2  khi x  2 
Câu 33. Cho hàm số f x   x  2 2 
, m là tham số. Có bao nhiêu giá trị của m để hàm  2 m
x4m6 khi x  2 
số đã cho liên tục tại x  2 ? A. 3 . B. 0 . C. 2 . D. 1 Lời giải Chọn D Ta có 2 x x
x  2 x   1  x  2  2 3 2 
lim f (x)  lim  lim  lim  x   1         x 2 2 4 x2 x2 x2 x2 x  2  2 x  2
lim f (x)  lim         2 m x 4m 6 2 2m 4m 6 x2 x2 2
f (2)  2m  4m  6
Để hàm số liên tục tại x  2 thì 2 2
lim f (x)  lim f (x)  f (2)  2m  4m  6  4  2m  4m  2  0  m  1 x 2 x 2  
Vậy có một giá trị của m thỏa mãn hàm số đã cho liên tục tại x  2 . 2
 3x  2x 1  2  , x  1
Câu 34. Cho hàm số f x 2   x 1
. Hàm số f x liên tục tại x 1 khi 0 4  m x  1  A. m  3 . B. m  3  . C. m  7 . D. m  7  . Lời giải Chọn A
Tập xác định D   , x  1  . 0 Ta có f   1  4  m .
Trang 10 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 2
3x  2x 1  2  x   1 3x  5
lim f x  lim  lim x 1  x 1   x   1  x   1 x 1   x   1  x   1  2
3x  2x 1  2 3x  5  lim  1 x 1   x   1  2
3x  2x 1  2
Hàm số f x liên tục tại x 1 khi và chỉ khi lim  x  f  
1  4  m  1  m  3 . 0 x 1  2
x  3x  2  khi x  1
Câu 35. Tìm giá trị của tham số m để hàm số f x 2   x 1
liên tục tại x  1 . mx  2 khi x  1  3  5  3 5 A. m  . B. m  .
C. m  . D. m  . 2 2 2 2 Lời giải Chọn D - Ta có: + f   1  m   2 .
+ lim f x  m   2.  x     1 2 x  3x  2
x 1 x  2 x  2 1
+ lim f x  lim  lim  lim  .   2 x     1 x     1 x 1   x  1  x   1  x 1 x  1 x 1 2 1 5
- Hàm số liên tục tại x  1  f  
1  lim f x  lim f x  m  2   m  .   x     1 x     1 2 2 2  x  4  2  khi x  0 2 
Câu 36. Cho hàm số ( ) x f x  
. Tìm giá trị thực của tham số a để hàm số f ( x) 5 2a  khi x  0   4
liên tục tại x  0 . 3 4 4 3 A. a   . B. a  . C. a   . D. a  . 4 3 3 4 Lời giải . Chọn D
Tập xác định: D   . x  
 2x  4 2 2 2 x  4  2 4 2 
lim f (x)  lim  lim 2 x0 x0 x0 2 x x  2 x  4  2 2 x  4  4 1 1  lim  lim  . x 0  2 2 x 0  2 4
x ( x  4  2) x  4  2 5 f (0)  2a  . 4 5 1 3
Hàm số f ( x) liên tục tại x  0  lim f (x)  f (0)  2a    a  . x 0  4 4 4 3 Vậy a  . 4
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ 2
x  2x  3 khi x  1
Câu 37. Cho hàm số f x  
. Tìm m để hàm số liên tục tại x  1. 0
3x m 1 khi x  1  A. m  1. B. m  3 . C. m  0 . D. m  2 . Lời giải Chọn C TXĐ D   Ta có f   1  2  m .
lim f x  lim 2
x  2x  3  2 . x 1  x 1 
Hàm số liên tục tại x  1  lim f x  f  
1  2  m  2  m  0 . 0 x 1  2
x  3x  2  khi x  2
Câu 38. Cho hàm số f (x)   x  2
. Hàm số liên tục tại x  2 khi a bằng a khi x  2  A. 1. B. 0 . C. 2 . D. 1  . Lời giải Chọn A
Hàm số liên tục tại x  2  lim f (x)  f (2) . x2 2 x  3x  2
Ta có f (2)  a, lim f (x)  lim
 lim(x 1)  1 . Do đó a  1 x2 x2 x2 x  2  3  x khi x  3 
Câu 39. Cho hàm số f x   x 1  2
. Hàm số liên tục tại điểm x  3 khi m bằng: mx  2 khi x  3  A. 2  . B. 4 . C. 4 . D. 2 . Lời giải Chọn A
Tập xác định D . 3  x
Ta có f 3  3m  2 và lim f x  lim lim   x 1 2      4  . x 3  x3 x 1  2 x3  
Hàm số đã cho liên tục tại điểm x  3  lim f x  f 3  3m  2  4   m  2 . x3 2  x 16  khi x  4
Câu 40. Tìm m để hàm số f x   x  4
liên tục tại điểm x  4 .
mx 1 khi x  4  7 7 A. m  . B. m  8 . C. m   . D. m  8  . 4 4
Lời giải Chọn A 2 x 16
Ta có lim f x  f 4  4m 1; lim f x  lim
 lim  x  4  8. x 4  x 4 x 4   x  4 x 4  7
Hàm số liên tục tại điểm x  4  lim f x  lim f x  f 4  4m 1  8  m  . x 4 x 4   4
Trang 12 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Câu 41. Tìm tất cả các giá trị của tham số m để hàm số
liên tục tại x  2 .
A. m  3 . B. m  2 .
C. m  2 .
D. Không tồn tại m . Lời giải Chọn A 2 x  2x x x  2
Ta có lim f x  lim  lim  lim x  2 . x 2 x 2 x 2 x 2 x  2 x  2     
lim f x  lim mx  4  2m  4 x 2 x 2  
Hàm số liên tục tại x  2 khi lim f x  lim f x  2m  4  2  m  3. x 2 x 2  
 x  3 mkhi x  1
Câu 42. Cho hàm số f x    . x  1 x 1 
Để hàm số liên tục tại
 thì giá trị của biểu 0 nkhi x  1 
thức m n tương ứng bằng: 3 1 9 A. . B. 1. C.  . D. . 4 2 4 Lời giải Chọn D Ta có: f   1  n. x m lim f x  3  2  lim . x 1
x1 x  
1  x  3  m 2 x  3  m
Hàm số liên tục tại x  1  lim f x   f   1  n  lim (1). x 1  x 1  x  
1  x  3 mm   2 lim f x 
tồn tại khi 1 là nghiệm của phương trình: 2 1  3  m  0  .  x 1 m  2  x  1 1 1
+ Khi m  2 thì   1  n  lim  n  lim  n  . x 1  x   1  x  3  2 x 1  x  3  2 4 1
+ Khi m  2 thì   1  n  lim
suy ra không tồn tại n. x 1 x  3  2 1 9
Vậy m n  2   . 4 4 3 2
x  6x 11x  6  khi x  3
Câu 43. Cho hàm số f x   x  3
. Tìm giá trị của m để hàm số liên tục tại m khi x  3  x  3? A. m  1. B. m  2 . C. m  3 . D. m  0 . Lời giải
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Chọn B
Ta có: f 3  m . 3 2
x  6x 11x  6
lim f x  lim  lim  2
x  3x  2  2 . x 3  x 3  x  3 x3
cos 3x  cos 7x
Câu 44. Giới hạn lim
. Tìm giá trị của m để hàm số liên tục tại x  3 ? 2 x0 x A. 40 . B. 0 . C. 4  . D. 20 . Lời giải Chọn B
cos 3x  cos 7x 2sin 5x sin 2x Ta có: lim  lim  2.5.2  20 . 2 x0 x 2 x0 x 2
x x  2  khi x  1 
Câu 45. Tìm m để hàm số f (x)   x 1
liên tục tại x  1. 2
mx  2m khi x  1    3   3   3  A. m  1  ;   . B. m   1 .
C. m    . D. m   1  ; ..  2   2   2  Lời giải Chọn A
Tập xác định D R . * 2 f ( 1
 )  m  2m * 2 2
lim f (x)  lim (mx  2m )  m  2m . x 1 x 1   2 x x  2
(x 1)(x  2)
* lim f (x)  lim  lim  lim (x  2)  3  . x 1 x 1   x 1 x 1 x 1 x 1   
Hàm số liên tục tại x  1
 khi và chỉ khi lim f (x)  lim f (x)  f ( 1  ) x 1 x 1   m  1 2 2
 m  2m  3
  2m m  3  0   . 3 m    2  3 
Vậy các giá trị của m là m  1  ;  .  2  2
x  3x  2  khi x  2
Câu 46. Tìm các giá trị của tham số m để hàm số f x 2   x  2x liên tục tại điểm
mx m 1 khi x  2  x  2 . 1 1 1 1 A. m  . B. m   . C. m   . D. m  . 6 6 2 2 Lời giải Chọn B 2 x  3x  2
x  2 x   1 x 1 1 Ta có: lim  lim  lim  . 2 x2 x2 x  2x x x  2 x2 x 2
f 2  3m 1 .
Trang 14 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 1 1
Để hàm số liên tục tại điểm x  2  3m 1   m   . 2 6 2  x  4  2  khi x  0 2  Câu 47. Cho hàm số   x f x  
. Tìm các giá trị thực của tham số a để hàm 5
2a  khi x  0   4
số f x liên tục tại x  0 . 3 4 4 3 A. a   . B. a  . C. a   . D. a  . 4 3 3 4 Lời giải Chọn D 5
+ Ta có f 0  2a  . 4 2 2 x  4  2 x  1  1
+ lim f x  lim  lim  lim    . 2 x0 x0 x0 2 x x  2
x  4  2 x0 2 4  x  4  2  5 1 3
Hàm số f x liên tục tại x  0
lim f x f 0  2a    a  . khi     x 0  4 4 4 2
ax 1  bx  2 1  khi x  3  1
Câu 48. Cho hàm số f x 4x  3x 1 2   , a, ,
b c   . Biết hàm số liên tục tại x  . c 1  2 khi x    2 2
Tính S abc . A. S  3  6 . B. S  18 . C. S  36 . D. S  1  8. Lời giải Chọn A
ax   bx
ax 12 bx22 2  2 a b  2 2 x  4bx  3 1 2 Ta có   . 3 4x  3x 1 2x  2 1  x  
1  ax 1  bx  2 2x  2 2 1  x   1  2
ax 1  bx  2
a b x  4bx  3  m2x  2 2 2 1 m  3  1  
Để hàm số liên tục tại x     b   3 . 2 a b  1   2  0 a  3 4 2   2 2
ax 1  bx  2 1
 2x 12x  3 Khi đó lim  lim 3 1 1 x 4x  3x 1 x 2x  2 1  x   1  2 3
x 1  3x  2 2 2  3  3  c  lim   2    c  4  . 1 x  x   2 3 2 1 3
x 1  3x  2 2  2
Vậy S abc  3   3   4    3  6 . 2  x 1  khi x  1
Câu 49. Tìm a để hàm số f x   x 1
liên tục tại điểm x  1. 0 a khi x  1 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
A. a  1.
B. a  0 .
C. a  2 . D. a  1  . Lời giải Chọn C
Tập xác định D R . f   1  a . 2 x 1
lim f x  lim  lim  x   1  2 . x 1  x 1  x 1 x 1 
f x liên tục tại x  1 khi và chỉ khi lim f x  f   1  a  2 . 0 x 1  2
x x  2  khi x  2
Câu 50. Tìm giá trị thực của tham số m để hàm số f (x)   x  2
liên tục tại x=2. m  khi x=2 
A. m  3.
B. m  1.
C. m  2. D. m  0. Lời giải Chọn A 2 x x  2
(x  2)(x 1) Ta có: lim  lim  lim(x 1)  3. x2 x2 x2 x  2 x  2
Hàm số liên tục tại x=2  lim f (x)  f (2)  m  3. x2 2
 2x  3x 1 khi x 1 
Câu 51. Để hàm số f x  2   x   1
liên tục tại x  1 thì giá trị m bằng m khi x  1  A. 0, 5 . B. 1,5. C. 1. D. 2 . Lời giải Chọn A f   1  m . 2 2x  3x 1  x   1 2x   1 2x 1 1
lim f x  lim  lim  lim  . x 1  x 1  2  x   x 1 1  2  x   x 1 1  2 2 1
Để hàm số f x liên tục tại x  1 thì lim f x  f   1  m  . x 1  2 2
x x  2  khi x  1
Câu 52. Cho hàm số f x   x 1
. Tìm tất cả các giá trị thực của tham số m để hàm số 3  m khi x 1 
gián đoạn tại x  1. A. m  2. B. m  1. C. m  2. D. m  3. Lời giải
Tập xác định của hàm số là .  2 x x  2
Hàm số gián đoạn tại x  1 khi lim f x  f   1  lim  3m x 1  x 1  x 1  x   1  x  2  lim
 3m  lim x  2  3m  3  3m m  1. x 1  x 1 x 1 
Trang 16 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
 1 x  1 x khi x  0  
Câu 53. Tìm tất cả các giá trị của m để hàm số   x f x  
liên tục tại x  0 . 1 xm  khi x  0   1 x
A. m  1.
B. m  2 . C. m  1. D. m  0 . Lời giải Ta có  1 x
lim f x  lim m   m 1   . x 0 x 0    1 x
 1 x  1 x  2  x 2 
lim f x  lim    lim  lim  1  . x 0 x 0    x      x0
x  1 x  1 x x0  1 x  1 x
f 0  m 1
Để hàm liên tục tại x  0 thì lim f x  lim f x  f 0  m 1  1  m  2 . x 0 x 0   axe 1 khi x  0   x
Câu 54. Cho hàm số f x  
. Tìm giá trị của a để hàm số liên tục tại x  0 . 0 1  khi x  0   2 1 1 A. a  1 . B. a  . C. a  1 . D. a   . 2 2 Lời giải
Tập xác định: D   . ax e 1 ax e 1
lim f x  lim  lim .a a . x0 x0 x0 x ax 1 1 f 0 
; hàm số liên tục tại x  0 khi và chỉ khi: lim f x  f 0  a  . 2 0 x0 2 2
ax  (a  2)x  2 khi x 1 
Câu 55. Cho hàm số f (x)   x  3  2
. Có tất cả bao nhiêu giá trị của a để hàm số  2
8  a khi x  1 
liên tục tại x  1 ? A. 1. B. 0 . C. 3 . D. 2 . Lời giải
Tập xác định: D  3;   . 2
ax  a  2 x  2
lim f x  lim . x 1  x 1  x  3  2  x  
1 ax  2 x  3  2  lim . x 1  x 1
 lim ax  2 x  3  2  4a  2 . x 1  f   2 1  8  a . a  0
Hàm số đã cho liên tục tại x  1 khi lim f x  f   1  a   2 4 2  8  a   . x 1  a  4 
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
Vậy có 2 giá trị của a để hàm số đã cho liên tục tại x  1 .  x  2  2  khi x  2
Câu 56. Giá trị của tham số a để hàm số y f x   x  2
liên tục tại x  2 . a  2x khi x  2  1 15 A. . B. 1. C.  . D. 4 . 4 4 Lời giải x  2  2 x  2 1 1
Ta có: lim f x  lim  lim  lim  . x2 x2 x2 x  2
x  2 x  2  2 x2 x  2  2 4 1 15
Hàm số liên tục tại x  2  lim f x  f 2  a  4   a   . x2 4 4 2
x 1 khi x  1
Câu 57. Hàm số f x  
liên tục tại điểm x  1 khi m nhận giá trị 0
x m khi x  1  A. m  2 . B. m  2 . C. m  1. D. m  1. Lời giải
Ta có lim f x  lim  2 x
 ; lim f x  lim  x m  1 m . Để hàm số liên tục tại x  1    1 2 0 x 1  x 1  x 1 x 1  
thì lim f x  lim f x  2  m 1  m  1. x 1 x 1  
 2x 1  x  5  khi x  4
Câu 58. Cho hàm số f x   x  4
. Tìm tất cả các giá trị thực của tham số a a  2 khi x  4 
để hàm số liên tục tại x  4 . 0 5 11 A. a . B. a   .
C. a  3.
D. a  2 . 2 6 Lời giải
2x 1  x  5 x  4 1 1
lim f x  lim  lim  lim  x4 x4 x4 x  4
x  4 2x 1  x  5 x4 2x 1  x  5 6
f 4  a  2 . 1 11
Hàm số liên tục tại x  4 khi: lim f x  f 4 
a  2  a   . 0 x4 6 6 2
x x 12  khi x  4
Câu 59. Tìm tham số thực m để hàm số y f x   x  4
liên tục tại điểm x  4  . 0
mx 1 khi x  4  A. m  4 . B. m  3 . C. m  2 . D. m  5 . Lời giải
Tập xác định: D   . Ta có:
Trang 18 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Điện thoại: 0946798489
TOÁN 11-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 2 x x 12
x  3 x  4
+ lim f x  lim  lim
 lim  x  3  7  . x4 x4 x  4 x4 x  4 x4 + f  4    4  m 1.
Hàm số f x liên tục tại điểm x  4
 khi và chỉ khi lim f x  f 4  4m 1  7 0 x4  m  2 .  3x 1  2  khi x  1
Câu 60. Tìm giá trị của tham số m để hàm số f x   x 1
liên tục tại điểm x  1. 0 m khi x  1  3 1 A. m  3 . B. m  1 . C. m  . D. m  . 4 2 Lời giải 3x  1  2 2 3x  1  2 3 3 Ta có lim  lim  lim  . x 1  x  1 x 1   x   1  3x 1  2 x 1  3x  1  2 4 3 Với f  
1  m ta suy ra hàm số liện tục tại x 1 khi m  . 4  x  3  2 khi  x    1 
Câu 61. Cho hàm số f xx 1  
. Tìm tất cả các giá trị của tham số thực m để 1  2 m m  khi  x   1   4
hàm số f x liên tục tại x  1 . A. m 0  ;1 .
B. m 0;   1 . C. m   1 . D. m   0 . Lời giải x  3  2 1 1 1
Ta có lim f x  lim  lim  ; f  
1  lim f x 2  m m  . x 1 x 1 x 1 x 1     x  3  2 4 x 1  4 1 1 m  1
Để hàm số f x liên tục tại x  1 thì 2 m m     . 4 4 m  0  2x a khi x  1 
Câu 62. Tìm a để hàm số liên tục trên  : f x 3 2
  x x  2x  2 khi x  1.   x 1 A. a  2  . B. a  1. C. a  2 . D. a  1  . Lời giải
 Khi x 1 thì f x  2x a là hàm đa thức nên liên tục trên khoảng   ;1 . 3 2
x x  2x  2
 Khi x  1 thì f x 
là hàm phân thức hữu tỉ xác định trên khoảng 1;   nên x 1
liên tục trên khoảng 1;   .
 Xét tính liên tục của hàm số tại điểm x  1, ta có: + f   1  2  a .
+ lim f x  lim 2x a  2  a . x 1 x 1  
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/
x x x   x   1  2 3 2 x  2 2 2 
+ lim f x  lim  lim  lim   .      2 x 2 3 x 1  x 1  x 1  x 1 x 1 x 1 
 Hàm số f x liên tục trên   hàm số f x liên tục tại x  1
 lim f x  lim f x  f  
1  2a 1  3  a  1. x 1 x 1   2
x x  2  khi x  2
Câu 63. Tìm tất cả các giá trị thực của m để hàm số f x   x  2
liên tục tại x  2 . 2 m khi x  2  A. m  3 .
B. m  1.
C. m   3 . D. m  1. Lời giải 2 x x  2
Hàm số f x liên tục tại  lim f x  f 2 2  lim  m 2
 3  m m   3 . x2 x2 x  2 2
x  4x  3  khi x  1
Câu 64. Tìm m để hàm số f (x)   x 1
liên tục tại điểm x  1  . mx  2 khi x  1   A. m  2 . B. m  0 . C. m  4 . D. m  4 . Lời giải 2 x  4x  3  x   1  x  3
Ta có: lim f x  lim  lim
 lim  x  3  2 .     x  1 x  1 x 1 x     1 x 1 x  1
lim f x  lim mx  2  m  2 .   x  1 x  1 f   1  m  2 .
Để hàm số đã cho liên tục tại điểm x  1 thì
lim f x  lim f x  f  
1  2  m  2  m  0 .   x  1 x  1 3  x  8  khi x  2
Câu 65. Cho hàm số f x   x  2
. Tìm m để hàm số liên tục tại điểm x  2 . 0
2m 1 khi x  2  3 13 11 1 A. m  . B. m  . C. m  . D. m   . 2 2 2 2 Lời giải
f 2  2m 1. x   x  2 2 3 x  2x  4 8 
lim f x  lim  lim  lim  2
x  2x  4  12 . x2 x2 x2 x2 x  2 x  2 11
Hàm số liên tục tại x  2  f 2  lim f x  2m 1  12  m  . 0 x2 2 2
 x  2x  8  khi x  2 
Câu 66. Cho hàm số f (x)   x  2
m . Biết hàm số f x liên tục tại x  2 . 0 2 2 m x  5mx khi x  2  
Số giá trị nguyên của m thỏa mãn yêu cầu bài toán là A. 3 . B. 2 . C. 1. D. 0 .
Trang 20 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/

Tài liệu liên quan: