Bài 2: Ước Lượng Khoảng Tin Cậy cho μ môn Xác suất thống kê| Trường Đại học Ngoại Thương

17:47, 27/01/2026
XSTK - Bài 2: Ước Lượng Khoảng Tin Cậy cho μ - Studocu
BÀI 2: ƯỚC LƯỢNG KHOẢNG
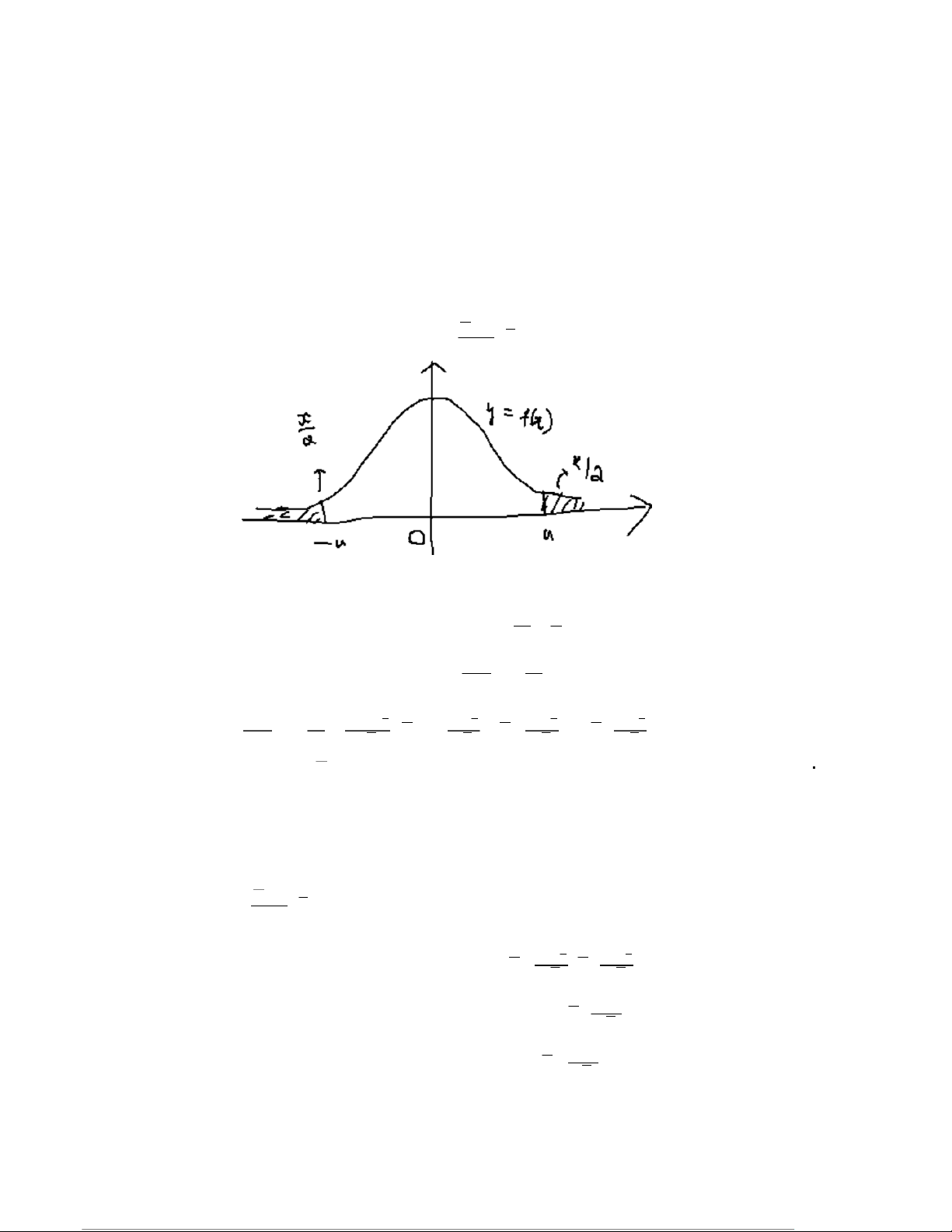
1. Ước lượng khoảng tin cậy cho μ X: EX=μ , VX=δ2 Trường hợp 1: X N (μ , δ2) G=X−μ √n N(0,1) δ
f(x) là hàm mật độ xs của Z N (0,1) { }
F(x) là hàm phân bố xs của Z Z>uX 2{ } P 2 2 2−uX P =1−α nn→X− 2 n<μ2→ −δ U α −u δ U α δ U α δ U α X (Có xs là1 √ √ √ √ −α ) 2 2 2 2 n
VD: Với α=90 % , X=15 →14.9<μ<15.1
BT: Giả sử đám đông X có EX =
μ chưa biết. Với độ tin cậy 1−
α hãy tìm khoảng tin cậy cho μ Giải TH1.1: G V = ( X X − ) μ =δ0 (Đã biết) 2 Xét: √n N(0,1) δ n;X+ n) δ U δ U
Khoảng tin cậy đối xứng cho α α μ với độ tin cậy là (X− với độ tin cậy là 1 √ √ −α (−∞; X +δ U 2 α n) 2
Khoảng tin cậy bên trái cho μ với độ tin cậy 1 −α là √ (X−δ Uαn;+∞)
Khoảng tin cậy bên phải cho μ với độ tin cậy 1 −α là √ 17:47, 27/01/2026
XSTK - Bài 2: Ước Lượng Khoảng Tin Cậy cho μ - Studocu
Gọi (θ1,θ2 ) là khoảng tin cậy cho kỳ vọng μ. Khi đó
θ1−θ2 được gọi là độ dài khoảng tin cậy,
θ1−θ2 được gọi là độ chính xác của khoảng tin cậy 2
1−α được gọi là độ tin cậy của ước lượng
VD: Cho 1 kho cung cấp sơn muốn ước lượng lượng sơn chứa trong 1 thùng được sản xuất từ
1 dây chuyền Quốc gia. Biết theo tính chất của công nghệ dây chuyê đó thì độ lệch tiêu chuẩn của một lượng sơn(
δ) là 0.08 thùng. Điều tra 1 mẩu gồm 50 thùng được lượng sơn trung bình là 0.97 thùng
(X) . Với độ tin cậy 99% (1 −α) hãy ước lượng:
a. Lượng sơn TB chứa trong 1 thùng
b. Lượng sơn tối thiểu chứa trong một thùng Giải
a. n=50,X=0.97,δ0=0.08,1−α=99%→α 2=0.05% G=X−μ Xét thống kê: √n N(0,1) δ Ta có khoảng tin cậy cho μ
với độ tin cậy 99% là: δUα δU α uα (X− 2 n;X+ 2 n) (Tra bảng ) √ √ 2 (0,97−2.576∗0 5 ,0 0; 8 0,97+2.576∗0,08 Hay 50) (phụ lục 8) √ √ hay(0.9408;0.9992)
b. Khoảng tin cậy bên phải cho μ
với độ tin cậy 99% là:
(X−δUαn;+∞ ) hay (0,97−2.326∗0,08 50;+∞ ) hay (0.944;+∞) √ √ TH2: Chưa biết VX=δ2{n≥30 0 n<30 G=X−μ Xét thống kê: √n T(n−1) δ Khoảng tin cậy đã cho μ với đồ thị tin cậy 1 −α là t(n−1;α 2).s t(n−1;α 2).s (X− n;X+ n) √ √ X+t ¿ (n−1;α).s n¿ khoảng tin cậy bên trái √
VD: Giá bán của 1 loại thiết bị (USD) trên thị trường là BNN có phân phối chuẩn. 1 người
định mua loại thiết bị này, khảo sát ngẫu nhiên tại 8 cửa hàng được giá bán trung bình là
137.75 USD với độ lệch tiêu chuẩn 7.98 USD độ tin cậy 90%. Hãy ước lượng giá bán thiết bị
này (độ lệch tiêu chuẩn đứng sau S) Giải
X=137.75$,n=8,S=7.98,1−α=90% 17:47, 27/01/2026
XSTK - Bài 2: Ước Lượng Khoảng Tin Cậy cho μ - Studocu Khoảng tin cậy đã cho
μ với độ tin cậy 90% là t(n−1;α 2).s t(n−1;α 2).s (X− n;X+ n) √ √ (137.75−1.895∗7. 89 ; 8 137.75+1.895∗7.98 Hay 8) √ √ Hay (132.4035;143.0965)
Chú ý: với trường hợp chưa biết δ20
nếu n≥30 , ta có thể thay được bởi μ, nhưng không được thay s với δ
2. Ước lượng khoảng tin cậy cho tỉ lệ p: Xét: XA (p) G=F−p Sử dụng thống kê: √n≈ N (0,1) √F (1−F ) Khi nf và
n (1−f )≥10 thì xấp xỉ là tương đối chính xác ¿ √f(1−f )
Khi đó bên phải n độ tin cậy 1− α cho phải là( f−uα n;1) √
VD: Trong đợt bầu cử tổng thống, phỏng vấn ngẫu nhiên 1600 thì được biết có 900 người sẽ
bầu cho A, n độ tin cậy 99%, hãy xem ứng cử viên A có trúng cử hay không? Giải α=0.01 n=1600,m=960,1−α=99%→{ f=m n
Ta có khoảng tiêu chuẩn bên phải cho tỉ lệ p với độ tin cậy 99% là (f−u √ α f(1−f ) n;1) hay (0.6−2.326 √0.6 (1−0.6 ) 1600;1) hay (0.37;1) √ √ 17:47, 27/01/2026
XSTK - Bài 2: Ước Lượng Khoảng Tin Cậy cho μ - Studocu