Bài giảng Chapter 6: Basic Passband Digital Modulations môn Điện tử - Viễn thông | Trường Đại học Khoa học Tự nhiên - Đại học Quốc gia Thành phố Hồ Chí Minh

Viet Nam National University Ho Chi Minh City University of Science
Faculty of Electronics & Telecommunications Chapter 6:
Basic Passband Digital Modulations Dang Le Khoa Email: dlkhoa@hcmus.edu.vn Outline – ASK, OOK, MASK – FSK, MFSK – BPSK, DBPSK, MPSK – MQAM, – OQPSK – Bit error rate. ASK, OOK, MASK ●
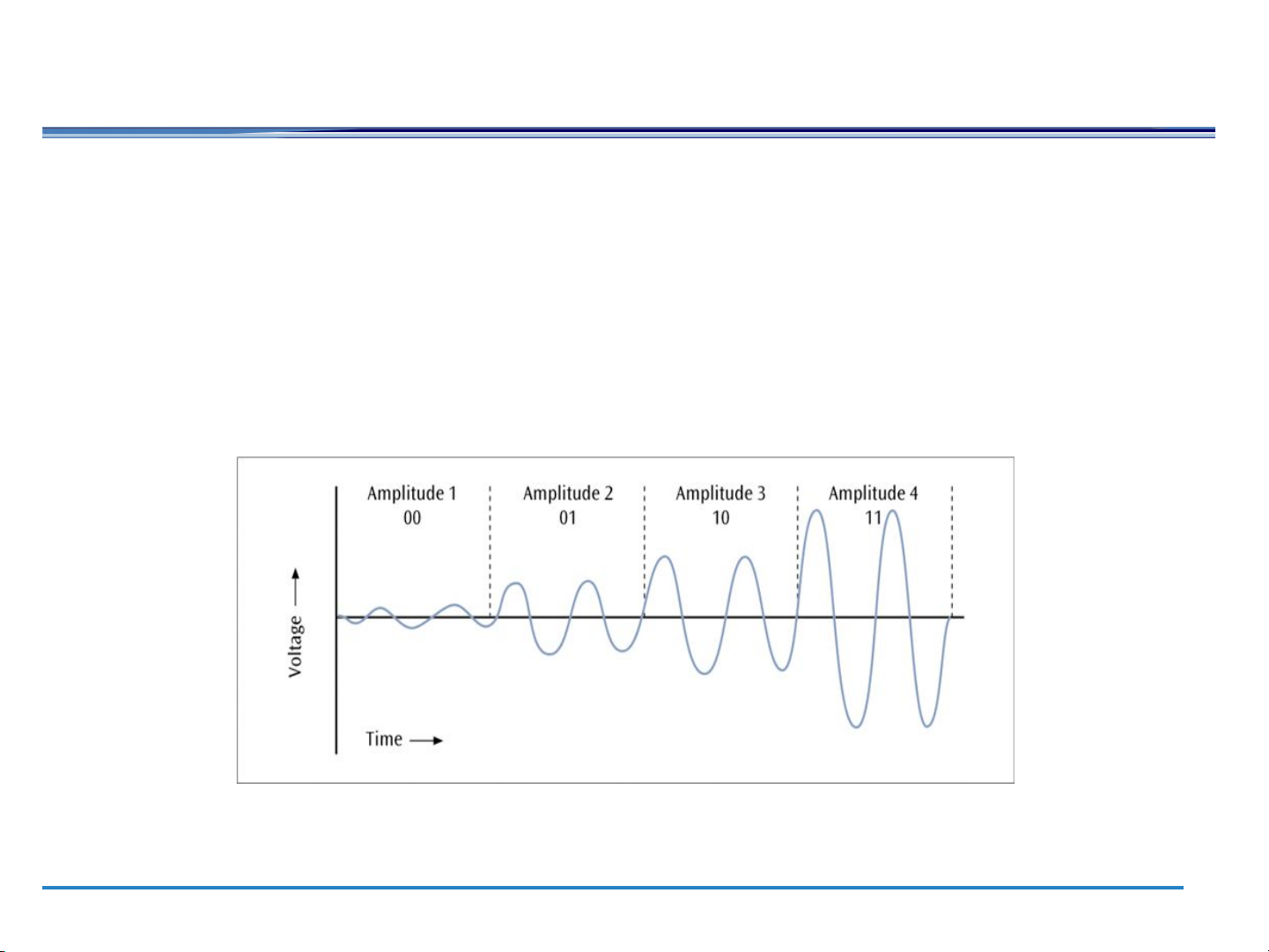
The amplitude (or height) of the sine wave varies to transmit the ones and zeros ●
One amplitude encodes a 0 while another amplitude encodes a 1
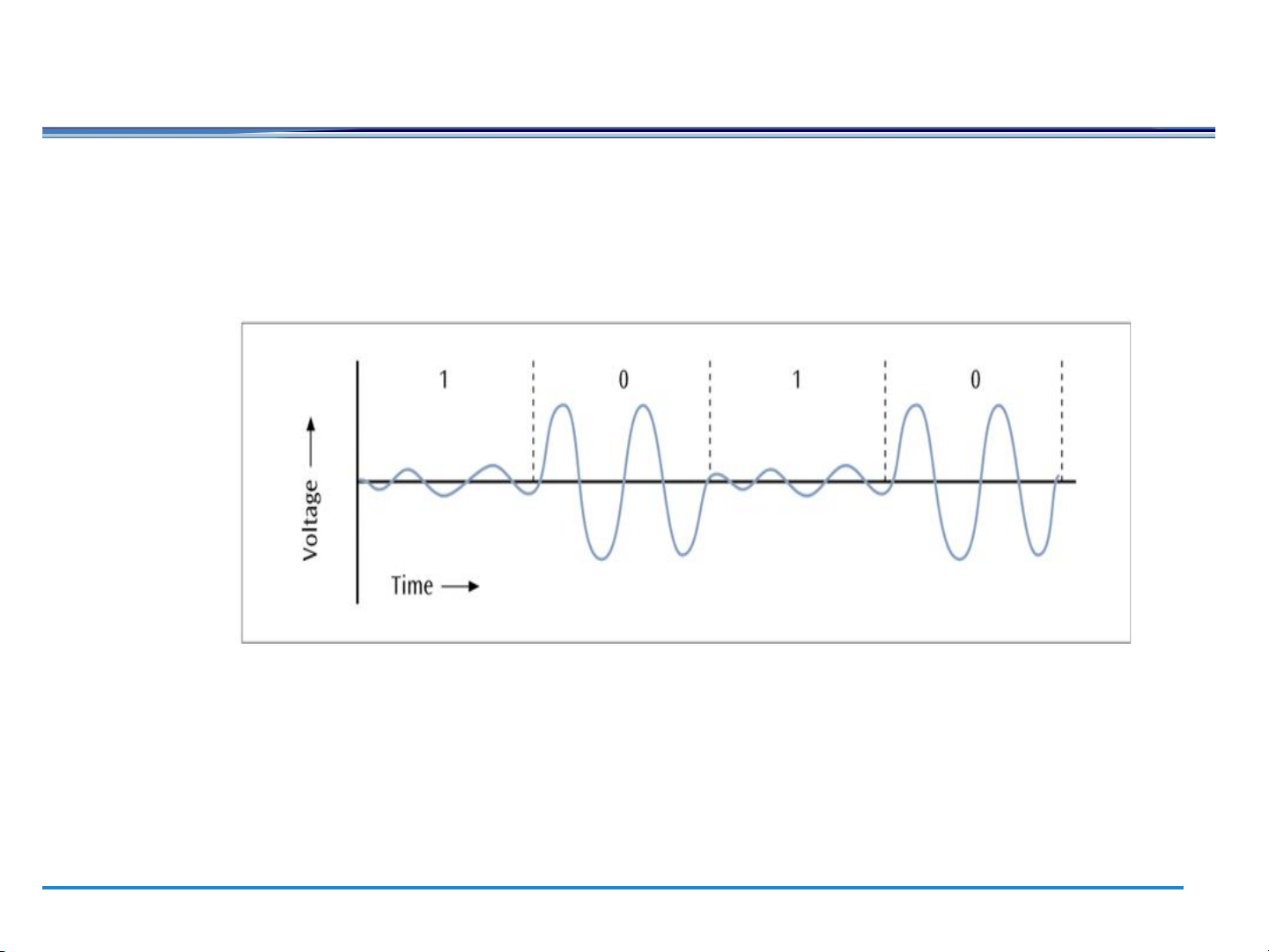
(a form of amplitude modulation) On-off keying On-off keying “0 (M=2): “1 ” ” 0 4
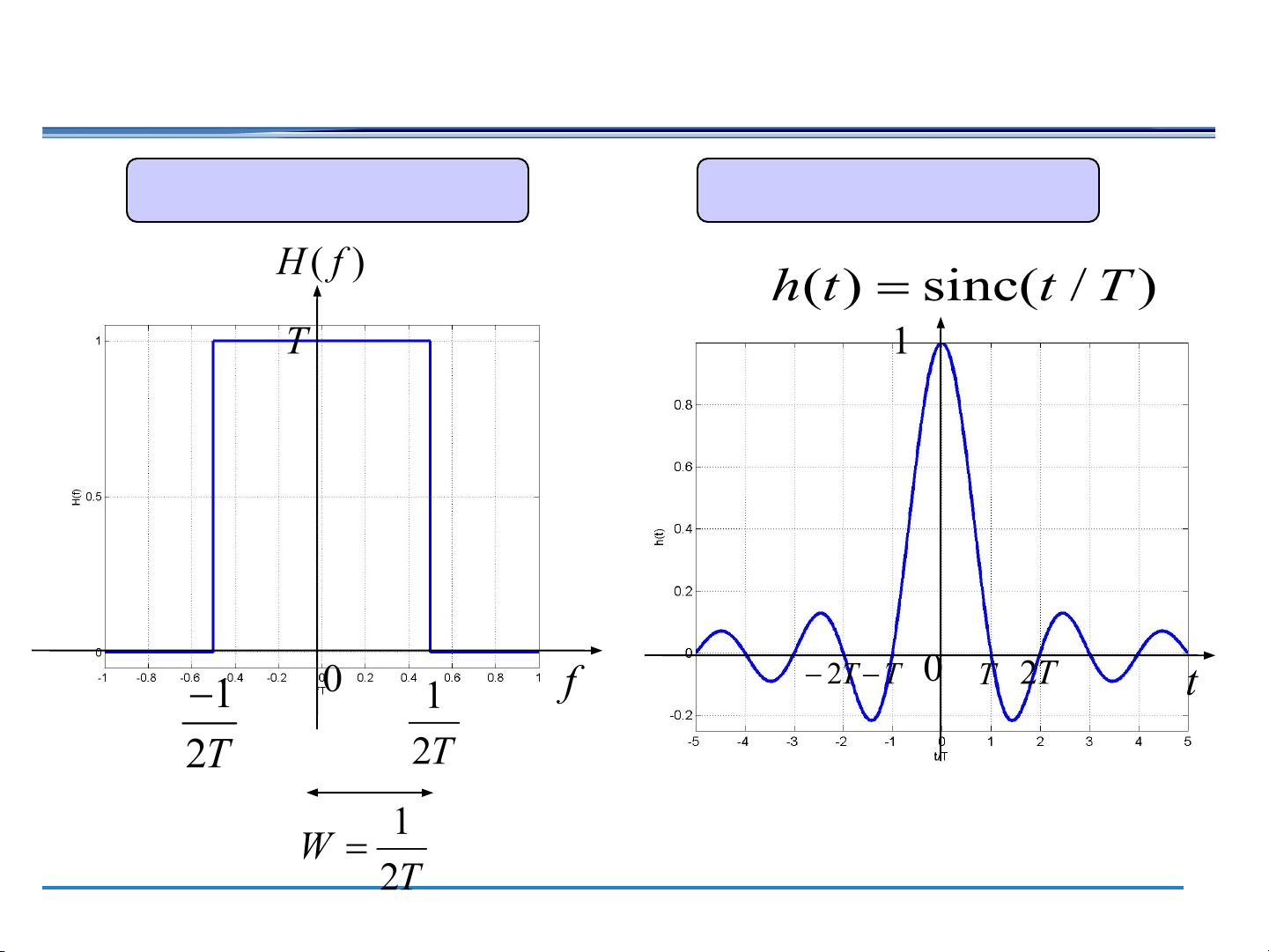
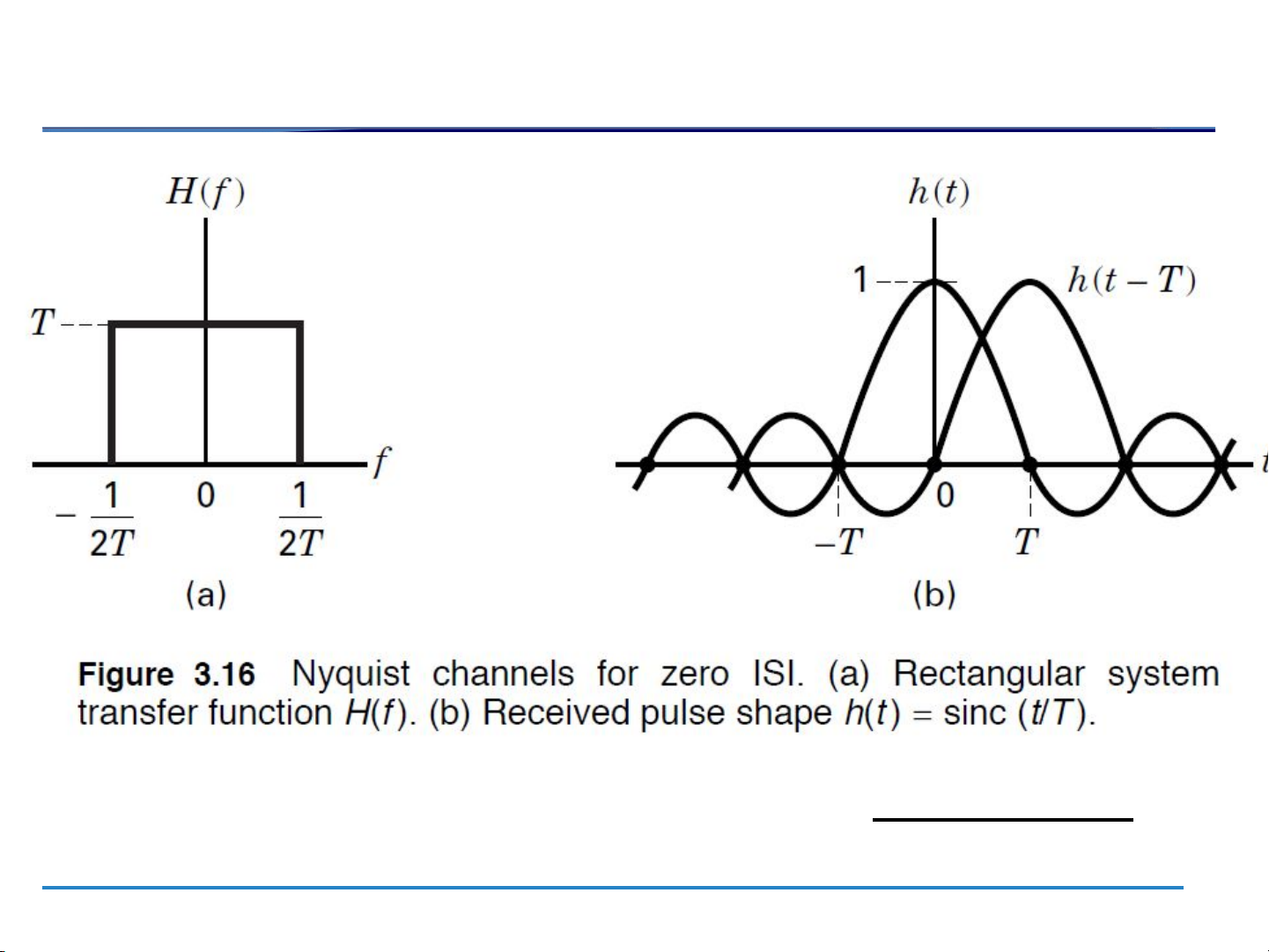
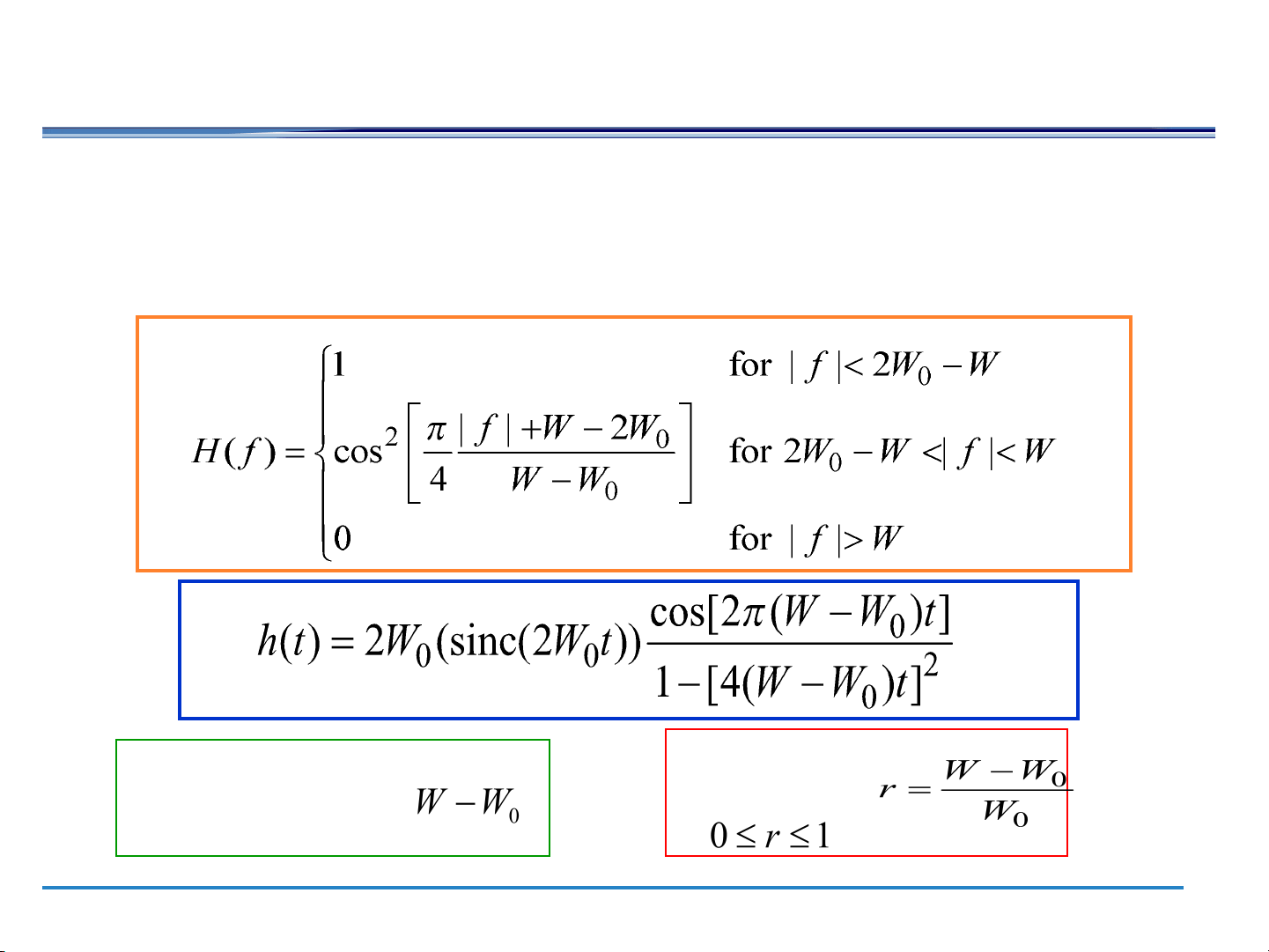
Ideal Nyquist pulse (filter) Ideal Nyquist filter Ideal Nyquist pulse 5
Nyquist pulses (filters): no ISI at the sampling time 6
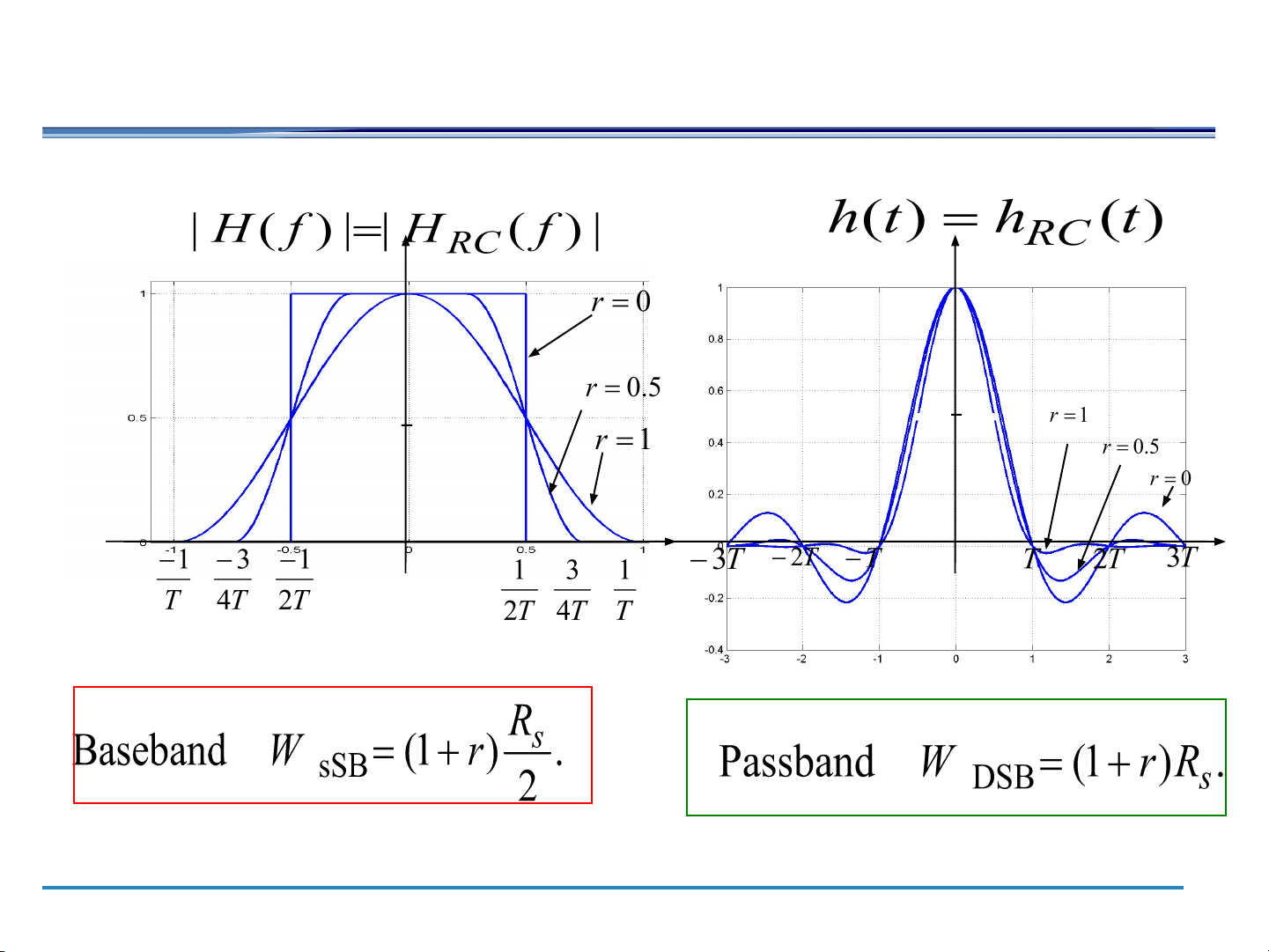
The raised cosine filter ● Raised-Cosine Filter
– A Nyquist pulse (No ISI at the sampling time) Excess bandwidth: Roll-off factor 7
The Raised cosine filter – cont’d 1 1 0. 0. 5 5 0 0 8
Binary amplitude shift keying, Bandwidth ●
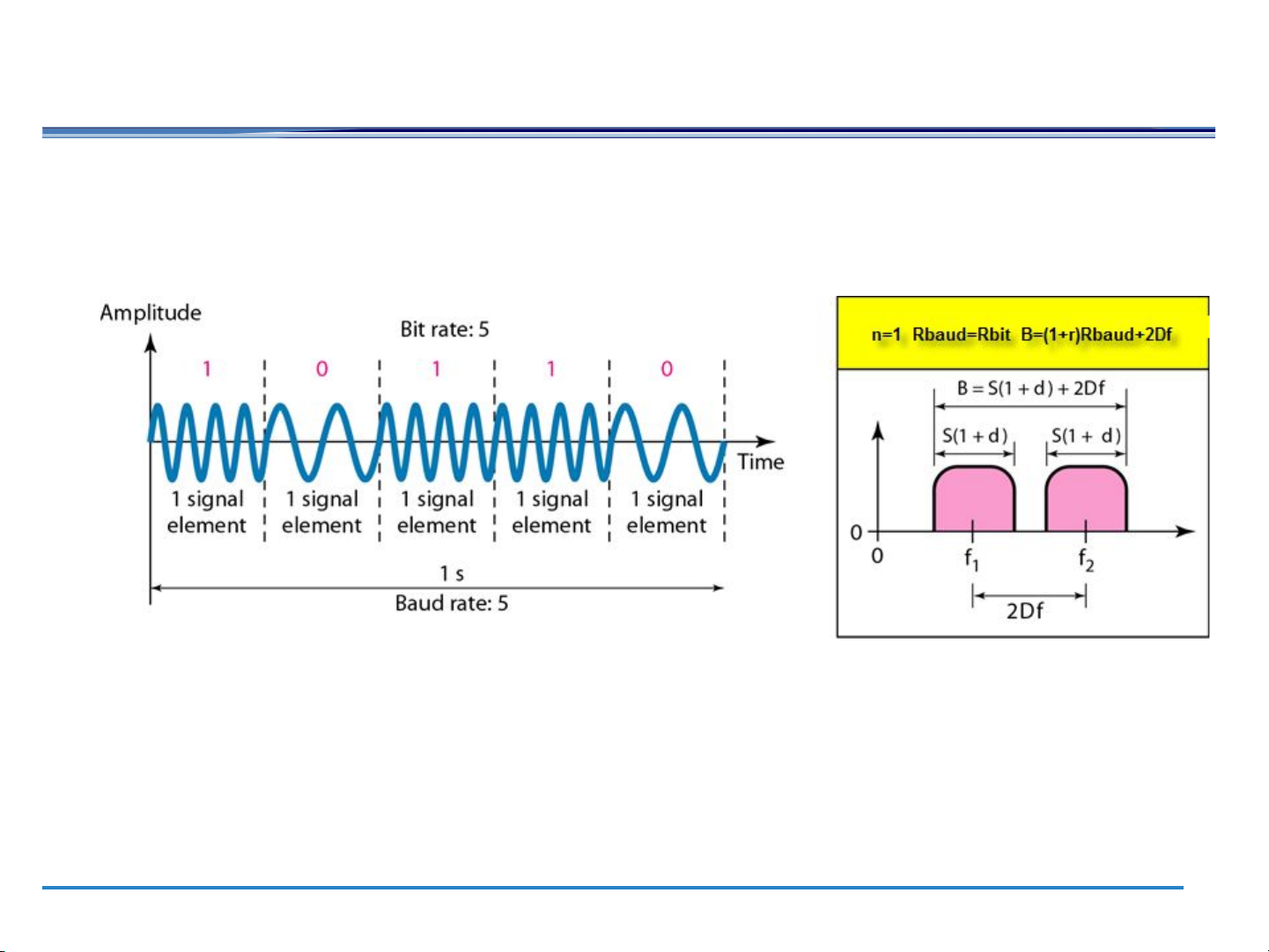
d ≥ 0 🡪 related to the condition of the line B = (1+r) R = (1+r) R DSB baud b
Implementation of binary ASK OOK and MASK ● OOK (On-OFF Key) – 0 silence.
– Sensor networks: battery life, simple implementation ●
MASK: multiple amplitude levels
Pro, Con and Applications ● Pro – Simple implementation ● Con
– Major disadvantage is that telephone lines are very susceptible to
variations in transmission quality that can affect amplitude
– Susceptible to sudden gain changes
– Inefficient modulation technique for data ● Applications
– On voice-grade lines, used up to 1200 bps
– Used to transmit digital data over optical fiber – Morse code – Laser transmitters Example ●
We have an available bandwidth of 100 kHz which spans from 200 to
300 kHz. What are the carrier frequency and the bit rate if we
modulated our data by using ASK with r = 1? ● Solution ●
The middle of the bandwidth is located at 250 kHz. This means that
our carrier frequency can be at fc = 250 kHz. We can use the formula
for bandwidth to find the bit rate (with n= 1 and r = 1). B = (1+r) R = 2 xR =100KHz baud b => R =50kbps b
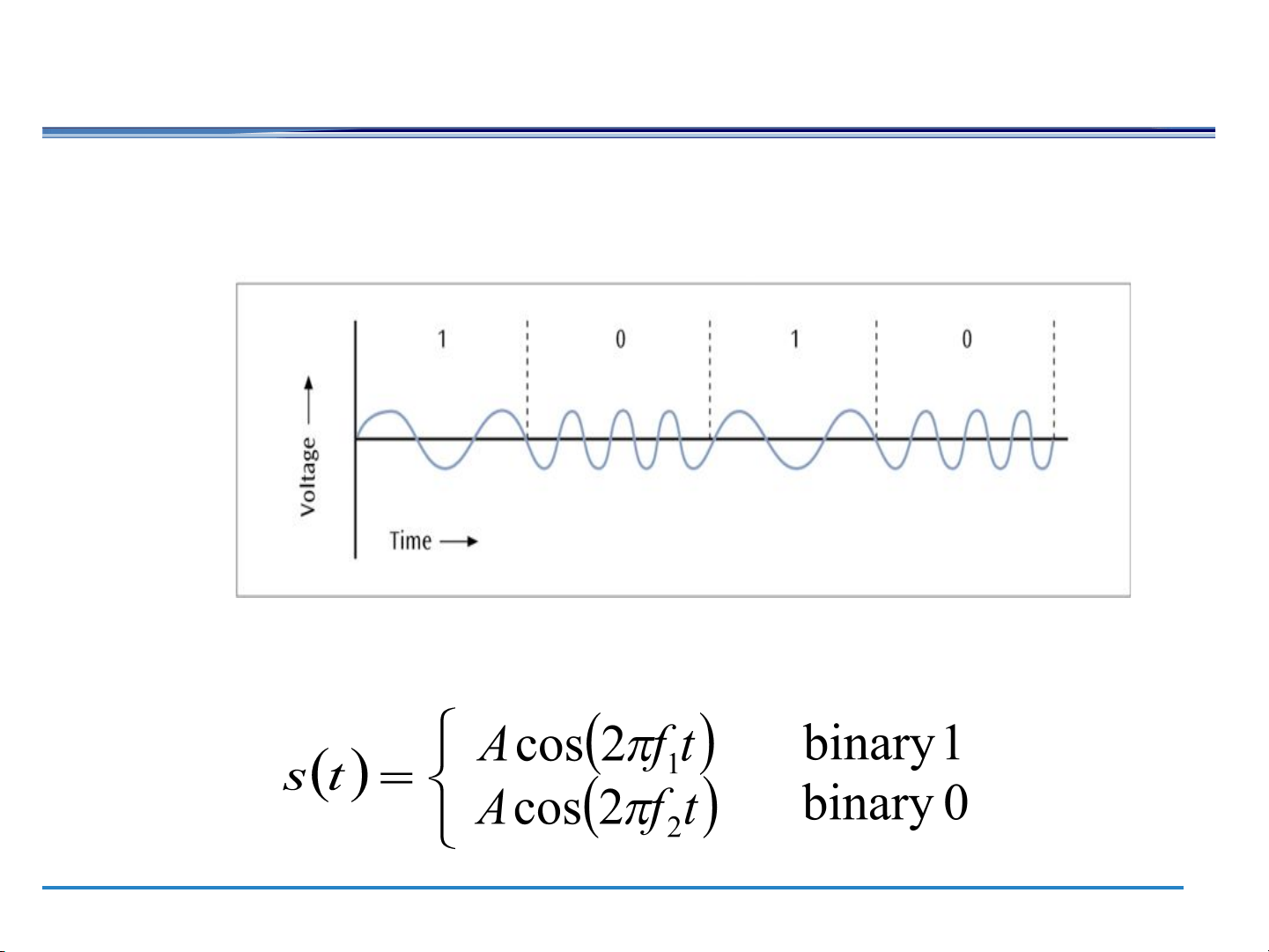
Frequency Shift Keying ●
One frequency encodes a 0 while another frequency encodes a 1
(a form of frequency modulation) ●
Represent each logical value with another frequency (like FM) FSK Bandwidth ●
Limiting factor: Physical capabilities of the carrier ●
Not susceptible to noise as much as ASK ● Applications
– On voice-grade lines, used up to 1200bps
– Used for high-frequency (3 to 30 MHz) radio transmission
– used at higher frequencies on LANs that use coaxial cable Example ●
We have an available bandwidth of 100 kHz which spans from
200 to 300 kHz. What should be the carrier frequency and the
bit rate if we modulated our data by using FSK with r= 1? ● Solution
– This problem is similar to Example 5.3, but we are modulating
by using FSK. The midpoint of the band is at 250 kHz. We
choose 2Δf to be 50 kHz; this means
B = (1+r) Rbaud+ 2Δf = 100KHz =>2xR = 2xR =50kHz b baud => Rb=25kbps EE 541/451 Fall 2007
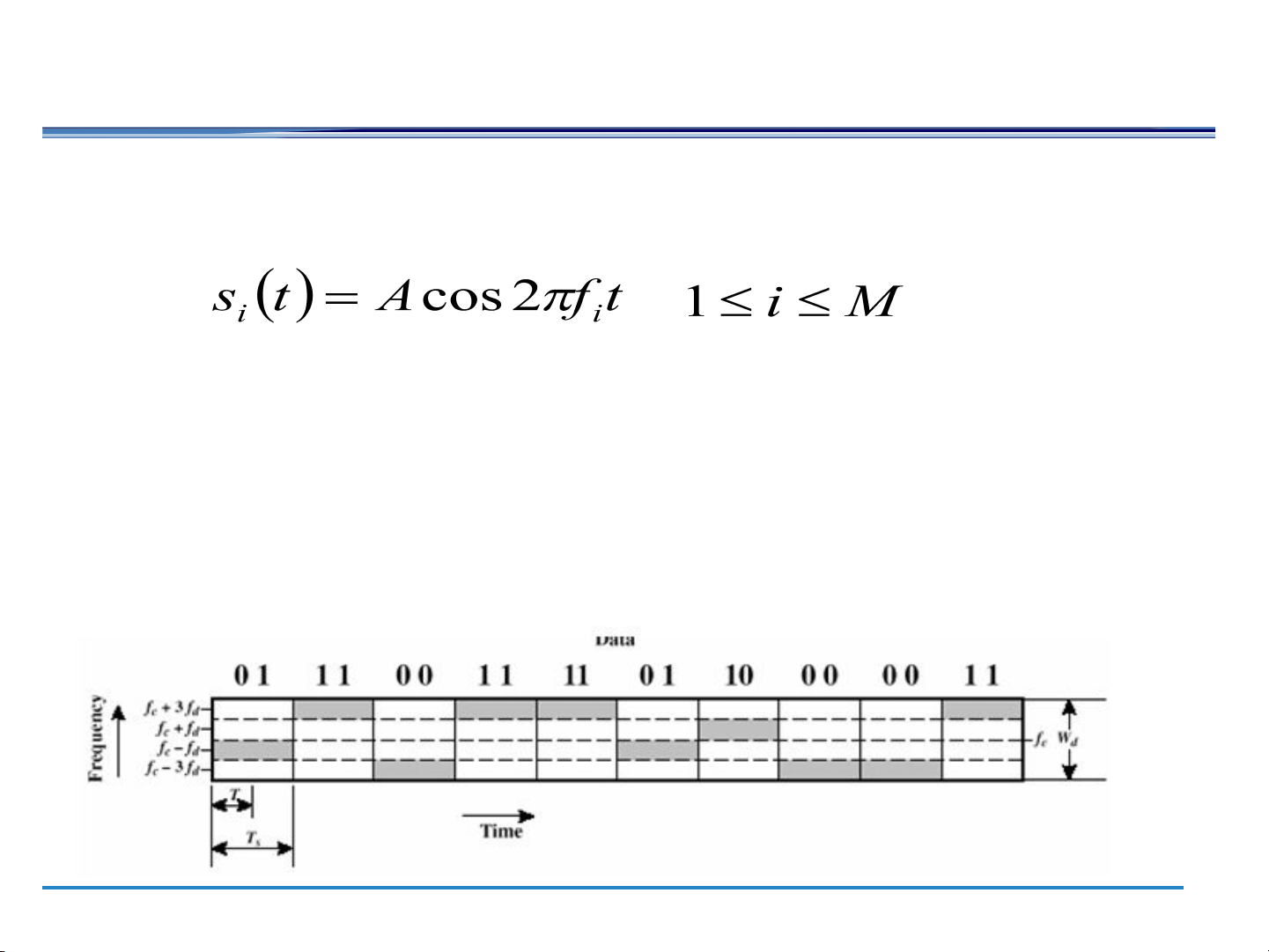
Multiple Frequency-Shift Keying (MFSK) ●
More than two frequencies are used ●
More bandwidth efficient but more susceptible to error
● f = f + (2i – 1 – M)f i c d
● f = the carrier frequency c
● f = the difference frequency d
● M = number of different signal elements = 2 n
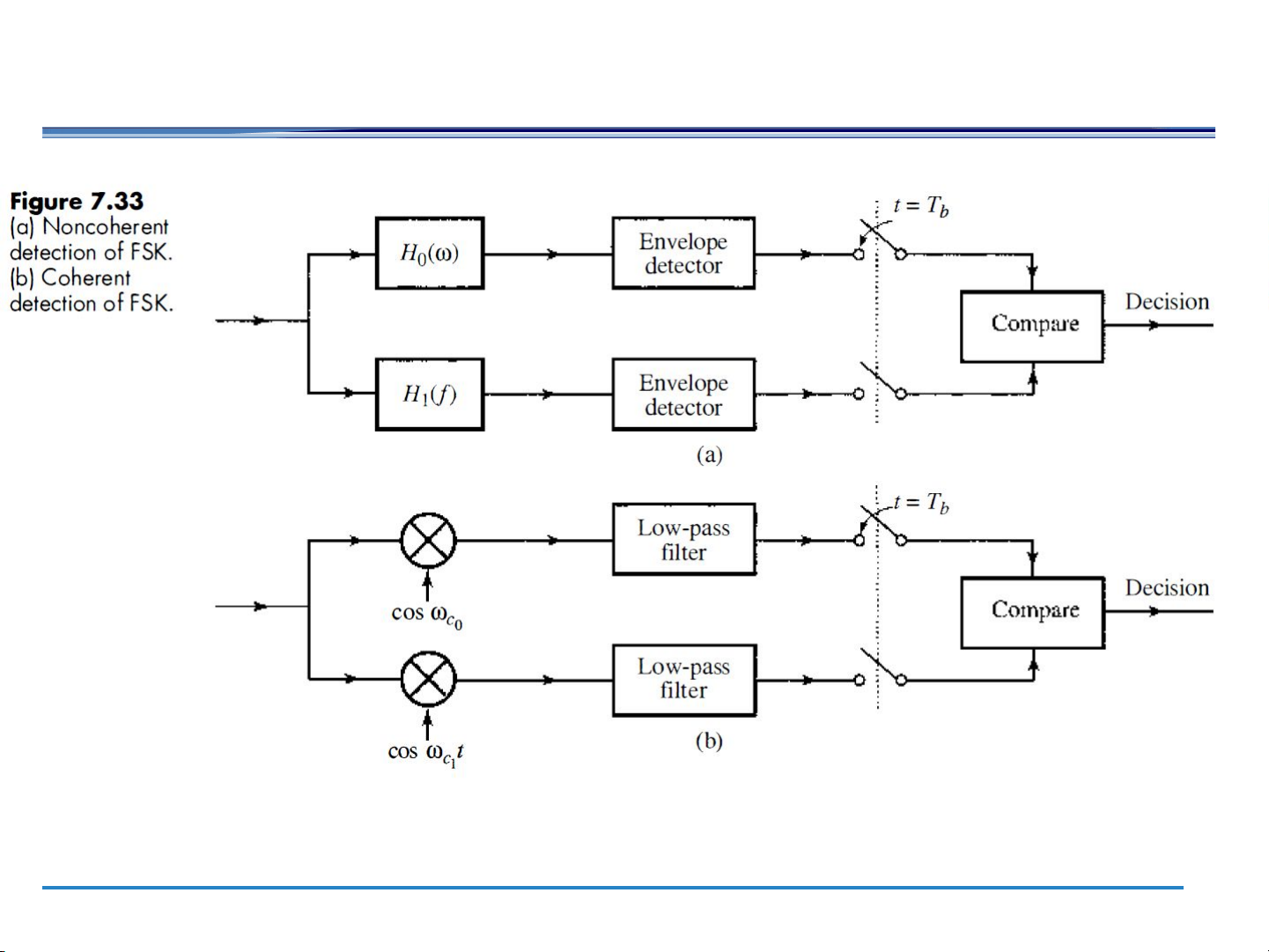
● n = number of bits per signal element FSK detection
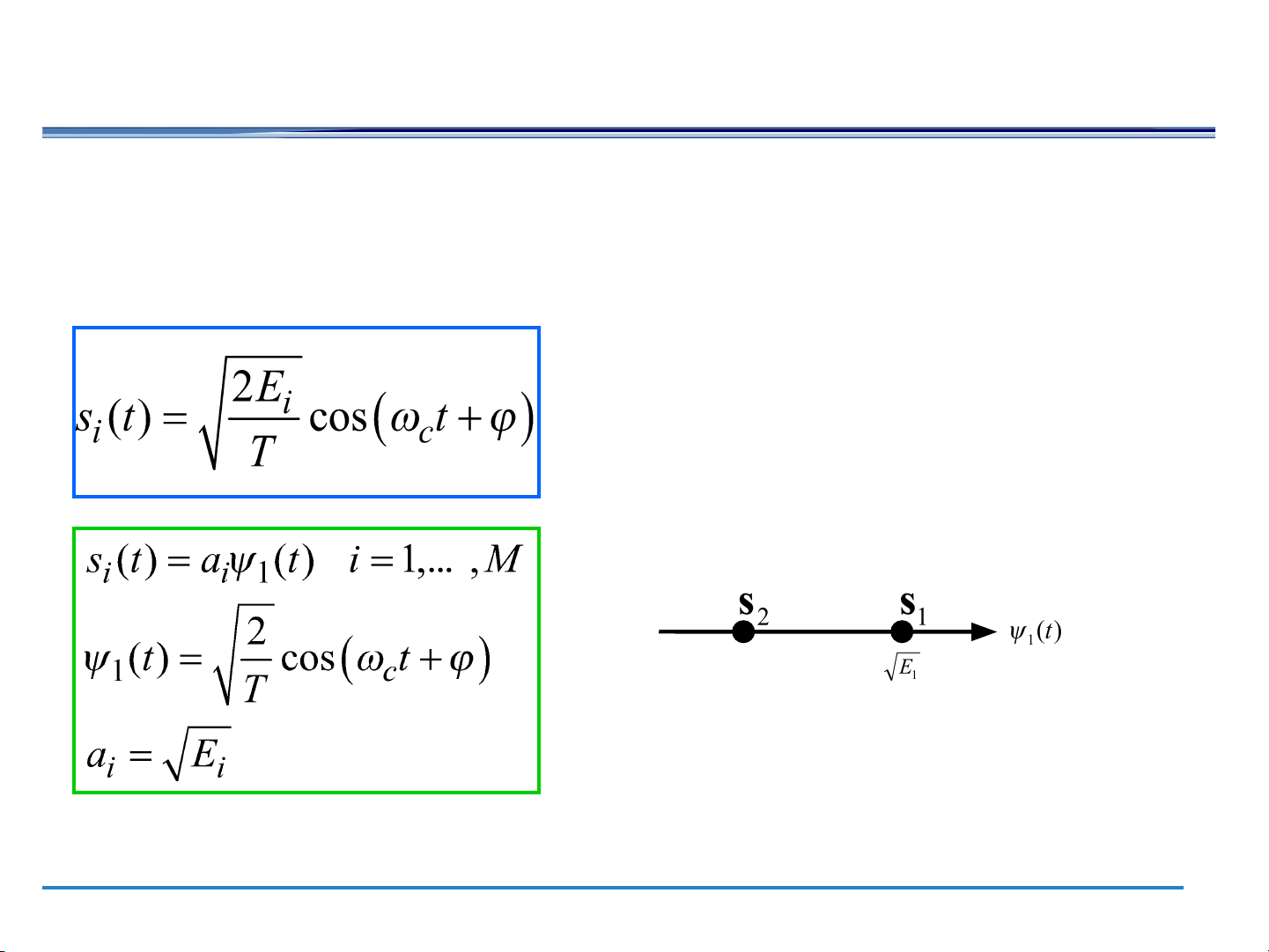
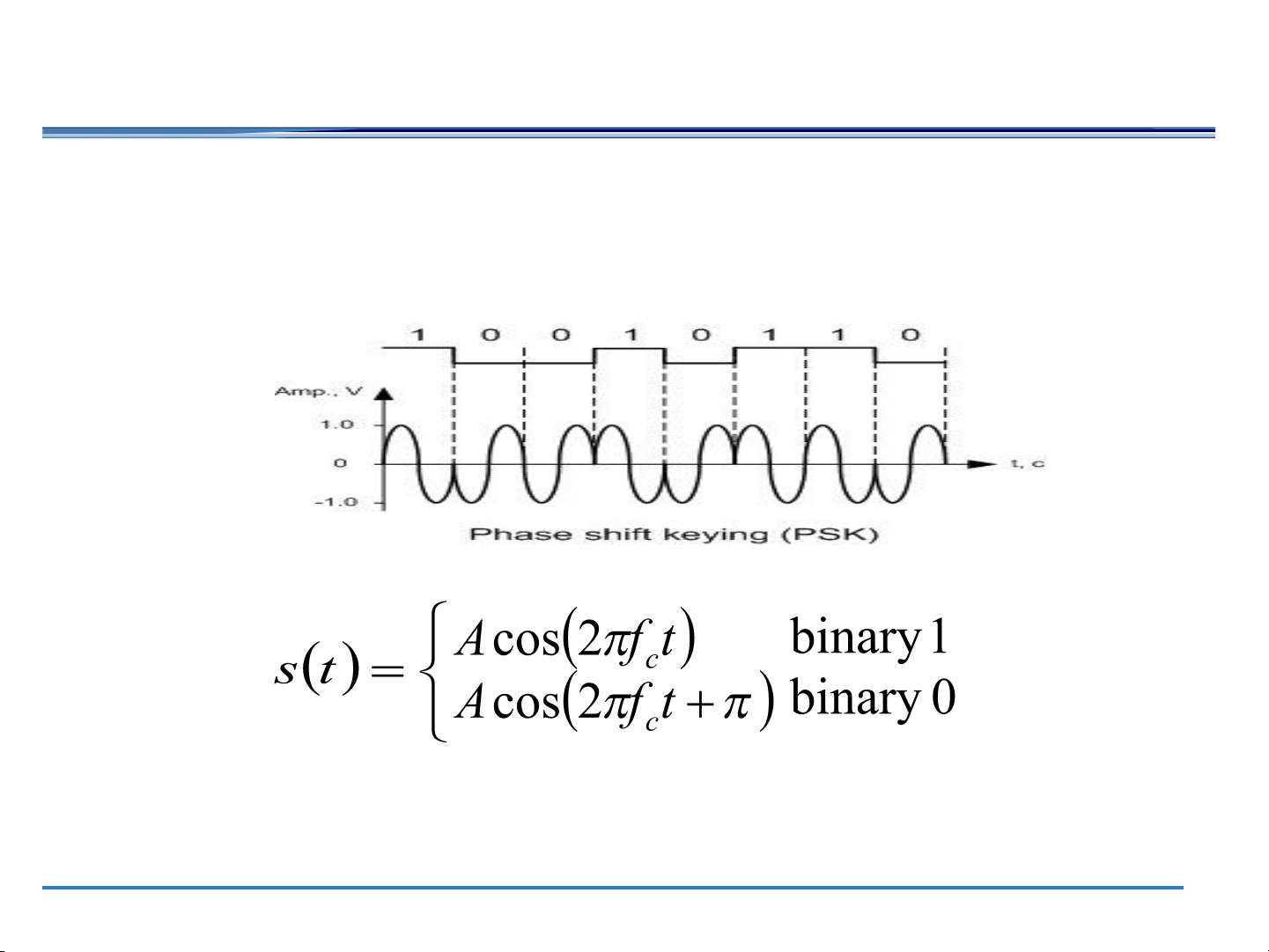
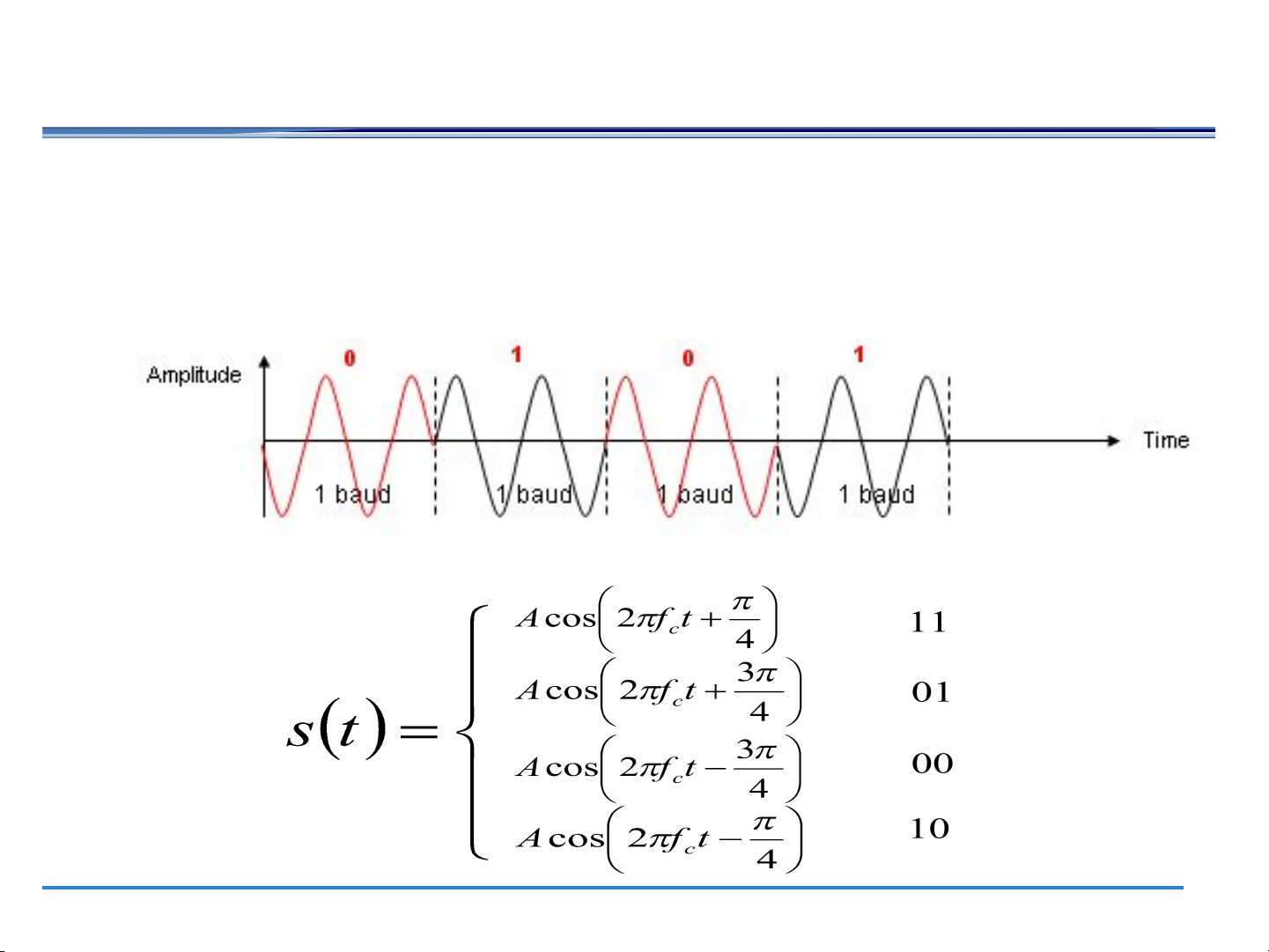
Phase Shift Keying ●
One phase change encodes a 0 while another phase change
encodes a 1 (a form of phase modulation) DBPSK, QPSK ● Differential BPSK
– 0 = same phase as last signal element
– 1 = 180º shift from last signal element ● Four Level: QPSK