Bài giảng Chapter 7: Introduction to Information Theory môn Điện tử - Viễn thông | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

Viet Nam National University Ho Chi Minh City University of Science
Faculty of Electronics & Telecommunications Chapter 7:
Introduction to Information Theory Dang Le Khoa Email: dlkhoa@hcmus.edu.vn Outline ⚫ Basic concepts ⚫ Information ⚫ Entropy ⚫ Source Encoding 11/13/2024 2 Basic concepts
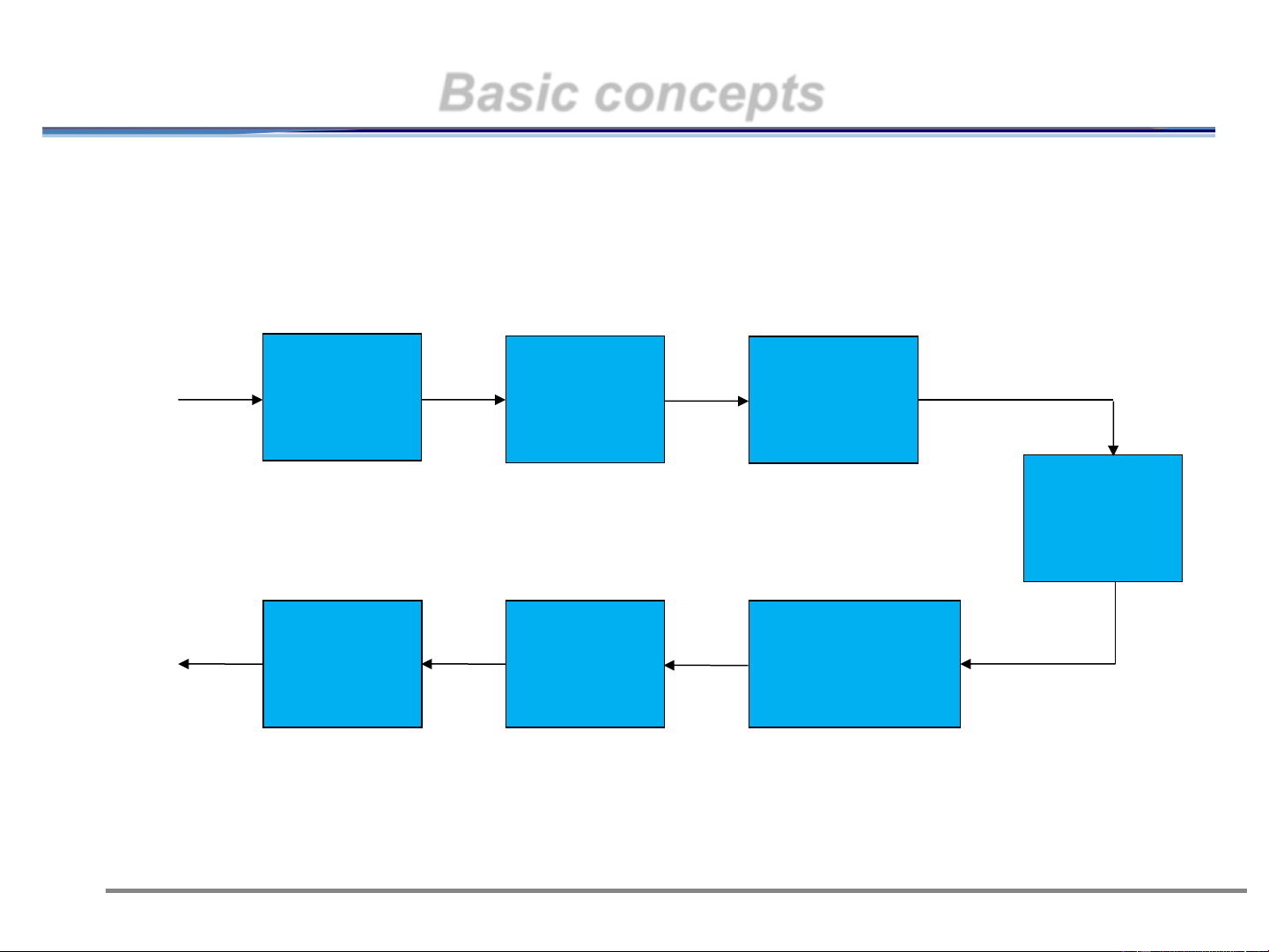
⚫ Block diagram of digital communication system Source Source Channel Modulator encoder encoder Noisy Channel Destination Source Channel Demodulator decoder decoder 11/13/2024 3
What is Information Theory?
⚫ Information theory provides a quantitative measure of source
information, the information capacity of a channel
⚫ Dealing with coding as a means of utilizing channel capacity for information transfer
⚫ Shannon’s coding theorem (Shannon’s noisy channel coding theorem):
“If the rate of information from a source does not exceed the
capacity of a communication channel, then there exists a
coding technique such that the information can be transmitted
over the channel with an arbitrarily small probability of error,
despite the presence of error” 11/13/2024 4
Information measure
⚫ Information Theory: how much information
– … is contained in a signal? – … can a system generate?
– … can a channel transmit?
⚫ Information is the commodity produced by the source for
transfer to some user at the destination
⚫ The less likely the message, the more information it conveys
⚫ How is information mathematically defined? 11/13/2024 5 Information
⚫ Let x be an event with p(x ) is the probability of the event j j
that x is selected for transmission j
⚫ If x occurred, we have j 1 I (x ) = log = − log p(x ) (1) j a p(x ) a j j units of information
◼ I(x ) is called self-information j  I(x )0 for 0 p(x )1 j j
 I(x )→0 for p(x )→1 j j
 I(x )>I(x ) for p(x )

j i j i 11/13/2024 6

Information ⚫ The base of the logarithm
– 10 →the measure of information is hartley
– e →the measure of information is nat
– 2 →the measure of information is bit
⚫ Examples: A random experiment with 16 equally likely outcomes:
– The information associated with each outcomes is:
I(xj)=-log2(1/16)=log216=4 bits
– The information is greater than one bit, since the probability of each outcome is much less than ½. 11/13/2024 7
Entropy and Information rate
⚫ Consider an information source emitting a sequence of symbols from
the set X={x ,x ..,x } 1 2 M
⚫ Each symbol x is treated as a message with probability p(x ) and self- i i information I(x ) i
⚫ This source has an average rate of r symbols/sec ⚫ Discrete memoryless source
⚫ The amount of information produced by the source during an arbitrary
symbol interval is a disrete random variable X.
⚫ The average information per symbol is then given by: M H ( X ) = { E I (x )} = − p x p x j  ( )log ( ) b it/symbol j 2 j (2) j 1 =
⚫ Entropy = information = uncertainty
⚫ If a signal is completely predictable, it has zero entropy and no information
⚫ Entropy = average number of bits required to transmit the signal 11/13/2024 8 Example
⚫ Random variable with uniform distribution over 32 outcomes
– H(X) = -  (1/32).log(1/32) = log 32 = 5
– # bits required = log 32 = 5 bits!
– Therefore H(X) = number of bits required to represent a random event
⚫ How many bits are needed for: – Outcome of a coin toss 11/13/2024 9 Entropy
⚫ The value of H(X) for a given source depends upon the
symbol probabilities p(x ) and M i ⚫ However,
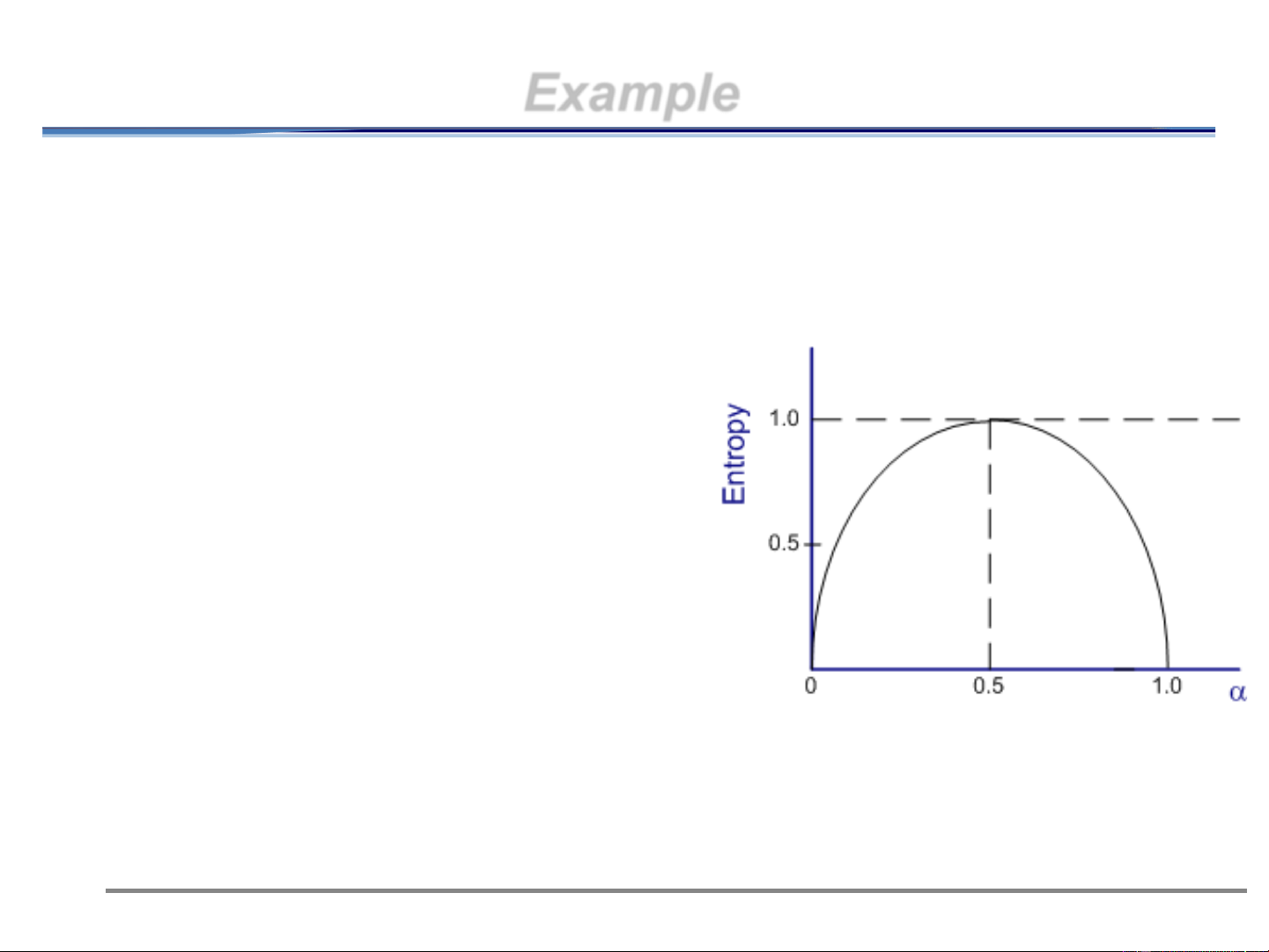
0  H ( X )  log M (3) 2
⚫ The lower bound corresponds to no uncertainty
⚫ The upper bound corresponds to maximum uncertainty,
occuring when each symbol are equally likely 11/13/2024 10 Example
⚫ For a binary source (M=2), p(1)=
and p(0)=1- = .
⚫ From (2), we have the binary entropy:
⚫ H(X)= -.log -(1-).log(1-) 11/13/2024 11
Source coding theorem
⚫ Information from a source producing different symbols
could be described by the entropy H(X)
⚫ Source information rate (bit/s):
R = rH(X) (bit/s) s
– H(X): source entropy (bits/symbol)
– r: symbol rate (symbols/s)
⚫ Assume this source is the input to a channel: – C: capacity (bits/symbol)
– S: available symbol rate (symbols/s) – S.C: bits/s 11/13/2024 12
Source coding theorem (cont’d)
⚫ Shannon’s first theorem (noiseless coding theorem):
– “Given a channel and a source that generates information at
a rate less than the channel capacity, it is possible to encode
the souce output in such a manner that it can be
transmitted through the channel”
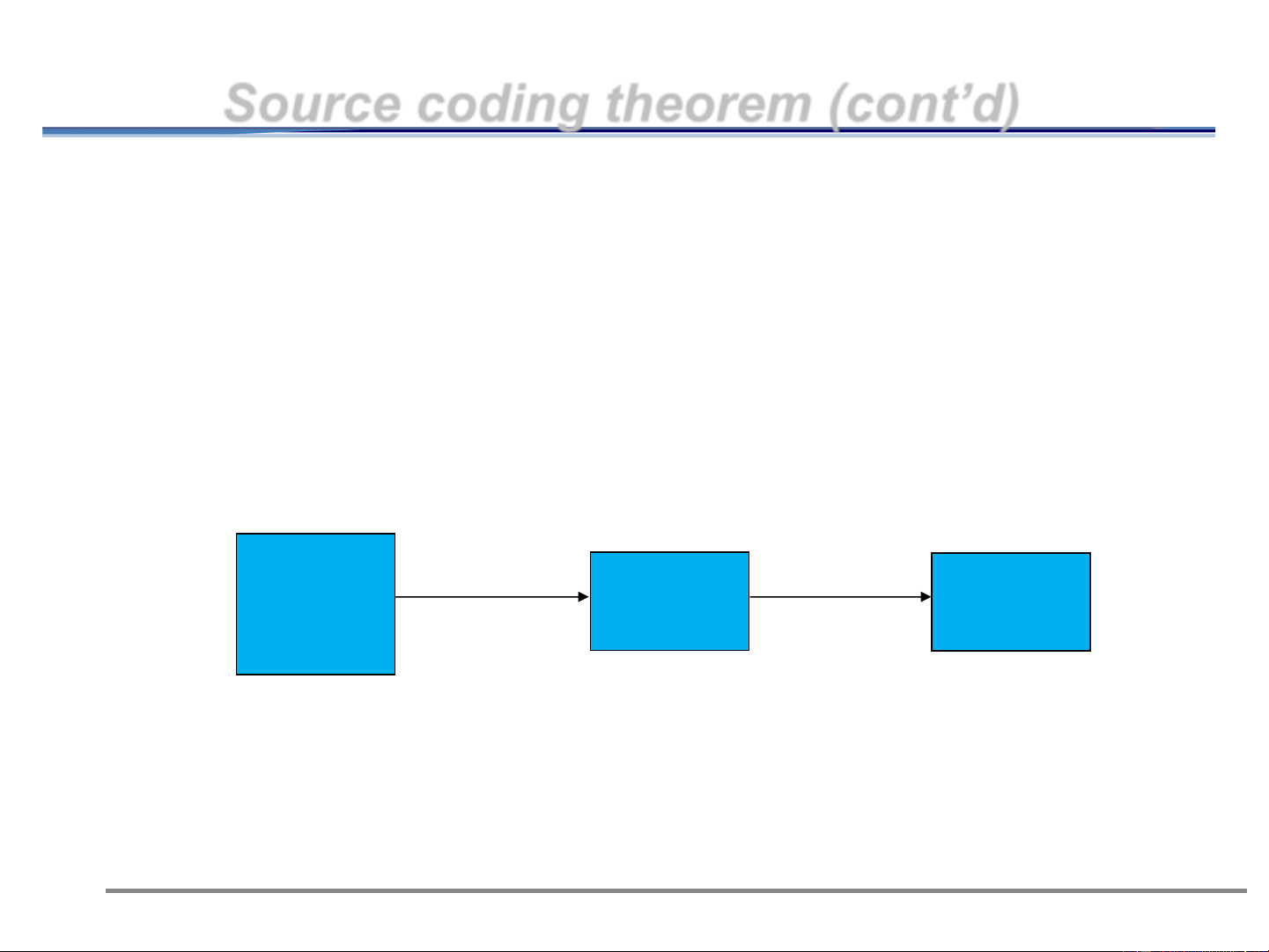
⚫ Demonstration of source encoding by an example: Discrete Source Binary binary encoder channel source Source symbol rate C = 1 bit/symbol r = 3.5 symbols/s S = 2 symbols/s SC = 2 bits/s 13 11/13/2024
Example of Source encoding
⚫ Discrete binary source: A(p=0.9), B(p=0.1)
⚫ Source symbol rate (3.5) >channel capacity (2) 
source symbols cannot be transmitted directly ⚫ Check Shannon’s theorem:
– H(X)=-0.1 log 0.1-0.9log 0.9=0.469bits/symbol 2 2
– R = rH(X) = 3.5(0.469)=1.642 bits/s < S.C = 2 bits/s s
⚫ Transmission is possible by source encoding to
decrease the average symbol rate 11/13/2024 14
Example of Source encoding(cont’d)
⚫ Codewords assigned to n-symbol groups of source symbols ⚫ Rules:
– Shortest codewords for the most probable group
– Longest codewords for the least probable group
⚫ n -symbol groups of source symbols # n th-order extension of original source 11/13/2024 15
First-Order extension Source P () Codeword [P()].[Number of Code symbol Symbols] A 0.9 0 0.9 B 0.1 1 0.1 L=1.0
⚫ Symbol rate of the encoder = symbol rate of source
⚫ Larger than that of the channel can accommodate 11/13/2024 16
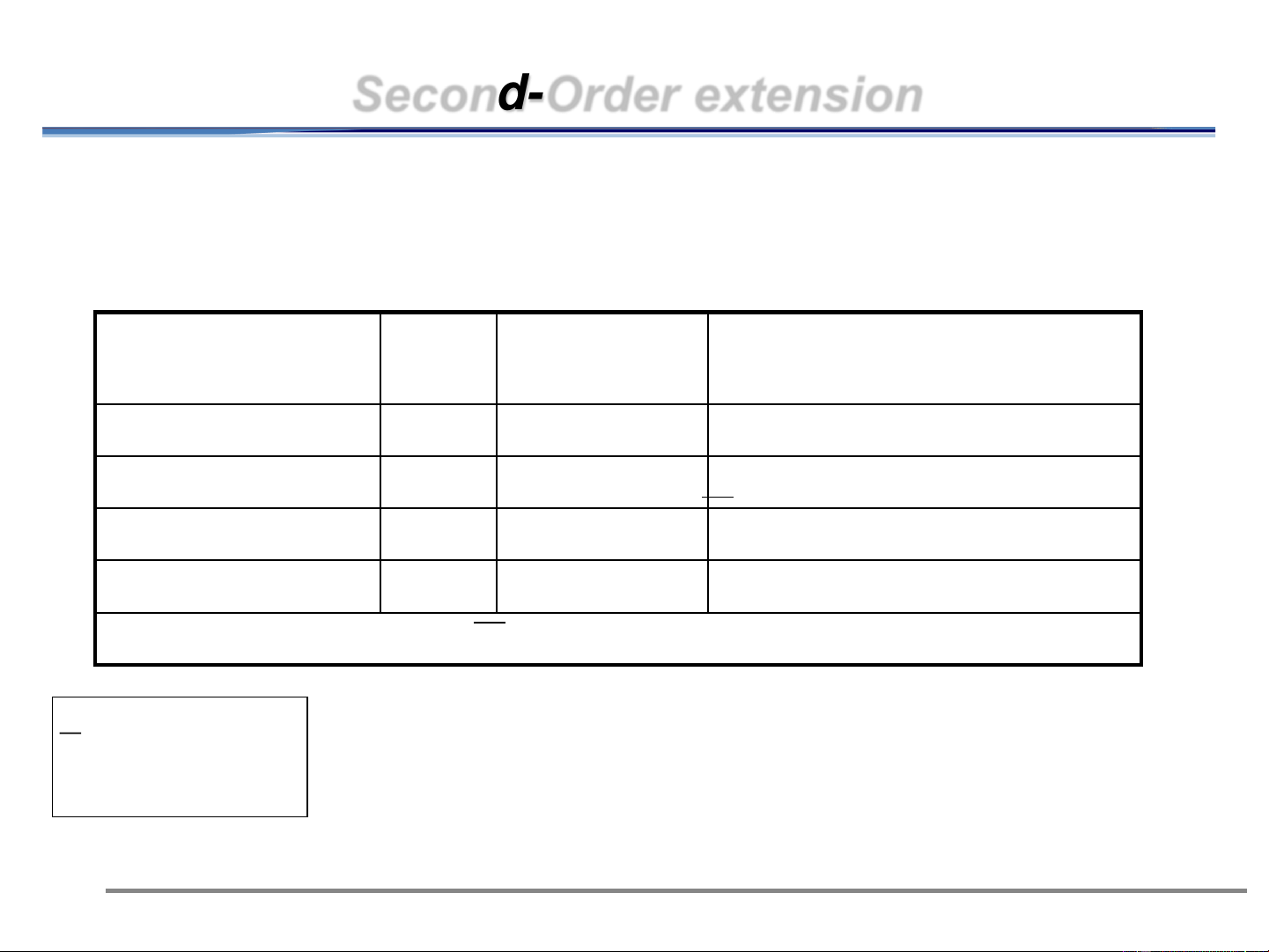
Second-Order extension
Grouping 2 source symbols at a time
The codeword is based on Shannon-Fano Coding
(explained in some slides later) Source symbol P ()
Codeword [P()].[Number of Code Symbols] AA 0.81 0 0.81 AB 0.09 10 0.18 BA 0.09 110 0.27 BB 0.01 111 0.03 L=1.29 n
L: the average code length 2
L =  p(x )*l i i
p(x ): probability of the i th symbol of the extended source i i 1 = 17
l : length of the codeword corresponding to the i th symbol i 11/13/2024
Second-Order extension L 29 . 1 = = co 645 . 0 de s ymbols/s u o rce s ymbol n 2
The symbol rate at the encoder output: L r = ( 5 . 3 ) 645 . 0 = 258 . 2 code symbols/sec >2 n
Still greater than the 2 symbols/second of the channel
So, we continue with the third-order extension 11/13/2024 18
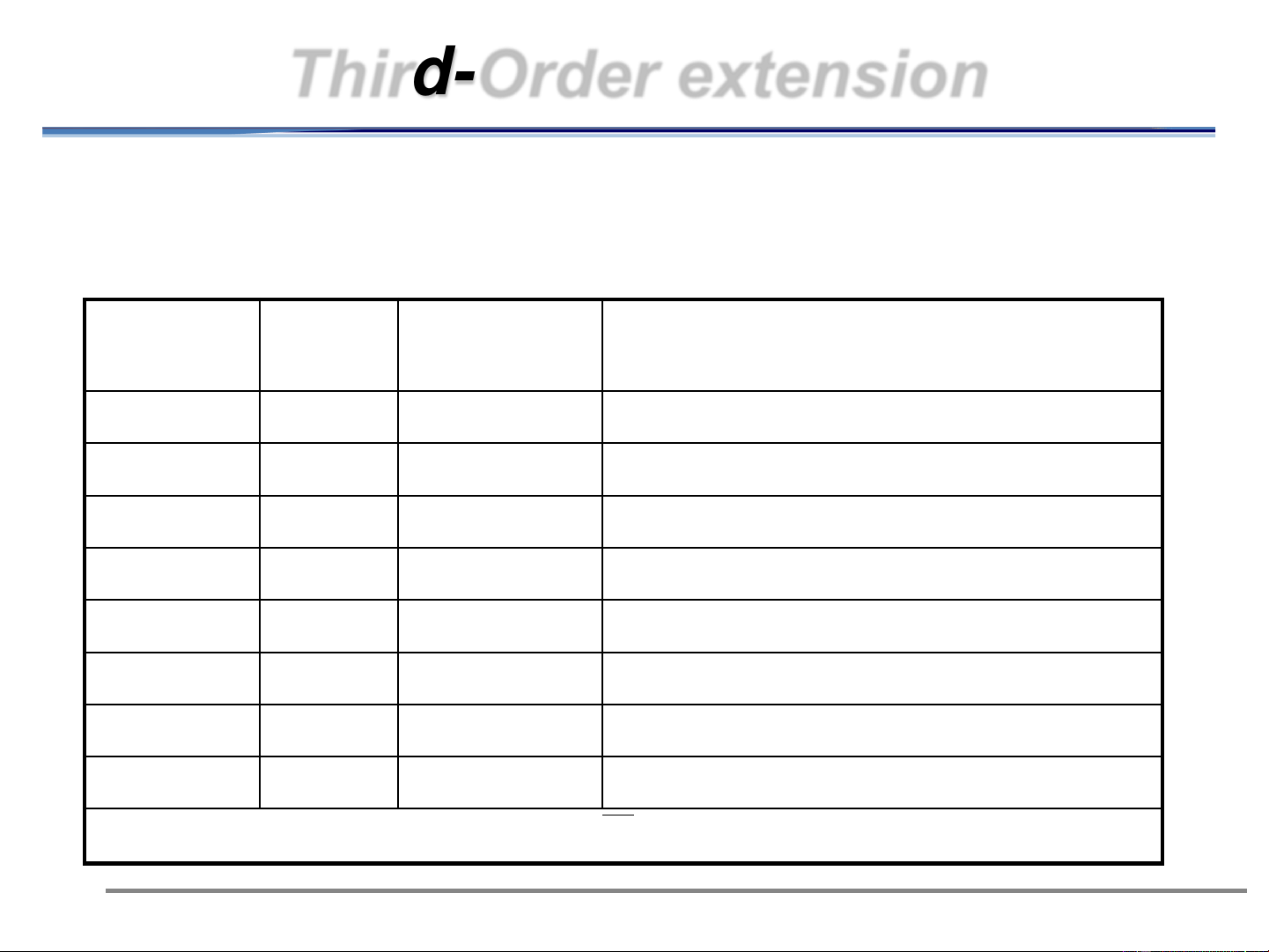
Third-Order extension
Grouping 3 source symbols at a time: Source P ()
Codeword [P()].[Number of Code symbol Symbols] AAA 0.729 0 0.729 AAB 0.081 100 0.243 ABA 0.081 101 0.243 BAA 0.081 110 0.243 ABB 0.009 11100 0.045 BAB 0.009 11101 0.045 BBA 0.009 11110 0.045 BBB 0.001 11111 0.005 L=1.598 11/13/2024 19
Third-Order extension L 598 . 1 = = 533 . 0 code symbols/source symbol n 3
The symbol rate at the encoder output: L r = ( 5 . 3 5 . 0 3 ) 3 = 8 . 1 64 co de s ymbols/s co e nd n
This rate is accepted by the channel 11/13/2024 20