Bài giảng Chương 1 - Mở đầu - Hàm nhiều biến - Giới hạn và liên tục - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Bài giảng Chương 1 - Mở đầu - Hàm nhiều biến - Giới hạn và liên tục - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

56 28 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2 (MAT1042)

Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Thông tin:

43 trang 5 tháng trước

Tác giả:

Profile Mai Nguyệt
GIẢI TÍCH II
Trường Công nghệĐại học
Đại học Quốc gia Hà nội
Giảng TS. Nguyễn Vănviên: Quang
E-mail: nvquang.imech@gmail.com
Đánh kiểm giá tra:
A: thành (40%) Điểm phần
o Điểm điểm tập chuyên cần, bài : 10%
o Điểm giữa thi kỳ: 30%
B: thi Điểm cuối kỳ (60%)
Điểm kết thúc môn học = A*0.4 + B*0.6
2 02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tài liệu:
1. Nguyễn Đình Trí. Toán học cao cấp, tập 3.
NXB Giáo dục, 2006.
2. Nguyễn Thủy Thanh. Bài tập giải tích, tập
1,2,3. NXB Giáo dục, 2002.
3. Trần Đức Long. Bài tập Giải tích, tập 1,2,3.
NXB ĐHQGHN, 2005.
4. Nguyễn Thừa Hợp. Giải tích, tập 1,2,3. NXB
ĐHQGHN, 2004.
5. James Stewart. Calculus, 7th Edition, 2010.
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
3
Nội dung:
• Chương 1: Mở đầu, giới hạn, liên tục
• Chương 2: Đạo hàm, vi phân
• Chương 3: Tích phân bội hai
• Chương 4 bội ba: Tích phân
• Chương 5: Tích phân đường
• Chương 6: Tích phân mặt
• Chương 7: Phương trình vi phân
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
4
1. Hàm hai biến
2. Mặt bậc hai
3. Giới hạn
4. Liên tục
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
5
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
6
Định nghĩa
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
7
Ví dụ
Hàm hai : biến
𝑓
𝑥, 𝑦 =
𝑥 + 𝑦 + 1
𝑥 − 𝑦
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
8
Ví dụ
Hàm hai : biến
𝑓
𝑥, 𝑦 = 𝑥
2
+ 𝑦
2
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
9
Ví dụ
Hàm hai : biến
2 2
1
, ( , ) (0,0)
( , )
0 , ( , ) (0,0)
x y
e x y
f x y
x y
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
10
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
11
Nhắc lại
Mặt paraboloid elliptic:
𝑧 =
𝑥
2
𝑎
2
+
𝑦
2
𝑏
2
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
12
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
13
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
14
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
15
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
16
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
17
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
18
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
19
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
20
Nhắc lại
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
21
Ví dụ
Cho 2 hàm số hãy xét các giá trị của nó khi tiến 𝑓 𝑥, 𝑦 , 𝑔(𝑥, 𝑦) (𝑥, 𝑦)
tới (0, 0).
𝑓
𝑥, 𝑦 =
sin (𝑥
2
+ 𝑦 )
2
𝑥
2
+ 𝑦
2
𝑔
𝑥, 𝑦 =
𝑥
2
− 𝑦
2
𝑥
2
+ 𝑦
2
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
22
Ví dụ
𝑓 𝑥, 𝑦 =
sin (𝑥
2
+ 𝑦 )
2
𝑥
2
+ 𝑦
2
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
23
Ví dụ
𝑔 𝑥, 𝑦 =
𝑥
2
− 𝑦
2
𝑥
2
+ 𝑦
2
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
24
Nhận xét
• 𝑓 𝑥, 𝑦 , 𝑔 𝑥, 𝑦 đều không xác định tại (0,0).
• Khi 𝑥, 𝑦 dần đến (0,0): các giá trị của 𝑓(𝑥, 𝑦) dần tới 1, các giá
trị của không tiến tới bất kỳ một giá trị nào.𝑔(𝑥, 𝑦)
• Dự đoán:
lim
(𝑥,𝑦)→(0,0)
sin (𝑥 +𝑦 )
2 2
𝑥
2
+𝑦
2
= 1.
lim
(𝑥,𝑦)→(0,0)
𝑥
2
−𝑦
2
𝑥
2
+𝑦
2
không tồn tại.
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
25
Định nghĩa giới hạn kép
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
26
0 0
, , ,
n n f n n
n n
x y D x y f x y a
 
0 0
( , ) ( , )
lim ( , )
x y x y
f x y a
Ký (kép): hiệu của giới hạn
Tính chất của giới hạn
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
27
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
28
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
29
Ví dụ
Dọc trục theo : 𝑂𝑥
lim
(𝑥,𝑦)→(0,0)
𝑥𝑦
𝑥
2
+ 𝑦
2
= lim
(𝑥,𝑦)→(0,0)
0
𝑥
2
= 0
Dọc trục theo : 𝑦 = 𝑥
lim
(𝑥,𝑦)→(0,0)
𝑥𝑦
𝑥
2
+ 𝑦
2
= lim
(𝑥,𝑦)→(0,0)
𝑥
2
2𝑥
2
=
1
2
Do : không (kép). đó tồn tại giới hạn
x
y
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
30
Chú ý
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
31
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
32
Ví dụ
Chọn 𝑦 = 𝑘𝑥, khi đó:
𝑓
𝑥, 𝑦 = 𝑓 𝑥, 𝑘𝑥 =
𝑘
1 + 𝑘
2
𝑓 𝑥, 𝑦 là vào một đại lượng phụ thuộc 𝑘, mà 𝑘 thay nên không đổi
tồn tại giới hạn .
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
33
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
34
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
35
Ví dụ
Đặt 𝑡 = 𝑥𝑦, khi đó thì : (𝑥, 𝑦) → (0,0) 𝑡 → 0
𝐼 = lim
𝑡→0
𝑡
1 − 1 + 𝑡
3
= −3
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
36
Ví dụ
Đặt 𝑡 = 𝑥
2
+ 𝑦, khi đó thì (𝑥, 𝑦) → (0,0) 𝑡 → 0:
𝐼 = lim
𝑡→0
𝑡
𝑡 + 9 − 3
= 6
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
37
Ví dụ
Sử dụng hệ độ tọa cực, đặt 𝑥 = 𝑟𝑐𝑜𝑠𝑡, 𝑦 = 𝑟𝑠𝑖𝑛𝑡.
Vì nên khi thì tùy ý.
𝑥
2
+ 𝑦
2
= 𝑟
2
, 𝑥 → 0, 𝑦 → 0 𝑟 → 0, 𝑡 → 𝑎, 𝑎
𝐼 = lim
(𝑟,𝑡)→(0,𝑎)
𝑟. 𝑐𝑜𝑠𝑡. 𝑟 𝑡
4
. 𝑠𝑖𝑛
4
𝑟
4
= lim
(𝑟,𝑡)→(0,𝑎)
𝑟. 𝑐𝑜𝑠𝑡. 𝑠𝑖𝑛
4
𝑡
= 0
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
38
Định nghĩa
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
39
Định nghĩa
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
40
Các phép toán: nhân, chia, hàm các cộng, trừ, lấy hợp hàm sơ cấp
là . hàm sơ cấp
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
41
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
42
Ví dụ
02-Apr-20
TS. Nguyễn Văn Quang
Đại học Công nghệ
- ĐHQGHN
43
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GIẢI TÍCH II
Trường Đại học Công nghệ
Đại học Quốc gia Hà nội
Giảng viên: TS. Nguyễn Văn Quang
E-mail: nvquang.imech@gmail.com
Đánh giá kiểm tra:
A: Điểm thành phần (40%)
o Điểm chuyên cần, điểm bài tập: 10%
o Điểm thi giữa kỳ: 30%
B: Điểm thi cuối kỳ (60%)
 Điểm kết thúc môn học = A*0.4 + B*0.6 TS. Nguyễn Văn Quang 02-Apr-20 2
Đại học Công nghệ - ĐHQGHN Tài liệu:
1. Nguyễn Đình Trí. Toán học cao cấp, tập 3. NXB Giáo dục, 2006.
2. Nguyễn Thủy Thanh. Bài tập giải tích, tập 1,2,3. NXB Giáo dục, 2002.
3. Trần Đức Long. Bài tập Giải tích, tập 1,2,3. NXB ĐHQGHN, 2005.
4. Nguyễn Thừa Hợp. Giải tích, tập 1,2,3. NXB ĐHQGHN, 2004.
5. James Stewart. Calculus, 7th Edition, 2010. TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 3 - ĐHQGHN Nội dung:
• Chương 1: Mở đầu, giới hạn, liên tục
• Chương 2: Đạo hàm, vi phân
• Chương 3: Tích phân bội hai
• Chương 4: Tích phân bội ba
• Chương 5: Tích phân đường
• Chương 6: Tích phân mặt
• Chương 7: Phương trình vi phân TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 4 - ĐHQGHN
1. Hàm hai biến
2. Mặt bậc hai
3. Giới hạn 4. Liên tụ c TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 5 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 6 - ĐHQGHN Định nghĩa TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 7 - ĐHQGHN Ví dụ Hàm hai biến: 𝑥 + 𝑦 + 1 𝑓 𝑥, 𝑦 = 𝑥 − 𝑦 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 8 - ĐHQGHN Ví dụ Hàm hai biến:
𝑓 𝑥, 𝑦 = 𝑥2 + 𝑦2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 9 - ĐHQGHN Ví dụ Hàm hai biến: 1   2 2   f ( , x y) x ye
, (x, y)  (0,0)
0 , (x,y)(0,0) TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 10 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 11 - ĐHQGHN Nhắc lại Mặt paraboloid elliptic: 𝑥2 𝑦2 𝑧 = + 𝑎2 𝑏2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 12 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 13 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 14 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 15 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 16 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 17 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 18 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 19 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 20 - ĐHQGHN Nhắc lại TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 21 - ĐHQGHN Ví dụ
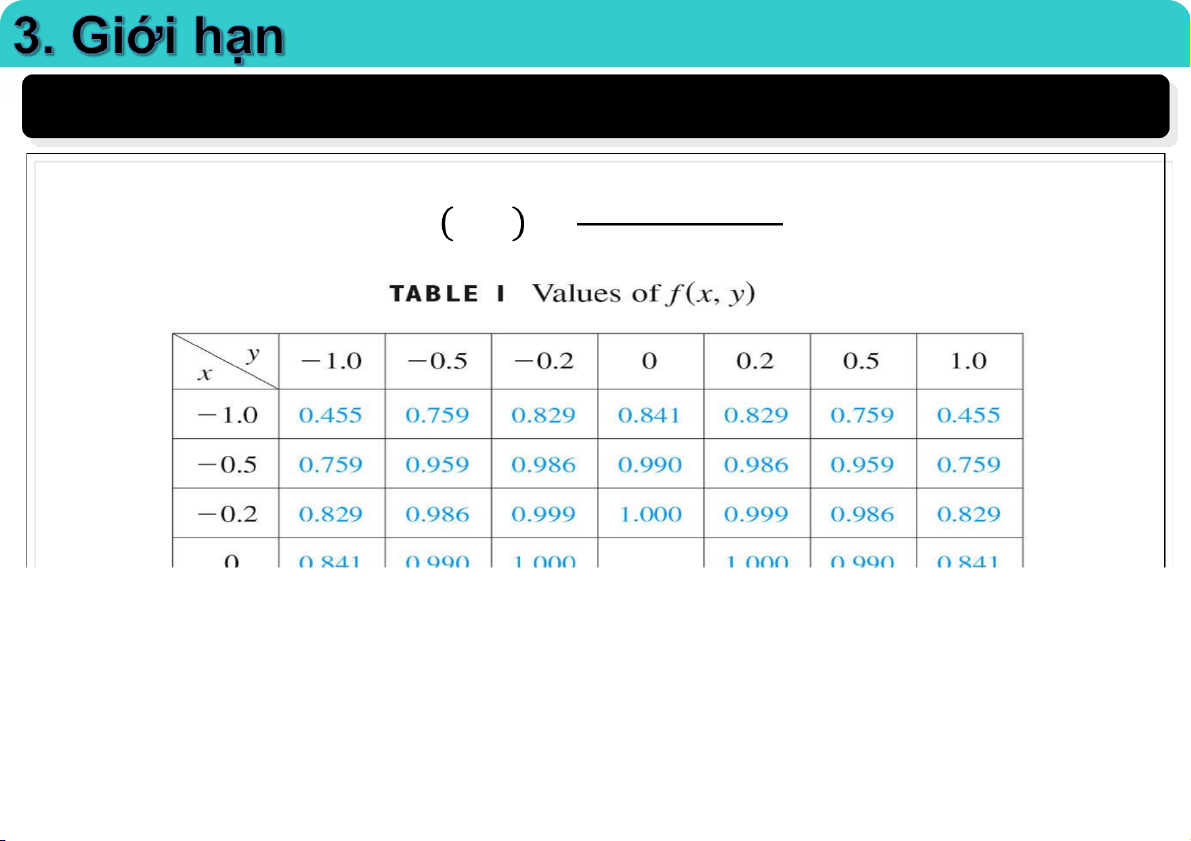
Cho 2 hàm số 𝑓 𝑥, 𝑦 , 𝑔(𝑥, 𝑦) hãy xét các giá trị của nó khi (𝑥, 𝑦) tiến tới (0, 0). sin (𝑥2 + 𝑦2) 𝑓 𝑥, 𝑦 = 𝑥2 + 𝑦2 𝑥2 − 𝑦2 𝑔 𝑥, 𝑦 = 𝑥2 + 𝑦2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 22 - ĐHQGHN Ví dụ sin (𝑥2 + 𝑦2) 𝑓 𝑥, 𝑦 = 𝑥2 + 𝑦2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 23 - ĐHQGHN Ví dụ 𝑥2 − 𝑦2 𝑔 𝑥, 𝑦 = 𝑥2 + 𝑦2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 24 - ĐHQGHN Nhận xét
• 𝑓 𝑥, 𝑦 , 𝑔 𝑥, 𝑦 đều không xác định tại (0,0).
• Khi 𝑥, 𝑦 dần đến (0,0): các giá trị của 𝑓(𝑥, 𝑦 ) dần tới 1, các giá
trị của 𝑔(𝑥, 𝑦) không tiến tới bất kỳ một giá trị nào. • Dự đoán: sin (𝑥2+𝑦2) lim = 1. (𝑥,𝑦)→(0,0) 𝑥2+𝑦2 𝑥2−𝑦2 lim không tồn tại.
(𝑥,𝑦)→(0,0) 𝑥2+𝑦2 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 25 - ĐHQGHN
Định nghĩa giới hạn kép
 x , y  D  x    0 , y0 
f x , y a n n f n n n n
Ký hiệu của giới hạn (kép): lim
f (x, y)  a (x,y ) (  0 x ,y0 ) TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 26 - ĐHQGHN
Tính chất của giới hạn TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 27 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 28 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 29 - ĐHQGHN Ví dụ Dọc theo trục 𝑂𝑥: y 𝑥𝑦 0 lim = lim = 0
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 (𝑥,𝑦)→(0,0) 𝑥2
Dọc theo trục 𝑦 = 𝑥: 𝑥𝑦 𝑥2 1 x lim = lim =
(𝑥,𝑦)→(0,0) 𝑥2 + 𝑦2 (𝑥,𝑦)→(0,0) 2𝑥2 2
Do đó: không tồn tại giới hạn (kép). TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 30 - ĐHQGHN Chú ý TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 31 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 32 - ĐHQGHN Ví dụ
Chọn 𝑦 = 𝑘𝑥, khi đó: 𝑘
𝑓 𝑥, 𝑦 = 𝑓 𝑥, 𝑘𝑥 = 1 + 𝑘2
𝑓 𝑥, 𝑦 là một đại lượng phụ thuộc vào 𝑘, mà 𝑘 thay đổi nên không tồn tại giới hạn. TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 33 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 34 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 35 - ĐHQGHN Ví dụ
Đặt 𝑡 = 𝑥𝑦, khi đó (𝑥, 𝑦) → (0,0) thì 𝑡 → 0: 𝑡 𝐼 = lim = −3 𝑡→0 1 − 3 1 + 𝑡 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 36 - ĐHQGHN Ví dụ
Đặt 𝑡 = 𝑥2 + 𝑦, khi đó (𝑥, 𝑦) → (0,0) thì 𝑡 → 0: 𝑡 𝐼 = lim = 6 𝑡→0 𝑡 + 9 − 3 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 37 - ĐHQGHN Ví dụ
Sử dụng hệ tọa độ cực, đặt 𝑥 = 𝑟𝑐𝑜𝑠𝑡, 𝑦 = 𝑟𝑠𝑖𝑛𝑡.
Vì 𝑥2 + 𝑦2 = 𝑟2, nên khi 𝑥 → 0, 𝑦 → 0 thì 𝑟 → 0, 𝑡 → 𝑎, 𝑎 tùy ý.
𝑟. 𝑐𝑜𝑠𝑡. 𝑟4. 𝑠𝑖𝑛4𝑡 𝐼 = lim (𝑟,𝑡)→(0,𝑎) 𝑟4 = lim
𝑟. 𝑐𝑜𝑠𝑡. 𝑠𝑖𝑛4𝑡 (𝑟,𝑡)→(0,𝑎) = 0 TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 38 - ĐHQGHN Định nghĩa TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 39 - ĐHQGHN Định nghĩa
Các phép toán: cộng, trừ, nhân, chia, lấy hàm hợ p các hàm sơ cấ p là hàm sơ cấ . p TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 40 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 41 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 42 - ĐHQGHN Ví dụ TS. Nguyễn Văn Quang 02-Apr-20 Đại học Công nghệ 43 - ĐHQGHN