Chương TÍCH PHÂN ĐƯỜNG, TÍCH PHÂN MẶT 3.
3.1. Tích phân đường loại một 3.1.1.
Định nghĩa tích phân đường loại một
Bài toán vật lý dẫn đến khái niệm tích phân đường loại một
Giả sử trong mặt phẳng tọa độ Oxy có một sợi dây AB rất mảnh (chỉ có độ dài, còn tiết diện
không đáng kể - coi như không có kích thước) có khối lượng riêng tại điểm (x,y) AB  được biểu diễn
bằng hàm số f(x,y) đơn trị, liên tục và không âm. Yêu cầu tìm khối lượng m của sợi dây AB.
Để tính m, chúng ta thực hiện như sau: Chia tùy ý AB thành n
cung nhỏ không dẫm lên nhau bởi
các điểm A  A0, A1, A2 …, A , n-1, An  B v
à ký hiệu độ dài của cung nhỏ Ai-1Ai là si (1  i  n). Trên
cung Ai-1Ai lấy tùy ý một điểm (xi,yi), nếu cung Ai-1Ai đủ nhỏ thì chúng ta có thể coi giá trị f(xi,yi)
không đổi trên cung Ai-1Ai; khi đó, khối lượng của cung nhỏ Ai-1Ai là mi  f(xi,yi).si.
Như vậy, nếu mọi cung Ai-1Ai (1  i  n) đủ nhỏ thì có thể coi khối lượng của sợi dây AB là n m = m f (x , y )  1 + m2 + … + mn
 f(x1,y1).s1 + f(x2,y2).s2 + … + f(xn,yn).sn =  . s i i i i=1 n Tổng  f (x , y ) 
. s sẽ có độ chính xác cao (tức là giá trị của biểu thức này càng gần khối lượng i i i i=1
thực m của sợi dây AB) nếu n càng lớn và tất cả các si (1  i  n) càng bé. Do đó, khối lượng m của n
sợi dây AB bằng giới hạn của tổng f (x , y ) 
. s khi n →  cùng với độ dài của mỗi cung nhỏ si (1 i i i i=1 n
 i  n) bé dần về 0, tức là m = lim trong đó  = max s  . →  f (x , y . ) s  i i i i 0 1 i  n i 1 = n→
Định nghĩa tích phân đường loại một
Cho đường cong phẳng L là cung AB trong mặt phẳng tọa độ Oxy và hàm số f(x,y) xác định,
đơn trị và liên tục với (x,y) AB. 
Chia cung AB thành n cung nhỏ tùy ý không dẫm lên nhau bởi các
điểm A  A0, A1, A2, …, An-1, An  B và ký hiệu độ dài của cung nhỏ Ai-1Ai là si (1  i  n). Trên n
cung Ai-1Ai lấy điểm (xi,yi) t ùy ý và lập tổng I f (x , y ). s . n =  i i  i i=1
Nếu khi n →  sao cho  = max s → 0 mà I → I là một giá trị hữu hạn, không phụ thuộc vào i n 1 i  n
cách chia cung AB và cách lấy điểm (xi,yi) trên cung Ai-1Ai thì giá trị hữu hạn I được gọi tích phân
đường loại một của hàm số f(x,y) trên cung AB (hay trên đường cong L) và ký hiệu là n
I = f (x, y)ds = f (x, y)ds = limI = lim f (x , y )  . s → n n →   i i i 0 i=1 AB L
Khi đó hàm số dưới dấu tích phân f(x,y) được gọi là khả tích trên cung AB (hay trên đường cong L), còn ds .
được gọi là vi phân cung
Nếu hàm số f(x,y) đơn trị và liên tục với (x,y)L thì nó khả tích trên đường cong L.
Hoàn toàn tương tự, chúng ta cũng định nghĩa tích phân đường loại một trên đường cong L trong
không gian 3 chiều, tức là I =  f (x, y,z)ds. L
3.1.2. Tính chất của tích phân đường loại một
Đối với tích phân đường loại một trên đường cong phẳng
(1) Tích phân đường loại một không phụ thuộc vào chiều tính tích phân từ A đến B hay ngược
lại, tức là f (x, y)ds = f (x, y)ds. AB BA 103
Các tính chất khác của tích phân đường loại một giống như các tính chất của tích phân xác định. (2) [f (x, y)+ f (x, y) d ] s = f (x, y)ds f (x, y)ds 1 2  + 1  2 L L L
(3)  f (x, y)ds =  f (x, y)ds (hằng số R) L L L  L = L  (4) f (x, y d
) s = f (x, y)ds + f (x, y)ds  1 2    L L =  L  1 2  1 L L2
Hoàn toàn tương tự đối với tích phân đường loại một trên đường cong trong không gian 3 chiều. 3.1.3.
Cách tính tích phân đường loại một Tính tích p t
hân đường loại một trên đường cong rong R2 (đường cong phẳng) x = x(t)
(1) Nếu đường cong phẳng AB được cho dưới dạng tham số  với a  t  b, y = y(t)
 ds = (dx)2 + (dy)2 = [x'(t d ) t]2 + [y'(t d
) t ]2 = x'(t)2 + y'(t)2dt b 2 2 và f (x, ) y = f ( ( x t), (
y t) ) với a  t  b, thì f (x, y)ds = f (x(t), y(t)) x'(t) + y'(t) dt.   AB a
(2) Nếu đường cong phẳng AB được cho bởi y = y(x) với a  x  ,
b khi đó chúng ta coi x là x = t
tham số t thì đường cong phẳng AB được cho dưới dạng tham số  với a  t  b y = y(t) d  t = dx  2  x'(t)= 1
 ds = 1+y'(x ) dx và f ( , x ) y = f(x, ( y x ) ) với a  x  b y'(t) = y'(x)  b 2 thì
f (x, y)ds = f (x, y(x)) 1 + y'(x) dx.   AB a
(3) Nếu đường cong phẳng AB được cho bởi x = x(y) với c  y  d, khi đó chúng ta coi y là x = x(t)
tham số t thì đường cong phẳng AB được cho dưới dạng tham số  với c  t  d y = t d  t = dy  2  x
 '(t) = x'(y)  ds = 1+ x'(y  ) dy và f (x, ) y = f(x( ) y , ) y với c  y  d y'(t)= 1  d 2
thì f (x, y)ds = f (x(y), y) 1+ x'(y) d . y   AB c
(4) Nếu đường cong phẳng AB được cho dưới dạng tọa độ cực r = r() với      trong hệ
x = r cos  = r()cos 
tọa độ cực (r,), khi đó 
và chúng ta coi  là tham số thì đường cong phẳng AB y = r sin = r  ( ) sin x = x  ( ) = r() cos
được cho dưới dạng tham số  với      y = y  ( ) = r  ( ) sin
 ds = (dx)2 + (dy)2 = [x'  ( )  d ]2 + [y'  ( ) 
d ]2 = x'()2 + y'  ( )2  d = r'  ( ) co  s − r  ( ) sin 
 2 +r'()sin + r  ( ) cos   2 d = [r  ( )]2 + [r'  ( )]2d và f (x, y) = f (r cos ,  r sin )  (     ) 104  thì f (x, y)ds = f (r cos ,
 r sin) r()2 + r'(  ) 2 d .    AB 
Tính tích phân đường loại một trên đường cong trong R3 x = x(t) 
(1) Nếu đường cong AB trong R3 được cho dưới dạng tham số y = y(t) với a  t  b  z =z(t)  thì f (x, , y ) z ds = f (x(t), y(t), (
z t)) x'(t)2 + y'(t)2 + z'(t)   2 dt AB  y = y(x)
(2) Nếu đường cong AB trong R3 được cho bởi các phương trình  với a  x  b z = z(x) b 2 2 thì f (x, , y ) z ds = f (x, y(x), (
z x)) 1 + y'(x) + z'(x)   dx AB a x = x(y)
tương tự, nếu đường cong AB trong R3 được cho bởi các phương trình  với c  y  d z = ( z y) d 2 2 thì f (x, , y z)ds = f (x(y), ,
y z(y)) 1 + x'(y)  + z'(y)    dy AB c x = x(z)
và tương tự, nếu đường cong AB trong R3 được cho bởi các phương trình  với p  z  q y = y(z) q 2 2
thì f (x, y, z)ds = f(x(z), y(z),z) 1 +x'(z) +y'(z)   dz AB p Lưu ý.
(1) Vì tích phân đường loại một không phụ thuộc vào chiều tính tích phân nên đối với giá trị của
hai cận của tích phân, giá trị nhỏ là cận dưới còn giá trị lớn hơn là cận trên.
(2) Nếu L là đường cong kín thì có thể dùng ký hiệu  f (x, )
y ds =  f (x, y)ds (L là đường cong L L
phẳng) và tương tự f(x, y, z)ds = f(x, y,z)ds (L là đường cong trong R3) . L L
Ví dụ 3.1. Tính I = xds, 
OA là cung của đường parabol y = x2 từ điểm O(0,0) đến điểm A(2,4). OA Bài giải.
Cung OA nằm trên đường parabol y = y(x) = x2 với 0  x  2 nên đồ thị của nó trong hệ tọa độ Descartes vuông góc Oxy là 2 2 2 2 1 2
Chúng ta có y’(x) = 2x  I =
xds = x 1 + y'(x) dx = x 1 + 4x dx = 1 + 4x2 d(x2 ) =     2 OA 0 0 0 2 1 1 1 2 2 + 1 1 + − 2 2 1 2 2 1 1 ( 4x 2 2 ) 2 17 17 1 . 1 + 4x d(4x ) = 1 ( + 4x ) d 1 ( + 4x ) = =   . 2 4 8 8 1 ( 2) + 1 12 0 0 0 105
Ví dụ 3.2. Tính I = (x2 2y)ds,  −
L là các cạnh của ABC có tọa độ các đỉnh trong hệ tọa độ L
Descartes vuông góc Oxy là A(1,1), B(3,1) và C(1,5) . Bài giải.
Đồ thị của ABC trong hệ tọa độ Descartes vuông góc Oxy là
Chúng ta có L = AB + BC + CA  I =  2 (x − 2y d ) s =  2 (x − 2 ) y ds +  2 (x − 2 ) y ds +  2 (x − 2 ) y ds L AB BC CA - Tính  2
(x − 2y)ds : Lấy làm tham số, x khi (x,y) A
 B thì y = 1 với 1 ≤ x ≤ 3 AB  f (x, ) y = f(x, y(x )  ) = x2 − 2y = x2 − . 2 1= x2 − 2 Chúng ta có 
y'(x) = 0  ds = 1+[y'(x)]2dx = 1 + 02dx = dx 3 3   2 2 x3 14  (x −2y)ds = (x −2)dx = −2x =     3 3   AB 1 1 - Tính  2
(x − 2y)ds : Lấy x làm tham số, khi (x,y) B
 C thì phương trình đường thẳng đi qua BC − − − − điểm B(3,1) v x x y y B B x 3 y 1 à điểm C(1,5) là =  =  y = 2 − x + 7 với 1 ≤ x ≤ 3 x − x y − y 1− 3 5 −1 C B C B
f (x, y) = f[x, y(x)] = x 2 − 2 − ( 2x + ) 7 = x 2 + 4x − 14 Chúng ta có   2 2 y'(x) = −2 ds = + 1 [y'(x)] dx = + 1 − ( ) 2 dx = 5dx 3 3   2 2 x 3 x2 10 5  (x − 2y)ds = (x + 4x− 1 ) 4 d 5 x = 5 + 4 − 1 x 4 = −      3 2  3 BC 1 1 - Tính  2
(x − 2y)ds : Lấy y làm tham số, khi (x,y) C
 A thì x = 1 với 1 ≤ y ≤ 5 CA
f (x, y) = f (x(y),y ) = x 2 − 2y =12 − 2y =1 − 2y Chúng ta có 
x'(y) = 0  ds = 1 +[x'(y)]2dy = 1 + 02dy = dy 5 5  (x 2 − 2y)ds = 1 ( − 2y)dy = (y − y2 ) = 2 − 0   1 CA 1 − − Như vậy, 2 14 10 5 46 10 5
chúng ta được I = (x − 2y d ) s = − − 20 =  . 3 3 3 L
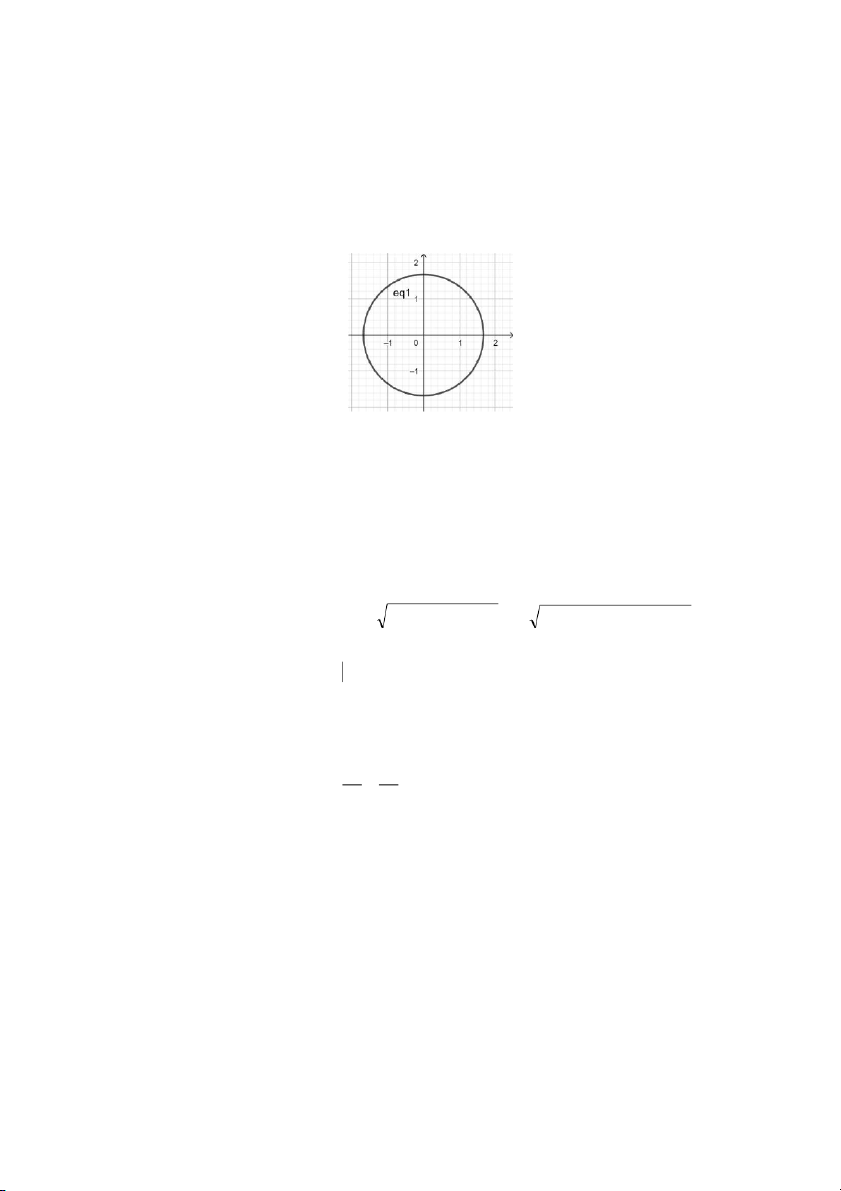
Ví dụ 3.3. Cho L là đường cong có phương trình trong hệ tọa độ cực (r,) là r = cos với 0    2 . 
(a) Vẽ đồ thị của L trong hệ tọa độ Descartes vuông góc Oxy.
(b) Tính I =  xds trong hệ tọa độ Descartes vuông góc Oxy khi  là tham số. L
(c) Tính I =  xds trong hệ tọa độ cực (r,) . L Bài giải.  x = r co  s
x = rcos = coscos = cos2  (a) Chúng ta có  mà r = cos   y = r sin  y = rsi  n = co  s si  n 106  x2 + y2 = (cos2 )2  + (cossin )2  = cos2 (  cos2  + sin2 )
 = cos2  = x , do đó phương trình 2 2    
của đường cong L trong hệ tọa độ Descartes vuông góc Oxy là 1 1 2 2 2
x + y = x  x −  + y =   .  2  2  1 
Phương trình này là phương trình của đường tròn có tâm 1 I  ,0 , bán kính R = và có đồ thị  2  2
x = rcos = coscos = cos2 
(b) Chúng ta có r = cos   ,  là tham số y = rsi  n = co  s si  n 2
f (x, y) = x  f (r cos, r sin ) = cos     , 2 , 2 2 2 2 2
ds = [x ()] +[y ()] d = (2cossin ) + (−sin  + cos ) d = d     2 2   2 1 2 1 1  I = xds = cos d   = 1 ( + cos2)d =  + sin2 = .     2 2  2  L 0 0 0
f (x, y) = x f (x( ), (
y ) ) = x( ) =r cos  = cos cos  =cos2 
(c) Chúng ta có r = cos  
ds = [r()]2 + [r'()]2  d = (co 
s )2 + (− sin )2 d =  d 2 2  2     2 1 1 1  I = xds = cos d   = 1 ( + cos2)d =  + sin2 = .     2 2  2  L 0 0 0
Ví dụ 3.4. Tính I = (2x + y − 2z)ds với AB là đoạn thẳng nối điểm A(1,–1,2) với điểm B(– AB
1,2,–1) trong hệ tọa độ Descartes vuông góc Oxyz. Bài giải.
Phương trình đường thẳng đi qua điểm A(1,–1,2) và điểm B(–1,2,–1) là x − x y − y z − z − − − − A A A x 1 y ( ) 1 z 2 = =  = = x − − − − − − − − − B xA yB yA z B z A 1 1 2 ( ) 1 1 2
Nếu lấy x làm tham số thì 3 1 3 1 x = x, y = − x + , z = x + với –1 ≤ x ≤ 1 2 2 2 2  3 1 3 1  5 1 f (x, , y ) z = x 2 + y − 2z = 2x − x + −  2 x +  = − x −  2 2 2 2  2 2    2 2 2 2 2 2 ds = (x') + [y'(x)] + z
[ '(x)] dx = 1 + (− 3 2 ) + (3 2 ) 22  dx = dx  2 1 1  5 1 22 22 1 22  x2  22  I = (2x + y− 2 ) z ds =  − x −  dx = − x 5 ( + ) 1 dx = − 5 + x = −      . −  2 2 2 2 4 2 2 AB 1 −1  −1
3.1.4. Ý nghĩa vật lý và ý nghĩa hình học của tích phân đường loại một
Nếu hàm số dưới dấu tích phân f(x,y) > 0 (đường cong phẳng L) hoặc f(x,y,z) > 0 (đường cong
không gian L) xác định và liên tục với mọi điểm trên đường cong, biểu thị khối lượng riêng của đường
cong tại điểm (x,y) của đường cong phẳng hoặc tại điểm (x,y,z) của đường cong không gian, thì khối
lượng m của đường cong L là m = f (x,y)ds hoặc m = f(x, ,y )zds(ý nghĩa vật lý). Đặc biệt, nếu L L 107
f(x,y) = 1 thì  ds (L là đường cong phẳng) hoặc nếu f(x,y,z) = 1 thì  ds (L là đường cong không L L
gian) là độ dài của đường cong L (ý nghĩa hình học).
Ví dụ 3.5. Tính chu vi của đường tròn L bán kính R. Bài giải.
Không mất tính tổng quát, có thể coi đường tròn L bán kính R có tâm tại gốc tọa độ O(0,0) của
hệ tọa độ Descartes vuông góc Oxy, khi đó phương trình của đường tròn L trong hệ tọa độ Descartes
vuông góc Oxy là x2 + y2 = R2 và đồ thị của nó là x(t) = R cost
Phương trình tham số của đường tròn x2 + y2 = R2 là 
(0 ≤ t ≤ 2), theo ý nghĩa y(t) = R sin t
hình học của tích phân đường loại một thì chu vi của đường tròn L bán kính R là C =  ds. L
Đường tròn L là đường cong phẳng khép kín nên bất kỳ điểm nào trên L cũng có thể được chọn
là điểm bắt đầu đồng thời là điểm kết thúc khi tính tích phân C =  ds . Để đơn giản, ta chọn điểm (x,y) L
= (R,0) là điểm bắt đầu đồng thời là điểm kết thúc, tương ứng với t = 0 và t = 2. x'(t) = − R sin t Chúng ta có 
 ds = x'(t)2 + y'(t) 2 dt = (−R sin t) 2 + (R cost) 2dt = Rdt y'(t) = R cost  2 2 2   C = ds = Rdt = R dt = Rt = 2R.    0 L 0 0 Bài tập
3.1. Tính I =  xyds L x2 y2
(a) L là cung của đường ellipse +
= 1 nằm trong góc vuông thứ nhất (x  0, y  0) của hệ a 2 b2
tọa độ Descartes vuông góc Oxy.
(b) L là các cạnh của hình chữ nhật OABC có tọa độ các đỉnh trong hệ tọa độ Descartes vuông
góc Oxy là O(0,0), A(4,0), B(4,2) và C(0,2).
(c) L là các cạnh của hình vuông |x| + |y| = a (a > 0). 3.2. Tính I =  2 (x + 2 y d ) s L
(a) L là đoạn thẳng nối điểm O(0,0) với điểm A(2,4) trong hệ tọa độ Descartes vuông góc Oxy.
(b) L là các cạnh của OAB có tọa độ các đỉnh trong hệ tọa độ Descartes vuông góc Oxy là O(0,0), A(1,1) và B( 1,1) – .
(c) L là đường có phương trình x2 + y2 = ax (a > 0) trong hệ tọa độ Descartes vuông góc Oxy. 108 3.3. Tính I =  2 x + 2
y ds với C là đường cong có phương trình trong hệ tọa độ cực (r,) là r = 4sin C
(0    ) . Vẽ đồ thị của đường cong C.
3.4. Tính các tích phân sau đây x = t  (a) I =  2yds , cung L c
ó phương trình tham số y = t 2 2 với 0 ≤ t ≤ 1. L  z = t 3 3 x = a cost  (b) I =  2 (x + 2 y + 2
z )ds , cung L là đường xoắn ốc có phương trình tham số y = a sin t L  z = bt a  0 với  và 0 ≤ t ≤ 2. b  0 (c) I =  2 ( 5 x − 2 y ) + 24xy + z ( − 2 ) 1 + d
4 s , L là giao tuyến của mặt trụ x2 + y2 = 4 với mặt L phẳng 2x – 3y + z = 1. (d) I =  2
x ds , L là giao tuyến của mặt cầu x2 + y2 + z2 2
= a (a > 0) với mặt phẳng x + y + z = 0. L
3.5. Tính khối lượng của sợi dây có phương trình a  x − x 
(a) là đường cong phẳng y =  a e + a e  
 với 0  x  a (a > 0), biết rằng khối lượng riêng của 2  
đường cong tại điểm (x,y) là f(x, y) =1 y . x = a cost 
(b) là đường xoắn ốc y = a sin t với 0  t  2, a = b = 1, biết rằng khối lượng riêng của sợi dây  z = bt
tại điểm (x,y,z) là f (x, , y ) z = x2 + y2 + z2 . x2
3.6. Tính độ dài cung có phương trình y = − ln x (1  x  e). 4 109