1. Định nghĩa, cách tính tích phân kép
2. Tọa độ cực
3. Ứng dụng hình học
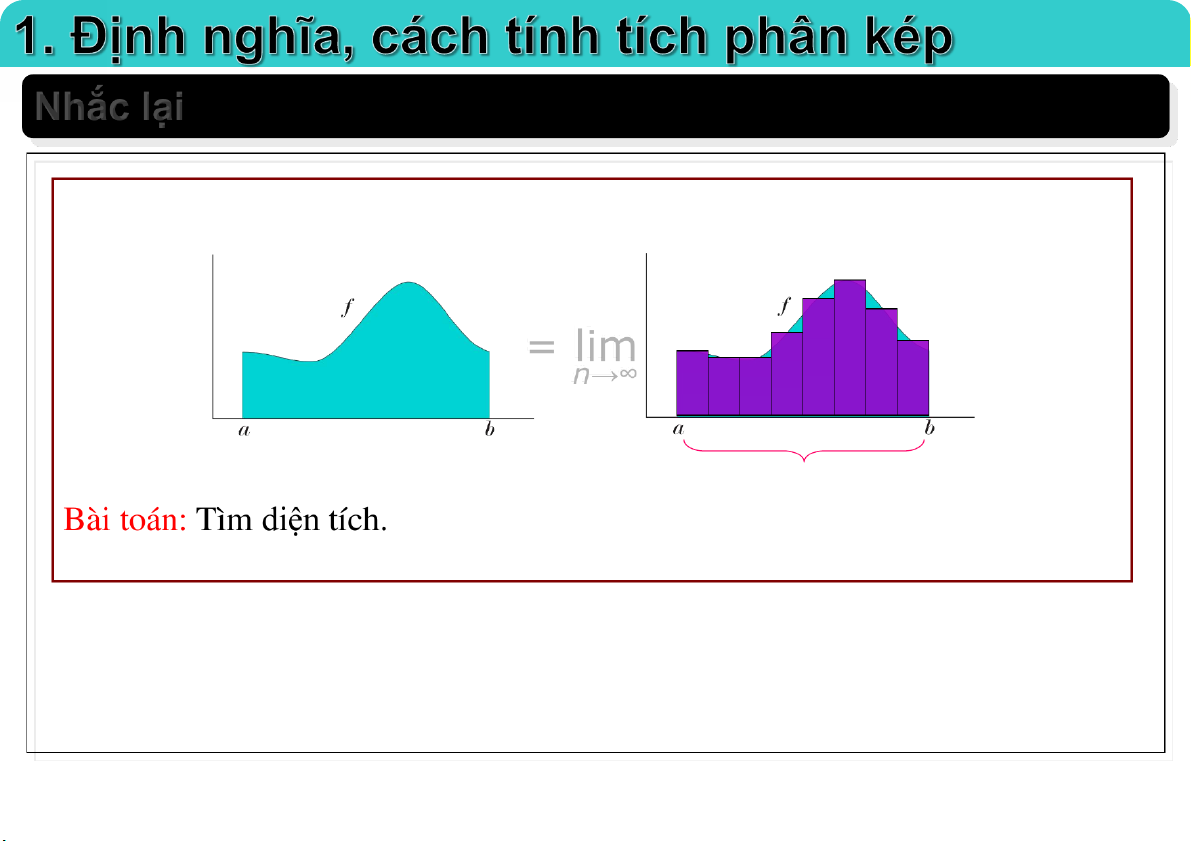
4. Ứng dụng cơ học Nhắc lại = lim n→∞ 23-Feb-21 TS. Nguyễn Văn Quang 2
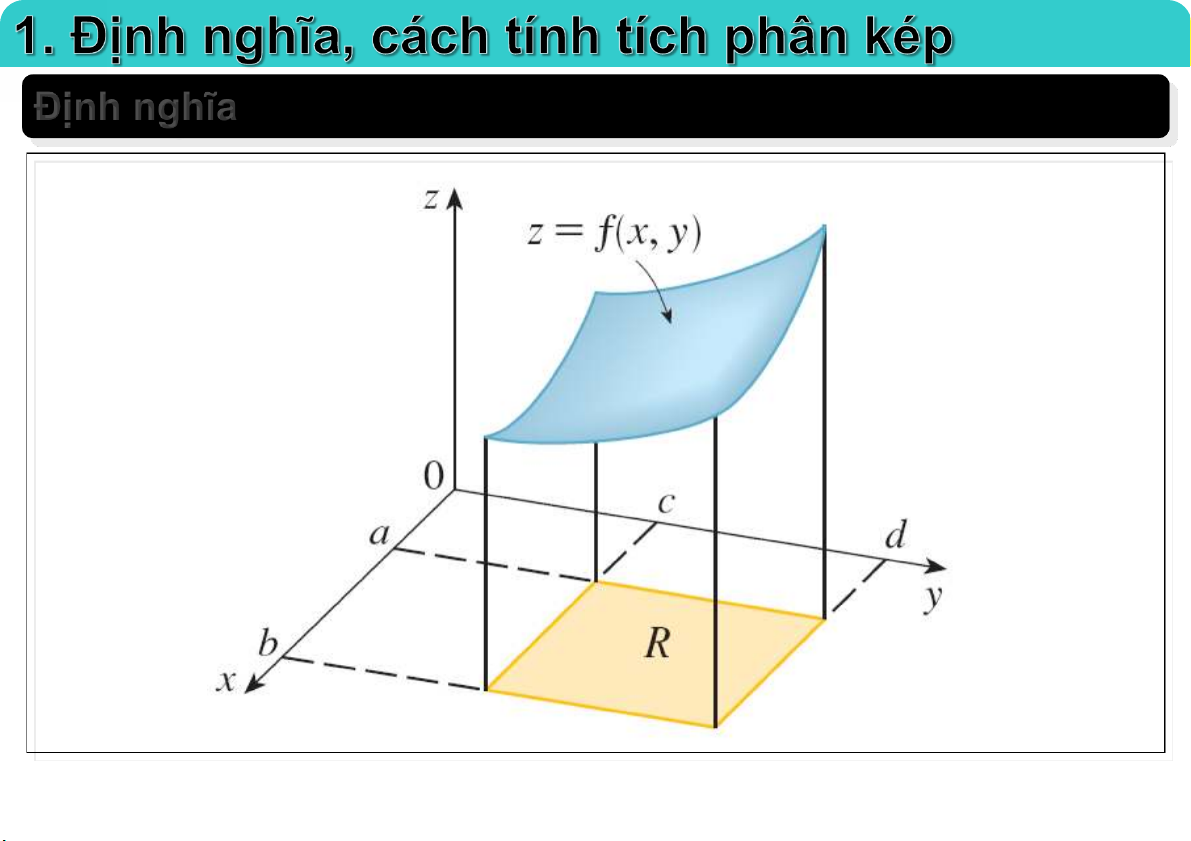
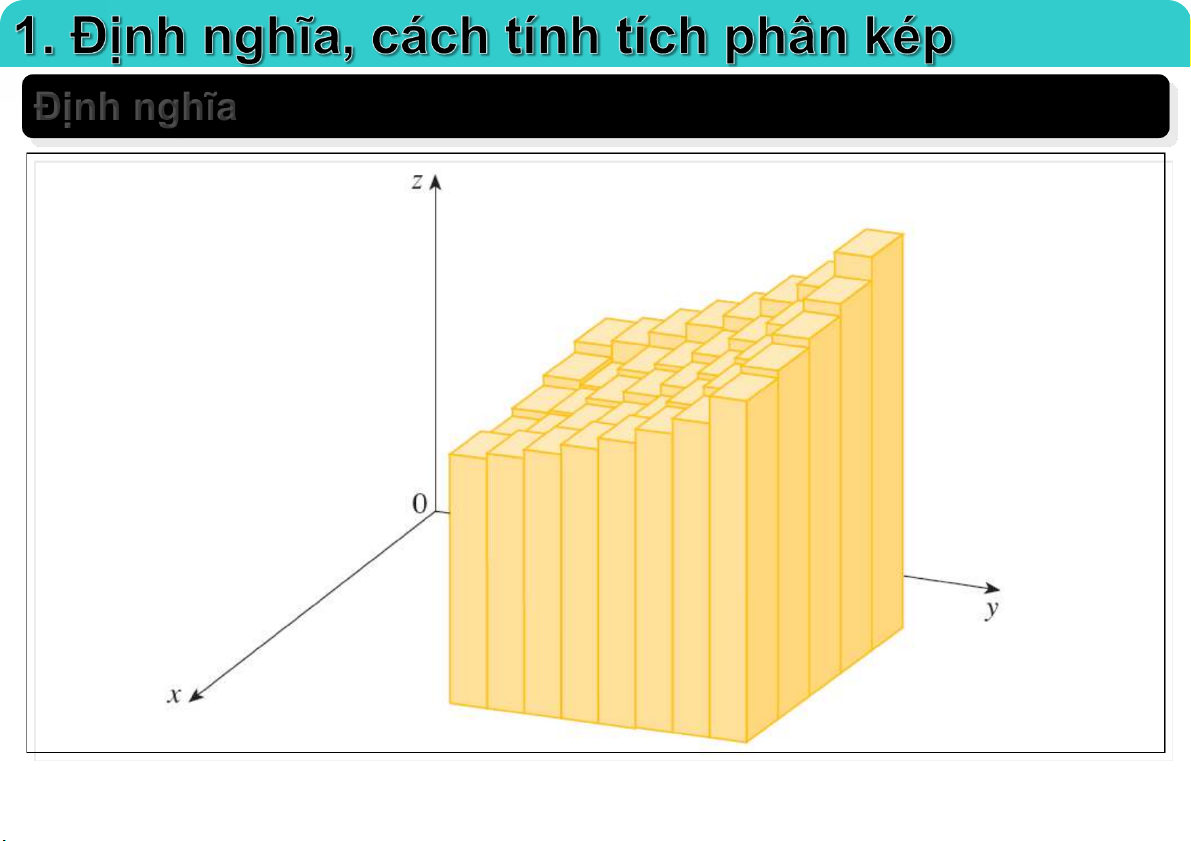
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 3
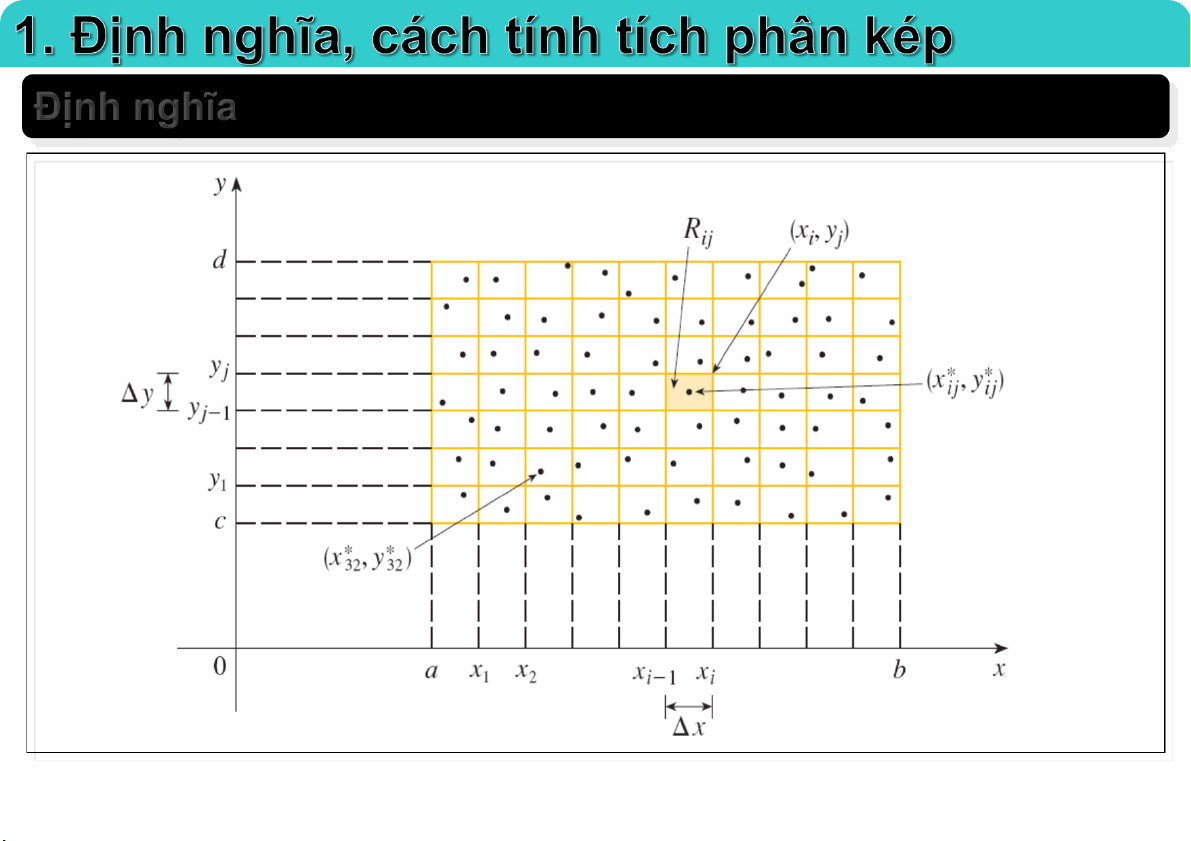
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 4
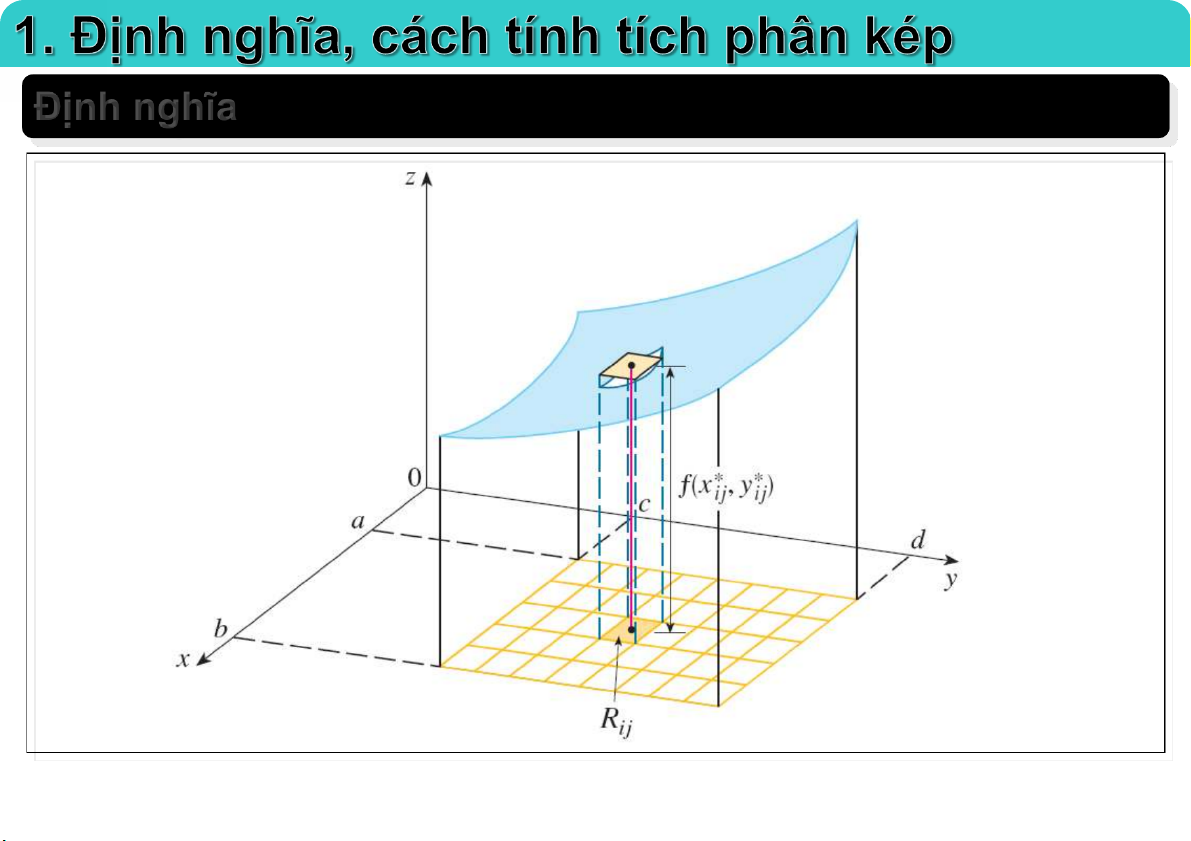
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 5
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 6
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 7
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Feb-21 TS. Nguyễn Văn Quang 8
Đại học Công nghệ - ĐHQGHN Định nghĩa
Do đó, D có thể được bao kín trong một miền chữ nhật C. y
Xác định hàm F(x,y) như sau: D C
 f (x, y) (x, y)  D F( , x ) y   x 0 ( , x ) y  D  n  
Nếu giới hạn: I  l i m  F ( M )  S 
tồn tại hữu hạn, thì ta nói hàm f(x,y) i C  i
n   i 1  
khả tích trên miền D. Ký hiệu: I  f ( , x ) y dxdy D 23-Feb-21 TS. Nguyễn Văn Quang 9
Đại học Công nghệ - ĐHQGHN Tính chất 23-Feb-21 TS. Nguyễn Văn Quang 10
Đại học Công nghệ - ĐHQGHN Ví dụ 2 2 23-Feb-21 TS. Nguyễn Văn Quang 11
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 12
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 13
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 14
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 15
Đại học Công nghệ - ĐHQGHN (Định tục miền đóng bị chặn 23-Feb-21 TS. Nguyễn Văn Quang 16
Đại học Công nghệ - ĐHQGHN 
a  x  b b g2 ( ) x R : 
I   f (x, y)dxdy   dx  f (x, y)dy g x  y   1( ) 2 g ( x) R a 1 g ( x) y g (x) 2 g (x) 1 a b x 23-Feb-21 TS. Nguyễn Văn Quang 17
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 18
Đại học Công nghệ - ĐHQGHN  c  y  d d 2 h ( y) R : 
I   f (x, y)dxdy   dy  f (x, y)dx h y  x   1( ) 2 h ( y) R c 1 h ( y) y d c h (y) 1 h (y) 2 x 23-Feb-21 TS. Nguyễn Văn Quang 19
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 20
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 21
Đại học Công nghệ - ĐHQGHN 1 5 4    . 2 6 3 23-Feb-21 TS. Nguyễn Văn Quang 22
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 23
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 24
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 25
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 26
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 27
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 28
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Tổng quát, xét phép đổi biến T từ mặt Ouv sang mặt Oxy:
𝑇(𝑢, 𝑣) = (𝑥, 𝑦)
với x và y liên hệ với u và v bởi:
𝑥 = 𝑔 𝑢, 𝑣 ; 𝑦 = ℎ(𝑢, 𝑣)
Có thể viết: 𝑥 = 𝑥(𝑢, 𝑣), 𝑦 = 𝑦(𝑢, 𝑣).
Giả sử T là một phép biến thỏa mãn: g và h có đạo hàm riêng bậc nhất liên tục. Nếu 𝑇(𝑢 , 𝑣 , 𝑦
được gọi là ảnh của điểm 1 1) = (𝑥1 1), thì (𝑥 , 𝑦 ) 1 1 (𝑢 , 𝑣 1 1).
Nếu không có 2 điểm nào có cùng chung 1 ảnh và ngược lại, thì ta gọi
T là đổi biến 1-1. 23-Feb-21 TS. Nguyễn Văn Quang 29
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Nếu T là đổi biến 1-1, nó sẽ có một phép biến đổi ngược 𝑇−1 từ mặt Oxy sang mặt Ouv.
Do đó, ta có thể tìm u và v theo x và y :
𝑢 = 𝐺(𝑥, 𝑦), 𝑣 = 𝐻(𝑥, 𝑦) 23-Feb-21 TS. Nguyễn Văn Quang 30
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Xét một hình chữ nhật nhỏ S trong mặt Ouv: ảnh của S là miền R trong mặt
Oxy. Một điểm trên cạnh biên của nó sẽ là: (𝑥 , 𝑦 , 𝑣 ) 0 0) = 𝑇(𝑢0 0 23-Feb-21 TS. Nguyễn Văn Quang 31
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Ta có vector vị trí của điểm (u, v):
𝒓(𝑢, 𝑣) = 𝑥 𝒊 + 𝑦 𝒋 = 𝑔(𝑢, 𝑣) 𝒊 + ℎ(𝑢, 𝑣) 𝒋
Phương trình của cạnh dưới của S là: 𝑣 = 𝑣0
Ảnh của nó được cho bởi hàm vector 𝒓(𝑢, 𝑣 ) 0 . 23-Feb-21 TS. Nguyễn Văn Quang 32
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Nếu một đường cong trong mặt phẳng cho bởi hàm vector:
𝒓(𝑡) = 𝑥(𝑡) 𝒊 + 𝑦(𝑡) 𝒋
với 𝑡 là tham số thì vector tiếp tuyến tại 𝑡 đối với đường cong không gian 0 này sẽ là: x  y 
r  x i  y j  i  j t t t 0 0 t  t 23-Feb-21 TS. Nguyễn Văn Quang 33
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Do đó vector tiếp tuyến tại (𝑥 , 𝑦 đối với đường cong ảnh này sẽ là: 0 0) x y
r  g (u , v ) i  h (u , v ) j  i  j u u 0 0 u 0 0 u u 23-Feb-21 TS. Nguyễn Văn Quang 34
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Tương tự, vector tiếp tuyến tại (𝑥 , 𝑦 ) đối với đường cong ảnh của cạnh trái 0 0 của (𝑢 = 𝑢0) là: x y
r  g (u ,v ) i  h (u ,v ) j  i  0 0 0 0 j v v v v v 23-Feb-21 TS. Nguyễn Văn Quang 35
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Ta có thể xấp xỉ miền ảnh 𝑅 = 𝑇(𝑆) bởi một hình bình hành xác định
bởi các vector cát tuyến: a  (
r u  u, v ) 0 0
 r(u , v ) 0 0
b  r(u , v   ) 0 0 v
 r(u , v ) 0 0 23-Feb-21 TS. Nguyễn Văn Quang 36
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Tuy nhiên, ( r u   , u v )  ( r u , v ) 0 0 0 0 r  lim u   u 0 u
Nên, r(u   ,
u v )  r(u , v )  u r . 0 0 0 0 u
Tương tự, r(u , v  v)  r(u , v )  v r . 0 0 0 0 v 23-Feb-21 TS. Nguyễn Văn Quang 37
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Điều này có nghĩa là ta có thể xấp xỉ R bởi một hình bình hành xác định bởi 2 vector ∆𝑢. 𝒓 ∆𝑣. 𝒓 𝑢 và 𝑣 . 23-Feb-21 TS. Nguyễn Văn Quang 38
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Vậy, có thể xấp xỉ diện tích của R bởi diện tích của hình bình hành này:
|(∆𝑢 𝒓 ) × (∆𝑣 𝒓 )| = |𝒓 × 𝒓 | ∆𝑢 ∆𝑣 𝑢 𝑣 𝑢 𝑣
Tích có hướng của 2 vector: i j k x y x x x y u u u v r r 0        k  k u v u u x y y y x y 0 v v u v v v 23-Feb-21 TS. Nguyễn Văn Quang 39
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Jacobian của biến đổi T cho bởi 𝑥 = 𝑔(𝑢, 𝑣) và 𝑦 = ℎ(𝑢, 𝑣) là: x x ( , x ) y u v
x y x y    ( , u ) v y y
u v v u u v
Với ký hiệu này ta có thể xấp xỉ một diện tích ∆A của R: ( , x y) ở đây Jacobian được A  u v (u,v)
tính tại (u0, v ). 0 23-Feb-21 TS. Nguyễn Văn Quang 40
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Tiếp theo, ta chia miền S trong mặt Ouv thành các hình chữ nhật nhỏ 𝑆 𝑖𝑗
và gọi ảnh của nó trong mặt Oxy là 𝑅 . 𝑖𝑗 23-Feb-21 TS. Nguyễn Văn Quang 41
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát
Áp dụng công thức xấp xỉ đối với 𝑅 ở trên, ta có xấp xỉ của tích phân 𝑖𝑗
2 lớp của f trên miền R như sau. f ( , x y)  dxdy R 
f (x , y )  A i j (x, y)  ở đây Jacobian được
f (g(u , v ), h(u , v )) u   v i j i j (u,v) tính tại (𝑢 , 𝑣 𝑖 𝑗).
Chú ý đây chính là tổng Riemann của tích phân: ( , x y)
f (g (u,v),h(u,v))  du dv (u, v) S 23-Feb-21 TS. Nguyễn Văn Quang 42
Đại học Công nghệ - ĐHQGHN Đổi biến tổng quát Định lý: 23-Feb-21 TS. Nguyễn Văn Quang 43
Đại học Công nghệ - ĐHQGHN Định nghĩa y 23-Feb-21 TS. Nguyễn Văn Quang 44
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 45
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 46
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 47
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 48
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 49
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 50
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 51
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 52
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 53
Đại học Công nghệ - ĐHQGHN 37  35 67 3   6 24 23-Feb-21 TS. Nguyễn Văn Quang 54
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 55
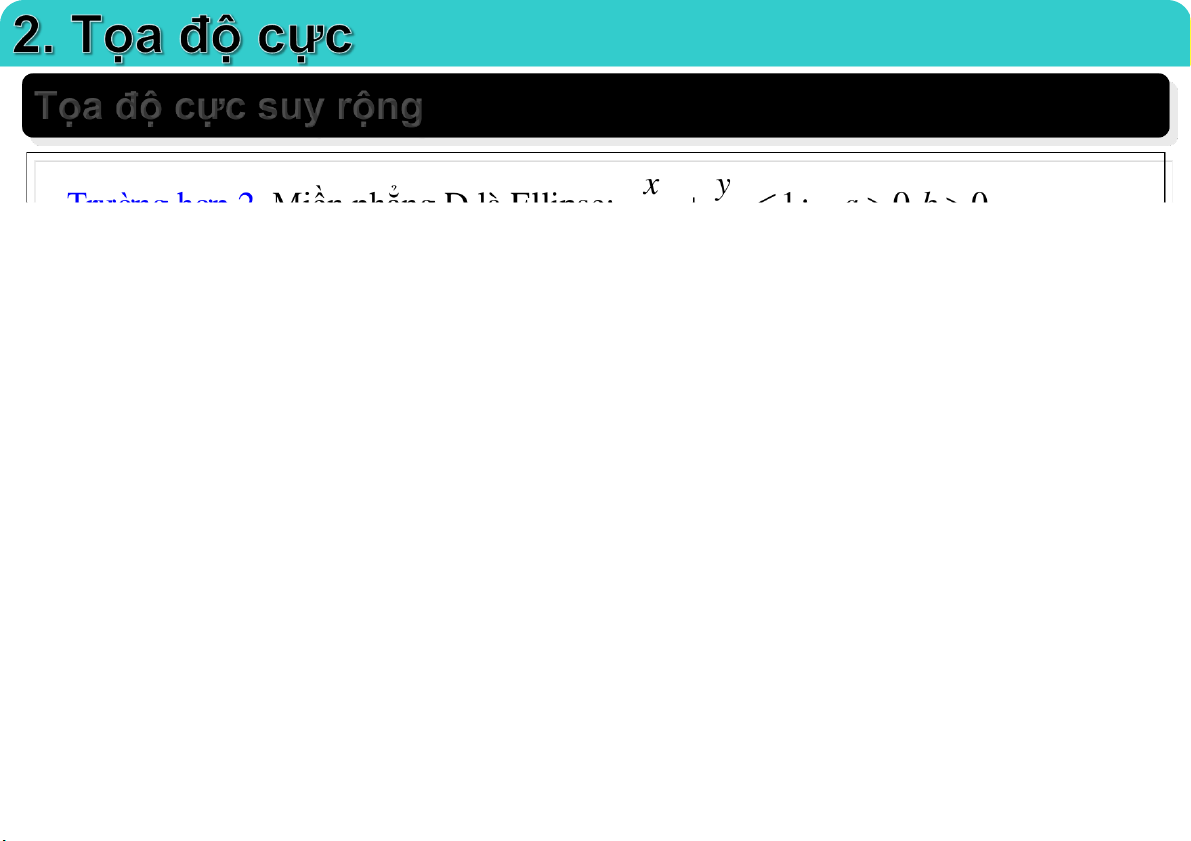
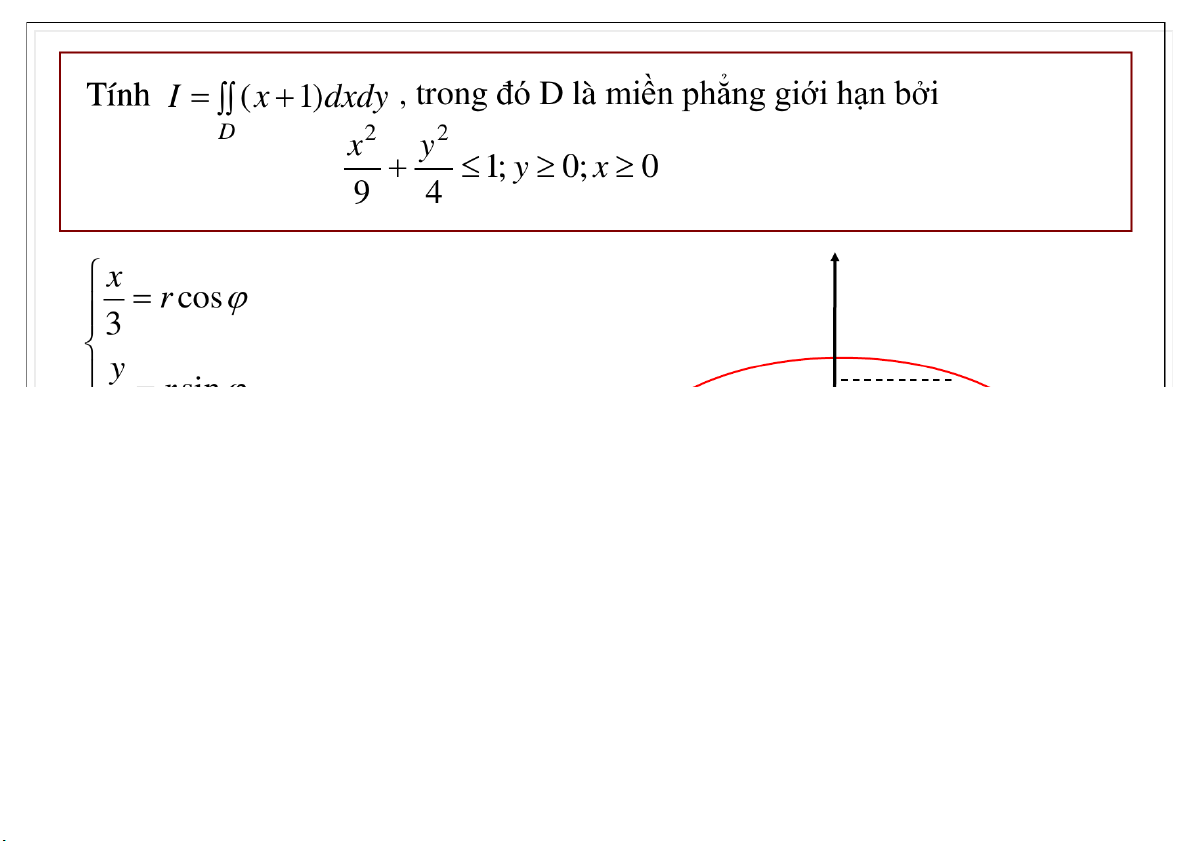
Đại học Công nghệ - ĐHQGHN Tọa độ cực suy rộng 23-Feb-21 TS. Nguyễn Văn Quang 56
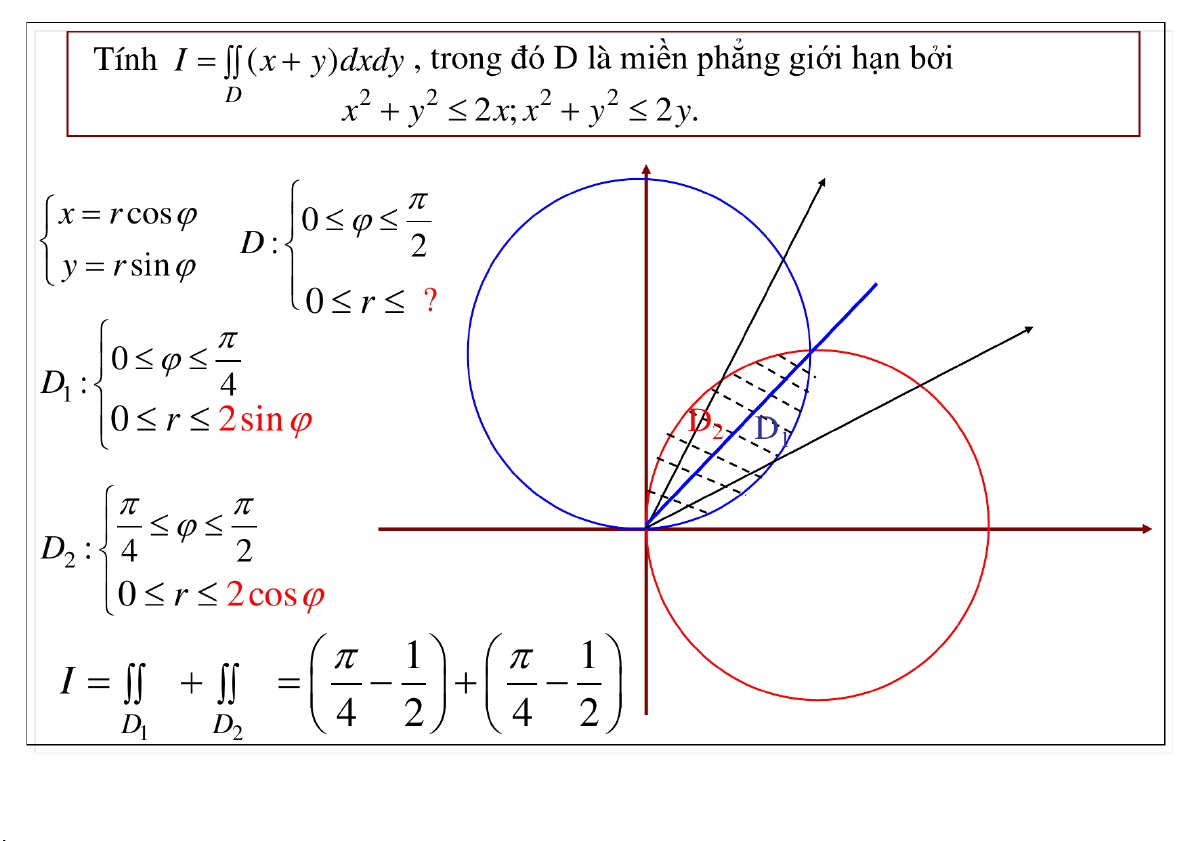
Đại học Công nghệ - ĐHQGHN Tọa độ cực suy rộng 2 2 23-Feb-21 TS. Nguyễn Văn Quang 57
Đại học Công nghệ - ĐHQGHN 32   8 3 23-Feb-21 TS. Nguyễn Văn Quang 58
Đại học Công nghệ - ĐHQGHN 3  6  2 23-Feb-21 TS. Nguyễn Văn Quang 59
Đại học Công nghệ - ĐHQGHN 3  2 23-Feb-21 TS. Nguyễn Văn Quang 60
Đại học Công nghệ - ĐHQGHN
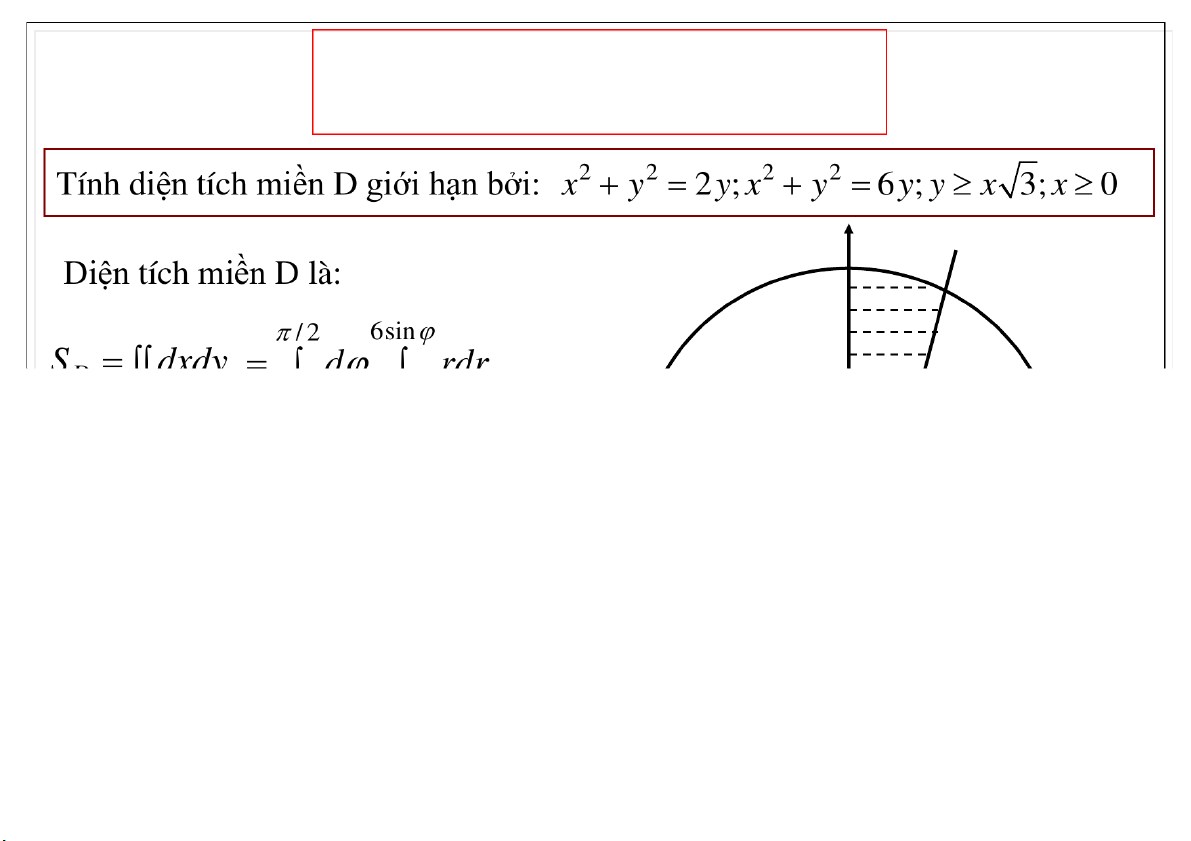
Diện tích miền D: S   dxdy D x D y 23-Feb-21 TS. Nguyễn Văn Quang 61
Đại học Công nghệ - ĐHQGHN Tính thể tích 23-Feb-21 TS. Nguyễn Văn Quang 62
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 63
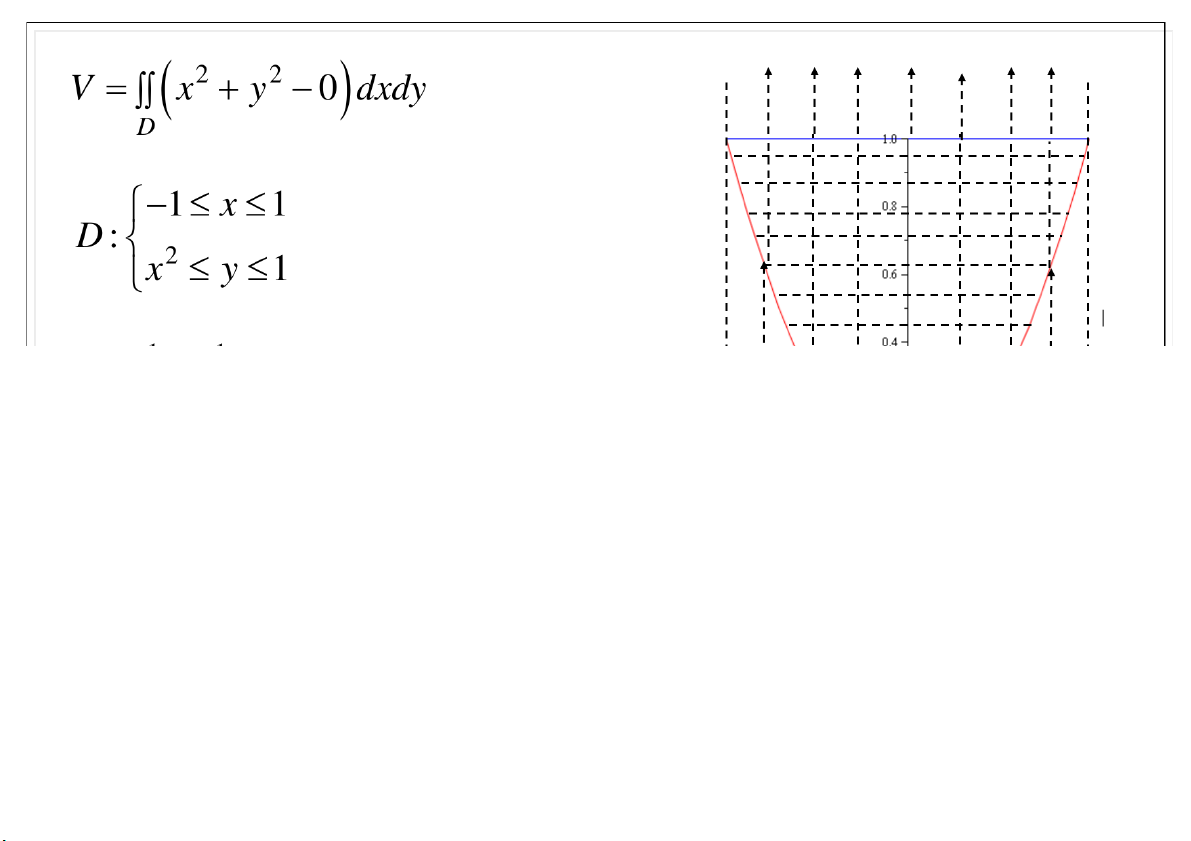
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Feb-21 TS. Nguyễn Văn Quang 64
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 65
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 66
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 67
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 68
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 69
Đại học Công nghệ - ĐHQGHN Diện tích mặt cong
Diện tích tương ứng: ∆𝑆 . 1, ∆𝑆2, ⋯ , ∆𝑆𝑛
Lấy điểm tùy ỳ P (x , y ,0)  D . i i i i
Tương ứng với điểm M (x , y , z )  S . i i i i i
Gọi Ti là mặt tiếp diện với Si tại Mi .
Và Ti là mảnh có hình chiếu xuống Oxy là D i 23-Feb-21 TS. Nguyễn Văn Quang 70
Đại học Công nghệ - ĐHQGHN Diện tích mặt cong
Véctơ pháp của S tại M : n     i
 z (x , y ), z (x , y ), x i i y i i 1 i 1 cos  i
z (x , y )  z x y   x i i  2 2 ( , ) 1  y i i  23-Feb-21 TS. Nguyễn Văn Quang 71
Đại học Công nghệ - ĐHQGHN 23-Feb-21 TS. Nguyễn Văn Quang 72
Đại học Công nghệ - ĐHQGHN (5 5 1)  6 23-Feb-21 TS. Nguyễn Văn Quang 73
Đại học Công nghệ - ĐHQGHN 23-Feb-21 74 23-Feb-21 75 23-Feb-21 76