Bài giảng Chương 4: Tích phân bội ba - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài giảng Chương 4: Tích phân bội ba - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 2 (MAT1042) 50 tài liệu
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 591 tài liệu
Tác giả:
Preview text:
1. Định nghĩa, cách tính tích phân bội ba
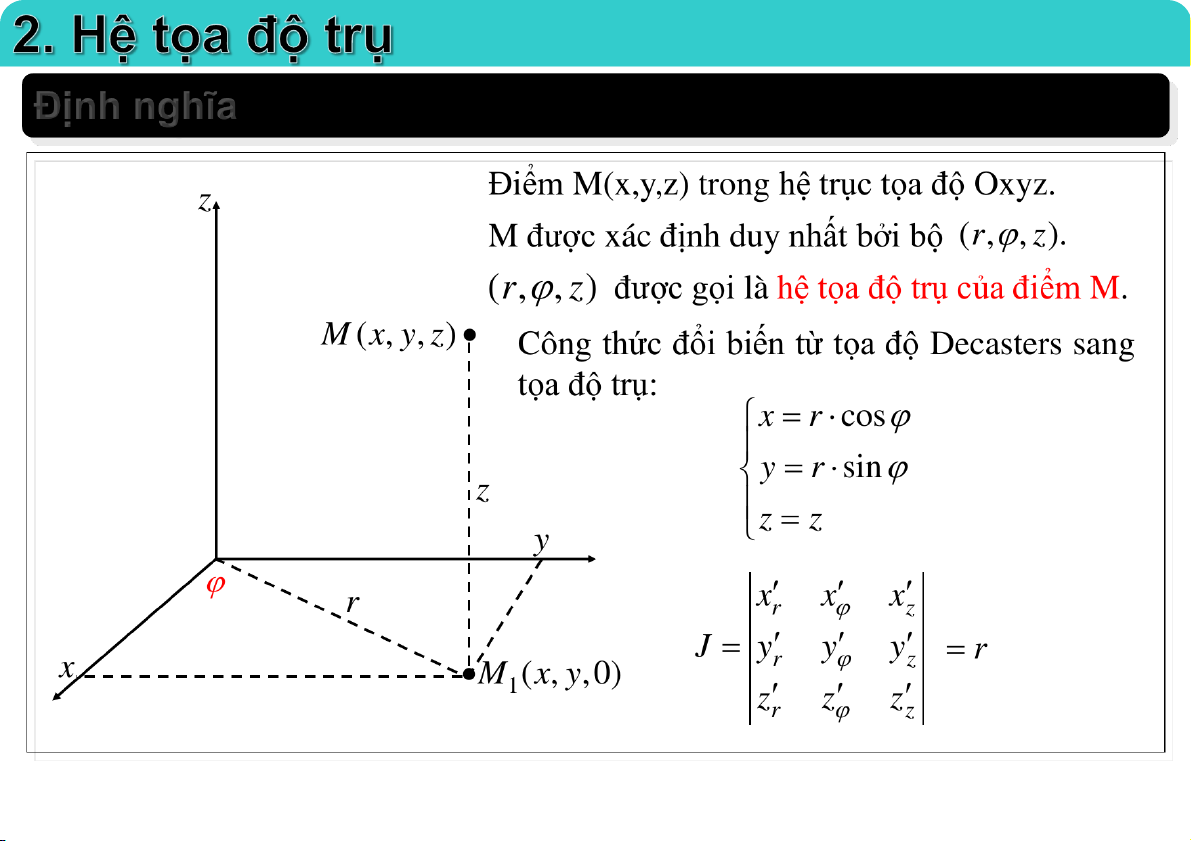
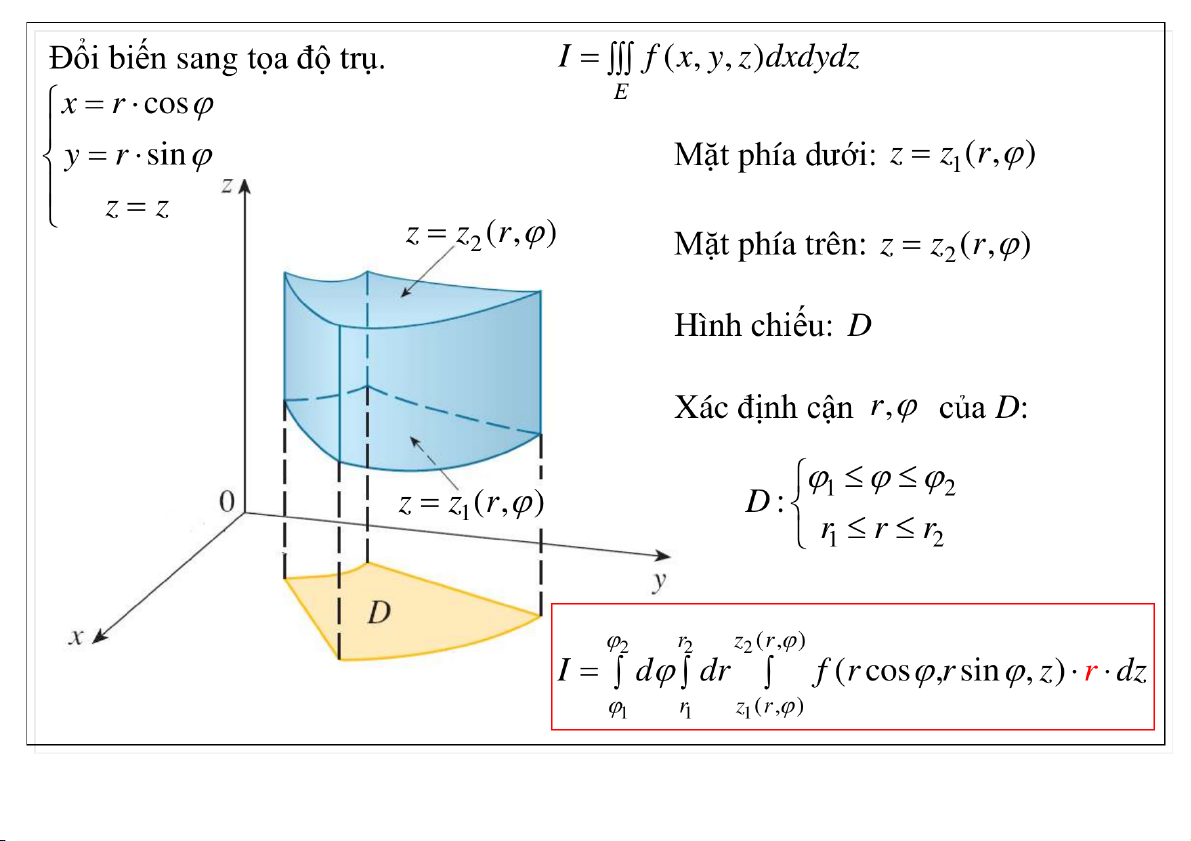
2. Hệ tọa độ trụ
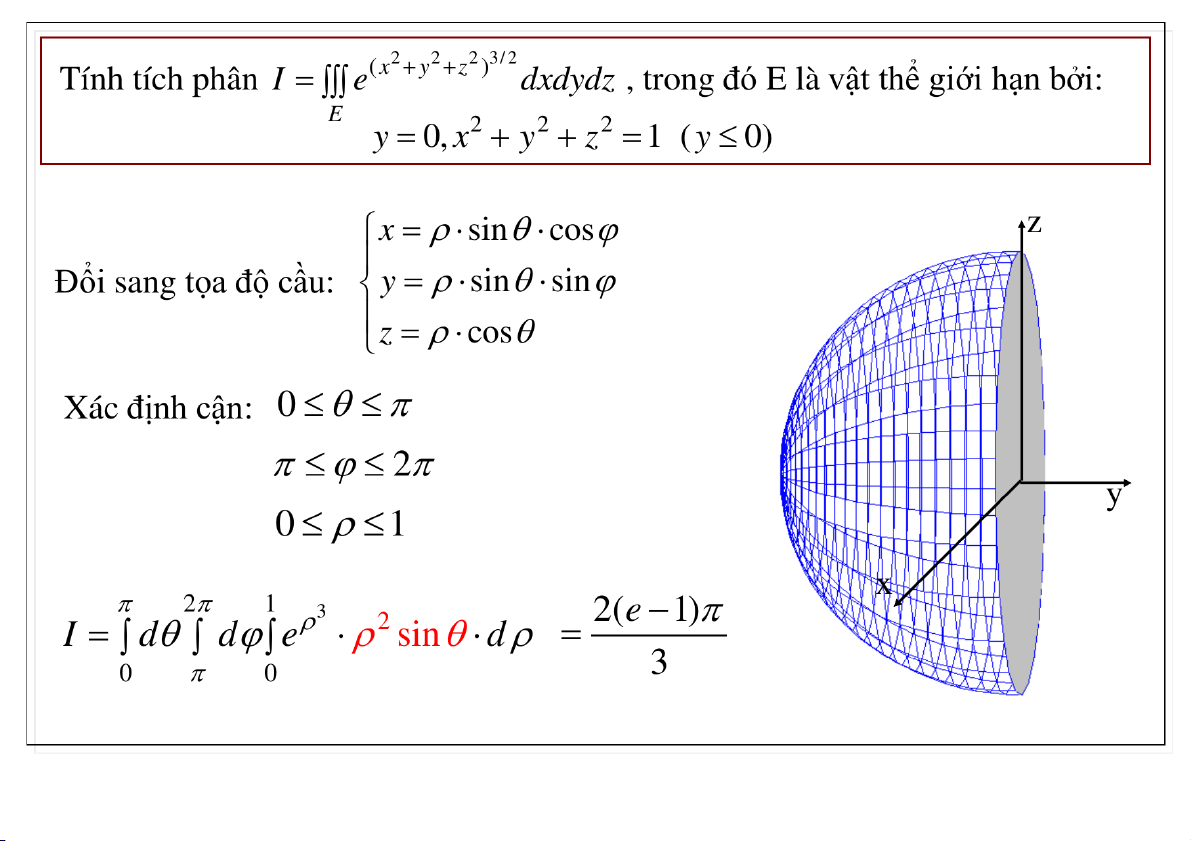
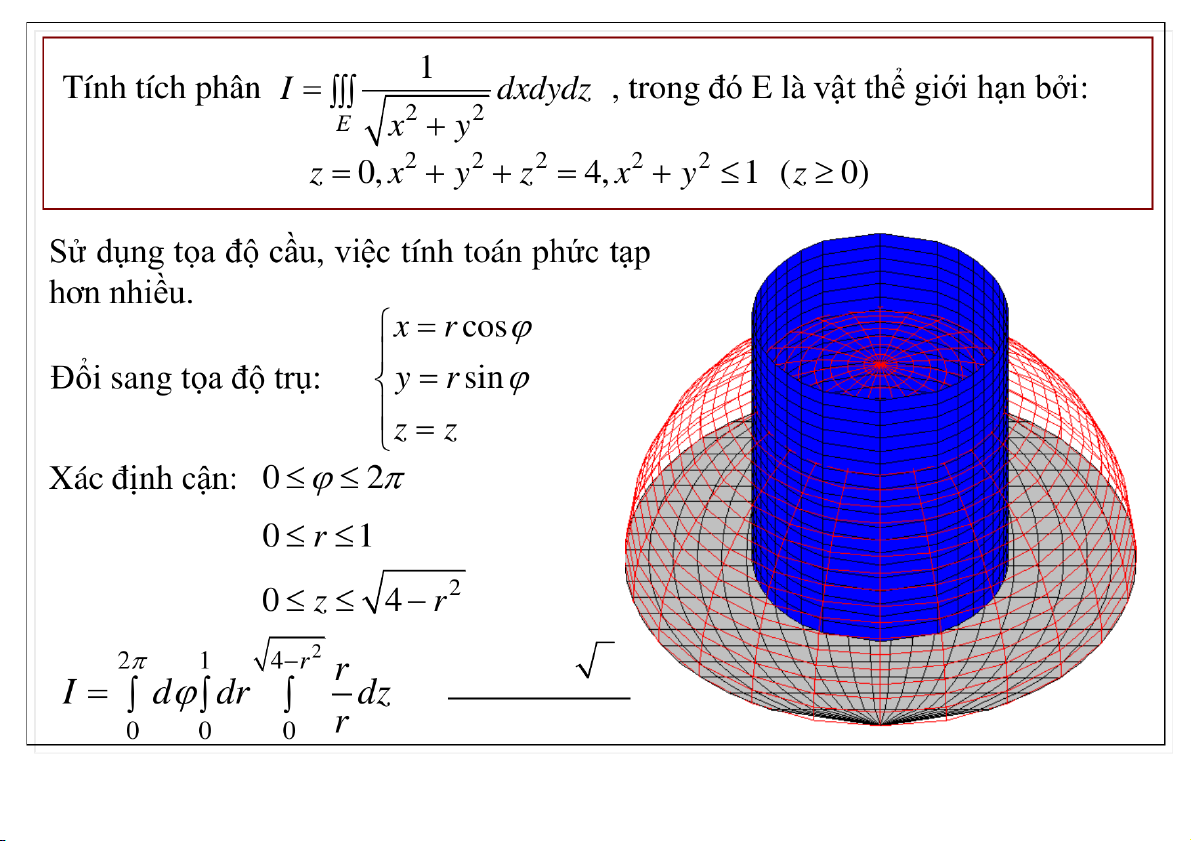
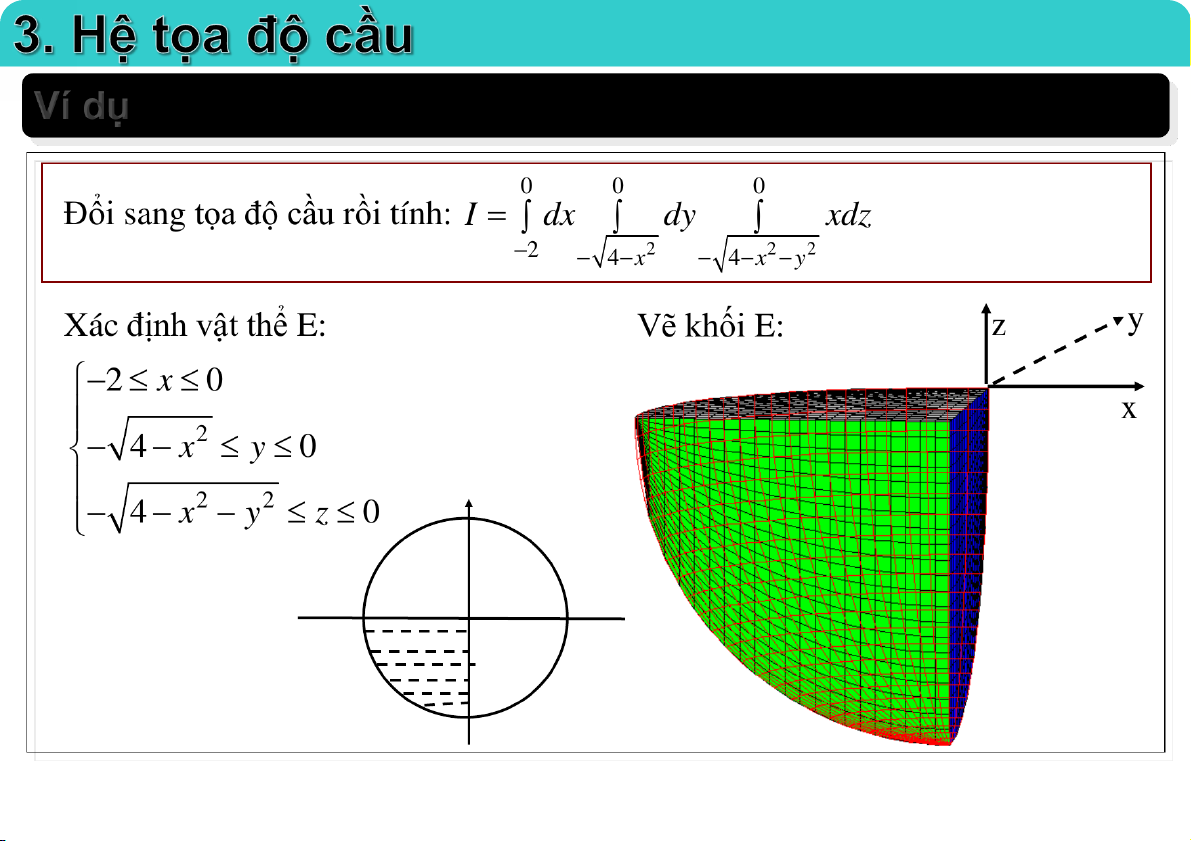
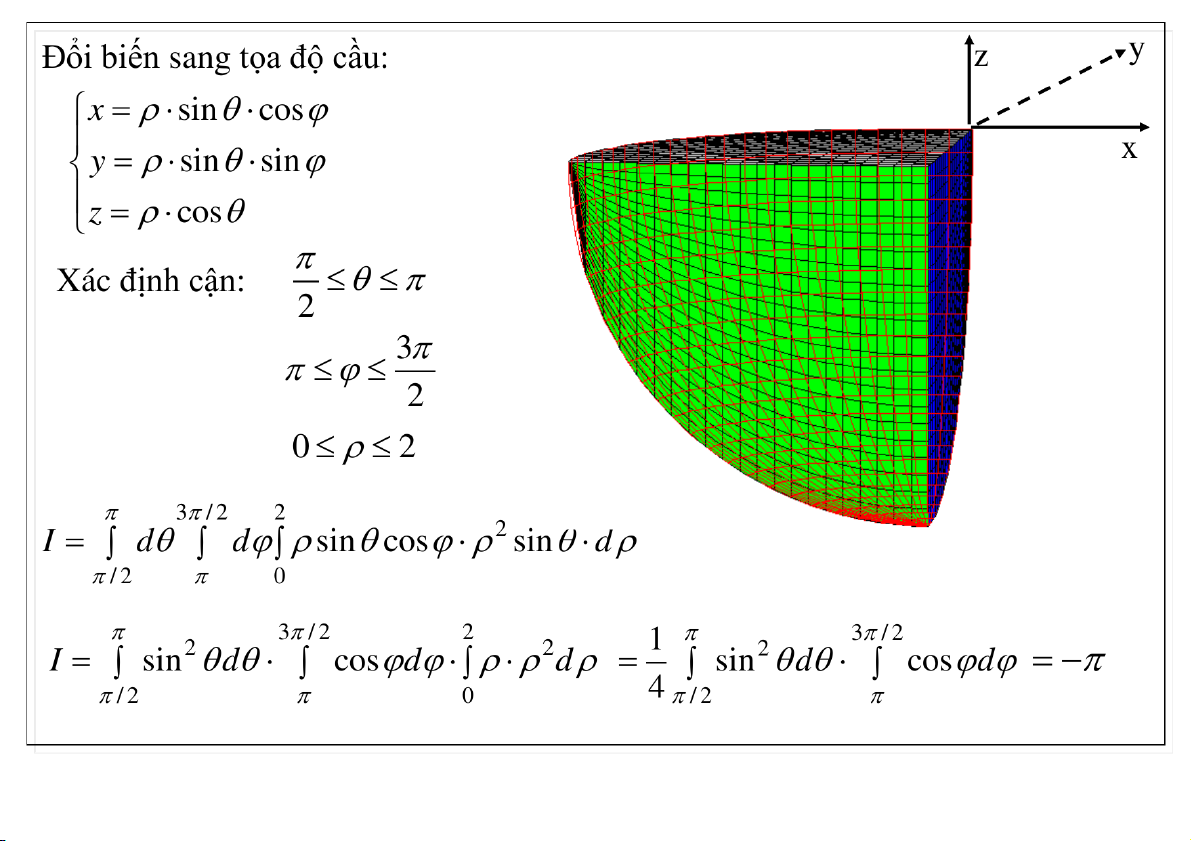
3. Hệ tọa độ cầu
4. Ứng dụng hình học 02-Apr-20 TS. Nguyễn Văn Quang 1
Đại học Công nghệ - ĐHQGHN Định nghĩa 02-Apr-20 TS. Nguyễn Văn Quang 2
Đại học Công nghệ - ĐHQGHN Tính chất 02-Apr-20 TS. Nguyễn Văn Quang 3
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 4
Đại học Công nghệ - ĐHQGHN
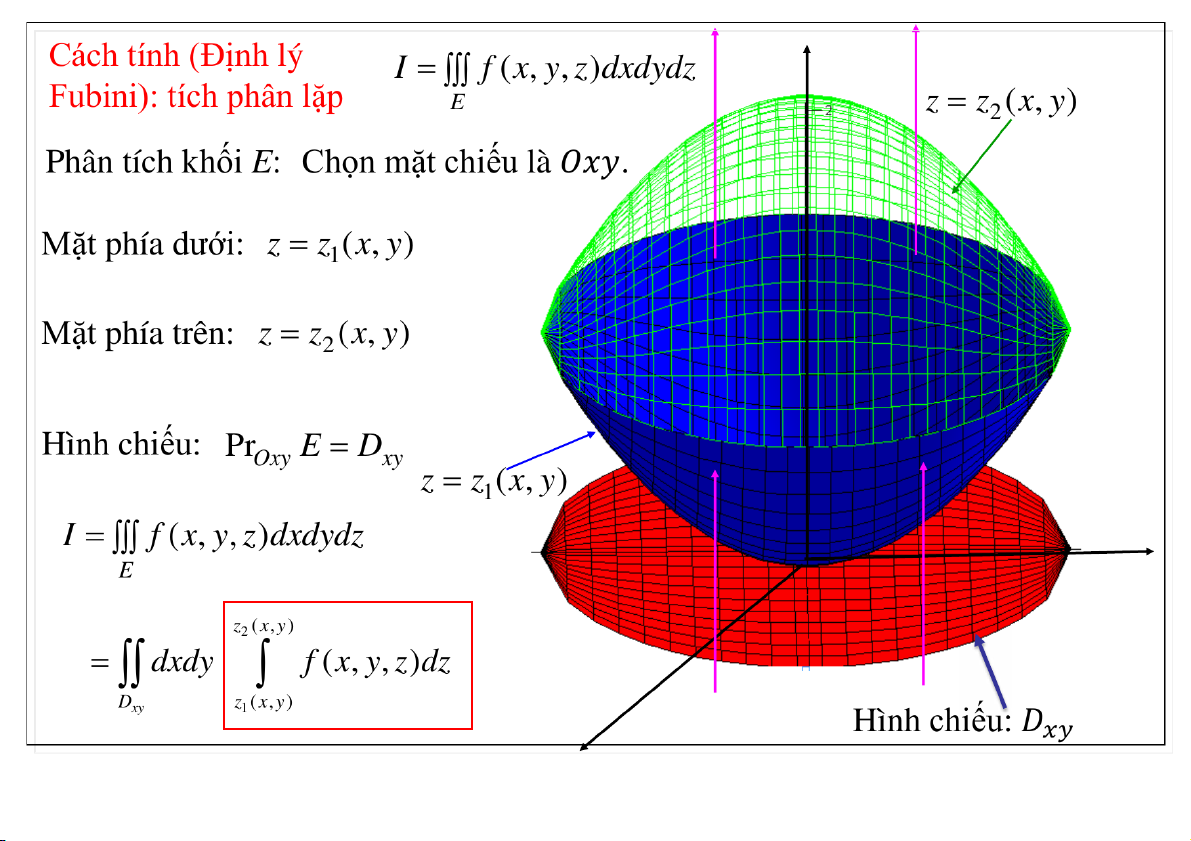
Cách tính – Định lý Fubini (tích phân lặp) Chú ý 02-Apr-20 TS. Nguyễn Văn Quang 5
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 6
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 7
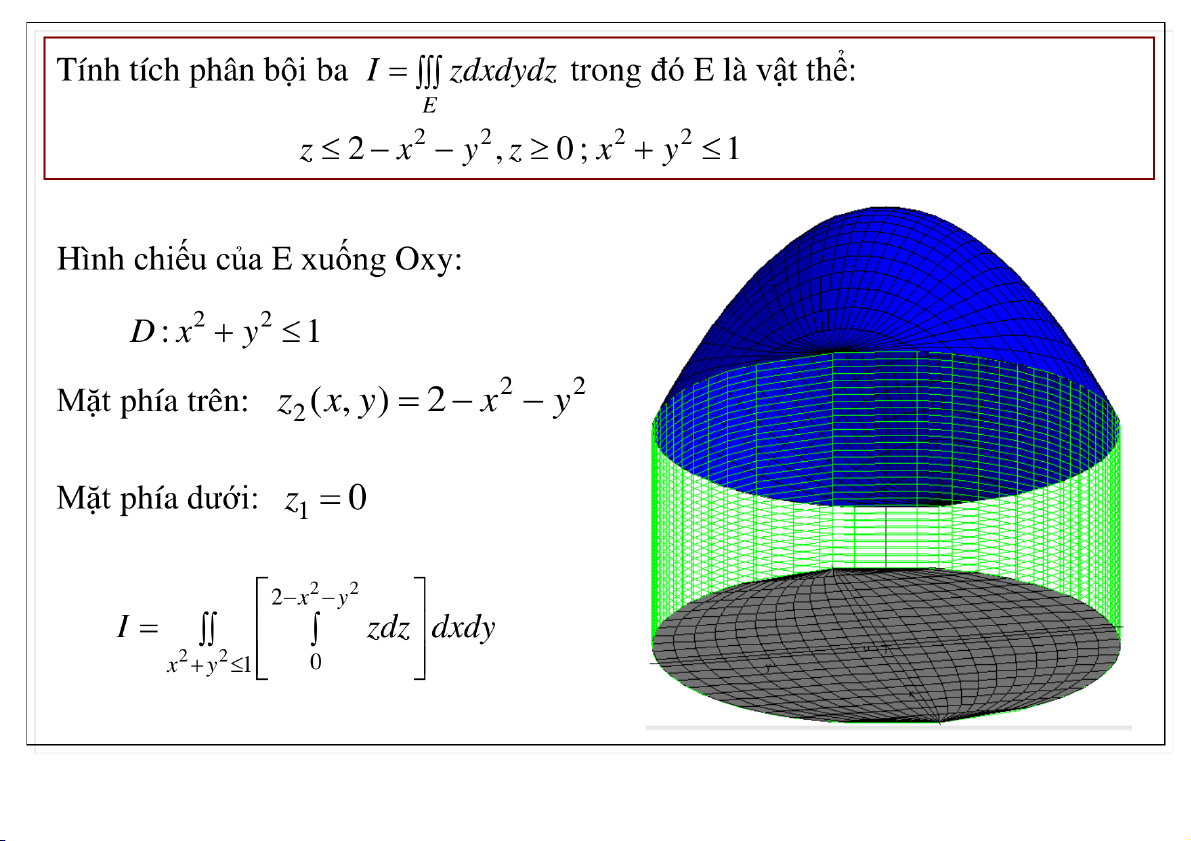
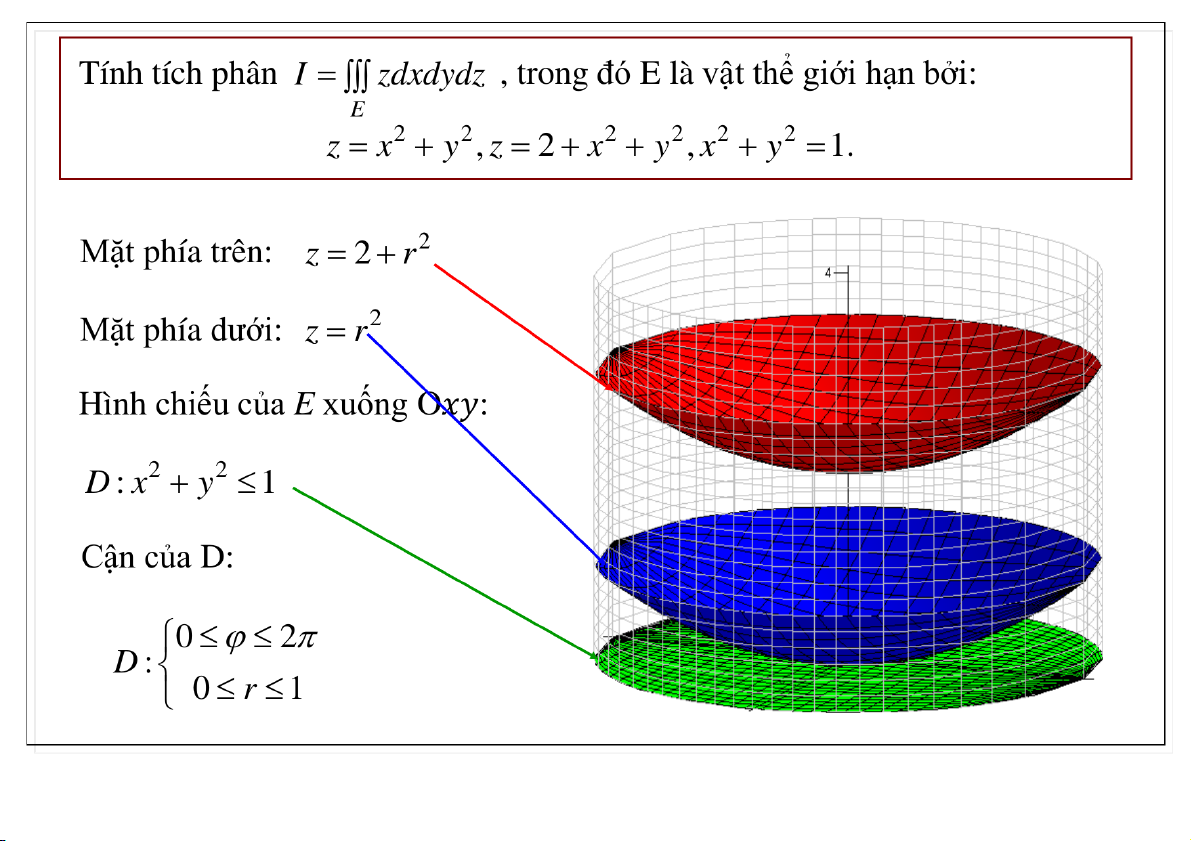
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 8
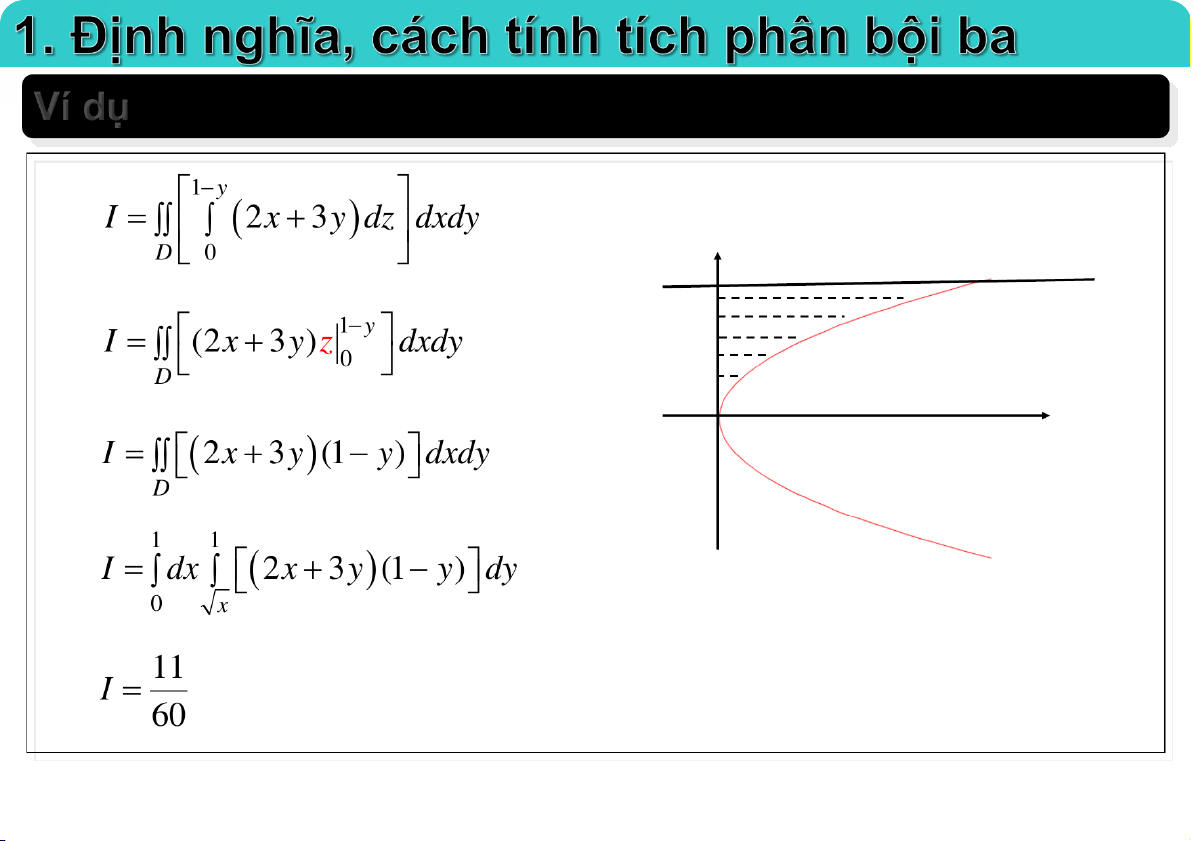
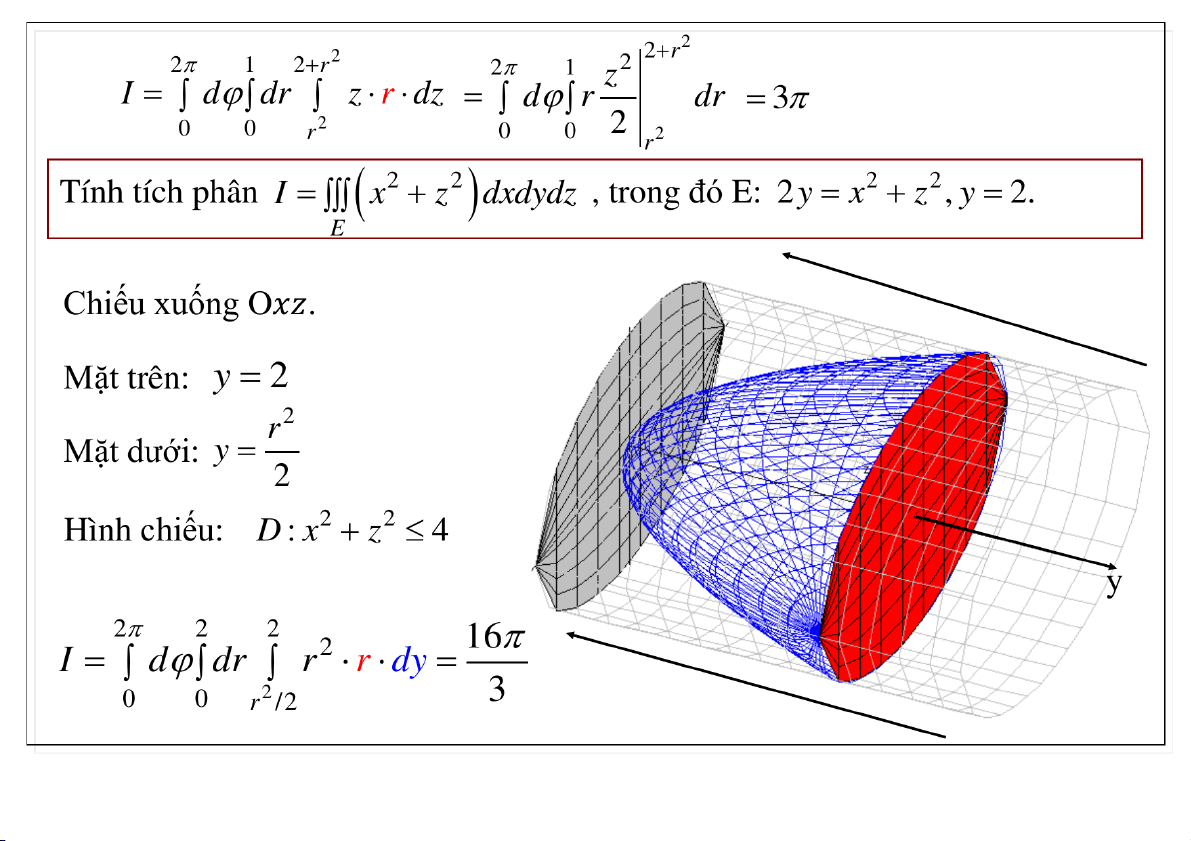
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 9
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 10
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 11
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 12
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 13
Đại học Công nghệ - ĐHQGHN
Đổi biến tổng quát Định lý:
Giả sử có phép đổi biến: 𝑥 = 𝑥 𝑢, 𝑣, 𝑤 , 𝑦 = 𝑦 𝑢, 𝑣, 𝑤 , 𝑧 = 𝑧(𝑢, 𝑣, 𝑤); sao cho
phép đổi biến này là 1-1 (có thể trừ trên biên), và 𝐽 ≠ 0 (có thể 𝐽 = 0 tại một số
điểm hữu hạn), khi đó:
𝑓(𝑥, 𝑦, 𝑧)𝑑𝑥𝑑𝑦𝑑𝑧 = 𝐸𝑥𝑦𝑧
𝑓(𝑥 𝑢, 𝑣, 𝑤 , 𝑦 𝑢, 𝑣, 𝑤 , 𝑧(𝑢, 𝑣, 𝑤)). 𝐽 . 𝑑𝑢𝑑𝑣𝑑𝑤 𝐸𝑢𝑣𝑤 Trong đó: 𝑥′ 𝜕(𝑥, 𝑦, 𝑧) 𝑢 𝑥′𝑣 𝑥′𝑤 𝐽 = = 𝑦′ 𝑦′ 𝑦′ 𝜕(𝑢, 𝑣, 𝑤) 𝑢 𝑣 𝑤
𝑧′𝑢 𝑧′𝑣 𝑧′𝑤 02-Apr-20 TS. Nguyễn Văn Quang 14
Đại học Công nghệ - ĐHQGHN Định nghĩa 02-Apr-20 TS. Nguyễn Văn Quang 15
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 16
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 17
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 18
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 19
Đại học Công nghệ - ĐHQGHN Định nghĩa 02-Apr-20 TS. Nguyễn Văn Quang 20
Đại học Công nghệ - ĐHQGHN Định nghĩa 02-Apr-20 TS. Nguyễn Văn Quang 21
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 22
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 23
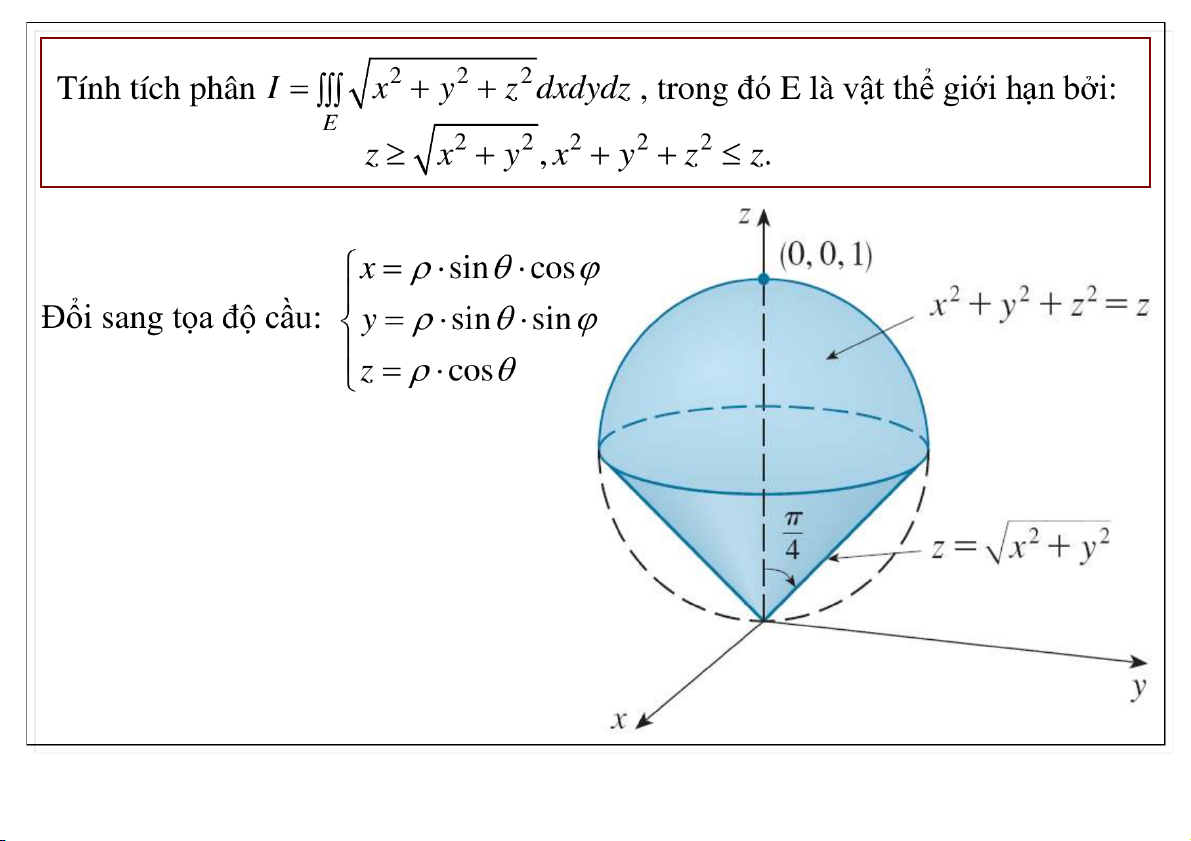
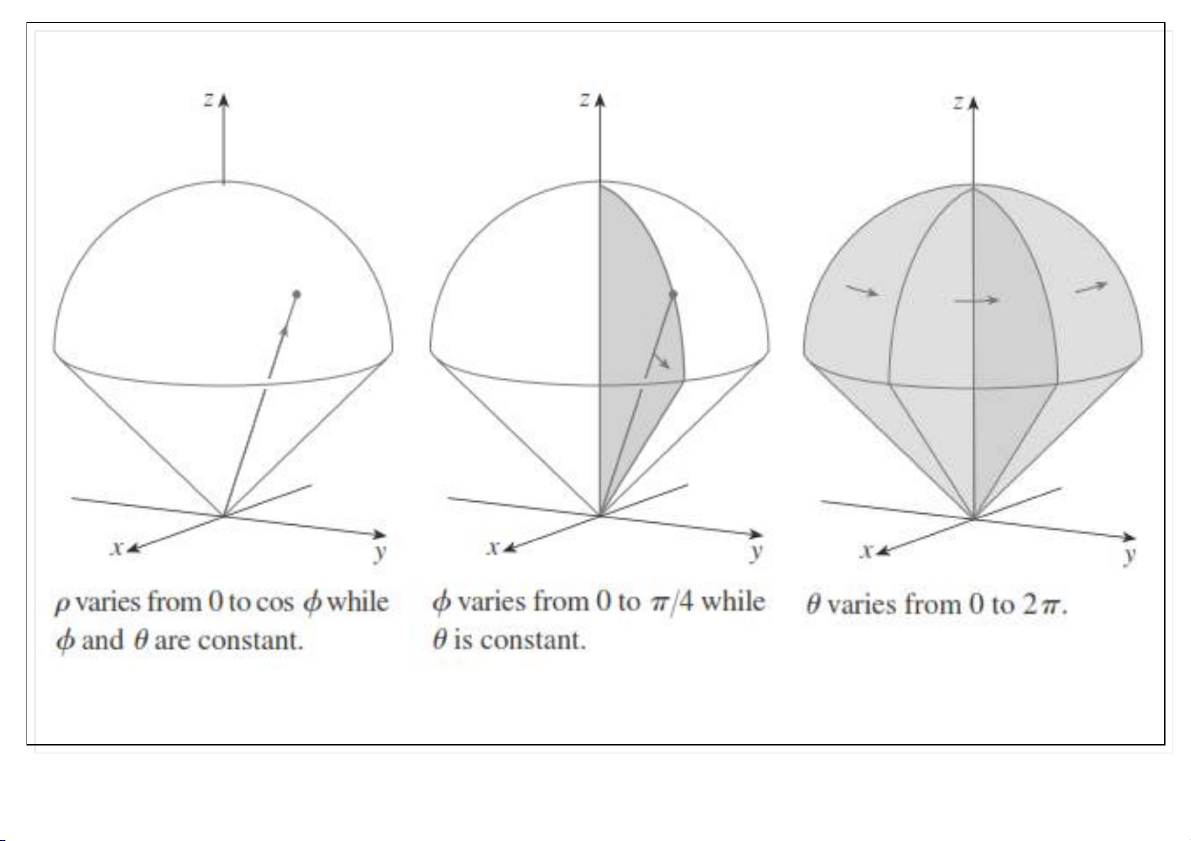
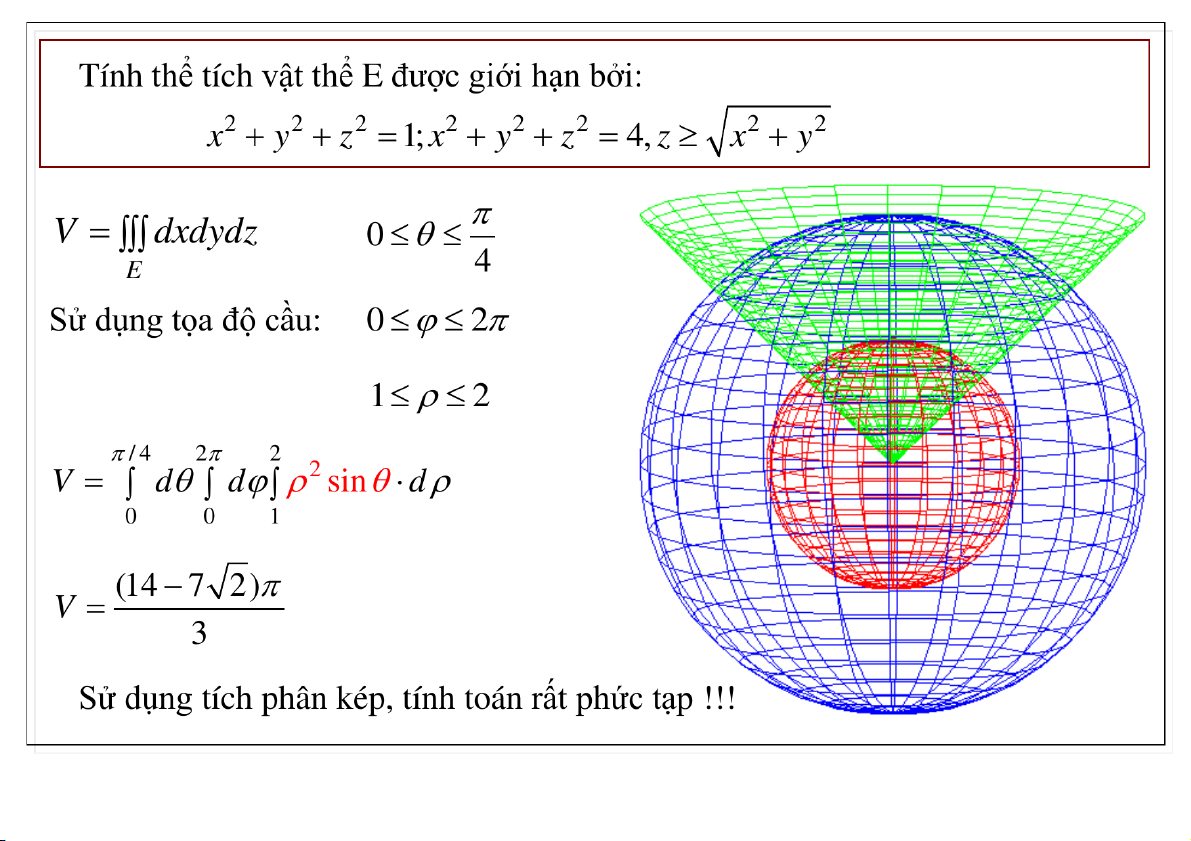
Đại học Công nghệ - ĐHQGHN Xác định cậ : n 0 4 0 2 0 cos / 4 2 cos 2 1 2
I d d sin d 0 0 0 10 80 02-Apr-20 TS. Nguyễn Văn Quang 24
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 25
Đại học Công nghệ - ĐHQGHN Cách 1: 5 12 02-Apr-20 TS. Nguyễn Văn Quang 26
Đại học Công nghệ - ĐHQGHN 5 12 02-Apr-20 TS. Nguyễn Văn Quang 27
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 28
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 29
Đại học Công nghệ - ĐHQGHN 5 12 02-Apr-20 TS. Nguyễn Văn Quang 30
Đại học Công nghệ - ĐHQGHN 2 3 3 3 02-Apr-20 TS. Nguyễn Văn Quang 31
Đại học Công nghệ - ĐHQGHN Ví dụ 02-Apr-20 TS. Nguyễn Văn Quang 32
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 33
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 34
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 35
Đại học Công nghệ - ĐHQGHN
Ứng dụng hình học của tích phân bội ba 02-Apr-20 TS. Nguyễn Văn Quang 36
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 37
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 38
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 39
Đại học Công nghệ - ĐHQGHN 02-Apr-20 TS. Nguyễn Văn Quang 40
Đại học Công nghệ - ĐHQGHN