Bài giảng Chương 5 - Tích phân đường - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Bài giảng Chương 5 - Tích phân đường - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

69 35 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Giải tích 2 (MAT1042)

Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

Thông tin:

55 trang 5 tháng trước

Tác giả:

Profile Mai Nguyệt
1. Tích phân 1 đường loại
2. Tích phân 2 đường loại
Định nghĩa
23-Mar-21 2 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Định nghĩa
23-Mar-21 3 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tính chất
23-Mar-21 4 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cách tính
23-Mar-21 5 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
2 2
1 1 1
2 2
( ) ( )
( ) ( )
i i i i i i i
i i
L A A x x y y
x y
xác trên cong có trình: định đường C phương
( , )f f x y
( ), .y y x a x b
Cách tính
23-Mar-21 6 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Theo công thức Lagrange (Định lý giá trị trung đối với bình) y x( ) trong đoạn
[ ]x
i–1
, x
i
, ta tìm được một giá trị 𝑥
𝑖
∗
∈[𝑥
𝑖−1
,𝑥
𝑖
] sao cho:
*
1 1
( ) ( ) ( ) ( )
i i i i i
y x y x y x x x
*
( )
i i i
y y x x
2 2
2
2 *
2 2
* 2 *
( ) ( )
( ) ( )
1 ( ) ( ) 1 ( ) (do 0)
i i i
i i i
i i i i i
L x y
x y x x
y x x y x x x
Cách tính
23-Mar-21 7 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Sau khi phép chia cong khi : thực hiện đường C, đó
2
* * *
1
( , ( )) 1 ( )
n
i i i i
i
f x y x y x x
2
* * *
1
lim ( , ) lim ( , ( )) 1 ( )
n
n i i i i
n n
i
C
I I I f x y dl f x y x y x x
 
Do : đó
Cách tính
23-Mar-21 8 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cách tính
23-Mar-21 9 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cách tính
23-Mar-21 10 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Khi , trình tham cung : đó phương số của C
( )cos , ( )sinx r y r
Định nghĩa
23-Mar-21 11 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Ví dụ
23-Mar-21 12 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Ví dụ
23-Mar-21 13 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 14 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 15 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 16 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 17 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 18 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 19 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
1 2
0I I I
23-Mar-21 20 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 21
Với đường đường thì cong C là cong
nằm mặt trụ trên .
0 t 4
TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
2 2
9 x y
Ta có trình : . phương mặt trụ
Bài toán
23-Mar-21 22 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cho một chất điểm M di chuyển dọc theo cung một phẳng 𝐴𝐵 từ
điểm A B tác : đến điểm dưới dụng của lực
𝐹 𝑀 = 𝑃 𝑀 .𝑖 + 𝑄 𝑀 .𝑗 , 𝑀 ∈ 𝐴𝐵
.
Hãy tính công W của lực đó sinh ra.
Bài toán
23-Mar-21 23 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Khi : đó
1
i i i i
A A x i y j
Lấy
1
( , ) .
i i i i i
M x y A A
Cung nên có coi nó nhỏ, thể xấp xỉ dây cung
1i i
A A
1i i
A A
và không và trên cung . đổi (về chiều độ lớn) đó
( )
i
F M
Do công sinh ra khi di đó, của lực chất điểm chuyển
từ 𝐴
𝑖−1
theo cung đến 𝐴
𝑖
sẽ xấp xỉ là:
1i i
A A
1
( ) ( ) ( )
i i i i i i i
F M A A P M x Q M y
Bài toán
23-Mar-21 24 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Do trên khi chính là công : đó, giới hạn của tổng 𝑛 →∞ của lực
1
lim ( , ) ( , )
n
i i i i i i
n
i
P x y x Q x y y

W=
Định nghĩa
23-Mar-21 25 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tính chất
23-Mar-21 26 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
đường loại
23-Mar-21 27 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cách tính
23-Mar-21 28 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tích phân đường loại 2 trong không gian
23-Mar-21 29 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tích phân đường loại 2 trong không gian
23-Mar-21 30 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Giả sử: 𝐅(𝑥,𝑦,𝑧) = 𝑃 𝑥,𝑦,𝑧 𝐢 + 𝑄 𝑥,𝑦,𝑧 𝐣 + 𝑅 𝑥,𝑦,𝑧 𝐤
là vector xác trên cung một trường định AB.
Tích phân trên cung là (công sinh ra khi di đường của F AB của lực F
chuyển một vật đường trên cong AB):
( ( )) '( )
F r F r r
AB AB
d t t dt
Ví dụ
23-Mar-21 31 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 32 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 33 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 34 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 35 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tham cong C qua số đường hệ tọa độ trụ:
Công thức Green
23-Mar-21 36 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Công thức Green
23-Mar-21 37 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Công thức Green
23-Mar-21 38 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 39 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 40 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 41 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 42 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Ví dụ
23-Mar-21 43 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Ví dụ
23-Mar-21 44 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
2 2
( , ) sin(2 )
x y
Q x y e xy
23-Mar-21 45 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 46 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tích phân không phụ thuộc đường lấy tích phân
23-Mar-21 47 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tích phân không phụ thuộc đường lấy tích phân
23-Mar-21 48 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 49 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 50 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 51 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tuy nhiên không tính câu a (theo A B theo I thể như đường thẳng từ đến trục
hoành), vì không liên D nào AB và tồn tại miền đơn chứa đường thẳng đường
cong kín bao quanh O cho P, Q và các gốc để ĐHR cấp 1 liên trên D.tục
b) , tích phân không A B. I phụ thuộc đường đi từ đến
Q P
x y
Nên ta tính tích phân theo trục hoành:
23-Mar-21 52 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Cách 3: Bổ sung thêm đoạn thẳng từ B A, vào tròn bao đến đưa đường (đủ nhỏ)
quanh O. công Green gốc Sử dụng thức đối với miền đa liên này.
trong : A(1,0), C(1,1), D(-1,1), E(-1,-1), F(2,-1), B(2,0).đó
Cách 2: Tìm hàm ) là vi phân toàn U(x,y phần của P x,y dx+Q x,y dy( ) ( )
2 2
2 2
( , )
( , )
(1)
(2)
x
y
x
U P x y
x y
y
U Q x y
x y
(1) ( , ) ( , ) ( )U x y P x y dx g y
2 2
ln( )
( , ) ( )
2
x y
U x y g y
(2) ( ) 0
g y
( )g y C
2 2
2
ln( )
( , )
x y
U x y C
(2,0)
(1,0)
( , )I U x y
(2,0) (1,0)U U
ln 4 ln1
ln 2
2
23-Mar-21 53 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
23-Mar-21 54 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
Tích phân không phụ thuộc đường lấy tích phân
23-Mar-21 55 TS. Nguyễn Văn Quang
Đại học Công nghệ - ĐHQGHN
| 1/55
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

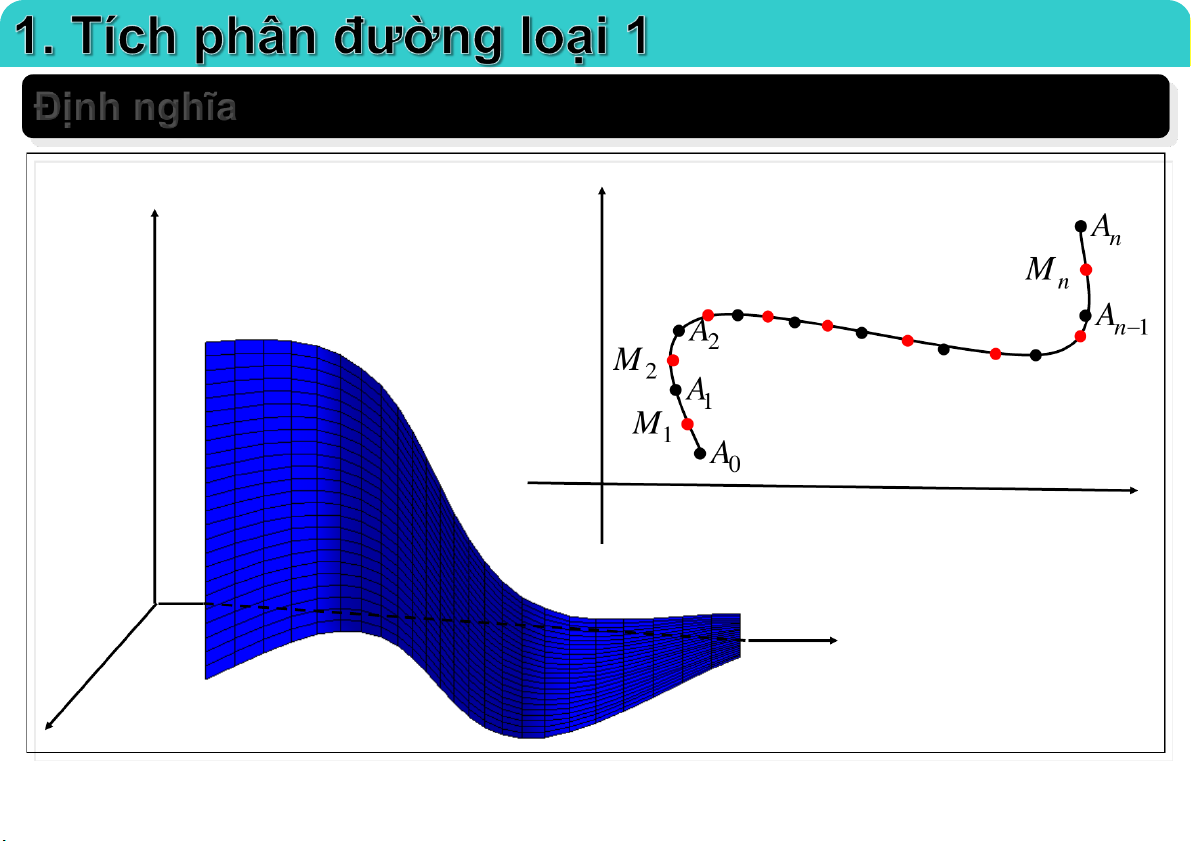
1. Tích phân đường loại 1
2. Tích phân đường loại 2 Định nghĩa 23-Mar-21 TS. Nguyễn Văn Quang 2
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Mar-21 TS. Nguyễn Văn Quang 3
Đại học Công nghệ - ĐHQGHN Tính chất 23-Mar-21 TS. Nguyễn Văn Quang 4
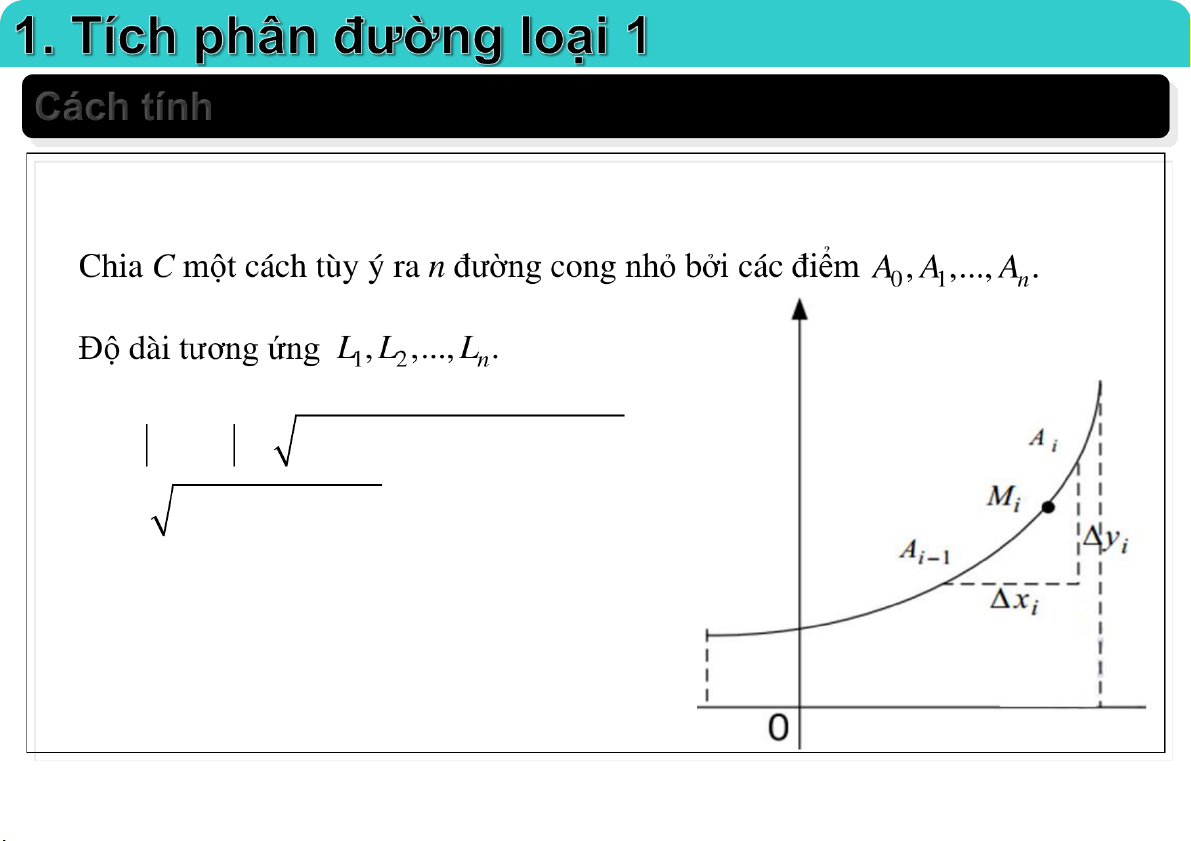
Đại học Công nghệ - ĐHQGHN Cách tính ff ( x ,
y ) xác định trên đường cong C có phương trình: y y(x), a x  . b 2 2
L A A  (x x )  ( y y ) i i1 i i i 1 i i1 2 2
 (x )  ( y  ) i i 23-Mar-21 TS. Nguyễn Văn Quang 5
Đại học Công nghệ - ĐHQGHN Cách tính
Theo công thức Lagrange (Định lý giá trị trung bình) đối với y(x) trong đoạn
[x , x ], ta tìm được một giá trị 𝑥 ∗ ∈[𝑥 i–1 i 𝑖 𝑖−1,𝑥𝑖] sao cho: *
y( x )  y( x )  y (
x ) (x x ) i i 1  i i i 1  *  y
  y (x )  xi i i 2 2  L  ( x  )  ( y  ) i i i 2 2 *
 (x )   y ( x )  x ii i  2 2 * 2 *
 1  y (x )  (x )  1  y (x )  x (do x  0)  iiii i 23-Mar-21 TS. Nguyễn Văn Quang 6
Đại học Công nghệ - ĐHQGHN Cách tính
Sau khi thực hiện phép chia đường cong C, khi đó: n 2 * * *
  f (x , y(x ))  1   y (x )  xi i i i   i 1  Do đó:  n 2  * * *
I  lim I I   f (x, y)dl  lim  f (x , y(x ))  1 y (x )  x n i i i i    n n C i 1    b
  f x y x   yx 2 ( , ( )) 1 ( ) dx a 23-Mar-21 TS. Nguyễn Văn Quang 7
Đại học Công nghệ - ĐHQGHN Cách tính 23-Mar-21 TS. Nguyễn Văn Quang 8
Đại học Công nghệ - ĐHQGHN Cách tính 23-Mar-21 TS. Nguyễn Văn Quang 9
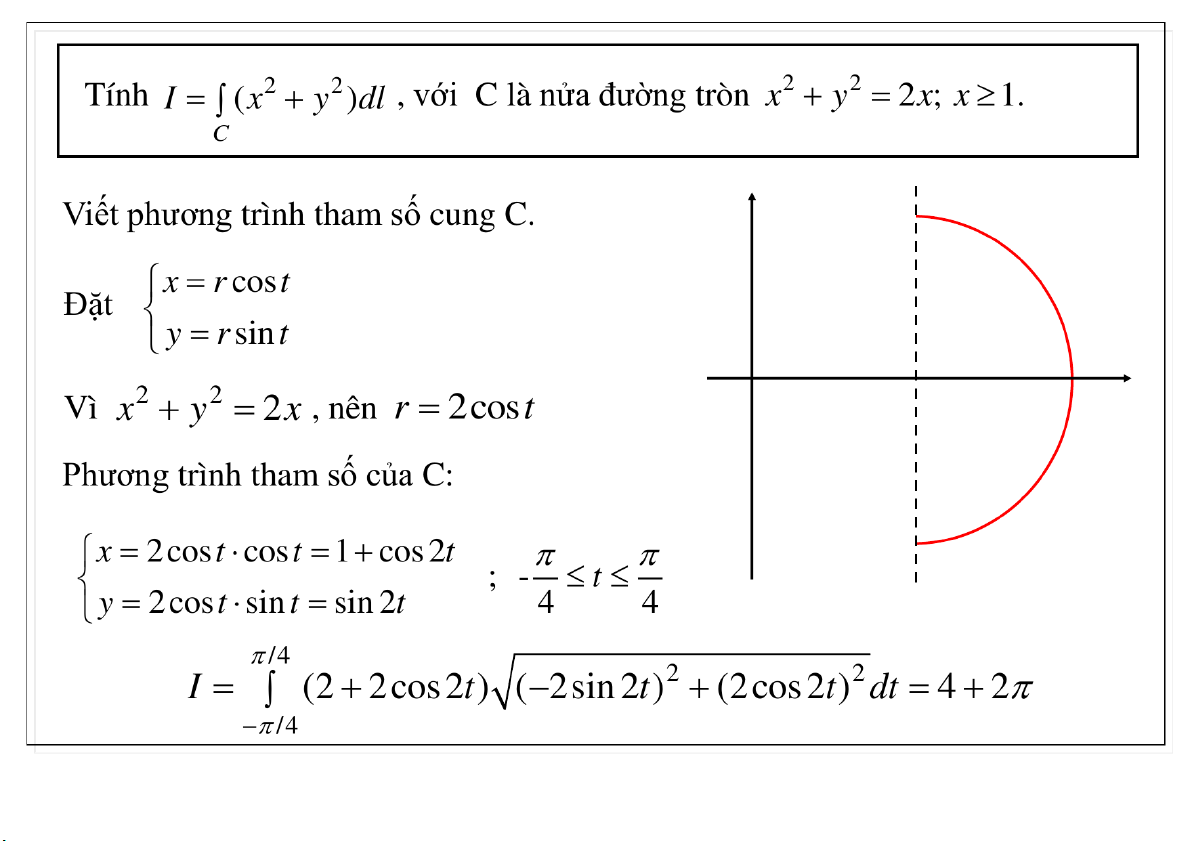
Đại học Công nghệ - ĐHQGHN Cách tính
Khi đó, phương trình tham số của cung C: x r( ) cos , y r( ) sin 23-Mar-21 TS. Nguyễn Văn Quang 10
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Mar-21 TS. Nguyễn Văn Quang 11
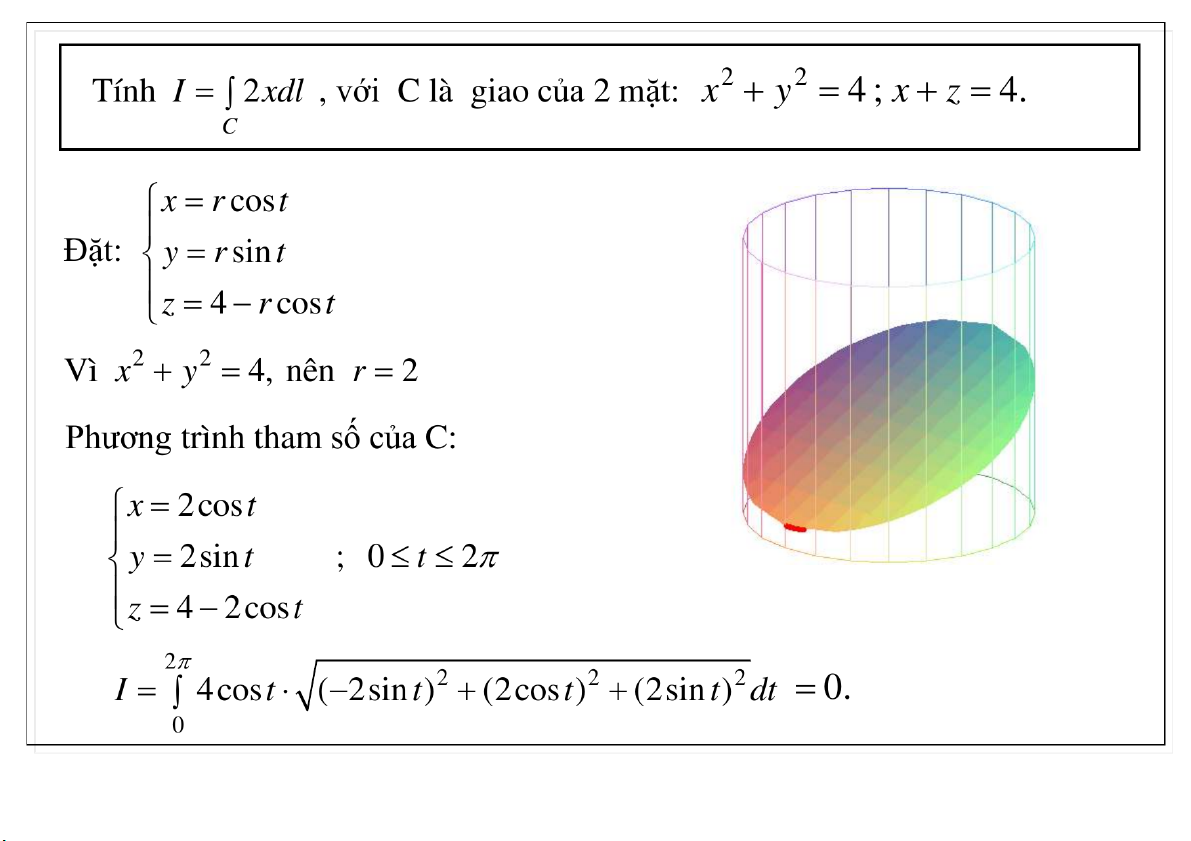
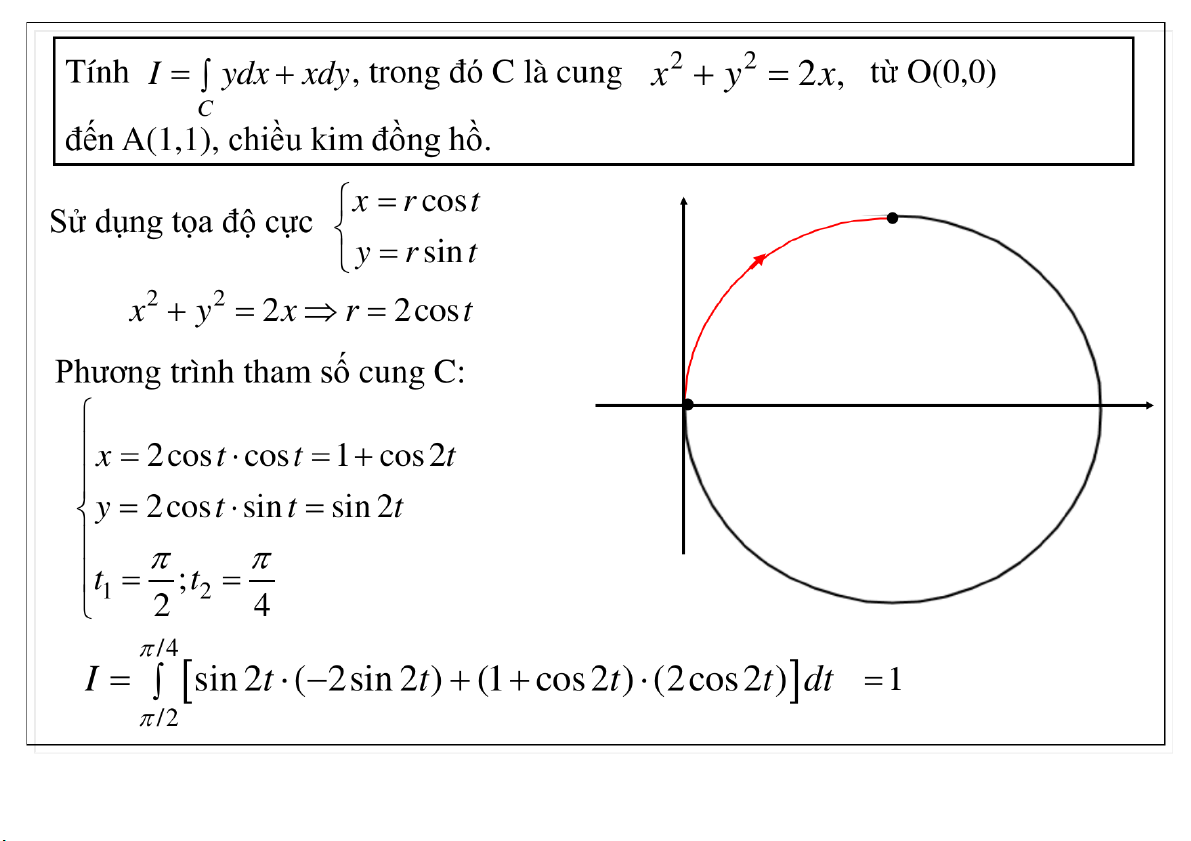
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Mar-21 TS. Nguyễn Văn Quang 12
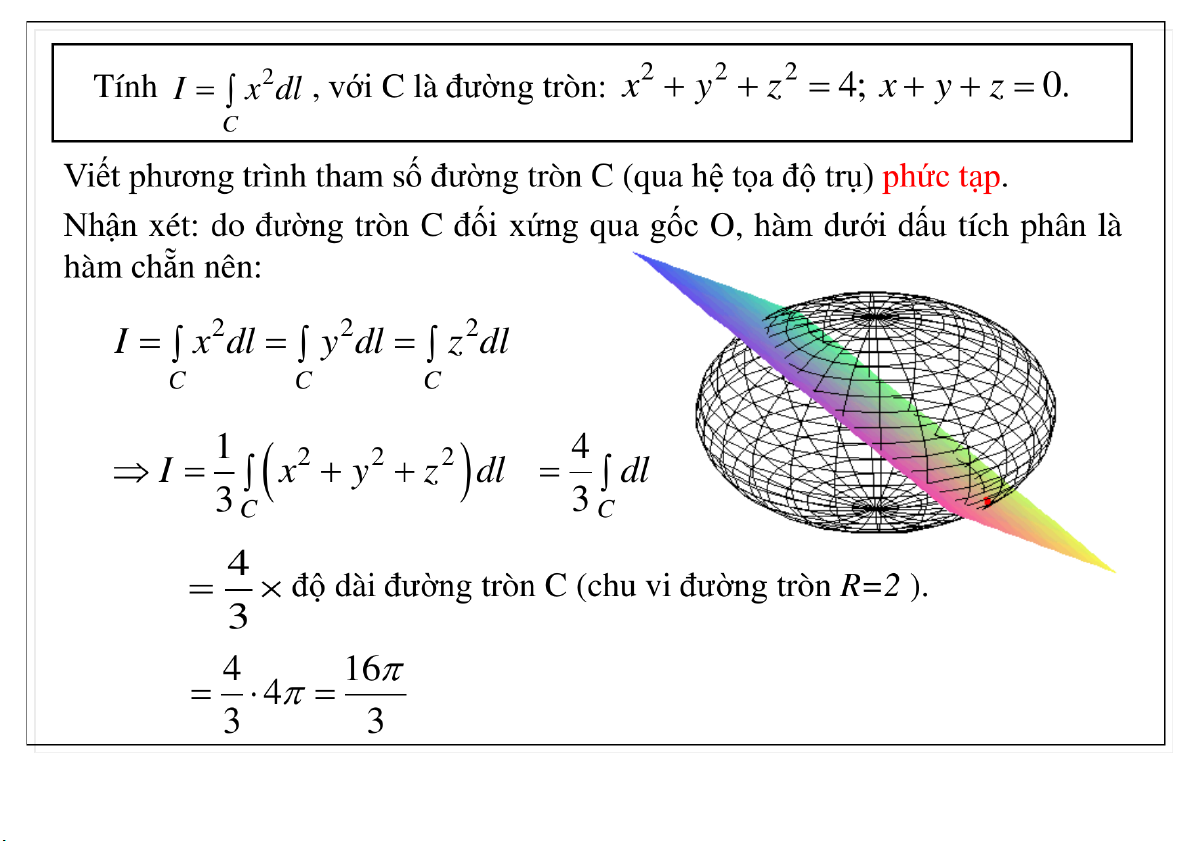
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Mar-21 TS. Nguyễn Văn Quang 13
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 14
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 15
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 16
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 17
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 18
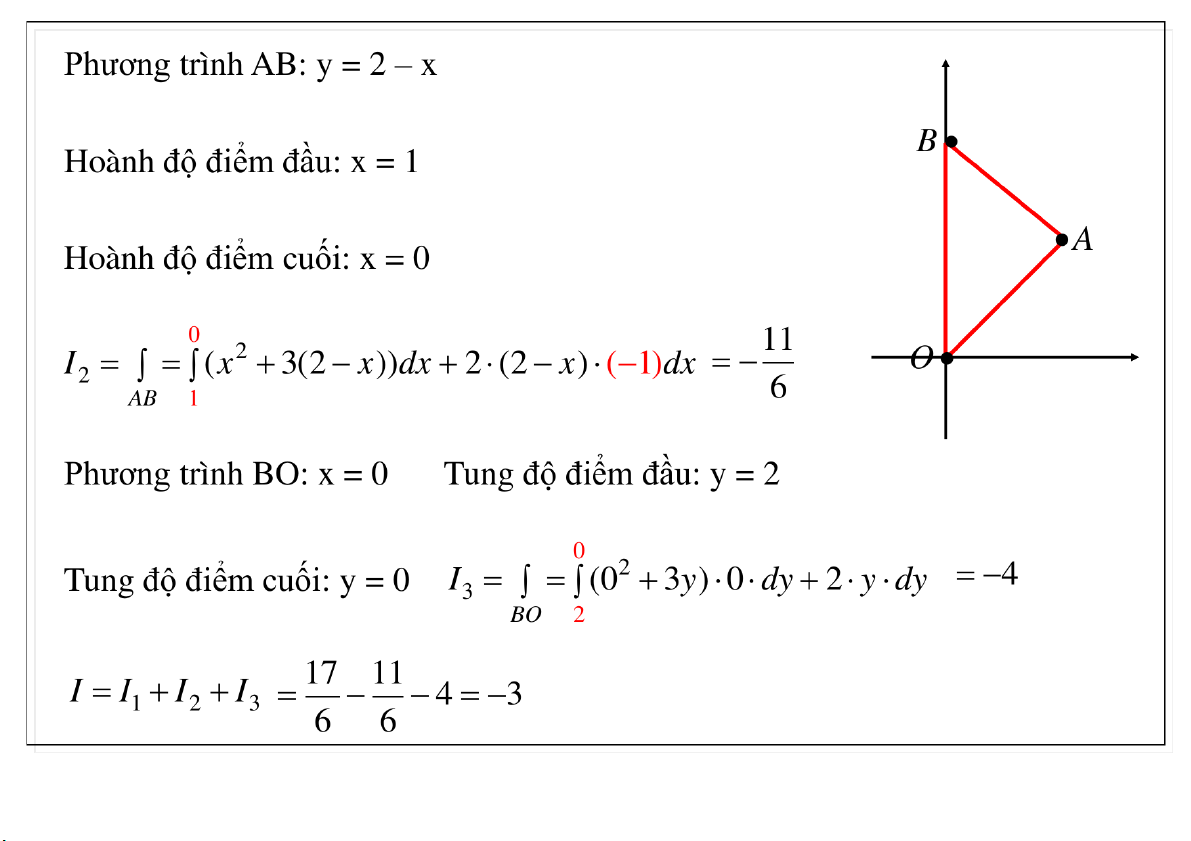
Đại học Công nghệ - ĐHQGHN
I I I  0 1 2 23-Mar-21 TS. Nguyễn Văn Quang 19
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 20
Đại học Công nghệ - ĐHQGHN 2 2
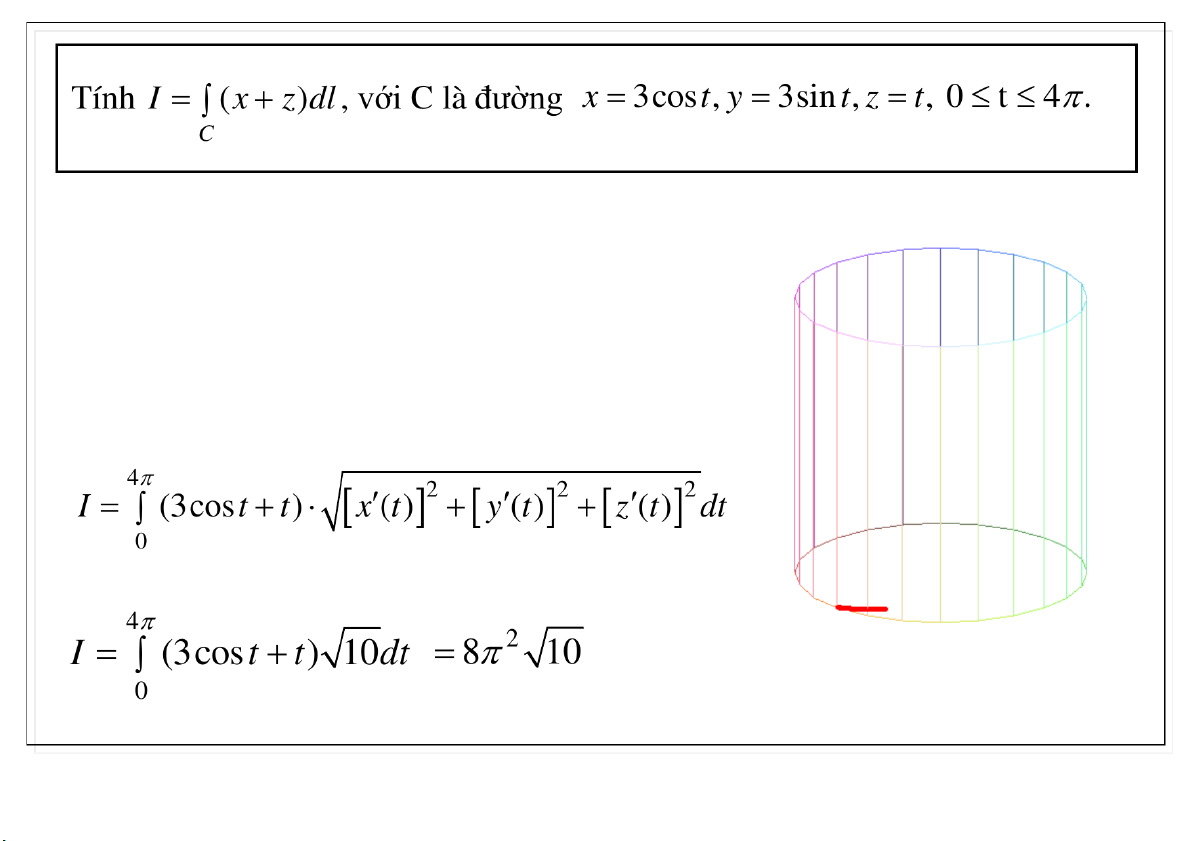
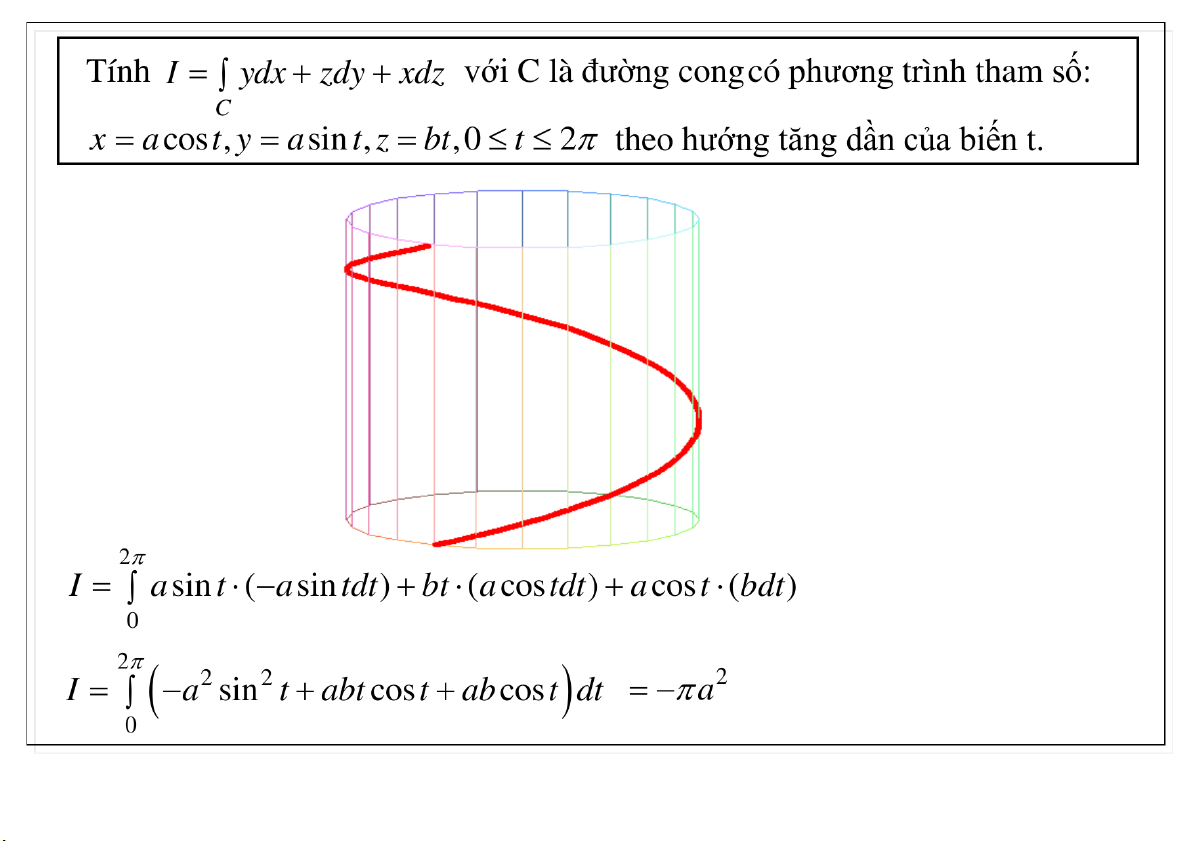
Ta có phương trình mặt trụ: xy  9 . Với 0  t  4
 thì đường cong C là đường cong nằm trên mặt trụ. 23-Mar-21 TS. Nguyễn Văn Quang 21
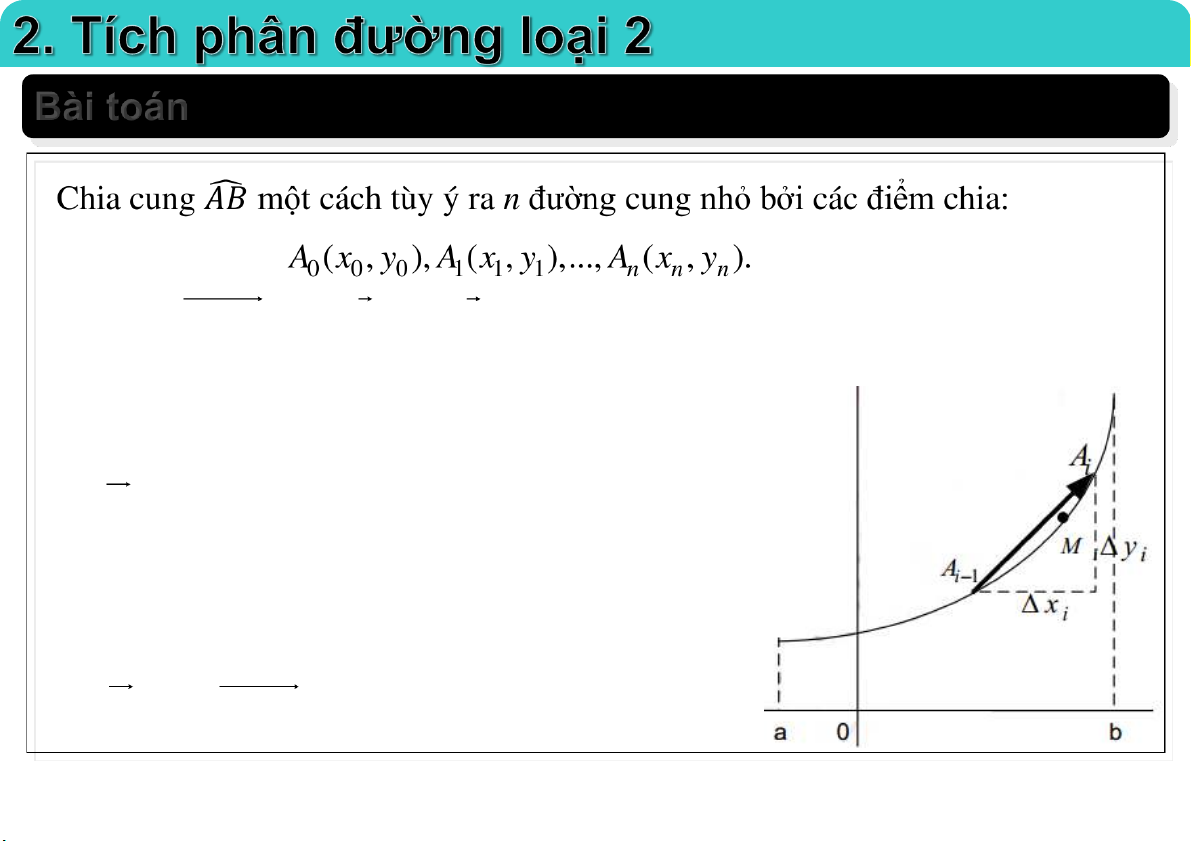
Đại học Công nghệ - ĐHQGHN Bài toán
Cho một chất điểm M di chuyển dọc theo một cung phẳng 𝐴𝐵 từ
điểm A đến điểm B dưới tác dụng của lực:
𝐹 𝑀 = 𝑃 𝑀 .𝑖 + 𝑄 𝑀 .𝑗 , 𝑀 ∈ 𝐴𝐵.
Hãy tính công W của lực đó sinh ra. 23-Mar-21 TS. Nguyễn Văn Quang 22
Đại học Công nghệ - ĐHQGHN Bài toán Khi đó: A A x i y j 1        i i i i Lấy M (
x , y ) A 1A . i i i ii Cung A
A nhỏ, nên có thể coi nó xấp xỉ dây cung A A i 1  i i 1  i và F (
M ) không đổi (về chiều và độ lớn) trên cung đó. i
Do đó, công của lực sinh ra khi chất điểm di chuyển
từ 𝐴𝑖−1 đến 𝐴 theo cung A A 𝑖 sẽ xấp xỉ là: i 1  i
F (M )  A A P(M )  x Q(M )  y i i1 i i i i i 23-Mar-21 TS. Nguyễn Văn Quang 23
Đại học Công nghệ - ĐHQGHN Bài toán
Do đó, giới hạn của tổng trên khi 𝑛 →∞ chính là công của lực: n
W= lim P(x , y )  x
  Q(x , y )  yi i i i i i n i 1  23-Mar-21 TS. Nguyễn Văn Quang 24
Đại học Công nghệ - ĐHQGHN Định nghĩa 23-Mar-21 TS. Nguyễn Văn Quang 25
Đại học Công nghệ - ĐHQGHN Tính chất 23-Mar-21 TS. Nguyễn Văn Quang 26
Đại học Công nghệ - ĐHQGHN đường loại 23-Mar-21 TS. Nguyễn Văn Quang 27
Đại học Công nghệ - ĐHQGHN Cách tính 23-Mar-21 TS. Nguyễn Văn Quang 28
Đại học Công nghệ - ĐHQGHN
Tích phân đường loại 2 trong không gian 23-Mar-21 TS. Nguyễn Văn Quang 29
Đại học Công nghệ - ĐHQGHN
Tích phân đường loại 2 trong không gian
Giả sử: 𝐅(𝑥,𝑦,𝑧) = 𝑃 𝑥,𝑦,𝑧 𝐢 + 𝑄 𝑥,𝑦,𝑧 𝐣 + 𝑅 𝑥,𝑦,𝑧 𝐤
là một trường vector xác định trên cung AB.
Tích phân đường của F trên cung AB là (công của lực F sinh ra khi di
chuyển một vật trên đường cong AB):
F dr   F(r(t)) r '(t)dt AB AB 23-Mar-21 TS. Nguyễn Văn Quang 30
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Mar-21 TS. Nguyễn Văn Quang 31
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 32
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 33
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 34
Đại học Công nghệ - ĐHQGHN
Tham số đường cong C qua hệ tọa độ trụ: 23-Mar-21 TS. Nguyễn Văn Quang 35
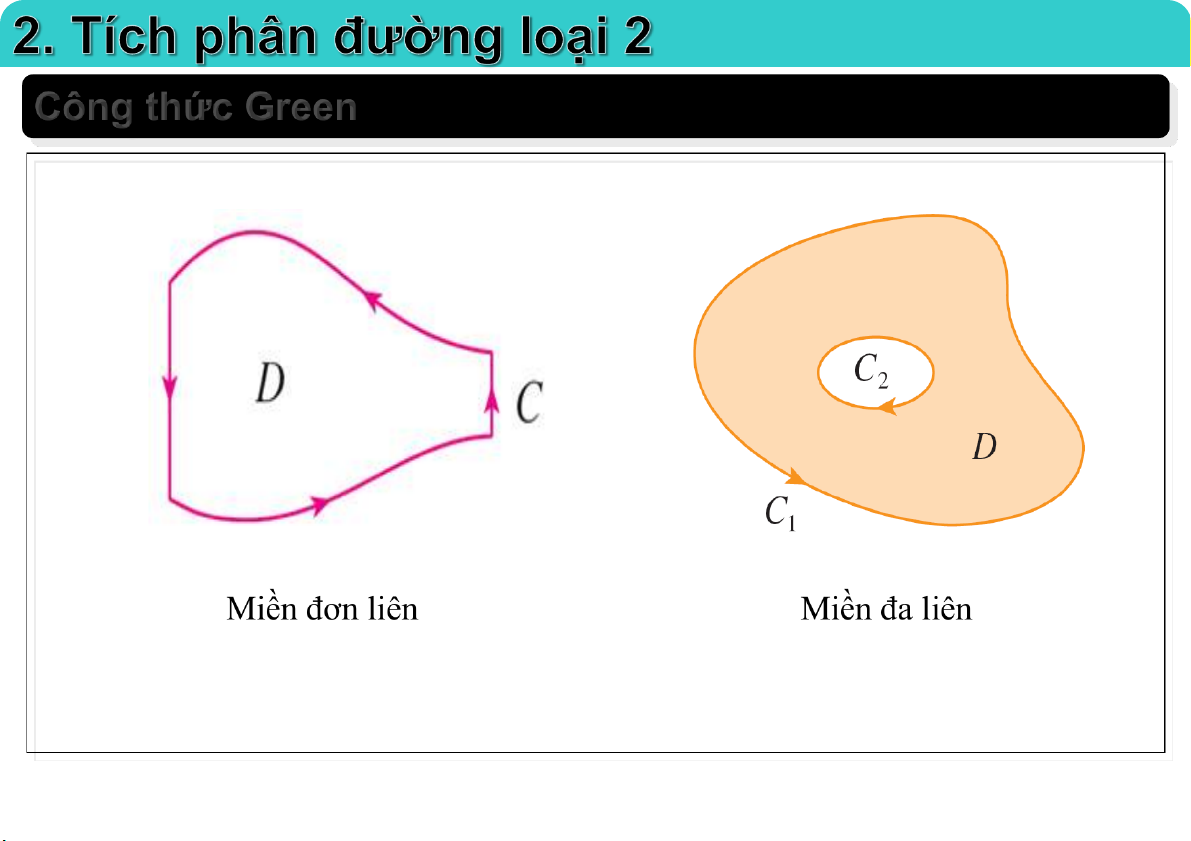
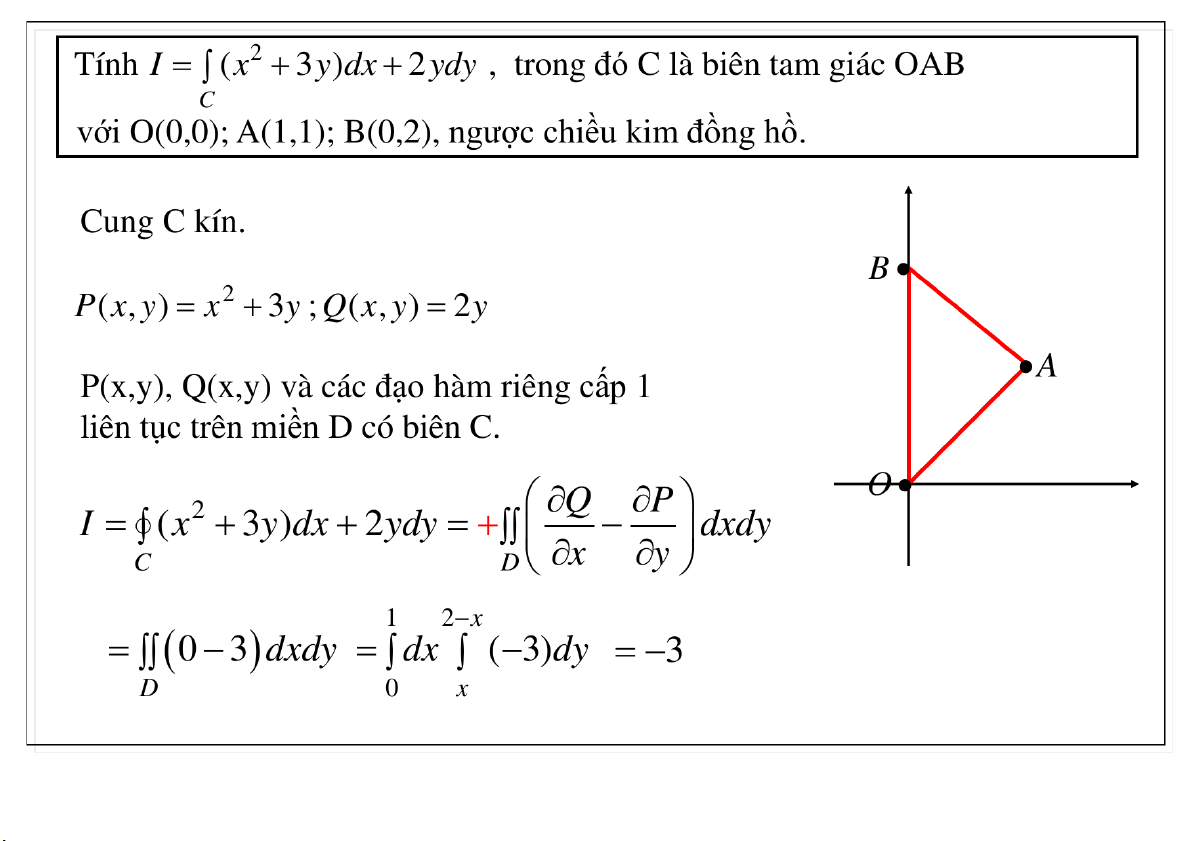
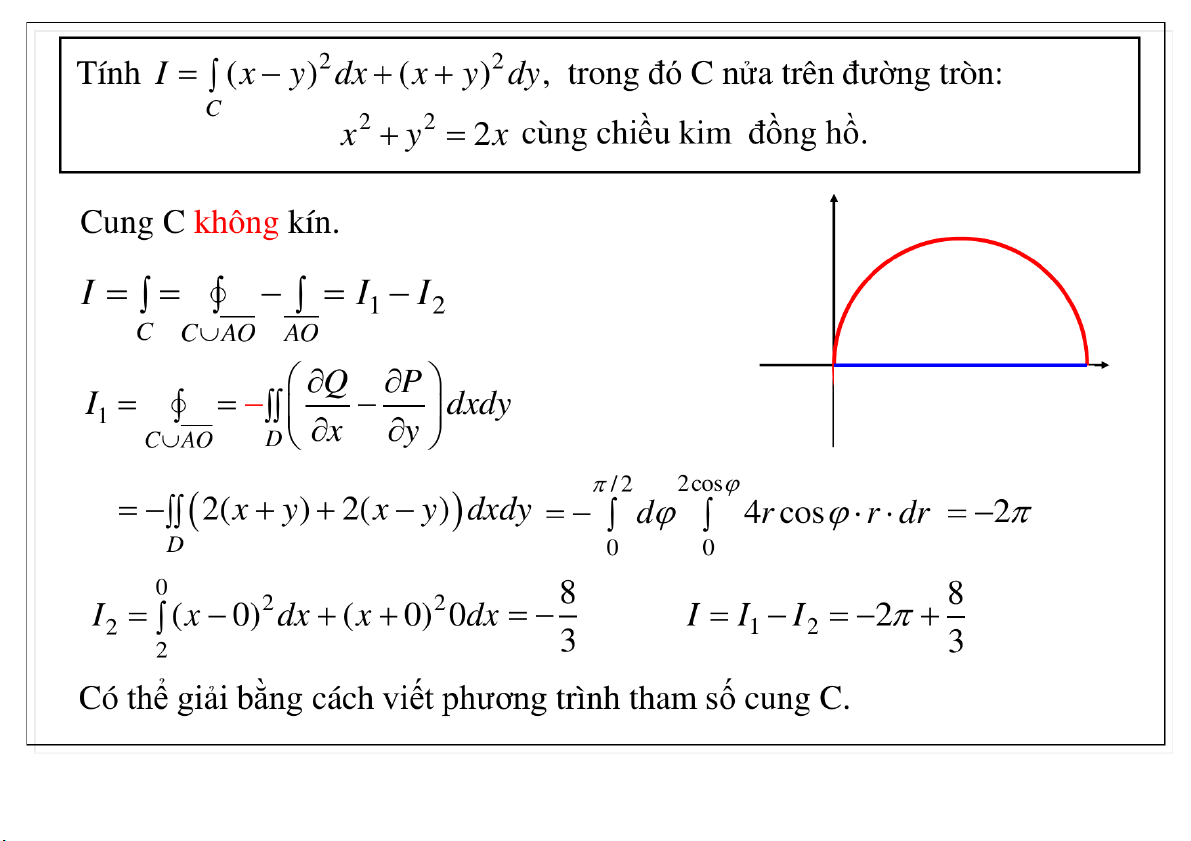
Đại học Công nghệ - ĐHQGHN Công thức Green 23-Mar-21 TS. Nguyễn Văn Quang 36
Đại học Công nghệ - ĐHQGHN Công thức Green 23-Mar-21 TS. Nguyễn Văn Quang 37
Đại học Công nghệ - ĐHQGHN Công thức Green 23-Mar-21 TS. Nguyễn Văn Quang 38
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 39
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 40
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 41
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 42
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Mar-21 TS. Nguyễn Văn Quang 43
Đại học Công nghệ - ĐHQGHN Ví dụ 2 2   ( , ) x y Q x y e sin(2xy) 23-Mar-21 TS. Nguyễn Văn Quang 44
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 45
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 46
Đại học Công nghệ - ĐHQGHN
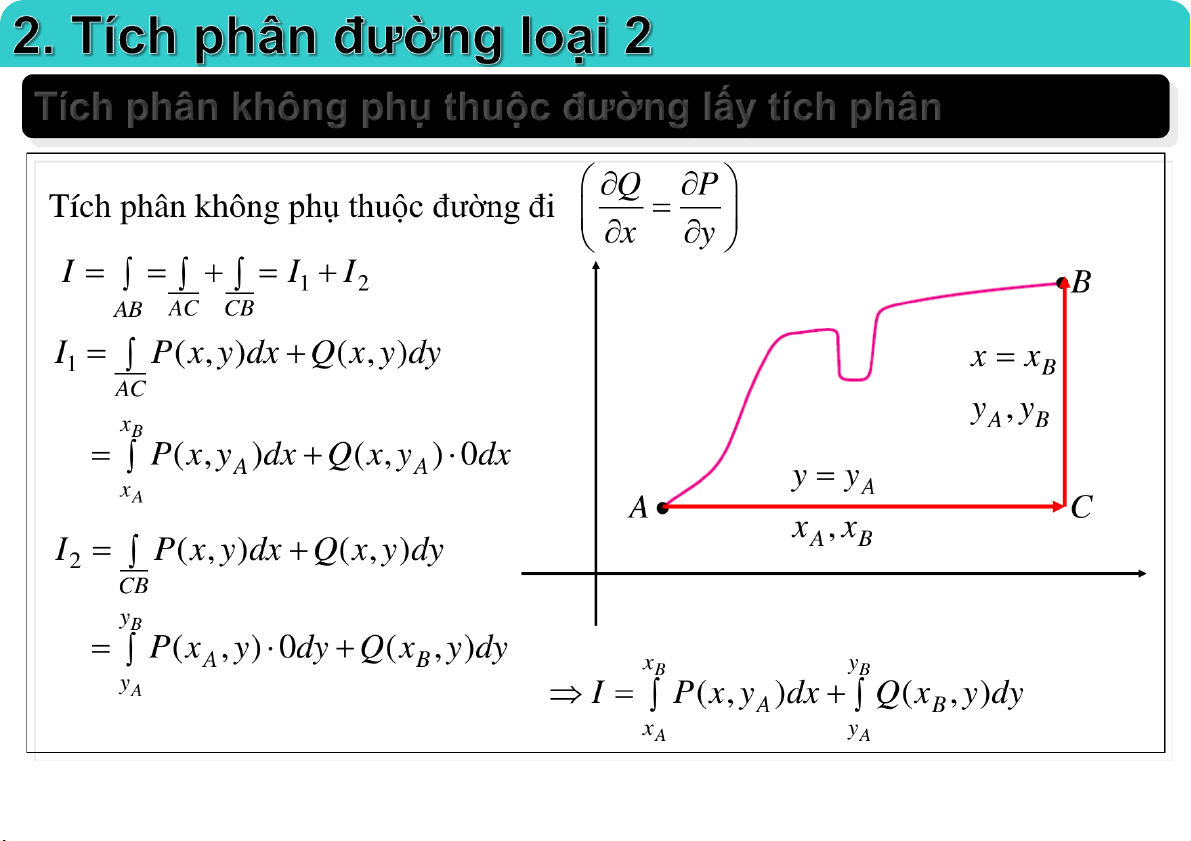
Tích phân không phụ thuộc đường lấy tích phân 23-Mar-21 TS. Nguyễn Văn Quang 47
Đại học Công nghệ - ĐHQGHN
Tích phân không phụ thuộc đường lấy tích phân 23-Mar-21 TS. Nguyễn Văn Quang 48
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 49
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 50
Đại học Công nghệ - ĐHQGHN
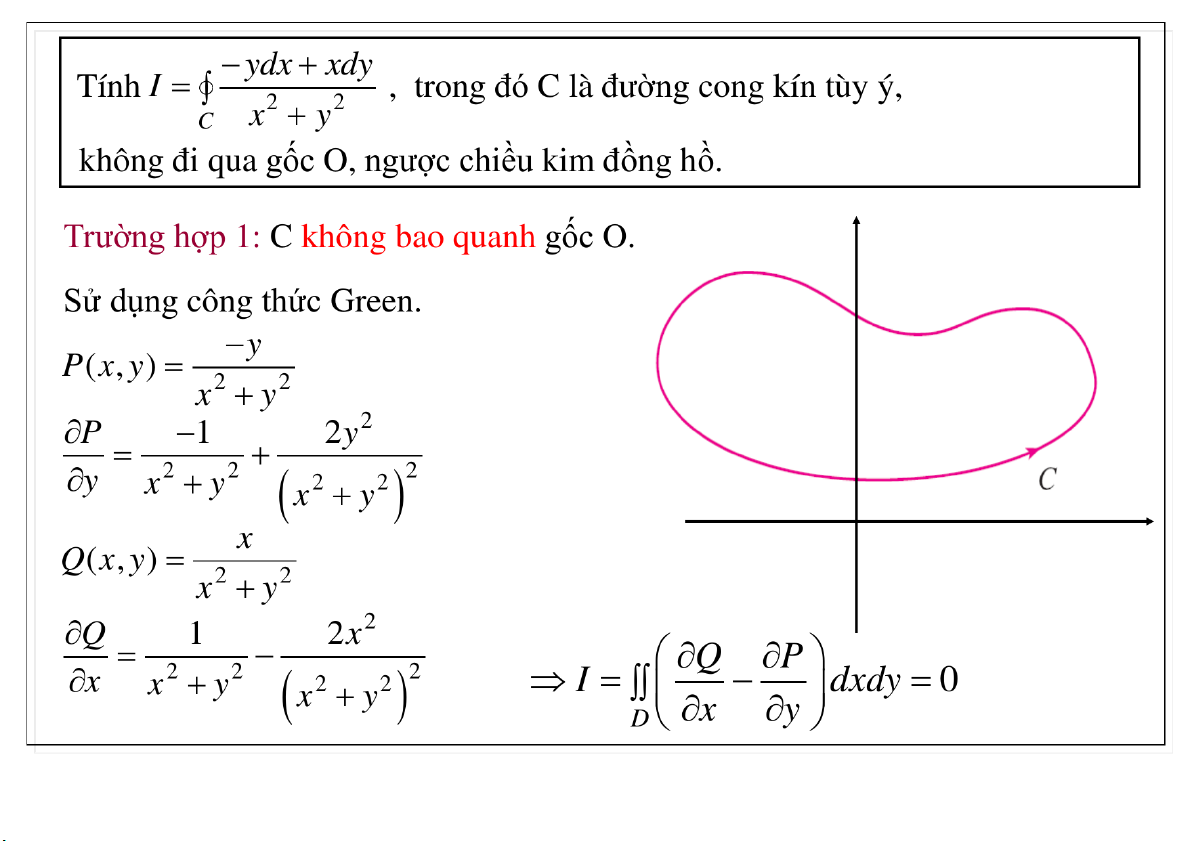
Nên ta tính tích phân theo trục hoành: QP  b)
 , tích phân I không phụ thuộc đường đi t ừ A đến B. xy
Tuy nhiên I không thể tính như câu a (theo đường thẳng từ A đến B theo trục
hoành), vì không tồn tại miền đơn liên D nào chứa đường thẳng AB và đường
cong kín bao quanh gốc O để cho P, Q và các ĐHR cấp 1 liên tục trên D. 23-Mar-21 TS. Nguyễn Văn Quang 51
Đại học Công nghệ - ĐHQGHN
trong đó: A(1,0), C(1,1), D(-1,1), E(-1,-1), F(2,-1), B(2,0).
Cách 2: Tìm hàm U(x,y) là vi phân toàn phần của P(x,y)dx+Q(x,y)dy    x U
P(x, y)       (1) (1) U(x, y)
P(x, y)dx g(y) x 2 2  x y  2 2 ln(x y )    y
U( x, y)   ( g y) U
Q(x, y)  (2) y 2 2  2  x y (2)  
g (y )  0  g(y)  C 2 2 ln(x y )
U (x,y)   C 2 (2,0) 
I U (x, y)  U(2,0)  ln 4 ln1 U(1,0)   ln 2 (1,0) 2
Cách 3: Bổ sung thêm đoạn thẳng từ B đến A, đưa vào đường tròn (đủ nhỏ) bao
quanh gốc O. Sử dụng công thức Green đối với miền đa liên này. 23-Mar-21 TS. Nguyễn Văn Quang 52
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 53
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 54
Đại học Công nghệ - ĐHQGHN
Tích phân không phụ thuộc đường lấy tích phân 23-Mar-21 TS. Nguyễn Văn Quang 55
Đại học Công nghệ - ĐHQGHN