Bài giảng Chương 6: Tích phân mặt - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội
Bài giảng Chương 6: Tích phân mặt - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Môn: Giải tích 2 (MAT1042) 50 tài liệu
Trường: Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội 591 tài liệu
Tác giả:
Preview text:
1. Tích phân mặt loại 1 2. Tích phân mặt loại 2 Định nghĩa
Cho hàm 𝑓(𝑥, 𝑦, 𝑧) xác định trên mặt cong 𝑆.
Chia 𝑆 thành 𝑛 mặt con: 𝑆1, 𝑆2, ⋯ , 𝑆𝑛 rời nhau (không chồng lên nhau).
Diện tích tương ứng: ∆𝑆1, ∆𝑆2, ⋯ , ∆𝑆𝑛.
Trên mỗi mặt 𝑆𝑖 lấy điểm 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) tùy ý. Lập tổng Riemann: 𝑛 𝐼𝑛 = 𝑓 𝑀𝑖 . ∆𝑆𝑖 𝑖=1
𝐼 = lim 𝐼𝑛, không phụ thuộc cách chia mặt cong 𝑆, và cách lấy điểm 𝑀𝑖. 𝑛→∞ 𝐼 =
𝑓 𝑥, 𝑦, 𝑧 𝑑𝑆 𝑆
được gọi là tích phân mặt loại 1 của hàm 𝑓(𝑥, 𝑦, 𝑧) trên mặt 𝑆. 23-Mar-21 TS. Nguyễn Văn Quang 2
Đại học Công nghệ - ĐHQGHN Tính chất
1. 𝑓(𝑥, 𝑦, 𝑧) liên tục trên mặt cong trơn 𝑆 thì khả tích trên 𝑆.
2. Diện tích của mặt 𝑆: 𝑑𝑆. 𝑆 3.
𝑘𝑓 + 𝑚𝑔 𝑑𝑆 = 𝑘 𝑓𝑑𝑆 + 𝑚 𝑔𝑑𝑆 𝑆 𝑆 𝑆
4. Nếu 𝑆 = 𝑆1 ∪ 𝑆2 thì: 𝑓𝑑𝑆 = 𝑓𝑑𝑆 + 𝑓𝑑𝑆. 𝑆 𝑆1 𝑆2 23-Mar-21 TS. Nguyễn Văn Quang 3
Đại học Công nghệ - ĐHQGHN Cách tính
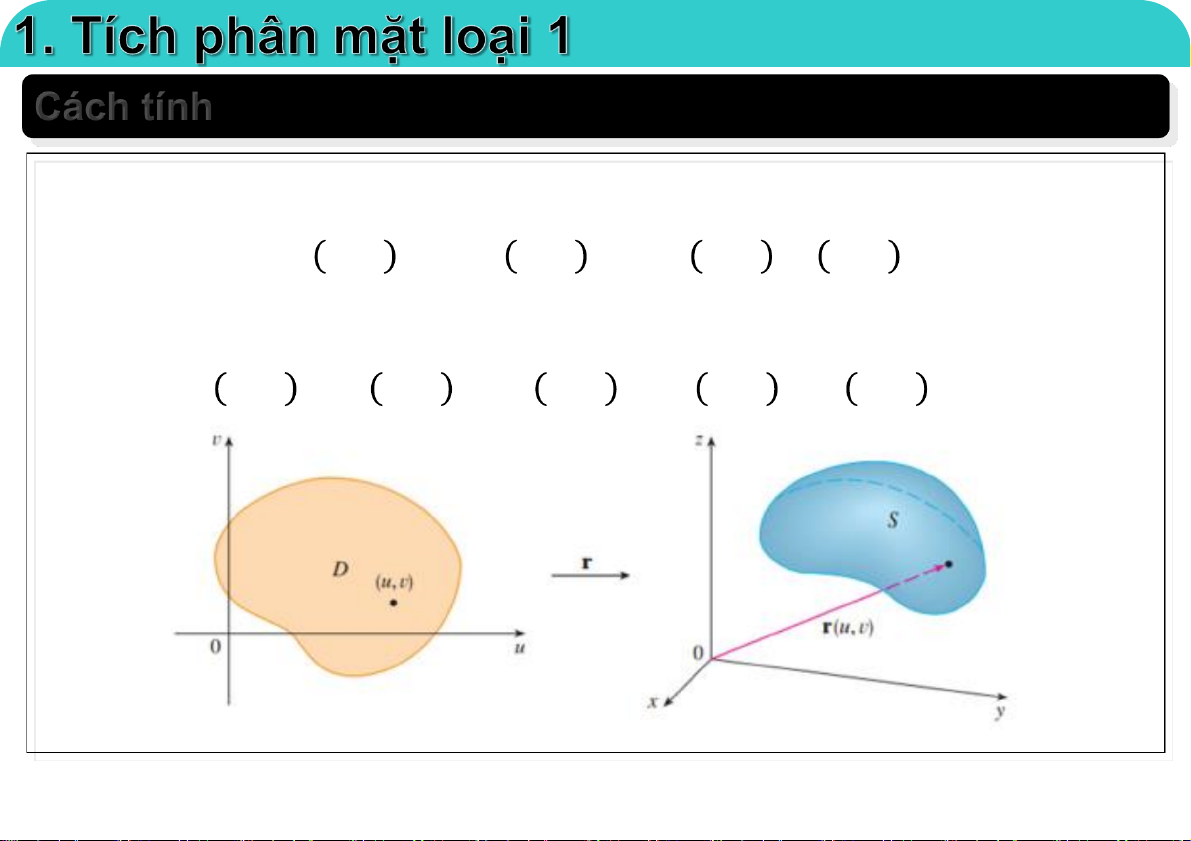
Phương trình tham số mặt cong S:
𝑥 = 𝑥 𝑢, 𝑣 , 𝑦 = 𝑦 𝑢, 𝑣 , 𝑧 = 𝑧 𝑢, 𝑣 ; 𝑢, 𝑣 ∈ 𝐷
Phương trình tham số hàm vector mặt cong S:
𝐫 𝑢, 𝑣 = 𝑥 𝑢, 𝑣 𝐢 + 𝑦 𝑢, 𝑣 𝐣 + 𝑧 𝑢, 𝑣 𝐤 ; 𝑢, 𝑣 ∈ 𝐷 23-Mar-21 TS. Nguyễn Văn Quang 4
Đại học Công nghệ - ĐHQGHN Ví dụ
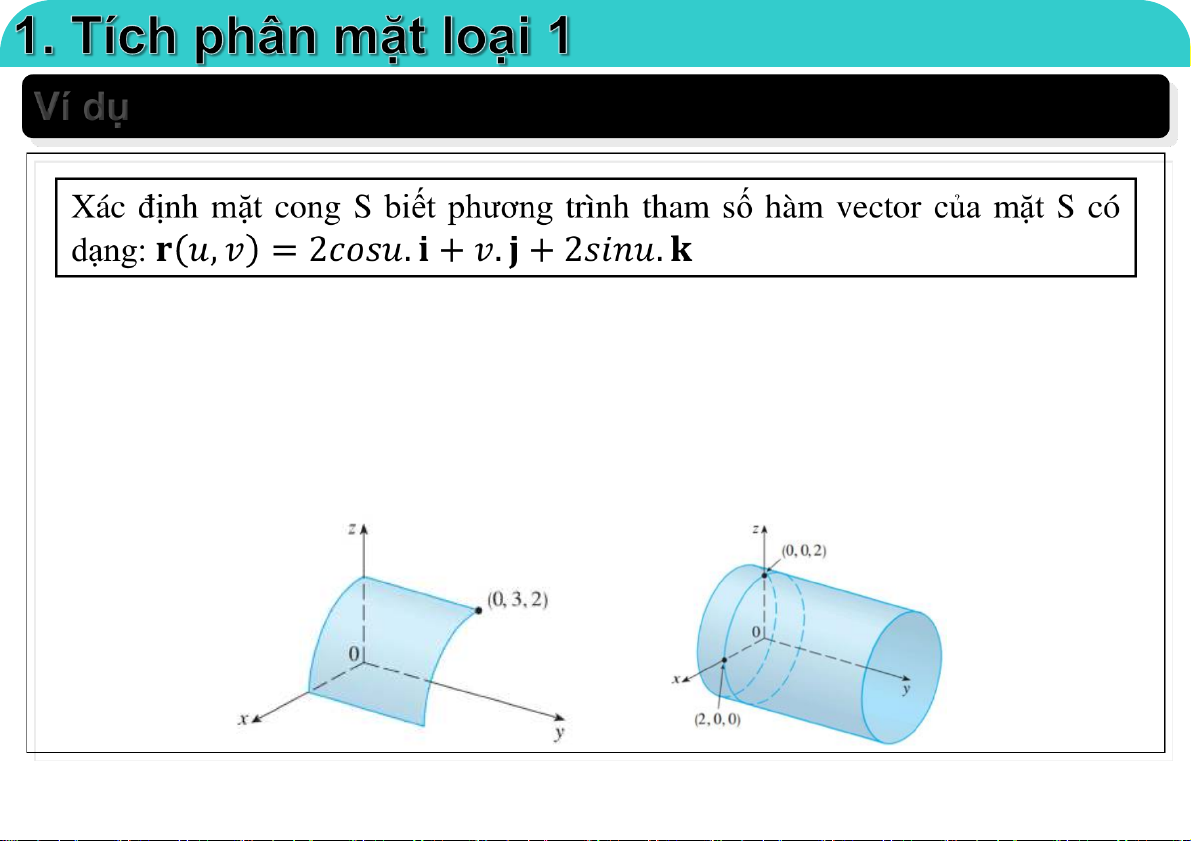
Phương trình tham số mặt cong S:
𝑥 = 2𝑐𝑜𝑠𝑢; 𝑦 = 𝑣; 𝑧 = 2𝑠𝑖𝑛𝑢
Do đó: 𝑥2 + 𝑧2 = 4, mặ S l t
à mặ ttrụ song song với trục Oy.
Nếu thêm điều kiện: 0 ≤ 𝑢 ≤ 𝜋/2,0 ≤ 𝑣 ≤ 3, mặt S có dạng: 23-Mar-21 TS. Nguyễn Văn Quang 5
Đại học Công nghệ - ĐHQGHN Ví dụ
Phương trình tham số mặt cong S:
𝑥 = 𝑥; 𝑦 = 𝑦; 𝑧 = 𝑥2 + 2𝑦2
Do đó phương trình tham số hàm vector của mặt cong S:
𝐫 𝑥, 𝒚 = 𝑥. 𝐢 + 𝑦. 𝐣 + (𝑥2 + 2𝑦2). 𝐤 23-Mar-21 TS. Nguyễn Văn Quang 6
Đại học Công nghệ - ĐHQGHN Cách tính
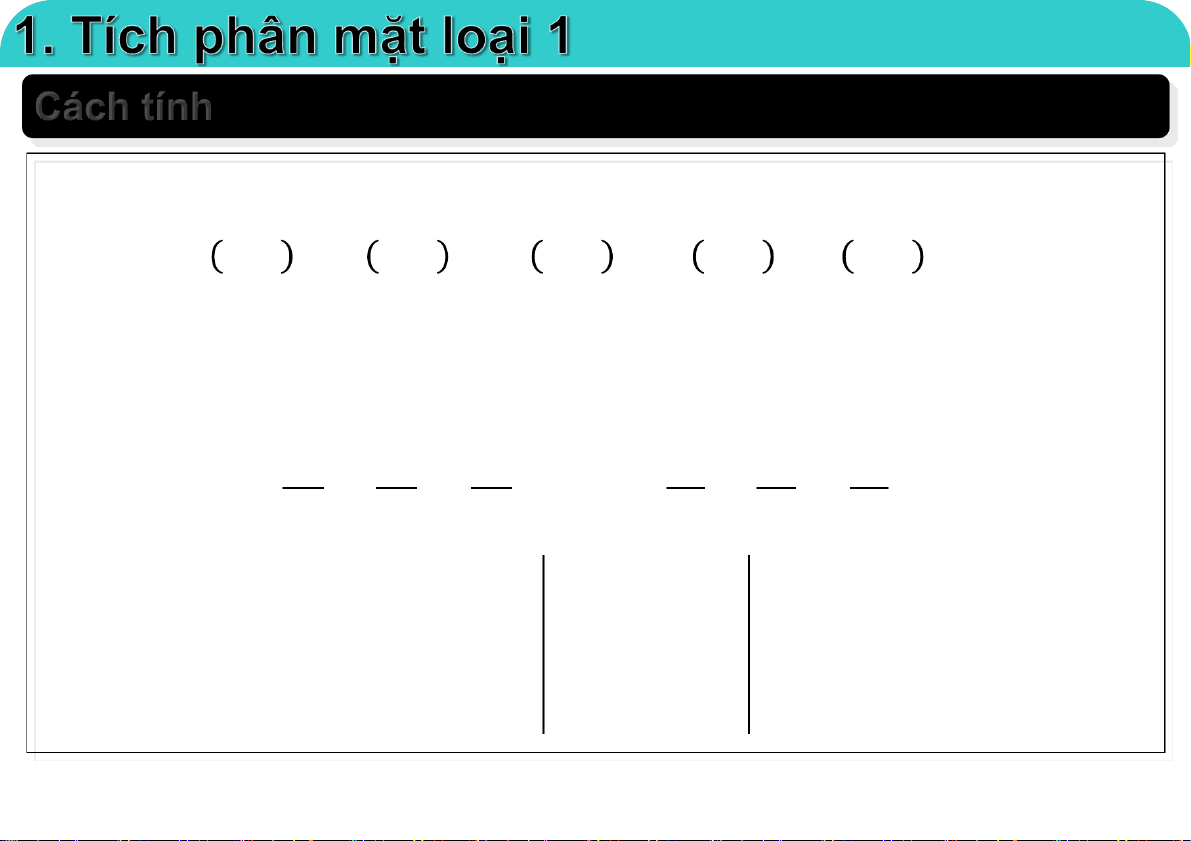
Giả sử mặt cong S có phương trình tham số hàm vector:
𝐫 𝑢, 𝑣 = 𝑥 𝑢, 𝑣 𝐢 + 𝑦 𝑢, 𝑣 𝐣 + 𝑧 𝑢, 𝑣 𝐤 ; 𝑢, 𝑣 ∈ 𝐷, khi đó: f ( , x ,y )z dS (f ( ,u )) vr | |r du r dv u v S D trong đó: x y z x y z r i j k ; r i j k u v u u u v v v i j k r r x y z u v u u u x y z v v v 23-Mar-21 TS. Nguyễn Văn Quang 7
Đại học Công nghệ - ĐHQGHN Ví dụ
Tham số hóa mặt cầu S bằng hệ tọa độ cầu:
𝑥 = 𝑅𝑐𝑜𝑠𝜑. 𝑠𝑖𝑛𝜃; 𝑦 = 𝑅𝑠𝑖𝑛𝜑. 𝑠𝑖𝑛𝜃; 𝑧 = 𝑅𝑐𝑜𝑠𝜃
𝐷 𝜑, 𝜃 = { 𝜑, 𝜃 : 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝜃 ≤ 𝜋}
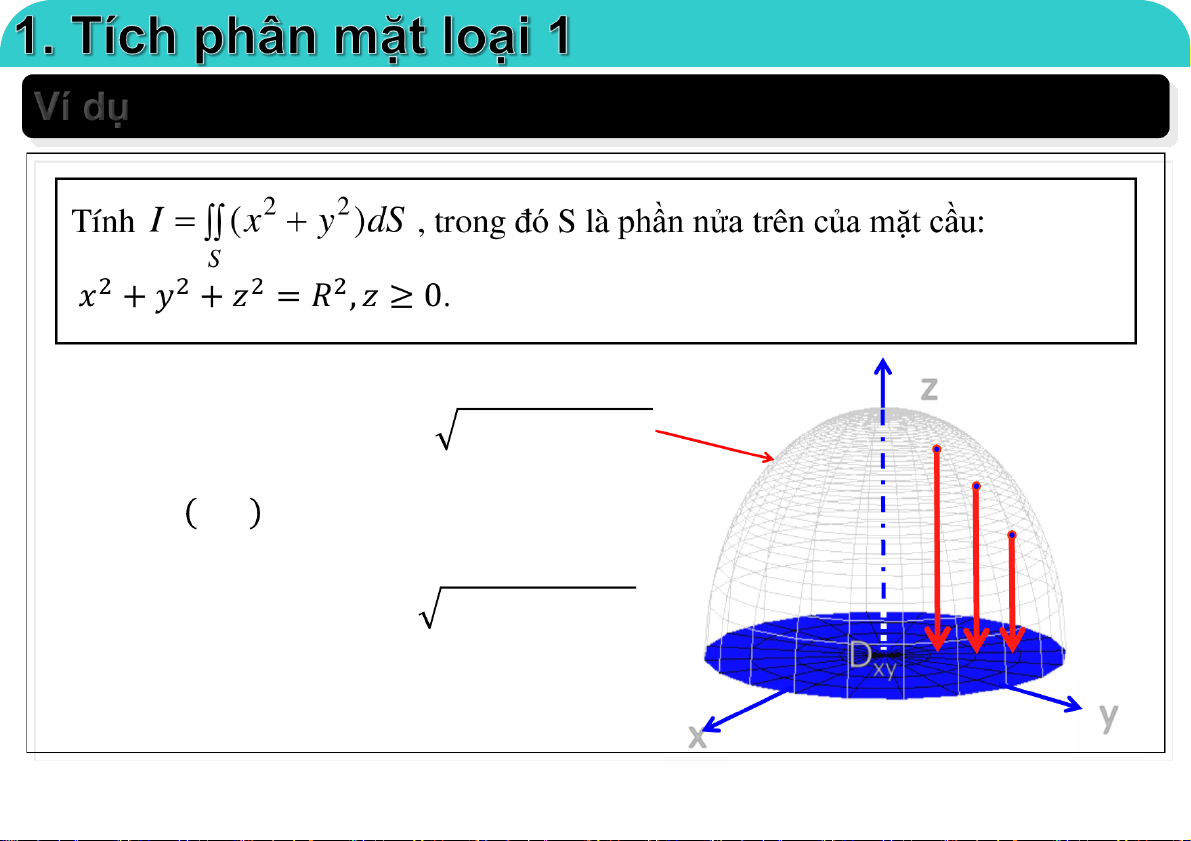
Tức là: 𝐫 𝜑, 𝜃 = 𝑅𝑐𝑜𝑠𝜑. 𝑠𝑖𝑛𝜃𝐢 + 𝑅𝑠𝑖𝑛𝜑. 𝑠𝑖𝑛𝜃𝐣 + 𝑅𝑐𝑜𝑠𝜃𝐤 r si R n sin i co R s sin j 0. k r c R os cos i s R in cos j s R in k 23-Mar-21 TS. Nguyễn Văn Quang 8
Đại học Công nghệ - ĐHQGHN Ví dụ i j k r r R sin sin R cos sin 0 Rcos cos Rsin cos sin R 2 2 2 2 2 c R os sin i si R n sin j sin R cos k Do đó: 2 | r r | R sin u v 2 2 Vậy: x dS ( c R os sin ) r r d d S ( D , ) 4 2 R (cos sin ) sin d d D ( , ) 23-Mar-21 TS. Nguyễn Văn Quang 9
Đại học Công nghệ - ĐHQGHN Ví dụ 2 4 2 3 R cos sin d d 0 0 2 4 2 3 R cos d sin d 0 0 2 1 2 (1 cos 2 ) d (sin sin cos ) d 2 0 0 4 2 R 1 1 3 sin 2 cos cos 2 2 0 3 0 4 4 R 3 23-Mar-21 TS. Nguyễn Văn Quang 10
Đại học Công nghệ - ĐHQGHN Ví dụ Cách 2:
Do các hàm dưới dấu tích phân là hàm chẵn, và mặt cầu đối xứng qua
các mặ tphẳng tọa độ. 𝐼 = 𝑥2𝑑𝑆 = 𝑦2𝑑𝑆 = 𝑧2𝑑𝑆 𝑆 𝑆 𝑆 Do đó: 𝐼 = 1
(𝑥2 + 𝑦2 + 𝑧2)𝑑𝑆 = 𝑅2 𝑑𝑆 = 4𝜋𝑅4 3 𝑆 3 𝑆 3 23-Mar-21 TS. Nguyễn Văn Quang 11
Đại học Công nghệ - ĐHQGHN Cách tính
Cho hàm 𝑓(𝑥, 𝑦, 𝑧) xác định trên mặt cong 𝑆: 𝑧 = 𝑧(𝑥, 𝑦).
Chia 𝑆 thành 𝑛 mặt con: 𝑆1, 𝑆2, ⋯ , 𝑆𝑛 rời nhau (không chồng lên nhau).
Diện tích tương ứng: ∆𝑆1, ∆𝑆2, ⋯ , ∆𝑆𝑛.
Trên mỗi mặt 𝑆𝑖 lấy điểm 𝑀𝑖(𝑥𝑖, 𝑦𝑖, 𝑧𝑖) tùy ý. Lập tổng Riemann: 𝑛 𝐼𝑛 = 𝑓 𝑀𝑖 . ∆𝑆𝑖 𝑖=1
Trong phần ứng dụng tích phân kép (tính diện tích mặt cong), ta có: 2 2 S z ( x, y) z ( , x ) y 1 (S ) i x i i y i i i D 2 2 z ( x , y) z ( , x ) y 1 x i i y i i x y 23-Mar-21 TS. Nguyễn Văn Quang 12
Đại học Công nghệ - ĐHQGHN Cách tính n Do đó: I f (M ) n i i S i 1 n 2 2 f ( x , y, z) z ( , x ) y z( ,x )y 1 i i i x i i y i i x i 1 n 2 2 f (x , y , z ( x, ) y ) z ( , x ) y ( z ,x )y 1 i i i i i x i i y i i x i 1 2 2 I lim I hay f ( , x , y ) z dS (f ,x ,y )z z z 1 n x y dxd n S x D y 2 2 f ( , x , y ( z ,x )y) z z 1 x y dxdy Dxy 23-Mar-21 TS. Nguyễn Văn Quang 13
Đại học Công nghệ - ĐHQGHN Cách tính z
1. Chiếu mặt cong 𝑆 lên mp Oxy S z = z(x,y)
Nếu 𝑆 có phương trình 𝑧 = 𝑧(𝑥, 𝑦)
và 𝑆 có hình chiếu trên mp Oxy là 𝐷𝑥𝑦 : y D O xy x
𝑓 𝑥, 𝑦, 𝑧 𝑑𝑆 =
𝑓 𝑥, 𝑦, 𝑧 𝑥, 𝑦 1 + (𝑧′ ′ )2
𝑥)2 + (𝑧𝑦 𝑑𝑥𝑑𝑦 𝑆 𝐷𝑥𝑦 23-Mar-21 TS. Nguyễn Văn Quang 14
Đại học Công nghệ - ĐHQGHN Cách tính
2. Chiếu mặt cong 𝑆 lên mp Oxz
Nếu 𝑆 có phương trình 𝑦 = 𝑦(𝑥, 𝑧)
và 𝑆 có hình chiếu trên mp Oxz là 𝐷𝑥𝑧 :
𝑓 𝑥, 𝑦, 𝑧 𝑑𝑆 =
𝑓 𝑥, 𝑦(𝑥, 𝑧), 𝑧
1 + (𝑦′)2 + (𝑦′)2𝑑𝑥𝑑𝑧 𝑆 𝑥 𝑧 𝐷𝑥𝑧
3. Chiếu mặt cong 𝑆 lên mp Oyz
Nếu 𝑆 có phương trình 𝑥 = 𝑥(𝑦, 𝑧)
và 𝑆 có hình chiếu trên mp Oyz là 𝐷𝑦𝑧 :
𝑓 𝑥, 𝑦, 𝑧 𝑑𝑆 =
𝑓 𝑥(𝑦, 𝑧), 𝑦, 𝑧
1 + (𝑥 ′ )2 + (𝑥′ )2𝑑𝑦𝑑𝑧 𝑆 𝑦 𝑧 𝐷𝑦𝑧 23-Mar-21 TS. Nguyễn Văn Quang 15
Đại học Công nghệ - ĐHQGHN Chú ý
Nếu hình chiếu của 𝑆 xuống mặt phẳng Oxy chỉ là một đường cong
(trường hợp này xảy ra khi 𝑆 là một mặt trụ có đường sinh song song
với trục Oz) thì phải chiếu 𝑆 xuống các mặt phẳng tọa độ khác,
không được chiếu xuống mặt phẳng Oxy. 23-Mar-21 TS. Nguyễn Văn Quang 16
Đại học Công nghệ - ĐHQGHN Ví dụ Z=3
𝐷𝑥𝑦 = { 𝑥, 𝑦 : 𝑥2 + 𝑦2 ≤ 9}
Phương trình mặt nón: 𝑧 = 𝑥2 + 𝑦2 𝜕𝑧 𝑥 𝜕𝑧 𝑦 = = 𝜕𝑥 𝑥2 + 𝑦2 𝜕𝑦 𝑥2 + 𝑦2 Z=0 23-Mar-21 TS. Nguyễn Văn Quang 17
Đại học Công nghệ - ĐHQGHN Ví dụ 𝐼 =
𝑥2 + 𝑦2 + 𝑧2 𝑑𝑆 = 2 𝑥2 + 𝑦2 2𝑑𝑥𝑑𝑦 𝑆 𝐷𝑥𝑦
Chuyển sang hệ tọa độ cực: 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝐷𝑟𝜑 = { 𝑟, 𝜑 : 0 ≤ 𝑟 ≤ 3,0 ≤ 𝜑 ≤ 2𝜋} 2𝜋 3 𝐼 = 2 2
𝑟2. 𝑟. 𝑑𝑟𝑑𝜑= 2 2 𝑑𝜑 𝑟3𝑑𝑟 = 81 2𝜋 𝐷𝑟𝜑 0 0 23-Mar-21 TS. Nguyễn Văn Quang 18
Đại học Công nghệ - ĐHQGHN Ví dụ Cách 2:
Tham số mặt S qua hệ tọa độ cầ : u
𝑥 = 𝜌𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃, 𝑦 = 𝜌𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃, 𝑧 = 𝜌𝑐𝑜𝑠𝜃 ; 𝜃 = 𝜋/4
Do đó: 𝑥 = 𝜌 𝑐𝑜𝑠𝜑, 𝑦 = 𝜌 𝑠𝑖𝑛𝜑, 𝑧 = 𝜌 2 2 2 𝐷 𝜌, 𝜑 =
𝜌, 𝜑 : 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝜌 ≤ 3 2 23-Mar-21 TS. Nguyễn Văn Quang 19
Đại học Công nghệ - ĐHQGHN Ví dụ i j k cos sin 1 r r 2 2 2 sin cos 0 2 2 cos sin i j k 2 2 2
Do đó: 𝐫𝜌 × 𝐫𝜑 = 𝜌2 + 𝜌2 = 𝜌 4 4 2 23-Mar-21 TS. Nguyễn Văn Quang 20
Đại học Công nghệ - ĐHQGHN Ví dụ 2 2 2 2 I (x y z ) dS d d S D( , ) 2 2 3 2 1 3 1 3 d d d d 2 D( , ) 2 0 0 81 2 23-Mar-21 TS. Nguyễn Văn Quang 21
Đại học Công nghệ - ĐHQGHN Ví dụ 𝐷 2 2
𝑥𝑦 = { 𝑥, 𝑦 : 𝑥 + 𝑦 ≤ 2}
Phương trình mặt S: 𝑧 = 2 − 𝑥2 − 𝑦2 𝜕𝑧 𝜕𝑧 = −2𝑥 = −2𝑦 𝜕𝑥 𝜕𝑦 2 2 𝜕𝑧 𝜕𝑧 𝑑𝑆 = 1 + +
𝑑𝑥𝑑𝑦 = 1 + 4(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦 𝜕𝑥 𝜕𝑥 23-Mar-21 TS. Nguyễn Văn Quang 22
Đại học Công nghệ - ĐHQGHN Ví dụ 𝐼 = 𝑧𝑑𝑆 = 2 − 𝑥2 − 𝑦2
1 + 4(𝑥2 + 𝑦2)𝑑𝑥𝑑𝑦 𝑆 𝐷𝑥𝑦
Chuyển sang hệ tọa độ cực: 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝐷𝑟𝜑 = { 𝑟, 𝜑 : 0 ≤ 𝑟 ≤ 2, 0 ≤ 𝜑 ≤ 2𝜋} 2𝜋 2
𝐼 = (2 − 𝑟2) 1 + 4𝑟2. 𝑟. 𝑑𝑟 𝜑 𝑑
= 𝑑𝜑 (2 − 𝑟2) 1 + 4𝑟2. 𝑟𝑑𝑟 𝐷𝑟𝜑 0 0 37 = 𝜋 10 23-Mar-21 TS. Nguyễn Văn Quang 23
Đại học Công nghệ - ĐHQGHN Ví dụ Cách 2:
Tham số mặt S qua hệ tọa độ trụ:
𝑥 = 𝜌𝑐𝑜𝑠𝜑, 𝑦 = 𝜌𝑠𝑖𝑛𝜑, 𝑧 = 2 − 𝜌2
Do đó: 𝑥 = 2 − 𝑧𝑐𝑜𝑠𝜑, 𝑦 = 2 − 𝑧𝑠𝑖𝑛𝜑, 𝑧 = 𝑧 𝐷 𝑧, 𝜑 =
𝑧, 𝜑 : 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝑧 ≤ 2 23-Mar-21 TS. Nguyễn Văn Quang 24
Đại học Công nghệ - ĐHQGHN Ví dụ i j k cos sin r r z 1 2 2 z 2 2 z 2 z sin 2 z cos 0 1 2 co z s i 2 sizn j 2 Do đó: 𝐫 = 9 − 𝑧 × 𝐫𝜑 = (2 − 𝑧) + 1 𝑧 4 4 23-Mar-21 TS. Nguyễn Văn Quang 25
Đại học Công nghệ - ĐHQGHN Ví dụ 9 I zdS z zdzd S D( , z ) 4 2 2 1 d z 9 4zdz 2 0 0 37 10 23-Mar-21 TS. Nguyễn Văn Quang 26
Đại học Công nghệ - ĐHQGHN Ví dụ z
𝑧 = 𝑅2 − 𝑥2 − 𝑦2 𝐷 2 2 2
𝑥𝑦 = { 𝑥, 𝑦 : 𝑥 + 𝑦 ≤ 𝑅 }
Phương trình mặt S: 𝑧 = 𝑅2 − 𝑥2 − 𝑦2 Dxy z 0 y x 23-Mar-21 TS. Nguyễn Văn Quang 27
Đại học Công nghệ - ĐHQGHN Ví dụ 𝜕𝑧 −𝑥 𝜕𝑧 −𝑦 𝑅 = ; = → 𝑑𝑆 = 𝑑𝑥𝑑𝑦 𝜕𝑥 𝑅2 − 𝑥2 − 𝑦2 𝜕𝑦 𝑅2 − 𝑥2 − 𝑦2 𝑅2 − 𝑥2 − 𝑦2
Chuyển sang hệ tọa độ cực: 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝐷𝑟𝜑 = { 𝑟, 𝜑 : 0 ≤ 𝑟 ≤ 𝑅, 0 ≤ 𝜑 ≤ 2𝜋} 2𝜋 𝑅 𝑅 𝑟3 𝐼 = 𝑟2.
. 𝑟. 𝑑𝑟𝑑𝜑 = 𝑅 𝑑𝜑 𝑑𝑟 𝑅2 − 𝑟2 𝑅2 − 𝑟2 𝐷𝑟𝜑 0 0 4𝜋𝑅4 = 3 23-Mar-21 TS. Nguyễn Văn Quang 28
Đại học Công nghệ - ĐHQGHN Ví dụ Cách 2: Tham số mặt cầ
u S qua hệ tọa độ cầ : u
𝑥 = 𝑅𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃, 𝑦 = 𝑅𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃, 𝑧 = 𝑅𝑐𝑜𝑠𝜃
𝐷(𝜑, 𝜃) = {(𝜑, 𝜃): 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝜃 ≤ 𝜋/2} 23-Mar-21 TS. Nguyễn Văn Quang 29
Đại học Công nghệ - ĐHQGHN Ví dụ i j k r r R sin sin R cos sin 0 Rcos cos Rsin cos sin R 2 2 2 2 2 c R os sin i sin R sin j sin R cos k Do đó: 2 | r r | R sin u v 2 2 2 2 Vậy: (x y ) dS R sin r r d d S ( D , ) 4 3 R sin d d D( , ) 23-Mar-21 TS. Nguyễn Văn Quang 30
Đại học Công nghệ - ĐHQGHN Ví dụ 4 3 R sin d d D ( , ) 2 /2 4 3 R d sin d 0 0 /2 4 2 2 R (cos 1)d(cos ) 0 /2 3 4 cos 2 R cos 3 0 4 4 R 3 23-Mar-21 TS. Nguyễn Văn Quang 31
Đại học Công nghệ - ĐHQGHN Ví dụ 23-Mar-21 TS. Nguyễn Văn Quang 32
Đại học Công nghệ - ĐHQGHN C x + y + z = 1 z = 1 – x – y S B D O xy A 23-Mar-21 TS. Nguyễn Văn Quang 33
Đại học Công nghệ - ĐHQGHN Ví dụ 𝐼 =
𝑥 + 𝑦 + (1 − 𝑥 − 𝑦) 1 + 1 + 1𝑑𝑥𝑑𝑦 B 𝐷𝑥𝑦 1 1−𝑥 Dxy 3 = 3 𝑑𝑥 𝑑𝑦 = 2 O A 0 0 23-Mar-21 TS. Nguyễn Văn Quang 34
Đại học Công nghệ - ĐHQGHN Ví dụ
Mặt S gồm 4 mặt của tứ diện OABC.
Tích phân 𝐼1 trên mặt ABC đã tính trong ví dụ trước.
Ta tính tích phân trên các mặt còn lại 𝑂𝐴𝐵 , 𝑂 𝐵𝐶 , 𝑂 𝐶𝐴. 𝐼2 𝐼3 𝐼4 23-Mar-21 TS. Nguyễn Văn Quang 35
Đại học Công nghệ - ĐHQGHN C S1 S3 B O S2 S4 A 23-Mar-21 TS. Nguyễn Văn Quang 36
Đại học Công nghệ - ĐHQGHN
Trên mặt OAB, phương trình của mặt là: z = 0.
Hình chiếu của mặt xuống Oxy là tam giác OAB. 1 1−𝑥 1 𝐼2 =
𝑥 + 𝑦 + 0 1 + 0 + 0𝑑𝑥𝑑𝑦 = 𝑑𝑥 𝑥 + 𝑦 𝑑𝑦 = 3 𝑂𝐴𝐵 0 0
Tích phân trên các mặt còn lạ itính tương t . ự 3 → 𝐼 = 1 + 2 23-Mar-21 TS. Nguyễn Văn Quang 37
Đại học Công nghệ - ĐHQGHN Ví dụ 2𝜋 𝑅 𝑅 𝑟 𝑆 = 𝑑𝑆 =
𝑑𝑥𝑑𝑦 = 𝑅 𝑑𝜑 𝑑𝑟 𝑅2 − 𝑥2 − 𝑦2 𝑅2 − 𝑟2 𝑆 𝐷 0 𝑥𝑦 0 = 2𝜋𝑅2
Diện tích toàn bộ mặt cầu bằng 2 lần diện tích nửa mặt cầu và bằng 4𝜋𝑅2. 23-Mar-21 TS. Nguyễn Văn Quang 38
Đại học Công nghệ - ĐHQGHN Ví dụ 2 z=1 z=0 23-Mar-21 TS. Nguyễn Văn Quang 39
Đại học Công nghệ - ĐHQGHN Cách tính
Các hàm P(x,y,z), Q(x,y,z), R(x,y,z) xác định trên mặt định hướng S : z (zx, ) y .
Vector pháp tuyến đơn vị hướng về phía dương của mặt S: n cos ,cos ,cos . 1 cos ,cos ,cos 2 2 2 2 2 2 1 z z 1 z z 1 z z x y x y x y dxdy 2 2 Mặt khác: dS 1 z z dxd .y cos x y Do đó, I P cos Q cos R cos dS S P z Q z R 1)dxdy . x y Dxy 23-Mar-21 TS. Nguyễn Văn Quang 55
Đại học Công nghệ - ĐHQGHN Cách tính
Cho 𝑆 là mặt định hướng có phương trình: 𝑧 = 𝑧(𝑥, 𝑦).
Hình chiếu của 𝑆 trên mp Oxy là miền 𝐷𝑥𝑦 .
Vector pháp tuyến: 𝐥 = 𝐴, 𝐵, 𝐶 = ±(−𝑧′ ′ 𝑥, −𝑧𝑦, 1).
Dấu (+) , (-) được chọn sao cho 𝐥 hướng về phía dương của mặt S.
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = (𝑃𝐴 + 𝑄𝐵 + 𝑅𝐶)𝑑𝑥𝑑𝑦 𝑆+ 𝐷𝑥𝑦 23-Mar-21 TS. Nguyễn Văn Quang 56
Đại học Công nghệ - ĐHQGHN Cách tính
Cho 𝑆 là mặt định hướng có phương trình: 𝑥 = 𝑥(𝑦, 𝑧).
Hình chiếu của 𝑆 trên mp Oyz là miền 𝐷𝑦𝑧 .
Vector pháp tuyến: 𝐥 = 𝐴, 𝐵, 𝐶 = ±(1, −𝑥 ′ ′ 𝑦 , −𝑥𝑧).
Dấu (+) , (-) được chọn sao cho 𝐥 hướng về phía dương của mặt S.
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = (𝑃𝐴 + 𝑄𝐵 + 𝑅𝐶)𝑑𝑦𝑑𝑧 𝑆+ 𝐷𝑦𝑧 23-Mar-21 TS. Nguyễn Văn Quang 57
Đại học Công nghệ - ĐHQGHN Cách tính
Cho 𝑆 là mặt định hướng có phương trình: 𝑦 = 𝑦(𝑥, 𝑧).
Hình chiếu của 𝑆 trên mp Oxz là miền 𝐷𝑥𝑧 .
Vector pháp tuyến: 𝐥 = 𝐴, 𝐵, 𝐶 = ±(−𝑦′ ′ 𝑥, 1, −𝑦𝑧).
Dấu (+) , (-) được chọn sao cho 𝐥 hướng về phía dương của mặt S.
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 = (𝑃𝐴 + 𝑄𝐵 + 𝑅𝐶)𝑑𝑥𝑑𝑧 𝑆+ 𝐷𝑥𝑧 23-Mar-21 TS. Nguyễn Văn Quang 58
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑥𝑑𝑦𝑑𝑧 + 𝑦𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 . Trong đó 𝑆+ là phía ngoài 𝑺+
của mặt cầu: 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2.
Tham số mặt S qua hệ tọa độ cầu:
𝑥 = 𝑅𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃
𝑦 = 𝑅𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃 ; 0 ≤ 𝜃 ≤ 𝜋, 0 ≤ 𝜑 ≤ 2𝜋 𝑧 = 𝑅𝑐𝑜𝑠𝜃 i j k r r R sin sin R cos sin 0 Rcos cos s R in cos s R in 2 2 2 2 2 c R os sin i sin R sin j sin R cos k 23-Mar-21 TS. Nguyễn Văn Quang 59
Đại học Công nghệ - ĐHQGHN Ví dụ
𝐫𝜑 × 𝐫𝜃 hướng vào trong mặt cầu, ngược hướng với phía ngoài của mặt cầu. Do đó: I ( ( F r, )) ( r )rd d D( , )
= 𝑅𝑐𝑜𝑠𝜑𝑠𝑖𝑛𝜃. 𝑅2𝑐𝑜𝑠𝜑𝑠𝑖𝑛2𝜃 + 𝑅𝑠𝑖𝑛𝜑𝑠𝑖𝑛𝜃. 𝑅2𝑠𝑖𝑛𝜑𝑠𝑖𝑛2𝜃 𝐷𝜑𝜃
+ 𝑅𝑐𝑜𝑠𝜃. 𝑅2𝑠𝑖𝑛𝜃𝑐𝑜𝑠𝜃 𝑑𝜑𝑑𝜃 = 2𝜋 𝜋 =
𝑅3𝑠𝑖𝑛𝜃𝑑𝜑𝑑𝜃 = 𝑅3 𝑑𝜑 𝑠𝑖𝑛𝜃𝑑𝜃 = 4𝜋𝑅3 𝐷𝜑𝜃 0 0 23-Mar-21 TS. Nguyễn Văn Quang 60
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑦𝑑𝑦𝑑𝑧 + 𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 𝑺+ .
Trong đó 𝑆+ là phía ngoài của vật thể được giới hạn bởi các mặt:
𝑧 = 1 − 𝑥2 − 𝑦2, 𝑧 = 0. 𝐼 =
𝑦𝑑𝑦𝑑𝑧 + 𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 𝑺+ =
= + 𝑦𝑑𝑦𝑑𝑧 + 𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 + 𝑺𝟏
+ + 𝑦𝑑𝑦𝑑𝑧 + 𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 𝑺𝟐 23-Mar-21 TS. Nguyễn Văn Quang 61
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 62
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 63
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 64
Đại học Công nghệ - ĐHQGHN Ví dụ Tính
(2𝑥 + 𝑦)𝑑𝑦𝑑𝑧 + (2𝑦 + 𝑧)𝑑𝑧𝑑𝑥 + (2𝑧 + 𝑥)𝑑𝑥𝑑𝑦 𝑺+ .
Trong đó 𝑆+ là phía phần của mặt phẳng 𝑥 + 𝑦 + 𝑧 = 3 nằm trong hình
trụ 𝑥2 + 𝑦2 = 2𝑥, phía dương là phía dưới nhìn từ hướng dương của Oz.
𝑆: 𝑧 = 3 − 𝑥 − 𝑦. Do đó: 𝑧′ ′ 𝑥 = 𝑧𝑦 = −1.
𝑆+ là phía dưới nhìn từ hướng dương của trục Oz.
Vector pháp tuyến của mặt 𝑆 có dạng: 𝐥 = (𝑧′ ′ 𝑥, 𝑧𝑦, −1). 𝐷 2 2 𝑥𝑦 =
𝑥, 𝑦 : 𝑥 + 𝑦 ≤ 2𝑥 23-Mar-21 TS. Nguyễn Văn Quang 65
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 66
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 = 𝑥 + 𝑧 𝑑𝑥𝑑𝑦 𝑆+
Trong đó 𝑆+ là phần của mặt phẳng 𝑧 = 2 − 𝑥 giới hạn bởi mặt
𝑧 = 𝑥2 + 𝑦2, phía dương là phía dưới nhìn từ hướng dương của trục Oz.
𝑆: 𝑧 = 2 − 𝑥. Do đó: 𝑧′ ′ 𝑥 = −1, 𝑧𝑦 = 0.
𝑆+ là phía dưới nhìn từ hướng dương của trục Oz.
Vector pháp tuyến của mặt 𝑆 có dạng: 𝐥 = (𝑧′ ′ 𝑥, 𝑧𝑦, −1). 1 9 𝐷 2 2 𝑥𝑦 =
𝑥, 𝑦 : 𝑥 + 𝑦 ≤ 2 − 𝑥 = { 𝑥, 𝑦 : (𝑥 + )2+𝑦2 ≤ } 2 4 23-Mar-21 TS. Nguyễn Văn Quang 67
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 68
Đại học Công nghệ - ĐHQGHN Ví dụ Tính I = 𝑦𝑧𝑑𝑥𝑑𝑦 ngoài của vật thể: 𝑆+ , trong đó 𝑆+ là phía
Ω: 𝑥2 + 𝑦2 ≤ 𝑅2; 𝑥 ≥ 0, 𝑦 ≥ 0, 0 ≤ 𝑧 ≤ ℎ
Mặt 𝑆 được chia thành 5 mặt gồm:
• Hai mặt đáy 𝑆1, 𝑆2.
• Hai mặt bên 𝑆3, 𝑆4 nằm trong mp: 𝑦 = 0, 𝑥 = 0. • Mặt trụ cong 𝑆5. 𝐼 = 𝑦𝑧𝑑𝑥𝑑𝑦 + 𝑆+ = + 𝑦𝑧𝑑𝑥𝑑𝑦 𝑺𝟏
+ + 𝑦𝑧𝑑𝑥𝑑𝑦+ + 𝑦𝑧𝑑𝑥𝑑𝑦 + 𝑺𝟐 𝑺𝟑
+ + 𝑦𝑧𝑑𝑥𝑑𝑦+ + 𝑦𝑧𝑑𝑥𝑑𝑦. 𝑺𝟒 𝑺𝟓 23-Mar-21 TS. Nguyễn Văn Quang 69
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 70
Đại học Công nghệ - ĐHQGHN 23-Mar-21 TS. Nguyễn Văn Quang 71
Đại học Công nghệ - ĐHQGHN Công thức Stokes
Giả sử mặt cong 𝑆 trơn, định hướng, có biên là đường cong 𝐶. Hàm số
𝑃, 𝑄, 𝑅, và các đạo hàm riêng cấp 1 của chúng liên tục trên mặt 𝑆 thì: 𝜕𝑅 𝜕𝑄 𝜕𝑃 𝜕𝑅 𝜕𝑄 𝜕𝑃
𝑃𝑑𝑥 + 𝑄𝑑𝑦 + 𝑅𝑑𝑧 = − 𝑑𝑦𝑑𝑧 + − 𝑑𝑧𝑑𝑥 + − 𝑑𝑥𝑑𝑦 𝜕𝑦 𝜕𝑧 𝜕𝑧 𝜕𝑥 𝜕𝑥 𝜕𝑦 𝐶+ 𝑆+
Sự phụ hợp về chiều lấy tích phân trên
đường cong C và phía dương của mặt S:
• Đi theo chiều lấy tích phân trên
đường cong C, mặt S nằm ở bên tay trái.
• Hướng từ chân lên đầu là hướng của
vecto pháp tuyến của mặt S. 23-Mar-21 TS. Nguyễn Văn Quang 72
Đại học Công nghệ - ĐHQGHN Công thức Stokes
Dạng vector: Cho trường vector 𝐅 = 𝑃𝐢 + 𝑄𝐣 + 𝑅𝐤, và mặt định hướng S có biên C. 𝐅 ∙ 𝑑𝐫 =
𝐫𝐨𝐭𝐅 ∙ 𝐧𝑑𝑆 𝐶 𝑆 Trong đó: r r n u v r r u v i j k rotF x y z P Q R 23-Mar-21 TS. Nguyễn Văn Quang 73
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
−𝑦2𝑑𝑥 + 𝑥𝑑𝑦 + 𝑧2𝑑𝑧 , trong đó 𝐶 là giao tuyến của 𝐶+
mặt 𝑥2 + 𝑦2 = 1 và mặt 𝑦 + 𝑧 = 2, chiều của 𝐶 như hình vẽ.
Ta có 𝑃 = −𝑦2, 𝑄 = 𝑥, 𝑅 = 𝑧2. Áp dụng công thức Stokes:
𝐼 = −𝑦2𝑑𝑥 + 𝑥𝑑𝑦 + 𝑧2𝑑𝑧 = 1 + 2𝑦 𝑑𝑥𝑑𝑦 𝑆+ 𝐶+
Trong đó 𝑆 là mặt định hướng, có vector pháp
tuyến hướng lên trên, nhìn từ phía dương của trục Oz. 23-Mar-21 TS. Nguyễn Văn Quang 74
Đại học Công nghệ - ĐHQGHN Ví dụ Do đó: 𝐼 = 1 + 2𝑦 𝑑𝑥𝑑𝑦 = 1 + 2𝑦 𝑑𝑥𝑑𝑦 𝑆+ 𝐷(𝑥,𝑦)
Chuyển sang hệ tọa độ cực: 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑖𝑛𝜑
𝐷 𝑟, 𝜑 = { 𝑟, 𝜑 : 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝑟 ≤ 1} 2𝜋 1 𝐼 =
1 + 2𝑟𝑠𝑖𝑛𝜑 . 𝑟. 𝑑𝑟𝑑𝜑 = 𝑑𝜑 1 + 2𝑟𝑠𝑖𝑛𝜑 𝑟𝑑𝑟 𝐷(𝑟,𝜑) 0 0 2𝜋 1 2 = +
𝑠𝑖𝑛𝜑 𝑑𝜑 = 𝜋 2 3 0 23-Mar-21 TS. Nguyễn Văn Quang 75
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
−𝑦2𝑑𝑥 + 𝑥𝑑𝑦 + 𝑧2𝑑𝑧 , trong đó 𝐶 là giao tuyến của 𝐶+
mặt 𝑥2 + 𝑦2 = 1 và mặt 𝑦 + 𝑧 = 2, chiều của 𝐶 như hình vẽ. Cách 2:
Tham số đường cong C qua hệ tọa độ trụ:
𝑥 = 𝑐𝑜𝑠𝜑, 𝑦 = 𝑠𝑖𝑛𝜑, 𝑧 = 2 − 𝑠𝑖𝑛𝜑 0 ≤ 𝜑 ≤ 2𝜋 2𝜋 𝐼 =
𝑠𝑖𝑛3𝜑 + 𝑐𝑜𝑠2𝜑 − (2 − 𝑠𝑖𝑛𝜑)2𝑐𝑜𝑠𝜑 𝑑𝜑 = 𝜋 0 23-Mar-21 TS. Nguyễn Văn Quang 76
Đại học Công nghệ - ĐHQGHN Ví dụ Tính
3𝑥 − 𝑦2 𝑑𝑥 + 3𝑦 − 𝑧2 𝑑𝑦 + 3𝑧 − 𝑥2 𝑑𝑧 , trong đó C là giao 𝐶
của mặt phẳng 2𝑥 + 𝑧 = 2 và mặt paraboloid 𝑧 = 𝑥2 + 𝑦2 ngược chiều kim đồng hồ nhìn t
ừ phía dương của trục Oz.
S là phần mặt 2𝑥 + 𝑧 = 2 nằm trong paraboloid.
Mặt S có phương trình: 𝑧 = 2 − 2𝑥.
S là mặt định hướng, phía trên của mặt S là phía dương, nhìn t
ừ phía dương của trục Oz.
Vector pháp tuyến của S là: 𝐥 = (2,0,1). 23-Mar-21 TS. Nguyễn Văn Quang 77
Đại học Công nghệ - ĐHQGHN Ví dụ Theo Stokes: 2 2 I )dx (3 y z )dy (3z x )dz C R Q P R Q P dydz dzdx dxdy S y z z x x y 2zdydz 2xdzdx 2ydxdy S 2(2 2x)2 2 . x 0 2 ydxdy Dxy 2 4 4x ydxdy 48 2 2 D (x,y ) : x 1 y 3 xy Dxy 23-Mar-21 TS. Nguyễn Văn Quang 78
Đại học Công nghệ - ĐHQGHN Ví dụ Tính
𝑥 + 𝑦 𝑑𝑥 + 2𝑥 − 𝑧 𝑑𝑦 + 𝑦𝑑𝑧 , trong đó C là giao của mặ t 𝐶
𝑧 = 𝑦2 và mặt 𝑥2 + 𝑦2 = 1, chiều của 𝐶 ngược chiều kim đồng hồ nhìn
từ phía dương của trục Oz.
S là phần mặt 𝑧 = 𝑦2 nằm trong hình trụ 𝑥2 + 𝑦2 = 1.
S là mặt định hướng, phía trên của mặt S
là phía dương, nhìn từ phía dương của trục Oz.
Vector pháp tuyến của S là: 𝐥 = (0, −2𝑦, 1). 23-Mar-21 TS. Nguyễn Văn Quang 79
Đại học Công nghệ - ĐHQGHN Ví dụ Theo Stokes: I x (2 x )zdy ydz C R Q P R Q P dydz dzdx dxdy S y z z x x y 2dydz 0dzdx 1dxdy S
Vì hình chiếu S xuống Oyz có diện tích bằng 0, nên 2dydz 0 I 1 dxdy S S I 1 dxdy 2 2 x y 1 23-Mar-21 TS. Nguyễn Văn Quang 80
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑦𝑑𝑥 + 𝑧𝑑𝑦 + 𝑥𝑑𝑧 , trong đó 𝐶 là giao tuyến của mặt cầ : u 𝐶
𝑥2 + 𝑦2 + 𝑧2 = 𝑅2 và mặt phẳng 𝑥 + 𝑦 + 𝑧 = 0, chiều của 𝐶 ngược
chiều kim đồng hồ nhìn từ phía dương của trục Oz.
Cách 1: S là phần mặt 𝑥 + 𝑦 + 𝑧 = 0 nằm trên mặt cầ
u 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2.
Ta có: 𝑃 = 𝑦, 𝑄 = 𝑧, 𝑅 = 𝑥. Theo Stokes: 𝐼 = −
𝑑𝑦𝑑𝑧 + 𝑑𝑧𝑑𝑥 + 𝑑𝑥𝑑𝑦 𝑆
S là mặt định hướng, phía trên của mặt S là phía
dương, nhìn từ phía dương của trục Oz. 23-Mar-21 TS. Nguyễn Văn Quang 81
Đại học Công nghệ - ĐHQGHN Ví dụ
Vector pháp tuyến của 𝑆: 𝐥 = (1,1,1).
Vector pháp tuyến đơn vị của 𝑆: 𝐧 = ( 1 , 1 , 1 ). 3 3 3 𝐼 = −3
𝑑𝑥𝑑𝑦 = −3. 𝐷𝑡(𝐷(𝑥, 𝑦)) = −3. 𝐷𝑡 𝑆 . 𝑐𝑜𝑠𝛾 𝐷(𝑥,𝑦) 1 = −3. 𝐷𝑡 𝑆 . = − 3𝜋𝑅2 3 23-Mar-21 TS. Nguyễn Văn Quang 82
Đại học Công nghệ - ĐHQGHN Ví dụ
Cách 2: Tham số hóa đường cong 𝐶.
Phương trình hình chiếu 𝐶1 của 𝐶 trên mp Oxy:
𝐶1: 𝑥2 + 𝑦2 + 𝑥𝑦 = 𝑅2/2.
Đưa dạng toàn phương 𝑓 𝜔 = 𝑥2 + 𝑦2 + 𝑥𝑦 về dạng chính tắc bằng phép biến đổi trực giao. 1 1/2
Ma trận của dạng toàn phương: 𝐴 = . 1/2 1 23-Mar-21 TS. Nguyễn Văn Quang 83
Đại học Công nghệ - ĐHQGHN Ví dụ Trị riêng của 1
𝐴: det 𝐴 − 𝜆𝐸 = 0 → 𝜆 = , 𝜆 = 3 . 2 2
Vector riêng của 𝐴: det 𝐴 − 𝜆𝐸 𝑥 = 0, 𝑥 = 𝑥1, 𝑥2 .
𝜆 = 1 : vector riêng 𝑎 = (−1,1). 2
𝜆 = 3 : vector riêng 𝑏 = (1,1). 2
Hệ vector riêng trực chuẩn: 1 , 1 , − 1 , 1 . 2 2 2 2 1 − 1
Ma trận trực giao: 𝑃 = 2 2 . 1 1 2 2 23-Mar-21 TS. Nguyễn Văn Quang 84
Đại học Công nghệ - ĐHQGHN Ví dụ 𝑥 𝑢
Phép đổi biến: 𝑦 = 𝑃 𝑣 𝑢 𝑣 𝜋 𝜋 𝑥 = − = 𝑢. 𝑐𝑜𝑠 − 𝑣. 𝑠𝑖𝑛 2 4 4 2 𝑢 𝑣 𝜋 𝜋 𝑦 = + = 𝑢. 𝑠𝑖𝑛 + 𝑣. 𝑐𝑜𝑠 2 2 4 4
Phép quay hệ trục Oxy sang Ouv một góc 𝛼 = 𝜋 4 .
Do đó 𝐶1 có phương trình: 3 1 𝑅2 𝑢2 𝑣2 𝐶1: 𝑢2 + 𝑣2 = ↔ + = 1. 2 2 2 𝑅 2 𝑅2 3 23-Mar-21 TS. Nguyễn Văn Quang 85
Đại học Công nghệ - ĐHQGHN Ví dụ
Dùng phép đổi biến qua hệ tọa độ cực suy rộng, đưa Ellipse trên v ề đường tròn: 𝑅 𝑢 =
𝑐𝑜𝑠𝜑, 𝑣 = 𝑅𝑠𝑖𝑛𝜑. 3
Do đó phép đổi biến đưa 𝐶1 về đường tròn: 𝑅𝑐𝑜𝑠𝜑 𝑅𝑠𝑖𝑛𝜑 𝑅𝑐𝑜𝑠𝜑 𝑅𝑠𝑖𝑛𝜑 𝑥 = − , 𝑦 = + . 6 2 6 2 23-Mar-21 TS. Nguyễn Văn Quang 86
Đại học Công nghệ - ĐHQGHN Ví dụ
Vậy phương trình tham số đường cong 𝐶: 𝑅𝑐𝑜𝑠𝜑 𝑅𝑠𝑖𝑛𝜑 𝑅𝑐𝑜𝑠𝜑 𝑅𝑠𝑖𝑛𝜑 −2𝑅𝑐𝑜𝑠𝜑 𝑥 = − , 𝑦 = + , 𝑧 = − 𝑥 + 𝑦 = 6 2 6 2 6 0 ≤ 𝜑 ≤ 2𝜋. 2𝜋 𝑐𝑜𝑠𝜑 𝑠𝑖𝑛𝜑 𝑠𝑖𝑛𝜑 𝑐𝑜𝑠𝜑 2𝑅2𝑐𝑜𝑠𝜑
𝑐𝑜𝑠𝜑 𝑠𝑖𝑛𝜑 𝐼 = −𝑅2 + + − − 6 2 6 2 6 2 6 0
2𝑅2𝑠𝑖𝑛𝜑 𝑐𝑜𝑠𝜑 𝑠𝑖𝑛𝜑 + − 𝑑𝜑 6 6 2 = − 3𝜋𝑅2. 23-Mar-21 TS. Nguyễn Văn Quang 87
Đại học Công nghệ - ĐHQGHN Công thức Gauss
Giả sử 𝑉 là khối đóng, giới nội trong 𝑅3 có biên là mặt trơn 𝑆. Nếu
các hàm số 𝑃, 𝑄, 𝑅 và các đạo hàm riêng cấp 1 của chúng liên tục trên khối 𝑉 thì: 𝜕𝑃 𝜕𝑄 𝜕𝑅
𝑃𝑑𝑦𝑑𝑧 + 𝑄𝑑𝑧𝑑𝑥 + 𝑅𝑑𝑥𝑑𝑦 ± + + 𝑑𝑥𝑑𝑦𝑑𝑧 𝜕𝑥 𝜕𝑦 𝜕𝑧 𝑆+ 𝑉
Dấu + : khi phía dương của mặt S là phía ngoài của khối 𝑉.
Dấu - : khi phía dương của mặt S là phía trong của khối 𝑉. 23-Mar-21 TS. Nguyễn Văn Quang 88
Đại học Công nghệ - ĐHQGHN Công thức Gauss
Dạng vector: Cho trường vector 𝐅 = 𝑃𝐢 + 𝑄𝐣 + 𝑅𝐤 xác định trên mặt
định hướng 𝑆. Ký hiệu: 𝜕𝑃 𝜕𝑄 𝜕𝑅 𝑑𝑖𝑣𝐅 = + + 𝜕𝑥 𝜕𝑦 𝜕𝑧 Khi đó: 𝐅 ∙ 𝑑𝐒 = 𝐅 ∙ 𝐧𝑑𝑆 =
𝑑𝑖𝑣𝐅𝑑𝑥𝑑𝑦𝑑𝑧 𝑆 𝑆 𝑉 23-Mar-21 TS. Nguyễn Văn Quang 89
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑥𝑧𝑑𝑦𝑑𝑧 + 𝑦𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑦𝑑𝑥𝑑𝑦 , trong đó 𝑆+ là phía 𝑆+
ngoài của các mặt: 𝑥 + 𝑦 + 𝑧 = 1, 𝑥 = 0, 𝑦 = 0, 𝑧 = 0.
Áp dụng công thức Gauss ta có: 𝐼 =
𝑥𝑧𝑑𝑦𝑑𝑧 + 𝑦𝑥𝑑𝑧𝑑𝑥 + 𝑧𝑦𝑑𝑥𝑑𝑦 𝑆+ =
𝑥 + 𝑦 + 𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉
Trong đó khối 𝑉 có các mặt là S. 23-Mar-21 TS. Nguyễn Văn Quang 90
Đại học Công nghệ - ĐHQGHN Ví dụ 𝐼 =
𝑥 + 𝑦 + 𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 1 1−𝑥 1−𝑥−𝑦 = 𝑑𝑥 𝑑𝑦 𝑥 + 𝑦 + 𝑧 𝑑𝑧 0 0 0 1 1−𝑥 1 1 = 𝑑𝑥
1 − (𝑥 + 𝑦)2 𝑑𝑦 = 2 8 0 0 23-Mar-21 TS. Nguyễn Văn Quang 91
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑥3𝑑𝑦𝑑𝑧 + 𝑦3𝑑𝑧𝑑𝑥 + 𝑧3𝑑𝑥𝑑𝑦 , trong đó 𝑆+ là phía 𝑆+
ngoài của mặt cầu: 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2. Theo công thức Gauss: 2𝜋 𝜋 𝑅 𝐼 = 3
𝑥2 + 𝑦2 + 𝑧2 𝑑𝑥𝑑𝑦𝑑𝑧 = 3
𝑑𝜑 𝑑𝜃 𝜌2𝜌2𝑠𝑖𝑛𝜃𝑑𝜌 𝑉 0 0 0 12𝜋𝑅5 = 5 23-Mar-21 TS. Nguyễn Văn Quang 92
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑧2𝑑𝑦𝑑𝑧 + 𝑥𝑑𝑧𝑑𝑥 − 𝑧𝑑𝑥𝑑𝑦 , trong đó 𝑆+ là mặt xung 𝑆+
quanh, phía dương là phía ngoài của vật thể được giới hạn bởi các
mặt: 𝑧 = 4 − 𝑦2, 𝑧 = 0, 𝑥 = 1, 𝑥 = 0. z Theo công thức Gauss: z=4-y2 𝐼 =
0 + 0 − 1 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 1 2 4−𝑦2 = −
𝑑𝑥𝑑𝑦𝑑𝑧 − 𝑑𝑥 𝑑𝑦 𝑑𝑧 𝑉 0 −2 0 y = −32/3 23-Mar-21 TS. Nguyễn Văn Quang 93
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 , trong đó 𝑆+ là phía dưới 𝑆+
của mặt: 𝑧 = 𝑥2 + 𝑦2, 0 ≤ 𝑧 ≤ 1 (nhìn từ phía dương trục Oz).
𝑆 chưa phải là mặt kín, nên ta bổ sung thêm mặt 𝐷. Biên của khối 𝑉 là
𝛿𝑉 = 𝑆 ∪ 𝐷. Trong đó D là miền hình tròn: 𝑧 = 1, 𝑥2 + 𝑦2 ≤ 1
𝛿𝑉+ là phía ngoài của khối 𝑉. Theo công thức Gauss ta có:
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 = 2
𝑥 + 𝑦 + 𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 𝛿𝑉+ 𝑉 23-Mar-21 TS. Nguyễn Văn Quang 94
Đại học Công nghệ - ĐHQGHN Ví dụ
Chuyển sang hệ tọa độ trụ: 𝑥 = 𝑟𝑐𝑜𝑠𝜑, 𝑦 = 𝑟𝑠𝑖𝑛𝜑, 𝑧 = 𝑧
𝑉 𝑟, 𝜑, 𝑧 = { 𝑟, 𝜑, 𝑧 : 0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝑟 ≤ 1, 𝑟 ≤ 𝑧 ≤ 1} 2
𝑥 + 𝑦 + 𝑧 𝑑𝑥𝑑𝑦𝑑𝑧 𝑉 2𝜋 1 1 𝜋
= 2 𝑑𝜑 𝑑𝑟 𝑟 𝑟𝑐𝑜𝑠𝜑 + 𝑟𝑠𝑖𝑛𝜑 + 𝑧 𝑑𝑧 = 2 0 0 𝑟 23-Mar-21 TS. Nguyễn Văn Quang 95
Đại học Công nghệ - ĐHQGHN Ví dụ Do đó:
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 = 𝜋 = 𝛿𝑉+ 2 =
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 + 𝑆+ +
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 𝐷+ Suy ra: 𝐼 =
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 = 𝑆+ = 𝜋 −
𝑥2𝑑𝑦𝑑𝑧 + 𝑦2𝑑𝑧𝑑𝑥 + 𝑧2𝑑𝑥𝑑𝑦 . 2 𝐷+ 23-Mar-21 TS. Nguyễn Văn Quang 96
Đại học Công nghệ - ĐHQGHN Ví dụ
Pt mặt định hướng 𝐷: 𝑧 = 1. Phía dương của mặt D là phía trên, do đó
vector pháp tuyến của mặt 𝐷: 𝐥 = (0,0,1). Vậy: 𝜋 𝜋 𝜋 𝜋 𝐼 = − 12. 1𝑑𝑥𝑑𝑦 = − 𝑑𝑥𝑑𝑦 = − 𝑆 . 2 2 2 𝐷 = − 2 𝐷 𝐷
Do 𝐷 là đường tròn có 𝑅 = 1, nên 𝑆𝐷 = 𝜋. 23-Mar-21 TS. Nguyễn Văn Quang 97
Đại học Công nghệ - ĐHQGHN Ví dụ Tính 𝐼 =
𝑦 + 𝑧 𝑑𝑦𝑑𝑧 + 𝑥 − 𝑧 𝑑𝑧𝑑𝑥 + 𝑧 + 1 𝑑𝑥𝑑𝑦 , trong đó 𝑆+ 𝑆+
là phía trên của nửa trên mặt cầu: 𝑥2 + 𝑦2 + 𝑧2 = 𝑅2 (nhìn từ phía dương trục Oz). Gọi 𝑆 2 2 2
1 là mặt: 𝑧 = 0, 𝑥 + 𝑦 ≤ 𝑅 , phía dương của 𝑆1 là phía dưới
(nhìn từ phía dương của trục Oz). Theo công thức Gaus: + =
1. 𝑑𝑥𝑑𝑦𝑑𝑧 ; khối 𝑉 có biên là các mặt 𝑆 và 𝑆1. 𝑆 𝑆1 𝑉 2𝜋𝑅3 2𝜋𝑅3 → 𝐼 = − −1. (0 + 1)𝑑𝑥𝑑𝑦 = + 𝑑𝑥𝑑𝑦 3 𝑥2+𝑦2≤𝑅2 3 𝑥2+𝑦2≤𝑅2 2𝜋𝑅3 = + 𝜋𝑅2 3 23-Mar-21 TS. Nguyễn Văn Quang 98
Đại học Công nghệ - ĐHQGHN