Tài liệu tham khảo
1) Toán cao cấp Tập 3 – Nguyễn Đình Trí (CB) – NXB Giáo Dục
2) Giải Tích, Tập I, II – Trần Đức Long, Nguyễn Đình Sang,
Hoàng Quốc Toàn – NXB ĐHQGHN
3) Giải Tích Toán học – Nguyễn Thủy Thanh – NXB ĐHQGHN
4) Calculus – Jame Stewart – 7th . 3/12/2020
Chương I: Hàm nhiều biến 2 Nội dung
• Chương I: Hàm nhiều biến (4b)
• Chương II: Tích phân bội (3b)
• Kiểm tra giữa học kỳ (1b) – Tuần 8 (20%)
• Chương III: Tích phân đường, tích phân mặt (4b)
• Chương IV: Phương trình vi phân (2b)
• Ôn tập cuối học kỳ (1b) – Tuần 15 3/12/2020
Chương I: Hàm nhiều biến 3
Chương I: Hàm nhiều biến
• Giới hạn và liên tục
 Tính giới hạn, chứng minh hàm số không tồn tại giới hạn
 Khảo sát liên tục của hàm 2 biến • Đạo hàm, vi phân
 Đạo hàm riêng hàm hợp, hàm ẩn
 Xét tính khả vi của hàm số
 Tìm vi phân toàn phần của hàm số, tính giá trị gần đúng • Cực trị
 Cực trị không điều kiện, cực trị có điều kiện  Bài toán min, max 3/12/2020
Chương I: Hàm nhiều biến 4 1. Hàm hai biến
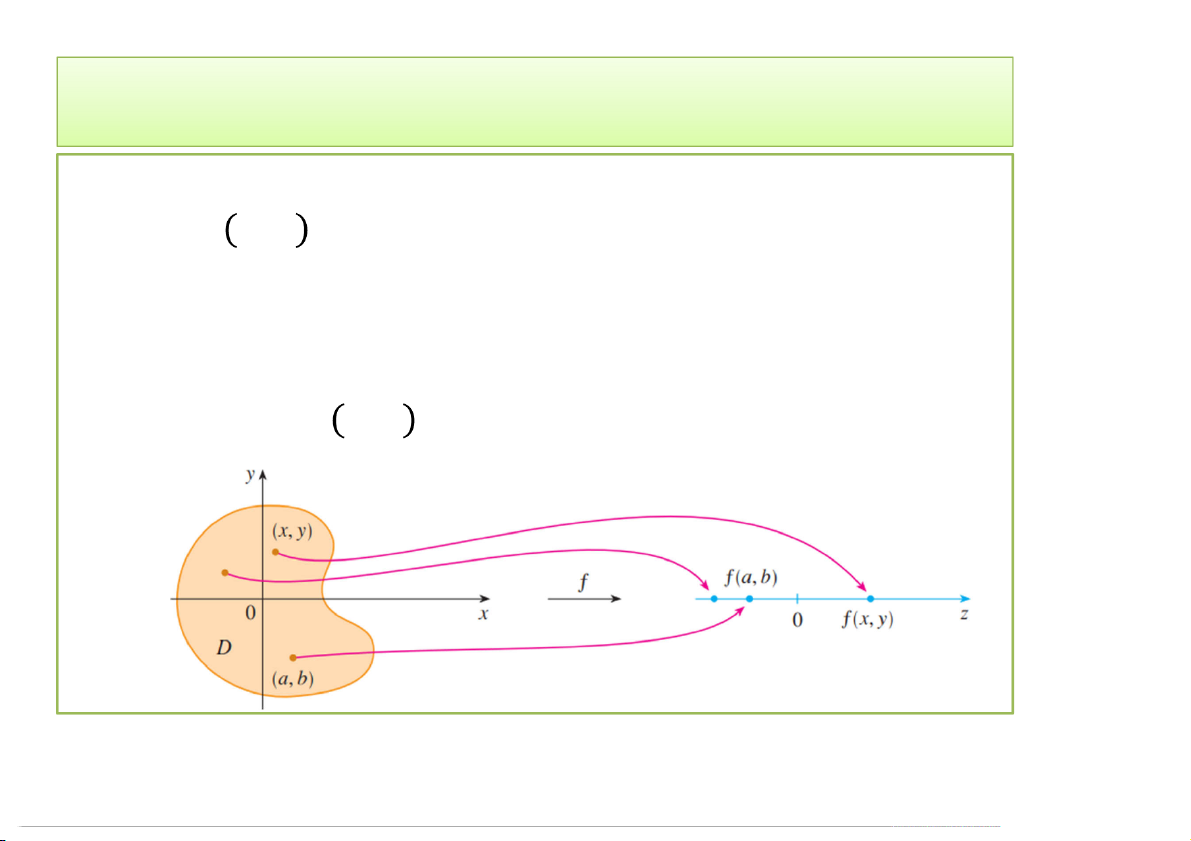
• Hàm hai biến f là một quy tắc cho tương ứng mỗi một cặp
số thực ,  ∈  ⊂  có duy nhất một số thực ký hiệu (, ).
:   →    (, ) → (, )
• Ký hiệu:  =  ,  |(, ) ∈ ; 3/12/2020
Chương I: Hàm nhiều biến 5 1. Hàm hai biến
• D - miền xác định: tập hợp tất cả những giá trị của x và y
sao cho biểu thức f(x,y) có nghĩa.
• Miền giá trị: tập hợp các giá trị mà hàm nhận được
 ≔  ∈ | =  ,  , (, ) ∈ 
• , : biến độc lập; : biến phụ thuộc.
• Giá trị của hàm tại điểm  ,  :   ,  hoặc (). 3/12/2020
Chương I: Hàm nhiều biến 6 1. Hàm hai biến
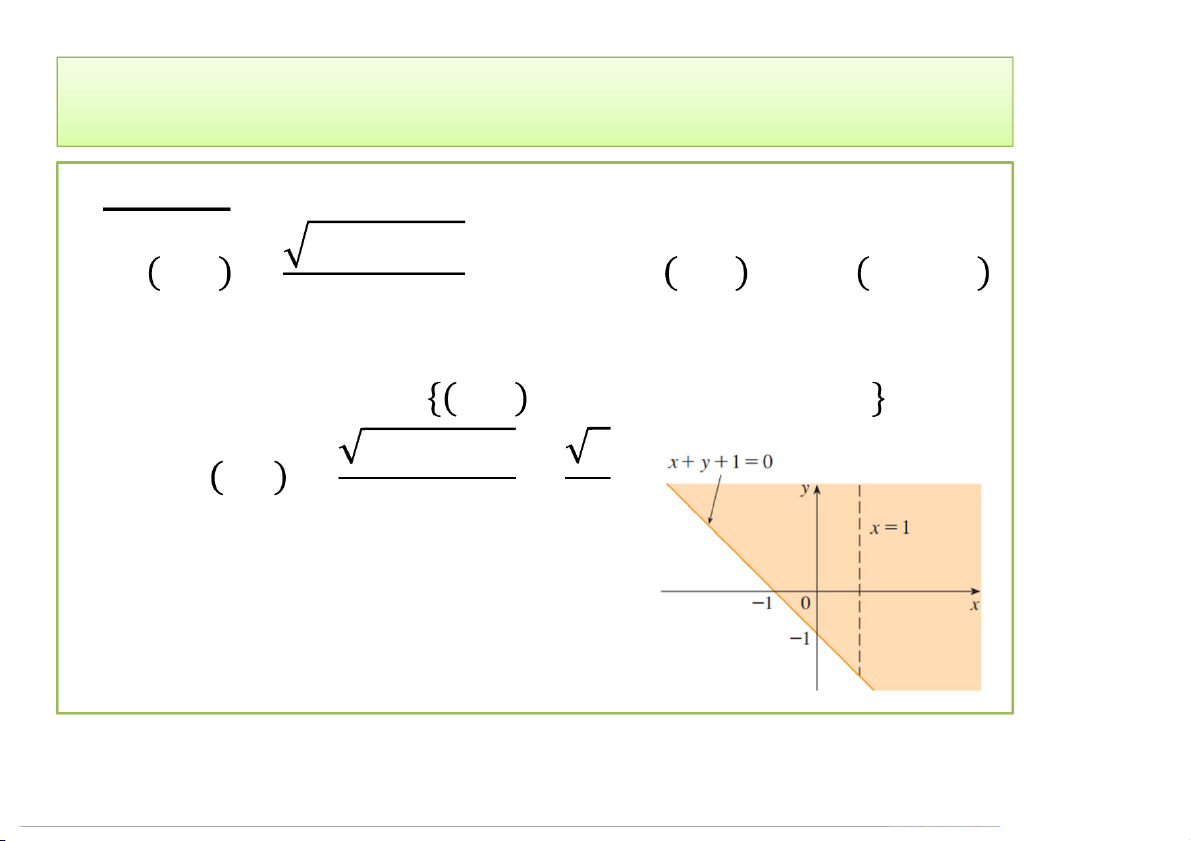
• Ví dụ 1. Tìm miền D và (3,2) của các hàm số sau:  +  + 1 ) ,  =
 − 1 ;       ) ,  =   −  Giải:
a) Miền xác định: = ,  | +  + 1 ≥ 0,  ≠ 1 3 + 2 + 1 6  3,2 = 3 − 1 = 2    3/12/2020
Chương I: Hàm nhiều biến 7 1. Hàm hai biến
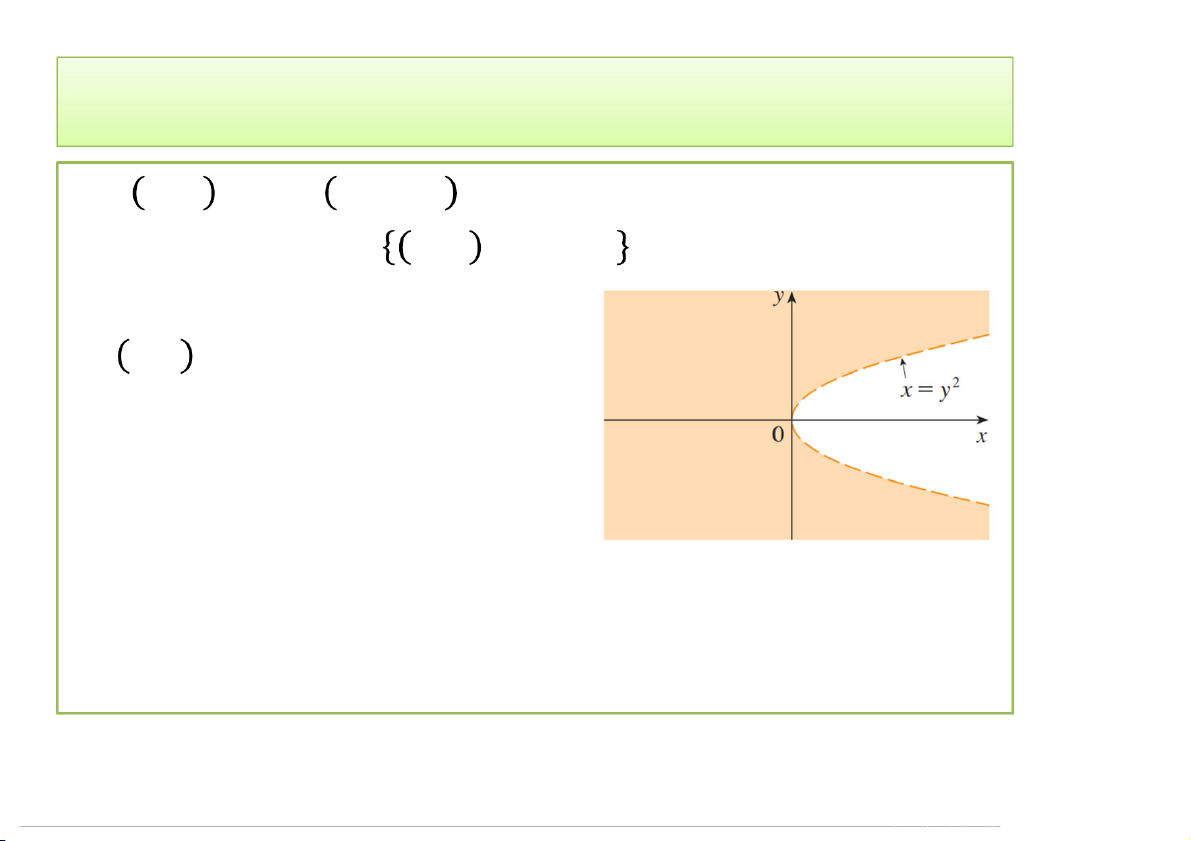
b)  ,  =   − 
Miền xác định:  = ,  | ≤    3,2 = 31 = 0. 3/12/2020
Chương I: Hàm nhiều biến 8 1. Hàm nhiều biến  Về mặt hình học:
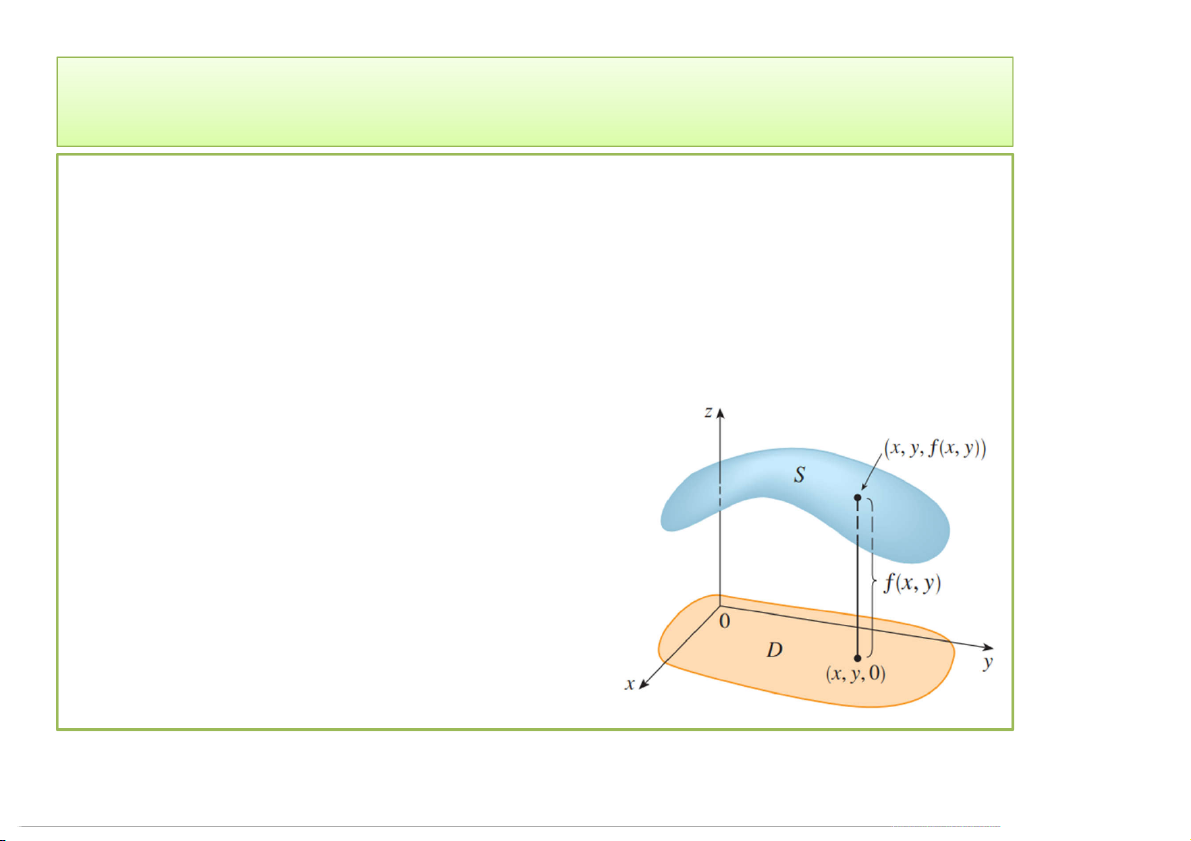
o Mỗi cặp số thực (, ): xác định một điểm P trên ().
o (): cao độ của điểm P trong không gian . o
Tập hợp các điểm trong 
mà tọa độ thỏa mãn phương
trình  = (, ): đồ thị của
hàm hai biến – 1 mặt trong
 mà hình chiếu vuông góc
của nó lên () là D. 3/12/2020
Chương I: Hàm nhiều biến 9 1. Hàm nhiều biến
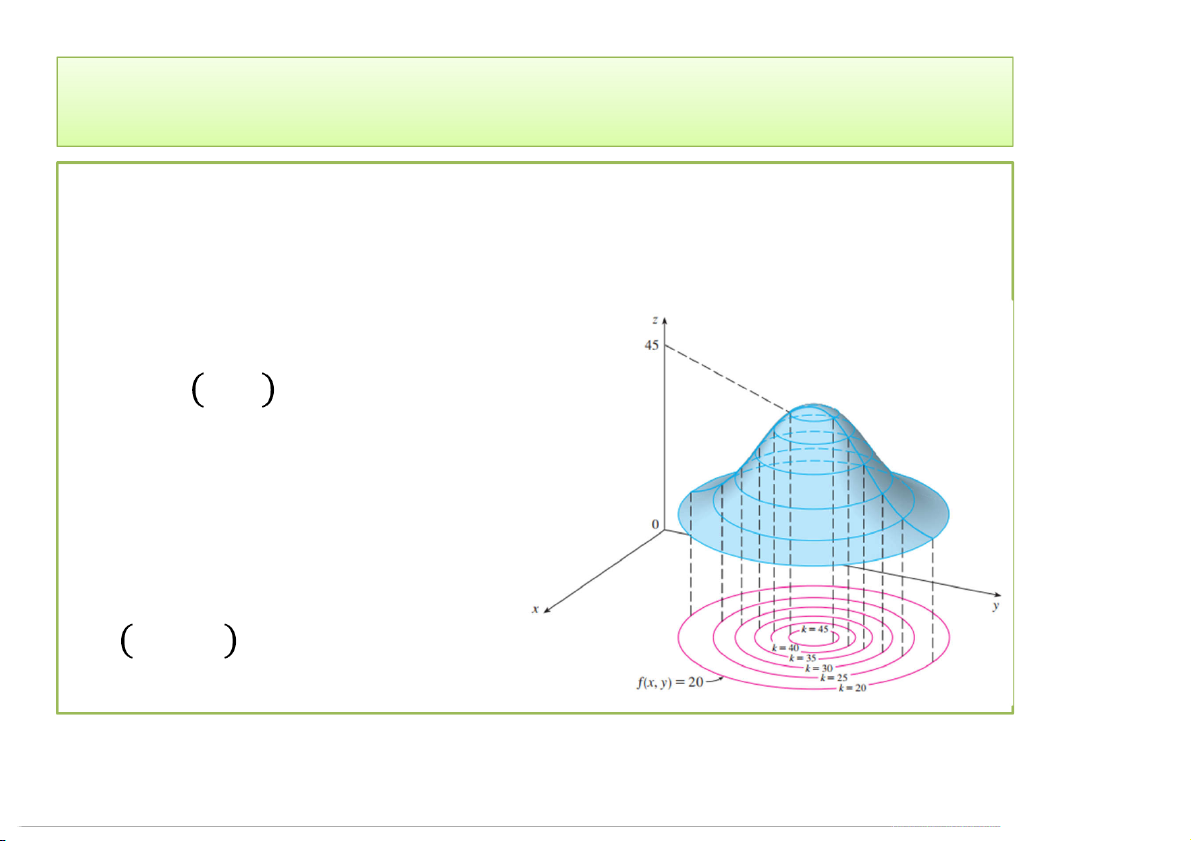
 Đường đồng mức, mặt đồng mức
• Đường đồng mức của hàm
 = (, ): Đường trên
() mà tại các điểm của
nó:  ,  =  (C: hằng số).
• Mặt đồng mức của hàm
 = (, , ) : mặt trong
 mà tại các điểm của nó
 , ,  =  (C: hằng số). 3/12/2020
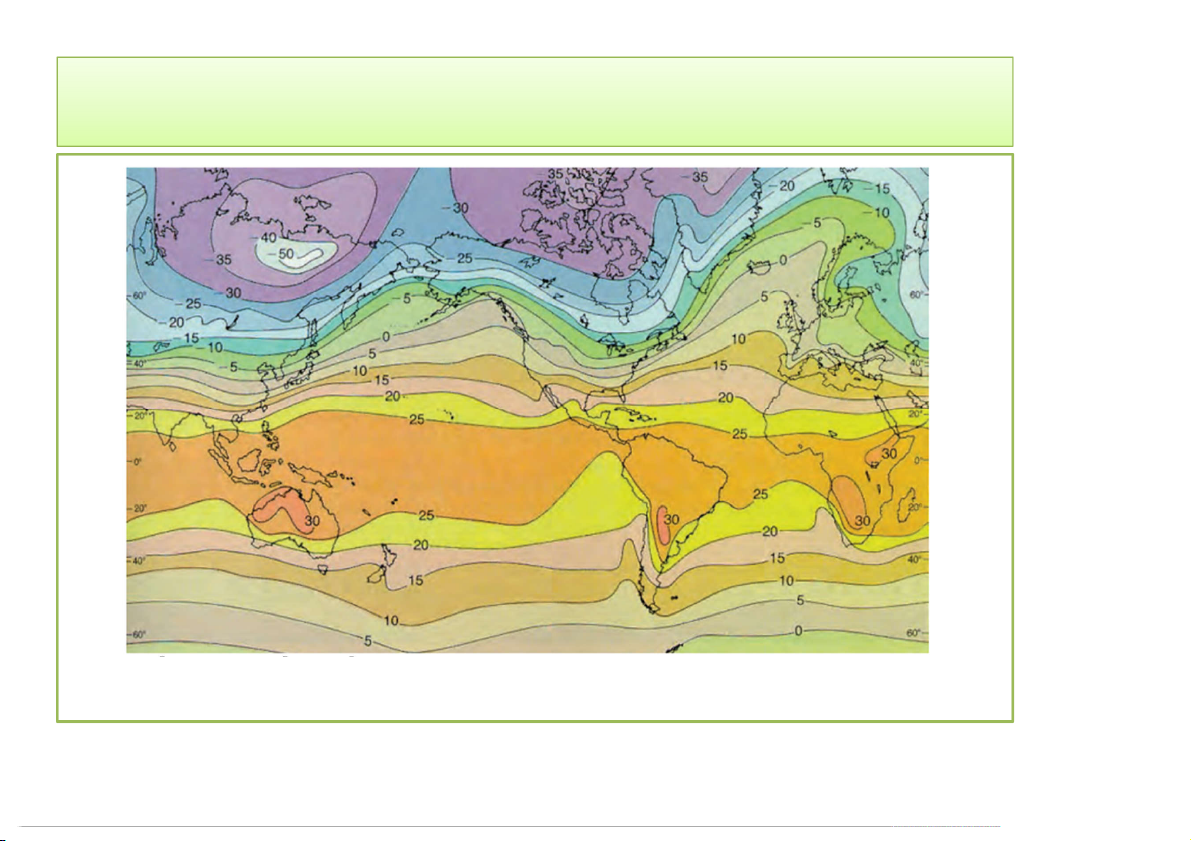
Chương I: Hàm nhiều biến 10 1. Hàm nhiều biến
Bản đồ thời tiết thế giới: nhiệt độ trung bình trong 1 tháng. 3/12/2020
Chương I: Hàm nhiều biến 11 1. Hàm nhiều biến
Ví dụ. Tìm đường mức của hàm:
(, ) = 4 + ;
Đường mức là đường  ,  = , C = const  
4 +  =  ⇔ /4 +  = 1
Vậy đường đồng mức là họ các đường elip có tâm tại
(0,0), các bán trục là: 2, ,(>0) 3/12/2020
Chương I: Hàm nhiều biến 12 1. Hàm nhiều biến
• Bản đồ đường mức và các đường tiến ngang tăng theo các đường mức 3/12/2020
Chương I: Hàm nhiều biến 13
2. Giới hạn và liên tục
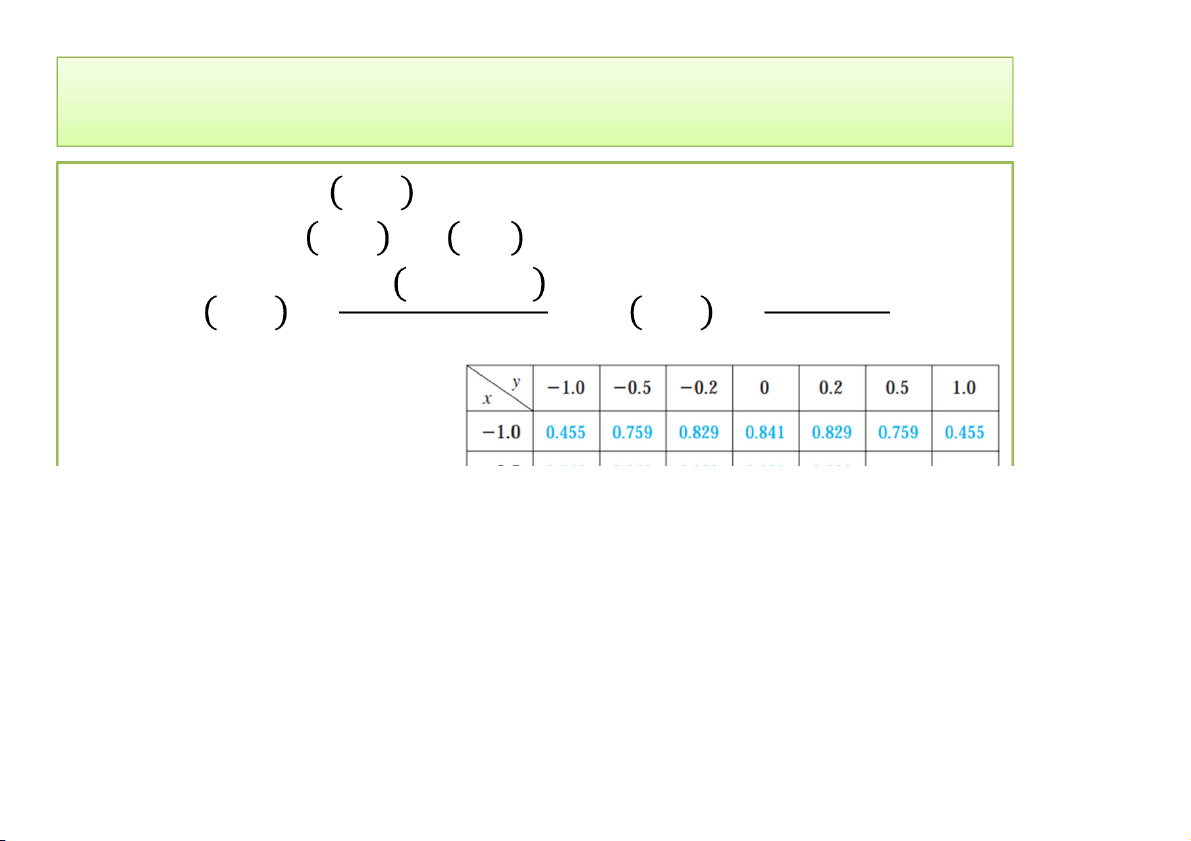
• Cho hai hàm  ,  , (, ), khảo sát các giá trị của các
hàm trên khi ,  → 0,0 :   +   − 
 ,  =  +  ;   , =  + 
Bảng giá trị của (, ) 3/12/2020
Chương I: Hàm nhiều biến 14
2. Giới hạn và liên tục
Bảng giá trị của g(, ) • Nhận xét:
 Tại (0,0):  ,  , (, ): không xác định;
 Khi ,  → 0,0 :  ,  → 1; (, ): không tiến tới 1 giá
trị cụ thể nào.   +  −  lim (,)→(,)
 +  = 1; ∄ lim
(,)→(,)  +  3/12/2020
Chương I: Hàm nhiều biến 15
2. Giới hạn và liên tục
• Giả sử hàm u = f(M) = f(x,y) xác định trên tập hợp D.
M0(a,b) là điểm cố định nào đó của mặt phẳng và
 → ,  →  ⇒  ,  →  ,  2 2 M , M x a y b 0 0 3/12/2020
Chương I: Hàm nhiều biến 16
2. Giới hạn và liên tục • Định nghĩa 1 (Cauchy) lim (, ) =  → Nếu: 0, 0 : M D : 0 M , M0 f M L . 3/12/2020
Chương I: Hàm nhiều biến 17
2. Giới hạn và liên tục • Chú ý rằng:
0 <  ,  <   : tập hợp các điểm M nằm trong
đường tròn tâm (a,b) bán kính   .
  có thể tiến tới  theo nhiều đường khác nhau. f x, y L : x, y a,b C 1 1 • Nếu: f x, y L : x, y a,b C lim f x, y 2 2 x, y a,b L L 1 2 3/12/2020
Chương I: Hàm nhiều biến 18
2. Giới hạn và liên tục • Định nghĩa 2 (Heine)
Số L: giới hạn của hàm f(M) tại điểm M0 nếu: M M n,M D, M M f M L n 0 n n 0 n Kí hiệu: lim f M L; lim f x, y L M M 0 x a y b 3/12/2020
Chương I: Hàm nhiều biến 19
2. Giới hạn và liên tục
 Giới hạn của hàm không phụ thuộc vào phương M tiến đến M0.
 Nếu M→M0 theo các phương khác nhau mà f(M) dẫn đến
các giá trị khác nhau thì hàm f(M) không có giới hạn.
 Số L: giới hạn của hàm f(M) khi  → ∞ nếu: 0, R 0 : M D : M ,0 R f M L . 3/12/2020
Chương I: Hàm nhiều biến 20
2. Giới hạn và liên tục
• Ví dụ 2. Chứng minh rằng:  −  ∄ lim
(,)→(,)  +  Giải.
Xét ,  → 0,0 theo trục Ox (y=0):   , 0 =  = 1
Xét ,  → 0,0 theo trục Oy (x=0): −
 0,  =  = −1 ≠ 1
Vậy không tồn giới hạn của hàm f(x,y) đã cho. 3/12/2020
Chương I: Hàm nhiều biến 21
1. Giới hạn và liên tục
• Dạng 1. Tính giới hạn kép lim f x, y lim f x, y lim f M L x 0 x x, y 0 x , 0 y M M0 y y0
• Ví dụ 1. Tính giới hạn 2 2x 3x 1 xy a) lim ; b) lim 2 2 2 x, y 1, 1 x,y 0,0 xy 3 x y xy 2 2 1 ) c lim ; d) lim x y sin x, y 0,0 2 2 x, y 0,0 x y xy 3/12/2020
Chương I: Hàm nhiều biến 22
1. Giới hạn và liên tục 2 2x 3x 1 1 a) lim 2 x, y 1, 1 xy 3 2 xy b) lim 2 2 x,y 0,0 x y
Cho ,  → 0,0 theo phương của đường thẳng y = kx k k f , x kx x 0 lim f , x kx . 2 2 x 0 1 k 1 k
Khi k khác nhau, ,  → 0,0 theo các phương khác
nhau, f(x,y) dần tới những giới hạn khác nhau.
 Giới hạn không tồn tại. 3/12/2020
Chương I: Hàm nhiều biến 23
1. Giới hạn và liên tục xy c) lim ; x, y 0,0 2 2 x y xy xy 0 f x, y x , lim x 0 2 2 x y y x,y 0,0 2 2 x y hoặc: xy 0 2 2 2 (nguyên lý kẹp) xy x y 0 xy 2 2 x y 2  Vậy: lim 0 x ,y 0,0 2 2 x y 3/12/2020
Chương I: Hàm nhiều biến 24
1. Giới hạn và liên tục 1 2 2 d ) lim x y sin x ,y 0,0 xy 2 2 1 2 2 0 x y sin x y xy 2 2 2 2 1 lim x y 0 lim x y sin 0 x,y 0,0 x,y 0,0 xy 1  Vậy 2 2 lim x y sin 0 , x y 0,0 xy 3/12/2020
Chương I: Hàm nhiều biến 25
1. Giới hạn và liên tục  Nhận xét
• Thông thường, đối với hàm phân thức, bậc của tử ≤ bậc
của mẫu: xét dãy điểm tiến tới điểm cần tính giới hạn theo các đường khác nhau.
• Nếu bậc của tử > bậc của mẫu: sử dụng nguyên lý kẹp Chú ý: a b a b a b 2 2 x y xy 2 3/12/2020
Chương I: Hàm nhiều biến 26 1. Giới hạn
• Dạng 2. Giới hạn lặp
Giả sử tồn tại lim (, ) = () với mỗi y cố định →
Nếu tồn tại lim () = , L được gọi là giới hạn lặp → Ký hiệu: lim lim (, ) → → Tương tự có: lim lim (, ) → → 3/12/2020
Chương I: Hàm nhiều biến 27 1. Giới hạn Chú ý: Nếu
1) Tồn tại giới hạn kép lim (, ) =  → →
2) Với mỗi y cố định, tồn tại lim (, ) → Thì ∃lim lim (, ) → →
lim (,) = lim lim (,) → → → → 3/12/2020
Chương I: Hàm nhiều biến 28 1. Giới hạn
 Ví dụ: Cho hàm số : 0, +∞ × 0, +∞ →  xác định
bởi công thức  ,  = . 
Tính các giới hạn lặp tại điểm (0,0). 
• Ta có: lim (, ) = lim =  − 1 → →  ⇒ lim  − 1 = −1
→ −  +  + lim (, ) = lim → →  +  =  + 1 ⇒ lim  + 1 = 1 →
Hai giới hạn lặp tồn tại nhưng khác nhau ⇒ ∄ lim (, ). → → 3/12/2020
Chương I: Hàm nhiều biến 29
1. Giới hạn và liên tục
• Ví dụ 2: Tính giới hạn 2 2 3 sin x y xy a) lim ; b) lim 2 6 2 2 x,y 0,0 x,y 0,0 2x 3 y x y 2 2 2 x y 2 1 1 2 c) lim ; d ) lim 1 xy x xy 2 x,y 0,2 2 x,y 0,2 x y 2 3/12/2020
Chương I: Hàm nhiều biến 30
1. Giới hạn và liên tục 3 xy a) lim ; 2 6 x,y 0,0 2x 3y k l Xét dãy điểm: x , y , 0,0 , n n n 3 n n
với k, l là các hằng số. 3 kl Khi đó: f x , y , n n n 2 6 2k 3l
Với mỗi cặp giá trị (k, l) khác nhau, f(x,y) dần tới những giá trị khác nhau. 3 xy  Vậy: lim 2 6 x, y 0,0 2 x 3 y 3/12/2020
Chương I: Hàm nhiều biến 31
1. Giới hạn và liên tục 2 2 sin x y b) lim 2 2 x, y 0,0 x y
• Đặt:  +  =  ∶  ,  → 0,0 ⟹  → 0 • Khi đó 2 2 sin x y sin t lim lim 1 2 2 x, y 0,0 t 0 x y t 3/12/2020
Chương I: Hàm nhiều biến 32
1. Giới hạn và liên tục 2 2 x y 2 1 1 c) lim 2 x,y 0,2 2 x y 2
• Đặt:  =   +  − 2 ,  ≥ 0, ,  → 0,2 :  → 0 • Khi đó: 2 2 2 x y 2 1 1 1 1 lim lim 2 2 x,y 0,2 2 0 x y 2 1 1 lim0 2 1 1 2 3/12/2020
Chương I: Hàm nhiều biến 33
1. Giới hạn và liên tục 2 2 d) lim 1 xy x xy x, y 0,2 • Ta có: 2 xy 2 y 2 1 2 1 x xy x y 2 1 xy x xy 1 xy xy 1 xy xy
• Đặt  = , ,  → 0,2 :  → 0 • Khi đó: 1 1 lim 1 xy xy lim 1 t t e x, y 0,2 t 0 2 2 y • Mà: 2 2 lim 2 lim 1 xy x xy e x, y 0,2 x, y 0,2 x y 3/12/2020
Chương I: Hàm nhiều biến 34
1. Giới hạn và liên tục
• Dạng 2. Khảo sát tính liên tục
Hàm số f(x,y) liên tục tại  ,  ∈  ⊂  nếu lim f x, y f x , y 0 0 , x y 0 x , y0
• Ví dụ 3. Xét tính liên tục của hàm số: 3 3 x y , ,x y 0,0 2 2 f x, y x y 0, , x y 0,0 3/12/2020
Chương I: Hàm nhiều biến 35
1. Giới hạn và liên tục
- Hàm f(x,y) liên tục với ∀(x, y) ≠ (0, 0).
- Xét tính liên tục của f(x,y) tại (0, 0): f(0,0) = 0, 2 2 3 3 x y x y x xy y x y 2 2 0 x xy y 2 2 2 2 2 2 x y x y x y Mà: 2 2 2 2 x xy y x y xy 2 2 x y 3 2 2 2 2 2 2 x y xy x y x y 2 2 3 3 x y x y 3 3 2 2 0 . x y x y 2 2 2 2 x y x y 2 2 3/12/2020
Chương I: Hàm nhiều biến 36
1. Giới hạn và liên tục 3 3 3 x y lim x y 0 lim 0 2 2 x, y 0,0 x, y 0,0 2 x y 3 3 x y lim 0 2 2 x, y 0,0 x y
Suy ra f(x, y) liên tục tại điểm (0,0).
 Vậy hàm số f(x,y) đã cho liên tục trên R2. Cách biến đổi khác: 3 3 3 3 x y x y 0 x y 2 2 2 2 2 2 x y x y x y 3/12/2020
Chương I: Hàm nhiều biến 37
1. Giới hạn và liên tục
• Ví dụ 4. Xét tính liên tục của hàm số: xy , , x y 0,0 2 2 f x, y x y 0 , , x y 0,0 Giải:
- Hàm f(x,y) liên tục với ∀(x, y) ≠ (0, 0).
- Xét tính liên tục của f(x,y) tại (0, 0): f(0,0) = 0, 3/12/2020
Chương I: Hàm nhiều biến 38
1. Giới hạn và liên tục • Mặt khác: 2 2 x y xy 1 1 2 2 xy x y 2 2 2 x y 2 1 1 Nhận thấy: l i m x 2 y 2 phụ thuộc vào α x,y 0,0 2 1 1 1 0 không tồn tại ≠ 0
 f(x,y) liên tục trên R2 nếu α >1, gián đoạn tại (0,0) nếu α ≤ 1 3/12/2020
Chương I: Hàm nhiều biến 39 3. Bài tập
• Bài tập. Tính các giới hạn sau: 2 2 x y 1) f , x y khi , x y 0,0 2 2 x y 2 xy 2) f , x y khi , x y 0,0 2 4 x y 2 2 2 2 x y 3) f , x y x y khi , x y 0,0 1 2 2 4) f , x y 1 xy x y khi , x y 0,0 3/12/2020
Chương I: Hàm nhiều biến 40 3. Bài tập 2 2 x y 5) f , x y khi , x y 0,0 2 2 4 x y 2 sin xy 6) f , x y khi , x y 0,3 x 3 3 sin x y 7) f , x y khi , x y 0,0 2 2 x y y 8) f , x y xarctan khi , x y 0,0 x 3/12/2020
Chương I: Hàm nhiều biến 41 3. Bài tập 2 2 1 x y 9) f , x y 1 cos y khi , x y 0,0 2 y x y cos x y 10) f , x y khi , x y 0,0 sin x y 2 2 1 x y 1 cos y 11) f , x y khi , x y 0,0 2 y x y 12) f , x y khi , x y , 2 2 x y 3/12/2020
Chương I: Hàm nhiều biến 42 3. Bài tập x y 13) f x, y khi x, y , 2 2 x xy y 2 x xy 14) f x, y khi x, y , 2 2 x y 2 y 15) f x, y xarctan khi x, y 0,0 x xsiny ysinx 16) f x, y khi x, y 0,0 2 2 x y 3/12/2020
Chương I: Hàm nhiều biến 43 3. Bài tập
• Bài tập. Khảo sát sự liên tục của các hàm số sau tại (0,0): 2 2 1 x y sin , x ,y 0,0 2 2 1) f x, y x y ; 0, x, y 0,0 x sin y y sin x , x,y 0,0 2 2 2) f x, y x y ; 0, x, y 0,0 3/12/2020
Chương I: Hàm nhiều biến 44 3. Bài tập 2 x y , x, y 0,0 4 4 3) f x, y x y ; 0, x, y 0,0 cos x y cos x y , xy 0, 4) f x, y 2xy 1, xy 0 3/12/2020
Chương I: Hàm nhiều biến 45 3. Bài tập
Cho hàm số  ,  = .. CMR tồn tại giới hạn lặp  3/12/2020
Chương I: Hàm nhiều biến 46 Hướng dẫn x y 13) lim 2 2 x x xy y y 2 2 2 2 2 x 2xy y x y 0 x xy y xy x y x y 1 1 0 0, x , y 2 2 x xy y xy x y . 3/12/2020
Chương I: Hàm nhiều biến 47