











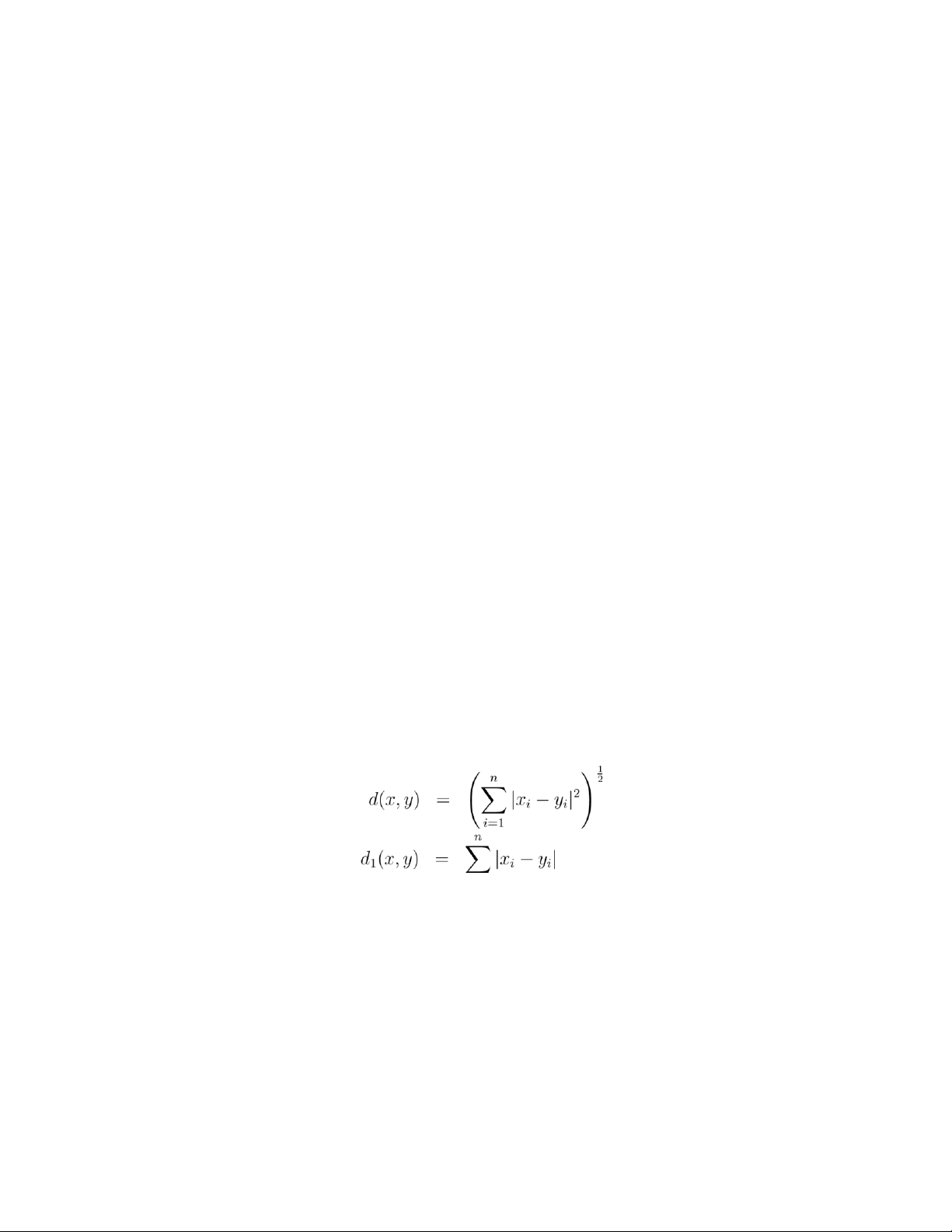






Preview text:
Mục lục
1 Không gian topo và không gian metric ......................................................................................... 3
1.1 Không gian topo ........................................................................................................................... 3
1.2 Không gian metric ...................................................................................................................... 13
1.3 Ánh xạ liên tục ............................................................................................................................ 29
2 Lí thuyết độ đo ............................................................................................................................... 36
2.1 Độ đo trên σ-đại số .................................................................................................................... 36
2.2 Mở rộng độ đo ............................................................................................................................ 50
2.3 Độ đo Lebesgue trên Rn ............................................................................................................. 63
3 Tích phân Lebesgue ....................................................................................................................... 74
3.1 Hàm đo được .............................................................................................................................. 74
3.2 Tích phân Lebesgue.................................................................................................................... 88
3.3 Mối quan hệ giữa tích phân Lebesgue và tích phân Riemann ........................................... 110
Tài liệu tham khảo ........................................................................................................................... 118 Chỉ mục 109 Chương 1
Không gian topo và không gian metric 1.1 Không gian topo
Trong toán học, tôpô là chuyên ngành liên quan đến những tính chất của không gian mà không
thay đổi qua những phép biến đổi liên tục, chẳng hạn như các sự biến dạng, sự xoắn, và sự kéo
giãn nhưng ngoại trừ việc xé rách và việc dán dính. Điều này có thể được nghiên cứu bằng cách
xem xét một họ những tập hợp con, được gọi là tập mở, thỏa mãn những tính chất nào đó và sẽ
biến tập hợp đã cho thành một không gian tôpô. Do đó, tôpô còn được mệnh danh là “hình học
của màng cao su”. Các đặc tính đó gọi là các bất biến tôpô.
Tôpô phát triển như là một chuyên ngành độc lập với hình học và lí thuyết tập hợp, mặc dù
chúng có các khái niệm như không gian, chiều và phép biến đổi. Những ý tưởng đầu tiên của ngành
học này thuộc về Gottfried Leibniz trong thế kỉ 17. Ông đã hình dung ngành “hình học của vị trí”
và “giải tích của nơi chốn”. Những định lí đầu tiên của tôpô có thể kể đến đó là Bài toán 7 cây cầu
và công thức đa diện của Leonhard Euler. Thuật ngữ tôpô được giới thiệu lần đầu bởi Johann
Benedict Listing trong thế kỉ 19. Tuy nhiên cho đến đầu thế kỉ 20 thì tôpô mới được phát triển. Vào
khoảng giữa thế kỉ 20 thì tôpô trở thành một chuyên ngành chính của toán học.
Tôpô có nhiều chuyên ngành hẹp, trong đó tôpô đại cương hay còn gọi là tôpô tậpđiểm, nghiên
cứu về những khái niệm và tính chất cơ bản của không gian tôpô và các khái niệm cơ bản khác.
Trong chương này chúng ta sẽ tìm hiểu những khái niệm và tính chất cơ bản của không gian tôpô.
Lập luận trong chương này chủ yếu liên quan đến các phép toán tập hợp. Về các phép toán tập
hợp và một số nội dung liên quan, người học đã được học ở trong các môn học như Nhập môn Toán cao cấp.
1.1.1 Định nghĩa (Tôpô). Giả sử tập hợp X ̸= ∅ và T là một họ những tập con của X thỏa mãn những điều kiện sau.
1. ∅,X ∈ T .
2. Hợp của một họ tùy ý những phần tử thuộc T là một phần tử thuộc T , nghĩa là nếu Gi ∈
T , i ∈ I thì Si∈ I Gi ∈ T .
3. Giao của hữu hạn phần tử bất kì thuộc T là một phần tử thuộc T , nghĩa là nếu
. Điều này tương đương với nếu A,B ∈ T thì Khi đó
1. T được gọi là một tôpô (topology) trên X, cặp (X,T ) được gọi là một không gian tôpô
(topological space) và còn được viết gọn là X.
2. Mỗi phần tử G thuộc T được gọi là một tập mở (open) của không gian tôpô X; mỗi phần
tử x của X được gọi là một điểm (point).
3. Tập con E của X được gọi là một tập đóng (closed) nếu X \ E là tập mở.
Tiếp theo là một số ví dụ minh họa cho khái niệm trên.
Hình 1.1: Vòng xuyến Mobius, một vật thể được nghiên cứu trong tôpô, là vật thể chỉ có một mặt và một cạnh 1.1.2 Ví dụ.
1. ∅ và X là những tập mở của mọi không gian tôpô.
2. ∅ và X là những tập đóng của mọi không gian tôpô.
3. Cho tập hợp X ̸= ∅, họ T = {∅,X} là một tôpô trên X và được gọi là tôpô thô.
4. Cho tập hợp X ̸= ∅, họ T = P(X) là một tôpô trên X và được gọi là tôpô rời rạc.
5. Cho X = R, họ T = {Si∈I(ai,bi) : ai,bi ∈ R,I bất kì } là một tôpô trên R và được gọi là tôpô thông
thường (usual topology) trên R. Trên R nếu không nói gì thêm thì ta luôn mặc định tôpô là tôpô thông thường. 6. Cho bất kì } là một tôpô
trên R2 và được gọi là tôpô Euclid (Euclidean topology) trên R2, ở đây .
Trên R2 nếu không nói gì thêm thì ta luôn mặc định tôpô là tôpô Euclid.
Trên mỗi tập hợp có thể trang bị những tôpô khác nhau. Để so sánh hai tôpô trên cùng một
tập hợp chúng ta sử dụng khái niệm sau.
1.1.3 Định nghĩa (So sánh hai tôpô). Giả sử T và σ là những tôpô trên X. Tôpô T được gọi là yếu
hơn (weaker) hay thô hơn (coarser) tôpô σ nếu T ⊂ σ. Khi đó tôpô σ cũng được gọi là mạnh hơn
(stronger) hay mịn hơn (finer) tôpô T .
1.1.4 Ví dụ. Tôpô thô là tôpô yếu nhất và tôpô rời rạc là tôpô mạnh nhất trên tập hợp X ̸= ∅.
Tính chất sau của tập đóng chính là đối ngẫu với tính chất của tập mở.
1.1.5 Mệnh đề. Kí hiệu F là họ tất cả các tập con đóng của không gian tôpô (X,T ). Khi đó
1. ∅ ∈ F và X ∈ F.
2. Giao của một họ con tùy ý những phần tử thuộc F là phần tử của F.
3. Hợp của hai phần tử tùy ý của F là phần tử của F.
4. G ∈ T khi và chỉ khi X \ G ∈ F.
Chứng minh. Suy trực tiếp từ Định nghĩa 1.1.1 và tính chất các phép toán tập hợp.
Những khái niệm sau mô tả vị trí tương đối giữa điểm và tập hợp trong một không gian tôpô.
1.1.6 Định nghĩa. Giả sử X là một không gian tôpô, E ⊂ X và x ∈ X.
1. Tập con U của không gian tôpô X được gọi là một lân cận (neighborhood) của điểm x nếu
tồn tại tập mở V trong X sao cho x ∈ V ⊂ U.
2. Tập con U của không gian tôpô X được gọi là một lân cận của E trong X nếu tồn tại tập mở
V ⊂ X sao cho E ⊂ V ⊂ U.
3. Điểm x được gọi là điểm trong (interior point) của E nếu E là một lân cận của x.
4. Điểm x được gọi là điểm ngoài (exterior point) của E nếu X \ E là một lân cận của x.
5. Điểm x được gọi là điểm giới hạn (limit point) của E nếu với mọi lân cận U của x ta có U
∩(E \{x}) ̸= ∅. Tập hợp các điểm giới hạn của E được gọi là tập dẫn xuất (derived set) của
E và kí hiệu là E′ hay Ed.
6. Điểm x được gọi là điểm dính (adherent point ) của E nếu với mọi lân cận U của x ta có U ∩ E ̸= ∅.
7. Điểm x được gọi là điểm biên (boundary point) của E nếu với mọi lân cận U của x ta có U
∩ E ̸= ∅ và U ∩ (X \ E) ̸= ∅. Tập hợp các điểm biên của E được gọi là biên (boundary) của
E và kí hiệu là ∂E.
8. Hợp của các tập mở chứa trong E được gọi là phần trong (interior) của E, kí hiệu là E0 hoặc IntE.
9. Giao của các tập đóng chứa E được gọi là bao đóng (closure) của E, kí hiệu là E hoặc ClE.
1.1.7 Nhận xét. Với mỗi điểm x ∈ X và tập con E của X chỉ xảy ra một và chỉ một trong 3 quan hệ:
x là điểm trong của E, x là điểm ngoài của E, x là điểm biên của E.
1.1.8 Ví dụ. Giả sử X = R và E = (0,1] ∪ {2}. Khi đó
1. E là lân cận của mọi x ∈ (0,1) và của mọi A ⊂ (0,1).
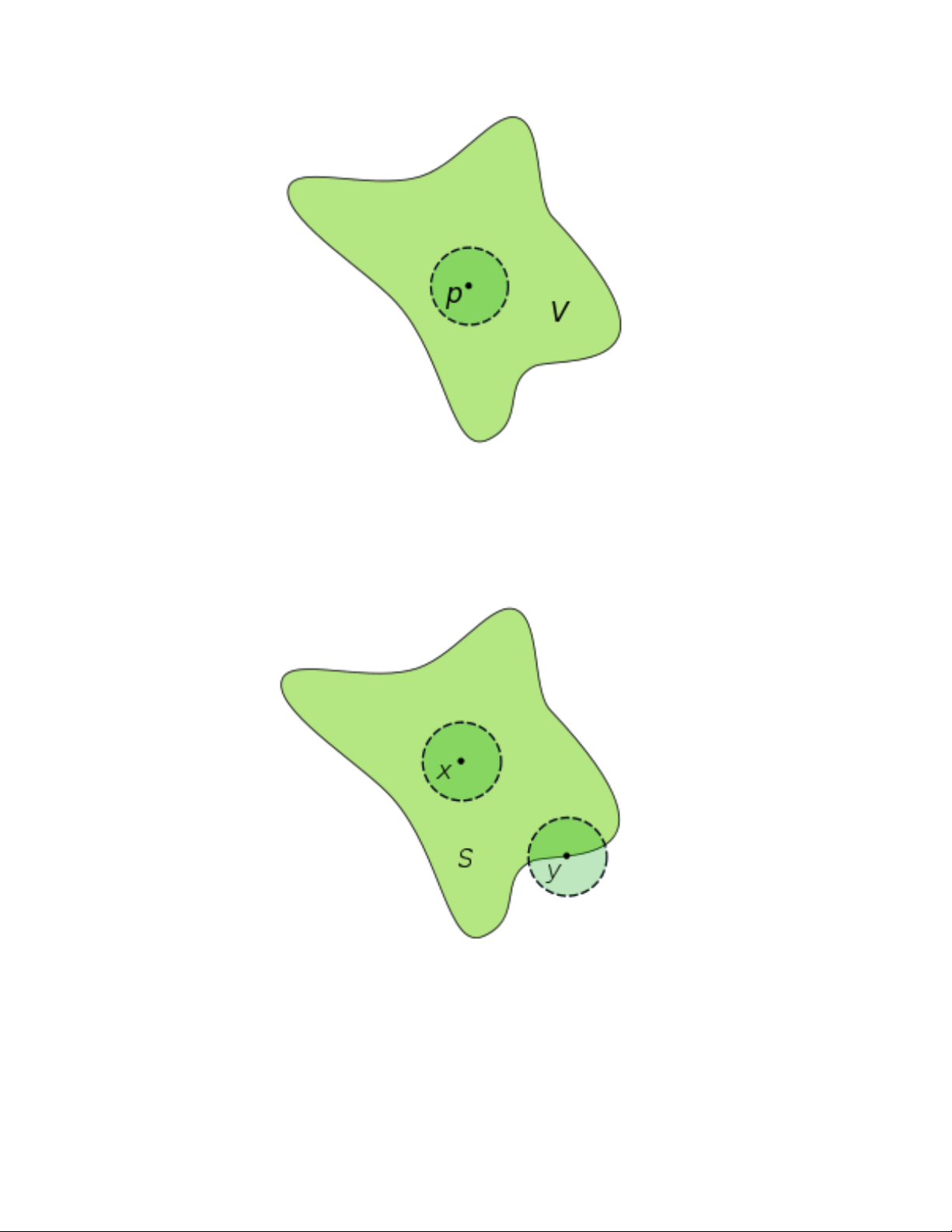
Hình 1.2: Lân cận V của điểm p
Hình 1.3: Điểm x là điểm trong của tập S, điểm y là điểm biên của tập S
2. Mọi x ∈ (0,1) là điểm trong của E.
3. Mọi x ∈ (−∞,0) ∪ (1,2) ∪ (2,∞) là một điểm ngoài của E.
4. Tập dẫn xuất của E là [0,1].
5. Tập các điểm dính của E là [0,1] ∪ {2}.
6. Tập các điểm biên của E là {0,1,2}.
7. IntE = (0,1). 8. E = [0,1].
Giải. Kiểm tra trực tiếp các điều kiện của định nghĩa.
Mệnh đề tiếp theo là những tính chất cơ bản của bao đóng, phần trong và biên của một tập hợp.
1.1.9 Mệnh đề. Giả sử X là một không gian tôpô và E,F ⊂ X. Khi đó
1. E là tập đóng bé nhất chứa E.
2. E đóng khi và chỉ khi E = E.
3. IntE là tập mở lớn nhất chứa trong và E.
4. E mở khi và chỉ khi E = IntE.
Chứng minh. (1). Theo Mệnh đề 1.1.5 thì E là đóng. Hơn nữa, E là tập đóng bé nhất chứa E theo
định nghĩa của bao đóng.
(2). Suy trực tiếp từ (1).
Lập luận tương tự cho các nội dung còn lại.
Để đặc trưng tính chất của một không gian tôpô, chúng ta có thể chỉ cần đặc trưng qua một
số phần tử của tôpô. Những phần tử đó được gọi là cơ sở của một không gian tôpô.
1.1.10 Định nghĩa. Giả sử (X,T ) là một không gian tôpô, x ∈ X và U(x) là họ tất cả các lân cận của x.
1. Họ B ⊂ T được gọi là cơ sở (base) của tôpô T nếu với mỗi x ∈ X và với mỗi lân cận U của x
tồn tại V ∈ B sao cho x ∈ V ⊂ U.
2. Họ σ những tập con của X được gọi là tiền cơ sở (subbase) của T nếu X = S{S : S ∈ σ} và họ
tất cả các giao hữu hạn những phần tử của σ lập thành một cơ sở của tôpô T .
3. Họ B(x) ⊂ U(x) được gọi là cơ sở lân cận (neighborhood system) tại điểm x ∈ X nếu với
mỗi U ∈ U(x) tồn tại V ∈ B(x) sao cho x ∈ V ⊂ U.
4. (X,T ) được gọi là không gian thỏa mãn tiên đề đếm được thứ hai (second countable space)
nếu T có cơ sở đếm được.
5. (X,T ) được được gọi là không gian thỏa mãn tiên đề đếm được thứ nhất (first countable
space) nếu tại mỗi điểm x ∈ X đều có cơ sở lân cận đếm được.
6. Tập con A của X được gọi là trù mật khắp nơi (everywhere dense) trong X nếu A = X.
7. (X,T ) được gọi là khả li (separable) nếu nó chứa một tập con đếm được và trù mật khắp nơi trong X.
1.1.11 Ví dụ. 1. Họ B = {(a,b) : a,b ∈ Q} là một cơ sở của tôpô thông thường trên R.
2. Họ σ = {(−∞,a),(b,∞) : a,b ∈ R} là một tiền cơ sở của tôpô thông thường trên tập các số thực R.
3. R là một không gian khả li vì có tập hợp Q các số hữu tỉ là tập đếm được và trù mật khắp nơi trong R.
4. R là một không gian thỏa mãn tiên đề đếm được thứ hai.
5. Tập số hữu tỉ Q trù mật trong R.
6. R là một không gian khả li.
Tiếp theo là một số tính chất cơ bản của cơ sở và cơ sở lân cận.
1.1.12 Mệnh đề. 1. Giả sử B ⊂ T . Khi đó B là cơ sở của tôpô T nếu và chỉ nếu với bất kì U ∈ T ta
có U là hợp của họ con nào đó những phần tử của B, nghĩa là tồn tại C ⊂ B sao cho U = SC∈C C.
2. Giả sử B là họ những tập con nào đó của X sao cho X = S{B : B ∈ B}. Nếu với mỗi U,V ∈ B
và với mỗi x ∈ U ∩ V tồn tại W ∈ B sao cho x ∈ W ⊂ U ∩ V thì tồn tại một tôpô T trên X sao
cho B là cơ sở của T .
3. Không gian tôpô có cơ sở đếm được là một không gian khả li.
Chứng minh. (1). Điều kiện đủ. Giả sử x ∈ X và U là lân cận mở bất kì của x. Vì U = Si∈I Bi với Bi ∈
B, i ∈ I và x ∈ U nên tồn tại Bi0 ∈ B sao cho x ∈ Bi0 ⊂ U.
Điều kiện cần. Giả sử B ⊂ T là cơ sở của tôpô T . Khi đó với U là tập mở bất kì của T và với
bất kì x ∈ U, vì B là cở sở nên có một lân cận Vx ∈ B sao cho x ∈ Vx ⊂ U.
Vì thế U ⊂ Sx∈U Vx ⊂ U và ta có U = Sx∈U Vx.
(2). Kí hiệu T là họ gồm các hợp tùy ý những phần tử của B. Khi đó T là một tôpô. Thật vậy,
ta có hợp tùy ý những phần tử thuộc T cũng là một phần tử thuộc T và ∅ ∈ T , X ∈ T .
Với U,V ∈ T ta cần chứng minh rằng U ∩ V ∈ T . Giả sử x ∈ U ∩ V , ta có x ∈ U và x ∈ V . Vì thế
tồn tại V1 ∈ B và V2 ∈ B sao cho x ∈ V1 ∩ V2. Theo giả thiết, tồn tại Wx ∈ B sao cho x ∈ Wx ⊂ V1 ∩
V2. Từ đó ta suy ra U ∩ V ⊂ Sx∈U∩V Wx ⊂ U ∩ V . Vì thế, U ∩V = Sx∈U∩V Wx. Điều đó chứng tỏ U ∩V
∈ T . Từ các giả thiết của mệnh đề ta có ngay B là cơ sở của tôpô T .
(3). Giả sử B là một cơ sở đếm được trong X. Với mỗi B ∈ B ta chọn phần tử
xB ∈ B. Khi đó A = {xB : B ∈ B} là đếm được. Bây giờ ta sẽ chứng minh rằng A = X.
Muốn vậy ta sẽ chứng minh rằng X \ A = ∅. Thật vậy, vì X \ A là tập mở trong X và (X \ A) ∩ A =
∅ ta suy ra X \ A không chứa phần tử B nào của cơ sở B. Bởi thế
X \ A = ∅. Do đó X = A và X khả li.
Như chúng ta đã biết, các tính chất Giải tích của R được đặc trưng qua giới hạn của dãy số.
Trong phần tiếp theo, chúng ta sẽ xét dãy trong không gian tôpô.
1.1.13 Định nghĩa (Dãy, dãy con và dãy hội tụ). Giả sử X là một không gian topo.
1. Ánh xạ x : N → X, x(n) = xn với mọi n ∈ N, được gọi là một dãy (sequence) trong X và kí hiệu
là {xn} hoặc là {xn}n∈N.
2. Nếu k : N → N là một hàm số tăng thì ánh xạ x◦k : N → X, x◦k(n) = xk(n) := xkn được gọi là
dãy con (subsequence) của dãy {xn}n∈N và kí hiệu là {xkn} hoặc là {xkn}n∈N
3. Dãy {xn}n∈N được gọi là hội tụ (convergent) đến điểm x ∈ X trong X nếu với mỗi lân cận U
của x, tồn tại n0 sao cho xn ∈ U với mọi n ≥ n0, kí hiệu là
. Khi đó điểm x ∈ X
được gọi là điểm giới hạn (limit point) của dãy {xn}n∈N.
1.1.14 Ví dụ. 1. Sự hội tụ trong Rn trong Giải tích cổ điển là sự hội tụ theo topo Euclid trên R.
2. Trong không gian topo rời rạc, mọi dãy là một dãy hội tụ.
Tiếp theo, chúng ta tìm hiểu về cấu trúc tôpô trên mỗi tập con của một không gian tôpô cho
trước. Lưu ý rằng trên mỗi tập hợp có thể có nhiều tôpô khác nhau, xem Ví dụ 1.1.2. Tuy nhiên,
chúng ta cần cấu trúc tôpô có “liên hệ” chặt chẽ với tôpô đã cho.
1.1.15 Bổ đề. Giả sử (X,T ) là một không gian tôpô và Y là một tập con khác rỗng của X. Khi đó
TY = {A : A = G ∩ Y,G ∈ T }
là một tôpô trên Y .
Chứng minh. Kiểm tra trực tiếp các điều kiện của Định nghĩa 1.1.1.
1.1.16 Định nghĩa (Không gian con). Giả sử (X,T ) là một không gian tôpô và Y là một tập con
khác rỗng của X. Khi đó tôpô TY xác định như trong Bổ đề 1.1.15 được gọi là tôpô cảm sinh
(induced topology) từ tôpô T và không gian tôpô (Y,TY ) được gọi là không gian tôpô con
(topological subspace) hay không gian con (subspace) của không gian tôpô (X,T ). 1.1.17 Ví dụ.
1. Không gian con N của R là một không gian tôpô rời rạc.
2. Không gian con [a,b] của R là không gian tôpô với tôpô có cơ sở
B = {[a,x) : x ∈ (a,b]} ∪ {(x,b] : x ∈ [a,b)} ∪ {(x,y) : x,y ∈ [a,b]}.
Tính chất cơ bản của không gian con được cho bởi mệnh đề sau.
1.1.18 Mệnh đề. Giả sử (X,T ) là một không gian tôpô và (Y,TY ) là một không gian con. Khi đó
1. Tập con U của Y mở theo TY khi và chỉ khi U = Y ∩ G với G mở theo T .
2. Tập con V của Y đóng theo TY khi và chỉ khi V = Y ∩ F với F đóng theo T .
Chứng minh. Áp dụng đặc trưng trong Bổ đề 1.1.15 và kiểm tra trực tiếp.
1.1.19 Nhận xét. 1. Nếu (Y,TY ) là một không gian con của không gian (X,T ) và (Z,TZ) là một
không gian con của (Y,TY ) thì (Z,TZ) là một không gian con của (X,T ).
2. Tương tự Mệnh đề 1.1.18 chúng ta có thể đặc trưng các loại tập con khác trong không gian
con qua tập con tương ứng trong không gian tôpô đã cho. 1.2 Không gian metric
Trong mục này chúng ta tìm hiểu một sự mở rộng của tập số thực R cùng với cấu trúc giá trị
tuyệt đối |x − y| hoặc tổng quát hơn, của không gian vật lí ba chiều với khoảng cách thông thường
với ba đặc trưng tiêu biểu: tính không âm, tính đối xứng và bất đẳng thức tam giác theo nghĩa
tổng độ dài hai cạnh thì lớn hơn độ dài cạnh còn lại.
Sự mở rộng trên cho chúng ta khái niệm không gian metric. Đặc biệt, mỗi metric sẽ sinh ra
một tôpô tương thích với nó và do đó mỗi không gian metric sẽ là một không gian tôpô.
1.2.1 Định nghĩa. Giả sử X ̸= ∅ và hàm d : X × X → R thỏa mãn các điều kiện sau.
1. Tính không âm: d(x,y) ≥ 0 với mọi x,y ∈ X và d(x,y) = 0 khi và chỉ khi x = y.
2. Tính đối xứng: d(x,y) = d(y,x) với mọi x,y ∈ X.
3. Bất đẳng thức tam giác: d(x,y) ≤ d(x,z) + d(z,y) với mọi x,y,z ∈ X. Khi đó
1. d được gọi là một metric hay khoảng cách (distance) trên X.
2. Tập hợp X cùng với một metric d xác định trên nó được gọi là một không gian metric và kí
hiệu là (X,d) hay đơn giản là X.
3. Các phần tử của X được gọi là điểm (point) và giá trị d(x,y) được gọi là khoảng cách giữa
hai điểm x và y.
4. Với A,B là những tập con khác rỗng của X, giá trị
d(A,B) = inf{d(x,y) : x ∈ A,y ∈ B}
được gọi là khoảng cách giữa các tập hợp A và B. Nếu A = {x} thì thay cho kí
hiệu d(A,B) ta viết là d(x,B) và gọi nó là khoảng cách từ điểm x đến tập hợp B. 5. Dãy {xn}
trong X được gọi là hội tụ (convergent) đến điểm a ∈ X nếu lim d(xn,a) =
n→∞ 0. Khi đó ta kí hiệu là
hay xn = a khi n → ∞. Một cách tương đương ta nói nếu với
mỗi ε > 0 tồn tại n0 ∈ N sao cho với mọi n ≥ n0 ta có d(xn,a) < ε. Điểm a được gọi là điểm
giới hạn (limit point) hay giới hạn (the limit) của dãy {xn}.
1.2.2 Nhận xét. Với mọi tập con A,B của không gian metric X ta có
1. d(A,B) = d(B,A);
2. 0 ≤ d(A,B) < ∞;
3. Nếu d(A,B) > 0 thì A ∩ B = ∅. Điều ngược lại nói chung không đúng.
1.2.3 Ví dụ. 1. Giả sử X = R và d(x,y) = |x−y| với mọi x,y ∈ R. Khi đó d là một metric trên R và được
gọi là metric giá trị tuyệt đối (absolute metric).
2. Không gian metric rời rạc. Giả sử X là một tập hợp tùy ý khác rỗng. Trên X ta xác định hàm d như sau ( 0 nếu
x = y d(x,y) = 1 nếu x ̸= y.
Khi đó d thỏa mãn các tiên đề của một metric. Không gian metric (X,d) này được gọi là
không gian metric rời rạc (discrete metric space).
3. Không gian Euclid Rn, Cn. Giả sử X = Rn (X = Cn) là tập hợp tất cả các bộ n số thực (tương
ứng, n số phức). Với hai phần tử bất kì x = (x1,...,xn) và y = (y1,...,yn) ta đặt ; ;
i=1 d2(x,y) =
sup |xi − yi|. 1≤i≤n
Kiểm tra trực tiếp ta có d,d1,d2 là các metric trên Rn và Cn. Không gian Rn và Cn được mặc
định với metric d và được gọi là không gian Euclid (Euclidean space).
4. Không gian các hàm liên tục C[a,b]. Giả sử [a,b] ⊂ R. Kí hiệu C[a,b] là tập hợp tất cả các hàm
giá trị thực xác định và liên tục trên đoạn [a,b]. Với bất kì x,y ∈ C[a,b] ta đặt
d(x,y) = sup |x(t) − y(t)|
a≤t≤b
Z b d1(x,y) = |x(t) − y(t)|dt. a
Khi đó d và d1 là những metric trên C[a,b], lần lượt được gọi là metric hội tụ đều (uniformly
convergent metric) và metric tích phân (integral metric) trên C[a,b].
Không gian C[a,b] luôn được mặc định với metric hội tụ đều.
1.2.4 Mệnh đề. Giả sử (X,d) là một không gian metric. Khi đó
1. Với x1,x2,...,xn ∈ X , d(x1,xn) ≤ d(x1,x2) + ··· + d(xn−1,xn).
2. Với x,y,u,v ∈ X, |d(x,y) − d(u,v)| ≤ d(x,u) + d(y,v).
3. Nếu A là tập con khác rỗng của không gian metric X và x,y ∈ X thì
|d(x,A) − d(y,A)| ≤ d(x,y).
Chứng minh. (1). Với n = 2 kết luận của định lí là hiển nhiên.
Với n = 3 kết quả suy từ bất đẳng thức tam giác. Giả sử định lí đúng với n−1. Khi đó với n
điểm bất kì x1,...,xn ∈ X, nhờ bất đẳng thức tam giác ta có
d(x1,xn) ≤ d(x1,xn−1) + d(xn−1,xn)
≤ d(x1,x2) + d(x2,x3) + ··· + d(xn−2,xn−1) + d(xn−1,xn).
(2). Áp dụng (1) cho 4 điểm x,y,u,v ta có
d(x,y) ≤ d(x,u) + d(u,v) + d(v,y).
Vì vậy ta nhận được d(x,y) − d(u,v) ≤ d(x,u) + d(y,v).
Thay đổi vai trò của x và u, y và v ta nhận được
d(u,v) − d(x,y) ≤ d(u,x) + d(v,y).
Từ đó ta suy ra |d(x,y) − d(u,v)| ≤ d(x,u) + d(y,v).
(3). Giả sử z là điểm tùy ý thuộc A. Khi đó ta có
d(x,z) ≤ d(x,y) + d(y,z).
Do đó d(x,A) ≤ d(x,y) + d(y,z) với mọi z ∈ A. Vì vậy ta nhận được
d(x,A) ≤ d(x,y) + d(y,A).
Thay đổi vai trò của x và y ta được
d(y,A) ≤ d(x,y) + d(x,A).
Từ đó ta nhận được bất đẳng thức cần chứng minh.
1.2.5 Bổ đề. 1. Giả sử (X,d) là một không gian metric, M là một tập con khác rỗng và dM(x,y) =
d(x,y) với mọi x,y ∈ M. Khi đó dM là một metric trên M.
2. Giả sử (X,dX) và (Y,dY ) là hai không gian metric. Khi đó các hàm d, d1 và d2 cho bởi công thức
với mọi x1,x2 ∈ X, y1,y2 ∈ Y là những metric trên X × Y .
1.2.6 Định nghĩa. 1. Metric dM trong Bổ đề 1.2.5.(1) được gọi là metric cảm sinh (induced metric)
bởi metric d trên M và không gian metric (M,dM) được gọi là không gian metric con (metric
subspace) hay không gian con (subspace) của không gian metric (X,d).
2. Metric d trong Bổ đề 1.2.5.(2) được gọi là tích (product) của các metric dX,dY . Không gian
(X × Y,d) được gọi là không gian tích (product space) của các không gian metric X và Y .
Tiếp theo là một số tính chất cơ bản của giới hạn dãy trong không gian metric. 1.2.7 Mệnh đề.
1. Trong không gian metric, mỗi dãy hội tụ chỉ có một giới hạn duy nhất.
2. Nếu lim xn = a và lim yn = b thì lim d(xn,yn) = d(a,b). n→∞ n→∞ n→∞
Chứng minh. (1). Giả sử ta có . Khi đó ta có
0 ≤ d(a,b) ≤ d(a,xn) + d(xn,b).
Cho n → ∞ ta suy ra d(a,b) = 0 hay a = b.
(2). Từ Mệnh đề 1.2.4.(2) ta có
|d(xn,yn) − d(a,b)| ≤ d(xn,a) + d(yn,b).
Vì vậy lim |d(xn,yn) − d(a,b)| = 0 hay lim d(xn,yn) = d(a,b). n→∞ n→∞
Tiếp theo, chúng ta sẽ chứng tỏ rằng mỗi metric sẽ sinh ra một tôpô tương thích với nó và
do đó mỗi không gian metric sẽ là một không gian tôpô với các tính chất tôpô như đã trình bày trong Chương 1.1.
1.2.8 Định nghĩa. Giả sử (X,d) là một không gian metric, a ∈ X và r ≥ 0.
1. Tập hợp B(a,r) = {x ∈ X : d(x,a) < r} được gọi là hình cầu mở (open ball) tâm a bán kính r.
2. Tập hợp B′(a,r) = {x ∈ X : d(x,a) ≤ r} được gọi là hình cầu đóng (closed ball) tâm a bán kính
r. Ta cũng kí hiệu hình cầu đóng tâm a bán kính r là B[a,r].
3. Tập hợp S(a,r) = {x ∈ X : d(x,a) = r} được gọi là mặt cầu (sphere) tâm a bán kính r.
4. Dãy các hình cầu đóng {Bn} với Bn = B[xn,rn], n ∈ N được gọi là thắt (decreasing nested) nếu
(a) Bn+1 ⊂ Bn với mọi n ∈ N. .
Mệnh đề sau chứng tỏ rằng trên mỗi không gian metric chúng ta có thể xây dựng một tôpô.
1.2.9 Mệnh đề. Giả sử (X,d) là một không gian metric và
Td = {G ⊂ X : với mỗi x ∈ G tồn tại rx > 0 sao cho B(x,rx) ⊂ G}.
Khi đó Td là một tôpô trên X, nghĩa là Td thỏa mãn các tính chất sau.
1. ∅ ∈ Td, X ∈ Td.
2. Nếu Gα ∈ Td, α ∈ Λ thì Sα∈Λ Gα ∈ Td. 3. Nếu .
Chứng minh. (1). Hiển nhiên.
(2). Giả sử x0 là điểm bất kì thuộc G = Sα∈Λ Gα. Khi đó tồn tại một chỉ số β ∈ Λ sao cho x0 ∈ Gβ.
Vì Gβ mở nên tồn tại một hình cầu mở B(x0,r) sao cho B(x0,r) ⊂ Gβ ⊂ G. Do đó x0 là điểm trong
của G. Bởi vậy G mở.
(3). Ta chỉ cần chứng minh cho trường hợp n = 2. Giả sử G1,G2 là hai tập hợp mở và x0 là điểm
bất kì thuộc G1 ∩ G2. Khi đó x0 ∈ G1 và x0 ∈ G2. Do đó tồn tại các hình cầu mở B(x0,r1) ⊂ G1 và
B(x0,r2) ⊂ G2. Lấy r sao cho 0 < r ≤ min{r1,r2}. Khi đó ta có B(x0,r) ⊂ G1 ∩G2, nghĩa là x0 là điểm
trong của G1 ∩G2. Bởi vậy G1 ∩G2 là tập hợp mở.
1.2.10 Định nghĩa (Tôpô sinh bởi metric). Giả sử (X,d) là một không gian metric. Khi đó họ Td
trong Mệnh đề 1.2.9 được gọi là tôpô sinh bởi metric d.
1.2.11 Nhận xét. 1. Nếu không giải thích gì thêm thì không gian metric (X,d) luôn được mặc định
là một không gian tôpô với tôpô sinh bởi metric d.
2. Các khái niệm và tính chất liên quan đến tôpô như tập đóng, tập mở, bao đóng, phần trong,
...trong không gian metric được hiểu là khái niệm tương ứng trong không gian tôpô với tôpô sinh bởi metric.
1.2.12 Ví dụ. 1. Metric giá trị tuyệt đối trên R, xem Ví dụ 1.2.3.(1), sinh ra tôpô thông thường trên
R, xem Ví dụ 1.1.2.(5) Chương 1.1.
2. Giả sử (X,d) là không gian metric rời rạc, xem Ví dụ 1.2.3.(2). Khi đó tôpô sinh bởi metric
rời rạc là tôpô rời rạc, xem Ví dụ 1.1.2.(4) Chương 1.1.
1.2.13 Mệnh đề. Giả sử (X,d) là một không gian metric. Khi đó
1. Hình cầu mở B(a,r) là tập mở trong không gian metric X. 2. Với mỗi
là một cơ sở lân cận tại x.
3. Họ B = Sx∈X B(x) là một cơ sở của tôpô Td.
4. Sự hội tụ của dãy trong không gian tôpô (X,Td) và sự hội tụ của dãy trong không gian metric
(X,d) là tương đương với nhau.
Chứng minh. (1). Giả sử x là điểm bất kì thuộc B(a,r). Khi đó d(x,a) < r. Lấy 0 < r′ < r − d(x,a). Lúc
đó ta có B(x,r′) ⊂ B(a,r). Thật vậy, với điểm y bất kì thuộc B(x,r′) ta có d(y,x) < r′. Do đó ta có
d(y,a) ≤ d(y,x) + d(x,a) < r. Vậy y ∈ B(a,r).
Điều này chứng tỏ mọi điểm x thuộc hình cầu mở B(a,r) là điểm trong của nó. Bởi vậy B(a,r) là tập mở.
(2). Theo (1) thì B(x) là một họ những lân cận tại điểm x. Giả sử U là một lân cận bất kì của x.
Khi đó tồn tại B mở sao cho x ∈ B ⊂ U. Do đó, tồn tại rx > 0 sao cho x ∈ B(x,rx) ⊂ B ⊂ U. Điều này
chứng tỏ B(x) là một cơ sở lân cận tại x.
(3). Suy trực tiếp từ (1) và (2).
(4). Áp dụng (3) và các định nghĩa hội tụ.
1.2.14 Mệnh đề (Đặc trưng tập đóng bởi dãy hội tụ). Tập con F của không gian metric X là đóng
nếu và chỉ nếu với mọi dãy {xn} ⊂ F mà .
Chứng minh. Điều kiện cần. Giả sử F là tập hợp đóng, {xn} là dãy bất kì trong F và
. Khi đó tập hợp G = X \F là mở. Giả sử b là điểm bất kì thuộc G = X \F, do G mở nên
tồn tại hình cầu mở B(b,r) ⊂ G. Mặt khác vì xn ∈/ G với mọi n = 1,2,... nên xn ∈/ B(b,r) với mọi n
= 1,2,... Bởi vậy ta có d(xn,b) ≥ r với mọi n = 1,2,... Điều này chứng tỏ rằng nếu b /∈ F thì b không
thể là giới hạn của dãy {xn}. Vì a là giới hạn của dãy {xn} nên a ∈ F.
Điều kiện đủ. Để chứng minh F đóng ta sẽ chứng minh rằng tập hợp G = X \ F là mở. Giả sử
ngược lại rằng G không mở. Khi đó tồn tại một điểm a ∈ G mà nó không là điểm trong của G. Lúc
đó với mọi n = 1,2,... ta có
, nghĩa là với mỗi n = 1,2,... tồn tại nhưng
xn ∈/ G. Khi đó ta có dãy {xn} ⊂ F sao cho
. Vậy a ∈ F. Điều này là vô lí.
1.2.15 Hệ quả (Đặc trưng bao đóng bởi dãy hội tụ). Giả sử (X,d) là một không gian metric và A ⊂ X. Khi đó
A = {x : tồn tại {xn} ⊂ A, lim xn = x}. n→∞
1.2.16 Mệnh đề. Mọi không gian metric đều là T4-không gian.
Chứng minh. Ta chỉ cần chứng minh rằng X là một không gian chuẩn tắc. Giả sử F là tập con đóng
bất kì trong không gian metric (X,d). Khi đó ta xác định hàm fF : X → R cho bởi công thức fF (x) =
d(x,F) = inf d(x,y) với mọi x ∈ X. y∈F
Hàm fF xây dựng như trên thoả mãn các điều kiện
1. fF (x) = 0 nếu x ∈ F. 2. fF (x) >
0 nếu x /∈ F. 3. fF liên tục.
Thật vậy, khẳng định (1) là hiển nhiên.
(2). Vì F đóng nên nếu x /∈ F thì tồn tại số r > 0 sao cho B(x,r) ∩ F = ∅. Từ đó suy ra d(x,y) ≥
r với mọi y ∈ F. Vì thế ta có fF (x) ≥ r > 0.
(3). Với bất kì x,y ∈ X, từ Mệnh đề 1.2.4.(3) ta có |d(x,F) − d(y,F)| ≤ d(x,y). Vì thế |fF (x) − fF
(y)| ≤ d(x,y) với mọi x,y ∈ X. Điều này kéo theo fF liên tục.
Bây giờ giả sử A, B là các tập đóng bất kì rời nhau trong X. Khi đó từ chứng minh trên ta suy
ra fA(x) + fB(x) > 0 với mọi x ∈ X. Đặt
với mọi x ∈ X.
ta có φ là hàm liên tục trên X, hơn nữa φ(x) = 0 với mọi x ∈ A và φ(x) = 1 với mọi x ∈ B. Đặt ,
Ta có U,V là các tập mở trong X lần lượt chứa A, B và U ∩ V = ∅.
Một tính chất quan trọng trong giới hạn của dãy số thực, còn được gọi là tiêu chuẩn Cauchy
đối với dãy số thực, nói rằng mọi dãy số thực {xn} hội tụ khi và chỉ khi với mỗi ε > 0 tồn tại n0 sao




