Bài giảng đồ họa môn Đồ họa kỹ thuật CTTT | Trường Đại học Bách Khoa Hà Nội

LỜI NÓI ĐẦU
Giáo trình Đồ họa kỹ thuât I nhằm phục vụ cho các cán bộ giảng dạy, sinh viên các
nghành kỹ thuật và các cán bộ kỹ thuật làm tài liệu giảng dạy, nghiên cứu, học tập và tra cứu.
Giáo trình này cung cấp các kiến thức cần thiết với mong muốn đồng hành với sinh viên
đạt các mục tiêu của học phần Đồ họa kỹ thuật I: Đọc hiểu được bản vẽ kỹ thuật, thiết lập
được bản vẽ kỹ thuật và sử dụng được phần mềm vẽ kỹ thuật tiên tiến.
Giáo trình này chia thành 3 phần:
Phần I: Hình học họa hình gồm 4 chương cung cấp những kiến thức hình học cốt lõi của
việc biểu diễn, làm cơ sở cho phần vẽ kỹ thuật - Chương 1: Phép chiếu
- Chương 2: Biểu diễn và sự liên thuộc
- Chương 3: Thay mặt phẳng hình chiếu
- Chương 4: Giao của các đối tượng
Phần II: Vẽ kỹ thuật gồm 4 chương trình bày các tiêu chuẩn, các loại hình biểu diễn, làm
cơ sở để thiết lập bản vẽ kỹ thuật
- Chương 1: Một số tiêu chuẩn về trình bày bản vẽ
- Chương 2: Các hình chiếu thẳng góc
- Chương 3: Hình chiếu trục đo
- Chương 4: Hình cắt, mặt cắt
Phần III: Vẽ kỹ thuật trên máy tính gồm 3 chương, cung cấp các kiến thức cần thiết để có
thể thiết lập bản vẽ trên máy tính . - Chương 1: Vẽ 2D - Chương 2:Tạo khối 3D
- Chương 3: Xuất bản vẽ, tạo hình cắt, mặt cắt
Mặc dù đã cố gắng để hoàn thành tài liệu một cách tốt nhất nhưng không tránh khỏi những
thiếu sót. Các tác giả mong muốn nhận được những ý kiến đóng góp của bạn đọc để lần
xuất bản sau được tốt hơn. Các tác giả. PHẦN 1
HÌNH HỌC HỌA HÌNH(HÌNH HỌA) Chương 1 PHÉP CHIẾU 1.1 PHÉP CHIẾU XUYÊN TÂM
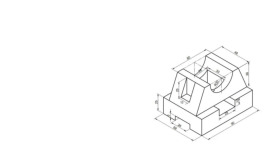
Cho một mặt phẳng i, gọi là mặt phẳng hình chiếu; một điểm S gọi là tâm chiếu. S không
thuộc i. Vẽ đường thẳng SA. Giao của đường thẳng SA và mặt phẳng i là điểm Ai.
Điểm Ai được gọi là hình chiếu xuyên tâm S lên mặt phẳng hình chiếu i (hình 1.1). Phép
chiếu xuyên tâm được sử dụng trong kiến trúc, hội họa.
Hình 1.1: Phép chiếu xuyên tâm Hình 1.2: Phép chiếu song song 1.2 PHÉP CHIẾU SONG SONG
Cho một mặt phẳng i, gọi là mặt phẳng hình chiếu; một đường thẳng s gọi là phương
chiếu. s không song song với i. Vẽ đường thẳng t đi qua điểm A và song song với s. Giao
của đường thẳng t và mặt phẳng i là điểm Ai. Điểm Ai được gọi là hình chiếu song song
theo phương s lên mặt phẳng hình chiếu i (hình 1.2). Phép chiếu song song có 3 tính chất cơ bản như sau:
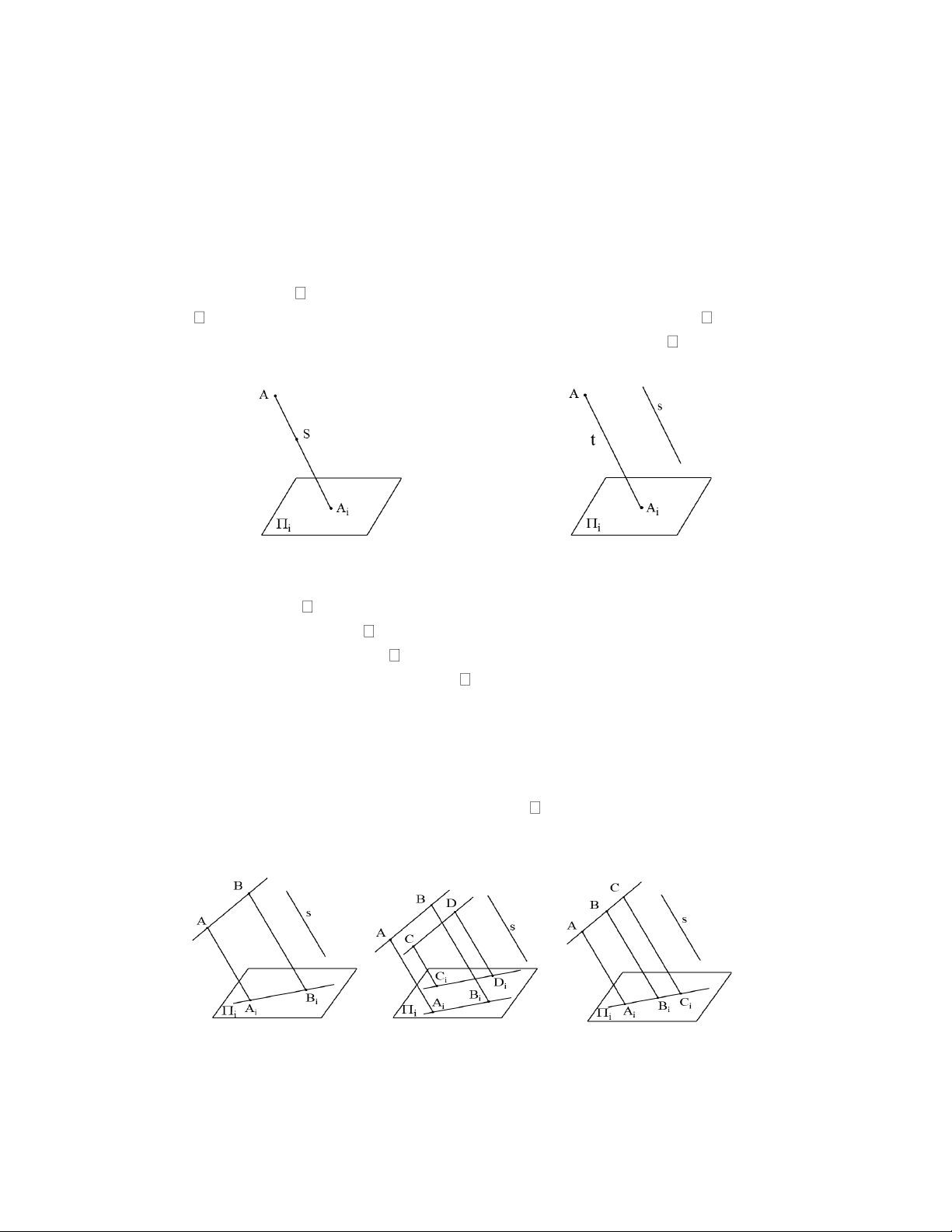
• Hình chiếu của một đường thẳng không song song với phương chiếu là một
đường thẳng. Trên hình 1.3 chiếu của AB là AiBi.
• Hai đường thẳng song song và không song song với phương chiếu thì hai hình
chiếu song song. Trên hình 1.4: AB//CD AiBi//CiDi.
• Phép chiếu song song bảo toàn tỉ số đơn của 3 điểm thẳng hàng (và không song
song với phương chiếu). Trên hình 1.5: AB:BC = AiBi:BiCi
Hình 1.3 Hình 1.4 Hình 1.5 1.3 PHÉP CHIẾU VUÔNG GÓC 1.3.1 Định nghĩa
Phép chiếu vuông góc là một trường hợp riêng của phép chiếu song song, trong đó phương
chiếu vuông góc với mặt phẳng hình chiếu (hình 1.6). Như vậy, để tìm hình chiếu vuông
góc của một điểm A có thể thực hiện như sau: Qua A vẽ một đường thẳng t vuông góc với
mặt phẳng hình chiếu i. Xác định giao điểm Ai của t và i. Ai chính là hình chiếu vuông
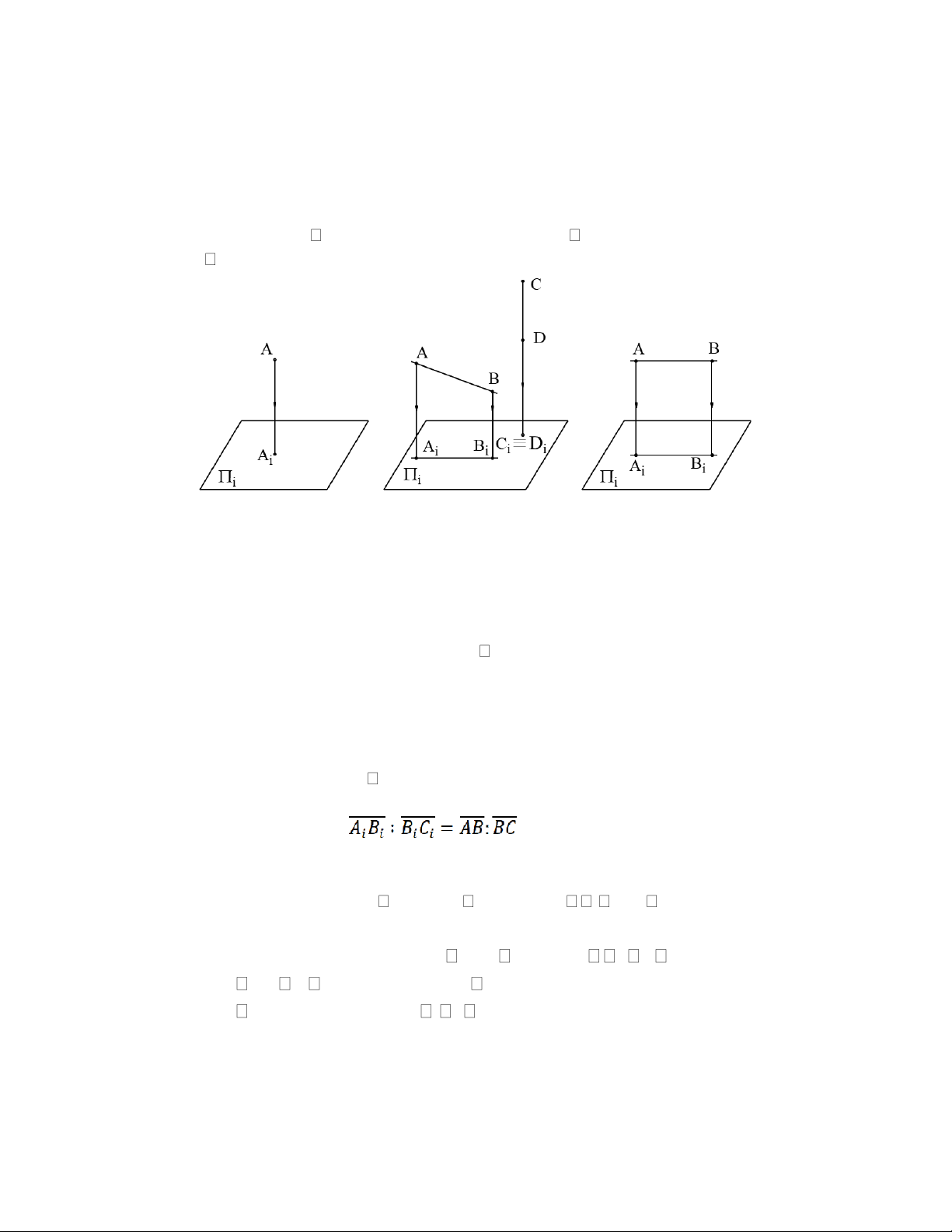
góc lên i của điểm A (hình 1.6). Hình 1.6 Hình 1.7 Hình 1.8 1.3.2 Tính chất
a) Hình chiếu của một đường thẳng nói chung là một đường thẳng.
• Hình chiếu của một đường thẳng không vuông góc với mặt phẳng hình chiếu
là một đường thẳng. Trên hình 1.7: hình chiếu của AB là AiBi. Độ dài đoạn
AiBi≤AB. Dấu ‘=’ xảy ra khi AB// i (hình1. 8).
• Hình chiếu của một đường thẳng vuông góc với mặt phẳng hình chiếu là một
điểm. Trên hình 1.7: hình chiếu của CD là CiDi trùng nhau.
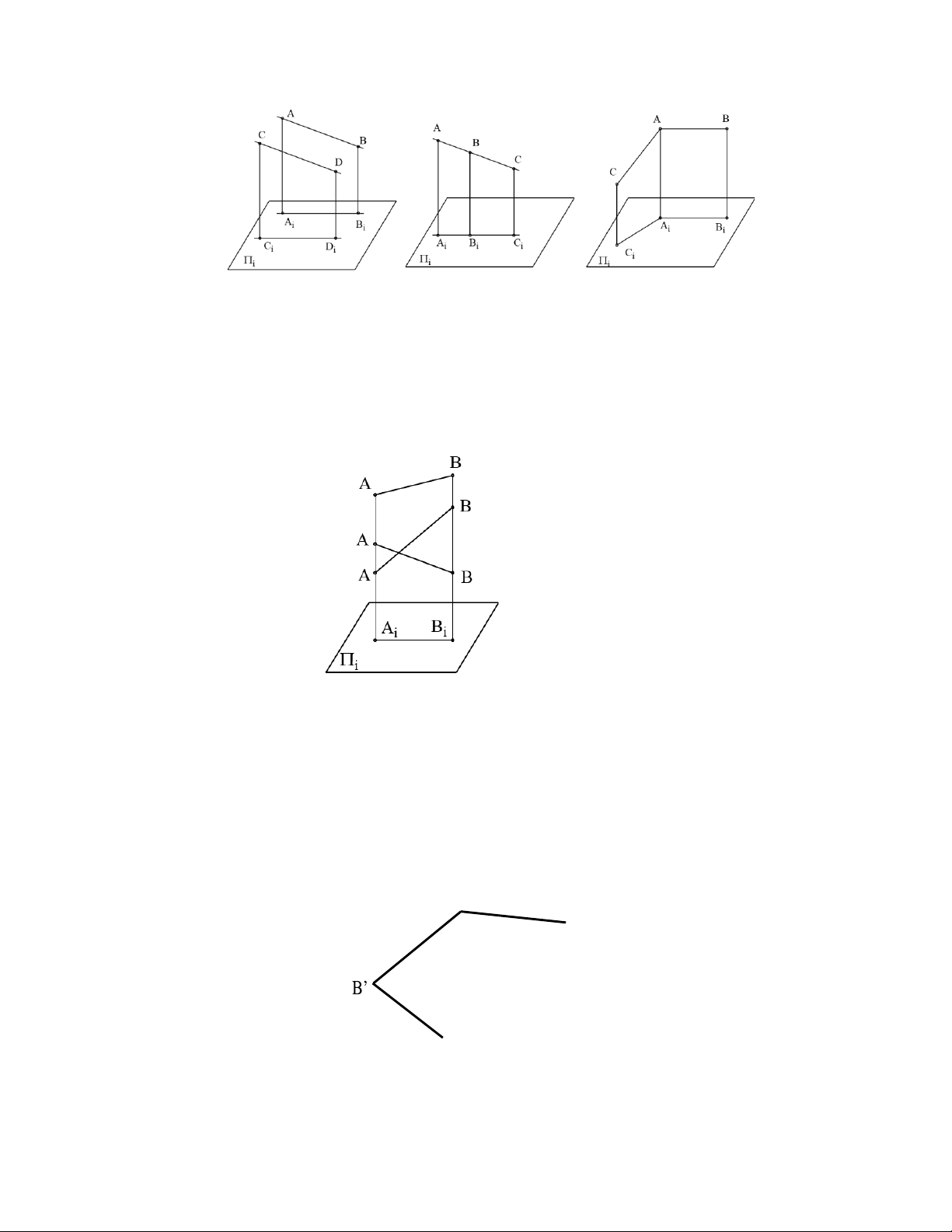
b) Hai đường thẳng song song với nhau và không vuông góc với mặt phẳng hình
chiếu thì hình chiếu tương ứng song song.
Trên hình 1.9: AB//CD AiBi//CiDi và AiBi/AB=CiDi/CD.
c) Phép chiếu vuông góc bảo toàn tỉ số đơn của 3 điểm thẳng hàng (Hình 1.10).
d) Hình chiếu của một góc vuông là một góc vuông chỉ khi có ít nhất 1 cạnh song
song với mặt phẳng hình chiếu, cạnh kia không vuông góc với mặt phẳng hình
chiếu. Trên hình 11: CA AB, AB// i, CA không i CiAi AiBi. Mở rộng:
• a,b là 2 đường thẳng bất kỳ, a b, a// i, b không i ai bi.
• ai bi, a b có ít nhất a hoặc b// i.
• ai bi, có ít nhất a hoặc b// i a b.
Hình 1.9 Hình 1.10 Hình 1.11 1.4
TÍNH PHẢN CHUYỂN CỦA HÌNH BIỂU DIỄN
Một hình biểu diễn một đối tượng trong không gian có tính phản chuyển khi từ hình biểu
diễn đó người ta có thể xác định được đối tượng và có nghiệm duy nhất. Nếu dùng phép
chiếu với chỉ một mặt phẳng hình chiếu thì hình biểu diễn sẽ không phản chuyển. Trên
hình 1.12 minh họa cho điều đó: đoạn thẳng AB có vô số nghiệm nếu cho biết hình chiếu
vuông góc của nó là AiBi.
Hình 1.12: Có vô số nghiệm AB CÂU HỎI ÔN TẬP
1. Phát biểu định nghĩa và tính chất của phép chiếu song song.
2. Phát biểu định nghĩa và tính chất của phép chiếu vuông góc.
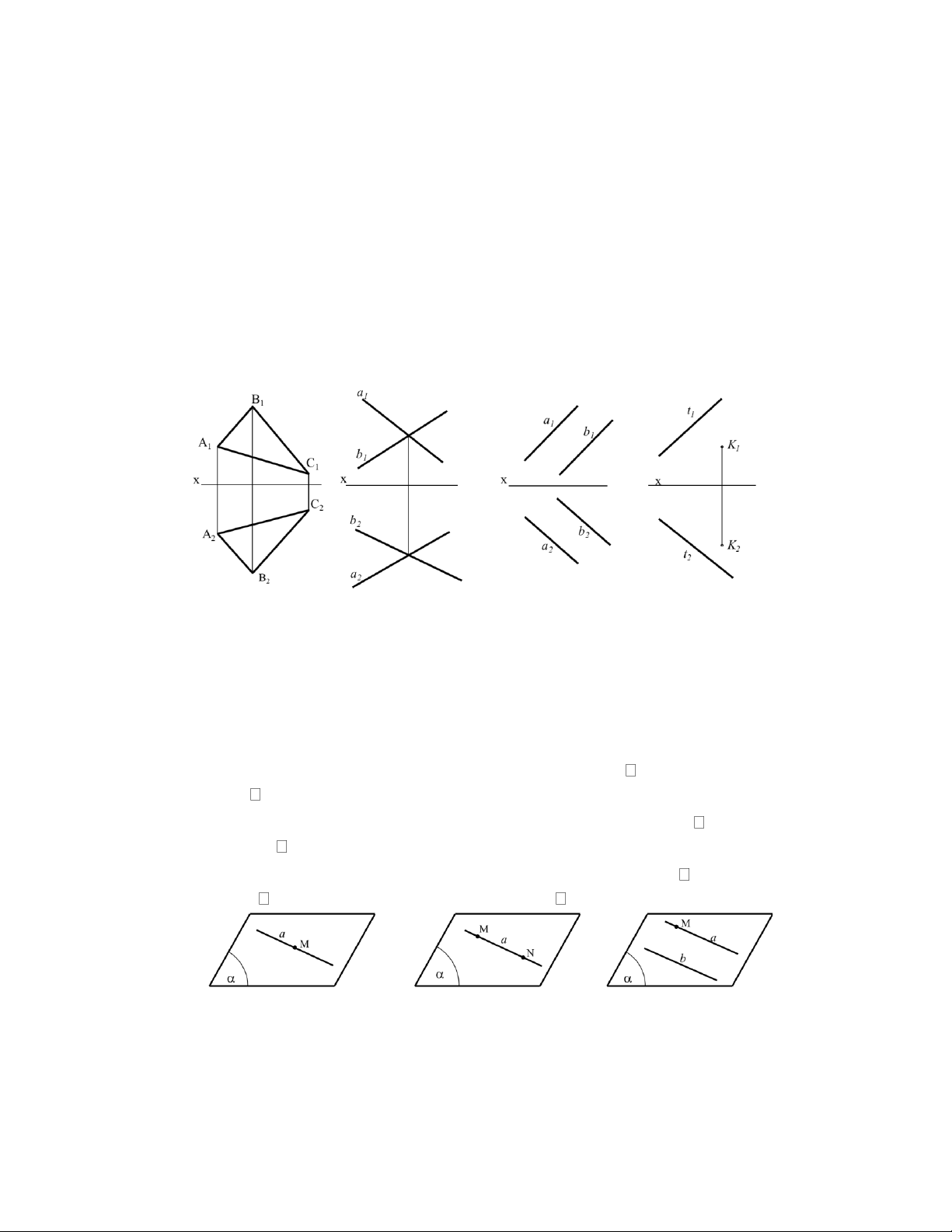
4. Biết rằng A’B’C’D’ là hình chiếu song song của các đỉnh một lục giác đều ABCDEF
trong không gian ( hình 1.13). Hãy vẽ đầy đủ hình chiếu song song của lục giác đó. C’ D’ A’ Hình 1.13 Chương 2
BIỂU DIỄN VÀ SỰ LIÊN THUỘC 2.1 ĐIỂM 2.1.1. Các khái niệm
Trong không gian, gọi mặt phẳng thẳng đứng là mặt phẳng hình chiếu đứng 1. Mặt phẳng
nằm ngang vuông góc với 1 gọi là mặt phẳng hình chiếu bằng 2. Mặt phẳng vuông góc
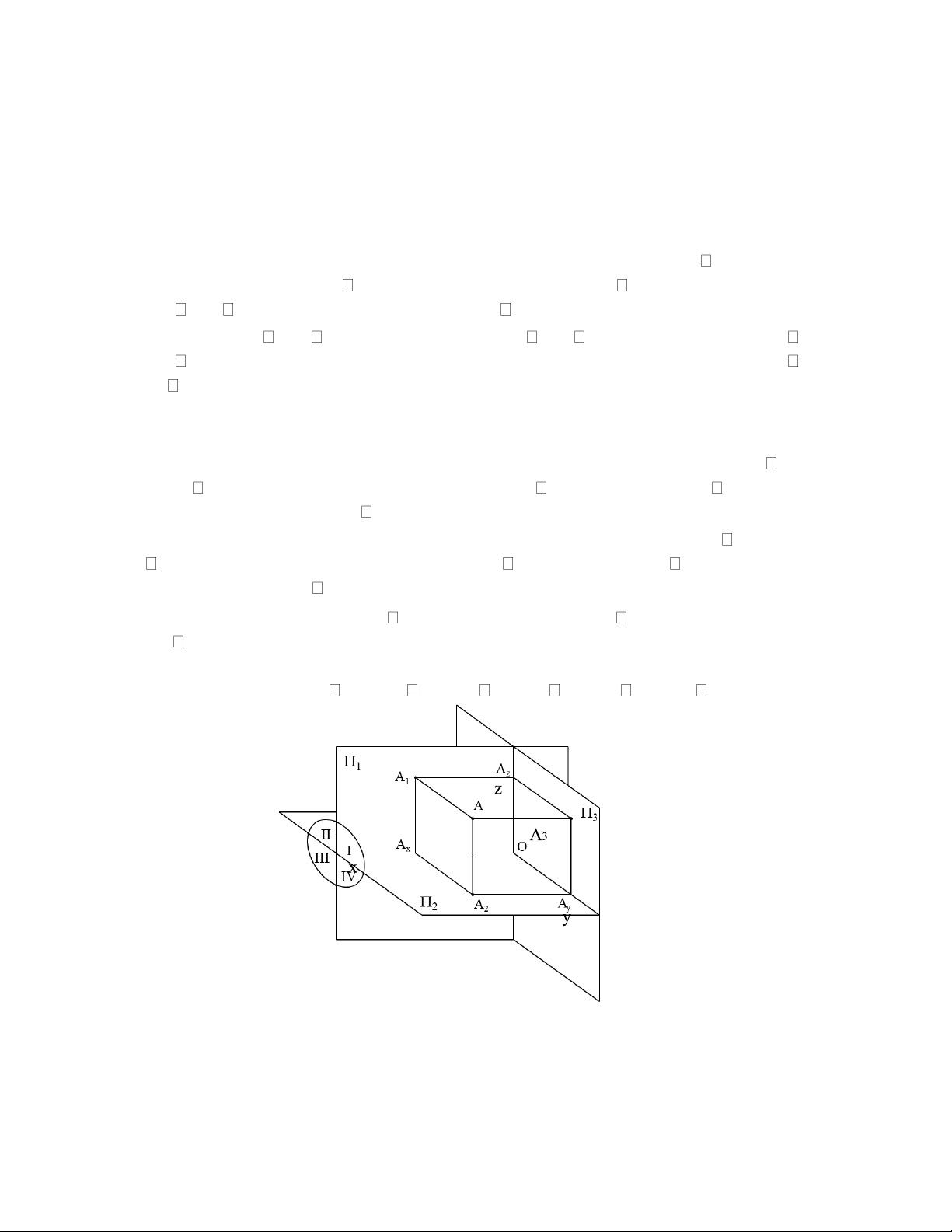
với 1 và 2 gọi là mặt phẳng hình chiếu cạnh 3 (hình 2.1).
Giao tuyến của 1 và 2 là trục x. Giao tuyến của 2 và 3 là trục y. Giao tuyến của 3
với 1 là z. Hiển nhiên là các trục x, y, z đôi một vuông góc với nhau. Hai mặt phẳng 1
và 2 chia không gian thành 4 góc gọi là các góc phần tư thứ I, II, III, IV. Mặt phẳng phân
giác của góc phần tư I và III gọi là mặt phẳng phân giác I, Mặt phẳng phân giác của góc
tư II và IV gọi là mặt phẳng phân giác II.
Độ cao của một điểm A là khái niệm đặc trưng cho vị trí tương đối của A so với 2. A
thuộc 2 thì độ cao bằng 0, ‘+’ khi A nằm phía trên 2, ‘-‘ khi A nằm dưới 2, Trị số độ
cao là khoảng cách từ A đến 2.
Độ xa của một điểm A là khái niệm đặc trưng cho vị trí tương đối của A so với 1. A thuộc
1 thì độ cao bằng 0, ‘+’ khi A nằm phía trước 1, ‘-‘ khi A nằm sau 1, Trị số độ xa là
khoảng cách từ A đến 1.
Hình chiếu vuông góc của A lên 1 gọi là hình chiếu đứng, lên 2 gọi là hình chiếu bằng,
lên 3 gọi là hình chiếu cạnh. Gọi giao của mặt phẳng (AA1A2) với trục x là Ax, giao của
y với mặt phẳng (AA2A3) là Ay, giao của z với mặt phẳng (AA1A3) là Az. Người ta đã
chứng minh được rằng x A1Ax, x A2Ax, y A2Ay, y A3Ay, z A1Az , z A3Az.
Hình 2.1: Hệ thống 3 mặt phẳng hình chiếu
2.1.2 Xây dựng đồ thức điểm
Đồ thức của điểm là một hình biểu diễn phẳng của điểm đó. Dựa vào đồ thức này, có thể
tìm lại được điểm trong không gian.
Để xây dựng đồ thức, từ hình không gian (hình 2.1) ta thực hiện như sau:
Quay 2 quanh trục x một góc 90 độ đến trùng 1, theo chiều quy định: nửa phía trước
của 2 quay xuống dưới. Hình chữ nhật OAxA2Ay quay theo và cuối cùng A1AxA2 thẳng
hàng, vuông góc với trục x.
Quay 3 quanh trục z một góc 90 độ đến trùng 1, theo chiều quy định: nửa phía trước
của 3 quay sang phải. Hình chữ nhật OAyA3Az quay theo và cuối cùng A1AzA3 thẳng
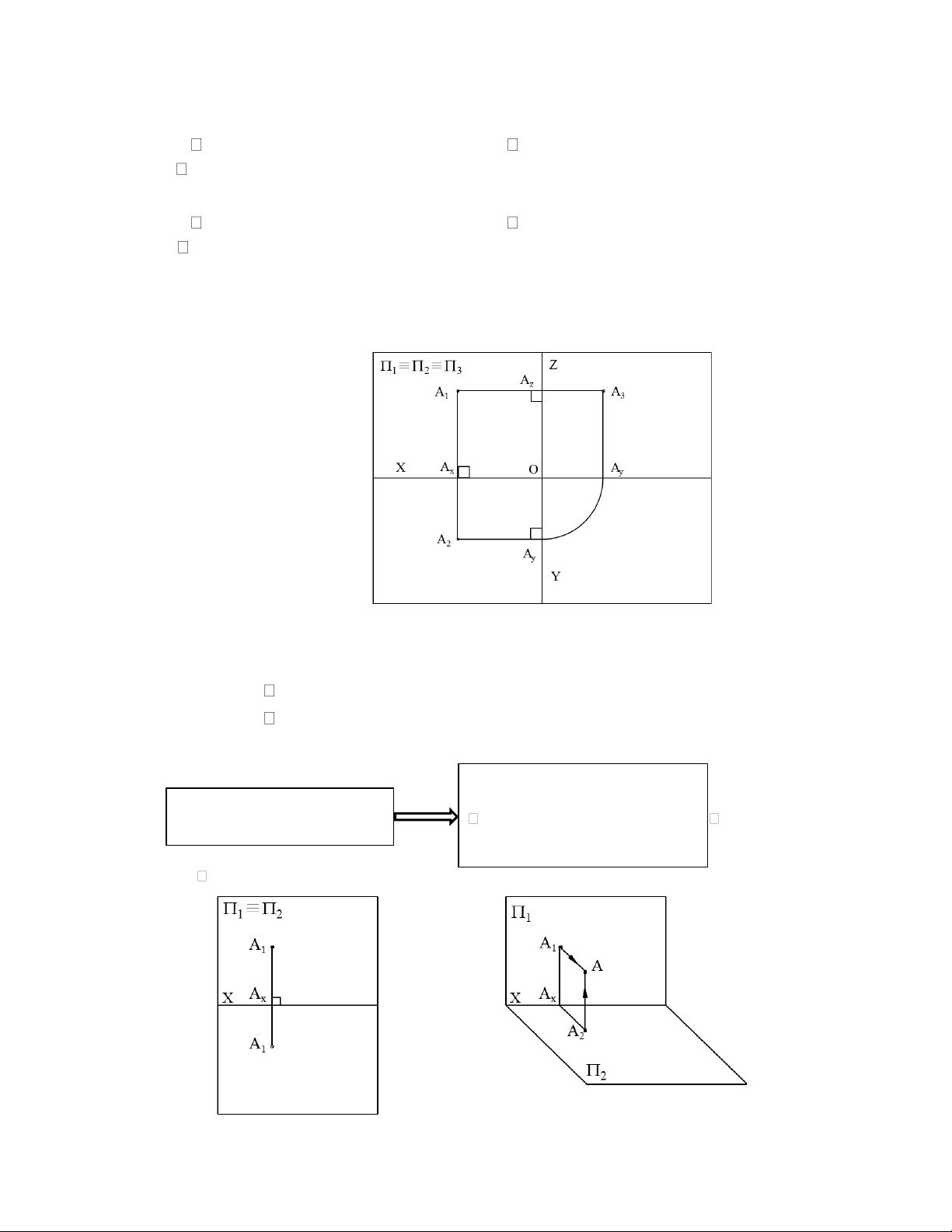
hàng, vuông góc với trục z. Hình 2.2 là kết quả cuối cùng, gọi là đồ thức của điểm trong
hệ thống 3 mặt phẳng hình chiếu vuông góc.
2.1.3 Tính chất của đồ thức
Hình 2.2 Đồ thức của điểm A
Đồ thức của một điểm A có các tính chất sau: • A1A2 x • A1A3 z • A2Ax=A3Az
• Biết A1A2 xác định được điểm A duy nhất:
Qua A 1 dựng đường vuông góc với
1 ; qua A2 dựng đường vuông góc với 2;
Biết 2 hình chiếu của điểm A chúng cắt nhau tại (hình 2.3) A.(Hình 2.4)
Quay 2 quanh trục x góc 90 độ. Hình 2.3 Hình 2.4
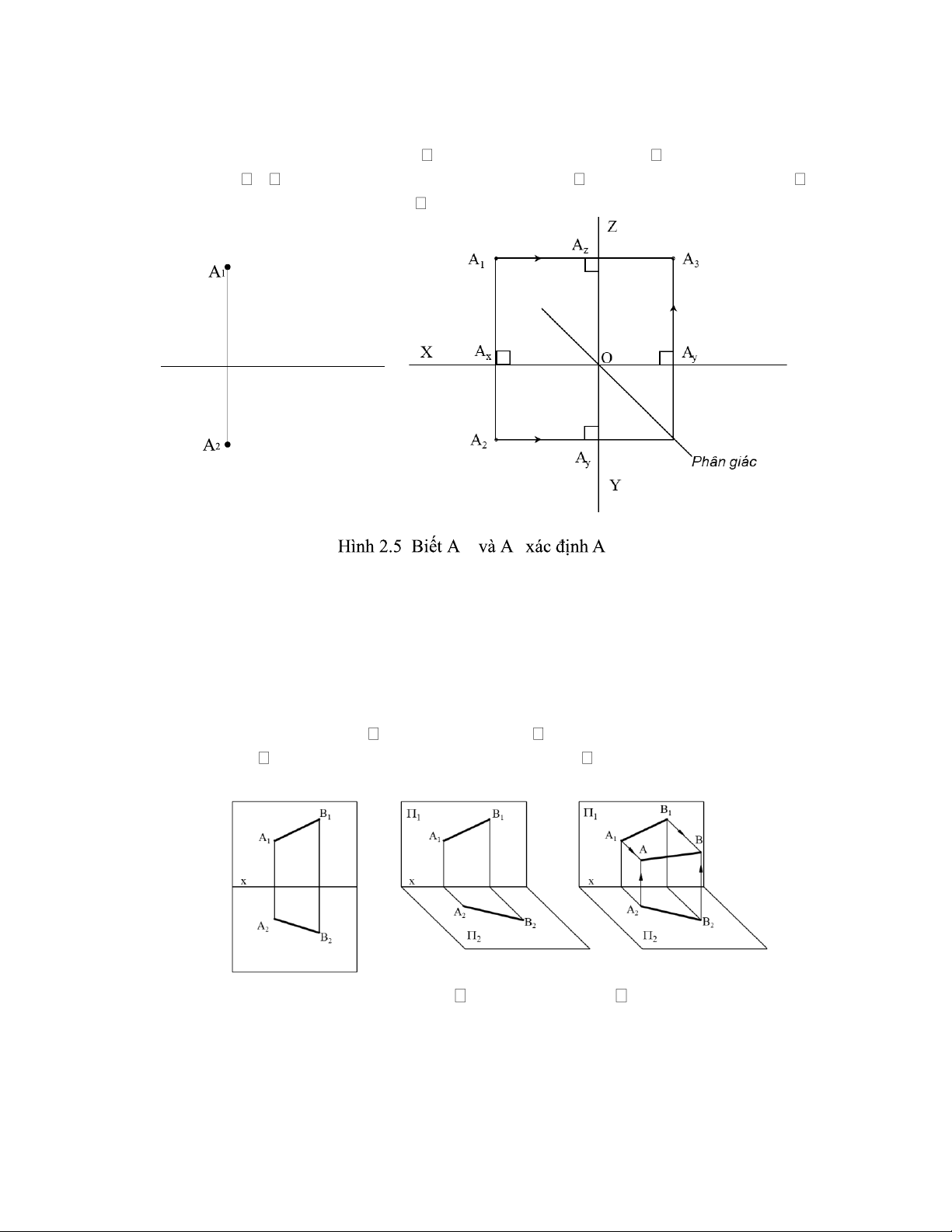
• Biết A1A2 xác định được A3 (hình 2.5).
Các bước xác định A3: Bước 1: Vẽ z x, vẽ phân giác góc II và IV Bước 2: qua A1 vẽ
đường A1Az z Bước 3: qua A2 vẽ đường thẳng A2Ay y đến cắt đường phân giác
Bước 4: Gióng vuông góc với trục x Đường gióng ở bước 2 và bước 4 cắt nhau là A3. 1 2 3 . 2.2 ĐƯỜNG THẲNG
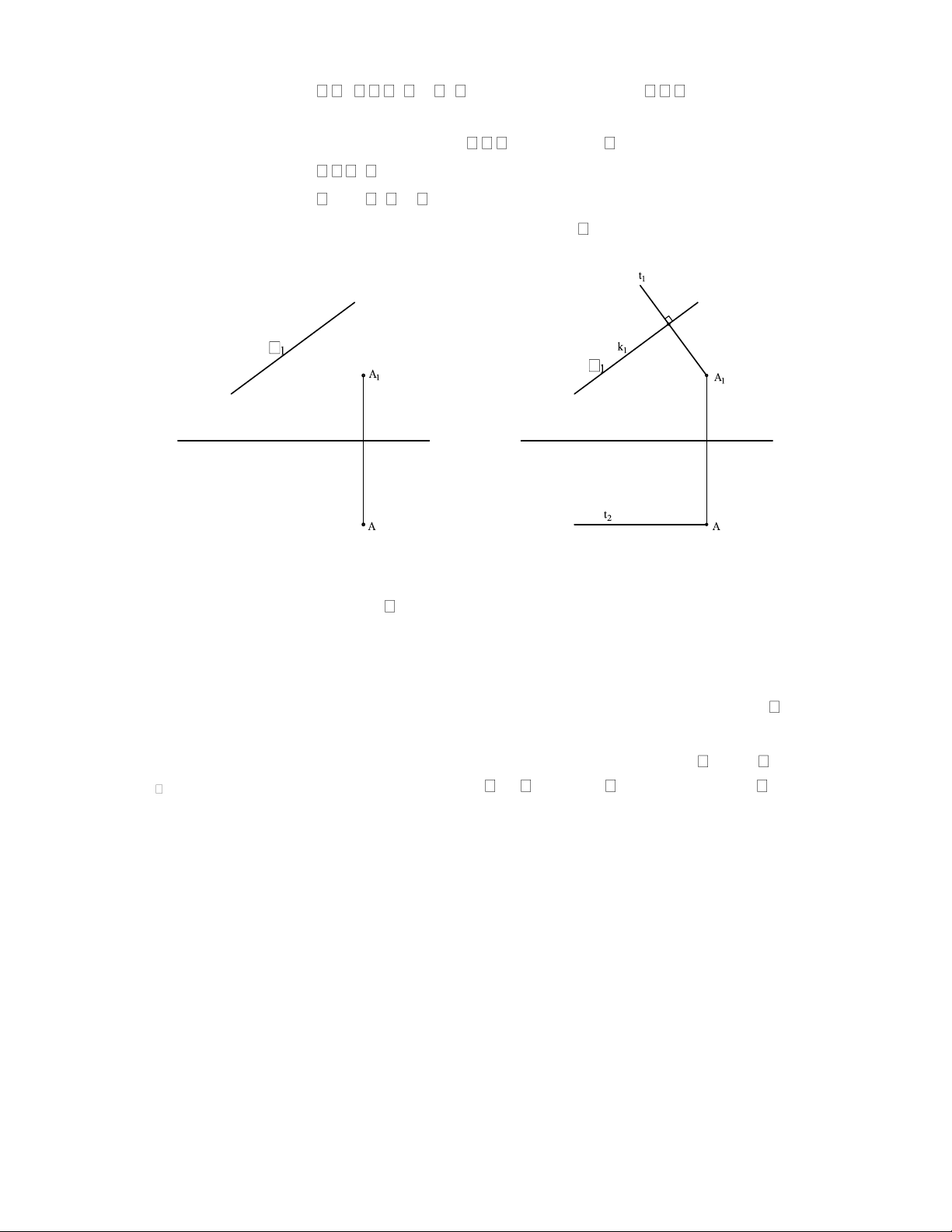
2.2.1 Biểu diễn đường thẳng. *
Trong mọi trường hợp, một đường thẳng xác định khi biết 2 điểm. Vì vậy có thể
biểu diễn một đường thẳng thông qua biểu diễn 2 điểm. Hình 2.6a là một ví dụ biểu diễn
đường thẳng bằng cách cho 2 điểm. Từ hình biểu diễn này, có thể xác định được AB trong
không gian bằng cách: Quay 2 về vuông góc với 1 (hình 2.6b), Qua A1, B1 vẽ các tia
vuông góc với 1 và qua A2, B2 vẽ các tia vuông góc với 2, chúng cắt nhau tương ứng là A,B (hình 2.6c).
a)Biểu diễn 2 điểm b) Quay 2 về vuông góc với 1 c) Tìm được AB
Hình 2.6: Biểu diễn đường thẳng thông qua biểu diễn 2 điểm
Hình 2.7a cũng là một ví dụ biểu diễn đường thẳng AB bằng 2 điểm A, B. Tuy nhiên đây
là một trường hợp đặc biệt: A1B1A2B2 nằm trên đường vuông góc với trục x. Trong trường
hợp này, AB song song với 3 và được gọi là đường cạnh. Tất nhiên là khi cho 2 điểm
như hình 2.7a, có thể xác định được A,B (hình 2.7b, 2.7c).
a) Biểu diễn 2 điểm b) Quay 2 về vuông góc với 1 c) Tìm được AB
Hình 2.7: Biểu diễn đường thẳng thông qua biểu diễn 2 điểm *
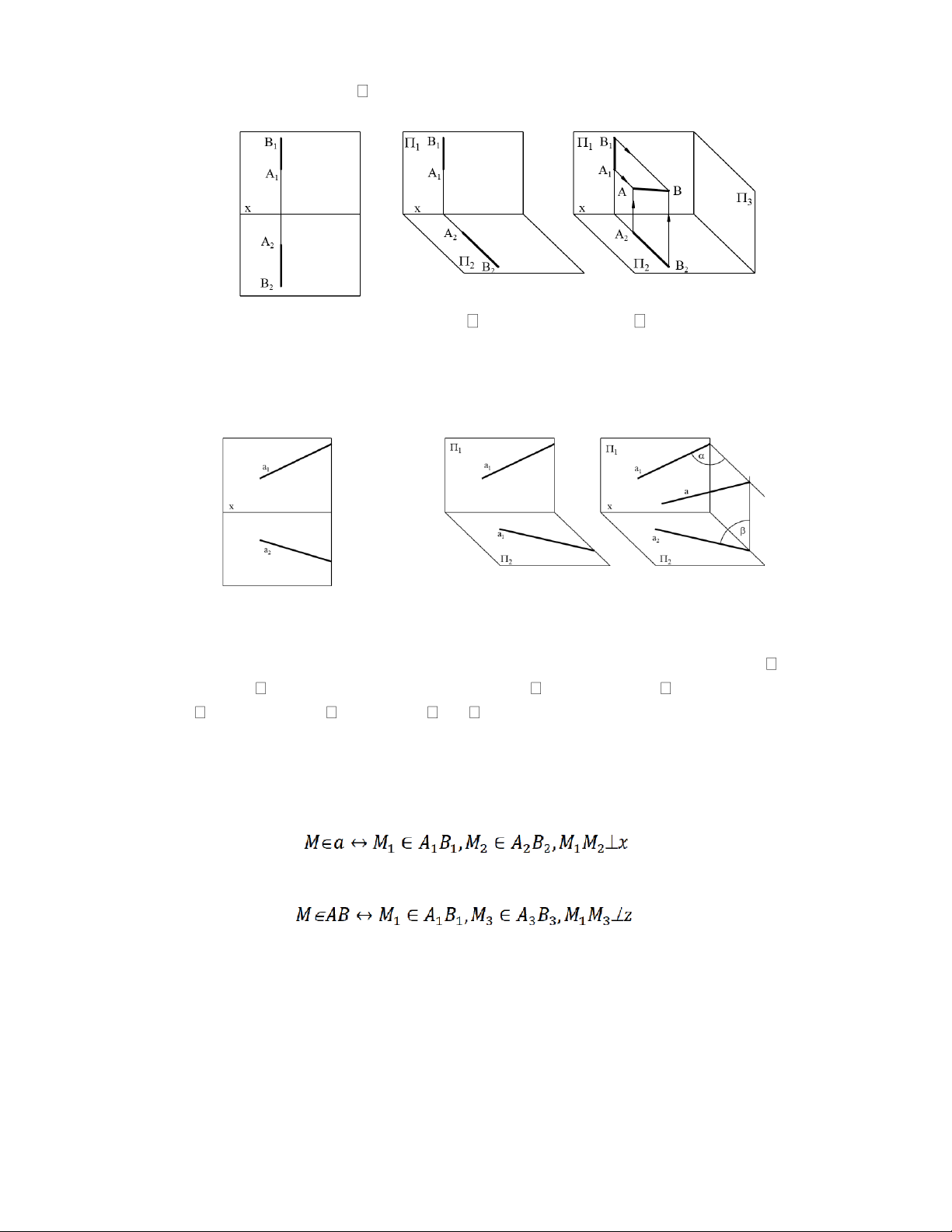
Có thể biểu diễn 1 đường thẳng bằng cách cho 2 hình chiếu của nó, với điều kiện
chúng không cùng vuông góc với x(hình 2.8a).
a) Biểu diễn a bằng 2 hình chiếu b) Xác định a trong không gian
Hình 2.8 Cho 2 hình chiếu của 1 đường thẳng, xác định được đường thẳng đó
Từ hình biểu diễn 2.8a, có thể xác định được a trong không gian bằng cách: Quay 2 về
vuông góc với 1 (hình 2.8b), Qua a1 vẽ mặt phẳng vuông góc với 1 và qua a2 vẽ mặt
phẳng vuông góc với 2. Giao của và là a (hình 2.8b).
2.2.2 Điều kiện điểm thuộc đường thẳng
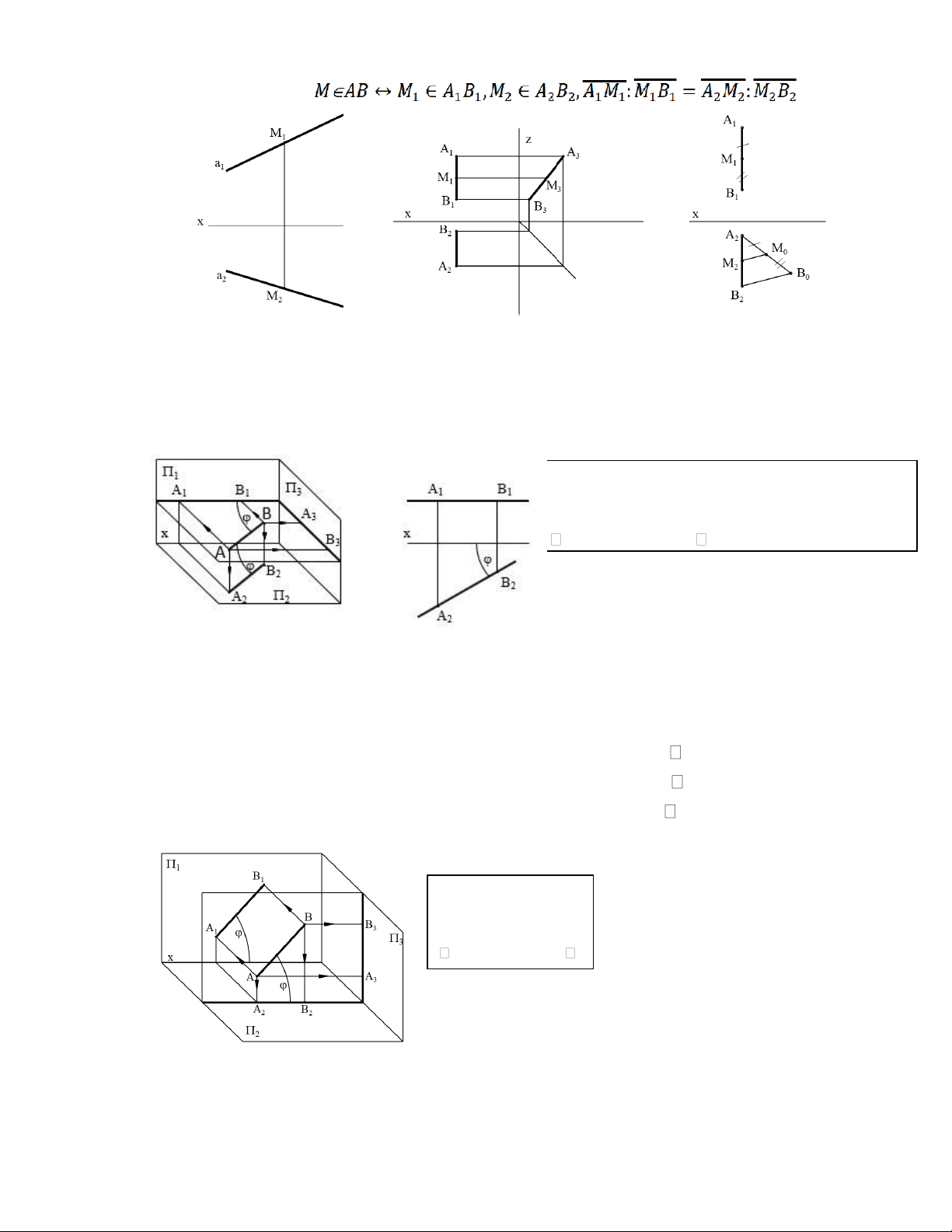
• Định lý 1(hình 2.9)- Điều kiện để điểm M thuộc đường thẳng a không phải là đường cạnh:
• Định lý 2(hình 2.10a)- Điều kiện để điểm M thuộc một đường thẳng AB là đường cạnh:
• Định lý 3(hình 2.10b)- Điều kiện để điểm M thuộc một đường thẳng AB là đường cạnh:
Hình 2.9 Hình 2.10a Hình 2.10b
2.2.3 Các đường thẳng có vị trí đặc biệt.
a) Đường bằng là đường thẳng song song với mặt phẳng hình chiếu bằng (hình 2.11). Tính chất: A1B1//x A2B2=AB là góc của AB và 1 Hình 2.11
b) Đường mặt là đường thẳng song song với mặt phẳng hình chiếu đứng (hình 2.12).
c) Đường cạnh là đường thẳng song song với mặt phẳng hình chiếu cạnh (hình 2.13).
d) Đường thẳng chiếu bằng là đường thẳng vuông góc với mặt phẳng 2 (hình 2.14).
e) Đường thẳng chiếu đứng là đường thẳng vuông góc với mặt phẳng 1 (hình 2.15).
f) Đường thẳng chiếu cạnh là đường thẳng vuông góc với mặt phẳng 3 (hình 2.16). Tính chất: A2B2//x A1B1=AB là góc của AB và 2 Hình 2.12 Hình 2.13 Hình 2.14 Hình 2.15 Hình 2.16
2.2.4 Vị trí tương đối của các đường thẳng.
Trong không gian, hai đường thẳng có thể cắt nhau, song song hoặc chéo nhau.
a) Hai đường thẳng cắt nhau
Việc kiểm tra hai đường thẳng có cắt nhau hay không được quy về việc kiểm tra hai đường
thẳng có chung nhau 1 điểm duy nhất hay không.
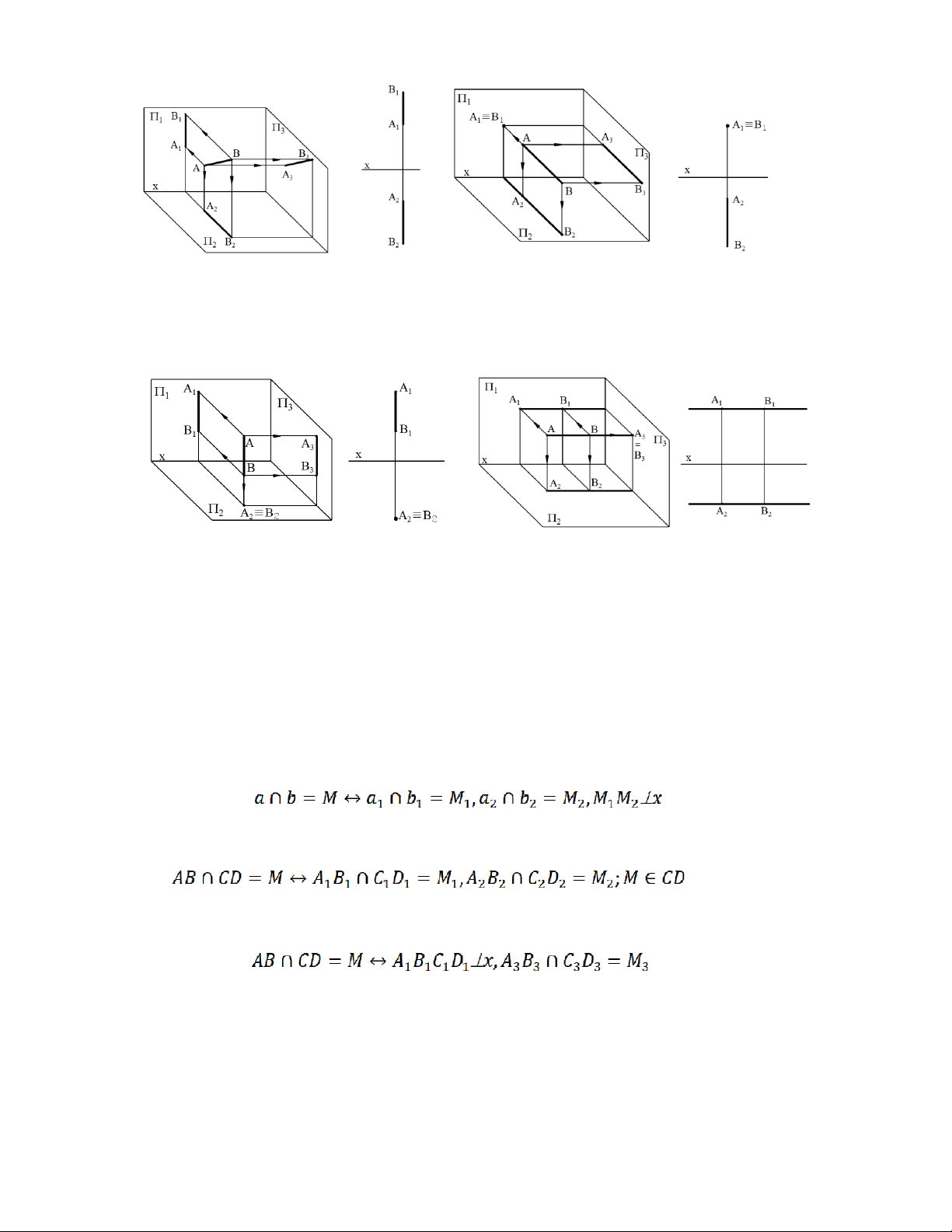
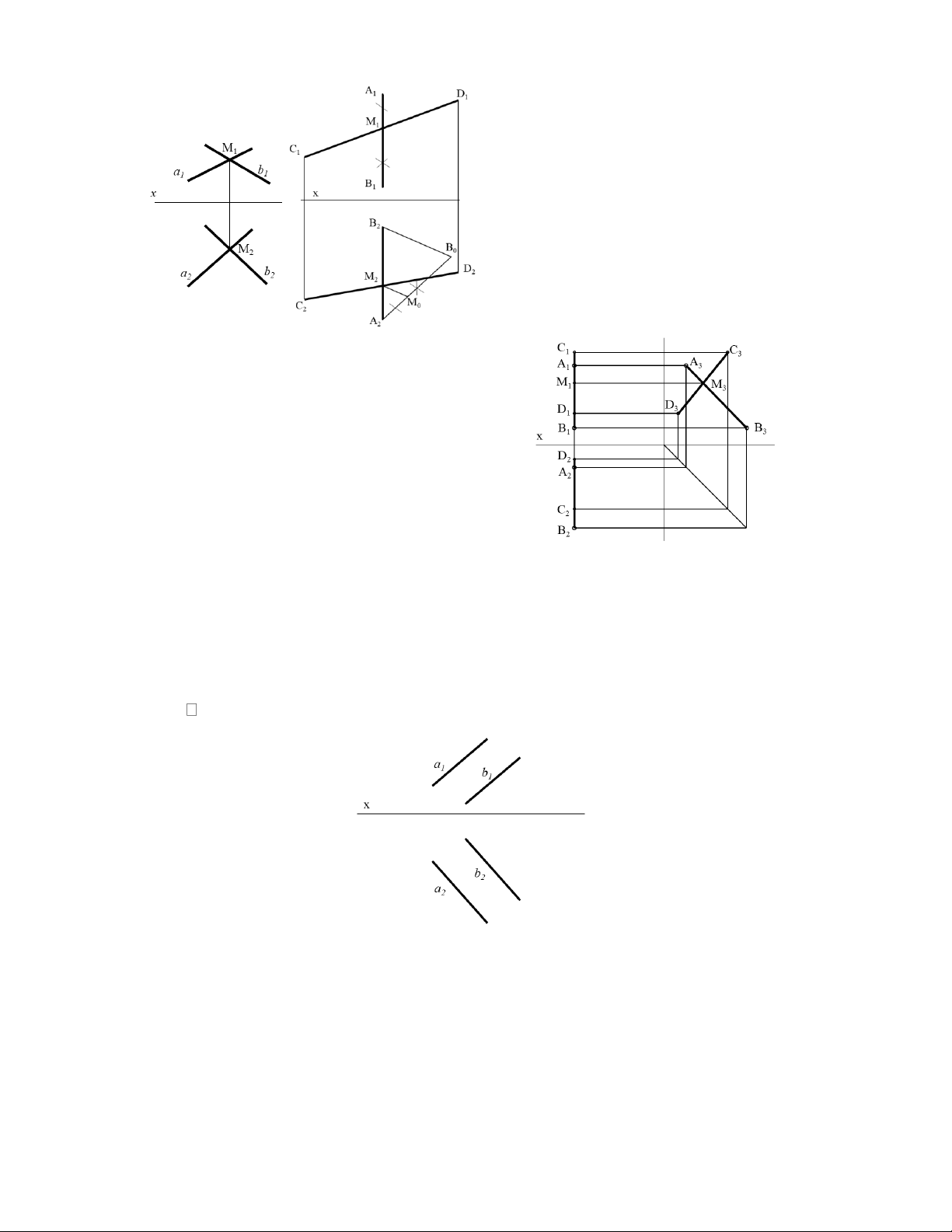
* Trường hợp hai đường thẳng bất kỳ, có thể sử dụng định lý sau: (hình 2.17).
* Trường hợp 1 trong hai đường là đường thẳng cạnh. Gọi AB là đường bất kỳ, CD là
đường cạnh. Ta có thể sử dụng định lý sau: (hình 2.18a).
Trong đó, để kiểm tra M thuộc CD hay không ta sử dụng các định lý trong mục 2.2.2.
* Trường hợp cả hai đường AB và CD đều là đường cạnh, có thể dùng định lý sau: (hình 2.18b).
Hình 2.17 Hình 2.18a Hình 2.18b
b) Hai đường thẳng song song.
Trên hình chiếu, việc kiểm tra hai đường thẳng có song song hay không dựa vào tính chất
2 của phép chiếu (đã trình bày ở trên).
* Trường hợp hai đưởng thẳng bất kỳ, có thể sử dụng định lý sau:
a//b a1//b1; a2//b2 (hình 2.19) Hình 2.19 Hình 2.20
* Trường hợp hai đường thẳng là 2 đường cạnh, có thế sử dụng định lý sau:
AB//CD A1B1//C1D1, A3B3//C3D3 (hình 2.20)
(Ngoài ra, có thể kiểm tra gián tiếp: Nối A-C và B-D. Nếu AC và BD cắt nhau hoặc
song song thì AB và CD song song với nhau.) c) Hai đường thẳng chéo nhau
Là hai đường thẳng không cắt nhau và không song song.
2.2.5 Hai đường thẳng vuông góc
Để giải các bài toán liên quan đến 2 đường thẳng vuông góc, cần sử dụng các định lý về
2 đường thẳng vuông góc:
• a,b là 2 đường thẳng bất kỳ, a b, a// i, b không i ai bi.
• ai bi, a b có ít nhất a hoặc b// i. D • a i
bi, có ít nhất a hoặc b// i a b. Ví dụ
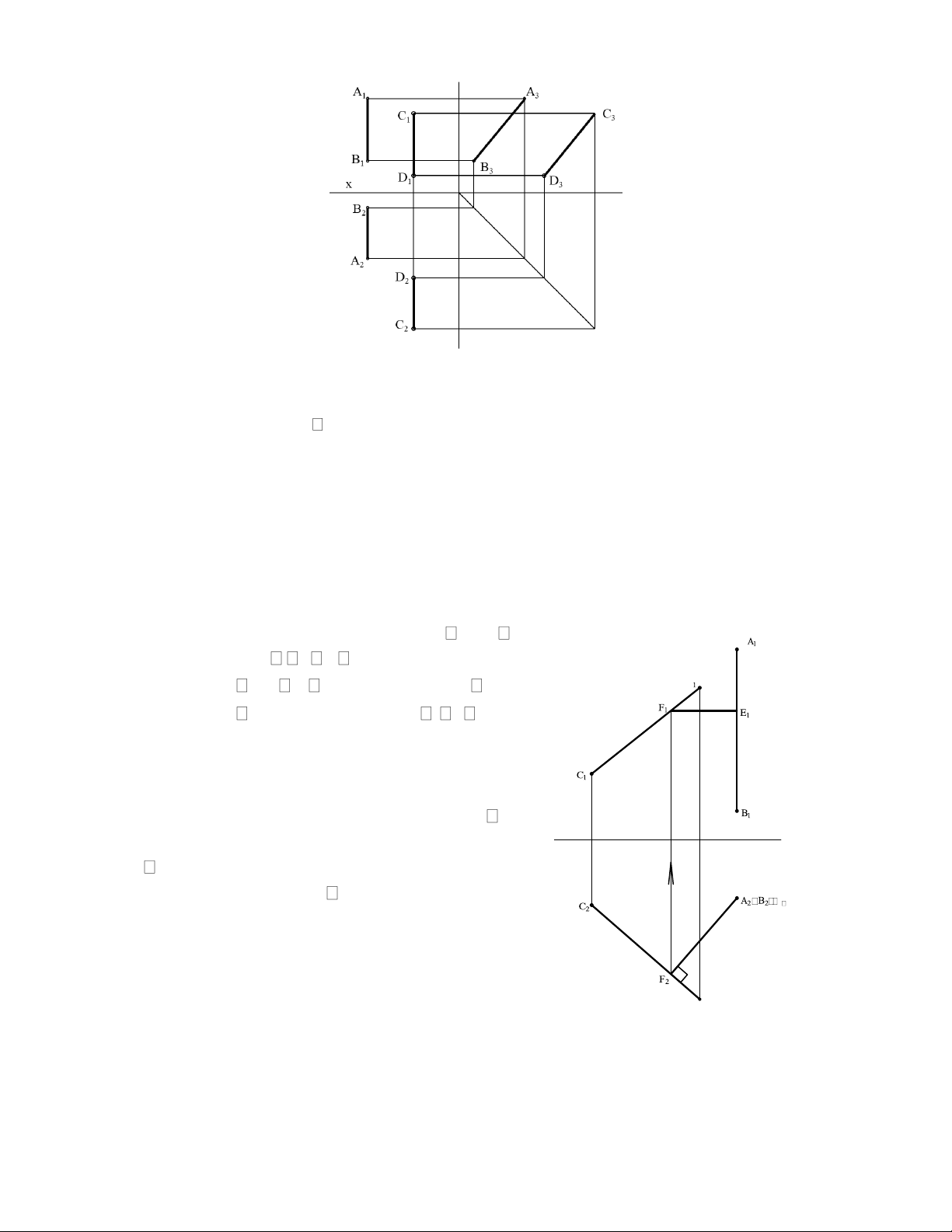
áp dụng: Vẽ đường vuông góc chung của
hai đường thẳng AB và CD (hình 2.21)
Giải: Gọi đường vuông góc chung là EF với E thuộc
AB, F thuộc CD. AB là đường vuông góc với 2 , EF
vuông góc với AB suy ra EF song song với
2. E thuộc AB nên E2 trùng A2. EF vuông góc với
CD, EF song song với 2 nên E2F2 vuông góc với
C2D2. Từ đó suy ra cách vẽ: Lấy E2 trùng A2. Từ E2
kẻ vuông góc với C2D2 tại F2. Từ F2 dóng về C1D1
được F1. Qua F1 kẻ song song với x, cắt A1B1 là E1. D 2 Hình 2.21 2.3.1 MẶT PHẲNG
2.3.1. Biểu diễn mặt phẳng
Để biểu diễn mặt phẳng chỉ cần chuyển đổi các phát biểu trong hình học không gian thành
phát biểu trên các hình chiếu. Trong không gian ta có các phát biểu sau:
- Cho 3 điểm không thẳng hàng xác định một mặt phẳng duy nhất.
- Cho 2 đường thẳng cắt nhau xác định duy nhất một mặt phẳng.
- Cho 2 đường thẳng song song xác định duy nhất một mặt phẳng.
- Cho 1 đường thẳng và một điểm không thuộc đường thẳng đó xác định duy nhất một mặt phẳng.
Các phát biểu đó được chuyển thành cách biểu diễn tương ứng trên hình chiếu như các
hình 2.22, hình 2.23, 2.24 và 2.25.
Hình 2.22 Hình 2.23 Hình 2.24 Hình 2.25
2.3.2 Điều kiện điểm, đường thẳng thuộc mặt phẳng
Có nhiều cách phát biểu điều kiện điểm, đường thẳng thuộc mặt phẳng. Có thể áp dụng 3
phát biểu sau đây để giải các bài toán điểm, đường thẳng thuộc mặt phẳng:
a) Phát biểu điều kiện *
Phát biểu 1: Điều kiện một điểm M thuộc một mặt phẳng là M thuộc một đường
thẳng a thuộc (hình 2.26). *
Phát biểu 2: Điều kiện một đường thẳng a thuộc một mặt phẳng là a đi qua 2
điểm M, N thuộc (hình 2.27). *
Phát biểu 3: Điều kiện một đường thẳng a thuộc một mặt phẳng là a đi qua một
điểm M thuộc và song song với một đường b thuộc (hình 2.28).
Hình 2.26 Hình 2.27 Hình 2.28 b) Bài tập áp dụng * Bài tập 1:
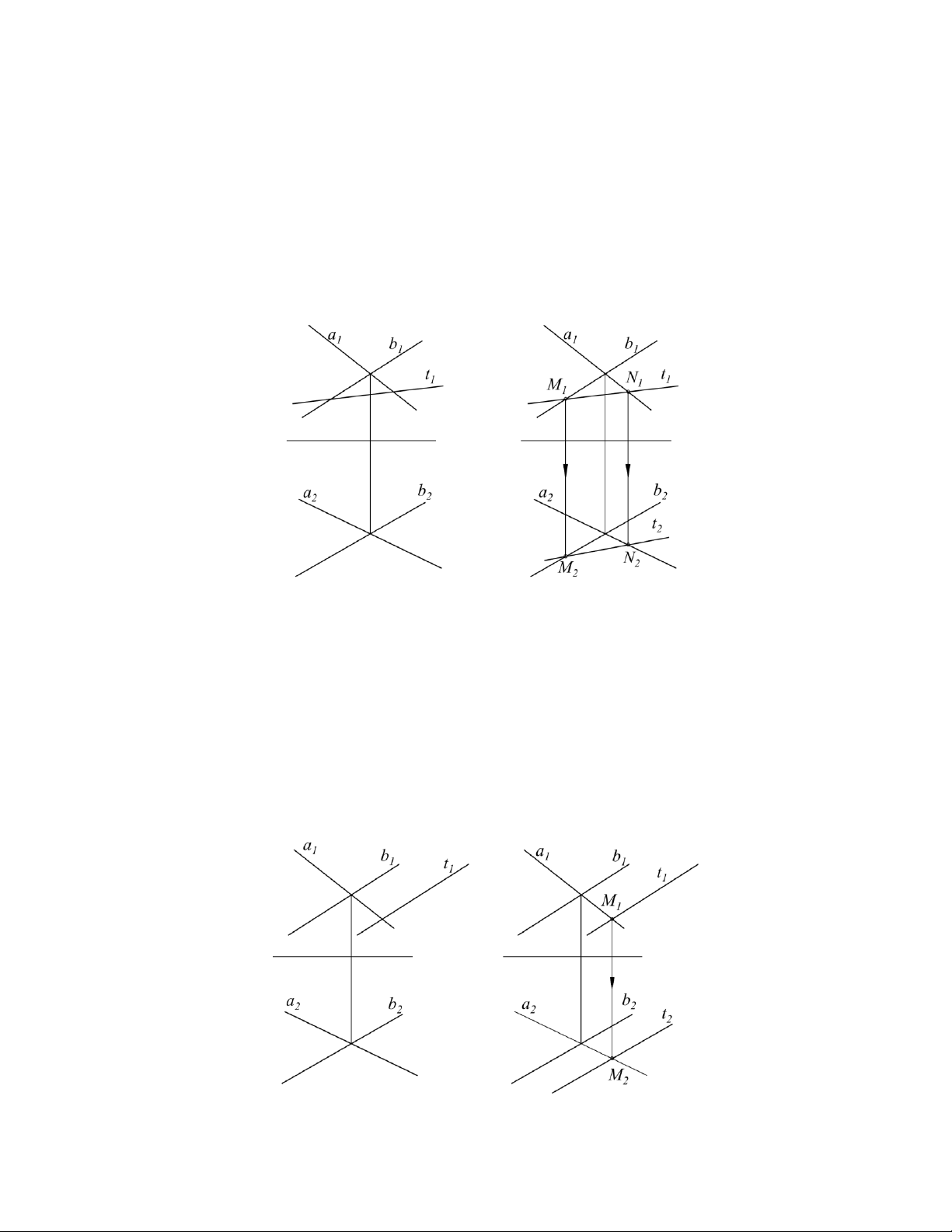
Biết rằng đường thẳng t thuộc mặt phẳng (a,b). Đã biết t1, tìm t2.
Phân tích đầu bài và hình vẽ: Theo hình của đầu bài, t1 cắt a1 và b1 nên ta dễ dàng áp dụng
phát biểu 2: Gọi giao của t1 với a1, b1 là N1, M1 và từ đó dóng về a2 và b2 tìm được N2, M2.
Nối M2N2 chính là t2 (hình 2.29). * Bài tập 2:
Biết rằng đường thẳng t thuộc mặt phẳng (a,b). Biết t1//b1, Tìm t2.
Phân tích đầu bài và hình vẽ: Theo hình của đầu bài, t1 // b1 nên ta sẽ áp dụng phát biểu 3:
Gọi giao của t1 với a1 là M1, từ đó dóng về a2 tìm được M2. Từ M2 vẽ t2 song song với b2 (hình 2.30). Hình 2.29 * Bài tập 3:
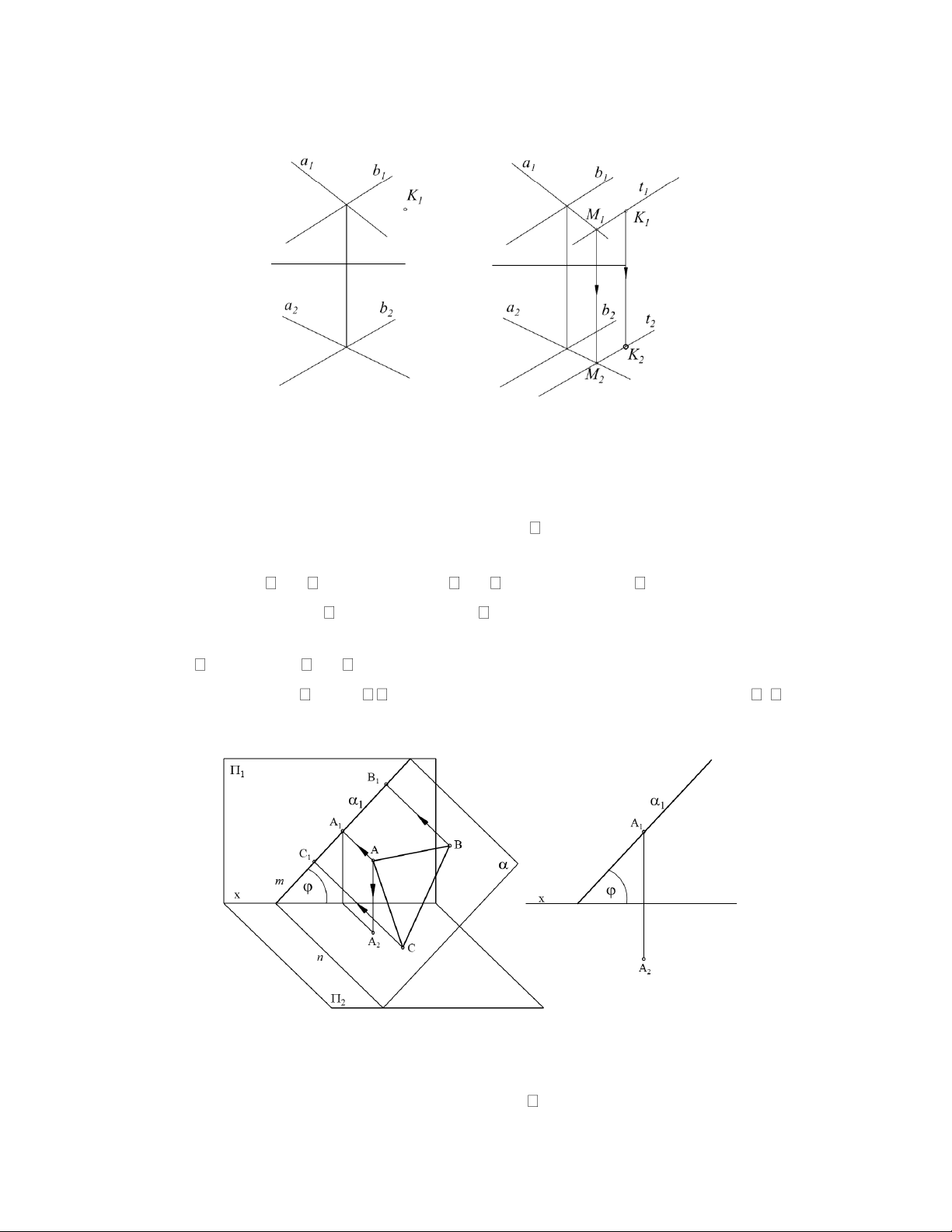
Biết rằng điểm K thuộc mặt phẳng (a,b). Đã biết K1, tìm K2.
Phân tích đầu bài và hình vẽ: Bài tập thuộc phần kiến thức điểm thuộc mặt phẳng, nên cần
áp dụng phát biểu 1. Qua một điểm, có thể vẽ được vô số đường thẳng trên mặt phẳng. Ta
có thể chọn vẽ qua K một đường t theo kiểu của bài tập 1(t1 qua K1 và cắt a1, b1) hoặc theo
kiểu bài tập 2(t1 qua K1 và //b1). Sau đó tìm được t2. Từ K1 dóng vuông góc với x đến t2, ta được K2( hình 2.31). Hình 2.30 Hình 3.31
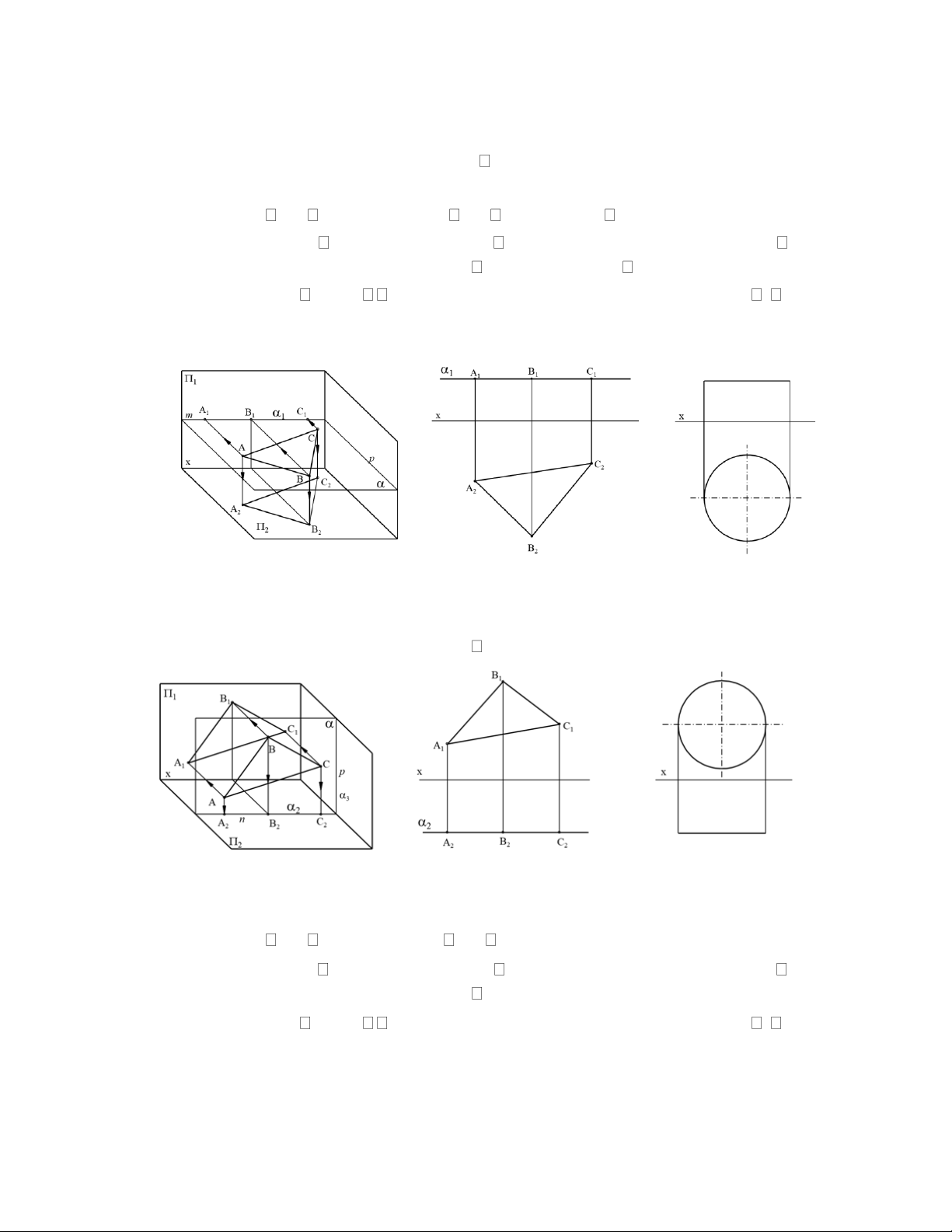
2.3.3 Các mặt phẳng có vị trí đặc biệt
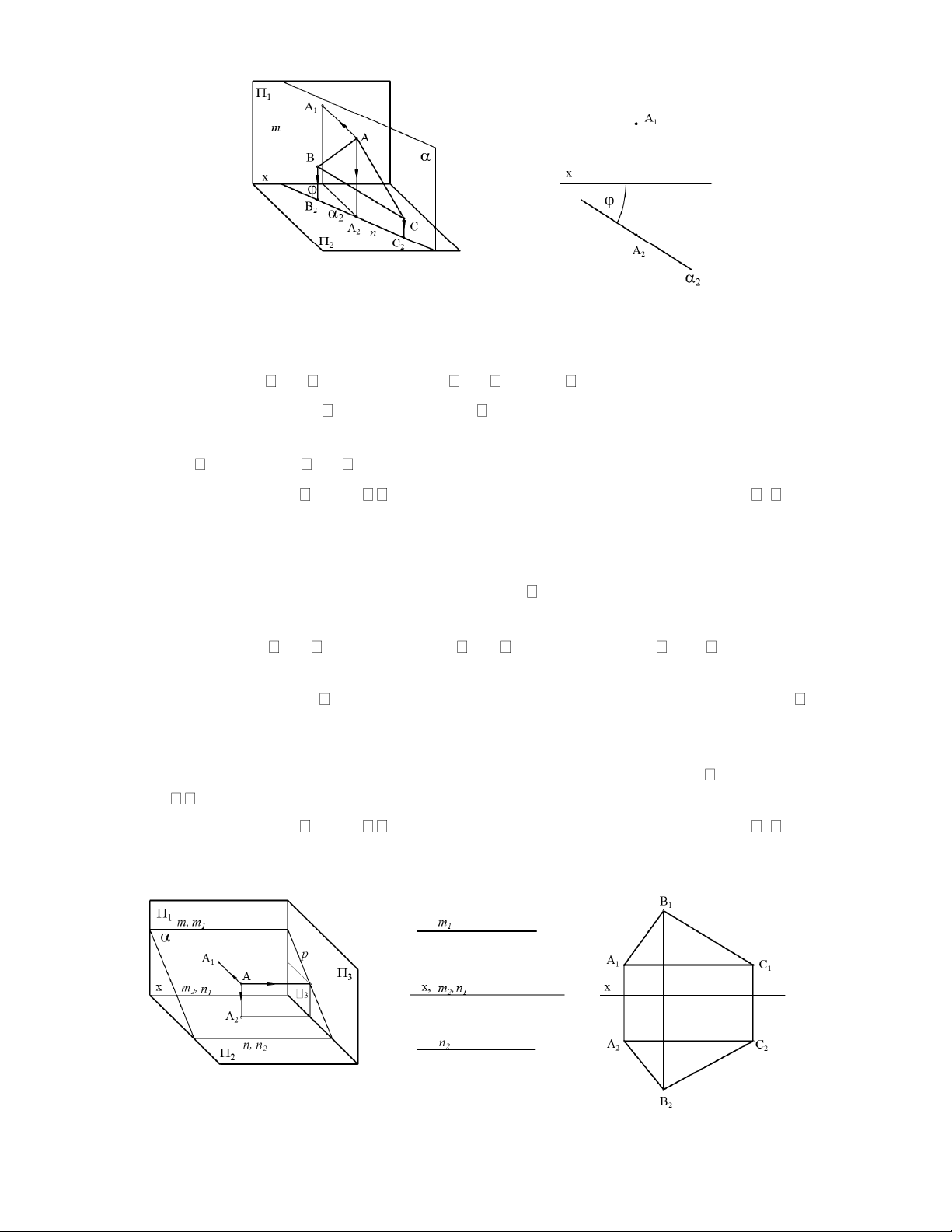
a) Mặt phẳng chiếu đứng
Mặt phẳng chiếu đứng là mặt phẳng vuông góc với 1(hình 2.32). Tính chất:
+ Gọi giao giữa và 1 là m, giao giữa và 2 là n. m bất kỳ, n x.
+ Hình chiếu đứng của là 1 đường thẳng 1 trùng với m. Hình chiếu bằng là toàn bộ mặt phẳng vẽ. + Góc là góc giữa và 2
+ Một điểm A thuộc thì A1
1. Một hình phẳng (đa giác, đường tròn, elip,…) thì
hình chiếu đứng là đoạn thẳng. Hình 2.32
b) Mặt phẳng chiếu bằng
Mặt phẳng chiếu bằng là mặt phẳng vuông góc với 2(hình 2.33). Hình 2.33 Tính chất:
+ Gọi giao giữa và 1 là m, giao giữa và 2 là n. m x, n bất kỳ.
+ Hình chiếu bằng của là 1 đường thẳng 2 trùng với n . Hình chiếu đứng là toàn bộ mặt phẳng vẽ. + Góc là góc giữa và 1
+ Một điểm A thuộc thì A2
2. Một hình phẳng (đa giác, đường tròn, elip,…) thì
hình chiếu bằng là đoạn thẳng.
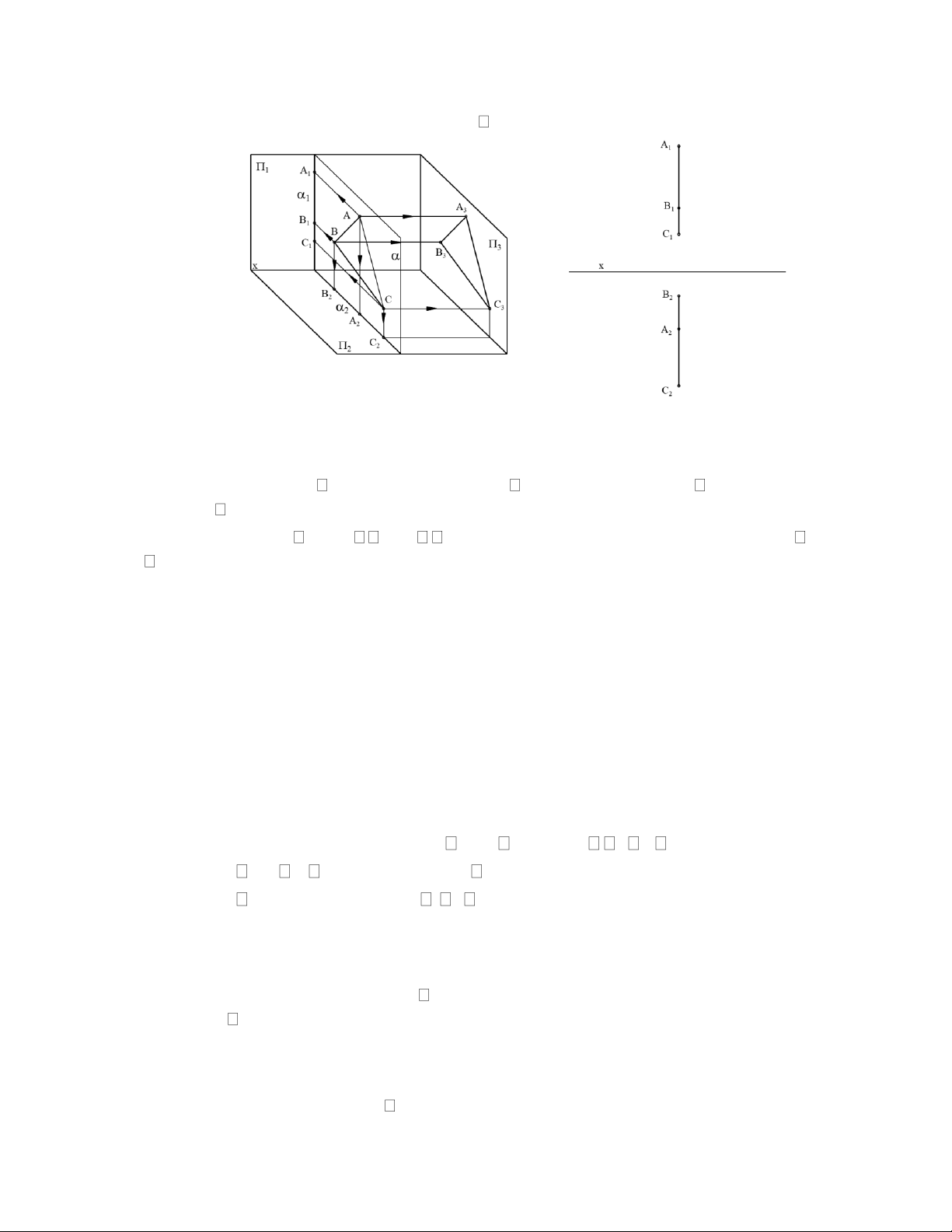
c) Mặt phẳng chiếu cạnh
Mặt phẳng chiếu cạnh là mặt phẳng vuông góc với 3(hình 2.34). Tính chất:
+ Gọi giao giữa và 1 là m, giao giữa và 2 là n và giao giữa với 3 là p. m//x, n//x, p bất kỳ.
+ Hình chiếu cạnh của là 1 đường thẳng (chính là p). Hình chiếu đứng và bằng của
là toàn bộ mặt phẳng vẽ.
+ Người ta thường biểu diễn mặt phẳng chiếu cạnh bằng cách cho 2 đường m, n(hình
2.35) hoặc biểu diễn mặt phẳng trong đó có một đường vuông góc với 3(hình 2.36: AC 3),…
+ Một điểm A thuộc thì A3
3. Một hình phẳng (đa giác, đường tròn, elip,…) thì
hình chiếu cạnh là đoạn thẳng. 3
Hình 2.34 Hình 2.35 Hình 2.36 d) Mặt phẳng bằng
Mặt phẳng bằng là mặt phẳng song song với 2. Tính chất:
+ Gọi giao giữa và 1 là m, giao giữa và 3 là p. m//x, p z (hình 2.37).
+ Hình chiếu đứng của là 1 đường thẳng //x( 1 trùng với m). Hình chiếu bằng của là
toàn bộ mặt phẳng vẽ. Hình chiếu cạnh của là 1 đường thẳng z (chính là p).
+ Một điểm A thuộc thì A1
1. Một hình phẳng (đa giác, đường tròn, elip,…) thì
hình chiếu đứng cạnh là đoạn thẳng còn hình chiếu bằng thì bằng hình thật(hình 2.38, 2.39)
Hình 2.37 Hình 2.38 Hình 2.39 e) Mặt phẳng mặt
Mặt phẳng mặt là mặt phẳng song song với 1(hình 2.40).
Hình 2.40 Hình 2.41a Hình 2.41b Tính chất:
+ Gọi giao giữa và 2 là n, giao giữa và 3 là p. n//x, p//z (hình 2.40).
+ Hình chiếu bằng của là 1 đường thẳng //x( 2 trùng với n). Hình chiếu đứng của là
toàn bộ mặt phẳng vẽ. Hình chiếu cạnh của là đường thẳng p.
+ Một điểm A thuộc thì A2
2. Một hình phẳng (đa giác, đường tròn, elip,…) thì
hình chiếu bằng, hình chiếu cạnh là các đoạn thẳng còn hình chiếu đứng thì bằng hình thật(hình 2.41a, 2.41b) f) Mặt phẳng cạnh
Mặt phẳng cạnh là mặt phẳng song song với 3(hình 2.42). Hình 2.42 Tính chất:
+ Hình chiếu đứng của và hình chiếu bằng của là những đường thẳng x. Hình chiếu
cạnh của là toàn bộ mặt phẳng vẽ.
+ Một điểm A thuộc thì A1 1, A2
2. Một hình phẳng (đa giác, đường tròn, elip,…)
thì hình chiếu đứng, hình chiếu bằng là các đoạn thẳng (hình 2.42) còn hình chiếu cạnh thì bằng hình thật.
3.3.4 Đường thẳng vuông góc với mặt phẳng
Để giải được các bài toán về đường thẳng vuông góc với mặt phẳng, chúng ta cần hai định
lý phát biểu về đường thẳng vuông góc với mặt phẳng trong không gian như sau:
• Đường thẳng vuông góc với mặt phẳng thì vuông góc với mọi đường thẳng thuộc mặt phẳng đó.
• Điều kiện để một đường thẳng vuông góc với một mặt phẳng là: đường thẳng đó
vuông góc với 2 đường thẳng cắt nhau thuộc mặt phẳng.
Ngoài ra chúng ta cũng cần áp dụng các định lý về hai đường thẳng vuông góc:
• a,b là 2 đường thẳng bất kỳ, a b, a// i, b không i ai bi.
• ai bi, a b có ít nhất a hoặc b// i.
• ai bi, có ít nhất a hoặc b// i a b.
Sau đây trình bày hai bài toán cơ bản về đường thẳng vuông góc với mặt phẳng. a) Bài toán cơ bản 1:
Cho một điểm A và một mặt phẳng . Qua A hãy vẽ một đường thẳng t vuông góc với mặt phẳng ).
Trường hợp thứ nhất: Mặt phẳng đã cho là mặt phẳng chiếu. Phân tích: (hình 2.43) •
t đi qua A t1 đi qua A1, t2 đi qua A2. • t , 1
t// 1 t2//x (Trong trường hợp 2, có thể lập luận tương tự) • Lấy 1 đường thẳng k k1 trùng với 1 • t t k •
t k, t// 1 t1 k1. Cách vẽ (hình 2.43):
Qua A2 vẽ t2 song song với x. Qua A1 vẽ t1 vuông góc với 1(hình 2.43). 2 2 Hình 2.43
Trường hợp thứ hai: Mặt phẳng (MNP) là mặt phẳng bất kỳ (hình 2.44).
Phân tích: Điều kiện một đường thẳng vuông góc với một mặt phằng là nó vuông góc với
2 đường thẳng cắt nhau của mặt phẳng đó. Để có thể áp dụng định lý về 2 đường thẳng
vuông góc ở trên, cần chọn một đường bằng và một đường mặt của mặt phẳng. Có thể đưa
về trường hợp thứ nhất nhờ phép thay mặt phẳng hình chiếu, biến đổi để mặt phẳng trở
thành mặt phẳng chiếu( sẽ trình bày ở chương sau).
Cách vẽ: Vẽ đường bằng MH và một đường mặt PF của mặt phẳng. MH// 2, MH t nên
t2 M2H2 . Từ A2 t2 vuông góc với M2H2. PF// 1, t PF nên t1 P1F1: Qua A1 vẽ t1 P1F1.
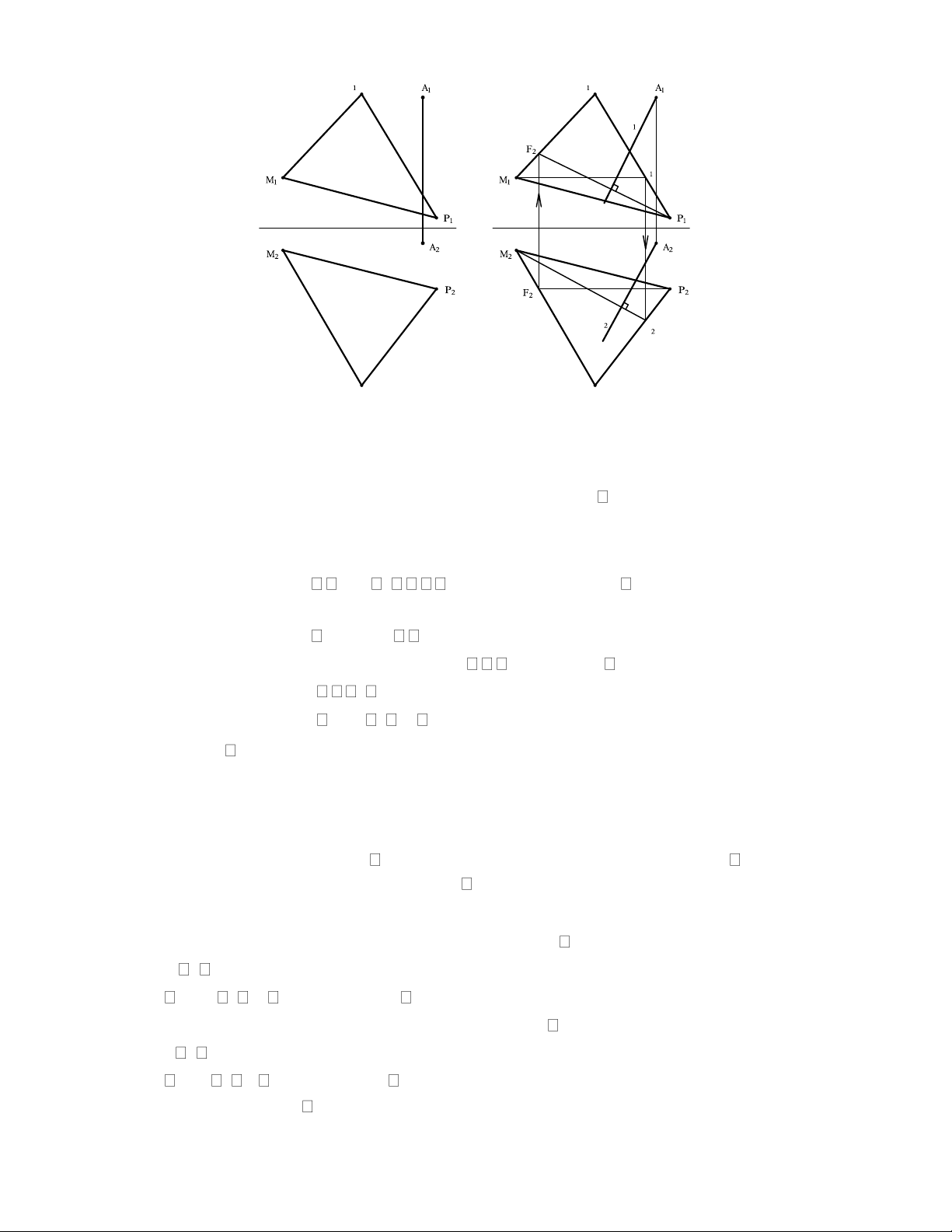
Đường thẳng t(t1, t2) thỏa mãn qua A và vuông góc với mặt phẳng (M,N,P). N N t H t H N2 N2 Hình 2.44 b) Bài toán cơ bản 2:
Cho một điểm A và một đường thẳng t. Qua A vẽ mặt phẳng vuông góc với t.
Trường hợp thứ nhất: Đường thẳng đã cho là đường bằng hoặc đường mặt.. Phân tích: • t, t// 1 1 (Trong trường hợp t//
2, có thể lập luận tương tự) • đi qua A
1 là một đường thẳng đi qua A1 • Lấy 1 đường thẳng k k1 trùng với 1 • t t k • t k, t// 1 t1 k1. Cách vẽ:
Qua A1 vẽ 1 vuông góc với t1(hình 2.45).
Trường hợp thứ hai: t là thẳng bất kỳ. Có thể đưa về trường hợp thứ nhất nhờ phép thay
mặt phẳng hình chiếu( sẽ trình bày ở chương sau) hoặc giải như sau: Phân tích:
Điều kiện để t vuông góc với là t vuông góc với hai đường cắt nhau thuộc . Chọn 2
đường đặc biệt, cắt nhau thuộc mặt phẳng : một đường bằng và một đường mặt. Cách vẽ (hình 2.46): •
Vẽ đường bằng h của mặt phẳng :
+ h// 1 h1//x: Qua A1 vẽ h1//x
+ t h, h// 2 h2 t2: Qua A2 vẽ h2 t2. •
Vẽ đường mặt f của mặt phẳng .
+ f// 2 f2//x: Qua A2 vẽ f2//x
+ t f, f// 1 f1 t1: Qua A1 vẽ f1 t1.
Kết luận: Mặt phẳng (h,f) là mặt phẳng đi qua A và vuông góc với t.