










































































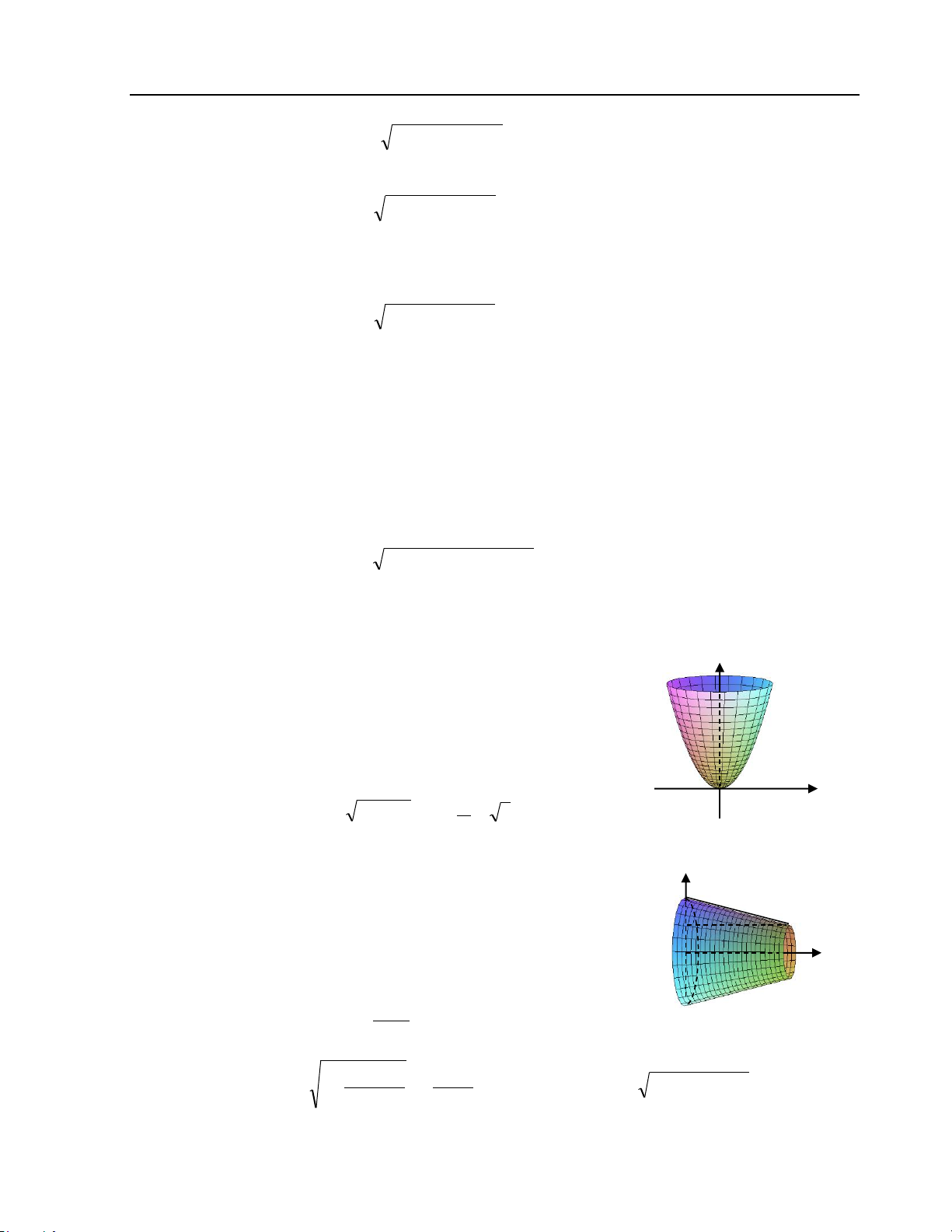
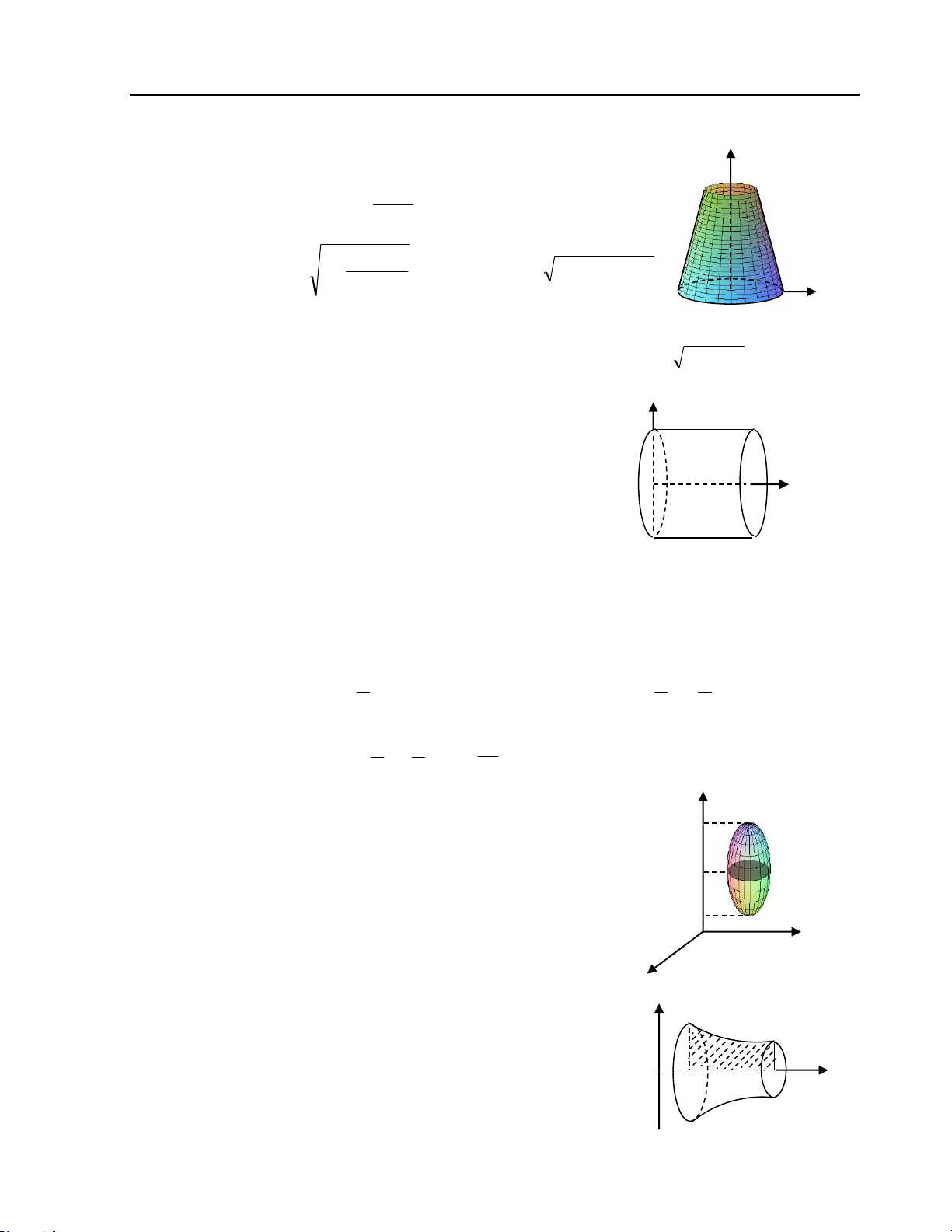
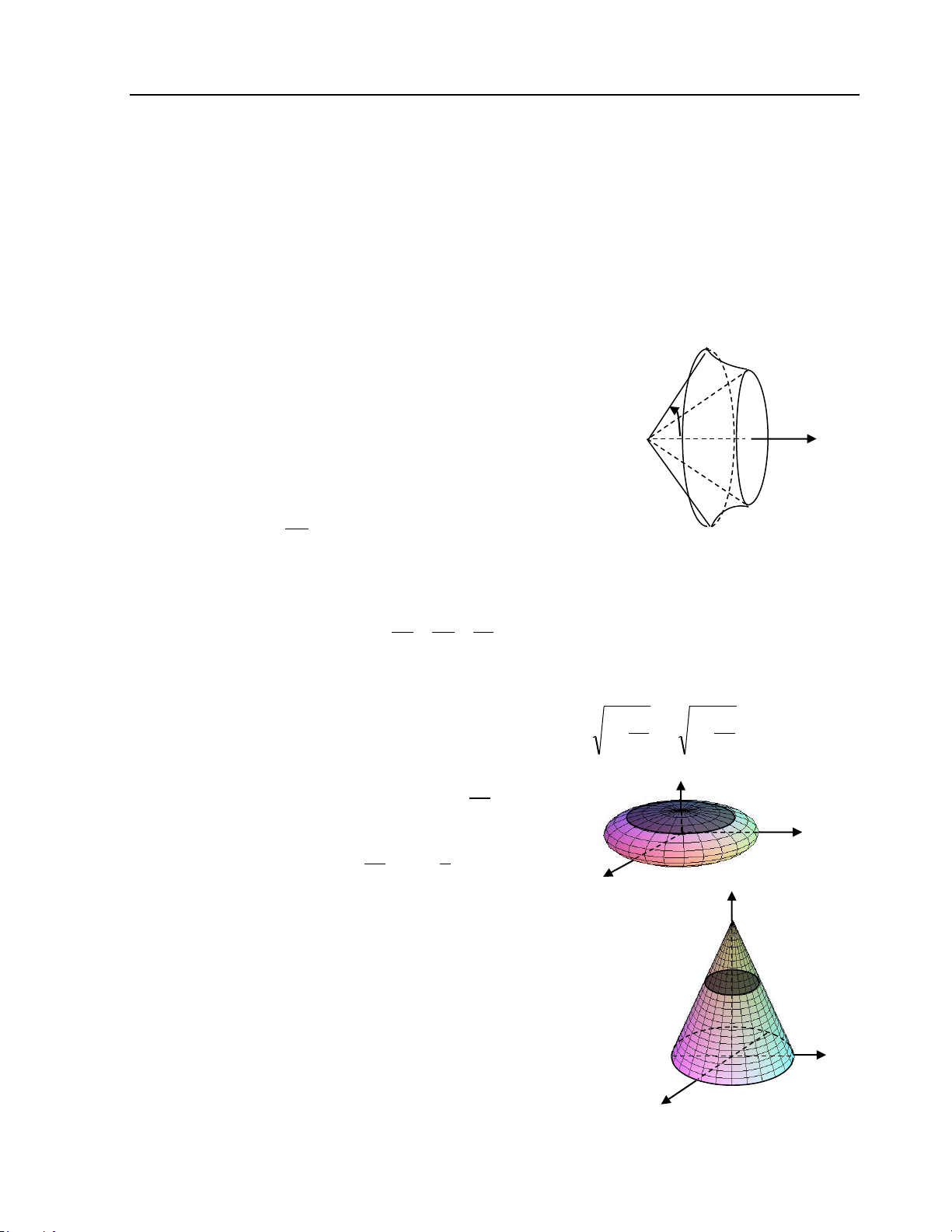
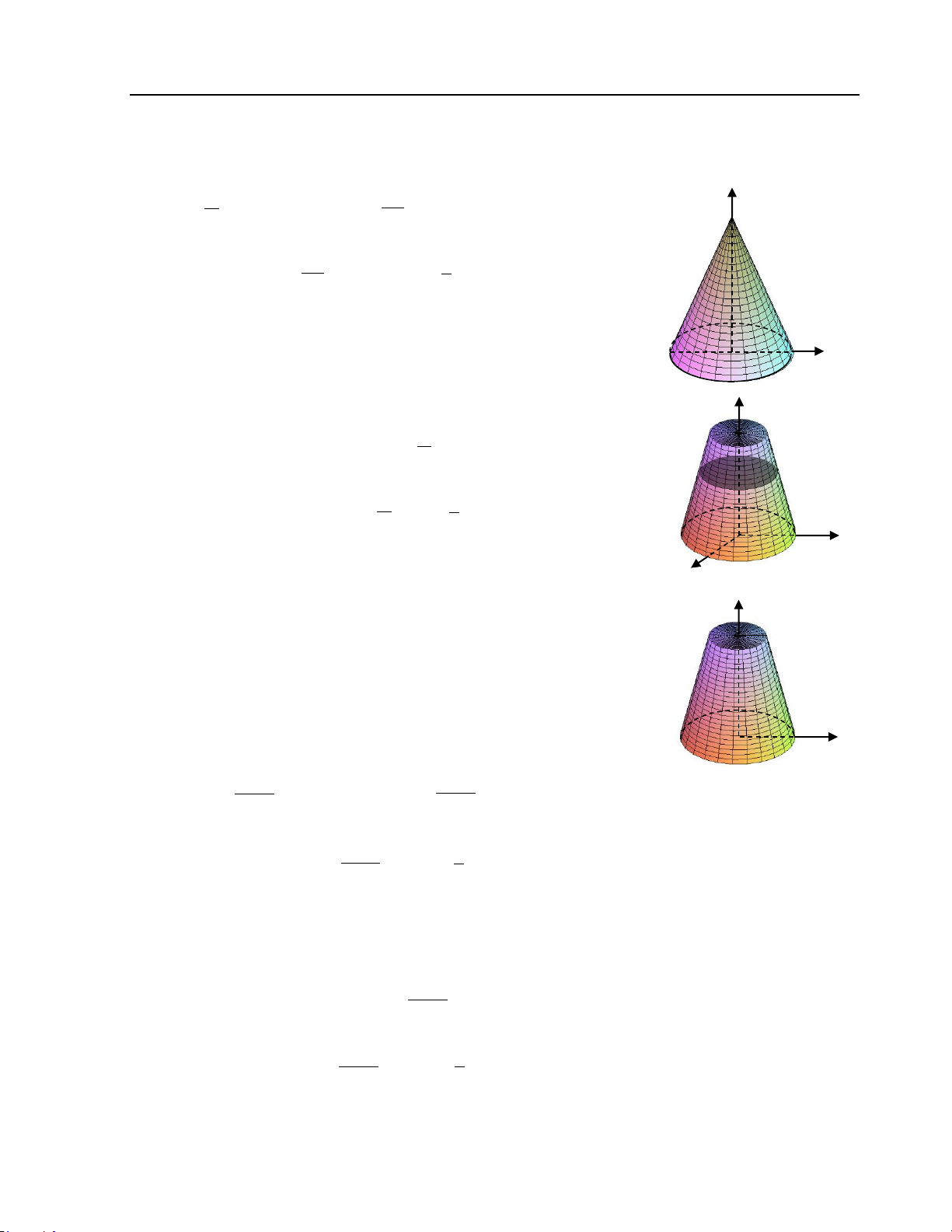



















































Preview text:
TRƯàNG ĐẠI HỌC Kþ THU¾T - CÔNG NGHỆ CẦN THƠ
KHOA KHOA HỌC CƠ BẢN BỘ MÔN TOÁN BÀI GIẢNG GIẢI TÍCH 1
(Dùng cho các lßp chuyên ngành kÿ thu¿t) Năm 2020
KHOA KHOA HỌC CƠ B¾N Tài liệu tham kh¿o chính
TÀI LIỆU THAM KHẢO CHÍNH
[1] Nguyễn Đình Trí (chủ biên): Toán học cao cấp tập 1, 2. NXB Giáo dục - Hà Nội 2005,
[2] Nguyễn Đình Trí (chủ biên): Bài tập Toán học cao cấp tập 1, 2. NXB Giáo dục - Hà Nội 2005,
[3] G.M Fichtengôn: Giáo trình phép tính vi tích phân tập 1, 2. NXB Giáo dục - Hà Nội 1969,
[4] Jean-Maria Monier: Giải tích tập 1, 2 NXB Giáo dục - Hà Nội 1999,
[5] Phan Quốc Khánh: Phép tính vi tích phân tập 1. NXB Giáo dục - Hà Nội 2000, 1
KHOA KHOA HỌC C¡ B¾N Mục lục MỤC LỤC
Tài liệu tham kh¿o chính ................................................................................................. 1
Mục lục ............................................................................................................................ 2
Chư¢ng 1: TÀP HþP – ÁNH X¾ – HÀM Sà MâT BIÀN .......................................... 6
1.1. TÀP HþP ............................................................................................................... 6
1.1.1. Khái nißm tÁp hÿp....................................................................................... 6
1.1.2. Các phép toán ............................................................................................. 7
1.1.3. Các kí hißu toán học th°ờng dùng .............................................................. 7
1.2. ÁNH X¾ ................................................................................................................ 8
1.2.1. Đßnh nghĩa và ví dā .................................................................................... 8
1.2.2. Các lo¿i ánh x¿............................................................................................ 9
1.3. HÀM Sà MâT BIÀN Sà .................................................................................... 10
1.3.1. Đßnh nghĩa ................................................................................................ 10
1.3.2. Các ph°¢ng pháp cho hàm sá ................................................................... 11
1.3.3. Các d¿ng hàm sá ....................................................................................... 12
1.3.4. Phép toán .................................................................................................. 12
1.3.5. Tính chÁt ................................................................................................... 14
1.3.6. Hàm s¢ cÁp ............................................................................................... 15
1.4. DÃY Sà VÀ GIäI H¾N CĂA DÃY Sà ............................................................ 17
1.4.1. Dãy sá ....................................................................................................... 17
1.4.2. Giåi h¿n căa dãy ....................................................................................... 18
1.4.3. Sá e ........................................................................................................... 20
BÀI TÀP CH¯¡NG 1 .................................................................................................. 21
Chư¢ng 2: PHÉP TÍNH VI PHÂN HÀM MâT BIÀN ................................................ 23
2.1. GIäI H¾N CĂA HÀM Sà .................................................................................. 23
2.1.1. Các đßnh nghĩa .......................................................................................... 23
2.1.2. Phép toán và tính chÁt ............................................................................... 27
2.1.3. Các giåi h¿n c¢ b¿n .................................................................................. 28 2
KHOA KHOA HỌC C¡ B¾N Mục lục
2.1.4. Vô cùng bé và vô cùng lån ....................................................................... 30
2.2. HÀM Sà LIÊN TĀC ........................................................................................... 31
2.2.1. Đßnh nghĩa và ví dā .................................................................................. 31
2.2.2. Phép toán và tính chÁt ............................................................................... 33
2.3. Đ¾O HÀM ........................................................................................................... 34
2.3.1. Đßnh nghĩa, ý nghĩa hình học và vÁt lý ..................................................... 34
2.3.2. Tính chÁt và phép toán .............................................................................. 36
2.3.3. Đ¿o hàm cÁp cao ....................................................................................... 37
2.3.4. Vi phân ...................................................................................................... 38
2.3.5. Các đßnh lý về giá trß trung bình ............................................................... 39
2.4. ĄNG DĀNG ........................................................................................................ 41
2.4.1. Tìm cÿc trß hàm sá .................................................................................... 41
2.4.2. Giá trß lån nhÁt và giá trß nhß nhÁt ............................................................ 42
2.4.3. Tính gần đúng nhờ vi phân ....................................................................... 43
2.4.4. Quy tắc L’Hopital ..................................................................................... 45
2.4.5. Công thąc Taylor ...................................................................................... 47
2.4.6. Kh¿o sát và v¿ đồ thß hàm sá theo tham sá trong tọa đã cÿc ................... 49
BÀI TÀP CH¯¡NG 2 .................................................................................................. 55
Chư¢ng 3: PHÉP TÍNH TÍCH PHÂN .......................................................................... 59
3.1. TÍCH PHÂN BÀT ĐÞNH .................................................................................... 59
3.1.1. Khái nißm tích phân bÁt đßnh .................................................................... 59
3.1.2. Các ph°¢ng pháp tính tích phân bÁt đßnh ................................................. 61
3.1.3. Mãt sá d¿ng tích phân bÁt đßnh ................................................................ 64
3.2. TÍCH PHÂN XÁC ĐÞNH .................................................................................... 72
3.2.1. Khái nißm tích phân xác đßnh ................................................................... 72
3.2.2. Ph°¢ng pháp tính tích phân xác đßnh ....................................................... 74
3.3. TÍCH PHÂN SUY RâNG ................................................................................... 78
3.3.1. Tích phân suy rãng lo¿i I .......................................................................... 78
3.3.2. Tích phân suy rãng lo¿i II ......................................................................... 80 3
KHOA KHOA HỌC C¡ B¾N Mục lục
3.4. ĄNG DĀNG ........................................................................................................ 83
3.4.1. Ąng dāng trong toán học .......................................................................... 83
3.4.2. Ąng dāng trong kỹ thuÁt ........................................................................... 91
BÀI TÀP CH¯¡NG 3 .................................................................................................. 94
Chư¢ng 4: LÝ THUYÀT CHUàI ................................................................................ 98
4.1. CHUàI Sà, Sþ HâI TĀ CĂA CHUàI Sà ........................................................ 98
4.1.1. Chuái sá .................................................................................................... 98
4.1.2. Chuái sá d°¢ng ....................................................................................... 100
4.1.3. Chuái đan dÁu ......................................................................................... 102
4.1.4. Hãi tā tuyßt đái và bán tā ....................................................................... 103
4.2. CHUàI LiY THĆA ......................................................................................... 104
4.2.1. Đßnh nghĩa .............................................................................................. 104
4.2.2. Miền hãi tā .............................................................................................. 105
4.2.3. Khai triển mãt hàm thành chuái ljy thća& ........................................... 107
4.2.4 Mãt vài ąng dāng để tính gần đúng ........................................................ 109
BÀI TÀP CH¯¡NG 4 ................................................................................................ 111
Chư¢ng 5: PH¯¡NG TRÌNH VI PHÂN ................................................................... 113
5.1. KHÁI NIÞM PH¯¡NG TRÌNH VI PHÂN ...................................................... 113
5.1.1. Mãt sá ví dā d¿n tåi ph°¢ng trình vi phân ............................................. 113
5.1.2. Đßnh nghĩa .............................................................................................. 113
5.2. PH¯¡NG TRÌNH VI PHÂN CÀP 1................................................................. 114
5.2.1. Đßnh nghĩa .............................................................................................. 114
5.2.2. Các ph°¢ng trình d¿ng khuyÁt ............................................................... 115
5.2.3. Mãt sá lo¿i ph°¢ng trình vi phân cÁp 1 khác& ..................................... 117
5.2.4 Ph°¢ng pháp tham sá hóa tßng quát để gi¿i PTVP cÁp 1 ...................... 128
5.3. PH¯¡NG TRÌNH VI PHÂN CÀP 2................................................................. 130
5.3.1. Đßnh nghĩa .............................................................................................. 130
5.3.2. Các ph°¢ng trình d¿ng khuyÁt ............................................................... 131
5.3.3. Ph°¢ng trình vi phân tuyÁn tính cÁp 2 .................................................... 136 4
KHOA KHOA HỌC C¡ B¾N Mục lục
5.4. HÞ PH¯¡NG TRÌNH VI PHÂN ...................................................................... 142
5.4.1. Khái nißm chung ..................................................................................... 142
5.4.2. Mãt vài ph°¢ng pháp gi¿i ....................................................................... 143
BÀI TÀP CH¯¡NG 5 ................................................................................................ 145 5
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số Chương 1:
T¾P HþP - ÁNH X¾ - HÀM SÞ 1.1. T¾P HþP
1.1.1. Khái niệm t¿p hÿp
Tập hợp (tập) là một trong những khái niệm cơ bản của toán học, không được
định nghĩa mà chỉ được mô tả qua các ví dụ.
Chẳng hạn: tập tất cả sinh viên của một lớp học, tập tất cả các số nguyên, tập tất
cả các điểm trên một đường thẳng, tập hợp tất cả các bàn ghế trong một hội trường, ...
Tập hợp thường được ký hiệu bởi các chữ cái La-tinh in: A, B, C, ..., X, Y, Z ...
Còn phần tử, ký hiệu bởi các chữ la tinh
thường: a, b, c, ..., x, y, z ...
Nếu x thuộc tập A thì viết x þ A (đọc là x thuộc A), còn y không thuộc tập A thì
viết y þ A hay y ÿ A (đọc là y không thuộc A).
Các cách xác định một tập hợp:
- Liệt kê, ví dụ: A = {a, b} để chỉ A gồm các phần tử a, b. Vậy a þ A, c ÿ A
- Chỉ ra tính chất, ví dụ: X = {x þ ℝ| x2 – 3x + 2 = 0}. Vậy 2 þ X, 5 ÿ X.
- Dùng biểu đồ Ven, vẽ một đường cong kín và phần tử thuộc tập hợp thì nằm
trong, phần tử không thuộc thì nằm ngoài phần mặt phẳng giới hạn bởi đường cong ấy.
Các tập hợp số:
Tập các số tự nhiên ký hiệu là ℕ, vậy 1, 2, 3, ... þ ℕ còn – 3; 7,52 ÿ ℕ.
Tập các số nguyên ký hiệu là ℤ, vậy 0, 2, 7 þ ℤ còn 0,15; 7,52 ÿ ℤ.
Tập các số hữu tỷ ký hiệu là ℚ, vậy 3,2; 0,4; 15 þ ℚ, còn 2 , ð ÿ ℚ.
Tập các số vô tỷ ký hiệu là I, vậy 2 , – 5 þ I còn 0; – 2; – 3,14 ÿ I
Tập số thực ký hiệu là ℝ = ℚ ø I
Tập không chứa một phần tử nào được gọi là tập rỗng (trống) và ký hiệu ö, 6
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số 1.1.2. Các phép toán
a) Tập con: Tập A được gọi là tập con của tập B và ký hiệu là A B nếu mọi phần tử
của tập A đều là phần tử của tập B.
Ví dụ: Nếu A = {1, 2, 3} và B = {0, 1, 2, 3, 4, 5} thì A B. A B
Hay ℕ ℤ ℚ ℝ A B
Chú ý: Với mọi tập A ta có: ö A và A A.
b) Bằng nhau: Hai tập A và B được gọi là bằng nhau và ký hiệu là A = B, nếu mọi x þ
A tương đương x þ B hay A B và B A.
Ví dụ: Nếu A = {1; 2} và B = {x þ ℝ| x2 – 3x + 2 = 0} thì A = B.
c) Phép hợp: Hợp của hai tập A và B là tập
A ø B = {x | x þ A ú x þ B} A B
d) Phép giao: Giao của hai tập A và B là tập A \ B A ø B A ÷ B
A ÷ B = {x | x þ A và x þ B}
e) Phép hiệu: Hiệu của hai tập A và B là tập B A
A \ B = {x | x þ A và x ÿ B} CBA
Ví dụ: Nếu A = {1, 2, 4, a} và B = {2, 3, a, b}
thì A ø B = {1, 2, 3, 4, a, b}, A ÷ B = {2, a} và A \ B = {1, 4}, B \ A = {3, b}
f) Phần bù: Nếu A B, thì B\A được gọi là phần bù của A trong B và ký hiệu là CBA
Ví dụ: Nếu A = {2, 4} và B = {1, 2, 3, 4} thì CBA = {1, 3}
g) Tích Descartes: Tích Descartes của các tập X1, X2, …, Xn là tập X = X1 × X2 ×…× Xn
= {x = (x1, x2,…, xn)| xk þ Xk}
Ví dụ: Nếu X = {1, 2}, Y = {a, b}. Thì X × Y = {(1, a), (1, b), (2, a), (2, b)}
Chú ý: Xn = {x = (x1, x2, ... , xn)| xk þ X} với n þ ℕ.
1.1.3. Các kí hiệu toán học th°ờng dùng
- <=: lượng phổ biến, đọc là x þ ℝ ta đều có x2 + 1 1
- <=: lượng tồn t¿i, đọc là x þ ℝ sao cho x2 – 3x + 2 = 0
- <!=: !x þ ℝ sao cho x + 6 = 0
- < =: x þ ℝ sao cho x2 + 1 = 0 7
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
- <=: hay Mệnh đề: <A B= nghĩa là: <A kéo theo B=.
Ví dụ: ABC đều ABC cân.
- <û=: Mệnh đề: <A û B= nghĩa là: <A tương đương B=.
Ví dụ: Tam giác đều û tam giác cân và có một góc có số đo bằng 600, hay <n
chia hết cho 2 và 3= û <n chia hết cho 6=.
- <&= hay <ù=: Thay cho liên từ .
Ví dụ: n chia hết cho 2 và 3, có thể viết n chia hết cho 2 & 3.
- <ú= thay cho liên từ .
Ví dụ: <n þ N, thì n lẻ hoặc n chẵn=, có thể viết <n þ N, thì n lẻ ú n chẵn=.
- Các chú ý: Cho mệnh đề P(x). Khi ấy P(x) là phủ đßnh của P(x).
Nếu <x, P(x)= là đúng (sai), Thì <x, P(x) = là sai (đúng)
Nếu <x, P(x)= là đúng (sai), Thì <x, P(x) = là sai (đúng)
- Ví dụ: <x þ R: x2 + 1 1= đúng. Khi ấy <x þ R: x2 + 1 < 1= sai.
<x þ R: x2 - 1 = 0= sai. Khi ấy <x þ R: x2 - 1 0= đúng
<n þ N: n < 10= đúng. Khi ấy <n þ N: n 10= sai
<x þ R: x2 + 1 = 0= sai. Khi ấy <x þ R: x2 + 1 0= đúng 1.2. ÁNH X¾
1.2.1. Định nghĩa và ví dÿ
Định nghĩa: Cho hai tập X và Y khác rỗng. Ánh xạ ö từ X vào Y là một quy tắc cho
tương ứng sao cho với mỗi phần tử x thuộc X ứng với một phần tử duy nhất y thuộc Y.
Khi đó X được gọi là tập nguồn, Y được gọi là tập đích, phần tử y ứng với x
(qua ö) được gọi là ảnh của x, còn x được gọi là tạo ảnh của y, ký hiệu y = f (x) và ánh xạ khi ấy được viết
f : X → Y
x y = f(x)
Các ví dụ: Nếu X = {a, b, c} và Y = {1, 2, 3, 4}
- Thì f: X → Y như sau: f(a) = 2, f(b) = 4, f(c) = 2 là một ánh xạ. 8
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
- Thì f: X → Y như sau: f(a) = 1, f(b) = 2 không là ánh xạ vì c þ X nhưng không
có y þ Y ứng với nó (không tồn tại).
- Thì ö: X → Y như sau: f(a) = 2, f(b) = 4, f(c) = 1, f(b) = 1 không là ánh xạ vì
b þ X ứng với 1 và 4 cùng thuộc Y (không duy nhất)
Các ánh x¿ đặc biệt
- Ánh xạ hằng: Ánh xạ f: X → Y được gọi là ánh xạ hằng nếu tồn tại c thuộc Y
sao cho mọi x thuộc X ta đều có f(x) = c.
Chẳng hạn xét X = {1, 2, 3, 4, 5} và Y = {a, b, c}, quy tắc f: X → Y như sau: f(1)
= f(2) = f(3) = f(4) = f(5) = c là ánh xạ hằng.
- Ánh xạ nhúng: Giả sử X Y, ánh xạ f: X → Y thoả mãn f(x) = x với x þ X
thì ö được gọi là ánh xạ đồng nhất.
Chẳng hạn xét X = {1, 2, 3} và Y = {1, 2, 3, 4, 5} quy tắc ö: X → Y như sau f(1)
= 1, f(2) = 2, f(3) = 3 là ánh xạ nhúng.
Đặc biệt: Ánh xạ nhúng từ X vào chính X được gọi là ánh xạ đồng nhất và ký hiệu là 1X. 1.2.2. Các lo¿i ánh x¿
a) Đơn ánh: Ánh xạ f: X → Y được gọi là đơn ánh, nếu bất kỳ x1 và x2 thuộc X mà x1
x2 thì f (x1) f (x2).
Ví dụ: Cho X = {1, 2, 3} và Y = {a, b, c, d}
Ánh xạ ö: X → Y xác định như sau: ö(1) = a, ö(2) = c, ö(3) = d là đơn ánh.
Ánh xạ ö: X → Y xác định như sau: ö(1) = b, ö(2) = d, ö(3) = b, ö(4) = a không
đơn ánh, vì 1 và 3 thuộc X, 1 3 nhưng ö(1) = ö(3)
b) Toàn ánh: Ánh xạ ö: X → Y được gọi là toàn ánh nếu với mỗi y thuộc Y đều tồn tại
x thuộc X sao cho ö(x) = y.
Ví dụ: Cho X = {1, 2, 3, 4} và Y = {a, b, c}
Ánh xạ f: X → Y theo quy tắc: ö(1) = a, ö(2) = b, ö(3) = c, ö(4) = b là toàn ánh.
Ánh xạ f: X → Y theo quy tắc ö(1) = b, ö(2) = c, ö(3) = b, ö(4) = c không toàn
ánh, vì tồn tại a þ Y nhưng không tồn tại x þ X sao cho ö(x) = a 9
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
c) Song ánh (hay ánh xạ 1 – 1): Ánh xạ ö: X → Y vừa đơn ánh vừa toàn ánh thì ö
được gọi là một song ánh.
Ví dụ: Cho X = {a, b, c, d} và Y = {³, ³, ´, ·} ánh xạ ö: X → Y như sau: ö(a) = ³, ö(b) =
³, ö(c) = ´, ö(d) = · là song ánh
d) Ánh xạ ngược: Nếu ö: X → Y là một song ánh. Khi ấy quy tắc g: Y → X với mỗi y
thuộc Y qua g ứng với x thuộc X thỏa ö(x) = y. Thì g là một ánh xạ từ Y đến X, được gọi
là ánh xạ ngược của ö và ký hiệu là ö –1.
Chú ý: Dễ dàng thấy rằng ö–1 cũng là song ánh và ánh xạ ngược của ö–1 là ö.
Ví dụ: Với song ánh trên, xét tương ứng ö–1: Y → X như sau: ö–1(³) = a, ö–1(ò) =
b, ö–1() = c, ö–1(·) = d là ánh xạ ngược của ö.
e) Ánh xạ hợp: Giả sử ö là một ánh xạ từ X vào Y và g là một ánh xạ từ Y vào Z. Khi
ấy với mỗi x thuộc X qua ö ứng với y thuộc Y sao cho y = ö(x). Từ y þ Y qua g ứng
với z thuộc Z sao cho z = h(x) = g(y). Như vậy với mỗi x þ X, tồn tại duy nhất z þ Z
sao cho z = h(x) = g(ö(x)) được gọi là ánh xạ tích của ö và g, và ký hiệu là h = goö.
Sơ đồ ánh xạ hợp : X ö Y h = goö g Z
Ví dụ: X = {1, 2, 3, 4}, Y = {a, b, c, d, m, n}, Z = {ñ, ò, , ô, õ}
ö: X → Y như sau: ö(1) = a, ö(2) = c, ö(3) = d, ö(4) = m
g: Y → Z như sau: g(a) = ³, g(b) = ³, g(c) = ³, g(d) = ò, g(d) = ñ, g(m) = ¸.
Khi ấy h = goö: X → Z như sau: h(1) = h(2) = ñ, h(3) = ò, h(4) = õ.
Chú ý: Nếu ö: X → Y là một song ánh, thì 1X = ö–1oö, 1Y = öoö–1
1.3. HÀM SÞ MÞT BIẾN SÞ 1.3.1. Định nghĩa
Định nghĩa: Hàm số (một biến số) là một ánh xạ ö từ tập X ≠ ö, X ℝ vào ℝ. X: miền xác định
Y = {y þ ℝ| x þ X: y = ö(x)}: miền giá trị 10
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
x þ X: đối số hay biến độc lập
y = ö(x): hàm số hay biến phụ thuộc
Ví dụ: y = ax + b được gọi là hàm bậc nhất, a được gọi là hệ số góc.
1.3.2. Các ph°¢ng pháp cho hàm sß
Phương pháp giải tích: Là cho hàm số dưới dạng một hay nhiều biểu thức.
üx +1 khi x ü 0 ÿ
Ví dụ: ö(x) = x2 – 3x + 2 (một biểu thức), ö(x) = 2
ýx −1 khi 0 x 1 (ba biểu thức) ÿ 3 x + 2 khi x þ þ 1
Phương pháp biểu đồ
Ví dụ: Tỷ lệ học sinh giỏi: 15%, khá: 20%, trung bình: 35%, yếu, kém: 30% của một
trường phổ thông trung học X năm học nào đó 35% 30% 30% 20% 20% 15% 15% 35% Y,k Tb Kh G
Phương pháp bảng: Là cho hàm số dưới dạng một bảng gồm 2 hàng (hay 2 cột), trong
đó hàng (hay cột) thứ nhất biểu thị giá trị của biến độc lập, còn hàng (hay cột) thứ hai
biểu thị giá trị tương ứng của hàm số
Ví dụ: Bảng giá trị hàm số y = 2x + 1 X 0 1 2 3 4 Y 1 3 5 7 9
Phương pháp đồ thị: Đồ thị của hàm y = ö(x) xác định trên X (X ö, X R) là tập Gö
= {M(x, y)| x þ X, y = ö(x)}. Khi x chạy khắp trong X, thông thường M vạch ra trong
mặt phẳng Oxy một đường cong nào đó, nên người ta thường nói đồ thị hàm một biến
là một đường cong. Vì vậy cho hàm số bằng phương pháp đồ thị là cho một đường cong nào đó. 11
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
Chú ý: M0(x0, y0) þ Gö nếu x0 þ X và y0 = y ö(x M
0). Trái lại M1(x1, y1) ÿ Gö nếu x1 ÿ X 0 y0 y = ö(x)
hoặc x1 þ X nhưng y1 ö(x1) . y M 1 1 Ví dụ: Hàm 2 2
y = R − x (R þ 0) hay O x0 x1 x 2 2 2
üx + y = R y ý
có đồ thị là nửa trên đường tròn þy 0 tâm O(0, 0), bán kính R. O x 1.3.3. Các d¿ng hàm sß
Dạng tường minh: y = ö(x) hay cho hàm số bởi một hay nhiều biểu thức đại số. ü2x + k 1 h ix ü 1
Ví dụ: y = 2x + 1, y = x2 - 3x + 1, ö(x) = ý … þ 2 x - k 3 h ix 1
üx = x(t)
Dạng tham số: ý (t - tham số)
þy = y(t)
Ví dụ: Phương trình tham số đường thẳng trong mặt phẳng Oxy đi qua M0(x0, y0) → → có vectơ chỉ
üx = x + a t
phương a = (a 0 1 1, a2) ñ là ý (t þ R).
þy = y + a t 0 2
Phương trình tham số đường tròn tâm O bán kính R > 0 trong mặt phẳng Oxy là:
üx = R cost ý (0 t 2ð).
þy = Rsin t
Phương trình tham số elip với các bán trục a, b > 0 trong mặt phẳng Oxy là:
üx = a cost ý (0 t 2ð)
þy = bsin t
Dạng hàm ẩn: F(x,y) = 0
Ví dụ: Phương trình hàm ẩn của đường thẳng là: Ax + By + C = 0 (A2 + B2 0).
Phương trình tham số đường tròn tâm O bán kính R > 0 là: x2 + y2 = R2. 1.3.4. Phép toán
a) Bằng nhau: Cho y = ö(x) và y = g(x) cùng xác định trên X. Khi ấy ö = g nếu x þ
X chúng ta có ö(x) = g(x). 12
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
Ví dụ: ö(x) = x2 - 3x + 2 và g(x) = (x – 1)(x – 2) là bằng nhau trên R
ö(x) = log3(x2) và g(x) = 2log3x khác nhau, vì miền xác định của ö là x 0 còn
miền xác định của g là x > 0. Nhưng nếu xét trên tập X = (0, + ∞) thì ö = g.
Chú ý: Hai đa thức bằng nhau nếu chúng cùng bậc và các hệ số tương ứng bằng
nhau. Chẳng hạn: ax2 + bx + c = 4x2 + 1 û a = 4, b = 0, c = 1.
b) Cộng, trừ, nhân và chia: ö g, ö.g, f được định nghĩa như sau: x þ X ta có: (ö g f f (x)
g)(x) = ö(x) g(x), (ö.g)(x) = ö(x).g(x), ( )(x) =
(với điều kiện g(x) 0 nên g g(x)
miền xác định của thương 2 hàm số có thể bị thu hẹp)
Ví dụ: Cho ö(x) = x2 – 2, g(x) = x + 1 có cùng miền xác định là R. Khi ấy:
(ö + g)(x) = x2 + x – 1 có miền xác định là R
(ö – g)(x) = x2 – x – 3 có miền xác định là R
(ö.g)(x) = (x2 – 2)(x + 1) = x3 + x2 – 2x – 2 có miền xác định là R 2 x − 2 ( f )(x) =
có miền xác định là R \ {–1} g x +1
c) Hàm hợp: Cho y = ö(x) xác định trên X và có miền giá trị Y, z = g(y) có miền xác
định G ù Y. Khi ấy z = g(ö(x)) được gọi là hàm số hợp của ö và g, ký hiệu: h = goö.
Đặc biệt (öoöoö…oö)(x) = ö(ö(ö…(ö(x))) và viết là ön(x)
Ví dụ: Cho ö(x) = 3x + 1 và g(x) = x2 – 3, khi ấy:
(goö)(x) = g(ö(x)) = (3x + 1)2 – 3 = 9x2 + 6x – 2
(ö0g)(x) = ö(g(x)) = 3(x2 – 3) + 1 = 3x2 – 8
ö2(x) = (öoö)(x) = ö(ö(x)) = 3(3x + 1) + 1 = 9x + 4
g2(x) = (gog)(x) = g(g(x)) = (x2 – 3)2 – 3 = x4 – 6x2 + 6
d) Hàm ngược: Cho y = ö(x) có miền xác định là X, miền giá trị là Y. Nếu ö là song
ánh thì ánh xạ ngược ö–1 là một hàm số và gọi là hàm ngược của ö và ký hiệu là y = ö–1(x).
Ví dụ: Nếu ö(x) = x3 thì ö–1(x) = x1/3, nếu ö(x) = 2x + 1 thì ö–1(x) = x −1 2 13
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
Chú ý: Đồ thị của hàm số y = ö(x) và hàm số ngược của nó y = ö–1(x) trong cùng hệ
tọa độ đối xứng nhau qua đường thẳng có phương trình: y = x . 1.3.5. Tính chất
a) Đơn điệu: Hàm y = ö(x) được gọi là đơn điệu tăng [tương ứng giảm] trong (a, b)
nếu x1, x2 þ (a, b) mà x1 < x2 thì ö(x1) ö(x2) [tương ứng ö(x1) ö(x2)]
Nếu bỏ dấu 88=99 trong các bất đẳng thức này thì ta có khái niệm tăng (tương ứng
giảm) nghiêm ngặt (hay thực sự)
Ví dụ: 1) Xét ö(x) = ax + b (a 0). Nếu a > 0: x1, x2 þ R và x1 < x2. Thì ax1 < ax2
ax1 + b < ax2 + b ö(x1) < ö(x2). Vậy ö(x) đơn điệu tăng trên R. Nếu a < 0: tương
tự ta chứng minh được ö(x) đơn điệu giảm trên R. ü 1 − khi x ü 0 ÿ
2) Hàm signx = ý 0 khi x = 0 ÿ 1 khi x þ þ 0
3) Hàm phần nguyên ö(x) = [x] (trong đó [x] là số nguyên lớn nhất thỏa [x]
x) đơn điệu tăng trên R
4) Hàm phần phân ö(x) = {x} = x – [x] tăng nghiêm ngặt trong từng bán
khoảng [n, n + 1) với n þ Z y y 2 y = [x] y 1 y = {x} 1 1 y = signx x O 1 2 3 - 1 O 1 2 x O x - 1 - 1
b) Bị chặn: Hàm y = ö(x) được gọi là bị chặn trên (tương ứng dưới) trên X. Nếu tồn tại
M þ R (tương ứng tồn tại m þ R) sao cho x þ X thì ö(x) M (tương ứng ö(x) g m)
Hàm y = ö(x) vừa bị chặn trên vừa bị chặn dưới trên X thì ta nói ö(x) bị chặn trên tập
X (tương đương tồn tại K > 0: x þ X ta có |ö(x)| K).
Ví dụ: Hàm số mũ y = ax (a > 0, a 1) bị chặn dưới bởi m = 0, không bị chặn trên;
Hàm y = 4 – x2 không bị chặn dưới, bị chặn trên bởi M = 4; 14
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
Hàm y = sinx và y = cosx bị chặn bởi K = 1; y = x3 không bị chặn trên và dưới;
Hàm phần nguyên y = [x] không bị chặn;
Hàm phần phân y = {x} bị chặn dười bởi m = 0 và bị chặn trên bởi M = 1
c) Chẵn, lẻ: Tập X ℝ được gọi là đối xứng (qua O) nếu –x þ X û x þ X. Hàm số y =
ö(x) xác định trên tập đối xứng X được gọi là chẵn [tương ứng lẻ] nếu mọi x thuộc X thì
ö(–x) = ö(x) [tương ứng ö(–x) = –ö(x)].
Ví dụ: ö(x) = x4 – 3|x| + 1, ö(x) = x2 + 4, ö(x) = ln|x| ... là các hàm chẵn.
ö(x) = x3 – 3x, ö(x) = ln(x + 2
1+ x ), signx, ö(x) = x|x| ... là các hàm lẻ.
Chú ý: Đồ thị hàm chẵn (tương ứng lẻ) tự đối xứng qua trục tung (tương ứng qua O)
d) Tuần hoàn: Hàm y = ö(x) xác định trên X ℝ được gọi là tuần hoàn nếu tồn tại số
thực l khác 0 sao cho x þ X thì x ± l þ X và ö(x + l) = ö(x). Nếu tồn tại T > 0 nhỏ nhất
thỏa mãn ö(x + T) = ö(x) với mọi x þ X thì T được gọi là chu kỳ tuần hoàn của ö(x) và
khi ấy ö(x) được gọi là hàm tuần hoàn có chu kỳ. Trái lại ö(x) là hàm tuần hoàn không chu kỳ.
Ví dụ: 1) Hàm y = sinx, y = cosx tuần hoàn với chu kỳ T = 2ð.
2) Hàm hằng ö(x) = C tuần hoàn không có chu kỳ. Vì với với bất kỳ số thực T >
0 và với mọi x þ R ta có ö(x + T) = ö(x) = C và tập số thực dương không có số bé nhất.
3) Hàm ö(x) = {x} tuần hoàn với chu kỳ T = 1, vì x þ R và n þ N ta có {x +
n} = {x} mà min{n| n þ N } = 1 > 0 ü 1 khi x þQ
4) Hàm Dirichlet: D(x) = ý
tuần hoàn không chu kỳ. þ 1 k − hi x þ I
Thật vậy x þ R và r þ Q. Nếu x þ Q, thì x + r þ Q D(x + r) = D(x) = 1, nếu x
þ I thì x + r þ I D(x + r) = D(x) = –1, mà tập Q+ không có số bé nhất. 1.3.6. Hàm s¢ cấp
Các hàm s¢ cấp c¢ bÁn
- Hàm hằng: y = C, miền xác định R, miền giá trị {C}, không tăng, không giảm.
- Hàm lũy thừa: y = x³, ³ þ R, miền xác định, miền giá trị và tính chất của nó phụ
thuộc ñ, đồ thị luôn luôn đi qua điểm A(1, 1). 15
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
Chú ý: Nếu ñ þ I, thì quy ước miền xác định của hàm lũy thừa y = xñ là [0, +õ) nếu ñ
> 0 và là (0, +õ) nếu ñ < 0.
- Hàm mũ: y = ax (a > 0, a 1), miền xác định R, miền giá trị (0, +∞), đồ thị luôn đi
qua A(0, 1), đơn điệu tăng (giÁm) nếu a > 1 (0 < a < 1). y y
y = logax (a > 1)
y = ax (a > 1)
y = ax (0 < a < 1) B x O 1 1 A x
y = logax (0 < a < 1) O
- Hàm lôgarit: y = logax (a > 0, a 1) là hàm ngược của y = ax miền xác định là (0,
+∞), miền giá trị R, đồ thị hàm y = logax và hàm y = ax đối xứng qua đường thẳng y =
x, luôn đi qua B(1, 0), đơn điệu tăng (giÁm) nếu a > 1 (0 < a < 1).
- Các hàm lượng giác
y = sinx, miền xác định R, miền giá trị: [ –1, 1], là hàm lẻ, tuần hoàn với T = 2ð.
y = cosx, miền xác định R, miền giá trị [–1, 1], là hàm chẵn, tuần hoàn với T = 2ð. ð
y = tanx, miền xác định R\{ +kð| kþZ}, miền giá trị R, là hàm lẻ, tuần hoàn với T= ð. 2
y = cotx, miền xác định R\{kð| k þ Z}, miền giá trị R, là hàm lẻ, tuần hoàn với T = ð.
- Các hàm lượng giác ngược
• y = arcsinx là hàm ngược của hàm y = sinx, có miền xác định [–1, 1], miền giá ù ð ð trị ù − ; ú
, đơn điệu tăng trên [–1;1] 2 2 ú û û üa = sinñ ÿ ð 3 ð
Chú ý: ³ = arcsina û ý ð
ð . Chẳng hạn: arcsin1 = , arcsin( ) = . − ñ ÿ 2 2 3 þ 2 2
• y = arccosx là hàm ngược của hàm y = cosx, có miền xác định [–1, 1], miền giá
trị [0, ð], đơn điệu giảm trên [–1, 1]. üa = cosñ ð 2 ð
Chú ý: ³ = arccosa û ý
. Chẳng hạn: arccos0 = , arccos = . þ0 ñ ð 2 2 4 16
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
• y = arctanx là hàm ngược của hàm y = tanx, có miền xác định R, miền giá trị ö ð ð ö − ÷
; ÷, đơn điệu tăng trên toàn trục, là hàm số lẻ. ø 2 2 ø üa = tanñ ÿ ð
Chú ý: ³ = arctana û ý ð
ð . Chẳng hạn: arctan( 1) = . − ü ñ ü ÿ 4 þ 2 2 y ð/2 y = arctanx x O - ð/2
• y = arccotx là hàm ngược của hàm y = cotx, có miền xác định R, miền giá trị (0,
ð), đơn điệu giảm trên toàn trục. üa = cotñ ð 3 ð
Chú ý: ³ = arccota û ý
. Chẳng hạn: arccot1 = , arccot = . þ0 ü ñ ü ð 4 3 3
- Hàm s¢ cấp: Sau khi thực hiện hữu hạn các phép toán cộng, trừ, nhân, chia và hợp
hữu hạn các hàm sơ cấp cơ bản được một hàm - gọi là hàm sơ cấp.
Ví dụ: y = 2x + 1, y = x2 – 3x + 2, y = sin2x, y = ex–1 ...
1.4. DÃY SÞ VÀ GIàI H¾N CĀA DÃY SÞ 1.4.1. Dãy sß
Định nghĩa: Dãy số là một ánh xạ u từ * vào .
Đặt u(n) = un, dãy số thường được viết dưới dạng khai triển là u1, u2, ..., un, ...
hoặc (u )õ . Khi đó u n n 1 =
1 được gọi là số hạng đầu tiên, u2 được gọi là số hạng thứ 2,..., un
được gọi là số hạng thứ n hay số hạng tổng quát của dãy số. õ
Ví dụ: Dãy ö 1 ö 1 1 1
÷ ÷ viết dưới dạng khai triển là 1, , , ..., , ... (1) ø n ø 2 3 n n 1 =
Dãy (2n −1)õ viết dưới dạng khai triển là 1, 3, 5, ..., 2n – 1, ... (2) n 1 = Dãy (1− 3 )
n õ viết dưới dạng khai triển là -2, -5, ..., 1 – 3n, ... (3) n 1 = 17
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số õ Dãy ö 1 ö 3 1 1− ÷
viết dưới dạng khai triển là 0, , ..., 1 - , ... (4) 2 ÷ ø n ø 4 2 n n 1 = õ Dãy ((– )
1 n−1 ) viết dưới dạng khai triển là 1, –1, 1, –1, ..., (–1)n1, ... (5) n 1 = õ Dãy ( – )
1 n−1 n) viết dưới dạng khai triển là 1, -2, 3, -4, 5, ..., (-1)n-1n, ... (6) n 1 = * Các tính chất
Đơn điệu: Dãy (un) được gọi là đơn điệu tăng (tương ứng giảm) nếu n þ * ta có un
< un+1 (tương ứng un > un+1)
Bị chặn: Dãy (un) được gọi là bị chặn trên (tương ứng dưới) nếu M þ (tương ứng
m þ ) sao cho n þ * ta có un f M (un g m). Một dãy vừa bị chặn trên vừa bị chặn
dưới thì được gọi là bị chặn (tương đương K > 0 sao cho với n þ *: |un| K )
Ví dụ: Dãy (1) giảm, bị chặn trên bởi M = 1, bị chặn dưới bởi m = 0
Dãy (2) tăng, bị chặn dưới bởi m = 1, không bị chặn trên.
Dãy (3) giảm, bị chặn trên bởi M = -2, không bị chặn dưới.
Dãy (4) giảm, bị chặn trên bởi M = 1, bị chặn dưới bởi m = 0
Dãy (5) không đơn điệu, bị chặn bởi K = 1.
Dãy (6) không đơn điệu, không bị chặn trên và dưới.
1.4.2. Giái h¿n cāa dãy
Định nghĩa 1: Số thực a được gọi là giới hạn của (un) khi n dần ra õ. Nếu với mỗi ¸ >
0 tùy ý, đều tồn tại N > 0 sao cho n þ thỏa n > N thì |un – a| < ¸ và viết limun = a.
Định nghĩa giái h¿n mở rßng:
Định nghĩa 2: Ta nói (un) dần ra +∞ khi n ra +õ nếu với mỗi A > 0 lớn tùy ý, đều tồn
tại N > 0 sao cho n þ mà n > N thì un > A, và viết limun = +∞.
Định nghĩa 3: Ta nói (un) dần ra -∞ khi n ra +õ nếu với mỗi A > 0 lớn tùy ý, đều tồn
tại N > 0 sao cho n þ mà n > N thì un < –A, và viết limun = –∞. +
Ví dụ: 1) lim 2n 1 = 1. Với mỗi ε > 0 bé tùy ý, đều N > 0: n þ mà n > N thì 2n 2n +1 − 1 1 1 1 1 < õ û
< õ û 2n > û n > . Từ đó chọn N = > 0 2n 2n õ õ 2 õ 2
2) lim(n2 – 1) = +∞. Với mỗi A > 0 lớn tùy ý, đều N > 0 sao cho n þ mà n
> N thì n2 – 1 > A û n > A +1 . Từ đó chọn N = A +1 > 0 18
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số ü k 0 hiñ þ 0 ÿ 3) lim 1 = ý 1 k hiñ = 0 ñ n ÿ þ+ õ k h iñ ü 0
Phép toán: Giả thiết các dãy (un) và (vn) có giới hạn. Ta có:
1) lim(un ± vn) = limun ± limvn,
2) lim(un.vn) = limun.limvn, u lim u 3) lim n n =
(với limvn 0) v lim v n n 4) v lim lim n u = lim n v u n n õ Các dạng vô định: 0 õ 0 0 õ − ; õ 0. ; õ ; ;1 ;0 ;õ 0 õ Tính chất:
1) Giới hạn của một dãy (nếu có) là duy nhất.
2) Một dãy có giới hạn thì bị chặn.
3) (un) đơn điệu tăng (tương ứng giảm) và bị chặn trên bởi M (tương ứng dưới bởi
m) thì có giới hạn và limun f M (tương ứng limun g m)
4) Nếu un < vn thì limun f limvn
5) (nguyên lý kẹp) Nếu un f vn f wn và limun = limwn = a. Thì limvn = a.
6) limun = 0 û lim|un| = 0
7) (Tiêu chuẩn cần và đủ Cauchy): Dãy (un) có giới hạn û với mỗi õ > 0, đều tồn
tại N > 0 sao cho với mọi n þ N, n > N và mọi p þ N ta có |un+p – un| < õ 3 1 2 + n + 3n -1 1 - 2 Ví dụ: 1) lim = lim n n = 1 2 n + n +1 1 1 1 + + 2 n n 1 1 n + + 1+ + 2 2 + ( 1 2) 1 + 2 2 2) lim n 2n = lim n = lim n = 3 3 n3 +1 + n 1 1 2 n(3 1 + + ) 1 3 1 + +1 3 n 3 n 19
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số
( n +1 - n)( n +1 + n) 3) lim( 1 n +1 - n ) = lim = lim = 0 n +1 + n n +1 + n
1.4.3. Sß e 1
* Cho (un) có un = (1 +
)n. Ta chứng minh {un} tăng và bị chặn trên. Thật vậy: n
- Áp dụng bất đẳng thức Cauchy cho n + 1 số: x 1
1 = 1, x2 = ... = xn = xn+1 = 1 + ta có: n 1 1 1+ 1 ( + ) + ... + 1 ( + ) n + n n n 1 1 2 1 n 1 + . 1 1 ( + ) 1 ...( + ) û (1 + ) n 1+ n +1 n n n +1 n n û 1 + 1 (1 + 1 ) 1 1 n 1 + û (1 +
)n+1 (1 + )n û un+1 g un. n +1 n n +1 n
Vậy (un) đơn điệu tăng 2 k
- Áp dụng bất đẳng thức: Với k = 1, 2, ..., n ta có (1 + 1 )k < 1 + k + (*). n n 2 n
Chứng minh (*) bằng phương pháp quy nạp theo k như sau
Với k = 1: (*) là 1 + 1 < 1 + 1 + 1 - đúng n n 2 n
Giả sử (*) đúng với k < n. Chứng minh (*) đúng cho k + 1, nghĩa là + 2 (k + ) 1
(1 + 1 )k+1 < 1 + k 1 + (**). n n 2 n 2 2
Do (*) nên (1 + 1 )k+1 = (1 + 1 )k(1 + 1 ) < (1 + k + k )(1 + 1 ) = 1 + k + k n n n n 2 n n n 2 n 2 + 2 + 2 (k + ) 1
+ 1 + k + k < 1 + k 1 + k + k + k + 1 = 1 + k 1 + n 2 n 3 n n 2 n 2 n 2 n 2 n n 2 n
Từ đó lấy k = n: (1 + 1 )n < 3. Vậy tồn tại limun. n
Người ta chứng minh được rằng mặc dù {un} Q, nhưng limun = e 2,718281... þ I. 1 ñ (n
* Tổng quát: Nếu lim³(n) = 0 thì lim[1 + ³(n)] ) = e 20
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số 1
Hay limò(n) = ∞ thì lim[1 + ]ò(n) = e ò (n) 1 ù 1 ù
Ví dụ: 1) lim(1 + 1 )n = lim 2 n (1+ )n = e0 = 1 2 n ú 2 n ú û û 3n - 2n 1 + 2n 1 + ù ù 3 2) lim(1 - 3 )n = lim - 3 - 3 ú 1 ( - ) ú = e 2 2n +1 2n +1 û û BÀI T¾P CH¯¡NG 1
Bài tập 1: Chứng minh 1. AøB = BøA 2. A÷B = B÷A
3. (AøB)÷C = (A÷C)ø(B÷C)
4. (A÷B)øC = (AøC)÷(BøC)
5. A B thì A÷C B÷C và X\B X\A
6. A÷B = Ø thì A\B = A, B\A = B.
Bài tập 2: Định nghĩa hiệu đối xứng của A và B là AB = (A\B) ø (B\A).
Chứng minh: AB = BA và AB = (AøB)\(A÷B)
Bài tập 3: Chứng minh công thức Der-Morgan: Nếu Aα X thì 1. CX(øAα) = ÷CXAα 2. CX(÷Aα) = øCXAα
Bài tập 4: Giả sử ö: X → Y là ánh xạ. Chứng minh:
1. A B ö(A) ö(B) 2. ö(A÷B) ö(A)÷ö(B) 3. ö(AøB) ö(A)øö(B)
4. A B ö-1(A) ö-1(B)
5. ö-1(B\A) = ö-1(B) \ ö-1(A)
6. ö-1(A÷B) = ö-1(A) ÷ ö-1(B)
7. ö-1(AøB) ö-1(A) ø ö-1(B)
Bài tập 5: Giả sử ö: X → Y, g: Y → Z là các ánh xạ và h = goö. Chứng minh:
1. h(A) = g(f(A)), A X
2. h-1(B) = ö-1(g-1(B)), B Z.
Bài tập 6: Tính các giới hạn sau: n + n + + 1. lim ( ) 2 - 3 2. lim (n ) 1 ! ! n n 1 + n 1 ( ) 2 - + 3 + (n + ) 1 - ! ! n 21
KHOA KHOA HàC C¡ BÀN
Chư¢ng 1: Tập hợp - Ánh x¿ - Hàm số 100 căn n 1 3. lim 2n -1 2 + 2 + ... + 2 + 4. lim õ n k =1 (k + ) 1 (k + ) 3 5. lim n 6. lim n 2 n +1 n2 + n n 7. lim õ 1 8. lim n! 2 n k =1 n + k n n k 9. lim õ
10. lim( 2 . 4 2 … n2 2 ) 2 k 1 = n 22
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến Chương 2:
PHÉP TÍNH VI PHÂN HÀM MÞT BIÀN
2.1. GIàI H¾N CĀA HÀM Sà
2.1.1. Các định nghĩa
a) Giới hạn tại một điểm
Đßnh nghĩa 1 (bằng ngôn ngữ õ - ô): Số thực L được
gọi là giới hạn của hàm số y = ö(x) xác định trên tập
X R khi x dần về số thực a, nếu với mỗi số thực õ
dương bé tùy ý, đều tồn tại số thực ô dương đủ nhỏ
sao cho với x X mà 0 < |x – a| < ô thì |ö(x) – L| <
õ và viết lim ö(x) = L hay ö(x) → L (x → a). x→a 2 4x −1 Ví dụ 1: 1 1 lim
= 2 vì với mỗi õ > 0, ô > 0: x ù mà 0 < |x– | < ô thì 1 x→ 2x −1 2 2 2 2 4x −1 (2x −1)(2x +1) õ õ − 1 1 2 < õ
− 2 < õ 2|x– |< õ |x– |< . Vậy ô = > 0. 2x −1 2x −1 2 2 2 2
Đßnh nghĩa 2 (bằng ngôn ngữ dãy): Số thực l được gọi là giới hạn của hàm số y = ö(x)
xác định trên tập X R khi x dần về số thực a, nếu với mọi dãy số thực (xn) X mà
limxn = a thì limö(xn) = l.
Chú ý: Từ định nghĩa này ta có, để chứng tỏ không tồn tại lim ö(x) ta cần chỉ ra hai dãy x→a
(xn) và (x’n) cùng thuộc X và cùng dần về a nhưng limö(xn) ù limö(x’n)
Ví dụ 2: Chứng minh không tồn tại 1 lim sin . x→0 x 23
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến Xét dãy (x 1 1 n) có xn =
và dãy (x’n) có x’n = cùng dần về 0, nhưng 2 ð n ð + 2nð 2
lim(sinxn) = 0, còn lim(sinx’n) = 1.
b) Giới hạn một phía
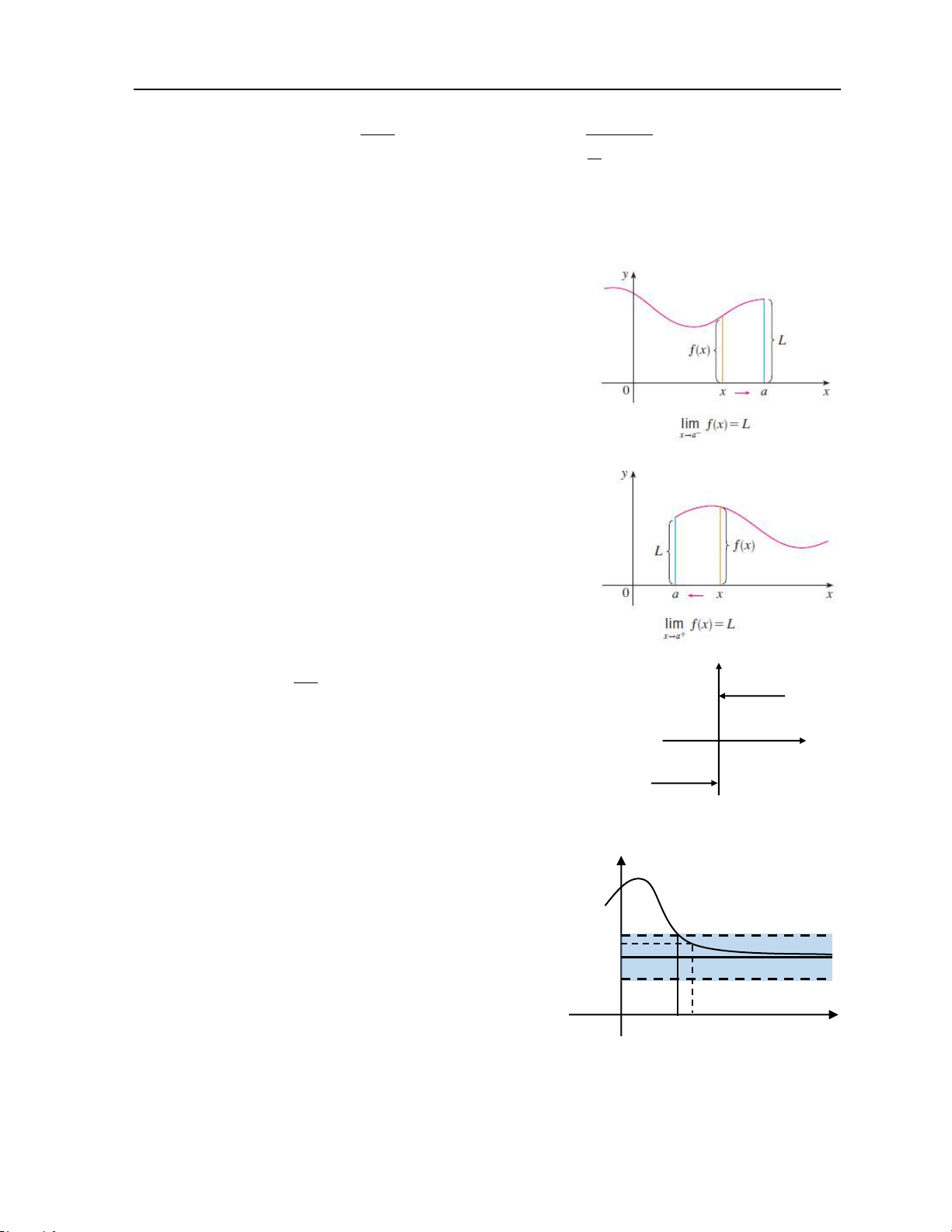
Đßnh nghĩa 1: Số thực L được gọi là giới h¿n trái của
hàm số y = ö(x) xác định trên X khi x dần về số thực
a, nếu với mỗi số thực õ dương bé tùy ý, đều tồn tại số
thực ô dương đủ nhỏ sao cho x X mà 0 < a – x < ô
thì |ö(x) – L| < õ và viết lim f (x) = L . x a− →
Đßnh nghĩa 2: Số thực L được gọi là giới h¿n phÁi của
hàm số y = ö(x) xác định trên X khi x dần về số thực
a, nếu với mỗi số thực õ dương bé tùy ý, đều tồn tại số
thực ô dương đủ nhỏ sao cho x X mà 0 < x – a < ô
thì |ö(x) – L| < õ và viết lim f (x) = L. x a+ → ü 1 − khi x ü 0 y
Ví dụ 3: Xét ö(x) = | x | = ý x þ 1 khi x þ 0 1
Ta có ngay lim f (x) = 1
− , lim f (x) =1. x x 0− → x 0+ → O
Đßnh lý: lim ö(x) = L khi và chỉ khi lim f (x) = lim f (x) = L . - 1 x→a x a− x a+ → →
c) Giới hạn mở rộng
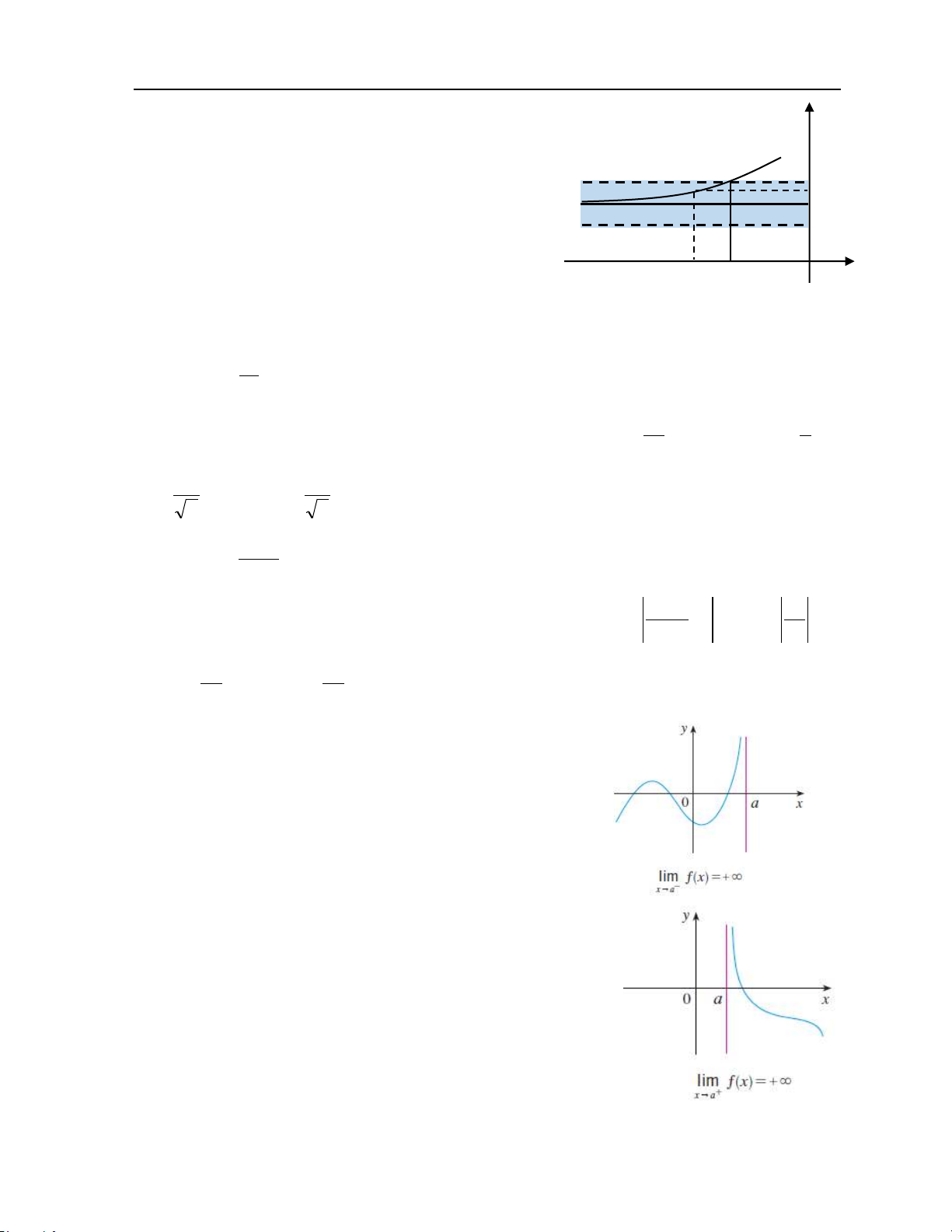
Đßnh nghĩa 1: Số thực L được gọi là giới hạn của
hàm số y = ö(x) xác định trên X khi x dần ra + ∞,
nếu với mỗi số thực õ dương bé tùy ý, đều tồn tại L+õ L
số thực B dương đủ lớn sao cho x X mà x > B
L–õ
thì |ö(x) – L| < õ, và viết lim ö(x) = L. x→+õ O B 24
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đßnh nghĩa 2: Số thực L được gọi là giới hạn của
hàm số y = ö(x) xác định trên X khi x dần ra –∞, L+õ
nếu với mỗi số thực õ dương bé tùy ý, đều tồn tại L
L–õ
số thực B dương đủ lớn sao cho x X mà x < –B
thì |ö(x) – L| < õ, và viết lim ö(x) = L. - B O x→-õ
Đßnh nghĩa 3: Nếu ta có lim f (x) = lim f (x) = L thì ta nói lim f (x) = L . x→+õ x→−õ x→õ Ví dụ 4: 1 lim = 0 2 x→õ x
Chứng minh: Với mỗi õ > 0, B > 0 sao cho x mà |x| > B thì | 1 – 0|< õ x2 1 2 > x õ 1 1 |x| > . Chọn B = . õ õ − Ví dụ 5: 2x 1 lim = 1 x→õ 2x −
Chứng minh: Với mỗi õ > 0, B > 0 sao cho x mà |x| > B thì 2x 1 −1 ü õ 1 ü õ 2x 2x
|x| > 1 . Chọn B = 1 . õ 2 õ 2
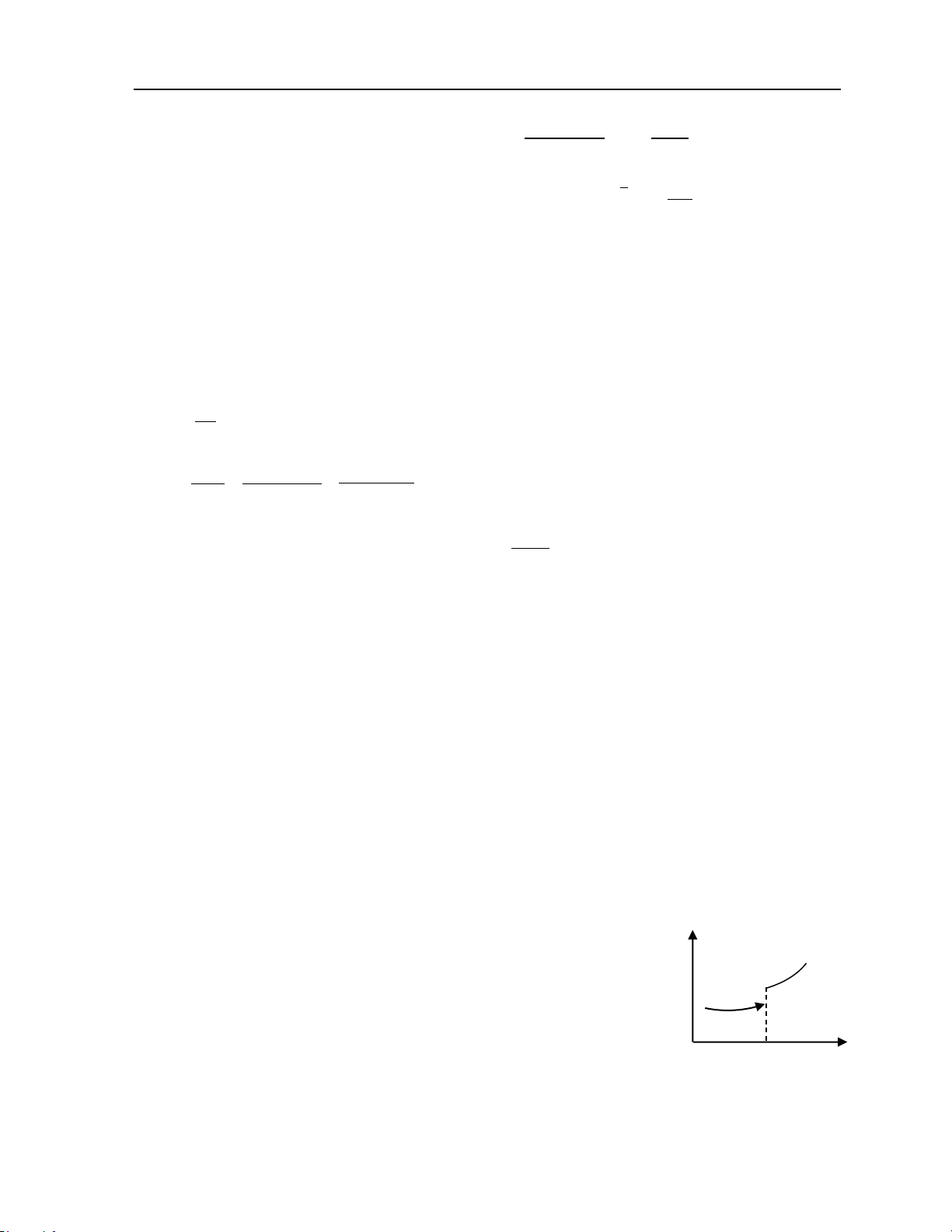
Đßnh nghĩa 4: Ta nói y = ö(x) xác định trên X có
giới hạn trái là +∞ khi x dần về số thực a, nếu với
mỗi số thực A dương lớn tùy ý đều tồn tại số thực ô
dương đủ bé sao cho x X mà 0 < a – x < ô thì
ö(x) > A và viết lim ö(x) = + õ. x a− →
Đßnh nghĩa 5: Ta nói y = ö(x) xác định trên X có
giới hạn phải là +∞ khi x dần về số thực a, nếu với
mỗi số thực A dương lớn tùy ý đều tồn tại số thực ô
dương đủ bé sao cho x X mà 0 < x – a < ô thì
ö(x) > A và viết lim f (x) = +õ. x a+ → 25
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đßnh nghĩa 6: Nếu ta có lim f (x) = +õ và lim f (x) = +õ thì ta nói lim f (x) = +õ . x a− → x a+ → x→a Ví dụ 6: 1 lim = + õ 2 x→0 x
Chứng minh: Với A > 0, ô > 0: x ù 0 mà 0 < |x| < ô thì 1 > A x2 < 1 |x| < 2 x A 1 1 . Vậy chọn ô = . A A
Đßnh nghĩa 7: Ta nói y = ö(x) xác định trên X có
giới hạn trái là – ∞ khi x dần về số thực a, nếu với
mỗi số thực A dương lớn tùy ý đều tồn tại số thực ô
dương đủ bé sao cho x X mà 0 < a – x < ô thì
ö(x) < - A và viết lim ö(x) = - õ. x a− →
Đßnh nghĩa 8: Ta nói y = ö(x) xác định trên X có
giới hạn phải là – ∞ khi x dần về số thực a, nếu với
mỗi số thực A dương lớn tùy ý đều tồn tại số thực ô
dương đủ bé sao cho x X mà 0 < x – a < ô thì
ö(x) < - A và viết lim ö(x) = - õ. x a+ →
Đßnh nghĩa 9: Nếu ta có lim f (x) = −õ và lim f (x) = −õ thì ta nói lim f (x) = −õ . x a− → x a+ → x→a
Đßnh nghĩa 10: Ta nói y = ö(x) xác định trên X dần về + ∞ khi x dần ra + ∞, nếu mỗi số
thực A dương lớn tùy ý, đều tồn tại số thực B dương đủ lớn sao cho x X mà x > B
thì ö(x) > A và viết lim ö(x) = + ∞. x→+õ
Đßnh nghĩa 11: Ta nói y = ö(x) xác định trên X dần về – ∞ khi x dần ra + ∞, nếu mỗi số
thực A dương lớn tùy ý, đều tồn tại số thực B dương đủ lớn sao cho x X mà x > B
thì ö(x) < - A và viết lim ö(x) = – õ. x→+õ 26
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đßnh nghĩa 12: Ta nói y = ö(x) xác định trên X dần về + ∞ khi x dần ra – ∞, nếu với
mỗi số thực A dương lớn tùy ý, đều tồn tại số thực B dương đủ lớn sao cho x X mà
x < – B thì ö(x) > A và viết lim ö(x) = + ∞. x→-õ
Đßnh nghĩa 13: Ta nói y = ö(x) xác định trên X dần về – ∞ khi x dần ra – ∞, nếu với
mỗi số thực A dương lớn tùy ý, đều tồn tại số thực B dương đủ lớn sao cho x X mà
x < – B thì ö(x) < – A và viết lim ö(x) = – ∞. x→-õ
2.1.2. Phép toán và tính chất a) Phép toán
Các giới hạn sau đây giả thiết là tồn tại. Ta có:
• lim[f (x) g(x)] = lim f (x) lim g(x) x→a x→a x→a
Điều kiện: vế phải khác dạng vô định ∞ – ∞.
• lim[f (x).g(x)] = lim f (x).lim g(x) x→a x→a x→a
Điều kiện: vế phải khác dạng vô định 0.∞. lim f (x) • f (x) lim = x→a
x→a g(x) lim g(x) x→a Đ õ
iều kiện: lim g(x) ù 0 và vế phải khác dạng vô định 0 hoặc . x→a 0 õ • lim g ( x
lim ö(x)g(x) = lim ö(x) ) x→a x→a x→a
Điều kiện: ö(x) > 0 và vế phải khác dạng vô định 00, 1õ, õ0.
• Nếu lim ö(x) = b và lim g(y) = c thì lim g(ö(x)) = c. x→a y→b x→a
b) Các tính chất
• Giới hạn (nếu có) của ö(x) khi x → a là duy nhất.
• Nếu ö(x) có giới hạn khi x dần về a thì ö(x) bị chặn trong khoảng J nào đó chứa a.
• Hàm số đơn điệu tăng (tư¢ng ứng giÁm) và bị chặn trên (tư¢ng ứng dưới) thì có giới hạn. 27
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
• Nếu ö(x) f g(x) trên X thì lim ö(x) f lim g(x). x→a x→a
• Nếu ö(x) f h(x) f g(x) và lim ö(x) = lim g(x) = L thì lim h(x) = L. x→a x→a x→a
• lim ö(x) = 0 lim |ö(x)| = 0 x→a x→a
• Nếu ö(x) là hàm sơ cấp xác định tại x0 R thì lim ö(x) = ö(x0). x→ 0 x
2.1.3. Các giái h¿n c¢ bản y a) Giới hạn sin x lim =1 P x→0 x M sin x
- Trước hết ta chứng minh: lim =1. x 0+ → x ð
Thật vậy, vì x → 0+ nên chỉ cần xét 0 < x < x 2 O H A x ð
Ta vẽ một phần tư đưßng tròn lượng giác á góc thứ nhất (ứng với 0 < x < ) 2
Giả sử độ đo AM = x, ta có HM = sinx, AP = tanx. Rõ ràng: S O . A HM x O . A AP
OAM < Squạt(OAM) < SOAP < OA2 <
sinx < x < tanx 2 2 2
cos x < 1 < 1 cosx < sin x < 1. sin x x sin x x
Cho x → 0+ và áp dụng nguyên lý kẹp suy ra sin x lim =1. x 0+ → x
- Tương tự: Đặt t = – x t → 0– và sin x sin t lim = lim = 1 x→ 0 - x t→ 0 + t sinñ (x)
- Tổng quát: Nếu lim ñ(x) = 0 thì lim = 1 x→a x→a ñ(x) x + a x − a − − 2cos sin Ví dụ 7: sin x sin a 0 x a lim (a ù 0, dạng ) = sin sin lim = 2 2 lim x→a x − a 0 x→a x − a x→a x − a x − a sin + = x a 2 lim cos . x→a 2 x − = cosa a 2 28
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến 2 2 x ö x ö − 2sin 1 ÷ sin ÷ 1 Ví dụ 8: 1 cos x 0 lim (dạng ) = lim 2 = lim ÷ 2 ÷ = 2 x→0 x 0 x→0 2 x 2 x→0 ÷ x ÷ ÷ ÷ 2 ø 2 ø Ví dụ 9: arcta x n 0 lim
(dạng ). Đặt t = arctanx x = tant; x → 0 khi t → 0 nên: x→0 x 0 arcta x n t tc t os 1 - ö sint ö lim = lim = lim = lim cost÷ ÷ = 1 x→0 x t→0 tant t→0 sin t t→0 ø t ø x b) Giới hạn ö 1 ö lim 1+ = ÷ ÷ e x→+õ ø x ø
Vì x → + ∞ nên chỉ cần xét x ó 1. Do x ó 1 n N sao cho n x < n +1 1 1 1
ü 1 + 1 < 1 + 1 f 1 + 1 n +1 x n n +1 x n n n x x n 1 + ö 1 ö ö 1 ö ö 1 ö ö 1 ö ö 1 ö 1+ ü 1+ 1+ 1+ ü 1+ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ ø n +1ø ø x ø ø x ø ø n ø ø n ø n x n 1 + ö 1 ö ö 1 ö ö 1 ö 1+ ü 1+ ü 1+ ÷ ÷ ÷ ÷ ÷ ÷ ø n +1ø ø x ø ø n ø n 1 + 1 − x n ö 1 ö ö 1 ö ö ö ö ö ö ö 1+ 1+ ÷ ÷ ÷ ÷ < 1 1+ ÷ ÷ < 1 1 1+ . 1+ ÷ ÷ ÷ ÷ . ø n +1ø ø n +1ø ø x ø ø n ø ø n ø
Cho n → + ∞ thì n + 1 → + ∞ và x → + ∞. Áp dụng nguyên lý kẹp suy ra điều phải chứng minh. ñ (x) ö ö Tổng quát: 1
lim ñ(x) = ± ∞ thì lim 1+ = ÷ ÷ e x→a x→a ø ñ(x) ø 1
hay lim ò(x) = 0 thì lim (1 + ò(x)) ò(x) = e x→a x→a x2 2 - ö sin x ö ÷ ÷ 1 1 2 ö ösin x 1 ö öø x ø Ví dụ 10: li ( m 1+ x2 ) 2 2 2 sin x (dạng 1õ) = 2 ÷ x lim 1 ( + x ) ÷ = 2 lim÷ 1 ( + x ) x ÷ = e x→0 x→0 ÷ ÷ x ÷ ÷ ø ø →0ø ø cos x 1 − 1 1 2 ö ö x 1 −
Ví dụ 11: lim (cosx) 2x (dạng 1õ) = cos x 1
lim÷[1+ (cos x −1)] − ÷ = 2 e x→0 x→0 ø ø 29
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến 1 Ví dụ 12: l 1 n( + x) 0 lim
= 1 (dạng ) = lim ln(1 + x) x = lne = 1 x→0 x 0 x→0 x e −1 Ví dụ 13: lim (dạng 1õ) x→0 x
Đặt t = ex – 1, ta có x = ln(t + 1) và khi x → 0 thì t → 0. x − Nên e 1 t 1 lim = lim = = 1 x→0 t→0 x ln(t +1) l 1 n( + t) lim t→0 t
2.1.4. Vô cùng bé và vô cùng lán
a) Vô cùng bé (VCB)
Đßnh nghĩa: ñ(x) được gọi là một VCB khi x → a nếu lim ñ(x) = 0 x→a
Ví dụ: sinx, x2 , 1 – cosx, tanx là các VCB khi x → 0.
x2 – 1, x2 – 3x + 2, x3 – 4x2 + 6x – 3 là các VCB khi x → 1
Phân lo¿i: Giả sử và
là hai VCB khi x → a. ñ(x) 0 Ta tính lim (dạng vô định ). x→ñ ò (x) 0 • ñ(x) Nếu lim
= L ù 0, thì ta nói ñ và ò là hai VCB cùng bậc.
x→a ò (x)
Đặc biệt L = 1 thì ta nói ñ và ò là hai VCB tương đương và viết ñ ò. • ñ(x) Nếu lim
= 0 thì ta nói ñ là VCB bậc cao hơn ò và viết ñ = O(ò).
x→a ò (x) ñ • (x) Nếu lim
= +∞ thì ta nói ñ là VCB bậc thấp hơn ò và viết ò = O(ñ).
x→a ò (x) • ñ(x) Nếu lim
không tồn tại thì ta nói ñ và ò không so sánh được.
x→a ò (x) −
Ví dụ: 1 – cosx và x2 là các VCB cùng bậc khi x → 0 vì 1 cos x 1 lim = 2 x→0 x 2
tanx sinx khi x → 0 vì sin x lim = lim cosx = 1 x→0 tan x x→0 30
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến 2 (x −1) x −1
(x – 1)2 = O(x2 – 3x + 2) khi x → 1 vì lim = lim = 0 . 2 x 1 → x 1 x − 3x + 2 → x − 2 | x
x| và x là các VCB không so sánh được khi x → 0 vì lim . x→0 | x |
Đßnh lý: lim ö(x) = L tồn tại VCB ñ(x) khi x → a sao cho ö(x) = L + ñ(x). x→a
Chú ý: Tích một đại lượng bị chặn với một VCB là một VCB (trong cùng quá trình ấy).
b) Vô cùng lớn (VCL)
Đßnh nghĩa: ò(x) được gọi là một VCL khi x → a nếu lim |ò(x)| = + ∞. x→a
Ví dụ: 1 , cotx, ... là các VCL (x → 0) 2 x 1 , 1 , 1
, ... là các VCL (x → 1) 1− x 2 x − 3x + 2 2 sin(x −1) Đß 1
nh lý: ò(x) là VCL khi x → a khi và chỉ khi
là VCB khi x → a. ò (x) 2.2. HÀM Sà LIÊN TþC
2.2.1. Định nghĩa và ví dÿ
Đßnh nghĩa 1: Hàm số y = ö(x) xác định trên X được gọi là liên tục tại x0 R nếu
chúng ta có lim ö(x) = ö(x0). x→x0
Chú ý 1: y = ö(x) liên tục tại x0 ö(x) thỏa 3 điều kiện sau:
• x0 X và ta tính được ö(x0).
• Tồn tại lim ö(x) = L (L R). x→x0 • ö(x0) = L.
Một trong 3 điều trên bị vi phạm thì ö(x) được gọi là gián đoạn tại x0. y
- Gián đoạn được gọi là gián đo¿n lo¿i 1 nếu
tồn tại các giới hạn một phía của ö(x) khi x dần về x0, y = ö(x)
đặc biệt trong gián đoạn loại 1 mà các giới hạn một
phía của ö(x) khi x dần về x O x x
0 bằng nhau thì điểm gián 0
đoạn ấy được gọi là bỏ được. 31
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Gián đoạn được gọi là gián đo¿n lo¿i 2 nếu một trong các giới hạn một phía của
ö(x) khi x dần về x0 không tồn tại.
Ví dụ 1: ö(x) = |x| liên tục tại x0 = 0 vì lim |x| = 0 = ö(0) x 0 → üsin x ÿ k hi x ù 0
Ví dụ 2: Xét sự liên tục của ö(x) = ý x tại x0 = 0. ÿþ A k ih x = 0 sin x
Ta có ö(0) = A và lim ö(x) = lim = 1. x→0 x→0 x
Vậy nếu A = 1 thì ö(x) liên tục tại x = 0; nếu A ù 1 thì ö(x) gián đoạn tại x = 0. üx2 - 1 x 1 ÿ
Ví dụ 3: Xét sự liên tục tại x1 = 1 và x2 = 2 của ö(x) = ý2x +1 1 ü x ü 2 ÿ þx + 3 x ó 2
o Tại x1 = 1: ö(1) = 0, lim ö(x) = lim (x2 – 1) = 0, lim ö(x) = lim (2x + 1) = 3. x 1− → x 1− → x 1+ → x 1+ →
Vậy không tồn tại lim ö(x) nên ö(x) gián đoạn tại x1 = 1. x 1 →
o Tại x2 = 2: ö(2) = 5, lim f (x) = lim (2x +1) = 5 , lim f (x) = lim (x + 3) = 5 . x 2− x 2− → → x 2+ x 2+ → →
Vậy lim ö(x) = 5 = ö(2). Nên ö(x) liên tục tại x2 = 2. x→2 2 ü x khi x 0
Ví dụ 4: Xét hàm số ö(x) = ý tại x0 = 0.
þcot x khi x þ 0 Ta có ö(0) = 0. Mà 2
lim f (x) = lim x = 0 và lim f (x) = lim cot x = +õ . x 0− x 0− → → x 0+ x 0+ → →
Vậy ö(x) gián đoạn tại x0 = 0.
Đßnh nghĩa 2: y = ö(x) được gọi là liên tục trái tại x0 R nếu lim f (x) = f (x ) . − 0 x→ 0 x
Đßnh nghĩa 3: y = ö(x) được gọi là liên tục phÁi tại x0 R nếu lim f (x) = f (x ) . + 0 x→ 0 x
Ví dụ 3 á trên, ö(x) không liên tục tại x1 = 1 nhưng liên tục trái tại đó.
Đßnh lý: Hàm y = ö(x) liên tục tại x0 ö(x) liên tục phải và trái tại x0. 32
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đßnh nghĩa 4: Hàm y = ö(x) liên tục tại mọi x thuộc (a, b) thì ö(x) được gọi là liên tục
trong (a, b). Hàm y = ö(x) liên tục trong (a, b), liên tục phải tại a và liên tục trái tại b
thì ö(x) được gọi là liên tục trên [a, b]. y B ö(b)
Chú ý: Ðồ thị của hàm y = ö(x) liên tục trên [a, b] là một A ö(a)
đưßng cong liền nối A(a, ö(a)) và B(b, ö(b)).
2.2.2. Phép toán và tính chất O a b x a) Phép toán
• Nếu các hàm số ö(x) và g(x) liên tục tại x0. Thì ö ± g, ö.g, f (điều kiện g(x0) ù g
0) liên tục tại x0.
• Nếu y = ö(x) liên tục tại x0, z = g(y) liên tục tại y0 với y0 = ö(x0). Thì z = g(ö(x)) liên tục tại x0.
• Nếu y = ö(x) liên tục tại x0 và có hàm ngược x = ö-1(y) với giả thiết y0 = ö(x0) ù
0. Thì hàm ngược liên tục tại y0. b) Các tính chất
• Nếu y = ö(x) là hàm sơ cấp xác định trên X. Thì ö(x) liên tục trên X.
• Nếu y = ö(x) liên tục trên [a, b], thì ö(x) bị chặn trên [a, b]. Nghĩa là K > 0 sao
cho x [a, b] ta có |ö(x)| K.
• Nếu y = ö(x) liên tục trên [a, b], thì ö(x) đạt giá trị nhỏ nhất m và lớn nhất M trên
đoạn đó. Nghĩa là x1, x2 [a, b] sao cho x [a, b] ta có m = ö(x1) f ö(x) f ö(x2) = M.
• Nếu y = ö(x) liên tục trên [a, b], thì ö(x) nhận mọi giá trị trung gian giữa giá trị
nhỏ nhất và lớn nhất. Nghĩa là C R mà m < C < M thì c [a, b] sao cho ö(c) = C.
• Nếu y = ö(x) liên tục trên [a, b] và ö(a).ö(b) < 0 thì c (a, b) sao cho ö(c) = 0. c) þng dụng
Ví dụ 1: Chứng minh rằng phương trình x.2x – 1 = 0 có nghiệm dương bé hơn 1. 33
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Chứng minh: Xét ö(x) = x.2x – 1 liên tục trên ℝ nên liên tục trên [0, 1] mà
ö(0)ö(1) = - 1 < 0 nên c (0, 1) sao cho: ö(c) = 0 c.2c – 1 = 0. Vậy c (0,
1) là nghiệm phương trình đã cho.
Ví dụ 2: Chứng minh rằng phương trình a b c + +
= 0 (a, b, c > 0 và ñ < ò < x −ñ x − ò x −
) có 2 nghiệm x1, x2 thỏa ñ < x1 < ò < x2 < .
Chứng minh: Giả thiết x ù {ñ, ò, } phương trình trên tương đương:
a(x – ò)(x – ) + b(x – )(x – ñ) + c(x – ñ)(x – ò) = 0
- Đặt ö(x) = a(x – ò)(x – ) + b(x – )(x – ñ) + c(x – ñ)(x – ò) ta có ö(x) là tam
thức bậc 2 nên ö(x) liên tục trên toàn trục. Từ đó ö(x) liên tục trên [ñ, ò];
ö(ñ) = a(ñ – ò)(ñ – ) > 0, ö(ò) = b(ò – )(ò – ñ) < 0.
Vậy x1 thỏa ñ < x1 < ò sao cho ö(x1) = 0.
- Tương tự xét ö(x) trên [ò, ] thì x2 thỏa ò < x2 < sao cho ö(x2) = 0. Điều phải chứng minh. 2.3. Đ¾O HÀM
2.3.1. Định nghĩa, ý nghĩa hình học và v¿t lý y
Cho đưßng cong (C) và M M
0 (C). Từ M0 kẻ
đưßng thẳng cắt (C) tại M khác M0, thì M0M được
gọi là một cát tuyến của (C). C t ò
Cho M chạy liên tục trên (C) về M M 0 nếu M0M 0 ñ H x
về vị trí tới hạn M0t thì M0t được gọi là tiếp tuyến của O (C) tại M0.
* Bài toán: Tính hệ số góc tiếp tuyến của (C): y = ö(x) tại M0(x0, y0) (C).
Giả sử M(x, y) (C), đặt x = x – x0 được gọi là số gia của biến.
ö = y = y – y0 = ö(x) – ö(x0) = ö(x0 + x) – ö(x0) được gọi là số gia của hàm. → → → → ò y = ( MH
Ox , M M ) và ñ = ( Ox , M t ). Khi ấy tanò = = . 0 0 M H x 0
Bây giß cho M → M0 suy ra M0M → M0t, x → 0 và ò → ñ. 34
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến Do y
y = tanx liên tục nên tanò → tanñ. Vậy tanñ = lim x→0 x
Đßnh nghĩa 1: Cho hàm số y = ö(x) xác định trong (a, b) và x0 (a, b). Nếu tồn tại f lim
và giới hạn này hữu hạn thì giới hạn ấy được gọi là đạo hàm của ö(x) tại x0 và x→0 x viết ö’(x0).
* Ý nghĩa hình học: Như ta đã biết tanñ chính là hệ số góc của tiếp tuyến M0t. Vậy từ
bài toán và định nghĩa trên suy ra: Đạo hàm của hàm số tại một điểm x0 bằng hệ số góc
của tiếp tuyến với đưßng cong tại điểm đó M0(x0, y0).
* Ý nghĩa vật lý: Giả sử có một vật chuyển động trên đoạn thẳng từ A đến B. Gọi s(t0)
là quãng đưßng vật đi được tại thßi điểm t0.
Trong khoảng thßi gian t, vật di chuyển được một đoạn: s = s(t0 + t) – s(t0).
Vậy vận tốc tức thßi của vật tại thßi điểm t0 là: + − s s(t t) s(t ) v(t0) = 0 0 lim = lim = s '(t ) 0 t →0 t →0 t t
Ví dụ 1: Tính đạo hàm của hàm ö(x) = x2 + 3x + 2. Xét tại x0 (tùy ý) thuộc R.
Cho x (tùy ý). Khi ấy ö = ö(x0 + x) – ö(x0) = [(x0 + x)2 + 3(x0 + x) + 2] – (x 2
0 + 3x0 + 2) = 2x0x + x2 + 3x = (2x0 + 3)x + x2 f = (2 f
x0 + 3) + x lim
= 2x0 + 3. Vậy ö’(x0) = 2x0 + 3. x x→0 x Đßnh nghĩa 2: Nếu tồn tại f lim
và giới hạn này hữu hạn thì giới hạn ấy được gọi là x 0− → x
đ¿o hàm trái của ö(x) tại x0 và viết ö’–(x0). Đßnh nghĩa 3: Nếu tồn tại f lim
và giới hạn này hữu hạn thì giới hạn ấy được gọi là x 0+ → x
đ¿o hàm phÁi của ö(x) tại x0 và viết ö’+(x0).
Ví dụ 2: Tính các đạo hàm trái phải của hàm số: ö(x) = |x| tại x0 = 0. f | x | 0 − f | x | 0 − lim = lim =1 nên ö’+(0) = 1; lim = lim = 1 − nên ö’–(0) = –1 x 0+ x 0 x + → → x x 0− x 0 x − → → x 35
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đßnh nghĩa 4: Nếu ö(x) có đạo hàm tại mọi x (a, b) thì ö(x) được gọi là có đạo hàm
trong (a, b). Nếu ö(x) có đạo hàm trong (a, b), có đạo hàm phải tại a và đạo hàm trái tại
b. Thì ö(x) được gọi là có đạo hàm trên [a, b].
2.3.2. Tính chất và phép toán
a) Tính chất:
• Hàm số y = ö(x) liên tục tại x0 có đạo hàm tại x0 khi và chỉ khi ö(x) có các
đạo hàm một phía tại x0 và ö’-(x0) = ö’+(x0). Khi ấy ö’(x0) = ö’-(x0) = ö’+(x0).
• Nếu ö(x) có đạo hàm tại x0 thì ö(x) liên tục tại x0. Trái lại không đúng (ví dụ
xét ö(x) = |x| liên tục tại x0 = 0 nhưng không có đạo hàm tại x0 = 0).
• Nếu y = ö(x) có đạo hàm trong (a, b). Khi ấy ö(x) đơn điệu tăng (tư¢ng ứng
giÁm) trong (a, b) ö’(x) g 0 (tương ứng ö’(x) f 0) trong (a, b). b) Phép toán • f
Nếu y = ö(x) và y = g(x) cùng có đạo hàm tại x0. Thì ö ± g, ög, (điều kiện g
g(x0) ù 0) cũng có đạo hàm tại x0 và
(ö g)’(x0) = ö’(x0) g’(x0)
(ög)’(x0) = ö’(x0).g(x0) + ö(x0).g’(x0) f
f '(x ).g(x ) − f (x ).g '(x ) ( )’(x0) = 0 0 0 0 g 2 g (x ) 0
• Nếu y = ö(x) có đạo hàm tại x0, z = g(y) có đạo hàm tại y0 với y0 = ö(x0). Khi
ấy z = h(x) = g(ö(x)) có đạo hàm tại x0 và h’(x0) = g’(y0).ö’(x0).
• Nếu y = ö(x) có đạo hàm tại x0 và có hàm ngược x = g(y). Thì hàm ngược
cũng có đạo hàm tại y 1
0 = ö(x0) và g’(y0) =
, điều kiện ö’(x0) ù 0. f '(x ) 0
c) Các đạo hàm cơ bản C’ = 0
(xñ)’ = ñxñ–1 (uñ)’ = ñ.u’uñ-1.
(ax)’ = axlna (au)’ = u’aulna. Đặc biệt: (ex)’ = ex (eu)’ = u’eu. 36
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến 1 ' 1 u' (log u a|x|)’ =
(loga|u|)’ =
. Đặc biệt (ln|x|)’ = (ln|u|)’ = x ln a u ln a x u
(sinx)’ = cosx (sinu)’ = u’.cosu
(cosx)’ = - sinx (cosu)’ = - u’.sinu 1 u' (tanx)’ =
= 1 + tan2x (tanu)’ =
= u’(1 + tan2u) 2 cos x 2 cos u 1 u' (cotx)’ = -
= - (1 + cot2x) (cotu)’ = -
= - u’(1 + cot2u) 2 sin x 2 sin u (arcsin 1 u'
x)’ = - (arccosx)’ =
(arcsinu)’ = - (arccosu)’ = 2 1- x 2 1- u 1 u'
(arctanx)’ = - (arccotx)’ =
(arctanu)’ = - (arccotu)’ = 2 1+ x 2 1+ u
2.3.3. Đ¿o hàm cấp cao
* Khái niệm: Cho hàm số y = ö(x). Khi ấy y’ = ö’(x) (nếu tồn tại) thì được gọi là đạo
hàm cấp một của ö(x).
Vì ö’(x) lại là hàm của x. Nên nếu tồn tại (y’)’ = (ö’(x))’ thì nó được gọi là đạo
hàm cấp 2 của ö(x) và ký hiệu là y”, y(2), ö”(x), ö(2)(x) …
Tổng quát, đạo hàm của ö(n–1)(x) được gọi là đạo hàm cấp n của ö(x) và ký hiệu
là y(n) hay ö(n)(x). Đạo hàm từ cấp 2 trá lên được gọi là đạo hàm cấp cao.
* Các ví dụ: Tính các đạo hàm cấp n của ö(x) sau
Ví dụ 1: ö(x) = ex. Khi ấy: n = 0, 1, 2, 3, ... thì ö(n)(x) = ex
Ví dụ 2: ö(x) = sinx ð
Khi ấy: ö(0)(x) = sinx = sin(x + 0. ) 2 ð
ö(1)(x) = cosx = sin(x + 1. ) 2 ð ð
ö(2)(x) = cos(x + 1. ) = sin(x + 2. ) 2 2 ... 37
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến ð
ö(n)(x) = sin(x + n. ) 2
Ví dụ 3: ö(x) = ln(1 + x). 1 Khi ấy: ö’(x) =
= (1 + x)-1 = (- 1) 1-1(1 - 1)!(1 + x)-1 1+ x ö(2)(x) = 1 − 2 (1+ x) ö(3)(x) = 2! 3 (1+ x) ... ö − (n)(x) = n 1 − (n 1)! ( 1 − ) (1+ x)n 2.3.4. Vi phân
a) Định nghĩa
Cho hàm số y = ö(x) xác định trong (a, b) và x0 (a, b). Cho x số gia x đủ bé
sao cho x0 + x (a, b). Nếu ö = A.x + O(x), trong đó A không phụ thuộc x và
O(x) là một VCB bậc cao hơn x khi x dần về 0. Thì A.x được gọi là vi phân của
ö(x) tại x0 và viết dö(x0) = A.x. Khi đó ta nói ö(x) khả vi tại x0.
Ví dụ: Cho ö(x) = x2 + 3x + 2, xét x0 (tùy ý) R.
Cho x tùy ý, ta có: ö = (2x0 + 3)x + (x)2.
Rõ ràng: A = 2x0 + 3 không phụ thuộc x, còn O(x) = (x)2 là VCB bậc cao
hơn so với x khi x → 0. Vậy dö(x0) = (2x0 + 3)x
Nhận xét: A = ö’(x0).
b) Mối liên hệ giữa đạo hàm và vi phân
* Đßnh lý: y = ö(x) khả vi tại x0 ö(x) có đạo hàm tại x0 và dö(x0) = ö’(x0)x. f ( ) f Do ö( O x
x) khả vi tại x0 ö = Ax + O(x) = A + lim = A. x x x →0 x
Vậy ö’(x0) = A và dö(x0) = ö’(x0)x.
* Hệ quÁ: Nếu ö(x) = x. Thì ö’(x) = x’ = 1 suy ra dö = dx = x. 38
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Vậy với hàm số y = ö(x) ta có dö(x) = ö’(x)x = ö’(x)dx. dy
Từ đó cách kí hiệu: ö’( df x) = hay y’ = . dx dx
c) Các công thÿc tính vi phân • f
Nếu ö(x) và g(x) cùng khả vi tại x0. Thì ö ± g, ö.g,
(điều kiện g(x0) ù 0) cũng g
khả vi tại x0 và có d(ö ± g)(x0) = dö(x0) ± dg(x0)
d(ö.g)(x0) = g(x0)dö(x0) + ö(x0)dg(x0) f d( )(
g(x )df (x ) - f (x )dg(x ) x 0 0 0 0 0) = g 2 g (x ) 0
• Nếu y = ö(x) khả vi tại x0, z = g(y) khả vi tại y0 với y0 = ö(x0).
Thì z = g(ö(x)) cũng khả vi tại x0 và dz(x0) = ö’(x0)g’(y0)dx
2.3.5. Các định lý về giá trị trung bình y
Định nghĩa: Hàm số y = ö(x) xác định trong (a, b) được y = ö(x)
gọi là đạt cực đ¿i (cực tiểu) đßa phư¢ng tại x0 (a, b) nếu
tồn tại (ñ, ò) thỏa mãn x0 (ñ, ò) (a, b) sao cho mọi x O x0 x 1 (ñ, ò) \{x x
0} ta có ö(x) < ö(x0) (tương ứng ö(x) > ö(x0)) .
Chú ý: Cực đại hay cực tiểu địa phương gọi chung là cực trß đßa phư¢ng hay gọi tắt là cực trị. a) Định lý Fermat:
Nếu y = ö(x) khả vi và đạt cực trị tại c (a, b). Thì ö’(c) = 0.
Chứng minh: Giả sử ö(x) đạt cực đại tại c (a, b). Khi ấy tồn tại (ñ, ò) thỏa c (ñ,
ò) (a, b) sao cho với x (ñ, ò) \ {c} ta có ö(x) < ö(c). f (c + x ) − f (c) f (c + x ) − f (c)
Do tồn tại ö’(c) nên lim = f '(c) = lim . x 0− x 0 x + → → x
Từ x → 0 suy ra c + x → c, nên với x đủ bé thì x = c + x (ñ, ò) và do đó ö(c
+ x) < ö(c) hay ö(c + x) – ö(c) < 0. f (c + x ) - f (c) f (c + x ) - f (c) Nên 0 f lim = ö’(c) = lim f 0. Vậy ö’(c) = 0. x→ 0 - x x→ 0 + x 39
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Chú ý: Trưßng hợp ö(x) đạt cực tiểu địa phương tại c, chứng minh tương tự. Tại điểm x
mà ö(x) không khả vi hoặc khả vi mà ö’(x) = 0, thì x0 được gọi là điểm dừng (hay điểm
tới hạn) của ö(x). b) Định lý Rolle:
Nếu y = ö(x) liên tục trên [a, b], khả vi trong (a, b) và ö(a) = ö(b). Thì c (a, b) sao cho ö’(c) = 0.
Chứng minh: Do ƒ(x) liên tục trên [a, b] nên x1, x2 [a, b] sao cho: ö(x1) = m =
min{ö(x)| x [a, b]} và ö(x2) = M = max{ö(x)| x [a, b]}
Trường hợp 1: Nếu m = M thì thì C R sao cho ö(x) ú C trên [a, b].
Khi đó ta lấy c tùy ý trong (a, b) đều có ö’(c) = 0
Trường hợp 2: Nếu m < M. Khi ấy x1 hoặc x2 (a, b).
Thật vậy giả sử x1 = a, thì m = ö(a) = ö(b) < M. Nên ö(x2) ù ö(a) = ö(b) nên x2 ù a,
b. Khi đó ta chọn c = x2, thì ö(x) đạt cực đại tại c. Vậy ö’(c) = 0
c) Định lý Lagrange:
Nếu y = ö(x) liên tục trên [a, b], khả vi trong (a, b). Thì c (a, b) sao cho ö’(c) = f b ( ) - f (a) . b - a
f (b) − f (a)
Chứng minh: Lập hàm phụ F(x) =
(x − a) – [ö(x) – ö(a)]. Dễ thấy F(x) b − a
thỏa các điều kiện của định lý Rolle, nên c (a, b) sao cho F’(c) = 0. Do F’( f b ( ) - f (a) x) =
- ö’(x), thay x bái c được điều phải chứng minh. b - a d) Định lý Cauchy:
Nếu y = ö(x) và y = g(x) cùng liên tục trên [a, b], cùng khả vi trong (a, b) và g’(x) ù f '(c)
f (b) − f (a)
0 trong (a, b). Thì c (a, b) sao cho: = g'(c)
g(b) − g(a)
f (b) - f (a)
Chứng minh: Lập hàm phụ (x) =
[g(x) – g(a)] – [ö(x) – ö(a)].
g(b) - g(a)
Dễ thấy (x) thỏa các điều kiện của định lý Rolle, nên c(a, b) thỏa ’(c) = 0. 40
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Do ’(x) = f (b) - f (a) g’(x) - ö’(x), thay x bái c được điều phải chứng minh.
g(b) - g(a) Các chú ý
• Nếu thêm điều kiện ö(a) = ö(b) thì định lý Lagrange trá thành định lý Rolle.
Nên định lý Rolle là trưßng hợp đặc biệt của định lý Lagrange.
• Nếu g(x) = x thì định lý Cauchy trá thành định lý Lagrange. Nên định lý
Lagrange là trưßng hợp đặc biệt của định lý Cauchy.
• à định lý Lagrange, đặt x0 = a, x = b – a suy ra b = x0 + x. Khi ấy tồn tại c
(a, b) tương đương tồn tại ñ (0, 1) sao cho c = x0 + ñ.x. Nên công thức á
định lý là ö = ö’(x0 + ñ.x)x. Đây là công thức số gia giới nội Lagrange.
Hệ quả: Nếu ö’(x) ú 0 trong (a, b). Thì ö(x) là một hàm hằng trong (a, b).
Chứng minh: Thật vậy, cố định x0 trong (a, b) và đặt ö(x0) = C. Ta chứng minh ö(x) ú
C trong (a, b).
Nếu x0 < x: Hiển nhiên ö(x) thỏa định lý Lagrange trên [x0, x]. Nên c (x0, x)
f (x) − f (x ) sao cho ö’(c) = 0
= 0 nên ö(x) – ö(x0) = 0 hay ö(x) = ö(x0) = C. x − x0
Nếu x < x0: Hoàn toàn tương tự chúng ta xét ö(x) trên [x, x0].
Vậy ö(x) ú C hay ö(x) là hàm hằng. 2.4. ĂNG DþNG
2.4.1. Tìm cực trị cāa hàm sá
* Bài toán: Tìm cực trị của hàm số y = ö(x) khả vi trên (a, b). * Phư¢ng pháp:
• Bước 1: Tìm điểm dừng bằng cách giải phương trình ö’(x) = 0. Giả sử phương
trình có n nghiệm x1, x2, ..., xn thuộc (a, b). (Tức là ta loại những nghiệm nằm ngoài (a, b)).
• Bước 2: Để kết luận tại xi hàm số có đạt cực trị hay không ta có 2 cách sau:
+) Cách 1: Xét dấu của ö’(x).
Nếu qua xi mà ö’(x) đổi dấu từ dương sang âm thì hàm số đạt cực đại tại xi. 41
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Nếu qua xi mà ö’(x) đổi dấu từ âm sang dương thì hàm số đạt cực tiểu tại xi.
Nếu qua xi mà ö’(x) không đổi dấu thì hàm số không đạt cực trị tại xi.
+) Cách 2: Tính ö”(xi):
Nếu ö”(xi) < 0 thì hàm số đạt cực đại tại xi.
Nếu ö”(xi) > 0 thì hàm số đạt cực tiểu tại xi.
Nếu ö”(xi) = 0 thì ta không kết luận. Tức hàm số có thể đạt cực trị hoặc không,
muốn biết có cực trị hay không thì ta phải quay lại sử dụng cách 1.
Ví dụ 1: Tìm cực trị của hàm số ö(x) = x3 – 3x2 – 9x + 1 trên (-4, 4).
GiÁi: ö’(x) = 3x2 – 6x – 9 = 0 x1 = - 1, x2 = 3. Cả 2 nghiệm đều thuộc (-4, 4) nên ta
có 2 điểm dừng. Mà ö”(x) = 6x – 6.
+) ö”(-1) = - 12 < 0 nên öCĐ(-1) = 6,
+) ö”(3) = 12 > 0 nên öCT(3) = - 26.
* Chú ý 1: Nếu hàm số y = f(x) không khả vi trên (a, b) thì ngoài việc tìm các điểm
dừng ra ta cần tìm thêm những điểm trên (a, b) mà tại đó hàm số không khả vi. Sau đó
ta kiểm tra xem f ’(x) có đổi dấu khi qua các điểm đó hay không rồi kết luận.
Ví dụ 2: Tìm cực trị của hàm số ö(x) = |x| trên (-4, 4).
GiÁi: Nếu x > 0 thì f (x) = x, khi đó f ’(x) = 1.
Nếu x < 0 thì f (x) = – x, khi đó f ’(x) = –1.
Trên (-4, 4), phương trình f ’(x) = 0 vô nghiệm. Tuy nhiên trên khoảng này có
một giá trị mà tại đó hàm số không khả vi là x = 0.
Theo trên ta có f ’–(0) < 0 và f ’+(0) > 0 nên hàm số đạt cực tiểu tại x = 0.
* Chú ý 2: Khi tìm cực trị của hàm số f (x) trên X R. Nếu hàm số đạt cực trị tại a thì
a phải là điểm trong của X.
Như vậy nếu tìm cực trị của f (x) trên [a, b] thì không có khái niệm đạt cực trị tại
2 đầu mút a và b, tức là ta làm giống như trên (a, b).
2.4.2. Tìm giá trị lán nhất và giá trị nhß nhất
* Bài toán: Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của y = ö(x) khả vi
trên [a, b]. 42
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến * Phư¢ng pháp:
• B°ác 1. Giải phương trình f ’(x) = 0. Giả sử có n nghiệm x1, x2, ..., xn [a, b].
(loại các nghiệm nằm ngoài [a, b]).
• B°ác 2. Tính các giá trị f (a), f (x1), f (x2),..., f (xn), f (b).
• B°ác 3. Giá trị lớn nhất, nhỏ nhất trong các giá trị đã tính á bước 2 là các giá trị max, min cần tìm.
* Chú ý: Nếu bài toán yêu cầu tìm GTLN, GTNN trên khoảng (a, b). Trước tiên ta
cũng giải phương trình f ’(x) = 0, sau đó ta lập bảng biến thiên của hàm số rồi kết luận.
Ví dụ 2: Ngưßi ta cử một liên lạc viên đi từ hạm đội ngoài khơi tại A đến đài chỉ huy
tại C trên bß biển. Biết khoảng cách từ A đến vị trí gần nhất trên bß tại B là 30 km,
khoảng cách BC là 40 km, trên biển liên lạc viên đi bằng canô máy với vận tốc 30
km/h còn trên đất liền đi bằng xe máy với vận tốc 50 km/h.
Hỏi điểm đổ bộ trên bß tại đâu thì nhanh nhất? B 30 A
GiÁi: Giả sử điểm đổ bộ trên bß tại D suy ra D BC (tại sao ?). x
Đặt BD = x (km) 0 f x f 40. 40 D Khi ấy AD = 2 2 AB + BD = 2
x + 900 , DC = 40 – x. 40 - x 2 x + Thßi gian đi là: ö( 900 40 - x x) = + C 30 50
Vấn đề x = ? thì ömin. 1 2 x x + Do ö’(x) = x - = 5 - 3 900 = 0 2
5x - 3 x + 900 = 0 30 2 x + 900 50 150 2 x + 900 90 x =
= 22,5 km (thỏa điều kiện 0 x 40). 4
Ta thấy f (0) = 1,8; f (40) = 1,67; f (22,5) = 1,6 fmin = 1,6
Vậy để đến nhanh nhất thì điểm đổ bộ cách B: 22,5 km.
Ví dụ 3: Từ một miếng tôn hình tròn tâm I, bán kính R > B m
0, ngưßi ta cắt bỏ quạt IAmB, sau đó cuốn lại sao cho IA A
ú IB để được hình nón. Hỏi cắt bỏ như thế nào thì hình I
nón có thể tích lớn nhất ? n 43
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
GiÁi: Giả sử cắt quạt IAmB còn lại quạt IAnB với độ đo là 2t (0 < t < ð). Khi ấy độ
dài quạt IAnB là l(IAnB) = 2tR.
Gọi bán kính đáy hình nón là r > 0 và chu vi đáy là C thì: C = l(IAnB) = 2tR = 2ð R
r nên r = t . Gọi chiều cao hình nón là h, theo Pitago: ð R h = 2 2 R − r = 2 2 ð − t ð 1 3
Vậy thể tích hình nón là R
V = ðr2h = t2 2 2 ð − t . 3 2 3ð Từ đó Vmax khi t2 2 2
ð − t lớn nhất ö(t) = t4(ð2 – t2) = ð2t4 – t6 lớn nhất.
Do ö’(t) = 4ð2t3 – 6t5 = 2t3(2ð2 – 3t2) = 0 khi t 6 0 =
ð (vì điều kiện 0 < t < ð). 3 ö ö
Vì f (0) = f (ð) = 0, 6 4 6 6 f ÷ ð ÷ = ð ÷
. Vậy Vmax khi t = ð. 3 ÷ 27 ø ø 3
2.4.3. Tính gần đúng nhờ vi phân
* Công thức: Cho hàm số y = ö(x) khả vi trong (a, b) và giả sử x0 (a, b). Khi ấy với
x đủ bé sao cho x0 + x (a, b). Thì ö = ö’(x0).x + O(x). Nhưng O(x) là VCB
bậc cao hơn so với x khi x → 0.
Nên ö = ö(x0 + x) – ö(x0) û ö’(x0).x ö(x0 + x) û ö(x0) + ö’(x0)x.
* Phư¢ng pháp (có 3 bước)
- Dựa vào yêu cầu của bài toán ta xác định ö(x), hàm này phải khả vi trong miền
cần xét và tính được ö’(x).
- Dựa vào dữ liệu bài toán, xác định x0, x.
- Áp dụng công thức thích hợp.
Ví dụ 1: Một miếng kim loại đồng chất hình vuông cạnh
là 20cm. Sau khi bị nung nóng cạnh đo được 20,10cm. Hỏi
diện tích tăng thêm bao nhiêu ?
GiÁi: Gọi cạnh hình vuông là x (cm) thì diện tích là S(x) = 0,1cm 20cm
x2 (cm2) hàm này khả vi và S’(x) = 2x. 44
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Đặt x0 = 20, x = 0,10. Thì diện tích tăng là: Stăng = S(20 + 0,10) – S(20) = S
Nên Stăng û S’(20) ô 0,10 hay Stăng û 2ô20ô0,10. Vậy Stăng û 4cm2
Ví dụ 2: Tính gần đúng A = 4 15 8 , 1
GiÁi: Xét ö(x) = 4 x , x > 0 hàm này khả vi và ö’(x) = . 4 3 4 x
Chọn x0 = 16, x = - 0,2 suy ra A = ö(16 + ( –0,2)) = ö(x0 + x) Nên A û ö( 1
x0) + ö’(x0).x. Hay A û 4 16 + (- 0,2). . Vậy A û 1,99375. 4 3 4 16
Ví dụ 3: Tính gần đúng B = sin59030’ ð ð
GÁi: Trước hết đổi 59030’ = 600 + (- 30’) + (- ) 3 360
Xét ö(x) = sinx hàm này khả vi và ö’(x) = cosx Đặ ð ð
t x0 = , x = -
suy ra B = ö(x0 + x) û ö(x0) + ö’(x0)x 3 360 ð ð ð ð ð 3 ð Hay B = sin( + (- )) û sin - .cos . Vậy B û - 3 360 3 360 3 2 720
Ví dụ 4: Tính gần đúng C = 0 , 2 13 +1 3 2 x Xét ö(x) = 3
x +1 , x > 0 hàm này khả vi và ö’(x) = 2 3 x + 1
Chọn x0 = 2, x = 0,01. Thì C = ö(x0 + x) û ö(x0) + ö’(x0)x. 3.22 Nên C û 23 +1 + .0,01. Vậy C û 3,02 2 23 +1
2.4.4. Quy tắc L’Hopital f (x) 0 õ
* Đßnh lý: Giả sử lim
có dạng vô định hoặc , các hàm ö(x) và g(x) khả vi.
x→a g(x) 0 õ f '(x) f (x) Khi ấy nếu lim = l thì lim = l.
x→a g'(x)
x→a g(x) 45
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến * Các chú ý
Chú ý 1: Quy tắc L’Hopital chỉ dùng cho hai dạng vô định trên, 5 dạng vô định còn lại
(0.∞, ∞ - ∞, 1∞, 00, ∞0) muốn sử dụng quy tắc L’Hopital thì ta phải biến đổi về một
trong hai dạng trên. Cụ thể: 0 õ
Nếu cần tính lim ö(x).g(x) (dạng 0.∞). Ta đưa về dạng hoặc bằng cách x→a 0 õ biến đổi f (x) g(x)
lim ö(x).g(x) = lim
hoặc lim ö(x).g(x) = lim . x→a x→a 1 x→a x→a 1 g(x) f (x) 0 õ
Nếu cần tính lim [ö(x) – g(x)] (dạng ∞ - ∞). Ta đưa về dạng hoặc bằng x→a 0 õ
cách quy đồng mẫu số hoặc nhân liên hợp.
Nếu cần tính lim ö(x)g(x) với ö(x) > 0 (một trong 3 dạng 1∞, 00 , ∞0). Ta biến đổi x→a như sau:
lim g ( x)ln f ( x
lim ö(x)g(x)= lim eg(x).lnf(x) = ) x a e →
và được: lim g(x).lnö(x) (dạng 0.õ). x→a x→a x→a
Riêng dạng 1õ có thể áp dụng số e á phần trước.
Chú ý 2: Có thể sử dụng quy tắc L’Hopital liên tiếp nhiều lần. f '(x) f (x)
Chú ý 3: Nếu lim
thì không được kết luận lim .
x→a g'(x)
x→a g(x)
* Các ví dụ: Tính các giới hạn sau 3 + − + 0 1 1 1 1 1 Ví dụ 1: 1 x 1 x lim (dạng ) = lim ( – ) = – = x→0 x 0 x→0 2 1+ x 3 2 3 1 ( + x) 2 3 6 ln x õ 1 Ví dụ 2: lim (dạng ) = lim = 0 x→+õ x õ x→+õ x 1 cos x 1
x cos x − sin x
Ví dụ 3: lim (cotx – ) (dạng ∞ - ∞) = lim ( – ) = lim x→0 x x→0 sin x x x→0 xsin x
cos x − xsin x − cos x −xsin x
−sin x − xcos x = lim = lim = lim = 0 x→0
sin x + x cos x
x→0 sin x + x cos x
x→0 2 cos x − x sin x õ Ví dụ 4: ln(tan x) lim sin .
x ln(tan x) (dạng 0.∞) = lim (dạng ) x 0+ → x 0+ → 1 õ sin x 46
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến ö − = 1 cos x ö sin x lim ÷ : ÷ = - − lim = 0 + 2 2 x→0 ø cos .
x tan x sin x ø + 2 x→0 cos x lim xln(sin x)
Ví dụ 5: lim (sin x)x (dạng 00) = x 0 e + → x 0+ → õ Ta có: ln(sin x) cos x lim .
x ln(sin x) (dạng 0.õ) = lim (dạng ) = lim − − x 0+ → + 1 x→0 x õ + 2
x→0 −x .sin x = x − lim . x cos . x
= 0 . Vậy lim (sinx)x = e0 = 1 x 0+ → sin x x→+0 1 1 1 ln(cos x) Ví dụ 6: 2
lim (cos x)x (dạng 1∞). Đặt y = (cosx) 2x lny = ln(cosx) = x 0+ → 2 x 2 x 0 − 1 1 - nên ln(cos x) sin x 1 lim ln y = lim (dạng ) = lim
= − . Vậy lim (cosx) 2x = e 2 + + 2 x→0 x→0 x 0 x 0+ → 2x cos x 2 x 0+ → 1 1 1 Ví dụ 7: ln(ln x)
lim (lnx) x (dạng ∞0). Đặt y = (lnx) x lny = ln(lnx) = nên x→+õ x x ln(ln x) õ 1 1 lim lny = lim (dạng ) = lim
= 0. Vậy lim (lnx) x = e0 = 1 x→+õ x→+õ x õ
x→+õ x ln x x→+õ x − sin x õ x − sin x Ví dụ 8: lim
(dạng ). Nếu dùng quy tắc L’Hopital thì lim =
x→+õ x + sin x õ
x→+õ x + sin x 1− cos x ð lim
không có giới hạn, vì lấy xn = 2nð và x’n = + 2nð cùng dần về +õ x→+õ 1+ cos x 2 nhưng lim1− cos x 1− cos x ' n = 0, lim n = 1 khác nhau. 1+ cos x 1+ cos x ' n n sin x 1−
Nếu tính trực tiếp bằng cách chia cả tử và mẫu cho x được lim x = 1. x→+õ sin x 1+ x
2.4.5. Công thăc Taylor
* Đßnh lý: Giả sử hàm số y = ö(x) có đạo hàm liên tục tới cấp n + 1 trong (a, b) và x0
(a, b). Khi ấy với mỗi x thuộc (a, b) đều tồn tại c nằm giữa x0 và x sao cho: n (k ) ( + ) 1 ö f (x ) ( f n (c) x) = õ 0 (x – x0)k +
(x – x0)n+1 (*) n + k =0 k! ( ) 1 ! 47
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến n (k f ) (x ) 0
* Chú ý: P(x) = õ
(x – x0)k là một đa thức bậc n và được gọi là đa thức Taylor, k =0 k! ( + ) 1 còn R f n (c) n(x) =
(x – x0)n+1 là đa thức bậc n + 1 và được gọi là phần dư thứ n. (n + ) 1 ! * Đặc biệt
- Nếu ö(n+1)(x) bị chặn, x đủ gần x0, n đủ lớn. Thì |Rn(x)| rất nhỏ nên ö(x) û P(x) n (k ) ( + ) 1 - Nếu x f ( ) 0 f n (c)
0 = 0, thì (*) là ö(x) = õ xk +
xn+1 – công thức Maclaurin n + k =0 k! ( ) 1 !
- Nếu a = x0, b = x, n = 0: Công thức Taylor trá thành công thức á định lý Lagrange.
* Các ví dụ: Khai triển Maclaurin các hàm sau
Ví dụ 1: ö(x) = ex
Vì k N ta có ö(k)(x) = ex, nên ö(k)(0) = 1. n c
Vậy ex = õ 1 xk + e xn+1 (0 < c < x) n + k =0 k! ( ) 1 ! c R n 1 +
Nếu x = R > 0 và 0 < c < R thì |R e e R n(x)| = | xn+1| → 0 (khi n → õ) (n + ) 1 ! (n + ) 1 ! n
Vậy ex û õ 1 xk với n đủ lớn. k =0 k! Đặ 1 1 1
c biệt: x = 1 thì e û 1 + 1 + + + ... + ! 2 ! 3 ! n
Ví dụ 2: ö(x) = sinx ð ð
Vì k N ta có ö(k)(x) = sin(x + k ) suy ra ö(k)(0) = sin(k ) hay 2 2 ü 0 khi k = 4q ÿ ÿ = + ü 0 k hi k = 2 m ö 1 khi k 4q 1 (k)(0) = ý = ý
0 khi k = 4q + 2 ÿ þ( ) 1 - m k hi k = 2 m +1 ÿþ 1 khi − k = 4q + 3 1 1 1 n sin(c + (n + ) 1 ð ) Vậy sin ( ) 1 -
x = x – x3 + x5 – x7 + ... + x2n+1 + x2(n+1) ! 3 ! 5 ! 7 (2n + ) 1 ! (2n + ) 2 ! 48
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến n k c + n + ð Hay sin sin( ( ) 1 ) x = õ ( )1 - x2k+1 +
x2(n+1) (c nằm giữa 0 và x) n + k =0 (2k + ) 1 ! (2 ) 2 ! 2 +2
Nếu |x| f R thì |r R k n(x)| f
, n = 2k + 1 → 0 khi n → ∞ nên rn(x) rất nhỏ khi (2k + 2)! n k
n đủ lớn. Vậy sinx û õ ( )1 - x2k+1 k =0 (2k + ) 1 !
Ví dụ 3: ö(x) = ln(1 + x).
Ta có: ö(0)(x) = ln(1 + x)
ö(k)(x) = (–1)k–1(k – 1)!(1 + x)–k
Nên ö(0)(0) = 0 và ö(k)(0) = (–1)k–1(k – 1)! với k = 1, 2, 3, … n k 1 - ( ) 1 - n 1 ( + c)-n 1-
Thay vào ta có: ln(1 + x) = õ ( )1 - xk +
xn+1, 0 < x < 1 n +1 k=1 k 1 n k 1 - Vì |R ( ) 1 - k n(x) | <
nên Rn(x) rất nhỏ khi n đủ lớn. Vậy ln(1 + x) û õ x n k =1 k
2.4.6. Khảo sát và v¿ đồ thị hàm sá theo tham sá và trong tọa đß cực
a) Khảo sát và vẽ đồ thị hàm số tham số
Như đã biết hàm một biến cho bái tham số có dạng x = (t), y = (t) với tham số thực t.
Để khảo sát và vẽ đồ thị của hàm dạng này, ta làm tương tự như hàm tưßng minh y = ö(x) như sau:
- Bước 1: Tìm miền xác định của x = (t), y = (t), xét tính chẵn lẻ và tuần hoàn …
- Bước 2: Xét chiều biến thiên của x = (t), y = (t), ta tính x’ = ’(t), y’ = ’(t).
Sau đó tìm điểm dừng của các hàm này và xét dấu của chúng để xác định
khoảng đơn điệu và cực trị (nếu có).
- Bước 3: Tìm tiệm cận
Nếu t → t0 mà (t) → a, (t) → õ thì x = a là phương trình tiệm cận đứng,
Nếu t → t0 mà (t) → õ, (t) → b thì y = b là phương trình tiệm cận ngang, 49
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến (t)
Nếu t → t0 mà (t) → õ, (t) → õ và lim
= A, lim ((t) - A(t)) = B thì y
t→t0 (t) t→t0
= Ax + B là phương trình tiệm cận xiên dy '(t) '(t) Chú ý: Do = nên khi t → t0 mà lim = k0 và lim (t) = x0, dx '(t)
t→t0 '(t) t→t0
lim (t) = y0, thì k0 là hệ số góc của tiếp tuyến tại M0(x0, y0) với đưßng cong. t→t0 2 - Bướ d y
c 4: Khoảng lồi lõm và điểm uốn, có
= " -' ' " . Từ đó tìm nghiệm và xét 2 dx 3 ( ')
dấu của nó để kết luận khoảng lồi lõm và điểm uốn của đồ thị.
- Bước 5: Vẽ đồ thị, làm các bước tương tự như hàm tưßng minh.
Ví dụ: Cho đưßng cong về dạng tham số sau đó khảo sát và vẽ đồ thị chúng 2 2 2
1. Đưßng Astroid x 3 + y 3 = a 3 (a > 0)
2. Lá Descartes x3 + y3 - 3axy = 0 (a > 0). 2 2 2 1 1 1
1. * Ta có x 3 + y 3 = a 3 (x 3 )2 + (y 3 )2 = (a 3 )2 . 1 1 1
Đặt X = x 3 , Y = y 3 , R = a 3 ta đưa Astroid về đưßng tròn X2 + Y2 = R2. X = üx = 3 Đặ ü R cost ÿ a cos t t tiếp ý (0 t 2ð). Nên ý
(0 t 2ð) - Đây là phương
þY = Rsin t ÿþy = a 3 sin t
trình tham số của Astroid.
* Khảo sát và vẽ đồ thị Astroid
- Miền xác định của hai hàm x = acos3t và y = asin3t là toàn trục, cùng tuần hoàn chu
kỳ T = 2ð, nên ta chỉ cần xét trên [0, 2ð]
- Chiều biến thiên: x’(t) = - 3asintcos2t, y’(t) = 3asin2tcost. Nên x’(t) = 0 và y’(t) = 0 ð khi t = k (k = 0, 1, 2, 3, 4) 2 dy y'(t) y'(t) y'(t) Chú ý : Do = = - tant lim = lim
= 0, nên tiếp tuyến tại t = 0 và dx x'(t)
t→0 x'(t) t ð → x'(t)
t = ð nằm ngang (song song với trục hoành) 50
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến ð y y'(t) y'(t) lim = lim
= - 1, nên tiếp tuyến tại t = . a ð 5ð t→ x'(t) t→ x'(t) 4 4 4
và t = 5ð song song với đưßng thẳng y = - x - a a 4 O x y'(t) y'(t) ð lim = lim
= õ, nên tiếp tuyến tại t = ð 3ð t→ x'(t) t→ x'(t) 2 2 2 - a
và t = 3ð thẳng đứng (song song với trục tung) 2 y'(t) y'(t) 3ð 7ð lim = lim
= 1, nên tiếp tuyến tại t = và t = song song với y 3ð 7ð t→ x'(t) t→ x'(t) 4 4 4 4 = x. T 0 ð ð 3ð 2ð 2 2 x’(t) 0 - 0 - 0 + 0 + 0 x(t) a a 0 0 - a y’(t) 0 + 0 - 0 - 0 + 0 y(t) A 0 0 0 - a 2 1 ð ð
- Khoảng lồi lõm, điểm uốn: d y =
, nên trong (0, ) và ( , ð) đồ thị là 2 dx a 3 cos4 t.sin t 2 2 3ð 3ð cung lõm, trong (ð, ) và (
, 2ð) đồ thị là cung lồi 2 2
2. * Nhận thấy vai trò x và y như nhau, nên đồ thị đối xứng qua đưßng thẳng y = x. 2 Đặ 3at 3at
t y = tx thì hàm số là x3 + t3x3 - 3atx2 = 0 suy ra: x = , y = 3 1+ t 3 1+ t
* Khảo sát và vẽ đồ thị lá Descartes 51
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
- Miền xác định của x(t) và y(t) là t ù - 1 3 1− 2t
- Chiều biến thiên: x’(t) = 3a
nên x’ = 0 khi t = 1 ứng với điểm (a 3 4 , a 3 2 ) 3 2 1 ( + t ) 3 2 3
y’(t) = 3a t(2-t ) nên y’ = 0 khi t = 0, 3 2 ứng với các điểm (0, 0), (a 3 2 , a3 4 ) 3 2 1 ( + t ) y
Khi t → õ thì x(t) và y(t) → 0
Khi t → - 1 - 0 thì x(t) → + õ, y(t) → - õ
Khi t → - 1 + 0 thì x(t) → - õ, y(t) → + õ O x
Nên chúng ta có bảng biến thiên sau đây T - õ - 1 0 1 3 2 + õ 3 2 x’(t) + | + + 0 - - x(t) a 3 4 0 a 3 2 - õ - õ y’(t) - | - + + - y(t) + õ a 3 4 a 3 2 0 - õ 2 3 4 1 ( 2 + t ) 1
- Khoảng lồi lõm, điểm uốn: Do d y = , nên - õ < t < - đồ thị là một 2 dx 3 3 3a 1 ( - 2t ) 3 2 1 cung lõm, còn
< t < + õ - đồ thị là một cung lồi 3 2 y(t) - Tiệm cận: lim
= lim (t) = - 1, lim (y(t) + x(t)) = lim (- a) = - a. t→ 1 − x(t) t→ 1 − t→ 1 − t→ 1 −
Vậy đưßng thẳng y = - x - a là tiệm cận xiên
b) Khảo sát và vẽ đồ thị hàm số trong tọa độ cực
* Hệ táa độ cực y
Trong mặt phẳng cho điểm O gọi là gốc cực và tia Ox gọi là tia M 52 yM r O xM x
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến →
cực. Hệ tọa độ cực là (O, Ox ). Với mỗi điểm M trong mặt phẳng khác → → →
O, ta hoàn toàn xác định được OM và = (Ox , OM ), đặt r = OM
Nếu quy ước r ó 0, 0 2ð - thì hệ táa độ cực được gái là hệ thông thường.
Gọi tọa độ cực của M trong hệ tọa độ này là M(r, ). Quy ước tọa độ của O là (0, 0)
* Phư¢ng trình đường cong trong hệ táa độ cực
Hệ thức F(r, ) = 0 hay r = ö() xác định một quan hệ giữa r và được gọi là
hàm số trong hệ tọa độ cực.
Đồ thị của hàm F(r, ) = 0 hay r = ö() xác định một đưßng cong nào đó được
gọi là đưßng cong trong hệ tọa độ cực
Ví dụ 1: Viết phương trình đưßng tròn tâm I(R, 0) bán kính R > 0 M
Giả sử M thuộc đưßng tròn. Khi ấy r = OM, đặt → → O
= ( Ox , OM ), A(2R, 0). Ta có OAM vuông tại M. A x
Nên ta có OM = OAcos. Vậy r = 2Rcos (0 2ð)
* Mối liên hệ giữa hệ táa độ Descartes và hệ táa độ cực
Bây giß ta đưa vào hệ tọa độ Descartes sao cho O là gốc tọa độ và Ox là trục üx = r cos
hoành. Khi ấy với M thuộc mặt phẳng ta có M(r, ) và M(xM, yM). Khi ấy: ý þy = r sin ÿür = x2 + 2 hay y ý .
ÿþtan = y / x
Đây là mối liên hệ giữa tọa độ Descartes và tọa độ cực.
* Khảo sát và vẽ đồ thị hàm số trong hệ tọa độ cực: Về phương pháp cũng tương tự như
khi xét hàm dạng tưßng minh hay hàm dạng tham số. Tuy nhiên chúng ta lưu ý một số vấn đề sau đây:
- Tính đối xứng
Nếu hàm số chẵn đối với thì đồ thị nhận trục cực (Ox) làm trục đối xứng.
Nếu hàm số lẻ đối với thì đồ thị nhận đưßng thẳng vuông góc với trục cực tại
O (trục Oy trong hệ tọa độ Descartes) làm trục đối xứng 53
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
- Tiếp tuyến: Giả sử C: r = ö() và M C với tiếp tuyến là Mt, ñ là góc hợp bái tiếp
tuyến với chiều dương trục cực, ñ là góc hợp bái OM và tiếp tuyến tanñ - tan
Khi ấy: ñ = ñ - nên tanñ = tan(ñ - ) = (*) t 1 + tanñ.tan ñ üx = r ( ) cos C
Mặt khác ta tham số hóa đưßng cong ý M r þy = r ( )sin ñ y
r'.sin + r.cos Nên tanñ = '( ) = (**) O x x'()
r'.cos - r.sin r()
Thay (**) vào (*) và tính được tanñ =
, từ đó tính được độ nghiêng của tiếp tuyến r'() tại M.
Ngoài ra chúng ta xét thêm tính đối xứng nếu có.
Ví dụ 2: Hình hoa hồng 3 cánh r = a.sin3, a > 0 ð ð
- Là hàm tuần hoàn chu kỳ T = 2ð , nên chỉ cần xét [- , ], nhưng r là hàm lẻ nên 3 3 3 đồ y thị đối = 5ð/6 = ð/6 ð
xứng qua trục tung nên chỉ cần xét [0, ] 3 x ð r 1 O
- Ta có r’ = 3a.cos3 = 0 khi = , tanñ = = tan3 6 r' 3
- Bảng biến thiên và đồ thị như sau: 0 ð/6 ð/3 r’ 3a + 0 - r A 0 0 tanñ 0 õ 0 54
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến BÀI T¾P CH¯¡NG 2
Bài tập 1: Tìm các giới hạn sau 2 20 (x − x − 2) 2
x + x + ... + xn - 1. n lim 2. lim x→2 3 10 (x −12x +16) x 1 → x -1
x − a + x − a 1 n +1 3. lim (a > 0) 4. lim ( - ) x a+ → 2 2 x − a x 1 → x -1 n 1 + x -1 5. lim ( 2 x + x +1 - 2 x - x +1 ) 6. lim x( 2 x +1 - x) x→+õ x→+õ 2 + + sin 7.
x sin x tan x ax lim 8. lim (a, b ù 0) x→0 2
2x cos x + x x→0 sin bx 1- cos + sin 1 9. x x lim (p ù 0, 1) 10. lim x.sin
x→0 1- cos px + sin px x→+õ x 1- cos x 1 11. lim
12. lim (cos x ) x x 0+ → 1- cos x x 0+ → ð 1 x ð 1
13. lim [1 + tan(x - )] 4x ð- 14. lim (sin ) x 1- ð x→ 4 x 1 → 2 4 1 2 + ö x + x 3 ö ln 1 ( x2 + ) 15. lim ÷÷ ÷÷ 16. lim x→+õ 2 ø x +1 ø x→0 x 2 + + + + 17. xsin x x 1 -1 1 x 3 - 1 x lim 18. lim x→0 2 x x→0 x
Bài tập 2: Xét sự liên tục của các hàm số sau trên R ü x -1 ü ð ÿ kh ix ù 1 cos x k h i x ü 1 1. ÿ ö(x) = 2 ý x -1 2. ö(x) = ý 2 ÿþ A kh ix = 1 ÿþ x - 1 k h ix ó1 ü1+ sin x k h ix ü 0 üx + 2 kh ix 1 - ÿ ÿ 3. ö(x) = ý2x + 1 k hi 0 x 1 4. ö(x) = ý x2 kh i -1 ü x ü 1 ÿ ÿ þcosð x k h ix þ 1 þ4 3 x + kh 1 ix ó 1
Bài tập 3: Định A, B để ö(x) liên tục trên R 55
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến üsin x k h i x ü - / ð 2 ü 2 x - 1 kh ix 1 - ÿ
1. ö(x) = ÿýAsin x + B k h i - / ð 2 x ð / 2 2. ö(x) = ýAx + B kh i - 1 ü x ü 1 ÿ ÿ þcos x k h i / ð 2 ü x ü +õ þ 3 x + kh 2 ix ó 1
Bài tập 5: Tính đạo hàm của các hàm số sau
1. y = x + x + x 2. y = earctanx 3. y = ln|cosx| 4. y = sin2x.cos3x 2 2 + + 3 1- x 5. y = 2 2 a a x
a + x - a ln (a ù 0) 6. y = 3 x 3 1+ x üax + k b h ix ü 1
Bài tập 6: Định a, b, c, d để ö(x) = ý
có đạo hàm tại x0 = 1. þcx + k d h ix þ 1
Hướng dẫn: Điều kiện cần để f(x) có đ¿o hàm t¿i x0 là ö(x) liên tục t¿i x0 và f’(x+c) = f’(x - c)
Bài tập 7: Tính y’ nếu
1. y = u(x)v(x) điều kiện u(x) > 0, u(x) ù 1. Từ đó tính y’ nếu: y = xx, y = (sinx)cosx
Hướng dẫn: Với ñ > 0 thì ñ = elnñ hoặc y = uv thì lny = vlnu
2. y = logu(x)|v(x)| điều kiện u(x) > 0, u(x) ù 1 và v(x) ù 0.
Từ đó tính y’ nếu y = log(2x+1)(x2 + 3x - 1), y = logsinxcosx ln v(x)
Hướng dẫn: logu(x)|v(x)| = lnu(x)
Bài tập 8: Chứng minh rằng hàm số
1. y = C1ex + C2e2x thỏa mãn y” - 3y’ + 2y = 0
2. y = (C1x + C2)ex thỏa mãn y” - 2y’ + y = 0
3. y = e-x(C1cos2x + C2sin2x) thỏa mãn y” + 2y’ + 5y = 0
Bài tập 9: Tính đạo hàm cấp n của các hàm sau 1. y = xex 2. y = (1 + x)ñ 3. y = xe-x 4. y = xlnx
Bài tập 10: Giả sử f(x) và g(x) cùng có đạo hàm tới cấp n. Tính (ö.g)(n) n Hướng dẫn: k 1- k k C
+ C = C và kết quÁ (f.g)(n) = õ k (n-k) (k C f g ) n 1 - n 1 - n n k =0
Bài tập 11: Chứng minh bất đẳng thức |arctx - arcty| |x - y| với x, y R 56
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến
Bài tập 12: Một xí nghiệp cần sản xuất những thùng hình hộp chữ nhật không nắp đậy,
đáy là hình vuông và thể tích cần đạt được là V. Hỏi kích thước thùng như thế nào thì
tiết kiệm nguyên liệu nhất?
Bài tập 13: Một ngưßi cần làm chiếc thùng hình trụ tròn xoay không có nắp đậy và thể
tích cần đạt được là V. Hỏi kích thước của thùng như thế nào thì tiết kiệm nguyên liệu nhất?
Bài tập 14: Một xí nghiệp cần sản xuất những thùng hình hộp có nắp đậy, đáy là lục
giác đều và thể tích cần đạt được là V. Hỏi kích thước thùng như thế nào thì tiết kiệm nguyên liệu nhất?
Bài tập 15: Từ một miếng tôn kích thước 1m ô 2m ngưßi
ta cắt bỏ 4 góc 4 hình vuông bằng nhau, sau đó gấp lai
theo đưßng gạch gạch (-----) về cùng môt phía để được
một hình hộp chữ nhật. Hỏi cắt như thế nào thì thể tích hộp
chữ nhật lớn nhất ? (hình bên)
Bài tập 16: Một liên lạc viên đi từ hạm đội ngoài khơi tại A đến đài chỉ huy trên bß
biển tại C. Biết khoảng cách từ A đến vị trí gần bß nhất tại B là 28km và BC = 45km,
trên biển ngưßi ấy đi bằng canô máy với vận tốc 30km/h còn trên đất liền đi bằng xe
máy với vận tốc 50km/h. Hỏi điểm đổ bộ trên bß á đâu thì nhanh nhất ?
Bài tập 17: Trong các hình chữ nhật nội tiếp hình tròn (có các đỉnh hình chữ nhật nằm
trên đưßng tròn) bán kính R > 0 khi nào có diện tích lớn nhất ?
Bài tập 18: Tính gần đúng nhß vi phân hàm một biến 1. 3 0 , 8 2 2. sin29045’ 3. cos60030’ 4. ln0,97 2 + 0 , 1 ( ) 2 2 + 3 5. ( 9 , 2 ) 5 7 6. ( 9 , 2 ) 5 2 - 5 0 , 1 ( 2 ) 2 3 -1
Bài tập 19: Một bồn hoa hình tròn bán kính 5m, nếu xây ra phía ngoài bao quanh nó bái
một lớp gạch dày 10cm. Hỏi diện tích xây bao quanh bồn hoa này là khoảng bao nhiêu?
Bài tập 20: Tìm các giới hạn sau bằng qui tắc L’Hopital 57
KHOA KHOA HàC C¡ BÀN Chư¢ng 2: Phép tính vi phân hàm một biến n 1- cos x -x + 1. x e e - 2cos x lim (n N) 2. lim x→0 n n x sin x 2 x→0 x 3 1- x - 1- x x - sin 3. x lim 4. lim x→0 4 5 1- x - 1- x x→0 3 x ln x n 5. x lim 6. lim (n N) x→ 0 + cot x x→+õ x e 1 1 1 7. lim ( - cot2x) 8. lim ( - ) x→0 2 x x→0 x x e -1 1 1 1 9. lim( − ) 10. lim x( x e - 1) x 1 → x-1 ln x x→+õ 1 11. lim sinxlnx 12. x lim x -1 x→ 0 + x 1 → 13. lim (sinx)arcsinx 14. lim (sinx)sinx x→ 0 + x→+0 1 1 15. x lim(sin x ln ) 16. x lim (ln x ln ) x→ 0 + x→+õ 1 17. lim x x 18. 2x ð - lim (tanx) x→+õ ð x→ -0 2 19. lim (x - ex) 20. lim (x - lnx) x→+õ x→+õ
Bài tập 21: Khảo sát và vẽ đồ thị các hàm sau (á đây a, h > 0)
üx = a(t − sint) 1. Đưßng xicloit: ý
2. Lá Descartes: x3 + y3 – 3xy = 0 þy = a 1 ( − cost) a ð
3. Đưßng xoắn hypebol r =
4. Đưßng hình tượng r =
5. Đưßng ốc sên Pascal r = 2acos + h
6. Đưßng Lemniscata r2 = 2a2cos2
7. Đưßng xoắn ốc Acsimet r = a
8. Đưßng xoắn lôgarit r = a.eh
9. Hoa hồng 4 cánh r = a.sin2
10. Hoa hồng tám cánh r = acos4 58
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Chương 3 : PHÉP TÍNH TÍCH PHÂN
3.1. TÍCH PHÂN B¾T ĐÞNH
3.1.1. Khái niệm tích phân b¿t đßnh
a) Định nghĩa
* Đßnh nghĩa 1: Hàm số y = F(x) được gọi là một nguyên hàm của hàm y = ö(x) trong
(a, b) nếu với x (a, b) ta có: F'(x) = ö(x).
* Ví dụ: F(x) = x2 + 3x - 1 là một nguyên hàm của ö(x) = 2x + 3
* Đßnh lý: F(x) là một nguyên hàm của ö(x) trong (a, b). Khi ấy G(x) là nguyên hàm
của ö(x) trong (a, b) khi và chỉ khi tồn tại C R sao cho G(x) = F(x) + C.
Do F(x) là nguyên hàm của ö(x) trong (a, b) F’(x) = ö(x) với x (a, b).
G(x) là nguyên hàm của ö(x) trong (a, b) G'(x) = ö(x) với x (a, b).
Vậy x (a, b) thì G'(x) - F'(x) = 0 [G(x) - F(x)]’ = 0 tồn tại C R sao
cho G(x) - F(x) ú C G(x) = F(x) + C.
* Đßnh nghĩa 2: Tập tất cả các nguyên hàm của ö(x) được gọi là tích phân bất định của
ö(x) và được ký hiệu là ö(x)dx.
- dấu tích phân, ö(x) và ö(x)dx - hàm số và biểu thức dưới dấu tích phân
* Nhận xét: Như vậy nếu y = F(x) là một nguyên hàm của y = ö(x) trong (a, b). Thì ö(x)dx = F(x) + C.
* Ví dụ: (3x2 + 4x + 5)dx = x3 + 2x2 + 5x + C
(4x3 + 6x2 - 8x + 3)dx = x4 + 2x3 - 4x2 + 3x + C
b) Các tính chất đơn giản
Giả thiết các tích phân nói dưới đây là tồn tại
- Tính chất 1: [ö(x) g(x)]dx = ö(x)dx g(x)dx
- Tính chất 2: kö(x)dx = kö(x)dx, k ù 0 59
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
- Tính chất 3: (ö(x)dx)' = ö(x) d(ö(x)dx) = ö(x)dx
- Tính chất 4: F'(x)dx = F(x) + C dF(x) = F(x) + C
- Tính chất 5: Nếu ö(x)dx = F(x) + C thì ö(t)dt = F(t) + C
c) Các công thức cơ bản
kdx = kx + C, k R ü 1 ñ + 1 x + k C hi ñ ù 1 - xñdx = ÿýñ +1 ÿþ l n | x | + C k hi ñ = 1 -
axdx = ax + C. Đặc biệt exdx = ex + C ln a sinxdx = - cosx + C ; cosxdx = sinx + C
1 dx = (1 + tan2x)dx = tanx + C 2 cos x
1 dx = (1 + cot2x)dx = - cotx + C 2 sin x
1 dx = arcsinx + C = - arccosx + C 2 1- x
1 dx = arctanx + C = - arccotx + C 2 1+ x
Các ví dụ: Tính các tích phân sau 2 x + 2
Ví dụ 1: I = (ex + sinx + tan2x +
)dx = (ex + sinx + tan2x + 1 + 1 )dx 2 1+ x 2 1+ x
= ex - cosx + tanx + arctanx + C Ví dụ 2: I = 1
dx = ( 1 + 1 )dx = tanx - cotx + C 2 cos x 2 + sin x 2 cos x 2 sin x 60
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 2 x + 3x + 2 Ví dụ 3: I =
dx =(1 + 3 + 2 )dx = x + 3ln|x| - 2 + C 2 x x 2 x x
3.1.2. Các ph°¢ng pháp tích phân b¿t đßnh
Ngoài phương pháp biến đổi và áp dụng trực tiếp các công thức cơ bản, ta còn
có 2 phương pháp thưßng dùng để tính tích phân.
a) Phương pháp đổi biến số
* Phư¢ng pháp: Nếu cần tính I = ö(x)dx, x = (t) là hàm số có hàm ngược và khả vi.
Thì I = ö((t)).'(t)dt.
Thay đổi vai trò x và t cho nhau: Từ I = ö((x))’(x)dx, đặt t = (x). Thì I = ö(t)dt.
* Các ví dụ: Tính các tích phân sau dx Ví dụ 1: I = . x ln . x ln(ln x)
Đặt t = lnx dt = dx nên I = dt . Đặt tiếp u = lnt du = dt . x t ln t t
Nên I = du = ln|u| + C. Vậy I = ln|ln(lnx)| + C. u
Ví dụ 2: I = xñ(axñ+1 + b)òdx trong đó a, b, ñ, ò ù 0, ñ ù - 1 Đặ 1
t t = axñ+1 + b dt = (ñ + 1)axñdx xñdx = dt. (ñ + ) 1 a ü 1 ò +1 t + k C h i ò ù 1 - 1 ÿÿ(ñ + ) 1 (ò + ) 1 a Từ đó I = tòdt = ý (ñ + ) 1 a ÿ 1 ln | t + | k C h i ò = 1 - ÿþ (ñ +1)a ü 1 ñ + ( 1 ax + ò+ b) 1 + k C h i ò ù 1 - ÿÿ(ñ + ) 1 (ò + ) 1 a Vậy I = ý ÿ 1 ñ + ln | 1 ax + b + | k C h i ò = 1 - ÿþ (ñ +1)a
Ví dụ 3: I = tanxdx 61
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Do I = sin x dx, đặt t = cosx dt = - sinxdx. Vậy I = - dt = - ln|t| + C cos x t
Thay t = cosx ta được I = - ln|cosx| + C. x x 1 ( + )
Ví dụ 4: I = e e dx 2 x 1- e Đặ +
t t = ex dt = exdx. Nên I = 1 t dt = 1 dt + t dt = arcsint + J. 2 1- t 2 1- t 2 1- t Trong đó J = t dt, đặt u = 2 t 1- t du = -
dt hay J = - du = - u J = - 2 1- t . 2 1- t 2 1- t Vậy I = arcsint - 2
1- t + C. Thay t = ex được I = arcsinex - x 1 e2 - + C n ln x Ví dụ 5: I = dx, n N x
Đặt t = lnx dt = dx nên I = tndt = 1 tn+1 + C. Vậy I = 1 lnn+1x + C x n +1 n +1
b) Phương pháp tích phân từng phần
* Phư¢ng pháp: Nếu u(x) và v(x) là hai hàm khả vi thì udv = uv - vdu.
* Các ví dụ: Tính các tích phân sau
Ví dụ 1: I = logaxdx (a > 0, a ù 1, x > 0) ü ü dx u = ln x du =
Ta có I = ln x dx = 1 lnxdx. Đặt ÿ ý ý x . ln a ln a þdv = dx ÿþv = x
Nên I = 1 (xlnx - dx) = 1 (xlnx - x) + C. ln a ln a
Vậy I = 1 x(lnx - 1) + C. Đặc biệt lnxdx = x(lnx - 1) + C ln a
Ví dụ 2: I = arcsinxdx 62
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân ü dx üu = arcsin x ÿdu = Cách 1: Đặt xdx ý ý 1 x2 - I = xarcsinx - þdv = dx ÿ 2 1- x þv = x Hay I = xarcsinx + 2
1- x + C (xem ví dụ 4 á trên)
Cách 2: Đổi t = arcsinx - t , x = sint nên dx = costdt. Từ đó I = t.costdt, 2 2 u = du = đặ ü t ü dt t ý ý
. Suy ra I = t.sint - sintdt = t.sint + cost + C, do - t þdv = costdt þv = sin t 2 nên cost = 2
1- sin t . Nên I = t.sint + 2 1- sin t + C. 2 Vậy I = xarcsinx + 2 1- x + C.
Ví dụ 3: I = arctanxdx ü dx u = Đặ ü arctan x du = t ÿ x ý ý + x2 1 . Nên I = xarctanx - dx = xarctanx - þdv = dx ÿ 2 1+ x þv = x 1 2 d 1
( + x ) = xarctanx - 1 ln(1 + x2) + C. 2 2 1 + x 2 Vậy I = xarctanx - ln 2 1+ x + C
Chú ý: Tư¢ng tự ta có thể đổi t = arctanx như ví dụ trên
Ví dụ 4: I = exsinxdx x x Đặ üu = e üdu = e dx t ý ý
. Nên I = - excosx + excosxdx þdv = sin xdx þv = -cos x x x Đặ üu = e üdu = e dx t tiếp ý ý
I = - excosx + (exsinx - exsinxdx) þdv = cos xdx þv = sin x
Hay I = ex(sinx - cosx) - I. Vậy I = 1 ex(sinx + cosx) + C 2 n ln x Ví dụ 5: I = dx, n N x 63
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân üu = n ln x ü n ln 1- du = n x n ln Đặt ÿ ÿ dx x ý dx ý x . Nên I = lnn+1x - n dx = lnn+1x - nI. ÿdv = x þ ÿ x þdv = ln x Vậy I = 1 lnn+1x + C n +1
Chú ý: Một số hàm sau không thể dùng các phư¢ng pháp trên để tính tích phân được: sin x , x 1 2
, e -x , sinx2, cosx2, exlnx ... vì người ta chứng minh được rằng các nguyên hàm của chúng không ln x
phÁi là một hàm s¢ cấp.
3.1.3. Mßt số dạng tích phân b¿t đßnh
a) Tích phân hàm hữu tỷ P(x) P(x) * D¿ng: I =
dx, với P(x) và Q(x) là hai đa thức,
(*) được gọi là phân thức Q(x) Q(x) (hay hàm hữu tỷ)
Nếu bậc P(x) < bậc Q(x) thì (*) được gọi là phân thức thực sự.
Nếu bậc P(x) bậc Q(x) thì (*) được gọi là phân thức chưa thực sự: Bằng phép
chia tử số cho mẫu số chúng ta đưa phân thức chưa thực sự về tổng một đa thức và một
phân thức thực sự, tích phân đa thức tính dễ dàng. P(x) P(x)
Nên ta chỉ cần tính I = dx trong đó
là phân thức thực sự. Q(x) Q(x)
* Phư¢ng pháp
- Bước 1: Phân tích Q(x) thành tích các nhân tử dạng x + a và x2 + px + q (với < 0) P(x) - Bước 2: Viết
dưới dạng tổng các phân thức đơn giản như sau: Q(x) P(x)
Nếu trong Q(x) có nhân tử dạng (x + a)k thì có tổng k phân thức: Q(x) A A A 1 + 2 + … + k x + a 2 (x + a) k (x + a) 64
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân P(x)
Nếu trong Q(x) có nhân tử dạng (x2 + px + q)k thì có tổng k phân thức: Q(x) M x + N M x + N M x + N 1 1 + 2 2 + ... + k k
x2 + px + q 2 2
(x + px + q) 2 k
(x + px + q)
- Bước 3: Sau đó tính các hệ số Ai, Mi, Ni bằng phương pháp đồng nhất hệ số.
Vậy để tính I ta chỉ cần tính tích phân các phân thức đơn giản dạng: + I dx Mx N k = , J dx trong đó k N k k = (x + a) 2 k
(x + px + q) dx Tính Ik = k (x + a) Nếu k = 1: I dx 1 = = ln|x + a| + C x + a Nếu k > 1: I 1 1 k = (x + a)-kdx = (x + a)1-k + C = - + C 1- k k 1 - (k - ) 1 (x + a) Mx + N Tính Jk = dx 2 k
(x + px + q)
Do = p2 - 4p < 0 nên x2 + px + q = (x + p )2 + - = (x + p )2 + ñ2, ñ2 = - và 2 4 2 4
đặt t = x + p dx = dt và (x2 + px + q)k = t2 + ñ2, 2
Mx + N = M(x + p ) + (N - M p ) = Mt + (N - M p ). 2 2 2 p
Mt + (N - M ) Nên J 2 tdt p dt k = dt = M + (N - M ) . 2 2 k t ( + ñ ) 2 k t ( 2 + ñ ) 2 2 k t ( 2 + ñ ) Hay J p tdt dt k = MJk1 + (N - M )Jk2. Trong đó Jk1 = và Jk2 = 2 2 k t ( 2 + ñ ) 2 k t ( 2 + ñ ) Tính J 1 du
k1: Đặt u = t2 + ñ2 thì du = 2tdt Jk1 = nên 2 k u J 1 1 k1 =
lnu + C = ln(x2 + px + q) + C nếu k = 1 2 2 65
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân - 1 2 - 1 k + + J u k (x px q) k1 = + C = + C nếu k > 1 2 1 ( - k) 1 ( 2 - k) dt Tính Jk2 = 2 k t ( 2 + ñ ) Nếu k = 1: J dt 12 =
. Đặt t = ñu dt = ñdu nên : 2 2 t + ñ J du 1 du 1 t p 12 = ñ =
= arctanu + C thay u = và t = x + . 2 2 (ñu) + ñ ñ 2 1+ u ñ ñ 2 2x + ñ 2x + p - Suy ra ta có J 1 p 1 12 = arctan + C = arctan + C ñ ñ 2 - 2 - 2 2 2 +ñ 2 Nếu k > 1: J 1 t ( ) - t 1 1 t k2 = dt = ( dt - dt) 2 ñ 2 2 k t ( +ñ ) 2 ñ 2 2 1 ( ) − + k t ñ 2 k t ( 2 + ñ ) 2 = 1 J 1 J (*). Với J (*) = t dt = tdt t . 2 ñ (k-1)2 - 2 ñ k k2 2 k t ( 2 + ñ ) 2 k t ( 2 + ñ ) üu = t üdu = dt Đặ ÿ ÿ t ý tdt ý 1 . Nên ÿdv = v = þ ( 2 + 2 k t ñ ) ÿþ 2 1 (
2 - k)(t + 2 k 1- ñ ) J (*) t 1 t t 1 k2 = + dt = + J 2 2 k 1 - (k-1)2. 1 ( 2 - k)(t +ñ ) 2(k - ) 1 2 2 k 1 - (t +ñ ) 2 2 k 1 - 1 ( 2 - k)(t +ñ ) 2(k - ) 1 Suy ra J 1 t 1 k2 = J - J 2 ñ (k-1)2 + 2 2 2 k 1 - (k-1)2 2ñ 1 ( - k)(t +ñ ) 2 ( 2 k - ) 1 ñ = t + 2k -3 J 2 2 2 k 1 -
(k-1)2: Đây là công thức truy hồi. 2ñ 1 ( - k)(t +ñ ) 2 ( 2 k - ) 1 ñ
Vậy chúng ta tính được Jk2 do đó tính được I.
* Các ví dụ: Tính các tích phân sau Ví dụ 1: I = 1 dx 2 x +10x + 7 1
(A + B)x + 5 ( A + 2B) Do 1 = = A + B = 2 x +10x + 7 (x + ) 2 (x + ) 5 x + 2 x + 5 (x + ) 3 (x + ) 2 66
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân A + B = ü 0
(A + B)x + (5A + 2B) = 0x + 1 1 1 ý A = , B = - þ5A + 2B = 1 3 3 x +
Vậy I = 1 ( 1 - 1 )dx = 1 (ln|x + 2| - ln|x + 5|) + C = 1 ln| 2 | + C. 3 x + 2 x + 5 3 3 x + 5 1 1 (x + ) 5 - (x + ) 2
Chú ý: Ví dụ 1 có thể làm nhanh h¢n bằng cách = . (x + ) 2 (x + ) 5 3 (x + ) 2 (x + ) 5 1 1 x + a Tổng quát I = dx = ln
+ C nếu a ù b
(x + a)(x + b) b - a x + b + Ví dụ 2: I = x 1 dx
x3 - 4x2 + 3x + Do x 1 = x + 1
= A + B + C =
x3 - 4x2 + 3x x(x - ) 1 (x - ) 3 x x -1 x - 3
(A + B + C) 2 x + ( 4
- A - 3B - C)x + 3A nên (A + B + C)x2 +(- 4A - 3D - C)x + 3A = 0x2 + x x(x - ) 1 (x - ) 3
ü A + B + C = 0 ÿ + 1. Suy ra 1 2
ý4A + 3B + C = 1
- A = , B = - 1, C = . Nên ÿ 3 3 þ3 A = 1
I = 1 dx - dx + 2 dx = 1 ln|x| - ln| x - 1| + 2 ln|x - 3| + ln|C| 3 x x -1 3 x - 3 3 3 3 x(x - ) 3 2 Vậy I = ln|C |. x -1
Ví dụ 3: I = x -1 dx. x3 + x x -1 Bx + 2 A x + + x Bx + = x -1 = A + C = ( ) 1 ( C) =
x3 + x x( 2 x + ) 1 x 2 x +1 x( 2 x + ) 1 üA + B = 0 (A + B) 2
x + Cx + A ÿ
(A + B)x2 + Cx + A = 0x2 + x - 1 nên ýC =1 A = x( 2 x + ) 1 ÿ þA = 1 - - 1, B = 1, C = 1. Vậy x + I = - dx +
1 dx = - ln|x| + x dx + 1 dx x 2 x +1 2 x +1 2 x +1 67
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân +
= 1 ln(x2 + 1) - ln|x| + arctanx + C = ln 1 2 x + arctanx + C. 2 | x |
Ví dụ 4: I = dx 4 2 x + x 2 2 x + Do 1 = 1 = ( ) 1 - x = 1 - 1 4 2 x + x 2 x ( 2 x + ) 1 2 x ( 2 x + ) 1 2 x 2 x +1
Nên I = ( 1 - 1 )dx = - 1 - arctanx + C 2 x 2 x +1 x Ví dụ 5: I = xdx 4 x + 5 2 x + 4 Đặ 1
t t = x2 2xdx = dt . Nên I = 1 dt = 1 dt = 1 ( 1 - t 2 2 t + 5t + 4 2 (t + ) 1 (t + ) 4 6 t + 1 1 C t +
)dt = 1 [ln(t + 1) - ln(t + 4)] + 1 ln|C| = 1 ln | | ( ) 1 (C ù 0). t + 4 6 6 6 t + 4 2 C x + Vậy I = 1 ln | | ( ) 1 (C ù 0) 6 2 x + 4
b) Tích phân các hàm vô tỷ ax + b
* Lo¿i 1: I = R(x, n
)dx, trong đó a hoặc p ù 0, n N, n 2, R(u, v) là hàm hữu px + q tỷ đối với u và v. n Đặ + + t t = ax b ax b qt - b n tn = x =
= (t) nên dx = ’(t)dt. px + q px + q n a - pt
Vậy R((t), t).’(t)dt - Đây là tích phân hàm hữu tỷ. dx Ví dụ 1: I = 3 x +1 - x +1
Đặt t = 6 x +1 x = t6 - 1 dx = 6t5dt, x +1 = t3, 3 x +1 = t2. 5 3 Nên I = 6 t
dt = 6 t dt = 6(t2 + t + 1 + 1 )dt 3 2 t - t t -1 t -1
Hay I = (6t2 + 6t + 6 + 6 )dt = 2t3 + 3t2 + 6t + 6ln|t - 1|) + C. t -1 68
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Thay t = 6 x + 1 ta được I = 2 x +1 + 3 3 x +1 + ln| 6 x +1 - 1|) + C 4 8
Ví dụ 2: I = x - x dx. x 1 ( 4 + x) 2 Đặt t = t - t t -1
8 x x = t8, dx = 8t7dt, 4 x = t2. Nên I = 8 t7dt = 8 dt = 8 t 1 ( 2 + t ) 2 1+ t
8 t dt - 8 1 dt = 4ln(1 + t2) - 8arctant + C. 2 1+ t 2 1+ t
Vậy I = 4ln(1 + 4 x ) - 8arctan 8 x + C Ví dụ 3: I = dx 3 2 (x - ) 1 (x + ) 1
Ta có I = x +1 dx 3 . . x -1 x +1 3 3 2 Đặt t = x +1 t + 1 2t t 3 x = , x + 1 = dt, dx = - 6 dt. x -1 3 t -1 3 t -1 3 2 (t - ) 1 3 2
Nên I = - 3t. t -1 . t dt = - 3 dt . 3 t 3 2 (t - ) 1 3 t -1 Bt + 2
A t + t + + Bt + Do 1 = 1 = A + C = ( ) 1 ( C)(t - ) 1 3 t -1 (t - ) 1 ( 2 t + t + ) 1 t -1 2 t + t +1 (t - ) 1 ( 2 t + t + ) 1 üA + B = 0 2 + + + + ÿ = (A B)t
(A - B C)t (A - C) 1 1 2
ýA - B + C = 0 A = , B = - , C = - 3 t -1 ÿ 3 3 3 þA - C = 1 t + t + +
I = - dt +
2 dt = - ln|t - 1| + 1 (2 )1 3 dt t -1 2 t + t +1 2 2 t + t +1 t +
= - ln|t - 1| + 1 2 1 dt + 3 dt 2 2 t + t +1 2 2 t + t +1
= - ln|t - 1| + 1 ln(t2 + t + 1) + 3 J. Trong đó 2 2 J = dt = dt = dt = 4 dt . 2 t + t +1 1 3 2t +1 3 2t +1 2 3 2 (t + ) + ( ) [( )2 + ] 1 ( )2 +1 2 2 4 3 3 69
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Đặt u = 2t +1 du = 2 dt dt = 3 du J = 2 3 du = 2 3 arctanu. 3 3 2 3 2 u +1 3
Thay u = 2t + 1 J = 2 3 arctan 2t + 1 . 3 3 3
Vậy I = - ln|t - 1| + 1 ln(t2 + t + 1) + 2t + 1 x +1 3 arctan + C, với t = 3 2 3 x -1 2 * Lo¿i 2: I = R(x,
ax + bx + c )dx, trong đó R(u, v) là hàm hữu tỷ đối với u, v và = b2 - 4ac ù 0.
- Nếu = b2 - 4ac > 0: ax2 + bx + c có 2 nghiệm phân biệt ñ, ò (giả sử x þ ñ) suy ra a(x - ò )
ax2 + bx + c = a(x -ñ)(x - ò ) = (x - ñ) . x -ñ a(x - ò Nên I = R(x, (x - ñ)
) )dx. Đây là tích phân vô tỷ loại 1 với n = 2. x -ñ
- Nếu = b2 - 4ac < 0: ax2 + bx + c > 0 với x R nên c > 0. Đặt ax2 + bx + c = tx + b − 2 c t. c x =
= (t) ax2 + bx + c = t(t) + c . t 2 − a
Vậy I = R((t), t(t) + c )’(t)dt. Đây là tích phân hữu tỷ. Ví dụ 1: I = dx (a > 0, |x| > a) = dx 2 2 x - a
(x - a)(x + a) 2 Trưß − +
ng hợp x > a: I = x - a . dx . Đặt t = x - a t2 = x a x = a1 t ,
x + a x - a x + a x + a 2 1- t 2 2
dx = 4atdt , x - a = 2at . Do đó I = t. 1- t . 4at dt = 2dt = ( 1 + 1 )dt. 2 2 1 ( - t ) 2 1- t 2 2at 2 2 1 ( - t ) 2 1- t 1- t 1+ t
Nên I = ln|1 + t| - ln|1 - t| + C = ln| t +1 | + C. t -1 x - a +1 - + +
Thay t = x - a I = ln| x + a | + C = ln| x a x a | + C, x + a x - a
x - a - x + a -1 x + a 70
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 2 + + 2 2 +
nhân liên hợp với mẫu được I = ln| ( x - a
x a ) | + C = ln| 2x 2 x - a | + C - 2a 2a = ln|x + 2 2
x - a | + C* (với C* = C - lna)
Trưßng hợp x < - a: Tương tự ta cũng có I = ln|x + 2 2 x - a | + C*
Ví dụ 2: I = dx (a > 0). 2 2 x + a 2 2 Đặ + + t 2 2 2at 2a 1 ( t ) 1 t
x + a = tx + a x = , dx = dt, 2 2 x + a = a . 2 1- t 2 2 1 ( - t ) 2 1- t 2 2 + Vậy I = 1- t . 2a 1 (
t ) dt = 2 dt = ln| t +1 | + C (ví dụ trên). a 1 ( 2 + t ) 2 2 1 ( - t ) 2 1- t t -1 2 2
Sau đó thay t = x + a - a và tính toán ta được I = ln(x + 2 2 x + a ) + C a
c) Tích phân các hàm lượng giác
Dạng I = R(cosx, sinx)dx. Trong đó R(u, v) là hàm hữu tỷ đối với u, v x 2dt 2 1- t 2t
* Tổng quát: Đặt t = tan x = 2arctant, dx = , cosx = , sinx = . 2 2 1+ t 2 1 + t 2 1+ t 2 1- Từ đó I = R(
t , 2t ) 2dt : Đây là tích phân hữu tỷ. 2 1 + t 2 1+ t 2 1+ t Ví dụ 1: I = dx
3 + 5sin x + 3cos x 2
Đặt t = tan x x = 2arctant dx = 2dt , sinx = 2t , cosx = 1- t nên 2 2 1+ t 2 1+ t 2 1 + t 2dt 2 2 I = 1 + t = dt
= dt = - 1 ln|3 + 5t| + C. 2 10t 3 - 3t 2 2 1 (
3 + t ) + 10t + 3 - 3t 3 + t 5 5 3 + + 2 2 1 + t 1 + t
Vậy I = 1 ln|3 + 5tan x | + C 5 2 * Đặc biệt:
R(sinx, - cosx) = - R(sinx, cosx) đặt u = sinx
R(- sinx, cosx) = - R(sinx, cosx) đặt u = cosx 71
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
R(- sinx, - cosx) = R(sinx, cosx) đặt u = tanx hoặc u = cotx cos3 x
Ví dụ 2: Tính I =
dx. Chúng ta có thể làm theo ít nhất 1 trong các cách sau, kết sin x
quả tưáng khác nhau, nhưng thật ra chúng như nhau (?) 2 - cos2 x 1- sin x
Cách 1: Đặt u = sinx du = cosxdx. Nên I = cosxdx = cosxdx = sin x sin x 1 u2 -
du = ( 1 - u)du = ln|u| - 1 u2 + C = ln|sinx| - sin2 x + C u u 2 2 2 2 - cos x cos x
Cách 2: Đặt u = cosx du = - sinxdx. Nên I = sinxdx = sinxdx 2 sin x 2 1- cos x 2
= u du = (u + u )du = 1 u2 + 1 ln|u2 - 1| + C. 2 u -1 2 u -1 2 2 Thay u = cosx đượ cos2 c I =
x + 1 ln(1 - cos2x) + C = 1 cos2x + ln|sinx| + C 2 2 2
- Cách 3: I = cos2x. cos x dx = (1 - sin2x)cotxdx = (cotx - sinxcosx)dx sin x
= cos x dx - 1 sin2xdx = ln|sinx| + 1 cos2x + C sin x 2 4
3.2. TÍCH PHÂN XÁC ĐÞNH
3.2.1. Khái niệm tích phân xác đßnh
a) Định nghĩa
* Bài toán: Tính diện tích <hình thang cong= D giới bái các đưßng y = ö(x) xác định,
liên tục và không âm trên [a, b], y = 0, x = a, x = b (a < b).
Giả thiết đã biết diện tích hình chữ nhật.
- Chia [a, b] thành n phần nhỏ bái các điểm chia x0 = a < x1 < x2 < ... < xn = b. Gọi Sk là n
diện tích Dk trên [xk-1, xk] (k = 1, 2, ..., n) thì S = õ S . k k =1
Đặt k = [xk-1, xk] và |k| là độ dài k, d = max{|k|, k = 1, 2, ..., n}.
- Nếu k đủ bé thì do ö(x) liên tục trên k nên ö(x) thay đổi không đáng kể.
Nên có thể coi ö(x) û ö(øk) với øk là điểm nào đó trong k nên Sk û ö(øk)|k| 72
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân n
- Từ đó S û õ f (øk)|k| (*) k =1
- Nhận xét (*) càng chính xác nếu các k càng nhỏ hay chính d càng nhỏ. n
Vậy theo quan điểm của giải tích thì S = lim õ f (øk)|k| d → 0 k=1
* Đßnh nghĩa: Cho hàm số y = ö(x) xác định trên [a, b].
- Chia [a, b] thành n đoạn nhỏ bái các điểm xo = a < x1 < x2 < ... < xn = b. Mỗi phép
chia như vậy được gọi là một phép phân hoạch , đặt k = [xk-1, xk], |k| = xk - xk-1 với
k = 1, 2, ..., n và d = max {|k|, k = 1, 2, ..., n}
- Chọn tùy ý điểm øk k (k = 1, 2, ..., n) n
- Lập tổng ó = õ f (ø ) | k
k|: Tổng này được gọi là tổng tích phân của hàm y = ö(x) k =1
lấy trên [a, b] ứng với phép phân hoạch và phép chọn các điểm øk.
- Nếu tồn tại lim ó = I, giới hạn này hữu hạn không phụ thuộc vào phép phân hoạch d → 0
và phép chọn các điểm øk. Thì giới hạn ấy được gọi là tích phân xác định của ö(x) trên b
[a, b] và viết I = f (x)dx. a
Khi ấy ö(x) được gọi là khả tích trên [a, b]
Cách gọi: - dấu tích phân, ö(x) và ö(x)dx - hàm số và biểu thức dưới dấu tích phân, a
là cận dưới, b là cận trên. b
* Ý nghĩa hình hác: Từ bài toán và định nghĩa trên suy ra S = f (x)dx a
b) Điều kiện khả tích
Đßnh lý 1: Nếu y = ö(x) liên tục trên [a, b] thì ö(x) khả tích trên [a, b]
Đßnh lý 2: Nếu y = ö(x) chỉ có hữu hạn điểm gián đoạn loại một trên [a, b] thì ö(x) khả tích trên [a, b]
Đßnh lý 3: Nếu y = ö(x) đơn điệu tăng (tư¢ng ứng giÁm) và bị chặn trên (tư¢ng ứng
dưới) trên [a, b] thì ö(x) khả tích trên [a, b] 73
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Đßnh lý 4: Nếu y = ö(x) khả tích trên [a, b] thì ö(x) bị chặn trên [a, b] c) Tính chất
Chúng ta giả thiết các tích phân nói đến là tồn tại. b a a
Tính chất 1: f (x)dx = - f (x)dx. Từ đó f (x)dx = 0 a b a b
Tính chất 2: m dx = m(b - a) a b b b
Tính chất 3: [ ö(x) g(x)]dx = f (x)dx g (x)dx a a a b b
Tính chất 4: k ö(x)dx = k f (x)dx a a b b
Tính chất 5: Nếu ö(x) g(x) trên [a, b] thì f (x)dx g (x)dx a a b c b
Tính chất 6: f (x)dx = f (x)dx + f (x)dx a a c b b
Tính chất 7: | f (x)dx| |ö(x)|dx a a b
Tính chất 8: ö(x) liên tục trên [a, b] thì c [a, b] sao cho ö(c) = 1 f (x)dx (định b - a a
lý trung bình của tích phân) b b
Tính chất 9: f (x)dx = f (t)dt a a
3.2.2. Ph°¢ng pháp tính tích phân xác đßnh
a) Công thức Newton – Leibnitz x
* Đßnh lý (Đ¿o hàm theo cận trên): Nếu y = ö(x) liên tục trên [a, b] thì (x) = f (t)dt a
là một nguyên hàm của ö(x) trên [a, b].
* Công thức: Nếu F(x) là một nguyên hàm của hàm ö(x) liên tục trên [a, b]. 74
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân b b
Thì f (x)dx = F(b) - F(a). Thưßng viết f (x)dx = F(x)| ba a a
* Các ví dụ: Tính các tích phân sau 1
Ví dụ 1: I = ( 3x2 + 4x + 1)dx = (x3 + 2x2 + x)| 10 = (1 + 2 + 1) - (0 + 0 + 0) = 4 0 e 2 e 2 x 2 e
Ví dụ 2: I = x -1dx = 1 1 1 ( x - )dx = ( - lnx)| e 1 = ( - 1) - = (e2 - 3) x x 2 2 2 2 1 1 3 cos 2x 3 2 2 cos x - sin x 3 1 1 Ví dụ 3: I = dx = dx = ( - ) dx = - (cotx + 2 2 2 2 2 2 sin . x cos x sin . x cos x sin x cos x 6 6 6 tanx) 1 1 3 = ( + 3 ) - ( 3 + ) = 0 6 3 3
b) Phương pháp đổi biến số b
* Phư¢ng pháp: Nếu cần tính I = f (x)dx; mà x = (t) là hàm khả vi trên [ñ, ò], có a ò
hàm ngược và a = (ñ), b = (ò). Thì I = f ((t))'(t)dt. ñ b
Thay đổi vai trò x và t cho nhau: Nếu I = f ((x))'(x)dx. Khi ấy đặt t = (x), mà a ò
ñ = (a), ò = (b). Thì I = f (t)dt ñ * Các ví dụ a
Ví dụ 1: Cho I = f (x)dx với y = ö(x) là hàm liên tục /[- a, a]. Chứng minh rằng -a a
I = 2 f (x)dx nếu ö(x) là hàm số chẵn, 0
I = 0 nếu ö(x) là hàm số lẻ. 75
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 0 a
Do I = f (x)dx + f (x)dx = I1 + I2 nên ta cần chứng minh I1 = I2 nếu ö(x) -a 0
chẵn và I1 = - I2 nếu ö(x) lẻ. 0 a
Xét I1, đặt t = - x dx = - dt và t: a → 0 nên I1 = f (- t)(- dt) = f (- t)dt. a 0 a
Nếu ö(x) chẵn: Thì ö(- t) = ö(t) nên I1 = f (t)dt = I2 I = 2I2 (đpcm) 0 a
Nếu ö(x) lẻ: Thì ö(- t) = - ö(t) nên I1 = - f (t)dt = - I2 I = 0 (đpcm) 0 1
Ví dụ 2: Tính I = x n(axn+1 + b)ñdx trong đó a, b ù 0, n N, ñ R 0 1
Đặt t = axn+1 + b t: b → a + b, dt = (n + 1)axndx, xndx = dt (n + ) 1 a a+b Vậy I = 1
tñ dt . Từ đó (n + ) 1 a a 1 1 I = ln|t|| a+b a b = ln|1 + | nếu ñ = - 1 (n + ) 1 a (n + ) 1 a b 1 ñ 1 + t ñ 1 + ñ 1 + + I = . | a+b (a b) - b b = nếu ñ ù - 1 (n + ) 1 a ñ +1 (n + ) 1 (ñ + ) 1 a R
Ví dụ 3: I = R2 - x2 dx, R > 0. 0
Đặt x = Rcost t: → 0, dx = - Rsintdt, 2 2 R - x = R 2 1- cos t = Rsint 2 0 0 Nên I = - 1 1 sin 2t 1
R 2sin2tdt = - R2 ( 1 - cos2t)dt = R2( - t 0 ) = R2. 2 2 2 2 4 2 2
c) Phương pháp tích phân từng phần b b b
* Phư¢ng pháp: udv = uv|a - vdu a a
* Các ví dụ: Tính các tích phân sau 76
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân e
Ví dụ 1: I = x lnxdx. 1 ü = dx du u = 2 e Đặ ü ln x ÿÿ t x x 1 1 1 ý ý . Vậy I = lnx| e e 1 -
x dx = e2 - x2|1 þdv = xdx ÿ 2 x 2 2 2 4 1 ÿv = þ 2
Hay I = 1 e2 - 1 (e2 - 1) = 1 (e2 + 1) 2 4 4
Ví dụ 2: I = x cosxdx. 0 u = du = Đặ ü x ü dx t ý ý . Vậy I = xsinx| 0 - sinx dx = cosx|0 = - 2. þdv = cos xdx þv = sin x 0 1
Ví dụ 3: I = x exdx. 0 u = du = 1 Đặ ü x ü dx t ý ý . Vậy I = xex| 1 x 1
0 - e dx = e - ex|0 = 1. þdv = exdx þv = x e 0 4 x Ví dụ 4: I = dx. 2 cos x 0 1
Đặt t = tanx x = arctant, t: 0 → 1, dt = dx . Nên I = arctantdt. 2 cos x 0 ü dt u = Đặ ü arctan t du = t ÿ ý ý + t 2 1 . þdv = dt ÿþv = t 1 1 Nên I = t.arctant| 1 t t 0 - dt = - dt , + 2 1 t 4 + 2 1 t 0 0
đổi biến u = 1 + t2 u: 1 → 2, du = 2tdt 2
Vậy I = - 1 du = - 1 lnu| 2 1 1 = - ln2 4 2 u 4 2 4 2 1
Chú ý: Có thể đặt u = x, dv = dx 2 cos x 77
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
3.3. TÍCH PHÂN SUY RÞNG
3.3.1. Tích phân suy rßng loại I * Các đßnh nghĩa
- Đßnh nghĩa 1: Cho hàm số y = ö(x) xác định trên [a, + õ), khả tích trên mọi [a, b] với b
b > a. Khi ấy lim f (x)dx được gọi là tích phân suy rộng của ö(x) trên [a, + õ) và ký b→+õ a +õ
hiệu là f (x)dx. Nếu giới hạn ấy tồn tại và hữu hạn (bằng I) thì ta nói tích phân trên a +õ
hội tụ (về I) và viết I = f (x)dx. a
Ta cũng nói ö(x) khả tích trên [a, + õ).
Trái lại thì tích phân trên được gọi là phân kỳ - Hình 1
- Đßnh nghĩa 2: Cho hàm số y = ö(x) xác định trên (- õ, b] và khả tích trên mọi đoạn [a, b
b] với a < b. Khi ấy lim f (x)dx được gọi là tích phân suy rộng của ö(x) lấy trên (- õ, a→-õ a b
b] và ký hiệu f (x)dx. Nếu giới hạn trên tồn tại và hữu hạn (bằng I) thì ta nói tích -õ b
phân trên hội tụ (về I ) và viết I = f (x)dx. -õ
Ta cũng nói ö(x) khả tích trên (- õ, b].
Trái lại thì tích phân trên được gọi là phân kỳ - Hình 2
- Đßnh nghĩa 3: Cho hàm y = ö(x) xác định trên R = (- õ, + õ). Khi ấy tích phân của +õ a +õ
ö(x) lấy trên R được định nghĩa là: f (x)dx = f (x)dx + f (x)dx, với a là số thực -õ -õ a
nào đó nếu vế phải có nghĩa. 78
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân a +õ
Nếu các tích phân f (x)dx và f (x)dx hội tụ (về I1 và I2 tương ứng). Thì -õ a +õ +õ
f (x)dx được gọi là hội tụ về I1 + I2 và viết I = I1 + I2 = f (x)dx. -õ -õ
Ta cũng nói ö(x) khả tích trong (- õ, + õ).
Trái lại thì tích phân trên được gọi là phân kỳ - Hình 3 y y y y = ö(x) y = ö(x) y = ö(x) O a a O b b x O x a x Hình 1 Hình 2 Hình 3
* Ví dụ: Xét sự hội tụ của các tích phân và tính nó nếu được +õ
Ví dụ 1: I = dx . + 2 1 x -õ +õ 0 +õ
Ta viết dx = dx + dx = I + 2 1 + I2 1 x + 2 1 x + 2 1 x -õ -õ 0 0 0 Trong đó I dx dx 0 1 = = lim
= lim (arctanx| ) = lim (- arctana) = + 2 a 1 x a→-õ + 2 1 x a→-õ a→-õ 2 -õ a +õ Tương tự I dx 2 = = . Vậy I = + 2 1 x 2 0 +õ
Ví dụ 2: I = dx , ñ R. ñ x 1 l
ü n x |a = lnt k h i ñ =1 t ü 1 0 ÿ ÿ k h iñ þ 1
Xét I(a) = dx = -1ñ - 1 ý ñ lim = ý1-ñ xñ x = t ñ ù t→+õ 1 ÿ k h i 1 ÿ 1 þ -ñ 1-ñ þ+ õ k h iñ 1 +õ
Vậy dx dx hội tụ khi ñ > 1 và phân kỳ khi ñ 1 ñ x 1
* Điều kiện hội tụ 79
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
- Đßnh lý 1: Nếu tồn tại số thực C > 0 sao cho với mọi số thực b (b > a) mà ta có b +õ
| f (x)dx| C thì f (x)dx hội tụ. a a
- Đßnh lý 2: Giả sử 0 ö(x) g(x) trên [a, + õ). Khi ấy: b b
Nếu g (x)dx hội tụ thì f (x)dx hội tụ, a a b b
Nếu f (x)dx phân kỳ thì g (x)dx phân kỳ. a a
3.3.2. Tích phân suy rông loại II * Các đßnh nghĩa
- Đßnh nghĩa 1: Cho y = ö(x) xác định trên [a, b) và khả tích trên mọi [a, b - ] (với mọi b -
thỏa 0 < < b - a). Khi ấy lim f (x)dx được gọi là tích phân suy rộng của ö(x) trên → 0 + a b
[a, b) và viết f (x)dx. Nếu giới hạn trên tồn tại và hữu hạn (bằng I) thì tích phân trên a b
được gọi là hội tụ (về I) và viết I = f (x)dx. Trái lại tích phân trên được gọi là phân a kỳ - hình 1.
Ta cũng nói ö(x) khả tích tren [a, b)
- Đßnh nghĩa 2: Cho y = ö(x) xác định trên (a, b] và khả tích trên mọi [a + , b] (với b
mọi thỏa 0 < < b - a). Khi ấy lim f (x)dx được gọi là tích phân suy rộng của ö(x) → 0 + a+ b
trên (a, b] và viết f (x)dx. Nếu giới hạn trên tồn tại và hữu hạn (bằng I) thì tích phân a b
trên được gọi là hội tụ (về I) và viết I = f (x)dx. Trái lại tích phân trên được gọi là a phân kỳ - hình 2.
Ta cũng nói ö(x) khả tích trên (a, b] 80
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
- Đßnh nghĩa 3: Cho y = ö(x) xác định trên [a, c) (c, b] trong đó a < c < b. Khi ấy ta b c b
định nghĩa f (x)dx = f (x)dx + f (x)dx nếu vế phải có nghĩa. a a c c b
Nếu các tích phân f (x)dx, f (x)dx hội tụ (về I1, I2 tương ứng). Thì ta nói a c b
f (x)dx hội tụ về I = I1 + I2. Trái lại tích phân trên được gọi là phân kỳ - hình 3. a
Ta cũng nói ö(x) khả tích trên [a, c) (c, b]
- Đßnh nghĩa 4: Cho y = ö(x) xác định trong (a, b). Khi ấy với bất kỳ c (a, b) ta định b c b
nghĩa f (x)dx = f (x)dx + f (x)dx nếu vế phải có nghĩa. a a c c b
Nếu cả 2 tích phân f (x)dx, f (x)dx hội tụ (về I1, I2 tương ứng). Thì ta nói a c b
f (x)dx hội tụ về I = I1 + I2. Trái lại tích phân trên được gọi là phân kỳ a
Ta cũng nói ö(x) khả tích trong (a, b) y y y y = ö(x) y = ö(x) y = ö(x) O O a b- b O a a+ b x x a c b x Hình 1 Hình 2 Hình 3
* Ví dụ: Xét sự hội tụ của các tích phân và tính nó nếu được 1
Ví dụ 1: I = dx . 2 1 - 1- x 0 1
Ta viết I = dx + dx = I1 + I2 2 2 1 - 1- x 0 1- x 81
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 0 0 I dx dx 1 = = lim
= lim (arcsinx|-1+0) = lim arcsin(- 1 + ) = 2 → 0 + 2 → 0 + → 0 + 2 1 - 1- x + 1 - 1- x 1 Tương tự I dx 2 = = . Vậy I = 2 2 0 1- x b
Ví dụ 2: I = dx với a < b, ñ R. (x - a ñ ) a b ñ - 1
Nếu ñ 0: Tích phân trên không suy rộng và I = dx = (b - a) (x - a ñ ) 1-ñ a
Nếu ñ > 0: Khi ấy với mọi thỏa 0 < < b - a. Ta xét
ü(x - a) |b = a
ln(b - a) - ln(a + k ) h iñ = 1 b ÿ + I() = dx = ý - 1 ñ - 1 ñ - 1 . b b a ñ (x - a ñ ) (x - a) | = ( - ) - a k h iñ ù a+ ÿ 1 þ + 1-ñ 1-ñ ü + õ k h iñ 1 Nên ÿ
lim I() = ý(b - ) -1ñ a . → 0 + ÿ k h iñ ü1 þ 1-ñ b
Vậy dx hội tụ khi ñ < 1, phân kỳ khi ñ 1 (x - a ñ ) a
* Chú ý 1: Ngưßi ta chứng minh được rằng bằng phép đổi biến thích hợp, đưa được tích
phân suy rộng loại 2 về tích phân suy rộng loại 1
* Chú ý 2: Trong chương trình môn Xác suất thống kê, đại lượng ngẫu nhiên liên tục
X nhận giá trị trong (- õ, + õ) được gọi là phân phối chuẩn nếu hàm mật độ xác suất 2 1 ( x- ) - +õ 1 - 2 có dạng ö(x) = e t 2 2ó
(, ó > 0). Khi ấy dựa vào tích phân Poisson 2 e dt = ó 2 -õ 2 ta tính được: +õ
- Kỳ vọng E(X) = x ö(x)dx = -õ +õ
- Phương sai D(X) = 2x ö(x)dx - E(X)2 = ó2 -õ 82
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 3.4. ỨNG DþNG
3.4.1. Ứng dÿng trong toán học
a) Tính độ dài đường cong Công thức
- Nếu (C): y = ö(x) và hàm này cùng đạo hàm của nó liên tục trên [a, b]. b
Thì l(C) = 1+ f '2 (x)dx a üx = (t) - Nếu (C): ý
và các hàm này cùng đạo hàm của chúng liên tục trên [ñ, ò]. þy =ù (t) ò
Thì l(C) = '2 t()+ù '2 t()dt ñ
- Nếu (C): r = r() và hàm này cùng đạo hàm của nó liên tục [ñ, ò]. ò
Thì l(C) = r2 ( ) + r'2 ( ) d ñ üx = (t) ÿ
- Nếu (C): ýy =ù (t) và các hàm này cùng đạo hàm của chúng liên tục trên [ñ, ò]. ÿ þz = ó(t) ò
Thì l(C) = '2 t()+ù '2 t()+ ó'2 t()dt ñ Các ví dụ
Ví dụ 1: Tính độ dài đưßng cong C: y = x2 với 0 x 4 4
Ta có l(C) = 1+ 2xdx, đặt t = 1+ 2x suy ra 1 x 3 và t2 = 1 + 2x nên dx = 0 3 tdt. Vậy 1 26
l(C) = 2tdt = 3 3 t | = 1 3 3 1
Ví dụ 2: Tính độ dài đưßng tròn bán kính R > 0.
- Phư¢ng pháp 1: Đưa đưßng tròn vào hệ tọa độ Oxy sao cho tâm đưßng tròn
trùng với gốc tọa độ O.
Phương trình tham số của đưßng tròn là x = Rcost, y = Rsint (0 t 2). 83
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 2
Ta có x’2 + y’2 = R2. Vậy l(C) = R dt = 2R. 0 x
- Phư¢ng pháp 2: Đưa đưßng tròn vào hệ tọa độ cực sao cho O
tâm đưßng tròn trùng với cực O. Khi ấy phương trình đưßng
tròn là r() = R, 0 2. Ta có r2() + r’2() = R2. 2
Vậy l(C) = R dt = 2R. 0
Ví dụ 3: Tính độ dài đưßng đinh ốc trụ tròn xoay: x = acost, y = asint, z = amt á đây a,
m > 0 và 0 t 2.
Ta có x’2 + y’2 + z’2 = a2cos2t + a2sin2t + a2m2 = a2(1 + m2). 2
Nên l(C) = a + 2
1 m dt = 2a 2 1+ m . 0
b) Tính diện tích hình phẳng Công thức y = ö(x)
- Nếu D giới hạn bái các đưßng: y D
+ y = ö(x) liên tục, không âm/a, b] x + y = 0, O a b + x = a, x = b. b
Thì dt(D) = f (x)dx a
* Nếu D giới hạn bái các đưßng: y y = ö(x)
+ y = ö(x) liên tục / [a, b] + y = 0 O a b x + x = a, x = b. b
Thì dt(D) = |ö(x)|dx. a y y = ö(x)
* Nếu D giới hạn bái các đưßng: y = ö(x) và y = g(x)
cùng liên tục trên [a, b], x = a và x = b. y = g(x) O a b x 84
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân b
Thì dt(D) = |ö(x) - g(x)|dx. a
* Nếu miền phẳng (D) với biên là đưßng cong kín, không tự cắt (L) có phương trình x b
= (t), y = ù(t), ñ t ò. Thì dt(D) = |ù t()' t() | dt a
* Nếu (D) là hình quạt cong trong hệ tọa độ cực giới hạn bái 2 tia cực: = ñ, = ò và
r = r() là đưßng cong liên tục trên [ñ, ò] và mọi tia cực chỉ cắt đưßng cong này không b
quá một điểm. Thì dt(D) = 1 r2 ( )d . 2 a Các ví dụ
* Ví dụ 1: Tính diện tích hình phẳng D giới hạn bái các đưßng y = x2 và x = y2. Rõ ràng x, y 0.
Phương trình hoành độ giao điểm x4 = x y y = x2
x = 0, x = 1, x2 x trên [0, 1] nên 1 x = y2 1 dt(D) = 2 1 ( x - x)dx = ( 3 x - x2)| 1 0 3 2 0 O 1 x Vậy dt(D) = 2 - 1 = 1 3 2 6
* Ví dụ 2: Tính diện tích hình phẳng D giới hạn bái các đưßng y = x3 và y = x
Do hai hàm số y = x3 và y = x là hai hàm lẻ nên đồ thị của chúng tự đối xứng
qua O. Nên D cũng đối xứng qua O.
Vậy ta chỉ cần tính một nửa phần x 0 là đủ
Phương trình hoành độ giao điểm: x3 = x x = 0, x = - 1, x = 1. Nên một nửa 1
phần x 0 thì 0 x 1, trên [0, 1] ta có x3 x. Vậy dt(D) = 2 1 ( x - x3)dx = 2( x2 - 2 0 1 x4)| 1 1 0 = 4 2
* Ví dụ 3: Tính diện tích hình Elip với các bán trục a, b > 0. 85
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 2 2
Phư¢ng pháp 1: Phương trình Elip x + y = 1. Do tính 2 2 a b
đối xứng nên chỉ cần tính 1/4 á góc thứ nhất: y = b 2 2 a − x a 2
(0 x ). Nên dt(E) = 4 b 2 a − 2 x dx = ab 2 a 0 x = Phư¢ng pháp 2: ü a cost
Phương trình tham số của Elip ý
(0 t 2). Nên ta có:
þy = bsin t 2 2 2
dt(E) = 4ab | −sint.sint | dt = 4ab 2
sin tdt = 2ab 1(− cos2t)dt = ab. 0 0 0
Chú ý: Nếu a = b thì Elip trở thành hình tròn và do đó dt(Tr) = R2.
* Ví dụ 4: Tính diện tích cardioid r() = 2(1 + cos) nằm trong hình tròn r() = 3.
Trong hệ tọa cực hai đưßng cong này cắt nhau tại y
A(3, - ) và B(3, ) và do tính chẵn của hai hàm này nên 3 3 3 dt(D) = 9 3 [ 1 ( 4 + 2 cos) + ] 9 d = + 5. x 2 0
c) Tính diện tích xung quanh vật thể tròn xoay Công thức
- Nếu mặt cong (S) do đưßng cong y = ö(x) có đạo hàm liên tục trên [a, b] quay một vòng xung quanh: y b y = ö(x) Ox thì S 2
xq = 2 | f (x) | 1+ f ' (x)dx a O a b b x Oy thì S 2
xq = 2 | x | 1+ f ' (x)dx a
- Nếu mặt cong (S) do đưßng cong x = (t), y = ù(t) có đạo hàm liên tục trên [ñ, ò] quay một vòng xung quanh: 86
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân ò Ox thì S 2 2
xq = 2 |ù t() | ' t() +ù ' t()dt ñ ò Oy thì S 2 2
xq = 2 | t() | ' t() +ù ' t()dt ñ
- Nếu mặt cong (S): r = r() liên tục trên [ñ, ò] quay một vòng xung quanh Ox. ò Thì S 2 2 xq = 2 r ( )sin r ( ) + r' ( ) d ñ Các ví dụ
Ví dụ 1: Tính diện tích mặt cầu tâm O, bán kính R > 0.
Phư¢ng pháp 1: Phương trình tham số nửa trên đưßng tròn tâm O, bán kính R > 0 là
üx = R cost ý (0 t ).
þy = Rsin t
Vậy dt(C) = 2 Rsint R2 2 sin t R2 2 cos tdt + = 2R2 sin d t t = 4R2. 0 0
Phư¢ng pháp 2: Trong hệ tọa cực mặt cầu như đưßng cong r = R /[0, ] quay một vòng y
xung quanh Ox. Nên dt(C) = 2R2 sin d t t = 4R2. 0
Ví dụ 2: Tính diện tích của đèn pha parabol có dạng tạo thành
bái parabolic y = x2 (0 x 1) quay một vòng quanh Oy. x 1 O
Ta có dt(S) = 2 x 1+ 2 4x dx = 5 ( 5 − ) 1 6 0
Ví dụ 3: Tính diện tích xung quanh mặt nón cụt tròn xoay với y
các bán kính đáy r, R và chiề A
u cao h, giả thiết 0 < r < R, h > 0. B
Phư¢ng pháp 1: Mặt nón cụt như đoạn thẳng AB, trong đó O
A(0, R), B(h, r) quay một vòng xung quanh trục hoành. h x
Phương trình AB: y = r - R x + R, 0 x h. h 2 h r − Nên S (r − R) ö R ö 2 xqnc = 2 1+ ÷
x + R÷dx = (r + R) 2
h + (r − R) . 2 h 0 ø h ø 87
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Phư¢ng pháp 2: Mặt nón cụt này như đoạn thẳng AB với A(R, 0), B(r, h) quay một vòng xung quanh Oy. y
Phương trình AB: y = h (x − R) với r x R. r − R 2 R Vậy S h 2 xqnc = 2 1 + = (r + R) 2
h + (r − R) . 2 xdx ( x
r − R) r O
Chú ý: Nếu r = R thì mặt nón cụt trở thành mặt trụ tròn xoay nên Sxqmtr = 2Rh.
Nếu r = 0 thì mặt nón cụt trở thành mặt nón tròn xoay nên S 2 xqn = R 2 h + R .
Ví dụ 4: Tính diện tích xung quanh mặt trụ tròn xoay y
bán kính R, chiều cao h (R, h > 0). A B
Mặt trụ trên như mặt tròn xoay do đoạn thẳng AB:
y = R / [0, h] quay một vòng xung quanh Ox. O h x h
Nên Sxqtr = 2 Rdx = 2Rh. 0
Ví dụ 5: Tính diện tích mặt tròn xoay do đưßng Cardioid: r = a(1 + cos) quay một
vòng xung quanh Ox (0 ).
Do r’2 + r2 = 4a2cos2 , rsin = a(1 + cos)sin = 4acos3 sin . 2 2 2 4 Vậy S 32 xq = 16a2 cos sin d = a2. 2 2 5 0 z
d) Tính thể tích vật thể b Công thức
- Nếu vật thể (V) trong Oxyz với a z b và cắt (V) bới z S(z)
mặt phẳng song song với Oxy tại mỗi z (a, b) được thiết a O b y
diện có diện tích là S(z). Thì tt(V) = S (z)dz. x a y
- Nếu (V) là vật thể tròn xoay do miền phẳng (D) giới hạn y = ö(x)
bái y = ö(x) liên tục trên [a, b], y = 0, x = a, x = b quay một O a b x vòng xung quanh: 88
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân b
Ox thì tt(V) = f 2(x)dx. a b
Oy thì tt(V) = 2 | xf (x) | dx . a üx = (t)
- Nếu (V) do phần phẳng giới hạn bái đưßng cong ý
(ñ t ò) quay một vòng þy =ù (t) ò
xung quanh Ox. Thì tt(V) = ù 2 t( ) ' t ( )dt r = r() ñ
- Nếu (V) do phần phẳng trong tọa độ cực giới hạn bái ò x
đưßng r = r()với 0 ñ ò quay một vòng xung ñ O quanh trục cực Ox. ò
Thì tt(V) = 2 r3 ( )sin d 3 ñ Các ví dụ 2 2 2 x y z
Ví dụ 1: Tính thể tích Ellipsoid + + 1 (a, b, c > 0). 2 2 2 a b c
Phư¢ng pháp 1: Nếu ta cắt (E) bái mặt phẳng song song với Oz và cắt trục Oz tại z (- c 2 2
< z < c) ta được thiết diện là Ellipse với các bán trục là a z z 1− , b 1− . 2 c 2 c 2
Nên diện tích thiết diện là ab(1 - z ). z 2 c y c ö z 2 ö O Vậy tt(E) = ab 4 ÷÷1− = a bc . 2 ÷ ÷dz c 3 −cø ø x z
Ví dụ 2: Tính thể tích hình nón tròn xoay với bán kính đáy
là R và chiều cao là h. à đây R, h > 0.
Phư¢ng pháp 1: Đưa hình nón vào hệ tọa độ Oxyz sao cho
đáy hình nón nằm trên Oxy, trục nằm trên Oz. y O x 89
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Nếu cắt hình nón bái mặt phẳng đi qua cao độ z với
0 < z < h và song song với Oxy thì tiết diện là hình tròn bán 2 y kính r = R R
(h − z) nên S(z) = 2 (h − z) . h 2 h A 2 h Vậy V R 2 nón =
(h − z) dz = 1 R2h. 2 h 3 0
Phư¢ng pháp 2: Hình nón này như vật thể tròn xoay do B x
OAB quay một vòng quay một vòng quanh Oy, với A(0, O h), B(R, 0). z
Phương trình AB: y = h(1 - x ), 0 x R. R 2R Vậy V ö x ö nón = 2h x 1− ÷ ÷ dx = 1 R2h. ø R ø 3 y 0 O x
Ví dụ 3: Tính thể tích hình nón cụt tròn xoay với các bán kính y đáy dướ C
i và trên là R và r, chiều cao là h (R, r, h > 0). B
Phư¢ng pháp 1: Đưa hình nón cụt vào Oxyz sao cho đáy lớn
nằm trong Oxy, trục nằm trên Oz. Cắt hình này bái mặt phẳng đi qua cao độ x
z (0 < z < h) được thiết diện là hình tròn có bán O A − 2 ö − kính r = R - R r R r ö
z nên S(z) = R − ÷ z ÷ . h ø h ø h 2 ö − Vậy V R r ö 1 nc = R − ÷
z ÷ dz = h(R2 + Rr + r2). ø h ø 3 0
Phư¢ng pháp 2: Hình nón cụt này như hình thang OABC với A(R, 0), B(r, h), C(0, h)
quay một vòng xung quanh Oy.
Phương trình AB: x = R + r − R y , 0 y h. h h 2 ö − Vậy V r R ö 1 nc = R + ÷
y ÷ dy = h(R2 + Rr + r2). ø h ø 3 0 90
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Phư¢ng pháp 3: Hình nón cụt này như hình thang OABC với A(0, R), B(h, r), C(h, 0)
quay một vòng xung quanh Ox. y A
Phương trình AB: y = r - R x + R, 0 x h. h B x h 2 O Vậy V ö r - R ö 1 C nc = ÷ x + R dx ÷ = h(R2 + Rr + r2). 3 0 ø h ø
Chú ý: Nếu r = R thi hình nón cụt trở thành hình trụ và dó đó tt(Tr) = R2h.
Nếu r = 0 thì hình nón cụt trở thành hình nón và do đó tt(N) = R2h/3.
Ví dụ 4: Tính thể tích tròn xoay do phần phẳng giới hạn bái đưßng Cardioid r = a(1 +
cos), 0 2 quay quanh trục cực Ox.
Do tính đối xứng nên ta chỉ cần tính một nửa 0 . Vậy V = 4 a3 16 1 ( + cos 3 ) sin d = a3. 3 3 0
Ví dụ 5: Tính thể tích hình cầu bán kính R.
Chúng ta có nhiều phương pháp tính. à đây ta đưa ra 2 phương pháp tương đối đơn giản một chút. x = Phư¢ng pháp 1: ü R cost
Hình cầu trên như nửa nửa hình tròn ý với 0 t quay
þy = Rsin t một vòng xung quanh Ox.
Vậy tt(C) = R3 3 4 sin d = R3. 3 0
Phư¢ng pháp 2: Hình cầu trên như nửa nửa hình tròn r = R với 0 quay một
vòng xung quanh trục cực Ox. Vậy tt(C) = 2 R3 4 sind = R3. 3 3 0
3.4.2. Ứng dÿng trong kỹ thu¿t
a) Tính khối lượng Công thức
- Nếu miền phẳng (D) với a x b, biết khối lượng tại hoành độ x là m(x). 91
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân b
Thì m(D) = m(x)dx. a
- Nếu vật thể (V) với a z b, biết khối lượng tại cao độ z là m(z). b
Thì m(V) = m(z)dz. a b
Đặc biệt: Nếu (L) là đo¿n thẳng thì ta coi nằm trên Ox, (L) = [a, b]và ò = ò(x). Thì m(L) = ò
(x)dx . a Các ví dụ y
Ví dụ 1: Tính khối lượng của đĩa kim loại (C) hình tròn tâm O,
bán kính R > 0. Biết tỷ khối là ò(x, y) = k(2R + x), k > 0.
Tại M(x, y) (C) độ dài dây cung song song với Oy là O x Là 2 2 2 R - x .
Nên khối lượng dây cung ấy là m(x) = 2k(2R + x) 2 2
R - x (- R x R). R
Vậy m(C) = 2k. (2R + x R2 )
− x2 dx = 2kR2. −R
Ví dụ 2: Tính khối lượng khối nón cụt tròn xoay, biết các bán
kính đáy, chiều cao lần lượt là r, R, h (với 0 < r < R, h > 0); z
nếu cắt nón cụt bằng mặt phẳng song song với đáy thì mọi
điểm thuộc thiết diện có cùng tỷ khối bằng 2 lần đưßng kính thiết diện tương ứng. y
Đưa hình nón cụt vào hệ tọa độ Oxyz sao cho đáy lớn O x
nằm nằm trong Oxy, trục nón cụt trên Oz. Khi ấy: nón cụt
như hình bên có 0 z h.
Giả sử cắt nón cụt bái mặt phẳng đi qua cao độ z (với 0 < z < h) và song song −
với Oxy thì thiết diện là hình tròn với bán kính r(z). Tính ra được r(z) = R - R r z và h 92
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
tỷ khối tại mỗi điểm trên thiết diện tương ứng là ò(z) = 4r(z). Nên khối lượng thiết diện 3 là: m(z) = 4r(z)S(z) = 4ö R − r ö ÷ R − z ÷ . ø h ø h − 3 Vậy m(V) = 4 ö R r ö ÷ R − z dz ÷ = h(R + r)(R2 + r2). 0 ø h ø
b) Mômen quán tính
Công thức: Nếu đoạn thẳng AB Ox, xA = a, xB = b và tỷ khối tại x [a, b] là ò = b
ò(x). Thì mômen quán tính đối với O là: I 2
O = x ò(x)dx . a
Ví dụ: Tính mômen quán tính đối với O của OA Ox, biết xA = 1 và ò(x) = 4x. 1 Ta có I 3 1
O = 4x dx = x4|0 = 1. 0
c) Mômen tĩnh và tọa độ trọng tâm (tâm khối lượng)
Công thức: Nếu đoạn thẳng AB Ox, xA = a, xB = b và tỷ khối tại x [a, b] là ò =
ò(x). Thì mômen tĩnh đối với O và tọa độ trọng tâm H là: b M M O
O = xò(x)dx , xH = . m(AB) a
Ví dụ: Tính mômen tĩnh đối với O và tọa độ trọng tâm H của một dây kim loại (K)
chiếm đoạn [0, 9] trên trục Ox, biết tỷ khối là ò(x) = 2x. 9 9
Ta có m(K) = 2xdx = 81; M 2
O = 2x dx = 486. Vậy xH = 6. 0 0
d) Công của một lực → →
Công thức: Công của lực F = P(x) i đẩy chất điểm O A → B x F
di chuyển trên đoạn thẳng AB Ox đi từ A đến B với xA = a, xB = b là: b
W = P(x)dx. a
Ví dụ: Một bình chứa đầy nước dạng hình nón tròn xoay thẳng đứng (hình bên) với bán
kính đáy là Rm, chiều cao là hm. Tính công để bơm hết nước ra khỏi bình qua mép trên. 93
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Đưa bình vào hệ tọa độ Oxyz sao cho đỉnh bình trùng
gốc tọa độ O, trục bình nằm trên Oz. Như vậy đáy bình nằm
trên mặt phẳng song song với Oxy có cao độ là h. h - z h
Xét mặt nước á độ cao z (0 < z < h) là hình tròn bán kính 2 z r(z) = R R
z nên diện tích là S(z) =
z2. Lực để thắng trọng h 2 h R 2
lực của phần nước này là F(z) = òg R z2. 2 h 2
Lượng nước này bơm lên một đoạn h - z nên: W(z) = òg R (h - z)z2. 2 h 2 h Vậy W = òg R 1
(hz2 − z3 )dz = ògR2h2. 2 h 12 0 BÀI T¾P CH¯¡NG 3
Bài tập 1: Tính các tích phân sau
1. I = (sinx + 3cosx - cot2x)dx 2. I = (3x4 + 7x3 - 5x)dx 2 3. I = ( x -1 - 3 )dx 4. I = cos2x dx 2 x + 1 2 1- x 2 cos x 2 .sin x
5. I = (ax + bx)2dx, với a, b > 0, a, b ù 1 6. I = x2(x - 1)3dx
Bài tập 2: Tính các tích phân sau 3x 1. I = dx 2. I = e dx -x 1+ e 2 x e +1 2 3. I = xdx 4. I = x dx 4 x + 2 2 x +1 5 (x - ) 1 3 2 x e arctan x 5. I = sin x dx 6. I = e dx 3 2 2 x x e + 1 94
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 7. I = dx 8. I = dx x 2 1- ln x x(x + ) 1 x
9. I = sin 2x dx, a R/{0} 10. I = e +1 dx 4 2 cos x - a x e -1
Bài tập 3: Tính các tích phân sau
1. I = xnlnxdx, n N
2. I = xnln2xdx, n N 3. I = x2e3xdx 4. I = x5e 3x dx 5. I = sin(lnx)dx 6. I = 2xarctan2xdx 7. I = arcsin x dx 8. I = arctan x dx 2 x 2 x 1 ( 2 + x )
9. I = ln(sin x) dx
10. I = xarctan x dx 2 sin x 2 3 1 ( + x ) 11. I = e x dx 12. I = sin x dx 2 1 + x 13. I = arcsin x . dx 14. I = . x arctan x dx 2 x 2 1- x 2 2 1 ( + x )
Bài tập 4: Tính các tích phân sau 1. I = dx 2. I = dx 2 x + 4x - 5 x( 2 x + ) 2 5 x + 3. I = x dx 4. I = ( ) 1 dx 6 x - 3 x - 2 2 x ( 2 x + ) 1 + 5. I = (x )
1 dx . Hướng dẫn: Đặt t = 1 + xex 6. I = dx x 1 ( x + xe ) x(x + 1) 1+ 4 3 x x + 7. I = x dx 8. I = 2 dx 1+ x 3 x + x + 2 9. I = dx 10. I = dx 2 x - x - 2 2 x + 2x + 2 sin x + sin3 11. I = dx 12. I = x dx
4sin x + 3cos x + 5 cos 2x -1 95
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân 3 13. I = dx 14. I = cos x dx 2 sin x + sin 2x 2 - 3cos x sin2 x + sin x
Bài tập 5: Tính các tích phân sau đây 2 1 1. I = |1 - x|dx 2. I = 15 x 1+ 8 x dx 0 0 1 2 1 3. I = x dx 4. I = xdx 1 ( + 4 x) 5 - 4x 0 1 - 7 3 1 5. I = x dx 6. I = 2x exdx 3 2 2 3 1 ( + x ) 0 e 1 7. I = (x + 1)lnxdx 8. I = 3 x e dx 1 0 ln 2 9. I = dx 10. I = dx 2 + cos x x e 1 ( + 2x e ) 0 0 ñ ñ
Bài tập 6: Nếu ö(x) là hàm số chẵn, thì f (x) dx = f (x d ) x
(với a > 0, a ù 1, ñ> 0) ax +1 ñ - 0
Bài tập 7: Xét tính hội tụ của các tích phân suy rộng sau (và tính nó nếu được) +õ +õ 1. -x xe dx 2. - x e dx 0 0 +õ +õ 3. dx 4. dx 2 x + 5x + 4 2 x + 6x + 9 0 0 +õ +õ 5. dx 6. dx x x +1 x ln x 3 e +õ +õ 7. cos xdx 8. ln xdx 0 1 2 1 n 9. xdx
10. ln x dx, n N 2 x 0 4 - x 0 2 2 11. xdx 12. dx 2 x -1 2 (x - ) 1 -2 0 96
KHOA KHOA HàC C¡ BÀN
Chư¢ng 3: Phép tính tích phân
Bài tập 8: Tính các diện tích D giới hạn bái các đưßng sau đây 1. y = x2 + 4, x - y + 4 = 0 2. y = 4x - x2 và y = 0
3. y = 2x2, y = 3 - x2, x = 2 4. y = 2x, y = 2, x = 0
5. y = x3 và tiếp tuyến với đưßng cong này tại điểm A(1, 1)
6. Phía ngoài đưßng parabolic: x2 = 4(1 - y) và phía trong đưßng tròn x2 + y2 = 4
Bài tập 9: Tính độ dài đưßng cong 1. y = 4x (0 x 1) 2 y = x2 + 4 (0 x 1) 3. y = x2 - 2 (|x| 2 )
4. y = lncosx (0 x /4)
5. Một đoạn đưßng đinh ốc trụ: x = acost, y = asint, z = amt (0 t 2, a > 0)
Bài tập 10: Tính thể tích vật thể tròn xoay
1. Do D giới hạn bái: y= 0, y = 2x - x2 quay một vòng quanh trục hoành và trục tung
2. Do hình tròn C: x2 + (y - a)2 R2 với 0 < R < a quay một vòng quanh trục hoành.
3. Do D giới hạn bái y = 1
, y = 0, x = 0 quay một vòng quanh trục hoành. 2 1 ( + x) 97
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
Chương 4: LÝ THUYẾT CHUÞI
Mở đầu: Có nhiều bài toán dẫn đến phải tính giá trị của hàm số tại một
điểm, tính tích phân nào đó hay tìm nghiệm một PTVP .v.v. Bằng phương pháp
trực tiếp hay phương pháp tích phân là rất khó khăn nếu không muốn nói là có
những bài không thể được. Nhưng nhß công cụ lý thuyết chuỗi, cụ thể việc khai
triển một hàm thành chuỗi lũy thừa thì công việc lại trá nên tương đối dễ dàng.
4.1. Chußi số, sự hội tụ của chußi số 4.1.1. Chußi số
a) Định nghĩa: Cho dãy số (un)n=1, 2,... , n,... . Khi đó tổng vô hạn u1 + u2 + ... + un +
... (1) được gọi là một chuỗi số và ký hiệu là õõu , các số hạng của dãy số (u n n) n=1
cũng được gọi là các số hạng tương ứng của chuỗi số. n
Với mỗi n N, Sn = u1 + u2 + ... + un = õu được gọi là tổng riêng thứ n k k =1
của chuỗi (1). Nếu tồn tại limSn = S (hữu hạn) thì ta nói chuỗi số (1) hội tụ về
tổng S và viết õõu = S, trái lại thì chuỗi (1) được gọi là phân kỳ. n n=1
Nếu chuỗi số (1) hội tụ về S thì rn = S - Sn được gọi là phần dư thứ n của
chuỗi số (1). Dễ dàng thấy rằng rn = õõu và limr n+k n = 0. k =1 n
Ví dụ 1. õõ 1 . Có S 1 1 1 1 n = õ = + + ... + n n +
n=1 n(n + ) 1
k =1 k (k + ) 1 1 2 . 3 . 2 ( ) 1 Do 1 = 1 - 1 nên S 1 1 n = 1 - ³ 1. Vậy õõ = 1 k(k + ) 1 k k +1 n +1
n=1 n(n + ) 1 ü 1- qn õ u khi q Ví dụ 2 ÿ 1 . 1 − õ nq u
(giả thiết u và q 0). Có Sn = õõu qk-1 = ý 1- q n 1 = n=1 ÿ þ n u kh iq = 1 - Nếu |q| < 1 thì limS u u n =
nên chuỗi trên hội tụ về S = 1- q 1- q 98
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
- Nếu |q| 1 thì limSn hoặc không tồn tại hoặc tồn tại bằng õ nên chuỗi trên phân kỳ.
Ví dụ 3. õõ( - 1)n-1 phân kỳ, vì không tồn tại lim(- 1)n-1 n=1 Ví dụ 4 + . 1 õõ 1 n 1 ln 1
( + ) phân kỳ, vì un = ln(1 + ) = ln = ln(n + 1) - lnn. n 1 = n n n n n Nên S 1 n = õ ln 1
( + ) = õ[ ln(k + 1) - lnk] = ln(n + 1) ³ + õ k 1 = k k = 1
b) Điều kiện hội tụ của một chuỗi
* Đßnh lý 1: (Điều kiện cần): Nếu õ õ u hội tụ thì limu n n = 0. n=1
Giả sử õõu = S limu n
n = lim(Sn - Sn-1) = S - S = 0. n=1
* Đßnh lý 2 (Điều kiện cần và đủ Côsi): õ õ
u hội tụ khi và chỉ khi với mỗi số thực n n=1
dương bé tùy ý, đều tồn tại N > 0 sao cho n N mà n > N và p N ta có:
|un+1 + un+2 + ... + un+p| <
Thật vậy õõu hội tụ {S n
n} có giới hạn > 0, N > 0 sao cho n n=1
N mà n > N và p N ta có |Sn+p - Sn| < |un+1 + un+2 + ... + un+p| <
* Chú ý: Nếu limun 0 thì õ õ
u phân kỳ. Nhưng limu u hội tụ. n n = 0 chưa hẳn õ õ n n=1 n=1 Ví dụ 5. 1 õõ 1 ln 1
( + ) có limln(1 + ) = 0 nhưng nó phân kỳ. n 1 = n n Ví dụ 6. 1
õõ (chuỗi điều hòa) có lim 1 = 0 nhưng nó phân kỳ. n=1 n n
Giải: Như đã biết (1 + 1 )n ý e nên (1 + 1 )n < e ln(1 + 1 )n < lne n n n +
nln(1 + 1 ) < 1 nln n 1 < 1 n[ln(n + 1) - lnn] < 1 ln(n + 1) - lnn < n n 1 n n õ 1
[ ln(k + 1) - lnk] < õ Sn > ln(n + 1) mà limln(n + 1) = + õ nên n 1 k k =1 k = 99
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi cũng có lim S 1 n = + õ. Vậy õ õ phân kỳ. n=1 n
c) Các tính chất
Tính chất 1: Nếu õõu và õõv hội tụ lần lượt về S Cu và õ õ (u n n u, Sv thì õ õ n n n=1 n=1 n=1 n=1
vn) hội tụ về CSu và Su Sv.
Nếu õõu phân kỳ và C 0 thì õõCu phân kỳ n n n=1 n=1
Tính chất 2: Tính hội tụ hay phân kỳ của một chuỗi số không thay đổi khi ta thay
đổi một số hữu hạn số hạng đầu tiên.
Chú ý: Với mọi C 0. Khi ấy õõu hội tụ (phân kỳ) õõCu hội tụ (phân kỳ). n n n=1 n=1
4.1.2. Chußi số d°¢ng
a) Định nghĩa: Chuỗi số õõu được gọi là chuỗi số dương nếu mọi u n n đều n=1 dương. * Nhận xét: Nếu õ õ
u là chuỗi số dương thì {S u hội tụ n
n} đơn điệu tăng, nên õ õ n n=1 n=1
khi và chỉ khi {Sn} bị chặn trên.
b) Các tiêu chuẩn so sánh hai chuỗi số dương
Cho hai chuỗi số dương õõu và õõv . n n n=1 n=1
* Tiêu chuẩn 1: Nếu un vn với n đủ lớn. Thì từ õ õ v hội tụ suy ra õ õ u hội tụ. n n n=1 n=1
Ngược lại từ õõu phân kỳ suy ra õõv phân kỳ. n n n=1 n=1
Ví dụ 7. Chuỗi õõ 1 phân kỳ vì 1 1 > 0 mà õõ 1 = 1 õõ 1 phân n + n=1 2n + 1 2 1 n 3 n=1 3n 3 n=1 n kỳ.
Ví dụ 8. Chuỗi õõ 1 hội tụ vì 1 < 1 mà õõ 1 hội tụ. n n + n n n=0 2 +1 2 1 2 n=0 2 un
* Tiêu chuẩn 2: Giả sử lim = K. Khi ấy vn 100
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
0 < K < + õ: Hai chuỗi cùng hội tụ hoặc cùng phân kỳ
K = 0: Từ õõv hội tụ suy ra õõu hội tụ n n n=1 n=1
K = + õ: Từ chuỗi õõv phân kỳ suy ra õõu cũng phân kỳ n n n=1 n=1 n
Ví dụ 9. Chuỗi õõ 1 hội tụ vì õõ 1 hội tụ và lim( 1 : 1 ) = lim 3 −1 = 1 n n n n − n n=1 3 −1 n=1 3 3 3 1 3
c) Các tiêu chuẩn hội tụ un 1+
* Tiêu chuẩn Dalămbe: Cho chuỗi số dương õ õ u và giả sử lim = l. n n=1 un
l < 1: chuỗi đã cho hội tụ
Khi ấy nếu l > 1: chuỗi đã cho phân kỳ
l = 1: không kết luận n n n+ Ví dụ 10. u
Chuỗi õõ10 hội tụ vì u 10 10 1 10 n 1 + n = , un+1 = = ³0 < 1. n + n + n=1 ! n ! n ( ) 1 ! u 1 n n n n+ Ví dụ 11. u
Chuỗi õõ 2 phân kỳ vì u 2 2 1 2n n 1 + n = , un+1 = = ³ 2 > 1. n + n + n=1 n n 1 u 1 n
* Tiêu chuẩn Côsi: Cho chuỗi số dương õ õ
u và giả sử lim n u = l. n n n=1
l < 1: chuỗi đã cho hội tụ
Khi ấy nếu l > 1: chuỗi đã cho phân kỳ
l = 1: không kết luận n
Ví dụ 12. Chuỗi õõö n ö n 1 ÷
÷ hội tụ vì lim n u = lim = < 1. n n=1 ø 2n + 1 ø 2n +1 2 n
Ví dụ 13. Chuỗi õõö 3n ö 3n 3 ÷
÷ phân kỳ vì lim n u = lim = > 1. n n + n=1 ø 2n + 5 ø 2 5 2
* Tiêu chuẩn tích phân Côsi: Nếu hàm số y = ö(x) liên tục, không âm và đơn điệu +õ
giảm trên [n, + õ) với n N. Khi ấy f (x)dx và õõ f (n) cùng tính chất hội tụ n n hoặc phân kỳ.
Ví dụ 14. Xét chuỗi õõ 1 . n=1 nñ 101
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
Nếu ñ 0 thì lim 1 0 nên chuỗi phân kỳ ñ n
Nếu ñ > 0 ta xét ö(x) = 1 là hàm liên tục, không âm, giảm trên [1, + õ). ñ x +õ Như đã biết 1 1 dx
hội tụ khi ñ > 1 và phân kỳ khi ñ 1. Do đó õõ xñ nñ 1 n=1
cũng hội tụ khi ñ > 1 và phân kỳ khi ñ 1
Ví dụ 15. Xét chuỗi õõ 1 , ñ R. ñ
n=2 n(ln n)
Nếu ñ < 0: Dễ thấy limun 0 nên chuỗi này phân kỳ
Nếu ñ = 0: Chuỗi là õõ 1 phân kỳ n=1 n Nếu ñ > 0: ö(x) = 1
là một hàm số liên tục, không âm, đơn điệu ñ x(ln x) giảm trên [3, + õ). üln(lnx) |t k h iñ = 1 +õ t ÿ 2
Xét dx và đặt I(t) = dx = ý(lnx) -1ñ x(ln )ñ x x(ln x)ñ |t k h iñ 1 2 2 ÿ þ (1-ñ) 2 üln(lnt) - ln(ln2 ) k h iñ = 1 ü + õ k h iñ 1 ÿ ÿ
Hay I(t) = ý(lnt) -1ñ - (ln ) 2 -1ñ lim I(t) = ý(ln2) -1ñ ÿ k h iñ 1 t³+õ ÿ k h iñ þ 1 þ (1- ñ ) þ 1-ñ +õ
Vậy dx hội tụ khi ñ > 1 và phân kỳ khi ñ 1 nên õõ 1 cũng x(ln )ñ x ñ n n(ln n 2 =2 )
hội tụ khi ñ > 1 và phân kỳ khi ñ 1.
4.1.3. Chußi đan dấu
a) Định nghĩa : Chuỗi đan dấu là một chuỗi có dạng õõ( - 1)n-1un trong đó tất cả n=1
các số hạng un đều dương (hoặc đều âm ) với n N.
à đây ta chỉ cần xét chuỗi đan dấu mà tất cả un > 0.
b) Tiêu chuẩn Lépnít: Chuỗi đan dấu õõ (- 1)n-1un với un > 0 hội tụ nếu unÿ 0. n=1 102
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi Ví dụ 16. õõ 1 1 1 1
( - 1)n-1 1 = 1 - + - + … + (- 1)n-1 + ... (chuỗi điều hòa n=1 n 2 3 4 n
đan dấu) là chuỗi đan dấu có 1 ÿ 0 nên chuỗi này hội tụ. n Ví dụ 17. õõ n 1 - ( ) 1 - tan
là chuỗi đan dấu, vì 0 < nên u > n+1 n 1 n = tan n 1 n=1 2 2 + 4 2 +
0 và unÿ 0 nên chuỗi này hội tụ
4.1.4. Hội tụ tuyệt đối và bán tụ
Trong mục này, chúng ta xét chuỗi số với un có dấu bất kỳ.
a) Định lý: Nếu õõ| u | hội tụ thì õõu cũng hội tụ. n n n=1 n=1
Chứng minh: Do õõ| u | hội tụ nên > 0, N > 0 sao cho n N, n > N và p n n=1
N ta có: |un+1| + |un+2| + ... + |un+p| < do |un+1 + un+2 + ... + un+p| |un+1| + |un+2|
+ .... + |un+p| |un+1 + un+2 + ... + un+p| < . Vậy õõu hội tụ n n=1 * Các chú ý
Chú ý 1: õõu hội tụ thì chưa chắc õõ| u | hội tụ. Nhưng õõu phân kỳ thì chắc n n n n=1 n=1 n=1
chắn õõ| u | phân kỳ. n n=1
Ví dụ 18. õõ n1- 1 n 1 1 ( ) 1 - hội tụ nhưng õõ 1 - | ( ) 1 - | = õ õ phân kỳ n=1 n n=1 n n=1 n
Chú ý 2: Nếu dùng tiêu chuẩn Dalambe hay Côsi mà kết luận õõ| u | phân kỳ. n n=1
Thì cũng suy ra được õõu phân kỳ. n n=1
b) Định nghĩa:
õõu được gọi là hội tụ tuyệt đối nếu õõ| u | hội tụ. n n n=1 n=1
õõu được gọi là bán tụ nếu õõu hội tụ còn õõ| u | phân n n n n=1 n=1 n=1 kỳ. 103
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
Ví dụ 19. õõ n1- 1 1 ( ) 1 - bán tụ còn õõ n 1 - 1 ( ) 1 -
hội tụ tuyệt đối vì õõ hội tụ. 2 2 n=1 n n=1 n n=1 n
Tổng quát: õõ n1- 1 ( ) 1 - . Khi ấy n=1 nñ ñ 0: chuỗi phân kỳ
0 < ñ 1: chuỗi bán tụ
ñ > 1: chuỗi hội tụ tuyệt đối
c) Các tiêu chuẩn hội tụ
* Tiêu chuẩn 1: (Dấu hiệu Aben) Nếu õ õ b hội tụ và {a n n} đơn điệu (tăng hay n=1
giảm) và bị chặn. Thì õõa b hội tụ. n n n=1
* Tiêu chuẩn 2: (Dấu hiệu Dirichle) Cho 2 dãy (an), (bn) thỏa anÿ 0 và tồn tại C >
0 sao cho n N ta có |Sn| = | õõb | C. Thì õõa b hội tụ. n n n n=1 n=1
* Tiêu chuẩn 3: (Hội tụ tuyệt đối) Nếu tồn tại dãy số dương (Cn) sao cho |un| Cn
với n N và õõC hội tụ. Thì õõu hội tụ tuyệt đối. n n n=1 n=1 4.2. Chußi luỹ thừa 4.2.1. Định nghĩa
Chuỗi lũy thừa tổng quát là một chuỗi hàm có dạng a0 + a1(x - a) + a2(x -
a)2 + ... + an(x - a)n + ... và ký hiệu là õõa (x - a)n trong đó các số a, a n n R. n=0
Chú ý: Nếu đặt t = x - a thì chuỗi lũy thừa có dạng chính tắc (chuẩn) õõ n a t . n n=0
Ngoài ra chuỗi hàm dạng õõ n
a f (x) , trong đó ö(x) là hàm nào đó được gọi là n n=0
chuỗi lũy thừa suy rộng. Vì nếu đặt t = ö(x) thì chuỗi trên thành õõ n a t nên ta n n=0
chỉ cần xét chuỗi lũy thừa dạng chuẩn õõ n a x (1) là đủ. n n=0 104
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi n n 1 -
Ví dụ: õõ n1- x x nx , õ õ , õõ
, ... là các chuỗi lũy thừa dạng chuẩn. 2 n=1 n=0 n +1 n=1 n n + n + õõ
1 (x - 5)n, đặt t = x - 5 thì ta được chuỗi õõ 1 tn 2 2 n=0 2n + 3 n=0 2n + 3 n õõ 1 ö 2x-1ö 2x -1 1 ÷ ÷ đặt t =
ta được chuỗi lũy thừa õõ tn 2 + x + 2 n=1 n ø x 2 ø 2 n=1 n 4.2.2. Miền hội tụ
a) Định nghĩa: Tập gồm tất cả các số thực x làm cho chuỗi (1) hội tụ được gọi là
miền hội tụ. Nếu gọi X0 là miền hội tụ của (1) thì hiển nhiên x0 = 0 X0. Ngoài ra, ta có định lý sau.
* Đßnh lý Abel: Nếu ñ 0, ñ X0 thì x R mà |x| < |ñ| ta đều có x X0. Chứng minh: Nếu x n n x0 n
0 0, |x0| < |ñ| thì õ
õ | a x | = õõ|a ñ |.| | . n 0 n ñ n=0 n=0 Do õõ n
a ñ hội tụ nên lim a n
nñn = 0 suy ra K > 0: n N ta có |anñn| n=0 K.
Đặt q = | x0 | thì 0 < q < 1 nên õõ| n
a x | là chuỗi số dương có |a n| ñ n 0 nx0 n=0 Kqn mà õõ n Kq hội tụ nên õ õ | n
a x | cũng hội tụ suy ra (1) hội tụ. Vậy x X n 0 0. n=0 n=0
* Hệ quÁ: Nếu (1) phân kỳ tại ò 0 thì (1) cũng phân kỳ tại x R mà |x| > |ò|.
* Miền hội tụ: Cho chuỗi (1) khi ấy xảy ra 1 trong 3 khả năng sau đây: - Một là: X n 0 = {0}. Ví dụ õ
õ (nx) , nếu x 0 thì limn n
| nx | = limn|x| = + õ n=1 nên õõ| |n nx phân kỳ suy ra õ õ ( )n
nx phân kỳ. Vậy X0 = {0}. n=1 n=1 ö x ön n x - Hai là: X | x | 0 = R. Ví dụ õ
õ ÷ ÷ , rõ ràng x R ta có limn = lim = n=1 ø n ø n n n 0 suy ra õõö x ö
÷ ÷ hội tụ tuyệt đối nên hội tụ. Vậy X0 = R. n=1 ø n ø n
- Ba là: X x
0 {0}, R. Ví dụ õ õ
hội tụ tại x = - 1 nhưng phân kỳ tại x = 1. n=1 n 105
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
Trong trưßng hợp này, ngưßi ta chứng minh được rằng R > 0 sao cho (1)
hội tụ với x R mà |x| < R và phân kỳ với x R mà |x| > R. Số R được gọi
là bán kính hội tụ của chuỗi. Khi ấy (- R, R) được gọi là khoảng hội tụ. Còn tại x
= R chuỗi hội tụ hay không, ta phải thay trực tiếp và xét bằng chuỗi số để kết luận.
Khi đó miền hội tụ của (1) có một trong 4 dạng: (- R, R), [- R, R), (- R, R]
hay [- R, R]. Trưßng hợp X0 = {0} ta quy ước R = 0, trưßng hợp X0 = R ta quy ước R = + õ.
b) Phương pháp tìm bán kính hội tụ: ü 0 k hi l = + õ Định lý: a Nếu lim| ÿ n 1
+ | = l hoặc lim n | a | = l. Thì R = ý+ õ k hi l = 0 a n n ÿ þ 1- l k hi ü 0 l ü + õ
Ví dụ 1. Tìm miền hội tụ của chuỗi õõ . n n x n=1 Giải: a + Do lim n 1 n 1 + = lim
= 1 R = 1. Tại x = 1 thì un = ( 1)nn có limun a n n
0 nên chuỗi phân kỳ tại x = 1. Vậy X0 = (- 1, 1) n
Ví dụ 2. Tìm miền hội tụ của chuỗi õõ x . 2 n n=1 ö 1 ö ÷1+ ÷ ø n ø Giải: Ta có lim 1 1 n a = lim = nên R = e. n n ö ö e ÷ + 1 1 ÷ ø n ø n n n n Tại x = e thì u ( e) e ö ö ö ö n = = ( 1)n . Do ÷ + 1 1 ÷ ý e ÷ + 1 1 ÷ < e 2 2 ö 1 n ö ö 1 n ö ø n ø ø n ø ÷1+ ÷ ÷1+ ÷ ø n ø ø n ø 2 n ö 1 ö
÷1+ ÷ < en. Nên |un| > 1 limun 0. Từ đó chuỗi phân kỳ tại x = e. ø n ø Vậy X0 = (- e, e) n 1 -
Ví dụ 3. Tìm miền hội tụ của chuỗi õõ x . n=1 n 106
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi Giải: a + Do lim n 1 n 1 + = lim = 1 R = 1. a n n n 1 - Tại x = - 1: õõ ( )1 -
hội tụ ; tại x = 1: õõ 1 phân kỳ. Vậy X0 = [- 1, 1) n=1 n n=1 n n 1 -
Ví dụ 4. Tìm miền hội tụ của chuỗi õõ x . 2 n=1 n 2 Giải: a Do lim n n 1 + = lim = 1 R = 1. a 2 (n + ) 1 n n 1 -
Tại x = 1: õõ 1 và õõ ( )1 - hội tụ. Vậy X 2 2 0 = [- 1, 1] n=1 n n=1 n
c) Tính chất của tổng một chuỗi lũy thừa: Nếu õõ n
a x hội tụ về S(x) với bán n n=0
kính hội tụ R > 0. Thì trong (- R, R) ta có:
i) S(x) là một hàm liên tục trong (- R, R).
ii) S(x) khả tích trên mọi [a, b] (- R, R) và: b b õ b a a
S(x)dx = õõ n a x dx = õ n a x dx= õ õ n
xn+1| b = õõ n (bn+1 - an+1). n n a n n 1 n n 1 a = a n 0 n=0 a =0 + =0 + x
Đặc biệt a = 0, b = x thì a S t ( )dt = õ õ n
xn+1 và chuỗi này cũng có bán n n 1 0 =0 + kính hội tụ là R.
iii) S(x) khả vi mọi cấp và S(k)(x) = õõn (n - 1)...(n - k + 1)an-kxn-k cũng có n=k bán kính hội tụ là R.
4.2.3. Khai triển một hàm thành chußi lũy thừa
* Đßnh lý: Giả sử ö(x) có đạo hàm mọi cấp trong (a, b) và x0 (a, b). Nếu K > 0
sao cho x (a, b) và n N mà |ö(n)(x)| < K. Thì x (a, b) ta có khai triển (n) f (x ) Taylor sau đây ö(x) = õõ 0 (x - x0)n (*) n=0 ! n (n) f ( ) 0
* Chú ý: Nếu x0 = 0 thì được gọi là khai triển Maclaurin: ö(x) = õ õ xn n=0 ! n
Ví dụ 5. Khai triển Maclaurin hàm ö(x) = ex.
Giải: Do ö(n)(x) = ex nên N > 0: |ö(n)(x)| eN, với x (- N, N) và ö(n)(0) = 1. 107
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi n Vậy ex = õõ x . n=0 ! n
Ví dụ 6. Khai triển Maclaurin hàm ö(x) = sinx. Giải:
Do ö(n)(x) = sin(x + n ) |ö(n)(x)| 1 và như ta đã biết 2 ü k 0 hi n = 4 q ÿ k 1 hi n = 4 q + ü 0 k hi n = 2 k ö 1 (n) ÿ (0) = sin(n ) = ý = ý 2 ÿ k 0 hi n = 4 q + 2 þ(-1 )k k hi n = 2 k + 1 ÿþ k 1 - hi n = 4 q + 3 n 3 5 7 n Vậy sinx = õõ ( )1 -
x2n+1 = x - x + x - x + ... + ( ) 1 - x2n+1 + ... n + n=0 (2n + ) 1 ! ! 3 ! 5 ! 7 (2 ) 1 !
Từ khai triển của hàm ö(x) = sinx ta có:
Đạo hàm hai vế ta được khai triển của ö(x) = cosx n 2 4 6 2 Vậy cosx = õõ ( )1 -
x2n = 1 - x + x - x + ... + (- 1)n x n + ... n=0 (2n)! ! 2 ! 4 ! 6 (2n)! (ix)n
* Công thức ¡le: Từ khai triển hàm cosx và sinx cosx + isinx = õ õ = e ix n=0 ! n
Vậy z = r(cos + isin) = rei. Từ đó cos + isin = ei : Công thức ơle
Đặc biệt: Nếu r = 1 và = . Thì ei = - 1 (mối liên hệ giữa 3 số e, i, )
Ví dụ 7. Khai triển Maclaurin hàm ö(x) = (1 + x)ñ, ñ R.
Giải: Ta có ö(n)(x) = ñ(ñ - 1)(ñ - 2)...(ñ - n + 1)(1 + x)ñ-n
ö(n)(0) = ñ(ñ - 1)(ñ - 2) ... (ñ - n + 1) ñ ñ ñ ñ
Vậy (1 + x)ñ = 1 + ñx + (ñ - )
1 x2 + ... + ( - )1...( -n+ )1 xn + ... ! 2 ! n
Chuỗi này có tên gọi là chuỗi nhị thức, bán kính hội tụ R = 1. 1 n
* Đặc biệt: Nếu ñ = - 1 thì
= 1 - x + x2 + ... + (- 1)nxn + ... = õõ ( )1 - xn. x +1 n=0 x x
+) Lấy tích phân 2 vế 1 dt = õõ ( )1
- n ntdt ta có khai triển của hàm ln(1 + x): 1+ t 0 n=0 0 n ln(1 + x) = õõ ( )1 - xn+1 n=0 n + 1 108
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi
+) Thay x bái x2 được 1 = 1 - x2 + x4 - x6 + ... + (- 1)nx2n = õõ ( )1 - n x2n, lấy 2 x +1 n=0 x õ x tích phân 2 vế 1 dt = õ( n 2 ) 1 - n
t dt ta được khai triển của hàm arctanx: + t 2 1 0 n=0 0 2 1 + arctanx = õõ x n ( ) 1 - n n + n=0 2 1 n
+) Cuối cùng nếu lấy x = 1 ta có õõ ( )1 - = (Chuỗi Lepnit) 4 n=0 2n + 1
4.2.4. Một vài ứng dụng để tính gần đúng
a) Tính gần đúng giá trị hàm số tại một điểm
Ví dụ 8. Tính cos50 chính xác đến 10-5 Giải: Do 50 ~ nên cos50 = cos 1 - 1 .( )2 hay cos50 0,99238. 36 36 ! 2 36
Ví dụ 9. Tính e chính xác đến 10-7 2 3
Giải: Do ex = 1 + x + x + x + ... + xn + ... ! 1 ! 2 ! 3 ! n Nên 1 1 1
e = 1 + 1 + 1 + + + ... + + ... (đây là định nghĩa khác của số e) ! 1 ! 2 ! 3 ! n Suy ra 1 1
e 1 + 1 + 1 + + + ... + 1 hay e 2,71828181… ! 1 ! 2 ! 3 1 ! 0
Ví dụ 10. Tính ln2 chính xác đến 10-5 2 3 4 5 6
Giải: Do ln(1 + x) = x - x + x - x + x - x + ... 2 3 4 5 6 2 3 4 5 6
Thay x bái - x được: ln(1 - x) = - x - x - x - x - x - x - ... trừ vế với vế 2 2 3 4 5 6 3 5 7
khai triển trên suy ra: ln1+ x = 2(x + x + x + x + ...) 1- x 3 5 7
Lấy x = 1 thì ln2 2( 1 + 1 . 1 + 1 . 1 + 1 . 1 + 1 . 1 ) hay ln2 0,69314 3 3 3 3 3 5 5 3 7 7 3 9 9 3
b) Tính gần đúng tích phân xác định 1 2
Ví dụ 11. Tính gần đúng I = - 2x e dx 0 109
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi n 2n
Giải: Do ex = õõ x . Thay x bái - x2 được e- 2x = õõ x ( ) 1 - n . Suy ra n=0 ! n n=0 ! n 1 1 1 2 2 2 x n 2 2 I = - 2x x n e
dx = õõ( - 1)n !n dx = õõ( - 1)n dx ! n 0 n= 0 0 n=0 0 1 = õ õ n 1 2n+1 n 1 2 ( ) 1 - x = õõ( )1 - 0 2n+1 n 0 n ( ! 2n + n=0 n ( ! 2n + ) 1 = ) 1 2
Lấy n = 2 được I 1 - 1 + 1 hay I 0,4644. 2 3 ! 1 . 2 . 3 5 ! 2 . 2 . 5 a
Ví dụ 12. Tính I = sin xdx x 0 2n 1 - 2n-2
Giải: Do sinx = õõ n−1 x sin x x ( ) 1 - = õ õ n−1 ( ) 1 - . Nên n=1 (2n - ) 1 ! x n=1 (2n - ) 1 ! a 2n-2 n 1 - a I = n 1 - x ( ) 1 - ( ) 1 - dx õõ = õ õ 2n x -2dx (2 - ) 1 ! n (2n - ) 1 ! 0 n=1 n =1 0 n 1 - n 1 - 2n-2 = õõ n1- ( ) 1 - ( ) 1 - a ( ) 1 - x2n-1| a 0 = õ õ n=1 (2n - ) 1 !(2n - ) 1 n=1 (2n - ) 1 !(2n - ) 1
Từ đây cho a giá trị cụ thể và n đủ lớn ta tính được giá trị cần thiết.
c) Tính gần đúng nghiệm PTVP
* Phư¢ng pháp hệ số bất đßnh
Ví dụ 13. Giải PTVP y” - x2y = 0 (1)
Giải: Ta tìm NTQ của PT (1) dưới dạng chuỗi lũy thừa. Giả sử y = õõ n C x (2). n n=0 Từ (2): y’ = õõ n 1 - nC x và y” = õ õ n-2 n(n - ) 1 C x . n n n=1 n=2
Thay y và y” vào (1) được: õõ n-2 n(n - ) 1 C x - õõ n+2 C x = 0 n n n=2 n=0
Hay 2.1.C2 + 3.2.C3x + õõ[(n + 4)(n + ) 3 C C xn+2 = 0 C n+ - ] 4 n 2 = 0, C3 = 0, n=0 C C C n 0 n+4 = , n = 0, 1, 2, … C4k = , C4k+1 = (n + ) 3 (n + 4) 3 4 . .7.8...(4k − ) 1 (4k) C1 , C4k+2 = C4k+3 = 0
4.5.8.9...(4k)(4k + ) 1 110
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi 4k 4k +1 Vậy y = C x x 0 õ õ + C1 õõ (C0, C1 R) k 0 . 9 . 8 . 5 . 4 ..(4k)(4k + k =0 . 8 . 7 . 4 . 3 ..(4k − ) 1 (4k) = ) 1
* Phư¢ng pháp đ¿o hàm liên tiếp
Ví dụ 14. Giải PTVP y" = y' - 1 . Với điều kiện y(1) = 1, y’(1) = 0 y x (n)
Giải: Giả sử NTQ có dạng y = ö(x) = õõ f ) 1
( (x - 1)n. Vấn đề ö(n)(1) = ? n=0 ! n
Từ điều kiện đầu suy ra ö(0)(1) = 1, ö(1)(1) = 0
Từ PT ta có: ö(2)(1) = 0 - 1 = - 1 1 1 2
Lấy đạo hàm 2 vế của PT đã cho được: y(3) = .yy -"y' + 1 y(3)(1) = 0 2 y 2 x
Tương tự suy ra ö(4)(1) = - 2, ö(5)(1) = - 3 ... 2 4 5
Vậy nghiệm của PT cần tìm là y = 1 - (x - )
1 - 2(x - )1 + (3x - )1 + ... ! 2 ! 4 ! 5 BÀI TẬP CH¯¡NG 4
Bài tập 1: Tính tổng riêng Sn và tổng S của các chuỗi sau (nếu được) 2n + n 1. õõ 1 2. õõ 3 n
n=1 n(n + 2) n=0 6 2n + 3. õõ 1
( n + 2 - 2 n +1 + n) 4. õ õ 2 2 n=1
n=1 n (n + ) 1
Bài tập 2: Dùng tiêu chuẩn so sánh, xét sự hội tụ của các chuỗi sau 1. õõsin 2. õõsin n n=1 2n n=1 2 n + 1+ n 3. õõ 1 4. õõ 2 n
n=1 n(n + 2) n=0 1 + 3
Bài tập 3: Dùng tiêu chuẩn Đalambe hay Côsi xét sự hội tụ của các chuỗi sau 1. õõ ! n 2. õõ (2n - )1 !! n n n=1 n n=1 3 . ! n (n + 2 n 3. õõ (2n) !! 3. õõ ) 1 n 2 n n n=0 2 . ! n n=1 n 3 111
KHOA KHOA HàC C¡ BÀN
Chư¢ng 4: Lý thuyết chuỗi n ö 2 + -1 ö 5. õõ ! n 6. n n õõ 2 n ÷÷ 2 ÷÷ 1 2 - 3 + n=1 n .e n= ø n n 4 ø 7. õõ 1 8. õõ 1 2 n=3 . n ln . n ln(ln n) n=1 n + n n + 9. õõ 1 - n 10. õõ 1 n=1 n n=2 ln n
Bài tập 4: Xét tính hội tụ, bán tụ, hội tụ tuyệt đối của các chuỗi sau n 1 - n + n 1 - n + 1. õõ 1 1 ( ) 1 - 2. õõ( )1 - n=1 2n + 3 n=1 n(n + 2) n n 1 - 2n + 3. õõ ö 1ö n ( ) 1 - ÷ ÷ 4. õõ n 1 - ( ) 1 - 3 n=1 ø 3n +1ø n=1 n +1 5. õõ n 1 - ( ) 1 - sin 6. õõ n 1 - ( ) 1 - sin n n=1 2n n=1 2
Bài tập 5: Tìm bán kính hội tụ của các chuỗi lũy thừa sau 1. õõ ! n 1 ( + 1 2 )n xn 2. õõ xn, ñ > 1 2 n n=1 n n=1 ñ ö p (2n - ) 1 ! ! ö n + n 3. õõ ö 1 ö ÷÷ ÷÷ xn, p R 4. õõ÷ ÷ xn n 1 2n + n=1 ø (2n) ! ! ø = ø 1ø
Bài tập 6: Tìm miền hội tụ của các chuỗi lũy thừa sau 1. õõ ! n xn-1 2. õõ 1 xn-1 n n n=1 n n=3 3 ln n 2 n 1 - 3. õõ ( ! n ) xn-1 4. õõ (x - ) 4 n=1 (2n)! n=1 n n n + 5.
ö n 1 ö ö 1- x õõ ö 1 ÷ ÷ ÷ ÷ 6. õõ n 1 - 1 ø 2 +1ø 1+ n n(x 2) n= n ø x ø =1 +
Bài tập 7: Tìm khoảng hội tụ và tính tổng của các chuỗi lũy thừa sau n 1. õõ x 2. õõ4n xn-1 n n=1 3 n=1 n 3. õõ n 1 - x ( ) 1 - 4. õõ n 1 - ( ) 1 - nxn-1 n=1 n n=1 112
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Chương 5: PH¯¡NG TRÌNH VI PHÂN
5.1. KHÁI NIÞM PH¯¡NG TRÌNH VI PHÂN
5.1.1. Một số ví dụ d¿n tới ph°¢ng trình vi phân
Ví dụ 1: Có một vật với khối lượng m rơi tự do trong không khí, giả sử sức cản của
không khí tỷ lệ với vận tốc rơi v(t) tại thßi điểm t với hệ số k > 0. Tính v(t).
Ta có khi vật rơi thì chịu tác động của các lực sau: Lực hút của trái đất là mg và
lực cản của không khí là kv(t). Theo định lý Newton: ma = F với a là gia tốc của vật rơi.
Vậy ta có phương trình m dv = mg - kv hay v’ + k v - g = 0. dt m
Ví dụ 2: Tìm phương trình đưßng cong (C): y = ö(x) thỏa mọi đoạn tiếp tuyến với
đưßng cong nằm giữa hai trục tọa độ bị tiếp điểm chia thành hai phần bằng nhau.
Giả sử M(x, y) tùy ý trên (C), tiếp tuyến với (C) tại M y
cắt hai trục tại A và B, góc hợp bái tiếp tuyến và chiều dương (C): y = ö(x)
trục hoành là ñ, hình chiếu của M xuống trục hoành là N. Từ B M
ý nghĩa hình học của đạo hàm ta có y’ = ö’(x) = tanñ= - ñ N A x O tan(MAN) = - MN . NA
Hiển nhiên NM = y và do AM = MB nên AN = NA = x.
Vậy chúng ta có y’ = - y . x 5.1.2. Định nghĩa
Khái niệm chung: Phương trình vi phân (PTVP) là một phương trình (PT) chứa
biến độc lập, hàm cần tìm và các đạo hàm nào đó của nó. Trong PTVP phải có đạo hàm
(nào đó) của hàm cần tìm.
Nếu hàm cần tìm là hàm một biến thì đạo hàm là thông thưßng và PT được gọi
là PTVP thưßng, còn nếu hàm cần tìm là hàm nhiều biến thì đạo hàm là đạo hàm riêng
và PT được gọi là PT đạo hàm riêng (hay PT Vật lý - Toán). 113
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Trong chương này chúng ta chỉ xét PTVP thưßng và gọi tắt là PTVP.
Cấp của PTVP là cấp cao nhất của các đạo hàm có mặt trong PT.
Nghiệm của PTVP là tất cả các hàm số thỏa mãn PT đã cho.
Sau này ta sẽ thấy ngoài hai loại nghiệm chính: Nghiệm tổng quát (NTQ) và
nghiệm riêng (NR), còn có một loại nghiệm khác nữa là nghiệm kỳ dị.
Chú ý: Bài toán tìm NR thưßng được gọi là bài toán Cauchy.
Ví dụ 1: PTVP cấp 1: (y’)2 - xy’ + y = 0 có NTQ là y = C(x - C), nếu cho C = 1 thì 2
được NR là y = x - 1. Ngoài ra còn có nghiệm kỳ dị y = x . 4
Ví dụ 2: PTVP cấp 1: y’ = 2
1- y có NTQ y = sin(x + C), nếu cho C = 0 thì NR là y =
sinx. Ngoài ra có nghiệm kỳ dị y = 1.
Ví dụ 3: PTVP cấp 2: (y’)2 + yy” = 0 có NTQ là y2 = C1x + C2, nếu cho C1 = 2, C2 = 1
thì NR là y2 = 2x + 1. Ngoài ra còn có họ nghiệm kỳ dị y = C.
Có PT chỉ có nghiệm kỳ dị hoặc vô nghiệm: Chẳng hạn PT |y’| + y2 = 0 chỉ có
nghiệm kỳ dị y = 0 hay PT (y’)2 + sin2y = 0 chỉ có họ nghiệm kỳ dị y = k, với k
Z, còn PT (y’)2 + ex = 0 hay PT (y”)2 + 1 = 0 vô nghiệm.
Sau đây chúng ta lần lượt xét một số loại PTVP cấp 1 và cấp 2. 5.2. PTVP CÀP 1 5.2.1. Định nghĩa
* PTVP cấp 1 là PTVP có dạng y’ = ö(x, y) hay F(x, y, y’) = 0.
* NTQ của PTVP cấp 1 là tất cả các hàm y = (x, C) hay (x, y, C) = 0 (trong đó C là
hằng số thực tùy ý) thỏa mãn PT đã cho.
* NR được lấy từ NTQ khi cho C một giá trị cụ thể nào đó, giá trị cụ thể ấy thưßng
được lấy từ điều kiện đầu y|x = x = y 0 0.
Ví dụ: PT y’ - y = 0 có NTQ là y = Cex với C ù 0 và có NR y = ex với C = 1 hay với
điều kiện đầu y|x = 0 = 1. Ngoài ra còn có nghiệm kỳ dị y ú 0. 114
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
5.2.2. Các ph°¢ng trình dạng khuyết
a) Dạng khuyết y: F(x, y’) = 0
* Trưßng hợp 1: y’ = ö(x).
- Cách giÁi: Lấy tích phân hai vế ta được y = ö(x)dx + C
- Ví dụ 1: Giải PT y’ = xlnx.
Tích phân 2 vế được y = xlnxdx + C = x(lnx - 1) + C
* Trường hợp 2: x = ö(y’).
- Cách giÁi: Đặt t = y’ thì x = ö(t), dx = ö’(t)dt, dy = y’dx = tdx = tö’(t)dt.
Từ đó y = tö’(t)dt + C = tö(t) - ö(t)dt + C. ÿüx = f t() Vậy NTQ của PT là ý (t là tham số)
ÿþy = tf t()- f(t)dt + C
- Ví dụ 2: Giải PT x = 3y’2 + 2y’ + 1.
GiÁi: Đặt t = y’ suy ra x = 3t2 + 2t + 1, dx = (6t + 2)dt,
dy = y’dx = tdx = (6t2 + 2t)dt nên y = (6t2 + 2t)dt + C = 2t3 + t2 + C. ÿüx = t2 3 + t 2 +1 Vậy NTQ là ý (t là tham số) ÿþy = t3 2 + t 2 + C
* Trường hợp 3: D¿ng F(x, y’) = 0 nhưng tham số hóa được: x = ö(t), y’ = g(t)
- Cách giÁi: Ta có dy =y’dx = g(t)ö’(t)dt, nên y = g(t)ö’(t)dt + C ÿüx = f t() Vậy NTQ của PT là ý (t là tham số)
ÿþy = g t() f '(t)dt + C
- Ví dụ 3: Giải PT x3 + y’3 = 3xy’ 2 3t
GiÁi: Đặt y’ = tx thì PT là x3(1 + t3) = 3tx2 hay x = 3t suy ra y’ = tx = . 3 1+ t 3 1 + t 2 3 2 3
Do đó dy = y’dx = 3t 3 . 1 (
3 - 2t ) dt, nên y = t . 1( 3 - 2t ) dt + C. 3 1 + t 3 2 1 ( + t ) 3 1 + t 3 2 1 ( + t )
Đặt u = 1 + t3 suy ra du = 3t2dt, 1 - 2t3 = 3 - 2u nên 115
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
y = 3 3 - 2u du + C = 9 du - 6 du + C = - 9 + 6 + C 3 u 3 u 2 u 2 2u u hay y = - 9 + 6 + C. 3 2 2 1 ( + t ) 3 1+ t ü = t3 x 1+ 3 Vậy NTQ là ÿÿ t ý ÿ 9 6 y = - + + C ÿþ ( 2 1 + t3 )2 1 + t3
b) Dạng khuyết x: F(y, y’) = 0
* Trường hợp 1: D¿ng y’ = ö(y) - dy
Cách giÁi: y’ = ö(y) dy = ö(y) dx = . dx f ( y)
Tích phân 2 vế được NTQ là x = dy + C f ( y)
- Ví dụ 4: Giải PT y’ = y2 + 1 dy dy
GiÁi: Ta có y’ = y2 + 1 dy = y2 + 1 dx = dx = + C dx 2 y + 1 2 y + 1
x = arctany + C y = tan(x - C).
* Trường hợp 2: D¿ng y = ö(y’)
- Cách giÁi: Đặt t = y’ y = ö(t), dy = ö’(t)dt, mặt khác dy = y’dx = tdx. Nên dx = ü f '(t) f ' t ( ) x = dt + C
, tích phân 2 vế được x = f ' t() dt + C. Vậy NTQ là ÿ ý t t t
ÿþy = f (t)
- Ví dụ 5: Giải PT y = y’ + lny’
GiÁi: Đặt t = y’ ta có y = t + lnt, dy = (1 + 1 )dt, hơn nữa dy = tdx. Nên tdx = (1 + 1 )dt t t
dx = ( 1 + 1 )dt dx = (1 + 1 )dt x = lnt - 1 + C. t 2 t t 2 t t ü 1
ÿx = lnt - + C Vậy NTQ là ý t
ÿþy = t +lnt 116
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
* Trường hợp 3: D¿ng F(y, y’) = 0 nhưng tham số hóa được: y =ö(t), y’ = g(t) - f '(t)
Cách giÁi: Do dy = ö’(t)dt và dy = g(t)dx nên ö’(t)dt = g(t)dx hay dx = dt. g(t) ü f '(t) ÿx = dt + C
Tích phân 2 vế được x = f '(t) dt + C. Vậy NTQ là ý g(t) g(t)
ÿþy = f (t)
- Ví dụ 6: Giải PT y2 + y’2 = 1
GiÁi: Đặt y = sint, y’ = cost. Từ đó dy = costdt và dy = y’dx = costdx. Nên costdt =
costdx. Từ đây xảy ra 2 khả năng sau:
Một là: cost ù 0 thì dt = dx nên t = x + C và do đó NTQ là y = sin(x + C),
Hai là: cost = 0 suy ra t = + k, nên y = 1 - Hai nghiệm này không thuộc 2
NTQ trên nên là 2 nghiệm kỳ dị.
5.2.3. Một số dạng PTVP cÁp 1
(Giải được bằng phương pháp cầu phương)
a) Phương trình tách biến (hay PT với biến phân ly)
* D¿ng: M(x)dx + N(y)dy = 0 (1)
* Cách giÁi: Tích phân 2 vế của (1) được M(x)dx + N(y)dy = C (hay ln|C|, C ù 0)
* Các ví dụ: Giải PTVP 1 Ví dụ 1: exdx +
dy = 0 với điều kiện y|x = 0 = 0 y +1 1
GiÁi: Tích phân 2 vế PT trên ta được exdx +
dy = C ex + ln|y + 1| = C. y + 1
Thay điều kiện y|x = 0 = 0 C = 1. Vậy NR cần tìm là ex + ln|y + 1| = 1 ydy
Ví dụ 2: xdx + = 0. 2 x +1 y + 3 ydy
GiÁi: Tích phân 2 vế xdx +
= ln|C| 1 ln(x2 + 1) + ln|y + 3| = ln|C| 2 x +1 y + 3 2 (y + 3) 2
x +1 = C. Vậy NTQ của PT đã cho là (y + 3) 2 x +1 = C 117
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Ví dụ 3: Theo định luật Newton, vận tốc nguội dần của một vật trong không khí tỷ lệ
với hiệu nhiệt độ của vật và không khí. Hãy tìm quy luật nguội dần của vật nếu nhiệt
độ không khí là 200C và sau 20 phút vật giảm từ 1000C xuống 600C. Hỏi sau bao nhiêu
lâu thì nhiệt độ của vật giảm còn 300C
GiÁi: Gọi nhiệt độ của vật tại thßi điểm t là T(t), hệ số tỷ lệ là . Ta có:
dT = (T - 20) dT = dt dT = dt + ln|C| ln|T - 20| = t + ln|C| dt T - 20 T - 20
ln|T - 20| = ln|C| + lnet ln|T - 20| = ln|Cet| T(t) = 20 + Cet.
Do T(0) = 100 C = 80 hay T(t) = 20 + 80et.
Lại do T(20) = 60 80e20 = 40 e20 = 1 20 = - ln2 = - ln 2 . 2 20 ln 2 ln 2
Vậy T(t) = 20 + 80e - t. -
20 . Nhiệt độ của vật còn 300 30 = 20 + 80e t. 20 ln 2 ln 2 - e - t. 1 ln 2 20 = e t. 20 = 2-3 - t = - 3ln2 t = 60’. 8 20
Ví dụ 4: Tốc độ phân hủy của Radium tỷ lệ với khối lượng của nó tại thßi điểm t. Biết
rằng lúc đầu khối lượng là m0 và sau 1.600 năm khối lượng ấy giảm còn một nửa. Hãy
xác định khối Radium tại thßi điểm t
GiÁi: Gọi khối lượng Radium tại thßi điểm t là m = m(t), hệ số tỷ lệ là k > 0.
Ta có dm = - km (do khối lượng giảm theo thßi gian). dt
Hay dm = - kdt suy ra m(t) = Ce-kt. Do m(0) = m0 nên C = m0 m(t) = m0e-kt m ln 2 - và m(1.600) = m ln 2 0 nên k = . Vậy m(t) = m0e t 1600 2 1600
* Chú ý: Các PT dạng sau đưa được về PT tách biến
- PT d¿ng: M1(x)N1(y)dx + M2(x)N2(y)dy = 0 (2) M (x) N ( y) Thật vậy PT (2) 1 dx + 2
dy = 0 (điều kiện M2(x)N1(y) ù 0). M (x) N ( y) 2 1 Đây là PT tách biến
Ví dụ 5: Tìm NR của PT: x(y2 - 1)dx + y(x2 + 1)dy = 0 với điều kiện y|x = 1 = 0 118
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
GiÁi: y = 1: là nghiệm kỳ dị y ù 1: PT x dx + y
dy = 0 2x dx + 2 y dy = 0 2 x +1 2 y + 1 2 x +1 2 y −1
2x dx + 2y dy = ln|C| ln(x2 + 1) + ln(y2 - 1) = ln|C| ln(x2 + 1)|y2 - 1| = 2 x +1 2 y −1
ln|C| (x2 + 1)(y2 - 1) = C.
Với điều kiện y|x = 1 = 0 ta có (12 +1)(02 - 1) = C C = - 2.
Vậy NR cần tìm là: (x2 + 1)(y2 - 1) = - 2
ax + by + c a b - PT d¿ng: y’ = ö( ) (3). Trong đó D = = 0 và b, b1 ù 0
a x + b y + c a b 1 1 1 1 1 a = Khi đó ü ka + + k R sao cho ax by c ý 1 PT (3) là y’ = ö( ). þb = kb
k(ax + by) + c 1 1
Đặt u = ax + by y = 1 (u - ax) y' = 1 (u' - a) thay vào PT (3) ta được u’ = b b + +
bö( u c ) + a hay g(u)du - dx = 0 với g(u) = bö( u c ) + a (đây là PT tách biến). ku + c ku + c 1 1 2x + 3y +1
Ví dụ 6: Giải PTVP y’ = . 4x + 6y + 5
GiÁi: Đặt u = 2x + 3y y = 1 u - 2 x nên y’ = 1 u’ - 2 . 3 3 3 3 u + u + u + u + Từ đó PT là 1 u’ - 2 =
1 u’ = 7 13 du = 7 13 2 5 du = 3 3 2u + 5 2u + 5 dx 2u + 5 7u +13 u + dx 14 35 du = 7dx. 7u +13
Tích phân 2 vế ta được (2 + 9
)du = 7dx + C 2u + 9 ln|7u + 13| = 7x + C. 7u +13 7
Cuối cùng thay u = 2x + 3y được NTQ của PT là 3x + 6y + 9 ln|14x + 21y + 13| = C. 7
b) Phương trình đẳng cấp cấp 1 * Hàm đẳng cấp 119
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
- Đßnh nghĩa: Hàm z = ö(x, y) được gọi là đẳng cấp cấp k (k = 0, 1, 2,...) nếu mọi số
thực t ù 0 ta có ö(tx, ty) = tkö(x, y) 2 2
Ví dụ 7: Hàm ö(x, y) = x - y đẳng cấp cấp 0 vì t ù 0: xy 2 2 2 2 2 2 2
ö(tx, ty) = t(x) -(ty) = t (x - y ) = x - y = t0.ö(x, y), tx t.y t 2xy xy 2 2 +
Hàm ö(x, y) = x
y đẳng cấp cấp 1 vì t ù 0: x - y 2 2 2 2 2 2 ö + + + (tx, ty) = t(x) t ( y) = t ( 2 x
y ) = t x y = t1.ö(x, y) tx - y t t(x - y) x - y 4 4
Hàm ö(x, y) = x + y đẳng cấp cấp 2 vì t ù 0: 2 2 x - y 4 4 + 4 4 4 + 4 4 ö(tx, ty) = (tx)
(ty) = t (x y ) = t2 x + y = t2.ö(x, y) 2 2 (tx) - (ty) 2 t ( 2 x - 2 y ) 2 2 x - y
* D¿ng: y’ = ö(x, y) trong đó ö(x, y) là là hàm đẳng cấp cấp 0, nghĩa là ö(x, y) với t ù
0 ta có ö(tx, ty) = ö(x, y). 1 y y
* Cách giÁi: Giả thiết x ù 0, lấy t =
suy ra PT là y’ = ö(1, ). Đặt u = y = xu, x x x
y’ = u + xu’, ö(x, y) = ö(1, u) nên PT là xu’ + u = ö(1, u), đặt g(u) = ö(1, u) - u thì PT
là: x du = g(u) hay du = dx , điều kiện g(u) ù 0. dx g(u) x
Đây là PT tách biến giải ra được u = (x, C).
Từ đó NTQ của PT đã cho là y = x(x, C) * Các ví dụ 2 y + 2xy
Ví dụ 8: Giải PT y’ = 2 x
GiÁi: PT y’ = ( y )2 + 2 y . Đặt u = y y = xu và y’ = xu’ + u và PT là xu’+ u = x x x
u2 + 2u x du = u2 + u du = dx du = dx . dx u2 + u x u(u + ) 1 x 120
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Tích phân 2 vế được du = dx + ln|C| ( 1 - 1 )du = dx + ln|C| u(u + ) 1 x u u +1 x
ln|u| - ln|u + 1| = ln|x| + ln|C| ln| u | = ln|Cx| u = Cx. u +1 u +1
Vậy NTQ của PT đã cho là y = Cx x + y
Ví dụ 9: Tìm đưßng cong (C) đi qua A(0, 1) sao cho tam giác y
tạo bái trục Oy, tiếp tuyến với đưßng cong tại M (C) và OM (C): y = ö(x) là tam giác cân đỉ B nh O M
GiÁi: Giả sử (C): y = ö(x) và M(x, y) (C), tiếp tuyến tại M x
với (C) cắt Oy tại B. Theo giả thiết OMB cân tại O. O
Phương trình tiếp tuyến tại M là Y = ö’(x)(X - x) + y Hay Y = y’(X - x) + y nên B(0, - xy’ + y). 2
Từ OB = OM suy ra - xy’ + y = 2 2 y y
x + y hay y’ = - 1+ . x 2 x
Đặt y = xu ta có y’ = u + xu’ u + xu’ = u - 2 1+ u x du = - 2 du dx du dx 1+ u = - = ln|C| - dx 2 1+ u x 2 1+ u x ln|u + 2 C
1+ u | = ln|C| - ln|x| u + 2 1+ u = y + 2 2 x + y = C x 2 2 - 2 y = C
x . Do (C) đi qua A(0, 1) nên C = 2. Vậy (C): y = 1 - x C 2 4
Ví dụ 10: Tìm dạng của gương hội tụ, biết các tia phản y T’
chiếu của các tia tới song song nhau hội tụ tại một điểm. S M
GiÁi: Giả sử các tia tới song song với Ox và các tia phản
chiếu hội tụ tại O. Do tính chất đối xứng nên gương phải do T P O x N
một đưßng cong nào đó quay quanh Ox. Ta đi xác định dạng đưßng cong này. 121
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Gọi M(x, y) là một điểm thuộc đưßng cong ấy, MT là tiếp tuyến, MN là pháp
tuyến, SM là tia tới, MP ⊥ Ox. Vì góc tới bằng góc phản xạ nên SMN = OMN
SMT' = OMT , SMT' = OTM (hai góc đồng vị) OMT cân (đỉnh O).
Theo ý nghĩa hình học của đạo hàm ta có y’ = tanOTM . Nhưng tan PM PM PM y OTM = = = = . TP TO-PO MO - PO
x2 + y2 + x Vậy y’ = y .
x2 + y2 + x
x2 + y2 + x 2 ö x ö
Bây giß coi x là hàm của y thì x’ = hay dx = x 1+ + . y dy ÷÷ ÷÷ ø y ø y
Đặt u = x x = yu x’ = u + yu’ hay u + yu’ = 2 du 1+ u + u y = y dy 2 du dy 1+ u = ln|u + 2
1+ u | = ln|C| + ln|y| u + 2 1+ u = Cy. 2 1+ u y
Thay u = x và tính toán ta được y2 = 2C*(x + 1 C*) trong đó C* = C-1. y 2
ax + by + c a b
* Chú ý: PT dạng y’ = ö( ), với b ù 0 và D = ù 0 đưa được về PT
a x + b y + c a b 1 1 1 1 1 đẳng cấp cấp 1. ü ax + by + c = 0
üx = x + h
Thật vậy nếu (h, k) là nghiệm của hệ ý ta đặt ý 1 . Thì
þa x + b y + c = 0 y = y + k 1 1 1 þ 1 ax + by PT đã cho là y 1 1 1' = ö(
) - Đây là PT đẳng cấp cấp 1. a x + b y 1 1 1 1 x + y -1
Ví dụ 4: Giải PT y’ = x - y +1 122
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân üx + y -1 = 0 üx = x
Dễ thấy (0, 1) là nghiệm hệ PT ý nên đặt ý 1 thì PT đã cho là þx - y +1 = 0 þy = y +1 1 y x + y 1 1 1’ = . x - y 1 1 Đặ y + t u = x x u 1 (với x 1 1
1 ù 0) y1 = x1u thì y1’ = x1u’ + u. PT là: x1u’ + u = x x - x u 1 1 1 2 + dx x 1+ u du 1+ u du 1 u 1- u 1 1u’ + u = x1 = - u x1 = du = 1- u dx 1- u dx 1- u 2 1+ u x 1 1 1 1-u dx dx du = du udu 1 1 + ln|C| -
= 1 + ln|C| arctanu - ln(u2 + 1) = 2 1+ u x 2 1+ 2 1+ x 2 1 u u 1 ln|x 2
1| + ln|C| arctanu - ln u + 1 = ln|Cx1| y y 2 y y Thay u = y 1 được arctan 1 - ln +1 [1 + ( 1 )2] = ln|Cx 1 1| arctan - x x 2 x x x 1 1 1 1 2 2 x + y y üx = x ln 1 1 = ln|Cx 1 2 1 1| arctan = ln|C| 2
x + y . Cuối cùng thay ý được | x | x 1 1 y = y -1 1 1 þ 1
NTQ của PT đã cho là: arctan y -1 = ln| C | 2 2 x + (y - ) 1 x x
c) Phương trình tuyến tính cấp 1
* D¿ng: y’ + p(x)y = q(x) (1). Trong đó p(x) và q(x) liên tục trên tập X R
Nếu q(x) ú 0 thì (1) được gọi là PT thuần nhất (PTTN): y’ + p(x)y = 0 (2)
Nếu q(x) ù 0 thì (1) gọi là PT không thuần nhất.
* Cách giÁi: Để giải PT (1) ta tuân theo 2 bước sau đây
- Bước 1: Tìm NTQ của PTTN (2) tương ứng y’ + p(x)y = 0
Rõ ràng y ú 0 là một nghiệm (kỳ dị) của PT (2)
Nếu y ù 0 thì PT (2) dy = - p(x)y dy = - p(x)dx. Tích phân 2 vế được y y
dy = - p(x)dx + ln|C| ln|y| = ln|C| - p(x)dx y = Ce-p(x)dx. y
Hiển nhiên có thể coi y ú 0 là một trưßng hợp đặc biệt khi C = 0. 123
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
- Bước 2: Coi y = Ce-p(x)dx cũng là nghiệm của (1) nhưng C = C(x) và tìm C(x)
(phương pháp biến thiên hằng số Lagrange).
Do y = C(x)e-p(x)dx y’ = C'(x)e-p(x)dx - C(x)p(x)e-p(x)dx.
Thay y, y’ vào (1) được C’(x)e-p(x)dx = q(x) hay C’(x) = q(x)ep(x)dx C(x) =
q(x)ep(x)dxdx + C*. Vậy NTQ của (1) là y = (q(x)ep(x)dxdx + C*)e-p(x)dx
* Các ví dụ
Ví dụ 1: Tìm NR của PT y’ - 2 y = x3 với điều kiện y|x = 2 = 4 x
Bước 1: PTTN tương ứng: y’ - 2 y = 0 x
y = 0: là nghiệm kỳ dị.
y ù 0: PT là dy = 2 y dy = 2 dx dy = 2 dx + ln|C| ln|y| = 2ln|x| + dx x y x y x
ln|C |. Vậy NTQ của PTTN là y = Cx2.
Bước 2: Coi y = C(x)x2 là NTQ của PT đã cho suy ra y’ = C’(x)x2 + 2xC(x). 2
Thay y và y’ vào PT đã cho ta được: C’(x)x2 = x3 hay C'(x) = x. Từ đó C(x) = x + C*. 2 2 4
Vậy NTQ của PT đã cho là y = ( x + C*)x2 hay y = x + C*x2 2 2 4 Từ điều kiện y| x
x=2 = 4 4 = 8 + 4C* C* = - 1. Vậy NR là y = - x2 2
Ví dụ 2: Một mạch điện có thế điện động E, điện trá R và hệ số tự cảm L (R, L không
đổi). Tìm cưßng độ dòng điện i sau khi đóng mạch t giây trong 2 trưßng hợp: E = E0
không đổi và E = E0cost, nếu biết i(0) = 0
Trong điện học ta đã biết thế điện động được tính như sau: E = Ri + L di . dt 124
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Từ đó PTVP của cưßng độ dòng điện là di + R i = E : Đây là PT tuyến tính dt L L R R
cấp 1 giải ra ta có NTQ là i = Ce - t dC E L và suy ra = e t L . dt L
Để tìm nghiệm của PT không thuần nhất, ta coi C = C(t) R R
Trường hợp 1: E = E E - E 0 0 0: Thì C = e t L + C* i = Ce t L + . R R R
Từ i(0) = 0 C* = - E E - 0 . Vậy i = 0 (1 - e t L ) R R Trường hợp 2: t + ñ E sin cos t R 0 E = E0cost: Thì C = ( eñt + C*) với ñ = L 2 2 + ñ L t +ñ ñ i = Ce-ñt + E sin cos t E 0 , do i(0) = 0 C* = - 0 . . L 2 2 +ñ L 2 2 +ñ
Vậy i = E sint +ñ cost ñ 0 ( - e-ñt). L 2 2 +ñ 2 2 +ñ E Hay i = 0
(sint + ñcost - ñe-ñt). Nếu t → + õ thì e-ñt → 0. L( 2 2 + ñ )
Nên có thể nói khi t đủ lớn thì i û E 0 (sint + ñcost) L( 2 2 + ñ )
d) Phương trình Bernoulli (hay PT đưa về tuyến tính)
* D¿ng: y’ + p(x)y = q(x)yñ (1) trong đó p(x), q(x) liên tục trên tập X R, ñ R
* Cách giÁi: Nếu ñ = 0 hoặc ñ = 1 thì (1) là PT tuyến tính cấp 1, nên ta giả thiết ñ ù 0, 1.
y=0: là nghiệm kỳ dị của (1) nếu ñ > 0 và không là nghiệm của (1) nếu ñ<0
y ù 0: Nhân 2 vế với y-ñ thì PT (1) y-ñy’ + p(x)y1- ñ = q(x).
Đặt z = y1-ñ z’ = (1 - ñ)y-ñy’ và PT là 1 z’ + p(x)z = q(x) hay tương đương 1-ñ
z’ + (1 - ñ)p(x)z = (1 - ñ)q(x) đây là PT tuyến tính cấp 1.
Giải ra được z = (x, C). Vậy NTQ của PT đã cho là y1-ñ = (x, C). * Các ví dụ 125
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Ví dụ 1: Giải PT y’ + 2y = exy2 (1). y = 0 là nghiệm
y ù 0 thì PT y-2y’ + 2y-1 = ex. Đặt z = y-1 z’ = - y-2y’ và PT là - z’ + 2z = ex
hay z’ - 2z = - ex (2): Đây là PT tuyến tính cấp 1. Giải (2) như sau:
Bước 1: PTTN: z’ - 2z = 0 dz = 2z dz = 2dx. Tích phân 2 vế được dx z
dz = 2dx + ln|C| ln|z| = ln|C| + 2x ln|z| = ln|C| + lne2x ln|z| = ln|C|e2x z
Vậy NTQ của PTTN là z = Ce2x.
Bước 2: Coi z = C(x)e2x là NTQ của PT (2) z’ = C’(x)e2x + 2C(x)e2x. Thay z
và z' vào PT (2) được: C’(x)e2x = - ex C’’(x) = - e- x C(x) = e- x + C*.
Vậy NTQ của PT (2) là z = (e- x + C*)e2x hay z = ex + C*e2x .
Thay z = y-1 được y-1 = ex + Ce2x. Vậy NTQ của PT (1) là y(ex + C*e2x) = 1.
Ví dụ 2: Tìm đưßng cong (C) biết tại mỗi điểm trên nó, y
pháp ảnh bằng trung bình cộng của bình phương các tọa (C): y = ö(x) độ của điểm đó. M(x, y)
Theo định nghĩa pháp ảnh tại M(x, y) (C) là PN . ñ
Do MNI vuông tại M và MP là đưßng cao suy ra MIN = I O P N x PN
PMN y’ = tanñ = PM
PN = yy’. Theo giả thiết PN = 1 (x2 + y2). Nên yy’ = 1 (x2 + y2) hay y’ - 1 y 2 2 2
= 1 x2y-1 : Đây là PT Bernoulli. 2
PT 2yy’ - y2 = x2. Đặt z = y2 z’ = 2yy’ và PT là z’ - z = x2: Đây là PT
tuyến tính cấp 1, giải ra ta được z = Cex - x2 - 2x - 7.
Vậy đưßng cong cần tìm có PT là y2 = Cex - x2 - 2x - 7 126
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
e) PTVP toàn phần
* D¿ng: M(x, y)dx + N(x, y)dy = 0 (1). Trong đó M(x, y), N(x, y) liên tục G R2 và tồn
tại hàm u(x, y) thỏa du = M(x, y)dx + N(x, y)dy trên G. M N
* Đßnh lý: PT (1) là PTVP toàn phần khi và chỉ khi = . y x
üu = M(x, y) ÿÿx * Cách giÁi: Do ý
. Nên u(x, y) = M(x, y)dx + T(y)
ÿu = N(x, y) ÿþy
Để xác định T(y) ta đạo hàm 2 vế theo y: T’(y) = N(x, y) - (M(x, y)dx)’y. Suy
ra tìm được T(y) và do đó tìm được u(x, y) = C.
Chú ý: Có thể tìm u(x, y) bằng cách khác như sau: Nếu A(x0, y0) thuộc tập xác đßnh của các hàm số M(x, x y
y), N(x, y) thì u(x, y) = M (x, y0)dx + N (x, y)dy + C. x0 y0
* Ví dụ 1: Giải PT (2x + 3y + 1)dx + (3x - 4y + 3)dy = 0. à
đây M(x, y) = 2x + 3y + 1, N(x, y) = 3x - 4y + 3 M = N = 3. y x
Nên đây là PTVP toàn phần, do đó tồn tại u(x, y) thỏa du = Mdx + Ndy u(x,
y) = (2x + 3y + 1)dx + T(y) u(x, y) = x2 + 3xy + x + T(y) T(y) = u(x, y) - x2 - 3xy - x. Đạ
o hàm 2 vế theo y được T’(y) = u - 3x = (3x - 4y + 3) - 3x = - 4y + 3. y
Từ đó T(y) = T’(y)dy + C = (- 4y + 3)dy + C = - 2y2 + 3y + C
Vậy NTQ của PT đã cho là u(x, y) = x2 - 2y2 + 3xy + x + 3y + C
* Thừa số tích phân: Một số PT (1) chưa là PTVP toàn phần, nhưng nếu tìm được hàm
F(x, y) nào đó thỏa F(x, y)M(x, y)dx + F(x, y)N(x, y)dy = 0 là PTVP toàn phần, thì
hàm F(x, y) được gọi là thừa số tích phân của PT (1).
Chẳng hạn, dễ thấy F = x3 là thừa số tích phân của PT 2siny2dx + xycosy2dy = 0
vì 2x3siny2dx + x4ycosy2dy = 0 là PTVP toàn phần 127
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
- Phư¢ng pháp tìm thừa số tích phân: Như ta biết điều kiện cần và đủ để PT (2) là
PTVP toàn phần là (FN ) = (FM ) F N + F N = F M + F M (3). Từ điều y x y y x x
kiện này, việc xác định F rất khó khăn. Vì vậy trong thực tế ngưßi ta thưßng tìm F dưới dạng hàm một biến.
Nếu F = F(x) thì (3) F N = dF M + F M dF = 1 ( M - N )dx y dx x F N y x
F(x) = eR(x)dx với R(x) = 1 ( M - N ). N y x Tương tự
nếu F = F(y) thì F(y) = eR(y)dy với R(y) = 1 ( N - M ). M x y
- Mệnh đề: Nếu PT (1) thỏa mãn điều kiện
i) 1 ( M - N ) chỉ phụ thuộc x. Thì PT có thừa số tích phân chỉ phụ thuộc x N y x
là F(x) = eR(x)dx với R(x) = 1 ( M - N )dx. N y x M
ii) Nếu 1 ( N -
) chỉ phụ thuộc y. Thì PT có thừa số tích phân chỉ phụ M x y
thuộc y là F(y) = eR(y)dy trong đó R(y) = 1 ( N - M )dy M x y
- Ví dụ 2: Giải bài toán Cauchy 2xydx + (4y + 3x2)dy = 0 với điều kiện y|0,2 = - 1,5
Dễ dàng thấy đây không là PT vi phân toàn phần nhưng thỏa điều kiện b. á 2 mệnh đề trên 1
( N - M ) = 1 (6x - 2x) = 2 . Nên F = e dy y = y2. Nên nhân 2 vế M x y 2xy y
PT với y2 được 2xy3dx + (4y3 + 3x2y2)dy = 0. Đây là PTVP toàn phần có NTQ là y4 +
x2y3 = C. Thay điều kiện đầu được y4 + x2y3 = 4,9275
5.2.4. Ph°¢ng pháp tham số hóa tổng quát để gi¿i PTVP cÁp 1 Khái niệm chung:
Xét PTVP cấp một F(x, y, y’) = 0, đặt p = y’ ta được F(x, y, p) = 0. Nếu coi F là
hàm của 3 biến x, y, p thì F(x, y, p) = 0 xác định một mặt cong nào đó có thể biểu diễu 128
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
dạng PT tham số tương ứng với PT ẩn trên x = (u, v), y = (u, v), p = ó(u, v). Chú ý rằng p = y’ hay dy = pdx. Từ đó du + dv = ó(u, v)( du +
dv): PTVP cấp 1 giữa u và v. u v u v ó -
Chẳng hạn coi v = v(u) thì dv = u u
. Từ đây có được v = v(u, C). du - ó v v
Vậy NTQ của PT đã cho là x = (u, v(u, C)), y = (u, v(u, C))
Sau đây ta xét 2 loại PT đặc biệt
a) Phương trình Lagrange
* D¿ng: A(p)y + B(p)x = C(p) với A(p), B(p), C(p) là các hàm khả vi của p = y’
* Cách giÁi: Nếu A(p) ù 0. Thì ta đưa PT về dạng y = (p)x + (p) = ö(x, p).
Đạo hàm 2 vế được p = (p) + [’(p)x + ’(p)] dp . dx
Bây giß coi x là hàm, p là biến độc lập thì PT trá thành PTVP tuyến tính cấp 1: dx +
'( p) x = '(p) . Giải ra được x = x(p, C). dp ( p) - p p - ( p)
Vậy NTQ của PT Lagrange là x = x(p, C), y = ö(x(p, C), p). Nếu từ đây khử
được p thì NTQ có dạng (x, y, C) = 0
* Ví dụ: Tìm NTQ của PT Lagrange y = 2xy’ + y’2
Ta viết lại PT là y = 2px + p2. Đạo hàm 2 vế theo x, coi y và p là hàm của x,
đồng thßi thay y’ bái p được p = 2p + 2(x + p) dp dx = - 2x - 2. Đây là PT tuyến dx dp p 3
tính cấp 1. NTQ của PT này là x = C - 2 p . Thay vào PT đầu ta được y = C 2 - p . 2 p 3 p 3
üx = C 2p - ÿÿ 2 p 3
Vậy NTQ dưới dạng tham số là ý ÿ 3 y = 2C p ÿ - þ p 3 129
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Chú ý: Để được PT tuyến tính trên phÁi giÁ thiết p ù 0, nếu p = 0 thì y’ = 0 hay y = C, thay vào PT ban
đầu ta thấy C = 0. Vậy y = 0 là nghiệm kỳ dß.
b) Phương trình Clairaut
* D¿ng: y = px + (p), giả thiết (p) là hàm khả vi của p = y’. Đây là trưßng hợp đặc biệt của PT Lagrange.
* Cách giÁi: Đạo hàm 2 vế (theo x): p = p + xp’ + ’(p)p’ [x + ’(p)]p’ = 0. Từ đó:
Hoặc p’ = 0 p = C. Thay vào PT đầu thì NTQ là y = Cx + (C).
Hoặc x + ’(p) = 0, từ đây ta có 2 cách để nhận cùng một nghiệm PT
(1) dạng tham số x = - ’(p), y = - p’(p) + (p)
(2) từ x + ’(p) = 0 suy ra p = (x) thay vào PT được y = x(x) + ((x)) là nghiệm.
* Ví dụ: Tìm đưßng cong biết tiếp tuyến của nó luôn lập với hai trục Ox, Oy một tam
giác có diện tích bằng 2.
Ta viết PT đưßng tiếp tuyến dạng đoạn chắn x + y = 1. a b
Khi ấy theo giả thiết ab = 4 hay b = 4 . Vậy PT tiếp tuyến là x + ay = 1. a a 4
Đạo hàm 2 vế theo x coi y là hàm 1 + ay' = 0 a2 = - 4 hay a = 2 1 - . a 4 y' y' x - y' Vậy PT là + y
= 1 hay y = xy’ + 2 - y' - Đây là PT Claius. 2 2 - y' NTQ là y = Cx + 2 1
- C . Đạo hàm NTQ theo C ta được 0 = x - C = - - C
1 . Từ đó y = - 1 + 2 xy = 1. Vậy đưßng cong là Hypebol xy = 1. 2 x x x 5.3. PTVP CÀP 2 5.3.1. Định nghĩa
* PTVP cấp 2 là PTVP có dạng y” = ö(x, y, y’) hay F(x, y, y’, y”) = 0.
* NTQ của PTVP cấp 2 là tất cả các hàm dạng y = (x, C1, C2) hay (x, y, C1, C2) = 0
(trong đó C1, C2 là các số thực tùy ý) thỏa mãn PT đã cho. 130
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
* NR được lấy từ NTQ bằng cách cho C1, C2 các giá trị cụ thể, các giá trị này thưßng y(x ) = được xác đị ü y
nh từ điều kiện đầu: ý 0 0
þy'(x ) = y 0 1
Ví dụ: PT y” - 3y’ + 2y = 0 có NTQ là y = C1ex + C2e2x.
Lấy C1 = C2 = 1 thì NR là y = ex + e2x và cũng tìm được NR trên bái điều kiện y( ) 0 = đầ ü 1 u ýþy'( )0 = 3
5.3.2. Các ph°¢ng trình dạng khuyết
a) Dạng khuyết y, y’: y” = ö(x)
* Cách giÁi: Tích phân 2 vế liên tiếp 2 lần
Tích phân lần thứ nhất được y’ = ö(x)dx + C1.
Tích phân tiếp lần thứ hai suy ra NTQ là: y = (ö(x)dx)dx + C1x + C2. * Các ví dụ
Ví dụ 1: Tìm NR của PT y” = 1 với điều kiện đầu y(0) = - 1, y’(0) = 1 2 cos x Ta có y’ = 1 dx + C 2
1 y’ = tanx + C1 y = tanxdx + C1x + C2. cos x
Hay NTQ của PT trên là y = - ln|cosx| + C1x + C2.
Từ điều kiện y’(0) = 1 suy ra C1 = 1 và y(0) = - 1 suy ra C2 = - 1.
Vậy NR cần tìm là y = - ln|cosx| + x - 1
Ví dụ 2: Một chiếc ôtô đang chạy với vận tốc 72 km/h thì thắng gấp với gia tốc không
đổi là a(t) = - 0,8m/s2. Hỏi ôtô chạy được bao nhiêu mét thì dừng hẳn?
Gọi quãng đưßng ôtô chạy được sau khi thắng t giây là S(t).
Theo vật lý S”(t) = a(t) hay S”(t) = - 0,8. Từ đó v(t) = S’(t) = S”(t)dt = - 0,8dt
= - 0,8t + C1 và S(t) = S’(t)dt = (- 0,8t + C1)dt = - 0,4t2 + C1t + C2.
Do v(0) = 72 nên C1 = 20 và S(0) = 0 nên C2 = 0. Vậy v(t) = - 0,8t + 20 và S(t) =
- 0,4t2 + 20t, khi dừng hẳn thì v(t) = 0 - 0,8t + 20 = 0 t = 25s.
Vậy quãng đưßng đi được sau khi thắng là S(25) = - 0,4.252 + 20.25 = 250 mét. 131
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Ví dụ 3: Một cái xà được giữ chặt một đầu mút (tại O) và xN
chịu tác dụng của một lực thẳng đứng P á đầu mút kia (là L) O x
xà dài a(m), trọng lượng của xà không đáng kể. Hãy xác định N
độ uốn tại điểm bất kỳ trên xà và tại L. L y
GiÁi: Ta chọn hệ tọa độ Oxy sao cho Ox nằm ngang theo trục
của xà lúc chưa bị biến dạng, còn Oy thẳng đứng từ trên
xuống (cùng phương của lực).
Xét thiết diện của xà tại điểm N(x).
Mômen uốn đối với thiết diện là M(x) = (a – x)P.
Mặt khác theo lý thuyết sức bền vật liệu thì M(x) = E.J , trong đó E là mômen R
đàn hồi phụ thuộc vào chất liệu làm xà, J là mômen quán tính của diện tích thiết diện
ngang của xà đối với đưßng nằm ngang đi qua trọng tâm của thiết diện và R là bán
kính cong của xà đã bị uốn. 2 3 / 2 +
Gọi y là độ uốn của xà thì R = 1 ( y' )
. Vì sự biến dạng nhỏ nên có thể bỏ " y qua y’2 1 , nên R =
. Vậy (a - x)P = E.J.y” hay y” = P (a - x). y" EJ
Do khi x = 0 thì độ uốn y = 0 và tiếp tuyến với trục nằm ngang trùng với Ox nên y( ) 0 = y’ = 0. Vậy điề ü 0 u kiện đầu là ý þy'( ) 0 = 0 3
Giải PT này được y = P (ax2 - x ) + C1x + C2. 2EJ 3 3 3
Thay điều kiện đầu ta được y = P (ax2 - x ). Tại L: y(a) = Pa 2EJ 3 3EJ
b) Dạng khuyết y: y” = ö(x, y’)
* Cách giÁi: Đặt p = p(x) = y’ p’ = y” và PT là p’ = ö(x, p) đây là PTVP cấp 1 giải ra
được p = p(x, C1) y’ = p(x, C1) từ đó y = p(x, C1)dx + C2. * Các ví dụ 132
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Ví dụ 1: Giải PT xy” = y’.ln y' x
GiÁi: PT y” = y' ln y' . Đặt p = p(x) = y’ p’ = y” và PT là p’ = p ln p . x x x x
Đây là PT tuyến tính cấp 1.
Đặt u = p p = xu p’ = xu’ + u thì PT là xu’ + u = ulnu hay x du = u(lnu - x dx 1) du
= dx . Tích phân 2 vế được du
= dx + ln|C1| ln|lnu - 1| = u(lnu - ) 1 x u(lnu - ) 1 x ln|C C x+ C x+ C x+
1| + ln|x| lnu = C1x + 1 u = 1 1 e p = y’ = x 1 1 e y = x 1 1 e dx + C2. du = u = ü dx Đặ ü x t ÿ ý ý 1 . þdv = C x+ e 1 C x+1 1 dx ÿv = e 1 dx þ C 1 Ta có: y = 1 x C x 1+ 1 C x+ 1 C x+ 1 C x+ 1 e - 1 1 e dx = x 1 1 e - 1 1 e + C2. C C C 2 C 1 1 1 1
Vậy NTQ cần tìm là: y = 1 x C x 1+ 1 C x+ 1 e - 1 1 e + C2 C 2 C 1 1
Ví dụ 2: Tìm dạng của một sợi dây đồng chất không bị dãn, y B A
dễ uốn bị gắn chặt á 2 đầu và chịu tác dụng của trọng lượng T của nó. M ñ
GiÁi: Chọn Oy là trục thẳng đứng đi qua điểm thấp nhất N N H P
của sợi dây, Ox là trục nằm ngang, gốc tọa độ O á phía dưới O x x
N cách N một khoảng nào đó.
Gọi M là điểm bất kỳ trên dây. Đoạn dây NM chịu tác dụng bái 3 lực: lực căng
H tại N có hướng song song với Ox, lực căng T tại M hướng theo tiếp tuyến với dây tại
điểm đó và trọng lực P của đoạn dây NM tại trọng tâm của đoạn này.
Gọi s là độ dài đoạn dây NM và d là tỷ trọng của dây, ta có P = sd. Do điều kiện
cân bằng của đoạn NM, nên Tsinñ = sdcosñ = H, suy ra tanñ = ds (*). H 133
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Gọi y = (x) là PT phải tìm của dây ANB thì đẳng thức (*) có dạng y’ = ds . H
Lấy đạo hàm 2 vế theo x được y” = d 2 d 1+ y' , đặt k = thì ta có y” = k 2 1+ y' . H H
Đây là PTVP cho dạng của sợi dây. Đặt y’ = p thì PT là p’ = k 2 dp 1+ p hay = 2 1+ p
kdx, tích phân 2 vế được ln(p + 2 1+ p ) = kx + C1
Vì N là điểm thấp nhất nên tiếp tuyến tại đây song song với Ox, nghĩa là y’(0) = 0 hay p(0) = 0, nên C1 = 0. Vậy ln(p + 2 1+ p ) = kx p + 2 1+ p = ekx 2 1+ p = ekx - p.
Bình phương 2 vế và rút gọn được p = y’ = 1 (ekx - e-kx). 2
Tích phân ta được: y = 1 (ekx + e-kx) + C2. 2k
Nếu chọn hệ tọa độ sao cho ON = 1 có y(0) = 1 nên C2 = 0 thì PT sợi dây là y k k x x -
= 1 (ekx + e-kx). Đặt a = 1 thì PT sợi dây là y = a (e a + e a ) 2k k 2
c) Dạng khuyết x: y” = ö(y, y’)
* Cách giÁi: Đặt p = p(y) = y’ y” = p’(y).y’ = p’.p PT là p’.p = ö(y, p): Đây là
PTVP cấp 1 giải ra ta được p = p(y, C dy 1) hay y’ = p(y, C1) = p(y, C1). dx Từ đó: dy = dx dy = dx + C dy 2 = x + C2 p(x,C ) p(x,C ) p(x,C ) 1 1 1 * Các ví dụ
Ví dụ 1: Giải PT (y’)2 + yy” = 0
GiÁi: Đặt p = p(y) = y’ y” = p’y’ = p’p và PT là p2 + yp’p = 0.
- p = 0 hay y = C là một họ nghiệm (kỳ dị) của PT đã cho.
- p ù 0 thì PT là p + yp’ = 0 hay y dp = - p dp = - dy . p p y 134
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân C C
Tích phân 2 vế được dp = - dy + ln|C 1 1 dy 1| p = . Từ đó y’ = = p y y y dx C 2 y
1 ydy = C1dx ydy = C1dx + C2 = C1x + C2. y 2 Vậy NTQ là y2 = C * * * *
1 x + C2 (trong đó C1 = 2C1, C2 = 2C2)
Ví dụ 2 (Bài toán về vận tốc vũ trụ cấp 2): Xác định vận tốc nhỏ nhất mà ta phải ném
một vật thẳng đứng sao cho vật không trá về trái đất, giả thiết sức cản của không khí không đáng kể.
GiÁi: Gọi khối lượng trái đất là M, khối lượng của vật là m và khoảng cách giữa tâm
trái đất và trọng tâm của vật là ném lên là r. Theo định luật hấp dẫn Newton thì lực hút
tác dụng lên vật là ö = Mm , trong đó là hằng số hấp dẫn. 2 r 2 2
PT chuyển động của vật là m d r = - Mm hay d r = - M (lưu ý gia tốc 2 dt 2 r 2 dt 2 r
được nói trong bài có giá trị âm). Ta sẽ giải PTVP trên với điều kiện đầu r(0) = 0,
dr (0) = v0, R là bán kính trái đất và v0 là vận tốc ném vật. dt 2
Đặt v(t) = dr , ta có d r = dv = v dv (vì dv = dv . dr = v dv ). dt 2 dt dt dr dt dr dt dr 2
Khi đó v dv = - M hay vdv = - M dr. Tích phân 2 vế: v = M + C1. dr 2 r 2 r 2 r 2 v
Từ điều kiện đầu v(0) = v 0 M 0 hay v(R) = v0 = + C1 2 R 2 v 2 2 Hay C M v v 0 M M M 0 1 = - + . Từ đó = + ( - ). Từ đây ta thấy có R 2 2 r 2 R R 2
thể nhỏ tùy ý khi r → + õ, nên điều kiện v > 0 được thực hiện với mọi r chỉ trong 2 2 trưßng hợp v M M M 2 0 - 0 hay v 2 0 2 v0 . 2 R R R 135
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân 3 m
Vậy vận tốc nhỏ nhất khi ném vật lên là v M 2 0 = với = 6,67.10-11 2 và R kg.s
R = 63.105m. Trên mặt đất thì r = R và gia tốc của trọng trưßng là g = 9,81 m/s2 nên từ
mg = mM suy ra M = gR2. 2 R Do đó v M 2 0 = = 5 8 , 9 . 2 1 6 . 3 1
. 0 û 11,2.103 m/s hay v0 û 11,2 km/s. R
Đây là vận tốc vũ trụ cấp 2.
5.3.3. PTVP tuyến tính cÁp 2
a) Sơ lược về số phức
* Đßnh nghĩa: Số phức là "số mới" có dạng z = a + ib trong đó a, b R và i được là
đơn vị ảo có tính chất i2 = - 1. Tập tất cả các số phức ký hiệu là C.
Chú ý: Quy đßnh 0.i = 0.
Rõ ràng mỗi một số thực a đều là một số phức vì a = a + 0i. Nên ta có R C.
Số thực 0 cũng được coi là số phức bằng không (0 = 0 + 0i).
* Phép toán số hác: Cho z1 = a1 + ib1, z2 = a2 + ib2 C. Khi ấy
z1 = z2 a1 = a2 và b1 = b2
z1 + z2 = (a1 + a2) + i(b1 + b2)
z1.z2 = (a1a2 - b1b2) + i(a1b2 + a2b1)
* Phép liên hợp: Nếu z = a + ib thì z = a - ib được gọi là liên hợp của z.
* Chú ý: Mọi số thực đều có căn bậc hai nói riêng và căn bậc chẵn nói chung. Chẳng
hạn: -1 = i, -16 = 4i, - 225 = 15i, …
* Nghiệm của PT bậc 2: Cho PT k2 + pk + q = 0 có = p2 - 4q. Khi ấy: p
Nếu > 0 thì PT có 2 nghiệm thực phân biệt k - 1,2 = . 2
Nếu = 0 thì PT có một nghiệm thực kép k p 0 = - 2 p i
Nếu < 0 thì PT có 2 nghiệm phức liên hợp k - - 1,2 = = ñ iò. 2
* Các ví dụ: PT k2 - 3k + 2 = 0 có a + b + c = 0 nên nghiệm là k1 = 1, k2 = 2 136
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
PT k2 + 2k + 10 = 0 có ' = - 9 < 0 nên nghiệm là k1,2 = - 1 3i.
PT k2 + 4 = 0 có ' = - 4 < 0 nên nghiệm là k1,2 = 0 2i
b) Khái niệm chung về PTVP tuyến tính cấp 2
* D¿ng: y” + p(x)y’ + q(x)y = ö(x) (1).
Nếu ö(x) ú 0 thì (1) là y” + p(x)y’ + q(x)y = 0 (2) và được gọi là PTTN
Nếu ö(x) ù 0 thì (1) được gọi là PT không thuần nhất.
* Tính chất về nghiệm
Tính chất 1: Nếu y1 và y2 là các nghiệm của PTTN (2). Thì y = C1y1 + C2y2 với C1,
C2 R đều là nghiệm của PTTN (2)
Tính chất 2: Hai hàm {y1, y2} được gọi là độc lập tuyến tính nếu từ C1y1 + C2y2 = 0 suy ra C1 = C2 = 0.
Đặc biệt: Nếu y1, y2 khả vi. Thì {y1, y2} độc lập tuyến tính khi và chỉ khi định
thức Wronski của nó W = y ' y ' 1 2 ù 0. y y 1 2
Tính chất 3: Nếu y1, y2 là các nghiệm độc lập tuyến tính của PTTN (2).
Thì y* = C1y1 + C2y2 là NTQ của PTTN (2).
Tính chất 4: Nếu y* là NTQ của PTTN (2) và Y là một NR của PT (1). Thì y = Y + y* là NTQ của PT (1)
Tính chất 5: Nếu Y1 là nghiệm PT y” + p1(x)y’ + q1(x)y = ö1(x),
Y2 là nghiệm PT y” + p1(x)y’ + q1(x)y = ö2(x).
Thì Y = Y1 + Y2 là nghiệm PT y” + p1(x)y’ + q1(x)y = ö1(x) + ö2(x).
c) PTVP tuyến tính cấp 2 hệ là hằng số
* D¿ng: y” + py’ + qy = ö(x) (1) trong đó p, q R.
Nếu ö(x) ù 0 thì (1) được gọi là PT không thuần nhất
Nếu ö(x) = 0 thì (1) là: y” + py’ + qy = 0 (2) được gọi là PTTN.
* Cách giÁi: Chúng ta tuân theo 2 bước sau đây 137
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Bước 1 (Tìm NTQ y* của PTTN tư¢ng ứng): Ngưßi ta chứng minh được rằng NTQ y*
của PT (2) có 3 dạng phụ thuộc vào 3 khả năng về nghiệm của PT đặc trưng k2 + pk + q = 0
Nếu PTĐT (3) có 2 nghiệm thực phân biệt k1, k2 thì y* = C1ek1x + C2e k2x.
Nếu PTĐT (3) có 1 nghiệm thực (kép) k0 thì y* = (C1x + C2)ek0x.
Nếu PTĐT (3) có 2 nghiệm phức ñ iò thì y* = eñx(C1cosòx + C2sinòx). Ví dụ: * PT y” + 3y’ + 2y = 0:
PTĐT k2 + 3k + 2 = 0 có nghiệm k1 = - 1, k2 = - 2 nên NTQ là y* = C1e-x + C2e-2x. * PT y” - 6y’ + 9 = 0:
PTĐT k2 - 6k + 9 = 0 có nghiệm kép k0 = 3 nên NTQ là y* = (C1x + C2)e3x.
* PT y” - 2y’ + 5y = 0: PTĐT k2 - 2k + 5 = 0 có hai nghiệm phức liên hợp k1,2 = 1 2i
nên NTQ là y* = ex(C1cos2x + C2sin2x)
Bước 2 (Tìm một NR của PT không TN): Về mặt tổng quát chúng ta sử dụng phương
pháp biến thiên hằng số Lagrange như sau:
Nếu y* = y(x, C1, C2) là NTQ của (2), thì ta cũng coi y* = y(x, C1(x), C2(x)) là
üC ' y + C ' y = 0 NTQ của (1) và tìm C 1 1 2 2 1(x) và C2(x) nhß hệ PT ý . Trong đó y1, y2 là þC ' y +
' C ' y '= f (x) 1 1 2 2
các nghiệm độc lập tuyến tính của (2). Sau khi tính được C1’(x), C2’(x) suy ra tính
được C1(x) và C2(x) rồi kết luận NTQ y* của (1).
Ví dụ 1: Giải PTVP y” - 3y’ + 2y = sinx. Dễ thấy y* = C1ex + C2e2x .
GiÁi: Do y1 = ex, y2 = e2x là 2 nghiệm độc lập tuyến tính của PTTN tương ứng vì vậy
ÿüC 'ex + C 'e2x = 0 C 1 2
1, C2 là nghiệm của hệ PT : ý .
ÿþC 'ex + C 2
'e2x = sin x 1 2
Suy ra C1’ = e-xsinx, C2’ = e-2xsinx Hay C 1 * 1 * 1 =
e-x(cosx + sinx) + C1 và C2 = e-2x(2sinx + cosx) + C2 2 2
Vậy NTQ của PT đã cho là: y = - 1 sinx + C * * 1 ex + C2 e2x 2 138
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Tuy nhiên, theo tính chất 4 á trên thì NTQ(1) = NTQ(2) + NR(1). Nên để tìm
NTQ của PT (1) ta đi theo 2 bước sau
Bước 1: Tìm NTQ y* của (2)
Bước 2: Tìm một NR Y của (1)
Kết luận: NTQ của (1) là y = y* + Y.
Sau đây, ta xét hai trưßng hợp đặc biệt của ö(x): vế phải của (1) cho phép ta tìm
một NR Y của (1) dễ dàng
Trường hợp 1: Nếu ö(x) = exP(x), R, P(x) là đa thức bậc n. Thì một NR của (1) là:
Y = exQ(x) nếu không là nghiệm của PT đặc trưng.
Y = exxQ(x) nếu là một nghiệm đơn của PT đặc trưng.
Y = exx2Q(x) nếu là nghiệm kép của PT đặc trưng.
Trong đó Q(x) là đa thức bậc n cần tìm bằng phương pháp hệ số bất định
Ví dụ 2: Giải PTVP y”+ 3y’ + 2y = ex(x - 1). à đây n = 1, = 1.
GiÁi: PTTN y” + 3y’ + 2y = 0: PTĐT k2 + 3k + 2 = 0 có 2 nghiệm phân biệt k1 = - 1,
k2 = - 2 nên y* = C1e-x + C2e-2x.
Do = 1 không là nghiệm của PTĐT nên Y = ex(Ax + B) Y’ = ex[Ax + (A +
B)], Y” = ex[Ax + (2A + B)].
Thay Y, Y’, Y” vào PT đã cho và rút gọn ta được 6Ax + (5A + 6B) = x – 1 6A = ü 1 1 11 1 11 ý A = , B = - . Từ đó Y = ex( x - ). þ5A + 6B = −1 6 6 6 36 Vậy NTQ của PT là: y = C 1 1e-x + C2e-2x + ex(6x - 11) 36
Ví dụ 3: Giải PTVP y” - 4y’ + 3y = 2ex. à đây n = 0, = 1.
GiÁi: PTTN y” - 4y’ + 3y = 0: PTĐT k2 - 4k + 3 = 0 có 2 nghiệm k1 = 1, k2 = 3 nên y* = C1ex + C2e3x.
Do = 1 là một nghiệm của PT đặc trưng nên Y = exxA Y’ = A(xex + ex), Y”
= A(xex + 2ex). Thay Y, Y’, Y” vào PT đã cho và rút gọn suy ra: - 2A = 2 hay A = - 1.
Từ đó: Y = - xex. Vậy NTQ của PT trên là: y = C1ex + C2e3x - xex
Ví dụ 4: Giải PTVP y” + 2y’ + y = e-x(2x + 1). à đây n = 1, = - 1. 139
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
GiÁi: PTTN y” + 2y’ + y = 0: PTĐT k2 + 2k + 1 = 0 có nghiệm kép k0 = - 1 nên y* = (C1x + C2)e-x.
Do = - 1 là nghiệm kép của PT đặc trưng nên Y = e- xx2(Ax + B) Y’ = [-
Ax3 + (3A - B)x2 + 2Bx]e-x, Y” = [Ax3 - (6A - B)x2 + (6A - 4B)x + 2B]e-x.
Thay Y, Y’, Y” vào PT trên và rút gọn ta được 6Ax + 2B = 2x + 1 ü6A = 2 1 1 1 1 ý
A = , B = . Nên Y = ( x3 + x2)e-x. þ2B = 1 3 2 3 2
Vậy NTQ của PT trên là: y = (C 1 1x + C2)e-x + (2x3 + 3x2)e-x 6
Trường hợp 2: Nếu ö(x) = eñx[P(x)cosòx + Q(x)sinòx] trong đó ñ, ò R, P(x) và Q(x)
là 2 đa thức, đặt n = max{bậc P(x), bậc Q(x)}. Thì một NR của (1) là:
Y = eñx[R(x)cosòx + S(x)sinòx] nếu ñ iò không là nghiệm PTĐT.
Y = eñxx[R(x)cosòx + S(x)sinòx] nếu ñ iò là nghiệm PTĐT.
Với R(x) và S(x) là hai đa thức bậc n cần tìm bằng phương pháp hệ số bất định.
Ví dụ 5: Giải PTVP y” - y = exsinx. à đây: n = 0, ñ iò = 1 i.
GiÁi: PTTN y” - y = 0: PTĐT k2 - 1 = 0 có nghiệm k = 1 nên NTQ y* = C1ex + C2e-x.
Do ñ iò = 1 i không là nghiệm PTĐT nên Y = ex(Acosx + Bsinx) Y’ =
ex[(A + B)cosx + (- A + B)sinx], Y” = ex(2Bcosx - 2Asinx).
Thay Y’, Y” vào PT: (2B - A)cosx + (- A + B)sinx = sinx. Suy ra ü- A+ 2B = 0 ý þ - 2A - B =1
hay A = - 2 , B = - 1 . Nên Y = - 1 ex(2cosx + sinx). 5 5 5 Vậy NTQ của PT là y = (C 1 1x + C2)ex - ex(2cosx + sinx) 5
Ví dụ 6: Giải PTVP y” + y = cosx. à đây n = 0, ñ iò = 0 i.
PTTN y” + y = 0: PT đặc trưng k2 + 1 = 0 có 2 nghiệm phức k = 0 i nên NTQ y* = C1cosx + C2sinx.
Do ñ iò = 0 i là nghiệm của PTĐT nên Y = x(Acosx + Bsinx) = Axcosx +
Bxsinx Y’ = (Bx + A)cosx + (- Ax + B)sinx, Y” = (- Ax + 2B)cosx + (- Bx - 2A) 140
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân 2B = thay Y, Y” vào PT ü 1
có: 2Bcosx - 2Asinx = cosx 1 ý A = 0, B = nên Y = þ2A = 0 2 x sinx. 2
Vậy NTQ của PT đã cho là y = C 1 1cosx + C2sinx + xsinx 2
Ví dụ 7: Giải PTVP của dao động đàn hồi không bị cản và có lực kích động tuần hoàn 2
là d x + a2x = psint (*). Với a, p, là các hằng số. à đây x là vị trí chất điểm dao 2 dt
động, a là tần số riêng của dao động, là tần số kích động, p là biên độ của lực kích động.
GiÁi: PT đặc trưng k2 + a2 có nghiệm phức k = ai.
Do đó NTQ của PTTN là x(t) = C1cosat + C2sinat = Csin(at + ñ). Khi ấy:
Nếu ù a: Ta tìm NR dưới dạng X(t) = Acost + Bsint, thay X, X’, X” vào
PT được A = 0, B = p . 2 2 a -
Vậy NTQ của PT (*) là x(t) = Csin(at + ñ) + p sint. 2 2 a -
Hay tổng dao động riêng của hệ với tần số a và dao động cưỡng bức với tần số .
Dao động cưỡng bức sẽ trùng pha với lực kích động nếu a > và lệch một góc
nếu a < . Biên độ của dao động cưỡng bức tỷ lệ với biên độ p của lực và với 1
. Do đó, biên độ sẽ rất lớn khi gần a. | 2 a - 2 |
Nếu = a: Ta tìm NR dưới dạng X(t) = t(Acost + Bsint). Thay X, X’, X”
vào PT ta được A = - p , B = 0. Vậy NTQ của PT (*) là x(t) = Csin(at + ñ) - 2a
p tcost. Số hạng thứ 2 cho thấy biên độ tăng đến + õ khi t → + õ. 2a 141
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
Vậy khi tần số riêng a của hệ trùng với tần số kích động thì có hiện tượng này
được gọi là sự cộng hưáng.
Chú ý: PT Euler sau x2y” + axy’ + by = 0 trong đó a, b R đưa được về PTTT cấp 2 hệ là hằng số.
Thật vậy, đặt t = ln|x| ta có y’ = dy = dy . dt = dy . 1 ; dx dt dx dt x 2
y” = d ö dy ö dy d ö dy 1 ö 1 dy
1 d ö dy ö dt 1 ö d y dy ö ÷ ÷ = ÷ . ÷ = - . + . ÷ ÷ . = - .
dx ø dx ø dx dx ø dt x ø 2 x dt
x dt ø dt ø dx 2 x ÷÷ 2 ÷÷ ø dt dt ø 2
Thay vào PT được: d y + (a - 1) dy + by = 0 hay y” + (a - 1)y’ + by = 0. 2 dt dt
Ví dụ 8: Giải PT x2y” + 2xy’ - 6y = 0 2
Đặt x = et ta được d y + dy - 6y = 0 hay y” + y’ - 6 = 0: Đây là PTTT thuần 2 dt dt
nhất cấp 2 hệ là hằng số có PT đặc trưng k2 + k - 6 = 0 k1 = 2, k2 = - 3. Vậy NTQ là y = C C2
1e2t + C2e-3t. Thay x = et được: y = C1x2 + . 3 x 5.4. HÞ PTVP 5.4.1. Khái nißm chung
üF (x, y ,..., y , y ',..., y ') = 0 k 1 n 1 n
* Hệ PTVP là một hệ PT có dạng ý . Trong đó yk = ök(x), k = þk = , 1 , 2 ...,n
1, 2, ... , n là các hàm theo biến x cần tìm.
Đặt y = (y1, y2, ..., yn), y’ = (y1’, y2’, ..., yn’) và F = (F1, F2, ..., Fn). Thì hệ PT có
thể viết được dưới dạng F(x, y, y’) = 0 với 0 = (0, 0, ..., 0).
* NTQ của hệ PTVP là tất cả các hàm y = (1(x, C1, C2, ..., Cn), 2(x, C1, C2, ..., Cn), ...,
n(x, C1, C2, ..., Cn)) thỏa hệ PT đã cho với C1, C2, ..., Cn R.
* NR được lấy từ NTQ ta khi cho C1, C2, ..., Cn các giá trị cụ thể. Các giá trị này thưßng
được cho bái điều kiện đầu. 142
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
5.4.2. Một vài ph°¢ng pháp gi¿i
Sau đây, chúng ta xét hai phương pháp thưßng gặp để giải một hệ PTVP và để đơn
giản ta hạn chế chỉ xét hệ gồm hai PT và hai hàm cần tìm.
a) Phương pháp khử ü y'= ) 1 (
(x, y, z)
* Phư¢ng pháp: Giả sử cần giải hệ PTVP ý þz'= (2)
(x, y, z)
Từ (1) chẳng hạn suy ra: y” = ’x + ’y.y’ + ’z.z’ (3) và z = g(x, y, y’)
Thay vào (2) suy ra z’ = (x, y, g(x, y, y’)) (4). Thay (4) vào (3) được:
y” = ’x + ’y.y’ + ’z.((x, y, g(x, y, y’))
Đây là PTVP cấp 2 hàm cần tìm là y, giải ra: y = ö(x, C1, C2).
Từ đó z = g(x, ö(x, C1, C2), ö’(x, C1, C2)).
üy = f (x,C ,C ) Vậy NTQ của hệ là: ý 1 1
þz = g(x, f (x,C ,C ), f '(x,C ,C )) 1 2 1 2
ü y'= x - y + z + (1 2x - 1 )
* Ví dụ: Tìm NR của hệ PT ý þz'= 6
- y + 4z - x + (2) 5
Từ PT (1) suy ra y” = - y’ + z’ + 2 (3) và z = y’ + y - 2x + 1 (4).
Thay vào (2): z’ = - 6y + 4(y’ + y - 2x + 1) - x + 5 z’ = 4y’ - 2y - 9x + 9.
Thay z' vào (3): y” = - y’ + 4y’ - 2y - 9x + 9 + 2 y” - 3y’ + 2y = - 9x + 11.
Đây là PTVP tuyến tính cấp 2 giải ra ta được NTQ là: y = C 9 1ex + C2e2x - x - 2 5 y’ = C 9 1ex + 2C2e2x - . 4 2 Thay y, y’ vào (4): z = 2C 13 19 1ex + 3C2e2x - x - 2 4
üy = C ex + 2x 9x 5 C e - - ÿÿ 1 2
Vậy NTQ của hệ PT đã cho là ý 2 4 . ÿ x 2 x 13x 19
ÿz = 2C e + 3C e - - þ 1 2 2 4 143
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
b) Phương pháp tổ hợp tích phân ÿüy'= ) 1 (
f ( y, z )
* Phư¢ng pháp: Chúng ta xét hệ PTVP ý ÿþz'= (2)
g( y, z ) f ( y, z)
Do y’ = dy , z’ = dz nên y' = dy . Lấy (1) chia cho (2): dy = dx dx z' dz dz g( y, z)
Đây là PTVP cấp 1 giải ra ta được: y = (z, C1) (3).
g((z,C ), z)
Lấy đạo hàm (3) theo x được y’ = ’ 1 z.z’ thay vào (2): z’ = . ' (z,C ) z 1
Đây là PTVP cấp 1. Giải ra: z = (x, C1, C2). Thay vào (3) được y = ((x, C1,
üy = ( (x,C ,C ),C ) C 1 2 1
2), C1). Vậy NTQ của hệ PT là ý .
þz = (x,C ,C ) 1 2 ü y y'= ) 1 ( ÿÿ y + 2z
* Ví dụ: Giải hệ PTVP ý ÿ z z'= (2) ÿþ y + 2z
Lấy (1) chia cho (2) vế cho vế được dy = y dy = dz dy = dz + dz z y z y z
ln|C1| ln|y| = ln|z| + ln|C1| y = C1z. C z C C x Thay vào (1): y' = x 1 suy ra y' = 1 y = 1 + C2 z = C z + 2z C + 2 C + 2 C + 2 1 1 1 1 C + 2 . C1
ü y = C x1 + C ÿÿ C + 2 Vậy NTQ của hệ là 2 ý 1
(điều kiện á đây C1 ù 0, - 2) ÿ = x z + C2 ÿþ C + 2 C 1 1
c) Phương pháp đưa về PTVP cấp cao üdx = ) 1 (
f (x, y ) ÿÿ dt
* Phư¢ng pháp: Giả sử hệ ý . ÿdy (2) ÿ
= g(x, y ) þ dt 144
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân 2 d x
Từ (1) đạo hàm 2 vế theo t:
= f . dx + f . dy hay x” = f x’ + f g(x, 2 dt x dt y dt x y
y) x” - f x’ - f g(x, y) = 0. Đây là PTVP tuyến tính cấp 2. x y
Giải ra được x = (t, C1, C2) rồi thay vào (1) ta có y = (t, C1, C2).
üx = (t,C ,C ) Vậy NTQ của hệ là ý 1 2
þy = (t,C ,C ) 1 2 üdx = 2x + (1) y ÿÿ dt
* Ví dụ: Tìm NTQ của hệ PTVP sau ý ÿdy (2) ÿ = -x + 4 y þ dt 2 Đạ d x o hàm 2 vế (1) theo t:
= 2 dx + dy hay x” = 2x’ + (- x + 4y). 2 dt dt dt
Từ (1) ta có y = x’ - 2x nên x” = 2x’ + (- x + 4x’ - 8x) x” - 6x’ + 9x = 0
Đây là PTVP tuyến tính cấp 2 thuần nhất hệ hằng số.
PTĐT k2 - 6k + 9 = 0 có nghiệm kép k0 = 3 nên x(t) = e3t(C1t + C2) x’ =
3e3t(C1t + C2) + e3tC1 = e3t(3C1t + C1 + 3C2) y = e3t(3C1t + C1 + 3C2) - 2e3t(C1t + C2) = e3t(C1t + C1 + C2). ÿüx(t) = e3t (C t + C )
Vậy nghiệm của hệ PT đã cho là ý 1 2 ÿþy(t) = e3t (C t + C + C ) 1 1 2 BÀI TÀP CH¯¡NG 5
Bài tập 1: Giải các PT khuyết sau 1. ey’ + y’ = x 2. xy’2 = 1 + y’ 3. y’ = 4 2
y -1 điều kiện y|x=0 = 0,5 4. y = ey’ - y’2
Bài tập 2: Giải các PT tách biến sau 1 1. 2 ln x dx + dy = 0 2. dx + y dy = 0 x y ln y 2 y + 3 145
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
3. xydx + (1 + y)(1 + x2)dy = 0 4. 2xydx + (1 + x2)dy = 0 5. x3e-ydx + (x4 + 1)ydy = 0 6. ylnxdx + xlnydy = 0 7. 2y’tanx = y
8. y y’ + ey = 0, y|x=2 = 0 ln y x
9. y’ = x + 2y -3
10. y’ = 2x - 2y -1 2x + 4y + 2 x - y + 2
Bài tập 3: Tìm đưßng cong trong mặt phẳng Oxy có tính chất: Diện tích của phần mặt
phẳng giới hạn bái trục hoành, phần đưßng cong từ điểm cắt trục hoành tới điểm có
tung độ y và đoạn thẳng song song với Oy ứng với tung độ y này tỷ lệ với yn, n N
Hướng dẫn: GiÁ sử đường cong C có PT: y = ö(x). Gái M0(x0, 0) là giao của C với trục hoành và x thuộc trục
hoành suy ra tung độ là y. Khi ấy dt(D) = kyn (k là hệ số tỷ lệ, k > 0), mặt khác x 1 y
dt(D) = f (x)dx. Nên ta có y’ = . (C): y = ö(x) 2 n kny - x y 0 1
Kết quÁ: y = k(x - x n (D) 0) 1 -
Bài tập 4: Giải các PT đẳng cấp cấp 1 sau O x0 x x 1. y’ = 2xy
2. xy’ln y = x + yln y 2 2 x - y x x 2 2 3. xy’sin y y - 2 + x = ysin y 4. y’ = x x x 2 x 5. y’ = y x + y + + tan y 6. y’ = - 2 2 1 x x x + y + 1
Bài tập 5: Giải các PT tuyến tính cấp 1 sau 1. y’ - y = 2lnx 2. y’ + y = ex x x 3. xy’ + 2y = 4x2 4. y’ + 2xy = x 2 - x e 5. y’ - y = xln2x
6. y’ + y = x2e 2x x ln x x
7. y’ + x +1y = 3xe-x 8. y’ + tany = x x cos y 9. y’ + ycosx = sinxcosx 10. y’ - ytanx = esinx 146
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân 11. y’(xcosy + sin2y) = 1 12. (xey - 1)y’ + ey = 0 13. (2xy + 3)dy - y2dx = 0 14. (y4 + 2x)y’ = y
Hướng dẫn: Câu 8: Nhân 2 vế với cosy, sau đó đặt z = siny. Câu 11, 12, 13, 14 coi x là hàm và y là biến độc lập.
Bài tập 6: Giải các PT Bernoulli sau x 1. y’ + y = -2 e y , y|x=0 = 0 2. xy’ - 2x2 y = 4y 3 x 3. y’ + y + = x2y4
4. y’ - x 1 y = x e x 3x 2 y 5. xyy’ - y2 = x4 6. y’ - 2xy = x3y2 7. y + x(1 + xy2)y’ = 0 8. 2y + x(xy2 - 6)y’ = 0
Hướng dẫn: Câu 7, 8 coi x là hàm và y là biến độc lập.
Bài tập 7: Giải các PTVP toàn phần sau y 1. 1 e dx dy
x (xdy - ydx) = 0, điều kiện y| + = 0 2 -2 = - 2 2. x x y
3. (x3 + 3xy2)dx + (3x2y + y3)dy = 0 4. y3dx + 3xy2dy = 0
Bài tập 8: Chứng tỏ F là thừa số tích phân của PTVP tương ứng và giải PT sau
1. ydx - xdy, F = 1 , F = 1 , F = 1 2 x 2 y 2 2 x + y
2. 2siny2dx + xycosy2dy = 0, F = x2
3. 2xydx + (3x2 + 4y)dy = 0, F = y2, điều kiện y|x=0,2 = - 0,2.
4. (1 + xy)dx + x2dy = 0, F = exy, điều kiện y| x=1 = 0.
Bài tập 9: Giải PT Lagrange và PT Clairaut sau (á đây p = y’) 1. y = (1 + x)p2 2. p2 = 4(xp - y)
Bài tập 10: Giải các PTVP khuyết (giảm cấp) sau 1. y” = xe-x 2. y” = xlnx
3. (x - 1)xy” – y’ = x(x - 1)2 4. y” = y’ + x 5. xy” = y’ + x2 6. xy” - 2y’ = x3 7. y” = y’ + (y’)3 8. y” - (y’)2 + y = 0 9. (y - 1)y” = 2(y’)2 10. y” = y’ey
Bài tập 11: Giải các PTTT cấp 2 hệ là hàm số 147
KHOA KHOA HàC C¡ BÀN
Chư¢ng 5: Phư¢ng trình vi phân
1. y” + 2 y’ + y = 0. Biết một NR là y sin x 1 = . x x
2. (2x - x2)y” - xy’ + y = 0, điều kiện y|x=1 = 0, y’|x=1 = 1. Biết một NR y1 = ex. 3. xy” - y = x2. 4. y” - 1 y’ + 1 y = 1. x 2 x
Bài tập 12: Giải PTTT cấp 2 thuần nhất sau 1. y” - 3y’ + 2y = 0 2. y” - 4y = 0 3. y” + 6y’ + 9y = 0 4. y” - 2y’ + y = 0 5. y” - 2y’ + 5y = 0 6. y” + 4y = 0
Bài tập 13: Giải các PTTT cấp 2 sau
1. y” + 5y’ + 6y = ex(2x + 1) 2. y” + 3y’ = e-x(3x + 4)
3. y” - 3y’ + 2y = ex(x + 2) 4. y” - 2y’ + y = 6ex
5. y” + 4y’ + 3y = (2x + 1)cosx 6. y” + y’ = - 20exsinx
7. y” - 2y’ + 2y = ex(2cosx - 4sinx) 8. y” - y = 6e2x + cosx
Bài tập 14: Giải hệ PTVP sau
üy'= y + z + 2x 1 -
üy'= y - z + x + 2 1. ý 2. ý þz'= 6
- y + 4z -x + 5
þz'= 3y -5z + 2x -1
üy'= y + z üy(0) = 0
üy' = 3y - z üy(0) =1 3. ý đ/k ý 4. ý đ/k ý
þz'= -2y + 4z þz(0) = 1 - þz' = 10 - 4z þz(0) = 5 üdx = üdx 3x - y = 4x + 5y ÿÿ ÿÿ 5. ý dt 6. ý dt ÿdy ÿdy ÿ = 4x - y = 4 - x - 4y þ dt ÿþ dt 148



