
















Preview text:
TẬP ĐOÀN BƯU CHÍNH VIỄN THÔNG
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG BÀI GIẢNG
GIẢI TÍCH HÀM NHIỀU BIẾN SỐ PTIT
PGS. TS. Phạm Ngọc Anh HÀ NỘI-2013 M l Lêi nãi ®Çu 6 Ch¬ng 1. Php tÝnh vi ph©n hµm nhiÒu biÕn sè 7 Rn 1.1. Kh«ng gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.1.1. C¸ php to¸n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.1.2. ChuÈn vµ hµm kho¶ng ¸h . . . . . . . . . . . . . . . . . . . . . . 7 1.1.3. T«p« . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 1.2. Hµm sè nhiÒu biÕn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.2.1. MÆt Çu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.2.2. MÆt elipxoit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.2.3. MÆt hypeboli mét tÇng . . . . . . . . . . . . . . . . . . . . . . . . 9 1.2.4. MÆt hypeboli hai tÇng . . . . . . . . . . . . . . . . . . . . . . . . 10 1.2.5. MÆt paraboloit-elipti . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1.2.6. MÆt tr . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.2.7. MÆt nãn bË hai . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.3. Giíi h¹n hµm hai biÕn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.4. Hµm liªn t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.5. §¹o hµm riªng vµ vi ph©n ¶u hµm nhiÒu biÕn sè . . . . . . . . . . . . . . 15 PTIT 1.5.1. §¹o hµm riªng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 1.5.2. Hµm kh¶ vi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.6. §¹o hµm theo ph¬ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18 1.7. Quan hÖ gi÷a ®¹o hµm theo ph¬ng vµ ®¹o hµm riªng . . . . . . . . . . . . 19 1.8. §¹o hµm riªng ña hµm hîp . . . . . . . . . . . . . . . . . . . . . . . . . 20 1.9. §¹o hµm riªng vµ vi ph©n Êp ao . . . . . . . . . . . . . . . . . . . . . . 21 1.10. C«ng thø T aylor ña hµm hai biÕn sè . . . . . . . . . . . . . . . . . . . . 23 1.1 1. Hµm Èn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 1.12. Cù trÞ ña hµm hai biÕn sè . . . . . . . . . . . . . . . . . . . . . . . . . . 27 1.12.1. Cù trÞ kh«ng ®iÒu kiÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 1.12.2. Cù trÞ ã ®iÒu kiÖn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 2 1.13. Gi¸ trÞ lín nhÊt vµ nhá nhÊt . . . . . . . . . . . . . . . . . . . . . . . . . . 33 1.13.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 1.13.2. Ph¬ng ph¸p t×m . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Bµi tËp h¬ng 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 Ch¬ng 2. TÝnh ph©n béi 41 2.1. TÝh ph©n ph thué tham sè . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.1.1. TÝh ph©n x¸ ®Þnh . . . . . . . . . . . . . . . . . . . . . . . . . . 41 2.1.2. TÝh ph©n suy réng . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2.2. TÝh ph©n kp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.2.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.2.2. §iÒu kiÖn kh¶ tÝh . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.2.3. C¸ tÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 2.2.4. §Þnh lý Fubini . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 2.2.5. C«ng thø ®æi biÕn . . . . . . . . . . . . . . . . . . . . . . . . . . 56 2.2.6. C«ng thø ®æi biÕn trong täa ®é ù . . . . . . . . . . . . . . . . . 58 2.2.7. ng dng ña tÝh ph©n kp . . . . . . . . . . . . . . . . . . . . . 59 2.3. TÝh ph©n béi ba . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 2.3.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63 PTIT 2.3.2. C«ng thø tÝnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64 2.3.3. Ph¬ng ph¸p ®æi biÕn . . . . . . . . . . . . . . . . . . . . . . . . . 66 Bµi tËp h¬ng 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 Ch¬ng 3. TÝh ph©n ®êng vµ mÆt 73 3.1. TÝh ph©n ®êng lo¹i mét . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 3.1.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 3.1.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 3.1.3. C«ng thø tÝnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73 3.2. TÝnh ph©n ®êng lo¹i hai . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 3.2.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78 3.2.2. NhËn xt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 3 3.2.3. TÝnh hÊt ¬ hä . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 3.2.4. C¸h tÝnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79 3.2.5. Chó ý . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 3.2.6. C«ng thø Green . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 3.2.7. §Þnh lý bèn mÖnh ®Ò t¬ng ®¬ng . . . . . . . . . . . . . . . . . . 85 3.3. TÝh ph©n mÆt lo¹i mét . . . . . . . . . . . . . . . . . . . . . . . . 90 3.3.1. C¸ kh¸i niÖm vÒ mÆt . . . . . . . . . . . . . . . . . . . . . . . . . 90 3.3.2. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 3.3.3. C«ng thø tÝnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92 3.4. TÝnh ph©n mÆt lo¹i hai . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 3.4.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 3.4.2. C¸h tÝnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95 3.5. Quan hÖ gi÷a ¸ tÝh ph©n . . . . . . . . . . . . . . . . . . . . . . 98 3.5.1. C«ng thø Stokes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98 3.5.2. C«ng thø Ostrogradski . . . . . . . . . . . . . . . . . . . . . . . . 100 3.6. V t¬ r«ta vµ trêng thÕ . . . . . . . . . . . . . . . . . . . . . . . 101 Bµi tËp h¬ng 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105 Ch¬ng 4. Ph¬ng tr×nh vi ph©n 110 4.1. Kh¸i niªm hung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 10 PTIT 4.1.1. C¸ bµi to¸n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 10 4.1.2. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 10 4.2. Ph¬ng tr×nh vi ph©n Êp 1 . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 4.2.1. §Þnh nghÜa vµ sù tån t¹i nghiÖm . . . . . . . . . . . . . . . . . . . 1 1 1 4.2.2. Ph¬ng tr×nh t¸h biÕn . . . . . . . . . . . . . . . . . . . . . . . . 1 12 4.2.3. Ph¬ng tr×nh tuyÕn tÝnh . . . . . . . . . . . . . . . . . . . . . . . . 1 14 4.2.4. Ph¬ng tr×nh Bernoulli . . . . . . . . . . . . . . . . . . . . . . . . . 1 16 4.2.5. Ph¬ng tr×nh vi ph©n toµn phÇn . . . . . . . . . . . . . . . . . . . . 1 18 4.3. Ph¬ng tr×nh vi ph©n Êp hai . . . . . . . . . . . . . . . . . . . . . . . . . 1 19 4.3.1. §Þnh nghÜa vµ sù tån t¹i nghiÖm . . . . . . . . . . . . . . . . . . . 1 19 4.3.2. Ph¬ng tr×nh khuyÕt . . . . . . . . . . . . . . . . . . . . . . . . . . 120 4 4.3.3. Ph¬ng tr×nh vi ph©n tuyÕn tÝnh Êp hai . . . . . . . . . . . . . . . 122 4.3.3.1. CÊu tró nghiÖm . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123 4.3.3.1. Ph¬ng tr×nh vi ph©n tuyÕn tÝnh Êp hai víi hÖ sè h»ng sè . . . . . . 126 4.4. HÖ ph¬ng tr×nh vi ph©n . . . . . . . . . . . . . . . . . . . . . . . . 134 4.4.1. HÖ ph¬ng tr×nh vi ph©n Êp 1 . . . . . . . . . . . . . . . . . . . . 134 4.4.2. Ph¬ng ph¸p gi¶i hÖ ph¬ng tr×nh vi ph©n Êp 1 . . . . . . . . . . . 135 4.4.3. Ph¬ng ph¸p gi¶i hÖ ph¬ng tr×nh vi ph©n Êp 1 víi hÖ sè h»ng sè . 136 Bµi tËp h¬ng 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137 Tµi liÖu tham kh¶o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143 PTIT 5 Lêi nãi ®Çu Trong ho¹t ®éng khoa hä vµ kü thuËt thêng gÆp nhiÒu vÊn ®Ò ã liªn quan ®Õn hµm nhiÒu biÕn sè vµ ¸ øng dng ña hóng. Do vËy , gi¶i tÝh hµm nhiÒu biÕn sè lµ mét m«n hä ®ang gi÷ mét vÞ trÝ quan träng trong ¸ lÜnh vù øng dng vµ trong hÖ thèng ¸ m«n hä ña Hä viÖn C«ng nghÖ Bu hÝnh ViÔn th«ng. C¸ kiÕn thø vµ ph¬ng ph¸p tiÕp Ën ña gi¶i tÝh hµm nhiÒu biÕn sè ®· hç trî hiÖu qu¶ ¸ kiÕn thø nÒn t¶ng ho ¸ m«n hä nh vËt lý, x¸ suÊt thèng kª, to¸n kü thuËt, to¸n rêi r¹ vµ ¸ m«n huyªn ngµnh kh¸. Bµi gi¶ng "Gi¶i tÝh hµm nhiÒu biÕn sè" ®î biªn so¹n l¹i theo h¬ng tr×nh qui ®Þnh ña Hä viÖn ho hÖ ®¹i hä huyªn ngµnh §iÖn tö-ViÔn th«ng-C«ng nghÖ th«ng tin víi h×nh thø ®µo t¹o theo tÝn hØ. Do ®èi tîng sinh viªn rÊt ®a d¹ng víi tr×nh ®é ¬ b¶n kh¸ nhau, hóng t«i ®· è g¾ng t×m ¸h tiÕp Ën ®¬n gi¶n vµ hîp lý ®Ó tr×nh bµy néi dung theo ph¬ng ph¸p dÔ hiÓu h¬n, nh»m gióp ho sinh viªn n¾m ®î ¸ kiÕn thø ¬ b¶n nhÊt. §Ó võa «n tËp, võa tù kiÓm tra kiÕn thø vµ ®Ó h×nh dung ®î mø ®é ña mét ®Ò thi hÕt m«n, sau mçi phÇn lý thuyÕt quan träng hóng t«i thêng ®a ra ¸ vÝ d minh häa hi tiÕt. Néi dung ®î hia thµnh 4 h¬ng. Ch¬ng 1 dµnh ho php tÝnh vi ph©n ña hµm nhiÒu biÕn sè. Ch¬ng 2 vµ 3 tr×nh bµy hi tiÕt vÒ tÝh ph©n ®êng vµ tÝh ph©n mÆt. Ph¬ng tr×nh vi ph©n vµ ¸ ph¬ng ph¸p gi¶i ®î ®a ra trong h¬ng 4. C¸ kh¸i niÖm vµ «ng thø ®î tr×nh bµy t¬ng ®èi ®¬n gi¶n vµ ®î minh häa b»ng nhiÒu vÝ d víi ¸ h×nh vÏ sinh ®éng. C¸ høng minh khã ®î lî bít ã hän lä ®Ó gióp ho gi¸o tr×nh kh«ng qu¸ ång kÒnh nhng vÉn ®¶m b¶o ®î, PTIT ®Ó tiÖn ho sinh viªn hä tËp huyªn s©u vµ tra øu ph v qu¸ tr×nh hä tËp ¸ m«n hä kh¸. Cuèi mçi h¬ng hä ®Òu ã ¸ bµi tËp ®Ó sinh viªn tù gi¶i nh»m gióp ¸ em hiÓu s©u s¾ h¬n vÒ lý thuyÕt vµ rÌn luyÖn kü n¨ng thù hµnh. T¸ gi¶ hy väng r»ng gi¸o tr×nh nµy ã Ýh ho ¸ em sinh viªn vµ ¸ b¹n ®ång nghiÖp trong qu¸ tr×nh hä tËp vµ gi¶ng d¹y vÒ m«n hä gi¶i tÝh hµm nhiÒu biÕn sè. T¸ gi¶ òng ¸m ¬n mäi ý kiÕn gãp ý ®Ó gi¸o tr×nh bµi gi¶ng nµy ®î hoµn thiÖn h¬n nh»m n©ng ao hÊt lîng d¹y vµ hä m«n hä nµy . 1 1/2013, T¸ gi¶: PGS. TS. Ph¹m Ngä Anh 6 Ch¬ng 1. php tÝnh vi ph©n hµm nhiÒu biÕn Rn 1.1. Kh«ng gian 1.1.1. C¸ php to¸n Cho hai v t¬
x = (x1, x2, ..., xn) ∈ Rn, y = (y1, y2, ..., yn) ∈ Rn. n Rn Khi ®ã, ta nh¾ l¹i ¸ php to¸n quen thué trong kh«ng gian hiÒu : + Php éng vµ trõ:
x ± y = (x1 ± y1, x2 ± y2, ..., xn ± yn). + Php nh©n v t¬ víi 1 sè thù:
λx = (λx1, λx2, ..., λxn), ∀λ ∈ R. + Php nh©n v« híng 2 v t¬:
hx, yi = x1y1 + x2y2 + ... + xnyn. x y x1y1 + x2y2 + ... + xnyn = 0. Khi ®ã, ta ã v t¬ vu«ng gã víi khi vµ hØ khi x 6= 0 y 6= 0 + Gã gi÷a 2 v t¬ vµ x¸ ®Þnh bëi «ng thø: x cos(x, y) = 1y1 + x2y2 + ... + xnyn .
px2 + x2 + ... + x2 py2 + y2 + ... + y2 1 2 n 1 2 n 1.1.2. ChuÈn vµ hµm kho¶ng ¸h. PTIT x = (x1, x2, ..., xn) ∈ Rn. x Cho v t¬ Khi ®ã, huÈn ña v t¬ lµ mét sè thù ®î ký kxk hiÖu bëi vµ ®î x¸ ®Þnh bëi q kxk = x2 + x2 + ... + x2 . 1 2 n ChuÈn ã ¸ tÝnh hÊt ¬ b¶n sau: kxk ≥ 0 ∀x ∈ Rn kxk = 0 x = 0 + vµ khi vµ hØ khi .
kλxk = |λ|kxk ∀x ∈ Rn, λ ∈ R + .
kx + yk ≤ kxk + kyk ∀x, y ∈ Rn + . x ∈ Rn y ∈ Rn Khi ®ã, kho¶ng ¸h gi÷a vµ ®î x¸ ®Þnh bëi «ng thø d(x, y) = kx − yk. 1.1.3. T«p«. x ∈ Rn, ǫ > 0 Cho . Khi ®ã 7
B(x, ǫ) = {y ∈ Rn : ky − xk < ǫ} x ǫ + gäi lµ h×nh Çu më ã t©m t¹i ®iÓm vµ b¸n kÝnh lµ . ¯
B(x, ǫ) = {y ∈ Rn : ky − xk ≤ ǫ} x ǫ + gäi lµ h×nh Çu ®ãng ã t©m t¹i ®iÓm vµ b¸n kÝnh lµ . x ∈ M ⊆ Rn B(x, ǫ) B(x, ǫ) ⊆ M + §iÓm gäi lµ ®iÓm trong, nªu tån t¹i mét h×nh Çu më sao ho . M M intM TËp hîp ¸ ®iÓm trong ña ®î gäi lµ phÇn trong ña vµ ký hiÖu bëi . M ⊆ Rn intM = M + TËp gäi lµ tËp më, nÕu . M ⊆ Rn x M ǫ > 0 B(x, ǫ) + Cho . §iÓm ®î gäi lµ ®iÓm biªn ña , nÕu víi mäi th× høa nh÷ng M M M ®iÓm thué vµ nh÷ng ®iÓm kh«ng thué . TËp hîp ¸ ®iÓm biªn ña ®î ký hiÖu lµ ∂M . M ⊆ Rn ∂M ⊆ M + TËp gäi lµ mét tËp ®ãng, nÕu . M ⊆ Rn α > 0 kxk ≤ α ∀x ∈ M + TËp gäi lµ bÞ hÆn bëi , nÕu . M ⊆ Rn M + TËp gäi lµ tËp ompat, nÕu lµ tËp ®ãng vµ bÞ hÆn. 1.2. Hµm sè nhiÒu biÕn ∅ 6= D ⊆ Rn Cho . Khi ®ã, ¸nh x¹ f : D → R x¸ ®Þnh bëi
x = (x1, x2, ..., xn) ∈ D 7−→ y = f(x1, x2, ..., xn) ∈ R D f ®î gäi lµ mét hµm sè nhiÒu biÕn, TËp ®î gäi lµ miÒn x¸ ®Þnh ña hµm sè . C¸ sè x1, x2, ..., xn f ®î gäi lµ ¸ biÕn sè ña hµm sè . R > 0 VÝ d 1.1. Cho . T×m miÒn x¸ ®Þnh ña hµm sè PTIT q f (x) =
R2 − x21 − x22 − ... − x2 . n Gi¶i. D Theo ®Þnh nghÜa, miÒn x¸ ®Þnh ®î x¸ ®Þnh bëi
D ={x ∈ Rn : R2 − x21 − x22 − ... − x2n ≥ 0}
={x ∈ Rn : kx − 0k2 ≤ R2} = ¯ B(0, R). R3 Díi ®©y lµ mét sè mÆt bË 2 thêng gÆp trong kh«ng gian . 1.2.1. MÆt Çu Ph¬ng tr×nh:
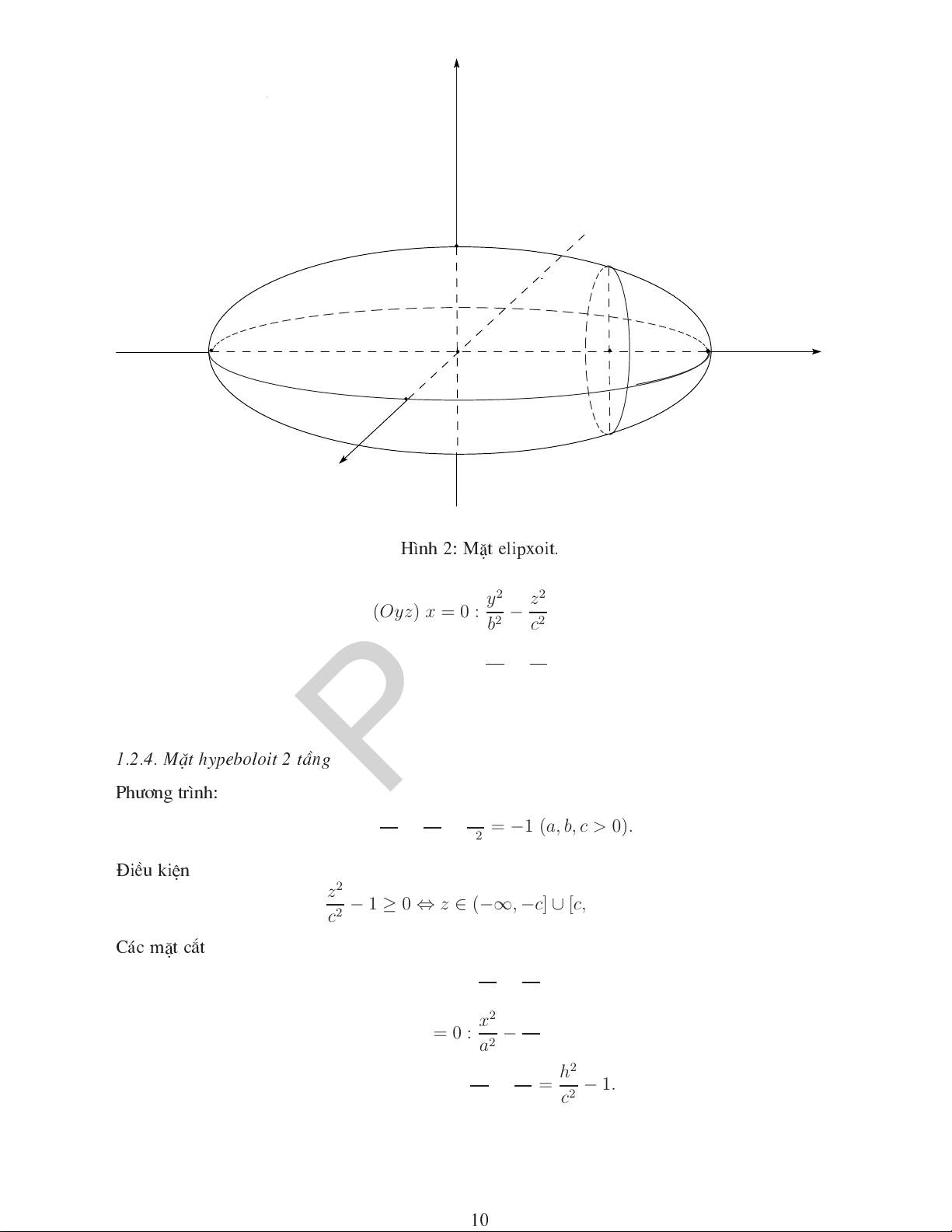
(S) = {(x, y, z) ∈ R3 : (x − a)2 + (y − b)2 + (z − c)2 = R2}. 8 z c I b y O a x H×nh 1: MÆt Çu. I(a, b, c) R (S) Khi ®ã, ®iÓm gäi lµ t©m vµ gäi lµ b¸n kÝnh ña mÆt Çu . 1.2.2. MÆt Elipxoit Ph¬ng tr×nh: x2 y2 z2 (E) : + + = 1 (a, b, c > 0). a2 b2 c2 PTIT C¸ mÆt ¾t x2 y2 (Oxy) z = 0 : + = 1. a2 b2 y2 z2 (Oyz) x = 0 : + = 1. b2 c2 x2 z2 (Oxz) y = 0 : + = 1. a2 c2 1.2.3. MÆt hypeboloit 1 tÇng Ph¬ng tr×nh: x2 y2 z2 (H1) : + − = 1 (a, b, c > 0). a2 b2 c2 C¸ mÆt ¾t x2 y2 (Oxy) z = 0 : + = 1. a2 b2 9 z c b y O a x H×nh 2: MÆt elipxoit. y2 z2 (Oyz) x = 0 : − = 1. b2 c2 x2 z2 (Oxz) y = 0 : − = 1. a2 c2 PTIT 1.2.4. MÆt hypeboloit 2 tÇng Ph¬ng tr×nh: x2 y2 z2 (H2) : + − = −1 (a, b, c > 0). a2 b2 c2 §iÒu kiÖn
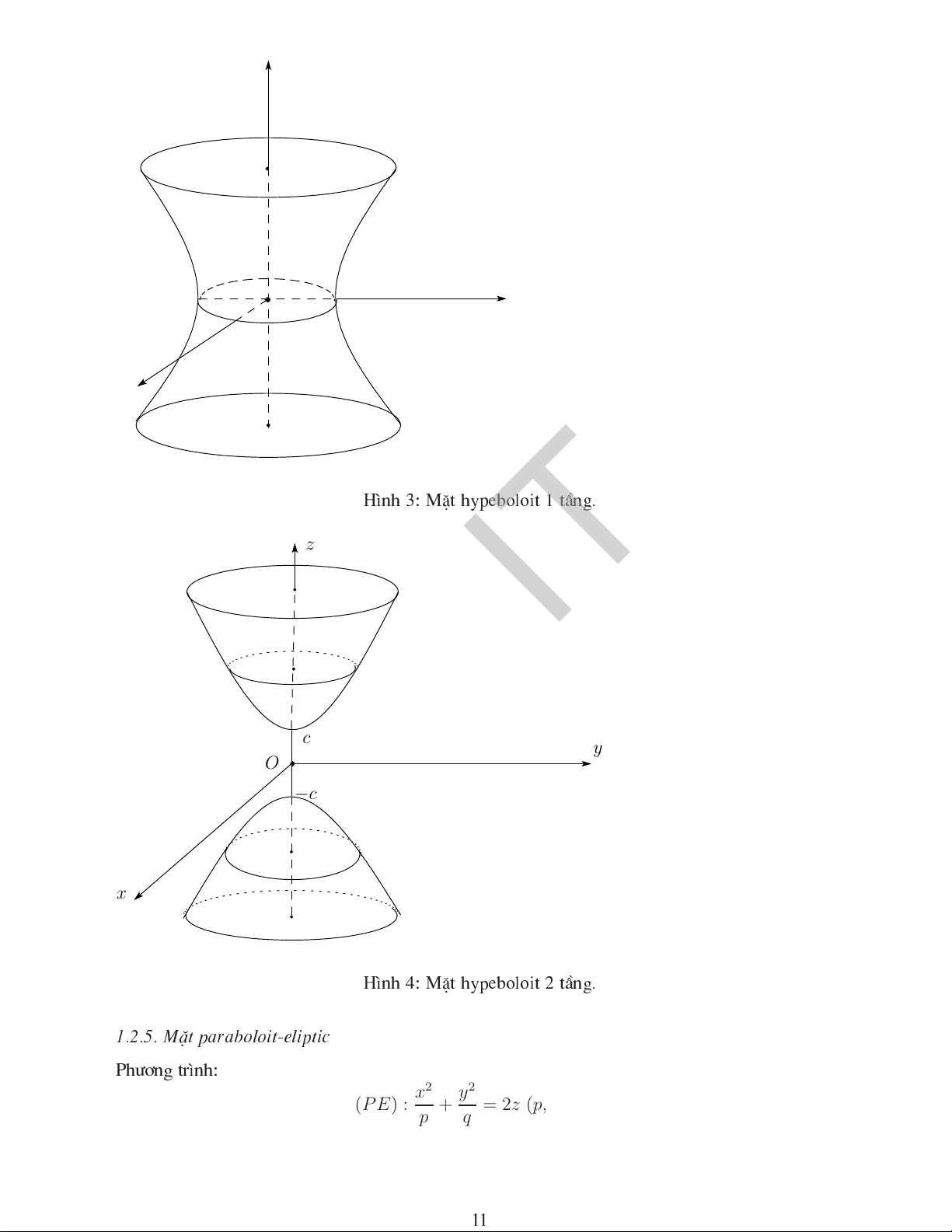
z2 − 1 ≥ 0 ⇔ z ∈ (−∞,−c] ∪ [c,+∞). c2 C¸ mÆt ¾t y2 z2 (Oyz) x = 0 : − = −1. b2 c2 x2 z2 (Oxz) y = 0 : − = −1. a2 c2 x2 y2 h2 (P ) z = h > c : + = − 1. a2 b2 c2 10 z b y O a x H×nh 3: MÆt hypeboloit 1 tÇng. z c y O PTIT −c x H×nh 4: MÆt hypeboloit 2 tÇng. 1.2.5. MÆt paraboloit-elipti Ph¬ng tr×nh: x2 y2 (P E) : + = 2z (p, q > 0), p q 1 1 z ≥ 0 víi ®iÒu kiÖn . C¸ mÆt ¾t (Oyz) x = 0 : y2 = 2qz. (Oxz) y = 0 : x2 = 2pz. x2 y2 (P ) z = h > 0 : + = 2h. p q z y O x H×nh 5: MÆt hypeboloit-elipti. PTIT 1.2.6. MÆt tr Ph¬ng tr×nh: (Tz) : f (x, y) = 0 Oz, song song víi tr (Ty) : g(x, z) = 0 Oy, song song víi tr (Tx) : f (y, z) = 0 Ox, song song víi tr f, g, h : D ⊆ R2 → R trong ®ã . 1.2.7. MÆt nãn bË hai Ph¬ng tr×nh: x2 y2 z2 (N) : + − = 0 (a, b, c > 0). a2 b2 c2 C¸ mÆt ¾t b (Oyz) x = 0 : y = ± z. c 12 z y O x Oz H×nh 6: MÆt tr song song . a (Oxz) y = 0 : x = ± z. c x2 y2 h2 (P ) z = h > 0 : + = . a2 b2 c2 1.3. Giíi h¹n hµm nhiÒu biÕn sè Rn §Ó hiÓu vÒ giíi h¹n hµm nhiÒu biÕn sè trong kh«ng gian , ta ã thÓ nghiªn øu th«ng qua {Mn} ⊂ R2 M0 ∈ R2 giíi h¹n ña hµm hai biÕn sè. Mét d·y ®iÓm ®î gäi lµ dÇn tíi ®iÓm , viÕt PTIT Mn → M0 n → ∞ lim Mn = M0 ǫ > 0 n(ǫ) t¾t lµ khi hay , nÕu víi mäi tån t¹i sè tù nhiªn sao n→∞ ho
Mn ∈ B(M0, ǫ) ∀n ≥ n(ǫ). lim xn = x0 lim yn = y0 Mn(xn, yn) → M0(x0, y0) Trong trêng hîp ®Æ biÖt: NÕu vµ th× ®iÓm n→∞ n→∞ n → ∞ khi . z = f (x, y) M0 ∈ R2 Cho mét hµm 2 biÕn sè x¸ ®Þnh trong l©n Ën ña ®iÓm ã thÓ trõ M0 m f (x, y) (x, y) M0(x0, y0) ®iÓm . Khi ®ã, sè ®î gäi lµ giíi h¹n ña hµm khi dÇn tíi , ký lim f (M) = m {Mn} ⊂ R2 lim Mn = M0 hiÖu , nÕu víi mäi d·y ®iÓm bÊt kú sao ho th× M →M0 n→∞ lim f (Mn) = m. n→∞ lim f (M) = m T a ã thÓ høng minh ®î r»ng: khi vµ hØ khi M →M0
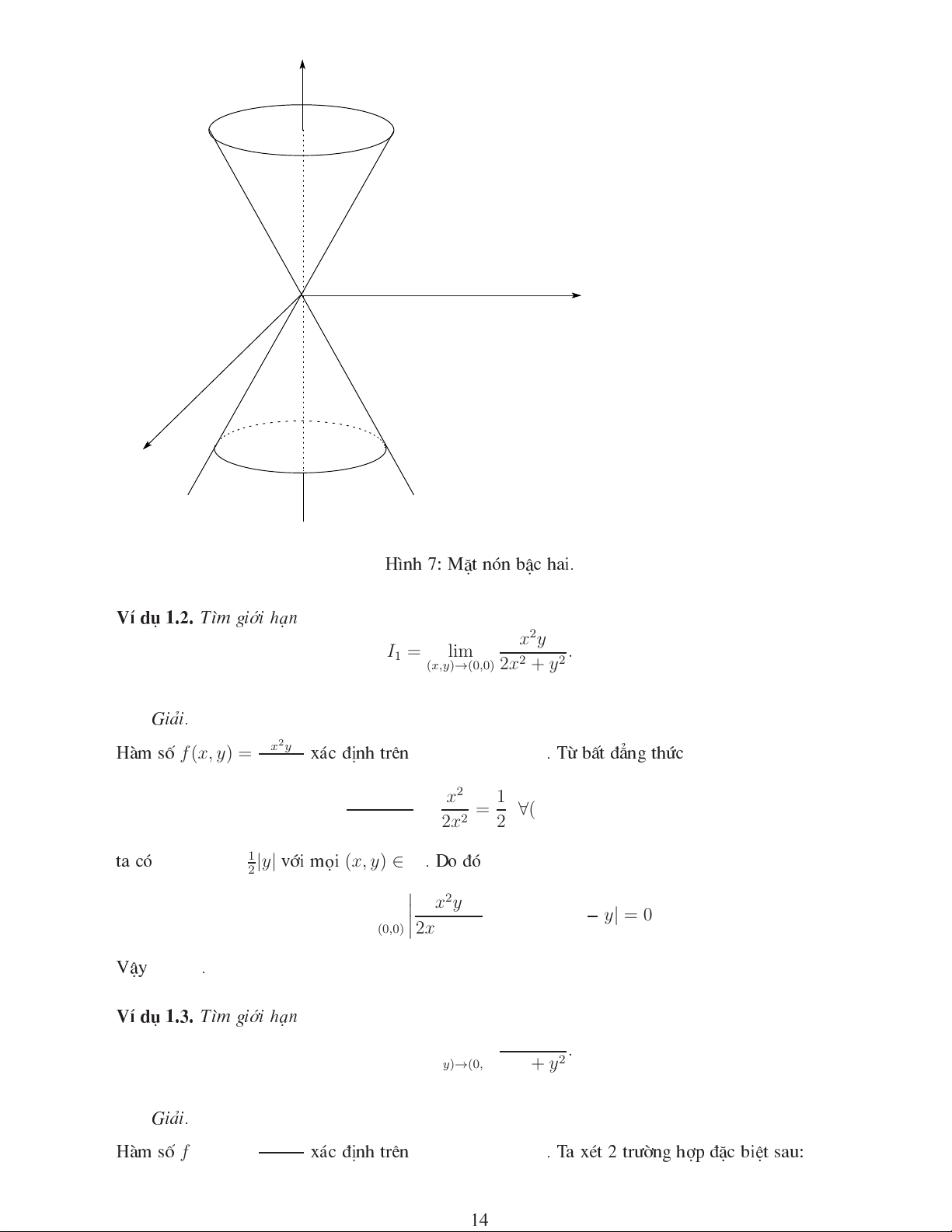
∀ǫ > 0, ∃δ > 0, ∀M ∈ B(M0, δ) ⇒ |f(M) − m| < ǫ. 13 z y O x H×nh 7: MÆt nãn bË hai. VÝ d 1.2. T×m giíi h¹n x2y I1 = lim . (x,y)→(0,0) 2x2 + y2 Gi¶i. f (x, y) = x2y D = R2\{(0, 0)} PTIT Hµm sè 2x2+y2 x¸ ®Þnh trªn . Tõ bÊt ®¼ng thø x2 x2 1 ≤ = ∀(x, y) ∈ D, 2x2 + y2 2x2 2 |f(x, y)| ≤ 1|y| (x, y) ∈ D ta ã 2 víi mäi . Do ®ã x2y 1 0 ≤ lim ≤ lim |y| = 0. (x,y)→(0,0) 2x2 + y2 (x,y)→(0,0) 2 I1 = 0 VËy . VÝ d 1.3. T×m giíi h¹n xy I2 = lim . (x,y)→(0,0) 2x2 + y2 Gi¶i. f (x, y) = xy D = R2\{(0, 0)} Hµm sè 2x2+y2 x¸ ®Þnh trªn . T a xt 2 trêng hîp ®Æ biÖt sau: 14 (x, y) ∈ d : y = x (x, y) → (0, 0) x → 0 + §iÓm . Khi ®ã khi vµ hØ khi . Khi ®ã, ta ã xy x2 1 I2 = lim = lim = . (x,y)→(0,0) 2x2 + y2 x→0 2x2 + x2 3 (x, y) ∈ d : y = 3x (x, y) → (0, 0) x → 0 + §iÓm . Khi ®ã khi vµ hØ khi . Khi ®ã, ta ã xy 3x2 3 I2 = lim = lim = . (x,y)→(0,0) 2x2 + y2 x→0 2x2 + 9x2 11 I2 Do vËy kh«ng tån t¹i. 1.4. Hµm sè liªn t z = f (x, y) D M0 ∈ D Cho hµm sè x¸ ®Þnh trªn miÒn vµ ®iÓm . Khi ®ã, f M0 + Hµm sè liªn t t¹i ®iÓm nÕu tån t¹i giíi h¹n lim f (M) = f (M0). M →M0 f D f M ∈ D + Hµm sè liªn t trªn miÒn nÕu liªn t t¹i mäi ®iÓm . f D ǫ > 0 δ > 0 + Hµm sè liªn t ®Òu trªn miÒn nÕu víi mäi , tån t¹i sao ho
∀(x, y), (x′, y′) ∈ D : k(x, y) − (x′, y′)k < δ ⇒ |f(x, y) − f(x′, y′)| < ǫ. B»ng ¸h dïng ®Þnh nghÜa, ta ã nhËn xt sau. f : D ⊆ R2 → R D f NhËn xt 1.4. + NÕu hµm liªn t ®Òu trªn miÒn , th× liªn t trªn miÒn
D. §iÒu ngî l¹i kh«ng ®óng. f D D f D + NÕu liªn t trªn miÒn vµ lµ tËp ompat, th× liªn t ®Òu trªn miÒn . PTIT f D f D + NÕu liªn t trªn miÒn ompat , th× ®¹t gi¸ trÞ lín nhÊt vµ nhá nhÊt trªn miÒn . 1.5. §¹o hµm riªng vµ vi ph©n toµn phÇn ña hµm nhiÒu biÕn sè z = f (x) D ⊆ Rn ¯ x = (¯ x1, ¯ x2, ..., ¯ xn) ∈ D Cho hµm sè x¸ ®Þnh trªn miÒn vµ ®iÓm . 1.5.1. §¹o hµm riªng
x1 7−→ f(x1, ¯x2, ..., ¯xn) x1 NÕu hµm mét biÕn sè ã ®¹o hµm t¹i , th× ®¹o hµm ®ã ®î gäi lµ f x1 ¯ x ®¹o hµm riªng ña theo Èn t¹i ®iÓm vµ ®î ký hiÖu ∂f f ′ (¯ x) (¯ x). x hay 1 ∂x1 f xi i = 1, 2, ..., n B»ng ¸h hiÓu t¬ng tù, ta òng ã ¸ ®¹o hµm riªng ña theo Èn ( ) t¹i ®iÓm ¯ x vµ ®î ký hiÖu ∂f f ′ (¯ x) (¯ x). x hay i ∂xi 15 VÝ d 1.5. T×m ¸ ®¹o hµm riªng ña hµm sè sau: f (x, y) = x2 tan(x3 + 2y). Gi¶i. ∂f 1 3x4 = 2x tan(x3 + 2y) + x2. .3x2 = 2x tan(x3 + 2y) + . ∂x cos2(x3 + 2y) cos2(x3 + 2y) ∂f 1 2x2 = x2. .2 = . ∂y cos2(x3 + 2y) cos2(x3 + 2y) 1.5.2. Hµm kh¶ vi f : D ⊆ Rn → R ¯ x = (¯ x1, ¯ x2, ..., ¯ xn) ∈ D Cho hµm nhiÒu biÕn vµ ®iÓm . x = (x1, x2, ..., xn) ∈ D + Víi mçi , ®Æt ∆x = x i i − ¯ xi. Khi ®ã ∆f = f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x 1 2 + ∆x2 n + ∆xn 1, ¯ x2, ..., ¯ xn) ¯ x ®î gäi lµ sè gia ña hµm sè t¹i ®iÓm . + NÕu sè gia ña hµm sè ã d¹ng ∆f = A1∆x + A + ... + A + α + α + ... + α , 1 2∆x2 n∆xn 1∆x1 2∆x2 n∆xn Ai(i = 1, 2, ..., n) ¯ x
∆x = (∆x , ∆x , ..., ∆x ) trong ®ã hØ ph thué vµo , kh«ng ph thué vµo 1 2 n PTIT vµ
lim αk = 0 ∀k = 1, 2, ..., n, ∆x→0 f ¯ x th× hµm sè ®î gäi lµ kh¶ vi t¹i ®iÓm . Khi ®ã df = A1∆x + A + ... + A 1 2∆x2 n∆xn f ¯ x ®î gäi lµ vi ph©n toµn phÇn ña t¹i ®iÓm . f D f ¯ x ∈ D + Hµm sè ®î gäi lµ kh¶ vi trªn miÒn , nÕu kh¶ vi t¹i mäi ®iÓm . f : D ⊆ Rn → R §Þnh lý 1.6. NÕu hµm ã ¸ ®¹o hµm riªng liªn t trong mét l©n Ën ña ¯ x ∈ D f ¯ x ®iÓm , th× sÏ kh¶ vi t¹i ®iÓm vµ ∂f ∂f ∂f df = (¯ x)∆ + (¯ x)∆ + ... + (¯ x)∆ . ∂x x1 x2 xn 1 ∂x2 ∂xn 16 Chøng minh: Theo ®Þnh nghÜa, ta ã ∆f =f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x 1 2 + ∆x2 n + ∆xn 1, ¯ x2, ..., ¯ xn) =f (¯ x1 + ∆x , ¯ x , ..., ¯ x ) − f(¯x , ..., ¯ x ) 1 2 + ∆x2 n + ∆xn 1, ¯ x2 + ∆x2 n + ∆xn + · · · + f (¯ x1, ¯ x2, ...¯ xn ) −1, ¯ xn + ∆x − f(¯x n 1, ¯ x2, ..., ¯ xn). θ1, θ2, ..., θn ∈ (0, 1) Theo «ng thø sè gia giíi néi, tån t¹i ¸ sè sao ho f (¯ x1, ..., ¯ xi , ..., ¯ x ) , ..., ¯ x ) −1, ¯ xi + ∆x − f(¯x i n + ∆xn 1, ..., ¯ xi, ¯ xi+1 + ∆xi+1 n + ∆xn ∂f = (¯ x , ..., ¯ x )∆ . ∂x 1, ..., ¯ xi−1, ¯xi + θi∆xi n + ∆xn xi i ¯ x Do ¸ ®¹o hµm riªng liªn t trong l©n Ën ña ®iÓm nªn ∂f ∂f (¯ x , ..., ¯ x ) = (¯ x) + α ∂x 1, ..., ¯ xi−1, ¯xi + θi∆xi n + ∆xn i(∆x), i ∂xi
lim αi(∆x) = 0 ∀i = 1, 2, ..., n trong ®ã . Do vËy , ®Þnh lý ®î høng minh. ∆x f (x, y, z) NhËn xt 1.7. T rong trêng hîp hµm 3 biÕn sè ã ¸ ®¹o hµm riªng liªn t trong l©n (x0, y0, z0) Ën ña ®iÓm , theo ®Þnh lý trªn, ta ã ∂f ∂f ∂f ∆f = (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z + α∆x + β∆y + γ∆z. ρ = p∆2 + ∆2 + ∆2 ǫ = 1 (α∆x+β∆y +γ∆z) §Æt x y z vµ ρ . Khi ®ã, theo bÊt ®¼ng thø Bunhia«pski, ta ã PTIT q 1
(α2 + β2 + γ2)(∆2 + ∆2 + ∆2) x y z |ǫ| = |α∆ = pα2 + β2 + γ2. ρ x + β∆y + γ∆z | ≤ p∆2 + ∆2 + ∆2 x y z Do ®ã lim ǫ = 0 (∆x,∆y,∆z)→0 vµ
α∆x + β∆y + γ∆z = o(ρ). Nh vËy ∂f ∂f ∂f ∆f ≈ (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z + o(ρ). ∆x, ∆y, ∆z Khi ¸ sè kh¸ nhá, ta ã ∂f ∂f ∂f ∆f ≈ (x (x (x ∂x
0, y0, z0)∆x + ∂y 0, y0, z0)∆y + ∂z 0, y0, z0)∆z. (1.1) 17 VÝ d 1.8. Dïng vi ph©n, tÝnh xÊp xØ gi¸ trÞ biÓu thø sau: 1, 02 S = arctan . 0, 95 Gi¶i: Tõ 1 + 0, 02 S = arctan 1 − 0,05
x0 = 1, y0 = 1, ∆x = 0, 02, ∆y = −0, 05 f (x, y) = arctan x ta ®Æt vµ y . Khi ®ã ∂f −y ∂f x = , = . ∂x x2 + y2 ∂y x2 + y2 Theo «ng thø (1.1) ho hµm sè ã 2 biÕn, ta ã ∂f ∂f ∆f ≈ (x (x ∂x 0, y0)∆x + ∂y 0, y0)∆y. Do ®ã S = ∆f + f (x0, y0) ∂f ∂f ≈ (x (x ∂x
0, y0)∆x + ∂y 0, y0)∆y + f(x0, y0) 1.0, 02 + 1.0, 05 = f (1, 1) + 2 π = + 0, 035 4 = 0, 82rad. PTIT 1.6. §¹o hµm theo ph¬ng d ∈ Rn Cho v t¬ . NÕu tån t¹i giíi h¹n (h÷u h¹n) f (¯ x + λd) − f(¯x) lim , λ→0 λ d f ¯ x th× giíi h¹n nµy ®î gäi lµ ®¹o hµm theo ph¬ng ña hµm t¹i ®iÓm vµ ®î ký hiÖu bëi Ddf (¯ x). Ddf (¯ x) f (x, y, z) = 2x + 3y + z2 VÝ d 1.9. T×m ®¹o hµm theo ph¬ng ña hµm sè , trong ®ã d = (1, 2, 0), ¯ x = (3, −1, 1) Gi¶i: 18 Ddf (¯ x) Theo ®Þnh nghÜa, ®¹o hµm ®î x¸ ®Þnh bëi «ng thø f (¯ x + λd) − f(¯x) Ddf (¯ x) = lim λ→0 λ
f (1 + 3λ, −1 + 2λ, 1) − f(3, −1, 1) = lim λ→0 λ
2(1 + 3λ) + 3(−1 + 2λ) + 12 − (2.3 + 3.(−1) + 12) = lim λ→0 λ = 12. Dùa vµo ®Þnh nghÜa, ta ã nhËn xt sau: {e1, e2, ..., en} Rn f (x) NhËn xt 1.10. Gi¶ sö lµ mét hÖ ¬ së trù huÈn trong , hµm sè tån t¹i D ¯ x ∈ D ¸ ®¹o hµm riªng trªn vµ . Khi ®ã ∂f De f (¯ x) = (¯ x) ∀i = 1, 2, ..., n. i ∂xi 1.7. Quan hÖ gi÷a ®¹o hµm theo ph¬ng vµ ®¹o hµm riªng f : D ⊆ Rn → R ¯ x ∈ D Cho hµm kh¶ vi t¹i ®iÓm . Khi ®ã, ®¹o hµm theo ph¬ng
d = (d1, d2, ..., dn) ®î x¸ ®Þnh bëi «ng thø: ∂f ∂f ∂f Ddf (¯ x) = (¯ x)d (¯ x)d (¯ x)d ∂x 1 + 2 + ... + n. (1.2) 1 ∂x2 ∂xn f ¯ x Chøng minh: Theo ®Þnh nghÜa, hµm sè kh¶ vi t¹i ®iÓm hay ∆f = A1∆x + A + ... + A + α + α + ... + α , 1 2∆x2 n∆xn 1∆x1 2∆x2 n∆xn ∆f = f (¯
x + ∆x) − f(¯x), Ai = ∂f (¯x), lim αi = 0 i = 1, 2, ..., n trong ®ã ∂x víi mäi . Dïng «ng i ∆x→0 ∆x = λdi thø trªn víi i , ta ã PTIT f (¯ x + λd) − f(¯x) Ddf (¯ x) = lim ∆x→0 λ
= lim (A1d1 + ... + Andn + α1d1 + ... + αndn) ∆x→0 ∂f ∂f ∂f = (¯ x)d (¯ x)d (¯ x)d ∂x 1 + 2 + ... + n. 1 ∂x2 ∂xn d = (−1, 3) ¯ x = (e, e2) VÝ d 1.11. T×m ®¹o hµm theo ph¬ng t¹i ®iÓm ña hµm sè f (x, y) = ln(x2 + y). Gi¶i. TÝnh ¸ ®¹o hµm theo ph¬ng ∂f 2x = , ∂x x2 + y ∂f 1 = . ∂y x2 + y 19 Khi ®ã ∂f 2x 1 (¯ x) = (¯ x) = , ∂x x2 + y e ∂f 1 1 (¯ x) = (¯ x) = . ∂y x2 + y 2e2 Theo «ng thø (1.2), ta ã ∂f ∂f Ddf (¯ x) = (¯ x)d (¯ x)d ∂x 1 + ∂y 2 1 1 = (−1) + 3 e 2e2 3 1 = − . 2e2 e 1.8. §¹o hµm riªng ña hµm hîp f : D ⊆ Rn → Rm g : f (D) → R h = gof : Cho hµm v t¬ vµ hµm sè . Khi ®ã hµm sè D → R ®î x¸ ®Þnh bëi gof (x) = g f (x) g f g ®î gäi lµ hµm hîp ña 2 hµm sè vµ . NÕu ¸ hµm sè , hµm sè trong täa ®é thµnh phÇn f x = (x1, ..., xn) f (x) ña vµ ¸ ®¹o hµm riªng ña hóng liªn t t¹i ®iÓm vµ t¬ng øng. Khi h ®ã ¸ ®¹o hµm riªng ña hµm hîp ®î x¸ ®Þnh bëi «ng thø ∂h ∂g ∂f ∂g ∂f ∂g ∂f = 1 + 2 + ... + m ∂x1 ∂f1 ∂x1 ∂f2 ∂x1 ∂fm ∂x1 ... PTIT ∂h ∂g ∂f ∂g ∂f ∂g ∂f = 1 + 2 + ... + m . ∂x (1.3) n ∂f1 ∂xn ∂f2 ∂xn ∂fm ∂xn Chøng minh: 20



