Bài giảng Giải tích hàm một biến số môn Giải tích | Học viện Công Nghệ Bưu Chính Viễn Thông
Bài giảng Giải tích hàm một biến số môn Giải tích | Học viện Công Nghệ Bưu Chính Viễn Thông
Môn: Giải tích (BAS1203) 18 tài liệu
Trường: Học viện Công Nghệ Bưu Chính Viễn Thông 1.8 K tài liệu
Tác giả:
Preview text:
BỘ THÔNG TIN VÀ TRUYỀN THÔNG
HỌC VIỆN CÔNG NGHỆ BƯU CHÍNH VIỄN THÔNG Bài giảng
GIẢI TÍCH HÀM MỘT BIẾN SỐ
Biên soạn: PGS. TS. Phạm Ngọc Anh PTIT Hà Nội, 2013 CuuDuongThanCong.com
https://fb.com/tailieudientucntt M l Lêi nãi ®Çu 6 Ch¬ng 1. Sè phø vµ giíi h¹n ña d·y sè 7 1.1. Sè thù . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.1. Më ®Çu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 1.1.2. C¸ tÝnh hÊt ña tËp sè thù . . . . . . . . . . . . . . . . . . . . . 9 1.2. Sè phø . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1.2.1. Më ®Çu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1.2.2. §Þnh nghÜa vµ ¸ php to¸n . . . . . . . . . . . . . . . . . . . . . 1 1 1.2.3. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.2.4. BiÓu diÔn h×nh hä . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.2.5. C«ng thø Moive . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.2.6. C¨n bË n ña sè phø . . . . . . . . . . . . . . . . . . . . . . . . 18 1.2.7. C«ng thø Euler . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 1.3. D·y sè thù . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 1.3.1. C¸ kh¸i niÖm ¬ b¶n . . . . . . . . . . . . . . . . . . . . . . . . . 22 1.3.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 1.3.3. C¸ php to¸n vÒ giíi h¹n . . . . . . . . . . . . . . . . . . . . . . 28 PTIT 1.3.4. D·y ®¬n ®iÖu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 1.3.5. Hai d·y kÒ nhau . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 1.3.6. D·y on . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34 1.3.7. D·y Cauhy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37 Bµi tËp h¬ng 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40 Ch¬ng 2. Php tÝnh vi ph©n ña hµm mét biÕn sè 44 2.1. C¸ kh¸i niÖm ¬ b¶n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2.1.1. Hµm mét biÕn thù . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2.1.2. Hµm sè h½n, lÎ . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2.1.3. Hµm sè tuÇn hoµn . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2.1.4. Hµm sè ®¬n ®iÖu . . . . . . . . . . . . . . . . . . . . . . . . . . . 44 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 2.1.5. Hµm sè bÞ hÆn . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 2.1.6. CËn trªn ®óng vµ Ën díi ®óng . . . . . . . . . . . . . . . . . . . 45 2.1.7. Hµm sè ngî . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 2.1.8. Hµm sè hypeboli . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 2.2. Giíi h¹n ña hµm mét biÕn sè . . . . . . . . . . . . . . . . . . . . . . . . 49 2.2.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.2.2. Quan hÖ gi÷a giíi h¹n ña d·y sè vµ giíi h¹n ña hµm sè . . . . . . 52 2.2.3. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52 2.2.4. C¸ php to¸n vÒ giíi h¹n . . . . . . . . . . . . . . . . . . . . . . 55 2.2.5. Giíi h¹n ña hµm ®¬n ®iÖu . . . . . . . . . . . . . . . . . . . . . . 55 2.3. §¹i lîng v« ïng b vµ v« ïng lín . . . . . . . . . . . . . . . . 56 2.3.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56 2.3.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 2.4. Hµm sè liªn t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 2.4.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57 2.4.2. TÝnh hÊt ®¹i sè . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58 2.4.3. Cù trÞ hµm liªn t . . . . . . . . . . . . . . . . . . . . . . . . . . 59 2.4.3. TÝnh hÊt bÞ hÆn . . . . . . . . . . . . . . . . . . . . . . . . . . . 61 2.5. Hµm liªn t ®Òu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 PTIT 2.5.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 2.5.2. Quan hÖ gi÷a tÝnh liªn t vµ liªn t ®Òu . . . . . . . . . . . . . . 62 2.6. §¹o hµm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 2.6.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65 2.6.2. C¸ «ng thø ña ®¹o hµm . . . . . . . . . . . . . . . . . . . . . . 66 2.6.3. §¹o hµm ña mét sè hµm th«ng dng . . . . . . . . . . . . . . . . . 66 2.6.4. §¹o hµm ña hµm ngî . . . . . . . . . . . . . . . . . . . . . . . 66 2.7. Vi ph©n ña hµm sè . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 2.8. §¹o hµm vµ vi ph©n Êp ao . . . . . . . . . . . . . . . . . . . . . . . . . 68 2.8.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68 2.8.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 3 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 2.8.3. C¸ ®Þnh lý vÒ hµm kh¶ vi . . . . . . . . . . . . . . . . . . . . . . 71 2.9. C«ng thø T aylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 2.9.1. §a thø T aylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76 2.9.2. PhÇn d T aylor . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77 2.9.3. C«ng thø khai triÓn T aylor . . . . . . . . . . . . . . . . . . . . . . 78 2.10. Quy t¾ L'Hospital . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80 2.1 1. Hµm låi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 Bµi tËp h¬ng 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82 Ch¬ng 4. Php tÝnh tÝh ph©n 96 4.1. TÝh ph©n x¸ ®Þnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 4.1.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96 4.1.2. Y nghÜa h×nh hä . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97 4.1.3. Tæng Darboux trªn vµ díi . . . . . . . . . . . . . . . . . . . . . . 97 4.1.4. C¸ ®iÒu kiÖn kh¶ tÝh . . . . . . . . . . . . . . . . . . . . . . . . 99 4.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 4.3. Mèi quan hÖ gi÷a nguyªn hµm vµ tÝh ph©n x¸ ®Þnh . . . . . . . . . . . . 104 4.3.1. Nguyªn hµm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104 4.3.2. Hµm theo Ën trªn . . . . . . . . . . . . . . . . . . . . . . . . . . . 105 4.3.3. C«ng thø Newton-Leibnitz . . . . . . . . . . . . . . . . . . . . . . 106 PTIT 4.4. C¸ ph¬ng ph¸p tÝnh tÝh ph©n . . . . . . . . . . . . . . . . . . . . . . . 107 4.4.1. Ph¬ng ph¸p ®æi biÕn . . . . . . . . . . . . . . . . . . . . . . . . . 107 4.4.2. Ph¬ng ph¸p tÝh ph©n tõng phÇn . . . . . . . . . . . . . . . . . . . 1 10 4.5. TÝh ph©n ña hµm ph©n thø h÷u tû . . . . . . . . . . . . . . . . . . . . . 1 1 1 4.5.1. C¸ d¹ng ¬ b¶n . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 1 4.5.2. Ph¬ng ph¸p ®ång nhÊt hÖ sè . . . . . . . . . . . . . . . . . . . . . 1 13 4.6. TÝh ph©n ña hµm lîng gi¸ . . . . . . . . . . . . . . . . . . . . . . . . 1 14 4.7. Mét vµi øng dng ña tÝh ph©n . . . . . . . . . . . . . . . . . . . . . . . . 1 17 4.7.1. TÝnh diÖn tÝh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 17 4.7.2. TÝnh ®é dµi ®êng ong . . . . . . . . . . . . . . . . . . . . . . . . 121 4.7.3. TÝnh thÓ tÝh ña vËt thÓ . . . . . . . . . . . . . . . . . . . . . . . . 123 4 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 4.7.4. TÝnh diÖn tÝh mÆt trßn xoay . . . . . . . . . . . . . . . . . . . . . 125 4.8. TÝh ph©n suy réng víi Ën v« h¹n . . . . . . . . . . . . . . . . . . . . . . 127 4.8.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127 4.8.2. C¸ ®iÒu kiÖn héi t ña tÝh ph©n suy réng víi Ën v« h¹n . . . . . 129 4.8.3. Héi t tuyÖt ®èi vµ b¸n héi t . . . . . . . . . . . . . . . . . . . . . 132 4.9. TÝh ph©n suy réng víi Ën h÷u h¹n . . . . . . . . . . . . . . . . . . . . . 133 4.9.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133 4.9.2. Quan hÖ gi÷a hai lo¹i tÝh ph©n suy réng . . . . . . . . . . . . . . . 135 4.9.3. C¸ ®Þnh lý héi t . . . . . . . . . . . . . . . . . . . . . . . . . . . 135 Bµi tËp h¬ng 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138 Ch¬ng 4. Chuçi sè vµ huçi hµm 146 4.1. Chuçi sè . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146 4.1.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146 4.1.2. C¸ ®iÒu kiÖn héi t . . . . . . . . . . . . . . . . . . . . . . . . . . 147 4.1.3. C¸ tÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148 4.2. Chuçi sè d¬ng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 4.2.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149 4.2.2. C¸ tiªu huÈn héi t . . . . . . . . . . . . . . . . . . . . . . . . . 149 PTIT 4.3. Chuçi ®an dÊu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154 4.3.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154 4.3.2. DÊu hiÖu héi t . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155 4.4. Chuçi hµm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 4.4.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156 4.4.2. C¸ ®iÒu kiÖn héi t ®Òu . . . . . . . . . . . . . . . . . . . . . . . 157 4.4.3. TÝnh hÊt ña huçi hµm héi t ®Òu . . . . . . . . . . . . . . . . . 161 4.5. Chuçi lòy thõa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164 4.5.1. §Þnh nghÜa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164 4.5.2. TÝnh hÊt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165 4.5.3. Quy t¾ t×m b¸n kÝnh héi t . . . . . . . . . . . . . . . . . . . . . 165 4.5.4. TÝnh héi t ®Òu ña huçi lòy thõa . . . . . . . . . . . . . . . . . . 167 5 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 4.5.5. Khai triÓn mét hµm sè thµnh huçi lòy thõa . . . . . . . . . . . . . 169 4.6. Chuçi Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 4.6.1. Chuçi lîng gi¸ . . . . . . . . . . . . . . . . . . . . . . . . . . . 171 2π 4.6.2. Khai triÓn Fourier ña hµm sè ã hu kú . . . . . . . . . . . . . 173 2T 4.6.3. Khai triÓn Fourier ña hµm sè ã hu kú . . . . . . . . . . . . . 175 4.6.4. Khai triÓn Fourier ña hµm sè x¸ ®Þnh trªn ®o¹n, kho¶ng . . . . . . 177 Bµi tËp h¬ng 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182 Tµi liÖu tham kh¶o . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 190 PTIT 6 CuuDuongThanCong.com
https://fb.com/tailieudientucntt Lêi nãi ®Çu Gi¶i tÝh hµm mét biÕn sè lµ mét m«n hä ®ang gi÷ mét vÞ trÝ quan träng trong ¸ lÜnh vù øng dng vµ trong hÖ thèng ¸ m«n hä ña Hä viÖn C«ng nghÖ Bu hÝnh ViÔn th«ng. C¸ kiÕn thø vµ ph¬ng ph¸p ña gi¶i tÝh hµm mét biÕn sè ®· hç trî hiÖu qu¶ ¸ kiÕn thø nÒn t¶ng ho ¸ m«n hä gi¶i tÝh hµm nhiÒu biÕn, vËt lý, x¸ suÊt thèng kª, to¸n kü thuËt, to¸n rêi r¹ vµ ¸ m«n huyªn ngµnh kh¸. Bµi gi¶ng "Gi¶i tÝh hµm mét biÕn sè" ®î biªn so¹n l¹i theo h¬ng tr×nh qui ®Þnh ña Hä viÖn ho hÖ ®¹i hä huyªn ngµnh §iÖn tö-ViÔn th«ng-C«ng nghÖ th«ng tin víi h×nh thø ®µo t¹o theo tÝn hØ. Do ®èi tîng sinh viªn rÊt ®a d¹ng víi tr×nh ®é ¬ b¶n kh¸ nhau, hóng t«i ®· è g¾ng t×m ¸h tiÕp Ën ®¬n gi¶n vµ hîp lý ®Ó tr×nh bµy néi dung theo ph¬ng ph¸p dÔ hiÓu h¬n, nh»m gióp ho sinh viªn n¾m ®î ¸ kiÕn thø ¬ b¶n nhÊt. Gi¸o tr×nh ®î hia thµnh 4 h¬ng. Ch¬ng 1 dµnh ho phÇn sè phø vµ giíi h¹n ña d·y sè. Ch¬ng 2 vµ 3 bao gåm ¸ néi dung vÒ hµm liªn t, php tÝnh vi ph©n vµ php tÝnh vi ph©n ña hµm mét biÕn. Ch¬ng 4 tr×nh bµy vÒ huçi sè, huçi hµm, huçi lòy thõa vµ huçi Fourier . C¸ kh¸i niÖm vµ «ng thø ®î tr×nh bµy t¬ng ®èi ®¬n gi¶n vµ ®î minh häa b»ng nhiÒu vÝ d víi ¸ h×nh PTIT vÏ sinh ®éng. C¸ høng minh khã ®î lî bít ã hän lä ®Ó gióp ho gi¸o tr×nh kh«ng qu¸ ång kÒnh nhng vÉn ®¶m b¶o ®î ®Ó tiÖn ho sinh viªn hä tËp huyªn s©u vµ tra øu ph v qu¸ tr×nh hä tËp ¸ m«n hä kh¸. Cuèi mçi h¬ng hä ®Òu ã ¸ bµi tËp ®Ó sinh viªn tù gi¶i nh»m gióp ¸ em hiÓu s©u s¾ h¬n vÒ lý thuyÕt vµ rÌn luyÖn kü n¨ng thù hµnh. T¸ gi¶ hy väng r»ng gi¸o tr×nh nµy ã Ýh ho ¸ em sinh viªn vµ ¸ b¹n ®ång nghiÖp trong qu¸ tr×nh hä tËp vµ gi¶ng d¹y vÒ m«n hä gi¶i tÝh hµm mét biÕn sè. T¸ gi¶ òng ¸m ¬n mäi ý kiÕn gãp ý ®Ó gi¸o tr×nh bµi gi¶ng nµy ®î hoµn thiÖn h¬n nh»m n©ng ao hÊt lîng d¹y vµ hä m«n hä nµy . 2/9/2013, T¸ gi¶: PGS. TS. Ph¹m Ngä Anh CuuDuongThanCong.com
https://fb.com/tailieudientucntt 7 Ch¬ng 1. Sè thù, sè phø vµ giíi h¹n ña d·y sè 1.1. Sè thù 1.1.1. Më ®Çu Nh¾ l¹i mét sè tËp hîp quen thué + TËp ¸ sè tù nhiªn N = {0, 1, 2, ...}. + TËp ¸ sè nguyªn Z = {0, ±1, ±2, ...}. + TËp ¸ sè h÷u tû p
Q = { : p ∈ Z, q ∈ N \ {0}}. q N ⊂ Z ⊂ Q T a ã . Q Trong tËp ¸ sè h÷u tû ã thÓ thù hiÖn ¸ php to¸n éng, trõ, nh©n vµ 0 Q ≤, ≥, = hia ho sè kh¸ . Trong ßn ã quan hÖ thø tù . Theo ng«n ng÷ ®¹i Q sè, ïng víi ¸ php to¸n vµ quan hÖ thø tù ®· ho lµ mét trêng ®î s¾p thø tù. Q Tuy nhiªn, tõ l©u ngêi ta ®· thÊy tËp ha ®Çy ®ñ. Ch¼ng h¹n, kh«ng ã 1 sè h÷u tû nµo biÓu diÔn ®é dµi ®êng ho ña mét h×nh vu«ng ã ¹nh b»ng 𠮬n vÞ, biÓu diÔn sè lµ tû sè gi÷a ®é dµi ña mét ®êng trßn vµ ®êng kÝnh ña PTIT nã. x x = p p, q ∈ Z, q 6= 0 Mét sè h÷u tû , b»ng ¸h viÕt q víi vµ thù hiÖn php p q hia ho , ta ã thÓ ®ång nhÊt víi d·y mµ sau ®©y sÏ ®î gäi lµ sè thËp ph©n: x = x0, x1x2... x0 ∈ Z
x1, x2, ... ∈ {0, 1, 2, ..., 9} trong ®ã vµ . Sè thËp ph©n nµy hoÆ h÷u h¹n, k xn = 0 ∀n > k tø lµ tån t¹i sè sao ho hay x = x0, x1x2...xk, p hoÆ v« h¹n tuÇn hoµn víi hu kú , tø lµ
x = x0, x1x2...xk xk x ...x x x ...x ... x x ...x . 1 k2 kp k1 k2 kp k1 k2 kp | {z } | {z } | {z } p p p CuuDuongThanCong.com
https://fb.com/tailieudientucntt 8 HiÓn nhiªn x x x = x 1 y 0 + + ... + , 10 10k hoÆ x x 1 x = x 1 y 0 + + ... + + x x ...x . . 10 10k k1 k2 kp 10k(1 − 10−p) Ngî l¹i, mäi sè thËp ph©n h÷u h¹n hay v« h¹n tuÇn hoµn ®Òu ®î biÓu diÔn Q díi d¹ng mét sè h÷u tû. Nh vËy , ta ã thÓ ®ång nhÊt tËp ¸ sè h÷u tû víi tËp ¸ sè thËp ph©n h÷u h¹n hay v« h¹n tuÇn hoµn. Mét ¸h tæng qu¸t, ta oi mäi sè thËp ph©n v« h¹n kh«ng tuÇn hoµn lµ mét sè míi vµ gäi lµ sè v« tû. TËp ¸ sè h÷u tû vµ v« tû gäi lµ tËp ¸ sè thù, ký R R hiÖu lµ . Mçi phÇn tû ña ®î gäi lµ mét sè thù. Cho sè thù x = x0, x1x2...
x0 ∈ Z, x1, x2, ... ∈ {0, 1, 2, ..., 9}. víi Khi ®ã x0 x [x] ®î gäi lµ phÇn nguyªn ña , ký hiÖu lµ , xn n x ®î gäi lµ phÇn thËp ph©n thø ña . m NÕu tån t¹i sè nguyªn sao ho m ≤ x < m + 1 PTIT m x ⌊x⌋ th× ®î gäi lµ sµn ña , ký hiÖu . m NÕu tån t¹i sè nguyªn sao ho m − 1 < x ≤ m m x ⌈x⌉ th× ®î gäi lµ trÇn ña , ký hiÖu . x, y ∈ R Gi¶ sö x = x0, x1x2... y = y0, y1y2... vµ x < y x0 < y0 k x0 = y0, ..., xk = yk T a viÕt nÕu hoÆ tån t¹i sao ho vµ xk+1 < yk+1 x = y xi = yi ∀i = 0, 1, ... . Hai sè b»ng nhau nÕu 1.1.2. C¸ tÝnh hÊt ña tËp sè thù + TÝnh s¾p thø tù CuuDuongThanCong.com
https://fb.com/tailieudientucntt 9 a, b a b a ≤ b Cho hai sè thù . Khi ®ã, vµ so s¸nh ®î víi nhau, tø lµ hoÆ a > b
a = a0, a1a2..., b = b0, b1b2... a 6= b . ThËt vËy , gi¶ sö . NÕu khi ®ã tån t¹i k ∈ N sao ho a0 = b0, ..., ak = bk nhng ak+1 < bk+1 ak+1 > bk+1. hoÆ a < b a > b Nh vËy hoÆ . + TÝnh trï mËt a, b a < b r ∈ Q a < r < b Cho 2 sè thù vµ . Tån t¹i sè h÷u tû sao ho . ThËt
a = a0, a1a2..., b = b0, b1b2... a < b k ∈ N vËy , ta gi¶ sö , tõ suy ra tån t¹i sao ho
a0 = b0, ..., ak = bk, ak+1 < bk+1. Khi ®ã, ta hän sè h÷u tû lµ a0, a1...akbk+1 b ∈ Q nÕu r = 1 (a b / 2
0, a1...akak+19 + a0, a1...akbk+10) ∈ Q, nÕu a < r < b tháa m·n . + TÝnh ®Çy ®ñ A ⊆ R Cho . Khi ®ã PTIT m ∈ R A m ≤ a ∀a ∈ A m ®î gäi lµ Ën díi ña nÕu . NÕu lµ Ën díi lín A m A nhÊt trong ¸ Ën díi ña th× ®î gäi lµ Ën díi ®óng ña , ký hiÖu m = inf A. M ∈ R A a ≤ M ∀a ∈ A M ®î gäi lµ Ën trªn ña nÕu . NÕu lµ Ën trªn nhá A m A nhÊt trong ¸ Ën trªn ña th× ®î gäi lµ Ën trªn ®óng ña , ký hiÖu M = sup A. sup A, inf A Theo tÝnh s¾p thø tù ña tËp sè thù, nªn nÕu tån t¹i th× lµ duy nhÊt. TÝnh tån t¹i ®î thõa nhËn bëi nguyªn lý ®ñ díi ®©y . R §Þnh lý 1.1. Mäi tËp on kh¸ rçng ña tËp sè thù ã Ýt nhÊt mét Ën trªn (t¬ng øng mét Ën díi) th× tån t¹i duy nhÊt Ën trªn ®óng (t¬ng øng Ën díi ®óng). CuuDuongThanCong.com
https://fb.com/tailieudientucntt 10 Q Q Chó ý r»ng tËp ¸ sè h÷u tû kh«ng ã tÝnh ®Çy ®ñ. VÝ d trong ã tËp A = {x : x2 < 2} Q kh«ng ã Ën trªn ®óng trong . + C¸ tËp sè thù th«ng dng. R - §o¹n trªn
[a, b] = {x ∈ R : a ≤ x ≤ b}. R - Nöa ®o¹n trªn
[a, b) = {x ∈ R : a ≤ x < b}, [a, +∞) = {x ∈ R : a ≤ x}. R - Nöa kho¶ng trªn
(a, b] = {x ∈ R : a < x ≤ b}, (−∞, b] = {x ∈ R : x ≤ b}. R - Kho¶ng trªn
(a, b) = {x ∈ R : a < x < b}, R = (−∞, +∞). a ∈ R ǫ > 0 - Cho vµ , kho¶ng
(a − ǫ, a + ǫ) = {x ∈ R : |x − a| < ǫ} = Bǫ(a) a ®î gäi lµ mét l©n Ën ña ®iÓm . 1.2. Sè phø PTIT 1.2.1. Më ®Çu R TËp sè thù ®· rÊt phong phó, xong nÕu ta xt ph¬ng tr×nh bË 2 ax2 + bx + c = 0, a 6= 0, a, b, c ∈ R ∆ := b2 − 4ac < 0 ë ®©y víi , th× ph¬ng tr×nh sÏ v« nghiÖm R trªn . §Ó më réng líp nghiÖm ña ph¬ng tr×nh nµy , ta më réng tËp sè thù C i thµnh tËp sè phø (ký hiÖu: ). Muèn x©y dùng tËp sè phø, ta quan t©m tíi sè i2 = −1 i tháa m·n , sè kh«ng ph¶i lµ sè thù vµ ®î gäi lµ ®¬n vÞ ¶o. 1.2.2. §Þnh nghÜa vµ ¸ php to¸n
• TËp sè phø lµ mét tËp hîp x¸ ®Þnh bëi
C := {z = a + bi : a, b ∈ IR, i2 = −1}. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 1 1 • z := a + bi a, b ∈ R z Cho sè phø víi (ßn gäi lµ d¹ng hÝnh t¾ ña ), khi ®ã a z z z ®î gäi lµ phÇn thù ña , ký hiÖu t¾t bëi Re (Real of ). b z z z ®î gäi lµ phÇn ¶o ña , ký hiÖu t¾t bëi Im (Image of ). √a2 + b2 z |z| ®î gäi lµ m«®un (ßn gäi lµ ®é dµi) ña , ký hiÖu t¾t bëi . a − bi z ¯ z Sè phø ®î gäi lµ sè phø liªn hîp ña sè phø , ký hiÖu t¾t bëi . −a − bi z Sè phø ®î gäi lµ sè phø ®èi ña sè phø . • x = x1 + x2i, y = y1 + y2i Cho 2 sè phø díi d¹ng hÝnh t¾ . C¸ php to¸n C trªn tËp sè phø ®î x¸ ®Þnh bëi ¸ quy t¾ sau: x + y = (x1 + y1) + (x2 + y2)i -Quy t¾ éng: .
x − y = (x1 − y1) + (x2 − y2)i -Quy t¾ trõ: .
x.y = (x1y1 − x2y2) + (x1y2 + x2y1)i -Quy t¾ nh©n: . -Quy t¾ b»ng nhau: x1 = y1 x = y ⇔ x2 = y2 1.2.3. TÝnh hÊt
(x + y) + z = x + (y + z) ∀x, y, z ∈ C. a) TÝnh hÊt kÕt hîp (víi php éng):
(xy)z = x(yz) ∀x, y, z ∈ C. b) TÝnh hÊt kÕt hîp (víi php nh©n): x + y = y + x ∀x, y ∈ C ) TÝnh hÊt giao ho¸n: . x(y+z) = xy+xz ∀x, y, z ∈ d) TÝnh hÊt ph©n phèi ña php nh©n víi php éng: C. PTIT x+ y = ¯ x+ ¯ y ∀x, y ∈ C e) . x.y = ¯ x.¯ y ∀x, y ∈ C f) . x.¯ x = |x|2 ∀x ∈ C g) .
(x) = ¯x ∀x, y ∈ C, y 6= 0 h) y ¯ y .
|x| ≥ 0 ∀x ∈ C, |x| = 0 ⇔ x = 0 i) .
|x.y| ≤ |x|.|y| ∀x, y ∈ C j) .
|x + y| ≤ |x| + |y| ∀x, y ∈ C k) . Chøng minh BiÓu diÔn ¸ sè phø díi d¹ng hÝnh t¾ vµ dïng ®Þnh nghÜa 1.2. C VÝ d 1.2. Gi¶i vµ biÖn luËn ph¬ng tr×nh sau trªn tËp ¸ sè phø ax2 + bx + c = 0 a 6= 0. víi CuuDuongThanCong.com
https://fb.com/tailieudientucntt 12 Gi¶i ∆ := b2 − 4ac Cã . ∆ = 0 x1 = x2 = −b. -NÕu , th× ph¬ng tr×nh ã nghiÖm kp 2a ∆ > 0 -NÕu , th× ph¬ng tr×nh ã 2 nghiÖm thù ph©n biÖt √ −b+ ∆ x1,2 = . 2a √ ∆ < 0
∆ = −(−∆) = (i −∆)2 -NÕu , th× . Khi ®ã, ph¬ng tr×nh ã 2 nghiÖm phø ph©n biÖt √ −b+i −∆ x1,2 = . 2a z = a−bi a, b ∈ R, b 6= 0 Im(z), Re(z), |z|. VÝ d 1.3. Cho sè phø a+bi víi . H·y tÝnh Gi¶i a − bi Nh©n ¶ tö sè vµ mÉu sè víi , ta ã (a − bi)2 z = a2 − b2i2 a2 − b2 − 2abi = a2 + b2 a2 − b2 −2ab = + .i a2 + b2 a2 + b2 p (z) = a2−b2 (z) = −2ab |z| = Re2(z) + Im2(z) = 1 Khi ®ã, Re a2+b2 , Im a2+b2 vµ . 1 2 VÝ d 1.4. BÊt ®¼ng thø Cauhy -Shwarz PTIT a1, a2, ..., an b1, b2, ..., bn Cho ¸ sè phø vµ . Khi ®ã n n n X X X | ai.bi|2 ≤ |ai|2. |bi|2. i=1 i=1 i=1 Chøng minh §Æt n n n X X X a = |ai|2, b = |bi|2, c = ai. ¯ bi. i=1 i=1 i=1 1 21.8.1789-23.5.18 57 , nhµ T o¸n hä ngêi Ph¸p Augustin Louis Cauhy sinh ra t¹i Paris ã h¬n 800 «ng tr×nh nghiªn øu liªn quan ®Õn tÊt ¶ ¸ lÜnh vù T o¸n hä, ®Æ biÖt lµ hµm hØnh h×nh, ph¬ng tr×nh vi ph©n, lý thuyÕt nhãm vµ ®¹i sè tuyÕn tÝnh. ¤ng òng ã nh÷ng «ng tr×nh vÒ thiªn v¨n vµ vËt lý, trong ®ã «ng ®Æt ¬ së to¸n hä ho lý thuyÕt ®µn håi. 2 25.1.1843-30.1 1.1 92 1, nhµ T o¸n hä ngêi §ø Hermann Shwarz hä T o¸n vµ Hãa ë Hä viÖn «ng nghiÖp Berlin, ë ®Êy «ng lµ hä trß ña Weierstrass. C¸ «ng tr×nh ña «ng liªn quan ®Õn hµm gi¶i tÝh, ¸nh x¹ b¶o gi¸, ph¬ng tr×nh ®¹o hµm riªng, lý thuyÕt thÕ vµ mÆt. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 13 b = 0 b1 = b2 = ... = bn NÕu th× , th× bÊt ®¼ng thø lu«n ®óng. b > 0 NÕu , th× theo tÝnh hÊt 1.3.e) vµ g), ta ã n n X X 0 ≤ |b.ai − c.bi|2 = (b.ai − c.bi)(b.ai − c.bi) i=1 i=1 n X =
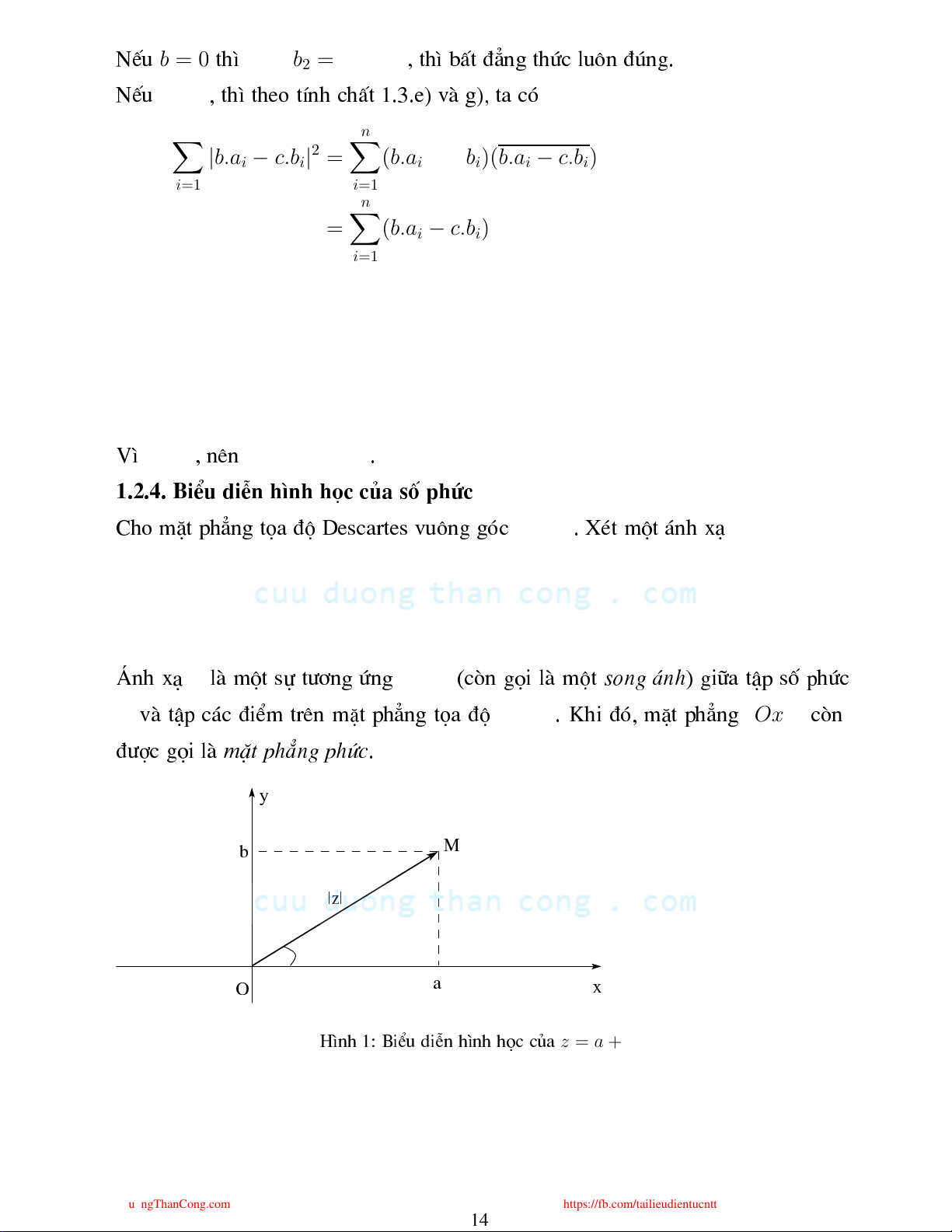
(b.ai − c.bi)(b.¯ai − c.¯bi) i=1 n n n n X X X X = b2 |ai|2 − bc ai.¯bi − bc ¯ai.bi + |c|2 |bi|2 i=1 i=1 i=1 i=1 = b2.a − b|c|2 = b(ab − |c|2). b > 0 a.b − |c|2 ≥ 0 2 V× , nªn . 1.2.4. BiÓu diÔn h×nh hä ña sè phø (Oxy) Cho mÆt ph¼ng täa ®é Desartes vu«ng gã . Xt mét ¸nh x¹ f : C → (Oxy)
z = a + bi 7→ f(z) = M(a; b) ∈ (Oxy) f 1 − 1 Ánh x¹ lµ mét sù t¬ng øng (ßn gäi lµ mét song ¸nh) gi÷a tËp sè phø C (Oxy) (Oxy) vµ tËp ¸ ®iÓm trªn mÆt ph¼ng täa ®é . Khi ®ã, mÆt ph¼ng ßn PTIT ®î gäi lµ mÆt ph¼ng phø. y M b |z| ϕ a x O z = a + bi H×nh 1: BiÓu diÔn h×nh hä ña CuuDuongThanCong.com
https://fb.com/tailieudientucntt 14 z ∈ C z2 ∈ iR z VÝ d 1.5. Cho tháa m·n z+i . H·y biÓu diÔn h×nh hä ña trªn mÆt (Oxy) ph¼ng phø . Gi¶i z = x + yi Gi¶ sö , khi ®ã z2 z2(¯ z − i) 1 = = .(x + yi)2(x − yi − i) z + i |z + i|2 |z + i|2 z2 ∈ iR Re z2 = 0 Gi¶ thiÕt ho z+i , ®iÒu ®ã ã nghÜa r»ng z+i hay
Re (x+yi)2(x−yi−i) = 0 ↔ x(x2−y2+2xy(y+1) = 0 ↔ x(x2+y2+2y) = 0. x = 0 x2 + (y + 1)2 = 1 M(x, y) Oy Hay hoÆ . Khi ®ã, ®iÓm n»m trªn tr hoÆ I(0, −1) R = 1 2 n»m trªn ®êng trßn t©m b¸n kÝnh . √ z OM = a2 + b2 = |z| Dùa vµo biÓu diÔn h×nh hä ña , ta ã vµ x = |z|. cos ϕ y = |z|. sin ϕ. z Do vËy , sè phø ã thÓ ®î viÕt l¹i r»ng z = |z|.(cos ϕ + i sin ϕ), PTIT ϕ z Arg(z) z ∈ C gäi lµ Agumen ña vµ ®î ký hiÖu bëi . Nh vËy víi mäi
z = |z|.[cos Arg(z) + i sin Arg(z)] z biÓu thø nµy ®î gäi lµ d¹ng lîng gi¸ ña .
Arg(z) ã mét vµi tÝnh hÊt sau: ϕ z ϕ + k2π (k ∈ Z) 1) NÕu lµ mét Agumen ña sè phø , th× òng lµ Agumen z Arg(z) 2π ña . Nh vËy ã thÓ sai kh¸ sè lÇn . Arg(¯ z) = −Arg(z) ∀z ∈ C 2) . z = |z|.(cos ϕ + i sin ϕ) ¯ z Chøng minh Gi¶ sö , theo ®Þnh nghÜa ña ta ã ¯
z = |z|.(cos ϕ − i sin ϕ) = |z|.[cos(−ϕ) + i sin(−ϕ)]. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 15 Arg(¯ z) = −ϕ = −Arg(z) 2 Do vËy .
Arg(z1.z2) = Arg(z1) + Arg(z2) ∀z1, z2 ∈ C 3) . Dïng quy n¹p to¸n hä, ta ã tæng qu¸t nh sau: Arg(zn) = n.Arg(z) ∀z ∈ C.
z1 = |z1|.(cos ϕ1 + i sin ϕ1), z2 = |z2|.(cos ϕ2 + i sin ϕ2) Chøng minh Gi¶ sö . Khi ®ã
z1.z2 = |z1|.|z2|.(cos ϕ1 + i sin ϕ1).(cos ϕ2 + i sin ϕ2)
= |z1|.|z2|.[cos ϕ1 cos ϕ2 − sin ϕ1 sin ϕ2 + i(sin ϕ1 cos ϕ2 + cos ϕ1 sin ϕ2)]
= |z1|.|z2|.[cos(ϕ1 + ϕ2) + i sin(ϕ1 + ϕ2)], Arg(z1 + z2) = ϕ1 + ϕ2 2 ta ã . B»ng ¸h høng minh t¬ng tù nh tÝnh hÊt 3), ta ã ¸ tÝnh hÊt sau: Arg(1) = −Arg(z) ∀z ∈ C 4) ¯ z .
Arg(z1 ) = Arg(z1) − Arg(z2) ∀z1, z2 ∈ C 5) z . 2
|z1 + z2| ≤ |z1| + |z2| ∀z1, z2 ∈ C Arg(z1) = 6) . DÊu '=' x¶y ra khi vµ hØ khi Arg(z2). a, b, c ∈ C
|a| = |b| = |c| = 1, a 6= c, b 6= c VÝ d 1.6. Cho sao ho . Chøng minh PTIT r»ng: c − b 1 b Arg = Arg . c − a 2 a (1.1) Gi¶i Tõ tÝnh hÊt 5), ta ã c − b 1 b c − b a (1.1) ⇔ Arg − Arg = 0 ⇔ Arg[( )2. ] = 0. c − a 2 a c − a b
Arg(z) = 0 ↔ z ∈ R ↔ ¯z = z z = ( c−b )2.a Tõ nhËn xt , ta ®Æt c−a b c − b a c − b ¯a 1 − 1 2 1 b − c a2 b c − b 2a ¯ z = ( )2. = ( )2. = c b a = = = z. c − a b c − a ¯b 1 − 1 1 a − c b a c − a b c a b 2 1.2.5. C«ng thø Moivre CuuDuongThanCong.com
https://fb.com/tailieudientucntt 16 z z = |z|(cos ϕ + i sin ϕ) Cho sè phø ®î biÓu diÔn díi d¹ng lîng gi¸ , ta 3 ã «ng thø Moivre
zn = |z|n(cos nϕ + i sin nϕ) ∀n ∈ N∗, z ∈ C. (1.2) Chøng minh n = 1 -Víi , (1.2) lu«n ®óng.
n = k zk = |z|k(cos kϕ + i sin kϕ) -Gi¶ sö (1.2) ®óng víi , . Khi ®ã,
zk+1 = zk.z = |z|k(cos kϕ + i sin kϕ).|z|(cos ϕ + i sin ϕ) = |z|k+1[cos kϕ cos ϕ −
sin kϕ sin ϕ+i(sin kϕ cos ϕ+cos kϕ sin ϕ)] = |z|k+1[cos(k+1)ϕ+i sin(k+1)ϕ]. n = k + 1 §iÒu nµy ã nghÜa r»ng (1.2) ®óng víi . Theo quy n¹p T o¸n hä, (1.2) 2 ®î høng minh. sin 10x cos 10x sin x, cos x VÝ d 1.7. H·y biÓu diÔn vµ theo ¸ hµm . Gi¶i n = 10, |z| = 1 Áp dng «ng thø Moivre víi , ta ®¹t ®î
(cos x + i sin x)10 = cos 10x + i sin 10x. (1.3) MÆt kh¸, theo «ng thø khai triÓn Newton n X (a + b)n = Ckan−kbk, n PTIT k=0 ta ã
(cos x + i sin x)10 =C010 cos10 x + iC110 cos9 x sin x + ... + i10C10 10 sin10 x.
= C010 cos10 x − C210 cos8 x sin2 x + ... − C10 10 sin10 x
+ i C110 cos9 x sin x − ... + C910 cos x sin9 x . (1.4) i2n = (−1)n KÕt hîp (1.3), (1.4) víi nhËn xt , ta nhËn ®î
sin 10x = C010 cos10 x − C210 cos8 x sin2 x + ... − C10 10 sin10 x 3 Abraham Moivre lµ mét nhµ T o¸n hä ngêi Anh, sinh ngµy 26.5.1667 t¹i Ph¸p. C¸ «ng tr×nh nghiªn øu ña «ng hñ yÕu liªn quan ®Õn lý thuyÕt x¸ suÊt. ¤ng ®î ã thÓ dî xem nh lµ ngêi ®i tiªn phong trong lÜnh vù T o¸n hä tµi hÝnh vµ T o¸n hä øng dng vµo nghiªn øu d©n sè. ¤ng mÊt ngµy 27.1 1.1754. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 17 vµ
cos 10x = C110 cos9 x sin x − C310 cos7 x sin3 x + ... + C910 cos x sin9 x. 2 n 1.2.6. C¨n bË ña mét sè phø z z = |z|(cos ϕ + i sin ϕ) Cho sè phø biÓu diÔn díi d¹ng lîng gi¸ . C¨n bË n z ña ®î x¸ ®Þnh bëi «ng thø √ p ϕ + k2π ϕ + k2π n z = n |z| cos + i sin k = 0, 1, 2, ..., n − 1, n n víi (1.5) p n
|z| ∈ R+ := {x ∈ R : x ≥ 0}. trong ®ã Chøng minh √
z0 = n z = |z0|(cosϕ0 + i sin ϕ0), zn Gi¶ sö tõ 0 = z suy ra
|z|(cos ϕ + i sin ϕ) = [|z0|(cos ϕ0 + i sin ϕ0)]n. Theo «ng thø Moivre,
|z|(cos ϕ + i sin ϕ) = |z0|n(cos nϕ0 + i sin nϕ0). Do ®ã |z| = |z0|n p |z0| = n |z| cos ϕ = cos nϕ0 ⇔ ϕ , k = 0, 1, .., n 0 = ϕ+k2π − 1. n sin ϕ = sin nϕ0 PTIT −1 C VÝ d 1.8. Dïng «ng thø (1.5), tÝnh ¨n bË 3 ña trªn . Gi¶i −1 = cosπ + i sin π −1 Tõ ta ã ¸ ¨n bË 3 ña lµ π + k2π π + k2π zk = cos + i sin k = 0, 1, 2. 3 3 víi −1 VËy ã ba ¨n bË 3 kh¸ nhau ña lµ √ π π 3 1 k = 0 ⇒ z0 = cos + i sin = + i, 3 3 2 2 3π 3π k = 1 ⇒ z1 = cos + i sin = −1, 3 3 √ 4π 4π 3 1 k = 2 ⇒ z2 = cos + i sin = − − i. 3 3 2 2 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 18 2 4 1.2.7. C«ng thø Euler (¥le)
eαi = cos α + i sin α ∀α ∈ R. VÝ d 1.9. TÝnh tæng n n X X An = cos(a + kb), Bn = sin(a + kb) a, b ∈ R, b / ∈ 2πZ. víi k=1 k=1 Gi¶i Dïng «ng thø Euler , ta ã n n n X X X An + iBn =
[cos(a + kb) + i sin(a + kb)] = ei(a+kb) = eai (eib)k. k=1 k=1 k=1 b / ∈ 2πZ Tõ gi¶ thiÕt , nªn tæng ¸ sè h¹ng ña mét Êp sè nh©n ®î x¸ ®Þnh bëi n n eib X − 1 (eib)k = eib . eib − 1 k=1 Do ®ã, theo «ng thø Euler vµ Moivre, ta ã n eib − 1
(cos(a + b) + i sin(a + b))[(cos b + i sin b)n − 1] An+iBn = ei(a+b) = eib − 1 cos b + i sin b − 1 nb sin nb nb sin nb PTIT = cos(a + b + ). 2 + i sin(a + b + ). 2 . 2 sin b 2 sin b 2 2 V× vËy , nb sin nb nb sin nb A 2 2 n = cos(a + b + ). , B ). . 2 n = sin(a + b + sin b 2 sin b 2 2 b / ∈ 2πZ sin b NhËn xt. Gi¶ thiÕt ho nªn
2 6= 0. Bµi to¸n trªn ßn ã thÓ gi¶i b»ng An Bn sin b → ¸h nh©n hoÆ víi 2 , sau ®ã ph©n tÝh "tÝh tæng". f : C → C VÝ d 1.10. T×m ¸nh x¹ tháa m·n f (z) + zf (−z) = 1 + z z ∈ C. víi mäi (1.6) 4 Nhµ T o¸n hä Thy SÜ Leonhard Euler sinh ngµy 15.4.1707 vµ mÊt ngµy 18.9.1783, «ng nghiªn øu ®Õn tÊt ¸ ¸ lÜnh vù ña T o¸n hä. ¤ng lµm ho gi¶i tÝh bay bæng nhê nh÷ng «ng míi ña php tÝnh vi ph©n vµ tÝh ph©n, «ng ph¸t triÓn h×nh hä vi ph©n vµ ã nh÷ng «ng tr×nh hµng ®Çu vÒ lý thuyÕt sè. ¤ng lµ ngêi s¸ng lËp ra lý thuyÕt liªn ph©n sè, «ng tr×nh ®î «ng bè vµo n¨m 1737. CuuDuongThanCong.com
https://fb.com/tailieudientucntt 19 Gi¶i z −z Thay bëi vµo (1.6), ta ã f (−z) − zf(z) = 1 − z. (1.7) f (−z) Khö tõ (1.7) vµo (1.6), ta nhËn ®î (1 + z2)f (z) = 1 + z2. z = i z = i -NÕu , th× thay vµo ph¬ng tr×nh tr×nh (1.6), ta thÊy ®óng víi mäi f (z) f (i) = α + iβ α, β ∈ R . Kh«ng mÊt tÝnh tæng qu¸t, ta ®Æt víi . z = −i z = −i -NÕu , th× thay vµo (1.6), ta nhËn ®î
f (i) + if (−i) = 1 + i ⇔ if(−i) = 1 + i − α − βi ⇔ f(−i) = 1 − β + (α − 1)i. z 6= +i f (z) = 1 -NÕu , th× . f (z) Nh vËy , hµm Çn t×m ã d¹ng 1 z 6= +i, nÕu f (z) = α + iβ z = i, nÕu 1 − β + (α − 1)i z = −i. nÕu z 6= 1, |z| = 1 x ∈ R VÝ d 1.11. Chøng minh r»ng: Víi mäi sè phø ®Òu tån t¹i z PTIT sao ho ®î biÓu diÔn díi d¹ng x + i z = . x − i Gi¶i Dùa vµo b¶ng biÕn thiªn díi ®©y vµ x −∞ +∞ 1 -1 y' 0 - 0 - + 1 0 y 0 -1 y = 2x H×nh 2: Hµm sè 1+x2 x2 − 12 2x 2 + = 1, x2 + 1 x2 + 1 CuuDuongThanCong.com
https://fb.com/tailieudientucntt 20
Tài liệu liên quan:
-
Đề mẫu-Đề minh họa thi kết thúc học phần môn giải tích 1 | Học viện Công Nghệ Bưu Chính Viễn Thông
19 10 -
Bài giảng Giải tích hàm nhiều biến số môn Giải tích | Học viện Công Nghệ Bưu Chính Viễn Thông
30 15 -
Đề minh họa thi kết thúc học phần môn Giải tích | Học viện Công Nghệ Bưu Chính Viễn Thông
35 18 -
Đề minh họa thi kết thúc học phần giải tích | Học viện Công nghệ Bưu chính Viễn Thông
26 13