BÀI GIẢNG GIẢI TÍCH PHẦN 2

BÀI GIẢNG GIẢI TÍCH PHẦN 2
Chương 1. TÍCH PHÂN BỘI
Bài 1. Tích phân bội hai (kép)
Bài 2. Tích phân bội ba
Bài 3. Ứng dụng của tích phân bội
Bài 1. Tích phân bội hai 1.2. Tích phân bội hai 1.2.1. Định nghĩa
Cho hàm số f (x,y) xác định trên miền D đóng và
bị chặn trong mặt phẳng Oxy .
Chia D thành n phần S i n như i ( 1,..., ) bài
toán mở đầu và lấy n điểm tùy ý M (x ,y ) S i i i i .
Bài 1. Tích phân bội hai Khi đó n I f (M ) S n i i i 1
được gọi là tổng tích phân của f (x,y) trên D .
Bài 1. Tích phân bội hai n Nếu I lim f (M ) S i
i tồn tại hữu hạn thì số n i 1
thực I được gọi là tích phân bội hai của hàm số
f (x,y) trên miền D , ký hiệu là I
f (x,y)dxdy D
Bài 1. Tích phân bội hai
Nếu tồn tại tích phân
f (x,y)dxdy , ta nói: D
• hàm số f (x,y) khả tích trên miền D ;
• f (x,y) là hàm dưới dấu tích phân;
• dx , dy là các vi phân lần lượt theo biến x và y .
Bài 1. Tích phân bội hai 1.2.2. Định lý
Hàm f (x,y) liên tục trong miền D đóng và bị
chặn thì khả tích trong D .
Bài 1. Tích phân bội hai
1.3. Tính chất của tích phân kép
Giả thiết rằng các tích phân dưới đây đều tồn tại.
• Tính chất 1
f (x,y)dxdy
f (u,v)dudv D D
Bài 1. Tích phân bội hai
• Tính chất 2 (f g)dxdy fdxdy gdxdy D D D k.fdxdy k fdxdy (k ) D D
Bài 1. Tích phân bội hai
• Tính chất 3
Nếu chia miền D thành D D bởi đườ 1 và 2 ng cong
có diện tích bằng 0 thì fdxdy fdxdy fdxdy D D D 1 2
Bài 1. Tích phân bội hai
1.4. PHƯƠNG PHÁP TÍNH
1.4.1. Đưa về tích phân lặp
a) Định lý (Fubini) Giả sử I
f (x,y)dxdy tồn tại, trong đó D D
{(x, y) : a x , b y (x) y y (x } ) 1 2 ,
Bài 1. Tích phân bội hai y (x ) 2 và với mỗi x
[a; b] cố định,
f (x,y)dy tồn tại. y (x ) 1 Khi đó, ta có: b y (x ) b y (x ) 2 2 I
f (x,y)dy dx dx
f (x,y)dy a y (x ) a y (x ) 1 1
Bài 1. Tích phân bội hai
Tương tự, nếu miền D là D
{(x,y) : x (y) x x (y), c y d} 1 2 thì d x (y) d x (y) 2 2 I
f (x,y)dx dy dy
f (x,y)dx c x (y) c x (y) 1 1
Bài 1. Tích phân bội hai Chú ý
1) Nếu miền D là hình chữ nhật, D {a x , b c y d} [a; b] [ ; c d], thì b d d b
f (x,y)dxdy dx fdy dy fdx D a c c a
Bài 1. Tích phân bội hai 2) Nếu miền D {a x , b y (x) y y (x } ) 1 2
và f (x,y) u(x . ) v(y) thì b y (x ) 2
f (x,y)dxdy u(x)dx v(y)dy D a y (x ) 1
Bài 1. Tích phân bội hai 3) Nếu miền D {x (y) x x (y), c y d} 1 2
và f (x,y) u(x . ) v(y) thì d x (y) 2
f (x,y)dxdy v(y)dy u(x)dx D c x (y) 1
4) Nếu D là miền phức tạp thì ta chia D ra thành những miền đơn giản.
Bài 1. Tích phân bội hai
VD 1. Tính tích phân I 2x cosy dxdy , D
trong đó miền D giới hạn bởi: 1 x 2, y . 4 2
VD 2. Tính tích phân I (2x y)dxdy , D trong đó D {y x 1 , y 2 y 0}.
Bài 1. Tích phân bội hai VD 3. Đưa I
f (x,y)dxdy D
về dạng tích phân lặp,
biết miền D được giới hạn bởi các đường: y x 1 và 2 y x 1.
VD 4. Tính tích phân I ydxdy , trong đó D
miền D giới hạn bởi các đường 2 y x 4, y 2x .
Bài 1. Tích phân bội hai
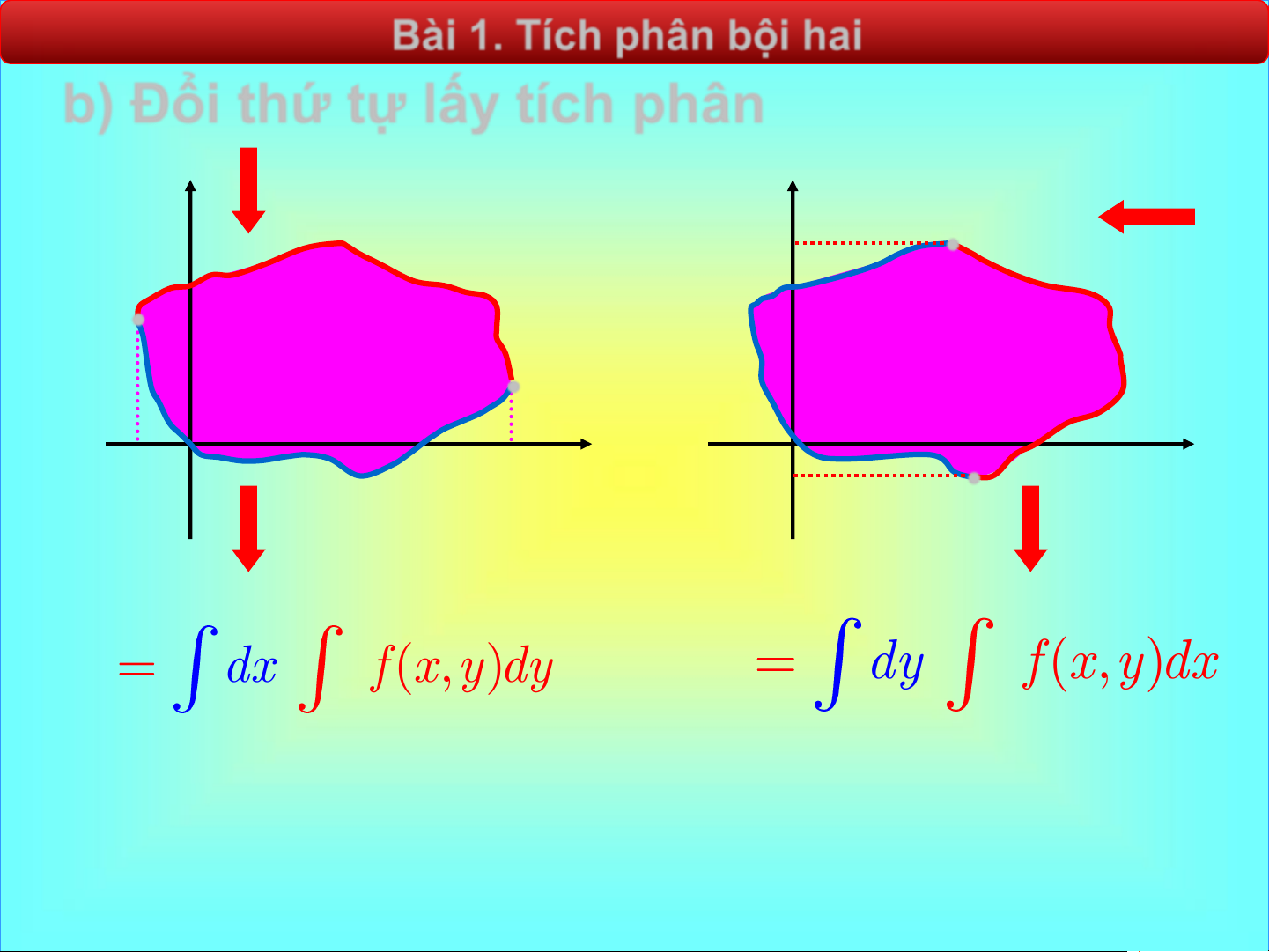
b) Đổi thứ tự lấy tích phân y y y (x) d 2 • x (y) • 1 x (y) 2 D D • a O b x O x c • y (x) 1 b y (x ) d x (y) 2 2 I dx
f (x,y)dy I dy
f (x,y)dx a y (x ) c x (y) 1 1
Bài 1. Tích phân bội hai
VD 5. Đổi thứ tự lấy tích phân trong tích phân sau 2 1 2 1 y I dy
f (x,y)dx . 1 2 2 1 y
VD 6. Đổi thứ tự lấy tích phân trong tích phân sau 2 0 x 1 1 1 x I dx
f (x,y)dy dx
f (x,y)dy . 1 0 0 0