Bài giảng Hàm số 1 biến môn Toán cao cấp | Trường Đại học Luật Thành phố Hồ Chí Minh

 Chương 1. Hàm số một biến số §1. Bổ túc về hàm số
§2. Giới hạn của hàm số
§3. Đại lượng vô cùng bé – vô cùng lớn §4. Hàm số liên tục
……………………………. §1. BỔ TÚC VỀ HÀM SỐ 1.1. Khái niệm cơ bản
1.1.1. Định nghĩa hàm số
• Cho X,Y   khác rỗng.
Ánh xạ f : X Y với x  y  f (x) là một hàm số. Khi đó:
– Miền xác định (MXĐ) của f, ký hiệu Df, là tập X.
– Miền giá trị (MGT) của f là:
G  y  f(x) x  X.
 Chương 1. Hàm số một biến số
– Nếu f (x1)  f(x2)  x1  x2 thì f là đơn ánh.
– Nếu f(X) = Y thì f là toàn ánh.
– Nếu f vừa đơn ánh vừa toàn ánh thì f là song ánh. VD 1.
a) Hàm số f :    thỏa  ( )  2x y f x là đơn ánh.
b) Hàm số f :   [0; )  thỏa 2 f(x)  x là toàn ánh. c) Hsố f : (0; )
   thỏa f(x)  lnx là song ánh.
• Hàm số y  f (x) được gọi là hàm chẵn nếu: f( x  )  f(x), x  D .f
• Hàm số y  f (x) được gọi là hàm lẻ nếu: f( x
 )  f(x), x  D .f
 Chương 1. Hàm số một biến số Nhận xét
– Đồ thị của hàm số chẵn đối xứng qua trục tung.
– Đồ thị của hàm số lẻ đối xứng qua gốc tọa độ. 1.1.2. Hàm số hợp
• Cho hai hàm số f và g thỏa điều kiện Gg  Df .
Khi đó, hàm số h(x)  (f  g)(x)  f[g(x)] được gọi là
hàm số hợp của f và g. Chú ý
(f  g)(x)  (g  f )(x). VD 2. Hàm số 2 2 2
y  2(x  1)  x 1 là hàm hợp của 2 f(x)  2x x và 2 g(x)  x  1.
 Chương 1. Hàm số một biến số 1.1.3. Hàm số ngược
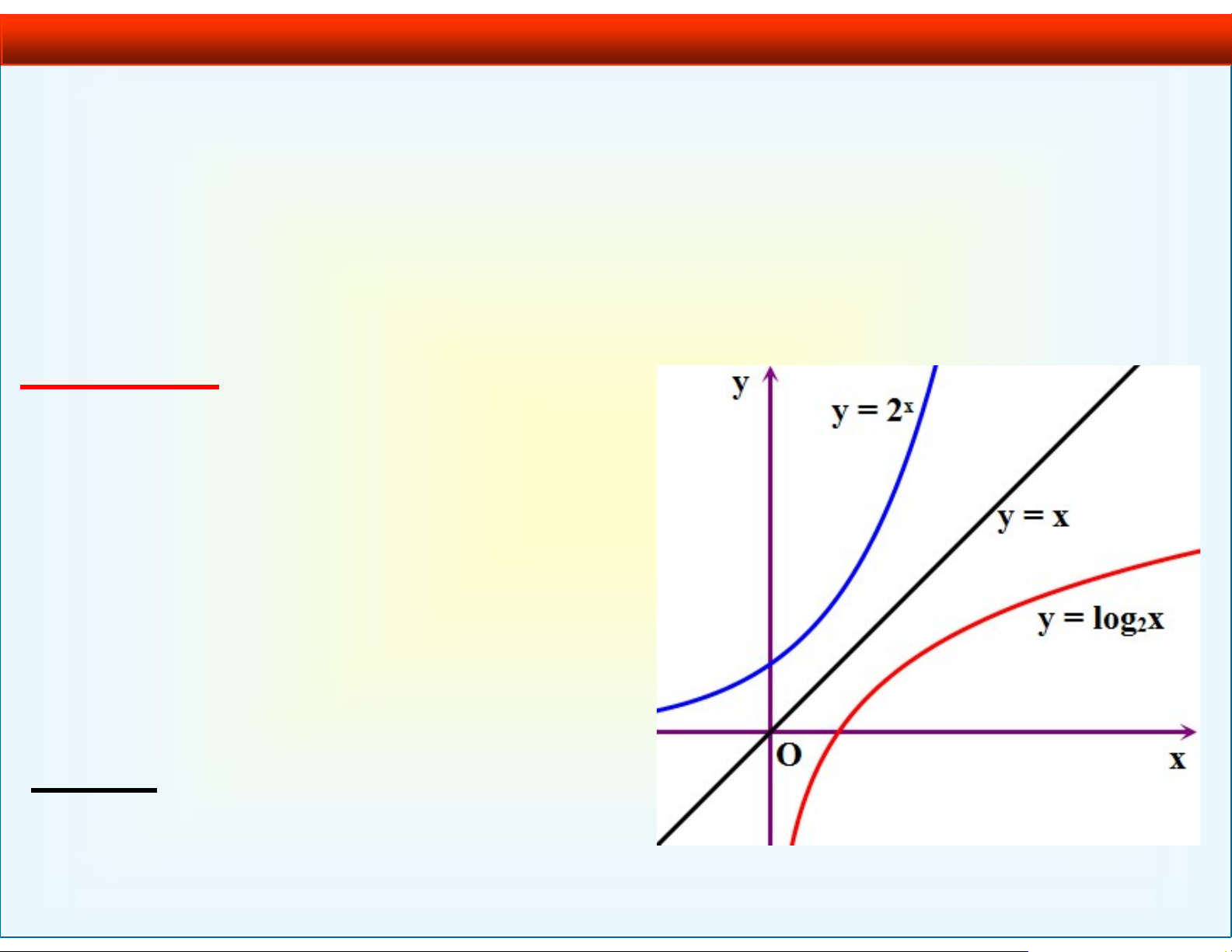
• Hàm số g được gọi là hàm số ngược của f, ký hiệu 1 g f   , nếu x  g(y), y  Gf . Nhận xét – Đồ thị hàm số 1 y f   (x)
đối xứng với đồ thị của hàm số y  f (x) qua đường thẳng y  x . VD 3. Cho ( ) 2x f x  thì 1
f  (x)  log2 x, mọi x > 0.
 Chương 1. Hàm số một biến số
1.2. Hàm số lượng giác ngược
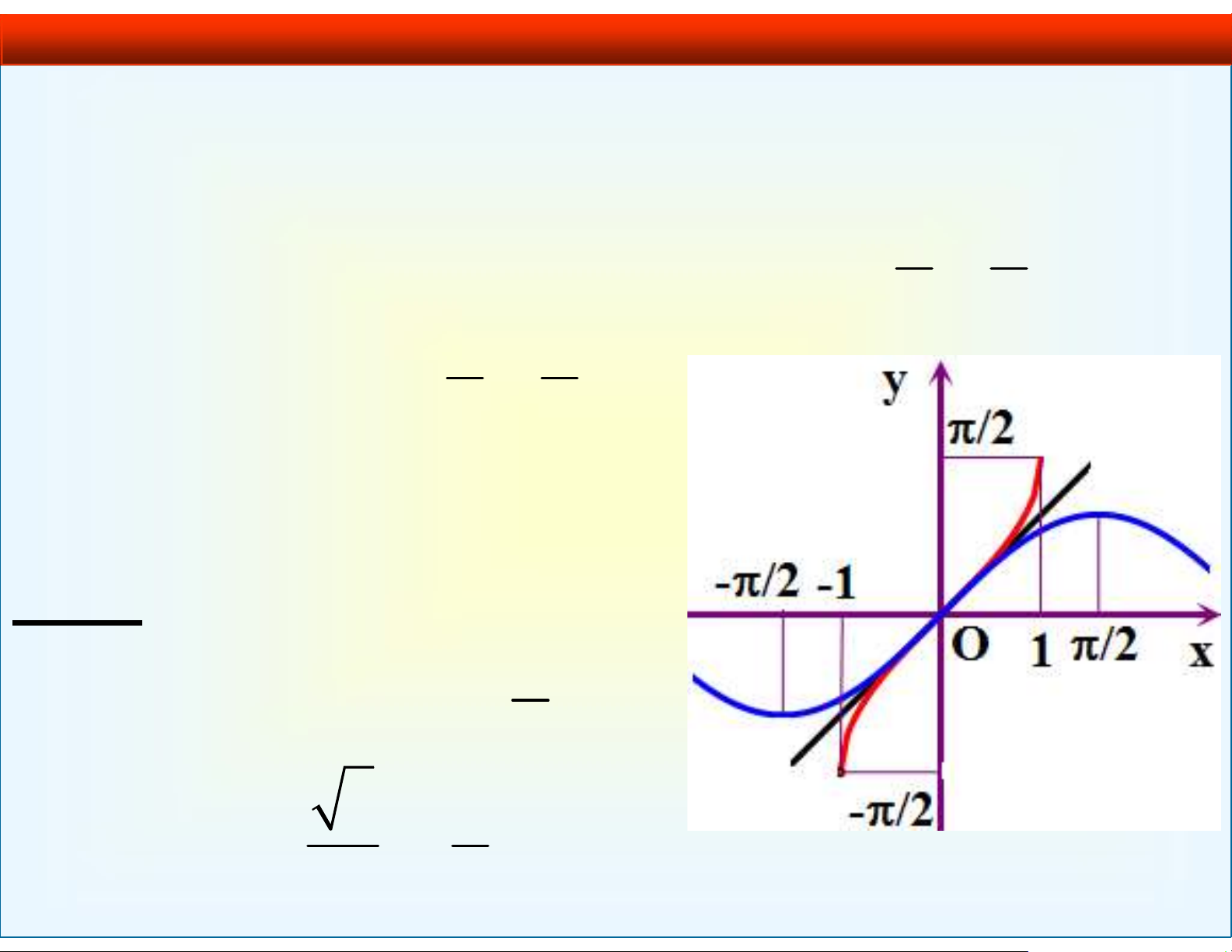
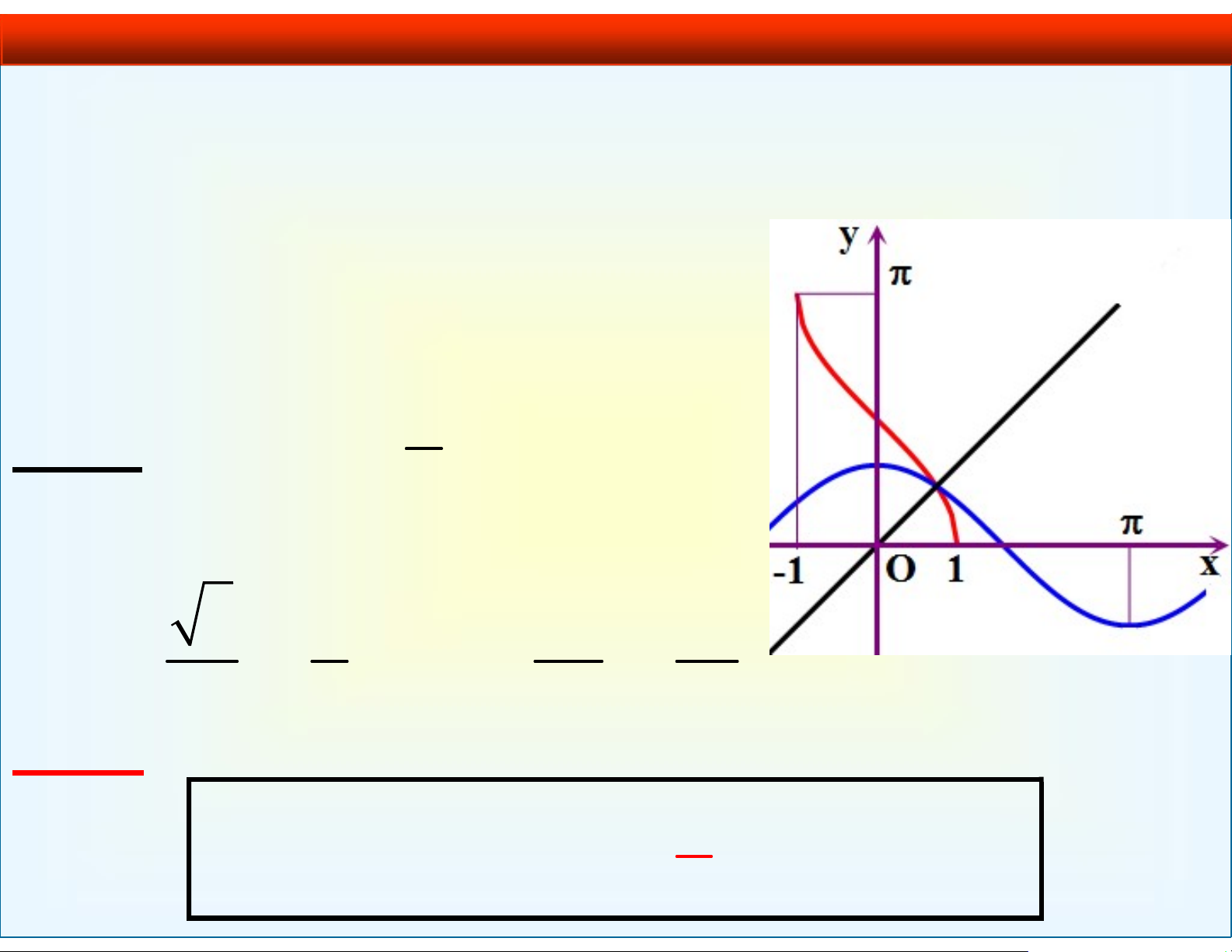
1.2.1. Hàm số y = arcsin x   
• Hàm số y  sin x có hàm ngược trên  ;   là 2 2       1 f  : [ 1  ; 1]   ;   2 2   x  y  arcsin x . VD 4. arcsin 0  0;  arcsin( 1  )   ; 2 3  arcsin  . 2 3
 Chương 1. Hàm số một biến số
1.2.2. Hàm số y = arccos x
• Hàm số y  cosx có hàm ngược trên [0; ] là 1
f  : [1; 1]  [0; ] x  y  arccosx .  VD 5. arccos 0  ; 2 arccos( 1  )  ; 3  1  2 arccos  ; arccos  . 2 6 2 3 Chú ý arcsinx arccosx    , x  [1; 1]. 2
 Chương 1. Hàm số một biến số
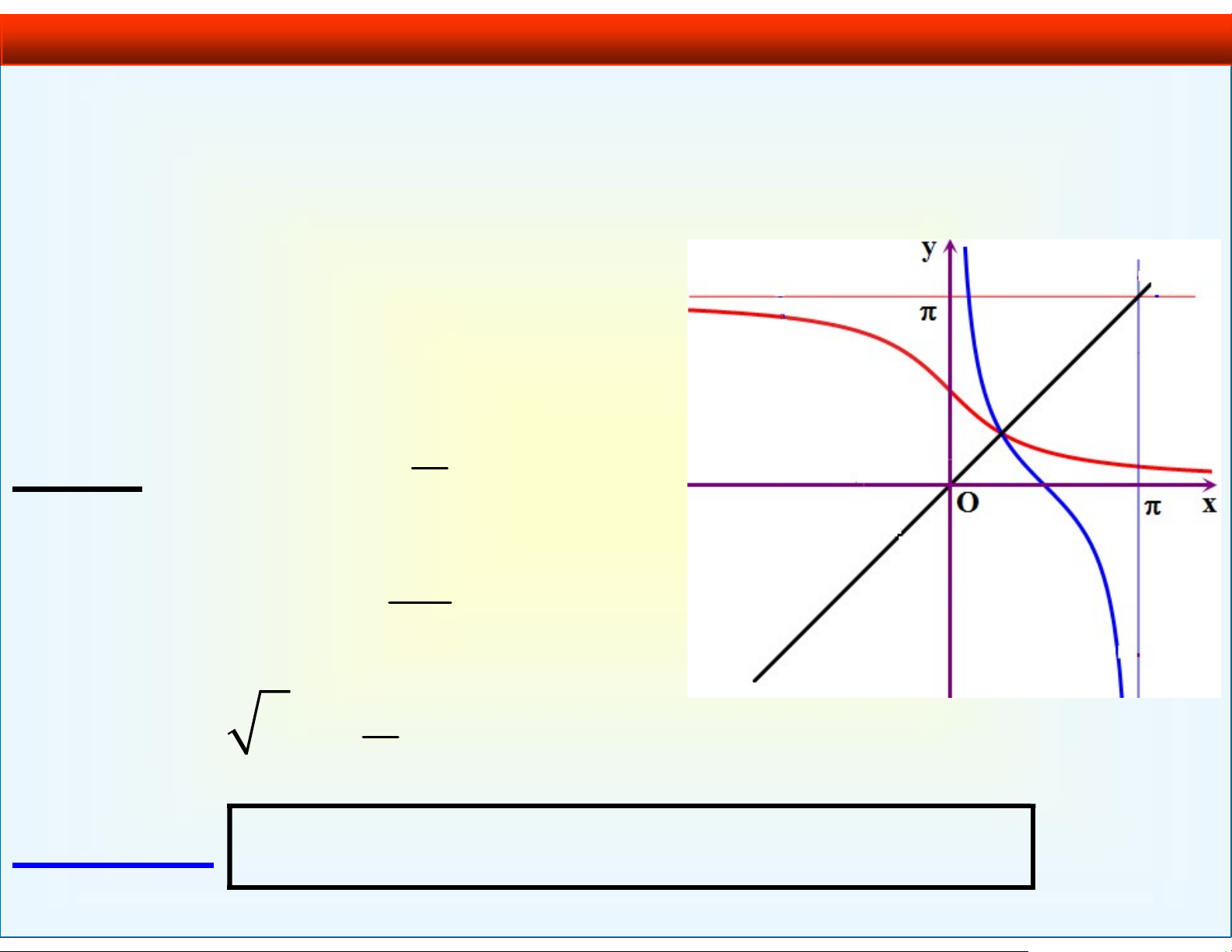
1.2.3. Hàm số y = arctan x   
• Hàm số y  tan x có hàm ngược trên   ;      là  2 2 1 f  :     ;    2 2 x  y  arctan x . VD 6. arctan 0  0;  arctan(1)   ; 4  arctan 3  . 3  
Quy ước. arctan  , arctan   . 2 2
 Chương 1. Hàm số một biến số
1.2.4. Hàm số y = arccot x
• Hàm số y  cotx có hàm ngược trên (0; ) là 1 f  :   (0; )  x  y  arc cotx .  VD 7. arc cot 0  ; 2 3 arc cot(1)  ; 4  arc cot 3  . 6 Quy ước. arc cot( )   0, arc cot( )   . 
………………………………………
 Chương 1. Hàm số một biến số
§2. GIỚI HẠN CỦA HÀM SỐ 2.1. Các định nghĩa Định nghĩa 1
• Cho hàm số f(x) xác định trên (a; b). Ta nói f(x) có giới
hạn là L (hữu hạn) khi x  x0  [a; b], ký hiệu
lim f (x)  L, nếu   0 cho trước ta tìm được   0 xx0
sao cho khi 0  x  x0   thì f (x) L  .
Định nghĩa 2 (định nghĩa theo dãy)
• Cho hàm số f(x) xác định trên (a; b). Ta nói f(x) có giới
hạn là L (hữu hạn) khi x  x0  [a; b], ký hiệu
lim f (x)  L, nếu mọi dãy {xn} trong (a; b) \ {x } mà xx 0 0 xn  x0 thì lim f(x ) n  L . n
 Chương 1. Hàm số một biến số
Định nghĩa 3 (giới hạn tại vô cùng)
• Ta nói f(x) có giới hạn là L (hữu hạn) khi x  ,
ký hiệu lim f (x )  L , nếu   0 cho trước ta tìm x 
được N > 0 đủ lớn sao cho khi x > N thì f (x )  L  .
• Tương tự, ký hiệu lim f (x )  L , nếu   0 cho x 
trước ta tìm được N < 0 có trị tuyệt đối đủ lớn sao cho
khi x < N thì f (x)  L  .
Định nghĩa 4 (giới hạn vô cùng)
• Ta nói f(x) có giới hạn là  khi x  x0, ký hiệu
lim f (x)  , nếu M  0 lớn tùy ý cho trước ta x x0
tìm được   0 sao cho khi 0  x  x0   thì f (x)  M .
 Chương 1. Hàm số một biến số
• Tương tự, ký hiệu lim f (x )   , nếu M  0 có trị x x0
tuyệt đối lớn tùy ý cho trước ta tìm được   0 sao cho
khi 0  x  x 0   thì f (x )  M .
Định nghĩa 5 (giới hạn 1 phía)
• Nếu f(x) có giới hạn là L (có thể là vô cùng) khi x  x 0
với x  x 0 thì ta nói f(x) có giới hạn phải tại x0 (hữu
hạn), ký hiệu lim f (x )  L hoặc lim f (x )  L . x x  0  0 x x 0
• Nếu f(x) có giới hạn là L (có thể là vô cùng) khi x  x 0
với x  x 0 thì ta nói f(x) có giới hạn trái tại x0 (hữu
hạn), ký hiệu lim f (x )  L hoặc lim f (x )  L . x x  0 0 x x 0
Chú ý. lim f (x )  L  lim f (x )  lim f (x )  L. x x    0 x x x x 0 0
 Chương 1. Hàm số một biến số 2.2. Tính chất
Cho lim f (x)  a và lim g(x)  b . Khi đó: xx0 xx0
1) lim [C .f (x)]  C .a (C là hằng số). xx0
2) lim [f (x)  g(x)]  a  b . xx0 3) lim [f (x)g(x)]  ab ; xx0 f(x) a 4) lim  , b  0; xx0 g(x) b
5) Nếu f (x)  g(x), x  (x0  ; x0  ) thì a  b.
6) Nếu f (x)  h(x)  g(x), x  (x0  ; x0  ) và
lim f (x)  lim g(x)  L thì lim h(x)  L . xx0 xx0 xx0
 Chương 1. Hàm số một biến số Định lý
Nếu lim u(x)  a  0, lim v(x)  b thì: xx0 xx0 v(x) lim[u(x)] b  a . xx0 2x  2x x 1
VD 1. Tìm giới hạn L  lim     . xx  3
A. L  9; B. L  4; C. L  1; D. L  0. 2. x  2x  x 1 Giải. Ta có:    2 L lim    2  B. xx  3
 Chương 1. Hàm số một biến số Các kết quả cần nhớ 1 1 1) lim   ,  lim  . x 0 x x 0   x n n 1 a x a x   . .a 2) Xét n n 1  0 L  lim , ta có: x m m 1  m b x  m b 1x  . .   0b a a) n L  nếu n  m; n b b) L  0 nếu n  m; c) L   nếu n  m . sinx tanx 3) lim  lim  1. x0 x x0 x
 Chương 1. Hàm số một biến số 4) Số e:  1 x lim 1       lim   1x1x  .e x x  x0  2  3 x x 
VD 2. Tìm giới hạn L  lim 1      . x 2  2x  1 A. L  ; B. 3 L  e ; C. 2 L  e ; D. L  1. 3x 2 2x. 2  2x 1   2x 1    3x  x  Giải. L  lim 3 1        . x  2  2x 1       
 Chương 1. Hàm số một biến số 3x 3x Khi x   thì  0, 2x.  3 2 2 2x  1 2x  1 2 2x 1    3 3 x x   3  lim 1     e  L  e  B. x 2  2x  1
 Chương 1. Hàm số một biến số1 VD 3. Tìm giới hạn 2 4 L  lim 1  tan x x . x 0  A. L  ; B. L  1; C. 4 L  e ; D. L  e . 1 2 .  1 tan x 4x   Giải. 2 2 tan L  lim  1  tan x x  x 0      2 1 tan  . x     1 4    x   2 2  4 tan  lim  1 tan x x   e C . x0    
………………………………………
 Chương 1. Hàm số một biến số
§3. ĐẠI LƯỢNG VÔ CÙNG BÉ – VÔ CÙNG LỚN
3.1. Đại lượng vô cùng bé a) Định nghĩa Hàm số (
 x) được gọi là đại lượng vô cùng bé (VCB) khi x  x0 nếu lim (
 x)  0 (x có thể là vô cùng). xx 0 0 VD 1. 3 (
 x)  tan sin 1x là VCB khi x 1  ; 1 (  x)  là VCB khi x  . 2 ln x
 Chương 1. Hàm số một biến số b) Tính chất của VCB 1) Nếu (  x), (
 x) là các VCB khi x  x0 thì (  x)  (  x) và (  x). (  x) là VCB khi x  x0. 2) Nếu (  x) là VCB và (
 x) bị chận trong lân cận x0 thì (  x). (  x) là VCB khi x  x0.
3) lim f (x)  a  f (x)  a  (  x), trong đó (  x) là x x  0 VCB khi x  x0.
 Chương 1. Hàm số một biến số c) So sánh các VCB • Định nghĩa (  x) Cho (  x), (
 x) là các VCB khi x  x0, lim  k . xx0 (  x) Khi đó: – Nếu k  0, ta nói (
 x) là VCB cấp cao hơn (  x), ký hiệu (  x)  0( (  x)).
– Nếu k  , ta nói (
 x) là VCB cấp thấp hơn (  x).
– Nếu 0  k  , ta nói (  x) và (  x) là các VCB cùng cấp.
– Đặc biệt, nếu k  1, ta nói (  x) và (  x) là các VCB
tương đương, ký hiệu (  x)  (  x).