-
Thông tin
-
Hỏi đáp
Bài giảng hướng dẫn làm bài tập Toán kinh tế | Đại học Tây Đô
Ngành Toán kinh tế là một ngành học có tính ứng dụng cao trong lĩnh vực kinh doanh, cụ thể là việc vận dụng kiến thức toán học vào việc phân tích các mô hình toán kinh tế nhằm hiểu rõ và nắm bắt được các quy luạt kinh tế trên thị trường. Toán ứng dụng trong kinh tế từ đó tạo ra tư duy nghiên cứu độc lập, năng lực tự học tập nhằm nâng cao trình độ chuyên môn để thích nghi với sự thay đổi của môi trường làm việc;...
Môn: Toán Kinh Tế (BG) 2 tài liệu
Trường: Đại học Tây Đô 170 tài liệu
Thông tin:
Tác giả:
Preview text:
lOMoARcPSD|45156089
Toan kinh te-2022 - Bài giảng hướng dẫn làm bài tập Toán kinh tế
Quản trị kinh doanh (Trường Đại học Tây Đô)
Studocu is not sponsored or endorsed by any college or university
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
&KѭѫQJ BÀI TOÁN QUI HOҤ&+78<ӂ17Ë1+
1.1 MӝWVӕví dөGүQÿӃQEài toán qui hoҥFKWX\ӃQWtQK
1.1.1 Bài toán lұSNӃKRҥFKVҧQ[XҩW
Công ty Toàn ThҳQJ dӵÿӏQKWURQJQăPNӃ KRҥFKVӁVҧQ[XҩW QORҥLVҧQ
phҭP631, SP2,…, SPn. BiӃWÿӏQKPӭFNLQKWӃ- kӻWKXұWPӭFGӵWUӳFiF\ӃX tӕ
sҧQ[XҩWYà lӧLQKXұQWUên mӛLÿѫQYӏVҧQSKҭP cho trong sau Các yӃXWӕ
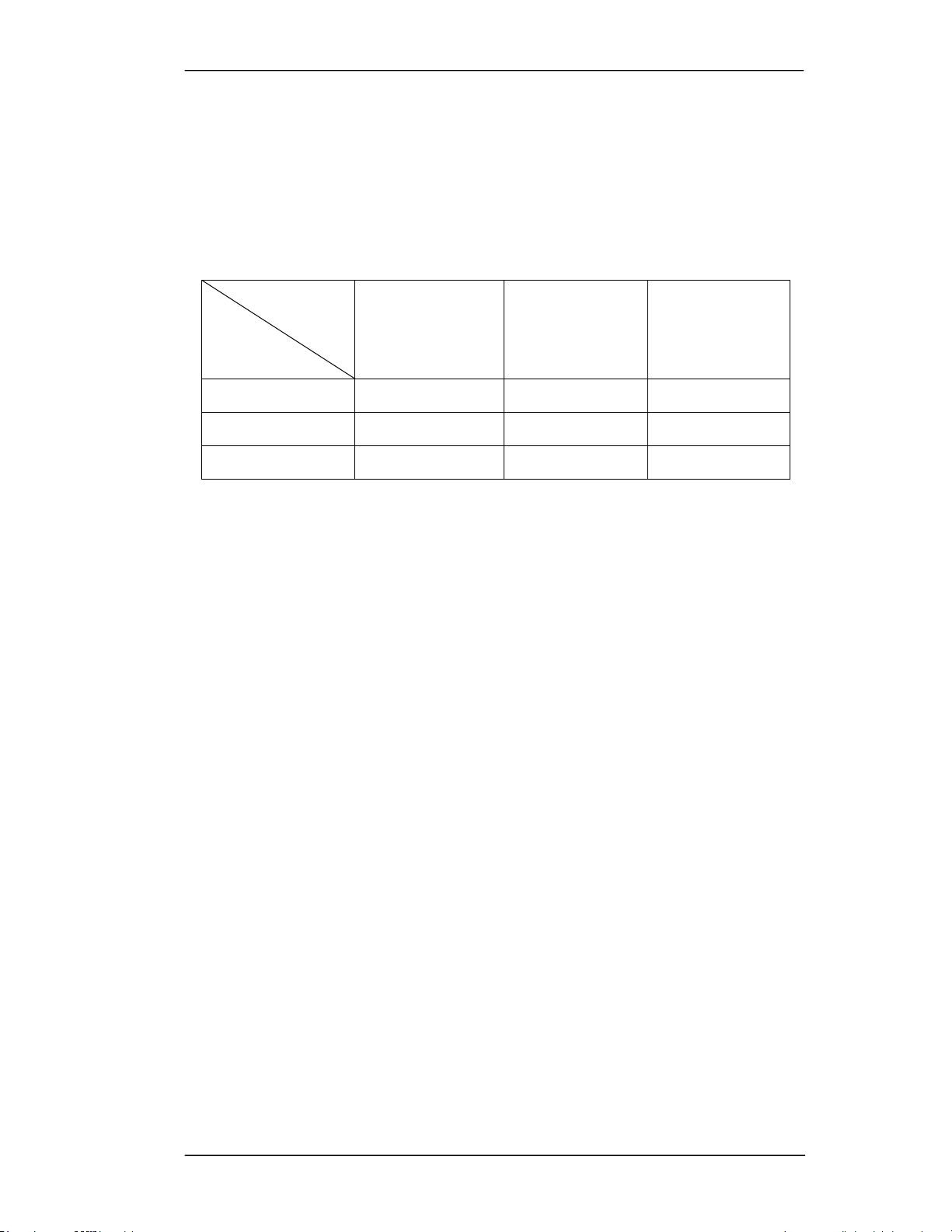
ĈӏQKPӭFNLQKWӃ- kӻWKXұW MӭFGӵWUӳ sҧQ[XҩW SP1 SP2 … SPn I1 b1 a11 a12 … a1n I2 b2 a21 a22 … a2n . . . . . . . . . . . . . . . Im bm am1 am2 … amn
LӧLQKXұQĈѫQYӏVҧQphҭP P1 P2 … Pn 7URQJÿy
I (i 1, 2,..., m) : Các yӃXWӕVҧQ[XҩW. i
b (i 1, 2,..., m) /ѭӧQJGӵWUӳFӫD\ӃXWӕsҧQ[XҩWthӭi . i
a (i 1, 2,..., ;
m j 1, 2,..., n) : MӭF WLêu hao cҫQ WKLӃW \ӃX Wӕ sҧQ [XҩW thӭ i ÿӇ ij
sҧQ[XҩWPӝWÿѫQYӏVҧQSKҭPORҥL j .
P ( j 1, 2,..., n) : LӧLQKXұQWKXÿѭӧFNKLEiQPӝWÿѫQYӏVҧQSKҭPORҥL j . j
Hãy xác ÿLQKVҧQOѭӧQJVҧQSKҭPWӯQJORҥLPà công ty Toàn Thҳng cҫQ
sҧQ[XҩWWURQJQăPVDRFKRWәQJOӧLQKXұQOӟQQKҩW
Ta chuyӇQQKӳQJ\êu cҫXYӅPһWNLQKWӃ thành mô hình toán hӑFQKѭVDX.
GӑL x , x ,..., x OjOѭӧQJVҧQSKҭP SP , SP ,..., SP WѭѫQJӭQJFҫQVҧQ[XҩW 1 2 n 1 2 n WURQJQăPNӃKRҥFK
TәQJOӧi nhuұQWѭѫQJӭQJYӟLNӃKRҥFKVҧQ[XҩWWUên là: P x P x ... P x 1 1 2 2 n n
VӟL\êu cҫXWӕLÿDKyDOӧLQKXұQ P x P x ... P x Max 1 1 2 2 n n 1
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
ĈӇVҧQ[XҩWUDOѭӧQJVҧQSKҭPFiFORҥLOà x , x ,..., x thì tәQJPӭFWLêu 1 2 n hao các yӃXWӕsҧQ[XҩWlà:
YӃX tӕsҧQ[XҩW loҥL a x a x ... a x 11 1 12 2 1n n
YӃXWӕsҧQ[XҩW loҥL a x a x ... a x 21 1 22 2 2n n
Ta có thӇ WKLӃW OұS WәQJ PӭF WLêu hao các yӃX Wӕ sҧQ [XҩW tӯQJ ORҥL QKѭ
trên. ӬQJYӟLNKҧQăQJGӵWUӳWӕLÿDFiF\ӃXWӕsҧQ[XҩW, ta có:
a x a x ... a x b 11 1 12 2 1n n 1
a x a x ... a x b 21 1 22 2 2n n 2
a x a x ... a x b 1 m 1 m 2 2 mn n m
Vì OѭӧQJ VҧQ SKҭP FҫQ VҧQ [XҩW WURQJ QăP Oj OѭӧQJ NK{QJ kP Qên
x , x ,..., x 0 . 1 2 n
1Kѭ Yұ\ Wӯ QKӳQJ \êu cҫX YӅ NLQK WӃ FӫD PӝW GRDQK QJKLӋS WD Fy WKӇ
chuyӇQ thành mô hình toán hӑF 7D chӑQ WKXұW WRiQ thích hӧS ÿӇ JLҧL Eài toán.
CuӕLFùng tӯFiFNӃWTXҧYӅPһWWRiQKӑFWDFKX\ӇQÿәLWKành các thông tin kӃW quҧYӅPһWNLQKWӃ
Tóm lҥL, viӋFӭQJGөQJEài toán QHTT vào trong thӵFWLӉQJӗPFiFEѭӟFVDX:
Tìm kiếm thông tin gốc: Là quá trình thu thұSFiFVӕOLӋXNLQKWӃ- kӻ
thuұW%ѭӟFQày khá quan trӑQJYì tҩWFҧFiFEѭӟFVDXGӵDYào các sӕOLӋXQj\ÿӇ
tính toán. Nó quyӃWÿLQKWtQKFKtQK[iFFӫDNӃWTXҧWKXÿѭӧF0ӛLEài toán kinh
tӃFөWKӇÿòi hӓLFiFWK{QJWLQJӕFNKiFQKDX
Xử lý số liệu: GӗPKDLJLDLÿRҥQ
LұSP{Kình toán: TӯQKӳQJVӕOLӋXvà các yêu cҫXYӅPһWNLQK
tӃ- kӻWKXұWWDFKX\ӇQWKành mô hình toán hӑFTa cҫQSKҧL thiӃWOұSFKtQK[iF
Yjÿҫ\ÿӫFiFÿLӅXNLӋQFӫDEài toán.
LӵDFKӑQWKXұWWRiQWKtFKKӧSYà giҧLEài toán: Ĉk\OjEѭӟFUҩW
quan trӑQJYì kӃWTXҧӣEѭӟFQày chính là lӡL giҧLFѫEҧQÿӇÿѭDUDJLҧLSKiSWӕL ѭXYӅPһWNLQKWӃ
Thông tin kết quả: Ta chuyӇQ ÿәL các thông tin toán hӑF WKành các thông tin vӅPһWNLQKWӃ 2
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
Ví dө Nhân dӏS7ӃW7UXQJ7KX[tQJKLӋSVҧQ[XҩWEiQK7UăQJPXӕQVҧQ[XҩWED
loҥL EiQK ĈұX [DQK WKұS Fҭm, bánh dҿR QKkQ ÿұX [DQK ĈӇ VҧQ [XҩW ED ORҥL
bánh này, xí nghiӋS FҫQ ÿѭӡQJ ÿұX EӝW WUӭQJ PӭW OҥS [ѭӣQJ « *Lҧ Vӱ Vӕ
ÿѭӡQJFyWKӇFKXҭQEӏÿѭӧFOjNJÿұXOà 300 kg, các nguyên liӋXNKiFPXӕQ
bao nhiêu cNJQJFy/ѭӧQJÿѭӡQJÿұXFҫQWKLӃWYà sӕWLӅQOãi khi bán mӝWFKLӃF
bánh cho mӛLORҥLFKRWURQJEҧQJVDX Bánh
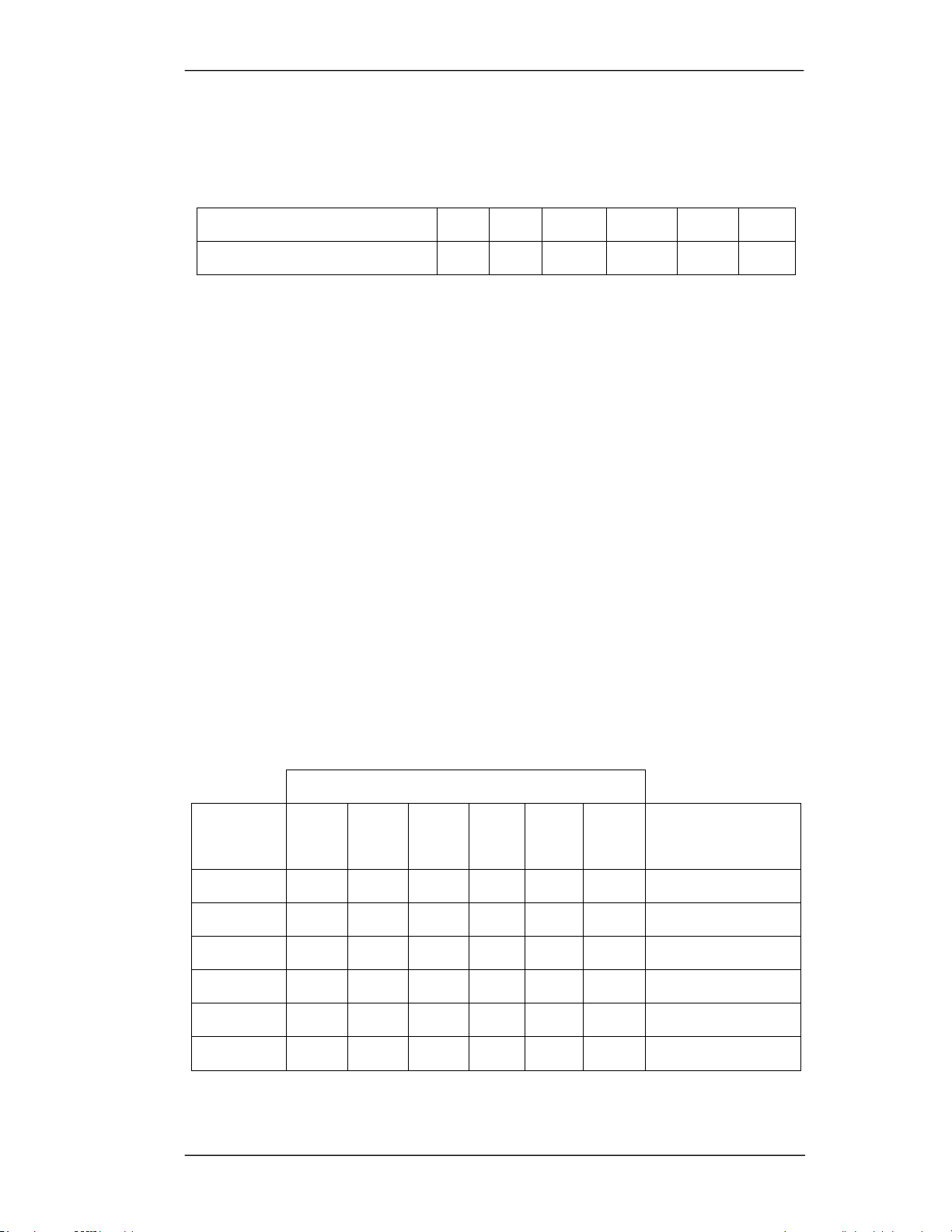
%iQKÿұX[DQK Bánh thұSFҭP Bánh dҿR Nguyên liӋX ĈѭӡQJ 500 kg 0,06 kg 0,04 kg 0,07 kg ĈұX 300 kg 0,08 kg 0 kg 0,04 kg Lãi 2 ngàn 1,7 ngàn 1,8 ngàn
CҫQOұSNӃhoҥFKVҧQ[XҩWPӛLORҥLEiQKEDRQKLrXFiLÿӇNK{QJEӏÿӝQJ
vӅÿѭӡQJÿұXYà tәQJVӕOãi thu ÿѭӧFOà lӟQQKҩWJLҧVӱVҧQ[XҩWEDRQKLêu cNJQJ bán hӃW
Phân tích: GӑL x , x , x lҫQOѭӧWOà sӕFKLӃFEiQKÿұX[DQKWKұSFҭPEiQKGҿR 1 2 3 QKkQÿұX[DQKVӁVҧQ[XҩW
TәQJVӕOãi thu ÿѭӧFOà: 2x 1, 7x 1,8x . 1 2 3
TәQJVӕOãi thu ÿѭӧFOà lӟQQKҩW 2x 1, 7x 1,8x max. 1 2 3
TәQJVӕÿѭӡQJFҫQWKLӃWOà: 0, 06x 0, 04x 0,07x 500 1 2 3
TәQJVӕÿұX[DQKFҫQWKLӃWOà: 0, 08x 0x 0, 04x 300 1 2 3
SӕOѭӧQJFKLӃFEiQKPӛLORҥLOà không âm nên: x , x , x 0 1 2 3
Vұ\WDFyÿѭӧFP{Kình cӫDEjLWRiQQKѭVDX
Ĉ. 2x 1,7x 1,8x max. 1 2 3
Ĉ. 0,06x 0,04x 0,07x 500 1 2 3
0,08x 0x 0,04x 300 1 2 3
Ĉ. x , x , x 0 . 1 2 3 3
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
1.1.2 %jLWRiQ[iFÿӏQKF{Qg thӭFSKDWUӝQ
CônJW\ FKăQ QX{L VƭQK1JX\ên cҫQ SKD WUӝQ PӝWORҥL WKӭF ăQ KӛQ KӧS
cho gia súc tӯ Q ORҥLQJX\ên liӋX WK{ NL1, NL2,…, NLn). Phân tích các nguyên
liӋXWUên, ta biӃWKjPOѭӧQJFiFGѭӥQJFKҩWFyWURQJWӯQJORҥLQJX\ên liӋX
ĈӗQJWKӡL, ta cNJQJELӃWFiF\êu cҫXYӅPӭFdinhGѭӥQJFҫQWKLӃWFKRJLD
súc vàÿѫQJLiFKRWӯQJORҥLQJX\ên liӋXFKRWURQJEҧQJVDX
+jPOѭӧQJGѭӥQJFKҩWFyWURQJWӯQJ Các loҥL MӭFFҫQ nguyên liӋX GѭӥQJFKҩW thiӃW NL1 NL2 … NLn I 1 b1 A11 a12 … a1n I 2 b2 A21 a22 … a2n . . . . . . . . . . . . . . . . . . I m bm am1 am2 … amn ĈѫQJLiQJX\rQOLӋX P1 P2 … Pn 7URQJÿy
I (i 1, 2,..., m) /ѭӧQJ GѭӥQJ FKҩW FҫQ WKLӃW FKR QKX FҫX VLQK WUѭӣQJ Yà phát i triӇn cӫDJLDV~F
b (i 1, 2,..., m) : MӭFGѭӥQJFKҩWFҫQWKLӃWSKҧLÿҧPEҧRYӅPһWGLQKGѭӥQJ i
NL ( j 1, 2,..., n) : Nguyên liӋX FiF ORҥL Gӵ ÿӏQK Vӱ GөQJÿӇ FKӃ ELӃQ WKӭF ăQ j hӛQKӧS
a (i 1, 2,..., ;
m j 1, 2,..., n) : +jP OѭӧQJ FiF FKҩW GLQK GѭӥQJ b chӭD WURQJ ij i nguyên liӋXORҥL j .
P ( j 1, 2,..., n) ĈѫQJLiQJX\rQOLӋXloҥL j . j
Yêu cҫX ;iF ÿӏQK SKҫQ OѭӧQJ WӯQJ ORҥL QJX\ên liӋX WURQJ WKӭF ăQ KӛQ
hӧS VDR FKR thӭF ăQ ÿҧm bҧR YӅ PһWGѭӥQJ FKҩW Yj ÿӗQJ WKӡL FKL SKt WKӭF ăQ thҩSQKҩW LұSP{Kình bài toán:
GӑL x , x ,..., x là phҫQOѭӧQJWӯQJORҥLQJX\ên liӋXFyWURQJWKӭFăQKӛQKӧS 1 2 n
Ta có tәQJFKLSKtQJX\ên liӋXWURQJJLiWKành thӭFăQOà: P x P x ... P x 1 1 2 2 n n 4
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
NhҵPFӵc tiӇXKyDFKLSKtQJX\ên liӋX P x P x ... P x Min 1 1 2 2 n n
VӟLSKҫQOѭӧQJWӯQJ ORҥLQJX\ên liӋX trong thӭFăQQKѭWUrQWD có hàm
OѭӧQJGѭӥQJFKҩWDi trong thӭFăQQKѭVDX TәQJPӭFGLQKGѭӥQJ D 1: a x a x ... a x 11 1 12 2 1n n 7ѭѫQJWӵÿӕL
a x a x ... a x vӟL D n n 2: 21 1 22 2 2
Theo yêu cҫXYӅPһWNӻWKXұW,ÿӇÿҧPEҧRVӵSKiWWULӇQWӕWFKRJLDV~FWKì
thӭF ăQ phҧL ÿҧP EҧR YӅ PһW FKҩW OѭӧQJ QJKƭD Oà phҧL WKӓD Pãn vӅ PһW GLQK GѭӥQJ9ì vұ\
a x a x ... a x b 11 1 12 2 1n n 1
a x a x ... a x b 21 1 22 2 2n n 2
a x a x ... a x b 1 m 1 m 2 2 mn n m
Ta cNJQJFy x ( j 1, 2,..., n) là phҫQOѭӧQJFiFORҥLQJX\ên liӋXWURQJWKӭF j
ăQKӛQKӧSGRÿy x , x ,..., x 0 . 1 2 n
Ví dөMӝW[tQJKLӋSOX\ӋQNLPPXӕQVҧQ[XҩWPӝWORҥLKӧSNLPYӟLEҥF
ÿӗQJQK{P1JѭӡLWDVӱGөQJFiFQJX\ên liӋXEҥFÿӗQJQK{PKӧS
kim A, hӧS NLP % KӧSNLP & +jP OѭӧQJ EҥF ÿӗQJ QK{PWURQJ FiF QJX\ên
liӋXWUên cNJQJQKѭJLiPӝWÿѫQYӏNKӕLOѭӧQJPӛLORҥL86'NJÿѭӧFFKRWURQJ bҧQJVDX Nguyên liӋX HӧSNLP HӧSNLP HӧSNLP BҥF ĈӗQJ Nhôm ChҩW A B C BҥF 100% 0 0 30% 50% 40% ĈӗQJ 0 100% 0 40% 20% 35% Nhôm 0 0 100% 30% 30% 25% Giá 1500 300 100 1000 1200 1100
Hãy lұSSKѭѫQJiQSKDWUӝQWKӃQjRÿӇJLiWKành sҧQSKҭPOà nhӓQKҩW
Phân tích: GӑL x j 1,...,6 lҫQOѭӧWOà khӕL OѭӧQJEҥF ÿӗQJQK{PKӧSNLP j
A, hӧSNLP B, hӧSNLP&WѭѫQJӭQJÿӇVҧQ[XҩW kg hӧSNLPFҫQWKLӃW
Giá thành 1 kg sҧQSKҭP1500x 300x 100x 1000x 1200x 1100x . 1 2 3 4 5 6 5
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
Giá thành 1 kg sҧQSKҭPFàng ít càng tӕW
1500x 300x 100x 1000x 1200x 1100x min 1 2 3 4 5 6
/ѭӧQJEҥFFKӭDWURQJNJVҧQSKҭP x 0,3x 0,5x 0,4x 0,2 1 4 5 6
/ѭӧQJÿӗng chӭDWURQJNJVҧQSKҭP x 0,4x 0,2x 0,35x 0,3 2 4 5 6
/ѭӧQJQK{PFKӭDWURQJNJVҧQSKҭP x 0,3x 0,3x 0,25x 0,5 3 4 5 6
Vұ\WDFyÿѭӧFP{Kình cӫDEjLWRiQQKѭVDX
Ĉ.1500x 300x 100x 1000x 1200x 1100x min 1 2 3 4 5 6
x 0,3x 0,5x 0,4x 0,2 1 4 5 6
Ĉ. x 0,4x 0,2x 0,35x 0,3 2 4 5 6
x 0,3x 0,3x 0,25x 0,5 3 4 5 6
Ĉ. x 0 j 1,...,6 . j
1.1.3 Bài toán cҳWQJX\ên liӋX
3KkQ[ѭӣQJHoàng Gia cҫQ thӵFKLӋQPӝWÿѫQÿһWKàng cung ӭQJFiFWҩP
thép theo các kích cӥYà sӕOѭӧQJFKRWURQJEҧQJVDX. Các tҩPWKpSQà\ÿѭӧFFҳW
ra tӯFiFWҩPWKpSFyNtFKFӥFKXҭQNtFKFӥÿѭӧFVҧQ[XҩW Các loҥL
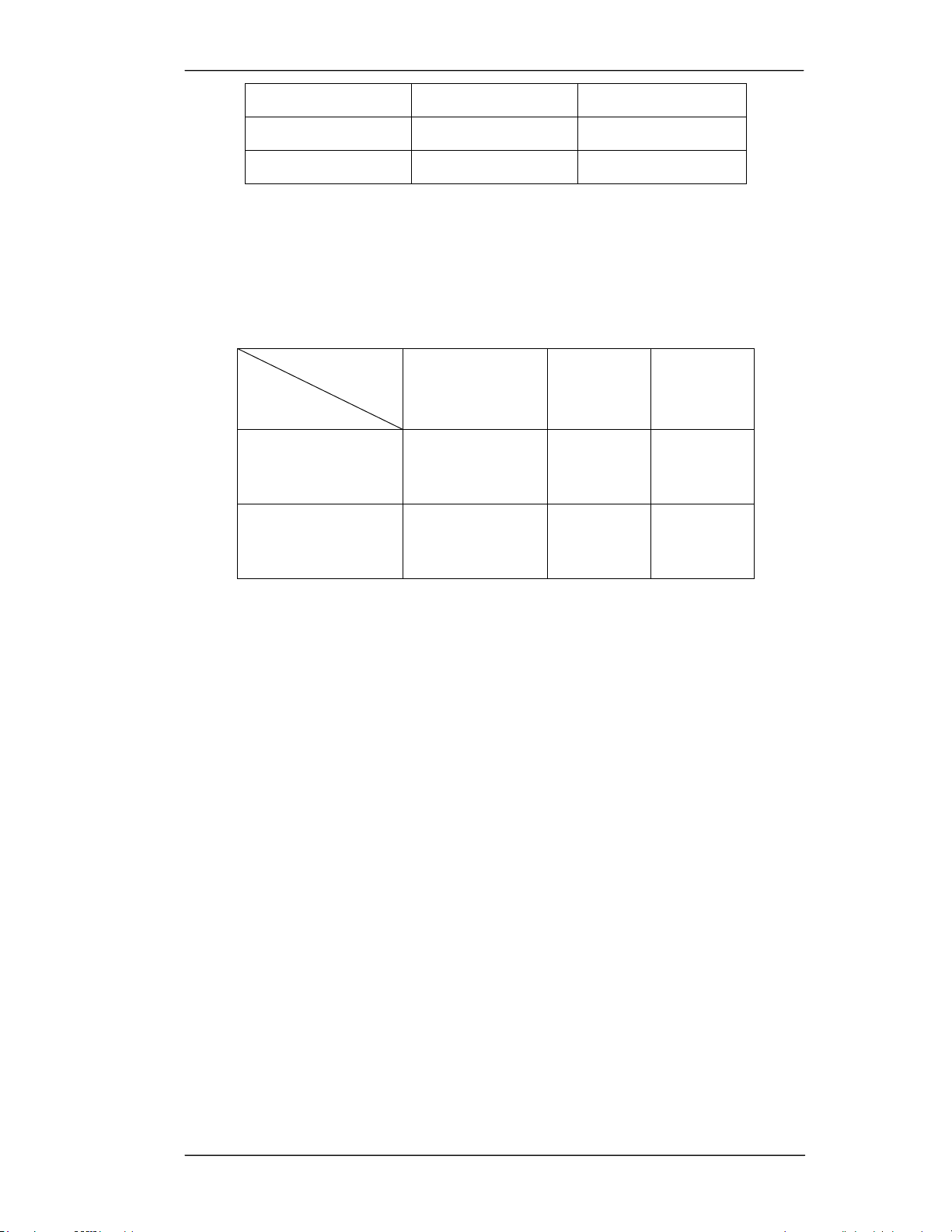
SӕOѭӧQJWKpSFҳWÿѭӧF&iFKFҳW MӭF\êu cҫX thép C1 C2 … Cn I1 b1 a11 a12 … a1n I2 b2 a21 a22 … a2n . . . . . . . . . . . . . . . . . . Im bm am1 am2 … amn PhҫQGѭUD&iFKFҳW P1 P2 … Pn 7URQJÿy
I (i 1, 2,..., m) : LoҥLWҩPWKpSFҫQFҳt thHRÿѫQÿһWKàng. i
b (i 1, 2,..., m) : MӭFFҫQWKLӃWWKHRÿѫQÿһWKàng. i
C (i 1, 2,..., n) : SӕFiFKFҳWKӧSOê i
a (i 1, 2,..., ;
m j 1, 2,..., n) : SӕWҩPWKpSFiFORҥLFҳWÿѭӧFWѭѫQJӭQJYӟLPӛL ij cách cҳW 6
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
P ( j 1, 2,..., n) : TәQJPӭF phӃOLӋXWѭѫQJӭQJYӟLWӯQJFiFKFҳW j
Yêu cҫX;iFÿӏQKSKѭѫQJiQFҳWWӕLѭXVDRFKRYӯDbҧRÿҧPWKӵFKLӋQÿӫ
sӕOѭӧQJWKHRÿѫQÿһWKàng vӯD ÿҧPEҧR WәQJSKӃOLӋXWәQJVӕWKpSGѭUDWӕL thiӇX
Lұp mô hình bài toán
GӑL x , x ,..., x là sӕWҩPWKép chuҭQÿѭӧFFҳWWKHRFiFFiFK C ,C ,...,C 1 2 n 1 2 n
VӟLSKѭѫQJiQFҳWWUên ta có tәQJPӭFSKӃOLӋXOà: P x P x ... P x 1 1 2 2 n n
NhҵPFӵFWLӇXKyDPӭFSKӃOLӋX P x P x ... P x Min 1 1 2 2 n n
MһWNKiFWDFyOѭӧQJWKpSFiFORҥL D FyÿѭӧFNKLWKӵFKLӋQSKѭѫQJiQFҳWWUên i là:
SӕWҩPWKpSORҥL: a x a x ... a x 11 1 12 2 1n n 7ѭѫQJ
a x a x ... a x tӵORҥL 21 1 22 2 2n n
ĈӇÿҧPEҧRFXQJӭQJVӕWҩPWKpSWKHRÿѫQÿһWKàng, ta phҧLFy
a x a x ... a x b 11 1 12 2 1n n 1
a x a x ... a x b 21 1 22 2 2n n 2
a x a x ... a x b 1 m 1 m 2 2 mn n m
Ta cNJQJFy x ( j 1, 2,..., n) là sӕWҩPWKpSFKXҭQÿѭӧFFҳWWKHRPӝWFiFKQào j
ÿyGRYұ\ x phҧLOà sӕNK{QJkPKD\ x , x ,..., x 0 . j 1 2 n
Ví dө1JѭӡL WDFҫQ FҳWQKӳQJWKDQK VҳWGjL PWKjQKÿRҥQGài 0,9m; 500
ÿRҥQGài 0,8m; 150ÿRҥQGài 0,6m. Hãy lұSP{Kình bài toán tìm phѭѫQJiQFҳW
sao cho sӕVҳWWKӯDtWQKҩW&KRUҵQJVӕOѭӧQJFiFWKDQKVҳWKLӋQFyOà rҩWOӟQ
Giải thuật thành lập bài toán quy hoạch tuyến tính như sau:
Bước 1: Xác định phương án.
ChҷQJKҥQSKѭѫQJiQWURQJEji toán lұSNӃKRҥFKVҧQ[XҩWOà bӝFiFVӕ
x chӍVӕÿѫQYӏVҧQSKҭP SP cҫQVҧQ[XҩW i i
Bước 2: Xác định hàm mục tiêu.
ChҷQJKҥQKàm mөFWLêu trong bài toán lұSNӃKRҥFKVҧQ[XҩWlà tәQJ
lӧLQKXұQWKXÿѭӧFnhiӅXQKҩW. 7
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
Bước 3: Xác định các ràng buộc.
1JRjLUDWK{QJWKѭӡQJFiFELӃQWURQJPӝWSKѭѫQJiQNLQKWӃWKѭӡQJ
NK{QJkPQrQWDWKѭӡQJFyWKêm các ràng buӝFYӅGҩX
1.2 Các dҥQJFӫa bài toán qui hoҥFKWX\ӃQWtQK
1.2.1 DҥQJ tәQJTXiWFӫa bài toán qui hoҥFKWX\ӃQWtQK
Ta thҩ\UҵQJFiFGRDQKQJKLӋSWKXӝFQKLӅXOƭQKYӵFNKiFQKDXFyQKӳQJ\êu
cҫXNKiFQKDXtrong viӋFÿӅUDFiFTX\ӃWÿӏQKÿӏQKOѭӧQJQhҵPWӕL ѭXKyDVҧQ
xuҩW NhӳQJ\êu cҫXQày có thӇÿѭӧFchuyӇQÿәL thành mô hình WRiQÿѭӧFWәQJ TXiWKyDQKѭVDX:
a) ĈLӅX NLӋQ WӕL ѭX KyD PhҧL WKӓD Pãn nhu cҫX YӅ PһW NLQKWӃ, bao gӗP KDL
WUѭӡQJKӧSFӵFÿҥLKyDKRһFFӵFWLӇXKyD
b) ĈLӅXNLӋQUàng buӝF: Là mӝWKӋJӗPFiFSKѭѫQJWUình hoһFEҩWSKѭѫQJWUình
bұFQhҩWxuҩWSKiWWӯQKӳQJÿòi hӓLFҫQÿѭӧFWKӓDPãn vӅPһWNӻWKXұW
c) ĈLӅXNLӋQYӅGҩX: XuҩWSKiWWӯ\êu cҫXWKӵFWLӉQOà các biӃQTX\ӃWÿӏQKphҧL không âm.
TӯÿyWDFydҥQJWәQJTXiWFӫDEài toán qui hoҥFKWX\ӃQWtQK. Ĉ. 1: c x c x ... c x Max (Min) 1 1 2 2 n n
a x a x ... a x b 11 1 12 2 1n n 1
a x a x ... a x b Ĉ. 21 1 22 2 2n n 2 2:
a x a x ... a x b 1 m 1 m2 2 mn n m Ĉ. n n 1
3: x , x ,..., x 0 1 2 1 n
HoһFWDFyWKӇYLӃWlҥLEjLWRiQGѭӟLGҥQJ n Ĉ. 1: z c x Max (Min) j j j 1 n Ĉ. 2: y a x b i m i ij j i 1,2,..., j 1 Ĉ. 3: x
0 j 1,2,..., n ;n n j 1 1
ĈLӅXNLӋQÿѭӧFgӑLOà hàm mөFWLêu. 8
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
HӋWKӕQJFiFSKѭѫQJWUình và bҩWSKѭѫQJWUình cӫDÿLӅXNLӋQJӑLOà các ràng buӝFcӫDEài toán.
ĈLӅXNLӋQJӑLOà các ràng buӝFYӅGҩX.
Tӯ bài toán dҥQJWәQJTXiWWD thҩ\FiFÿLӅXNLӋQFyWKӇOjFiFSKѭѫQJWUình,
bҩWSKѭѫQJWUình vӟLFiFGҩXWKHRFKLӅXNKiFQKDX ,
và có thӇÿiӅXNLӋQ
có mӝWVӕELӃQNK{QJEҳWEXӝFNK{QJkPVì vұ\,ÿӇWKXұQWLӋQKѫQWURQJYLӋF
[iFÿӏQKSKѭѫQJiQ tӕLѭXWDFyWKӇFKX\ӇQEài toán dҥQJWәQJTXiWEҩWNì thành
bài toán qui hoҥFKWX\ӃQWtQKGҥQJ chính tҳFYà dҥQJFKXҭQ.
1.2.2 DҥQJFKtQKWҳFFӫa bài toán qui hoҥFKWX\ӃQWtQK
Bài toán qui hoҥFKWX\ӃQWtQKGҥQJWәQJTXiW nӃXWKӓDPãn các ÿLӅXNLӋQVDX
ÿѭӧFJӑLOà bài toán qui hoҥFKWX\ӃQWtQKGҥQJFKtQKWҳF
Các hӋVӕEên vӃSKҧLFӫDFiFSKѭѫQJWUình thuӝFÿLӅXNLӋQOà nhӳQJVӕ
không âm b 0, i 1, 2,..., m . i
HӋWKӕQJFiFÿiӅXNLӋQJӗPFiFSKѭѫQJWUình.
Các biӃQ x 0, j 1,2,...,n j
Mô hình bài toán qui hoҥFKWXyӃQWtQKGҥQJFKtQKWҳF Ĉ. 1: c x c x ... c x Max (Min) 1 1 2 2 n n
a x a x ... a x b 11 1 12 2 1n n 1
a x a x ... a x b Ĉ. 21 1 22 2 2n n 2 2:
a x a x ... a x b 1 m 1 m2 2 mn n m
Ĉ.3: x , x ,..., x 0 1 2 n Hay ta có thӇYLӃWOҥL: n Ĉ. 1: z c x Max (Min) j j j 1 n Ĉ. 2: y a x b i m i ij j i 1,2,..., j 1 Ĉ. 3: x
0 j 1,2,...,n j
Tӯ PӝW Eài toán qui hoҥFK WX\ӃQ tính dҥQJ WәQJ TXiW WD Fy WKӇ ÿѭa vӅ GҥQJ
chính tҳFWѭѫQJÿѭѫQJWKHRFiFKVDX 9
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
a) 7UѭӡQJKӧSÿLӅX NLӋQFKѭD WKӓa:.KL ÿLӅXNLӋQFKѭDWKӓDcó nghƭDOà
tӗQWҥLtWQKҩW mӝWb QjRÿykPJLҧVӱE i k< 0).
a x a x ... a x b k1 1 k 2 2 kn n k
ĈӇÿѭDYӅGҥQJFKtQKWҳF, ta nhân 2 vӃcӫDSKѭѫQJWUình cho -1.
a x a x ... a x b k1 1 k 2 2 kn n k
MuӕQWKӓDPãn ÿLӅXNLӋQFӫDEài toán có dҥQJÿҷQJWKӭF
GiҧVӱWDFy a x a x ... a x b . k1 1 k 2 2 kn n k
7URQJWUѭӡQJ KӧSQày ta trӯÿLYӃWUiLFӫDEҩWSKѭѫQJWUình mӝWELӃQSKө[n+1
GѭѫQJ.ӃWTXҧWDELӃQGҩX thành dҩX, hay ta có dҥQJSKѭѫQJWUình:
a x a x ... a x x b k1 1 k 2 2 kn n n 1 k
1JѭӧFOҥLWDFӝQJWKêm vào vӃWUiLFӫDEҩWÿҷQJWKӭFPӝWELӃQSKө xn 1
GѭѫQJ.ӃWTXҧOà ta biӃQEҩWÿҷQJWKӭFWKjQKÿҷQJWKӭF
Tóm lҥLĈӇWKӓDPãn ÿLӅXNLӋQWUên, ta cӝQJWKêm biӃQ xn 1 vào vӃWUiLFӫDEҩW
SKѭѫQJ WUình và hӋ Vӕ FӫD ELӃQ xn 1 là 1 hoһF - WѭѫQJ ӭQJ YӟL GҩX FӫD EҩW
SKѭѫQJWUình là hoһF . Ví dө
ĈѭDÿLӅXNLӋQFӫDEài toán sau vӅGҥQJFKtQK tҳF
x 2x x 5 1 2 3
2x 3x 5x 6 1 2 3
x 2x x x 5 Ta có dҥQJFKtQKWҳF 1 2 3 4
2x 3x 5x x 6 1 2 3 5
Chú ý: Các biӃQSKө x , x trong hàm mөFWLêu có hӋVӕEҵQJNK{QJ 4 5
b7UѭӡQJKӧSÿLӅXNLӋQFKѭDWKӓD: TӭFOà có mӝWVӕELӃQEҳWEXӝFNK{QJ âm thuӝFÿLӅXNLӋQ
ĈӇÿҧPEҧRÿLӅXNLӋQFӫDEài toán là tҩWFҧFiFELӃQ x 0, ta sӁWKD\PӛLELӃQ i
không ràng buӝFYӅGҩX EҵQJKDLELӃQUàng buӝFYӅGҩXJLҧVӱELӃQ x không 1
ràng buӝFYӅGҩXWDWKD\ x x x vӟL x 0, x 0). 1 1 1 1 1 10
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
1.2.3 DҥQJFKuҭQ cӫa bài toán qui hoҥFKWX\ӃQWtQK
Bài toán qui hoҥFKWX\ӃQWtQKGҥQJFKtQKWҳFQӃXWKӓDWKrPÿLӅXNLӋQVDX
ÿѭӧFJӑLOà bài toán qui hoҥFKWX\ӃQWtQKGҥQJFKXҭQ ĈK 1: c x c x ... c x Min 1 1 2 2 n n
1x 0x ... 0x ... a x b 1 2 m 1n n 1
0x 1x ... 0x ... a x b Ĉ. 1 2 m 2n n 2 2:
0x 0x ... 1x ... a x b 1 2 m mn n m
Ĉ.3: x , x ,..., x 0 1 2 n
HӋVӕFӫDFiFELӃQWURQJÿLӅXNLӋQFӫDEài toán lұSWKành mӝWPDWUұQ
ÿѫQYӏ(FyFҩSEҵQJVӕSKѭѫQJWUình.
Các biӃQ WURQJÿLӅX NLӋQ FӫD Eài toán có hӋ sӕ OұS WKành mӝW PD WUұQ
ÿѫQYӏ(JӑLOà biӃQFѫEҧQFiFELӃQFòn lҥLJӑLOà biӃQNK{QJFѫEҧQ
TұSKӧSFiFELӃQTX\ӃWÿӏQK x , x ,..., x thӓDPãn ÿLӅXNLӋQYà 3 gӑLOà 1 2 n
lӡLJLҧLKRһFSKѭѫQJiQFӫDEài toán.
3KѭѫQJiQ X (x , x ,..., x ) vӟLFiFELӃQNK{QJFѫEҧQEҵQJNK{QJJӑL 1 2 n
OjSKѭѫQJiQFӵFELrQSKѭѫQJiQFѫEҧQFӫDEài toán.
3KѭѫQJiQFӵFELên thӓDPãn ÿLӅXNLӋQJӑLOjSKѭѫQJiQWӕLѭX–SKѭѫQJ án cuӕLFùng ta cҫQWìm.
Chú ý: NӃX ӣ GҥQJ FKtQK WҳF, hӋ Vӕ FӫD FiFELӃQ WURQJ ÿLӅX NLӋQ FӫD Eài
toán không lұSWKành mӝWPDWUұQÿѫQYӏWKì ta cӝQJYào mӝWELӃQJLҧNK{QJkP
là biӃQFѫEҧQӣQKӳQJUàng buӝFFKѭDFyELӃQFѫEҧQ.KLÿyKӋVӕFӫDELӃQQày
ӣKàm mөFWLêu là M (sӕGѭѫQJUҩWOӟQÿӕLYӟLEài toán cӵFWLӇXKyDKD\–0ÿӕL vӟLEài toán cӵFÿҥLKyD
1.3 MӝWVӕEài toán ӭQJGөQJ
1.3.1 Bài toán phân bәYӕQÿҫXWѭ
MӝWQKjÿҫXWѭFyWӍÿӗQJPXӕQÿҫXWѭYjROƭQKYӵFFKӭQJNKRiQ
công trái, gӣLWLӃWNLӋPYà bҩWÿӝQJVҧQ%LӃWOãi suҩWKҵQJQăPFӫDFiFOƭQKYӵF ÿҫXWѭQKѭVDX 11
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế LƭQKYӵFÿҫXWѭ Lãi suҩWKjQJQăP ChӭQJNKRiQ 20% Công trái 12% GӣLWLӃWNLӋP 10% BҩWÿӝQJVҧQ 15%
1JRjLUDÿӇJLҧPWKLӇXPӭFÿӝUӫLURQKjÿҫXWѭFKRUҵQJNK{QJQrQÿҫX
WѭYjRFKӭQJNKRiQYѭӧWTXiWәQJYӕQÿҫXWѭFòn ÿҫXWѭYjRF{QJWUiLYj
gӣLWLӃW kiӋPSKҧLtWQKҩWOà 25% tәQJYӕQÿҫXWѭYjWLӅQJӣLWLӃWNLӋPSKҧLtWQKҩW là 100 triӋXÿӗQJ
Hãy lұSNӃKRҥFKSKkQEәYӕQÿҫXWѭVDRFKRWәQJWKXQKұSKjQJQăPOjOӟQ nhҩW GiҧL
GӑL x j 1,..., 4 lҫQOѭӧWOà sӕWLӅQWULӋXÿӗQJÿҫXWѭYjR chӭQJNKRiQ j
công trái, gӣLWLӃWNLӋPYà bҩWÿӝQJVҧQ
TәQJWKXQKұSKjQJQăPOjOӟQQKҩW 0, 2x 0,12x 0,1x 0,15x max 1 2 3 4
TәQJVӕWLӅQÿҫXWѭNK{QJYѭӧWTXiVӕWLӅQKLӋQFy x x x x 2.000 1 2 3 4
ĈLӅXNLӋQYӅVӕWLӅQÿҫXWѭYjRFKӭQJNKRiQ
x 0, 4(x x x x ) 0,
6x 0,4x 0,4x 0,4x 0 1 1 2 3 4 1 2 3 4
ĈLӅXNLӋQYӅVӕWLӅQÿҫXWѭYjRF{QJWUiLYjJӣLWLӃWNLӋP
x x 0, 25(x x x x ) 0,
25x 0,75x 0,75x 0,25x 0 2 3 1 2 3 4 1 2 3 4
ĈLӅXNLӋQYӅVӕWLӅQJӣLWLӃWNLӋPWӕLWKLӇX x 100 3
ĈLӅXNLӋQNK{QJkPFӫDFiFNKRҧQÿҫXWѭ x 0 j 1,...,4 j
Vұ\WDFyÿѭӧFP{Kình cӫDEjLWRiQQKѭVDX
Ĉ. 0,2x 0,12x 0,1x 0,15x max 1 2 3 4
x x x x 2.000 1 2 3 4 Ĉ. 0,6x 0, 4x 0, 4x 0, 4x 0 1 2 3 4
0,25x 0,75x 0,75x 0,25x 0 1 2 3 4 x 100 3
Ĉ. x 0 j 1,...,4 . j 12
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
1.3.2 Bài toán xӃSFDOàm viӋF
Xí nghiӋS QKӵD %ình Minh chuyên sҧQ [XҩW ÿӗ QKӵD KRҥW ÿӝQJ JLӡ
mӛLQJj\ÿrP&ăQFӭYào nhu cҫXWLêu thөWUên thӏWUѭӡQJ[tQJKLӋS[iFÿӏQKVӕ
OѭӧQJF{QJQKkQFҫQWKLӃWFKRWӯQJJLDLÿRҥQVҧQ[XҩWFKRWURQJEҧQJVDX ThӡLJLDQWURQJQJày 3-7 7-11 11-15 15-19 19-23 23-3 SӕOѭӧQJF{QJQKkQFҫQWKLӃW 250 270 300 280 220 200
GiҧVӱ[tQJKLӋSVӁEӕWUtPӛLFDOàm viӋFOLên tөFJLӡYà hӋVӕOѭѫQJWUҧ
FKRF{QJQKkQWURQJFiFFDWKD\ÿәLQKѭVDXFDKRҥWÿӝQJQҵPWURQJNKRҧQJ
thӡLJLDQWӯ-17 giӡWKì hӋVӕOѭѫQJWUXQJEình là 1, các ca còn lҥL cӭOӋFKQJRài
giӡKành chánh 2 giӡthì hӋVӕOѭѫQJWăQJOrQ
Hãy xác ÿӏQKSKѭѫQJiQEӕWUtFiFFDOàm viӋFYӟLPөFWLêu cӵFWLӇXKyD
tәQJTXӻOѭѫQJWURQJWUѭӡQJKӧSÿҧPEҧRVӕF{QJQKkQYà quӻOѭѫQJWKҩSQKҩW
Yêu cҫXOұSP{Kình toán hӑFFӫDEài toán trên. GiҧL
GӑL x là sӕFông nhân cҫQFyÿӇEҳWÿҫXFD 1
GӑL x là sӕF{QJQKkQ cҫQFyÿӇEҳWÿҫXFD. 2
GӑL x là sӕF{QJQKkQ cҫQFyÿӇEҳWÿҫXFD. 3
GӑL x là sӕF{QJQKkQ cҫQFyÿӇEҳWÿҫXFD. 4
GӑL x là sӕF{QJQKkQ cҫQFyÿӇEҳWÿҫXFD. 5
GӑL x là sӕF{QJQKkQ cҫQFyÿӇEҳWÿҫXFD. 6
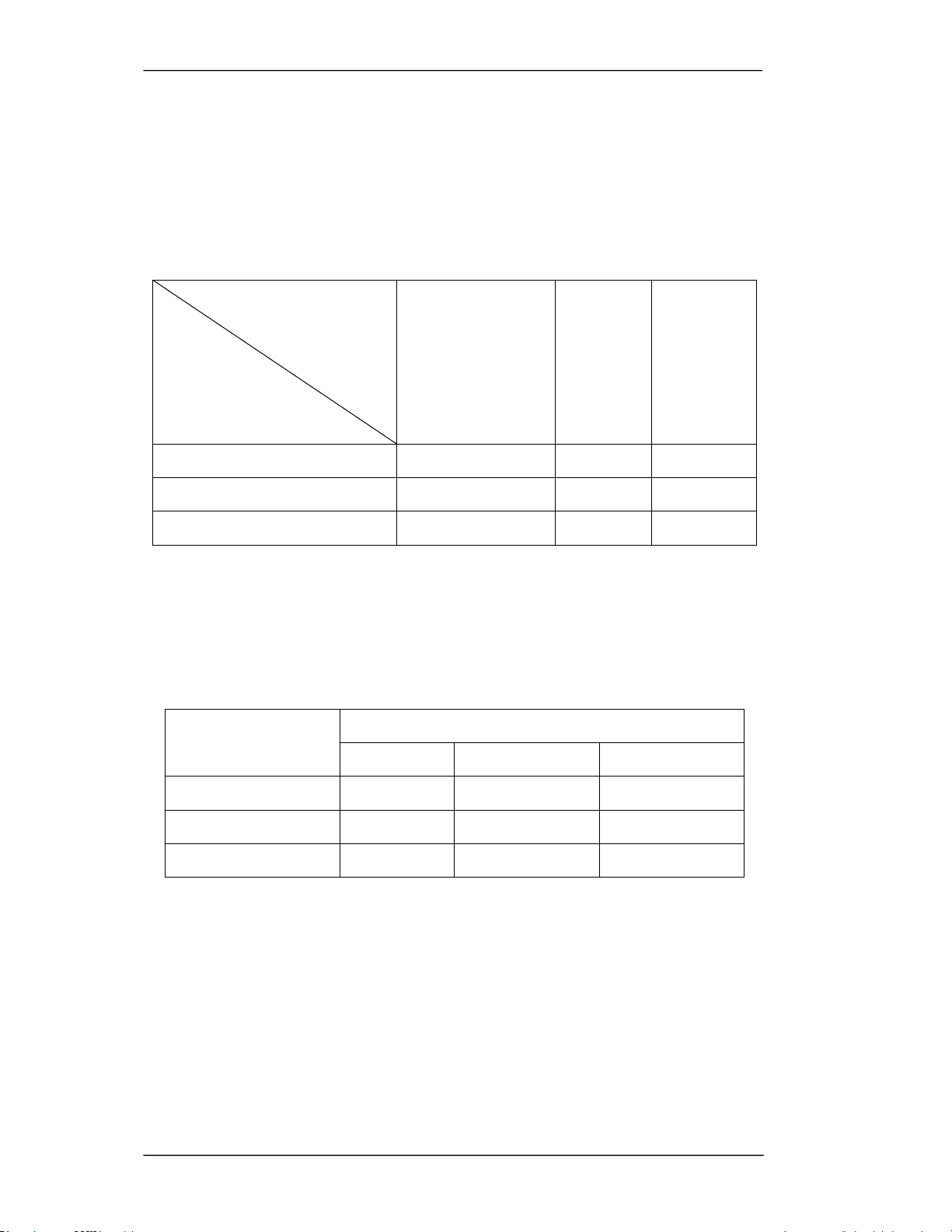
SӕFDOàm viӋFWURQJPӝWQJj\ÿrP Công nhân tӕL *LDLÿRҥQ C1 C2 C3 C4 C5 C6 thiӇX 3-7 X X 250 7-11 X X 270 11-15 X X 300 15-19 X X 280 19-23 X X 220 23-3 X X 200
Ta có bҧQJKӋVӕOѭѫQJQKѭVDX 13
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế C1 C2 C3 C4 C5 C6 1,2 1 1,1 1,3 1,5 1,4
z 1, 2x x 1,1x 1,3x 1,5x 1, 4x min 1 2 3 4 5 6
x x 250 1 6
x x 270 1 2
x x 300 2 3
x x 200 5 6 x 0, j 1,..,6 j
1.3.3 Bài toán bӕWUtVҧQ[XҩW - vұQFKX\ӇQ
MӝWcông ty có hai nhà máy cùng sҧQ[XҩWPӝWORҥLVҧQSKҭPFXQJFҩSUD
thӏWUѭӡQJ&KLSKtVҧQ[XҩWWҥLPӛLQKà máy ӣPӛLWKiQJÿӅXNKiFQKDX*LҧVӱ
công ty chӍFXQJFҩSVҧQSKҭPFKRKDLFӱDKàng cӫDPình vӟLJLiEiQOҿWҥLPӛL
cӱDKàng cNJQJNKiFQKDX7URQJNǤNӃKRҥFKF{QJW\PXӕQWӕLÿDKyDOӧLQKXұQ
thông qua viӋFEӕWUtVҧQxuҩW-vұQFKX\ӇQYӟLJLҧÿӏQKOjOѭӧQJKjQJEiQUDÿ~QJ
QKѭGӵEiR6ӕOLӋXYӅQăQJOӵFVҧQ[XҩWFKLSKtVҧQ[XҩWOѭӧQJKàng bán ra và
giá bán ӣFiFÿӏDÿLӇPFKRELӃWQKѭVDX Tháng 1 2 3 1ăQJOӵFVҧQ[XҩWVҧQSKҭP 160 200 150 Nhà máy A Chi phí sҧQ[XҩWÿVS) 12 14 10 1ăQJOӵFVҧQ[XҩWVҧQSKҭP 150 200 180 Nhà máy B Chi phí sҧQ[XҩWÿVS 12 13 11 *LiEiQÿVS 20 22 21 CӱDKàng 1 /ѭӧQJEiQVҧQSKҭP 180 190 200 *LiEiQÿVS 21 22 20 CӱDKàng 2 /ѭӧQJEiQVҧQSKҭP 120 200 120
Chi phí vұQFKX\ӇQPӝWÿѫQYӏVҧQSKҭPWӯFiFQKjPi\ÿӃQFiFFӱDKàng OjÿӗQJ 14
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế CӱDKàng 1 CӱDKàng 2 Nhà máy A 3 4 Nhà máy B 2 5
Hãy lұS P{ Kình toán hӑF FӫD EjL WRiQ WUrQ WURQJ WUѭӡQJ KӧS VҧQ [XҩW
tháng nào tiêu thөKӃWWKiQJÿy GiҧL
Ta có: Giá vӕQ &KLSKtVҧQ[XҩWFKLSKtYұQFKX\ӇQ LӧLQKXұQ *LiEiQ– Giá vӕQ ThӭWӵ 1 2 3 SҧQ[XҩW C H1 5x 5x 8x 11 12 13 A C H 2 5x 4x 6x 21 22 23 C H1 6x 7x 8x 31 32 33 B C H 2 4x 4x 4x 41 42 43
GӑL x (i 1,..., 4; j 1,...,3) là sӕOѭӧQJVҧQSKҭPWLêu thө. ij
z 5x 5x 8x 5x 4x 6x 11 12 13 21 22 23
6x 7x 8x 4x 4x 4x max 31 32 33 41 42 43
T x x 160 1: 11 21
A T x x 200 2: 12 22
T x x 150 3: 13 23
Cung T x x 150 1: 31 41
BT x x 200 2: 32 42
T x x 180 3: 23 43
T x x 180 1: 11 31
A T x x 190 2: 12 32
T x x 200 3: 13 33
Câu T x x 120 1: 21 41
BT x x 200 2: 22 42
T x x 120 3: 23 43 15
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế x 0,
(i 1,...,4; j 1,...,3) ij BÀI TҰ3&+ѬѪ1* 1.
MӝWWәVҧQ[XҩWÿӏQKWUӗQJEӕQORҥLE{QJ+ӗQJ+XӋ/D\ѫQ&~F&KLSKt
trung bình cho 100 bông hoa mӛL ORҥL YӅ OѭӧQJ SKkQ KӳX Fѫ OѭӧQJ SKkQ KyD
hӑF Vӕ QJày công, diӋQ WtFK ÿҩW FNJQJ QKѭ WLӅQ Oãi thu vӅ ÿѭӧF FKo trong bҧQJ sau: Chi phí cho 100 bông Tài nguyên ĈѫQYӏ HӗQJ HuӋ /D\ѫQ Cúc ĈҩW ha 0,001 0,002 0,003 0,001 Công ngày 0,02 0,01 0,3 0,01 Phân hӳXFѫ tҩQ 0,005 0,004 0,003 0,006 Phân hóa hӑF tҩQ 0,004 0,002 0,003 0,004 Lãi ÿӗQJ 20.000 25.000 28.000 29.500
BiӃWWәQJVӕF{QJGӵWUӳQJày; diӋQWtFKKDSKkQKӳXFѫ7SKkQ
hóa hӑF7&ҫQOұSNӃKRҥFKWUӗQJVDRFKRWәQJVӕOãi thu ÿѭӧFOà lӟQQKҩW Hãy lұSP{Kình bài toán. 2.
Hai loҥL VҧQ SKҭP$ Yà B cҫQ ÿѭӧF VҧQ [XҩW TXD PӝW KӋ WKӕQJ OLên tөF
máy. ThӡLJLDQKRҥWÿӝQJFӫDPӛLPi\WURQJQJày là 10 giӡ+DRSKtWKӡLJLDQ
ÿӇKRàn thành tӯQJF{QJÿRҥQvà lӧLQKXұQWKXÿѭӧFWUên mӛLÿѫQYӏVҧQSKҭP
tӯng loҥLFKRWURQJEҧQJGѭӟLÿk\: SҧQ Phút/sҧQSKҭP LӧLQKXұQÿѫQYӏ phҭP Máy 1 Máy 2 Máy 3 ÿӗQJ A 10 6 8 20 B 5 20 15 30
Tìm lӡLJLҧLWӕLѭXYӅ OѭӧQJVҧQSKҭP PӛLORҥLFҫQVҧQ[XҩW +ãy lұS P{Kình toán hӑFEài toán trên. 3.
Công ty VҥQ+ѭQJcó thӇTXҧQJFiRVҧQSKҭPFӫDQyEҵQJFiFKVӱGөQJKDL
SKѭѫQJWLӋQNKiFQKDXOà radio và tivi. GiӟLKҥQYӅFKLSKtTXҧQJFiRFӫDF{QJW\
là 100 triӋX ÿӗQJWKiQJ %LӃW PӛL SK~W TXҧQJ FiR WUên radio là 5 triӋX ÿӗQJ Yà
trên tivi là 1 triӋXÿӗQJ&{QJW\PXӕQWKӡLJLDQTXҧQJFiRtrên radio ít nhҩWOà
gҩSÿ{LWKӡLJLDQVӱGөQJSKѭѫQJWLӋQTXҧQJFiROà tivi. Qua kӃWTXҧQJKLên cӭX 16
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
hiӋXTXҧFӫDFiFORҥLSKѭѫQJWLӋQTXҧQJFiRWKì sӱGөQJSKѭѫQJWLӋQTXҧQJFiR
là tivi làm cho sҧQ OѭӧQJ WLêu thө ÿѭӧF WăQJ JҩS OҫQ VR YӟL TXҧQJ FiR WUên
UDGLR;iFÿӏQKWKӡLJLDQTXҧQJFiRWӟLѭXWUrQPӛLSKѭѫQJWLӋQUDGLRYà tivi) và
vӟLSKkQEәWKӡLJLDQQKѭYұ\FKLSKtTXҧQJFiROà bao nhiêu mӛLWKiQJ"+ãy lұS mô hình bài toán trên. 4.
Công ty Bao Bì DѭӧFFҫQVҧQ[XҩWEDORҥLKӝSJLҩ\ÿӵQJWKXӕF B ÿӵQJ 1
thuӕF B YjÿӵQJ³4XLVkPÿҥLEәKRjQ´ĈӇVҧQ[XiWFiFORҥLKӝSQày, công ty 6
dùng các tҩPEìa có kích thѭӟFJLӕQJQKDX0ӛLWҩPEài có 5 cách cҳWNKiFQKDX Cách HӝS B HӝS B 1 6 HӝS4XLVkP 1 12 0 2 2 0 7 4 3 8 0 3 4 1 6 2 5 9 2 0
Theo kӃKRҥFKVӕKӝS B phҧLFyOà 1500; sӕKӝS B phҧLFyOà 1000; sӕKӝS4XL 1 2
sâm tӕLWKLӇXOà 2000. CҫQSKѭѫQJiQFҳWVDRFKRWәQJVӕWҩPEìa phҧLGùng là ít
nhҩW+ãy lұSP{Kình bài toán. 5.
MӝW [t QghiӋS GӋW Fy ORҥL VӧL &RWWRQ .DWH 3RO\HVWHU YӟL NKӕL OѭӧQJ
WѭѫQJӭQJOà 3 tҩQWҩQYà 4,2 tҩQ&iFQJX\ên liӋXVҧQ[XҩWNKiFYjODRÿӝQJ
có sӕOѭӧQJOӟQ;tQJKLӋSFyWKӇVҧQ[XҩWUDORҥLYҧL$%&YӟLPӭFWLêu hao
các loҥLVӧLÿӇVҧQ[XҩWUDmӝWPpWYҧLFiFORҥLFKRWURQJEҧQJVDX
LoҥLVӧLWLêu hao (gam)/1 m vҧL LoҥLVӧLJDP A B C Cotton 200 200 100 Kate 100 200 100 Polyester 100 100 200 LӧLQKXұQPQJjQÿӗQJ 35 48 25
Hãy lұSP{Kình toán hӑFFӫDEài toán trên.
a. ;iFÿӏQKVӕPpWYҧLPӛLORҥLFҫQVҧQ[XҩWWӕLÿDKyDOӧLQKXұQ
b. Giҧ Vӱ OѭӧQJ YҧL ORҥL $ WLêu thө tW QKҩW JҩS OҫQ YҧL ORҥL & Yà loҥL % không quá 2/3 vҧLORҥL$ 17
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
13. Công ty vұQWҧL &ҫQ 7Kѫ QKұQ PӝW KӧSÿӗQJYұQFKX\ӇQ Jҥo cho công ty
;1. OѭѫQJWKӵF0HNRQJ /ѭӧQJ JҥRÿѭӧFFKXyӇQWӯ NKR7Uà Nóc, PhөQJ
HiӋSYà CҫQ7KѫÿӃQÿӏDÿLӇPQKұQOà Thành phӕ+ӗ&Kt0LQK6yF7UăQJYà
VƭQK/RQJ/ѭӧQJJҥRWҥLFiFNKRFҫQJLDRYjOѭӧQJJҥRFҫQQKұQWӕLWKLӇXWҥL
FiFNKRÿӃQYà chi phí vұQFKX\ӇQQJjQÿӗQJWҩQWӯFiFNKRJLDRÿӃQFiF kho nhұQFKRWURQJEҧQJVDX 1ѫLQKұQKàng
/ѭӧQJFҫQQKұQ Tp. Hӗ&Kt0LQK 6yF7UăQJ VƭQK/RQJ 500T 800T 600T 1ѫLFKX\ӇQKàng ÿL/ѭӧQJGӵWUӳ Trà Nóc: 1.000T 200 130 90 PhөQJ+LӋS300T 80 30 60 CҫQ7Kѫ700T 40 70 35
Yêu cҫX[iFÿӏQKNӃKRҥFKYұQFKX\ӇQVDRFKRÿҧPEҧRÿӫKàng và tәQJ
chi phí vұQFKX\ӇQQKӓQKҩWHãy lұSP{Kình toán hӑFFӫDEài toán trên.
14. Cѫ Vӣ mӝF Hoàng Minh dӵ ÿӏQKVҧQ [XҩW Eàn, tӫJKӃ %LӃW ÿӏQKPӭF WLêu
hao các yӃXWӕ VҧQ [XҩW Yà lӧL QKXұQ NKL Oàm ra mӝW VҧQ SKҭP FKR WURQJ EҧQJ sau:
Hao phí yӃXWӕVҧQ[XҩW6ҧQSKҭP YӃXWӕVҧQ[XҩW Bàn Tӫ GhӃ /DRÿӝQJQJày) 2 0.5 3 &KLSKtÿ 200 50 350 LӧLQKXұQÿ 40 10 60
&ăQFӭYào nhu cҫXWUên thӏWUѭӡQJELӃWUҵQJNKLVҧQ[XҩWVӕEàn và sӕJKӃ
phҧLWXkQWKHRWӍOӋ;tQJKLӋSFyVӕODRÿӝQJOjQJj\F{QJTXLÿәLUD
sӕQJày công) và sӕYӕQOà 120 triӋXÿӗQJ+ãy lұSNӃKRҥFKVҧQ xuҩWWӕLѭXYj
lұSP{Kình toán hӑFFӫDEài toán trên.
15. ĈӇ sinh sӕQJPӝWQJj\ ÿrP PӛLQJѭӡLFҫQ tWQKҩWJ SURWLW J OLSLWYà
420g gluxit. GiҧVӱELӃWKjPOѭӧQJFiFFKҩWWUên có trong 1g thӭFăQ$%Yà C QKѭVDX 18
Downloaded by Long Lê (lelong28032006@icloud.com) lOMoARcPSD|45156089
Bài giảng Toán kinh tế
HàmOѭӧQJFiFFKҩWGLQKGѭӥQJ ChҩWGLQKGѭӥQJ MӭFcҫQWKLӃWJ) trong 1g thӭFăQ A B C Protit (g) 70 0.1 0.2 0.3 Lipit (g) 30 0.1 0.1 0.55 Gluxit (g) 420 0.7 0.6 0.55 *LiPXDJDPÿӗQJ 4 6 5
Hãy xiFÿӏQKFiFKPXDWKӭFăQÿӇFKӃELӃQNKҭXSKҫQăQVDRFKRÿҧPEҧR
mӭFWӕLWKLӇXGLQKGѭӥQJPӝWQJj\ÿrPYjFKLSKtPXDWKӭFăQWKҩSQKҩW<êu
cҫXOұSP{Kình toán hӑFFӫDEài toán trên.
16. 3KkQ[ѭӣQJEDREì cӫDF{QJW\%LELFDFҫQVҧQ[XҩWORҥLKӝSJLҩ\NtFK cӥ
khác nhau cho công viӋFÿyQJJyLVҧQSKҭPEiQKQJӑWĈӇVҧQ[XҩWFiFKӝSJLҩ\
Qj\SKkQ[ѭӣQJVӱGөQJFiFWҩPEìa có kích thѭӟFJLӕQJQKDX0ӛLWҩPEìa có 5
cách cҳWNKiFQKDXÿӇFҳWWKành 3 loҥLKӝSJLҩ\QKѭÿѭӧFFKӍUDWURQJEҧQJVDX ÿk\
Sӕ hӝSJLҩ\PӛLORҥLWҩPEìa Cách cҳW HӝSJLҩ\ORҥL HӝSJLҩ\ORҥL HӝSJLҩ\ORҥL Cách 1 10 2 4 Cách 2 0 12 2 Cách 3 5 8 0 Cách 4 6 2 3 Cách 5 1 7 6
SӕKӝSJLҩ\PӛLORҥLWӯYLӋFFҳWPӝWWҩPEìa theo tӯQJFiFKFҳW
Theo kӃKRҥFKFҫQVҧQ[XҩWEiQKQJӑWVӕKӝSJLҩ\ORҥLYà 2 cҫQWKLӃW
WѭѫQJӭQJOà 1.000 và 1.500 hӝS6ӕKӝSJLҩ\ORҥLFҫQWKLӃWNK{QJtWKѫQ
và không nhiӅXKѫQKӝS+ӓLSKkQ[ѭӣQJEDREì nên cҳWWKHRSKѭѫQJiQ
nhu thӃQjRÿӇQKҵPWӕLWKLӇXKyDVӕWҩPEìa. Yêu cҫXOұSP{Kình toán hӑFFӫD bài toán trên. 17.
Công ty VIFON sҧQ[XҩWPì ăQOLӅQPӛLJyLFyWUӑQJOѭӧQJWӏQKOà 80g. Giҧ
sӱ ELӃW UҵQJ KjP OѭӧQJ FiF FKҩW Fy WURQJ FiF QJX\ên liӋX FKӃ ELӃQ FKR WURQJ bҧQJVDX: 19
Downloaded by Long Lê (lelong28032006@icloud.com)