-
Thông tin
-
Hỏi đáp
Bài giảng môn Vật liệu điện_Phạm Hồng Thịnh| Bài giảng môn Vật liệu điện| Trường Đại học Bách Khoa Hà Nội
Nội dung chính của thuyết cấu tạo nguyên tử theo mô hình Borh được hiểu như sau: điện tử quay quanh hạt nhân theo một quỹ đạo tròn. Ở điều kiện bình thường (nhiệt độ phòng) điện tử nằm trên quỹ đạo gần hạt nhân nhất, vị trí này ứng với mức năng lượng thấp nhất của nguyên tử hay còn gọi là trạng thái dừng (ground state).
Đại học Bách Khoa Hà Nội (2.8 K)
Bài giảng môn Vật liệu điện_Phạm Hồng Thịnh| Bài giảng môn Vật liệu điện| Trường Đại học Bách Khoa Hà Nội
Nội dung chính của thuyết cấu tạo nguyên tử theo mô hình Borh được hiểu như sau: điện tử quay quanh hạt nhân theo một quỹ đạo tròn. Ở điều kiện bình thường (nhiệt độ phòng) điện tử nằm trên quỹ đạo gần hạt nhân nhất, vị trí này ứng với mức năng lượng thấp nhất của nguyên tử hay còn gọi là trạng thái dừng (ground state).
Môn: Vật liệu điện hust
Trường: Đại học Bách Khoa Hà Nội
Thông tin:
Tác giả:
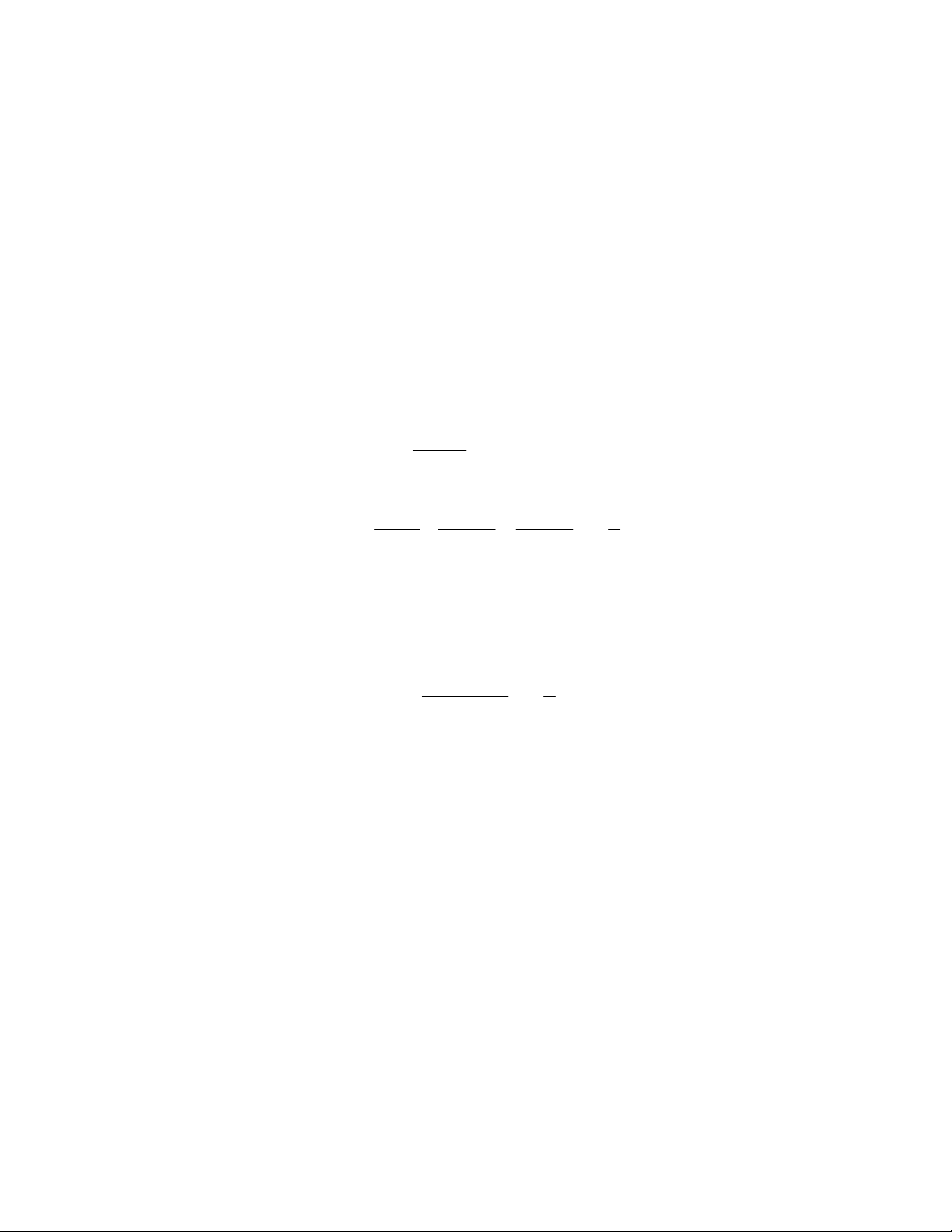
Preview text:
Trường Đại học Bách Khoa Hà nội
Khoa Điện- Bộ môn Hệ thống điện BÀI GIẢNG MÔN VẬT LIỆU ĐIỆN
Biên soạn: TS Phạm Hồng Thịnh TS Trần Văn Tớp Hà nội, tháng 10-2006
Chương I: CẤU TẠO VẬT CHẤT .................................................................................... 1
I.1. Cấu tạo nguyên tử..................................................................................................... 1
I.1.1. Thuyết cấu tạo nguyên tử của Borh................................................................... 1
I.1.2. Thuyết cơ học lượng tử của nguyên tử.............................................................. 3
I.2. Cấu tạo phân tử và các dạng liên kết ........................................................................ 8
I.2.1. Liên kết ion........................................................................................................ 9
I.2.2. Liên kết cộng hoá trị........................................................................................ 11
I.2.3. Liên kết kim loại.............................................................................................. 12
I.2.4. Các liên kết thứ cấp ......................................................................................... 13
I.2.5. So sánh các liên kết ......................................................................................... 15
I.2.6. Cực tính của liên kết và độ âm điện ................................................................ 17
I.2.8. Cấu trúc tinh thể và khuyết điểm trong mạng tinh thể .................................... 18
I.3. Lý thuyết phân vùng năng lượng trong vật rắn ...................................................... 24
I.3.1. Mức năng lượng Fermi .................................................................................... 24
I.3.2. Lý thuyết vùng năng lượng. Kim loại, điện môi và chất bán dẫn ................... 26
I.4. Phân loại vật chất theo độ dẫn điện và từ tính........................................................ 28
I.4.1. Phân loại vật chất theo độ dẫn điện ................................................................. 28
1.4.2 . Phân loại vật liệu theo độ từ tính ................................................................... 29
Chương II: VẬT LIỆU DẪN ĐIỆN VÀ BÁN DẪN ĐIỆN............................................. 30
II.1. Tính dẫn điện của kim loại.................................................................................... 30
II.1.1. Các điện tích chuyển động ............................................................................. 30
II.1.2. Dòng điện ....................................................................................................... 30
II.1.3. Mật độ dòng điện, vận tốc chuyển động của các điện tích và điện dẫn suất của
vật liệu....................................................................................................................... 31
II.2. Điện trở và điện trở suất........................................................................................ 34
II.2.1. Tính tuyến tính của định luật Ohm................................................................. 34
II.2.2. Sự phụ thuộc của điện trở suất và độ linh hoạt vào nhiệt độ ......................... 34
II.2.3. Điện dẫn của kim loại sạch ............................................................................ 36
II.2.4. Điện dẫn của hợp kim .................................................................................... 37
II.3. Tính chất vật lý của kim loại................................................................................. 37
II.3.1. Nhiệt độ và nhiệt lượng nóng chảy ................................................................ 37
II.3.2. Tính dẫn nhiệt................................................................................................. 37
II.3.3. Giãn nở nhiệt ................................................................................................. 38
II.3.4. Vẻ sáng của kim loại ...................................................................................... 38
II.4. Tính chất hoá học của kim loại ............................................................................. 38
II.5. Tính chất cơ học của kim loại ............................................................................... 38
II.5.1. Độ bền ............................................................................................................ 38
II.5.2. Độ đàn hồi ...................................................................................................... 38
II.5.3. Độ dẻo ............................................................................................................ 38
II.6. Vật liệu có điện dẫn cao ........................................................................................ 38
II.6.1. Đồng............................................................................................................... 39
II.6.2. Nhôm.............................................................................................................. 42 II.6.3.
So sánh tính chất của đồng và nhôm......................................................... 44
II.6.4. Các kim loại khác...................................................................................... 45 II.7. Các
vật liệu điện trở suất cao ............................................................................ 47 II.7.1. Các
hợp kim điện trở suất cao................................................................... 47 II.7.2. Các
hợp kim điện trở suất cao và bền nhiệt.............................................. 47
II.8. Vật liệu bán dẫn..................................................................................................... 47
II.8.1. Bán dẫn tinh khiết (intrinsic semiconductor) ................................................. 48
II.8.2. Bán dẫn tạp chất (extrinsic semiconductor) ................................................... 50
Chương III- VẬT LIỆU TỪ VÀ SIÊU DẪN ................................................................... 52
III.1. Một số khái niệm cơ bản...................................................................................... 52
III.1.1. Các đơn vị cơ bản ......................................................................................... 52
III.1.2. Một số định lý về từ trường .......................................................................... 53
III.2. Khái niệm về tính chất từ của vật liệu ................................................................. 56
III.2.1. Tính chất từ của nguyên tử ........................................................................... 56
III.2.2. Các thành phần của mô men từ nguyên tử.................................................... 58
III.3. Phân loại vật liệu từ ............................................................................................. 59
III.3.1. Vật liệu nghịch từ (diamagnetism) ............................................................... 60
III.3.2. Vật liệu thuận từ (paramagnetism) ............................................................... 60
III.3.3. Vật liệu sắt từ (ferromagetism) ..................................................................... 62
III.3.4. Vật liệu phản sắt từ (antimagnetism)và ferit từ (ferrimagnetism) ................ 66
III.4. Tổn hao từ ............................................................................................................ 67
III.4.1. Tổn hao từ trễ................................................................................................ 67
III.4.2. Dòng điện và tổn hao Foucault ..................................................................... 68
III.4.3. Tổn hao từ dư................................................................................................ 68
III.5. Tác dụng của từ trường ........................................................................................ 68
III.5.1. Hiệu ứng Hall................................................................................................ 68
III.5.2. Hiệu ứng Kelvin (Hiệu ứng bề mặt) ............................................................. 69
III.6. Vật liệu siêu dẫn................................................................................................... 70
III.6.1. Nhiệt độ tới hạn............................................................................................. 71
III.6.2. Hiệu ứng Meissner........................................................................................ 72
III.6.3. Từ trường tới hạn và phân loại vật liệu siêu dẫn .......................................... 74
III.6.4. Lý thuyết BCS............................................................................................... 75
III.6.5. Mật độ dòng điện tới hạn .............................................................................. 77
III.6.6. Ứng dụng của vật liệu siêu dẫn..................................................................... 78
Chương IV- CÁC QUÁ TRÌNH ĐIỆN LÝ CỦA ĐIỆN MÔI ......................................... 81
IV.1. Nhắc lại các khái niệm cơ bản về tĩnh điện ......................................................... 81
IV.1.1. Định luật Coulomb ....................................................................................... 81
IV.1.2. Điện trường và định luật Gauss .................................................................... 81
IV.1.3. Thông lượng của cường độ điện trường ....................................................... 82
IV.1.4. Liên hệ giữa điện thế và điện trường. Phương trình Poisson-Laplace ......... 83
IV.2. Điện môi đặt trong điện trường không đổi .......................................................... 85
IV.2.1. Lưỡng cực điện............................................................................................. 85
IV.2.2. Hiện tượng phân cực..................................................................................... 89
IV.2.3. Điện trường nội bộ........................................................................................ 92
IV.2.4. Phương trình Clausius-Mosotti..................................................................... 94
IV.2.5. Mô hình Onsager và mô hình Kirwood ........................................................ 96
IV.3. Điện môi đặt trong điện trường thay đổi ............................................................. 97
IV.3.1. Hàm đáp ứng điện môi trong điện trường thay đổi ở miền thời gian ........... 98
IV.3.2. Hàm đáp ứng điện môi trong miền tần số. Quan hệ Kramers-Kronig........ 101
IV.3.3. Định nghĩa về hằng số điện môi phức và góc tổn hao DELTA.................. 103
IV.3.4. Hiện tượng điện môi nghỉ (dielectric relaxation) ....................................... 105
IV.3.5. Phân cực tiếp giáp trong điện môi không đồng nhất- Mô hình Maxwell-
Wagner.................................................................................................................... 110
IV.3.6. Sự phụ thuộc của tổn hao điện môi vào nhiệt độ........................................ 112
Chương V- ĐIỆN MÔI KHÍ........................................................................................... 114
V.1. Phóng điện trong điện môi khí............................................................................ 114
V.1.1. Các quá trình hình thành điện tích trong điện môi khí................................. 114
V.1.2. Các quá trình trên điện cực âm (cathode) .................................................... 116
V.1.3. Các quá trình trung hòa điện tích trong điện môi khí .................................. 117
V.1.4. Phóng điện chọc thủng của chất khí trong điện trường đồng nhất (đều) ..... 118
V.1.5. Phóng điện chọc thủng của chất khí trong điện trường không đồng nhất.... 127
V.1.6. Phóng điện chọc thủng của chất khí ở điện áp xung.................................... 134
V.2. Điện môi chân không .......................................................................................... 138
V.2.1. Các quá trình giải thoát điện tử trong chân không....................................... 139
V.2.2. Các cơ chế gây ra hiện tượng phóng điện chọc thủng trong chân không .... 142
V.2.3. Các yếu tố ảnh hưởng lên trị số điện áp phóng điện chọc thủng trong chân
không....................................................................................................................... 144
V.3. Cách điện SF6...................................................................................................... 146
V.3.1. Các tính chất cơ bản của SF6........................................................................ 146
V.3.2. Phóng điện chọc thủng trong SF6................................................................. 147
V.3.4. Hỗn hợp của SF6 với các khí khác .............................................................. 148
V.4. Lựa chọn cách điện thể khí ................................................................................. 149
Chương VI- ĐIỆN MÔI LỎNG...................................................................................... 152
VI.1. Hiện tượng dẫn điện của điện môi lỏng............................................................. 152
VI.1.1. Chất lỏng cực tính và không cực tính......................................................... 152
VI.1.2. Quá trình điện dẫn nội tại của môi.............................................................. 152
VI.1.3. Điện dẫn do các điện tích sinh ra ở lớp tiếp giáp........................................ 156
VI.2. Quá trình phóng điện chọc thủng trong chất lỏng ............................................. 159
VI.2.1. Lý thuyết phóng điện điện tử...................................................................... 159
VI.2.2. Lý thuyết phóng điện bởi các phần tử chất rắn........................................... 159
VI.2.3. Lý thuyết phóng điện gây bởi các lỗ hổng (cavitation) và bọt khí (bubble)161
VI.2.4. Nghiên cứu quá trình phóng điện bằng phương pháp quang học- lý thuyết về
streamer................................................................................................................... 162
VI.2.5. Các tính chất cơ bản của cách điện lỏng..................................................... 165
VI.2.6. Các yếu tố ảnh hưởng đến điện áp chịu đựng............................................. 166
VI.3. Một số cách điện lỏng thông dụng..................................................................... 171
VI.3.1. Dầu mỏ........................................................................................................ 172
VI.3.2. Hydrocarbone tổng hợp .............................................................................. 172
Chương VII- CÁCH ĐIỆN RẮN................................................................................... 177
VII.1. Tính chất điện môi............................................................................................ 177
VII.1.1. Hằng số điện môi....................................................................................... 177
VII.1.2. Điện trở suất .............................................................................................. 177
VII.1.3. Tổn hao điện môi....................................................................................... 178
VII.2. Phân loại cách điện rắn..................................................................................... 178
VII.2.1. Phân loại theo thành phần hóa học............................................................ 178
VII.2.2. Phân loại theo ứng dụng............................................................................ 179
VII.2.3. Phân loại theo nhiệt độ chịu đựng ............................................................. 179
VII.3. Phóng điện chọc thủng trong điện môi rắn....................................................... 180
VII.3.1. Cơ chế điện tử (electronic breakdown) ..................................................... 180
VII.3.2. Cơ chế phóng điện nhiệt (thermal breakdown) ......................................... 182
VII.3.3. Cơ chế phóng điện cơ điện (electromechanical breakdown) .................... 186
VII.3.4. Một số cơ chế phóng điện chọc thủng của chất rắn trong thực tế ............. 187
VII.4. Một số cách điện rắn thông dụng ..................................................................... 191
VII.4.1. Điện môi giấy ............................................................................................ 191
VII.4.2. Mica và các sản phẩm của mica ................................................................ 191
VII.4.3. Thủy tinh ................................................................................................... 192
VII.4.4. Gốm cách điện........................................................................................... 192
VII.4.5. Polymer ..................................................................................................... 193
CHƯƠNG VIII: CÁCH ĐIỆN NGOÀI TRỜI ............................................................... 203
VIII.1. Giới thiệu về cách điện ngoài trời................................................................... 203
VIII.1. 1. Vai trò của cách điện............................................................................... 203
VIII.1.2. Tính chất vật liệu...................................................................................... 204
VIII.1.3. Một số chủng loại cách điện ngoài trời tiêu biểu..................................... 204
VIII.2. Cơ chế gây ô nhiễm bề mặt............................................................................. 207
VIII.2. Cơ chế phóng điện bề mặt............................................................................... 208
VIII.2.1. Độ ẩm bề mặtt .......................................................................................... 209
VIII.2.2. Trường hợp vật liệu thích nước (hydrophilic) ......................................... 210
VIII.2.3. Trường hợp vật liệu ghét nước (hydrophobic)......................................... 213
VIII.3. Các tính chất ảnh hưởng lên trị số phóng điện bề mặt.................................... 214
VIII.3.1. Ảnh hưởng của phần tử hòa tan ............................................................... 215
VIII.3.2. Ảnh hưởng của phần tử không hòa tan .................................................... 215
VIII.3.2. Ảnh hưởng đường kính trung bình đối với cách điện thích nước............ 216
VIII.3.3. Quá điện áp quá độ................................................................................... 217
VIII.3.4. So sánh giữa điện áp xoay chiều và một chiều ........................................ 218
VIII.4. Các biện pháp cải thiện phóng điện bề mặt .................................................... 218
VIII.4.1. Mũ đỡ (Booster shed)............................................................................... 219
VIII.4.2. Mở rộng vùng mũ (shed extender)........................................................... 219
VIII.4.3. Phủ bằng một lớp khác (coating) ............................................................. 220
VIII.4.4. Lau rửa ..................................................................................................... 220
CHƯƠNG I: CẤU TẠO VẬT CHẤT I.1. CẤU TẠO NGUYÊN TỬ
I.1.1. THUYẾT CẤU TẠO NGUYÊN TỬ CỦA BORH
Hình I.1: Mô hình nguyên tử Borh (lấy từ trang http://phys.free.fr/modbohr.htm)
Nội dung chính của thuyết cấu tạo nguyên tử theo mô hình Borh được hiểu như
sau: điện tử quay quanh hạt nhân theo một quỹ đạo tròn. Ở điều kiện bình thường (nhiệt
độ phòng) điện tử nằm trên quỹ đạo gần hạt nhân nhất, vị trí này ứng với mức năng lượng
thấp nhất của nguyên tử hay còn gọi là trạng thái dừng (ground state). Khi điện tử nằm
trong một quỹ đạo, hệ không lấy thêm hoặc mất đi năng lượng. Khi nhận thêm năng
lượng điện tử sẽ di chuyển đến một quỹ đạo mới, xa hạt nhân hơn, lúc này nguyên tử có
năng lượng lớn hơn năng lượng ban đầu và khi đó điện tử ở trạng thái kích thích (excited
state). Ngược lại nguyên tử có thể bức xạ năng lượng để chuyển từ trạng thái kích thích
có mức năng lượng cao về trạng thái kích thích có mức năng lượng thấp hơn. Tuy nhiên
các điện tử không thể nằm trên những quỹ đạo bất kỳ mà nó chỉ được phép chuyển động
trên những quỹ đạo cách hạt nhân những khoảng cách nhất định, nói cách khác khi
chuyển từ quỹ đạo này sang quỹ đạo khác năng lượng mà điện tử nhận hoặc bức xạ ra là
những đại lượng cố định (hay còn gọi là năng lượng được lượng tử hóa-quantized). Trạng
thái kích thích tiếp theo của mức năng lượng dừng gọi là trạng thái kích thích thứ nhất,
trên nữa là trạng thái kích thích thứ hai và cứ tiếp tục như thế. Mức năng lượng ion hóa là
mức năng lượng mà khi đó điện tử không còn liên kết với hạt nhân nữa để trở thành điện
tử tự do và hậu quả là nguyên tử trở thành ion dương. Ở mức năng lượng lớn hơn mức
năng lượng ion hóa, các điện tử có các mức năng lượng liên tục chứ không còn gián đoạn 1
Pham Hong Digitally signed by Pham Hong Thinh DN: cn=Pham Hong Thinh, c=VN, Thinh ou=Bo mon HTD
Reason: I am the author of this document
Date: 2007.02.28 13:32:09 +07'00'
như trong trường hợp nó liên kết với hạt nhân. Ví d ụ trong
nguyên tử hidro mức năng lượng ion hóa là 13,6eV. Mặt khác các nguyên tử cũng nhận
thêm điện tử để trở thành ion âm.
Như vậy nguyên tử chuyển từ trạng thái này sang trạng thái khác bằng cách nhận
thêm hoặc bức xạ một lượng tử có độ lớn bằng hiệu năng lượng giữa hai trạng thái và có độ lớn: ΔW = Wm - Wn = h.f (I.1)
Với f là tần số của bức xạ và h=6,624.10-34 J.s là hằng số Plank
Năng lượng toàn phần của điện tử trong nguyên tử bao gồm động năng T và thế
năng U. Thế năng U gây bởi tương tác của điện tử với hạt nhân và có trị số U=-eV trong
đó e=1,602. 10-19 là điện tích của điện tử còn V là điện thế do hạt nhân gây ra tại nơi đặt
điện tử. Vì điện tích của hạt nhân là qhạt nhân=Ze (Z là số thứ tự nguyên tử của nguyên tố
trong bảng hệ thống tuần hòan) nên thế năng gây lên điện tử cách hạt nhân khoảng cách r được tính bằng: Ze U = − e (I.2) r
Do vậy năng lượng toàn phần của điện tử được tính bằng: m v2 2 e Ze
E = T + U = − (I.3) 2 r
Điện tử chuyển động trên một quỹ đạo tròn là do lực tương tác Coulomb giữa
điện tử và hạt nhân đã truyền cho nó một lực hướng tâm, để điện tử chuyển động ổn định
trên quỹ đạo tròn lực hướng tâm cân bằng với lực ly tâm nên ta viết được: 2 2 m v e Ze = (I.4) 2 r r
Từ đó ta xác định được bán kính chuyển động của quỹ đạo: 2 Ze r = (I.5) 2 m v e
Mô hình nguyên tử Bohr hạt nhân là khu vực có mật độ vật chất dày đặc nhất,
khối lượng của nguyên tử xấp xỉ bằng khối lượng của hạt nhân do khổi lượng của các
điện tử không đáng kể. Hạt nhân bao gồm hai loại hạt: proton mang điện tích dương và
neutron không mang điện. Hình vẽ 1.1 chỉ biểu diễn một cách tương đối cấu tạo của
nguyên tử vì trong thực tế bán kính của hạt nhân nhỏ hơn bán kính của nguyên tử khoảng 100 000 lần.
Mô hình Bohr tương tự như mô hình hệ mặt trời với mặt trời tương đương với hạt
nhân còn các điện tử giống như các hành tinh trong hệ mặt trời. Tuy nhiên trong hệ mặt 2
trời thì quỹ đạo của các hành tinh được coi như nằm trên một mặt phẳng và tương tác
giữa các hành tinh chỉ do lực hấp dẫn và do đó các hành tinh luôn hút nhau. Trong khi đó
trong mô hình Bohr quỹ đạo của các điện tử không nằm trên mặt phẳng và tương tác giữa
hạt nhân và các điện tích có thể là tương tác hút hoặc đẩy tùy theo dấu của điện tích.
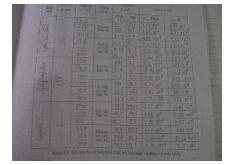
Bảng 1.1 mô tả các đặc tính chính của các phần tử cơ bản trong mô hình nguyên tử Bohr. Hạt Khối lượng Điện tích Mô men từ Spin I.32 L ýthuyế vùngă lượng. K im loạ, điệnm ô vàchất bándẫ..26¶ (C) (A.m2) Photon 0 0 0 0 Neutron 1,675.10-27 0 -9,64.10-27 1/2
Proton 1,673.10-27 1,602.10-19 1,41.10-26 1/2
Điện tử 9,101.10-31 -1,602.10-19 6,27.10-24 1/2
Bảng 1.1: Đặc tính của các phần tử cơ bản trong mô hình Bohr
I.1.2. THUYẾT CƠ HỌC LƯỢNG TỬ CỦA NGUYÊN TỬ
Như vậy nếu ta chấp nhận mô hình Bohr như một mô hình mô tả cấu tạo của
nguyên tử bằng các phần tử cơ bản nhất của vật chất, các tính chất của nguyên tử sẽ được
quyết định bởi: số nguyên tử Z (số điện tử hoặc số proton trong nguyên tử trung hòa),
khối lượng nguyên tử, phân bố trong không gian của điện tử trên quỹ đạo quay quanh hạt
nhân, năng lượng của điện tử trong hạt nhân và khả năng cho hoặc nhận thêm điện tử của
nguyên tử để tạo thành các ion dương hoặc âm. Nếu hai yếu tố đầu phụ thuộc vào bản
chất của từng loại nguyên tử thì ba yếu tố sau phụ thuộc vào các điều kiện ngoài như lực
cơ học, trường điện từ và nhiệt độ. Do đó để xác định được ảnh hưởng của các điều kiện
ngoài lên đặc tính của vật chất ta cần phải nắm được các đặc tính của điện tử.
Để mô tả một cách chi tiết và chính xác các đặc tính của điện tử người ta dùng
thuyết cơ học lượng tử. Như đã đề cập trong mô hình Bohr sự chuyển động của điện tử
trên các quỹ đạo của nguyên tử là gián đoạn chứ không liên tục, cơ học cổ điển trong đó
điện tử có thể tồn tại trên các quỹ đạo có bán kính bất kỳ không thể giải thích được điều
này. Tuy mô hình Bohr đã thành công rực rỡ trong việc giải thích cấu tạo của nguyên tử
hydro, nhưng nó không giải thích được cấu tạo của các nguyên tử phức tạp có từ hai điện
tử trở lên (từ He). Vì vậy cơ học lượng tử kế thừa từ các giả thiết trong mô hình Bohr để
đưa ra mô hình toán học mô tả sự tương tác của các điện tử, proton và neutron trong nguyên tử.
Một trong những điểm cơ bản trong cơ học lượng tử là lưỡng tính sóng hạt của
điện tử. Tính chất sóng của điện tử được thể hiện trong hiện tượng giao thoa còn tính chất
hạt thể hiện trong vị trí của nó trong quỹ đạo của nguyên tử. Tính chất của một điện tử
trong nguyên tử có thể được mô hình hóa bằng cách coi nó như một sóng năng lượng. 3
Cấu tạo của nguyên tử được mô tả một cách đầy đủ qua phương trình biểu diễn sóng hay còn gọi là hàm sóng.
1. Hàm sóng của một điện tử tự do
Để đi vào chi tiết hàm sóng trước tiên ta xét một sóng phẳng đơn sắc trong vật lý
cổ điển có vận tốc góc ω lan truyền theo chiều dương của trục x được biểu diễn bằng hàm sóng de Broglie:
ψ (x,t) =ψ sin(kx − t ω ) (I.6) o
Trong đó ψ0 là biên độ của sóng, k=2π/λ là số sóng (wave number), λ là bước
sóng, tần số góc ω=2πf, còn vận tốc sóng c= λf=ω/k.
Chúng ta biết rằng phương trình truyền sóng trên chính là một nghiệm của
phương trình vi phân cấp 2: 2 2 1 ∂ ψ ∂ ψ = (I.7) 2 2 2 c t ∂ x ∂
(ký hiệu ∂ chỉ vi phân theo một biến khi coi biến kia là hằng số)
Trong không gian ba chiều hàm sóng ψ là một hàm phụ thuộc vào bốn biến x,y,z
và t hay được biểu diễn là ψ(x,y,z,t). Phương trình vi phân ban đầu khi đó có dạng: 2 2 2 2 1 ∂ ψ ∂ ψ ∂ ψ ∂ ψ = + + (I.8) 2 2 2 2 2 c t ∂ x ∂ y ∂ z ∂
Xét chuyển động của một điện tử tự do (không chịu tác dụng của ngoại lực) di
chuyển với tốc độ không đổi v. Gọi khối lượng của điện tử là me, điện tử có động lượng
p=mev và năng lượng cũng chính là động năng của điện tử: 1 2 E = m v (I.9) 2 e
Ta có thể viết được mối quan hệ giữa năng lượng và động lượng của điện tử: 1 2 E = p (I.10) 2me
Các đại lượng p và E đặc trưng cho bản chất hạt của điện tử. Mặt khác bản chất
sóng của điện tử được biểu diễn qua các đại lượng như bước sóng λ và tần số f. Mối quan
hệ giữa các đại lượng trong hai bản chất sóng-hạt được gọi là quan hệ de Broglie- Einstein: h p = và E = hλ (I.11) λ
Sử dụng quan hệ de Broglie- Einstein, hàm sóng ψ(x,t) của điện tử tự do với
lưỡng tính sóng hạt được Shrodinger viết trong không gian một chiều như sau: 4 2 2 ∂ψ η ∂ ψ iη = − (I.12) 2 t ∂ 2m x ∂ h trong đó η = = 10 . 054 , 1
−39 J s. còn gọi là hằng số Dirac 2π
Nghiệm đơn giản nhất của phương trình này có dạng: ⎛ p E ⎞ ⎛ p E ⎞
i( px−Et ) / η
ψ (x,t) = cos⎜ x − t ⎟ + isin⎜ x − t ⎟ = e (I.13) ⎝ η η ⎠ ⎝ η η ⎠
Đây chính là hàm sóng của một điện tử tự do
2. Hàm sóng của một điện tử đặt trong điện trường
Giả sử điện tử đặt trong trường nào đó có thế V(x), khi đó năng lượng toàn
phần của điện tử sẽ bao gồm động năng T=p2/2me và thế năng V(x): 1 2
E = T + V =
p + V (x) (I.14) 2me
Khi đó hàm sóng Schodinger viết cho điện tử sẽ có dạng: ψ 2 ∂ η ∂ ψ 2 iη = − +V (x ψ ) (I.15) t ∂ 2 2 m x ∂ e
Trong không gian ba chiều nó có dạng: ψ 2 ∂ η ⎛ ∂ ψ 2 ∂ ψ 2 ∂ ψ 2 ⎞ iη = − + +
+V (x, y, z ψ ) (I.16) t ∂ 2 ⎜⎜ 2 2 2 m ⎝ x ∂ y ∂ z ⎟⎟ ∂ e ⎠
Nếu biết dạng cụ thể của hàm V(x,y,z), thay vào phương trình trên ta sẽ giải để
tìm được dạng ψ(x,y,z) và E, nghĩa là xác định được trạng thái và năng lượng của điện tử.
3. Ý nghĩa toán học của hàm sóng
Hàm sóng Schodinger áp dụng cho mọi hạt sơ cấp, để đi vào tìm hiểu ý nghĩa của
hàm sóng ta xét trường hợp hạt là một photon. Xét một khối hộp nhỏ thể tích dV=dxdydz
trong không gian ba chiều bao quanh điểm M, gọi xác suất tìm thấy một hạt trong thể tích
này ở thời điểm t là P(x,y,z,t)dxdydz. Đại lượng P(x,y,z,t) được gọi là xác suất xuất hiện
hạt trong đơn vị thể tích hay còn gọi là mật độ xác suất. Mặt khác theo quan điểm sóng
cường độ sáng tại M tỉ lệ bình phương với biên độ dao động, như thế xác suất xuất hiện
hạt trong đơn vị thể tích dV được tính bằng:
P(x, y, z,t)dxdydz = ψ (x, y, z,t 2 ) dV (I.17)
Trong toàn bộ không gian chúng ta chắc chắn phải tìm thấy hạt, do đó xác suất
trong toàn bộ không gian phải là 1:
ψ (x, y, z,t) 2 = 1 ∫∫∫ dV (I.18)
Điều kiện này còn được gọi là điều kiện chuẩn hóa của hàm sóng 5
Như vậy nếu trong cơ học cổ điển từ phương trình của Newton ta có thể xác định
chính xác quỹ đạo và động lượng của hạt ở mọi thời điểm thì trong cơ học lượng tử hàm
sóng Schodinger chỉ cho phép suy ra xác suất xuất hiện của hạt tại một vị trí nào đó trong
không gian ở một trạng thái nào đó. Nói một cách khác là hàm sóng mang tính thống kê.
4. Cấu tạo nguyên tử Hidro
Chúng ta sẽ dùng hàm sóng Schrodinger để giải thích cấu trúc nguyên tử của
hydro. Xét một nguyên tử hydro gồm một proton nằm ở trung tâm và điện tử quay xung
quanh nó và cách một khoảng r, khối lượng nguyên tử nằm chủ yếu ở proton nên ta bỏ
qua khối lượng điện tử. Lực hút Coulomb tác dụng lên điện tử và điện tử có thế năng: 1 e2 V (r) = − (I.19) 4πε r 0
Khi điện tử chuyển động trong trường lực thế V(r) ở trạng thái dừng tức là ứng
với một năng lượng xác định, cơ học lượng tử đã chứng minh rằng hàm sóng của nó có dạng: i − Wt
ψ (x, y, z,t) = e η ψ (x, y, z) (I.20)
Như vậy phương trình Schodinger cho chuyển động của điện tử có là hàm không
phụ thuộc vào thời gian có dạng: 2 2 2 2 η ⎛ ∂ ψ ∂ ψ ∂ ψ ⎞ − + +
+ [V (r) − E]ψ = 0 (I.21) 2 ⎜⎜ 2 2 2 ⎟⎟ m ⎝ ∂x ∂y ∂z ⎠
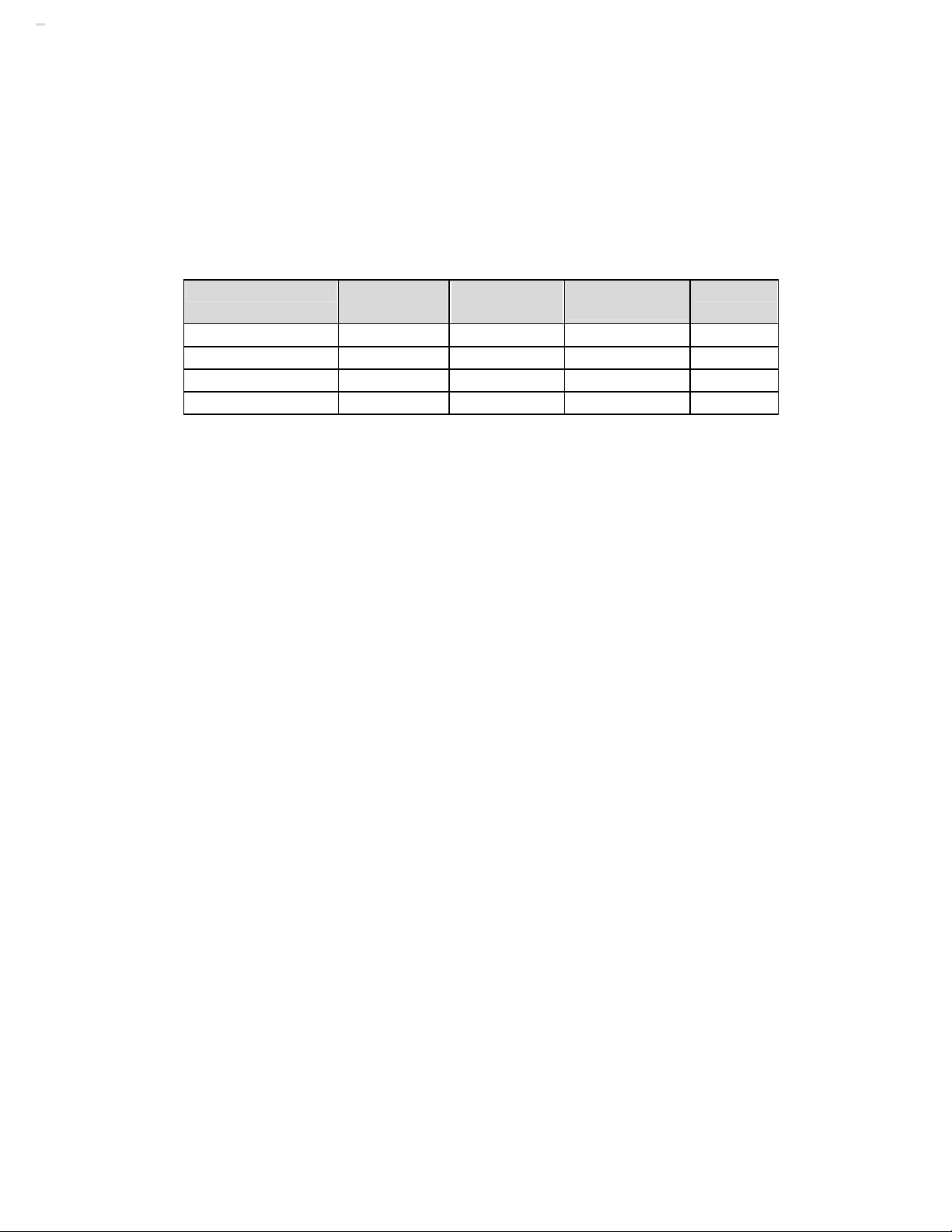
Do tính đối xứng cầu của hệ nên ta giải phương trình Schodinger trong hệ tọa độ
cầu và do vậy hàm sóng sẽ là hàm ψ(r,θ,φ) (hình I.2). Phương trình (1.21) khi đấy có dạng: 2 η ⎡ 1 ∂ ⎛ ∂ψ ⎞ ∂ ⎛ ∂ψ ⎞ ∂ ψ ⎤ ⎡ e ⎤ 2 1 1 2 1 2 ⋅ ⎜r ⎟ + ⋅ ⎜sinθ ⎟ + ⋅ + ⋅ + E ψ = 0 ⎢ ⎥ ⎢ ⎥ 2 2 2
m ⎣r ∂r ⎝ ∂r ⎠ r sin 2 θ ∂r ⎝ ∂θ ⎠ r sin2 2 θ ∂ϕ 4 ⎦ ⎣ πε r 0 ⎦ (I.22)
Hình I.2: Hệ tọa độ cầu với giả thiết hạt nhân nằm tại vị trí O 6
Giải phương trình này trong hệ tọa độ cầu bằng cách phân ly biến số theo đó đặt
ψ(r,θ,φ)=R(r).Y(θ, φ) với các điều kiện :chuẩn hóa, hàm sóng là liên tục và khả vi trong
không gian. Chú ý rằng do tính chất lượng tử nên các điều kiện trên chỉ đúng với một số
giá trị E nhất định gọi là giá trị riêng của năng lượng (eigenvalue hoặc valeur propre).
Các trạng thái ứng với mỗi giá trị năng lượng riêng này được gọi là trạng thái riêng, còn
hàm sóng ứng với mỗi trạng thái riêng này còn được gọi là hàm riêng
(eigenfunction)(cách giải cụ thể tham khảo trang http://scienceworld.wolfram.com). Kết
quả ta được thu được:
ψ (r,θ,φ) = R (r)Y (θ,φ) (I.23) nl lm
Với Rnl(r) và Ylm(θ,φ) là các hàm phức tạp theo n, l, m trong đó n=1, 2, 3...; l=0, 1,
2...,n-1 còn m là số nguyên (±1, ±2,...). Với n, l, m đặc trưng cho các giá trị riêng của các
phương trình vi phân từng phần với R và Y theo các điều kiện trên (điều kiện chuẩn hóa, liên tục, khả vi...)
Phần Rnl(r) gọi là hàm sóng cầu (radial wave function) có giá trị xác định bằng
các giá trị của n và l, n và l được gọi là số lượng tử đặc trưng cho từng trạng thái riêng, cụ
thể n là số lượng tử chính còn l là số lượng tử orbital. Phần Ylm(θ,φ) được gọi là hàm
sóng góc (angular wave funtion) miêu tả trạng thái quay của điện tử xung quanh hạt nhân
trong đó số lượng tử l đặc trưng cho vận tốc quay của điện tử xung quanh hạt nhân (hay
chính là biên độ của mô men xung lượng góc) còn m đặc trưng cho hướng của vectơ
xung lượng góc. Các trị số l và m nhận giá trị nguyên chứng tỏ cả biên độ và hướng của
mô men xung lượng góc nhận các giá trị gián đoạn.
Mỗi trạng thái nhất định của điện tử đuợc đặc trưng bởi hàm sóng ψ(r,θ,φ) ứng
với các trị số của số lượng tử chính là quỹ đạo (orbital) của điện tử, nghĩa là từ đó ta xác
định được vị trí, động năng và thế năng của điện tử. Ở trạng thái dừng năng lượng của
điện tử là thấp nhất ứng với n=1, l=0 và m=0, người ta tính được hàm sóng của nguyên tử có dạng: 1 ⎛ 1 ⎞3/ 2 ⎛ r ⎞ ψ (r,θ,φ) = exp (I.24) 100 ⎜⎜ ⎜⎜− ⎟⎟ ⎟⎟ π ⎝ r r 0 ⎠ ⎝ 0 ⎠ 2 4πη ε với 0 r = − (I.25) 0 2 m e e
Còn năng lượng ứng với trạng thái này tính được: 4 m e 1 E e = − ⋅ (I.26) 2 2 2 8η ε n 0
Với n=1 ta tính được E0=-2,18.10-18J=-13,6eV 7
Các thực nghiệm đã tìm ra mức năng lượng thấp nhất của nguyên tử hydro chính xác là -13,6eV.
Xác suất quan sát thấy điện tử ở khoảng cách từ r đến r+dr so với hạt nhân có giá trị:
P (r)dr = ψ (r 2 ) 4 r 2 π dr (I.27) 100 100
Khoảng cách r ứng với xác suất tìm thấy điện tử lớn nhất được ước lượng bằng
cách đạo hàm P theo r, tức là cho dP/dr=0, ta tìm được r=r0. Như vậy quỹ đạo ở trạng thái
dừng ứng với nơi có xác suất tìm thấy điện tử lớn nhất chính là r0 tính bằng công thức
(I.27) và bằng 0,529.10-10m.
Ta thấy trạng thái lượng tử của một điện tử được mô tả bằng ba số lượng tử n, l và
m. Tuy nhiên các thực nghiệm tiến hành vào những năm 1920 đã xác nhận thêm những
tính chất khác của điện tử: dụng cụ thí nghiệm tinh vi đã phát hiện ra quang phổ vạch của
hydro không phải là là một vạch đơn mà là do nhiều vạch nhỏ sít lại tạo thành, thí nghiệm
thứ hai khi hướng một chùm nguyên tử bạc vào trong một từ trường không đều thì chùm
nguyên tử này bị tách thành hai chùm khác nhau. Những hiện tượng này gợi ý rằng ngoài
chuyển động xung quanh hạt nhân, điện tử còn tham gia vào chuyển động riêng của chính
nó. Tính chất này được gọi là spin và được đặc trưng bởi số lượng tử spin ms=±1/2. Do
vậy ta đi đến kết luận trạng thái lượng tử của một điện tử được đặc trưng bởi bốn số
lượng tử n, l, m và ms. 5. Tổng quát
Cách giải tìm hàm sóng trong phần trên có thể áp dụng cho các hệ nguyên tử khác
khác bằng cách thay trị số e bằng Ze với Z là số thứ tự của nguyên tố trong bảng
Mendeleev. Cấu trúc điện tử của nguyên tử có được áp dụng cho tất cả các nguyên tử,
được hình dung như sau: Các điện tử có các mức năng lượng gián đoạn thay đổi từ E0 là
mức năng lượng cơ bản đến 0 là mức năng lượng ứng với năng lượng ion hóa của nguyên
tử. Ở mỗi trị số En trong khoảng này tương ứng với n2 trạng thái của điện tử, từ trạng thái
n này ta có thể xác định được mật độ xác suất xuất hiện của điện tử cũng như quỹ đạo
(orbital) của nó. Các giá trị này (n, xác suất, quỹ đạo) càng xa hạt nhân thì năng lượng
của điện tử càng tiến gần đến năng lượng ion hóa của nguyên tử. Các điện tử nằm ở xa
hạt nhân này liên kết yếu với hạt nhân và là nguyên nhân gây ra hiện tượng dẫn điện trong vật liệu.
I.2. CẤU TẠO PHÂN TỬ VÀ CÁC DẠNG LIÊN KẾT
Năng lượng liên kết của một phân tử là năng lượng tối thiểu để tách các nguyên tử
của chúng và đưa chúng ra một khoảng cách đủ lớn để chúng không còn tương tác với 8
nhau nữa. Năng lượng liên kết thường được biểu diễn bằng đơn vị eV/mol hoặc kJ/mol (1kJ/mol=1.037. 10-2eV/mol).
Tuỳ theo vị trí trong bảng Mendeleev, các nguyên tử liên kết với nhau bằng các
liên kết hoá trị với các bản chất khác nhau. Theo độ mạnh yếu của liên kết hoá trị người
ta chia làm các loại liên kết hoá trị mạnh và liên kết hoá trị yếu. Liên kết hoá trị mạnh bao
gồm liên kết ion, liên kết cộng hoá trị và liên kết kim loại. Trong khi đó liên kết hoá trị
yếu bao gồm liên kết Van der Waals và liên kết hydro. Liên kết ion và liên kết cộng hoá
trị đặc trưng cho các oxít và sunphít trong khi các điện môi chủ yếu được tạo thành từ các
liên kết Van der Waals và hydro. Rất ít phân tử được tạo thành từ một loại liên kết duy
nhất, chúng thường có từ hai đến ba loại liên kết trong đó có một loại liên kết mạnh hơn
cả. Ví dụ trong tinh thể Ga As thì liên kết cộng hoá trị mạnh hơn hai lần so với liên kết
ion, trong khi đó phân tử NaCl thì liên kết ion chiếm tới 94% sau đó mới đến liên kết
cộng hoá trị. Còn Silicum thì cấu tạo thuần tuý là liên kết cộng hoá trị. Đặc tính của từng
loại vật chất như điện, cơ, lý, hóa…do liên kết chủ yếu trong nó quyết định. Sau đây ta đi
vào chi tiết từng loại liên kết. I.2.1. LIÊN KẾT ION
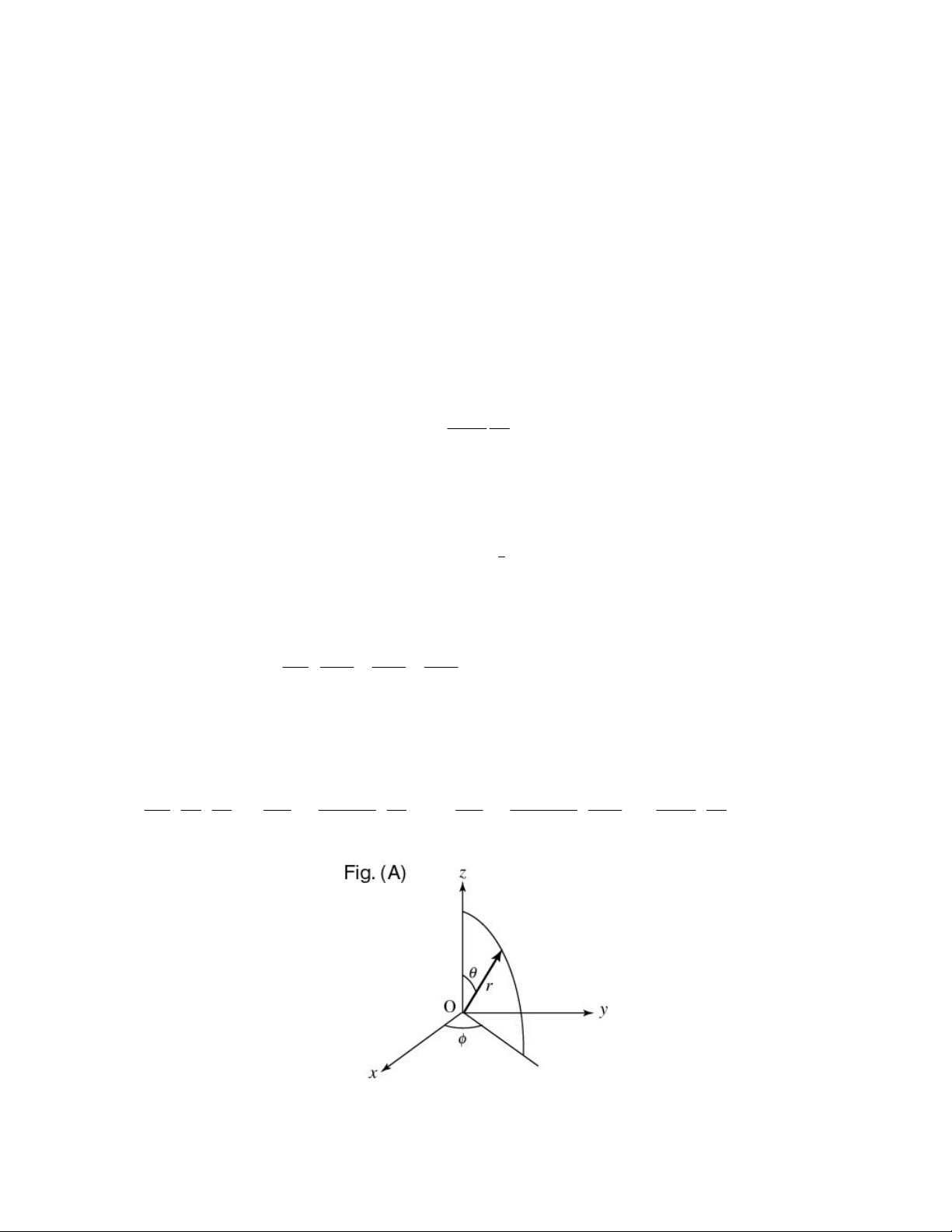
Liên kết ion được hình thành từ sự trao đổi điện tử giữa các nguyên tử, các
nguyên tử này trao hoặc nhận điện tử để hình thành nên cấu hình điện tử giống như một
khí hiếm. Ví dụ như trong phân tử NaCl: nguyên tử kim loại kiềm Na có một điện tử ở
lớp ngoài cùng liên kết yếu với hạt nhân luôn có xu hướng nhường điện tử này đi để tạo
thành cation Na+ và nguyên tử halogen Cl có lớp ngoài thiếu một điện tử nên sẵn sàng
nhận điện tử do nguyên tử Na nhường để trở thành anion Cl- có cấu hình ổn định. Liên
kết ion gây bởi lực hút Coulomb giữa các ion tích điện trái dấu từ quá trình cho nhận kể
trên. Tương tác hút giữa hai ion i và j mang điện tích Zie và Zje (với e là điện tích cơ bản
và Z là hoá trị của từng ion, đối với Na+ thì Z=+1 và đối với Cl- thì Z=-1) được hiểu như
sau: ở khoảng cách giữa hai ion là rij các ion hút nhau bằng lực hút Coulomb với trị số: Z Z i j 2 F = ± e (I.28) c rij 9
Hình I.3: Liên kết ion trong phân tử và cấu trúc tinh thể NaCl
Ngoài ra một ion tạo xung quanh nó một điện trường, điện trường này làm phân
cực các ion khác và tạo thành lực hút giữa hai ion, tuy nhiên trị số lực hút này được bỏ
qua do nó rất nhỏ so với lực Coulomb. Khi các ion tiến sát gần nhau mà các lớp điện tử
bên ngoài phủ lên nhau khi đó tương tác đẩy sẽ xảy ra (người ta gọi là lực đẩy ở khoảng
cách ngắn do liên kết giữa hai nguyên tử được giải thích là do sự tạo thành của lực hút
giữa chúng, tuy nhiên chúng bao giờ cũng giữ một khoảng cách là r=r0, điều này được
giải thích theo phương pháp cổ điển là có sự tồn tại một lực đẩy ở khoảng cách ngắn, ở
khoảng cách r=r0 thì lực hút và lực đẩy sẽ bù trừ cho nhau). Lực tương tác đẩy được Born
giả thiết là tỉ lệ nghịch với r -n
ij theo tỉ lệ rij với n tương đối lớn . Vị trí cân bằng của các
ion ứng với khoảng cách giữa các ion mà các tương tác hút-đẩy cân bằng. Như vậy thế
năng ứng với tương tác giữa hai ion được tính bằng công thức: Z Z B e2 i j 2 ij ¦ W = ± e + (I.29) ij n r r ij ij
Ở thành phần thứ nhất của biểu thức bên phải, dấu + ứng với trường hợp lực đẩy
của các ion cùng dấu và dấu - ứng với trường hợp hút của các ion trái dấu.
Bij là hằng số Born cho cặp ion
Năng lượng tổng cộng của một tinh thể ion tính bằng tổng của thế năng tất cả các
cặp ion trong tinh thể. Gọi r là khoảng cách giữa hai ion cạnh nhau và rij=r.pij, thế năng
của tinh thể được tính như sau: 1 W = W (I.30) p ∑ ij 2 i≠ j Tương đương với: ⎡ 1 e2 Z Z B ⎤ Me2 Z 2 B W = ∑ ⎢ ± + ⎥ = + (I.31) p ( ) i j ij n n n 2 i≠ j r p ⎢ r p r ⎣ ⎥ r ij ij ⎦ 10
Hệ số Z2=ZiZj để áp dụng phương trình này cho những tinh thể chứa các ion có
giá trị khác nhau. Hệ số Z2 phụ thuộc vào từng loại tinh thể, nó có giá trị 1 đối với tinh
thể NaCl, MgF2, giá trị 4 đối với MgO, TiO2.
Hệ số M gọi là hằng số Madelung, nó không có thứ nguyên, chỉ phụ thuộc vào
từng dạng tinh thể và được xác định bằng phương pháp toán học và được tính cho nhiều
tinh thể khác nhau ví dụ NaCl=1,747565; CsCl=1 v..v.
Ở khoảng cách cân bằng r0 giữa hai ion, hằng số B được tính qua điều kiện ∂Wp/∂r=0, ta được: 1/(n− ) 1 ⎛ nB ⎞ r ≡ r = ⎜− ⎟ (I.32) 0 2 2 ⎝ MZ e ⎠ trong đó: 2 2 Z Me 1 − B = n r (I.33) 0 n
Năng lượng tại vị trí cân bằng: Z 2 E 2 Z 2Me2 Me2Z 2 ⎛ 1 ⎞ W = − = 1 (I.34) p0 ⎜ − ⎟ r nr r 0 0 0 ⎝ n ⎠
Số mũ n được tính từ hệ số nén của tinh thể, nó phụ thuộc vào tích phân bậc hai
của Wp và được tính có giá trị là 9 cho tất cả các tinh thể. Để tính năng lượng của tinh thể
người ta dùng đại lượng W0=-NAvWp0, mà W0 là đại lượng dương đại diện cho nhiệt
lượng để tạo thành một gam phân tử, như vậy: N Me2Z 2 1 Av ⎛ ⎞ W = (I.35) 0 ⎜1− ⎟ r0 ⎝ n ⎠
Như vậy năng lượng tinh thể lớn hơn năng lượng Coulomb với tỉ lệ 1/n, nghĩa là khoảng 10%.
Một đặc điểm quan trọng khác của liên kết ion là đẳng hướng (không định
hướng), ví dụ trong liên kết NaCl thì cation Na+ hút với các anion Cl- bên cạnh mình ở tất
cả các hướng với độ lớn bằng nhau. Số ion bị hút bởi một ion được coi là mốc (reference)
chỉ phụ thuộc vào tỉ số giữa bán kính của hai ion.
I.2.2. LIÊN KẾT CỘNG HOÁ TRỊ
Giống như liên kết ion, liên kết cộng hoá trị cũng làm cho cấu hình điện tử của
các nguyên tử tham gia liên kết giống như một khí hiếm. Tuy nhiên cơ chế của hai liên
kết này khác nhau ở chỗ không có sự trao đổi điện tử từ nguyên tử này sang nguyên tử
khác mà các nguyên tử góp chung một số điện tử. Thuật ngữ “cộng hóa trị” xuất phát từ
việc liên kết được hình thành từ các điện tử hóa trị ở lớp ngoài cùng của nguyên tử. Loại 11
liên kết này thường xảy ra đối với các tinh thể gồm các nguyên tử giống nhau như O2, H2 v..v..
Để có một khái niệm cụ thể về liên kết cộng hóa trị, ta xét trường hợp liên kết
trong phân tử H2. Giả sử trong khỏang cách tương đối lớn có hai nguyên tử hydro:
nguyên tử A gồm hạt nhân a và điện tử 1 và nguyên tử B gồm hạt nhân b và điện tử 2.
Hai nguyên tử này có thể coi là cô lập, xác suất để điện tử 1 ở gần hạt nhân b và 2 gần hạt
nhân a là rất nhỏ. Khi hai nguyên tử lại gần nhau, xác suất chuyển điện tử đến các hạt
nhân của nguyên tử kia tăng lên. Khi khoảng cách bé (nhỏ hơn 50 Ao) sự phủ lớp mây
điện tử của các nguyên tử tăng lên rõ rệt, tần số chuyển động của điện tử đạt tới 1014s-1.
Với khoảng cách nhỏ như vậy, sự phủ tăng kèm theo tần số trao đổi của các điện tử tăng
đến mức không thể nói rằng điện tử 1 thuộc về nguyên tử A và điện tử 2 thuộc về nguyên
tử B. Một trạng thái mới đã xuất hiện không phải là hệ hai nguyên tử cô lập mà vấn đề là
các điện tử ở trạng thái này là các điện tử chung cho cả hai hạt nhân.
Dạng liên kết hình thành giữa hai nguyên tử có cấu hình giống hệt nhau như trong
trường hợp phân tử H2, trong đó đôi điện tử dùng chung không thuộc về nguyên tử nào
được gọi là liên kết cộng hoá trị không cực. Trường hợp liên kết hính thành bởi các
nguyên tử có cấu hình khác nhau, các điện tử dùng chung bị lệch về một nguyên tử nào
đó được gọi là liên kết cộng hoá trị có cực. Phân tử HCl là một ví dụ về dạng liên kết này.
Hình I.4: Liên kết cộng hóa trị trong phân tử H2
I.2.3. LIÊN KẾT KIM LOẠI
Tinh thể kim loại được cấu tạo từ một mạng lưới các ion dương cố định nằm trong
một biển (hay đám mây) điện tử rất linh động (sea of electron hoặc electron cloud). Các
điện tử trong “biển” này có xác suất liên kết giống nhau đối với tất cả các ion dương ở lân
cận. Do đó liên kết kim loại vừa có sự chia sẻ điện tử (giống liên kết cộng hoá trị) nhưng
lại đẳng hướng (giống liên kết ion). Đám mây điện tử linh động này giải thích cho tính
dẫn điện và dẫn nhiệt cao của kim loại. Năng lượng của liên kết kim loại nhỏ hơn năng
lượng của liên kết ion và liên kết cộng hoá trị. 12
Hình I.5: Mô hình liên kết kim loại với các ion dương cố định ở nút mạng liên kết với “biển điện tử” xung quanh
I.2.4. CÁC LIÊN KẾT THỨ CẤP
Các liên kết chính trong vật liệu thường là một trong ba liên kết kể trên bởi sự cho
nhận điện tử hoặc góp chung điện tử và chúng được gọi là liên kết sơ cấp, năng lượng
liên kết của các loại liên kết này thường nằm trong khoảng từ 200 đến 700kJ/mol. Liên
kết thứ cấp khác liên kết sơ cấp ở chỗ là chúng không có sự cho nhận hay góp chung điện
tử mà liên kết thứ cấp được hình thành từ lực hút giữa các điện tích âm và điện tích
dương. Liên kết thứ cấp bao gồm liên kết Van der Waals và liên kết hydro.
1. Liên kết Van der Waals
Trong liên kết sơ cấp, các nguyên tử đều có xu hướng tạo nên cấu hình điện tử
của các nguyên tử khí hiếm bằng cách cho nhận hoặc chia sẻ điện tử. Thực tế thì các
nguyên tử vẫn có thể tạo thành liên kết với nhau mà không cần cho nhận hay chia sẻ điện
tử, ví dụ như ở nhiệt độ thấp các nguyên tử khí hiếm đều liên kết với nhau để tạo thành
dạng dạng lỏng hay rắn. Như vậy phải có một loại liên kết nào đó hình thành giữa các
nguyên tử khí hiếm ở nhiệt độ thấp, mà ta biết rằng cấu trúc đối xứng hoàn hảo của các
điện tử trong nguyên tử khí hiếm không tạo ra bất kỳ điện trường nào bên ngoài chúng.
Liên kết đó được gọi là liên kết Van der Waals hay là một dạng của liên kết thứ cấp.
Thực tế là cấu trúc đối xứng của các điện tử trong nguyên tử khí hiếm chỉ là trị số
trung bình trong thời gian. Ở một thời điểm bất kỳ, xác suất một nguyên tử khí hiếm có
mômen lưỡng cực p1≠0 là không bằng không. Và điện trường E gây nên bởi lưỡng cực p1
cảm ứng lên một nguyên tử cách nó khoảng cách r một mô men lưỡng cực p2 có trị số: p2=αE (I.36)
với α là hệ số phân cực của nguyên tử bị cảm ứng mô men lưỡng cực p2.
Liên kết Van der Waals tạo bởi lực hút giữa p1 và p2, lực này có trị số: 13 3p p r F 1 2 = − (I.37) 2πε r 4 r 0
Thế năng Ws của hệ tạo bởi hai lưỡng cực này được biểu diễn bằng: r r 2 3p αp 2αp 1 1 1 1
W = F.dr'= . dr'= − . (I.38) s ∫ ∫ 4 3 2πε r 2πε r ∞ ∞ πε r 0 0 (4 0 )2 6
Số nguyên tử càng nhiều, thì các mô men lưỡng cực tức thời càng lớn. Điều này
lý giải hiện tượng nhiệt độ chảy (melting temperature) của các hydrocarbon có công thức
hóa học CnH2n+2 càng tăng khi n tăng. Trong các vật chất mà liên kết Van der Waals
chiếm phần lớn thì năng lượng liên kết (hay nhiệt độ sôi hoặc nhiệt độ chảy) tăng với Z
(số thứ tự trong bảng tuần hoàn).
Liên kết Van der Waals có mặt trong tất cả các vật liệu nhưng nó rất yếu so với
các liên kết sơ cấp. Năng lượng liên kết của liên kết VdW thường nhỏ hơn 40kJ/mol. Nó
là nguyên nhân dẫn tới sự hoá lỏng hay sự hoá rắn của các khí như H2, N2, O2… 2. Liên kết hydro
Liên kết hydro là được hình thành bởi lực hút giữa nguyên tử hydro liên kết với
một nguyên tử mang điện tích âm của một nguyên tố và một nguyên tử mang điện tích âm
của một nguyên tố khác. Thông thường nguyên tử mang điện tích âm ở đây là O, N hoặc
F vì nguyên tử của chúng mang điện âm còn nguyên tử hydro do cấu tạo lớp điện tử
ngoài cùng trong liên kết với một nguyên tố khác đã trở thành tích điện dương. Ví dụ rõ
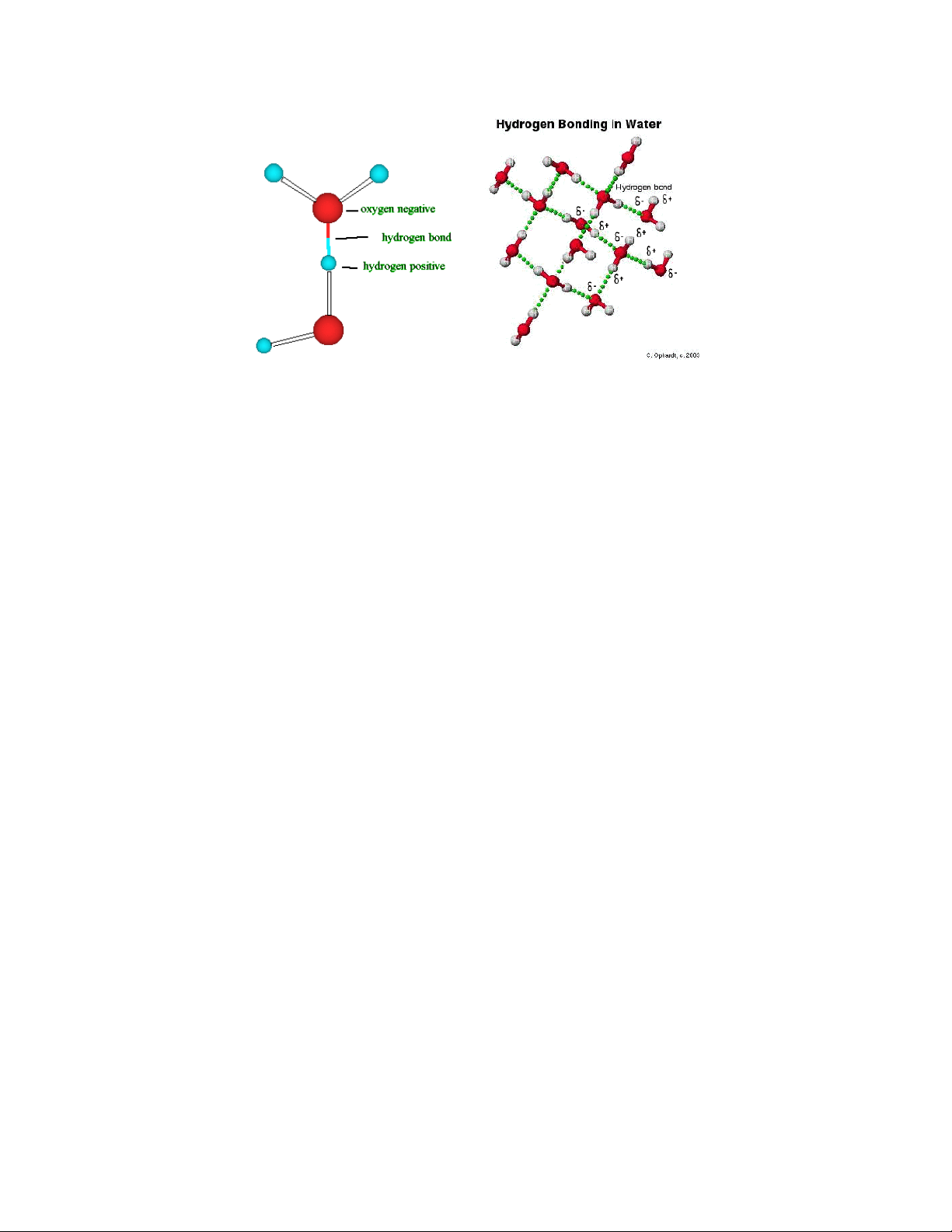
nhất trong tự nhiên là liên kết giữa các phân tử nước: khi ta đưa hai phân tử nước vào
cạnh nhau chúng liền dính lại với nhau đó là do liên kết hydro đã hình thành giữa chúng.
Thật vậy trong nguyên tử hydro lớp điện tử xung quanh nó (gồm chỉ 1 điện tử) rất mỏng
nên nó giống như tích điện dương yếu. Còn oxy lớp điện tử xung quanh nó rất dày (2 lớp
với 8 điện tử) nên nó giống như tích điện âm yếu. Sự khác nhau về dấu giữa hai điện tích
này tạo nên lực hút giữa chúng, đó chính là liên kết hydro. Khả năng tạo liên kết hydro
với nước là một trong những đặc tính quan trọng của vật liệu. Nếu chúng không tạo thành
liên kết hydro với nước ta gọi là chúng có tính ghét nước (hydrophobic), còn ngược lại là
tính thích nước (hydropholic). Một số vật chất ghét nước có chất béo và dầu, trong khi
thích nước phải kể đến đường hoặc cồn.
Liên kết hydro là một loại liên kết định hướng rõ rệt (có nghĩa là năng lượng liên
kết phụ thuộc vào góc liên kết). Năng lượng liên kết có thể dao động từ 1kJ/mol cho đến 40kJ/mol. 14
Hình I.6: Liên kết hydro trong phân tử nước và cấu trúc của nước trong tự nhiên
I.2.5. SO SÁNH CÁC LIÊN KẾT
Liên kết thường gặp nhất là liên kết Liên kết Van der Waals, nó xuất hiện trong
mọi trường hợp và là loại liên kết yếu nhất với năng lượng liên kết dưới 40kJ/mol và
thường bị che lấp bởi các loại liên kết khác mạnh hơn. Về trị số của năng lượng liên kết
thì Van der Waals và liên kết hydro có cùng bậc.
Liên kết ion là loại liên kết điển hình, thường gặp trong các chất vô cơ trong các
hợp chất kim loại với halogen, oxyt, kim loại, sulphua... Liên kết ion cũng thường gặp
trong các kim loại chuyển tiếp (cadimi, celen, nitri...). Năng lượng liên kết ion lớn hơn
hẳn của liên kết Van der Waals. Vì thế vật rắn cấu tạo từ liên kết ion hình thành lên mạng
tinh thể ion có nhiệt độ nóng chảy cao. Ở nhiệt độ thấp, điện dẫn điện tử rất yếu vì các
điện tử bị gắn chặt vào các ion, các tinh thể ion có tính chất của các điện môi. Nhưng ở
nhiệt độ cao do chuyển động mạnh của các ion, nên điện dẫn ion xuất hiện.
Liên kết cộng hoá trị ít có mặt trong các chất hữu cơ và thường hay gặp trong các
hợp chất vô cơ. Liên kết này dẫn đến sự tạo thành tinh thể hoá trị điển hình như Al, Ge...
Năng lượng của liên kết ion thường khá cao khong 106 J/mol. Do vậy các chất có liên kết
hoá trị có điểm nóng chảy cao và nhiệt dung riêng lớn.
Liên kết kim loại xuất hiện do tạo thành các điện tử hoá trị góp chung cho , đặc
trưng cho kim loại điển hình. Năng lượng liên kết cùng bậc với với liên kết cộng hoá tri.
Trong khi bản chất hóa học của nguyên tử được xác định bởi số proton và neutron
trong hạt nhân nguyên tử, thì bản chất liên kết nguyên tử được xác định bởi cách hành xử
của các điện tử trên quỹ đạo của nguyên tử. Sự phân loại vật liệu được dựa vào bản chất
của liên kết trong nguyên tử. Ba loại liên kết sơ cấp mạnh nhất là nguyên nhân làm cho
chất rắn có tính kết dính mạnh:
a. Liên kết ion do sự cho nhận điện tử để tạo thành các cặp ion trái dấu và chúng
được liên kết với nhau bằng lực hút Coulomb. Khoảng cách ổn định giữa các ion là do 15