4/28/2022 TÍCH PHÂN MẶT 1. Mặt tham số 2. Tích phân mặt loại I
3. Ứng dụng tích phân mặt loại I để tính diện tích mặt cong 4. Tích phân mặt loại II Calculus: pages 1070 - 1108 4/28/2022 Thaodt 1 1
1. Mặt tham số (Parametric surfaces)
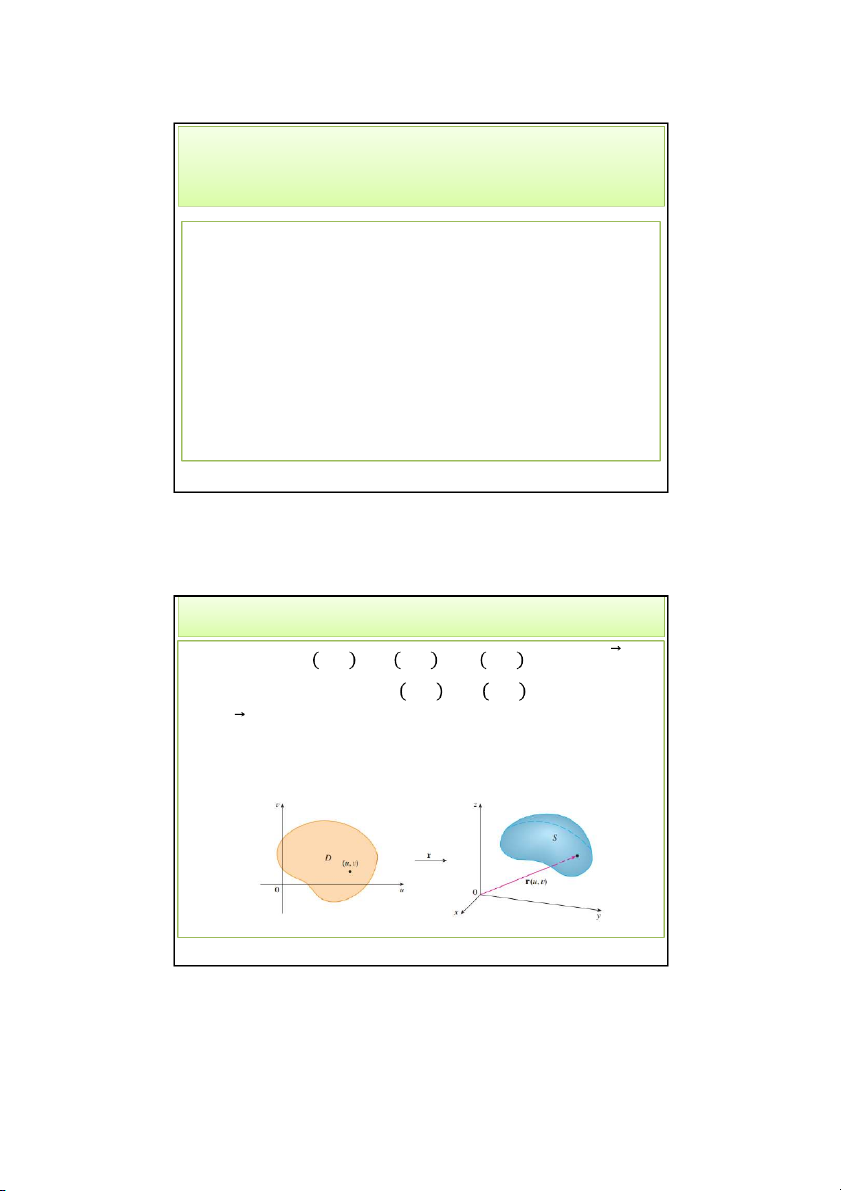
 Hàm véc-tơ 𝑟 𝑢, 𝑣 = 𝑥 𝑢, 𝑣 𝚤 + 𝑦 𝑢, 𝑣 𝚥 + 𝑧(𝑢, 𝑣)𝑘
o là một ánh xạ 𝑅 ⊃ 𝐷 ∋ 𝑢, 𝑣 ↦ 𝑟 𝑢, 𝑣 ∈ 𝑅,
o 𝚤, 𝚥, 𝑘 là các véc-tơ đơn vị trên các trục Ox, Oy, Oz
o 𝑥, 𝑦, 𝑧 là các thành phần của hàm 𝑟, 𝑥, 𝑦, 𝑧 là các hàm của 2 biến 𝑢, 𝑣 trong D. 4/28/2022 Thaodt 2 2 1 4/28/2022
1. Mặt tham số (Parametric surfaces)
o Tập hợp tất cả các điểm 𝑥, 𝑦, 𝑧 ∈ 𝑅 thỏa mãn:
𝑥 = 𝑥 𝑢, 𝑣 , 𝑦 = 𝑦 𝑢, 𝑣 , 𝑧 = 𝑧 𝑢, 𝑣 (2) là một mặt tham số
o Phương trình (2): phương trình tham số 4/28/2022 Thaodt 3 3
1. Mặt tham số (Parametric surfaces)
 Ví dụ 1. Xách định mặt có phương trình véc-tơ:
𝑟 𝑢, 𝑣 = 2𝑐𝑜𝑠𝑢. 𝚤 + 𝑣. 𝚥 + 2𝑠𝑖𝑛𝑢. 𝑘
• Từ phương trình vec-to đã cho, rút ra được phương trình tham số:
𝑥 = 2𝑐𝑜𝑠𝑢, 𝑦 = 𝑣, 𝑧 = 2𝑠𝑖𝑛𝑢 Mọi điểm trên mặt có: 𝑥 + 𝑧 = 4
Nghĩa là tiết diện song song với mặt phẳng xz (y: hằng số
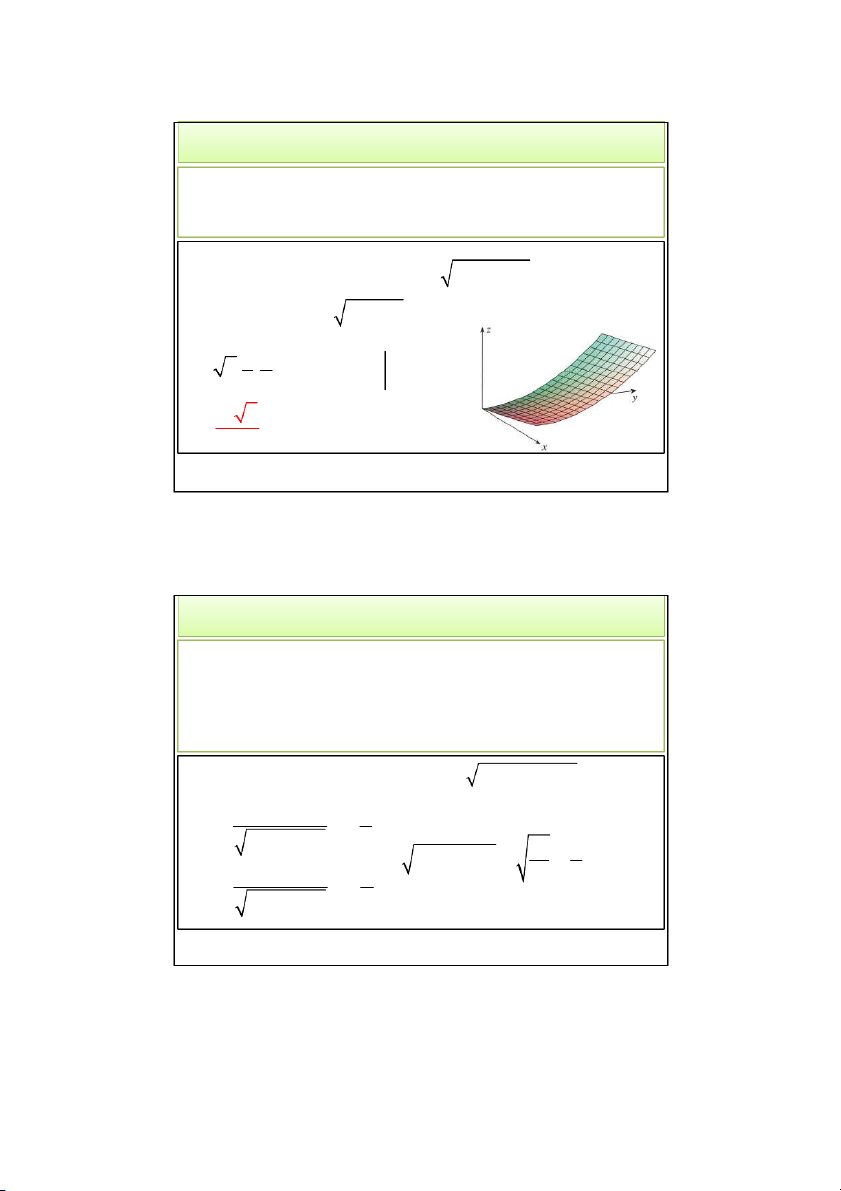
)là một đường tròn, tâm nằm trên Oy, bán kính 2. 4/28/2022 Thaodt 4 4 2 4/28/2022
1. Mặt tham số (Parametric surfaces)
𝑟 𝑢, 𝑣 = 2𝑐𝑜𝑠𝑢. 𝚤 + 𝑣. 𝚥 + 2𝑠𝑖𝑛𝑢. 𝑘
Do 𝑦 = 𝑣 và không bị giới hạn khoảng của v nên mặt cong
là 1 hình trụ tròn có bán kính bằng 2, trục là Oy.
Nếu giới hạn u, v trong miền:
0 ≤ 𝑢 ≤  , 0 ≤ 𝑣 ≤ 3, ta được:  4/28/2022 Thaodt 5 5 2. Tích phân mặt loại I
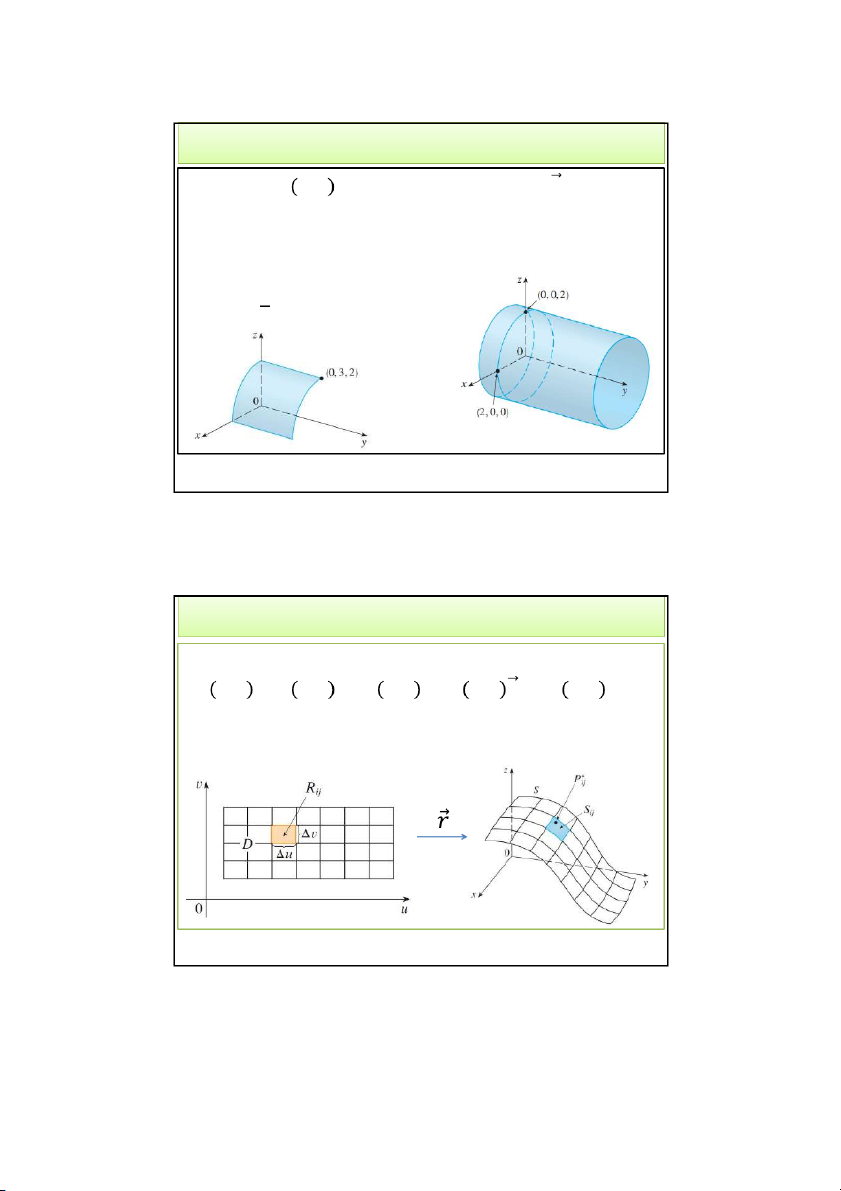
• Giả sử mặt S có phương trình véc-tơ:
𝑟 𝑢, 𝑣 = 𝑥 𝑢, 𝑣 𝚤 + 𝑦 𝑢, 𝑣 𝚥 + 𝑧 𝑢, 𝑣 𝑘, 𝑢, 𝑣 ∈ 𝐷
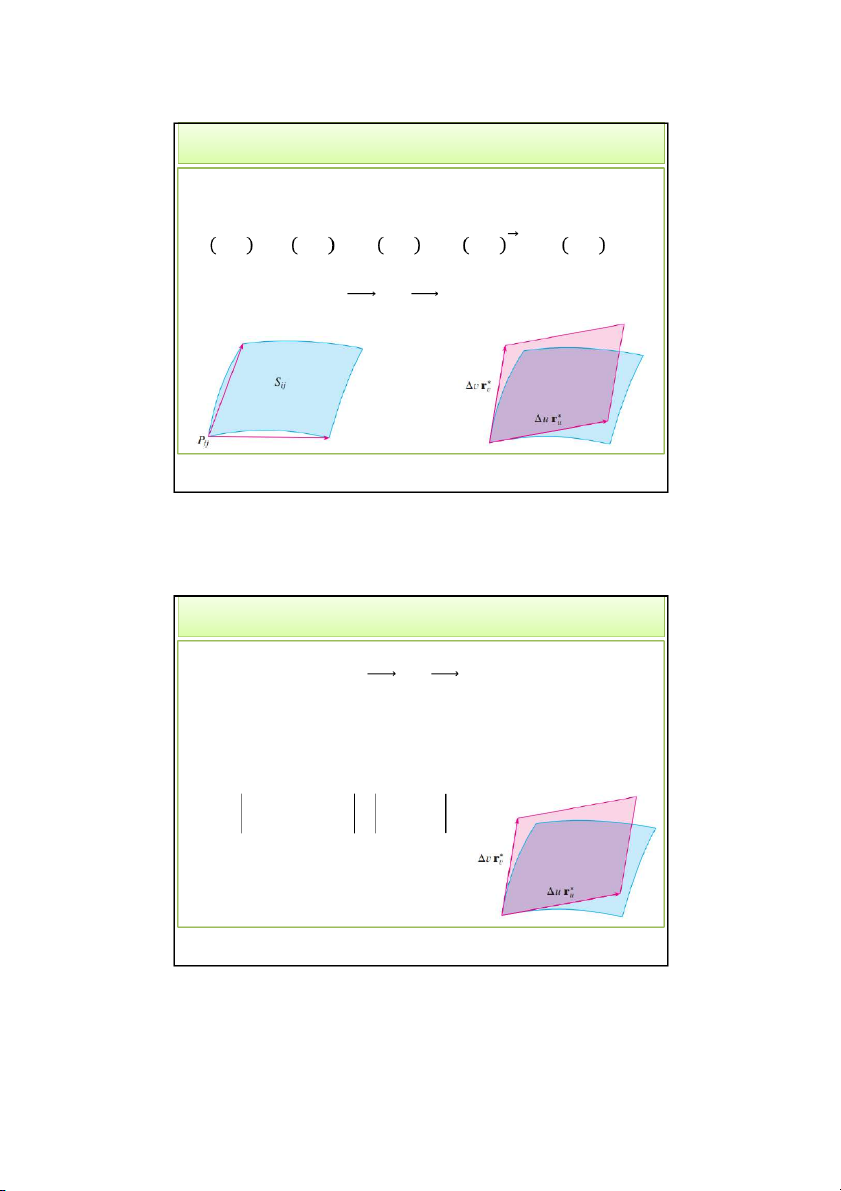
Giả sử miền D là hình chữ nhật, chia D thành các hcn 𝑅 , 
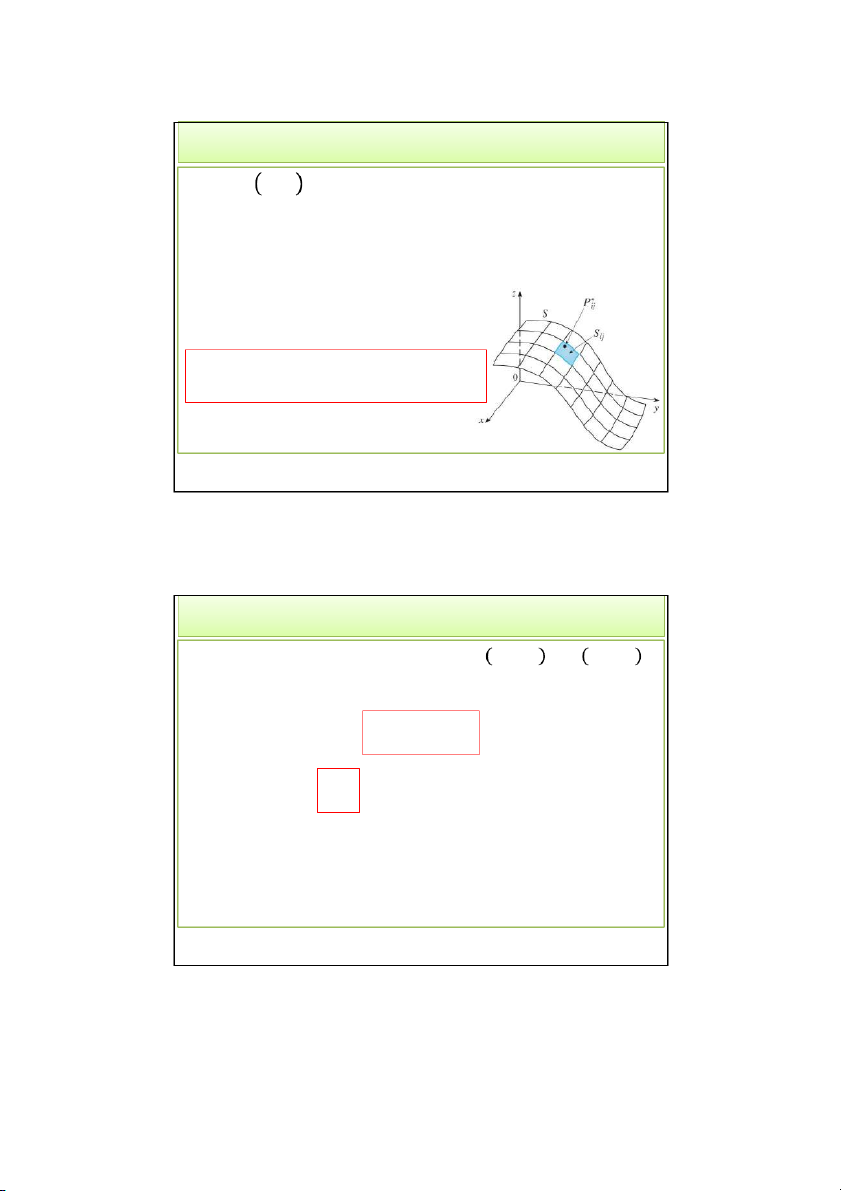
khi đó mặt S được chia tương ứng thành các mảnh 𝑆. 4/28/2022 Thaodt 6 6 3 4/28/2022 2. Tích phân mặt loại I • Tính 𝑓 𝑃∗
tại mỗi mảnh, nhân với diện tích  ∆𝑆 của mảnh đó. m n f  * P S   ij  • Lấy tổng Riemann: ij i1 j1 m n
• Nếu  lim  f  * P S   L ij  ij m,n   Thì i 1 j 1 m n lim  f  * P S   f x, y, z dS ij  ij    m ,n i1 j1 S Tích phân mặt loại I 4/28/2022 Thaodt 7 7 2. Tích phân mặt loại I
• Nếu mặt S có khối lượng riêng tại 𝑀 𝑥, 𝑦, 𝑧 là 𝜌 𝑥, 𝑦, 𝑧 , Khối lượng của mặt S:   x,y,zdS S • Tích phân mặt
dS cho ta diện tích của mặt S. S
• Tích phân mặt loại I có tính chất giống tích phân kép. 4/28/2022 Thaodt 8 8 4 4/28/2022 2. Tích phân mặt loại I  Diện tích mặt
• Xét mặt S có phương trình véc-tơ:
𝑟 𝑢, 𝑣 = 𝑥 𝑢, 𝑣 𝚤 + 𝑦 𝑢, 𝑣 𝚥 + 𝑧 𝑢, 𝑣 𝑘, 𝑢, 𝑣 ∈ 𝐷
• Xấp xỉ 2 biên của mảnh 𝑆 bởi 2 véc-tơ, các véc-tơ này lần
lượt xấp xỉ bởi ∆𝑢𝑟∗, ∆𝑣𝑟∗ 4/28/2022 Thaodt 9 9 2. Tích phân mặt loại I
• Khi đó mảnh 𝑆 được xấp xỉ bởi hình bình hành có các -
cạnh là các véc-tơ ∆𝑢𝑟∗, ∆𝑣𝑟∗
• Hình bình hành này nằm trong mặt phẳng tiếp diện của S tại 𝑃.
• Diện tích của hình bình hành:     * * * * S  ur ' , vr '  r ' ,r '       uv ij u v u v        
Trong đó: r'  x' i y' j z' k u u u u     r'  x' i y' j  z' k v v v v 4/28/2022 Thaodt 10 10 5 4/28/2022 2. Tích phân mặt loại I
• Diện tích mặt S được xấp xỉ bằng: m n   * *  r' ,r'  u v   u v   i 1 j 1
• Để độ chính xác tốt hơn: 𝑚, 𝑛 → ∞
 Vậy: Diện tích mặt S được xác định bởi biểu thức:   * *  r' ,r'  dudv  u v   D
Nếu mặt S: 𝑟 𝑥, 𝑦 = 𝑥, 𝑦, 𝑧(𝑥, 𝑦) 𝑟󰆒 󰆒 󰆒 󰆒 󰆒 󰆒 󰆒 󰆒
 = 1,0, 𝑧 ; 𝑟 = 0,1, 𝑧 ⇒ 𝑟, 𝑟 = −𝑧, −𝑧, 1 4/28/2022 Thaodt 11 11 2. Tích phân mặt loại I
2.2. Cách tính tích phân mặt loại I
Xét mặt S cho bởi phương trình 𝑧 = 𝑓(𝑥, 𝑦): hàm liên
tục, có các 𝑧′, 𝑧′ liên tục trong miền đóng giới nội D (hình  chiếu của S lên Oxy) f  x y zdS  f  x y zx y '2 '2 , , , , , 1  z  z dxdy x y S D
 Ví dụ 2. Tính tích phân ∬ 𝑦𝑑𝑆  trong đó S là mặt:
𝑧 = 𝑥 + 𝑦, 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 2 4/28/2022 Thaodt 12 12 6 4/28/2022
2.2 Cách tính tích phân mặt loại I
 Ví dụ 2. Tính tích phân ∬ 𝑦𝑑𝑆  trong đó S là mặt:
𝑧 = 𝑥 + 𝑦, 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 2 • Ta có: ' ' 2
z  1, z  2y  dS  1 1 4y dxdy x y 1 2 2 I  ydS  y 2  4y dydx   00 S 1 2  
I  2. .  1 2y  2 1 3/2 2 dx 0 8 3  0   13 2 I  3 4/28/2022 Thaodt 13 13
2.2 Cách tính tích phân mặt loại I
 Ví dụ 3. Tính tích phân sau với S là mặt cầu 𝑥 + 𝑦 +
𝑧 = 1, 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑧 ≥ 0: 2 z   2 2 x  y dS S
Từ phương trình mặt cầu rút ra: 𝑧 = 1 − 𝑥 − 𝑦   x x ' z    x  2 2 1  x   y z 1 1 '2 '2   1 z  z   , z  0 x y 2    ' y y z z z    y 2 2  1 x  y z  4/28/2022 Thaodt 14 14 7 4/28/2022
2.2 Cách tính tích phân mặt loại I • Suy ra: 2 I  z   2 2 x  y  2 2 dS  1 x  y   2 2 x  y dxdy 2  S D
• Trong đó, miền D là ¼ hình tròn tâm O bán kính 1 thuộc góc phần tư thứ nhật.
• Chuyển sang tọa độ cực:  /2 1  1 2 3 2 3 I  d 1 r r dr  1  r r dr 2    0 0 0 2 
• Đặt 𝑟 = 𝑠𝑖𝑛𝑡, 0 ≤ 𝑡 ≤ , suy ra   I2 15 4/28/2022 Thaodt 15 15 Tích phân mặt loại I
• Ví dụ 4: Tính ∬ 𝑥𝑑𝑆 
, trong đó S là mặt cầu đơn vị 𝑥 + 𝑦 + 𝑧 = 1.
• HD: Tham số hóa mặt cầu: 𝑥 = sin 𝜙 cos 𝜃 , 𝑦 = sin 𝜙 sin 𝜃 , 𝑧 = cos 𝜙 ,
0 ≤ 𝜙 ≤ 𝜋, 0 ≤ 𝜃 ≤ 2𝜋
⇒ 𝒓 𝜙, 𝜃 = sin 𝜙 cos 𝜃 𝒊 + sin 𝜙 sin 𝜃 𝒋 + cos 𝜙 𝒌 Từ đó suy ra:
𝒓󰆒,𝒓󰆒 = sin𝜙
Áp dụng CT tính tích phân mặt: 4/28/2022 Thaodt 16 16 8 4/28/2022 Tích phân mặt loại I
 𝑥𝑑𝑆 =  sin𝜙 cos 𝜃  𝒓′, 𝒓′ 𝑑𝐴    
=   sin 𝜙 cos 𝜃 sin𝜙 𝑑𝜙𝑑𝜃     4𝜋
=  cos 𝜃 𝑑𝜃  sin 𝜙 𝑑𝜙 = 3   4/28/2022 Thaodt 17 17 Tích phân mặt loại I
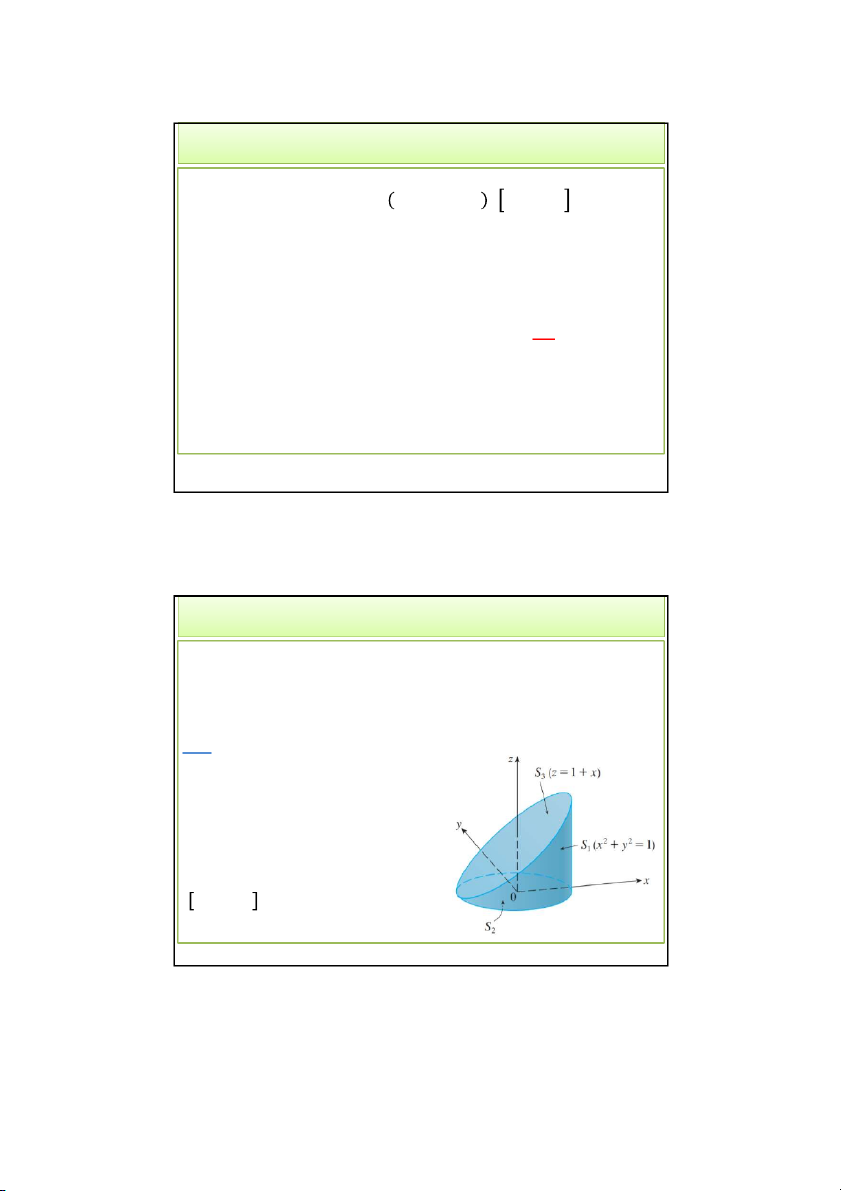
Ví dụ 6. Tính ∬ 𝑧𝑑𝑆 
, trong đó S là mặt bao gồm mặt
𝑆 cho bởi mặt trụ 𝑥 + 𝑦 = 1, 𝑆 là đĩa tròn 𝑥 + 𝑦 ≤ 1
nằm trong mặt phẳng 𝑧 = 0, và 𝑆 là mặt phẳng 𝑧 = 1 + 𝑥. HD:
𝑆: sử dụng các tham số 𝜃 và z.
𝑥 = cos 𝜃 , 𝑦 = sin 𝜃 , 𝑧 = 𝑧 Khi đó: 0 ≤ 𝜃 ≤ 2𝜋
0 ≤ 𝑧 ≤ 1 + 𝑥 = 1 + cos 𝜃
𝒓󰆒,𝒓󰆒 = (cos𝜃 , sin 𝜃 , 0) 4/28/2022 Thaodt 18 18 9 4/28/2022 Tích phân mặt loại I • Tiếp ví dụ 6:
 𝑧𝑑𝑆 =  𝑧| 𝒓󰆒 󰆒 , 𝒓  |𝑑𝐴      3𝜋
=   𝑧𝑑𝑧𝑑𝜃 = 2   Trên mặt 𝑆: 𝑧 = 0  𝑧𝑑𝑆 = 0  4/28/2022 Thaodt 19 19 Tích phân mặt loại I
Trên mặt 𝑆: 𝑧 = 1 + 𝑥 ⇒ 𝑧′ = 1, 𝑧′ = 0
 𝑧𝑑𝑆 =  1 + 𝑥 2𝑑𝐴  
Chuyển sang tọa độ cực:  
 1 + 𝑥 2𝑑𝐴 = 2  1 + 𝑟. cos 𝜃 𝑟𝑑𝑟𝑑𝜃 = 2𝜋    3 ⇒  𝑧𝑑𝑆 =  2 + 2 𝜋 4/28/2022 Thaodt 20 20 10 4/28/2022 3. Tích phân mặt loại II
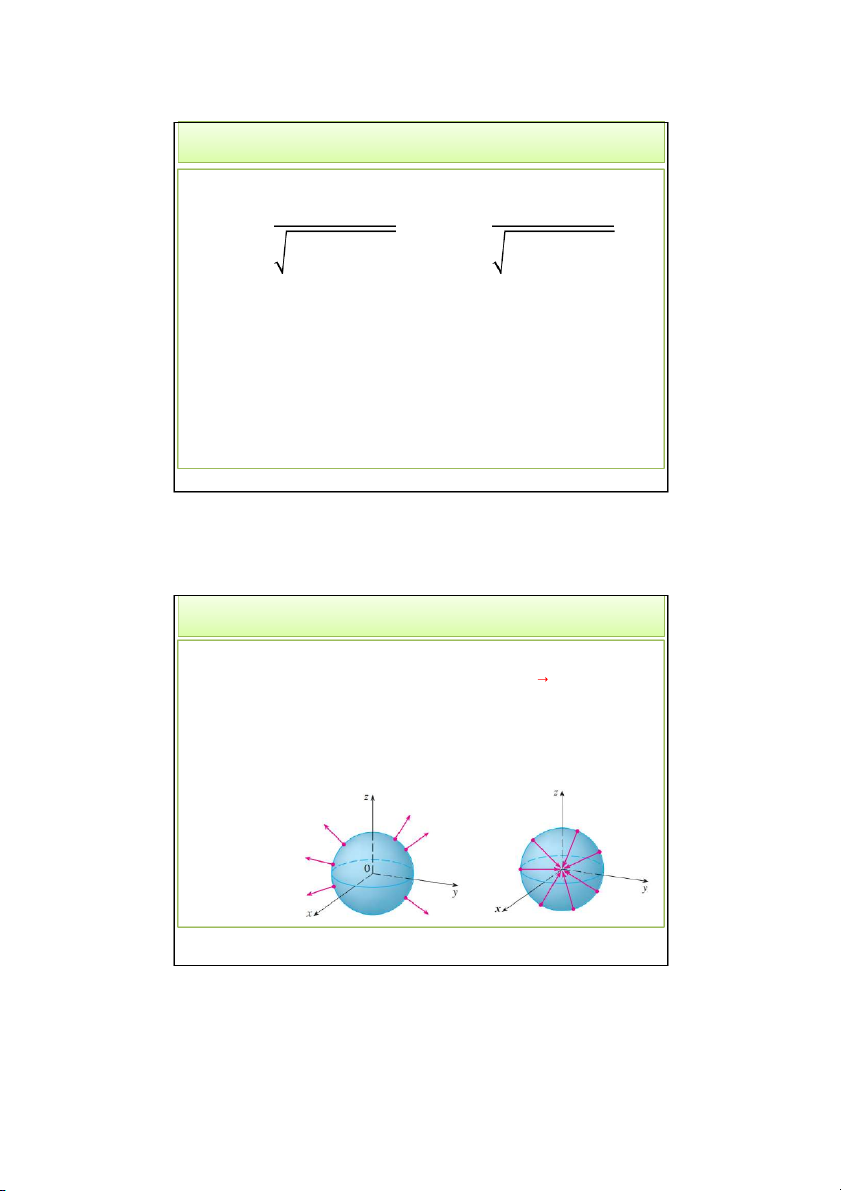
 3.1. Mặt định hướng
• Cho mặt S, tại mỗi điểm chính quy M của S, có 2 véc-tơ pháp tuyến 𝑛, 𝑛′.
• Nếu tại mỗi điểm M của S, 1 véc-tơ 𝑛 có thể biến thiên
liên tục trên S: S định hướng được
• Hướng của S: hướng của 𝑛 4/28/2022 Thaodt 21 21 3. Tích phân mặt loại II
• Dải Mobius là 1 ví dụ của mặt không định hướng được 4/28/2022 Thaodt 22 22 11 4/28/2022 3. Tích phân mặt loại II
 3.2. Tích phân mặt loại II
• Ở phần này chỉ xét những mặt định hướng được (2 mặt)
• Tại mỗi điểm trong mặt sẽ có 2 véc- tơ pháp tuyến đơn vị. 4/28/2022 Thaodt 23 23 3. Tích phân mặt loại II
 3.2. Tích phân mặt loại II
• Nếu mặt S có phương trình 𝑧 = 𝑓(𝑥, 𝑦), hay:
𝑟 𝑥, 𝑦 = 𝑥. 𝚤 + 𝑦. 𝚥 + 𝑓 𝑥, 𝑦 . 𝑘 Véc-tơ pháp tuyến: 𝑙 = 𝑟󰆒 󰆒 󰆒 󰆒
, 𝑟 = −𝑓 , −𝑓, 1 l 4/28/2022 Thaodt 24 24 12 4/28/2022 3. Tích phân mặt loại II
• Véc-tơ pháp tuyến đơn vị:
−𝑓󰆒𝒊 − 𝑓󰆒𝒋 + 𝒌
󰆒𝒊 + 𝑓󰆒𝒋 − 𝒌 𝒏   𝑓   = ; 𝒏𝟐 = 1 + 𝑓󰆒 󰆒 󰆒  + 𝑓󰆒 1 + 𝑓 + 𝑓 Hay:
𝒏 = (cos 𝛼 , cos 𝛽 , cos 𝛾)
Với 𝛼, 𝛽, 𝛾 là góc giữa 𝒍 và các trục Ox, Oy, Oz; 4/28/2022 Thaodt 25 25 3. Tích phân mặt loại II
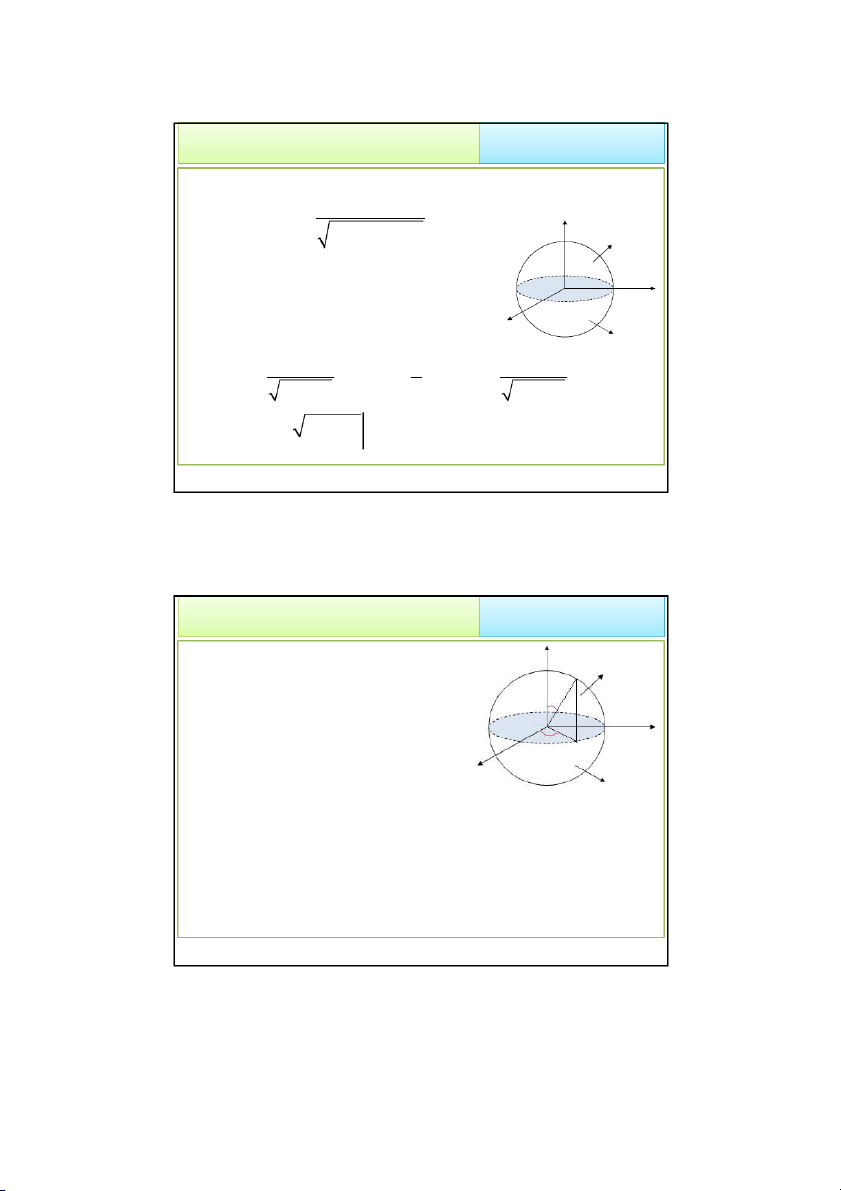
• Đối với mặt thông thường,
Hướng dương là hướng mà thành phần của 𝑘 trong véc-tơ
pháp tuyến đơn vị dương.
• Đối với mặt đóng (mặt S vao vật thể E)
Hướng dương là hướng mà véc-tơ pháp tuyến hướng ra ngoài vật thể 4/28/2022 Thaodt 26 26 13 4/28/2022 3. Tích phân mặt loại II
 Xét mặt S là 1 mặt có hướng với véc-tơ đơn vị n
• Giả sử có 1 dòng chất lỏng có mật độ 𝜌 𝑥, 𝑦, 𝑧 , trường
vận tốc 𝒗(𝑥, 𝑦, 𝑧) chảy qua mặt S
• Lượng chất lỏng chảy qua 1 đơn vị diện tích trong 1 đơn vị thời gian là: 𝜌𝒗
• Nếu chia S thành các mảnh nhỏ 𝑆
• Lượng chất lỏng chảy qua 𝑆
theo hướng của n trong 1 đơn vị thời
gian: 𝜌𝒗. 𝒏 𝐴 𝑆 4/28/2022 Thaodt 27 27 3. Tích phân mặt loại II
• Lượng chất lỏng chảy qua S: xấp xỉ bằng tổng lượng chất
lỏng chảy qua các mảnh con 𝑆 
  ,x ,y z.v ,x ,y z.n ,x ,y zdS  FdS  . F ndS   S S S
F  .v  P x, y,z i Q x,y,z j R x,y,z k
n là véc-tơ pháp tuyến đơn vị;
- Tích phân mặt loại II (thông lượng của F chảy qua S)
- Nếu ta đổi hướng mặt S thì tích phân mặt loại II đổi dấu
(do cosin chỉ hướng của n đổi dấu)
- Tích phân mặt loại II có tính chất tương tự tích phân kép 4/28/2022 Thaodt 28 28 14 4/28/2022
3.3. Cách tính tích phân mặt loại II  Cách tính
• Nếu mặt S cho bởi phương trình 𝑧 = 𝑓 𝑥, 𝑦 , 𝑥, 𝑦 ∈ 𝐷: r x y z  x y ' r   ' f  'r  f x x y  ' , , , : 1,0, ; 0,1, y
→ 𝑙 = 𝑟′ × 𝑟′ = −𝑓󰆒,−𝑓󰆒,1
Suy ra 2 véc-tơ pháp tuyến đơn vị tương ứng:
−𝑓󰆒𝒊 − 𝑓󰆒𝒋 + 𝒌
𝑓󰆒𝒊 + 𝑓󰆒𝒋 − 𝒌 𝒏      = ; 𝒏𝟐 = 1 + 𝑓󰆒 󰆒 󰆒 󰆒  + 𝑓 1 + 𝑓 + 𝑓 𝑑𝑆 = 1 + 𝑓󰆒 󰆒  + 𝑓 𝑑𝑥𝑑𝑦 4/28/2022 Thaodt 29 29
3.3. Cách tính tích phân mặt loại II ⇒ 𝑭. 𝒏. 𝑑𝑆
−𝑓󰆒𝒊 − 𝑓󰆒𝒋 + 𝒌
= ± 𝑃𝒊 + 𝑄𝒋 + 𝑅𝒌 .   . 1 + 𝑓󰆒 󰆒  + 𝑓 𝑑𝑥𝑑𝑦 1 + 𝑓󰆒 󰆒  + 𝑓
= ±𝑭. 𝒍𝑑𝑥𝑑𝑦 = ± −𝑃𝑓󰆒 󰆒
 − 𝑄𝑓 + 𝑅 𝑑𝑥𝑑𝑦 Vậy:
 𝑭𝑑𝑺 =  𝑭.𝒏. 𝑑𝑆 = ±  −𝑃𝑓󰆒 󰆒
 − 𝑄𝑓 + 𝑅 𝑑𝑥𝑑𝑦   
D: miền hình chiếu của S lên Oxy
Nếu hướng dương là ↑: 𝒏𝟏, nếu ↓: 𝒏𝟐 4/28/2022 Thaodt 30 30 15 4/28/2022 3. Tích phân mặt loại II  3.3. Cách tính
• Nếu mặt S cho bởi hàm véc-tơ 𝒓 𝑢, 𝑣 : 𝐼 =  𝑭. 𝒏𝑑𝑆 𝒓 =  𝑭. , 𝒓 𝒓 𝑑𝑆 , 𝒓   𝒓
=  𝑭(𝑟(𝑢, 𝑣). , 𝒓 𝒓
. 𝒓,𝒓 𝑑𝑢𝑑𝑣 , 𝒓  =  𝑭. 𝒓 dS , 𝒓 𝑑𝑢𝑑𝑣  4/28/2022 Thaodt 31 31
3.3. Cách tính tích phân mặt loại II
• Ví dụ: Tính TP trên mặt S của 𝑭 = 𝑥𝑦𝒊 + 𝑦𝑧𝒋 + 𝑧𝑥𝒌, S là
một phần của mặt paraboloid 𝑧 = 4 − 𝑥 − 𝑦 nằm bên
trên hình vuông 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1, hướng dương là hướng lên trên. 4/28/2022 Thaodt 32 32 16 4/28/2022
3.3. Cách tính tích phân mặt loại II
• Giải: Theo bài cho ta có:
𝑭 = 𝑥𝑦𝒊 + 𝑦𝑧𝒋 + 𝑧𝑥𝒌 → 𝑭 = 𝑥𝑦, 𝑦𝑧, 𝑧𝑥
𝑧 = 4 − 𝑥 − 𝑦 → 𝑧󰆒 󰆒
 = −2𝑥, 𝑧  = −2𝑦
Hướng dương hướng lên trên ⇒ 𝒍 = 2𝑥, 2𝑦, 1
𝐷 = 𝑥, 𝑦 0 ≤ 𝑥 ≤ 1, 0 ≤ 𝑦 ≤ 1} ∬ 𝐹𝑑𝑆  =
 2𝑥𝑦 + 2𝑦 4 − 𝑥 − 𝑦 + 𝑥 4 − 𝑥 − 𝑦 𝑑𝑥𝑑𝑦  4/28/2022 Thaodt 33 33
3.3. Cách tính tích phân mặt loại II
 Ví dụ 3. Tính ∬ 𝑭. 𝑑𝑺 
, trong đó 𝑭 = 𝑦𝒊 + 𝑥𝒋 + 𝑧𝒌, S là
phía ngoài của paraboid 𝑧 = 1 − 𝑥 − 𝑦, 0 ≤ 𝑧 ≤ 1. • Theo bài cho ta có: 𝑃 𝑥, 𝑦, 𝑧 = 𝑦, 𝑄 𝑥, 𝑦, 𝑧 = 𝑥,
𝑅 𝑥, 𝑦, 𝑧 = 1 − 𝑥 − 𝑦 𝑓 󰆒 󰆒  = −2𝑥; 𝑓 = −2𝑦 Hình chiếu của S lên Oxy
là hình tròn tâm O, bán kính 1: 𝑥 + 𝑦 ≤ 1 4/28/2022 Thaodt 34 34 17 4/28/2022
3.3. Cách tính tích phân mặt loại II • Áp dụng công thức: FdS    ' '  P.f  Q. f  R dxdy x y  S D • Suy ra: I 
y  x  x y  2 2 2 2  1 x  y d  xdy    D I   2 2 4xy 1 x  y dxdy D
• Chuyển sang tọa độ cực: 2  1 I     2 2
1 4r sin cos r rdrd  I  0 0 2 4/28/2022 Thaodt 35 35 2. Tích phân mặt loại II Cách tính
 Ví dụ 4. Tính ∬ 𝑭. 𝑑𝑺 
, trong đó 𝑭 = 𝑦𝒊 + 𝑥𝒋 + 𝑧𝒌, S là
phía ngoài của vật thể E giới hạn bởi 𝑧 = 0 và paraboid
𝑧 = 1 − 𝑥 − 𝑦
• Mặt 𝑆 = 𝑆 + 𝑆 Do đó: . F dS  . F dS  . F dS  I  I    1 2 S 1 S S2 Trong đó: 𝜋 𝐼 = 2 4/28/2022 Thaodt 36 36 18 4/28/2022 2. Tích phân mặt loại II Cách tính
• Mặt S : là hình tròn có phương trình . 2 𝑥 + 𝑦 ≤ 1
Véc tơ pháp tuyến của S2 (hướng dương): 𝑛 = 0,0, −1 Do đó: . FdS    z  dxdy  0dxdy  0  2 S D D Vậy:   F.dS  F.dS  F.dS   0     2 2 S 1 S 2 S 4/28/2022 Thaodt 37 37 2. Tích phân mặt loại II Cách tính
Ví dụ 4. Tính tích phân sau với S là phía ngoài mặt cầu
𝑥 + 𝑦 + 𝑧 = 𝑅:
𝐼 =  𝑥𝑑𝑦𝑑𝑧 + 𝑦𝑑𝑧𝑑𝑥 + 𝑧𝑑𝑥𝑑𝑦 
 Hướng dẫn: Mặt 𝑆 = 𝑆 + 𝑆
𝑆 = 𝑅 − 𝑥 − 𝑦
𝑆 = − 𝑅 − 𝑥 − 𝑦 4/28/2022 Thaodt 38 38 19 4/28/2022 2. Tích phân mặt loại II Cách tính • Xét trên mặt 𝑆: 2 2 2 ' x '  y
S : z  R  x  y ; z  , z  1 x 2 2 2 y 2 2 2 R  x  y R  x  y   x y   n   , ,1 2 2 2 2 2 2  R x y R x y        • Suy ra: xdydz  ydxdz  zdxdy  1 S  2 2  2 x  y R 2 2 2    R  x  y dxdy  dxdy   2 2 2  2 2 2 D R  x  y D R  x  y   4/28/2022 Thaodt 39 39 2. Tích phân mặt loại II Cách tính • Xét trên mặt S : 2 x y 2 2 2 ' '
S : z   R  x  y ; z  , z  2 x 2 2 2 y 2 2 2 R  x  y R  x  y   x y   n   , , 1   2 2 2 2 2 2  R x y R x y        xdydz  ydxdz  zdxdy  2 S  2 2  2 x  y R 2 2 2    R  x  y dxdy  dxdy   2 2 2  2 2 2 D R  x  y D R  x  y   4/28/2022 Thaodt 40 40 20 4/28/2022 2. Tích phân mặt loại II Cách tính
Trong đó D là hình tròn tâm O(0,0) bán kính R 2 Vậy: R I  2 dxdy 4  2 2 2 D R  x  y
Chuyển sang tọa độ cực: x  rcos  ,0  r  , R 0   2 y  r sin  2 2 R R 1 R 1 2 I  2 rdrd   .2.2 R d     2 2 R  r 4  0 0 2 2 0 2 2 R  r 2 R  r R 2 2 2 3 2     R .2 R  r  4R   0   4/28/2022 Thaodt 41 41 2. Tích phân mặt loại II Cách tính  Cách 2. Tham số hóa mặt cong: x  R sin cos 
y  R sin sin , 0   ,0   2 z  R cos  ' r        
Rcos cos , Rcos sin , Rsin  ' r         R sin sin ,Rsin cos ,0 ' ' r  r              2 2 2 2 2 R sin cos , R sin sin , R sin cos 
F  Rsin cos,Rsin sin,R cos 4/28/2022 Thaodt 42 42 21 4/28/2022 2. Tích phân mặt loại II Cách tính ' ' 3 3 2 3 3 2 3 2 F. r
 ,r   R sin  cos   R sin  sin   R cos  sin     3  R sin  Khi đó: I  xdydz  ydzdx  zdxdy 4 S 2  2  3 3  R sind d  R d sin d     0 0 0 0 3  3  2   R .cos  4 R 0 4/28/2022 Thaodt 43 43
Exercise 1. Evaluate the surface integral
• ∬ 𝑥𝑦𝑧𝑑𝑆 
, S is the part of the plane 𝑧 = 1 + 2𝑥 + 3𝑦
that lies above the rectangle 0,3 × [0,2]. • ∬ 𝑥𝑦𝑑𝑆 
, S is the triangular region with vertices (1,0,0), (0,2,0) and (0,0,2). • ∬ 𝑦𝑧𝑑𝑆 
, S is the part of the plane 𝑥 + 𝑦 + 𝑧 = 1 that lies in the first octant.   • ∬ 𝑦𝑑𝑆 𝑥  , 0 ≤ 𝑥 ≤ 1,  , S is the surface 𝑧 =   + 𝑦  0 ≤ 𝑦 ≤ 1). 4/28/2022 Thaodt 44 44 22 4/28/2022
Exercise 1. Tính: Evaluate the surface integral • ∬ 𝑥𝑧𝑑𝑆 
, S is the part of the cone 𝑧 = 𝑥 + 𝑦 that
lies between the planes 𝑧 = 1 and 𝑧 =3. • ∬ 𝑧𝑑𝑆 
, S is the surface 𝑥 = 𝑦 + 2𝑧, 0 ≤ 𝑦 ≤ 1, 0 ≤ 𝑧 ≤ 1. • ∬ 𝑦𝑑𝑆 
, S is the part of the paraboloid 𝑦 = 𝑥 + 𝑧 that
lies inside the cylinder 𝑥 + 𝑦 = 4. 4/28/2022 Thaodt 45 45 Tính: 4/28/2022 Thaodt 46 46 23