












Preview text:
TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
BÀI 1: TÍNH ĐƠN DIỆU VÀ CỰC TRỊ CỦA HÀM SỐ ........................................................................ 2
A. KIẾN THỨC CƠ BẢN CẦN NẮM ....................................................................................................... 2
B. CÁC DẠNG TOÁN ................................................................................................................................. 7
Dạng 1: Xét định đơn điệu của hàm số cho bởi công thức ..... Lỗi! Thẻ đánh dấu không được xác định.
Dạng 2: Xét tính đơn điệu dựa vào bảng biến thiên, đồ thị .... Lỗi! Thẻ đánh dấu không được xác định.
Dạng 3: Tìm tham số m để hàm số đơn điệu .................. Lỗi! Thẻ đánh dấu không được xác định.
Dạng 4: Ứng dụng tính đơn điệu để chứng minh bất đẳng thức, giải phương trình, bất phương
trình, hệ bất phương trình ............................................... Lỗi! Thẻ đánh dấu không được xác định.
Dạng 5: Tìm cực trị hàm số cho bởi công thức .............. Lỗi! Thẻ đánh dấu không được xác định.
Dạng 6: Tìm cực trị dựa vào bảng biến thiên, đồ thị .... Lỗi! Thẻ đánh dấu không được xác định.
Dạng 7: Tìm m để hàm số đạt cực trị tại một điểm x0 cho trước . Lỗi! Thẻ đánh dấu không được xác định.
Dạng 7: Toán thực tế ........................................................ Lỗi! Thẻ đánh dấu không được xác định.
C. GIẢI BÀI TẬP SÁCH GIÁO KHOA ................................................................................................... 7
D. BÀI TÂP TRẮC NGHIỆM 4 PHƯƠNG ÁN ................... Lỗi! Thẻ đánh dấu không được xác định.
PHẦN 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ..................... Lỗi! Thẻ đánh dấu không được xác định.
PHẦN 2. CỰC TRỊ CỦA HÀM SỐ ................................... Lỗi! Thẻ đánh dấu không được xác định.
E. CÂU TRẮC NGHIỆM ĐÚNG SAI ................................... Lỗi! Thẻ đánh dấu không được xác định.
F. TRẢ LỜI NGẮN ................................................................. Lỗi! Thẻ đánh dấu không được xác định.
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT HÀM SỐ
BÀI 1: TÍNH ĐƠN ĐIỆU VÀ CỰC TRỊ CỦA HÀM SỐ
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Tính đơn điệu của hàm số
Nhắc lại vể tính đổng biến, nghịch biến của hàm số
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f (x) xác định trên K .
Hàm số y = f (x) gọi là đồng biến (tăng) trên K nếu với mọi x , x thuộc K mà x < x thì 1 2 1 2
f (x < f x . 1 ) ( 2)
Hàm số y = f (x) gọi là nghịch biến (giảm) trên K nếu với mọi x , x thuộc K mà x < x thì 1 2 1 2
f (x > f x . 1 ) ( 2)
Nếu hàm số y = f (x) đồng biến trên K thì đồ thị của nó đi lên từ trái sang phải (Hình 1a).
Nếu hàm số y = f (x) nghịch biến trên K thì đồ thị của nó đi xuống từ trái sang phải (Hình 1 b).
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K .
Ví dụ 1. Tìm các khoảng đơn điệu của hàm số y = f (x) có đồ thị cho ở Hình 2. Lời giải
Hàm số đồng biến trên các khoảng ( 2
− ;1) và (5;8) , nghịch biến trên khoảng (1;5).
Tính đơn điệu của hàm số
Tổng quát, ta có kết quả sau đây:
Cho hàm số y = f (x) có đạo hàm trên K .
Nếu f (′x) > 0 với mọi x thuộc K thì hàm số y = f (x) đồng biến trên K .
Nếu f (′x) < 0 với mọi x thuộc K thì hàm số y = f (x) nghịch biến trên K .
Ví dụ 2. Chứng minh rằng hàm số ( ) x g x =
nghịch biến trên khoảng (1;+∞) . x −1 Lời giải 1
Hàm số xác định trên (1;+∞). Ta có g (′x) = −
< 0 với mọi x∈(1;+∞) . 2 (x −1)
Vậy g(x) nghịch biến trên khoảng (1;+∞).
Chú ý: Khi xét tính đơn điệu của hàm số mà chưa cho khoảng K , ta hiểu xét tính đơn điệu của hàm số đó
trên tập xác định của nó.
Từ kết quả trên, để xét tính đơn điệu của hàm số y = f (x) , ta thực hiện các bước sau:
Buớc 1. Tìm tập xác định D của hàm số.
Buớc 2. Tính đạo hàm f (′x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f (′x) bằng 0
hoặc đạo hàm không tồn tại.
Buớc 3. Xét dấu f (′x) và lập bảng biến thiên.
Buớc 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
Ví dụ 3. Xét tính đơn điệu của các hàm số sau: a) 3 2
f (x) = −x + 3x b) 1
g(x) = x + c) 3
h(x) = x . x Lời giải a) Xét hàm số 3 2
f (x) = −x + 3x .
Tập xác định: D = . Ta có 2 f (′x) = 3 − x + 6 ;
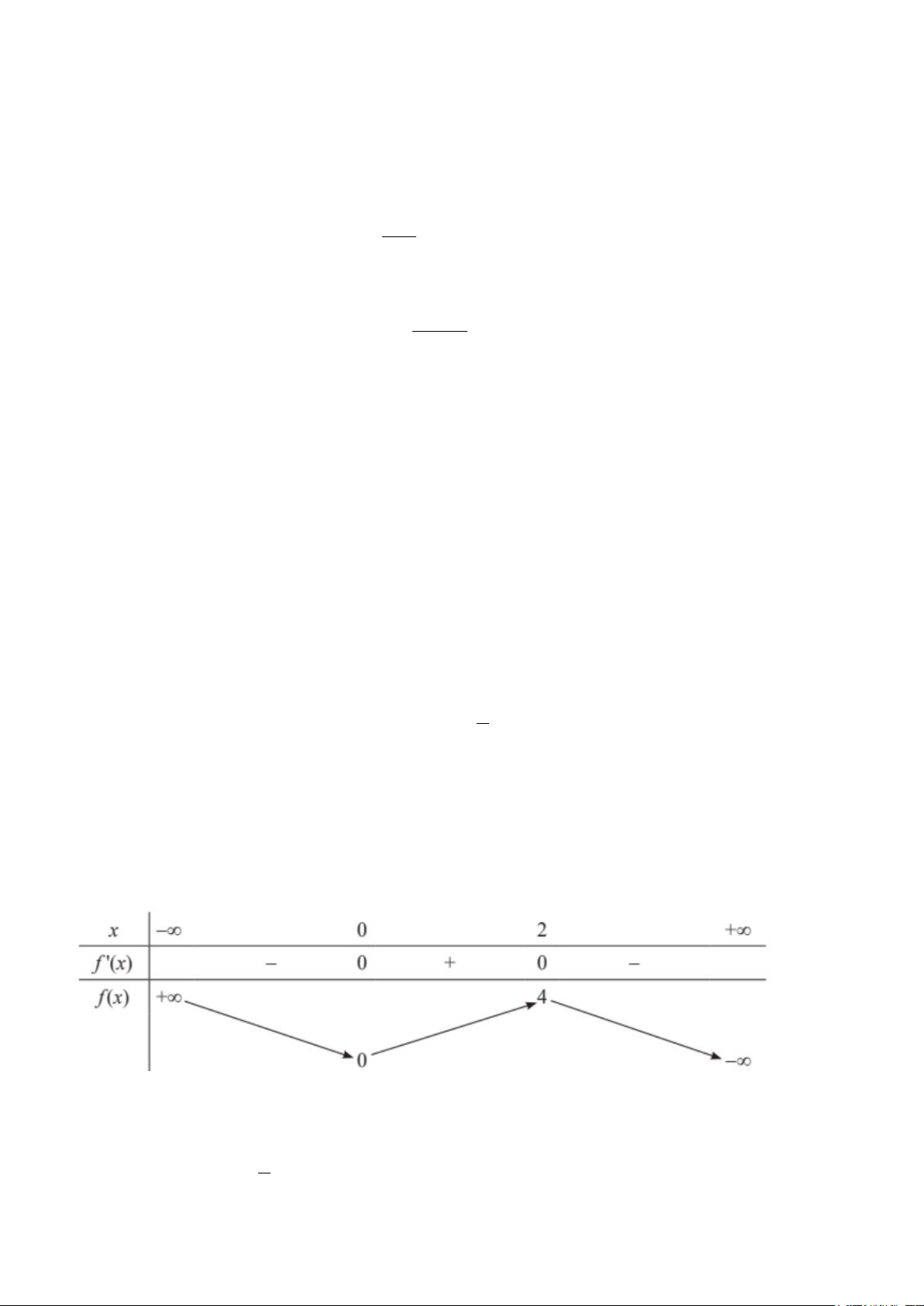
x f (′x) = 0 ⇔ x = 0 hoặc x = 2 . Bảng biến thiên: Vậy hàm số 3 2
f (x) = −x + 3x đồng biến trên khoảng (0;2) , nghịch biến trên các khoảng ( ; −∞ 0) và (2;+∞) . b) Xét hàm số 1
g(x) = x + . x
Tập xác định: D = \{0}. 2 1 −1 Ta có (′ ) =1 x g x − = . Vì 2
x > 0 với mọi x ∈ \{0} nên g (′x) cùng dấu với 2 x −1. 2 2 x x Ta có 2
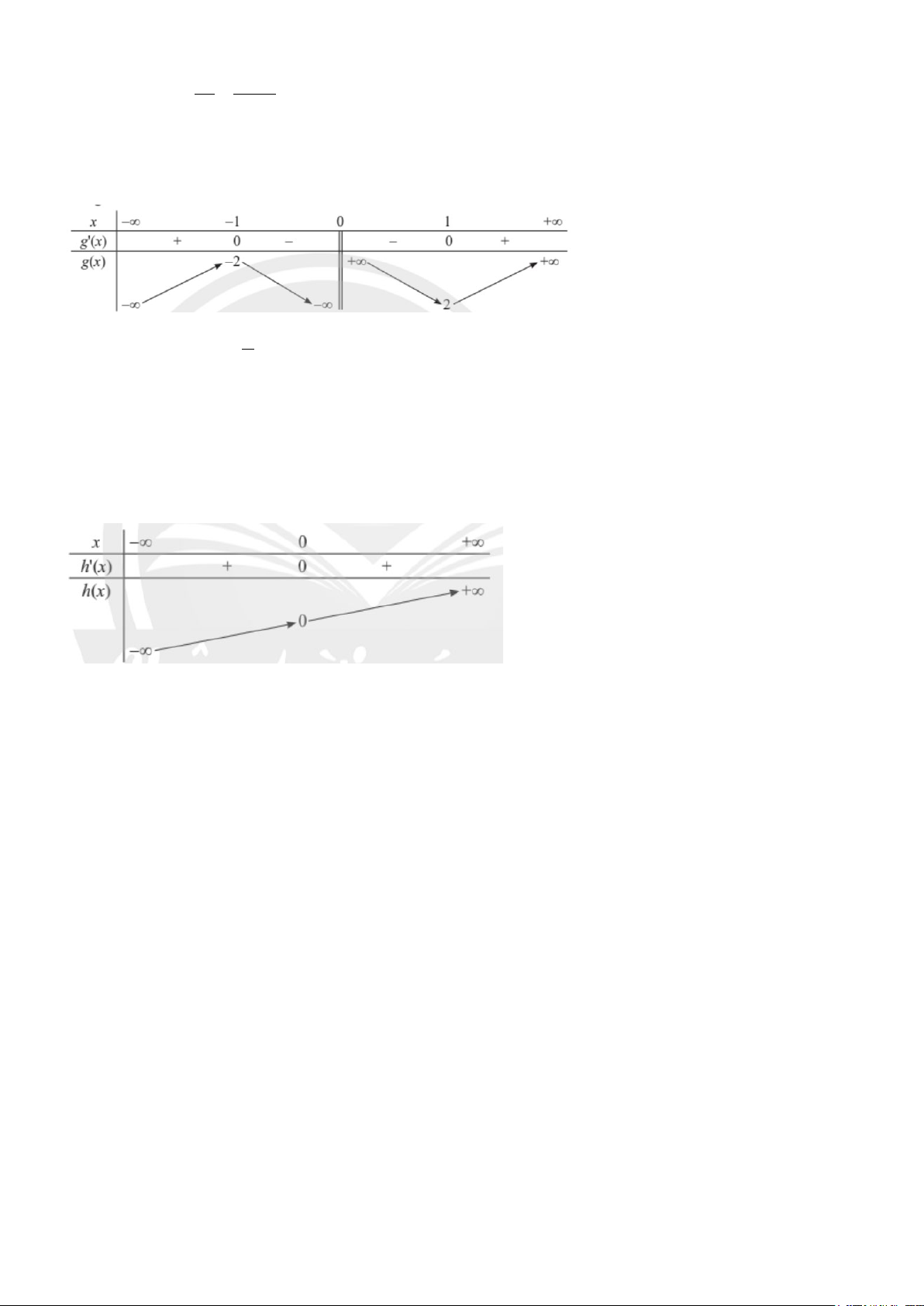
g (′x) = 0 ⇔ x −1 = 0 ⇔ x = 1 − hoặc x =1. Bảng biến thiên: Vậy hàm số 1
g(x) = x + đồng biến trên các khoảng ( ; −∞ 1)
− và (1;+∞) , nghịch biến trên các khoảng x ( 1; − 0) và (0;1) . c) Xét hàm số 3
h(x) = x .
Tập xác định: D = . Ta có 2
h (′x) = 3x ;h (′x) = 0 ⇔ x = 0 . Bảng biến thiên: Vậy hàm số 3
h(x) = x đồng biến trên . Chú ý:
a) Nếu hàm số y = f (x) có đạo hàm trên K, f (′x) ≥ 0 với mọi x∈ K và f (′x) = 0 chi tại một số hữu
hạn điểm thì hàm số đồng biến trên K .
b) Nếu hàm số y = f (x) có đạo hàm trên K, f (′x) ≤ 0 với mọi x∈ K và f (′x) = 0 chi tại một số hữu
hạn điểm thì hàm số nghịch biến trên K .
c) Nếu f (′x) = 0 với mọi x∈ K thì hàm số không đổi trên K .
2. Cực trị của hàm số
Khái niệm cực trị của hàm số
Cho hàm số y = f (x) xác định trên tập hợp D và x ∈ D . 0
- Nếu tồn tại một khoảng ( ;
a b) chứa điểm x và ( ;
a b) ⊂ sao cho f (x) < f (x với mọi 0 ) 0 D x∈( ; a b) \{x thì
f x được gọi là giá trị cục đại của hàm số 0}
x được gọi là một điểm cục đại, ( 0 ) 0
y = f (x) , kí hiệu y . CD
- Nếu tồn tại một khoảng ( ;
a b) chứa điểm x và ( ;
a b) ⊂ sao cho f (x) > f (x với mọi 0 ) 0 D x∈( ; a b) \{x , thì
f x được gọi là giá trị cục tiểu của hàm số 0}
x được gọi là một điểm cưc tiểu, ( 0 ) 0
y = f (x) , kí hiệu y . CT Chú ý:
a) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị của hàm số. Giá trị cực đại và giá trị cực
tiểu được gọi chung là giá trị cưc trị (còn gọi là cưc trị) của hàm số.
b) Nếu x là một điểm cực trị (điểm cực đại, điểm cực tiểu) của hàm số y = f (x) thì ta cũng nói hàm số 0
y = f (x) đạt cực trị (cực đại, cực tiểu) tại x . 0
c) Hàm số có thể đạt cực đại và cực tiểu tại nhiều điểm trên D .
d) Nếu x là điểm cực trị của hàm số y = f (x) thì điểm M (x ; f x là một điểm cực trị của đồ thị 0 ( 0)) 0
hàm số y = f (x) .
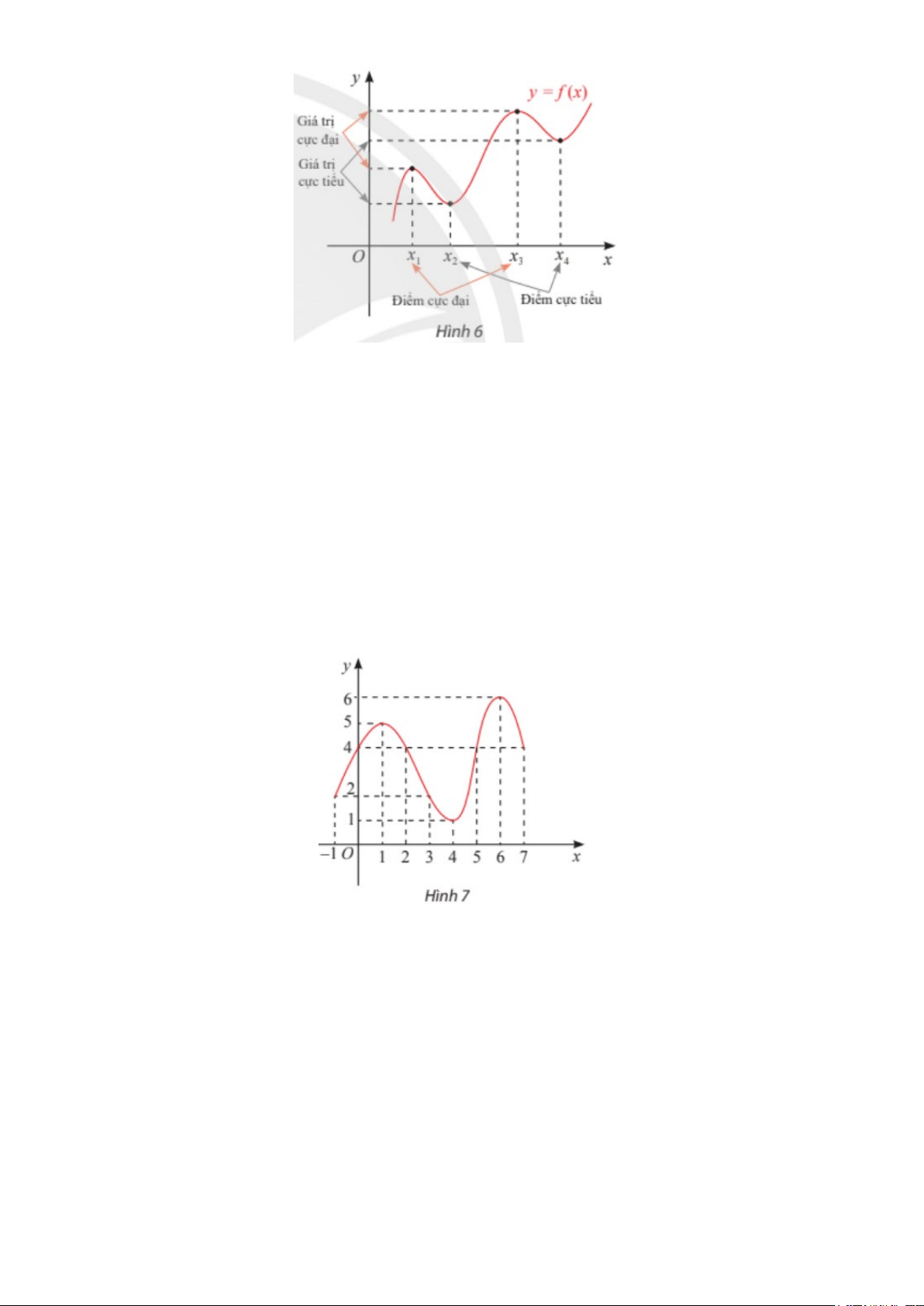
Ví dụ 4. Tìm cực trị của hàm số y = f (x) có đồ thị được cho ở Hình 7. Lời giải
Hàm số y = f (x) có:
- x =1 là điểm cực đại vì f (x) < f (1) với mọi x∈(0;2) \{1}, y = f = ; CÐ (1) 5
- x = 6 là điểm cực đại vì f (x) < f (6) với mọi x∈(5;7) \{6}, y = f = ; CD (6) 6
- x = 4 là điểm cực tiểu vì f (x) > f (4) với mọi x∈(3;5) \{4}, y = f = . CT (4) 1
Tìm cực trị của hàm số
Cho hàm số y = f (x) liên tục trên khoàng ( ;
a b) chứa điểm x và có đạo hàm trên các khoảng (a; x và 0 ) 0
(x ;b . Khi đó: 0 )
- Nếu f (′x) < 0 với mọi x∈( ; a x và ′
> với mọi x ∈(x ;b thì hàm số = đạt cực tiểu tại 0 ) 0 ) f (x) 0 y f (x) điểm x ; 0
- Nếu f (′x) > 0 với mọi x∈( ; a x và ′
< với mọi x ∈(x ;b thì hàm số = đạt cực đại tại 0 ) 0 ) f (x) 0 y f (x) điểm x . 0
Ví dụ 5. Tìm cực trị của hàm số 3 2
f (x) = 2x − 9x − 24x +1. Lời giải
Tập xác định: D = . Ta có 2
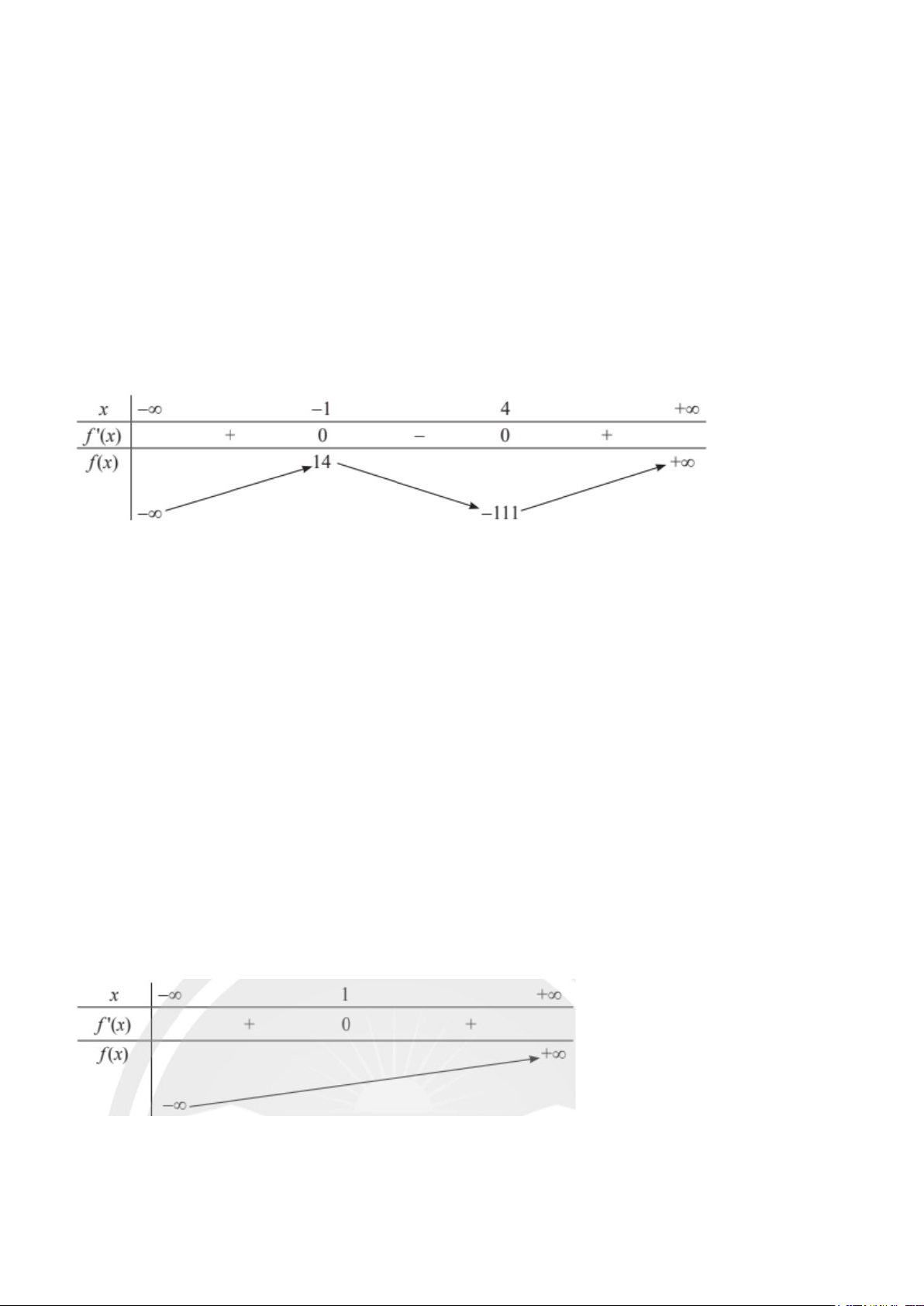
f (′x) = 6x −18x − 24 ; f (′x) = 0 ⇔ x = 1 − hoặc x = 4 . Bảng biến thiên:
Vậy hàm số đạt cực đại tại x = 1
− , giá trị cực đại là f ( 1)
− = 14 ; hàm số đạt cực tiểu tại x = 4 , giá trị cực tiểu là f (4) = 111 − .
Nhận xét: Từ kết quả trên, để tìm cực trị của hàm số y = f (x) , ta thực hiện các bước sau:
Buớc 1. Tìm tập xác định D của hàm số.
Buớc 2. Tính đạo hàm f (′x) của hàm số. Tìm các điểm x thuộc D mà tại đó đạo hàm f (′x) bằng 0
hoặc đạo hàm không tồn tại.
Buớc 3. Lập bảng biến thiên của hàm số.
Bước 4. Từ bảng biến thiên kết luận về cực trị của hàm số.
Ví dụ 6. Tìm cực trị của hàm số 3 2
f (x) = x − 3x + 3x − 4 . Lời giải
Tập xác định: D = . Ta có 2
f (′x) = 3x − 6x + 3 ; f (′x) = 0 ⇔ x =1. Bảng biến thiên:
Vậy hàm số không có cực trị. Chú ý:
a) Nếu f ′(x = 0 và ′ không đổi dấu khi x qua điểm 0 ) f (x)
x thì hàm số không có cực trị tại x . 0 0
b) Nếu f (′x) không đồi dấu trên khoảng K thì f (x) không có cực trị trên khoảng đó.
B. GIẢI BÀI TẬP SÁCH GIÁO KHOA
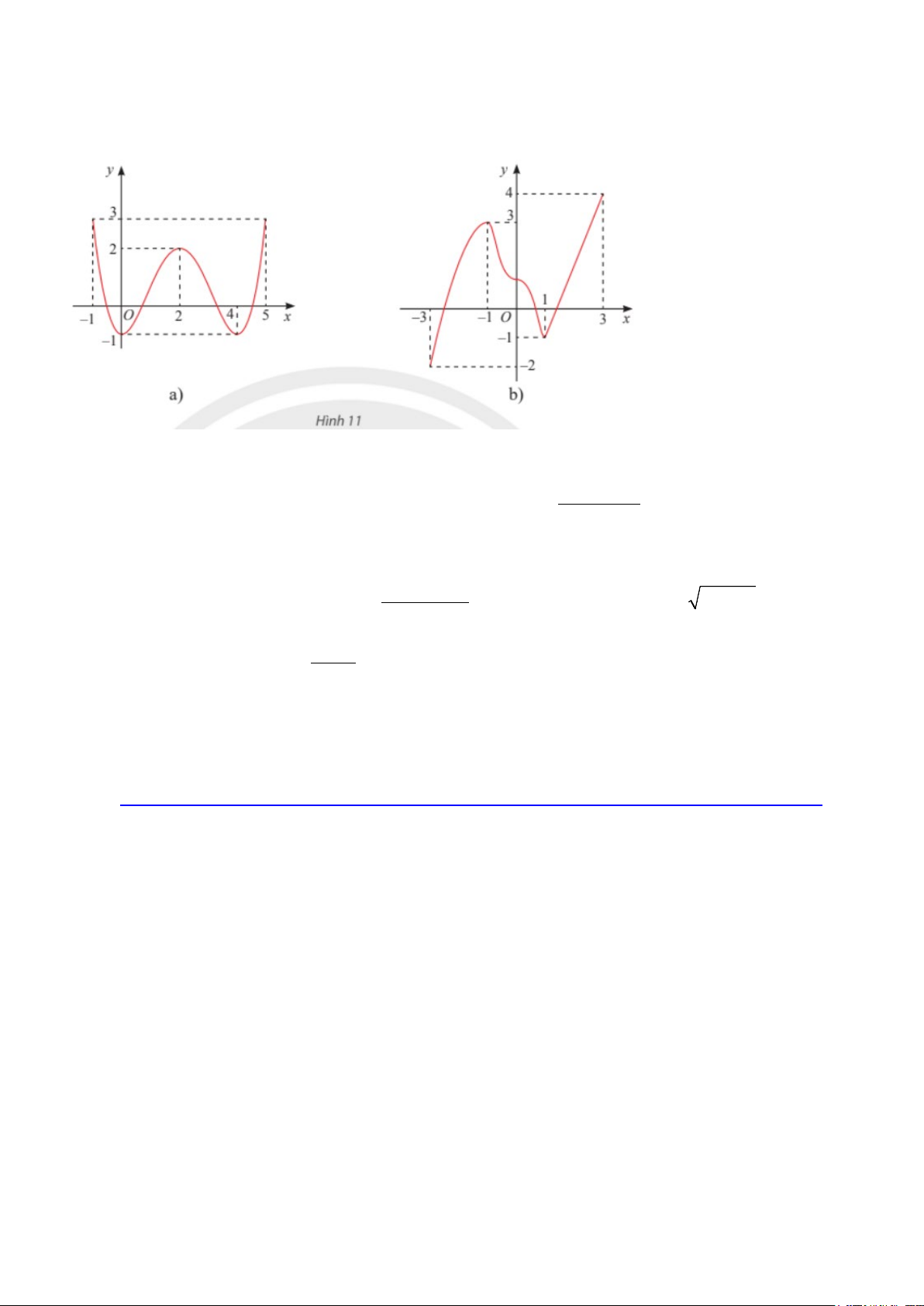
1. Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
2. Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: 2 x − 2x − 7 а) 3 2
y = 4x + 3x − 36x + 6 ; b) y = . x − 4
3. Tìm cực trị của các hàm số sau: 2 x −8x +10 a) 3 2
y = 2x + 3x − 36x +1; b) y = ; c) 2 y = −x + 4 . x − 2
4. Chứng minh rằng hàm số 2x +1 y =
nghịch biến trên từng khoảng xác định của nó. x − 3
5. Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức 3 2
f (x) = 0,01x − 0,04x + 0,25x + 0,44 (tỉ USD) với x là số năm tính từ 2010 đến 2017(0 ≤ x ≤ 7) .
(Theo: https://infographics.vn/interactive-xuat-khau-rau-quadu-bao-bung-no-dat-4-ty-usd-trong-nam- 2023/116220.vna)
a) Tính đạo hàm của hàm số y = f (x) .
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
6. Xét một chất điểm chuyển động dọc theo trục Ox. Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số 3 2
x(t) = t − 6t + 9t với t ≥ 0 . Khi đó x (′t) là vận tốc của chất điểm tại thời điểm t , kí hiệu
v(t);v (′t) là gia tốc chuyển động của chất điểm tại thời điểm t , kí hiệu a(t) .
a) Tìm các hàm v(t) và a(t) .
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
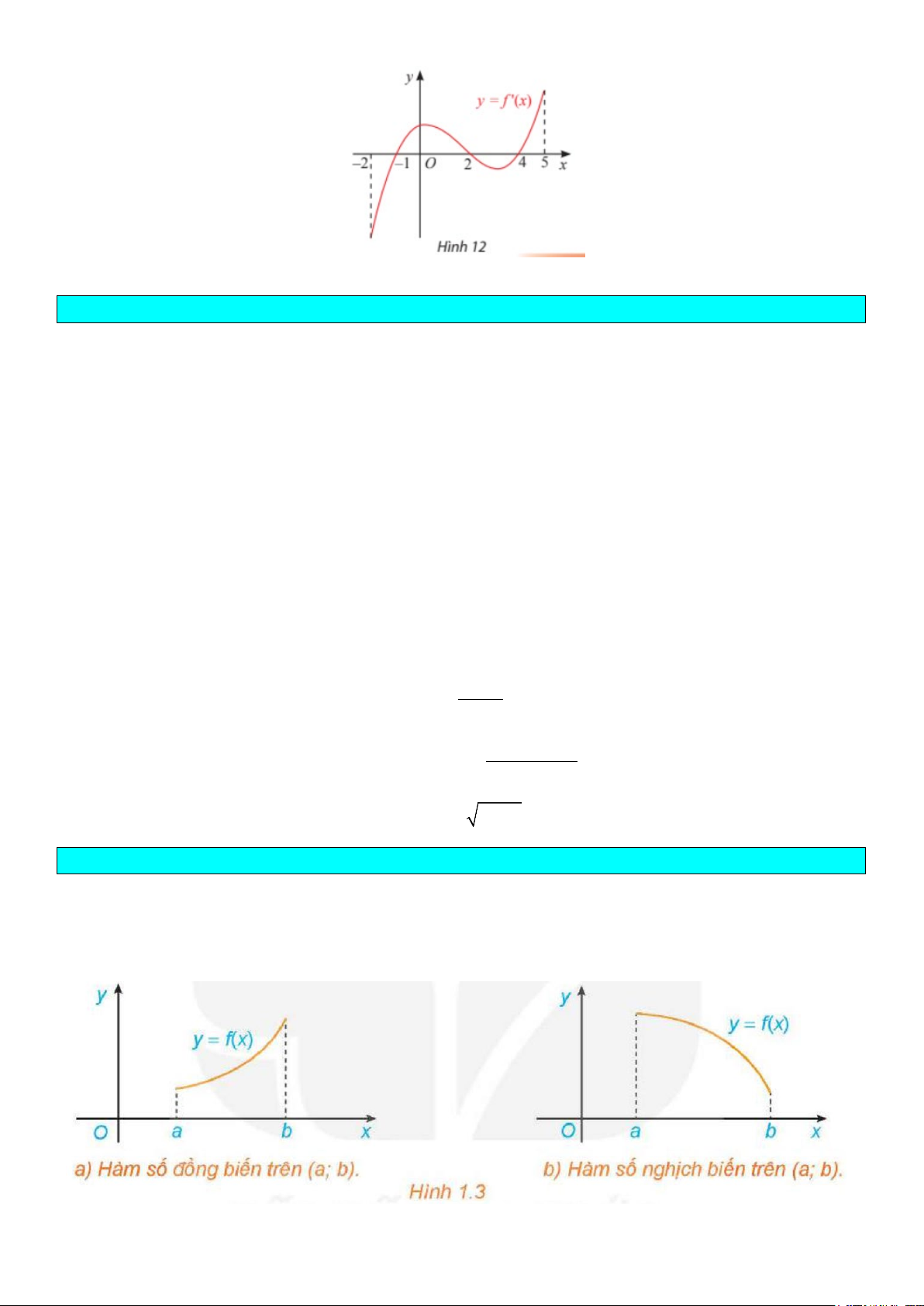
7. Đạo hàm f (′x) của hàm số y = f (x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của
hàm số y = f (x) . C. CÁC DẠNG TOÁN
Dạng 1: Xét định đơn điệu của hàm số cho bởi công thức 1.1 Phương pháp
Bước 1: Tìm tập xác định D .
Bước 2: Tính đạo hàm y′ = f (′x) .
Bước 3: Tìm nghiệm của f (′x) hoặc những giá trị x làm cho f (′x) không xác định.
Bước 4: Lập bảng biến thiên.
Bước 5: Kết luận.
1.2 Ví dụ minh họa
Câu 1. Tìm các khoảng đồng biến, nghịch biến của hàm số 3 2
y = x − 3x +1.
Câu 2. Tìm các khoảng đơn điệu của hàm số 4 2
y = x − 2x .
Câu 3. Tìm các khoảng đơn điệu của hàm số 3x +1 y = . 1− x 2
Câu 4. Tìm các khoảng nghịch biến của hàm số: −x + 2x −1 y = . x + 2
Câu 5. Tìm các khoảng đơn điệu của hàm số 2
y = x 4 − x .
Dạng 2: Xét tính đơn điệu dựa vào bảng biến thiên, đồ thị 2.1 Phương pháp
Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải (H.1.3a).
Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải (H.1.3b).
2.2 Ví dụ minh họa
Câu 1. Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
a) Từ đồ thị hàm số trên hãy vẽ bảng biến thiên
b) Tìm các khoảng đồng biến và nghịch biến.
Câu 2. Cho hàm số y f x có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây? .
Câu 3. Cho hàm số y = f (x) xác định và liên tục trên và có bảng biến thiên
Tìm các khoảng đồng biến của hàm số y = f (2x + ) 1 .
Dạng 3: Tìm tham số m để hàm số đơn điệu 3.1. Phương pháp Xét hàm số bậc ba 3 2
y = f (x) = ax + bx + cx + d.
– Bước 1. Tập xác định: D = .
– Bước 2. Tính đạo hàm 2
y′ = f (′x) = 3ax + 2bx + . c a = > ′ a f x 3 0
+ Để f (x) đồng biến trên ⇔ ( )
y′ = f (′x) ≥ 0, x ∀ ∈ ⇔ ⇒ m ? 2 ∆ = − ≤ ′ b ac f x 4 12 0 ( ) a = < ′ a f x 3 0
+ Đề f (x) nghịch biến trên ( )
⇔ y′ = f (′x) ≤ 0, x ∀ ∈ ⇔ ⇒ m ? 2 ∆ = − ≤ ′ b ac f x 4 12 0 ( )
Lưu ý: Dấu của tam thức bậc hai 2
f (x) = ax + bx + . c a > 0 a < 0
• Để f (x) ≥ 0, x ∀ ∈ ⇔
⋅ • f (x) ≤ 0, x ∀ ∈ ⇔ ⋅ ∆ ≤ 0 ∆ ≤ 0 +
Xét hàm số nhất biến = ( ) ax b y f x = ⋅ cx + d
– Bước 1. Tập xác định: \ d D = − ⋅ c . a d − . b c
– Bước 2. Tính đạo hàm y′ = f (′x) = ⋅ 2 (cx + d)
+ Để f (x) đồng biến trên D ⇔ y′ = f (′x) > 0, x ∀ ∈ D ⇔ . a d − .
b c > 0 ⇒ m ?
+ Để f (x) nghịch biến trên D ⇔ y′ = f (′x) < 0, x ∀ ∈ D ⇔ . a d − .
b c < 0 ⇒ m ?
Cô lập tham số m , tức là biến đổi f (′x,m) ≥ 0(≤ 0) ⇔ g(x) ≥ m(≤ m) .
Bước 1. Xác định tham số để hàm số f xác định trên khoảng đã cho.
Bước 2. Tính f (′x,m) .
Bước 3. Để giải bài toán dạng này, ta thường sử dụng các tính chất sau.
Nếu hàm số đồng biến trên ( ; a b) thì
f (′x) ≥ 0, x ∀ ∈[ ;
a b] → g(x) ≥ h(m), x
∀ ∈[a;b] ⇔ min g x ≥ h m . a b ( ) ( ) [ ; ]
Nếu hàm số đồng biến trên ( ; a b) thì
f (′x) ≤ 0, x ∀ ∈[ ;
a b] → g(x) ≤ h(m), x
∀ ∈[a;b] ⇔ min g x ≤ h m . a b ( ) ( ) [ ; ] 3.2. Ví dụ minh họa
Câu 1. Tìm m để hàm số 3
y = x + (m + ) 2
1 x + 3x + 2 đồng biến trên .
Câu 2. Tìm điều kiện của m để hàm số y = ( 2 m − ) 3 x + (m − ) 2 1
1 x − x + 4 nghịch biến trên khoảng ( ; −∞ +∞) . 1 m ;1 ∈ − 2 + Câu 3. Cho hàm số mx 4m y =
với m là tham số. Tìm m để hàm số nghịch biến trên các khoảng xác x + m định.
Dạng 4: Ứng dụng tính đơn điệu để chứng minh bất đẳng thức, giải phương trình, bất phương
trình, hệ bất phương trình 4.1. Phương pháp
1. Nếu hàm số y = f (x) liên tục và đơn điệu trên D thì f (x) = 0 có ít nhất một nghiệm.
2. Nếu hàm số f (x), g(x) liên tục và đơn điệu trên D thì f (x) = g(x) có ít nhất một nghiệm.
3. Nếu f (x) liên tục và đơn điệu trên D và u,v ∈ D thì phương trình f (u) = f (v) ⇔ u = v . 4.2. Ví dụ minh họa
Câu 1. Giải phương trình 2017 3 2 x
+ x − 6x +13x − 9 = 0 .
Câu 2. Giải phương trình sau x − −
x − = ( x − )5 −( x − )5 2 1 5 2 5 2 2 1 .
Câu 3. Giải phương trình 3 2
x + 3x + 4x + 2 = (4x + 6) 4x + 5 .
Dạng 5: Tìm cực trị hàm số cho bởi công thức 5.1. Phương pháp
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f ′(x) . Tìm các điểm tại đó f ′(x) bằng 0 hoặc f ′(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
5.2. Ví dụ minh họa
Câu 1. Tìm cực trị của hàm số 3 2
y = x −3x −9x +1.
Câu 2. Tìm cực trị của hàm số 3 2 y = 2
− x −3x − 6x +1.
Câu 3. Tìm cực trị của hàm số 4 2
y = x + 4x +1.
Câu 4. Tìm cực trị của hàm số y = ( − x)3 ( x − )2 1 3 8 . Câu 5.
Cho hàm số f (x) có đạo hàm f ′(x) 3 = x (x − )
1 (x − 2),∀x ∈ . Số điểm cực trị của hàm số đã cho là.
Dạng 6: Tìm cực trị dựa vào bảng biến thiên, đồ thị 6.1. Phương pháp
- Nếu f ′ (x) đổi dấu qua x ∈ D thì x là cực trị. Cụ thể: 0 0
+Nếu f ′ (x) đổi dấu từ + sang – thì x là điểm cực đại. 0
+Nếu f ′ (x) đổi dấu từ - sang + thì x là điểm cực tiểu. 0 - Chú ý:
+ Hàm số đạt cực trị tại: x =
+ Điểm cực trị của hàm số là: x =
+ Giá trị cực trị của hàm số là: y =
+ Cực trị của hàm số là: y =
+ Điểm cực trị của đồ thị hàm số: ( ; x y) 6.2. Ví dụ minh họa
Câu 1. Cho hàm f (x) có bảng biến thiên như sau:
a) Giá trị cực tiểu của hàm số.
b) Điểm cực đại của đồ thị hàm số.
Câu 2: Cho hàm số y = f (x) liên tục trên với bảng xét dấu đạo hàm như sau:
Hỏi hàm số y = f (x) có bao nhiêu điểm cực trị?
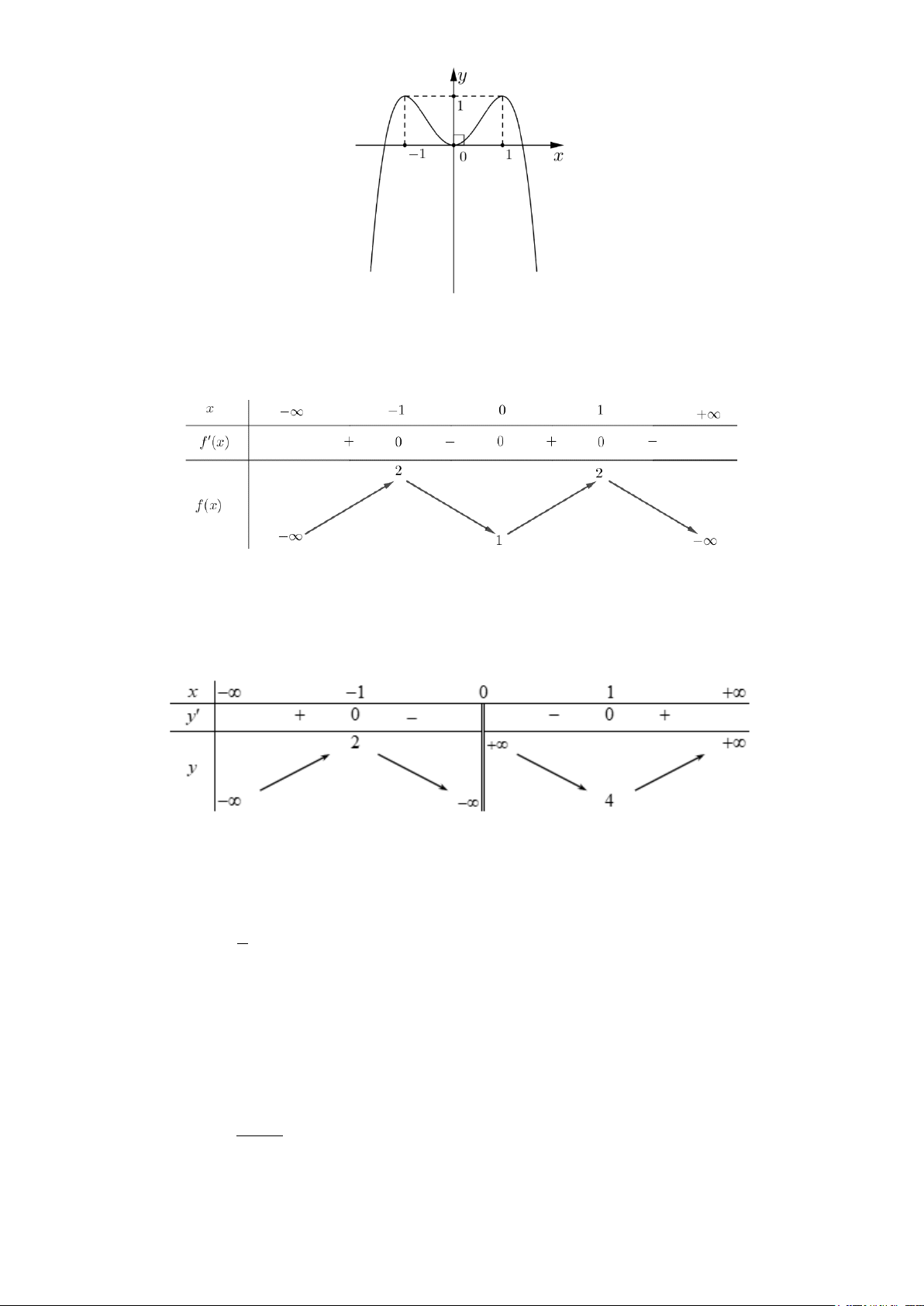
Câu 3: Cho hàm số y = f (x) liên tục trên và có đồ thị như hình bên. Hỏi hàm số có bao nhiêu điểm cực trị? y -1 O 1 x -1 -2
Câu 4: Cho hàm số y = f (x) xác định, liên tục trên đoạn [ 2;
− 2] và có đồ thị là đường cong trong
hình vẽ bên. Hàm số f (x) đạt cực đại tại điểm nào dưới đây?
Câu 5: Biết rằng hàm số f (x) có đạo hàm là f (x) = x(x − )2 (x − )3 (x − )5 ' 1 2
3 . Hỏi hàm số f (x) có
bao nhiêu điểm cực trị?
Câu 6: Cho hàm số y = f (x) có đạo hàm liên tục trên và hàm số y = f ′(x) có đồ thị như hình vẽ bên.
Tìm điểm cực tiểu của hàm số
Dạng 7: Tìm m để hàm số đạt cực trị tại một điểm x0 cho trước 7.1. Phương pháp
Bước 1. Tính y '(x , y '' x 0 ) ( 0)
Bước 2. Giải phương trình y '(x = 0 ⇒ m? 0 )
Bước 3. Thay m vào thử lại 7.2. Ví dụ minh họa
Câu 1. Tìm m để hàm số 3 2
y = x − 2mx + mx +1 đạt cực tiểu tại x = 1
Câu 2. Tìm tất cả các giá trị thực của tham số 1 m để hàm số 3 2
y = x − mx + (m + )
1 x −1 đạt cực đại tại 3 x = 2 −
Câu 3. Tìm tất cả tham số thực m để hàm số y = (m − ) 4 x − ( 2 m − ) 2 1
2 x + 2019 đạt cực tiểu tại x = 1 − .
Dạng 8: Toán thực tế
Câu 1. Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số 25t +10 N(t) =
,t ≥ 0 trong đó N(t) được tính bằng nghìn người. t + 5
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N (′t) và lim N(t) . Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng t→+∞
nhưng sẽ không vượt quá một ngưỡng nào đó.
Câu 2. Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất
định) tuân theo quy luật logistic được mô hình hoá bằng hàm số 5000 f (t) = ,t ≥ 0 1+ 5 t e−
trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm
f (′t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?.
Câu 3. Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính
xấp xỉ bằng công thức 3 2
f (x) = 0,01x − 0,04x + 0,25x + 0,44 (tỉ USD) với x là số năm tính từ
2010 đến 2017(0 ≤ x ≤ 7) .
a) Tính đạo hàm của hàm số y = f (x) .
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Câu 4. Xét một chất điểm chuyển động dọc theo trục Ox . Toạ độ của chất điểm tại thời điểm t được xác định bởi hàm số 3 2
x(t) = t − 6t + 9t với t ≥ 0 . Khi đó x (′t) là vận tốc của chất điểm tại thời
điểm t , kí hiệu v(t);v (′t) là gia tốc chuyển động của chất điểm tại thời điểm t , kí hiệu a(t) .
a) Tìm các hàm v(t) và a(t) .
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?.
Câu 5. Thể tích V (đơn vị: centimét khối) của 1 kg nước tại nhiệt độ T (0 C ° ≤ T ≤ 30 C ° ) được tính bởi công thức sau: 2 3
V (T) = 999,87 − 0,06426T + 0,0085043T − 0,0000679T .
Hỏi thể tích V (T),0 C ° ≤ T ≤ 30 C
° , giảm trong khoảng nhiệt độ nào?.
Câu 6. Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi
Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0(s)
cho đến khi tên lủa đẩy được phóng đi tại thời điểm t =126( s) , cho bởi hàm số sau: 3 2
v(t) = 0,001302t − 0,09029t + 23
( v được tính bằng ft / s,1 feet = 0,3048 m )
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho
đến khi tên lửa đẩy được phóng đi?.
D. BÀI TÂP TRẮC NGHIỆM 4 PHƯƠNG ÁN
PHẦN 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
Câu 1: Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 1; − 0). B. ( ; −∞ − ) 1 . C. (0; ) 1 . D. (0;+ ∞).
Câu 2: Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A. (1;+ ∞) . B. ( 1; − 0) . C. ( 1; − ) 1 . D. (0 ) ;1 .
Câu 3: Cho hàm số y = f (x) có bảng biến thiên như sau:
Hàm số nghịch biến trong khoảng nào? A. ( 1; − ) 1 . B. (0; ) 1 . C. (4;+∞) . D. ( ;2 −∞ ) . Câu 4: Hàm số 1 3 2
y = x − x − 3x + 2019 nghịch biến trên 3 A. ( 1; − 3). B. (−∞;− ) 1 . C. (−∞;− ) 1 và (3;+ ∞) . D. (3;+ ∞). Câu 5: Hàm số 3 2
y = −x + 3x − 2 đồng biến trên khoảng A. (0;2). B. (−∞;0) . C. (1;4). D. (4;+ ∞) . Câu 6: Hàm số 5 − 2x y = nghịch biến trên x + 3 A. R\ 3 . B. R . C. ( ; −∞ 3 − ) . D. (3;+∞) . − Câu 7: Cho hàm số x 2 y =
. Mệnh đề nào dưới đây đúng? x +1
A. Hàm số nghịch biến trên khoảng ( ;
−∞ +∞) B. Hàm số nghịch biến trên khoảng ( 1; − +∞)
C. Hàm số nghịch biến trên khoảng ( ; −∞ − )
1 D. Hàm số đồng biến trên khoảng ( ; −∞ − ) 1 2 Câu 8: x + x − Cho hàm số 2 3 y =
. Phát biểu nào sau đây là đúng? x +1
A. Hàm số đồng biến trên khoảng (2;4) .
B. Hàm số nghịch biến trên khoảng ( ; −∞ +∞) .
C. Hàm số nghịch biến trên các khoảng ( ; −∞ − ) 1 và ( 1; − +∞) .
D. Hàm số đồng biến trên khoảng ( ; −∞ − )
1 và nghịch biến trên khoảng ( 1; − +∞) .
Câu 9: Cho hàm số y = f (x) có đạo hàm f ′(x) = 2
x + 1, ∀x∈ . Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng (1;+∞)
B. Hàm số nghịch biến trên khoảng (−1;1)
C. Hàm số đồng biến trên khoảng (−∞;+∞) D. Hàm số nghịch biến trên khoảng (−∞;0) Câu 10: Cho hàm số 1 3 1 2
y x x 12x1. Mệnh đề nào sau đây là đúng? 3 2
A. Hàm số đồng biến trên khoảng 3;4.
B. Hàm số đồng biến trên khoảng 4;.
C. Hàm số nghịch biến trên khoảng ;4 .
D. Hàm số nghịch biến trên khoảng 3;.
Câu 11: Cho hàm số y = f (x) có đạo hàm f ′(x) = x(x − )3
2 , với mọi x∈ . Hàm số đã cho nghịch
biến trên khoảng nào dưới đây? A. (1; 3). B. ( 1; − 0) . C. (0; ) 1 . D. ( 2; − 0) .
Câu 12: Hàm số y = f (x) có đạo hàm 2
y′ = x . Mệnh đề nào sau đây đúng?
A. Hàm số nghịch biến trên .
B. Hàm số nghịch biến trên (− ;0
∞ ) và đồng biến trên (0;+∞).
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên (− ;0
∞ ) và nghịch biến trên (0;+∞).
Câu 13: Cho hàm số y = f (x) liên tục trên và có đạo hàm f ′(x) = ( − x)2 (x + )3 1 1 (3− x) . Hàm số
y = f ( x) đồng biến trên khoảng nào dưới đây? A. ( ) ;1 −∞ . B. ( ; −∞ − ) 1 . C. (1;3). D. (3;+ ∞) .
Câu 14: Hàm số nào dưới đây đồng biến trên khoảng ( ; −∞ +∞) ? − + A. x 1 y = B. 3
y = x + x C. 3
y = −x −3x D. x 1 y = x − 2 x + 3
Câu 15: Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau
Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ( ; −∞ 2
− ) B. Hàm số đồng biến trên khoảng ( 2; − 0)
C. Hàm số đồng biến trên khoảng ( ;0 −∞ )
D. Hàm số nghịch biến trên khoảng (0;2)
Câu 16: Cho hàm số y = f (x) có bảng xét dấu của đạo hàm như hình vẽ. Hàm số đã cho nghịch biến
trên khoảng nào dưới đây? A. (1;+ ∞) . B. (−∞ ) ;1 . C. ( 1; − + ∞) . D. (−∞;− ) 1 . Câu 17: Cho hàm số 2
y = x −1 . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (1;+∞).
B. Hàm số nghịch biến trên khoảng ( ;0 −∞ ) .
C. Hàm số đồng biến trên khoảng (0;+∞).
D. Hàm số đồng biến trên ( ; −∞ +∞) . Câu 18: Hàm số 4
y = 2x +1 đồng biến trên khoảng A. 1 ; −∞ − B. 1 − ;+∞ C. (0;+∞) D. ( ;0 −∞ ) 2 2
Câu 19: Trong các hàm số sau, hàm số nào vừa có khoảng đồng biến vừa có khoảng nghịch biến trên tập + xác định của nó. (Ι) 2x 1 . y = , (ΙΙ) 4 2 .
y = −x + x − 2 , (ΙΙΙ) 3 . 3
y = x + x − 4. x +1
A. (Ι);(ΙΙΙ) .
B. (Ι) & (II ) .
C. (ΙΙ);(ΙΙΙ). D. (II) .
Câu 20: Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x − 2x , x
∀ ∈ . Hàm số y = 2
− f ( x) đồng biến trên khoảng A. ( 2; − 0) . B. (0;2) . C. (2;+∞) . D. ( ; −∞ 2 − ) . Lời giải Chọn B
Ta có: y′ = − f ′(x) 2 2 = 2
− x + 4x > 0 ⇔ x ∈(0;2) . Suy ra: Hàm số y = 2
− f ( x) đồng biến trên khoảng (0;2) Câu 21: Cho hàm số 1 4 2
y = x − 2x −1. Chọn khẳng định đúng. 4
A. Hàm số nghịch biến trên các khoảng ( 2; − 0) và (2;+∞).
B. Hàm đồng biến trên các khoảng ( ; −∞ 2 − ) và (0;2) .
C. Hàm số đồng biến trên các khoảng ( 2; − 0) và (2;+∞) .
D. Hàm số nghịch biến trên các khoảng ( ; −∞ 2 − ) và (2;+∞). Câu 22: Hàm số 4 2
y = −x + 4x +1 nghịch biến trên mỗi khoảng nào sau đây? A. ( 2;+∞).
B. (− 3;0);( 2;+∞).
C. (− 2;0);( 2;+∞) . D. (− 2; 2). Câu 23: Cho hàm 2
y = x − 6x + 5 . Mệnh đề nào sau đây là đúng?
A. Hàm số đồng biến trên khoảng (5;+∞).
B. Hàm số đồng biến trên khoảng (3;+∞).
C. Hàm số đồng biến trên khoảng (−∞ ) ;1 .
D. Hàm số nghịch biến trên khoảng ( ; −∞ 3).
Câu 24: Tìm tất cả các khoảng đồng biến của hàm số 2
y = 9 − x . A. (0;+∞). B. ( ;0 −∞ ) . C. ( 3 − ;0) . D. (0;3).
Câu 25: Tìm khoảng đồng biến của hàm số y = −x + sin x . A. ∅ . B. ( ;2 −∞ ) . C. . D. (1;2) .
Câu 26: Cho hàm số y = xln x . Chọn khẳng định sai trong số các khẳng định sau:
A. Hàm số đồng biến trên khoảng (0;+∞).
B. Hàm số đồng biến trên khoảng 1 ; +∞ . e
C. Hàm số có đạo hàm y′ =1+ ln x .
D. Hàm số có tập xác định là D = (0;+∞) .
Câu 27: Cho hàm số y = sin x + cos x − 3x . Chọn khẳng định đúng trong các khẳng định sau.
A. Hàm số đồng biến trên .
B. Đồ thị hàm số đi qua gốc tọa độ.
C. Hàm số có điểm cực trị.
D. Hàm số nghịch biến trên . 1
Câu 28: Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số 3 2
f (x) = x + mx + 4x + 3 đồng biến 3 trên . A. 5 . B. 4 . C. 3 . D. 2 .
Câu 29: Cho hàm số y = − 3 x − 2
mx + (4m + 9)x + 5 , với m là tham số. Hỏi có bao nhiêu giá trị nguyên
của m để hàm số nghịch biến trên khoảng (−∞;+∞) A. 5 B. 4 C. 6 D. 7
Câu 30: Tập hợp tất cả các giá trị của tham số m để hàm số 3
y = x + (m + ) 2
1 x + 3x + 2 đồng biến trên là A. [ 4; − 2]. B. ( 4; − 2) . C. ( ; −∞ 4
− ]∪[2;+∞). D. ( ; −∞ 4 − ) ∪(2;+∞) . Câu 31: Cho hàm số 1 3 2
y = − x + mx + (3m + 2) x +1. Tìm tất cả giá trị của m để hàm số nghịch biến trên 3 . m ≥ 1 − m > 1 − A. . B. 2 − ≤ m ≤ 1 − . C. 2 − < m < 1 − . D. . m ≤ 2 − m < 2 −
Câu 32: Hỏi có bao nhiêu số nguyên m để hàm số y = ( 2 m − ) 3 x + (m − ) 2 1
1 x − x + 4 nghịch biến trên khoảng ( ; −∞ +∞) . A. 0 B. 3 C. 2 D. 1
Câu 33: Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số hàm số 1 y = ( 2 m − m) 3 2
x + 2mx + 3x − 2 đồng biến trên khoảng ( ; −∞ + ∞) ? 3 A. 4 . B. 5. C. 3. D. 0 .
Câu 34: Số các giá trị nguyên của tham số m trong đoạn [ 100 − ;100] để hàm số 3 2
y = mx + mx + (m + )
1 x − 3 nghịch biến trên là: A. 200 . B. 99. C. 100. D. 201.
Câu 35: Giá trị của tham số 1 m sao cho hàm số 3 2
y = x − x − (3m + 2) x + 2 nghịch biến trên đoạn 3
có độ dài bằng 4 là A. m =1. B. 1 m = .
C. m = 4 . D. 1 m = . 2 3
Câu 36: Tất cả các giá trị thực của tham số m để hàm số 3
y = x + (m − ) 2 2 3
1 x + 6(m − 2) x + 2017 nghịch biến
trên khoảng (a;b) sao cho b − a > 3 là m < 0
A. m < 0 . B. .
C. m > 6.
D. m = 9 . m > 6 Câu 37: Gọi 1
S là tập hợp các giá trị của tham số m để hàm số 3
y = x + (m + ) 2 1 x + 4x + 7 3 nghịch biến
trên một đoạn có độ dài bằng 2 5. Tính tổng tất cả phần tử của S. A. 2 − . B. 2 . C. 1 − . D. 4 .
Câu 38: Tìm tất cả các giá trị thực của tham số 1 1 m sao cho hàm số 3 2
y = x − mx + 2mx − 3m + 4 nghịch 3 2
biến trên một đoạn có độ dài là 3? A. m = 9 .
B. m =1;m = 9 − . C. m = 1; − m = 9 . D. m = 1 − .
Câu 39: Tìm các giá trị của tham số m 1 để hàm số 3 2
y = x − mx + (2m − )
1 x − m + 2 nghịch biến trên 3 khoảng ( 2; − 0)..
A. m >1. B. 1 m ≤ − . C. 1 m < − .
D. m = 0. 2 2 3
Câu 40: Biết rằng hàm số x y = + (m − ) 2 3
1 x + 9x +1 nghịch biến trên (x ; x và đồng biến trên các 1 2 ) 3
khoảng còn lại của tập xác định. Nếu x − x = 6 thì giá trị m là: 1 2 A. 4 − và 2 .
B. 1+ 2 và 1− 2 . C. 4 − . D. 2 .
Câu 41: Tìm tất cả các giá trị thực m để f (x) 3 2
= −x + 3x + (m − )
1 x + 2m − 3 đồng biến trên một khoảng
có độ dài lớn hơn 1. 5 5
A. − < m < 0 .
B. m > − .
C. m ≥ 0 .
D. m ≤ 0 . 4 4
Câu 42: Hàm số = ( + )3 + ( + )3 3 y x m
x n − x đồng biến trên khoảng ( ;
−∞ + ∞) . Giá trị nhỏ nhất của biểu thức P = ( 2 2
4 m + n ) − m − n bằng − A. 16 − . B. 4 . C. 1. D. 1 . 16 4 Câu 43: Cho hàm số mx − 2m − 3 y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của x − m
m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S . A. Vô số B. 3 C. 5 D. 4 mx + 4m
Câu 44: Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m x + m
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S . A. 4 B. Vô số C. 3 D. 5 2
Câu 45: Có bao nhiêu giá trị nguyên của tham số x + m
m để hàm số y =
đồng biến trên từng khoảng x + 4 xác định của nó? A. 5. B. 3. C. 1. D. 2 .
Câu 46: Tìm tất cả các giá trị thực của tham số mx − m để hàm số 4 y =
nghịch biến trên từng khoảng x − m xác định của nó. m ≤ 2 − m < 2 − A. . B. 2
− < m < 2 . C. . D. 2
− ≤ m ≤ 2 . m ≥ 2 m > 2

