Bài giảng Vectơ và hệ tọa độ trong không gian môn Toán 12

Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
VECTƠ VÀ HỆ TỌA ĐỘ TRONG KHÔNG GIAN VECTƠ VÀ CÁC PHÉP T OÁN TRONG KHÔNG GIAN 1 Vectơ trong không gian ● Kí hiệu
chỉ vectơ có điểm đầu A, điểm cuối B.
● Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của nó. Kí hiệu là .
● Giá của vectơ là đường thẳng đi qua điểm đầu và điểm cuối của vectơ đó.
● Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
● Nếu hai vectơ cùng phương thì chúng có thể cùng hướng hoặc ngược hướng.
● Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Nếu hai vectơ , bằng nhau thì ta viết là .
● Hai vectơ được gọi là đối nhau nếu chúng có cùng độ dài và ngược hướng.
● Vectơ đối của được kí hiệu là .
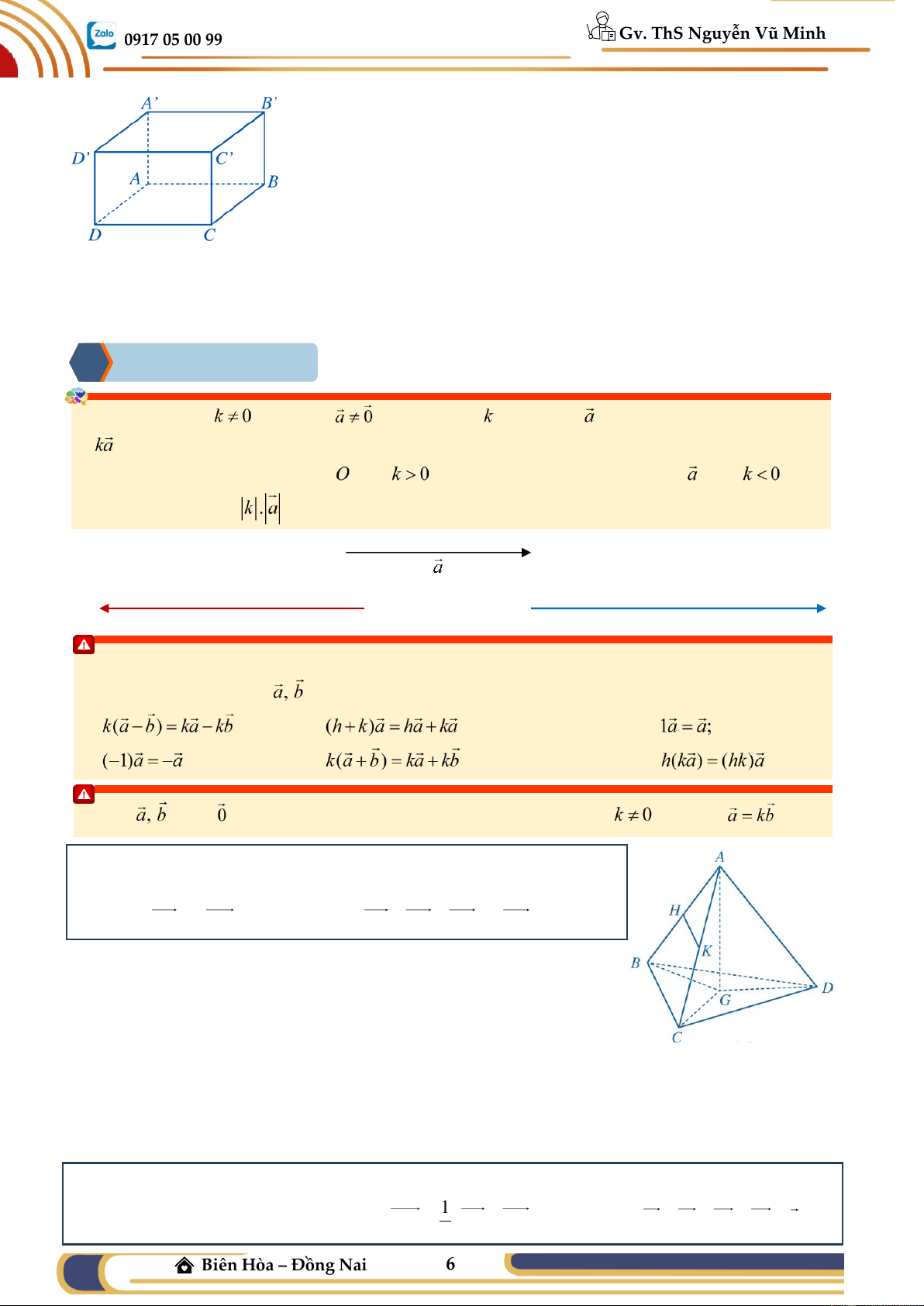
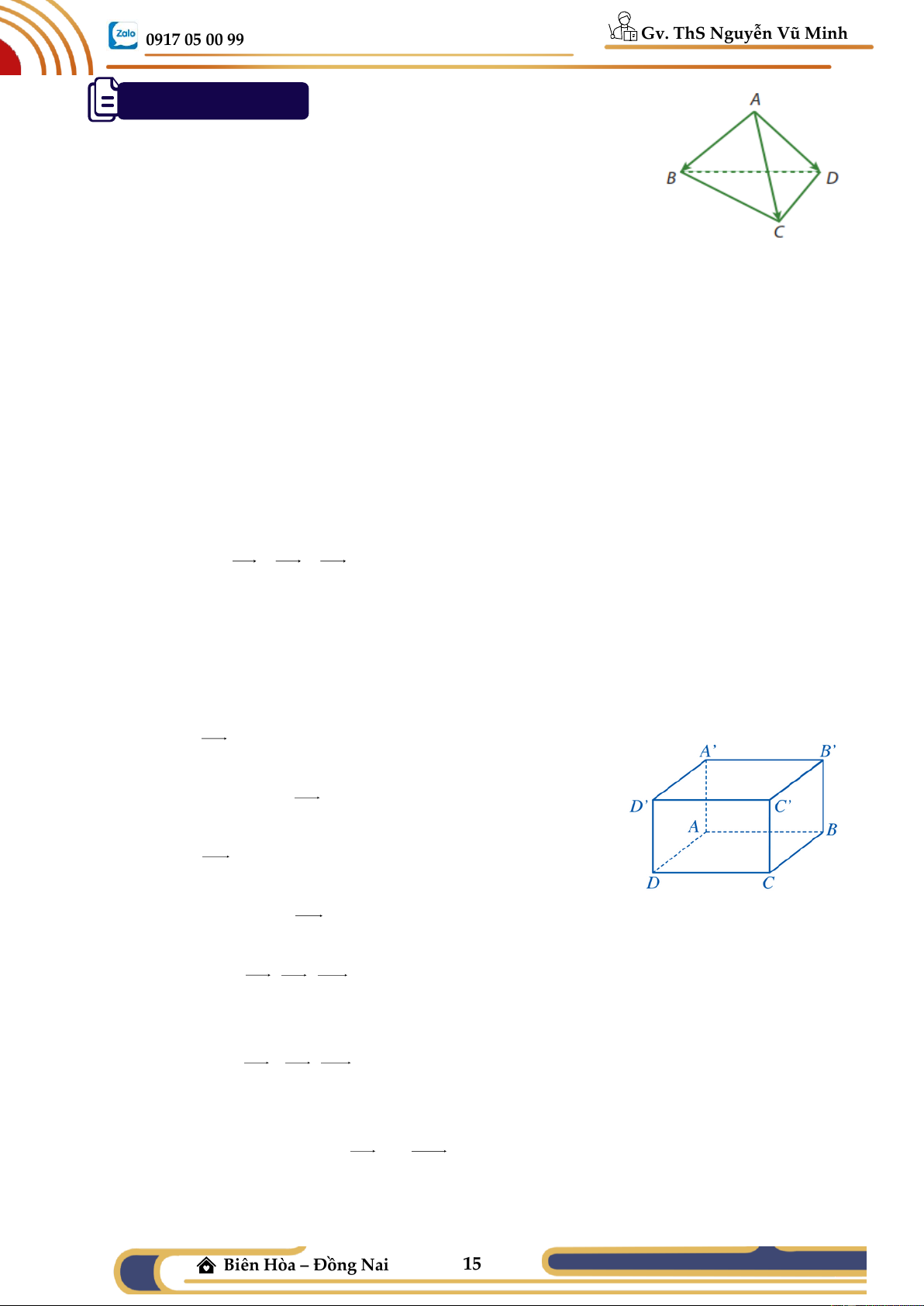
Ví dụ 01: (SGK CD) Cho hình hộp ABC .
D A' B 'C ' D ' . Hãy chỉ ra ba
vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vectơ đó: a) Bằng vectơ AD ;
b) Là vectơ đối của vectơ AD .
Biên Hòa – Đồng Nai 1
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
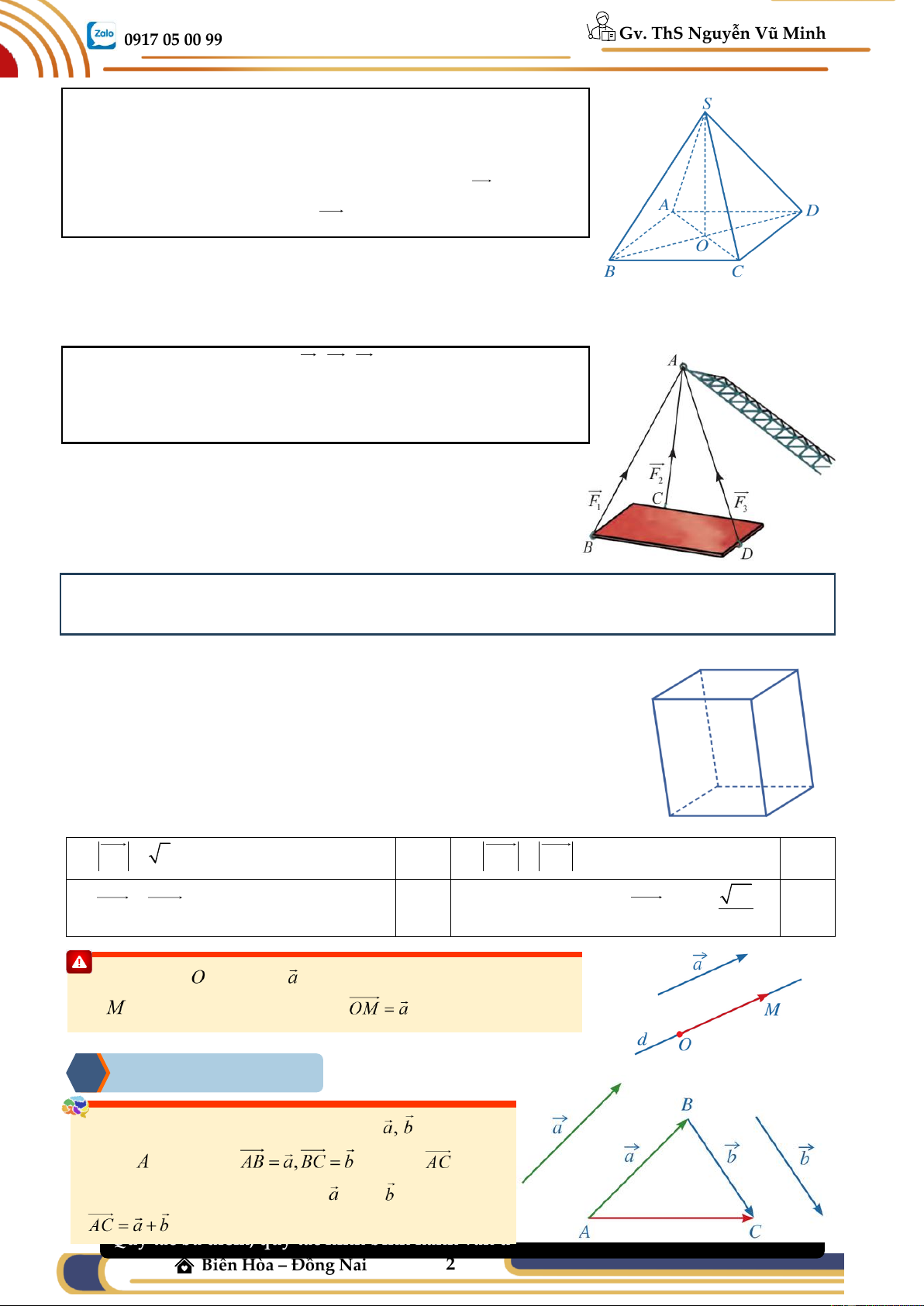
Ví dụ 02: (SGK CTST) Cho hình chóp tứ giác đều S.ABCD .
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy.
b) Tìm các vectơ có độ dài bằng độ dài của vectơ SA .
c) Tìm các vectơ đối của vectơ CB .
Ví dụ 03: Cho biết ba vectơ F , F , F biểu diễn lực căng của 1 2 3
các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba
vectơ này có cùng nằm trên một mặt phẳng không?
Ví dụ 04: Cho hình hộp chữ nhật ABC .
D A' B 'C ' D ' có AB = 1, AD = 2 và AA' = 3 . Gọi M là
trung điểm của CC ' . Xét tính đúng, sai của các mệnh đề sau a) BD = 5 .
b) BC ' = AB ' . 29
c) A' B = C ' D .
d) Độ dài của véc tơ AM bằng . 2
Cho điểm và vectơ . Khi đó, tồn tại duy nhất điểm trong không gian sao cho . 2 Tổng v à hiệu hai vectơ
Trong không gian, cho hai vectơ . Lấy một điểm tuỳ ý, vẽ . Vectơ được
gọi là tổng của hai vectơ và , kí hiệu là .
Quy tắc ba điểm, quy tắc hình bình hàn
h vẫn đúng với các vectơ trong không gian.
Biên Hòa – Đồng Nai 2
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) Quy tắc ba điểm
Quy tắc hình bình hành
Với ba điểm A, B, C ta có
Nếu ABCD là hình bình hành thì ta có
AB + BC = AC .
AB + AD = AC .
Ví dụ 01: Cho hình lăng trụ AB .
C A' B 'C ' . Tìm các vectơ tổng
BA + A'C ', BC + AA' .
Ví dụ 02: Cho tứ diện ABCD. Chứng minh rằng
a) AB + CD = AD + CB ;
b) AC + DB = AB + DC .
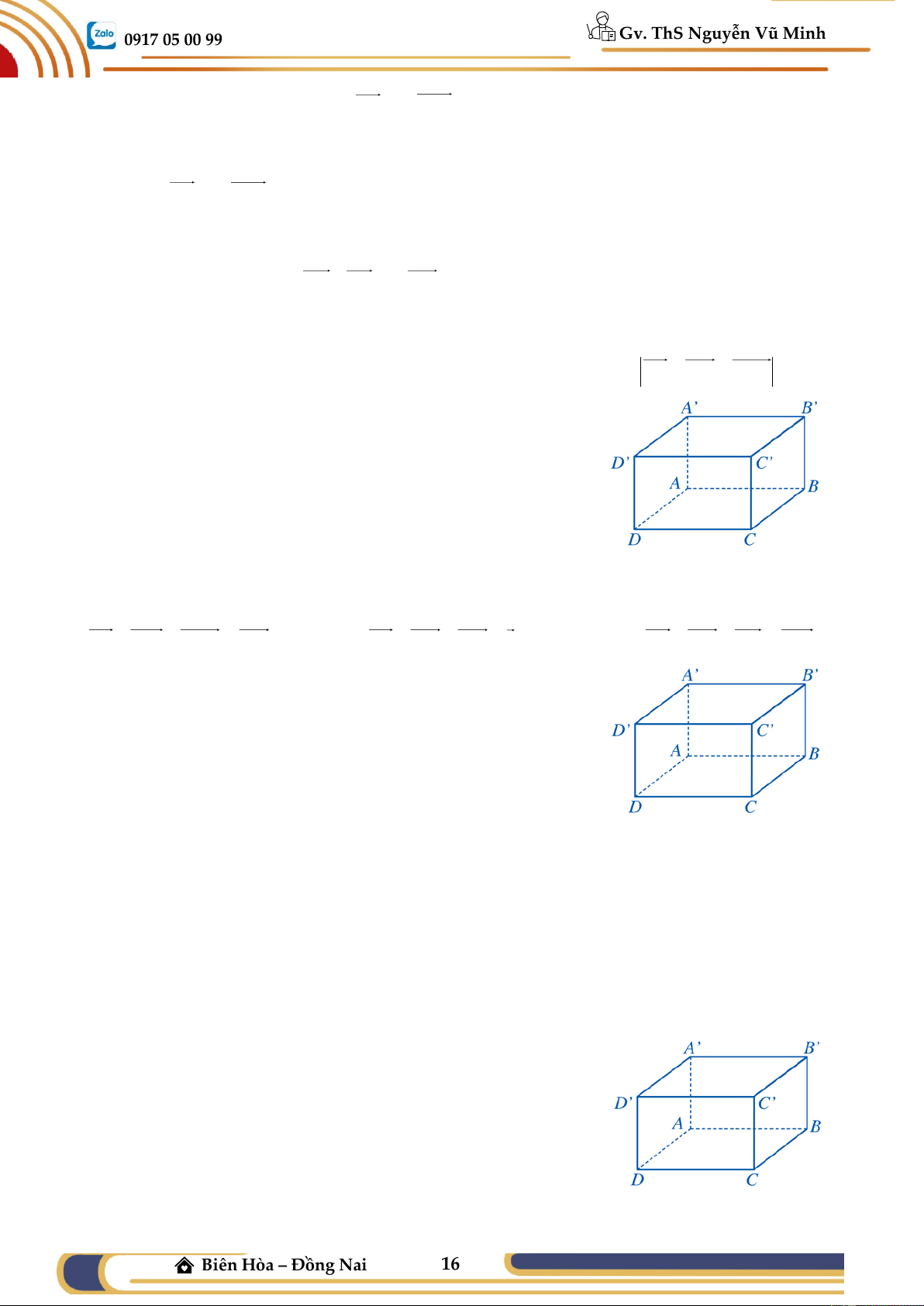
Ví dụ 03: Cho hình hộp ABC .
D A' B 'C ' D ' .
a) Tìm liên hệ giữa: AB + AD và AC; AC + AA và AC ;
b) Từ đó, hãy suy ra rằng: AB + AD + AA' = AC '
Ví dụ 04: Cho hình hộp ABC .
D A' B 'C ' D ' . Chứng m
inh rằng: B ' B + AD + CD = B ' D Quy tắc hình hộp
Biên Hòa – Đồng Nai 3
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Cho hình hộp ABCD.A’B’C’D’, khi đó ta có
Ví dụ 05: Cho hình hộp ABCD.EFGH. Tìm các v
ectơ: a) CB + CD + CG ;
b) AB + CG + EH .
Ví dụ 06: Ba lực F , F , F cùng tác động vào một vật có phương đôi một vuông góc và có độ 1 2 3
lớn lần lượt là 2 N;3 N; 4 N . Tính độ lớn hợp lực của ba lực đã cho.
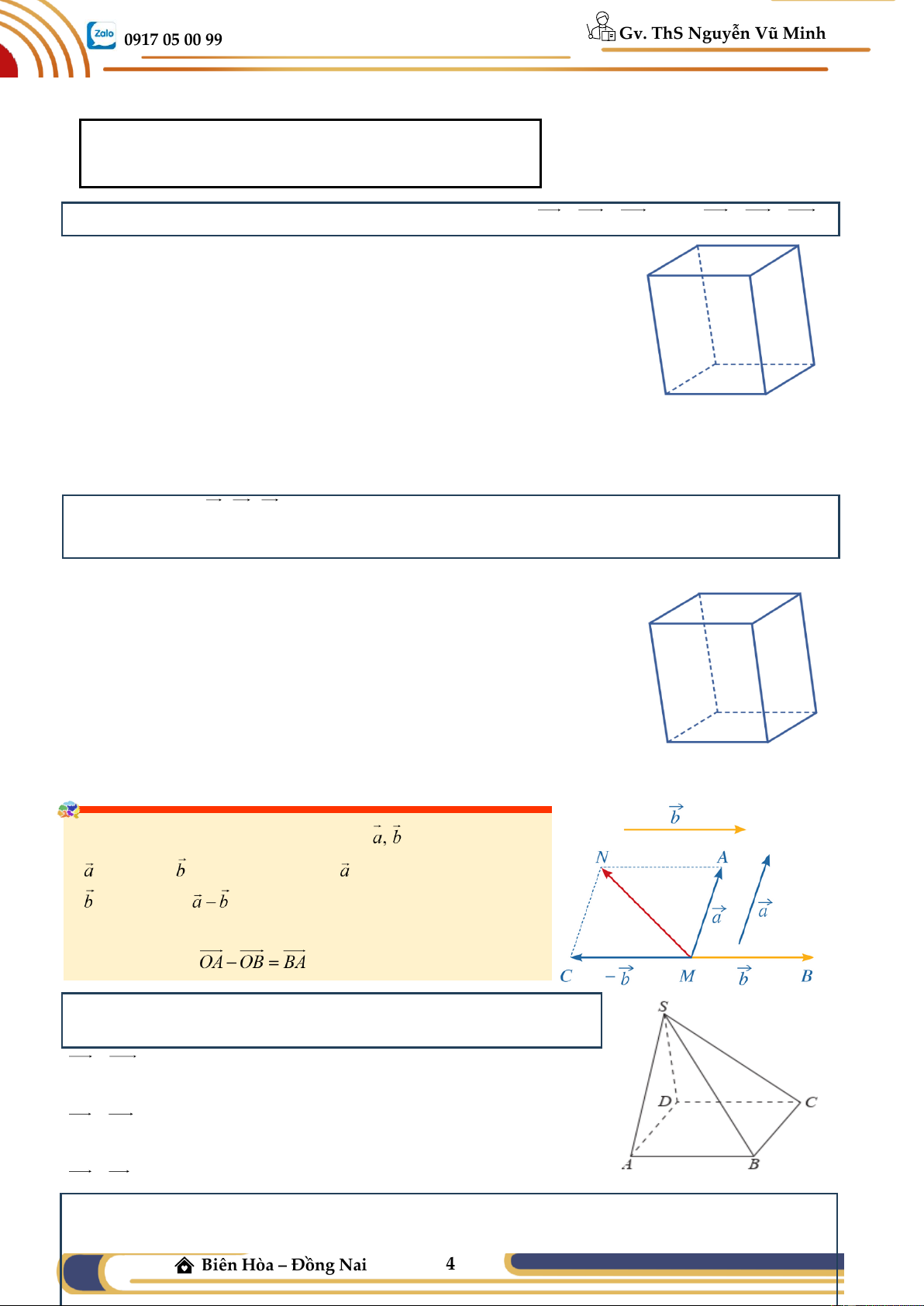
● Trong không gian, cho hai vectơ . Hiệu của vectơ
và vectơ là tổng của vectơ và vectơ đối của vectơ , kí hiệu là .
● Với ba điểm O, A, B trong không gian, ta có: (Quy tắc hiệu).
Ví dụ 01: Cho hình chóp S.ABCD có đáy là hình bình hành. Khi đó: AS − DC = CS − DA = SD − SB =
Ví dụ 02: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung
điểm của AB, CD. Chứng minh rằng:
Biên Hòa – Đồng Nai 4
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
a) AM và CN là hai vectơ đối nhau;
b) BN và DM là hai vectơ đối nhau;
c) SD − BN − CM = SC ;
d) SC − AM − AN = SA .
Ví dụ 03: Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:
a) BM + AC + ND ;
b) AD − AM + NC .
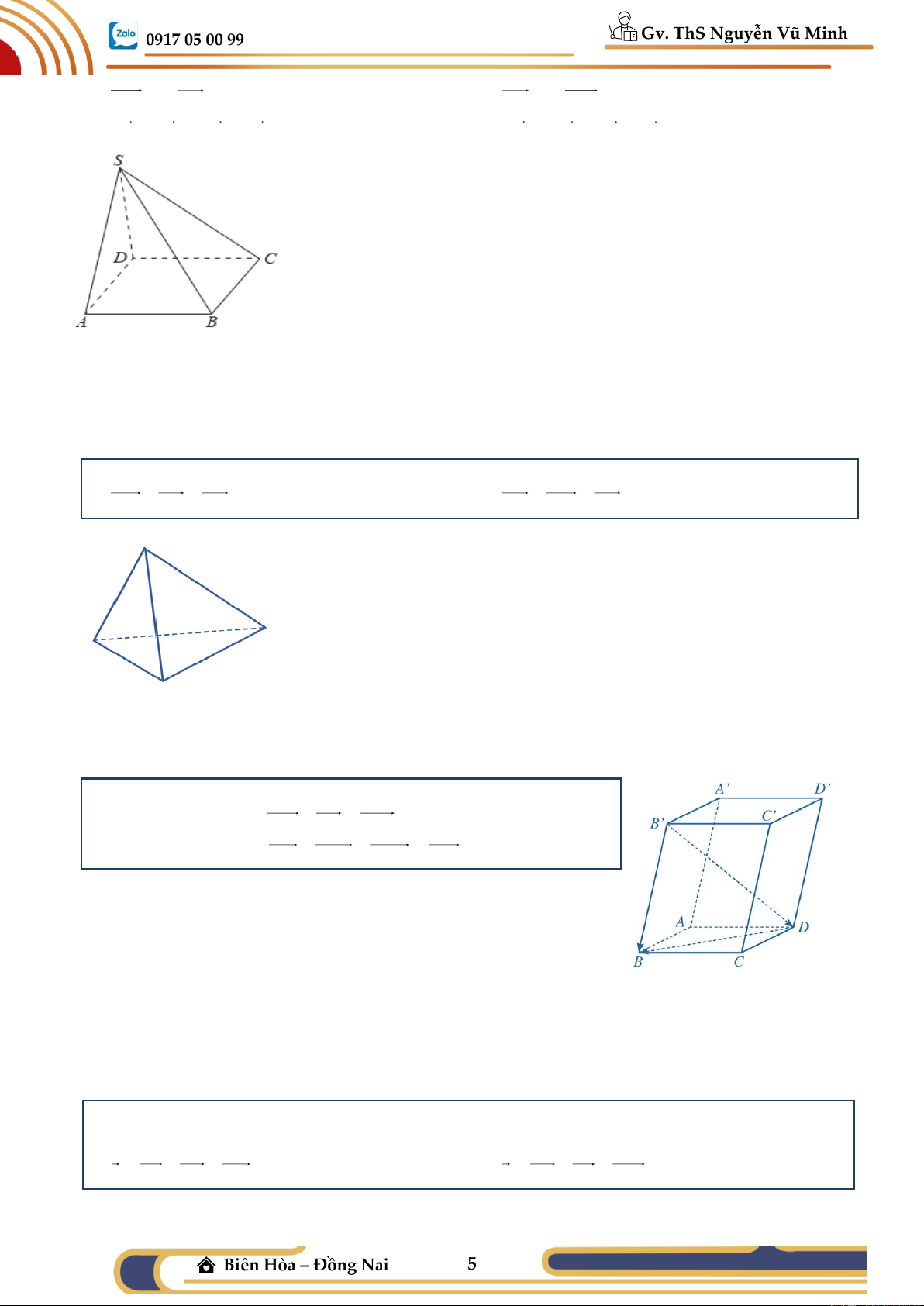
Ví dụ 04: Cho hình hộp ABC .
D A' B 'C ' D ' .
a) Chứng minh rằng: B ' B − DB = B ' D .
b) Chứng minh rằng: BB ' − C ' B ' − D 'C ' = BD ' .
Ví dụ 05: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) a = BA + BC + BB ';
b) b = BC − BA + C ' A .
Biên Hòa – Đồng Nai 5
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) 3 Tích vec tơ với một số ● Cho số thực và vectơ
. Tích của số với vectơ là một vectơ, kí hiệu là
, được xác định như sau:
Cùng hướng với vectơ nếu ,
ngược hướng với vectơ nếu ; ● Có độ dài bằng
Phép nhân một số với một vectơ trong không gian có các tính chất sau: (Với hai vectơ bất kì và hai số thực h, k) ; ; ; Với
khác là cùng phương khi và chỉ khi có một số thực sao cho .
Ví dụ 01: Cho tứ diện ABCD có G là trọng tâm của tam giác BCD.
Gọi H, K lần lượt là trung điểm củ a các cạnh AB, AC. Chứng minh
rằng: a) BC = 2HK ;
b) AB + AC + AD = 3AG .
Ví dụ 02: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, I là 1
trung điểm MN. Chứng minh rằng: a) MN = (AB + DC) ;
b) IA + IB + IC + ID = 0 . 2
Biên Hòa – Đồng Nai 6
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 03: Cho tứ diện ABCD. Lấy G là trọng tâm tam giác BCD. Các phát biểu nào sau đây là đúng hay sai?
a) GB + GC + GD = 0
b) GA + GB + GC + GD = 0
c) CB + CD = 3CG
d) AB + AC + AD = 3AG
Ví dụ 04: Cho hình lăng trụ AB .
C A' B 'C ' có M là trung điểm của BB ' . 1
Đặt CA = a, CB = b, CC ' = c . Chứng minh rằng AM = b − a + c . 2
Ví dụ 05: Cho hình hộp ABC .
D A' B 'C ' D ' . Gọi G là trọng tâm tam giác AB ' D ' . Chứng minh
rằng A'C = 3A'G .
Biên Hòa – Đồng Nai 7
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 06: Cho hình chóp S.ABCD , có ABCD là hình
bình hành tâm O . Tam giác SAC đều cạnh bằng 7 cm.
Khi đó, tính SA + SC
Ví dụ 07: Cho hình lăng trụ tam giác ABC.A′B′C′, gọi M, N lần
lượt là trung điểm của AB và AC.
a/ Hai vectơ MN và B C
  có cùng phương không? Có cùng 1
hướng không? Giải thích vì sao MN = B C   ? 2
b/ Gọi O là giao điểm của AB’ và A’B. Chứng minh rằng CC = ( 2 − )OM .
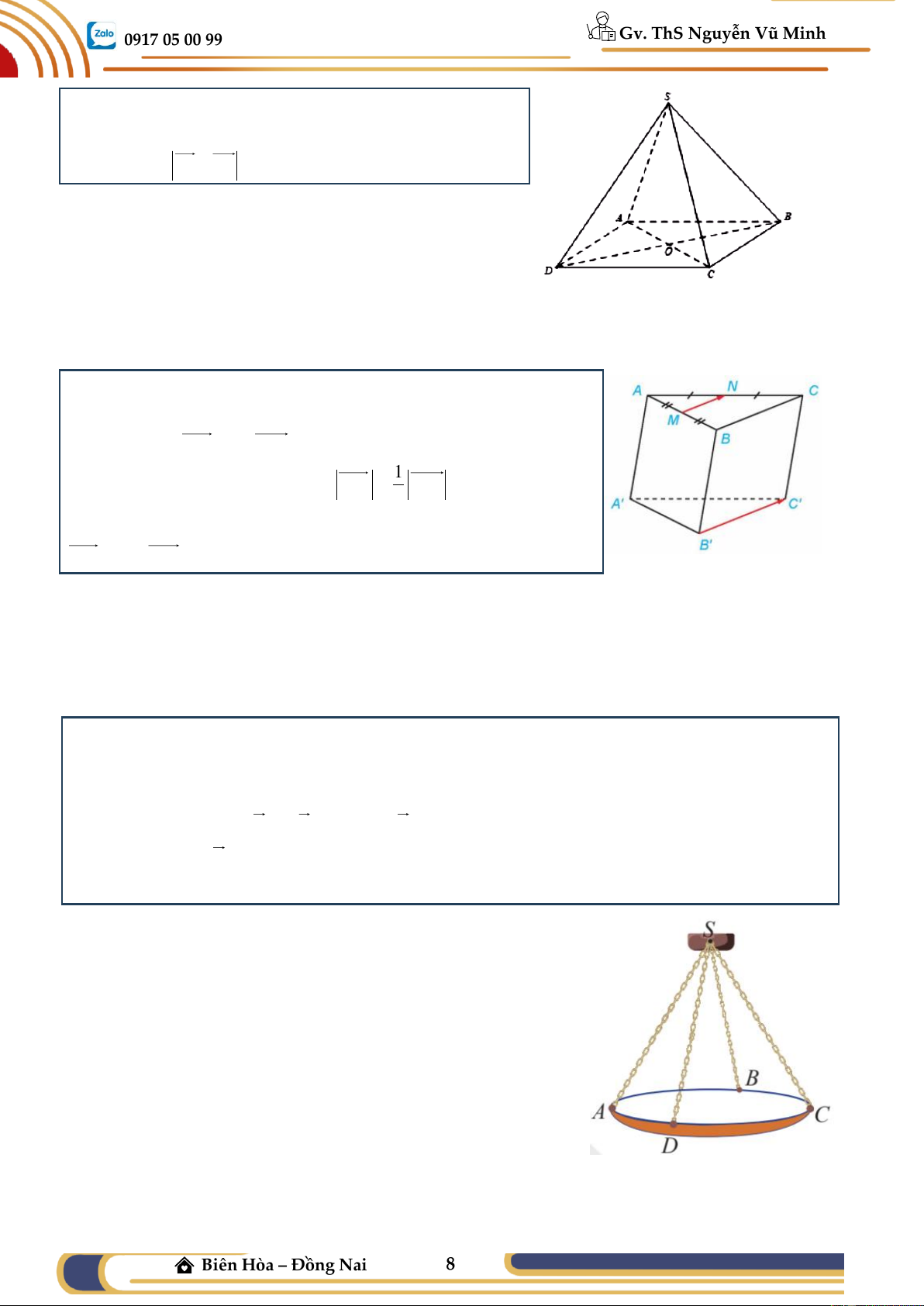
Ví dụ 08: (CTST) Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn
được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có o ASC = 60 .
a) Sử dụng công thức P = mg trong đó g là vectơ gia tốc rơi tự do có độ lớn 10 m/s2, tìm độ
lớn của trọng lực P tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Biên Hòa – Đồng Nai 8
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
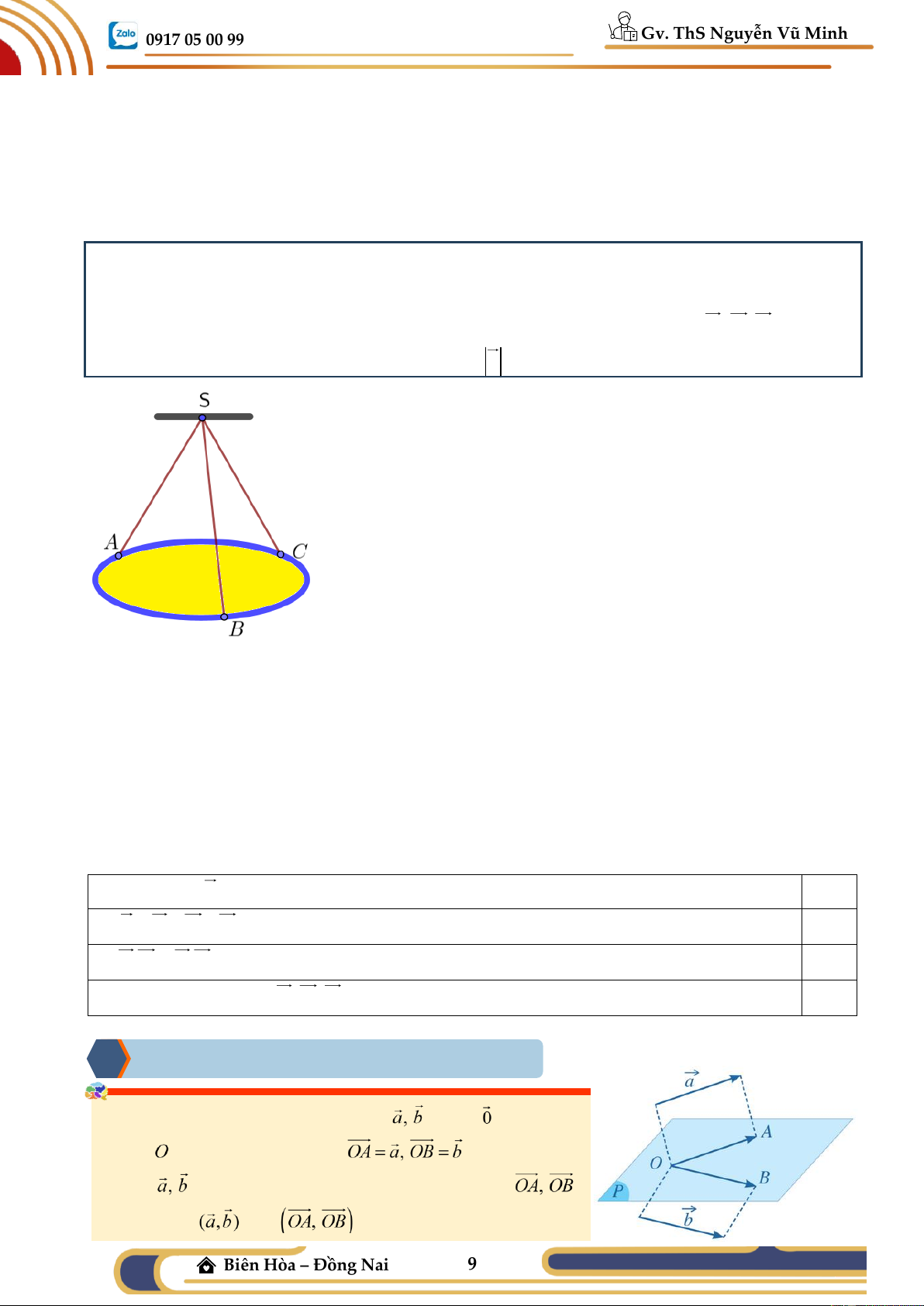
Ví dụ 09: Một chiếc đĩa kim loại khối lượng 4,5 (kg) được treo bởi ba sợi dây không dãn S , A S ,
B SC sao cho S.ABC là hình chóp đều có o
ASB = 60 (hình vẽ). Khối lượng dây không
đáng kể; lực căng của mỗi sợi dây S , A S ,
B SC đặt tại điểm S tương ứng là F , F , F có độ lớn 1 2 3
bằng nhau. Lấy độ lớn của gia tốc trọng trường 2 g = 9,8(m/s ) .
a) Trọng lực P của hệ vật có độ lớn bằng 34,3 (N).
b) P = F + F + F . 1 2 3
c) F .F  F .F . 1 2 1 3
d) Độ lớn của các lực F , F , F bằng 14, 7 (N) . 1 2 3 4 Tích vô hướng c
ủa hai vectơ trong không gian
Trong không gian, cho hai vectơ khác . Lấy một
điểm tuỳ ý và vẽ hai vectơ . Góc giữa hai vectơ
trong không gian là góc giữa hai vectơ , kí hiệu là hay .
Biên Hòa – Đồng Nai 9
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
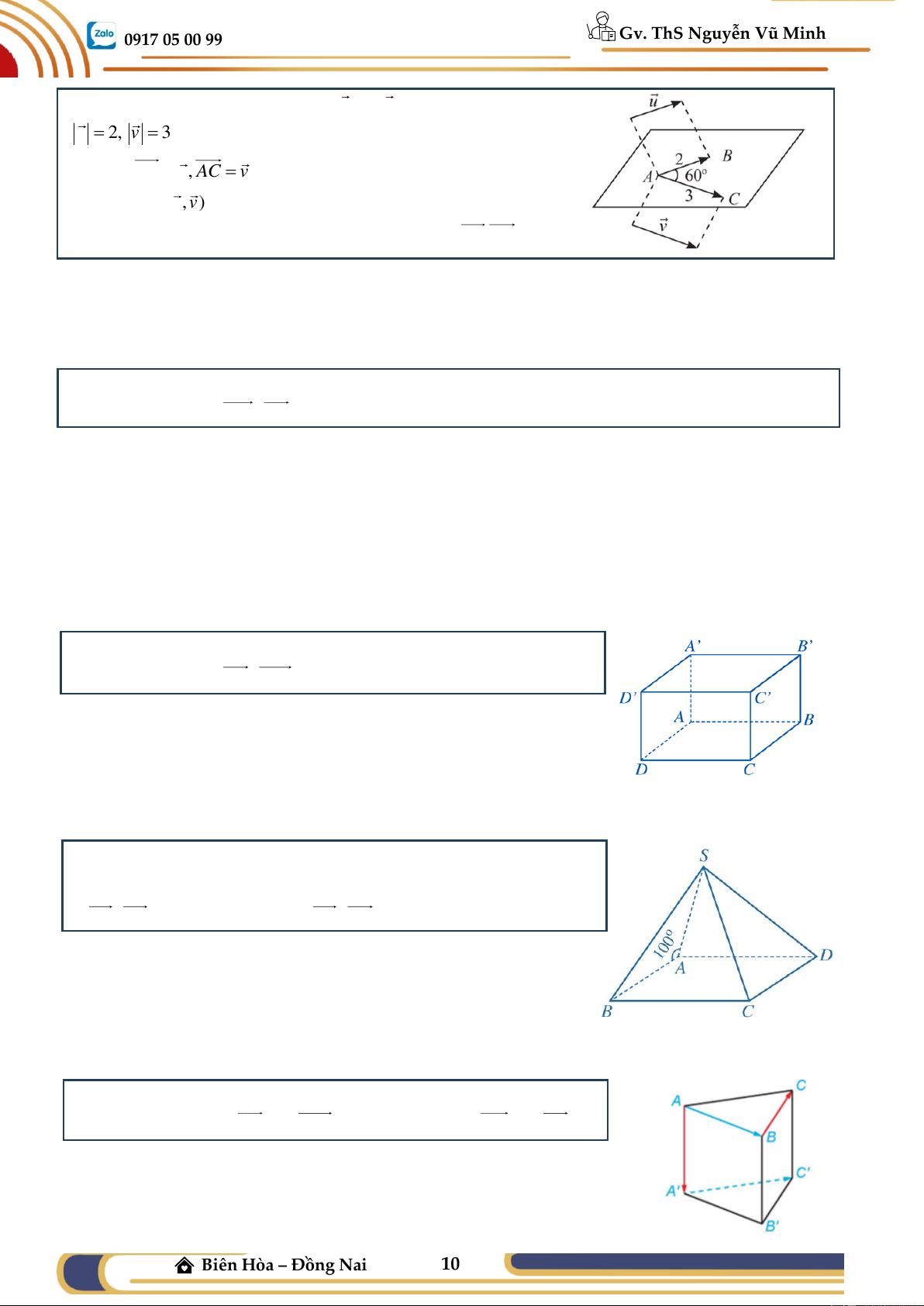
Ví dụ 01: Trong không gian, cho u và v thoả mãn
u = 2, v = 3. Lấy một điểm A bất kì, gọi B và C là hai điểm
sao cho AB = u, AC = v . Giả sử o BAC = 60 .
a) Tính góc (u, v) ;
b) Trong mặt phẳng (ABC) , tính tích vô hướng A . B AC .
Ví dụ 02: Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Hãy tính
góc giữa hai vectơ MN, BD .
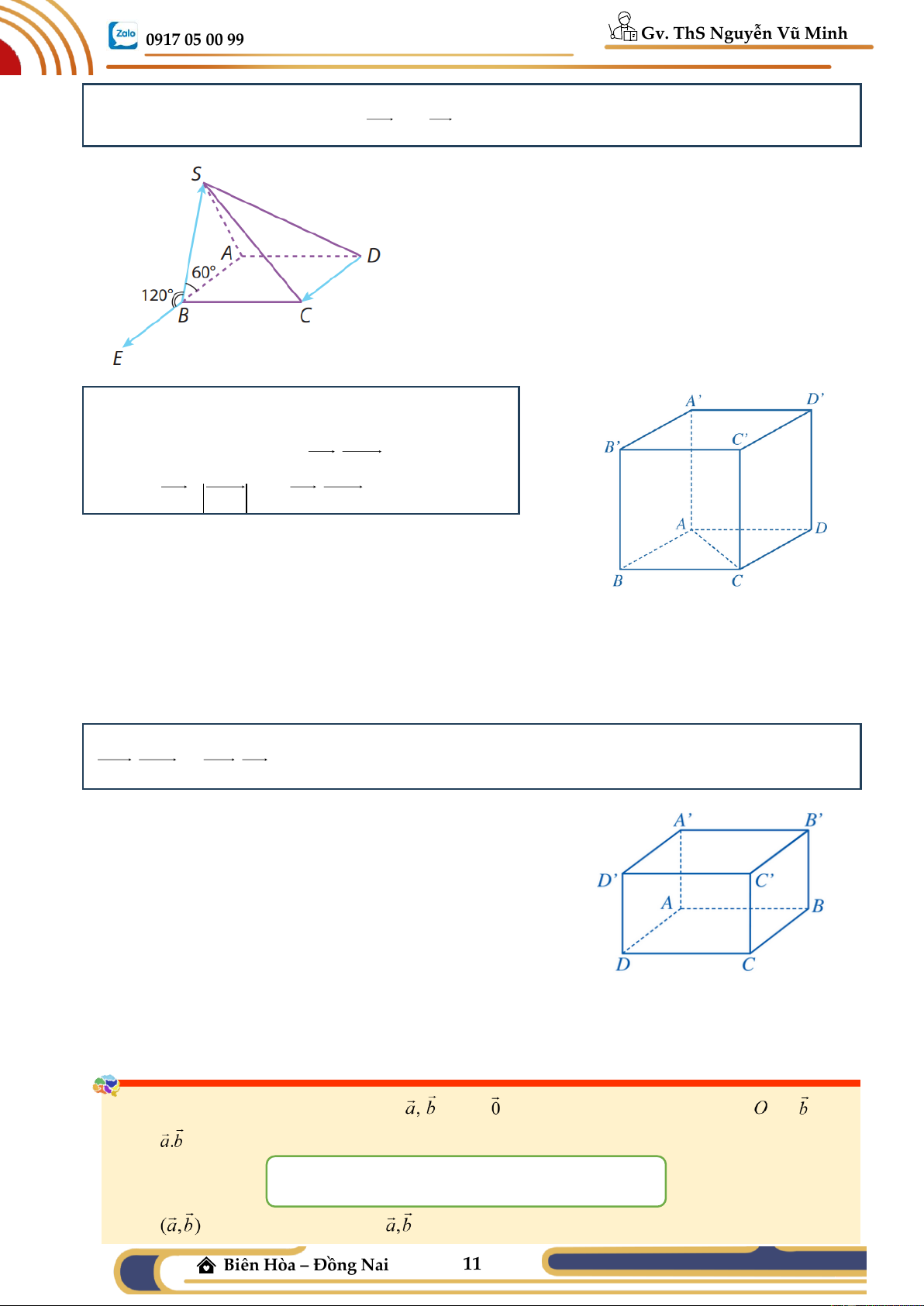
Ví dụ 03: (SGK CD) Cho hình lập phương ABC .
D A' B 'C ' D ' . Tính
góc giữa hai vectơ B , D B 'C .
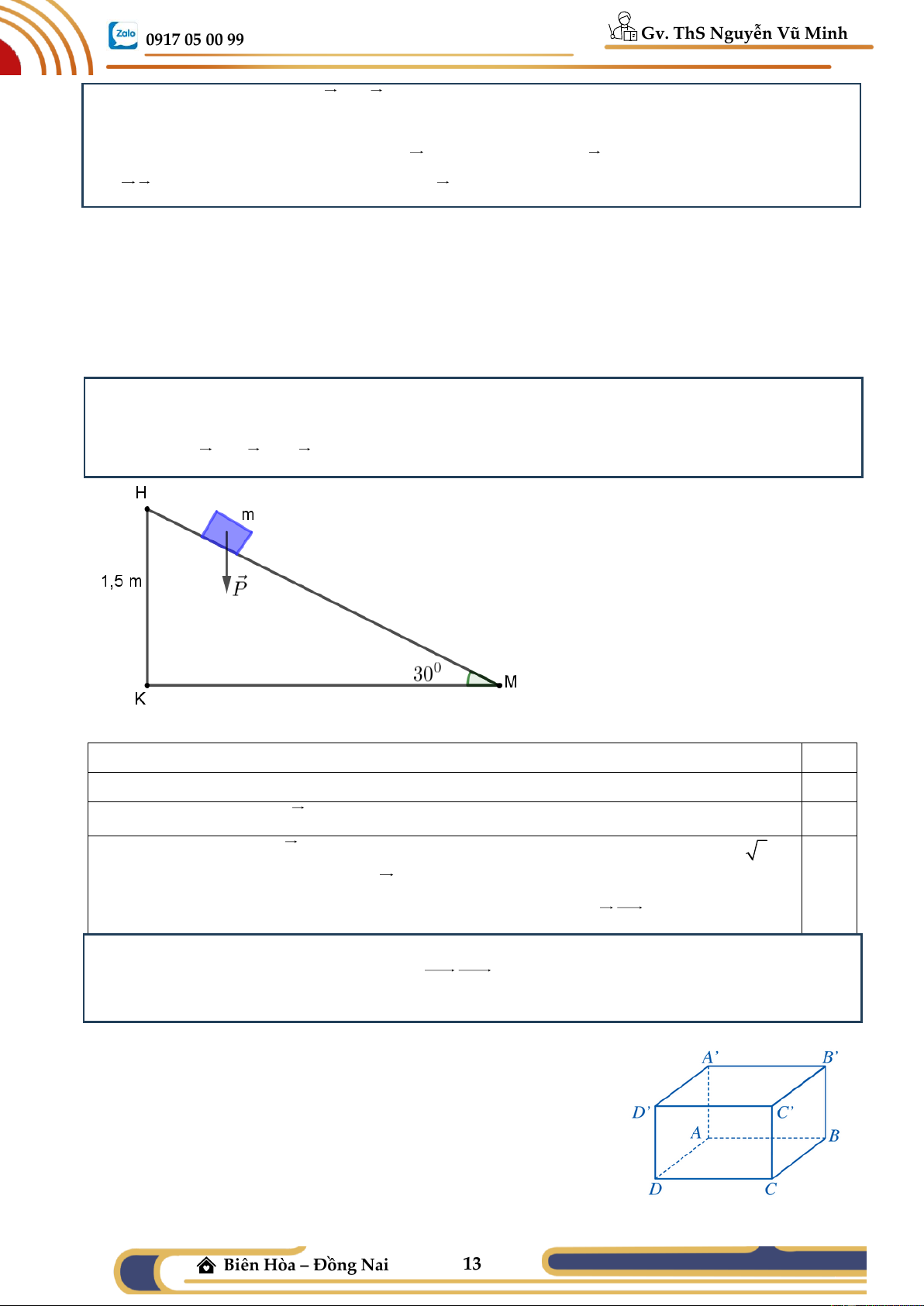
Ví dụ 04: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và o
SAB = 100 . Tính góc giữ a hai vectơ. a) AS, AB ; b) AS, CD ;
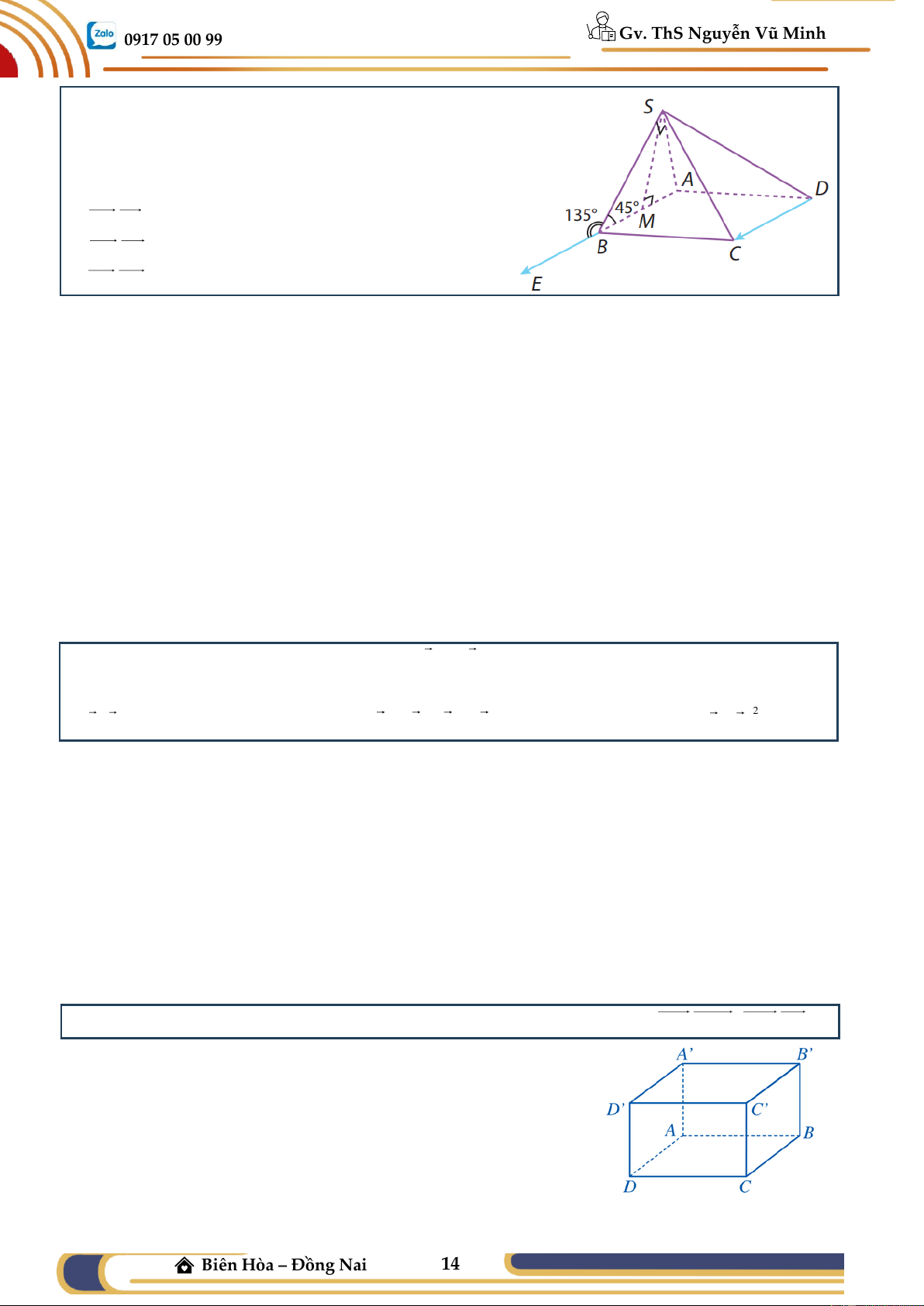
Ví dụ 05: Cho hình lăng trụ tam giác đều ABC.A’B’C’.
Tính các góc giữa: a) AB và AC ;
b) AA và BC .
Biên Hòa – Đồng Nai 10
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 06: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và mặt bên SAB là tam
giác đều. Tính góc giữa hai vectơ DC và BS .
Ví dụ 07: Trong không gian, cho hình lập phương ABC .
D A' B 'C ' D ' có độ dài cạnh bằng 3 cm.
a) Tính góc giữa hai vectơ AC, A' D '.
b) Tính | AC | . A' D ' .cos ( AC, A' D') .
Ví dụ 08: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Tính các góc ( A' ,
D B 'C '); ( AD', BD) .
● Trong không gian, cho hai vectơ
khác . Tích vô hướng của hai vectơ và , kí hiệu
, là một số thực được xác định bởi công thức: ở đó là góc giữa hai vectơ .
Biên Hòa – Đồng Nai 11
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
● Với các vectơ bất kì
và số thực tuỳ ý, ta có: (tính chất giao hoán); (tính chất phân phối); ; , trong đó . ● Ngoài ra, . ● Nếu là hai vectơ khác thì .
Ví dụ 01: Trong không gian, cho hai vectơ a,b tạo với nhau một góc o 50 và a = 7 dm ,
b = 5 dm . Khi đó, hãy tính a.b ?
Ví dụ 02: Cho tứ diện đều ABCD có cạnh bằng a và M là trung điểm của CD.
a) Tính các tích vô hướng A . B AC, A . B AM ;
b) Tính góc ( AB,CD) .
Ví dụ 03: (SGK CTST) Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết
rằng, cầu trượt có góc nghiêng so với phương nằm ngang là 300 (Hình mnih họa).
Biên Hòa – Đồng Nai 12
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
a) Tính độ lớn của trọng lực P = mg tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do có
độ lớn là g = 9,8 m/s2.
b) Cho biết công A (J) sinh bởi một lực F có độ dịch chuyển d được tính bởi công thức
A = F.d . Hãy tính công sinh bởi trọng lực P khi em nhỏ trượt hết chiều dài cầu trượt.
Ví dụ 04: Một vật khối lượng m = 10(kg) trượt trên mặt phẳng nghiêng so với mặt đất một góc o
30 từ độ cao HK=1,5 (m) . Giả sử mặt phẳng nghi
êng không có ma sát và vật chỉ bị tác dụng
bởi trọng lực P = .
m g với g là véc tơ gia tốc rơi tự do của vật có độ lớn được lấy bằng 2 10 (m/s )
a) Hướng chuyển động của vật là hướng từ H xuống K .
b) Chiều dài quãng đường HM là 3 (m).
c) Độ lớn của trọng lực P là 100 (N) .
d) Công của trọng lực P làm vật ở trên trượt từ vị trí H đến mặt đất bằng 150 3 (J)
(Cho biết công A (J) sinh bởi lực F (N) làm vật dịch chuyển một đoạn thẳng từ C
đến D có độ dài tính bằng mét, được tính theo công thức A=F.CD )
Ví dụ 05: Cho hình lập phương ABC .
D A' B 'C ' D ' có cạnh bằng a . Gọi M , N lần lượt là trung
điểm của A ' D ' và C ' D '. Tích vô hướng 2
MN.C ' B = .
n a ( n là số thập phân). Giá trị của n bằng bao nhiêu?
Biên Hòa – Đồng Nai 13
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Ví dụ 06: Cho hình chóp S.ABCD có đáy ABCD là
hình bình hành. Mặt bên ASB là tam giác vuông cân
tại S và có cạnh AB = a . Gọi M là trung điểm của AB . Hãy tính: a) DC.BS ; b) DC.AS ; c) DC.MS .
Ví dụ 07: Trong không gian, cho hai vec tơ a và b cùng có độ dài bằng 1. Biết góc giữa hai
vec tơ đó là 45o, hãy tính: a) a . b
b) (a + 3b).(a − 2b) c) ( + )2 a b
Ví dụ 08: Cho hình lập phương ABC .
D A' B 'C ' D
' có cạnh bằng a . Tính A' .
B D 'C '; D ' . A BC
Biên Hòa – Đồng Nai 14
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT) Bài tập tự luận
Bài tập 01: Cho hình tứ diện đều ABCD có độ dài cạnh bằng 2.
a) Có bao nhiêu vectơ có điểm đầu và điểm cuối là đỉnh của tứ
diện? Liệt kê tất cả những vectơ đó?
b) Có bao nhiêu vectơ có điểm đầu là A và điểm cuối là đỉnh của tứ diện? Liệt kê tất cả những vectơ đó.
c) Trong các vectơ tìm được ở câu b), những vectơ nào có giá nằm trong mặt phẳng (ABC).
d) Tính độ dài của các vec tơ tìm được ở câu b).
e) Bạn Lan nói: " AB = AC = AD vì các vectơ này có cùng độ dài và cùng hướng (từ trên xuống
dưới)". Khẳng định của bạn Lan có đúng không? Vì sao?
Bài tập 02: Cho hình hộp ABCD.A'B'C'D' có AB = 2, AD = 3 và AA' = 4.
a) Hãy chỉ ra ba vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho ba vectơ đó: ● Bằng vectơ AD ;
● Là vectơ đối của vectơ AD ;
● Bằng vectơ AA ;
● Là vectơ đối của vectơ AA ;
b) Trong các vectơ AC , AD , AD , hai vectơ nào có giá cùng nằm trong mặt phẳng (ABCD).
c) Trong các vectơ AB , AD , AD , hai vectơ nào có cùng độ dài.
d) So sánh độ dài của hai vectơ AB và D C   .
Biên Hòa – Đồng Nai 15
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
e) Nhận xét gì về giá của hai vectơ AB và D C   .
f) Hai vectơ AB và D C
  có cùng phương không? Có cùng hướng không?
g) Tính độ dài của các vectơ BB , BD và BD .
Bài tập 03: Cho hình lập phương ABC .
D A' B 'C ' D ' cạnh bằng a . Tìm AB + CC ' − D ' A'
Bài tập 04: Cho hình hộp ABC .
D A' B 'C ' D ' ' Chứng minh rằng:
a) AB + DD ' + C ' D ' = CC ' ;
b) AB + CD ' − CC ' = 0 ;
c) BC − CC ' + DC = A'C .
Bài tập 05: Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và
cùng có cường độ là 7N. Tính cường độ của hợp lực.
Biên Hòa – Đồng Nai 16
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Bài tập 06: Cho hình lăng trụ tam giác AB .
C A' B 'C ' có AA' = a, AB = b, AC = c . Chứng minh
rằng B 'C = c − a − b và BC ' = a − b + c .
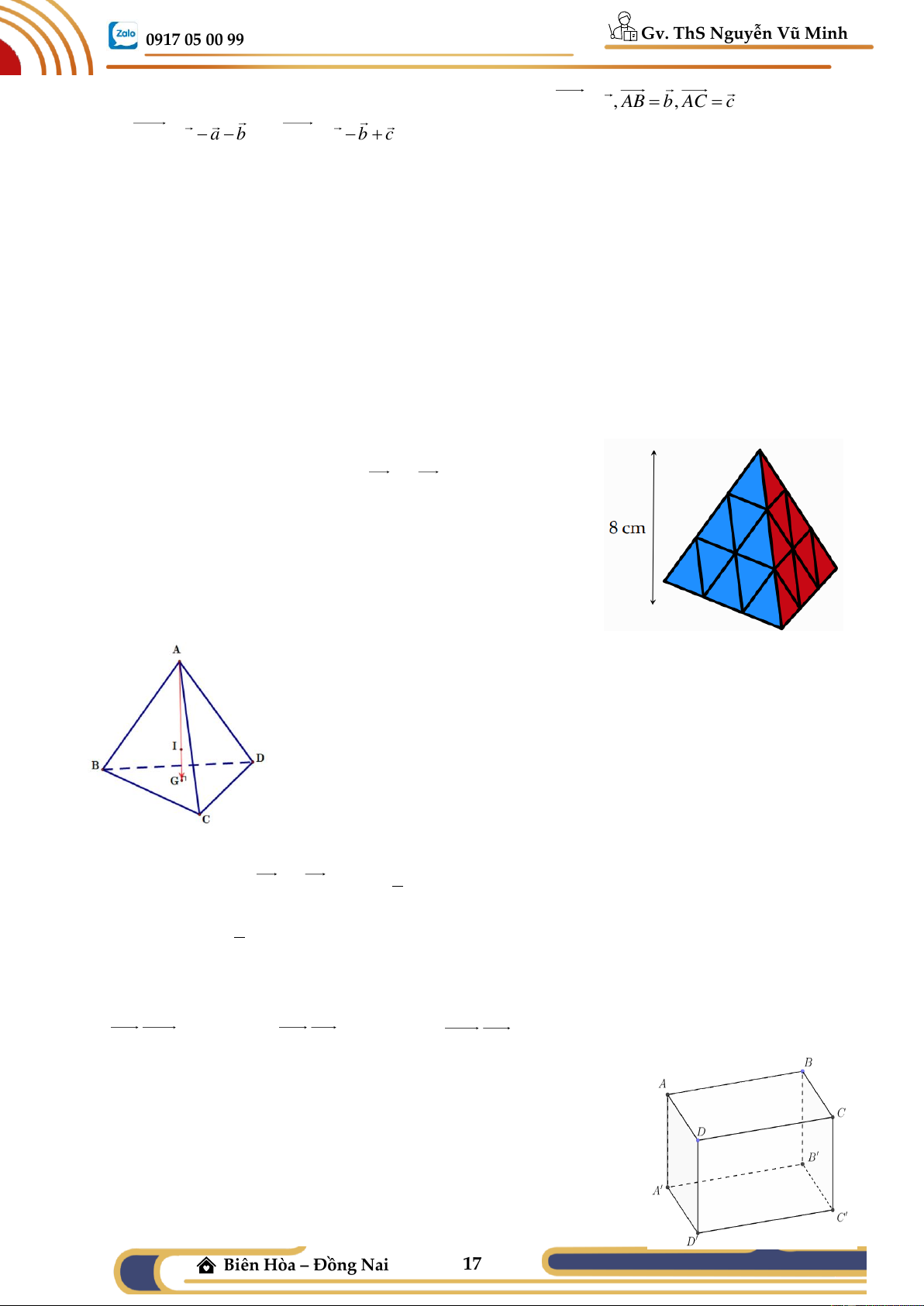
Bài tập 07: (SGK KNTT) Ta đã biết trọng tâm của tứ diện
ABCD là một điểm I thoả mãn AI = 3IG , ở đó G là trọng tâm của B
 CD. Áp dụng tính chất trên để tính khoảng cách
từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều
đến một mặt của nó, biết rằng chiều cao của khối rubik là 8 cm .
Lời giải: Đáp số: 2cm.
Đặt tên khối rubik là tứ diện đều ABCD có G là trọng tâm tam giác BCD , I là trọng tâm tứ 1
diện ABCD . Do đó, AI = 3IG  IG =
AG . Vì chiều cao của rubik bằng 8 cm nên 4 1
AG = 8 cm  IG =
.8 = 2( cm) . Vậy khoảng cách từ trọng tâm của một khối rubik (đồng chất) 4
hình tứ diện đều đến một mặt của nó bằng 2 cm .
Bài tập 08: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy tính:
a) AB .AC ; b) AB .BD ;
c) AC .BB .
Biên Hòa – Đồng Nai 17
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Bài tập 09: Cho hình chóp S.ABCD . Gọi I là trọng tâm của tam giác ABC và J là trọng tâm
tam giác ADC. Chứng minh rằng 2SA + SB + 2SC + SD = 3(SI + SJ ) .
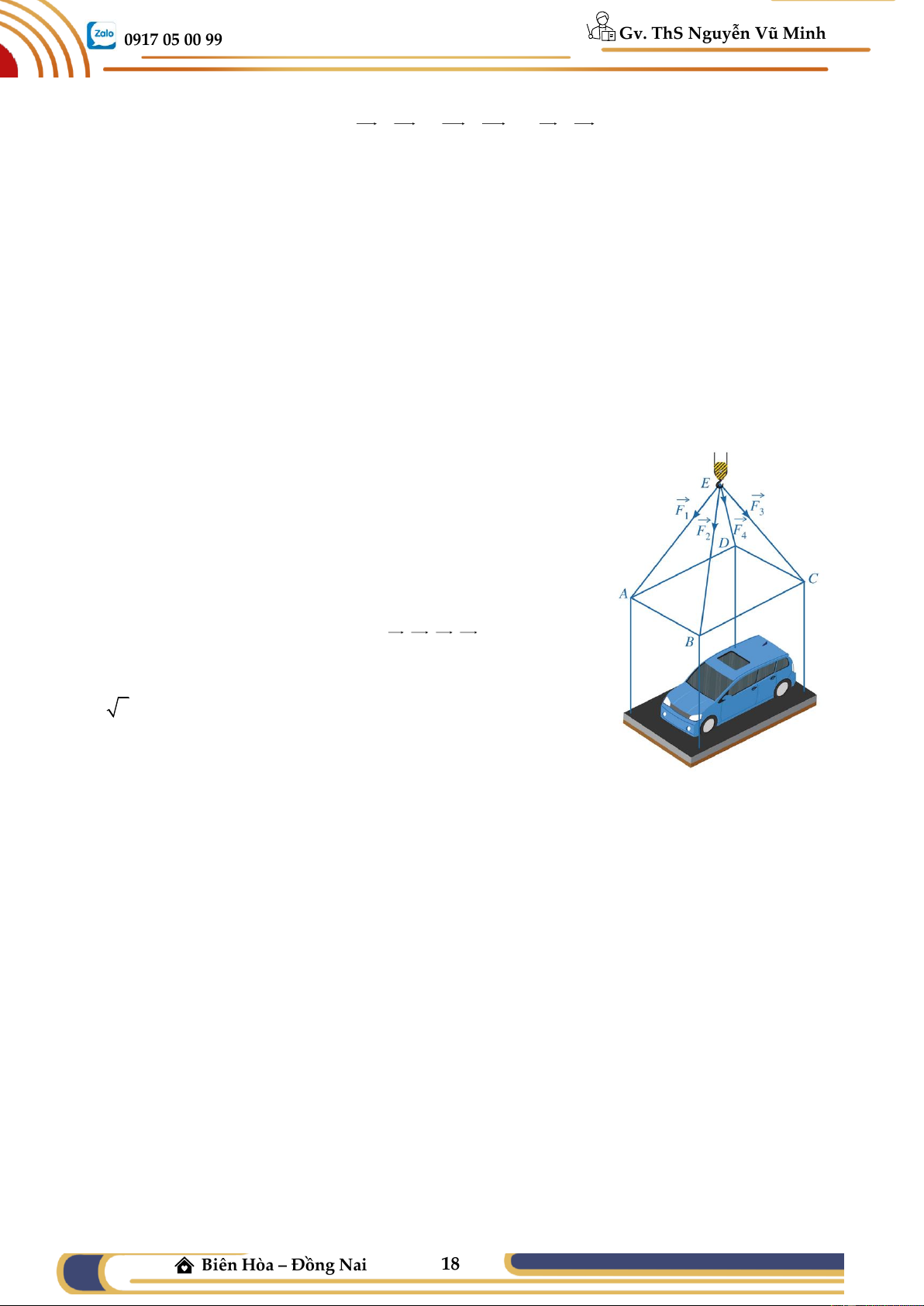
Bài tập 10: Một chiếc ô tô được đặt trên mặt đáy dưới của một
khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật
ABCD , mặt phẳng ( ABCD) song song với mặt phẳng nằm ngang.
Khung sắt đó được đặt vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp E ; A E ;
B EC; ED bằng nhau và cùng tạo với mặt
phẳng ( ABCD) một góc  . Chiếc cần cẩu kéo khung sắt lên theo
phương thẳng đứng. Biết các lực căng F ; F ; F ; F đều có cường 1 2 3 4
độ là 4800 N , trọng lượng của hệ gồm cả khung sắt và xe ô tô là
7200 6 N . Tính sin (làm tròn kết quả đến hàng phần trăm).
Bài tập 11: Một thùng hàng container được móc cẩu bởi 4 sợi dây cáp được móc vào 4 đầu của
thùng hàng (như hình vẽ minh họa). Các sợi dây cáp đó được buộc vào móc P của chiếc cần
cẩu sao cho các đoạn dây cáp PA, PB, PC, PD có độ dài bằng nhau và cùng tạo với mặt phẳng
( ABCD) một góc bằng o
45 . Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính
trọng lượng của thùng hàng container (làm tròn đến hàng đơn vị), biết rằng các lực căng của
các sợi dây cáp đều có cường độ là 1200 N.
Biên Hòa – Đồng Nai 18
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Bài tập 12: Cho tứ diện ABCD có AC và BD cùng vuông góc với AB. Gọi M, N lần lượt là trung
điểm của hai cạnh AB, CD. Chứng minh rằng: 1
a) MN = (AC + BD) ; b) MN.AB = 0 . 2
Bài tập 13: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt bên ASB là tam giác
vuông cân tại S và có cạnh AB = a. Gọi M là trung điểm của AB. Hãy tính: a) DC.BS b) DC.AS c) DC.MS
Biên Hòa – Đồng Nai 19
Gv. ThS Nguyễn Vũ Minh
0917 05 00 99 (Toán – Vật Lí THPT)
Bài tập 14: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các 1 1 1
điểm thuộc các cạnh SA, SB sao cho SE = S , A SF = S .
B Chứng minh rằng EF = DC . 3 3 3
Bài tập 15: Cho tứ diện ABCD có G là trọng tâm của tam giác BCD. Gọi H, K lần lượt là trung
điểm của các cạnh AB, AC. Chứng minh rằng: a) BC = 2HK ;
b) AB + AC + AD = 3AG . 2
Bài tập 16: Cho hình chóp S.ABC. Điểm M thuộc cạnh SA và SM = SA. 3
a) Viết hệ thức liên hệ giữa các cặp vectơ SM và SA , MA và AS ; 2
b) Tìm điểm N sao cho MN = − BA . 3
Biên Hòa – Đồng Nai 20