Ôn kiến thức, luyện kỹ năng bài giảng đồ thị, bảng biến thiên của hàm số

Tài liệu gồm 62 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập trắc nghiệm ôn kiến thức, luyện kỹ năng bài giảng đồ thị, bảng biến thiên của hàm số môn Toán 12 THPT (kết hợp ba bộ sách giáo khoa Toán 12 chương trình mới: Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức Với Cuộc Sống).Mời bạn đọc đón xem!

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung

Môn: Toán 12

Thông tin:

62 trang 1 tháng trước

Tác giả:

Profile Lê Phương
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
B
B
À
À
I
I
G
G
I
I
Ả
Ả
N
N
G
G
Đ
Đ
Ồ
Ồ
T
T
H
H
Ị
Ị
,
,
B
B
Ả
Ả
N
N
G
G
B
B
I
I
Ế
Ế
N
N
T
T
H
H
I
I
Ê
Ê
N
N
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
7
7
/
/
2
2
0
0
2
2
4
4
2
Ô
Ô
N
N
K
K
I
I
Ế
Ế
N
N
T
T
H
H
Ứ
Ứ
C
C
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
Đ
Đ
Ồ
Ồ
T
T
H
H
Ị
Ị
,
,
B
B
Ả
Ả
N
N
G
G
B
B
I
I
Ế
Ế
N
N
T
T
H
H
I
I
Ê
Ê
N
N
C
C
Ủ
Ủ
A
A
H
H
À
À
M
M
S
S
Ố
Ố
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG
1 FILE
NHẬN DIỆN ĐỒ THỊ CÁC HÀM SỐ THƯỜNG GẶP
1 FILE
XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ THÔNG QUA ĐỒ THỊ
1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ
3
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT KHẢO SÁT ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
I
. SƠ ĐỒ KHẢO SÁT HÀM SỐ
Sơ đồ khảo sát hàm số
( )y f x
:
1. Tìm tập xác định của hàm số.
2. Xét sự biến thiên của hàm số:
- Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có).
- Tính đạo hàm
y
. Tìm các điểm mà tại đó
y
bằng 0.
- Lập bảng biến thiên; xác định chiều biến thiên, cực trị của hàm số(nếu có).
3. Vẽ đồ thị hàm số
- Vẽ các đường tiệm cận (nếu có).
- Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục tọa độ ( trong trường hợp đơn
giản),…
- Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Chú ý. Đồ thị hàm số
( )y f x
giao với trục hoành tại những điểm có hoành độ là nghiệm của phương trình
( ) 0
f x
, giao với trục tung tại điểm có tung độ là
(0)f
nếu
0
thuộc tập xác định của hàm số đó.
II. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ ĐA THỨC BẬC BA
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
3 2
3 4
y x x
.
1) Tập xác định:
.
2) Sự biến thiên
- Giới hạn tại vô cực:
lim , lim
x x
y y
 
 
.
-
2
3 6y x x
,
2
0 3 6 0 0
y x x x
hoặc
2
x
.
- Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng
( ;0)
và
(2; )
, nghịch biến trên khoảng
(0;2)
.
Hàm số đạt cực đại tại
0, 4
CĐ
x y
; hàm số đạt cực tiểu tại
2, 0
CT
x y
.
3) Đồ thị
- Giao điểm của đồ thị với trục tung:
(0;4)
.
- Giao điểm của đồ thị với trục hoành:
Xét phương trình
3 2 2
3 4 0 ( 1)( 2) 0
x x x x
1 2.
x x
Vậy đồ thị hàm số giao với trục hoành tại hai điểm
( 1;0)
và
(2;0)
.
- Đồ thị hàm số đi qua các điểm
( 1;0),(2; 0),(0;4)
và
(1;2)
.
Vậy đồ thị hàm số
3 2
3 4
y x x
được cho ở Hình.
Quan sát đồ thị ở Hình, ta thấy đồ thị đó có tâm đối xứng là điểm
(1;2)
I
.
4
Ví dụ 2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
3 2
3 4 2y x x x
.
1) Tập xác định:
.
2) Sự biến thiên
- Giới hạn tại vô cực:
lim , lim
x x
y y
 
 
.
-
2
3 6 4
y x x
;
0 , .
y x
- Bảng biến thiên:
Hàm số nghịch biến trên khoảng
( ; ) 
.
Hàm số không có cực trị.
3) Đồ thị
- Giao điểm của đổ thị với trục tung:
(0; 2)
.
- Giao điểm của đồ thị với trục hoành:
Giải phương trình
3 2
3 4 2 0
x x x
ta được
1x
. Vậy đồ thị hàm số giao với trục hoành tại điểm
(1;0)
.
- Đồ thị hàm số đi qua các điểm
(1;0),(0;2), (2; 2)
.
Vậy đồ thị hàm số
3 2
3 4 2y x x x
được cho ở hình
Tâm đối xứng của đồ thị hàm số đó là điểm
(1;0)
I
.
Nhận xét: Trong trường hợp tổng quát, đồ thị của hàm số bậc ba
3 2
( )
y f x ax bx cx d
( 0)
a
có tâm
đối xứng là điểm
;
3 3
b b
I f
a a
. Hoành độ
3
b
a
của tâm đối xứng đó là nghiệm của phương trình
0
y

.
III KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA MỘT SỐ HÀM PHÂN THỨC HỮU TỈ
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
( , )
ax b
y c ad bc
cx d
0 0
Sử dụng sơ đồ khảo sát hàm số, ta có thể khảo sát sự biến thiên và vẽ đồ thị hàm số
( , )
ax b
y c ad bc
cx d
0 0
. Ta sẽ tìm hiểu qua một số ví dụ sau đây.
Ví dụ 3. Khảo sát sự biến thiên và vẽ đồ thị hàm số
x
y
x
2 1
1
1) Tập xác định
\ 1
2) Sự biến thiên
5
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận
lim ,lim
x x
y y

1 1
. Do đó, đường thẳng
x
1
là tiệm cận đứng của đồ thị hàm số
lim ,lim
x x
y y
 
2 2
Do đó, đường thẳng
y
2
là tiệm cận ngang của đồ thị hàm số
'y
x
2
3
0
1
với mọi
x
1
Bảng biến thiên
Hàm số nghịch biến tên mỗi khoảng
; 1
và
;
1
.
Hàm số không có cực trị.
3) Đồ thị
Giao điểm của đồ thị với trục tung:
;
0 1
Giao điểm của đồ thị với trục hoành:
;
1
0
2
Đồ thị hàm số đi qua các điểm
; , ;
1
0 1 0
2
; , ; , ; , ;
5
2 1 2 5 4 4 3
2
Vậy đồ thị hàm số
x
y
x
2 1
1
được cho ở hình 21.
Quan sát đồ thị ở Hình 21, đồ thị đó nhận giao điểm
;
I
1 2
của hai tiệm cận của đồ thị hàm số làm tâm đối
xứng và nhận hai đường phân giác của góc tạo bởi hai tiệm cận đó làm trục đối xứng.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2
0; 0
ax bx c
y a m
mx n
Sử dụng sơ đồ khảo sát hàm số ta có thể khảo sát sự biến thiên và vẽ đồ thị của hàm số
2
( 0; 0;
ax bx c n
y a m
mx n m
không là nghiệm của đa thức
2
ax bx c
). Ta sẽ tìm hiểu qua một số ví dụ
sau đây.
Ví dụ 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2
1
1
x x
y
x
Tập xác định :
\ 1
Sự biến thiên
Giới hạn tại vô cực và các đường tiệm cận:
Ta viết hàm số đã cho dưới dạng :
1
1
y x
x
x
lim y

x
lim y

1x
lim y
1x
lim y
Do đó đường thảng
1x
là tiệm cận đứng của đồ thị hàm số.
1 1
( ) 0, ( ) 0
1 1
x x x x
lim y x lim lim y x lim
x x
   
.
Do đó đường thẳng
y x
là tiệm cận xiên của đồ thị hàm số.
6
Ta có
2
2
2
'
1
x x
y
x
;
2
0
' 0 2 0
2
x
y x x
x
Bảng biến thiên
x
0
1
2

'y
+ 0 -
y
1


3
Hàm số đồng biến trên mỗi khoảng
;0
và
2;
; nghịch biến trên mỗi khoảng
0;1
và
1;2
Hàm số đạt cực đại tại
0; 1
CÐ
x y
; đạt cực tiểu tại
2; 3
CT
x y
.
Đồ thị
Giao điểm của đồ thị với trục tung:
0; 1
.
Đồ thị hàm số không cắt trục hoành.
Đồ thị hàm số đi qua các điểm
1 3
0; 1 , ; .
2 2
3 3 7 7
1; , 2;3 , ; 3; .
2 2 2 2
và
Vậy đồ thị hàm số
2
1
1
x x
y
x
được cho ở Hình 23.
Quan sát đồ thị ở Hình 23, đồ thị đó nhận giao điểm
1;1
I
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận
hai đường phân giác của các góc tạo bởi hai đường tiệm cận
đó làm trục đối xứng.
7
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
NHẬN DIỆN CÁC ĐỒ THỊ HÀM SỐ THƯỜNG GẶP
_____________________________________
NHẬN DIỆN ĐỒ THỊ HÀM SỐ ĐA THỨC
Bài toán 1. Đồ thị của hàm số
3 2
f x ax bx cx d
có dạng như hình vẽ. Hệ số a không thể bằng
A.3 B. 2 C. 1 D. – 4
Lời giải. Đồ thị của hàm số
3 2
f x ax bx cx d
với
0
a
nên a không thể bằng – 4.
Bài toán 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3 y x x
. B.
3
3 y x x
. C.
4 2
2
y x x
. D.
4 2
2
y x x
.
Lời giải. Đồ thị của hàm số bậc ba với
0
a
nên
3
3 y x x
.
Bài toán 3. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
3
3y x x
. B.
2
2y x x
. C.
3
3y x x
. D.
2
2y x x
.
Lời giải
Dựa vào bảng biến thiên trên, ta nhận thấy đây là hàm số bậc ba có dạng
3 2
y ax bx cx d
với
0
a
.
Mà
3 2
lim
x
ax bx cx d


0
a
. Do đó có duy nhất hàm số
3
3y x x
thoả mãn.
Bài toán 4. Hàm số nào dưới đây có bảng biến thiên như sau?
A.
4 2
2y x x
. B.
3
3y x x
. C.
4 2
2y x x
. D.
3
3y x x
.
Lời giải
Từ BBT ta nhận thấy hàm số có hai điểm cực trị và đồng biến trên khoảng
1; .
Do đó hàm số là hàm đa
thức bậc ba có hệ số
0.
a
Bài toán 5. Đồ thị của hàm số
3 2
f x ax bx cx d
có dạng như hình vẽ. Giá trị d không thể bằng
8
A.2 B. 3 C. 4 D. 0
Lời giải. Đồ thị hàm số không đi qua gốc tọa độ nên
0
d
.
Bài toán 6. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2y x x
. B.
3
3y x x
. C.
3
3y x x
. D.
4 2
2y x x
.
Lời giải. Đồ thị hàm số bậc ba đi qua gốc tọa độ nên
3
3y x x
.
Bài toán 7. Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
3
3 1y x x
. B.
4 2
1
y x x
. C.
2
1y x x
. D.
3
3 1y x x
.
Lời giải
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba
3 2
y ax bx cx d
nên loại phương án B và C
Dựa vào đồ thị, ta có
lim 0
x
y a


nên loại phương án A
Bài toán 8. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới?
A.
3
1
2
2
y x x
. B.
3
1
2
2
y x x
. C.
4 2
1
2
2
y x x
. D.
4 2
1
2
2
y x x
.
Lời giải
Đồ thị đã cho là đồ thị hàm số bậc ba có hệ số bậc ba
0
a
. Chọn B.
Bài toán 9. Đồ thị của hàm số
3 2
f x ax bx cx d
có dạng như hình vẽ. Giá trị
0
f
bằng
A.1 B. 0 C. 2 D. 4
Lời giải. Đồ thị hàm số đi qua gốc tọa độ nên
0 0
f
.
9
NHẬN DIỆN ĐỒ THỊ HÀM SỐ PHÂN THỨC HỮU TỶ
Bài toán 1. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
2 1
x
y
x
D.
2
3 1
x
y
x
Lời giải. Đồ thị hàm số bậc hai/bậc nhất và có tiệm cận đứng
1
2
x
nên
2
2 1
x
y
x
.
Bài toán 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
3
1
x x
y
x
D.
2
3 1
x
y
x
Lời giải. Đồ thị hàm số nhận tiệm cận xiên
2y x
như hình vẽ nên
2
3
1
x x
y
x
.
Bài toán 3. Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực.
Tính giá trị biểu thức
2d c
c
.
A.2 B. 3 C. 4 D. 1
Lời giải. Đồ thị có tiệm cận đứng
2 2
1 1 1
d d c c c
x d c
c c c
.
Bài toán 4. Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực. Mệnh đề nào
dưới đây đúng?
10
A.
0,y x
B.
0, 1y x
C.
0, 1y x
D.
0,y x
Lời giải. Hàm số nghịch biến và có tiệm cận đứng
1x
, suy ra
0, 1y x
.
Bài toán 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
x
y
x
D.
2
3
1
x
y
x
Lời giải
Đồ thị hàm số có tiệm cận xiên
1y x
và đi qua điểm
0;1
nên
2
1
x
y
x
.
Bài toán 6. Đường cong ở hình bên là đồ thị của hàm số
ax b
y
cx d
với
, , ,a b c d
là các số thực. Mệnh đề nào
dưới đây đúng?
A.
y 0, 1x
B.
y 0, x 1
C.
y 0, x 2
D.
y 0, 2
Lời giải
Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, Hàm số nghịch biến vậy chọn B
Bài toán 7. Hình vẽ bên dưới là đồ thị của hàm số nào
11
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2 3
1
x
y
x
. D.
2 5
1
x
y
x
.
Lời giải
Đồ thị hàm số cắt trục Oy tai điểm có tọa độ
0;1
nên chọn phương án B.
Bài toán 8. Đồ thị hàm số sau có đường tiệm cận xiên là
A.
y x
B.
1y x
C.
2 1y x
D.
2y x
Lời giải
Đường tiệm cận đã cho đi qua
0;1
và song song với đường phân giác góc phần tư thứ nhất nên
1y x
Bài toán 9. Đường cong trong hình là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
. B.
2 1
2 2
x
y
x
. C.
4 2
3y x x
. D.
3 2
3y x x
.
Lời giải
Hình vẽ trên là đồ thị của hàm số dạng
0; 0
ax b
y c ad bc
cx d
Loại phương án C, D
Ta thấy: Đồ thị có đường tiệm cận đứng là
1
x
và đường tiệm cận ngang là
1y
Phương án B: Đồ thị có đường tiệm cận đứng là
2
x
loại B
A đúng.
Bài toán 10. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1
a
có đồ thị như hình bên). Mệnh đề nào dưới
đây đúng?
A.
' 0, 1
y x
. B.
' 0, 1
y x
. C.
' 0,y x
. D.
' 0,y x
.
Lời giải
Ta có :
1
x a
y
x
2
1
' 0, 1
1
a
y x
x
12
Do
1
a
nên dấu “
” không xảy ra.
Hàm đơn điệu không phụ thuộc vào
a
.
Bài toán 11. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2 3
1
x
y
x
. D.
2 5
1
x
y
x
.
Lời giải. Hàm số đồng biến và có tiệm cận đứng, tiệm cận ngang lần lượt là
1; 2
x y
.
Kết luận hàm số
2 1
1
x
y
x
.
Bài toán 12. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1
a
) có đồ thị như trong hình bên. Mệnh đề
nào dưới đây đúng?
y
x
O
A.
' 0,
y x R
. B.
' 0, 1 y x
. C.
' 0,
y x R
. D.
' 0, 1 y x
.
Lời giải
Ta có TXĐ:
\ 1
D R
và
2
1
' 0, 1
( 1)
a
y x
x
và đồ thị là đường đi xuống trên từng khoảng xác định nên
hàm số đã cho nghịch biến trên mỗi khoảng xác định.
Bài toán 13. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
A.
1
1
x
y
x
. B.
2 1
1
x
y
x
. C.
2
1
1
x x
y
x
D.
2
2 1
1
x x
y
x
Lời giải
Đồ thị hàm số có tiệm cận xiên
y x
nên
2
1
1
x x
y
x
.
13
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ THÔNG QUA ĐỒ THỊ
_____________________________________
Bài toán 1. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A.
0, 0, 0, 0
a b c d
B.
0, 0, 0, 0
a b c d
C.
0, 0, 0, 0
a b c d
D.
0, 0, 0, 0
a b c d
Lời giải
- Dựa vào hình dáng của đồ thị suy ra hệ số
0
a
.
- Đồ thị cắt trục
Oy
tại điểm có tung độ âm nên
0
d
.
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình
2
3 2 0
y ax bx c
có 2 nghiệm
1 2
,x x
trái dấu kéo theo
3 . 0 0a c c
.
- Mặt khác
1 2
0 0
2 3
x x b
b
a
.
Bài toán 2. Đồ thị của hàm số
2
1
x a
y
x
dưới đây có dạng như đường cong trong hình vẽ bên. Khi đó
A.
0
a
B.
1
a
C.
2
a
D.
1
a
Lời giải
Đồ thị hàm số đi qua gốc tọa độ nên
0a
.
Bài toán 3. Hình vẽ bên là đồ thị hàm số
ax b
y
cx d
.
.
Mệnh đề nào dưới đây đúng?
A.
0
ad
và
0
bd
. B.
0
ad
và
0
ab
. C.
0
bd
và
0
ab
. D.
0
ad
và
0
ab
.
Lời giải
14
Đồ thị hàm số giao với trục
Ox
tại điểm có hoành độ
b
x
a
, giao với
Oy
tại điểm có tung độ
b
y
d
.
Dựa vào hình vẽ ta có
0 0
0
0
0
0 0
b b
ab
a a
ad
b b bd
d d
.
Trong các phương án chỉ có phương án B thỏa mãn.
Bài toán 4. Cho hàm số
3 2
y ax bx cx d
có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào
đúng?
A.
0, 0, 0
ab bc cd
B.
0, 0, 0
ab bc cd
C.
0, 0, 0
ab bc cd
D.
0, 0, 0
ab bc cd
Lời giải
Từ dáng điệu của đồ thị ta có ngay được:
lim ; lim 0
x x
y y a
 

.
Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên
0
d
.
Ta có:
2
' 3 2
y ax bx c
Mặt khác dựa vào đồ thị ta thấy phương trình
' 0
y
có hai nghiệm trái dấu và tổng hai nghiệm này luôn dương
nên
0
0
2
0
3
ac
c
b
b
a
(do
0
a
). Do đó:
0, , 0
ab bc cd
.
Bài toán 5. Cho hàm số
ax b
y
cx d
có đồ thị như trong hình bên dưới. Biết rằng
a
là số thực dương, hỏi trong
các số
, ,b c d
có tất cả bao nhiêu số dương?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Nhìn vào đồ thị ta thấy
tiệm cận ngang
a
y
c
nằm trên trục hoành nên
0
c
(vì
0
a
)
tiệm cận đứng
d
x
c
nằm bên trái trục tung nên
0.
d
c
Suy ra
0
d
(vì
0
c
)
giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên
0.
b
d
Suy ra
0
b
(vì
0
d
). Vậy
0, 0
c d
Bài toán 6. Cho hàm số
6
ax
f x
bx c
, ,
a b c
có bảng biến thiên như sau:
15
Trong các số
, ,a b c
có bao nhiêu số âm?
A.
0
. B.
3
. C.
1
. D.
2
.
Lời giải
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là đường thẳng
2
x
và tiệm cận ngang là đường thẳng
1
y
.
Suy ra
2
1
c
b
a
b
0
0
bc
ab
1
0, 0, 0
2
0, 0, 0
b c a
b c a
Lại có hàm số nghịch biến trên mỗi khoảng xác định
2
6
0
ac b
f x
bx c
6ac b
.
Ta thấy
1
không thể xảy ra do nếu
0
b
thì
6 0
ac b
; và
2
có thể xảy ra do nếu
0, 0
c a
thì
6 0
b ac
. Vậy trong các số
, ,a b c
có hai số âm.
Bài toán 7. Đồ thị trong hình bên dưới là của hàm số
ax b
y
x c
(với
, ,a b c
).
Khi đó tổng
a b c
bằng
A.
1
. B.
1
. C.
2
. D.
0
.
Lời giải
Đồ thị hàm số
ax b
y
x c
có đường tiệm cận ngang
y a
, đường tiệm cận đứng
x c
và cắt
Oy
tại điểm
0;
b
c
. Từ đồ thị hàm số ta có đường tiệm cận ngang
1
y
, đường tiệm cận đứng
1x
và cắt
Oy
tại điểm
0; 2
. Từ đó suy ra:
1 1 1
1 1 1
2 2
2
a a a
c c c
b b c b
c
. Vậy
1 1 2 0
a b c
.
Bài toán 8. Hàm số
2
1
x ax b
y
x
có đồ thị như hình vẽ bên. Tính giá trị
2 3a b
.
16
A.4 B. 5 C. 2 D. 1
Lời giải
Theo đồ thị ta thấy
0; 2
2 2
2 3 4
4 4 2 1
2;4
A C
b b
a b
a b a
B C
.
Bài toán 9. Hàm số
2
1
x ax b
f x
x
có đồ thị như hình vẽ bên. Xác định góc tạo bởi đường tiệm cận xiên của
đồ thị hàm số
1
f x
và trục tung.
A.
45
B.
60
C.
30
D.
20
Lời giải
Theo đồ thị ta thấy
0; 2
2 2
2 3 4
4 4 2 1
2;4
A C
b b
a b
a b a
B C
.
Khi đó
2
2 2 2
1 1
1 1
x x
y x f x x
x x x
.
Đường tiệm cận xiên
1y x
, đường này tạo với trục tung một góc
45
.
Bài toán 10. Cho hàm số
, ,
1
ax b
y a b c
cx
có bảng biến thiên như sau:
Tập các giá trị
b
là tập nghiệm của bất phương trình nào dưới đây?
A.
3
8 0.
b
B.
2
4 0.
b
C.
2
3 2 0.
b b
D.
3
8 0.
b
Lời giải
Đồ thị hàm số
1
ax b
y
cx
có đường tiệm cận đứng là đường thẳng
1
x
c
và đường tiệm cận ngang là đường
thẳng
a
y
c
.
Nhìn vào bảng biến thiên, ta thấy
1
1 1c
c
và
2 2
a
a
c
(vì
1c
).
Ta có
2
1
a bc
y
cx
.
Vì hàm số đã cho đồng biến trên các khoảng
; 1
và
1;

nên
3 3
2
0 0 2 0 2 8 8 0
a bc
y a bc b b b b
bx c
.
Vậy tập các giá trị
b
là tập nghiệm của bất phương trình
3
8 0.
b
17
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ
BÀI TOÁN ĐỒ THỊ HÀM SỐ CHỨA THAM SỐ
_____________________________________
Bài toán 1. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ . Gọi
S
là tập hợp tất cả các giá trị
nguyên của tham số
m
để phương trình
sin 3sin
f x x m
có nghiệm thuộc khoảng
0;
. Tổng các phần
tử của
S
bằng.
A.
9
. B.
10
. C.
6
. D.
5
.
Lời giải
Dựa vào đồ thị hàm số ta có
3 2
3 1 ; 3 3
f x x x f x x
.
Đặt
sin 1 1
u x u
. Xét hàm số
sin 1 1
u x u
.
cos ; 0 , 0;
2 2
u x u x k do x gt x
Bảng biến thiên :
Suy ra
0; 0;1 0 1x u u
.
Vậy dựa vào bảng biến thiến ta có với mỗi
0;1 :sin
u pt x u
có 2 nghiệm
0;
x
Và
1 sin 1u x u
có một nghiệm kép
2
x
.
Khi đó phương trình
sin 3sin 3 3
f x x m f u u m f u u m
Xét hàm số :
3g x f x x
2
3; 0 3 3 3 3 2
g x f x g x f x x x
.
Bảng biến thiên
x

2
0 1
2
g x
0
|
|
0
g x

1 4 2
1 -4

1 4 2
Dựa vào bảng biến thiên ta có với
0;1
x
thì phương trình
3
f x x m
có nghiệm khi :
1 0 4 1 4; 3; 2; 1;0
g m g m m
tổng các giá trị của
:10
m
.
18
Bài toán 2. Cho hàm số
y f x
. Đồ thị hàm
y f x
như hình vẽ
Đặt
3
3 3
g x f x x x m
, với
m
là tham số thực. Điều kiện cần và đủ để bất phương trình
0
g x
đúng với
3; 3
x
là
A.
3 3
m f
. B.
3 0
m f
. C.
3 1m f
. D.
3 3
m f
.
Lời giải
3 3
0 3 3 0 3 3
g x f x x x m f x x x m
.
Đặt
3
3 3h x f x x x
. Ta có
2
3 3 3
h x f x x
. Suy ra
3 3 3 6 0
3 3 3 6 0
0 3 0 0
1 3 1 0
h f
h f
h f
h f
Từ đó ta có bảng biến thiên
Vậy
3 3 3
g x m g x h f
.
Bài toán 3. Cho hàm số
y f x
có đồ thị như hình vẽ
Có bao nhiêu số nguyên
m
để phương trình
3
2 6 2
f x x m
có 6 nghiệm phân biệt thuộc đoạn
1; 2
?
A.
1
. B.
0
. C.
2
. D.
3
.
Lời giải
Xét hàm số
3
2 6 2
g x x x
trên đoạn
1; 2
.
x
3
0
1
3
h
0
h
3
h
0
h
3
h
19
2
1
6 6 0
1
x
g x x
x
Ta có bảng biến thiên như sau
Đặt
3
2 6 2
t x x
, với
1; 2
x
thì
2;6
t
.
Dựa vào bảng biến thiên, ta có nhận xét với mỗi giá trị
0
2;6
t
thì phương trình
3
0
2 6 2
t x x
có hai
nghiệm phân biệt
1; 2
x
và tại
0
2
t
thì phương trình
3
0
2 6 2
t x x
có một nghiệm duy nhất.
Với nhận xét trên và đồ thị hàm số trên đoạn
2;6
thì phương trình
3
2 6 2
f x x m
có 6 nghiệm phân
biệt thuộc đoạn
1; 2
khi và chỉ khi phương trình
f t m
có 3 nghiệm phân biệt trên nửa khoảng
2;6
.
Bài toán 4. Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2 sin
2
m
f x f
có đúng 12 nghiệm phân biệt
thuộc đoạn
;2
?
A.
3.
B.
4.
C.
2.
D.
5.
Lời giải
Ta có bảng biến thiên của hàm số
2 siny g x x
trên đoạn
;2
Phương trình
2 sin
2
m
f x f
có đúng 12 nghiệm phân biệt thuộc đoạn
;2
khi và chỉ khi phương
trình
2
m
f t f
có 2 nghiệm phân biệt
0;2
t
.
Dựa vào đồ thị hàm số
y f x
suy ra phương trình
2
m
f t f
có 2 nghiệm phân biệt
0;2
t
khi và chỉ
20
khi
27
0
16 2
m
f
0 2
0 4
2
3 3
2 2
m
m
m m
.
Do
m
nguyên nên
1;2
m
. Vậy có 2 giá trị của
m
thoả mãn bài toán.
Bài toán 5. Cho hàm hàm số
y f x
có bảng biến thiên như hình vẽ dưới
Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
1
f x m
có
6
nghiệm phân biệt.
A.
12
. B.
198
. C.
6
. D.
190
.
Lời giải
Đặt
2
1
t x
, điều kiện
1t
, từ đó phương trình trở thành
f t m
,
1t
.
Do
1t
nên ta xét bảng biến thiên của hàm
y f t
trên
1;

như sau:
Bảng biến thiên của hàm số
y f t
trên
1;

là
Cứ mỗi nghiệm
1t
cho được hai nghiệm
x
, do vậy để phương trình
2
1
f x m
có
6
nghiệm phân biệt thì
phương trình
f t m
cần có
3
nghiệm
1t
. Dựa bảng biến thiên của hàm
y f t
ở trên ta có điều kiện
3 10
m
, mặt khác
m
nguyên nên
4;5;6;7;8;9
m
.
Vậy có
6
giá trị nguyên
m
thỏa mãn bài toán.
Bài toán 6. Cho hàm số
( )y f x
xác định trên
\ 0
và có bảng biến thiên như hình vẽ. Số giá trị nguyên
của
m
để phương trình
2 3 0
f x m
có đúng
2
nghiệm phân biệt là
A. 2. B. 1. C. 4. D. 3.
| 1/62
| | Tải xuống

Có thể bạn quan tâm:

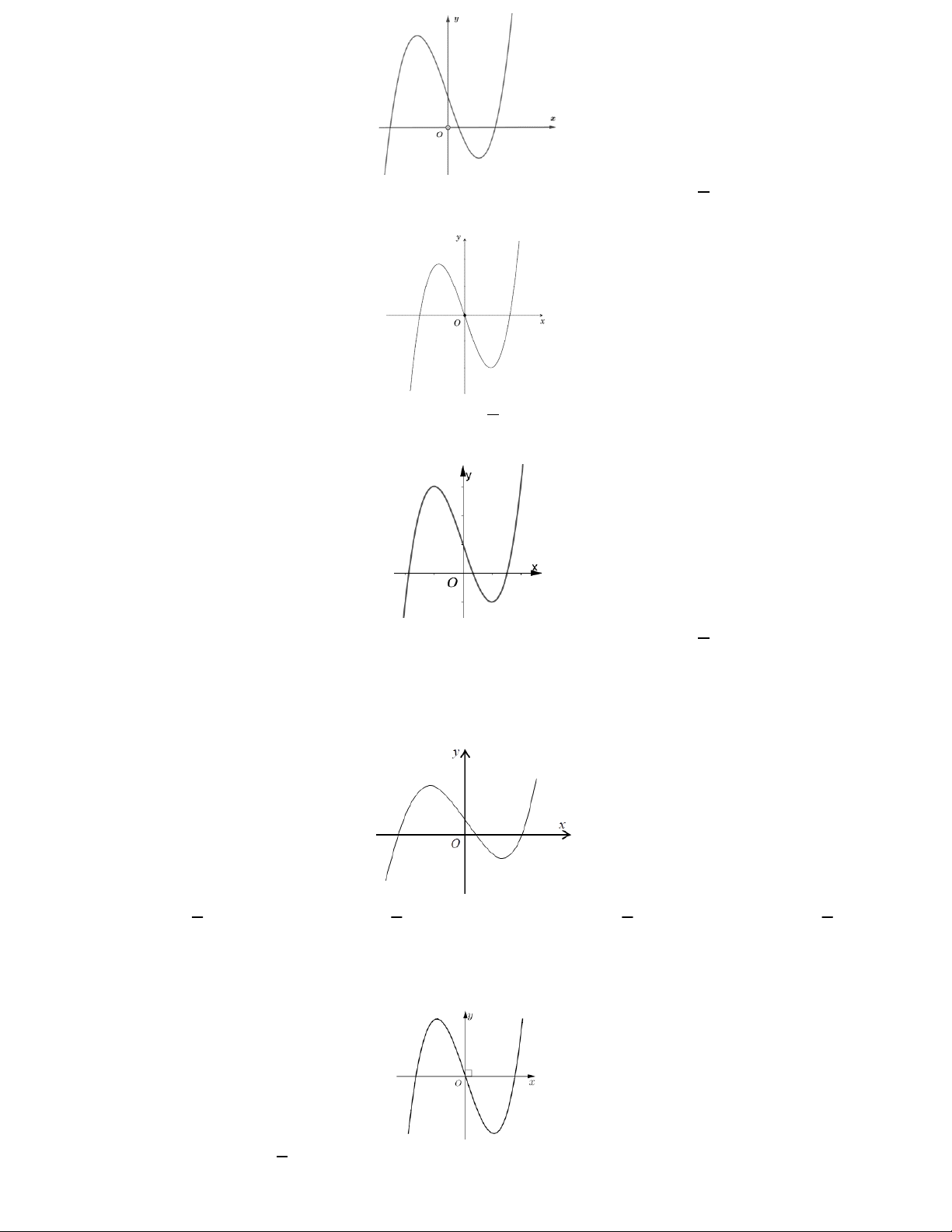
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________
------------------------------------------------------------------------------------------
ÔN KIẾN THỨC TOÁN 12 THPT BÀI GIẢNG
ĐỒ THỊ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 7/2024 1
ÔN KIẾN THỨC TOÁN 12 THPT
ĐỒ THỊ, BẢNG BIẾN THIÊN CỦA HÀM SỐ
__________________________ DUNG NỘI DUNG LƯỢNG 1 FILE
NHẬN DIỆN ĐỒ THỊ CÁC HÀM SỐ THƯỜNG GẶP 1 FILE
XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ THÔNG QUA ĐỒ THỊ 1 FILE
CÁC BÀI TOÁN CHỨA THAM SỐ 2
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
LÝ THUYẾT KHẢO SÁT ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
I. SƠ ĐỒ KHẢO SÁT HÀM SỐ
Sơ đồ khảo sát hàm số y f (x) :
1. Tìm tập xác định của hàm số.
2. Xét sự biến thiên của hàm số:
- Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận (nếu có). - Tính đạo hàm 
y . Tìm các điểm mà tại đó  y bằng 0.
- Lập bảng biến thiên; xác định chiều biến thiên, cực trị của hàm số(nếu có). 3. Vẽ đồ thị hàm số
- Vẽ các đường tiệm cận (nếu có).
- Xác định các điểm đặc biệt của đồ thị: cực trị, giao điểm của đồ thị với các trục tọa độ ( trong trường hợp đơn giản),…
- Nhận xét về đặc điểm của đồ thị: chỉ ra tâm đối xứng, trục đối xứng (nếu có).
Chú ý. Đồ thị hàm số y f (x) giao với trục hoành tại những điểm có hoành độ là nghiệm của phương trình
f (x)  0 , giao với trục tung tại điểm có tung độ là f (0) nếu 0 thuộc tập xác định của hàm số đó.
II. KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ ĐA THỨC BẬC BA
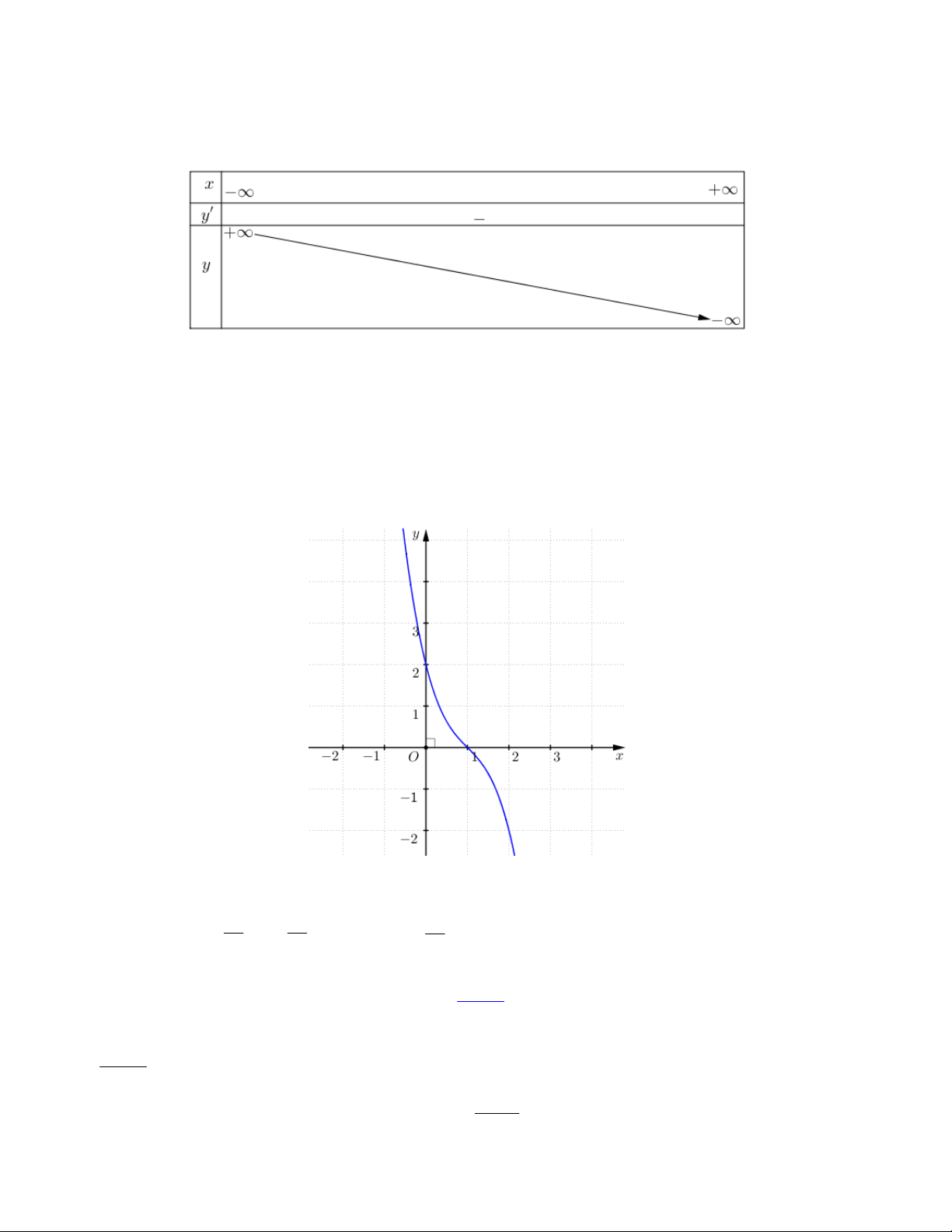
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số 3 2
y x  3x  4 . 1) Tập xác định:  . 2) Sự biến thiên
- Giới hạn tại vô cực: lim y  , lim y   . x x -  2
y  3x  6x ,  2
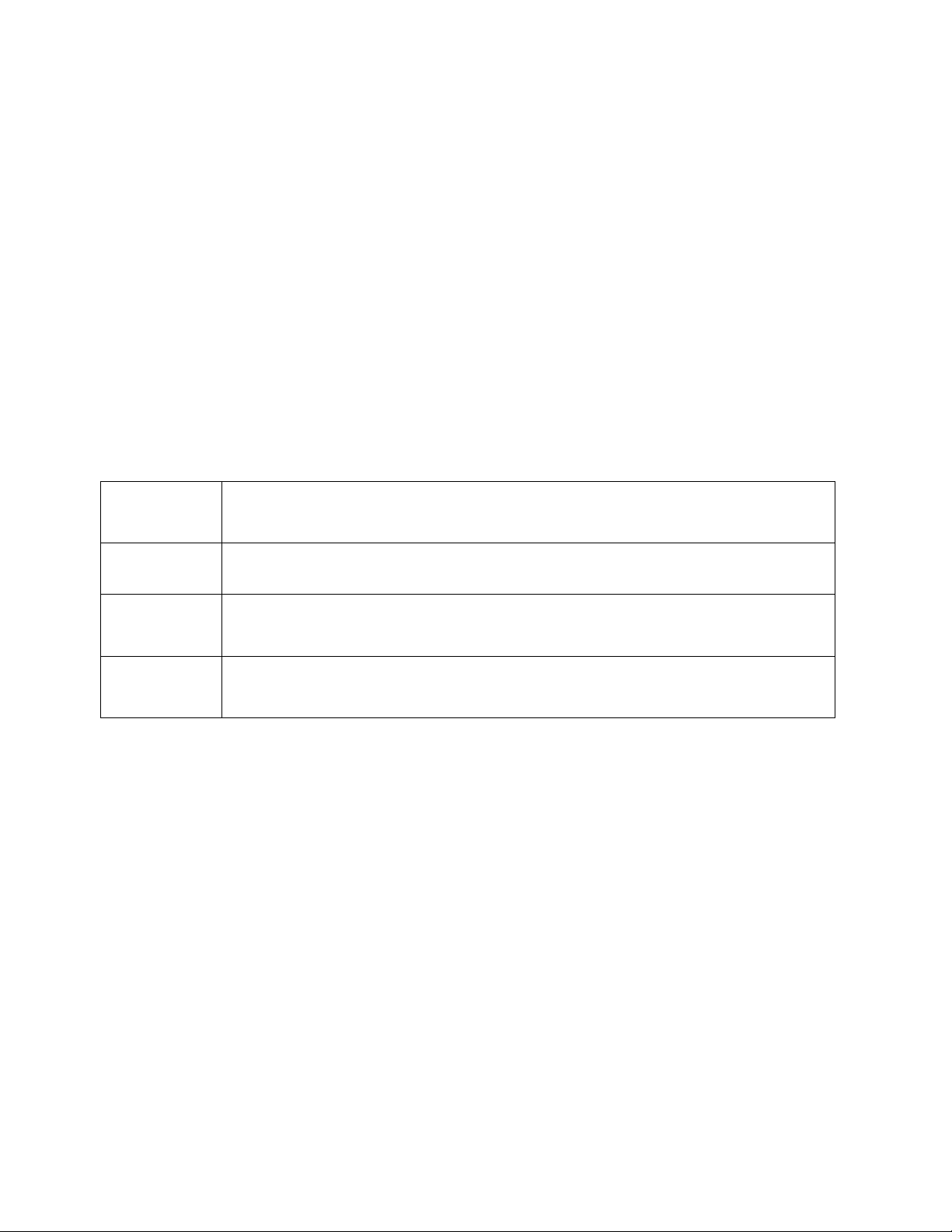
y  0  3x  6x  0  x  0 hoặc x  2 . - Bảng biến thiên:
Hàm số đồng biến trên mỗi khoảng ( ;
 0) và (2; ) , nghịch biến trên khoảng (0; 2) .
Hàm số đạt cực đại tại x  0, y
 4 ; hàm số đạt cực tiểu tại x  2, y  0 . CĐ CT 3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; 4) .
- Giao điểm của đồ thị với trục hoành: Xét phương trình 3 2 2
x  3x  4  0  (x 1)(x  2)  0  x  1   x  2.
Vậy đồ thị hàm số giao với trục hoành tại hai điểm (1; 0) và (2;0) .
- Đồ thị hàm số đi qua các điểm ( 1
 ; 0), (2; 0), (0; 4) và (1; 2) . Vậy đồ thị hàm số 3 2
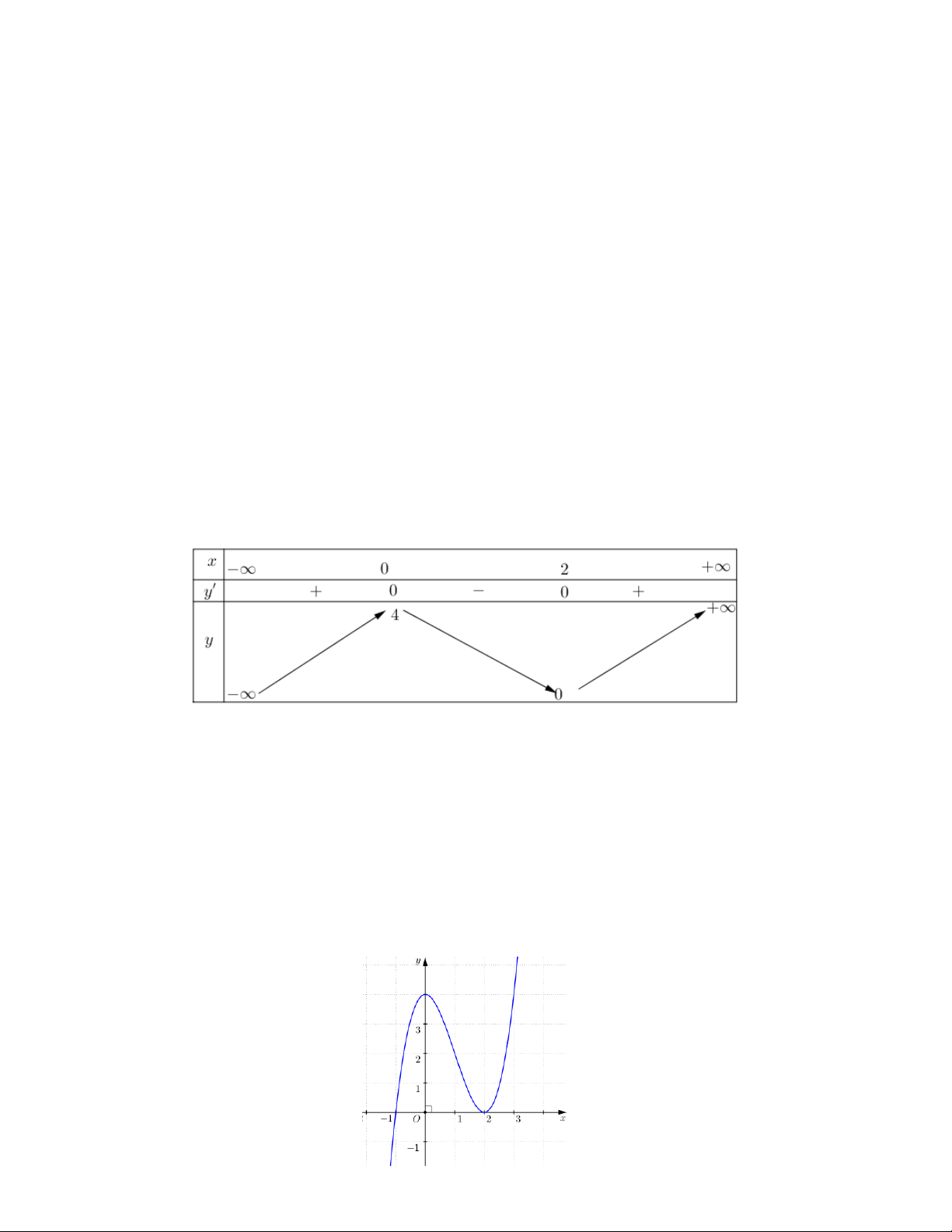
y x  3x  4 được cho ở Hình.
Quan sát đồ thị ở Hình, ta thấy đồ thị đó có tâm đối xứng là điểm I (1; 2) . 3
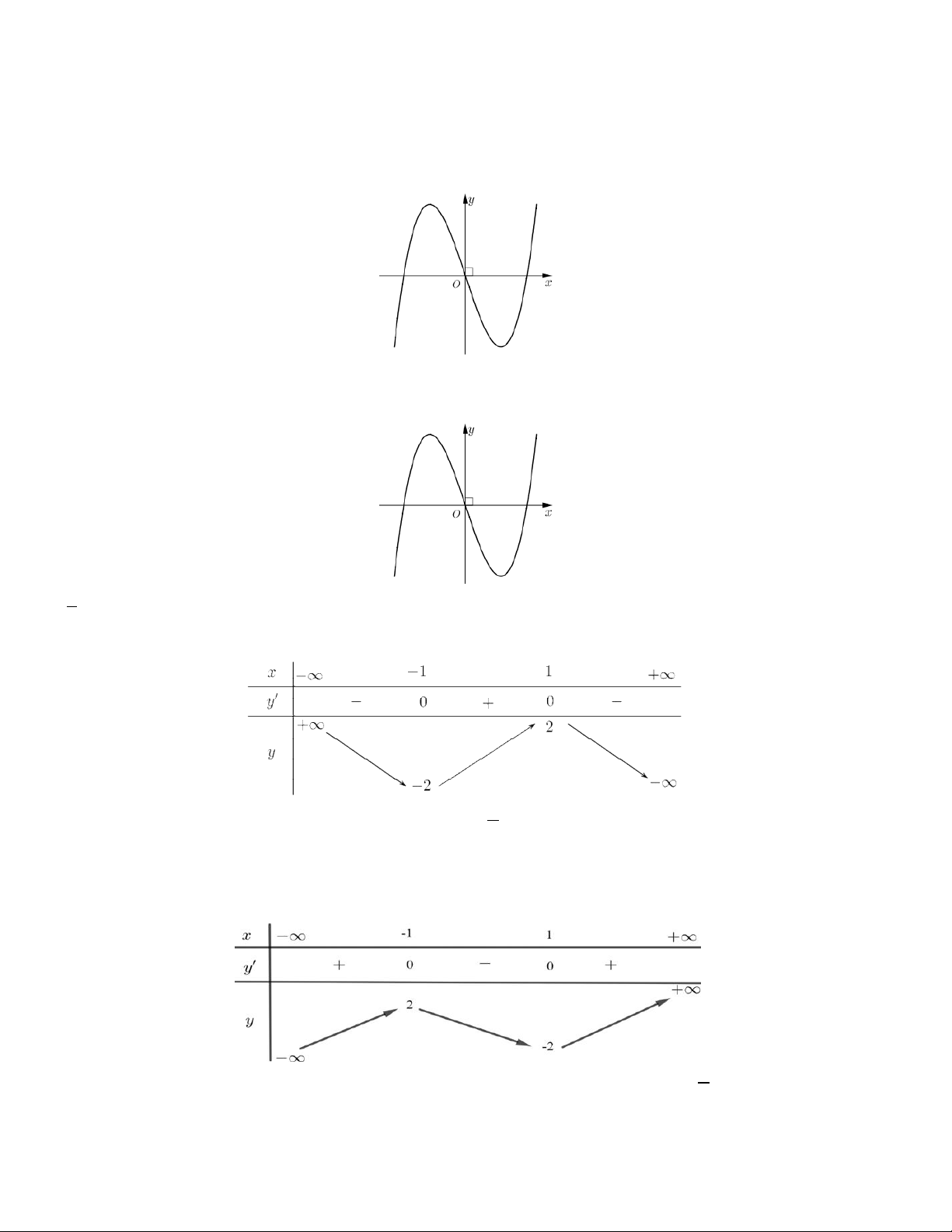
Ví dụ 2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số 3 2
y  x  3x  4x  2 . 1) Tập xác định:  . 2) Sự biến thiên
- Giới hạn tại vô cực: lim y  , lim y   . x x -  2 y  3
x  6x  4 ; y  0 , x  .  - Bảng biến thiên:
Hàm số nghịch biến trên khoảng (; ) .
Hàm số không có cực trị. 3) Đồ thị
- Giao điểm của đổ thị với trục tung: (0; 2) .
- Giao điểm của đồ thị với trục hoành: Giải phương trình 3 2
x  3x  4x  2  0 ta được x  1. Vậy đồ thị hàm số giao với trục hoành tại điểm (1; 0) .
- Đồ thị hàm số đi qua các điểm (1; 0), (0; 2), (2; 2) . Vậy đồ thị hàm số 3 2
y  x  3x  4x  2 được cho ở hình
Tâm đối xứng của đồ thị hàm số đó là điểm I (1; 0) .
Nhận xét: Trong trường hợp tổng quát, đồ thị của hàm số bậc ba 3 2
y f (x)  ax bx cx d (a  0) có tâm  bb  b
đối xứng là điểm I  ; f      . Hoành độ 
của tâm đối xứng đó là nghiệm của phương trình y  0 . 3a   3a   3a
III KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA MỘT SỐ HÀM PHÂN THỨC HỮU TỈ ax b
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y  (c  ,
0 ad bc  0) cx d
Sử dụng sơ đồ khảo sát hàm số, ta có thể khảo sát sự biến thiên và vẽ đồ thị hàm số ax b y  (c  , 0 ad bc  )
0 . Ta sẽ tìm hiểu qua một số ví dụ sau đây. cx d 2x 1
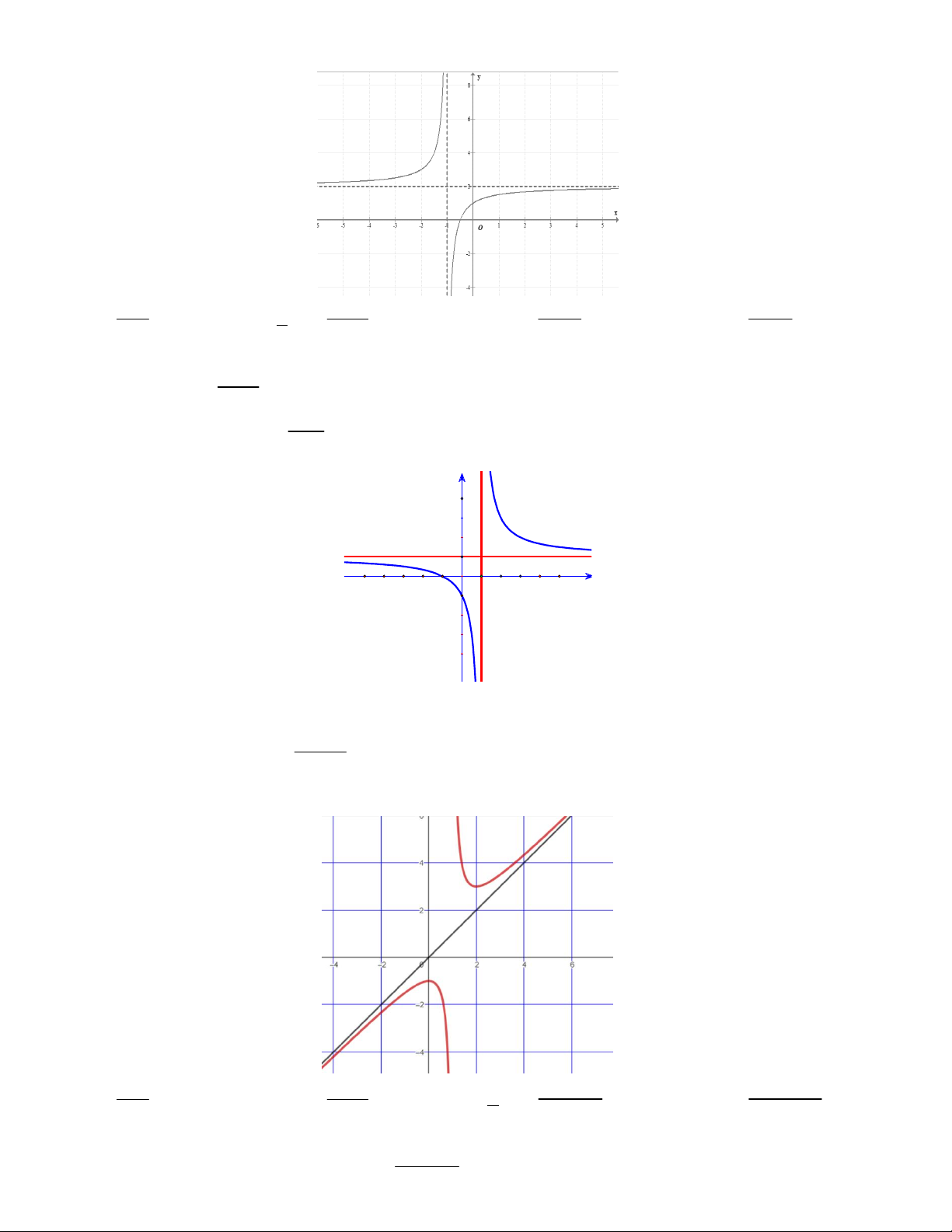
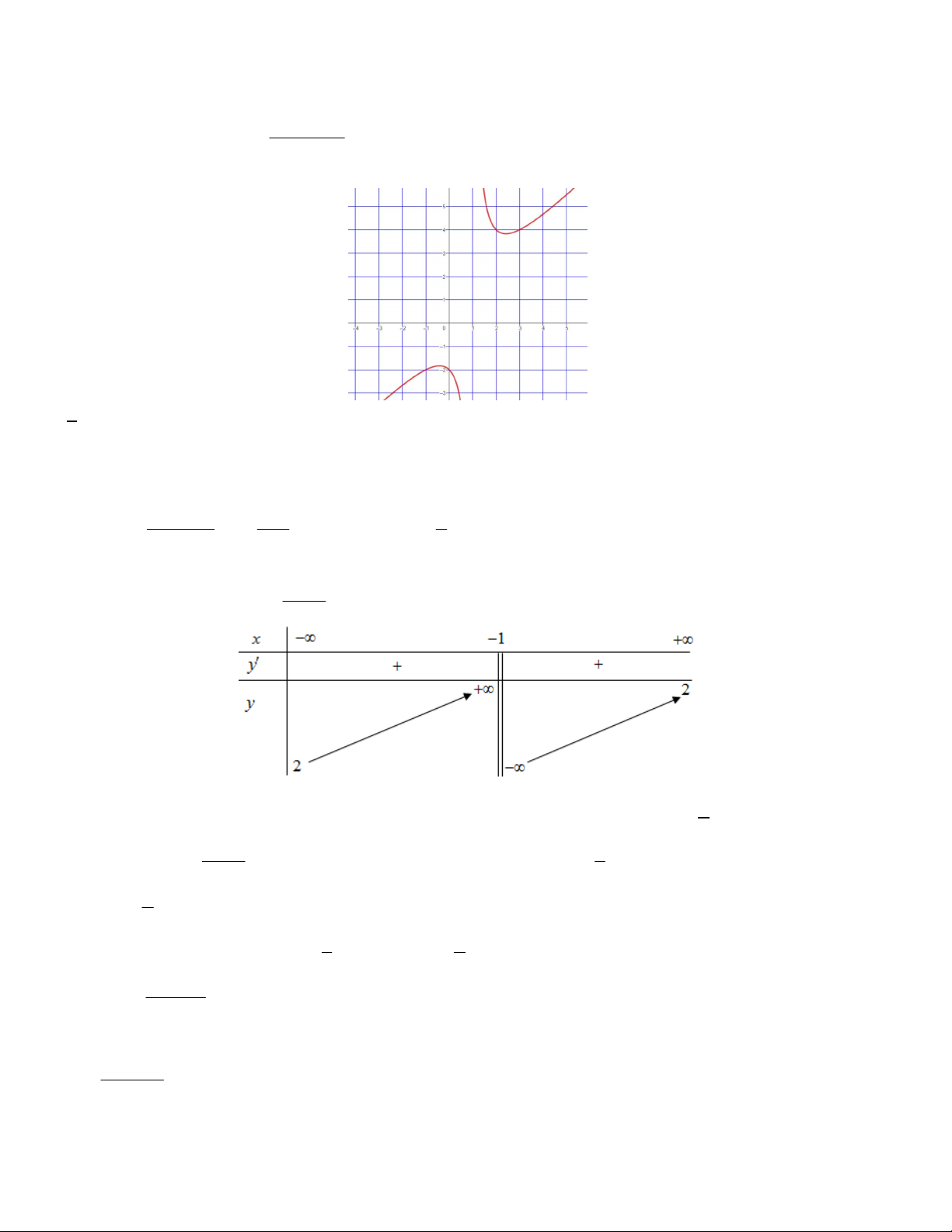
Ví dụ 3. Khảo sát sự biến thiên và vẽ đồ thị hàm số y x 1
1) Tập xác định  \   1 2) Sự biến thiên 4
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận lim y   ,
 lim y   . Do đó, đường thẳng x  1 là tiệm cận đứng của đồ thị hàm số   x1 x1 lim y  ,
2 lim y  2 Do đó, đường thẳng y  2 là tiệm cận ngang của đồ thị hàm số x x 3 y ' 
 0 với mọi x  1  2 x   1 Bảng biến thiên
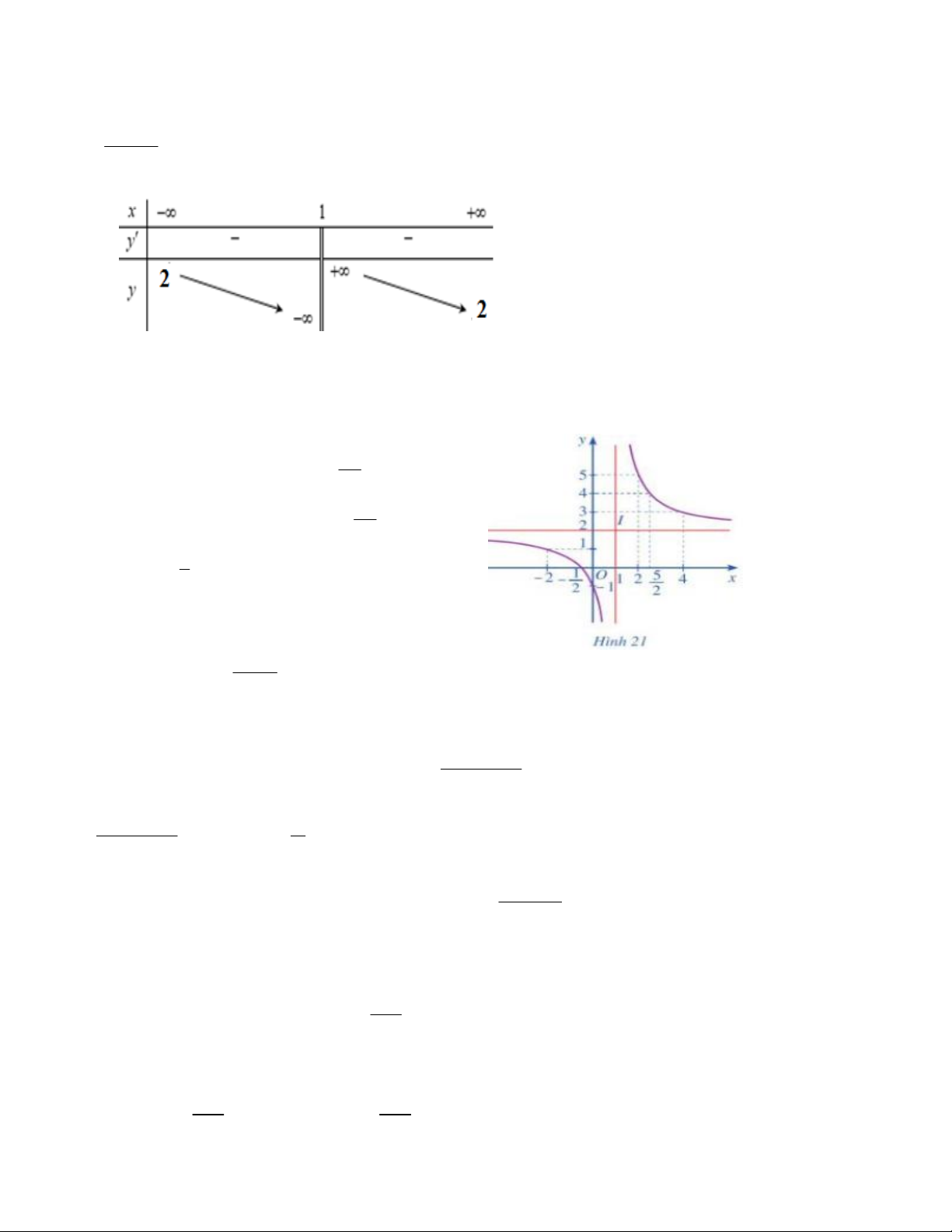
Hàm số nghịch biến tên mỗi khoảng  ;   1 và  ; 1 .
Hàm số không có cực trị. 3) Đồ thị
Giao điểm của đồ thị với trục tung: 0;  1 1 
Giao điểm của đồ thị với trục hoành:  ;    0  2  1 
Đồ thị hàm số đi qua các điểm0;  1 , ;    0  2  5  2;  1 ,2;  5 , ;  4 ,4;    3 2  2x 1
Vậy đồ thị hàm số y  được cho ở hình 21. x 1
Quan sát đồ thị ở Hình 21, đồ thị đó nhận giao điểm I 1; 
2 của hai tiệm cận của đồ thị hàm số làm tâm đối
xứng và nhận hai đường phân giác của góc tạo bởi hai tiệm cận đó làm trục đối xứng. 2
ax bx c
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y
a  0;m  0 mx n
Sử dụng sơ đồ khảo sát hàm số ta có thể khảo sát sự biến thiên và vẽ đồ thị của hàm số 2
ax bx c n y
(a  0; m  0; 
không là nghiệm của đa thức 2
ax bx c ). Ta sẽ tìm hiểu qua một số ví dụ mx n m sau đây. 2 x x 1
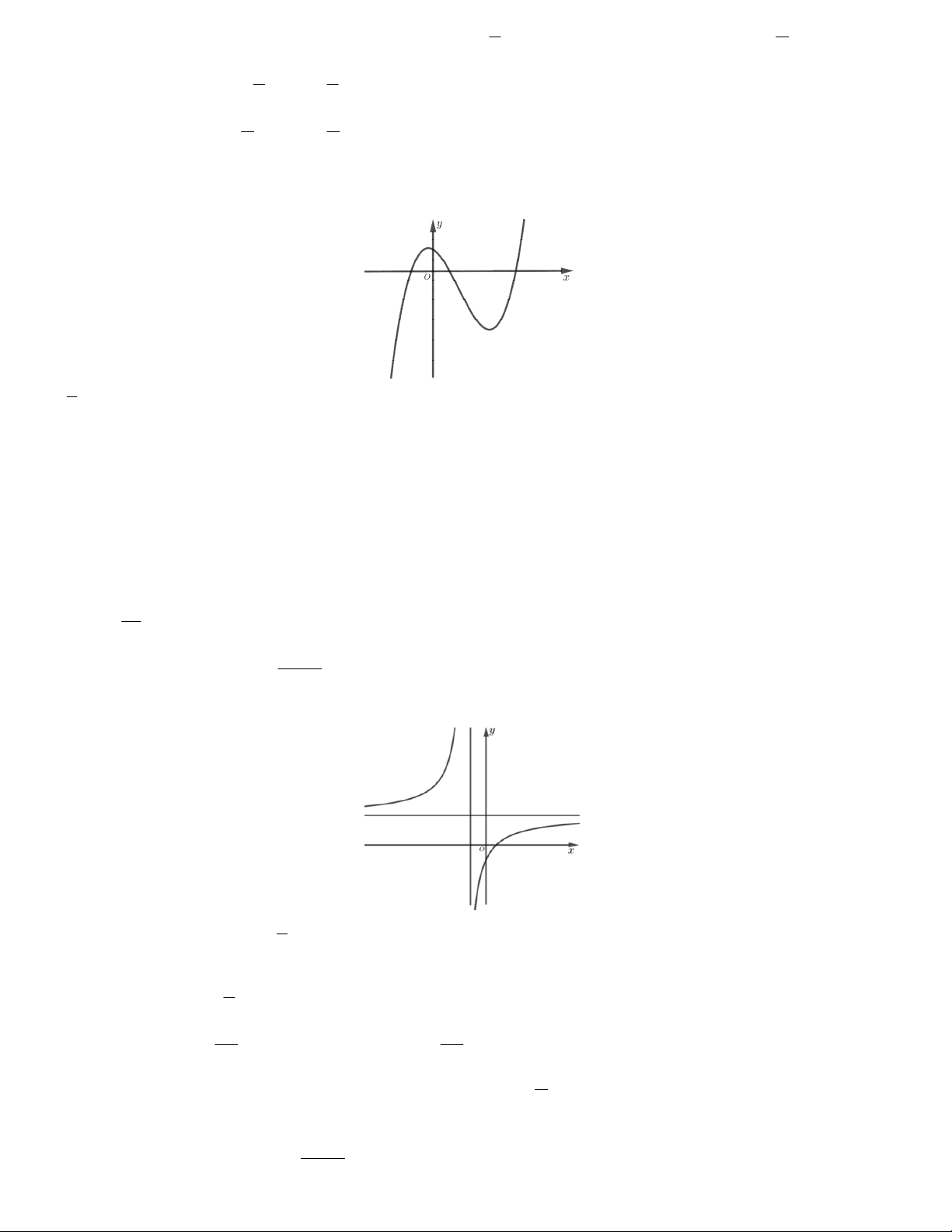
Ví dụ 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số y x 1
Tập xác định :  \   1 Sự biến thiên
Giới hạn tại vô cực và các đường tiệm cận: 1
Ta viết hàm số đã cho dưới dạng : y x x 1
lim y   lim y   lim y   lim y   x x x 1  x 1 
Do đó đường thảng x 1 là tiệm cận đứng của đồ thị hàm số. 1 1
lim ( y x)  lim
 0, lim ( y x)  lim  0 . x
x x 1 x
x x 1
Do đó đường thẳng y x là tiệm cận xiên của đồ thị hàm số. 5 2 x  2xx  0 Ta có y '  ; 2
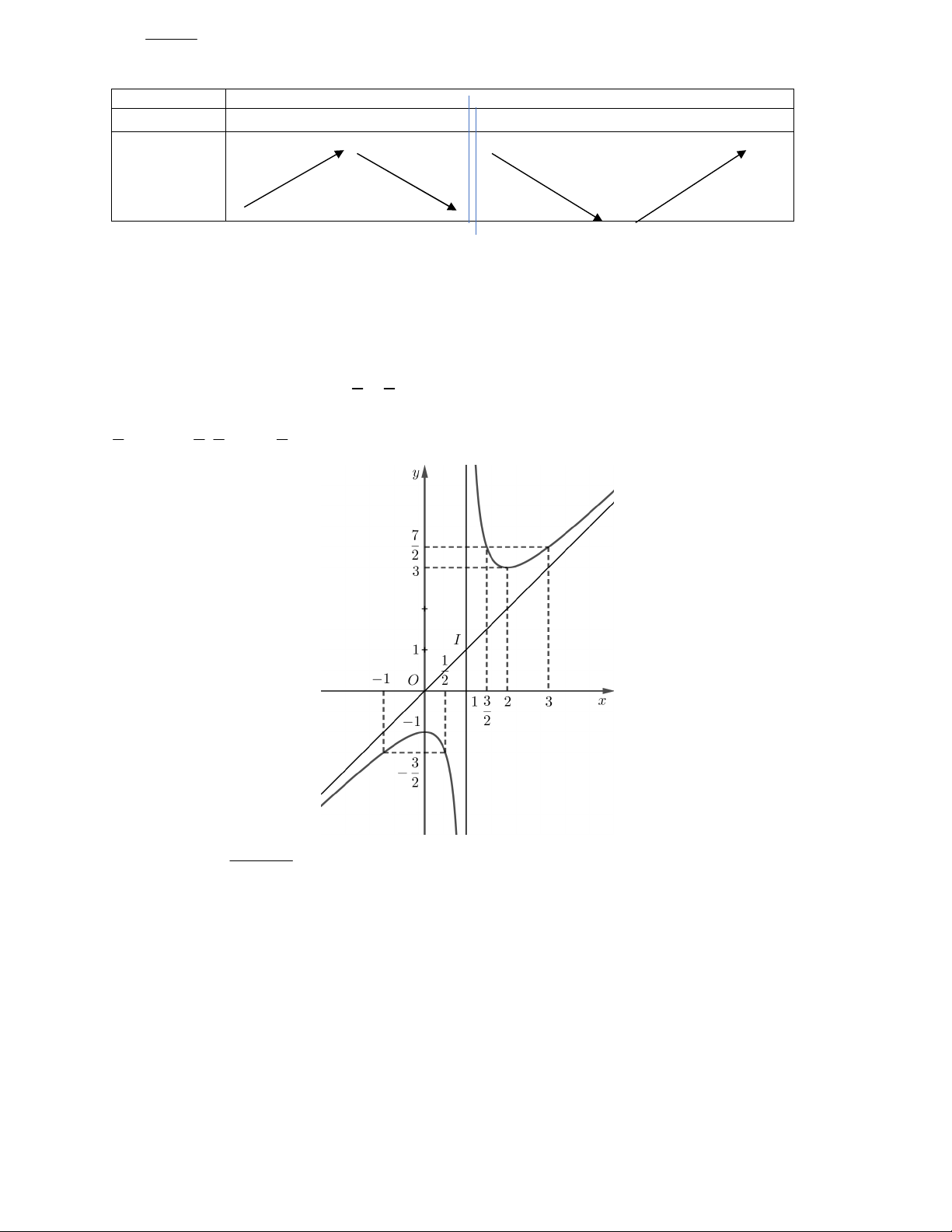
y '  0  x  2x  0    x  2 1 x  2  Bảng biến thiên x  0 1 2  y ' + 0 - y 1    3 
Hàm số đồng biến trên mỗi khoảng  ;
 0 và 2;   ; nghịch biến trên mỗi khoảng 0  ;1 và 1;2
Hàm số đạt cực đại tại x  0; y
 1; đạt cực tiểu tại x  2; y  3 . CÐ CT Đồ thị
Giao điểm của đồ thị với trục tung: 0;  1  .
Đồ thị hàm số không cắt trục hoành.  1 3 
Đồ thị hàm số đi qua các điểm 0;   1 , ;  .    2 2   3   3 7   7  1  ;  ,   2;  3 , ; và 3; .      2   2 2   2  2 x x 1
Vậy đồ thị hàm số y  được cho ở Hình 23. x 1
Quan sát đồ thị ở Hình 23, đồ thị đó nhận giao điểm I 1;  1
của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận
hai đường phân giác của các góc tạo bởi hai đường tiệm cận
đó làm trục đối xứng. 6
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
NHẬN DIỆN CÁC ĐỒ THỊ HÀM SỐ THƯỜNG GẶP
_____________________________________
NHẬN DIỆN ĐỒ THỊ HÀM SỐ ĐA THỨC
Bài toán 1. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Hệ số a không thể bằng A.3 B. 2 C. 1 D. – 4
Lời giải. Đồ thị của hàm số   3 2
f x ax bx cx d với a  0 nên a không thể bằng – 4.
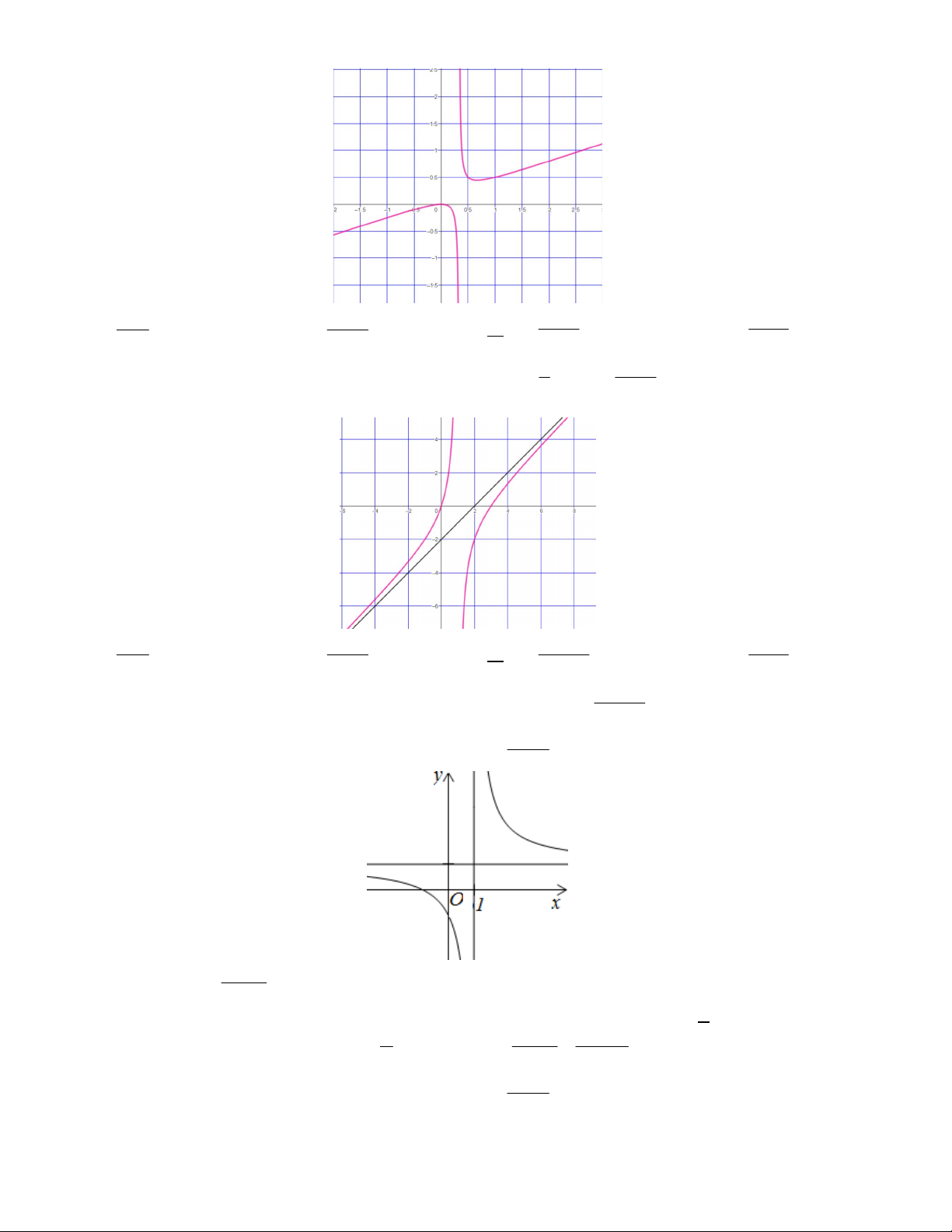
Bài toán 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y x  3x . B. 3
y  x  3x . C. 4 2
y x  2x . D. 4 2
y  x  2x .
Lời giải. Đồ thị của hàm số bậc ba với a  0 nên 3
y x  3x .
Bài toán 3. Hàm số nào dưới đây có bảng biến thiên như sau? A. 3
y x  3x . B. 2
y x  2x . C. 3
y  x  3x . D. 2
y  x  2x . Lời giải
Dựa vào bảng biến thiên trên, ta nhận thấy đây là hàm số bậc ba có dạng 3 2
y ax bx cx d với a  0 . Mà  3 2
lim ax bx cx d     a  0 . Do đó có duy nhất hàm số 3
y  x  3x thoả mãn. x
Bài toán 4. Hàm số nào dưới đây có bảng biến thiên như sau? A. 4 2
y x  2x . B. 3
y  x  3x . C. 4 2
y  x  2x . D. 3
y x  3x . Lời giải
Từ BBT ta nhận thấy hàm số có hai điểm cực trị và đồng biến trên khoảng 1;  . Do đó hàm số là hàm đa
thức bậc ba có hệ số a  0.
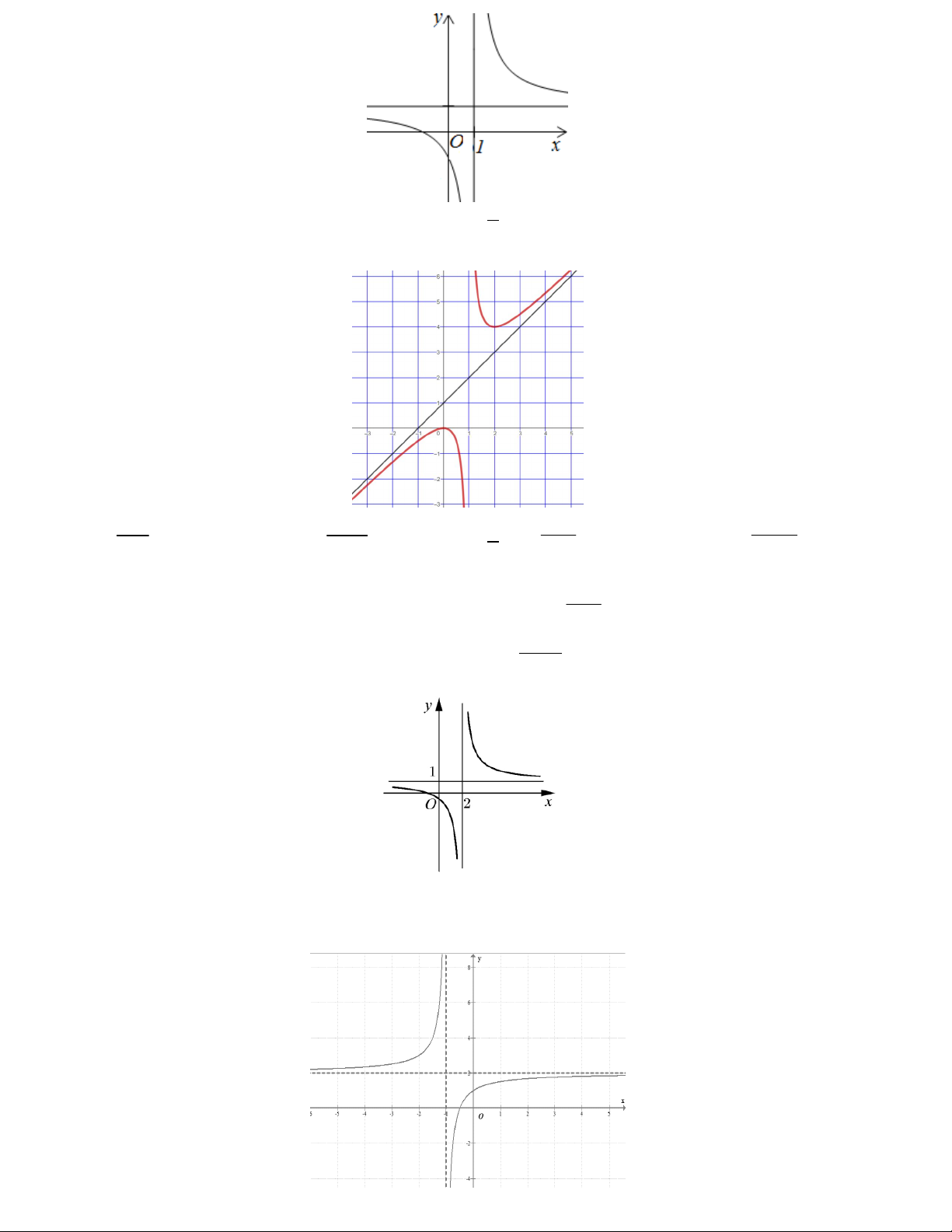
Bài toán 5. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Giá trị d không thể bằng 7 A.2 B. 3 C. 4 D. 0
Lời giải. Đồ thị hàm số không đi qua gốc tọa độ nên d  0 .
Bài toán 6. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y x  2x . B. 3
y  x  3x . C. 3
y x  3x . D. 4 2
y  x  2x .
Lời giải. Đồ thị hàm số bậc ba đi qua gốc tọa độ nên 3
y x  3x .
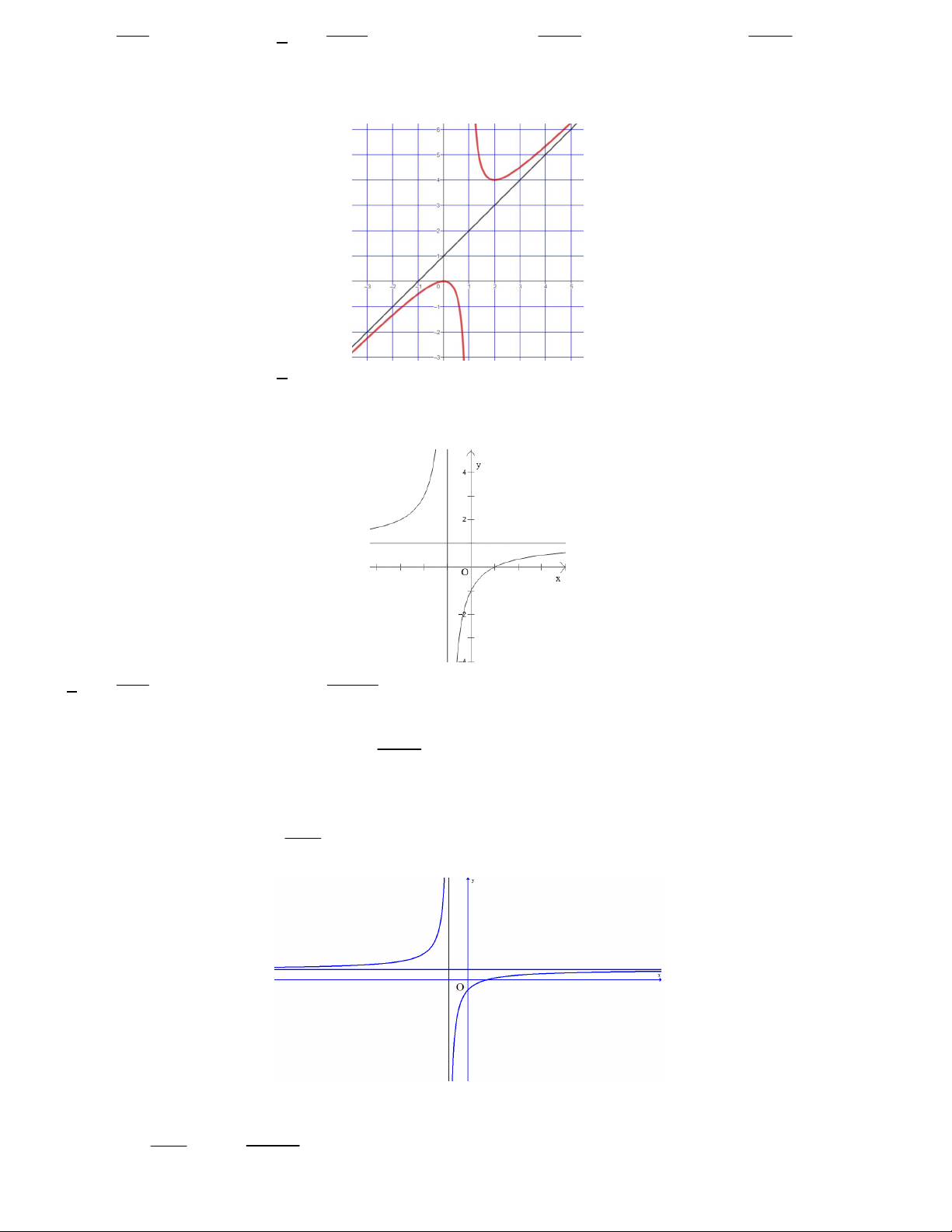
Bài toán 7. Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây? A. 3
y  x  3x 1. B. 4 2
y x x 1. C. 2
y  x x 1. D. 3
y x  3x 1. Lời giải
Đồ thị đã cho có hình dạng của đồ thị hàm số bậc ba 3 2
y ax bx cx d nên loại phương án B và C
Dựa vào đồ thị, ta có lim y    a  0 nên loại phương án A x
Bài toán 8. Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên dưới? 1 1 1 1 A. 3
y  x  2x  . B. 3
y x  2x  . C. 4 2
y  x  2x  . D. 4 2
y x  2x  . 2 2 2 2 Lời giải
Đồ thị đã cho là đồ thị hàm số bậc ba có hệ số bậc ba a  0 . Chọn B.
Bài toán 9. Đồ thị của hàm số   3 2
f x ax bx cx d có dạng như hình vẽ. Giá trị f 0 bằng A.1 B. 0 C. 2 D. 4
Lời giải. Đồ thị hàm số đi qua gốc tọa độ nên f 0  0. 8
NHẬN DIỆN ĐỒ THỊ HÀM SỐ PHÂN THỨC HỮU TỶ
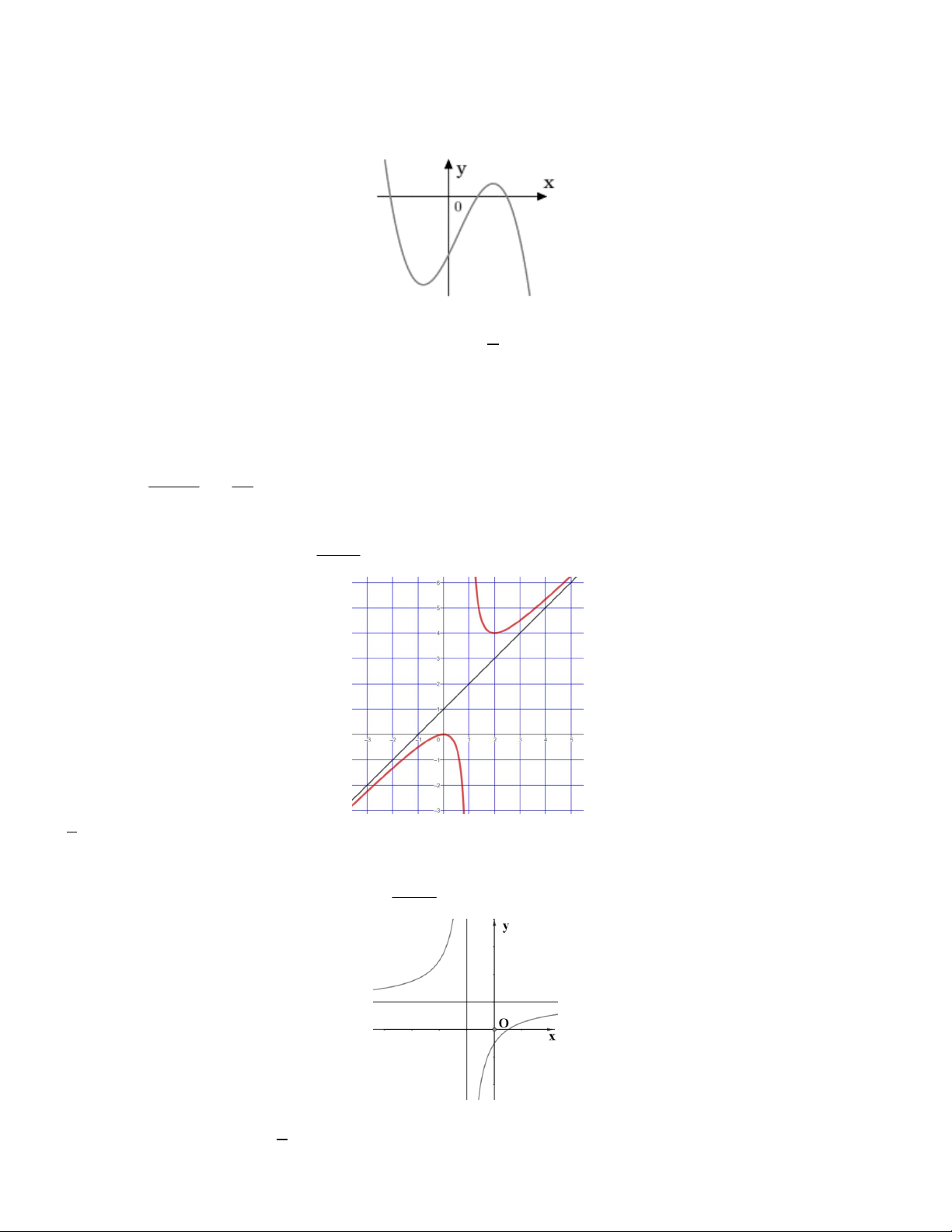
Bài toán 1. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? x 1 2x 1 2 x 2 x A. y  . B. y  . C. y  D. y x 1 x 1 2x 1 3x 1 1 2 x
Lời giải. Đồ thị hàm số bậc hai/bậc nhất và có tiệm cận đứng x  nên y  . 2 2x 1
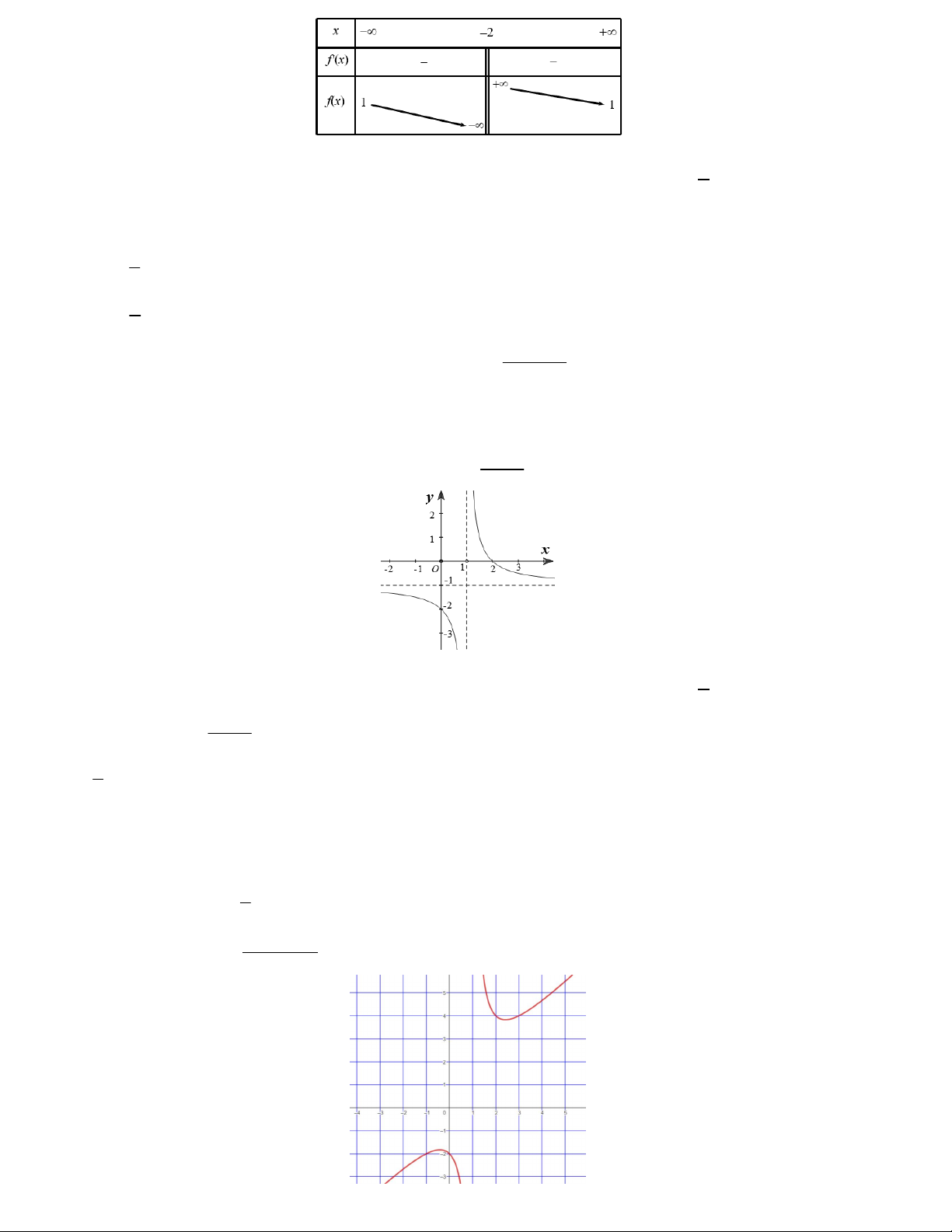
Bài toán 2. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên x 1 2x 1 2 x  3x 2 x A. y  . B. y  . C. y  D. y x 1 x 1 x 1 3x 1 2 x  3x
Lời giải. Đồ thị hàm số nhận tiệm cận xiên y x  2 như hình vẽ nên y  . x 1 ax b
Bài toán 3. Đường cong ở hình bên là đồ thị của hàm số y
với a, b,c, d là các số thực. cx d d  2c
Tính giá trị biểu thức . c A.2 B. 3 C. 4 D. 1 d d  2cc  2c
Lời giải. Đồ thị có tiệm cận đứng x  1  
 1  d  c    1. c c c ax b
Bài toán 4. Đường cong ở hình bên là đồ thị của hàm số y
với a, b,c, d là các số thực. Mệnh đề nào cx d dưới đây đúng? 9
A. y  0,x   B. 
y  0,x  1 C. 
y  0,x  1
D. y  0,x  
Lời giải. Hàm số nghịch biến và có tiệm cận đứng x  1 , suy ra 
y  0,x  1 .
Bài toán 5. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên? 2 2 x 1 2x 1 x x  3 A. y  . B. y  . C. y  D. y x 1 x 1 x 1 x 1 Lời giải 2 x
Đồ thị hàm số có tiệm cận xiên y x 1và đi qua điểm 0;  1 nên y  . x 1 ax b
Bài toán 6. Đường cong ở hình bên là đồ thị của hàm số y
với a,b,c,d là các số thực. Mệnh đề nào cx d dưới đây đúng? A.  y  0,x  1 B.  y  0,x  1 C.  y  0,x  2 D.  y  0,  2 Lời giải
Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, Hàm số nghịch biến vậy chọn B
Bài toán 7. Hình vẽ bên dưới là đồ thị của hàm số nào 10 x 1 2x 1 2x  3 2x  5 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1 Lời giải
Đồ thị hàm số cắt trục Oy tai điểm có tọa độ 0 
;1 nên chọn phương án B.
Bài toán 8. Đồ thị hàm số sau có đường tiệm cận xiên là A. y x
B. y x  1
C. y  2x  1
D. y x  2 Lời giải
Đường tiệm cận đã cho đi qua 0 
;1 và song song với đường phân giác góc phần tư thứ nhất nên y x  1
Bài toán 9. Đường cong trong hình là đồ thị của hàm số nào dưới đây? x 1 2  x 1 A. y  . B. y  . C. 4 2
y x  3x . D. 3 2
y x  3x . x 1 2x  2 Lời giải ax b
Hình vẽ trên là đồ thị của hàm số dạng y
c  0;ad bc  0  Loại phương án C, D cx d
Ta thấy: Đồ thị có đường tiệm cận đứng là x  1 và đường tiệm cận ngang là y  1
Phương án B: Đồ thị có đường tiệm cận đứng là x  2  loại B  A đúng. x a
Bài toán 10. Biết hàm số y
( a là số thực cho trước, a  1 có đồ thị như hình bên). Mệnh đề nào dưới x 1 đây đúng? A. y '  0, x   1 . B. y '  0, x   1.
C. y '  0, x   .
D. y '  0, x   . Lời giải x a 1 a Ta có : y   y '   0, x   1 x 1  x  2 1 11
Do a  1 nên dấu “  ” không xảy ra.
Hàm đơn điệu không phụ thuộc vào a .
Bài toán 11. Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? x 1 2x 1 2x  3 2x  5 A. y  . B. y  . C. y  . D. y  . x 1 x 1 x 1 x 1
Lời giải. Hàm số đồng biến và có tiệm cận đứng, tiệm cận ngang lần lượt là x  1  ; y  2 . 2x 1
Kết luận hàm số y  . x 1 x a
Bài toán 12. Biết hàm số y
( a là số thực cho trước, a   1 ) có đồ thị như trong hình bên. Mệnh đề x 1 nào dưới đây đúng? y O x
A. y'  0,xR.
B. y '  0,x 1.
C. y'  0,xR.
D. y '  0,x 1. Lời giải 1   a
Ta có TXĐ: D R \   1 và y ' 
 0,x 1 và đồ thị là đường đi xuống trên từng khoảng xác định nên 2 (x 1)
hàm số đã cho nghịch biến trên mỗi khoảng xác định.
Bài toán 13. Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên x 1 2x 1 2 x x 1 2 x  2x 1 A. y  . B. y  . C. y  D. y x 1 x 1 x 1 x 1 Lời giải 2 x x 1
Đồ thị hàm số có tiệm cận xiên y x nên y  . x 1 12
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT
ĐỒ THỊ HÀM SỐ, BẢNG BIẾN THIÊN
XÁC ĐỊNH HỆ SỐ CỦA HÀM SỐ THÔNG QUA ĐỒ THỊ
_____________________________________
Bài toán 1. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?
A. a  0, b  0, c  0, d  0
B. a  0, b  0, c  0, d  0
C. a  0, b  0, c  0, d  0
D. a  0, b  0, c  0, d  0 Lời giải
- Dựa vào hình dáng của đồ thị suy ra hệ số a  0 .
- Đồ thị cắt trục Oy tại điểm có tung độ âm nên d  0 .
- Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình 2
y  3ax  2bx c  0 có 2 nghiệm x , x trái dấu kéo theo 3 .
a c  0  c  0 . 1 2 x x b - Mặt khác 1 2    0  b  0 . 2 3a 2 x a
Bài toán 2. Đồ thị của hàm số y
dưới đây có dạng như đường cong trong hình vẽ bên. Khi đó x 1 A. a  0 B. a  1 C. a  2 D. a  1  Lời giải
Đồ thị hàm số đi qua gốc tọa độ nên a  0 . ax b
Bài toán 3. Hình vẽ bên là đồ thị hàm số y  . cx d .
Mệnh đề nào dưới đây đúng?
A. ad  0 và bd  0 .
B. ad  0 và ab  0 .
C. bd  0 và ab  0 .
D. ad  0 và ab  0 . Lời giải 13 b b
Đồ thị hàm số giao với trục Ox tại điểm có hoành độ x  
, giao với Oy tại điểm có tung độ y  . a dbb   0  0     ab  0 a a
Dựa vào hình vẽ ta có       ad  0 . b b bd  0  0    0    d   d
Trong các phương án chỉ có phương án B thỏa mãn.
Bài toán 4. Cho hàm số 3 2
y ax bx cx d có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng?
A. ab  0,bc  0, cd  0
B. ab  0,bc  0, cd  0
C. ab  0, bc  0, cd  0
D. ab  0,bc  0, cd  0 Lời giải
Từ dáng điệu của đồ thị ta có ngay được:  lim y   ;
 lim y    a  0 . x x
 Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên d  0 . Ta có: 2
y '  3ax  2bx c
Mặt khác dựa vào đồ thị ta thấy phương trình y '  0 có hai nghiệm trái dấu và tổng hai nghiệm này luôn dương ac  0  c   0 nên  2b  
(do a  0 ). Do đó: ab  0,bc ,  cd  0 .   b  0    3a ax b
Bài toán 5. Cho hàm số y
có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi trong cx d
các số b, c, d có tất cả bao nhiêu số dương? A. 1 . B. 2 . C. 0 . D. 3 . Lời giải
Nhìn vào đồ thị ta thấy a
 tiệm cận ngang y
nằm trên trục hoành nên c  0 (vì a  0 ) cdd
 tiệm cận đứng x
nằm bên trái trục tung nên
 0. Suy ra d  0 (vì c  0 ) c c b
 giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên  0. d
Suy ra b  0 (vì d  0 ). Vậy c  0, d  0 ax  6
Bài toán 6. Cho hàm số f x 
a,b,c   có bảng biến thiên như sau: bx c 14
Trong các số a,b, c có bao nhiêu số âm? A. 0 . B. 3 . C. 1. D. 2 . Lời giải
Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là đường thẳng x  2
 và tiệm cận ngang là đường thẳng y  1 .  c  2  b bc  0
b  0,c  0, a  0   1 Suy ra      aab  0
b  0,c  0, a  0  2  1    bac  6b
Lại có hàm số nghịch biến trên mỗi khoảng xác định f  x 
 0  ac  6b . bx c2 Ta thấy  
1 không thể xảy ra do nếu b  0 thì ac  6b  0; và 2 có thể xảy ra do nếu c  0, a  0 thì
6b ac  0 . Vậy trong các số a,b, c có hai số âm. ax b
Bài toán 7. Đồ thị trong hình bên dưới là của hàm số y  (với a, , b c   ). x c
Khi đó tổng a b c bằng A. 1  . B. 1. C. 2 . D. 0 . Lời giải ax b
Đồ thị hàm số y
có đường tiệm cận ngang y a , đường tiệm cận đứng x c
 và cắt Oy tại điểm x cb  0; 
 . Từ đồ thị hàm số ta có đường tiệm cận ngang y  1
 , đường tiệm cận đứng x  1 và cắt Oy tại điểm  c   a  1 a  1 a  1    0; 2
  . Từ đó suy ra: c  1  c  1  c  1 . Vậy a b c  11 2  0 . b b  2c    b  2 2       c 2
x ax b
Bài toán 8. Hàm số y
có đồ thị như hình vẽ bên. Tính giá trị 2a  3b . x 1 15 A.4 B. 5 C. 2 D. 1 Lời giải A
 0; 2  C  2  bb   2 Theo đồ thị ta thấy     
 2a  3b  4 . B
 2; 4  C
4  4  2a b a  1     2
x ax b
Bài toán 9. Hàm số f x 
có đồ thị như hình vẽ bên. Xác định góc tạo bởi đường tiệm cận xiên của x 1
đồ thị hàm số f x   1 và trục tung. A. 45 B. 60 C. 30 D. 20 Lời giải A
 0; 2  C  2  bb   2 Theo đồ thị ta thấy     
 2a  3b  4 . B
 2; 4  C
4  4  2a b a  1     2 x x  2 2 2 Khi đó y   x
f x   1  x 1 . x 1 x 1 x
Đường tiệm cận xiên y x 1, đường này tạo với trục tung một góc 45 . ax b
Bài toán 10. Cho hàm số y
a ,b,c   có bảng biến thiên như sau: cx 1
Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. 3 b  8  0. B. 2 b  4  0. C. 2
b  3b  2  0. D. 3 b  8  0. Lời giải ax b 1
Đồ thị hàm số y
có đường tiệm cận đứng là đường thẳng x  
và đường tiệm cận ngang là đường cx 1 c a thẳng y  . c 1 a
Nhìn vào bảng biến thiên, ta thấy 
 1  c  1 và
 2  a  2 (vì c  1). c c a bc Ta có y  . cx  2 1
Vì hàm số đã cho đồng biến trên các khoảng ;  
1 và 1;   nên a bc 3 3 y 
 0  a bc  0  2  b  0  b  2  b  8  b  8  0 . bx c2
Vậy tập các giá trị b là tập nghiệm của bất phương trình 3 b  8  0. 16
PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI TOÁN KHẢO SÁT HÀM SỐ LỚP 12 THPT ĐỒ THỊ HÀM SỐ
BÀI TOÁN ĐỒ THỊ HÀM SỐ CHỨA THAM SỐ
_____________________________________
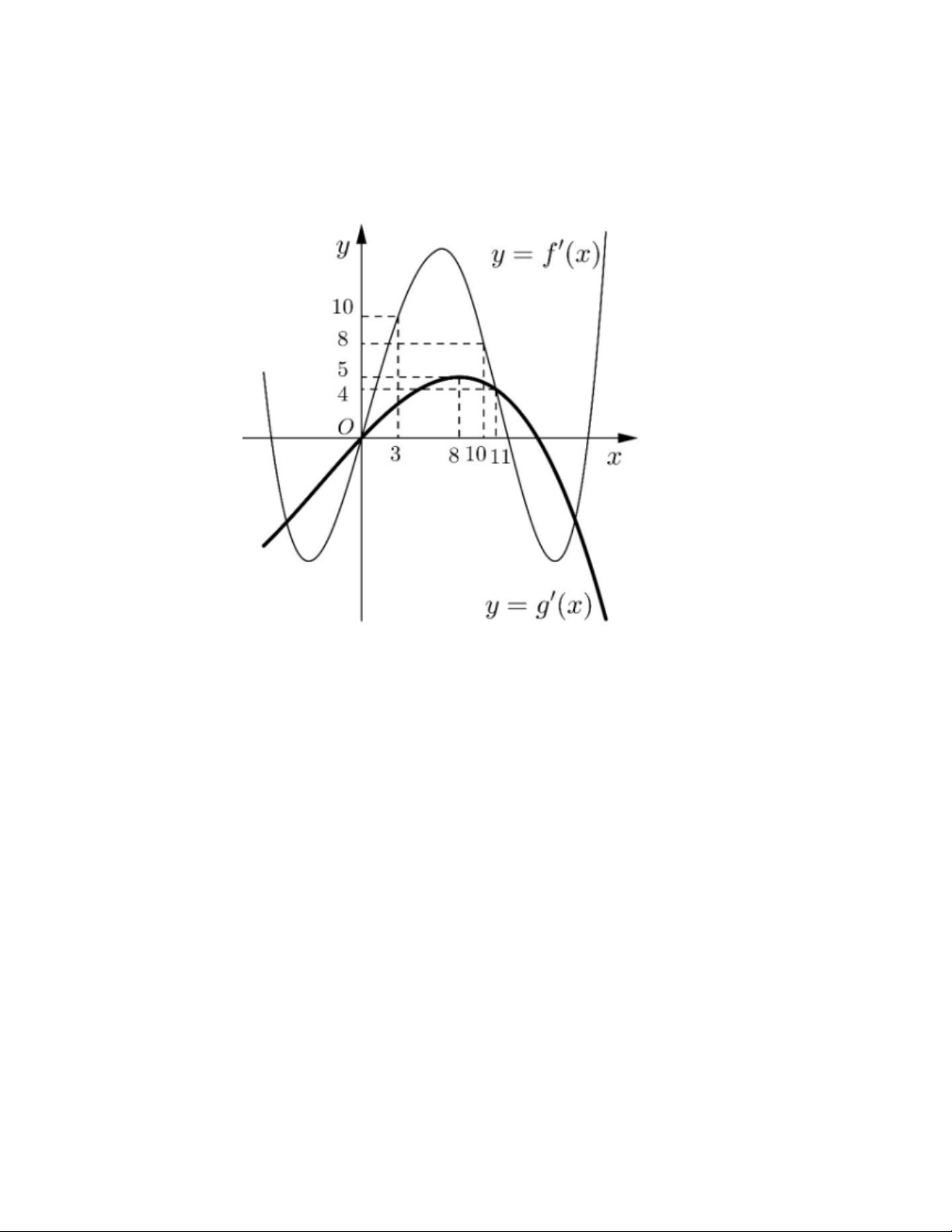
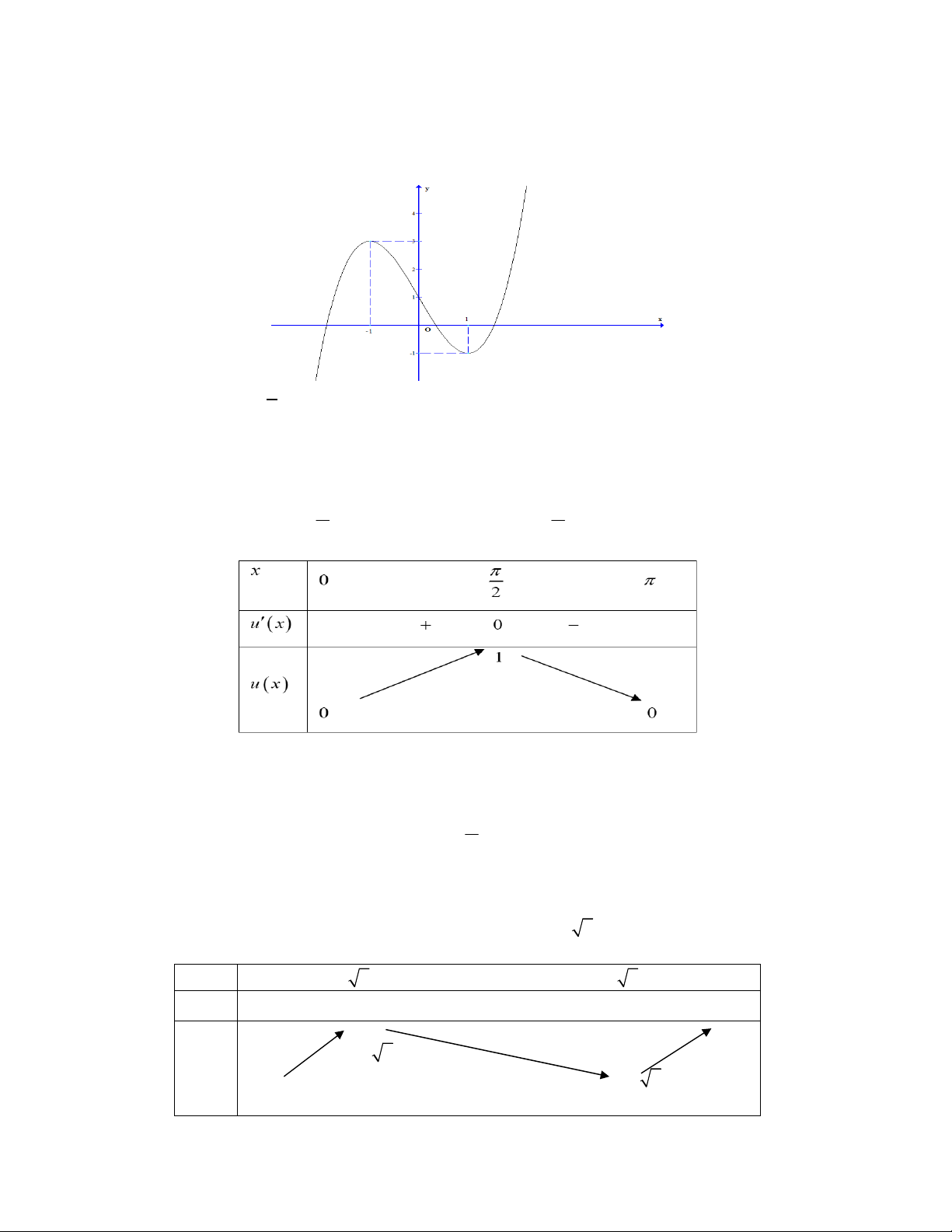
Bài toán 1. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ . Gọi S là tập hợp tất cả các giá trị
nguyên của tham số m để phương trình f sin x  3sin x m có nghiệm thuộc khoảng 0;  . Tổng các phần tử của S bằng. A. 9 . B. 10 . C. 6  . D. 5  . Lời giải
Dựa vào đồ thị hàm số ta có f x 3  x x f  x 2 3 1 ;  3x  3.
Đặt u  sin x  1   u  
1 . Xét hàm số u  sin x  1   u   1 .   u  cos ;
x u  0  x
k , do x  0;   gt   x  2 2 Bảng biến thiên :
Suy ra x  0;   u 0  ;1  0  u  1.
Vậy dựa vào bảng biến thiến ta có với mỗi u 0 
;1  pt :sin x u có 2 nghiệm x  0;  
Và u  1  sin x u  1 có một nghiệm kép x  . 2
Khi đó phương trình f sin x  3sin x m f u  3u m f u  3u m
Xét hàm số : g x  f x  3x
g x  f  x 
g x   f  x 2 3; 0
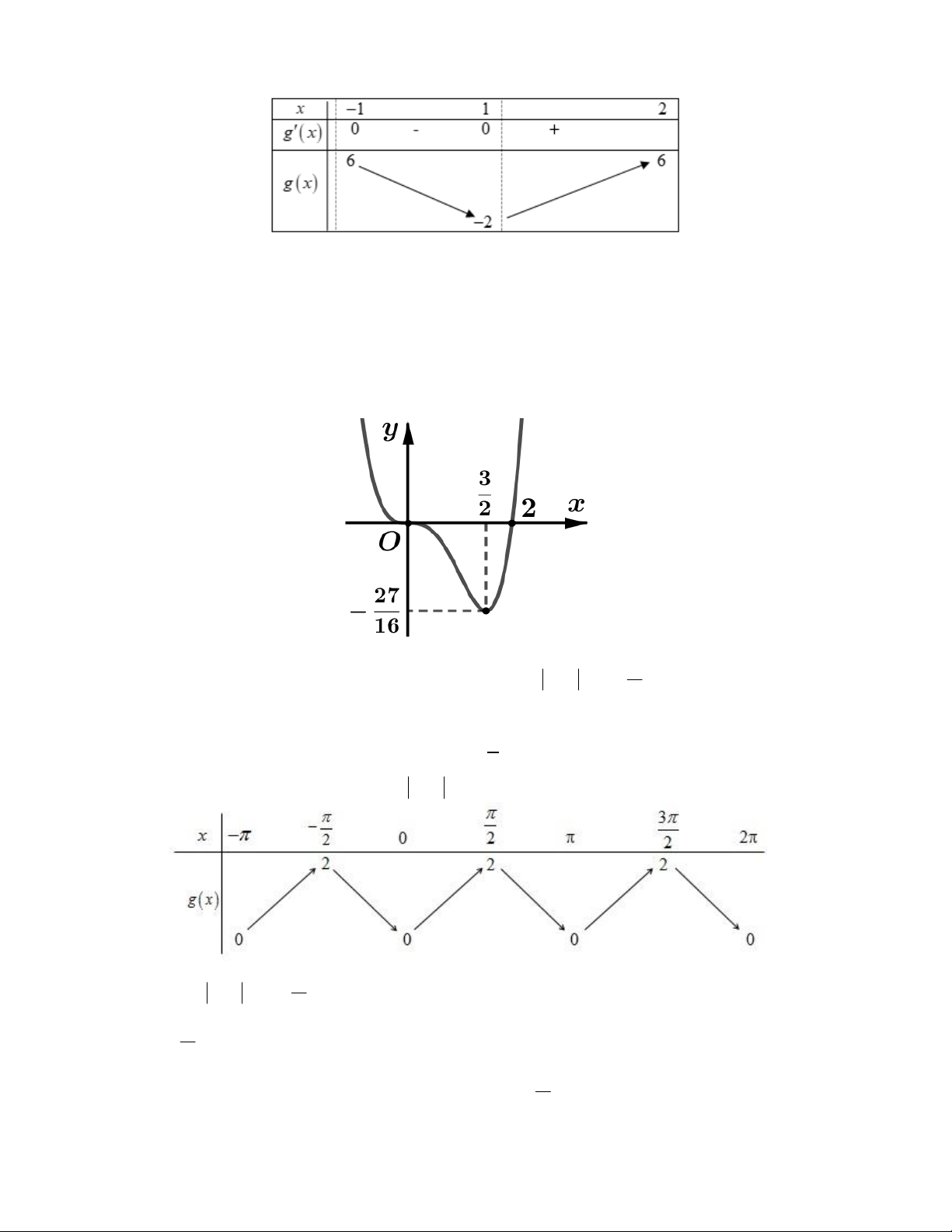
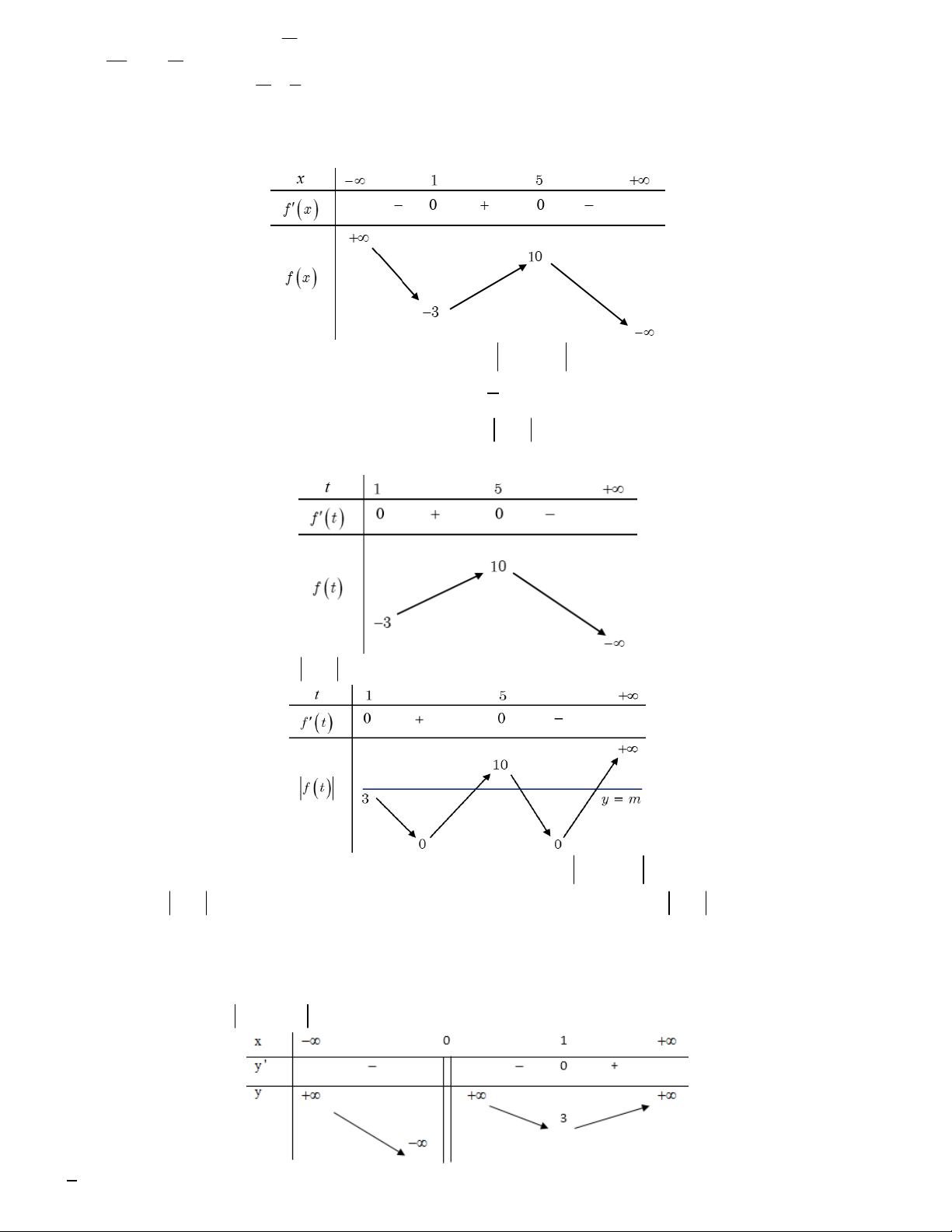
 3  3x  3  3  x   2 . Bảng biến thiên x   2 0 1 2 
g x  0  |  |  0   1 4 2 1 -4
g x  14 2
Dựa vào bảng biến thiên ta có với x  0 
;1 thì phương trình f x  3x m có nghiệm khi : g  
1  m g 0  4
  m  1  m  4  ;  3;  2; 1; 
0 tổng các giá trị của m :10 . 17
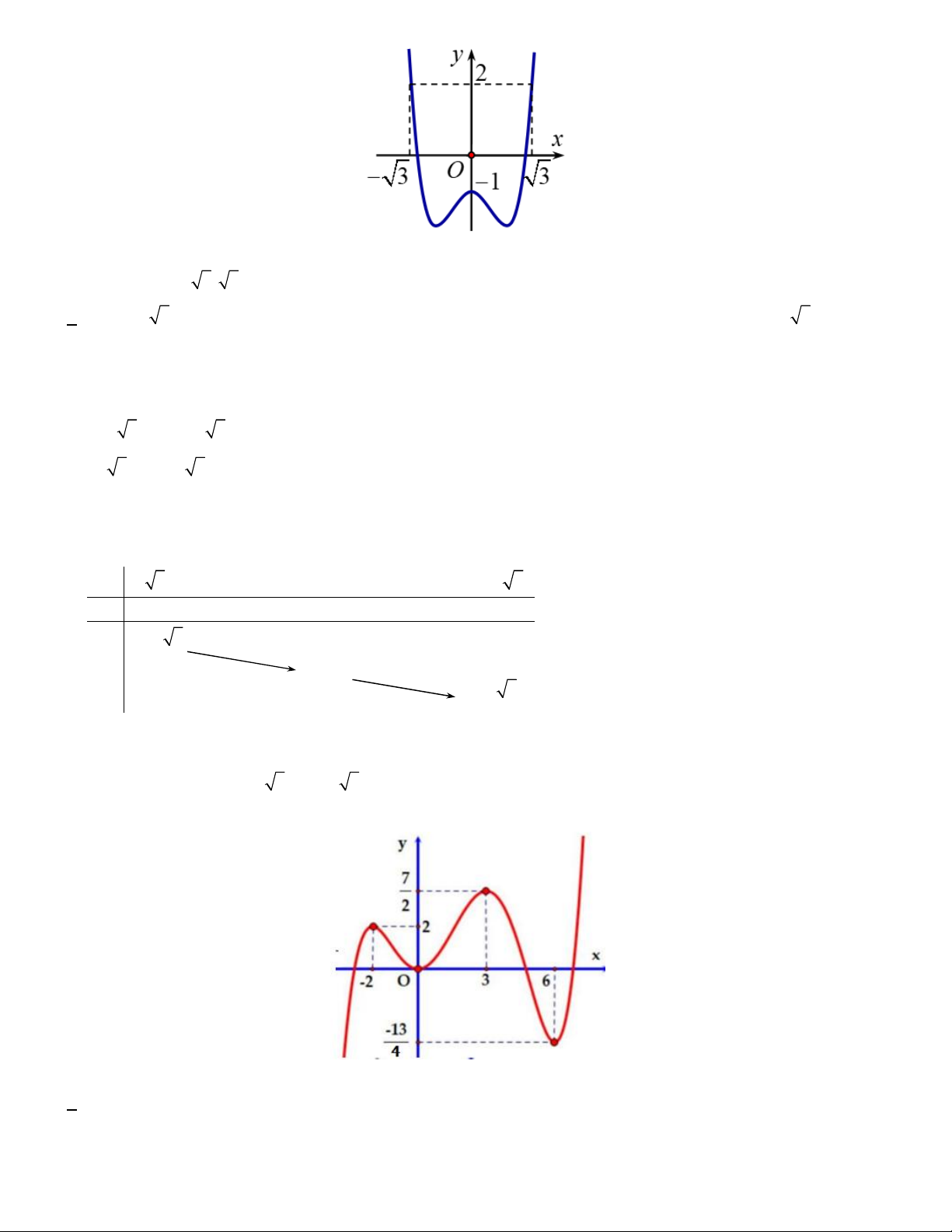
Bài toán 2. Cho hàm số y f x . Đồ thị hàm y f  x như hình vẽ
Đặt g x  f x 3 3
x  3x m , với m là tham số thực. Điều kiện cần và đủ để bất phương trình g x  0 đúng với x    3; 3 là  
A. m  3 f  3 .
B. m  3 f 0 .
C. m  3 f   1 .
D. m  3 f  3 . Lời giải
g x   f x 3
x x m   f x 3 0 3 3 0 3
x  3x m .
Đặt h x  f x 3 3
x  3x . Ta có h x  f  x 2 3  3x  3 . Suy ra
h 3  3 f  3  6  0  
h 3  3 f  3  6  0 
h0  3 f 0  0  h  1  3 f   1  0 
Từ đó ta có bảng biến thiên x  3 0 1 3 h  0  h  3 h h 0 h  3
Vậy g x  m g x  h  3  3 f  3 .
Bài toán 3. Cho hàm số y f x có đồ thị như hình vẽ
Có bao nhiêu số nguyên m để phương trình f  3
2x  6x  2  m có 6 nghiệm phân biệt thuộc đoạn 1; 2? A. 1. B. 0 . C. 2 . D. 3 . Lời giải
Xét hàm số g x 3
 2x  6x  2 trên đoạn 1; 2. 18  x  1 g x 2
 6x  6  0   x  1  
Ta có bảng biến thiên như sau Đặt 3
t  2x  6x  2 , với x  1
 ; 2 thì t  2  ;6.
Dựa vào bảng biến thiên, ta có nhận xét với mỗi giá trị t  2  ; 6 thì phương trình 3
t  2x  6x  2 có hai 0   0
nghiệm phân biệt x  1
 ; 2 và tại t  2  thì phương trình 3
t  2x  6x  2 có một nghiệm duy nhất. 0 0
Với nhận xét trên và đồ thị hàm số trên đoạn  2
 ;6 thì phương trình f  3
2x  6x  2  m có 6 nghiệm phân
biệt thuộc đoạn 1; 2 khi và chỉ khi phương trình f t   m có 3 nghiệm phân biệt trên nửa khoảng  2  ;6 .
Bài toán 4. Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ.  m
Có bao nhiêu giá trị nguyên của tham số m để phương trình f 2 sin x   f   có đúng 12 nghiệm phân biệt  2  thuộc đoạn    ; 2 ? A. 3. B. 4. C. 2. D. 5. Lời giải
Ta có bảng biến thiên của hàm số y g x  2 sin x trên đoạn    ; 2   m
Phương trình f 2 sin x   f   có đúng 12 nghiệm phân biệt thuộc đoạn  
 ; 2 khi và chỉ khi phương  2   m
trình f t   f   có 2 nghiệm phân biệt t 0;2 .  2   m
Dựa vào đồ thị hàm số y f x suy ra phương trình f t   f   có 2 nghiệm phân biệt t 0;2 khi và chỉ  2  19  m 0   2 27  m    0  m  4 2 khi   f  0       . 16  2  m 3 m  3      2 2
Do m nguyên nên m 1; 
2 . Vậy có 2 giá trị của m thoả mãn bài toán.
Bài toán 5. Cho hàm hàm số y f x có bảng biến thiên như hình vẽ dưới
Có bao nhiêu giá trị nguyên của tham số m để phương trình f  2 x  
1  m có 6 nghiệm phân biệt. A. 12 . B. 198 . C. 6 . D. 190 . Lời giải Đặt 2
t x 1, điều kiện t  1, từ đó phương trình trở thành f t   m , t 1.
Do t  1nên ta xét bảng biến thiên của hàm y f t  trên 1; như sau:
Bảng biến thiên của hàm số y f t  trên 1; là
Cứ mỗi nghiệm t 1 cho được hai nghiệm x , do vậy để phương trình f  2 x  
1  m có 6 nghiệm phân biệt thì
phương trình f t   m cần có 3 nghiệm t 1. Dựa bảng biến thiên của hàm y f t  ở trên ta có điều kiện
3  m  10 , mặt khác m nguyên nên m 4;5;6;7;8;  9 .
Vậy có 6 giá trị nguyên m thỏa mãn bài toán.
Bài toán 6. Cho hàm số y f ( )
x xác định trên  \  
0 và có bảng biến thiên như hình vẽ. Số giá trị nguyên
của m để phương trình f 2x  3  m  0 có đúng 2 nghiệm phân biệt là A. 2. B. 1. C. 4. D. 3. 20