69 trang 3 lượt tải

Bài tập bổ trợ Toán 11 chương hàm số lượng giác và phương trình lượng giác

6

Tài liệu gồm 69 trang, được biên soạn bởi thầy giáo Nguyễn Trung Trông, tuyển tập các bài tập bổ trợ môn Toán 11 chương hàm số lượng giác và phương trình lượng giác.

Chủ đề: Tài liệu chung Toán 11 83 tài liệu

Môn: Toán 11 3.5 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/69
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
1
CHỦ ĐỀ 1:
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
I. LÝ THUYẾT CƠ BẢN
1. Hệ thức lượng giác cơ bản
2 2
sin cos 1
tan .cot 1, ,
2
k k
2
2
1
1 tan , ;
2
cos
k k
2
2
1
1 cot ,
sin
k k
2. Giá trị lượng giác của các góc có liên quan đặc biệt
Góc đối nhau (
và
)
Góc bù nhau (
và
)
cos cos
sin sin
tan tan
cot cot
sin sin
cos cos
tan tan
cot cot
Góc phụ nhau (
và
2
)
Góc hơn kém
(
và
)
sin cos
2
cos sin
2
tan cot
2
cot tan
2
sin sin
cos cos
tan tan
cot cot
3. Công thức lượng giác
a. Công thức cộng
cos cos cos sin sin
a b a b a b
sin sin cos cos sin
a b a b a b
cos cos cos sin sin
a b a b a b
sin sin cos cos sin
a b a b a b
tan tan
tan( )
1 tan .tan
a b
a b
a b
tan tan
tan( )
1 tan .tan
a b
a b
a b
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
2
Chú ý:
sin cos 2 sin 2 cos
4 4
sin cos 2 sin 2 cos
4 4
a a a a
a a a a
b. Công thức nhân đôi, công thức hạ bậc
Công thức nhân đôi Công thức hạ bậc
sin 2 2 sin .cos
2 2
2
2
cos 2 cos sin
2 cos 1
1 2 sin
2
2 tan
tan 2
1 tan
2
2
2
1 cos 2
sin
2
1 cos 2
cos
2
1 cos 2
tan
1 cos 2
d. Công thức biến đổi tích thành tổng, tổng thành tích
Biến đổi tích thành tổng Biến đổi tổng thành tích
1
cos .cos cos cos
2
1
sin .sin cos cos
2
1
sin .cos sin sin
2
a b a b a b
a b a b a b
a b a b a b
cos cos 2 cos cos
2 2
a b a b
a b
cos cos 2sin sin
2 2
a b a b
a b
sin sin 2 sin cos
2 2
a b a b
a b
sin sin 2 cos sin
2 2
a b a b
a b
4. Hàm số lượng giác
a) Hàm số chẵn, hàm số lẻ
Hàm số
y f x
có tập xác định là
D
+) Hàm số
y f x
được gọi là hàm số chẵn nếu
x D x D
f x f x
+) Hàm số
y f x
được gọi là hàm số lẻ nếu
x D x D
f x f x
Chú ý: +) Đồ thị hàm số lẻ nhận gốc
O
làm tâm đối xứng
+) Đồ thị hàm số chẵn nhận trục tung là trục đối xứng
b) Hàm số tuần hoàn
Hàm số
y f x
xác định trên tập hợp D, được gọi là hàm số tuần hoàn nếu có số
0
T
sao cho với mọi
x D
ta có
x T D
và
f x T f x
.
Nếu có số dương
T
nhỏ nhất thỏa mãn các điều kiện trên thì
T
gọi là chu kì của hàm số
tuần hoàn đó.
Chú ý:
+) Hàm số
sin , cos
y x y x
tuần hoàn với chu kì
2
T
+) Hàm số
tan , cot
y x y x
tuần hoàn với chu kì
T
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
3
+) Hàm số
sin
y A ax b
và
cos , , 0
y A ax b A a
tuần hoàn với chu kì
2
T
a
+) Hàm số
tan
y A ax b
và
cot , , 0
y A ax b A a
tuần hoàn với chu kì
T
a
c) Đồ thị và tính chất của các hàm số lượng giác
sin
y x
+) Tập xác định
+)Tập giá trị:
1;1
, có nghĩa là
1 sin 1,
x x
.
+) Hàm số tuần hoàn với chu kì
2
+) Hàm số đồng biến trên mỗi khoảng
2 ; 2
2 2
k k
và nghịch biến trên mỗi
khoảng
3
2 ; 2
2 2
k k
,
k
.
+) là hàm số lẻ, đồ thị là đường hình sin nhận gốc tọa độ
O
là tâm đối xứng
d) Đồ thị và tính chất của các hàm số lượng giác
cos
y x
+) Tập xác định
.
+) Tập giá trị:
1;1
, có nghĩa là
1 cos 1,
x x
.
+) Hàm số tuần hoàn với chu kì
2
+) Hàm số đồng biến trên mỗi khoảng
2 ; 2
k k
và nghịch biến trên mỗi
khoảng
2 ; 2
k k
,
k
.
+) là hàm số chẵn, đồ thị là đường hình sin nhận
Oy
làm trục đối xứng
e) Đồ thị và tính chất của các hàm số lượng giác
tan
y x
+) Tập xác định:
\
2
k k
+) Tâp giá trị là
.
+) Hàm số tuần hoàn với chu kì
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
4
+ Hàm số đồng biến trên mỗi khoảng
; ,
2 2
k k k
.
+ là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ
O
làm tâm đối xứng
f) Đồ thị và tính chất của các hàm số lượng giác
cot
y x
+) Tập xác định:
\ k k
.
+) Tập giá trị:
.
+) Hàm số tuần hoàn với chu kì
+) Hàm số nghịch biến trên mỗi khoảng
; ,k k k
.
+) là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ
O
làm tâm đối xứng
5. Phương trình lượng giác cơ bản
a. Phương trình
sin
x m
+) Trường hợp 1:
1
m
thì phương trình vô nghiệm.
+) Trường hợp 2:
1
m
thì phương trình có nghiệm.
2
sin sin ,
2
x k
x k
x k
.360
sin sin ,
180 .360
x k
x k
x k
2
sin sin ,
2
f x g x k
f x g x k
f x g x k
Chú ý:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
5
sin 0
sin 1 2
2
sin 1 2
2
x x k
x x k
x x k
b. Phương trình
cos
x m
+) Trường hợp 1:
1
m
thì phương trình vô nghiệm.
+) Trường hợp 2:
1
m
thì phương trình có nghiệm.
2
cos cos ,
2
x k
x k
x k
.360
cos cos ,
.360
x k
x k
x k
2
cos cos ,
2
f x g x k
f x g x k
f x g x k
Chú ý:
cos 0
2
cos 1 2
cos 1 2
x x k
x x k
x x k
c. Phương trình
tan
x m
Phương trình
tan
x m
luôn có nghiệm với mọi
m
tan tanx x k k
tan tan 180x x k k
tan tanf x g x f x g x k k
d. Phương trình
cot
x m
Phương trình
cot
x m
luôn có nghiệm với mọi
m
cot cotx x k k
cot cot 180x x k k
cot cotf x g x f x g x k k
PHẦN BÀI TẬP BẮT BUỘC
Chủ điểm: Giá trị lượng giác của một cung
Dạng 1. Đơn vị đo góc
Câu 1. a) Đổi từ độ sang rađian các số đo sau:
360 ; 450
;
b) Đổi từ rađian sang độ các số đo sau:
11
3 ;
5
.
Câu 2. Đổi số đo cung tròn sang số đo độ:
a)
3
4
b)
5
6
c)
32
3
d)
3
7
e)
2, 3
f)
5,6
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
6
Câu 3. Đổi số đo cung tròn sang số đo radian:
a)
45
b)
150
c)
72
d)
75
Dạng 2. Độ dài cung tròn
Câu 4. Một đường tròn có bán kính
20
cm
. Tìm độ dài của các cung trên đường tròn đó có số đo
sau:
a)
12
; b) 1,5 ; c)
35
; d)
315
.
Câu 5. Một đường tròn có bán kính
36
m
. Tìm độ dài của cung trên đường tròn đó có số đo là
a)
3
4
b)
0
51
c)
1
3
Câu 6. Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây.
a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.
b) Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính
của bánh xe đạp là
680
mm
.
Dạng 3. Mối liên hệ giữa góc hình học và góc lượng giác
Câu 7. Trên đường tròn lượng giác, xác định điểm
M
biểu diễn các góc lượng giác có số đo sau:
a)
2
3
; b)
11
4
; c)
150
; d)
225
.
Câu 8. Cho góc lượng giác
,
Ou Ov
có số đo
5
. Hỏi trong các góc
6
5
,
9
5
,
11
5
,
31
5
,
14
5
, những góc nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc
đã cho.
Câu 9. Hãy tìm số đo
của góc lượng giác
,
Ou Ov
với
0 2
, biết một góc lượng giác
có cùng tia đầu và tia cuối với góc đó có số đo là:
a)
29
4
b)
128
3
c)
2003
6
d)
18,5
Câu 10. Hãy tìm số đo
của góc lượng giác
,
Ou Ov
0 360
biết một góc lượng giác
có cùng tia đầu và tia cuối với nó có số đo:
a)
395
b)
1052
c)
972
d)
20
Dạng 4. Dấu các giá trị lượng giác của góc
Câu 11. Cho
0 90
. Xét dấu của các biểu thức sau:
a)
sin 90
A
. b)
cos 45
B
.
c)
cos 270
C
. d)
cos 2 90
D
.
Câu 12. Cho
0
2
. Xét dấu của các biểu thức sau:
a)
cos
A
. b)
tan
B
.
c)
2
sin
5
C
. d)
3
cos
8
D
.
Dạng 5. Rút gọn biểu thức lượng giác
Câu 13. Rút gọn các biểu thức sau:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
7
a)
cos cos 2 cos 3
2
A x x x
b)
7 3
2 cos 3 cos 5 sin cot
2 2
B x x x x
c)
3
C 2 sin sin 5 sin cos
2 2 2
x x x x
d)
3 3
D= cos 5 sin tan cot 3
2 2
x x x x
Câu 14. Rút gọn biểu thức
sin cos cot 2 tan
2 2
A
Câu 15. Rút gọn biểu thức
3
3 7
tan cos sin
2 2 2
3
cos tan
2 2
B
Câu 16. Rút gọn biểu thức
2
sin tan
1
cos 1
x x
A
x
.
Câu 17. Rút gọn biểu thức
cos
tan
1 sin
x
A x
x
Câu 18. Đơn giản biểu thức
4 4 2
sin cos 2cos
A x x x
Câu 19. Đơn giản biểu thức
4 4
6 6 4
sin 3 cos 1
sin cos 3 cos 1
x x
B
x x x
Câu 20. Đơn giản biểu thức
2
2
1 2 sin
2 cos 1
x
D
x
Câu 21. Đơn giản biểu thức
6 6 4 4
2 sin cos 3 sin cos
E x x x x
Dạng 6. Tính giá trị lượng giác của góc lượng giác
Câu 22. Tính các giá trị lượng giác của góc
, biết:
a)
1
cos
5
và
0
2
; b)
2
sin
3
và
2
;
c)
tan 5
và
3
2
d)
1
cot
2
và
3
2
2
.
Câu 23. Cho biết một giá trị lượng giác, tính các giá trị lượng giác còn lại
a)
4
cos , 270 360
5
a a
. b)
5
sin ,
13 2
a a
.
c)
3
tan 3,
2
a a
. d)
cot15 2 3
.
Câu 24. Cho biết một giá trị lượng giác, tính giá trị của biểu thức, với:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
8
a)
cot tan 3
, sin , 0
cot tan 5 2
a a
A khi a a
a a
.
b)
2 2
2 2
sin 2 sin .cos 2 cos
, cot 3
2 sin 3 sin .cos 4 cos
a a a a
C khi a
a a a a
.
c)
cot 3 tan 2
cos
2 cot tan 3
a a
G khi a
a a
.
d)
sin cos
tan 5
cos sin
a a
H khi a
a a
.
Câu 25. Thực hiện các yêu cầu sau
a) Cho
4 4
3
3 sin cos
4
x x
. Tính
4 4
sin 3 cos
A x x
.
b) Cho
4 4
1
3 sin cos
2
x x
. Tính
4 4
sin 3 cos
C x x
.
c) Cho
4 4
7
4 sin 3 cos
4
x x
. Tính
4 4
3 sin 4 cos
C x x
.
Câu 26.
)
a
Cho
1
sin cos
5
x x
. Tính
sin , cos , tan , cot .
x x x x
)
b
Cho
tan cot 4.
x x
Tính
sin , cos , tan , cot .
x x x x
Câu 27. Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương (tức là áp lực
máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi
tại thời điểm
t
được cho bởi công thức:
( ) 80 7 sin ,
12
t
B t
trong đó
t
là số giờ tính
từ lúc nửa đêm và
( )
B t
tính bằng
mmHg
(milimét thuỷ ngân). Tìm huyết áp tâm trương
của người này vào các thời điểm sau:
a) 6 giờ sáng; b) 10 giờ 30 phút sáng c) 12 giờ trưa; d) 8 giờ tối.
Dạng 7. Chứng minh đẳng thức
Câu 28. Chứng minh các đẳng thức:
a)
4 4 2
cos sin 2 cos 1
; b)
2 2
2
2
cos tan 1
tan
sin
.
Câu 29. Chứng minh các đẳng thức:
a)
3 3
sin cos
1 sin cos
sin cos
a a
a a
a a
. b)
2 2
sin cos tan 1
1 2sin cos tan 1
a a a
a a a
.
c)
4 4 6 6 2 2
sin cos sin cos sin .cos
a a a a a a
.
Câu 30. Cho
tan 2
và
3
2
. Chứng minh rằng
2
sin 2cos 2 5
5
sin .cos 2 sin 2
HỆ THỐNG CÂU HỎI TRẮC NGHIỆM
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Số đo theo đơn vị rađian của góc
315
là
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
9
A.
7
2
. B.
7
4
. C.
2
7
. D.
4
7
.
Câu 2. Cung tròn có số đo là
5
4
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau
đây.
A.
5
. B.
15
. C.
172
. D.
225
.
Câu 3. Cung tròn có số đo là
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau
đây.
A.
30
. B.
45
. C.
90
. D.
180
.
Câu 4. Góc có số đo
2
5
đổi sang độ là:
A.
0
135
.
B.
0
72
.
C.
0
270
.
D.
0
240
.
Câu 5. Góc có số đo
0
108
đổi ra rađian là:
A.
3
5
. B.
10
. C.
3
2
. D.
4
.
Câu 6. Góc có số đo
9
đổi sang độ là:
A.
0
25
.
B.
0
15
.
C.
0
18
.
D.
0
20
.
Câu 7. Cho
2
2
a k
. Tìm
k
để
10 11
a
A.
7
k
. B.
5
k
. C.
4
k
. D.
6
k
.
Câu 8. Một bánh xe có
72
răng. Số đo góc mà bánh xe đã quay được khi di chuyển
10
răng là:
A.
60
. B.
0
30
. C.
0
40
. D.
50
.
Câu 9. Đổi số đo góc
0
105
sang rađian.
A.
7
12
. B.
9
12
. C.
5
8
. D.
5
12
.
Câu 10. Số đo góc
0
22 30’
đổi sang rađian là:
A.
5
. B.
8
. C.
7
12
. D.
6
.
Câu 11. Một cung tròn có số đo là
0
45
. Hãy chọn số đo radian của cung tròn đó trong các cung
tròn sau đây.
A.
2
B.
C.
4
D.
3
Câu 12. Góc có số đo
24
đổi sang độ là:
A.
0
7
.
B.
0
7 30 .
C.
0
8
.
D.
0
8 30 .
Câu 13. Góc có số đo
0
120
đổi sang rađian là:
A.
2
3
. B.
3
2
. C.
4
. D.
10
.
Câu 14. Trên đường tròn bán kính
15
r
, độ dài của cung có số đo
50
là:
A.
180
15.l
. B.
15
.
180
l
C.
180
15. .50
l
. D.
750
l
.
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
10
Câu 15. Cho bốn cung (trên một đường tròn định hướng):
5 25 19
, , ,
6 3 3 6
, Các cung nào có điểm cuối trùng nhau:
A.
và
;
và
. B.
, ,
. C.
, ,
.
D.
và
;
và
.
Câu 16. Cho
L
,
M
,
N
,
P
lần lượt là điểm chính giữa các cung
AB
,
BC
,
CD
,
DA
. Cung
có mút đầu trùng với
A
và số đo
3
4
k
. Mút cuối của
ở đâu?
A.
L
hoặc
N
. B.
M
hoặc
P
. C.
M
hoặc
N
. D.
L
hoặc
P
.
Câu 17. Trên đường tròn bán kính
5
r
, độ dài của cung đo
8
là:
A.
8
l
. B.
8
r
l
. C.
5
8
l
. D. kết quả khác.
Câu 18. Một đường tròn có bán kính
10
R cm
. Độ dài cung
40
o
trên đường tròn gần bằng
A.
11cm
. B.
13cm
. C.
7cm
. D.
9cm
.
Câu 19. Biết một số đo của góc
3
, 2001
2
Ox Oy
. Giá trị tổng quát của góc
,
Ox Oy
là:
A.
3
,
2
Ox Oy k
. B.
, 2
Ox Oy k
.
C.
,
2
Ox Oy k
. D.
, 2
2
Ox Oy k
.
Câu 20. Cung nào sau đây có mút trung với B hoặc B’?
A.
0 0
90 360
a k
. B.
0 0
–90 180
a k
.
C.
2
2
k
. D.
2
2
k
.
Câu 21. Cung
có mút đầu là
A
và mút cuối là
M
thì số đo của
là:
A.
3
2
4
k
. B.
3
2
4
k
. C.
3
4
k
. D.
3
4
k
.
Câu 22. Trên hình vẽ hai điểm
,
M N
biểu diễn các cung có số đo là:
A.
2
3
x k
. B.
3
x k
.
C.
3
x k
. D.
.
3 2
x k
.
Câu 23. Trên đường tròn lượng giác gốc A, cho điểm M xác
định bởi sđ
3
AM
. Gọi
1
M
là điểm đối xứng của M
qua trục
Ox
. Tìm số đo của cung lượng giác
1
.
AM
A. sđ
1
5
2 ,
3
AM k k
B. sđ
1
2 ,
3
AM k k
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
11
C. sđ
1
2 ,
3
AM k k
D. sđ
1
,
3
AM k k
Câu 24. Góc lượng giác nào sau đây có cùng điểm cuối với góc
7
4
?
A.
4
. B.
4
. C.
3
4
. D.
3
4
.
Câu 25. Có bao nhiêu điểm
M
trên đường tròn định hướng gốc
A
thỏa mãn
2
6 3
k
AM
,
k
.
A.
6
. B.
4
. C.
3
. D.
8
.
Câu 26. Cho
2
a
. Kết quả đúng là
A.
sin 0
a
,
cos 0
a
. B.
sin 0
a
,
cos 0
a
.
C.
sin 0
a
,
cos 0
a
. D.
sin 0
a
,
cos 0
a
.
Câu 27. Trong các giá trị sau,
sin
có thể nhận giá trị nào?
A.
0,7
. B.
4
3
. C.
2
. D.
5
2
.
Câu 28. Cho
5
2 .
2
a
Chọn khẳng định đúng.
A.
tan 0, cot 0.
a a
B.
tan 0, cot 0.
a a
C.
tan 0, cot 0.
a a
D.
tan 0, cot 0
a a
.
Câu 29. Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết
quả sau đây.
A.
cot 0
. B.
sin 0
. C.
cos 0
. D.
tan 0
.
Câu 30. Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả
sau đây.
A.
cot 0
. B.
tan 0
. C.
sin 0
. D.
cos 0
.
Câu 31. Cho
7
2
4
.Xét câu nào sau đây đúng?
A.
tan 0
. B.
cot 0
. C.
cos 0
. D.
sin 0
.
Câu 32. Xét các mệnh đề sau:
I.
cos 0
2
. II.
sin 0
2
. III.
tan 0
2
.
Mệnh đề nào sai?
A. Chỉ I. B. Chỉ II. C. Chỉ II và III. D. Cả I, II và III.
Câu 33. Xét các mệnh đề sau đây:
I.
cos 0
2
. II.
sin 0
2
. III.
cot 0
2
.
Mệnh đề nào đúng?
A. Chỉ II và III. B. Cả I, II và III. C. Chỉ I. D. Chỉ I và II.
Câu 34. Cho hai góc nhọn
và
phụ nhau. Hệ thức nào sau đây là sai?
A.
cot tan
. B.
cos sin
. C.
cos sin
. D.
sin cos
.
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
12
Câu 35. Trong các đẳng thức sau, đẳng thức nào đúng?
A.
0
sin 180 – – cos
a a
. B.
0
sin 180 – sin
a a
.
C.
0
–s
i
i 0n
18 s n
a a
. D.
0
–s
o
i 0n
18 c s
a a
.
Câu 36. Chọn đẳng thức sai trong các đẳng thức sau
A.
sin cos
2
x x
. B.
sin cos
2
x x
.
C.
tan cot
2
x x
. D.
tan cot
2
x x
.
Câu 37. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
cos cos
x x
. B.
sin sin
x x
.
C.
cos cos
x x
. D.
sin cos
2
x x
.
Câu 38. Khẳng định nào sau đây là sai?
A.
sin sin
. B.
cot cot
.
C.
cos cos
. D.
tan tan
.
Câu 39. Khẳng định nào sau đây đúng?
A.
sin sin .
x x
B.
cos cos .
x x
C.
cot cot .
x x
D.
tan tan .
x x
Câu 40. Chọn hệ thức sai trong các hệ thức sau.
A.
3
tan cot
2
x x
. B.
sin 3 sin
x
x
.
C.
cos 3 cos
x
x
. D.
cos cos
x x
.
Câu 41. Cho biết
1
tan
2
. Tính
cot
A.
cot 2
. B.
1
cot
4
. C.
1
cot
2
. D.
cot 2
.
Câu 42. Trong các công thức sau, công thức nào sai?
A.
2 2
sin cos 1
. B.
2
2
1
1 tan ,
2
cos
k k
C.
2
2
1
1 cot ,
sin
k k
. D.
tan cot 1 ,
2
k
k
.
Câu 43. Cho
3
sin
5
và
2
. Giá trị của
cos
là:
A.
4
5
. B.
4
5
. C.
4
5
. D.
16
25
.
Câu 44. Cho
4
cos
5
với
0
2
. Tính
sin
.
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
13
A.
1
sin
5
. B.
1
sin
5
. C.
3
sin
5
. D.
3
sin
5
.
Câu 45.
Tính
biết
cos 1
A.
k k
. B.
2k k
.
C.
2
2
k k
. D.
2k k
.
Câu 46. Cho
2
cos
5
2
. Khi đó
tan
bằng
A.
21
3
. B.
21
5
. C.
21
5
. D.
21
2
.
Câu 47. Cho
tan 5
, với
3
2
. Khi đó
cos
bằng:
A.
6
6
. B.
6
. C.
6
6
. D.
1
6
.
Câu 48. Cho
3
sin 90 180
5
. Tính
cot
.
A.
3
cot
4
. B.
4
cot
3
. C.
4
cot
3
. D.
3
cot
4
.
Câu 49. Trên nửa đường tròn đơn vị cho góc
sao cho
2
sin
3
và
cos 0
. Tính
tan
.
A.
2 5
5
. B.
2 5
5
. C.
2
5
. D.
1
.
Câu 50. Cho
1
sin
3
và
2
. Khi đó
cos
có giá trị là.
A.
2
cos
3
. B.
2 2
cos
3
. C.
8
cos
9
. D.
2 2
cos
3
.
Câu 51. Cho
1
sin cos
2
x x
và 0
2
x
. Tính giá trị của
sin
x
.
A.
1 7
sin
6
x
. B.
1 7
sin
6
x
. C.
1 7
sin
4
x
. D.
1 7
sin
4
x
.
Câu 52. Cho
3 sin cos
sin 2 cos
x x
P
x x
với
tan 2
x
. Giá trị của
P
bằng
A.
8
9
. B.
2 2
3
. C.
8
9
. D.
5
4
.
Câu 53. Cho
tan 2
x
.Giá trị biểu thức
4 sin 5 cos
2 sin 3 cos
x x
P
x x
là
A.
2
. B.
13
. C.
9
. D.
2
.
Câu 54. Cho tam giác
ABC
đều. Tính giá trị của biểu thức
P cos , cos , cos ,
AB BC BC CA CA AB
     
.
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
14
A.
3
P
2
. B.
3
P
2
. C.
3 3
P
2
. D.
3 3
P
2
.
Câu 55. Cho
tan 2
a
. Tính giá trị biểu thức
2 sin cos
sin cos
a a
P
a a
.
A.
2
P
. B.
1
P
. C.
5
3
P
. D.
1
P
.
Câu 56. Cho
3
sin
5
và
0 0
90 180
. Giá trị của biểu thức
cot 2 tan
tan 3cot
E
là:
A.
2
57
. B.
2
57
. C.
4
57
. D.
4
57
.
Câu 57. Cho
tan 2
. Giá trị của
3 sin cos
sin cos
A
là:
A.
5
. B.
5
3
. C.
7
. D.
7
3
.
Câu 58. Biết
tan 2
và
180 270
. Giá trị
cos sin
bằng
A.
3 5
5
. B.
1 –
5
. C.
3 5
2
. D.
5 1
2
.
Câu 59. Biểu thức
2 2 2 2 2
cos .cot 3 cos – cot 2 sin
D x x x x x
không phụ thuộc
x
và bằng
A. 2. B.
–2
. C. 3. D.
–3
Câu 60. Đơn giản biểu thức
2
2 cos 1
sin c
os
x
x x
A
ta có
A.
cos sin
A x x
. B.
cos – sin
A x x
.
C.
sin – cos
A x x
. D.
sin – cos
A x x
.
Câu 61. Biểu thức:
2003
cos 26 2 sin 7 cos1, 5 cos cos 1,5 .cot 8
2
A
có kết quả thu gọn bằng:
A.
sin
. B.
sin
. C.
cos
. D.
cos
.
Câu 62. Đơn giản biểu thức
A cos sin cos sin
2 2 2 2
, ta có:
A.
2 sin
A a
. B.
2 cos
A a
. C.
sin – cos
A a a
. D.
0
A
.
Câu 63. Biểu thức
sin cos cot 2 tan
3
2 2
P x x x x
có biểu thức rút
gọn là
A.
2 sin
P x
. B.
2 sin
P x
. C.
0
P
. D.
2 cot
P x
.
Câu 64. Cho tam giác
ABC
. Đẳng thức nào sau đây sai?
A.
A B C
. B.
cos cos
A B C
.
C.
sin cos
2 2
A B C
. D.
sin sin
A B C
.
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
15
Câu 65. Đơn giản biểu thức
A cos sin
2
, ta có
A.
in
cos
s
A a a
. B.
2 sin
A a
. C.
o
sin
c s
–
A a a
. D.
0
A
.
Câu 66. Cho A, B, C là ba góc của một tam giác không vuông. Mệnh đề nào sau đây sai?
A.
tan cot
2 2
A B C
. B.
cot tan
2 2
A B C
.
C.
cot cot
A B C
. D.
tan tan
A B C
.
Câu 67. Rút gọn biểu thức
3
cos sin tan .sin 2
2 2
A
ta được
A.
cos
A
. B.
cos
A
. C.
sin
A
. D.
3 cos
A
.
PHẦN II. BÀI TẬP ĐÚNG/ SAI
Câu 1. Đổi số đo của các góc sang radian. Khi đó:
Mệnh đề Đúng
Sai
a)
30
6
rad
b)
15 1
12
rad
c)
11
132
15
rad
d)
13
495
4
rad
Câu 2. Đổi số đo của các góc sang độ. Khi đó:
Mệnh đề Đúng
Sai
a)
3
135
4
rad
b)
0, 5
360
rad
c)
31
27
2
rad
d)
4 229,18
rad
Câu 3. Biểu diễn góc lượng giác trên đường tròn lượng giác. Khi đó:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
16
Mệnh đề Đúng
Sai
a)
125
là điểm
M
thuộc góc phần tư thứ thứ II
b)
405
là điểm
N
thuộc góc phần tư thứ III
c)
19
3
là điểm
P
thuộc góc phần tư thứ II
d)
13
6
là điểm
Q
thuộc góc phần tư thứ IV
Câu 4. Biểu diễn góc lượng giác trên đường tròn lượng giác. Khi đó:
Mệnh đề Đúng
Sai
a)
36 36
,
0
k
k
là điểm
M
thuộc góc phần tư thứ
II
b)
,
60 180
k
k
là các điểm
1 2
,
M M
thuộc góc phần tư thứ
II
và
IV
c)
2 ,
4
kk
là
M
thuộc góc phần tư thứ
III
d)
2
,
6
kk
là bốn điểm
, , ,
M N P Q
thuộc góc phần tư thứ
, , ,
I II III IV
Câu 5. Các mệnh đề sau đúng hay sai?
Mệnh đề Đúng
Sai
a)
1127 , 313
có cùng điểm biểu diễn trên đường tròn lượng giác
b)
1127 , 674
có cùng điểm biểu diễn trên đường tròn lượng giác
c)
61 19
,
5 5
có cùng điểm biểu diễn trên đường tròn lượng giác
d)
61 23
,
5 4
có cùng điểm biểu diễn trên đường tròn lượng giác
Câu 6. Các mệnh đề sau đúng hay sai?
Mệnh đề Đúng
Sai
a)
756 , 324
có cùng điểm biểu diễn trên đường tròn lượng giác
b)
324 ,36
có cùng điểm biểu diễn trên đường tròn lượng giác
c)
36 ,216
có cùng điểm biểu diễn trên đường tròn lượng giác
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
17
d)
41 15
,
7 7
có cùng điểm biểu diễn trên đường tròn lượng giác
Câu 7. Trong hình vẽ bên, ta xem hình ảnh đường tròn trên một bánh lái tàu thuỷ tương ứng với
một đường tròn lượng giác.
Mệnh đề Đúng
Sai
a)
Công thức tổng quát biểu diễn góc lượng giác
( , )
OA OB
theo đơn vị radian:
( , ) 2 ( );
4
OA OB k k
b)
Công thức tổng quát chỉ ra góc lượng giác tương ứng với bốn điểm biểu diễn
là
, , ,
A C E G
theo đơn vị radian là
( )
3
k k
c)
Công thức tổng quát chỉ ra góc lượng giác tương ứng với hai điểm biểu diễn là
,
A E
theo đơn vị độ là:
180 ( )
k k
d)
Công thức tổng quát biểu diễn góc lượng giác
( , ) ( , )
OA OC OC OH
theo đơn
vị radian:
2 ( )
4
k k
Câu 9. Các mệnh đề sau đúng hay sai?
Mệnh đề Đúng
Sai
a)
Điểm biểu diễn của góc lượng giác có số đo
218
là điểm
M
thuộc góc phần
tư thứ III của đường tròn lượng giác thoả mãn
218
AOM
b)
Điểm biểu diễn của góc lượng giác có số đo
405
là điểm
N
thuộc góc phần
tư thứ IV của đường tròn lượng giác thoả mãn
45
AON
c)
Điểm biểu diễn của góc lượng giác có số đo
25
4
là điểm
P
thuộc góc phần
tư thứ I của đường tròn lượng giác thoả mãn
4
AOP
d)
Điểm biểu diễn của góc lượng giác có số đo
15
2
là điểm
(0; 1)
Q
thuộc đường
tròn lượng giác thoả mãn
2
AOQ
Câu 10. Tính được các giá trị lượng giác của góc
2
3
k
(biết
k
). Khi đó:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
18
Mệnh đề Đúng
Sai
a)
3
sin
2
b)
1
cos
2
c)
tan 3
d)
3
cot
3
Câu 11. Cho
0 90
. Khi đó:
Mệnh đề Đúng
Sai
a)
sin 90 0
A
b)
cos 45 0
B
c)
tan 270 0
C
d)
cos 2 90 0
D
Câu 12. Cho biết
3 4
sin , cos
5 5
. Và các biểu thức:
sin sin( )
2
A
;
cos( ) cot
2
B
. Khi đó
Mệnh đề Đúng
Sai
a)
cos sin
A
b)
cos tan
B
c)
27
20
A B
d)
29
20
A B
Câu 13. Biết:
1
cos
4
x
với
0
2
x
. Khi đó:
Mệnh đề Đúng
Sai
a)
sin 0
x
b)
15
sin
4
x
c)
tan 15
x
d)
1
cot
15
x
Câu 14. Cho
0
2
. Khi đó:
Học để khẳng định mình!
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương
19
Mệnh đề Đúng
Sai
a)
cos( ) 0
A
b)
tan( ) 0
B
c)
2
sin 0
5
C
d)
3
cos 0
8
D
Câu 15. Biết:
2
sin ,
3 2
. Khi đó:
Mệnh đề Đúng
Sai
a)
cos 0
b)
5
cos
3
c)
2
tan
5
d)
5
cot
2
Câu 16. Biết: cot 2 1,0
2
. Khi đó:
Mệnh đề Đúng
Sai
a)
cos 0
sin 0
b)
tan 2 1
c)
2 2
sin
2
d)
2 2
cos
2
ĐỀ ÔN TẬP BÀI 1: “GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC”
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Góc có số đo
24
đổi sang độ bằng
A.
7
. B.
7 30
. C.
8
. D.
8 30
.
Câu 2. Một đường tròn có đường kính là
50 cm
. Độ dài của cung tròn trên đường tròn có số đo
là
4
bằng (làm tròn đến hàng đơn vị):

Tài liệu khác của Toán 11

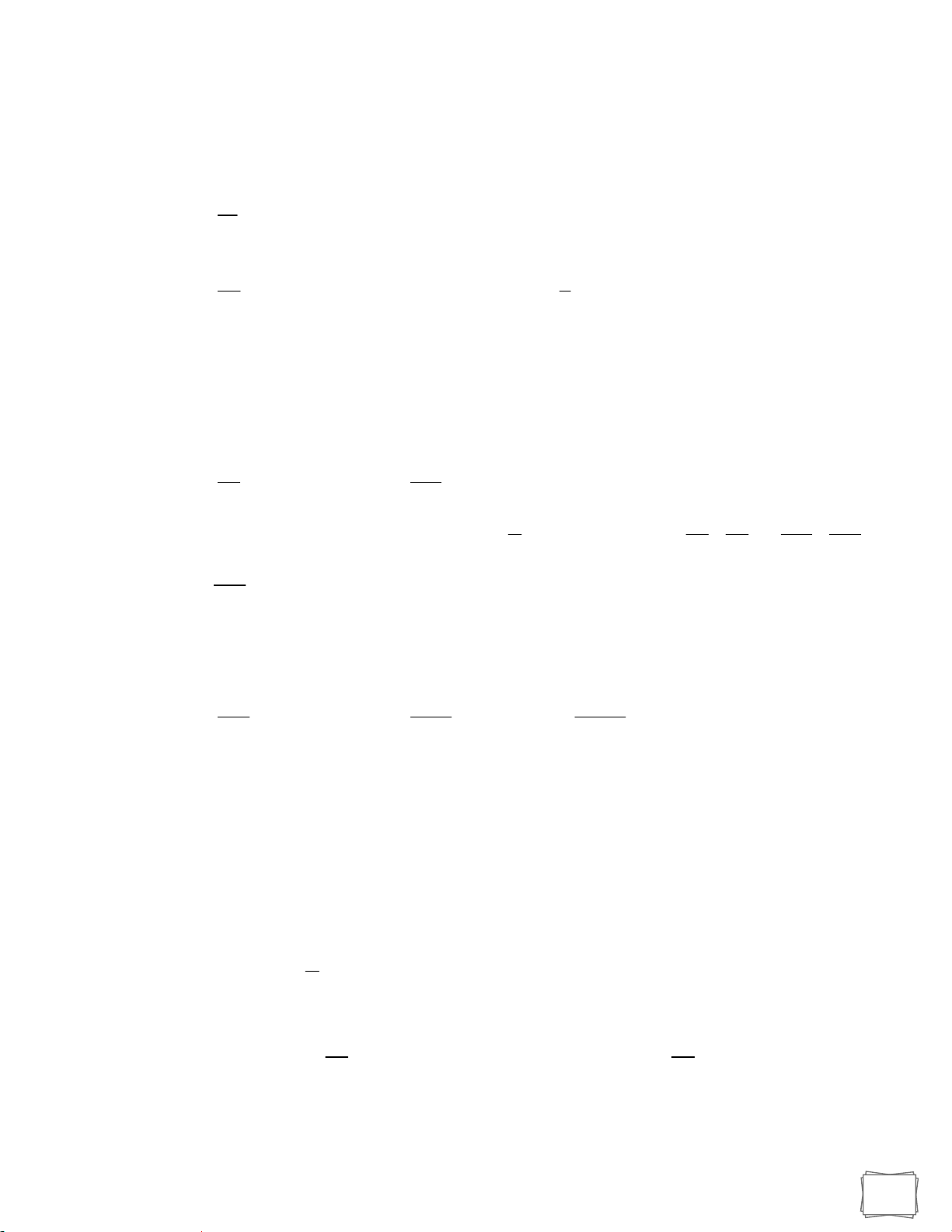
Preview text:

Học để khẳng định mình! CHỦ ĐỀ 1:
HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC I. LÝ THUYẾT CƠ BẢN
1. Hệ thức lượng giác cơ bản  2 2 sin   cos   1     tan .
 cot  1,   k ,k      2     1  2 1  tan       k ,  k   ; 2 cos   2   1 2 1  cot     k ,  k   2   sin 
2. Giá trị lượng giác của các góc có liên quan đặc biệt Góc đối nhau (  và   )
Góc bù nhau (  và    ) cos     cos
sin    sin sin     sin
cos    cos tan     tan
tan    tan cot     cot
cot    cot 
Góc phụ nhau (  và   ) 2
Góc hơn kém ( và    )   sin   sin    sin      cos   2 
cos    cos   cos 
    sin 
tan    tan   2   
cot    cot tan     cot  2    cot 
    tan  2 
3. Công thức lượng giác a. Công thức cộng
cosa b  cosa cosb  sina sinb sina b  sina cosb  cosa sinb
cosa b  cosa cosb  sina sinb sina b  sina cosb  cosa sinb tana  tan tan(  ) b a b  tana  tanb tan(a b)  1  tana.tanb 1  tana.tanb
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 1
Học để khẳng định mình!     sina  cosa  2 sin a        2 cos a          4     4  Chú ý:      sina  cosa  2 sin a   
     2 cos a          4    4
b. Công thức nhân đôi, công thức hạ bậc Công thức nhân đôi Công thức hạ bậc sin 2  2sin .  cos 2 1  cos2 2 2
cos2  cos   sin  sin   2 1  cos2 2  2cos  1 2 cos   2  1  2sin  2 2 1  cos2 tan    2tan  1  cos2 tan 2  2 1  tan 
d. Công thức biến đổi tích thành tổng, tổng thành tích
Biến đổi tích thành tổng
Biến đổi tổng thành tích a  b a b 1 cosa  cosb  2cos cos cosa.cosb cos 2 2
 a b cosa b     2  a b a b 1 cosa  cosb  2sin sin sina.sinb cos  2 2  a b cosa b     2  1 a  b a b sina.cosb sin sina  sinb  2 sin cos
 a b sina b     2  2 2 sin sin 2cosa b sin a b a b     2 2 4. Hàm số lượng giác
a) Hàm số chẵn, hàm số lẻ
Hàm số y  f x có tập xác định là D  x   D  x   D
+) Hàm số y  f x được gọi là hàm số chẵn nếu  f   x    f x  x   D  x   D
+) Hàm số y  f x được gọi là hàm số lẻ nếu  f   x    f x
Chú ý: +) Đồ thị hàm số lẻ nhận gốc O làm tâm đối xứng
+) Đồ thị hàm số chẵn nhận trục tung là trục đối xứng b) Hàm số tuần hoàn
Hàm số y  f x xác định trên tập hợp D, được gọi là hàm số tuần hoàn nếu có số T  0
sao cho với mọi x  D ta có x T  D và f x T  f x.
Nếu có số dương T nhỏ nhất thỏa mãn các điều kiện trên thì T gọi là chu kì của hàm số tuần hoàn đó. Chú ý:
+) Hàm số y  sin x,y  cosx tuần hoàn với chu kì T  2
+) Hàm số y  tan x,y  cotx tuần hoàn với chu kì T  
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 2
Học để khẳng định mình! 2
+) Hàm số y  A sinax b và y  Acosax b,  ,
A a  0 tuần hoàn với chu kì T  a 
+) Hàm số y  A tanax b và y  Acotax b,  ,
A a  0 tuần hoàn với chu kì T  a
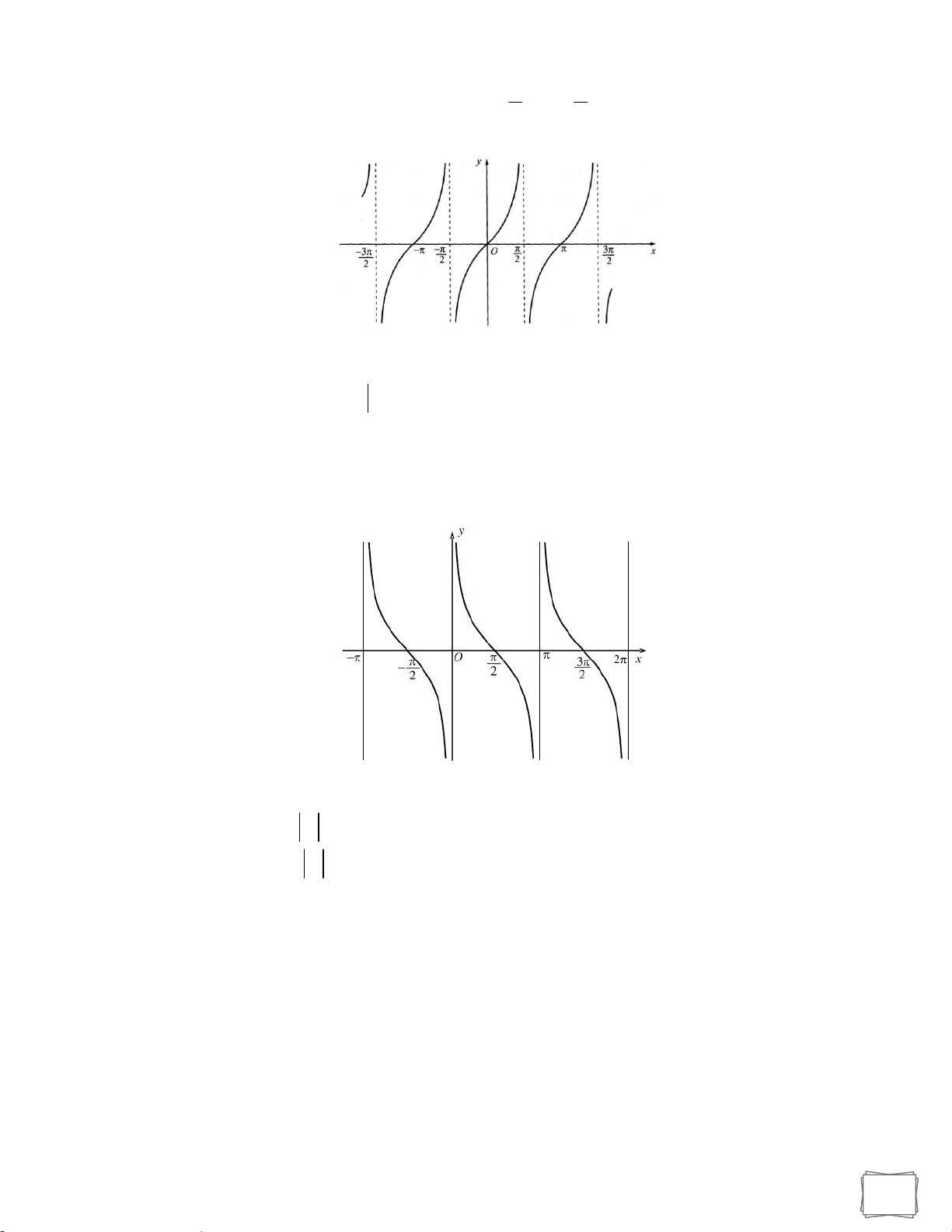
c) Đồ thị và tính chất của các hàm số lượng giác y  sinx +) Tập xác định  +)Tập giá trị:  1  ;1   , có nghĩa là 1   sinx  1, x    .
+) Hàm số tuần hoàn với chu kì 2    
+) Hàm số đồng biến trên mỗi khoảng    k2;  k2 
và nghịch biến trên mỗi  2 2   3  khoảng   k2 ;   k2  ,k   . 2 2 
+) là hàm số lẻ, đồ thị là đường hình sin nhận gốc tọa độ O là tâm đối xứng
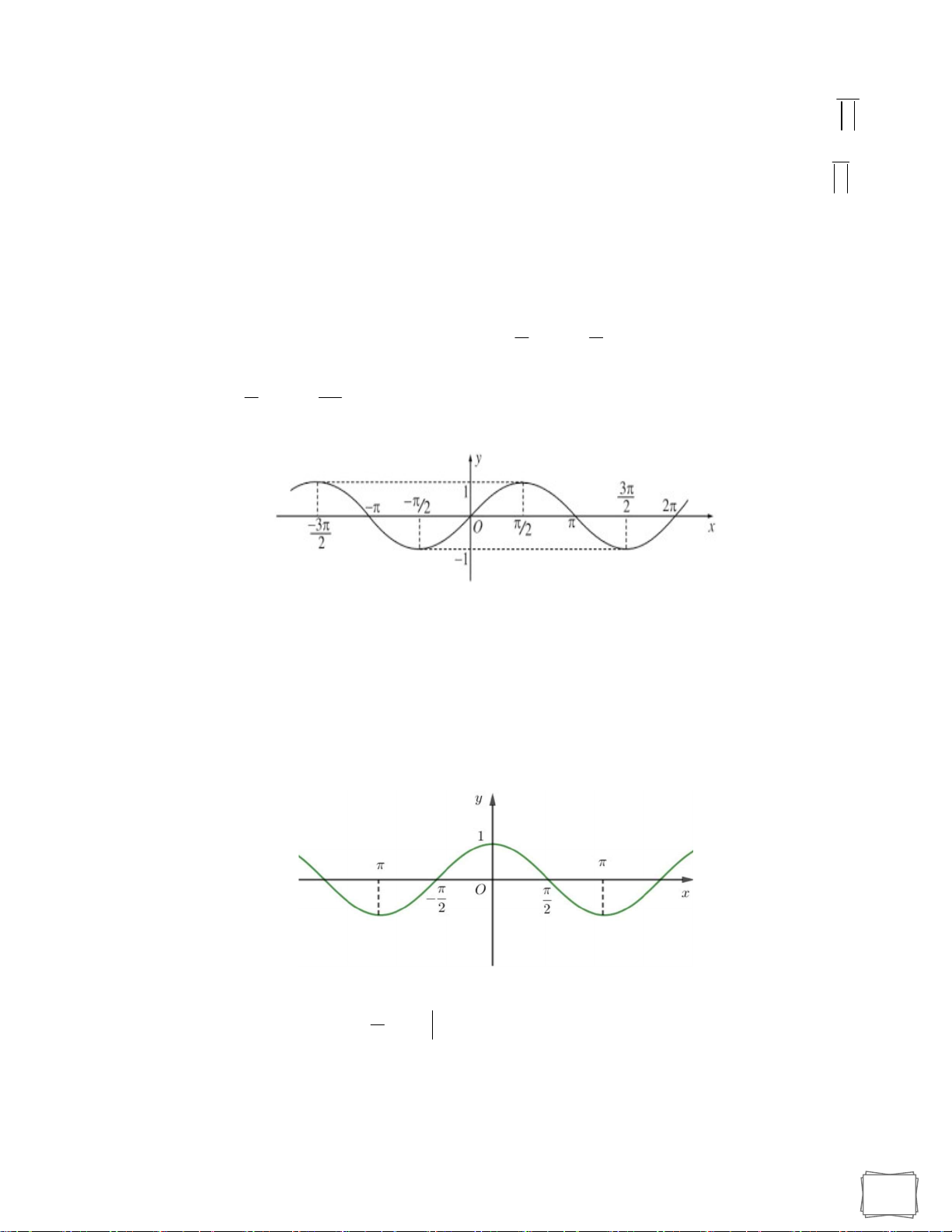
d) Đồ thị và tính chất của các hàm số lượng giác y  cosx +) Tập xác định  . +) Tập giá trị:  1  ;1   , có nghĩa là 1   cosx  1, x    .
+) Hàm số tuần hoàn với chu kì 2
+) Hàm số đồng biến trên mỗi khoảng  
  k2;k2 và nghịch biến trên mỗi khoảng k2 ;
   k2,k  .
+) là hàm số chẵn, đồ thị là đường hình sin nhận Oy làm trục đối xứng
e) Đồ thị và tính chất của các hàm số lượng giác y  tan x  
+) Tập xác định:  \  k k     2      +) Tâp giá trị là  .
+) Hàm số tuần hoàn với chu kì 
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 3
Học để khẳng định mình!    
+ Hàm số đồng biến trên mỗi khoảng    k;  k,   k    .  2 2 
+ là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
f) Đồ thị và tính chất của các hàm số lượng giác y  cotx
+) Tập xác định:  \ k k  . +) Tập giá trị: .
+) Hàm số tuần hoàn với chu kì 
+) Hàm số nghịch biến trên mỗi khoảng k;  k,k  .
+) là hàm số lẻ, đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
5. Phương trình lượng giác cơ bản
a. Phương trình sin x  m
+) Trường hợp 1: m  1 thì phương trình vô nghiệm.
+) Trường hợp 2: m  1 thì phương trình có nghiệm. x    k2  sinx sin     ,   2  k x k      
 x k.360  sinx sin      , k   
x  180    k.360  f x  g x k2
 sin f x  singx         
f x   gx ,k   k2 Chú ý:
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 4
Học để khẳng định mình! sinx  0  x  k sinx  1  x    k2 2 sinx  1   x     k2 2 b. Phương trình cosx  m
+) Trường hợp 1: m  1 thì phương trình vô nghiệm.
+) Trường hợp 2: m  1 thì phương trình có nghiệm. x    k2  cosx cos    ,  2  k x k      
 x k.360  cosx cos     , k    x      k.360  f x  g x  k2 
cos f x  cosgx          f x  g  x ,k   k2 Chú ý: cosx  0  x    k 2 cosx  1  x  k2 cosx  1   x    k2
c. Phương trình tan x  m
Phương trình tan x  m luôn có nghiệm với mọi m
 tanx  tan   x    k k  
 tanx  tan   x    k180 k  
 tan f x  tangx  f x  gx k k   d. Phương trình cotx  m
Phương trình cotx  m luôn có nghiệm với mọi m
 cotx  cot  x    k k  
 cotx  cot  x    k180 k  
 cot f x  cotg x  f x  g x k k  
PHẦN BÀI TẬP BẮT BUỘC
Chủ điểm: Giá trị lượng giác của một cung Dạng 1. Đơn vị đo góc
Câu 1. a) Đổi từ độ sang rađian các số đo sau: 360 ; 4  50; 11
b) Đổi từ rađian sang độ các số đo sau: 3 ;   . 5
Câu 2. Đổi số đo cung tròn sang số đo độ: 3 5 32 3 a) b) c) d) e)2, 3 f) 5,6 4 6 3 7
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 5
Học để khẳng định mình!
Câu 3. Đổi số đo cung tròn sang số đo radian: a) 45 b) 150 c) 72 d) 75
Dạng 2. Độ dài cung tròn
Câu 4. Một đường tròn có bán kính 20 cm . Tìm độ dài của các cung trên đường tròn đó có số đo sau:  a) ; b) 1,5 ; c) 35 ; d) 315 . 12
Câu 5. Một đường tròn có bán kính 36m . Tìm độ dài của cung trên đường tròn đó có số đo là 3 1 a) b) 0 51 c) 4 3
Câu 6. Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây.
a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.
b) Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính
của bánh xe đạp là 680 mm .
Dạng 3. Mối liên hệ giữa góc hình học và góc lượng giác
Câu 7. Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau: 2 11 a) ; b)  ; c) 150 ; d) 225. 3 4  6 9 11 31
Câu 8. Cho góc lượng giác Ou,Ov có số đo . Hỏi trong các góc , ,  , , 5 5 5 5 5 14 
, những góc nào là số đo của một góc lượng giác có cùng tia đầu, tia cuối với góc 5 đã cho.
Câu 9. Hãy tìm số đo  của góc lượng giác Ou,Ov với 0    2, biết một góc lượng giác
có cùng tia đầu và tia cuối với góc đó có số đo là: 29 128 2003 a) b)  c)  d) 18,5 4 3 6
Câu 10. Hãy tìm số đo  của góc lượng giác Ou,Ov 0    360  biết một góc lượng giác
có cùng tia đầu và tia cuối với nó có số đo: a) 395 b) 1052 c) 9  72 d) 20
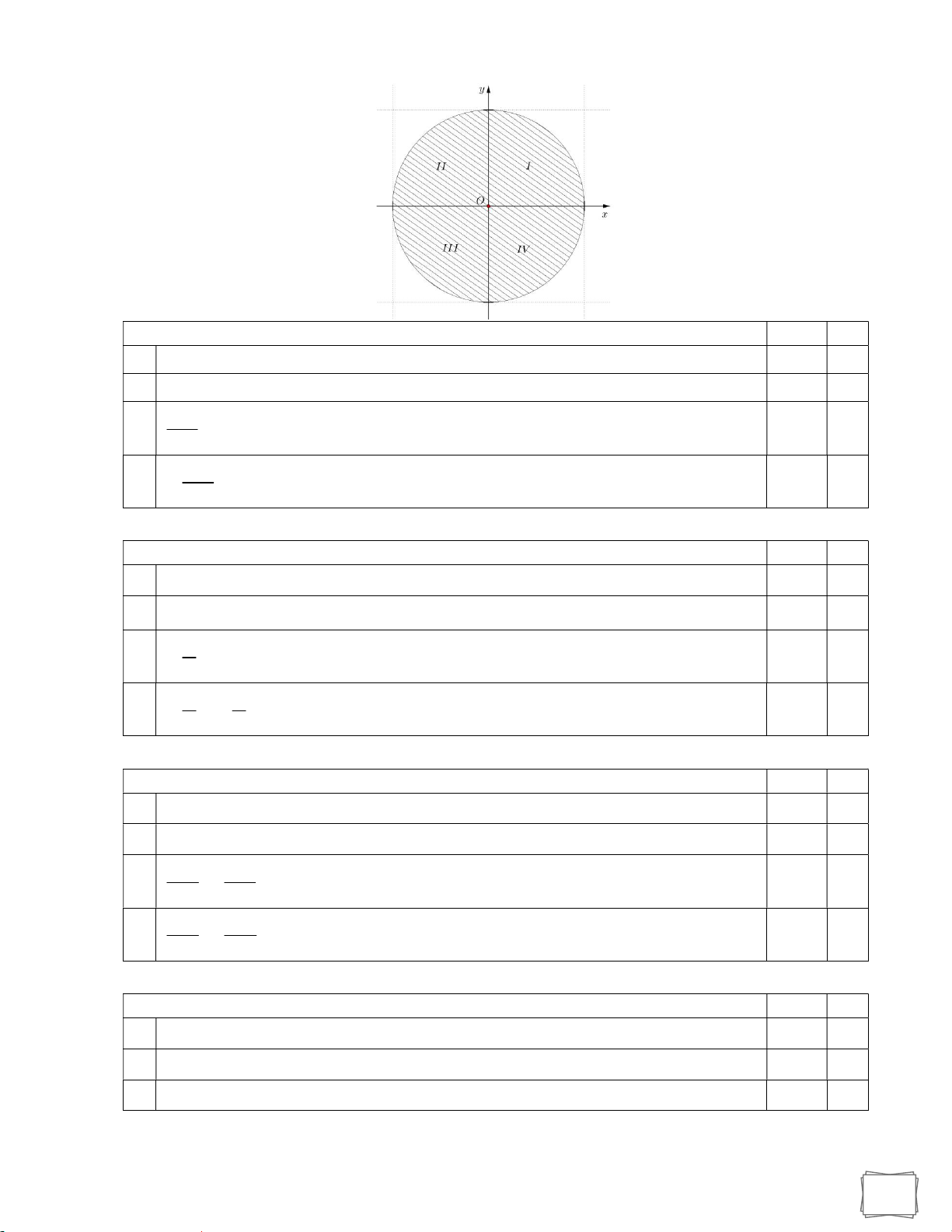
Dạng 4. Dấu các giá trị lượng giác của góc
Câu 11. Cho 0    90. Xét dấu của các biểu thức sau: a) A  sin  90   .
b) B  cos  45.
c) C  cos270  . d) D  cos2  90   . 
Câu 12. Cho 0    . Xét dấu của các biểu thức sau: 2
a) A  cos  .
b) B  tan  .  2  3 c) C  sin       D  cos   5 . d)  8 .
Dạng 5. Rút gọn biểu thức lượng giác
Câu 13. Rút gọn các biểu thức sau:
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 6
Học để khẳng định mình!  
a) A  cos  x  cos  
2 x cos3 x   2          b) B  x   x 7 3 2cos 3cos  5sin  x cot     x   2     2                  c) x     x 3 C 2sin sin 5  sin  x cos        x 2   2    2  3     3 
d) D= cos5 x sin  x tan     x  cot      3 x 2   2        
Câu 14. Rút gọn biểu thức A  sin   cos   cot  
2 tan   2     2    3           3 7 tan cos      sin            2   2     2 
Câu 15. Rút gọn biểu thức B       3  cos  tan          2     2  2 sinx  tanx 
Câu 16. Rút gọn biểu thức A       1   cosx  1  . cosx
Câu 17. Rút gọn biểu thức A  tan x  1  sinx
Câu 18. Đơn giản biểu thức 4 4 2
A  sin x  cos x  2cos x 4 4 sin x  3cos x 1
Câu 19. Đơn giản biểu thức B  6 6 4
sin x  cos x  3cos x 1 2 1  2sin x
Câu 20. Đơn giản biểu thức D  2 2cos x 1
Câu 21. Đơn giản biểu thức E   6 6 x  x  4 4 2 sin cos 3 sin x  cos x
Dạng 6. Tính giá trị lượng giác của góc lượng giác
Câu 22. Tính các giá trị lượng giác của góc  , biết: 1  2 
a) cos   và 0    ;
b) sin   và     ; 5 2 3 2 3 1 3
c) tan   5 và     d) cot   và    2 . 2 2 2
Câu 23. Cho biết một giá trị lượng giác, tính các giá trị lượng giác còn lại 4 5 
a) cosa  , 270  a  360 . b) sina  ,  a   . 5 13 2 3 c) tana  3,  a    . d) cot15  2  3 . 2
Câu 24. Cho biết một giá trị lượng giác, tính giá trị của biểu thức, với:
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 7
Học để khẳng định mình! cota  tana 3  a) A  ,khi sina  , 0  a  . cota  tana 5 2 2 2
sin a  2sina.cosa  2cos a b) C  , khi cota  3  . 2 2
2sin a  3sina.cosa  4 cos a cota  3tana 2 c) G  khi cosa   . 2cota  tana 3 sina  cosa d) H  khi tana  5. cosa  sina
Câu 25. Thực hiện các yêu cầu sau a) Cho 4 4 3 3sin x  cos x  . Tính 4 4 A  sin x  3cos x . 4 b) Cho 4 4 1 3sin x  cos x  . Tính 4 4 C  sin x  3cos x . 2 c) Cho 4 4 7
4 sin x  3cos x  . Tính 4 4 C  3sin x  4 cos x . 4 1
Câu 26. a) Cho sin x  cosx  . Tính sin x, cosx, tan x,cotx. 5
b) Cho tanx  cotx  4. Tính sinx, cosx, tanx,cotx.
Câu 27. Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp tâm trương (tức là áp lực
máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi t 
tại thời điểm t được cho bởi công thức: B(t)  80  7 sin
, trong đó t là số giờ tính 12
từ lúc nửa đêm và B(t) tính bằng mmHg (milimét thuỷ ngân). Tìm huyết áp tâm trương
của người này vào các thời điểm sau: a) 6 giờ sáng;
b) 10 giờ 30 phút sáng c) 12 giờ trưa; d) 8 giờ tối.
Dạng 7. Chứng minh đẳng thức
Câu 28. Chứng minh các đẳng thức: 2 2 cos   tan  1 a) 4 4 2
cos   sin   2cos  1; b) 2  tan  . 2 sin 
Câu 29. Chứng minh các đẳng thức: 3 3 sin a  cos a 2 2 sin a  cos a tana 1 a)  1  sina cosa . b)  . sina  cosa 1  2sina cosa tana  1 c) 4 4 6 6 2 2
sin a  cos a  sin a  cos a  sin a.cos a . 3
Câu 30. Cho tan   2 và     . Chứng minh rằng 2 sin   2cos 2 5   2 sin .  cos  2sin   2 5
HỆ THỐNG CÂU HỎI TRẮC NGHIỆM
Phần I. Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Số đo theo đơn vị rađian của góc 315 là
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 8
Học để khẳng định mình! 7 7 2 4 A. . B. . C. . D. . 2 4 7 7 5
Câu 2. Cung tròn có số đo là
. Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau 4 đây. A. 5 . B. 15 . C. 172. D. 225 .
Câu 3. Cung tròn có số đo là . Hãy chọn số đo độ của cung tròn đó trong các cung tròn sau đây. A. 30 . B. 45 . C. 90 . D. 180 . 2 Câu 4. Góc có số đo đổi sang độ là: 5 A. 0 135 . B. 0 72 . C. 0 270 . D. 0 240 . Câu 5. Góc có số đo 0 108 đổi ra rađian là: 3  3  A. . B. . C. . D. . 5 10 2 4 
Câu 6. Góc có số đo đổi sang độ là: 9 A. 0 25 . B. 0 15 . C. 0 18 . D. 0 20 . 
Câu 7. Cho a   k2 . Tìm k để 10  a  11 2 A. k  7 . B. k  5 . C. k  4. D. k  6 .
Câu 8. Một bánh xe có 72 răng. Số đo góc mà bánh xe đã quay được khi di chuyển 10 răng là: A. 0 60 . B. 0 30 . C. 0 40 . D. 0 50 . Câu 9. Đổi số đo góc 0 105 sang rađian. 7 9 5 5 A. . B. . C. . D. . 12 12 8 12 Câu 10. Số đo góc 0
22 30’ đổi sang rađian là:   7  A. . B. . C. . D. . 5 8 12 6
Câu 11. Một cung tròn có số đo là 0
45 . Hãy chọn số đo radian của cung tròn đó trong các cung tròn sau đây.    A. B.  C. D. 2 4 3  Câu 12. Góc có số đo đổi sang độ là: 24 A. 0 7 . B. 0 7 30. C. 0 8 . D. 0 8 30. Câu 13. Góc có số đo 0 120 đổi sang rađian là: 2 3   A. . B. . C. . D. . 3 2 4 10
Câu 14. Trên đường tròn bán kính r  15 , độ dài của cung có số đo 0 50 là: 180 15 180 A. l  15. . B. l   . C. l  15. .50. D. l  750.  180 
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 9
Học để khẳng định mình! 5  25 19
Câu 15. Cho bốn cung (trên một đường tròn định hướng):    ,  ,   ,  6 3 3 6
, Các cung nào có điểm cuối trùng nhau:
A.  và  ;  và  . B. ,  , . C. , , .
D.  và  ;  và  .
Câu 16. Cho L , M , N , P lần lượt là điểm chính giữa các cungAB , BC , CD ,DA . Cung  3
có mút đầu trùng với A và số đo   
 k . Mút cuối của  ở đâu? 4 A. L hoặc N . B. M hoặc P . C. M hoặc N . D. L hoặc P . 
Câu 17. Trên đường tròn bán kính r  5 , độ dài của cung đo là: 8 r 5 A. l   . B. l   . C. l   . D. kết quả khác. 8 8 8
Câu 18. Một đường tròn có bán kính R  10cm . Độ dài cung 40o trên đường tròn gần bằng A. 11cm . B. 13cm . C. 7cm . D. 9cm . 
Câu 19. Biết một số đo của góc Ox Oy 3 , 
 2001 . Giá trị tổng quát của góc Ox,Oy 2 là:  A. Ox Oy 3 ,   k .
B. Ox,Oy    k2 . 2  
C. Ox,Oy   k.
D. Ox,Oy   k2 . 2 2
Câu 20. Cung nào sau đây có mút trung với B hoặc B’? A. 0 0 a  90  k360 . B. 0 0 a  –90  k180 .   C.    k2 . D.     k2 . 2 2
Câu 21. Cung  có mút đầu là A và mút cuối là M thì số đo của  là: 3 3 3 3 A.  k2 . B.   k2 . C.  k . D.   k . 4 4 4 4
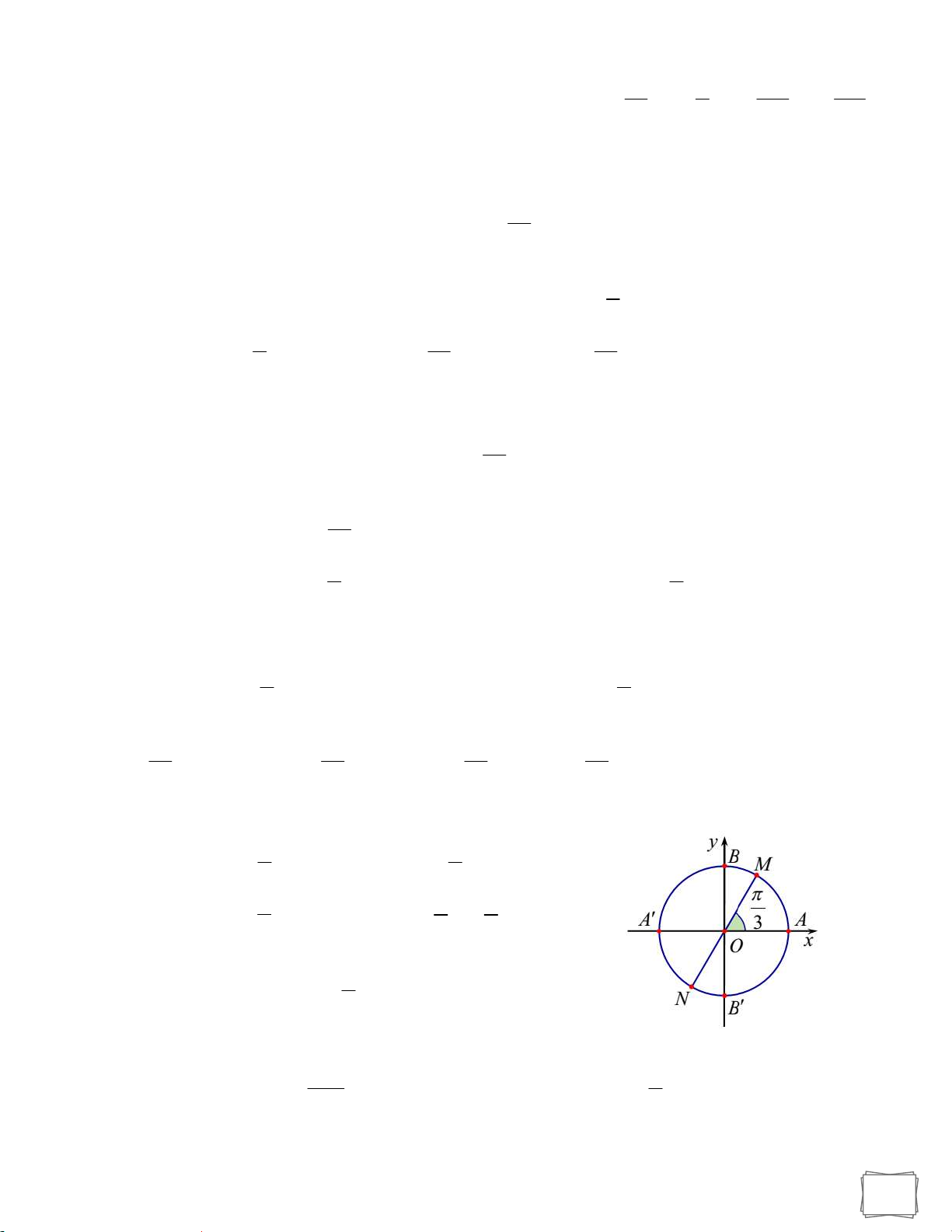
Câu 22. Trên hình vẽ hai điểm M,N biểu diễn các cung có số đo là:   A. x   2k . B. x    k . 3 3    C. x   k . D. x   k .. 3 3 2
Câu 23. Trên đường tròn lượng giác gốc A, cho điểm M xác  định bởi sđAM 
 . Gọi M là điểm đối xứng của M 3 1 
qua trục Ox . Tìm số đo của cung lượng giác AM . 1  5     A. sđ AM   k2 ,  k   B. sđ AM   k2 ,  k   1 3 1 3
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 10
Học để khẳng định mình!       C. sđ AM   k2 ,  k   D. sđ AM   k ,  k   1 3 1 3 7
Câu 24. Góc lượng giác nào sau đây có cùng điểm cuối với góc ? 4   3 3 A.  . B. . C. . D.  . 4 4 4 4 k
Câu 25. Có bao nhiêu điểm M trên đường tròn định hướng gốc A thỏa mãn  2 AM     , 6 3 k  . A. 6 . B. 4 . C. 3 . D. 8 .  Câu 26. Cho
 a   . Kết quả đúng là 2 A. sina  0 , cosa  0 . B. sina  0 , cosa  0 . C. sina  0 , cosa  0 . D. sina  0, cosa  0 .
Câu 27. Trong các giá trị sau, sin  có thể nhận giá trị nào? 4 5 A. 0  ,7. B. . C.  2 . D. . 3 2 5 Câu 28. Cho 2 a    
. Chọn khẳng định đúng. 2 A. tana  0, cota  0. B. tana  0, cota  0. C. tana  0, cota  0. D. tana  0, cota  0 .
Câu 29. Ở góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây. A. cot  0 . B. sin   0 . C. cos   0 . D. tan   0 .
Câu 30. Ở góc phần tư thứ tư của đường tròn lượng giác. hãy chọn kết quả đúng trong các kết quả sau đây. A. cot  0. B. tan   0. C. sin   0 . D. cos   0 . 7 Câu 31. Cho
   2 .Xét câu nào sau đây đúng? 4 A. tan   0. B. cot  0. C. cos   0 . D. sin   0 .
Câu 32. Xét các mệnh đề sau:      
I. cos    0     
. II. sin    0. III. tan    0. 2  2  2  Mệnh đề nào sai? A. Chỉ I. B. Chỉ II. C. Chỉ II và III. D. Cả I, II và III.
Câu 33. Xét các mệnh đề sau đây:       I. cos     0      .
II. sin    0 . III.cot    0 .  2  2   2  Mệnh đề nào đúng? A. Chỉ II và III. B. Cả I, II và III. C. Chỉ I. D. Chỉ I và II.
Câu 34. Cho hai góc nhọn  và  phụ nhau. Hệ thức nào sau đây là sai? A. cot  tan  .
B. cos   sin  . C. cos   sin  . D. sin   cos  .
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 11
Học để khẳng định mình!
Câu 35. Trong các đẳng thức sau, đẳng thức nào đúng? A.  0
sin 180 – a  – cosa. B.  0
sin 180 – a  sina . C. sin 0 180 – a  sina . D. sin 0 180 – a  cosa .
Câu 36. Chọn đẳng thức sai trong các đẳng thức sau    
A. sin  x  cosx    . B. sin  x  cosx .  2  2     
C. tan  x  cotx    . D. tan  x  cotx .  2  2 
Câu 37. Trong các mệnh đề sau, mệnh đề nào đúng? A. cos x    cosx .
B. sinx    sinx .  
C. cos x  cosx .
D. sin  x  cosx  .  2 
Câu 38. Khẳng định nào sau đây là sai? A. sin     sin . B. cot     cot. C. cos     cos. D. tan     tan.
Câu 39. Khẳng định nào sau đây đúng? A. sin x    sinx. B. cos x    cosx. C. cot x    cotx. D. tan x    tanx.
Câu 40. Chọn hệ thức sai trong các hệ thức sau. 3  A. tan  x  cotx  .
B. sin3  x  sinx .  2 
C. cos3  x  cosx . D. cos x    cosx . 1
Câu 41. Cho biết tan   . Tính cot 2 1 1 A. cot  2 . B. cot  . C. cot  . D. cot  2 . 4 2
Câu 42. Trong các công thức sau, công thức nào sai? 1    A. 2 2 sin   cos   1. B. 2 1  tan       k ,  k    2 cos   2  1  k  C. 2 1  cot     k ,
 k   . D. tan   cot  1  ,k   . 2   sin   2  3 
Câu 43. Cho sin   và     . Giá trị của cos là: 5 2 4 4 4 16 A. . B.  . C.  . D. . 5 5 5 25 4 
Câu 44. Cho cos   với 0    . Tính sin  . 5 2
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 12
Học để khẳng định mình! 1 1 3 3 A. sin   . B. sin    . C. sin   . D. sin    . 5 5 5 5
Câu 45. Tính  biết cos   1
A.   k k  .
B.   k2 k  . 
C.    k2 k  . D.   
  k2 k  . 2 2  
Câu 46. Cho cos        . Khi đó tan  bằng 5 2  21 21 21 21 A. . B.  . C. . D.  . 3 5 5 2 3
Câu 47. Cho tan   5 , với     . Khi đó cos bằng: 2 6 6 1 A.  . B. 6 . C. . D. . 6 6 6 3
Câu 48. Cho sin   90    180 . Tính cot . 5 3 4 4 3 A. cot  . B. cot  . C. cot   . D. cot   . 4 3 3 4 2
Câu 49. Trên nửa đường tròn đơn vị cho góc  sao cho sin   và cos   0 . Tính tan  . 3 2 5 2 5 2 A. . B. . C. . D. 1 . 5 5 5 1 
Câu 50. Cho sin   và     . Khi đó cos có giá trị là. 3 2 2 2 2 8 2 2 A. cos    . B. cos   . C. cos   . D. cos    . 3 3 9 3 1
Câu 51. Cho sin x  cosx  và 0 x 
  . Tính giá trị của sinx . 2 2 1 7 1 7 1 7 1 7 A. sin x   . B. sin x   . C. sin x   . D. sin x   . 6 6 4 4 3sin x  cosx Câu 52. Cho P 
với tanx  2. Giá trị của P bằng sinx  2cosx 8 2 2 8 5 A. . B.  . C. . D. . 9 3 9 4 4 sin x  5cosx
Câu 53. Cho tanx  2.Giá trị biểu thức P  là 2sinx  3cosx A. 2 . B. 13 . C. 9  . D. 2  .
Câu 54. Cho tam giác ABC đều. Tính giá trị của biểu thức      
P  cosAB,BC cosBC,CA cosC ,AAB.
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 13
Học để khẳng định mình! 3 3 3 3 3 3 A. P  . B. P   . C. P   . D. P  . 2 2 2 2 2sina  cosa
Câu 55. Cho tana  2 . Tính giá trị biểu thức P  . sina  cosa 5 A. P  2. B. P  1. C. P  . D. P  1  . 3 3 cot  2tan Câu 56. Cho sin   và 0 0
90    180 . Giá trị của biểu thức E    là: 5 tan   3cot 2 2 4 4 A. . B.  . C. . D.  . 57 57 57 57 3sin  cos
Câu 57. Cho tan   2 . Giá trị của A    là: sin   cos 5 7 A. 5 . B. . C. 7 . D. . 3 3
Câu 58. Biết tan   2 và 180    270 . Giá trị cos   sin  bằng 3 5 3 5 5 1 A.  . B. 1 – 5 . C. . D. . 5 2 2 Câu 59. Biểu thức 2 2 2 2 2
D  cos x.cot x  3cos x – cot x  2sin x không phụ thuộc x và bằng A. 2. B. –2 . C. 3. D. –3 2 2cos x 1
Câu 60. Đơn giản biểu thức A  ta có sin x  cosx A. A  cosx  sinx . B. A  cosx – sin x . C. A  sin x – cosx . D. A  sin x – cosx . Câu 61. Biểu thức:   A        2003 cos 26 2sin 7  cos1,5  cos            cos  
 1,5.cot 8  2 
có kết quả thu gọn bằng: A. sin  . B. sin  . C. cos . D. cos.                           
Câu 62. Đơn giản biểu thức A cos  sin   cos  , ta có:        sin         2 2  2    2  A. A  2 sina . B. A  2 cosa . C. A  sina – cosa . D. A  0 .       
Câu 63. Biểu thức P  sin  x cos  x cot  
2 x tan 3 x  có biểu thức rút 2     2  gọn là A. P  2 sin x . B. P  2  sin x . C. P  0 . D. P  2 cotx .
Câu 64. Cho tam giác ABC . Đẳng thức nào sau đây sai? A. A  B C   .
B. cosA  B  cosC . A  B C C. sin  cos .
D. sinA  B  sinC . 2 2
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 14
Học để khẳng định mình!  
Câu 65. Đơn giản biểu thức A  cos     sin     , ta có  2 
A. A  cosa  sina . B. A  2 sina . C. A  sina – cosa . D. A  0 .
Câu 66. Cho A, B, C là ba góc của một tam giác không vuông. Mệnh đề nào sau đây sai? A  B   C A  B   C A. tan   cot  . B. cot   tan .  2  2  2  2
C. cotA  B  cotC .
D. tanA  B  tanC .      3 
Câu 67. Rút gọn biểu thức A  cos   sin   tan     .sin  ta được     2  2   2  A. A  cos  . B. A  cos  . C. A  sin  . D. A  3 cos  .
PHẦN II. BÀI TẬP ĐÚNG/ SAI
Câu 1. Đổi số đo của các góc sang radian. Khi đó: Mệnh đề Đúng Sai a) 30   rad 6 b) 15      1     rad    12 c)  11 132   rad 15 d)  13 4  95    rad 4
Câu 2. Đổi số đo của các góc sang độ. Khi đó: Mệnh đề Đúng Sai a) 3 rad 135  4 b)  rad 0,5    360 c) 31 rad 27  2 d) 4rad 229,18   
Câu 3. Biểu diễn góc lượng giác trên đường tròn lượng giác. Khi đó:
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 15
Học để khẳng định mình! Mệnh đề Đúng Sai
a) 125là điểm M thuộc góc phần tư thứ thứ II
b) 405là điểm N thuộc góc phần tư thứ III c) 19
là điểm P thuộc góc phần tư thứ II 3 d) 13 
là điểm Q thuộc góc phần tư thứ IV 6
Câu 4. Biểu diễn góc lượng giác trên đường tròn lượng giác. Khi đó: Mệnh đề Đúng Sai a) 36 k360 
,k   là điểm M thuộc góc phần tư thứ II b) 60 k180  
,k   là các điểm M ,M thuộc góc phần tư thứ II và IV 1 2 c)    k2 ,
 k   là M thuộc góc phần tư thứ III 4 d)  k   
,k   là bốn điểm M,N,P,Q thuộc góc phần tư thứ I,II,III,IV 6 2
Câu 5. Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a) 1127, 313 
có cùng điểm biểu diễn trên đường tròn lượng giác
b) 1127,674 có cùng điểm biểu diễn trên đường tròn lượng giác c) 61 19 ,  
có cùng điểm biểu diễn trên đường tròn lượng giác 5 5 d) 61 23 ,  
có cùng điểm biểu diễn trên đường tròn lượng giác 5 4
Câu 6. Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai a) 756, 324 
có cùng điểm biểu diễn trên đường tròn lượng giác b) 324,36 
có cùng điểm biểu diễn trên đường tròn lượng giác
c) 36,216 có cùng điểm biểu diễn trên đường tròn lượng giác
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 16
Học để khẳng định mình! d) 41 15 ,  
có cùng điểm biểu diễn trên đường tròn lượng giác 7 7
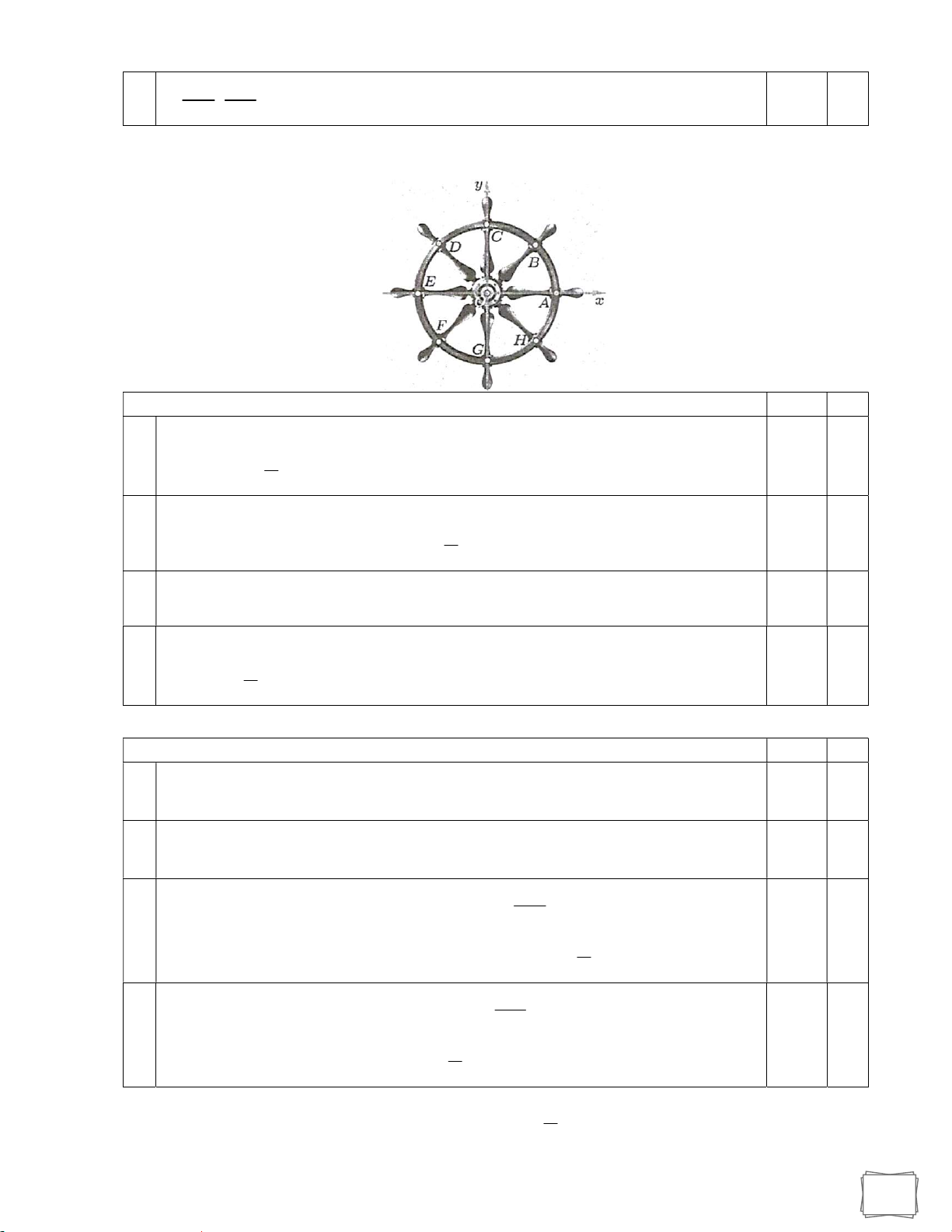
Câu 7. Trong hình vẽ bên, ta xem hình ảnh đường tròn trên một bánh lái tàu thuỷ tương ứng với
một đường tròn lượng giác. Mệnh đề Đúng Sai
a) Công thức tổng quát biểu diễn góc lượng giác (O , A OB) theo đơn vị radian: (O , A OB)    k2 (  k  ); 4
b) Công thức tổng quát chỉ ra góc lượng giác tương ứng với bốn điểm biểu diễn  là ,
A C,E,G theo đơn vị radian là k (k  ) 3
c) Công thức tổng quát chỉ ra góc lượng giác tương ứng với hai điểm biểu diễn là ,
A E theo đơn vị độ là: k180(k  ) 
d) Công thức tổng quát biểu diễn góc lượng giác (O , A OC) (OC,OH) theo đơn  vị radian:  k2 (  k  ) 4
Câu 9. Các mệnh đề sau đúng hay sai? Mệnh đề Đúng Sai
a) Điểm biểu diễn của góc lượng giác có số đo 218 là điểm M thuộc góc phần
tư thứ III của đường tròn lượng giác thoả mãn  AOM 218 
b) Điểm biểu diễn của góc lượng giác có số đo 405 
là điểm N thuộc góc phần
tư thứ IV của đường tròn lượng giác thoả mãn  AON 45   c) 25
Điểm biểu diễn của góc lượng giác có số đo
là điểm P thuộc góc phần 4
tư thứ I của đường tròn lượng giác thoả mãn  AOP   4 d) 15
Điểm biểu diễn của góc lượng giác có số đo là điểm Q(0; 1  ) thuộc đường 2
tròn lượng giác thoả mãn  AOQ    2 
Câu 10. Tính được các giá trị lượng giác của góc  
 k2 (biết k  ). Khi đó: 3
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 17
Học để khẳng định mình! Mệnh đề Đúng Sai a) 3 sin    2 b) 1 cos   2 c) tan  3 d) 3 cot   3 Câu 11. Cho 0  90   . Khi đó: Mệnh đề Đúng Sai a) A sin 90    0 b) B cos 45    0 c) C tan270     0 d) D cos2 90    0 3 4  
Câu 12. Cho biết sin   ,cos    . Và các biểu thức: A  sin    sin(  ); 5 5 2    B  cos(  )  cot        . Khi đó 2  Mệnh đề Đúng Sai a) A  cos   sin  b) B  cos   tan  c) 27 A  B  20 d) 29 A  B   20 1
Câu 13. Biết: cosx  với 0 x    . Khi đó: 4 2 Mệnh đề Đúng Sai a) sin x  0 b) 15 sinx   4 c) tanx  15 d) 1 cotx   15 
Câu 14. Cho 0    . Khi đó: 2
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 18
Học để khẳng định mình! Mệnh đề Đúng Sai
a) A  cos(  )  0
b) B  tan(  )  0 c)  2  C  sin       0   5  d)  3  D  cos       0   8  2 
Câu 15. Biết: sin   ,     . Khi đó: 3 2 Mệnh đề Đúng Sai a) cos   0 b) 5 cos   3 c) 2 tan    5 d) 5 cot   2 
Câu 16. Biết: cot  2  1,0    . Khi đó: 2 Mệnh đề Đúng Sai a) c  os  0  s  in  0  b) tan  2 1 c) 2 2 sin    2 d) 2 2 cos   2
ĐỀ ÔN TẬP BÀI 1: “GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC”
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.  Câu 1. Góc có số đo đổi sang độ bằng 24 A. 7 . B. 7 3  0 . C. 8 . D. 8 3  0 .
Câu 2. Một đường tròn có đường kính là 50cm. Độ dài của cung tròn trên đường tròn có số đo 
là bằng (làm tròn đến hàng đơn vị): 4
GV: Nguyễn Trung Trông - ☎ :0983.286.750 - Trường THPT Xuân Phương 19

Tài liệu liên quan: