Bài tập chương I: Cơ Sở logic
I. MỆNH ĐỀ, BIỂU THỨC LOGIC Câu 1:
Cho p, q và r là các mệnh đề:
p: Bạn nhận được điểm giỏi trong kỳ thi cuối khoá.
q: Bạn làm hết các bài tập trong giáo trình.
r :Bạn đạt giỏi ở lớp.
Hãy dùng các kí hiệu p, q, r và các ký hiệu phép toán logic để viết các mệnh đề sau:
a) Bạn đạt giỏi ở lớp nhưng không làm hết các bài tập trong giáo trình.
b) Bạn nhận được điểm giỏi trong kỳ thi cuối khoá,bạn làm hết các bài tập trong giáo trình
và bạn đạt loại giỏi ở lớp.
c) Để được công nhận loại giỏi ở lớp bạn cần phải được điểm giỏi ở kỳ thi cuối khoá.
d) Bạn đạt loại giỏi ở lớp nếu và chỉ nếu bạn làm hết các bài tập trong giáo trình hoặc nhận
được điểm giỏi trong kỳ thi cuối khoá. Câu 2:
Gọi P,Q,R là các mệnh đề sau: P: ABC là tam giác cân Q: ABC là tam giác đều
R: Tam giác ABC có ba góc bằng nhau
Hãy viết các mệnh đề sau:
a) Nếu ABC là tam giác đều thì ABC là tam giác cân
b) ABC không phải là tam giác cân thì ABC là tam giác đều.
c) ABC là tam giác cân và ABC không phải tam giác đều
d) Tam giác ABC có ba góc bằng nhau thì ABC là tam giác cân. Câu 3:
P := “Mai đang học Lí”
Q := “Mai đang học Hoá”
R := “Mai đang học Anh văn”
Hãy viết các mệnh đề dưới đây dưới dạng hình thức trong đó sử dụng các phép toán
a) Không đúng là Mai đang học Anh văn hay Hoá mà không học Lí
b) Mai không học Hoá lẫn Anh văn nhưng đang học Lí 1
Câu 4: Rút gọn các biểu thức logic sau :
a) A = (r  q) (p  q  r) (p  q  r)
b) B = (x  y)  (z  y  x)  (z  y  x)
c) C = (x  y)  ((z  x)  y)
d) D = (x  y)z  (x  z)(y  z) ) e
E = x y → ( y → x)
Câu 5: Cho p,q,r là các biến mệnh đề. Chứng minh: a) b) c)
Câu 6: Cho p, q, r là các biến mệnh đề. Không lập bảng chân trị, chứng minh:
a)( p  q  r)  ( p → q  ( p  r)
b) (p→q)  (¬q)  (q→r)  (¬q ¬p)
c) (p¬ (qr)) ¬ (p→ q)  (p¬r)
d) (¬p→r)(q→r)(p→q)→r
e) (¬p˅q)∧(p→r)p→(q∧r)
f) (p → q) ∧ ¬q ∧ (q → r) ⇔ ¬q ∧ ¬ p
g) (p ∧ q) ∨ r ⇔ (p → ¬q) ∧ ¬ r
h){[( p → r)  (q → r)] → ( p → q)}  ( p  q  r ) i) 
 (p q  r)→ q]→ (p r )  (p q r)
j) [p → (q  r)]  [r → (q → p)]
k) ( p → q)  p  q
Câu 7: Không lập bảng chân trị, sử dụng các công thức tương đương logic để chứng minh các
biểu thức logic sau là đúng :
a) (p∧q) → q 2 b) (p∧q) → p
c) p→(¬p→p) d) ¬ (p v ¬q)→¬p e) p→ (q→(p∧q))
II. VỊ TỪ, LƯỢNG TỪ Câu 1:
Cho Q(x, y) là ký hiệu của câu “ x = y + 3”. Xác định giá trị chân lý của các mệnh đề Q(1, 2) và Q(3, 0). Câu 2:
Xác định giá trị chân lý của∀P(x) ,trong đó P(x) là diễn đạt “x2<10” và không gian khảo sát
gồm các số nguyên dương không lớn hơn 4. Câu 3:
Cho các vị từ trên không gian là tập số thực như sau: P(x) = {x ≥ 0) Q(x) = {x2 ≥ 0} R(x) = {x2- 3x -4 = 0} S(x) = {x2- 3 > 0}
Xác định giá trị đúng, sai của những mệnh đề sau: a) ∀x [Q(x) → S(x)] b) ∀x [R(x) ∨ S(x)] c) ∀x [R(x) → P(x)] Câu 4:
Cho P(x, y) là câu “x + y = y + x”. Xác định giá trị đúng, sai của ∀x ∀y P(x, y) với không gian
được khảo sát đối với từng biến đều là các số thực. Câu 5:
Cho Q(x, y) là câu “x + y = 0”. Xác định giá trị đúng, sai của Ǝy ∀x Q(x, y) và ∀x Ǝy Q(x, y)
với không gian được khảo sát đối với từng biến đều là các số thực. Câu 6:
Cho Q(x, y, z) là diễn đạt “x + y = z”. Xác định giá trị đúng,sai của ∀x∀y Ǝz Q(x, y, z) và
Ǝz∀x∀y Q(x, y, z) với không gian được khảo sát đối với từng biến đều là các số thực. 3
Câu 7:Xét các câu sau, trong đó ba câu đầu là tiền đề và câu thứ tư là một kết luận đúng.
“ tất cả các chim ruồi đều có màu sặc sỡ”
“ không có con chim ruồi lớn nào sống bằng mật ong”
“ những chim ruồi không sống bằng mật ong đều có màu xám” “ chim ruồi là nhỏ”
Gọi P(x), Q(x), R(x) và S(x) lần lượt là các câu “ x là chim ruồi”, “x là lớn”, “x sống bằng mật
ong”, và “x có màu sặc sỡ”. Giả sử không gian được khảo sát là tất cả các loài chim, hãy diễn
đạt các câu trong suy lý bằng P(x), Q(x), R(x), S(x) và các lượng từ.
Câu 8: Viết dạng phủ định của A và xét chân trị 3
a) A = "x  R,| x |= −x ' n n 1 b) A " x R, n N , 2 x 2 + =       " 2 2
c)A = "x  , R y  ,
R (x = y ) → (x = y)" 2
d)A = "x  , Q y  ,
R (x + 2x −15) y = 0" 2 2 )
e A = "x  , R y  ,
Q x + 4x  y + 7"
) = "  ,  ,  2y f A x R y R x −3" 2 2
g)A = "x  , R y  ,
R (x  y ) → (x  y)"
III. NGUYÊN LÝ QUY NẠP
Câu 1:CM: 𝟐𝒏 < 𝒏!∀n ≥ 4
Câu 2: Cho n ∈ 𝑵, n ≥ 𝟐. Chứng minh rằng 𝑷𝒏 = 𝒏 bằng tích của các số nguyên tố.
Câu 3: Chứng minh 1+3+…+(2n-1) = 𝒏𝟐với mọi số nguyên dương n.
Câu 4: Chứng minh rằng (𝟏 + 𝟏 𝒏 ⁄ )𝒏2.
Câu 5:Chứng minh rằng n  2 , ta có : 𝒂𝒏 = (𝒏 + 𝟏)(𝒏 + 𝟐) … . (𝒏 + 𝒏) ⋮ 𝟐𝒏 4
IV. QUI TẮC SUY DIỄN
Câu 1: Cho p,q,r,s,t,u là các biến mệnh đề. Kiểm tra sự đúng đắn của các suy luận sau: a) p→ r ⌐p→ q q→ s -------------------  ⌐r→ s b) p p→ q ⌐s→r r→ ⌐q ----------  st c) p q→r p→⌐r --------- ⌐q
d) { ⌐s [(⌐pq) →r]  ⌐u  r→(st)] ( u⌐t)]}  p e) [p→(q→r)] (t→q) ⌐s ps --------------  ⌐r→⌐t 5 f) p→q r→s (sq) →( pt) t→⌐p ------------------  ⌐(pr) g) t → u r → (s  t) (p q ) → r (s  u ) ____________  p 6 1 BÀI TẬP CHƯƠNG 2
I. Tập hợp – các phép toán trên tập hợp.
Câu 1 : Giả sử A = {1,{1},{2}}. Hãy chỉ ra các khẳng định đúng trong số các khẳng định dưới đây : a) b) c) d) e) f)
Câu 2 : Hãy liệt kê các phần tử trong các tập hợp dưới đây : = 1+ (−1)n A | n  N  1  B = n + n 1;2;3;5;  7   n   1  C =  n  1;3;5;7;9;11  2   n + n 
Câu 3 : Xét các tập hợp con của Z :
A = 2m +1 m  Z, B =2n + 3 n  Z
C =2 p − 3 p  Z, D = 3r +1 r  Z
E = 3s + 2 s  Z, F = 3t − 2 t  Z
Hãy xác định các khẳng định đúng trong số các khẳng định sau đây a) A = B b) A = C c) B = C d) D = E e) D = F f) E = F
Câu 4 : Trong số các tập hợp dưới đây, tập hợp nào khác ? a) b) c) d) e) 2 f)
Câu 5 : Xét 4 tập hợp con của tập hợp vũ trụ A = {1,2,3,4,5}, B = {1,2,4,8} C = {1,2,3,5,7}, D = {2,4,6,8}
Hãy xác định các tập hợp dưới đây: a) (A B)C b) A(B C)
c) C  D d) C  D
e) ( A  B)  C f) A  (B C) g) (B C)
 D h) B  C  D
i) ( A  B)  C  D
Câu 6 : Dùng các quy luật của Lý thuyết tập hợp để đơn giản các biểu thức dưới đây:
a) A  (B  A)
b) A  B  ( A B C)
Câu 7: Cho A,B,C,D là các tập hợp, chứng minh rằng:
a) A  (B − A) = 
b) ( A − C )  (C − B) = 
c) A − B = A  B
Câu 8: Cho A = {1,5}và B = {a, b, c, d}. Tìm a. A × B b. B × A c. A2
Câu 9: Cho tập A = { a, b, c }, B = { x, y }, C = { 0, 1 }. Tìm a. A×B×C b. B×B×B 3
Câu 10: Giả sử tập vũ trụ U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Biểu diễn các tập dưới đây bằng các xâu bit. a. {3, 4, 5} b. {1, 3, 6, 10} c. {2, 3, 4, 7, 8, 9}
Câu 11: Dùng tập vũ trụ như bài tập trên , tìm các tập biểu diễn bới các xâu sau: a. 11110 01111 b. 01011 11000 c. 10000 00001
Câu 12: Cho U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Hãy dùng các xâu bit để tìm giao và
hợp của tập A = {2, 4, 5, 7, 8, 10} và B = {1, 3 ,4, 6, 7, 8 ,9} .
II. Nguyên lý cộng. Nguyên lý nhân. Nguyên lý chuồng bồ câu.
Câu 1: Một sinh viên có thể chọn một đề tài từ 1 trong 3 danh sách các đề tài. Số
đề tài trong 3 danh sách các đề tài lần lượt là 23, 15, 20. Hỏi sinh viên có bao
nhiêu cách để chọn 1 đề tài.
Câu 2: Trong đoạn từ 1 đến 1000 có bao nhiêu số hoặc là số lẻ hoặc là số chính phương?
Câu 3: Đếm số xâu nhị phân độ dài 8 có hai bit đầu 00 hoặc 11.
Câu 4: Có bao nhiêu xâu nhị phân độ dài 8 không chứa 6 số 0 liền nhau?
Câu 5: Có bao nhiêu xâu nhị phân độ dài 10 hoặc bắt đầu bởi 3 số 1, hoặc kết thúc bởi 4 số 0?
Câu 6: Một lớp học có 5 sinh viên nữ, 10 sinh viên nam. Có bao nhiêu cách chọn
ra 2 sinh viên bao gồm 1 nam và 1 nữ tham gia vào đại hội sinh viên? 4
Câu 7 : Người ta có thể ghi nhãn cho những chiếc ghế trong một giảng đường
bằng một chữ cái và số nguyên dương không vượt quá 100. Bằng cách như vậy,
nhiều nhất có bao nhiêu chiếc ghế có thể được ghi nhãn khác nhau?
Câu 8: Cho tập X={1,2,3,4,5,0}. Hỏi có bao nhiêu số tự nhiên có 3 chữ số khác nhau chia hết cho 2.
Câu 9: Có bao nhiêu xâu nhị phân có độ dài n.
Câu 10: Một mã gồm 6 ký tự, trong đó gồm 3 chữ cái rồi đến 3 chữ số. Hỏi có bao nhiêu mã khác nhau?
Câu 11: Chứng tỏ rằng trong một lớp có 30 sinh viên thì ít nhất có 2 sinh viên có
tên bắt đầu bằng cùng một chữ cái?
Câu 12: Số các học viên của một lớp học ít nhất là bao nhiêu để ít nhất hai học
viên có số điểm như nhau trong kỳ thi môn Toán học rời rạc, nếu dự định thang điểm là 0->10?
Câu 13: CMR: Trong số những người có mặt trên trái đất, phải tìm được hai người
có hàm răng giống nhau. (Giả sử trên hành tinh có trên 6 tỉ người)
Câu 14: Trong 45 học sinh làm bài kiểm tra không có ai bị điểm dưới 2, chỉ có 2
học sinh được điểm 10. CMR: Ít nhất cũng tìm được 6 học sinh có điểm kiểm tra
bằng nhau (điểm kiểm tra là một số tự nhiên từ 0 đến 10)
Bài 15: Số lượng mã vùng tối thiểu phải là bao nhiêu để đảm bảo cho 25 triệu mấy
điện thoại trong một bang ở Bắc Mỹ có số điện thoại khác nhau, nếu mỗi số đó
gồm 10 chữ số.( Giả sử số điện thoại có dạng NXX-NXX-XXXX, trong đó 3 chữ
số đầu là là mã vùng, N là 1 chữ số có giá trị từ 2 đến 9, và X từ 0 đến 9).
Bài 16: Có 5 loại học bổng khác nhau, hỏi rằng phải có ít nhất bao nhiêu sinh viên
để chắc chắn rằng có ít ra là 6 sinh viên cùng nhận một loại học bổng.
III. Hoán vị, tổ hợp và chỉnh hợp. Công thức nhị thức Newton.
Câu 1: Gọi Pn là số hoán vị của n phần tử. Chứng minh: a) Pn – Pn-1= (n – 1)Pn-1
b) 1 + P1+ 2P2+ 3P3+ … + (n – 1)Pn-1= Pn
Câu 2: Nhóm 10 ứng cử viênvào 3 vị trí (Trưởng phòng, Phó phòng và Thư kí)
a) Hỏi có bao nhiêu cách bổ nhiệm 3 người vào 3 vị trí trên? 5
b) Hỏi có bao nhiêu cách chọn ra 3 người để xếp vào 3 vị trí trên?
Câu 3: Một lớp học có 40 học sinh gồm 25 namvà 15 nữ. Có bao nhiêu cách lập ban cán sự lớp gồm: a) 3 học sinh.
b) 3 học sinh gồm 1 nam và 2 nữ
c) 3 học sinh trong đó có ít nhất 1 nam.
Câu 4: Một tạp chí thể thao định cho ra 22 kì báo chuyên đề về 22 đội bóng. Mỗi
kì chỉ viết về 1 đội bóng. Hỏi có bao nhiêu cách sao cho:
a) Kì báo đầu tiên nói về đội bóng A?
b) Hai kì báo liên tiếp nói về 2 đội bóng A và B?
Câu 5: Có 4 nữ sinh tên là Huệ, Hồng, Lan, Hương và 4 nam sinh là An, Bình,
Hạnh, Phúc cùng ngồi quanh một bàn tròn có 8 chỗ.
a) Hỏi có bao nhiêu cách sắp xếp biết nam và nữ ngồi xen kẽ nhau?
b) Hỏi có bao nhiêu cách sắp xếp nếu nam và nữ ngồi xen kẽ nhau nhưng hai bạn
Hồng và An không chịu ngồi cạnh nhau?
Câu 6: Mỗi người sử dụng máy tính dùng password có 6 -> 8 ký tự. Các ký tự có
thể là chữ số hoặc chữ cái, mỗi password phải có ít nhất 01 chữ số. Tìm tổng số
password có thể có?( phân biệt chữ hoa chữ thường)
Câu 7: Cho 7 điểm trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng
a) Có bao nhiêu đường thẳng mà mỗi đường thẳng đi qua 2 trong 7 điểm nói trên?
b) Có bao nhiêu tam giác với các đỉnh là 3 trong 7 điểm nói trên ?
Câu 8: Cho 2 đường thẳng song song d1 và d2.Trên d1 lấy 17 điểm phân biệt, d2 lấy
20 điểm phân biệt.Có bao nhiêu cách để tạo thành 1 tam giác? 12 Câu 9: Tìm  1 
hệ số x8 trong khai triển 1+    x 
Câu 10: Tìm số hạng chứa x37 trong khai triển (x2 – xy)20
Câu 11: Tìm hệ số của số hạng không chứa x trong khai triển: 7 f ( x)  1  3 = x +   4  x  6
Câu 12: Tìm số hạng đứng giữa trong các khai triển sau( + )21 3 x xy
Câu 13: Tìm hệ số của x8 trong khai triển đa thức của:  + x ( − x) 8 2 1 1   
IV. Hoán vị lặp và tổ hợp lặp.
Câu 1: Có bao nhiêu chuỗi ký tự khác nhau có thể lập được từ các chữ trong từ
MISSISSIPPI, yêu cầu phải dùng với tất cả các chữ (độ dài chuỗi là 11).
Câu 2: Một dãy bit gồm 4 bit: 2 bit ở trạng thái 0, 2 bit ở trạng thái 1. Hỏi có bao nhiêu dãy bit khác nhau?
Câu 3: Với các chữ số 0; 1; 2; 3; 4; 5; 6 lập được bao nhiêu số có 10 chữ số mà
trong mỗi số chữ số 2 có mặt đúng 3 lần, chữ số 4 có mặt đúng 2 lần và các chữ số
khác mỗi chữ số có mặt đúng 1 lần.
Câu 4: Trong một cửa hàng có bán 3 mẫu nón: nam, nữ, trẻ em. Hỏi có mấy cách
để chọn 2 cái nón trong cữa hàng đó?
Câu 5: Giả sử ta có 3 đầu sách : Toán, Tin, Lý và mỗi đầu sách có ít nhất 6 bản
photocopy. Hỏi có bao nhiêu cách chọn ra 6 quyển?
Câu 6: Sếp 42 quyển sách vào 3 ngăn tủ. Hỏi có bao nhiêu cách sếp sao cho:
a. Ngăn tủ nào cũng có sách?
b. Có ít nhất 1 ngăn tủ không có sách?
c. Ngăn thứ 2 phải có 10 quyển sách?
d. Tổng số sách ngăn 2 và ngăn 3 là 18?
Câu 7: Tìm số cách xếp 30 viên bi giống nhau vào 5 bình khác nhau, biết rằng
bình 1 chứa ít nhất 5 viên bi, bình 2 và 3 chứa nhiều nhất 6 viên?
Câu 8: Phương trình: x + x + x + x =10 có bao nhiêu bộ nghiệm nguyên không 1 2 3 4 âm?
Câu 9: Cho phương trình x + y + z + t = 20. Phương trình có bao nhiêu bộ nghiệm
nguyên thỏa x ≥ 1, y > 2, z > 3, t > 4.
BÀI TÂP CHƯƠNG 3 I. QUAN HỆ 2 NGÔI
Bài 1: Cho A = {1, 2, 3, 4, 8}, B = {1, 2, 3, 4}. Liệt kê tất cả các phần tử của A x B có
quan hệ R, trong đó (a, b)  R nếu và chỉ nếu : a) a > b b) a là ước của b c) a là bội của b d) a = b3
Bài 2: Trên tập A={-1,0,2,3,4} ta xét quan hệ hai ngôi như sau: xRy ⇔ x2 - 3x = y2 - 3y
a) Liệt kê các phần tử của quan hệ R trên A.
b) Tìm tập hợp X có vô hạn phần tử để R là một quan hệ trên X. Giải thích?
Bài 3: Trên tập hợp A={-2,-1,0,2,3}, ta xét quan hệ hai ngôi R như sau: x R y ⇔ x2 - 2x = y2 - 2y
a) Liệt kê các phần tử của quan hệ R trên A.
b) Tìm tập hợp X có vô hạn phần tử để R là một quan hệ trên X. Giải thích?
Bài 4: Liệt kê tất cả các cặp trong quan hệ R = {(a, b) | (2a = b̭) ˅ (b = 2a)} trên tập
{1, 2, 3, 4, 5, 6}. Biểu diễn quan hệ trên dưới dạng đồ thị và dưới dạng ma trận.
Bài 5: Đối với mỗi quan hệ được cho dưới đây trên tập {1, 2, 3, 4}, hãy xác định xem
nó có phản xạ, đối xứng, bắc cầu không ? a) {(1, 2), (2, 3), (3, 2)}
b) {(1, 1), (2, 2), (3, 3), (4, 4)}
c) {(1, 3), (1, 4), (2, 3) ,(3, 1), (3, 2) , (4,1),}
Bài 6: Xác định xem quan hệ R trên tập loài người có phản xạ, đối xứng, phản đối
xứng, bắc cầu hay không, với (a, b)  R nếu và chỉ nếu. a) a và b cùng chiều cao. b) a là bố b.
c) a không phải là bạn của b.
Bài 7: Xác định xem quan hệ R trên tập tất cả các số thực có tính phản xạ, đối xứng,
phản đối xứng, bắc cầu hay không, với (x, y)  R nếu và chỉ nếu: a) x = 2y b) x + y = 2 c) xy ≥ 0
Bài 8: Cho quan hệ R = {(a, b) a > b } trên tập các số nguyên, tìm quan hệ ngược từ
tập B đến tập A và quan hệ bù của R. (Quan hệ ngược từ tập B đến tập A, được ký hiệu là , 1 − R
là tập các cặp được sắp {(b, a) (a, b)  R}. Quan hệ bù 𝑅 ̅ là tập các cặp
được sắp {(a, b) (a, b)  R})
Bài 9: Cho quan hệ R = {(a, b)  b chia hết cho a} trên tập các số nguyên dương. Tìm 1 − R và 𝑅̅.
Bài 10: Trên tập A={1,2,3,4}, cho các quan hệ R1 = {(a,b)| a là ước của b},
R2 = {(a,b)| a = b2}, R3 = {(a,b)| a = b}. Tìm: a) R1  R2 b) R1 \ R3 c) R1  R2  R3
Bài 11: Cho các quan hệ trên tập gồm các số thực
R1 = {(a, b)  R2a > b}, quan hệ “lớn hơn”,
R2 = {(a, b)  R2a  b}, quan hệ “lớn hơn hoặc bằng”,
R3 = {(a, b) R2a < b}, quan hệ “nhỏ hơn”,
R4 = {(a, b) R2a  b}, quan hệ “nhỏ hơn hoặc bằng” Tìm: a) R1  R2 b) R2  R4 c) R1  R3
Bài 12: Có bao nhiêu quan hệ trên tập {a, b, c, d} có chứa cặp (a, a)?
Bài 13: Tìm sai lầm trong chứng minh định lý sau:
Định lý : Cho R là quan hệ trên tập A có tính chất đối xứng và bắc cầu. Khi đó,
R có tính chất phản xạ.
Chứng minh: Cho a A. Lấy phần tử b  A sao cho (a, b)  R. Vì R là đối xứng
nên (b, a)  R. Bây giờ sử dụng tính chất bắc cầu của R, ta suy ra rằng (a, a) R, vì (a, b)  R và (b, a) R.
Bài 14: Biểu diễn các quan hệ trên tập {1, 2, 3} dưới đây bằng ma trận 0 – 1(với các
phần tử được liệt kê theo thứ tự tăng dần). a) {(1, 1), (1, 2), (1, 3)}
b) {(1, 2), (2, 1), (2, 2), (3, 3)}
c) {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)} d) {(1, 3), (3, 1)}
Bài 15: Biểu diễn các quan hệ trên tập {1, 2, 3, 4} dưới đây bằng ma trận 0 – 1(với các
phần tử được liệt kê theo thứ tự tăng dần).
a) {(1, 2), (1, 3), (1, 4), (2, 3), (2,4), (3, 4)}
b) {(1, 1), (1, 4), (2, 2), (3, 3), (4, 1)}
c) {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2), (4,3)}
d) {(2, 4), (3,1), (3, 2), (3,4)}
Bài 16: Liệt kê các cặp được sắp trong quan hệ trên tập {1, 2, 3} tương ứng với các
ma trận dưới đây (trong đó các cột và hàng tương ứng với các số nguyên được liệt kê theo thứ tự tăng). 1 0 1 a) [0 1 0] 1 0 1 0 1 1 b) [1 1 0] 0 1 1 1 0 1 c) [0 0 1] 0 0 1
Bài 17: Liệt kê các cặp được sắp trong quan hệ trên tập {1, 2, 3, 4} tương ứng với các
ma tr6n dưới đây (trong đó các cột và hàng tương ứng với các số nguyên được liệt kê theo thứ tự tăng). 1 0 0 0 a) 0 0 1 0 [1 1 0 1] 0 0 0 1 1 0 1 0 b) 0 0 1 1 [1 1 0 1] 0 0 1 0 1 0 0 0 c) 1 0 1 1 [1 1 0 1] 1 0 1 1
Bài 18: Làm thế nào để xác định được tính phản xạ, tính phản xứng của một quan hệ,
thông qua ma trận biểu diễn của nó? Áp dụng : 1 1 1 [0 1 1] 0 0 1
Bài 19: Hãy xác định xem các quan hệ được biểu diễn bởi các ma trận dưới đây có
phản xạ, không phản xạ, đối xứng, phản đối xứng, bắc cầu hay không? 1 0 1 a) [0 0 1] 0 0 1 1 1 1 b) [1 1 1] 0 0 0 1 0 1 0 c) 0 1 1 1 [1 1 1 0] 0 1 0 1
Bài 20: Cho R là một quan hệ được biểu diễn bởi ma trận : 0 1 1     M = 1 1 0 R    1 0 1   
Tìm ma trận biểu diễn quan hệ R, 1− R
Bài 21: Cho R1 và R2 là hai quan hệ trên tập A được biểu diễn bằng các ma trận: 0 1  0 0 1  0     M = 1 1 1 , M = 0 1 1 R R 1   2   1 0  0 1 1      1 a. R1  R2, R1  R2 b. R1\ R2, R2\ R1
Bài 22: Vẽ các đồ thị có hướng, biểu diễn quan hệ R = {(a, a), (a, b), (b, c),
(c, b), (c, d), (d, a), (d, b)}.
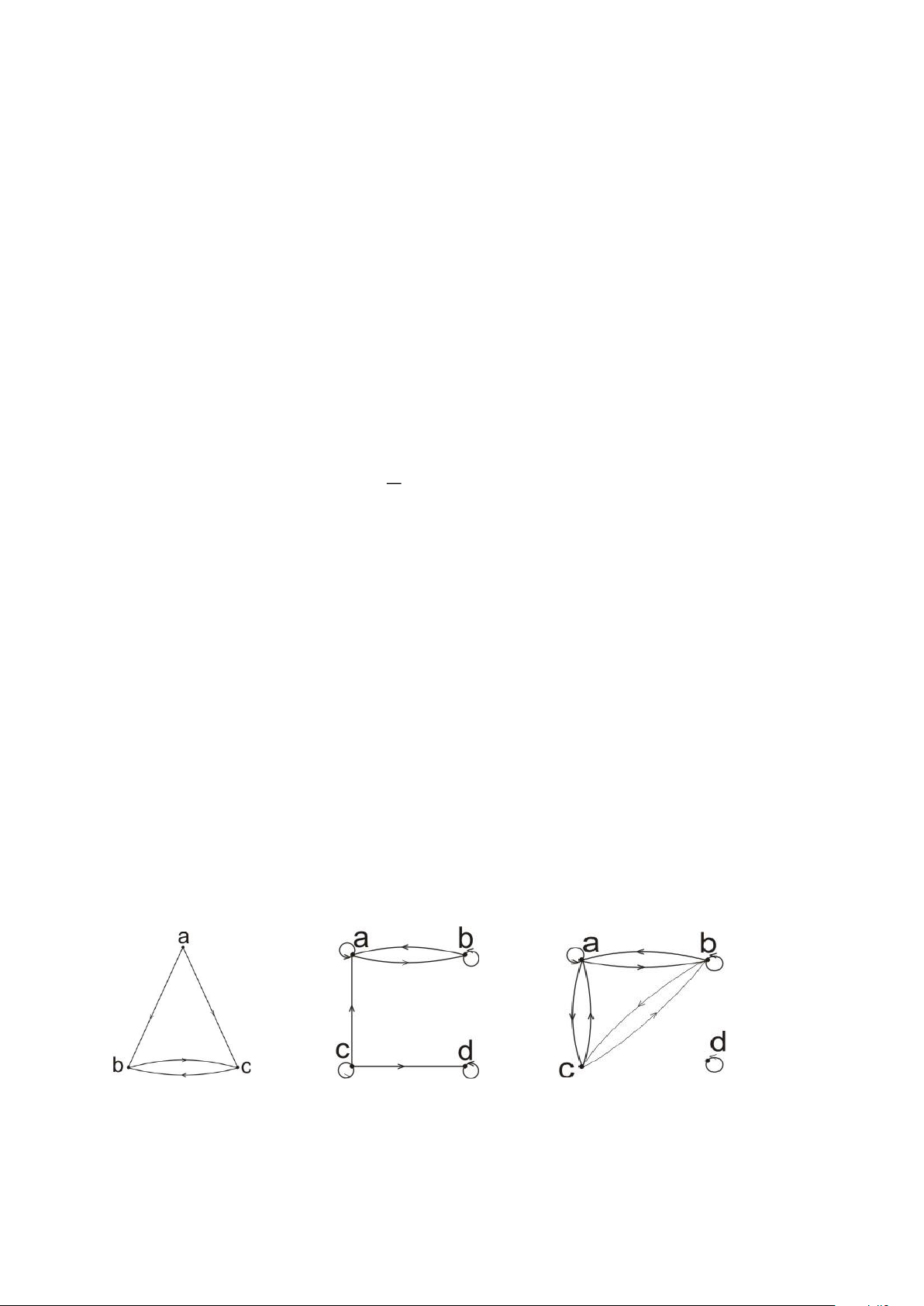
Bài 23: Hãy liệt kê các cặp được sắp trong các quan hệ được biểu diễn bởi các đồ thị có hướng. a. b. c.
Bài 24: Hãy xác định xem các quan hệ được biểu diễn bởi các đồ thị có hướng được
cho trong « Bài 13 » có phản xạ, đối xứng, phả xứng, bắc cầu hay không?
Bài 25: Cho đồ thị có hướng biểu diễn hai quan hệ. Làm thế nào để có thể tìm được
đồ thị có hướng biểu diễn quan hệ được tạo thành từ hợp, giao, hiệu đối xứng của các quan hệ trên.
II. QUAN HỆ TƯƠNG ĐƯƠNG
Bài 1: Các quan hệ nào trong số các quan hệ sau đây trên tập A= {0, 1, 2, 3} là quan
hệ tương đương? Xác định các tính chất nào của một quan hệ tương đương mà quan hệ này không có.
R1={(0, 0), (1, 1), (2, 2), (3, 3)}
R2={(0, 0), (0 , 2), (2, 0), (2, 2), (2, 3), (3, 2), (3, 3)}
R3={(0, 0), (1, 1), (1, 2), (2, 1), (2, 2), (3, 3)}
R4={(0, 0), (1, 1), (1, 3), (2, 2), (2, 3), (3, 1), (3,2),(3, 3)}
R5={(0, 0), (0, 1), (0, 2),(1, 0), (1, 1), (1, 2), (2, 0), (2, 2),(3, 3)}
Bài 2: Các quan hệ nào trong số các quan hệ sau đây (trên tập con người) là quan hệ
tương đương. Xác định các tính chất nào của một quan hệ tương đương mà quan hệ này không có.
R1={(a, b) a và b cùng tuổi }
R2={(a, b)a và b có cùng bố mẹ}
R3={(a, b)a và b đã gặp nhau}
R4={(a, b)a và b nói cùng một thứ tiếng}
Bài 3: Các quan hệ nào trong số các quan hệ sau đây (trên tập tất cả các hàm từ Z đến
Z) là quan hệ tương đương. Xác định các tính chất nào của một quan hệ tương đương
mà quan hệ này không có. R1={(f, g) f(1) = g(1)}
R2={(f, g)f(0) = g(0) hoặc f(1) = g(1)}
R3={(f, g)f(x) – g(x) = 1, x  Z }
R4={(f, g)f(x) – g(x)  Z, x  Z}
R5={(f, g)f(0) = g(1) và f(1) = g(0)}
Bài 4: Giả sử A là một tập khác rỗng và f là một hàm số xác định trên A. Giả sử R là
một quan hệ trên A gồm tất cả các cặp (x, y) với f(x) = f(y). Chứng minh rằng R là
một quan hệ tương đương trên A. Xác định các lớp tương đương của R.
Bài 5: Chứng minh rằng quan hệ R chứa tất cả các cặp (x, y) trong đó x và y là các
xâu bit có chiều dài bằng hoặc lớn hơn 3 và có 3 bit đầu tiên như nhau là một quan hệ
tương đương trên tập tất cả các xâu bit có chiều dài lớn hơn hoặc bằng 3.
Bài 6: Chứng minh rằng sự tương đương của các mệnh đề là một quan hệ tương
đương trên tập tất cả các mệnh đề phức hợp.
Bài 7: Cho R là quan hệ trên tập tất cả các cặp có thứ tự hai số nguyên dương sao cho
((a, b), (c, d))  R nếu và chỉ nếu a*d = b*c. Chứng minh rằng R là một quan hệ tương đương.
Bài 8: Xác định xem các quan hệ được biểu diễn bởi các ma trận được cho dưới đây
có là quan hệ tương đương hay không? 1 0 1 0 1 1 1 0 1 1  1       a b 0 1 0 1 c 1 1 1 0 ) 0 1  1 , )  , ) 1 0 1 0 1 1 1 0 1 1    1     0 1 0 1 0 0 0 1
Bài 9: Xét quan hệ tương đương T = {(x, y)∈ 2 R x – y ∈ Z}.
a) Xác định lớp tương đương của 1 đối với quan hệ T.
b) Xác định lớp tương đương của ½ đối với quan hệ T.
Bài 10:Trên tập số nguyên Z, xét quan hệ hai ngôi T như sau:
∀x,y ∈ Z, xTy ⇔ x − y là số chẵn.
T có phải là một quan hệ tương đương hay không ? Vì sao ?
Nếu T là một quan hệ tương đương, hãy tìm các lớp tương đương và tập hợp thương.
Bài 11: Cho A={-2,-1,0,1,2,3,4,5}, xét quan hệ hai ngôi R trên A như sau: xRy ⇔ x - 3y chẵn.
a) Chứng minh R là quan hệ tương đương.
b) Tìm các lớp tương đương [1]R, [2]R .
Bài 12: Cho m là số nguyên dương và xét quan hệ hai ngôi R trên Z như sau:
∀a,b ∈ Z, aRb ⇔ a-b chia hết cho m
a) CMR: R là quan hệ tương đương.
b) Hãy tìm các lớp tương đương và tập hợp thương.
(Chú ý: Quan hệ R trên gọi là quan hệ đồng dư modulo m trên tập các số nguyên Z,
ký hiệu bởi  (mod m), còn được viết lại như sau:
∀a,b ∈ Z, a  b (mod m)⇔k ∈ Z: (a-b) = k.m )
Bài 13: Tìm lớp tương đương của quan hệ đồng dư modulo 8 trên tập Z chứa phần tử 0? chứa phần tử 1?
Bài 14: Xét quan hệ R trên tập số nguyên Z được định nghĩa như sau:
∀m,n∈ Z, mRn ⇔ "m cùng tính chất chẵn lẻ với n".
Chứng minh R là quan hệ tương đương.
Bài 15: Trên tập hợp số tự nhiên N, ta xét quan hệ hai ngôi R như sau: x R y ⇔ x2 - y2 chẵn
a) Chứng minh R là quan hệ tương đương trên N.
b) Tìm phân hoạch của tập N theo quan hệ R.
III. QUAN HỆ THỨ TỰ
Bài 1: Trên tập hợp X, ta xét quan hệ hai ngôi sau: x R y ⇔ x2 + 3x ≤ y2 + 3y
a) Nếu X = R thì R có những tính chất nào? Giải thích.
b) Nếu x = N thì R có phải là quan hệ thứ tự không? Giải thích.
Bài 2: Trong các tập hợp sắp thứ tự dưới đây, cho biết tập hợp nào sắp thứ tự tốt:
a) (N, ≺) b) (Z,≺) c) (Q,≺) d) (Q+,≺)
e) (P, ≺) trong đó P là tập hợp các số nguyên tố.
f) (A, ≺) trong đó A ≠ ∅ là một tập con hữu hạn của Z.
Bài 3: Cho R là quan hệ hai ngôi trên tập số phức C được xác định như sau:
(a, b) R (c, d) ⇔ a ≤ c và b ≤ d
a) CMR: R là một quan hệ thứ tự trên C.
b) R có phải là toàn phần không?
Bài 4 : Cho ⋮ là quan hệ “chia hết” trên tập số nguyên Z.
(∀a,b ∈ Z, a ⋮ b ⇔k ∈ Z: a = k.b)
a) Chứng minh ⋮ là một quan hệ thứ tự trên Z.
b) Quan hệ thứ tự ⋮ trên Z có phải là toàn phần không?
Bài 5: Cho tập A = {1, 2, 3, 4, 5}. Cho R là quan hệ trên A và R = {(1,1); (2,1); (2,2);
(2,4); (3,1); (3,2);(3,3); (3,4); (3,5); (4,4); (5, 5)}.
a) R có là quan hệ tương đương? quan hệ thứ tự? Vì sao?
b) Nếu quan hệ R trên A là quan hệ thứ tự, vẽ biểu đồ Hasse cho (A, R).
Bài 6: Cho tập A = {1, 2, 3, 4} và các quan hệ R1 ={(1, 1); (2, 2); (3, 3); (4, 4)} và R2
= {(1, 1); (2, 2); (3,1 ); ( 3, 3); (3, 4); (4,1); (4, 4)} trên A.
a) Xác định xem các quan hệ trên có là quan hệ thứ tự trên A?
b) Nếu quan hệ nào là quan hệ thứ tự, hãy vẽ biểu đồ Hasse cho quan hệ đó trên A.
Bài 7: Cho (A, |) là tập hợp sắp thứ tự, trong đó A= {2, 4, 5, 10, 12, 20, 25}, quan hệ |
trên A là quan hệ “ước số của” (∀a,b ∈ A, a | b ⇔k ∈ Z: b = k.a)
a) Vẽ biểu đồ Hasse cho (A, |).
b) Dựa vào biểu đồ Hasse tìm phần tử tối đại, tối tiểu của A.
Bài 8: Cho ( A, ≤ ) là tập hợp sắp thứ tự, trong đó A là tập các chuỗi nhị phân có độ
dài bằng 3, quan hệ ≤ là quan hệ “nhỏ hơn hoặc bằng” thông thường.
a) Vẽ biểu đồ Hasse cho (A, ≤ )
b) Dựa vào biểu đồ Hasse tìm phần tử tối đại, tối tiểu của A.
c) Dựa vào biểu đồ Hasse tìm phần tử lớn nhất, nhỏ nhất của A.
Bài 9: Cho X ={2; 4; 6; 8; 10; 14; 16; 15; 20; 30; 36; 40; 60}. Trên X cho quan hệ | là
quan hệ “ước số của”.
a) Vẽ biểu đồ Hasse (X, | ).
b) Tìm phần tử tối đại, tối tiểu của X.
Bài 10: Trong các trường hợp sau, hãy tìm các phận tử lớn nhất, nhỏ nhất, tối đại, tối
tiểu (nếu có) của các tập hợp đã cho với quan hệ thứ tự tương ứng. Vẽ các biểu đồ Hasse.
a) U30 = {𝑛 ∈ 𝑁 | 𝑛 |30} với quan hệ ước số |.
b) X ={2; 3; 4; 6; 8; 10; 80} với quan hệ ước số |.
c) X = {1, 2, 3, 4, 6, 8, 10, 11} với quan hệ R được xác định như sau:
xRy ⇔ x = y hay x < y – 1
Bài 11: Cho tập hợp X = {2, 5, 8, 10, 20, 40} và ⋮ là quan hệ “chia hết” trên X.
a) Chứng tỏ R là quan hệ thứ tự. Vẽ biểu đồ Hasse cho (X, ⋮ ).
b) Tìm các phần tử tối đại và tối tiểu của X.
c) Tìm các phần tử lớn nhất và nhỏ nhất của X.
Bài 12: Cho tập X = { 1, 2, 3, 4, 5}. Cho R và S là 2 quan hệ 2 ngôi trên tập X có ma
trận biểu diễn lần lượt là: 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 0 AR = 1 1 1 1 1 , AS = 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 [0 0 0 0 1] [1 1 1 1 1]
CMR : R và S là quan hệ thứ tự trên tập X. Hãy vẽ biểu đồ Hasse cho các quan hệ này.
Câu 13: Cho S={1, 2, 3, 5, 6, 10, 15, 30} (các ước số lớn hơn 0 của 30). Hãy vẽ biểu
đồ Hasse cho (S,|) và (S, ⋮).
Câu 14: Vẽ biểu đồ Hasse cho S với quan hệ thứ tự tương ứng.
a) (S = {1, 2, 3, 4, 5, 6, 7, 8}, ⋮)
b) (S = {1, 2, 3, 6, 12, 24, 36, 48}, |)