-
Thông tin
-
Hỏi đáp
Bài tập chương 3 môn cấu trúc rời rạc - Đại học công nghệ thông tin- ĐHQGTPHCM
I. QUAN HỆ 2 NGÔI
Bài 1: Cho A = {1, 2, 3, 4, 8}, B = {1, 2, 3, 4}. Liệt kê tất cả các phần tử của A x B có quan hệ R, trong đó (a, b) R nếu và chỉ nếu :
a) a > b
(a,b) thuộc R | a>b
R= {(2,1),(3,1),(4,1), (8,1),(8,2),(8,3) (8,4), (3,2), (4,2), (4,3)}
Tài liệu này bổ ích. Mời bạn đọc đón xem
Môn:
Cấu trúc rời rạc 29 tài liệu
Trường:
Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh 451 tài liệu
Thông tin:
20 trang
4 tháng trước
Tác giả:
Bài tập chương 3 môn cấu trúc rời rạc - Đại học công nghệ thông tin- ĐHQGTPHCM
I. QUAN HỆ 2 NGÔI
Bài 1: Cho A = {1, 2, 3, 4, 8}, B = {1, 2, 3, 4}. Liệt kê tất cả các phần tử của A x B có quan hệ R, trong đó (a, b) R nếu và chỉ nếu :
a) a > b
(a,b) thuộc R | a>b
R= {(2,1),(3,1),(4,1), (8,1),(8,2),(8,3) (8,4), (3,2), (4,2), (4,3)}
Tài liệu này bổ ích. Mời bạn đọc đón xem
85
43 lượt tải
Tải xuống
Môn: Cấu trúc rời rạc 29 tài liệu
Trường: Trường Đại học Công nghệ Thông tin, Đại học Quốc gia Thành phố Hồ Chí Minh 451 tài liệu
Thông tin:
20 trang
4 tháng trước
Tác giả:
lOMoARcPSD|44990377
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
BÀI TÂP CHƯƠNG 3
I. QUAN HỆ 2 NGÔI
Bài 1: Cho A = {1, 2, 3, 4, 8}, B = {1, 2, 3, 4}. Liệt kê tất cả các phần tử của A x B có
quan hệ R, trong đó (a, b) R nếu và chỉ nếu :
a) a > b
(a,b) thuộc R | a>b
R= {(2,1),(3,1),(4,1), (8,1),(8,2),(8,3) (8,4), (3,2), (4,2), (4,3)}
b) a là ước của b
(a,b) thuộc R | a là ước của b
R= {(1,1),(1,2),(1,3)(1,4) (2,2) (2,4) (3,3)}
c) a là bội của b
(a,b) thuộc R | a là bội của b
R= {(1,1),(2,1),(2,2) (3,1) (3,3) (4,1) (4,4) (8,1) (8,2) (8,4) }
d) a = b
3
R= {(1,1),(8,2)}
Bài 2: Trên tập A={-1,0,2,3,4} ta xét quan hệ hai ngôi như sau:
(x-y) (x+y+3)=0
a) Liệt kê các phần tử của quan hệ R trên A.
R= {(-1,-1), (0,0), (2,2), (3,3) (4,4) }
b) Tìm tập hợp X có vô hạn phần tử để R là một quan hệ
trên X. Giải thích? R = {(x,x) , ( x, -3-x) x thuộc R }
Bài 3: Trên tập hợp A={-2,-1,0,2,3}, ta xét quan hệ hai ngôi R như sau:
a) Liệt kê các phần tử của quan hệ R trên A.
R= {(-2, -2), (-1, -1), (0,0) ,(2,2), (3,3), (0,2), (2,0), (-1,3), (3, -1)}
b) Tìm tập hợp X có vô hạn phần tử để R là một quan hệ trên X. Giải thích? R
= {(a,a), (a;2-a) a thuộc N}
Bài 4: Liệt kê tất cả các cặp trong quan hệ R = {(a, b) | (2a = ) (2b = a)} ˅ b
trên tập {1, 2, 3, 4, 5, 6}. Biểu diễn quan hệ trên dưới dạng đồ thị và
dưới dạng ma trận.
R= { (1,2), (2,1), (2,4), (4,2), (3,6) ,( 6,3) }
Bài 5: Đối với mỗi quan hệ được cho dưới đây trên tập A={1, 2, 3, 4}, hãy xác định
xem nó có phản xạ, đối xứng, bắc cầu không ?
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
a)
* không có tính phản xạ. Vì
* không có tính đối xứng.
Vì * không có tính bắc cầu.
Vì
b) {(1, 1), (2, 2), (3, 3), (4, 4)}
c) {(1, 3), (1, 4), (2, 3) ,(3, 1), (3, 2) , (4,1),} không có tính
phản xạ. Vì có tính đối xứng. Vì
Bài 6: Xác định xem quan hệ R trên tập loài người có phản xạ, đối xứng, phản đối
xứng, bắc cầu hay không, với (a, b) R nếu và chỉ nếu.
a) a và b cùng chiều cao. Không phản xạ, kh đối xứng, kh bắc cầu
b) a là bố b. phản xạ, đối xứng, bắc cầu
c) a không phải là bạn của b. Đối xứng, kh bắc cầu
Bài 7: Xác định xem quan hệ R trên tập tất cả các số thực có tính phản xạ, đối xứng,
phản đối xứng, bắc cầu hay không, với (x, y) R nếu và chỉ nếu:
a) x = 2y kh pxa, kh dxung, kh bcau, pxung
b) x + y = 2 kh pxa, dxung, bcau, kh pxung
c) xy ≥ 0 pxa, dxung, bcau, kh pxung
Bài 8: Cho quan hệ R = {(a, b) a > b } trên tập các số nguyên, tìm quan hệ ngược từ
tập B đến tập A và quan hệ bù của R. (Quan hệ ngược từ tập B đến tập A, được ký
hiệu là , là tập các cặp được sắp {(b, a) (a, b) R}. Quan hệ bù là tập các cặp
được sắp {(a, b) (a, b) R})
R1
Bài 9: Cho quan hệ R = {(a, b) b chia hết cho a} trên tập các số nguyên dương.
Tìm và .R
1
Bài 10: Trên tập A={1,2,3,4}, cho các quan hệ R1 = {(a,b)| a là ước của b},
R2 = {(a,b)| a = b
2
}, R3 = {(a,b)| a = b}. Tìm:
a) R1 R2
b) R1 \ R3
c) R1 R2 R3
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Bài 11: Cho các quan hệ trên tập gồm các số thực
R1 = {(a, b) R
2
a > b}, quan hệ “lớn hơn”,
R2 = {(a, b) R
2
a b}, quan hệ “lớn hơn hoặc bằng”,
R3 = {(a, b) R
2
a < b}, quan hệ “nhỏ hơn”,
R4 = {(a, b) R
2
a b}, quan hệ “nhỏ hơn hoặc bằng” Tìm:
a) R1 R2
b) R2 R4
c) R1 R3
Bài 12: Có bao nhiêu quan hệ trên tập {a, b, c, d} có chứa cặp (a, a)?
Bài 13: Tìm sai lầm trong chứng minh định lý sau:
Định lý : Cho R là quan hệ trên tập A có tính chất đối xứng và bắc cầu. Khi đó,
R có tính chất phản xạ.
Chứng minh: Cho a A. Lấy phần tử b A sao cho (a, b) R. Vì R là đối xứng
nên (b, a) R. Bây giờ sử dụng tính chất bắc cầu của R, ta suy ra rằng (a, a) R, vì (a,
b) R và (b, a) R.
Bài 14: Biểu diễn các quan hệ trên tập {1, 2, 3} dưới đây bằng ma trận 0 – 1(với các
phần tử được liệt kê theo thứ tự tăng dần). (vẽ)
a) {(1, 1), (1, 2), (1, 3)}
b) {(1, 2), (2, 1), (2, 2), (3, 3)}
c) {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}
d) {(1, 3), (3, 1)}
Bài 15: Biểu diễn các quan hệ trên tập {1, 2, 3, 4} dưới đây bằng ma trận 0 – 1(với các
phần tử được liệt kê theo thứ tự tăng dần).
a) {(1, 2), (1, 3), (1, 4), (2, 3), (2,4), (3, 4)}
b) {(1, 1), (1, 4), (2, 2), (3, 3), (4, 1)}
c) {(1, 2), (1, 3), (1, 4), (2, 1), (2, 3), (2, 4), (3, 1), (3, 2), (3, 4), (4, 1), (4, 2),
(4,3)}d) {(2, 4), (3,1), (3, 2), (3,4)}
Bài 16: Liệt kê các cặp được sắp trong quan hệ trên tập {1, 2, 3} tương ứng với các ma
trận dưới đây (trong đó các cột và hàng tương ứng với các số nguyên được liệt kê theo
thứ tự tăng).
a)
b)
c)
Bài 17: Liệt kê các cặp được sắp trong quan hệ trên tập {1, 2, 3, 4} tương ứng với các
ma tr6n dưới đây (trong đó các cột và hàng tương ứng với các số nguyên được liệt kê
theo thứ tự tăng).
a)
b)
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
c)
Bài 18: Làm thế nào để xác định được tính phản xạ, tính phản xứng của một quan hệ,
thông qua ma trận biểu diễn của nó? Áp dụng :
Tất cả các phần tử trên đường chéo của ma trận bằng 1 = > phản xạ (dòng
i cột j )
Bài 19: Hãy xác định xem các quan hệ được biểu diễn bởi các ma trận dưới đây có
phản xạ, đối xứng, phản đối xứng, bắc cầu hay không?
a)
b)
Có phần tử trên đường chéo của ma trận không bằng 1 = > => không phản xạ
Vậy mọi I,j,z nếu => bắc cầu
c)
Tất cả các phần tử trên đường chéo của ma trận bằng 1 = > phản xạ
Bài 20: Cho R là một quan hệ được biểu diễn bởi ma trận :
0 1 1
MR 1 1 0
1 0 1
Tìm ma trận biểu diễn quan hệ RR,
1
(Xem kí hiệu bài 8).
Bài 21: Cho R1 và R2 là hai quan hệ trên tập A được biểu diễn bằng các ma trận:
0 1
1
0 0
, MR2 0
1
1
0
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
MR1 1
1
0
1
0
1
1
1
1
a. R1 R2, R1 R2
b. R1R2, R2 R1
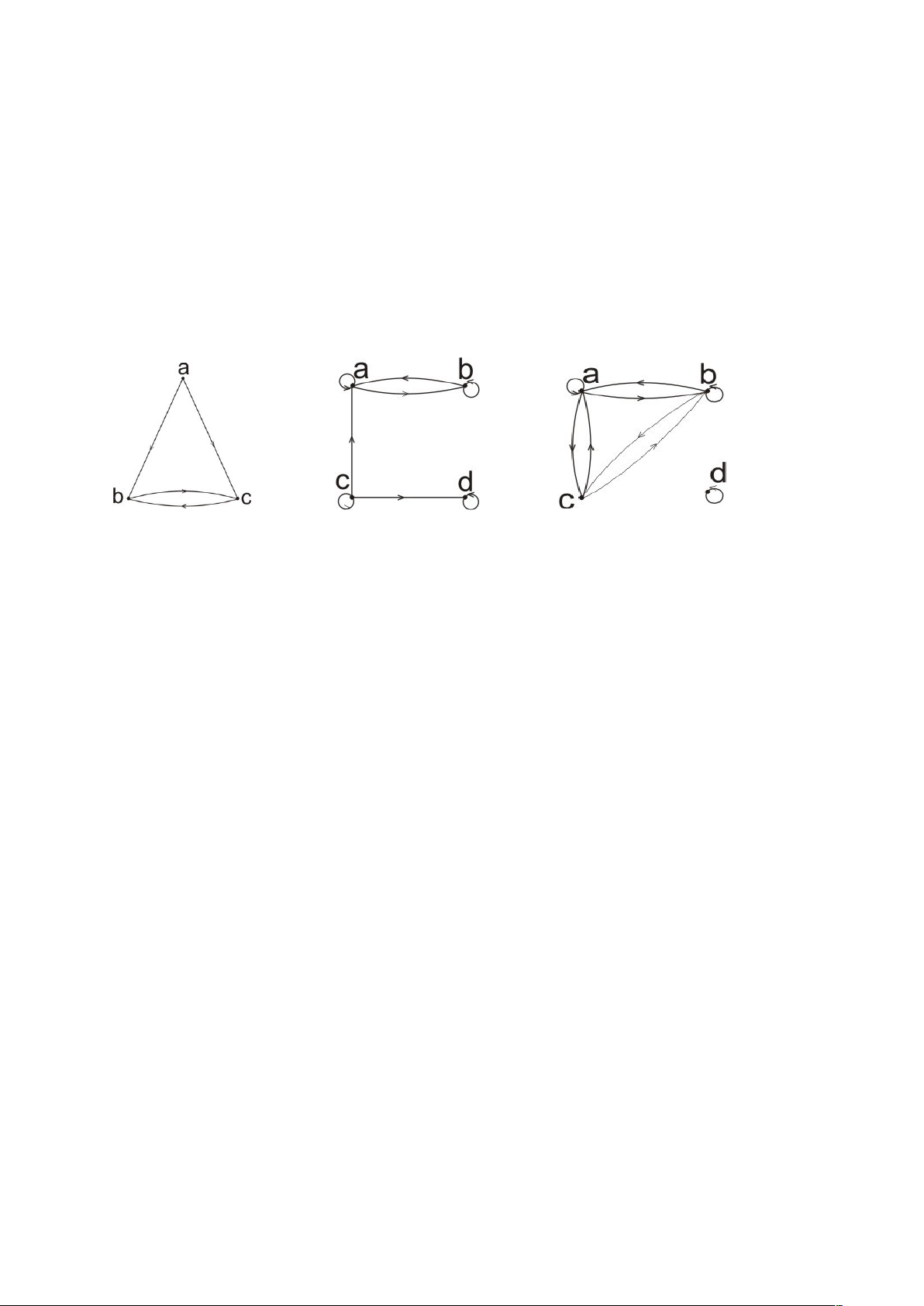
Bài 22: Vẽ các đồ thị có hướng, biểu diễn quan hệ R = {(a, a), (a, b), (b, c), (c,
b), (c, d), (d, a), (d, b)}.
Bài 23: Hãy liệt kê các cặp được sắp trong các quan hệ được biểu diễn bởi các đồ thị
có hướng.
a. b. c.
Bài 24: Hãy xác định xem các quan hệ được biểu diễn bởi các đồ thị có hướng được
cho trong « Bài 13 » có phản xạ, đối xứng, phản xứng, bắc cầu hay không?
Bài 25: Cho đồ thị có hướng biểu diễn hai quan hệ. Làm thế nào để có thể tìm được đồ
thị có hướng biểu diễn quan hệ được tạo thành từ hợp, giao, hiệu đối xứng của các
quan hệ trên.
II. QUAN HỆ TƯƠNG ĐƯƠNG
Bài 1: Các quan hệ nào trong số các quan hệ sau đây trên tập A= {0, 1, 2, 3} là quan
hệ tương đương? Xác định các tính chất nào của một quan hệ tương đương mà quan hệ
này không có.
R1={(0, 0), (1, 1), (2, 2), (3, 3)}
R2={(0, 0), (0 , 2), (2, 0), (2, 2), (2, 3), (3, 2), (3, 3)}
R3={(0, 0), (1, 1), (1, 2), (2, 1), (2, 2), (3, 3)}
R4={(0, 0), (1, 1), (1, 3), (2, 2), (2, 3), (3, 1), (3,2),(3, 3)}
R5={(0, 0), (0, 1), (0, 2),(1, 0), (1, 1), (1, 2), (2, 0), (2, 2),(3, 3)}
R1,R3 tương đương với nhau
Bài 2: Các quan hệ nào trong số các quan hệ sau đây (trên tập con người) là quan hệ
tương đương. Xác định các tính chất nào của một quan hệ tương đương mà quan hệ
này không có.
R1={(a, b) a và b cùng tuổi }
R2={(a, b)a và b có cùng bố mẹ}
R3={(a, b)a và b đã gặp nhau}
R4={(a, b)a và b nói cùng một thứ tiếng}
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Bài 3: Các quan hệ nào trong số các quan hệ sau đây (trên tập tất cả các hàm từ Z đến
Z) là quan hệ tương đương. Xác định các tính chất nào của một quan hệ tương đương
mà quan hệ này không có.
R1={(f, g) f(1) = g(1)}
R2={(f, g)f(0) = g(0) hoặc f(1) = g(1)}
R3={(f, g)f(x) – g(x) = 1, x Z }
R4={(f, g)f(x) – g(x) Z, x Z}
R5={(f, g)f(0) = g(1) và f(1) = g(0)}
Bài 4: Giả sử A là một tập khác rỗng và f là một hàm số xác định trên A. Giả sử R là
một quan hệ trên A gồm tất cả các cặp (x, y) với f(x) = f(y). Chứng minh rằng R là
một quan hệ tương đương trên A. Xác định các lớp tương đương của R.
Bài 5: Chứng minh rằng quan hệ R chứa tất cả các cặp (x, y) trong đó x và y là các
xâu bit có chiều dài bằng hoặc lớn hơn 3 và có 3 bit đầu tiên như nhau là một quan hệ
tương đương trên tập tất cả các xâu bit có chiều dài lớn hơn hoặc bằng 3.
Bài 6: Chứng minh rằng sự tương đương của các mệnh đề là một quan hệ tương
đương trên tập tất cả các mệnh đề phức hợp.
Bài 7: Cho R là quan hệ trên tập tất cả các cặp có thứ tự hai số nguyên dương sao cho
((a, b), (c, d)) R nếu và chỉ nếu a*d = b*c. Chứng minh rằng R là một quan hệ tương
đương.
Bài 8: Xác định xem các quan hệ được biểu diễn bởi các ma trận được cho dưới đây
có là quan hệ tương đương hay không?
1 0 1 0 1 1 1 0 a) 0 1 1 , )
1
1 1
b 0 1 0 1 , ) c 1 1 1 0
1 0 1 0 1 1 1 0
1 1 1
0 1 0 1 0 0 0 1
Bài 9: Xét quan hệ tương đương T = {(x, y) ∈
R
2x – y ∈ Z}.
a) Xác định lớp tương đương của 1 đối với quan hệ T.
b) Xác định lớp tương đương của ½ đối với quan hệ T.T = {(x, y) ∈
R bình x – y ∈ Z}.
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
(1)(2)(3) => T có quan hệ tương đương
= { x => { -3,-1,-2,0,1,2,3,…}
=> { -3/2,-1/2, ½, 3/2 , 5/2,…}
Bài 10:Trên tập số nguyên Z, xét quan hệ hai ngôi T như sau:
∀x,y ∈ Z, xTy ⇔ x − y là số chẵn.
T có phải là một quan hệ tương đương hay không ? Vì sao ?
Nếu T là một quan hệ tương đương, hãy tìm các lớp tương đương và tập hợp thương.
x-x = 0 là số chẵn => xTx => có tính phản xạ
xTy -> x-y là số chẵn -> y –x là số chẵn => yTx => có tính đối xứng
->
x-z = (x – y) + (y –z) -> x-z là số chẵn -> xTz
Có tính bắc cầu
T là một quan hệ tương đương
[0]
T
= {bZ/ bT0} = {b Z/b-0 là số chẵn} = {…-6,-4,-2,0,2,4,6…}
[1]
T
= {bZ/ bT1} = {b Z/b-1 là số chẵn}
= {…-5,-3,-1,1,3,5,…}
[-1]
T
= {bZ/ bT-1} = {b Z/b+1 là số chẵn}
= {…-5,-3,-1,1,3,5,…}
[2]
T
= {bZ/ bT2} = {b Z/b-2 là số chẵn}
= {…-6,-4,-2,2,4,6,…}
[2k+1]
T
= {bZ/ bT 2k+1} = {b Z/b-(2k+1) là số chẵn}
= {…-5,-3,-1,1,3,5,…}
[2k]
T
= {bZ/ bT2k} = {b Z/b-2k là số chẵn}
= {…-6,-4,-2,0,2,4,6…}
Vậy tập hợp thương là
Z/T = { [2k+1]
T
,[2k]
T
|kZ}
Bài 11: Cho A={-2,-1,0,1,2,3,4,5}, xét quan hệ hai ngôi R trên A như sau:
xRy ⇔ x - 3y chẵn.
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
a) Chứng minh R là quan hệ tương đương.
b) Tìm các lớp tương đương [1]
R
, [2]
R
.
(1)
(2)
=> y -3x = y – 3( 3y +2k) = -8y-6k chia hết 2
=> y-3x là số chẵn = > yRx=> R có tính đối xứng
(3)
b)
Bài 12: Cho m là số nguyên dương và xét quan hệ hai ngôi R trên Z như sau:
∀a,b ∈ Z, aRb ⇔ a-b chia hết cho m
a) CMR: R là quan hệ tương đương.
b) Hãy tìm các lớp tương đương và tập hợp thương.
(Chú ý: Quan hệ R trên gọi là quan hệ đồng dư modulo m trên tập các số nguyên Z,
ký hiệu bởi (mod m), còn được viết lại như sau:
∀a,b ∈ Z, a b (mod m) k ⇔ ∈ Z: (a-b) = k.m )
Bài 13: Tìm lớp tương đương của quan hệ đồng dư modulo 8 trên tập Z chứa phần tử
0? chứa phần tử 1?
Bài 14: Xét quan hệ R trên tập số nguyên Z được định nghĩa như sau:
∀m,n ∈ Z, mRn ⇔ "m cùng tính chất chẵn lẻ với n". Chứng
minh R là quan hệ tương đương.
a) m có cùng tính chất chẵn lẻ với n nghĩa là có k thuộc Z sao cho m+n = 2k
hoặc m -n =2k
• Tính phản xạ
• Tính đối xứng
• Tính bắc cầu
Vậy mRu=> R có tính bắc cầu
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
(1)
(2)
= > yRx=> R có tính đối xứng
(3)
Bài 15: Trên tập hợp số tự nhiên N, ta xét quan hệ hai ngôi R như sau:
x R y ⇔ x
2
- y
2
chẵn
a) Chứng minh R là quan hệ tương đương trên N.
b) Tìm phân hoạch của tập N theo quan hệ R.
a)
(1)
(2)
= > yRx=> R có tính đối xứng (3)
b)
[0]
R
= {N/ bT0} = { N/-0 là số chẵn} = {0,2,4,…}
[1]
R
= {N/ bT1} = { N/-1 là số chẵn}
= {1, 3, 5, 7,…}
[2]
R
= { N/ bT2} = { N/ -4 là số chẵn} ={0,2,4,6…}
[3]
R
= { N/ bT3} = { N/ -9 là số chẵn}
={1,3,5,7,… }
[4]
R
= { N/ bT4} = { N/ -16 là số chẵn}
={0,2,4,6,8… }
[2k+1]
R
= {N/ bT 2k+1} = { N/-( là số chẵn}
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
= {1,3,5,…}
[2k]
R
= {N/ bT2k} = { N/ - là số chẵn}
= {0,2,4,6…}
Vậy tập hợp thương là N/R = { [2k+1]
R
,[2k]
R
|kN}
Vậy phân hoạch của tập N= [2k+1]
R
[2k]
R
III. QUAN HỆ THỨ TỰ
Bài 1: Trên tập hợp X, ta xét quan hệ hai ngôi sau:
x R y ⇔ x
2
+ 3x ≤ y
2
+ 3y
a) Nếu X = R thì R có những tính chất nào? Giải thích.
Ta có:
Tính phản xạ xRx thì
0 <= 0 (thỏa)
Tính đối xứng xRy
với or
b) Nếu x = N thì R có phải là quan hệ thứ tự không? Giải thích.
Tính phản xạ
xRx thì 0 <= 0 (thỏa)
Tính đối xứng xRy
với
or
Bài 2: Trong các tập hợp sắp thứ tự dưới đây, cho biết tập hợp nào sắp thứ tự tốt:
a) (N) số tự nhiên N là tập hợp được sắp tốt vì có phần tử nhỏ nhất là 0
b) (Z,) số nguyên Z không là tập hợp tốt vì không có phần tử nhỏ nhất
c) (Q,số hữu tỉ Q không là tập hợp tốt
d) (Q+,) số hữu tỉ Q dương không là tập hợp tốt vì là phân số
e) (P, ) trong đó P là tập hợp các số nguyên tố.
P tập hợp tốt vì có phần tử nhỏ nhất là 2
e) (A, ) trong đó A là một tập con hữu hạn của Z.
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
A là tập tốt vì A hữu hạn nên A luôn có phần tử nhỏ nhất
Bài 3: Cho R là quan hệ hai ngôi trên tập số phức C được xác định như sau:
(a, b) R (c, d) ⇔ a c và b d
a) CMR: R là một quan hệ thứ tự trên C.
Theo nguyên lí kẹp a=c, b=d => R có tính phản xứng
=> R có tính bắc cầu R
có quan hệ thứ tự trên C
b) R có phải là toàn phần không?
Ta chọn x0 = (3,2) thuộc C và y0= (1,4) thuộc C
MÀ ta thấy x0 không có quan hệ R với y0 vì 3>1 và 2<4
Y0 không có quan hệ R với x0 vì 1<3 và 4>2 Vậy
R không là quan hệ thứ tự toàn phần
Bài 4 : Cho là quan hệ “chia hết” trên tập số nguyên Z.
(∀a,b ∈ Z, a b k ⇔ ∈ Z: a = k.b)
a) Chứng minh là một quan hệ thứ tự trên Z.
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
b) Quan hệ thứ tự trên Z có phải là toàn phần không?
Bài 5: Cho tập A = {1, 2, 3, 4, 5}. Cho R là quan hệ trên A và R = {(1,1); (2,1); (2,2);
(2,4); (3,1); (3,2);(3,3); (3,4); (3,5); (4,4); (5, 5)}.
a) R có là quan hệ tương đương? quan hệ thứ tự? Vì sao?
b) Nếu quan hệ R trên A là quan hệ thứ tự, vẽ biểu đồ Hasse cho (A, R).
Bài 6: Cho tập A = {1, 2, 3, 4} và các quan hệ R1 ={(1, 1); (2, 2); (3, 3); (4, 4)} và R2
= {(1, 1); (2, 2); (3,1 ); ( 3, 3); (3, 4); (4,1); (4, 4)} trên A.
a) Xác định xem các quan hệ trên có là qudan hệ thứ tự trên A?
R không tồn tại phần tử nhỏ nhất
Phần tử tối thiểu 2,3
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Phần tử tối đại 1,2
Không tồn tại phần tử lớn nhất
b) Nếu quan hệ nào là quan hệ thứ tự, hãy vẽ biểu đồ Hasse cho quan hệ đó
trên A.
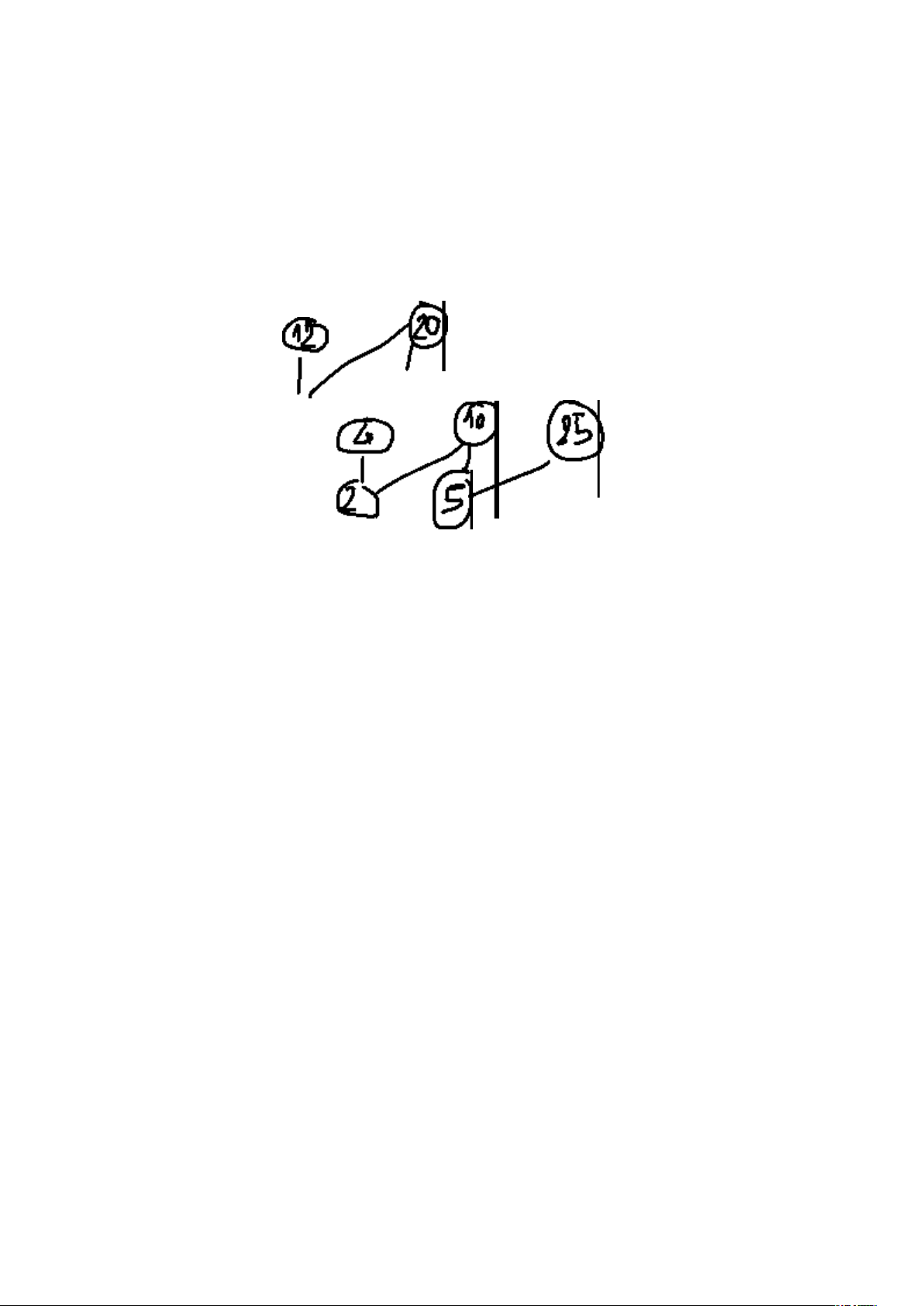
Bài 7: Cho (A,) là tập hợp sắp thứ tự, trong đó A= {2, 4, 5, 10, 12, 20, 25}, quan hệ |
trên A là quan hệ “ước số của” (∀a,b ∈ A, a | b k ⇔ ∈ Z: b = k.a)
a) Vẽ biểu đồ Hasse cho (A,).
b) Dựa vào biểu đồ Hasse tìm phần tử tối đại, tối tiểu của A.
Phần tử tối đại: 20,25,12
Phần tử tối thiểu: 2,5
KHông có phần tử lớn nhất và nhỏ nhất
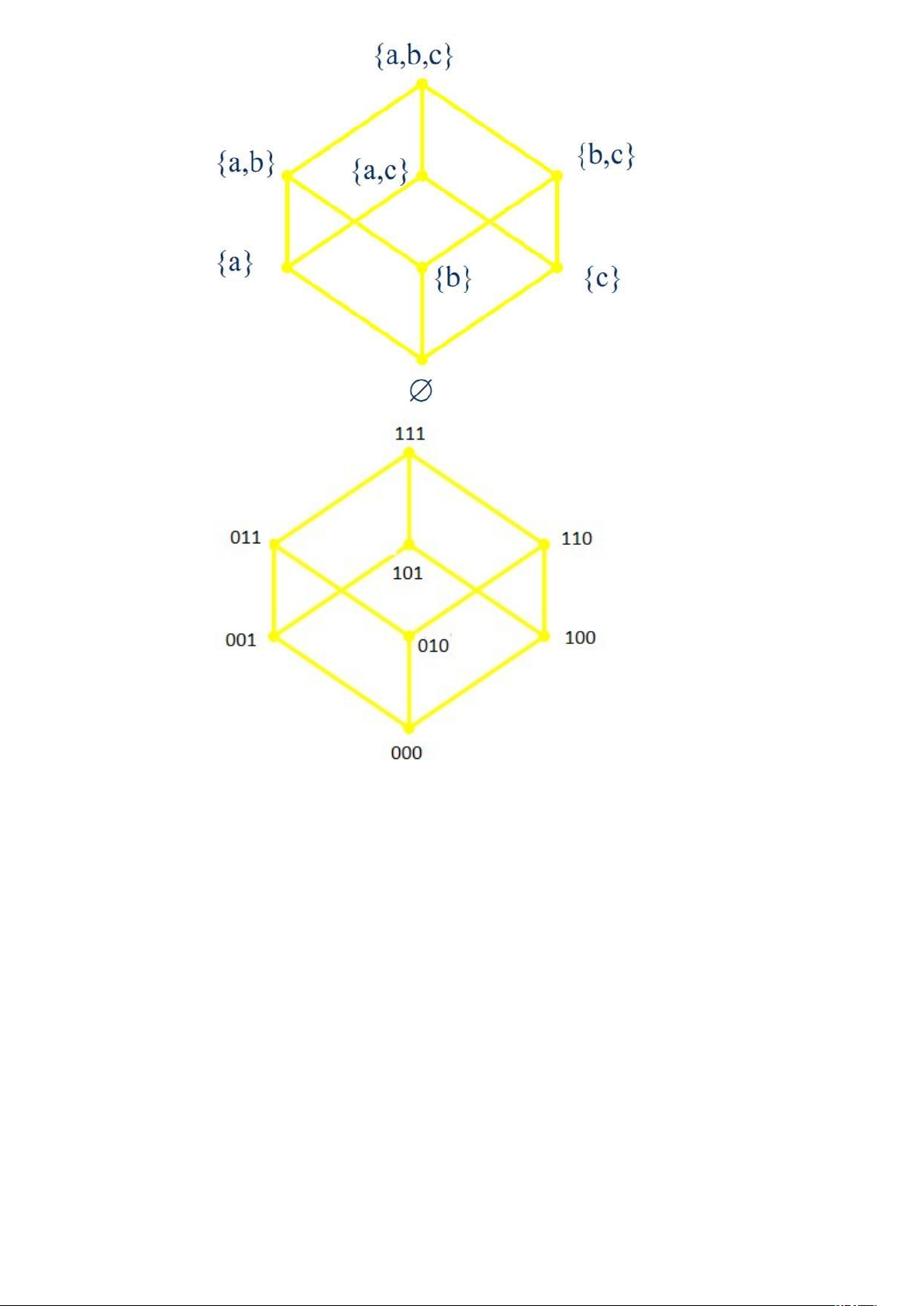
Bài 8: Cho ( A, ≤ ) là tập hợp sắp thứ tự, trong đó A là tập các chuỗi nhị phân có độ
dài bằng 3, quan hệ ≤ là quan hệ “nhỏ hơn hoặc bằng” thông thường.
a) Vẽ biểu đồ Hasse cho (A, ≤ )
b) Dựa vào biểu đồ Hasse tìm phần tử tối đại, tối tiểu của A.
c) Dựa vào biểu đồ Hasse tìm phần tử lớn nhất, nhỏ nhất của A.
• Các phần tử của (A, ≤) là (A, ≤) = {000;001;010;011; 100; 101;
110; 111}.
• Vẽ biểu đồ Hasse cho (A, ≤)
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
• Từ biểu đồ Hasse ,111 là phần tử tối đại duy nhất và 000 là phần tử
tối tiểu duy nhất .
• Từ biểu đồ Hasse ,111 là phần tử lớn nhất và 000 là phần tử nhỏ
nhất
Bài 9: Cho X ={2; 4; 6; 8; 10; 14; 16; 15; 20; 30; 36; 40; 60}. Trên X cho quan hệ | là
quan hệ “ước số của”.
a) Vẽ biểu đồ Hasse (X, | ).
b) Tìm phần tử tối đại, tối tiểu của X.
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Bài 10: Trong các trường hợp sau, hãy tìm các phận tử lớn nhất, nhỏ nhất, tối đại, tối
tiểu (nếu có) của các tập hợp đã cho với quan hệ thứ tự tương ứng. Vẽ các biểu đồ
Hasse.
a) U
30
với quan hệ ước số |.
Tối thiểu: 1 tối đại:30, lớn nhất 30 , nhỏ nhất 1
b) X ={2; 3; 4; 6; 8; 10; 80} với quan hệ ước số |.
Tối thiểu 2,3 tối đại 80, 6 không có lớn nhất và nhỏ nhất
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
c) X = {1, 2, 3, 4, 6, 8, 10, 11} với quan hệ R được xác định như sau:
xRy ⇔ x = y hay x < y – 1
Phần tử tối thiểu 1,2 Phần tử tối đại : 10,11 không có lớn nhát và bé nhất
Bài 11: Cho tập hợp X = {2, 5, 8, 10, 20, 40} và là quan hệ “chia hết” trên X.
a) Chứng tỏ R là quan hệ thứ tự. Vẽ biểu đồ Hasse cho (X, ).
b) Tìm các phần tử tối đại và tối tiểu của X.
c) Tìm các phần tử lớn nhất và nhỏ nhất của X.
tối thiểu: 40 tối đại là 5,2 phần tử nhỏ nhất là 40, không có phần tử lớn nhất
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
Tính phản xạ:
lOMoARcPSD|44990377
Bài 12: Cho tập X = { 1, 2, 3, 4, 5}. Cho R và S là 2 quan hệ 2 ngôi trên tập X có ma
trận biểu diễn lần lượt là:
AR =, AS =
CMR : R và S là quan hệ thứ tự trên tập X. Hãy vẽ biểu đồ Hasse cho các quan hệ này.
S= { (1,1) ;(1,3) ;(1,4); (2,2) (2,3),(2,4) (3,3) (3,4) (4,4) (5,1)(5,2) (5,3) (5,4) (5,5)
Tối đại và lớn nhất 2, tối thiểu 5,1
• Cmr R quan hệ thứ tự trên X.
• + Ta có:
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Mii=1, i
M11=M22=M33=M44=M55=1, với I
• R có tính phản xạ (1) Tính phản xứng:
+ Ta có:
Mij=0 hoặc Mji=0, nếu i khác j
M12=0 M13=0 M14=0 M15=0 M23=0 M25=0 M41=0 M42=0 M43=0 M45
=0 M51=0 M52=0 M53=0 M54=0
• R có tính phản xứng (2) Tính bắc cầu:
+ Ta có:
Mij=Mjz=Miz, với i, j, z
• M21 khác M13 khác M23
• R có không tính bắc cầu (3)
(1)(2)(3) => R k quan hệ thứ tự trên X
R={ (1,1) ,(2,1), (2,2) , (2,4) , (3,1), (3,2) (3,3) (3,4) (4,4) (5,5) }
Phần tử tối thiểu và nhỏ nhất 3 tối đại 1,4 , 5 không tồn tại lớn nhất
• Cmr S quan hệ thứ tự trên X:
• Tính phản xạ:
+ Ta có:
Mii=1, i
M11=M22=M33=M44=M55=1, với I
• S có tính phản xạ Tính phản xứng:
+ Ta có:
Mij=0 hoặc Mji=0, nếu i khác j
M12=0 M15=0 M21=0 M25=0 M31=0 M32=0 M35=0 M41=0 M42=0
M42=0 M45=0
• S có tính phản xứng Tính bắc cầu:
M14=1
M42=0
M12=0
• S k có tính bắc cầu
• S k có quan hệ trên R
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
lOMoARcPSD|44990377
Câu 13: Cho S={1, 2, 3, 5, 6, 10, 15, 30} (các ước số lớn hơn 0 của 30). Hãy vẽ biểu
đồ Hasse cho (S,|) và (S, ).
(S,|)
Tối đại và lớn nhất : 30
Tối thiểu và nhỏ nhất: 1
(S, )
Tối đại và lớn nhất : 1
Tối thiểu và nhỏ nhất: 30
Câu 14: Vẽ biểu đồ Hasse cho S với quan hệ thứ tự tương ứng.
a) (S = {1, 2, 3, 4, 5, 6, 7, 8}, )
b) (S = {1, 2, 3, 6, 12, 24, 36, 48}, |)
Downloaded by Ph??ng Linh (nguyenphuonglinh281104@gmail.com)
Bấm Tải xuống để xem toàn bộ.